Это копия, сохраненная 1 июня 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.


Аксиоматизация понятия «триангулированная категория с комплексами RHom» приводи к необходимости рассматривать дифференциальные градуированные (DG-) категории. Структура DG-категории должна быть в разумном смысле согласована с триангулированной структурой. Во-первых, когомологии комплексов RHom должны быть естественно изоморфны группам Ext в триангулированной категории. Далее, имеются два способа определения высших композиций Масси. Один исходит из DG-структуры, другой — и триангулированной. Естественно ожидать, что для DG-структуры, согласованной с триангулированной, оба способа должны приводить к одному ответу.
http://mi.mathnet.ru/msb1196
Предыдущий: >>346772 (OP)
Для начинающих: >>349176 (OP)
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
46. https://arhivach.org/thread/156244/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
46. https://arhivach.org/thread/156244/

Math for Welders is a combination text and workbook designed to help welding students learn and apply basic math skills. The basic concept behind each math operation is explained at the opening of the unit. Next, students are given clear instruction for performing the operation. Each unit includes a variety of weldingrelated practice problems to reinforce what the students have learned. The practice problems are identical to the types of problems the students will be required to solve in a welding shop.
Да оба они не умеют в юмор. На картинке его нет, на картинке препод, преподающий дворникам, говорит, что больше чем на 3000 они рассчитывать не могут. В чём юмор?
Хочу запилить анонимный опросник для посетителей треда. Никто не против? Google Forms подойдёт - он вроде не требует аккаунта для респондентов?
Стал сомневаться, могу ли я в юмор. Тебе действительно объяснить шутку с моей точки зрения? Или у тебя мета-юмор такой?
По крайней мере ОП понимает.
Попробуй - у меня вроде без авторизации катит.
https://docs.google.com/forms/d/1Z8oRvLbVAqPozmHH1quswfu4ht6aAA0jcHPzOhww2gk/viewform?fbzx=1430905225422334000
Ручаюсь анусом опубликовать результаты.
20 гигов матёшки http://rghost.ru/8CXZw7ttB
Юмор, значится в том, что пик вызывает аналогию с ситуацией, когда на лекции по какой-либо математической дисциплине лектор формулирует/задаёт вопрос аудитории являющийся наводкой на фундаментальную теорему(либо следствием её). И ответ лектора обычно немного шокирует т.к. эта теорема даёт неочевидный учащимся результат. С другой стороны, этот результат может быть очень абстрактным и трудным для восприятия.
Ещё юмор/ассоциация в том, что лектор страдает общим "синдромом" преподавателей/учёных - считает свой предмет очевидно нужным и полезным, хотя на деле он довольно таки оторван от жизни и реалий обучающихся. И в предмете у него "элементарно" и "очевидно, что..." в связи с высоким лвлом погружённости в предмет, когда аудитория просто выпадает в осадок.
Слишком усложнил на мой взгляд. Но автор мог иметь ввиду именно это. Плохая шутка, непродуманная.
>Слишком усложнил на мой взгляд.
Возможно. Я изложил все ассоциации, которые породил этот пик. Может это слишком специфичная шутка.
>Плохая шутка, непродуманная.
А мне наоборот, очень понравилась.
А, по-моему, он уже в идеальном состоянии.
Все равно не понял. А какой теоремы следствие, что дворники получают 3000 тыс? Это очень мало. 13 тыс. ближе к реальности. Расценки правильные. Откуда 3 тыс?
Три тыщи никто никогда не получал в 21-м веке же. ну может молодые математики, но не дворники в дс Поэтому подумалось, может это тонкий намек на какую-то константу из уравнения . наконец-то то я беседую наравных в серьезном математическом треде!
А если подмосковье/милионники/прочие мухосрански взять? А вообще мне кажется цифра 3к - это либо такая МРОТ была, либо мемчик.
Да, че то про мухосрански я не подумал, подразумевал дс.
лоль, нихуя сварщиков грузят. сложнее им чем дворникам даже! show your work!
Правильно пишут. Но во всём нужна мера. В системе обучения должна быть дифференциация по уровню способностей и целей(будущая профессия/предполагаемая область деятельности). Зачем умному ботанику ебать мозги примерами 2+2x2, когда он их давно понял и ему пора двигаться дальше, он хочёт в абстракции? А будущим сварщикам - это в самый раз может оказаться.
Куну из 2005-го, ушел далар. Проверь.
Ещё забыл добавить, формулировка вопроса напоминает https://en.wikipedia.org/wiki/Constant_problem
Функция зарплаты дворника = константа на при любых значениях агрументов.(как бы подразумевается)
Русский математик Вербицкий уже атакован трансвеститом!
Есть другие мнения, ознакомься с ними.
Допустим, нужно найти предел последовательности
>lim(1/(n+1/n), n->inf
пользуясь только бесконечно малыми последовательностями.
Очевидно, что
>(lim(1/n), n->inf) = 0
Теперь суть вопроса. Можно ли решение этого предела записать так:
>(lim(1/(n+1/n), n->inf) = (lim(1/n), n->inf) = 0
Как вообще такие вещи принято оформлять?
А, да, пропустил одну. То есть все точь-в-точь так и пишут в тетрадках? ну я имею ввиду то что будет если скормить это вольфраму
Пошёл на хуй.
Го мне в чат, и те припас.
И как записать тоже самое только вместо степени умножение?
>И как записать тоже самое только вместо степени умножение?
n!
>Как одним выражением написать n^(n-1)^(n-2)^...^1?
ХЗ. Ввести новое обозначение: степенной факториал ^!, лол.
У тебя как скобки расставлены? Здесь это важно. Если лесенка из степеней - то наверно нужно новое обозначение. Если (n(n-1(n-2(...))1) - перемножь показатели и логарифмируй.
>n!
>Ввести новое обозначение: степенной факториал ^!
n! = 1·...·(n-2)·(n-1)·n;
n^(n-1)^(n-2)^...^1 =
n^((n-1)·(n-2)·...·1) =
n^(1·...·(n-2)·(n-1)) =
n^((n-1)!) =
n^(n!/n); ага

^ — очень интересный знак. Скобки обычно ставятся не как у тебя: a ^b ^c, а наоборот: a^ b^ c. Как будто читается не слева направо, а справа налево. В этом и множественный смысл есть, пространство отображений из А в Б записывается Б^А, порядок реверсирован. То есть с современной (современной ли?) точки зрения сначала берётся степень, а только потом то, что в неё возводится.
вбей "2^2^2^2" в гугл.
Калькулятор как-бы намекает, что:
2^2^2^2 = 2^(2^(2^2)) = 65536
Можешь вбить "2 ^2 ^2 ^2" и "2^ 2^ 2^ 2".
Имелись в виду, варианты калькуляторов, где порядок вычисления степеней - не такой, как в гугл-калькуляторе. Ну и где есть пространства отображений, реверс порядков и другие знаки.
Ок, я просто запутался в порядке из-за твоего идиотского примера с превращением ^ в ×, который тупо неправильный (2^2^2=16; 2×2×2=8), а вообще свойственном для порядка, противоположного правильному: (a^b)^c=a^(b×c).
Значит гугл-калькулятор - балабол?
И
2^2^2^2 ≠ 2^(2^(2^2));
2^2^2^2 = ((2^2)^2)^2 = 2^(2·2·2) = 2^8 = 256;
Я тогда в уме, двойку, в четвертую возвёл.
Арнольдчую этого!
Просто он Рыбникова посмотрел и узнал, что умножение это суммирование. А возведение в степень - умножение!
Это значит, что он не предназначен для серьёзной математики - а больше для бытовых/инженерных расчётов наверное ;)
Кстати, в питоне и фортране(операция двойная звёздочка) порядок вроде "правильный". Инверсия предполагаемого порядка(т.к. для + и x "правильный"/логичный порядок обратен даже в случае некоммутативности, к примеру если рассматривать матрицы) происходит именно для возведения степени.
>2^2^2^2 = 2^(2·2·2) = 2^16 = 65536
фикс.
1) 2^2^2^2 ≠ 2^(2^(2^2));
2) 2·2·2 ≠ 16;
2^2^2^2 = ((2^2)^2)^2 = 2^(2·2·2) = 2^8 = 256;
На виндовом калькуляторе такое не прокатит.

Между прочим, вполне разумная идея. Рыбников приблизился к открытию тропической арифметики. В тропической арифметике обычное сложение заменяется на сложение по модулю 2, умножение - на обычное сложение, а возведение в степень - на обычное умножение.
https://ru.wikipedia.org/wiki/Тропическая_геометрия
Это у того анона что-то в голове переклинило. Из-за флюидов Рыбникова, наверное. Там вместо сложения просто максимум.
Задам тут вопрос, надеюсь, не обоссыте. Гуглил сегодня, ничего подобного не нашёл. Ищу таблицы с числами от одного до 12, чтобы были привязаны к числу 12. То есть, блин, как объяснить. Ну типо 16 ричной системы, только 12 ричная. Числа должны быть в рандомном порядке, без разницы, сколькизначные. хоть 10-ти. То есть тупо таблицы с числами, которые привязаны к числу 12. Надеюсь, понятно объяснил. Буду благодарен.
2 чаю с нефтью, тебе ЛаМпОвЫй АнОнЧеК, теперь реальные анонимасы кто нонконформист и не-быдло должны стать гуманитариями я считаю, а все кто матёшку учат зашквареное путинское быдло. Тут кстати только последние седят, я пробовал, им уже ничего не обьяснишь, у них фимозг на весь мозг уже более чем на половину, эту проблему мы с трухекками обсуждаем в этом тренде >>349176 (OP)
>должны стать гуманитариями я считаю
Я уже недели две как в лингвач перекатился. Тут засилье рачья просто одолело.
Перекатись окончательно.
так ничего нового, стадный менталитет в этой стране всегда был, узость выбора, типа все читают одну книгу, мечтать о бали или мальдивах, других мест нет, и таких много примеров. другое дело, что никогда бы я не подумал что и в выборе "кульной" научки тоже может быть стадность, но почему бы и нет. возможно какой-нибудь популярный ютюб канальчик рассказал им про STEM. за другой стороной окопов кстати тоже приколько наблюдать. видели как тут у анона пару дней назад пукан порвало, из-за того что "недостойные дибилы" учебники качают из торентов. он размахивал костылем как фронтовик, у которого спиздили военный кителек - вы суки не воевали, нахуя погоны нацепили, пидорасы ряженые!
Интересные интерпретации у тебя
А что тебе мешает и дальше няшиться со своей физикой и информатикой? Ебучие социоблядки приходят к тебе домой, отрывают тебя от серьезных занятий серьезной наукой, заставляют тебя читать науч.поп и говорить о всякой мейнстримной хуйне?
Похоже, что у тебя комплекс не-такого-как-все. Ебучие социоблядки разрушили твои представления о собственной исключительности, вторгнувшись в твой идеализированный манямирок.
Числа разные, написал же. Хоть 5 значные. Просто чтоб привязаны к 12 числу были.
А эти не разные?
>351561
Мне нужны готовые таблицы с рандомными числами. Может, вы сайты знаете, где такие таблицы есть. Ничего найти не могу.
Юзай конвертеры
http://planetcalc.ru/375/
http://calculatori.ru/perevod-chisel.html
Если же ты имеешь в виду таблицы степеней, вида:
http://inf.e-alekseev.ru/text/Schisl_perevod.html
то считай их сам.
Вот последняя ссылка похоже, только большие таблицы с 12 столбцами или подобное. Чтоб было разделение на 12 каких-либо групп или подобное.
Бляяяя, он че трансфоб? Фу, пидораха, я-то думал Вербит нормальный пацан.
12-ричная система счисления. Таблица степеней.
n (степень) 12^n
0 1
1 12
2 144
3 1728
4 20736
5 248832
6 2985984
7 35831808
8 429981696
9 5159780352
10 61917364224
11 743008370688
и т. д.
Где вот такие таблицы достать? Можно какие-нибудь параметры, харрактеристики. да что угодно, хот ьатомарные массы соединений. Главное, чтоб по 12 столбцов было. Таблицы вот как эти>>351581
>чтоб числа только большие были и рандомные.
Какой нахрен рандом?
В сих таблицах всё вполне закономерно.
Таблица Пифагора, если речь идёт о умножении.
Результат перемножения и сложения цифр выражается в цифрах этой же системы исчисления. Никакого рандома здесь.
К чему тебе рандом? Задай алгоритм деривации, что-ли, блеать?..
Каков запрос, таков ответ.

Не совсем понятно, что значит "привязаны к 12 числу" и как это связано с "разделение на 12 каких-либо групп" и "По 12 столбцов либо вдоль либо поперёк".
Ты хочешь что-то, вроде пикрелейтед "карты кодов"?
Если да, нужны следующие параметры:
1. Основание системы счисления, в которой будут выражаться числа.
2. Количество разрядов чисел для выбора минимального и максимального.
3. Количество самих чисел. (Кратное 12-ти, если ты хочешь 12 столбцов)
Всё.
Да, это пойдёт. Где такие таблицы можно в инете посмотреть?
Система исчисления любая - любые натуральные числа, как на твоей таблице. Без всяких дробей, степеней и прочего. Можно со знаком минуса, без разницы. Привязка к числу 12 любая, будь то 12 столбиков, 12 ячеек. В твоей таблице в идеале после 12 строки надо обрезать и всё. Получится как раз то, что нужно.
Где ты взял эту таблицу, где еще такие посмотреть можно?
>Привязка к числу 12 любая, будь то 12 столбиков, 12 ячеек.
Значит, один из параметров - задан. Количество чисел - 12.
>Система исчисления любая - любые натуральные числа, как на твоей таблице.
Ты не задал остальные параметры.
Вдруг, ему это, жизненно-важно?..
С хуяли ты делаешь такие выводы? Если не знаешь, не говори.
Окей.
Количество столбцов 64.
В каждом столбце должны быть рандомные числа от одного до 12 в разном порядке через запятую. Количество чисел в столбце до 24.
Ну, няша, что, сильно тебе мозг взорвал? Я же сказал, просто таблицы и всё. Всё равно ты мои идеи не знаешь.
https://www.random.org/integers/?num=1536&min=1&max=12&col=64&base=10&format=html&rnd=new
Держи свои 64 столбца, по 24 рандомных числа в каждом, от 1 до 12.

Еще забыл добавить, как самому такое генерировать в двух словах? Простите, что ваш тред тут засоряю, мне просто нигде больше спросить.
Просто обновляй ту страницу.
И ещё, укажи количество разрядов, кое-что интересное ещё подкину.
Блин, я, наверно, туповат для вашего треда умняш, что такое разрядность? Если объяснишь, я напишу.
А, блять, сорри. Тогда так. Я всё в голове уже перепутал. Но тебе благодарен, что ты сделал для меня эту чудесную таблицу. Если ты не против, я немношко подумаю, что еще в ней доработать можно. Ну, скажем, пускать будут числа не до 12, а до 84. То есть в столбиках пусть будут числа от 1 до 84, а сами столбики будут пусть раз в 10 длиннее вниз. Такое можно?
Ты хотел кодовую карту, а теперь хочешь неведомую поебнятину какую-то.
И да, ты так и не указал количество разрядов.
2 разряда же, ну. То есть такая же таблица, которую ты мне сделал, но чтоб числа в столбиках были от 1 до 84 и столбики были вниз далеко, ну то есть например пусть будет 84 знака вниз, чтоб теоретически там расположились все числа от одного до 84. В длину пусть будет так же, 16 столбиков. Так понятней, няша?
Ты, кстати, близок примерно к истине. Но всё намного интересней. Ты еще не представляешь, чт ов себе числа прячут.
>>351628
>>351626
кун
Так так так, что тут у нас...
Ага, 16 столбиков, по 84 строки, 1344 рандомных числа от 1 до 84.
>2 разряда
1-9 это уже 1 разряд, так что двухразряднче числа должны быть от 10 до 84.
>чтоб теоретически там расположились все числа от одного до 84
Рандомизация значений в от 1 до 84 в этих твоих столбиках - как-бы исключает уникальность чисел, да.

Ну да, в смысле в столбиках не обязательно должны быть все числа по порядку от 1 до 84, это понятно. Пусть алгоритм сам выберет из диапазона от 1 до 84 любые числа в разном порядке и заполнит пустые клеточки. Столбик вниз должен быть ровно на 84 значения. В длинну должен быть 16 столбцов, это подходит. Ну, как ты мне сделал. Очень тебе благодарен, если честно. Вот. Если сможешь еще и эту штуку сделать, у я даже не знаю, принесу сюда ориджинал фото какое-нибудь из моей коллекции, я по Европе путешествовал много. Вот. Жду кароче, анончик :3
Да я уже въехал, лол. Я же не совсем валенок. Просто запрос у меня такой, да, специфический. А вы всё равно тут скучаете, хоть мне поможете.
Да, забыл добавить, ноля не должно быть, разумеется. Ну так, на всякий.
Держи, и вали. Весь тред засрал.
16 столбцов ×84 строки = 1344 значения от 1 до 84.
https://www.random.org/integers/?num=1344&min=1&max=84&col=16&base=10&format=html&rnd=new
1 столбец × 84 строки = 84 значения от 100000 до 999999 (кодовая карта 84-х рандомных, 6-значных чисел)
https://www.random.org/integers/?num=84&min=100000&max=999999&col=1&base=10&format=html&rnd=new

Спасибо! :3 И чего ты такой злой, лол. Не сердись, ты помог человеку. Держи фотачку
Ладно, я ушёл. Спасибо всем за помощь.
Погуглил. Испания. Барселона. Искупительный храм Святого Семейства (Саграда Фамилия). Строение Антонио Гауди. :3
Чтоб ты всрался, с этой фоткой, что там в треде, про хойну.
3 + 3 +3 = 3 + (3 + 3) = (3 + 3) + 3 = 9
3 3 3 = 3 (3 3) = (3 3) 3 = 27
но
3 ^ 3 ^ 3 = (3 ^ 3) ^ 3 != 3 ^ (3 ^ 3) почему
нотация Кнута ≠ ɐɯʎнʞ ʁиǹɐɯон
пздц
Это как?
х3, антуан, мейби, теория категорий занимает центральное место в современной математике, она также нашла применения в информатике, логике и в теоретической физике. О сим глаголит педивикия. А там хуле я тебе, в общем, смотри сам.
Это дает формальное обоснование тому, что объект = морфизмы в него (из него).
Поэтому можно определять (и изучать объекты) как представимые функторы. Простые примеры, например, якобиан или схема Гилберта. В топологии вот пространства Эйленберга-Маклейна.

Это полноценная аксиоматика, альтернатива ZFC?
Спрошу тогда - раз такая тема пошла
Почему https://ru.wikipedia.org/wiki/Тетрация и последующие гипероператоры теряют непрерывность, в чём фундаментальнальная причина? Почему вообще при "наращивании" гипероператоров теряются какие-либо базовые свойства(н-р умножение->некоммутативное возв. в степень)?
P.S. Школота уже не знает, как перевести число в позиционную систему счисления по другому основанию. Я опечален.
Я что-то не пойму, аноны. Как доказать, что секвенциально компактное пространство - компактное?
Множество всех написанных математических статей.
Гранты, стипухи. В промежутках - члены подсасывать.

Ищем значение п-й в точке a=3 для ф-ции у=x^2.
По X: a+x. По Y строим значение dy/dx т.е. отношение (f(a+x) - f(x)) / (a+x). Начинаем с a+x = 4 и постепенно х приближаем к а (3). Первые три точки задают "тренд" в виде линии, и видно куда сходится предел графически. Синяя точка и есть значение предела, где получается 0/0, а на самом деле f(3) = 6. По линии можно видеть, что вообще тут происходит. Никогда не видел таких графиков в учебниках. Обычно на словах, через формулы, или чертят секущие/касательные к самой ф-ции.
Удвою запрос. Нельзя на этой доске, да ещё и в этом треде выкладывать такое без соуса.
Какова пракладная сторона высера из оп-поста?
>1% женщин больны раком груди. У 80% женщин, больных раком груди, маммограмма верно выявляет наличие заболевания; кроме того, она даёт ложный положительный результат (то есть, неверно показывает наличие рака) для 9.6% здоровых женщин.
У какого процента женщин, маммограмма которых дала положительный результат, есть рак груди?
Запишите ответ с точностью до одного знака после десятичной точки (знак процента не нужен)
Можно получать денежки от государства и срать офисобыдлу в рот, попивая чаёк с печеньками и занимаясь любимым делом.

Байес, плиз. Для этого достаточно салфетки и общей сообразительности.
Incorrect Response
Воспользуйтесь формулой Байеса
Вот и в математике для ньюфагов не смогли решить.
Введём несколько событий.
A1 - рак есть
A2 - рака нет
B - результат теста положительный
Запишем данные нам вероятности.
P(A1) = 0.01
P(B | A1) = 0.8
P(B | A2) = 0.096
Найти нужно P(A1 | B).
Ясно, что A1 и A2 образуют полную группу.
Поэтому P(A2) = 1 - 0.01 = 0.99
По формуле полной вероятности имеем:
P(B) = P(B | A1)P(A1) + P(B | A2)P(A2) = 0,8×0,01 + 0,096×0,99 = 0,10304
По формуле Байеса:
P(A1 | B) = P(A1) × P(B | A1) / P(B) = 0,01×0,8/0,10304 ≈ 0,078.
То есть ответ - у 7.8%.
Correct Response
Верно, спасибо.
А вот еще задача.
Какова вероятность того, что при независимом подбрасывании двух симметричных шестигранных кубиков хотя бы на одном из них выпадет больше трёх очков? Запишите точный ответ в виде десятичной дроби.
У меня получилось 0.5, то есть в половине случаев. Почему мой ответ инвалид?
Исходов, при которых на первом кубике выпадает больше трёх очков, 18 штук.
Исходов, при которых на втором кубике выпадает больше трёх очков, тоже 18 штук.
Исходов, при которых на обоих кубиках выпадает больше трёх очков, девять штук.
По формуле включений-исключений, исходов, при которых хотя бы на одном кубике выпадает больше трёх очков, 18+18-9=27 штук.
Всего исходов 36. Значит, ответом буде число 27/36 = 0.75.
Ты даун, блядь, ёбаный. 0.777 – это более точная версия 7.8%. 0.1 – ещё более грубое округление. Я думал, что ты приебался к оформлению, и намекнул, что ты сам мог бы округлять. Ты вообще хотя бы понимаешь, что спрашиваешь? Что такое процент, вероятность, формула Байеса? Если нет, нахуя ты спрашиваешь?
> при независимом подбрасывании двух симметричных шестигранных кубиков хотя бы на одном из них выпадет больше трёх очков
Тут даже думать о Байесе не хочется. Короче есть 4 равновероятных сценария: на кубике А выпадает 1..3 и на кубике Б выпадает 1...3; А 4..6 и Б 4...6; А 1...3 Б 4...6; А 4...6, Б 1...3. Условию удовлетворяет 3 сценария из четырёх, это 0.75.
> Почему мой ответ инвалид?
Потому что ты инвалид ума, наверное. Откуда ты взял 0.5?
> Откуда ты взял 0.5?
>хотя бы на одном из них выпадет больше трёх очков
1, 2, 3, 4, 5, 6
0.5
Я же не спорю, что я тупой, зачем ты злишься.
Спасибо.
Это вероятность для одного кубика. У тебя их два. Каждый из этих двух кубиков может выпасть либо с результатом больше 3, либо с результатом не больше 3. Поскольку тут всего два равновероятных варианта для каждого броска кубика, можно свести задачу к более понятному дебилам случаю монеток. Представь, что ты бросаешь 2 монетки. Какова вероятность, что хотя бы одна монетка из двух упадёт орлом? Подумай сам своей головой, потом посмотри спойлер: первая может упасть орлом или решкой; вторая может упасть орлом или решкой. Из этого получается, что у нас четыре варианта: орёл-орёл, орёл-решка, решка-орёл, решка-решка, 3/4 из них соответствуют условию. Итого вероятность 0.75.
> Я же не спорю, что я тупой, зачем ты злишься.
Мне плевать, споришь ты или нет. И на тупость тоже плевать, меня раздражает абсурдный подход. Ты же не понимаешь слов, в которых тебе дана задача, и просишь других людей её решить. Но просто собрать ответы к вопросам – плохой способ понять тему.
Вот смотри, анон выше написал
> Исходов, при которых на первом кубике выпадает больше трёх очков, 18 штук.
Ты понимаешь, почему их 18? Откуда взялось 18, а откуда – 36? Не понимаешь.
> По формуле включений-исключений
Ты можешь нагуглить эту формулу, но сможешь ли ты понять, откуда взялся этот метод и почему его надо применить к этой задаче? Не сможешь.
Никогда не симулируй понимание. Раз пришёл задавать тупые вопросы, спрашивай именно о том, что ты не понимаешь, тогда ты сможешь выстроить твёрдое интуитивное понимание. Не
> У какого процента женщин, маммограмма которых дала положительный результат, есть рак груди?
> Запишите ответ с точностью до одного знака после десятичной точки (знак процента не нужен)
А:
> что такое процент? что такое положительный результат в данной задаче? что такое формула байеса? что такое точность до n-го знака после десятичной точки?
и на все эти вопросы ответ будет: гугли прямо в этой формулировке, сука
>первая может упасть орлом или решкой; вторая может упасть орлом или решкой. Из этого получается, что у нас четыре варианта: орёл-орёл, орёл-решка, решка-орёл, решка-решка, 3/4 из них соответствуют условию. Итого вероятность 0.75
Спасибо за пояснение, я даже не подумал об этом.
>>351999
>Ты понимаешь, почему их 18?
Я нагуглил это формулу еще перед заходом сюда, но не осилил.

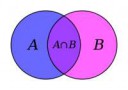
Всё это крайне примитивно и формулы, строго говоря, не нужны (в некоторых других задачах они удобны). В данных задачах рассматривается тема полной вероятности: есть ряд возможных взаимно исключающих исходов, совокупная вероятность которых равна 1 (или 100%, ведь процент это просто одна сотая или 0,01; это не более чем синонимы). Иными словами, какой-то один и только один из этих исходов неизбежно произойдёт. В случае с кубиками исходов 36: это все возможные сочетания результатов первого и второго кубика (1 и 1, 1 и 2, 1 и 3... можешь посчитать на салфетке, вариантов 36, что можно было бы получить сразу из 6*6, вот тебе даже картинка). Тебе задаётся вопрос о том, какая доля этих вариантов соответствует условию. Смысл формулы Байеса сводится к выяснению данной величины.
Я упростил задачу, воспользовавшись тем, что для данного условия не обязательно рассматривать каждое число на кубике отдельно, поэтому и вариантов получается 4, а не 36. Так получится делать не всегда.
Формула включений-исключений применялась тем аноном только потому, что нам нужно избежать повторного учёта одних и тех же вариантов. Мы не можем сложить все случаи, когда условию удовлетворяет бросок первого кубика (18), когда условию удовлетворяет бросок второго (18) и когда удовлетворяют оба кубика (9), потому как эта третья величина – есть просто пересечение первого и второго наборов. Чтобы получить реальное общее количество удовлетворяющих случаев, надо из суммы первых двух вычесть их пересечение. Смотри на иллюстрацию из вики, представляй, как фигуры разделяются, думай, как правильно узнать площадь общей фигуры, если мы знаем площадь А, площадь Б и площадь пересечения. Если так не дойдёт, то никак не дойдёт. Подумай вот о чём: в этой логике фигура не может «дважды покрывать» одно и то же пространство – если положить на пол ковёр и на него ещё один, нигде не выступающий за край первого, то общая покрытая площадь ковра не изменится.
Числа округляются до нужного знака (даются с точностью до n-го знака) так: берётся (знак+1), если он больше или равен 5, то округляется вверх (то есть мы прибавляем единицу к указанному знаку), если 0-4 то вниз (ничего не прибавляем). Например: 17 округлить до десятков. 17 = 10+7. 7>4, округляем до десятка, получили 10+10=20. 1.452, округлить до второго знака после десятичного разделителя: 1.450+0.002, 2<4, округляем, 0.002 теперь приравнено к нулю, получилось 1.45.


Всё это крайне примитивно и формулы, строго говоря, не нужны (в некоторых других задачах они удобны). В данных задачах рассматривается тема полной вероятности: есть ряд возможных взаимно исключающих исходов, совокупная вероятность которых равна 1 (или 100%, ведь процент это просто одна сотая или 0,01; это не более чем синонимы). Иными словами, какой-то один и только один из этих исходов неизбежно произойдёт. В случае с кубиками исходов 36: это все возможные сочетания результатов первого и второго кубика (1 и 1, 1 и 2, 1 и 3... можешь посчитать на салфетке, вариантов 36, что можно было бы получить сразу из 6*6, вот тебе даже картинка). Тебе задаётся вопрос о том, какая доля этих вариантов соответствует условию. Смысл формулы Байеса сводится к выяснению данной величины.
Я упростил задачу, воспользовавшись тем, что для данного условия не обязательно рассматривать каждое число на кубике отдельно, поэтому и вариантов получается 4, а не 36. Так получится делать не всегда.
Формула включений-исключений применялась тем аноном только потому, что нам нужно избежать повторного учёта одних и тех же вариантов. Мы не можем сложить все случаи, когда условию удовлетворяет бросок первого кубика (18), когда условию удовлетворяет бросок второго (18) и когда удовлетворяют оба кубика (9), потому как эта третья величина – есть просто пересечение первого и второго наборов. Чтобы получить реальное общее количество удовлетворяющих случаев, надо из суммы первых двух вычесть их пересечение. Смотри на иллюстрацию из вики, представляй, как фигуры разделяются, думай, как правильно узнать площадь общей фигуры, если мы знаем площадь А, площадь Б и площадь пересечения. Если так не дойдёт, то никак не дойдёт. Подумай вот о чём: в этой логике фигура не может «дважды покрывать» одно и то же пространство – если положить на пол ковёр и на него ещё один, нигде не выступающий за край первого, то общая покрытая площадь ковра не изменится.
Числа округляются до нужного знака (даются с точностью до n-го знака) так: берётся (знак+1), если он больше или равен 5, то округляется вверх (то есть мы прибавляем единицу к указанному знаку), если 0-4 то вниз (ничего не прибавляем). Например: 17 округлить до десятков. 17 = 10+7. 7>4, округляем до десятка, получили 10+10=20. 1.452, округлить до второго знака после десятичного разделителя: 1.450+0.002, 2<4, округляем, 0.002 теперь приравнено к нулю, получилось 1.45.
Хуёво пояснил, на самом деле, там даже есть описки. Но это не проблема. И школа не проблема.
Дело не в пояснениях, а в вопросах. Научись задавать вопросы о непонятном, и ты сможешь сам для себя делать простые пояснения. Обычные люди почти никогда не умеют думать. Они не думают о том, какова в действительности задача, каковы те понятия, модели и явления, о которых их спросили, как они связаны – а сходу перебирают догадки о решении конкретного поставленного вопроса, ищут, каким эзотерическим трюком получить число, которое впишется в бланк ответа; ты буквально именно и это делал, полагая, что 7.8 верное решение, а 7.777 это «не смогли решить». Таким образом всё соревнование обычных людей в образовании сводится к тому, чтобы выяснить, у кого лучшая память на правила и формулы, описывающие манипуляции с символами. Это изнурительный мартышкин труд, поведение китайской комнаты. Нужно быть выше этого.
Нужно только тем, кому нужно.
У тех, кто поверхностно относится к математике и другим наукам, зачастую актуальны все время другие задачи, например социальные. Как расположить к себе того то, как напиздеть тому то, как себя повести, как решать проблему с вот тем чуваком, как исполнить или сформулировать поручение.
Математику всерьез могут задрачивать только асоциальные граждане. Чтоб строить норм модели, нужно о них думать,много думать. У большинства же нет времени/сил/желания это делать, когда есть задачи посложнее и поважнее в рамках социальной обезьяньей житухи. Да да, посложнее. Ибо социальная житуха, если ее формулизовать- это неебическая система нелинейных уравнений. Которую считать надо насухую,мозгом.
Не уподобляйся тупой двачегрязи. Никаких оправданий тут нет: я не тот анон во-первых, во-вторых я с тобой согласен почти во всем. "надо быть выше" - вот на что ответил. Надо то оно надо, если тебе больше не о чем думать. Но большинству объективно просто не до формирования норм моделей. И оно тебе должно нравиться-ведь именно своим абстрактным и системным мышлением ты и выделяешься на фоне большинства.
Выделяешь на фоне выделенных тобой обычных людей.
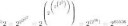
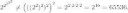
>P.S. Школота уже не знает, как перевести число в позиционную систему счисления по другому основанию. Я опечален.
http://inf.e-alekseev.ru/text/Schisl_perevod.html
Это тебе.
А пикчи - вам. >>351336>>351315>>351314
Алсо, обратите внимание, что в тетрации количество повтора возведения в степень пишется слева от числа. Ага.
>>351964
Кстати, в своём роде поддвачну, только интересует не прикладная сторона, а общематематическая. Триангулированные категории это только для топологии/алгема штука?
Я думаю, что твой расчёт времени не верен
Ты просто потворствуешь своей лени и строишь охуительные теории социального взаимодействия, анон про "надо быть выше", не говорит о уровне Перельмана или другого проф.математика, а об уровне просто разумного человека, который время тратит разумно, если придётся усвоить математику, то лучше усвоить хорошо, затрат умственных больше, но по времени тоже самое + тебе социально взаимодействовать надо не 24/7 ты чем занимаешься,что строишь какие-то охуительные планы манипуляций?
Сомнительные со всех сторон аргументы у тебя
Я (последний пост >>352010) полагаю, что самая малоинтересная вещь в жизни – это тупить на лекциях и получать тройки по матеше. Я ненавидел её в школе (хотя там были отличные учителя), боялся в универе (там были преподы похуже), с трудом зубрил аккурат к экзаменам и забывал после них, поступил в аспирантуру и только тогда понял, насколько вся эта чепуха (арифметика, школьная алгебра, базовый тервер, статистика, начала матанализа) естественна, а кроме того тривиальна и самоочевидна, стоит лишь немного (на уровне минут, очень редко – полчаса) подумать вместо того, чтобы избегать под предлогом неинтересности. И какие красивые идеи разворачиваются дальше. Виноват только я сам, что не старался увидеть в математике то, чем она является, что предпочитал быть тупым (да, это возможно – видеть себя тупее, чем на самом деле) и загонял её в быдлокатегории мещанского опыта, в муторный неизящный подбор отгадок. Я жалею, что уже поздно, выбрана другая область и я не буду иметь с математикой ничего общего. Если бы по крайней мере биоинформатика... Ну, не всем дано. Впрочем, теперь я хотя бы могу видеть этот отблеск идеальных категорий на логических паззлах, которые предоставляются жизнью.
Но это так, сопли, а прагматика состоит в том, что учиться с пониманием и проще и эффективнее, чем без оного. Слово иксперту по обучаемости: https://www.scotthyoung.com/blog/2016/03/14/learning-fast/
Гарри поттер и методы рациональности, лол.
Вообще тебе надо понять, что «математика» это просто слово. Есть идеи. Они излагаются математическим языком, но сами по себе не зависят ни от какой дисциплины и значков. В книжке с картинками Thinking Physics почти нет чисел или формул, но там тоже есть подобные идеи.
Арнольд в «науке математике...» попробовал пояснить красоту идей, но я не уверен, что эта популяризация имеет большой смысл.
Есть книжки типа «думай как математик» или «Великая математика» - первая вообще полезна, вторая чистое популяризаторство.
Мне очень понравились некоторые задачи в Mathematics for computer science (курс MIT) и простые тексты betterexplained.com по исчислению.
Но на самом деле я не знаю, когда и за что ты зацепишься. Я не знаю, как это происходит. И не разбираюсь в математике. Спроси местных анонов, что их увлекло в детстве. Какой бы там ни был IQ, вряд ли они в 10 лет с энтузиазмом дрочили Демидовича.

А тв их игнорируй. Много ведь обиженок злых на двачах, которые не могут в силу умственной инвалидности придумать способов привлечь внимание, кроме агро уровня каментов пикабу. Но ты ведь не такой.
В таком случае всё же хотелось бы получить ответ на вопрос: "Что такое математика: наука или метод описания действительности сродни языку?"
>поступил в аспирантуру и только тогда понял, насколько вся эта чепуха (арифметика, школьная алгебра, базовый тервер, статистика, начала матанализа) естественна, а кроме того тривиальна и самоочевидна
Ты только в аспирантуре дошел до того, что школьник, который собирается на мат-фак понимает уже в десятом классе. Чем ты так возгордился? Тут плакать надо.
Я и плачу, собственно. Меня утешает только то, что большинство зарвавшихся школьников с матфака, вроде тебя, нихуя не достигло в математике ввиду недостаточных способностей. Догадаться о ней всё же мало.
>нихуя не достигло в математике ввиду недостаточных способностей
Ты думаешь, если достиг просветления в понимании прописных истин, то уже имеешь достаточно способностей вершить великие дела? Много вас таких по весне оттаяло.
Чтобы заниматься математикой, не нужно ничего кроме того, на чем можно писать. Поэтому на доске много математиков (и мамкиных феласафов еще).
Дефайн наука,описание,действительность.
Можно сказать, что математика и есть действительность. С помощью математики были предсказаны и описаны многие физические явления действительности, о которых до мат.вывода не было даже предположений. Начиная от радиоволн, заканчивая виртуальными частицами и зоопарком стандартной модели. Т.е. вот написали формул, преобразовали их по законам математики-и вылезли члены какие то. А потом оказывается, что этим членам соответствует реальное дерьмо. И чем не наука? Это просто лол описание?
Это символ Галлии. Ничего не означает, просто охуенно выглядит.
Но даже из твоего описания следует, что математика - это удобочитаемый для человека язык. Да, геометрия в большинстве своих направлений - это не только язык, но всё равно описание и передача. Да, с помощью математики можно что-то предсказывать. Но только с помощью, лишь используя инструментарий.
Ты о каких членах и почему математики о них думают, если это просто одно из понятий математики?
Дефайн наука. Пока что ты пишешь несвязный набор слов, в котоом угадывается отсутствие способности пользоваться русским языком.
Нет, не думаю. Строго говоря, я считаю своё положение безнадёжным и это очевидно из моих постов.
Но также я думаю, что ты тупенький высокомерный уже не школяр. Если тебе так сложно даётся понимание русского языка, то ты почти наверняка останешься посредственностью в математике. Распространённый мемчик про аутистов является не более чем мемчиком, практически все люди с высоким интеллектом хорошо понимают, что говорят окружающие. Фон Нейман бы не писал такой хуйни, как ты.
>>352058
Математику можно рассматривать как язык (символьную систему, позволяющую формулировать пропозиции), но тогда нам придётся принять, что вселенная основана на символьной системе, что абсурдно.
Простые числа, отношение длины окружности к её диаметру и прочие математические константы и их отношения – это реальность предельно фундаментального характера, и сколько бы раз ни возникал существенно абстрактный разум, он должен к ним приходить. Символьная сторона не важна, и суть исчисления была одинаковой, пусть Лейбниц и придумал более удобную форму записи, чем Ньютон.
Как говорил мой батя, математика – наука об идеях. Разрабатываемый и совершенствуемый математиками корпус понятий можно уподобить языку, поскольку он фиксирует наши знания об этих идеях. Но тогда мы имеем дело с символьной системой, настолько не похожей на все прочие, что я считаю более уместной параллель с научным методом. Научный метод – для изучения проявленной реальности. Математический «язык» – для идеальной. Различия этих двух реальностей, собственно, всё и объясняют.
Подобная философия не слишком полезна, конечно.
Физика не считает, что вселенная основана на символьной системе. Просто вселенная устроена достаточно строго, чтобы наблюдения могли описываться математически точными записями и это позволяло делать такие же точные выводы на основе оных записей.
>точными
Ты уже отсасываешь, остановись. Суть вселенной в неопределённости, она не может быть точной, хоть заупишись своим математическим языком.
> Суть вселенной в неопределённости
А, так ты настоящий шизик, суть вселенной прозрел интуитивно. Съёбываю.
/thread
Определенно ты дегенерат.
Есть. Период полураспада – чертовски определённая вещь. Абсолютно определённая. Что иронично ввиду того, что распад отдельного атома предсказать невозможно. Это говорит нам кое-что о связи «определённости» и «неопределённости», чего мещанскими мозгами, бездумно повторяющими штампы ньюэйджерского характера про «квентовая мехоника, куд кудах тах тах фсё случайно прост!11» не понять. Для этого нужно мыслить математически. И так со всем остальным, рили.
А теперь уёбывай.
>>ничтожество
По делу - у тебя АНГСТ.
По делу - дефайн наука. Если справишься без википедии, то может и поддержу с тобой спор, вдруг поумнеешь.
Ты уёбывай, сука. Определён у него период полураспада, лол. Засунь свой атом водорода в гравитационный колодец и наблюдай, какой он охуительно определённый. Хотя постойте-ка! Мы и и так в гравитационном колодце и нихуя не знаем, каково это жить за ним.
> Определён у него период полураспада, лол.
Лол – оружие дегенерата.
> Засунь свой атом водорода в гравитационный колодец
В твою мамашу лучше.
Ты провалил тест.
Сам придумай.
По делу, сука, по делу давай!
Ты же хуй простой, без математического образования, тебе ли судить о том, кто чего добьется в математике? Строишь тут из себя байроновского персонажа, говно ебаноё. Разобрал основы алгебры и считаешь себя охуенным гуру, разделил, блять, всех на обычных и необычных - избранных, которые умеют думать. Охуеть вообще. Через три месяца тебе надоест математика и ты уже будешь писать подобные восторженные отзывы в другом загоне, о какой-нибудь другой хуйне для избранных.
> Ты же хуй простой, без математического образования, тебе ли судить о том, кто чего добьется в математике?
Конечно, я могу судить об этом, что за жалкий визг и попытка сыграть в илитарность. В идеальном случае мне даже не нужно стараться, за меня всё сделают другие математики, научная иерархия довольно прозрачна. Но то, что ты туповат и от баттхерта слепнешь, видно уже сейчас.
> разделил, блять, всех на обычных и необычных - избранных, которые умеют думать
Ряд простых экспериментов подтверждает, что людей действительно можно разделить таким образом, и это действительно не имеет отношения к образованию, а лишь к пониманию ими того факта, что думать надо. По моим наблюдениям, большинство не понимает, что надо, и поэтому может быть определено как обычные.
А неслабо ты загорелся, я погляжу. Что, реально посредственность? Дрочил-дрочил, пыхтел-пыхтел и теперь должен охранять свой статус от нелегитимных посягательств?
Эта агрессия пиздец как глупо выглядит.
Да, ето так. Но не глупее твоего сиплого квохтания о «куда полез блеаа, хули возомнил, сука ты кто такой нахуй, чё выёбываешься, тебе ли судить, ёмана» и проч. Выглядишь как нищий замкадский инженер предпенсионного возраста, пытающийся на кухне со стопочкой самоутвердиться разговорчиками о гуманитариях. Зажатая, нервная зверушка, тебе действительно припекает от того простого факта, что я позволяю себе этот максимализм. Ты ведь даже не стебёшься высокомерно над восторженным дурачком, а суетливо пытаешься опустить в грязь. Какие после этого могут быть разговоры о том, добьёшься ты чего-то или нет?
Ну давай, расскажи, что ты там достиг. Я извинюсь, если окажется, что я ошибся.
я лох ни суди строга ти прав
>>даже не стебёшься высокомерно над восторженным дурачком, а суетливо пытаешься опустить в грязь.
Зачем контору спалил? Вдруг он сейчас решит задачу сравнения разных типов текстового поведения в зависимости от самооценки\компетенции и поймет, что палит свой долбоебизм? Кто будет развлекать анона?
>Дрочил-дрочил, пыхтел-пыхтел и теперь должен охранять свой статус от нелегитимных посягательств?
Но это и есть математика, сперва ты дрочишь и пыхтишь над учебниками, потом пишешь свои по большому счёту нахуй никому не нужные статейки и, время от времени, стараешься всем доказать всем, что ты занимаешься нужным делом.
Риск, да.
Можно сделать правило: как только долбоёб додумывается до рационального анализа своего поведения (частный случай умения думать) и таким образом перестаёт быть долбоёбом, он должен пойти и привести нового долбоёба.
>>352108
Иии так мы доказали, что математика = наука.
Так мы доказали, что ты долбоёб без образования.
Ну, давай у обезьяны попросим пользовательскую доску создать.
>какая самая острая научная проблема сейчас стоит перед математиками?
Очевидно же. Это плохой уровень сопутствующей математико-методической литературы. Давно уже пора провести реформу в этом направлении.
Но ведь полно мат. статей в открытом доступе.
Посоны нужен учебник по методам оптимизации, мне нужно освоить сиплекс метод метод искусственного базиса, метод лагранжа.
Хуй его знает. Это важно?
Большинство полезных ништяков из математики пришли не в результате целенаправленного поиска, а просто потому что.
Взял пацан, подифференцировал уравнения максвелла - получил уравнения. А там тип волны. Их искали? - Нет. А теперь сидим, как фуфелы, сидим тут с вайфаями и мобилами, с радио и тв, с интернетом и спутниками.
Математика дает ништяки как подарки на новый год. Глупо задавать вопрос - над какой проблемой работают, т.к. это не важно. Важно разнообразие изучаемых проблем и их связь с физикой. А так пусть считают там и выводят всякую дичь - занятие благородное.
Проблем, кстати, дохуя - сжатие информации, пэ равно эн пэ - навскидку. Или взять чисто прикладные проблемы с нелинейностями всякими в системах диффуров - там вообще поле, я так понимаю, непаханное. Цивилизация будет рада любому новому методу, который позволит считать системы быстрее\точнее. Думаешь там все уже расписали? Нихуя.
Я не математик конечно- не в курсе деталей, но мне и то время от времени приходится видеть, насколько математика важна и каких ништяков оттуда можно ожидать, какие ништяки там очень желанны и какие появляются время от времени. Пусть про них в сраных вк-пабликах "пра науку для быдла" не пишут.
Речь идет не о прикладных профитах, а о важности проблемы в рамках самой математики. Например как был кипиш вокруг оснований математики, тогда это было важнейшей проблемой.
О, будешь тут вечером или завтра? Хочу обсудить одну мульку.
Давно грызет простая мысль - большую часть курса дефолтного вышмата (матан, линал, урматы-вычматы, теорвер и стохи, логика) можно донести до студента более ярко и красочно, чем это делается в стандартных вузовских курсах. Мне самому оно не шибко надо, но сдается мне, что если б изложение бакалаврской математики снабжалось яркими визуализациями и четко подобранными примерами, то качество СТЕМ-кадров было бы получше.
Вопрос в том - такое положение вещей (сухость в изложении начал математики) это педагогическая необходимость-сговор, чтоб, например, студенты сами тужились и строили в голове образы и структуры и биндили их к реальным проблемам, либо математики на кафедрах просто ленятся врубить фантазию и добавить красок в материал?
Очевидно идешь в википедию и смотришь проблемы тысячелетия и так далее.
Почему тебя это интересует? По-моему прикладные задачи всяко важнее и интереснее, коль скоро они реально повышают продуктивность и делают жизнь даже сраного хиккана сытней.
Зачем мне проблемы тысячелетия, если я прошу проблемы в данный момент?
Быстро ты объявился. Как оно, многого уже добился на своём реформаторском поприще?
Ты смотрел стандартные западные учебники, например, Calculus: early transcendentals? Они очень красочные и во многом прекрасные (строго говоря, я вообще теку от качества лучших англоязычных изданий).
Есть мнение, что это связано с бесплатным образованием в СССР и платным на Западе. В совке было рациональнее набрать 9000 долбоёбов на илитный факультет, позволить им обломать зубы о Фихтенгольца или Ландавшица, отсеять не сумевших и дальше тратить бабло только на самых талантливых, которые отобьют вложения, запилив бонбуэ. В Штатах студенты покупают себе образование.
Тв не один задавался этим вопросом.
https://www.quora.com/Why-are-Soviet-mathematics-physics-textbooks-so-insanely-hardcore-in-comparison-to-US-textbooks
>>352122
Меня это не интересует, я не тот, кто спросил. Я восторженный дурачок ИТТ и не понимаю современного состояния математики. Но всё же очевидно, что делать домашку важнее, чем сидеть на дваче или катать в лолец, однако недолюди катают в лолец с большим интересом. Это я в терминвх хиккана поясняю, что интерес и практическая значимость зачастую имеют отрицательный коэффициент корреляции.
>Здесь уже указали, что математика помогла в поиске новых направлений для экспериментальных исследований, однако, таким же образом воздух помог поиску новых направлений, и является более фундаментальным явлением, нежели математика, значит вся ваша математика - это воздух, и наука, соответственно, тоже воздух.
Можно быть воздушной планетой...
говорят софт такой есть le coq. математический софт "петух". теоремы доказывает. определяет число N
Да, можно. Хотя математика это не только наука.
Математика даёт объективные знания о действительности, будь то действительность алгоритмов, игр или квантовых переходов. Помимо этого она даёт гораздо больше знаний о разных абстрактных соотношениях понятий, которые не относятся прямо к физической действительности, но они не произвольны и таким образом не запутывают нас: мы можем определить, имеет ли смысл тот или иной матметод в том или ином приложении.
Кроме того все остальные науки опираются на математику, поэтому некорректно требовать именно от математики «самостоятельной научности».
Вопрос закрыт?
Вот ты соснул.
>>можно ли считать символы объективными знаниями о действительности
Наука вся в символах. Результаты любого эксперимента-слова,графики,символы. На вход мозгу дается набор образов(наблюдений), на выход-числа и высказывания.
Любые знания об атомах=символы. В виде чисел на дисплее приборов, в виде чисел,на которые указывает стрелка. Любая теория любой науки по определению=символы.
Единственный разумный критерий, который ты родить оказался не в силах: может ли считываемый мозгом набор символов в данной теории формировать ожидания, которые будут полюбому реализованы? Какач теория из всего множества текстов (предположение,набор символов) формирует наиболее надежные ожидания относительно наблюдаемого явления?
Очевидно, что математика(ее отдельные результаты, как и положено) формировала и продолжает ыормировать правильные ожидания, позволяющие выбирать более и более продуктивный вектор действия.
>>>Символы изначально рождены субъектом, в противовес явлениям, не привязанным к субъекту, и уже позже описанных символами.
В пхарашу, ублюдок мать твою, со своим дуализмом. Еще о науке тут попездываешь.
>>как дисциплину без экспериментов над явлениями мира и без возможности опровергнуть конечное доказательство экспериментом
Тебе уже пояснили за эксперимент. Взяли уравнения максвелла, преоьразовали-предсказали и экспериментально подтвердили волны поля. Взяли уравнения паули, преобразовали-получили предположение о вирт.частицах,подтвердили. Таких примеров тонна.
>>поиске новых направлений для экспериментальных исследований,
Оче плохо. Не "новые направления" подсказала, а предсказала реальные существенные явления.
Нет, водник.
Математика - не наука, вы заебали уже. Просто по определению. Мамины матиматики не могут взять и посмотреть определение, слишкам, да?
Я другой анон. Просто крапку принёс.
У "науки" нету чётко фиксированного определения, как и у любой достаточно широкой области человеческой культуры. Математика имеет очень много признаков науки, но некоторых не имеет.
>>352183
Хватит маневрировать уже.
Это не значит, что она хуже или нинужна, просто не наука в отличии от физики, например.
>>352166
С момента открытия простых чисел, прошло 2000 лет прежде чем их начали использовать в криптографии.
Математика – наука изучающая понятия количества, пространства, изменения и структуры.
Сейчас он тебе скажет, что
> понятия количества, пространства, изменения и структуры
не имеют отношения к действительности, каким-то хуем. Ведь действительность – это то, что может лизнуть и осмыслить обезьяна, например камешки и хуи, а не абстрактные универсальные свойства мира.
А пространство это не разновидность структуры? "Структура пространства". Хм.
Физика и химия науки потому, что изучают наш объективный мир. Можно ставить эксперименты и проверять теории, это и есть наука. Математика же сама в себе и занимается скорее манямирами.
Действительность, это когда мамин матиматик отказывается видеть различия между физикой/химией и математикой. Ведь для науки-то эксперименты нинужны, го лучше сразу в философию.
Есть же какое-то определение, типа наука - это то, что можно опровергнуть или что-то типа того. В контексте холиворзов против альтернативщиков.
Оно не нужно, определения суть произвольные, математики это прекрасно знают. Математика - наука.
>Физика и химия науки потому, что изучают наш объективный мир.
Изучение включает построение мат. моделей для точного анализа и описания явлений.
>Можно ставить эксперименты и проверять теории, это и есть наука.
Математика – единственная наука, которая опирается на понятие доказательства (в заданной аксиоматике). Кроме того это единственная наука где было математически доказаны грани её (аксиоматики) применимости.
>Математика же сама в себе и занимается скорее манямирами.
Почти верно. Самодостаточность математики присутствует, но применимость её инструментов (корректность которых доказана) – неоспорима.
Пошёл нахуй.
>Изучение включает построение мат. моделей для точного анализа и описания явлений.
Именно, там где мат.модель разойдётся с реальность, там и кончается применимость теории, но мат.аппарату будет похуй.
Ещё раз, математика - не наука, просто инструмент.
>Почти верно. Самодостаточность математики присутствует, но применимость её инструментов (корректность которых доказана) – неоспорима.
Не всё можно применять, например. Лишь малую часть. Всё остальное уже манямир математики.
>Именно, там где мат.модель разойдётся с реальность, там и кончается применимость теории
Что потребует построения другой модели.
>но мат.аппарату будет похуй.
Не всегда.
>Ещё раз, математика - не наука, просто инструмент.
Это наука, инструменты которой используются в других науках. Объекты изучения этой науки я назвал. Помимо эксперимента – доказательство.
>Не всё можно применять, например. Лишь малую часть. Всё остальное уже манямир математики.
«Малой» я бы эту часть не назвал, но в остальном, с точностью до стилистики ты прав.
>верная логическая импликация == эксперимент
Охуеть просто.
>мат.аппарату не похуй на что-то
Вот это да.
Это не наука, я тебе уже пояснил, экспериментов в ней нету.
>Что потребует построения другой модели.
Это называется физика/химия. Математическая модель самодостаточна у неё нет нужды в реальности.
>>верная логическая импликация == эксперимент
>Охуеть просто.
?
>>мат.аппарату не похуй на что-то
>Вот это да.
То есть что такое (например) краевые условия ты не знаешь.
>Это не наука, я тебе уже пояснил, экспериментов в ней нету.
Есть. Помимо экспериментов есть доказательства.
>Это называется физика/химия. Математическая модель самодостаточна у неё нет нужды в реальности.
У «реальности» есть нужда в ней.
Помимо каких экспериментов?
Какие такие эксперименты в математике?
Ты с физикой не путаешь?
>То есть что такое (например) краевые условия ты не знаешь.
То есть, ты вот так вот берёшь и начинаешь уже с реальностью свою математику сверять?
>У «реальности» есть нужда в ней.
Мат.модели это вещи в себе, у них нет никакой нужды, как только ты определил определения и операции между ними, всё остальное должно логически вытекать из этого и пусть даже это не согласуется с реальностью.
Ну, и на языке математики можно написать кучу бредовых, но верных утверждений. Математика - язык, инструмент, искусство, как тебе угодно, но не наука.
>Какие такие эксперименты в математике?
Чем, кроме печения в сраке воннаби-попперианцев, доказательство хуже эксперимента? Да ничем. Задача четырёх красок, например, имела все черты большой науки и большого эксперимента. После появления в физике МЫСЛЕННЫХ экспериментов твои рассуждательства вообще смешны.
>Какие такие эксперименты в математике?
Подтверждающие гипотезу или опровергающие её. Надеюсь ты не рассматриваешь исключительно эксперименты на материальной основе?
>То есть, ты вот так вот берёшь и начинаешь уже с реальностью свою математику сверять?
Конечно. Если условия построенной модели не удовлетворяются «реальностью», значит модель ей неадекватна. Модель арифметики без числа 5 неадекватна реальным задачам на вычисление.
>>У «реальности» есть нужда в ней.
>Мат.модели это вещи в себе, у них нет никакой нужды, как только ты определил определения и операции между ними, всё остальное должно логически вытекать из этого и пусть даже это не согласуется с реальностью.
>Ну, и на языке математики можно написать кучу бредовых, но верных утверждений. Математика - язык, инструмент, искусство, как тебе угодно, но не наука.
Полностью согласен со всем кроме последнего предложения.
Тем что тебе всё таки приходиться прибегать к реальным экспериментам, одних "маняэкспериментов" не хватит. Со своими МЫСЛЕННЫМИ маняэкспериментами ты дальше богословов не уйдёшь.
>доказательство хуже эксперимента?
Просто пиздец.
>>352211
Построенная модель будет самодостаточна. Баттхёрт будет только у тебя, когда она с реальностью разойдётся, но математически она будет корректна.
А comp. sci тоже не наука, кстати? Если наука то сразу вопрос - а какие там эксперименты? По-моему ты путаешь "наука" с "естественная наука".
Согласен, я ещё забыл про гуманитарные науки, православные, подожду пока ты дополнишь список.
Исторический науки
Молодец, сам себя опроверг.
Молодец, теперь ты ещё и путаешь CS и Theoretical CS.
>>352213
Ты какой-то странный.
Математическое утверждение = гипотеза.
Доказательство/опровержение и его повторение сообществом математиков = эксперименты.
Доказательство никакой не мысленный маняэксперимент, а вполне материальный набор символов на бумаге/экране, составленный по определенным правилам. То, что достаточное количество экспертов после ознакомления с изначальным экспериментом сумели его повторить и подтвердить, что он корректен, дает основания для его принятия.
Совершенно не понимаю, в чем разница - считать количество решений в целых числах у вполне определенного уравнения или считать ускорение свободного падения.
Вот есть у нас, скажем, двойка. Её можно определить как множество M = {∅; {∅}}.
Почему 2 + 2 = 4, а вот M∪M = {∅; {∅}}, то есть |M∪M| = 2?
Сначала определяется инкремент по формуле inc(x) = {x} U x, а сложение определяется как единственная функция plus:NxN->N, что plus(x,0)=x, plus(x,inc(y))=inc(plus(x,y))
>Совершенно не понимаю, в чем разница - считать количество решений в целых числах у вполне определенного уравнения или считать ускорение свободного падения.
Это ты какой-то странный
А всё почему? Потому что вы постите без саги, поэтому всплывает этот, а не специально созданный для этого парашный тред https://2ch.hk/sci/res/349176.html (
https://www.dartmouth.edu/~matc/MathDrama/reading/Hamming.html
Описанное тобой - это коллегиальная проверка синтаксической корректности текстов.
Э. Ландау. "Основы анализа". Прочитай это, там всего лишь горстка страниц.
Кококо ссылаться на кого-то другого. Кудахтахтах если кто-то другой говорит что-то, значит это истина в последней инстанции. Цыпцыпцып нельзя иметь своё мнение, нужно только ссылаться на что-то.
Написал с сагой как советовали.
>>352300
За вами очень интересно наблюдать (и делать выводы), у вас «всё что абстрактно то божественно». Ну что же, грозу тоже колесницей Зевса объясняли, это в порядке вещей. Замечу лишь, что «эксперимент» – это не только колбы приборы (как в мультиках) и лабораторный журнал, и механистическое понимание мироздания было актуально в XIX веке.
аноны, умоляю
спасибо
>Я говорил лишь про критерии научности-ненаучности,
Приведи пожалуйста их ещё раз, в шуме я их не увидел.
>и привел яркий пример аналогии с научностью богословия, который показывает абсурдность квалификации математики как науки.
Ну я могу здесь начать размахивать разнообразными «приложенияии» математики в различных научных и инженерных областях, но это уже пошло и неинтересно. Самое интересное, что схожие черты между математикой и ммм... "изучением бога" (sic!) есть. Но как в том анекдоте «есть один нюанс»: Во-первых математика не является догматом (нет, аксиомы догмами не являются), во-вторых в математике присутствует консистентность (а точнее непротиворечивость) и преемственность её положений. В третьих математика является динамической постоянно развивающейся наукой (и пусть г-н Гроттендик утрёт слёзы в своём «плаче Ярославны»), в четвёртых пресловутая строгость доказательства (вплоть до контринтуитивности) это пожалуй аспект присутствующий только в этой науке и наконец в пятых математика никоим образом не касается вопросов морали, этики, нравственности и прочих «человеческих» факторов (и слава богу).

Матаны, а как пятое решается? Я что-то сообразить не могу.
можешь, пожалуйста, сказать как решаются остальные
братан, помоги, прошу, очень нужно
какое пятое?
Если это так, то на двощах обитают исключительно дауны и школьники. Что, впрочем, неудивительно.
>Библия - это не какая-то там маняидея, это символы на бумаге-экране
Которые трактуются не пойми как по непонятно каким правилам (история показывает, что обычно трактуются так, как выгодно церкви). Утверждения относительно библии поэтому не фальсифицируемы и не верифицируемы. В математике есть и то и другое.
>Ты не понимешь, потому что
Ну, давай. Объясни мне разницу. Предположим, уравнение смоделировано электрической цепью и задачу мы формулируем как задачу про конкретную электрическую цепь. Любое уравнение можно смоделировать вполне себе обычным физическим процессом.
В общей, давай еще раз. Чем математика отличается от физики? Эксперименты есть, наблюдения есть (множество теорий и утверждений изменилось из-за проводения наблюдений над объектами и нахождения противоречий), фальсифицируемость есть, верифицируемость есть, предсказательная сила есть.
А то ты, в основном, толсто кукарекаешь и утверждаешь "Вы не понимаете, потому что тупые, а объяснять я не буду"
Первокурсник закукарекал.
>а человек - это всевышний, наблюдающий себя из человеческого тела.
Я один про "Лёха, помоги выбраться из собаки подумал"?
Функция меры.
Какие-нибудь научные журналы за статьи платят хотя бы копейки?
> Какие-нибудь научные журналы за статьи платят хотя бы копейки?
Кекнул, это ты должен ещё дополнительно платить за публикацию.
Ебать. Что за хуйня ебучая? Пиздец, блядь. Правда что ли? Ебануться. Я тебе не верю. Это же охуеть можно, я за свой труд платить им ещё должен? Хуетень. Так не может быть.
Ты бы хотел маленького Хокинга?
Это нормально, ведь математики не биологи и даже не физики, они занимаются только им одним интересной хуйнёй и не всем везёт так, что впоследствии эта хуйня оказывается полезной в какой-нибудь теории струн (впрочем, тоже бесполезной) или в криптографии (а вот это уже ништяк). Так как математики не стремятся и не приносят пользы другим, они должны платить за возможность растиражировать свои фантазии.
>В математике нет фальсификации, я не могу опровергнуть теорему пифагора экспериментально, эксперимента нет изначально.
Ясно. Понятно. Только ничего, что куча математических теорем была опровергнута? Ничего, что куча из них была опровергнута совершенно экспериментально. И теорему Пифагора ты тоже модешь попытаться опровергнуть.
В общем, ты подебил. С дальнейшей шизофазией тоже спорить бессмысленно.
Это касается всех учёных, маня. Платить тебе за твою охуенно важную работу один хуй никто не будет, более того ещё и взнос потребуют "за обслуживание". Всё потому что публиковать учёным-мочёным статьи нужнее, чем журналам печатать какого-то очередного васю пупкина.
> В моих маняфантазиях я могу представить маняэкперимент, в котором я маняопровергнул теорему пифагора - это будет чисто математический эксперимент
Нет, не будет. Или ты где-то ошибся. Видишь ли, мань, вся сила математики в том, что она отражает идеальные и инвариантные признаки вселенной. Ну, вот никак не возможно себе представить, пользуясь математическим методом, что отношение длины окружности к радиусу на плоскости будет не 2 пи r. Либо непредставимо, либо не окружность, либо не на плоскости, либо ошибка.
> Еще раз напоминаю про разницу между названием и действием - нельзя скушать слово "яблоко", нельзя выебать мамку по переписке
Поэтому математика – не маняфантазии, дурачок. Ты можешь сказать, как что-то представил, но не можешь этого представить, если это противоречит математике.
> вселенная едина и неделима
Хуина.
Да, это всё очень любопытно, но расскажи мне, как ты представишь, что (1+1/n)^n при n ===> бесконечность – не будет стремиться к e. Просто кукарекнуть, что «представляю», недостаточно. Давай, попробуй подтвердить свою позицию, что математика ненаучна. Поставь эксперимент и распиши ходы своего представления.
Я утверждаю, что какие бы числа ты ни брал, покуда ты выполняешь вычисления честно, (опираясь на элементарную самоочевидность, например, что 1=1 и 10=10) – результат, не соответствующий верному, будет непредставим. Если это нечто наподобие религии, то ты сможешь просто помыслить ересь и сразу окажешься победителем.
Еще раз. Моделируешь все на аналоге компьютере. Эксперимент, опровергающий/подтверждающий теорему Пифагора это электрическая цепь, составленная по определенным правилам, при подаче на которую некоторой определенной последовательности 0 и 1, загорается лампочка.
Все это совершенно независимо от наших фантазий и абсолютно объективно (даже объективнее физики, где обработка показаний эксперимента гораздо более субъективна). И абсолютно математично.
Поэтому все твои аналогии с богословием говно собачье.
Можно сделать электрическую цепь с лампочкой. Лампочка загорается тогда и только тогда, когда на вход цепи подан никео-цареградский символ веры. Если есть отличие хотя бы в одном знаке - лампочка не горит.
Значит, эта система способна определять крест. Дальше что, дебик? Ты слишком туп для этой проблемы.
Система, которая проверяет синтаксическую корректность никео-цареградского символа веры,
ничем не отличается от системы, которая проверяет синтаксическую корректность теоремы Пифагора.
И столь же научна.
Мудак, я ещё раз повторю: попробуй выполнить условия в >>352464, а потом кудахчи о синтаксисе.
Утверждение, что lim (1+1/n)^n при n->Inf равно e - это всего лишь строка символов, которая ничем не хуже любой другой строки символов той же самой длины.
> ничем не хуже любой другой строки символов той же самой длины.
Окей. lim (1+1/n)^n при n->Inf равно 4.5
Приступай к доказательству.
Это операция со значком. Математика – операции с идеями. Идея лимита вполне понятна. Ты можешь переопределить lim, а можешь насрать себе на голову. Все это поймут.
>>352500
> Тебе сначала нужны цифры, потом тебе нужно понятие измерения, акт измерения окружности, также, тебе нужна идеальная окружность, то есть, понятие этой окружности
Всё это здорово, но независимо от того, существуют ли люди, обладающие подобными знаниями, природа окружности не изменяется.
> Нигде в мире не существует идеальной окружности
Фронт любого волнового процесса. Сечение звезды. Существует бесконечное количество окружностей, чья неидеальность пренебрежима. Это нелепое возражение.
> идея, это мысль в голове
Не каждая идея является всего лишь мыслью в голове. Я могу помыслить, как ебал твою мать. Я могу помыслить, что два раза по два – четыре. Только дегенерат не увидит фундаментальной разницы между этими мыслями.
> Отсюда простой факт - в мире есть огромное кол-во вещей, похожих на окружность, у которых отношение радиуса к диаметру - не 2 пи эр
А то. Я тебе больше скажу, у идеальной окружности отношение радиуса к диаметру – тоже не 2 пи эр, а 1/2. Ты натурально дегенерат, филолог небось?
> Поставлю свечку у иконы, помолюсь богоматери, и представлю
Ну распиши, что ты там представляешь. Ну давай, что ты жмёшься.
Ты не видишь разницы между «сказать» и «сделать», живёшь в мирке пустых декламаций, поэтому твои попытки борцунствовать с математикой некогерентны.
>Господь расставит все на свои места.
Понятно.
Смотри, чувак, я понимаю тебя. Ты слишком тупой для математики, IQ не хватает, ну бывает такое, ввиду этого для тебя непостижимы простейшие абстрактные понятия. Ты понимаешь, что апельсин – это апельсин, его можно сожрать. Ты выучился тому факту, что слово есть слово, его можно сказать, записать, переставить в нём буквы, пока оно не станет непонятным. Но это примерно твой потолок абстрагирования. Ты смутно замечаешь, что другие люди умнее, быстрее соображают, могут не только заниматься демагогией, но и предсказывать некоторые результаты, будто бы пользуясь божественным откровением. Это вызывает у тебя неприязнь, ты в стиле фрейдовского младенца пытаешься убедить себя и весь мир, что нету никакой истинной абстракции выше твоего потолка, что есть только высказывания о такой абстракции, только претензии на её понимание; кто-то претендует на понимание Бога, кто-то на понимание математики, но и то и другое является не более чем словами, не более чем претензией, броском в непостижимое.
Ну, не совсем так. Это ты ограничен словами, а не мы и не мир вокруг.
Надо просто принять, чувак, что есть области знания, для которых недостаточно читать книжки или остроумно отгавкиваться. Есть вещи, которые физически для тебя непостижимы, они просто не помещаются в твою головёнку. Знаю, сейчас ты продумываешь, как изящно это перепишешь в виде богословского довода, типа я сектант. Это предсказуемо. Но это просто признак твоей ограниченности. Если я возьму тебя за руку и проведу от идеи тождества (1=1) до выведения указанного лимита – для тебя это будет ровно то же, как если бы я от тождества довёл до необходимости покаяться. Я понял, что ты так мыслишь, но умные люди мыслят не так, для них в рассуждении нет произвольности, они действительно осознают все безусловно истинные переходы на том же уровне, на котором ты можешь осознать, что вещь тождественна самой себе.
Нет способа доказать достаточно тупому двухмерному существу, что существует трёхмерное пространство: для него события в трёх измерениях выглядят как просто какая-то хуйня с появляющимися и исчезающими признаками, и опираясь на свой опыт он принимает, что так и есть, что это просто ересь и наёбка. Так и с тобой.
>Господь расставит все на свои места.
Понятно.
Смотри, чувак, я понимаю тебя. Ты слишком тупой для математики, IQ не хватает, ну бывает такое, ввиду этого для тебя непостижимы простейшие абстрактные понятия. Ты понимаешь, что апельсин – это апельсин, его можно сожрать. Ты выучился тому факту, что слово есть слово, его можно сказать, записать, переставить в нём буквы, пока оно не станет непонятным. Но это примерно твой потолок абстрагирования. Ты смутно замечаешь, что другие люди умнее, быстрее соображают, могут не только заниматься демагогией, но и предсказывать некоторые результаты, будто бы пользуясь божественным откровением. Это вызывает у тебя неприязнь, ты в стиле фрейдовского младенца пытаешься убедить себя и весь мир, что нету никакой истинной абстракции выше твоего потолка, что есть только высказывания о такой абстракции, только претензии на её понимание; кто-то претендует на понимание Бога, кто-то на понимание математики, но и то и другое является не более чем словами, не более чем претензией, броском в непостижимое.
Ну, не совсем так. Это ты ограничен словами, а не мы и не мир вокруг.
Надо просто принять, чувак, что есть области знания, для которых недостаточно читать книжки или остроумно отгавкиваться. Есть вещи, которые физически для тебя непостижимы, они просто не помещаются в твою головёнку. Знаю, сейчас ты продумываешь, как изящно это перепишешь в виде богословского довода, типа я сектант. Это предсказуемо. Но это просто признак твоей ограниченности. Если я возьму тебя за руку и проведу от идеи тождества (1=1) до выведения указанного лимита – для тебя это будет ровно то же, как если бы я от тождества довёл до необходимости покаяться. Я понял, что ты так мыслишь, но умные люди мыслят не так, для них в рассуждении нет произвольности, они действительно осознают все безусловно истинные переходы на том же уровне, на котором ты можешь осознать, что вещь тождественна самой себе.
Нет способа доказать достаточно тупому двухмерному существу, что существует трёхмерное пространство: для него события в трёх измерениях выглядят как просто какая-то хуйня с появляющимися и исчезающими признаками, и опираясь на свой опыт он принимает, что так и есть, что это просто ересь и наёбка. Так и с тобой.

>теория категорий пришла на смену UML http://category-theory.livejournal.com/26862.html
Таки что, это правда просто продвинутый UML?
> я призер городской олимпиады по математике, и областной по физике
Ты пиздобол, конечно же.
>Не будет никакой разницы. Одни правила - другие правила. У одного человека свои правила - у другого другие правила
> Ты не попытался проверить мои знания
Попытался и проверил. Тебе предложено рассказать, что ты там представляешь, чтобы вместо математически верного результата выходил неверный. Вместо этого ты начал пиздеть. Ты не попытался изменить правила – твоей лучшей попыткой было изменить значения, приписать значку «лимит» другой смысл; но это глупо, поскольку ты просто меняешь выражение на иное. Слова про боженьку и так далее невалидны, это описание некоторых внешних признаков рассуждения, а не рассуждение как таковое: ты рассказываешь, по каким мотивам даёшь неверный результат, как можно отмахнуться от критики, а не о взаимодействии чисел. Если математика является набором произвольных правил, то давай, создай другую математику с другим произвольным набором правил. Раз уж объяснить лимит на основе здравого смысла можно школьнику – при данном условии для этого не потребуется, я думаю, рассматривать вопросы типа аксиом математики.
Выше тебе дан лимит. Представляй. На входе числа, в процессе числа, на выходе числа. Единственное, что от тебя требуется – согласованность системы и чтобы число на выходе не равнялось e.
> теория категорий пришла на смену UML http://category-theory.livejournal.com/26862.html
> вход 250 рублей
Просто ушлые интерпринёры рубят бабло с монетизации очередной модной идеи.
Хипстерьё хавает.
Ты опять не попытался даже изобразить рассуждение, ты просто написал символ. Но математика не занимается символами. Итак, Ꮬ равен 2,7182...
Ты ровно никак не возразил против трансцендентной истинности математики.
> По-моему у тебя серьезные проблемы с обучаемостью
Это не то, что ты можешь говорить из своего жалкого положения, манипулируя символами и не улавливая, чем символ отличается от идеи.
Я уже который день в избранном вижу, что в мат треде новые посты, захожу посмотреть, думаю вдруг че-то интересное, а тут опять эти уебаны.
Графики с координатами их точек пересечения.
Потому что сажица-матушка
С чего это ты взял? Не он.
нет
И чего?
>Математика – операции с идеями
Нет, с текстами. С точки зрения аппаратного прувера с лампочкой, математика - это формальная теория, в которой нет ничего кроме синтаксиса.
Проблема в том, что «аппаратный прувер с лампочкой» — искусственное создание, которое появилось совсем недавно. А математика — творение (по крайней мере в каком-то из слабых смыслов) человеческого ума, который намного более мощная и древняя конструкция.
В этом треде для проверки математики был предложен прувер с лампочкой. Я настаиваю, что этот прувер способен проверить только синтаксическую корректность математических доказательств - как раз в духе Гильберта. Эпистемологически такой прувер ничуть не отличается от прувера, который способен проверить лишь синтаксическую корректность никео-цареградского символа веры. Более того, можно построить прувер-объединение, который считает никео-цареградский символ веры столь же синтаксически корректным, сколь и математические доказательства. Я понимаю, что эта идея кажется вам странной, собеседник, но я всё-таки надеюсь на рациональное обсуждение. Если вы читали Юдковского, то попрошу потратить некоторое время над размышлением над моими словами, если вы решите написать ответ. В противном случае не берите в голову.
Хуёвского.
> Я настаиваю
Настаивай в другом месте.
Модер, убери отсюда это уёбище, ещё раз, если можно.
кстати, забавно то, что он использует слово «синтаксис» в некотором уничижительном смысле, типа того, что существование иных формальных систем, с менее строгими, чем в математике, правил, что-либо доказывает или опровергает
Юдковский рекомендовал банить долбоёбов.
Мы сейчас обсуждаем именно аргумент прувера с лампочкой.
Прувер с лампочкой, которая загорается при синтаксической корректности входного текста, ничем не лучше прувера с лампочкой, которая загорается при синтаксической корректности входного текста, - это одно и то же. Прувер для математики ничем не лучше прувера для символа веры.
Если существование прувера с лампочкой для математических текстов обосновывает ценность математики, то существование прувера с лампочкой для никео-цареградского символа веры обосновывает ценность никео-цареградского символа веры.
Одного лишь наличия прувера с лампочкой недостаточно, чтобы счесть математику чем-то превосходящим богословие. Нужны дополнительные аргументы.
Ты тут даун, блядь. Не отвечай ему.
> Одного лишь наличия прувера с лампочкой недостаточно, чтобы счесть математику чем-то превосходящим богословие
Превосходящим богословие в чём именно, ебанашка? Попробуй хоть раз сформулировать конкретно и содержательно, что ты доказываешь.
>в чём именно
В соответствии набору признаков понятия "наука", разумеется.
>что ты доказываешь
Вздорность идеи "математика - наука, потому что для её доказательств существуют синтаксические пруверы".
>В соответствии набору признаков понятия "наука", разумеется.
Наука – частный случай познавательной деятельности. Сведения науки менее достоверны, чем сведения математики. Более того, если биологи путём тысяч измерений откроют, что радиус деревьев относится к длине окружности деревьев примерно как 6.3, математику не нужно даже видеть деревья, чтобы сказать точнее, к какому числу будет стремиться это отношение при бесконечных измерениях. Может ли религия, или любая иная формальная система кроме математики, делать такие утверждения? Могут ли биологи сами понять, почему отношение стремится к указанному математиком числу? Если нет, то я не вижу смысла для математики быть чем-то таким примитивным, как наука.
Да, как-то так, если угодно. Следующую олимпиарду выигрывай по основам православной культуры, гений. Думаю, тебе будет без разницы.
Ты с несколькими разными людьми разговариваешь. Как минимум с тремя.
На обычную логику предикатов.

хех

Конечно, только точку еще какую-нибудь надо отметить.
Итак, вы окончили матшколу или просто где-то нахватались до базового уровня математической культуры.
Херачим кое-как (т.е. необязательно все вдоль перечитывать, просто на сносном уровне понимать про большую часть в книге и нормально выучить основы).
кс). Вот эволюция учебников. Паралельные вещи учатся одновременно.
ALG1. Винберг
ALG2 Aluffi (просто проглядеть уже выученное и начать учить гомологическую алгебру)
ALG3. Атья-Макдональд
ALG4. Гельфанд-Манин
ANAL1. Зорич (1 том)
ANAL2. Львовский, анализ
ANAL3. Рандомный учебник комплана
TOP1. Виро, топология (пока не освоишься с теоретикомножественным формализмом, т.е. достаточно нескольких глав)
TOP2. Хатчер или Фоменко/Фукс
ALGEM1. Набор мотивации разной из геометрических введений. Например, первые несколько глав Шафаревича Алгебраическая геометрия.
ALGEM2. Хартсхорн до посинения.
CG1. Вуазен Теория Ходжа и комплексная алгебраическая геометрия.
Итого порядка 11-13 книжек (так как многие книги читаются далеко не полностью).
Поздравляю! Вы охуенны и пиздаты, владеете бэкграундом достаточным, чтобы дальше учить, что пожелаете. Еще пара-тройка узкоспециализированных книжек и вы можете читать статьи, вести научную работу, поступать в топовые аспирантуры без зазрений совести.
Казалось бы можно за месяц одну книжку прочитать? Следовательно, за первые полтора курса все это учится. А дальше становишься оверпавер богом, который разбирается во всех современных областях и уезжает заграницу под аплодисменты.
Объясните, почему очень мало тюдей так делает, и работает это все только в теории? Я то распиздяй, которому лень с кровати даже подняться. Но есть же товарищи, которые каждый день делают зарядку или работают с утра до вечера. Казалось бы пару-тройку часов математике нормальные люди вполне себе могут уделить.
При этом после освоения матшкольника идейных трудностей не должно же быть (так что на талант и прочее не свалить).
Итак, вы окончили матшколу или просто где-то нахватались до базового уровня математической культуры.
Херачим кое-как (т.е. необязательно все вдоль перечитывать, просто на сносном уровне понимать про большую часть в книге и нормально выучить основы).
кс). Вот эволюция учебников. Паралельные вещи учатся одновременно.
ALG1. Винберг
ALG2 Aluffi (просто проглядеть уже выученное и начать учить гомологическую алгебру)
ALG3. Атья-Макдональд
ALG4. Гельфанд-Манин
ANAL1. Зорич (1 том)
ANAL2. Львовский, анализ
ANAL3. Рандомный учебник комплана
TOP1. Виро, топология (пока не освоишься с теоретикомножественным формализмом, т.е. достаточно нескольких глав)
TOP2. Хатчер или Фоменко/Фукс
ALGEM1. Набор мотивации разной из геометрических введений. Например, первые несколько глав Шафаревича Алгебраическая геометрия.
ALGEM2. Хартсхорн до посинения.
CG1. Вуазен Теория Ходжа и комплексная алгебраическая геометрия.
Итого порядка 11-13 книжек (так как многие книги читаются далеко не полностью).
Поздравляю! Вы охуенны и пиздаты, владеете бэкграундом достаточным, чтобы дальше учить, что пожелаете. Еще пара-тройка узкоспециализированных книжек и вы можете читать статьи, вести научную работу, поступать в топовые аспирантуры без зазрений совести.
Казалось бы можно за месяц одну книжку прочитать? Следовательно, за первые полтора курса все это учится. А дальше становишься оверпавер богом, который разбирается во всех современных областях и уезжает заграницу под аплодисменты.
Объясните, почему очень мало тюдей так делает, и работает это все только в теории? Я то распиздяй, которому лень с кровати даже подняться. Но есть же товарищи, которые каждый день делают зарядку или работают с утра до вечера. Казалось бы пару-тройку часов математике нормальные люди вполне себе могут уделить.
При этом после освоения матшкольника идейных трудностей не должно же быть (так что на талант и прочее не свалить).
> Объясните, почему очень мало тюдей так делает, и работает это все только в теории?
Потому что твоя алгебраическая геометрия никому нахуй не нужна.
> Казалось бы можно за месяц одну книжку прочитать?
> Львовский
> за месяц
Слишком толсто.
Что-то не понял. Нашел вот это
и вот это
В первом только алгебра и геометрия, а во втором только лекции, а где задачи?
> Почему толсто?
Может потому что он содержит в себе 3 семестра НМУ?
> Короче, обучение в НМУ и на матфаке
То есть ты в течение 3х семестров проходил это 2 раза, в НМУ и на матфаке, и говоришь что это осваивается за месяц с 1 раза? Нихуя ты умный.
Пусть V - конечномерное векторное пространство над C и dim V >= 2. Пусть T - линейный оператор на V и λ - его собственное число. Тогда U = im (T - λI) инвариантно относительно T.
Доказательство, которое я прочитал, такое: Пусть u ∈ U.
Тогда Tu = (T − λI)u + λu, где каждый вектор, очевидно, принадлежит U. Мне это доказательство совсем не нравится. Я вижу, что оно верно, но это просто трюк. То есть, если заранее не знать, что U должно быть инвариантно, то никогда не заметишь. Есть какая-то настоящая причина того, что U инвариантно относительно T? В идеале хотелось бы геометрическую интерпретацию.
Нельзя это доказать так:
T(T-λ)=TT-Tλ=TT-λT=(T-λ)T
?
При чём тут вообще конечномерность и собственные числа.
Как ваши дела? Студент-недоучка воннаби-алгебраист по-прежнему беснуется?
Да ты и сам нюфаня, чего уж там.
Разумеется, это не все, что нужно знать. Но то, что там, знать нужно. И после этого можно уже читать что-то продвинутое (очень часто из прериквизитов только 2-3 главы Хартсхорна).
Поэтому не понял. Или ты предлагаешь какого-нибудь Liu взамен?
Sheldon Axler: Linear algebra done right. 5 глава, доказательство того, что матрица над C может быть приведена к верхнетреугольному виду.
>Sheldon Axler: Linear algebra done right.
>
>Theorem: Suppose V is a complex vector space and
>T ∈ L(V). Then T has an upper-triangular matrix
>with respect to some basis of V.
>Proof: We will use induction on the dimension of V.
>Clearly the desired result holds if dimV = 1. Suppose
>now that dimV > 1
А вообще верно, доказывать правильно нужно просто пользуясь тем что T-\lambdaI и T перестановочны, там какая-то хуета вместо этого.
Бамп вопросу
Сомневаюсь, что люди, учащиеся/учившиеся на матфаке ВШЭ, сидят в un, потому что это помойка, на которой только и делают что просят посчитать интеграл.
И чем ты лучше них?
Они, наверное, даже не знают, что такое гомологии...
Взять, например, теорему Ролля -
"Если вещественная функция, непрерывная на отрезке [a; b] и дифференцируемая на интервале (a; b), принимает на концах отрезка [a,b] одинаковые значения, то на интервале (a; b) найдётся хотя бы одна точка, в которой производная функции равна нулю".
Почему непрерывность берут на отрезке, а дифференцироуемость на интервале?
Шафаревич совершенно точно не подходит (там схем и когомологиий слишком мало).
То, что по твоей ссылке подходит, но вроде не особо отличается от Хартсхорна.
Потому что мы хотим уметь брать производную внутри точки, котрую найдём, а она лежит в интервале.
Какое животное?
0) В большинстве учебников производную определяют только во внутренней точке области определения, уверен ли ты до конца, что понимаешь, что значит выражение "функция f : [a..b] -> R дифференцируема в точке a"? Если уверен, что понимаешь, то гоу дальше.
1) Довольно очевидный факт, что у такой вот функции всегда есть экстремум внутри интервала (для его доказательства дифференцируемость не нужна).
1.2) Во внутренней точке экстремума такой вот функции производная 0: делаются очевидные локальные рассуждения вида: если не 0, то чуть пошевелим точку (вправо и влево ТУТ ДОКАЗАТЕЛЬСТВО СЛОМАЕТСЯ, ЕСЛИ БРАТЬ НЕ ВНУТРЕННЮЮ ТОЧКУ, А КОНЦЫ ОТРЕЗКА) и увидем, что f(x)-f(x0) разных знаков, значит не экстремум.
1.3) Так как мы пытаемся найти точку, в которой производная 0, то, очевидно, для подобных рассуждений мы можем вообще вместо условия "f дифференцируема на интервале (a..b)" написать условие "f дифференцируема в некоторой окрестности некоторого внутреннего экстремума".
1.4) Но, очевидно, что такие условия нахуй никому не нужны, ибо непрактичны, поэтому мы их ослабляем до "f дифференцируема на всём интервале (a..b)".
2) Почему бы тогда уже ослабить не до отрезка [a..b]? Кому впизду впёрлись функции, котороые непрерывны на [a..b], дифференцируемы на (a..b) но не дифференцируемы в точках a и b, ведь они убер-аномальны, скорее всего? Как там выглядела функция, график которой - единичная полуокружность? sqrt(1-x^2)? Wait, oh shi...
Инженерия, программирование, моделирование
Потому что доказательство теоремы Ролля основано на использовании леммы Ферма. Лемма Ферма справедлива только для двусторонних окрестностей. У концов отрезка, понятно, окрестности только односторонние.

Анон, проверь моё доказательство, пожалуйста.
>Некоторое множество попарно непересекающихся отрезков прямой покрасили в белый цвет. Может ли так случиться, что на любом отрезке есть белая точка? (Точка отрезком не считается).
Пусть M - семейство, элементами которого являются множества непересекающихся отрезков. Упорядочим M по включению, т.е. если a - множество непересекающихся отрезков, b - множество непересекающихся отрезков и a подмножество b, то a < b.
Пусть m1 < m2 < ... < mn < ... - цепь в M.
Объединение ∪m множеств m1, m2, ... , mn, ... тоже будет множеством попарно непересекающихся отрезков, причём для любого i верно mi < ∪m.
По лемме Цорна, в M существует хотя бы один максимальный элемент. Обозначу его U.
Покрасим отрезки из U в белый цвет. Тогда на любом отрезке вещественной прямой есть белая точка. В самом деле, если на некотором отрезке белых точек нет, то этот отрезок не пересекается ни с одним из отрезков U, поэтому его можно добавить к U, что противоречит максимальности U.
Ошибки есть?
> Ошибки есть?
> Покрасим отрезки из U в белый цвет. Тогда на любом отрезке вещественной прямой есть белая точка.
Каким образом ты перешел от М к "любому отрезку вещественной прямой"? Если ты покрасил U то ты можешь утверждать что любой из отрезков входящих в какое-то множество из семейства M является белым. Но не любой отрезок вещественной прямой. Чтобы делать такое утверждение как у тебя, тебе (как минимум) нужно показать каким образом ты можешь разбить вещественную прямую на множество попарно непересекающихся отрезков.
Задача в том, чтобы выбрать на прямой какое-то множество попарно не пересекающихся отрезков W так, чтобы для любых чисел p и q отрезок [p;q] пересекался хотя бы с одним из отрезков W.
Я не утверждаю, что любой отрезок прямой является элементом U. Я утверждаю, что какой бы ты отрезок ни взял на прямой, он пересечётся хотя бы с одним из отрезков, входящих в U.
А как ты хочешь? Непрерывности на (a, b) недостаточно, нужна непрерывность и в концах отрезка. А вот дифференцируемость на концах отрезка необязательна, поэтому берут (a, b).

Не читал твое доказательство, но ответ на эту задачу: так случиться может. Очевидный пример: множество Кантора (с той разницей, что при построении вместо отбрасывания открытого интервала посередине нужно красить соответствующий отрезок в белый цвет).
Я видел твой пост, но он показался мне недостаточно строгим. Решил доказать существование без конструирования вспомогательных объектов.
Отбрасывается интервал, если взять отрезок то у тебя получится пересечение - после первого отбрасывания у тебя получится три пересекающихся отрезка, один из которых белый.
То есть ты в множество Кантора не веришь?
>>353907
Че непонятного?
1) [1/3, 2/3] красим в белый цвет
2) [1/9, 2/9] и [7/9, 8/9] красим в белый цвет
и т. д.
Меня смущают слова и т.д., которые ты использовал. В приведённой формулировке у тебя остался непокрашенным любой отрезок из (2/9; 1/3).

Либо ты просто тролль, либо у тебя реально очень низкий уровень математической культуры, если ты не понимаешь как перевести слова "и т. д." в формализованный текст. Я это за тебя делать не собираюсь. Слова "и т. д." в моем построении формализуются точно так же как и в построении множества Кантора, о чем я тебе говорил еще в прошлом треде.
Тогда формализуй же их, и закончим с этим. Как видишь, не только я тебя не понял.
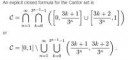
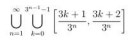
Окей.
1) Открываем статью на вики про множество Кантора, видим там пикрелейтед 1.
2) После секундных размышлений получаем явную формулу для подмножества [0, 1], покрашенного в белый цвет (пикрелейтед 2).
Так яснее.
Медленно вникаю в электричество, входит туго в том числе потому, что матана не хватает.
Где можно взять все в легкоусвояемой форме эти роторы с лапсианами?
Что рекомендуете по физике? Быстро погуглив узнал что есть Фейнмановские лекции, Берклиевский курс, Ландавшиц, Савельвев и Сивухин.
На каком уровне объяснить? Просто совсем на школьном уровне как-то долго выйдет. Хотя можно, просто это будет этакая научно-популярная лекция, а не короткое объяснение.
Тебя интересуют именно обозначенные определения или примеры вообще? Можно привести более простые примеры, но там легко обойтись без категорий в каждом конкретном случае.
Например, что такое произведение двух пространств X и Y? Это такое пространство, что задать отображение в него это все равно, что задать отображения и в X и в Y (представь плоскость как произведение двух прямых, задать туда отображение это все равно что задать отображение по x и по y координатам). Лемма Йонеда утверждает, что если такое пространство есть, то оно единственно с точностью до изоморфизма, так что это свойство полностью его определяет. А также, что отображения между ним и другим объектом Z это все равно что сопостовления парам отображений в X и Y отображений в Z. Поэтому он не только однозначно задается этим свойством, но еще и отображения между ним и другими пространствами описываются в терминах этого свойства.
Поэтому такое описание во всех смыслах полно и порой оказывается гораздо удобнее определения ручками. Даже в данном случае оно дает некоторое понимание, так как произведения бывают не только у геометрических объектов, но и у, скажем, групп. И вообще во многих ситуациях. И для всех них определение будет одинаковым в терминах представимого функтора (хотя в каждом конкретном случае несложно предъявить явную конструкцию, которая не сильно хуже).
А в некоторых случаях такое определение практически единственное разумное. Так как явная конструкция громоздкая, непонятно, чем мотивирована, а по существу не используется (используется только свойство).
Погоди, вот я так понимаю, что есть универсальное свойство, которое абузится вкривь и вкось, позволяя определять вещи с точностью до изоморфизма (те самые произведения, копроизведения, и ещё вагон с маленьким прицепом всякой ерунды) Универсальное свойство кагбе строится на том, что отображение между парой объектов (или множеством объектов) определяет конструкцию. Например, моноид с точностью до изоморфизма определяется множеством его элементов и всё в таком духе, а Йонеда, стало быть, подводит законодательную базу под этот беспредел, утверждая, что объект характеризуется отображениями в него (из него - в зависимости от формулировки) Это вполне в категорном духе, кажется, изучать чёрные ящики без внутренней структуры/каких-то элементов исключительно с помощью тыкания стрелочек в этот ящик и тем, как он относится с другими объектами. В частности, представляющий объект - это пробное тело, а функтор, сопоставляющий множество стрелочек в (из) пробное тело - это как представление извучаемого объекта в терминах морфизмов. Нет?
Да.
Йонеда показывает, что объект можно изучать как черный ящик, основываясь только на стрелках в другие ящики (из других ящиков).
Это полезно потому что порой естественно возникает именно представление объекта в терминах морфизмов, а не сам объект со внутренней структурой.
А порой мы вообще делаем наоборот и интересуемся именно функтором каким-нибудь полезным, а потом уже очень радуемся, если находим объект его представляющий, так как это позволяет больше узнать про свойства функтора.
Это не Лемма Йонеды даёт. А сам функтор Йонеды такое свойство имеет
Хотя тоже вроде понятно. Пусть 2 каких-нибудь отрезка в U пересекаются. Пусть A - элемент цепи содержащий 1й отрезок, B - элемент цепи, содержащий 2й отрезок. Тогда элемент цепи max(A, B) содержит оба этих отрезка. Противоречие.
Кстати, я немного объебался. В задаче же просят не [0, 1] покрасить в белый цвет, а всё R. Но это ничего. Для каждого четного n покрасим в белый цвет отрезок [n, n + 1]. А для каждого нечетного покрасим так, как я написал.
http://www.euclideanspace.com/maths/discrete/category/concrete/monoid/index.htm
Заценил так, что весь сайт - это то что мне нужно.


Русского достаточно для изучения математики вплоть до исследовательского уровня.
Нормас. Правда уже про инфинити-категории и прочее лурьейобство на русеке один хуй ничего нема, поди. Да и то, что есть, старовато а в переводе Маклейна ошибка на ошибке. Но для знакомства с очобой сгодится. В фиглише тоже есть проблемы (amnestic/forgetful functors - по названию одно и то же, почитай, а по определению не совсем; то, что в ACC называют квазикатегориями, оказывается, вовсе не квазикатегории, ну и так ещё до кучи всякого разного)
Заебёшься публиковаться зарубежом. Начиная с задроча терминов (я это на собственном опыте проходил, правда, с английского на немецкий, для лекций надо), а во-вторых, если ты учишь только на русском, то с англ. у тебя проблемы, работаешь в рашке в НИИ Говна и без протекции ничего не опубликуешь.
>>354986
Нехуй тут обсуждать. Здесь всё как с русским на компе - поставил инглиш в ОС и всех приложухах и даже не обсуждается.
> поставил инглиш в ОС и всех приложухах
ВЫБРОСИЛ ИЗ ДОМА ВСЕ КНИЖКИ НА РУССКОМ
@
НАДПИСИ НА ВСЕХ УПАКОВКАХ ЧТО ПОЯВЛЯЮТСЯ ДОМА ЗАКЛЕИВАЕШЬ СПЕЦИАЛЬНО ЗАГОТОВЛЕННЫМИ ПОЛОСОЧКАМИ И ПЕРЕПИСЫВАЕШЬ ПО-АНГЛИЙСКИ
@
ИГНОРИРУЕШЬ МАМКУ, РЕАГИРУЕШЬ ТОЛЬКО КОГДА ОБРАЩАЕТСЯ К ТЕБЕ НА ЛОМАНОМ РУГЛИШЕ
@
ПИЗДИШЬ КОТА КОГДА ОН НЕ ОТЗЫВАЕТСЯ НА НОВОЕ БЕЛОЕ ИМЯ
@
ИЛИТА
Но он прав.
Они клёвые.
Алгебрами Ли заниматься.
pre-algebra+algebra1+geometry(планиметрия)+algebra2
Эти программы равны или нет?
Если есть возможность ответьте поподробней, если не равны то насколько сильно.
Не совсем понимаю что ты имеешь в виду.
Наверное базовый, ну в смысле обычная общеобразовательная школа


Математическое образование в России делится на два разных уровня - базовый и профильный. Кроме того, оно делится на основное общее ака неполное среднее (до 9 класса включительно) и среднее полное общее (10-11 классы).
Я буду ориентироваться на https://www.khanacademy.org/math/linear-algebra
Среднее полное общее базового уровня - это Early math, Arithmetic, Pre-algebra, Basic geometry, Algebra I, Geometry (чисто на бумаге; все существующие учебники геометрии отвратительны и не покрывают стандарт по сути) и вдобавок к планиметрии стереометрия, Algebra II (кроме разделов sequences and series и конических сечений; комплексные числа часто не изучают, хотя они входят в стандарт), Trigonometry и Precalculus (только разделы Trigonometric equations и Vectors; вдобавок школьники учат таблицу производных и первообразных). Статистика и вероятность не изучается на практике, хотя в стандарт входит.
Профильный уровень вдобавок к этому содержит Differential calculus и Integral calculus, а также невообразимое количество какого-то мусора.
Реально изучающиеся вещи можно посмотреть в содержаниях учебников, выложенных на http://www.alleng.ru/edu/math1.htm
Спасибо добрый анон, схоронил твой пост.
Занимаюсь математикой на английском, какие-нибудь подводные камни? Ну в смысле это жеж математика, ее и инопланетянин поймет.
Просто реально больше качественного контента.
>какие-нибудь подводные камни?
Будут некоторые проблемы с переводом терминов. См. http://trv-science.ru/2014/03/11/ni-odin-lingvist-ne-ugadaet/
Даже с простым словом "отрезок" уже возникает путаница.
Что это за ноунейм?
Ну я рили учил ингриш для доступа к контенту, фильмы, мультфильмы, игры, вот это все, ну и математика туда же. Так что пусть себя оправдывает.
Мне всегда казалось что чтобы выебываться на грязных крестьян нужно говорить на французском при этом покачивая ладонью так как будто в ней зажат гипотетический бокал белого шардоне.
Шардоне прозрачное с лёгким желтоватым оттенком, который придаётся напитку дубовыми щепками больше чем виноградом. Понял, чернь?
Спасибо за статью, я конечно же об этом думал, но все время приходил к выводу, что задания нам будут давать в письменном виде, а когда написано на бумаге, то проблем не должно быть, а переводить на русский мне не придется.
Нужна ручка специальная. Только если на доске мелом.

Существуют же всякие программы и сайты для решения математических уравнений и задач.
Насколько хороши эти программы? Все ли известные математические проблемы могут решать такие программы? Если не все то почему? Математика ведь дедуктивна (кроме статистики наверное)
Почему школьники до сих пор ебут себе мозги математикой вместо того чтобы установить себе такую программу и ебать математичку в рот своим маленьким прыщавым необрезанным фимозным хуйчишкой?
Сам я инвалид по математике, поэтому и спрашиваю.
Если есть инфа по теме дайте ссылочку плес (можно на муриканском)
>Все ли известные математические проблемы могут решать такие программы?
Нет конечно.
>Если не все то почему?
Потому что компьютеру нужен алгоритм решения, причем зачастую эффективный, а не просто тупой перебор, который будет работать миллиарды лет, а людишки даже с таким читом как интуиция не все в состоянии осилить.
>Почему школьники до сих пор ебут себе мозги математикой вместо того чтобы установить себе такую программу и ебать математичку в рот своим маленьким прыщавым необрезанным фимозным хуйчишкой?
Во-первых потому, что программы чаще всего выдают только ответ, а не человекоподобное описание решения, потому как и решают не как люди. А математичка будет проверять решение, а не ответ. Во-вторых, даже если школьник найдет программу, генерирующую решение задачи, оно с большой вероятностью по оформлению будет выглядеть не как то, которое рассказывала математичка и которое воспроизвели отличники и списывавшие у них по старинке двоечники. То есть палево, после обнаружения которого обоссать шибко умного не составит труда. А чтобы изготовить беспалевную подделку, с должным оформлением, надо-таки понимать, что где менять, а что - оставлять. Что есть труд неблагодарный, по сложности сопоставимый с честным решением задачи. Бездумно списать у отличника куда проще и надежнее. В-третих, если кого они и выебут в рот, то только себя, потому что матеша нужна им самим куда больше, чем математичке. Незнание матеши закрывает дорогу к куче технических наук, а вместе с ними к огромной горе годных вакансий. Сложно нанести такой же вред для своего будущего, не уча какой-то другой школьный предмет.
Спасибо
Это копия, сохраненная 1 июня 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.