Это копия, сохраненная 28 сентября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.




Топология не составляет исключения. Это не просто компендиум прикольных словечек.
Предыдущий: >>350917 (OP)
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
46. https://arhivach.org/thread/156244/
47. https://arhivach.org/thread/159628/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
46. https://arhivach.org/thread/156244/
47. https://arhivach.org/thread/159628/
Ебанутый что ли? Это лучший писатель учебников по математике на всём постсовке.
Заебись.
Пишем с сагой, опускаем тред

Просто добавил ещё одну книжечку, которую нигде не мог найти.
Список книг http://pastebin.ru/0GwfJtXk
Раздача http://rghost.ru/7rCxBWGhR
Вот у нас есть формула Герона для треугольника. Есть для четырёхугольника. И она по идее должна вычислять площадь для любых треугольников и четырёхугольников, то есть она универсальная. А вчера я обнаружил, что: если мы скармливаем этой формуле ромб, то результат получится такой, как если бы мы искали площадь квадрата со стороной данного ромба. Сначала я подумал, а что, если у меня в задаче и должен был получиться квадрат? Но потом я пошёл к общему виду и получил, что формула сводится к площади квадрата:
Если сторона = a, полупериметр = 4a/2 = 2a, площадь, согласно формуле Герона = sqrt(a^4) = a^2.
В чём может быть ошибка? Или же получается, что формула не работает для ромба?

Ошибка в том, что ты используешь формулу для вписанных в окружность четырёхугольников. Используй общую.
>Есть для четырёхугольника.
Откуда? Её не может быть для любого 4-угольника чисто по сторонам, потому что они деформируются.
> для вписанных в окружность четырёхугольников
Ааа, точно, я и забыл про это ограничение. Спасибо.
Пидорасы, сэр.
Кто «мы»?
А что такое обратный элемент?
А если идти по такой логике: сколько в числе 5, например, содержится нулей? Бесконечно много. Значит, 5/0 = бесконечность.
>А что такое обратный элемент?
Обратный элемент к элементу а, по определению является элемент b такой что ab=ba=1. Если предполагать что у нуля есть обратный элемент то мы очень многое теряем, если не всё, что касается поля действительных чисел. Другими словами идти по такому пути неконструктивно.
>А если идти по такой логике
Это не логика, а шизофрения.
Ну а почему для того, чтобы на число можно было делить, оно должно иметь обратное ему число?
Как же вы заебали, пидорасы. Дели сколько влезет. Другое дело, что ответ тебе никто говорить не будет.
Тогда 1 тоже специальное число, так как обратно само себе. Кроме того 0 и 1 выходит родственники - оба являются identities для соотв. сложения и умножения. Но нуль не повезло - делить на него нельзя. Интересно эта теория верная на межпланетном уровне? Может у инопланетян и нуля то нет.
Анон, как доказать, что замыкание - это множество всех предельных точек?
Замыкание множества M - пересечение всех замкнутых надмножеств M.
Предельная точка множества M - точка, любая проколотая окрестность которой пересекается с M.
Точка прикосновения множества M - точка, любая окрестность которой пересекается с M. Замыкание - это не множество всех предельных точек. Замыкание - это множество всех точек прикосновения.
В самом деле. Пересечение любого семейства замкнутых множеств замкнуто, следовательно, замыкание замкнуто. Множество замкнуто тогда и только тогда, когда его дополнение открыто, следовательно, дополнение замыкания открыто. Множество открыто тогда и только тогда, когда вместе с каждой своей точкой содержит некоторую её окрестность. Из "тогда" следует, что если точка обладает окрестностью, не пересекающейся с замыканием (то есть входящей в дополнение), то точка не принадлежит замыканию, и потому если точка принадлежит замыканию, то каждая её окрестность пересекается с замыканием, то есть каждая точка замыкания - точка прикосновения. Из "только тогда" следует, что если точка не обладает окрестностью, целиком лежащей в дополнении замыкания, то она не является элементом дополнения замыкания и потому является элементом замыкания, то есть каждая точка прикосновения - точка замыкания. Десу.
Вообще - нельзя. Пусть f(x) = 0. Это липшицево отображение. Пусть мы знаем, что f(a)-f(b) = 0. Тогда a и b могут быть какими угодно.
> замыкание - это множество всех предельных точек?
Во-первых, это неверно. Изолированные точки тоже входят в замыкание.
Во-вторых:
> как доказать
Сначала докажи, что множество замкнуто <=> оно содержит все свои предельные точки.
Потом тупо в лоб проверяешь равенство двух множеств.

Очень сложно. Если вообще возможно.
Прямо сходу невозможно. Сначала надо уровень математической культуры повысить. Для этого нужно потратить несколько тысяч часов.

Вся известная мне инфа содержится в https://en.wikipedia.org/wiki/Affine_arithmetic
Можешь в https://en.wikipedia.org/wiki/Category:Numerical_analysis покопаться, вдруг найдёшь что-то.

В противоречивой теории можно доказать любое утверждение, которое можно сформулировать. Поэтому такая теория не представляет ценности.
A→(A∨B) - аксиома. Здесь A и B - формулы. Возможно, эта аксиома нуждается в комментарии.
A→B суть ¬A∨B - определение.
Пусть имеются теоремы A и ¬A. Пусть B - произвольная формула. Рассмотрим вывод.
1. A - по условию
2. ¬A - по условию
3. ¬A → (¬A∨B) - аксиома.
4. ¬A∨B - модус поненс к 2 и 3.
5. A→B - определение импликации к 4.
6. B - модус поненс к 1 и 5.
> Поэтому такая теория не представляет ценности.
Говори только за себя. Непротиворечивая теория в свою очередь обладает неполнотой. Прикладные задачи таковы, что полнота бывает ценнее непротиворечивости.
>Непротиворечивая теория в свою очередь обладает неполнотой.
Чушь. Логика предикатов непротиворечива и полна. https://ru.wikipedia.org/wiki/Теорема_Гёделя_о_полноте
>ценнее непротиворечивости
В противоречивой системе что бы ты ни спизданул, отрицание этого будет истинным.
>Чушь. Логика предикатов непротиворечива и полна
Лол, ну конечно она непротиворечива и полна, потому что предикаты - это смысл ВЫСКАЗЫВАНИЙ. Если я делаю высказывание, оно автоматически эквивалентно истинной формуле в логике предикатов. Высказывание это может быть противоречивым при анализе его в более сложной системе, но оставаться истинным в предикатах. Так что ты сам-то почитай внимательно про неполноту, подумай, почему там есть слова "в любой достаточно сложной системе"
А знаешь, что значит работать в логике предикатов? Это значит, что у тебя даже нет операции сложения. А как только вводишь сложение, ты сразу теряешь истинность многих и многих формул.
Но на практике, знаешь как происходит? Никого не ебет противоречивость. Люди просто идут в неизведанное и достают оттуда новое знание.
>Чушь. Логика предикатов непротиворечива и полна
Лол, ну конечно она непротиворечива и полна, потому что предикаты - это смысл ВЫСКАЗЫВАНИЙ. Если я делаю высказывание, оно автоматически эквивалентно истинной формуле в логике предикатов. Высказывание это может быть противоречивым при анализе его в более сложной системе, но оставаться истинным в предикатах. Так что ты сам-то почитай внимательно про неполноту, подумай, почему там есть слова "в любой достаточно сложной системе"
А знаешь, что значит работать в логике предикатов? Это значит, что у тебя даже нет операции сложения. А как только вводишь сложение, ты сразу теряешь истинность многих и многих формул.
Но на практике, знаешь как происходит? Никого не ебет противоречивость. Люди просто идут в неизведанное и достают оттуда новое знание.
>Прикладные задачи таковы, что полнота бывает ценнее непротиворечивости.
Разумеется. Например, в политике, дипломатии, религии и многих других уважаемых прикладных вещах. Я бы даже сказал, что в них противоречивость сама по себе весьма ценна, мало кто без нее обходится.
>Люди просто идут в неизведанное и достают оттуда новое знание.
А потом голословно спорят десятки лет с противоречащими друг другу знаниями. Или, что еще хуже, даже не спорят, а просто публикуют все подряд, после чего наука превращается в помойку на полвека, которую потом приходится разгребать потомкам.
школьники не могут в сокращения, такие дела
Грустный тралль ест сам себя. Душераздирающее зрелище. Иа.
Нет, разумеется, речь о таких вещах, как поиск в дереве. Тебе не нужно никакой суммы, чтобы пройтись по вершинам бинарного дерева, нужен только список. Поиск может привести к новому знанию?
Там не то же самое деление, что и деление в вещественных числах, там от операции деления - одно название.
В вещественных числах не то же самое деление, что и в рациональных числах, там от операции деления - одно название.
У тебя ошибка в восприятии, а демагог почему-то я. Whatever.
Смотря в какой аксиоматике.
Спасибо за колеса, лол
Я именно таким его и представлял.

Пример слева.

Те же википидоры говорят, что sin(x)'=cos(x). Открываю калькулятор в виндовсе, cos(5,5) = 0.99. Где я наебался?
Синус воспринял как радианы, а косинус — как градусы.
Точно так же ведут себя настоящие учёные. Проблемы?
Объясните мне, в чем отличие правила индукции в Primitive Recursive Arithmetic от традиционной аксиоматизации индукции. Я не понимаю, как работает это правило без квантификаторов. Там же либо подразумевается forall, либо получается несвязанная переменная.
PRA replaces the axiom schema of induction for first-order arithmetic with the rule of (quantifier-free) induction:
From f(0) and f(x) -> f(S(x)), deduce f(y), for any predicate f.
это стероедовед, друг тесака?
В PRA можно элиминировать все кванторы.
Почитай про Floop/bloop. Вот bloop - это язык пограммирования без неопределённых циклов. Вот на нём можно рализовать любую примитивную рекурсивную функцию.
Если добавить while, то программы будут страдать от Halting problem.
Нет, ну я понимаю, что такое примитивно рекурсивная функция. Меня конкретно вот этот >>357006 параграф смущает.

Есть задачка и формула пикрелейтед, я пытался решить с помощью этой формулы, но валидатор пишет, что формула для n дней, а не n и более.
Пытался гуглить, но ничего не нашел.
Может кто знает нужную для моей задачи формулу?
Спасибо.
Ну и? В стандартной схеме индукции у тебя формула с квантором. А тут без. Умеешь отличать безкванторные формулы от формул с квантором?
Нет :(
Я не понимаю, что вообще разумеется под
> From f(0) and f(x) -> f(S(x)), deduce f(y), for any predicate f.
Я вижу тут два квантора (на y и f), а их тут нет. Как это?
В обычной схеме у тебя выводится формула \forall n. phi [n]
А тут безкванторная формула
Простой пример:
forall n. n + 1 > n
можно тривиально убрать квантор, будет n + 1 > n - формула с одной свободной переменной.
Или exists n . n² - 4 = 0 эквивалентно n = 2 \lor n = -2
Тут квантор уже не уберёшь так просто.
В PRA f(y) можно вывести достаточным количеством применений импликации. Поэтому PRA считается формализацией финитизма кстати.
Зависит от того, что ты понимаешь под формальным методом. Но так да, в подавляющем большинстве неприкладных областей математики стандартом являются детально прописанные доказательства (не формальные конечно, но сводящиеся к шагам которые математики разбирающиеся в этой области могут разбить до совсем уж тривиальных логических переходов, что далее, при достаточных усилиях, видимо, может быть превращено в формальное доказательство).
Совеобразный раздел примата, сильно навешенный анализом, функаном, теорией меры, стохастикой и таких штук.
>можно тривиально убрать квантор, будет n + 1 > n - формула с одной свободной переменной.
Я и не понимаю, что нам с этой свободной переменной теперь делать. Это корректное выражение получается? Переименование как работает? Короче, я понимаю, что я очень сильно затупливаю с чем-то очевидным и элементарным, так что сейчас прочитаю скачанную пдфку по теме и потом уже задам нормально вопрос, если он еще останется.
> f(0) f(x) -> f(x')
> ----------------------
> f(t)
Я не понимаю, что это значит. :(
Или в википедии:
> Например, в целочисленной арифметике формула \exists x (x >= 0 \land a + x = b) эквивалентна формуле b >= a
Я понимаю, что бы значило, например, \exists x (x >= 0 \land a + x = b) <-> b >= a, а что значит "b >= a" - не понимаю.
Ну, если ты сказал, что есть такой неотрицательный х, что прибавь его к b, получишь a, то стало быть b >= a. Вот и всё. На тривиальных формулах всё слишком очевидно.
>если ты сказал, что есть такой неотрицательный х, что прибавь его к b, получишь a, то стало быть b >= a
Так это и получается "\exists x (x >= 0 \land a + x = b) <-> b >= a". Что это значит мне понятно. Мне непонятно, что значит "b >= a". И что означает несвязанная переменная t в правой части правила вывода.
Это вся задача.
В правиле вывода, я же сказал. Прочитай еще раз тот пост, на который ты отвечал, самое начало: >>357245
Ну это и значит, что если формула верна для единицы, и верен переход, то верна эта же формула для ЛЮБОГО t, you pick it. А вот формула ДЛЯ ВСЕХ Х, ЧТО-ТО ОТ Х не верна. Нету тотальности и объемлемости, грубо говоря, как в станлдартной схеме.
Представь, что ты можешь за конечное число шагов доказать эту формулу просто применяя импликацию достаточное число раз.
Разберись, чем безкванторные формулы отличаются от формул с кванторами
Да ты охуел!
Не понял. Че гуглить-то надо?
\ref{метка} — вставит в текст только номер формулы. Обвязку типа традиционных скобочек делаешь самостоятельно.
\begin{equation}
формула
\label{метка}
\end{equation} — сама формула.
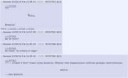
А, бля, у меня просто стоит расширение, которое отображает формулы, я думаю че за хуйня, лол
>Ну это и значит, что если формула верна для единицы, и верен переход, то верна эта же формула для ЛЮБОГО t
Ну... для любого... без кванторов... для любого... Блин :(
> А вот формула ДЛЯ ВСЕХ Х, ЧТО-ТО ОТ Х не верна
Ну так ведь твое n+1 > n, например, и означает, что для всех n верно, что n+1>n. Хоть и нет квантора, но нам его приходится подразумевать для придания смысла выражению.
> Представь, что ты можешь за конечное число шагов доказать эту формулу просто применяя импликацию достаточное число раз.
Я понимаю, что имеется в виду; я не понимаю, как это работает. Мы можем для какого-то конкретного значения t доказать f(t) цепочкой импликаций, но здесь-то имеется в виду не конкретное t, а любое, произвольное T. Я понимаю, что означает переменная под квантором, понимаю, что означает переменная не под квантором, встречающаяся и в левой, и в правой части правила, а что означает просто повисшая переменная в правой части не понимаю.
> Разберись, чем безкванторные формулы отличаются от формул с кванторами
Можешь посоветовать что-то прочитать на эту тему?
>что означает просто повисшая переменная в правой части не понимаю.
Свободная переменная.
Например, уравнение с параметром x²-a=0 имеет, допустим, свободный параметр a.
На
>Можешь посоветовать что-то прочитать на эту тему?
Трудно так с куста сказать. Можно по Quantifier elimination погуглить
Нет, мы про другое.
>>357631
Я, разумеется, погуглил еще в самом начале нашего разговора, но там все-таки немного про другое - мой вопрос гораздо более простого уровня, согласись?
Ты долбаёб или гумус? Задачу сформулируй нормально.
Я не о том. Ладно, проехали.
то есть Hom(Spec B, Spec A), разумеется
chi_A (T)
где chi_A - характеристическая функция множества A гильбертова пространства H, а T - оператор на этом пространстве?
Дохуя где видел и нигде норм. определения нет.
Да нееее. Не то.
ну так и что? ясное дело, что по морфизму колец иожно построить морфизм спектров в обратную сторону. А почему такое отображение на морфизмах биекция?
Мне лектор ВШЭ сказал, что задача сформирована правильно.
Давай, назови его долбоебом или гумусом.
Во-первых, задача сформулирована некорректно. Связь биномиального распределения и распределения Пуассона, как и другие асимптотические утверждения, не является панацеей, которую можно направо-налево использовать для чёрт знает как сформулированных задач.
Во-вторых, fun fact: p(X > 4) = 1 - p(X < 5).
Зачем ему? Он же иканамист. Он слышал только про смуззи и антикафе.
Какие работы?
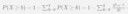
Твой преподаватель считает, что каждый человек обязан знать, что случайная величина, равная количество спам-писем в день подчиняется распределению Пуассона. Ты ведь понимаешь, что конкретно этот момент - это вопрос мат. моделирования а не математики? и решение, собственно, у тебя на пике, чего ещё надо?
Посоветую её не читать.
It is useful to use the language of category theory and observe that Spec is a functor. Every ring homomorphism f : R → S induces a continuous map Spec(f) : Spec(S) → Spec(R) (since the preimage of any prime ideal in S is a prime ideal in R)
То есть по каждому морфизму в Ring мы имеем морфизм в Spec, отсюда эквивалентность категорий (биекция в hom).
У кассы кто угодно может стоять, в этом нет чего-то плохого.
Мне не понятно, почему это биекция. Ты опять просто построил некоторое отображение, но почему оно эпи? почему моно?
На курсере есть немного.
Ясно.
у стоящих у кассы доход сравним с математегами, так что мушку спили чуток, ваннаби гроденьтик
не ну честно, лолирую с попыток унизить тупых студентов, обещая им в случая фейла на поприще точных наук маленькую зарплату )))
Плоскость можно спроектировать на прямую, но это не значит что все функции на плоскости - поднятия с прямой.
Бросишь читать на первом же томе.
http://libgen.io/search.php?req=nicolas+bourbaki&open=0&res=25&view=simple&phrase=1&column=def
Полного набора ещё нигде нет. Недавно вышла новая книга, её ещё не спиратили.

Но херр, немецкий его задавил ближе к 20-му веку. Зачем Вы предлагаете мне книгу на английском и заводите дискуссию о роли Франции, м-сье Картан? Это не патриотично.
Мсье Оур, я вам никаких английских книг не предлагал. Это сделал вон тот предатель - предлагаю отправить его на гильотину, пока он еще кому-нибудь их не предложил.
Премного благодарю, м-сье!
Не обращайте внимания, м-сье, это Гротендик.
Да, тоже неоднократно о таком слышал. Интересно, насколько эффективно использовать математические статьи для изучения иностранных языков?
Я только более-менее грамматику подтянул. Сейчас пытаюсь читать учебник по биологии на английском — идет очень тяжело из-за огромного количества специфической лексики.
Что за EGA, если не секрет?
А насчет франца не знаю даже. Там ведь иногда не только определения и теоремы, но и объяснения, которые должны быть максимально понятны читателю.
https://en.wikipedia.org/wiki/Éléments_de_géométrie_algébrique
> но и объяснения, которые должны быть максимально понятны читателю
Математическая литература максимально просто в плане языка пишется. Мне хватало гугл-транслейта, например, для французского. Тяжелее будет в геометрии/топологии, где автор будет стараться приводить аналогии.
Ого, это же уже совсем ад. Кстати, труды Гротендика по алгему еще достаточно актуальны, как я понимаю?
Смотря для кого. Если тебе интересен алгем, то да.
> mathematics as a hole

Да, полет нормальный, т.к. по матлогу уже некоторые вещи были известны. Не знаю, как дальше.
Первая книга бурбаков - это просто философия (первая глава) и пачка определений для следующих книг (вторая, третья и четвёртая главы). Актуальность имеют следующие книги, первая - чисто техническая.
мимошёл
А можно это сконвертить под гряземонки?
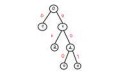
построить усеченное дерево функции F(x)^W, если y(t) есть 3-я цифра после запятой в двоичном разложении числа 1/28.
Как строится это дерево? У меня есть число 1/28, которое при переводе в двоичную систему счисления стало 0,00[001]^W, я нахожу y(1)=0, y(2)=0, y(3)=1, но как построить усеченное дерево? Я накидал что-то, как понял сам, и хочу спросить у анона - а правильно ли это?
Для этого надо с ним устроить перестрелку кожаными пулями в темном переулке
Применение это нежелательная стадия. Спроси у погромистов. Применение - это баги, вопросы тупых кастомеров и тд. Лучше оставаться на уровне чистого искусства.
Без гомологической алгебры нельзя нормально работать с когомологиями. А без когомологий жизни нет.
На полную катушку все используется в теоретической физике, струны там всякие.
В некоторой мере влезает во всевозможные области. Например, в Big Data сейчас пытаются применять топологические методы, естественно, с когомологиями. Ну, или эллиптические кривые в криптографии. Тут какой-никакой алгем и без когомологий и Римана-Роха тяжело будет всякие вещи обосновывать.
Ну, и самый глупый, наверное, пример. Вот хочешь ты для вектор-функции v(x), заданной на каком-то пространстве (например, на плоскости без одной точки), найти такую функцию F(x), что Grad F (x) = v (x). Это крайне важно бывает в самой банальной механике. Какие условия обеспечивают ее существование? Есть очевидное условие на производные, так как частные производные коммутируют. Но дальше уже возникает чисто топологическое препятствие - первые когомологии Де-Рама нашего пространства.
Последнее, наверное, можно изложить как-то рабоче-крестьянски, но это убьет все понимание и значительно все усложнит в нетривиальных примерах.
Теорем пруверы ссут тебе в спектр кольца.
>используется
>струны там всякие
>используется
Лол
>Например, в Big Data сейчас пытаются применять топологические методы, естественно, с когомологиями.
Как человек, непосредственно работающий над Big Data проектами, могу тебе только сикнуть в еблецо.
https://en.wikipedia.org/wiki/Topological_data_analysis
Я не утверждал, что это уже является чем-то стандартным.
Вот я сколько натыкаюсь на упоминание когомологий во всяких книжках - столько читаю фразу о том, что это дохуя важно, дохуя вопросов к ним сводится, и т.п. Но! Ни разу не видел четких и убедительных примеров, подтверждающих этот тезис. Нету, так сказать, платинового ответа на платиновый вопрос.
Вот хоть ты давай, шагни дальше остальных. Напиши ответ на все времена. Возьми пример какой-нибудь более-менее интересной и естественной задачи (чтобы нам тоже стало интересно узнать на нее ответ), реши его без когомологий, покажи, как это трудно, нудно и ебано. И следом реши его с когомологиями, быстро, легко и естественно. А лучше два-три таких примера. Вот тогда этот вопрос в какой-то мере можно будет считать закрытым. Мне лично особенно интересно про
>эллиптические кривые в криптографии
Не тот анон, но вот лично мне всё это помогло взглянуть на знакомые вещи с другой стороны, особенно в калибровочных теориях и квантовой теории поля. За криптографию и проч. не скажу, не разбираюсь.
Потому что то, что применяется, является вычислимым. Произвольные топологические пространства и структур на них такими не являются.
Странный вопрос. Тебе нужны применения в математике или в быту? Если в математике, то без них реально жизни нет, практически нет областей, которые без них обходятся.
Если в быту то вопрос эквивалентен вопросу о пользе математики вообще из-за предыдущего замечания.
Про применение эллиптических кривых в криптографии написано и на википедии, суть простая. А для того, чтобы понимать что-то про эллиптические кривые над конечными полями нужны когомологии.
Ну вот пошли маневры.
>Тебе нужны применения в математике или в быту
В математике.
>Если в математике, то без них реально жизни нет, практически нет областей, которые без них обходятся.
Где пруфы? Нам нужны пруфы, Билли.
>Про применение эллиптических кривых в криптографии написано и на википедии, суть простая.
Про их применение в криптографии я знаю без всякой википедии. Мне потому и интересно, что ж такого суперважного я упустил с этими самыми когомологиями.
>А для того, чтобы понимать что-то про эллиптические кривые над конечными полями нужны когомологии.
Что-то - это что? При-ме-ры мне нужны. Например, помогут ли они ввести на эллиптических кривых групповой закон? Потому что вот он для криптографии еще как нужен, в отличие от чего-то другого, например.
Вот давай я покажу что я хочу увидеть. Щас обосную, чем полезно в математике понятие нормы алгебраического числа.
Кольцо целых чисел, как известно, факториально: в нем можно выделить набор т.н. простых чисел, в произведение которых раскладывается любой необратимый элемент кольца. Думаю, не нужно говорить, насколько это свойство важно в дальнейшем, сколько вещей на это опирается. В теории чисел активно рассматриваются алгебраические расширения поля Q, в частности, поля вида Q[sqrt(d)], где d - свободное от квадратов целое число. Естественно, там бы тоже хотелось, чтобы кольцо целых (т.е. Z[sqrt(d)]) было факториально, это было бы очень удобно.
Итак, задача 1:
Дано кольцо Z[sqrt(d)]. Как понять, факториально оно или нет?
Покажем, чем здесь полезна норма, на двух примерах. Кольцо Z факториально, а кольцо Z[sqrt(-5)] - нет: 6 = 2 x 3=(1+sqrt(-5))(1-sqrt(-5)), причем ни одно из этих разложений не раскладывается дальше, т.е. нету однозначного разложения на множители. Пока запомним эти два примера, а пояснять и доказывать их будем чуть позже.
Что нам нужно знать про норму?
1) Явная формула: N(a + b sqrt(d)) = a^2 - d b^2. Для комплексных чисел d = -1, и норма имеет вид a^2 + b^2 - все сходится.
2) Мультипликативность: N(A B) = N(A) N(B)
Вернемся к примерам, а именно к разложению числа 6 в Z[sqrt(5)]. Возьмем нормы от всего написанного: N(a + b sqrt(-5)) = a^2 + 5 b^2; N(6) = 36, N(2) = 4, N(3) = 9, N(1 +- sqrt(-5)) = 1 + 5 = 6. То есть исходные равенства превращаются в 36 = 4 х 9 = 6 х 6.
Как показать, что дальше разложить нельзя?
Без норм мы могли бы воспользоваться методом неопределенных коэффициентов, т.е. предположить, скажем, что число 2 раскладывается на два множителя, 2 = (a + b sqrt(-5)) (c + d sqrt(-5)), записать равенства на коэффициенты при 1 и sqrt(-5), немного повозиться и показать, что таких целых a, b, c, d не существует. Не самый простой и удобный способ, а самое главное с трудом допускающий обобщение: для каждого кольца и элемента придется возиться заново.
Что же будет с нормами? С нормами видно, что если бы число 2 раскладывалось на два множителя, то раскладывалась бы на два множителя (в кольце уже целых чисел) и его норма: 4 = 2 х 2 разложение 1 х 4 не годится: нормой 1 обладают только обратимые элементы кольца, в нашем случае 1 и -1. Это значит, что у наших множителей была бы норма 2. А есть ли хоть одно число с нормой 2? Нет, и это легко показать: пусть a^2 + 5 b^2 = 2, отсюда, поскольку a и b целые, b = 0, иначе левая часть будет уже больше пяти, ну а a^2 = 2 не имеет целых решений. Все то же самое можно проделать для всех остальных множителей в том равенстве, доказав тем самым, что дальше на множители разложить нельзя, т.е. кольцо не факториально.
Рассмотрим теперь пример Z. Посчитаем норму какого-нибудь числа, скажем, числа 1+i: N(1+i) = 2. Оно простое: если предположить, что оно раскладывается на множители, то разложатся и их нормы, а число 2 - простое в кольце целых чисел. То же самое можно сказать про числа 1+2i и 2+i: у них норма 5 - простое число. А, например, у числа 2 норма 4. Чтобы найти его разложение, уже понятно, что надо искать числа с нормой 2. Мы уже такое находили: 2 = (1+i)(1-i). А методом неопределенных коэффициентов все было бы дольше и сложнее. Если же мы попробуем разложить пятерку, то нас ждет подвох: 5 = (1+2i)(1-2i) = (2+i)(2-i). Но это лишь подвох, поскольку в Z обратимыми элементами являются не только +-1, но еще и +-i, и если умножить, скажем, 1-2i на i, то получим 2+i - то же самое разложение.
Мимоходом мы решили задачу 2:
Как разложить число на множители, и, если кольцо факториально, как показать, что данное число - простое?
Теперь мы знаем ответ: если норма числа - простое число, то оно само простое в этом кольце. Если норма не проста, нужно разложить норму на множители и искать числа с такими нормами: найдутся - вероятно, сможем разложить, не найдутся - число простое. Без норм, т.е., скажем, тем же методом неопределенных коэффициентов, мы не увидим разницы между всеми этими вещами.
Вот такого рода штуку я хочу увидеть про когомологии. Можно менее развернуто.
Ну вот пошли маневры.
>Тебе нужны применения в математике или в быту
В математике.
>Если в математике, то без них реально жизни нет, практически нет областей, которые без них обходятся.
Где пруфы? Нам нужны пруфы, Билли.
>Про применение эллиптических кривых в криптографии написано и на википедии, суть простая.
Про их применение в криптографии я знаю без всякой википедии. Мне потому и интересно, что ж такого суперважного я упустил с этими самыми когомологиями.
>А для того, чтобы понимать что-то про эллиптические кривые над конечными полями нужны когомологии.
Что-то - это что? При-ме-ры мне нужны. Например, помогут ли они ввести на эллиптических кривых групповой закон? Потому что вот он для криптографии еще как нужен, в отличие от чего-то другого, например.
Вот давай я покажу что я хочу увидеть. Щас обосную, чем полезно в математике понятие нормы алгебраического числа.
Кольцо целых чисел, как известно, факториально: в нем можно выделить набор т.н. простых чисел, в произведение которых раскладывается любой необратимый элемент кольца. Думаю, не нужно говорить, насколько это свойство важно в дальнейшем, сколько вещей на это опирается. В теории чисел активно рассматриваются алгебраические расширения поля Q, в частности, поля вида Q[sqrt(d)], где d - свободное от квадратов целое число. Естественно, там бы тоже хотелось, чтобы кольцо целых (т.е. Z[sqrt(d)]) было факториально, это было бы очень удобно.
Итак, задача 1:
Дано кольцо Z[sqrt(d)]. Как понять, факториально оно или нет?
Покажем, чем здесь полезна норма, на двух примерах. Кольцо Z факториально, а кольцо Z[sqrt(-5)] - нет: 6 = 2 x 3=(1+sqrt(-5))(1-sqrt(-5)), причем ни одно из этих разложений не раскладывается дальше, т.е. нету однозначного разложения на множители. Пока запомним эти два примера, а пояснять и доказывать их будем чуть позже.
Что нам нужно знать про норму?
1) Явная формула: N(a + b sqrt(d)) = a^2 - d b^2. Для комплексных чисел d = -1, и норма имеет вид a^2 + b^2 - все сходится.
2) Мультипликативность: N(A B) = N(A) N(B)
Вернемся к примерам, а именно к разложению числа 6 в Z[sqrt(5)]. Возьмем нормы от всего написанного: N(a + b sqrt(-5)) = a^2 + 5 b^2; N(6) = 36, N(2) = 4, N(3) = 9, N(1 +- sqrt(-5)) = 1 + 5 = 6. То есть исходные равенства превращаются в 36 = 4 х 9 = 6 х 6.
Как показать, что дальше разложить нельзя?
Без норм мы могли бы воспользоваться методом неопределенных коэффициентов, т.е. предположить, скажем, что число 2 раскладывается на два множителя, 2 = (a + b sqrt(-5)) (c + d sqrt(-5)), записать равенства на коэффициенты при 1 и sqrt(-5), немного повозиться и показать, что таких целых a, b, c, d не существует. Не самый простой и удобный способ, а самое главное с трудом допускающий обобщение: для каждого кольца и элемента придется возиться заново.
Что же будет с нормами? С нормами видно, что если бы число 2 раскладывалось на два множителя, то раскладывалась бы на два множителя (в кольце уже целых чисел) и его норма: 4 = 2 х 2 разложение 1 х 4 не годится: нормой 1 обладают только обратимые элементы кольца, в нашем случае 1 и -1. Это значит, что у наших множителей была бы норма 2. А есть ли хоть одно число с нормой 2? Нет, и это легко показать: пусть a^2 + 5 b^2 = 2, отсюда, поскольку a и b целые, b = 0, иначе левая часть будет уже больше пяти, ну а a^2 = 2 не имеет целых решений. Все то же самое можно проделать для всех остальных множителей в том равенстве, доказав тем самым, что дальше на множители разложить нельзя, т.е. кольцо не факториально.
Рассмотрим теперь пример Z. Посчитаем норму какого-нибудь числа, скажем, числа 1+i: N(1+i) = 2. Оно простое: если предположить, что оно раскладывается на множители, то разложатся и их нормы, а число 2 - простое в кольце целых чисел. То же самое можно сказать про числа 1+2i и 2+i: у них норма 5 - простое число. А, например, у числа 2 норма 4. Чтобы найти его разложение, уже понятно, что надо искать числа с нормой 2. Мы уже такое находили: 2 = (1+i)(1-i). А методом неопределенных коэффициентов все было бы дольше и сложнее. Если же мы попробуем разложить пятерку, то нас ждет подвох: 5 = (1+2i)(1-2i) = (2+i)(2-i). Но это лишь подвох, поскольку в Z обратимыми элементами являются не только +-1, но еще и +-i, и если умножить, скажем, 1-2i на i, то получим 2+i - то же самое разложение.
Мимоходом мы решили задачу 2:
Как разложить число на множители, и, если кольцо факториально, как показать, что данное число - простое?
Теперь мы знаем ответ: если норма числа - простое число, то оно само простое в этом кольце. Если норма не проста, нужно разложить норму на множители и искать числа с такими нормами: найдутся - вероятно, сможем разложить, не найдутся - число простое. Без норм, т.е., скажем, тем же методом неопределенных коэффициентов, мы не увидим разницы между всеми этими вещами.
Вот такого рода штуку я хочу увидеть про когомологии. Можно менее развернуто.
И да, в книжках вещи типа этой описывались бы фразой в духе "понятие нормы сводить вопросы о делимости в алгебраических расширениях полей к вопросам о делимости в исходном поле, например, определять факториальность кольца Z[sqrt(d)]". Это чистая правда и самая суть, но это нихуя не показательно для ньюфага, а разжеванных примеров нигде нет, остается только верить на слово.
>Кольцо целых чисел, как известно, факториально: в нем можно выделить набор т.н. простых чисел, в произведение которых раскладывается любой необратимый элемент кольца
Самое важное пропустил - однозначно раскладывается
>
Вернемся к примерам, а именно к разложению числа 6 в Z[sqrt(5)]
В Z[sqrt(-5)], конечно
фиксы 2
По-моему, это платный функционал вольфрам альфы, в математике этого нет.
Классификация векторных расслоений, например. Канонический пример - монополь Дирака как связность на расслоении U(1)->X->R^3/{0}.
Я даже, честно говоря, не знаю, как можно посчитать их без когомологий с коэффициентами в п_n и классифицирующих пространств.
>Канонический пример - монополь Дирака как связность на расслоении U(1)->X->R^3/{0}.
Кто такой, чем знаменит? Вот про факториальность я сказал, почему это важно.
Не обязательно приводить пример того, что без когомологий не считается. Лучше привести пример того, что с ними делается заметно проще.
> Вот про факториальность я сказал, почему это важно.
Твоё объяснение по сути заключается в этом
> Думаю, не нужно говорить, насколько это свойство важно в дальнейшем, сколько вещей на это опирается.
Точно так же можно сказать, что связности - одна из центральных тем современном геометрии, думаю не надо объяснять и.т.п.
Ты реально похоже хочешь примеров в какой-нибудь элементарщине типа планиметрии - ну тогда разочарование, потому что их вроде нет. А если и есть - то несистемно, а только в качестве забавных отдельных фактов. Гомологическая алгебра - это техника "верхних" наук, можно конечно объяснять что типа это позволяет посчитать A, а это нужно, потому что позволяет понять B, а это применяется в C. Но и A и B и C обитают в этой "верхней" части, поэтому после каждого такого объяснения ты будешь задавать вопрос "А зачем нужно A/B/C?" и это может продолжаться бесконечно.
Нет. Я хочу диньги заробатывать. Кто будет покупать гомологии?
Двачую вот этого. >>359557
Попробуй сейчас объяснить охуенность нормы алгебраического числа человеку, который не знает, что такое кольцо. Вот ты требуешь того же.

>Гомологическая алгебра - это техника "верхних" наук, можно конечно объяснять что типа это позволяет посчитать A, а это нужно, потому что позволяет понять B, а это применяется в C. Но и A и B и C обитают в этой "верхней" части, поэтому после каждого такого объяснения ты будешь задавать вопрос "А зачем нужно A/B/C?" и это может продолжаться бесконечно.
Нет, не бесконечно. Верхние области выкристаллизовались из изучения нижних, например, теория Галуа, из которой рукой подать в алгебраическую ТЧ, в алгебраическую геометрию и т.д., связана с вопросом о разрешимости уравнения в радикалах, по сути школьного вопроса о том, как решить полиномиальное уравнение. То есть это доставляет пример того, что некоторые наиболее сложные вопросы нижней области могут укатиться в верхнюю, и потому-то верхняя область и нужна. Если ты не знаешь об этой связи между верхними и нижними областями, значит, ты сам не понимаешь, зачем эти самые верхние области нужны, т.е. математики не знаешь.
А объяснить, почему единственность разложения на множители в кольце целых чисел так важна, труда вообще не составляет - просто начать перечислять все вещи, в которых вылезают простые числа. Мне действительно надо это делать?
>>359576
Я же не запрещаю объяснить, что такое кольцо. И, кстати, в рассмотренных мною примерах ничего, кроме определения кольца, по сути не требовалось. Какие-то стандартные вещи типа "почему Z[sqrt(d)] образует кольцо" я опустил, потому что никому, кто это знает, не составит труда это пояснить. И вообще зачем нужно понятие кольца - тоже это просто тип, к которому относятся много структур, возникающих в математике, типа как в биологии много организмов бывают животными, много - растениями, ну и т.д. То есть по сути оно выделяется исключительно для удобства, как техника обобщения: если что-то доказать для колец вообще, то это автоматически будет верно для всех "реальных" математических структур, которые можно отнести к кольцам. А к кольцам можно отнести много математических структур, и про кольца доказать удается много чего, т.е. выигрыш от такого подхода налицо. Короче, не вижу проблемы.

>Гомологическая алгебра - это техника "верхних" наук, можно конечно объяснять что типа это позволяет посчитать A, а это нужно, потому что позволяет понять B, а это применяется в C. Но и A и B и C обитают в этой "верхней" части, поэтому после каждого такого объяснения ты будешь задавать вопрос "А зачем нужно A/B/C?" и это может продолжаться бесконечно.
Нет, не бесконечно. Верхние области выкристаллизовались из изучения нижних, например, теория Галуа, из которой рукой подать в алгебраическую ТЧ, в алгебраическую геометрию и т.д., связана с вопросом о разрешимости уравнения в радикалах, по сути школьного вопроса о том, как решить полиномиальное уравнение. То есть это доставляет пример того, что некоторые наиболее сложные вопросы нижней области могут укатиться в верхнюю, и потому-то верхняя область и нужна. Если ты не знаешь об этой связи между верхними и нижними областями, значит, ты сам не понимаешь, зачем эти самые верхние области нужны, т.е. математики не знаешь.
А объяснить, почему единственность разложения на множители в кольце целых чисел так важна, труда вообще не составляет - просто начать перечислять все вещи, в которых вылезают простые числа. Мне действительно надо это делать?
>>359576
Я же не запрещаю объяснить, что такое кольцо. И, кстати, в рассмотренных мною примерах ничего, кроме определения кольца, по сути не требовалось. Какие-то стандартные вещи типа "почему Z[sqrt(d)] образует кольцо" я опустил, потому что никому, кто это знает, не составит труда это пояснить. И вообще зачем нужно понятие кольца - тоже это просто тип, к которому относятся много структур, возникающих в математике, типа как в биологии много организмов бывают животными, много - растениями, ну и т.д. То есть по сути оно выделяется исключительно для удобства, как техника обобщения: если что-то доказать для колец вообще, то это автоматически будет верно для всех "реальных" математических структур, которые можно отнести к кольцам. А к кольцам можно отнести много математических структур, и про кольца доказать удается много чего, т.е. выигрыш от такого подхода налицо. Короче, не вижу проблемы.
Пи нельзя представить конечной десятичной дробью разумной длины (то есть такой, что её можно записать от руки на листе бумажки). Следовательно, пи невычислимо.
>В математике.
Ну, ок.
Начнем сразу с имбы, если веришь в полезность коммутативной алгебры, а судя по твоему примеру с факториальностью, веришь.
Алгебра:
Локализация локального регулярного кольца регулярно. Это реально много лет не могли доказать, пока не появился достаточно серьезный аппарат гомологической алгебры и интерпретация регулярности в его терминах.
Без всяких "более удобно" или "понимание", просто не могли и все.
При этом теорема крайне важная для коммутативной алгебры и алгебраической геометрии.
Топология:
Даже странно что-то говорить. (ко)Гомологии являются одним из основных инвариантов топологических пространств. Например, доказать, что R^n не гомеоморфно R^m для m не равного n проще всего с помощью них. Ну, или теорема Брауэра, что непрерывное отображение n-мерного шара в себя имеет неподвижную точку (кстати, используется экономистами для доказательства существования равновесия в разных ситуациях). Можно использовать гомотопические группы, но они несколько сложнее все-таки. Или, чтобы, например, корректность понятия эйлеровой характеристики без гомологий доказать, я не представляю, как ебаться придется.
Или, например, характеристические классы отвечают на многие естественные вопросы Например, является ли данное многообразие границей какого-то еще. Или можно ли построить сечение у данного векторного расслоения.
Сложнее придумать теорему в топологии, в доказательстве которой не участвуют (ко)гомологии.
Алгебраическая геометрия:
Тут дела чуть ли не лучше/хуже, чем в топологии. Чуть ли не все инварианты по природе своей когомологические. Первое, что приходит на ум, теорема Римана-Роха, без которой можно только сосать хуй.
Теория чисел:
Гипотезы Вейля можно сформулировать совершенно элементарно. При этом вопрос достаточно естественный: "Как устроены количества решений нашей системы уравнений над разными конечными полями". А тут целая теория этальных когомологий, построенная на аналогиях с более стандартными теориями когомологий. Отдельно укажу одно простое следствие: теорема Хассе. Количество точек на эллиптической кривой над полем из q элементов отличается от q+1 не более чем на 2sqrt(q).
Еще когомологии Галуа ебошат в ТЧ.
Мне лень продолжать, если честно. Напоследок про эллиптические кривые.
>помогут ли они ввести на эллиптических кривых групповой закон
Да. Групповой закон появляется из-за того, что эллиптическая кривая с отмеченной точкой естественно изоморфна своей группе Пикара. Это очевидное следствие Римана-Роха, для которого нужны когомологии.
Если вводить закон напрямую геометрически, то, например с ассоциативностью будет знатная ебля (в особенности над конечным полем, а именно этот случай нас и интересует). Cкорее всего придется использовать какую-нибудь теорему Безу, а ее тоже доказывают с помощью когомологий. А еще работать все будет только в форме Вейерштрасса с фиксированным нулем.
>в отличие от чего-то другого, например.
Нужны не только формулы для алгоритмов, но и обоснования, почему эти алгоритмы хороши и оценки на то, насколько они хороши. Для этого что-то еще надо знать кроме закона сложения. Как минимум уметь давать оценку на количество точек. Признай, все эти формулы не имели бы смысла, если на кривых было бы ничтожно мало точек над конечными полями. И тут внезапная теорема Хассе, которая следует из весьма глубокой теории, которая целиком и полностью мотивирована приложениями когомологий, которые были до неё.
>В математике.
Ну, ок.
Начнем сразу с имбы, если веришь в полезность коммутативной алгебры, а судя по твоему примеру с факториальностью, веришь.
Алгебра:
Локализация локального регулярного кольца регулярно. Это реально много лет не могли доказать, пока не появился достаточно серьезный аппарат гомологической алгебры и интерпретация регулярности в его терминах.
Без всяких "более удобно" или "понимание", просто не могли и все.
При этом теорема крайне важная для коммутативной алгебры и алгебраической геометрии.
Топология:
Даже странно что-то говорить. (ко)Гомологии являются одним из основных инвариантов топологических пространств. Например, доказать, что R^n не гомеоморфно R^m для m не равного n проще всего с помощью них. Ну, или теорема Брауэра, что непрерывное отображение n-мерного шара в себя имеет неподвижную точку (кстати, используется экономистами для доказательства существования равновесия в разных ситуациях). Можно использовать гомотопические группы, но они несколько сложнее все-таки. Или, чтобы, например, корректность понятия эйлеровой характеристики без гомологий доказать, я не представляю, как ебаться придется.
Или, например, характеристические классы отвечают на многие естественные вопросы Например, является ли данное многообразие границей какого-то еще. Или можно ли построить сечение у данного векторного расслоения.
Сложнее придумать теорему в топологии, в доказательстве которой не участвуют (ко)гомологии.
Алгебраическая геометрия:
Тут дела чуть ли не лучше/хуже, чем в топологии. Чуть ли не все инварианты по природе своей когомологические. Первое, что приходит на ум, теорема Римана-Роха, без которой можно только сосать хуй.
Теория чисел:
Гипотезы Вейля можно сформулировать совершенно элементарно. При этом вопрос достаточно естественный: "Как устроены количества решений нашей системы уравнений над разными конечными полями". А тут целая теория этальных когомологий, построенная на аналогиях с более стандартными теориями когомологий. Отдельно укажу одно простое следствие: теорема Хассе. Количество точек на эллиптической кривой над полем из q элементов отличается от q+1 не более чем на 2sqrt(q).
Еще когомологии Галуа ебошат в ТЧ.
Мне лень продолжать, если честно. Напоследок про эллиптические кривые.
>помогут ли они ввести на эллиптических кривых групповой закон
Да. Групповой закон появляется из-за того, что эллиптическая кривая с отмеченной точкой естественно изоморфна своей группе Пикара. Это очевидное следствие Римана-Роха, для которого нужны когомологии.
Если вводить закон напрямую геометрически, то, например с ассоциативностью будет знатная ебля (в особенности над конечным полем, а именно этот случай нас и интересует). Cкорее всего придется использовать какую-нибудь теорему Безу, а ее тоже доказывают с помощью когомологий. А еще работать все будет только в форме Вейерштрасса с фиксированным нулем.
>в отличие от чего-то другого, например.
Нужны не только формулы для алгоритмов, но и обоснования, почему эти алгоритмы хороши и оценки на то, насколько они хороши. Для этого что-то еще надо знать кроме закона сложения. Как минимум уметь давать оценку на количество точек. Признай, все эти формулы не имели бы смысла, если на кривых было бы ничтожно мало точек над конечными полями. И тут внезапная теорема Хассе, которая следует из весьма глубокой теории, которая целиком и полностью мотивирована приложениями когомологий, которые были до неё.
>теорема Римана-Роха, без которой можно только сосать хуй
Эта теорема не входит в российский стандарт для студентов-математиков и обычно не изучается в вузах. Статья про неё отсутствует в рувики. Так, для справки.
мимошёл
>А еще работать все будет только в форме Вейерштрасса с фиксированным нулем.
Вот тут я знатно запизделся. Беру эти слова назад
Ну вообще да, это многое говорит о рувики и о российском матобразовании, имхо.
>Алгебра:
>Локализация локального регулярного кольца регулярно.
Не знаю, что такое, погуглю. Звучит разумно.
>Топология:
Это все хорошо, но сама топология достаточно далека от привычных мне областей. В смысле, доказываемые там охуительно важные утверждения редко применимы к моим баранам. Поскольку я хочу увидеть, как применяется техника и насколько это естественно получается, давай более подробные пояснения на простые вещи типа
>доказать, что R^n не гомеоморфно R^m для m не равного n
>непрерывное отображение n-мерного шара в себя имеет неподвижную точку
>корректность понятия эйлеровой характеристики
У этого я хотя бы могу оценить теоретическую/практическую значимость, не вставая с дивана. И все это хотя бы с намеком на то, как придется возиться без когомологий, дабы я оценил профит от всего этого. А то ведь знаешь, можно просто переформулировать на другой язык, а там все будет ничуть не проще, тогда возникнет вопрос: а нахрена?
>Первое, что приходит на ум, теорема Римана-Роха, без которой можно только сосать хуй.
Вполне доказывается "в явном виде", без когомологий. Может, не в настолько общих терминах, но в достаточных для возни с эллиптическими кривыми. А значимость возни со всякими обобщениями "из верхних областей" тогда придется осознавать отдельно, т.е. вопрос "а нахрена" это не снимет. Короче, идею доказательства в студию, буду сравнивать.
>Теория чисел:
>Гипотезы Вейля можно сформулировать совершенно элементарно. При этом вопрос достаточно естественный: "Как устроены количества решений нашей системы уравнений над разными конечными полями".
Ну сформулировать - это здорово, а что насчет доказать?
>Отдельно укажу одно простое следствие: теорема Хассе. Количество точек на эллиптической кривой над полем из q элементов отличается от q+1 не более чем на 2sqrt(q).
Давай. Вот на это я бы посмотрел. В картофельных книжках вроде было не очень сложно. На вики какой-то пиздец, а лезть за книжками мне в данный конкретный момент лень. Пиши, а я отыщу и сравню с картофельной версией.
>Да. Групповой закон появляется из-за того, что эллиптическая кривая с отмеченной точкой естественно изоморфна своей группе Пикара. Это очевидное следствие Римана-Роха, для которого нужны когомологии.
Это да, но я говорю: теорема Римана-Роха в достаточном виде доказывается и "так".
>Нужны не только формулы для алгоритмов, но и обоснования, почему эти алгоритмы хороши и оценки на то, насколько они хороши. Для этого что-то еще надо знать кроме закона сложения. Как минимум уметь давать оценку на количество точек. Признай, все эти формулы не имели бы смысла, если на кривых было бы ничтожно мало точек над конечными полями. И тут внезапная теорема Хассе, которая следует из весьма глубокой теории, которая целиком и полностью мотивирована приложениями когомологий, которые были до неё.
Ну если речь только о теореме Хассе, то про нее я уже сказал. И если речь только про то, что на кривой достаточно много точек, то это интуитивно тривиальная вещь, поскольку если кривая y^2 = x^3 + a x + b выбирается случайно равновероятно, то левая часть должна бы быть квадратичным вычетом или невычетом также случайно равновероятно, а вычетов и невычетов поровну. Ну так вот и получается, что поскольку точки идут парами (x, y) и (x -y), то в половине случаев точек нет, а в другой половине - есть две, плюс точка на бесконечности = q+1. Это, ясное дело, не доказательство ни разу, но годное интуитивное пояснение: опять таки, чтобы точек оказалось ну оче мало, левая часть должна быть невычетом куда чаще, чем вычетом, а у этого должна быть ну оче малая вероятность, т.е. с точки зрения практики на такие кривые должно быть пофиг. Т.е. строгие оценки на количество точек позволят только дать строгие оценки на время работы алгоритма, а на практике все должно будет работать уже сейчас.
А вообще я что-то не припомню, где там нужны оценки на количество точек. Разве что, может быть, при вычислении порядка группы точек на элл. кривой. И то это вещь весьма стандартная и обособленная, настолько, чтобы просто относиться к ней по принципу "it works". Может еще в алгоритме Ленстры (факторизация с помощью элл. кривой). В общем, хочу больше пояснений по этому моменту.
Тем не менее спасибо за столь обстоятельный ответ.
>Алгебра:
>Локализация локального регулярного кольца регулярно.
Не знаю, что такое, погуглю. Звучит разумно.
>Топология:
Это все хорошо, но сама топология достаточно далека от привычных мне областей. В смысле, доказываемые там охуительно важные утверждения редко применимы к моим баранам. Поскольку я хочу увидеть, как применяется техника и насколько это естественно получается, давай более подробные пояснения на простые вещи типа
>доказать, что R^n не гомеоморфно R^m для m не равного n
>непрерывное отображение n-мерного шара в себя имеет неподвижную точку
>корректность понятия эйлеровой характеристики
У этого я хотя бы могу оценить теоретическую/практическую значимость, не вставая с дивана. И все это хотя бы с намеком на то, как придется возиться без когомологий, дабы я оценил профит от всего этого. А то ведь знаешь, можно просто переформулировать на другой язык, а там все будет ничуть не проще, тогда возникнет вопрос: а нахрена?
>Первое, что приходит на ум, теорема Римана-Роха, без которой можно только сосать хуй.
Вполне доказывается "в явном виде", без когомологий. Может, не в настолько общих терминах, но в достаточных для возни с эллиптическими кривыми. А значимость возни со всякими обобщениями "из верхних областей" тогда придется осознавать отдельно, т.е. вопрос "а нахрена" это не снимет. Короче, идею доказательства в студию, буду сравнивать.
>Теория чисел:
>Гипотезы Вейля можно сформулировать совершенно элементарно. При этом вопрос достаточно естественный: "Как устроены количества решений нашей системы уравнений над разными конечными полями".
Ну сформулировать - это здорово, а что насчет доказать?
>Отдельно укажу одно простое следствие: теорема Хассе. Количество точек на эллиптической кривой над полем из q элементов отличается от q+1 не более чем на 2sqrt(q).
Давай. Вот на это я бы посмотрел. В картофельных книжках вроде было не очень сложно. На вики какой-то пиздец, а лезть за книжками мне в данный конкретный момент лень. Пиши, а я отыщу и сравню с картофельной версией.
>Да. Групповой закон появляется из-за того, что эллиптическая кривая с отмеченной точкой естественно изоморфна своей группе Пикара. Это очевидное следствие Римана-Роха, для которого нужны когомологии.
Это да, но я говорю: теорема Римана-Роха в достаточном виде доказывается и "так".
>Нужны не только формулы для алгоритмов, но и обоснования, почему эти алгоритмы хороши и оценки на то, насколько они хороши. Для этого что-то еще надо знать кроме закона сложения. Как минимум уметь давать оценку на количество точек. Признай, все эти формулы не имели бы смысла, если на кривых было бы ничтожно мало точек над конечными полями. И тут внезапная теорема Хассе, которая следует из весьма глубокой теории, которая целиком и полностью мотивирована приложениями когомологий, которые были до неё.
Ну если речь только о теореме Хассе, то про нее я уже сказал. И если речь только про то, что на кривой достаточно много точек, то это интуитивно тривиальная вещь, поскольку если кривая y^2 = x^3 + a x + b выбирается случайно равновероятно, то левая часть должна бы быть квадратичным вычетом или невычетом также случайно равновероятно, а вычетов и невычетов поровну. Ну так вот и получается, что поскольку точки идут парами (x, y) и (x -y), то в половине случаев точек нет, а в другой половине - есть две, плюс точка на бесконечности = q+1. Это, ясное дело, не доказательство ни разу, но годное интуитивное пояснение: опять таки, чтобы точек оказалось ну оче мало, левая часть должна быть невычетом куда чаще, чем вычетом, а у этого должна быть ну оче малая вероятность, т.е. с точки зрения практики на такие кривые должно быть пофиг. Т.е. строгие оценки на количество точек позволят только дать строгие оценки на время работы алгоритма, а на практике все должно будет работать уже сейчас.
А вообще я что-то не припомню, где там нужны оценки на количество точек. Разве что, может быть, при вычислении порядка группы точек на элл. кривой. И то это вещь весьма стандартная и обособленная, настолько, чтобы просто относиться к ней по принципу "it works". Может еще в алгоритме Ленстры (факторизация с помощью элл. кривой). В общем, хочу больше пояснений по этому моменту.
Тем не менее спасибо за столь обстоятельный ответ.
Числа, которые не могут быть записаны на листочке А4, не нужны. Ими нечего считать.
Мы следим за тобой.
> давай более подробные пояснения на простые вещи
>И все это хотя бы с намеком на то, как придется возиться без когомологий, дабы я оценил профит от всего этого.
Прости, но читать курс топологии как-то не входит в мои планы. Тем более изучать труды предков, которые доказывали все комбинаторными разбиениями. Во всех этих теоремах гомологии самый простой способ, который я знаю. За подробностями - Хатчер.
>Вполне доказывается "в явном виде", без когомологий.
Вот тут я требую четкой формулировки и ссылки на доказательство. Напоминаю, что поле у нас может быть конечным.
>Короче, идею доказательства в студию
Слева написана эйлерова характеристика пучка, соответствующего дивизору (из двойственности Серра). При прибавлении точки она увеличивается на 1, так как эйлерова характеристика аддитивна на коротких точных последовательностях, как и значение справа. Итого достаточно доказать для нуля, а это верно по определению. За подробностями - Хартсхорн
>а что насчет доказать?
В смысле? Этальные или кристаллические когомологии единственный известный человечеству способ доказывать эти гипотезы.
Вообще мне все это напоминает какой-то странный троллинг. Такого набора знаний, как у тебя, просто не бывает (ни малейшего представления о топологии при каких-то знаниях о другой математике, знания из алгема, чудом избегающие когомологии).
В общем, скажи какие у тебя бараны.
>Вот тут я требую четкой формулировки и ссылки на доказательство. Напоминаю, что поле у нас может быть конечным.
Да пожалуйста. http://www.mi.ras.ru/~prokhoro/teach/crypt.pdf
>В общем, скажи какие у тебя бараны.
Все понятно из ссылки. В мехматской программе все это когомологическое добро заботливо выкинуто. Я и хочу понять, как проще - изучить весь этот геометрический аппарат (понятно ведь, что мало просто заучить определение, нужен еще джентльменский набор примеров и теорем, чтобы этим хоть как-то пользоваться), или чистить все вилкой. Ну то есть, я почти уверен, что с обобщающей теорией проще, но вы этого продемонстрировать не можете, тогда возникает вопрос, а что вы, собственно, можете? Мне как-то чужда мысль о том, чтобы изучать какой-то аппарат, и потом им не пользоваться, или пользоваться для таких же вещей, которые сначала надо изучить, т.е. априори нахуй не нужных. Математика связна, цельна, простое связано со сложным, практика с теорией, и математик должен всегда уметь это продемонстрировать, иначе это либо аутист какой-то конкретной области, которому покласть на все остальное, в том числе и на историю развития этой самой области, либо еще хуже - пиздабол, нахватавшийся умных слов, который сам в принципе ничего не умеет, кроме как книжку пересказывать. Я уже рад, что увидел одного, кто может генерировать осмысленный текст, а не неинформативное НУЖНО, просто хочу более развернутой аргументации, чтобы не дрочить страниц двадцать понятий и определений, а сразу уловить суть, пусть и в упрощенном виде, на пальцах и для дебилов.
Итак, давай, вот все говорят, что когомологии суть инварианты топологических пространств. Какой профит можно поиметь с инварианта? Например, можно сравнить инварианты у двух вещей: если они разные, значит и вещи в каком-то смысле разные. Думаю, в этом суть
>доказать, что R^n не гомеоморфно R^m для m не равного n
Можно, наверное, еще рассмотреть процесс, при котором какая-то хуевина изменяется, а ее инвариант - нет, тогда можно будет показать, что начальная и конечная хуевины каким-то образом связаны, или наоборот, прийти к противоречию и показать, что они не связаны. Думаю, в этом суть доказательства
>непрерывное отображение n-мерного шара в себя имеет неподвижную точку
Какие еще техники использования когомологий есть, что они позволяют получить? Я хочу увидеть, что это систематический инструмент для делания того-то и того-то (как я про нормы сказал >>359549), а не просто клевая штука, с помощью которой повезло решить две с половиной задачи из теории пониже, а вся высокая теория, ее обрамляющая, напилена просто "шоб было".
>Вот тут я требую четкой формулировки и ссылки на доказательство. Напоминаю, что поле у нас может быть конечным.
Да пожалуйста. http://www.mi.ras.ru/~prokhoro/teach/crypt.pdf
>В общем, скажи какие у тебя бараны.
Все понятно из ссылки. В мехматской программе все это когомологическое добро заботливо выкинуто. Я и хочу понять, как проще - изучить весь этот геометрический аппарат (понятно ведь, что мало просто заучить определение, нужен еще джентльменский набор примеров и теорем, чтобы этим хоть как-то пользоваться), или чистить все вилкой. Ну то есть, я почти уверен, что с обобщающей теорией проще, но вы этого продемонстрировать не можете, тогда возникает вопрос, а что вы, собственно, можете? Мне как-то чужда мысль о том, чтобы изучать какой-то аппарат, и потом им не пользоваться, или пользоваться для таких же вещей, которые сначала надо изучить, т.е. априори нахуй не нужных. Математика связна, цельна, простое связано со сложным, практика с теорией, и математик должен всегда уметь это продемонстрировать, иначе это либо аутист какой-то конкретной области, которому покласть на все остальное, в том числе и на историю развития этой самой области, либо еще хуже - пиздабол, нахватавшийся умных слов, который сам в принципе ничего не умеет, кроме как книжку пересказывать. Я уже рад, что увидел одного, кто может генерировать осмысленный текст, а не неинформативное НУЖНО, просто хочу более развернутой аргументации, чтобы не дрочить страниц двадцать понятий и определений, а сразу уловить суть, пусть и в упрощенном виде, на пальцах и для дебилов.
Итак, давай, вот все говорят, что когомологии суть инварианты топологических пространств. Какой профит можно поиметь с инварианта? Например, можно сравнить инварианты у двух вещей: если они разные, значит и вещи в каком-то смысле разные. Думаю, в этом суть
>доказать, что R^n не гомеоморфно R^m для m не равного n
Можно, наверное, еще рассмотреть процесс, при котором какая-то хуевина изменяется, а ее инвариант - нет, тогда можно будет показать, что начальная и конечная хуевины каким-то образом связаны, или наоборот, прийти к противоречию и показать, что они не связаны. Думаю, в этом суть доказательства
>непрерывное отображение n-мерного шара в себя имеет неподвижную точку
Какие еще техники использования когомологий есть, что они позволяют получить? Я хочу увидеть, что это систематический инструмент для делания того-то и того-то (как я про нормы сказал >>359549), а не просто клевая штука, с помощью которой повезло решить две с половиной задачи из теории пониже, а вся высокая теория, ее обрамляющая, напилена просто "шоб было".
> Числа, которые не могут быть записаны на листочке А4, не существуют.
Починил, не благодари.
мимо-последовательный-ультрафинитист
Существуют числа, которые не могут быть записаны на одном листочке А4, но могут быть записаны на двух листочках. Такие числа не нужны.
>тогда возникает вопрос, а что вы, собственно, можете?
Ради интереса задай этот же вопрос теории множеств. То есть несомненно, что теория множеств используется всюду. Но что вообще может теория множеств сама по себе? Теорему Кантора-Бернштейна доказать разве что.
Что вообще такое "можете", какой смысл ты вкладываешь в это слово? Ты реквестируешь сборник упражнений на гомологии?
Я вполне пояснил, что имеется в виду под "можете". Раз более высокая теория обобщает и расширяет более низкую, значит, задачи более низкой теории она должна решать легко. Если не можете решать легкие задачи - значит, не можете вообще никакие. Я преувеличиваю, конечно, но сами понимаете, профессор, который не может решить задачку школьника, сразу вызывает вопрос - а что он вообще может? Понятно, что подлый школьник мог спросить великую теорему Ферма, но кого ебет-то? И уж тем более если это произошло, надо уделить этому вопросу повышенное внимание, как минимум крепко запомнить сей курьезный случай, а не отмахиваться, мол, школопроблемы.
>Ради интереса задай этот же вопрос теории множеств. То есть несомненно, что теория множеств используется всюду. Но что вообще может теория множеств сама по себе? Теорему Кантора-Бернштейна доказать разве что.
Теория множеств-то - это как раз самое днище, лол, в том смысле, что она извлекается из самого низа, из философии и наблюдений реального мира, а вся математика строится уже на ней. Понятно, что от нее не потребуешь много чего содержательного: когда модель полностью описывает объект, она становится ему эквивалентна, т.е. все, что может сказать модель - все это можно увидеть непосредственно на объекте. Соответственно, чем ближе к полному описанию, тем меньше возможности для добычи новой информации. С когомологиями-то явно дело обстоит не так, это довольно высокий уровень абстракции.
>Существуют числа, которые не могут быть записаны на одном листочке А4, но могут быть записаны на двух листочках.
Пока ты мне не предъявишь конкретный пример такого числа, я буду считать тебя платонистом и религиозным фанатиком аксиоматического подхода, буду насмехаться и потешаться над тобой.
Это не запись числа. Число - это десятичная дробь.
>Спор двух студентиков о говне и моче и их применении.
> 2016
> ёбля с нерелейтед топологическими пространствами и их нерелейтед инвариантами
> невычислимо
> спорят о применении
Если уж и говорить о реальном применении высоких областей на практике -- то это automated reasoning.
Это из калибровочных теорий поля.
Монополь Дирака - просто первый встречающийся пример такого подхода.
Лагранжиан, использующийся в электромагнетизме, инвариантен с точностью до действия группы U(1), то есть - домножения на e^-iф. И когда мы хотим найти поле, удовлетворяющее уравнениям Максвелла, и удовлетворяющее U(1)-калибровочной инвариантности, мы можем рассмотреть расслоение из некоторого пространства в то пространство, которое мы хотим описать (наблюдаемое, собственно), переводящее группу U(1)~S^1 в точку.
Все такие расслоения классифицируются группой Z (утверждение, активно использующее гомотопии и гомологии, на самом деле - буквально утверждение о гомотопических группах пространств, конкретно - классифицирующего пространства для группы U(1)).
Если на этих расслоениях ввести связность, можно вывести поле монополя (=закон Кулона). И, в частности, то, что он квантуется.
Это только один из примеров. На самом деле такой подход используется во всех калибровочных теориях. В квантовой хромодинамике, например, лагранжиан инвариантен относительно действия группы SU(3). Есть даже теории, инвариантные относительно E8.
>the composition of any two consecutive maps is zero
Как композиция функций может быть числом? Вы там ебанулись совсем? Почему, блядь, нельзя писать понятным языком? Что тут подразумевается под нулем?
Всё отображается в ноль. Пропускается через ноль (нулевой объект в категории).
>Вы там ебанулись совсем? Почему, блядь, нельзя писать понятным языком?
Язык отличный, проблема в тебе.
В какой категории? Всех групп? Всех абелевых групп? Всех групп чейн комплекса? А если в этой категории нет нулевого объекта?
Чтобы определить комплекс и его (ко)гомологии тебе нужно по сути знать только что такое ядра/образы/фактор-объекты и нулевой объект. Обычно для гомологической алгебры ограничиваются абелевыми категориями.
Ноль - это не всегда число.
>>359896
Ладно, понял. Не понимаю только почему чейн комплекс определяется именно так, как он определяется. Как пришли к такому определению? Почему там последовательность ...A_2, A_1, A_0, A_{-1}, A_{-2}..., а не А_0, А_1,... ведь мощность множества целых и натуральных чисел одинакова? Почему последовательность бесконечная, а не конечная? Почему не трансфинитная? Почему именно "abelian groups or modules", почему не какие-то другие алгебраические структуры? Почему решили упомянуть, что композиция любых двух последовательных дифференциалов дает нулевой объект?
Т.е. для меня пока это все выглядит как взятое с потолка. Почему надо изучать чейн комплексы определенные именно таким способом, почему другие схожие определения (например, когда последовательность конечна) не заслуживают внимания?
>Почему именно "abelian groups or modules", почему не какие-то другие алгебраические структуры?
Без коммутативности ядра и образы мммм... не равны? [Нормальные подгруппы не то же самое, что подгруппы. А в абелевом случае разница стирается. По-моему это вообще одна из ключевых особенностей коммутативности.] Поэтому нельзя разделить одно на другое (а ядра/образы = гомологии). d^2=0 <=> образы попадают в ядра (и можно измерить разницу, разделив).
>Почему последовательность бесконечная, а не конечная?
Можно сделать конечной, подставив нули (как пространства). Да и никто не запрещает на конечные смотреть.
Вообще, dd=0 в куче мест встречается. Например, берёшь полусферу и смотришь на границу (d). Это окружность. А вот у неё границы нет (у отрезка, который тоже 1D граница — пара точек). И так всегда будет. Граница границы = 0.
В книгах такое написано.
Сам в этом ничего не понимаю, тоже начинающий.
Упражнения помогают понять зачем нужны теоремы и как их использовать. Доказательства теорем помогает понять почему они верны.
>Да пожалуйста
Она доказана только для эллиптических кривых. Даже сформулирована только для них (ибо написано |-D|, а не |K-D|). При этом доказательство занимает в два раза больше места, чем доказательство общего случая по модулю когомологий.
И вообще там как раз на 20 страниц больше, чем у Хартсхорна о том же.
>Можно, наверное,
Удачи. Жду картофельного доказательства.
Еще больше интересно про корректность эйлеровой характеристики.
>Все понятно из ссылки.
Если под ссылкой ты понимаешь алгем какой-то, пускай даже сильно геометрический, то чистить все вилкой не получится. Та же теорема Римана-Роха для кривых, якобиан, группа Пикара имеет когомологическое описание, которое позволяет ее просто считать во многих случаях над комплексными числами (экспоненциальная точная последовательность).
В конце концов опять таки когомологии это выжный инвариант, который несложно посчитать, но по которому можно классифицировать и изучать многообразия. Критерий Кастельнуово рациональности поверхности, например. Теорема, что любое векторное расслоение на P^1 разложимо. А также подсчет этого самого разложения в конкретных случаях.
Давай я объясню, почему они естественно вылазят в алгеме. Мы хотим изучать линейные и вообще векторные расслоения на многообразиях. Больше всего нас интересуют глобальные сечения у расслоения. Но есть проблема, которая приводит собственно ко всей теории когомологий. При сюрьективном отображении расслоений глобальные сечения отображаются не сюрьективно. Поэтому для точной последовательности 0->E->F->G->0 векторных расслоений мы не можем извлечь информацию о глобальных сечения одного из расслоений по двум другим. На этот вопрос отвечает теория когомологий, дополняя последовательность 0->Г(Е)->Г(F)->Г(G)
справа членами H^i, делаяя последовательность точной. Поэтому из когомологий E и G мы уже получаем много информации о Г(F), например, если H^1(Е)=0, то отображение будет обязательно сюрьективно.
Но я и так знаю, зачем мне нужны теоремы. Допустим, у меня есть цель разбираться в какой-то области, которую я сейчас не понимаю. Я сначала по диагонали просмотрел пару книг, почитал википедию, а потом начал подробно изучать материал. При этом я разбираюсь с тем, что используется для доказательства дальнейших результатов и пропускаю то, что не используется.
>Она доказана только для эллиптических кривых.
А курс как раз только про эллиптические кривые.
>При этом доказательство занимает в два раза больше места, чем доказательство общего случая по модулю когомологий.
>И вообще там как раз на 20 страниц больше, чем у Хартсхорна о том же.
Ну я скачал книгу, посмотрел сам. Та же идея - доказывать индукцией, переходя от дивизора D к дивизору D+P. Весьма вероятно, что картофельная версия - просто адаптированная эта. Ну а так, нихрена не на 20 страниц больше. В хартсхорновском доказательстве ссылки на 5 утверждений ранее, всякие упражнения, теоремы и т.п. А там свои ссылки на предыдущие утверждения, и т.д. То есть если честно собрать все это вместе, то же самое и выйдет. И это не считая терминологии, всяких этих пучков-небоскребов и т.п. В картофельной версии достаточно элементарной алгебры. И вообще, по сути, основной инструмент в доказательстве Хартсхорна - эйлерова характеристика, а когомологии как таковые используются только для базы индукции D=0. Ну так случай D=0, вероятно, можно доказать без привлечения когомологий (Прохоров же смог), т.е. они здесь не необходимы. Более того, нулевые и первые группы когомологий, насколько мне помнится из беглого чтения всякой лабуды, являются какими-то другими важными группами, которые можно определить и без использования когомологий. А поскольку в доказательстве только они и использовались, это еще раз намекает на то, что когомологии как таковые тут не нужны, сама суть доказательства сводится не к ним. Короче, этот пример не показателен. Доказательство здесь проще из-за эйлеровой характеристики, не из-за когомологий.
>Можно, наверное,
>Удачи. Жду картофельного доказательства.
>Еще больше интересно про корректность эйлеровой характеристики.
Этот комментарий говорит о том, что ты вообще не понял, что я писал.
>Если под ссылкой ты понимаешь алгем какой-то, пускай даже сильно геометрический, то чистить все вилкой не получится.
Не алгем, а
>Эллиптические кривые и криптография
>Мы хотим изучать линейные и вообще векторные расслоения на многообразиях.
Почему?
>Больше всего нас интересуют глобальные сечения у расслоения.
Почему?
>Она доказана только для эллиптических кривых.
А курс как раз только про эллиптические кривые.
>При этом доказательство занимает в два раза больше места, чем доказательство общего случая по модулю когомологий.
>И вообще там как раз на 20 страниц больше, чем у Хартсхорна о том же.
Ну я скачал книгу, посмотрел сам. Та же идея - доказывать индукцией, переходя от дивизора D к дивизору D+P. Весьма вероятно, что картофельная версия - просто адаптированная эта. Ну а так, нихрена не на 20 страниц больше. В хартсхорновском доказательстве ссылки на 5 утверждений ранее, всякие упражнения, теоремы и т.п. А там свои ссылки на предыдущие утверждения, и т.д. То есть если честно собрать все это вместе, то же самое и выйдет. И это не считая терминологии, всяких этих пучков-небоскребов и т.п. В картофельной версии достаточно элементарной алгебры. И вообще, по сути, основной инструмент в доказательстве Хартсхорна - эйлерова характеристика, а когомологии как таковые используются только для базы индукции D=0. Ну так случай D=0, вероятно, можно доказать без привлечения когомологий (Прохоров же смог), т.е. они здесь не необходимы. Более того, нулевые и первые группы когомологий, насколько мне помнится из беглого чтения всякой лабуды, являются какими-то другими важными группами, которые можно определить и без использования когомологий. А поскольку в доказательстве только они и использовались, это еще раз намекает на то, что когомологии как таковые тут не нужны, сама суть доказательства сводится не к ним. Короче, этот пример не показателен. Доказательство здесь проще из-за эйлеровой характеристики, не из-за когомологий.
>Можно, наверное,
>Удачи. Жду картофельного доказательства.
>Еще больше интересно про корректность эйлеровой характеристики.
Этот комментарий говорит о том, что ты вообще не понял, что я писал.
>Если под ссылкой ты понимаешь алгем какой-то, пускай даже сильно геометрический, то чистить все вилкой не получится.
Не алгем, а
>Эллиптические кривые и криптография
>Мы хотим изучать линейные и вообще векторные расслоения на многообразиях.
Почему?
>Больше всего нас интересуют глобальные сечения у расслоения.
Почему?
>Ну а так, нихрена не на 20 страниц больше
Я не про доказательство, а про эллиптические кривые вообще.
>эйлерова характеристика
Эйлерова характеристика пучка, а не топологического пространства, тут без когомологий не обойтись.
>Этот комментарий говорит о том, что ты вообще не понял, что я писал.
Наверное. Мне показалось, что ты пытаешься что-то доказать.
>Почему?
Это уже вопрос на уровне "Зачем мы хотим изучать кольца". Это естественные геометрические объекты, которые много где возникают.
>Почему?
Потому что это самое простое, что мы можем о нем спросить. А еще они задают отображение в P^n, если они вообще имеются.
>Эллиптические кривые и криптография
В таком случае, наверное, можно обойтись и картофаном, если воспользоваться несколькими утверждениями как черными ящиками или поверить в них (все равно веримв в P не равно NP). Если честно, я не готов обстоятельно это обсуждать, так кака я это специально не изучал. Впрочем, это какая-то слишком узкая тема да еще и на стыке математики с другой наукой.
Тебе все еще нужны пояснения за математику вообще, а не криптографию? Если так, то могу еще раз подумать и обновить список относительно элементарно формулирующихся теорем, про которые я на 100 процентов уверен, что без когомологий их не решить. Особенно если ты скажешь, какие области признаешь.
Да видно же что этот мемчик интересуется какой-то "криптографией", а не наукой. Просто его обманул видимо этот "рекламный пример" (по мнению многих, именно по этому и плохой) про то что "алгем применяется в криптографии".
.>Допустим, у меня есть цель разбираться в какой-то области,
Каков твой критерий "разбирательства"?
>по диагонали просмотрел пару книг, >почитал википедию
Получил поверхностное представление, об опыте речь даже не начиналась.
>а потом начал подробно изучать материал.
В чём заключается изучение?
>разбираюсь с тем, что используется для доказательства дальнейших
>пропускаю то, что не используется.
Так действует человек, имеющий опыт и решавший задачи. Если так подходить к теме с самого начала – будет в лучшем случае поверхностное представление.
Да хуй знает, насколько он рекламный. Я просто недостаточно хорошо разбираюсь в вопросе. Просто мне казалось очевидным, что надо достаточно много знать про эллиптические кривые над конечными полями, чтобы доказывать разные теоремы про алгоритмы шифрования и атак.
Еще люди пытаются использовать многомерные абелевы многообразия. И для некоторых якобианов гиперэллиптических кривых даже получили какой-то профит в плане производительности.
Пусть читает Бурбаков в оригинале!

Просто не ожидал, что в библиотеке завода есть такие книжки! Завод моссельмаш. Работяги. Синька. Кватернионы. Это ли не подвох!
Как зачем? Без них теорему Фробениуса не докажешь. Еще спроси, зачем токарю теорема Фробениуса.
Там сцылка на полный курс https://www.lektorium.tv/course/22939. Но я хз, зачем оно тебе. Я и сам-то слабо понимаю, о чём там.
>Наверное. Мне показалось, что ты пытаешься что-то доказать.
Я попытался предположить техники, которые позволяют воспользоваться когомологиями для чего-нибудь. Я хочу увидеть в них систематический инструмент, нежели магию, которая иногда работает.
>Это естественные геометрические объекты, которые много где возникают.
Где? Мне сколько раз повторять, что я хочу примеров? Что я хочу видеть, как все то, чего я не знаю, связано с тем, что я знаю? А оно связано. Просто если связи действительно весьма тонкие и далекие, то можно не торопиться это учить.
>А еще они задают отображение в P^n, если они вообще имеются.
Вот это уже больше похоже на ответ. Я понимаю, что с отображения в P^n можно поиметь профит, но все равно хотел бы парочку примеров, это демонстрирующих, для полноты представления. Теорем каких-нибудь охуительных или сорт оф.
>Тебе все еще нужны пояснения за математику вообще, а не криптографию?
За математику вообще. Просто ты меня спросил, какие у меня бараны, а я тебе ответил. Вообще меня интересует ТЧ. Она-то как раз хорошо демонстрирует связь между простым и сложным. Ну а в криптографии иногда всплывают всякие вещи типа такой http://eprint.iacr.org/2013/673.pdf . То есть вот кто-то придумал алгоритм, но обосновать толком его скорость не смог. А потом кто-то другой пришел и пояснил по-хардкору, что вот-де для не-куммеровых расширений поля работать не будет, надо вот так-то переделать. И тут становится интересно, каким образом он умудрился выкопать, что надо рассмотреть именно не-куммеровы расширения, ведь в исходном алгоритме даже близко ничего такого не обсуждалось. Очевидно, для этого надо что-то понимать на качественно более высоком уровне. Вот мне и интересно, например, когомологии входят в этот уровень, или они все-таки лежат уровнем выше и лучше пока поизучать нечто другое, более близкое к указанной теме. Потому что у вас там напилено столько всякого, что за несколько лет не разгребешь, если хвататься за первое попавшееся.
Кватернионы ориентации - для 3-х мерных деталей, чтобы при верчении не возникал gimbal lock. Поэтому новые станки проградуированы именно в кватернионах. Но действительно непонятно нахуя заставляют столько теории учить.
токарь-лобовик 5-го разряда
Просто стереотипы про пьянь относятся прежде всего к фрезеровщикам. Те конечно дно. А лобовики как правило головастые ребята.
Фрезировщики - это типа картофан токарного дела.

Cварщикам еще и инглиш нужно знать, потому что пикрил учебника на русском просто нет.
В чем разница? Ты станок лобовой видал? Там от станины до оси шпинделя рукой не дотянешься. И планшайба размером с копыто слона! Там СМЕКАЛОЧКА нужна, brute force под картофан не получится.
Шок! Сенсация! Рома Михайлов прокрадывается во сны к анону и учит гомотопическому хаосу!
Охуенно же!
>Я хочу увидеть в них систематический инструмент,
Чтобы увидеть систематический инструмент надо разбираться в топологии. Иначе в любом случае получится набор каких-то магических примеров. Но вот тебе систематическая техника, которая привела к доказательству гипотез Вейля в ТЧ. Теорема Лефшеца https://en.wikipedia.org/wiki/Lefschetz_fixed-point_theorem
Она часто позволяет оценить количество неводвижных точек отображения в себя. Например, из нее следует, что эйлерова характеристика равна количеству нулей сечения касательного расслоения, а следовательно, например, нельзя причесать ежа.
Сейчас ты спросишь, зачем изучать количество неподвижных точек, а также как именно это реализуется с помощью теоремы Лефшеца?
>Где?
В математике! Прости, но я уже пояснил, что это вопрос уровня, зачем нужны кольца. В той же мере, в какой я не готов читать курс по топологии, я не готов читать курс по алгему.
Касательноек расслоение, кокасательное, канонический пучок, нормальное расслоение. И так далее. Это все естественные многообразия, которые естественно изучать. Не менеее естественно, чем факториальность колец.
>но все равно хотел бы парочку примеров, это демонстрирующих, для полноты представления.
Отображение в P^n = выбор n+1 глобальных порождающих сечений в линейном расслоении.
Например, если канонический пучок очень обилен, то имеется естественное выделенное вложение в P^n многообразия (с точностью до линейного автоморфизма), а любой его автоморфизм является линейным.
>Вообще меня интересует ТЧ
Гипотезы Вейля. ОК? Это тот самый пример, про который уверен на 100%. Еще Class Field Theory, которое я не готов содержательно объяснять в виду своей некомпетентности.
В общем, прости, но ты требуешь систематической техники, но не знаешь почти никакой математики. В такой ситуации я могу лишь приводить отдельные элементарно формулирующиеся теоремы. Потому что рассказывать про то, зачем нужны линейные расслоения или топологические пространства, это уже слишком.
>и лучше пока поизучать нечто другое, более близкое к указанной теме.
Я уже сказал, что недостаточно компетентен в вопросах криптографии. И я не знаю нужно ли конкретно тебе учить когомологии. Ты спросил про математику. Я уже заебался приводить примеры областей математики и важных теорем в них, где без когомологий не обойтись. Ты в этих областях не разбираешься и просишь свести все к чему-то простому. Но если свести, то жалуешься, что не видишь общей техники. Откуда ты увидешь общую технику, если мы уже спустились на несколько уровней?
>Я хочу увидеть в них систематический инструмент,
Чтобы увидеть систематический инструмент надо разбираться в топологии. Иначе в любом случае получится набор каких-то магических примеров. Но вот тебе систематическая техника, которая привела к доказательству гипотез Вейля в ТЧ. Теорема Лефшеца https://en.wikipedia.org/wiki/Lefschetz_fixed-point_theorem
Она часто позволяет оценить количество неводвижных точек отображения в себя. Например, из нее следует, что эйлерова характеристика равна количеству нулей сечения касательного расслоения, а следовательно, например, нельзя причесать ежа.
Сейчас ты спросишь, зачем изучать количество неподвижных точек, а также как именно это реализуется с помощью теоремы Лефшеца?
>Где?
В математике! Прости, но я уже пояснил, что это вопрос уровня, зачем нужны кольца. В той же мере, в какой я не готов читать курс по топологии, я не готов читать курс по алгему.
Касательноек расслоение, кокасательное, канонический пучок, нормальное расслоение. И так далее. Это все естественные многообразия, которые естественно изучать. Не менеее естественно, чем факториальность колец.
>но все равно хотел бы парочку примеров, это демонстрирующих, для полноты представления.
Отображение в P^n = выбор n+1 глобальных порождающих сечений в линейном расслоении.
Например, если канонический пучок очень обилен, то имеется естественное выделенное вложение в P^n многообразия (с точностью до линейного автоморфизма), а любой его автоморфизм является линейным.
>Вообще меня интересует ТЧ
Гипотезы Вейля. ОК? Это тот самый пример, про который уверен на 100%. Еще Class Field Theory, которое я не готов содержательно объяснять в виду своей некомпетентности.
В общем, прости, но ты требуешь систематической техники, но не знаешь почти никакой математики. В такой ситуации я могу лишь приводить отдельные элементарно формулирующиеся теоремы. Потому что рассказывать про то, зачем нужны линейные расслоения или топологические пространства, это уже слишком.
>и лучше пока поизучать нечто другое, более близкое к указанной теме.
Я уже сказал, что недостаточно компетентен в вопросах криптографии. И я не знаю нужно ли конкретно тебе учить когомологии. Ты спросил про математику. Я уже заебался приводить примеры областей математики и важных теорем в них, где без когомологий не обойтись. Ты в этих областях не разбираешься и просишь свести все к чему-то простому. Но если свести, то жалуешься, что не видишь общей техники. Откуда ты увидешь общую технику, если мы уже спустились на несколько уровней?
>У меня в юности был один знакомый анон. Он неправильно жил, употреблял там всякие препараты. И вот один раз он увидел Рому Михайлова во сне, который сказал "ЗАДАВАЙ МНЕ ЛЮБЫЕ ВОПРОСЫ"
Начну с конца.
>Я уже заебался приводить примеры областей математики и важных теорем в них, где без когомологий не обойтись. Ты в этих областях не разбираешься и просишь свести все к чему-то простому. Но если свести, то жалуешься, что не видишь общей техники. Откуда ты увидешь общую технику, если мы уже спустились на несколько уровней?
Очень просто. Выделить из доказательства чего-то простого лежащий в его основе прием, и потом привести примеры, когда этот прием работает где-то еще, в высоких областях. Примеры я приводил уже
>Например, можно сравнить инварианты у двух вещей: если они разные, значит и вещи в каком-то смысле разные.
>рассмотреть процесс, при котором какая-то хуевина изменяется, а ее инвариант - нет, тогда можно будет показать, что начальная и конечная хуевины каким-то образом связаны, или наоборот, прийти к противоречию и показать, что они не связаны.
Или, скажем, как твой пример с теоремой Римана-Роха: была найдена числовая характеристика, которая равномерно изменяется при шаге индукции это больше похоже на утверждение наоборот: изучали эйлерову характеристику, обнаружили вот такое ее поведение, потом переписали этот факт в других терминах, и получили теорему Римана-Роха. То есть теперь, зная это, ничего не мешает поизучать другую какую-нибудь штуку, посмотреть на ее поведение, и если что-то найдется, переписать это в других терминах, и получить теорему Анона - это и есть выделение техники из доказательства.
Если такое выделение техники невозможно, значит, связь с простыми вещами именно "магическая", т.е. отсутствие какого-то общего приема, там хуяк, тут хуяк, и вуаля. Картофельные доказательства часто таким грешат, например.
Вообще это странно. Если ты не мыслишь в таких терминах, то как ты понимаешь и запоминаешь всякие доказательства? Я имею в виду, какую пользу это тебе приносит, если ты просто заучиваешь их? А если не заучиваешь, почему не можешь пояснить?
>Прости, но я уже пояснил, что это вопрос уровня, зачем нужны кольца.
Но я могу пояснить, зачем нужно кольцо, какие понятия оно обобщает и какие допускает обобщения, какие профиты мы поимеем с такого обобщения, где такая структура естественно возникает, и привести какие угодно примеры, а ты почему-то нет. Например, слабо ответить на такой тупой вопрос: почему нужно рассматривать поле, а не две группы с разными операциями? В чем разница, для чего этот дополнительный термин, что он дает? Видимо, слабо.
Вообще опять же странно. Разве это не первое, с чего нужно начинать что-то объяснять? Мы вводим новую сущность - нахуя мы ее вводим? Чтобы была? Чтобы доказать кучу безразличных фактов про нахуй не нужную сущность? В этом ты видишь суть математики? Печально, если это так.
>Это все естественные многообразия, которые естественно изучать. Не менеее естественно, чем факториальность колец.
Это не ответ. Ты видишь эту естественность, потому что изучал это, а я не вижу. Так, может, и надо ее продемонстрировать, чтобы я тоже увидел?
Вот я залез на вики и сразу нашел ответ:
>Более сложный пример — это касательное расслоение гладкого многообразия: каждой точке на многообразии сопоставляется касательное пространство к многообразию в этой точке.
Что мешало сразу так сказать? Мне, как картофанщику, не особо надо пояснять, зачем рассматривать в каждой точке касательное пространство. Интересно только, что нам дает такая "совмещенная" структура, хотя бы элементарные утверждения для нее, а если рассмотреть их на примере вот этого самого касательного расслоения - так и вообще отлично. Заодно почти наверняка получится какой-то нетривиальный, если не пользоваться понятием векторного расслоения, факт. Впрочем, я уже нашел такой факт, ты его озвучил.
>Сейчас ты спросишь, зачем изучать количество неподвижных точек
Да, спрошу. Я увидел, да и до этого представлял себе, зачем нам знать, есть ли неподвижные точки вообще. А вот зачем знать, сколько их? Впрочем, если неподвижные точки отображения соответствуют нулям сечения касательного расслоения, то тогда понятно.
В общем ладно, я уже чувствую некоторое раздражение, поэтому спасибо за беседу.
Начну с конца.
>Я уже заебался приводить примеры областей математики и важных теорем в них, где без когомологий не обойтись. Ты в этих областях не разбираешься и просишь свести все к чему-то простому. Но если свести, то жалуешься, что не видишь общей техники. Откуда ты увидешь общую технику, если мы уже спустились на несколько уровней?
Очень просто. Выделить из доказательства чего-то простого лежащий в его основе прием, и потом привести примеры, когда этот прием работает где-то еще, в высоких областях. Примеры я приводил уже
>Например, можно сравнить инварианты у двух вещей: если они разные, значит и вещи в каком-то смысле разные.
>рассмотреть процесс, при котором какая-то хуевина изменяется, а ее инвариант - нет, тогда можно будет показать, что начальная и конечная хуевины каким-то образом связаны, или наоборот, прийти к противоречию и показать, что они не связаны.
Или, скажем, как твой пример с теоремой Римана-Роха: была найдена числовая характеристика, которая равномерно изменяется при шаге индукции это больше похоже на утверждение наоборот: изучали эйлерову характеристику, обнаружили вот такое ее поведение, потом переписали этот факт в других терминах, и получили теорему Римана-Роха. То есть теперь, зная это, ничего не мешает поизучать другую какую-нибудь штуку, посмотреть на ее поведение, и если что-то найдется, переписать это в других терминах, и получить теорему Анона - это и есть выделение техники из доказательства.
Если такое выделение техники невозможно, значит, связь с простыми вещами именно "магическая", т.е. отсутствие какого-то общего приема, там хуяк, тут хуяк, и вуаля. Картофельные доказательства часто таким грешат, например.
Вообще это странно. Если ты не мыслишь в таких терминах, то как ты понимаешь и запоминаешь всякие доказательства? Я имею в виду, какую пользу это тебе приносит, если ты просто заучиваешь их? А если не заучиваешь, почему не можешь пояснить?
>Прости, но я уже пояснил, что это вопрос уровня, зачем нужны кольца.
Но я могу пояснить, зачем нужно кольцо, какие понятия оно обобщает и какие допускает обобщения, какие профиты мы поимеем с такого обобщения, где такая структура естественно возникает, и привести какие угодно примеры, а ты почему-то нет. Например, слабо ответить на такой тупой вопрос: почему нужно рассматривать поле, а не две группы с разными операциями? В чем разница, для чего этот дополнительный термин, что он дает? Видимо, слабо.
Вообще опять же странно. Разве это не первое, с чего нужно начинать что-то объяснять? Мы вводим новую сущность - нахуя мы ее вводим? Чтобы была? Чтобы доказать кучу безразличных фактов про нахуй не нужную сущность? В этом ты видишь суть математики? Печально, если это так.
>Это все естественные многообразия, которые естественно изучать. Не менеее естественно, чем факториальность колец.
Это не ответ. Ты видишь эту естественность, потому что изучал это, а я не вижу. Так, может, и надо ее продемонстрировать, чтобы я тоже увидел?
Вот я залез на вики и сразу нашел ответ:
>Более сложный пример — это касательное расслоение гладкого многообразия: каждой точке на многообразии сопоставляется касательное пространство к многообразию в этой точке.
Что мешало сразу так сказать? Мне, как картофанщику, не особо надо пояснять, зачем рассматривать в каждой точке касательное пространство. Интересно только, что нам дает такая "совмещенная" структура, хотя бы элементарные утверждения для нее, а если рассмотреть их на примере вот этого самого касательного расслоения - так и вообще отлично. Заодно почти наверняка получится какой-то нетривиальный, если не пользоваться понятием векторного расслоения, факт. Впрочем, я уже нашел такой факт, ты его озвучил.
>Сейчас ты спросишь, зачем изучать количество неподвижных точек
Да, спрошу. Я увидел, да и до этого представлял себе, зачем нам знать, есть ли неподвижные точки вообще. А вот зачем знать, сколько их? Впрочем, если неподвижные точки отображения соответствуют нулям сечения касательного расслоения, то тогда понятно.
В общем ладно, я уже чувствую некоторое раздражение, поэтому спасибо за беседу.
>почему нужно рассматривать поле, а не две группы с разными операциями? В чем разница, для чего этот дополнительный термин, что он дает?
Кстати, а расскажи, пожалуйста. Зачем, по-твоему, нужно понятие поля?
мимозаинтересовался
Сколько не читаю - не могу из понять, слишком абстрактны. Желательно и за математическую составляющую, так и применение в программировании. Спасибо, аноны.
Функтор и два простых ест. преобразования. Не используется, конечно же. Как и 99% всего остального абстрактного бреда. Только кукареки уже сто лет в обед, как кококонужны каты в программировании, за тарелкой маминого борща и обсёры в пижаму по ночам.
Это великолепно, только можно теперь нормальным языком, я слабо понял это бессвязный бред
А что за мемчик с борщеедством? Настоящие модные программные парни, не осиливающиене заморачивающиеся монадами не едят борщи, только всё смусси с маффинами?

Пруфы чего?
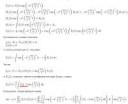
Не. Наоборот.
Лол, забавно он в конце сказал "ясно".
Это действительно эндофунктор и пара его естественных преобразований.
Видимо имелось в виду, что о таких вещах написано много статей во всяких бложеках, хабрах и ещё чёрт знает где. Написано хачкеледетьми прежде всего. Но зачем им это надо, они и сами не знают. Просто модно, загадочно звучит и быдло уважаетне понимает. Писать говнокод можно и без этого, а само по себе знание о категориях от этого никак не спасает, равно как этому и не способствует.
Так и вербитарии ноют постоянно, как плохо что тупая вата не даёт им преподавать моноидальные категории в пятом классе. Они даже сильнее ужаленные, постоянно письма какие-то малюют.
Но Арнольд то ебнутый безотносительно матеши. Послушай какуйю хуйню он несет. Даже жирик менее категоричен по сравнению с ним лол.
Лол, одного из основателей НМУ, одного из последних оплотов науки для вербитят, обозвали картофанщиком.
Ну в основатели то он подался по другим причинам, потому что его из МГУ пидорнули, (или некомфортно там стало). Он как раз и хотел мгушные картофанские традиции в НМУ внедрить, но дело его не победило.
Он не совсем ебанутый. Это неправильный термин, потому что ебанутыми становятся всё-таки без механических травм мозга. Правильнее сказать, что он повреждённый.
Фигаси, я думао вы аноны шутите про повреждение мозга. Стал гуглить, вот что нашел:
http://www.ega-math.narod.ru/Arnold3.htm#intro
Не знаю что произошло пока, но дело серьезное :)
>Что мешало сразу так сказать?
Потому что неизвестно, что ты знаешь, а что нет. Знать теорему Римана-Роха и вместе с тем не знать, что такое касательное пространство - это очень, очень странно.
Касательные пространства нужны потому, что любое поле - это в точности вектора на касательном пространстве. Но вид они иметь могут произвольный, однако лагранжиан выбранной модели задаёт тебе классы того, какими они могут быть. Вот затем, чтобы вытащить свойства полей (а значит, в частности, гравитации и электромагнетизма), и нужны характеристические классы векторных расслоений, а для них - гомологии.
Общий механизм рассуждений на примере простейшей U(1)-калибровки я уже описал. Дальше уже идут всякие теории Янга-Миллса.
>>359802-кун
Капица подпездывает постоянно, хотя по маразматической роже видно, что нихуя не понимает.
А, ну это объясняет, почему он не может сконцентрироваться на чем-то одном, а постоянно выдает кучу рандомных несвязных мыслей.
Это насколько нужно быть необразованным скотом, чтобы о герметизме узнавать от Арнольда.
Может, там Мур-Пенроуза инверс?
>пучок
Слушай, можешь, пожалуйста, на пальцах объяснить "аксиому склейки" для пучка. Я туповат и понимаю, что предпучок — это контрвариантный функтор, но как дело доходит до аксиомы склейки — сразу теряюсь.
Ну на "перехлёстах" множеств функции должны совпадать. Вроде, понятно же.
То есть это хуже, чем о сексе узнавать от родителей?
из стандартных оборотов есть
primary maximum - главный максимум.
relative maximum - относительный максимум.
а вообще от контекста зависить.
>Так и вербитарии ноют постоянно, как плохо что тупая вата не даёт им преподавать моноидальные категории в пятом классе. Они даже сильнее ужаленные, постоянно письма какие-то мал
Петух закукарекал!
Малюют не "верюбитарии", а нормальные студенты, ибо охуевшие профессоры-выбегаллы в Вышке читают им свою ОФИГИТЕЛЬНО ИНТЕРЕСНУЮ область глубоко вместо того, что придерживаться адекватной(которой, конечно, нету) программы
Анализ читают как на мехмате, то есть очень подробно. Я кстати не буду писать как Вербицкий что классических аналитиков надо сжигать на костре, но фишка в том, что это лишь один из множества разделов математики.
Почему "динамический системы"(диффуры+механика) есть в обязательной программе, а алгебраической геометрии нет?
Почему интегралы изучаются подробно(а не выделяются в спецкурсы, например, "Методы вычисления интегралов"), а нету обязательного курсы по анализу на многообразиях?
Нет теории Галуа в обязательных, а также алгебраической топологии. Это всё важные математические предметы, как минимум, не менее важные, чем классический анализ.
То есть если бы в обязательной программе читалась алгебраическая топология, теория Галуа, алгебраическая геометрия, анализ на многобразиях, дифференциальная геометрия и Риманова геометрия наряду с анализом, то вопросов бы не возникало, но это не возможно.
Почему-то охуевшая профессура выкидывает дофига математических наук, а вместо этого читает ОЧЕНЬ ПОДРОБНО классический анализ и динамсистемы(которые не относятся к науке "динамические системы") Чем они лучше?
А чем лучше дискретная математика? Логика? Дифгем не всем нужен, да. Алгем не всем нужен, да. Но и матлогика не всем нужна, а её читают. И диффуры с механикой не всем нужны, а их читают. И настолько подробный классический анализ тоже не всем нужен, а его читают.
А студенты за то, чтобы читали самый минимум, нужный специалисту-математику, после которого(минимума) уже студент будет выбирать специализацию, и пойдёт хоть диффуры решать, хоть алгебраической геометрией заниматься. Или матлогикой, если ему понравится.
>Так и вербитарии ноют постоянно, как плохо что тупая вата не даёт им преподавать моноидальные категории в пятом классе. Они даже сильнее ужаленные, постоянно письма какие-то мал
Петух закукарекал!
Малюют не "верюбитарии", а нормальные студенты, ибо охуевшие профессоры-выбегаллы в Вышке читают им свою ОФИГИТЕЛЬНО ИНТЕРЕСНУЮ область глубоко вместо того, что придерживаться адекватной(которой, конечно, нету) программы
Анализ читают как на мехмате, то есть очень подробно. Я кстати не буду писать как Вербицкий что классических аналитиков надо сжигать на костре, но фишка в том, что это лишь один из множества разделов математики.
Почему "динамический системы"(диффуры+механика) есть в обязательной программе, а алгебраической геометрии нет?
Почему интегралы изучаются подробно(а не выделяются в спецкурсы, например, "Методы вычисления интегралов"), а нету обязательного курсы по анализу на многообразиях?
Нет теории Галуа в обязательных, а также алгебраической топологии. Это всё важные математические предметы, как минимум, не менее важные, чем классический анализ.
То есть если бы в обязательной программе читалась алгебраическая топология, теория Галуа, алгебраическая геометрия, анализ на многобразиях, дифференциальная геометрия и Риманова геометрия наряду с анализом, то вопросов бы не возникало, но это не возможно.
Почему-то охуевшая профессура выкидывает дофига математических наук, а вместо этого читает ОЧЕНЬ ПОДРОБНО классический анализ и динамсистемы(которые не относятся к науке "динамические системы") Чем они лучше?
А чем лучше дискретная математика? Логика? Дифгем не всем нужен, да. Алгем не всем нужен, да. Но и матлогика не всем нужна, а её читают. И диффуры с механикой не всем нужны, а их читают. И настолько подробный классический анализ тоже не всем нужен, а его читают.
А студенты за то, чтобы читали самый минимум, нужный специалисту-математику, после которого(минимума) уже студент будет выбирать специализацию, и пойдёт хоть диффуры решать, хоть алгебраической геометрией заниматься. Или матлогикой, если ему понравится.
>Анализ читают как на мехмате
Как в совке, а не как на мехмате. Лично общался с экономистами и прочими менеджерами, которые тешили себя теплой мыслью - "а нам матан как математикам читают!" Долбоебы. .
Анализ преподают везде хуево: типичным представителям - слишком много, интересующимся людям - не в той форме. Не говоря уже про устаревшую формулировку.
Сам отучился шесть лет на околоматематике и все интересные разделы приходилось читать самому в англоязычных книгах. Убежден, что образование в нашей Федерации хуевое, что складывается из всего: учебников, преподавателей и ЦА. Могу читать статьи про алгебраическую топологию потому, что я - молодец. Спасибо, блядь, за нихуя.
Двачую!
Нужно пересмотреть программу математического образования. На своём горьком опыте испытал, отстутствии теории групп в обязательной программе. Кроме того, есть же ещё дискретный математики, которых и в Независимом нет.
http://math.stackexchange.com/questions/469688/riemann-integrable-improperly-but-not-lebesgue-integrable
А при чём тут интегрируемость по Лебегу к измеримости? Нет, конечно понятно откуда звон - но это не он.
>>361143
Ну странный вопрос немного, без предположения измеримости ты не сможешь решить те задачи, которые этого предположения требуют. Но интуитивно, конечно, можно представлять, что все "нормальные" функции измеримые.
- "Молодой человек, у вас в презентации запятых не нашлось, а ещё и в слове "дезоксирибонуклеиновая" семь ошибок, шли бы Вы, не позорились." Удивлённые учёные его спрашивают:
- "Ты ещё, что за хуй?", а он в ответ:
- "Я такой же учёный как и вы, только я лучше и умнее всех вас, потому что вы все используете язык моей науки - филологии".
Правда, такая ситуация была бы необычной и крайне забавной? А ТЕПЕРЬ ПОЯСНИТЕ ЗА КАКИМ ХЕРОМ НА ВСЕХ НАУЧНЫХ КОНФЕРЕНЦИЯХ СИДЯТ МАТЕМАТИКИ С ТОЧНО ТАКИМИ ЖЕ ПРАВАМИ, КАК У ФИЛОЛОГОВ?
Математика - это даже не наука и она вообще не нужна в науке. Её изучение можно ограничить 8-ми классами средней школы, ведь остальное даже не понадобиться ни в жизни, ни в естественных науках.
Я - биолог и я должен за каким-то хуем изучать математику, ТОЛЬКО по причине того, что античные фанатики и средневековые фанатики назвали её царицей наук для изучения своего богословия.
Из-за вонючей математики и логики у меня из группы отчислили треть человек. Сейчас мой одногруппник, который два года получал "отлично" за курсачи по неоламаркизму и у которого уже даже были планы стать учёным и на 50% завершённый дисер, вынужден работать в макдаке, чтобы заработать на взятку для военкомата, потому что не смог сдать математику и логику.
Математику даже ненавидели и презирали Ландау и Нобель. Последний даже не стал вносить их в номинацию на премии.
Пора уже выкинуть этот верунский бред с корабля науки.

Obvious trolling aside, я согласен с тезисом о том, что в современном мире лучше ограничить знакомство с математикой восемью классами, или меньше того - ни слова про квадратные уравнения, иррациональные числа и уж тем более производные и проч.
Ну а ты, конечно, тролль толстый для всякого, кто знаком с перечнем логических ошибок, что, думаю, не редкость в этом треде.
Создайте отдельный тред ненависти к математике и сидите в нём. В этом треде благородные доны изобретают категорный аналог равенства Планшереля, а также слушают нашиды.
Saleelul sawarim
Nasheedul ubah...
Математика - это не про числа и треугольники, математика - это вообще любое системное знание. Поэтому любая наука действительно либо уже математика, либо потенциально математика; то же, где математики нет и не может быть - не наука, а в лучшем случае набор разрозненных фактов типа книги о вкусной и здоровой пище. Ну а в образовательном процессе математика выступает в качестве последнего барьера, отсеивая уже совсем конченных.
>А ТЕПЕРЬ ПОЯСНИТЕ ЗА КАКИМ ХЕРОМ НА ВСЕХ НАУЧНЫХ КОНФЕРЕНЦИЯХ СИДЯТ МАТЕМАТИКИ С ТОЧНО ТАКИМИ ЖЕ ПРАВАМИ, КАК У ФИЛОЛОГОВ?
Вот математику больше делать нечего, как приходить и слушать вашу хуету. Такое может быть, только если его специально пригласили, ну в таком случае все вопросы к тому, кто пригласил.
>Из-за вонючей математики и логики у меня из группы отчислили треть человек.
>Пора уже выкинуть этот верунский бред с корабля науки.
Господа, перед вами яркий пример юношеского максимализма: вместо того, чтобы решать свои собственные проблемы (добиваться упрощения мат. программы на своем гумусфаке до уровня "8 класса средней школы"), поциент экстраполирует их до проблем всего мира (нужно изгнать математику из всех наук вообще). Ну что ж, пожелаем ему удачи в их решении.
Покормил

Хз, как определить крутость математика, от математики тоже далековат, но Концевича, Воеводского и Фоменко знаю.
По твоему крутой - это мускулистый альфач eбущий тянок?
А ну-ка давай список "реальных задач" для любителя теории категорий.
Я честно никогда не понимал, кто решает, что что-то реальная математика, а что - "лингвистика и онанизм ума".
Какой критерий? Применимость?
А если я хуй простой, который может делать только что-то абстрактное в неделю раз. (Инженером быть? Доказывать свою нужность псевдонаучными статейкам?)
Вот честно я сейчас думаю о том, что вообще блять делать дальше по жизни.
Чтобы быть математиком - надо обладать нехуёвой энергией и яростной верой, что то, что ты делаешь - не бесполезная ерунда.
Честно - просто накипело, сейчас заканчиваю универчик, и не хочу всю молодость ходить под малоуважаемыми старикашками, говорящими мне что делать и обещающими мне только гарант рованную бедность.
Да и вообще бля - кто идёт преподавать за гроши? Идейные? Так вот идейные - это самые твердолобые и редкостные мудаки.
Мне хотелось бы быть как можно более независимым и при этом заниматься техническими вещами и иметь адекватные деньги за это. (Это, конечно, некорректно поставленная задача, лол, нужен регуляризатор Тихонова)
Вывод пока - заканчивать вузик и ебашить прогером. Да только я чувствую себя идиотом, проебавшим несколько лет.
Да.
>экономистами и прочими менеджерам
>матан как математикам
>образование хуевое
Что сказать то хотел? Матан как математикам нужен только математикам.
Кек, в /po нашлась эта паста. Там то хоть срач длинный получился.
Пошёл нахуй
Тут не "матаногоспода", а нормальные пацаны, считающие когомологическую размерность Нетеровых схем
Матан не нужен
Ты спам. Умри.
функция: f: C^n -> C называется голоморфной, если
ее производная Df: C^n->C является гомоморфизмом векторных пространств над C
Кто-нибудь, привыкший к гомоморфизмам векторных пространств над С, может привести мне пример, когда функция бесконечно дифференцируема, но не голоморфна (и показать, почему ее производная - не гомоморфизм)
Я понимаю, что надо от уравнений Коши-Римана отплясывать, но может кто-нибудь напишет? А для нескольких переменных?
за Х принимаешь неизвестное. это основной принцип. про шапку и фальшивую купюру можешь решить? понимаешь почему именно такой ответ? еще про поляйца хорошая задача. там тоже Х неизвестно.
Меня тут уже 15 минут мотает по первому кольцу, как отсюда выйти?
Понятия не имею, как заставить справочную систему считать матан. А в математике напиши Series и нажми F1.
ненетеровых
Видишь ли, анон, не бывает доказательства самого по себе. Если ты просишь доказать что-то, ты должен объяснить, что предполагается доказанным. Из каких конкретно утверждений мне следует вывести тебе закон Гаусса? И укажи точную формулировку, которая тебя интересует.
Если тебе нужно вывести его из закона Кулона - почитай какого-нибудь Сивухина за электричество.
Из теоремы кранца-начиханца
>Вывод пока - заканчивать вузик и ебашить прогером.
Заработаешь кучу денег, а потом умрешь, славная будет жизнь.
Максвел в треде, все в эфир.
В эфире развлекательное капитал шоу "Поле Чудес" и я его ведущий Леонид Якубович
http://lvlb.ru/Void/Continuum.html
Говно какое-то.
>Анон, а если в категории есть произведение и копроизведение, то обязательно ли оно должно быть определено для произвольного семейства объектов?
Нет, с какой стати-то? Если для двух есть, то и для конечного числа есть, а между конечным и бесконечным большая разница. Например, дроби, морфизмы из порядка (>=→), конечные супы есть, а бесконечных — нет (вообще говоря).
>Это семейство может быть несчётным?
Почему бы и нет? Вещественные числа с порядком (верхние|нижние грани), множества и несчетные пересечения.
Скорость возрастания показательной функции больше степенной, значит такие натуральные числа существуют, но как указать их явно?
2. Математическая статистика- область в которой активно работают ученые, или сугубо прикладная вещь, в которой уже все, или почти все известно?
3. Вот берем типичного хорошего студента 2-3 курса с мехмата МГУ и ФУПМ физтеха... сильно ли разнятся их познания в математике?
1. Неизвестно. Учёные не рассказывают, а у не-ученых нет квалификации, чтобы понять.
2. Статистика - отдельная наука, в которой крутится так много денег, что финансово всю остальную математику можно считать маленьким её разделом.
3. Сильно.
1. Ок
2. Там реально люди пишут научные работы и эти работы реально двигают эту науку, а не "бла-бла-бла"?
3. Победитель международной олимпиады школьников по математике, поступивший на ФУПМ- нонсенс?
1) Интеруниверсальная теория Мочидзуки-Тейхмюллера, некоммутативная геометрия, квантовые группы, теория высших топосов. Вообще "раздел" - очень мутное понятие, любое направление исследований и идеи вокруг него можно воспринимать как раздел, то, чем я занимаюсь можно сказать тоже придумали недавно относительно.
2) Реально пишут научные работы и двигают науку. Известно многое, но задач - ещё больше.
3) Мне кажется, что при должном характере: вообще абсолютно поебать где учиться - лишь бы интеллектуальный климат хороший был. Вполне возможно, что тебе "высокая математика", которая очень сильно от "олимпиадной" отличается - не понравится, кстати. Тем более в Москве НМУ есть, чего ещё нужно?
Еще один мимопроходил врывается в тред.
1. Почему-то заинтриговало название "некоммутативная геометрия". Можно "так сказать в общих чертах" объяснить что это такое?
2. Я тут так понял, что-то типа стоматологов в меде- вроде как не совсем врач, а бабла много
3. Понимаю, что идиотский вопрос... а вот(гипотетически) очень хочется человеку, чтобы в процессе учебы хоть немного приобщиться к некоммутативной геометрии... ему куда поступать?
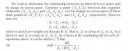
1. Не знаю, могу в общих чертах рассказать что такое некоммутативная топология и некоммутативная теория вероятностей.
Некоммутативная топология строится примерно так: сначала выясняется, что категория хаусдорфовых компактных пространств полностью (анти)эквивалентна категории коммутативных унитальных С-алгебр. А потом задаётся вполне логичный вопрос, а какие пространства "соответствуют" некоммутативным С-алгебрам? Ну и на этом пути начинают делать "словарик" из соответствий понятий между С-алгебрами и топологией:
унитальность и коммутативность <-> хаусдорфов компакт
AW алгебры <-> экстремально несвязные пространства
связность <-> отсутствие проекций
и так далее. Затем в чисто стрелочных терминах пытаются задать топологические структуры (гомотопии, фундаментальные группы) на С-алгебрах. Получается неплохо.
2. Вроде того.
3. Поступать в любое место, где есть люди, которые занимаются некоммутативной геометрией. А они есть почти везде: MIT, Принстон, Гарвард, любое другое место высокого класса* ...
>>365072
Квантовыми деформациями алгебр Кунца и их устойчивостью.
Финансовая аналитика, крупные IT компании (анализ web-графов и трафика), вообще в любую крупную корпорацию, на самом деле.
Не знаю. НМУ ещё есть.
Взял из головы. Думал, что не может же быть все так просто. Но ты прав.
Отображение несет информацию о том, какие множества в декартовом произведении идут в каком порядке, то есть у нас есть i-я координата. Буквы в определении частной производной и неважны.
Нет же, не несёт. Нельзя узнать, является ли данное множество декартовым произведением каких-либо множеств.
Ты о чём вообще. Если у тебя есть конкретная функция f : R^n -> R (где n фиксировано и ты его знаешь), то ты легко можешь определить её проекцию.
О, я вижу, ты тут котегориями размахиваешь. Поясни за аргумент Экманна-Хилтона.
Не слышал даже о нём раньше сорян 3: Я всё-таки люблю, когда структуры побольше, всякие моноиды, полугруппы и прочая абстрактная алгебра - мне совершенно неблизки.
Тоже открытая проблема https://en.wikipedia.org/wiki/Square_root_of_2
>It is not known whether √2 is a normal number, a stronger property than irrationality, but statistical analyses of its binary expansion are consistent with the hypothesis that it is normal to base two.[21]
Это для всех иррациональных чисел? Или есть какое нибудь чилсо, в котором определена или хотябы существует хоть какая нибудь оценка вероятности появления цифр?
Если ты под "вероятностью" имеешь в виду частоту появления цифр, то в статье https://en.wikipedia.org/wiki/Normal_number есть большое количество примеров как нормальных, так и ненормальных чисел. Но частота появления цифр, двуграмм из цифр, триграмм из цифр и т.д. - это ещё не признак того, что цифры этого числа дадут хороший генератор случайных чисел.
такие интервалы используются в тфкп
https://en.wikipedia.org/wiki/Extended_real_number_line
Тао строит теорию меры на полупрямой [0..inf] (на которой не всегда возможно вычитание, которое, впрочем, в теории меры не нужно особо). Про его подход можешь почитать в Preface тут http://www.faculty.jacobs-university.de/poswald/teaching/RealAnal2/handouts/TaoMeasureTheory.pdf
>зашёл в тред математиков
>читаю буквари на пафосном слоге
Ты где математику учил? В воскресной школе для горняков, в русском селе под Нижним, в 1920-м?
Сама математика существует только в разностях. Не будет любых размерностей ("динамика" лишь общий случай размерностей, включающий в себя частности, в виде неких постоянных величин, например (не имеющих параметров временной оси).
Стыдно должно быть писать такие ОП-посты в тредах про математику на серьёзных щях. А за тред спасибо, в общем.
Чего почитать, имея школьные знания и курс математики из экономического вуза? Чтобы лучше ориентироваться в математике в целом.
Гугли mit mathematics for computer science, там все для дебилов объясняется.
Число 0.101001000100001000001... иррационально. Вероятность появления в нём цифр 2-9 равна нулю.
Так-то он прав, просто это взгляд на природу математики со стороны. даже не берусь конкретизировать с какой - философия или когнитивная наука, хз. Это же естественно - основа мышления строится на объективизации, на отделении одних объектов от других. Другое дело, причем тут ОП-пост и чего он на него гонит.
http://ium.mccme.ru/postscript/s16/topology3-problems-manifolds-4.pdf ?
Научите, пожалуйста
Я всё прощу
Тебе же сказали, долбоёб, любая проколотая окрестность. Только должна быть у каждой точки центральная система окрестностей, счётная, например. Точка на прямой не имеет предельных точек, которые ей не принадлежат.
Никто не умер. Все ботают. Кстати, почему в литературе нигде нет внятного определения дифференциала функции Rm->R? Даже в английской википедии хуйня какая-то написана. Внятного - такого, чтобы теорема о дифференциале композиции без лишних слов доказывалась. Везде торчит o-малое, с которым приходится ебаться.
Не знаю. Но когда в доказательстве теоремы о производной композиции имеется, как у Львовского во второй части, целая страница выкладок, объясняющих поведение o-малого, и лишь в конце маленькая приписочка типа "а это доказывает теорему" - это не гуд.
exp(-((y-x)^2)/(4ta^2))/(y+a)^2 dy from -inf to inf
Вольфрам и маткад меня нахуй послали.
Через клетки Шуберта.
Посмотри, например, вот здесь: http://www.mi.ras.ru/~kazarian/papers/homology05.pdf (66 страница)
Мне кажется, что единственное внятное определение - как проекция из кольца R[e]={(a,b)}={a+be}, где e^2=0. То есть через НЕСТАНДАРТНЫЙ АНАЛИЗ, да.
Ночешь, чтобы что-то "по жизни пригодилось" - иди в ПТУ или подмастерьем каким.
Мне пригодилось, петух ту тупой. Мне.
о-малое, совершенно адекватный и понятный аналитический концепт, не понимаю, в чём может быть проблема.
Я не он, но технически, o(f(x)) при x->a - это класс функций g таких, что g(x)/f(x) -> 0 при x -> а. Когда пишут hui + o(f(x)) при x->a на самом деле имеют в виду hui + g(x), где g принадлежит описанному классу.
что не комплексный? сначало убедится что интеграл существует хотя бы в смысле главного значения, затем использовать теорему о вычетах
да только тут будет полувычет, но это такое
можно подробнее?


>>367852
Пожалуйста, давайте работать с общим случаем, в дифференциальном исчислении R->R никаких проблем нет. Ваши определения нельзя элементарно обобщить на функции в R^n, для этого приходится возиться с нормами, из-за чего происходит много неприятных вещей - вместо равенств возникают нестрогие неравенства, например. И в доказательстве теоремы о дифференциале композиции приходится работать с нормой функции, аргументом которой является хитровыебанное выражение. Пикрелейтед.
Обобщаются напрямую без изменений.
Доказательство в учебнике странное. Вполне можно обойтись без введения эпсилонов и дельт.
Напрямую они обобщаться не могут - хотя бы потому, что в определении o-малого фигурирует умножение функций, а в R^n умножения нет.
Если можно, то покажи, пожалуйста.
Этого недостаточно. Такое определение слишком слабое, чтобы доказать теорему о производной дифференциала. Если о-малое определено с использованием норм, можно оценивать "хвосты", которые получаются из-за использования о-малых. А без норм оценка невозможна.
Это эквивалентно, в конечномерных пространствах если последовательность векторов покоординатно стремится к нулю, то стремится к нулю и по норме.
Лол. О производной композиции, конечно.
Окей. Пусть есть две функции f и g, для простоты R^n -> R^n. f дифференцируема в точке a, g дифференцируема в точке b := f(a). Это значит, что есть такие линейные операторы f' и g', что f(a+h)-f(a) = f'(h) + o(h), g(b+m)-g(b) = g'(m) + o(m). Нужно доказать, что g∘f дифференцируема в a, и её производная есть g'∘f'.
Согласно определению o-малого, речь идёт вот о чём.
Существует такая функция p: R^n -> R, что
f(a+h)-f(a) = f'(h) + p(h)×h
и lim p(h) = 0 при h->a
Существует такая функция q: R^n -> R, что
g(b+m)-g(b) = g'(m) + q(m)×m
и lim q(m) = 0 при m->b
Нужно доказать, что существует такая функция r: R^n -> R, что
(g∘f)(a+k) - (g∘f)(a) = g'(f'(k)) + r(k)×k,
и lim r(k) = 0 при k->a.
Как это сделать?
Я тебе отвечу чуть позже.
Логичнее писать
f = o(g) при B
если ||f|| = o(||g||) при В.
Про теорему о композиции дифференциалов напишу чуть позже.
Зачем тебе вообще красивое доказательство этой формулы? Ты же не вспоминаешь как это утверждение доказывается, когда его применяешь. Это в алгебре все взаимосвязано и если медитировать над доказательствами, то сможешь легко доказывать с нуля большую часть утверждений, а матан - это bag of tricks, смирись. Многие доказательства в матане не дают вообще никакой интуиции, они приводятся для порядка, чтоб не оступаться от аксиоматического метода. Какую, например, важную идею иллюстрирует вывод формулы Тейлора? Никакой. Я его прочитал 1 раз и забыл через пару дней, потому что он никак не помогает в применении самой формулы.
> происходит много неприятных вещей
> хитровыебанное выражение
Это же матан, в нем вообще никаких приятных вещей не происходит. Чего ты ожидал?

Меня не интересуют многочисленные задачки, связанные с матаном. Мне интересна именно внутренняя структура. Я рассматриваю дифференциальное исчисление как красивое архитектурное сооружение, и я вижу, что это сооружение очень интуитивно и логично. Анализ воспринимается как bag of tricks только потому, что красота его внутренней структуры скрыта за уёбищным изложением.
Производная - это линейный оператор, то есть многочлен первой степени, который приближает функцию. Ряд Тейлора (он же производная Пеано) - это многочлен степени n>=1, который приближает функцию. Коэффициенты этого многочлена - операторы (если выбран базис, то матрицы). За тейлором и дифференциалом скрывается одна и та же идея - приближение функции многочленом.
К сожалению, эту идею сложно увидеть. В курсе анализа сначала отдельно рассматривают функции R->R, а производной называют число (которое вообще-то просто является матрицей линейного оператора, и вот этот-то линейный оператор и важен на самом деле). Затем отдельно рассматривают матрицу Якоби, опять-таки без упоминания о том, что эта матрица на самом деле является матрицей некоторого линейного оператора. Затем, снова отдельно, рассматривают ряд Тейлора. Никто не объясняет, что все эти вещи - на самом деле одна и та же вещь. Не знаю, почему так.
Казалось бы, так просто сделать всё по уму: по аналогии с производной Фреше сконструировать обобщённую производную Пеано, назвать эту производную рядом Тейлора (первый член этого ряда Тейлора назвать сильным дифференциалом), и с помощью этой обобщённой производной Пеано доказать все очевидно возникающие теоремы. Если хочется, то ввести вдобавок производную Гато. Хз, почему так не делают.
Хз. У Рудина не лучше, например.
> пикрелейтед
Там речь об определениях. Если заменить определние какого-нибудь фундаментального объекта на другое, то дохуя чего изменится, красивые определения - это действительно очень важно. Если заменить одно доказательство на другое то не изменится вообще ничего. Математик не обязан знать доказательства всех результатов, которыми он пользуется,
> потому что память человеческая очень ограничена, увы.
Не соглашусь. Доказательства - это то, что связывает одно определение с другим, и доказательства ценны никак не меньше, чем определения. Концептуально правильные доказательства лично меня волнуют, очень даже.
Ты меня не слушаешь и повторяешь принятую в определенных кругах мысль, никак ее не аргументируя. Я тебе излагаю просто свой взгляд. В математике есть смысл тратить на что-то время, если тебе это интересно или неинтересно, но ты этим занимаешься из каких-то утилитарных соображений. Если руководствоваться утилитарными соображениями, то я уже объяснил, почему утверждение про производную композиции проще запомнить. Если руководствоваться интересностью, то непонятно, зачем вообще искать какие-то красивые доказательства в матане: если тебе нравится, когда все естественным образом получается и все со всем связано, то занимайся областями математики, где по дефолту все так и не надо по многу часов гуглить, чтоб найти красивое доказательство.
> доказательства ценны никак не меньше, чем определения
Я совсем не понимаю эту мысль. Я ее и раньше читал, но никакой аргументации не встречал.
Опять же, для чего нужны доказательства? Если кто-то открывает что-то новое, то доказательства нужны, чтобы убедиться в истинности, а если ты читаешь учебник (тем более по такому старому предмету как классический матан), ты можешь сделать разумное предположение, что автор учебника тебя не наебывает и утверждения в учебнике действительно верные. В этой ситуации не нужно вникать в доказательства всех утверждений. Скажем, я знаю, что вещественные числа определяются как классы эквивалентности фундаментальных последовательностей, но я никогда не проделывал это построение своими руками, я ж не ебанутый. Если доказательство лучше помогает понять какой-то объект, оно нужно. Скажем, в общей топологии лучше разобраться со всеми основными доказательствами. Я думаю это понятно, не буду расписывать. А вот в матане - крайне сомнительно. Если мне, например, покажется некрасивым и неконцептуальным доказательство того, что (R, L, m), где L - измеримые по Лебегу множества а m - мера Лебега на R, является пространством с мерой, я с этим смирюсь, потому что если посмотреть на определение пространства с мерой и сопоставить это с интуитивными представлениями о длине, то понятно, что по-другому и быть не может и если бы эти свойства не выполнялись, то мера Лебега никому была бы не нужна.
Ты меня не слушаешь и повторяешь принятую в определенных кругах мысль, никак ее не аргументируя. Я тебе излагаю просто свой взгляд. В математике есть смысл тратить на что-то время, если тебе это интересно или неинтересно, но ты этим занимаешься из каких-то утилитарных соображений. Если руководствоваться утилитарными соображениями, то я уже объяснил, почему утверждение про производную композиции проще запомнить. Если руководствоваться интересностью, то непонятно, зачем вообще искать какие-то красивые доказательства в матане: если тебе нравится, когда все естественным образом получается и все со всем связано, то занимайся областями математики, где по дефолту все так и не надо по многу часов гуглить, чтоб найти красивое доказательство.
> доказательства ценны никак не меньше, чем определения
Я совсем не понимаю эту мысль. Я ее и раньше читал, но никакой аргументации не встречал.
Опять же, для чего нужны доказательства? Если кто-то открывает что-то новое, то доказательства нужны, чтобы убедиться в истинности, а если ты читаешь учебник (тем более по такому старому предмету как классический матан), ты можешь сделать разумное предположение, что автор учебника тебя не наебывает и утверждения в учебнике действительно верные. В этой ситуации не нужно вникать в доказательства всех утверждений. Скажем, я знаю, что вещественные числа определяются как классы эквивалентности фундаментальных последовательностей, но я никогда не проделывал это построение своими руками, я ж не ебанутый. Если доказательство лучше помогает понять какой-то объект, оно нужно. Скажем, в общей топологии лучше разобраться со всеми основными доказательствами. Я думаю это понятно, не буду расписывать. А вот в матане - крайне сомнительно. Если мне, например, покажется некрасивым и неконцептуальным доказательство того, что (R, L, m), где L - измеримые по Лебегу множества а m - мера Лебега на R, является пространством с мерой, я с этим смирюсь, потому что если посмотреть на определение пространства с мерой и сопоставить это с интуитивными представлениями о длине, то понятно, что по-другому и быть не может и если бы эти свойства не выполнялись, то мера Лебега никому была бы не нужна.
Зачем постоянно гуглить, если красивое доказательство я могу просто придумать самостоятельно, как следует продумав имеющиеся некрасивые доказательства? И мне нравится именно дифференциальное исчисление, а не какая-то другая конструкция.
>Я совсем не понимаю эту мысль.
Аксиомы и определения можно выбирать произвольно, любой набор слов может быть постулирован. Ценность у системы из аксиом и определений появляется только тогда, когда об этой системе доказано некоторое количество красивых теорем (что понимать под красотой - см. эссе "Плач математика"). Термины, определения терминов, аксиомы и теоремы называются теорией. В ходе исторического развития теории определения терминов меняются, становясь всё более понятными. Некрасивые доказательства заменяются красивыми, аксиомы заменяются более красивыми эквивалентными. В конце концов вся теория становится настолько простой и красивой, что становится всего лишь одним цельным математическим объектом, который можно объяснить всем.
Такой путь прошли, например, вещественные числа. Древние греки писали толстые книги о теории "величин", в средние века мыслители изобретали абстрактное сложение, в новое время учёные спорили о реальности отрицательных чисел (причём некоторые люди в комплексные числа верили, но в отрицательные нет). А в наши дни вся эта теория, некогда большая и богатая, редуцировалась до всего лишь трёх слов: "непрерывное упорядоченное поле". Понятие числа прочно вошло в нашу культуру и изучается с пелёнок.
Я надеюсь, что это же ждёт и все современные математические теории, в частности матан, - они станут всего лишь двумя-тремя терминами и будут усваиваться ещё в детских садах.
День арнольда же.
> будут усваиваться ещё в детских садах.
IBM Watson и улица сезам кажется над этим работают. cognitive learning вот это все
>Скажем, я знаю, что вещественные числа определяются как классы эквивалентности фундаментальных последовательностей, но я никогда не проделывал это построение своими руками, я ж не ебанутый
А зря. Важная конструкция, не плохо было бы руку набить. Или тебе поебать на p-адические числа в теории чисел, и формальные окрестности в алгебраической геометрии.
>>367859
>хитровыебанное выражение
>целая страница выкладок
Ты сильно преувеличиваешь сложность выкладок в матане. Это несложная техника, которую надо выучить один раз (как езду на велосипеде), чтобы строго излагать совершенно очевидные доказательства и определения. Типа люди этому в школе без проблем обучаются.
Например, необходимая тебе теорема о композиции на человеческом языке звучит так.
Дифференциал отображения F в точке это линейное отображение DF, что F = DF + хуйня
Если F = DF + хуйня, а G = DG + хуйня, то так как хуйня(G) = хуйня и DF(хуйня)=хуйня, то F(G)=DF(DG+хуйня)+хуйня=DF(DG)+хуйня.
Любой человек, который обучился соответствующему навыку, переведет это рассуждение в доказательство из Львовского.
Вещественные числа не нужны физике и непредставимы в ЭВМ. Одного этого уже достаточно, чтобы отправить их на свалку истории.
>которую надо выучить один раз
Это неверно. Я не хочу ничего учить, я хочу видеть. Например, тривиально и без всяких выкладок видно, что композиция непрерывных функций непрерывна: если f(X)⊂g(Y) и g(Y)⊂O, то f(X)⊂O.
>на человеческом языке звучит так
На самом деле не совсем так, кстати.
> Или тебе поебать на p-адические числа в теории чисел, и
По-моему, логично, что чтобы понять p-адические числа, нужно заниматься p-адическими числами, а не строить вещественные. В любом, случае, мне это действительно неинтересно. Я для себя не вижу никаких причин заниматься теорией чисел и алгебраической геометрией кроме того, что это модно.
Зубрить не надо, а запоминать надо. В конечном итоге, ты все равно что-то запоминаешь.
Записал хуёво. Нормальная запись: D(f o g) = Df Dg, просто эдакая "фнукториальность дифференциала". Нытьё того куна действительно непонятно, неосилятор, видимо.
С каким из перечисленных мной фактов ты не согласен?
Доказательство очень простое. И не отличается от одномерного случая почти ничем. А в одномерном доказательство простое.
Некрасивое.
У нас в институте за такие вопросы убивают нахуй.
Хочу.
Я пишу статью по континуум-гипотезе.
http://lvlb.ru/Void/Continuum.html
Хотелось бы услышать советы и критику.
Спасибо.
Бамп, не молчите пожалуйста, скажите, что вы об этом думаете, это же анонимная борда...
что именно непонятно?
Это копия, сохраненная 28 сентября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.