Это копия, сохраненная 20 мая 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.



И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
И. М. Гельфанд, С.М. Львовский, А. Л. Тоом: “Тригонометрия”. Название говорит само за себя. Много геометрических и физических интерпретаций + комплексные числа, как бонус.
Я.П. Понарин: “Элементарная геометрия” в двух томах. Собственно, первый том - это планиметрия(это раздел геометрии, изучающий фигуры в двумерном пространстве, т.е. на плоскости), а второй том - это стереометрия(это раздел геометрии, который изучает фигуры вне одной плоскости(не двумерное пространство), т.е. в пространстве).
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”.
М. М. Постников: “Теорема Ферма. Введение в теорию алгебраических чисел”.
Виленкин: "Рассказы о множествах".
С. Гроссман, Дж. Тернер: “Математика для биологов”.
А. Ю. Калинин, Д. А. Терешин: “Геометрия”, 10-11 классы. Годный учебник.
А. Д. Александров, А. Л. Вернер, В. И. Рыжик: “Геометрия”. Учебник для 10-11 классов. Базовый и углубленный уровни. Говорят, что годный. Хотя не проверял. На первый взгляд годный.
В. В. Ткачук: “Математика - абитуриенту”. Один из лучших учебников для поступающих в ВУЗы.
Г. Н. Яковлев: “Пособие по математике то для поступающих в ВУЗы”. Туда же.
С. Б. Гашков: “Современная элементарная алгебра”.
В. И. Арнольд: “Обыкновенные дифференциальные уравнения”.
Э. Б. Винберг: “Курс алгебры”.
Н. Стинрод Первые понятия топологии
Список литературы для начинающих физиков:
В. И. Яковлев: “Физика”.
Я. Б. Зельдович: “Высшая математика для начинающих и ее приложения к физике”, “Высшая математика для начинающих физиков и техников”.
Г. С. Ландсберг: “Элементарный учебник физики” в трех томах.
Интересное:
Я. П. Понарин: “Алгебра комплексных чисел в геометрических задачах”.
В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”
В. И. Арнольд: “Вещественная алгебраическая геометрия”
А. А. Заславский: “Геометрические преобразования”.
В. Акопян, А. А. Заславский: “Геометрические свойства кривых второго порядка”.
В. И. Арнольд: “Геометрия комплексных чисел, кватернионов и спинов”.
В. В. Прасолов: “Геометрия Лобачевского”.
В. Г. Сурдин: “Динамика звездных систем”.
Д. В. Аносов: “Дифференциальные уравнения: то решаем, то рисуем”.
М. А. Шубин: “Математический анализ для решения физических задач”.
В. В. Прасолов: “Наглядная топология”.
Д. В. Аносов: “От Ньютона к Кеплеру”.
Виро, Иванов, Нецветаев, Харламов: “Элементарная топология”.
Так же есть очень интересные и полезные ресурсы:
Библиотечка "Квант": www.math.ru/lib/ser/bmkvant
Высшая математика просто и доступно, по 2 курс включительно: mathprofi.net
Алсо, продолжаем обсуждать и дополнять список.
Avec plaisir:
С. Маклейн: "Категории для работающего математика"
Р. Голдблатт: "Топосы. Категорный анализ логики"
А. Хэтчер: "Алгебраическая топология"
О. Я. Виро, Д. Б. Фукс: "Введение в теорию гомотопий. Гомологии и когомологии"
Д. Мамфорд: "Красная книга о многообразиях и схемах"
Д. Пойа - Математическое открытие
Л. Кэрролл - Логическая игра
>ТЕПЕРЬ БАНАНОВЫЙ
Это отсылка к Банандину из ПКА?

вербицтвую этого анона!
telegram.me/matan_for_everyone
А в комплексной?
:с
Они и в математике то очень не везде нужны.
Что?
А что тогда создавать?? Твои предложения
Вид бинарного отношения f371 при котором для любого x существует единственный y так что (x, y) ∈ f.
В силу единственности y запись (x, y) ∈ f эквивалентна f(x) = y
Нормальная подгруппа определяется в группе (инвариантна по сопряжению). Идеал — подмодуль, если рассматривать кольцо как модуль над собой.
Так тебе надо учебники читать тогда. Что именно непонятно? Нормальная подгруппа — это про группы, идеал — это про кольца.
Так кольцо же от группы только наличием еще одной операции отличается.
В нормальной подгруппе H группы G результат сопряжения gH не обязательно включен в H
В идеале I кольца R для любого x∈ I, y ∈ R xy ∈ I
http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal Teichmuller Theory IV.pdf
http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal Teichmuller Theory III.pdf
http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal Teichmuller Theory II.pdf
http://www.kurims.kyoto-u.ac.jp/~motizuki/Inter-universal Teichmuller Theory I.pdf
толсто.
>>349308
Я один это голосом Пахома прочитал?
Я английский не знаю
Спасибо
>В нормальной подгруппе H группы G результат сопряжения gH не обязательно включен в H
Лол, как не обязательно-то? Поэтому она и нормальная, что все элементы вида a^-1Ha=H.
Есть линейное отображение из пространства в поле. Проверь, что сложение и умножение на скаляр этого отображения позволяет ввести структуру векторного пространства линейных функционалов. Вот тебе собряженное пространство.
Я говорю о gH (косет).
Как может быть отображение из пространства в поле? Я думал пр-во НАД полем? Поле это же цифирки. R например
Возьми R^2. Пусть есть отображение (x,y) - x. Вот тебе отображение из R^2 в R.
Голдблатт не очень, кста. Маклейна можно на Гельфанда-Манина поменять (и категории, и гамалогии тапалогии выучишь).
Очень сложный вопрос, это за пределами современной математики.
>>349311
Чем отличается 2 от 1? Только на единицу больше.
Ладно, ты меня раскусил. Я не Мочидзука. И работы его не читал, поскольку английский не знаю.
Может тогда хоть скажите в каком направление двигаться чтобы найти нули.
Линейный функционал — это просто линейное отображение из пространства в поле.
Одна операция и две операции — принципиальная разница. Одно + или × понять не так уж сложно. А вот + и × вместе — это ад. Взаимодействие этих двух знаков — одна из самых загадочных вещей в математике
Все, понял. На вики написано, что это одно и то же.
ты чеё лох чтоли кокие нули хааааа
Идеал - это из теории колец, а нормальные подгруппы - из теории групп. Вроде бы очевидно.
я имею ввиду я в ООП немного могу, а тут посмотрел на вашу алгебру и подумал - да это же ОХУЕННО! это оно!

Дело не только в "позже-раньше", если убрать всю болтовню то принципы ООП действительно следуют из таких областей математики как теория типов и абстрактная алгебра.
заплакал. почему? мозг испорчен ооп?
Другой интерфейс.
Ну, извини. Читаю несколько источников параллельно. Одни авторы начинают с колец, другие с групп. Я смотрю, что понятия нормальной подгруппы и идеала очень похожи, поэтому и спросил. Мне нигде не говорили, что в группах идеалов не бывает.
sigh
Группы, моноиды, полугруппы, кольца, модули, векторные пространства - это разные классы объектов.
Магму забыл, алгебру и лупу Муфанг.
В чем тогда суть отличия, если опустить тот факт, что это понятия, определенные на разных классах объектов.
Ты совсем не об этом. Я про теорию групп вообще как другой подход.
А так почему нет - от полугруппы вниз до полей, вполне можно наследовать друг от друга. А вот модуль -> поле -> алгебра это уже составные объекты. Например "пространство над полем" Или "модуль на кольцом". Разве не так?
Так.
И нормальные подгруппы и идеалы — это ядра. С этой точки зрения это одно и то же. В их конкретных описаниях тоже есть сходство, например, идеалы стабильны под действием всего кольца умножением, нормальные подгруппы — под действием вей группы сопряжением. Нормальные подгруппы замкнуты относительно умножения внутри себя, идеалы — относительно сложения внутри себя.
Но умножение и сопряжение, сложение и умножение — разные вещи, на этом уровне я не видел аналогий, даже вышеописанное сходство явно выписанным не видел.
Если нужна площадь чего-то ровного типа квадрата - пользуйся алгеброй (умножением). Если кривое - нужен интеграл. Разбиваешь на маленькие кусочки, притворяешься что они прямоугольные и суммируешь их площади. Как то так
Это определенный интеграл, я знаю, а я говорю про неопределенный. Т.е. я говорю про первообразную функцию.
>Нормальные подгруппы замкнуты относительно умножения внутри себя
А если групповая операция - сложение?
Множество со структурой группы всегда замкнуто относительно групповой операции. Подгруппа - та же группа, только внутри другой группы.
+ значит коммутативно
× значит некоммутативно
В основном. Коммутативные=абелевы группы — не группы по сути. Вся идеология меняется. Группа — там умножение, некоммутативно, если коммутативно — это уже кольца и модули (что почти одно и то же).
Не ну просто из определения производной, даешь приращение f(x+h) и тд. попробуй для x^2. Просто дроби, 5-й класс. Сокращаешь туда-сюда и получишь 2х. Или можно геометрически думать. Касательная к параболе в точке есть прямая.
Вот и я об этом. У тебя просто написано, что она замкнута относительно умножения.
А какая разница, лол. И то, и то — бинарные операции с аксиомами. Просто договорились, что для абелевых будем писать "+", для остальных — "*". Чисто конвенциональная разница.
В смысле не касательная прямая, она всегда прямая лол, а если из тангенсов угла наклона построить график то будет прямая. Это иесть производная
Ну как это какая разница? А если группу относительно арифметического сложения рассматривать, тут уже совсем не одно и то же.
Производная это скорость изменения функции, относительно какой-либо переменной, это я понимаю. Ну, пусть будет функция х^2-3x+1, как же узнать производную без таблицы? И что есть "даешь приращение"?
И что у меня не то? Коммутативность — такое важное свойство, что объекты, отличающиеся им, обладают принципиально другими свойствами. То, что коммутативная группа — это тоже группа, это, конечно, так, но это всё равно, что сказать, что тор(=бублик) — это множество.
Относительно любой групповой операции. Умножение - только одна из. Это касается и аддитивных, и мультипликативных групп, и вообще каких угодно.
>>349398
> + значит коммутативно
> × значит некоммутативно
Нихуя это не значит. Это вопрос соглашений и не более того. Просто традиционно абелевы группы вводят используя "кагбе сложение", а неабелевы - на "кагбе умножении". Но значки + и × здесь используются чисто символически и в общем случае они ни к чему не обязывают. Можно заменить + и × на # и @ или ещё что-то более прикольное.
Подставь вместо x x+ε, отними то, что было, раздели на ε, преобразуй и посмотри, что будет когда ε —> 0.
Зачем нам что-то подставлять? И что такое ε? И зачем потом делить? Как и что преобразовать?
>Нихуя это не значит. Это вопрос соглашений и не более того.
Всё, что есть в мире и говорится на языке — вопрос соглашений. Эти знаки употребляются не только в контексте групп и даже не только в контексте чисто абстрактной алгебры, а наделяются многими конкретными смыслами.
Ты че, ты че? Я это в лекциях Вавилова видел. Под бинарной групповой операцией можно понимать что угодно. В том числе и обычные арифметические операции.
Тут сложно записать аккуратно и наглядно, посмотри формулу определения производной как предела
И из этого ты делаешь вывод, что любая группа (М, +) априори коммутативна, только потому что операцию обозначили как "+"? А ты прикольный.
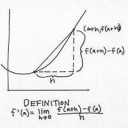
Пикрил запись тебе знакома? Это и есть определение отношения приращения ф-ции к приращению аргумента. Теперь возьми самую просто ф-цию например x^2 и подставь в эту формулу и выведи что получится
что такое предел знаешь? сможешь простенький предел решить с h->0 ? (это стрелочка от h)
А ты не прикольный, а просто тупой. Речь не про логические импликации, а про реальное использование. Кстати, можешь показать пример того, что обозначается +, но некоммутативно?
Знакома, но я опять не понимаю что на ней написано... Я тупой, блядь, не понимаю нихуя. Кучу учебников уже просмотрел но не понял.
Да нормально, ты не тупой, просто нужно читать вдумчиво, в учебниках то нихуя не объясняют. Ты понимаешь смысл выражения "отношение приращения ф-ции к приращению аргумента"? Конкретно на графике y=x^2? Показывает как быстро растет парабола. То есть мы даем какое то приращение по х и смотрим что получилось по y. А потом делаем это приращение все меньше и меньше. В этом идея предела. Этого даже ньютон с лейбницем не знали. Коши придумал сто лет спустя.
Понимание — это не дискретный пареключатель, а непрерывный процесс. Точнее, что-то посередине. Оно прогрессирует в течение больших промежутков времени.
Есть разница между
1)Кто-то не вдумчиво читает
2)В учебниках нет определений и теорем с доказательствами
>Ты понимаешь смысл выражения "отношение приращения ф-ции к приращению аргумента"?
Это значение от двух точек на графике функции. Мы выбираем 2 любые точки на функции по х и узнаем их значения еще и по у. Потом узнаем разницу и делим полученное значение от у на полученное значение от х. Я правильно понимаю? Это так ведь? И извини за мой уебанский стиль речи.
Рассмотрим симметрическую группу S4. Обозначим композицию подстановок... Никак не обозначим. Эта группа некоммутативна. Помимо тривиальной подгруппы у ней есть ещё альтернирующая подгруппа A4 и клейновская K4. Но по твоей логике, на множествах образующих этих групп должна быть какая-то операция "+", ведь они коммутативны! Ну что тут скажешь.
ну так и сделай просто пример по формуле тупо подставь x^2 вместо f, обычная дробь же. все что нужно потом это отбросить слагаемые что в нуль обращаются при h->0. и все
м? ЧЕ?
Правильно понимаешь. Показывает как быстро растет твоя функция. Идея в том, чтобы эти две точки были как можно ближе друг к другу, иначе получается погрешность. В идеале они вообще слились в нулевое приращение, но тода будет неопределенность 0/0. Но тебе можно этим не париться а просто подставить ф-цию в формулу для определения производной через предел и самому убедиться.
Как это может показать то, как быстро растет моя функция? Что за формула? Как ее вывели?
A4 и K — это индивидуальные исключения.
Мы говорим о разных вещах.
Операция там скорее композиция. В чём разница между композицией и умножением? С композицией связан геометричекий образ.
Повторяю в n-ый раз: я имею в виду то, как это реально представляется в голове, а не в учебнике «определение группы и абстрактная точка зрения на алгебру для начинающих».
>Этого даже ньютон с лейбницем не знали. Коши придумал сто лет спустя.
И как они тогда придумали интеграл и производную?
Формула на пике что выше. Она выражает ровно то что ты сказал словами. h - это и есть приращение, или "разница". Просто это приращение стремится к нулю. Чтобы получить скорость изменения ф-ции (рост, т.е. производную) но в точке, а не на отрезке. Вот и все что нужно понимать. Через эту формулу (и еще есть ее вторая разновидность) и выводятся производные простейщих ф-ций
Ну про интегралы еще греки древние знали а может и китайцы. В смысле вычисление площадей методом деления и суммирования. Ньютон придумал обобщенный аппарат но он не был строг, я забыл подробности но они там с лейбницом говном обмазывались много лет, длиннее любого треда на двачах. А потом они оба кони двинули, дым осел, пришел коши и все формализовал.
Лол, а мне группы самосовмещений фигур в пространстве мультипликативным языком рассказывали, да и во всех учебниках, что я видел тоже мультипликативный язык.
Ты не делаешь то что я тебе предлагаю сделать потому что тебе в лом, или даже не знаешь как подступиться?
а шо перекот уже грядет?
Я просто пока собираюсь понять, как к этому пришли. Ибо я не понимаю как это делать вообще никак.
Лол, какие исключения? Откуда исключения? Операция - это просто операция, а значок "+" - иногда просто значок и ничего больше. В частности это "иногда" имеет место в тегории групп. Арифметика арифметикой, а теория групп теорией групп. Если явно не сказано, что группа (G, +) аддитивна, ты не имеешь права предполагать, что групповая операция - это арифметическое сложение, хотя бы потому что природа элементов вообще прозвольна и это может быть что-то, для чего арифметическое сложение, как таковое, не имеет смысла, то есть, не числа даже. Абстракция, ты можешь в неё? The same holds for "×", btw.
К слову, не стоит забывать, что в контексте арифметики и умножение коммутативно. Если у тебя что-то там представляется в голове, напиши об этом книгу и может даже из этого что-то выйдет. Но не тащи, пожалуйста, свои странные представления в уже имеющуюся теорию, она без них прекрасно себя чувствовала.
Ну мы же выше уже договорились, как к этому пришли. Через приращения. И уменьшение размера этого приращения до нуля. Что отражается в формуле на пике.
Потому что группы — это и есть изучение × (обратимого), а изучение + это скорее модули.
Но нет, это ведь совершенно не важно, просто договорённость!

Не понимаю что там на пике. Я только понял, что качество хуевое, и больше ничего. Сейчас все пытаюсь по учебнику вдуплить, но не получается.
Слушай, ну это же то что нужно. На одной страничке то, о чем мы тут пытаемся говорить. Какое качество хуевое? Печати? Что тебе там непонятно?
Короче, почему там указана ОПРЕДЕЛЕННАЯ БЛЯДЬ ТОЧКА СУКА, но обозначена она КАК ЦЕЛАЯ БЛЯДЬ ФУНКЦИЯ СУКА???
>Лол, какие исключения? Откуда исключения?
Объекты, настолько редкие и интересные, что их разумно рассматривать отдельно.
>Арифметика арифметикой, а теория групп теорией групп.
>арифметическое сложение
Сложение — вещь намного более широкая, чем арифметика. У тебя не понятие группы шире моего, а понятие + и × уже. Векторы, например, тоже складывают, коммутативно.
>Если явно не сказано, что группа (G, +) аддитивна, ты не имеешь права предполагать, что групповая операция - это арифметическое сложение
Перечитал. Что за шиза. Сказано, что (G, +) аддитивно?
В общем, я воспринимаю умножение и сложение широко, по факту употребления в математике, как объекты не менее абстрактные, чем само понятие группы, а ты ограничиваешься числами и воспринимаешь группу как объект более высокого уровня абстракции чем + и ×.
Заебало писать.
Че то у тебя каша какая-то. Тебе нужно с записью разобраться. Есть функция, есть точка на функции.
Допустим f(x)=x^2. Это функция. А есть точка x0. Ее значение f(x0). Если x0=3, f(3) = 9. Или в чем у тебя трудность?
Так ты шизик безграмотный просто. Ты разницу в записи бинарных операций хочешь выдать за серьезное концептуальное различие, а его нет — зато есть договоренность записи, чтобы математикам полегче было книжки и статьи читать.
>Ее значение f(x0)
Это как?
>f(3) = 9
Это понятно.
Там написано, что нужно формулу 3 для х, подставить в формулу 2. Зачем?
А так же там указана определенная(!) точка х, потом она называет вдруг переменной, потом мы её обозначаем, как функцию. Я вообще нихуя не понял что за ахинея.
Согласен с тобой, не понятно о чём спор, ошибся же он
А то, все используют это так, но это совершенно не важно!
Это важно. То, как какая-то концепция фактически используется как раз важнее всего. Явно выписанные определения нужны просто чтобы закодировать и зафиксировать принятое использование.
> Объекты, настолько редкие и интересные, что их разумно рассматривать отдельно.
Почему абелевы группы представляются тебе чем-то исключительным?
> Перечитал. Что за шиза. Сказано, что (G, +) аддитивно?
По твоей логике именно так и должно быть, хотя ничего такого сказано не было. Но вообще это, конечно же, не так. Кажется, ты начал что-то понимать.
> В общем, я воспринимаю умножение и сложение широко, по факту употребления в математике, как объекты не менее абстрактные, чем само понятие группы, а ты ограничиваешься числами и воспринимаешь группу как объект более высокого уровня абстракции чем + и ×.
Это совсем не так. В группах есть групповая операция. Она может обозначаться любым значком, приглянувшимся или кажущимся целесообразным данному автору (либо вовсе не обозначаться, типа juxtaposition): +, ×, ⋅, ∘, •, и даже вот такими смищными значками ⊕, ⊗.
Ну вот, блядь, заставил лезть в таблицу символов. А каково авторам книг по теории групп должно быть, постоянно лазить за этим говном в таблицу символов при наборе текста на компутере?
Да нет такого. Просто какой-то парень навроде Галуа использовал плюсик, решили по такому случаю и дальше плюсик ставить. Все, просто история. Артин в своей книжке по алгебре негодует с термина "unit", что очень неудачно, но исторически так сложилось, он это признает. Ты же вокруг "identity" и "unit" настрочил бы эзотерики: мол, одно есть нейтральное, второе — обратимое, и где-то внутри лежит ключик.
f(x0) это тоже самое что f(3) или f(хуй) например. значение ф-ции в точки x0.
забудь про формулы 2 и 3. смотри сразу на 4. это и есть суть.
Где-то на следующей странице должна быть формула через пределы. Что за учебник кстати, какой класс?
Взять хотя бы сложение.
2+2+2=6 и 23=6. Но 23=8, поскольку 222=8. Под умножением в учебнике написано сумирование. Но умножение, это другая операция. Например 210=1024, 53=125 и т.д.
>Почему абелевы группы представляются тебе чем-то исключительным?
Где я такое написал? A4 — исключительна. K — тоже, отдельное название чему попало не дадут.
>Но вообще это, конечно же, не так.
То есть по-твоему «аддитивность» и «использование знака +» — не одно и то же?
>Это совсем не так. В группах есть групповая операция. Она может обозначаться любым значком, приглянувшимся или кажущимся целесообразным данному автору (либо вовсе не обозначаться, типа juxtaposition): +, ×, ⋅, ∘, •, и даже вот такими смищными значками ⊕, ⊗.
С абстрактной точки зрения. В реальности у этих значков индивидуальные смыслы, контексты использования, подразумеваемые свойства.
>Ну вот, блядь, заставил лезть в таблицу символов. А каково авторам книг по теории групп должно быть, постоянно лазить за этим говном в таблицу символов при наборе текста на компутере?
Боюсь, авторы книг по теории групп используют TeX и пишут обычными символами.
Я 11 класс. А это "Шнейдер В. Е. и др. Краткий курс высшей математики."
Я смотрю и не понимаю как это действует. Я просто не понимаю схуяли на точке там функцию взяли. У меня уже боль в жопе начинается.

Настолько удачная, что ни один учебник не обходится без обсуждения контекста. На пикрил Атья, Макдональд.
Ну и что. Интуитивно это означает, что всё рассматривеатся с точностью до обратимых, по модулю обратимых, то есть подразумевается некая факторизация, при которой обратимые уходят в 1, поэтому и «единицы». По каким-то неподвластным моему разуму причинам такая факторизация явно не указывается, хотя это, скорее всего, возможно и легко.
А, понял я тоже пытаюсь вперед забегать, думал может в 11-м этот учебник Я честно говоря только по интернетам да двощам, в книжках все как-то стремно для меня, я сразу тупить начинаю. Видео и картинки помогают.
Погоди, как схуяли на функции точку взяли, но функция же вся из точек состоит. Или о чем ты вообще. Производная же в точке например.
> Где я такое написал? A4 — исключительна. K — тоже, отдельное название чему попало не дадут.
Ну, в принципе, это типичные абелевы группы, какими-то совершенно экстраординарными свойствами кроме этого они не обладают. Они достаточно просты, чтобы рассказывать о них ньюфагам во всяческих введениях. А ты почему-то назвал их уникальными.
> То есть по-твоему «аддитивность» и «использование знака +» — не одно и то же?
Бинго! Но только не по-моему, а вообще, "в реальности", как ты пишешь, лол.
> С абстрактной точки зрения. В реальности у этих значков индивидуальные смыслы, контексты использования, подразумеваемые свойства.
В какой реальности? В реальности композиций морфизмов категорий (∘)? В реальности тензорных произведений (⊗)? В реальности градуированных структур (⊕)? Может в реальности прямого произведения множеств (×)? Какая из этих реальностей более "реальна"? Важен контекст, правильно? А ты вот свои прямолинейные и бесхитростные, как табуретка, понятия о "+" и "×" тащишь в группы без оглядки. Не надо так делать.
> Боюсь, авторы книг по теории групп используют TeX и пишут обычными символами.
Я знаю. Кайнд оф шутка.
>>349475
Ну да.
>Ну, в принципе, это типичные абелевы группы, какими-то совершенно экстраординарными свойствами кроме этого они не обладают.
А вот и нет. Ядра знака перестановки обычно простые, насколько я помню, A4 единственная не простая. Да и вообще для альтернированных разве быть абелевой — обычное дело? Интуитивно они должны быть неабелевыми.
В целом, все объекты малой конечной мощности обладают какими-то особенными свойствами.
>Бинго! Но только не по-моему, а вообще, "в реальности", как ты пишешь, лол.
А вот это уже действительно странно, то, что ты так считаешь. Насколько я помню, во всех учебниках «аддитивность» употребляется в смысле «аддитивная запись».
Этот пустопорожний «спор» ни о чём начинает заёбывать.
>>349475
На идеологическом уровне это происходит потому, что модули над фиксированным кольцом — по сути коммутативная структура.
>Бинго! Но только не по-моему, а вообще, "в реальности", как ты пишешь, лол.
Жаль, потому что это одно и то же на самом деле. Ты просто не понимаешь сказанного.
Я уже понял. Дело в том, что не пояснили кое-что. Показали бы, проиллюстрировали, что f(x)=f(x0+Δx), теперь понятно откуда эта функция. Мы узнаем приращение и эту определенную точку через приращение. Вот и все.
Ну и отлично, видишь - ты в общем-то сам разобрался. А еще хороший способ - не зацикливайся на одной картинке, одном учебнике. Учебников дофига на вебе да и просто поиск помогает!
>во всех учебниках «аддитивность» употребляется в смысле «аддитивная запись»
Как раз-таки везде аддитивная подгруппа - подгруппа, в которой групповая операция совпадает с операцией сложения.
С моей точки зрения «аддитивная запись» и «операция сложения» — это одно и то же. Однако ты, насколько я понимаю, считаешь знак «+» и слово «сложение» принципиально разными вещами. Дескать, знак — это просто бессмысленный значок, который можно заменить хоть на пиктограмму дилдака, а вот слово «сложение» — это совсем другое, это настоящее сложение. Одно — это договорённость, другое — труъ. Хотя, казалось бы, в чём разница между словом и знаком? Ни один здоровый математик не обозначит сложение в модуле умножением, некоммутативный + — страшная редкость, но это же не важно.
1. Допустим, решение ОДУ методом разделения переменных - можно сделать без нотации dy/dt - и как обосновать перетасовывания дифференциалов по разные стороны равенства? Где-то встречал мнение, что эта нотация ущербна(правда не очень понял, осознавая её удобства). Подозреваю юзается инвариантность формы первого дифференциала(нам не важно что y - функция от t, а не наоборот, к примеру).
2. В интеграле фигурирует выражение f(x)dx. А что если вместо dx взять величину g(dx) -> 0 при dx -> 0 к примеру g(x)=x^k, e^x-1 и.т.д. и рассмотреть суммы, аналогичные интегральным - будут ли они существовать, сводиться к интегралам или у них своя собственная атмосфера?
Добавочка:
3. Почему https://ru.wikipedia.org/wiki/Тетрация и последующие гипероператоры теряют непрерывность, в чём фундаментальная причина? Почему вообще при "наращивании" гипероператоров теряются какие-либо базовые свойства(н-р умножение->некоммутативное возв. в степень).
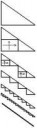
4. Ну и конечно, платина - лестничка пикрил/aka Troll Pi vs вычисление Pi приближением окружности правильными многоугольниками. Как строго обосновать, почему работают многоугольники и не работает лестница?
В прошлом обсуждении пришли к тому, что лестница сходится к линии по метрике d_0, но не d_1, а многоугольники - по d_0, d_1. Значит, отсюда ноги растут?
> Ядра знака перестановки обычно простые, насколько я помню, A4 единственная не простая. Да и вообще для альтернированных разве быть абелевой — обычное дело? Интуитивно они должны быть неабелевыми.
> В целом, все объекты малой конечной мощности обладают какими-то особенными свойствами.
Да, извини, анон. Не знаю, что на меня нашло. Такую хуйню сморозил, что теперь хоть убейся от стыда.
Нет, не прикалываюсь.
Аноны, пример такого отображения - это просто ф-ция двух переменных, типа z = f(x,y) ?
http://m.youtube.com/watch?v=j2LTRE6sX2o
начало
Мимо-стремящийся
Не понять производную может только тупое хуйло, коим и является тот чел.
Да ладно тебе. Я вот лично думаю, что тупить - это нормально. Важно не то, как долго ты "тупишь", а сколько ты усилий приложил для того, чтобы что-то понять. Ведь в конце концов у него получилось. В математике важен последовательный подход.
Но зачем учить школьный курс? Это же бессмысленно
Время является очень важным ресурсом. Его "В конце концов" никому не нужно,лол. Другое дело, если он мат. учит для себя, но опять же стоит-ли это делать, если дифур решить не может.
Вот я ему терпеливо сообщений 10 не меньше послал. А мне за сливочный интеграл так хуй чего и объяснили.
ну какой-то пиздеж там был явно, типо учебник полистал
Этим школьным курсом был тифаретник
анонимус изучает топологию
Нет, я у него поспрашивал, он топологию и линал прошёл в 1 семе, во втором взялся за алгеом, но он шизик кажется
Проиграл.
Нужны более общие теоретические задачи с доказательствами
Есть, но они пьют Зелёную Марку. Точнее уже выпили и не в состоянии помочь тебе.
Вот есть представление mq+a чисел, делящихся на m с остатком a. По этой хероте строится разбиение на классы. Почему мне в книжке втирают, что для остатка a=1 класс будет: -mq+1, ..., 1, ..., ..., mq+1? В области отрицательных значений должно же быть -mq-1, а не плюс.
Мне кажется, нужно писать -(mq+1), тогда и остаток положителен получается. Просто если как в книжке писать, то, к примеру, класс по модулю 3 должен для остатка 1 быть ..., -3х2+1=-5, ... То есть остаток от целочисленного деления 5 на 3 равен 2, а это противоречит условию, где остаток=1.
>То есть остаток от целочисленного деления 5 на 3 равен 2
Ты делишь не 5 на 3, -5 на 3. Просто такое определение, остаток отрицательных чисел - положительное число.
Объясни, плиз, а то я туповат. Зачем такое определение? Не понимаю почему мой пример не верен.
https://ru.wikipedia.org/wiki/Деление_с_остатком
>Это условие обеспечивает однозначность результатов деления с остатком для всех целых чисел
Но ведь -3х2+1=-5, остаток 1 никак не получается же. Я не понимат. :(
Почитать определения не хочешь?
Почитай ещё определений, заебал тут тупые вопросы спрашивать, ты так никогда нихуя не выучишь, будешь очередным нытиком неосилятором
Ну чего ты? Все я прочитал, просто я с этим определением не согласен. Но не верю, что я умнее книжек. Вот и прошу пояснить.
Ну мне кажется, что такое определение только мракобесие в себе несет. Скорее всего, я не прав. Но ведь никто не пояснил на примере, который я привел почему я не прав. Вот я и не могу понять.
Тред для высокомерных мудаков ниже по течению. А здесь люди ньюфагам помогают.
Понял твою мысль, ананасик. Пойду втыкать в определение, может осенит просветление.
Привет, жируша :3
Тебя мамка наругает, за то что т ы на двоче сидишь.
>:)
>Ясно.
Ох, да ты же ананасик :)
Ну, что же ты так быстро, я думал ты способнее
Давай, попытайся ещё :))
Вопрос-то простой и годный. И столько бугурта, бэ-стайл говна .
-5=-2x3+1=-1x3-2. Т.е. мы берем наименьшее частное(в отриц. числах это будет большее по модулю), чтобы остаток был >0. Тем более, остатки-претенденты -2 и 1 равны с точностью до +/- делителя(тройки). Но нам удобнее выбирать остаток положительным, чтобы деление было однозначно(частное -2 или -1 в твоем примере). Понятно объяснил?
А мне вот непонятно - троль ты или нет. Давай сначала - какой у тебя вопрос? Почему остаток не может быть отрицательным, так?
Анон, у меня сейчас благодаря тебе все в голове перевернулось. Я как-то абсолютно по-другому до этого воспринимал свой пример. Про округление в меньшую сторону я понял давно, но такой подход казался мне лишенным всякой логики. Сейчас я как будто из другого измерения на этот пример посмотрел и противоречие улетучилось. Спасибо огромное! Не уверен, что с этим представлением я полностью разобрался, но как минимум стало намного легче. Пойду спать, может со свежей головой все вообще очевидным покажется. :3
В равнобедренную трапецию ABCD вписана окружность с центром О. Найдите диагональ трапеции, если средняя линия равна √6, а угол AOD=135°, где AD - бо’льшее основание. Удачи всем.
Я не согласен. Я совсем не разбираюсь в основаниях, но интуитивно же понятно, что такое "понимание".
Понять доказательство утверждения означает быть способным при желании полностью его формализовать. В доказательствах всегда есть пропущенные шаги (иначе было бы невозможно читать). Понимание заключается в способности заполнить все эти пропущенные шаги так, чтобы доказательство представляло собой полностью формализованный текст. Делать этого, конечно, не надо.
Определение - это сокращенная запись какого-то знакосочетания. Понимать сокращенную запись означает знать все другие сокращения, которые в ней используются.
Математические тексты состоят из определений и утверждений.
>Я не согласен. Я совсем не разбираюсь в основаниях, но интуитивно же понятно, что такое "понимание".
«интуитивно же понятно»
Всё интуитивно понятно всем. В какой-то степени, ведь понимание — не бинарный переключатель.
Это кстати, свойственно далеко не только пониманию. Часто непрерывное считают дискретным, а дискретное — непрерывным.
>Понять доказательство утверждения означает быть способным при желании полностью его формализовать.
1. В лучшем случае это всего лишь одна грань понимания.
2. Я не знаю, что такое «формализовать». Или надо сказать «не понимаю»?
>Определение - это сокращенная запись какого-то знакосочетания.
Для меня смысла в этом предложении 0. Например, всё что пишется — это знакосочетания. Что такого особенного в значках?
>Понимание заключается в способности заполнить все эти пропущенные шаги так, чтобы доказательство представляло собой полностью формализованный текст.
И много людей такое могут? Хотя бы в отношении ограниченного количества более-менее серьёзных теорем? В такой интерпретации «понимание» — чрезвычайно редкая вещь.
>Понимать сокращенную запись означает знать все другие сокращения, которые в ней используются.
>Понимать это — означает знать то.
>Математические тексты состоят из определений и утверждений.
«Математические тексты» из чего только не состоят.
С какой стати речь идёт исключительно о математике? «Объяснять» слова надо в естественном контексте.
Корень разногласия:
я: знание не дерево,
ты: знание — дерево.
> Зачем такое определение?
Поставим каждому числу в соответствие его класс эквивалентности. Будем обозначать эти классы как [0], [1], ..., [m - 1]. То есть, например, 0, m и -m принаджежат одному классу [0].
Оказывается, можно складывать и вычитать эти классы. Мы ожидаем следующего:
1) [a] + = [a + b mod m]. То есть если мы выберем любые x из [a] и y из , то x + y mod m будет принадлежать [a + b mod m].
2) [a] - = [a - b mod m].
3) [a] + [a] = [a]
4) [a] - [a] = [a]
5) [a] + [0] = [a]
Если бы остатки были такими, как ты хочешь, так бы сделать не получилось. Например, 1 и -1 принадлежали бы [1], но 1 + -1 = 0 не принадлежит [1].
Разметка проебалась. Там где пусто, я писал b в квадратных скобках.
Ой, бля, забей.
>Controversy has existed on issues of mathematical pedagogy.
>У пидагогав БОМБАНУЛО
А есть какие-нибудь более конструктивые книжки без баттхёрта школьных учителей?
Батхерт батхертом, а это довольно таки нишевое говнецо.
Я только одну норм книжку видел
https://books.google.co.uk/books?id=HmJ1CgAAQBAJ&printsec=frontcover&dq=Nonstandard+Analysis+for+the+Working+Mathematician&hl=en&sa=X&ved=0ahUKEwikma3lm9LLAhXlfHIKHcDiCSMQ6AEIKDAA#v=onepage&q=Nonstandard Analysis for the Working Mathematician&f=false
Спасибо, почитаю.
Можно ли выучить математику по википедии?
1) Верно ли, что если Ax+By=Cz, где A,B,C,x,y,z — натуральные и x,y,z>2, то A,B,C имеют общий простой делитель?
2) Какое наибольшее количество непересекающихся окружностей единичного радиуса можно разместить на сфере радиуса R?
3) Можно ли заполнить 7-мерное пространство равными 7-мерными гиперкубами так, чтобы никакие два гиперкуба не имели целой общей 6-мерной гиперграни?
4) Существует ли простая группа, которая не является трансфинитно сверхпростой?
5) Существует ли нетривиальный узел, полином Джонса которого является таким же, как и у тривиального узла?
За 100 на киви могу оформить
Если в каждой школе нормально преподавать математику, люди думать научатся, а это нахуй не нужно, потому что тогда за императора никто не проголосует и не получится спокойно распиливать бабки с нефти.
Мне одноклассник, который недавно решил все задачи на Всеросе по математике еще в 6 на уроках музыки гиперкубы рисовал

За АСГУ.
За Перельмана
Он здесь чем-то на Китано похож.
кстати я только благодаря вашим вайпам сподобился посмотреть, кто это такой. это охуенно. не догадывался, что ТАКОЕ може быть. "непрерывный - это когда потекло".
Мне больше интересно, кто такое хуйло в мгу пускает и зачем вообще с ним спорят (сколько будет 2x3 например). Это же блять егор кузмич лигачев, во кто это. Блять аноны, почему мы тут, как из этой страны съебаться?
8?
А какая разница?
HSE на факультете математики. Но есть подводные камни:
https://youtu.be/4s8wpYde8dU
А ваще как Ромка Михайлов сказал: иди на мехмат не ради содержания основной программы, а ради погружения в среду и ради общаги конечно же
>подводные камни
Вышка сама по себе говно, тут секрета нет. Охуенность любого конкретного места делают люди, а не вывеска. На матфаке это преподавательский состав и способные студенты.
Это двачер на видео? ЧСВ такое ЧСВ. Стрелочки ему дорисовали и лишили красного диплома суки.
Так математика для начинающих же. Вон там ведь с треугольником то задачу решили
У тебя-то очевидная домашка.
Почему?
Пытаюсь понять структуру математики.
Вот вроде все начинается с арифметики, но!
Математика это дедукция насколько я понимаю, а где математические доказательства арифметики из которых можно делать дедуктивные выводы? Это те самые foundations and philosophy?
Т.е. в школе нас учат воспринимать арифметику на веру потому что понять те самые foundations and philosophy трудно, и для этого нужны знания в математике? Ну и плюс арифметика весьма очевидна, ну или как это сказать... понятна по своей природе и легко проверяема.
Или все таки математика начинается с допущений?
Не могу найти норм материал по данной теме, матанон дай если не жалко.
Современная классификация математических теорий из разных разделов - это про топосы. Топосы Гротедника например. Топосы сейчас так же революционны, как в свое время генетика. Трудно переоценить их роль в унификации теории математики. В кратце - теория множеств дидов устарела. На смену ей пришла теория категорий. Топосы - это своего рода унифицирующие пространства, "мостики", связывающие различные теории. За основу там берется геометрическая логика, но тащемта все геометрические теории - это объекты чисто синтаксической природы. То есть система доказательств опирается на геометрические секвенции. Эта геометрическая логика как бы дает нам язык, при помощи которого пилятся теории топосов. Не только формулируются, а именно пилятся. Разумеется концепции какой-то конкретной модели могут быть интерпретированы через теории множеств, но это подход всратых дидов, а все знают, что четкие пацанчики уже давно пользуются категориальными структурами. Ведь у них для любой геометрической теории есть соответствующий классифицирующий топос - своего рода ДНК математической теории. Фишка в том что, именно синтаксис служит объединяющим костылем. Понятно, что классический подход дидов на основе теории множеств какбе подразумевает эквивалентность семантической и синтаксической компоненты (теоремы полноты, вот это все). Но важно понимать, что в теории моделей, основанный на топосах, естественным образом проявляется хуева туча различных семантик, и тогда очевидно что ключевую роль играет именно синтаксический подход.
Совсем просто - унификация теорий - через топосы-мостики - геометрическая логика первична - главенствует синтаксический подход, который разруливает многообразие семантик. Ну и может факультативно посмотри еще на лемму Йонеды. Вот и все.
Молодец.
Пару минут ликбеза по теорверу в гугле - и ты в шоколаде. Но так и быть, решение: события у рандом-человека группа крови на рукаве 1,2,3,4 образуют полную группу.
Событие "безопасно перелить ему кровушки" - это сумма попарно несовместных событий обозначенных плюсиками(произведение различных пар независимых событий i*j, где i и j - номера групп(являющиеся номерами строк и столбцов в матрице) крови донора-реципиента - вероятность которой = произведению) в табличке - значит можно спокойно просуммировать эти произведения - полученный результат и есть ответ.
Спасибо тебе матанон, я далеко не все конечно же понял, но все равно спасибо.
Короче, сделал для себя вывод, что для упрощения легче воспринимать некоторые правила как аксиомы, и не ебать себе мозги, если когда-нибудь лягу в дурку, то там то я и займусь всякой метаматематикой и т.д.
>Т.е. в школе нас учат воспринимать арифметику на веру потому что понять те самые foundations and philosophy трудно, и для этого нужны знания в математике?
Не то, чтобы трудно(для старшеклассника, разумеется) - а скорее накладно и бесполезно с точки зрения практики.
Если хочешь ознакомиться с аксиоматикой арифметики - бери аксиоматику и построение вещественных чисел(они обычно сильно урезаные, без тонкостей и технических деталей в начале курса матана идут). Ещё опционально можно поверхностно, в плане обозначений/определений ознакомиться с теорией множеств и предикатами - на этом языке-нотации всё формулируется, в дальнейшем пригодится. Хотя вполне можно обойтись естественным языком на данном этапе.
https://ru.wikipedia.org/wiki/Вещественное_число#.D0.90.D0.BA.D1.81.D0.B8.D0.BE.D0.BC.D0.B0.D1.82.D0.B8.D1.87.D0.B5.D1.81.D0.BA.D0.B8.D0.B9_.D0.BF.D0.BE.D0.B4.D1.85.D0.BE.D0.B4
Можно просто пробежаться, посмотреть вообще что это.
Знаменитое здесь, благодаря кое-кому, строгое определение N можешь взять по Пеано.
https://ru.wikipedia.org/wiki/Аксиомы_Пеано
Ну и вот ещё немного из базового
https://ru.wikipedia.org/wiki/Основная_теорема_арифметики
https://ru.wikipedia.org/wiki/Китайская_теорема_об_остатках
Книгу с достаточно строгой, но в то же время доступной формой изложения по арифметике, к сожалению подсказать немогу.
Впрочем, первый том Бурбаки должен подойти. Шутка про баян
Ну или Principia Mathematica. Тоже шутка, но не про баян
Только вчера у нас пациент из дурки сбежал. Везде искали, а он на дваче свои фантазии льет!
>топосы, которые нужны 3.5 логикам
>геометрическая логика
>тут же лемма йонеды, которая вообще про вложение категории в категорию функторов из нее в set
Больной, вернитесь в палату.
> >тут же лемма йонеды, которая вообще про вложение категории в категорию функторов из нее в set
> Больной, вернитесь в палату.
Что не так-то?
Лемма Йонеды нужна и полезна, используется везде. Топосы нужны 3.5 логикам, потому что пучков за глаза хватает для математики.
1/10, 1/100, 1/1000.
>и ради общаги конечно же
А что с общагами, какая-то особая атмосфера? Насколько я знаю первые курсы они живут в ФДСе, что там? Расскажи.
Есть линейное дифур 2 го порядка, приводящееся к канон виду. Знаю, что любое уравнение с постоянными коэф может быть приведено к канон виду с помощью линейного преобразования и тип уравнения не меняется при невырожденной замене переменных.
сам алгоритм нахождения :
1)привести к квадратичной форме методом Лагранжа
2)ввести новые переменные
3)найти матрицу преобразования
4)транспонировать
5)выполнить искомую замену
На практике просто, в теории ступор, преподу нужно объяснить почему вводятся новые переменные во втором шаге.
Ходи на пары, внимательно слушай, делай домашки. На первом курсе будет сложно из-за большого количества разнородной информации. Где-то к концу второго курса заметишь аналогии и связи между всем этим, казалось бы несвязным материалом. Да и опыт решения появится, к терминам привыкнешь. Символику обсуждают, напоминают, если забудешь. Ничего страшного нет, главное не запускать. Правда я это понял не сразу и почти полностью проебланил первый курс, потом самостоятельно пришлось нагонять, что гораздо сложнее.

Так и не понял что на что умножать. Можно подробнее?
Не грусти, ты просто тупой.
Что, блядь?
На сколько я понял, няша. Тупые должны поддерживать друг друга:
P(x)=P(1)1/4+P(2)2/4+P(3)2/4+P(4)4/4
Поправьте, если неправильно пжл.

---> un/
Он, наверное, имел ввиду общагу в общем смысле. Чтобы жить было где. А в фэдосах пиздец, как в Ираке после бомбежек. Одна из худших общаг при МГУ.
Мне кажется чтобы разобраться, нужно начинать с аксиом Пеано и дать определение N.
Мочедзука - такой же ебанько, как его односельчанин который придумал свою версию теории струн с 25 вложенными пространствами. А может это даже его родственник. Его доказательство не опирается ни на один известный метод. Он там навертел 10500 страниц абстрактной хуйни, которую сам же и придумал. Ее нельзя ни подтвердить ни опровергнуть, потому что никто нихуя не понимает, что это вообще. Поебень короче, не парься.
>Мочедзука - такой же ебанько, как его односельчанин который придумал свою версию теории струн с 25 вложенными пространствами.
Совершил революционное открытие/доказал теорему, долгое время считавшуюся одной из главных проблем математики. В /сци/ нассали на лицо потому, что слишком сложно.
>>350849
Неправильно, но на верном пути. Вместо кол-ва плюсиков в столбцах деленных на 4 - надо брать в столбцах сумму тех вероятностей, которые отмечены плюсом.
P(x)=P(1)^2+P(2)x(P(1)+P(2)) + ...
Учите теорвер, дети - я сам его толком не знаю, но на таком уровне(точнее чуть выше) его освоил. Много где пригождается.
Мне кажется понимает только один Фесенко. Беда в том, что он никому объяснить не может.
>/sci, мат. тред
До:
>Отвечай МРАЗЬ!
После:
>Мне кажется чтобы разобраться, нужно начинать с аксиом Пеано и дать определение N.
Попробуй навернуть Coq, формально определить "метаиндукцию" и доказать некорректность аксиом Пеано, а также прочих аксиоматик.
Так и шо, Мочесуке уже дали таки премию Клэя, как Грише? Или все еще вникают? Когда следующий воркшоп?
Да. Больше не грузи домашкой, плиз. Полно ведь годных справочных материалов "для чайников", "для самых маленьких" с похожими разобранными примерами.
Не надо кипиш поднимать. Он теперь меньше палится. А может у меня детектор дал сбой.
Не путай тупость/ум и знание/незнание предмета. "Многознание уму не научает". Удачи в освоении наук.

Только вместо cosh и sinh лучше используй sh, ch. Остальное впадлу, спать хочу.
А теперь доказывай. Не докажешь - всю жизнь будешь слыть беспруфным кукаретиком.
Ананасы, а вам не кажется, что путь по которому большинство изучает математику совершенно неправилен?
Допустим та же "Алгебра" Шень, начинается со свойств сложения и умножения, но при не вводятся понятия: натурального числа, множества, системы счисления и т.д.. Почему книги посвященные математике не начинаются с математической логики, которая позволила бы доказывать изученное?
Ну вот можно прочтя того же Шень/Шеня доказать основную теорему арифметики, например? О математической индукции там и речи нет, по мат. логике тоже ничего. В чем смысл тогда зубрить математику, когда нет четкого понимания на чем она строится, как доказывать ее положения и т.д.?

>но при не вводятся понятия: натурального числа, множества, системы счисления и т.д..
Ага, ведь любой математический учебник должен определять и доказывать все используемые понятия, на ZFC-основаниях.
Спасибо, ты реально помог, и даже существенно повлиял на мое мировоззрение.



>>351157
Не кажется. То, что нет мат. индукции и задач на неё - это конечно плохо.
>>но при не вводятся понятия: натурального числа, множества, системы счисления и т.д.
Это больше к мат. логу, арифметике и основаниям, чем к алгебре. Ньюфагам это не нужно, лишний объём информации(все эти ZFC, предикаты в деталях и.т.д.) и они этого могут не понять. На крайняк можно про это прочитать на википедиях/учебниках по мат. логу/
основаниям.
Закон божий вернули - можно и Киселёва вернуть.
Конечно
НОД системы этих чисел задан в условии же. Зачем тут Евклид?
Мне эта задача, на самом деле, видится как вариация основной теоремы арифметики, только вместо неприводимых тут взаимно простые и доказательства единственности не требуется.
Чем вы тут заняты вообще? НОД=1 эквивалентно существует линейная комбинация = 1. В целых числах умножение выражается через сложение, так что это то же самое, что используя + и - можно дойти до 1. А единица уж порождает всё.
Задача сформулирована для группы целых чисел. Подозреваю, что это группа относительно сложения. Других операций, следовательно, там нет. Опять же не дано точного описания объекта, подразумеваемого под системой натуральных чисел с НОД=1. Вот {3, 7} - это система натуральных чисел с НОД=1? Все множество целых чисел оно породить не может.
7-3-3=1 1+1+1+...+1 (n раз) = n, взять - — -n. Всё Z покрывается. Или у тебя свои представления о +–группе Z, в которые - не входит?
a и b - система образующих, если любой элемент можно представить в виде ((-)a х (-)b) х n.
Там ведь ещё оранжевый есть для двачеров!
Я не умею в формулы на дваче. А еще возможно, что ты прав, и {3, 7} являются-таки системой образующих. 7-3-3=1, 7+7-3-3-3-3=2, ... Блиа, а че я тупил тогда все это время? В общем, все-равно это надо доказать, а я не знаю с какой стороны подступиться.
>В общем, все-равно это надо доказать, а я не знаю с какой стороны подступиться.
Для того, чтобы «доказать» по крайней мере нужно «определение» НОД.
Кстати бурбаки таки пользуются интуитивной индукцией в логике формальных систем.

Бурбакистская мафия не нужна.
Параметры звена - время обработки/продуцирования и потребности в компонентах.
Как понимаю, структура является деревом, есть идея начиная с низа цепочки высчитать НОД по уровню исходя из времени операции узла. Но что-то явно не так.
Изучай линейное программирование.
здесь
У какого процента женщин, маммограмма которых дала положительный результат, есть рак груди?
Это школьная задача, тебе максимум, что надо знать, что сумма вероятностей 100.
гугли формулу умножения вероятностей
Зачем тебе нужен был ответ этой задачи?
>кроме того, она даёт ложный положительный результат (то есть, неверно показывает наличие рака) для 9.6% здоровых женщин.
Не понимаю это предложение
Я так понимаю ты ответ вбиваешь на сайтик, а сайтик тебе пишет верно или нет?
Тогда ты мог неправильно забить ответ, который был
Если условие задачи верно понял
0,01-0,010,2-0,990,096
>>351818
Запишите ответ с точностью до одного знака после десятичной точки (знак процента не нужен)
Все не так просто, как вы думали, поэтому и пиздец.
Ой ли? Мне кажется, тут без Баеса не обойтись

Это полноценная аксиоматика, альтернатива ZFC?
Это не альтернатива ZFC, а вообще отдельный раздел современной математики, который, среди прочего, позволяет изложить и основания. Категории часто называют метаязыком, чем-то, что позволяет описать математику, то есть математические объекты, включая, естественно, и множества.
В общем, категория - это достаточно абстрактная штука, в которую можно завернуть множества, множества со структурой (группы, алгебры, векторные пространства, топологии), небо, Аллаха и даже самого Маклейна с Эйленбергом. Прелесть категории в том, что внутренняя структура объекта остаётся нераскрытой сама по себе. Для того, чтобы изучить объект категории, нужно не лезть в его нутряности, а изучить, как он ведёт себя по отношению к другим объектам (изучить морфизмы этого объекта). Морфизмы - это не то обобщение отображений, не то что (на самом деле, морфизм может быть как объектом, так и функцией - в общем, тоже штука абстрактная)
Вот простой пример: рассмотрим категорию Set всех малых множеств. Класс объектов этой категории (обозначается Ob(Sets)) состоит из совокупности всех малых множеств, как нетрудно догадаться. Там есть и одноэлементные множества, синглтоны (обозначается для краткости 1). Множество морфизмов в этой категории - обычные функции на множества (обозначается Mor(Set)). Возьмём произвольный объект этой категории, Х и изучим все морфизмы hom (1, X). Они будут представлять собой множество функций f : 1 → X. Такое отображение можно назвать "выделением элемента Х", а множество морфизмов таким образом даст нам совокупность таких выделений. Множества довольно скучные объекты сами по себе. Любое множество характеризуется своими элементами. Но это именно то, что нам и надо. Только что мы изучили объект "множество", изучив множество его морфизмов.
Это очень просто пример, но вот приблизительно так это и работает. Можно изучать целые классы объектов, можно изучать даже сами категории средствами теории категорий. Но это очень общий инструмент. В частных проблемах использование категорий вряд ли оправдано. Это всё равно, что пытаться через телескоп читать книгу. Таким образом, категории позволяют исследовать целые совокупности объектов едиными и иногдя даже не лишёнными няшностями методами, выяснять их некоторые общие свойства. До кучи, категории позволяют переформулировать теорию множеств на категорном языке и, как считают некоторые категорные хуесосеры, это более модно, стильно, молодёжно, чем методы теоретикомножественных дидов.
Это не альтернатива ZFC, а вообще отдельный раздел современной математики, который, среди прочего, позволяет изложить и основания. Категории часто называют метаязыком, чем-то, что позволяет описать математику, то есть математические объекты, включая, естественно, и множества.
В общем, категория - это достаточно абстрактная штука, в которую можно завернуть множества, множества со структурой (группы, алгебры, векторные пространства, топологии), небо, Аллаха и даже самого Маклейна с Эйленбергом. Прелесть категории в том, что внутренняя структура объекта остаётся нераскрытой сама по себе. Для того, чтобы изучить объект категории, нужно не лезть в его нутряности, а изучить, как он ведёт себя по отношению к другим объектам (изучить морфизмы этого объекта). Морфизмы - это не то обобщение отображений, не то что (на самом деле, морфизм может быть как объектом, так и функцией - в общем, тоже штука абстрактная)
Вот простой пример: рассмотрим категорию Set всех малых множеств. Класс объектов этой категории (обозначается Ob(Sets)) состоит из совокупности всех малых множеств, как нетрудно догадаться. Там есть и одноэлементные множества, синглтоны (обозначается для краткости 1). Множество морфизмов в этой категории - обычные функции на множества (обозначается Mor(Set)). Возьмём произвольный объект этой категории, Х и изучим все морфизмы hom (1, X). Они будут представлять собой множество функций f : 1 → X. Такое отображение можно назвать "выделением элемента Х", а множество морфизмов таким образом даст нам совокупность таких выделений. Множества довольно скучные объекты сами по себе. Любое множество характеризуется своими элементами. Но это именно то, что нам и надо. Только что мы изучили объект "множество", изучив множество его морфизмов.
Это очень просто пример, но вот приблизительно так это и работает. Можно изучать целые классы объектов, можно изучать даже сами категории средствами теории категорий. Но это очень общий инструмент. В частных проблемах использование категорий вряд ли оправдано. Это всё равно, что пытаться через телескоп читать книгу. Таким образом, категории позволяют исследовать целые совокупности объектов едиными и иногдя даже не лишёнными няшностями методами, выяснять их некоторые общие свойства. До кучи, категории позволяют переформулировать теорию множеств на категорном языке и, как считают некоторые категорные хуесосеры, это более модно, стильно, молодёжно, чем методы теоретикомножественных дидов.
А, забыл добавить. Какая категория обходится без стрелок и будет ли теория без коммутативных диаграмм теорией категорий? Вряд ли. Дык вот, морфизм - это просто стрелка. А её конкретная природа зависит от самой категории. Стрелки между целыми категориями называются функторами ("морфизмы категорий") Например, U : Grp → Set, это так называемый забывающий функтор, который сопоставляет каждой группе её множество-носитель. Вложение категории C в категорию функторов C → Set (если быть точнее, то Сор - двойственная к С категория, хотя есть и ковариантная формулировка) является темой леммы Йонеды (тут анон кратко поясняет о чём это >>351739)


Короче спрашиваю тут, как на первой пикче получили производную таким способом, и как на второй пикче определили что и куда в уравнении ставить, что икс под игреком?
Ты даун что ли?

>Это не альтернатива ZFC, а вообще отдельный раздел современной математики, который, среди прочего, позволяет изложить и основания. Категории часто называют метаязыком, чем-то, что позволяет описать математику, то есть математические объекты, включая, естественно, и множества.
Не понял. Это такая же аксиоматика, как и ZFC, которую можно записать на языке логики первого порядка?

Ну вот ZFC записывается логикой первого порядка, которая находится в плане "определяемости/неопределяемости" ниже некуда.
А как выглядит формализация теории категорий? Или там не заморачивались этим и по формальности она уровня наивной теории множеств?
Да.
Этот ответ инвалид, математик.
На первой предполагают, что у — сложная функция, а дальше по правилу дифференцирования сложной функции.
Вот ссылочка для второй пикчи, смотришь "производная параметрически заданной функции".
http://www.mathprofi.ru/proizvodnye_neyavnoi_parametricheskoi_funkcii.html
Нет.
Нет.
Какой-то список слишком неструктурированный, Винберг рядом с Шенем странно смотрится, по крайней мере. Подкину пару совсем уж для начинающих + выскажу своё мнение о них.
Ted Sundstrom "Mathematical reasoning writing and proof" - мне кажется отличная книга для первого чтения по математике. В ней объясняется, собственно, что такое математическео доказательство, математический факт и каким образом их можно придумывать. Начала теории множеств.
Гельфанд Шень "Алгебра", - курс как бы для начинающих, а как бы есть и действительно сложные задачи и темы, а также задачи, требующие изрядного количества смекалки. Поэтому читать можно, но если некоторые упражнения будут сложными - то скипать их. Охватывает весь курс школьной алгебры за вычетом тригонометрии.
Следующие книги Шеня: "Космография", "Геометрия", "Вероятность", "Игры", "Индукция", "Простые и составные", "Программирование" (чуть более сложные "Анализ в 57 школе" и "Экспонента и логарифм"). В духе "Алгебры" брошюрки на 10-30 страниц, дозировка простых и сложных задач аналогичная.
Если кому-то полезно, могу ещё подобного написать.
Давай.
> для начинающих математиков
> В. И. Арнольд: “Обыкновенные дифференциальные уравнения”.
Лол. Ты ее открывал вообще? Это graduate level. Если, конечно, рассуждать как Вербит, типа в 11 классе все уже знают че такое диффеоморфизм и касательное пространство, то тогда да, это книга для начинающих.
>Вот {3, 7} - это система натуральных чисел с НОД=1? Все множество целых чисел оно породить не может.
Этот не знает о чём говорит, не слушайте школьника.
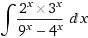
> Все множество целых чисел оно породить не может.
Это утверждение и оно неверное. {7,3} порождает все целые так же как любая другая пара взаимнопростых.
Разобрался уже, спасибо.
Не он, но поясню. Хороший учебник с отвратительными задачами. Для задач смотри НМУшные листки Локтева/Елагина.
Здравствуйте, я даун-аутист и я прочитал 1 том Фейнмана. Прдкиньте учебники и страницы в них (sic!), где можно попрактиковатт все, что указано в первом томике. Желательно, чтобы там тоже были решения да понагляднее
Тебе задачник или что? Объясняешь действительно как даун-аутист.
Читал, давай ещё.
Курсы Винберга и Констрикина - лучшие курсы по алгебре на русском языке (почему-то с книгами по алгебре на русском дикая напряжёнка).
Мне стиль Винберга очень нравится - очень хорошая подача материала в том смысле, что почти все определения очень хорошо мотивированы, и читать его мне было действительно приятно и легко. На самом деле - это одна из немногих книг по математике которые я прочитал от начала до конца. Есть много "отходов в сторону", в том плане, что главы 7 11 12 мне кажутся излишними и их можно скипать. Упражнения действительно по большей части простые, но я бы не сказал, что прорешав большую их часть вы будете плохо знать линейную и коммутативную алгебру (по крайней мере их азы), но если хочется чего-то сверх, то я при изучении линейной алгебры прорешивал этот листок, например http://verbit.ru/MATH/Teaching/Ginzburg-listok-1986.pdf которого мне хватило с головой (последние 4 до сих пор не решил 3:).
Констрикина Манина ("Линейная алгебра и геометрия") не читал, но когда-то бегло просматривал, мне он показался более сухим и формализованным, а также перегруженным лишними определениями и фактами - что плохо для первого учебника (не очень понятно на чём акцентировать внимание). А ещё он хуже свёрстан (вроде как даже не ЛаТеХ).
По-поводу учебников на английском: есть краткая рецензия от одного из немногих шарящих чуваков на dxdy на некоторые из них http://dxdy.ru/post1097114.html#p1097114 сам ни один из них не читал, но мнению того чувака полностью доверяю.
Ах да, ещё и Винберг и Констрикин требуют хорошие знания в школьной алгебре на уровне того, что вы понимаете что такое многочлен, что такое рациональные и на интуитивном уровне - что такое действительные числа, откуда берутся решения для квадратных уравнений и, в частности, формулы Виета.
Что скажешь за Городенцева? Его учебник показался не таким уж простым, посмотрел потом лекцию, не один я не врубался сразу, хотя думал, что все остальные сразу и всё понимают, как только прозвучали определения и теоремы, лол
Я пытался читать у него что-то по представлениям: мне не сильно понравился его стиль, мне кажется, он переоценивает читателя и во многих доказательствах опускает некоторые места, которые следовало бы разжёвывать. Сейчас посмотрел его учебник алгебры - мне кажется подбор материала не очень как для первого учебника, есть много специфических тем, которые на самом-то деле не сильно так чтобы must have. Но знаю многих крутых, по моему мнению, математиков-студентов, которые считают его учебник очень качественным, так что такое вот.
Представь себе ньюфага, который читает его первую лекцию, и думает, что всё это надо сразу понимать, если бы я не видел его лекций, то думал бы, что я самый тупой из его читателей
Не толсти, это был вопрос, в котором содержался пример, поясняющий суть непонимания. Пример не верный, да. Спасибо, Кэп.

Гм, Кострикина я имел ввиду курс алгебры в трех частях (+задачник). Там как линейная алгебра, так и общая.
Просто мне повезло спиздить эти книжки, собираюсь по ним наконец-то нормально освоить алгебру.
Немного читал уже, сухим он точно не показался, Винберг суше на мой вкус. (Хотя его я только немного читал, когда мне начала теории групп понадобились. Как же у меня бомбануло от того что он определил сначала Абелевы группы, а только потом общее определение дал)
У Городенцева очень сложный учебник с упором на быстрый старт в алгебраической геометрии (у Городенцева все рассчитано на быстрый старт в алгебраической геометрии).
>>352442
На dxdy очень хорошие рекомендации. Я почти все эти учебники потрогал, так что поясню:
Dummit&Foote, Abstract Algebra — хороший, много примеров, задач, но страшно скучный, его нужно держать как справочник.
M.Artin, Algebra — американский Винберг. Группы Ли, упор на геометрию (классические линейные группы это все). Задачи неудачные.
Gallian, Contemporary Abstract Algebra — не читал.
Rotman A First Course in Abstract Algebra — не читал.
Advanced Modern Algebra — читал главы про введение в гомологическую алгебру, Ротман сильно разжевывает. Задачи слишком простые для уровня учебника.
Aluffi, Algebra, Chapter 0 — если ты в состоянии ее осилить, бери и забывай про остальные книжки из списка.
Herstein, Abstract Algebra — не читал.
Topics in Algebra — прекрасные задачи, отбор материала очень устарел, почти что Ван дер Варден
Дочитать его 1 книгу и можно начинать АГ?
Хотя тут был первак, который во втором семе учил АГ
Для аг тебе нужна топология и анализ еще. Тот же Городенцев основы аг (до схем) дает на втором году обучения (впрочем, как и остальные лекторы в НМУ).
В числителе не 1.
Вкусовщина же, возможно из-за того что Винберг был моим вторым серьезным учебником я слегка предвзят.
Да там слово "идеал" появляется почти в конце. Винберг не тем хорош. Он хорошо объясняет и приводит кучу примеров. Категории ты и так возненавидишь в гомологической алгебре, не надо торопиться.
А как так получилось, что группы играют важную роль во всяких там электро-/хромодинамиках и струнах?
Это как раз то, чем я занимаюсь. Грубо говоря, Фон Нейман пытался аксиоматизировать квантовую механику, чтобы она стала разделом математики, как какая-нибудь геометрия. В квантовой механике есть объекты следующего типа: удовлетворяющие CCR соотношению (ab - ba = 1, соотношение бозонного типа) и удовлетворяющие CAR соотношению (ab + ba = 1, соотношение фермионного типа) и встаёт естественный вопрос - а любые ли две алгебры, которые более-менее адекватные и имеют смысл и в которых есть пара элементов удовлетворяющих CCR соотношению изоморфны? Оказалось - что любые, Фон Нейман это доказал. А требование, чтобы эти алгебры имели представления хотя бы в замкнутых операторах - очень естественное, как раз и означает "имеет физический смысл", примерно так.
Ну это более менее классика и только один вопрос теории представлений. А про алгебры Гекке всякие можешь пояснить, каким образом они к физике?
Нет, к сожалению, я занимаюсь некоторыми некоммутативными обобщениями CCR и СAR, в квантовые группы пока не лез.
Почему в одних книгах говорят, что простые числа - числа, делящиеся только на себя и на единицу, а в других приводят определение через такую вот делимость? Эти определения не эквивалентны? Плюс, вот 8 делит 16 х 37, но при этом 8 же не простое число. Поясни, пожалуйста.
> Плюс, вот 8 делит 16 х 37, но при этом 8 же не простое число.
Но 8 может делить так же 2 х 4, и отсюда не будет следовать, что либо 8 делит 2, либо 8 делит 4.
>Почему в одних книгах говорят, что простые числа - числа, делящиеся только на себя и на единицу, а в других приводят определение через такую вот делимость? Эти определения не эквивалентны?
Эквивалентны.
>Но 8 может делить так же 2 х 4, и отсюда не будет следовать, что либо 8 делит 2, либо 8 делит 4.
Теперь я совсем запутался.
Что вы вообще такое несете?
Простое число это то, которое делится на себя и на единицу.
Если a*b делится на x, то что-то из этого, либо а либо b делится на x.
Это ж свойство типа.
> математическому моделированию и оптимальному управлению
> с математикой у меня не ахти
Нененене. Сначала тапалогии, потом гамологии, а потом уже своё картофанное говнецо.
У этого учебника ключевое слово "wrong". Лучше взять Акслера или Хофмана, Кунце (в обоих учебниках плохая нотация: nullspace вместо kernel и тому подобное).
Splitting field theorem.
Кажется, теперь понимаю. Но зачем такое хитрожопое определение? Чем деление только на 1 и на себя хуже?
>Если a*b делится на x, то что-то из этого, либо а либо b делится на x.
>Это ж свойство типа.
Это определение простого элемента. Даже Вавилов на лекциях это говорил.
Это определение простого идеала, оставаясь в целых числах, общепринятое определение всё-таки другое (хотя не важно ведь, на самом деле).
ОП ты няша
думаю стоит еще упомянуть из интересных "Три жемчужины теории чисел" (http://ilib.mccme.ru/djvu/hinchin-3zhem.htm), хотя бы за теорему Ван дер Вардена об арифметических прогрессиях.
(-F+B)(-D+H)(-D+C)(-C+-G)(-A+-B)
Должно приводится к одночлену, но я не ебу как. При раскрытии скобок, формула только разрастается.
Это копия, сохраненная 20 мая 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.