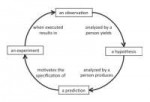
>В любой науке ровно столько науки, сколько в ней математики.
>В любой математике ровно столько математики, сколько в ней вычислимости.
Предыдущий, тонет тут: https://2ch.hk/math/res/25624.html (
Архивач: https://arhivach.cf/thread/369697/
(У кого не открывается - попробуйте HTTP.)
 407 Кб, 480x726
407 Кб, 480x726>Как начать веровать в исключённое третье?
>Сначала обдумай "парадокс лжеца", а затем - "теоремы Гёделя о неполноте",
>после этого - можешь возомнить логический элемент полным по Гёделю и удивиться.
>Аххах, если лжец сказал, что он бздит - значит он не выдувает бздо,
и он вполне правдиво сказал, что он пердит - а значит пиздит.
А если он биздит, что он пздит, то он правду говорит что он подпёздывает.
Раз он правду говорит про то, что он попёрдывает, то он либо не лжец (ну, правда же),
либо таки лжец и правдиво утверждает, что таки врёт.
Тут кстати, тоже закон исключённого третьего. И третьего не дано.
Или таки дано? Лол...
 93 Кб, 850x400
93 Кб, 850x400Основание математики существует лишь одно - теория типов Мартина-Лёфа.
Вот тут смотри революционные открытия:
https://ru.wikipedia.org/wiki/Филдсовская_премия#Список_лауреатов
https://ru.wikipedia.org/wiki/Абелевская_премия#Лауреаты
https://ru.wikipedia.org/wiki/Премия_Тьюринга#Лауреаты_премии_Тьюринга
В частности - премии за решение задач тысячелетия:
https://ru.wikipedia.org/wiki/Задачи_тысячелетия
А также, решённые проблемы Гильберта:
https://ru.wikipedia.org/wiki/Проблемы_Гильберта
О, давно не было.
Не пойму чё-т в чём парадокс, если лжец пиздит, то он шо так, шо так - пиздит, даже если не пиздит и правду говорит о том, что он пиздит - всё-равно он пиздит.
Там, кстати, кто-то выпилился даже из-за этого логического элемента. Диодор Кронос, кажется.
Тут, внутри статьи, инфа: https://ru.wikipedia.org/wiki/Евбулид
>вычилсть знак ((100!)!))! у пи, значит, нам ничего не известно об этом знаке, то есть нельзя сказать одназначно ответить - эта цифра 3 или нет. Тут кроме двух ещё и третий вариант может быть.
А разве это математическое высказывание? Насколько я помню, совокупность всех цифр числа пи даже множеством не будет, ведь для множества должно быть для любой вещи в мире известно, принадлежит ли она множеству или нет.
Нам не известно. Но в принципе выяснить можно. Есть алгоритм, вычисляющий пи. Мы можем представить, что он завершился.
Но на данный момент это не истина и не ложь, а значит не является логическим высказыванием.
Ну в смысле "знак ((100!)!))! у пи это 3" не истина и не ложь. А логическое высказывание всегда либо истинно, либо ложно.
А вдруг Вася Пупкин знает быстрый способ узнавать любой знак пи? Для него это тоже не истина и не ложь? Он же может проверить.
Всё-таки мне кажется, что "не знаешь пока" под всегда не подпадает.
Ещё Аристотель обо всём этом написал, когда создавал логику. "Завтра будет гроза" по Аристотелю не является логическим высказыванием, потому что объективного истинностного значения этим словам приписать нельзя. А с пи не так, не может получиться такого, что у двух разных людей два разных числа пи. Как только пи определено, все знаки в его десятичной записи у любых двух людей обязательно будут одинаковые.
Отказываться на уровень доантичных греков - это, конечно, сильно.
Тут же дело не в объективности, в отдельно взятом селе гроза одновременно для всех людей будет или не будет. Пример с пи как по мне это то же самое, только приправлено математичностью дабы вызвать больший конфуз.
В математику как бы вводится понятие времени, что уже настораживает, смахивает на чей-то софистический прикол если честно.
Это не то же самое, поскольку с грозой реально непонятно, пока завтра не наступит, а с пи - просто не хватает вычислительного скилла, хотя объективно уже всё предопределено определением числа пи. Дело именно в объективности.
Люди мыслят доисторическими категориями, не осилив даже Аристотеля.
Тут разные взгляды могут быть, привязка к вычислительному скиллу тоже ведь ерунда какая-то, получается, что истинность этого высказывания зависит от того, в какой век человек его прочёл? И вообще, ну хорошо, пока не вычислили, вот вычислим и узнаем наверняка, но до вычислений в каком состоянии находится высказывание? В третьем, получается, в состоянии неопределённости, откуда третье состояние возьмётся в логике с двумя состояниями?
До вычислений оно тоже было истинным (или ложным). Потому что с неизбежностью вытекает из определения числа пи, никакой свободы вариантов тут нет.
![68747470733a2f2f7062732e7477696d672e636f6d2f6d656469612f436[...].jpeg](/math/big/thumb/40955/15306698482290s.jpg) 64 Кб, 600x439
64 Кб, 600x439Молодцы какие.
kjk
>со своим петросянством про то что Мартин-Леф величайший математик
Себя имеешь в виду? Утверждать что Мартин-Лёф – математик это само по себе петросянство. Всё остальное ad absurdum.
>операционная семантика лучше платоновского мира идей
Мы уже выяснили в треде про философию математики, что ты раздяешь веру в мир идей, поскольку являешься рационалистом. Картезианский (или кантианский, или мартин-лёфовский) рационализм подразумевает реализм в смысле Платона, поскольку основан на идее объективности.
>что операционная семантика
В хаскелле, кстати, она отсутствует. Недавно читал статью в блоге Харпера про это.
>но уже видно что это сила
С 2011 видно. Как появятся математически содержательные результаты – приходи. Пока ты сойбой-хипстер и вместо математики изучаешь кубические пруверы, смузи.
> В хаскелле, кстати, она отсутствует.
Потому что там денотационная семантика. Что является просто слегка другим взглядом на одну и ту же вычислимость. Ну и операционная семантика и в хаскеле делается без проблем при желании. Остальной твой бред и комментировать лениво.
> Картезианский (или кантианский, или мартин-лёфовский) рационализм подразумевает реализм в смысле Платона, поскольку основан на идее объективности.
У тебя конечно же, есть цитаты Мартин-Лефа, которые подтверждают эти твои кукареканья. Поэтому ты же их приведешь? Ну или как вариант, ходи дальше обоссаным, про охранника написать не забудь, это же твой основной аргумент, опровергающий mltt.
По цитатам Мартина Льва ты у нас спец. При чём настолько, что философию Канта изучаешь исключительно через них (как и любую другую философию).
Что конкретно тебе надо пруфануть? Что идея объективности подразумевает платоновский реализм? Или что рационализм подразумевает идею объективности?
Достаточно грамотному человеку и то и другое должно быть понятно, но, так и быть:
https://en.wikipedia.org/wiki/Objectivity_(philosophy)
A proposition is generally considered objectively true (to have objective truth) when its truth conditions are met without biases caused by feelings, ideas, opinions, etc., of a sentient subject.
Умеющему читать человеку этого уже достаточно. В предыдущих тредах один анон не мог понять, почему свобода воли подразумевает реализм (= веру в мир идей).
Потому что свобода воли позволяет мыслящему субъекту осуществлять выбор вне зависимости от внешних обстоятельств.
Аналогично, идея объективности позволяет утверждениям быть истинными в абсолютном смысле. То есть, должен быть единый стандарт, позволяющий различать, что всегда истинно, а что нет. Где он располагается? В мире идей, конечно.
Plato's idealism was a form of metaphysical objectivism, holding that the Ideas exist objectively and independently.
Plato's definition of objectivity can be found in his epistemology, which takes as a model mathematics, and his metaphysics, where knowledge of the ontological status of objects and ideas is resistant to change.
Ниже указан другой интересный момент:
Strong versions of this claim hold that there is only one correct description of this reality. If it is true that reality is mind-independent, then reality might include objects that are unknown to consciousness and thus might include objects not the subject of intensionality.
В прошлый раз тебе не удалось вникнуть в понятие интенциональности у Брентано.
Напомню:
Brentano described intentionality as a characteristic of all acts of consciousness that are thus "psychical" or "mental" phenomena, by which they may be set apart from "physical" or "natural" phenomena.
Every mental phenomenon includes something as object within itself, although they do not all do so in the same way. In presentation something is presented, in judgement something is affirmed or denied, in love loved, in hate hated, in desire desired and so on. This intentional in-existence is characteristic exclusively of mental phenomena. No physical phenomenon exhibits anything like it. We could, therefore, define mental phenomena by saying that they are those phenomena which contain an object intentionally within themselves.
Понятие интенциональности делает возможной феноменологическую редукцию. Мы можем отождествить предмет, находящийся в естественной установке, с восприятием данного предмета в сознании. Это буквально одно и то же. Субъект и объект (в смысле Декарта), материальный мир и мир явлений, mind and body, etc.
Почему можем? Сознание обладает интенцией, всякая мысль направлена на какой-то предмет и нельзя мыслить беспредметно. Это и есть феноменология.
Если же ты позволяешь себе мыслить беспредментно, и "реальность" у тебя может включать что-то непознаваемое, не поддающееся интенции, как например трансцендентальное у Канта, то ты и есть платонист. По определению. Здесь не с чем спорить. Трансцендентальное, находящееся за пределами возможного опыта знание, может быть только в другой реальности, независимой от этой, в реальности мира идей, абсолютных истин и прочих Аллахов. Читай Канта в общем, там всё это описано.
Естественно тебе было непонятно назначение и смысл феноменологии, если ты даже её осознаешь проблему трансцендентного в философии Канта. Проблему, которую успешно решила феноменология. В отличие от менее успешных попыток неокантианства типа Когена и других.
Что касается цитат, то ты уже приводил одну, в которой Мартин-Лёф обсирается, показав своё незнание термина "эпистемология".
На этом разговор в принципе можно закрыть, если для тебя ни одна книга или статья это не аргумент, а бред полоумного шизофреника, к тому же неграмотного – аргумент.
Ещё раз: меня не волнует, что недоучка Лёф понимает под рационализмом или какие ещё маняназвания для давно существующих дисциплин вроде семиотики придумал сойбой Маннури (сингнификс, лол).
Твой кумир не знает философии и не читал Канта. Цитата из произведений Лефа аргументом является только для тебя, т.к. ничего сложнее ты не осилишь. Можешь вертеться сколько угодно с переопределением терминов под себя, спорить с бредом шизофреников не вижу смысла, мне в данном случае интересна философия, а не сектоведение. Поэтому я говорю о Канте, а не о том, как его попытался понять жопочтец Лёф.
По цитатам Мартина Льва ты у нас спец. При чём настолько, что философию Канта изучаешь исключительно через них (как и любую другую философию).
Что конкретно тебе надо пруфануть? Что идея объективности подразумевает платоновский реализм? Или что рационализм подразумевает идею объективности?
Достаточно грамотному человеку и то и другое должно быть понятно, но, так и быть:
https://en.wikipedia.org/wiki/Objectivity_(philosophy)
A proposition is generally considered objectively true (to have objective truth) when its truth conditions are met without biases caused by feelings, ideas, opinions, etc., of a sentient subject.
Умеющему читать человеку этого уже достаточно. В предыдущих тредах один анон не мог понять, почему свобода воли подразумевает реализм (= веру в мир идей).
Потому что свобода воли позволяет мыслящему субъекту осуществлять выбор вне зависимости от внешних обстоятельств.
Аналогично, идея объективности позволяет утверждениям быть истинными в абсолютном смысле. То есть, должен быть единый стандарт, позволяющий различать, что всегда истинно, а что нет. Где он располагается? В мире идей, конечно.
Plato's idealism was a form of metaphysical objectivism, holding that the Ideas exist objectively and independently.
Plato's definition of objectivity can be found in his epistemology, which takes as a model mathematics, and his metaphysics, where knowledge of the ontological status of objects and ideas is resistant to change.
Ниже указан другой интересный момент:
Strong versions of this claim hold that there is only one correct description of this reality. If it is true that reality is mind-independent, then reality might include objects that are unknown to consciousness and thus might include objects not the subject of intensionality.
В прошлый раз тебе не удалось вникнуть в понятие интенциональности у Брентано.
Напомню:
Brentano described intentionality as a characteristic of all acts of consciousness that are thus "psychical" or "mental" phenomena, by which they may be set apart from "physical" or "natural" phenomena.
Every mental phenomenon includes something as object within itself, although they do not all do so in the same way. In presentation something is presented, in judgement something is affirmed or denied, in love loved, in hate hated, in desire desired and so on. This intentional in-existence is characteristic exclusively of mental phenomena. No physical phenomenon exhibits anything like it. We could, therefore, define mental phenomena by saying that they are those phenomena which contain an object intentionally within themselves.
Понятие интенциональности делает возможной феноменологическую редукцию. Мы можем отождествить предмет, находящийся в естественной установке, с восприятием данного предмета в сознании. Это буквально одно и то же. Субъект и объект (в смысле Декарта), материальный мир и мир явлений, mind and body, etc.
Почему можем? Сознание обладает интенцией, всякая мысль направлена на какой-то предмет и нельзя мыслить беспредметно. Это и есть феноменология.
Если же ты позволяешь себе мыслить беспредментно, и "реальность" у тебя может включать что-то непознаваемое, не поддающееся интенции, как например трансцендентальное у Канта, то ты и есть платонист. По определению. Здесь не с чем спорить. Трансцендентальное, находящееся за пределами возможного опыта знание, может быть только в другой реальности, независимой от этой, в реальности мира идей, абсолютных истин и прочих Аллахов. Читай Канта в общем, там всё это описано.
Естественно тебе было непонятно назначение и смысл феноменологии, если ты даже её осознаешь проблему трансцендентного в философии Канта. Проблему, которую успешно решила феноменология. В отличие от менее успешных попыток неокантианства типа Когена и других.
Что касается цитат, то ты уже приводил одну, в которой Мартин-Лёф обсирается, показав своё незнание термина "эпистемология".
На этом разговор в принципе можно закрыть, если для тебя ни одна книга или статья это не аргумент, а бред полоумного шизофреника, к тому же неграмотного – аргумент.
Ещё раз: меня не волнует, что недоучка Лёф понимает под рационализмом или какие ещё маняназвания для давно существующих дисциплин вроде семиотики придумал сойбой Маннури (сингнификс, лол).
Твой кумир не знает философии и не читал Канта. Цитата из произведений Лефа аргументом является только для тебя, т.к. ничего сложнее ты не осилишь. Можешь вертеться сколько угодно с переопределением терминов под себя, спорить с бредом шизофреников не вижу смысла, мне в данном случае интересна философия, а не сектоведение. Поэтому я говорю о Канте, а не о том, как его попытался понять жопочтец Лёф.
>Ну и операционная семантика и в хаскеле делается без проблем при желании
Ага, ну я так и понял, что Харпер дурак (впрочем ты наверняка даже не знаешь, кто это), и тебе виднее. Ты же у нас в перерывах между просмотром аниме и работой охранником прувер написал.
Отклеилась ссылка.
Впрочем я склоняясь к мнению, что твоё знание теории типов такое же, как знание математики или философии, то есть отсутствует полностью. Скорее всего пишешь случайные фразы невпопад, периодически вставляя ключевые слова своей секты, типа: "идеи сигнифики воплощены в программе spikgram Миколова". Учитывая что никакой сигнифики не существует и это просто ещё один пример твоей путаницы в терминах, можно примерно оценить содержание остальных пассажей.
А, игнорирование аргументации, понятно. Старый приём, уже видели.
>Ты даже прочитать, что тебе пишут, неспособен.
Смешно слышать от человека, которому шесть в шести тредах объяснили одно и то же, а всё равно непонятно.
Я уже показывал ранее что Лёф некомпетентен в этой области, банально неграмотен и несёт хуйню. При этом, когда я утверждаю что-то про Канта, тебе требуется цитата из Лёфа как подтверждение. Как болезнь называется?
Аллах запретил читать всё книжки, кроме написанных конструктивистами? Или что? Что ты ничего больше не читал мне прекрасно видно, интересует почему. Боишься увидеть несостоятельность своего учения? А как же интеллектуальная честность, о которой писал кумир Поппер?
> Я уже показывал ранее что Лёф некомпетентен в этой области, банально неграмотен и несёт хуйню.
Ну разумеется, ты один умный. И уже опроверг mltt. Ладно, ещё раз: какие есть цитаты Мартин-Лефа, связывающие mltt и платонизм, ты это утверждал
>>41226
> Картезианский (или кантианский, или мартин-лёфовский) рационализм подразумевает реализм в смысле Платона, поскольку основан на идее объективности.
Поэтому обосновывай. Как вариант, можешь и дальше жопой крутить, у тебя это хорошо получается. Но тогда ты и сам должен понимать, что ты клоун и занимаешься клоунадой.
>>41277
> При этом, когда я утверждаю что-то про Канта, тебе требуется цитата из Лёфа как подтверждение. Как болезнь называется?
Пиздежь хронический, т.к с моей стороны никогда не было и не могло быть требований обосновать Канта через Мартин-Лефа, ты там совсем заболел, такую хуйню нести? С тобой все ясно, защищаешь свой сломанный манямир в котором бездушная машина не может в математику, а человек якобы может в этой области что-то чего не может алгоритм.
И кто не умеет читать? Я написал про рационализм, а не про mltt.
>связывающие mltt и платонизм
>рационализм подразумевает реализм в смысле Платона
То есть ты даже не видишь, что цитируешь.
Ты сам называл себя рационалистом в предыдущих тредах. И не только себя, например, по твоему мнению, Брауэр тоже был рационалистом. При чём тут mltt? Под mltt понимается любое утверждение, которое ты напишешь тут, что ли?
Я показал, что рационализм подразумевает платонизм. Смешно будучи платонистом кукарекать потом про веру, аллахов и т.д.
>стороны никогда не было и не могло быть требований обосновать Канта через Мартин-Лефа
О чём речь тогда? Философии Лёфа не существует в принципе. Началось же с того, что ты начал писать про Канта несколько тредов назад, мол кантианство отлично укладывается в МЛТТ. У тебя это так работает: святой сослался (Лёф в данном случае) – значит хорошая, годная философия. Как Ваник сослался на Поппера, а Маннури на Витгенштейна
А то, что это и есть тот самый платонизм, о котором ты негативно отзываешься уже три-четыре года, как бы и не важно. Главное что святые пишут и кого упоминают, цитаты святых, содержание же данных идей или концептов не существенно.
>бездушная машина не может в математику, а человек якобы может в этой области что-то чего не может алгоритм
С отправной точкой зрения конструктивизма я не спорил, кстати, никогда. Она по сути совпадает с феноменологией. Понятие примордиальной интуиции у Брауэра, акты интуиционизма. По существу, Брауэр здесь переоткрыл то, о чём уже написали Брентано и Гуссерль.
Посылки хорошие, только с выводами не очень.
Решение ограничить математику операциями, выполняемыми на машине Тьюринга, перекладыванием палочек это уже over the top nonsense. Совершенно не понятно, как можно думать подобным образом и при этом знать хоть что-нибудь содержательное из математики после 1870-х.
Требование построимости в этом роде похоже на фальсификационизма Поппера: никакая содержательная теория ему удовлетворять просто не может.
Опять же, использование гомологической алгебры и даже (infty, 1)-категорий никак не требует реализма в смысле Платона. Обоснованием теории категорий служит скорее прагматизм Пирса. О чём хорошо написано у Kromer'а в Tool & object, уже приводил ссылки.
То есть это ложная альтернатива, в принципе. Либо перекладываешь палочки, либо плутонист. Вовсе нет. Об этом ещё Мах писал.
И кто не умеет читать? Я написал про рационализм, а не про mltt.
>связывающие mltt и платонизм
>рационализм подразумевает реализм в смысле Платона
То есть ты даже не видишь, что цитируешь.
Ты сам называл себя рационалистом в предыдущих тредах. И не только себя, например, по твоему мнению, Брауэр тоже был рационалистом. При чём тут mltt? Под mltt понимается любое утверждение, которое ты напишешь тут, что ли?
Я показал, что рационализм подразумевает платонизм. Смешно будучи платонистом кукарекать потом про веру, аллахов и т.д.
>стороны никогда не было и не могло быть требований обосновать Канта через Мартин-Лефа
О чём речь тогда? Философии Лёфа не существует в принципе. Началось же с того, что ты начал писать про Канта несколько тредов назад, мол кантианство отлично укладывается в МЛТТ. У тебя это так работает: святой сослался (Лёф в данном случае) – значит хорошая, годная философия. Как Ваник сослался на Поппера, а Маннури на Витгенштейна
А то, что это и есть тот самый платонизм, о котором ты негативно отзываешься уже три-четыре года, как бы и не важно. Главное что святые пишут и кого упоминают, цитаты святых, содержание же данных идей или концептов не существенно.
>бездушная машина не может в математику, а человек якобы может в этой области что-то чего не может алгоритм
С отправной точкой зрения конструктивизма я не спорил, кстати, никогда. Она по сути совпадает с феноменологией. Понятие примордиальной интуиции у Брауэра, акты интуиционизма. По существу, Брауэр здесь переоткрыл то, о чём уже написали Брентано и Гуссерль.
Посылки хорошие, только с выводами не очень.
Решение ограничить математику операциями, выполняемыми на машине Тьюринга, перекладыванием палочек это уже over the top nonsense. Совершенно не понятно, как можно думать подобным образом и при этом знать хоть что-нибудь содержательное из математики после 1870-х.
Требование построимости в этом роде похоже на фальсификационизма Поппера: никакая содержательная теория ему удовлетворять просто не может.
Опять же, использование гомологической алгебры и даже (infty, 1)-категорий никак не требует реализма в смысле Платона. Обоснованием теории категорий служит скорее прагматизм Пирса. О чём хорошо написано у Kromer'а в Tool & object, уже приводил ссылки.
То есть это ложная альтернатива, в принципе. Либо перекладываешь палочки, либо плутонист. Вовсе нет. Об этом ещё Мах писал.
> С отправной точкой зрения конструктивизма я не спорил, кстати, никогда. Она по сути совпадает с феноменологией. Понятие примордиальной интуиции у Брауэра, акты интуиционизма. По существу, Брауэр здесь переоткрыл то, о чём уже написали Брентано и Гуссерль.
Скорее, Павлов. Все, что у Брауэра написано про примордиальную интуицию, укладывается в понятие абстракции условного рефлекса (стимул, ещё стимул, их временнАя ассоциация и выведение свойств путем рассмотрения) . Уже хотя бы потому, что речь об интеллекте человека, высшей нервной деятельности, а это одни рефлексы, ничего другого там нет и быть не может. Феноменологию тут можно приделать при желании, но смысла нет. Естественнее нейрофизиологию, т.к повторюсь, речь у Брауэра изначально об интеллекте и его свойствах.
> Посылки хорошие, только с выводами не очень.
Ты просто не понимаешь предмет. Выводы Брауэра прямо следуют из его же посылок, ничего другого оттуда вывести просто невозможно.
> Решение ограничить математику операциями, выполняемыми на машине Тьюринга, перекладыванием палочек это уже over the top nonsense.
Это прямое следствие возможностей человека, свойств и ограничений его интеллекта, точнее его рефлекторной природы, с чего и начал Брауэр. Машина Тьюринга просто модель этого.
> А то, что это и есть тот самый платонизм, о котором ты негативно отзываешься уже три-четыре года, как бы и не важно. Главное что святые пишут и кого упоминают, цитаты святых, содержание же данных идей или концептов не существенно.
Факт прежде всего в том, что mltt и вычислимость, как и интуиционизм Брауэра никакого платонизма не подразумевают. Важно это, а не то, как и к каким моим словам тебе хотелось бы придраться.
>Уже хотя бы потому, что речь об интеллекте человека, высшей нервной деятельности, а это одни рефлексы, ничего другого там нет и быть не может
О, вы биолог? Или просто на Савельева дрочишь?
Теорема Геделя говорит о том, что всякая теория либо неполна, либо противоречива.
Представим теорию, содержащею всевозможные логически теории. Она не может быть полной из-за Теоремы Геделя. Но она не является противоречивой(из-за отборки теорий логичностью)
Это исходит из того, что мы можем образовать новую теорию, склеив две старые.
Как варианты избежать этого парадокса?:
Логичные теории в результате их объединения, могут стать нелогичными. Тогда, нужно привести контрпример.
>Теорема Геделя говорит о том, что всякая теория либо неполна, либо противоречива.
Лжёшь, уёбок. Названная тобой теорема справедлива только для класса формальных арифметик. А полноту, например, исчисления предикатов самолично Гёдель и доказал, это так называемая "теорема Гёделя о полноте".
https://ru.wikipedia.org/wiki/Теорема_Гёделя_о_полноте
https://www.youtube.com/watch?v=shGIXO69BlQ
Видео, где Вассерман говорит о невозможности Бога(причина всех причин) из-за Теоремы Геделя.
А материальный мир является частным случаем формальной арифметики? Он говорит, что у него есть пруфы.
Достаточно, чтобы теория включала в себя формальную арифметику.
> Видео, где Вассерман говорит о невозможности Бога(причина всех причин) из-за Теоремы Геделя.
Онотоле таки опроверг Аллаха?
В том, что он не пристрелил тебя как собаку, когда ебал твою мамашу-шлюху, говно. Никогда не упоминай имя Геделя. Быдло, которое не прочитало ни одного учебника логики, не имеет права даже думать об этом человеке. Сдохни, тварь, мудак. Ненавижу тебя.
Я настолько с него сгорел, что даже отвечать не стал. А ты считай мои мысли выразил. Мерси.
Ну например теорему Ферма. Не только и не столько категориями, конечно, но без категорий бы не получилось.
![023b08300d2df77e9e25955093acf9f6[1].jpg](/math/big/thumb/40955/15312663210670s.jpg) 107 Кб, 700x528
107 Кб, 700x528>Теорема Геделя говорит о том, что всякая теория либо неполна, либо противоречива.
>>41355
>Названная тобой теорема справедлива только для класса формальных арифметик.
>А полноту, например, исчисления предикатов самолично Гёдель и доказал, это так называемая "теорема Гёделя о полноте".
>>41356
>Вассерман говорит
>>41357
>Вассерман извинился
Ох ничего себе, вот это спор!
Я раньше тоже рассматривал любую систему, любую теорию и любую структуру из формул
как систему формальную - просто потому что существует их формализация.
Мне нравится непротиворечивость и полнота по Гёделю системы логики вычислений первого порядка.
Логику второго порядка, рассматривать не хочу, ибо хоть она и расширяет логику первого порядка,
но по её определению - это формальная система! А значит она может быть либо противоречивой, либо неполной.
Так вот, аноны, есть какие-нибудь онлайн или оффлайн трансляторы какого-нибудь текста
из бредогенератора - в логику исчисления предикатов первого порядка?
И да, можно ли на её основе, вообще производить всякую мыслительную деятельность и даже разговаривать?
Логических операций у неё не так много, всего 4, пикрелейтед,
плюс две скобки, запятая, и два квантора - квантор всеобщности и квантор существования.
Итого - 9 символов. Они, помимо переменных всяких, могут кодироваться лишь 4-мя битами,
и обрабатываться каким-то 4-х битным процессором.
Если это единственная логика, способная дать возможность
перепроверять структурируемую в режиме реального времени информацию,
в частности различные высказывания и выражения - сводя их к этой логике,
я думаю стоило бы вшить в башку чётырехбитный квантовый компьютер, под видом микронаушника,
чтобы, ну, чтобы правду как-бы Боженька нашёптывал, без всяких проводов. И заебись.
![023b08300d2df77e9e25955093acf9f6[1].jpg](/math/big/thumb/40955/15312663210670s.jpg) 107 Кб, 700x528
107 Кб, 700x528>Теорема Геделя говорит о том, что всякая теория либо неполна, либо противоречива.
>>41355
>Названная тобой теорема справедлива только для класса формальных арифметик.
>А полноту, например, исчисления предикатов самолично Гёдель и доказал, это так называемая "теорема Гёделя о полноте".
>>41356
>Вассерман говорит
>>41357
>Вассерман извинился
Ох ничего себе, вот это спор!
Я раньше тоже рассматривал любую систему, любую теорию и любую структуру из формул
как систему формальную - просто потому что существует их формализация.
Мне нравится непротиворечивость и полнота по Гёделю системы логики вычислений первого порядка.
Логику второго порядка, рассматривать не хочу, ибо хоть она и расширяет логику первого порядка,
но по её определению - это формальная система! А значит она может быть либо противоречивой, либо неполной.
Так вот, аноны, есть какие-нибудь онлайн или оффлайн трансляторы какого-нибудь текста
из бредогенератора - в логику исчисления предикатов первого порядка?
И да, можно ли на её основе, вообще производить всякую мыслительную деятельность и даже разговаривать?
Логических операций у неё не так много, всего 4, пикрелейтед,
плюс две скобки, запятая, и два квантора - квантор всеобщности и квантор существования.
Итого - 9 символов. Они, помимо переменных всяких, могут кодироваться лишь 4-мя битами,
и обрабатываться каким-то 4-х битным процессором.
Если это единственная логика, способная дать возможность
перепроверять структурируемую в режиме реального времени информацию,
в частности различные высказывания и выражения - сводя их к этой логике,
я думаю стоило бы вшить в башку чётырехбитный квантовый компьютер, под видом микронаушника,
чтобы, ну, чтобы правду как-бы Боженька нашёптывал, без всяких проводов. И заебись.
> Так вот, аноны, есть какие-нибудь онлайн или оффлайн трансляторы какого-нибудь текста
> из бредогенератора - в логику исчисления предикатов первого порядка?
> И да, можно ли на её основе, вообще производить всякую мыслительную деятельность и даже разговаривать?
Это ещё Лейбниц хотел сделать. Более современные попытки - семантика Монтегю и ещё пара примеров. Но все это простые примеры формального представления разговорного текста, а не его фактическая формализация, т.е вывод любой возможной языковой конструкции из формальных правил. Последнее невозможно, что прямо следует из теории 5 уровней языка Маннури. Исчисление предикатов это язык 5 уровня, тогда как разговорный это 1-2 уровень. Последующие уровни выводимы из предыдущих, но предыдущие не сводимы к последующим, т.к считай, являются их подмножествами. Поэтому легко и просто разговорным языком описать исчисление предикатов, но сам разговорный язык к ним не сведешь.
Для чего же весь язык сводить, если можно было бы отдельные языковые высказывания
(те самые формальные правила из языковых конструкций)
последовательно сводить и перепроверяя их непротиворечивость, полноту и истинность,
а также наличие этих свойств - у целых конструкций из этих высказываний, которые побольше будут.
При необходимости, же, отвергать их, дополняя при этом, к полноте, да так чтоб непротиворичиво было и правлиьно всё, с последующей конвертацией этого дополнительного уточнения - в языковую конструкцию.
>При необходимости, же, отвергать их, дополняя при этом, к полноте, да так чтоб непротиворичиво было и правлильно всё,
>с последующей конвертацией этого дополнительного уточнения - в языковую конструкцию.
Не учёл, что языковая конструкция, описывающая это дополняющее уточнение,
может быть настолько сложной, многогранной и разомкнутой в другие конструкции,
что памяти не хватит её воспринять языком.
Ты описал любой язык с зависимыми типами, оно примерно так и работает.
 898 Кб, 487x560
898 Кб, 487x560Тот клован, который тут серет на тему "конструктивизм ита кудахтер саенс, конструктивных доказательств нет" либо этого сойбоя косплеит, либо сам он и есть. Сходу даже и не скажешь, в каком из этих вариантов больше деградантства
 26 Кб, 644x800
26 Кб, 644x800> Это ты вербита-то сойбоем назвал?
> Знатно я проиграл, конечно.
Поплачь теперь, вот горе, сойбоя сойбоем назвали. "Теорема о неподвижной точке неверна", чего блядь? Надеюсь, он хотя бы теорему о веерах имел в виду...
Ты двачь-то затроллил уже, маленький? А то я не понимаю бомбить мне или нет.
> У него степень PhD,
Как у любого индуса или китайца из гугла. Я и говорю, тайпикал магистр кукольных наук.
> "Теорема о неподвижной точке неверна", чего блядь? Надеюсь, он хотя бы теорему о веерах имел в виду...
Ты же безграмотен, погуглил бы хоть о чем идет речь, лол. Вербицкий здесь полностью прав и теорема Брауэр о неподвижной точке действительно неверна в конструктивном анализе. Бывают конструктивные функции из квадрата [0,1]x[0,1] в себя без конструктивных неподвижных точек.
 36 Кб, 604x340
36 Кб, 604x340> Вербицкий здесь полностью прав и теорема Брауэр о неподвижной точке действительно неверна
Обокакался твой профессор соевых наук, https://madiot.fr/coq100/ доказательство этой теоремы в коке за нумером 36, код по ссылке оттуда.
> Много ли индусов выступают на Международном конгрессе математиков с докладом?
На коворкингах со смузи-то? Постоянно.
Здесь дан контрпример, который я упомянул http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=dan&paperid=28506&option_lang=rus . И его наличие означает, что формализации на которые ты ссылаешься по тем или иным причинам не допускают конструктивной интерпретации.
> https://madiot.fr/coq100/ доказательство этой теоремы в коке за нумером 36
Кстати, если бы ты хотя бы посмотрел на свою собственную ссылку, то обнаружил бы, что собственно формализации в Coq там нет.
Просто хотел продемонстрировать то, что ты не разбираешься в вещах о которых говоришь. И да, если бы ты взглянул на этот "конструктивный вариант теоремы Брауэра", то заметил бы, что там даже не утверждается существование каких-либо неподвижных точек.
> Просто хотел продемонстрировать то, что ты не разбираешься в вещах о которых говоришь.
Нет, ты. Погугли хотя бы, конструктивное доказательство теоремы о неподвижной точке есть на каждом углу, и только один сойбой, что самое смешное, из рашки, у себя в бложике пишет, что она неверна.
> Демагогия. По ссылке, что ты привёл, этого нет.
Тебе на гугл ссылку дать? Даже в педивикии доказательство есть. То, что я принёс, там доказательство для HOL и ещё каких-то пруверов. Но раз преподобный (((сойбой))) сказал, что теорема неверна, значит так и есть, даже?
Раньше я считал конструктивиста хотя бы минимально грамотным собеседником. Но наехать на мкм - это за гранью.
>(((сойбой)))
Ты еще и /pol/-тард или это кто-то залетный порочит доброе имя конструктивиста?
Как на коке это доказать? Чтобы он сам доказал.
(и я даже знаю, откуда ты взял эту задачу)
> http://archive-pml.github.io/martin-lof/pdfs/Bibliopolis-Book-retypeset-1984.pdf со 2 по 7 страницы
На русском есть?
>3734
> Тип - это конструктивный объект, который есть элемент самого себя
Хуй проссышь, конструктивный объект это ж вроде неопределяемое понятие?
Формулировка "быть элементом" разве не предполагает наличие теории множеств, которая тут как бы избегается?
Это ж высер обезумевшего конструктуха. Лучше не пытайся это понять. Если же тебе так хочется с ним на одну волну, можешь попробовать каждый день читать святые писания Брауэра и Мартина-Лефа и молиться вычислительному смыслу. Возможно, через пару лет сможешь уверовать, если в дурку не заберут.
>Формулировка "быть элементом" разве не предполагает наличие теории множеств
"Тип" имеет тип "Тип", он об этом. (На самом деле N : Type, Type : Type1, etc)
Дано: Любые комплексные числа m,k. Для них (m-k)/(m-k)=1. Следовательно для m=k: 0/0=1.
Как понять где начинается 0, а где просто эквивалентная трансформация без подстановки.
лучше просто убей себя.
Значит ли это, что когда пиздуешь в ноль, там трансформеры активизируются?
Че за индус на втором пике? На википедии посмотрел - вроде ничего великого.
Скорее всего да, уже дошли до предела мозга. Дальше только всякие технически сложные доказательства на компе, которые со временем ни один чел не осилит.
Увы, правда. То же самое касается всех наук вообще. Время науки прошло, всё открыто, всё сделано. Предел человеческих возможностей достигнут.
Нет конечно, математика жила, живёт, и будет жить вечно, под вечный же аккомпанемент неосиляторов-жопоголиков, не отличающих науку от спорта. Если что-то и загнётся, что точно не математика.
Со временем происходит процесс упрощения математического знания, именно благодаря которому и возможно продвижение вперед, потому что люди умнее не становятся. Математика отличается от спорта, прежде всего, высоким уровнем контакта с трансцендентными, высшими источниками и изящными мирами, которые дают ей нескончаемый запас МАНЫ, НАДЕЖДЫ, ПРОЦВЕТАТЕЛЬНОЙ ЭНЕРГИИ. Шоколадные медальки — подачка плебсу, обиженным люмпенам, которые не видят. Сферы остаются нетронутыми, собственно, ничем, кроме любовью. А теперь съеби отсюда и возвращайся только когда осмыслишь. Можешь ебануть арматурой себе по башке — мысли потекут быстрее.
Блин, еще раз вопрос задам. Что еще за индус-математик на 2 пике? Сриниваса Рамануджан Айенгор . Какой-то крупный математик своего времени( таких много), но чтоб прям величайший?
Да и Пифагор вроде не такой уж крутой математик( хоть и известный). Он кроме теоремы пифагора ничего не доказал( которую к слову и не он доказал вовсе).
Возможно, про спорт такого бреда пишут меньше, потому что за него всё-таки кто-то готов платить?
>>42291
Разрешим этот спор как мужчины — доставайте свои кошельки.
Идите своей дорогой, ебланы. A mathematician is so rare an animal that he deserves to be preserved, be it only on the score of curiosity. А вас, вальяжно заваливающихся в чужой монастырь со «скрытым» намерением доебаться я всегда презирал. Вместе с молящимися на силиконовые гробы истеричками переводчик-стайл, орущими о «конце математики» и «великом кризисе».
Я знаю, поэтому мы с тобой тут и сидим, правда?
Но почему?
Формальная система - это алгоритм, продуцирующий последовательность высказываний (каждое высказывание из этой последовательности является теоремой в данной формальной системе).
Действительно, ведь суть формальной системы - в возможности получать теоремы, а то, каким именно образом эти теоремы получены (через аксиомы и правила вывода; или же, например, через продуцирование высказываний в логике 0-го порядка и проверку их на тавтологичность через таблицы истинности) - вторично. Ну а в силу счётности всех доказательств очевидно, что для любой классической формальной системы сущ.алгоритм, продуцирующий ВСЕ теоремы этой формальной системы.
К вопросу зачем это нужно - теорема Гёделя при таком определении становится гораздо более ясной. Если бы у нас была формальная система, доказывающая все истинные (и только истинные) высказывания арифметики, то был бы и алгоритм U, продуцирующий все истинные высказывания арифметики. А так как вопрос остановки того или иного алгоритма равноценен истинности или ложности определённого арифметического высказывания, то наличие алгоритма U дало бы возможность решить проблему остановки, что невозможно.
Конструктивненько. Сейчас местному шизику подпечет, опять будет про охранников писать, из /pr его выгнали ссаными тряпками, а тут некому. Суть в том, что есть разница в том, что считать истинным высказыванием. С нормальной точки зрения это построимый, вычислимый терм, с точки зрения религии - непротиворечивый в некоем наборе аксиом (заповеди Цермело-Френкеля, например). Результат будет разным, хотя и алгоритмически выводимым. Только в случае заповедей, проблемы останова не будет, т.к есть заповедь об исключенном третьем.
Быдло забыли спросить. Ебет. Какаго-то индуса сраного записали в топ 10 велиайшших математиков всех времен. Нехорошо
>>42503
То что ты описал это в целом стандартный взгляд на первую теорему Гёделя о неполноте с точки зрения теории рекурсии. Отмечу, что в близком духе можно доказать теорему Тарского о невыразимости истины (нет арифметической формулы T(x) такой что для каждого арифметического предложения F она истинна на коде F если и только если F истинно).
Впрочем, вторую теорему Гёделя о неполноте (никакая непротиворечивая теория не доказывает свою непротиворечивость) так видимо не доказать.
 84 Кб, 780x410
84 Кб, 780x410Недавно наткнулся на статью о японском математике Синъити Мотидзукида да, я тот еще слоупок , что мол этот товарисч доказал abc-гипотезу, создав при этом теорию, которую никто не понимает, кроме 3,5 таких же шизофреников и выложил доказательство в открытый доступ. Вооружившись старым добрым англо-русским словарем решил почитать введение. Единственное что я понял если , конечно правильно понял, это то что Мотидзуки решил запить собственные математические структуры скомпелив самые разнообразные области математики. Так вот у меня к знающим математикам вопрос такой, а с помощью каких , собственно, областей математики Мотидзуки создал интер-универскальную теорию и доказал abc-гипотезу ? Ведь как я знаю, он эксперт по теории чисел , да по алгебраической геометрии ( спасибо вике ), а в его теории задействованы элементы из абсолютно разных областей, никак с вышеперечисленными не связанные.
 3,2 Мб, webm,
3,2 Мб, webm,480x360, 0:30
> с помощью каких , собственно, областей математики Мотидзуки создал интер-универскальную теорию и доказал abc-гипотезу ?
Теория чисел, гамалогии, тапалогии. У него ж есть статья, где он объясняет свою теорию через интеграл Гаусса. Была ещё статья, где iuteich объясняется с помощью видеорелейтед анимца.
>создав при этом теорию, которую никто не понимает, кроме 3,5 таких же шизофреников
>3,5
>Так вот у меня к знающим математикам вопрос такой, а с помощью каких , собственно, областей математики Мотидзуки создал интер-универскальную теорию и доказал abc-гипотезу ?
Спроси у тех 3,5.
Понял, на что похоже, когда напьёшься в хлам и пытаешься уснуть.
Это в корне неверно. "Несомненные интуиции" - это миф. Наши интуиции уточняются, шлифуются по мере развития как мышления, так и математики. Когда-то всем казалось несомненной интуицией возможность существования только евклидовой геометрии. Интуитивисты часто обвиняют нас в "вере в бесконечности", хотя на самом деле религиозная вера свойственна скорее им - вера в непогрешимые математические интуиции.
Взгляд на математику как на науку, открывающую идеальные несомненные истины, в отличие от ненадёжных эмпирических наук, где мы всегда вынуждены пользоваться лучшей теорией из имеющихся, зная, что однажды может появиться лучшая теория, описывающая физическую реальность, также ложен. Критерием "истинности" может быть только практика. Мы пользуемся законом исключения третьего не потому, что считаем его несомненной истиной, а потому, что на данный момент нет лучшей альтернативы той логике, которая включает закон исключения третьего. Те "математики", которые строятся без закона исключения третьего, пока не принесли никакой пользы и только пытаются отнять у нас те несомненно полезные результаты, которые даёт "классическая" математика.
Нынешняя классическая математика возможно однажды будет заменена лучшей альтернативой (также, как Общая теория относительности заменила Ньютонов закон гравитации) - но только тогда, когда эта лучшая альтернатива появится. Интуитивисты же большей частью подобны современникам Ньютона, которые говорили бы "эта теория неверна, т.к. дальнодействие абсурдно; ничто не может действовать на расстоянии, так что Ньютон неправ", не предлагая лучшей альтернативы и игнорируя те огромные практические результаты, которые давала теория Ньютона.
Математика - довольно "странная" наука, так как она исследует что-то очень абстрактное - абстрактные структуры. Поэтому неудивительно, что её постоянно пытаются свести к чему-то более конкретному: интуитивисты - к психологии (во всяком случае, к той части психологии, которую они считают непогрешимой), конструктивисты - к вычислениям, формалисты - к оперированию символами. Конечно, математика связана со всеми этими областями, она пользуется и интуициями, и вычислениями, и формальным методом как мощными инструментами. Но нельзя заменить суть математики каким-то одним её "методом".
Это в корне неверно. "Несомненные интуиции" - это миф. Наши интуиции уточняются, шлифуются по мере развития как мышления, так и математики. Когда-то всем казалось несомненной интуицией возможность существования только евклидовой геометрии. Интуитивисты часто обвиняют нас в "вере в бесконечности", хотя на самом деле религиозная вера свойственна скорее им - вера в непогрешимые математические интуиции.
Взгляд на математику как на науку, открывающую идеальные несомненные истины, в отличие от ненадёжных эмпирических наук, где мы всегда вынуждены пользоваться лучшей теорией из имеющихся, зная, что однажды может появиться лучшая теория, описывающая физическую реальность, также ложен. Критерием "истинности" может быть только практика. Мы пользуемся законом исключения третьего не потому, что считаем его несомненной истиной, а потому, что на данный момент нет лучшей альтернативы той логике, которая включает закон исключения третьего. Те "математики", которые строятся без закона исключения третьего, пока не принесли никакой пользы и только пытаются отнять у нас те несомненно полезные результаты, которые даёт "классическая" математика.
Нынешняя классическая математика возможно однажды будет заменена лучшей альтернативой (также, как Общая теория относительности заменила Ньютонов закон гравитации) - но только тогда, когда эта лучшая альтернатива появится. Интуитивисты же большей частью подобны современникам Ньютона, которые говорили бы "эта теория неверна, т.к. дальнодействие абсурдно; ничто не может действовать на расстоянии, так что Ньютон неправ", не предлагая лучшей альтернативы и игнорируя те огромные практические результаты, которые давала теория Ньютона.
Математика - довольно "странная" наука, так как она исследует что-то очень абстрактное - абстрактные структуры. Поэтому неудивительно, что её постоянно пытаются свести к чему-то более конкретному: интуитивисты - к психологии (во всяком случае, к той части психологии, которую они считают непогрешимой), конструктивисты - к вычислениям, формалисты - к оперированию символами. Конечно, математика связана со всеми этими областями, она пользуется и интуициями, и вычислениями, и формальным методом как мощными инструментами. Но нельзя заменить суть математики каким-то одним её "методом".
>Наши интуиции уточняются, шлифуются по мере развития как мышления, так и математики.
Верно, и интуиционизм как раз и представляет такое уточнение, такую шлифовку традиционной (постренной на вере в божественное) "математики".
"постренной на вере в божественное"
Считать бесконечность чем-то "божественным" - это личная проблема интуиционистов. Интуиционизм выступает здесь как подобный солипсизму вид бесплодной гиперкритики (мы не можем доказать существование внешнего мира помимо субъективных ощущений, следовательно, нужно выбросить все теории, основанные на "вере" в существование внешнего мира).
Интуиционист подобен астроному, который считал бы, что утверждать, будто Вселенная так велика, как следует из современной астрофизики - религиозная вера. Можно же предположить более "экономное" описание реальности - наша солнечная система - это "гигантский планетарий", за пределами которого ничего нет. Возможно даже описать "физические законы" такой компактной Вселенной (законы поведения такого планетария), которые оказались бы излишним усложнением более простых законов физики.
>Математика - довольно "странная" наука, так как она исследует что-то очень абстрактное - абстрактные структуры.
Слишком сложное пояснение. И ничего странного в этой науке нет. Математика нужна для того чтобы решать уравнения. Все теории нужны только чтобы дать ответ, когда уравнение(или система уравнений) имеет решение, при каких условиях уравнение имеет единственное решение, при каких его можно вычислить и как.
Неравенства -- это частный случай уравнений, где ничего неравно.
> Главное заблуждение интуитивистов заключается в том, что математика по их мнению - это наука, которая должна открывать некие несомненные, абсолютные истины,
Первое предложение и уже хуйня. Дальше читать смысла не вижу. И да, интуиционизм это называется, название хоть осильте, потом лезьте со своими маняопровержениями.
> куска математики, который по-мнению интуитивистов построен на "несомненных интуициях".
> Это в корне неверно. "Несомненные интуиции" - это миф. Наши интуиции уточняются, шлифуются по мере развития как мышления, так и математики. Когда-то всем казалось несомненной интуицией возможность существования только евклидовой геометрии.
А, вот ещё интересно, где вы долбаебы вычитали про какие-то "несомненные интуиции", тут уже не первый дегрод эту хуйню несёт, явно это откуда-то, не сами же вы придумали. Откуда вы это взяли? Тоже хочу почитать.
> Ну или не боготворил, но спиздил всю философию, это еще называют "повлял".
И что он у Шопенгауэра спиздил? Повлиять на него много кто повлиял, Кант тот же. Но Брауэр никогда бездумно не пиздил идеи, если и использовал или отвергал что-то, то обоснованно.
А причём тут основания вообще? То, о чем ты пишешь - это идентификация систем. Система в общем случае это совокупность измеримых и связанных друг с другом параметров. Динамическая система - это когда эти параметры меняются со временем. Любая динамическая система представима в виде моделей типа NARMAX, т.е в простейшем случае - в виде матриц Ганкеля.
"Концепции симметрии как основополагающему аспекту природы противостоит концепция абстрактной вычислимости, предполагающей дискретную природу вселенной. В более романтических терминах, вопрос о природе вселенной стоит так: является ли вселенная гигантским компьютером? Более точно, превосходят ли законы природы возможности абстрактного вычисления? "
"Если такая парадигма победит, это будет означать, что во вселенной могут происходить только вычислимые процессы. Это является довольно проблематичным, поскольку имеется много примеров, где элементы описания не могут быть перечислены конечным числом шагов тьюринговского типа. Некоторые невычислимые процессы подобного рода обсуждались выше. Очевидно, что если мы не готовы принять «вычислимую» вселенную в виде тьюринговской машины и в то же время верим, что познаваемость мира зависит от вычислительной мощи человеческой технологии, нам придется искать расширение понятия вычислимости."
"Очевидно, что если мы не готовы принять «вычислимую» вселенную в виде тьюринговской машины и в то же время верим, что познаваемость мира зависит от вычислительной мощи человеческой технологии, нам придется искать расширение понятия вычислимости."
Вычисление -- это измышление об предмете.
Алгоритм -- это единица вычисления.
Интуиционизм -- это попытка описать пространства, минимальными основаниями.
По всей видимости, всякие вычисления сводятся к дискретному, прерывному.
Потому что, мысль является частным случаем натурального числа.
Такой закон. Говорить о непознаваемом бессмысленно.
Но нам точно известно, что рассуждения образуют натуральное множество.
Мы встречаемся, с такими вещами повсеместно.
Например, число легко описать двоичной системой счисления.
Логику легко описать двоичной системой счисления.
Механику легко описать двоичной системой счисления.
А вот... Понятия цвета. Какие цифры не были бы на конвейере. Ты никогда не сможешь описать красный или зеленый.
Математика, информатика занимается измерениями. Ведь, исключительно в рамках измерениях возможно размышление.
Измерения появляются тогда, когда существуют взаимоисключающие состояния.
Истина и ложь. Пример дискретной, конечной измеримости.
Это одномерное пространство.
В определении бита, единицы информации сказано...
Двойственность является требованием, для наличия информации.
Другими словами, информация появляется там, где появляются измерения.
И элементарной(битом) информацией будет единичный заряд двоичной системы счисления.
Взаимоисключающие состояния дают нам возможность познавать вещи и предметы.
> А вот... Понятия цвета. Какие цифры не были бы на конвейере. Ты никогда не сможешь описать красный или зеленый.
Про RGB кодирование ты не слышал, разумеется.
 284 Кб, 600x591
284 Кб, 600x591Ну вот, уже до тезиса Черча-Тьюринга-Дойча додумались. Мейлру познавательный.
RGB использует физические понятия(определенным образом отражают свет в физическом мире).
Также, цвет является измеримым, но само явление как таково непознаваемо.
Каждому цвету можно сопоставить число, частоту электромагнитных колебаний. Но это не достаточно.
> Также, цвет является измеримым, но само явление как таково непознаваемо.
Про фотоны, фоторецепторы слышал что-нибудь?
>Вычисление в математике является аналогом измерения в физике.
Нихуя, потому что вычисление это априорное синтетическое явление, а измерение -- апостериорное аналитическое. По-разному задействуется категориальный аппарат мышления при формирований представлений об этих объектах, значит, они разной природы и даже близко не являются аналогами. мимопиздоёб
Ding an Sich, братуха ёба
Вопрос, является ли определенно размышление априорным или апостериорным, является вопросом биологов.
Биологическая теория познания, ставит крест на то, что является изначально присуждено природой,а что в результате опыта.
Генотип и фенотип. Говорят, что древние племена воспринимают далекие предметы, как маленькие. И тяжело представляют концепцию числа. Говорит ли это об опытности в математических изысканиях?
Я говорю про цвет, который вижу.
Никогда, НИ ПРИ КАКИХ УСЛОВИЯХ, не смогу описать зеленый слепому.
Он может узнать, что это определенная электромагнитная волна, что это определенные колебания света.
Но это ничего не даст. НИЧЕГО.
Нельзя. Это будет подобно тому, как странник обойдя весь мир, поведает свою историю. Ты просто не будешь там, информация донесется до тебя, но не ЧУВСТВА.
Ведь, ЧУВСТВА передать невозможно.
Измерения - вычисления
Модели - вычисления
Из этого следует. Элон Маск прав. Мы живем в симуляции.
Не передаст. Зеленый цает нельзя описать, математически. Вкус колбасы, нельзя.
Лишь свойство наличности и отсутствия.
Либо эпифеномены, всякие побочные продукту.
Прозаист описывающий ландшафт, занимается вычислениями выдуманных миров.
> Аноним 07/09/18 Птн 16:18:50 №428
Симуляция -- это искусственное проектирование систем.
Познание является симуляцией, создает отображение мира вокруг. Ведь присутствует субъект.
Наш мир может тоже быть симуляцией, а не только знания. Например, в случае, если мир создан Богом(разумным началом, не естественным, а искусственным), наш мир является симуляцией.
Скоро дойдём до эволюционной эпистемологии
А о том, что индивидуальное цветовое восприятие зависит от того, как именно твой мозг обрабатывает сигналы, ты же догадываешься? И о том, что у тебя не может быть уверенность, что другие люди воспринимают RGB(255,0,0) так же, как и ты?
априорное синтетическое явление
Ага, особенно когда ты будешь вычислять что-то на квантовом компьютере
Так рассуждать, у меня вообще не может быть ни в чем уверенности. Солипсизм как есть. Лень объяснять, в чем ты проебался, веруй дальше во что ты там веруешь.
> Динамическая система - это когда эти параметры меняются со временем.
А разве это не когда последующее состояние системы зависит от предыдущего?
Математики, сэр.
>Симуляция -- это искусственное проектирование систем.
Cимуляция — это отображение одной физической системы на другую физическую систему и вычисление с помощью неё. Даже простые числа отображение одной физической системы на другую.
https://indicator.ru/news/2018/09/06/prostye-chisla-kvazikristall/
Если перестать различать естественное и искусственное, то получается, симуляция -- это отображение.
Очевидно, познание или созерцания -- симуляция.
Ведь, перед непосредственной записью стоит интерпретатор.
А, если мы видим объктивно, тогда мы просто воспринимаем через интерпретатор, который не имеет искажений. Т.е тоже симуляция с нулевой искаженностью.
Примером симулирования будет поход в туалет. Когда человеку сопоставляется факт мочеиспускания.
Или, например, всякий секс является симуляцией. Ведь, двум партнерам сопоставляется набор биологических действий.
 20 Кб, 398x273
20 Кб, 398x273Биология является описательной наукой.
Там видят, и делают выводы.
Чтобы увидеть, режут.
Вычислением становится не сам факт обретение знания, а использования знания, чтобы обрести новое.
Знаешь свойство белков, выводишь новое.
Ботаника, аграрная промышленность, медицина, скотоводство. Везде нужно вычислять.
Интерпретация, это то знание, которое мы получаем, прежде, чем обретаем возможность о нем размышлять. В данном контексте.
Ты будешь отрицать то, что индивидуальные особенности колбочек твоей сетчатки глаза или твоей зрительной коры мозга вносят коррективы в твоё восприятие RGB(255,0,0)?
>Из его интуиционизма следует и тезис Чёрча-Тьюринга-Дойча и даже квантово-волновой дуализм.
Каким образом квантово-волновой дуализм из него следует?
Уж во всяком случае коррелятом того или иного феноменального опыта являются определённые информационные процессы в мозгу, а не длина волны света, падающего на сетчатку. Последнее лишь отчасти верно потому, что наша сетчатка, свойства колбочек, глазных нервов, да и устройство мозга ПРИМЕРНО одинаково (и то, всё же со индивидуальными особенностями).
Открой уже для себя разницу между объективным и субъективным. Так вот, длина волны фотона обьективна, а её восприятие может и отличаться для субъектов в зависимости от их индивидуального опыта. У чукчей вон 11 названий для сортов снега в зависимости от цвета, и они их не путают. А для человека, не живущего в снегах, разницы никакой.
Я об этом и говорю. Есть огромная разница между объективным и субъективным.
>Про RGB кодирование ты не слышал, разумеется.
RGB-кодирование объективно. Феноменальные переживания субъективны. И потому феноменальное переживание красного цвета невозможно зашифровать в какой бы то ни было кодировке или системе символов.
Вполне возможно, что множество всех возможных феноменальных переживаний несчётно или вообще превышает любой кардинал (являясь уже не множеством, а чем-то большим - классом), а потому невозможно прямое соответствие между феноменальными переживаниями и конечными словами в алфавите с конечным числом символов.
На самом деле нет разницы никакой, поскольку ты интроецируешь свой эмпирический опыт. Объект ДЛЯ ТЕБЯ является объектом только в момент взаимодействия с тобой, а по факту это просто то, как твой организм проецирует НЕЧТО на твой аппарат созерцания. Мы просто по умолчанию принимаем, что существует нечто за пределами нас, поскольку мы в состоянии категоризировать некоторые свои представления как внешние, это имманентная черта нашего сознания. Моё послание всем математикам жи есть: не лезь бля дибил сука ебаный. Разрабатывайте формальные системы, генерализуйте абстрактные представления, занимайтесь синтаксисом формальных систем. Семантикой занимаются фелосафы.
Мимо-феласаф
> Моё послание всем математикам жи есть: не лезь бля дибил сука ебаный. Разрабатывайте формальные системы, генерализуйте абстрактные представления, занимайтесь синтаксисом формальных систем. Семантикой занимаются фелосафы.
Ну что ты за долбоклюй. Брауэр для философии математики сделал больше, чем может любой философ. Даже Кант оказался неправ во многом, что касается математики.
>занимайтесь синтаксисом формальных систем. Семантикой занимаются фелосафы.
Самые важные результаты математической логики достигнуты именно на стыке синтаксиса и семантики. Смотри Теорию моделей:
https://ru.wikipedia.org/wiki//Теория_моделей
А ещё тогда вопрос, в интуиционизме используется принцип индукции? Потому что возникает впечатление, что в рамках этой концепции он просто неприемлем. Джон Локк бы одобрил
> А я правильно понимаю, что в интуиционизме закон исключённого третьего считается хуйнёй, потому что тот факт, что никто до сих пор не представил тезис, который был бы одновременно истинным и ложным, не значит, что это в принципе невозможно?
Нет. В интуиционизме сключенное третье верно в случаях, когда его можно доказать. Но не как общий принцип, в который веруется априори. Это вытекает из свойств конструктивного отрицания, т.е для утверждения "А или не А" должно быть построено доказательство А или же построено доказательство того, что построение А невозможно.
Тут скорее наоборот - есть случаи, когда мы не можем доказать ни истинности суждения, ни его ложности. Например, "гипотеза континуума" - в середине XX века было доказано, что мы не можем в рамках теории множеств доказать ни истинности этой теории, ни её ложности.
Отрицание как ЛОГИЧЕСКАЯ ОПЕРАЦИЯ вообще по определению предполагает бинарность высказывания с формальной точки зрения, вне зависимости от содержания. Т.е. если ты специально не выёбывался с антиномиями, то отрицание по своей сути и определению предполагает исключённое третье. Если это НЕ ТАК, то С ХУЯ в интуиционизме используется принцип ДВОЙНОГО ОТРИЦАНИЯ? Ведь, фактически, без принципа исключённого третьего ты не имеешь права считать операцию отрицания идемпотентной по умолчанию, значит, тебе нужно доказать, что ¬¬A эквивалентно A, что ¬¬¬¬A эквивалентно A, и так далее. Доказать это без индукции на основе идемпотентности А невозможно, а если идемпотентность предполагается, тогда закон исключённого третьего должен приниматься за аксиому как встроенный в определение отрицания. Ебанутая концепция этот интуиционизм, вот что я скажу, пацаны
>С ХУЯ в интуиционизме используется принцип ДВОЙНОГО ОТРИЦАНИЯ
Он и не используется. Ура, я всё правильно понял. Вы меня заинтересовали этой хуйнёй, я поботаю что-нибудь на тему
>Ебанутая концепция этот интуиционизм, вот что я скажу, пацаны
Это так, я лично так и не понял чем же двойное отрицание отличается от обычного и если у нас есть только истина и ложь, то чему ещё может быть равно не не А, кроме как А. Но всё же эти треды повлияли на меня, я стараюсь теперь всегда где возможно использовать конструктивное доказательство.
> Отрицание как ЛОГИЧЕСКАЯ ОПЕРАЦИЯ вообще по определению предполагает бинарность высказывания с формальной точки зрения, вне зависимости от содержания. Т
Нет. Помимо "истинно" и "ложно" возможны другие варианты - "неизвестно", " хуй его знает", "в настоящее время неизвестно" итд. Я же говорю, тут все дело в свойствах конструктивного отрицания. В машине Тьюринга кроме результативного или безрезультатного останова возможен ещё и третий вариант - безостановочная работа. И вопрос когда что получится, в общем случае неразрешим. Хотя с формальной точки зрения, или остановится или нет. В чем и разница между формализмом и вычислимостью. Поэтому классическая логика не формализует понятие алгоритма, а просто затыкает проблему останова невычислимым (как общий принцип) верованием в исключение третье.
Что такое отрицание?
!0=1
!1=0
Рассмотрим двойное отрицание.
!!1
Подставим, вместо "!1" знак "0"
Получаем !(!1)=!0=1
Что такое отрицание?
Если поставить под сомнение все, останется лишь знание о том, что это явление.
Тогда отрицание, это порождение нового явление из прошлого.
Говоря об существовании отрицания, мы говорим, что для каждого предмета есть другой предмет, называемый !предметом.
Кстати, вроде, Арнольд приводил примеры естественной речи, где понятие отрицания выходила за рамки теории высказываний.
В таком случае, закон двойного отрицания абсолютно требуемый.
Автоморфизм -- это пример отрицания себя(т.е работает закон !1=1)
Если эндоморфизм -- это отображения в себя.
А изоморфизм -- это прямые, для которых существуют обратные отображения.
Тогда автоморфизм -- это эндоморфизм, являющийся изоморфизмом.
В многозначных логиках может. В нечёткой логике разрешим парадокс лжеца - он говорит правду и неправду в соотношении 50/50%. Этот и похожие парадоксы характерны только для бинарной логики.
>>42973
Я так понял, что закон исключённого третьего не должен приниматься на веру в конкретных случаях, -- в которых пресуппозиция предполагает наличие третьего варианта, а чувак, разрабатывающий ту или иную систему, не видит этого и пытается напялить на всё булеву алгебру, следовательно, классическую логику. Буквально, когда ты неправильно подобрал формальный инструментарий для конкретного случая
> Я так понял, что закон исключённого третьего не должен приниматься на веру в конкретных случаях,
Не должен приниматься на веру как общий принцип, априори истинный всегда, как аксиома. В случаях, когда доказать его можно, в нем нет ничего страшного.
Истинность вовсе не равноценна доказуемости в формальной системе. Смотри, например, теорему Гёделя о неполноте, доказывающую, что для любой формальной системы существует истинное, но недоказуемое в рамках этой формальной системы предложение.
fix - для непротиворечивой формальной системы с арифметикой
> Истинность вовсе не равноценна доказуемости в формальной системе.
В чем и проблема такой религии как формализм. Веруется, что есть какая-то высшая истинность, независимая от самого математического объекта и существующая в платоновском мире идей например. Конструктивно же это не так, истинность это то же самое, что доказуемость, вычислимость, построимость. Поэтому конструктивная система может быть полна максимум в смысле Тьюринг-полноты. Из этого же вытекает невозможность формализации интуиционизма, т.к такая формализация одновременно решала бы и проблему останова, а это невозможно. Разумеется, эту невозможность можно заткнуть исключенным третьим и внешней по отношению к системе аксиоматикой, постулирующей какую-то истину, независимую от математики.
>истинность это то же самое, что доказуемость, вычислимость, построимость.
>полна максимум в смысле Тьюринг-полноты.
назовем это аксиомами конструктивной математики, постулирующими какую-то истину, независимую от математики
 118 Кб, 811x1147
118 Кб, 811x1147По не помню какому разу объяснять, чем аксиомы отличаются от выводимых свойств, в чем разница между аксиомой и теоремой? Спасибо, не интересно.
Но ведь формализм как раз таки отрицает понятие математической истины помимо доказуемости в формальной системе. С этой точки зрения для формалиста вполне возможен случай, когда A не является истинным, (НЕ A) не является истинным, (A ИЛИ (НЕ A)) является истинным. Из истинности последнего не следует, что какое-то из первых должно быть истинно. Во всяком случае именно так утверждают Бурбаки в первых же главах своего Трактата.
Исключенное третье в формализме истинно потому что Гильберт так скозал, безотносительно того, можем ли мы доказать истинность его составляющих (А или не А), т.е это априорная истинность, независимая от возможности доказательства. Конструктивно же А или не А истинно только если мы можем построить А или доказать, что А непостроимо.
да, это я понимаю. Для формалистов истинность зависит исключительно от произвольно выбранных аксиом (тех самых "я так сказал" и тех теорем, что могут быть выведены из них по произвольно выбранным правилам вывода). В этом смысле чистый формализм является прямой противоположностью платонизма, так как сводит математику к чистому синтаксису, отказываясь интерпретации этого синтаксиса вне манипуляции знаками.
Останов может быть результативным или безрезультатным (программа вывалится с ошибкой итд). Вместе с отсутствием останова это уже три а не два варианта. Далее, если нам неизвестен алгоритм для какой-то задачи, это не является доказательством, что такого алгоритма нет принципиально. Т.е мы не можем сказать, возможен такой алгоритм или нет, отсутствие само по себе не доказывает невозможности.
Но безотносительно к нашей возможности доказать остановку алгоритма и рассматривая в качестве алгоритмов классические алгоритмы Тьюринга, можно ли сказать, что любой алгоритм либо останавливается, либо не останавливается?
Значит, интуиционизм/конструктивизм - хуйня. Я ещё могу понять аргументы против актуальных бесконечностей, аксиомы выбора и всего такого прочего, но утверждать, что относительно алгоритма мы не можем сказать, что он либо остановится, либо нет - это уже имхо перебор.
да, и не надо втирать, что за моей уверенностью в том, что алгоритм либо останавливается, либо нет, стоит вера к какие-то платонические сущности.
Почему не надо? Ты сам себе уже всё объяснил.
> Значит, интуиционизм/конструктивизм - хуйня. Я ещё могу понять аргументы против актуальных бесконечностей, аксиомы выбора и всего такого прочего, но утверждать, что относительно алгоритма мы не можем сказать, что он либо остановится, либо нет - это уже имхо перебор.
Ты не можешь понять, что суть того, что ты перечислил это одно и то же. Затыкание проблемы невычислимой хуйней. Да, про любое математическое выражение можно сказать, что оно либо равно 42, либо не равно. И это даже действительно так. Но, какая с этого польза, зачем такое высказывание математике, какое оно вообще имеет отношение к математике? Это чистая демагогия и детский сад уровня "купи слона".
> да, и не надо втирать, что за моей уверенностью в том, что алгоритм либо останавливается, либо нет, стоит вера к какие-то платонические сущности.
А это она и есть, вера в платонические сущности. Ты веруешь во что-то, что в общем случае из самого алгоритма невыводимо. Т.е во что-то, не связанное с алгоритмом, а в какую-то общую истину, априори верную, вне связи с тем, о чем она вообще. Платонизм и есть в его худшей религиозной форме.
> Не понимаю
Именно. Все дело в свойствах конструктивного отрицания. Оно работает не так, как классическое, отсутствие доказательства А не подразумевает "не А" автоматически. "Не А" так же должно быть построено, только тогда оно принимается. Т.е конструктивно отсутствие доказательства не значит вообще ничего и ровно ничего не доказывает. Поэтому исключенное третье верно только тогда, когда может быть построено, а не априори как какая-то заповедь, как это принято классически.
> unconstructed(мол вот когда вычислим, тогда и поговорим)
А так оно и есть. В конструктивизме внезапно рассматриваются только конструкции, а не аксиомы, заповеди и платоновские идеи оторванные от построения.
Как раз, платоновский мир идей конструктивизм обойти не может.
Просто конструктивизм предлагает альтернативный список. Включая в мир идей только могущие к строительству идеи
Идеи в данном случае - лишние сущности, конструктивизму не нужные, т.к он может и без них. А то ведь такие идеи можно назвать барабашками или сепульками и потом утверждать, что конструктивизм не может обойти теорию сепулек. Только все это демагогия уровня детского сада.
>отсутствие доказательства А не подразумевает "не А"
А в классическрй разве подразумевает? Тогда бы, скажем, гипотеза Римана была бы ложна, ведь нет доказательства. Хотя в жизни такая логика как раз работает, отсюда все эти бремя доказательства и тп.
>А так оно и есть.
Хм, я понял кажется, инт логика изначально, ещё до всех манипуляций, проверяет конструктивность высказывания, а уже только потом выясняет истинно оно или ложно. Ну здраво так-то.
>инт логика
Ну конечно сама логика ничего не проверяет, просто её область применимости только конструктивные сущности, думаю ты понял меня.
Потому, что алгоритм либо останавливается, либо не останавливается!
Если я докажу, что из того, что он останавливается, следует A, и докажу, что из того, что он не останавливается, следует A, значит A верно в любом случае. Значит A истинно. И для этого мне не нужно знать, остановится ли алгоритм или нет - достаточно того, что одно из двух обязательно верно.
>Вне связи с тем, о чем она вообще
Нет, я говорю про конкретные вещи. Если передо мной - конкретный сформулированный алгоритм, я в любом случае знаю, что он либо останавливается, либо не останавливается.
т.е. у тебя тезис черча выводимое свойство? вера твоя сильна. Да и остальные выводимые свойства такие забавные, возьмем вместо аксиомы выбора аксиому хуевого выбора, вместо полноты хуевую полноту, и оп-ля у нас построимая математика (в которой правда построить нихуя нельзя, даже ебаный анализ дальше 19 века не продвинулся).
Смотри, ты видишь алгоритм, например:
1. Мальчик берет ящик из Точки А
2. ТОТ ЖЕ мальчик кладет ящик в точку B.
(1. Перейти в пункт 2
2. Завершить)
Как ты определишь, является ли он конечным или бесконечным?
"Конечность -- это то, чему наблюдатель может сопоставить натуральные числа в прямом эфире".
1. Перейти в пункт 2
2. Перейти в пункт 1
Этот алгоритм пример бесконечен? Мы всегда можем верить в наблюдателя, который сможет завершить этот алгоритм.
Но, чтобы такое могло быть, мы должны принять аксиому:
1. Всегда есть выход из вычислений. И он заключен в неведомой природе. Всякий алгоритм конечен.
Тогда, наш второй алгоритм, пройдет какое-то кол-во циклов, но должен будет завершиться, согласно природе нашего мира.
Нету бесконечных алгоритмов. Нету симулякров из постмодернисткой философии. Нету копий несуществующих идей.
Реальность творится во мгновения.
Тогда, получается вопрос. Каким образом происходит то, что происходит? Каким образом образуется форма(которая обязывает сразу быть реализованной).
Вот-вот, шаг... И формы не было, но она возникла.
Есть строители. Числа строят наблюдатели.
Откуда у них способности создавать формы?
Откуда у них дар творения? Они же простые наблюдатели.
Они творят, используя ВЫСШИЕ СИЛЫ. Очевидно, мир создал их такими, ТВОРЯЩИМИ. Но творящими не вопреки, а сомиром.
Смотри, ты видишь алгоритм, например:
1. Мальчик берет ящик из Точки А
2. ТОТ ЖЕ мальчик кладет ящик в точку B.
(1. Перейти в пункт 2
2. Завершить)
Как ты определишь, является ли он конечным или бесконечным?
"Конечность -- это то, чему наблюдатель может сопоставить натуральные числа в прямом эфире".
1. Перейти в пункт 2
2. Перейти в пункт 1
Этот алгоритм пример бесконечен? Мы всегда можем верить в наблюдателя, который сможет завершить этот алгоритм.
Но, чтобы такое могло быть, мы должны принять аксиому:
1. Всегда есть выход из вычислений. И он заключен в неведомой природе. Всякий алгоритм конечен.
Тогда, наш второй алгоритм, пройдет какое-то кол-во циклов, но должен будет завершиться, согласно природе нашего мира.
Нету бесконечных алгоритмов. Нету симулякров из постмодернисткой философии. Нету копий несуществующих идей.
Реальность творится во мгновения.
Тогда, получается вопрос. Каким образом происходит то, что происходит? Каким образом образуется форма(которая обязывает сразу быть реализованной).
Вот-вот, шаг... И формы не было, но она возникла.
Есть строители. Числа строят наблюдатели.
Откуда у них способности создавать формы?
Откуда у них дар творения? Они же простые наблюдатели.
Они творят, используя ВЫСШИЕ СИЛЫ. Очевидно, мир создал их такими, ТВОРЯЩИМИ. Но творящими не вопреки, а сомиром.
Если математик был картинкой, то он, что ли, не мог бы вычислять?
Мне кажется, наибольшим странным представляет интерес(с точки зрения мистики), это однашаговые или безшаговые доказательства.
Например, доказать, что а=а.
1. "=" обладает свойством рефлексивности, т.е aRa есть истина, и
a и a являются частными случаями левых/правых аргументов "=", следовательно a=a истинно.
Доказать, что точка, на которую смотрит наблюдатель(на статической картинке), является той же самой точкой.
1. Точка, является нульмерным пространством, не имеющим измерений. Но, если точка принадлежит высшим измерениям, то обретает атрибуты именно их. Если наблюдатель после нескольких экспериментов на статику, соотносит одной точки те же самые атрибуты, то это точка является равной той(если соотнести время наблюдателя с реальностью) Атрибуты точки будет звать расположением. Подобное наблюдение обоюдности в себе, заключена лишь мистика, не больше. Невозможно конструктивно доказать, что А является А. Если ты видишь А и А.
Мы не можем написать алгоритм того, как мы распознаем лица своих родителей, и отличаем монитор от собаки. Но алгоритмы есть?? Они используют,(я практически уверен), физические теории, не только математические.
1
Аксиома выделение. Наблюдатель может сопоставить мирозданию пространства(теории). Истинность вечна неопределенна. Но теории обладают следующими структурами:
1. Эквивалентность, ==, ~
2. Теоремы. То, что не сказано в аксиомах
3. Редукция. Если у нас есть некоторое общее, тогда, мы можем подставить в него частное, и использовать свойства общего.
4.Натуральные числа, количество аксиом, количество теорем, етс...
5.Ссылка на интуицию, магичность
6.Ошибки вычислителей
7.Статус, выгодность, эстетика.
8. Сложность.
9. Высказывания, являющиеся одновременно истинными. Высказывания, которые истины для любого.Концепция истины/лжи, двоичности
10.
>>40966
>>42980
Суть парадокса:
Парадокс лжеца — утверждение «То, что я утверждаю сейчас — ложно» (либо «Я лгу», либо «Данное высказывание — ложь»).
Если это высказывание истинно,
значит, исходя из его содержания,
верно то, что данное высказывание — ложь;
но если оно — ложь,
тогда то, что оно утверждает, неверно;
значит, неверно, что данное высказывание — ложь,
и, значит, данное высказывание истинно.
Таким образом, цепочка рассуждений возвращается в начало.
Заметьте, не обязательно, чтобы эту фразу сказал лжец. Ведь о говорящем человеке, в условии - ничего не сказано.
Сама же попытка разобраться в истинности высказывания - представляет из себя рекурсивную булеву функцию.
http://rextester.com/DKMBA30473
Если ещё короче, то вот: https://bash.im/quote/268036
#define TRUE FALSE
#define FALSE TRUE
То есть если сравнить функцию попытки разобраться,
с функцией вычисления числа знаков числа пи,
подмечая закономерность чередования единиц и нулей,
то можно сказать, что задача установления окончательной истинности высказывания - невычислима в принципе.
> Если передо мной - конкретный сформулированный алгоритм, я в любом случае знаю, что он либо останавливается, либо не останавливается.
Какая разница, что ты знаешь? Тебе выше написали, конструктивное доказательство это построение. А то что ты знаешь, что нет бога кроме Винни-Пуха а Карлсон пророк его, это твоё дело.
>>43067
> т.е. у тебя тезис черча выводимое свойство?
Рекомендую погуглить откуда он вообще взялся, вместо того чтобы кукарекать.
>>43048
> А в классическрй разве подразумевает?
Да, в этом суть исключённого третьего.
>>43062
> Если я докажу, что из того, что он останавливается, следует A, и докажу, что из того, что он не останавливается, следует A, значит
Значит, решишь проблему останова. Пробуй.
> И для этого мне не нужно знать, остановится ли алгоритм или нет - достаточно того, что одно из двух обязательно верно.
Верно только то, что построимо/вычислимо. Тебе знать вообще ничего не нужно, плоти нологи и все. Но если речь о конструктивном доказательстве, твоя вера ничего не решает без построения.
>Да, в этом суть исключённого третьего.
Ну тогда ведь всё, что не доказано, то ложно получается. Нет, ты что-то путаешь, тогда ответ на все открытые проблемы ложь автоматом, этого не может быть.
Я имел в виду, что исключенное третье как общий принцип, аксиома, не требует доказывать А или не А, т.к считается что все равно или или, безотносительно того есть ли доказательство или его нет.
Задолбали все со своим исключением третьего.
Например, натуральные, целые, рациональные, действительные, комплексные, квартерионы, октавы, вектора, функции, множества, категории, отображения, етс.
к
Это все то, что обладает бесконечным количеством вариантов, а не одним. Вместо числа "5", может стоять "f(x)" или "12+5i".
Другими словами, в каждом разряде бесконечное разнообразие вариантов.
В отличии простой и самой минимальной дихотомии истина/ложь. Где всего два варианта.
 10 Кб, 276x183
10 Кб, 276x183> В отличии простой и самой минимальной дихотомии истина/ложь. Где всего два варианта.
Тут был клован, который за несколько лет так и не понял в чем отличие актуальной бесконечности от потенциальной. Ты, я вижу, не понимаешь чем отличается конструктивная логика Гейтинга от таблицы Тарского в самом элементарном вопросе - исключенное третье. В связи с чем вопрос - откуда вы лезете это на самом деле так сложно - просто прочитать?
>чем отличие актуальной бесконечности от потенциальной
Актуальная уже существует, а потенциальной нету, но она может стать актуальной после некоторых действий!?
>Рекомендую погуглить откуда он вообще взялся, вместо того чтобы кукарекать.
Он взялся, чтобы решить невозможность построения финитной математики просто отсеканием некоторой ее части. "Ваша математика не математика, математика это теория вычислимости" - донеслось со стороны конструктивистопараши.
https://en.wikipedia.org/wiki/List_of_undecidable_problems
А ты уже научился решать конструктивно такие проблемы как "[0,1] компактно" или или теорему о среднем значении? Или на 2018 год эти проблемы до сих пор открыты?
Теперь понятно.
>> Если я докажу, что из того, что он останавливается, следует A, и докажу, что из того, что он не останавливается, следует A, значит
>Значит, решишь проблему останова. Пробуй.
Проблема останова этим не решается. Я по-прежнему не знаю, остановится ли алгоритм B или не остановится. Но я знаю, что A истинно, если A следует как из того, что алгоритм остановится, так и из того, что алгоритм не остановится.
Мне не нужны какие-то "конструктивные доказательства". Мне нужны работающие доказательства. Закон исключения третьего работает, даже если кому-то это не нравится. Интуитивисты подобны солипсистам, которые отрицали бы любые научные теории об объективном мире, потому что мы вообще не можем доказать, что объективный мир существует.
Верно. В мире (в том числе математическом) есть объективно истинные вещи, даже если мы не способны узнать или доказать их истинность. Истинность чего-то не зависит от нашей способности узнать эту истину.
Возможно есть объективная истина, а возможно нету. Проверить это невозможно.
Главная претензия к конструктивизму его бесполезность в современной математике. Программа Лэндлендса, syz-гипотеза, abc-гипотеза, гипотеза Пуанкаре, тропическая геометрия, все они базируются на сотнях и тысячах теорем, доказанных классической математикой с использование аксиомы выбора и без конкретного построения. У этих теорем просто нет конструктивных доказательств, никто этим не занимается, потому что обьем огромный, а конструктивные методы тяжелы и уродливы (стоит только взглянуть на конструктивную топологию, например, и попытаться в ней что-то доказать).
Конструктивизм -- это основа прикладного знания, основа всех желаний, основа всего на свете.
Колгоморов говорил, что конструктивизм -- это искусство решение задач, искусство исполнения желаний.
Построение позволяет обратиться к миру в мире, и стать чудным странником во мгле большой. Рваться и недоверять. Убивать и нероптать.
Становись конструктивистом, ведь с ним Божий замысел.
Все знают, что математика -- это раздел линейной алгебры, а именно, частный случай модуля над кольцом.(куда делся тот шизик?)
http://krotov.info/libr_min/05_d/oy/ch_05.htm
"Сложные и автономные абстрактные категории объективно существуют и являются частью структуры реальности. Существуют логически необходимые истины об этих категориях, которые и составляют предмет математики. Однако, эти истины невозможно знать определенно. Доказательства не дают их выводам определенность. Обоснованность конкретной формы доказательства зависит от истинности наших теорий о поведении объектов, с помощью которых мы осуществляем доказательство. Следовательно, математическое знание наследственно производно и полностью зависит от нашего знания физики. Постижимые математические истины - это в точности то бесконечно малое меньшинство, которое можно передать в виртуальной реальности. Однако непостижимые математические категории (например, среды Кантгоуту) тоже существуют, т.к. они сложным образом появляются в наших объяснениях постижимых категорий."
> знаю, что A истинно, если A следует как из того, что алгоритм остановится, так и из того, что алгоритм не остановится.
Т.е веруешь в это. Доказательства кто нет.
>>43098
> Мне не нужны какие-то "конструктивные доказательства". Мне нужны работающие доказательства. Закон исключения третьего работает, даже если кому-то это не нравится
Ну да, работает, когда нужно заткнуть чем-то невычислимую проблему. Других задач у него никогда не было.
>>43099
> Верно. В мире (в том числе математическом) есть объективно истинные вещи, даже если мы не способны узнать или доказать их истинность. Истинность чего-то не зависит от нашей способности узнать эту истину.
Ну то есть опять все скатили к вере в то, что что-то есть. Это платоновский мир идей в худшем виде.
> аксиомы выбора и без конкретного построения. У этих теорем просто нет конструктивных доказательств, никто этим не занимается, потому что обьем огромный, а конструктивные методы тяжелы и уродливы (стоит только взглянуть на конструктивную топологию, например, и попытаться в ней что-то доказать).
Естественно, доказать что-то нетривиальное сложно. Гораздо проще заткнуть проблемные места заповедями исключённого третьего и выбора.
> Актуальная уже существует, а потенциальной нету, но она может стать актуальной после некоторых действий!?
Потенциальная бесконечность существует в виде правил построения, например, множества N. Актуальная "существует" в виде заповеди, в мире идей Платона или в священном писании.
Понятно, что любая пара матриц либо вырождена, либо нет.
Не существует алгоритма, который для любой пары матриц решает, вырождена ли эта пара.
> Не существует алгоритма, который для любой пары матриц решает, вырождена ли эта пара.
Зато существует заповедь исключённого третьего, которой можно заткнуть невычислимую проблему. И вроде как все доказали, ну ведь правда же, если пошёл посрать, то или встретишь динозавра, или нет. Истинное высказывание, хуй оспоришь.
> ну ведь правда же, если пошёл посрать, то или встретишь динозавра, или нет
Всё так и есть. Не вижу здесь парадоксов.
Суть в методах, а не в нетривиальности. Пример тому, что решения уравнения 3 степени и выше не могли придумать почти 20 веков, потому что со времен греков принципиально отказывались принимать в расчет иррациональные числа. Вот просто такое ограничение, нисхуя, как запрет на xor. Ферма никогда не смог бы решить свою теорему, используя дремучие методы элементарной арифметики. Используя методы конструктивизма мы оставляем себя в том же отсталом положении науки 19 века.
> Всё так и есть. Не вижу здесь парадоксов.
А парадоксов и нет, есть бесполезность. Ты или не ты чуть выше кукарекал >>43119 что конструктивизм бесполезен, так вот тебе настоящая бесполезность - зачем вообще математика, если любое возможное выражение априори либо равно 42, либо нет. Заповедь исключённого третьего делает бесполезной вообще все.
>>43122
> Используя методы конструктивизма мы оставляем себя в том же отсталом положении науки 19 века.
Начнём с того, что это не так.
>так вот тебе настоящая бесполезность - зачем вообще математика, если любое возможное выражение априори либо равно 42, либо нет.
Верно, что любое выражение равно 42 либо нет. А при чем тут бесполезность?
> Верно, что любое выражение равно 42 либо нет. А при чем тут бесполезность?
А при том, что зачем вообще математика, если все что угодно можно приравнять к "42 или не 42"? Это ж верный ответ в любом случае. И т.о это готовое решение вообще всех математических проблем - от открытых до ещё даже не сформулированных.
>полезность
Субъективная штука, та же теория категория и прочая абстрактная гомологическая чепуха бесполезные вещи бесполезная с точки зрения дидов штука. Хейтя конструктивизм и аргументируя свой хейт его, как тебе кажется, бесполезностью ты уподобляешься дидам с закостеневшим разумом.
> просто нет конструктивных доказательств, никто этим не занимается, потому что обьем огромный
Так если бы у конструктивизма было бы больше последователей и объём перестал бы быть проблемой, но им никто не занимается.
>объём
Ну и вообще, конечно будет объём, почти всегда на порядок сложнее найти конструктивное доказательство, чем заюзать "отпротивное" и вуаля, всё готово.
А откуда ты знаешь, что потенциальная бесконечность существует? Ты проверил все числа, чтобы утверждать, что для каждого существует число большее? Это какой-то стрёмный платонизм.
>А при том, что зачем вообще математика, если все что угодно можно приравнять к "42 или не 42"?
Ты задал вопрос, математика на него ответила. А зачем тебе потребовалось сравнивать всё что угодно с 42 уже дело десятое.
>И т.о это готовое решение вообще всех математических проблем - от открытых до ещё даже не сформулированных.
Неверно. От того, что нам известно, что число pi^e либо равно 42 либо нет не становиться известным рационально или трансцендентно оно.
Бред. Даже в рамках конструктивизма можно сказать, что любое число равно самому себе. И на этом математика заканчивается? Другие свойства чисел тебя после этого больше не интересуют?
Ты до сих пор не понял, чем существование математического объекта отличается от потенциальной бесконечности, для тебя поди пиздец откровение, что ответ на твой вопрос - сами правила построения того же типа N.
>>43134
> Неверно. От того, что нам известно, что число pi^e либо равно 42 либо нет не становиться известным рационально или трансцендентно оно.
Ну либо рационально/трансцедентно, либо нет. Что ты как маленький.
> Даже в рамках конструктивизма можно сказать, что любое число равно самому себе
Чего?
> Другие свойства чисел тебя после этого больше не интересуют?
Ну для любого числа они либо есть, либо их нет. И это таки истинное высказывание же.
Число равно самому себе. Это всегда верно, так что математику можно закрывать. У меня есть решение всех твоих математических вопросов.
Именно так выглядит твоя логика.
>Ну либо рационально/трансцедентно, либо нет
Из задачи уже известно, что либо либо. Эта задача другого типа, где нужно конкретно указать один из двух вариантов, а не доказать, что один какой-то из двух вариантов возможен в отличие от задачи про 42.
Двачую. Странно что конструктивисты со своим гиперскептицизмом верят в то, что их правила построения работают всегда, не применив их ко всем числам. Тот же Есенин-Вольпин, который не верил в существование триллиона, был более последователен
>Начнём с того, что это не так.
Ну что ж, где я могу найти конструктивные учебники по дисциплинам 20ого века: алгебраической геометрии, алгебраической топологии, дифференциальной топологии? Все чем можно заниматься конструктивисту, это передоказывать теоремы 200-летней давности.
Нет.
С конструктивной точки зрения даже не существует предмета доказывания - алгоритма построения изучаемых объектов нет.
Разве что Дарвина за смерть от старости в попытках конструктивно доказать теорему Коши о промежуточном значении.
 84 Кб, 521x500
84 Кб, 521x500ЕРОХЕ СЕКТАНТЫ ДАЮТ МИЛЛИОНА ЗА НЕВЫЧИСЛИМУЮ ХУЙНЮ, КОТОРАЯ НА УРОВНЕ ВЕРЫ В АЛЛАХА
@
ЕРОХА ОТКАЗЫВАЕТСЯ И СТАНОВИТСЯ ИЗВЕСТНЫМ НА ВЕСЬ МИР-БУНТАРЁМ, А К ЕГО НЕВЫЧИСЛИМОЙ ПАРАШЕ ОБЩЕСТВО ПРИКОВАЛО ВНИМАНИЕ, ПЫТАЯСЬ ПОНЯТЬ
@
НОУНЕЙМ-СЫЧОВ МАРГИНАЛ ОТ МИРА МАТЕМАТИКИ СГОРАЕТ НА СТУЛЕ В БУДКЕ ОХРАНИКА ДОКАЗЫВАЯ НА MA@L.RU ОЧЕВИДНЫЕ ЕМУ ОДНОМУ ИСТИНЫ
@
БРАУЗЕР НА НЕБЕ ВМЕСТЕ С АЛЛАХОМ СМОТРИТ С ЕХИДНОЙ УЛЫБКОЙ НА СВОЕГО ПОТОМКА
> Ты не ответил на вопрос про бесполезность здесь >>43134
Ответил. Вся математика сводится к тому, что я там описал, если из неё убрать требование вычислимости результата. А вот к чему ты понес, что конструктивно все числа равны сами себе и это якобы как-то свидетельствует против конструктивного подхода, это у тебя надо спросить. Хотя особого смысла в этом нет, ещё что-то прокукарекаешь.
>Вся математика сводится к тому, что я там описал
С чего ты взял? Посмотри любое доказательство от противного. В таком доказательстве новая информация, нетавтологическая, получается неконструктивными методами.
бля, я понял.
Конструктивистами становятся те, у кого в принципе с логикой плохой - не только математической...
> 1. Думаю, надо доказать, что если a изоморфно a', b изоморфно b' и a>b, то a'>b' (предположить иное и получить противоречие
Пусть, a, b - произвольные натуральные
числа.
Рассмотрим с = ab.
a < c
Пусть f - изоморфизм первой полугруппы во вторую.
Надо доказать, f(a) < f(с).
Предположим от противного, что
f(a) >= f(с).
Тогда
f(a) >= f(ab) = f(a)f(b)
Сократим левую и правую часть на f(a) (в полугруппе четных чисел с единицей можно сокращать и слева и справа на один и тот же сомножитель).
1 >= f(b).
b - произвольное натуральное число, f(b) меньше либо равное единице. Но меньше единицы оно быть не может, следовательно равно единице.
То есть всякое натуральное число изоморфизмом f переводится в единицу. Получается противоречие.
Не ошибся ли я где-нибудь?
К слову, а почему в данном случае не может быть изоморфизма f для которого при некоторых a и b таких, что a<b выполняется f(a)>f(b)?
Так, анон, я нашёл решение.
1~1 в силу единственности нейтрального элемента.
Теперь пусть p~a, где p-простое число.
Легко показать, что a должно быть вида 2b, где b - либо простое число (не равное 2) либо 1. Действительно,
p^2 ~ 4(b^2)
p^2 может быть представлено в виде произведения двух отличных от 1 чисел лишь единственным образом, значит, это должно быть верно и для 4(b^2) (т.е. 4(b^2) должно единственным образом раскладываться на 2 чётных числа).
Любое натуральное число Z отличное от 1 представляется как произведение n простых чисел, следовательно Z~T, где T = (2^n)b1b2..bn, где каждое bi либо равно 1 либо нечётное простое число.
Значит во втором множестве, с которым устанавливается изоморфизм, могут быть только такие числа, при разложении которых на простые степень двойки не меньше чем общее количество нечётных простых. Т.е. число вида 18 = 23*3 во втором множестве отсутствует, значит изоморфизм невозможен.
на каком этапе? может сумбурно объясняю.
Если мы возьмём в N простое число, то ему может быть изоморфно лишь число вида 2*p, где p - простое нечётное или 1 - это понятно? Это главная идея в доказательстве.
Потому что если числу p изоморфно 2ab, то числу
pp изоморфно 22aabb
pp может быть представлено в натуральных только как произведение pp (если не учитывать единицу). А 22aabb = (2ab)(2ab) = (2aa)(2bb) = (2a)(2aab) = (2b)(2aa*b). То есть операция умножения была бы явно не изоморфна.
Обсудили тысячу раз. Отменить всё после сложения дробей или изучать гамологии-тапалогии в 9 классе.
Мне на ум приходит ассоциация что имея какое-то правило мы можем его повтроять(применять повтроно), это и есть эта абстракция?
> в тексте часто упоминается абстракция повторяемости и повторения, не уверен что я правильно это понимаю, объясните значение.
Индукция штоле? Цитату давай
Добавляешь аксиому выбора или слабую версию аксиом выбора и просто берешь элементы по одному.
> Наука рассматривает повторяемость во времени явлений, качественно различных, но взаимно согласованных. Это выделение наблюдаемой и повторяемой идеи возникает из внерелигиозного разделения субъекта и не достигнутой достижимости, которая утверждается как нечто иное. Разум пытается постичь эту достижимость через немедленно достижимые сущности с помощью математической системы понятий, порожденной абстракцией повторяемости.
.....
>Остается вопрос, неоспоримы ли логические принципы хотя бы в математических системах, свободных от живого содержания, т. е. в системах, порожденных постулированной абстракцией повторяемости и повторения, абстрактной интуицией времени и первичной математической интуицией
Речь об условном рефлексе. Брауэр нигде не употреблял этот термин, но из его описания это очевидно, даже в твоих отрывках. Повторяемость в данном смысле - связь во времени любых событий, явлений, независимых друг от друга, но которые можно связать друг с другом в смысле системы. Например, как с собаками Павлова, звонок - кормление. После нескольких повторений этих качественно разных явлений возникает устойчивая реакция слюноотделения на звонок. Рефлексы можно получить и на любые другие события, связанные только их повторяемостью во времени. Убираем конкретное содержимое рефлексов, получаем общую их форму, т.е интуицию времени, ведь эти события не связаны ничем, кроме временнОй связи их в одну систему типа "если а то б". Брауэр совершенно правильно это явление ставил в основу любой науки и вообще мышления. По-сути, Павлов писал о том же, но другими словами и с другой целью.
Тогда никак. С zf совместимо существование бесконечных множеств, не содержащих счетных подмножеств.
Ого, даже так. А где можно почитать про это? И еще: означает ли это что в ZF у счетного множества может быть бесконечное но не счетное подмножество?
Спасибо за развернутую простынку люблю простыни, твой послы про познавание условными рефлексами звучит убедительно(кинул палку, упала, кинул палку, упала, в конце концов связываешь эти явления), но тогда не затруднит ли тебя пояснить твою позицию по поводу оснований, ведь если оуководствоваться этим принципом то основания должны строиться не на копротивлении каким нибудь там аксиомам или построениями всего на целых числах, а на удобности описания конкретных задач и базовые аксиомы могут быть совершенно любыми(квантовая логика, неэвклидова геометрия), лишь бы это хорошо вписывалось в ту область, для которой понадобилась математика
> если оуководствоваться этим принципом то основания должны строиться не на копротивлении каким нибудь там аксиомам или построениями всего на целых числах, а на удобности описания конкретных задач и базовые аксиомы могут быть совершенно любыми(квантовая логика, неэвклидова геометрия), лишь бы это хорошо вписывалось в ту область, для которой понадобилась математика
Дело в том, что математику вообще нельзя строить на логических аксиоматиках, т.к они не могут быть полными и непротиворечивыми одновременно. И т.о построенная на них математика будет такой же дырявой. Тут так никто и не понял, что интуиционизм Брауэра это не ещё одна нескучная аксиоматика, а вообще другой подход к построению математики. И суть его в том, что поскольку математика это продукт мыслительной деятельности человека, а не какие-то платоновские миры идей, то и правильные основания математики могут быть построены только из элементов мыслительной деятельности человека. Из работ Павлова известно, что это в любом случае рефлексы. Брауэр дошёл до этого без Павлова, более того, с абсолютно противоположной стороны, но речь у него о том же самом. Основания на то и основания, что все остальное должно быть построимо на их основе, хоть любая геометрия, хоть что.
И как тогда выглядят самые базовые кирпичики построения математических теорий? С чего начинать?
 1 Мб, 1468x1129
1 Мб, 1468x1129> И как тогда выглядят самые базовые кирпичики построения математических теорий? С чего начинать?
Интуиция времени же, абстракция рефлекса, общая его форма и свойства. Если вкратце - первый акт, пикрелейтед. Если в подробностях - 2ая часть диссертации Брауэра.
че за туити? че за единство туитей?он чё, гегельянец штоли
>связь во времени любых событий, явлений, независимых друг от друга, но которые можно связать друг с другом в смысле системы. Например, как с собаками Павлова, звонок - кормление.
https://ru.wikipedia.org/wiki/Апофения
К чему это? Условные рефлексы будешь опровергать или что?
Это психология, но причём здесь математика? Очевидно, что многие математические абстракции сформировались под влиянием интуиций, опосредованных опытом, но математика начинается там, где эти абстракции отрываются от своих корней.
Для того, чтобы знать геометрию, не нужно изучать, как механизмы психики формируют у нас пространственные отношения. И даже если мы механизмы нашей психики поменяем, геометрия не перестанет существовать как абстрактная наука.
теория первого порядка, порождаемая одной аксиомой «(для любого x)P(x)», непротиворечива и полна, логика первого порядка непротиворечива и полна(теорема гёделя о полноте)
Я знаю про теорему о полноте. Как знаю и то, что теории, удовлетворяющие ей, не могут быть основаниями математики. Думаю, что и ты это знаешь. Так к чему тогда троллинг тупостью?
>>44044
> Это психология, но причём здесь математика?
Вот бы сейчас пересказывать вторую часть диссертации Брауэра. Там подробно и с примерами на твой вопрос отвечено.
>логических аксиоматиках, т.к они не могут быть полными и непротиворечивыми одновременно.
логические аксиоматики могут быть полными и непротиворечивыми одновременно
> Так к чему тогда троллинг тупостью?
 10 Кб, 223x225
10 Кб, 223x225> логические аксиоматики могут быть полными и непротиворечивыми одновременно
Ты это уже писал. Речь изначально шла об основаниях, в частности о том, что такие аксиоматики не могут быть основаниями.
>>44047
> Как будто твой интуиционизм полон.
Интуиционизм полон и непротиворечив только в том, что с помощью него можно построить. И это единственная возможная а математике полнота и непротиворечивость одновременно. Все, что есть за его рамками - два стула геделевской теоремы о неполноте. Все это уже сто раз обсуждалось, дальше можно по непомню какому разу вспомнить универсальную машину Тьюринга, существование алгоритмически неразрешимых проблем, которые не разрешимы никак вообще и так далее.
> полные и непротиворечивые логические аксиоматики не могут быть основаниями
> логические аксиоматики не могут быть полными и непротиворечивыми
тогда точнее выражай свои мысли, это разные вещи и ты написал именно второе
да и могут они быть основаниями, другое дело, что в них мало чего можно выразить, вместо нормальной математики получится кастрированная, но в целом им ничего не мешает быть основаниями
Ты сначала разберись, что такое основания и зачем они. Вместо того, чтобы нести хуйню, ок?
> логические аксиоматики не могут быть полными и непротиворечивыми
да как ты смеешь после того обсёра мне ещё что-то говорить быдло
Чучелок, речь шла об основаниях. Пиздец ты тупое хуйло. Слов нет. Сам обосрался, ещё что-то кукарекает.
ты пытаешься извернуться просто, ты чётко написал, что логические аксиоматики не могут быть полными и непротиворечивыми и именно поэтому они не могут быть основаниями, ты написал хуйню, ты обосрался и пытаешься теперь выставить так, будто ты имел ввиду другое
> логические аксиоматики не могут быть полными и непротиворечивыми и именно поэтому они не могут быть основаниями
> математику вообще нельзя строить на логических аксиоматиках, т.к они не могут быть полными и непротиворечивыми одновременно|
это в точности что ты написал, так что иди нахуй, демагог тупой
Ну ты и убогое говно. Тебе ещё раз говорят - аксиоматики, удовлетворяющие теореме о полноте, не могут быть основаниями. Это факт, ещё Гильберт писал, что исчисления высказываний недостаточно.
>только в том, что с помощью него можно построить.
То есть для математики он не годится, ибо она к интуиционистским построениям отнюдь не сводится.
>Тебе ещё раз говорят - аксиоматики, удовлетворяющие теореме о полноте, не могут быть основаниями
это не то же самое, что логические аксиоматики не могут быть полными и непротиворечивыми
> То есть для математики он не годится, ибо она к интуиционистским построениям отнюдь не сводится.
Сводится. А то, что не сводится - это религия, всякая вера в платоновские идеи и прочие невычислимые заповеди.
Перечислимость и вычислимость то же самое или не? Теорема Гёделя о неполноте говорит, что множество истинных формул теории с определёнными свойствами неперечислимо, так? Почему это к интуиционистской логике не относится, там же алгоритм и перечислимость основы всего.
> Перечислимость и вычислимость то же самое или не?
Не.
> Теорема Гёделя о неполноте говорит, что множество истинных формул теории с определёнными свойствами неперечислимо, так? Почему это к интуиционистской логике не относится, там же алгоритм и перечислимость основы всего.
Начнём с того, что интуиционизм Брауэра и интуиционистская логика Гейтинга это разные вещи. Последнее - это формальная система.
> Последнее - это формальная система.
> И как, относится к ней результат Гёделя?
А типа ты не знаешь, что он относится к любой формальной системе? Брауэр задолго до Гёделя назвал логику Гейтинга "интересным но бесплодным примером".
> Не к любой же. Но я уловил.
Естественно, за исключением тех формальных систем, к которым относится теорема о полноте. Я думаю, вещи самоочевидные из контекста фразы вполне можно опускать. Так же и с машиной Тьюринга, все ее упоминания в этом треде относятся к универсальной машине Тьюринга, как и вообще понятие тьюринг-полноты.
Так же, я думаю об этом как о расширении уже существующей теории, а не замене старых понятий на новые. Например, был бы у нас континуальный алфавит, мы бы каждому символу поставили в соответствие элемент континуального множества и потом перечислили бы их. Так-то существует же континуальный ординал, а по ординалам можно проходить, они линейно-упорядочены, для каждого есть следующий и тд. Можно как-то сопоставить каждому ординалу, меньшему несчётного, элемент множества. Оно и фундировано, можно трансфинитную индукцию применять. Вроде бы всё ок, но вот мы например идём от 0 до w, алгоритм перечисляет элементы, перечисляет, а как он поймёт, что нам нужно перепрыгнуть через бесконечность и начать считать уже от w? Никак. А хотелось бы, чтобы мог.
О, а можно, чтобы машин было много, одна перечисляет все предельные ординалы, w, w^w, w^w^w, w^w^w^w..., счётное число других перечисляет промежуточные между w и w^w например, w, w^2, w^3..., между w^w и w^w^w так же w^w2, w^w3, ... w^w^w и тд, потом следующие перечисляют более мелкие уровни, короче нужно очень много машин Тьюринга и будет норм.
Ну да, у нас есть континуум последовательностей нулей и единиц и пусть у нас есть континуум машин Тьюринга, которые занимаются их перечислением, тогда всё будет четко.
Профит в том, что можно вернуться в 19 век и пытаться доказать теорему о среднем значении.
И крякает тоже как непрофит
Никаких оснований нет и не будет. Математика это просто интуиция вбитая людям в голову эволюцией. Просто вот для выживания обезьянам полезно было и всё. нахуй надо какие-то там основания искать, работает и похуй.
Ты сейчас все аспекты человеческой жизни описал разом.
Ты написал хуйню. Ты даже не понимаешь, что такое основание и зачем, но при этом своё школьное мнение имеешь.
>даже не понимаешь, что такое основание
Область в которой работают полтора шизика-нематематика Лефа.
>и зачем
Попил бюджета на грантах.
> Область в которой работают полтора шизика-нематематика Лефа.
Мань, не тебе, кловану, судить кто математик, а кто нет.
> Абстракция отождествления состоит в предположении о возможности однозначного и не вызывающего сомнений решения вопроса о (графическом) равенстве или различии любых двух рассматриваемых нами конструктивных объектов, а также о возможности полного отвлечения от мелких различий, имеющихся между графически равными объектами. Случаи, когда указанные предположения не выполняются, заранее исключаются из рассмотрения. > Так, при рассмотрении слов в некоемом алфавите мы исключаем из рассмотрения случаи, когда не можем прочитать слово (вследствие неразборчивости почерка или, например, вследствие повреждения запоминающего устройства ЭВМ, в которое слово было занесено).
А ведь я думал об этом будучи подростком или даже ребёнком. В итоге я разочаровался в каких-то идеалистических представлениях и понял, что мир не идеален, пришёл к делегированию ответственности и всему такому. А ведь это более общий принцип... Видимо действительно надо почистить себе голову математикой, философией.
И да
> Абстракция потенциальной осуществимости состоит в отвлечении от границ наших конструктивных возможностей в пространстве, времени и материале. Случаи, когда находящихся в нашем распоряжении средств недостаточно для осуществления требующихся построений, заранее исключаются из рассмотрения.
Знаю, эта тема раскрыта даже в предисловии к первому тому бурбаков. Но у них скорее неполнота, чем противоречивость, они и сами не утверждали, что всю математику можно свести к теории множеств. Т.е тут изначально нельзя говорить об основаниях, т.к основания это то, к чему сводима вся возможная математика, а не местами.
> Перестань читать жопой
К чему ты вообще это высрал? Что-то сообщить хотел или что? Хуле вы тупые такие, никак не получается просто мимо поста пройти, обязательно нужно ответить, даже если сказать нечего?
Расслоился от этого.
Последний абзац вообще порадовал. Почитали бы Дьёдонне, Кутателадзе для начала. Они хорошо пояснили (особенно Дьёдонне), почему трактат именно такой и почему все эти обвинения глупы.
Можно рассматривать их на том уровне абстракции, на котором они одинаковые.
А что если предметов не существует? Какое у нас право обобщать свои ощущения, сенсорную информацию?
>какое у нас право их обобщать и считать?
Никакого. Ведь предметы, как и числа, не существуют.
>Ведь все предметы разные, какое у нас право их обобщать и считать?
В этом состоит претензия? Ну ты наделяешь предметы неким свойством 'числа', смысл которых в том, что они как-то сравниваются и считаются.
Имеется в виду, что вообще-то числа это нечто, что имеет свойства сравнения и операций друг с другом. Это их определение, если угодно (определение есть перечисление свойств). Ну вот наборы предметов или просто предметы ты сравниваешь, проводишь над ними операции. А теперь возвращаемся к определению чисел. А это любая хуйня, которая сравнивается и считается. Являются ли предметы такой хуйней, которая считается и сравнивается? Да. Ну значит предметы и их наборы являются в каком-то смысле смысле числами.
Юный алгебраист эзотерик
>Ну значит предметы и их наборы являются в каком-то смысле смысле числами.
Комплексные валенки на месте?
https://www.youtube.com/watch?v=5QO-rOJHW0M
Че это за хуйня
Бля я забыл, что тут секта кококонструктивистов (читай: погромисты с низкими способностями к абстрактному мышлению)
Скажи мне лучше, несектант, я тут собираюсь по Генцевскому исчислению секвенций простенький прувер написать, но где-то наткнулся, что мол по формуле понять верна она или нет в каком-то исчислении это алгоритмически неразрешимая задача. Бля, там вроде просто всё, однозначно, не понимаю, где может быть затык, поясни, есть ли смысл время тратить или это реально неразрешимая задача?
Правила вывода в любом прувере, да и в любой теории типов это и есть исчисление секвенций Генцена-Правитца. Разница с неконструктивной логикой только в том, что в ней истинность задана соотв аксиомами, а конструктивно в правиле вывода заключение может быть истинным только в случае истинности посылок, а не автоматически согласно заповедям Гильберта. Т.о возвращаясь к изначальному вопросу - алгоритмически такое исчисление разрешимо только для логик и систем, полных по Гёделю. Пропозишен калькулюс, арифметика Пресбургера, вот это все. Уже исчисление предикатов этим условиям не соответствует, не говоря о более сложных логиках. Причём, неважно о конструктивных логиках речь или нет, заповеди против геделевской неполноты не помогают. Зачем тебе такой велосипед, непонятно, все давно есть в коке, в т.ч тактики, гарантированно решающие любую задачу, сформулированую в полных по Гёделю системах.
>Т.о возвращаясь к изначальному вопросу - алгоритмически такое исчисление разрешимо только для логик и систем, полных по Гёделю. Пропозишен калькулюс
А, понятно, ну отлично, тогда есть смысл запариваться.
>>46036
>Зачем тебе такой велосипед
Да просто, побаловаться, читал про исчисление секвенций, подумал, что в принципе довольно несложно запилить, ну и захотел запилить. В общем, спасибо за исчерпывающий ответ.
> исчисление предикатов этим условиям не соответствует,
Разве? Вроде оно полно по Гёделю, у него даже теорема есть соответствующая(о полноте исчисления предикатов). Но я не эксперт, я только вкатываюсь в логику, до понятий вычислимости, разрешимости и тд ещё далеко, они сильно дальше будут.
Элемент типа. N если речь про натуральные числа итд.
Да хз, я по Шеню иду, мне норм. Кстати, наткнулся тут на аксиому Лукашевича, ((P -> Q) -> R) -> ((R -> P) -> (S -> P)), и типа ей можно заменить по сути все аксиомы классической логики. Хочу вывести сам то дело, но даже на первой A -> (B -> A) несколько дней залипал и ничего не вышло. Это сильно сложно, мб там сотня страниц вывода? Где можно посмотреть на док-во самого Лукашевича? И ещё вопрос, в инт логике закона Пирса нет как я понимаю, а он выводится из этой аксиомы тоже, выходит эта аксиома не подходит для инт логики. Тогда есть ли такая универсальная аксиома в инт логике?
Спасибо.
>Гёдель вкатывался в логику с учебника Гильберта-Акермана.
Книга Гильберта-Аккермано на Гёделя влияние очевидно имела. Но почти уверен, что он начал заниматься логикой до её выхода. Диссертация в которой он доказал теорему о полноте датируется 1929 годом, а первое издание Гильберта-Аккермана 1928.
На всякий случай отмечу, что это использовать эту книгу в качестве учебника не стоит. Она была написана до фундаментальных открытий в логике в 1930-х годов. И в целом, просто исходя из тех соображений, что вместе с предметом хорошо также выучить актуальную терминологию и обозначения, я бы не рекомендовал учить логику по учебникам написанным до 1970-х.
>Проблема в том, что эти самые работы Гёделя хер прочтёшь просто так.
Так и работы какого-нибудь Коши или Лагранжа хер прочтешь просто так. Так ли нужно их читать?
мимокрок
>Проблема в том, что эти самые работы Гёделя хер прочтёшь просто так.
Так их чтение, как впрочем и любых других известных старых математических работ, может быть осмыслено либо для изучения вопросов истории математики, либо чтобы выяснить математически интересные детали, которые могли быть утеряны в более поздних изложениях. Но не очень ясно зачем это может быть нужно кому-нибудь кроме профессиональных логиков и историков науки. Благо Гёдель написал не так много статей и, если я не упускаю из виду какую-нибудь его малоизвестную работу или две, все они достаточно хорошо известны и их результаты были многократно переизложены.
>>47757
Нет, за редкими исключениями.
француз в трежде, все в круассан
речь скорее о том, что базовые факты современного анализа тогда были открытиями и подавались соответственно.
Изоморфизма чего?
часто можно услышать, мол, "теория категорий это не теория, а язык", т.е. в ней ничего особо не доказывается. но это не совсем точно.
повседневная реальность такова, что многие утверждения из различных разделов математики (скажем, описывающие функториальность или универсальность чего-нибудь) доказываются с помощью одних и тех же рассуждений, отличающихся только терминологией, относящейся к разделу.
теория категорий же все эти рассуждения унифицирует, надстроив подходящий абстрактный фреймворк, который позволяет их все все единым образом формулировать. так, освоив теорию категорий, можно везде, где надо, писать лишь "верно по абстрактной чепухе сиречь, в рамках теории категорий" и больше уже не доказывать
я не знаю, как дела в алгебраической геометрии (мне она, в основном, неведома), где утверждения, так кажется, уже с самого начала формулируются на языке категорий и там и остаются
один умный алгебраический геометр сказал, что теория категорий позволяет в вашей теории всё разложить по полочкам, навести в ней в порядок, и т.д.
фреймворк производных категорий позволяет записать производный функтор композиции двух функторов, не упоминая всуе спектральную последовательность (которую приходится строить попутно доказывая множество лемм если ты хочешь сидеть в обычных комплексах).
и всё же я не знаю, что в производных категориях можно реально вычислить
А напомните, что наш конструктивист думает про HoTT и CubicalTT?
У него даже книжка есть.
>доказываются с помощью одних и тех же рассуждений, отличающихся только терминологией
Ну так в том языковая функция и заключается, чтобы унифицировать терминологию разных областей математики.
Ну так можно сравнивать лошадь с верблюдом или упряжку лошадей с самолетом, как вообще качественные сравнения, или сравнения по существу отражаются на числах? Или это работает только для количественных сравнений?
>Ну значит предметы и их наборы являются в каком-то смысле смысле числами.
Ага, а в каком-то смысле число планет во Вселенной = Юлий Цезарь.
В смысле, что когда числа являются объектами, без уточнения объектами какого рода, то нет логических оснований отказываться
от подобных выражений.
 33 Кб, 400x400
33 Кб, 400x400После праздников не протрезвел ещё? Или с чего тебя так от элиминатора пустого множества пробрало? Вычислительный смысл упомянутого тобой правила в том, что если мы допускаем существование пруф-обьекта для пустого множества или что то же самое для абсурдной пропозиции, то пропозициональная функция с таким пруф-обьектом истинна. Но поскольку пустое множество не может содержать элементов, то и пропозициональной функции в вышеупомянутом случае мы построить так же не можем. Уж такие то вещи и школьникам должны быть очевидны же.
>если мы допускаем существование пруф-обьекта для пустого множества или что то же самое для абсурдной пропозиции, то пропозициональная функция с таким пруф-обьектом истинна
Ты просто написал словами то что уже было написано формулой. Если два раза написать одно и то же оно не становится более верным от этого. Ты либо давай показывай мне машину Тьюринга соответственную этой аксиоме, либо так прямо и говори - уверовал, слава кококонструктивизму и Браузер пророк его.
 957 Кб, 1280x720
957 Кб, 1280x720Начнём с того, что это не аксиома, а правило вывода. И его суть в том, что пустое множество оно, внезапно, пусто! Ибо любой другой вариант приводит к возможности доказать что угодно. Машины Тьюринга у меня нету, есть вон код для агды. Собственно, все что я сказал выше, только более формально и с возможностью проверить. Без всяких верований, с отрицания которых в математике и возник интуиционизм.
>это не аксиома, а правило вывода
В смысле? ⊥ → A? Аксиома же, правило вывода одно, модус поненс. Или я тебя не понял?
>Ибо любой другой вариант приводит к возможности доказать что угодно
ну это откровенная брехня, вот тебе другой вариант:
https://www.illc.uva.nl/Research/Publications/Reports/PP-2016-23.text.pdf
>поорали над его "неформализуемостью алгоритма" про которую он любит постоянно повторять.
Есть ссылка?
> В смысле? ⊥ → A? Аксиома же, правило вывода одно, модус поненс. Или я тебя не понял?
В конструктивной логике нет аксиом, только правила вывода. Модус поненс соответствует элиминаторе импликации.
>>48619
Фантазии клоуна. Понятие алгоритма неформализуемо из-за проблемы останова, если ты и этого не понимаешь, что ты тут вообще забыл? Какие там "программисты с меня орали", когда? Тамошние чумаходы в дискретку могут один из десяти, куда им до высоких материй типа машины Тьюринга хотя бы.
>>48620
> Нее, мне интересно, как с него программисты орали.
Никак.
>В конструктивной логике нет аксиом, только правила вывода
Что за конструктивная логика? В интуиционистской одно правило вывода. Алсо если у тебя только правила вывода и нет аксиом, то из чего тогда вывод происходит?
> Так вроде же не нужно никакой полноты по Тьюрингу, не? Idris там разные...
Что значит нужно-ненужно? Все зависит от задачи. "Разные идрисы" нужны для написания абсолютно корректного софта либо для доказательства корректности любой выразимой в них типизации. Очевидно, что будь они полными по Тьюрингу это было бы невозможно из-за проблемы останова. Поэтому формализовать там можно только некоторую часть из всех возможных алгоритмов, в которых точно нет ничего, что могло бы поставить вопрос об их останове. Системы и теории полные по Тьюрингу тоже не формализуют общее понятие алгоритма и опять же из-за проблемы останова. Из работ Тьюринга же известно, что эта проблема никак вообще совсем нерешаема и т.о формализация общего понятия алгоритма невозможна. Ну есть ещё секта свидетелей сверхтьюринговых вычислений, но это уже психиатрия, а не математика
>В конструктивной логике нет аксиом, только правила вывода.
Ок, чем обосновано использование более сильного чем нужно ex falso и отсутствие правила вывода LEM?
Объясни как вообще этот случайный набор символов относится к exfalso, как из него можно доказать произвольное утверждение имея на руках дно? Будешь сыпать дальше случаными перестановками из любимых слов вроде "вычислительный смысл" или хуйнешь еще один на угад выбранный кусок кода из либ агды?
>>48623
>Понятие алгоритма неформализуемо из-за проблемы останова
О, петух опять закукарекал о своем любимом. Вот статья в которую я тебя уже тыкал носом
https://en.wikipedia.org/wiki/Algorithm#Formalization
На что ты вскукарекнул неформализуемо потому что браузер/тьюринг/проблема останова/случайный набор слов в случайном порядке и якобы все это есть в статье. Один наивный мимокрок попросил петуха привести прямую цитату из статьи в таком случае и тут внезапно наш петушок ушел в полную несознанку, будто его ветром сдуло. За всех программистов не могу сказать, но я с этого поорал знатно. Что скажешь теперь?
>>48624>>48633
Удваиваю оба вопроса.
> Удваиваю оба вопроса.
Мозги купи, удваивать не придётся. Спрашивать что такое конструктивная логика и схуяли там исключённого третьего нет, это вообще за гранью. Проще уж считать это толстотой.
> Объясни как вообще этот случайный набор символов относится к exfalso, как из него можно доказать произвольное утверждение имея на руках дно?
Я ж даже пропозициональную функцию упомянул. Вам все разжевываешь, ложишь за щеку, а в ответ такое. Я конечно же могу сослаться на параграф 6.1 из книги programming in Martin-Lof type theory, где это разбирается, но какой смысл, для тебя математика это китайская грамота. Ты даже не поймешь, как из нотации в упомянутом параграфе получается код с картинки выше.
> За всех программистов не могу сказать, но я с этого поорал знатно. Что скажешь теперь?
То же самое и скажу, что по твоей ссылке хуйня, не относящаяся к формализации алгоритма как явления. Я тебе даже конкретный термин приводил, Entscheidungsproblem, формализация алгоритма это решение этой проблемы Гильберта, а не то, что в учебнике по дискретке для похапе макак из ПТУ написано. Так вот, Тьюринг доказал, что проблема эта не разрешима.
>Проще уж считать это толстотой.
Конечно проще быть петушком и вилять хвостом чем разобраться в вопросе и нормально на него ответить.
>Я конечно же могу сослаться
И вдруг внезапно но закономерно выяснится что там ничего связанного с твоим говнокодом нет и ты снова обосрался.
Где же прямые цитаты? Нет. Только петушок обосравшийся виляет хвостом.
>>48640
>формализация алгоритма это решение этой проблемы Гильберта
>, а не то, что в учебнике
Ну если у тебя для всего свои собственные понятия, а не те что в учебниках у всех остальных людей в мире с этого бы и начинал. Прости но у меня словаря для перевода с петушиного на человеческий нет, поэтому очень тяжело понимать о чем вообще твои высеры.
Ты думаешь, мне интересно по сотому разу объяснять азы? Зря ты так думаешь. Подсказать мне не жалко, а что-то доказывать ананимному долбаебу с мейлру, не понимающему почему в конструктивной логике нет исключённого третьего, зачем мне это?
> очень тяжело понимать о чем вообще твои высеры.
Тебе это тяжело понимать потому что у тебя мозгов нет. Проблема не во мне и уж тем более не в тех источниках, на которые я ссылаюсь, просто ты слишком тупой. Это не трагедия на самом деле, чем раньше ты это поймешь, тем быстрее сможешь перестать гореть от того, что не осилил что-то.
>а что-то доказывать ананимному долбаебу с мейлру, не понимающему почему в конструктивной логике нет исключённого третьего, зачем мне это?
Так ты нихуя не доказал, ты все время уходишь от ответа. Во-первых, докажи сначала, что в конструктивной логике нет исключенного третьего, а именно с ссылкой на учебник или статью, иначе будучи обоссан, когда я принесу тебе модель с конструктивной классической логикой.
Во-вторых, если ты имеешь в виду все-таки интуиционистскую аксиоматику, обьясни, почему нельзя ослаблять другие аксиомы. (подозреваю, по религиозным и историческим причинам)
 481 Кб, 640x480
481 Кб, 640x480> Так ты нихуя не доказал, ты все время уходишь от ответа
Я не виноват, что ты ответы не понимаешь.
> Во-вторых, если ты имеешь в виду все-таки интуиционистскую аксиоматику,
Куда ты лезешь, господи. Ты полторы строчки кода из агды не понял, с чего ты решил что поймешь чем конструктивная логика Гейтинга отличается от интуиционизма Брауэра? Тебе в сотый раз говорят, что ни там ни там нет никакой аксиоматики, ты ж даже не понимаешь чем аксиома отличается от правила вывода, про пропозициональные функции ты вообще узнал несколькими постами выше, ну как узнал, прочитал название такое, теперь будешь кукарекать что я ничего о не доказал. Ты правду пиши - это ты ничего не понял.
> обьясни, почему нельзя ослаблять другие аксиомы. (подозреваю, по религиозным и историческим причинам)
Какие аксиомы? Элиминатор пустого множества? Это не аксиома.
Да в смысле толстотой? Я искренне не понимаю, о какой конструктивной логике речь и из чего происходит вывод, если аксиом нет.
 10 Кб, 223x225
10 Кб, 223x225Я выше уже упоминал книшку programming in Martin-Lof type theory, под конструктивной логикой я имею в виду то, что там описано во 2ой главе, т.е интерпретацию логических констант по Брауэру-Гейтингу-Колмогорову, (BHK). Под логическим выводом без аксиом, соответственно, имею в виду натуральную дедукцию Генцена-Правитца, 5ая глава там же. Опять же, с оговоркой, что конструктивно "аксиома" это правило вывода без посылок, с одним заключением. Как будто все это уже сто раз не написано даже в этом треде.
>конструктивная логика Гейтинга
Неси пруфы, что это понятие где-нибудь употребляется, кроме твоей головы. Любую литературы, плиз, а не очередной пиздеж.
>ты ж даже не понимаешь чем аксиома отличается от правила вывода
не понимаю. Смотри аксиома:
A -> B
правило вывода:
/(A - > B)
в чем отличие, если заменить одно на другое? Станет "конструктивнее"?
>Какие аксиомы? Элиминатор пустого множества? Это не аксиома.
в своей агде ты "доказал" EFQ, согласно изоморфизму карри-говарда это может быть тогда и только когда, когда это является теоремой интуиционистской логики, ну а в интуиционисткой логике это эквивалентно одной из аксиом. Или ты не согласен?
>исчисление секвенций
Ааа, дошло наконец. Ну там тоже ведь аксиомы есть, если секвенция состоит из одних переменных, причём какая-то встречается в левой и правой части, то тогда секвенция называется аксиомой. Ну короче это ж backward chaining inference machine, а мы тут про форвард чейнинг. Мы начинаем с аксиом, а ты к ним приходишь ( или к контрпримеру), ну правильно, тв же типа пруверами занимаешься, отсюда такое непонимание друг друга. Гильберт стайл мышление vs Генцен стайл. Пойду посру.
>Тебе это тяжело понимать потому что у тебя мозгов нет.
Маня, ну признайся уже что тут то ты совершенно неоспоримо обдристался. Хватит приговаривать
>Нет это не говно! Это шоколад!
Показывай прямые цитаты где приравнивали бы понятие "формализация" и entscheidungsproblem. Только я более чем уверен что их нет и не может быть нигде кроме твоего бредящего сознания. Это как назвать твердое - теплым, или зеленое - сладким.
Этот вопрос не дает мне покоя уже давно - кто блядь такой
>Правитц
>Как будто все это уже сто раз не написано даже в этом треде.
Ссылку?
Полистал немного эту твою книжку и вот что меня несколько беспокоит - как-то у них перемешаны понятия типа и множеств. Но ведь даже школьнику в наше время известно что тип и множество - это совсем не одно и тоже. Как же так, конструшок?
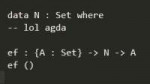 3 Кб, 262x148
3 Кб, 262x148Почему вариант проще (пикрелейтед) было не написать?
Только уже даже из синтаксических особенностей уже видно что этот случай добавлен искусственно поверх остальных правил. В таком случае ссылаться на него все равно что вынимать аксиомы из черной коробочки и говорить при этом - ну как же мои аксиомы могут быть не верны ведь я же их вынул из черной коробочки.
 8 Кб, 891x29
8 Кб, 891x29Это кстати уже другой анон писал. (Я бы в свою очередь совсем не отказался бы посмотреть на классическую конструктивную теорию).
>пропозициональные функции
Хм, думал что это тоже что предикаты, самые базовые понятия в общем то. Но по тому как яростно петух виляет хвостом ясно что у него опять какая то своя задумка, может прямиком из собственного делирия, может из первого издания диссертации браузера.
>натуральную дедукцию
>исчисление секвенций
Ебать я жопой читаю, увидел имя Генцена и мозг автоматом подставил. Почитал про натуральную дедукцию, да, там принципиально нет аксиом, она для того и создавалась, одни только правила вывода, ты прав. Спасибо, теперь я разобрался.
> Неси пруфы, что это понятие где-нибудь употребляется, кроме твоей головы. Любую литературы, плиз, а не очередной пиздеж.
Спроси ещё почему таблица Менделеева или пистолет глок так называется. Не, я тебе серьёзно говорю - твой уровень это голова дай денег и говняк треды, чего ты тут забыл, непонятно.
> в своей агде ты "доказал" EFQ, согласно изоморфизму карри-говарда это может быть тогда и только когда, когда это является теоремой интуиционистской логики, ну а в интуиционисткой логике это эквивалентно одной из аксиом. Или ты не согласен?
Там нет аксиом. Упомянутое тобой построение сводится только к другим построениям и категорическим / гипотетическим суждениям MLTT. Ничто из этого нельзя назвать аксиомами, т.к их истинность зависит только от вычислительного содержания, а не существует априори в мире идей.
>>48663
> Полистал немного эту твою книжку и вот что меня несколько беспокоит - как-то у них перемешаны понятия типа и множеств. Но ведь даже школьнику в наше время известно что тип и множество - это совсем не одно и тоже. Как же так, конструшок?
Мешанина только у тебя в голове, в книге чётко разделяются понятия типа, множества и арности (по Фреге). Достаточно не читать попой. Тип более общий объект чем множество, поэтому любое множество это тип, но не любой тип это множество. Конструктивно множество задается исчерпывающими правилами формирования элемента и равенства между элементами. Если тип задан так же, то вычислительно он является множеством. По этой причине например, N : Set в агде ровно то же самое, что N : Type в идрисе, т.к и там и там N определено одинаково.
>>48665
> (Я бы в свою очередь совсем не отказался бы посмотреть на классическую конструктивную теорию).
Конструктивная логика была предложена Гейтингом в 1928 году. Он, к слову, сразу сказал, что она не формализует интуиционизма (попробуй подумать почему ,и причём тут entscheidungsproblem и формализация алгоритма). Брауэру она не зашла, он назвал её "интересным, но бесплодным примером". Именно эта логика лежит в основе MLTT и вообще любого конструктивизма.
> Неси пруфы, что это понятие где-нибудь употребляется, кроме твоей головы. Любую литературы, плиз, а не очередной пиздеж.
Спроси ещё почему таблица Менделеева или пистолет глок так называется. Не, я тебе серьёзно говорю - твой уровень это голова дай денег и говняк треды, чего ты тут забыл, непонятно.
> в своей агде ты "доказал" EFQ, согласно изоморфизму карри-говарда это может быть тогда и только когда, когда это является теоремой интуиционистской логики, ну а в интуиционисткой логике это эквивалентно одной из аксиом. Или ты не согласен?
Там нет аксиом. Упомянутое тобой построение сводится только к другим построениям и категорическим / гипотетическим суждениям MLTT. Ничто из этого нельзя назвать аксиомами, т.к их истинность зависит только от вычислительного содержания, а не существует априори в мире идей.
>>48663
> Полистал немного эту твою книжку и вот что меня несколько беспокоит - как-то у них перемешаны понятия типа и множеств. Но ведь даже школьнику в наше время известно что тип и множество - это совсем не одно и тоже. Как же так, конструшок?
Мешанина только у тебя в голове, в книге чётко разделяются понятия типа, множества и арности (по Фреге). Достаточно не читать попой. Тип более общий объект чем множество, поэтому любое множество это тип, но не любой тип это множество. Конструктивно множество задается исчерпывающими правилами формирования элемента и равенства между элементами. Если тип задан так же, то вычислительно он является множеством. По этой причине например, N : Set в агде ровно то же самое, что N : Type в идрисе, т.к и там и там N определено одинаково.
>>48665
> (Я бы в свою очередь совсем не отказался бы посмотреть на классическую конструктивную теорию).
Конструктивная логика была предложена Гейтингом в 1928 году. Он, к слову, сразу сказал, что она не формализует интуиционизма (попробуй подумать почему ,и причём тут entscheidungsproblem и формализация алгоритма). Брауэру она не зашла, он назвал её "интересным, но бесплодным примером". Именно эта логика лежит в основе MLTT и вообще любого конструктивизма.
>Спроси ещё почему таблица Менделеева или пистолет глок так называется. Не, я тебе серьёзно говорю - твой уровень это голова дай денег и говняк треды, чего ты тут забыл, непонятно.
Ну у пистолета глок есть чертеж, а таблица менделеева существует в виде рукописи. Теперь я жду "конструктивную логику" в любом виде, хотя бы в виде ссылки. Можешь просто назвать труд Гейтинга, где я могу прочитать это словосочетание.
>Ничто из этого нельзя назвать аксиомами, т.к их истинность зависит только от вычислительного содержания, а не существует априори в мире идей
Борьба с невидимыми платониками идет полным ходом. Ну тогда к изначальному вопросу: почему используется система "изоморфная" данным аксиомам, а не минимальной логике, например, simply typed λ? И почему тогда не использовать classical type theory?
> Ну тогда к изначальному вопросу: почему используется система "изоморфная" данным аксиомам, а не минимальной логике, например, simply typed λ? И почему тогда не использовать classical type theory?
У тебя даже не каша в голове, а узбекский плов как минимум... Все смешалось в доме облонских. Даже по таким вопросам видно, что ты вообще не представляешь о чем говоришь. Какая-то общая картина происходящего должна быть, тогда уже можно задавать вопросы по непонятным моментам, а у тебя чистая шизофазия - какие-то аксиомы нашёл там где их никогда не было (в натуральной дедукции), абсолютно ебнутый вопрос почему вместо MLTT не используют простую типизированную лямбду (к слову, стораз было говорено почему - stlc по изоморфизму Карри-Говарда соответствует исчислению высказываний, абсолютно недостаточному для тех целей, для которых нужна MLTT), будешь спрашивать источник этого? Так тоже сто раз ссылался на Барендрегта. Итд итп, сказка про белого бычка итт.
>Если тип задан так же, то вычислительно он является множеством
Можешь мне показать код на агде такого вида
1 множество четных чисел
2 множество чисел x таких что x mod 4 = 0 или x mod 4 = 2
3 демонстрацию того что эти два множества равны
?
Алсо, конструшок, раз ты решил основательно выходить из клозета, это ведь ты в сае писал охуительные истории про word2vec? Что это такая охуенная вещь что прям скоро за тебя думать будет, только нужно больше данных и на каждый недоуменный контр-аргумент отвечал можнозделать?
>т.к их истинность зависит только от вычислительного содержания, а не существует априори в мире идей
Что мешает сформулировать аксиому, или если у тебя так люто бомбит - правило вывода без посылок:
lem: A \/ -A
и объявить lem ее "высчислительным смыслом"?
> Можешь мне показать код на агде такого вида
Возьми да сделай.
> это ведь ты в сае писал охуительные истории про word2vec?
Про этот подход скорее. Потому что такая задача ставилась еще Маннури и т.н "венским кружком" в 20х годах прошлого века. И вот, первые реализации пошли, века не прошло. Word2vec только первый шаг, сейчас уже есть гораздо более интересная вещь - starspace, это я бы назвал вторым шагом в правильную сторону. Вот только с чего ты взял, что мне будет интересно опровергать твои петушиные "аргументы", высосанные непонятно откуда? Думаешь, мне не похуй что в интернете кто-то несёт хуйню?
Ты не понимаешь нихуя, в том числе что такое вообще "вычислительный смысл". Хотя в вышеупомянутой книжке про MLTT это есть. То, что ты описал, сделать не запрещается, более того, это уже сделано в том же коке. Почему это неприменимо в общем случае, думаю объяснять бесполезно.
 74 Кб, 600x429
74 Кб, 600x429>>48769
Уже трех простых фактов (твои требования пруфов что интуиционистскую / конструктивную логику предложил Гейтинг, школьный вопрос, почему вместо всего этого нельзя использовать простую типизированную лямбду, а так же абсолютно ебнутое предложение "объявить вычислительным смыслом" терма его название) достаточно для понимания, что передо мной еблан, обсуждать с которым конструктивизм это то же что обсуждать Достоевского в оригинале с тем, кто русского алфавита не знает. Мне-то похуй, про что писать посты на мейлру, про хохлов, пыню или Брауэра, но тебе самому с себя и своих потуг не смешно, ты серьёзно считаешь, что прямо борешься с конструктивизмом и что-то там кому-то доказываешь своими потоками хуеты?
Т.е прямые указания на твою абсолютную некомпетентность в теме, на которую ты пытаешься спорить, для тебя вообще не аргумент? Что ж ты за королева колхозная?
> слову, стораз было говорено почему - stlc по изоморфизму Карри-Говарда соответствует исчислению высказываний, абсолютно недостаточному для тех целей, для которых нужна MLTT
цели это построение конструктивной брауэрской маняматетики? в stlc вполне себе формализуется минимальная логика, где уже возможно работать, и ты так и не ответил на вопрос, зачем нужно усилять ее EFQ. Потому что это "интуитивно ясно" и "не нуждается в обосновании"?
>ко-ко-ко-кукарек
Лучше уже съеби писать про хохлов, как собирался, пиздлявая маня. Ссу на петуха.
Где копать идеи связанные с подобным подходом?
P.S: Начинающих тред что-то прям мимо моего вопроса совсем, поэтому сюда запостил.
тебе надо на специальную секретную доску /schizo, её, казалось бы, нет на дваче, но ты найдёшь. там ответят, только не бросай поиски!
Браузеру так же говорили, а теперь он главный кумир петухов на дваче.
>Алсо, конструшок, раз ты решил основательно выходить из клозета, это ведь ты в сае писал охуительные истории про word2vec?
Наверное тот же шизик, который в /pr писал, что strong AI решённая проблема, просто больше слоёв сеточки нахуярить нужно. Ну и закономерно был обоссан.
Существуют ли задачи для которых может быть получен некоторый результат при помощи натуральной дедукции(или исчисления секвенций), а в рамках Гильбертовского вывода этот же результат не выводим для этой же задачи. Если таких нет задач, то мне кажется странным наличие стольких разных подходов к одному и тому же. Я прочитал на вики, что Гентзен хотел построить вывод более похожий на есстественное мышление, но без практической разницы в доказательствах я не понимаю зачем это нужно. Или это просто классификации видов доказательств ?
Метод резолюий и табличная техника это самостоятельные виды доказательств или частные случаи Гильбертовского вывода ?
https://en.wikipedia.org/wiki/List_of_undecidable_problems
Вот список задач, которые не могут быть решены, но нигде не скзано что они Тьюринг не вычислимые. Бывают задачи которые Тьюринг вычислимые, но при этом всё равно не решаемые в плане, что для них нельзя придумать алгоритм достоверно находящий ответ за конечное число шагов на любых данных ?
 59 Кб, 575x595
59 Кб, 575x595Дополню свои вопросы. Вот картинка с вики из статьи Propositional_proof_system и текст под ней:
>Describes the hierarchy of different proof systems, when there's an arrow A->B then there is a translation from every proof in system A to system B with at most a polynomial increase in length, a dotted arrow means we don't know whether there is a translation or not. Lastly if two systems are written in the same bubble then it means that A<->B in the same sense as above.
Как правильно понимать картинку ? Табличная техника позволяет построить доказательства, которые не возможно построить другими системами с картинки ? Т. е. могут существовать задачи на доказательство, которые можно решить только при помощи табличной техники и ни метод резолюций ни натуральная дедукция не позволяют их решить ?
Этот же пик на вики:
https://en.wikipedia.org/wiki/Propositional_proof_system#/media/File:Proofstrength.png
>Существуют ли задачи для которых может быть получен некоторый результат при помощи натуральной дедукции(или исчисления секвенций), а в рамках Гильбертовского вывода этот же результат не выводим для этой же задачи.
Не знаю, что ты называешь задачами. Но разница между секвенциальным, гильбртовским и естественными выводами, скажем для классической пропозициональной логики, состоит в том, что это разные форматы доказательств, а вот множества доказуемых формул совпадают (это множество и известно как классическая пропозициональная логика).
>Метод резолюий и табличная техника это самостоятельные виды доказательств или частные случаи Гильбертовского вывода ?
Это другие виды доказательств.
>Вот список задач, которые не могут быть решены, но нигде не скзано что они Тьюринг не вычислимые. Бывают задачи которые Тьюринг вычислимые, но при этом всё равно не решаемые в плане, что для них нельзя придумать алгоритм достоверно находящий ответ за конечное число шагов на любых данных ?
Я не знаю, что ты называешь "Тьюрин вычислимой" задачей.
>>49249
Эта картинка из науки про системы доказательств для пропозициональной классической логики. Наличие обычной стрелочки от системы P к Q иллюстрирует наличие полиномиального алгоритма, который по данному Q-выводу строит P-вывод той же формулы.
У тебя каша в голове. Если интересует логика лучше почитай какой-нибудь учебник, например Верещагин-Шень хорош для первого знакомства с логикой.
Вот бы можно было перенестись на машине времени лет на тридцать назад или когда там самый хайп был вместе с конструхом и послушать его охуительные истории в духе
> экспертные системы умееют вообще все что угодно
> любую проблему можно решить достаточным количеством if'ов, это же очевидно
> ты нихуя не понимаешь кукареку
> нужно только дописать еще if'ов
> а вообще придумали такую охуенную штуку prolog - там даже if'ов не надо писать, он все за тебя делает
Спасибо за ответы. Я почитал какой-то учебник и вроде понял что к чему.
>что ты называешь "Тьюрин вычислимой"
Мне на первом курсе в информатике говорили такое слово, я думал оно на слуху.
https://en.wikipedia.org/wiki/Computability_theory#Turing_computability
Мне не нужно сильно вдаваться в это. Перефразирую вопрос так. Если для задачи не может быть составлен алгоритм дающий верный ответ на любом наборе данных за конечное число шагов, то(далее впорос) все такие задачи попадают в одну категорию или есть классификация таких задач, например, по причинам невозможности нахожденя алгоритма ?
Мне конечно стало интересно про исключённое третье. Даже учебник Клини почитал. Почему интуиционисты считают что при помощи мат. индукции нельзя доказать что для всех элементов бесконечного множества свойство P(или не P) истинно ? Типа нужно обязательно до последнего элемента по индукции дойти, а это не возможно при их взгляде на бесконечность ?
Табличный метод хорош всем, кроме случаев, когда он не работает. У тебя табличка бесконечно растет, например. Тут-то и начинается современная логика.
>я думал оно на слуху
Дебич, тут местным Тьюринг как второй батя родной. Ты просто нахватался терминов которых нихуя не понимаешь и пытаешься из них что-то криво слепить. Тебе на это и указывают.
А первый батя Чёрч.
Есть еще такое понятие - полуразрешимость
https://en.wikipedia.org/wiki/Decidability_(logic)#Semidecidability
> Мне конечно стало интересно про исключённое третье. Даже учебник Клини почитал. Почему интуиционисты считают что при помощи мат. индукции нельзя доказать что для всех элементов бесконечного множества свойство P(или не P) истинно ? Типа нужно обязательно до последнего элемента по индукции дойти, а это не возможно при их взгляде на бесконечность ?
Причём тут индукция? Вот есть число пи. Как ты по индукции докажешь, существует ли там последовательность, являющаяся датой рождения и смерти пыни? Проблема в том, что кроме "А" и "не А" существуют варианты "хуй знает", " в данный момент неизвестно А или нет" итд.
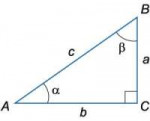 13 Кб, 250x203
13 Кб, 250x203Представь что ты крутишь гипотенузу фиксированной длины 1 от 0 до 90 градусов. Каждому углу будут соответствовать единственные значения катетов. Составив таблицу значений угла и соответствующих значений катетов ты сможешь определять углы, зная только длину одного из катетов.
Допустим у тебя есть треугольник T с гипотенузой с и катетом b, тебе нужно найти угол альфа. Таблицей ты воспользоваться не можешь, т.к. c не равен 1. Но ты можешь воспользоваться подобием треугольников. Пусть T' треугольник подобный T, имеющий гипотенузу c'=1. Найдя в нём b', ты сможешь по таблице определить уголок. Составим пропорцию:
c/c'=b/b' => c=b/b'. Выражаем от сюда b', b'=b/c. Это выражение b/c называют косинусом.
С синусом аналогично.
>Возможно ли понимать математику, или ты просто вбиваешь себе все эти формулы на подкорку, и пользуешься?
Ты ничего кроме школьных учебников не открывал?
>и не могу, голова аж закипает, а ни на шаг не продвигаюсь в задаче
Это нормально. Я, пытаясь "изобрести", то есть понять как придумали косинус/синус, сам потратил немало времени. Обычно хорошо думается перед тем как заснуть.
Расскажи, как ты его изобретаешь.
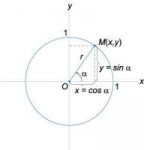 10 Кб, 322x334
10 Кб, 322x334В школе нам тоже через треугольники и гипотенузы объясняли тригонометрию. Синусы какие-то, катеты, тангенсы, углы еще эти - то в градусах, то в радианах измеряются. Не въехал. Принципиально не зубрил, то что не понимал (за это в аттестате одни тройки). Вся школьная тригонометрия мимо пролетела.
Потом в универ поступал на механический. Мамка мне репетитора по математике наняла. Репетиторша мне показала, где на круге найти эти косинусы-синусы. Сразу всю тригонометрию въехал.
Есть окружность, с радиусом = 1. Центр окружности - начало координат. Длина окружности - 2pi. Если на окружности взять точку и соединим ее с началом координат - получим угол между точкой и осью X. Проекция точки на ось X - косинус, Проекция на ось Y - синус. Всё.
>Обычно хорошо думается перед тем как заснуть.
"Гипногогию" гугли. Нормальная тема.
 67 Кб, 542x464
67 Кб, 542x464>существует ли там последовательность, являющаяся датой рождения и смерти пыни?
Погоди, это плохой пример. В учебнике(забавный факт что лишь в одном) сказано что высказываниями могут быть только такие предложения которые однозначно принимают значение истина или ложь.
А вот есть же утверждения которые можно проверить на бесконечном множестве путём, например, мат. индукции. На пике цитата из учебника Клини. Брауэр считает, что закон исключённого тртьего не спасает тот факт что, иногда можно доказать его наличие путём рассуждения(мат. индукции или любым другим видом док-ва) Т.е. к бесконечным множествам закон исключённого тртьего вообще не применим. Вот мне стало интересно чем его не устраивали док-ва типа мат. индукции для бесконечных множеств ?
https://en.wikipedia.org/wiki/First-order_logic#Completeness_and_undecidability
Не могу понять одновременную полноту и неразрешимость логики предикатов. С одной стороны полнота - тождественно истинное предложение выводимо, с другой стороны не разрешимость - сущетвуют такие предложения что для них нетспособа проверить истина они или ложь. Так если она истина значит всё таки должен быть способ это вывести(из полноты следует). Не врубаюсь, помогите растолковать этот момент ?
ABCDE... - Это число, которое мы получаем переумножив все простые числа, "A", "B", "C", "D" и тж.
За каждым числом идет следующее.
Значит за числом ABCDE... идет
ABCDE...+ 1.
Делителями числа будут все множители составляющие его. Для ABCDE... Это "A', "B", "C", "D", "E".
Если B не делится на A, то в A должен быть множитель, которого нет в B. Это можно вывести. Рассматривая совокупности букв, как умножение. Деление - Это изьятия буквы из множества букв.
ABCDE не делится на ABCDE...+ 1(меньшее не делится на большое).И ABCDE...+ 1 существует. Значит в ABCDE...+ 1 должен быть множитель которого нет ABCDE. Но мы определили, что ABCDE - Это множество всех простых чисел, а оказывается есть еще один множитель. Значит противоречие.
КОНСТРУКТИВИСТЫ ДОЛЖНЫ ИСРПАВИТЬ ЭТО ГОВНЯННО4 ДОКАЗАТЕЛЬСТВО.
По сути, это доказательство говорит, про невозможность структуры. Ведь из внутренней структуры следует внешнее.
Но если из внутреннего следует внешнее, это не значит бесконечность.
((ВСЕ -> НЕ ВСЕ) -> бесконечность)
Ложь.
Что такое ВСЕ и как оно может включать НЕ ВСЕ?
Мне кажется тут математика превращается в мистику.
Здесь мы должны есть Тело Бога во время причастия(самый главный ритуал православия).
 291 Кб, 388x550
291 Кб, 388x550> А вот есть же утверждения которые можно проверить на бесконечном множестве путём, например, мат. индукции. На пике цитата из учебника Клини. Брауэр считает, что закон исключённого тртьего не спасает тот факт что, иногда можно доказать его наличие путём рассуждения(мат. индукции или любым другим видом док-ва)
Тут все та же разница между актуальными бесконечностями и потенциальными. Из того, что на каком-то конкретном бесконечном множестве N например что-то можно доказать индукцией, вообще никак не следует, что принцип индукции это высшая истина, работающая как общий принцип, оторванный от конкретного построения. Я вон выше приводил пример кода из MLTT, там рекурсия задается над элементами некоторых конкретных множеств, общего правила рекурсии там нет. Так и с исключенным третьим. То, что оно доказуемо в каких-то случаях, не повод тащить его в математику как общий принцип, заповедь, тем более как незыблемую часть оснований.
Ну вообще да, ничего кроме учебников не открывал особо, да и преподавали просто ультрадерьмово. Вообще, я не стремлюсь всё знать, я стремлюсь к некому пониманию предмета, чтобы самому достраивать необходимые знания.
Предложи что-то лучше. Желательно, подкрепи это отчётливой строгостью и логичностью. Тут критиков просто куча, но ни одного разработчика универсальной системы.)
>критиков просто куча, но ни одного разработчика
Жиза пиздец. В какой раздел не зайди — критики, советчики. Но никто нихуя не делает. Бесполезны, ни на что не способны. Могут лишь потреблять, пиздить чужое и делать вид, что являются специалистами. Перфекционисты, не отточившие до совершенства ни единой мельчайшей способности — сапожники без сапог. Жрут лишь готовое, переваривают и делятся "собственным" мнением. Не думают над ответом: правда, ложь, истина — похуй, высирают своё "мнение", по поводу и без. Делать не умеют, но зато есть мнение. Важное, охуенное. Заебешься отделять особей с "мнением" от тех кто решил подумать и сказать, а не мнением своим поделиться.
Че блядь несете, пидарасы. Просто хотел уточнить немного на самом деле макнуть конструшка в очередной раз в говно идет ли речь об индукции на натуральных числах или еще какой неизвестной мне "всеобщей" индукции. Я такой "всеобщей" индукции что то не припомню. В каждой теории когда возникает необходимость постулируется ад-хок структурная индукция.
В этом смысле конструшки посасывают еще глубже потому что они одним большим махом сразу веруют что методы для работы с любым сколь угодно сложным индуктивным типом (в том числе с само-ссылками на себя и на другие типы) не могут не существовать. Вот они как разу получается веруют в великую индукцию.
Не забывай, это тоже твоё мнение. А пока от тебя sci hub-ом не пахнет.
Пошёл ты на хуй со своим мнение, чмоня. Когда свою аксиоматику выведешь, тогда только попробуй что-то писать об индукции. Ты, блядь, логику для гуманитариев осиль сперва, хуеплёт, и только потом Чёрча коснись, чтобы не выглядеть обоссаным петушком. <Прекрасное обсуждение для математиков>
А может наш конструктивист скинет репозиторий, где он там с HoTT что-то фигачит?
 539 Кб, 1452x1127
539 Кб, 1452x1127https://www.youtube.com/watch?v=21qPOReu4FI
не универсум?
Моя версия - рассматривать умножение и деление чисел, как единую сущность, множество (одно число, разбитое на процессы).
То есть 2+3 × 5 это 2+ множество 3 × 5, нельзя отодрать 3 от множества и сложить ее с немножеством "2", а потом умножить на 5. При операциях вычитания и сложения мы можем представить течение времени - последовательно, друг за другом выполняем операции с ОДИНАКОВЫМИ сущностями. При операциях деления и умножения мы имеем, по сути, одну сущность, которую, чтобы сложить или вычесть, сначала нужно привести к ОДИНАКОВОСТИ одного числа. Как то так.
Просвещайте.
Если тебе для похромирования, то Types and Programming Languages и 4 книжки SF тебе хватят с лихвой.
Потом уже можно изучать hott, cubical type theory
Мне бы с философской/логической позиции.
Аноны, давайте рассмотрим одно из таких оснований математики, как полный перебор.
Алгоритм полного перебора - даёт гарантированный ответ в виде искомого (подбираемого) значения,
но алгоритм полного перебора - экспоненциальный.
Это значит, что при увеличении битовой длины подбираемого числа, количество вариантов перебора растёт по экспоненте.
Давайте попытаемся хоть как-то оптимизировать полный перебор, и запилим универсальный брутфорс?!!
Выкладываю код функции-генератора обратных чисел на уменьшающихся отрезках,
и функции для брутфорса числа x, основанного на этом генераторе:
https://rextester.com/XCYS63908
Видно, что при N = 2^6 = 64 число x, лежащее в пределах от 0 до N,
подбирается за количество итераций, значительно меньшее, нежели N = 64.
Видно, что в массиве сгенерированных чисел - 128 чисел, так как +x и -x для каждого полинома.
Видно, что:
одно из двух первых чисел, всегда меньше (N/2) = 32,
одно из первых четырех чисел - всегда меньше (N/4) = 16,
одно из первых восьми чисел - всегда меньше (N/8) = 8,
и так далее...
Поэтому, видно, что вся суть подбора - сводится к поиску именно наименьшего числа в группе сгенерированных чисел.
Также видно, что количество "мусора" - растёт экспоненциально.
Именно это свойство обратных чисел и ускоряет брутфорс...
Не очень понятно, правда, как вся эта херня связана с "методом ветвей и границ":
https://ru.wikipedia.org/wiki/Метод_ветвей_и_границ
но больше похоже на вариацию алгоритма Baby-step-giant-step:
https://ru.wikipedia.org/wiki/Алгоритм_Гельфонда_—_Шенкса
Аноны, как можно эту шнягу оптимизировать?
Мне кажется, что числа в массиве, имеют свойства повторяться.
Может быть их отсеять как-то можно, например, с использованием простых чисел?
Так давайте же заебеним - универсальный алго для брутфорса!
Быть может, он будет ещё и полиномиальным! Лол.
Я уже вижу повторы в массиве. Особенно это наглядно видно, если разбить массив так:
2 числа, 2 числа, 4 числа, 8 чисел, 16 чисел, 32 числа...
Эти повторы ещё нагляднее - в Notepad++, где подсветка есть, при клике на число.
Не знаю, можно ли с помощью простых чисел отсеять как-то эти повторы,
но видно, что вторая половина каждой строчки - это (64 минус числа из первой половины).
Может это поможет оптимизировать алго, уменьшив длину массива...
Сама идея - охуенно ускоряет перебор, но массив этот, он всё-равно пиздато растёт - по экспоненте, бля.
Можно ли, с помощью каких-то закономерностей - убрать "мусор" с массива, и выявить наименьшее число, или "вероятно-наименьшее",
ну или хотя-бы сделать так, чтобы числа в массиве не повторялись...
Конечно же, с учётом того, что теоретически, длина массива может быть велика...
Аноны, давайте рассмотрим одно из таких оснований математики, как полный перебор.
Алгоритм полного перебора - даёт гарантированный ответ в виде искомого (подбираемого) значения,
но алгоритм полного перебора - экспоненциальный.
Это значит, что при увеличении битовой длины подбираемого числа, количество вариантов перебора растёт по экспоненте.
Давайте попытаемся хоть как-то оптимизировать полный перебор, и запилим универсальный брутфорс?!!
Выкладываю код функции-генератора обратных чисел на уменьшающихся отрезках,
и функции для брутфорса числа x, основанного на этом генераторе:
https://rextester.com/XCYS63908
Видно, что при N = 2^6 = 64 число x, лежащее в пределах от 0 до N,
подбирается за количество итераций, значительно меньшее, нежели N = 64.
Видно, что в массиве сгенерированных чисел - 128 чисел, так как +x и -x для каждого полинома.
Видно, что:
одно из двух первых чисел, всегда меньше (N/2) = 32,
одно из первых четырех чисел - всегда меньше (N/4) = 16,
одно из первых восьми чисел - всегда меньше (N/8) = 8,
и так далее...
Поэтому, видно, что вся суть подбора - сводится к поиску именно наименьшего числа в группе сгенерированных чисел.
Также видно, что количество "мусора" - растёт экспоненциально.
Именно это свойство обратных чисел и ускоряет брутфорс...
Не очень понятно, правда, как вся эта херня связана с "методом ветвей и границ":
https://ru.wikipedia.org/wiki/Метод_ветвей_и_границ
но больше похоже на вариацию алгоритма Baby-step-giant-step:
https://ru.wikipedia.org/wiki/Алгоритм_Гельфонда_—_Шенкса
Аноны, как можно эту шнягу оптимизировать?
Мне кажется, что числа в массиве, имеют свойства повторяться.
Может быть их отсеять как-то можно, например, с использованием простых чисел?
Так давайте же заебеним - универсальный алго для брутфорса!
Быть может, он будет ещё и полиномиальным! Лол.
Я уже вижу повторы в массиве. Особенно это наглядно видно, если разбить массив так:
2 числа, 2 числа, 4 числа, 8 чисел, 16 чисел, 32 числа...
Эти повторы ещё нагляднее - в Notepad++, где подсветка есть, при клике на число.
Не знаю, можно ли с помощью простых чисел отсеять как-то эти повторы,
но видно, что вторая половина каждой строчки - это (64 минус числа из первой половины).
Может это поможет оптимизировать алго, уменьшив длину массива...
Сама идея - охуенно ускоряет перебор, но массив этот, он всё-равно пиздато растёт - по экспоненте, бля.
Можно ли, с помощью каких-то закономерностей - убрать "мусор" с массива, и выявить наименьшее число, или "вероятно-наименьшее",
ну или хотя-бы сделать так, чтобы числа в массиве не повторялись...
Конечно же, с учётом того, что теоретически, длина массива может быть велика...
<b>What is a mathematical structure?</b>
If you think about a mathematical structure, then it's basically a set of objects or elements, which we call a "set." A set is a collection of all the possible objects or elements that can occur in a given set. It is a collection of all possible objects or elements that are elements of another set. You can think of a set as a box of chocolates. If you open a box of chocolate and find a piece of candy, you can easily identify it as a piece of chocolate (and therefore, that candy is an element of that set of chocolate) but if you open a box of chocolates with no chocolate or just some chocolate, you might be confused.
> Great Mathematicians
До чего же отстойный уебанский список. Максвелла нет, а Энштейн, известный молодёжи главным образом за копипейст работ Максвелла с незначительно дополненным списком приложений его математического аппарата к разным материальным сущностям, есть.
Матемач, можете помочь с логикой.
В общем чтобы нам определить некую дедукцию, нам надо определить некое множество аксиом. Множество аксиом это некоторое множество правильно составленных формул. И тут начинаются проблемы. Ведь значит в множество акисом может входить формулы с открытыми переменными.
И вот к моему вопросу автор дает даже задачу.
1) Σ = {∀xP (x, x),
P (u, v),
P (u, v) → P (v, u),
P (v, u) → P (u, u)}
Σ можество аксиом для языка L {P} с одним символом P для обозначения некого предиката. Так вот у меня вопрос на счет второй аксиомы, как вторая формула P (u, v) может быть аксиомой? Ее переменные не замкнуты кванторами. Что вообще может обозначать эта аксиома? Как она может иметь истинность?
Правильно ли я понимаю, что когда автор вводит формулу с открытыми переменными как аксиому то он намекает что эта формула верна под всеми функциями переменными в данной структуре. Но если это и так, то нельзя ли было написать вместо этого P (u, v) это ∀u∀vP (u,v)?
 1,1 Мб, 683x1024
1,1 Мб, 683x1024





![15425765483860[1].png](/math/big/thumb/40955/15426392835290s.jpg)


