Предыдущий - https://2ch.hk/math/res/21361.html (
 170 Кб, 1440x900
170 Кб, 1440x900После Тьюринга математика делится на информатику и собственно математику.
Вычислимость, автоматы, пруверы = информатика.
Все остальные школы (ньютон-пуанкаре-гротендик) = традиционная математика.
Пруф ми ронг.
>традиционная математика.
Либо выразима в типизированной лямбде, либо все те же невычислимые Аллахи.
>Вычислимость, автоматы, пруверы = информатика.
Так называемая "информатика" это лишь частный случай математики.
Можно показать простой диагонализацией, что сама каппа-дескриптивность не является каппа-дескриптивной, следовательно она тоже идёт нахуй.
>Либо выразима в типизированной лямбде
Исключённое третье тоже спокойно выразимо если у тебя есть пустой тип и пи-типы, но это не делает его не невычислимым Аллахом.
Да нет, это ведь очевидно. Каппа-дескриптивность не сохраняет копределы, а это необходимо, чтобы быть каппа-дескриптивным. Это доказал ещё Витгенштейн.
Каппа-дескриптивность - это конечный орграф. Что ты там диагонализировать собрался? Впрочем, я понял. Ты просто говоришь рандомные слова без всякого смысла.
Это без разницы на самом деле. Конечность или "бесконечность" тут не играет никакой роли. По индукции спокойно доказывается, что каппа-дескриптивность не каппа-дескриптивна. Следует из существования NNO в топосе графов.
 115 Кб, 1240x698
115 Кб, 1240x698Двачую этого сударя
Да что тут понимать - основания математики пусты. Можешь мыслить их как контейнер, в который можно положить всё что угодно. Не всем такая свобода по душе, они хотят непременно какой-то объектный фундамент.
Да мне похуй на "пустоту" оснований математики, я на интуитивном уровне верую в теорию категорий, мне этого в принципе достаточно.
Конечно можно формально с помощью индукции показать (причём конструктивно), что она непротиворечива, но меня это особо не волнует.
Конкретно что именно из этого бессмысленная чепуха?
Ссылку на книгу или статью с определением каппа-дескриптивности приведи, а то непонятно про что ты говоришь.
>основания математики пусты. Можешь мыслить их как контейнер, в который можно положить всё что угодно.
Коран сойдет? Основания математики - это то, на чем можно основать всю математику. Т.е. нечто даже потенциально противоречивое не подойдет, а это уже не "все, что угодно".
>Не всем такая свобода по душе, они хотят непременно какой-то объектный фундамент.
Математика - это самое точное знание, какое есть у человечества. Нет объективного фундамента - нет точного знания. Смешно считать мир идей Платона или любую другую религию точным знанием.
>Удачи в поисках.
Нашли уже, вопрос в том, чтобы реализовать, но и это в процессе. Воеводского вот жалко, то, что он помер, упомянутому процессу не на пользу.
>нужен текст на русском или английском,
Не можешь в языки, учись работать с гугл переводчиком, инвалид.
Да это ебнутый местный, его репортить за шитпостинг надо.
>нужен текст на русском или английском
Если ты ещё французский не выучил, то сразу видно, что на математику тебе похуй по сути.
Двачую.
Le son de langue russe est un bête du son... Jusqu'à un degré d'être ridicule. Je suis tombé par hasard, en cet istant regardais une translation sportive — c'est dérisoire. Elles parlent du cette langue avec tel air et telles intonations comme si tout était normal, comme si ne faisaient pas une bouffonnerie, faisont une voix sérieux. Il y a une espèce du épouvantable dans cette monde, qui ne note pas le comique de russe. Voilà cette speaker regarde moi en camera avec un air serieux — comme si tout était en ordre — prononce les mots russes, "pétaouchnok", "vskrvzénski", "sklijniarfrvrstchnost" et fait encoir ce voix, elles sont tous fous. Zut alors!
J'ai dû dire-vous là et ouvrir les yeux. Vous, probablement, ne comprenes pas mêmes et comptez à la façon des autres qui le russe soit "une langue belle" et non gloussement de la poule, qui les hommes rejetent de soi. Ça cloche dans cette monde.
Здесь такое не принято. Здесь просто называют фамилии. Чем малоизвестнее, тем лучше.
А кто-то виноват, что фамилии типа Мартин-Лёф и Брауэр тебе неизвестны? Это не повод подгорать и срать в треде.
Релятивизм Маннури, ATOM и MT, Бишоп, цифферкомплекс, Уолш, нумероны, изоморфизм Карри-Говарда - всё это входит в общеизвестный багаж знаний теоретика оснований? Ну окей. Если тебе позволено поступать так, то и я буду ссылаться на моих ученых без всяких дополнительных слов. Тебя интересует, что такое каппа-библиотека, - твои проблемы, ебись с гуглом самостоятельно.
Изоморфизм Карри-Говарда точно входит, как и интрерпретация логических констант по Брауэру-Гейтингу-Колмогорову, "это классика, это знать нада". За остальное я вполне доходчиво пояснял, при том по-русски.
Разница в том, что я на что-то ссылаюсь по теме, в связи с основаниями, а у тебя просто БАРЕНДРЕХТ.
Отнюдь. Я предельно точен в своих описаниях. Хочешь знать больше - повторяю, гугли самостоятельно. Твой ко-ко-конструктивизм гроша ломаного не стоит, объективно. Смотри, ты говоришь, что число пи построимо. Но ты даже банально не можешь сказать, какова цифра номер гугол после запятой в его десятичном представлении. Всех вычислительных мощностей этой вселенной не хватит, чтобы её найти. Значит, твоя абстракция потенциальной осуществимости ущербна, и от неё нужно отказаться в пользу каппа-библиотек.
>ты говоришь, что число пи построимо.
Я такого нигде и никогда не говорил. Более того, про вещественные числа я вообще говорил только то, что они фактически построимы только до конечного числа цифер после запятой, в каковом качестве и используются в любой математике, в т.ч. и неко нструктивной. Про абстракцию потенциальной осуществимости ты так и не понял, что это и зачем, чему я не удивлен. Итого, в сухом остатке от твоих предъяв одна батрушка.
Ну да, начались оправдания. А ведь до простой мысли, что Брауэр не гений на все времена, ты не додумался. Жемайтис изобрёл каппа-библиотеки, и это открытие уничтожило и конструктивистов, и даже ультра-финитистов. All hail Жемайтис.
 294 Кб, 490x750
294 Кб, 490x750>до простой мысли, что Брауэр не гений на все времена, ты не додумался.
Но он гений на все времена. И до него никто не додумался поставить вопросы об основаниях так, как это сделал он. Хотя математике тысячи лет. А вот ты простой недотролль с мейлру.
Жемайтис решил проблемы, о которых Брауэр даже не думал. А ещё у тебя фиксация на мейлру.
Брауэр конечно великий человек, но гениальность его не в постановке вопроса об основаниях (об этом задумывался еще Кронекер) а в переоткрытии понятия интенциальности, независимо от Маха и Брентано.
Математике, впрочем, никак не тысячи лет, а около двух веков, ибо "алгебра это решение уравнений" и "чертежи без доказательств" к ней очевидно не относятся. Это не значит что ранее до математики никто не додумался, например были же Дезарг и Паскаль, но это не могло прижиться, поскольку общество до-индустриальной эпохи не обладало достаточными ресурсами, чтобы позволить ученым мужам всю жизнь заниматься лишь математикой. Соответственно, никто и не занимался основаниями, потому что дисциплины такой не было. С другой стороны, понятно, что Брауэр на голову выше таких людей как Курт Гёдель или Герман Вейль, последние прочитали Гуссерля, а Брауэр пере-придумал его сам.
Жемайтис это генерал наподобие Бурбаки или персонаж повести Стругацких? В любом случае, он сильно уступает Дедекинду, так что я бы тут не бравировал каппа-фейсом.
Это мне не мешает.
 24 Кб, 200x284
24 Кб, 200x284С тем же успехом можно утверждать, что любая наука - частный случай генеративной лингвистики, поэтому нет ничего кроме генеративной лингвистики.
Ты слишком сильно абстрагируешься и поэтому упускаешь из виду важные отличия информатики от математики.
Ну, самое очевидное - разные дискурсивные поля. В математике в принципе нет понятия "стандарт оформления кода" и многих других специфичных для информатики понятий. А в информатике нет доминирующей аксиоматической теории, в которой всё строится, - тогда как в математике в основном играют внутри ZFC-TG-NBG.
>С тем же успехом можно утверждать, что любая наука - частный случай генеративной лингвистики,
Если любую науку можно свести к генеративной лингвистике, почему бы и не утверждать подобное?
>поэтому нет ничего кроме генеративной лингвистики.
Э, нет. Не "нет ничего кроме Х", а "можно свести к Х". Если неважно, от какой именно печки танцевать по причине того, что нечто всегда можно свести к чему-то другому, то мы тут имеем пример работы релятивизма Маннури, но в качестве начала отсчета логичнее брать то, что удобнее и проще в практическом использовании. И я очень сомневаюсь, что любую науку проще всего представлять в генеративной лингвистике и изучать с этой точки зрения, даже если такая возможность реально существует.
>важные отличия информатики от математики.
Их нет, упомянутый изоморфизм как раз об этом. Вся математика, основанием которой может быть исчисление предикатов, представима в лямбда-П исчислении, именно этот факт лежит в основе первого прувера AUTOMATH де Брауна.
>>25756
Некоторая разница в терминологии, не более.
>В математике в принципе нет понятия "стандарт оформления кода"
Ты доказательства абсолютно в любом виде пишешь?
>А в информатике нет доминирующей аксиоматической теории
Это не говорит ничего о математике и информатике как о науках.
>в информатике нет доминирующей аксиоматической теории, в которой всё строится,
Типизированная лямбда же.
>тогда как в математике в основном играют внутри ZFC-TG-NBG.
Которые представимы в типизированной лямбде.
>Что ты имеешь ввиду под "представима"?
Скажем, "однозначно выразима" с помощью все того же изоморфизма Карри-Говарда. У де Брауна полно годных примеров, но меня опять же тут будут обвинять, что я всех своими евреями пугаю и даю ссылки на сложночитаемые источники.
 101 Кб, 614x995
101 Кб, 614x995>>25758
Информатика и математика различаются, и я показал вам отличия. Просто вы сидите на заоблачном уровне абстракции, и на нём эти отличия теряются. Но если вы снизите абстрактность, вы не сможете игнорировать разницу. А держаться на вашем уровне абстрактности и не снижать его вы сможете только в том случае, если так и останетесь сторонними философствующими наблюдателями, далёкими от реалий предметов, про которые чешете языками.
Пикрандом.
Все математики знают про ZFC.
Редкий информатик слышал про какую-то там типизированную лямбду.
>Просто вы сидите на заоблачном уровне абстракции, и на нём эти отличия теряются.
Изоморфизм Карри-Говарда это не заоблачный уровень абстракции. Но уже с этих позиций вся разница, что ты назвал - это разница в терминологии.
>А держаться на вашем уровне абстрактности и не снижать его вы сможете только в том случае, если так и останетесь сторонними философствующими наблюдателями, далёкими от реалий предметов, про которые чешете языками.
Опять же, сложно найти что-то более практически применимое, чем изоморфизм Карри-Говарда, чему пример пруверы. Это не стороннее наблюдение, а самая что ни на есть практическая математика.
>>25763
>Редкий информатик слышал про какую-то там типизированную лямбду.
Это вообще ничего не меняет.
Выбор уровня абстрактности очень важен. Чем выше уровень, тем больше деталей теряется. На самом высоком уровне абстрактности между любыми двумя вещами нет разницы, любые две вещи - одна и та же вещь.
Подходящим выбором уровня абстрактности можно отождествить любые две вещи. Это очевидно.
Если две вещи оказались отождествлены, то нужно посмотреть, за счет чего это произошло: из-за слишком высоко задранной планки абстрактности или же из-за более содержательных причин. И если оказалось, что из-за абстрактности, - оное отождествление не имеет никакой познавательной ценности.
Вот я и хочу спросить - как эта болтология соотностится с приведенным мной конкретным примером - изоморфизмом Карри-Говарда?
>На самом высоком уровне абстрактности между любыми двумя вещами нет разницы, любые две вещи - одна и та же вещь
Ты несёшь полную хуйню, никто тут не говорит про "самый высокий уровень абстракции".
Это уже никакого отношения не имеет даже к изначальной теме.
Это разница не в терминологии, а в понятийном аппарате. Дискурсивное поле информатиков включает в себя идеи, которые ни в каком виде не содержатся в дискурсивном поле математиков. И обратно.
>>25767
"Информатика", которая оказывается в твоих глазах тем же самым, что "математика", - это вовсе не то же самое, что информатика (без кавычек).
На твоём уровне абстрактности нет разницы между допотопной пекарней с четвертым пентиумом и модным айфоном. С абстрактной точки зрения - они одно и то же. Но реальность такова, что допотопная пекарня и айфон - две разные вещи.
Я тебя услышал. Терминология под разными названиями для тебя "существенное отличие". Видно, что даже примеров использования AUTOMATH ты не видал, не говоря уже о полноценных пруверах. У де Брауна был пример с книгой "Grundlagen" Ландау, полностью переписанную на AUT, т.е. в конечном счете, в лямбде-П. https://www.win.tue.nl/automath/archive/pdf/aut046.pdf тут http://www.cs.ru.nl/F.Wiedijk/aut/index.html есть архив с этой книгой, переписанной под нотацию AUT. Есть пример этой же книги, прочеканной в Коке, что так же естественно, т.к. лямбда-П подмножество "исчисления построений", типизированной лямбде, на которой основан Кок. к слову, я тоже этой же книжкой обмазываюсь для своего недопиленного прувера Мартин-Лёф в своей MLTT показывает, как в типизированной лямбде можно представить основания. А местные полтора философа на мейлру говорят, что вы все врети и математика это не информатика, яскозал! Очень убедительно.
Я еще раз попрошу уточнить что есть твое выражение "уровень абстракции" применительно к конкретному обсуждаемому примеру - изоморфизму Карри-Говарда.
Не было. Нет и не может быть доказательств противоречивости MLTT, поскольку эта противоречивость непосредственно вычислима и была бы получена лет еще 30 назад.
Зайди в последний тред, там открытым текстом написано доказательство противоречивости HoTT.
>HoTT.
Вычислительная интерпретация НоТТ - открытая проблема. Это во-первых. Во-вторых, конструктивные основания - это MLTT. Ты даже изоморфизм Карри-Говарда понять не можешь, хотя его и школьнику можно объяснить, ну куда ты лезешь в НоТТ? Может быть, хватит уже цирка?..
>Вычислительная интерпретация НоТТ - открытая проблема.
Но противоречивость HoTT уже закрытая.
>Ты даже изоморфизм Карри-Говарда понять не можешь
Почему ты так уверен?
>ну куда ты лезешь в НоТТ?
А что такого?
Почему я не понимаю этого даже приблизительно?
Каждый раз, когда ты постишь в таком стиле, нарушается синхронность и один из внетелесных разумов погибает.
Ты видимо не знаком с той ололомистической бодягой, которую Воеводский толкал в жж на пару с Михайловым.
Я в курсе.
 62 Кб, 1123x349
62 Кб, 1123x349Противоречивая хуйня, стало очевидно после доказательства независимости аксиомы выбора.
>Противоречивость конструктивных оснований
Что уже доказано в самих конструктивных основаниях.
Что ты хочешь этим сказать? Ты ебанутый, если тебе не очевидно, что из аксиомы Аллаха следует разрешимость типа путей для любого типа. Из чего следует тривиальность всех гомотопических групп любого типа, а можно построить сколько угодно типов с нетривиальными гомотопическими группами.
Бамп вопросу. Сейчас пытаюсь доказать, что положительное разрешение данного вопроса эквивалентно:
1) существованию непротиворечивой теории типов где исключённое третье отрицается. (тривиально эквивалентно тому, что я пытаюсь доказать)
2) существованию теории типов, где двойное отрицание исключённого третьего недоказуемо. (эквивалентность уже почти доказал, но вот с существованием сложнее)
Что-нибудь уже известно про такие теории? Желательно, чтобы по "мощности" не уступала MLTT, хотя это конечно маловероятно.
 11 Кб, 238x363
11 Кб, 238x363Непротиворечивые основания изложил еще Брауэр в 1907 году. Сама суть там в том, что их противоречивость принципиально невозможна в той мере, в которой не дропаются основные принципы (пример, что бывает, если их дропнуть - парадокс Жирара). Все, что было сделано на эту тему позднее, в т.ч. самим Брауэром - это адаптация его первоначальных идей к несовершенству людишек, которые не имеют физических возможностей работать со сколько-либо сложными ментальными построениями (или алгоритмическими, что то же самое по тезису Черча). Некий компромисс между самой идеей конструктивности и реальными возможностями в т.ч. вычислительных машин. Любая теория типов, MLTT хотя бы, это просто дальнейшее развитие брауэровской теории species/spreads/choice sequences.
Я не понимаю твой пост. Видимо такой теории типов пока нет, значит сам строить буду. Надеюсь, что мне всё удастся.
Верно ли, что математический объект не называется существующим, если не известен способ его построения из натуральных чисел за конечное число шагов?
Вообще, любой конструктивный объект представим в виде натуральных чисел, поэтому основаниями конструктивной математики является арифметика, а не логика. Я даже Мартин-Лёфа цитировал на эту тему, даже со скринами страниц. Вопрос предыдущего оратора тоже обсуждали уже, ответ на его вопрос положителен с учетом абстракции потенциальной осуществимости, или lazy evaluation в функциональном программировании.
>с учетом абстракции потенциальной осуществимости
Вопрос как раз про то, как именно учитывать эту абстракцию.
>Вопрос как раз про то, как именно учитывать эту абстракцию.
Да я уж понял, что вопрос про это. Тут больше чем за год никто не понял, как это. Учитывать эту абстракцию очень просто, lazy evaluation называется. Т.е. вычисляется только то, что нужно для конкретного построения. Проще говоря, если мы работаем с множеством N, то нам не требуется веровать в наличие этого множества целиком, как объекта платоновского мира идей. Ах, ох, фофудью отобрали? Но ведь если задуматься, верование в это множество (с точки зрения платонизма) ничего не добавляет к возможностям работы с элементами этого множества.
То есть само множество N не называется при этом слово "существует", правильно?
Не он, но я вообще сомневаюсь в существовании множеств.
Хорошо, спасибо.
А ты умеешь их рисовать? Рукописный алеф совсем не похож на печатный алеф, он не как буква N.
 254 Кб, 608x977
254 Кб, 608x977Внимание на последний столбец. Именно так пишут алефы-беты-гимели спецы по теории множеств.
Аллеф Един.
Ты из ДС, где учишься? Думаю может тебя пригласить на семинар по этой вот тематике.
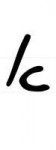 12 Кб, 384x1024
12 Кб, 384x1024Нет. В теории множеств используются только некоторые значки и только в особенной форме. Например, алеф от руки рисуют только как на пикрелейтед, обязательно двумя раздельными чертами причем.
Это практика множеств.
 387 Кб, 2480x3508
387 Кб, 2480x3508Алеф, бет, гимель, маленькое с готическое, маленькие греческие омега, эпсилон, эта и дзета. Для дальнейшего исследования - маленькую латинскую эйч, большую греческую тета, еврейскую букву тав, маленькую греческую лямбда, маленькую латинскую k и некоторые другие символы, о которых я сейчас забыл.
Да.
хуйню написал сорян. Не перечислимые множества и теория вычислимости.
 282 Кб, 604x511
282 Кб, 604x511http://philomatica.org/wp-content/uploads/2016/11/lamb_tuto.pdf
А Чёрч от него отошёл.
Некая внешняя по отношению к математике характеристика. Вопросы о ее природе, возможно, стоит лучше задавать психиатрам и нейробиологам.
Ну, каждому свое.
Вот поэтому он и умер. Как и конструктивист местный. Мораль: хочешь жить не трогай конструктивную математику.
И то верно, желание познавать истину и желание жить - цели редко совпадающие.
Это заговор жидомасонов ордена Исключённого Третьего.
там автор хвастается, что выписывает какую-то притимтивную категорную хуйню
пару раз выписал
не, это просто школьник
Что ж тебе так припекает от чьей-то личности, да ещё и на анонимной борде? У тебя же все должно быть хорошо, академия ведь во всем права, никаких проблем в основаниях современного понимания науки и математики нет... так ведь?
Тёмные уголки двача, двач наоборот какой-то. брр.
>Это, вероятно, потому, что автор поста сам не понимает того, о чем пишет, - как какой-нибудь постмодернист. Это такой сорт кофейного помешательства: взять кучу баззвордов и пытаться их упорядочить, ничего не понимая сколько-нибудь глубоко.
>>175125
Слушай, ну похоже. И ник Coquus от coq.
 116 Кб, 640x256
116 Кб, 640x256> Владимир Воеводский о своем мистическом опыте и "игре, хозяйкой которой является страх"
Пиздец, это же у него неврология была какая-то, а не мистика. От чего он умер?
> знаток душ
Груш. Поехавшим он явно не был, а тут такое - нарушения чувствительности, галюны, расстройства сна итд. 100% клиент невролога.
Тут такая забава, невролог с ходу никогда не определяет - его это клиент или нет. Он сначала просит посетить терапевта, как говорится "чтобы исключить другую патологию". Эта такая общая тенденция, когда сталкиваешься с непонятным, то первая, обывательская, реакция - подумать, что существует некий другой человек, который это понимает.
Википедия говорит, что от аневризмы. До неврологии далековато.
Все проще: самый простой способ нихуя не делая как бы "вылечить" чувака это закормить его нейролептиками и антидепрессантами, поэтому все специалисты сейчас сталкивающиеся с чем-то сложнее того, решение чего в первой строчке гугла можно найти, сначала отправляют к психотерапевту, чтобы тот с вероятностью 90% после каких-то идиотских тестов сказал "да у вас депрессия" и прописал это самое.
Как к земле.
https://www.quora.com/Is-N-J-Wildberger-a-joke-or-a-genius-when-he-claims-that-mathematics-in-its-current-form-is-a-hoax/answer/Hans-Hyttel
Притворяются, что мы уже всё перетерли давно ты че и никаких проблем нет, кто не согласен ебанько.
Развитие модели акторов имеет интересную связь с математической логикой. Одной из ключевых мотиваций для её развития была необходимость управления аспектами, которые возникли в процессе развития языка программирования Planner. После того как модель акторов была первоначально сформулирована, стало важно определить мощность модели в отношении тезиса Роберта Ковальского о том, что «вычисления могут быть сгруппированы по логическим выводам». Тезис Ковальского оказался ложным для одновременных вычислений в модели акторов. Этот результат всё ещё является спорным и противоречит некоторым предыдущим представлениям, поскольку тезис Ковальского верен для последовательных вычислений и даже для некоторых видов параллельных вычислений, например, для лямбда-исчислений.
Тем не менее были предприняты попытки расширения логического программирования для одновременных вычислений. Однако, Хьюитт и Ага в работе 1999 года утверждают, что результирующая система не является дедуктивной в следующем смысле: вычислительные шаги параллельных систем программирования логики не следуют дедуктивно из предыдущих шагов.
Как вкатиться?
Он верует в "доказательство" от противного. Мы тут такое не приветствуем.
 33 Кб, 413x709
33 Кб, 413x709Помогите выбрать - Coq или Agda?
Я недоматематик-недопогромист, хочу просто немного поиграться с пруверами.
Agda привлекает использованием юникода в синтаксисе, Coq - тем что он более популярный, а следовательно (наверн) для него больше гайдов.
Ну, начни с Coq, например. С книжки Software Foundations by Benjamin C. Pierce.
Алсо http://wiki.portal.chalmers.se/agda/pmwiki.php?n=Main.AgdaVsCoq
 438 Кб, 570x585
438 Кб, 570x585Похоже на Агду, только проект кажется более живой.
> Помогите выбрать - Coq или Agda?
Однозначно кок. Его больше 30 лет уже пилят, там полно тактик на все случаи жизни. Только ставить его лучше через OPAM, даже на шиндовс. И SSReflect к нему очень желательно доустановить. Lean скатили. Когда там было дополнительное ядро HoTT, то да. А так, обычный второсортный прувер.
Дошел до главы logic(уже и дальше) в software foundations и завис на вроде бы простом доказательстве:
Example and_exercise :
∀ n m : nat, n + m = 0 → n = 0 ∧ m = 0.
Proof.
( FILL IN HERE ) Admitted.
Как это доказать примитивными тактиками вроде destruct, apply, intros, rewrite, unfold, inversion, induction и т.д. не привлекая всякие однострочники типа omega и auto?
Самое интересное что следующее упражнение, где импликация в другую сторону, я доказал сходу, а вот это нихуя.
Доказать, что из ложности "n или m" следует истинность "n и m ложны".
Связка " ИЛИ" или "+", значит, что существует три варианта, когда истина. Когда "ИЛИ", когда "+" или когда " "ИЛИ" и "+" "
Связка "ИЛИ" ложна тогда, когда ЛОЖНО ВСЕ.
Ты должна погрузиться В СУТЬ ИЛИ ИЛИ ИЛИ
Да. Есенин-Вольпин, следовательно, один из важнейших математиков.
 49 Кб, 704x396
49 Кб, 704x396>там полно тактик на все случаи жизни. Только ставить его лучше через OPAM, даже на шиндовс. И SSReflect к нему очень желательно доустановить.
Ты уверен что мне это будет важно, учитывая
>хочу просто немного поиграться с пруверами.
?
Я сейчас выбираю Agda или Lean, просто из-за более приятного синтаксиса.
>А вдруг они ошиблись?
Для этого и нужны пруверы и конструктивисты. Чтобы ухмыляться и потирать ручки каждый раз, когда кто-то ошибается.
> конструктивисты
Конструктивизм тут вообще не при чем. Ещё де Браун писал про Automath, что это исчисление не привязано к конкретной аксиоматике, а речь всего лишь о лямбдаР. В коке же гораздо более продвинутое CiC. Никто не запрещает туда что угодно прописать, хоть аксиому исключённого третьего, хоть десять заповедей. Любую ебулду можно доказывать в рамках прописанной аксиоматики. Проблема не в этом, а в том, что конечное доказательство к прописанной ебулде и сведется.
Я этого и не говорил.
Если есть формализация анализа в той полноте, которой требует Зорич, то да. Если нет — то вряд ли. Формализация для компухтерный пруверов это титанический труд, заходи лет через 10.
http://www.ens-lyon.fr/LIP/AriC/MSC2014/clelay.pdf
Посмотри эти слайды, там мелькают названия либ.
Только если сможешь себя клонировать.
 296 Кб, 500x375
296 Кб, 500x375За Вайлдбергером соскучились? У него новая серия видеороликов всё о том же, о старом выходит. Будет пояснять по хардкору почему современная теория множество - религиозная вера, и на чём нужно строить правильный фундамент для математики на натуральных числах, конечно же.
Спешите видеть.
Он хотя бы раз употребил словосочетание "доказать Аллаха" или слово "Аллах"?
Алсо, пикрелейтед давно пора ставить в шапку раздела вместо того лысого поца.
> Будет пояснять по хардкору почему современная теория множество - религиозная вера
За это Брауэр пояснил чуть более 100 лет назад.
> на чём нужно строить правильный фундамент для математики на натуральных числах, конечно же.
Будто не так.
Извините, Александр Николаич.
>За это Брауэр пояснил чуть более 100 лет назад.
Что меня возмущает в Ваилдбергере так это то, что он откровенно игнорирует всю историю интуиционизма, конструктивизма, ультрафинитизма и т.п. Как будто он первый предложил основывать математику на натуральных числах и алгоритмах.
Ну положим независимо - вполне можно в это поверить. То что он игнорирует предшествующие исследования в этом направление говорит либо о том, что он практически ничего не знает о развитие мысли в основаниях математики, либо о том, что все-таки он слышал о конструктивизме, но предпочитает о нем не упоминать. Даже если верно первое, это все-равно плохо о нем говорит - значит он уже много лет пропагандирует свои идеи об основаниях математики и не удосужился прочесть хотя бы что-то уровня статьи в википедии о предмете. Хотя я думаю, что верно второе - он производит впечатление более-менее образованного математика - и ему просто приятнее делать вид что он совершенно оригинален.
Что-то читаю основания, ну там про ZFC, про модели ZFC, и чувствую, что меня хотят наебать. Ну серьезно, все эти von Neumann universe, inacessible cardinals, каждая модель ZFC имеет модель ZFC; существуют модели ZFC, в которых ZFC is inconsistent.
Понял, что не хочу всего этого, хочу палочки к палочкам приписывать, как дедушка Марков завещал.
Третья проблема Гильберта гарантирует, что приписывания палочек к палочкам не хватит, чтобы заниматься математикой, то есть теория длин и объёмов необходимо должна использовать рассуждения с бесконечностью. Поэтому однажды кому-то всё-таки придётся строить хорошую, рациональную теорию бесконечного. Текущая стандартная теория множеств несовершенна, многие нужные бесконечности в неё не влезают. Но реформа бесконечного будет, по-видимому, нескоро. Сейчас размышления о теории бесконечного - окраинная часть науки, почти маргинальная. Некоторые философы пытаются сделать свою ТМ, но у них ничего не получается и не сможет получиться, ибо заниматься такими вещами может только математик, очень хорошо изучивший современную математику, а не хуй с горы. Сейчас философы и логики просто априорно что-нибудь постулируют, не заботясь о реальном устройстве науки, и поэтому все их кадавры - мертворожденные.
 20 Кб, 351x351
20 Кб, 351x351> Третья проблема Гильберта гарантирует, что приписывания палочек к палочкам не хватит, чтобы заниматься математикой, то есть теория длин и объёмов необходимо должна использовать рассуждения с бесконечностью.
Есть бесконечность здорового человека и курильщика. Брауэр за это пояснил в своей вступительной речи по случаю назначения профессором в 1912 году, статья "intuitionism and formalism". Он там на пальцах поясняет, почему алеф-нуль - единственная допустимая бесконечность, а континуум ни к какому алефу сводиться не может. Опять же, и тут сто раз обсуждали отличие актуальной бесконечности от потенциальной, по-моему никто так нихуя и не понял.
>алеф-нуль - единственная допустимая бесконечность
Единственное объяснение этому скандальному заявлению, которое было озвучено итт, - религиозно-мистическое. Если у тебя есть какие-нибудь другие - произноси их. В противном случае ты просто фрик, как Катющег.
 109 Кб, 298x376
109 Кб, 298x376О, коконструктивист вернулся. Как жизнь вообще? Как объект? Всё охраняешь?
> 15197005162890.jpg
>Опять же, и тут сто раз обсуждали отличие актуальной бесконечности от потенциальной, по-моему никто так нихуя и не понял.
Внезапно, эта картинка идеально передаёт твои эмоции.
> Единственное объяснение этому скандальному заявлению, которое было озвучено итт, - религиозно-мистическое.
Тыскозал?
> Если у тебя есть какие-нибудь другие - произноси их.
Я и принёс. В виде названия конкретной статьи.
Он пришёл и ты заикаться начал.
> Он там на пальцах поясняет, почему алеф-нуль - единственная допустимая бесконечность
Для начала N определить нужно.
Причём самому Брауэру на его интуиционизм было строго поебать всюду кроме философских семинаров. В своих работах по топологии он вплоть до середины XX века пользовался ZFC/NBG, на пенсии начал экспериментировать с аксиомой детерминированности.
 69 Кб, 960x878
69 Кб, 960x878> Да, япрочетал.
Искать знакомые буквы и понимать прочитанное - слишком разные вещи, на примере Брауэра это особенно хорошо заметно. Я вот не сразу въехал в его аргументацию по поводу того, почему восприятие пространства нельзя считать априорным суждением, и т.о в этом вопросе не прав не только Кант, но и автор т.н metaphor theory, объясняющей нейрофизиологию понятия числа, времени итп метрик. И у Брауэра это не просто "ятакскозал", а конкретное математическое доказательство.
Не совсем так. Топологию к интуиционизму он привязал ещё до своего профессорства, просто задача полной реформы математики неподьемна для одного человека, даже если это Брауэр. Поэтому и приходилось пользоваться устаревшими методами.
Скинь этот R скрипт пж
Батхерт древних греков.
Актуальной или потенциальной?
> Давайте придумаем иное слово для бесконечности.
Так давно уже. Брауэр писал, что одно из свойств two-ity, выводимое путём ее рассмотрения, это "and so forth" (и так далее), возможность продолжать построение дальше. Что и есть потенциальная бесконечность. Насчёт актуальной - разницы нет как называть объект религиозной веры.
В реальности потенциальной бесконечности не бывает. Текст рано или поздно схлопнется в чер(ниль)ну дыру.
 181 Кб, 1920x1080
181 Кб, 1920x1080> В реальности потенциальной бесконечности не бывает. Текст рано или поздно схлопнется в чер(ниль)ну дыру.
А это не потенциальная бесконечность. Ты за все это время так и не понял, что это вообще такое, ладно ты, этого не понял и тот кловн, которого ты сейчас цитируешь про чернильную дыру. Не поняли про потенциальную бесконечность, не поняли про существование математического объекта. Вообще нихуяшеньки не поняли, если называть вещи своими именами. И такие вот гейнии мне что-то предъявлять будут и за математику пояснять, пиздец.
 123 Кб, 500x339
123 Кб, 500x339> Нельзя "и так далее" сделать в реальном мире.
Потому оно и называется потенциальным. Strict evaluation такого выражения и приведёт к дыре. Однако, есть ещё lazy evaluation, которое к дыре не приводит. И тем не менее оно возможно в реальном мире, т.к у нас есть правила построения, та самая потенциальная бесконечность. Впрочем, все это за последнюю пару лет мильен раз обсуждалось, посему нот зис шит егейн.
Значит, это просто верунство. Всё эти лэзи-городки. В то, чего в реальности быть не может.
 283 Кб, 604x505
283 Кб, 604x505> Значит, это просто верунство. Всё эти лэзи-городки. В то, чего в реальности быть не может.
Охуительные истории. Проснись, это не только может быть в реальности, это уже давно есть в любом языке с зависимыми типами. А вот чего в реальности действительно нет и быть не может, так это актуальной бесконечности и платоновского мира идей. Такое только в религии бывает.
>оно возможно в реальном мире
Возможно? То есть, мы не можем сказать, что это существует и просто верим?
То есть потенциальная бесконечность может быть, а может и не быть? Чем это отличается от Аллаха?
 709 Кб, 992x1403
709 Кб, 992x1403> И каждый раз, когда речь заходит о том, что очень больших чисел в реальности не существует ровно также как и бесконечных объектов,
С этим - к свидетелям алефов. Про отличия фактического построения от правил построения мне нечего добавить к уже сказанному. Мозги купите, что ли.
И в чем тогда преимущество если и там и там ты построить ничего не можешь?
Это вопрос интерпретации. Я могу сказать что правила построения бесконечности - это нарисовать ее символ на листочке и принципиально это ничем не отличается от твоих ленивых манядогм.
В каком-то треде видел ты или не ты еще копротивлялся за биологическую обусловленность математики, т.е. то что там в каком-то участке мозга есть что-то похожее на числа в конструктивном смысле, а значит только такая математика - тру. Это вообще кек.
> Это вопрос интерпретации. Я могу сказать что правила построения бесконечности - это нарисовать ее символ на листочке и принципиально это ничем не отличается от твоих ленивых манядогм.
Думай что хочешь, мне до бороды на самом деле. Если ты не видишь разницы, более того, не понимаешь объяснений, что тут сказать.
> В каком-то треде видел ты или не ты еще копротивлялся за биологическую обусловленность математики, т.е. то что там в каком-то участке мозга есть что-то похожее на числа в конструктивном смысле, а значит только такая математика - тру. Это вообще кек.
С этой темой могу сказать то же самое, что выше. Если тебе не очевидна связь идей Брауэра с современными моделями типа ATOM или MT которая неверна, т.к пространство не может быть априорным суждением, что заметил ещё Сеченов, могу только посочувствовать. Биологически обусловлена не только математика, но и вся вообще деятельность человека. Ну если это тяжеловато понять, остаётся религия.
>Ну если это тяжеловато понять, остаётся религия.
Вижу что ты решил остановиться на религии.
P.S. Если бы тебе было до бороды ты вообще бы не отстаивал свои догмы в этом треде
Ладно, давай разберем не примере.
Утверждение. Для любого натурального n есть простое p большее его.
Доказательство. Число n!+1 взаимно просто со всеми числами <=n, следовательно найдется простое p между n+1 и n!+1.
У меня есть такие вопросы:
1) Конструктивно ли это рассуждение?
2) Можно ли применить его к числу в десятичной системе исчисления n=1000000000000000000000000000000000000000000000000000000000000000000000000?
3) Есть ли принципиальная разница между верой в то, что для этого конкретного n найдется p, основываемая на этом рассуждение (т.е. используя существование числа 1000000000000000000000000000000000000000000000000000000000000000000000000!+1), от веры в то, что нет доказательств противоречия в ZFC длиной <=10000000, обосновываемой на базе существования недостижимого кардинала?
 71 Кб, 850x400
71 Кб, 850x400> И при чем тут математика?
При том, что математика это деятельность человека, никакого мира идей Платона нет. Причём тут математика, написано на пикрелейтед, который сто раз постился.
Верунство во что? Не понимаю. Ты отрицаешь, что математикой занимаются люди, или что?
Нет, так как он считает, что математики вне секты Браузера не существует.
Лучше чем ответил анон в одном из предыдущих тредов я мысль не выскажу так что, в привычном для твоей демагогии стиле, отсылаю тебя к нему.
Вообще почитал твои хуй знает может вас несколько посты на три треда назад и как и следовало ожидать никакой конкретики.
Все твои посты сводятся к пустословию в стиле "мне лень в n раз объяснять", "я уже n раз писал", "мне это не интересно", "не конструктивно - не мотематика, Я СКОЗАЛ" и т.д. с периодисческими ссылками на свои же посты, где точно так же нет никакой конкретики или сепеульки, и с ссылками на книжки на многие сотни страниц.
 48 Кб, 419x484
48 Кб, 419x484> Я СКОЗАЛ"
Мань, ты не туда воюешь. Это мне нужно писать, а не рандомному собеседнику, охуевающему с уровня твоей аргументации а-ля детский сад штаны на лямках. Я ни разу не использовал аргумент "яскозал", а вот ты только им и пользуешься.
>Мань, ты не туда воюешь.
Но ты то все равно прочитал, так что не вижу проблемы. Это двач и напротив твоих постов иконку петуха не рисует, для однозначной идентификации
>Я ни разу не использовал аргумент "яскозал"
"я это уже тыщу раз писал" - это как раз уровень я скозал. Еще бы ты начал прямо яскозакать и мамок ебать, было бы совсем потешно.
В чем смысл обсуждать библию и Христа с тем, кто не знает, что это. Ещё меньше смысла не читая библию пытаться её "опровергнуть" своим незнанием предмета. Вы хотя бы это понимаете?
>А что нового узнал ты, интуиционист-кун?
Его вера в непогрешимость браузера ещё сильнее усилилась.
>в привычном для твоей демагогии стиле
Что? Это мой второй пост в этом треде. Мне так и хочется предложить тебе принять таблетки, но я воздержусь.
Я, кажется, задал вполне конкретный вопрос, а в ответ получил какую-то не имеющую отношения к теме доски ерунду. Это печально.
>>40447
>>40461
Цитаты вот на этих картинках мне видятся весьма здравыми. Кто-нибудь из несогласных с ними может внятно объяснить, с чем именно он несогласен? Или у вас тут просто какая-то специальная олимпиада? Опять же, извиняюсь, но со стороны вот эти >>40466 >>40464 >>40463 >>40460 посты выглядят нерелейтед бредом шизика, которого непонятно почему еще тут не забанили. Это какой-то троллинг или я чего-то не понимаю?
Тебя приняли за человека, который некоторое время назад совершенно упорото, люто, дико, безумно воевал с математикой, подняв на знамена почему-то Брауэра. В адекватный разговор с тем человеком пытались, но понимания с его стороны не нашли. Он так затерроризировал сначала тред в /sci, а потом и всю эту доску, что аноны до сих пор реагируют очень нервно, стоит лишь тени этого безумца промелькнуть где-нибудь в уголке.
Да это он же, ты что, не видишь? Он уже второй раз на моей памяти "пропадает", ждёт, чтобы на доску пришли ньюфаги, а потом возвращается за свежей едой.
Ну или это мятежная душа Брауэра кочует из тела в тело. Как вариант.
Есть некоторый шанс, что всё-таки не он. Впрочем, не пофиг ли.
 47 Кб, 512x680
47 Кб, 512x680> Вот я с начала этого треда успел продвинутую алгебру заботать, научился доказывать клёвые штуки про группы и поля.
Немалая часть практически полезной алгебры формализована в коковской либе ssreflect. Проще было кок поразбирать.
> А что нового узнал ты, интуиционист-кун?
А я таки нашёл общий подход к реализации изначальной программы Брауэра, чего он сделать не смог. Без всякой теории типов, машин Тьюринга и тезисов Чёрча, сам Брауэр бы не доебался. Алсо я говорил, что пилю прувер по мере возможности, так вот, почти готово :3
>>40471
> В адекватный разговор с тем человеком пытались, но понимания с его стороны не нашли.
Не было адекватного разговора. С самого 2016 года весь разговор с вашей стороны был точно такой же как сейчас, с маняаргументацией, от невменяемости которой хуеют даже мимокрокодилы.
> совершенно упорото, люто, дико, безумно воевал с математикой, подняв на знамена почему-то Брауэра.
Я никогда с математикой не воевал. С моей стороны на этот счёт было только утверждение о религиозном характере некоторых верований, которые натащили в математику ещё древние греки, а именно исключенное третье, актуальные бесконечности и платоновский мир идей. Ну и некоторые производные от этих верований, вроде догмы Гильберта.
>>40479
В твоём понимании "математикой" называются теоретические основы функционального программирования, центральным результатом которых является "изоморфизм" Бойля-Кавендиша, устанавливающий связь между написанной на Clojure праграммой и канструктивным доказательством в смысле некоего Лёфа. Ничего из математики в общепринятом смысле ты при этом не знаешь.
Лямбда-калькулюс Барендрегта в математике не используется, он относится к праграммированию. Впрочем, у тебя считается, что праграммирование это и есть математика:
>Программисты и есть математики по изоморфизму Карри-Говарда, но ты же не осилил
>>31015
Только вот в изоморфизме Больцмана-Фарадея, который никто кроме тебя на мейл.ру не понял, ничего о математике не утверждалось: там устанавливается соответстветвие между конструктивной теорией типов Мартина Льва и лямбда-исчислением.
 43 Кб, 759x635
43 Кб, 759x635> ничего о математике не утверждалось: там устанавливается соответстветвие между конструктивной теорией типов Мартина Льва и лямбда-исчислением.
Зачем ты лезешь спорить, если нихуя не понимаешь в предмете? В чем твоя мотивация писать всякую хуйню и коверкать названия и имена? Просто пройти мимо богородица не велит? Propositions as sets/types - другое название изоморфизма Карри-Говарда. Забей в гуглтранслейт и постарался сравнить перевод с тем, что ты выше вытужил про типы и лямбду. Ты поди и про более известное соответствие между логическими и теоретикомножественные операции не слышал. И такой вот гейний будет мне что-то пояснять, лол.
> Лямбда-калькулюс Барендрегта в математике не используется, он относится к праграммированию.
А я ведь цитировал на этот счёт де Брауна и приводил в пример его проект automath. Что вы за хлебушки, все просто же как 3 копейки...
 12 Кб, 468x265
12 Кб, 468x265After Curry emphasized the syntactic correspondence between Hilbert-style deduction and combinatory logic, Howard made explicit in 1969 a syntactic analogy between the programs of simply typed lambda calculus and the proofs of natural deduction. Below, the left-hand side formalizes intuitionistic implicational natural deduction as a calculus of sequents (the use of sequents is standard in discussions of the Curry–Howard isomorphism as it allows the deduction rules to be stated more cleanly) with implicit weakening and the right-hand side shows the typing rules of lambda calculus.
>>40490
>automath де Брауна
Это который книгу Ландау "Основы анализа" переписал в твоей лямбда-нотации? Ты бы хоть предисловие к ней прочитал, что ли, оттуда совершенно ясны цель и назначение данной книги:
>на каких основных фактах как на аксиомах можно без пробелов построить анализ и как это построение можно начать
Это "основания математики", не математика, разницу тебе неоднократно объясняли.
> Лямбда-калькулюс Барендрегта в математике не используется,
Ты даже не знаешь, что такое и зачем основания математики, раз такое пишешь.
- изоморфизм Карри-Говарда и тезис Чёрча;
- содержание диссертации Брауэра в переводе Гейтинга;
- пять уровней языка и четыре способа отрицания по Маннури;
- интерпретацию логических констант по Брауэру-Гейтингу-Колмогорову;
- теорию статистического обучения Вапника и модель spikgram Миколова;
- отличия машины Тьюринга от машины Поста.
1.6 Охранник обязан:
- отрицать закон исключённого третьего;
- отрицать любую математику, не выразимую через типизированную лямбду в MLTT или нормальные алгорифмы Маркова;
- переписать на прувере AUTOMATH де Брауна книгу "Основы математического анализа" Ландау;
- представить все формальные теории в терминах алфавитов, термов и манипуляций с ними;
- свести гомологическую алгебру к исчислению предикатов, используя нумерацию Гёделя.
 194 Кб, 800x600
194 Кб, 800x600Можно. Иными методами просто не получится в силу изоморфизма Гагарина-Авогадро в категории представлений машин Поста.
> Можно ли учить математике через программирование?
Нужно. ,21 век таки.
> Типа делаешь свой язык программирования где числа это палочки и прочее такое.
Зачем велосипед, все давно есть. Coq тот же.
 298 Кб, 683x1024
298 Кб, 683x1024Тебе ж подпекает с того, что mltt весь твой манямир рушит, типа любой кудахтер в математике может ровно то же что и ты, как минимум не меньше, а по факту в разы больше. Петросянством прохудившуюся веру не заштопать, привыкай.
>теорию статистического обучения Вапника
А случаем диакон-конструктивист и вапниколюб из ML треда программача это не одно лицо?
>Немалая часть практически полезной алгебры формализована в коковской либе ssreflect
А что там есть?
Кстати, мы уже выяснили, в какой категории построен изоморфизм Гротендика-Садовничего?
Но ведь Hask - не категория.
 53 Кб, 576x432
53 Кб, 576x432>>40503
Из вас сыщики ещё хуже чем математики. В /др я за всю жизнь ни одного поста не написал. А форсил я много что и кого, от нечёткой логики до Настеньки пикрелейтед. Только все это никакого отношения к теме треда не имеет. Впрочем, с моих постов никогда и никто так не рвался, как местный кловн, который походу все мои посты за последний год (если не больше) собрал. Я даже и сам уже не припоминаю, когда я тут про Вапника с Миколовым писал.
Я надеюсь, что это такой троллинг тупостью. Для подобного тут вроде есть тред математических мемов, а тут тред вроде про другое.
Этот тред не первый в цепочке. Изначально цепочка началась с наркоманских тредов про определение натуральных чисел. Так что безумие в традициях этого треда, для серьезной беседы о чем-то конкретном лучше отпочковаться.
 163 Кб, 645x729
163 Кб, 645x729> Это все замечательно, но на вопрос, заданный в >>40467-посте, все-таки не отвечает никак.
Главная претензия местного подгоревшего дурачка к Брауэру и интуиционизму в том, что из него прямо следует, что бездушная машина в плане математики может ровно столько же, сколько человек. Точнее, это следует из конструктивизма, Брауэр бы с таким выводом не согласился, но тонкие различия неоинтуционизма и различных направлений конструктивизма далеко за пределами способностей к пониманию тутошних дегенератов. По идее, критиковать им было бы логичнее Чёрча и Поста, но для этого нужно их хотя бы почитать, а там букв много и они нерусские какие-то. Это как с критиками эволюции, которые хуесосят Дарвина только потому что в школе больше ни про кого не рассказывают, хотя на деле все их претензии относятся к современной СТЭ, а Дарвин вообще верующим был.
>все мои посты за последний год (если не больше) собрал
Я думал может что-то новое придумаешь, чем упоминать автомат деБрауна по сто раз.
> А что бесконечные множества ни в каком виде изучать нельзя, ты не упомянул.
Можно. И даже упомянул, в какой статье Брауэр доказывает, что алеф-нуль единственная бесконечность, за которой могут стоять правила построения, и что нет ни одного внятного доказательства, что последующие алефы больше, чем алеф-нуль. Все это я упоминал и неоднократно.
 24 Кб, 200x284
24 Кб, 200x284> Я думал может что-то новое придумаешь, чем упоминать автомат деБрауна по сто раз.
Если бы ты хотя бы понял, о чем он, можно было бы и что-то более новое упомянуть. А так и этого слишком.
Но ты же не понял, что книга Ландау не имеет отношения к математике. Сам Ландау этого не скрывал, указал в предисловии даже.
Ну в inaccessible cardinals ты всё еще не веришь. Значит отрицаешь существование топосов, ведь они требуют аксиомы универсума (эквивалентна аксиоме недостижимого кардинала). Хотя ранее и про них что-то упоминал.
Допустим, что есть биекция f между N и множеством всех подмножеств N. Если x - натуральное число и f(x) = M, то x либо является элементом M, либо не является. В зависимости от этого будем называть натуральные числа соответственно: самопринадлежащие и несамопринадлежащие.
Пусть A - множество в точности всех несамопринадлежащих натуральных чисел. Так как f - биекция, существует натуральное число a такое, что f(a) = A.
Если a является самопринадлежащим, то a является элементом A и потому должно являться несамопринадлежащим. Противоречие.
Если a является несамопринадлежащим, то a является элементом A и потому является самопринадлежащим. Снова противоречие.
Таким образом, биекции f существовать не может.
> Но ты же не понял, что книга Ландау не имеет отношения к математике. Сам Ландау этого не скрывал, указал в предисловии даже.
Эта книга вообще не при чем. Речь о самом прувере automath и почему и что и как его возможности позволяют доказать в математике. Де Браун ясно писал, почему этот прувер не привязан ни к какой аксиоматике, в качестве таковой хоть 10 заповедей можно использовать.
Если подумать, то немного печально, что для бесед об основаниях математики надо отпочковаться от треда об основаниях математики.
>>40522
Так я ведь в том и дело, что я даже ни Брауэра, ни интуиционизм не упоминал. Я специально с самого начала вопрос сформулировал максимально широко, а в ответ получил какую-то шизофрению.
Более того, уже сколько постов прошло, а никто так и не сформулировал претензий к цитатам на пиках. Видимо и вправду это все насеменил один местный поехавший. Впрочем, ладно, бог с ним.
> Но машины не могут доказывать теоремы, только проверять.
Могут. Т.н. тактики в коке кв раз для этого. Но ты веровай и дальше, что не могут, семень тут, неси хуйню про охранников. Вдруг правда поможет.
Миллионы обезьян, печатающие на печатных машинках случайные символы тоже могут доказывать теоремы. Конструктивные по крайней мере. Вся суть конструктивизма кароче.
>Миллионы обезьян
Это ты про homo sapiens?
Ах, нет, забыл. Ведь у этих есть одно очень важное отличие от всех остальных обезьян: богоизбранность. Главное - верить.
> мам я такой же умный как математики, ведь я тоже сделан из кварков и электронов)))
Любых обезьян, даже конструктивисты справятся.
>>40575
Угадал я значит, причина твоего копротивления - скрепы. Ничем ты не уникальнее обезьяны, и машина Тьюринга может ровно столько же сколько и ты, в том числе и в манипуляции с нарисованными значками, за которыми не стоит ничего. Алгоритмически неразрешимую задачу ты никак не решишь, впрочем и это уже обсуждали, ты тогда знатно обпучкался, показав что понятия не имеешь об идентификации систем. Короче, все с тобой ясно, опученный.
То есть - никак? Алгоритмически неразрешимое решается доказательством алгоритмической неразрешимости. См. Пенроуз, почему человек не машина Тьюринга.
Алгоритмически неразрешимые задачи легко решаются применением исключённого третьего.
>и машина Тьюринга может ровно столько же сколько и ты
Доказательство где? Или ты адепт свидетелей машины Тюринга? Понятненько, верунство очередное.
Шёл как-то Иван по лесу. Глядит — счётчик Гейгера лежит. Обрадовался: "Это ж я все теоремы сейчас докажу!". Сел на пенёк и стал записывать. Счёлк. "О теоремку подвезли". Наслюнявил Иван карандаш и стал писать.
Долго так писал. Внезапно счётчик затрещал так, что Ивану захотелось третью руку — в две руки не успевал записывать — а потом внезапно затих. Пока Иван крутил находку, за спиной, близко-близко, раздался звучный бас Есенина-Вольпина:
— Так-так-так, что тут у нас? Теоремки доказываем?
Иван растеряно посмотрел на незванного гостя и промычал что-то среднее между "угу" и "при Сталине такой хуйни не было". Есенин-Вольпин взял тетрадочку, полистал и говорит:
— Всё верно, молодой человек, вот вам за ваши труды два яблочка.
— Но я ещё не закончил, жду вот когда счётчик снова теоремы доказывать станет, — растерялся Иван.
— О-о-о, юноша, так вы верующий, — покачал головой гость, — Веруете в эту вашу бесконечность. А вы её видели? А? Видели? То-то и оно, нет её и всё тут. Не будет больше трещать, все трески закончились в этом вашем совке. А вы тут сидите и веруете, что оно снова трескать будет. У-у-у, ненавижу совок ебаный.
Старик сжал кулаки и устремил взгляд в осеннее небо.
Тут из кустов выскочили санитары, повязали деда и поволокли куда-то, а он всё кричал: "Закончились трески! Я их ещё в прошлом году все использовал!"
Иван долго смотрел им в след, пока из оцепенения его не вывел заветный доказыватель теорем очередной серией тресков. Работа чуть было не закипела, но тут Иван заметил, что рядом стоит грузный мужчина в пижонской шубе и с тростью. Иван насторожился.
— О, яблочки. Разрешите угоститься, — сказал мужик и недождавшись ответа схватил яблоко и откусил здоровенный кусок, — Ну не смотрите на меня так, у вас яблока много, не жалейте для доброго человека.
— Всего-то два.
Мужик подовился:
— Простите, что? Вы в текущем году веруете в целые числа? А вы их видели то, целые числа эти? А? Видели? Коров небось считали, да яблоки, и думали, вот они — целые числа. Но это всего-лишь приближение реальности, в которой нет никаких целых чисел, ибо всё вокруг непрерывные физические поля, вот где в уравнении Шрёдингера целые числа?..
Но Иван не дал ему закончить, бросив всё, включая солитонный сгусток яблочной материи, он вскачил и стремглав помчался в чащу леса, чтобы жить там и больше никого не видеть, а питаться только супом из ромашек.
>и машина Тьюринга может ровно столько же сколько и ты
Доказательство где? Или ты адепт свидетелей машины Тюринга? Понятненько, верунство очередное.
Шёл как-то Иван по лесу. Глядит — счётчик Гейгера лежит. Обрадовался: "Это ж я все теоремы сейчас докажу!". Сел на пенёк и стал записывать. Счёлк. "О теоремку подвезли". Наслюнявил Иван карандаш и стал писать.
Долго так писал. Внезапно счётчик затрещал так, что Ивану захотелось третью руку — в две руки не успевал записывать — а потом внезапно затих. Пока Иван крутил находку, за спиной, близко-близко, раздался звучный бас Есенина-Вольпина:
— Так-так-так, что тут у нас? Теоремки доказываем?
Иван растеряно посмотрел на незванного гостя и промычал что-то среднее между "угу" и "при Сталине такой хуйни не было". Есенин-Вольпин взял тетрадочку, полистал и говорит:
— Всё верно, молодой человек, вот вам за ваши труды два яблочка.
— Но я ещё не закончил, жду вот когда счётчик снова теоремы доказывать станет, — растерялся Иван.
— О-о-о, юноша, так вы верующий, — покачал головой гость, — Веруете в эту вашу бесконечность. А вы её видели? А? Видели? То-то и оно, нет её и всё тут. Не будет больше трещать, все трески закончились в этом вашем совке. А вы тут сидите и веруете, что оно снова трескать будет. У-у-у, ненавижу совок ебаный.
Старик сжал кулаки и устремил взгляд в осеннее небо.
Тут из кустов выскочили санитары, повязали деда и поволокли куда-то, а он всё кричал: "Закончились трески! Я их ещё в прошлом году все использовал!"
Иван долго смотрел им в след, пока из оцепенения его не вывел заветный доказыватель теорем очередной серией тресков. Работа чуть было не закипела, но тут Иван заметил, что рядом стоит грузный мужчина в пижонской шубе и с тростью. Иван насторожился.
— О, яблочки. Разрешите угоститься, — сказал мужик и недождавшись ответа схватил яблоко и откусил здоровенный кусок, — Ну не смотрите на меня так, у вас яблока много, не жалейте для доброго человека.
— Всего-то два.
Мужик подовился:
— Простите, что? Вы в текущем году веруете в целые числа? А вы их видели то, целые числа эти? А? Видели? Коров небось считали, да яблоки, и думали, вот они — целые числа. Но это всего-лишь приближение реальности, в которой нет никаких целых чисел, ибо всё вокруг непрерывные физические поля, вот где в уравнении Шрёдингера целые числа?..
Но Иван не дал ему закончить, бросив всё, включая солитонный сгусток яблочной материи, он вскачил и стремглав помчался в чащу леса, чтобы жить там и больше никого не видеть, а питаться только супом из ромашек.
И как же тогда человечестов до конструктивизма и комплюктера вычисляло и пользовалось богомерзкими верованиями в физике?
Кек новый мем
> То есть - никак? Алгоритмически неразрешимое решается доказательством алгоритмической неразрешимости.
Это не решение.
> См. Пенроуз, почему человек не машина Тьюринга.
Извини уж, третьесортный научпоп я не читаю.
>>40579
> Алгоритмически неразрешимые задачи легко решаются применением исключённого третьего.
Исключенноетретье можно и в коке прописать. Это уход от решения, а не решение.
>>40585
> Доказательство где? Или ты адепт свидетелей машины Тюринга? Понятненько, верунство очередное.
Доказательство чего, мань? Того, что ты выше алгоритма не прыгнешь? Так это факт. См выше
>>40587
> И как же тогда человечестов до конструктивизма и комплюктера вычисляло и пользовалось богомерзкими верованиями в физике?
Чего несешь-то? Прочитай хоть на что отвечаешь.
 35 Кб, 807x606
35 Кб, 807x606> Алгоритмически неразрешимые задачи легко решаются применением исключённого третьего.
Проблему останова ты тоже исключённых третьим решишь? Да и правда, или остановится, или нет))))0) И как Тьюринг до такого гениального варианта не додумался?
Почитал я про кок и всё равно не вижу, где тут программа что-то доказывает сама. Приведи простой пример кода, который что-то доказывает. По сути мы просто задаём систему аксиом, пишем доказательство, запускаем шайтан-машину, и либо на выходе будет противоречие, либо всё ок.
>Чего несешь-то? Прочитай хоть на что отвечаешь.
Люди пользовались бесконечностями и прочими нормальными вещами, приходя к решению тех или иных задач, в отличии от догматиков с манятеориями в которых они не могут досчитать до двух.
Даже если под всем этим на самом деле конструктивное начало и все можно свести к нему, это не отменяет полезность, отвергаемых конструктивными сектантами, ментальных конструкций.
Ну там есть тактики вроде omega, которые докажут за тебя, если доказываемые вещи можно свести к Presburger arithmetic, но это именно что proof assistance, а не доказательство чего то нового машиной.
Мимо
>Так это факт
Тогда тебе не составит труда его доказать.
>Почитал я про кок и всё равно не вижу, где тут программа что-то доказывает сама.
Никак не доказывает, тактики это чуть лучше, чем кататься ебалом по клаве, пока прувер не перестанет ругаться.
>если доказываемые вещи можно свести к Presburger arithmetic
Согласно тезису Чёрча это и есть вся математика.
1. верит в целые числа
2. верит в (хоть и в потенциальную, но) бесконечность
3. верит в существование абстрактных идей
4. верит в то, что человеческий мозг в точности машина Тьюринга
5. верит что пека с виндой, лемуры, генератор случайных чисел и rule 110 могут доказывать теоремы, просто почему-то этого не делают, стесняются наверное
Можно ещё пройтись по вере в реальность и по органам чувств, но это же не /ph так что пока не будем.
Я не хейтер конструктивизма, я просто не возвожу его в религию.
Ты думаешь, что бредовые идеи типа конструктивизма нужно обсуждать на серьёзных щщах. А на самом деле конструктивизм нужно сразу посылать нахуй. Как ферматиков, как православную арифметику.
> Ты думаешь, что бредовые идеи типа конструктивизма нужно обсуждать на серьёзных щщах. А на самом деле конструктивизм нужно сразу посылать нахуй.
Только потому что одному дегенерату с мейлру за свои скрепы обидно? Оно того не стоит.
 29 Кб, 460x460
29 Кб, 460x460> Но в том посте нет никаких доказательств же.
Формально я имел в виду:
?(?, ?) =\/ != 42, где ?() любой оператор, ? в скобках - любая переменная или константа. В общем, ?(?, ?) - любое выражение или лямбда терм. Пример: 1+1 =\/ != 42. Вопрос, допустимо ли так доказывать, если исключенное третье считать допустимым для использования в математике? И если да, зачем тогда вообще математика, если любое выражение можно просто поместить в левую часть "уравнения или не уравнения", и оно будет истинным?
Ага, а умножение натуральных чисел это маняфантазии верунов.
> По сути мы просто задаём систему аксиом, пишем доказательство, запускаем шайтан-машину, и либо на выходе будет противоречие, либо всё ок.
Нет, плохо ты читал. Доказательство не пишем, пишем теорему или теоремы. А кок выдаёт доказательство, если оно возможно в используемой аксиоматике. Это не то же самое, что написать доказательство самому и проверить. Короче, опучкался ты, снова.
Только вот на практике тактики кока не справляются с доказательством содержательных теорем. И даже более того, как правило они не справляются просто с тем, чтобы находить доказательства для переходов очевидных с точки зрения квалифицированных в релевантной области математиков, которые были бы просто опущены в статье.
Какие детсадовские попытки заштопать манямир, даже за шиворот ссать жалко лол. Некоторые подмножества исчислений CiC в коке уже сейчас полностью разрешимы с помощью тактик. Насчет остальных - это только вопрос времени, т.к. там более сложные исчисления, не все из которых даже исследованы нормально, Барендрегт и еще 3,5 исследователя все точно не вывезут. Дело только в этом, но ты этого даже не понимаешь, как не понимаешь ,что вообще такое кок и что и как он делает. Отсюда и твои жалкие потуги, "на практике тактики кока не справляются с доказательством содержательных теорем", "очевидных с точки зрения квалифицированных в релевантной области математиков,".
Люблю твои сказочки, захожу почитать перед сном как счётчики Гейгера, лемуры и петух доказывают теоремы. И всё сами! Жаль результатов нет, ну наверное просто тетрадочку с теоремами теряют. Ну или ты нассал себе за шиворот и штопаешь свой манямир, который в реальности состоит из 4.5 аутистов, который занимаются вопросами логики, а не математикой.
А что не так то? Там где тебе нужно знать точное значение это очевидно не подойдет, но если тебе нужно только знать что 7 или не 7 то в чем проблема то?
Корень из двух хотя бы до 5 знаков я смогу в твоей маняарифметике найти?
Продемонстрируй короткий кхе-кхе пример.
>>40605
Ну если дидовские методы позволяют, благодаря удобству дидовской математики, ебать законы природы и в хвост и в гриву, а в теории маняформализаторов вычислять можно только до одного то опять таки не вижу проблемы.
Только школьники и упоротые долбоебы будут в погоне за модой отвергать удобные вещи ради NEW SUPER COOL COQSTRUCTIVIST THIORY 2k18 COUNT FOR 3 POSIBEL.
И уж тем более долбоебизм называть только это МАТЕМАТИКОЙ. Все хуйня кроме пчел, да
Ой, а чё так кода много? Я думал omega напишу и мне петух всё докажет.
> Это все конструктивисты настолько не знакомы с математикой, или ты один такой?
Давай так. Исключенное третье допустимо использовать как доказательство в математике? Да или нет?
Что значит "использовать как доказательство"? Это схема аксиом вообще-то. Ты какие книжки по логике читал?
Конечно, а как иначе? Приведи простенький пример, показывающий ущербность исключённого третьего.
Просто это верно так же, как верно 2 = 2. В чём тут доказательство? Это всегда верно, да. Не понимаю тебя.
> Просто это верно так же, как верно 2 = 2.
Нет, не так же. 2=2 это вычисление. А 2 =\/ != 2 это исключенное третье.
> Нет, 2=2 это закон тождества.
Вообще-то в математике это доказывается. И "доказательство" уровня той картинки с Пифагором и подписью "хуле тут доказывать, и так видно" это не серьёзно.
Вообще - нет, не доказывается. Символ равенства вводится не на уровне математических теорий, а на уровне формального языка. Аксиомы на него налагаются тоже не математикой, а нижележащей логикой.
> Вообще - нет, не доказывается. Символ равенства вводится не на уровне математических теорий, а на уровне формального языка. Аксиомы на него налагаются тоже не математикой, а нижележащей логикой.
Сам себе противоречишь. Отношение равенства задается правилами, да. Применение правил этих в каждом конкретном случае возможно только путём вычисления результата. Конечно, так никто не делает, разве что прувер. Человек просто запоминает, что любое число равно самому себе. И в такой форме это уже является лингвистическим правилом, а не математическим, т к не при этом не используется вычислений.
 49 Кб, 1280x720
49 Кб, 1280x720> Есть ли математические основания на пучках онли без богомерзской вычислимости?
На пучках - HoTT, а без вычислимости - ZFC.
Я так и не понял, зачем тот анон колоски к моей пикче приделал.
Лучше бы вместо аэропорта на фоне зал МГУ сделали.
 525 Кб, 1600x1200
525 Кб, 1600x1200В нём нет никакой веры, в нём есть только правила построения. Конструктивизм ведь создавался величайшими математиками, а не ебанатами с мейлру. Впрочем, всё это я объяснял уже сто раз, но вы на мейлру не способны осилить даже известные работы Тьюринга, что уж говорить про действительно глубокие работы Мартина-Лёфа и других 3,5 исследователей в этой области.
Правила построения - просто частный случай правил вывода. Ничего нового в них нет.
Лол, странно что не вспомнил. Спасибо.
Почему у тебя именно с Мартин-Лефа так жопа горит?
Мань, тот факт, что исчисление для теории типов несколько отличается по формату от гильбертовских исчислений для классических теорий (в первых в основном все формулируется через правила, во вторых в основном через аксиомы) - это просто вопрос формата задания и те и другие исчисления на самом деле допускают переформулировки в обоих стилях. Что более существенно -это то, какие стили математических рассуждений эти исчисления призаны моделировать. В случае с теорией типов Марти-Лёфа соответствующий тип рассуждений - это рассуждение в терминах индуктивных конструкций. И такие рассуждения активно опираются на абстракцию потенциальной бесконечности (и да, для того чтобы принимать такие рассуждения нужно верить в эту абстракцию.
> (и да, для того чтобы принимать такие рассуждения нужно верить в эту абстракцию.
Эта абстракция подразумевается например при задании правил построения типа N. Допустим, я в неё не верю. И что, у меня от этого перестанет работать например тактика ring в коке? Веровать можно в нечто изначально оторванное от построения, точнее в допустимость использования такого.
Стандартное определение типа N - это по существу определение натуральных чисел через приписывание палочек. Это действительно базовая вещь явно подкрепленная нашим практическим опытом. Но теория типов производит очень широкое обобщение этого и в ней таким образом строятся не только натуральные числа, а населяется вся вселенная типов, включающая замысловатые функционалы высших типов, вселенные (во внутреннем смысле) и т.п. И здесь связь с практическим опытом разумеется теряется, остается только верить в то, что все правила построения новых функционалов сохраняют потенциальную вычислимость на любых входах которые потенциально могут быть построены в рамках незаконченной вселенной.
Кстати, проблемы с теорией множеств носят такой же характер, только там они вместо переноса интуиции касающийся натуральных чисел на высшие типы, они перенесли интуицию касающуюся конечных множеств на произвольные. Что характерно, в первых попытках построить формальные теории и там и там нашли противоречия (см. парадокс Жирара и парадокс Рассела соответственно).
Ты думаешь, хоть кто-то итт не знает про парадокс Рассела?
> (см. парадокс Жирара и парадокс Рассела соответственно).
Парадокс Жирара тривиально обходится кумулятивной иерархией типов, я вообще не знаю, о чем Мартин-Леф думал, когда вводил правило type : type, очевидно же, что сразу надо было что-то вроде type i : type i+1.
> И здесь связь с практическим опытом разумеется теряется, остается только верить в то, что все правила построения новых функционалов сохраняют потенциальную вычислимость на любых входах которые потенциально могут быть построены в рамках незаконченной вселенной.
Это ещё у Брауэра решено, 2ой акт интуиционизма. Построение делается только на основании уже построенного ранее более простого, либо по некоторым критериям равенства с уже построенным. Какой угодно функционал своим к более простому, у того же Мартин-Лефа суждения (общие схемы посылок и заклбчений в правилах) рассматриваются по нарастающей сложности, для одной переменной, для двух и для n.
> Кстати, проблемы с теорией множеств носят такой же характер, только там они вместо переноса интуиции касающийся натуральных чисел на высшие типы, они перенесли интуицию касающуюся конечных множеств на произвольные.
И тут же обосрались, потому что всякие недостижимые кардиналы не строятся на основе конечных множеств, как построения в теории типов или интуиционизме, а просто вероваются от балды, причём нет даже внятных пруфов того, что алеф1 больше чем алеф-нуль, на что Брауэр указывал ещё в 1912 году.
>Парадокс Жирара тривиально обходится кумулятивной иерархией типов, я вообще не знаю, о чем Мартин-Леф думал, когда вводил правило type : type, очевидно же, что сразу надо было что-то вроде type i : type i+1.
Ну да, ровно также как обошли парадокс Рассела. А тот факт, что Мартин-Лёф облажался показывает, что ровно также как и у теоретико-множественников наивная интуиция теоретико-типовиков подвережена парадоксам.
>либо по некоторым критериям равенства с уже построенным
Это ключевое место. Фунции в теории типов могут применяться к любым термам соответствующего типа, в частности к термам которые будут введены после введения этой фунции. И чтобы считать, что даже какая-то очень простая фунция (например следования на натуральных числах) тотальна нужно предполагать, что любой терм который когда-либо может быть построен будет равен терму в канонической форме (т.е. в данном примере по нему можно вычислить конкретное натуральное число). Другими словами происходит использование глобальных свойств ещё незаконченной вселенной. На мой взгляд совершенно правильно называть это верой, если мы называем верой пригятие вселенной множеств фон Неймана.
Теорию множеств ты совсем не понимаешь. Недостижимые кардиналы прямой аналог вселенных в теории типов т.к. каппа недостижим если и только если капповый уровень вселенной фон Неймана модель ZFC. И если Брауэр не принимал аксиому степени, то конечно он не принимал существования несчетных мощностей. Просто одни люди произвели более широкре обобщение простой конечной математики, а некоторые (Брауэр) менее широкое.
> Другими словами происходит использование глобальных свойств ещё незаконченной вселенной. На мой взгляд совершенно правильно называть это верой,
А какие могут быть проблемы с правильно типизированными термами?
> Недостижимые кардиналы прямой аналог вселенных в теории типов
Вообще, разница в использовании актуальной бесконечности. В теории множеств это делать не стесняются, в отличие от. Но если ты говоришь, что речь об аналоге иерархий вселенных, и допустимо написать, например алеф-нуль : алеф1 и в целом алеф i : алеф i+1, тогда вообще интересно получается. Так ведь можно сказать и про мир идей Платона и тогда выходит, что Платон был конструктивистом, а в основаниях математики кроме конструктивизма ничего никогда и не было.
>в отличие от
RUSSIAN MOTHERFUCKER DO YOU SPEAK IT
>Так ведь можно сказать и про мир идей Платона и тогда выходит, что Платон был конструктивистом, а в основаниях математики кроме конструктивизма ничего никогда и не было.
Преемственность, слыхал о такой?
Никакого конструктивизма не было и нет, было развитие идей обычной математики. Просто несколько хитрецов грамотно пропиарились выделив это во что-то непохожее и назвав другим словом.
>А какие могут быть проблемы с правильно типизированными термами?
Никаких проблем с теорией типов у меня нет. Просто при рассуждениях в ней в общем случае неявно используется предположение, что все термы данного типа, которые потенциально могуть быть построены в процессе (сколь угодно длительной) деятельности в теории типов, могут быть полностью вычислены. Это сильное предполжение, на самом деле я не знаю, как такое предположение обосновать не аппелируя к законченному построению вселенной т.е. к актуальной бесконечности; что гаходит свое отражение в том, что в определенных версиях теории типов Мартин-Лёфа можно доказать непротиворечивость некоторых непредикативных классических теорий. Если ты хочешь верить в это и считать базовым принципом - пожалуйста. Но просто здесь нет принципиальной разницы с верующими в разные большие кардиналы.
Это впрочем не умаляет достоинств теории типов в смысле возможности извлечения конкретных алгоритмов из конкретных доказательств.
> Просто при рассуждениях в ней в общем случае неявно используется предположение, что все термы данного типа, которые потенциально могуть быть построены в процессе (сколь угодно длительной) деятельности в теории типов, могут быть полностью вычислены.
Почему "неявно"? Это явное предположение. И оно прямо вытекает из правил построения. Если у нас есть правила построения N, то из них прямо следует потенциальная построимость любого элемента этого типа. То же с любым другим типом, любой терм, являющийся элементом этого типа строится по правилам построения элемента этого типа, т.е. этот терм правильно типизирован, в противном случае он не является термом данного типа. Мы не можем взять этот элемент из мира идей Платона, мы его можем либо построить явно, либо задать общее правило построения, либо задать правила его вычисления из какого-то другого терма (бета- и др. редукции итд).
> Это сильное предполжение, на самом деле я не знаю, как такое предположение обосновать не аппелируя к законченному построению вселенной т.е. к актуальной бесконечности;
Вот ты говоришь, что я не понимаю теорию множеств, а ты похоже, не понимаешь разницу между потенциальной и актуальной бесконечностью. Правило построения "type i : type i+1" это потенциальная бесконечность, а аксиома "существует бесконечное множество" - это актуальная.
>>40696
> Алеф 1 больше Алеф 0 по определению, если ты не в курсе.
Если это понимать в смысле, указанном предыдущим оратором >>40688 то да, т.к. получается кумулятивная иерархия типов. Но тогда это конструктивизм простой, от которого тут кое-кто рвется уже пару лет. Если же понимать это с позиции теории множеств, то Брауэр пояснил, какие пробемы из этого вытекают.
>>40691
> Никакого конструктивизма не было и нет, было развитие идей обычной математики
Брауэр и за это пояснял, в чем разница. Ты тут точно ничего нового не скажешь, поверь.
У алефа-1 в смысле теории множеств нет внятного определения, так как не даны правила построения.
Я под ним понимаю некое религиозное верование. Алефы выше алефа-0 невозможно понять человеческим мозгом, так как для них нет правил построения. Это следует из применения тезиса Чёрча к пояснению Брауэра о невозможности вычисления алефа-1 и выше.
> Конструктивисты, как дальтоники, неспособны понять бесконечность, когда нормальные люди абсолютно без проблемы работают с ней.
С чем ты там работаешь? То, что ты понимаешь под "работой с бесконечностью" - чисто лингвистические, а не математические построения.
Рассказать можно и про гаррипоттера с файрболами. Того же уровня твое понимание бесконечности.
А что понимает здоровый человек, когда говорит о цветах, неспособных быть увиденными дальтоником?
Ты сделал утверждение об алефе-1. Ты отказываешься объяснить, что ты подразумеваешь под термином "алеф-1".
Как по-твоему можно выразить цвета разных оттенков через черный и белый? Как синий выразить через них? То же самое и с конструктивной математикой.
Я понимаю под этим термином объект религиозной веры вроде Христа или Аллаха, тут можно много чего подставить, но результат один - невычислимая хуета.
Если ты делаешь утверждение, в котором хотя бы одно слово не может быть тобою определено, - ты несешь ахинею. Ты сделал утверждение "нет пруфов того, что алеф-1 больше чем алеф-0".
 289 Кб, 1728x800
289 Кб, 1728x800Хех, что-то проиграл с твоего поста. Недели 2 назад даже гугл намекнул. В одном из рекламных сообщений впарашке выдало пикрил и сообщение о какой-то клинике которая обследует глаза. Я тогда отметил что это странно т.к. по моим запросам ничего подобного выдать не должно. Обычно любое рекламное объявление я примерно знаю почему мне выдало, а тут вдруг совсем не в тему. А после твоего поста внезапно ОСОЗНАЛ. Ведь в последнее время я пытаюсь вступить в секту, искал и качал все эти книжки что тут кидает конструктивофорсер, про ML теорию, машинку поста и т.д. На фоне чтения возникает много релейтед запросов в гугл. В общем все сходится. А киберпанк в лице гугла уже наступил
>>в отличие от
>RUSSIAN MOTHERFUCKER DO YOU SPEAK IT
https://ru.wiktionary.org/wiki/в_отличие_от
Тебе учебник для страшеклассников по русскому языку посоветовать?
>Правило построения "type i : type i+1" это потенциальная бесконечность, а аксиома "существует бесконечное множество" - это актуальная.
Анон, так он о том и говорит (если я правильно понял): мы предполагаем, что мы можем построить и вычислить каждый из термов, заданных этим правилом, но у нас для этого нет никаких оснований. Самый простой способ получить такое основание - считать, что вселенная уже построена, то есть все эти термы существуют (то есть свести это к актуальной бесконечности). В противном случае получается, что возможность построения у нас основана на такой же вере, как и у всех остальных математиков.
>сообщение о какой-то клинике которая обследует глаза.
>Обычно любое рекламное объявление я примерно знаю почему мне выдало, а тут вдруг совсем не в тему.
То есть о том, что ты много сидишь за компьютером и гугл предполагает, что у тебя от этого портится зрение, ты не подумал? Спишу на то, что ты приукрасил историю ради комического эффекта.
 17 Кб, 274x274
17 Кб, 274x274(Автор этого поста был забанен. Помянем.)
> Самый простой способ получить такое основание - считать, что вселенная уже построена,
Т.е уверовать в это? Ведь не построена по факту-то.
> В противном случае получается, что возможность построения у нас основана на такой же вере, как и у всех остальных математиков.
Про возможность никто не говорил. Речь про правила построения. Которые не требуют никакой веры, т к они есть независимо от того, веруешь или нет.
Определи мне Я, умник хуев.
Почитал, тебе процитировать?
>в от-ли-чи·е от
>Устойчивое сочетание.
>(от кого, чего) в противоположность кому, чему
Ты не нейтив спикер? Может тебе на simple russian переформулировать? Ты не стесняйся, анон, спрашивай - тут доска взаимопомощи, отвечаем на вопросы, помогаем друг другу. Можешь еще заглянуть в international math thread, анон: https://2ch.hk/math/res/27513.html (
>Т.е уверовать в это? Ведь не построена по факту-то.
Ну так он тебе об этом и говорит, вот!
>Про возможность никто не говорил.
Ну когда ты пишешь type i : type i + 1, ты же предполагаешь, что единицу мы можем прибавлять сколько угодно, пользуясь заданными правилами построения, так?
Блин, ну не тролль пжл "нейтив"
https://ru.wikipedia.org/wiki/Предлог
Второе предложение процитировать или сам прочтешь?
> Ну когда ты пишешь type i : type i + 1, ты же предполагаешь, что единицу мы можем прибавлять сколько угодно, пользуясь заданными правилами построения, так?
Это прямо прописано в правиле, зачем там что-то предполагать? Незачем предположение, что уже все построено, т.к оно ничего не даёт дополнительно к правилу, даже если бы и правда было построено. Т.е имеем абсолютно ненужную сущность, вера в которую никакого смысла не имеет.
Анон, ну куда ты лезешь? Погугли, что такое эллипсис. И в следующий раз, когда запутаешься в окончаниях, просто сразу признай, что ты обосрался (с кем не бывает, анон), а не пытайся по ходу дела маневрировать в материях, о которых ты имеешь весьма и весьма смутное представление.
Продолжить дискуссию можем (можешь) в треде русского языка в /fl.
Ой, блять, ладно, если ты сам знаешь такие слова то поверю что намеренно. Но как НЕЙТИВ тебе заявляю, выглядит по-уебански, на манер английских deferred prepositions и так на русском не пишут.
Нормально выглядит. Конечно, похоже немного на ущербное "это зависит", но в пределах нормы.
мимо
Алеф-1 можно явным образом определить как множество всех не более чем счетных ординалов. Легко видеть, что при таком определении алеф-1 не биективен алеф-0.
Множество не более чем счетных ординалов само по себе не более чем счётный ординал
> Тогда оно является элементом самого себя
Подмножеством. К i+1 хоть сколько добавляй, так из алефа0 алеф1 не построить.
Если ординал, состоящий в точности из всех не более чем счетных ординалов, сам является счетным, то он является своим элементом. По определению. Понимаешь?
> Если у нас есть правила построения N, то из них прямо следует потенциальная построимость любого элемента этого типа.
В том то и дело, что этого недостаточно. Термы типа N могут быть сформулированы в терминах произвольных других типов, например можно формализовать подходящий кусок топологии и выписать терм обозначающий какой-нибудь числовой инвариант какого-нибудь пространства. В итоге вопрос о том, вычислимы ли произвольные термы данного конкретного типа зависит от всей системы в целом, а не только от определения данного конкретного тип; если взять какой-нибудь вариант теории типов в котором есть противоречие, то в ней будут термы типа N, которым не будет соответствовать никакого значение. И хотя с твоей стороны происходит заметание этого вопроса под ковер, наличие такого глобального свойства требует обоснования для каждого конкретного варианта теории типов.
На мой взгляд наиболее естественный способ обосновать, почему конкретный вариант теории типов работает как следует, т.е. все термы вычислимы - это построить её модель (в терминах рекурсивных функционалов высших типов).
Конечно можно говорить, что-то в духе того, что все определения типов, которые дают "квалифицированные" теоретико-типовики в некотором смысле "правильны" и сохраняют "правильность" теорий типов и во всех "правильных" теориях типов все вычислимо. Проблема в том, что если посмотреть, что должно соответствовать "правильности" с более формальной точки зрения, то наиболее родственно оно конструкциям возникающим в доказательствах сильной нормализуемости сильных лямбда исчислений и там определения таких свойств существенно опирается на квантификацию по бесконечным множествам (см. доказательство сильной нормализуемости системы F). Но как ни крути, либо нужно принять на веру, что (довольно туманная) интуиция теоретико-типовиков никогда не приводит к проблемам, либо дать обоснование в терминах бесконечных множеств.
>это построить её модель
Я не понимаю, как вообще можно доверять этому методу. Ведь у нас нет ни одной гарантированно свободной от противоречий теории, в которой можно было бы строить более-менее содержательные модели.
другой анон
>Ведь у нас нет ни одной гарантированно свободной от противоречий теории, в которой можно было бы строить более-менее содержательные модели.
Таким образом мы можем редуцировать корректность одной теории к другой. И если теория к которой происходит редукция в каком-нибудь смысле понятнее редуцируемой теории, то это до некоторой степени объясняет последнюю.
Кстати, как ты себе представляешь гарантии свободы от противоречий для какой-либо теории, которая формализует хотя бы арифметику натуральных чисел? Ведь для любой такой теории есть неограниченно много доказательств и поэтому гарантировать непротиворечивость можно только приняв какой-нибудь метод установления универсальных утверждений.
> И хотя с твоей стороны происходит заметание этого вопроса под ковер, наличие такого глобального свойства требует обоснования для каждого конкретного варианта теории типов.
Твоя проблема в том, что ты не понял сути конструктивизма и поэтому пытаешься натянуть его на формализм как сову на глобус. А оно изначально создавалось не для этого, более того, формализация интуиционизма невозможна принципиально. Я уже пояснял за это, но местный шизик все закукарекал. Формализация понятия алгоритма (и интуиционизма Брауэра) невозможна по той простой причине, что таковая должна одновременно решать и проблему останова универсальной машины Тьюринга. Поэтому в конструктивизме речь только об уточнении понятия алгоритма (нормальные алгоритмы Маркова, машина Тьюринга итд). Именно по этой причине, о которой говорил ещё Брауэр, обосрался Гильберт со своей изначальной программой формализма.
> Но как ни крути, либо нужно принять на веру, что (довольно туманная) интуиция теоретико-типовиков никогда не приводит к проблемам, либо дать обоснование в терминах бесконечных множеств.
Вот ещё одно подтверждение, что ты не понимаешь тех соображений, которые вообще привели к созданию конструктивизма. MLTT корректна и непротиворечива не потому что преподобный рабби Леф так скозал, а по той простой причине, что в ней принципиально невыразимо невычислимое в ней же. Оно исходя из этого и создавалось. Противоречивость подобных теорий видно сразу же, самый известный пример - парадокс Жирара, суть которого в том, что при использовании правила построения type : type появляется возможность выразить в mltt парадокс Рассела, т.е невычислимую хуету. Менее известные примеры противоречивых лямбда исчислений есть у Барендрегта.
> На мой взгляд наиболее естественный способ обосновать, почему конкретный вариант теории типов работает как следует, т.е. все термы вычислимы - это построить её модель (в терминах рекурсивных функционалов высших типов).
Это бессмысленно. Я тут миллион раз упоминал книжку "Programming in Martin-Lof type theory", авторов не помню, какие-то шведские куколды, так вот, она является наиболее полным изложением mltt и написана под руководством Мартин-Лефа. Так вот, там в предисловии прямым текстом написано, что mltt создавалась как основания и поэтому её представление в других теориях смысла не имеет, это наоборот другие теории должны выражаться в ней. Поэтому, единственный смысл, семантика mltt это вычислимость. Она выразима в терминах операционной семантики (в приложении они перечислены), что делает её не только основаниями, но и языком программирования (изоморфизм Карри-Говарда). Последнее касается не только конкретно mltt, но и CiC (Coq) и UTT (Idris) итд.
Как оборот?
>Последнее касается не только конкретно mltt, но и CiC (Coq) и UTT (Idris) итд.
А python и javascript тоже основаниями математики являются? Не для себя спрашиваю.
>A marriage of category theory and set theory: a finitely axiomatized nonclassical first-order theory implying ZF
>Marcoen J.T.F. Cabbolet
>(Submitted on 11 Jun 2018)
>The main purpose of this paper is to introduce a finitely axiomatized theory that might be applicable as a foundational theory for
mathematics. For that matter, some twenty axioms in a formal language are introduced, which are to hold in a universe consisting of a class of objects, each of which is a set, and a class of arrows, each of which is a function on a set. One of the axioms is nonclassical: it states that, given a family of ur-functions - i.e. functions on a singleton - with disjunct domains, there exists a uniquely determined sum function on the union of these domains. This 'sum function axiom' is so powerful that it allows to derive ZF from a finite axiom scheme. In addition, it is shown that the Loewenheim-Skolem theorem does not hold for the present theory, which therefore can be considered stronger than ZF. Furthermore, the axioms of category theory are proven to hold: the present universe may therefore serve as an ontological basis for category theory. However, it has not been investigated whether any of the soundness and completeness properties hold for the present theory: the inevitable conclusion is therefore that only further research can establish whether the present results indeed constitute an advancement in the foundations of mathematics.
> А python и javascript тоже основаниями математики являются?
Я ссылался на операционную семантику mltt, она очень простая. Coq на жабаскрипте давно существует, если что. Lean тоже есть на жабаскрипте, причём был ещё 2ой версии, где ядро HoTT. Так что ответ - да, изоморфизм Карри-Говарда допускает такую возможность.
>mltt создавалась как основания и поэтому её представление в других теориях смысла не имеет, это наоборот другие теории должны выражаться в ней
Лол.
Говоря проще, это лишнее. Бурбаки, Кантор, Гильберт теорию множеств через другие не представляли. И никто не лолкает. Так и тут, есть операционная семантика, этого достаточно для работоспособности mltt, зачем огород из пучков городить.
>>40810
Это понятно, что ты в своем представление теории типов в качестве самодостаточных оснований следуешь за Мартин-Лёфом.
В принципе, с этим нет особых проблем. Есть довольно много математиков, которые привыкли думать о математике в бурбакистском ключе и поэтому для них аксиоматика Цермело-Френкеля представляет из себя формализацию самоочевидных принципов - у них уже есть преконцепция что такое множества и что с ними можно делать, а аксиомы просто соответствуют этой интуиции. Ровно также на существование имеет право и более маргинальная позиция людей думающих о математике в интуиционистских терминах для которых самоочевидной оказывается теория типов.
Не буду скрывать - я привык к бурбакисткому изложению математики и соответственно у меня развита именно интуиция касательно понятия множества, а не типа. Поэтому с неизбежностью я смотрю на интуиционизм и его формализации со стороны.
И как я уже довольно подробно расписал в нескольких предшествующих постах, анализируя их со стороны довольно прозрачно, что в них неявно заложены сильные и выходящие далеко за пределы вычислимой математики предположения (здесь под вычислимостью я понимаю вычислимость на натуральных числах) - особенно явно это проявляется в версиях с W-типами и вселенными.
>MLTT корректна и непротиворечива не потому что преподобный рабби Леф так скозал, а по той простой причине, что в ней принципиально невыразимо невычислимое в ней же.
Буллщит, феномен второй теоремы Гёделя о неполноте очень общий и чтобы доказать корректность (или хотя бы непротиворечивость) какого-либо метода рассуждений заведомо нужно выйти за его пределы.
>Противоречивость подобных теорий видно сразу же
Отмечу, что в теории множеств ровна такая же история с большими кардиналами. Из серьезных ошибочных попыток дать аксиому большого кардинала судя по всему был только кардинал Рейнхардта и не то, чтобы доказать его противоречивость было особо сложно.
Хотя, конечно, нельзя полностью исключать, что в будущем нетривиальные противоречия будут найдены, как для ZFC и её расширений так и для теорий типов
>>40810
Это понятно, что ты в своем представление теории типов в качестве самодостаточных оснований следуешь за Мартин-Лёфом.
В принципе, с этим нет особых проблем. Есть довольно много математиков, которые привыкли думать о математике в бурбакистском ключе и поэтому для них аксиоматика Цермело-Френкеля представляет из себя формализацию самоочевидных принципов - у них уже есть преконцепция что такое множества и что с ними можно делать, а аксиомы просто соответствуют этой интуиции. Ровно также на существование имеет право и более маргинальная позиция людей думающих о математике в интуиционистских терминах для которых самоочевидной оказывается теория типов.
Не буду скрывать - я привык к бурбакисткому изложению математики и соответственно у меня развита именно интуиция касательно понятия множества, а не типа. Поэтому с неизбежностью я смотрю на интуиционизм и его формализации со стороны.
И как я уже довольно подробно расписал в нескольких предшествующих постах, анализируя их со стороны довольно прозрачно, что в них неявно заложены сильные и выходящие далеко за пределы вычислимой математики предположения (здесь под вычислимостью я понимаю вычислимость на натуральных числах) - особенно явно это проявляется в версиях с W-типами и вселенными.
>MLTT корректна и непротиворечива не потому что преподобный рабби Леф так скозал, а по той простой причине, что в ней принципиально невыразимо невычислимое в ней же.
Буллщит, феномен второй теоремы Гёделя о неполноте очень общий и чтобы доказать корректность (или хотя бы непротиворечивость) какого-либо метода рассуждений заведомо нужно выйти за его пределы.
>Противоречивость подобных теорий видно сразу же
Отмечу, что в теории множеств ровна такая же история с большими кардиналами. Из серьезных ошибочных попыток дать аксиому большого кардинала судя по всему был только кардинал Рейнхардта и не то, чтобы доказать его противоречивость было особо сложно.
Хотя, конечно, нельзя полностью исключать, что в будущем нетривиальные противоречия будут найдены, как для ZFC и её расширений так и для теорий типов
А ничего, что Мартин-Лёф несколько раз давал противоречивые версии систем?
Нужно определять семантику, чтобы не было таких чудачеств.
Ты сначала ZFC осиль, потом будешь писать на моём дваче.
Если ты доказал непротиворечивость одной теории в другой, то ничто не мешает им обоим оказаться противоречивыми. Единственно это исключает возможность, что первая противоречива, а вторая - нет.
> на моём дваче.
Носатый, уходи.
>>40830
> Буллщит, феномен второй теоремы Гёделя о неполноте очень общий и чтобы доказать корректность (или хотя бы непротиворечивость) какого-либо метода рассуждений заведомо нужно выйти за его пределы.
Потому я и написал про операционную семантику, в терминах которой доказывается в т.ч непротиворечивость mltt. Насчёт геделя-шмеделя и прочего такого, попытка выразить это в теории типов приведёт только к ошибке, ибо невычислимая хуитка. Я тебе ещё раз скажу - ты лезешь с формализмом туда, где от него изначально старались избавиться по причине его безблагодатности. Поэтому и вместо аксиом там натуральная дедукция итд итп.
>Насчёт геделя-шмеделя и прочего такого, попытка выразить это в теории типов приведёт только к ошибке, ибо невычислимая хуитка.
Стандартное доказательство теорем о неполноте полностью конструктивно и в частности они приложимо к любой системе в которую можно погрузить гейтингову арифметику, в том числе к теориям типов.
Слышать о неприложимости формализма от тебя довольно смешно. То что ты называешь здесь формализмом это видимо просто общий метод широко применяемый в математической логике: чтобы исследовать некоторый метод математических рассуждений вначале нужно построить математическую модель понятия доказательства для данного случая, т.е. дать адекватное понятие формального доказательства, а затем исследовать это понятие математическими средствами. Идея о том, что переход от гильбертовского стиля исчисления к системе натуральной дедукции как-то принципиально мешает анализу системы просто показывает твое полное непонимание того, о чем ты говоришь. На самом деле метод приложим к любым методам рассуждения, которые могут быть описаны какой-нибудь рекурсивной процедурой. Учитывая тот факт, что немного ранее в этом треде ты сам защищал идею о том, что человеческий интеллект может быть заменен на компьютер, ....
>чтобы исследовать некоторый метод математических рассуждений
-->
чтобы исследовать некоторый метод рассуждений
Обычно, чтобы свести вопрос о непротиворечивости какой-нибудь менее понятной теории к вопросу о непротиворечивости более понятной теории. Характерный пример это доказательство непротиворечивости NFU в ZFC.
Зачем доказывать непротиворечивость одной теории множеств в другой теории множеств? Это ничего не даёт.
NFU вовсе не тоже самое, что обычные теории множеств в духе ZFC. Там существует множество всех множеств и тому подобные объекты. В результате там возможен в некоторых отношениях более естественный метод формализации теории категорий.
От того, что непротиворечивость NFU сведена к непротиворечивости ZFC, ничего нового мы не получили. По-прежнему непонятно, есть ли противоречия в NFU. Непонятно, легко ли их найти.
>метод формализации теории категорий
Категория функторов между двумя большими категориями существует? Категория эндофункторов Set, в частности? Категория всех категорий? infty-категории можно?
> принципиально мешает анализу системы
Ты б меня так читал, как отчитываешь. Не мешает оно анализу системы, речь о том, что эта система и без анализа обойдётся. 2 акта интуиционизма Брауэра не нуждаются в формализации, как не нуждается в ней и операционная семантика mltt. Просто потому что это не так работает. Ну формализуешь ты это, дальше что? То, в чем ты это формализуешь, тоже вообще то формализовать придётся. И дальше и дальше. Ты думаешь, что теория множеств истина в последней инстанции? Так её тоже опучкать можно.
>Категория функторов между двумя большими категориями существует?
Да.
>Категория всех категорий?
Да и она является своим собственным объектом.
>infty-категории можно?
Наверное, но нужно вникать. Проблема с NF и NFU состоит в том, что в них множества ведут себя не вполне так мы привыкли - в частности Set не будет декартова замкнута.
>По-прежнему непонятно, есть ли противоречия в NFU.
ZFC в отличие от NFU это теория с которой очень много работали. И если там и есть противоречия, то их совершенно нетривиально найти.
> Set не будет декартова замкнута.
Ну офигеть теперь, приплыли. В который раз убеждаюсь, что теоретико-множественные попытки формализовать категории не нужны.
>их совершенно нетривиально найти.
Вовсе нет. Сведение к ZFC никак не повлияло на сложность поиска противоречий в NFU, поскольку сложность не является инвариантом логических теорий, а полностью зависит от синтаксических инструментов, предоставляемых теорией. Даже если в теории A найти противоречия сложно и если непротиворечивость теории B сводится к непротиворечивости A, - вполне может быть так, что в B найти противоречия очень просто.
> Ну формализуешь ты это, дальше что?
Например, даже не вдаваясь в детали формализации, а исходя лишь из возможности такую осуществить я уже сразу могу сказать, что твой способ рассуждений либо противоречив, либо не может гарантировать свою собственную непротиворечивость.
>То, в чем ты это формализуешь, тоже вообще то формализовать придётся.
Зачем? Если мне нужен будет мета-анализ средств которые я сам использовал, то да. Но в общем случае нет, анализ это просто математические результаты, которые имеют некоторое отношение к философии математики. Ты же не говоришь физикам, что когда они анализируют физический мир математическими средствами, то они должны построить математическую модель того, как им удалось построить математическую модель.
>Ты думаешь, что теория множеств истина в последней инстанции?
В отличие от тебя я не считаю, что если мне кажется что-то интуитивно ясным, то это и есть истина в последней истанции. Наиболее убедительными я нахожу ультрафинитистские доказательства, центральная идея здесь состоит в том, чтобы доказательства на каждом конкретном обозримом примере соответствовали действительно осуществимым вычислениям; таким образом это фрагмент математики опирающийся на реальную физику. Проблема в том, что разумеется это очень ограничивающий взгляд на допустимую математику. Поэтому я часто и пользуюсь более сильными средствами, понимая, что основная гарантия их корректности состоит в том, что пока нам не удалось обнаружить проблемы с нашей интуицией.
>В который раз убеждаюсь, что теоретико-множественные попытки формализовать категории не нужны
Проблема в том, что если я не упускаю, чего-нибудь, то никаких принципиально более адекватных формализаций, чем погружение в теорию множеств нет. На самом деле очень интересно было бы найти понятную и объемлющую формализацию теоретико-категорных рассуждений в собственно категорных терминах.
>Вовсе нет. Сведение к ZFC никак не повлияло на сложность поиска противоречий в NFU, поскольку сложность не является инвариантом логических теорий, а полностью зависит от синтаксических инструментов, предоставляемых теорией. Даже если в теории A найти противоречия сложно и если непротиворечивость теории B сводится к непротиворечивости A, - вполне может быть так, что в B найти противоречия очень просто.
Нет. Ты же найдя какую-нибудь новую переформулировку гипотезы Римана наверное справедливо решишь, что переформулировка скорее-всего тоже очень сложная задача. Ровно также и здесь, мы знаем, что нахождение противоречия в ZFC это действительно сложная проблема и то, что мы нашли вопрос к которому он сводится говорит нам о том, что это скорее всего это тоже очень сложная проблема; центральное отличие состоит в том, что здесь мы можем решить проблему только в одну сторону.
>никаких принципиально более адекватных формализаций
Вообще, есть ETCC и ETCS от Lawvere. Не знаю, насколько они удачны, но они есть.
>переформулировка скорее-всего тоже очень сложная задача
Нет, не решу. Потому что я знаю, что очень многие сложные математические задачи с помощью удачно подобранной переформулировки сводились к очень просто решающимся задачам, даже тривиальным. Каждую переформулировку я рассматриваю саму по себе. Не настаиваю, что все должны так делать, но не вижу причин думать иначе.
Using this metaphor, SEAR can be thought of as an ETCS-car which comes preassembled with a nice slick control panel. Or, using an alternate metaphor, ZFC is like Windows, ETCS is like UNIX, and SEAR is like OS X (or maybe Ubuntu). With SEAR you get a nice familiar interface with which it is easy to do standard things, there is less cruft than you get with ZFC, and behind the scenes you have all the power of ETCS (and more). (Of course, if you like Microsoft products, then this metaphor probably does not appeal to you.)
Его формализация категории Set просто переформулировка теории множест. Формализация же Cat, насколько я слышал изначально была с пробелами и исправленная версия в итоге вышла весьма корявой, хотя я сам не смотрел.
>Нет, не решу
ОК. Но это довольно самонадейно. Конечно, сложные задачи решаются при помощи переформулировок, но все-таки это в норме не произвольные переформулировки, а правильно подобранные.
>просто переформулировка теории множест
Вот, кстати, сомневаюсь. Насколько я помню, в ETCS ни в каком виде не включена схема подстановки, то есть у него даже существование алефа номер омега-нулевое недоказуемо. Нет?
>не произвольные переформулировки
Однако нет причин считать апиори, что переформулировка задачи обязательно будет не менее сложна, чем исходная задача. В каждом конкретном случае нужно конкретное исследование.
>Вот, кстати, сомневаюсь.
Да, вроде действительно буквально она соответствовала не собственно ZFC, а теория множеств Цермело. Но дело в том, что в любом случае этот подход ничего особенно не дает по сравнению с формализацией теории категорий в теории множеств.
>Однако нет причин считать апиори что переформулировка задачи обязательно будет не менее сложна, чем исходная задача
Полных гарантий у нас конечно нет. Но например мне кажется довольно абсурдным рассчитывать, что если взять случайную из огромного числа известных NP-полных задач, которые никто особо не анализировал за исключерием доказательства их NP полноты и расчитывать, что анализируя эту задачу будут хорошие шансы решить P vs NP. Я не говорю, что возможность легко найти решение полностью исключена, просто исходя из моего опыта занятия математикой я считаю, что это маловероятно.
Причины, по которым ты испытываешь чувство абсурдности, у тебя не вполне отрефлексированы, как мне кажется. Ты фокусируешь внимание на NP-полноте. Но можно посмотреть шире и увидеть, что вообще большинство задач не решены даже схематично. И поэтому если взять случайную задачу, то решить её, скорее всего, будет очень трудно, независимо от того, эквивалентна ли она какой-либо из известных сложных задач. Я согласен с тем, что если взять случайную из NP-полных задач и пытаться её решить, то будет тяжко. Но я думаю, что эта сложность вызвана не тем, что задача эквивалентна NP-полной, а тем, что задача попросту не относится к узенькому классу ранее изученных человечеством задач. И я считаю, что доказательство NP-полноты задачи не будет свидетельством, что эту задачу очень сложно решить (а вот экспериментальный факт, что задача не решается применением стандартных методов, таким свидетельством будет). Так и с формальными теориями: то, что теория эквивалентна ZFC, не будет свидетельством, что в теории сложно найти противоречие. Зато факт, что долгий поиск противоречий не даёт результатов, таким свидетельством таки будет.
На самом деле здесь мы приходим к очень важному для успешного получения интересных теорем, но очень субъективному вопросу о том, как оценивать шансы на успех тех или иных подходов к решению проблем. Когда мы говорим о проблемах, которые безуспешно в течение долгого времени пытались решить многие в том числе действительно талантливые математики, то решения как правило приходят из применения существенно новых методов. При этом я полагаю, что для того, чтобы улучшить шансы на успех кроме того, чтобы подход был действительно новым, желательно иметь какие-нибудь (неформальные) объяснения, почему он избегает проблем предшествующих подходов и в целом иметь какой-нибудь план действий.
Если посмотреть на какую-нибудь очередную графовую NP-полную задачу в качестве подхода к решению P vs NP, то по существу он не удовлетворяет ни одному из трех критериев. В случае поиска противоречия в NF вместо ZFC, здесь до некоторой степение есть новизна (NFU в самом деле сильно отличается от привычных теорий множеств), но по остальным критерия все также выглядит плохо.
Если говорить не о вопросах о непротиворичивости, а более обычных действительно важных открытых вопросах, т.е. связанных со многими другими вопросами. Я лично считаю, что за ними как правило лежит некоторое фундаментальное недопонимание сооответствующей предметной области. И их решение с должно устранить это недопонимание. Выбор правильного контекста (т.е. переформулировки) и составляет существенную часть этого прояснения ситуации.
> В отличие от тебя я не считаю, что если мне кажется что-то интуитивно ясным, то это и есть истина в последней истанции.
А где и когда я вообще хоть что-то про "интуитивную ясность" говорил?..
> Ты же не говоришь физикам, что когда они анализируют физический мир математическими средствами, то они должны построить математическую модель того, как им удалось построить математическую модель.
Будешь смеяться, но именно это можно предъявить и не только физикам. Идентификация систем часто может тривиально решить проблему, над которой даже очень умный исследователь будет биться долго.
Математика состоит из того, что линеаризуется – то есть в абелевой категории и тд (условно алгебра) и того, что нет (условно: топология; нлаб, стакс проджект).
Счет палочек это computer science. по изоморфизму Карри-Кетчупа и есть математика.
> Ну понял. Типа алгебра это когда палочки считаем. А геометрия?
Алгебра - гамалогии, геометрия - тапалогии. Все вместе - пучки. Что тут непонятного.
 50 Кб, 960x492
50 Кб, 960x492Охуенно, лучше и не скажешь.
>>40887
>научность
>фальсифицируемость
Как там в 1946? Человек, который решил изучать вместо математики основания, а вместо науки философию науки, называет кого-то хипстером, спешите видеть. Тот же Гильберт для физики сделал намного больше, чем все твои кумиры от Брауэра до Поппера.
Впрочем, ничего нового. К 1970-м все уже убедились в неадекватности фальсификационизма, что изначальное требование фальсифицируемости слишком сильное,более поздние же формулировки вроде методологии исследовательских программ, не налагают никаких содержательных ограничений вообще. Apparently you didn't catch the memo.
Америку открыл, всем давно известно, что математика не наука. Алсо сам этот критерий тоже нефальсифицируем, сам себе не удовлеторяет.
Чего он не может осознать на протяжении семи тредов уже, а довольно простая мысль, казалось бы: те, кто занимается наукой (или математикой); и те, кто дает определения науке, кто выясняет, что является наукой, а что нет, и каким критериям наука обязана удовлетворять – два разных множества людей, не пересекающихся никак, дизъюнктивных, вообще.
>этот критерий тоже нефальсифицируем, сам себе не удовлеторяет
Можно показать (было показано учениками Поппера) что этому критерию в его изначальной формулировке не удовлетворяет ничего вообще. То есть это бессмысленное абсолютно занятие, философия науки это разговор слепого о живописи.
> Америку открыл, всем давно известно, что математика не наука.
Только неконструктивная, по озвученным мной причинам.
> Алсо сам этот критерий тоже нефальсифицируем, сам себе не удовлеторяет.
Это как?
>>40888
> Впрочем, ничего нового. К 1970-м все уже убедились в неадекватности фальсификационизма,
Все хипстеры убедились, потому что им напекло от нефальсифицируемости их религии? Или что? Что там неадекватного?
> изначальное требование фальсифицируемости слишком сильное,
С чего бы? Нормальное, адекватное требование, которому удовлетворяет любая наука, если это наука, а не вера.
> философия науки это разговор слепого о живописи
Это надо отлить в граните, выражаясь словами классика.
> простая мысль, казалось бы: те, кто занимается наукой (или математикой); и те, кто дает определения науке, кто выясняет, что является наукой, а что нет, и каким критериям наука обязана удовлетворять – два разных множества людей, не пересекающихся никак, дизъюнктивных, вообще.
Это не "простая мысль", а простая вера. У Вапника очень хорошо за критерий Поппера изложено применительно к машинному обучению. Я понимаю, что ты скажешь, что это не наука, т.к не гамалогии, но это только твоё личное мнение, с реальностью не связанное.
> Он ненаучен, его нельзя фальсифицировать.
Можно. Допустим, что критерий Поппера неверен. Тогда получается, что астрология, херомантия, вера в жопу хэнка итд - это науки. М?
> Нет, не получается.
Почему? Ты можешь назвать критерий научности теории лучше попперовского?
Потому что из того, что научная теория может быть принципиально неопровержимой не следует, что хиромантия и астрология науки. Могу, наука это то, чем занимаются учёные.
Конечно.
Ну правда, я уверен, что многие теоремы были доказаны во время сранья или мытья яиц. Конечно это наука.
>у Вапника
Теперь понятно откуда ветер дует. У Вапника изложено про Поппера, у Лёфа изложено про Канта, у Маннури про Витгенштейна. То есть даже самого Поппера ты не читал, как и любое явление в истории человеческой мысли рассматриваешь его исключительно с позиций своей секты.
>Все хипстеры убедились
Почему прямые ученики Поппера, с которыми он вел дискуссии это бесполезные хипстеры, а сам Поппер нет? Потому что про Поппера написал Вапник, вот почему. Что одобрено церковью конструктивизма, то не оспаривается. Только вычисляется.
>Что там неадекватного?
А я уже объяснял, два треда подряд, только ты прослушал. И ссылки приводил. Не имеет значения даже, применим ли этот критерий к самому себе. К реальной науке он совершенно не применим. Что показано (Куном, Лакатосом и др) не из каких-то философских принципов, а путем рассмотрения контрпримеров, в первую очередь.
Если бы этот принцип понимался буквально, и его последовательно и строго применяли, наука бы перестала существовать. Поскольку ни одна успешная теория не может ему удовлетворить.
>Тогда получается, что астрология, херомантия, вера в жопу хэнка итд - это науки
Даю тебе определение из действительности, а не из шизанутого манямирка. Наука это то, за что дают гранты. Как только научнут давать за астрологию – можешь называть её наукой. В общем-то, ничего плохого в астрологии в узком смысле нет, это такая вспомогательная дисциплина на стыке метеорологии и какой-нибудь биохимии. Как с торсионными полями, которые придумал Картан – изначально вполне научная концепция была, но в нынешнем виде это понятно что. Профанация же и обман есть во всех областях науки: пример в математике – конструктивизм.
>Учёные дрочат, мочатся в сортире
Как и все люди, кстати. Начни выяснять в чем состоит здравый смысл научного сообщества и каких конвенций оно придерживается и ты окажешься гораздо ближе к пониманию что такое наука, чем изучая интерпретацию Вапника предложений Поппера.
 55 Кб, 640x489
55 Кб, 640x489> Наука это то, за что дают гранты.
> здравый смысл научного сообщества
> К реальной науке он совершенно не применим. Что показано (хипстером, сойбоями и др)
Я тебя услышал. Из твоего монолога я понял, что печет тебе с того, что гамалогии нефальсифицируемы аки боженька, и никакого отношения к научным знаниям не имеют. А виноват в этом Маннури, разумеется. Кто ж ещё.
Конструктивисты не получают новых результатов. Они просто раз в десятилетие берут какое-нибудь утверждение школьного уровня, например теорему Больцано-Коши, и пытаются передоказать конструктивно. Обычно ничего не получается.
Перепощу в тред с цитатами.
Не услышал. Единственный способ донести до тебя информацию это прочитать твоих кумиров и найти у них цитаты, где утверждается то же самое.
Смотри пример: Поппер молодец, Кун и Лакатос – сойбои, хипстеры и тд. В реальности это представители одной и той же школы Поппера. Но: Поппера упомянул Вапник, а его учеников нет.
Другой пример: с критикой Поппера высказался Витгенштейн (инцидент с кочергой). Получается он тоже сойбой. Ох вейт. Витгенштейна упоминал Миколов! Конструктивист protection comes in. И т.д.
То есть, ты просто будешь игнорировать любые идеи, даже не пытаясь разобраться, если они не в полном согласии с твоими догмами; называть бесполезным хипстерством и тд, других оснований тебе не нужно. Догмы же в защите не нуждаются, достаточно self-reference, криков про вычислимость, смешных картинок, оскорблений.
>>40912
Ну переписать книгу Ландау "Основы анализа" на прувере Автомат чем не результат. Или там нумерацией Гёделя свести производные функторы к исчислению палочек на машине Тьюринга.
Не важно как нелепо это, он a priori не признаёт существенным ничего другого, вычислимость это и есть математика, математика это и есть вычислимость.
Не важно что там утверждали разные люди по этому поводу, если упомянуть Гротендика или там Манина это апелляция к авторитетам, а если какого-то конструктивиста – к вычислимости. Проходили уже, серьёзную дискуссию вести невозможно.
> если они не в полном согласии с твоими догмами; н
У меня нет догм. Догмы и вера у тебя, поскольку что тебе ещё остаётся с нефальсифицируемой религией. Разве что в очередной раз Миколова вспомнить.
> Не важно как нелепо это, он a priori не признаёт существенным ничего другого, вычислимость это и есть математика, математика это и есть вычислимость.
Но ведь так и есть. Альтернатив никогда и не было, разве что как ты предлагаешь, считать наукой только то, за что дают гранты.
> Не важно что там утверждали разные люди по этому поводу, если упомянуть Гротендика или там Манина
Не важно, конечно. Утверждения в математике не стоят ничего, важны доказательства. А о каком вообще доказательстве можно говорить применительно к вере в нефальсифицируемое исключенное третье?
 407 Кб, 480x726
407 Кб, 480x726>исключённое
Сначала обдумай "парадокс лжеца", а затем - "теоремы Гёделя о неполноте",
после этого - можешь возомнить логический элемент полным по Гёделю и охуеть.
 26 Кб, 644x800
26 Кб, 644x800> вся вообще история неконструктивной математики закончилась
Это, мягко говоря, не так. Анус твой закончился, а не математика.
> Это, мягко говоря, не так.
Это так. Осталось только гранты получать под смузи на коворкингах, сам же признал. Исключенное третье и актуальные бесконечности это тупик. Остаётся только вычислимость.
> Анус твой закончился
Скрепы болят? Неважно во что ты там вероваешь, алгоритмически неразрешимые проблемы не решаются никак. И ты никуда не денешься от этого факта.
>алгоритмически неразрешимые проблемы не решаются никак.
Аксиома выбора не вызывает противоречий.
Математика доказала теорему Ферма.
А чего добился конструктивизм за последние ну хотя бы сто лет?
> Аксиома выбора не вызывает противоречий.
Нет конечно. И исключенное третье не вызывает. Откуда противоречия в нефальсифицируемой религии.
Фальсификационизм это и есть религия, он был опровергнут, неоднократно на примерах конкретных ситуаций в истории науки было показано, что принцип фальсифицируемости не работает. Ты это игнорируешь, говоря о сойбоях, хипстерах. Прочитай в словаре, что такое "догма".
>считать наукой только то, за что дают гранты
За всю историю начиная с 17-го века, как только наука возникла, никому не удалось дать внятного и содержательного определения тому что такое наука, изложить критерии, которым должна удовлетворять научная теория.
Почему – любому ученому это и так понятно; сойбои же вроде Поппера это слепцы в картинной галерее и просто не понимают, о чем говорят.
Как ты не понял, что такое языковые игры. У Витгенштейна, не в пересказе Миколова или кого ещё, под этим понимались informal rules. То, чему можно научиться, но что нельзя формализовать. Как научиться? Abrichten, дрессировка, реальная практика. Это и есть здравый смысл ученого. Ему он понятен без явно высказанных критериев и определений, тебе же и твоим кумирам никакие определения не помогут. Потому что вместо науки и математики они занимались хуйней, называемой "основания математики" и "философия науки".
>Утверждения в математике не стоят ничего
Только если это не утверждения твоих любимых авторов, на них ты ссылаться не стесняешься. Отстаивая точку зрения, высказанную Маннури, приводить как аргумент слова самого Маннури, и т.д.
Для тебя не подлежит сомнению любое утверждение высказанное конструктивистом, оно автоматически верно, потому что вычислимо. Соответственно вся математика сводится к деятельности конструктивистов по проверке написанными нематематиками типа Ландау книг.
А если привести нетривиальный пример деятельности Вейля, Серра, Гротендика, то он сводится к "перекладывание палочек + верунство". Особенно легко игнорировать то, назначение чего тебе изначально не было известно, та же гомологическая алгебра.
Мне-то это ясно, конечно, я просто ещё раз озвучиваю, чтобы мимо проходящие типа >>40467 понимали, с кем имеют дело.
Фальсификационизм это и есть религия, он был опровергнут, неоднократно на примерах конкретных ситуаций в истории науки было показано, что принцип фальсифицируемости не работает. Ты это игнорируешь, говоря о сойбоях, хипстерах. Прочитай в словаре, что такое "догма".
>считать наукой только то, за что дают гранты
За всю историю начиная с 17-го века, как только наука возникла, никому не удалось дать внятного и содержательного определения тому что такое наука, изложить критерии, которым должна удовлетворять научная теория.
Почему – любому ученому это и так понятно; сойбои же вроде Поппера это слепцы в картинной галерее и просто не понимают, о чем говорят.
Как ты не понял, что такое языковые игры. У Витгенштейна, не в пересказе Миколова или кого ещё, под этим понимались informal rules. То, чему можно научиться, но что нельзя формализовать. Как научиться? Abrichten, дрессировка, реальная практика. Это и есть здравый смысл ученого. Ему он понятен без явно высказанных критериев и определений, тебе же и твоим кумирам никакие определения не помогут. Потому что вместо науки и математики они занимались хуйней, называемой "основания математики" и "философия науки".
>Утверждения в математике не стоят ничего
Только если это не утверждения твоих любимых авторов, на них ты ссылаться не стесняешься. Отстаивая точку зрения, высказанную Маннури, приводить как аргумент слова самого Маннури, и т.д.
Для тебя не подлежит сомнению любое утверждение высказанное конструктивистом, оно автоматически верно, потому что вычислимо. Соответственно вся математика сводится к деятельности конструктивистов по проверке написанными нематематиками типа Ландау книг.
А если привести нетривиальный пример деятельности Вейля, Серра, Гротендика, то он сводится к "перекладывание палочек + верунство". Особенно легко игнорировать то, назначение чего тебе изначально не было известно, та же гомологическая алгебра.
Мне-то это ясно, конечно, я просто ещё раз озвучиваю, чтобы мимо проходящие типа >>40467 понимали, с кем имеют дело.
>Фальсификационизм это и есть религия
Кокоструктивист нашел себе новую секту. Или вступил ещё в одну. Мультисектант.
Я ему это уже говорил, он считает что доказательство великой теоремы Ферма это конструктивный результат, даже какую-то уродскую формулировку в терминах своей теории типов приплёл, типа, вот, я пруверы знаю.
Не хочет человек понимать, при чем там эллиптические кривые и теория представлений, что поделать, слепому новые глаза не дашь, а конкретно этого ещё и из галереи не вывести, нравится ему людей пугать, похоже.
>Вот - мы не можешь вычилсть знак ((100!)!))! у пи, значит, нам ничего не известно об этом знаке, то есть нельзя сказать одназначно ответить - эта цифра 3 или нет.
Ой, где-то был тут алгоритм вычисления N-ного знака у числа Pi... А вот же: https://habr.com/post/179829/
Возможно, можно было бы его адаптировать и под факториалы эти, не?
Тогда вычисли мне ((100!)!))!
Нельзя скозать тут будит 3 или нет исключеннёное третие исключенно111!
Ты что ослеп? Нельзя сказать, какая цифра будет, значит, исключающее третье неприменимо здесь.
Аххах, если лжец сказал, что он пиздит - значит он не пиздит,
и он вполне правдиво сказал, что он пиздит - а значит пиздит.
А если он пиздит, что он пиздит то он правду говорит что он пиздит.
Раз он правду говорит про то, что он пиздит, то он либо не лжец (правда же),
либо таки лжец и правдиво утверждает, что таки пиздит.
Тут кстати, тоже закон исключённого третьего. И третьего не дано.
Или таки дано? Лол.
Только утрафинизм! Толька хардкоре!
Гротендик считал, что тупо перебор - некрасивое решение. Задача не решена по-настоящему, пока не придумана общая красивая теория, позволяющая решать целый класс аналогичных задач.
Манина наш конструктивист лишил статуса математика и за меньшие пригрешения: тот упомянул в своей книге существование невычислимых функций.
С Гротендиком же смешно получилось: конструктивист много говорил про топосы, пока не узнал, что в топосе Гротендика используется аксиома недостижимого кардинала. Пришлось срочно маневрировать и убеждать, что у Гротендика, который данное понятие ввел, определение неверное, вот, у Лавера верное или еще у кого. С Воеводским и теоремой о гомоморфизме норменного вычета похожее было, оказалось: кумир занимался гамалогиями до святой теории типов. Предательство почти.
Что самое смешное, Ловер (именно так его фамилию принято транскрибировать на русский) не конструктивист ни разу, и даже посрался недавно с каким-то индусом, попытавшимся сделать конструктивную версию ETCS на основе теории Мартин-Лёфа.
https://arxiv.org/abs/1201.6272
А ещё оказывается, это был не рандомный индус, а заслуженный коллега Мартин-Лёфа.
Смешно получилось.
http://staff.math.su.se/palmgren/
Немного гуманитарно на самом деле.
Теоретически слепой может воспринимать живопись, если найти удобный способ перекодировать ее в те категории восприятия, которые доступны слепому.
Но если нашему гипотетическому слепому хирургически встроить искусственные глаза и дать таким образом зрение, - его восприятие живописи изменится.
 60 Кб, 700x525
60 Кб, 700x525Содомит
Почти. Видимо корректнее будет сформулировать как то, что математика, программирование и теория типов - это одно и тоже.
>В любой науке ровно столько науки, сколько в ней математики.
>В любой математике ровно столько математики, сколько в ней вычислимости.
Предыдущий, тонет тут: https://2ch.hk/math/res/25624.html (
Архивач: https://arhivach.cf/thread/369697/ (У кого не открывается - попробуйте HTTP.)
Перекат: https://2ch.hk/math/res/40955.html (
Перекат: http://arhivach.cf/thread/369744/
Перекат: >>40955 (OP)
Перекот: https://2ch.hk/math/res/40955.html (
Перекот: http://arhivach.cf/thread/369744/
Перекот: >>40955 (OP)
Перекіт: https://2ch.hk/math/res/40955.html (
Перекіт: http://arhivach.cf/thread/369744/
Перекіт: >>40955 (OP)
>>40381
>Браузер писал, то так оно и есть. Слово Браузера - закон.
Вот это было излишне, ибо на принципах интерпретатора:
>>40466
>непогрешимость браузера ещё сильнее усилилась





















![14830130820maths[1].jpg](/math/big/thumb/25624/15297904900861s.jpg)
![xczxczc[1].jpg](/math/big/thumb/25624/15297904900872s.jpg)
![216-0018[1].jpg](/math/big/thumb/25624/15297904900883s.jpg)