Это копия, сохраненная 13 января 2022 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
Тред для обсуждения определения N, конструктивизма, интуиционизма, Грэя, петухов.
N = {0, 1, 2, 3, ...}.
Я нихуя не понял? N определяется через кардиналы или кардиналы через N? Именно об этом верещал N-шизик?
Лол, надо мне пойти поспать.
Определили же с помощью языка, который каждый трактует как хочет.
Наоборот важно владение независимыми от трактовок знаниями.
Капитан [sppoiler]К[/spoiler]О.
Она субъективная только в предпочтениях в выборе областей. Тут спорят о вкусах? К какому результату стремятся спорящие?
>>38
О, это гораздо больший спор, чем вы думаете. Это спор фактически о том, что есть математика: наука или ненаука?
Если содержать её основания на вере, то наукой математика никак считаться не может (и я совсем не говорю, что это плохо, возможно, даже наоборот), в противном случае - это всё-таки наука.
Это спор обо всём, что есть.
Допустим вы определили, что такое наука. И что такое "ненаука". Возникает закономерный вопрос - в какой внешней системе вы дали им определения?
Если эта система - естественный язык, то уверяю: вас легко могут понять не так или вывернуть наизнанку смысл, сделать неверный вывод из ваших фраз... Практичнее - движение наоборот - определение физических, в частности языковых, явлений в математике с её-то стремлением к непротиворечивости.
Как построение моделей теорий Ловера в теории категорий. Кстати, домен этих функторов это же КАТЕГОРИЯ ТЕОРИЙ.
fix: домены
Ну и что там? Типа Рыбникова?
http://baaltii1.livejournal.com/198675.html
http://baaltii1.livejournal.com/200269.html
Это заслуживает отдельного треда в силу своей меметичности.
Причём следует очень чётко разделять научную работу в этой области
и
их личные, Владимира или Романа, филосовское, психологическое и наркотическое самопознание.
Репутацию и личную жизнь эти дела подмачивают СИЛЬНО. Поэтому не надо так, ребят, оно того не стоит.
Вкину тезис. Любое неконструктивное определение N тривиально сводится:
- либо к любому конструктивному определению (алгорифм Маркова, нумералы Черча, ...) т.к. н-р подсчет кардиналов множеств ничем не лучше подсчета счетных палочек или функций следования от 0.
- либо к любой рандомной фуфлософии (яскозал) или религии (я верую в хуйню, и ты так делай).
 62 Кб, 1200x979
62 Кб, 1200x979Ну что, потомки, N определили уже?
 94 Кб, 271x311
94 Кб, 271x311Филдсовский лауреат В. Воеводский (на картинке в танке) разрабатывает и внедряет новые основания математики с помощью компьютерной системы Кок (игра слов: Кок = петух).
Под танком -- специалисты по классической теории множеств Цермело-Френкеля. Нововведения Воеводского оставят их за бортом.
Не шарю за основания, но если Вован к успеху придет, задавит всех адептов ТМ, то учебники переписывать будут? Будут ли нас потомки называть дедами, реконструирующими математику 20века?
Конструктивные основания - естественное продолжение работ Брауэра. В принципе, отличие от неконструктивных оснований в том, что выкинули всякую фофудью, нарушающую вычислимость. И вуаля, оказалось что математику можно построить на комплюктере. Такой-то нежданчик.
Мне пропустить его и сразу за Воеводского браться?
Нормально успехи, я способный очень
>К психиатрам я с этим не обращался. Как-то с самого начала было ясно, что это никакая не шизофрения.
А надо бы, почти по всем критериям подходит.
Согласно МКБ-10 должен наблюдаться хотя бы один из следующих признаков:
Эхо мыслей (звучание собственных мыслей), вкладывание или отнятие мыслей, открытость мыслей окружающим.
Бред овладения, воздействия, или пассивности, отчётливо относящийся к телу или конечностям, мыслям, действиям, или ощущениям; бредовое восприятие.
Галлюцинаторные голоса, комментирующие или обсуждающие поведение больного; другие типы «голосов», идущих из различных частей тела.
Устойчивые бредовые идеи, которые культурно неадекватны, нелепы, невозможны и/или грандиозны по содержанию.
Либо должны наблюдаться по крайней мере два из следующих «меньших» симптомов:
Стойкие галлюцинации любой сферы, сопровождающиеся лабильным или неполностью сформированным бредом, но без выраженного аффекта; либо постоянные, навязчивые сверхценные идеи.
Неологизмы, шперрунги, разорванность речи.
Кататонические расстройства, такие как возбуждение, застывание или восковая гибкость, негативизм, мутизм и ступор.
Достоверные и последовательные изменения общего качества поведения, проявляющиеся утратой интересов, бесцельностью, поглощенностью собственными переживаниями, социальным аутизмом.
Негативные симптомы (но не обусловленные при этом депрессией или фармакотерапией), которые могут быть выражены
апатией
бедностью или неадекватностью эмоциональных реакций
социальной отгороженностью
социальной непродуктивностью.
При этом указанные симптомы должны отмечаться не менее месяца. Состояния, отвечающие данным критериям, но продолжающиеся менее месяца, классифицируются как острое шизофреноподобное психотическое расстройство (F23.2 с добавочным четвёртым знаком, обозначающим характер расстройства), а если они впоследствии продолжаются свыше месяца, то диагноз изменяется (перекодируется) на соответствующую форму шизофрении.
 88 Кб, 940x498
88 Кб, 940x498Вброшу тезис. И Воеводский, и Михайлов не настоящие, просто позеры. Вот Михайлов ездил в Индию, учил язык, да. Какой? Бенгали, в Калькутте.
Типичный индоевропейский язык, такой же как французский примерно, или английский. Охуеть самопознание, да? Мог бы ездить в Бангалор, Ченнаи, изучать тамильский, каннада, читать поэзию Бхагавата Пурана, Канака Даса, но нет, ему надо в самую не индийскую часть индии, тьфу, блядь.
Ничем не отличается от фитоняшек, увлекающихся йогой.
А Воеводский чем занимался после Филдса? Эволюционной биологией, популяционной генетикой? Ну пиздец, еще бы историей занялся. Где же было его чутье визионера?
Математика все еще ждет своих героев.
>>43
Наука или не наука это путь к определению понятия "определение".
Просто дело вот в чём: есть геометрия Римана, Лобачевского и Евклида, и все они работают. То есть в математике можно выдумать любую хуйню, главное что внутренних противоречий не было. Таким образом вопрос вот в чём: что в математике применимо к естественным наукам и технике, а что нет. И зачем заниматься тем, что неприменимо? Между тем замечу: часто бывает что мне, как физику, очень помогают функции, которые математики исследовали до внедрения их в естественные науки. Ну и математики это дёшево. Им синхротронов и микроскопов не надо.
>в математике можно выдумать любую хуйню, главное что внутренних противоречий не было.
Можно. Только это и будет хуйня, если без противоречий, то неполная. А если полная, то с противоречиями.
>в математике можно выдумать любую хуйню, главное что внутренних противоречий не было. Таким образом вопрос вот в чём: что в математике применимо к естественным наукам и технике, а что нет.
Все, что непротиворечиво, объективно существует.
Ох, лол, спервадобейся
>Все, что непротиворечиво, объективно существует.
Что значит "объективно существует" в математике?
>Является термом в языке первого порядка.
Т.е. может быть записан с помощью конечного числа знаков.
>Обнаружь мне круг, пожалуйста.
Луна на небе круглая. Отклонения от идеального круга необнаружимы невооруженным глазом -> их нет.
Вся живая природа - фракталы. Евклидовых геометрических примитивов там довольно мало, но если потрудиться - можно найти.
При наблюдении с Земли невооруженным глазом.
Посложней бы чего-нибудь загадал. Те же логарифмы, например...
Вот и замечательно.
Спор материалистов с идеалистами решается очень просто. Все, что математически непротиворечиво, объективно существует. Если мы не можем воспринимать, к примеру, 12-мерное финслерово пространство-время - это наши половые трудности.
И картинка клёвая и тезис очень похож на правду. Провокация, да. Ну хули, система воеводский+ работает, значит её лучше не трогать.
Да вроде да, но у нас бомбит, что мы ноунеймы и мало чего можем, а у гопников с наркоманами что-то получилось.
>Все, что математически непротиворечиво, объективно существует. Если мы не можем воспринимать, к примеру, 12-мерное финслерово пространство-время - это наши половые трудности.
Где все это "объективно существует"? Покажи.
Мамке своей показал? Забегу вперед, все равно в итоге все сведется к формулам и т.п. формальным нотациям, которые сами по себе конструктивные объекты (что показал Мартин-Лёф), естественно, возможен вариант что эти формулы простая поебень не проходящая проверку типов из-за нарушающих вычислимость верований.
Значит ты обосрался со своими обызаниями нас верунами. Ты веришь в какие-то потенциальные построения числа Грэмма, на которые просто не хватит атомов во свеленной, а в фотоны не веришь. Для них же нет правил построения.
Как какую, я показываю тебе, что твоя ко-ко-констктивная параша не применима к реальному миру. Все, что не подтверждено эксперементом в реальном мире - основанна на вере, поэтому твоя вскукареки по поводу верунства не имеют никаких весомых оснований. Теперь понял, к чему я упомянил физику? Я понимаю, что у тебя ограниченные уственные способности в силу юнного возраста.
Ты можешь просто пройти мимо моих постов? Совсем не обязательно что-то кукарекать в ответ, уверяю.
Чем тебе так не нравятся мои посты? Ты конечно, можешь, как всегда обозвать меня и попытася увести разговор в другую сторону, но скажи почему ты так не хочешь отвечать на мои вопросы? Тебе больно из-за того, что у тебя нет подходящего ответа?
 16 Кб, 552x414
16 Кб, 552x414>простая поебень не проходящая проверку типов из-за нарушающих вычислимость верований
>нарушающих вычислимость верований
Чёт сложно. Я вот верю что 5 это деревянная тумбочка, например, а 3 - это мой братишка.
 31 Кб, 600x315
31 Кб, 600x315Тебе уже сто раз сказано, что фотон это не математический объект. Возможно, есть его математическая модель. Что именно из написанного тебе не понятно?
Раз математический объыекты находятся в сторонке от реального мира, то почему ты так упорно называешь, все верунами?
Ты опять переходишь на личности и уходишь от конструктивного диалога. Просто признайся, что ты необоснованно кричишь о вере.
А я вот знаю что Бог есть. Может несколько странно, но я знаю. Могу обосновать. В культы и всякую хрень не приглашаю.
И так, что есть мы.Мы не есть протоны, нейтроны и электроны. Мы есть нечно иное. Потому что протоны, нейрноы и электроны они все логичны. С вероятнлсью.
Значит мы нечто иное что не известно. Но сколько электронов во вселенной? банальный ответ-один.
А при чём здесь капитализм, товарищ?
То, чтоим позволено говорить-быть-творить?
Нет-нет, по крайней мере я не из тех, кто стремится задавить творчество, я от такого подавления удовольстивия не получу. Не из породы силовиков и других кхм доминаторов.
Да и всяко раньше подковёрные интриги были жёстче.
Или я совсем непонял или капитализм тут не причём.
Добра
Просто ты аутист и не уловил иронии, все нормально, не покидайте палаты.
Это всего лишь гипотеза, шутка даже больше. Типо один электрон пробегает всю вселенную от рождения до смерти а потом движется обратно во времени. Гугли диаграммы Фейнмана.
>>840
Вобщем объясню подробнее. Мы, наше самосознание, наше Я есть некий другой вид материи. Который находится в том числе в нашей телесной оболочке. Далее я не имею права рассказывать (не поминай имя Господа своего в суе).
Хорошо, начнём с простого. Покажи мне в природе число, прямую, точку, плоскость. Математика это просто язык для колличественного описания вселенной. И объективность его именно такая же, как и объективность другого языка. Впрочем, я не думаю что стоит предавать этому большое значение.
>Покажи мне в природе число, прямую, точку, плоскость.
А ты можешь показать, что их не существует?
>математика это просто язык для колличественного описания вселенной.
>язык
М-да. Сильное завяление, которое ещё нужно доказать.
>И объективность его именно такая же, как и объективность другого языка
Опять же, на каких основаниях ты это говоришь?
Ты написал, что
>математика это просто язык для колличественного описания вселенной.
Это тоже вера, верно? Или нет?
Я википедия тоже согласна, кстати.
>Язык — сложная знаковая система, естественно или искусственно созданная и соотносящая понятийное содержание и типовое звучание (написание).
>соотносящая понятийное содержание и типовое звучание (написание)
Да иди ты нахуй из раздела, говно уманитарное, у меня сука по русскому 50 баллов на ЕГЭ в 2003-м было. Я не на экзамене, грамотно писать не обязан. "Нет ничего по сути-доебеись до грамматики", правило демагога номер там какое-то.
>Сначало может научишься большие буквы использовать?
>Нет ничего по сути-доебеись до грамматики
ебать даун отмороженный, ссу тебе еще раз на ротеш))))
РЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯ
Дело в том, что математика не узучает вселенную, она изучает саму себя. На вселенную ей похуй. Так что она не может бьть языком для количественного описания вселенной.
Неправ в чём? Приведи его цитату.
>Так что она не может бьть языком для количественного описания вселенной.
Так получается что физики и инженеры зря её используют?
Представь себе мужика, который делает молотки. И вот его интересуют только параметры молотка, причем в отрыве от всего, лишь бы в результате получился инструмент, которым можно что-то ударить. И он делает разные молотки Клейна, проектирует многомерные молотки, проверяет возможность решения вопроса ударности в разных параметрах молотка. А тебе надо узнать каким молотком можно забить гвоздь. Конечно, результаты этого мастера будут для тебя полезны, но тем не менее ты проверяешь все в виде эксперимента, да еще и материалы из которых ты делаешь реальны, так что твоя область совершенно другая.
То есть молоток - это язык? Разве молоток не записывается на языке молотковедения, а? Как бы в этом же и состоит единственная задача этого самого молотковедения, не?
Математика не описывает реальный мир. Его описывают мат-модели, созданные с помощью её аппарата, но которые к ней самой отношения не имеют. Она прекрасно без них проживёт.
Физики пользуются мат-моделями для построения своих теорий.
Ты не согласен с тем, что математики поебать на реальный мир? И на вселенную тем более.
Не её используют, а мат-модели созданные на её основе.
>Физики пользуются мат-моделями для построения своих теорий
с точностью до наоборот. физики придумывают матнматику чтобы описать свои физические модели. математики начинают дрочить на эти модели, но как из дрочки не рождаются дети, так и умствования математиков ничего не дают
>зики придумывают матнматику чтобы описать свои физические модели. математики начинают дрочить на эти модели, но как из дрочки не рождаются дети, так и умствования математиков ничего не дают
И ведь не поспоришь! Гротендик небось создавал свои схемы под впечапелением от закона Кулом. А Рамануджан вывел формулу разбиений считая атомную массу водорода. ))))))))
Ох а как же математики любят дрочить на физические модели в каждой книжке по абстрактной албере висит таблица Менделеева)))))
Никогда не казалось странным, что простых конечных чисел бесконечно много, а простых конечных групп нет?
Настоящая математика это пока не признанная область естествознания, как химия или биология.
A_100, хули. Там элементов больше, чем в Монстре
Угораешь по спорадическим группам?
Мы когда-то М24 строили через коды Галея и системы Штейнера, надо бы освежить в памяти, а то не помню нихуя.
Блядь, охуеть, выебите меня, кто-нибудь, срочно!
 271 Кб, 1097x1221
271 Кб, 1097x1221Какой-то дебил писал этот текст, ей-богу. Обосновывать некорректность математической теории тем, что у нас чернила кончатся и ночью кто-то придет и что-то нам напишет - это по-моему диагноз.
Вавилов? Не знал что он платонист. Я сразу линейную алгебру стал читать, много интересного в первом томе?
Конструктивизм это не математическая теория. Это вера в возможность конструктивного построения, о чем и говорит вавилов.
Ок. Обосновывать невозможность конструктивного построения... и далее по тексту. Чернила тут не при чем, как ты конструктивизм не назови.
Как ни при чём? Констурктивисты при таком построении подразумивают, что у них бесконечный запас чернил.
Чувак, извини, но "не". "Подразумевают". Глаза же слезятся от такого, ей-богу.
Какое отношение чернила имеют к мысленным конструкциям?
Ты в галаза ебёшься? Даже в тексте написанно, что они подразумивают, что процесс можно неограниченно продолжать.
Да, твоего аргумента я не вкурил. А тот анон вряд ли это имел в виду, он какой-то поехавший походу.
То есть ты утверждаешь, что все мысленные конструкции равноценны в плане удобства и интуитивности? Это ведь очевидно не так, разве нет?
Идея потенциальной бесконечности ака потенциальной построимости ничуть не более реалистична, чем идея актуальной бесконечности, в этом суть.
И какое это имеет отношение к моему утверждению о том, что "доказывать" несостоятельность мыслительных конструкций с помощью чернил - маразм и шизофазия? Ты того, не подменяй тут предметы обсуждения.
>"доказывать" несостоятельность мыслительных конструкций с помощью чернил
Ну конструктивисты пытаются доказать с помощью реального мира несостоятельность актуальной бесконечности.
Чернила показывают, что против конструктивистов можно обернуть их собственный генеральный аргумент: обвинение в нереалистичности.
>>2198
Удобство, интуитивность и истинность это разные вещи. Для меня возможность оперировать с бесконечными множества так же интуитивна, как и предполагать что-то на бесконечной ленте. Но бесконечные множества удобнее, т.к. из них вылилась вся настоящая математика, отказываться от них -- вступать в клуб конструктивистов-чуханов и доказывать заново вещи типа коши-буняковского, бесконечности простых чисел, etc...
Но если речь идет об истинности, мы должны давать какой-то критерий. Если критерий построимость в реальности и отсутствие аксиом, как предполагает невидимый собеседник вавилова, то по этому критерию конструктивизм ничем не отличается от обычной математики.
Евклидово доказательство бесконечности простых чисел удовлетворяет стандартам конструктивизма, т.к. оно не является доказательством от противного, и, следовательно, не использует закона исключенного третьего.
Конструктивизм изначально возник как реакция на чисто экзистенциальные доказательства типа канторовского диагонального аргумента. Когда доказывается существование чего-то, что нельзя построить.
>т.к. оно не является доказательством от противного
С дуба рухнул? Оно является доказательством от противного. "Предположим, что простых чисел конечное количество. Перемножим их и прибавим единицу. Полученное число будет простым, пришли к противоречию."
Вавилов пишет, что против конструктивистов можно обернуть их же аргумент. Про что пишешь ты?
Еще раз. Я не призываю никого быть сторонниками (или противниками) конструктивизма. Я лишь утверждаю, что автор того текста на картинке - либо маразматик, либо демагог (и вредитель).
Про критерий построимости, который состоит в "реальности" чего-то там, я вообще первый раз слышу. Даже ультрафинитисты не говорят о "реальности".
Нет, он не пишет такого. Он пишет ахинею про чернила. К конструктивистам это не имеет отношения. Я про это.
>вредитель
Ну блядь начался сталинизм.
>>2209
Именно это он пишет. Приводя конкретный пример, как это делается. Более того, аргумент про чернильную дыру кажется убедительным той подсекте конструктивистов, которая называется ультрафинитисты, они его принимают и большие числа не разрешают. А ты ничего на этот аргумент не можешь возразить, лишь только шокированно пишешь про "демагогию" и "вредительство".
> сталинизм
Ой, а иронию мы как будто уже не улавливаем.
>>2211
Что "именно это"? Ахинею про чернила? Так я об этом и говорю!
И про ультрафинитистов я уже сказал. Не надо их мешать с обычными конструктивистами, это разные взгляды. А ты все в кучу смешал. Более того, аргумент ультрафинитистов не имеет отношения к ахинее на пике. Они говорят про свойства больших чисел, а не про какие-то чернила.
>>2213
Бро, так у меня к его мнению претензий никаких. Я настаиваю на том, что аргумент его - демагогический и некорректный.
Если мы допускаем, что где-то на бесконечности закон исключенного третьего мистическим образом перестаёт работать, почему бы нам не допустить чернильную дыру?
Допусти чернильную дыру, назови это чернилизмом и вперед, доказывать теоремы. Конструктивизм тут при чем?
>Полученное число будет простым
Нету такого перехода там, и твое рассуждение не является доказательством. Мы утверждаем, что полученное перемножением n простых и прибавлением единицы к произведению число не может делиться ни на одно из меньших простых чисел, поскольку в остатке от деления будет единица.
Доказательство верно и в том случае, если мы не предполагаем, что число всех простых чисел конечно. У нас есть процедура, которую можно повторять. Возьми достаточно большое n, рассуждение по-прежнему верно. Никакой контрадикции не требуется.
>Возьми достаточно большое n, рассуждение по-прежнему верно
Это не так.
>Нету такого перехода там
Если бы противоречия не было, то ты получил бы алгоритм генерирования простых чисел. Мол, достаточно перемножать первые n простых и прибавлять единичку. Проблема в том, что полученное таким образом число M на самом деле не будет простым, вообще говоря. Например, 235711*13+1 делится на 59. Если не предполагать, что число M является произведением _всех_ простых чисел, то доказательство не пройдёт - остаётся шанс, что M делится на простое число, расположенное между n-ым простым числом и M.
вопрос только в том, как определить произведение n простых. Как мы его строим?
https://oeis.org/A066576
Да что ты. Произведение первых семи простых плюс один тоже не простое, мрожешь проверить. Поэтому я и оговорил "достаточно большое n".
Никак, потому что это неправда.
Алсо, какие же вы тупые, в сотый раз повторяю, что мне плевать на конструктивизм, меня бесит Вавилов- пиздабол и демагог.
>что мне плевать на конструктивизм
Так сильно плевать, что ты сидишь в тредике и защищаешь его.
>меня бесит Вавилов- пиздабол и демагог.
То же можно сказать о Брауэре.
Пруфай возможность построения такого n.
Выше по треду. Я предложил не заниматься религиозными войнами и дешевыми софисткими трюками, а обращать внимание на качество рассуждения.
Аргумент Вавилова - не дешёвый. Этот аргумент (в реальном мире нельзя написать много черточек) настолько убедителен, что убедил часть конструктивистов.
Не ибу, кто есть кто, кто конструктивист, а кто нет, но от писанины про чернила выпал нахуй. Пиздец, кончится время, бумага, гравитация нахуй. Чёрточку нарисовать можем? -Можем. Если написали N чёрточек, то ещё 1 можно написать? - Можно. Тогда сколько угодно чёрточек можно написать, ёпта.
Точно так же можно обосновать аксиому выбора.
Пусть M - множество. Выберем в нём элемент и скажем, что он < всех других элементов. Выберем второй элемент, не равный первому. Скажем, что он < всех других элементов, но > первого. И так для любого ординала, пока множество M не исчерпается. Убедительно? А конструктивисты не верят.
>А конструктивисты не верят.
Наркоман ты. Конструктивность аксиомы выбора сто раз обосновывали, Мартин-Лёф тот же. В конструктивной математике аксиома выбора - доказуемая теорема. Зато в ZFC нет даже внятного доказательства этой аксиомы, в нее веровать надобно. А вы и веруете.
Петушок!
>Конструктивность аксиомы выбора сто раз обосновывали
Этак у вас скоро и ZFC конструктивной станет.
 246 Кб, 736x732
246 Кб, 736x732>у вас скоро и ZFC конструктивной станет.
Так уже. https://coq.inria.fr/V8.2pl1/contribs/ZFC.html
>В конструктивной математике аксиома выбора - доказуемая теорема
И давно? Потому что для конечного числа множеств этот факт вывел еще Цермело, но конструктивисты как всегда впереди планеты всей.
>>2347
>кроме непрерывных кризисов оснований и парадоксов это ни к чему не приведет
Открываешь любую статью топового математика типа там Тао, Громова, Атьи, Лэнглендса, Терстона, Уайлза, etc. Считаешь количество утверждение, использующих неконструктивную индукцию и закон исключенного третьего. Открываешь любой учебник по алгебре, анализу или геометрии graduate уровня. Делаешь то же самое.
Выходит, что большинство математиков и не слышали о каком-то кризисе, что неудивительно, ведь конструктивная догма поставит крест на работе всей их жизни.
>большинство математиков и не слышали о каком-то кризисе,
Потому что любая практически применимая математика конструктивна по своей сути. Иначе ее просто нельзя было бы применять. Неконструктивные верования, нарушающие вычислимость, встречаются только в неконструктивных основаниях. Закон исключенного третьего никто не отменяет в случаях, когда он доказуем непосредственно.
>любая практически применимая математика конструктивна по своей сути
На самом деле эти слова бессмысленны, лишены какого-либо смысла вообще. Невозможно понять, что они значат. Т.е. тут ничего не утверждается.
>Невозможно понять, что они значат.
С точки зрения умственно неполноценного дебила вроде тебя - несомненно.
Ахахахах, где-то была паста "how to отвечать, как конструктивист". Реквестирую её. Она полностью обличает демагогию.
Также, в тред призывается парень с фотонами.
Вот практический пример, я инженер, мне надо посчитать площадь круга. Где мне найти конструктивное доказательство этого факта?
>я инженер, мне надо посчитать площадь круга.
>конструктивное доказательство этого факта
>я инженер
>доказательство этого факта
Ну то, что ты дебил - очевидно и доказательств не требует.
 152 Кб, 1121x621
152 Кб, 1121x621>Где мне найти конструктивное доказательство этого факта?
Какого факта? Формула площади круга - конструктивный объект. Круг тоже, поскольку его как-то же построили.
Площадь круга равна pr^2. С классическим анализом мне не приходится брать это на веру.
>Формула площади круга - конструктивный объект.
Значит должно существовать конструктивное доказательство этого факта.
— Потому.
— Ты ебанутый?
— На это неоднократно давался ответ.
— Ты можешь доказать формулу Гаусса?
— Твоя вера не нужна.
— Пошёл нахуй, ебанашка.
— Ты не воспринимаешь объективные аргументы.
— Какие?
— Хватит спрашивать одно и то же.
— Ты издеваешься. Ты не можешь писать это всерьёз.
— Я не виноват, что ты такой тупой.
>существующие во времени и пространстве
И тут из-за горизонта выплыла, ехидно улыбаясь, ЧЕРНИЛЬНАЯ ДЫРА
>Значит должно существовать конструктивное доказательство этого факта.
Ну круг же существует. Его радиус измерим, число пи тоже существует (в виде аппроксимации практически целесообразным числом знаков после запятой). Все это существующие и измеримые конструктивный объекты. Это и есть доказательство. Или тебе нужно какое-то мистическое доказательство, в отрыве от конкретного объекта?
>Поверь, что они существуют, просто поверь!
Ясно. Все еще надеюсь на конструктивное доказательство, типа пикрелейтед, сводящие элементарные теоремы анализа к нерешенной в конструктивном мирке теореме Ферма.
Напишу еще раз, быть может русский для тебя не родной.
Мне необходимо конструктивное доказательство факта, что площадь круга равна pr^2.
Вот как выглядят неконструктивные доказательства:
https://en.wikipedia.org/wiki/Area_of_a_circle#Modern_proofs
В сотый раз спрашиваю: какое отношение математика имеет к "реальному миру"?
Ты выше аргумент Вавилова прочти, он говорит, что у конструктивистов есть много ОЧЕВИДНЫХ аксиом, которые так не называются.
 61 Кб, 600x450
61 Кб, 600x450>Вот как выглядят неконструктивные доказательства:
Я думал, ты дебил. А ты дебил. Дифиченто, что именно тебе непонятно >>2394 в фразе что "конструктивный объект - это конечная конфигурация знаков, в том числе формула и доказательство в формальной системе"? Что именно неконструктивного в тех формулах, которые ты по своей одаренности называешь неконструктивными? Что неконструктивного в построенном по ним круге?
>>2469
>какое отношение математика имеет к "реальному миру"?
А к какому миру она имеет отношение, скоморох? К загробному? Ты совсем тутуру что ли? Даже неконструктивные аксиомы, в которые вы веруете, это конечные конфигурации знаков, только нарушающий вычислимость и т.о. всего лишь неправильный конструктивный объект, соответствующий пустому типу при проверке. Любое ментальное построение - результат работы ЦНС, т.е. все тот же реальный мир. Почему кому-то неочевидны настолько простые вещи? Тебе лет сколько? 9?
>>2568
>Это правда, что там нет аксиомы выбора?
Неравда. Я же цитировал Мартин-Лёфа >>2348 НоТТ основана на MLTT. Единственная разница - в конструктивной математике аксиома выбора - это доказуемая теорема, а не взятая с потолка аксиома как в ZFC.
Отрицание аксиомы выбора не имеет к HoTT прямого отношения, HoTT это фреймворк, который может дать приют и подобным извращенцам.
>>2572
>НоТТ основана на MLTT
Основана, но...
https://homotopytypetheory.org/2015/01/11/hott-is-not-an-interpretation-of-mltt-into-abstract-homotopy-theory/
>Единственная разница - в конструктивной математике аксиома выбора - это доказуемая теорема, а не взятая с потолка аксиома как в ZFC.
Тут стоит добавить, что модель Воеводского неконструктивна. И еще раз, не понимаю, зачем говорить о доказательстве слабой аксиомы выбора, если она выводится из ZF?
>Что неконструктивного в построенном по ним круге?
А почему получится круг? Почему именно число pi? А какая формула для n-мерного случая?
Или по-твоему достаточно предъявить построение "хуй знает чего", а потом утверждать, что это мол круг? Давай я тебе построю рандомную хуиту и с помощью интегрирования найду площадь, это тоже конструктивный пруф?
Местный конструктивист прав касательно этого доказательства того, что площадь круга pi*r^2.
В самом деле, в этом доказательстве не происходит ничего неконструктивного. Определение pi вполне конструктивно, значения интегралов определены конструктивным образом и т.д. Твои претензии в духе:
>А почему получится круг? Почему именно число pi? А какая формула для n-мерного случая?
Во-первых, не имеют никакого отношения к вопросу конструктивности и с тем же успехом могут быть применены к доказательству и без заявки на конструктивность. Во-вторых, все они разрешаются аккуратным выписыванием определений и увеличением подробности доказательства.
Другое дело, что в самом деле нет конструктивного доказательства того, что все непрерывные функции достигают своего максимума/минимума и даже того, что они принимают все свои промежуточные значения. И это действительно составляет коренной недостаток конструктивного анализа.
Я все-таки надеялся, что конструктивист знает понятие интеграла, хотя бы то, что давали в школе.
Тут два тонких вопроса. Во-первых конструктивное определение пи, насколько я знаю, это пи до определенного знака, что совершенно не вносит ясности.
Во-вторых как определить интеграл без фундаментальных лемм классического анализа, и что можно им посчитать? Везде, где фигурирует бесконечность, конструктивная математика дает прокол.
Не должна, я как бы на это и намекаю, привет. /аутист-мод
>>2475
К акисиомам у меня нет претензий; у меня претензии к его идиотскому или осознанно вводящему в заблуждение балабольству про чернила. Привет.
>>2570
Неавторитетный источник.
>>2572
Привет, Кококонтсруктивист. Ты настолько ослеплен своим фанатизмом, что даже не заметил, что я спорю как раз с противниками конструктивизма в этом итт треде. Впрочем, тебе же похуй, лишь спиздануть чего-нибудь, лол. Цирк с конями.
По содержанию: математика имеет отношение к миру идеалов Платона, например. А реальным миром занимается физика. Называть, например, сказки Андерсена реальностью из-за того, что они, мол, результат работы ЦНС - это редкое клоунство и аутизм, если честно.
Я не прихожу. Почему ты приходишь?
Почему ты считаешь аргумент Вавилова балабольством? Он ничем не отличается от аргументов конструктивистов и призван высмеять их.
Я тыщу раз уже отвечал на этот вопрос выше по треду.
Ладно, выпиши явно "аргументы конструктивистов", о которых ты говоришь, чтобы разговор был предметным.
>Мы не имеем оснований, считает Брауэр, утверждать, к примеру, что каждое из множеств некоторой совокупности множеств либо конечно, либо бесконечно, ибо такое утверждение предполагает наличие процедуры отображения любого множества из этой совокупности либо на начальный отрезок натурального ряда, либо его или его части, — на множество чисел натурального ряда в целом. Некто может возразить в том смысле, что существует объективное положение дел, независимое от наблюдателя, и что на самом деле все-таки существует только одно из двух: либо A, либо не-А Эти возражения, считает Брауэр, исходят из незаконной объективации математических истин, из метафизического предположения, что и после того, как человечество будет уничтожено, они будут существовать наряду с законами природы. Г. Вейль писал в поддержку этой идеи Брауэра: «Принцип исключенного третьего для таких утверждений (для утверждений принадлежности или непринадлежности некоторого свойства всем числам натурального ряда) мог бы быть справедливым для Бога, способного обозревать все натуральные числа как бы единым взором, но не для человеческой логики».
>Брауэр был убежден, что логические законы не являются абсолютными истинами, не зависящими от того, к чему они прилагаются. Возражая против закона исключенного третьего, он настаивал на том, что между утверждением и его отрицанием имеется еще третья возможность, которую нельзя исключить. Она обнаруживает себя при рассуждениях о бесконечных множествах объектов. Допустим, что утверждается существование объекта с определенным свойством. Если множество, в которое входит этот объект, конечно, то можно перебрать все объекты. Это позволит выяснить, какое из следующих двух утверждений истинно: "В данном множестве есть объект с указанным свойством" или же: "В этом множестве нет такого объекта". Закон исключенного третьего здесь справедлив. Но когда множество бесконечно, его объекты невозможно перебрать. Если в процессе перебора будет все-таки найден объект с требуемым свойством, первое из указанных утверждений подтвердится. Но если найти этот объект не удастся, ни о первом, ни о втором из утверждений нельзя ничего сказать, поскольку перебор не проведен до конца. Закон исключенного третьего здесь не действует: ни утверждение о существовании объекта с заданным свойством, ни отрицание этого утверждения не является истинным.
Если в нашей критике дозволен Боженька-Переберун, то в ней также должна быть дозволена и чернильная дыра, согласись.
>Мы не имеем оснований, считает Брауэр, утверждать, к примеру, что каждое из множеств некоторой совокупности множеств либо конечно, либо бесконечно, ибо такое утверждение предполагает наличие процедуры отображения любого множества из этой совокупности либо на начальный отрезок натурального ряда, либо его или его части, — на множество чисел натурального ряда в целом. Некто может возразить в том смысле, что существует объективное положение дел, независимое от наблюдателя, и что на самом деле все-таки существует только одно из двух: либо A, либо не-А Эти возражения, считает Брауэр, исходят из незаконной объективации математических истин, из метафизического предположения, что и после того, как человечество будет уничтожено, они будут существовать наряду с законами природы. Г. Вейль писал в поддержку этой идеи Брауэра: «Принцип исключенного третьего для таких утверждений (для утверждений принадлежности или непринадлежности некоторого свойства всем числам натурального ряда) мог бы быть справедливым для Бога, способного обозревать все натуральные числа как бы единым взором, но не для человеческой логики».
>Брауэр был убежден, что логические законы не являются абсолютными истинами, не зависящими от того, к чему они прилагаются. Возражая против закона исключенного третьего, он настаивал на том, что между утверждением и его отрицанием имеется еще третья возможность, которую нельзя исключить. Она обнаруживает себя при рассуждениях о бесконечных множествах объектов. Допустим, что утверждается существование объекта с определенным свойством. Если множество, в которое входит этот объект, конечно, то можно перебрать все объекты. Это позволит выяснить, какое из следующих двух утверждений истинно: "В данном множестве есть объект с указанным свойством" или же: "В этом множестве нет такого объекта". Закон исключенного третьего здесь справедлив. Но когда множество бесконечно, его объекты невозможно перебрать. Если в процессе перебора будет все-таки найден объект с требуемым свойством, первое из указанных утверждений подтвердится. Но если найти этот объект не удастся, ни о первом, ни о втором из утверждений нельзя ничего сказать, поскольку перебор не проведен до конца. Закон исключенного третьего здесь не действует: ни утверждение о существовании объекта с заданным свойством, ни отрицание этого утверждения не является истинным.
Если в нашей критике дозволен Боженька-Переберун, то в ней также должна быть дозволена и чернильная дыра, согласись.
Ты сейчас на полном серьезе пытаешься обосновать метафизический аргумент Вавилова против конструктивизма тем, что Вейль однажды употребил метафору в тексте о принципе исключенного третьего?
Это либо аутизм, либо стопроцентная жирнота. Извини, но я не вижу у нас common ground для интересного разговора. Предлагаю сойтись на том, что мы друг друга не поняли.
Конструктивисты отвергают принцип исключенного третьего, основываясь на идее, что человек не может перебрать все элементы бесконечного множества. Эта идея столь же нелепа, сколь и идея, что слишком большие числа обязаны схлопнуться в чернильную дыру.
То есть от предыдущего аргумента про Боженьку ты отказываешься?
По поводу этого твоего поста: я чисто формально, несодержательно контраргументирую. Человек действительно не может перебрать все элементы бесконечного множества. То есть конструктивисты основывают свое рассуждение на истинной посылке.
Числа же не могут схлопнуться в чернильную дыру, поскольку числа - абстрактный мыслительный конструкт, отличный от их изображения чернилами, карандашом или чем-то другим. Получается, что в этом случае рассуждение основано на ложной посылке.
И повторю в сто десятый раз: мне плевать на конструктивистов, моя претензия - к демагогу Вавилову.
Это один аргумент, на мой взгляд.
Конструктивисты утверждают, что не в человеческих силах перебрать все элементы бесконечного множества. Вавилов утверждает, что не в человеческих силах написать 10^10^10 палочек. Если первое принимается к рассмотрению, то и второе следует принять к рассмотрению; никакой демагогии.
Одни аппелируют к ментальным моделям, а другой - к физическим ограничениям материального мира, еще раз повторяю. Числа - это про ментальные модели или про материальный мир, ответь мне сам? Числами занимается математика или физика?
Я уж молчу про то, что ты извратил его аргумент и представил его ультрафинитистом, а ультрафинитизм - вполне "законная" точка зрения, там нет никаких нелепостей.
Конструктивисты апеллируют именно к физическим ограничениям. Перебрать все элементы бесконечного множества невозможно лишь в физическом мире. Ибо ментальную модель, в которой операция перебора всех элементов бесконечного множества возможна, построить очень легко: нужно лишь вполне упорядочить это множество и пробежаться по нему трансфинитной индукцией, то есть совершить совершенно стандартное в обычной теории множеств движение ушами. Конструктивисты запрещают такие модели именно из-за их несоответствия физическому миру, отнюдь не по каким-либо иным причинам.
Я с самого начала называл аргумент Вавилова ультрафинитистским. Более того, про ультрафинитистов я в его же книге и вычитал, если не ошибаюсь.
upd: ошибаюсь. Но неважно, аргумент всё равно ультрафинитистский.
Так в стандартном формализме типа Гильберта речь идёт только о строках и некоторым базовым операциям над ними (чистые подстановки, правила вывода, ...). То, как ты интерпретируешь такую работу со строками - это неважно абсолютно, основаниям это никак не повредит.
То есть мне твой аргумент про "пробегание по трансфинитному множеству" видится подобным такому: "я не могу себе представить R^4 столь же ясно, как и R^3 R^2 R^1, а значит линейная алгебра неправильная", но чтобы работать с линейной алгеброй ничего представлять не нужно - подобные представления нужны тебе исключительно в твоих педагогическо-образовательных целях, а на уровне оснований нужно только уметь, опять же, работать со строками символов (выводить следствия из аксиом векторного пространства, например).
Я вслед за Вавиловым анализирую конструктивистское табу на закон исключенного третьего и точно так же прихожу к выводу, что причины этого табу, как их излагают конструктивисты, именно в невозможности перебрать все элементы бесконечного множества в физической реальности. Частные рассуждения о боженьке-переберуне лишь подкрепляют мою уверенность.
Мне, как и Вавилову, непонятно, почему конструктивисты не изгоняют из своей математики все остальные неосуществимые в физической реальности вещи. Я, как и Вавилов, отнюдь не возражаю против формальных теорий, лишь указываю на непоследовательность конструктивистов.
А, я понял. Думал ты наоборот конструктивист, который думает, что основания в классической математике стоят на "вере в аксиомы и бесконечные множества", а не на преобразованиях строк.
Ну причины этого табу понятны. Они хотят чтобы любая теорема утверждающая существование некоторого (для простоты положим) рационального числа явно предъявляла алгоритм его построения. То есть у них сильно бомбит от ситуаций, когда есть некоторая теорема существования некоторого числа с некоторыми свойствами, но при этом она не даёт способа взять это число и выписать на бумажке цифрами, ну и они тогда спрашивают: "А в каком смысле это число тогда существует, если мы не можем взять его и выписать?". Вопрос резонный вполне, но мне конструктивный подход кажется просто-напросто неудобным для усвоения. Хотя, быть может, я просто привык.
А Вавилов палки перегибать очень любит.
>математика имеет отношение к миру идеалов Платона, например.
И где этот мир, покажи. Или мне в него уверовать надобно?
>>2886
>Конструктивисты апеллируют именно к физическим ограничениям. Перебрать все элементы бесконечного множества невозможно лишь в физическом мире.
А в каком возможно? Вот эта простая вещь, что для неконструктивной математики нужны какие-то особенные манямиры, не имеющие отношения к объективной действительности, это разве не шизофрения? О каких мирах-то вы толкуете, жалкие веруны? Если нам нужно что-то посчитать, то все, что у нас есть для этого - объективная действительность.
>>2890
>Они хотят чтобы любая теорема утверждающая существование некоторого (для простоты положим) рационального числа явно предъявляла алгоритм его построения.
Ну а как иначе-то? С каких хуев мне веровать в слонопотама или в математический объект, который может существовать в каком-то смысле, отличном от возможности или хотя бы алгоритма его построения?
> Аристотель в него веровал, и вы так делаете
>веровал
А вот и манька. В фотоны тоже верим?
>Принимать же этот частный принцип как нечто общее и незыблемое - это не просто вера, а противоречие с математикой
Жду примеры противоречий.
>швято веровать
Ясно, кто кричал про швабодку.
> несмотря даже на то, что он нарушает вычислимость.
Почему мы не должны класть хуй на вычислимость? Зачем нам веровать в то, что всё кроме вычислимости ненужная хуета?
>Почему мы не должны класть хуй на вычислимость?
Класть хуй на вычислимость = класть хуй на математику. На остальное отвечал уже.
>класть хуй на математику
Ну и правильно же.
Хуй ложу и ебу бесконечными множествами как хочу - потому что могу.
>это разве не шизофрения
Как что-то плохое, ты просто завидуешь.
>О каких мирах-то
Быдлу не понять.
>Класть хуй на вычислимость = класть хуй на математику
Cильное заявления. Только вот оно нихуя не значет, поскольку не ты можешь привести аргументов в его пользу.
>На остальное отвечал уже.
Ах да, кукареки мани.
Так я примерно о том же - неконструктивная математика это не математика.
>>2938
Опять же, поясню - манямиры и шизофрения это не что-то плохое, это просто не математика.
>>2940
>не ты можешь привести аргументов в его пользу.
Я их в каждом посте привожу, только ты их не воспринимаешь. Не судьба значит, просто смирись.
>Я их в каждом посте привожу, только ты их не воспринимаешь.
Потмоу что, твои агрументы лишь школьные вскареки и могут убедить школьников. Старайся лучше.
>Так я примерно о том же - неконструктивная математика это не математика.
Ну раз анон с мейлача так сказал, значит так и есть.
Проффесора и академики с тобой не согласны, они бы обоссали тебя, если бы не были культурными.
>Ясно.
>уровня РАЕН не нужны.
Ну да, Вавилов просто тупой школьник. И чего его не устраивают твои аргументы?
>Вавилов просто тупой школьник
Что-то вроде, да.
Этот его, как вы это называете, "тралирование" чернилами и прочим - как раз уровень школьника.
Так это анончики же, то есть - дебилы и черви-пидоры по определению.
Странно что этот твой академик - точно такое же говно.
>Школота, школота never change.
Хех. А ведь ты это нет ты уже несколько постов подряд повторяешь. Школьник ;3
>Или мне в него уверовать надобно?
Но ты же в него уже уверовал, когда тебе разъяснили земной аналог такой идеи как "число". Что этим идеальным числом можно яблоки посчитать. К этому миру, кстати, относится и машина Тьюринга с бесконечной лентой, ограничивая которой математику, ты просто ставишь идеальный мир в более узкие рамки.
>который может существовать в каком-то смысле, отличном от возможности или хотя бы алгоритма его построения?
Как, например, pi, e, ln, lg, sin, cos, R...
Зачем ты хуйню несешь?
>Как, например, pi, e, ln, lg, sin, cos, R...
И что из этого неконструктивно? Пи? Или ты веруешь, что синус может существовать в каких-то манямирах, вне конкретного своего значения?
>К этому миру, кстати, относится и машина Тьюринга с бесконечной лентой, ограничивая которой математику, ты просто ставишь идеальный мир в более узкие рамки.
Мне уже надоело объяснять рзницу между такими математическими абстракциями как потенциальная и актуальная бесконечность. Если тебе даже это непонятно, о чем тут вообще можно говорить? О погоде разве что. Я уже не говорю о разнице между машиной Тьюринга и универсальной машиной Тьюринга. Ты же даже не шаришь в том, что пытаешься использовать в качестве аргументов, это вообще пиздец полный. Может ли существовать что-то бесполезнее школьника, который на мейлру мне поясняет о неконструктивности машины Тьюринга?
>Может ли существовать что-то бесполезнее школьника, который на мейлру мне поясняет о неконструктивности машины Тьюринга?
Может. Например - ты, метающий бисер на мейлопараше перед школодегенератами.
>И что из этого неконструктивно
Все. Ничего из этого нельзя построить. Теорема Линдемана-Вейерштрасса. Их существование доказывается, но построить их нельзя. В конструктивной математике они значит вообще не существуют.
>сли тебе даже это непонятно, о чем тут вообще можно говорить?
Так ты не объяснил чем же одна лучше другой. По мне они равнозначны. В сотый раз расскажешь про то, что нельзя выбрать из бесконечного множества что-то, зато можно производить это что-то бесконечное количество раз, и это намного убедительнее? Не понимаю почему.
Позабавлюсь-ка и я со школьником. Педофил я или где? :3
>Теорема Линдемана-Вейерштрасса.
>Теорема Линдемана — Вейерштрасса, являющаяся обобщением теоремы Линдемана, доказывает трансцендентность большого класса чисел.
>Трансцендентное число — это вещественное или комплексное число, не являющееся алгебраическим — иными словами, число, которое не может быть корнем многочлена с рациональными коэффициентами
Отсюда вывод: для нашего школотуна построить - это только и исключительно многочлены и их корни.
Ну да что со школобыдла взять - дебил же, вполне в медицинском смысле.
Можете объяснить мне как полному профану, полнейшему? Вот на пальцах и без лишнего ололоканья и внутренних непонятных мне мемчиков.
Кто в математике кто? Как относиться к конструктивистам? Чем они недовольны? Кто более прав? К какому лагерю относится группа Бурбаки? Кто такие структуралисты? Кто среди математических школ самый благоразумный?
Я очень хочу разобраться, но из-за обилия инсайдерских шуточек и жаргона я с трудом въезжаю и в тред, и в математику вообще.
>Кто в математике кто? Как относиться к конструктивистам? Чем они недовольны? Кто такие структуралисты?
wiki:Foundations of mathematics
wiki:Philosophy of mathematics
>Кто более прав? Кто среди математических школ самый благоразумный?
You decide.
>К какому лагерю относится группа Бурбаки?
Это размытый вопрос. Назовём их теоретико-множественными формалистами.
>>3003
google:Алгоритмы вычисления числа pi
wiki:Gauss–Legendre algorithm
>вполне конструктивный объект?
Это бессмысленное разделение.
Все объекты - вполне конструктивны.
Ибо действительно неконструктивный объект человечки представить/подумать/написать/сказать просто не в состоянии.
Скромнее будь, так-то.
Ну так в классическом формализме типа Гильберта вообще объектов нету, есть только утверждения и доказательства. Это, как мне кажется, с точки зрения конструктивизма вполне приемлимо.
Не нашел ни одного алгоритма, который на выходе бы давал пи. Все они выдают рациональные числа.
Видишь ли, я задал этот вопрос, потому что указанные тобой статьи кажутся мне слишком трудными для вхождения. Я надеялся, что на этой доске есть кто-то, достаточно хорошо шарящий, чтобы простыми словами объяснить как смотреть например на направления философии математики.
>You decide.
Опять же, проще начать с чьего-то мнения, чем со своего. В чужом мнении кроме информации сразу груда мета-информации.
Не понял твоей мысли.
>>3012
Вероятность того, что кто-то сейчас напишет тебе качественное эссе об основаниях математики КРАЙНЕ МАЛА. Я ещё чего-нибудь простого поищу, но вообще говоря, если чувствуешь, что не осиливаешь тонкостей, то может ты пока просто не дорос до этого (абсолютно без всякого снобизма)?
> то может ты пока просто не дорос до этого
Ну разумеется я не дорос, и я пытаюсь найти какую-то протоптанную тропу, чтобы пройти по ней, в надежде, что после этого я научусь топтать тропы сам.
Бывало у тебя такое, что ты вроде как морально готов что-то понять, но не хватает какой-то одной мелкой детали, или двух-трёх? И нужен совет кого-то, кто уже прошарен.
Википедия привела меня к очередному шизонаправлению:
https://en.wikipedia.org/wiki/Computable_analysis
чувствую ответы на мои вопросы где-то там, в референсах
Да нет, ответ на вопрос о том, что такое вычислимое число (а именно их используют в конструктивной математике) где-то в районе первого семестра курса мат.логики.
>>3016
Можешь читануть введение в Вавилове "Не совсем наивная теория множеств", только он очень любить передёргивать и говнить всё, чего не понимает. А по-нормальному конечно начать надо с курса мат.логики и потом переходить ко всяким экзотикам.
>говнить всё, чего не понимает
Конструктивисты так делают, ты чего. Даже актуальную бесконечность не могут понять и говнят.
Да мне вообще кажется, что метафизической разницы между классикой и конструктивизмом никакой нету.
Я закончил курс матана, матлогики, немного алгебры, я в общем знаю теорию множеств.
Я бы хотел понять общую, большую картинку математики. Типа вот почему конструктивисты петухи? И кто не петух? Кто находится в прямом антогонизме с ними?
Вот я, допустим, знаю матан. Пока я его учил, меня совершенно не ебали ни конструктивисты. ни структуралисты, ни неоплатонисты. Я вообще не понимал, с чего сыр бор. Теперь я вижу, что людей это нихуёво загоняет. Чего же я не догоняю блять?
 100 Кб, 358x604
100 Кб, 358x604>в классическом формализме типа Гильберта вообще объектов нету, есть только утверждения и доказательства. Это, как мне кажется, с точки зрения конструктивизма вполне приемлимо.
Я же цитировал Мартин-Лёфа по поводу того, что формулы и формализмы, записанные конечным числом символов - конструктивные объекты. Другое дело, что при проверке типов они могут приводить к пустому типу из-за всяких нарушающих вычислимость аксиом и т.п.
>>3019
>Даже актуальную бесконечность не могут понять
Ты что ли можешь? Думаешь, узнал псевдоумное слово и типа понял, школотрон?
>>3021
>мне вообще кажется
Крестись, если кажется. Интуиционизм просто не твое, бывает.
>>3022
Речь в основном о разных подходах к основаниям, на каких принципах строить математику в принципе. И так уж получилось, что формализм и логицизм для этой цели не подошел, т.к. все уперлось в кризис оснований, парадоксы и все такое. Брауэр же показал, очему так получилось и что конкретно надо править в консерватории, чтобы такой хуйни не было.
Брауэр интуиционист? То есть, он отвергает математические объекты, которые не понятны интуитивно, так? Типа бесконечности.
>т.к. все уперлось в кризис оснований, парадоксы и все такое
Очередной раз:
1) какой кризис?
2) какие парадоксы?
>не понятны интуитивно, так? Типа бесконечности.
С точки зрения малолетнего долбоеба - несомненно.
Чувак, мы поняли, что ты так крут, что можешь представить себе бесконечность. Я надеюсь, ты после этого признания тебя в качестве гения успокоишься и уйдёшь из треда делать свои гениальные дела.
 653 Кб, 1709x744
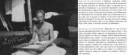
653 Кб, 1709x744Брауэр - основоположник интуиционизма как такового.
>он отвергает математические объекты, которые не понятны интуитивно, так? Типа бесконечности.
Не совсем. Отвергаются объекты, которые невозможно построить или задать правила для их построения. Бесконечность как свойство потенциально бесконечного построимого объекта (N, например) не отвергается. Отвергается бесконечность актуальная, т.е. бесконечность сама по себе, в отрыве от конкретного объекта. То же для принципа исключенного третьего - он отвергается как общий принцип, когда он доказуем непосредственно - никто его не отвергает. Чистые ментальные конструкции по Брауэру на основе 1 и 2 актов интуиционизма можно по тезису Черча считать аналогами алгоритмических конструкций, поэтому по-сути, Брауэр отвергал то, что сейчас можно назвать "нарушающим вычислимость".
>>3028
>1) какой кризис?
Оснований.
>2) какие парадоксы?
Полно их, же. Забыл еще упомянуть неполноту либо противоречивость любой формальной системы по Геделю.
 18 Кб, 887x84
18 Кб, 887x84Ты слишком высокого мнения о нём, за много тредов просто очевидно, что этот человека из computer science или вообще без образования, потому что он и понятия не имеет о классической математике. Прочитал в жизни несколько научно-популярных книжек, а ля "очерки по конструктивной математике" и пытается осилить HoTT, хотя я уверен, он даже задачку пикрелейтед не осилит.
https://arxiv.org/pdf/1211.2851v4.pdf
тогда и у новых оснований кризис?
>Полно их, же.
Неси сюда.
>Отвергаются объекты, которые невозможно построить или задать правила для их построения.
Разве это не определение конструктивизма?
>Отвергается бесконечность актуальная, т.е. бесконечность сама по себе, в отрыве от конкретного объекта.
Спасибо, это один из тех маленьких нюансов. которые мешают мне понимать философию математики.
>тогда и у новых оснований кризис?
Конструктивная математика тем и хороша, что при правильном использовании никаких кризисов и парадоксов быть не может. При неправильном - бывает, но легко обходится, как парадокс Жирара для первой версии MLTT. В брауэровском интуиционизме ничего такого не может быть в принципе, т.к. за первокультурную математику он считал только чистые ментальные построения на основе актов интуиционизма, даже интуиционистскую логику Гейтинга считал не первокультурным явлением. НоТТ же слишком новая область, чтобы говорить о кризисах и парадоксах, возможно что-то и выплывет со временем и то только потому что забили на заветы Брауэра.
>Неси сюда.
В педивикии забанили? Да в любой книге по матлогике все перечислено.
>>3039
>Разве это не определение конструктивизма?
Конструктивизм это по-сути допиленный подход Брауэра, из которого выкинули его акты интуиционизма, солипсизм, и добавили формализма, что сделал еще Гейтинг. Тут уж каждый интерпретировал как мог, н-р отдельно выделяют русский конструктивизм (Колмогоров, Марков, вот это все). Но существование в математике к построению приравнял Брауэр.
>Конструктивная математика тем и хороша, что при правильном использовании никаких кризисов и парадоксов быть не может
Т.е. теоремы Геделя неприменимы к ней и можно сделать самоверифицирующую систему?
И про парадоксы ZFC я не нашел. Был парадокс Рассела, но его поправили аксиомой регулярности. В MLTT нет аналогов такой аксиоме? Парадокс Банаха-Тарского это вообще не парадокс.
>Т.е. теоремы Геделя неприменимы к ней и можно сделать самоверифицирующую систему?
Да. Мартин-Лёф пояснял почему так, пикрелейтед 1.
>>3046
>Говоришь так, как будто это парадокс.
Это хуже парадокса. Это как два стула - на одном неполнота точеная, на другом противоречивость дроченая. И вся ваша неконструктивная математика по-сути, выбор на какой стул сесть самому, на какой мамку посадить.
>>3047
В основном, мемас. Первая культура - т.е. чистая математика. Остальное - прикладная и т.д. По Брауэру же (пикрелейтед 2) матматика первого уровня - чистые ментальные конструкции. Второй уровень - формализация первого и т.д.
Ты похоже, начинаешь что-то понимать, лол. Я, во-первых, уже раз 10 цитировал Мартин-Лёфа по поводу того что любая формула, записанная конечным числом знаков - это конструктивный объект. Более того, вся практически используемая математика конструктивна, иначе ее нельзя было бы использовать в практических целях. Даже таблица умножений конструктивна, хотя никто это особо не оговаривает. Неконструктивность по-сути начинается там, где идет по пизде вычислимость, т.е. когда начинаются всякие верования в актуальные бесконечности и т.д. А вычислимое всегда конструктивно.
>Да. Мартин-Лёф пояснял почему так, пикрелейтед 1.
Ну это какой-то философский бред, ты мне притащи что-то типа такого:
http://r6.ca/Goedel/goedel1.html
Только с противоположными выводами.
Так утверждение о существовании актуальной бесконечности - это не верования. Это тоже конечная строка символов.
>Так утверждение о существовании актуальной бесконечности - это не верования. Это тоже конечная строка символов.
Да. Но проверка типов этой последовательности приведет к пустому типу, т.к. строить там нечего. Так-то и слово "Аллах" тоже конечная последовательность символов.
>>3055
Там не философский бред. Канта с его аналитическими и синтетическими суждениями он приплел больше для иллюстрации, там суть в разных подходах. То, что в неконструктивной логике просто предполагается априори, в конструктивнй доказывается непосредственно построением типа/множества. Полная статья http://archive-pml.github.io/martin-lof/pdfs/Martin-Lof-Analytic-and-Synthetic-Judgements-in-Type-Theory.pdf
>Более того, вся практически используемая математика конструктивна, иначе ее нельзя было бы использовать в практических целях.
остался единственный вопрос: почему неконструктивные доказательства работают и дают верные предсказания. Или все великие математики занимались какой-то херней и построили огромный хрустальный замок?
Я же говорю, неконструктивность - это то, что нарушает вычислимость. Если что-то можно построить алгоритмически, с каких хуев это что-то считать неконструктивным? Ты головой-то подумой.
Погоди, разве теорема Гёделя о неполноте не касается ЛЮБОЙ математики? Вообще, любого языка описания. Я думал, что неполнота — это принципиальная неразрешимая особенность языков.
>По Брауэру же (пикрелейтед 2) матматика первого уровня - чистые ментальные конструкции
Что понимается под ментальными конструкциями? Что-то типа неясных интуитивных предчувствий? Речь идёт о психологических штуках?
что-то я не вижу, что автор строит где-то PRA. Вот тебе еще ссылка, где конструктивно строят результат Геделя
https://ncatlab.org/nlab/show/incompleteness+theorem
>Да. Но проверка типов этой последовательности приведет к пустому типу, т.к. строить там нечего. Так-то и слово "Аллах" тоже конечная последовательность символов.
Я не мыслю в таких терминах, в FOL вообще нету типов, есть только строки и правила вывода из строк. В конструктивизме марковского типа разве тоже не просто нормальные алгорифмы/машины тьюринга без всяких типов?
Теорема Ферма, например. Результат ее проверен вычислительно, но само ее доказательство неконструктивно.
>Погоди, разве теорема Гёделя о неполноте не касается ЛЮБОЙ математики? Вообще, любого языка описания. Я думал, что неполнота — это принципиальная неразрешимая особенность языков.
Там фишка в том, что алгоритм, по которому строится (и может быть проверен на корректность) конструктивный объект сам по себе является конструктивным объектом, который может быть проверен на корректность. Правила проверки на корректность - тоже конструктивный объект, который можно проверить на корректность.
>Что понимается под ментальными конструкциями? Что-то типа неясных интуитивных предчувствий? Речь идёт о психологических штуках?
Ну это в 3х словах не объяснить, речь о базовой интуиции времени, как функции ЦНС (нумеронов в правой нижней префронтальной коре - rIPC), ес-но, Брауэр всего этого знать не мог, но он таки сделал правильный выбор. Первичное построение на основе базовой интуиции времени - это two-ity, далее по второму акту интуиционизма - веера и виды (типа множеств и континуума). Как из всего этого построить математику - отдельная тема, вот тут http://gen.lib.rus.ec/book/index.php?md5=1F429F7BAC43FFFDB0EC4A5157EFEECD очень грамотно все рассмотрено. Но если не заморачиваться со взглядами конкретно Брауэра на этот вопрос, то ментальное построение это то же самое, что алгоритмическое построение (пик 3).
>>3064
>в FOL вообще нету типов, есть только строки и правила вывода из строк. В конструктивизме марковского типа разве тоже не просто нормальные алгорифмы/машины тьюринга без всяких типов?
Есть жи изоморфизм Карри-Говарда. Можно и без типов, но с типами удобнее. Логика первого порядка не подходит для камплюктеров, напрямую ее там использовать нельзя, отсюда необходимость костылей типа логики Хоара. В MLTT изначально все на типах, хотя по-сути те же строки и правила вывода. Это вопрос разных представлений одного и того же на самом деле.
>напрямую ее там использовать нельзя, отсюда необходимость костылей типа логики Хоара. В MLTT изначально все на типах, хотя по-сути те же строки и правила вывода. Это вопрос разных представлений одного и того же на самом деле.
А в metamath proof explorer какие костыли, кроме того, что там всё мета-? Скрины страничек почитаю обязательно. Что думаешь о HoTT?
>Там фишка в том, что алгоритм, по которому строится (и может быть проверен на корректность) конструктивный объект сам по себе является конструктивным объектом, который может быть проверен на корректность. Правила проверки на корректность - тоже конструктивный объект, который можно проверить на корректность.
Т.е. вся фишка в том, чтобы использовать МЕТААЛГОРИТМ. А кто МЕТАЛГОРИТМ проверять будет?
 42 Кб, 800x333
42 Кб, 800x333>Что думаешь о HoTT?
Конструктивные основания жи, дело Брауэра живет и процветает, скоро всю математику на компьютере можно будет строить.
>metamath proof explorer
Не очень понял, что это вообще. Вроде бы и не язык с зависимыми типами. Хитрое там доказательство "1+1=2", поди и определения N нету. Вот правильный проект https://leanprover.github.io/ есть онлайн-вариант с учебником https://leanprover.github.io/tutorial/
>>3070
>МЕТААЛГОРИТМ
Че? Фишка в том, что любая стадия такой проверки, начиная с самого объекта - конструктивный проверяемый объект. На языке с зависимыми типами можно проверить сам этот язык с зависимымии типами, например. И все, круг замыкается, все построимо, проверяемо, выводимо и полно.
Это охуенно интересно, дружище, спасибо за ликбез. Теперь мне есть что почитать. Если можешь посоветовать ещё статей и книг на поднятые темы, особенно для таких профанов, как я, буду очень благодарен.
Алсо, правильно ли я понимаю, что философские школы проходят своеобразный путь эволюции: сначала от восприятия математики как формальной игры с цепочками символов, затем к рассмотрению воображаемых объектов, которые обозначаются символами, затем к рассмотрению и объектов и психики, которая их порождает? Типа как бы к всё более многомерному взгляду? Сорян. надеюсь, я не слишком криво выражаюсь.
>ещё статей и книг на поднятые темы
Вот годная книжка http://gen.lib.rus.ec/book/index.php?md5=F54C47275837DBC876940E067DB9FF0E пояснение за MLTT с нуля.
>Алсо, правильно ли я понимаю, что философские школы проходят своеобразный путь эволюции: сначала от восприятия математики как формальной игры с цепочками символов, затем к рассмотрению воображаемых объектов, которые обозначаются символами, затем к рассмотрению и объектов и психики, которая их порождает? Типа как бы к всё более многомерному взгляду?
Вряд ли, это скорее со стороны можно все представить в виде чего-то такого.
>Конструктивные основания жи, дело Брауэра живет и процветает, скоро всю математику на компьютере можно будет строить.
Хватит обманывать людей. Открываем HoTT 3.4, 3.8 и убеждаемся в обратном.
>>3073
> те самые два стула неконструктивной математики.
Теорема Геделя доказывается без исключенного третьего, без аксиомы выбора. Что в ней неконструктивного?
>Поэтому этот ваш metamath proof explorer не дотянет до языков с зависимыми типами
Да и на кой он нужен, если можно использовать язык с зависимыми типами и строить там ZFC с блекджеком и бесконечностям?
Представил бесконечность конечным числом символов, и чернильной дыры не образовалось. Вопросы?
>я в общем знаю теорию множеств
Скорее не знаешь, чем знаешь. Аксиомы NBG воспроизвести можешь? Аксиомы ZFC? Ультрафильтр можешь определить?
>Аксиомы ZFC?
1. Пустое множество существует.
2. Хотя бы один бесконечный ординал существует.
3. Для любого множества объединение его элементов существует.
4. Для любой пары множеств неупорядоченная пара существует.
5. Для любого множества булеан существует.
6. Два множества равны титтк они состоят из одних и тех же элементов.
7. Одноместный предикат, заданный на множестве, - коллективизирующий.
8. Двуместный предикат, первый аргумент которого задан на множестве, - коллективизирующий по второму аргументу.
9. В непустом множестве есть элемент, не пересекающийся с этим множеством.
10. Всякая сюръекция имеет сечение.
Правильно?
>Представил бесконечность конечным числом символов, и чернильной дыры не образовалось. Вопросы?
Проверка типов что даст? Правильно, жопу. Я уже приводил пример - "Аллах" тоже конечная последовательность символов. Никто не запрещает использовать нарушающие вычислимость верования, результатом проверки такого типа все равно будет пустой тип, т.к. в подобных последовательностях символов не содержится ничего для построения того, что эта последовательность символов выражает. Как итог - построения и нет, получаем дырку от бублика.
>>3096
>В каком месте начинаются проблемы?
Проблемы начинаются ровно в том месте, когда бесконечность постулируется без конкретного потенциально бесконечного объекта.
Зачем ты вообще лезешь что-то отвечать в этот тред, если даже не понимаешь о чем говоришь? Пиздуй в /б, там и неси хуйню. Тут тематика вообще-то.
Зарепортил срущего петуха.
Если твоя проверка типов показывает жопу на обычном математическом объекте - проблема в твоей проверке типов. Это очевидно.
 27 Кб, 400x366
27 Кб, 400x366Серьёзно, о какой проверке типов речь?
Что такое "проверка типов", о которой тут так много говорят?
>Проблемы начинаются ровно в том месте, когда бесконечность постулируется без конкретного потенциально бесконечного объекта.
А в классической математике оперируют самой бесконечностью? Есть примеры?
>говорит "Срущий петух ожидаемо перешел к угрозам."
>при этом сам угрожает всем репортами
Тяжело тебе с самим собой, наверное, да и с людьми. Лицемерие никогда не сближает с окружающими.
Без интернета же. Вопрос в том, достаточно ли глубоко ты знаешь теорию множеств, чтобы в твоей речи свободно присутствовали серьёзные теоретико-множественные понятия. Обычно люди, которые говорят о знании теории множеств, подразумевают умение брать объединения-пересечения-произведения конечного количества множеств и фейлятся уже при попытке определить произведение бесконечного семейства.
Ну давай, ну чего ты.
Ладно.
>вот почему конструктивисты петухи?
Потому что они верят, что аксиомы математических теорий нельзя выбирать произвольно и что некоторые аксиомы - харам. По каким-то причинам они решили напасть на аксиому выбора (на другие аксиомы не нападают, видимо, только из-за того что ничего о них не знают). Что отсутствие аксиомы выбора означает недоказуемость наличия в каждом бесконечном множестве счётного подмножества и непустоты бесконечных декартовых произведений, а также отсутствие классической иерархии алефов, их не волнует. В то, что кумулятивная иерархия верумов является стандартной интерпретацией теории множеств, они не верят тоже. Общую топологию они просто ненавидят. Как-то аргументировать свою позицию отказываются либо аргументируют её ещё более сектантскими загонами.
Трипфажить начать, что ли. Часто отвечают за меня.
> По каким-то причинам они решили напасть на аксиому выбора
Ну не по "каким-то" а по вполне определённым. Нельзя просто взять и выбрать что-то, не уверившись, что твой выбор вообще возможен. Это очень слабое место.
Сколько платишь за услуги репетитора?
Точно так же можно напасть на какую-нибудь другую аксиому. Например, на аксиому подстановки.
Понимаешь, у тебя критика конструктивистов довольно бессмысленная. Ты говоришь мол "посмотрите, эти петухи не признают мою топологию, мои счётные подмножества! правда дебилы?" Но это не аргумент. Как раз потому и не признают, что доказательства на основе аксиомы выбора слишком опрометчивы. То есть, ты не привёл критику их позиций, ты привёл личное возмущение.
Это напоминает спор между атеистом и верующим. Один говорит, что аксиома верна, второй говорит, что не верна. И тот и другой пердят в лужу.
Хотя, конструктивисты не пердят в лужу. На их стороне как минимум интуитивное представление о том, что невозможно сделать какой-то там абстрактный выбор, если нет уверенности, что он вообще возможен. Я вот не математик, а мне это вполне понятно. Что ты этому противопоставишь?
>невозможно сделать какой-то там абстрактный выбор, если нет уверенности
>нет уверенности
Верун, please.
Живёшь в ожидании модера? Ты в детском саду, наверное, был из тех мерзких детей, которые постоянно крысили воспиталке и хныкали "вот сичас васпитатильница придёт!"
Проблема в том, что конструктивисты отказываются аргументировать свои взгляды. От аксиомы выбора можно отказываться в некоторых случаях, я и сам отказываюсь иногда. Если хочется поизучать большие кардиналы, можно отказаться от выбора в пользу аксиомы детерминированности. Так что сам по себе отказ от выбора не вызывает у меня возмущения.
Видишь ли, мне не нужно что-то противопоставлять тому, что тебе кажется неинтуитивной какая-то аксиома. Ибо ZFC - это по определению теория первого порядка с равенством, имеющая вот такие вот аксиомы. У меня нет нужды как-то мотивировать определение и, в частности, делать его согласующимся с твоей интуицией.
Меня немного беспокоит репортер, который вмешивается в разговор.
Быстрее, а то срущий петух вместо тебя модером станет.
Быстрее подавай заявку! Не терпится порвать тебе пукан проксями.
>хочется поизучать большие кардиналы
Слушай, меня интересуют ординалы и вся вот эта их охуительная иерархия. Что посоветуешь почитать для плавного вхождения?
Манин. Доказуемое и недоказуемое.
Архангельский. Канторовская теория множеств.
Мендельсон. Введение в математическую логику и теорию множеств.
Jech. Set theory, third millenium edition. Вышла недавно, разительно отличается от первых двух редакций, на русский не переведена.
Это по классической ТМ. По дескриптивной можешь навернуть Кановея, он пишет на русском.
>>3170
Куратовский-Мостовский используют довольно-таки оригинальный подход и нестандартную нотацию. В доказательствах они широко используют комбинаторику. Вряд ли это хорошая книга.
>>3171
Там об ординалах как раз-таки мало написано.
От души, братуха, спасибо.
>На их стороне как минимум интуитивное представление о том, что невозможно сделать какой-то там абстрактный выбор
И контринтуитивное отрицание закона исключенного третьего.
Утверждение: Конструктивист петух или конструктивист не петух. Но зная, что конструктивист петух, мы не можем определить истинность этого утверждения! Для этого нужен конструктивный алгоритм определения петушиности в общем случае.
Мы знаем, что это ложь, что конструктивист не петух. Но из этого знания мы не можем заключить, что конструктивист петух, потому что двойное отрицание выводится из исключенного третьего.
В итоге отпадает большинство доказательства "от противного".
Почему контринтуитивное? Сокращение двойного отрицания это совершенно бредовая на интуитивном уровне операция.
Вот прикинь, ты подходишь к своей тёлке и спрашиваешь "Мань, как тебе секс со мной? Хорошо? Или не очень хорошо?"
Маня мнётся, не хочет отвечать. Ты настаиваешь.
"Нет, Мань, ну скажи? Не хорошо разве было?"
Наконец Маня отвечает тебе "Ну, не не хорошо".
Чувствуешь разницу между "не не хорошо" и "хорошо"? Думаю, у тебя от её ответа на месте бы бомбануло, и мистер вялый на всю жизнь с тобой.
Теперь понятно, почему ты такой злой и кидаешь на всех репорты. Я думаю, тебе стоит познакомиться с прелестями мастурбации, пока ты совсем не утратил человеческий облик.
Ты пытаешься аргументировать модальностью фразы? Совершенно бредово было бы, если бы ты маню расспрашивал было ли хорошо, а потом расспросил дополнительно было ли ей плохо, а потом узнал бы еще критерии оценки и попытался доказать независимость этих критериев от аксиомы выбора. Маня бы сразу поняла, что ты или долбоеб или конструктивист, что в общем-то одно и то же.
При этом я не могу представить ситуации, когда утверждение верное в классическое логике, но неверное в интуитивной, что-то принципиально меняет в фактической ситуации, что в принципе и очевидно, ведь классическая логика более сильная.
> Совершенно бредово было бы, если бы ты маню расспрашивал было ли хорошо, а потом расспросил дополнительно было ли ей плохо
Между прочим, недурная стратегия.
>При этом я не могу представить ситуации, когда утверждение верное в классическое логике, но неверное в интуитивной, что-то принципиально меняет в фактической ситуации
Верно, затруднительно привести подобные примеры. Их, скорее всего, и не будет никогда. Но знаешь, спускать на тормозах проблему по этой причине это всё равно, что признать теорему доказанной за счёт компьютерной проверки брутфорсом по всем значениям переменных. Вроде на практике верна, но не хватает полнейшей аналитической убеждённости.
s/сильная/слабая
Так интуитивная логика не воспринимает аналитических доказательств и всегда требует потенциальный брутфорс. Сама математика на ней превращается в поиск конкретного алгоритма, в алгоритмическую науку. Вся математическая интуиция, методы оценок и доказательства существования, это все переходит в разряд "математики гипотез". Гипотезу любой может, как Уайлс или Перельман, а вот алгоритм найти это другое дело.
Нужен результат. Под этим подразумевается решение уравняшек. Вы сказали, что 10 проблема Гильберта не имеет решений - поэтому будем разводить философию. Если она Вам так нравиться - занимайтесь этим. Никто не мешает Вам.
Про алгебру говорите, но алгебраические методы не используете. Рисование стрелочек это не алгебра. Там всегда надо прийти к формализованной записи и доказательства всех утверждений. Получается так, что человек может проучиться лет 8 и всё равно не сможет решить уравняшку. Нужно ли это кому то? Если можно ему рассказать небольшой курс и он их будет спокойно решать. Не все конечно, но очень многие - а заодно и системы нелинейных уравняшек.
Можно сколько угодно кричать, что не надо их решать, но потребности остановить так не получиться. Можете всё удалять и ругать. Со временем это со стороны будет выглядеть как банда психов не даёт решать уравняшки. Видите ли они решили, что написанная формула не должна существовать и теперь ведут борьбу с ней.
Наш мир построен на формулах. Философская болтавня забывается или опровергается, но формулы раз появившись уже не исчезают. Это только с виду они кажутся слабыми.
У меня есть результат - то есть формулы. Поэтому вся Ваша философская болтавня должна быть уничтожена. Это то, что я добиваюсь и то, что обязательно произойдёт! Решайте уравняшки.
Как ты прав, Андрюша!
>Вся математическая интуиция, методы оценок и доказательства существования, это все переходит в разряд "математики гипотез"
А можно подробнее про математическую интуицию? Как математики приходят к тем или иным теориям? Какие есть философские взгляды на этот процесс? Как приходит конструктивист и как приходит ну какой-нибудь там алгебраист?
Попробуйте в яндекс/гугл картинках ввести HoTT
я чот прихуел
https://yandex.ru/images/search?text=hott
это получается такой намек: "нехуй, петушара, гейской хуйней заниматься, вот лучше на баб подрочи"
ко-ко-кошники официально унижены
Простите, вставлю свои пару копеек. Я примерно могу понять, откуда претензии к теории множеств, и даже пассажи в духе "теория множеств это психическое заболевание". На мой взгляд, это одно из самых охуенных изобретений человечества. То есть вот сам образ такого мышления, набор инструментария. Изобретение недопиленное, находится в доработке. Кроме того, рвёт мозг неподготовленным людям. Теория множеств открывает двери в целый мир потрясающих гипотез и результатов.
Чувак пишет, мол можно придумать какую угодно теорию. Так да, блять, в том и дело. МОЖНО. Никто блять не запрещает, на то математика и нужна, чтобы делать построения даже такие, которые вообще крайне далеки от бытового опыта. Если ты способен придумать охуенную теорию — придумывай, никто не запрещает. Если ты обезьяна, у которой мозги перегреваются от любого нетривиального воздействия, то ну могу посоветовать, скажем, пойти паять электросхемы.
Теория множеств — это рывок над пошлятиной и бытовухой. Это просто охуенно. Кто не может с ней совладать, тот просто слишком зашорен и погряз в болоте. Я уверен, есть какие-то психологические причины, почему одни люди могут в ТМ, а другие нет. Мне кажется, у последних есть что-то вроде болезненной зацикленности на своих мыслительных процессах. В итоге это выливается в бессмысленные кукареки типа "хватет феласофствавать!!!111". Ну не можешь, не лезь, пидрила.
>Кто не может с ней совладать, тот просто слишком дебил и дегенерат
Пиши правильно, толераст хуев.
Малоизвестные математики. Манин известен тем, что работал в одном институте с великим Кострикиным, а Гротендик вообще известен только за то, что придумал считать 0 натуральным числом.
Ты ебанулся, "малоизвестные"? Гротендик придумал всю современную математику почти в одиночку. Зарепортил тролля.
На самом деле Гротендик известен лишь тем, что как-то однажды ляпнул, что 57 — не очень большое простое число. С тех пор число 57 называется Гротендик.
Серьёзно? Почему в википедии написано совсем другое? Гротендик редактировал?
(успокойся, сумасшедший)
Манин кстати когда его выгнали с мехмата в 57ой преподавал, пока родители одной девочки не пожаловались
Отец спросил девочку, что такое жорданова нормальная форма, а она показала, как Манин вводил.
Ах ты содомит.
Ты настолько тупой, что у меня просто нет слов.
>По каким-то причинам они решили напасть на аксиому выбора
Кукарекать так после того, как я постил конструктивное доказательство аксиомы выбора, как и все прочее накукареканное в твоем посте говорит только о том, что ты малолетний дебил, не могущий даже в чтение. Сам выдумал себе врагов и сам с ними успешно борешься в своих манямирах, а о конструктивизме представлений вообще не имеешь, даже самых общих.
> у тебя критика конструктивистов довольно бессмысленная.
Я там вообще критики не увидел, если что. Одно непонимания темы, на которую предыдущий оратор пытается еще и рассуждать. Газификация луж всё это.
Ты даже не считаешь нужным попытаться понять, что имел в виду под интуиционизмом Брауэр, хотя я сто раз цитировал его 1 и 2 акты интуиционизма. Но, при этом ты что-то там критикуешь. И ты даже не понимаешь ,что критикуешь ты свое непонимание вопроса, считая интуиционизм чем-то вроде своих школьных "интуитивных" представлений о чем-то, считаешь, что это и имеется в виду в интуиционизме. И с чем тут спорить? С твоим незнанием предмета? Нахуй надо, сначала сам хоть пойми, что ты пытаешься "оспаривать", потом что-то заявляй.
По существу в том посте утверждается, что интуиционисты отрицают аксиому выбора. Это утверждение верно или неверно?
 167 Кб, 782x543
167 Кб, 782x543>>3331
>интуиционисты отрицают аксиому выбора. Это утверждение верно или неверно?
А ты сам как думаешь, после того как я постил >>2348 конструктивное доказательство аксиомы выбора? Если интуиционисты ее прямо доказывают и в конструктивной математике это никакая не аксиома, а доказуемая теорема?
Идет заяц и читает книгу по логике. Тут навстречу волк:
- Слышь, заяц, а что читаешь?
- Книгу по логике
- А что это?
- Ну смотри. У тебя спички есть?
- Есть
- Если есть спички, то ты куришь.
- Ну, курю
- Если ты куришь, то деньги есть.
- Ну, есть.
- Если есть деньги, значит работаешь.
- Ну, работаю.
- Если работаешь, то много денег зарабатываешь.
- Ну.
- Если много денег, то и телки есть.
- Ну есть.
- Если телки есть , то ты с ними спишь.
- Допустим, сплю.
- Если ты спишь с телками, то ты не импотент.
Волк:
- Ух ты, круто. Дай почитаю.
Идет по лесу , читает и встречает Медведя. Медведь:
-Волк, что читаешь?
-Книгу по логике.
-А что это?
-Ну смотри. У тебя спички есть??
-Не-а
-Значит ты импотент!
Жирный шрифт - пример аналитического суждения, конструктивный подход. Наклонный шрифт - пример синтетического суждения, неконструктивный подход.
Идет заяц и читает книгу по логике. Тут навстречу волк:
- Слышь, заяц, а что читаешь?
- Книгу по логике
- А что это?
- Ну смотри. У тебя спички есть?
- Есть
- Если есть спички, то ты куришь.
- Ну, курю
- Если ты куришь, то деньги есть.
- Ну, есть.
- Если есть деньги, значит работаешь.
- Ну, работаю.
- Если работаешь, то много денег зарабатываешь.
- Ну.
- Если много денег, то и телки есть.
- Ну есть.
- Если телки есть , то ты с ними спишь.
- Допустим, сплю.
- Если ты спишь с телками, то ты не импотент.
Волк:
- Ух ты, круто. Дай почитаю.
Идет по лесу , читает и встречает Медведя. Медведь:
-Волк, что читаешь?
-Книгу по логике.
-А что это?
-Ну смотри. У тебя спички есть??
-Не-а
-Значит ты импотент!
Жирный шрифт - пример аналитического суждения, конструктивный подход. Наклонный шрифт - пример синтетического суждения, неконструктивный подход.
Это утверждение называется слабая аксиома выбора и она выводится из остальных аксиом ZF.
Хотя не, это даже что-то более слабое.
Это аксиома конечного выбора. https://mathoverflow.net/questions/32538/finite-axiom-of-choice-how-do-you-prove-it-from-just-zf
Бармен-интуиционист спросил бы:
- У тебя есть собака?
- Нет.
- У тебя нет собаки?
- Да.
- Это значит, что ты пидор!
В неконструктивной логике правила принимаются априори, тогда как в конструктивной (интерпретация логических констант по Брауэру-Гейтингу-Колмогорову) только в случае существования соответствующих правилам конструктивных пруф-объектов. Истинное суждение в конструктивизме т.о. должно быть непосредственно доказуемо, иначе оно не принимается. Пример - тот же закон исключенного третьего. Он конструктивно приемлем только в тех случаях, когда доказуем. А не сам по себе, потому что "Аристотель в него веровал, и ты так делай".
Ну, я в сказанном не вижу ничего такого, что следовало бы критиковать. Есть ли у классических математиков реальные причины бомбить по поводу конструктивизма, кроме той, что это задевает их чувства?
Я читал у Пенроуза какую-то критику конструктивизма, но не понял её тогда, слишком молод был, а сейчас вряд ли найду. Он писал что-то на тему того, что конструктивизм налагает чрезмерные ограничения и вместо чистоты математики по факту культивирует запутанность и что-то там ещё. Не помню, к сожалению.
Для того, чтобы понять о чем он говорит, надо открыть книгу по конструктивному анализу, конструктивной топологии (pointless), да и вообще любое реальное применение конструктивных оснований к математике.
Обнаружится, что простейшие доказательства элементарных теорем сводятся к нетривиальной комбинаторике, поиску алгоритмов, и даже зависимости от теоремы Ферма (которая доказана только неконструктивно).
А все потому, что интуиционистская логика более сильная, чем обычная. Самый обычный пример, это доказательство иррациональности двух. Классическое школьное доказательство использует аксиому исключенного третьего. Без нее, это довольно нудно доказываемое утверждение (см. примечание на стр. 14):
https://arxiv.org/pdf/1110.5456v1.pdf
А отрицание аксиомы выбора добавляет еще больше огня, ведь огромное количество простых утверждений становятся в общем случае неверными:
https://en.wikipedia.org/wiki/Axiom_of_choice#Equivalents
При этом конструктивисткая математика занимается только подтверждением результатов классической в частном случае. Зачем это нужно? Математик, работающий в любой современной области, просто не сможет работать так.
> огромное количество простых утверждений становятся в общем случае неверными
Так что если они и есть неверные в общем случае? И однажды это где-то как-то вылезет?
Стоит вчитаться, ведь речь идет о существовании базиса векторного пространства и об обратимости справа сюръективной функции.
>где-то как-то вылезет
Удивительно, что за 150 лет существования линейной и абстрактной алгебры, не было найдено такого контрпримера!
>Мехмат отзывает 500 000 своих выпускников по причине того, что во втором томе Фихтенгольца на странице 196 в формуле 56 отсутствует нормирующий оператор
Конструктивный, построимый по заданным правилам объект, удовлетворяющий заданным же условиям. Число, вектор, список, как простейшие примеры. Важна еще разница между каноническими и неканоническими элементами, но объяснять лениво, гуглится все элементарно.
>>3350
Ты главное игнорируешь - конструктивная математика построима и доказуема на компьютере, в т.ч. и с немалой степенью автоматизации. Хотя тут во многом все еще в зачаточном состоянии. Теорему 4х красок так и доказали, сколько с ней еблась бы классическая математика - никому не известно.
>>3351
>что если они и есть неверные в общем случае? И однажды это где-то как-то вылезет?
Они в общем случае как раз неверные и есть. Поскольку доказать их именно для общего случая возможности нет, т.к. эти утверждения опираются на нечто принципиально невычислимое. Брауэр именно это и показал, что все проблемы в математике из-за того, что некоторые вещи просто принимаются на веру.
>Ты главное игнорируешь - конструктивная математика построима и доказуема на компьютере
В чем тут отличие от неконструктивной? С принятием двух дополнительных аксиом ZFC построим и доказуем на компьютере.
При этом HoTT отличается, например, удобной, но избыточной аксиомой унивалентности. Почему бы и ее не выбросить?
>Теорему 4х красок так и доказали, сколько с ней еблась бы классическая математика - никому не известно.
Классическая математика дала возможность перебора за допустимое время как минимум.
>возможность перебора за допустимое время как минимум.
И что неконструктивного в конструктивном переборе, м?
>В чем тут отличие от неконструктивной?
В том, что в неконструктивной есть нарушающие вычислимость допущения. В остальном конструктивно все, что можно построить.
>И что неконструктивного в конструктивном переборе, м?
Тебе кажется это очевидным, но на самом деле конструктивное доказательство появилось много после самого доказательства. Самому перебору предшествует рассуждение:
https://en.wikipedia.org/wiki/Four_color_theorem#Summary_of_proof_ideas
>все проблемы в математике
Вот, началось. Ну-ка, о каких проблемах в математике идёт речь? Огласите весь список.
Конструктивная математика его не решает. Метод теории типов это метаматематической подход, когда мы используем более сильную систему.
Ты бы ещё иррациональность корня из 2 проблемой назвал. Этот "кризис" сто лет назад закончился, сейчас он живёт только в статьях второсортных философов.
Объясни в чем разница:
1) Мы проверяем непротиворечивость ZFC средствами более сильной формальной системы. (например, в с помощью HoTT)
2) Мы проверяем непротиворечивость конструктивистской аксиоматики средствами более сильной формальной системы.
3) Мы проверяем непротиворечивость какой-то аксиоматики его собственными средствами. По известной теореме она неполна.
По вашему треду трудно понять, что харам, а что зашквар.
Все 3 - примеры синтетических суждений. Я уже неоднократно пояснял за аналитические суждения >>3333 Неполнота любой формальной системы - причина невозможности вывести из этой системы доказательства логических констант. Их можно только построить непосредственно, и уже в таком виде принимать, как это делается в случае интерпретации логики по Брауэру-Гейтингу-Колмогорову. Такая логика полна и непротиворечива, что показал Мартин-Лёф. Эти два геделевских стула с неполнотой точеной и противоречиостью дроченой - удел формально-аксиоматических построений.
Мочизука слишком мутный перец, вряд ли тута кто-то знаком с его доказательством настолько, чтобы грамотно за него раскидать. Сам Мочизука в сентябре месяце выдал статью http://www.kurims.kyoto-u.ac.jp/~motizuki/Alien Copies, Gaussians, and Inter-universal Teichmuller Theory.pdf где поясняет за свою теорию с точки зрения вычисления гауссова интеграла. Надо полагать, при желании можно было бы попробовать изложить все это в виде типов и проверить в прувере. Но те, кто понимает Мочизуку, видимо, слишком просветленные для такой слесарной работы.
Теория чисел жи. Просто абстракций слишком много, в т.ч. придуманных самим Мочизукой, все эти анабелиоиды, фробениоиды, эталь-тета функции и т.д. Мыслить в терминах таких уровней абстракции, мало кто может.
 1,7 Мб, 2715x2748
1,7 Мб, 2715x2748И вообще-то, это верно для любой теоремы. То есть, я не понимаю, в чём в целом сложность математики для народа. В том, что нужно обладать большой математической эрудицией? Ну так её теоретически можно достичь, это экстенсивная проблема, а не интенсивная, вопрос времени, а не какой-то недоступной для мозга сложности. Доказательство действительно базируется на конструкциях, которые состоят из конструкций поменьше и так далее. Почему все в один голос говорят, что в доказательство abc-гипотезы трудно въехать?
>Такая логика полна и непротиворечива, что показал Мартин-Лёф.
тащи сюда формальное доказательство. "Предположил" не считается.
Решил поставить над собой эксперимент. Собираюсь понять доказательство Мочезуки. Уровень в математике на отметке "знаю, что такое интеграл и группа". Не могу похвастаться высоким IQ. Буду прилагать максимум усилий, по-честному стараться и идти с несгибаемой волей к своей цели. Прошу всех мне помочь советами, с чего начинать и куда двигаться. Пока что я вообще не вдупляю, о чём там. Постараюсь отчитываться о прогрессе.
Ты что-то в своей жизни делал на протяжении нескольких лет? Ну вот допустим ты учился в школе. А потом учился в институте хотя бы два курса. Чтобы понять доказательство теоремы Стокса, тебе надо открыть его и прочитать. А теперь представь себе маугли, которого надо научить пониманию этого доказательства. Трудно ли это? Это ведь экстенсивная проблема!
Проблема в основном в том, что нужно неблохо ориентироваться и мыслить в областях, связанных с основной задачей, н-р такой, как Мочизукино доказательство. Во всех областях. А это требует времени. В итоге, прискорбно, но оценка Фесенко (один из тех, кто проверил мочизукино доказательство) - 10 лет для математика-аспиранта, чтобы понять мочизукины выкладки - это правда. Альтернативный вариант - >>3388 нечто вроде lazy evaluation, займет минуты построения модели, ну и дни/недели чтобы разобраться.
>>3393
> Собираюсь понять доказательство Мочезуки. Уровень в математике на отметке "знаю, что такое интеграл и группа". Не могу похвастаться высоким IQ. Буду прилагать максимум усилий, по-честному стараться и идти с несгибаемой волей к своей цели.
По оценке Фесенко - 10 лет + путь до аспиранта-математика.
>>3392
http://archive-pml.github.io/martin-lof/pdfs/Martin-Lof-Analytic-and-Synthetic-Judgements-in-Type-Theory.pdf
Во-первых, аналогия не совсем правильная. Маугли не знает человеческой речи и, как считают современные нейролингвисты, если до определённого возраста человек не постигает логику языка, то уже и не сможет постичь. Есть вполне объективные физиологические барьеры для этого. Язык Мочезуки нам полностью доступен, мы знаем все слова, мы знаем правила грамматики. Так что мы как раз в положении студента-второкурсника, а не маугли.
Я не спорю, что это трудно, но есть совершенно явный и прямой путь, как понять доказательство. Нет ничего принципиально скрытого.
>In August 2012, Shinichi Mochizuki released a series of four preprints on Inter-universal Teichmuller Theory which is then applied to prove several famous conjectures in number theory, including Szpiro's conjecture, the hyperbolic Vojta's conjecture and the abc conjecture.
Вот эти четыре документа. Я, правда, пока не могу их найти.
>Я, правда, пока не могу их найти.
Лол, ты ж в гугл не можешь, думаешь, сможешь в IUTT? http://www.kurims.kyoto-u.ac.jp/~motizuki/papers-english.html в самом низу.
На момент, когда ты написал это пост, я уже нашёл эту страницу, так что видишь, я не так безнадёжен)
Ещё хочу добавить к своему посту. Конечная цель эксперимента в том, чтобы мочь ответить ИТТ на вопросы хотя бы по философии доказательства.
>Конечная цель эксперимента в том, чтобы мочь ответить ИТТ на вопросы хотя бы по философии доказательства.
Для этого Мочизука не нужон. Есть такая тема, как теория доказательств жи.
Я про конкретно его доказательство. Чтобы понимать бегло, что откуда следует и что означает.
Опять кидаешь какую-то лекцию. Демонстрирую как выглядит формальное доказательство полноты:
https://arxiv.org/abs/1110.1614
однако такое доказательство подтверждает мою точку зрения, а не твою. Поэтому неси своё.
Если ты не впитал теорию чисел с молоком матери, то ты дальше программы второго курса и не пройдешь.
В твоей статье доказывается полнота логики первого порядка в случае, если она основывается на BHK-интерпретации (Брауэра-Гейтинга-Колмогорова) логических констант, так? Это и есть то, о чем я толкую.
С помощью пруверов, видимо, т.к. приводится код. Т.е. с помощью изоморфизма Карри-Говарда в конечном счете. Не?
Там доказывается полнота логики первого порядка. Этот факт для классической логики называется теоремой о полноте. Мне же нужна другая слегка другая теорема:
https://math.stackexchange.com/questions/14709/what-is-the-difference-between-gödels-completeness-and-incompleteness-theorems
Падажжи, ты ж о каком-то метаязыке говорил? А оказывается, достаточно всего лишь BHK-интерпретации логических констант, и все, полнота логики первого порядка уже доказуема в прувере.
В жизни вообще ничего "принципиально скрытого" нет, и магии никакой не существует. Это ведь рассуждение уровня "вот мы знаем, что такое капитализм, деньги нам полностью доступны; значит нет никаких проблем стать миллионером". Формально вроде бы правильно, но совершенно бессмысленно.
Плохое сравнение. Богатыми люди становятся обычно из-за влияния факторов, которые для практических целей можно считать случайными и почти непредсказуемыми.
Богатыми люди обычно становятся из-за того, что у них богатые родители. А неуч - это твоя мамка. Тебе тут не место с такими манерами.
А твоя мамка научила тебя выгонять людей с анонимных форумов? Хуйца сосни, раз привык уже.
 140 Кб, 639x436
140 Кб, 639x436И опять приходим к тому же самому - тебе нужны какие-то теоремы, оторванные от конкретных конструктивных объектов. Суть-то неполноты в том, что никакой формальной системой ты не выведешь все возможные случаи, их можно получить только построением и последующей проверкой типов. Без этого имеем ситуацию как в анекдоте выше "нет спичек - это значит что ты пидор". Если мы исходя из этой системы допустим, что не имеющий спичек - не пидор, то доказать это в данной системе мы не сможем, т.к. у нас есть только формальное правило "нет спичек = пидор". В случае же BHK-интерпретации логических констант мы просто проверяем обе части этой формулы (строим соответствующий тип) и получаем готовое построение (тип опять же) для конкретного случая, конструктивный пруф-объект. Получаем непосредственно, а не выводим из каких-то общих правил, не связанных с конкретным случаем.
Совсем что ли? Я пример привожу понятный. Где я науку опровергаю? Ты даже в таком изложении не понимаешь о чем речь, к чему тогда комментировать лезешь? Ты же даже не понял о чем пост вообще. Пиздец, со школотой поселили.
Ты приводишь какие-то рассуждения уровня Поехавшего. Какие-то спички, пидоры. О чём ты вообще? Ладно, допустим, твои слова осмысленны. Тогда ты задал недостаточный уровень рекурсии. Что такое тип, в твоём понимании? Что такое BHK-интерпретация? Что такое пруф-объект? Что такое проверка типов?
 298 Кб, 683x1024
298 Кб, 683x1024>Ты приводишь какие-то рассуждения уровня Поехавшего.
Ну раз школьнику с мейлру так кажется, то ладно.
>Что такое тип, в твоём понимании? Что такое BHK-интерпретация? Что такое пруф-объект? Что такое проверка типов?
Вот я об этом и говорю. Ты же азов не знаешь, а лезешь что-то пояснять и кого-то поучать. Речь об MLTT, мое понимание типа и всего остального из перечисленного соответствует стандартным определениям из конструктивной теории типов Мартин-Лёфа.
 25 Кб, 800x1200
25 Кб, 800x1200>разнесу тебя в пух и прах.
Смешной такой, пиздец. Ты для начала хоть попытайся понять о чем там.
 82 Кб, 1077x215
82 Кб, 1077x215Для начала я уже вычитал, что аргумент Вавилова значим и для Мартин-Лёфа. Разве что чернильной дыры нет.
MLTT это не только математическая теория, но еще и язык программирования. Очень странно было бы программировать чернильные дыры. Это в неконструктивной математике легко все берега потерять, а-ля "Остапа понесло" - ехала актуальная бесконечность через закон исключенного третьего, а тут все должно быть построимо и без нарушений вычислимости.
Посмотрим. Пока что выяснилось, что все кудахтания про "демагога" Вавилова выше по треду были бессовестными.
Мартин-Лёф свободно оперирует конструкциями, которые подозрительно напоминают обычные, наивные множества. А именно, если K - категория, то Мартин-Лёф не может предъявить алгоритм, перечисляющий все элементы K, но для разных штук вправе сказать, являются ли они объектами K или не являются. Похоже, Вавилов-то был прав во всём.
Я не знаю, кто такой Вавилов, но во многих языках с зависимыми типами котягории используются наотличненько, что было бы физически невозможно, если бы это нарушало вычислимость.
 1,3 Мб, 1432x1080
1,3 Мб, 1432x1080Толстый доктор наук, луркоёб и автор своих "конкретных" книжек типа вон той >>2136.
http://www.mathnet.ru/rus/person21987
Божечки, твой пикрелкхейтед к "аргументу Вавилова" не имеет отношения. И разберись уже наконец, как соотносятся конструктивизм и ультрафинитизм.
>>3491
Относится, конечно. Невозможность построить некоторые числа на бумажке, руками, непосредственно по определению, - именно она заставляет Мартин-Лёфа разделять элементы множеств на канонические и неканонические. Число Вавилова 10^10^10 - неканонический элемент множества натуральных чисел, так как его на бумажке не построить, ибо бумажка схлопнется в чернильную дыру. А вот числа 1 = 0', 4=0'''', 10 = 0'''''''''' являются каноническими.
 22 Кб, 600x309
22 Кб, 600x309Окей. Вечером продолжу.
Я не обиделся. У тебя мания величия всего лишь. Надеюсь, тебе не слишком рвёт сраку тот факт, что я всё ещё тут, о хозяин анонимной доски.
Строить мы ГДЕ должны? По Брауэру все просто, мы строим в воображении. А вот в реальной жизни мы строим ГДЕ-ТО. Строим в теории типов минимальную логику, в ней логику первого порядка, в ней арифметику, вот какая у нас цепочка получилась!
>мы просто проверяем обе части этой формулы (строим соответствующий тип)
"Проверяем", но без формальной системы? Как только ты берешь в руки спичку и куда-то ее кладешь, ты уже действуешь в рамках формальной системы, хочешь ты этого или нет.
Мой мессадж хэз кам акросс, так что у меня ни единого повода для каких бы то ни было негативных эмоций.
Петушок, у тебя бомбануло, когда тебя всего лишь назвали неучем за слабую аргументацию, причём настолько, что ты до сих пор не можешь успокоиться. Какие-то "манеры" призвал на помощь. Ясно, что когда тебя в школе в унитаз башкой макали, ты тоже причитал "вам здесь не место, это храм знания!"
>Богатыми люди обычно становятся из-за того, что у них богатые родители.
А это реально неуч написал. Гугли теорию хаоса, обезьяна.
 18 Кб, 282x360
18 Кб, 282x360>Строить мы ГДЕ должны? По Брауэру все просто, мы строим в воображении. А вот в реальной жизни мы строим ГДЕ-ТО. Строим в теории типов минимальную логику, в ней логику первого порядка, в ней арифметику, вот какая у нас цепочка получилась!
Суть в том, что все последующие построения в конструктивной математике опираются только на предыдущие. Тут вообще нет никакой разницы между Брауэром с его актами интуиционизма и Мартин-Лёфом с его тетраграмматоном MLTT (4 формы суждений, 4 формы гипотетических суждений, 4 формы интерпретации суждений, 4 вида правил для всех операций, 4 различных типа - Pi, Sigma, W, U). И как у Брауэра в итоге всё можно свести к two-ity, так и в MLTT все сводится к начальным суждениям и пруф-объектам для них.
>"Проверяем", но без формальной системы?
Система в данном случае зависит от конкретного построения, нет ножек - нет конфетки нет построения - нет и непустого вывода из пустоты. В неконструктивной же логике все опирается на сами правила вывода, безотносительно их применимости в данном конкретном случае.
>В неконструктивной же логике все опирается на сами правила вывода, безотносительно их применимости в данном конкретном случае.
Что весьма печально для прувера, но не для человека. Применимость означает "изоморфизм Карри-Говарда" и наоборот.
Для реальной работы конструктивная математика просто более сильная система аксиом. Можно опускаться дальше:
https://en.wikipedia.org/wiki/Reverse_mathematics
Это копия, сохраненная 13 января 2022 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
















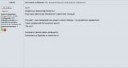


![The-Multiradial-Representation-of-Inter-universal-Teichmüll[...].webm](/math/big/thumb/22/14795678288700s.jpg)
![Mózg Rozjebany HD oryginał - YouTube [360p].webm](/math/big/thumb/22/14795678290661s.jpg)
