Это копия, сохраненная 13 ноября 2023 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
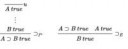
>The state after the second "intros" command, looks like:
> A : Prop
> proof_of_A : A
> ============================
> A
> Now, we can talk about "Prop". "proof_of_A" is a proof. It has type "A", which means that "A" is something that could have a proof. In logic, that is called a "proposition". Since the proposition "A" has type "Prop", "Prop" must be the type of propositions.
Поясните, как у утверждения может быть тип? В чем смысл?
Ну, прямо следующий абзац же об этом... Или я твоего вопроса не понял? Если бы у пропозишнов не было типа, ты бы не смог доказывать никакие утверждения о пропозишнах. Он там и дает примеры: можно сказать "для всех натуральных чисел, если число меньше пяти, то меньше и шести", а можно сказать "для всех пропозишнов, если у нас есть пропозишн, то он у нас есть".
http://adam.chlipala.net/cpdt/html/Universes.html
https://coq.inria.fr/refman/Reference-Manual006.html#Cic
По второй ссылке определение: получается, что "тип" - это сорт, а сорт - это Проп, Сет или Тип_ай для натурального ай.
 4 Кб, 240x240
4 Кб, 240x240Кук не нужон, зашквар же. Есть няшный LEAN http://leanprover.github.io/ в том числе с браузерным вариантом https://leanprover.github.io/tutorial/?live и учебником https://leanprover.github.io/tutorial/ онлайн и в пдф. Помимо прочего, это первый прувер с ядром на HoTT - гомотопической теории типов, но основное ядро CiC, как и у Кука.
>Поясните, как у утверждения может быть тип? В чем смысл?
Изоморфизм Карри-Говарда жи есть. Пропозишены/формулы как типы/множества. Я в прошлом треде сколько годноты на эту тему спалил быдлу, а все зря. Например, http://archive-pml.github.io/martin-lof/pdfs/Bibliopolis-Book-retypeset-1984.pdf со 2 по 7 страницы
 225 Кб, 1425x740
225 Кб, 1425x740>что такое тип?
Тип - это конструктивный объект, который есть элемент самого себя. Да, в общем случае это приводит к парадоксу Жирара (по-сути, все тот жи парадокс Рассела), что было показано для первого варианта MLTT, поэтому сейчас там все немного хитрее - иерархия вложенных универсумов - U. Подробности опять же в вышеупомянутой книге, либо в учебнике по LEAN. Если не интересны философические объяснения - считай тип множеством, элементы которого определены заданными правилами.
У тебя мания величия походу, бро.
> полная и выводимая по Геделю
Что очевидно, ведь теорема Гёделя распространяется только на те системы, где можно построить PRA.
Предыдущий тред.
>В итоге получается логическая система, полная и выводимая по Геделю
Ну сколько можно распространять дезинформацию?
>полная
Она не полна т.к. к ней вполне применимы теоремы Гёделя о неполноте, в частности, она не может ни доказать, ни опровергнуть утверждение о своей собственной непротиворечивости. Напомню, что полнота означает, что всякое предложений либо доказуемо, либо опровержимо. Если теория обладает таким свойством только для специального класса предложений, а не для всех предложений своего языка, то называть это полнотой некорректно.
>выводимая по Геделю
Не то, чтобы я прочел все работы Геделя, но я видел этот термин тоько у тебя, почти уверен, что ввел его вовсе не Гедель - ссылку на Геделя в студию, если придерживаешься другой точки зрения.
>>3744
>Что очевидно, ведь теорема Гёделя распространяется только на те системы, где можно построить PRA.
На самом деле теоремы Геделя о неполноте распространяются и на более слабые системы (1-ую так и вовсе можно доказать в арифметике Робинсона). Кроме того, эквациональная версия PRA (для которой тоже имеют место обе теоремы о неполноте) погружается в интуиционистскую теорию типов.
>в частности, она не может ни доказать, ни опровергнуть утверждение о своей собственной непротиворечивости.
Для этого есть проверка типов, ведь по изоморфизму Карри-Говарда все утверждения в конструктивной логике соответствуют своим типам. Т.е. такая система как MLTT сама по себе конструктивный объект.
>Не то, чтобы я прочел все работы Геделя, но я видел этот термин тоько у тебя, почти уверен, что ввел его вовсе не Гедель - ссылку на Геделя в студию, если придерживаешься другой точки зрения.
Естественно, ты видел этот термин только у меня, ты ведь упорно игнорируешь его источник - статьи Мартин-Лёфа, где все это не только описано, но и разжевано на элементарных примерах. http://archive-pml.github.io/martin-lof/pdfs/Martin-Lof-Analytic-and-Synthetic-Judgements-in-Type-Theory.pdf и http://archive-pml.github.io/martin-lof/pdfs/Meanings-of-the-Logical-Constants-1983.pdf
>Напомню, что полнота означает, что всякое предложений либо доказуемо, либо опровержимо.
Спасибо, я знаю что такое полнота. Интерпретация логических констант по Брауэру-Гейтингу-Колмогорову полна именно в этом смысле, поскольку любое суждение в ней либо построимо, либо абсурдно и т.о. соответствует пустому множеству своих пруфов (типу по изоморфизму Карри-Говарда).
 101 Кб, 499x734
101 Кб, 499x734 8 Кб, 950x128
8 Кб, 950x128Шарящий в мат.логике анон, ответь.
Может ли теоретически получиться так, что ZFC непротиворечива, однако омега-противоречива, и если так, то возможно ли было бы эту омега-противоречивость некими метаматематическими методами (вроде тех, что использовал Гёдель) доказать?
Если кратко, то может. Будучи точным, вопрос о том, что значит "может ли теоретически получиться" довольно тонкий.
Например, используя вторую теорему Гёделя о неполноте можно показать, что если непротиворечива ZFC + omega-Con(ZFC), то непротиворечива и теория ZFC + Con(ZFC+Сon(ZFC)) + not omega-Con(ZFC).
Доказать это можно довольно просто. Покажем, что ZFC + omega-Con(ZFC) доказывает Con(ZFC+Сon(ZFC)). Рассуждаем в ZFC + omega-Con(ZFC). Очевидно, из omega-Con(ZFC) следует Con(ZFC). Но так как Con(ZFC) арифметическое предложение, то omega-Con(ZFC) влечет искомое Con(ZFC+Сon(ZFC)). Также отметим, что рассуждая аналогично дальше мы получим Con(ZFC+Сon(ZFC+Сon(ZFC))).
Отсюда из непротиворечивости ZFC + omega-Con(ZFC) следует непротиворечивость ZFC + Con(ZFC+Сon(ZFC)). В силу второй теоремы Гёделя о неполноте, ZFC + Con(ZFC+Сon(ZFC)) не доказывает Con(ZFC+Con(ZFC+Сon(ZFC))) и тем самым непротиворечива теория ZFC + Con(ZFC+Сon(ZFC))+ not Con(ZFC+Con(ZFC+Сon(ZFC))). В силу того, что мы уже видели, что в ZFC предложение omega-Con(ZFC) влечет Con(ZFC+Con(ZFC+Сon(ZFC))), мы заключаем, что ZFC + Con(ZFC+Сon(ZFC))+ not Con(ZFC+Con(ZFC+Сon(ZFC))) доказывает not omega-Con(ZFC). Таким образом, непротиворечива теория ZFC + Con(ZFC+Сon(ZFC)) + not omega-Con(ZFC).
Спасибо, анон!
Отсюда даже виден дальнейший ход того, как можно было бы доказать omega-Con(ZFC) - доказав неким образом верность арифметического выражения, эквивалентного not Con(ZFC+Con(ZFC+Сon(ZFC)))
fix: доказать not omega-Con(ZFC)
Я на самом деле переусложнил. Для ответа на твой вопрос нужно было лишь доказать непротиворечивость ZFC + Сon(ZFC) + not omega-Con(ZFC). Что требовало немного меньше усилий.
-(-(-A V B) V (C V (D V E))V(-(-D V A) V (C V (E V A))
Понимаю, что достаточно было бы вывести из этой схемы три стандартные схемы логики высказываний, из которых уже доказуемо всё остальное, но вообще не представляю как это делать.
Статью, в которой это доказывается, найти не могу:
Meredith Carew A.. Single axioms for the systems (C, N), (C, O) and (A, N) of the two-valued propositional calculus. The journal of computing systems, vol. 1 no. 3 (1953), pp. 155–164.
Да никакой он не божественный. Мало того, что конструктивистов с кое-кем другим перепутал, так еще и ночью у него там кто-то символы дорисовывает. Теорем-пруверы, оказывается, опираются на тысячи неявных предположений - вот оно как! Просто черная магия и сильный ИИ какие-то.
> Теорем-пруверы, оказывается, опираются на тысячи неявных предположений - вот оно как!
Вавилов тенденциозен, но собственно критика того, что конструктивность так называемой конструктивной математики довольно условна и опирается на то, что допускаются явно физически нереализуемые вычисления остается. В чем, в конце-концов, утверждение об обрывании последовательностей Гудстейна конструктивнее, чем утверждение о возможности удвоить шар путем перемещения конечного числа частей, учитывая, что ни одно из них не является физически реализуемым.
>Да нормальный парень он, просто платонист.
Проблема не в том, что он платонист, а в том, что его заносит и он выдает мало адекватную аргументацию против несимпатичных ему позиций. Например теже "тысячи неявных аксиом" нужные конструктивной математике или что теорема Гёделя о неполноте говорит о "генерации некоторого специального вида текстов" (и ничего не говорит о математике).
Но, впрочем, пишет увлекательно (хотя, отчасти, это следствие того, что он выдвигает совершенно скандальные тезисы).
Да, видимо так, просто потому что сомнения в реальности математических объектов однозначно являются большой помехой, когда реально занимаешься доказательством теорем.
Хотя, разумеется, это касается только собственно математиков. Философы математики, не являющиеся, а тем более никогда не являвшиеся действующими математиками вполне могут не быть платонистами ни в какой степени.
 54 Кб, 453x679
54 Кб, 453x679>пик
Какой же этот клоун неосилятор, господи. Он бы хоть попытался разобраться в том, что критикует. Вместо того, чтобы мазать калом математиков, до которых ему как до Луны пешком и всё лесом. Впрочем, наверное, я слишком многого хочу от рашкованского быдлана. Сто раз уже было сказано об абстракции потенциальной осуществимости, общей для всей математики, но нет. Дебилы будут кукарекать про чернильные дыры. Дебил, он на то и дебил, чтобы не понимать очевидного. В частности, что число 10^10^10^...^10 относится к натуральным исходя из конструктивно определенных правил построения N. В частности, у этого числа есть предваряющее его 10^10^10^...^10-1 и следущее за ним 10^10^10^...^10+1 Т.о., хотя данное число физически и непостроимо, о его свойствах (принадлежности к N) мы можем судить из вышесказанного. И еще раз - абстракция потенциальной осуществимости, она общая для всей математики, какого хуя за нее предъявляют только конструктивизму? Если об этом еще Евклид писал? Вот этой своей обличающей писаниной этот ваш вавилов вообще что и кому доказал? Практическое применение у нее какое? С MLTT все ясно, при интерпретации логических констант по Колмогорову это по факту готовая спецификация для языка программирования с зависимыми типами, который может служить для доказательства теорем на компьютере. При интерпретации этих же логических констант по Брауэру-Гейтингу MLTT может служить конструктивными основаниями математики. А вот эта ваша вавиловщина, какие у нее задачи? Парашу тралить?
>>5932
>критика того, что конструктивность так называемой конструктивной математики довольно условна и опирается на то, что допускаются явно физически нереализуемые вычисления остается.
Он просто про MLTT не слышал, если слышал, то не читал, если читал, то не понял, если понял, то не так.
Ой, какая милота эта ваша грязноштанная математика. "Яскозал, что это буржуазная теория и вы так делайте". На самом же деле, а не в калмунистических манямирах, есть нейрофизиологические данные, доказывающие сводимость натурального числа к восприятию времени, о чем писал еще Брауэр. Т.н. модель ATOM Уолша. Ну, цитата Кронекера про бога хуета, конечно.
>о чем писал еще Брауэр.
Ох и давно я этого не слышал.
>есть нейрофизиологические данные, доказывающие сводимость натурального числа к восприятию времени
Пруф?
>Пруф?
Пишу жи
>>6117
>Т.н. модель ATOM Уолша.
Ссылочка на РТ пабмед - https://www.ncbi.nlm.nih.gov/pubmed/14585444
Нейровизуализация - объективные данные, они не могут быть хуйней, они либо что-то показывают, либо нет. По этой теории, на которую ты ссылаешься, я тоже пояснял уже. Там авторы сами себе противоречат, результаты нейровизуализации у них показывают связь в обоих направлениях, но в одном меньше, чем в другом, из чего они от балды заключают, что то направление, по которому корелляция меньше - это метафора и его на самом деле не существует. Еще раз скажу, в их же статье показана реальная корелляция на реальной нейровизуализации. Т.е. исходя из их же данных, они просто дополнили результаты Уолша, показав несимметричность пространственно-временных отношений, т.е. фиолетовый, зеленый и розовый кружочки на втором пике >>6117 должны быть разных диаметров, чтобы точнее показывать реальную картину.
Поздравляю всех любителей кококатегорий с Новым Годом! Дорогие подгорающие и сотрудничающие с администрацией красные петушки, я очень рад, что вы есть:3
 9 Кб, 180x280
9 Кб, 180x280Советую пик-релейтед. Книжка посовременнее, и изложено всё яснее и компактнее.
 190 Кб, 2540x728
190 Кб, 2540x728Там, например, вся логика высказываний строится на основе всего 3 схем аксиом.
Не читал, но...
1) часть серии из десятков книг
2) в названии серии "applied"
3) в названии "an introduction"
4) ОДИН АВТОР
5) в аксиомах ниже - символ точки поставлен так, что совершенно непонятно, что же он обозначает. НИКОГДА такое не встречал.
Предполагаю, что книга - говно, перехожу к дегустации.
Фу, буэ, действительно говно. Ты откуда такой выполз, что советуешь это? Сам что-ли нашёл. Небось первокур ВУЗ-а с непрофильной математикой?
Прежде всего это содержательно-аксиоматический метод. Он употребляется, когда изучается род структур, удовлетворяющих одному и тому же списку свойств. Например, один род структур составляют группы, другой род структур — кольца, третий род структур — структуры Пеано и т.п. Под аксиомами при этом понимаются просто конкретные условия, которым должна удовлетворять любая из структур изучаемого рода. Эти условия понимаются содержательно и записываются на рабочем математическом языке, например на русском или английском. Впрочем, часто аксиомы какого-либо рода структур записывают и на точном логико-математическом языке, но понимают содержательно как утверждения о структурах; для одних структур эти аксиомы могут быть истинны, а для других — ложны.
И где же тут вера кокококонсруктивист?
 102 Кб, 696x919
102 Кб, 696x919>И где же тут вера
Сейчас бы веруну за веру пояснять на подтираче. Ты ж очевидных вещей не видишь, что такому объяснишь. Самый очевидный пример веры - как раз матлогика. Вот есть логические константы, например А. Есть их комбинации. Например "А или не А". Последнее, например, считается истиной, невзирая ни на что. А если подумать головой, а не как обычно, то с каких хуев-то? Если у нас нет конкретного построения, на основании которого мы можем показать свойства А или не А, то надо веровать что все равно это правило истинно для всех возможных случаев априори. Отсюда и неполнота по Геделю - мы делаем предположение, недоказуемое в общем случае. Простейший пример - расеянский автопром. Пусть А будет высказыванием "дверь закрыта", не А - соответственно "дверь открыта". Так есть еще вариант "дверь не закрыта", не сводящееся к открытой двери, т.к. формально-то она выглядит закрытой, но она и не закрыта, т.к. если прислониться - вывалишься из таза к хуям. Но формально у нас только 2 варианта - "А или не А". Совсем другое дело - интерпретация логических констант по Гейтингу. В этом случае мы можем принять А только в случае наличия доказательства А (наличия пруф-объекта, принадлежащего к множеству А и т.о. доказывающего, что множество А ненулевое). Так же и с "не А", мы это принимаем только в случае доказательства того, что множество А пустое (т.е. не содержит никаких объектов). Никакой веры не требуется, требуется только построение. Собственно, к матлогике как формальным правилам еще при Гильберте были большие претензии, отсюда и необходимость создания других подходов к вопросу ощущалась еще в начале 20 века, что н-р привело к созданию натуральной дедукция Генценом и т.д. Аксиоматическая матлогика была фейлом уже во времена ее создания, просто Гильберт яскозал что можно вот так формализовать все, потому что до этого у него получилось формализовать геометрию. Ну и догма Гильберта, конечно. Тут уже чистая религия.
Приведи пример в математике, когда закон исключающего третьего не выполняется. Без теоремы генделя о неполноте.
Во всех случаях, когда нет построения, доказывающего свойства "А" или "не А", остается только веровать, что этот закон выполняется (т.к. непосредственно мы не можем этого заключить). Это вообще не математический закон, а онтологический. Аристотель в него веровал, и ты так делай.
Закон исключенного третьего утверждает, что для любого A верно A или не A.
Отрицание закона исключенного третьего утверждает, что существует такое A, что верно A и не A.
Предъяви такое A.
>мам, вот они веруны, ну скажи
Наличие в формальной системе каких-либо законов регулируется только правилами вывода.
>>8036
В твоём вопросе ошибка, ведь при сокращении двойного отрицания ты неявно подразумеваешь, что верен закон исключения третьего.
Отрицание закона исключенного третьего - это утверждение, что верно не(А или неА) = неА и ненеА.
Отрицанием "неB" я обозначаю то, что определена вычислимая функция из пустого множества в множество B.
В такой формулировке на роль А подходит пустое множество.
Это и есть искомый контрпример существования интерпретации интуиционисткой логики, которую нельзя расширить до интерпретации классической логики.
(ну и да, под верностью С я понимаю существование вычислимой функции из одноэлементного множества - в С)
Ты же, скорее всего, говоришь, что "Пропозициональная логика лучше, чем логика предикатов!", что весело. Ведь если проводить аналогию с молотком и микроскопом, то ты предлагаешь смотреть на инфузорий в молоток.
Однако - спасибо за провокационный вброс, мне понравилось.
>Отрицание закона исключенного третьего утверждает, что существует такое A, что верно A и не A.
Хуйню не неси, пожалуйста. Прочитай, что ты написал и подумай головой. Ты же даже дизъюнкцию не понимаешь, о каком интуиционизме с тобой говорить вообще? Сам написал хуйню, сам опроверг, ахаха кококонструктивисты соснули. Детский сад блядь, штаны на лямках.
p.p.p.s. - я не он, и хз что он там насчёт Аристотеля и онтологий говорил. Не могу утверждать, что он сказал либо верно, либо неверно. Может он сказал, что он лжёт. И как тогда решить - верно или неверно? Надо мне было именно так, по-Антисфенофски возразить.
другие аксиомы логики тоже онтологические. Уверуем же.
 38 Кб, 506x170
38 Кб, 506x170>Так есть еще вариант "дверь не закрыта", не сводящееся к открытой двери, т.к. формально-то она выглядит закрытой, но она и не закрыта, т.к. если прислониться - вывалишься из таза к хуям
Эх щас бы естественным языком формальную логику опровергать...
Приходит к конструктивисту мамка и спрашивает: тебе суп или котлеты? А он такой: мать ты че охуела такое спрашивать ты че под гильберта легла...
>Аксиоматическая матлогика была фейлом уже во времена ее создания
кто б создателям HoTT рассказал, они еще новые аксиомы придумали, дебичи
Тег для раздела вроде должен автоматом добавляться же. Или надо админа стукнуть, чтобы он его добавил?
Допустим, есть N утверждений, про которые известно, что они должны быть истинными. Требуется предоставить набор аксиом и определений такой, что в нём каждое из N утверждений будет теоремой, причем аксиомами будут далеко не все из этих N утверждений (желательно - ни одно).
Допустим, есть N утверждений, про которые известно, что они должны быть истинными. Требуется предоставить набор аксиом и определений такой, что в нём каждое из N утверждений будет теоремой, причем аксиомами будут далеко не все из этих N утверждений (желательно - ни одно).
А я ведь всю книгу прочёл, по совету с двача. В конце было ощущение, что меня протроллили. Хуже книги по логике я просто не встречал
Разве об этом тред?
>различие "больших и малых категорий" осталось, но я надеюсь, что всё же откажутся вскоре и от этого
Чистая педагогика же. Отказываться тут не получится, нужно новое поколение, которое со школы обучено категориям.
>Потому что ебать себе мозги по-поводу оснований в 2к17 это уже такая же пошлятина как и ебать себе мозги по поводу того, что первичнее - материализм или идеализм.
Я тебя помню. У тебя подход к вопросу о том, что важно в математике - это что-то в духе отождествления важного с модным. Вполне понятно, почему с таким мировоззрением тебе претят основания, онтологические вопросы вообще, как и вероятно остальная философская проблематика. Но вообще, для остальных людей (более склонных к независимым суждениям) такого рода вопросы часто могут быть важнее.
>хотя на начальном уровне всё же различие "больших и малых категорий" осталось, но я надеюсь, что всё же откажутся вскоре и от этого
Эта дурацкая терминология - это последствие неудачного выбора подразумеваемого метода формализации в теории множеств на основе классов. Но изначально это все было весьма полезно т.к. не было хорошей независимой интуиции о категориях и допустимых рассуждениях о них так что апелляция к разработанному аппарату теории множеств была полезна. Хотя стоит отметить, что если, например, подразумевать формализацию в теории множеств на основе принципа отражений, то все выходит существенно более гладко (хотя здесь есть недостаток в виде относительно больших требований к знаниям теории множеств). С другой стороны, разумеется, все это было важно в основном на начальном этапе разработки теории категорий, сейчас, когда неформальные представления о том, какого рода рассуждения корректны хорошо разработаны, заморачиваться вопросом о формализации куда менее важно.
>если бы не было вот этого вот дискурса классической логики и попыток свести всю математику к формальным теориям, то никому бы не казалось, что абстракция алгоритма или конструктивного типа чем-то проще или сложнее, чем абстракция множества.
Нет, конечно. Алгоритм на текущий день (исторически это, разумеется, было скорее наоборот) можно считать непосредственной абстракцией от программы на компьютере. Это гораздо боле приближенно к обычной жизни, чем множества или конструктивные типы (я бы сказал, что лишь немного сложнее понятия натурального числа).
>Потому что ебать себе мозги по-поводу оснований в 2к17 это уже такая же пошлятина как и ебать себе мозги по поводу того, что первичнее - материализм или идеализм.
Я тебя помню. У тебя подход к вопросу о том, что важно в математике - это что-то в духе отождествления важного с модным. Вполне понятно, почему с таким мировоззрением тебе претят основания, онтологические вопросы вообще, как и вероятно остальная философская проблематика. Но вообще, для остальных людей (более склонных к независимым суждениям) такого рода вопросы часто могут быть важнее.
>хотя на начальном уровне всё же различие "больших и малых категорий" осталось, но я надеюсь, что всё же откажутся вскоре и от этого
Эта дурацкая терминология - это последствие неудачного выбора подразумеваемого метода формализации в теории множеств на основе классов. Но изначально это все было весьма полезно т.к. не было хорошей независимой интуиции о категориях и допустимых рассуждениях о них так что апелляция к разработанному аппарату теории множеств была полезна. Хотя стоит отметить, что если, например, подразумевать формализацию в теории множеств на основе принципа отражений, то все выходит существенно более гладко (хотя здесь есть недостаток в виде относительно больших требований к знаниям теории множеств). С другой стороны, разумеется, все это было важно в основном на начальном этапе разработки теории категорий, сейчас, когда неформальные представления о том, какого рода рассуждения корректны хорошо разработаны, заморачиваться вопросом о формализации куда менее важно.
>если бы не было вот этого вот дискурса классической логики и попыток свести всю математику к формальным теориям, то никому бы не казалось, что абстракция алгоритма или конструктивного типа чем-то проще или сложнее, чем абстракция множества.
Нет, конечно. Алгоритм на текущий день (исторически это, разумеется, было скорее наоборот) можно считать непосредственной абстракцией от программы на компьютере. Это гораздо боле приближенно к обычной жизни, чем множества или конструктивные типы (я бы сказал, что лишь немного сложнее понятия натурального числа).
>Я тебя помню.
Ты меня не можешь помнить.
>Но вообще, для остальных людей (более склонных к независимым суждениям)
>Это гораздо боле приближенно к обычной жизни, чем множества или конструктивные типы
Самая большая загадка на свете: почему люди, позицианирующие себя как рационально-мыслящие-с-независимыми-суждениями упорнее всего талдычат одни и те же догмы? Не загадка никакая, конечно, примерно понятно из какого желания ноги у независимо-судящих растут.
>Ты меня не можешь помнить.
Технически я не могу исключать, что ошибаюсь, но определенно у меня был небольшой диалог с аноном с явно родственной позицией и похожим стилем.
>позицианирующие себя как рационально-мыслящие-с-независимыми-суждениями
Да бог с тобой, я лишь подчеркивал то, что идея о сведение ценности исключительно к моде - это, в сущности, радикальная позиция состоящая в полном отказе от самостоятельных суждений (по данному вопросу).
> талдычат одни и те же догмы
Если у тебя все-таки есть аргументы почему это довольно очевидно наблюдение несостоятельно, то можешь поделиться.
>Отказываться тут не получится, нужно новое поколение, которое со школы обучено категориям.
Думаю, что в любом случае учить сразу категориям, в обход множеств, неэффективный подход. Дело в том, что очень похоже, что основной набор интуиций касательно категорий (в независимом от теории множеств контексте) заметно сложнее чем набор интуиций для самих множеств. В пользу этого явно говорит то, что набор формальных аксиом для теории множеств более-менее вразумителен, а вопрос о аксиоматизации категории Cat, если мне не изменяет память, провисел открытым полтора десятилетия, в итоге был решен, но аксиоматизация оказалась весьма сложной и в итоге никакой заметной популярностью не пользуется.
>Если у тебя все-таки есть аргументы почему это довольно очевидно наблюдение несостоятельно, то можешь поделиться.
Аргументы должны быть у тебя почему оно состоятельно. (Бремя доказательства) Сразу скажу, что аргумент эта же ачивидно - не очень сильный.
>Да бог с тобой, я лишь подчеркивал то, что идея о сведение ценности исключительно к моде - это, в сущности, радикальная позиция состоящая в полном отказе от самостоятельных суждений (по данному вопросу).
Я ни к чему "ценность" не сводил, так как не понимаю, что слово "ценность" значит.
>набор формальных аксиом для теории множеств более-менее вразумителен
Объясни, пожалуйста, чем мотивированы
а) аксиома подстановки
б) аксиома регулярности
Это простая часть. Проблема состоит в том, чтобы очертить допустимые методы формации новых категорий, не опираясь на аппарат теории множеств. И если доводить дело до честного выписывания набора аксиом, то выходит сложно (сложнее чем с множествами).
>>9624
a) если некоторая коллекция является множеством, то всякая коллекция того же или меньшего размера тоже множество;
б) множества и вселенная фон Неймана - это одно и тоже.
Но строго говоря, это аксиомы, которые были добавлены на позднем этапе разработки теории множеств и если их выбросить, то получится теория вполне подходящая для погружения обычной математики, но плохо подходящая для собственно теоретико-множественных исследований. В силу этого они отражают боле "продвинутые" интуиции.
Ладно, у меня нет особенного желания ввязываться в пустой спор с человеком, который в основном занимается словесной эквелибристикой, а не содержательной аргументацией своей позиции.
>Ачивидно, что алгоритм понятнее и проще, чем множество
>Почему?
>А почему нет?
>Ты сделал утверждение, ты и обосновывай
>Пропало всякое желание с тобой разговаривать, эквилибрист словесный
yaasno
>Это простая часть. Проблема состоит в том, чтобы очертить допустимые методы формации новых категорий
Вот у меня два вопроса всегда
1) Зачем их очерчивать?
2) Почему останавливаются только на первой итерации и не очерчивают допустимые методы очерчивания допустимых методов образования новых категорий?
1)Чтобы различать корректные рассуждения и некорректные. Для практики обычного математика аксиоматизация, как правило, здесь избыточна и в подавляющем большинстве случаев понимания получаемого из разбора большого числа допустимых построений и нескольких приводящих к парадоксам вполне достаточно. Хотя, конечно, не исключено, что например однажды может прийти на рецензию статья, где ошибка кроется в построение парадоксальность которого не ясна из рассмотренных примеров.
2)Без комментариев.
Почему без комментариев? Почему корректность важна, а корректность корректности "без комментариев"? Что это за фашизм такой?
Я же говорю, тебе прежде всего хочется заниматься словесной эквилибристикой. Речь шла о обучении теории категорий, ты же для полемических целей акцентируешь внимание на совершенно очевидно иррелевантном здесь вопросе.
>Проблема состоит в том, чтобы очертить допустимые методы формации новых категорий, не опираясь на аппарат теории множеств.
Таки да. Но тут такая штука , что просто так взять и раз и навсегда очертить математику и успокоится ( как хотел Гильберт, например) ведь не получится. Точнее, оно может и получится, только смысла тогда особого в категориях нет - тут теория множеств как раз лучше послужит, как статичная система.
Как по мне, весь смак категорий в том, чтобы не мешать творческой ( а для упоротых платонистов - исследовательской) составляющей процесса. Т.е. да - ты можешь наворотить лютейшую хуйню не оглядываясь ни на кого, лишь бы ты сам видел в этом смысл. Тогда вопрос корректности выходит за рамки формализма - это уже вопрос того, как другие относятся к твоей работе.
Ну а прелесть еще в том, что по сути даже школьную программу менять не надо. Просто математика должна начинаться с показа объектов и морфизмов и слов типа "ну вот в целом это и есть математика". Дети сначала нихуя не поймут, конечно. И дальше все пусть идет по старому, но каждая пройденная тема, хоть в алгебре, хоть в геометрии, должна кончаться показом соответствующей категории. И вот так постепенно к концу школы до некоторых действительно дойдет, что значит абстракция и конструирование. А это уже будет лютейшим вином, как по мне.
Почему каждый хуй мечтает отреформировать школьную программу? Т.е. вообще каждый, поголовно.
Потому что фундамент
потому что хочется как-то связать ее с математикой, а так они лишь имеют одинаковое название. Почему бы просто не переименовать школьный предмет в "практические вычислительные навыки".
Проблема есть. Но исправить это далек не просто, особенно если говорить об общеобразовательной школе и тем более, если заходить с позиций математика с ограниченным/отсутствующим опытом преподавания рядовым школьникам. Например, уверен, что план
>Просто математика должна начинаться с показа объектов и морфизмов и слов типа "ну вот в целом это и есть математика". Дети сначала нихуя не поймут, конечно. И дальше все пусть идет по старому, но каждая пройденная тема, хоть в алгебре, хоть в геометрии, должна кончаться показом соответствующей категории. И вот так постепенно к концу школы до некоторых действительно дойдет, что значит абстракция и конструирование.
полностью провалится и просто никто ничего не поймет (включая преподавателей математики). Думаю, что это провалится и в матшколах.
Можно вспомнить колмогоровскую реформу школьного курса геометрии в рамках которой например простая замена термина "равенство фигур" на более корректный "конгруэнтность фигур" привела к большим проблемам с пониманием содержания школьниками.
Из своего ограниченного опыта преподавания в кружках школьникам 5-7 классов могу сказать, что навык восприятия абстрактных конструкций находится на низком уровне и развивается медленно. Например, задачи которые сводятся к тому или иному разбору конкретных случаев даются школьникам куда легче, чем задачи где нужно дать, пусть и тривиальное, но общее рассуждение.
 45 Кб, 1292x1962
45 Кб, 1292x1962Колмогоровская реформа была гораздо более радикальной, нежели просто замена термина "равенство" на термин "конгруэнтность". Например, он определил вектор как изометрию плоскости/пространства, буквально такими словами. Естественно, что учителя его не поняли.
>то чувство, когда искренне не понимаешь, что не так
как вектор то определять правильно? как стрелочку с хвостиком?
Столбец.
Неориентированный отрезок - это неупорядоченная пара точек плоскости.
Ориентированный отрезок - это упорядоченная пара точек плоскости.
Два ориентированных отрезка называются эквивалентными, если совмещаются параллельным переносом.
Свободные векторы - классы множества ориентированных отрезков по этому отношению эквивалентности.
ну и с какого хуя такой подход верный? эти определения не дают никакой интуиции: определи теперь сумму векторов, разнообразные произведения, получится вообще невыносимая поебень.
Вот это проиграл с теоретико-множественных дидов, лил.
Что там определять? Правило треугольника очень простое. А "вектор это изотропия пространства" хуйня какая-то. Много векторов = много изотропий? Сумма векторов = сумма изотропий? Это тоже не даёт никакой интуиции. Поебень непонятная. Никогда школьник не вдуплит это.
>>9778-кун
ну можно сказать просто "группа", это совсем простое понятие.
Суммой ориентированного отрезка (ab) и ориентированного отрезка (bc) называется ориентированный отрезок (ac).
Пусть x и y - свободные векторы. Выберем в x представителя (pq). Найдем в y ориентированный отрезок (qr), начало которого равно q. Суммой x и y называется класс эквивалентности отрезка (pq)+(qr). Определение не зависит от выбора представителя, очевидно.
Пусть векторы определены как изометрии плоскости. Ну и как определить тогда сумму?
>Пусть векторы определены как изометрии плоскости.
Это неправильное определение - хочется отождествить вектора с параллельными переносами, а кроме них изометриями являются еще повороты и отражения.
Как композицию биекций, но не мат. школьникам такое будет очень сложно переварить. Им ещё придётся строить заново геометрическую интуицию. Ещё школьнику понятно будет что такое параллельный перенос конкретных фигур и векторов, но преобразования всей плоскости будет сложнее понять.
В общем всем реформаторам предлагаю пойти в обычную школу, взять там обычных школьников и попытаться им рассказать что-то на вашем любимом языке. в рамках факультатива
Существуют фс, которые могут подтвердить собственную непротиворечивость, именно этот факт и заставил гильберта верить.
Но ведь они доказывают не собственную непротиворечивость, а непротиворечивость "маленькой модели самой себя", то есть тут происходит расщепление на "большую ФС" и "маленькую ФС внутри большой ФС" и "большая ФС" не может, вообще говоря, провести отождествление "маленькой ФС" с самой собой. То есть тут размахивают руками и говорят о какой-то "эффективной непротиворечивости", дескать да, формально не можем отождествить, но мы-то понимаем как оно на самом деле. Ну так мы и раньше понимали как оно на самом деле, без программ Гильберта всяких.
У Гильберта не стояло задачи обосновать корректность финитных методов - они как раз и были очерчены таким образом, чтобы быть куском математики, который признается всеми математиками (не уверен, были ли в те времена ультрафинитисты, которые и с этим были не согласны, но в любом случае они никогда не были чем-то большим, чем незначительное меньшинство). Была проблема с более абстрактными теоретико-множественными методами в свете парадоксов теории множеств и вполне заметного числа математиков, которые эти методы отвергали. Гильберт хотел защитить теоретико-множественные методы от этих нападок, сведя их к финитным. Насколько я понимаю, Гильберт не был точен в формулировках целей так как в силу ошибочных предположений считал, что можно достичь "всего и сразу". Тем не менее, видимо главным здесь было доказать финитными средствами, что всякое теоретико-множественное доказательство финитного факта преобразуется в финитное доказательство того же факта.
>>9926
>Существуют фс, которые могут подтвердить собственную непротиворечивость, именно этот факт и заставил гильберта верить.
Во времена Гильберта ничего такого известно не было. Современные же примеры совершенно экзотичны.
Понятно. То есть, если грубо, этот аргумент в каком-то роде должен был быть социальным, а не метафизическим.
Видимо так.
Но строго говоря, я Гильберта не читал (и не факт, что он непосредственно об этом пишет), а просто пересказываю интерпретации, которые слышал.
 167 Кб, 782x543
167 Кб, 782x543У Гильберта получилось (и надо признать, годно получилось) аксиоматически построить геометрию. Этот успех заставил его уверовать, что и с арифметикой и вообще со всем остальным можно так же. Но реальность оказалось несколько сложнее, что прямо показывает нам сомнительную ценность таких экстраполяций от одного-пары частных случаев оптом и априори на все остальные как закон исключенного третьего, например. То же самое можно сказать про т.н. "догму Гильберта", это же чистая религия.
Если начать применять этот принцип
>прямо показывает нам сомнительную ценность таких экстраполяций от одного-пары частных случаев оптом и априори на все остальные
последовательно (т.е. отказываться от индукции вообще), то и от модус поненс нужно отказаться.
>Только конструктивные объекты, только хардкор.
Ну это вера из двух частей:
- вера в тезис черча, так что любая математическая задача может быть сведена к алгоритму
- вера в непогрешимость вычислительной техники (тот же модус поненс по сути)
о вере в функциональные типы. Еще разок: у нас есть эмпирический закон, что транзисторы ведут себя определенным образом. Остается только верить, что они будут вести себя так и дальше. Согласно этой вере вычисление всегда предсказуемо. А дальше по изоморфизму карри-говарда модус поненс может быть сведен к функциональным типам.
Теперь у нас есть такой же закон исключенного третьего. Эмпирически он всегда выполнен для вычислимых объектов. В чем же дело? Почему нельзя в него верить?
>у нас есть эмпирический закон, что транзисторы ведут себя определенным образом. Остается только верить, что они будут вести себя так и дальше.
Именно что эмпирически. Зачем верить, если есть факты?
>закон исключенного третьего. Эмпирически он всегда выполнен для вычислимых объектов. В чем же дело? Почему нельзя в него верить?
Потому что он невычислим в общем случае. А на конечных множествах его и Брауэр не отрицал.
>Зачем верить, если есть факты?
Математик и физик доказывают теорему о том, что все нечетные числа - простые. Математик: - 1 - простое, 3 - простое, 5 - простое, 7 - простое, 9 - не простое. Это контрпример, значит теорема неверна. Физик: - 3, 5 и 7 - простые, 9 - ошибка эксперимента, 11 - простое и т.д. Возьмем ещё несколько случайно выбранных нечетных чисел. 17 - простое, 19 - простое, 23 - простое... Теорема доказана.
>Потому что он невычислим в общем случае
Это доказанный факт?
Но вернемся к >Зачем верить, если есть факты
На 2017 год закон исключенного третьего всегда работал для любых математических объектов.
Высказывание - моя мамка старше меня и моложе, например. Вообще, логика времени нужна, а не пространства.
Невыводимая формула, конечно, отличный пример.
>На 2017 год закон исключенного третьего всегда работал для любых математических объектов.
Для любых, на которых его можно показать непосредственно. Т.е. на любых построимых, вычислимых, в общем случае - конструктивных объектах. Хватит тупить уже, самому тебе не надоело нести хуйню?
Я сказал просто для любых. Утверждение, доказанное в классической логике, всегда может быть доказано в интуитивистской. (эмпирический факт)
Классическая логика - это просто синтаксические правила. Считается, что они истинны для всех случаев оприори. Конструктивная - манипуляции с конструктивными объектами, действие правил распространяется только на конструктивные объекты.
 54 Кб, 586x253
54 Кб, 586x253Ты оперируешь какими-то бредовыми определениями. Классическая логика это интуитивистская + LEM. Собственно, нахера я опять пересказываю HoTT?
>Ты оперируешь какими-то бредовыми определениями.
Ты не слышал про интуиционстскую логику Гейтинга, интерпретацию логических констант по Брауэру-Гейтингу-Колмогорову, изоморфизм Карри-Говарда, раз уж называешь "мои" определения бредовыми. Видимо, и про MLTT мало что знаешь. Но при этом лезешь в НоТТ. Это напоминает школьников из треда про машинное обучение и нейросети в /пр - не зная даже азов уровня учебников Вентцель и Зорича/Фихтенгольца, лезут читать ISLR и т.д. Итог закономерен.
 32 Кб, 564x151
32 Кб, 564x151HoTT не нужны никакие пререквизиты, она предназначена для математиков, желающих изучить новые основания. Читателю не нужно знать даже, что такое теория типов, а все твои исторические термины он может изучить в википедии.
Пока что я могу судить, что ты до сих пор не удосужился открыть HoTT и почитать, раз я должен вычитывать правильные определения за тебя.
>>9941
Я хотел бы переделать свой ответ. Мне кажется ты говоришь не про то, ибо если бы программа Гильберта действительно бы заключалась в
>всякое теоретико-множественное доказательство финитного факта преобразуется в финитное доказательство того же факта.
то, естественно, она была бы успешной. Ведь есть тупо теорема о том, что ZFC доказывает те же самые арифметические утверждения, что и PA (я её запомнил как "теорема об элиминации"), значит дело тут не в том.
>HoTT не нужны никакие пререквизиты
Ой, все. Там самая первая глава - изложение MLTT. Для MLTT не нужны пререквизиты? И как, много ты там понял?
> Ведь есть тупо теорема о том, что ZFC доказывает те же самые арифметические утверждения, что и PA (я её запомнил как "теорема об элиминации"), значит дело тут не в том.
Такой теоремы нет. В силу второй теоремы Гёделя о неполноте, предполагая непротиворечивость PA, верно обратное. В ZFC несложно доказать, что PA непротиворечива (рассмотреть натуральные числа с функциями сложения, умножения и следования и показать, что это модель PA), но по второй теореме Гёделя о неполноте PA не доказывает собственную непротиворечивость.
Извиняюсь, перепутал с другой теоремой о том, что ZFC+CH доказывает те же самые арифм. утверждения, что и ZFC.
Мне всю книгу скринить надо, чтобы ты ее тут прочитал? Книга начинается с пояснения, что такое тип, что такое теория типов, что такое суждение. Кому нужны такие пояснения? Вестимо, что математикам, кому знакомы общие понятия наивной теории множеств и гомотопической алгебры. Далее идет сравнение с классическими основаниями.
Читателю, знакомому с MLTT, рекомендуют вообще читать первую главу по диагонали.
 2,7 Мб, webm,
2,7 Мб, webm,480x360
Ты в моих постах триггеры выискиваешь, чтобы потом гореть с них? Зачем? Это же обычная терминология.
которые кроме тебя никто не употребляет.
https://www.google.ru/?gfe_rd=cr&ei=ev2VWIOMNoqBZI_LlcgF#newwindow=1&q="интерпретацию+логических+констант"
https://www.google.ru/?gfe_rd=cr&#newwindow=1&q="акт+интуиционизма"
https://www.google.ru/?gfe_rd=cr#newwindow=1&q="Брауэру-гейтингу"
А ты хорош. Но интуиционизм тоже неплох
>>10339
Пиздец. А ниче, что по этой теме на русском языке полторы книжки и есть? Мне, может быть, использовать термин meaning of the logical constants, использующийся Мартин-Лёфом http://people.inf.elte.hu/divip/AgdaTutorial/Further_Reading/Meanings_and_justification.pdf и авторами Programming in
Martin-Löf’s Type Theory? Ты правда аутист какой-то, сам себе придумываешь триггеры, чтобы потом с них на батрушку высаживаться.
-Дохуя-это сколько?
- Иди вдоль рельсов и считай шпалы. Когда досчитаешь до "а ну его
нахуй"-это будет как раз половина.
На твоем пикрелейтеде же вполне четко и понятно даны ответы на твои вопросы. Не очень понятно, что именно непонятно. Вот он говорит: пусть у нас есть ребенок и функция следования для него, которая берет ребенка и дает ребенка в следующий момент времени. То есть р, р', р''- это все ребенки, но интуитивно ясно, что после некоторого (неопределенного) количества применений этой операции результат уже никак ребенком быть не может. Это он и постулирует утверждением под номером три. Я просто пересказываю текст еще раз, да.
Ну а про "и так далее" и вовсе говорить нечего. Определим натуральные числа: 1, 2, 3 и так далее. Ну ты понял.
Пример с ребенком дурной какой-то, что-то уровня парадокса лысого или парадокса кучи. Такое решается с помощью нечеткой логики, функция следования и потенциальная осуществимость тут вообще не при чем.
>Ну а про "и так далее" и вовсе говорить нечего. Определим натуральные числа: 1, 2, 3 и так далее. Ну ты понял.
И что тут не так?
> что тут не так
Это не определение.
> тут вообще не при чем
Ну как они не при чем, если он об этом и говорит? Никто же не спорит, что эти ситуации можно смоделировать в рамках дефолтной модели. Это у него просто философский аргумент такой: вот, посмотрите - понятие, которые мы принимаем за интуитивно ясное, на самом деле работает совсем не так, а эдак.
Не более дурной, чем пример с брадобреем в кое-какой другой некогда популярной теории.
>>10795
1. Если убрать с головы волосатого человека один волосок, он не станет лысым. Начнём убирать с головы человека волосы по одной штучке за раз; через некоторое время получим лысого человека. Таким образом, имеем антиномию. Объекты, обладающие такой антиномией, будем называть собственно ультрафинитистскими.
2. К собственно ультрафинитистским объектам не применима абстракция потенциальной осуществимости. Они обладают тем свойством, что по ходу итеративного процесса перестают быть равными себе, какими они были до начала процесса.
3. Не существует доказательств, что объекты, используемые в метаматематических построениях, не являются собственно ультрафинитистскими.
4. Пользуясь случаем, передаю привет чернильной дыре.
>1. Если убрать с головы волосатого человека один волосок, он не станет лысым. Начнём убирать с головы человека волосы по одной штучке за раз; через некоторое время получим лысого человека. Таким образом, имеем антиномию. Объекты, обладающие такой антиномией, будем называть собственно ультрафинитистскими.
Тут нет никакой антиномии, просто бинарная логика неприменима к подобным задачам, т.к. мы не можем в точности указать, с какого конкретно количества волос считать человека лысым. Непрерывная функция принадлежности вопрос снимает полностью, т.к. появляется возможность считать человека лысым и волосатым в какой-то степени от 0 до 1. Не понимаю, зачем тащить в такие задачи какой-то ультрафинитизм, когда все элементарно сводится к нечетким множествам.
>>10808
>Это не определение.
А что это? 0:N, if a:N then succ(a):N, закон построения (функция следования).
А где гарантия, что "бинарная логика" применима к основным умозрительным объектам метаматематики, таким как строка символов, алфавит, возможность в любой момент времени ввести новую, не использованную ранее букву?
В случае конечных объектов можно проверить непосредственно, применима или нет. В общем случае, безотносительно возможности построения, никакой гарантии, только вера.
>С какими-то можем, с какими-то нет. Так-то 10^100^1000^10000 тоже натуральное число.
Выходит, конструктивная математика основанна на вере ?
Я уже столько раз писал про марковскую абстракцию потенциальной осуществимости, что даже не помню сколько раз конкретно. И чем конструктивный объект отличается от потенциально существующего, писал не меньше. С себя начни, если такие простые вещи понять не можешь.
проговаривать название != писать
Ну у тебя и пичот.
>марковскую абстракцию потенциальной осуществимости
Вера. Обычная вера в то, что алгоритм может работать верно и выдавать нужные результаты, при этом не останавливаясь. Раз можно проверить потенциальное сущствование только конечное количество объектов, в нашем случае чисел, то как проверить, что алгоритм верен?
> С себя начни, если такие простые вещи понять не можешь.
Ты опять берёшь и уходишь от ответа, мань.
>Выходит, конструктивная математика основанна на вере ?
Мозг конструирует для нас реальность. И мы в нее верим, а что ещё остается делать?
В алгоритмы веровать не нужно. Алгоритм либо работает правильно и выдает правильный результат, либо он работает неправильно и выдает результат, доказывающий абсурдность предположения, что алгоритм работает правильно. Любой алгоритм сводится к типизированной лямбде, корректность его можно проверить методами MLTT, опять же, про интерпретацию логических констант и изоморфизм Карри-Говарда я писал достаточно, чтобы тут у какого-то кловна жопа горела с этой терминологии.
>Алгоритм либо работает правильно и выдает правильный результат, либо он работает неправильно и выдает результат, доказывающий абсурдность предположения, что алгоритм работает правильно.
Разве это не закон исключённого третьего? Ты берёшь и веруешь в то, что твой алгоритм работет либо правильно либо неправильно? Чем эта вера отличается от веры в аллаха?
>Разве это не закон исключённого третьего? Ты берёшь и веруешь в то, что твой алгоритм работет либо правильно либо неправильно? Чем эта вера отличается от веры в аллаха?
Пиздец. А я ведь специально сформулировал отрицание именно в интуиционистском смысле. Но что можно объяснить школьнику на батрушке. Закон исключенного третьего это "А или не А". "А" в данном случае означает "у нас есть пруф-объект, подтверждающий, что А не пусто, а:А". "не А" можно представить в двух вариантах: "у нас есть пруф-объект, доказывающий, что построение А неосуществимо, б:Б" и "у нас нет нихуя". В классическом смысле оба этих случая равнозначны. В интуиционизме допустимо только доказательство через конкретное построение, т.е. только первый вариант. Тогда как второй не доказывает ничего, т.к. это не построение. В интуиционизме закон исключенного третьего не принимается как общее правило по простой причине - у нас нет построений А или построений, отрицающих А на все возможные случаи. Поэтому закон исключенного третьего, принимаемый априори - чистая вера.
Охуенный у тебя манямирок, в котором все алгоритмы всегда выдают результат. Нам бы всем не помешал такой.
> Пустой тип как результат проверки
> результат
Ты так говоришь, будто проблема остановки решена. Я не против твоих ХоТТов, да и в споре не участвую, но никогда не пиши хуйню вроде
>Алгоритм либо работает правильно и выдает правильный результат, либо он работает неправильно и выдает результат
Алгоритм может начать работу и никогда не завершиться, и никакие методы проверки, в том числе MLTT не выдадут на таком алгоритме никакого ответа, они просто зависнут.
Никто не спорит с тем, что существуют алгоритмически неразрешимые задачи.
>никакие методы проверки, в том числе MLTT не выдадут на таком алгоритме никакого ответа, они просто зависнут.
Сам хуйню пишешь, а мне запрещаешь. Не зависнет ничего, в худшем случае просто не будет чекаться и все. Защита от такой хуйни есть во всех пруверах, подход разный, правда.
>Защита от такой хуйни есть во всех пруверах, подход разный, правда.
Охуеть защита - внешним образом прерывать процесс. Мы тут про основания математики, ты подался рассуждать про хаки в софте.
 966 Кб, 2592x1944
966 Кб, 2592x1944Кстати, подумалось вдруг. А ведь постулат "всегда можно сделать ещё один шаг" прямо противоречит аксиоме выбора. В самом деле, рассмотрим множество возможных букв на листе бумаги и упорядочим его булеан по включению. Очевидно, любая цепь мажорируется своим объединением. Тогда по лемме Цорна есть максимальный элемент - должно существовать множество букв, к которому уже нельзя добавить ни одной буквы. Но ультрафинитисты говорят, что к любому множеству букв на листе можно, исхитрившись, дорисовать ещё одну букву. Противоречие. Аналогичное доказательство для шагающего человека оставим читателю в качестве упражнения.
Any комментс?
В частности, рассмотрим конечное множество, скажем, из 5 элементов и рассмотрим "шаг" обогащения подмножества множества одним элементом. Это неприменимо ко всему множеству. Шах и мат ультрафинитисты.
Это уже толстовато.
Если ты возьмёшь объединение всех букв, то добавить новую букву уже не получится (только одну из старых). Например, если к множеству букв {x,y,z} добавить букву x, всё равно будет множество {x,y,z}
Нет, тут под буквой понимается рисунок на листе бумаги, не пересекающийся с другими рисунками.
H A L T I N G
P R O B L E M
Вообще, насколько нужно быть наивным, что веровать в то, что машина тьюринга - это неебаца вычислитель, который может вычислить всё что вообще можно вычислить. Ещё скажи что я на квантово-астрально-тёмноматериальном компьютере в 20 000 веке н.э. всё ещё не смогу решить проблему останова.
Тупые транзистерные говна вообще дико примитивны. Тупая машина даже не догоняет что такое бесконечность, что блять нет смысла её строить, т.к. это займёт бесконечно времени. И даже если вместо самой бесконечности, ты просто даёшь ей конечный объект, но задашь ему свойства бесконечности, тупая машина решит доказать эти свойства и суко начнёт таки строить сраный бесконечный терм. Более того, даже нет возможности заставить одну тупую машину проследить за другой тупой машиной, чтоб та не строила бляцкий бесконечный терм. Быть констуктивистом, это значит верить в то, что вот этот вот примитив, типа МТ - это настолько серьёзный формализм, что на его основании можно кукарекать о глобальных вещах, типа существования/несуществования вообще. Даже гипервычисления преодолевают halting problem, но конструктивисту религия не позволит об него мараться.
Также, менее интересно, но тоже интересно все-же основание геометрии. Ранее думал, что аксиомы Гильберта, но краем уха в википедии прочитал, что там еще какие-то есть после Гильберта.
Проблема оснований математики успешно решена сто лет назад. Оказалось, что основания не нужны.
Как же так? Я так вообще ничего не могу изучать, например.
 111 Кб, 480x380
111 Кб, 480x380>нужно быть наивным, что веровать в то, что машина тьюринга - это неебаца вычислитель, который может вычислить всё что вообще можно вычислить.
Машина тьюринга, как и любое равнообъемное ей уточнение понятия алгоритма (каноническая система Поста, лямбда-исчисление Черча, нормальный алгорифм Маркова и т.д.) - это именно неебаца вычислитель, которым можно вычислить все, что вообще в принципе вычислимо. То, что нельзя вычислить на машине Тьюринга, хуй ты вообще вычислишь.
>Ещё скажи что я на квантово-астрально-тёмноматериальном компьютере в 20 000 веке н.э. всё ещё не смогу решить проблему останова.
Нет, не сможешь. Тьюринг предлагал мысленный эксперимент - машина Тьюринга со встроенным оракулом, несуществующим всемогущим боженькой, который может решать алгоритмически неразрешимые задачи (пейпер: Turing, Alan (1938). Systems of Logic Based on Ordinals) Так вот, у такой машины с боженькой так же остается нерешенной проблема останова. Мораль? Проблема останова - это не проблема машины Тьюринга как таковой, а проблема существования в принципе невычислимых проблем.
>>13696
>Тупая машина даже не догоняет что такое бесконечность, что блять нет смысла её строить,
Будто ты догоняешь, умник. Или твое понимание бесконечности чем-то отличается от веры в нее. Брауэр именно об этом и писал, что проблема математики (кризис оснований н-р) в том, что там полно обобщений на общие, в т.ч. бесконечные случаи того, что работает на случаях конечных. Невычислимую же хуйню никак ты не вычислишь. Отказ от конструктивного подхода в данном случае манярешение уровня пикрелейтед, если проблему игнорировать - авось само как-нибудь рассосется. А хуй там плавал, не рассосется ничего.
Конструктивный подход запрещает неконструктивные доказательства. Т.е. доказательства, отличные от построимого объекта-доказательства. Отрицание должно быть построено, только тогда оно истинно констркутивно.
>Даже гипервычисления преодолевают halting problem, но конструктивисту религия не позволит об него мараться.
Гипервычисления - самая религия и есть. Полтора фрика уверовали, что можно объебать машину Тьюринга по вычислительным возможностям, при этом пока нет даже внятных теоретических обоснований, как это сделать. Все на уровне добрых намерений.
>>13748
Машина Тьюринга - тупое примитивное картофанское говно, а не формализм. Как и тезис Чёрча-Тьюринга, который любой здравомыслящий человек стесняется использовать в диалоге, усиляя его хотя бы до тезиса - Дойча.
>Нет, не сможешь.
Приплыли, умозаключение хуйзнает скольки летней давности лысой обезьяны с космической песчинки Земля - вершина теоретической вычислимости во Вселенной.
Любая МТ, что недетерменированная, что с оракулом - говно. И при чём тут боженька, если
Постулируется, что оракул способен решить определённые проблемы разрешимости за один такт машины Тьюринга.
что достаточно сильное ограничение.
Даже НМТ всё ещё обсирается работать с бесконечностями. Если Вселенная бесконечна, бесконечность нужно использовать для вычислений, МТ сосёт в них, следовательно МТ сосёт впринципе. Хотя причём тут бесконечности, она даже на квантмехе уже рыгает.
>Будто ты догоняешь, умник.
Ну я не зависаю, когда ей оперирую, и мне хватает мозгов её не вычислять, а тупая тразистерная железяка - зависает. Если Вселенная таки бесконечна, то о ней нужно иметь возможность размышлять, а тупое транзистерное говно не могёт осознать что это. У машины абдукции нет, интуиции нет, абстракции нет, нихуя нет, можно маневрировать символьными вычислениями, до тех пор пока транзистерное говно не попытается что-то "доказать". А как оно может доказать - правильно, только построив. Пиздец примитив.
> То, что нельзя вычислить на машине Тьюринга, хуй ты вообще вычислишь.
Тебе напомнить, почему этот говнтезис - всего лишь тезис?
>Отказ от конструктивного подхода в данном случае манярешение
Маневрирование - это тупизм уровня древних греков, типа верю только в то что вижу, и числа чтоб перечислять существующие объекты. Не даром эти дауны застряли со своим ультрафинитизмом в жопе и площадь круга определить не могли, не говоря уже о пределах, производных и так далее. Кстати, иррациональные числа тоже не существуют? Напоминаю, что транзистерное говно зависнет, осторожно. Развитие в математике началось именно с момента, когда за неё взялись европейцы, которые любят бесконечность и не ссуца о ней размышлять, потмоу что она им естественна и интуитивно понятно. Быть конструктивным математиком = быть ссыклом из древней греции, где весь мир пластичен и точечен, и даже глядя в небо на звёзды нужно себя уверять, что это всего навсего отдельно стоящие исчислимые объекты, а не бесконечные неизмиримые и невычислимые дали.
>>13748
Машина Тьюринга - тупое примитивное картофанское говно, а не формализм. Как и тезис Чёрча-Тьюринга, который любой здравомыслящий человек стесняется использовать в диалоге, усиляя его хотя бы до тезиса - Дойча.
>Нет, не сможешь.
Приплыли, умозаключение хуйзнает скольки летней давности лысой обезьяны с космической песчинки Земля - вершина теоретической вычислимости во Вселенной.
Любая МТ, что недетерменированная, что с оракулом - говно. И при чём тут боженька, если
Постулируется, что оракул способен решить определённые проблемы разрешимости за один такт машины Тьюринга.
что достаточно сильное ограничение.
Даже НМТ всё ещё обсирается работать с бесконечностями. Если Вселенная бесконечна, бесконечность нужно использовать для вычислений, МТ сосёт в них, следовательно МТ сосёт впринципе. Хотя причём тут бесконечности, она даже на квантмехе уже рыгает.
>Будто ты догоняешь, умник.
Ну я не зависаю, когда ей оперирую, и мне хватает мозгов её не вычислять, а тупая тразистерная железяка - зависает. Если Вселенная таки бесконечна, то о ней нужно иметь возможность размышлять, а тупое транзистерное говно не могёт осознать что это. У машины абдукции нет, интуиции нет, абстракции нет, нихуя нет, можно маневрировать символьными вычислениями, до тех пор пока транзистерное говно не попытается что-то "доказать". А как оно может доказать - правильно, только построив. Пиздец примитив.
> То, что нельзя вычислить на машине Тьюринга, хуй ты вообще вычислишь.
Тебе напомнить, почему этот говнтезис - всего лишь тезис?
>Отказ от конструктивного подхода в данном случае манярешение
Маневрирование - это тупизм уровня древних греков, типа верю только в то что вижу, и числа чтоб перечислять существующие объекты. Не даром эти дауны застряли со своим ультрафинитизмом в жопе и площадь круга определить не могли, не говоря уже о пределах, производных и так далее. Кстати, иррациональные числа тоже не существуют? Напоминаю, что транзистерное говно зависнет, осторожно. Развитие в математике началось именно с момента, когда за неё взялись европейцы, которые любят бесконечность и не ссуца о ней размышлять, потмоу что она им естественна и интуитивно понятно. Быть конструктивным математиком = быть ссыклом из древней греции, где весь мир пластичен и точечен, и даже глядя в небо на звёзды нужно себя уверять, что это всего навсего отдельно стоящие исчислимые объекты, а не бесконечные неизмиримые и невычислимые дали.
Гипервычисления, это когда ты взял и перешагнул через манямирок про всемогущую МТ, не более.
 462 Кб, 752x1083
462 Кб, 752x1083>Гипервычисления, это когда ты взял и перешагнул через манямирок про всемогущую МТ, не более.
Но никто ведь не перешагнул. Как говорится, убьют - тогда и приходите.
>>13769
>Если Вселенная бесконечна,
А если не бесконечна? Насколько я понимаю, точного ответа на этот вопрос пока нет.
>Ну я не зависаю, когда ей оперирую, и мне хватает мозгов её не вычислять,
Ты так думаешь просто. Точнее, веруешь. Бесконечность невычислима, если ты нарисовал значок бесконечности и думаешь, что вычислил что-то - ты ебешь мозги самому себе. С таким же точно успехом можно пририсовать квантор существования к символу Аллаха и считать, что чего-то доказал.
>Тебе напомнить, почему этот говнтезис - всего лишь тезис?
Опровергнуть его все равно нечем, нравится тебе это или нет.
>Развитие в математике началось именно с момента, когда за неё взялись европейцы,
Которые ее и доразвивали до кризиса оснований, с которым уже больше 100 лет нихуя не могут поделать. Только один европеец (пикрелейтед) показал выход из этого тупика.
> А как оно может доказать - правильно, только построив.
А как можно доказать, не построив? Уверовать, что доказал? Расскажи.
 21 Кб, 400x382
21 Кб, 400x382>Человеку сразу ясно, что при правильной игре белых будет ничья.
Человеку, знающему правила шахмат. И да, программы, умеющие в шахматы, перебором тоже не пользуются, там все сложнее. Так что пример вообще не в тему.
Пример иллюстрирует суть того, что под капотом бесконечности. Человеку ясно, почему будет так. Конструктивисты же - негодуют и требуют полного перебора.
>Пример иллюстрирует суть того, что под капотом бесконечности.
Пиздец. Шахматы - это не совсем бесконечность, во-первых. Во-вторых, это потенциально построимая бесконечность, т.к. есть правила ее построения (собственно, правила шахмат). Итого, шахматы со всеми возможными вариантами ходов - конструктивный объект. Что не имеет ничего общего с актуальной бесконечностью. Именно поэтому возможны программы, хорошо играющие в шахматы, более того, они совершенствуются, посколько суть таких алгоритмов - некоторая оптимизация выбора вариантов ходов. Хуйня пример, говорю же.
Какая разница?
>потенциально построимая бесконечность
Как машина убедиться в том, что этот конструктивный объект действительно обладает задаными свойствами (свойством бесконечности)?
А как ты сам убеждаешься в существовании у бесконечности свойства бесконечности (неограниченности/непрерывности)?
Начинаю строить эту бесконечность и зависаю, очевидно же.
 55 Кб, 715x544
55 Кб, 715x544Конечность либо потенциальная бесконечность прямо следует из правил построения. Например, пикрелейтед правила построения множества N. Оно бесконечно в силу того, что для каждого a:N можно построить следующее за ним число через функцию следования succ(a):N.
>Проблема оснований математики успешно решена сто лет назад. Оказалось, что основания не нужны.
Чего? Это кто сказал, что основания не нужны?
Любой нормальный человек так скажет. Никаких нерешенных, острых проблем в основаниях сейчас нет. Всё закрыто.
>Никаких нерешенных, острых проблем в основаниях сейчас нет.
Да острых проблем нет. Но вовсе не оказалось, что "основания ненужны." Острых проблем нет потому что, фактически, произошла рецепция идей аксиоматической теории множеств в общематематическую культуру, разумеет, в сильно адаптированной форме. Аксиоматическая же теория множеств и была одним из подходов к преодолению кризису оснований начала 20-го века.
Острых проблем нет, да и вообще проблем нет, если не считать довольно странные исследования о всяких там континуумах Суслина и diamond-принципе.
Период, когда исследования в области оснований были важны и интересны буквально каждому математику, закончился ещё в первой половине двадцатого века. В наше время основания не нужны в том смысле, что новые статьи по основаниям не читает никто кроме трёх с половиной теоретиков оснований, а переписывания учебников на каком-то радикально новом языке в обозримом будущем вовсе не ожидается.
>странные исследования о всяких там континуумах Суслина и diamond-принципе.
Теория множеств и правда довольно выхолостилась на текущий момент.
> да и вообще проблем нет
Есть, конечно (я имею ввиду проблемы философии математики на которые потенциально могут пролить свет математические исследования). Например: 1. Что означает, что два доказательства по-существу одинаковые/разные? 2. Какие аксиомы на самом деле нужны в обычной математике (не логике)? 3. Какова правильная формализация теоретико-категорных построений?
Насколько я представляю ситуацию, по поводу 1. Ничего особенно убедительного до сих пор сделано не было. По вопросу 2. уже достигнут большой прогресс (см. обратная математика), тем не менее еще много чего можно сделать. По поводу более частного вопроса 3., некоторый прогресс безусловно имеется, но полностью удовлетворительной системы еще сформулировано не было.
>В наше время основания не нужны в том смысле, что новые статьи по основаниям не читает никто кроме трёх с половиной теоретиков оснований,
И собственно чем это отличается от многих других разделов математики? Ну и мода вещь приходящая - можно вспомнить, как недавно заметное количество алгебраических топологов потянулось заниматься теориями типов.
>а переписывания учебников на каком-то радикально новом языке в обозримом будущем вовсе не ожидается.
Ну собственно да, острой нужды в этом нет и не ожидается.
3. Вопрос неактуален. Очевидно, что для ∞-категорий оснований нет. Но они и не нужны никому, кроме сторонников веры, что у всего должно быть первопорядковое основание. Люди, которые пользуются инфинити-категориями, в основаниях не нуждаются.
>Люди, которые пользуются инфинити-категориями, в основаниях не нуждаются.
Учитывая, что вполне заметная их часть - это люди занимающиеся построениями моделей гомотопических теорий типов, тезис выглядит более чем сомнительно.
Вопрос вообще простой. Есть у нас какая-то теория поля с лагранжианом $L = d_{\mu} \phi d^{\mu} \phi \ans - m|\phi|^2 - g|\phi|^4 $. Почему этот ебанный раздел все-еще не может в тех!?
>И да, программы, умеющие в шахматы, перебором тоже не пользуются
Схуяли? Да, там все сложнее, но в основе самый что ни на есть перебор.
[math] L = d_{\mu} \phi d^{\mu} \phi \ans - m|\phi|^2 - g|\phi|^4 [/math]
Толстота.
И замени строку
> // @include /^https?:\/\/2ch\.(hk|pm|re|tf|wj)/(sci|test)/
на
// @include /^https?:\/\/2ch\.(hk|pm|re|tf|wj)/(sci|math|test)/
спасибо
А что не так? N петух в свое время правильно говорил, что аксиомы Пеано исходят из того, что нам уже дано натуральное число. Формального определения нету. Не считая бурбаковского аутизма.
 50 Кб, 1217x433
50 Кб, 1217x433Схуяли чушь-то? Ты их читал? Давай разберем по частям.
- как видим, 1ая аксиома гласит, что 1 это натуральное число.
- далее определяется то, что в конструктивной математике называют функцией следования succ().
- далее некоторые свойства единицы, равенства и индукция.
Нигде нет определения, что такое единица, она просто вводится в 1ой аксиоме как готовый объект, в остальных аксиомах определяются некоторые ее свойства. Отсюда и вопрос - где формальное определение того, что есть 1? Нету его. Конструктивно я могу сказать, что по Маркову единица, как и любое натуральное число, является словом в алфавите |. Либо могу приплести нумералы Черча. Во всех этих случаях я даю конструктивное определение натуральному числу. Аксиомы же Пеано по-сути представляют собой правила построения N, не определяя явно, что есть натуральное число.
>Ты их читал?
Более того, я могу их сформулировать по-человечески.
Непустое множество M называется множеством натуральных чисел, если:
1. Задана функция f:M→M.
2. Задана функция g:M→M.
3. Для любых x,y∈M верно, что f(x)=f(y).
4. Для любого m∈M верно, что g(m) ≠ f(m)
5. Для любых x,y∈M верно, что g(x)=g(y) → x=y.
6. Для любого X⊂M верно, что [f(M)⊂M ∧ ∀x [x∈X→g(x)∈X]]→X=M.
Функция f называется функцией выделения единицы. Единственный элемент множества f(M) обозначается 1.
Функция g называется функцией следования.
Но твои правила с тем же успехом можно считать описанием множества вещественных чисел, конкретно N они не определяют. В отличие от моих конструктивгых определений конкретно множества N.
И да, единицу ты вводишь как уже предсуществующий объект, без определения его формально.
Нет, структуре вещественных чисел описанная мной структура не изоморфна.
>>13992
Структура Пеано - это то, чем могут обладать разные множества. Как структура группы. Ты же не жалуешься, что в аксиомы группы входит аксиома нейтрального элемента?
Я могу предъявить по крайней мере одно множество, обладающее структурой Пеано.
>Структура Пеано - это то, чем могут обладать разные множества.
Т.е. ты согласен, что это не определение конкретно N, а некие условия, под которые могут подпадать разные множества. Но тогда получается, что определения натурального числа из аксиом Пеано никак не следует.
>Нет, структуре вещественных чисел описанная мной структура не изоморфна.
А множеству дедекиндовых сечений?
>а некие условия, под которые могут подпадать разные множества
Именно так. Впрочем, в классе всех множеств, подпадающих под аксиомы Пеано, есть подкласс канонически выделенных множеств. Все такие множества изоморфны.
>никак не следует
Тогда тебе следует говорить, что из определения векторного пространства не следует определение вектора, лол. А из определения тензорного произведения - определение тензора. Натуральное число - это просто элемент некоторого множества со структурой Пеано, так же как вектор - элемент некоторого векторного пространства.
>множеству дедекиндовых сечений
Все множества со структурой вещественных чисел изоморфны.
>Натуральное число - это просто элемент некоторого множества со структурой Пеано,
Но если структурой Пеано могут обладать разные множества, а не только N, то твое заявление нуждается в пруфе изоморфности всех принципиально возможных множеств, обладающих структурой Пеано, согласись. Иначе опять же, формального определения нет.
Мы можем говорить о векторах, хотя не все векторные пространства изоморфны. Надо просто указывать пространство, которому принадлежит вектор. С натуральными числами точно так же - нельзя говорить о сферическом натуральном числе в вакууме, нужно указывать множество со структурой Пеано, элементом которого является это число.
>нужно указывать множество со структурой Пеано, элементом которого является это число.
Т.е. все то же множество N и его элемент - натуральное число. Определения которого у нас нет. Вот и пришли к тому, с чего начали.
>нельзя говорить о сферическом натуральном числе в вакууме,
Но ведь именно в этом суть формально-аксиоматического подхода. Из которого, в частности, следует истинность закона исключенного третьего - "А или не А", априори и безотносительно того, что есть "А" и "не А".
>Определения которого у нас нет.
Почему же? Есть определение канонического представителя класса изоморфных множеств со структурой Пеано, я могу его привести.
>именно в этом суть формально-аксиоматического подхода
Вот слово "вектор" для тебя законно?
>Есть определение канонического представителя класса изоморфных множеств со структурой Пеано, я могу его привести.
Но это не обязательно множество N или изоморфное ему, как мы выяснили выше, так? Сам же пишешь, что нужно явно указывать конкретное множество.
>Вот слово "вектор" для тебя законно?
Мы говорим об определении базового понятия - N. Вектор таковым не является, это просто подмножество векторного пространства, природа которого не конкретизируется его определением.
>или изоморфное ему
Почему же, обязательно. В стандартной теории множеств под натуральными числами, если не оговорено противное, понимается не просто какое-нибудь случайно выбранное множество со структурой Пеано, но одно вполне конкретное множество с такой структурой. Я могу его определить, если хочешь.
>подмножество
Опечатка?
>Вектор таковым не является
Термины "вектор" и "натуральное число" находятся на одном онтологическом уровне. Ни один из них не является более базовым, чем другой.
>В стандартной теории множеств под натуральными числами, если не оговорено противное, понимается не просто какое-нибудь случайно выбранное множество со структурой Пеано, но одно вполне конкретное множество с такой структурой. Я могу его определить, если хочешь.
Определи.
>Термины "вектор" и "натуральное число" находятся на одном онтологическом уровне. Ни один из них не является более базовым, чем другой.
Э, нет. Всю конструктивную математику можно свести к натуральным числам, т.к. к ним сводится любой конструктивный объект, как это показано у Мартин-Лёфа. Про вектор того же самого сказать нельзя, т.к. в общем случае это вообще почти все что угодно.
>Определи
Натуральными числами называется такое множество N, что
1. ∅∈N.
2. Если x∈N, то [x∪{x}]∈N.
3. В N нет собственных подмножеств со свойствами 1-2.
Существование такого множества гарантируется аксиомами ZFC. Понятно, что любые два множества со свойствами 1-3 неизбежно будут равны, т.е. существует в точности одно-единственное множество натуральных чисел.
>вектор того же самого сказать нельзя
Вещественные числа - это векторное пространство, т.е. каждое вещественное число - вектор. Натуральные числа можно определить как подмножество вещественных чисел, см. анализ Зорича. Таким образом, всякое натуральное число - вектор, и всё, что сводится к натуральным числам, сводится и к векторам.
Кек. Ты тредом, похоже, ошибся.
Всякий элемент N - это множество вида {∅, {∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}}, ... }. Но вообще вторая аксиома - это просто формула ∀x[x∈N → [x∪{x}]∈N]. Ты ведь знаешь, что такое квантор, да?
Множество, единственным элементом которого является пустое множество.
По определению,
0 := ∅
1 := {∅}
2 := {0,1} = {∅, {∅}}
3 := {0,1,2}
4 := {0,1,2,3}
5 := {0,1,2,3,4}
6 := {0,1,2,3,4,5}
7 := {0,1,2,3,4,5,6}
8 := {0,1,2,3,4,5,6,7}
9 := {0,1,2,3,4,5,6,7,8}
Чтобы определить остальные числа, удобно воспользоваться десятичной позиционной системой счисления.
На каждой итерации ординалов фон Неймана и нумералов Черча получается одно и то же натуральное число.
Её считают не только математики.
Прикинь.
Тсс. Пусть думают, что мы умеем вычислять пустоты.
Не так назвал значит. Суть не меняется, пусть будет каждый последующий ординал фон Неймана равен каждому последующему нумералу Черча при условии отсчета их с нуля.
Элементарно. Есть две равнозначные системы. Одна из них конструктивная. Что можно сказать о второй?
В общем случае - ничего. Иначе придётся признать конструктивным любое доказательство с использованием аксиомы выбора, для которого есть конструктивная альтернатива.
 80 Кб, 565x650
80 Кб, 565x650В общем случае - конструктивно все, что вычислимо/построимо и наоборот. Если что-то можно вычислить либо построить, или хотя бы дать правила для построения, то это что-то конструктивно.
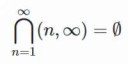 5 Кб, 227x115
5 Кб, 227x115Выходит, ординалы фон Неймана конструктивны.
Сразу оговорюсь, что сам лично не стою на конструктивистских позициях.
Но насколько я понимаю, можно конструктивно показать, что данное бесконечное пересечение в самом деле описывает пустое множество, в том смысле что можно показать, что всякое число не принадлежит по крайней мере одному из пересекаемых множеств. При этом надо понимать, что с конструктивной точки зрения, нет причин полагать, что пересечение всякой последовательности допустимых совокупностей будет допустимо. Разумеется, в зависимости от сорта конструктивизма, здесь возможны разные уточнения.
big intersection
Вопрос, как и ответ, со стакэксченджа. Интересует, как это доказывает конструктивная математика.
 135 Кб, 1527x749
135 Кб, 1527x749Его доказательство требует незначительной доработки напильником. В итоге получается программа, печатающая все простые числа.
База: напечатать 2.
Шаг: пусть напечатаны числа p1, ..., pn; проверяем все числа от pn + 1 до Пpi + 1 на простоту и печатаем наименьшее простое.
Выкладка Евклида выглядит теперь так: если все числа от pn+1 до Пpi составные, то Пpi + 1 простое. Это вполне себе конструктивно.
а как конструктивно определить пересечение ряда множеств?
Затем, что в оригинальной формулировке разбирались случаи, является ли некоторое множество A конечным или бесконечным. Но это не конструктивно. Допустим, что множество A задается программой, которая по любому числу говорит "да" или "нет". Но в общем случае нельзя только по программе вычислить, конечно или бесконечно задаваемое ей множество.
Все, уже понял.
>готовая спецификация для языка программирования с зависимыми типами, который может служить для доказательства теорем на компьютере.
Этот язык кто-то уже реализовал?
 157 Кб, 350x480
157 Кб, 350x480>Теорема Геделя о неполноте не говорит, что конструктивная математика не работает?
Не говорит. В конструктивной математике всё выводимо, поскольку логические константы - это не просто буковы, которых много, а пруф-объекты, элементы своих типов/множеств. BHK-интерпретация логических констант и изоморфизм Карри-Говарда используются вместо абстрактной аксиоматики, в которой можно выразить недоказуемое в этой аксиоматике. Тогда как в случае конструктивной логики мы имеем дело только с построимыми объектами, доказуемыми, выводимыми и вычислимыми.
>>15309
>Этот язык кто-то уже реализовал?
Их полно в настоящее время, вышеупомянутый Coq >>15180 хотя бы. Проблема в том, что для работы с ними нужно понимание всей подноготной, лежащей в основе, иначе сложно оценить возможности, предоставляемые такими языками. Поэтому навыков быдлокодерства недостаточно. Первый успешный пример подобного языка - AUTOMATH де Брауна, это конец 60-х годов. Но там по факту всего лишь один из вариантов типизированной лямбды, MLTT, PTS, CoC, на которых основаны современные пруверы гораздо бодрее в этом плане.
Никак, это алгоритмически неразрешимая задача. Тьюринг это наглядно показал в примере машины Тьюринга с оракулом. Даже если у нас есть некий боженька, могущий в решение алгоритмически неразрешимых задач, проблема останова машины Тьюринга с встроенным боженькой все равно остается. Существуют алгоритмически неразрешимые, невычислимые задачи, это факт, с которым ничего не поделаешь.
Как же Тьюринг доказал теорему об остановке? Он использовал неконструктивную математику для этого? В рамках конструктивной математики это сделать нельзя?
>Как же Тьюринг доказал теорему об остановке?
Он доказал, что это алгоритмически неразрешимая проблема.
Верно, он доказал, что проблема остановки - неразрешимая проблема. Меня интересует само доказательство. Оно везде приводися как доказательство от противного, что вроде бы недопустимо в конструктивной математике, так?
>>15327
А ты можешь предложить метод, не сводящийся к алгоритмическому, т.е. в общем случае к все той же машине Тьюринга?
Мой вопрос был лишь в том, является ли само доказательство теоремы об остановке конструктивным, и если нет - возможно ли построить его так, чтоб оно было конструктивным и если невозможно, то понять почему. Я конечно вообще нуб, но сейчас это выглядит так, как будто доказательство этой теоремы конструктивными методами невозможно по причинам, которые из этой же теоремы и выводятся. Т.е. во время доказательства теоремы, мы применяем следсвия из неё, что как бы странно, ведь мы её ещё не доказали.
Чего несешь? Изоморфизм Карри-Говарда - построение множества конструктивных пруф-объектов. Наличие таких построений есть конструктивное доказательство возможности рассматривать пропозишены как множества пруф-объектов.
...при условии, что у нас доказан изоморфизм Карри-Говарда. Но именно его мы доказываем.
HoTT и UniMath, таким образом, ― фреймворк для “делания математики” как программирования. Основное преимущество состоит в том, что он, буквально gets equality right. Т.е. понятие “равенства” впервые в истории математики описывает равенство объектов в настолько же сильном смысле, как оно используется на практике в неформальных доказательствах. Это преимущество достигается за счет использования топологического инструментария По-сути, Воеводский сводит все здание математики к топологическим операциям. Формальной основой для теории Воеводского явилась конструктивная теория типов Мартина-Лефа. Открытие Воеводского состояло в том, что он нашел геометрическую (гомотопическую) интерпретацию теории типов, позволившую исследовать богатую структуру отношений тождества, которая без этой интерпретации оставалась “невидимой”: тип a = b теперь интерпретируется не как тип доказательства равенства a и b, а как тип сохраняющих структуру обратимых переходов от a к b. При этом аксиома унивалентности Воеводского постулирует равенство объектов, между которыми может быть установлена эквивалентность, ― как равные рассматриваются изоморфные, гомеоморфные и другие гомотопически эквивалентные структуры.
Идея использования HoTT также в качестве математического основания физических и других естественно-научных теорий, мотивируется формальным характером теории типов и аксиомы унивалентности, что позволяет смотреть на HoTT и UniMath не только как на геометрическую теорию, но и как на своего рода геометризованную “логику” [Hartnet, 2015].
HoTT и UniMath, таким образом, ― фреймворк для “делания математики” как программирования. Основное преимущество состоит в том, что он, буквально gets equality right. Т.е. понятие “равенства” впервые в истории математики описывает равенство объектов в настолько же сильном смысле, как оно используется на практике в неформальных доказательствах. Это преимущество достигается за счет использования топологического инструментария По-сути, Воеводский сводит все здание математики к топологическим операциям. Формальной основой для теории Воеводского явилась конструктивная теория типов Мартина-Лефа. Открытие Воеводского состояло в том, что он нашел геометрическую (гомотопическую) интерпретацию теории типов, позволившую исследовать богатую структуру отношений тождества, которая без этой интерпретации оставалась “невидимой”: тип a = b теперь интерпретируется не как тип доказательства равенства a и b, а как тип сохраняющих структуру обратимых переходов от a к b. При этом аксиома унивалентности Воеводского постулирует равенство объектов, между которыми может быть установлена эквивалентность, ― как равные рассматриваются изоморфные, гомеоморфные и другие гомотопически эквивалентные структуры.
Идея использования HoTT также в качестве математического основания физических и других естественно-научных теорий, мотивируется формальным характером теории типов и аксиомы унивалентности, что позволяет смотреть на HoTT и UniMath не только как на геометрическую теорию, но и как на своего рода геометризованную “логику” [Hartnet, 2015].
 43 Кб, 574x369
43 Кб, 574x369Применимость = доказательство. Конструктивные системы вычислимы и выводимы сами из себя, без внешних дополнений. Именно это делает конструктивную логику полной по Геделю. Любая конструктивная аксиоматика - сама по себе конструктивный объект, правила вывода в ней - тоже. Поэтому корректность системы выводима из нее самой. Это азы, так-то. Именно подобные свойства конструктивных логик, того же изоморфизма Карри-Говарда, дают возможность строить проверяемые доказательства теорем, а интерпретация логических констант по Колмогорову - и писать абсолютно корректные программы на языках с зависимыми типами.
>>15436
Истину копипастишь. НоТТ - очень крутая вещь, но в зачаточном состоянии пока что.
Почему она в таком состоянии? Что там пока не так? Сколько это будет продолжаться?
 61 Кб, 600x450
61 Кб, 600x450Потому что это очень новое направление конструктивной математики. И сколько бы выдающихся умов над ней не работали, все равно за какие-то несколько лет невозможно проделать всю работу. В НоТТ книге описаны открытые проблемы. Радует, что с самого начала эту теорию пилили очень правильно - сразу в пруверах, чтобы поменьше аутизма, побольше фактического материала. Да и все доказательства с самого начала проверены, это значит, что в дальнейшем не вылезет никакой нежданчик, который просто не заметили сразу. По хорошему, нужны сразу пруверы с ядром на НоТТ, но такой пока что только один - LEAN.
 661 Кб, 1000x1334
661 Кб, 1000x1334Быстрее окамл установить чем ждать пока оно загрузится.
>что в дальнейшем не вылезет никакой нежданчик, который просто не заметили сразу
А тут PA возьми и окажись противоречивой (а соответственно и все мало-мальски сильные теории типов). Или найдется ошибка в ядре Coq. Ну или, скажем, систематическая ошибка во всех процессорах архитектуры x86, что повлекло положительную проверку неверных доказательств. Последнее, положим, выглядит крайне маловероятно. Но тем не менее, формализация на компьютере не дает абсолютных гарантий.
Что "интуиционистскому" понятию интуитивной ясности можно предъявить этот упрек, видно из той критики, какой сами "интуиционисты" подвергли канторовскую актуальную бесконечность. Основанием этой критики стало для них положение, будто в математике невозможно осуществить построение, которое сделало бы нас обладателями интуитивно ясного понятия о бесконечности как о бесконечности завершенной, сполна данной, предлежащей уму.
Мы показали выше, что, вводя в учение о множествах понятие актуальной бесконечности, Кантор, далекий от "интуиционизма" и даже избегающий прямых ссылок на интуицию, не ограничивается разъяснением, что понятие об актуально бесконечном он вводит посредством точного определения. Он указывает, что понятие это представляется его уму в своем объективном содержании совершенно непосредственно и с полной внутренней ясностью. Но эта характеристика совпадает с "интуиционистской" характеристикой интуиции. Актуально бесконечное Кантора – объект интеллектуальной интуиции ничуть не меньше, чем конструктивные результаты "интуиционистов". Почему же в таком случае это канторовское понятие отвергается, признается неосуществимым в мысли?
Канторовская интуиция актуальной бесконечности лишена обязательности в глазах "интуиционистов". Они отказались признать за ней непосредственность и совершенную ясность внутреннего видения, на которые ссылался, как мы видели, Георг Кантор. Это разногласие существенно не только для математики, но и для гносеологии. Оно показывает, что в самом понятии интеллектуальной интуиции не было безусловной ясности и существовала возможность, а следовательно, и опасность субъективной иллюзии. И это не удивительно. Ссылка на непосредственность интеллектуальной интуиции используется в редукции математического обоснования. Но она не может быть последней инстанцией в философской редукции происхождения знания. Для гносеологического объяснения интеллектуальная интуиция не беспредпосылочное абсолютное начало знания, а его среднее звено. Его последующие звенья – положения, обосновывающиеся на интеллектуальной интуиции. Его первичное звено, составляющее предмет исследования уже не математики и вообще не специальных наук, а теории познания, – материальная практика общественного человека в ее историческом развитии. Интуиция как функция человеческого познания имеет свою историю. Корни этой истории глубоко уходят в почву практики. По верному разъяснению итальянского математика и логика Энрикеса, первоначальные математические интуиции, например в геометрии, "возникли путем идеализированного опыта, который неоднократно повторялся при состоянии интеллекта, предшествовавшем полному развитию сознания" (6, 16).
Без обращения к гносеологическому критерию практики исходное для "интуиционизма" Брауэра и Вейля понятие интуиции становится шатким. На нем могут быть основаны только субъективные построения, а не система объективного научного знания. Возникает оправданное сомнение в способности "интуиционистов" убедить нас в том, что результаты их построений – нечто большее, чем субъективное творчество, что они составляют науку. Выходит, что отказ "интуиционистов" признать правомерность чрезвычайно обширных и хорошо разработанных частей математики как не допускающих "интуиционистского" ("конструктивного") обоснования – отказ, мотивированный строгостью логических требований, сочетается с далеко не строгой и не ясной выработкой центрального для всей этой школы понятия – понятия самой интуиции. Поле исследований, взывающих к точности и безупречной логической строгости, обволакивается туманом субъективистской неопределенности. Первые "интуиционисты" остались в плену своего идеализма – вполне догматического и метафизического.
Их идеализм был не только догматичен и не только метафизичен по методу, неспособному применить генетическую точку зрения к самому явлению интуиции в человеческом мышлении. Он, кроме того, был агрессивен по своей направленности и нетерпим. Правильно утверждая, что построение в математике подчиняется логике решения проблем, отличной от классической, "интуиционисты" типа Брауэра и Вейля полагали, будто только эта логика имеет право на признание в математике. Вразрез с этой точкой зрения академик А.Н.Колмогоров показал, что между принципами классической логики и принципами "конструктивной" логики "интуиционизма" не существует отношения исключающего противоречия: "интуиционистская" логика есть логика новой и особой области исследования, ею не исключаются принципы доинтуиционистской логики; они лишь подвергаются ограничению там, и только там, где это ограничение вызывается своеобразием исследуемой области объектов.
Что "интуиционистскому" понятию интуитивной ясности можно предъявить этот упрек, видно из той критики, какой сами "интуиционисты" подвергли канторовскую актуальную бесконечность. Основанием этой критики стало для них положение, будто в математике невозможно осуществить построение, которое сделало бы нас обладателями интуитивно ясного понятия о бесконечности как о бесконечности завершенной, сполна данной, предлежащей уму.
Мы показали выше, что, вводя в учение о множествах понятие актуальной бесконечности, Кантор, далекий от "интуиционизма" и даже избегающий прямых ссылок на интуицию, не ограничивается разъяснением, что понятие об актуально бесконечном он вводит посредством точного определения. Он указывает, что понятие это представляется его уму в своем объективном содержании совершенно непосредственно и с полной внутренней ясностью. Но эта характеристика совпадает с "интуиционистской" характеристикой интуиции. Актуально бесконечное Кантора – объект интеллектуальной интуиции ничуть не меньше, чем конструктивные результаты "интуиционистов". Почему же в таком случае это канторовское понятие отвергается, признается неосуществимым в мысли?
Канторовская интуиция актуальной бесконечности лишена обязательности в глазах "интуиционистов". Они отказались признать за ней непосредственность и совершенную ясность внутреннего видения, на которые ссылался, как мы видели, Георг Кантор. Это разногласие существенно не только для математики, но и для гносеологии. Оно показывает, что в самом понятии интеллектуальной интуиции не было безусловной ясности и существовала возможность, а следовательно, и опасность субъективной иллюзии. И это не удивительно. Ссылка на непосредственность интеллектуальной интуиции используется в редукции математического обоснования. Но она не может быть последней инстанцией в философской редукции происхождения знания. Для гносеологического объяснения интеллектуальная интуиция не беспредпосылочное абсолютное начало знания, а его среднее звено. Его последующие звенья – положения, обосновывающиеся на интеллектуальной интуиции. Его первичное звено, составляющее предмет исследования уже не математики и вообще не специальных наук, а теории познания, – материальная практика общественного человека в ее историческом развитии. Интуиция как функция человеческого познания имеет свою историю. Корни этой истории глубоко уходят в почву практики. По верному разъяснению итальянского математика и логика Энрикеса, первоначальные математические интуиции, например в геометрии, "возникли путем идеализированного опыта, который неоднократно повторялся при состоянии интеллекта, предшествовавшем полному развитию сознания" (6, 16).
Без обращения к гносеологическому критерию практики исходное для "интуиционизма" Брауэра и Вейля понятие интуиции становится шатким. На нем могут быть основаны только субъективные построения, а не система объективного научного знания. Возникает оправданное сомнение в способности "интуиционистов" убедить нас в том, что результаты их построений – нечто большее, чем субъективное творчество, что они составляют науку. Выходит, что отказ "интуиционистов" признать правомерность чрезвычайно обширных и хорошо разработанных частей математики как не допускающих "интуиционистского" ("конструктивного") обоснования – отказ, мотивированный строгостью логических требований, сочетается с далеко не строгой и не ясной выработкой центрального для всей этой школы понятия – понятия самой интуиции. Поле исследований, взывающих к точности и безупречной логической строгости, обволакивается туманом субъективистской неопределенности. Первые "интуиционисты" остались в плену своего идеализма – вполне догматического и метафизического.
Их идеализм был не только догматичен и не только метафизичен по методу, неспособному применить генетическую точку зрения к самому явлению интуиции в человеческом мышлении. Он, кроме того, был агрессивен по своей направленности и нетерпим. Правильно утверждая, что построение в математике подчиняется логике решения проблем, отличной от классической, "интуиционисты" типа Брауэра и Вейля полагали, будто только эта логика имеет право на признание в математике. Вразрез с этой точкой зрения академик А.Н.Колмогоров показал, что между принципами классической логики и принципами "конструктивной" логики "интуиционизма" не существует отношения исключающего противоречия: "интуиционистская" логика есть логика новой и особой области исследования, ею не исключаются принципы доинтуиционистской логики; они лишь подвергаются ограничению там, и только там, где это ограничение вызывается своеобразием исследуемой области объектов.
Это не определения. Это нонсенс.
Когда в конструктивных исследованиях будут открыты новые интересные математические факты? Какие теоремы доказаны конструктивистами? Где интуиционистские теоремы Пуанкаре? Где интуиционистские интегральчики?
Even though most mathematicians do not accept the constructivist's thesis, that only mathematics done based on constructive methods is sound, constructive methods are increasingly of interest on non-ideological grounds. For example, constructive proofs in analysis may ensure witness extraction, in such a way that working within the constraints of the constructive methods may make finding witnesses to theories easier than using classical methods. Applications for constructive mathematics have also been found in typed lambda calculi, topos theory and categorical logic, which are notable subjects in foundational mathematics and computer science. In algebra, for such entities as toposes and Hopf algebras, the structure supports an internal language that is a constructive theory; working within the constraints of that language is often more intuitive and flexible than working externally by such means as reasoning about the set of possible concrete algebras and their homomorphisms.
Physicist Lee Smolin writes in Three Roads to Quantum Gravity that topos theory is "the right form of logic for cosmology" (page 30) and "In its first forms it was called 'intuitionistic logic'" (page 31). "In this kind of logic, the statements an observer can make about the universe are divided into at least three groups: those that we can judge to be true, those that we can judge to be false and those whose truth we cannot decide upon at the present time" (page 28).
Проинтегрируй sin конструктивно.
Ясно все с вашим анализом.
... возможны и необычные с традиционной точки зрения функции: напр., построена к. ф., всюду определенная, непрерывная на единичном сегменте и не ограниченная на нем (см. [17]). Не имеет аналогов в традиционном анализе и теорема, согласно к-рой всякая к. ф. конструктивно непрерывна в любой точке, в к-рой она определена (см. [18]).
...
Так, доказана невозможность следующих алгоритмов (в смысле одного из уточнений понятия алгоритма): 1) распознающего для произвольного конструктивного действительного числа равно оно нулю или нет; 2) находящего для каждой сходящейся к. п. р. ч. то к. д. ч., к к-рому она сходится; 3) находящего для каждой совместной системы линейных уравнений (над полем к. д. ч.) какое-либо ее решение; 4) находящего для каждой непрерывной кусочно линейной знакопеременной функции корень этой функции; 5) находящего для всякой непрерывной кусочно линейной на единичном сегменте функции ее интеграл Римана по этому сегменту. К этому же кругу результатов принадлежит и следующая теорема, полностью решающая вопрос о возможности эффективного перехода от одной системы счисления к другой: алгоритм, находящий для всякой m-ичной конструктивной дроби равную ей n-ичную конструктивную дробь, возможен тогда и только тогда, когда множество простых делителей псодержится в множестве простых делителей т(см. [6]). (В частности, возможен алгоритм перехода от десятичной системы счисления к двоичной, но невозможен алгоритм перехода от двоичной системы к десятичной.)
Для конечной двоичной дроби алгоритм очевиден.
Для периодической тоже.
Видимо там речь идёт о каких-то специфичных дробях.
Актуальная бесконечность - ясная ментальная контрукция, мыслить её элементарно, если ты не инвалид с МТ вместо мозга, - это просто одновременное пребывание всех объектов, вроде бесконечной вселенной или бесконечности углубления в атом. При этом это одновременное существование само легко абстрагируется до объекта. Человеческий мозг не мыслит шагами и вычислениями, он мыслит зависимостями и отношениями. А ты просто даун-футуролух с машин лёрнингом головного мозга, которому бомбит что из транзистерных говен не сделать сознания, сколько мощностей не докидывай.
Но речь всего лишь о том, что ментальная конструкция "ещё один шаг", такая же идеалистическая: нет совершенно никаких причин считать её более обоснованной, чем актуальную бесконечность.
>Брауэр совершенно точно определяет, что есть праинтуиция, на которой основаны все дальнейшие построения.
Будьте добры, приведите это определение.
Я нигде не говорил что пользователей актуальной бесконечности надо репрессировать. Что я говорил и буду говорить по этому поводу, так это то, что актуальная бесконечность это не математика, а религия, поскольку она не вычислима и в нее надобно веровать. Ок, веруйте. Но это не математика. По делу я как раз много говорю, просто не в коня корм, как говорится, что и взять с мейлру. В частности, сто раз объяснял, почему манядоказательства с актуальной бесконечностью это религия, а не математика. Но это и Брауэр объяснял еще в 1907 году.
Я его приводил даже в виде картинок. Ну и цитаты самого Брауэра, разумеется. Толку'то хуй. Сложна слишком, наверное.
>поскольку она не вычислима и в нее надобно веровать
А разве вера только в вычислимое не является верой?
Вычислимость является математикой и работает без всякой веры, т.к просто вычтсляется. Вера начинается там, где заканчивается вычислимость и построимость. Построение, оно просто есть, без всякой дополнительной веры.
Еще раз. Абстракция потенциальной осуществимости по Маркову или трансфинитная индукция (конкретно по Мартин-Лёфу) - это бесконечность, взятая из правил построения объекта. Бесконечность, ассоциированная с правилами построения, о ней можно говорить только в контексте таких правил. Абстракция актуальной бесконечности - это бесконечность, не ассоциированная ни с чем, т.к. нет никаких общих правил ее получения. "Еще один шаг" построим в случае наличия правил построения, некая бесконечность сама по себе - вера уровня боженьки.
Но объект же нельзя построить используя его правила построения. Ты можешь только верить что потенциально это возможно.
>Но объект же нельзя построить используя его правила построения.
Тебе слово "абстракция" о чем-то вообще говорит? Или lazy evaluation?
Ещё раз, конструктивный объект [1, 2, ..] - нельзя построить. Он живёт только у тебя в голове. ∞ - тоже живёт только у тебя в голове, так в чём проблема?
∞ - это просто результат вычисления [1, 2, ..] на любом сверхтьюринговом вычислителе. ∞ - это, когда все шаги были сделаны.
Актуальную бесконесноть очень легко мыслить, для этого достаточно ощущать мир как безграничную протяжённость одновременно пребывающих объектов. Для потенциального 4хмерного существа наш 3хмерный мир с шагами выглядит как полностью развёрнутый, где нет никакого до, сейчас, дальше и ещё дальше, они прибывают все вместе.
>Актуальную бесконесноть очень легко мыслить
Все, что угодно очень легко мыслить. Однако, если мыслимое не имеет правил построения, то это не ментальная конструкция в смысле интуиционизма, не построимый объект (хотя бы в виде абстракции потенциальной осуществимости такого построения), а значит и не математика.
>на любом сверхтьюринговом вычислителе
Которые, как показал Тьюринг еще в 30-х годах, невозможны даже с оракулом, ага. Я тебя услышал.
![quote-one-cannot-inquire-into-the-foundations-and-nature-of[...].jpg](/math/big/thumb/3694/14927995492490s.jpg) 71 Кб, 850x400
71 Кб, 850x400МТ, как и конструктивная логика Гейтинга, например, не формализует интуиционизм Брауэра. Гейтинг даже объяснял, почему. Но там не для мейлру объяснние, тут даже в разницу между актуальной и потенциальной бесконечностью не могут или в понимание пикрелейтед цитаты. С другой стороны ты все равно не назовешь ничего вычислимого, что не сводилось бы к машине Тьюринга. У тебя на этот счет нет ничего кроме веры, что МТ это что-то плохое.
>Однако, если мыслимое не имеет правил построения, то это не ментальная конструкция в смысле интуиционизма, не построимый объект
А у самих правил построения есть правила построения?
Ты бы лучше на палочках пояснял.
Взяли одну палочку | - конструктивный объект
Дорисовываем палочки | к |.. - конструктивный процесс.
В теории палочки можно дорисовывать бесконечно. Но лучше применять какое-то кодирование, вводить уже систему счисления и тд.
Потенциальная бесконечность это процесс рисования палочек.
Актуальная бесконечность это когда мы возьмем какую-то группу палочек, можно обозначить за n и удвоим ее, например.
То есть, потенциальная бесконечность может быть эдакая лишь последовательная от чего-то и к чему-то, а актуальную бесконечность можно вырвать и сделать что-то согласно правилам. Выбор некоторой бесконечности оставляем за наблюдателям правил.
Но это я с дивана пишу. Я вообще больше мамин философ.
Твой вопрос тупой.
Все тупые вопросы я буду игнорировать.
(Автор этого поста был предупрежден.)
А почему тупой? Тем, что тебе не нравится и ломает твою маня-идеологию?
>Все тупые вопросы я буду игнорировать.
Веруны тоже игнорируют доказтельство того, что в их книжках полная туфта.
(Автор этого поста был предупрежден.)
Есть. И я даже сто раз писал об этом с цитатами. Сами правила тоже конструктивный объект, как и результаты вывода по ним. Все выводимо и проверяемо, никакой веры.
Это какой'то подгоревший пишет. Про правила вывода сто раз все разжевано уже с цитатами, даже в этом треде выше. Суть в том, что все выводимо из самих конструктивных объектов.
Нет, ты не понял. Актуальная бесконечность это бесконечность сама по себе, не связанная ни с каким объектом, ни с какими правилами построения чего'либо.
>Все выводимо и проверяемо, никакой веры
Только в рамках аксиом, принятых в данной конкретной математической системе, и только по принятым в ней же правилам вывода из них.
Да и то. Обычно с периодическим маханием руками "да, вот тут у нас обнаружился неудобный парадокс, ну и хрен с ним, будем обходить это место".
Да ты и правда не очень умный. Тебе же говорят, сами правила тоже конструктивные объекты, как и вывод по ним. Корректность вывода в таких системах,, это так же конкретное построение.
И никаких парадоксов со времен самого Брауэра. Т.н парадокс Жирара фиксится элементарно введением иерархии вложенных универсумов вместо неконструктивного общего правила, который его и вызывал. Других антиномий вообще не завезли.
Ну и в чем тогда преимущество по надежности перед, "религией" (теорией множеств). И там и там, неаккуратная формализация приводила к парадоксам. И там и там все пофиксили переходом к предикативным построениям. Иными словами не видно, чтобы интуиция касательно интуиционистской математики давала меньше сбоев, чем интуиция касательно теоретико-множественной.
Очень важное, хотя и не единственное преимущество конструктивного подхода - его автоматизируемость, в частности, непосредственная реализуемость на комплюктере, без дополнительных костылей, прямо в соответствии с колмогоровской интерпретацией логических констант и изоморфизмом Карри-Говарда (программы как доказательства). С неконструктивными аксиоматиками так не выйдет, комплюктер ты веровать не заставишь, а невычислимое оно и в африке невычислимое, правил для его вычисления нет. Причем, как сказано выше, проверяемы на корректность и сами правила проверки на корректность, что означает тотальную корректность и выводимость той же MLTT. С ZFC ничего даже близко подобного не выйдет, хотя костыльные реализации и возможны, все через те же типы, н-р в Coq'е.
>И там и там, неаккуратная формализация приводила к парадоксам.
К слову, интуиционизм Брауэра не формализуем, о чем говорил в т.ч. создатель интуиционистской логики Гейтинг, и парадоксов там не было, нет и не может быть принципиально, поскольку это не какая-то там формальная система.
Я говорил о том, естил у консрктивного объекта правило построение правил построения? И правил построения есть ли правила построение правил построения правил построения?
>в частности, непосредственная реализуемость на комплюктере
Ну смотри, в теории множеств я могу доказать, например, что всякий фильтр расширяется до ультрафильтра, что вполне подходит под твое замечание про отсутствующую реализации на компьютере. В тоже время MLTT, и многих других естественных интуиционистских теориях, несложно доказать, что для всюду определена супер-экспоненциальная функция (supexp(0)=1, supexp(n+1)=2^{supexp(n)}). Но не то, чтобы вычисление supexp(10) могло быть реализовано на реальном компьютере. То есть эта реализуемость в общем случае носит совершенно абстрактный характер. Если же хочется реализуемость на реальном компьютере, то нужна вычислимость с адекватной сложностью. Но если хочется доказать, например, что некоторые объекты не просто существуют, а могут быть найдены за полиномиальное время, то дополнительные усилия потребуются и в конструктивных и в некоструктивных системах.
Все есть. Меня правда, несколько подзаебало пояснять в пустоту. Если бы ты понимал такие темы как интерпретация логических констант по Брауэру-Гейтингу-Колмогорову, натуральная дедукция Генцена-Правитца, изоморфизм Карри-Говарда, куб типизированных лямбда-исчислений а-ля Черч Барендрегта, наконец-таки MLTT, то м.б. что-то и вынес бы из моих объяснений. А так, все это выглядит как лекция в детском саду про мочидзукину теорию пространств Тейхмюллера.
>>15757
Закон исключенного третьего все равно придется выбросить, т.к. он невычислим. Но, если мы выкидываем из некоей аксиоматики невычислимую хуету, остается что-то более-менее заменимое на конструктивную логику.
Большинство алгоритмически неразрешимых проблем доказовались таковыми путём сведения к проблеме остановки, неразрешимость которой вроде как доказана. Но доказана она неконструтивно, вот в чём проблема.
Кстати, доказательство, что задача определения того, является ли частично рекурсивная функция с данным описанием общерекурсивной или нет, алгоритмически неразрешима - так же проведено неконструтивно.
Получается, что в рамках конструктивной логики вообще нет доказательств существования алгоритмически неразрешимых проблем?
Ты бы хоть погуглил, что вообще есть кончтруктивная математика. Конструктивное доказательство - это построение.
Ну и отказ от правила исключения третьего. Следовательно - отказ от доказательства от противного. Все доказательства того, что проблема алгоритмически неразрешима - проводятся от противного, как, например, доказательство теоремы останова у Тьюринга.
Мой вопрос, как в конструктивной математике доказать что та или иная проблема алгоритмически неразрешима? Это вообще возможно?
> отказ от доказательства от противного
Если у тебя есть утверждение вида "не А", например, "не (разрешимо что-то)", то ты имеешь полное конструктивное право сказать "предположим, что A, приведем к противоречию и вуаля". Это только с точки зрения классической математики может показаться, что тут что-то противное, а так вообще-то в любом варианте "не A" можно считать синонимом "если А, то ложь". А нельзя наоборот, A доказывать через приведение "не А" к противоречию.
Поэтому все утверждения о неразрешимости доказываются в конструктивной логике безо всяких проблем.
Я в каждом втором посте говорю о конструктивной интерпретации логических констант. Любое доказательство допустимо, если оно построимо, никто не против принципа исключенного третьего в случаях когда он доказуем. То же про конструктивное отрицание и т.д. есть отказ от веры в общие принципы без общего метода их построения, а вовсе не какие'то догмы уроынч 'отказа от принципа исключенного третьего потому что богородица не велит'.
Конструктивная математика примечательна тем, что это настоящая математика, построимая и вычислимая. Без мутных верований в невычислимые вещи, от которых одни кризисы и неполнота.
Конструктивная математика примечательна тем, что доказательства и объекты строятся из одного и того же материала, а в классической математике они строго разделены.
Допустим, у тебя есть выражение sqrt (ln 1/x). Оно в программистских терминах выбрасывает исключения, то есть на самом деле оно в классической математике формально означает следующее:
case (case (if x != 0 then 1/x else \bot) of
| \bot -> \bot
| t -> if t > 0 then ln t else \bot
end) of
| \bot -> \bot
| t -> if t >= 0 then sqrt t else \bot
end
и к этому выражению еще нужно прицепить доказательство того, что оно не равно \bot для интересующих тебя x.
А в конструктивной математике sqrt (ln 1/x) означает let z <- div(1,x,доказательство x != 0),
y <- ln(z, доказательство z > 0)
in sqrt(y, доказательство y >= 0).
Вот поэтому большинство proof checker'ов основаны на конструктивной логике. Даже если пришить к ним пятую ногу закон исключенного третьего, они все равно по сути конструктивны.
Ну и чем принципиально отличается
if(x != 0) и if(t >= 0)
от
(доказательство x != 0) и (доказательство z > 0)
?
Из пустое в порожнее, ей богу.
Как раз однородность потеряна, вмето ондородной программы на термах, получили неоднородную с термами и типами (доказательствами).
Нет, это как раз математика. Быдлокод это невычислимые маняаксиомы, в которые по причине их невычислимости остается только веровать.
Математика = вычислимость. Иначе это не математика.
Ты постишь в прямом смысле быдлокод и называешь его математикой. Быдлокод - не математика, поэтому ты вызываешь ненависть.
 60 Кб, 600x433
60 Кб, 600x433>бисконечность рабаты посчитать нимогут=(
Ты будто можешь, чучело. Еще раз, для самых одаренных математиков: пририсовывание квантора существования к символу Аллаха не является математическим доказательством Аллаха. Что тут непонятно-то? Дебилы, блядь. Думают, нарисовали значки бесконечности, закона исключенного третьего и т.д. и что-то этим доказали.
>>16029
Еще один гейний математики.
Квантор существования не может быть пририсован к Аллаху, потому что Аллах - терм. А квантор существования может быть навешен только на соотношение.
>>16132
Ок, вставив терм "Аллах" в любое соотношение с квантором существования, мы ничего не докажем.
По какому правилу вставим? Нельзя просто так заменить связанную букву на произвольный терм. Под квантором вообще не может стоять терм, например.
Смотри, пусть у тебя есть слово, которое является соотношением, обозначим это слово значком f.
Пусть в слово f свободно входит буква, обозначаемая как x.
Так вот.
Ты не можешь просто так взять и написать (∃x)f.
Единственный законный способ получить соотношение (∃x)f - воспользоваться одним из правил вывода теории, в которой ты работаешь.
Ясно, что это не навешивание квантора на терм.
> иррациональных чисел
с чего бы? sqrt(2), например, вполне вычислим (как система стягивающихся интервалов).
> анализа
По крайней мере с непрерывными функциями все хорошо.
Лучше Брауэра никто пока не определил что есть существование в математике. Более того, обычно ответом на этот вопрос являются жалкие оправдания, уровня "ито философия, а не математика!!111". С чего бы? О какой вообще математике можно говорить, если нет даже внятного определения, в каком именно случае мы можем сказать, что математический объект существует и в каком смысле следует понимать его существование? Это тот вопрос, с которого должна начинаться математика. Собственно, точку зрения Брауэра я уже приводил >>15731
Да, один момент. Это было написано Брауэром во времена, когда Гедель еще пешком под стол ходил, и никакой теоремы о неполноте сформулировано не было. Это уже позже было доказано, что работая с математикой как с языком ее представления (одним из возможных), так или иначе встает проблема двух стульев, на одном из которых противоречивость точеная, на другом - неполнота дроченая. Гильберт со своей программой формализации арифметики присел сразу на оба стула, бурбаки предпочли помереть (даже с официальным некрологом), т.к. со своим трактатом тоже рано или поздно приблизились бы к упомянутым стульям, что было отмечено даже в предисловии переводчика первого тома про теорию множеств.
Определение Брауэра неадекватно математической практике. Со времен Евклида математики успешно работали с объектами, которые не умели строить, и даже не пытались строить.
>Со времен Евклида математики успешно работали с объектами, которые не умели строить, и даже не пытались строить.
Например? Какие это объекты?
 31 Кб, 489x471
31 Кб, 489x471- конструктивный объект - это всегда некое слово в некоем алфавите.
- конечные слова в конечных алфавитах можно прямо занумеровать натуральными числами, лексикографическим упорядочиванием, геделевской нумерацией, не суть.
- т.о. всю конструктивную математику можно напрямую свести к арифметике. Поэтому вся конструктивная математика вычислима, а единственными адекватными основаниями математики является арифметика. Не логика.
Вопрос, можно ли вычислить нечто, не сводимое вышеупомянутым либо каким-то другим способом к арифметике?
> это всегда некое слово в некоем алфавите.
Что такое алфавит и что такое слово?
>- т.о. всю конструктивную математику можно напрямую свести к арифметике. Поэтому вся конструктивная математика вычислима, а единственными адекватными основаниями математики является арифметика. Не логика.
Нельзя же доказать непротиворечимость арифметики её же соственными методами. Разве нет? И если каждая такая конструктивная математика сводится к арифметике, то нам остаёться верить в её непротеворичивость?
>Нельзя же доказать непротиворечимость арифметики её же соственными методами. Разве нет?
Формально-аксиоматически нельзя, у меня так программа Гильберта проебалась. Конструктивно можно.
>Что такое алфавит и что такое слово?
Писал не единожды, с примерами.
>Писал не единожды, с примерами.
Ещё раз напиши.
>Формально-аксиоматически нельзя, у меня так программа Гильберта проебалась. Конструктивно можно.
И как? Разве это не будет формальной системой?
>Ещё раз напиши.
Простейший пример: алфавит из одного знака |, слово в этом алфавите - натуральное число, н-р |||| = 4.
>Разве это не будет формальной системой?
Опять же, про интерпретации логических констант сто раз писано, и в чем разница между чисто формальным и конструктивным подходом на примере синтетических и аналитических кантовских суждений, даже лекцию Мартин-Лёфа приносил, тоже не один раз.
>Простейший пример: алфавит из одного знака |, слово в этом алфавите - натуральное число, н-р |||| = 4.
Я не понимаю, как это отличается от формального определения N? Мы говорим, что существует знак, который рассматриваем, как еденицу и вместо его сложения с другими знаками, как с числами рисует еденицы. Правда, как это отличается от формального определения?
>Опять же, про интерпретации логических констант сто раз писано, и в чем разница между чисто формальным и конструктивным подходом на примере синтетических и аналитических кантовских суждений, даже лекцию Мартин-Лёфа приносил, тоже не один раз.
Ты можешь привести конкретный пример, почему твоё определение N не формальная система? А не отсылать куда-то? Я хочу услышать твоё объяснение этому.
Например, с отрицательными числами. До XIX века об их существовании велись ожесточеннейшие споры. Даже Гаусс был вынужден отражать нападки философствующих околоматематиков, кричавших, что отрицательных чисел нет. Тем не менее, работать с отрицательными числами умели все. Речь именно об отрицательных, комплексные числа отдельная история. В XIX веке была предложена строгая теория отрицательных чисел, и спорщики заткнулись.
Отрицательное число - слово в алфавите - |. Это конструктивные объекты. Пример мимо.
>>16293
>Я не понимаю
В этом все дело. Разница в интерпретации логических констант. Чуть выше ИТТ уже выяснили, что единственным адекватным определением N можно считать ординалы фон Неймана, там же выяснили, что это те же нумералы Черча, вид сбоку. Т.е. конструктивная система.
>В этом все дело. Разница в интерпретации логических констант. Чуть выше ИТТ уже выяснили, что единственным адекватным определением N можно считать ординалы фон Неймана, там же выяснили, что это те же нумералы Черча, вид сбоку. Т.е. конструктивная система.
Ты не понял. Я хочу, чтобы ты объяснил, почему это не формальная система. Если ты говоришь, что выше дано такое объяснение, то приведи на него ссылки и прокоментируй его.
ЛЮБУЮ формальную систему можно рассмотреть как множество конечных слов в некотором алфавите - на которое наложено несколько дополнительных условий.
>>16292
ЛЮБУЮ формальную систему можно рассмотреть примерно таким же образом, разве что алфавит будет более богат.
>>16295
ЛЮБОЙ математический объект - слово в некотором алфавите. Теоретически достаточно всего одного символа, кстати. На практике используются более богатые алфавиты.
Я это уже писал >>14128 Вопрос был не в этом, а в том, как невычислимую хуитку типа закона исключенного третьего или актуальную бесконечность представить в такой же форме? Очевидно, что если знак бесконечности считать символом / термом / словом в некоем алфавите, то у него должны быть правила вычисления в канонический элемент множества или типа. Т.к. сам этот знак не является каноническим элементом. А таковых правил не существует. Вот и приплыли.
Читал я ваших бурбаков. У меня даже бумажная книшка есть. Ты расскажи, как ты неканонический элемент в канонический вычислять будешь, если правил вычисления нет? Значками играться можно сколько угодно, в итоге придем либо к противоречию, либо к неполноте, что есть свойства любой формальной системы, сводящейся к синтетическому суждению (опять же возвратимся к лекции Мартин-Лёфа).
Ты говоришь как человек, который не читал/не понял первую главу Бурбаки.
Давай разберемся вместе, если ты не против.
Читал и понял. Я уже сто раз говорил в чем разница. В конструктивной системе выразимо только то что там доказуемо, отсюда геделевская полнота. В формальной системе можно выразит то, чего в ней нельзя доказать, т.к для доказательства требуется что'то помимо нее. Это прямое следствие интерпретации логических и др констант.
Да.
К какому конкретно положению первой главы Бурбаки у тебя возникают претензии?
Тебе ж говорят, такой подход изначально ущербен, из'за геделевой неполноты либо противоречивости формальных систем, оторванных от построения. Самый простой пример, закон исключенного третьего, истинный с формально'аксиоматической точки зрения. Он невычислим в общем случае.
Ты вот з бурбаков поясняешь, а походу и предисловие даже не читал, где написано то , о чем я тебе толкую. Бурбаки даже не упомянули, что весь их подход в итоге в геделя и упирается.
Бурбаки предложили математику, в которой любой математический объект построим как конечное слово в некотором алфавите. То есть осуществили в точности твою мечту. Если тебя не устраивает их подход - назови первое же предложение первой главы Бурбаки, с которым ты не согласен.
Сейчас бы по сотому разу объяснять самые азы. Ты так и не понял что такое построение математического объекта. У бурбаков речь о построении вообще не идет, а язык рассматривается только как синтаксис. По бурбакам противоречие это синтаксическая ошибка. Выражение на бурбаковском языке не обязательно построимо, даже если и выразимо на нем. Пример все тот же, закон исключенного третьего. В нем нет ошибок по бурбакам, но он не вычислим и не построим. Я уже не знаю как проще объяснить, про интерпретации логических констант тцт вообще не воспринимают.
Математические объекты по Бурбаки и есть слова. Каждый математический объект построим точно в том же смысле, в каком натуральное число построимо из палочки |.
Ты просто не понял. Знакосочеетания бурбаков это просто синтаксис. В котором выразима любая хуйня, сколь угодно непостроимая. Хоть знак бесконечности, хоть закон исключенного третьего. У них нет понятия выводимости, пруф'объектов, базиса и т.п. у Мартин'Лефа в лекции разница рассмотрена подробно, ссылку я сто раз давал и своими словами пояснял.
Аллах="Аллах". Аллах и есть слово в конечном алфавите. Это просто слово, никакого иного смысла в нём нет.
В конструктивной математике кроме синтаксиса есть семантика, в т.ч номинальные дефиниции и правила вычисленичя неканонических объектов в канонические. Поэтому палочки и т.д можно вычислить в натуральные числа, а знакосочетания бурбаков вычислимы только когда выражают канонические объекты. Слово 'Аллах' невычислимо ни во что, так же как и закон исключенноно третьего, хотя и то и другое выразимо в бурбаковской нотации.
 24 Кб, 329x400
24 Кб, 329x400Так я уж на пальцах пытаюсь объяснить, зачем нужен изоморфизм Карри-Говарда и конструктивные интерпретации логических констант. И что ты хочешь на русском языке нагуглить? Лекция Мартин-Лёфа на английском, как и термины типа canonical, non-canonical constants, nominal definition и т.д. Ты главное пойми - если бы все было так просто, как тебе кажется, то изначальная программа Гильберта по формализации арифметики не провалилась бы. А метаматематика, которую ты у бурбаков в первой главе увидел - это уже шаг к конструктивизации математики. Отсюда и некоторое сходство типа наличия алфавитов, знаков, знакосочетаний. Но без вышеупомянутых вещей типа BHK-интерпретации и изоморфизма Карри-Говарда, такой подход мало чем интересен, опять же сто раз писал почему - возможны синтаксические выражения, не имебщие под собой объектов-построений, типа закона исключенного третьего. Я про эту лекцию говорю http://archive-pml.github.io/martin-lof/pdfs/Martin-Lof-Analytic-and-Synthetic-Judgements-in-Type-Theory.pdf и это еще http://archive-pml.github.io/martin-lof/pdfs/Meanings-of-the-Logical-Constants-1983.pdf
Допустим. Определи BHK-интерпретацию и изоморфизм Карри-Говарда, о которых ты так много говоришь. И сделай это, пожалуйста, корректно, без утверждений о навешивании квантора существования на Аллаха. По твоей ссылке какой-то Кант с тучками вместо определений.
>Определи BHK-интерпретацию и изоморфизм Карри-Говарда,
Определения есть на каждом углу, начиная с педивикии. https://en.wikipedia.org/wiki/Brouwer–Heyting–Kolmogorov_interpretation https://en.wikipedia.org/wiki/Curry–Howard_correspondence Зачем мне все это копипастить? Лучше спроси, если что-то непонятно.
Подожди, то есть палочки - это не натуральные числа? А что такое "натуральные числа" тогда?
Не пидорские.
 13 Кб, 300x269
13 Кб, 300x269Как свидетель теории множеств замечу, что
1. Нельзя говорить о сферической построимости в вакууме.
2. В стандартной аксиоматике (ZFC плюс-минус классы) нельзя доказать, что мощность континуума равна алеф1. Опровергнуть это также нельзя. Поэтому тот, кто говорит, что мощность континуума равна алеф-1, не разбирается в современной дефолтной теории множеств.
Однако мы ввели специальные числа бет (вторая буква еврейского алфавита). Легко доказать, что мощность континуума равна бет-1.
3. Зависит от того, как ты определяешь минус. Аналогия с натуральными числами здесь не работает, и определение должно быть ясным, внятным.
>Нельзя говорить о сферической построимости в вакууме.
Что значит "сферической в вакууме"? Построимость полностью определяется правилами построения, которые так же являются конструктивным объектом, и т.д., я об этом сто раз писал.
>Легко доказать, что мощность континуума равна бет-1.
Вот так маневр, не слыхал. Судя по педивикии, бет1 это булеан алеф0 (2^алеф0), или я не так понял?
>Аналогия с натуральными числами здесь не работает, и определение должно быть ясным, внятным.
А что работает? Так-то сложнее придумать что-то внятнее и яснее арифметики. Если речь об алеф0, который есть кардинал N, то почему для работы с ним нельзя использовать натуральные числа? Шаманство какое-то, не?
1. Определения на бочку.
2. Бет1 - это 2^ℵ0. Мощность булеана счетного множества, если угодно.
3. Сложение кардиналов вполне естественно. Вычитание не настолько интуитивно и потому должно быть определено строго.
>Определения на бочку.
Определение чего? Построения? Сто раз уже обсуждали, тут так никому и не зашло. И через акты интуиционизма Брауэра, и через BHK интерпретацию и изоморфизм карри-Говарда. Бесполезно ж, как в том анекдоте "и унитаз приносил, и жопу показывал, все равно бумагу не продали".
>Сложение кардиналов вполне естественно. Вычитание не настолько интуитивно и потому должно быть определено строго.
Вопрос в том, есть ли изоморфизм между кардиналами и натуральными числами. Если есть, то какой число соответствует кардиналу алеф0? Если нету, то о чем тут вообще говорить.
1. написал же в посте даже.
2. ну, скажем, соответствие между кардиналами и соотв. им натуральными числами. Оно есть?
1. "Построение - это ...". Где у тебя написаны такие слова? Не вижу.
2. Класс кардиналов настолько велик, что даже не является множеством. Натуральные числа можно отождествить с точками ℵ0.
Множество кардиналов конечных множеств изоморфно множеству ординалов конечных множеств. Для натуральных чисел Card(n) = Ord(n)
Операцию вычитания можно ввести не всегда. Даже на множестве натуральных чисел ты не можешь вычесть большее из меньшего. Множество кардиналов также не образует группу по сложению, поэтому вычитание в общем случае на множестве кардиналов ввести нельзя. Впрочем, поскольку из x + 1 = алеф0 следует, что x = алеф0, то можно сказать, что алеф0 - 1 = алеф0. А вот однозначно определить алеф0 - алеф0 нельзя, также как нельзя, например, делить на 0.
 50 Кб, 448x448
50 Кб, 448x448Подскажите пожалуйста какие из теорий учитывают время.
Ну типа:
a = 1; a is 1
a =? 2; a will be 2
a ?= 0; a was 0
А то чет после знакомства с хаскелем, изучая английский я понял что там никак особо не учитывается время. Ну и в прологе вроде тоже.
Ну раз уж ты знаком с хаскелем, то наверняка знаешь, что переменные можно замутить через state-монаду.
Да. Ну это само в глаза бросилось после пролога, хаскеля и инглиша.
>>16709
Спасибо, это то что нужно похоже.
>>16710
Дело не в этом. Дело в том что нынче мое чувство прекрасного очень страдает если я созерцаю логическую систему, но не вижу того что она учитывает времени. Пикрелейтед кароч.
А сейчас мне хочется какой нибудь работающий язык программирования пощупать на LTL или CTL. Ну или/и книжек годных по ним. Но я не математик, просто программирование немного знаю.
Плюс может знаете куда оно все нынче развилось, может что новее есть, включающее TL в себя. Типа помеси нечеткой и темпоральной логики, такое что то.
Я не особо шарю, но судя по этому треду его теория как то не очень программируется. Ну и мне не осилить чистый матан, вот то что можно потыкать в coq, agda или lean еще может быть как нибудь когда нибудь, а то что сильно оторвано от программирования уже сложновато.
Ну и я еще инглиш не выучил сильно дальше элементарной повседневности.
я имею в виду структуру (<,+). Там изоморфизм один-в-один
Чистый неоинтуиционизм Брауэра программируется только на мозгах создающего субъекта, это да. Но его формализации типа конструктивной математики уже программируются запросто, т.к есть ВНК интерпретация логических крюонстант и изоморфизм Карри'Говарда, на которых основаны перечимленные тобой пруверы. Кому как, конечно, лично мне проще понимать что'то когда представляешь, откуда растут ноги, зачем это ыообще было нужно и т.д
Он построен на восприятии человеком простарнства, т.е. ставшего, но не времени, т.е. становления.
Ты читать не умеешь? Я вполне определенно написал про время, столь же определенно об этом написано и у Брауэра, н'р первый акт интуиционизма
 633 Кб, webm,
633 Кб, webm,1280x720
Ну не могу я прочитать даже ту страницу текста что ты мне скинул. Кинешь упрощенный вариант на русском - прочитаю.
У меня еще первая сушка сейчас вдобавок и ощущения при попытке сосредоточенно думать о чем то напоминают попытку точно навести гуляющий по всему экрану прицел в каком нибудь шутане.
Ща погуглил эту математику и:
>Абстрактность конструктивной математики проявляется в систематическом применении двух основных отвлечений: абстракции отождествления и абстракции потенциальной осуществимости.
>Абстракция отождествления состоит в предположении о возможности однозначного и не вызывающего сомнений решения вопроса о (графическом) равенстве или различии любых двух рассматриваемых нами конструктивных объектов, а также о возможности полного отвлечения от мелких различий, имеющихся между графически равными объектами. Случаи, когда указанные предположения не выполняются, заранее исключаются из рассмотрения. Так, при рассмотрении слов в кириллическом алфавите мы исключаем из рассмотрения случаи, когда не можем прочитать слово (вследствие неразборчивости почерка или, например, вследствие повреждения запоминающего устройства ЭВМ, в которое слово было занесено).
>Абстракция потенциальной осуществимости состоит в отвлечении от границ наших конструктивных возможностей в пространстве, времени и материале. Случаи, когда находящихся в нашем распоряжении средств недостаточно для осуществления требующихся построений, заранее исключаются из рассмотрения.
Она вообще же не подходит для работы с чем то реальным. Первый абзац отметает всякие там нейронные сети и нечеткие логики. Второй это полное и тотальное возложение болта на имеющиеся в распоряжении ресурсы. Как математика оно может и заебись, но с реальной точки зрения оно никогда не будет эффективно работать на пк, а мне это важно.
> В связи со сказанным, в конструктивной математике под «существованием» конструктивного объекта понимается его потенциальная осуществимость — то есть наличие в нашем распоряжении метода, позволяющего воспроизводить этот объект любое потребное число раз. Такое понимание резко расходится с пониманием существования объекта, принятым в теоретико-множественной математике. В теории множеств факт постоянного рождения и исчезновения конструктивных объектов не находит никакого выражения: с её точки зрения, подвижные реальные объекты являются лишь «тенями» вечно существующих в некотором фантастическом мире статичных «идеальных объектов» (и только эти «идеальные объекты» и следует якобы рассматривать в математике).
Тут мне не совсем ясно. Но мне надо что бы один объект был фактически чем то не одним и тем же во времени. Т.е. сегодня А = 1, завтра все то же А = 2 уже, ну и вообще всему что я захожу, лол.
Ну и что бы выражение А = А + 1 могло быть верным. Типа что бы новое А стало равно старому А плюс единице.
Короче связь с реально работающими, эффективными(!) по ресурсам системами очень и очень важна мне.
 633 Кб, webm,
633 Кб, webm,1280x720
Ну не могу я прочитать даже ту страницу текста что ты мне скинул. Кинешь упрощенный вариант на русском - прочитаю.
У меня еще первая сушка сейчас вдобавок и ощущения при попытке сосредоточенно думать о чем то напоминают попытку точно навести гуляющий по всему экрану прицел в каком нибудь шутане.
Ща погуглил эту математику и:
>Абстрактность конструктивной математики проявляется в систематическом применении двух основных отвлечений: абстракции отождествления и абстракции потенциальной осуществимости.
>Абстракция отождествления состоит в предположении о возможности однозначного и не вызывающего сомнений решения вопроса о (графическом) равенстве или различии любых двух рассматриваемых нами конструктивных объектов, а также о возможности полного отвлечения от мелких различий, имеющихся между графически равными объектами. Случаи, когда указанные предположения не выполняются, заранее исключаются из рассмотрения. Так, при рассмотрении слов в кириллическом алфавите мы исключаем из рассмотрения случаи, когда не можем прочитать слово (вследствие неразборчивости почерка или, например, вследствие повреждения запоминающего устройства ЭВМ, в которое слово было занесено).
>Абстракция потенциальной осуществимости состоит в отвлечении от границ наших конструктивных возможностей в пространстве, времени и материале. Случаи, когда находящихся в нашем распоряжении средств недостаточно для осуществления требующихся построений, заранее исключаются из рассмотрения.
Она вообще же не подходит для работы с чем то реальным. Первый абзац отметает всякие там нейронные сети и нечеткие логики. Второй это полное и тотальное возложение болта на имеющиеся в распоряжении ресурсы. Как математика оно может и заебись, но с реальной точки зрения оно никогда не будет эффективно работать на пк, а мне это важно.
> В связи со сказанным, в конструктивной математике под «существованием» конструктивного объекта понимается его потенциальная осуществимость — то есть наличие в нашем распоряжении метода, позволяющего воспроизводить этот объект любое потребное число раз. Такое понимание резко расходится с пониманием существования объекта, принятым в теоретико-множественной математике. В теории множеств факт постоянного рождения и исчезновения конструктивных объектов не находит никакого выражения: с её точки зрения, подвижные реальные объекты являются лишь «тенями» вечно существующих в некотором фантастическом мире статичных «идеальных объектов» (и только эти «идеальные объекты» и следует якобы рассматривать в математике).
Тут мне не совсем ясно. Но мне надо что бы один объект был фактически чем то не одним и тем же во времени. Т.е. сегодня А = 1, завтра все то же А = 2 уже, ну и вообще всему что я захожу, лол.
Ну и что бы выражение А = А + 1 могло быть верным. Типа что бы новое А стало равно старому А плюс единице.
Короче связь с реально работающими, эффективными(!) по ресурсам системами очень и очень важна мне.
>Она вообще же не подходит для работы с чем то реальным. Первый абзац отметает всякие там нейронные сети и нечеткие логики.
Начнем с того, что это не так. Во-первых, любая нейросеть это в любом случае конструктивный объект, иначе ее невозможно было бы реализовать, тем более на капплюктере. Про нечеткую логику могу сказать, что существует конструктивная нечеткая логика, разработанная Атанассовым, есть даже крайне годная книжка http://gen.lib.rus.ec/book/index.php?md5=6503D14B49A5ED76608DB72793718885 если ты вообще в курсе, что такое нечеткая логика, то главная разница с конструктивным вариантом в том, что в последнем используется конструктивное отрицание, т.е. явно заданное и построимое. Это значит, что для нечеткого множества должна быть явно задана не только функция принадлежности, но и функция непринадлежности, которая в обычной нечеткой логике считается равной 1-функция принадлежности. Функция принадлежности + функция непринадлежности не должны в сумме превышать единицу, естественно. Но могут быть меньше единицы, что невозможно в обычной нечеткой логике.
>Тут мне не совсем ясно.
Это уже дебри какие-то. Речь о требовании, чтобы конструктивный объект всегда был одним и тем же построением, единица должна быть единицей вчера и через 100 лет. С классической точки зрения странное требование, да.
>Ну и что бы выражение А = А + 1 могло быть верным. Типа что бы новое А стало равно старому А плюс единице.
Суть в том, чтобы один и тот же конструктивный объект был одним и тем же. Никто не запрещает присваивать новые значения переменной.
>с реальной точки зрения оно никогда не будет эффективно работать на пк, а мне это важно.
С реальной точки зрения, это вообще единственное, что может работать на пк. Т.к. на пк возможны только построимые объекты. Любая программа на любом языке программирования - это конструктивный объект и тривиально сводится к типизированному лямбда-исчислению. Большинство вещей не называются конструктивными, хотя и являются таковыми. Таблица умножения конструктивный объект, однако никто и никогда не называет ее конструктивной таблицей умножения.
>Она вообще же не подходит для работы с чем то реальным. Первый абзац отметает всякие там нейронные сети и нечеткие логики.
Начнем с того, что это не так. Во-первых, любая нейросеть это в любом случае конструктивный объект, иначе ее невозможно было бы реализовать, тем более на капплюктере. Про нечеткую логику могу сказать, что существует конструктивная нечеткая логика, разработанная Атанассовым, есть даже крайне годная книжка http://gen.lib.rus.ec/book/index.php?md5=6503D14B49A5ED76608DB72793718885 если ты вообще в курсе, что такое нечеткая логика, то главная разница с конструктивным вариантом в том, что в последнем используется конструктивное отрицание, т.е. явно заданное и построимое. Это значит, что для нечеткого множества должна быть явно задана не только функция принадлежности, но и функция непринадлежности, которая в обычной нечеткой логике считается равной 1-функция принадлежности. Функция принадлежности + функция непринадлежности не должны в сумме превышать единицу, естественно. Но могут быть меньше единицы, что невозможно в обычной нечеткой логике.
>Тут мне не совсем ясно.
Это уже дебри какие-то. Речь о требовании, чтобы конструктивный объект всегда был одним и тем же построением, единица должна быть единицей вчера и через 100 лет. С классической точки зрения странное требование, да.
>Ну и что бы выражение А = А + 1 могло быть верным. Типа что бы новое А стало равно старому А плюс единице.
Суть в том, чтобы один и тот же конструктивный объект был одним и тем же. Никто не запрещает присваивать новые значения переменной.
>с реальной точки зрения оно никогда не будет эффективно работать на пк, а мне это важно.
С реальной точки зрения, это вообще единственное, что может работать на пк. Т.к. на пк возможны только построимые объекты. Любая программа на любом языке программирования - это конструктивный объект и тривиально сводится к типизированному лямбда-исчислению. Большинство вещей не называются конструктивными, хотя и являются таковыми. Таблица умножения конструктивный объект, однако никто и никогда не называет ее конструктивной таблицей умножения.
>любая нейросеть это в любом случае конструктивный объект, иначе ее невозможно было бы реализовать, тем более на капплюктере
Wrong. Компьютер не может даже в бесконечные десятичные дроби. Реализация на компьютере - просто приближение. Если на компьютере получилось приблизить какой-то объект, этот объект не становится конструктивным.
>всегда был одним и тем же построением
Причем в общем случае невозможно проверить, являются ли или не являются два построения одним и тем же построением. Так что требование заведомо невыполнимое.
>Если на компьютере получилось приблизить какой-то объект, этот объект не становится конструктивным.
Зато конструктивно его приближение. А если сам этот объект непостроим в силу бесконечности или еще чего-то невычислимого, то он и не существует. Хотя, можно и веровать что существует, но тогда встает вопрос, в каком смысле.
>в общем случае невозможно проверить, являются ли или не являются два построения одним и тем же построением.
Чего несет. Есть правила построения, есть методы проверки равенства конструктивных объектов, есть наконец объект построенный по правилам. Проверка т.о. тривиальна.
>есть методы проверки равенства конструктивных объектов
В общем случае даже невозможно выяснить, равны ли два конструктивных вещественных числа.
Блин, да мне конкретная реализация нужна на компьютере что бы её тыкать.
И пока я свой путь вижу так: haskell -> agda -> lean/coq
Либо это книга должна быть где решаются более менее конкретные задачи через вот это вот твое. А голую теорию мне не на что наматывать и никак я её не могу воспринимать, увы.
Потому что такому алгоритму придётся работать бесконечно долго - пока не построит оба числа и не сравнит их посимвольно. А алгоритм должен давать ответ за конечное время.
А хаскель и агда тебе зачем? Тыкай сразу кок, там все нужное есть. Книги, опять же по коку никто не отменял.
>>16999
>Потому что такому алгоритму придётся работать бесконечно долго - пока не построит оба числа и не сравнит их посимвольно. А алгоритм должен давать ответ за конечное время.
То, что континуум непостроим, еще Брауэр показал на примере актов интуиционизма. Это верующие придумали специальную ебулду - бет1, и написали, что она типа имеет мощность континуума. А я типа прочитал и должен уверовать, потому что проверить все равно невозможно, т.к. даже правил построения этой специальной ебулды нет. Вот тебе и неконструктивная математика.
Нельзя. Если алгоритм рекурсивен (а обычно так и есть), то он на каждом последующем шаге использует результат вычислений на предыдущем шаге. И просто так нельзя сказать, дают ли два алгоритма один и тот же результат или не дают, - нужно проделать вычисления. В конструктивной математике вещественное число - это алгоритм, который принимает на вход натуральное n и печатает первые n цифр вещественного числа; такой алгоритм должен быть определен для любого n. Такой алгоритм работает конечное время, и всё хорошо. Но чтобы сравнить два вещественных числа, в общем случае нужно запустить два соответствующих алгоритма бесконечно много раз - по одному разу для каждого натурального n - и сравнить результаты. Что требует бесконечного времени.
>>17001
Хватит кривляться. Жалко смотрится.
Нет, не нужно. Достаточно сравнить алгоритмы. Существуют системы типов, в которых несравнимые из-за проблемы останова алгоритмы не могут быть типизированы.
Возьми алгоритм, который каким-нибудь образом считает корень из 2.
Возьми итерационную формулу Герона для корня из 2.
Как ты будешь выяснять, равны ли два числа, определяемые этими алгоритмами?
Хаскелл нужен хотя бы затем что он еще язык программирования. Агда вроде некст лвл от него. А ну еще ща Идрис же. А петушка и лен, по хотту который, мне пока наверно не осилить.
У меня кароч очень все плохо с математическим бэграундом, но что то если по тихому если кодить от простого к сложному, то со временем идеи доходят.
А можно книжек по этим штукам? По 2-3 на каждую из тем. Одну для совсем конченых дебилов которые математики не нюхали толком, ну научпоп какой нибудь интересный. Вторую уже 50/50 человеческую/сверхчеловеческую математическую. А третью уже совсем для конченых сверхлюдей.
Ну и русский язык пока в приоритете, к сожалению.
Между первыми курсами и более крутой алгеброй можно почитать Ю. А. Бахтурин «Основные структуры современной алгебры» или Paolo Aluffi "Algebra: Chapter 0", чтобы настроиться. И любую книгу для программистов по теории типов (тот же Пирс).
Тут: http://maxim.livejournal.com/479716.html
Если с математикой до этого особо не разбирался, могу порекомендовать вторую главу Шилова, "Конечномерные линейные пространства" http://libgen.io/book/index.php?md5=22E05893136F1547705B6453A265601B
"" Следует отметить, что проблема распознавания равенства двух произвольных вещественных чисел является алгоритмически неразрешимой, а потому при конструктивном понимании математических суждений утверждение
«любые два вещественных числа или равны, или не равны»
оказывается ложным. Соответственно, теоретико-множественное представление об атомарности континуума (его составленности из чётко отделённых друг от друга точек) не переносится в конструктивную математику ""
Я уже сто раз написал, что континуум непостроим. Еще Брауэру это было известно. И уж континуум точно не сводится ко всякой религии типа алефов и бетов1. Однако, если мы рассматриваем вещественные числа с конечным числом знаков, проблемы нет никакой вообще.
>при конструктивном понимании математических суждений утверждение «любые два вещественных числа или равны, или не равны» оказывается ложным.
В тех случаях, когда это утверждение непосредственно доказуемо построением, то оно не может быть ложным конструктивно, как и закон исключенного третьего.
>если мы рассматриваем вещественные числа с конечным числом знаков
Конструктивисты не рассматривают вещественные числа с конечным числом знаков. Даже сраные ультрафинитисты так не делают. У тебя уже совсем какой-то радикализм.
Хаскель - это прекрасно, научишься жить без переменных, зато с монадами. Опыт весьма полезный для кока и прочего, будешь, например, фолдить налево и направо вместо того, чтобы пытаться писать циклы.
Но! собственно к доказыванию чего бы то ни было хаскель не имеет никакого отношения. Изучи хотя бы для начала классическую пропозициональную логику (она и в конструктивной математике для булевских значений точно так же работает).
Но в хаскеле же выразимо исчисление конструкций, СоС? Где'то видел даже реализацию млтт на нем.
"вещественные числа с конечным числом знаков" - это рациональные числа. Но ты же не запретишь конструктивистам рассматривать такие числа, как корень из двух?
В таком случае мы опять упираемся в абстракцию потенциальной осуществимости, от которой у местной школуйни непрекращающаяся батрушка из'за непонимания в чем разница с актуальной бесконечностью.
Не совсем, в хаскеле нету dependent types, а попытки их присобачить через typeclasses - то еще извращение.
См. https://wiki.haskell.org/Dependent_type
Но даже если какие-то индуктивные конструкции в хаскеле есть, то это еще не значит, что про них что-то доказывать можно, так же как далеко не всякий язык с типом boolean содержит проверялку доказательств пропозициональной логики.
Есть абстракция потенциальной осуществимости - нет алгоритма для проверки равенства двух чисел.
Ну и что? Можно подумать, эта проблема разрешима с неконструктивным подходом. Алгоритмически неразрешимые задачи не разрешимы ничем другим тоже.
Ты, наверно, имеешь в виду TypeInType. Это прикольно, но все-таки не dependent types.
А почему средствами самого языка не сделать? В зависимых типах нет никакого волшебства, только лямбда термы.
У нас есть полноценный предельный переход, использующий няшненькую актуальную бесконечность. А у вас нету, азаза.
Придумали очередную хуйню в надежде исправить ситуацию с невычислимой проблемой и рады. Сама'то проблема никуда не денется, если ее подкрасить пердельным переходом, а по факту заниматься самым махровым финитизмом с ограниченным числом знаков после запятой.
Это называется не хуйня, а математика.
У твоей секты даже вменяемых книжек нет с доказательствами.
Невычислимая хуйня называется 'хуйня' а не математика. Секта это когда веруют, что в математикке можно и без вычислимости. Книжки ты все равно не осилишь, хотя я сто раз ссылки давал.
Волшебство как раз есть, и вот оно в чем.
Почему "массив длины 120" и "массив длины 5!" - это один и тот же тип? Потому что (компилятор запускает рекурсивную функцию) 5!=5432=120. Ура?
Пока еще не ура. Есть две проблемы. Первая в том, что типы могут зависеть от параметров, значение которых на этапе компиляции неизвестно. Почему "массив длины 120n" - тот же тип, что "массив длины n5!"? А вот компилятор и не знает, почему. Значит, где-то рядом должно лежать доказательство.
Вторая проблема в том, что тип "массив длины f(x)" может быть вообще не определен, если f зависает.
Вот поэтому языки типа кока идеально подходят для зависимых типов: ничего никогда не зависает и всегда можно рядом положить доказательство. А хаскель ни одним из этих двух свойств не обладает.
 142 Кб, 628x685
142 Кб, 628x685Угу, наверно, тут кажется смотрел и там нету.
https://www.linux.org.ru/news/opensource/12611764
>>17270
А потому что не до этого наверно, пацаны пилят функциональный, но практичный язык. А сейчас самый тренд, по моему, это запиливание наиболее простого способа использования многоядерных процессоров.
>Поддержка превращения do-нотации в код, использующий класс Applicative вместо Monad.
>Applicative не накладывает ограничений на последовательность выполнения, что позволяет автоматически распараллеливать участки кода.
С точки зрения математики это изменение вообще вроде как даже вредное, а вот с точки зрения практичности и современных реалий оно нужное достаточно.
Ну вон предисловие к tapl'y годно отражает философию такого подхода.
>>17314
Потому что хаскелл это в первую очередь язык программирования заимствующий и адаптирующий некоторые концепции из математики под себя.
А кок и подобные это в первую очередь теорем пруверы которые врятли как то оптимизированы для эффективного программирования, но по части матана и построения всякого разного абстрактного они гораздо глубже конечно.
И смешивать их пока не стоит, имхо. Цели у них разные достаточно.
Оп, ты пилишь перекат? Как думаешь, есть ли смысл про х-ли и теорию категорий отдельный тред создать?
Можещь рассказать, почему труды Мартин'Лефа это гуманитарные манярассуждения, а твои кукареканья на мейлру нет?
Ты так и не ответил, что гуманитарного у Мартин'Лефа в млтт. А неконструктивные теории множеств и правда бесполезны из'за невычислимых аксиом типа исключенного третьего
Твои теории - это не математика. Это воинствующая философия, это ультиматум математикам. Ты пытаешься заставить всех превратиться в конструктивистов, но не аргументируешь это никак. Если бы твои теории были бы полезны и мощны, то математики бы сами стали на твою точку зрения. Но твои теории бестолковы, а твои требования вздорны. Ты не можешь обогатить математику. Более того, ты и не хочешь её обогащать. Ты требуешь от неё отказаться.
Проблема только в том, что ты кукарекаешь вместо того, чтобы попытаться понять, что единственный мой тезис в том, что математика должна быть вычислимой, иначе это не математика, что доказал кризис основпний. Так и бывает, когда в математику тащат всякую религию. Ну а то, что ты Мартин'Лефа не осилил не говоря о Брауэре, это чисто твои сложности.
К математике твои безумные идеи никакого отношения не имеют. Ни сам Брауэр, ни его культисты никакой математики (не то что интересной математики, а вообще хоть какой-нибудь математики) создать не смогли.
Ты уже какой раз свое незнание используешь как доказательство. Если лично ты чего'то не понимаешь, это ничего не доказывает.
Допустим, я чего-то не знаю и скрытая, потаённая конструктивистская математика действительно есть. Ну так покажи же её.
inb4 очередная философия
Эту тему почти никто и никогда не пытался популяризовать, практически все что есть это не для начинающих, более того, на английском. Вон, предыдущий оратор так нихуя и не понял. Но, немного годноты из области "по-проще" все же есть. Во-первых, переводная книжка создателя конструктивной логики и ученика Брауэра, Гейтинга http://gen.lib.rus.ec/book/index.php?md5=EF2FA380D0496F56F759C39EAA1A5459 во-вторых, конструктивный подход к основаниям крайне годно описан у Френкеля, того самого, который один из создателей ZFC, http://gen.lib.rus.ec/book/index.php?md5=1EC5F0DF018488D368BB3CB9D4EE279B 4ая глава. Хотя и заметно, что Френкель не сторонник (мягко говоря) этих идей, таки его уровень как математика сказывается - очень грамотно пояснил.
Толсто.
 979 Кб, 2592x1944
979 Кб, 2592x1944А, ну еще Марков, "Нормальные алгорифмы" и есть книжка даже для младших школьников, Успенский "Машина Поста". Пикрелейтед тоже весьма годная книжка, но я бы не назвал ее "попроще".
> конструктивной теории множеств
А что это? Если ты представляешь себе ZFC без закона исключенного третьего, так это совсем не то.
Конструктивно множества можно определить как функции (по объекту возвращают да или нет) или предикаты (каждому объекту соответствует утверждение). И это абсолютно разные вещи! С классической точки зрения это примерно как вычислимые и перечислимые множества.
А дальше можно развести какую-никакую теорию, но так как вся вселенная счётна, то кардинально не повыпендриваешься.
>Конструктивно множества можно определить как функции (по объекту возвращают да или нет) или предикаты (каждому объекту соответствует утверждение).
Конструктивно множества определяется через правила построения всех его элементов. Множество, определенное через функцию принадлежности (характеристическую) элементов - это самый что ни на есть классический подход.
Любые теоретические основания приходится строить на непроверяемых утверждениях. Современным аналогом утверждения пифагорейцев о том, что всё строится из целых чисел, является тезис Чёрча-Тьюринга о том, что любое вычисление в принципе может быть проделано машиной Тьюринга. Если когда-нибудь будут изобретены способы совершать сверхтьюринговые вычисления, то для большинства современных математиков (занимающихся основаниями) это станет таким же шоком, как для пифагорейцев - иррациональность числа √2
>Если когда-нибудь будут изобретены способы совершать сверхтьюринговые вычисления, то для большинства современных математиков (занимающихся основаниями) это станет таким же шоком, как для пифагорейцев - иррациональность числа √2
С какой стати?
>Любые теоретические основания приходится строить на непроверяемых утверждениях.
Не любые. Брауэр как раз от такого подхода и отказался.
То, что ты написал, эквивалентно предикату принадлежности. А именно, если есть предикат P, то можно перечислить все элементы, перечислив все доказательства и проверяя, доказывают ли они утверждения вида P(x). Обратно, если есть перечисляющая функция, то можно написать предикат P(x)="существует шаг, на котором эта функция выдаёт x".
Вот вроде неплохой курс для самых маленьких от основ лямбда-исчисления к теме "12. Генценовское (секвенциальное) исчисление для интуиционистской логики высказываний. Теорема об устранении сечения." Я начал смотреть вроде неплохо, нет проклятия знаний. Но почему-то есть только 12 лекций из 15, не хватает следующих:
13. Интуиционистская логика первого порядка. Система естественного вывода и генценовское (секвенциальное) исчисление.
14. Введение в теорию типов. Зависимое произведение типов и соответствие (по Карри–Говарду) с интуиционистским квантором всеобщности. Исчисление индуктивных конструкций (CIC); система Coq для формализации математических доказательств на ЭВМ.
15. Применение λ-исчисления в языкознании: категориальные грамматики, семантика Монтегю.
 289 Кб, 459x441
289 Кб, 459x441Что-то он сходу за типизированную лямбду пояснять начал, толком не рассказав про апплиацию, абстракцию, альфа и бета редукции как явления вообще. Думаю у самых маленьких по ходу этих лекций полно вопросов будет.
 30 Кб, 480x360
30 Кб, 480x360Короче, посмотрел минут 15, нахуй. Если уже знаешь о чем речь, то зайдет. В противном случае скорее всего будет пикрелейтед. Лучше уж сразу вот над этим медитировать http://ttic.uchicago.edu/~dreyer/course/papers/barendregt.pdf
 140 Кб, 920x960
140 Кб, 920x960Ну так надо haskell/(o)caml/idris(?) -> tapl -> потом языки которые сможешь хотя бы неполноценно осилить зная tapl: agda/coq/lean/может еще варианты какие -> потом добираешь нужный математический бэкграунд в hott, mltt и книжках которые нужны что бы их осилить.
Перед этим можно попердолиться в scheme и sicp'om если хаскелл сложна.
Ну это мой план такой, лол.
 31 Кб, 600x206
31 Кб, 600x206Более подходящий пик.
А ты сам что про тезис Чёрча-Тьюринга думаешь?
Это в следующей лекции.
https://colah.github.io/posts/2015-09-NN-Types-FP/
Вот, думаю тому парню с конструктивной математикой будет интересно. Автор рассматривает нейросети с помощью функционального программирования, теории типов и мельком вспоминает, что хорошо было бы рассмотреть с точки зрения гомотипической теории типов. Там есть и другие интересные статьи, в частности, нейросети и топология, но я до них еще не дошел.
у меня вопрос:
вы тут что против платонического мира идей?
сорян за сажу, если против хотелось бы услышать доводы, да и за тоже хотелось бы услышать
ну ебана, тред оснований математики, а ты не знаешь в чем разница между платоном и аристотелем?
Просто с беглого чтения треда я понял что тут в целом натсроены против платона.
Да я только залез сюда.
Анон, ты мне друг, но истина дороже: оба имеют самое прямое отношение к основаниям классической математики. Платон сформулировал, где находятся и как существуют невычислимые числа - в мире идей, конечно же. Аристотель создал первую формальную логику, дожившую до Ренессанса без изменений. Не фиг тут, короче.
> В мир идей, конечно же, нужно уверовать.
Еще в душу вселенной, какой же платонист без мировой души.
> А аристотелева логика для математики бесполезна, это Гильберт доказал.
Ну это все равно что сказать, что интегральное исчисление показало бесполезность методов Евклида для вычисления площадей и объемов. Теперь-то они, конечно, не нужны, а всё-таки Евклид красава. А аристотелева логика в современном варианте - это примерно содержимое детской книжки "Логическая игра" Кэрролла. Конечно, когда у тебя есть нормальное исчисление предикатов, оно уже не надо; но ведь кто-то переиздает же Кэрролла для детишек, значит, нужно.
>Тезис Чёрча — Тьюринга — Дойча
Довольно смутная гипотеза. Из того, что мы знаем о квантовой физике в настоящий момент, следует, что любое вычисление, которое делает квантовый компьютер, может сделать и машина Тьюринга (хотя для некоторых вычислений ей и потребуется для этого гораздо больше времени).
Однако теория множеств не предполагает существование "платоновского мира идей". Напротив, если, например, почитать "Теорию множеств" Бурбаки (классический теоретико-множественный трактат), то они там ясно дают понять, что не признают никакого другого понятия математической истины кроме как выводимости формулы определённого вида в определённой формальной математической системе. При этом разные формальные системы будут доказывать разные (возможно, даже противоположные) формулы, которые в рамках соответствующих формальных систем будут "истинными". Можно сказать, что формализм в математике - это противоположность платоновского идеализма, так как формалистов совершенно не интересуют вопросы "реального существования" математических объектов. Вопросы же эти интересуют как раз интуиционистов и конструктивистов, для которых математический объект "реально существует", если его можно конструктивно построить. Грамотные конструктивисты критикуют классическую теорию множеств не за мнимый "идеализм", а напротив, за то, что доказываемые в формальной теории множеств формулы оказываются совсем оторванными от какого бы то ни было реального содержания (например, в теории множеств доказывается формула существует множество A, обладающее определёнными свойствами, при этом о том, как построить такое множество нам остаётся неизвестно). Таким образом, формальная теория множеств строит излишние цепочки силлогизмов, которые можно рассматривать как чистую схоластику. Ну и у некоторых остаётся подозрение, что кроме излишних схоластических выводов могут оказаться построены и совсем уж некорректные (например, ZFC может оказаться омега-противоречивой), хотя пока никаких явных некорректных выводов в ZFC не выявлено.
"даже с точки зрения формалиста, есть
нечто, что оказывает большее влияние на направления математической
мысли, нежели человеческий разум."
Логики, поясните за одну вещь (сам я не логик, поэтому прошу прощения за возможно некорректные термины).
Можно ли в формальной арифметике 1-го порядка (с классической логикой, включающей закон исключения третьего и проч.) доказать существование числа, обладающего неким свойством, которое мы конструктивно не можем построить?
Или более общий вопрос. Допустим, у нас есть теория 1-го порядка, для которой существует конструктивная модель, и все аксиомы в этой теории могут быть подтверждены конструктивными построениями в этой модели. Есть подозрение, что, если мы можем доказать в этой теории существование объекта n, то мы можем его в нашей модели и конструктивно построить.
Как кажется, в теориях первого порядка классическая логика полностью согласуется с воззрением конструктивистов "существовать значит быть построенным", и менять для этого логику (например, убирая закон исключения третьего) необходимости нет.
Так ли это или я ошибаюсь?
Нет, платонизм - это когда на нас влияет реальный нефизический мир, а не реальный физический мир
Во времена платона не было разницы, а сейчас есть. Суть в том что мы открываем, а не изобретаем.
Возможно, это слишком искусственное разграничение. Ведь даже конструктивисты согласятся, что мы открываем свойства конструктивных объектов (даже если сами объекты мы изобрели). В то же время приведённая цитата из Роббинса говорит о том, что физический мир влияет на то, что определённые математические конструкции оказываются более ценными, чем другие, так как, например, более помогают нам в науке. Однако тот же инструментарий математического анализа можно строить разными способами (как строили его по разному Ньютон и Лейбниц). Поэтому открыли мы математический анализ или изобрели? И какие именно его аспекты открыли, а какие изобрели?
Курс по пучкам для нубов; тут мужик рассказывает про категории.
Не только разными способами, а, наверное, бесконечным количеством разных способов. Суть в том что единого понятия мат. анализа. нет. И какие бы мы способы не избрали, принципы будут открываться одни и те же(и базироваться на одних и тех же). Так же как например уже в самих операциях сложения и т.д. действительных чисел заложена конепция комплексных чисел.
Можно вот еще что сказать, представь что нам нужно проверить инопланетян на разумность, не логично ли выдать им информацию о натуральных числах и ожидать иррациональных и вообще всего остального.
Вся суть платонизма в современных терминах сводится именно к материализму, не взирая на многие элементы идеализации, понятно что точка в геометрии не соответствует ей в физике, но понятие точки в нас взялось именно из физической.
Дополню: арнольд, например, понимал математику как часть физики, не знаю конечно на сколько весь остальной его треп правдив.
Ну в такой трактовке, думаю, платонистами в той или иной мере являются все математики - и конструктивисты, и формалисты.
Однако, как я заметил здесь >>17529
главная претензия конструктивистов к теории множеств заключается вовсе не в платонизме последних, а в схоластичности выводов классической теории множеств.
> доказать существование числа, обладающего неким свойством, которое мы конструктивно не можем построить?
Да. Например, мы не можем конструктивно решить проблему остановки. Рассмотрим следующее свойство числа:
P(x) = x = 2^k, где k - останавливающаяся программа или x = 3^k, где k - зависающая программа
Это свойство невычислимо. Тем не менее, в зависимости от того, что делает программа номер 0, либо 2, либо 3 обладает этим свойством.
> то мы можем его в нашей модели и конструктивно построить.
Это правда в следующем смысле: если ExP(x) - теорема интуиционистской арифметики без свободных переменных, то также теоремой является P(t) для некоторого терма t. Если в P нет кванторов, то ExP(x) может быть даже и теоремой классической арифметики. Но вот если в P есть кванторы...
> менять для этого логику (например, убирая закон исключения третьего) необходимости нет.
Ну вот допустим ты привел предположение Ax~P(x) к противоречию, то есть доказал ~Ax~P(x). Что дальше? Классическая математика подсказывает, что ExP(x), а где ты этот x конструктивно возьмёшь?
Да, я, если честно, тоже там думаю. На данный момент квантовые компьютеры, которые хотят сделать, не способны на сверхтьюринговые вычислениями. Да и вообще, объяснять одну загадку (возможность сверхтьюринговых вычислений) другой загадкой (квантовые компьютеры) не очень умно. Просто решил закинуть этот тезис, хоть и самому он не очень нравится
>Например, мы не можем конструктивно решить проблему остановки
Зато неконструктивно можем, сведя ее у исключенному третьему, "или остановится или нет)))". И почему-то никого не беспокоит, что это "решение"-то уровня /б, никакого значения не имеющее, ни теоретического ни тем более практического.
>>17528
Но тут же есть какой-то верующий, кукарекующий что Тьюринг петух и его машина ненужна, т.к. квантовые вычисления бла-бла-бла. Мне вот тоже этот момент не очень понятен, что есть такого в квантовых вычислениях, не сводящегося к вычислениям неквантовым. Вычисления, они и в африке вычисления, безотносительно метода, разве нет?
Почему на правила вывода в формальных системах накладывают такое ограничение, что число их должно быть конечно? По-моему, как и в случае с аксиомами, достаточно, чтобы правила вывода составляли перечислимое множество, которое даже не обязательно должно быть эффективно разрешимым.
Ведь вся суть формальных систем - в том, чтобы множество теорем составляли перечислимое множество. Думаю, что и должно быть общим определением формальной системы, а уж с помощью каких алгоритмов это множество определяется (в частности, введение самих таких понятий как аксиомы и правила вывода) - это уже частности.
А чего ты привязался к классикам насчет неполноты, разве интуиционистская арифметика может доказать собственную непротиворечивость?
Арифметика Гейтинга - это конструктивный объект, как и все другие конструктивные объекты, служащий в т.ч. контекстом для всех возможных построимых выводов из него. И как для любого другого конструктивного объекта, любой такой вывод можно сделать не обращаясь к чему-то внешнему. В конструктивной системе заведомо непостроимо то, что из нее не выводимо и наоборот - нельзя вывести то, что нельзя построить. Это классически можно нарисовать закон исключенного третьего, а дальше как знаешь, никого не ебет, как ты его будешь доказывать в случае, когда построимое доказательство невозможно. Насчет непротиворечивости, любая конструктивная система непротиворечива, поскольку в таковой невозможно построить что-то и одновременно свести возможность такого построения к абсурду.
> И как для любого другого конструктивного объекта, любой такой вывод можно сделать не обращаясь к чему-то внешнему.
Ты, кажется, плохо понимаешь, что такое неполнота. Для того, чтобы сформулировать теорему о неполноте, нужно две системы - "маленькая" и "большая", большая - это наш обычный язык (скажем, арифметика), а маленькая - это модель большой, реализованная в ней самой (погугли coq-in-coq, например). Теорема Гёделя говорит, что большая система не может доказать непротиворечивость маленькой, и для арифметики Гейтинга эту теорему никто не отменял. Твои попытки избавиться от обращения к внешнему (к большой системе с точки зрения маленькой) неубедительны, поскольку большая и маленькая система изоморфны.
> любая конструктивная система непротиворечива,
Сферическая логика в вакууме непротиворечива, потому что любой терм типа ложь можно доредуцировать до конструкторов, а их в типе ложь нет. Но арифметика - ни разу не сферическая логика в вакууме, оттого и неполнота.
Но если система выводима из себя, как из контекста, то и противоречивость ее так же выводима непосредственно, т.е. построима.
аргументируй
Допустим, у меня есть алгоритм, с помощью которого я получаю бесконечную последовательность формул, и каждую такую формулу я считаю теоремой. Чем плоха такая формальная система?
Не в каждой формальной системе возможен алгоритм, выдающий все теоремы и только теоремы.
Что такое "выводима из себя, как из контекста"?
"Противоречивость построима" - в смысле ложь доказуема?
Ты о чем вообще?
Теорема - это по определению и есть то, что выдаёт алгоритм формальной системы. Ты путаешь "теорему" с "истинным высказыванием". Действительно, не все формальные системы полны - в сильных формальных системах не каждое "истинное высказывание" является "теоремой".
Объясни, пожалуйста, что ты понимаешь под алгоритмом формальной системы. В моём представлении формальная система - это ориентированный граф, в котором вершинами являются формулы, и стрелка из вершины A в вершину B есть тогда и только тогда, когда [тут описываются т.н. "правила вывода"]. Некоторые формулы называются аксиомы (между прочим, из любой вершины есть стрелка в каждую аксиому). Пути, начинающиеся в аксиомах, называются доказательствами. Формула называется теоремой, если ею оканчивается какое-нибудь доказательство.
Каждое доказательство формальной системы может быть верифицировано алгоритмом (который проверит это доказательство по строчкам и скажет - да, действительно, это доказательство корректно). Из этого следует, что и все аксиомы, и правила вывода тоже должны быть проверяемы алгоритмом. Поэтому мы, например, не можем сказать "возьмём в качестве аксиом нашей формальной системы все истинные предложения о натуральных числах". Просто потому, что нет такого алгоритма, который мог бы проверить истинность или ложность каждого предложения.
А поскольку множество доказательств счётно (каждое доказательство - конечная последовательность символов), то мы можем запустить алгоритм, который будет последовательно продуцировать корректные доказательства таким образом, что каждое корректное доказательство на каком-то этапе будет выведено. А значит, можно запустить алгоритм, который будет продуцировать теоремы, причём все теоремы (каждая теорема будет иметь некий конечный номер n). Естественно, имея формулу, сказать заранее, является ли она теоремой, то есть будет ли она выведена нашим алгоритмом или не будет, нельзя. Более того, этого нельзя в общем случае эффективно проверить, так как наш алгоритм работает бесконечно долго.
Но в целом для любой формальной системы ситуация выглядит так: существует алгоритм, который продуцирует только теоремы и при этом все теоремы. Доказательством при этом в общем случае можно считать указание на номер, под которым данная теорема будет выведена (так как здесь мы уже можем эффективно, за конечное время проверить, действительно ли n-ая теорема, выдаваемая алгоритмом, есть наша формула).
По-моему, именно такая, алгоритмическая точка зрения, даёт наиболее общее понятие формальной системы и теорем (всякие аксиомы, правила вывода - это частности; на самом деле, не так уж и важно, как именно наш алгоритм работает).
Спасибо.
Это копия, сохраненная 13 ноября 2023 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.