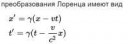Это копия, сохраненная 21 октября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

Если вы хотите задать вопрос типа "как мне взять этот интеграл", это не сюда. Вам нужен тред "для начинающих", он плавает неподалёку.
Предыдущий: >>355215 (OP)
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
46. https://arhivach.org/thread/156244/
47. https://arhivach.org/thread/159628/
48. https://arhivach.org/thread/165872/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
46. https://arhivach.org/thread/156244/
47. https://arhivach.org/thread/159628/
48. https://arhivach.org/thread/165872/
Наверное, глупый вопрос, но мало ли, может узнаю что-то новое... Куда поступать в этой стране если хочется обмазываться мат статистикой?
А про это лучше спрашивать в /u/.
Поошел нахуй.
В бакалавриат или в магистратуру? В бакалавриат все равно куда, потому что нормальной статистики в бакалавриате быть не может: для нее нужно знать теорвер, для теорвера нужно знать теорию меры и довольно много классического матана, потому что без теории меры и интеграла Лебега тупо даже статьи на википедии не понять. То есть поступать надо туда, где именно матана много. Если вопрос про магистратуру, то я хз.
Открою тебе секрет, если сидеть на жопе, то даже колтех даст столько же, сколько какая-нибудь региональная российская шарага.
f:R->{0,1}.
Для любого x: f(x) = 0, если гипотеза Римана верна, и f(x) = 1 в противном случае.
Функция которая ставит 1 или 0 машине Тьюринга если она останавливается или нет.
А тот еблан какую-то хуйню написал.
Я с прикладной математики собираюсь поступить в магу по чистой. Вообще в требованиях у большинства мест написано что-то вроде "undergraduate on mathematics or related fields", так шо может пронесёт :3
У тебя охуенные представления о вычислимости. Сегодня функция невычислимая, а завтра кто-то докажет гипотезу Римана и она станет вычислимой? Не писал бы хуйни, коль не шаришь.
Ладно, не буду.
Лично я пожарил картошки.

Каждый должен делать свои подобные списки, пользоваться готовыми - бесполезно, зашквар и картофан.
может я не прав, но мне всегда казалось, что этот раздел... скажем так.... меньше связан с другими разделами, чем другие разделы... как-то так
>Наверное, глупый вопрос
ОП так старался описать суть этого треда, но первый же еблан доказал, что шапок ЭТО НЕ СЮДА никто не читает лол
pi=4-p2h
>>368397
Нам нужен 2ch.hk/math, будет формироваться своя аудитория, без анальной мерзкой мочи и залётных из таких https://2ch.hk/sci/res/341186.html (
Приветик :3
Смотри внимательнее в ю. Там сильная алгебраическая школа.
http://dobrochan.com/u/res/147901.xhtml#i147901 магистратура
>>368432
Без лишнего шума безусловно надо подтирать только очевидный спам и вайпы. В остальных случаях польза сомнительна, а баттхерт неиллюзорен.
Даже любой откровенный урод >>368432 имеет право быть услышанным всеми, без удаления его мнения.
Моча не нужна.
Вот, двачую.
Достаточно не кормить троллей. Все.
Нет. В /b это происходит из-за соответствующей аудитории - мат. тред, соседствующий с КРЫМАТРЕДОМИ, ТНН, ЕОТ, РУЛЕТАЧКА и прочим говном, мягко говоря, не очень. Можно просто сформировать свою аудиторию и модератор не будет нужен.
Кстати по-моему мат. тред в /sci/ это эдакий аналог "столовки" или "курилки", в которой разные прошаренные посоны могут посидеть и попиздеть на околофилософские темы. С этой перспективы обсуждение оснований и (да-да-да!) определения N мне кажется вполне уместным тут.
Давно здесь не был, но раньше как не зайду, атк всеь тред засран аксиоматикой пеано и прочим непотребством.
двачую. особенно если есть два треда
>эдакий аналог "столовки" или "курилки", в которой разные прошаренные посоны могут посидеть и попиздеть на околофилософские темы.
По-моему ты сейчас описал всю чистую математику.
Когда приходят "философы".
Аксиоматика Пеано - это, конечно, атавизм и непотребство, но все-таки с ней приходится иметь дело, согласись.
Можно вообще индуцировать o-обсуждение для любого ординала o.
А эта чего не устраивает? Или агенты ГУЛАГа до нас и на пользовательской доске доберутся?
А по-моему она абсолютно адекватно отражает нашу интуицию относительно N.
Можно сделать какую-нибудь математическую мелкоборду, хостинги сейчас дешёвые, рублей двести в месяц. Но меня не HTML с php интересовали, а гамалогии, так что я хуй и нихуя не умею.
Абу не даст отдельную доску, что в принципе логично.
Да чем тебя доброчан-то не устраивает?! Бесплатно хостит любой тред, защищает от вайпа и ддоса, практикует матан капчу по праздникам.
Так будем N определять без преград, активность как вулкан раскочегарится. Тут же водой заливают быстро.
Смотрел я на эти чаны, там же в сумме 3.5 человека. Ну не интересно иметь скорость 1-2 поста в сутки.
Да, на мелкоборде то же самое. Я же говорю не о том, чтоб чаи с ними пить, а о том, чтобы использовать это как хостинг для треда.
Имхо активность нормальная, стабильно живущие два треда.
А осенью-зимой, до прихода анального мочерирования и когда был один мат. тред., мат. треды часто уходили в бамплимит за два-три дня - то есть, средняя скорость постинга ~20 в час, что абсолютно нормально для такой ограниченной от большинства темы, как математика.
Предлагаю генераторам объединиться и создать лабораторию имени двачей.
Для лаборатории нужны пробирки, а из генераторов собирается гидроэлектростанция. Чему вас только в этих ваших бауманках учат!
Я тут один вообще, лол.
А да, ты прав, это я загнул про генераторов конечно. Я пишу про <censored> а ты моча и меня трешь.
(Это я сам себе пишу, я сам моча, и сейчас все тут сотру)
Брать часть суммы за контрпример.
ЛОВИТЕ ФИЗИКА
Вот вам пример - "хей матаны", типа новый анон вкатился. Но кол-во постеров осталось 16. Моча забыла ай пи сменить.
Да я тут целый день сижу, ёба, мне нужно великие дела творить, а я как долбоёб 3:
Лол.
Ну так знаем, групповая взаимная прокрастинация.
Я-то думал он москвич, я-то думал - наш мужик! А он, сука, не Гротендик, а какой-то Гротендик.
Что за хуй? Чем знаменит)0
Естественно. Реклама сторонних ресурсов жи.
Это не какой-то определённый список, это просто 20 гигов книг.
>>368503
Суть в том, что если будет свой раздел - можно эвакуировать н-петухов и ниспровергателей математики в специальный фрический тред.
Их и так можно эвакуировать.
У форчковцев примерно такая же беда с "решите домашку плиз" и "1 =/= 0.(9)" тредами. Я бы хотел сидеть на такой чисто математической интернациональной борде. Такая, которая заполняла бы пустое пространство в интернете между с dxdy с одной стороны и mathoverflow/stackexchenge с другой.
Но ведь н-петух не занимался ничем таким. Он указал на объективно существующие недостатки, а потом набежали школьниики и началось "ахаха лол матиматику опровергает".
Еще год назад с посонами собирались пилить, да так и не собрались. Все равно бы не взлетело. Да, я пидораха, ну убейте меня теперь, что.
Н-петух, ты заебал, твои "недостатки" были осознаны и отрефлексированы ещё в венском логическом кружке. Очень хорошо, конечно, что ты пришёл к постановке этого круга вопросов самостоятельно, но не стоит думать, что ты первый.
Я не н-петух. А н-рпетух и не говорил, что он первый. Он кнуебку пытался объяснить, да тот так и не уловил.
Макака совсем ебанулась, кстати, и сделала какую-то невводимую капчу. Я так и не понял, что туда надо писать. Вангую, что скоро ее введут и в тематике, и на этом мое общение с этим сайтом закончится.
Я и есть кнуёбок, сириусли. Я с самого начала говорил, что дискурсы разные: над этими вопросами можно рефликсировать с логико-философских позиций, а не с позиций современного подхода к формальной математике (формализм/плюрализм, по сути) - с которых всё предельно недвузначно. В ZFC никаких парадоксов и порочных кругов нету.
Ох, лол, ну надо же. Да на самом деле мы с тобой в каком-то из тредов вроде бы коротко говорили и сошлись на том, что друг друга поняли.
В зфц парадоксов пусть и нет, но и на роль основания она не подходит, а чисто формалистический подход ведет к моральному разложению.
Привет ^^
>В зфц парадоксов пусть и нет, но и на роль основания она не подходит, а чисто формалистический подход ведет к моральному разложению.
Ну тут надо разделять задачи. Есть задача "подогнать основания понадёжнее", а есть задача "научиться математике". Вторая, конечно, никак с первой не пересекается, почти. А первую задачу формализм решает довольно неплохо. ПО крайней мере в отличии от идеологической жвачки интуиционизма Брауэра и конструктивизма Маркова он даёт какие-никакие прочные основания и довольно стойкий к критике.
Или ты про эффекты, когда утилитарное понимание числа не совпадает с РА потому что можно подогнать многочлен, который не имеет корней "на самом деле", но это в РА недоказуемо?
Недавно, кстати, нашёл такую статью об основаниях http://logic.harvard.edu/koellner/TM.pdf сам недочитал ещё, но годная дико (там, вроде, плюрализм критикуется, но до критики я пока ещё не дошёл), может кому ещё интересна будет.
капча наоборот до сих пор была невводимая, котрая для иностранных адресов. а вот только что смотрю поменялась на более читаемую. видно как в /b капчу ввели недавно, битарды охуели.
Мунин?
Его отец - украинский анархист Сашка Шапиро.
https://ru.wikipedia.org/wiki/Шапиро,_Александр_Петрович
>В ZFC никаких парадоксов и порочных кругов нету.
Зато есть так называемые "абсолютно неразрешимые проблемы" вроде континуум-гипотезы и прочих аксиом Мартина. В ZFC не существует не только доказательства этих проблем - в ZFC не существует даже наводящих соображений для этих проблем. Просто не существует даже философских причин, по которым эти гипотезы нужно принимать или отвергать.
Ну про "не существует философских причин" я бы не говорил так громко. В остальном: и что? Это никак не отменяет того, что ZFC - это синтаксически очень определённая штука, и что идея формального подхода к основаниям математики состоит в редуцировании любого рассуждения к синтаксису ZFC.
>"не существует философских причин" я бы не говорил так громко
Почему? Ведь всё то, что обычно принято называть здравым смыслом, уже отражено в ZFC. Абсолютно неразрешимые проблемы выходят за рамки здравого смысла.
Ну в статье которую я приводил есть аргументы. Например, Con(ZFC) не зависит от ZFC, поэтому ZFC+Con(ZFC) и ZFC+(не Con(ZFC)) как бы абсолютно равноправные теории, но в первую как-то верится больше, а в статье, вроде, есть какие-то более серьезные метаматематические аргументы в пользу того, что первая теория "лучше".
Потом, есть стандартный аргумент с теоремой Мятисевича: мы можем построить в ZFC многочлен P который (с точки зрения метатеории и здравого смысла вообще) не будет иметь корней, но про который ZFC не сможет доказать, что он корней не имеет.
Про аргументы касательно CH я знаю меньше. На вики перечислены же. Для платонистов, например, CH - серьезная мировоззренческая проблема, не в плане каких-то теорий и значков, а в плане того, удовлетворяют ли правильные множества этой CH или нет. Вот если меня на каком-то онтологическом уровне спросили бы об истиности CH, я бы ответил, из какого-то "онтологического максимализма" что ли.
>но в первую как-то верится больше
Не факт. Проблема континуума в том, что требуется указать такой ординал n, что алеф-n равен c. Доказано, что n>0. Континуум-гипотеза утверждает, что n=1. Но почему бы не предположить, что n=ω0?
Физики и про дифференциальные формы и когомологии де Рама зачастую не слышали, они вообще долбоёбы.
Представь. Ты учёный-физик. Сидишь на практикуме по механике, решаешь задачу:
На концах невесомой нерастяжимой нити, перекинутой через легкий неподвижный блок, подвешены два груза, массы которых равны 100 и 200 г. В начальный момент времени грузы покоятся на высоте 2 м от пола. Пренебрегая трением, определите ускорение грузов, натяжение нити при движении грузов и время, за которое груз массой 200 г достигнет пола.
Ну и на кой чёрт тебе нужна тут теория множеств? Граммы множеством моделировать?
На самом деле физикам не нужно ничего сложнее символьной арифметики (включая таблицы производных и изображений). Физики просто подставляют числа в готовые формулы, в этом и заключается суть их науки.
>Физики просто подставляют числа в готовые формулы
А разве большинство математиков так не делают?
Нет. Математики вообще крайне редко видят числа. Даже теоретико-числовики. Особенно теоретико-числовики.
Лол.
у нормального физика, вместо циферек, буковки, а циферки подставляются в самый последний момент.

Суть в том, что физик - это просто тупой механизм. Легко можно написать программу, которая будет решать задачи из книжки пикрелейтед не хуже физика. Вся деятельность физика - ритуальное совершение раз и навсегда определённых, канонiзированных манипуляций над коротенькими текстами.
http://dxdy.ru/post773884.html#p773884
ну это конечно толстота, человека который про физику слышал на заднем дворе..
Хелемский лекции по функционалному анализу, там вроде самое нормальное фурье на группах компактных вводится.
ну как и у математиков, где-то на 3 курсе, научкой начинает заниматься народ, практикумы уже к концу подходят если не подошли.
Школьник, съеби в ун.
Можем мат-мемы обсудить.
У математиков в принципе нет хуйни типа "взять сто интегралов на время".
Просто обожаю её! Каждый день ем.
В пидорашковуз я поступал, да. Ушёл после первого курса. Представляете, эти уроды вздумали меня пытать принудительной физкультурой. Физкультурой!
Любая контрольная. Помню была контрольная в том семестре на 1 пару, где надо было посчитать 4 полных дифференциала второй степени от двух переменных от неявных функций. Точнее там не тупо посчитать, а в приложениях это требовалось.
>>368595
Неосилятор детектед. Хз у нас физра просто охуенная - летом бассейн, зимой лыжи.
Разумеется. Я математик. Какого чёрта я должен тратить драгоценные часы своей жизни на хуйню?
Нет, разумеется. Это ненужный маразм.
Принудительная физкультура - зло, это утверждение верно независимо от моей личности.
Нет, верно. Если человек пришёл учиться математике, то его следует учить математике, а не заставлять подпрыгивать под угрозой отчисления.
Кроме того, в рашковузах она есть. Ей заставляют заниматься три курса, и на неё отводится больше часов, чем на алгебру, топологию и множества вместе взятые.
Во-первых, три. Во-вторых, даже если есть справка, всё равно заставят отрабатывать. Писать сочинения про гантелю или играть в шахматы.
Везде по разному, видимо. У нас 2. И если притащил справку, то можно не ходить и доклад скачать в нете.
В универ идут получать высшее образование, а не учиться математике.
Бамп вопросу.
Норм, я их знаю.

Странно, вот это вроде звучит как раз для даунов.
Сап, Пифагоры, ткните носом как называлась теорема о том, что бесконечность натуральных чисел меньше бесконечности вещественных [0,1], а то совсем из головы вылетело.
Диагональный метод Кантора.
"Мир как воля и представление" Шопенгауэра в гугле был где-то годный пересказ, погляди.
Ну можешь еще обмазаться статьей про Гиперреальность на вики и почитать кого-то из авторов, но последнее лучше не делать. А так собственно и все представление. Ну, еще можешь навернуть про жестокий театр Антонена Арто.
>>368792
Нет науки про теорию (на самом есть, но это То что нельзя называть).
>Я не хочу ничего учить, я хочу видеть
Видишь ты в нестрогом рассуждении, которое я привел. Оно несложное.
Все становится страшным, когда мы переводим это на формальный язык матана. Но трудности здесь ближе к лингвистическим. Примерно столь же сложным было бы утверждение о композиции непрерывных функций, если бы ты решил провести действительно строгое и формальное доказательство. В итоге получилось бы нагромождение кванторов и логических символов. Однако же у тебя нет сомнений, что при желании ты мог бы без особого интеллектуального труда его выписать, так как владеешь аппаратом формальной логики.
По сути в любой науке математической есть такая полулингвистическая техника. Она не делает доказательства сложнее, только страшнее на первый взгляд.
В матане это техника выписывания эпсилонов и дельт с соответствующими оценочками и приговорами про достаточно большое N повсюду.
В топологии, например, доказательство любой гомотопической эквивалентности (даже в общем виде) это страшные на вид рассуждения, которые однако всегда делаются одинаково, поэтому не являются существенной трудностью.
Это, кстати, не лингвистические трудности, это недостаток абстракции, если уж по-хорошему.
мимо
В теории меры строят свои аналоги производных и интеграла, которые концептуально ничем от "обычных" производных и интеграла, известных из анализа не отличаются, но с ними удобно работать на уровне доказательств.
Нет, весь матан построить нельзя. Например нет аналога интегрирования по частям для интеграла Лебега.
В смысле? Какие абстракции позволяют в матане избежать ебли с оценочками?
Вообще-то да, топология действительно позволяет сдать в дурдом большую часть эпсилонов с дельта.
Покажи мне с помощью тензоров как доказать правило дифференцирования сложной функции хотя бы в одномерном случае.
Kek.
Придумывать примеры к определениям, ещё можно писать что-то типа "intuition for thingname" в гугле и иногда что-то тоже полезное пишут.
Зависит от времени, которое ты потратишь. У всех разные техники, но основная идея в том, что чтобы понять какой-то объект, надо самому с ним работать.
Прочитав определение, можно придумывать примеры, можно подумать, зачем вообще этот объект нужен, какие у него свойства, можно придумать какую-то геометрическую интерпретацию.
С доказательствами сложнее. Каждый раз при прочтении доказательства думать о том "как можно было до этого додуматься" - довольно неблагодарный труд, потому что часто встречаются трюковые доказательства. Ты можешь тратить многие часы на попытки придать доказательству глубинный смысл и прочувствовать его, на поиск более красивых доказательств, но выхлоп в плане понимания от этого довольно слабый.
В конечном итоге, все зависит от времени, которое ты готов потратить. Если ты готов по несколько дней медитировать над 5ю страницами текста, то можешь делать все описанное выше и у тебя будет глубокое понимание. Но если ты будешь так дотошно читать все математические тексты, ты ниче не успеешь.
Полезно во время решения задач какать. Я только так и могу решать, по другому не выходит.
φ.
Это зависит от области и от человека. Просто пробуй разные методы и потом через какое-то время попробуй порефлексировать и оценить. Есть люди, которым надо картинку, есть люди, которые видят уродливую формулу на полстраницы и им сразу все понятно.
Посмотри ИППИ, Премолаб, ИПУ и соответствующие кафедры в университетах ДС.
>>368315
Сука, ещё один. Не обязательно понимать интеграл Лебега, чтобы заниматься статистикой. В статистике как не странно нужно хорошо владеть теорией матриц и методами (функционального)анализа.
Есть три игральные кости, с цифрами от 1 до 6. Ну кароч обычные игральные кости. Вопросы:
Какова вероятность выпадения комбинации 123? В любом порядке: 321, 231, 132.
Как её рассчитать?
Равна ли вероятность выпадения трёх одинаковых цифр вероятности выпадения трёх разных?
эксперимент проводится в вакууме
> Какова вероятность выпадения комбинации 123?
3/(6^3)
> Как её рассчитать?
Возьми любой учебник для даунов и прочитай первые несколько страниц.
> Равна ли вероятность выпадения трёх одинаковых цифр вероятности выпадения трёх разных?
Нет. 3 одинаковых:
6/(6^3)
3 разных: (6 x 5 x 4) / (6^3).
Нужных комбинаций шесть.
123 132 213 231 312 321
Всего комбинаций 63.
Вероятность выпадения нужной комбинации 6/63 = 1/36.
А ну да, я чет посмотрел на
> В любом порядке: 321, 231, 132
и почему-то подумал, что их 3, лол
На одном пики, на другом хуи, а третьем что? Картофан или тапалогии и гамалогии или может быть Рыбников? Этот вопрос не даст мне сегодня заснуть.
У меня есть мечта, что когда-нибудь Рыбников напишет книгу "тапалогии и гамалогии древних русов" и тогда я наконец-то смогу их освоить.
Пространства кручёные.
Бамп
Неважно. Моя мысль заключалась в том, что прежде чем серьезно заниматься статистикой, надо пару лет позаниматься другими разделами математики.




Пока могу посоветовать Начала православной арифметики, что-то уровня Рыбникова или выше.
Да иди ты нахуй со своей репой.
лол
с натуры?
Только очень малая часть совр. мат. аппарата юзается физиками. Ну, топология, дифф. геометрия, С*-алгебры, группы, кое-что из алгебраич. геометрии, твисторы, супералгебры (причем многое уже было самой физикой и мотивировано, лол). То, что реально работает и зарекомендовало себя. Ну и таки да, есть ряд отмороженных маргинальщиков, которые занимаются ёба-сверхматематизацией физики и выдристывают статейки в духе "а вот давайте-ка этальных когомологий сюда применим, диаграмм и морфизмов навернём и скажем - воооот, а мы тут у мамы математику к физике применяем, а вы говорите,что эти конструкции нинужныы!". (Нет нужды говорить,что 99% этих статеек оседают на днище журналов и arxiv'ов, никем не замеченные.)
Во, годная тема для срача же!
Во-первых как сверхрадикальный формалист заявлю противоположное утверждение: ровно те методы, что форсят и находят применения в физике, тупо потому, что других нету. Если бы все форсили интегралы, то 95% людей брало бы интегралы, а всей остальной математикой занималась бы кучка маргиналов. Wait, oh shi...
Во-вторых, даже если бы в математике использовалось 0.01% всех конструкций - это уже её бы целиком оправдывало, как фундаментальную область знаний.
В-третьих. 99% любых статеек оседают на днище arxiv'oв никем не замеченные, так что глупый аргумент совершенно.
В-четвёртых. В математике, спустя десятилетия остаются только те идеи и конструкции, которые оказались наиболее мощными - упрощают значительную часть доказательств, даёт новые исчисления и формализмы, позволяют подключить иной тип интуиции. Если "бесконечная аутичная игра в бисер" не приведёт в итоге к значительным сдвигам в наиболее важных проблемах математики - об этой игре забудут, и начнут создавать другую. А может и не начнут.
Во-первых, форсятся универсальные вычислительные методы. Всё остальное должно выиграть в "аутичную игру в бисер".
>>369082
Во-вторых, Витгенштейн например некотировал физику, но котировал матаны.
В-третьих, 99% всех работ не становится классикой из-за обширности самих математики и физики. Всегда найдётся долбаёб, который прочтёт йоба-статью.
>Во-первых, форсятся универсальные вычислительные методы. Всё остальное должно выиграть в "аутичную игру в бисер".
Ну так если бы форсили матан не на пределах, а на кольце eps^2=0, например, то именно это считали бы "универсальным вычислительным методом", а матан на пределах - хуйнёй для маргиналов.
Остальные два пункта не понял.
Почему?

поможешь, антон ?
Пиздуц в тред к начинающим со своей школьной хуйнёй.
В комплексных, условия для сходимости почленного дифференцирования/интегрирования намного проще формулируются чем в анализе на R, но без равномерности никак.
Я обсирал, привет. Напишу развёрнутый ответ чуть позже.
Равномерная сходимость вменяемо изложена в книгах Бурбаки. Они ввели понятие "равномерная структура".
Da.
Любая метрика появляется из некоторой нормы?
Нет, только для которой выполняется закон парллелограма: ||a+b||^2 + ||a-b||^2 = 2||a||^2 + 2||b||^2
Нет, метрика может быть задана вообще не на линейном пространстве. Например, дискретная метрика (расстояние между любыми двумя неравными точками = 1) не может быть индуцировано нормой.
> Нет, метрика может быть задана вообще не на линейном пространстве.
А есть какое-нибудь такое же необходимое и достаточное условие как для нормы и скалярных произведений?
Предметрика на некотором ЛП порождена некоторой нормой титтк она инвариантна относительно сдвигов и d(0,lambda x) =|lambda| d(0,x)
преднормой*
Можно вполне продвинуть некоторые области функ. анализа, теорию фреймов например. (Про РАН ничего не знаю)
Я тут внезапно призадумался, и должно быть это платиновый вопрос, но если учесть что все числа кроме рациональных "не настоящие", чему равна длина диагонали квадрата со стороной в одну единицу? Можете ткнуть как Валдбергер выкручивается из этого канандрума?
Вилдбергера не смотрел (вернее смотрел, но только его лекции по АТ), но как выкручиваться - понятно, отождествлять корень из двух с алгоритмом (основанным на рациональных числах) который его вычисляет.
Получается мы возьмем треугольник и у двух его сторон длина это единица, а у третей - это уже только алгоритм. Как-то это противоестественно.
У двух сторон длина тоже алгоритм, только более простой: выводящий последовательность из "1".
В таком случае можно сделать вот что.
Последовательность рациональных чисел называется фундаментальной, если для всякого рационального числа ε>0 существует такой номер n, что для любых двух членов последовательности с номерами, большими n, их разность по модулю меньше ε.
Две фундаментальные последовательности x1, x2, ... и y1, y2, ... называются эквивалентными титтк последовательность x1, y1, x2, y2, ... является фундаментальной.
Это отношение является отношением эквивалентности. Множество всех фундаментальных последовательностей разбито, таким образом, на классы эквивалентности.
И в чём проблема?
Проблема в том, что класс эквивалентности фундаментальных последовательностей для Вилдбергера онтологически неосязаемая и несуществующая вещь.
Типа да; некоторым машина тьюринга кажется чем-то намного более понятным, чем какие-то там классы эквивалентности. Ну и понятно по каким сображениям им так кажется. Класс эквивалентности - нечто очень абстрактное и заоблачное, а алгоритм - написал на пэхапэ нажал Ctrl+F5 и на экране хуярят приближения к квадратному корню - чё может быть более осязаемым чем это?
>>369960
Вычислимое вещественное число (хотя это у конструктивистов, у Вилдберга всё радикальнее, видимо).
Я вот какой достаточно простой аргумент припомнил.
Количество действительных чисел несчетно. Количество машин Тьюринга - счетно. Значит просто нет столько алгоритмов чтобы все эти числа воспроизвести. Значит их не существует.
Что скажите?
Я скажу, что это https://ru.wikipedia.org/wiki/Парадокс_Скулема
>среди элементов M нет такого f, что в модели M оно удовлетворяло бы свойствам биекции между w и P(w)
Посмотри, где работали Филдсовские лауреты.
Спойлер: ИППИ первая по числу лауреатов в мире%%%
Очень напоминает начально-конечные объекты категории. Рядышком определяют предикат и получают что-то вроде логики. Думаю, подобным образом можно определить алгоритм.
>>369869
Так-то вещественные числа можно определить как пополнение рациональных или предел p-адических. Алгоритм? Не уверен, что до определения Валдбергера дотягивает.
Мат. физика и статистика(не курятник машинного обучения) там вроде не плохая.
Школьник, притухни.
А какое у него определение? Пополнение рациональных эквивалентно вещественным числам, вряд ли W этого не знает.
курятник?
Охуенный чувак на видео, только после его лекции о теории Галуа, я хоть как-начал вникать в теорию груп.
Я пишу статью по проблеме континуума.
http://lvlb.ru/Void/Continuum.html
Прошу советов и критики.
Спасибо.
Не, всё ещё шизофазия не имеющая отношения к математике, а уж тем более мета-.
>Заметим, что мощность множества N0 больше мощности множества N, и равна ω+1.
Это неправда. Доказательство знают все, кто знает слово "мощность множества".
ну если вы назовете натуральное число, которое можно записать бесконечной последовательностью единиц например, то я очень удивлюсь
в канторовской таблице существуют элементы не принадлежащие множеству натуральных чисел
Условно говоря это все, что не содержит в конце бесконечную последовательность нулей, т.е натуральные записываются как:
1000(0)
0100(0)
1100(0)
0010(0)
etc.
В канторовской таблице вообще не натуральные числа, а последовательности из нулей и единиц. То, что последовательность из нулей и единиц у которой почти все элементы нули можно отождествить с натуральным числом - никакой роли не играет.
Ничего не понял. Можешь изъяснятся не обрывками фраз, а цельными утвержденими?
Ну да, множество последовательностей из 0 и 1 имеет континуальную мощность. И что?
Ну вот есть например множество целых чисел
Считается, что оно счетно. Это не так.
Примем за натуральный ряд вышеописанные числа, а в качестве отрицательных - антиэлементы, заканчивающиеся всеми единицами.
Очевидно, что мощность натурального ряда такая же, как и мощность отрицательных.
Однако мощность целых больше, чем мощность натуральных или отрицательных отдельно.
Т.к вы не можете назвать натуральное число даже заканчивающееся бесконечной последовательностью единиц.
Там еще много всяких таких, например заканчивающееся бесконечной последовательностью 010101(01), тоже туда же.
Ты построил инъекцию из натуральных чисел в целые, не являющуюся биекцией, и сделал отсюда вывод что биекций между натуральными и целыми числами не существует, всё правильно понял?
я не строил ничего из натуральных в целые, это невозможно.
можно построить биекцию из натуральных в отрицательные, но нельзя из натуральных в целые
Почему?
Построил биекцию между своим членом и твоей щекой, проверяй.
Во первых когда ты говоришь о отображении X в Y то образ - в Y. Во вторых, биекция это взаимно-однозначное соответствие.
проверил, ничего нет, строй еще
Колмогоров Фомин - элементы теории функций и функционального анализа хорошая книга.
Так я и построил, бери обратное.
0 -> 0
i > 0 -> 2i - 1
i < 0 -> -2i
>>370362
> В общем я не сомневался
Ты не понял самые основы и бросился метать претенциозные заявления. Уж не гуманитарий ли ты по образованию?
Из целых я строю в положительные целые. Заметь что ничто не отображается в число меньше нуля.
Да, и ты походу путаешь местами образы и прообразы.
Ты понимаешь, что x -> y означает что x переходит в y?
x = 3 = 2i - 1, отсюда y = i = 2.
т.е. 3 -> 2.
Машинное обучение в том виде, в котором оно существует в массах это прикладная статистика + методы оптимизации + что-то из алгоритмов. Поэтому исследования сводятся к придумыванию новой архитектуры, эвристики, кодированию и сравнения своих результатов. Обычно никаких оценок на ошибку классификаций и тому подобное, а если есть, то наследуются напрямую из используемых методов.
В противовес этому конечно есть работы в духе ВЧ-размерности, или подходят алгебраически к теории, рассматриваю категорию алгоритмов классификации, или всякие непараметрические методы, где выводятся какие0нибудь оценки на случайные матрицы.
> Машинное обучение в том виде
Это у нас или вообще?
> В противовес этому конечно есть работы в духе ВЧ-размерности, или подходят алгебраически к теории, рассматриваю категорию алгоритмов классификации, или всякие непараметрические методы, где выводятся какие0нибудь оценки на случайные матрицы.
А есть что почитать по научному подходу?
Тут не простое непонимание, тут непонимание + претензии на гениальность и разрушение основ математики, откуда полное нежелание что-либо слушать. Пусть пиздует в тред для начинашек.
> W этого не знает
Поэтому не уверен.
Реквестую фанов W пояснить за его определение алгоритма.
Может из методических соображений пойдёт читать на вики о парадоксе матиматиков со шляпами(или туфлями)? Если не трол, то должно дойти.
> Это у нас или вообще?
Ну это глобальный тренд. Но вообще говоря машинное обучение придумали русские из ИПУ как раз кампания Вапника и Червоненкинса.
> есть что
Есть конечно, но я не спец здесь. Вот оригинальная статья по ВЧ-размерности.
Vapnik and A. Chervonenkis. "On the uniform convergence of relative frequencies of events to their probabilities." Theory of Probability and its Applications, 16(2):264–280, 1971
Про алгебраические методы кто-то из ВЦ РАН(Рубаков или Рудаков, например).
Хочешь вскрыть тему? Иди в /pr/ там есть отдельный тред под это.
привет.
Вчера спать пошел, вы предлагаете перевести четные в отрицательные, а нечетные в положительные, да это действительно будет работать, в обе стороны.
Я думаю, что вопрос в недостижимости полного покрытия бесконечного множества другим бесконечным, буду пытаться как то описать это.
Спасибо.
Добавил в статью раздел проблемы.
Но ведь существование бесконечного количества несчетных множеств среди бесконечной последовательности бесконечных последовательностей нулей и единиц доказано.
Доказано, только целые не биективно отображаются в последовательности, так что никакого противоречия.
А что вы скажете на счет несчетности N0?
Представимо, как N U {0}, где 0- бесконечная последовательность нулей.
|N0| = омега+1
Что тебе мешает взять учебник и почитать?
N0 (это, в общем-то и называется обычно натуральными) так же счётно как N, как Z+, Z- или Q.
Дохуя-то дохуя, но так и инварианты могут состоять из охуенно бесконечных серий.
Ну и на практике, известны-ли тогда может многообразия у которых всё-всё из широко известного сегодня (гомотопические группы, гомологии и когомологии, K-функторы всякие, бордизмы, и.т.п.) совпадает, а они не гомотопны?
Как посчитать интеграл Лебега для простой функции на интервале от нуля до бесконечности?
1) Тебя наебали, простая функция - это конечная линейная комбинация характеристических функций измеримых множеств, а тут очевидно не конечная.
2) Давай распишем f(x) = Sum[n=1..inf] 1_[n..n+1] 1/[n!]. Стало что-то понятнее, мммм?
>>370785
Типа того, бля, только это не простая функция, серьезно абсолютно, не троллирую. Привет.
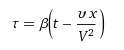
Потому что вся петушня была сосредоточена вокруг взятия интегралов нуфагами. А с созданием новго треда все перешли туда и тут лишь изредка отписываются.
Что за интегралы у нуфагов? Я думаю, неактивные, потому что на харкаче сейчас в целом ядерный пиздец.
Хм, забавно, выходит где-то у того парня должна была быть и верхняя формула, ведь это система диффуров, и без первого смысла нет?
> "как мне взять этот интеграл", это не сюда
>Вам нужен тред "для начинающих", он плавает неподалёку.
>Сап, Пифагоры, ткните носом как называлась теорема о том, что бесконечность натуральных чисел меньше бесконечности вещественных [0,1], а то совсем из головы вылетело.
человек книгу открыть не может
HeT.
Опять ты.
>>371053
Прямой - это приведение матрицы к ступенчатому виду. Forward и backward substitution вместо образуют обратный ход. Типа мы нашли разложние LU = PA. Это прямой ход. Теперь когда мы решаем LUx = Pb - это обратный ход. Когда мы решаем Ly = Pb - это forward substitution (потому что находим сначала y_1, потом y_2, и т. д.). Когда мы решаем Ux = y - это backward substitution (потому что находим сначала x_n, потом x_{n - 1}, и т. д.).
Короче, я решил это называть "подстановка вперед" и "подстановка назад".
>геометрию в раздел физики
Не смеши людей. Математика строится на логических выводах из аксиом и первичных неопределяемых понятиях, геометрия ничем в этом смысле не отличается от остальных разделов математики.
Физика же - экспериментальная наука, строящая модели в попытке описать окружающий мир, при этом пытаясь опровергнуть или подтвердить свои модели.
Математика же вообще никак не обязана описывать окружающий мир - она работает с идеальными абстрактными объектами.
Пока ты школьник, она тебе нужна, чтобы не пойти в армию. Если ты школьник поумнее, то она тебе нужна, чтобы прокачать мозги и возвыситься над биомассой, это поможет в будущем, и не только при занятиях наукой.
Если ты уже не школьник, и при этом не знаешь о разнообразных приложениях математики в науке и технике, то у меня для тебя очень плохие новости.
>Имеет мощность n, n бесконечно
Ты уж определись, что чему равна мощность, либо мощность равна n, или она бесконечна?
Пока что твой вопрос вообще бессмысленен.
А по-моему вполне осмысленный вопрос. Ответ - да, доказывать по трансфинитной индукции.
Ну-ка докажи заведомо ложное утверждение, где говорится что одновременно мощность равна n, и при этом что она бесконечна?
Шиза какая-то, "n" - это просто значок, который ввел тот кун специально для указания бесконечной мощности.
n - это просто число, поэтому если мощность равна n, то значит множество конечно.
Опять ты, петух, сможешь доказать корректность формулировки этого пидора >>371228 или ты просто спиздануть решил.
Что объяснить? Что такое "объединение к множеств мощности к", где к - бесконечное кардинальное число?
Чего ты разорался, я не твой оппонент.
Да, опиши построение объединения к множеств мщности к, где к - бесконечное кардинальное число.
Да я спокоен, мне просто искренне непонятно, что непонятно. У нас есть семейство попарно непересекающихся множеств V_i, где i пробегает некоторое семейство индексов I. Их объединением Union[i \in I] V_i, называется множество, содержащее все элементы V_i для каждого i. Если теперь Card = Card[V_i] = к то мы получим объединение к множеств мощности к.
Ну да, понял.
>n - это просто число, поэтому если мощность равна n, то значит множество конечно.
Ебать ты дебил.
>возвыситься над биомассой, это поможет в будущем, и не только при занятиях наукой
Сисадмины-таки гордо возвышаются над биомассой? Где ещё она поможет?
Знают, конечно, что не админ - то за теорему Атьи-Зингера поясняет и по высшим топосам угарает.
>>371288
google: "set equipotent to it cartesian product"
сопромат тоже работает с идеальным абстрактными телами - сплошными теломи, теор. мех. так вообще со сплошыми абсолютно твёрдыми телами.
>школьник поумнее
this inb4 скромность зашкаливает (нет)
можешь привести примеры, на счёт того что возвыситься над биомассой? Может просто логики достаточно? Или математика поможет чтобы логику повысить?
Тебе нужно конкретизировать вопрос. Зачем нужна для кого? Это просто некоторая область деятельности, по которой некоторые люди угарают. Некоторые любят в зал ходить и штангу жать, а некоторые любят сидеть и пытаться разбираться в КК-теории.
Господи, да вся физика - это модели и идеальные объекты, только принципиальное отличие от математики в том, что они должны давать предсказания, согласующиеся с экспериментом. От математики этого не требуется.
Кхе-кхе, то есть формализация натуральных чисел (а вместе с ней, кстати, - и вся математика) не должна давать результаты, согласующиеся с экспериментом? Ну-у, кхе-кхе. Когда вы уже кончитесь.
Святая толстота, конечно не должна, математические утверждения не экспериментом доказывают.
Ты наверное просто инженер или что хуже гуманитарий?
Ты правда думаешь, что кому-то интересно от тебя слышать о теоремах и топосах? Это нужно сдать на экзаменах и забыть.
В админы иди.
Мне жаль, что ты не понял, что там написано.
А что, решения линейного оде с переменными коэффициентами с гладкой правой частью не обязательно гладкие?
Ссылка случайна
У однородных ведь правая часть 0. Так что очень понятно, какие дифуры ты рассматриваешь.
*не очень
Аноны.
Есть пианино, 88 клавиш.
Существуют ли для него бесконечные способы создавать композиции?
Что происходит с числом стремящимся к бесконечности, но не являющимся ей в высших размерностях? Проклятие размерность, as is have
Получается, если число классов стремится к бесконечности, то и число будет стремиться к ней?
>>371377
А что в высших разрядностях произойдет? Если разрядность будет стремиться к бесконечности, то число будет стремиться к нулю?
Первые координат m-мерной точки это числа от 1 до 88, которые могут повторяться. n+1 до m просто зануляем. Вот и всё.
>Существуют ли для него бесконечные способы создавать композиции?
Да, более того их количество несчетно.
А что означает в этом случае равенство? Я нагуглил, что две дроби равны, если у них совпадает каждая цифра.
ОДЕ это "обычные дифуры", а не однородные.
Аноны, представьте, что мы совершаем какое-либо действие и каждый раз делаем это в 1000 раз медленнее, чем в прошлый.
Времени - бесконечность.
А количества действий? Когда время станет бесконечным, мы же не сможем совершить действие?
Мне хочется разобраться в определении вещественных чисел через десятичные дроби. Относительно какого отношения эквивалентности 0.(9) и 1 эквивалентны?
Если ты определяешь вещественные числа как классы эквивалентности по пределам последовательностей Коши, то тогда запись 1 и 0.(9) просто обозначают один и тот же класс эквивалентности (потому что 0.9, 0.99, 0.999... - последовательность Коши с пределом 1)
Нет, я определяю вещественные числа по-другому, как строки цифр. Мне нужно именно это определение.
Но ведь равенство определено как совпадение всех цифр.
> вещественные числа как строки цифр.
Это не определение вещественных чисел. Есть 2 способа определить вещественные числа: через сечения Дедекинда и как классы эквивалентности фундаментальных последовательностей.
>>371476
Ну попробуйте определить на множестве строк цифр операции сложения и умножения так, чтобы это было полем. Protip: you can't
С чего это вдруг множество конечных песен несчетно? Сперва пронумеруем все песни из одной ноты, потом из двух и тд.
Зачем тогда рассматривал бесконечные песни?
Пусть вещественные числа определены как строки.
Теорема. Непустое ограниченное сверху множество положительных вещественных чисел имеет супремум.
Доказательство. С цифрами до запятой всё ясно, потому что ограниченное сверху множество целых чисел имеет максимум. Трудности с цифрами после запятой. Построим число, у которого до запятой стоит ранее полученный максимум, а после запятой - дробь, сконструированная следующим способом. Рассмотрим множество всех первых цифр после запятой. Напишем её на первое место после запятой. Оно имеет наибольшую. Рассмотрим множество всех вторых цифр после запятой. Оно имеет наибольшую. Напишем её на второе место после запятой. И так далее. Супремум построен.
Аналогично, ограниченное снизу множество положительных вещественных чисел имеет инфимум. Для отрицательных чисел инфимум - это супремум соответствующих положительных, а супремум - инфимум.
Ясно, что если каждое число из множества M не больше a, то и супремум M не больше a.
Назовём n-ым приближением числа s число, у которого целая часть совпадает с целой частью s, а хвост после запятой обрывается на n-м знаке. Пусть a и b - два числа. Рассмотрим множество M, состоящее из сумм их 1-го приближения, 2-го приближения, 3-го приближения и т.д. Каждый элемент M меньше чем a+b+2, значит, M ограничено сверху и у него есть супремум. Этот супремум называется суммой чисел a и b.
Аналогично определяется произведение, умножение и частное.
Назовём два вещественных числа равными, если для любого e>0 их разность меньше e. Это равенство - отношение эквивалентности. Нетрудно показать, что классы эквивалентности согласованы с арифметическими операциями.
Полем будет фактормножество с этими арифметическими операциями.
> Пусть вещественные числа определены как строки.
А потом ты их определяешь как классы эквивалентности
> Назовём два вещественных числа равными, если для любого e>0 их разность меньше e. Это равенство - отношение эквивалентности. Нетрудно показать, что классы эквивалентности согласованы с арифметическими операциями.
И что, эта уродливая хуйня лучше чем классы эквивалентности фундаментальных последовательностей рациональных чисел?
В столбик, пятый класс.
>>371548
Множество произведений приближений (ab) и c совпадает со множеством произведений приближений a и (bc), так как для конечных дробей (ab)c = a(bc).
Пусть a, b и c - конечные десятичные дроби.
Тогда они представимы в виде обыкновенных.
Соответственно pa/qa, pb/qb, pc/qc.
Нужное утверждение вытекает из ассоциативности умножения целых чисел.
Ассоциативность умножения целых чисел я доказывать не буду.
>А потом ты их определяешь как классы эквивалентности
Нет, определяю как строки.
>И что, эта уродливая хуйня лучше чем классы эквивалентности фундаментальных последовательностей рациональных чисел?
"уродливое" теперь значит "некорректное"?
И в чем проблема? Число = предел рациональных дробей, заданных префиксами такой записи. Тогда 0.999999... очевидно = 1.
Глубоко мыслишь, фраерок.
Кстати да, хороший ответ.
Нормальное, логнормальное, Коши, биномиальное, равномерное - вот это всё.
> Mathematica есть, в любом случае.
У меня её нет, и по возможности хотелось бы просто чтобы сайт был и всё.
По набору данных нельзя выяснить распределение. Распределение вообще нельзя выяснить. Можно лишь предположить, что набор данных соответствует такому-то распределению, и потом вычислить, на сколько процентов это предположение истинно.
Это что такое и как оно влияет на появление квадрата? Объясни, пожалуйста, я совсем тупой.
Почему в формулах для пирамид нет кубический степени? Вообще в стереометрии, насколько я помню, третья степень нигде не фигурирует.
А КУБ?!
Этот вопрос за пределами возможностей современной науки.
Вчера на твитче ввели систему токенов для поощрения стримеров. Но дело не в ней, а в проценте комиссии.
За 1.4$ покупается 100 токенов. Стример же обменивает 100 токенов на 1$. Какая получается комиссия? 40/100 или 40/140?
Что такое процент комиссии? Дай точное определение.
Бля, покупаешь 1 хуйню за 1.4, продаешь продаешь 1 хуйню за 1.
Ну в полтора раза меньше, значит почти писят процентоов
Скалярное произведение - базовая бинарная операция (. , .) на векторах гильбертова пространства.
Теорема Пифагора в общем случае формулируется и верна для произвольного гильбертова пространства. Её формулировка -- если (v, w) = 0, то (v, v) + (w, w) = (v - w, v - w). Всё. Тащем-то, это очевидное утверждение, для его док-ва достаточно раскрыть правую часть.
Скалярное произведение вектора с собой = длина вектора в квадрате.
Ебать ты доступно объяснил, даже второкласснику будет ясно.
Я ничего не понял. Как мне раскрывать правую часть, если ты даже определения этой операции не привел?
Определение скалярного произведения входит в определение гильбертова пространства:
https://en.wikipedia.org/wiki/Hilbert_space#Definition
Нотки бугурта слышны в твоих попытках оскорбить. К несчастью для тебя тебя обоссали с небольшой высоты, но все же с высоты к.ф.-м.н.
Толстовато.
>А что, решения линейного оде с переменными коэффициентами с гладкой правой частью не обязательно гладкие?
К чему этот вопрос? Ни ответ да, ни ответ нет не будет означать ровно никак, что математика хоть как-то должна согласовываться с реальностью.
С реальностью сверяют физические модели. Физические законы выраженные математических в уравнениях и граничных условиях, должны соответствовать реальности.
То есть если физическая модель такова, что решение уравнений не проходит проверку экспериментом - значит не математика чему-то там не соответствует, а физическая модель неправильна. Надо менять модель.
Ну если тебе не сейчас не нужны, то в восьмом классе понадобятся. Вы просто пока не проходили это.
Весь анализ и вообще всю математику, имеющую какие-то приложения, можно построить без вещественных чисел, обсыхай.
А теперь ты такой берешь и доказываешь без теоремы Пифагора, что на евклидовой плоскости (то есть на той, где действует пятый постулат) можно ввести скалярное произведение для векторов, где длина отрезка будет модулем вектора.
Как из твоего утверждения, возможно ложного, следует, что действительные числа не нужны.
В девятом классе будете доказательства проходить.
Тебя хотят сказать, что даже если и можно обойтись без вещественных чисел, очевидно из этого не следует, что они не нужны.
Ну, даже если оставить в стороне тот факт, что "ненужно" - это известный фразеологизм с вполне понятным значением, то получается следующее: математика без приложений - не нужна (тавтология), а раз вещественные числа в математике с приложениями можно заменить более простой конструкцией, то и они не нужны (Оккам).
Пиздец, нахуй нужны эти постулаты? Ты из какого века-то? Все культурные люди работают с R^n.
Однако математика без приложений нужна математике с приложениями.
Невозможно понять метод множителей Лагранжа не понимая, что такое многообразие и не умея с ним обращаться, даже если вычислительная процедура не требует метода Лагранжа. К слову, утверждать, что иррациональности на уровне даже квадратных корней и тригонометрии не нужны в прикладной математике - это вообще топ кек: вычисление квадратных корней в современные процессоры вшито уже на аппаратном уровне, просто потому, что их дохуя где используют.
> даже если вычислительная процедура не требует метода Лагранжа
даже если вычислительная процедура метода множителей Лагранжа не требует понимания многообразий.
Демагогия уровня /б/.
Процессоры и с рациональными числами не работают, это просто набор транзисторов преобразовывающий одни электрические сигналы в другие.
Ясно.
Ты типа решил выебнуться знанием того, что floating point arithmetic происходит на сопроцессоре?
Это копия, сохраненная 21 октября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.