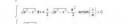Это копия, сохраненная 18 апреля 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.


То есть рассказать, что такое "система вещей" по Гильберту, что такое аксиомы.
Далее нужно ввести элементы логики.
Объяснить, что такое предикат, что такое функциональный символ, что такое квантор и т.д.
Теория множеств вводится так.
Существует система вещей, называемых множествами.
Для них задано логическое отношение "быть элементом".
Всякая вещь A либо является элементом вещи B, либо не является.
Кроме того, для этих вещей задано отношение равенства с традиционными свойствами:
рефлексивность, симметричность, транзитивность, подстановочность.
Далее нужно дать несколько определений.
1. Множество называется пустым, если никакое множество не является его элементом.
2. Множество называется индуктивным, если хотя бы одно пустое множество является его элементом и если оно вместе с каждым элементом x содержит элемент {x}.
3. A называется подмножеством B, если всякий элемент A является элементом B.
В таком случае B называется надмножеством A.
4. Вместо того, чтобы говорить "множество множеств", мы часто будем говорить "семейство множеств".
5. Пусть M - семейство. A называется объединением M, если каждое множество из M - подмножество A и каждый элемент A - элемент хотя бы одного элемента M.
6. Семейство называется регулярным, если в нём есть такое множество, что каждый его элемент не входит в семейство.
7. Непустое C называется неупорядоченной парой A и B, если каждый элемент C равен либо A, либо B.
8. Пусть A и M множества.
Пусть каждое подмножество A является элементом M.
Пусть каждый элемент M является подмножеством A.
Тогда M называется "булеан A" или "множество всех подмножеств A".
9. Пусть M - множество, P - высказывание о его элементах, N - подмножество M.
Мы говорим, что N удовлетворяет P, если для всякого n из N высказывание P(n) истинно.
10. Пусть, в тех же обозначениях, N удовлетворяет P.
Пусть любое подмножество M, которое удовлетворяет P, является подмножеством N.
Мы говорим, что P выделяет множество N из множества M.
Или что N выделено предикатом P из M.
11. Пусть f - функциональный символ от двух аргументов.
Если вещь можно подставить в этот символ в качестве первого аргумента, то мы говорим, что функциональный символ осмыслен на этой вещи.
Мы говорим, что функциональный символ корректен на множестве M, если функциональный символ осмыслен на каждом элементе M.
Мы говорим, что функциональный символ является истинным функциональным высказыванием об M, если он корректен на M.
12. Мы говорим, что функциональный символ f, корректный на M, преобразует множество M во множество N, если
а) для всякого m из M существует единственный n из N такой, что f(m, n) истинно
б) для всякого n из N существует элемент m из M такой, что f(m, n) истинно
13. Пусть есть функциональный символ, корректный на M. Пусть существует такое N, что f преобразует M в N.
Тогда мы говорим, что f является преобразованием M.
Далее нужно сказать, что вещи нашей системы подчиняются следующим аксиомам (Цермело-Френкеля с выбором).
1. Два множества равны тогда и только тогда, когда первое является подмножеством второго и второе является подмножеством первого.
2. Для всякого множества всякое высказывание о его элементах выделяет подмножество.
3. Существует пустое множество.
4. Существует индуктивное множество.
5. Для любых двух множеств, не обязательно разных, существует неупорядоченная пара.
6. Для всякого множества существует булеан.
7. Для всякого семейства множеств существует объединение.
8. Всякое истинное функциональное высказывание о множестве является преобразованием множества.
9. Всякое непустое семейство регулярно.
10. Для всякого семейства непустых множеств существует множество, содержащее ровно по одному элементу из каждого множества семейства.
Прошлый: >>340433 (OP)
1. https://arhivach.org/thread/18638/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
1. https://arhivach.org/thread/18638/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
Этой фотографии больше лет, чем некоторым школьникам из /b/.
Вроде разные. N-петух не дал определения определению, а Толстота дал.
Тред математики - ядро /sci.
Лол.
Вычислите:
a(2,3+1,6)=4,22,3+b
Задача за 5 класс
Сложна
https://ru.wikipedia.org/wiki/Таблица_математических_символов
https://en.wikipedia.org/wiki/List_of_mathematical_symbols
дарю ссылки
Ну смари правильное решение
a (2,3 + 1,6) = 4,2 2,3 + b
a 2,3 + а 1,6 = 4,2 2,3 + b
а = 4,2
b = a 1,6 = 4,2 *1,6 = 6,72
С какого хуя а = 4,2?
Нет.
Он лох.
Лол, это же моя фраза. Я её придумал, сучёныш!
Лол, ньюфажек, это не тян, а переодетый еврей.
у тебя нихуя не понятно воще, ты что сука чистый математик? У меня -4.6а-9.66=-9.66 и -4.6а=-19.32 от тебя.
Может кто что посоветует для того чтобы как то понимать математику и уметь решать?
Спасибо
>Les Éléments de mathématique restent, encore à ce jour, inachevés.
Лол, видимо, будет ещё продолжение.
>Springer
А вот это плохо. У них говённое качество принта.
Ты почему не на уроках?
mathprofi, если ты совсем даун
Спасибо.

Че? В каком ещё 8-м классе?
дерьмо
*в восьмом часе.
лол вот это реал дил труъ, и как всегда американец, а рашкованы только по двачам тупят, даже и близко никого нет!
Ну хуй знает. Яу тоже вот как в девяностые осел в некоммунистической СШАшке, утёкши из не менее некоммунистического Гонконга, так и не собирается оттуда съезжать, судя по всему. И он такой не один. Мурикане оне сука многонациональные. Почему-то пакинстанцы и иранцы тоже не не родине реализуются, как и рашкованы зачастую. В общем под изучение ситуации нужен грант. А без гранта тут нехуй даже обсуждать.
Так он же в австралии рос и математическим соком наливался. Можно в принципе заключить, что он и там реализовался, если бы в сшаку не переехал. Но хуй знает, все равно в австралии, что и в рашке, никто не реализовывается. Только в сшаке почему-то. Даже не в гейропе.
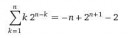
Что значит "вывести сумму ряда"? Ты задание напиши нормально, от себя хуйни не выдумывай.


Хм. Все равно разница как-то неочевидна. Вот пикрелейтед - это фазовое пространство или пространство состояний и почему?
То чем ты мучаешься называется общим словом динамические системы. И да, по второй ссылке я не так понял, думал, что под этим подразумевается конфигурационное пространство, а там какая то хуета из теории управлений.
Нет, я хочу сказать, что лучше оперировать понятием динамическая система, в том числе потому что она хорошо определена.
Именем своей мамаши называй. Еба, не существует такого понятия, просто такого нет забудь. Это же картофан ебаный, ты чё педор ашка не понимаишь??

>не существует такого понятия, просто такого нет забудь
Да неужели. Динамические системы, описываемые дифурами, обычно представляются в виде своего фазового пространства, тот же учебник Арнольда на этом построен. Далее, именно таким образом можно представить модели лотки-вольтерры и т.п. околоэкологическую хуйню. Далее, читаю я пикрелейтед и что вижу - большинство моделей экологических процессов построено на пространстве состояний из теории управления. В т.ч. та же модель лотки-вольтерры. Я и хочу понять, в чем разница, есть она вообще или это одно и то же? В соотв. статьях в педивикии об этом вообще нет ничего, в других местах так же не нашел. Тут возможны 2 варианта - либо "ЭТО БЛЯДЬ КЛАССИКА, ЭТО ЗНАТЬ НАДА!!", либо (что нереально) этот вопрос до меня никем не ставился в принципе.
Возьми формулу для $$\sum_{k=1}^{n} x^{-k}$$ геометрическая прогрессия и вычисли производную, это будет формула для суммы из производных $$\sum_{k=1}^{n} -kx^{-k-1}$$. Домножь на $$-x^{n+1}$$ - получишь сумму для $$\sum_{k=1}^{n} kx^{n-k}$$. Подставив, например, x=2 обнаружишь своё равенство. Вообще, для того чтобы творить такую грязь гугли производящие функции, норм такая тема дискретки, полезная для современной математики в том числе.
1) Есть динамическая система.
2) В чем разница ее представления в виде фазового пространства и в виде пространства состояний?
Тралей, школуйню и прочее хуепутоло сразу нахуй, интересен ответ по-существу.
Пока нет.
Вербитоблядь закукарекала заместо авроры))



Если ты ещё тут, объясни, пожалуйста, каждый шаг. Почему ты делал именно так, а не иначе?
Блять, иди в /un лучше, там тебе распишут решение. Задачка твоя тривиальная, решатся методом мат. индукции. Загугли метод математической индукции, посмотри примеры решения подобных задач. Ну ты даун что ли совсем?
В сигсах, братишка, в сигмах.
Очвидно, решение этой задачи по индукции не имеет никакой ценности, потому что если бы ответ не был заранее посчитан, ты бы до него никогда не догадался.
Бля ты правда тупой или притворяешься? Есть ряд sum kn^(n-k), надо найти closed form для этого выражения.
В смысле, понятно вообще что сделано? Или ты спрашиваешь почему именно так? Ну это суть всей этой техники, взять известную сумму/ряд (в данном случае конечную геом.прогрессию) и интегрированием/дифференцированием/умножением/сложением получить требуемую сумму/ряд. Тогда выражение суммы/ряда, если оно есть, получается соответствующей последовательностью действий с выражением для исходной суммы/ряда, которая известна.
>>344640
Но..там же теневое исчисление с такими штуками бывает, алгебра хопфа даже на полиномах есть!
>Но..там же теневое исчисление с такими штуками бывает, алгебра хопфа даже на полиномах есть!
Это вообще о чем? "Алгебра Хопфа на полиномах" это я понимаю афинная групповая схема, а все остальное про что?
Ладно, я уже сам нашел. Вопрос меняется на зачем оно нужно и где про него написано.
Можно без производных и производящих функций, а также мат. индукций на отъебись.
Попробуй представить выражение под суммой как сумму(умножение на целое - это сумма). И нарисовать сию двойную сумму по слагаемым в виде матрицы - по строкам будут внутренние суммы(выйдет-таки треугольник). Далее выполни суммирование сначала по строкам(треугольник схлопнется в одну строчку)Увидишь геометрическую прогрессию ты, а потом суммируй эту строчку. Надеюсь, я ясно разьяснил. Сии операции можно выполнить/записать путем перестановочек знак сумм и выкрутасов с индексами, но это довольно сложно осознать неискушенному в матанах.
Такой вот алгебраический хинт ушами.
inbefore картофан
Почему эллиптические кривые так важны и пропиарены, а кривые уравнений высших степеней нет? Лишь потому что уравнения 3 степени легко решать?
Потому что они сыграли ключевую роль в доказательстве теоремы Ферма.
https://en.wikipedia.org/wiki/Fermat's_Last_Theorem#Connection_with_elliptic_curves
Надо срочно проверить один картофельный интеграл, я хоть и справился, но чёта думаю, что мог обосраться жиденько.
ничем, просто функционалом чаще называют отображение из какого-то функционального пространства на действительную прямую
ну окей, тащемта если ты меня поправил, тогда поясни мне вот что, а то я хуй простой
Какие ещё есть поля кроме действительных и комплексных чисел? Часто вижу, что теоремы доказываются, скажем, для произвольного поля, но примеров полей, кроме вышеперечисленных, не дают.
Поле - это любой объект, удовлетворяющий аксиомам. Q, С и R лишь частные примеры. Если хочется "не очень традиционных" полей, можешь рассмотреть поле вычетов по модулю p Zp или любое расширение С, R, чего угодно ещё.
Вся математика опирается на три фундаментальных значения: ноль, единица и бесконечность.
Иди нахуй.
>Придумай применение
Так если реальное применение находят только какие-то частные примеры кривых или поверхностей, то чем тогда оправдывается пафос алгема как "центральной науки"?
>то чем тогда оправдывается пафос алгема как "центральной науки"?
Твоей тупостью и тупостью тебе подобных, которые считают, что в математике есть что-то центральное.
> чем тогда оправдывается пафос алгема как "центральной науки"?
Какой пафос? Почему центральной? Что ты несёшь вообще?
В алгеме, кстати.
Но мы же их получили эквивалентными преобразованиями, как при преобразовании обычных выражений. Когда мы оперируем подобным образом над алгебраическими выражениями дополнительно проверять не надо - выражения тождественны. А тут у нас вроде бы тождество, а при проверке оно может оказаться ложным.
В чём заложена скрытая разница? Может мы упускаем/подразумеваем какие-то детали предельных переходов?
>Но мы же их получили эквивалентными преобразованиями, как при преобразовании обычных выражений.
В них тоже не учитывалась сходимость.
>Когда мы оперируем подобным образом над алгебраическими выражениями дополнительно проверять не надо - выражения тождественны.
Спорно. Можно например переопределить отношение '='. То есть снова необходимо учитывать модель. В простых случаях она используется по умолчанию.
>А тут у нас вроде бы тождество,
Формальное.
>а при проверке оно может оказаться ложным.
Более того при различных видах топологий (fine-coarse) - сходимость может быть, а может не быть. Но опять: формальные ряды – игнорируют сходимость.
Не слушай уебков тебе отвечавших, они ничего не знают. Эллиптические кривые важны и пропиарены в основном из-за того, что это абелево многообразие, т.е. на них есть естественная структура группы (если выбрать точку, которая будет нулем). С комплексной точки зрения просто тор. По сути это самый простой из нетривиальных примеров многообразий, который еще можно совершенно в-наглую пощупать и очень много узнать.
Но в алгеме и комплексной геометрии, конечно, еще куча куча многообразий не менее пропиаренных. А вне так много шума из-за разных применений в криптографии и теории чисел (которые обычно следуют из группового закона).
Спс, аллах тебя не забудет.
Да потому что у них очень абстрактное мышление, оторванное не то, чтобы от трёхмерного пространства, но и, в некоторых конкретных случаях, от реальности вообще. Та же самая новая хронология Фоменко, теория струн, а в более запущенных случаях (вроде моего) - математическое устройство мира(т.е. все, что мы видим в мире - это сложные уравнения, возможно заложенные кем-то изначально, но не все уравнения в природе нам дано понять/узнать)
Смотря что за фигня, и как придумал.
Можно сказать с большой степенью уверенности, что то, что ты придумал уже отражено в том или ином виде в научных публикациях или математической литературе. Так что не спеши радоваться.
Так математики, а не "математики". Те кто кончил вузик, пошёл на постгредуейт/аспирантуру, и далее по накатанной. Кто встроен в систему, короч.
1) сходил в офис
2) сделал никому не нужную хуйню
3) пришёл домой
4) ???
5) ЗАРПЛАТА
6) повторяешь 1) - 5) в течении 50 лет
7) умираишь
Вряд ли удастся впечатлить тню какой-нибудь математической поеботой, если ты об этом, но если и не об этом, то всё равно напишу. Для большинства из них математика - это такой себе вид задротства, вроде мморпг или сборки кубика-рубика 11✕11, только с цифрами и фигурками. Ты произведёшь впечатление чудака: "какой ненормальный, зачем он рассказывает про свои гомологии, странный" - подумает тня.
Другое дело физика, биология или психология, - в общем те дисциплины, которые находятся на острие практической науки и активно популяризируются. Если ещё и речь хорошо поставлена и тема актуальна, то успех тебе гарантирован.

>Другое дело физика, биология или психология
Какие отчаянные фантазии. Да тот же самый результат, если эта "наука" не имеет отношения к модному айфончико-ориентированному околоайти, бинарным опционам или прочей чепухе, которая неразрывно связана с доходом от 50к$ в месяц.
Толсто у тебя за щекой
>имеет отношения к модному айфончико-ориентированному околоайти, бинарным опционам
Это по большому счету относится к совсем уж ванильным тпшкам. Я скорее имел ввиду обычных няшек-стесняшек из университетов средней руки.
Есть. Это вся математика, которая не касается понятий бесконечности и непрерывности.

>>345120
Вы совершенно ничего не понимаете в тянках. Да и о произведении впечатления вообще. Совершнно не важно чем ты занимаешься и о чем говоришь. Это с равной вероятностью может быть воспринято как унылое задротство и как охуенная.
Кстати, вбрасываю вполне себе солидного математика, выходца из России.
Это с равной вероятностью может быть воспринято как унылое задротство и как охуенная интеллектуальность в зависимости от харизмы и предпочтений собеседника.
Нет, разумеется. Такого раздела нет. Математические объекты не делятся по своей природе на "дискретные" и "непрерывные". Есть совершенно неожиданные примеры такого рода недвойственности. Например, в науке Громова группы можно представить в виде графа Кэли и изучать с помощью... метрической топологии.
Ты намекаешь на то, что тням похуй, что им говорят, главное слышать плавно текущую речь и видеть смазливое ебальце перед собой? Так это вроде понятно. А что если ты не является обладателем ни того ни другого?
>Математические объекты не делятся по своей природе на "дискретные" и "непрерывные".
Ты так говоришь будто есть математические боги, которые запрещают делить объекты на "дискретные" и "непрерывные". Если смотреть с позиции, - что если что-то из одной области можно каким-то образом представить в другой области, то тогда области нельзя отличить; выйдет так, что из математики и вовсе нельзя выделить ни одного раздела.
Маттрахер.
А множества не делятся на счётные и континуальные.
В России это возможно? Доход неважен, лишь бы после получения диплома хватало на еду и снимать жильё.
При этом меня не интересует статистика, теория вероятностей и прочая поебень - в экономическую контору не пойду.
Сейчас второй курс столичного ВУЗ-а средней руки. Преподы ретрограды сумасшедшие, могу спросить только у вас.
А недолбоёбам готов преподавать? Можно ещё умудриться работать не преподавая где-то в стекловке, в смысле не обязательно каждый год браться вести курс лекций семестровый, но какая-то педагогическая практика всё равно будет когда ты будешь учиться в аспирантуре, например.
>хачу заниматься исследованиями, пока низнаю какими и нахуя они
>это, это и это сразу нахуй
>вы токо оплатите мне хату и ништяки
>а я пока двач поскролю
Соус автора
А что ты запоминать собрался: формулы, теоремы, значки? Без понимания, как всё получается и для чего служит, тебе это не нужно. Сгенерировать что-либо новое ты будешь неспособен. А воспроизведение материала по памяти по большому счету нахуй никому не нужно. Всегда можно открыть учебник и посмотреть, что требуется.
Убери бесконечность.
Воображение и культурная база

>1.Сформируйте систему линейных уравнений (то есть задайте матрицу коэффициентов A и свободный вектор b) для многочлена первой степени, который должен совпадать с функцией f в точках 1 и 15. Решите данную систему с помощью функции scipy.linalg.solve. Нарисуйте функцию f и полученный многочлен. Хорошо ли он приближает исходную функцию?
Я решил, получилось 3.43914511, -0.18692825
Второе часть не могу понять
>2.Повторите те же шаги для многочлена второй степени, который совпадает с функцией f в точках 1, 8 и 15. Улучшилось ли качество аппроксимации?
Где взять многочлен второй степени?
Водофан и картовка.
В натуре. Постоянно ссылается и цитирует, а говорил, что против постоянного цитирования.
https://youtu.be/fJJ4W-0ATn8?t=1352
22:32
Ну поскольку я потратил время на прочтение, получите рецензию.
Не зная Вашей даты рождения и соответственно Вашего гороскопа, а как известно любому астрологу, человек обычно рассказывает только свой гороскоп ;))
Отмечу следующее. Книга написана достаточно живо и красочно, что намекает на хорошие аспекты венеры с меркурием. При этом есть концепция - узор(фрактальность, склейка), что вероятно говорит о пребывании планет в знаке стрельца.
Перечисление - эпилепсия, паранойя, шизофрения, говорит о выделенности тем для автора.
Что такое эпилепсия, как неосознанные выплески энергии. В отличие от маниакальности, когда энергия направлена на какую-то цель. То есть проблемы с Марсом и/или Плутоном. Ну и собственно весь текст, скорее описательный, что говорит о преобладании нейтральных и женских энергий. Кстати аватарка с преобладанием оранжевого, говорит об активности 2 чакры и энергиях Меркурия и Венеры. Короче основная точка сборки Вашей личности - там.
Параноидальность - о желании понять структуру мира, это выделенность Сатурна. А шизофрения как раскол - о слабой проработке и осознанности энергий сверхличных планет Урана и Плутона.
-Почему планковская длина считается абсолютным нулем
-Зачем нужны тахионы если есть суперсимметрия
-Почему гравитация не квантуется в если есть гравитоны
-Почему космические тела вращаются вокруг собственной оси
-Почему электрон не падает на ядро теряя энергию
Это лишь разные виды узоров. Зачем нужны узоры, каждый сам видит для себя. Физика она как индия, там все есть, каждый берет что хочет.
>>345444
Одна рыба.
А кого?
Обоснуй. 1 не делится на 3. Он выбросил рыбу и забрал себе треть нихуя.
Остальные не смогут сделать также.
Минимальный улов естественно достигается, если каждый рыбак забрал минимально возможное число рыбешек, а именно одну. Мне лень считать.
> неподеленый улов
Который за одну ночь уменьшился в три раза? Рыбак после сна забывает все что произошло в прошлый день?
Аноны, что-то еще про про продавца шапок есть! Типа фальшивую купюру ему дали и нужно узнать насколько он попал. Или наоборот, покупатель попал. Кто помнит? Охуетельно сложная задача, 100 ответов и все неверные. Кажется просто, а ведь нескольких лет мехмата уровень!
Что нет? Улов не уменьшился? Или рыбак забывает? Улов не может не уменьшится по условию задачи. Про склероз у рубака ничего не написано.
У мужика кепка-пятиклинка стоит 200 рублей, покупатель хочет купить её, но у него только 500. Подзывает мужик мишу вербитского, выпидоренного за космополитизм из вышки и говорит: "Беги, еврейка, скорее к тетё маше, разменяй". Побежал миша со всей прыти, всё разменял на сотки, прибежал обратно. Отдал мужик сдачу и кепку, сидит, отдыхает. Через полчаса заходит тётя маша и говорит, что купюра фальшивая, мужику пришлось заплатить всё из своего кармана. Был конец рабочего дня, мужик наказал вербитскому выяснить в чём дело и определить до завтра где же его наебали, а сам домой пошёл. Помоги мишке найти сумму наёба.
> сумму наёба
Проеб - пятсот фальшивых рублей. Если сможет их кому-то впарить как пятисотку, то не проебал. Если за половину - проебал 250. Не сможет - 500.
Тут получается диофантово уравнение
8x - 27y = 38. НОД(8,27) = 1, следовательно оно неразрешимо в целых числах.
>Вопрос: какое наименьшее число удовлетворяет исходному количеству выловленной рыбы?
Ответ: никакое
Покупатель наварил 300 рублей плюс шапку. Значит продавец очевидно попал на 300 плюс смотря как считать стоимость шапки.
Стоимость шапки - цена шапки, так как продавец проебал возможность ее продать за нормальные деньги.
Ну тогда 300 + 200 = пицот
Что именно нет?
Соседка осталась при своих, да или нет?
Покупатель наварил 300 руб плюс шапку, да или нет?
Продавец отдал соседке своих 300 плюс потерял шапку, которую мог бы продать за 200, да или нет?
Обоснуй, а то пока мне кажется что это просто пидора ответ.
Нет.
Блин ! Ну , что Вы все соседские деньги , соседские деньги ....!
Вместе с остатком , вместе с остатком ..... ! Какие они к чертям соседские ? Какой к чёрту остаток ?
Ребята это деньги ПОКУПАТЕЛЯ !!!! Реальные или фальшивые выяснится позже . Соседка лично своего ни чего не давала ! Её роль заключается всего лишь в размене денег. И продавец всего лишь вернул 15 р. его же денег ( покупателя ) , только уже реальных . А продавец заработал уже свои личные , кровные 10 р. с продажи шапки . В результате обнаружения фальшивки Продавец отдаёт свои кровно заработанные 10 р. и добавляет свои же 15 р. и отдаёт соседке ( 25 р. ). Вы спросите почему соседке ? Потому что она их получила в данном случае от продавца , а не от покупателя . Кроме того продаётся одна шапка , не 10 и не 1000 и не .....
А именно одна из условия задачи и цена ей 10 р . В результате афёры продавец имеет фальшивую купюру в 25.р которая ни кому не нужна !!!! Продавец остался и БЕЗ ШАПКИ И ЕЩЁ ОТДАЛ СВОИ 25 р.
Ущерб продавцу составляет 35 р.
Вы зациклились на элементарных действиях . Получил , отдал . Получил , отдал !!! А ведь я вам изначально говорил обратите внимание на условие задачи : Один продавец ( сам по себе ) , ОДНА шапка ( понимаете ОДНА У ЭТОГО продавца ). Стоит конкретные 10 р.
Я ведь разжёвывая Вам не зря приводил варианты . В варианте ЖУЛИК – ПРОДАВЕЦ ( без размена) , продавец теряет 25 р . В варианте ЖУЛИК – ПРОДАВЕЦ ( с разменом в магазине розничной торговли ) , продавец теряет 25 р. Читайте выше мои комментарии .
В третьем варианте ( конкретные условия задачи ) в процессе сделки фальшивые деньги номиналом в 25 р. ЖУЛИКА (ДЕНЬГИ ЖУЛИКА ,А НЕ СОСЕДКИ ) плавно перетекают через продавца к соседке , где они удачно меняются на реальные и опять через продавца возвращаются к Жулику в виде ПРОДАННОЙ шапки и реальных 15 р. ПРОДАВЕЦ ПОЛУЧАЕТ ЧЕСТНО ЗАРАБОТАННЫЕ 10 р. С ПРОДАЖИ ШАПКИ. ХОРОШЕНЬКО ЗАПОМНИТЕ !!!! ЭТА ДЕСЯТКА УЖЕ ЕГО СОБСТВЕННОСТЬ !!! ЭТО ДЕНЬГИ НЕ СОСЕДКИ КОТОРЫЕ ПРИШЛИ ПОСЛЕ РАЗМЕНА , ЭТО ДЕНЬГИ КОТОРЫМИ РАСПЛАТИЛСЯ ЖУЛИК ЗА ШАПКУ .
Поэтому как только к этой десятке Вы прибавляете ещё свои 15 р.( есть у продавца в данный момент ещё свои деньги или их нет РОЛИ НЕ ИГРАЕТ ) и отдаёте ( или 10 р. и будете должны 15 р. ) соседке 25 р. ПРОДАННАЯ ВАМИ ШАПКА ИЗ СТАТУСА ПРОДАННОЙ ПЛАВНО ПЕРЕХОДИТ В СТАТУС ДАРОМ ОТДАННОЙ !!!!! НЕТ ШАПКИ , НА РУКАХ ФАЛЬШИВЫЕ 25 р. Ну и на сколько Вас нагрели ????
Ребята Вы зацикливаетесь на деньгах , ДАЛ ,РАЗМЕНЯЛ ,ОТДАЛ , ВЕРНУЛ – фигурируют конкретные суммы . И в тот же момент Вы теряете из виду саму шапку . ШАПКА – ТОВАР С КОНКРЕТНОЙ ЦЕНОЙ , ВМЕСТО ШАПКИ – ТОВАРА ПРОДАВЕЦ ПОЛУЧАЕТ ДЕНЬГИ – ПРИБЫЛЬ . И ЕСЛИ ОТДАТЬ ДЕНЬГИ – ПРИБЫЛЬ ,ДА ЕЩЁ ДОБАВИТЬ СВОИ , ТО ПРОДАВЕЦ ТОВАР – ШАПКУ ПРОСТО ОТДАЛ ДАРОМ !!!!! ( НЕ ЗАБЫВАЕМ РЕЧЬ ИДЁТ О КОНКРЕТНОЙ СДЕЛКЕ ЖУЛИК – ПРОДАВЕЦ -(РАЗМЕН )- ПРОДАВЕЦ -ЖУЛИК ).
В данном случае ШАПКА досталась ЖУЛИКУ даром , а соседка урвала 25 р .
10 рыб.
Мой ответ на все ваши предположения: нет. Вы не достигли правильного ответа.
Внимание, правильный ответ: наименьшим числом, удовлетворяющим заданным условиям, является (-2). Рыбаки выловили -2 рыбы или две антирыбы.
Спасибо за внимание, глупцы, моё дело сделано, Я ухожу.
Ты охуел? Чем тебя например не устраивает -29 рыб? А, сука?
не выражается в элементарных функциях, а так выражается через функцию ошибок, путем интегрирования по частям.
>свербицкий
а почему мишу тут так не любят? он конечно скандалист и русофоб, но математик же международной пробы. у него индекс цитирования кстати - огого, выше кажется только у арнольда был.
как думаете аноны, он где-то с арнольдом одного уровня или все-таки уступает? за сколько бы он решил сто задачек арнольда?

1 сентября 1997 года, в результате деления на ноль в компьютеризированной управляющей системе крейсера USS Yorktown (CG-48) Военно-морского флота США произошло отключение всех машин в системе, в результате чего двигательная установка корабля прекратила свою работу
А бурбаки няшки. Особенно готично-лысый Гротендик и Вейль со своими гипотезами.
Хранцузского школьника спросили, сколько будет 2+3? Он ответа не знал, но ответил как его научила бурбакомафия: 3+2, так как сложение коммутативно.
байка от арнольда
25 рыб
следовательно оно неразрешимо в целых числах.
Скорее: следовательно - оно имеет бесконечно много решений в целых числах при любой правой части.
А почему вопрошающий счёл, что ответом на вопрос "сколько будет 2+3" не является "3+2"? Школьник, типа, должен был угадать слово, которое загадал вопрошающий?
Пусть сначала научатся точно формулировать вопросы, и только потом спрашивают.
Да, тут я обосрался. Перебором остатков можно подобрать частное решение (25,6).
Нихуя он не международной пробы, да и какое это имеет значение? Важны ведь только результаты. Арнольд, например, международной пробы. Доказывал проблемы Гильберта, унижал бурбаков и прочее быдло, за что ему посмертный рейхспект. Миша решит максимум 2 задачи из тривиума, для него ведь это зашквар. Есть три категории математиков. Первая это так называемая первая культура(низший сорт, 1 уровень). У них принято считать, что самое главное - это новая абстрактная теория. Такая себе чистая математика. На уровень выше стоят прикладники и формалисты, которые пытаются получить результаты в разных областях теми методами, которые есть, и разрабатывают новые, только если это необходимо. Ну и третья категория самая немногочисленная, это такие себе полубоги по типу Перельмана, которые доказывают проблемы специальными детализированными методами.


Нихуя не понимаю смысл производной. Вот например дефолтная ЕГЭшная задача. Правильно ли я думаю?
1. Производительность рабочих есть некоторая функция, а значит у это функции есть график.
2. Нужно найти максимум на это графике. Если, например, мое время не ограниченно, то я могу просто подставлять все значения в функцию и рано или поздно я получу этот максимум.
3. Очень долго производить такие вычисления. Поэтому вместо самой функции можно рассмотреть её аппроксимацию или проще говоря спрямление этой функции.
4. Получив вместо кривой функции обычную прямую или что-то похожее намного проще понять где у неё максимум.
Для этого и нужна производная?
Почему тогда, это спрямление пик 2 вообще не похоже на оригинал пик 1?
https://www.youtube.com/watch?v=Erzf5ktLkMw&index=3&list=PLowFPHQVq5qPL_Nmx5sITxbzoou_k-gO8
ALLO, DAUN, ETO TI?
Смысл производной в том, что она показывает скорость изменения функции в точке.
Значит ты дурак.
Открываешь тетрадку тгда и считаешь производную из функции х², может поймешь.
Хотя ладно, поясню дураку почему он дура. Жди пять минут пока я набираю
>Смысл производной в том, что она показывает скорость изменения функции в точке
Блядь, где строгое математическое определение, гильберт тебя за ногу?
>Нихуя он не международной пробы
Давеча он представлял Россию на International Congress of Mathematicians.
Пусть есть вещественная функция f.
Пусть есть отрезок [a;b].
Изменением функции f на этом отрезке называется число f(b) - f(a).
Длиной отрезка называется число h = b-a.
Средней скоростью изменения функции называется изменение функции, делённое на длину отрезка.
Символьно, fсредняя ba = (f(b) - f(a)) / (b-a).
Средняя скорость определена для отрезка. Но что если нас интересует скорость в точке? Нужно использовать предельный переход.
Скоростью функции в точке a называется fсредняя ba, когда b стремится к a. Или, эквивалентно, когда расстояние h между b и a стремится к нулю.
То есть fв точке a = limh→0(f(a+h) - f(a))/h
Тебя бы грузовик переехал - ты бы ещё не так ебанулся.

Ты делаешь следующие рассчеты (1+0.1)²-1²/0.1
Посчитаем в лоб. 1.1²=1.21, 1²=1
1.21-1=0.21/0.1=2.1
Вроде все просто.
А если тебе надо узнать насколько измениться значение функции если к единице добавить одну миллиардную, или даже какую то охуллиардную, что тогда? Теперь уже кучу ноликов писать сильно долго, неудобно, да и ошибиться можно. Заменим теперь цифры буквами.
Получится (х+у)²-х/у²=х²+2ху+у²-х²/у=2ху+у²/у=2х+у
Если теперь подставить вместо букв цифры, то можно увидеть, что прибавление охуллиардной части не сильно влияет на результат, а именно 2+почти ноль.
Что значат эти цифры?Это и есть скорость и величина изменения функции по направлению оси икс.

Нахуй строгость. Он сперва понять должен что от него хотят, а потом уже строгость
> можно рассмотреть её аппроксимацию
Апроксимируют когда функция не известна, а есть только несколько ее значений. У тебя же функция известна, следовательно никаких апроксимаций не нужно.
Твои графики это ни какие не "спрямления". Первый рисунок это график целевой функции, на которой нужно найти максимум. Только у тебя там как-то оси перепутаны, более показателней было бы х по горизонтали пустить. Второй график это график производной функции. На нем интрестно нулевое значение, которое соответсвует экстремуму функции.
Лол блядь
Двачую
Максимум/минимум функции это значение функции при котором соседние участки имеют меньшее/большее значение чем в точке максимума/минимума. Этим такие точки отличаются от максимума/минимума вообще. В функции х³-х игрек может быть каким угодно большим, но минимум и максимум у нее в районе х=-/+0.5774.
Находятся они по значению производных. Берем производную. Она будут равна 3х²-1=у. Подставлем у=0, так как в этих точках функция обращается в ноль и не изменяется, и находим корни уравнения. Они равны +/-0.5774.
Но ты не знаешь какое именно число отвечает максимуму какое минимуму. Для этого берем производную от производной и подставляем туда найденные значения. Она равна у=6х. При подставленных найденых корнях производная будет отрицательной при отрицательном значении корня и положительной, растущей, при положительном. Знак найденного корня никак не показывает минимум это или максимум. Для наглядности найди критические точки у функции х³-х²-х.
>Сами её методы - хуйня, переходящая во что-то осмысленное только в алгебраической форме.
У тебя получилось объяснение в духе вербитопомазанного: хуйня - просто потому что не алгем, и не то, что нам велит любить Миша.
Но, на самом деле, ты же ничего не пояснил. Почему её методы хуйня безотносительно алгебраической формы?
>Зачем людям знать о таком недоразумении, как Евклид и о его работах
Хотя бы потому, что он первый начал использовать аксиоматически построенную теорию. А такого подхода придерживается сейчас вся современная математика.
Если функция в какой-то точке имеет экстремум, то в этой точке производная равна нулю. Поэтому чтобы найти наибольшее значение, тебе нужно вычислить значения функции во всех точках, где производная равна нулю и на границах области определения (если она ограничена) и выбрать максимум.
Потому что там не 2 = 4, а 0 = 0.
Ты видмо не понимаешь всей глубины проблемы. Очевидно: любое произвольное значение умножить на (0) = любое другое произвольное значение умножить на (0). (0) сокращаем так как он в скобках, следовательно любое произвольное значение = любое другое произвольное значение. То есть даже бесконечность = 1, а 1 = 0, следовательно бесконечность = 0. Такие дела.
Всегда получалось. А физика, биология и психология - лженауки. Нахуй все, оставьте только математику. Ахахаха!!!! Глупый шкальнек!!! Весь мир будет у ног математиков!!!
меня понесло
Нет. Дурак. Пробей в поиске.
Какое понятие ты считаешь неясным?
Пацаны, накидайте баек про ебанутых советских математиков. Давайте сравнивать ебанутость на международном уровне!
Рассказ очевидца с mathoverflow про дуэль арнольда с французами в 2001-м. Из арнольда бы хороший двачер получился
I was there. Arnol'd is one of my big mathematical heros, but I found the whole thing really sad. It was in French, but my French is decent. Arnol'd began his part with a phrase I've heard him say before: “In Russia it is impolite to talk ill of the dead, so I will not talk about Bourbaki” and then he proceeded to lambast Bourbaki in as nasty a way as you've ever read in any of his writings. I just felt like hanging my head. It was embarrassing watching him insult French Mathematics in front of 500 French men and saying things that seemed silly. It went on from there, Serre with a kind of sad understated dignity, not fighting, Arnol'd wanting a fight, hurling insults. The two barely even addressed each other. And yes, he did mention Toth, and if memory serves, he stated that Toth was probably Thales and had most likely come up with Newton's inverse square law. For me, the whole event was sad, embarrassing, and myth-crushing. Well, us mathematicians, we are all humans.
Математики этой страны были ебанутыми задолго до советов.
>еще в 20-х гг. консервативные механики вроде Чаплыгина пренебрегали этими новыми науками, считали их западной чушью. П.С.Александров рассказывал мне, что Чаплыгин запретил П.Урысону включать новую тогда общую теорию относительности в его аспирантский экзамен. Это - наша специфическая русская черта - склонность к консерватизму, к отрыву от мировой науки. Даже Чебышев в XIX в., при своем блестящем аналитическом таланте был патологическим консерватором. В.Ф.Каган рассказывал, что будучи молодым приват-доцентом он встретил старого Чебышева, пытался поведать ему о современной геометрии и т.д., а тот презрительно высказался о новомодных дисциплинах типа римановой геометрии и комплексного анализа. Созданная им школа была сильной, но и с сильной склонностью к провинциализму.
http://aspirant.rggu.ru/article.html?id=50768
Это эссе тоже ебанутый человек написал, кстати, - Сергей Петрович Новиков. Боговерчик, ватник и просто интересная личность.
Тоже самое что и ибычная производная, только там джве переменных.
Ближайший аналог это системы линейных уравнений. Там вроде тоже нихуя не понятно, но если выразить икс через игрек, то система вполнетрешается. Тут так же, только одна-две-N реременных считаеются постоянными, вокруг которых вычисляется одна свободная переменная.
Тоже толсто

>>345749
Алсо, вот это тоже твой пост. Ты уже не первый тред засираешь своей тупостью, я специально скриню.
Вот тебе ссылочка и виктпедии, чтобы ты хоть как то мог связать свой поток сознания.
Частная производная - это производная вдоль вектора, когда в качестве вектора рассматривается вектор из наперёд выбранного зафиксированного базиса.
А интеграл это площадь под кривой в пределах оси икс. Дальше что? Определение как суммы бесконечно малых неправильное?
Не съезжай с темы.
Чем конкретно математическое, без маняпространств, определение частной производной написанное мной так, чтобы даже конченый смог понять, тебя не устраивает?
Ты не говоришь, что такое частная производная.
Ты говоришь всего лишь о синтаксических преобразованиях.
Ты описываешь операцию, которую следует применять к строке символов, чтобы получить другую строку символов.
Это тупо.
Тебя спрашивают о смысле строк символов, а не о синтаксических манипуляциях.
Поэтому частная производная - это производная вдоль вектора из наперед заданного базиса.
Точка.
Свои "одна-две-N реременных считаеются постоянными" засунь себе в жопу.
Я не хочу реформировать школы, я хочу убить всех методистов.
а весь бред, что выше-ниже, ничего? уровня sci?
нет, не про пикрил, а просто про интересную личность. да, книжица эта пиздец ацкий, выкини ее нахуй. возьми какой-нибудь нормальный вводный учебник для инженеров, желательно на английском языке. вот на таком примерно уровне
https://www.cengagebrain.com.au/content/9781285233260.pdf
Аксиоматика в стиле Евклида это куча безумных аксиом и тонна работы, которая была доделана только Гилбертом. И после этого ты еще нихуя даже не сможешь доказать, ибо методы сильно нетривиальные.
Базовая же линейная алгебра оперирует только важными и простыми понятиями, из которых все очевидно выводится. Сейчас одного семестра линейной алгебры хватит, чтобы узнать, понять и научиться решать больше, чем любой великий геометр древности
Собственно, вся суть Арнольда. Прилюдно обмазывается говном, а все терпят из уважения к научным результатам.
>а все терпят
А все получают особое, извращённое эстетическое удовольствие, как от просмотра хорошего копро-порно.
Толсто. Такая хуйня не нужна математикам, потому что там акцент на ручном решении кучи дифуров. Такая хуйня не нужна инженерам, потому что в 2016 году есть мат по, в которое вбиваешь дифур и он решается.
Собираешься своей массой пронзить пространство и время?
ну так то да, тогда и калькулюс нахуй не нужен. тогда нужно уточнить, что именно анон хочет получить в итоге.
Надто товсто.
Это все нужно для формирования мышдения. Ну и чтобы в случае ядерной войны можно было сразу создать интегральное исчисление, а не разбивать круг на отрезки нулевой длинны для нахождения пи.
да нухй вообще инженерам мышление, есть же компьютеры. нужно просто обучать ремеслу - какие кнопки нажимать
1-й семестр - задачки решать про торговца шапками и фальшивую купюру
>Сейчас одного семестра линейной алгебры хватит, чтобы узнать, понять и научиться решать больше, чем любой великий геометр древности
И кто тебя сейчас заставляет учить евклидову геометрию? На мат.факах нет такого предмета. Геометрия есть - только дифференциальная. Такую геометрию Миша вам не запрещает?
И да, ты не ответил на вопрос, чем плоха евклидова геометрия безотносительно алгебраической формы?
>На мат.факах нет такого предмета
Есть на всех матфаках страны, кроме одного. Называется "аналитическая геометрия".
Да никто не заставляет. Ты попросил объяснить, почему она говно и ненужна, я объяснил.
Я не тот анон, так что не знаю, что подразумевалос под алгебраической формой.
что такое 247-я школа? УO? short bus?
>Ты попросил объяснить, почему она говно и ненужна, я объяснил.
Что ты объяснил? Вот это:
>Аксиоматика в стиле Евклида это куча безумных аксиом и тонна работы
При желании, это можно сказать о любой аксиоматике. Да и чем аксиомы Евклида безумнее аксиом, скажем, ZFC?
Не решение, а понимание сути как они работают.
А суть лучше всего понимается если их решать максимально подробно. Это не то же самое что просто решать.
Просто решать это написать что интеграл х² равен х³/3. Подробно решать это вывести почему интеграл х² равен х³/3
> Подробно решать это вывести почему интеграл х² равен х³/3
Зачем ему выводить этот интеграл? Вот, например, я первокурсник и прошел основную теорему матана. Какое дополнительное понимание мне даст вычисление интеграла от x^2?
пределы нужно инженерам объяснять? а вывод формул дифферецирования через пределы? а пруфы?
Пусть предмет A горячий и белый, а предмет B холодный и чёрный.
По твоей логике, если бы предмет A был чёрным, то он был бы холодным.
На вопрос отвечай. Конкретный же вопрос задал. Представь, что я первокурсник, который прочитал теорему и ее доказательство
https://ru.wikipedia.org/wiki/Теорема_Ньютона_—_Лейбница
Что мне должно дать вычисление интеграла от x^2?
Так ведь ты затем и пришёл в ВУЗ, чтобы изучить теорему Ньютона-Лейбница. Ты знал, куда шёл, и знал (должен был знать), чему тут будут учить. Уж не знаю, зачем тебе понадобилось изучать это.
Не подменяй понятия. Еще раз спрашиваю, пасанчик с падика на одной волне с перельманом или нет?
>>345805
Ты чиьаешь плохо? Я уже ответил что тебе ничего. Разве что поможет корочки получить и пойти потом капчевать не по специальности с офиса за 20к, или сколько там офисные отбросы получают сейчас!?
> Так ведь ты затем и пришёл в ВУЗ, чтобы изучить теорему Ньютона-Лейбница.
Ну, верно, я ее изучил, понял как считать интегралы. А интеграл от x^2 нахуя считать?
>>345808
Поздравляю, тебе получилось затроллить меня своей тупостью, у меня реально бомбит.
Блджадь, в случае линала это нихуя не тонна работы и совершенно не безумно. Я тебе за пять минут определю, что такое евклидово пространство, прямые и прочее говно через линал, начав с натуральных чисел. Каждое определение будет прозрачным и использующимся во всех областях математики (поле, векторное пространство, билинейная форма).
После чего любая классическая теорема по геометрии будет практически очевидной.
А теперь сравни с вот этим
https://ru.wikipedia.org/wiki/Аксиоматика_Гильберта
Вот честно скажи, ты их воспроизведешь? Они хоть где-то еще появляются?
И сравни потом, насколько проще и надежнее сослаться на линейность и несложный счет, чем хуярить кучу дополнительных построений?
Напомню тебе, что это ты доказываешь, что если заставить пасанчика сыграть достаточное количество партий в шахматы, то он превратится в Пуанкаре.
Еще раз повторяю, специально для контуженных с бронепоезда. Лично тебе знания сути работы интегрального исчисления ничего не дадут.
Не всем же надо знать как получается электричество в проводе, чтобы включить лампочку. Но вот когда провод где то замыкает...
Ты подмениваешь понятия. Я писал про математический склад мышления, а не про стратегическое планирование. Не пиши мне больше.
Определяй и доказывай. Назвался груздем...
>После чего любая классическая теорема по геометрии будет практически очевидной.
Серьёзно? Классические теоремы геометрии: теорема Наполеона Бонапарта, теорема Монжа, теорема Сальмона, теорема Микеля. Ты обломаешься уже на формулировках.
Как скажешь.
Сука, ну какой же ты даун. Я знаю суть работы интегрального исчисления, понимаешь? Я могу вычислить интеграл от многочлена. Вопрос в том, нахуя мне вычислять интеграл от x^2?
Я высказал тут >>345812 все что хотел и не буду повторять все трижды.
Могу только добавить что если ты, таки да, знаешь как и что работает, ты бы расписал как получается интеграл из функции квадрата. Все.
Я тебе объясню ход мыслей нормального человека.
1) Многочлен - непрерывная функция. Непрерывные функции интегрируемы.
2) Из линейности интеграла следует, что
integral sum a_k x^k = sum a_k integral x^k
3) Интеграл от x^k можно посчитать по формуле Ньютона-Лейбница. Легко догадаться, что первообразная x^k - это x^(k+1) / (k + 1).
Ход мыслей долбоеба: ну кароч надо вычислить интеграл от sin 666x + x^1488, чтобы понять как работает интегрирование))0
Где?
Вот ты и показал свой уровень владения дискуссией и математикой. Никаких доказательств и обоснований, только три предложения, которые каким то магическим образом вместили чуть ли не полторы тысячилетия развития математики, как тебе кажется.
Я рад что больше мне не придется с тобой разговаривать.
Все, что я написал, общеизвестно. Если ты не можешь доказать что-то из этого или не знаешь, что именно надо гуглить, то ты просто даун. Это все проходят на 1 курсе.
Вот есть область целостности R, а есть элементы x1,...,xn, которые ей принадлежат. Так вот, говорится, что если dR=x1R+...+xnR имеет место, то d=gcd(x1,...,xn). И все бы ничего, но я, блиа, никак не могу понять как делитель может равняться сумме того, что он делит. Алсо, кажется мне, что я не правильно понимаю смысл написанного. Помогай, помогач!
Все кроме Салмона совсем просто. Особенно, Бонапарт насмешил, на фикипедии говно написано геметрическое, хотя всем очевидно, что через комплексные числа это делается за секунду.
Не сумме, а линейной комбинации. Там могут быть отрицательные коэффициенты. Никогда не слышал про алгоритм Евклида?
Увы, не слышал. Математикой увлекся недавно. Мне почему-то хочется d назвать общим кратным x1,...,xn. Я совсем конченный? x1R,...,xnR - это, вроде, идеалы. Это что-нибудь меняет?
наполеона сообщник

Судя по тому, что в книге используется теория категорий, - явно кто-то молодой, резвый, наглый.
Поворот на 60 градусов = умножение на корень шестой степени из единицы. Центр правильного треугольника = сумма вершин делить на три. Так что хуяришь начало координат как тебе удобнее и делаешь пару-тройку тривиальных арифметических действий.
А чому себе, а не тебе, например?
>Поворот на 60 градусов = умножение на корень шестой степени из единицы. Центр правильного треугольника = сумма вершин делить на три. Так что хуяришь начало координат как тебе удобнее и делаешь пару-тройку тривиальных арифметических действий.
И что за говно ты высрал, кокормист? Вычисли координаты равносторонних треугольников, построенных на сторонах произвольного треугольника относительно какой хочешь системы координат.
Пиздос, ты ебанутый или как?
Треугольник ABC, пускай 0 в А. Пусть B и С задаются комплексными числами z_1,z_2. Тогда AB достраивается числом z_1w, AC достраивается числом z_2(w^-1), BC достраивается числом z_1+(z_2-z_1)*w. Где w первообразный корень шестой степени из 1. Теперь очевидно считаешь центры и проверяешь, что разности отличаются домножением на w.
>теория категорий
>явно кто-то молодой
Ты ебанулся, категории уже с 40-хх годов активно используются.
>все
Да тут не считая мимокрокодилов человек 5 постит по-моему. И во всем саентаче один и тот же стиль, то есть те же люди. Сколько тут всего народу, человек 20 в хороший день?
Но это 90% мимикроки? А костяк так сказать, стержень, это 2-3 мегапостера, которые друг с другом срутся?
И тем не менее каждый мат.тред набирает минимум по сто постеров до бамп лимита. Хотя меня тоже это удивляет, кто все эти люди? Может Абу постеров накручивает, чтобы придать вес доске.
Ну та, хз что это за статистика, может с проксями мутят
Все ли нетривиальные нули дзета-функции лежат на прямой Re(z)=1/2?
Риман, замолчите, вы умерли. Обратитесь в институт Клэя.
ну спорно, может и не все, а просто не нашли еще опровергающего алгоритма. всего то требуется найти решение для интеграла через численные методы, а никто не ищет, ибо компьюетрных мощностей не хватает. можно через хадуп попробовать.
как сто, я вижу 96. это шо такое пацаны? выпиливают постеров?
Когда найдешь тогда и поговорим(то есть никогда)
И ничего он не ебанут, просто биологию не знает. Математичен ли мир - не известно. Но вот все восприятие мира - это сплошная математика. Вот взять зрение. Мы же не видим фотоны. Фотоны падают на группы нейронов сетчатки, те - генерируют сигнал. В мозге все сигналы обрабатываются, например, выявляются границы объектов. Вы же понимаете, что нет таких фотонов, которые несут информацию "я означаю границу этого объекта" независимо от наблюдателя.
Причем тут биология?

Пуанкаре стал гением потому, что переболел дифтериеей типо же
Кокая мощная аргументация. Сразу видно что после ядерной войны сможешь с нуля построить всю высшую математику.
Да.
--> /b
Так я и спрашиваю - в каком векторном пространстве элемент не n-tuple? Или наоборот, над каким полем должно быть определено в.п. чтобы элемент считался n-tuple? Что-то про координатные системы?
А, вот нашел ответ. Все-таки вектор это прежде всего геометрическое понятие, а все остальное - булшит.
The proper treatment of calculus for functions of several
variables requires vector ideas; the budding statistician and
the coming physicist need them; modern analysis is unthink-
able without the notion of linear dependence and all that flows
from it. Throughout these courses the infusion of a geomet-
rical point of view is of paramount importance. A vector
is geometrical; it is an element of a vector space, defined
by suitable axioms—whether the scalars be real numbers or
elements of a general field. A vector is not an
n
-tuple of
numbers until a coordinate system has been chosen. Any
teacher and any text book which starts with the idea that vec-
tors are
n
-tuples is committing a crime for which the proper
punishment is ridicule. The
n
-tuple idea is not ‘easier,’ it is
harder; it is not clearer, it is more misleading. By the same
token, linear transformations are basic and matrices are their
representations
В бесконечномерном пространстве вектор - не n-tuple. Бесконечномерные пространства встречаются очень часто. Например. R - бесконечномерное пространство над полем рациональных чисел. Но базис этого пространства не то что не конечен - он даже несчётен.
Конечномерные векторы превращаются в n-tuple только после фиксации в векторном пространстве какой-то системы координат. В двух разных системах координат одна и та же n-tuple может соответствовать двум разным векторам, один и тот же вектор может иметь две разные n-tuple. Вектор и n-tuple - разные вещи. Правильнее думать, что над каждым полем K для любого натурального числа n существует "модельное пространство энок", и что любое пространство над K с dim = n изоморфно модельному пространству n-ок, причём многими разными способами.
>>346028
Вектор - это элемент векторного пространства. Векторное пространство - это абелева группа, на которой действует поле. Абелева группа - это движения какого-то объекта.
Всю не всю, но матан на уровне 17 века смогу.
Возьми, например, пространство последовательностей в R. Понятно, я думаю, как складывать последовательности друг с другом и как умножать их на скаляр.
Разумеется. Гамма-функция называется.
Чтобы математики не доебывались, что ты не знаешь, что такое вектор.
Единственный смешной математический анекдот, который я когда-либо встречал:
Emil Artin (1898–1962) was famous for the extremely clear and
extraordinarily well presented lectures that he always gave without
any notes. One day, midway in a proof, he suddenly hesitated and
said: “this conclusion is trivial”. After a few seconds, he repeated:
“it is trivial, but I no longer know why”. He then thought about
the question for another minute and said: “I know that it is trivial,
but I no longer understand it”. He reflected on it a few moments
more and finally said: “excuse me, I have to look at my lecture
notes”. He then left the room and came back ten minutes later
saying: “it really is trivial”.
(Witnessed by Prof. Josef Schmid, Fribourg)
Бамп, посоны.
У этого анекдота борода больше чем у Перельмана.
Ох ебта, надо неделю над этим думать.
Другими словами, определение вектора через n-tuple ни чем не "обобщеннее" определения вектора из школьной геометрии как отрезка прямой имеющего величину и направление? А просто его алгебраибическая интерпретация? То есть всегда из тюпла можно построить геометрический вектор, если "мерность" пространства позволяет конечно? Я думал n-tuple это прямо так абстрактно, что все.
>всегда из тюпла можно построить геометрический вектор
Сначала нужно указать базис пространства. Одна и та же энка может быть координатами любого из векторов пространства, какого конкретно - зависит от базиса.
>это прямо так абстрактно, что все
Хочешь вменяемо определить векторное пространство - воспользуйся понятием "модуль над кольцом" и скажи, что векторное пространство - это модуль над полем. Поле - это частный случай кольца.
Ну да, я имел ввиду R^n, эвклидово (или декартово?!) пространство со стандартным базисом. А что такое эвклидово пространство без указания базиса?
Сколько тебе лет? Ответь честно.
Векторы в математике - это то, что ты можешь складывать и умножать на числа. Твои тюплы можно рассматривать как векторное пространство, но точно так же и функции на R (все/гладкие/полиномиальные/и.т.д), которые тюплами не являются, можно рассматривать как векторное пространство, потому что их можно умножать на числа и складывать.
>постоянно теряются какие-то знаки или скобки или числа.
Может ты даун. У них подобные проблемы. Проверься у доктора.
Такое уже устарело. В наши дни люди пытаются формализовать математику полностью, чтобы кодить теоремы на каком-нибудь идрисе вместо описания их словами.
Рассел, но его трактат "Principia Mathematica" провалился. В наши дни формализацией математики занимается программистский проект с говорящим названием "Петух" (coq по-французски), успехов нет.
Книги Бурбаки - единственный успешный проект такого рода.
Зачем, если есть Бурбаки. Подобные проекты не из воздуха появляются, нужно, чтобы назрела необходимость. Такого пока не произошло, хотя, по-моему, намечается. Конечно, появились компьютеры, по этому поводу уже сказали.
Ах да, категории тоже появились, это один из ингридиентов слова «намечается». Но одних категорий маловато. Впрочем, человечеству скоро будет не до этого. Война (вариант — катастрофа, кризис, коллапс...) начнётся, закончится, тогда и будет Бурбаки 2.0, в соответствии с первой версией.

Смысл? На тех же основаниях получится то же, что у бурбаков, но хуже. Вот если бы кто-нибудь осилил изложение всей математики с позиции пикрелейтед, то могло бы получиться нечто отличающееся от бурбаков. Но вряд ли кто осилит.
Что еще раз показывает, что программисты - петухи.
>В наши дни формализацией математики занимается программистский проект с говорящим названием "Петух" (coq по-французски), успехов нет.
Кто тебе сказал, что успехов нет?
Тогда почему его ещё не используют все чистые математики? В чём вообще может заключаться полезность "Coq"?
In Soviet Russia математик овладевает галоперидол.
Он говорит что маняматикой надо заниматься ради маняматики, а это плохо. Априорного знания быть не моожет, яскозал.
Но конечно же тут он возразит что две пересекающиеся прямые в н-мерном пространстве лежат в одной плоскости, этажиачивидна.
Хуйню написал. да.
Понимаю.
Ящитаю что занятие математикой ради математики это тупик и загнивание.
Тот же спор о струне принес больше в математику чем нынешние попытки натянуть теорию струн на реальность.
С ним можно вывести любую элементарную теорему?


http://math.stackexchange.com/questions/46060/the-categories-set-and-ens
Ens от слова Ensebmble
>Тогда почему его ещё не используют все чистые математики?
Потому что не все могут в него. Те, кто может - используют. Ты про гомотопическую теорию типов и Воеводского слышал?
>В чём вообще может заключаться полезность "Coq"?
В машинном доказательстве теорем, во-первых. Потом, написание кода, работающего строго по заданным спецификациям, т.е. программное обеспечение без глюков и ошибок. Ты и этого не знал?
>Например, (1, 1) и (-1, 1) - базис R^2.
Ну это я кажись понимаю. Берем стандартный базис (1,0) (0,1) и поворачиваем на 45 CCW?
Да не пацаны, я хоть и школьник, но не совсем даун (кажется), я понимаю что такое базис (по-крайней мере в координатном пространстве), я просто похоже хуйню спросил, потому что заморочился >>346343
>сначало нужно задать базис
и споткнулся я об "задать". т.е. является ли базис как бы "intrinsic property" любого в.п. В результате тупо через гугл
"every vector space has a basis" -- 9000 хитов.
Успокоился.
Любое конечномерное векторное пространство однозначно определяется размерностью n и поэтому изоморфно этим твоим тьюплам K^n, в этом смысле никаких (конечномерных) векторных пространств кроме K^n нет. Просто изоморфны они не одним способом - это и есть выбор базиса.
Кстати а поясни по хардкору за эти мои любимые тюплы.
>Конечномерные векторы превращаются в n-tuple только после фиксации в векторном пространстве какой-то системы координат.
Что есть в твоем понимании n-tuple?
Как я понимаю это же просто абстрактный упорядоченный список каких угодно элементов. Вот есть у меня какое-то абстрактное в.п. уровня /b.
То есть в нем - хоть пики точеные, хоть хуи дроченые. А базис я вообще не знаю какой.
Разве не может у меня быть тюпл дроченых хуев? Он же вектор?
тюпл дроченых хуев - это охуенный подарок был бы EOT на 8 марта
Ты ебанут? Всё правильно он сказал. Для любого целого положительного числа n и любого поля K есть только одно векторное пространство размерности n над полем K, с точностью до изоморфизма.
>>346394
Я не он, но поясню. Хуи должны образовывать абелеву группу. Ты должен быть в состоянии сложить два хуя и для каждого хуя найти минус хуй.
Пацаны вы охуенны! Я копипастаю ваши ответы, и пойду гуглить пару дней. Потом мамке расскажу, какой я у нее математик.
Открой учебники и прочитай нормальные определения, зачем ты хуйней страдаешь?
n-tuple - это элемент декартова произведения каких-то n множеств.
Второй вопрос я не понял.
Алсо, я не он >>346390 , он вообще пиздец отбитый.
> Любое конечномерное векторное пространство однозначно определяется размерностью n
Тогда бы говорили, что векторное пространство - это натуральное число.
У меня учебников хоть жопой жуй. Постоянно натыкаюсь на "подразумеваемые понятия". Толкования требуют как тора с талмудом. n-tuple видимо имеет разные определения в разных областях
https://ru.wikipedia.org/wiki/Кортеж_(информатика)#.D0.92_.D0.BC.D0.B0.D1.82.D0.B5.D0.BC.D0.B0.D1.82.D0.B8.D0.BA.D0.B5
Вот здесь все понятно написано. Кортеж это и есть tuple.
>>346395
> Для любого целого положительного числа n и любого поля K есть только одно векторное пространство размерности n над полем K, с точностью до изоморфизма.
Возьмем пространство, у которого вектора из R^n, а скаляры из Q и возьмем пространство, у которого вектора из Q^n, а скаляры из Q. Они не могут быть изоморфны, потому что в первом пространстве несчетное число векторов, а во втором - счетное.
Упс, я объебался, R^n над Q бесконечномерное.
>у которого вектора из R^n, а скаляры из Q
Вот здесь у тебя проблема. Ты можешь взять произвольную абелеву группу и рассмотреть её как модуль над угодным тебе полем, с этим проблем нет. Rn образует абелеву группу, это тоже верно. Но кто сказал, что размерность Rn над полем Q будет равна n? Она не будет. Уже размерность R над Q не только не конечна, но даже несчётна.
Если выбрать каноничных представителей для каждой размерности и каноничный набор сюрьекций и вложений между ними, то получим, что категория конечномерных векторных пространств и линейных отображений между ними расслоена в групоидах над категорией симплексов - см.
https://ncatlab.org/nlab/show/simplex+category
и https://ncatlab.org/nlab/show/fibration+fibered+in+groupoids
Вроде бы есть Монастырский М.И. Топология калибровочных полей и конденсированных сред. Судя по оглавлению, необходимый бэкграунд там излагается, судя по названию, оно по теме. Больше сказать не могу
Спасибо, пока гуглил, наткнулся на любопытные обсуждения.
Есть у Рубакова две книжки называются "Классические калибровочные поля". Там есть кое-что, но приложения тривиальные в духе спонтанного нарушения симметрии. Тем не менее весь групповой формализ, который ты встретишь в кондесированных средах там присутствует кроме, может быть, обсуждения конформной группы.
Иногда говорят отображение в/на, но это тоже не всегда удобно.
> у натуральных чисел нет нетривиальных эндоморфизмов
Если ты хочешь чтобы это соответсвие было функториально, то есть.
Наложение.
Я что-то не улавливаю.
Если ты хочешь чтобы соответствие натуральные <-> конечномерные пространства было функториально, то категория целых должна просто копироваться с категории векторных пространств, таким образом морфизмы в этой категории это множество матриц n x m. Автоморфизмы из n в n это обратимые n x n матрицы.
Я и не говорил, что строю соответствие между двумя категориями, наоборот я хотел показать, что это разные категории. Если определить категорию натуральных чисел как пишешь ты, то безусловно они будут эквивалентны. Но первоначальное утверждение было
>Тогда бы говорили, что векторное пространство - это натуральное число.
и я хотел продемонстрировать, чем же конкретно отличается категория векторных пространств от натуральных чисел.
А именно: симплициальная категория имеет в качестве объектов множество натуральных чисел, а в качестве морфизмов неубывающие отоьражения множеств {0,1,...,m}->{0,1,...,n}. Все эти морфизмы можно разложить в композицию двух типов отображений n->(n-1) и n->(n+1), отвечающих проекции симплекса на i-ю грань или включению i-й грани в симплекс.
Тогда выберем набор 'каноничных' n-мерных пространств для каждого n и набор каноничных вложений и проекций R^n->R^(n+1) или R^n->(n-1), отвечающих вышеописанным отображениям. В таком случае любое линейной отображение можно представить в виде композиции обратимого отображения (приводящего базис к "каноничному") и композиции этих вложений/проекций.
Теперь сопоставим каждому в.п. его размерность, а каждому лин. отображению композицию соответствующих ему отображений включения грани/проекции на грань в симплициальной категории.
Тогда нетрудно видеть, что слой этого функтора (т.е. набор объектов, отображаемых в заданный объект и с набором морфизмов, которые отображаются в тождественный морфизм в категории-цели) над любым нат. числом есть категория n-мерных пространств с морфизмами-обратимыми отображениями. Эта категория является группоидом (это значит, что каждый морфизм в ней обратим). В свою очередь это значит, что первоначальная категория расслоена в группоидах (на самом деле только pre-fibered, потому что нужно выбрать cleavage, но это детали).
Таким образом разница между категорией в.п. и категорией нат. чисел состоит в наличии в первой у каждого объекта нетривиальных автоморфизмов - что я и хотел показать.
Я и не говорил, что строю соответствие между двумя категориями, наоборот я хотел показать, что это разные категории. Если определить категорию натуральных чисел как пишешь ты, то безусловно они будут эквивалентны. Но первоначальное утверждение было
>Тогда бы говорили, что векторное пространство - это натуральное число.
и я хотел продемонстрировать, чем же конкретно отличается категория векторных пространств от натуральных чисел.
А именно: симплициальная категория имеет в качестве объектов множество натуральных чисел, а в качестве морфизмов неубывающие отоьражения множеств {0,1,...,m}->{0,1,...,n}. Все эти морфизмы можно разложить в композицию двух типов отображений n->(n-1) и n->(n+1), отвечающих проекции симплекса на i-ю грань или включению i-й грани в симплекс.
Тогда выберем набор 'каноничных' n-мерных пространств для каждого n и набор каноничных вложений и проекций R^n->R^(n+1) или R^n->(n-1), отвечающих вышеописанным отображениям. В таком случае любое линейной отображение можно представить в виде композиции обратимого отображения (приводящего базис к "каноничному") и композиции этих вложений/проекций.
Теперь сопоставим каждому в.п. его размерность, а каждому лин. отображению композицию соответствующих ему отображений включения грани/проекции на грань в симплициальной категории.
Тогда нетрудно видеть, что слой этого функтора (т.е. набор объектов, отображаемых в заданный объект и с набором морфизмов, которые отображаются в тождественный морфизм в категории-цели) над любым нат. числом есть категория n-мерных пространств с морфизмами-обратимыми отображениями. Эта категория является группоидом (это значит, что каждый морфизм в ней обратим). В свою очередь это значит, что первоначальная категория расслоена в группоидах (на самом деле только pre-fibered, потому что нужно выбрать cleavage, но это детали).
Таким образом разница между категорией в.п. и категорией нат. чисел состоит в наличии в первой у каждого объекта нетривиальных автоморфизмов - что я и хотел показать.
Поправка
>в качестве объектов множество натуральных чисел
в качестве объектов множество неубывающих последовательностей нат. чисел
>отоьражения множеств
отображения множеств.
На самом деле здесь есть небольшая неточность - нам нужно рассматривать не категорию всех симплексов, а только категорию невырожденных симплексов, т.е. не являющихся гранью. Иначе придется иметь дело с "вырожденными векторными пространствами" которые имеют размерность меньше n, но должны бы считаться n-мерными следуя нашим определениям. Переход к невырожденным симплексам исправляет проблему.
Не вкатишься. Проботай стандартный институтский курс вроде Кострикина или Винберга.
Математика = алгебра. Дебил, что ли?
Алгебра является универсальным языком математики, что поделать.

>Дебил, что ли?
-->
>Ананасики, я даун
>Проботай стандартный институтский курс вроде Кострикина или Винберга
Спасибо. Скачал Винберга. Количество учебников к прочтению начинает пугать, попробую читать все параллельно.
>>346458
Спасибо. Хотя мне до категорий еще как до Австралии.
Алсо, ловите чихающего тюленя.
А смысл читать несколько? Во всех учебниках излагается стандартный материал. Ленг (современное издание, а не 1967 года) и Aluffi Algebra chapter 0 в этом смысле просто самые полные. Кострикин лично мне не нравится, слишком сильно вязнет в деталях и почти не излагает современные разделы. Винберг, Artin и т.п. undergraduate курсы примерно эквивалентны друг другу, можно читать любой.
Считать теорию категорий "продвинутым" предметом тоже по-моему неправильно - никаких содержательных результатов там нет, это просто язык современной математики. Все что реально может из нее понадобиться - несколько утверждений о сопряженных функторах и лемма Йонеды. Даже читать по ней какие-нибудь пособия я считаю излишним.
Смотря что считать нетривиальным результатом. Для меня это такой, который бы привёл к решению некой математической проблемы, не относящейся изначально к области теории категорий. Вот например методами теории моделей передоказали mordell lang conjecture. Хотелось бы услышать о чем-то подобном в теории категорий.
>лемма Йонеды
А я ведь загуглил что это такое. Лол, вроде как это обобщение теоремы Кэли. Но если теорему Кэли я понимаю и, наверное, смогу доказать, то в формулировке этой леммы я даже слова в осмысленные словосочетания связать не могу.
Во-первых, я не понял, при чем здесь теорема Кэли. Во-вторых, она же в уме доказывается.
Что такое функтор C->Set? Это отображение, ставящее в соответствие каждому объекту X из C множество F(X), каждому морфизму f:X->Y отображение множеств F(f):F(X)->F(Y) так, что сохраняется ассоциативность и единичный элемент. Представимый функтор имеет вид Hom(A,X) для некого объекта A (здесь используется малость С, т.к. Hom должен быть множеством). Пусть теперь дано преобразование Hom(A,-)->F, поставим ему в соответствие образ в F(A) тождественного морфизма id_A из Hom(A,A). Наоборот, пусть задан элемент a из F(A). Тогда данному g:A->X поставим в соответствие F(g)(a) из F(X). Легко проверить, что это удовлетворяет определению естественного преобразования, а также что эти две конструкции обратны друг другу. Вот и лемма Йонеды.
>она же в уме доказывается
Предварительно нужно потратить некоторое время на понимание определений. А так да, ничего сложного.
Sets, категория всех малых множеств, не является малой категорией. Класс её объектов есть собственный класс, ибо. Ens инкапсулирует подмножества какого-то множества, не являющегося собственным классом (т.е., это не универсум во всяком случае).
>при чем здесь теорема Кэли
Википедия так говорит.
>она же в уме доказывается
Если ты разобрался в теории групп, а я только начал разбираться. Плюс я не знаю что такое функтор, что такое морфизм и т д, поэтому такое определение леммы для меня малоинформативно.
Пойду, короче, Винберга читать. Может поумнею.
Морфизм - это стрелка между объектами категории. В разных категориях природа морфизмов различается. В Set это функции на множествах, в Grp гомоморфизмы, в Mat(K) это матрицы с коэффициентами из K. Функтор - морфизм целых категорий. Технически функтор состоит из функции объектов и функции морфизмов. Пусть A и B категории, тогда функтор F : A -> B сопоставляет объекту A из A объект B из B и морфизму объектов f : A -> A' из A морфизм объектов g : B -> B' из B. Функторы обязаны сохранять тождественные морфизмы, т.е., если idA : A -> A, то F(idA) = idB (а след-но прицепом и изоморфизмы). Ещё они схороняют композицию морфизмов.
Изи.
> неубывающие отображения множеств
> n->(n-1)
Я не понял.
Но вообще твоя категория - это если просто повыкидывать из категории каноничных пространств все морфизмы, кроме одного для каждых двух пространств так чтобы это осталось категорией. У такой категории изоморфизмов, конечно, нет, но при чём тут она?
гамологии)
>Морфизм - это стрелка между объектами категории
Я стрелку только в смысле отображения знаю. Морфизм - это отображение?
>Функтор - морфизм целых категорий.
Звучит, вроде бы, понятно, но очень уж туманно. Где взять разжеванные для даунов примеры?


Оформил решение в техе - сразу видно что ты продвинутый малый. Следующий шаг - верифицируешь решение в петухе (Coq) - и никаких вопросов не останется. А Львовский со своими выпуклостями пусть на хуе крутится.
Петух это, конечно, смешно, но вопрос-то был не об этом. Суть упражнения была в какой-то фишке, которую я не понял.
Вот, например, статья по векторным пространствам: https://en.wikipedia.org/wiki/Vector_space
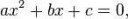

>это все имеет какой-то практический смысл
Разумеется. Нахождение корней уравнений это база ВСЕГО.
Вот пример. Допустим, мы знаем уравнение изменение координаты какого-то тела с течением времени:
x = x0 + v0t + at^2/2
где x0 - начальная координата тела, v0 - начальная скорость тела, a - ускорение, они нам заданы.
Решая квадратное уравнение, мы можем найти в какой момент времени тело будет в точке x.
К примеру, 5 + 2t + 3t^2 = 6 - в наших терминах будет означать, что тело начало движение в точке с координатой x0 = 5 м, начальной скоростью v0 = 2 м/с и ускорением 6 м/с^2. Нам интересно, в какой момент времени тело окажется в точке x=6. Решая это уравнение, находим, что t=1/3
>Прибавлять скорость к ускорению. Физика так не работает, лол.
Бессмысленный набор текста, что тебя беспокоит?
>что тебя беспокоит?
Что скоро может третья мировая начаться, что цены на бананы в три раза поднялись, а годных бананов и вообще не найти стало, что очки новые покупать надо, а я не знаю где и какой марки, что я до сих пор формализм Ламбека не освоил, и прочее по мелочи.
Ничего, что применение ln дает неравенство (третья формула в решении), которое по определению означает вогнутость?
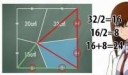
В точности 28.
Из внутренней точки, являющейся общим концом нарисованных отрезков, проведём по отрезку в каждую из вершин квадрата. Дальше вспомним, что площади треугольников одной высоты на равных основаниях равны. Дальше элементарно.
>>346595
Вы блядь серьёзно? Это же ёбаная трапеция. Хуле вы не применяете соответствующие формулы?

Разве BC не равно AD
Обычные, сука, прямоугольные трапеции!
Это же, ёбта, математики тред. Хуле тут все такие тупые? Хотя что это я, это же математики тред.
У трапеций оба основания должны быть параллельны. Ты тут параллельность видишь?
Формулу можно использовать всё равно.
Почему?
Таблица производных, в которых дана функция y и для неё y'. Интеграл берется от f(x) с учетом, что f(x)=y' и вычисляется у.
Почему оно означает вогнутость?
Тебя в un забанили что ли или в гугле?
Это копия, сохраненная 18 апреля 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.