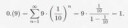Это копия, сохраненная 15 февраля 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

Метрическое пространство, в котором для каждого ε> 0 существует конечная ε-сеть, называется вполне ограниченным.
Пример. Для стандартной метрики на R множество рациональных чисел — ε-сеть для любого ε > 0.
Метрика ρ на множестве X называется вполне ограниченной, если (X,ρ) — вполне ограниченное метрическое пространство.
Топологическое пространство, гомеоморфное вполне ограниченному метрическому пространству, называется метризуемым вполне ограниченной метрикой.
Множество называется относительно компактным, если его замыкание компактно.
Теорема Хаусдорфа о компактности гласит, что для относительной компактности подмножества M метрического пространства X необходимо, а в случае полноты пространства X и достаточно, чтобы при любом ε>0 существовала конечная ε-сеть из элементов множества M.
Полное метрическое пространство компактно тогда и только тогда, когда для любого ε> 0 в нём существует компактная ε-сеть.
Предыдущий: >>327435 (OP)
Гайды:
http://pastebin.com/ZaHYuqpy - от какого-то анона
http://imperium.lenin.ru/~verbit/MATH/programma.html - оригинальный вербит
http://verbit.ru/Job/HSE/Curriculum/all.txt - побитый жизнью вербит
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
Не один. И почему "который"? Всего лишь с 2014.
и если ты когда-то посмотрел какие-то годные видеолекции, неважно по какой математической науке, просьба тут поделиться (почему-то с видео и учебником понимается лучше чем просто с учебником)
> http://verbit.ru/Job/HSE/Curriculum/all.txt - побитый жизнью вербит
Поясните, это реальная программа матфака? Просто поначалу эта программа недоступна всем, кроме тех, кто учился в мат школах. В обычных школах же математической культуры нихуя нет и вообще умение доказывать теоремы считается чем-то эзотерическим и недоступным простым смертным. Весь 10-11 класс прорешивают варианты егэ.
Чтобы изучать общую топологию, конечно, никаких предварительных знаний не нужно, но нужен определенный уровень математической культуры. А если человек в своей жизни ничего не доказывал, как он может изучать топологию?
> чисто на практическом уровне хочется понимать
Ну изучай просто алгоритмы. В любом учебнике по алгоритмам или в любом курсе в начале рассказывают это "для самых маленьких".
{ x | a <= x <= b, a < b }?
Мне кажется, что нельзя, но почему так?
Если ты про Колмогорова, то http://rghost.ru/6CQsN8PVP
>>330136
Нет, это не программа матфака. Это предложения Миши по реформе программы матфака. В настоящее время руководство матфака послало Мишу и его программу в жопу, так как "шыбо сложна", "STUDENTY NASHEGO FAKULTETA SOVSEM NE ZNAJUT KLASSICHESKOGO ANALIZA" и типа все должны ебаться в функции Бесселя.
Но ведь даже программа Вербицкого далеко не покрывает все области анализа, топологии, дифференциальной геометрии, дискретной математики, теории вероятностей и других областей математики.
Программа Вербицкого и не должна покрывать всё. Программа Вербицкого (старая) - это, по задумке Вербицкого, минимум, которого достаточно для более-менее осмысленного чтения современных научных статей. Алсо, вероятность и статистика - это уже давно самостоятельная большая наука, почти независимая от математики.
не совсем понял вопрос, но чем тебе не нравится ситуация с отрезком [1;+бесконечность)? b=1, а = меньше 1. и всегда можно выбрать x который будет между 1 и а
Это сам Вербуша так сказал? А то, сдаётся мне, она просто методически дебильна.
> b=1, а = меньше 1. и всегда можно выбрать x который будет между 1 и а
Не понял, что это означает
ну вот ты спрашивал про то, как можно разбить множество действительных чисел так, чтобы в одном подмножестве b был нижней границей одного подмножества, а был вернхей границей другого подмножества, а х тусил где то между ними. если я понял тебя правильно, то вот тебе пример такого разбиения R : отрезки (-бесконечность;1) [1;+бесконечность. скобка) означает не включая, а скобка [ включая. b тогда будет 1, "а" будет типа верхним пределом первого отрезка. но между а и b всегда можно впиздячить какой нить x, т.к. множество R несчетно. про это говно в подробностях написано в трех томнике для первокуров, забыл уже как называется, на языке вертится
>Просто поначалу эта программа недоступна всем, кроме тех, кто учился в мат школах.
Так матфак, по задумке, это и есть заведение для илитариев, которые учились в мажорных лицеях в питере или москве и имели возможность посещать все эти сунц и нму со школьных лет.
Нет, я спросил как представить R в виде объединения непересекающихся множеств такого вида.

Пиздос, третий тред подряд уже никто не может ответить.
Можно ли получить все рациональные числа, допустим, на отрезке [0;1] итеративной процедурой взятия "суммы двоечника" соседних точек, начиная с множества из двух концов {0/1,1/1} или нельзя?
Как будто хорошие сунцы и лицеи есть только там.
>>330136
Знаешь чем отличается специалист от неспециалиста? Специалист нарабатывает опыт, при этом информацию он получает не только из общеизвестных источников, но и из дополнительных. Знаешь, чем учёный отличается от специалиста? Учёному нравится искать такие источники.
В задумке скорее да, но на практике нет. Насколько я понимаю, выпускники сильных матшкол составляют там не более половины студентов. И надо сказать, что половине с худшим бэкграундом и так приходится весьма тяжело.
ну вот так и представь. чтобы еще веселее было вот разбиение (-inf;0) и (0;+inf). а функция например f(x)=1/x. в точке 0 она не определена ну никак. потому что на ноль делить нельзя. с другой стороны делить на любое другое чесло можно. х из твоего вопроса в данном случае будет 0.
> Знаешь чем отличается специалист от неспециалиста? Специалист нарабатывает опыт, при этом информацию он получает не только из общеизвестных источников, но и из дополнительных. Знаешь, чем учёный отличается от специалиста? Учёному нравится искать такие источники.
Ну все эти пафосные речи относятся только ко взрослым людям. На 1 курсе студентам обычно 16-17 лет.
Если бы R можно было разбить на непересекающиеся отрезки, то тогда не возникала бы проблема 0,(9) = 1.
вспомнил учебник - фихтенгольц. первая прям глава. сам отбитый
нельзя. рациональное чесло это то, которое представимо в виде q/n где q целое а n натуральное. в промежутке между 0 и 1 нет таких кроме его границ. ну или я тебя не понял. если не понял то можно.
Перешёл по ссылке через тор, вдруг ты и есть Вербуша и собираешь наши данные.
И что же я вижу? А вижу я бомбёжь какого-то препода по поводу незнания студентами классического анализа. А классический анализ - это ведь 10-11 класс. Так при чём тут бакалавриат, если школа не учит? Единственным выходом я вижу вполне законное введение дополнительных к ЕГЭ испытаний при поступлении.
Вербуша же ничего интересного не говорит. Хотелось бы увидеть
>послало Мишу и его программу в жопу, так как "шыбо сложна"
потому что я пока что виду всего лишь констатацию того, что из школ приходят ущербные, не знающие даже Алимова.
Или я не прав?

Под классическим анализом этот препод понимает пикрелейтед. 10-11 класс, говоришь?
Задачники где у него, еба. Заебали со своими талмудами. Некоторые не совсем очевидные моменты проще всего понимаются именно при решении задач. Передайте ему кто-нибудь, пусть добавит задачники.
Фурье 11, про Бесселя не помню, асимптоты тоже 11. По крайней мере, в Алимове есть.

Дедушка в треде? За последние двадцать лет школьную программу сильно подкорректировали. Пикрелейтед - задачи из ЕГЭ-2016.
Это уровень обычных смертных, тащи продвинутый. Сейчас же 2 уровня вроде.
Ты глупый.
А могло всё так хорошо начаться.
Мы по другому поводу срёмся.
Во всяком покрытии R непересекающимися отрезками не больше чем счётное количество элементов.
Пруф: каждый отрезок содержит рациональное число, что позволяет инъективно отобразить семейство отрезков в Q.
Теорема Серпинского. Если континуум X можно покрыть счётным семейством {Xi} попарно не пересекающихся замкнутых множеств, то самое большее одно из множеств Xi не пусто.
Пруф: Энгелькинг, "Общая топология", стр. 526.
Какой гайд тебя устроит? Как по мне надо к каждой книжке писать на что она направлена, чтобы дауны не срали друг на друга зря и мимо.
Например зельдович это чисто прикладная математика, исключительно для понимания физики. Фихтенгольц базовый курс для плавного вхождения в высшую математику, т.д.
Я доказываю что |P(A)| = 2^|A|, A - конечное множество, что и требовалось доказать.
Пусть A - конечное множество мощности |A| = n.
Занумеруем его элементы a1, a2, ... , an.
Рассмотрим множество всех строк из 1 и 0 длины n.
Всякая такая строка задаёт конкретное подмножество в A.
Не менее очевидно, что всякое подмножество в A описывается одной конкретной строкой.
Таких строк, очевидно, 2n.
Я вообще не понимаю, почему всяких инженеров заставляют считать интегралы по всяким Зельдовичам? Надо просто сказать, мол, вот Mathematica, вот Matlab, вот Maple. Нужные значки ищете, вбиваете, получаете ответ. Сейчас инженерская программа по математике - это какой-то полнейший долбоебизм в духе "что делать, если я окажусь на необитаемом острове и там не будет компьютеров".
Просто преподы ничему другому научить в принципе не могут.
Отмечу, что Зельдовича я никогда не читал, я говорил про обобщенного Зельдовича, то есть, про учебник, в котором не дают всех доказательств и задачи заключаются в вычислении.
Нет, не ясно. Бесконечные множества не похожи на конечные. Например, удалением из плоскости счётного количества открытых окружностей может быть получена любая замкнутая плоская фигура, например, замкнутый квадрат. Но удаление конечного количества окружностей напоминает всего лишь лепку пельменей.
Её нельзя доказать или опровергнуть с помощью ZFC. Лично мне она не нравится, поэтому она ложна.
Да, но по-моему мы доказывали когда-то как раз то, о чем тот анон спрашивал.

Пиздос, у меня в мат.кружке за такое убивают.
Это Мартин доказал. Лично я верую, что аксиома Мартина ложна. Кто не согласен, с тем готов подискуртировать в стиле средневековых профессоров философии (истинной считалась концепция того профессора, ученики которого сумели избить учеников всех других профессоров).
Ты меня обижаешь :-(
обьясняю - всякие интегралы с дифурами нужны не только для рассчетов в матлабе. рассказывают про это говно в общих чертах и просят чтобы ты доказывал общие вещи, а так же считал их, чтобы у тебя сложился определенный склад мышления. ну и вообще это хорошая тренировка для мозгов. такие вот мамкины инжИнеры, которые только на сосачах инжИнеры, а ирл хуи простые, не могущие в институтский матан, по сути своей и не инженеры нихуя. почему? у меня в быдловузике связи пол потока кукарекало - зачем нам ебаные производные, тем более каких то сраных логарифмов. подвывать начали, когда пришлось исходя из матана, рассказанного ранее, считать электрические цепи с привлечением комплексных чисел. те, кто не могли в матан, не могли и в эти расчеты. апофеоз же подобной херни был на защите диплома - один такой вот долбоеб очень бугуртил с фразы из пояснительной записки к диплому - "затухание на всем участке спроектированного мной участка связи составило не более 20 дециБелл". Че мне делать говорил, сказать то этот набор слов я смогу, но я не понимаю что это значит - 20 дециБелл? конечно же он знал определение Белла, знал так же что там логарифм, и то, как на первом курсе кукарекал что логарифмы не нужны. даже не вижу смысла приводить какие либо другие примеры, этот просто каноничен.
> просят чтобы ты доказывал общие вещи
это хорошо
> а так же считал их
это плохо (если не для этого не привлекаются мат пакеты)
> ну и вообще это хорошая тренировка для мозгов
С такими аргументами можешь нахуй идти
Чтобы знать определения, совсем на нужно решать Демидовича. "Тренировка для мозгов" - это миф.
этот илитарий порвался, несите следующего
Ньютон-то, конечно, решил 4000 интегралов из Демидовича. Не решив 4000 интегралов математику понять невозможно
Да, тренировка для мозгов - это миф. Люди, которые используют эту фразу, подразумевают, что мозг можно накачать как качают мышцы и от этого резко поумнеть, и что для качания мозга нужно пользоваться Демидовичем. На самом же деле тот, кто решит Демидовича, не научится ничему, кроме как решать Демидовича.
Тогда уж по областям лучше составить: алгебра, анализ, теория множеств/логика, прикладная математика, высшая математика (ентри-левел).
У меня вопрос http://ru.onlinemschool.com/math/library/vector/angl/
>Пример 1. Найти угол между векторами
>Найдем скалярное произведение векторов:
>a·b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
1) Почему это называется произведением (умножением?) и стоит точка (умножение) если на самом деле там плюсуется.
2) Что делать, если у меня векторы {0, 0} и {0, 1}. У меня получается деление на ноль. ЧЯДНТ?

Демидович - это книга, задачки из которой решают все, кроме немногих избранных.
это не тред вопросов от ньюфагов
почитай faq в шапке, там специально указаны адреса по которым такое можно спрашивать и получать ответы
и это действительно работает, то есть можно написать, и тебе ответят
> Почему это называется произведением (умножением?) и стоит точка (умножение) если на самом деле там плюсуется
разберись с тем что такое множество, декартово произведение, отображение, бинарная операция, почитай книжку "гиперкомплексные" числа примерно до момента где определяют скалярные и векторные произведения
У тебя не вектор там, а точка(вырожденный вектор). Как ты собрался определить угол между точкой и вектором?
Читаешь в википедии статью "векторное пространство". Потом читаешь в википедии статью "скалярное произведение"
Ну мы с тем аноном говорили не про Демидовича конкретно. Демидович -
это метафора бесполезного архаичного говна, которое существует в программе для унижения студентов. Видимо, ты аутист, раз у тебя проблемы с абстрактным мышлением и пониманием метафор собеседника.
А я смотрю, ты из этих, из касты униженных. Видно сам Демидович восстал из могилы и надругался над тобой.
Ага. Я сам себя наебал. Я для точек углы хотел, пойду переписывать.
Ну а куда еще.
Давай ты мне расскажешь, нахуя мне решать примеры из Демидовича, если это время я могу потратить на изучение алгебры или топологии или еще какой-нибудь интересной и актуальной области?
это был его дед. тот еще сукин сын.
>>330336
обьясняю - смоги решить хотя бы сраного демидовича, прежде чем идти дальше. а то много вас таких сыроежкиных развелось, хочу говорит диплом защитить, а что такое затухание в 20 дециБелл не знаю, потому что демидовичи ниже меня по статусу.
>>330292
нахуй можешь идти ты. ну или можешь в приемную комиссию сходить, авось возьмут учится, тогда и без моих обьяснений всё поймешь
бугурты про миф и умение решать демидовича - тренировка для мозгов не миф, после институского курса по матану реально стал мыслить по другому. решив именно демидовича да, научишся решать только демидовича. а решив учебник "математика для 5 ого класса", научишся решать только его. ну вообще числа складывать, чтобы быть в состоянии освоить математику 6ого. с демидовичем так же - можешь не решать, один хер не поймешь концепций того, что будет дальше. те кто не могли в матан радовались когда начался теорвер, т.к. кончился мат анализ. так им казалось пока, внезапно не оказалось что функция вероятности есть производная функции выборок(сча могу пиздеть, просто помню что че то одно было производной чего то другого) и как же эти выблядки рвались. не говоря уже о всяких свертках - там вообще было лютое непонимание того что происходит, потому что демидовича не решали. да и вообще конечно можете не решать, деградируйте как завещал лебедев.
>>330290 кун
> хотя бы сраного демидовича,
Демидович очень сложный и требует 1000 человекочасов. Нахуя мне его решать?
В демидовичах нет ничего про 20 дБ, в демидовичах есть только интегралы; прорва их.
не совсем с ним согласен, но удвою. К тому же там куча задач с геометрическим смыслом.
>математика для 5ого класса слишком сложный и требует 1000 человекочасов. Нахуя мне его решать?
исправил не благодори
И всё же, какова конкретная польза от Демидовича? "Тренировка для мозгов" нефальсифицируема по Попперу.
Ндааааа, ну ты и обсос. Ты серьезно считаешь, что люди, которые против нарешивания примеров из Демидовича, не понимают, что такое производная или что такое логарифм? Ты сам-то можешь определение логарифма сформулировать?
20 дБм в демидовиче нет. он и не посвящен дециБеллам. он посвящен тому, чему посвящен. в нем так же нет инфы, о том, что куча всяких теорем и прочего говна по другим предметам, на старших курсах, содержит приемы из матанализа. который видимо по демидовичу и предлагают вам изучать. но можете и не решать, это никому кроме вас не надо же.
Нет, старшие курсы не содержат ничего, что содержалось бы в демидовиче, но не содержалось бы в учебнике.
где волшебное слово?
У Пеано.
N-петух, а как ты отличаешь корректное определение N от некорректного? Ты, получается, можешь ответить на вопрос, принадлежит какой-то элемент N или не принадлежит?
Тебе необязательно решать всего демидовича. Это очевидно.
Господи, вы такой идиотский срач развели на полтреда. Для того, чтобы как следует уложить абстракции в голове, нужно использовать их на практике. Это общеизвестный факт.
Разумеется никто в реальной жизни не берет интегралы руками. Как никто (как правило) и не доказывает уже доказанные теоремы, например. Давайте не будем доказывать теоремы на мехмате, зачем? Нет же никакой тренировки мозгов. Более того, давно изобретены калькуляторы - зачем проходить арифметику в школе? Это же пустая трата времени.
Глупый спор, не относящийся к теме треда, короче. Я считаю, что вас всех следует забанить, а этот тред - удалить ввиду критической концентрации рака. Зарепортил.
Доказывать теоремы - хорошо. Решать примерчики из Демидовича - нехорошо. Хороший задачник для математика - Кириллов-Гвишиани, в нём задачи на доказательство, а не на числодрочку.
Я хз на самом деле. В школе задрачивал геометрию и задачи на док-во чего либо мне дико нравились. А вот задачи из "алгебры" всегда бесили, у меня даже 3 в аттестате по алгебре стоит, лол. Причем я тогда считал, что геометрия дно, а алгебра тащит. Олимпиадки хуядки это только подтверждали. Пришел я в топовый вузик и что я вижу, продолжение школьной алгебры, задачки на док-во никому в хуй не уперлись.
>Доказывать теоремы - хорошо. Решать примерчики из Демидовича - нехорошо.
Нет, хорошо и то, и другое. Перечитай пост, на который ты отвечаешь. Я там про это написал. Из твоих слов следует, что ты не понял, что я написал.
>>330403
>Пришел я в топовый вузик
>задачки на док-во никому в хуй не уперлись.
>топовый вузик
Как бы тебе сказать, братан...

Я считаю, что тратить время своей жизни на тысячи примеров типа пикрелейтед не нужно.
Сам Гаусс, между прочим, не брезговал интегральчики решать, сохранились его дневники с кучей подобных записей. А вот школьник считает, что это ненужная хуйня.
Гаусс жил давно, в его время это не было зашкваром.
Это твои личные проблемы, которые не имеют отношения к Демидовичу, высшему образованию и математике. Создай об этом тред в /b, если хочешь.
> Для того, чтобы как следует уложить абстракции в голове, нужно использовать их на практике.
Верно.
> Давайте не будем доказывать теоремы на мехмате, зачем? Нет же никакой тренировки мозгов.
Теоремы нужно доказывать не для тренировки мозгов, а для того чтобы > как следует уложить абстракции в голове
Вычислительные задачи из Демидовича ничего не помогают уложить в голове. Это наследие тех времен, когда не было компьютеров и интернета.
> Тебе необязательно решать всего демидовича. Это очевидно.
Лучше вообще ни одной задачи не решать. Я, конечно, все 4000 задач не читал, но из пары сотен, которые я прочитал, ни одной полезной задачи я не увидел.
Это надо постараться, чтобы из нгу отчислили. Если ты не с фф или фена.
Ты совсем тупой да? Во времена Гаусса
1) Не было компов
2) Один человек мог полностью изучить не только математику, а вообще все существующие науки.
Второе неверно выражено: один человек мог аккумулировать знания, считающиеся научными.
>Теоремы нужно доказывать не для тренировки мозгов, а для того чтобы > как следует уложить абстракции в голове
Я не знаю, что ты подразумеваешь под "тренировкой мозгов". Я под этим подразумеваю именно укладывание в них абстракций.
> Это наследие тех времен, когда не было компьютеров и интернета.
Преподавание арифметики в школе - это наследие тех времен, когда не было компьютеров и интернета.
Короче, мне неинтересно по десять раз повторять тезисы, которые я изложил в своем первом посте, так что я сваливаю.
Плохая аналогия, вот преподавание кучи задротских методов устного счёта - это наследие тех времён, когда не было калькуляторов. Потому их сейчас и не преподают.
> Преподавание арифметики в школе - это наследие тех времен, когда не было компьютеров и интернета.
И как это вообще связано с Демидовичем? Тебя че, в начальной школе заставляли тратить сотни часов на умножение и деление чисел в столбик, несмотря на то, что алгоритм деления в столбик и элементарные свойства умножения тебе уже давно были понятны?
> Я не знаю, что ты подразумеваешь под "тренировкой мозгов". Я под этим подразумеваю именно укладывание в них абстракций.
Я под тренировкой мозгов подразумеваю повышение способности мозга усваивать новое и создавать новое. При вычислениях эта способность теряется, вычисления отупляют.
Математика развивается во времени. Несколько тысяч лет назад математики вообще не было.
Если брать определение математики из википедии "Матема́тика — наука о структурах, порядке и отношениях", то математика была всегда. Универсальный язык, прочее говно. Вообще забавно, что под наукой ты подразумеваешь только один из языков.
Математика - сильнее, чем язык. Она позволяет не только формулировать утверждения, но и проверять их истинность.
>Ты серьезно считаешь, что люди, которые против нарешивания примеров из Демидовича, не понимают, что такое производная или что такое логарифм?
Почему ты пишешь так, словно все люди, которые против Демидовича, либо понимают, либо не понимают?
Странные у тебя представления о языках. Проверь утверждение: "Я ебал твою мать".
Ну, я надеюсь, что все люди в этом треде понимают.
Проверил тебе за щеку.
Я бы сказал, что у тебя ещё нос не дорос, но это было бы ложным суждением, ведь я не знаю ни тебя, ни того, с кем спит моя мать.
> ведь я не знаю ни тебя, ни того, с кем спит моя мать.
Exactly. А математика при должном усердии позволяет проверить практически (по модулю всяких логических забубонов) любое утверждение, формулируемое на её языке, не имея никакой априорной информации.
>Тебя че, в начальной школе заставляли тратить сотни часов на умножение и деление чисел в столбик, несмотря на то, что алгоритм деления в столбик и элементарные свойства умножения тебе уже давно были понятны?
Представь себе, в начальной школе к этим темам дается на отрешать энное количество примеров. Для умножения и деления существуют простые универсальные алгоритмы по одному на каждую из этих задач, а для интегральчиков таких простых универсальных алгоритмов нет вскудахнувшему про алгоритм Риша предлагается решить по нему хотя бы одну задачу, а есть только несколько общих техник, поэтому надо сначала освоить каждую из них, потом научиться их комбинировать, и наконец, научиться определять, где что выстрелит. Это такая же энтрилевельная базовая техника, как разложение разности степеней на множители или бином Ньютона, и используется она не столько для того, чтобы интегральчики считать там-то как раз надо матпакетами пользоваться, сколько в доказательствах. Нету пока таких компьютерных инструментов, которые за тебя поковыряют интегральчик этими техниками и дадут более удобную его форму или скажут, что таковой нет. А пока этого нет, без чутья никуда, а оно без практики не вырабатывается.
При должном усердии я могу доказать, что ты ебал мою мать. Но будет ли это истинным? Нет, ни математическими методами, ни словесными. Более того, математическими доказать будет этот факт намного сложнее, потому что вероятность события будет крайне мала. Математика как язык несовершенна. Особенно в руках дилетанта, изучившего лишь основы, но считающего себя нативом.
Математически, утверждение: "Я ебал твою мать" вообще невозможно сформулировать, ты можешь только построить некую математическую модель которая формализует этот вопрос. Но процесс формализации - несовершенен, и математика за него не отвечает, за него отвечает человек, и если модель даст неправильный ответ - то тут вина не модели, а человека.
>При должном усердии я могу доказать, что ты ебал мою мать. Но будет ли это истинным?
Только средствами русского языка - не сможешь. Ты сможешь только привести аргументы в пользу истинности/ложности утверждения, но это ли есть то, что мы понимаем под "проверкой истинности средствами языка"?
Заранее нельзя сказать, является ли утверждение логическим забубоном. Более того, ZFC тоже является логическим забубоном. То есть ты в ходе любой проверки просто придёшь к логическому забубону.
Ты понимаешь, что уметь виртуозно обращаться с интегралами нужно не во всех областях? Это нужно в какой-нибудь мат физике. Зайди на arxiv.org в какую-нибудь алгебраическую топологию и попробуй найти там статью, в которой есть знак интеграла.
Молодец, понимаешь, что математика ущербна, если не построена на вероятностях.
Зоопидор опять выбрался.
>истинной считалась концепция того профессора, ученики которого сумели избить учеников всех других профессоров
Пруфсы.
>Ты понимаешь, что уметь виртуозно обращаться с интегралами нужно не во всех областях?
Если ты сразу знаешь, что ты будешь заниматься теми областями, в которых аналитический метод не применяется, то и иди учиться туда, где будут учить именно им. К Вербиту там или куда еще. Если ты пришел туда, где дают что-то типа общего математического образования, то учи и не возникай.
>Это нужно в какой-нибудь мат физике.
Везде, где можно заебашить интегральчик, то есть хоть даже ТЧ.
В России образовательная деятельность без лицензии является административным преступлением. Лицензию можно получить только если ты следуешь программе, утвержденной Минобром. Нельзя так просто взять и начать изучать алгебраическую топологию.
Ещё бы, иначе бы гроздью расцвели конторки модной-молодёжной учёбы без интегралов "по вербиту", которые де факто занимались бы просто продажей дипломов.
>Рыночек быстро бы порешал, у какого университета дипломы имеют вес, а кто просто торгует понтами.
Но в реальности он ничего не решает на самом деле. До сих пор приходится расчищать наследие великой швободки, закрывая периодически парашные говновузы.
Нет, не лицемерие. Ты хочешь получить образование, а жалуешься на то, что не дают бумажку.
Кроме того, у вас есть всякие вышки и НМУ, так что вы имеете куда больше, чем негры.

Эти говновузы существуют только благодаря покровительству чиновников. Например, университет профсоюзов, ректор которого на прикреплённой фотке (реально так ответил своей студентке, был скандал), корефанится лично с Путиным. На то и существует.
>>330471
Я хочу получить математическое образование, а не картофельное.
>>330472
Алгебраическая геометрия.
http://www.mi.ras.ru/index.php?c=pubs&id=19549&l=0
http://www.mathnet.ru/person/19549
https://zbmath.org/authors/?q=kaledin.dmitry-b
http://arxiv.org/find/math/1/au:+Kaledin_D/0/1/0/all/0/1
>Я хочу получить математическое образование, а не картофельное.
Тогда я тем более не понимаю, зачем тебе нужна минобровская бумажка.
> Эти говновузы существуют только благодаря покровительству чиновников.
Да, точно так же и новым владельцам свободных от стандартов школ, разбогатевшим на дураках тоже захочется бюджетных денежек.
В этой стране степень дают за успехи в жарке картофеля. Нужна степень в этой стране и не хочешь воевать с Минобром - жарь картофель и не возникай. Нужна не в этой - ты знаешь что делать.
вай нот?
Нам очень жаль тебя, но варианты есть только такие.
Сейчас же по результатам егэ поступают. Можно пройти при желании. На повышенную стипу вполне можно жить, я не понимаю.
Понимаю только, что ебал твою мать.
Это значит что он слишком сложный для меня/я дурак?
Есть что то попроще или зельдович и так простой как два пальца?
Ну как, вербит советует - значит канон.
Это значит, что он пишет непонятно. Читай места, которые понимаешь, на остальное забей.
Изначально читал физику Сивухина. В первом же томе механики дошел до интегралов и решил их выучить, чтобы понимать о чем он.
На двощах посоветовали Зельдовича, Кушнера, Фихтенгольца и Зорича. Я по диагонали посмотрел оглавление и решил что зельдович это именно то что мне нужно.
Например он пишет "Умножение х на С равносильно делению х на 1/С" и дальше переводит разговор в другое русло.
Зачем надо было это говорить а потом съезжать. Я пытаюсь найти связь между этим и следующим абзацем.
Ты не на районе, надо было, значит надо.
Дальше он про умножение икса на числа меньше единицы ведет речь, о том что функция в таком случае сжимается по оси икс пропорционально этому самому числу.
Прочитай статью на википедии "определенный интеграл". Для понимания этой статьи надо знать, что такое предел. Тоже прочитай на википедии. Этого будет достаточно для твоих целей.
Что значит "понимать"? Для математиков понимание какого-то объекта означает способность доказывать утверждения об этом объекте. Не думаю, что тебе это надо.
Короче читай Зорича или Рудина. Не удивляйся, что в среднем будет уходить 1 час на страницу. Так и должно быть.
Но я ведь не математик нихуя, а физик. Ну по крайней мере хочу быть физиком. И немножко химиком.
Понимать в значение осознавать что именно ввиду имеет Сивухин когда говорит что "производная расстояния по скорости равна ускорению".
У Зорича сразу идет какая то логическая симфолика. Это меня немного напрягает.
Ну скопипасти полностью абзац, который тебе непонятен, что ты над нами издеваешься.
Я хочу начать читать Зорича. Прям вдохновился, цель себе поставил. Немножко пробежал глазами - вроде все, как надо, синтаксический онанизм, все дела. Какие ресурсы мне следует иметь под рукой, чтобы не забросить все это на втором параграфе от осознания собственной тупости?
Мне там все понятно, но не сразу. Приходится по два-три раза перечитывать чтобы понять что и к чему. Я про это и спрашиваю, это норма что я перечитываю два сраных абзаца на десять предложений по два раза или нет.
Поему у меня тогда с химией и той же физикой таких проблем не было? Я как начал читать, так и продолжаю, не перечитывая каждые пару слов по два раза с мыслями "что за хуйня блять?".
>читаю физику Сивухина
Изучение теоретической физики без знания предела - это вообще законно? Или я что-то перепутал и Сивухин написал ещё что-то на общедоступном уровне?
Вообще-то он утверждает "производная расстояния по времени равна скорости" и не делает более сложных утверждений.
Есть операция "штрих по букве", которая перерабатывает один набор букв в другой набор букв по правилам таблицы производных. Цифры, символы +, - и другие я тоже отношу к буквам. Под буквой обычно понимается x, но вместо икс может стоять любая буква.
В механике каждая физическая величина, - расстояние, скорость, ускорение, - есть набор букв. Сивухин утверждает, что если применить операцию "штрих по тэ" к набору букв, которым записано расстояние, то получится набор букв, которым записана скорость. Если же применить операцию "штрих по тэ" к набору букв, которым записана скорость, то получится набор букв, которым записано ускорение.
Физики не думают о производной в точке как о пределе чего-то, и тем более не думают о производных функциях как о функциях, которые каждой точке сопоставляют производную в этой точке. Они строго придерживаются концепции "набор букв, которым записана физическая величина". В физике дифференцирование (и интегрирование, и разложение в ряд) - это чисто буквенные операции, чисто манипулирование строками букв.
Почему физические величины вообще можно описывать строками букв, физики никогда не размышляют, предпочитая вычислять, а не философствовать.
Не знаю о чем ты, но первую сотню страниц я легко прочитал.
Я еще раз повторяю, я хочу понимать смысл того что эти самые буквы обозначают и как они переходят в другие беквы.
Вот я например понял что импульс это первичная характеристика движения тела, а кинетическая энергия интеграл от импульса по скорости.
Если еще короче и непонятнеё, я хочу понимать СУТЬ
Книг, написанных специально ради объяснения сути, не написано. Физики уже несколько веков не занимаются метафизикой, и само слово из респектабельного термина, обозначающего описание принципов физической науки и концептуальных связей между физическими понятиями, превратилось в зашкварное словечко из арсенала колдунов. Ты выбрал очень трудное направление деятельности. Удачи.
Нельзя быть превосходным математиком, не будучи гениальным логиком.
можно
Быть гениальным логиком просто - достаточно пройти тест http://hr-portal.ru/pages/hu/logika.php на тридцать баллов.
То есть предлагаешь изучать математическую логику перед всеми остальными разделами математики?
Сдал этот тест на 27. Мне не стать великим математиком?
Нельзя быть гениальным логиком, не будучи великим философом.
Ахуительные истории, впрочем ничего нового.
С каких пор Сивухин стал теоретической физикой, вы там совсем ебанулись? Всю жизнь это общефиз был
Чем отличается
> 9. Джон всегда либо урдит, либо мурлит.
от
> b. Джон иногда урдит, а иногда мурлит;
Точнее как вообще интерпретировать второе? Ни разу не встречал такой логической связки.
> 21. Найдено множество останков быдлозавров. Но все они очень плохо сохранились.
Чет сиранул
> 25. Информация о том, что завтрашнее совещание будет посвящено альным утятам, оказалась ложной.
Прочитал как "анальным утятам".
Ну это опять-таки смотря что читать. А мат.ан. труден (первоначально), не волнуйся.
>Вклеиваешь вдоль центральной окружности
Лол, охуенные у тебя задачи просто. Ничего, что если вклеивать по средней линии, то
а) Не получается гладкое многообразие, поэтому хуй тебе, а не когомологии де Рама.
б) Даже если забыть про это и считать сингулярные, то лента мебиуса ретрагируется на среднюю линию, так что задача тривиально, ибо получим тот же тор с k дырками.
Даже если ты хотел вклеивать по граничной окружности, то все равно задача тривиальна, ибо последовательность Майера-Виеториса.
Так что иди-ка нахуй. Даже не знаю, что у тебя спросить в ответ, раз уж ты подохуел.
Посчитай когомологии де Рама гладкой кубической гиперповерхности в CP^3. Посмотрим, можешь ли ты для первокурсника решить задачу, а не для школоты.
Быдло не может в модальную логику.
Во втором случае Джон может не делать ни того ни другого.
Программу изначально решил начать с теории множеств, элементов дискретной математики, теории алгоритмов и математической логики, потому что эти области не предполагают изначальных знаний.
В итоге изучил эти темы с помощью уже восьми прочитанных книг, решил много задач, только теперь появилась трудность говоря о самой программе.
Я читал, что невозможно стать хорошим математиком, не прочитав классику, потому, следующие книги в моей программе - три тома Рассела "Принципы математики". Я встречался и тем мнением, что читать логицизм Рассела будет пустой тратой времени, но опять-таки, например, двухтомник по этой же теме Гильберта, который я прочитал перед этим, мне очень понравился. Вопрос: читать ли всё-таки эти три тома от Рассела или сразу переходить к алгебре?
> Составил для себя программу из многих учебников для изучения почти всех высших аспектов математики (под сто загруженных книг).
Малореалистично.
>Я читал, что невозможно стать хорошим математиком, не прочитав классику,
Это полная глупость. Классика в математике имеет лишь исторический интерес, гораздо важнее читать актуальные учебники.
Типичный дурачок с псевдотехнического факультета. Классику нужно читать для понимания того, как работает то или иное что-нибудь. Например, если бы ты почитал про историю появления и развития интегралов, ты бы их понял намного быстрее.
>загруженных книг
>уже восьми прочитанных книг, решил много задач
Пиздос. Как ты это делаешь? Восемь книг это больше половины НМУ, если что. Чтобы не быть голословным даже перечислю: Зорич, Винберг, Львовский, Виро, Хатчер, рандомный учебник комплана, Атья-Макдональд, Хартсхорн.
>>330625
>Классику нужно читать для понимания того, как работает то или иное что-нибудь
Что несешь? Классики сами нихуя не понимали. Они в адовом бреду и муках нашли что-то интересное, чтобы потомки это осознали и запилили по-человечески. Если их читать, то только запутаешься и потратишь безумное количество времени. Это вообще основная задача математики развиваться, чтобы излагать все вещи проще, понятнее, короче. Когда-то нужно было потратить всю жизнь на изучение матанализа (и при этом ничего не понимать и писать доказательства и неверных утверждений), сейчас хватает одного семестра. А хороший олимпиадник унизит любого великого геометра древности во всех возможных вопросах.
>Классики сами нихуя не понимали
Так и ты нихуя не понимаешь, и актуальные учёные нихуя не понимают. В этом-то и суть науки, чтобы нихуя не понимать и постоянно улучшать.
Разумеется, никто на абсолютное понимание чего-то не претендует. Но авторы современных хороших учебников понимают несоизмеримо больше классиков. Черт возьми, даже при живом классике сейчас так бывает. Ну, т.е. человек открыл новую безумно крутую область, другой математик прониксяя и стал разбираться. А в итоге через несколько лет второй уже гораздо лучше осознал, что на самом деле означают идеи пришедшие первому первому в голову, и в итоге в предмете разбирается гораздо лучше.
Естественно больше. Но больше - не значит лучше. Может это тупиковый путь, а ты и не узнаешь, как повернуть в другое русло, не ознакомясь с предыдущими шагами.
Нет! Именно лучше. Что бы это слово ни значило. Ну, т.е. даже на уровне глупого практического критерия "Может ли человек отличать верные утверждения от неверных" или менее проверямого "Насколько концептуальны доказательства и определения"
Пуанкаре долго не понимал разницы между Pi_1 и H_1. После Ньютона/Лейбница еще долго классики делали просто неверные утверждения через шаг (не говоря уже о том, что гладкость, непрерывность и аналитичность для них были понятиями примерно из одной области), в топологии на начальном участке доказательства были сугубо технической пиздецовой работой с триангуляциями ручками. Так вообще везде.
> Может это тупиковый путь, а ты и не узнаешь, как повернуть в другое русло, не ознакомясь с предыдущими шагами.
И вообще ты делаешь какое-то совершенно непонятное предположение, что начало какого-то пути находится у того места, которое указали первым.
Я совсем не говорил о начале пути, я говорил о каком-то неправильном повороте.
зачем рассела читать? он не был математиком, более того и логик из него был не очень.
Это ты спроси у анона, который хочет его прочесть. Я просто указал, что был перевод на русский. Лично я думаю, что Вайтхеда Рассела стоит читать только в случае, если всерьез озаботился историей логики и основаниями математики.
Может они и не оцифрованы но твердую копию я видел.
>Перевод I тома книги на русский вышел в 2004 году, II тома — в 2005 году, III тома — в 2006 году. Перевод был выполнен под редакцией Г. П. Ярового и Ю. Н. Радаев
Это я с зельдовича скопировал просто.
Насколько эти основания основательны? Я имею ввиду если я дам это своему сыну-шестикласснику, он нормально в этом разберётся?
Совершенно основательны. Материал книги не предполагает никаких предварительных знаний. Можно дать кому-угодно, кто умеет читать и он должен разобраться.
К чему это ваше "лол", молодой человек?
Алгебра.
Чтобы научить детей рисовать хуйцы.
Закрой их и открой алгебру Шеня.
Но ведь ты не изучал теорию множеств, в отличие от меня. Там проясняется суть функции, как таковой.
следующий шаг после этих графиков функций 7-8класса - алгебра и начала анализа. в началах анализа фапают на эти графики и исследуют их. учат как строить графики любой злоебучей функции, а не только тех, которые проходят в 7-8м классах. это в свою очередь надо например для того, чтобы считать еще на следующем шаге всякие работы сил, которые в свою очередь являются площадями под определенными графиками. например изменение силы от времени. но эта зависимость в свою очередь за частую бывает не известна и не выразима в простых функциях типа х^2. или вообще не известна, известны только значения силы в определенные моменты времени. ну и тогда используют всякие интерполяции и ряды фурье, чтобы эту зависимость можно было представить с максимальной точностью. дрочат сперва в 7-8м классе на просто графики, чтобы дальше не было вопросов о графиках вообще. так же дрочат демидовичем ребят немного по страше, чтобы у них на старших курсах вообще не возникало вопросов о решении тех задач, которые есть в демидовиче. и так же в 5м классе дрочат на деление и сокрашение дробей, чтобы когда познакомился с определением рационального числа не смотрел на него пуская слюни, а принял душевно как уже прекрасно известную с 5 класса дробь. такие дела
Раз уж ты такой умный, то скажи мне, в школах до сих пор изучается только то, как построить график исходя из цифр, или всё же наконец-то хоть где-нибудь введено изучение обратного процесса, когда ученикам показывают как читать график и выражать в цифрах?
Вот смотри, я тебе даю какой-то объект, а ты мне сможешь сказать, принадлежит он N или не принадлежит. Получается ты знаешь, что такое N.
Ну нет. Возьми например, неравенство Коши-Буняковского-Шварца. Сначала его доказали для обычных векторов в C^n и стандартного скалярного произведения, потом для каких-то там функций, когда скалярное произведение - это интеграл. И нахуя тебе доказывать все эти частные случаи через какие-то невнятные трюки с суммами и интегралами? Просто открой статью на википедии про это неравенство и прочитай доказательство всех этих случаев в 6 строчек.
Это взаимно-однозначное соответствие элементов одного множества с другим множеством!
>>330746
Вот этого не слушай, он уже который тред засирает своей мелкобуквенной тупостью, у него просто какое-то когнитивное расстройство.
Если интересует школьный материал, то решай вот эти листки
http://www.mccme.ru/free-books/yaschenko/v08book-08.pdf
http://www.mccme.ru/free-books/yaschenko/v08book-09.pdf
Там в конце есть все решения. То есть, если че, сможешь себя проверить. Вопросы задавай если че.
Разве не смешно?
Кэт. Собственной персоной.
> ТАм же весб учебник учат как цыферки подставлять вместо переменных и графики рисовать, чё это за говно, я это и без учебника же могу блять.
То есть человек жалуется, что обычный школьный учебник написан для тупых. Ну я ему нормальный источник дал, по которому можно учиться математике.
Да, интуитивно. Но ты опять забыл, что ты это советуешь парню, который начинает с учебника за 7 класс.
Человек пришел, просит дать нормальные учебники, мы ему помогаем. А ты говоришь, что это хуйня, надо про яблоки, Петю и Ваню читать, строить графики, упрощать выражения с многочленами. Вот из-за таких как ты я поступил в свое время не на матфак, а на другую совсем специальность, потому что думал, что математика говно и ни один психически здоровый человек не станет ей заниматься.
Пусть f ⊂ X × Y. Говорят, что f — функция из X в Y, если
(x, y1) ∈ f ∧ (x, y2) ∈ f ⇒ y1 = y2.
Вместо (x, y) ∈ f пишут f(x) = y.
Немножечко Коши, для серда и души.
Сначала будет тяжело, мозг будет охуевать, если раньше подобное не читал. Так и должно быть. Главное поначалу не пропускать непонятных мест и разбираться с каждым символом.
>>330527
Википедию, возможно. Но вообще, никакие сторонние ресурсы не нужны, Зорич не предполагает никаких предварительных знаний.
Первые 3 главы, наверное, будет сложно. Я бы советовал начинать сразу с той главы, где вводится определение предела, а потом по необходимости возвращаться в первые 3 главы.


Да, он заострил на этом внимание. Но ничего хуже и скучнее (это при том, что изложение Бурбаки я нахожу довольно интересным) нынешнего учебника по математике для седьмого класса я не видел. И нет, я не множества задач, я против их полной безыдейности. От ученика просто требуется зазубрить алгоритм и как ебучий шакал использовать его в однотипных заданиях, пока не сдохнешь.
В то время как в предложенных листках >>330781 задания не настолько однотипны, на одной теме не "топчутся", как иной раз бывает в школе, да и всё-таки решить их можно с любым уровнем подготовки. Да посмотри же - они правда элементарны.
Годная книжка, никто не спорит.
Сколько элементов в множестве:
а) {1}, {Вася}; ???
>изложение Бурбаки я нахожу довольно интересным
Сукааа, потекло с монитора в заблаговременно подготовленный таз.
Шкварок теперь нажарю...
Так то проблема не только школы, но и вуза. В СПбГУ вон тоже задачи задрачивают перваки.
(Коля, Вася, Леша), (Коля, Вася, Петя), (Коля, Леша, Петя),
(Леша, Вася, Коля), (Леша, Вася, Петя), (Леша, Коля, Петя),
(Петя, Вася, Коля), (Петя, Вася, Леша), (Петя, Коля, Леша)
ВОТ ООНОО! ВОТ ОТВЕТ!!!
Зачем тебе знать, почему кристалл рос так, а не иначе, если тебя интересует сам кристалл?
Что значит "сам"? Мне же интересно как именно построены его связи, чтобы знать, где именно можно его использовать, даже если я обычный ювелир.
>Верно ли, что множество летающих крокодилов является
подмножеством множества учеников 7 «В» класса 57-й школы
Нихуя не понял
>Поскольку множество летающих крокодилов пусто
Почему?
Ну от туда и фраза про
>Поскольку множество летающих крокодилов пусто
По тому что оно не задано или чё?
Эти рассуждения, коненчо, не являются математическими. Имеется в виду, что-то вроде "в реальном мире летающих крокодилов не существует, поэтому множество летающих крокодилов пусто".
Ну эти листки нестрогие, конечно. Они просто развивают математическую интуицию. Ты же не можешь дать восьмикласснику аксиоматическую теорию множеств. Люди которые изучают аксиоматическую теорию множеств, уже знакомы с наивной теорией множеств и имеют какой-никакой кругозор в различных разделах математики.
Ты лох.
С чего бы это летающие крокодилы неважны и как это они связаны со школьниками?
Там аллигаторы, не путай.
Нет, я просто указал тебе на нестыковку и возможность изменения вариативного ряда.
Летающие крокодилы нахуй неважны, как и все конкретные объекты в математике. Важны их отношения. К этому книга и прививает.
Да с чего бы не важны-то? Летающие крокодилы важнее школьников. Даже математически, потому что именно про них вопрос, а не про школьников.
С чего бы вдруг? Если ты не можешь выделить из двух подмножеств важнейшее, то зачем ты советуешь именно эти задачи?
Математика - не место для твоего жизненного опыта. Одно множество не может быть важнее другого именно потому что про него встречается вопрос. Более того, в математическом смысле понятия "важнее", говоря о множествах, вообще не существует.
Математика вот уже полтора века устремляет свой взор не на объекты, а на их взаимодействие между собой. Тебе должно быть похуй на летающих крокодилов.
Лол. То есть, вопрос "верно ли что множество является подмножеством" - это для тебя не степень важности?:
Фу таким быть. Неудивительно, что ты не можешь использовать вероятностную математику.
//подкрался сзади и нанёс 2 удара в голову правой кнопкой мыши
Как что-то плохое.
Правда.
У нас одна любовь и одна только жизнь.
Я не он и не такой умный, как он, но да, в егэ сразу же были такие задания, если мне память не изменяет, то есть уже лет десять в школах это обязано изучаться.
Википедия - это само собой. Я имел в виду, может быть нужны какие-нибудь практические книжки, задачники там, не знаю. Обычно же дают учебник + задачник + рабочую тетрадь\методичку\конспект\хэндаут.
В любом случае, спасибо за совет.
Там и сейчас уютно, но очень много школьников и первокуром, поэтому всяких няшных интересных разговоров мало, в основном просто "допоможите решить".
>>330944
Создавай. Только N-определяющих банить не надо.
Вообще, вы заебали гнать на N-петуха. Про интуиционизм не слышали? Про конструктивизм? Про ультрафинитизм? Честное слово, заебали со своим невежеством. Вот вам с вики:
> Edward Nelson criticized the classical conception of natural numbers because of the circularity of its definition. In classical mathematics the natural numbers are defined as 0 and numbers obtained by the iterative applications of the successor function to 0. But the concept of natural number is already assumed for the iteration.
Нельсон - не хуй простой, а принстонский профессор математики: https://web.math.princeton.edu/~nelson/
Короче, создайте кто-нибудь уже доску, модерируемую не по тематике, а по уровню ведения дискуссии.
Мы бы всё решили, говоря о правилах тематической доски. Только вот, кажется, ебучая обезьяна запретила создавать новые. Попробуйте сами - https://2ch.hk/boardrequest.html (
Википедия это лицемерство. Вместо того что бы государства скинулись и сделали публичную энциклопедию, устроили говно на палочке.
Википедия это расточитльная трата человеческого труда. Правит кто то правит, говнюк стирает это, правит кто то другой, и ещё один говнюк стирает.
Самый нервотрёпный проект столетия это говновикипедия.
Нет. Проблема ведь решилась, модпок пробудился.
И, пожалуй, обсуждение личностей пора завершать.
Дискусия перетекет в ноократию.
>Государства в таких проектах нинужны.
Но они же правят в таких проектах данные и цензоров на зарплате предоставляют для таких проектов.
Какие результаты в теории множеств must have?
Не плачь ничто, утри свои слёзы, многие люди представляют из себя ничто, но они же не плачут!
Очень плохое утешение, ведь я хочу быть лучше, чем все остальные.
Хочешь с тобой моя тянка тяночка тянучка перепихнется в обмен на твою квартиру?
Еще очевидные теорема Кантора-Бернштейна и лемма Цорна. Из остального, хотя это менее широко используется, можно добавить базовые результаты о вполнеупорядочиваниях - теорема о том что из двух вполнеупорядочиваний одно всегда вкладывается в качестве начального отрезка в другое и теорема Цермело.
Ещё теорема о том, что отношения эквивалентности взаимно однозначно соответствуют разбиениям.
Как доказать что 0,(9) не равно единице?
Но они равны. Мнемонически: не существует числа между 0,(9) и 1, значит, логическое выражение 0,(9) < 1 ложно.
Бля,жопу проиграл(
Нехуй было рождаться человеком.
Объясни пожалуйста, я не могу достичь понимания
Так он докажет, что равны.
Представь, что количество девяток в числе 0,(9) не просто стремится к бесконечности, а уже равно ей.
Значит, при сверхточных расчетах,например, в космонавтике и прочем, 0,(9) принято принимать за единицу, 1,(9) за 2 и так далее?
Сорян,анон,если надоел. Просто реально этот вопрос не даёт покоя. Не обессудь,больше не буду беспокоить
Я этого уже не помню,а может и не знал вообще, и поэтому спросил в надежде на понятный ответ,зачем сагать сразу
0.9 = sum_{n=1}^\infty 9(1/10)^{-n} = 9\frac{1/10}{1 - 1/10} = 1.
Что и требовалось доказать.
Причем здесь ТМ?
В формуле все прозрачно и очевидно. Если тебе нет, у меня для тебя плохие новости.
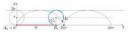
длина отрезка между точками касания производящего круга с направляющей
прямой в моменты времени 0 и t
(отрезка OBt, см. рис.2) равна
длине дуги Bt At, «прокатившейся» по этому отрезку
Рисунок посмотрел но не понял что имеется ввиду.
Вот теперь понял. Я не на ту кривую смотрел, да и написано там непонятно.
Вроде прочитал и чего то понял. Спасибо.
В смысле мучить? Я от математики не устаю вообще. Если мне какая-то область интересна, я могу с утра встать и весь день ее изучать пока спать не лягу и потом еще так же. Ну примативному быдлу не понять.
Ты дурак и не понимаешь в чем состоит деятельность математиков (или просто зеленый). Впрочем это совершенно верно, что если некоторый математик заменяется использованием пакетов компьютерной математики, то он тупой ебанат. Кстати, университетскую программу от всего этого вычислительного мусора уже давно пора почистить.
Почему?
Интересный образец! Что именно ты делаешь с утра до ночи, примат?
Суть математиков - глупые и ненужные занятия. Стране нужны токари, а ебанаты всё свои формулы надрачивают.
После чего недоумевать какого хрена пакетная функция даёт относительную погрешность больше 0.2. О теореме сходимости итерационного метода я вообще молчу.
Таких «пакетников», которые нетвёрдо зная мат. часть вызывают функции какие надо и не надо – увольняют.
Чет проиграл с матанобыдла.
Лол, я как раз за большую глубину изучения материала в противовес имеющейся до сих пор в программах длительной отработке навыков исполнения алгоритмов решения стандартных задач, которые с большим успехом выполняют эти самые пакеты.
В любом случае, проблемы с пакетами и решениями по-старинке - это все в основном релевантно для "низшей касты" прикладников. Нормальным математикам задачи в которых пакеты помогают нужно решать весьма редко.
Зачем ты тогда вообще отвечаешь? Если мне, допустим, непонятно, почему 0.(9) = 1, то как мне может быть "прозрачно и очевидно" то, что ты написал? Если не можешь объяснить - так и скажи, а не начинай вот это свое "вы все дураки".
Мало ли что случается. Например. Вот доказываешь ты теорему и никак не приходит в голову концептуально-правильное обоснование какого-нибудь перехода. Но при этом виден путь доказательства этого перехода через какие-нибудь комбинаторные оценки. Для того, чтобы произвести эти оценки могут потребоваться, скажем, методы аналитической комбинаторики. Вот и всплывут какие-нибудь задачки в которых есть толк от пакетов.
Я не полностью загринтекстил. Короче, все чаще и чаще пакеты нужны.
По аналогии с Евклидовым расстоянием.
Были б нужны токари - уже были бы, долбоеб, не могущий в рынок.
Зачем ты мне даешь ссылку на викистатью? Я тебя прошу показать, почему выполняется это равенство, а ты даешь мне ссылку на статью.
Счет какого-то частного говна в координатах тебе точно в этом не поможет. И опять у тебя какие-то неправильные аналогии. Математика это не история. И не кристалл. То говно, которое раньше было, уже в кристалле никак не отражено, оно было послано нахуй, так как говно. Ну, не знаю. Можешь думать, что это карта, которую все точнее изображают. Ты же не будешь исследовать черновые карты, чтобы понять, почему картографы пошли по такому пути. Да потому что лучше местность исследовали, блджадь.
Можешь предъвить хоть один пример, где работы классиков дали хоть что-то полезное? Да та же алгебраическая геометрия пошла из попыток взять какие-то интегралы. Естественно, это случайность, смыла изучать это нет, с тем же успехом она могла возникнуть сотней других способов.
Никого, он может только истерить в сети
Чтобы ты сначала прочёл что такое ряд, сумма ряда, сходимость ряда и (возможно) сам попробовал бы ответить на свой вопрос.
Не зная этих понятий – тяжело точно объяснить.
Как сказать по-английски, что отображение зануляется, ну например на каком-нибудь тензоре?
>>331353
Что-то я поторопился, вот тут все есть
https://en.wikipedia.org/wiki/Annihilator_(ring_theory)
Не могу такого сказать. Но отбрасывать всё только из-за давности было бы глупым, ведь нынешний путь может оказаться ложным.
Да ты охуел что ли? Напиши ещё в /d давай, там нас рассудят, глянув айпишники.
А не боишься в таком случае, гандон ебучий?
Пусть модеры действительно посмотрят и забанят к чертям тебя, ведь у этих двух постов разные IP.
Рака тебе и твоей семье. Мразь тупая.
Только посмотрите на уёбка. Я загнал скотину в угол, а она упирается. Но я взял её за вымя и буду выкручивать его, пока тварь не подохнет вместе со своей наглой лживостью.
Тот пост мой, я писал его вчера и точно знаю, точно помню.. Я жду мочепарашу, чтобы сука провалилась со стыда.
Я, блядина ты тупая, помню, как я вчера перед сном своими руками с телефона печатал этот текст: "Что значит "сам"? Мне же интересно как именно построены его связи, чтобы знать, где именно можно его использовать, даже если я обычный ювелир" и своими глазами видел окошко: "Сообщение отправлено".
Я желаю тебе сдохнуть за ложь.
Модер тупорылый просто такой же, как и ты. Решил издеваться.
Но меня то, мрази, не переубедить. Я знаю, что тот пост мой.
1) Это интересно.
А многим интересна поклейка танчиков, анализ литературы, программирование или просто обсуждение сплетен. Интерес - физиологический процесс, организм вырабатывает нейромедиаторы, которые вызывают ощущение эйфории, что называется в простонародье увлечением, интересом и удовольствием. Добиться выброса необходимых нейромедиаторов можно и более простыми путями.
Вывод: математика бесполезна.
2) Математика развивает мозг.
Развитие - не самоцель. Мозг - это просто кусок мяса, который скоро умрет. Так что его развитие это вовсе не аргумент. У любого развития должна быть конечная цель, ради которой человек тратит свое время.
Вывод: математика бесполезна.
3) Математика полезна для общества и в конечном итоге повышает уровень жизни, т.к. позволяет создавать новые технологии.
Но лично ты ничем не полезен. А если хочется работать на благо людей, то надо было становиться врачом и принимать людей бесплатно. В технологиях так же нет смысла, поскольку тот же интернет большинство людей используется не для саморазвития, а для прожигания времени. Точно так же можно было бы тратить время, выжигая линзами на скамейках матерные слова. Все современные информационные технологии направлены на анализ большого количества мусора и извлечения из него полезной информации. В этом нет смысла, потому что мусор надо просто игнорировать.
Вывод: ты бесполезен.
4) Математика позволяет находить больше тем для интересного общения.
А многие люди ничего не узнают кроме сплетен и расписания поездов/самолетов, и тем не менее счастливы (возможно, слово "счастливы" тебя сейчас покорежило по причине, которую ты сам понимаешь). Эндорфин у них вырабатывается и без математики.
Вывод: математика бесполезна.
5) У человека должно быть хобби, дело по вкусу и цель в жизни.
Многие успешные счастливые люди не имеют хобби. Цель в жизни - это симулякр, созданный, чтобы скрывать правду о том, что цели и смысла в жизни нет. Ты в любом случае умрешь и будешь забыт, как бы ни пытался засветиться в истории. Кроме того, в настоящей математике очень много тупой скучной рутины, поэтому в работе математика нет ничего интересного.
Вывод: математика бесполезна.
6) Математика дисциплинирует.
Многие успешные счастливые люди ведут распущенный образ жизни, играют в игры, смотрят много сериалов, бухают и радуются жизни.
Вывод: математика бесполезна.
7) Математика позволяет найти непыльную работу.
Частично согласен. Обучение математике превратилось в бизнес. Люди просто зарабатывают, обучая математике тех, кто имел неосторожность по еще советской футуристической романтике податься в эту бесполезную науку. Тем не менее, даже менеджеры зарабатывают больше математиков, а высококвалифицированные управленцы могут зарабатывать и по 500к в месяц, потому что оптимизировать производство и снизить расходы - это тебе не лекции студентам читать.
Вывод: математика бесполезна.
8) Математика применяется в ИТ.
Но в самом ИТ нет необходимости. Даже если в мире вдруг пропадут все компьютеры, люди некоторое время побугуртят, а потом все придет в норму. Компьютеры - еще одна ненужная, навязанная обществом потребления ценность.
Вывод: математика бесполезна.
9) Математика развивает ум. Парень/девушка, не знающая теорему Вейерштрасса, не может быть интересна молодым людям.
Практика показывает обратное, и лишь замкнутый ригидный шизоид, сказавший эту фразу, верит в нее и отказывается принимать реальность.
Вывод: математика бесполезна.
10) МАТЕМАТИКА ОЧИНЬ ВОЖНА НО Я НЕЗНАЮ КАК ЕТО ДОКОЗАТЬ!1!!
Большинство работ по математике пишутся в стол или только ради получения научного звания. Пример - сингулярные случайные величины и теорвер на группах. Многие из придуманных математиками понятий не имеют к реальному миру никакого отношения, и просто лежат на свалке истории. А то, что полезно, то рутинно и скучно.
Вывод: математика бесполезна.
1) Это интересно.
А многим интересна поклейка танчиков, анализ литературы, программирование или просто обсуждение сплетен. Интерес - физиологический процесс, организм вырабатывает нейромедиаторы, которые вызывают ощущение эйфории, что называется в простонародье увлечением, интересом и удовольствием. Добиться выброса необходимых нейромедиаторов можно и более простыми путями.
Вывод: математика бесполезна.
2) Математика развивает мозг.
Развитие - не самоцель. Мозг - это просто кусок мяса, который скоро умрет. Так что его развитие это вовсе не аргумент. У любого развития должна быть конечная цель, ради которой человек тратит свое время.
Вывод: математика бесполезна.
3) Математика полезна для общества и в конечном итоге повышает уровень жизни, т.к. позволяет создавать новые технологии.
Но лично ты ничем не полезен. А если хочется работать на благо людей, то надо было становиться врачом и принимать людей бесплатно. В технологиях так же нет смысла, поскольку тот же интернет большинство людей используется не для саморазвития, а для прожигания времени. Точно так же можно было бы тратить время, выжигая линзами на скамейках матерные слова. Все современные информационные технологии направлены на анализ большого количества мусора и извлечения из него полезной информации. В этом нет смысла, потому что мусор надо просто игнорировать.
Вывод: ты бесполезен.
4) Математика позволяет находить больше тем для интересного общения.
А многие люди ничего не узнают кроме сплетен и расписания поездов/самолетов, и тем не менее счастливы (возможно, слово "счастливы" тебя сейчас покорежило по причине, которую ты сам понимаешь). Эндорфин у них вырабатывается и без математики.
Вывод: математика бесполезна.
5) У человека должно быть хобби, дело по вкусу и цель в жизни.
Многие успешные счастливые люди не имеют хобби. Цель в жизни - это симулякр, созданный, чтобы скрывать правду о том, что цели и смысла в жизни нет. Ты в любом случае умрешь и будешь забыт, как бы ни пытался засветиться в истории. Кроме того, в настоящей математике очень много тупой скучной рутины, поэтому в работе математика нет ничего интересного.
Вывод: математика бесполезна.
6) Математика дисциплинирует.
Многие успешные счастливые люди ведут распущенный образ жизни, играют в игры, смотрят много сериалов, бухают и радуются жизни.
Вывод: математика бесполезна.
7) Математика позволяет найти непыльную работу.
Частично согласен. Обучение математике превратилось в бизнес. Люди просто зарабатывают, обучая математике тех, кто имел неосторожность по еще советской футуристической романтике податься в эту бесполезную науку. Тем не менее, даже менеджеры зарабатывают больше математиков, а высококвалифицированные управленцы могут зарабатывать и по 500к в месяц, потому что оптимизировать производство и снизить расходы - это тебе не лекции студентам читать.
Вывод: математика бесполезна.
8) Математика применяется в ИТ.
Но в самом ИТ нет необходимости. Даже если в мире вдруг пропадут все компьютеры, люди некоторое время побугуртят, а потом все придет в норму. Компьютеры - еще одна ненужная, навязанная обществом потребления ценность.
Вывод: математика бесполезна.
9) Математика развивает ум. Парень/девушка, не знающая теорему Вейерштрасса, не может быть интересна молодым людям.
Практика показывает обратное, и лишь замкнутый ригидный шизоид, сказавший эту фразу, верит в нее и отказывается принимать реальность.
Вывод: математика бесполезна.
10) МАТЕМАТИКА ОЧИНЬ ВОЖНА НО Я НЕЗНАЮ КАК ЕТО ДОКОЗАТЬ!1!!
Большинство работ по математике пишутся в стол или только ради получения научного звания. Пример - сингулярные случайные величины и теорвер на группах. Многие из придуманных математиками понятий не имеют к реальному миру никакого отношения, и просто лежат на свалке истории. А то, что полезно, то рутинно и скучно.
Вывод: математика бесполезна.
>математика бесполезна.
>ты бесполезен.
Лол, никто и не отрицает. Всем похуй на это. Ты залетный тут что ли?
>"Я никогда не делал чего-нибудь «полезного». Ни одно мое открытие не принесло или могло бы принести, явно или не явно, к добру или к злу, малейшего изменения в благоустройстве мира." (Г. Г. Харди)
Нигилист в треде, все в агностицизм.
Но мне просто нравится математика, не нравится ничего другого.
>Добиться выброса необходимых нейромедиаторов можно и более простыми путями.
Эти пути приведут к разрушению человеческой личности.
Вообще, все поста рассуждения строятся на основе глупейшего постулата, не раз упомянутого в самом тексте: "технологии не нужны".
Но ведь я поставил себе самоцель - развитие науки и технологий - и это главное. Отсутствие объективного смысла и цели не избавляют меня от возможности представить себе их и следовать им.
Некорректные рассуждения.
>У любого развития должна быть конечная цель, ради которой человек тратит свое время.
С чего взял? большой процент нашей деятельности направлен на улучшение условий жизни , но ведь МЫ ВСЕ УМРЕМ)))0!! КАКОЙ СМЫСЛ, МЫ ВСЕГО ЛИШЬ КУСКИ МЯСА!!))001
>ты бесполезен.
Все еще мыслишь субъективными категориями, лол.
> Эти пути приведут к разрушению человеческой личности.
Т.е., человеческая личность - это баланс между динамикой среды и динамикой гормонов? Думаю, что только отчасти, всё-таки. Думаю, и в гормональной буре личность способна отстроить себе островок инвариантности (неизменности относительно вопроса "кто я?") в мозгу.
Но какова будет субъективная цена такой личности?
Дай угадаю, тебе 13-17 лет, окружающие тебя не понимают, много думаешь о смысле жизни и не находишь удовлетворительных ответов? Не переживай, это пройдет. У всех разумных людей такой период бывает. Постарайся только не перерезать вены по-настоящему.
А определение N, срач по поводу авторства поста с привлечением модератора, школьные задачи и Демидович тебя не смущают?
Маттреды давно уже пробили дно
тупой вопрос
если хочется деньги то наверное можно отучиться пару-тройку лет на мехмате и идти в актуарии
можно и без этого, но там вроде как стремятся брать из мажорных вузов
ну а если хочется изучать математику то вопроса зачем не стоит
Тогда в повара иди будешь яйца в крутую варить.
Может.
Проблема Коллатца, как я понимаю - это наиболее простой из найденных в свое время Уламом открытых вопросов о глобальных свойствах динамических систем, задаваемых функциями аналогичного рода (из натуральных в натуральные, составленными из нескольких линейных, ограниченных на арифметические прогрессии). В таком контексте вопрос уже не лишен некоторой естественности. Вполне не исключено, что такого рода вопросы можно погрузить в некоторый красивый контекст и решить их там.
Насчет проблемы 196 мне в возможность связи с красивой математикой верится меньше.
>Насчет проблемы 196 мне в возможность связи с красивой математикой верится меньше.
Это смотря что считать красивой математикой. Если вдруг найдется функция, которая будет принимать значения близкие к числам предположительно не образующим никогда палиндром - это будет красивая математика?
Это зависит от того, что за функция. Но разумеется да, красивость (интересность и т.п.) математики вещь весьма субъективная. Кто-то ведь и без всяких дополнений считает, что эти две проблемы красивые и интересные (например, по той причине, что это сложные проблемы с лаконичной формулировкой в тривиальных терминах).
Да в общем-то и не важно какая функция. Чем меньше область её изначального применения будет связана в самой проблемой (это может быть даже какое-нибудь физическое распределение), тем интереснее математика, на мой взгляд.
Это копия, сохраненная 15 февраля 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.