Это копия, сохраненная 22 февраля 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
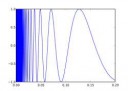
It can be defined as the graph of the function sin(1/x) on the half-open interval (0, 1], together with the origin, under the topology induced from the Euclidean plane:
T = { (x, sin 1/x) : x∈(0;1] } ∪ { (0,0) }.
The topologist's sine curve T is connected but neither locally connected nor path connected. This is because it includes the point (0,0) but there is no way to link the function to the origin so as to make a path.
The space T is the continuous image of a locally compact space (namely, let V be the space {−1} ∪ (0, 1], and use the map f from V to T defined by f(−1) = (0,0) and f(x) = (x, sin(1/x)) for x > 0), but T is not locally compact itself.
The topological dimension of T is 1.
Предыдущий: >>323534 (OP)
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429 - текущий

В целях самообразования решил начать задрачивать тему исключительно для себя. Поэтому прошу какой-нибудь учебник для чайников или видеокурс от А до Я, знакомящий человека с матаном, чтобы с объяснием тех или иных понятий и их значении в жизни. Вот нахуя людям нужен тот же интеграл? Я не знаю, но мне интересно. Ведь не из пальца же высосано. А вдруг лучше начну этот мир понимать
Перелопатил ютюб и трекеры, но там абсолютное большинство всех уроков уже рассчитаны на хорошее понимание школьного курса, а на школьные учебники у меня фобия
И. Гельфанд А. Шень – Алгебра
> А вдруг лучше начну этот мир понимать
Не начнешь. Ты не ту науку для этого выбрал. Почитай занимательную физику какую-нибудь.
А про интеграл можешь в википедии глянуть.
Математика не нужна в целях самообразования. Чтобы по-настоящему освоить программу первых курсов вуза, нужно потратить тысячи часов.
Тысячи - это ты загнул.
С вероятностью x -> 0 длина цепочки будет равна длине всей серии бросков (если монетка по нормальному распределению будет орлы и решки выкидывать).
Также с вероятностью x -> 0 длина цепочки будет равна единице. А между единичной и полной длиной будет находиться горб вероятностей до 50%.
>Сумма двух положительных иррациональных чисел может быть рациональным числом.
Можете дать пример такой суммы?
Хотя не, неправильно.
Да. 2-√2 - положительное и иррациональное.
√2 - положительное и иррациональное.
2-√2 + √2 = 2.
В таком случае я хотел бы увидеть доказательство того, что 2-√2 иррационально.
на самом деле да.
у меня действительно есть сомнения, что 2.(0) - 1.4142135623730950488… иррациональное число например. Вдруг это будет просто бесконечное рациональное. Ведь мы не знаем с какой величины начинается процесс последовательного вычитания(т.к не знаем последнюю цифру иррационального числа).
ну и что из этого следует? Значит так, вопрос состоит в том, почему Q-I не может быть обычной периодической дробью.
У тебя какое-то определение рационального числа не то, забей ты на эти периодические дроби, они для чуханов.
Мог.
√2 иррационально.
-√2 иррационально.
2 рациональное.
-2 рациональное.
Сумма двух рациональных - рациональное число по определению.
Предположим, что 2-√2 рациональное число.
(2-√2) + (-2) - сумма двух рациональных и потому рациональное.
Но оно равно -√2.
Противоречие. Значит, предположение ошибочно.
Примеров Много. Терем Мало. Нарезка по 45 минут.
Есть вот такая вещь(http://wayback.archive-it.org/3671/20150528171650/https://www.extension.harvard.edu/open-learning-initiative/abstract-algebra) Лекции в Гарварде,
всю хочу посмотреть, но руки не доходят слить видео.
Теорем*
Много это сколько?

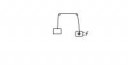
Вот допустим такую ситуацию, есть мотор который поднимает И опускает груз. Проблема в том если мотор отключиться груз упадет. Мне нужен механизм который бы фиксировал груз когда веревку когда мотор отключен что груз не падал. Также этот механизм не должен мотору поднимать и опускать груз.
Повесть на веревку шайбу, а веревку продень через трубку. Шайба зацепится за трубку и зафиксирует веревку.
ну и конечно же ты просто школьник, не слышавший о торможении двигателем, потому что школьников не пускают в автошколу? конечно будет ограничение на вес груза, который двигателем можно будет держать на весу, но это уже вопрос параметров задачи
что нибудь в духе - вероятность вытащить из 1 набора эту ебень 4/13 . набора 4. т.е. можно умножить на 4 что числитель что знаменатель. а можно и не умножать, потому что один хер 4 потом можно сократить.
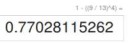
С 4 наборами вероятность же больше. На пике мой вариант, но я не уверен. И ещё одна задач.
Есть 5 наборов по 13 карт. Из первого набора взяли одну из 4 карт больших 10 далее буду называть их картинки, а из остальных по рандомной карте. Если задача с пика решена правильно, то вероятность их совпадения 1-(12/13)^4 Потом заново взяли 5 наборов и на этот раз вытащили 2 картинки и 3 рандомные карты. Какая вероятность что что хоть одна рандомная карта совпала хоть с одной из картинок. Будет ли она расти с ростом числа вытащенных картинок?
Посчитай 1 - вероятность того, что нет ни одной карты больше десятки. Это стандартный трюк.
Я смотрел и решал задачи. В принципе ок, но легче просто Артина так прочесть.
То есть 1 - (9/13)4 = 22000/28561
Виленкин. Рассказы о множествах.
Я просто под него засыпаю очень быстро, плюс пока читаешь, забываешь, что читал до этого.
Самый охуенный это Шень. Потом Куратовский. После них можно Вавилова наебнуть.

Шень. Достаточно легко читается, много выносится в задачи на самоконтроль.
Ответов, конечно, нет, но если что-то остаётся не ясным всегда можно разрбрать задачу всем тредом.
Блять, почему до сих пор не запилили удобный ресурс, на котором можно было бы сначала заносить задачи из какой-нибудь книги, а потом люди бы постили свои решения и обсуждали их, а придя к консенсусу - аккуратно оформляли в латехе ответ и оставляли потомкам? Я дваж года жду такой сайт.
Накидайте таких книжек плз. Особенно интересует дискретная математика и алгоритмы.

А зачем, если можно сделать удобную и доступную всем систему?
У меня, собственно, и баттхёрт от того что эти задачи много раз разбирались, но остались пылиться в архивах вузиков, либо просто в скомканных листочках полетели в мусорку.
Вузики, конечно, всё равно нужны, зато вопросов к преподу будет оставаться куда меньше.
Такой сайт был бы просто, блять, охуителен.

Наука мертва. Пикрелейтед - выжившие математики.
тут не в годах дело, я имею ввиду вообще какие-нибудь добротные советские учебники
Годный матан 30-х это вероятно Харди. Алгоритмы, классика это Хопкрофт и Ко. Ну и Кнут.

Поиск задач?
Список книг -> номера задач, очевидно же. Поиск как таковой не очень нужен будет.
>>328099
>>328111
>>328121

Иди нахуй. Конечно те кто просто хочет найти решение тоже будут таким сайтом пользоваться, но мне он кажется нужным с позиции человека который реально интересуется математикой, но не всегда может решить задачи из учебников/не уверен в правильности решения.
А тут будет возможность даже при остутствии решения обсудить задачу с другими людьми.
Ну и дроч на перфектционизм - разобрать, оформить и занести в базу все задачи из интересующего учебника,
https://www.coursera.org/learn/galois
Для ЛЮБОГО эпсилон потому что. ЛЮБОГО.
Ну возьми, например, epsilon_1 в первом определении и положи его равным epsilon /2, где epsilon - для второго. Так понятнее станет?
Была идея такой сделать, но с нынешних позиций - он нахуй никому не нужен будет.
Бесконечно малый - это очень неопределенное понятие об которое математики ХХ века часто спотыкались и набивали шишки. Концепция предела в том, чтобы заменить "бесконечно малые" на "сколь угодно (но конечно) малые". Попробуй решить такое упражнение для начала: доказать, что следующие определения "у последовательности x_n предел - это число А" эквивалентны:
\forall eps>0 \exists N \forall n > N ( |x_n - A| < eps)
\forall eps>0 \exists N \forall n > N ( |x_n - A| < eps^5+ln(1+eps) + 2*eps)
Забирай свои аватарки и уёбывай.
Никак, это для красоты сделано.
Да.
Почему поля не расчерчены красной ручкой? Мариванна заругает же.
> об которое математики ХХ века
скорее XVIII века, в начале XIX-го Коши уже в целом разобрался, как аккуратно подходить к делу.
Тебе надо доказать что для всех n,m больше какого-то N выполнится |x_n-x_m|<эпсилон. Забудь про бесконечно малые. Эпсилон это обычное вещественное положительное число. Берем любой такой эпсилон.
1) первая последовательность (та которая x_n) имеет предел
2) значит, для любого бета>0 найдется такой N1, что для любого n>N1 выполнится |x_n-b|<бета
3) так как это правда для любого бета, мы можем взять частный случай когда бета = эпсилон пополам. Перечитай теперь первый абзац в моем посте, чтобы не забыть о чем речь Тогда для всех n больше какого-то N1:
|x_n-b|<эпсилон/2
4) вторая последовательность имеет предел
5) знаит, для любого бета>0 найдется такой N2, что для любого m>N2 выполнится |x_m-b|<бета
6) так как это правда для любого бета, мы можем взять частный случай когда бета = эпсилон пополам. Тогда для всех m больше какого-то N2:
|x_m-b|<эпсилон/2
7) Если из N1, N2 выбрать больший и назвать его N обычно это записывают так: N=max(N1, N2), то для n,m>N одновременно выполнится
|x_n-b|<эпсилон/2
|x_m-b|<эпсилон/2
8) Берем любой эпислон, для него находим N1, N2
тогда для любых m,n>N, N=max(N_1, N_2) будет правдой что:
|x_n-b|<эпсилон/2
|x_m-b|<эпсилон/2
|x_n-b|+|x_m-b|<эпсилон
Например sha-256:
>Предварительная обработка:
>m := message ǁ [единичный бит]
>m := m ǁ [k нулевых бит], где k — наименьшее неотрицательное число, такое что (L + 1 + K) mod 512 = 448, где L — число бит в сообщении (сравнима по модулю 512 c 448)
Ведь A | 0 = A.
Да. В принципе, любое понятие можно определить на голой логике первого порядка. Но зачем.
Примем, что имеется достаточно сильная логика первого порядка, чтобы развить некоторую теорию моделей.
Мыслим две системы вещей.
1. Объекты.
2. Стрелки.
Мыслим следующие операции.
1. dom сопоставляет каждой стрелке объект.
2. cod сопоставляет каждой стрелке объект.
3. id сопоставляет каждому объекту стрелку.
4. композицию стрелок, которая сопоставляет двум стрелкам f и g таким, что dom g = cod f, стрелку g∘f.
Аксиомы таковы.
1. dom(id(a)) = a
2. cod(id(a)) = a
3. dom g∘f = dom f
4. cod g∘f = cod g
5. если можно взять композицию g∘f и композицию h∘(g∘f), то можно взять композиции h∘g и (h∘g)∘f, и причём h∘(g∘f) = (h∘g)∘f
6. если dom f = x, то id(x)∘f = f
7. если cod f = x, то f∘id(x) = f
Категорией называются любая модель для вышеназванного.
> Да. В принципе, любое понятие можно определить на голой логике первого порядка. Но зачем.
Ну это всё равно что сказать якобы аксиоматика ZFC всего лишь цепочки символов, а не множества.

> Да. В принципе, любое понятие можно определить на голой логике первого порядка.
А натуральное число можно в ней определить???
Нет. В формальной системе система вещей означает алфавит. Например, когда говорят, что есть две системы вещей - это означает, что есть два алфавита, скажем, большие латинские буквы и маленькие латинские буквы. Когда есть три системы вещей - это значит, что будут использоваться три алфавита.

Алфавит - это понятие, которое относится к метаматематике. Предполагается, что ты достаточно разумен, чтобы не считать "алфавит" чем-то непонятным. Пикрелейтед.
Какие-то манёвры итт. Я достаточно разумен, чтобы и теорию множеств понимать. Нахера мне тогда вообще нужна убогая формальная система?
Ну раз ты постоянно свою фотокартчку возле параши постишь, я тоже решил что не надо стеснятся.
Формальная система нужна только тогда, когда в твоём понимании возникают парадоксы. Пока парадоксов нет - не нужна. В алфавите, насколько мне известно, парадоксов не найдено.
Ты попал в замкнутый круг - просто перенёс определяемые понятия на метауровень с гнилой отмазкой якобы на нем его все и так знают. Это чит же.
Это бред, ты бы ещё математические задачки предложил на чертежах решать - там же все понятно и противоречий никто пока находил.
Чтобы выровнять, не? Длина после будет k.
Тут не воспринимают Трактат как книжку, которую можно прочитать. Местным дебилам кажется, что это такой мемчик, чтобы троллить ньюфагов.
Не переносит, а отделяет ненужное, берёт достаточную часть целого.
Одно дело просто говорить про конкретную "систему вещей", и другое про все "системы вещей" в принципе, включая те, которые содержат сами себя и прочие парадоксальные объекты.
> прочитать
> Бурбаки
Ещё бы не казалось, только особо отмороженные дауны клюнут на такую толстоту.
Хотя судя по тем кускам, что читал я Бурбаки прочесть можно, но я бы не назвал это особенно здравым занятием. Ведь Бурбаки писали не совсем учебник, а учебник, который демонстрирует возможность построить здание математики с нуля. Надо сказать, что вышло у них куда человечнее, чем у их предшественников занимавшихся второй задачей (Principia Mathematica). Но как бы то ни было, лучше найти хорошие учебники, не пытающиеся быть чем-то ещё.
Царских путей в науки нет.
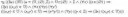
В трактате все математические теории описываются на основании аксиоматической теории множеств в духе крайней абстракции. Например, определение обыкновенного натурального числа 1 в «Теории множеств» даётся следующим образом:
Bourbaki term1.gif
Причём, учитывая, что в этой записи уже сделаны сокращения (например, пустое множество ∅ определяется в языке теории множеств Бурбаки как Bourbaki empty.gif[6]), мы получаем, что полная запись обыкновенной единицы состоит из 2 409 875 496 393 137 472 149 767 527 877 436 912 979 508 338 752 092 897 знаков и 871 880 233 733 949 069 946 182 804 910 912 227 472 430 953 034 182 177 связей[7], то есть полная запись терма, обозначающего единицу, заняла бы сто миллиардов квинтиллионов квинтиллионов книг [8]. Такой уровень абстракции (причём в трактате, не посвящённом исключительно математической логике) не мог не вызвать нарекания.
Они не строят математику с нуля, там как минимум натуральные числа и аксиома бесконечности необходимы.
Квантор "существует" в другую сторону пишется. Ты пытаешься найти количественный ответ, то есть явно выписать N, а суть в том, что тебе надо тупо заметить, что вот то самое eps^5 + ln(1+eps) + 2eps -> 0 (в смысле первого определения) при eps->0. Поэтому в твоём предыдущем вопросе, даже если не заменять eps на eps/2, абсолютно неважно, получишь ты оценку |x_n-x_m| < eps или |x_n-x_m| < 2eps.
>>328372
Так это только "теория множеств", остальные трактаты вполне адекватны, но, мне кажется, дико устарели и ненужны.
>>328293
>>328377
Большинство членов группы не уделяло достаточного внимания таким разделам математики, как дифференциальные уравнения, теория вероятностей, математическая физика, а также разделам прикладной математики, таким как численные методы или математическое программирование. В наибольшей степени это относится к их коллективному трактату.
Надрачивать математику ради математики!? Нет, спасибо. Я лучше посчитаю еще этих мягких французскх интегралов, да выпью метод наименьших квадратов.
>Большинство членов группы не уделяло достаточного внимания таким разделам математики, как дифференциальные уравнения, теория вероятностей, математическая физика, а также разделам прикладной математики, таким как численные методы или математическое программирование. В наибольшей степени это относится к их коллективному трактату.
Да дело даже не в том, что они актуарные и прикладные темы стороной проходят, просто устаревшая терминология и не туда смещённые акценты режут глаз.
Пиздёжь. Любое сознание перед началом любой мыслительной деятельности должно быть способно осмысливать отдельный объект, а значит интуитивно понимать что такое ОДИН конкретный объект. Так что твоё определение тоже таковым не является, а только лишь переформулировкой уже имеющегося объекта в других терминах.
Ты уж определись, невозможно или можно но сложно.
Я не говорю что нужно, это собственно сами бурбаки и рассел пиарили свое говно, якобы там все из одной логики выводится.
Невозможно ТОЧНО определить, можно только через три пизды колено ПРИМЕРНО определить что ты там имеешь ввиду.
>>328397
Первое правило трактата - никогда не говори о трактате.

Давай теперь объясни мне как выглядит винтовая лестница без привлечения слова спираль, бурбакодаун. Выведи мне определение винтовой лестницы без абстракций. Бурбакомрази же смогли вывести математику чисто на абстракциях, так ведь!? А тут фигня такая. У тебя получится обосраться вывести, я верю в тебя.
используй интерполяцию квадратичным полимоном тогда умник блять.или разложи тейлором до большей степени чем 3. суть тейлора в том что значение будет точным при бесконечной степени а не при третьей
Ну про бесконечность зы загнул. Просто с повышением степени повышается точность.
Это конкретный объект, который тебе показывают и говорят - это винтовая лестница. А спираль тут не нужна, она нужна твоей мамке чтобы ее почаще можно было сношать без залёта (мне бы не хотелось платить алименты).
PS Если хочешь юзать абстрактное понятие спирали, то ты не имеешь права пиздеть будто дал определение винотовой лестницы из одной логики. Ты ОБЯЗАН явно увказать, что вся твоя теория построена на исходном интуитивно понимаемом понятии спирали.
Мне то приближение нужно, чтоб поменьше членов, а не бесконечные степени. И полином всегда даёт точность лучше тейлора(на выбранном интервале), при членах одинаковой степени. Я подумал, вдруг скрытый смысл есть, а я просто не понимаю. Ну ладно.
МРАЗЬ.
Я и не пытаюсь определить винтовую лестницу без абстракций.
Да, я забыл уточнить что ты не можешь мне показать саму винтовую лестницу. Как и нарисовать, ибо абстракция.
Как я и предполагал, намек на то что не надо дрочить вприсядку в попытке вывести теорему о милиционерах, законы кранца-начиханца, шницель-птуцера и бабкина-няньского исключительно в абстракциях. Всякая абстракция опирается на реальность, хоть каплю.
Я в Электроника не полезу, увольте.
> Я и не пытаюсь определить винтовую лестницу без абстракций.
Я уже писал, тогда ты должен (по первому требованию) огласить весь список используемых абстракций на которые опирался в своих построениях и не говорить, что всё вывел из чистой логики. При этом сказать что ты дал определение винтовой лестницы можно с большой натяжкой, поскольку ты заюзал гораздо более мощное абстрактное понятие спирали.
Вероятность 0 но событие не невозможное.
Не вижу где я там обосрался? Двое со мной согласились, а остальные куда-то сдриснули после первой же волны моих ответов. Даже здесь обсуждение гораздо дальше продвинулось.
Я по первому требованию даже государству ничего не должен.
Но так как ты даун, который читает посты жопой, и при чем выборочно, мне проще и легче послать тебя определять N чем вести конструктивный диалог.
С таким подходом тебе даже математик отрицающий формальный метод пошлёт. К тому же ты пытаешься бесконтрольно задействовать произвольные абстракции при построении математических теорий, за такое вообще бьют по морде.
Где именно с тобой согласились? Я увидел, например:
>ИМХО, формальная система не имеет право задаваться вопросом, откуда взялись те инструменты, которыми она располагает на этапе её формирования.
то что тебе пытались вдолбить на протяжении кучи тредов.

>ты пытаешься бесконтрольно задействовать произвольные абстракции при построении математических теорий, за такое вообще бьют по морде.
>защищает бурбаки
Ты ему на примерах поясняй, он туго всасывает.
> ИМХО, формальная система не имеет право задаваться вопросом, откуда взялись те инструменты, которыми она располагает на этапе её формирования.
Эту глупость я ему простил, в конце поста он в правильном направлении про строки стал рассужда. Плюс после этого мы с ним в ЛС попереписывались, где он со мной согласился.
> то что тебе пытались вдолбить на протяжении кучи тредов.
Если формальная система строится для ОБОСНОВАНИЯ, то эта отмазка не прокатит. Ты не можешь обосновать что-то этим же предметом.
Это вообще было третье лицо, я ему сам ответил что его определение лишь простая переформулировка.
Обосновал тебе в кадык с левой и висок с правой, но толку то? Ты и так "обоснованный" к хуям.
Жду по адресу улица Пушкина дом Колотушкина. Докажу с пруфами.
Алсо, тамошний эскперт хи 0 вообще сразу со мной согласился. Так что попизди мне тут про обсёр.
Вот тут я не выдержал и рассмеялся.
Обосновал тебе за щёку, проверяй.
Как ты заебал даун. Прочитай уже определение вероятностного пространства и вероятности.
ежедневно практически.
Несовершенность математики и её невозможность поспевать за реальностью видна везде - например, до сих пор модели на математической основе не могут точно описать даже относительно простые по устройству циклоны, спрогнозировать с хоть сколь-нибудь большой вероятностью погоду на неделю вперёд, что тогда говорить о квантовом или релятивистском мире?
В конце концов, что мешает людям сделать вместо математического аппарата такую систему, в коей доказательства точно так же, как в реальном мире, можно было бы проводить эмпирическим методом?
Математика настолько несовершенна, что даже не может дать корректного определение натурального числа.
интригал в частности позволяет считать площади фигур, у которых стороны не из отрезков прямых, а из кусков параболы например.
Мимокрокодил, который хотел спросить про интегралы в физике, а тут такой цирк.

>Нужна например МАТЕМАТИКА РУСОВ
Эта которая настоящая двадцатиричная?
Так её кроме пятёрки волхвов никто не знает.
Давайте подумаем, какая основа могла бы быть у такой системы, дабы в самой её структуре имел место сугубо эмпирический метод доказательств, соответствующий реальному физическому миру?
Мне перво-наперво видится важность полного отсутствия аксиоматического метода, постулатов и прочих безусловностей, на которых только в свою очередь и строится математика.

Примитивных экспериментоблядушек предлагаем отправить на помойку вместе с их вульгарным эмпиризмом.

Это был мой пост. И это то, как Бурбаки определял число 1, пикрелейтед. Вполне типичное определение, в современных учебниках матана определяют так же. Полную запись, все эти тау-тау, какой-то посторонний человек выписал, сам Генерал такой фигнёй не страдал.
Да, твою реакцию можно понять. Как можно понять боль и слёзы всех математиков, когда они поймут то, что уже давно лежит на поверхности - математика является по сути бесполезной, тривиальной и полностью зацикленной на абстрактной своей структуре, которую сама же и создала. Математика - изыск первичной человеческой деятельности - счёта, - аппарат которой несостоятелен для описания хоть сколь-нибудь более сложных вещей, что говорить об описании всего, грамотного описания главного - современной физики?
Видится необходима создания нового аппарата и я сейчас думаю, каким он должен быть и, что самое главное, на чём должен основываться, чтобы достичь эмпиризма.
>я сейчас думаю, каким он должен быть и, что самое главное, на чём должен основываться
Вот как придумаешь - так и приходи. А сейчас кукаретиков тут и без тебя хватает.
Просто пора признать, что математика является проявлением человеческого мышления. Она полностью определена структурой и работой мозга, глубокозаложенными шаблонами. Это явно прослеживается в желании вводить интуитивно понятные конструкции. Возможно, такая отправная точка уже реализована в какой-то степени в теории множеств, но надо копать глубже, чтобы понять всю силу, с одной стороны, и ограниченность, с другой стороны, математического подхода.
Но ведь невозможно работать в изоляции, суть человеческой науки как раз заключается в совместном решении насущных проблем. Человек - социальное существо и необходимо обсуждать возможные решения, развивать с другими людьми возникшие идеи и в то же время бороться за новаторство.
Только в своей идее я уверен полностью - математика изжила себя, она погибла, тем не менее, используется всем миром вследствие ретроградности и естественного нежелания настолько кардинально (как же не хотел употреблять это мерзкое математическое словечко) менять вообще всё, над чем работают десятки тысяч людей и перечёркивать во много то, чего они "добились", отказываться от того, за что великие мыслители (а математику я за науку больше не считаю - потому они и мыслители, а не именуются учёными) посвятили всю свою жизнь. Но важно понять, что их труды не пропадут, ведь с другой стороны они достигли главного - осознания и понимания законов природы, заменяются на новые только разработанные ими математические модели, а не сама суть, состоящая в описании мира.
Не секрет, что прорыв в области человеческих знаний и человеческой науки тождественен (снова неприятно употреблять это слово) новому взгляду на вещи - самым известным примером являются работы Эйнштейна. Он сделал то, чего до него не делал ещё никто - отверг постулаты Ньютона. Точно так же и я отвергаю способность математики грамотно описать сложный мир. Стоя на заре новой науки, я также обратил внимание на то, что математика начала развиваться "сама в себя"; любая долговременная научная человеческая работа в конечном счёте начинает "затягиваться" в свою структуру, - тем самым создаётся иллюзия развития, которая порабощает молодые умы и никакая либерализация новых поколений не помогает - в итоге нужна всего одна, случайная идея и готовность к переменам всего одного человека. На самом деле эта иллюзия - стагнация, ставшая ужасно вредной после начал квантовой и релятивистской эр. Математика "загнулась" в дебри, которые сама же глупым образом итеративно создала.
Но точно так же, как Эйнштейн взглянул по-новому только на физику, но не на саму математику, её описывающую, описанная выше проблема развития в направлении "само в себя" только часть раковой опухоли полумёртвого организма, под названием "математика". Её абстрактная модель и, особенно, аксиоматизация - первопричина и главный недостаток всего, не позволяющий в должной мере описать реальны физический мир.
Необходим новый, антииндуктивный и полностью независимый от постулатов систематизированный аппарат - антипод математики - и теперь, раз мы коснулись развития науки, возникает один из фундаментальных вопросов: после основания синтаксиса новосозданной системы мы будем переводить на новый язык уже имеющиеся математические модели или же кардинально заново формулировать правильные модели на новом языке?
Мне кажется первый подход изначально совершенно неверным, потому что тогда возникает шанс создать ещё один изыск - наткнуться ещё раз на ошибки прошлых лет - изыск, схожий с математикой по структуре и противоречащий сам себе же ввиду изначально эмпирического синтаксиса; если мы будем выступать просто в качестве интерпретатора, то не получится создать аппарат, который истинно опирался бы на эмпирическую систему.
Нужно воссоздать все ещё раз. Один раз. Нужно описать в новой науке и создать модели всех физических законов - от закона Архимеда до силы Казимира. Но мы не начнём сначала, не вернёмся на прежний путь - у нас будет основа, заключающаяся в единственном, что нам дала математика - понимании аналитического характера. Мы будем изредка смотреть на труп математики, анализировать её гематомы и узнавать их причины, дабы избегать уже сделанных ошибок и, что самое главное на пути формирования нового описательного аппарата, формализировать своё понимание и быстрее создавать на той формализации основы новых моделей, для доказательства которых не будет нужен прямой опыт - нужно будет проводить доказательства только "на бумаге" - реальный опыт станет только эстетическим этюдом.
После основания синтаксиса нового аппарата для описания мира мы сможем создать новую модель известных нам физических законов и при упорном труде этот срок будет вмещать буквально в полтора десятилетия, а затем откроем новые.
Главный вопрос сейчас - как удовлетворить эмпирические требования новой системы. Важно начать решать фундаментальные вопросы основания нового аппарата.
Мы стоим на пороге исключительной науки, великих открытий и свершений.
Но ведь невозможно работать в изоляции, суть человеческой науки как раз заключается в совместном решении насущных проблем. Человек - социальное существо и необходимо обсуждать возможные решения, развивать с другими людьми возникшие идеи и в то же время бороться за новаторство.
Только в своей идее я уверен полностью - математика изжила себя, она погибла, тем не менее, используется всем миром вследствие ретроградности и естественного нежелания настолько кардинально (как же не хотел употреблять это мерзкое математическое словечко) менять вообще всё, над чем работают десятки тысяч людей и перечёркивать во много то, чего они "добились", отказываться от того, за что великие мыслители (а математику я за науку больше не считаю - потому они и мыслители, а не именуются учёными) посвятили всю свою жизнь. Но важно понять, что их труды не пропадут, ведь с другой стороны они достигли главного - осознания и понимания законов природы, заменяются на новые только разработанные ими математические модели, а не сама суть, состоящая в описании мира.
Не секрет, что прорыв в области человеческих знаний и человеческой науки тождественен (снова неприятно употреблять это слово) новому взгляду на вещи - самым известным примером являются работы Эйнштейна. Он сделал то, чего до него не делал ещё никто - отверг постулаты Ньютона. Точно так же и я отвергаю способность математики грамотно описать сложный мир. Стоя на заре новой науки, я также обратил внимание на то, что математика начала развиваться "сама в себя"; любая долговременная научная человеческая работа в конечном счёте начинает "затягиваться" в свою структуру, - тем самым создаётся иллюзия развития, которая порабощает молодые умы и никакая либерализация новых поколений не помогает - в итоге нужна всего одна, случайная идея и готовность к переменам всего одного человека. На самом деле эта иллюзия - стагнация, ставшая ужасно вредной после начал квантовой и релятивистской эр. Математика "загнулась" в дебри, которые сама же глупым образом итеративно создала.
Но точно так же, как Эйнштейн взглянул по-новому только на физику, но не на саму математику, её описывающую, описанная выше проблема развития в направлении "само в себя" только часть раковой опухоли полумёртвого организма, под названием "математика". Её абстрактная модель и, особенно, аксиоматизация - первопричина и главный недостаток всего, не позволяющий в должной мере описать реальны физический мир.
Необходим новый, антииндуктивный и полностью независимый от постулатов систематизированный аппарат - антипод математики - и теперь, раз мы коснулись развития науки, возникает один из фундаментальных вопросов: после основания синтаксиса новосозданной системы мы будем переводить на новый язык уже имеющиеся математические модели или же кардинально заново формулировать правильные модели на новом языке?
Мне кажется первый подход изначально совершенно неверным, потому что тогда возникает шанс создать ещё один изыск - наткнуться ещё раз на ошибки прошлых лет - изыск, схожий с математикой по структуре и противоречащий сам себе же ввиду изначально эмпирического синтаксиса; если мы будем выступать просто в качестве интерпретатора, то не получится создать аппарат, который истинно опирался бы на эмпирическую систему.
Нужно воссоздать все ещё раз. Один раз. Нужно описать в новой науке и создать модели всех физических законов - от закона Архимеда до силы Казимира. Но мы не начнём сначала, не вернёмся на прежний путь - у нас будет основа, заключающаяся в единственном, что нам дала математика - понимании аналитического характера. Мы будем изредка смотреть на труп математики, анализировать её гематомы и узнавать их причины, дабы избегать уже сделанных ошибок и, что самое главное на пути формирования нового описательного аппарата, формализировать своё понимание и быстрее создавать на той формализации основы новых моделей, для доказательства которых не будет нужен прямой опыт - нужно будет проводить доказательства только "на бумаге" - реальный опыт станет только эстетическим этюдом.
После основания синтаксиса нового аппарата для описания мира мы сможем создать новую модель известных нам физических законов и при упорном труде этот срок будет вмещать буквально в полтора десятилетия, а затем откроем новые.
Главный вопрос сейчас - как удовлетворить эмпирические требования новой системы. Важно начать решать фундаментальные вопросы основания нового аппарата.
Мы стоим на пороге исключительной науки, великих открытий и свершений.
Точно так же как никакой науки кроме математики не существует, просто по определению, потому что всё системное что возникает в других областях оказывается оперированием некоторыми абстрактными понятиями по определённым правилам; так же и здесь. Если твой новый антиматематический охуительный систематизированный аппарат будет не просто шизофазией рыбникова, а чем-то содержательным - он будет просто в сущности (возможно, новой) математической теорией.
Софист детектед. Жонглировать терминами можешь продолжать в пизде своей мамаши; мы занимаемся обсуждением содержательных аспектов новой науки.
Тот анон произвел пустые спекуляции. Но пустыми они были в основном по той причине, что никакой "новой науки" разумеется тобой не предложено. Все что можно здесь в твоих постах видеть - это ни чем не подкрепленные мечтания. В такой ситуации, разумеется, никакое "обсуждение содержательных аспектов новой науки" не возможно в силу отсутствия последней.
Я и говорю про содержательные аспекты. Когда ты не просто говоришь что произошло A или произошло B, а задаёшься вопросами почему это происходит и как устроено это не может быть ничем иным кроме как математическим рассуждением. Ты можешь не использовать те же объекты, которые используют всё остальные люди на земле, называть целые числа монадами, а вместо абелевых групп использовать жопу своей мамашки-шлюхи, но если ты ограничиваешься некими правилами - это математика, никуда тебе не деться.
Я ничего не предлагал, ты меня перепутал.
>>328546
>это не может быть ничем иным кроме как математическим рассуждением
Пруф или нахуй.
> если ты ограничиваешься некими правилами - это математика
Замечательно. То есть вождение автомобиля или поедание йогурта - это математика?
Идите-ка вы с такими определениями.
>Я ничего не предлагал
Ровно об этом я и говорю (на всякий, если ты не автор того длинющего поста выше, он тоже не предлагал) и поэтому здесь нечего содержательно обсуждать.
Автор того длиннющего поста выше предлагал обсудить альтернативы аксиоматическому методы. Он так подробно это описал, а ты все равно не понял, глупышка.
Безусловно он об том, что у него конкретных предложений нет более-менее явно сказал. Я же просто хочу обратить внимание на важный вывод от сюда состоящий в том, что и содержательного обсуждения в такой ситуации быть не может.
> Замечательно. То есть вождение автомобиля или поедание йогурта - это математика?
А что, сам акт вождения или поедания йогурта это занятие наукой? Нет, речь шла о рассуждении.
С такой грамматикой содержательное обсуждение и вправду проблематично.
>>328557
> речь шла о рассуждении
Замечательно. То есть любой философ является математиком?
Ну собственно видно, что аргументов в пользу того, что здесь возможно что-то кроме мечтаний и прочих фантазий у тебя нет - комментировать здесь больше нечего.
Я как раз на "нечего добавить - съеби" и намекал. Рад, что мы друг друга поняли.
Сдрачивай отсюда, кловун.
Опять выходишь на связь, Нео?
У нас тут будки с телефонами попрятали, так чшто будь осторожней в этой части матрицы, братишка.
Чему соответственны бесконечно вложенные матрицы и почему их не используют? Никакой информации в гугле абсолютно нет.
Суть в их нужном использовании.
>Необходим новый, антииндуктивный и полностью независимый
Шизик детектед, и еще было не лень такую простыню накатать. Математика дедуктивна, мань
Абсолютно. Но никто не будет строить новую математику и не собирается этого делать.
Индукцию в некоторой системе можно исключить, не исключив при этом скрывающейся чёткой основы, а даже наоборот - часть конструктивизма.
T-1({x}) + T-1({y}) = T-1({x + y}), при условии, что x и y имеют непустые прообразы относительно T?
Я придерживаюсь позиции, что числа правда стоит рассматривать только и только вкупе с объектами, имеющими физическое представление - никакой абстракции не должно быть. Чисел не существует.
Как*, простите.
>>328642
Да, вычти из прообраза x+y любой прообраз y (благо, он существует). Получится прообраз x.
Я могу предложить обсудить математику. Вот мой вопрос: что такое оператор набла? Какова теория таких операторов, представителем какого сорта вещей является этот оператор? Какие теоремы доказаны об этих "наблах", если их больше, чем одна конкретная набла? Википедия предлагает только пару формул, но смысла наблы не раскрывает.
Индукция существует только в абстрактной математической модели.
Я не дурак! Я взял этих тварей за вымя и буду выкручивать его, пока глупцы не смогут предоставить корректное определение самого важного в математике.
И все? Ты жрешь тонны говна и спишь около параши, видя пеано во сне, только для того чтобы потролить? Тебе больше сказать нечего? Например, что такого важного в определении N?
Троллингом занимается Вербицкий, твоя мамаша-шлюха и все, кто не может дать определение N. Это по-детски.
Я обсуждают серьёзнейший вопрос. Ты есть ничто, мразь, и лицемерно со стороны таких же тупых ублюдков не иметь корректного определения множества N.
Прекрати вилять сракой и отвечай на вопрос, что важного в определении N, пока я тебя не забанил?
Пеано определил N задолго до тебя, иди чтоли учебники почитай, а то нихуя не читаю, приходят и кукарекают.
А что, собственно, не так с пеановским определением эн?
>нихуя не читаю
По Фрейду. Какой же ебанат, лол.
>>328744
>пока я тебя не зобанел!!!!!
ХА-ХА-ХА-ХА! ХА-ХА-ХА! БЛЯДЬ! Это вообще нонсенс. Подзалупная хуйня угрожает мне, лол! Насосался в треде моего хуя, а теперь восстал!
Математика самоценности не имеет, петушки. Потому и важно определить ту степень формализма, с помощью которой будет возможно увидеть картину ясно, чтобы ориентироваться на это потом и при этом не стать жертвой противоречивости.
> вычти из прообраза x+y любой прообраз y (благо, он существует). Получится прообраз x.
Что это вообще? Что это показывает? Я не вижу, почему это показывает, что T-1({x + y}) - подмножество T-1(x) + T-1(y).
Нахуй тут идешь только ты, петушок :3
Сдрачивай отседова, упырь.
>>328771
Чтобы доказать равенство множеств, мы должны доказать два включения.
Пусть a и b таковы, что T(a) = x, T(b) = y.
Тогда T(a+b) = T(a) + T(b) = x+y.
Поэтому a+b - элемент прообраза x+y.
В одну сторону включение доказано.
Докажем в другую.
Пусть c таково, что T(c) = x+y.
Поскольку x имеет непустой прообраз, пусть a таково, что T(a) = x.
Положим b = c-a.
Тогда x+y = T(c) = T(a+c-a) = T(a+b) = T(a) + T(b) = x+T(b).
Отсюда y = T(b).
То есть b - элемент прообраза y.
Поэтому всякий элемент прообраза x+y имеет вид a+b, где a - элемент прообраза x, b - элемент прообраза y.
Так что да, верно.
тут вроде всё написано https://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D0%B5%D1%80%D0%B0%D1%82%D0%BE%D1%80_%D0%BD%D0%B0%D0%B1%D0%BB%D0%B0
>>328751
оператор набла это производные первого порядка по всем осям. производные в свою очередь показывают скорость изменения чего либо с измененем чего либо. например есть у тебя зависимость координаты тела от времени. производная будет показывать скорость, с которой тело двигалось. набля в частном случае трехмерного пространства - это вектор, у которого соответствующие компоненты это производные по осям - иксу, игреку, зэту. длине ширине высоте. ну и как бэ всё. оператор такой. с его помощью можно отобразить градиент - скорость изменения чего либо с изменением расстояния. например давления воды с глубиной. чем глубже тем больше давление. градиент соответственно будет направлен вниз. градиент же это вектор, который получается после скалярного произведения наблы на функцию, показываюшую какое давление на каждой глубине. мало в вике именно про наблу написано, потому что оператор в данном случае как операция, например умножение. какие теоремы про умножение есть? да никаких. или наоборт овер дохуя. только в этой куче теорем главное не умножение, а то, про что теорема, умножение же в них выступает как операция
Потому что любой элемент из T^{-1}({x + y}) лежит в T^{-1}(x) + T^{-1}(y): возьми этот элемент a и любой b из T^{-1}(y), тогда найдётся c = a - b из T^{-1}(x) и a = b + c лежит в T^{-1}(x) + T^{-1}(y).
Спасибо, понял.
Я не совсем понимаю, что значит "оператор". Какие операции с оператором определены? Как мы можем умножать оператор на что-то? Что это вообще за фигня? И притом в той же вики есть заметки наподобие "ну вот мы тут его как бы умножаем, но вы же понимаете, что на самом деле это не умножение".
Если честно, я и d/dx нотацию не очень понимаю. Зачем мы пишем d два раза, да еще и ставим черту, будто это дробь? Когда мы пишем, что набла = {d/dx, ...}, чем у нас это d/dx является? Раньше мы использовали это как часть выражения, а теперь у нас это выступает как самостоятельный объект.
Далее, зачем мы пишем эту глупость с d/dx на i, d/dy на j и так далее? Это же бессмысленно, зачем нам писать это три раза, почему нам не писать это в обобщенной форме?
Извините, но я не понимаю; объясните. Да, и у нас был курс физики, но там это все считалось "интуитивно понятным", иди решай задачи.
>что значит "оператор"
Сопоставляет одним объекты другие.
>я и d/dx нотацию не очень понимаю.
Стоит воспринимать как единый символ.
>чем у нас это d/dx является?
Оператором дифференцирования.
>Далее, зачем мы пишем эту глупость с d/dx на i, d/dy на j и так далее
Чтобы показать, что после применение оператора набла, получается вектор.
Набла - это не простой оператор. Наблу можно векторно умножать на вектор. Простой оператор нельзя.
>Сопоставляет одним объекты другие.
Чем это отличается от функции?
> Стоит воспринимать как единый символ.
Я имел в виду избыточность и странность такой нотации.
> Оператором дифференцирования.
То есть набла - множество из трех операторов? Любое ли множество операторов является оператором? Как у нас получается, что {d/dx_1, ..., d/dx_n} = de_1/dx_1 + ... + de_n/dx_n? Это же абсурд, я не понимаю.
> Чтобы показать, что после применение оператора набла, получается вектор.
Не понял. Что значит "чтобы показать"?
Вообще ничего твой пост не прояснил, если честно, извини.
>я и d/dx нотацию не очень понимаю.
это потому что школьник и не проходил мат анализ, производные и прочие пределы по жесткому. можно писать дельта f(x)делить на дельта х при дельта х стремящемся к нулю. или вместо дельта d - типа бесконечно малую дельта. d/dx без f(x) в числителе как бы говорит что не важно какая f(x) будет, подставляй любую. ну как умножение * а что будет с двух сторон от умножения уже не особо важно. тут так же, только набля это (d/dx,d/dy,d/dz) типа надо некую функцию f(x,y,z) отдельно продифференциировать по иксу игреку и зету. нотация просто удобный способ писать определение производной. удобный потому, что когда будешь решать уравнения настоящие, а не на определение смотреть, можно будет числитель и знаменатель сокращать например по обычным правилам, т.е. df(x) в числителе и знаменателе можно зачекрнуть, не особо задумываясь что это бесконечно малая разность.
чем умножение отличается от функции? тем же и оператор отличается от функции)
>Я имел в виду избыточность и странность такой нотации.
я тут >>328839 пояснил за нотацию
>набла - множество из трех операторов?
не из трех. из количества измерений. если у тебя 1 измерение, то из одного. если 5 то 5.
и не множество, а есть пространство, пусть трех мерное. набла - это вектор, показывающий скорость изменения твоего чего угодно - функции поля и т.д. по всем трем направлениям. или по 10 если направлений 10.
да и вообще прочитай >>328839
Этот пост отнюдь не добавляет понимания, к сожалению.
>это потому что школьник
Неверно.
> d/dx без f(x) в числителе
Еще раз: это не дробь, делением тут не пахнет, числителя тут нет. Эта нотация confusing и вводит в заблуждение. Я не понимаю, почему не писать например d_x(f, a) для первой производной по икс в точке а, и т.д.
>>328843
> чем умножение отличается от функции?
Умножение - это и есть функция.
> пояснил за нотацию
Не пояснил.
> не из трех.
Я дальше в общем случае написал, ну следующее предложение же.
> набла - это вектор
Так оператор, вектор или множество операторов? Любой ли вектор является оператором?
Извини, но ты совершенно ничего не пояснил, и твои посты полны внутренних противоречий. Спасибо за попытку, но для меня это оказалось абсолютно бесполезным.
Оно ждёт невероятно. Пламя ждёт.
он за собой даже подчистить не может, о чем ты
Докажи.
Я только сру на даунов-школьников вроде тебя и ебу ваших шлюховатых мамок. В неподмытый анал, а потом они слизывают своё же говно с моего члена.
И я не троллю, мне действительно интересны основания математики.
░░█▌░░░░░░░░░░░░░░░▀██████░░░
░█▌░░░░░░░░░░░░░░░░███████▌░░
░█░░░░░░░░░░░░░░░░░████████░░
▐▌░░░░░░░░░░░░░░░░░▀██████▌░░
░▌▄███▌░░░░▀████▄░░░░▀████▌░░
▐▀▀▄█▄░▌░░░▄██▄▄▄▀░░░░████▄▄░
▐░▀░░═▐░░░░░░══░░▀░░░░▐▀░▄▀▌▌
▐░░░░░▌░░░░░░░░░░░░░░░▀░▀░░▌▌
▐░░░▄▀░░░▀░▌░░░░░░░░░░░░▌█░▌▌
░▌░░▀▀▄▄▀▀▄▌▌░░░░░░░░░░▐░▀▐▐░
░▌░░▌░▄▄▄▄░░░▌░░░░░░░░▐░░▀▐░░
░█░▐▄██████▄░▐░░░░░░░░█▀▄▄▀░░
░▐░▌▌░░░░░░▀▀▄▐░░░░░░█▌░░░░░░
░░█░░▄▀▀▀▀▄░▄═╝▄░░░▄▀░▌░░░░░░
░░░▌▐░░░░░░▌░▀▀░░▄▀░░▐░░░░░░░
░░░▀▄░░░░░░░░░▄▀▀░░░░█░░░░░░░
░░░░█▄▄▄▄▄▄▄▀▀░░░░░░░▌▌░░░░░░
NNNNNNNNNNNNNNNNNNNNNNNNNN

жаль, что только ты у параши

>бу ваших шлюховатых мамок. В неподмытый анал, а потом они слизывают своё же говно с моего члена.
>Я не тролю.
Оно не является определением потому, что использует индукцию ("и т.д."). Все равно что точку определять по евклиду.
Мне действительно интересно.
Но ведь индукция и натуральные числа это одно и то же. Поясни подробнее, что ты имеешь в виду.
Уебок, схуяли я тролль??? Тролль это тот, кто выдвигает заведомо ложные утверждения для лулзов. Приведи хотя бы один пример ложного высказывания с моей стороны?
Именно, что одно и тоже. Почему я и говорю, что это не корректное определение в математическом смысле.
Почему некорректное? Мы вводим для интуитивного понятия индукции некий идеальный объект, являющийся ее выражением. Что неправильного в таком подходе?
Нет, "индукция" понимается как исходное, неопределяемое понятие, а натуральные числа являются идеальным (и определенным!) случаем индукции. Разве нет?
От души
Сука, ПРЕКРАТИ, Я ЩА УМРУ ОТ СМЕХ.
> Приведи хотя бы один пример ложного высказывания с моей стороны?
Не получится, потому что с твоей стороны слышатся не высказывания, а только вскукареки.
ИТТ ты продолжаешь сосать, так как не можешь ответить зачем тебе определение определения N.
Ну раз так, то определение N это аксиомы пеано, что и требовалось доказать.
Ну он же сказал, что считает аксоимы Пеано неудовлетворительным определением N, не тупи.
Чего тут конкретизировать? Ты взял и положил абстракцию индукции как исходное понятие, потом применив его к единице и операции конструирования следующего элемента построил натуральный ряд. Т.е. в данном случае у тебя N является частным случаем индукции.
>>328974
Ты дурак, а зачем вообще в математике что-то определяют, может лучше чертежи рисовать и линейкой всё доказывать???
Аксиомы Пеано не являются определением потому что без интуитивного понимания индкции (которое они пытаются определить) просто не работают.
Нет, ты все-таки немного не так интерпретируешь. Еще раз: я не применяю индукцию к единице, чтобы получить натуральные числа; натуральные числа - это и есть индукция. Не частный случай, а сама индукция. Натуральные числа выражают формально интуитивное понятие индукции. Ок? Здесь все выглядит справедливо.
>>328999
Ну так у тебя есть мысли по поводу того, какое более "простое" понятие можно использовать для определения индукции?
> Не частный случай, а сама индукция. Натуральные числа выражают формально интуитивное понятие индукции. Ок? Здесь все выглядит справедливо.
Я согласен с этим и в начале дискуссии почти дословно точно так же и писал, но на этот раз решил выразиться осторожнее чтобы не стали требовать доказать что из натурального ряда следует индукция.
> Ну так у тебя есть мысли по поводу того, какое более "простое" понятие можно использовать для определения индукции?
Думаю это невозможно, так как в математике нельзя работать с бесконечностями без какой либо интуитивной формы бесконечности. А потенциальная бесконечность индукции это и есть минимальная (самая слабая) бесконечность, поэтому приходится принимать ее как исходное неопределяемое понятие.

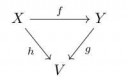
Пусть X, Y и V - множества и f, g, и h - такие функции, что gf != h. Тогда эта диаграмма некоммутативна.
Я тоже в свое время над этим долго тупил, пока мне не рассказали. Почему-то по запросу "example of non commutative diagram" ничего не гуглится.
лох

>>328810
> Какие операции с оператором определены?
Операторы образуют векторное пространство.
> Зачем мы пишем d два раза, да еще и ставим черту, будто это дробь?
Физики поднасрали. Та нотация, о которой говорил я, называется "нотацией Эйлера", и является единственной разумной нотацией. Любой, кто использует d/dx нотацию, является физиком, пидором и просто вредителем.
> Далее, зачем мы пишем эту глупость с d/dx на i, d/dy на j и так далее?
Это действительно бессмысленно, опять физики поднасрали.
>>328834
> Как у нас получается, что {d/dx_1, ..., d/dx_n} = de_1/dx_1 + ... + de_n/dx_n?
Никак не получается, в русской вики опять ошибка. Да, мне стыдно, но я не буду ее исправлять, потому что лень.
Если кому-то интересно, вот здесь отличные лекци: http://ocw.mit.edu/courses/mathematics/18-02-multivariable-calculus-fall-2007/
В частности, пятая неделя. Алсо, какие же классные у них лекторы, блин!
>Чем это отличается от функции?
Функции это как правило отображения из R->R, или R^{n}->R. Операторы в более общем случае это отображением из произвольного множества в другое множество.
>Я имел в виду избыточность и странность такой нотации.
Есть еще нотация, типа d_{x} ну или для частных d красивое с индексом, который обозначает по какой переменной идет дифференцирование.
>{d/dx_1, ..., d/dx_n} = de_1/dx_1 + ... + de_n/dx_n
Это твои додумки, в той же википедии, никто орты не дифференцирует.
>Не понял. Что значит "чтобы показать"?
Что набла при действии на вектор, дает вектор.
>Та нотация, о которой говорил я, называется "нотацией Эйлера", и является единственной разумной нотацией
Это какая?
Эйлера.
T-1({x}) = a s.t. T(a) = {x}
T-1({y}) = b s.t. T(b) = {y}
{x + y} = {x} + {y}
= T(a) + T(b)
= T(a + b)
T-1({x + y}) = T-1(T(a + b))
= a + b
= T-1({x}) + T-1({y})
>Вот мой вопрос: что такое оператор набла?
Вид векторного оператора. Будучи применённым разными способами к многомерной функции, он показывает её характеристики (градиент, дивергенцию, ротор).
https://en.m.wikipedia.org/wiki/Del
Что такое "существует"? Число – математический объект.
Спишь ещё что-ли? Конечно. Можно представить виде дроби. Например 0.(3) - это 1/3
До завтра!
Так это же легко.
зачем своего ебаря постишь?
господи, это охуительная шутка. молодец
Но ведь там нету индукции, все доказано абстрактно, как раз то что хочет петушара.
Потому что чирвячок :3
Блять. Эх. А можешь ссылку на результат скинуть, друг?
Совсем дурак, да?
Да. Пусть дробь имеет вид a,b(c). (с) можно найти как сумму геометрической прогрессии со знаменателем с/10^n.
А, ступил. a1/(1-q) рационально.
У нее период устраняется вычитанием. То есть пусть x = 7.(39), тогда 100x=739.(39) и 99x=732.
Замечательная группа талантливых математиков, которой не повезло превратиться в мем.
Меня и не интересует entry-level. Я сильно продвинутый.
Стоит ли изучать их литературу или полно книг лучше?
Если ты продвинутый, то без труда прочитаешь все их книги. Их там не больше пятидесяти, и они наполнены общеизвестным контентом (строго говоря, именно они и сформировали канон общеизвестного).
"Сильно продвинутые" даже если тут сидят, вопросов такого типа – не задают.
a, b, c откуда? Натуральные, целые, рациональные, вещественные, комплексные? Или это вообще не числа?
Поплыл, потонул, выкарабкался, весной опять поплывёт.
2*2+2 скоква??
Такс такс, што тут у нас, ахах, математикоблядь разорвалась от прикладной математики, найс)
20
Без определения N не ответить никак.
В КАКОЙ АЛГЕБРЕ?
Подойди к преподавателю и прямо и без обиняков ему об этом скажи. Если ты действительно неплох в интересных разделах, то тебя пожалеют и поймут. Ну, а ежели нет - увы.
Я не неплох. Просто после вот этих всяких задач теряется мотивация к занятию математикой, а что с этим делать — не знаю.
Я не хочу быть чистым математиком. Я учусь на физике. Я хочу просто быть теоретически-подготовленным и понимать современные идеи математики и их роль для физики. Да и перепоступить я не могу по нескольким весомым причинам.
>современные идеи математики и их роль для физики
Математика новее XIX века в физике не используется. Физики не осилили даже теорию множеств.
>Я учусь на физике.
Так бы сразу и сказал. Наверни еще немного этого ароматного говна, да выпей мочи. И не забывай страдать.
> Математика новее XIX века в физике не используется
намеренное преувеличение в духе арнольда?
Слово "множество" в учебниках физики не встречается вообще. Это было бы невозможно, если бы физики использовали теорию множеств. Но физики не используют теорию множеств.
физики топологию используют
определи мне топологию без множеств
я чего-то упускаю, или это старая добрая сосачерская традиция - спорить ради спора?
Просто покажи учебник физики, в котором есть слово "множество".
https://books.google.ru/books?id=3kUoBwAAQBAJ&pg=PA19&lpg=PA19&dq=%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0+%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE&source=bl&ots=K4S0iTPh2w&sig=NW6IQpHlhd2gOjWZPpk50J6SRq4&hl=en&sa=X&ved=0ahUKEwiw38ry7bHKAhVLjCwKHYFQA8kQ6AEIMzAD#v=onepage&q=%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0%20%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE&f=false
иди нахуй
https://books.google.ru/books?id=nV3-AgAAQBAJ&pg=PA48&lpg=PA48&dq=%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0+%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE&source=bl&ots=DJt26IzBFv&sig=wf0vgHnH5gVnxlvJLDNY7t_1FgQ&hl=en&sa=X&ved=0ahUKEwiw38ry7bHKAhVLjCwKHYFQA8kQ6AEIVTAI#v=onepage&q=%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0%20%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE&f=false
Ты просил
> Просто покажи учебник физики, в котором есть слово "множество".
Ты получил это. Теперь жри.
Это матфизика. Распространённая среди несведущих ошибка, основывающаяся на похожести по звучанию. На самом деле это не физика, а такой раздел современной математики, в котором люди занимаются инвариантами узлов, представлениями и прочим облизыванием несвежих хуёв.
зачем ты отвечаешь
он же вообще уходит в сторону от темы, ты посмотри с чего все началось
с того что в физике, якобы не используется математика позже XIX века
ему ответили что это не так
он начал про учебники
причем тут блядь учебники вообще
речь о науке, о взрослых дядях которые зарабатывают на хлеб физикой, каким боком тут сраные учебники для студентов
Что "это"? Учебник - это гиперссылка? Ты совсем дебил? Ты понимаешь слово "определение"? Съеби обратно на свою физикопарашу, короче.
Учебники по ссылке. Впрочем, я уже понял, что разговора о теории множеств в физике не получится.
Ты определил "учебник" перечислением? То есть на языках, кроме пидоранского, учебников нет. Отлично. Физикодебилы во всей своей красе.
Учебник является не словом формальной теории, но объектом реального мира, и не может быть определён иначе как демонстрацией большого количества примеров и контрпримеров.
>и не может быть определён иначе как демонстрацией большого количества примеров и контрпримеров.
Ну если у тебя вместо мозгов говно твоей мамаши - то это справедливо, да.
> Ты сделал верное утверждение, так что ты соснул
Господи, откуда вы такие вылазите? Физик, съеби уже на свою парашу, тебя еще в прошлом треде опускали.
Давай разберём утверждение "эта импликация истинна, так что ты соснул".
Предположим, что эта импликация истинна. Тогда ты соснул. Но это - как раз то, о чём говорит эта импликация. Таким образом, ты соснул.
лол
к чему тут это?
ты в состоянии понимать на какие посты ты отвечаешь?
ты читать еще в состоянии?
Это все наигранное мне кажется. Как можно обожать математику. Это просто есть, и все. Можно проявлять интерес, а можно не.
У тебя говноглюки. Иди нахуй.
Ты что, дурак?
Бамп вопросу.
Если ты символьный дроч осилить не можешь, зачем ты вообще пришел в математику? Хоть здесь многие и плюются от этого вида деятельности, но он весьма полезен, достаточно привести в пример Рамануджана.
Вся теория поля суть алгебраическая топология, так что иди нахуй, тупорылое чмо, сраный дегеннрат, пидорас и членокастрат
А что не так? Ленинская философия хорошо с математикой согласуется. Или ты либеральный пидорас???
Пиздец, быдло. Насколько недоразвитыми нужно быть, чтобы использовать в качестве ругательства такие слова, как "пидорас" и "либерал"?
Либеральный пидорас.
Математика это вообще дроч вприсядку математиков исключительно ради математики.
>не имеет никакого отношения к действительности.
Вся суть нынешней маняфизики.
Спасибо эйнштейну, что разделил физику на до и после, на Ъ физиков и на эксприментаторов с теоретиками.
Нет, потому как результаты по типу >>329650
не являются адекватными ни в какой формальной системе и в здравом смысле. Но чистые математики уже наверстали груду говённых теорий и доказательств в предположении верности гипотезы Римана.
>Вся суть нынешней маняфизики.
Неосиляторы пожаловали
>Спасибо эйнштейну, что разделил физику на до и после, на Ъ физиков и на эксприментаторов с теоретиками.
Толсто, попробуй тоньше
>в предположении верности гипотезы Римана.
Забавно, что этот результат не зависит от гипотезы Римана. Хотел понтануться, в итоге обосрался, как мило стекает говнина с твоей штанины.
ТЕОРИЮ относительности веревел в разряд аксиом уже? Волновую функцию объяснил?
>ТЕОРИЮ относительности веревел в разряд аксиом уже?
Ускорители работают, все считается, все более менее работает, пока метрика не перестает быть метрикой Минковского.
>Волновую функцию объяснил?
А че там объяснять? Или ты про маняфилософские рассуждения? Оставим их маняфилософам.
Еще раз, для абстрактных математиков, теория относительности остается теорией, так как пока не найдено прямых фактов того что пространство искривляется. Ллинзирования звездами света и подобное это только косвенные наблюдения.
А волновая функция так это вообще затычка в теории прямиком от бора, чтобы электрон нельзя было зафиксировать у ядра водорода.
>Ллинзирования звездами света и подобное это только косвенные наблюдения.
Этого вполне достаточно.
>А волновая функция так это вообще затычка в теории прямиком от бора
Хуйню какую-то спизданул. Иди учебников наверни, прежде чем позориться.
В чтении.
Так ведь теория - это не гипотеза. Ты ещё скажи, что теория колец - это же всего лишь теория.
Если достаточно, почему теория все еще теория?
>>329691
Как правило, большинство исследователей считает, что стандартным методом проверки теорий является прямая экспериментальная проверка («эксперимент — критерий истины»). Однако часто теорию нельзя проверить прямым экспериментом (например, теорию о возникновении жизни на Земле), либо такая проверка слишком сложна или затратна (макроэкономические и социальные теории), и поэтому теории часто проверяются не прямым экспериментом, а по наличию предсказательной силы — то есть если из неё следуют неизвестные/незамеченные ранее события, и при пристальном наблюдении эти события обнаруживаются, то предсказательная сила присутствует.
На самом деле взаимоотношение «теория — эксперимент» более сложное. Поскольку теория уже отражает объективные явления, ранее проверенные экспериментом, то нельзя делать подобные выводы. В то же время, поскольку теория строится на основе законов логики, то возможны заключения о явлениях, не установленные ранними экспериментами, которые и проверяются практикой. Однако, эти выводы необходимо уже называть гипотезой, объективность которой, то есть перевод этой гипотезы в ранг теории, и доказывается экспериментом. В этом случае эксперимент не проверяет теорию, а уточняет или расширяет положения этой теории.
Обобщая, прикладная цель науки — предсказывать будущее как в наблюдательном (аналитическом) смысле — описывать ход событий, на который мы не можем повлиять, так и в синтетическом — создание посредством технологии желаемого будущего. Образно говоря, существо теории в том, чтобы связывать воедино «косвенные улики», вынести вердикт прошлым событиям и указать, что будет происходить в будущем при соблюдении определённых условий.
>>329693
У меня от тебя ТЕМНАЯ МАТЕРИЯ и КРИВАЯ ВРАЩЕНИЯ ГАЛАКТИК
>бавно, что этот результат не зависит от гипотезы Римана. Хотел понтануться, в итоге обосрался, как мило стекает говнина с твоей штанины.
Где пруф-то? Результат связан на прямую, например. Дзета-функция в точке -1 и есть сумма натурального ряда.
Только вот незадача, в квантовом мире,будущее не определяется однозначно настоящим.
>У меня от тебя ТЕМНАЯ МАТЕРИЯ и КРИВАЯ ВРАЩЕНИЯ ГАЛАКТИК
Кто говорил, что ОТО должно описывать всё-всё? Это тебе не единая теория всего, уж извини.
Почему тогда теория, а не гипотеза? Или там в физическом кружке дураки сидят, грамоты не знают?
>Результат связан на прямую, например.
Гипотеза Римана: Все нетривиальные нули дзета-функции имеют действительную часть, равную 1/2.
Вывод соотношения на дзера(-1) не использует это предположение.
То что касается гравитации, есть много различных исследований, ведущихся в этом направлении.
>>329705
Эксперименты были поставлены, гипотеза потверждена, кривизна пространства показана.
Ясно, тебе просто нечего сказать в оправдание теории.
И опять таки, если нашли подтверждения что теория/гипотеза верна, почему слово теория не уберут из названия?
А ты умён, где и на кого учишься?
Общество физиков приятней чем логиков.
>Вывод соотношения на дзера(-1) не использует это предположение.
Пахнешь чистым математиком. Такое, засохшее, но ранее жиденькое желтое говно, которое ты носишь в кармане, хитро замаскировав его дешевым парфюмом. Наивно полагаешь, что солидные господа в пальто не заметят, что ты обосрался опять, но их не наебёшь.
Значит больше не буду тебе отвечать.
Я например некромант, воскресил твою мать, чтобы её трахнуть.

Порой мне кажется, что модерация - это не так уж и плохо.
Переполнение оперативки, хороший научный текст и так ее до предела нагружает, а если на чужом языке то еще и переводы надо помнить или в словарь лазить.
Как что-то плохое.
Просто следует создать два математикотреда: этот и тот, в котором мы будем определять N.
Кстати, это я еще вчера начал весь этот срач про физиков. Не думал, что вброс окажется таким удачным, хе-хе. Извини, я не со зла.
Ты не понял, под N-тредом я имел в виду хороший тред, а под этим тредом - плохой тред.
Ты дурак? Нет ничего лучше саморегулирующегося сообщества. Я давно был модератором на этих досках и просто не видел смысла в бане и удаления сообщений - в результате эти тупые ублюдки меня отстранили.
Тупой просто.
Саморегулирующееся сообщество, по своему смыслу, предполагает возможность саморегуляции. Но у анона нет способа пидорнуть из треда фрика.
http://pastebin.com/ZaHYuqpy
>Из развлекательного:
Нахуя это? Тебе 13 лет?
>Собственно математика:
>Алгебра. Гельфанд И.М., Шень А.Х.
>Парадоксы теории множеств. И. В. Ященко (в первый раз нормально чего-то не дочитать или не понять что-то)
>Теорема Абеля в задачах и решениях. В. Б. Алексеев.
>Высшая математика для начинающих физиков и техников. Зельдович Я.Б., Яглом И.М.
Комбинаторика. Виленкин Н.Я.
Таки 13. Это книги уровня 9-го класса.
И зачем эти советы в конце? Для этого есть /fl/. Да и вообще, умение читать мат. литературу на английском - считается само собой разумеющимся.
Ты можешь например тупо взять и переделать этот гайд на свой вкус, я даже рад буду. Ну или нахуй пойти если ты пришел просто повыебываться.
Не нужно это говно. Тред и так превратился в "реши домашку" и "помоги школьнику разобраться с определением предела" не считая поехавших разной степени ебанутости.
Такой гайд в шапке будет привлекать ещё больше школоты.
Они все равно не съебут в /un. Да впрочем плевать, зато теперь есть что в ответ писать таким вот >>328130>>328325>>327444
До слез, сука.
Давайте конфоблядствовать. Создадим анально огороженную конфу и будем дрочиться.
Конфа быстро умирает, архив вести неудобно, нужны клиенты помимо браузера и лишние телодвижения с регистрацией.
Давайте
>Тред и так превратился
Тред уже который месяц подряд не выходил из режима "я весёлый траль, сматрите чё ещё придумал". Домашки это, в общем, было бы неплохо.
Конфу в скайпе
Либо трудности и преграды, либо ананимнасть и трали. Это два стула, от них никуда не деться.
С чего это она должна съебать если говноеды её подкармливают, да она сама прекрасно поддувается? Она несколько месяцев уже тут.
Есть другие борды.
>"я весёлый траль, сматрите чё ещё придумал"
Ничего нового. Таких можно просто игнорить.
Заходишь в тред. Скроллишь немного, определяешь, что нить обсуждения визуально стала похожа на б/ - посты в три слова, мамкоёбство. Закрываешь и уходишь. А в образовавшееся таким образом свободное время, можешь заняться самообразованием или самоудовлетворением.
>для начинающих или нет?
Для самых маленьких.
Он устарел, безнадежно. Математическая номенклатура, там использующаяся, на данный момент никем и нигде не употребляется. Сейчас трехтомник представляет собой не столько математико-практическое, сколько историческое значение.
> Скроллишь
> определяешь
Трата времени. Трата времени. Проще просто сделать чтобы дебсов не было.
Я таки, наоборот, описал способ, как сэкономить время. У тебя гораздо больше времени уйдет на бесплодные попытки изгнать неугодных. Проще и практичнее - забить на них.
Да, ты аппелируешь к "эффективности" при этом подменяя результат, распространённая ошибка. Тогда, рассуждая так, ещё проще просто не заходить в этот тред - ещё больше времени экономится.
Да потому что в /un их никто не ждет. /un - это такой /soc, только про универчики тип)) Говно короче. Понятно, что спрашивают они в тематических тредах.
Модератор, закрепи тред тупых вопросов и явственно обозначь в шапке, что решить домашку и бог в четвертом измерении - это вот сюда. А фрики как-нибудь сами отрегулируются, ящитаю.
>>329877
Куда ты хочешь переехать? В /b?
Ну, кстати, есть scrollback.io, без клиентов и прочей параши, но с бриджами в телеграмы и ирц.
Даже у Вербицкого в комментах (даже во времена разрешенных анонов и безудержного спама) такого цирка не было.
Давай так сделаем. Пусть у тебя есть тор S^1 X S^1 с k проколами. В каждый прокол ты вклеиваешь лист Мёбиуса. Вклеиваешь вдоль центральной окружности. Вычисли когомологии де Рама вторые и первые получившегося гладкого многообразия, петух.
Предлагай же. Я не против, но мне кажется, что проще создать пользовательскую доску, или как это называется. Абуняша же запилил что-то такое. Создай математическую доску и модерируй ее. Я поддерживаю тебя.
Это копия, сохраненная 22 февраля 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.


























