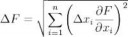Это копия, сохраненная 16 января 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

Древнегреческие математики не считали единицу числом, а понятия нуля у них вовсе не существовало. По этой причине утверждения о целых числах содержали в себе несколько аналогичных формулировок для случаев, когда рассматриваемые числа равны или не равны единице, что можно видеть у Эвклида, когда он излагает свой алгоритм нахождения наибольшего общего делителя («Начала», книга 7, предложения 1 и 2) — он вынужден формулировать два предложения вместо одного (предложение 1 излагает случай, когда наибольший общий делитель равен 1, а предложение 2 — когда не равен).
За прошедшие две тысячи лет люди освоили понятия нуля и единицы, но страх перед ними остался.
Далее я привожу список разнообразных верных утверждений, вызывающих отторжение под влиянием этого страха.
У пустого множества есть ровно один эндоморфизм — пустая функция. Вообще, из пустого множество в произвольное есть ровно одна функция — функция с пустой областью определения. (А из произвольного непустого множества в пустое функций нет.)
Натуральные числа — это те, которые используются при счёте.
Это определение я услышал в пятом классе. Счёт — это вычисление мощностей конечных множеств. Пустое множество конечное, стало быть число 0 — натуральное. По-другому думают только ретрограды и мракобесы.
Классическое проявление страха перед нулём — нумерация всего и вся с единицы, хотя зачастую более естественно нумерация последовательными натуральными числами, начиная с минимального — нуля, а часто наиболее естественным вариантом является отказ от нумерации.
Некоторые сумасшедшие продолжают утверждать, будто 0^0 не определено. Особенно популярно это мнение в среде жёстких аналитиков. (И вообще, жёсткий анализ (в противоположность мягкому) — это один из основных источников мракобесия в математике, как отметил один из моих знакомых.) Обосновывают они его следующим аргументом: функция (x,y) → x^y не является непрерывной в точке (0,0). Однако запись многочленов и рядов в форме ∑_k a_k x^k возможна только и исключительно при условии, что 0^0 = 1. Формула бинома (x+y)^n = ∑_k {n\choose k} x^k y^{n-k} верна для всех n≥0 и произвольных x и y также только при условии, что 0^0 = 1 (иначе надо потребовать, что x≠0, y≠0 и если n=0, то x+y≠0). Количество отображений из n-элементного множества в m-элементное равно m^n — смотри замечание выше про эндоморфизмы пустого множества. Отсюда тоже получаем, что 0^0 = 1. Список можно продолжать до бесконечности.
Сумма пустого множества чисел есть 0. Произведение пустого множества чисел есть 1. Упражнение: вычислите значение башни степеней x^{y^{z^…}} для пустого семейства чисел.
Нулевое векторное пространство имеет пустой базис и обладает ровно одним эндоморфизмом — нулевым. Определитель эндоморфизма нулевого векторного пространства равен 1, а его матрицей будет пустая матрица (матрица с пустым множеством строк и столбцов). Морфизмы из нулевого или в нулевое векторное пространство будут иметь пустое множество столбцов или строк.
Произведение пустого семейства объектов (или предел пустой диаграммы) есть терминальный объект, копроизведение пустого семейства объектов (или копредел пустой диаграммы) есть начальный объект. Тензорное произведение (в моноидальной структуре) пустого семейства объектов есть моноидальная единица. В частности, тензорное произведение пустого семейства векторных пространств есть основное поле.
Норму гомоморфизма нормированных пространств f: X→Y часто определяют как sup_{x∈X: x≠0} ‖f(x)‖/‖x‖ или как sup_{x∈X: ‖x‖=1} ‖f(x)‖. Эти определения не работают в случае X=0, а также, если допускаются полунормы, в случае если полунорма нулевая. Правильное определение, работающее во всех случаях, в том числе и для полунорм: ‖f‖=sup_{x∈X: ‖x‖≤1} ‖f(x)‖.
Конъюнкция пустого семейства утверждений истинна, дизъюнкция пустого семейства утверждений ложна. Объединение пустого семейства множеств есть пустое множество. Пересечение пустого семейства множеств есть класс всех множеств (или универсум, или другой аналогичный объект — зависит от используемых теоретико-множественных оснований). Например, топология на множестве X — это семейство его подмножеств, замкнутое относительно произвольных объединений и конечных пересечений внутри X.
Забывающий функтор из категории пунктированных множеств в категорию морфизмов множеств, интерпретирующий пунктированное множество A как морфизм из одноэлементного множества в A, имеет левый сопряжённый функтор. Значение этого функтора на объекте A→B обозначается B/A и называется фактормножеством множества B по множеству A. (Здесь имеет место очевидная волность речи.) В случае A=∅ имеем B/∅=B⊔*, объединение B и одноэлементного множества, тем самым фактормножество иногда может быть больше исходного множества, а факторотображение может не быть сюръективным.
Весьма показательна ошибка, которую сделал Hartshorne в своём учебнике алгебраической геометрии в определении предпучка — он определяет предпучок абелевых групп как предпучок абелевых групп в обычном смысле, удовлетворяющий дополнительному условию F(∅)=0. Это вызывает проблемы уже на элементарном уровне (нельзя определить постоянный предпучок обычным образом, непонятно как определить предпучок со значениями в произвольной категории), а куча утверждений про предпучки (например, про универсальные копополнения) становятся просто неверными.
На самом деле это условие является следствием аксиом пучка. Действительно, для произвольной категории C предпучок со значениями в C — это контравариантный функтор из противоположной категории открытых множеств данного топологического пространства в C, а пучок — это предпучок, удовлетворяющий свойству спуска: конус спуска произвольного покрытия произвольного открытого множества является предельным конусом. Если взять пустое покрытие пустого множества, получаем, что значение пучка на пустом множестве является терминальным объектом.
Желаю всем читателям избавиться от своего страха перед нулём и единицей, если он у них есть, и пользоваться этими понятиями свободно, без дополнительных оговорок.
Предыдущий: >>314306 (OP)
Я вот учу производные и мне пишут про вычисление формулы касательной графика функции в точке.
Собственно, зачем нужна эта касательная прямая? Если функция периодическая, касательная невозможна?
В чем заключается твое "изучение" производной, если ты не можешь понять ее определение?
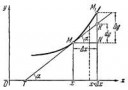
ну если точнее то это дэ игрек на дэ икс
то есть предел дельта игрек делить на дельта икс при дельта икс стремящемся к нулю
что тебя не устраивает
траллируешь? это обычное школьное определение
оно вполне работает, его хватает чтобы исследовать функции R->R
Напиши тогда определение.
это ты меня траллируешь
сначала производная у тебя это дельта игрек
потом дельта игрек по дельта икс
потом dy / dx
остаётся только сказать, что производная - это производная
ебануться, одним словом
> сначала производная у тебя это дельта игрек потом дельта игрек по дельта икс
ну это не я писал, извини. Я тоже почти школьник
> потом dy / dx
ну мы согласны что это правильно? Я понял что ты правильно возбухаешь, достаточно добавить из рисунка что это не просто L=NM1/NM а предел L при NM->0
В физике производная - это дельта игрек / дельта икс, причём dy равняется дельта игрек. Точка.
Математики со своими пределами идут нахуй.
>Нестандартный анализ — альтернативный подход к обоснованию математического анализа, в котором бесконечно малые — не переменные величины, а особый вид чисел.
Что это такое и с чем его едят?
Не секрет, что раньше(давным давно) использовался аппарат бесконечно малых чисел, при помощи него(сам аппарат не был строгим) получались вполне адекватные результаты. Потом была изобретена теория пределов и от бесконечно малых отказались. Однако, как оказалось можно придать им строгий вид.
>Математики со своими пределами идут нахуй.
Ах ты мой маленький первокурсник вузика имени залупина, как многое тебе еще предстоит узнать.
Чтолу чше САМОМУ учить, аппарат бесконечно малых или пределы? И в чем разница первого и второго? Как по мне это одно и то же.
пределы, нестандартный анализ - вещь довольно специфичная и если ты не математик, то абсолютно не нужная.
Но ведь надо их выучить если хочешь покорять дифференциалы и интегралы, а потом лагранжианы и операторы набла, так!?
нестандартный анализ для этого не требуется, описанное тобой покрывается I томом Зорича, можешь заглянуть
Какая разница, что было у Ньютона? Важно, как сейчас есть в физической практике. В физике Δy всегда равно dy, а предельный переход не используется никогда. Математики должны смириться, что их лимиты никому не нужны.
Открой учебник физики. Там не говорят "для всякого эпсилон". Когда надо, там просто используют бесконечно малые приращения. Лишь изредка что-нибудь разлагают в ряд (Маклорена, разумеется; другие ряды придумали аутисты).
Дон двачито эль даунито.
Ты не бойся. Ты открой книгу и своими глазами посмотри. Ну не используются лимиты в физике, не используются. Там только бесконечно малые.
Зачем мне определять какую-то последовательность? Я всегда могу разбить физическое тело на бесконечно малые кусочки, а потом проинтегрировать обратно.
Ну ладно. Пусть у тебя скорость в зависимости от времени изменяется по закону f(t). Тебе надо найти пройденное расстояние в промежутке времени от [t1 до t2]. Что такое атом времени?
То есть у тебя будет отдельное определение определенного интеграла для плотности, отдельное для скорости, отдельное для плотности вероятности и т.д.?
> С заделом на программирование
99% программистов математика не нужна вообще (арифметики за 1-4 класс достаточно). Есть смысл заниматься математикой только если тебе интересно.
Ну хз, погугли "Mathematics for computer science".
Несмотря на то, что ты школьник и быдлан, я тебе отвечу. Твои представления о математике на уровне 16 века. Понятно, что суть не меняется, от того, что ты дал формальное определение определенного интеграла, но использовать нормальные математические понятия - это удобно. Это язык, который разрабатывался веками. Люди использовали разные подходы, чтобы формализовать матан, и выбрали самый удобный. В учебниках по физике для 1 курса мухосранского пту не встретишь слова "lim", потому что авторы принимают во внимание уровень читателя и апеллируют к интуиции; так сказать, объясняют "in layman's terms".
Как минимум нужна Евклидова геометрия, алгебра и начала анализа(на уровне матшколы), матлогика и опыт в решении сложных задач.
Ну я говорил про 99%, а 99% работают в энтерпрйзе или в вебе. Там не нужно ничего кроме арифметики, это факт.
Ну и просто прикольных задач, для которых не нужны сильно знания выше 1-2 курса техновуза
Верно ли, что любое бесконечное множество A можно разбить на два непересекающихся множества B и C так, что |A| = |B| = |C|?

мимо-пропустил 2 (из 2х) семинара по этой теме
>В учебниках по физике для 1 курса мухосранского пту
Ни в одном учебнике физики не встретишь слова lim.
Просто тупо ни в одном. Нету таких учебников.
Да, верно.
Нет, в физике нет никаких направленностей. Это просто операция, обратная разбиванию тела на бесконечно малые кусочки.
интеграл Лебега определяется не через направленности
За интеграл Лебега с тобой говорить я не буду.
>Нет, в физике нет никаких направленностей.
Нам лично на лекциях вводили интеграла Римана как предел при N->inf И максимальный ранг разбиения -> 0, потому что про направленности не принято говорить на физических факультетах.
Не так много читал по матану литературы, но где видел - о направленностях ни слова не было упомянуто
Ну это довольно современный подход, не спорю, что в приложениях не нужно, но мне лично было неприятно от условия что максимальный ранг разбиения -> 0

ай красава
Нам лично рассказывали, а так среди русских учебников, в начале учебника Хелемского по функану есть небольшая ремарка про направленности
>На физических факультетах не используются пределы.
Я так то с физфака, не поверишь используются.
И почему это я должен не определять "бесконечно малые кусочки"? Какие у них свойства? Типа меньше таких кусочков уже нет? Я, например, считаю, что в жизни объекта с такими свойствами не существует. В математике ты тоже не сможешь определить объект с такими свойствами, чтобы он имел смысл.
> Интеграл - это бесконечная сумма.
Что такое бесконечная сумма? Как мы можем бесконечно складывать числа? Даже если представить, что можем, то откуда мы знаем, что в итоге мы получим конечное число?
> Правила интегрирования даны в таблице. Её нужно просто выучить.
Как там в 50х годах? Для этого давно есть математическое ПО. Оно все сделает лучше и быстрее чем ты.
>>317400
Вот зачем ты пиздишь? Я вообще даже не физик, просто погуглил сейчас какие есть учебники по физике и в первом же учебнике увидел слово "lim". Арнольд: "Математические методы классической механики".
Не, просто ты реально перетолстил. Правда весь спор мы не уточняем о какой физике мы говорим? О теоретической? О матфизической? Или о физике для экспериментаторов?
Интеграл жи есть предел
И че мне твой телескоп-то епта? Нахуя мне твой частный случай? Сформулируй мне определение бесконечной суммы без предела и докажи, например, что
1 + 1/2 + 1/4 + ... = 2.
Да, к слову, как мы можем знать, что в итоге получим конечно число ?
Получили - значит можно, блять.
Та же хуйня что и с лопиталем, если разъебошили и получили ответ, значит можно было
А на кой хуй ? предыдущий мой пост о том, что если получили что-то, значит можно было.
Если получили результат, то нахуй доказывать что его можно получить ?
Т.е. мы получили сумму ряда и после этого должны доказать, что ее можно получить ?
Ничего странного не находишь ?
что тебе не нравится ?
Если ответ был получен, то значит его можно получить и не нужно после получения ответа доказывать что его можно получить, если ты не страдаешь дцп
да хоть с точностью 10^(-100500) вычислил, какая нахуй разница ? Что ты хочешь сейчас услышать ?
Кому ты пиздишь? Может, в курсе "высшая математика" и используются, но в физике никаких пределов тупо нет.
>>317421
Ты пришёл не учить, а учиться. Тебе говорят, что бесконечно малые кусочки есть. Что математики не могут там чего-то определить - проблемы математиков, пусть стараются лучше.
Бесконечная сумма - это когда ты разбил объект на бесконечно малые кусочки, потом как-то вычислил число от каждого кусочка и просуммировал обратно. Это работает по таблице интегралов. Что работает - практика подтверждает. Не будет работать, сделаем новую таблицу.
Учебник Арнольда не известен физикам. Его читают только некоторые упоротые нерды из НМУ.
>>317424
Савельев. Сивухин. Иродов.
Дай мне ссылку на то, как получается этот результат без определения суммы ряда через предел.
Зачем она нужна, эта ваша касательная? Какой смысл с нее?
Вычисли мне сумму ряда
1 + 1/2 + 1/3 + 1/4 + 1/5 + ...
с любой точностью, какая тебе покажется достаточной. Пока не вычислишь, в тред не пиши.
Собственно сумма ряда обратных квадратов, к примеру ( вроде как ) без определения пределов выводится, доволен ?)
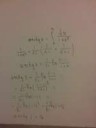
Смотри, я получил ответ, и теперь, если бы я был тобой, т.е долбоебом, я бы говорил, что арктангенс 1 это нуль
Про телескоп этот хз хз
> Это работает по таблице интегралов
Это-то понятно. А нахуя ты нужен, если вместо тебя комп может посчитать интегралы?
Становится жарка
чтобы сказать компу что именно считать, хуле
Стоп, ты же отрицаешь пределы, маня, ты уж определись. Заводить свой комплюктер и вперед вычислять ряд.
Не пизди. В любом нормальном университете про Арнольда не слышали. Предел физикам не нужен нахуй, они не пользуются пределами.
> Собственно сумма ряда обратных квадратов, к примеру ( вроде как ) без определения пределов выводится, доволен ?)
С точки зрения Эйлера, безусловно. Но я не верю.
Я, между прочим, задал намного более простой вопрос
> докажи, что 1 + 1/2 + 1/4 + ... = 2.
и жду ответа.
Арнольд известен только математикам. Для физиков Арнольд бесполезен. Это аутизм, а не физика.
А че такое "расходится" и "сходится"? Давай линк на определение без пределов.
тебя в школе не учили на множители раскладывать многочлены ? ути-пути бедняжка
Ищи ошибку, хуесос
Предельнул тебе ускорение, скорость, т.д. прямо в глотку
Я не отрицаю пределы, я говорю о том, что можно получив ответ, сказать, что его можно получить. Обратного я не утверждаю, равно как и того, что для получения того факта, что ответ получить можно его обязательно найти
Возможно даже N семёна.
да, пардон, тупанул, прогрессия то :D
иди учись раскладывать многочлены, лалка.
Ну или закинь в следующий вброс ошибку поинтереснее
Предположим ты не знаешь ничего о гармоническом ряде, как ты можешь сказать можешь ты вычислить его сумму или нет?
> Я не отрицаю пределы, я говорю о том, что можно получив ответ, сказать, что его можно получить.
Как ты получил ответ-то епта? Тебе конкретный вопрос задали. Ты понимаешь, что ты все, поехавший?
Я учу, что такое гармонический ряд, вывожу его за 2,5 минуты и ебашу.
Интересно, как же в твоем понимании считать значения дзеты от нечетных целых чисел ?) Или побежишь к компуктеру
Я утверждаю, что математика со всем её аутизмом (пределами, множествами, теоремами) для физики нахуй не нужна и не используется в физике никак. В физике своя, нормальная терминология, не опирающаяся на математику.
Ненененене, я жду от тебя правильного разложения, а то мало ли твоих умственных способностей не хватит и на это ?
Возразить по существу на: "Я утверждаю, что Х"? Возражаю: я утверждаю, что математика в физике нужна и используется в физике.
Только чур онлайн-сервисами то не пользоваться, а то ведь не научишься никогда считать ^_^
окей без теоремы Мермина — Вагнера нельзя обосновать существование бозе-конденсации в двумерном пространстве.
Я тебе уже все сказал.
То есть ты признаёшь, что я прав и лимиты в физике не упоминаются. Ты обзываешь меня только потому что тебе печёт от моей правоты. В физике нет лимитов, смирись.
Например, множество целых чисел можно разбить на на два непересекающихся множества четных и нечетных. Как решить эту задачу не прибегая у примерам, а исходя из общей терминологии?
+1
Я вот существование решения х+1 = 2 всегда проверяю экспериментально перекладыванием палочек и загибанием пальчиков, а то вдруг клятая жидоматематика соврёт.
>>317496
>То есть ты признаёшь, что я прав и лимиты в физике не упоминаются.
google: Искажение в собственную пользу. Искажение самовозвеличения. Когнитивные искажения
чую тут запрятанную аксиому выбора.
> Как решить эту задачу не прибегая у примерам, а исходя из общей терминологии?
Ну я не смог решить, когда задался этим вопросом, я просто нагуглил ответ на вопрос.
При чём здесь когнитивные искажения? Просто поставь эксперимент и убедись, что я прав.
Ключевое слово - обосновать.
неприятные вопросы, он игнорирует, это норма
Открыл учебник Спивака http://alpha.math.uga.edu/~shifrin/Spivak_physics.pdf увидел лимит на 38-40 страницах, что дальше делать?
ти што это жи моняфонтазии мотимотикоф , нит леметоф, нит, я скозол
Ну это просто нерусский учебник. Спивак, Арнольд - по фамилиям же видно, что они жиды, их читают только другие жиды из НМУ. А жидовские всякие лимиты нам в Россеюшке не нужны.
>Это не учебник физики. Это учебник геометрии.
Извини пожалуйста, а как отличать учебники физики от учебников геометрии? Я вот не умею
Да долой жидов, только водка только духовность
Когда есть чертежи и нет никакого физического смысла - это учебник геометрии.

>>317534
Пикрелейтед с математической точки зрения есть ахинея. Вы не увидите здесь слова лимит, зато увидите не известный математикам "элементарный путь". Суть бесконечно малую длину, которую свободно можно интегрировать и которая неизвестным для математиков образом равна проекции другой бесконечно малой величины.
Физика = теоретическая физика + экспериментальные подтверждения теорий. То есть учебник по физике - это учебник по теоретической физике с ремарками вида "Сэрр Жан-Поль Ван-Дам проверял эту модель 700 раз экспериментально в году эдак 1542 - вроде работает, поэтому есть смысл в неё верить".

Надо сделать что-то типа вебмрелейтед, только с Пеано, Вербицким, Гротендиком и другими.
Это вопрос в строгости изложения, учебники по анализу для ПТУ тоже примерно так же выглядят.
Все учебники физики выглядят именно так. "Строгость" - это мем аутистов от математики. В физике используется своя собственная математика, не похожая на математику, которую делают математики.
>Все учебники физики выглядят именно так.
Ну не все, вот Арнольда и Спивака в пример приводили. Выглядят так большинство учебников по понятным причинам, - гораздо проще "уловить общую суть" модели, чем вдаваться в тонкие детали.
>В физике используется своя собственная математика, не похожая на математику, которую делают математики.
Да нет, такая же точно математика используется.

...бесконечно порожденные....бесконечно представленные...гомотопическое пространство.....группы....
Смелое заявление, давай проверим. Сколько раз за этот год ты использовал понятие внешнего дифференциала дифференциальной формы? В штуках.
>>317543
В физике есть процесс разбивания физического тела на бесконечно малые. Математически эта операция бессмысленна.
В математике есть множества. В учебниках физики множества не используются никогда.
>гомотопическое пространство
А вот и позёры пришли, нихуя не понимающие в предмете, зато фапающие на Михайлова.
Лимтопетушок, плиз.
>В физике есть процесс разбивания физического тела на бесконечно малые. Математически эта операция бессмысленна.
Приведи пример, я поясню.
>В математике есть множества. В учебниках физики множества не используются никогда.
Они не используются никогда в том же смысле, в котором они не используются в алгебраической топологии, операторных алгебрах, теории чисел, анализе на многообразиях и прочих разделах математики, изучающих довольно богатые структуры. Множества дают основания для математики (одни из возможных!), а для достаточно богатой теории, в принципе, абсолютно не важно на каких основаниях её строить и понимать ли функцию как множество пар или как стрелку в какой-то категории.
>В математике есть множества. В учебниках физики множества не используются никогда.
А так ты тот петух, который тред создавал, помню тебя.
>использовал понятие внешнего дифференциала дифференциальной формы?
Как то надо было потоки векторных полей считать, там это прекрасно пригодилось, ибо, каким-то чудом, все выражалось аналитически. В штуках? Хм ну интергалов 7-8 было.
А так из последнего с чем столкнулся, счет топологических индексов, что напрямую меня закинуло во владения гомотопической топологии
> В учебниках физики множества не используются никогда.
Я утверждаю, что натуральные числа не используются никогда. Используются их записи в различных системах счисления.
Что либо ты не используешь теорему Стокса чаще раза в год, либо ты не считаешь теорему Стокса как-то связанной с дифференциальными формами.
>Например, разбиение заряженного кольца на бесконечно малые бусины с целью посчитать поле.
Ну так не разбивай а говори сразу "возьмём такой-то интеграл", и не пострадает строгость. Проблемы не вижу в упор.
>>317565
Не знаю как тот физик-кун, но я четыре раза прочёл и не смог вникнуть в логику поста.
Если ты считаешь, что можешь "работать в физике" и не использовать теорему Стокса, то у меня для тебя плохие новости.
теоретической*
>Я разбиваю кольцо на бесконечно малые бусины. Эта операция имеет физический смысл. Я не буду от неё отказываться только потому, что аутисты от математики считают её неприемлемой.
Ты какой-то ебанутый. Предположим я маломерный тополог (хотя я не являюсь им). И в учебнике по топологии читаю: "склеим круг по диаметрально противоположным точкам его границы", - захожу на двач и такой "ко-ко-ко, в топологии совершенно другой язык, чем в математике, вот например там есть "склейка пространств", которая в математике смысла не имеет", - и мне совершенно нормальные люди отвечают, - "ну говори не "склеить по противоположным точкам" а "взять фактортопологию по отношению эквивалентности, которое не различает каждую точку границы и диаметрально противоположную точку" ", и я такой - "склейка имеет топологический смысл, я не буду от неё отказываться только потому, что математики-аутисты считают что это не строго", - и господа совершенно справедливо ссут мне в лицо (как я тебе сейчас). Есть интуитивные образы, а есть их строгая формализация и вполне можно существовать мысля интуитивными образами, но при этом, при особой нужде, формализуя их с достаточной строгостью в виде математических конструктов.
у него вся физика теорема стокса, о чем тут говорить, это как сказать, что вся математика это теорема Атьи-Зингера
Ты не предлагаешь синонимов для операции разбиения кольца на бусины. Ты предлагаешь вообще отказаться от этой операции, хотя она очень важна для понимания смысла.
Ну например так: если мы считаем какую-то величину F(C) для кривой С (которая суть некое отображение I:[0..1]->R^3), которая аддитивна и "слабо зависит от шевелений". (Тобишь по сути у нас определён линейный непрерывный функционал на пространстве кривых).
То фразу "разобьём кривую на бесконечно малые участки элементарных путей посчитаем F на каждом участке и затем проинтегрируем" можно заменить на "возьмём кусочно линейную кривую C_eps, отличающуюся от нашей не более чем на eps, посчитаем F(C_eps) а затем возьмём lim(eps->0) F(C_eps)".
Почему?
ну ты должен уметь работать с простыми алгебраическими действиями, а потом уже лезть в общую алгебру

Мда, смеяться или плакать. 1-ый пост
Ну и что что она строго монотонна по x? Почему для меньших/больших значений функции не может быть того же предела?

Почему |f(x) -f(y)| = |x-y-(sinx-siny)| что =
|x-sinx-y+siny|? Это очепятка или так и надо?
Если сделать таки правильно, то можно ли будет уничтожить минус у |siny - sinx| и сделать его = |sinx - siny|. Или из-за модулей это вообще похуй?
И откуда он берет в предпоследнем выражении 2|(x-y)/2| > 2|sin((x-y)/2)*cos((x-y)/2)|? Просто типа по логике, чтобы получить дельта или тут что-то более хитрое?
Какое-то странное решение, трюковое. Я такое не люблю. Я тебе предлагаю так решить:
1) Найди где-нибудь доказательство следующего известного утверждения. Пусть X и Y - метрические пространства, X компактно и f - непрерывная функция из X в Y. Тогда f равномерно непрерывна на X.
2) Докажи, что сумма непрерывных функций непрерывна.
3) x и sin(x) - непрерывные функции, поэтому f(x) = x + sin x тоже непрерывна.
4) Так как R компактно, f(x) равномерно непрерывна
в том то и дело, что надо доказывать монотонность не внутри предела, а самого предела
1. Думаю, там опечатка, должно быть |x-y+(sinx-siny)|
2.
>Откуда он берет в предпоследнем выражении 2|(x-y)/2| > 2|sin((x-y)/2)*cos((x-y)/2)|?
Там <=, а не <.
cos(?)<=1
|sin(x)|<=|x|
Что тут неясного?
>>317639
>трюковое
Решение в лоб, через определение непрерывности же. Ты решаешь, как математик, а это скорее всего задачка не для математиков.
>4) Так как R компактно, f(x) равномерно непрерывна
Как мне помнится, само R некомпактно, а вот его пополнение элементами +inf -inf компактно.
> ешение в лоб, через определение непрерывности же. Ты решаешь, как математик, а это скорее всего задачка не для математиков.
Ну это как-то странно. Зачем вот тебе доказывать, что x + sin x равномерно непрерывна? Если, скажем, тебе понадобится доказать, что 2x + cos(x) или 3x + sin(x) + cos(x) равномерно непрерывны, ты опять будешь через определение равномерной непрерывности и тригонометрические трюки доказывать?
Может быть, автор упражнения думал, что без этого упражнения ты не поймешь определения равномерной непрерывности.
>>317650
> R некомпактно
Да, чет я проебался. Надо подумать еще, как нормально доказать.
Да, там опечатка
И как доказать? В лоб что-то не получается.
Если f и g равномерно непрерывны, то f+g - равномерно непрерывная. Любая периодическая непрерывная функция равномерно непрерывная, так что всё очевидно тащемта.
поэтому
lim n^1975/(n^x - (n-1)^x) = lim n^1975/(x n^(x-1) + O(n^(x-2)) = lim 1/(x n ^(x-1976) + O(n^(x-1977) )
и поэтому предел существует только при x=1976
Численно
можно руками оценить один из корней


Спасибо.
А пикрелейтед случайно не знаешь как решить? Я вывел формулу для a_n и собираюсь тупо в лоб найти предел. a_n = p_n / p_{n-1}. Формула для p_n на пикрелейтед 2. Но по идее должно как-то изи решаться.

Ебать, я представляю, как еще лет 20 назад люди вручную считали эту хуйню
Кто 20 лет назад считал это вручную, тот и до сих пор считает вручную, лол.
Сокращать тебя не учили, я погляжу!?
Это не самая тривиальная на свете идея, на самом деле. К тому же ты не показал, что предел существует.
И хули? Я за 10 секунд написал прогу и увидел, что предел 1 + sqrt(2). Надо вообще-то еще доказать, что предел существует.
Чётные члены образуют возрастающую последовательность, а ненчётные - убывающую.
Что-то нашел вроде
http://www.uni.bsu.by/arrangements/inputinmath/themes/theme3.pdf
Но я, кстати, даже не знал, что это называется "цепная дробь" пока >>317715 не сказал.
Да что там искать, посмотри, что чётные и нечётные члены образуют монотонные ограниченные последовательности поэтому имеют предел, и понятно какой.
ты мне это ёпта в глаза скажи
Посмотрел видосы. Этот Yair Minsky такой няшный.
https://www.youtube.com/watch?v=VnyGuiGpYf8
Нет. Если ты будешь доказывать равномерную непрерывность синуса через определение, тебе придется использовать тот же самый тригонометрический трюк

Ладно там когда 1/x, может и видно разницу. А так хуй пймешь, почему пидор вольфрам выдает разные значения. Как с этим бороться?
Итак, матаны, раз я задал треду направление на пределы, поясните не немножко.
Производная это формула касательной прямой к графику функции!? Смысл касательной? Что она показывает, зачем нужна?
Интеграл это формула графика соответствующего данной касательной?! Почему тогда интеграл называют сумму бесконечно малых? Поясните мне что и где я не понял.
Ты вместо того чтобы все действия над функцией сперва проделать сразу туда предельное значение ебашишь.
Надо же раскрывать скобки, отнимать все что можно и сокращать. А то у тебя предел при икс стремящимся к нулю (1+2)^x/ будет равно нулю, а не какому то там бесконечному ряду.
А хули ты, вместо того чтобы посмотреть любой нормальный учебник, задаёшь тупые вопросы на харкаче, а?
Я читаю вот зельдовича. Это нормальный учебник? Или тебе просто западло написать пару предложений?
в душе не ебу, кто этот твой зельдович-хуёвич, но везде в курсах матана 1-го семестра производная определяется как предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю, если таковой, конечно, существует.
А теперь скажи мне, нахуя я это написал?
Это
>производная определяется как предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю
я и так знал.
Но у зельдовича пишеться что по формуле производной какой то функции можно провести касательную в произвольно выбранной точке графика функции.
Смотри короче:
Есть интеграл Римана: предел сумм Римана, сумма Римана это такая вещь: разбиваешь отрезок (не обязательно на равные отрезки), определяешь диаметр разбиения (наибольшая разница между соседними точками), потом на каждом отрезке отмечаешь точку "x1, x2, x3,... ", теперь мы сделали отмеченное разбиение, теперь нужно составить сумму Римана: f(x1)(x2-x1)+f(x2)(x3-x2)+...
Это и есть "собственный интеграл Римана", есть всякие требования для того, чтобы можно было его определить (функция должна быть ограничена и проч.), но писать подробно не стану.
Есть такое понятие "неопределенный интеграл" от f(x) - это просто класс (множество) функций F(x), таких, что F'(x)=f(x)
Есть теорема Нюьтона-Лейбница: она как раз говорит, что если взять неопределенный интеграл от f(x), получить F(x), то:
"F(x2)-F(x1)= интегралу Римана от функции f(x) на отрезке [x1,x2]"
Забыл написать, что интеграл Римана определяется, если устремить диаметр разбиения к нулю для этого тоже куча теорем доказывается
>Ну тоесть, интеграл, сферический в вакууме, это сумма бесконечно малых.
Да иди ты нахуй с такими "АБСРАКЦИЯМИ". Тебе дали чёткое определение, нет блядь, нужно его переиначить, используя какую-то даже самому себе непонятную терминологию. Залил тебе в рот сумму бесконечно малых.
Ньютон-Лейбниц только для непрерывных выполняется.
>>317988
Вообще производную можно тремя способами воспринимать:
1) (физический смысл) Если у нас у частицы, двигающейся по прямой в момент времени t координата x(t), то x'(t) - это скорость частицы в момент времени t. Ещё один образ - если у нас частица движется под действием некоторых сил, то если в момент времени t все эти силы "отключить", то частица полетит равномерно и прямолинейно с некоторой скоростью - эта "элементарная" скорость - и есть производная.
2) (геометрический смысл) f'(x0) это тангенс угла наклона касательной к графику функции f(x) в точке x0
3) (аппроксимационный смысл) Производная в точке f'(x0) - это линейное отображение, наилучшим образом приближающее f в точке x0. Например, если нужно посчитать sqrt(4+0.00001) то есть смысл в первом приближении считать sqrt(4)+sqrt'(4) 0.00001 = 2 + 1/8 0.00001
>>317996
А я вот убеждён, что мотивировки и интуитивные образы как минимум столь же важны, сколь и важны чёткие определения.
На ровном месте лопнул. Проверь давление в шинах прежде чем ехать дальше.
>>317997
Значит по физическому смыслу это значение функции в точной точке, по геометрическому тангенс треугольника с гипотенузой проходящей касательно к выбранному графику это что получается, значение будет путешествовать по кривой тангенса?, а аппроксимационный вычисление значений функций в произвольной точке?
>Значит по физическому смыслу это значение функции в точной точке, по геометрическому тангенс треугольника с гипотенузой проходящей касательно к выбранному графику это что получается, значение будет путешествовать по кривой тангенса?, а аппроксимационный вычисление значений функций в произвольной точке?
Я не понял ни одного вопроса, но скорее всего ты меня понял неправильно. Попробуй читануть начало параграфа V.1 в "Математическом анализе" Зорича, там всё по мотивировкам расписано лучше, чем у меня.
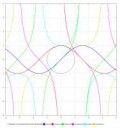
Ну вот ты говоришь что геометрически это значение тангенса угла наклона касательной к графику в некой точке.
Тангенс имеет свой личный график, который тянется из минус бесконечности в плюс бесконечность как макаронина. Значит значение производной функции будет равняться значению тангенса для этого угла в этой точке!?
Если коротко, производная это тангенс угла касательной функции в некой точке.
Это значение будет равно обычному тангенсу треугольника, проходящему в этой точке.
>Значит значение производной функции будет равняться значению тангенса для этого угла в этой точке!?
Да
Хорошо. Интеграл тогда что такое, кроме определения разница между двумя значениями одной функции.
Предлгаешь взять множество "тян" и рассчитать вероятность измены?
>>318014
>для этого угла в этой точке!?
для какого этого? есть у тебя парабола. к каждой точке параболы можно провести касательную. касательная это ПРЯМАЯ. эта ПРЯМАЯ пересекает где то ось x. пересекает под каким то углом. так вот ПРОИЗВОДНАЯ это тангес именно этого угла. и никакого отношения к графику тангенсов не имеет вообще. наглядный пример это синус, у которого производная косинус.
интеграл неопределенный это первообразная функции. все остальное уже дальше. а первообразная, это функция, для которой данная функция является производной. в примере синуса и косинуса, если косинус это производная от синуса, то синус это неопределенный интеграл от косинуса
если ехать дальше, возьмем и зададимся задачей отыскать площадь криволинейной трапеции, у которой нижнее основание это ось х от 1 до 2, левый бок это перпендикуляр из х=1 до параболы, правый бок это перпендикуляр из х=2 до параболы. парабола это у=х^2
как искать площадь фигур с границами из отрезков прямых(треугольнык, прямоугольник и т.п.) мы знаем, поэтому тут мы сделаем так - разобьем эту криволинейную параболу на много много маааленьких отрезков. настолько маленьких, что кусочек параболы в каждом из этих отрезков будет как прямой, и тогда у нас будет куча мелких прямоугольников. вычисление определенного интеграла по сути это суммирование этих маленьких прямоугольников. по другому интегрирование. а еще есть дифференциирование. это как раз процесс разбиения на эти маленькие прямоугольнички любой криволинейной поеботы. в процессе дифференциирования в свою очередь всплывает производная. т.к операции дифференциирования и интегрирования взаимообратны. как сложение и вычитание, умножение и деление, возведение в степень и вычисление корня.
я просто обьяснение растянул на два поста)))
че то типа корня квадратного из суммы квадратов разностей. типа ((32,42 - -1)^2+(-7,42-7)^2)^0,5
на бумаге отметь точки, потом линейкой отмерь, офк тебе линейки не хватит чтобы от одного конца до другого довести, поэтому придется несколько раз линейку прикладывать последовательно.
Чтобы длину узнать, сложишь то, что получится на линейке, погрешность: нужно знать погрешность самой линейки, и по формуле пикрелейтед считать "Погрешность косвенных воспроизводимых измерений", т.е если делал N измерений и получил X1, X2, X3... длины, то длина линейки это просто сумма, а для погрешности: (dX1^2+dX2^2+...)^(1/2)
Ну это не точный метод измерения, линейка все-таки не такая уж и точная, да и есть неучтенные факторы (можно линейку криво приложить)
Есть человечный способ >>318038
>>318024
>>318025
Мне щас свой конспект лень искать чтобы писать все подробно, поэтому напишу примерно.
Короче решали интеграл какой то, я решил так как ты написал, тобишь получил конкретное число. Когда я это показал лектору он сказал что все хуйня и не правильно и у меня должен был получиться интервал значений от 6.8 до 7.2. Что это такое было?
А как в методичке? Напиши тогда решение методички.
По моему тут вполне подходит уравнение прямой про штаны.
я чет даже не представляю что это даже могло быть. матан у меня был лет 10 назад. какие то общие вещи помню, а чтоб интеграл вываливался в интервал значений.... лучше покажи пример, обьясню что это было. если конечно сам пойму
может под интегралом параметр какой то был? и он был под синусом например. синус может принимать значения от -1 до 1. вот мол меняя параметр будет скачек от 6.8 до 7.2 . конечно скорее всего это не твой случай, показывай пример
Что-то туплю долго над вопросами: является ли семейство множеств множеством? Почему?
Это аксиоматическое понятие, потому и туплю. Верно ли, что если множество А является элементом множества В, то множество В есть семейство множеств? Алсо, верно ли, что булеан множества есть семейство множеств?
Пусть M - множество множеств.
Пусть I - множество.
Каждая сюръективная функция f:I->M называется семейством множеств над M.
Мы говорим, что множество x является элементом семейства f, если x является элементом множества M. Мы говорим, что множество x входит в семейство f с индексом i, если f(i) = x. Множество может входить в семейство более чем с одним индексом. В таком случае мы говорим, что у нас есть несколько экземпляров множества x.
Семейство множеств является множеством, так как любая функция является множеством. В теории множеств ZFC любой объект является множеством.
>Верно ли, что если множество А является элементом множества В, то множество В есть семейство множеств?
Нет.
>Алсо, верно ли, что булеан множества есть семейство множеств?
Нет.
Главное свойство семейства - наличие множества индексов. Нет индексов - нет и семейства.
Тем не менее, с помощью одного технического трюка каждое множество можно рассматривать как семейство.
А именно, пусть M - множество.
В качестве I возьмём само M.
Рассмотрим тождественную функцию f: M->M такую, что f(x) = x.
Тогда f будет семейством над M. Мы будем иногда называть такие семейства самоиндексированными, потому что каждый элемент является своим же индексом.
А как ты определяешь семейство множеств? Так же как >>318490? Я, например, определяю просто, по-деревенски:
https://ru.wikipedia.org/wiki/%D0%A1%D0%B5%D0%BC%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%BE_(%D0%B7%D0%BD%D0%B0%D1%87%D0%B5%D0%BD%D0%B8%D1%8F)
>>318446
>Верно ли, что если множество А является элементом множества В, то множество В есть семейство множеств?
нет, не верно. контр пример такое множество B в котором только один элемент это множество, а все остальные тупо элементы. в кодинге это очень удобно. чисто допустим что массив это множество. каждый элемент массива это какое то число. множество множеств это массив массивов получится. такой массив, у которого элементы сами по себе массивы. так вот любой массив массивов(множество множеств) будет массивом(множеством). но из этого совершенно не следует что каждый элемент мимокрокового массива массивов будет массивом. может быть так что только один элемент будет массивом, остальные тупо числами. или любая другая комбинация. например один элемент массива массивов(множества В) может быть сам массивом массивов, другой просто числом, третий массивом и так далее. и, как видишь, из того что один из элементов массива массивов будет сам массивом совсем не следует что все остальные элементы множества В будут именно такими же
дополню, верно только то, что в множестве Б можно выделить подмножества. каким угодно способом. в том числе и пустые подмножества. и обмазываться ими до бесконечности)
Кроме того, что ты, очевидно, не знаком с аксиоматической теорией множеств, на которую указывал анон выше, ты еще и говоря о кодинге подразумеваешь недоязыки с динамической типизацией.
>а все остальные тупо элементы
"тупо элемент" - это тоже множество. В теории множеств нет ничего кроме множеств.
Ты сказал хуйню. "Тупо элементов", не являющихся множествами, нет.
То есть вопрос "является ли A семейством множеств" имеет не больще смысла чем "каким шрифтом нужно писать A - обычным или каллиграфическим?"
> "каким шрифтом нужно писать A - обычным или готическим?"
Пофиксил. В целом верно, но ты так говоришь как будто это для кого-то неочевидно.
Нет. Аксиома конструктивности не входит в ZFC.
Собственно, это вопрос о том, как читать книги. Как при чтении математической литературы понять, какие результаты должно быть легко получить, а какие представляют собой сжатый и вылизанный результат долгой работы? Если, допустим, теорема названа чьей-то фамилией, то я особо долго не пытаюсь сам ее доказать, потому что скорее всего она содержит хитрый трюк (или несколько) и для доказательства нужно проявить смекалочку. А если теорема не названа ничьей фамилией, то я долго пытаюсь сам ее доказать и если не удается, то у меня возникает ощущение, что я плохо разбираюсь в материале.
>если какие-то результаты не названы чьей-то фамилией, ...
... то математики просто забыли, кто первым их получил.
Конкретно полярное разложение придумал Кронекер, по-моему.
> Одно и то же множество может входить в семейство несколько раз.
что за хуйня? Почему на этого петуха ещё не нассали.
Видимо, он думает, что
> Пусть M - множество множеств.
> Пусть I - множество.
> Каждая сюръективная функция f:I->M называется семейством множеств над M.
Первый раз такое вижу.
> Алсо, верно ли, что булеан множества есть семейство множеств?
> Нет.
Короче, он поехавший просто.
Все знают, что такое indexed family. Но при чем тут это? Очевидно, тот анон спрашивал про
https://en.wikipedia.org/wiki/Family_of_sets
Он не мог быть настолько тупым. Очевидно, что он спрашивал про индексированное семейство.
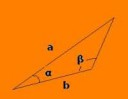
Дано стороны a, b и угол бетта. Найти угол альфа. См. картинку
Теорема синусов.
a / sin(/beta) = b / sin(/gamma), где /gamma = Pi - /alpha - /beta
Дальше разберешься.
Тогда
Pi - /alpha - /beta = arcsin(b sin(/beta) : a)
/alpha = -Pi + /beta +arcsin(b sin(/beta) : a)
Так?

Ты хочешь сказать, что выражения нет, потому что /gamma может быть и тупым?
Если угол /beta - тупой, то решение одно, если острый, то может возникнуть ситуация, когда треугольник определен неоднозначно, т.е. 2 варианта.
(попробуй построить его по данным двум сторонам и несмежному углу)
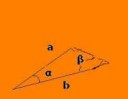
>Может возникнуть ситуация, когда треугольник определен неоднозначно
На картинке эта ситуация?

Да. Причем на этом рисунке ты можешь еще построить один треугольник со сторонами a, b и углом /beta.
Пикрелейтед.
>>318516
>>318490
Я тот анон, что спрашивал про семейство множеств.
Суть вопроса в том, чтобы для себя разделять множества, в которые:
1. В качестве элементов входят собственно элементы множеств (множества в обычном смысле).
2. В качестве элементов входят множества (семейства множеств).
Речь шла не об индексированных семействах, а о явлении множества, которое может в качестве элемента содержать в себе другое множество. Таким образом данное множество будет семейством.
Не существует примитивов. Нет каких-то элементов, которые не являлись бы множествами. Любой объект - это множество. Число 5 - множество. Функция - множество. Отношение - множество.
Это уже все отвлеченные выдумки. Аксиоматически определяется множество и элемент, который может содержаться в нем или не содержаться. Явно не указывается. что сам элемент обязан быть множеством. Конкретно по вышеописанным критериям можно привести два примера множеств:
1. A={a,b} , a, b Є R
2. 2^A
В таком случае первое будет множеством, которое не содержит в себе множеств в качестве элементов, а второе — семейством множеств, которое содержит в себе множества в качестве элементов.
Спасибо, помог.
На общеизвестный факт?
>Таким образом, в канонических аксиоматических теориях множеств ZF и ZFC урэлементы не упоминаются вовсе.
https://ru.wikipedia.org/wiki/Урэлемент
> Нет каких-то элементов, которые не являлись бы множествами.
Ты еще скажи, что теорию категорий не используешь.
Где это сказано? Из приведенной тобой выше ссылки следует, что элементы могут быть множествами, но не обязаны ими быть. Более того, ты упускаешь тот факт, что во многих случаях понятия, определяемые как множества (те же функции, например) могут рассматриваться как элементы без учета их природы как множеств, лишь потому, что в рассматриваемом случае нас не волнует, что функция это некое подмножество прямого произведения, нас волнует сама функция. Такая замена вполне нормальна.

Это сказано в любом нормальном учебнике.
Любой объект, который может быть элементом множества, но не является множеством, является урэлементом по определению урэлемента. Урэлементов нет.
Абстрактное множество A={a}. Множество А определено списком его элементов, из которого не следует, что a это множество. Потому в данном случае говорить, что А это семейство нет смысла.
Не спрашивай хуйню. Случайное число, блядь, у него.
Случайность перпендикулярна трансцендентности.


Я думаю, случайное число будет трансцендентным с вероятностью 1. Это должно быть как-то связно с тем, что множество алгебраических чисел счетно.
Бумп вопросу, времени нет, спаситипамагити плз.
Нормальный учебник теории множеств - это учебник, в котором явно сформулированы аксиомы теории множеств на языке явно сформулированной формальной теории. Школьные учебники нормальными не являются.
Да, нетрансцендентных чисел счётное множество.
Тыкаем пальцем в числовую ось, вероятность попасть в алгебраическое число равна нулю в силу их счетности и вложенности в континуальное множество.

В аксиоматике ZFC ничего не говорится о том, что элемент есть множество. Алсо Куликов. Л "Алгебра и теория чисел" составлен для преподавания математики в университетах. Там детально освещаются все необходимые для главных в этом учебнике разделы. Потому наивно думать, что такой важный момент как тождество элемента множеству был бы упущен, если бы это действительно было так.
Но я не спорю с тобой о том, что один учебник лучше другого. Было бы прекрасно, если бы ты назвал ряд учебников, которые ты считаешь нормальным.и Всегда приятно читать "нормальную" литературу.
Высказанное мной. Да, любой объект в ZF (и с выбором, и без) является множеством. Я не утверждаю при этом, что множество a - это то же самое, что множество {a}, - отнюдь, это два разных множества. Я утверждаю, что любой объект является множеством в ZF (а в чуть менее популярной NBG любой объект является классом), объектов другой природы нет, урэлементов нет. Причины этого расписаны в книжке Френкеля (который F в ZF) по второй ссылке.
Как ты заебал. Естественно, не любой объект - множество. Я в основаниях не разбираюсь, но если использовать теорию категорий, то точно есть объекты, не являющиеся множествами.
> Там детально освещаются все необходимые для главных в этом учебнике разделы. Потому наивно думать, что такой важный момент как тождество элемента множеству был бы упущен, если бы это действительно было так.
Во-первых, схуяли он важный? Твой вопрос - абсолютно бесполезная философская хуйня, что-то на уровне определения N.
Во-вторых, объекты не берутся из ниоткуда, они конструируются с помощью определенных правил. Конструируя из множеств, ты не получишь какую-то ебалу, ты всегда получишь множество.
Во второй части поста я имел в виду тот случай, когда мы не используем теорию категорий.
Только ясность появилась, так ты пришел и просрал все. Может, все дело в том, что
>в основаниях не разбираюсь
?
>Во-первых, схуяли он важный?
Важен он потому, что необходимо понимать природу объектов, с которыми работаешь. В противном случае и производные считать можно, не думая над тем, что это такое вообще.
>Во-вторых, объекты не берутся из ниоткуда
А это и не утверждалось.
Традиционная теория категорий (в формулировке Маклейна, например) строится на аксиоматике NBG. В этой аксиоматике каждый объект является классом. Классы бывают двух типов: собственные и несобственные. Собственные классы не могут быть элементами классов. Несобственные классы могут быть элементами других классов. Несобственные классы иногда называют множествами. Собственные классы - это очень большие классы. Настолько большие, что не могут из-за этого являться множествами. Например, класс всех множеств - собственный.
Тем не менее, элементов, которые сами не являлись бы множествами, нет и в NBG.
> Важен он потому, что необходимо понимать природу объектов, с которыми работаешь. В противном случае и производные считать можно, не думая над тем, что это такое вообще.
Ну давай тогда определяй, что такое "буква". Ты же с математическими текстами работаешь, а они из букв состоят.
Не мне определять, что такое "буква".
Но ведь понятие "атомарных" объектов разве не имеет смысла? Понятно, что если любой элемент является множеством, то получим бесконечную последовательность множеств, каждое из которых есть подмножеством исходного множества (элемент которого рассматривался). Для простоты и ясности можно заменить бесконечную последовательность множеств элементом и говорить о его принадлежности какому-нибудь множеству, которое интересует нас в конкретной ситуации. Такой подход имеет смысл?
>Но ведь понятие "атомарных" объектов разве не имеет смысла?
Ну оно вполне осмыслено, но не слишком полезно. Ровно по этой причине от него отказались в мэйнстримной аксиоматической теории множеств.
Что ты содержательно хотел сказать дальше в посте я не понял.
В каком плане не очень полезно? Если нас интересует конкретное множество, от которого мы будем отталкиваться, то что "не полезного" в том, чтобы рассматривать его как совокупность атомарных понятий, если природа самих элементов в данном случае нас не интересует? Пример: теория чисел рассматривает числа, как атомарные понятия, так как теорию чисел не интересует то, что такое число, интерес представляют их свойства. В то же время, для математического анализа такого атомарного представления о числах недостаточно, потому вводятся другие понятия, определяющие числа. Так вот: делает ли такой подход к числам в теории чисел саму теорию "не полезной"? Если нет, то в чем она выражается, эта "не полезность"?
В классических теориях множеств атомарных объектов нет.
Есть аксиома: если x и y - множества, то существует множество {x,y}.
Из неё вытекает простая теорема: если x - множество, то существует множество {x}.
Пустое множество ∅ существует по ещё одной аксиоме.
Поэтому существуют множества
∅
{∅}
{∅, {∅}}
{∅, {∅}, {∅, {∅}}}
и так далее. Можно объявить, что ∅ есть число 0, {∅} есть число 1, {∅, {∅}} есть число 2, {∅, {∅}, {∅, {∅}}} есть число 3 и так далее (каждое последующее число есть множество всех предшествующих чисел). Действуя таким способом, мы можем доказать существование любого конечного количества натуральных чисел, десяти или миллиона. Бесконечное же множество всех натуральных чисел существует по аксиоме бесконечности.
Таким образом, имея лишь одно пустое множество, с помощью аксиом ZF мы можем доказать существование бесконечного количества разных объектов. Нам не требуется вводить какие-то логические атомы, ведь пустое множество и аксиомы ZF дают нам достаточно объектов, чтобы занумеровать все молекулы во вселенной.
>>318765
Числа - это тоже множества. Как вводить натуральные числа, я показал. Все остальные числа легко строятся как теоретико-множественные конструкции из натуральных чисел.
Спасибо, разъяснил довольно детально.
То есть натуральное число есть семейство пустых множеств?
> Если нас интересует конкретное множество, от которого мы будем отталкиваться, то что "не полезного" в том, чтобы рассматривать его как совокупность атомарных понятий, если природа самих элементов в данном случае нас не интересует
В контексте формализации на основе теории множеств ставился вопрос о принципиальной возможно формализовать те или иные области. С такой постановкой нет никакого вреда в том, чтобы числа были не праэлементами и с формальной точки зрения сами имели какие-то элементы. Для "концептуально-правильной" формализации теория множеств в любом случае (хоть с праэлемнтами, хоть без них) подходит слабо. Не зря же люди в наши времена разрабатывают теории типов.
> теории типов
да мне бы теорию множеств осилить. К тому же, всегда интересовала структурная иерархия разделов математики. Вдаваться в дебри каждого раздела не так доставляет.
Почему пустых? Множество, элементом которого является пустое множество, не есть пустое множество.
∅ - пустое множество. {∅} - уже не пустое множество.
Да, неправильно выразился. По сути же, в таких семействах нет ничего, кроме пустого множества и множеств, содержащих пустое множество. Именно это я и имел в виду.
Тогда да. Иными словами, числом 0 объявляется пустое множество, числом 1 - {0}, числом 2 - {0,1}, числом 3 - {0,1,2}, числом 4 - {0,1,2,3} и так далее.
В таком случае, верно ли для конечных множеств, что мощность множеств отождествляется с самим множеством?
Зависит от того, как определены кардинальные числа. Это уже тонкости. В принципе, конечные кардиналы без проблем можно отождествить с конечными ординалами, а конечные ординалы - с натуральными числами. В таком случае мощность множества 4 будет самим этим множеством 4, например.
В какой аксиоме ZFC искать объяснение того, что какое-то множество может называться "слишком большим" и не подходить по этой причине под определение множества?
>Иными словами, мы хотим ввести понятие ординала как класса изоморфизмов вполне упорядоченных множеств, то есть класса эквивалентности, основанного на отношении «изоморфности с сохранением порядка». При таком подходе, однако, существует одна техническая сложность: определенный таким образом класс эквивалентности оказывается слишком большим, чтобы подходить под определением множества с точки зрения стандартной формализации теории множеств по Цермело-Френкелю.
это следует не напрямую из аксиом ZFC, а от противного. Мол, если бы существовал такое множество всех множеств A, то для него A = 2^A, что противоречило бы известной теореме.
Ситуация красивее. В ZFC просто нет аксиом, благодаря которым большие множества могут существовать. ZFC не предоставляет инструментов, с помощью которых можно доказать существование класса эквивалентности вполне упорядоченных множеств. ZFC не запрещает существование больших множеств явно, но и не предоставляет какой-либо возможности доказать их существование.
Запрещает. Можно доказать, что не существует множества всех ординалов, множества всех одноэлементных множеств, множества всех множеств и т.п.
Класс эквивалентности вполне упорядоченных множеств был бы множеством всех множеств в понимании наивной теории множеств? Разве нельзя было бы построить множество, большее чем класс эквивалентности таких множеств, тем самым показывая, что это не самое большое множество?
Множество, строго большее данного всегда можно построить - это и есть 2^A. Правда там в одном месте нужна пидорская аксиома выбора.
на том, что 2^A вложено в A (так как что угодно вложено в A, даже небо, даже аллах)
Ну то же парадокс Рассела, не? Исходя из теоремы Кантора, можно сказать, что множества всех множеств не существует, но разве из этого следует, что какое-либо явно заданное семейство (типа класса эквивалентности вполне упорядоченных множеств) не существует? Оно же не содержит в себе все множества, а лишь те, которые эквивалентны вполне упорядоченным.
ну с классом эквивалентности вполне упорядоченных множеств может и не всё так просто, сходу сложно говорить, если по чесноку
Но ващет, по моему мнению, ко всей этой хери нужно относиться несколько проще. Если у тебя есть какое-то множество, то изъёбывайся с ним как хочешь, с чистой совестью бери его подмножество по любому предикату. Но если никакого начального множества нет, то и не пытайся выебонить такими понятиями как множество всех множеств, его подмножествами и пр. Бог против этого.
Доказывается не несуществование, а существование. На основе какой аксиомы ты считаешь, что существует такой класс?
Я говорю про обычную повседневную практику. Если существование некоторого объекта не доказано, то его стараются не использовать. Пожалуй, правильнее назвать это чем-то вроде презумпции. Теория считается законченной только тогда, когда вопрос о существовании её основных объектов однозначно решён. Доказать несуществование какого-то множества можно, да.
Предполагаю, что существует бесконечное множество, элементами которого есть вполне упорядоченные множества, эквивалентные между собой. Но так как сама аксиома предполагает, что каждый последующий элемент должен включать в себя предыдущий, то такое ее использование неверно и из этого следует, что такое множество построить нельзя?
всё не так. Аксиома бесконечности говорит о существовании не абстрактного бесконечного множества, а вполне конкретного СЧЁТНОГО. Фактически, она говорит, что существует натуральный ряд. Всё.
Аксиома бесконечности утверждает, что существует по крайней мере одно непустое множество M такое, что если x∈M, то x∪{x}∈M. Множество M называется индуктивным.
>>318817
На самом деле натуральный ряд может оказаться собственным подмножеством M. Никто ведь не говорит, что ℕ∉M. Натуральные числа получаются из M по схеме выделения подмножеств.
Точнее говоря, аксиома бесконечности утверждает существование по крайней мере одного трансфинитного предельного ординала, но вовсе не говорит, что этим ординалом является именно ω.
но ты и сам сказал, что, пользуясь другими аксиомами, можно выделить и неё натуральный ряд, так что всё однохуйственно
Поэтому она называется аксиомой бесконечности, а не просто счётности.
Просто педантизм, сорри.
>>318818
То есть, вы хотите сказать, что я не могу построить произвольно большое множество потому, что аксиоматика ZFC позволяет мне работать лишь с определенным типом множеств индуктивным посредством вводимых операций для множества? Иными словами, множества всех множеств не получится, потому что данные средства мне этого не обеспечат?
нет, множества всех множеств построить не получится не потому что их существование не следует из ZFC, а потому что его существование бы противоречило ZFC.
А как определить, какое множество является слишком большим, а потому ему нет места в рамках ZFC?
Точнее, аксиоматика ZFC позволяет тебе доказать существование лишь тех множеств, которые ты сможешь построить из индуктивного множества средствами, предоставленными ZFC. Это очень мощные средства. Из индуктивного множества, существующего по аксиоме, можно получить бесконечные неиндуктивные множества, и даже бесконечную иерархию бесконечностей. Однако не для всякого множества его существование может быть доказано или опровергнуто средствами ZFC. Изучением множеств, лежащих за пределами ZFC, занимается малопопулярная и практически бесполезная в наши дни наука о large cardinals.
>>318825
Для произвольного множества нет алгоритма, позволяющего просто и быстро решить, может ли существование оного множества быть доказано на основе ZFC или же войти в противоречие с этими аксиомами. Проще говоря - никак.
Спасибо, доступно объяснил.

Охуеть. Просто охуеть. Обращаюсь сюда за помощью: Короче, пилю значит код, и натыкаюсь на необходимость решить одно маленькое, сука, уравнение для того, чтобы физический движок скомпилировать.
y"=2y^3
Ну, блять, думаю изич нахуй. Это же ссаное ДУ из моей говношарашки, которую сто лет в обед окончил.
А хуй там был. Бернулли не работает. Ни однородным, ни линейным ни неоднородным не является нахуй. Вольфрам тоже нахуй спотыкается, даже общее решение не может найти. Рот ебал короче.
Я даже не знаю. Может математикач знает, каким методом эту хуету решать нужно? Мне само решение не нужно, просто скажите каким методом, ну или прочитать где?
>>318837
http://eqworld.ipmnet.ru/en/solutions/ode/ode0301.pdf
Например. Сдаётся, хуёво оно решается.
А эти квадратные скобки в -1/2 степени - это просто единица деленная на квадратный корень?
Да.

1. Откуда брать n и k в задаче пикрелейтед.
2. При разложении в ряд Тейлора в конце ставят о-малое от х в какой-то степени. Как понять в какой - типа по порядку просто? Вот например ln(1+x) = x - x^2/2 + o(x^3?) или как?
n же число интервалов разбиения, не ?
Если да - то либо юзеру доверяй, либо программно в завис-ти от abs(b-a)
если правильно понял, то подумай, когда погрешности складываются и что значит K раз по эпсилон
ну да можно найти без гемора только x=x(y)
Зачем? Если он даже не желает уточнить, алгебраические или физические поля он имеет в виду, то нет смысла ему отвечать вообще.
Твоя правда.
Друзья, я совсем не математик. Не знал, что меня можно понять двояко. Читая статью про группы Галуа на вики, увидел словосочетание "теория полей". Судя по всему, это и правда поля классов.
>>319073
Для ньюфага не слишком сложно? А то я сейчас только советские учебники по группам для школьников читаю.
Ой, сажа приклеилась.
Нет, это классический учебник общей алгебры для ньюфагов. Если всё-таки покажется сложным, можешь сначала прочитать трёхтомник Кострикина или, опционально, томик Винберга, но в них, предупреждаю, избыточно много информации.
После ван дер Вардена имеет смысл прочитать книжку Ленга.
Спасибо большое.
>>318830
Я тебе его решил: y(x) = _C2JacobiSN((Ix+_C1)*_C2, I)

(1+a1 x) (1+a2 x) ... (1+an x)
Где-то была формула, не знаю где искать.
да,это ссаное ду второго порядка. http://www.mathprofi.ru/differencialnye_uravnenija_vtorogo_poryadka.html читай, там всё расжевано
Феллер пойдёт?
он имеет в виду, что уравнение не содержит икса и есть способы его решить, однако это не отменяет того факта, что эта срань решается только в эллиптических функциях.
Думаю он не это имеет в виду, а просто не сильно разбирается в уравнениях, а про эллиптические функции и вовсе не слышал.
У тебя нет общего члена чтобы можно было что-то записать в виде сигма-нотации. Наверное ты путаешь с чем-то другим.
то что ты долбоеб сомнений нет, но так, ради профилактики собственного долбоебизма, реши сей диффур с помощью ссылки, которую ты скинул.
долбоеб ты. сперва делаем подстановку z=y^3. тогда z''=6y'', получили уравнение z''/6=2z или блять z'' -12z=0. дальше паста из примера 1 из ссылки. составим и решим характеристическое уравнение:
u^2-12=0;U=+-(12)^1/2, Всё, что осталось сделать – записать ответ, руководствуясь формулой : формулу возьмешь из примера 1. там и x и y. а то что вы обмудки до подстановки не додумались это ваши сугубо обмудочные проблемы.
провался на саентаче лiл
тем более сам решай
ок. моя вина, дифуры видел 10 лет назад. но сука один хуй вот вам http://www.mathprofi.ru/odnorodnye_diffury_pervogo_poryadka.html на том же блять ресурсе с описанием корректной замены.
суки, я даже сам заморочился, вам правило нашел. бляди. Случай 2. Уравнение вида y′′=f(y)
Здесь правая часть уравнения зависит только от переменной y. Вводим новую функцию p(y), полагая y′=p(y). Тогда можно записать:
y′′=ddx(y′)=dpdx=dpdydydx=dpdyp,
и уравнение принимает вид:
dpdyp=f(y).
Решая его, находим функцию p(y). Затем находим решение уравнения y′=p(y), то есть функцию y(x).
http://www.math24.ru/%D0%BF%D0%BE%D0%BD%D0%B8%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5-%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BA%D0%B0.html
открою страшную тайну, таким образом ты получишь x=x(y) в виде эллиптического интеграла который потом надо обращать. К чему я всё это, если не знаешь, не лезь.
причем здесь это вообще? какая то демагогия, вместо решения задачи. демагогия и хамство
ты влез со своей ссаной ссылкой не разобравшись вообще в чем суть дела, т.е ты поступил, как говноед.

> обоссали как нерадивого десятикласника, за то что не умеет продифференцировать y в кубе как сложную функцию
> кококо я вас затралил коко вы все картофаны дефуры нинужны вообще!! пок пок пок кукарек
Кажется классического вербиторебёнка поймал, скорее сачок.
x (1- x^2/2 + x^4/4 ....)
пусть y = 1 - x^2/2 + x^4/4 - ...
y' = (-x + x^3 - x^5+....) = -x (1 - x^2 + x^4 - ...) = -x/(1+x^2)
y = интеграл(х/(1+x^2)) с такой константой, чтобы y(0) = 1
Ну а зачем нужно деление с остатком? Где вот оно может пригодиться нематематику? Делимость, конечно, можно понять и без этих понятий, но изучать надо именно в таком порядке.
Ты считаешь, что человек, который профессионально занимается криптографией, может не знать, что такое кольцо?
А как в терминах евклидовых колец формулируется квадратичный закон взаимности Гаусса и вообще весь этот сюжет с квадратичными вычетами (символы Лежандра, символы Якоби)? А вообще тот, кто считает, что общий случай нужно учить предварительно не ознакомившись с частными и не прочувствовав их специфику - интеллектуальный мастурбатор и мразь. Ненавижу тебя. В рот ебал.
двачую, нахую вэртел
В википедии посмотри, например.
> А как в терминах евклидовых колец формулируется квадратичный закон взаимности Гаусса и вообще весь этот сюжет с квадратичными вычетами (символы Лежандра, символы Якоби)?
А нахуй формулировать этот картофан? Там уже все изучено.
> А вообще тот, кто считает, что общий случай нужно учить предварительно не ознакомившись с частными и не прочувствовав их специфику - интеллектуальный мастурбатор и мразь.
Зависит от того, какие частные случаи. Скорее всего, то, что ты имеешь в виду под частными случаями, - ебучий картофан и никакого интереса из себя не предствляет. В частности, деление целых чисел с остатком не представляет интереса.
для тебя, но не для первоклассника. все зависит от погруженности человека в тему. а предыдущий оратор говорил о каких либо вообще общих знаний, что надо мол от частного к общему переходить в любом случае. а не с высоты матана издеваться над школьниками
ньютон наверное потому и умер, что остановился на пол пути, так и не дойдя до релятивизма. а то сейчас бы с нами жил. мне например эти кольца сами по себе нахер не сдались, хоть и тех вузик кончал. ни там не проходили ни по работе ну совсем кольца не нужны. конечно я узнавал на вике что это, но какой то особой необходимости в них погружатся не имею
>мне например эти кольца сами по себе нахер не сдались
Что поделать, большинство людей не являются учёными.
Уважаемые посетители данного ресурса, возник неоднозначный вопрос. Какой раздел высшей алгебры самый высокий?
Раздел так и называется, высшая математика. Любую книгу с таким названием возьми - охуеешь от происходящего. Доступно только элите.
тут дрочат на zfc
Высшая теория топосов.
Кракур?
Маняврирования уровня "обоссай".

Истину говоришь, посему пускай эту ёбаную математику учёным и преподают
Ну так в универ не иди, в путяжке тебя максимум производными помучают.
в пятом классе проходят дроби как правило и прочую простоту, если человек не способен усвоить даже этого, то он уже по определению дегенерат.
Пролёт. ВУЗ я бросил. Математику любил. На олимпиадки всякие там ездил по городам России, с переменным успехом выступал. Вообще вузовский уровень преподавания математики крайне низкий, и сами олимпиады были не сложными
А чё удивляться. Среди математиков много шизофреников. Шизофрения - королева математики. Шиза у меня обострилась. Хиккую щас да колёса пью
Не чувак, ты не прав. Шизофрения - это типо наследственное. Так что занимаясь матаном ты не станешь шизофреником, если только не имеешь предрасположенности (ну как Нэш, да?). Вообще от матана можно, конечно, конкретно ебнуться, но ебнуться можно от любой науки, если переусердствовать
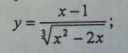
1. Это ведь не нечетная и не четная функция?
2. У производной нет нулей, лол. И вторая производная еще хуже.
Что с этим делать, как исследовать?
смотрю на задания одногруппников и слезы наворачиваются не совсем конечно, но все же
Это копия, сохраненная 16 января 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.