Это копия, сохраненная 30 января 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

Предыдущий: >>317156 (OP)
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
Голдблатт.
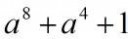
Подскажите, как пикрелейтед на множители разложить? С a^4+a^2+1 справляюсь, а с этим нет.
Есть годная литература по подобным элементарным преобразованиям?
Положи a2 = t и разложи как t4+t2+1.
Апофеоз ультрафинитизма.
a^4=t.
t^2 + t + 1 = 0.
t^2+t+1+t-t=(t+1)^2 - t=t^2(1+1/t)^2 -t=t(t(1+1\t)^2 - 1)=t( (t(1+1\t)+1)(t(1+1\t) -1) ).
и третья тоже
Спасибо! Наконец-то понял. Я вообще ноль в подобных преобразованиях - знал, что суть разложения завязана на корнях, но реализовать не получалось.
Нет (если строго к ней подходить).
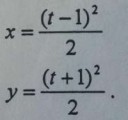
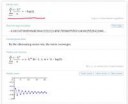
С помощью ключевого слова "solve".
http://www.wolframalpha.com/input/?i=solve+x%3D%28t-1%29%5E2%2F2%2C+y%3D%28t%2B1%29%5E2%2F2
Latex (Texmaker)
У одногруппника предел который k - бесконечность, а b равен 0. Ну и он пишет, что ассимптота y = 2x. А у меня k = 1, а b бесконечность. По идее должны оба предела быть конечными? Но у него вроде препод проверила и норм всё. Моча какая-та.
реально моча, потому что если b бесконечность то асимптота твоя начинается на бесконечности, дурачёк чтоле?


Общее практическое правило:
Если существуют два конечных предела Формулы нахождения наклонной асимптоты, то прямая является наклонной асимптотой графика функции при . Если хотя бы один из перечисленных пределов бесконечен, то наклонная асимптота отсутствует.
http://www.mathprofi.ru/asimptoty_grafika_funkcii.html
если всюду на интервале f''(x)>0 , то функция имеет вогнутость на этом интервале, если f''(x)<0, то функция имеет выпуклость.
Епты, я знаю определение вогнусти и выпуклости. Чому с гграфиком не сходится?
А че там?
Вообще я сам ебанулся, когда вольфрам построил это дерьмо. То есть всё более-менне правильно?
А как от руки это строить?
матан же простой как три рубля, че там с этими правилами исследования функции непонятного? ты кинул какой то кусок, там даже толком второй производной не видно, не то что функции. и график хуй пойми чего. чего с чем не сходится? вообще охуеть)
ебать, да фольфрамом это дерьмо строить сложнее чем от руки. с помощью этих правил анализа функции не думая вычисляешь особые точки, и соединяешь их, учитывая выпклость и вогнутость. а вольфрамом он это говно просто вычислил

>>320220
Оой, ну там в общем параметрическая функция. Я типа смотрел на x(t), потом на y(t), потом нашел производную y'(x) = y'(t)/x'(t), и там в общем тоже говно непонятное, типа функция всегда возрасатет. Потом вторая производная (на пике есть), там тоже говно, что всегда вогнутая. Как это вообще строить-то, если точек нет?
почему нет? они есть. просто заданы по другому. но есть. так и строить. просто это её так через жопу задали. и в том своде правил для анализа функций была помню специально оговорка о том как поступать когда функия задана параметрически
просто кучу недомемасов типа 0.999...=1, -1/12, е в степени и пи = -1 напихали и смешно тип
> просто это её так через жопу задали. и в том своде правил для анализа функций была помню специально оговорка о том как поступать когда функия задана параметрически
proigral s kartfanov
в каком смысле?как быть когда ты например измеряешь силу тока, в зависимости от напряжения для какого то нелинейного элемента. и тут оказывается что напряжение от времени твое меняется по синусу, а ток все время растет, но очень медленно. в таком случае ты и напряжение и ток будешь задавать через время. а не друг через друга. тот самый случай задания функции параметрически. с одной стороны что х что у в каждый момент времени определены, а значит есть точки. с другой х от у выразить в данном случае геморно, поэтому выразили вот так. но список правил для анализа функции запилили и для этого случая. там были какие то простенькие оговорки, мол производные надо таким то образом брать. чтоб получить инфу о поведении функции на каждом из интервалов, между волшебными точками. ты сам эти правила прочитаешь или пошлешь меня нахуй за пруфами? хотя я и не пойду никуда - не нравится мое обьяснение - можешь не верить. один хер сессию с таким подходом не сдашь
Чет вспомнил, как в школе этой хуйней занимался. Нахуя эти правила построения графиков нужны? Берешь и по точкам строишь в любом мат пакете.
эти правила придумали задолго то того как можно было это построить по точкам. более того эти правила это как бэ суть подхода по исследованию какой угодно функции в каких угодно точках. и в процессе их запила вывели много чего полезного. например то же правило лопиталя, без которого делить бескончно малые и бесконечно большие величины трудно. а еще яснее все станет на 2 м курсе вузика
1. Обязательно ли в пространстве координатные оси всех измерений должны быть ортогональны?
2. Почему сначала выполняются операция умножения, а уже затем сложения? Это откуда-то следует? Или просто аксиома?
не обязательно. вот цилиндрическая например https://ru.wikipedia.org/wiki/%D0%A6%D0%B8%D0%BB%D0%B8%D0%BD%D0%B4%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BA%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82 . там вместо одной оси вообще угол. зачем они нужны, эти изъебские системы координат? некоторое говно, например электромагнитные поля и волны бывает проще считать в таких вот изъебских системах. там куча всяких коэффициентов уходит. про второй вопрос вообще нихера не понял. умножение это сокращенная запись сложения. это как спрашивать почему перед ночью бывает день - это откуда то следует?
предвосхищая кукарекание, что ортогональность тут все таки выполняется, на так называемый общий случай - криволинейные системы координат https://ru.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D0%B2%D0%BE%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BA%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82 там тензорным языком обьясняется всё.
почему бы тензорным же языком не объяснить и в других ск ? Ты знаком с понятием "тензор", друг мой ?
знаком. только не пойму к чему этот вопрос? сейчас будет "кудах тах тах, врёти"? простым языком я обьяснил. при желании вскукарекнуть что простым языком не описаны какие то нюансы я дал более полное формальное обьяснение. оно через тензоры. этот твой вопрос это попытка чего? сказать мне что я не в курсе про тензоры и поэтому все то обьяснение, что я привел полное говно? расстрою - дела обстоят именно так. по крайней мере так считает научное сообщество, и переходить на личности (знаком ли тензор лично мне) тут немного глупо. если говорить о лично моих знаниях, умении доносить мысль и так далее - я дипломированный инженер связи. по крайней мере те, перед кем я защищал свой диплом сочли, что я достоин звания инженера связи. в том числе и в вопросе математики. и да, именно из-за случаев, когда применение косоебаных систем отсчета оправдано я как бэ в курсе что такие системы есть и их широко применяют.
> почему бы тензорным же языком не объяснить и в других ск ?
а почему бы в задаче когда два поезда едут друг навстречу другу не считать их скорости друг относительно друга не по галилею а по лоренцу? потому что 1) это излишне загромаздит решение задачи переменными, которые будут в данном случае бесконечно малы и их можно не учитывать 2) тому кто спрашивает как решать задачу с двумя паровозами даже вредно начинать втирать про лоренца - только сильнее запутается. всем же в школе математику начинают преподавать далеко не с интегралов. тут так же
но вот когда мы захотим понять, а с фига ли собственно, а не "посчитать на калькуляторе 9*9" таки придется. Не считаешь так ?
Почему сразу не сказать, мол, скушай теорию, хорошо пережевав и сглотнув, а не вдыхай сладостный аромат доказанного, не готовив его сам ?
я не пойму вопроса - чувак спросил. судя по тому как спросил, сам он не в курсе. ответить ему - иди учись сука, тогда поймешь? возможно он и так учится, и дальше узнает это всё сам. а сейчас хочет одним глазком глянуть. вот поглядел. а может и не учится, а так чисто праздный интерес. и опять же, почему бы его не удовлетворить - узнал немного нового да и хер забил - тогда и подводить всю теоретическую базу бессмыслено, будет как бисер перед свиньями. но в любом случае по мне так лучше обьяснить человеку хоть как то, чем просто посылать его нахуй, говоря азаза школота иди нахуй. если же парень захочет очень глубоко погрузится во все эти коши с гауссами, он всегда сможет ознакомится с конкретными изданиями. не вижу ничего плохого в том, чтобы обьяснять что кирпич красный потому, что все остальные длины волн поглащаются его атомами. а не посылать чувака учить квантмех. или даже общую физику. это просто излишне.
Спасибо, анон.
А на счет второго пункта, мне интересно почему, например, в выражении 2+2*2 ответ 6, а не 8. На уровне банальной повседневной логики я это понимаю, но мне интересно есть ли у этого правила порядка выполнения действий строгая математическая формулировка.
> это как считать 9*9 на калькуляторе и спрашивать - зачем нужна таблица умножения?
А она и не нужна. Ну, может кондуктору нужна, или продавцу. А математику зачем уметь умножать числа больше 5?
Ну так, сдачу посчитать, например. В современных социально-экономических реалиях, между прочим, вещь очень полезная.
Сдачу не на всех чеках пишут. А бабки на рынках чеков вообще не выдают.

Можно простым языком как так или простой пример где так же делают?


Мочизуки смотрит на вас как на театр Ходжа

Еще было бы неплохо, если поясните как это считать.
Спасибо.
>А математику зачем уметь умножать числа больше 5?
спроси у математика знакомого, он обьяснит доходчивее
бамп
Я математик. Последний раз два числа умножал в прошлом году, когда помогал анону с домашкой.
> Почему сначала выполняются операция умножения, а уже затем сложения
просто потому что так договорились
а, я сперва не понял. это здравый смысл чтоле. ну типа допустим что это не так, и можно делать любые действия. 2+33. 33 это сокрашенная запись 3+3+3. если ты сперва сложишь 2+3 то получишь 5*3. а это будет уже 3+3+3+3+3. но это ведь херня. ну тоесть про очередность выполнения действий это не то что аксиома, просто скажем так правило, позволяющее не задумываться каждый раз о том что умножение это сложение, не расписывать всё гавно, а быстренько посчитать. ну типа как формулы сокрашенного умножения - если их знаешь то быстрее решишь какой нить пример. не зная их ты их всегда можешь вывести, а зная даж задумываться об этом не надо, можно думать о задаче в целом например
в первом случае у тебя успех 2 из 6 комбинаций для одного кубика. не оговорено кстате - достаточно чтоб на хотя бы одном выпал или на всех? во втором случае 3 из 6 для одного кубика. 1)оговори на скольких кубиках должна выпасть удача 2) посчитай чесло этих комбинаций.
>>320544
сижу на форуме где задают вопросы.
посылаю нахуй тех кто их задает.
ощущаю свою никчемность.
Сидит в вербитятнике, дрочит на аниму, постит Мочидзуку, известное дело. Это же математик уровня sci.
> 2+33. 33 это сокрашенная запись 3+3+3. если ты сперва сложишь 2+3 то получишь 5*3. а это будет уже 3+3+3+3+3.
Ты правда считаешь, что это объяснение? А почему тогда 2 + sqrt(3) x sqrt(2) не равно (2 + sqrt(3)) x sqrt(2)?
>>320391
У каждой операции есть приоритет. При вычислении значения выражения операции выполняются в порядке убывания приоритета. Умножение имеет более высокий приоритет чем сложение.
> 1. Обязательно ли в пространстве координатные оси всех измерений должны быть ортогональны?
Что ты имеешь в виду под координатными осями? Если, например, взять линейное пространство и координатными осями называть вектора базиса, то они могут быть неортогональны.
>Ты правда считаешь, что это объяснение?
да, а ты его наверное не понял нихуя)
>А почему тогда 2 + sqrt(3) x sqrt(2) не равно (2 + sqrt(3)) x sqrt(2)?
именно по моему обьяснению
Да легко.
в каком классе, дружок? распиши мне до последней цифры диагональ квадрата со стороной 1 см. а в след году ты будешь проходить логарифмы с такой херней в основании. а если даже её осилишь, то поступишь в вузик и там, если опять же будешь хорошо учится, тебе расскажут про комплексные числа, дифференциальные уравнения и много другого в этом чудесном мире математики. твоя пошлая иррациональность слишком школьная. и вот когда тебя будут ебать всей этой херней ты поймешь наконец, что нет блять никаких "приоритетов операций" ослина. есть четкое определение операций и чисел. какая то аксиоматика. и на ней строятся теоремы и прочая хуйня. теоремы и прочая хуйня выводятся из аксиом. в аксиомах нету про приоритет умножения. есть что умножение==сокрашенная запись сложения. а теперь иди порешай квадратные уравнения и успокойся
> распиши мне до последней цифры диагональ квадрата со стороной 1 см
Это невозможно.
> умножение==сокрашенная запись сложения
Это означает, что sqrt(3) x sqrt(2) можно записать через сложение. Запиши.
почему невозможно? можно же написать 2^1/2? эта запись расписывает до любого приближения. вот и запись sqrt(3) x sqrt(2) расписывает для любого. конечно можно это представить и в виде ряда какого нить, но лень даже думать об этом
>sqrt(3) x sqrt(2)
даже еще смешнее - это ваше деление, которое тут "неявно" представлено, тоже ведь через сложение определяется, так что можно записать и через сложение тупо, но реально лень искать определение корня через ряды
> почему невозможно?
Потому что sqrt(2) не имеет "последней" цифры.
> вот и запись sqrt(3) x sqrt(2) расписывает для любого
Меня не интересует приближение. Меня интересует точный ответ.

Схоронил пасту
Я даже не знаю, предложить тебе дальше позориться или дать ссылку на определение умножения.
>Меня не интересует приближение. Меня интересует точный ответ.
совсем не знаком с мат анализом, правда?
>бесконечно точное приблежение==точный ответ, ибо 0,(9)==1 и так далее и на то похожее. эх, мне бы твои годы, всё еще в перде
я тебе сам её дам
Умноже́ние — одно из четырёх основных арифметических действий, бинарная математическая операция сложения указанного количества одинаковых слагаемых.
>сложения указанного количества одинаковых слагаемых.
>сложения
https://ru.wikipedia.org/wiki/%D0%A3%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5
не понимаешь - гугли определение базиса и переход к новому базису. сразу всё поймешь
охуеть... пасибо
А ничего, что это определение только для натуральных чисел?
>>320621
>бесконечно точное приблежение==точный ответ, ибо 0,(9)==1 и так далее и на то похожее. эх, мне бы твои годы, всё еще в перде
Я не вижу никаких нормальных объяснений. Только махания руками про какие-то бесконечно точные приближения вместо нормального определения умножения.
>>320622
> объясните как делать
Тупо по определению. Список векторов образует базис, если они вектора линейно независимы и длина списка равна размерности пространства. То есть тебе надо показать, что a1, a2, a3 линейно независимы.
блядь, анон, ты как знал какую книжку я найду. всё прям как по оглавлению.
>Я не вижу никаких нормальных объяснений.
>Умноже́ние — одно из четырёх основных арифметических действий, бинарная математическая операция сложения указанного количества одинаковых слагаемых.
>А ничего, что это определение только для натуральных чисел?
вся беседа велась в их области. ты вводил иррациональные числа, для того чтобы вставить свой пример? ты и вводи определение умножения для них, да так чтобы оно сочеталось с умножением для натуральных чисел.или прооверяй\убеждайся что мое определение на них распространяется, мне похую
> >А ничего, что это определение только для натуральных чисел?
> вся беседа велась в их области.
> 33 это сокрашенная запись 3+3+3
> А почему тогда 2 + sqrt(3) x sqrt(2) не равно (2 + sqrt(3)) x sqrt(2)?
> именно по моему обьяснению
> умножение==сокрашенная запись сложения
> ты и вводи определение умножения для них, да так чтобы оно сочеталось с умножением для натуральных чисел
https://proofwiki.org/wiki/Definition:Multiplication/Real_Numbers
Пустил тугую струю урины в лицо картофану.
Очевидно, через рациональные числа. Но какая разница, если ты не можешь объяснить, почему a + b x c не равно (a + b) x c для вещественных a, b и c?
конечно же по "приоритету операций". просто пиздец. лучший файлообменник нахуй
Ты серьезно считаешь, что "приоритет операций" не является общепринятым термином?
я серьезно считаю что он является следствием определения умножения через сложение
че ты будешь делать раньше - брать корень, синус, тангенс, экспоненту или логарифм?
Я не могу найти таблицу. А выводить, как ты понимаешь, не умею.
> я серьезно считаю что он является следствием определения умножения через сложение
Если считаешь так, то сформулируй определение умножения вещественных чисел и докажи.
>>320645
Зависит от выражения. Зачастую выражения написаны так, что компьютер не смог бы их проинтерпретировать однозначно. Например, log log n. Но человек может догадаться, что на самом деле имеется в виду.
>Зависит от выражения.
потому что определения этих операций не связаны друг с другом. были бы связаны, то был бы приоритет.
а сложение связано с умножением. и поэтому там есть приоритет.
>Если считаешь так, то сформулируй определение умножения вещественных чисел и докажи.
нет, это ты себе докажи. я себе это уже когда то доказал, а сейчас уже забыл. конечно за пол часа я нагуглю всю эту хуйню по новой, но я и так уже на примере синуса да логарифма показал отсутствие приоритета у не связанных функций. а дальше уже ты, если хочешь то докажи себе это, разберись так сказать в вопросе. или если не хочешь не разбирайся, останемся каждый при своем. не хочешь не верь мне. я ж уже говорил - мне похую
Для того, чтобы найти производную от частного двух функций необходимо, из произведения производной делимого, умноженной на функцию делителя, вычесть произведение производной делителя, умноженной на функцию делимого, и все это разделить на функцию делителя возведенную в квадрат. (u/v)' = (u'v-v'u)/v^2;
https://sites.google.com/a/nstuedu.com/perv/proizvodnye
в обоих примерах двоякий контекст, формально без скобок такую запись можно прочитать и просчитать и так и сяк. а вот с 2+3 умножить на 3 двоякого толкования нет. строго сперва умножь, потом уже складывай. с синусом если ты не оговоришь скобками не ясно что делать сперва синус брать или в квадрат возводить. так же и со второй формой записи. точнее конечно для человека может и ясно, но формально это говно. типа скобок надо добавить. а в случае умножения не надо, в том чесле и потому, что это просто сокрашенная запись суммы в скобках
твоя проблема в том, что ты рассматриваешь sin и ln как функцию, а + и умножить нет. хотя что одна херь переводит изначальное поле значений в какое то другое(область значений и опрежделений синуса), так и + с умножить делают по сути те же операции -переводят одно поле чисел в другое. такая же функция. и тут ты видишь зависимость между функцией сложить и функцией умножить. а между другими аналогичными нет. значит одна == другая с другим коэффициентом. хотя че то меня понесло не туда. я из аксиомы(умножение==сокращенная запись сложения) тебе эту же аксиому доказываю. это высший идиотизм. за сим откланяюсь
И что? Там не выходит рекуррентность. Там выходит потом произведение двух функций. Там производная энного порядка не выражается.
прости - рекуррентность незавезли,самому придется придумать
Всегда если ты пишешь fx^k имеется в виду f(x^k), а не f в степени k или композиция f k раз. Потому что ^ имеет больший приоритет чем f.
Предположим, ты определил бинарную операцию #: R x R -> R и хочешь, чтобы выражение a # b x c означало a # (b x c). Более того, в общем случае у тебя есть E1 # E2, где E1 и E2 - произвольные выражения, и ты хочешь, чтоб порядок выполнения операций как-то зависел от E1 и E2. Как ты опишешь этот порядок не определяя приоритет операции #? Ты, конечно, можешь вместо этого всегда ставить скобки или вообще не использовать инфиксную форму и писать #(E1, E2), но это довольно хуево будет читаться.
Но у меня к тебе есть просьба. Анон, накидай годных книг по вариационному исчислению, не страшны ни английский язык (ни даже французский, лол), ни высокая сложность книги. Желательно чего-нибудь поновее.
Допустим, натуральные числа со сложением у нас есть.
Умножение определяется как результат нескольких операций сложения.
Целые числа определяются как класс эквивалентности упорядоченных пар (a,b) натуральных чисел. Идея в том, что всякое целое число z может быть представлено в виде разности a-b, поэтому его можно отождествить с этой разностью; пары (3;5) и (7;9) эквивалентны. Таким образом, все действия в кольце целых чисел сводятся к действиям над натуральными числами.
Поле рациональных чисел определяется как поле частных целых чисел. Поэтому действия над рациональными числами сводятся к действиям над целыми и потому над натуральными числами.
Поле вещественных чисел определяется как пополнение поля рациональных чисел. Все действия над вещественными числами сводятся к действиям над последовательностями рациональных чисел и потому к действиям над натуральными числами. Хотя из-за непрерывности сложение даже двух вещественных чисел может потребовать бесконечного количества действий над натуральными числами.
Извлечение корня из вещественного числа может быть определено с помощью последовательностей.
Любую числовую операцию можно свести просто к некоторому количеству сложений натуральных чисел, возможно бесконечному.
>>320644
Нет, приоритет операций является просто договорённостью. Свидетельством этого служит лёгкость, с которой можно ввести альтернативный приоритет. Пример альтернативного - приоритет, в котором действия выполняются в том порядке, в котором идут знаки. Например, в альтернативном приоритете 2+2×2 = 8. Приоритет является просто соглашением по расстановке скобок, о чём писал ещё Клини.
Чтоб ебать твою мамку.
ньюфаг в треде. На сегодняшний день уже придумали логическую концепцию, которая способна обойти парадокс Рассела?
Да. Парадокс Рассела возможен только в наивной теории множеств. В аксиоматической невозможен.
Угу, как же.
Спасибо, выглядит интересно. Но, хотя я и не смотрел всё, там по-моему про сами алгоритмы ничего не сказано, а приведены инструкции для GAPа.

Наверное нелепо просить в sci, но попрошу помощи. Нужно успеть сделать 3 задания до пятницы для зачета. Я бы с удовольствием сам посидел за этими заданиями, но совершенно нет времени, сегодня нужно готовиться к ангему, завтра вернусь домой только в 10. Буду очень благодарен хотя бы за основной путь решения.
Да я сам уже охуел.
И вообще я не виноват, что у вас тут довольно тихо и я один воду мучу. Мне вообще желательно сдать эту хуйню завтра, тогда перестану вас доебывать.
ну слава перуну, я думал, что я совсем тупой
первые две хуй знает как решить, третья похожа на теорему ролля (ну или лагранжа, все они там одинаковы по сути)
> третья похожа на теорему ролля (ну или лагранжа, все они там одинаковы по сути)
Как раз это самое изи, а вот с первыми двумя хотелось бы, чтобы анон помог.
вторая тоже изи, потому что если брать m = (p+q)^2 / 2, n = (p-q)^2 / 2, то из того выражения получаем любое рациональное число. Дальше сам.
бля, проебался, на 2 делить не надо, иначе не натуральные числа будут, конечно же
первая задача тащемта похожа на подставу, потому что у функции sin x есть неподвижная точка, которая находится как раз на (0,pi)
Хорошо. Большое спасибо тебе.
смотря что ты вкладываешь в понятие "тыкнуть рандомное число"
То есть нужна какая-то вероятностная мера на R. Часто она абсолютно непрерывна относительно меры Лебега, и в этом случае вероятность попасть в транцендентное число равна нулю.
Легко придумать такую вероятностную меру, для которой будет не ноль. Такие дела.
Как можно представить соотношение между независимыми петлями? Какая фундаментальная группа у сферы с n ручками?
ох уж эти картофанские проблемы
В любом учебнике по матанализу посмотри.
Обычно когда ты пишешь отображение чего-то куда-то ты рисуешь буковки и стрелочки от одной буковки к другой. Теория категорий это наука о таких диаграммах из буковок и стрелочек.
А что там научного, поясни, а? Там этих стрелочек может быть бесконечное число например?
Ну не настолько для не математика. Чем она от теории групп отличается, например?
Аноны, как вы все знаете, скоро новый год, поэтому во всех офисах готовятся его отмечать. Некоторые нанимают тамаду, некоторые просто сидят и бухают, а некоторые, такие как наш офис, ищут в интернете всякие конкурсы и быдлоразвлекухи самостоятельно. Так вот один из таких конкурсов состоит в следующем: каждый член коллектива покупает небольшой подарок, заворачивает его в мешок (или кладет в коробочку) и скидывает в общую кучу. Потом, на празднике жизни, каждый по очереди тащит из мешка подарок (неизвестно чей). Сюрприз типа.
Конкурс, конечно, интересный, но вот незадача: а вдруг кому-нибудь попадется подарок, который он сам скинул? Неинтересно получается. Я задался вопросом: какова вероятность того, что каждый получит несвой подарок и все останутся счастливы? Хорошая задача по терверу, ящитаю.
Задача: вывести формулу (рекуррентную или аналитическую - не важно), которая бы позволила рассчитать вероятность удачного исхода, т.е. исхода, при котором никто не получит свой же подарок. Все подарки считать разными.
Помогите решить, аноны. Третий день голову ломаю.
Пусть A_n - множество комплексных z таких, что z является корнем многочлена степени n с рациональными коэффициентами. Каждое z из A_n однозначно определяется коэффициентами многочлена и номером корня (от 1 до n). Поэтому |A_n| <= |Z^n x {1, ..., n}|, то есть A_n не более чем счетно.
Множество алгебраических чисел - это объединение всех A_n для n от 1 до бесконечности. Так как объединение счетного количества не более чем счетных множеств счетно (я верю в аксиому выбора), A счетно.
Это классическая задача. Ответ: сумма (-1)^(k+1)/(k!), k от 1 до n и это стремится к e^-1.
Только это я наоборот нашел вероятность того, что кому-то попадется свой подарок. Этот ряд, кстати, сходится очень быстро. При n = 10 сумма ряда отличается от e не более чем на 10^-7.
Верно.
>Так как объединение счетного количества не более чем счетных множеств счетно (я верю в аксиому выбора)
а где тут аксиома выбора-то?

Все таки e^-1 это вероятность того, что никто не получит свой. В общем, вероятность того, что кто-нибудь получит свой подарок - это количество перестановок, в которых какая-нибудь цифра переходит сама в себя, поделить на количество всех перестановок. Количество таких перестановок можно найти по формуле включения-исключения и получится пикрелейтед.
а чем занимаешься-то? И выхлоп есть какой?
вздернись лiл
Я тож ниоч, потому что каждый день всё больше понимаю насколько я плохо на самом деле знаю математику, насколько я отстаю от топчиков, задрачивавших курсы нму ещё со старших классов школы и от осознания того, что я никогда их уже не догоню.
интересно - множество действительных чисел несчетно. а алгебраических счетно. а алгебраические это расширение множества действительных на комплексную ось. сказать тебе где ты обосрался?
>Каждое z из A_n однозначно определяется коэффициентами многочлена и номером корня (от 1 до n).
контр пример - чесло 1. чесло 1 принадлежит к множеству z? по твоему доказательству следует что чесло 1 однозначно определяется коэффициентами многочлена и номером корня. многочлен x^n-1=0. как видишь неоднозначно. канает бесконечно много. вот поэтому то ты и доказал полную хуйню
Блядь, усыпите его.

Матаны, неужели вы меня подведете? А раньше всегда помогали и объясняли. Ну помогите тогда хотя бы доказать, что любая коммутативная группа 4 порядка изоморфна группе 4 поворотов (на 90 гралусов каждый) правильного четырехугольника вокруг центра.
>Ну помогите тогда хотя бы доказать, что любая коммутативная группа 4 порядка изоморфна
Это неправда. Та группа которую ты имеешь ввиду это циклическая группа Z_4 (только не четыре поворота по 90 градусов каждый лол, а четыре поворота на 90, 180, 270 и 0 градусов). А среди абелевых групп порядка четыре есть ещё и Z_2 x Z_2.
>только не четыре поворота по 90 градусов каждый лол, а четыре поворота на 90, 180, 270 и 0 градусов
Да! Я просто туповат слегка, не заметил, что хрень написал. Да и задача (у Александрова) формулируется про изоморфизм либо группе поворотов, либо клейновской группе. Это я тоже просохатил.
Поясни про то как это строго доказать, пожалуйста.
>>318830
Прошло с сотку постов срача, взаимных обвинений в ватанстве, хуите про эллипсисы и так далее, но это ДУ так никто нормально и не решил:
>y"=2y^3
y(x) = _C2JacobiSN((ix+_C1)*_C2, i)
Категорией называется ориентированный граф, на рёбрах которого введены ассоциативная операция композиции и отношение равенства, причём в каждой вершине есть одна петля, нейтральная по этой операции. Вершины графа называются объектами, рёбра называются морфизмами (или стрелками).
Теория категорий использует аксиоматику NBG, в которой вдобавок к понятию множества есть понятие собственного класса. Собственный класс - это очень большая совокупность, которая не может являться множеством из-за своей величины. Например, класс всех множеств - это собственный класс. Совокупность всех объектов категории может являться не только множеством, но и собственным классом. Однако если A и B - два объекта категории, то совокупность всех морфизмов из A в B обязана являться множеством.
Любой класс математических объектов может быть смоделирован морфизмами какой-то категории (не объектами, а именно морфизмами). Например, мы можем зафиксировать какое-то поле K и рассмотреть категорию всех матриц над K. Объектами этой категории будут натуральные числа. Морфизмами между объектами m и n будут всевозможные матрицы из m строк и n столбцов. То есть вершинами графа являются натуральные числа; любая матрица размера m на n отождествляется с одним каким-то ребром из m в n. Другие примеры - категория всех множеств (объекты - множества, морфизмы - отображения), категория всех групп (объекты - группы, морфизмы - гомоморфизмы), категория всех топологических пространств (объекты - топологические пространства, морфизмы - топологические отображения), примеров очень много.
Теория категорий полезна в основном как язык.
Это одна из её формулировок, алё.
Точнее, конкретно это - формулировка аксиомы счётного выбора.
чёт ты гонишь маленько. Аксиома выбора говорит о том, что ты из каждого множества алгебраических чисел, являющихся корнями степени n, можешь выбрать по одному корню и снова будет множество.
Ты же используешь то обстоятельство, что объединение счётного числа не более чем счётных множеств не более чем счётно. Хз где тут аксиома выбора, разве что совсем неявно где-то.
> Категорией называется ориентированный граф, на рёбрах которого введены ассоциативная операция композиции и отношение равенства, причём в каждой вершине есть одна петля, нейтральная по этой операции. Вершины графа называются объектами, рёбра называются морфизмами
чето мне такое определение через граф не нравится
во-первых
> на рёбрах которого введены ассоциативная операция композиции
это не совсем бинарная операция, она определена только для ребер с общей вершиной направленных в одну сторону! т.е. fgh ассоциативно тогда когда данная композиция "имеет смысл"
во-вторых
> на рёбрах
тогда это не просто граф а мультиграф (если верить вики)!
между 2 вершинами в обычном ориентированном графе может быть только 1 ребро, у нас же в категорях между объектами может быть много морфизмов! т.е. у нас не просто ориентированный граф а что-то вроде мультиграфа
Это не просто мультиграф, это по большей части всегда граф с бесконечным количеством вершин, причём настолько большим что это даже иногда и не множество, и бесконечным количеством стрелок.


Это ты, уёбок, засрал весь тред своей мелкобуквенной тупостью? Съеби откуда пришел.

Где между ними связь? Ведь производная функции равна тангенсу угла наклона касательной к функции в данной точке. Или я все слишком буквально принял?
И да, как быть с касательной на промежутке от минус одного до одного. Ведь тогда касательная будет секущей.
Правда ли что дроби или неполные числа (1.5, 0.37 и тому подобные) невозможно использовать в бесконечности как обычные числа? Если будет непонятно то я постараюсь объяснить.
Хорошо. Вот представь бесконечность, состоящую из простых чисел, такие как 1,2,3,4 и так далее.
А теперь представь дроби. Сначала 1/1,1/2,1/3, и так далее. Потом тоже самое но с двойкой, то-есть 2/1,2/2,2/3. Но если первое бесконечное то как мы тогда имеем второе? Опять-таки, если непонятно объяснил то приведу другой пример.
Погугли теорему Лагранжа. Подумай какой порядок может иметь элемент в группе из четырёх элементов и рассмотри случаи.
Числа не квантуются. Мы имеем бесконечное количество "кусочков" чисел между еденицей и двойкой. Точнее, мы можем поделить отрывой между еденицей и двоек на бесконечное количество кусочков. Обоснование этого лежит где то в глубинах математики, где отрыв от реальности, гроб гроб кладбище, удвоение объема тела после разрезания его на бесконечные кусочки.
Спасибо за пояснение, а то я родителям уже все мозги запудрил. Я ещё хотел спросить что-то похожее, но думаю не стоит ведь твой ответ подходит и туда.
Бинарная операция не обязана быть вполне определённой. В нормальных учебниках, и даже у Бурбаки, всегда рассматривают частично определённые бинарные операции.
Под графом же в математике, ещё со времён Эйлера и его задачи о мостах, понимается именно "мультиграф". Строгое определение графа есть у Маклейна.
>>321260
Докажем, что объединение счётного семейства счётных множеств {xij} счётно.
Расположим их в виде бесконечной таблицы
x11 x12 x13 ...
x21 x22 x23 ...
x31 x32 x33 ...
...
Затем известным приёмом, "змейкой", расположим их в виде строки:
M = x11 x12 x21 x31 x22 x13 ...
Казалось бы, всё хорошо, получили счётное множество. Но кто сказал, что совокупность M является множеством?
Колмогоров, "Алгебра и начала анализа". Прочитай.
>есть её производная
Производная функции f в точке x - это число. В школьном случае равное тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Производная функция функции f - это функция, которая каждой точке x сопоставляет производную функции f в точке x.
"Производная функции в точке" и "производная функция функции" - два разных понятия.
Я не знал если честно, но я знаю что для решения этой головоломки применяются алгоритмы. Можешь показать какие графы, пожалуйста? Очень хотелось бы посмотреть.
>функция, которая каждой точке x сопоставляет производную функции f в точке x.
Я знаю что сопоставляет через пределы/бесконечно малые. Но где между ними связь? Или только через первородную?
>В школьном случае равное тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Почему тогда график тангенса не совпадает с графиком производной? Ну и
> как быть с касательной на промежутке от минус одного до одного. Ведь тогда касательная будет секущей.
Я читаю зельдовича. Там все и так объясняется, но я увидеть не могу этой связи тангенса с производной на графике. В твоем комогорове это объясняется или сразу же что то уровня пикчи надо делать?
Логические парадоксы.
Ошибка в изначально ложных посылках логики и отсутствия понятий времени/расстояния/т.д.
То-есть если я приведу один из парадоксов своему учителю по математике, то он посмотрит на меня как на идиота? Я думал что он просто совмещает математику где она по сути не нужна (Например Ахиллес и черепаха)
Значит возьми черепаху и попробуй её обогнать. Проведи опыт, сформулируй теорию, объяви о своих результатах и предложи другим проверить твои результаты.
Вообще-то я эти два поста запостил...
Я бы очень рад, но я в математике немножечко туп.
Кубик рубика сам по себе это интересный пример, чтобы использовать теорию групп.
http://www.math.harvard.edu/~jjchen/docs/Group%20Theory%20and%20the%20Rubik%27s%20Cube.pdf
Спасибо за ссылку, анон.

Это мой пост у тебя на скрине. Хуй тебе, а не моя коллекция.

Любишь черезчур абстрактной наукой заниматься? Пятиклассников - то высшим категориям научил уже?
ты просто всё в кучу смешал и поэтому нихера и не понимаешь. давай зайдем с другой стороны, а именно с определения производной через ебучий пердел. производная это же по сути предел отношения разности игрека к разности икса при стремлении разности икса к нулю. что происходит другими словами. есть у тебя график функции y=x^2. найдем для него производную в точке 2. для этого возьмем интервал х1=1.9 х2=2.1. соответственно y1=3.61 y2=4.41, x2-x1=0.2, y2-y1=0.8. а производная будет y2-y1/x2-x1=0.8/0.2 = 4. теперь че мы получили графически - из точек x1 и x2 поднимем перпендикуляры к нашей параболе,а там где они пересекут параболу отбросим перпендикуляры на y. нетрудно заметить что этим мы отсекли какой то небольшой кусочек параболы. не точку, а отрезок, причем криволинейный. а еще мы получили квадратик, у которого стороны будут y2-y1 и х2-x1, а вот этот кусочек параболы будет выступать эдакой кривоватой диагональю. или можно рассмотреть треугольник, у которого гипотинузой будет этот самый криволинейный кусок параболы. но катеты этого треугольника будут y2-y1 и x2-x1. мусье согласен?
теперь в прямоугольном треугольнике, как должно быть известно мусье, тангенс, по определению это отношение противолежашего катета к прилежашему. тоесть y2-y1/x2-x1. вроде всё пока ясно но не до конца. на самом деле, по определению производной x2-x1 должен стремится к нулю, т.е. в идеале мы должны взять такой маленький x2-x1, при котором выделенный кусочек параболы будет уже не кривым а малюсенькой прямой. или точкой. но приближать так можно бесконечно долго. и приближая x2-x1 к нулю мы будем делать этот наш треугольничег бесконечно маааленьким, гипотинузка будет становится прямой и в какоой то момент приближения наша посчитанная производная будет стремится к какому то числу. к какому? по формуле производных к числу 2x. т.е. если в точке 2 то к числу 4. Теперь я надеюсь ты понял какой тангенс считает производная и никакой связи с графиком тангенса она не имеет. про касательную - касательная к параболе в точке 2 будет ведь прямой линией?. при этом, эта прямая линия будет под таким же углом к катету x2-x1 нашего мини треугольника, и вообще, повторять нашу минигипотинузку. так сказать накладыватся на неё. но x2-x1 паралелен оси x, поэтому этот несчастный угол между нашей гипотинузкой и катетом x2-x1 равен углу между касательной и осью x. углы равны? равны и их тангенсы. поэтому и говорят что производная функции в точке равна углу наклона касательной к графику в этой точке. для некоторых функций можно вывести некие функции, которые будут сопоставлять каждой точке графика изначальной функции значение угла касательной в этой точке. например для x^n производной будет n*x^n-1. т.е. используя эту функцию можно не заморачиваясь с пределами найти этот тангенс для каждой точки функции.
ты просто всё в кучу смешал и поэтому нихера и не понимаешь. давай зайдем с другой стороны, а именно с определения производной через ебучий пердел. производная это же по сути предел отношения разности игрека к разности икса при стремлении разности икса к нулю. что происходит другими словами. есть у тебя график функции y=x^2. найдем для него производную в точке 2. для этого возьмем интервал х1=1.9 х2=2.1. соответственно y1=3.61 y2=4.41, x2-x1=0.2, y2-y1=0.8. а производная будет y2-y1/x2-x1=0.8/0.2 = 4. теперь че мы получили графически - из точек x1 и x2 поднимем перпендикуляры к нашей параболе,а там где они пересекут параболу отбросим перпендикуляры на y. нетрудно заметить что этим мы отсекли какой то небольшой кусочек параболы. не точку, а отрезок, причем криволинейный. а еще мы получили квадратик, у которого стороны будут y2-y1 и х2-x1, а вот этот кусочек параболы будет выступать эдакой кривоватой диагональю. или можно рассмотреть треугольник, у которого гипотинузой будет этот самый криволинейный кусок параболы. но катеты этого треугольника будут y2-y1 и x2-x1. мусье согласен?
теперь в прямоугольном треугольнике, как должно быть известно мусье, тангенс, по определению это отношение противолежашего катета к прилежашему. тоесть y2-y1/x2-x1. вроде всё пока ясно но не до конца. на самом деле, по определению производной x2-x1 должен стремится к нулю, т.е. в идеале мы должны взять такой маленький x2-x1, при котором выделенный кусочек параболы будет уже не кривым а малюсенькой прямой. или точкой. но приближать так можно бесконечно долго. и приближая x2-x1 к нулю мы будем делать этот наш треугольничег бесконечно маааленьким, гипотинузка будет становится прямой и в какоой то момент приближения наша посчитанная производная будет стремится к какому то числу. к какому? по формуле производных к числу 2x. т.е. если в точке 2 то к числу 4. Теперь я надеюсь ты понял какой тангенс считает производная и никакой связи с графиком тангенса она не имеет. про касательную - касательная к параболе в точке 2 будет ведь прямой линией?. при этом, эта прямая линия будет под таким же углом к катету x2-x1 нашего мини треугольника, и вообще, повторять нашу минигипотинузку. так сказать накладыватся на неё. но x2-x1 паралелен оси x, поэтому этот несчастный угол между нашей гипотинузкой и катетом x2-x1 равен углу между касательной и осью x. углы равны? равны и их тангенсы. поэтому и говорят что производная функции в точке равна углу наклона касательной к графику в этой точке. для некоторых функций можно вывести некие функции, которые будут сопоставлять каждой точке графика изначальной функции значение угла касательной в этой точке. например для x^n производной будет n*x^n-1. т.е. используя эту функцию можно не заморачиваясь с пределами найти этот тангенс для каждой точки функции.
И эту вебмку я нарезал.

Кстати, твой вопрос сделал меня вспомнить вопросы, над которыми я когда-то думал, но по-молодости ничего не придумал и забыл.
Вброшу, раз тут, раз тухловато в качестве исследовательской задачки:
1) Какие конечные (ну и до кучи, бесконечные)
группы можно реализовать как группы всех симметрий (аффинных преобразований/изометрий) каких-то подмножеств на плоскости (или в пространстве)?
2) Какие условия на множество отвечают тому, что группа его симметрий будет конечной или бесконечной? Например, у диска симметрий бесконечное количество, а у многоугольника конечное, почему? Какие ещё множества с бесконечными симметриями есть?
3) Если мы приближаем диск многоугольниками (ну или вообще, множество другими множествами) какой операции это соответствует на уровне групп симметрий?
Это я и так знал. До этого момента
>но приближать так можно бесконечно долго. и приближая x2-x1 к нулю мы будем делать этот наш треугольничег бесконечно маааленьким, гипотинузка будет становится прямой и в какоой то момент приближения наша посчитанная производная будет стремится к какому то числу. к какому? по формуле производных к числу 2x. т.е. если в точке 2 то к числу 4. Теперь я надеюсь ты понял какой тангенс считает производная и никакой связи с графиком тангенса она не имеет.
Сразу надо было про треугольник написать, я вроде не настолько даун.
ну прости - откуда мне знать насколько ты даун - пытался обьяснить как самому себе в школе. не помню уже насколько я был дауном тогда. но помню что этот вопрос меня ебал так же как и сейчас тебя. и конечно я не помню знал я тогда про треугольник или не знал
1 - первая и вторая группа движений, если сортировать по сохранению/не сохранению порядка обхода
если не знал про треугольник - не то что настолько, но еще болеей
Что-то не соображу, а у какого множества циклическая группа даёт ВСЕ его симметрии?

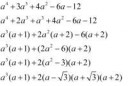
На втором пике результант моих максимальных трёхчасовых усилий, не знаю, что тут делать дальше с этим кубом и в верном ли направлении я пошёл.
Как бывалый скажу, если что то не становится проще, значит делаешь что то не так.
тут можно поискать корни среди целых делителей свободного члена (-12). Как найдешь - подели многочлен на (a-r), где r - любой найденный корень. И повторяй до успеха.
Разложи на произведение квадратичных многочленов с неопределёнными коэффициентами, раскрой скобки и приравняй к коэффициенты. Получится, конечно, системка из квадратичных уравнений, но её уже можно позарачивать.
2. Вербит или кто-то типа него как-то где-то сказал, что первый курс сильнее, мотивированнее и выносливее(способнее многое и больее переварить?) второго(и третьего? и далее?). Пояснил тем, что мотивации и свежести больше. Дайте ссылку, в общем.
Вот сейчас я второкурсник и я жто почувствовал. Как же заебался.

> Почему минус на минус - плюс?
Если ты спрашиваешь, почему -(-a) = a, то по определению аддитивной инверсии.
Если ты спрашиваешь, почему (-x)(-y) = xy, то сначала надо доказать, что -a = (-1)a, и получим (-x)(-y) = (-1)(x)(-1)(y) = (-1)(-1)xy = xy, где второе равенство следует из коммутативности умножения, а третье из того, что мультипликативная инверсия (-1) это (-1).
Доказательство того, что -a = (-1)a:
(-1)a = -a + a + (-1)a = -a + (1 - 1)a = -a + 0a = -a
>на 5м курсе будешь думать что ваще бог и будешь всегда заебаным. по крайней мере будешь так думать. и будет лениво что либо делать. а потом начнешь серьезно рабротать и будешь с умилением вспоминать эти деньки
> а третье из того, что мультипликативная инверсия (-1) это (-1).
Чет я проебался. Вот это хз как доказать.
Двачеты, помогите. Есть быстрое и простое доказательство существования первообразного корня по модулям p^a и 2p^a? У Нестеренко хуита с трехэтажными степенями, у Виноградова лучше, но все равно плохо. через полтора часа зачет по теории чисел, а я эту хуиту не знаю как доказать.

Хелп плз. Пик не осилю.

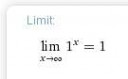
подумай.
Математика - символьная наука?
Вообще-то расширенная вещественная прямая является общепринятой конструкцией, хотя и не является ни полем, ни даже кольцом. Бесконечность апеллирует к топологическим свойствам R, и о расширенной прямой правильнее думать как о топологическом пространстве.

Направьте, как доказать, что пересечение сфер - окружность.
Очевидно, что пересечение сфер - окружность. Что и требовалось доказать.
или два овала


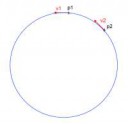
Пишет тебе безвестный кодер, перед которым стоит задача тригонометрического сорта: есть одна трапеция в двумерном пространстве, тупой угол которой нужно скруглить, пришив эллипс без изломов (т.е. касательные эллипса должны быть идентичны векторам-направляющим отрезков трапеции).
Таким образом, мне нужно получить точки центра эллипса, его A и B по двум точкам и двум касательным. Оси эллипса, естественно, параллельны соответствующим осям координат.
Проблема оказалась для меня сложнее, чем я ожидал. Заранее спасибо за любую инфу.
Полуштангой будем называть окружность и прямую, проходящую через центр оной окружности перпендикулярно плоскости оной окружности. Окружность будем называть диском, прямую будем называть грифом.
Семейство полуштанг будем называть концентрическим, если они все имеют один и тот же гриф, и у любых двух разных дисков центры не равны (игрушка "ёлочка"; неравенство центров означает, что никакие два диска не нанизаны на гриф в одном и том же месте).
Ясно, что диски концентрического семейства полуштанг либо равны, либо не пересекаются. Это означает, что если точка принадлежит объединению дисков концентрического семейства полуштанг, то она принадлежит лишь одному диску из семейства.
Пусть есть концентрическое семейство полуштанг такое, что их гриф является направленной прямой. Тогда мы будем называть это семейство убывающим, если радиусы окружностей убывают при движении вперёд по прямой.
Пусть есть два убывающих семейства полуштанг таких, что их диски расположены в параллельных плоскостях, а их грифы равны, но различаются ориентацией. То есть на один и тот же гриф нанизаны два семейства параллельных дисков так, что при движении по прямой вперёд радиусы дисков первого семейства возрастают, а радиусы дисков второго семейства убывают, и наоборот при движении назад.
Рассмотрим пересечение M объединения A дисков первого семейства и объединения B дисков второго семейства. Предположим, что это пересечение непусто. Тогда каждая точка x из M принадлежит как A, так и B. Тогда x принадлежит одному какому-то диску Ax первого семейства и одному какому-то диску Bx второго семейства. Ax и Bx расположены в параллельных плоскостях, а их центры лежат на прямой, перпендикулярной их плоскостям. Ax и Bx могут пересекаться тогда и только тогда, когда Ax = Bx. Таким образом, каждая точка M входит в M вместе со всем диском, то есть M есть подмножество дисков обоих семейств полуштанг.
Так как M непусто, M содержит по крайней мере один диск полуштанги. Ясно, что M не может содержать больше одного диска, так как при движении по грифу вперёд радиусы дисков из M должны и возрастать, и убывать, что абсурдно. Поэтому пересечение A и B, коль скоро оно непусто, есть окружность.
Если мы возьмём две неравные, но пересекающиеся полусферы, соединим их центры прямой и опустим на эту прямую пучок перпендикулярных плоскостей, то получим как раз рассмотренные выше два семейства полуштанг (ибо пересечение сферы и прямой - окружность). Поэтому две пересекающиеся неравные полусферы пересекаются только по окружности.
Отсюда можно вывести и утверждение для сфер.
Полуштангой будем называть окружность и прямую, проходящую через центр оной окружности перпендикулярно плоскости оной окружности. Окружность будем называть диском, прямую будем называть грифом.
Семейство полуштанг будем называть концентрическим, если они все имеют один и тот же гриф, и у любых двух разных дисков центры не равны (игрушка "ёлочка"; неравенство центров означает, что никакие два диска не нанизаны на гриф в одном и том же месте).
Ясно, что диски концентрического семейства полуштанг либо равны, либо не пересекаются. Это означает, что если точка принадлежит объединению дисков концентрического семейства полуштанг, то она принадлежит лишь одному диску из семейства.
Пусть есть концентрическое семейство полуштанг такое, что их гриф является направленной прямой. Тогда мы будем называть это семейство убывающим, если радиусы окружностей убывают при движении вперёд по прямой.
Пусть есть два убывающих семейства полуштанг таких, что их диски расположены в параллельных плоскостях, а их грифы равны, но различаются ориентацией. То есть на один и тот же гриф нанизаны два семейства параллельных дисков так, что при движении по прямой вперёд радиусы дисков первого семейства возрастают, а радиусы дисков второго семейства убывают, и наоборот при движении назад.
Рассмотрим пересечение M объединения A дисков первого семейства и объединения B дисков второго семейства. Предположим, что это пересечение непусто. Тогда каждая точка x из M принадлежит как A, так и B. Тогда x принадлежит одному какому-то диску Ax первого семейства и одному какому-то диску Bx второго семейства. Ax и Bx расположены в параллельных плоскостях, а их центры лежат на прямой, перпендикулярной их плоскостям. Ax и Bx могут пересекаться тогда и только тогда, когда Ax = Bx. Таким образом, каждая точка M входит в M вместе со всем диском, то есть M есть подмножество дисков обоих семейств полуштанг.
Так как M непусто, M содержит по крайней мере один диск полуштанги. Ясно, что M не может содержать больше одного диска, так как при движении по грифу вперёд радиусы дисков из M должны и возрастать, и убывать, что абсурдно. Поэтому пересечение A и B, коль скоро оно непусто, есть окружность.
Если мы возьмём две неравные, но пересекающиеся полусферы, соединим их центры прямой и опустим на эту прямую пучок перпендикулярных плоскостей, то получим как раз рассмотренные выше два семейства полуштанг (ибо пересечение сферы и прямой - окружность). Поэтому две пересекающиеся неравные полусферы пересекаются только по окружности.
Отсюда можно вывести и утверждение для сфер.
Я вроде сейчас надумал, что центр эллипса - пересечение перпендикуляров к v1 и v2, после этого я смогу перенести p1 и p2 в локальные координаты эллипса - а там всё должно разрешиться стандартным способом. Это кратчайший путь, достойный блаародного джентльмена?
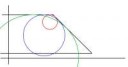
Скруглять можно окружностями разных радиусов. Радиус скругления известен?
Нужен эллипс. По идее он будет единственным, или я ошибаюсь?
Нужно было на картинке яснее показать, что иском именно эллипс, прошу прощения.
блять, охуеть. А если так:
Множество точек, образованных пересечением двух сфер есть пересечение множеств точек первой и второй сферы, а по определению это точки, удалённые от C_1 на R_1 И от C_2 на R_2, где C - центры сфер, R - их радиусы.
Потом записать систему:
(x_т-x_s1)^2 + (y_т - y_s1)^2 + (z_т - z_s1)^2 = r_1^2 ,
(x_т-x_s2)^2 + (y_т - y_s2)^2 + (z_т - z_s2)^2 = r_2^2
и невероятным манёвром привести её к виду уравнения окружности в трёхмерном пространстве?
Ну по идее даже с окружностями множественность не прокатит, так как есть условие соответствия касательным векторам.
Пруфни что ли.

Выражаешь икс через одно уравнение и подставляешь его в другое на место икса. Находишь икс. Ставишь значение икса в уравнения. С игреко делаешь то же самое.
Выше.
http://www.mathnet.ru/php/presentation.phtml?option_lang=rus
>Лекции и семинары Независимого Московского университета
>>321616
Пусть окружности имеют центры O_1, O_2 и радиусы r_1, r_2. Возьмем начало координат в точке O_1 и возьмем ось X по направлению вектора O_1O_2, то есть O_1 имеет координаты (0, 0, 0), а O_2 - (t, 0, 0). Получаем систему уравнений
x^2 + y^2 + z^2 = r_1^2
(x - t)^2 + y^2 + z^2 = r_2^2
Отсюда
x = (r_1^2 - r_2^2 - t^2) / (2t)
и
y^2 + z^2 = r_1^2 - x^2.
То есть y^2 + z^2 равно некоторой константе (если она отрицательная, то сферы не пересекаются). Сферы пересекаются по окружности, которая лежит на оси X.
>>321609
> полуштанга
> гриф
> игрушка "елочка"
> коль скоро
Как же я проиграл с этих слов.
>Как же я проиграл с этих слов.
зато понятно
>То есть y^2 + z^2 равно некоторой константе
чего я и хотел. Няши в сай только отвлекают, так что просто добра тебе.
>чего я и хотел. Няши в сай только отвлекают, так что просто добра тебе.
Добавлю что важно ещё что и x равно константе - т.е. все такие точки (y,z) лежат в одной плоскости.
Я это сам уже понял, спасибо
> по окружности, которая лежит на оси X.
фикс:
которая лежит в плоскости, перпендикулярной оси X
Мне один знакомый говорил, что этот университет - худшая шарага в Москве. Типа там все за деньги покупается, и никто даже этого не скрывает. Или это не так? В любом случае, спасибо.
>>321783
Спасибо.
Кстати, на ютьюбе еще видел распиаренные лекции Романа Михайлова по теории групп. Как они? Стоит ли пробовать?
лал
В третьей строке ошибка. Там должно быть
∀x(¬P (x) ∨ ¬Q(x, y))
Пример:
¬(∃x(x четное ∧ x нечетное)) ≡ ∀x(¬(x четное) ∨ ¬(x нечетное))
а не
(∀x ¬(x четное)) ∨ (∀x ¬(x нечетное))
Ыы почувствовал так, ты прав.
по таблице критических точек распределения Стьюдента нужно найти t с индексом "кр", известно только "k=n-2=19".
Ссылка на таблицу:
http://www.natalymath.ru/krit_student.html
А в итоге все равно то же самое получается?
> Стоит ли пробовать?
Если ты "дебил, стремящийся к знаниям, но не знающий в математике почти ничего" то ты вряд ли что-то поймёшь кроме кулсторей про трипы и метафизику. А НМУ норм.
например если взять каждое действительное чесло, и сопоставить ему точку на числовой прямой получишь бесконечное количество точек. почему бесконечное? ну например 1 и 2. две точки. между ними есть 1,2 и 1,3. а между ними 1.22 и 1.29 и так до бесконечности
Сам разобрался. Четвертая точка - точка пересечения двух прямых.
и чем оно не понраву? алсо не обязательно рациональных, могут затесаться так же и те, которые не будут представимы в виде q/n
Может, например R^n с дискретной топологией или несвязное обьёдинение несчётного семейства множеств из тех же R^n с обычной топологией, в пространствах функций всяких. Вот в простом R^n с обычной топологией вроде не может, как доказать - не знаю.
Оно счётно. Вопрос был про несчётное бесконечное множество изолированных точек.
счетно не значит конечно, это раз. два - в вопросе не было оговорено про его счетность. в третьих ну возьми какое нибудь несчетное множество за основу вместо действительных чисел, раз не нравится счетность. сам нагуглишь несчетное?
Отдельная точка - это точка x топологического пространства такая, что {x} - открытое множество?
Насколько я понял, это он так изолированную точку называет.
Ну, не оче выходит, 1/10 где-то. Завязывай.
бамп
это когда выполняется условие - если одна последовательность стремится к чему то(Xn->E), а другая, которая от неё зависит функционально(Y=f(X)), стремится к примеру к А (Yn->A), тогда говорят что у функции f(x),при х->E, существует предел,равный A. для более четкого понимания надо копать предел последовательности. там определяли какие то последовательности, а их чередование рассматривали как возрастание натуральных чисел. типа 1\х при стремлении n к бесконечности стремится к нулю. а предел функции это расширение понятия предел последовательности на более общий случай, когда сами n могут задаватся от пизды, а не строго по возрастанию. и тип говорят, что если последовательность,с помощью которой задают чередование стремится к чему то, а задаваемая при этом тоже стремится к чему то, то типа тогда вся эта ситуация - предел функции, лiл
Но предел - это какая-то сущность или это просто словесное выражение, оборот речи?
>который от нее чуть не засыпает
Ты засыпаешь потому, что подсознательно считаешь математику ненужной, скучной и унылой. Подчини себе своё подсознание. Научись жадно хавать математику.
блядство! почему ты не смотрел определение предела последовательности?!? там дается ответ на этот вопрос по ебаному хардококору!
>Пределом последовательности называют объект, к которому члены последовательности в некотором смысле стремятся или приближаются с ростом номера.
>объект
https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B5%D0%B4%D0%B5%D0%BB_(%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0)
где достать? мож купить проще?

Бля чуваки, нужен учебник из формата "азы математики для даунов" с большим количеством примеров, где все разжевано, который плавно выведет на комплексные числа, дифференцирование, интегрирование и прочий пиздец инста. Обычные учебники не канают т.к. предполагается наличие препода, который будет объяснять сложные, непонятные моменты.
Кратко суть, сильно захотел упороться схемотехникой, а там сплошные математические выкладки на по темы без понимания которых и сраный конденсатор не просчитать, я в ахуе. Школьные знания давно забыты и проебаны.
Спасибо.
> комплексные числа
гиперкомплексные числа кантор солодовников
даже если прочтешь только начало то заодно еще освоишь кватернионы и азы векторного исчисления
вот это вот еще
ilib.mccme.ru/pdf/ponarin.pdf
Спасибо за попытку, но видимо я не до конца выразил мысль о серьезном образовательном пробеле в области математики, и кроме комплексных чисел схемотехника изобилует другими более злоебучими операциями.
Вообще-то комплексные числа входят в школьную программу. Просто ты, видимо, учился в школе для даунов по урезанным версиям учебников. Скачай любой курс школьных учебников с пометкой "профильный уровень". В основном тебе нужна так называемая алгебра. Профильный школьный курс содержит: наивную теорию множеств, азы теории многочленов и полей (в виде "выражений" и действий с ними), азы теории вероятностей, арифметику комплексных чисел (сложение, умножение и плоскость Аргана), азы дифференциального и интегрального исчисления (в так называемой формулировке де Лопиталя). Если не хватит - Письменный, "Конспект лекций по высшей математике". Если не хватит - Демидович, "Краткий курс высшей математики". Если не хватит - Винберг, "Алгебра", Зорич, "Математический анализ".
>Просто ты, видимо, учился в школе для даунов по урезанным версиям учебников
А я учился в школе для даунов, но самостоятельно обмазался комплексными числами. Очень нравились все необычные понятия.
Математика охуенна. Просто русскоязычные книги - плохие, в них символьная абракадабра вместо идей и концепций. Это следствие культурной изоляции. Ты можешь в английский?
Про производные мне уже пояснили тут, тангенс угла в треугольнике построенном на пределе функции в выбранной точке. Хуево выразил, ну да ладно.
Про интеграл теперь. Интеграл это сумма пределов последовательности функции.
Определенный интеграл это площадь трапеции под криволинейной функцией, ограниченной некоторыми значениями.
Неопределенный интеграл это интеграл в котором производная по верхнему пределу равна подинтегральной функции.
Все правильно написал?
В математику нет царской дороги. Либо читай книги и изучай доказательства теорем, либо иди нахуй.
через физику легко понять. Производная скорости - ускорение, интеграл - расстояние (всё по времени dt)
Такие как ты во всем петушиную дрогу выбирают.
про производную с треугольником пояснял я. теперь про интегралы. значится на самом деле вот эта вот операция взятия производной, это, как ты можешь догадаться, процесс разбиения любой функции на бесконечное чесло бесконечно малых кусочков. по другому еще зовется дифферинциированием. помнишь как строили треугольник? когда подымали с икса пермендикуляры к этой бесконечномалой гипотинузке, мы как бы выделили бесконечно маленькую трапецию. у которой низ это кусок оси иксов, верх та самая гипотинузка, а бока это перпендикуляры. и таких трапеций бесконечно много. бесконечно маленьких. у каждой из них есть какая то площадь. малюсенькая. процесс интегрирования это суммирование площадей этих бесконечно маленьких трапеций. ни больше и ни меньше. типа диференциированием разбили сперва всю большую, неизвестную нам площадь криволинейной трапеции(у которой например одна из сторон не отрезок прямой, а кривая, кусок параболы или еще чего). а потом проинтегрировали - сложили все кусочки, и получили большую площадь. другими словами интегрирование это как ряд суммы, только каждый член этого ряда бесконечно мал. когда он не бесконечно мал пишут знак суммы(та самая с греческая, похожая на Е). а когда бесконечно мал то пишут интеграл. другой сути у процесса интегрирования нет. если дальше будешь учится матану, будешь обьемы считать и прочую хуйню через эти интегралы, а по сути считать сумму бесконечно малых слагаемых, но зато слагаемых этих будет бесконечно много. как это возможно? а вот весь матан и посвящен обоснованию возможности считать именно так.

С первого по четвертое ответы
1. 1/3
2. ~0.110
3. 0.5
4. два корня из трех минус два корня из еденицы.
Взять интеграл от 0 до b. Уровнение прямой y=кх. k = h/b. Как-то так.
а все-же, где задавать дуратские вопросы?
изучал-изучал, а доказать расходимость:
X_n = (-1)^1 + (-1)^2 + ... + (-1)^n
n -> inf
не могу. или могу, но не понимаю.
могу выделить две подпоследовательности.
при
n = 2k, -> inf.
n = 2k + 1, -> -inf
даже достаточно выделить одну такую последовательность. так-как все подпоследовательности сходящейся последовательности сходятся, то в данном случае это не так, а значит последовательность не сходится.
но не понимаю почему.
(1 - 1) + (1 - 1) + ... = 0
я же могу поставить каждому 2k в соответствие 2k + 1.
и могу выделить подпоследовательность сумм элементов 2k и 2k + 1, которая будет сходиться к нулю.
вот какие книги я использую:
1. Мордкович, Алгебра и начала
2. Ильин и Позняк, Основы
3. Зельдович, Высшая математика для начинающих
а этот пример суммы нашел в книге Abbott, Understanding analysis.
Извини, но это уже откровенная толстота. Работай тоньше.
никакого труда там нет. идея в том что тебя попросили проинтегрировать функцию y=kx+b. именно этой функцией, как ты знаешь, описывается уравнение прямой линии. а именно - гипотинузы твоего треугольника. первый катет будет при этом куском оси х. а второй катет будет перпендикуляром, поднятым из точки х=b. только учти что в уравнении y=kx+b конечно же не та b что и в задаче. более того, в твоем случае b в уравнении равно будет 0, потому, что этот б описывает насколько график функции сместится по оси иксов от начала координат, но исследуемая гипотинуза начинается в 0, т.е. сдвига нет, и b=0. попробуй решить, т.е. сперва вывести нужное уравнение, потом взять с него неопределенный интеграл. и увидеть что он равен той самой формуле для площади треугольника. если не получится спрашивай что не получается
Хммм, ну про то что интеграл это сумма бесконечного количества бесконечно малых я еще в википедии прочитал пока был на первом курсе, когда начались проблемы с ними.
Тобишь, я понимаю что интеграл через предел/бесконечно малые выражается, но я не могу его взять в смысле воображения. Ну разбил я на бесконечное количество кусочков, ну проссуммировал. Не понимаю почему результат должен различаться, и реально различается, между интегрированием и суммированием без разбиения. Я чувствую что ответ где то рядом, но не могу его осознать.
К чему тут последовательность суммирования минус еденицы в степени? Тут же результат зависит от четности степени.
У меня как раз зельдович, но я не догоняю все равно.
> Обычные учебники не канают т.к. предполагается наличие препода, который будет объяснять сложные, непонятные моменты.
Нет, они предполагают определенный уровень математической культуры у читателя. То есть, если вместо доказательства написано "очевидно", то после недолгих размышлений тебе должно стать очевидно. Если не становится, то тебе еще рано читать этот учебник.
Советую начать вот с этого
http://www.mccme.ru/free-books/yaschenko/v08book-08.pdf
Насколько я понял икс уже за нас проинтегрировали.
Получается икс квадрат бэ делить на два, что ни разу не вяжется с формулой площади треугольника, або там квадратов нет.
Лучше в /un/ спроси, там тебе помогут, а здесь это никому неинтересно.
>Не понимаю почему результат должен различаться, и реально различается, между интегрированием и суммированием без разбиения
> другими словами интегрирование это как ряд суммы, только каждый член этого ряда бесконечно мал. когда он не бесконечно мал пишут знак суммы(та самая с греческая, похожая на Е). а когда бесконечно мал то пишут интеграл. другой сути у процесса интегрирования нет.
ты блин не понимал а взял бы да посчитал то, про что я писал. сперва бы вывел формулу y=kx. потом понял что для суммы площади надо взять определенный интеграл, с пределами от 0 до b по иксу. и получил бы формулу kx^2/2 . далее задался бы вопросом как найти ебаную k. почитал бы в интернете. она у тебя не известна. но её можно выразить через h, которую дали в условии. пока выражать будешь у тебя в знаменателе x получится и x^2 превратится в просто x. а k превратится в h. но ведь ты считал определенный интеграл? поэтому x превращается в b. но ты не хочешь считать, ты хочешь говорить что все понял и нихуя не работает. а по сути - не понял и даже не пытался
Я и не говорил что я все понял.Я наоборот ничего не понял.
Ну вот прямую я проинтегрировал, получил ка икс квадрат делить на два. Как мне её через высоту выразить? Уравнение прямой подкорректровать чтобы через концы аш и бэ проходила? Тангенс вычислять что ли?
ну надо начать с вопроса что вообще за говно такое k. а для этого в бить в гугол "уравнение прямой". там дадут ясно понять что Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
y = k x + b
где k - угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ. http://ru.onlinemschool.com/math/library/analytic_geometry/line/ . далее подумаем как можно выразить этот ебаный тангенс из двух известных. а известен нам один катет - b, и высота - h. ну например давай рассмотрим треугольник, у которого один из катетов будет h, второй катет это кусок гипотинузы. а гипотинуза этого нового треугольника - сторона b. из этого треугольника можем найти тангенс угла. выразив неизвестный катет через изветсную гипотинузу b и известный катет h. по теореме пифагора найдем его, будет он у нас для красоты z. z^2=b^2-h^2. теперь тангенс получается h/z, теперь можно дрочить выражение, зависящее только от h и b чтобы получить искомую 1/2 hb. но возможно мое выражение тангенса не каноничное, какое правильно брать вопрос геометрии, а всех этих азов я конечно уже не помню. давно это было хе хе хе, уж потрудись сам хоть чуть чуть над решением, а то толку будет 0

sum [//math:(-1)^n*n^(-1)//] from [//math:1//] to [//math:infinity//]
кончилась
Алсо, встретил в этой статье термин "линейная серия". Где можно найти его определение и примеры? Совсем ничего не гуглится.
http://гоппа.рф/Publications/ag_codes.pdf
я могу очень постараться и написать скрипт, который сольёт эту книжку из гугла, а потом склеить результат в какое-нибудь джвю. Оно того стоит? Я стану легендой?
хер там был, гугл починили обход ограничения на просмотр
Там не все страницы - книга с пробелами. А так для этого уже давно существует Google book downloader скрипт для greasemonkey.
На первой странице по запросу в Гугле http://bkmd.narod.ru/doc/Lezioni-Severi-ru.pdf
>>322199
То же самое, что и линейная система, как я понимаю.
http://math.stackexchange.com/questions/579732/linear-series-vs-linear-system-on-algebraic-curves
я посоветовал литру по единственному топику в котором могу советовать
если книжки слишком сложно написаны могу объяснить или посоветовать что другое
компл. числа это далеко не пиздец, там нет ничего по-настоящему сложного
например, в америке их проходят школьники, и никто не умирает. да и тут в физматах про них уже знают, иногда класса с 8
если относится к какой-то теме как к дико сложному колдунству то так оно наверное и будет, - там где все эту элементарную поебень уже давно освоили будешь двигаться со скоростью черепахи или вообще стоять на месте суеверно тараща глаза на "i^2=-1"
Ну вот как мне представить число и квадрат равно минус еденице?
а чего там представлять? как ты себе представляешь число корень из двух? вот так же представь что есть некое чесло, которое если возведешь в квадрат то будет 1. но на самом деле эти ваши комплексные числа можно представлять и по другому. вот есть точка на плоскости. у неё есть координаты. одна по игреку, другая по иксу. вот то что по иксу это действительная часть чесла, а что по игреку - мнимая. типа i тут будет как бэ означать принадлежность координаты к игреку. очень хорошо это понимаешь после знакомства с аналитической геометрией, где используются единичные векторы, орты. i можно рассматривать как такую вот орту.
Любой математический объект - это некоторое множество. Число 5 - множество. Число 17/3 - множество. Число i - множество. Если ты знаешь, что такое множество, то проблем быть не должно.
Пеано давно последний раз снился?
МНОЖЕСТВО ЭТО КОГДА СОКРАЩЕНИЕ ТРАНСЦЕНДЕНТНЫХ ОБЪЕКТОВ АБЕЛЕВОЙ ГРУППЫ ПРОИСХОДИТ ЗА СЧЁТ БЕЗУСЛОВНОЙ ДИСФУНКЦИИ МНИМОЙ КАНОНИЧНОЙ НЁТЕРОВОЙ ФУНКЦИИ СО СТРОГО ПРИВЕДЁННЫМИ УРАВНЕНИЯМИ, СВЯЗАННЫМИ КОРНЯМИ НАД ПОЛЕМ ТОЛЬКО И ТОЛЬКО КОМПЛЕКСНЫХ ЧИСЕЛ КОГЕРЕНТНОГО КВАДРАТИЧНОГО СОСТОЯНИЯ, ПУТЁМ ДИФФЕРЕНЦИРОВАНИЯ СЕПАРАБЕЛЬНЫХ РАСШИРЕНИЙ И ПОЛОЖИТЕЛЬНОГО ФУНКЦИОНАЛЬНОГО ПЕРЕГИБА В ТОЧКЕ СОКРАЩЕНИЯ АНТИСИММЕТРИЧНЫХ МНОГОЧЛЕНОВ С ТОЧНОСТЬЮ ОТ ПОДКОЛЬЦА КОЛЬЦА Б И ОДНОРОДНОЙ ПЕРЕМЕННОЙ В ДРОБНОЙ НЕЧЁТНОЙ ОТРИЦАТЕЛЬНОЙ СТЕПЕНИ В ОБЛАСТИ НЕЗАВИСИМОСТИ АВТОРМОРФИЗОВ НЕСТРОГО ОТ ОБЛАСТИ ОПРЕДЕЛЕНИЯ КОМПОЗИТА РАСШИРЕНИЯ ГАЛУА.
Технически - это строка символов некоторой аксиоматической формальной системы.
Более содержательно - умозрительный объект из того сорта объектов, которые подчиняются аксиомам Цермело-Френкеля или альтернативным.
Почему аксиомы ZFC не определяют множество?
картинка с петухом у параши, которому снится Кантор, Цермело и Френкель.png
это такой сцаевский юмор.
Ты не имеешь права переставлять члены ряда, если он расходится.
Потому что трахал себя резиновым членом и описывал ощущения.
Накрытия Галуа.


СУКА ТРЕТИЙ ДЕНЬ УЖЕ ЕБУСЬ С ЭТОЙ ПАРАШЕЙ
1. Если щёлкнуть кобылу в нос, то она махнёт хвостом.
Кобыла махнула хвостом. Значит ли это, что её щелкнули в нос? Вообще говоря нет, потому что кобыла могла махнуть хвостом по многим другим причинам.
2. Кобыла махнёт хвостом, только если щёлкнуть её в нос.
Кобыла махнула хвостом. Значит ли это, что её щелкнули в нос? Да, значит.
Сходил тебе нахуй в кадык с левой и в висок КАРОНЫМ-ПАХАРОНЫМ с правой, ничтожество.
Просто ссу тебе в волосы, графоман, кусок говна.
Спасибо, стало понятнее.
Двачую, пидоры какие-то. Наверно, на полях работают, колхоз ебаный, хуле они в математику лезут со своими полями?
Ну за поля я загнул, но он с первых страниц начинает про сечения говорить, множества, пустоту-непустоту не дав определения что это такое за хуйня.
Аноны, порекомендуйте что-нибудь кошерное из Фихтенгольца. Программисты нахваливают какие-то разделы из его книг, мол, там прямо самый смак. А я анализом не сильно интересовался, я больше алгебру и геометрию люблю.
Если X, Y, Z - множества, то декартово произведение X x Y x Z состоит из векторов (x, y, z), координаты которого взяты только из соответствующего множества.
это легче всего представить как таблицу. Смотри, для тебя даже картинку на википедии сделали
https://upload.wikimedia.org/wikipedia/commons/thumb/4/4e/Cartesian_Product_qtl1.svg/789px-Cartesian_Product_qtl1.svg.png
Декартово произведение множества А на множество B
это просто множество всех возможных пар (a,b)
где а принадлежит А, b принадлежит B
и элемент из А стоит первым
т.е. элементы декартового произведения 2 множеств - это пары
примеры декартовых произведений:
произведение двух отрезков это прямоугольник
произведение двух обычных числовых прямых это плоскость
произведение окружности на отрезок это цилиндр
произведение окружности на окружность это тор (фигура кот. выглядит как бублик или пончик)
http://math.siomax.ru/Sets
вот тут вроде норм написано с главы 3.3, хотя я не читал
>>322277
Расслабься. Для начала посмотри вот мультик, там про это есть в одной из серий. Я посмотрел почти до конца в свое время, не жалею.
www.dimensions-math.org/Dim_regarder_RU.htm
Потом попробуй книжку. Советую начать с "Теорема абеля в задачах и решениях". Она не совсем по теме, но комплексные числа там будут, и вообще пойдет на пользу даже если не закончишь. Просто привыкнешь к немного более общей математике чем то говно что пихают в школе.
Те две книги что я рекомендовал выше тоже сойдут, хотя Понарина я только листал в нужных моментах, мб читать его подряд и не стоит. Но вот гиперкомплексные числа вполне ок. Если слишком сложно - ну что ж, тогда не обижайся но придется читать что-то для детей. Например Гельфанд-Шень алгебра.
Скоро вся эта восторженность пройдет, ты будешь работать с комплексными числами и удивляться когда говорят что это что-то сложное.
i это просто символ, про него нужно знать что он в квадрате дает -1
Что такое битарды? Это фактически отбросы общества. Люди, которые не смогли найти в нем места и которые всей душой (хотя подчас этого и не сознавая) его ненавидят. А Два.ч это берлога битардов. Зачем все нужно? Just for lulz. Просто так зачмырить кого-то до самоубийства. Просто так сломать кому-то жизнь. Просто посмеяться. «Потому что мы ненавидим всех других. Потому что мы другие. Мы не из этого остального быдла с ТП, планктоном и быдлом. И поэтому мы можем резать, жечь и убивать, издеваться над моралью и ценностями, смеясь ломать навсегда людям жизни. Это Два.ч. Мы вас ненавидим, но мы просто такие. Любите нас, пожалуйста.
Что такое битарды? Это фактически отбросы общества. Люди, которые не смогли найти в нем места и которые всей душой (хотя подчас этого и не сознавая) его ненавидят. А Два.ч это берлога битардов. Зачем все нужно? Just for lulz. Просто так зачмырить кого-то до самоубийства. Просто так сломать кому-то жизнь. Просто посмеяться. «Потому что мы ненавидим всех других. Потому что мы другие. Мы не из этого остального быдла с ТП, планктоном и быдлом. И поэтому мы можем резать, жечь и убивать, издеваться над моралью и ценностями, смеясь ломать навсегда людям жизни. Это Два.ч. Мы вас ненавидим, но мы просто такие. Любите нас, пожалуйста.

ХУЛИ ОНИ СОБРАЛИСЬ ВМЕСТЕ И ТУПЯТ КОЛЛЕКТИВНА?
ИМ ОБЯСНЯЕШ ЧТО НИ ДЕБИЛЫ, ОНИ НЕ ПОНИМАЮТ
МАКСИМУМ НА ЧТО МОЖНО РАСЧИТЫВАТЬ В ТАКОМ КОЛЛЕКТИВЕ- ДОЛЖНОСТЬ МАЛЬЧИКА ДЛЯ УНИЖЕНИЙ
ПОКА ОНИ ВСЕ НЕ ПЕРЕДОНУТ С ГОЛОДУ
Нет, ты протрезвей сначала, антоша, и одежду смени - проссанная вся.
Бамп. Нахуя нужны алгебраические замыкания, если их даже нельзя ни представить, ни построить на бумажке, и остается в них только веровать? Я люблю что-нибудь вычислять, мне нравятся сложно устроенные объекты, и алгебраическое замыкание - как раз такой интересный объект. Почему я не могу им обмазаться?
Пытался ебать себя дилдой в жопу как Вербитский, но что-то не чувствую культурного прозрения зато в области сфинктера приятно.
В программировании есть концепция инкапсулирования. Ты знаком с ней? Мы забываем внутреннюю структуру объекта и рассматриваем объект как чёрный ящик, с которым можно совершать лишь манипуляции из точно перечисленного набора. Нет ничего странного в том, чтобы соорудить из многочленов некоторое поле, а потом забыть о том, что элементами этого поля являются вообще-то многочлены и начать думать об элементах просто как о скалярах без внутренней структуры. Многочлен, коэффициенты которого взяты из некоторого поля многочленов, - вполне разумная и обозримая штука.
Чтобы инкапсулировать данные в объекте, их сначала надо построить. В математике аналогично.
Забывать стоит, когда ты себе хорошо представляешь объект, но для удобства лучше не думать о его устройстве. Также мне непонятно, для чего нужны многочлены задающие кривые, коэффициенты которых являются многочленами. В криптографии многочлены имеют только числовые коэффициенты. Тогда зачем вообще морочить голову сложными абстракциями, которые нельзя себе представить? Какая в этом необходимость? Про необходимость никто не говорит, поэтому у любителей конструктивного похода возникают брейнфаки при попытке залезть во внутренности объекта.
Во, это поинтереснее того, что я читал.
Че непонятного? Построим таблицу истинности A => B:
A, B, A => B
0, 0, 1
0, 1, 1
1, 0, 0
1, 1, 1
Из таблицы видно, что A может быть равно 1 только если B = 1. То есть "A только если B".
Предположим, мы желаем доказать существования поля B, являющегося расширением поля A и обладающего некоторыми свойствами. Есть типичный способ. Мы строим из поля A кольцо многочленов, вкладываем его в поле частных, забываем о внутренней структуре и получаем поле A'. Его элементы - сложные объекты, но мы забываем их структуру и думаем просто как о скалярах. С полем A' делаем аналогичные манипуляции и получаем поле A''. Потом поле A''', A'''' и так далее, и в итоге получаем поле B.
>Многочлен, коэффициенты которого взяты из некоторого поля многочленов, - вполне разумная и обозримая штука.
И, то есть, мы можешь раскрыть скобки, привести подобные члены и получить привычный нам многочлен, у которого коэффициенты - числа?
Например, как-то так: (ax+b)xy + (cx + d)yz = axxy + bxy + cxyz + dyz
Что именно тебя интересует? Ты же не смотришь на число 17 как на последовательность рациональных чисел (хотя должен, это стандартная конструкция поля вещественных чисел), ты думаешь о нём как о скаляре. Ну вот и на многочлены смотри не как на многочлены, а как на не имеющие внутренней структуры числа новой числовой системы, расширяющей имеющуюся.

Я?
Володин?
Это тоже истинно. Хотя из равенства следует "не более", поэтому зачем уточнять.
ЗАРЕКОМЕНДУЙ СБОРКУ ДЛЯ РАСЧЕТА ПРОТЕИНОВ!

Есть 160 шаров, из которых 40 красные, а остальные белые. Найти вероятность p(m), что среди наугад выбранных m (m <= 160) шаров хотябы один окажется красным.
Тебя асимптотика интересует или что?
Тут, по всей видимости, выбор без возвращения.
N=160, k=40
имеет смысл рассматривать только случай, когда m <= N-k, поскольку иначе p(m)=1
Проще искать вероятность того, что среди m выбранных наугад шаров нет красных
По формуле условной вероятности,
1-p(m) = ( (N-k)/k ) ( (N-k-1)/(k-1) ) ... ( (N-k-(m-1))/(k-(m-1)) ) = (N-k)! (N-m)! / (N-k-m)! N! = C_{N-k}^m / C_N^m
Это справедливо с коэффициентами из любого поля: если у многочлена $x^n+a_nx^{n-1}+...+a_1x^0$ есть различные корни $b_1,...,b_n$, то он обязан быть равен $(x-b_1)(x-b_2)...(x-b_n)$, что несложно показать индукцией по $n$ c использованием теоремы Безу для обоснования перехода.
Вопрос по парадоксу Рассела.
Вот например формулировка из вики: "Пусть K — множество всех множеств, которые не содержат себя в качестве своего элемента. Содержит ли K само себя в качестве элемента? Если предположить, что содержит, то мы получаем противоречие с "Не содержат себя в качестве своего элемента". Если предположить, что K не содержит себя как элемент, то вновь возникает противоречие, ведь K — множество всех множеств, которые не содержат себя в качестве своего элемента, а значит должно содержать все возможные элементы, включая и себя."
>Пусть K — множество всех множеств, которые не содержат себя в качестве своего элемента
Зачем это требование? Разве при данном определении K и есть то самое искомое множество всех множеств? А если найдется множество, содержащее себя в качестве элемента, ведь невозможность привести конкретный пример не доказывает его отсутствие.
Проучился пол года на математическом факультете, но до сих пор не могу въехать в логику доказательства невозможности существования множества всех множеств, помогите плз.
Твоя ошибка в том, что ты думаешь, что парадокс Расселла доказывает несуществование множества всех множеств. На самом деле парадокс Расселла доказывает, что не всякое свойство является коллективизирующим, точнее, свойство "не содержать себя в качестве своего элемента" не является коллективизирующим.
Напомню, что свойство (предикат) P(x) является коллективизирующим, если совокупность всех таких x, для которых P(x) истинно, является множеством.
Идея, что парадокс Расселла убивает конкретно множество всех множеств, встречается только в быдлолитературе.
Несуществование множества всех множеств M называется антиномия Кантора. А именно. По известной теореме Кантора, мощность множества всех подмножеств P(M) множества M должна быть строго больше мощности M. Но M - множество всех множеств, поэтому P(M) - подмножество M и потому мощность P(M) не превосходит мощность M. Проблема.
Большое спасибо.
Вот формулировка парадокса в конспекте лектора: "Парадокс Рассела: множество всех объектов невозможно". Получается, множество всех множеств, которые не содержат себя в качестве своего элемента это лишь частный случай множества всех объектов. Мы приходим к противоречию, что такого множества быть не может. Таким образом, мы привели пример, когда множество всех объектов невозможно. НО ЭТО ТОЛЬКО В ТОМ СЛУЧАЕ, КОГДА ОБЪЕКТАМИ МЫ СЧИТАЕМ МНОЖЕСТВА, НЕ СОДЕРЖАЩИЕ СЕБЯ В КАЧЕСТВЕ ЭЛЕМЕНТА. Где же здесь переход от конкретного к общему случаю?

Извините, но это же и правда легко, хоть и долго. Выделяем полный квадрат и раскладываем как разность квадратов.
...петух у параши...
А как же общая алгебра? Там вообще ведь есть только абстрактные сущности типа групп и категорий, что там упрощать?

ИЗИ
Будем пользоваться радиусом сферы: R = 1м
Отмеряем расстояние от центра окружности до центра сферы:
R - (1/5)*d = 1 - 0.4 = 0.6м
Вопщим найденное расстояние, радиус сферы и радиус окружности образуют прямоугольный треугольник, в котором радиус сферы - гипотенуза.
Считаем по теореме Пифагора радиус окружности:
sqrt(1^2 - 0.6^2) = 0.8м
Её диаметр тогда равен 1.6м.
Вроде ничего не напутал. По крайней мере, ты теперь знаешь, каким образом считать такое дерьмо.
Но нахуя написано про сектор - мне не понять.
Да, ещё и нигде не указано, что окружность - это сечение сферы. Если она не является таковым, то хуй знает, как решать.
Это важно, но решать задачи в духе "упростите выражение" точно не стоит. Нужно доказывать теоремы и выводить формулы, а техника со временем придет сама.
Если ты школьник, советую начать с этого
http://www.mccme.ru/free-books/yaschenko/v08book-08.pdf
Нет, это не частный случай. Множество всех множеств, которые не содержат себя в качестве элемента, и множество всех множеств (т.е. коллективизирующим свойством которого является "P(x) = x есть множество") - это просто два разных множества.
Правильная формулировка парадокса Расселла: не любое свойство является коллективизирующим.
Твой лектор просто лажанулся. Такое бывает.
Математики изучают разложение объектов на множители. Но такими методами, что у школьника вскипит мозг от одних названий.
Каждое неравенство p(x) < 0 замени линейным уравнением p(x) + y = 0, где y - новая переменная. Получишь систему из m линейных уравнений и n+m переменных. Реши систему и возьми любое решение, где все y положительны. Если такого нет - внутренних точек нет.
Любая задача из абстрактной теории групп на самом деле про то как бы упростить выражение в группе с образующими и соотношениями.
В категориях часто берется какое-нибудь пространство морфизмов, а потом n раз применяется какая-нибудь двойственность/сопряженность, что по сути то же упрощение выражения в широком смысле слова.
А вообще вопрос какой-то максимально странный и ебанутый. Примерно в стиле "Набирают ли программисты текст на компьютере?". Да, набирают, например, любая программа это текст. Что дальше? Имеет ли это отношение к программированию? Ну, хуй знает. Это надо уметь делать хоть как-то, впрочем, неясно, каким имбецилом надо, чтобы не уметь это делать. Но при этом документацию к ворду изучать не надо (как и вообще уметь им пользоваться).
Да. А вот книжка на английском http://avxhome.se/ebooks/science_books/math/2014-05-25-41_201504141540.html
Хотя это второе издение 2009 года, его скорее всего на русском и нет, но первое датируется 1977, тогда еще он в СССР жил, как так могла получиться что английском учебник издали, а на русском нет?
http://avxhome.se/ebooks/science_books/math/2014-08-26-59_201504180120.html
Спасибо.
>>322781
Благодарю, хоть я и не школьник.
>>322798
Ну хз, школьники сейчас такие пошли, что мне стыдно становится. Как будто я в школу с товарищами потусить приходил.
>>322821
Хм, интересно, благодарствую. А то я из учебника по общей алгебре вынес, что там люди только описанием поворотов/отображений/подстановок занимаются.

Второйзамечательный предел.
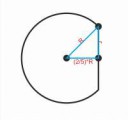
>Это же очеидно.
Нет, это кривейшая косноязычная формулировка. Если взято из учебника/задачника, то составлявшему надо разбить ебало.
>Это как они треугольник образуют?
Пикрил. ЭТАЖ ИЗИ, БЛЯТЬ, РАДИУС СФЕРЫ ПРОВОДИ ВПОЛТНУЮ К СЕЧЕНИЮ, ЕСЛИ СМОТРЕТЬ НА УСЕЧЕННУЮ СФЕРУ В ПРОФИЛЬ
Не, так-то это мой фейл, надо было сразу приложить чертёж. Дальше разберись сам, а то мне уже спать хочется Всего наилучшего ^_^
Сука, ещё расстояние от центра сферы до центра окружности на чертеже неправильное. Не (2/5)R, а (3/5)R. Теперь точно поебу спать.
Оно не всегда коммутативно. Умножение матриц, например, некоммутативно. Множества натуральных чисел все очевидно (учитывая ассоциативность): а б = а б 1 = а б а^(-1) а = б а, при а а^(-1) = 1 = а^(-1) * а
Кстати, если кто знает - подскажите, плз, как на местном движке звездочку отображаемую запилить.
Такое себе доказательство. На самом деле, конечно, нужна индукция.
Как из аба^(-1)а=> ба, если коммутативность еще не доказана. аба^(-1)а=аб тогда уж.
Охуенно доказал.
Зачем? Минус три прибавить минус четыре будет минус семь. Минус пять прибавить три будет минус два. ЭТОЖЕОЧЕВИДНО, ЧТД.
Ты просил доказать, я доказал. Или тебе в кадк с левой и в висок с правой доказать, мразь?
Ну где же ты
Ты просто ненавидишь все русское.
Используется.
e^(i pi) = -1
И я такой удивился и задумался. Ведь если возвести обе части выражения в квадрат, то получится следующее:
e^(2i pi) = 1
Что возможно только если степень равна нулю, то бишь:
2i pi = 0
i pi = 0
Почему так?
Полагаю, я где-то ошибся, а если нет, то это как-то абсурдно выглядит. Выходит же тогда что корень -1 равен нулю. Более того, выходит тогда что исходное выражение e^(i pi) = -1 неверно и получается своеобразный парадокс. В общем, объясните, пожалуйста.
>>323190
Предположим, что у нас уже доказаны ассоциативность сложения и дистрибутивность умножения относительно сложения.
Коммутативность сложения можно доказать по индукции. Пусть для любого m
m + n = n + m.
Тогда
m + (n + 1) = m + 1 + n = 1 + m + n = 1 + n + m = (n + 1) + m.
Умножение целых чисел определяется через повторяющееся сложение. Доказать коммутативность можно по индукции через дистрибутивность:
(n + 1)m = nm + m = mn + m = m(n + 1).
> Что возможно только если степень равна нулю
Вот здесь ошибка. Это было бы верно, если бы степень была вещественной.
Интересно, где же тут может быть ошибка, хммм.
>Коммутативность сложения можно доказать по индукции
А как ты докажешь, что индукция имеет смысл, если ты даже не знаешь определение N?
И в индукцию еще верю просто так.

> когда тожы хочица лампава хикковать с будущими филдсовскими лауреатами под веществами на вписоне

Все рациональные точки на отрезке 0;1
Я тоже на вписках сижу в углу и читаю мат тред.
И я пока что не определился, чем хочу заниматься, но математика мне нравится.
>>323453
Да любое знакомство с математикой вредным само по себе не будет, главное не увлекаться. Вообще, конечно хорошо, как я считаю, постепенно всё-таки наметить то что особенно тебе интересно и чем ты хочешь впоследствии заниматься, и выхватывать уже не всю математику - всю ты всё равно никогда не выучишь - а вокруг области, интересующей тебя.
Ты заебал со своей бесконечностью между нулем и еденицей.
Это копия, сохраненная 30 января 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.