Это копия, сохраненная 5 января 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

Области применения включают в себя общую топологию, теорию меры, коммутативную алгебру, алгебраическую геометрию, алгебраическую топологию, топологические векторные пространства, операторные алгебры и многие другие.
Предыдущий: >>311874 (OP)
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. http://arhivach.org/thread/109198/
30. http://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
Вот это а0а1 мне покоя не дает. Почему "умножить", а не "сложить"? Ведь к изначальному положению мы прибавляем 120 градусов, а не домножаем! Объясните, пожалуйста.
Это всего лишь обозначение бинарной операции. В данном случае t : X • X -> X, где X -- множество «поворотов», то есть { a0, a1, a2 }. Двум поворотам ставится в соответствие третий, например t(a0, a1) = a1, ибо можно считать значением t поворот, получающийся последовательным применением поворотов-аргументов. Можешь обозначить t звёздочкой/плюсом/кружком и записывать в инфиксной форме. Суть не в этом, а в том, что есть какая-то операция. На то, что у тебя градусы прибавляются, а не домнажаются, также смотреть не надо. В данном случае ты работаешь уже не с градусами (числами), а с некоторыми абстрактными объектами-поворотами, хотя, как я сказал выше, можешь обозначить операцию плюсом и складывать повороты, суть от этого не изменится.
Умножение или сложение это всего лишь обозначение операции в группе, значок. Можно рисовать звёздочку между аргументами, можно точку, можно плюсик, можно маленький хуец, а можно вообще ничего не рисовать. Обычно сложением обозначают операцию в абелевой (т.е. коммутативной, от перемены мест операций результат не меняется) группе, группа преобразований чего-либо как правило не абелева (матрицы, если ты знаешь что это такое, например, перемножаются некоммутативно), поэтому здесь используется обозначение умножения, а не плюсик сложения.

Понимание постепенно придёт. Возможно, тебе стоит уделить некоторое внимание теории множеств и определению отображения (в Зориче можешь глянуть). Ты должен чётко понимать, с какими объектами работаешь и какие отображения рассматриваешь. В том посте твоя ошибка была в том, что ты отождествил объект-«поворот» и число-«градус». Да, между ними есть некоторая связь, но это разные объекты. Хотя, наверно, об этом рано говорить, если ты только начал читать учебник.
>Поясните, пожалуйста, подчеркнутое.
По определению. Напомню. Если A = B = C, операция внутренняя. Если A = C или B = C, операция внешняя. Из того, что A = B = C, следует, что A = C так же, как следует, что B = C. Следовательно, свойства внутренней операции влекут свойства внешней, то есть любая внутрення операция является внешней. Возможно, это покажется нелогичным, но можешь принять это как игру слов/определений. Можешь пока не думать об этом.

Научись рассказывать не только о достоинствах, но и о недостатках задвигаемой теории, мгазь.
Это вербит написал, а не оп.
https://en.wikipedia.org/wiki/Complete_Heyting_algebra
Алгебра Гейтинга H - это ограниченная решетка (то есть существуют 0 и 1), такая, что для всех a, b ∈ H существует наибольший элемент x ∈ H такой, что a∧x ≤ b. Этот элемент называется относительным псевдо-дополнением к a и обозначается a → b.
Полная алгебра Гейтинга - это алгебра Гейтинга, которая полна как решётка.
Множество всех открытых множеств топологического пространства, упорядоченное по включению, образует полную алгебру Гейтинга.
Множество всех подмножеств данного множества, упорядоченное по включению, образует полную алгебру Гейтинга.
Полные алгебры Гейтинга являются объектами трёх разных категорий: категории CHey, категории локалей Loc, категории фреймов Frm.
Существует функтор O из категории топологических пространств Top в категорию локалей. Любая локаль имеет топологическое пространство, наилучшим образом её приближающее, оно называется спектром локали. Существует функтор S из Loc в Top, служащий правым сопряжённым функтором для O.
На русском языке об этом нет ни одного документа.
>На русском языке об этом нет ни одного документа.
О чем? Например в "Теории решеток" Биркгофа есть глава о полных решетках в которых рассматриваются полные брауэровы решётки, что есть суть теже гейтинговы алгебры.
>На русском языке об этом нет ни одного документа.
Этот западнец порвался, несите следующего.
О локалях и фреймах, вестимо.
Оно называется "эрмитово пространство".
Читаю Киселева и ничего не понимаю, может быть существуют учебники полегче, совсем для ньюфагов? Начал знакомство с матаметикой с учебника арифметики.
лол. Я про математика из Петербурга.
Я думаю, что да.
Пусть T = 0. Тогда, очевидно, у него нет собственных значений кроме нуля.
Пусть у T нет собственных значений кроме 0. Существует базис V из собственных векторов T. Назовем его v_1, ..., v_n. Так как для любого j: T(v_j) = 0, T = 0.

Просто я придумал свое доказательство пикрелейтед, потом посмотрел то, что в учебнике, а оно какое-то абсолютно упоротое.
Вот мое. Пусть (a, v) - собственная пара T. Тогда
a||v||2 = <av, v> = <Tv, v> = 0.
То есть a = 0. Так как любое собственное число T равно 0, T = 0.
Очевидно, нет. Возьми любой ненулевой нильпотентный оператор.
[0 0
1 0]
Нашел ошибку у себя
> Существует базис V из собственных векторов T
http://imperium.lenin.ru/~verbit/MATH/programma.html
Тут список дается, начиная с первого курса только.
Утилитаристы не нужны. Благодаря математике ты видишь сегодняшний мир таким как он есть, этого достаточно.
0.(9) = 1 - пришли к противоречивую. Так по твоему. Давай без мозгоебства. Мне действительно интересен вразумительное доказательство того, что это не верно.
Кто тебе сказал, что кто-то кому то что-то должен? Ты не прихуел? Каждый делает лишь то, что хочет.
Ты вопрос задай нормально. Что ты имеешь ввиду под 99999... Сумму бесконечного ряда? так в классическом смысле она не сходится. Определи правило суммирования, тогда можно будет о чём-то говорить.
Я иммею ввиду лишь то, что происходит в этом видео. Не больше и не меньше https://www.youtube.com/watch?v=x-fUDqXlmHM
Ты можешь просто съебать? Тебе уже 100 раз объянили, что нет такого объекта как ...9999. Если ты можешь его определить так, чтобы он имел смысл и сможешь доказать, что с ним можно делать операции, которые делаются в этом видео, то напиши. Если не можешь, то иди на хуй.
>ключевые результаты, которые повсеместно используются
Такой вещи не существует. Каждый результат самоценен и используется в лучшем случае в двух-трёх местах.
>Что подразумевается под "Оператор А, действующий из V в W"
Берешь элемент из векторного пространства V, предположим v, действуешь на него оператором A, получаешь элемент Av, который принадлежит векторноиу пространству W

Всегда пожалуйста!
А что тебе не нравится в этом утверждении, и с чем должно противоречить? Оно получается как предел по норме |a+1|_10=0, соответственно, проблемы могут возникнуть только с нормой, а не с алгебраическими операциями. Возникающие проблемы - неоднозначность разложения и отсутствие правильного деления.
Вот, например, в учебнике есть утверждение о том, что у самосопряженного оператора все собственные значения вещественные. Во-первых, на это утверждение не ссылаются последующие утверждения. Во-вторых, его можно доказать самому через минуту размышлений. Зачем надо было его включать? Мне не жалко, просто если такие вещи убрать, то можно сократить материал раза в 2-3 без потери глубины. И такое я замечал во всех учебниках.
В нормальных учебниках подобное выносится в упражнения.
Тебя уже обоссали в прошлом треде с твоими p-адическими числами, за которые ты не смог пояснить по понятиям. Что такое 0.9999... в р-адических, уёба?
А давай так, пока мы тебе всем тредом в рот не нассали ты даёшь определение того, что такое "вещественное число", потом того, что такое "...999", а потом уже задаёшь свои невероятно тупые вопросы.
А давай так, пока мы тебе всем тредом в рот не нассали ты даёшь определение того, что такое "п-адическое число", потом того, что такое "0.999..." в п-адических числах, а потом уже делаешь свои невероятно тупые умозаключения.
> Вот эта твоя гайка, петрович, которую ты завернул когда капот монтировал, она людям что-нибудь дала? Она спасла мир от войн, накормила миллионы? НЕ НУЖНО!

>3a) Показать, что метрика есть непрерывная функция на метрическом пространстве с этой же метрикой.
>искусственную сложность, неебические задачи
>материал слишком простой для понимания.
HA-HA-HA, oh you.
Ну это я как раз решил, если ты читал.
3б) Нужно по сути показать, что: тождественное отображение Id : (X',d') -> (X,d) непрерывно <-> топология (X',d') тоньше, чем (X,d). Однако это проверяется тупо по определению, прообраз любого открытого множества в (X,d) относительно Id открыт в (X',d'), значит, в (X',d') открытых множеств, как минимум, не меньше, чем в (X,d).

Чисто гипотетически, из википедии, я нашел ответ, но алгебраически я туплю.
Для второго надо ведь просто завести дельту под степень, разложить степенной двучлен и потом просто отнять исходную функию и сокртить все что с дельтой, чтобы получить 4X^3.
Для третьего что делать? Засунуть дельту в скобки и разложить как квадратный трехчлен? Или засунуть изначальную функцию в какую то букву и решать так же как в первом случае?
Четвертый и пятый вроде все просто, надо только в конце свести дробь к общему знаменателю.
А к шестому я подсказку не понял.
Раскрыть скобки, взять предел. Пределы отношения многочленов брать не учили, что ли?
>А к шестому я подсказку не понял.
Она довольно недвузначная. Умножь на ту самую сумму числитель и знаменатель, раскрой скобки, посмотри что выйдет.
Ты чё ты чё..
У тебя странное самообучение. Понятие "производная" - более сложное, чем понятие "предел", так как опирается на него (по крайней мере в классическом подходе). А так выходит что ты пытаешься найти "не знаю что, не зная как".
Я про отношение многочленов. Тобишь что это и как его и куда.
Предел я более менее усвоил, отношение функции с малым приращением к самой функции.
>Предел я более менее усвоил, отношение функции с малым приращением к самой функции.
Это как раз производная.
Раскрой всевозможные скобки в числителе выражения (x+1+delta)^2-(x+1)^2/delta и возьми предел delta->0..
Задачи на метризуемость того или иного пространства это по большей части задачи на использование одноимённого критерия https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D1%80%D0%B8%D0%B7%D1%83%D0%B5%D0%BC%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE . Не обязательно нужно эту метрику руками строить.
А почему RxR с лексикографическим порядком - нормальное пространство? Или ты не про теорему Тихонова о метризуемости?
((x+1)+delta)^2 например. Можешь даже замену сделать a=x+1 и b=delta, если тебе так удобнее.
Потом еще раз открывать а после всех делов?
А то у меня получилась херня какая то.
(x+1)^2+2Δx+Δx^2-(x+1)^2/Δx=2Δx+Δx^2/Δx=~0
Я сперва подставил буквы, раскрыл с буквами и потом вместо буковок поставил исходные цифры. Вроде все правильно сделал.
Вроде нет. Должно было выйти (x+1)^2 + 2 delta (x+1) + delta^2 - (x+1)^2 / delta
Ага, вижу ошибку свою.
Но ведь потом две дельты икс плюс один все равно становятся крайне малы и остается только квадрат минус квадрат. Их тоже раскрывать?
Ну я до этого еще не дошел. Это только страниц через 100 будет.
Распиши мне как для дауна, а то я не понимаю.
Результат должен быть (x+1)^2 + 2 (x+1) + delta - (x+1)^2?
[ (x+1+delta)^2-(x+1)^2 ]/delta =
[ (x+1)^2 + 2 (x+1) delta + delta^2 - (x+1)^2 ]/delta =
[ 2 (x+1) delta + delta^2]/delta =
[ 2 (x+1) + delta]
при delta -> 0 получаем просто 2 (x+1).
А вообще с такими вопросами в образовач (un), а не в саентач: тут на школьные дз агрятся.
Это в какой такой школе пределы и производные проходят?
Да и в ун сидят три с половиной долбоеба которым интереснее обсуждать кто в какуй универ поступит чтобы соснуть меньше чем другие.
>Это в какой такой школе пределы и производные проходят?
Да во всех, вроде, в 10-11 классах есть предмет такой: "алгебра и начала анализа", вот в "началах анализа" и проходят. Хотя я не знаю как оно на практике, сам учился на физ.мате, а не в обычной школе.
В моей школе такого нет. Только матрицы и связанные с ними примеры раздрачиваем.
Кстати, вполне очевидно, что RxR с лексикографическим порядком - не пространство со счётной базой. В частности, множества вида
U_x0 = {(x0,y) \in R^2 : 0<y<1}
образуют несчётную систему непересекающихся открытых множеств. Поэтому теорема Урысона неприменима.
Ну там же в условии дано что, Х' - метрическое пространство. Или не обязательно метрическое? Из контекста непонятно.
А Х со штрихом это что?
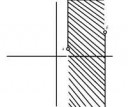
Чого ти несёшь? Открытое множество a<x<b в лексикографическом порядке выглядит как пикрелейтед. Всё тут со счётной базой, всё отделяется, всё регулярно.
За щекой проверь.
Это не база. Например, нельзя представить множество {(pi,x) : 0<x<1} в виде объединения элементов базы.
Оно приближается множествами {(an,x), 0<x<1} где an - последовательность рациональных, сходящаяся к pi.
Что значит "приближается"? База - это когда любое открытое множество в виде объединения представить можно, покажи мне семейство множеств из твоей базы, объединение которых даст {(pi,x), 0<x<1}.
Или нет, немного не то написал, в моих обозначениях это будут множества c a_n=(x_n, 0), b_n = (y_n, 1) где x_n и y_n сходящиеся к пи последовательности снизу и сверху соответственно.
Между (2/3,0) и (1,1) будет элемент (3/4,12482384234), например, ты это осознаешь?

Короче, вот че я придумал. Буду признателен, если проверишь на предмет ошибок.
Будем обозначать открытый шар в метрике $d$ с центром $x$ радиуса $\varepsilon$ как $B_d(x, \varepsilon)$. Надо показать, что для любого $x$ и любого шара $B_d(o, \varepsilon)$, содержащего $x$, найдется базисный элемент $X'$ $U$ такой, что $x \in U$ и $U \subset B_d(x, \varepsilon)$. Выберем любой $x_0 \in X$ и шар, в котором он содержится. Без потери общности можно считать, что $x_0$ - центр шара (если нет, можно взять шар с центром в $x_0$, целиком содержащийся в большем шаре, и найти нужный базисный элемент для него). Пусть радиус шара равен $\varepsilon$.
Выберем $y_0 \in B_d(x_0, \varepsilon/3)$. Определим $d_{y_0}: X' \to \mathbb{R}$ как $d_{y_0}(x) = d(x, y_0)$. Я знаю, что если функция непрерывна, то она непрерывна по каждой координате, то есть $d_{y_0}$ непрерывна. Поэтому можно выбрать базисный элемент $X'$ $U$ такой, что $x_0 \in U$ и $d_{y_0}(U) \subset B_d(d_{y_0}(x_0), \varepsilon/3)$ (по теореме 18.1(d), пикрейлейтед), то есть $\forall u \in U: d(x_0, y_0) - \varepsilon/3 < d(u, y_0) < d(x_0, y_0) + \varepsilon/3$.
По неравенству треугольника
$$d(x_0, u) \leq d(x_0, y_0) + d(y_0, u) < d(x_0, y_0) + d(x_0, y_0) + \varepsilon/3 < \varepsilon/3 + \varepsilon/3 + \varepsilon/3 = \varepsilon.$$
То есть, мы показали, что $U \subset B_d(x_0, \varepsilon)$.
Хотя да, именно такие множества и не получится представить.
Я какую-то хуйню написал, начиная с выбора $y_0$ (там еще ошибка в том, что не факт, что такое $y_0$ можно выбрать). Лучше вот так.
Определим $d_{x_0}: X' \to \mathbb{R}$ как $d_{x_0}(x) = d(x, x_0)$. $d_{x_0}$ непрерывна. Выберем базисный элемент $X'$ $U$ такой, что $x_0 \in U$ и $d_{x_0}(U) \subset B(d_{x_0}(x_0), \varepsilon) = B(0, \varepsilon)$. Это можно сделать по (18.1). Таким образом, $\forall u \in U: d(x_0, u) < \varepsilon$, т.е. $U \subset B_d(x_0, \varepsilon)$.
Там задания как я понял для поступления. Энивей нашел литературу в каком-то блоге.
Мало ли кто ещё искать будет
http://heller.ru/blog/2010/04/ium-in-details/
Тебе, тупому дауну, уже на пальцах все показали, а до тебя даже определение дойти не может. Если ты и способен кого то обоссать, то только себя и свою мамку.
Успокойся уже ущербный. Просто признай свою умственную неполноценность и не мешай людям общаться.
Сорян, сейчас прочту.
И таки в p-адических числах нету чисел с "бесконечной дробной частью".
Да, всё верно.

Какого хуя? То есть, исходя из этого, можно определённо точно сказать, что каждое целое число - лишь какая-то дробь с бесконечным порядком, которая стремится к вот к целому числу.
Что не так? Где я не прав? Прав ли Фихтенгольц или пидор-защеканец?

Пора напомнить твое место
Защеканец немножк.
Каждое вещественное число - это класс эквивалентности бесконечных десятичных дробей. Бесконечные десятичные дроби 1.000.... и 0.999... входят в один и тот же класс.
Кстати, ты врёшь, что читаешь Фихтенгольца.
Может всё же есть где-то? Очень нужно, препод чмо, не на что ровняться без решений задач.
Лучше пропусти эту главу. Есть более хорошие способы определения R, чем десятичные дроби.
Сейчас на примере корней расскажу, какое свойство R самое важное. У Q этого свойства нет. Возьмем, например, множество рациональных чисел x таких, что x2 < 2. В поле Q у него нет точной верхней грани, потому что корень из 2 - иррациональное число. При этом нам хочется, чтобы оно имело точную верхнюю грань.
Можно построить такое поле R, которое содержит Q в качестве подполя и в котором операции сложения и умножения совпадают с операциями в Q и у любого ограниченного сверху множества есть sup, а у любого ограниченного снизу - inf. То, как строится R, нет смысла читать, потому что построение довольно длинное и нигде тебе не пригодится. С другой стороны, если интересно или если ты не можешь поверить в это свойство (хотя в школе это свойство используют в течение 11 лет), то почитай.
С помощью описанного свойства можно доказать, например, что Q плотно в R (то есть, что между любыми двумя вещественными числами найдется рациональное), что существует корень n-й степени из произвольного положительного числа. Можно определить расстояние на плоскости от точки x до множества A как inf{расстояние от x до a, где a - элемент A}. Мы знаем, что множество {расстояние от x до a, где a - элемент A} ограничено снизу нулем (расстояние всегда неотрицательное) и поэтому имеет точную нижнюю грань.
Что касается десятичных чисел, то их лучше воспринимать просто как форму записи и не задумываться об этом.
> Вижу фигу, что дескать 0.(9) есть 1.
Это правда. Но ниче такого тут нет, потому что это просто форма записи.
> То есть, исходя из этого, можно определённо точно сказать, что каждое целое число - лишь какая-то дробь с бесконечным порядком, которая стремится к вот к целому числу.
Ну можно и так сказать. Например, 1 = 1.(0). Не вижу ниче такого. Но лучше определять вещественные числа как я выше написал.
Забыл написать, как воспринимать десятичную форму записи. Десятичную форму записи нужно воспринимать так, что число, которое в этой форме записано, равно тому, что перед запятой + сумма dn10-n, n от 1 до бесконечности, где dn - n-я цифра после запятой.
Что такое сумма бесконечного ряда, потом прочитаешь.
Допустим, мы определили C как множество чисел вида a + bi, где a и b вещественные и i2 = -1. Очевидно, такое определение никуда не годится, потому что непонятно, почему вообще должно существовать такое число i.
Допустим, мы определили C как R2. Как R может быть подмножеством R2?
То есть ты определяешь C вот так
> множество чисел вида a + bi, где a и b вещественные и i2 = -1
? Откуда ты знаешь, что такое число i существует? Из какого множество берется это i?
Открой книжку хорошую и посмотри как определяются комплексные числа через упорядоченные пары, как они умножаются. Оттуда будет следовать существование i.
Ну я знаю про это определение.
> Допустим, мы определили C как R^2. Как R может быть подмножеством R^2?
R туда вкладывается изоморфно, т.е R=(0,R)<(R,R). Если занимаешься математикой, такие недоговорки будут сплошь и рядом, ошибок в
этом, привыкай.
Темы каждой борды рано или поздно вырождаются в то, о чем удобно спорить.
Мне грустно, котаны.
Мне грустно, котаны.
Он прав, это всего лишь ссаные стрелочки, без теории множеств и функций это говно даже интуитивной интерпретации не имеет. Баловство одно, короче.
Ну это понятно. Просто одно дело, когда какую-нибудь статью читаешь и там незначительная ошибка/недоговорка, а другое дело, когда читаешь определение чего-то такого базового и простого как C и в английской и русской википедии такая же недоговорка.
>>не всякому символу (десятичной дроби) соответствует число
Всякому (если целая часть конечная).
По построению Зорича — не всякому.
http://edu.alnam.ru/book_z_math1.php?id=22
(в конце страницы)
В том числе для символа 0.(9) нет соответствующего числа.
Ссылка вставилась не так. Нажмёшь внизу 67, окажешься на 61 стр. Там внизу.
Можешь лучше? И что в нём плохого?
>>315060
Если интересно, то вот как это реализовано в metamath proof explorer: есть множество "модель вещественных чисел, реализованная в виде сечений Дедекинда", - http://us.metamath.org/mpegif/df-nr.html - это "временное множество" единственная цель которого - определить C как квадрат этого множества с некоторой структурой : http://us.metamath.org/mpegif/df-c.html после чего, R определяется как "модель сечений дедекинда" x {0} - http://us.metamath.org/mpegif/df-r.html и доказывается абсолютно строго это самое включение: http://us.metamath.org/mpegif/axresscn.html
>>315092
Для матана на многообразиях нужны, а другим профессионально заниматься не особо осмысленно, мне кажется.
>>315073
>>315087
Это дело вкуса и эстетство.
Ну это же преподаватель матанализа, зачем ты с ним так строго? Ему сочувствовать надо, он же не виноват в том что он преподаватель матанализа?
Да знаю я это. В прошлом треде похожий вопрос я же и задавал. Надеюсь, в этот раз будут ещё какие-то мнения. Просто у меня недавно вышел спор на эту тему. Каждый ли прикладной математик — математик? Любой ли преподаватель математических дисциплин — математик? Можно ли считать математиком человека, не знающего, к примеру, теории категорий/пучков/топосы/спектры/когомологии/etc?
Я напишу что я думаю: мне кажется красота математики как раз и состоит в том, что её "актуарная часть" связана с "фундаментальной частью", при этом связана обоюдно - идёт постоянная двухсторонняя подпитка. И для нормального развития математики нужны как прикладники так и фундаменталисты, поэтому, мне кажется, критерий должен быть максимально общий, вида: "решает математические задачи, формулирует свои результаты по схеме определение-доказательство-теорема - значит математик". Таки дела.
>И для нормального развития математики нужны как прикладники так и фундаменталисты
Я думаю мир стал бы прекраснее без картофанного матана.
Если бы в мире не было картофанного матана, ты бы щас не за пекой сидел, а в поле пахал на барина.
>решает математические задачи, формулирует свои результаты по схеме определение-доказательство-теорема - значит математик
А как узнать, что он что-то доказывает? Как вообще искать работы современных учёных? Как узнать, когда у человека последний раз были какие-то научные результаты?
И что такое в твоём понимании математические задачи? К примеру, улучшение каких-то алгоритмов в численных методах — математическая задача? А моделирование потоков вокруг стержней реактора?
>Как вообще искать работы современных учёных? Как узнать, когда у человека последний раз были какие-то научные результаты?
Google scholar, arxiv.
> К примеру, улучшение каких-то алгоритмов в численных методах — математическая задача?
Грубо говоря, всё то, что может быть "сформулировано при помощи аксиом ZFC при достаточном усердии", соответственно, если при улучшении алгоритма доказаны какие-то оценки - то это математический результат, а если это эвристическое размахивание руками вида "проверели на 1000 случаях на данных такой-то компании - вроде работает быстро", - то не математический.
>>315125
Uhh, знал бы ты для решения какой задачи Мочидзука свою теорию строил...
> Uhh, знал бы ты для решения какой задачи Мочидзука свою теорию строил..
Я не >>315128, но я думаю, что он ее строил не потому, что хотел доказать abc-гипотезу (хотел, конечно, но это не главное).
" https://youtu.be/hQLxmSgL0yI?t=1355 "
>А моделирование потоков вокруг стержней реактора?
Это комплексный результат. Оценка адекватности модели, то есть насколько модель соответствует реально наблюдаемым процессам - это, по сути, экспериментальная физика, а вот если получена содержательная информация о самой модели математическими методами - то это математический результат.
>>315133
Мне кажется это было основной мотивацией. Я смотрел лекции Михайлова и в них он как раз говорил о том, что очень часто мощные фундаментальные теории строились вокруг решения конкретных задач, и даже если они задачу не решали, они оказывались интересны сами по себе. Это именно то, что я хотел сказать.
Если когда-нибудь эта связь будет утрачена (фундаментальные математики будут "свысока" смотреть на конкретные задачи), то новые фундаментальные теории не будут столь глубокими. Если вообще будут.
Все вопросы, является ли кто-то X-истом решаются сообществом X-истов. Причём, вес имеет не только мировое, но и любое более-менее крупное сообщество, например региональное: российское или американское. И в российском, и в американском математических сообществах, человека, занимающегося численными методами пока признают математиком, а в сообществе читателей вербитятника, например, - нет. Но население его бложика само по себе три с половиной рашкофобских школьника, так что его мнение вряд ли можно считать весомым.
Мне кажется его вопрос был о каком-то "вселенском, абстрактном алгоритме" распознавания математической работы, а не о практических аспектах. Так-то понятно, что если большинство математиков называют результат математическим, то наверное так-то оно и есть. Но бывают и спорные случаи, например, что делать с теоремами, которые доказаны пруверами? Гротендик не признавал доказательство теоремы о четырёх красках, например.
Ничего не проебалось.
>Google scholar, arxiv.
Спасибо, учту. А всякие индексы там можно посмотреть, а то я не нашёл?
Ладно, в этом направлении я понял твою точку зрения. А что скажешь насчёт обязательного минимума для математика?
>>315138
>а в сообществе читателей вербитятника, например, - нет
Не скажу, что отношусь к ним. Если честно, весь этот спор вышел, из-за того что мне начали рассказывать, какой %преподаватель-нейм% крутой математик, на что у меня возникло странное чувство… в общем, негодование. Вот я и захотел узнать, можно ли считать рандомного преподавателя математиком, если он занимается чем-то прикладным. Во всяком случае я не могу поставить таких людей в один ряд с людьми, занимающимися, так скажем, теоретической математикой. Совершенно разные уровни.
>>315139
В общем, да, примерно так.
>Спасибо, учту. А всякие индексы там можно посмотреть, а то я не нашёл?
Пикрил.
>Во всяком случае я не могу поставить таких людей в один ряд с людьми, занимающимися, так скажем, теоретической математикой. Совершенно разные уровни.
Ну, ты это зря. Вот Гротендик писал в своих "Урожаях и Посевах", - что гонор и высокомерие - это очень плохо и недостойно. И рассказывал случай тоже про то, как какой-то чувак просил его рецензию, а он даже смотреть не стал, аргументировав тем, что там картофан какой-то и он всё это уже видел. И вот он некоторую часть книги убивается по-поводу того, как это было неправильно. А вообще есть вот Тао, который теорвером, теорией чисел и комбинаторикой в последнее время занимается, филдсовский лауреат, на секундочку. У него тоже "не тот же уровень", что и у людей, которые занимаются пучками и высшими топосами?
>А что скажешь насчёт обязательного минимума для математика?
Мне кажется, что в современных реалиях, недостижимый идеал - это если после обучения ты можешь ответить на любой вопрос из http://www.math.harvard.edu/graduate/quals/topics/ без предварительной подготовки. Достижимый идеал - это новый куррикулум Вербицкого (который вполне адекватен) - http://verbit.ru/Job/HSE/Curriculum/all.txt
>что гонор и высокомерие
Да нет, ты не подумай, у меня нет ни гонора, ни высокомерия, ибо себя я тем более не могу назвать математиком. Может быть, никогда им и не стану. Тут вопрос в другом скорее. Я бы сказал, вопрос в авторитете. Когда смотришь на людей, которые реально занимаются математикой, получают какие-то результаты, и на людей, которые преподают, но об их заслугах ты ничего не знаешь, непроизвольно проводишь деление. Это всё субъективно, но у меня вообще исчезает всякое уважение к преподавателю, если он не стремится проявить себя как учёный. И как таких преподавателей назвать математиками? Наверно, я не прав. Но апеллировать к своим внутренним ощущениям я тоже не могу. Вот я и пытаюсь рационально объяснить свои чувства.
>>315150
Интересно, посмотрю.
Где на такой вопрос найти ответ?
Я готов страдать ради красоты
>Морис Клайн
Утрата определённости или что? Там в общих чертах же. Интересно, может кто-то с подробностями разбирал конкретные теории прошлого.
> Это всё субъективно, но у меня вообще исчезает всякое уважение к преподавателю, если он не стремится проявить себя как учёный.
А если, допустим, человек понимает, что не может работать наравне с топовыми специалистами (а 99.9% людей не могут), но не имитирует научную деятельность, публикуя работы по каким-то малоактуальным и не особо интересным проблемам (типа "метод решения вот этого дифура, который возник, когда я моделировал явление, когда мы с женой шли по берегу и было туманно"), а делает что-то реально полезное? Например организация всяких конкурсов и олимпиад среди школьников мне кажется очень важным делом. Даже отвечать на вопросы на math.stackexchange - важное дело.
> Но население его бложика само по себе три с половиной рашкофобских школьника
Сходу могу назвать человек пять-десять серьезных математиков, которые сидят там. И неисчислимое количество студентов/аспирантов/молодых постдоков.
>делает что-то реально полезное?
Значит, это хороший преподаватель. Такие у меня вызывают уважение. Таких мало, ибо я в основном вижу лишь высокомерие со стороны преподавателей, словно они пытаются студентам доказать, как много они знают и какие мы тупые. Оно, конечно, так, но зачем?
>ут), но не имитирует научную деятельность, публикуя работы по каким-то малоактуальным и не особо интересным проблемам (типа "метод решения вот этого дифура, который возник, когда я моделировал явление, когда мы с женой шли по берегу и было туманно"),
Актуальность - это по сути характеристика того, насколько твоя работа потенциально может помочь всяким топовым математикам на вершине социальной пирамиды, - то есть характеристика чисто социальная; а интересно, мне кажется, может быть и с методами решения дифуров при моделировании каких-то там процессов (в конце концов, в чём фундаментальное отличие дифуров, моделирующих явления при туманной погоде, от Навье-Стокса, моделирующего какие-то там потоки в жидкостях?). Я считаю, что для нормального функционирования математического здания нужны и те, кто на подсосе у Великих (филдсовских лауреатов, IHES, макс планк) и занимаются актуальной и сверхсовременной(тм) математикой, и те, кто задрачиваются всю жизнь по проблеме Борсука, и какие-нибудь шизики, чья жизненная мечта построить "правильную теорию множеств", при том эта "правильность" дефенируется лишь их внутренним разумением и интуицией.
>>315180
Это плохие преподаватели и плохие люди. А бывают и хорошие.
>занимаются актуальной и сверхсовременной(тм) математикой, и те, кто задрачиваются всю жизнь по проблеме Борсука, и какие-нибудь шизики, чья жизненная мечта построить "правильную теорию множеств"
Они абсолютно равноценны.
>Для матанализа они и не нужны
Немного странная позиция. Зачем что-то оценивать по нужности для матанализа? Матанализ не самоценен, вовсе нет. Напротив, это необходимость изучать матанализ должна быть обоснована. Студент учится, чтобы стать учёным - читать и писать научные статьи. Зачем студенту нужен матанализ?
Назови. И в каком смысле "сидит"?
> что для нормального функционирования математического здания нужны и те, кто на подсосе у Великих
Ну и хуйли с того? Для нормального функционирования еще и мусорщики нужны и чистильщики сортиров.
Есть граф, в котором вершины раскрашены в какие-то цвета. Каждому цвету c поставим в соответствие целое t[c]. Перекрашивание вершины v из c1 в c2 происходит следующим образом:
1) Если t[c1] = 0, такая перекраска невозможна.
2) Если t[c1] = 1 и после перекраски будет существовать ребро, у которого оба конца имеют цвет c1, такая перекраска невозможна.
2) v перекрашивается из c1 в c2.
3) t[c1] уменьшается на 1.
4) t[c2] увеличивается на 1.
Есть простой (без петель и кратных ребер) неориентированный граф, все вершины которого покрашены в 1, t[1] = 2, t[2] = 0. Нужно научиться за полиномиальное от количества вершин в графе время определять, можно ли перекрасить все вершины в цвет 2 по описанным выше правилам.
Собственно, эта задача - обобщение задачи о волке, козе и капусте, которых надо переправить на другой берег так, чтобы никто никого не съел. Только животных здесь много и перевозчика 2; один их них может перевозить, а другой следить за животными на берегу.
Графьям не гоже превозкой скота и снеди заниматся. Пшел отсюда, смерд.
Я нормально сформулировал задачу. Последний абзац - это не условие. Так что не выебывайся.
Но ведь граф это исходное понятие, у маклейна через него категории определяются, вы их любите.
Формулировка в начале непонятна вообще. Почему нельзя три раза подряд перевезти с первого на второй бере, если ничего плохого не происходит? Где там второй перевозчик?
Задача же про перевозчика тривиальна, так как почти всегда нельзя. Граф вражды должен быть почти пустым, так как на береге без перевозчика он должен быть пустым, а за раз перевозим не более двух. Так что с одним перевозчиком получается граф, в котором все ребра соединены с одной из двух фиксированных вершин. Если два перевозчика (один из которых может только следить), то видимо что-то в стиле двудольного плюс две вершины.
Ну хуй знает, попробуй Френкеля, Основания теории множеств. Так есть разборы старых теорий.
Прости, я может быть туплю, но я не понимаю, как можно доказать теорему Банаха-Тарского без аксиомы выбора. Можешь простыми словами разъяснить?
> то видимо что-то в стиле двудольного плюс две вершины.
Да, это ответ. Ну не совсем ответ конечно. По идее надо доказать, что граф двудольный без двух вершин <=> граф можно перекрасить таким образом. Но вообще это правильно.
Example.
Я чет проебался. Забыл, что помимо перекраски можно для любого с1 такого, что t[c1] >= 1 и любого с2 сделать следующее:
1) уменьшить t[c1] на 1;
2) увеличить t[c2] на 1.
Просто хотел нормально задачу сформулировать, а не в терминах козы и капусты, но чет не очень получилось.
Если в аксиоматике теории множеств (скажем, в ZFC) аксиому пустого множества заменить на противоположную ей (любому множеству принадлежит хотя бы один элемент), будет ли такая аксиоматика непротиворечива? Какие примечательные утверждения, аналогичные утверждениям теории множеств, будут в ней выводимы, а какие - нет?

Любое построение вещественных чисел должно быть эквивалентно остальным построениям (в которых 0,(9) вполне существует. То, что 0,(9) не строится по Зоричу я не увидел, может тупой сильно.


Что означает algebra в топологии? То и означает, алгебру?
>будет ли такая аксиоматика непротиворечива?
Нет.
Пусть M - множество.
Положим P(x) как x != x и воспользуемся схемой выделения, применив P(x) к M. Получим пустое множество, что противоречит аксиоме.
Кстати, аксиома пустого множества вытекает из аксиомы существования бесконечного множества и схемы выделения.
А что будет, если убрать схему выделения? Потому что это выглядит как чит в данном случае.
Умрёт понятие "подмножество".
Да здесь же просто дрочеры википедии сидят, а не математики. Кстати, кого сегодня обоссываем, господа?
Историков.
> к нестандартному анализу
Без задач.
Успенского "Что такое нестандартный анализ" читни. Ну или там "Прикладной нестандартный анализ" Дэвиса.
Определение предела, ты имел в виду, наверное.
Бесконечность особый случай. Предел в точке a равен + бесконечности, если для любого M > 0 найдется такая окрестность а, что для всех x в этой окрестности f(x) > M. В случае - бесконечности предел определяется аналогично.
Книги
Я его не читал, но я тоже так считаю. Чтобы читать и различать символы между собой, нам нужны конечные строки. Работая с конечными строками, мы используем натуральные числа.
Ты про лекции фрика Босса, в которых упоминается Господь Боженька?
Илитизм в исполнении несведующего школьника в такой достопочтенной тематике как /sci/ выглядит уморительно и нисколько не обидно. Таким эффективнее в би заниматься.
Помогите решить пример, пожалуйста. В интернете ничего не нашел:
Линейный оператор f: V3->V3 в базисе (i,j,k) имеет матрицу А.
Описать геометрический смысл оператора, если задана А.
В данном случае A - единичная матрица.
Оператор оставляет все точки пространства на месте. Это тождественное преобразование пространства, ни одна точка не двигается.
Спасибо!
Я правильно понимаю, что тогда оператор с матрицой
(1)(0) (0)
(0)(-1)(0)
(0)(0) (-1)
инвертирует j и k, оставляя i на месте?
Еще раз спасибо, все понятно.
можно ли разделить плоскость с двумя выколотыми точками на непересекающиеся окружности? Ни одна окружность не может проходить через выколотую точку.
Чому без задач? Разве такой подход не упрощает многое?
Нет. Без аксиомы выбора нельзя даже доказать, что любое бесконечное множество содержит счётное подмножество.
Стоит ли ставить все деньги или по одной копейке, если количество денег прямо влияет на шанс выиграша? Например, одна копейка дает шанс выигрыша половину процента, две копейки процент, двадцать копеек десять процентов и так до сотки.
Сразу скажу что до сотки доводить шансы не выгодно, выигрыш маленький.
Без размера выигрыша дискуссия не имеет смысла. Сформулируй задачу в математических терминах.
Допустим выигрыш две копейки, с шансом на сто копеек.
Я вообще мимо проходил и решил спросить, так что не могу в термины.
>так что не могу в термины.
Здесь не телепаты сидят, поэтому если хочешь получить ответ - придётся учиться.
Допустим ты ставишь ставку A.
Каков будет выигрышь и какова будет вероятность выигрыша если выражать его/её через A?
Вообще я сейчас полистал второй том - задачки довольно интересные.
Здорово у етбя получается. А когда -бесконечность, f(x) разве не должна быть меньше M?
Есть что нибудь по мат физике для уравнения теплопроводности, где для дубоватых ребят разжаловано все что то можно и нельзя.
С аналитическим решением и численым явным.
Ну я же написал что в минус бесконечности определяется аналогично, то есть тебе нужно просто немного подправить определение. Очевидно, что да, должна быть меньше.
Пусть R - кольцо, I - идеал, a и b - элементы R.
I прост <=> если ab принадлежит I, то a принадлежит I или b принадлежит I.
Причём I не равно R.
>если ab принадлежит I, то a принадлежит I или b принадлежит I
Как из этого условия следует, что факторкольцо по такому идеалу не имеет делителей нуля? Может ли в каких-то случаях оказаться, что произведение элементов a и b, не принадлежащих идеалу, принадлежит идеалу? Как это объяснить?
>>315568
Фактор кольцо по простому идеалу не поле, это область целостности.
Поле это фактор по максимальному идеалу. Любое поле - область целостности, поэтому любой максимальный идеал - простой, но не наоборот.
Вообще, все эти фактормемчики правильно себе представлять так: если ты факторизуешь по идеалу/нормальной подгруппе/подмодулю/etc, заданному каким-то выражениями, то ты по сути строишь новый объект, где у тебя есть дополнительные соотношения между элементами, а именно, эти выражения, участвующие в идеалах - ноль (ну или единица, если мы говорим о группах - нейтральный элемент короч).
Поэтому простота идеала "если ab принадлежит I, то a принадлежит I или b принадлежит I" означает "если выражение ab равно нулю, то либо a = 0 либо b = 0" что и означает по определению, что делителей нуля нет. Конечно, это всё доказывается строго с нудным расставление чёрточек над буквами, но суть в этом.
Множество всех окружностей нулевого радиуса с центрами в каждой точке покрываемого пространства.
Не думал, что есть кто-то настолько тупой, что он не догадается, что точка не считается окружностью в этой задаче, и что надо это явно прописывать.
Пусть I - такой идеал в кольце R. Нуль кольца R обозначим как 0.
Введём отношение эквивалентности ~ следующим образом.
Пусть a и b - элементы R. a~b, если a-b ∈ I.
Это действительно отношение эквивалентности.
Поэтому оно разбивает R на классы эквивалентности.
Далее докажем, что класс эквивалентности нуля равен I.
Известно, что 0 ∈ I, так как I - идеал.
Пусть x ∈ I. Тогда x = x-0, то есть x-0 ∈ I, то есть x~0.
Пусть x~0. Тогда x-0 ∈ I, то есть x ∈ I.
Напомню некоторые свойства факторкольца по идеалу.
Факторкольцо состоит из классов эквивалентности.
Класс эквивалентности элемента x обозначим как [x].
Будем говорить, что x является представителем класса [x].
[a] = тогда и только тогда, когда a~b.
Операции в факторкольце сводятся к операциям в R над представителями классов.
Нулём факторкольца служит класс эквивалентности нуля [0].
По ранее доказанному, I = [0].
Докажем, что в факторкольце по I нет делителей нуля.
Предположим, [a] = [0].
По определению умножения, [a] = [ab], то есть [ab] = [0].
По определению равенства классов, ab~0.
Так как [0] = I, ab ∈ I.
Значит, a ∈ I или b ∈ I, то есть [a] = [0] или = [0].
Что и требовалось доказать.
Пусть I - такой идеал в кольце R. Нуль кольца R обозначим как 0.
Введём отношение эквивалентности ~ следующим образом.
Пусть a и b - элементы R. a~b, если a-b ∈ I.
Это действительно отношение эквивалентности.
Поэтому оно разбивает R на классы эквивалентности.
Далее докажем, что класс эквивалентности нуля равен I.
Известно, что 0 ∈ I, так как I - идеал.
Пусть x ∈ I. Тогда x = x-0, то есть x-0 ∈ I, то есть x~0.
Пусть x~0. Тогда x-0 ∈ I, то есть x ∈ I.
Напомню некоторые свойства факторкольца по идеалу.
Факторкольцо состоит из классов эквивалентности.
Класс эквивалентности элемента x обозначим как [x].
Будем говорить, что x является представителем класса [x].
[a] = тогда и только тогда, когда a~b.
Операции в факторкольце сводятся к операциям в R над представителями классов.
Нулём факторкольца служит класс эквивалентности нуля [0].
По ранее доказанному, I = [0].
Докажем, что в факторкольце по I нет делителей нуля.
Предположим, [a] = [0].
По определению умножения, [a] = [ab], то есть [ab] = [0].
По определению равенства классов, ab~0.
Так как [0] = I, ab ∈ I.
Значит, a ∈ I или b ∈ I, то есть [a] = [0] или = [0].
Что и требовалось доказать.
Нет, не буду. Если ты даже условие не в состоянии понять, то как ты задачу решишь?
Гильберта на тебя нету, интуицист проклятый.
Ну или хотя бы дайте определение алгебры, заданной образующими и соотношениями.
Пусть M - множество конечных последовательностей десятичных цифр. Например, 001 ∈ M, 99231 ∈ M.
Назовём бесконечную последовательность десятичных цифр w последовательностью Борхеса, если для любого m∈M верно, что m является подпоследовательностью w.
Существует ли хоть одна последовательность Борхеса?
Всякий элемент M можно считать числом в одиннадцатеричной системе счисления (не в десятеричной, чтобы сохранить ведущие нули). Поэтому M счётно.
Для всякого элемента m∈M определено натуральное число l(m) - его длина.
Пусть f - биекция между ℕ и M.
Построим вспомогательную последовательность g(n) таким образом.
g(0) = 0,
g(n) = g(n-1) + l(f(n)), если n>0.
Теперь легко построить последовательность h такую, что подпоследовательность f(i) стоит в ней на месте, начинающемся номером g(i).
Последовательность h и будет нужной нам вавилонской библиотекой.
Тащемта никаких особых секретов тут и нет. Просто берешь и без задней мысли строишь последовательность. Может ты имел в виду, что нужно явным образом построить последовательность, то есть иметь возможность вычислить, какая цифра у нее стоит на n-й позиции?
Можно взять пространство образующих, равную самой алгебре. Кстати, если эта алгебра конечна, то порожденная ей тензорная алгебра тоже конечна, так как ее базис состоит из всех возможных мономов исходного базиса. Но что делать с пространством соотношений?
Пару дней уже не могу решить.
N-петух, перестань семёнить.
Каждый день я хожу с большим черным мешком по земле и собираю натуральные числа. На два полных мешка уходит целый день. Но когда я прихожу домой и сваливаю свое богатство в ванную.... Ммммм....
>Во что переходит вращение треугольника на 120
при всевозможных внутренних автоморфизмах группы
симметрий треугольника?
При автоморфизмах, порожденных отражениями, у меня получился переход во все другие отражения. Но при автоморфизме, порожденном одним поворотом на 120 градусов получился переход в тот же поворот. При автоморфизме, порожденном другим поворотом, получился переход в отражение. Я где-то ошибся, или просто не надо было рассматривать автоморфизмы, порожденные поворотами?


https://www.youtube.com/watch?v=GfUKL30pG08
При автоморфизме, порождённом поворотом, поворот должен перейти в поворот. Это же просто последовательность поворотов туда крутишь, сюда. Вообще, каждый поворот по идее и должен в себя переходить.
Ну он же объясняет в видео.
Mean - это средневзвешенное, считается как ты показал.
Median - это значение, которое меньше ровно половины всех элементов выборки.
Можно ли понимать под тензорным произведением факторпространство прямого произведения по некоторому пространству? Какому?
Какие из перечисленных пространств изоморфны между собой V⊕V, V⊗V, V×V?
>меньше ровно половины
Тут ответ 26. А он больше 40 равен 50 и меньше 80 элементов выборки. А половина выборки это 85 элементов. Значит такого элемента нет.
Если есть повторяющиеся элементы выборки - то просто берешь среддний из отсортированного списка элементов выборки.
Это используется потому что медиана в отличии от меаны оценка стабильная. Т.е. если у тебя будет выборка из 100 элементов, 99 из них будут иметь значения из множества [-1,0,1] и один элемент будет иметь значение допустим 10000 - то среднее будет сильно смещено, а медиана будет как раз где-то в этом множестве. Таким образом сатисты борятся с выбивающимися значениями (полученными, к примеру, по ошибке, из-за сбоя оборудования или чего еще).
Всё понятно. Спасибо.
Двачую вопрос
В книги Прасолова элементы теории гомологий более сотни задач.
Накастовал тебе в ротик своих дум.
Насовал в твою мамашку своего ТЕЛА
В общем случае в completely regular пространстве Y пространства C(Y) и C(Y; c) - это distinct joint topological invariants of Y and E.
Я не знаю, что такое completely regular и distinct joint topological invariants, но думаю тебе уже должен стать понятен смысл.
Анон, я знаю, как перевести всю фразу, кроме того, что я подчеркнул: distinct joint topological invariants. Мне понятно каждое слово по отдельности, и даже попарно, но у этого словосочетания есть какой то математический смысл, потому и написал сюда, надеясь на то, что придёт анон-математик и спасёт меня. Весь остальной текст просто для того, чтобы был виден контекст фразы.
для не математика --- да.
Есть кайнда общий методологический принцип такой: любой "образовательный" курс в модных нынче на западе интернет-школках от молодых-шутливых-прогрессивных говно на уровне научпопа для 11классников. По крайней мере по математике и более-менее классическим наукам, может своей бизнес-хуите они и нормально учат, не знаю.
Но в оп-посте написано:
" Как побочный эффект, отпадает всякая необходимость в аксиоме выбора, лемме Цорна и им подобных."
Для конечного произведения суммы двух пространств - ничем. Для бесконечного - отличаютя. Грубо говоря, сумма векторных V_i пространств - это все такие строки того же размера, что и количество слагаемых в сумме такие, что на i-ом пространстве стоит элемент из V_i и на почти всех (кроме конечного числа) местах стоят нули. Произведение - то же самое, но требование, чтобы на почти всех местах стояли нули уже не нужно.
>>315706
>Можно ли понимать под тензорным произведением факторпространство прямого произведения по некоторому пространству? Какому?
>Можно ли понимать под тензорным произведением факторпространство прямого произведения по некоторому пространству? Какому?
Нельзя. Тупо по размерностям не подходит.
>Какие из перечисленных пространств изоморфны между собой V⊕V, V⊗V, V×V?
V⊕V и V×V
Она отпадает только локально, в конкретно этом разделе общей топологии.
И к чему ты это кукарекнул, ммм, уёба?

Вроде разобрался.
По поводу второго вопроса: вот, что написано у Миши в листочках по алгебре. Интересное определение. Я так понял, что это из теории представлений и связано с заданием алгебры с помощью образующих и соотношений. Пространство образующих --- прямое произведение. Пространство соотношений --- пространство, порожденное соотношениями линейности.
Кстати, никто не хочет со мной порешать эти листочки до января?
Ошибся, пространство образующих свободно порождено парами из сомножителей прямого произведения (т.е. суммой произведений конечного числа элементов пары).
Я не понял, что такое пространство образующих и что такое пространство соотношений, впервые в жизни слышу эти слова в таком порядке.
Векторное пространство, свободно порождённое парами векторов из пространств V,W - это не то же самое, что и произведение векторных пространств. Там значок "х" между V и W понимается не как произведение векторных пространств, а как декартовое произведение множеств (которое никакого отношения не имеет к произведению векторных пространств), а значок < S >, где S - любое множество, понимается как векторное пространство с базисом S.
Миша как всегда сверхаккуратен в формулировках.
Ну как хочешь. Если хоть капелька обучаемости есть - на таком уровне и на уровне стандартной программы вуза всегда эффективнее читать книжки самому, а вопрошать насчёт непонятного где-то в интернетике.
Я опять запутался. Чем отличается декартово произведение от прямого произведения для векторных пространств?
Да верно он вс в общем понял же, не путай нюфага.
Тензорное произведение - это фактор типа декартового точнее свободно-порождённого им векторного пространства по тем соотношениям.
Декартово произведение AxB - это вообще нечто такое, что не сохраняет структуру векторных пространств, то есть это тупо операция на множествах. Собственно, это просто множество пар. (a,b) где a \in A, b \in B.
Произведение векторных пространств VxW - это множества пар вида (v,w) где v \in V, w \in W. С покоординатными операциями:
(a,b)+(c,d) = (a+c,b+d), lambda(a,b) = (lambda a, lambda b). То есть это векторное пространство тоже.
Если S - любое множество без структуры, то множество комплекснозначных функций на S, принимающих ноль почти во всех, кроме конечного числа, точек - это векторное пространство <S> с базисом S. В терминах Миши - свободно порождённое элементами множества S пространство.
Теперь понятно в чём отличие векторного пространства с базисом V x W (в смысле декартового произведения), или, в терминах Миши, свободно порождённого парами (v,w) \in VxW пространства, от произведения векторных пространств. Например, в произведении векторных пространств есть равенство (a,b)+(c,d)= (a+c,b+d) а в векторном пространстве с базисом V x W (в смысле декартового произведения) - такого равенства нет. (a+c,b+d), (a,b), (c,d) - элементы не связанные никакой структурой. Отфакторизовав это пространство по нужному идеалу мы можем получить тензорное произведение.
Судя по вопросу
>Я опять запутался. Чем отличается декартово произведение от прямого произведения для векторных пространств?
понял не совсем верно.
Спасибо.
В жизни ни разу ничего не доказывал. Не понимаю даже принципа как это делается.
а тут какая-то хрень, какие-то многообразия, шо и несет https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%A1%D1%82%D0%BE%D0%BA%D1%81%D0%B0
Та, что ты считаешь нормальной, рассчитана на студентов технических специальностей, не собирающихся изучать математику, ну или физиков конца позапрошлого века.
А как же конкретно отфакторизуем? Какое там отношение эквивалентности?
Чтобы начать ничего особого не нужно, просто интерес и желание докопаться. Мне (не всегда но все же) хватает для решения элементарных задач где надо доказать утверждение.
Попробуй начать с детских книжек. Реймонд Смаллиан (принцесса или тигр итп) например.
А как же доказательства "Пускай ... , то ..."?
Как научится то? Если я просто буду перечитывать теорему, то вряд ли мне что-то вдруг на ум придет.
Начни действительно с книг Саллмана "Как же называется эта книга", "Принцесса или тигр" и такое всё, а там, возможно, самому станет понятно.
>Докажите, что в коммутативной группе всякая подгруппа является нормальной подгруппой.
По определениям получилось, что если a - элемент подгруппы N, то gag^{-1} = gg^{-1}a = a. То есть внутренние автоморфизмы оставляют элементы нормальной подгруппы неподвижными?
У меня в примере получилось, что N - подгруппа вращений треугольника, то автоморфизмы, порожденные вращениями, оставляют неподвижными другие вращения, но автоморфизмы, порожденные отражениями, уже могут переводить одно вращение в другое.
Судя по тому, что формально из a при отображении всегда получается a, этого быть не должно.
>Читайте, дети, Хартсхорна
Хм, сегодня в автобусе его читал, а пару дней назад обсуждал с преподавательницей. Изучение только систем уравнений это как-то кисло для дисциплины такого уровня.
>Изучение только систем уравнений это как-то кисло для дисциплины такого уровня.
Какое-то странное утверждение. Если дисциплина "такого уровня" и разрослась из "систем уравнений", то что значит "кисло"? Значит системы уравнений отнюдь не так просты, как тебе кажется.
Ничего не понимаю в алгебраической геометрии, но из обрывков информации, которые я имею у меня сложилось впечатление, что она гораздо глубже, нежели просто "методы для решения полиномиальных уравнений". Скорее, если мыслить себе геометрию, порождаемую функциями C^{(0)} как "обычную (метрическую, риманову) геометрию", геометрию, порождаемую функциями C^{(\infty)} как "дифференциальную геометрию", множество линейных функций - как "линейную геометрию", то алгебраической геометрии бы соответствовала алгебра полиномов. И правильно смотреть на неё как на изучение "полиномиальных объектов" вообще, точно так же как дифференциальная геометрия изучает "объекты со структурой дифференцирования" а линейная геометрия изучает "линейные объекты".
Почему умножение одной трети на одну треть дает одну девятую, а ту же треть делить на треть дает единицу? Ведь треть от трети это будет как раз одна девятая.
Определение. Произведение дроби a/b и дроби c/d есть дробь ac/bd. Точка.
В /un/
Если есть некоторый многочлен от линейного оператора на V, т. е. оператор вида
anTn + ... + a2T2 + a1T + a01V,
где 1V - тождественное преобразование V, то его можно разложить на множители как многочлен. Почему так?
В статье на википедии написано, что вместо поля кольцо многочленов можно опредлить над любым коммутативным кольцом. Меня смущает то, что композиция линейных операторов не коммутативна.
Алсо, я пока что не проходил кольца и все такое, только линейную алгебру. Без этих знаний можно понять ответ на вопрос или стоит временно принять это дело на веру?
Нет ни одной причины там сидеть, ничего интересного там не происходит. Тут вопросы интересней.
когда ты умножаешь 2 на 3, ты берешь двойку 3 раза
когда ты умножаешь 1/3 на себя, ты "берешь 1/3" 1/3 раз, получается 1/9
когда делишь, ты считаешь сколько раз 1/3 уместится в 1/3
примерно так должны в младших классах объяснять
помню там кто-то ловера советовал по теоркату, очень хорошая книжка
длинная только больно, функторы только в середине книги
как раз математик был работающий вроде (arxiv читал и все такое)
a_i это элементы поля или тоже линейные операторы?
Если первое то
> композиция линейных операторов не коммутативна
это конечно так, но композиция оператора самого с собой (и, следовательно, любой свое степени с любой степенью) очень даже коммутативна, это следствие ассоциативности на самом деле. Соответственно кольцо таких полиномов это просто некий фактор обычного кольца полиномов.
Нас тралят и смеются с нас.
Я его как-то рекомендовал, потом почитал Гельфанда, Манина - рекомендую его (там нет леммы Ионеды, но про нее можно в вики прочесть).
Давайте добавим в пасту книги, от которых надо предостеречь ньюфагов. Я начну:
1) Демидович
2) Кнут, Конкретная математика
Эти книги особенно опасны тем, что их искусственная сложность может создать иллюзию, что они нужны, и что если не получается вычислить интеграл от 1 переменной, то чем-то более современным заниматься точно не получится.
>Эти книги особенно опасны тем, что их искусственная сложность может создать иллюзию, что они нужны, и что если не получается вычислить интеграл от 1 переменной, то чем-то более современным заниматься точно не получится
Двачую этого. Интегралы брал в 9 классе и даже по просьбе решил на 5 контрольную какой-то 40-летней тетке в вечерней школе в далеком 2008. Когда я туда пришел, никто даже ничего не заподозрил и не спросили документы о том, учусь ли я там или нет.
Ну если кто-то не может понять и научиться применять довольно простой материал, разжеванный везде где только можно, то современная математика действительно не для него.
>Демидович
Кто-то похуй. Матан и есть матан.
>Кнут, Конкретная математика
Да. Кнут вреден и не нужен.
Зависит от того, сколько раз я мог бы ответитить и от конечного количества возможных вариантов ответа.
Я программист и ненавижу Конкретную математику. Задачи там нормальные, но текст читать абсолютно невозможно. Стиль повествования у него просто невыносимый, этакая смесь художественной и технической литературы. К тому же он концентрирует внимание не на природе вещей, а на трюках типа "вот сюда подставим, здесь сделаем вот такую замену, тут домножим".
Просто программисты - дауны с комплексом быдлокодера, который они сами культивируют в своей среде. Я, например, охуительно понял сортировку merge sort из книги Анания Левитина, а от Кнута проблевался.
Очень много где в настоящей математике доказательства "трюковые" в той или иной степени. Доказательства в 2.5 строчки или доказательства, получающиеся "шевелением мизинца", зачастую, чистая удача.
> Насколько вы хорошие математики, кстати, чтобы советовать, что нужно математику, а что нет?
Ну паста не претендует на правильность, это просто мнение.
FAQ, я считаю, надо запилить, потому что есть вопросы, которые повторяются из треда в тред. Вот че я написал: http://pastebin.com/8Sna4WYn
Скажем, что существует непустое множество S, элементы которого называются осмысленными формулировками.
Скажем, что существует непустое множество A, элементы которого называются возможными ответами.
Вопросом Mes называется следующий набор данных.
1. Непустое конечное множество M, являющееся подмножеством A, элементы которого называются вариантами ответа
Положим, что на M введено отношение линейного порядка.
2. Точка e∈M, называемая правильным ответом
3. Точка s∈S, называемая формулировкой вопроса
Рассмотрим класс Q вопросов.
Рассмотрим функцию ans: Q → A, которая каждому вопросу Mes сопоставляет его правильный ответ e.
Рассмотрим функцию quiz: Q → 2A×S, которая каждому вопросу Mes сопоставляет пару Ms, то есть (варианты ответа, формулировка).
Функцию f: 2A×S → A такую, что f∘quiz = ans, мы будем называть рациональным агентом.
Классы вопросов, для которых существует рациональный агент, будем называть правильно построенными вопросами.
Пусть на картинке написан правильно построенный вопрос.
Тогда один из четырёх вариантов ответа является правильным ответом, и существует рациональный агент, отвечающий на этот вопрос по его формулировке s.
Существование такого рационального агента, однако, противоречит аксиоме фундирования, так как из формулировки следует, что он должен быть своим (наследственным) элементом. Поэтому предположение, что на картинке правильно построенный вопрос, противоречит ZFC. ZFC - единственный инструмент, которым я располагаю. Поэтому у меня нет техники, с помощью которой можно изучать этот рациональный агент.
>Очень много где в настоящей математике доказательства "трюковые" в той или иной степени. Доказательства в 2.5 строчки или доказательства, получающиеся "шевелением мизинца", зачастую, чистая удача.
Хотя это правда зачастую так, но это недоработки. Если какая-то область понята по-настоящему хорошо, то в ней нет места трюкам - содержательные идеи оказываются отражены в определениях, доказательства же проводятся естественным и ожидаемым образом.
мимо-гротендик
>ZFC - единственный инструмент, которым я располагаю.
https://en.wikipedia.org/wiki/Aczel's_anti-foundation_axiom
Просвещайся.
>общая топология
Доказательство леммы Урысона нетрюковое? То есть конструкция той непрерывной функции, разделяющей два замкнутых множества - каждый, кто об этом думал, придумал сам?
>теория категорий
Там вообще все доказательства дико трюковые, из-за чего у меня бомбит немерянно. Взять ту же эквивалентность определений adjoint функтора. Или, из простого, доказательство того, что два базиса одного и того же объекта имеют одинаковую мощность - ебался n часов с ним.
Вполне возможно, что просто я тупой, конечно (а я действительно тупой).
Мне он не нравится. То, что геометрическая прогрессия - это-то конечно правильно, но это куда более мощное средство, и вполне резонно задать вопрос: а почему сумма бесконечной геометрической прогрессии именно такая? Тут, мне кажется, гораздо резоннее пояснить человеку, что 0.(9) и 1.0 - это просто кодирования вещественных чисел, а не сами эти числа. И при построении этого кодирования мы сами же кодируем одно и то же число дробями 0.(9) и 1.0 и истинная причина почему так получается, потому что мы сами же и определили вещественные числа как нечто такое, в чём нету бесконечно малых (аксиома Архимеда) а если бы 0.(9) и 1.0 кодировали разные числа, то 1.0 - 0.(9) нам сразу бы дало это самое "бесконечно малое" число.
То же самое с 1+2+3+... не объяснен смысл и мотивировки этих определений.
Школогайд вроде норм, хотя не знаю, осилил бы я его будучи человеком, ничего не понимающим в математике.
>Доказательство леммы Урысона нетрюковое?
Да, оно естественным образом восстанавливается из формулировки. По крайней мере я, прямо сейчас, не помня доказательства, за несколько минут его восстановил. Дело в том, что доказательства всех базовых теорем (я разумеется говорил только о них) это просто комбинации нескольких тривиальные манипуляций с данными понятими, основанных непосредственно на определениях.
>каждый, кто об этом думал, придумал сам?
Конечно нет - нужен некоторый уровень математической культуры. Сложно представить ситуацию, когда человек освоил общую топологию, а потом, хотя может вспомнить доказательства большинства классических результатов, не может вспомнить доказательство леммы Урысона.
В теории категорий временами часто возникают несколько тяжеловесные конструкции, но там нигде, из того с чем я знаком (примерно половина Маклейна и, на всякий случай, с общим понятием базиса я не знаком) для доказательств не нужны какие-то оригинальные идеи, всегда достаточно лишь тщательного анализа условия (да, это может требовать времени, я, например, пол дня провозился с леммой Йонеды).
Невозможно объяснить, чему равна какая-то бесконечная последовательность, не используя понятия предела. А когда ты знаешь определение определа, определить сумму ряда и вывести формулу для геометрической прогрессии очень просто. Формула выводится следующим образом.
Используем школьную формулу для an - bn (можно найти здесь http://math.stackexchange.com/questions/11618/algebraic-identity-an-bn-a-b-sum-limits-k-0n-1-akbn-1-k ).
Дальше
sum q^k от 0 до n = (1 - q^{n + 1}) / (1 - q) (по предыдущей формуле)
Предел этой суммы при n -> \infty равен 1 / (1 - q).
> Тут, мне кажется, гораздо резоннее пояснить человеку, что 0.(9) и 1.0 - это просто кодирования вещественных чисел, а не сами эти числа. И при построении этого кодирования мы сами же кодируем одно и то же число дробями 0.(9) и 1.0 и истинная причина почему так получается, потому что мы сами же и определили вещественные числа как нечто такое, в чём нету бесконечно малых (аксиома Архимеда) а если бы 0.(9) и 1.0 кодировали разные числа, то 1.0 - 0.(9) нам сразу бы дало это самое "бесконечно малое" число.
По-моему, это сильно путано и неконкретно.
> То же самое с 1+2+3+... не объяснен смысл и мотивировки этих определений.
Ну я сам не знаю, какой смысл работать с "суммами" расходящихся рядов. Просто этот вопрос всплывает постоянно и он уже заебал.
Забыл добавить: то, что нужно посчитать сумму ряда, следует напрямую из определения позиционной системы счисления. А системы счисления в школе проходят на информатике.
Верно.
алсо x>y <=> y<x, так что твой вопрос это "x>y => x=y", что неверно.
Алсо, чем учебник Зорича лучше Садовничего-Сендова?
Теорема Нёбелинга—Понтрягина: всякое нормальное пространство $X$ со счётной базой размерности $\dim X=n$ гомеоморфно подмножеству пространства $\mathbb R^{2n+1}$.
>Алсо, чем учебник Зорича лучше Садовничего-Сендова?
Второй учебник не смотрел, но из общих соображений: Зорич - не даун, а вот насчёт Садовничего большие сомнения.
Побуду капитаном. Любые два векторных пространства одинаковой конечной размерности n над одним и тем же полем изоморфны. В частности, n-мерное пространство над R изоморфно Rn.
Есть теорема о существование борелевского изоморфизма между любыми несчётными польскими пространствами (в частности, такими являются все $\mathbb{R}^n$).
Яро вдругорядь реку я: учитнитесеся об Камынина. Камынин весьми красив статен толст.
>вот это интересно, можно подробнее?
Чуть подробнее. Можно интересоваться не собственно топологией, а борелевскими сигма алгебрами, которые из неё получаются (наименьшее семейство подмножеств пространства, содержащее все открытые и замкнутое относительно операций дополнения и объединения счётных семейств). Оказывается, что несмотря на разнообразие топологий, для большой класс пространств является борелевски изоморфными (т.е. существую биекции такие, что образы и прообразы борелевских множеств борелевские). Подробнее написано, например, здесь http://ncatlab.org/nlab/show/Polish+space
Я думаю, надо для каждого диаметра найти эту вероятность и проинтегрировать по полуокружности. То есть проведем диаметр под углом alpha. Вероятность того, что все точки будут по первую сторону от диаметра равна (1/2)^n. По вторую сторону тоже. Чтобы получить искомую вероятность надо как-то проинтегрировать.
То есть получается что-то типа интеграла (1/2)^(n-1) d alpha от 0 до pi.
Я не уверен в подробностях, потому что я дебил-погромист. Че гуглить, чтобы научиться это решать и строго объяснять решение?
СУУУУКАААА. Как же долго я ебался с этой формулой. Спасибо, наукач, ты как всегда выручаешь в сложный момент.
Когда я слушал курс по терверу, нам препод эту шутку рассказал 8435767389678 раз и она даже в 1 раз не была смешной.

http://www.gap-system.org/Manuals/pkg/guava3.11/doc/chap5.html#X857EFE567C05C981
Кто-то занимался в этой системе? Каким образом можно разобраться в причине ошибки и пофиксить код?
В релизах только четвертая версия. http://www.gap-system.org/Releases/index.html
Спасибо за интересную задачу, ебался с ней пару часов. Пробовал и через условные вероятности, но самое простое в итоге - через вариационный ряд.
Пусть X_1,X_2,...,X_n - независимые равномерно распределённые на [0,1]
Тогда X_(1),X_(2),...,X_(n) - их вариационный ряд
Событие, когда все точки лежат на в одной полуокружности, это такое событие, когда
max( X_(2)-X_(1), X_(3)-X_(2), ..., X_(n)-X_(n-1), 1+X_(1)-X(n) ) >= 1/2
По-моему и не должна зависеть. Но я условие не читал.
тащемта щас попробовал решить через условные вероятности, какая-то хуита получается реккурентная.
xi_k - длина минимального куска окружности, соединяющего все точки X1,...,Xk (с нормировкой 1)
Тогда
Prob( xi_{k+1} <= t | \xi_k ) = 1{ \xi_k <= t } (2t - \xi_k)
Поэтому
Prob( xi_{k+1} <= t ) = \int_0^t (2t-x) dF_k(x)
хер знает, как отсюда в общем виде решение вывести.
Петух здесь только один.
Пусть S - линейный оператор на конечномерном пространстве V с положительно определенным скалярным произведением <, >. Нужно доказать, что если S - изометрия, то SжS = idV, где Sж - сопряженный к S оператор. Уже известен тот факт, что если S - изометрия, то <Su, Sv> = <u, v> для любых u, v из V.
Вот доказательство из учебника:
Для любых u, v:
<(SжS - idV)u, v> = <(SжS)u, v> - <u, v> = <Su, Sv> - <u, v> = 0.
Тогда
<(SжS - idV)u, (SжS - idV)u> = ||(SжS - idV)u||2 = 0
для любых u, то есть SжS - idV = 0.
Я тоже доказал это утверждене, перед тем как прочитать доказательство в учебнике, но мое доказательство заметно длиннее. Как научиться такие пиздатые трюки делать? Как конкретно можно было догадаться, что нужно рассмотреть <(SжS - idV)u, v>?. Вообще в алгебре я очень часто такие трюки вижу.
Смекалочка
Зачем какие-то id-ы.
<S-star S u, v> = (определение сопряженного оператора) <S u, S v> = (определение изометрии) <u,v>
Если для всех u,v <Au,v> = <Bu,v> то A=B, следовательно S-star S = Id.

А, ну я проебался, не всю ситуацию рассказал. Изометрия в книге определяется как отображение, которое сохраняет норму, есть теорема пикрелейтед и она доказывается так:
a => b => c => d => e => a.
То есть это автор так доказывал b => c (как будто он не знает, что b => a).
Согласен, что намного удобнее заметить, что b => a (это вообще очевидно) и применить рассуждения
>>316759
Просто, видимо, автор захотел выебнуться хитрым трюком.

>имеет в этой окрестности производные до (n−1) порядка включительно
Вот как определить, производную до какого порядка имеет функция?
Берёшь и без задней мысли дифференцируешь, пока получается. Главное - не забыть перед этим накатить картофана.
Ну вот, а если функция имеет производные до n-го порядка в точке, то она имеет производную производной производной ... (n раз) ... производной.

к=1

Математики, извините, если спрашиваю слишком много, но у меня пикрилейтед.
Я пролежал приличную долю семестра в больничке и теперь пытаюсь нагнать упущенное, однако осилить Фурье не могу. Четвёртое задание я сам решил, но мне нужно его как-то проверить, а для этого мне нужен чужое решение, чтобы их сравнить.
Помогите плиз, желательно чтобы Фурье был с объяснением действий, чтобы было легче разобраться.
Спроси на math.hashcode
Прямо напиши в общих чертах что ты уже решил и спроси правильно ли, и как вообще решать следующий
Чтобы аккуратно писать там формулы можно использовать латех
Вот в этом онлайн редакторе есть все символы и значечки
https://www.codecogs.com/latex/eqneditor.php
набиваешь там формулы, копируешь и вставляешь в свой вопрос обернув слева и справа значками $$
Тут кто-то короткий фак для нубов делал, включите туда эту инструкцию
можете подредактировать
>Зачем какие-то id-ы
Чтобы доказать вот это
>Если для всех u,v <Au,v> = <Bu,v> то A=B
Ибо надо вычесть и посмотреть на скалярный квадрат.
То есть для 1 точки ответ 1/2? Предположим, что эта формула верна для n >= 3. Очевидно, что для 3х точек ответ не 3/8. Возьмем любую из трех точек и проведем через нее диаметр. Вероятность того, что оставшиеся 2 точки будут по одну сторону от проведенного диаметра, равна 1/2. А искомая вероятность не меньше этой.
вроде обсчитался, 2n/2^n
Лил, если зафиксирован базис, то достаточно заметить, что <A e_j, e_i> - это элемент на месте (ij) в матрице оператора А.
Ортонормированный, естественно.

Они актуальны, но учиться по ним не стоит
Точно с них?
У меня друг с матфака ВШЭ хорошо разбирается во всяких топологиях, группах и т.п., но учился по современной литературе.
Или в Бурбаки все абсолютно фундаментально и полезно? Просто я хочу добиться как можно более глубокого чувства каждого раздела и связи между этими разделами, чтобы как можно свободнее математически мыслить, ну ты понял.

Вообще не люблю задачи, почему в каждом тексте нужно обязательно дристануть этими задачками ебаными. Только время на них зря тратить. Некоторые совсем ебанутые уже их в научные статьи суют.
Алсо, может посоветуете годноты по теории Галуа. Но только чтобы там было без гротендиков и пучков, или хотя бы не сразу.
Ну это сделано для того, чтобы не засорять текст рутинными и очевидными доказательствами.
Ну есть рекомендации Вербита по программе матфака http://verbit.ru/Job/HSE/Curriculum/all.txt например, учебнике, по мне, там порекомендованы ничёшные (но я бы кое-что поменял).
Вот я сейчас читаю и решаю Munkres "Topology", вообще годно. Чтобы начать читать, не нужно знать вообще ничего, даже теория множеств там дается в первой главе.



Там кроме собственно функции еще дается определение пары и графика (на которых основано определение функции). Ну и как подмножество декартова произвеения множеств функция тоже разбирается очень подробно.
Мне показалось трудно читать человеку с низким левелом математической культуры
даже матшкольнику-младшекурснику, и то сложно
Для более "взрослых" может и ок.

>даже теория множеств там дается в первой главе.
Да любой автор считает своим долгом в первых главах обсосать теорию множеств и определение функции, даже если в дальнейшем требуется знание ещё кучи материала чтобы читать основной текст учебника.
Своими словами написать не можешь значит идешь в деревенский туалет типа сортир, жрать говно ведрами.
>матшкольнику-младшекурснику, и то сложно
Разве? Если матшкольнику давали теорию и сведения об основаниях математики то должно быть норм.
Множество пар где для левого элемента есть единственный правый.
>>316797
Спасибо! Похоже, охуительный пакет для алгеброгеометрической теории кодирования. Есть где-нибудь кратное введение в основы гуавы? Например, почему где-то требуется ставить две точки с запятой, а где-то хватает одной?
Алсо, реквестирую теорему о ядре следа в конечных полях. Та, что о количестве элементов в ядре. Нигде не могу найти.
guava - отдельный пакет в GAP для всяких криптографий и наоколо (читай: библиотека). GAP - открытая оболочка, для которой все подряд пишут разные интересные математические тулзы. Другие системы компьютерной алгебры часто подключают GAP со всеми его пакетами, так как он достаточно функционален (точно знаю про Magma и Sage; вроде Maxima еще). На сайте есть подробная документация; как ты уже видел, по отдельным пакетам есть описания функций, которые туда входят. Возможно, по разным конкретным вопросах можно легко найти всякие гайды и книжечки.
Каждый вызов функции заканчивается ";". Двойная ";;" не будет выдавать результат в консоле (посмотри разницу на тех же скринах сверху).
След - линейное отображение большого поля НА маленькое, если смотреть на них как на векторные пространства (или как на абелевые группы даже). Далее вспоминаем первую теорему о гомоморфизме.
Двачую реквест.
спасибо, выглядит годно, пошел погружаться.
https://en.wikipedia.org/wiki/Rank%E2%80%93nullity_theorem
Конкретно эта- не знаю, но это простое следствие теоремы о гомоморфизме.
Evans
Так там суть в том, что все без упоминания базисов. Хорошая книжка, наверное.
Иначе можно просто перемножить А и А^t и не писать каких-либо теорем и доказательств.

А то в предложенном преподшей вроде не все есть, да и написано криво.
Это не определение, просто понятие функции исходное и неопределяемое (как и N). Пара по сути это и есть выражение соответствия и наоброт.
Неопределяемых понятий не бывает. Бывают технические термины - просто набор символов, который можно без каких-либо потерь заменить на любой другой нигде не задействованный набор символов. В технических терминах нет смысла, они ничего не значат сами по себе, это просто бессмыслица, никакого "интуитивного понимания" они не имеют. Когда мы накладываем на технические термины какие-то синтаксические ограничения, мы тем самым определяем некоторое понятие.
Идею, что есть какие-то неопределяемые понятия, придумали ебанутые на всю голову, безумные, алогичные школьные учителя.
>>317008
Первое очевидно, A=B. Остальное Игошин.

>понятие функции исходное и неопределяемое (как и N).
Ну что же ты так, братишка. Ладно N, теперь еще и функция. Что там еще неопределяемое, чтобы в картинку добавить?
>Пара по сути это и есть выражение соответствия и наоброт.
Ну. Соответствие. Почему это не определение, если как раз-таки однозначное определение?
N петушок как всегда незаметен.
Я вот учу производные и мне пишут про вычисление формулы касательной графика функции в точке.
Собственно, зачем нужна эта касательная прямая? Если функция периодическая, касательная невозможна?
Это копия, сохраненная 5 января 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.