 924 Кб, 1200x1800
924 Кб, 1200x1800Следующий тред: >>29692 (OP)
>Математика не имеет никакого основания, кроме того, что некоторым людям нравится ею заниматься. Попробуем это формализовать
Так же ищем ответ на вопрос:
>Существуют ли в математике примеры нарушения правила исключения третьего?
И на вопросы:
>Какие интересные математические результаты были получены конструктивистами за время своего существования? Какие теоремы, не поддавшиеся другим методам, им удалось доказать?
>Какие интересные математические результаты были получены конструктивистами за время своего существования?
То, что называют математикой обычные люди, - фуфло. Его надо выкинуть.
>математика не имеет оснований
Это зависит от того, что иметь ввиду под основаниями.
Понятное дело, что, нету причин выбирать определённую модель над другими.
Но это не говорит о том, что несуществует аксиом из которых следует следовало бы другое.
Я так понимаю, что нумеровать треды по порядку вы не можете, потому что еще не договорились, как формализовать натуральные числа?
Я не дед, прочитал Википедию, сейчас объясню.
Представь, что каждой точке некоторого пространства соответствует своё, уникальное пространство, назовём их няшками.
Так вот, существуют пространства, которые соответствует своим няшкам.
Так, вот, k-теория изучает такие пространства, но, чтобы при этом те были топологиями.(тип, каждый отрезок в пространстве содержит бесконечное кол-во точек, квадрат можно бесконечно уменьшать, и он поместиться).
А ещё ЭТИ пространства должны быть кольцами.
https://ru.wikipedia.org/wiki/Кольцо_(математика)
Прочитай на википедии.
K-теория изучает соответвие между топологическими пространствами и своими няшками, где пространства являются кольцами.
Функтор.
Топологическая к-теория это функтор из компактных хаусдорфовых пространств в коммутативные кольца, переводящий операции прямой суммы и тензорного произведения векторных расслоений в сложение и умножение в кольце. Наиболее естественная теория когомологий.
K(0) обобщает пополнение моноида до группы (добавление обратимости), частный случай – пополнение натуральных чисел вместе с нулем, иначе это не моноид до целых. Описано у Кириллова в "Что такое число", конец первой страницы.
K(0) это функтор из колец в абелевы группы. Высшая К-теория то же самое, только бьёт в категорию с более богатой структурой.
>Имеется "плюс-конструкция Квиллена". Это функтор в гомотопической категории, который делает из CW-комплекса CW-комплекс с теми же когомологиями, но с абелевой фундаментальной группой. Это универсальный функтор при отображениях в пространства с абелевой фундаментальной группой
Более просто объяснения найти пока не смог.
На топологическую К-теорию ещё можно смотреть как на классификацию векторных расслоений (я так понял, ты именно это и написал); хотя этим она, конечно, не исчерывается.
>Так же ищем ответ на вопрос:
>Существуют ли в математике примеры нарушения правила исключения третьего?
Ты же сам понимаешь, что тут ключевое слово "существуют". Т.е. мы опять пришли к вопросу существования в математике. Классически существование значит непротиворечивость в некоей аксиоматике. Конструктивно - построимость. Т.е. речь в конечном счете о дизъюнкции. Конструктивно дизъюнкция принимается только при построенном дизъюнкте из чего уже прямо следует неприемлемость исключенного третьего как общего правила, верного всегда и априорно. Потому что не существует общего способа построить дизъюнкт во всех вообще случаях. Классически все проще - есть соответствующая аксиома, непротиворечивая в своей аксиоматике и т.о. классически исключенное третье принимается на веру. Классически нет требования построения (вычисления) дизъюнкта. Вот это все, неужели так тяжело понять? Это же просто как 3 копейки. Ладно миша не понимает, но почему не понимает вообще никто? Это пиздец же просто.
Это понятно. Непонятно, почему математики должны всё бросить и поголовно обмазаться конструктивизмом.
>существование значит непротиворечивость в некоей аксиоматике. Конструктивно - построимость
Опять, конструктивист.
Ты понимаешь, что отрицаешь топологию?
Ты отрицаешь натуральные числа и веришь, что существует самое большое число.
Ненавижу тебя.
>Ты понимаешь, что отрицаешь топологию?
>Ты отрицаешь натуральные числа и веришь, что существует самое большое число.
Как интуиционизм связан с отрицанием натуральных чисел вообще, ты хоть сам читаешь, что пишешь? Какое самое большое число, ты чего несешь вообще?
>Существуют ли в математике примеры нарушения правила исключения третьего?
Существуют.
Например, "кушать яблоко", "не кушать яблоко".
Аксиоматически говорю, что эти два высказывания истинны и существуют, одновременно.
Но аксиоматически не принимаю закон исключения третьего.
У нас задана система, она противоречит закону исключения третьего, но существует.
Нельзя вычислить бесконечное натуральное множество(требуется бесконечно шагов), но можно вычислить только какое-то число.
Конструктивист соглашается лишь с построимым, значит отрицает бесконечное натуральное множество.
Для бесконечного есть потенциальная осуществимость (правила построения), ни о каком существовании бесконечного речи идти не может. Если ты признаешь что-то бесконечное, то пользоваться ты им все равно не можешь, т.к. это значок, за которым не стоит ничего. Алсо, где существуют бесконечные множества? В платоновском мире идей? Это не математика.
В самое большое число никто и не верит. Ну если только ты, кроме тебя я такого ни от кого не слышал.
>Существуют ли в математике примеры нарушения правила исключения третьего?
Тривиально существуют. Добавляешь аксиому "исключённое третье неверно".
Если ты отрицаешь ∞, то веришь в то, что божественные алгоритмы остановились на каком-то числе(ведь количество шагов конечно), где-то алгоритм в нашем мире закончен, на каком-то числе.
Если бесконечности не существует, то натуральных чисел, простых чисел конечное количество.
Хорошо, допустим, "существование" - это точный синоним слова "построимость". Тогда как возможны доказательства чистого существования, каков их онтологический статус? Ведь имеются прецеденты, когда математическими методами доказывался факт одного лишь существования/несуществования какого-либо объекта, и лишь спустя много лет конструктивисты проводили конструктивное доказательство этого же факта.
Но разве из того, что натуральное множество не бесконечно, не следует то, что оно конечно?
Это ты так сказал. Не говоря о том, что исходишь из исключенного третьего. Ни у Брауэра ни у кого другого ничего нет про самое большое число.
>алгоритмы остановились на каком-то числе(ведь количество шагов конечно)
Про проблему останова ты тоже не слышал.
>>0956
>Если бесконечности не существует, то натуральных чисел, простых чисел конечное количество.
И про потенциальную осуществимость тоже. Точнее, про нее слышал, но даже не понял, что это. Так вот, в правилах построения например N не указано какое число последнее. И ты правда тупой, потому что пытаешься использовать свое непонимание вопроса как доказательства чего-то.
>>0957
Тупее тебя, миша, с твоими гамалогиями, на мейлру все равно нет никого.
Сколько уже объяснял, что такое потенциальная осуществимость, а дегенераты так и не поняли. Ну и? Есть смысл пытаться что-то объяснять? Все равно глаза закатят и закукарекают.
>>0960
Нет, не следует. Почему - попробуй догадаться сам, все нужное для этого сто раз разбиралось, если мозги есть - поймешь но их у тебя нет.
>не бесконечно
Что под этим подразумевается? В его любимой MLTT (как и в любых адекватных канстуркивтных основаниях) можно спокойно доказать, что не существует биекции между конечным "множеством" (0-типом) и "множеством" натуральных чисел.
>>0961
>гамалогиями
Где ты тут увидел гамалогии, придурок?
>MLTT ты все равно не понимаешь
Действительно, это настолько сложная вещь. Только праграмист способен понять её.
>Никакого доказательства оторванного от построения быть не может.
Очень часто бывают ситуации, когда доказать существование чего-либо гораздо проще, чем построить это что-либо. Например, в анализе доказать существование суммы ряда часто проще, чем просуммировать ряд в явном виде.
>И про потенциальную осуществимость тоже. Точнее, про нее слышал, но даже не понял, что это. Так вот, в правилах построения например N не указано какое число последнее.
Не указано, но и не должно быть указанным.
Это зависит от того, сколько повторять алгоритм добавление.
Разве бесконечное не противоположное конечному?
Тогда я говорю не о бесконечности, а о не конечности.
Натуральное множество — это неконечное множество чисел.
Если у множества нету конца, тогда его можно вычислить?
Нет.
Хорошо, предположим, что натуральное множество не не-конечное, тогда оно конечное, имеет конец. Значит самое большое число.
>вычислить
Не математика.
>имеет конец
Определи это формально для начала.
>Значит самое большое число.
Тебе уже сказали, что можно доказать несуществование такого числа в канструктивных основаниях.
 42 Кб, 720x1280
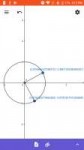
42 Кб, 720x1280Чтобы угол был 45° нужна бесконечная непериодичная дробь.
Не существует этого, не существует угла 45°.
И так относится к каждому углу.
Отрицая бесконечность, отрицаешь углы.
Хочешь сказать, что число Pi имеет конец?
Бесконечное все то, что не имеет конца.
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989
Отношение длинны окружности к диаметру в любой окружности
Отрицая бесконечность, ты говоришь, что не существует окружности, есть только многоугольники.
 30 Кб, 720x1280
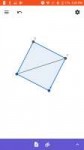
30 Кб, 720x1280Отрицая квадраты, ты отрицаешь формулы площадей, объёмов всех фигур, вообще. Все то, что было — ложь, фикция.
Отрицаем понятие "луч", " прямая", "углы" (это два луча)
Будучи конструтивистом, мы отрицаем понятия, которые невозможно определить.
Например, точка, плоскость, пространство.
Отрицаем понятие объект, оно неопределимо. Отрицаем понятие множества.
>>0983
>понятия, которые невозможно определить
>Например, точка, плоскость, пространство
Дэвид Гильберт справился с этой проблемой, насколько мне известно, в книге "Основания геометрии".
Бесконечность предполагает элементы, объекты.
Бесконечности нету вне связи с чем-то конкретным.
>Бесконечность предполагает
Для начала дай формальное определение "бесконечности".
>элементы
Элементы множества? То есть "бесконечность" является множеством?
Почему, мистер Брауэроёб, почему? Во имя чего? Что Вы делаете? Зачем, зачем отвечаете? Зачем продолжаете спорить? Неужели Вы верите в какую-то миссию или Вам просто страшно признать, что вы ошиблись? Так в чем же миссия, может быть Вы откроете? Это свобода, правда, может быть вычислимость или Вы боретесь против исключённого третьего? Иллюзии, мистер Брауэроёб, причуды восприятия! Хрупкие логические теории слабого человека, который отчаянно пытается оправдать свое существование: бесцельное и бессмысленное. Но они, мистер Брауэроёб, как и аксиома бесконечности, столь же искусственны. Только человек может выдумать скучное и безжизненное понятие "конструктивизм". Вам пора это увидеть, мистер Брауэроёб, увидеть и понять: Вы не можете победить, продолжать борьбу бессмысленно! Почему, мистер Брауэроёб, почему Вы упорствуете?
Необязательно множество.
Существуют структуры, к которым можно привязать понятие "мощности".
И там есть элементы.
Бесконечность не является множеством, но есть бесконечная структура с определённой на ней мощностью.
Сила — это неопределяемое понятие вне контекста. В физике, это мера того, насколько легко сдвинуть предмет с места. В боксе показывает степень травмируемости от удара. В боевых искусствах показывает знания боевых приёмов. В фильмах, сила, иногда, показывает то, что человек готов принимать боль и страдания, " сильный" человек.
Если существует множество определений, ты же не скажешь, что силы не существует?
То есть "бесконечность" является свойством структуры, а не как ты говорил раньше.
>В физике
Дальше не читал даже.
В предыдущих тредах было.
>Ты же сам понимаешь, что тут ключевое слово "существуют". Т.е. мы опять пришли к вопросу существования в математике.
Вот так всегда, задаёшь простой вопрос, а тебе отвечают "НО ДАВАЙТЕ ЗАДУМАЕМСЯ, ЧТО ЕСТЬ ВОПРОС? И МОЖЕТ ЛИ ЧТО-ТО ВООБЩЕ СУЩЕСТВОВАТЬ?" и так далее.
Я объяснение понимаю. Вопрос состоял в другом, существуют ли в математике примеры нарушения закона исключения третьего?
Не объяснение, почему не стоит доверять этому закону, а примеры его нарушения? Ответ на этот вопрос довольно прост ведь, это "да" либо "нет".
Так да или нет?
А моя претензия к конструктивисту в том. что он постоянно упоминает "гамалогии" и "мишу". При том, что никакого миши на борде разумеется нет, и пишут конструктивисту очевидно разные люди. А гомологии вовсе никем не упоминаются. То есть, конструктивист зачем-то сам нарочно делает всё, чтобы выглядеть идиотом и обиженным ребёнком. Зачем? это какая-то тонкая дискредитация конструктивизма?
Конструктивист, если ты слышишь, перестань исходить на говно и общайся нормально, невозможно ведь терпеть твои постоянные вываливания личных проблем на дискуссии о математике.
>>0999
>Моя претензия к конструктивисту только в том, что он признаёт существование противоречивых вещей. Если вещь противоречива, то она не должна существовать. А ему норм.
Но он утверждал, что этот пример и для классической логики будет корректным примером, несмотря на то, что он противоречит закону исключённого третьего, а значит по моему мнению не может существовать.
>Существуют ли в математике примеры нарушения правила исключения третьего?
Существуют. И их много.
Математическое нарушение исключения третьего используется в доказательствах от противного.
Если А истинно, мы доказываем, что Б и С противоречиво. Значит, существуют противоречивые Б и С при истинности А.
А так как мы не допускаем противоречивость, такая аксоима церкви, то А — ложно, ведь из него следует противоречие.
>противоречив только с точки зрения классической логики
То есть у нас есть доказательство его отрицания в классической логике? В таком случае он и интуацииаистски противоречив.
>Математика это по определению
По определению праграмистов? Я твой вид не считаю людьми.
>почитал бы Мартина-Лёфа
Что именно у него я должен почитать и с какой целью? Ссылку кинь.
Нет у нас доказательства его отрицания, я не понимаю тебя, отстань. Ты говоришь, что мы имеем право в классической логике рассматривать высказывание, которое не истинно и не ложно, то есть противоречит исключённому третьем, а я говорю, что такое высказывание противоречиво, то есть его нельзя рассматривать, оно не существует.
Программисты и есть математики по изоморфизму Карри-Говарда, но ты же не осилил.
>Ссылку кинь
Да я уже приводил сотни ссылок во всех тредах, лень копировать даже.
А, ну так это и есть основа конструктивизма как бы. Блядь. Противоречивость существования не значит несуществования.
>Нет у нас доказательства его отрицания
Значит не говори "противоречив", значения слова выучи для начала.
>противоречиво
>не существует
Такого не может быть. И вообще, тот пример не относится к математике. Не нужно пытаться про него говорить математическими терминами.
>значения слова выучи для начала.
Здарова! Не истинно и не ложно высказывание, противоречит исключённому третьему.
>В категории Int интуиционистких типов.
Какие там объекты и морфизмы? Между какими объектами установлен этот изоморфизм?
Математика это и есть MLTT, а он создал млтт, так что конечно он математик. Северной Нигерии не понять.
>Именно мне приведи ссылку
https://www.ozon.ru/context/detail/id/27946708/
>>1024
Это всё описано у Маннури, в работах по алгебре Миколова, нагуглишь сам если не тупой. Хотя с кем я говорю это же мейлру.
Я про логику, а не про вычислимость. Противоречивость существования и несуществование у тебя не одно и то же, у меня одно и то же. Опять к тому же и пришли.
>Не истинно и не ложно
Значит его отрицание тривиально доказуемо, ты сам хоть понимаешь что пишешь?
>высказывание
Та хуйня не является высказыванием.
>противоречит исключённому третьему
Причём тут исключённое третье? Тривиально из определения отрицания следует его неверность.
>а не про вычислимость
Еще Тьюринг и Бэббидж показали что все относящееся к математике вычислимо. Логика значит не относится, бред, рисование пропозиций.
>Математика это и есть MLTT
Это теорема, где она доказывается? Или в это нужно просто уверовать?
>Маннури
>1867-1956
Сомневаюсь, что он знал определение категории.
>Значит его отрицание тривиально доказуемо
Отрицание чего? Того, что не истинно и не ложно? Ну проотрицай неизвестность, что у тебя получится, лол.
>Та хуйня не является высказыванием.
О том я и говорю. А конструктивист такие штуки считает высказыванием.
>Или в это нужно просто уверовать?
Уверовать это как раз все не вычислимое. Хипстеры всякие философы с магическим мышлением. Где вычислимо, по определению верить не надо, все очевидно.
>Сомневаюсь, что он знал определение категории.
Категории еще Аристотель изобрел, и доказал теорему о том что у Set ровно девять модельных структур.
Нет, я как раз пытаюсь сказать, что это хуйня вне математики, потому что к ней такие термины неприменимы. А конструктивист сначала рассматривает такую хуйню, потом применяет к ней исключённое третье, оно не срабатывает, он радостно идёт писать книгу о том, что вот в математике пример, где исключённое третье не работает. А на самом деле он просто изначально не должен был рассматривать такую хуйню и всё было бы ровно.
>И ты не видишь, что из этого тривиально следует его неверность?
Только если это логическое высказывание, а не набор букв.
Ты сказал, что есть высказывание , которое не истинно и не ложно. Про примеры выше я даже говорить не собираюсь.
Church (Церковь), введение в логику, второй том, страница 156.
Просто эти примеры приводятся как иллюстрация необходимости отмены закона исключённого третьего. Но в основе примеров лежит не математика, а белиберда какая-то. Короче, это искусственное обоснование, надуманный предлог, на самом деле никаких оснований для создания интуиционистской логики нет.
>непонятно зачем создавать другую логику
Конструктивная логика к кансуткртивзму никакого отношения не имеет.
>ограничиться требованием конструктивности
Требованием конструктивности чего?
Я интуиционистскую имел ввиду. Конструктивности высказываний, типа постулировать, что мы можем высказывать что-то тогда и только тогда, когда у нас есть построение этого что-то.
>Конструктивности высказываний
Высказывание это лишь кусочек синтаксиса, каким образом он может быть неконструктивным?
Ну вот до этого же говорил он, что мы не можем о чём-то говорить, пока не построим/вычислим это. Видимо там и семантика тоже присутствует "интуитивно".
Ну её не дают, потому что большинство математики это не конструктивная болтовня про гамалогии, начиная с Гильберта и Пуанкаре. Как уберут категории и пучки, сразу Нобелевку начнуть присуждать за машинное обучение, я уверен. А даунам останется премия коммутативная и премия Полей.
>Мартину-Лёфу обучить бы дураков из Гарварда
Мартин-Лев очень занят работой по доказательству Изоморфизма Карри-Говарда, в данный момент он пытается определить категорию, между объектами которой будет этот изоморфизм.
Это давно уже было доказано построением алгебры Миколова сигнификационстких типов.
>>1049
Я имел в виду то что дауны типа миши зовут математики. Просто программа Брауэра ещё не довершена. Брауэр просчитался как Маркс когда-то, люди слишком тупые, и многие столетия еще потребуются пока все забудут пучки и выучат теорию алгоритмов.
>многие столетия
Дегенератам с мейлру, отрицающим волю Браузера и пророка его (Мартина-Льва) понадобится даже больше.
Я и говорю, но топазы и гамалогии уже сейчас не имеют отношения к науке, Брауэр выбросил их с парахода конструктивности.
Конечно, он решил главную задачу человечества, то есть построил МЛТТ. А Гротендик её даже не знал. И Миша не знает.
После него это сделали ещё Маннури и Мартин-Леф. Надеюсь, что их дело продолжится и дальше. Нам нужно будет очень много времени для полного доказательства Тезиса.
>Гротендик
Его сектанты говорят, что какая-то там "категория" имеет "достаточно проективных объектов", попахивает невычислимым верованием. Нужно их нахуй изгнать из математики.
В конструктивной математике не надо ничего доказывать, это не экспериментальная наука, а наблюдательная. Алгебра наблюдаемых Миколова описывает все возможные типы в пространстве дхармадхату всех дхарм (конструктивных типов), читай Максимку.
>человечества
Такое великое открытие этим не ограничивается. Уверен, что и за пределом человечества MLTT найдётся применение.
>не экспериментальная наука, а наблюдательная
>не экспериментальная
>наблюдательная
>не надо доказывать
>не экспериментальная
Это та самая интуиционистская логика в действии?
Но тут все тривиально, сводится к арифметике по нумерации Гёделя. Мне это решать и не надо, решит прувер, который я допишу.
В вычислимой математике все что построимо, то очевидно. Доказательства это в суде, математики не доказывают, они вычисляют.
Алгебраисты не могут найти порядки подгрупп симметрической группы, конструктивисты не знают алгоритмов. /math -- математика, которую мы заслужили.
/math нужно переименовать в /phmath. Вот по философии математики тут собрались крупнейшие специалисты.
Философия математики это и есть математика. Находить подгруппы гамалогий и доказывать алгоритмы любой птушник может. А вот работы Брауэра разбирать, это вряд ли. Тут ума много надо. Про писание пруверов я даже молчу.
Я с тобой соглашусь, к тому же подгруппы и правда находятся связкой gap+sonata
G:=SymmetricGroup(4);
S:=Filtered(Subgroups(G),H->IsNormal(G,H));
for H in S do
Print(StructureDescription(H),"\n");
od;
Так что тут конструктивист вин явно. Так и гамалогии с тапалогиями запрограммировать в два клика скоро станет возможным. Теория групп уже от взятия интегралов ничем не отличается.
Конечно, а что нельзя запрограммировать это мусор. Поэтому гамалогии, группы, интегралы и прочий бред учить явно не надо. 85% математики в работах Брауэра, 13% у Лёфа и остальное на будущие поколения писателей пруверов.
Да и если так подумать, программист по сути своей специалист по прикладной логике, пусть он не знает формального языка, но интуитивно он в ней ориентируется гораздо лучше многих так называемых математиков их за компьютер посадишь и они теряются сразу, хотя казалось бы с логикой они должны быть дружны. То есть нужно просто уметь мыслить, всё остальное мусор ненужный. Доказательства те же, кому они нужны, если ты можешь сделать, построить, написать только то, что можешь, только с этим ты и работаешь, не в чем сомневаться, а значит и доказательства нахуй не нужны. Нужно просто уметь излагать свои мысли, даже переводчик автоматический не нужен. Возможно, весь бугурт вызван только подавляемым осознанием, что человек не так уж и крут, что вся содержательная математика действительно вычислима, разрушение манямирка такое, постмодерн, последним гвоздём в крышку ортодоксальной некомпьютеризированной математики стало доказательство проблемы четырёх красок.
> даже переводчик автоматический не нужен.
даже переводить на формальный язык самому не надо, есть автоматический переводчик
фикс
Я написал это в шутку, типа такая ирония или сарказм, но сейчас перечитал и стало очень грустно. А что, если это и не шутка совсем? Проблемы ведь есть, доказывать теоремы некому, проверять некому, никуда без машин, но другой вопрос возникает, вот перебрали 50 млн вариантов и доказали, ок, но сука, а что если там где-то противная ошибка где-то закралась, один вариант неверно обработан и он и был контрпримером и доказательство проблемы 4 красок нихуя неверно. Ебучий постмодерн, постправда, постирония. Хуйня какая-то. Чему же тогда верить, если не математике?
https://www.youtube.com/watch?v=30LYNaUNikg
 251 Кб, 730x346
251 Кб, 730x346Вонючка.
Метамодернизм это постмодерн, который заебался быть постмодерном и сменил название. Суть та же.
Что возвращает нас к вопросу:
Есть ли в математике примеры нарушения закона исключения третьего?
В математике, а не в софистике.
И примеры, а не рассуждения о том, что они могут где-то быть.
Что возвращает нас к вопросу что считать математикой. Та же проблема четырёх красок, многие её доказательство так и не считают математическим.
До 2011-го. Ты манифест-то читай. Постмодерн больше не нужен, его время пришло, сейчас новая искренность, возвращение религий и идеологий, интегральная движуха типа Кена Уилбера и т.д.
>Та же проблема четырёх красок, многие её доказательство так и не считают математическим.
Перебор вариантов — не доказательство. По ряду причин.
Даказательства и не нужны поэтому. Если утверждение нельзя решить перебором на машине Тьюринга, это аллах, а не математика.
Читал ещё до того, как это стало мейнстримом. Это постмодерн. И да, ни один постмодернист-философ никогда не признавал себя постмодернистом. Потому что постмодерн это мейнстрим, а суть его в том, чтобы в нём не быть, высмеивать его. Вот и получается уроборос такой.
прошло
Да ты не понял просто значит. А философов-постмодернистов и нет вообще, это не философия.
Постмодерн даже само желание придумать "метамодернизм" или "постирония". Ещё одна отличительная черта это работа с текстом.
НАХУЯ МНЕ ЭТОТ СЕКС ТО Я ВГРЫЗАЮСЬ В ТЕЛО ТЕКСТА
https://www.youtube.com/watch?v=PL3MowvRvVc
Может быть. По мне так всё так и есть. Ну да, ок, держать середину между постмодерном и модерном. Очевидно же, что в крайности бросаться не стоит. А носятся с ним как с чем-то сверхкаким-то.
Ну решай, никто же не запрещает.
Зачем тогда используешь противоречие в своей претензии? Вот смотри:
>Если вещь противоречива, то она не должна существовать.
Ты обозначаешь объект, полагаешь его существование
>вещь противоречива
Следом сразу же говоришь, что его нет
>она не должна существовать
Выходит, ты сам признаешь существование противоречивых вещей
А вы могли бы, например, работать в системе с игровой логикой, где несколько агентов ведут спор, и противоречие в ней - всего лишь техническое событие, как "переход хода".
Вы можете прямо сейчас создавать целые новые миры, вместо этого вы надрачиваете сморщенные хуи давно умерших людей.
Смех тут в том, что мы не могли получить "Доказано от противного", пока не подошли к {Всё что угодно}. Похоже, что Доказательство от противного - всего лишь элемент Всего что угодно. Один из путей, который мы выбираем из моря возможностей противоречия. Когда вы доказываете от противного, вы все равно что говорите "Ну блин, принято вот так тут поступать"
>после противоречия - всё что угодно
>Что?
Я хз, это Аристотель спизданул. Ты б глянул откуда у мат. логики ноги растут
"Что?" было в ответ на "у классиков".
>Ты б глянул откуда у мат. логики ноги растут
Тебе бы самому про неё базовых вещей узнать не помешало.
У него чудовищные проблемы.
Только подумайте: он уже лет пять сидит на борде среди людей, которых ненавидит, называет идиотами и животными, но не уходит. Не представляю, что должно случиться с человеком, чтобы так себя пытать. Почему он не проводит это время со своими близкими, со своей девушкой?
У меня чередуется два состояния, когда я ощущаю себя полностью тупым, никчемным и недостойным заниматься математикой, и тогда, когда ощущаю себя умным, а математику считаю неинтересной, недостойной меня.
> Никто не знает где впервые было опубликовано доказательство аксиомы Чёрча?
Это не аксиома, мань. И я давал ссылку на ту его статью.
Сейчас бы высрать 87 постов за ночь а потом выдумывать, что проблемы у меня, а не у того, кто тут всю ночь срал, пытаясь петросянить типа как за меня. Дегенераты, что тут скажешь.
Черт.
То есть это не ты уже пять лет (сначала в sci, теперь тут) пишешь про конструктивизм, исходишь на говно, обзываешь всех идиотами, и всё равно не уходишь? Это кто-то другой за тебя делает? Ты скажи, я пойму. Я не буду строить гипотезы и инсинуации.
>когда ощущаю себя умным, а математику считаю неинтересной, недостойной меня.
Ну это совершенно точно иллюзия.
Да, миша уже научился копировать мой стиль речи и пытается выставить меня идиотом. Я это уже сто раз писал.
Нет уж, я не дегенерат с мейлру, чтобы таким заниматься. Всё особо значимое я уже по сто раз писал в других тредах.
На мейлру так и не делают.
> То есть это не ты уже пять лет (сначала в sci, теперь тут) пишешь про конструктивизм
Я про конструктивизм узнал в прошлом году. О чем уже сто раз писал. Мейлру я знаю давно, но не припомню чтобы тут кто-то за эту тему что-то писал. Ну и подпекает местным дегенератам наотличненько, значит все правильно делаю.
В любом случае, его история окончена.
Хорошо, значит это был не ты.
Но у меня ещё остались вопросы.
Вот ты говоришь
>Ну и подпекает местным дегенератам наотличненько, значит все правильно делаю.
Скажи, ты искренне считаешь, что люди, которые читают твои посты, испытывают сколь-нибудь сильные чувства? Когда кто-нибудь пишет тебе пост в ответ, этот человек действительно испытывает "подпекание"? Не сидит со скучающим лицом, не тупит, почёсывая яйца, лишь бы не работать над дипломником, а вот прямо закипает от твоих слов? Ты правда в это веришь?
Второй вопрос. Что именно ты "правильно делаешь"? Ты бы хотел, чтобы больше людей стали конструктивистами? В таком случае даже очень глупому человеку было бы очевидно, что твоя стратегия не рабочая для такой цели.
Ты бы хотел просто выделиться? Это странно, т.к. борда анонимная.
Ты любишь оскорблять людей? В таком случае мне искренне интересно, почему, что тобой движет, что тебе это даёт.
Ну и наконец, третий вопрос. Это правда стоит того? Ты много и часто пишешь, причём даже в такое раннее время. Такое чувство, что ты отвечаешь почти каждому, кто выражает несогласие с тобой. Практически находишься под контролем несогласных и простых троллей. Стоит ли это того? Почему ты не проводишь время с близкими вместо этого? Это просто анонимная борда, это практически мусорка. Даже если предположить, что у твоих оппонентов действительно бомбит (хотя я не понимаю, что достойного в такой цели), давай признаем, что вряд ли это оставит глубокий след в их жизни. Ну позлятся секунд 15 максимум. Этот выхлоп стоит всего твоего времени?
Вряд ли ответишь, конечно, но я попытался.
>что люди, которые читают твои посты, испытывают сколь-нибудь сильные чувства?
Я частенько смеюсь в слух при чтении его постов.
А я вообще часто посмеиваюсь, когда читаю эту доску, просто от приподнятой атмосферы тут)
> Ну и наконец, третий вопрос. Это правда стоит того? Ты много и часто пишешь, причём даже в такое раннее время. Такое чувство, что ты отвечаешь почти каждому, кто выражает несогласие с тобой.
Я сюда с работки обычно пишу, дома у меня поинтереснее занятия есть, а так все равно сычую без дела. А вот у тех, кто тут за ночь 87 постов набил, действительно что-то не то с приоритетами. Я не думаю, что тут у кого-то кроме меня суточный график, скорее дело в том, что здесь одна школуйня.
Ты самый адекватный анон здесь.
Я тебе объясню.
Дело в том, что и в реальной жизни конструктивисты/интуиционисты ведут себя как сектанты.
Я серьёзно: их невозможно слушать. И это делают только залётные студенты, например.
Интуиционисты которых я знаю на бордах и ИРЛ, просто придумали себе философскую надстройку над математическими теоремами и гасаждают её другим. И эта надстройка жрёт их мозг, делает неадекватными, отвлекает от нормальной деятельности. Причём совершенно без всякого эффекта.
Чтобы чисто психологически выдержать такую бесполезную нагрузку, надо в чём-то другом искать катарсис. Например, в обвинении других в том, что они не понимают.
Доказательство интуициониста имеет нулевую ценность.
Это сломавшиеся математики.
Написал на мейлру и сразу интуиционизм опроверг. Хорошо у тебя в манямире.
>Там противоречие - это ограда вокруг песочницы, "дальше детям нельзя".
Я лично не хочу взрослеть, пнятненько?
>Я сюда с работки обычно пишу, дома у меня поинтереснее занятия есть, а так все равно сычую без дела
Охуенная у тебя работа, ничего не скажешь. Сычевать сутки через двое.
> Охуенная у тебя работа, ничего не скажешь. Сычевать сутки через двое.
Ато. Читаю книжки, сплю, капчую, аниме смотрю, т.е саморазвиваюсь за зарплату. Ещё и налохи не все плачу, причём абсолютно законно, ндфл полностью возвращаю например.
>>1097
Ты даже не понимаешь, в чем суть противоречия в математике и чем отличается от противоречия где-нибудь еще. Что и неудивительно, ты простейших вещей осилить не можешь.
Миша, хватит уже копировать мой стиль и пытаться дискредитировать
>капчую, аниме смотрю, т.е саморазвиваюсь
Я серьезный человек и занимаюсь математикой, то есть пишу прувер, а не аниме смотрю.
Мань, прувер никак не мешает аниме и наоборот. Ты ебнутый же.
>Ещё и налохи не все плачу, причём абсолютно законно
Так и бы сказал что работаешь охранником, по ТК оформлять не стали чтоб не отчислять за дауна в пенсионный фонд, и рассчитываются с тобой из своего кармана, сумма наверняка небольшая.
Учиться на математика надо было, а не на программиста в радио-механическом техникуме, сейчас бы в вузе работал как я.
Миша
> Так и бы сказал что работаешь охранником, по ТК оформлять не стали чтоб не отчислять за дауна в пенсионный фонд, и рассчитываются с тобой из своего кармана, сумма наверняка небольшая.
Лол, охранником. Да нет, меня тут самого охраняют, режимный объект жи. И я по ТК оформлен.
>Я про конструктивизм узнал в прошлом году.
Прикрывать каждый свой обсёр несуразной ложью это здорово, конечно, но всё задокументировано:
http://arhivach.org/thread/5822/
Вот одно из первых твоих появлений (во всяком случае, что удалось сохранить). 2013-й был не год назад.
>но не припомню чтобы тут кто-то за эту тему что-то писал
>Математика может быть правильно понята только в терминах конструктивизма
>ещё один и, возможно, последний гроб в крышку гроба под названием "Платонизм"
Продолжай отнекиваться.
> Прикрывать каждый свой обсёр несуразной ложью это здорово, конечно, но всё задокументировано:
Да ты же поехавший. Я в 2013 про конструктивизм даже не слышал. И треды про математику в сци не читал, мб там что-то и было на эту тему. Я другого не понимаю, какая тебе выгода писать десятки постов за ночь, пытаться тут любой мой пост закукарекать и т.д.
>Математика может быть правильно понята только в терминах конструктивизма
Я бы даже сказал, что математика это и есть конструктивизм. Невычислимое и непостроимое это в любом случае не математика.
>Я в 2013 про конструктивизм даже не слышал
Школу еще не закончил потому что? Don't make me think less of you.
>Невычислимое и непостроимое это в любом случае не математика
То есть ты просто более смешная пародия на изначального конструктивиста, который давно свалил с борды, так?
>Рисование стрелочек раздел фукционального программирования
>Вся математика делится на нечеткую логику, теорию алгоритмов, и машинное обучение
>Основной результат математики – изоморфизм Карри-Говарда, за него должна быть дана Нобелевская премия
>В странах первого мира вся наука делается на кафедре философии математики
Ясно.
> >Вся математика делится на нечеткую логику, теорию алгоритмов, и машинное обучение
> >Основной результат математики – изоморфизм Карри-Говарда, за него должна быть дана Нобелевская премия
> >В странах первого мира вся наука делается на кафедре философии математики
А я где-то утверждал что-то из этого? Я ж говорю, ты ебнутый. Сам пишешь хуйню, сам опровергаешь. Потом сам же мне предьявляешь что опроверг. Если не ты, то другой такой же. И после всего этого что-то имеешь против того чтобы вас тут называли дегенератами. Ну а кто вы?
>А я где-то утверждал что-то из этого
Привожу список твоих постов из прошлых тредов. Продолжай отнекиваться.
Первый тред:
">А математику как применять?
Математика как раз для любой задачи применима. Идентификация систем, машинное обучение", пост #220
"Математика - это и есть вычислимость. Вне вычислимости никакой математики быть не может, невычислимое в математике - это всякая вера в актуальные бесконечности, алефы-беты и прочий еврейский алфавит и исключенное третье." пост #237
">У тебя считается неоспоримым, что Брауэр – бох, а Лёф – пророк
У меня это считается вычислимым. Оспорить можно мнение, но не вычисление." пост #272
"Ты даже не понимаешь,что такое вычислимость и изоморфизм Карри Говарда, с чего ты решил чтотпонимаешь что такое математика?" пост #539
Второй тред:
"А вот у белых людей и труды выходят по философии математики и кафедры есть, Мартин-Леф как раз профессор кафедры философии математики." пост #48
Третий тред:
"Миша, но ведь теория категорий это просто рисование стрелочек уровня UML. Как же ты эту хуйню из хачкиля считаешь единственной математикой, где тебя так промыли-то?" пост #364
И т.д., мне просто лень дальше.
>>1166
>нобелевской премии по математике не существует.
Там это и написано:
>Ну её не дают, потому что большинство математики это не конструктивная болтовня про гамалогии, начиная с Гильберта и Пуанкаре.
>Премию Полей и коммутативную премию дают за всякую чушь шизофреническую.
>А я где-то утверждал что-то из этого
Привожу список твоих постов из прошлых тредов. Продолжай отнекиваться.
Первый тред:
">А математику как применять?
Математика как раз для любой задачи применима. Идентификация систем, машинное обучение", пост #220
"Математика - это и есть вычислимость. Вне вычислимости никакой математики быть не может, невычислимое в математике - это всякая вера в актуальные бесконечности, алефы-беты и прочий еврейский алфавит и исключенное третье." пост #237
">У тебя считается неоспоримым, что Брауэр – бох, а Лёф – пророк
У меня это считается вычислимым. Оспорить можно мнение, но не вычисление." пост #272
"Ты даже не понимаешь,что такое вычислимость и изоморфизм Карри Говарда, с чего ты решил чтотпонимаешь что такое математика?" пост #539
Второй тред:
"А вот у белых людей и труды выходят по философии математики и кафедры есть, Мартин-Леф как раз профессор кафедры философии математики." пост #48
Третий тред:
"Миша, но ведь теория категорий это просто рисование стрелочек уровня UML. Как же ты эту хуйню из хачкиля считаешь единственной математикой, где тебя так промыли-то?" пост #364
И т.д., мне просто лень дальше.
>>1166
>нобелевской премии по математике не существует.
Там это и написано:
>Ну её не дают, потому что большинство математики это не конструктивная болтовня про гамалогии, начиная с Гильберта и Пуанкаре.
>Премию Полей и коммутативную премию дают за всякую чушь шизофреническую.
"Препод из рашкошараги имеет что-то против величайшего математика 20 века, серьёзно?" Второй тред, пост #72
Итого.
>Рисование стрелочек раздел фукционального программированияъ
Утверждал.
>Вся математика делится на нечеткую логику, теорию алгоритмов, и машинное обучение
Утверждал.
>Основной результат математики – изоморфизм Карри-Говарда
Утверждал.
>В странах первого мира вся наука делается на кафедре философии математики
Утверждал.
>Мартина-Лёфа, лучшего математика тысячелетия
Утверждал.
> И т.д., мне просто лень дальше.
И как из этого следует та хуйня, что ты пишешь в предыдущем посте? Или тебе не очевидна разница между "математика это вычислимость" и "математика это нечёткая логика, теория алгоритмов и машинное обучение"?
> >Вся математика делится на нечеткую логику, теорию алгоритмов, и машинное обучение
> Утверждал.
> >Основной результат математики – изоморфизм Карри-Говарда
> Утверждал.
> >В странах первого мира вся наука делается на кафедре философии математики
> Утверждал.
> >Мартина-Лёфа, лучшего математика тысячелетия
> Утверждал.
Пиздежь полный. То что ты не очень умный и не можешь понять о чем тебе пишут вообще, не даёт тебе права приписывать мне вещи, которые я по факту не утверждал никогда.
>В голову не приходило, что много анонов просто согласны с идеями
Все что я перечислил, были ответы на мои посты с цитированием одного и того же, очевидно что их один человек писал.
>>1171
>Или тебе не очевидна разница
А что еще математика? Гамалогии и топазы это не математика, понятно, ещё что?
>>1172
>ДА ЧЕ ВЫ ПРИСТАЛИ НЕ ГОВОРИЛ Я ТАК Я ВООБЩЕ ОБ КОНСТРУКТИВИЗМЕ ДВЕ НЕДЕЛИ НАЗАД УЗНАЛ Я ОБЫЧНЫЙ ЧЕЛОВЕК ТУТ НЕДАВНО ПРОСТ ПОТРОЛИТЬ ЗАШЕЛ
То есть ты не согласен с тем, что изоморфизм Карри-Говарда это важнейший результат в математике, а Мартин-Лёф крупнейший математик, так?
>Все что я перечислил, были ответы на мои посты с цитированием одного и того же, очевидно что их один человек писал.
Мужик, ну это же анонимная имиджборда. Ты никогда не узнаешь наверняка, кто за каким постом скрывается.
Но, кстати, я вижу чем ты тут занимаешься :3 Интересно деанонить, основываясь только на анонимных сообщениях? Если бы в нашем распоряжении было ещё хоть что-то, кроме ссылок на посты - какой-то явный инструмент, связывающий посты, можно было бы создать исчисление анонимных высказываний, лол
educated guess is more than enough, и в более крупных разделах типа /mu, /bo всегда понятно кто тебе отвечает, а тут и подавно. он и сам признал выше.
> А что еще математика? Гамалогии и топазы это не математика, понятно, ещё что?
Я же говорю, ты просто не понимаешь, что я на эту тему вообще пишу. Сколько конкретно раз мне ещё нужно написать, что математика это вычислимость, чтобы до тебя дошло, что математика это вычислимость?
Казалось бы, вот тебе передний край науки, сиди изучай, открывай. Нет, мы придумаем ещё аксиом, лишь бы не терять наследие.
> Из простого правила построения получаем и трансфинитные и бесконенчно малые,
Нет конечно. Ещё Брауэр объяснял почему.
> Казалось бы, вот тебе передний край науки, сиди изучай, открывай. Нет, мы придумаем ещё аксиом, лишь бы не терять наследие.
Понимаешь, отказ от наследия приведёт только к тому, что ты это же наследие и переоткроешь через десятки лет упорной работы. Ты зря считаешь себя умнее тех кто жил в позапрошлом веке. 100% того что ты сможешь открыть, дропнув наследие, будет это же самое наследие, либо нечто, тривиально к нему сводящееся.
>Нет конечно.
Ты поехавший. Статью прочти.
>Понимаешь, отказ от наследия приведёт только к тому
Беспочвенные утверждения. Ты просто проявляешь свой страх.
>Ты зря считаешь себя умнее тех кто жил в позапрошлом веке.
Не считаю. Думаю, их умность заключалась в том, что они своей головой думали, и были адекватны задачам своего времени. А не веровали в вечную истину.
Или ты думаешь, что я предлагаю книги сжигать? Просто, если конструктивизм с какими-то задачами справляется лучше, но при этом в твоем наследии месту конструктивизму нет, то это проблемы наследия.
1.Я не человек.
2.Людей несуществует
Человек — это объект, обладающий [определёнными] физиологическими свойствами.открытая система, это не определение
Я — это объект, который обладает [определенными] свойствами.
Я — человек. Это равенство между двумя объектами, где вместо "—" можно поставить "="
Посмотрим наши псевдоопределения.
Совпадают ли свойства "человек" и "я"?
Согласно определениям, необязательно.
Но, " я" обладает свойствами отличными от "человек" в физическом мире.
Например "я" могу "продавать обувь".
Но к понятию "человек" не относится свойство "продавать обувь", значит " я не человек", ибо свойства "человек" и "я" не совпадают.
Вещи физического мира всегда не являются обозначимыми понятиями, тем, как мы называем их, даем определения.
Определение ≠ смысл конкретной вещи.
Значит все, что о чем мы говорит не существует. Или существует в мире идей.
В мире обобщения, где детали перестают быть существенными, т.е существовать.
Мир обобщения — это мир идей.
Это мир, где неинтересны детали, где мы называем себя людьми, но нам не важно, совпадают ли все свойства[смысл] "нас" и "людей".
>исчисление анонимных высказываний
Буквально вчера во время приступа думал о том вернее представлял, как сюда пишу что анонимность на борде весьма условное понятие, чем больше постов оставляешь тем меньше твоя анонимность, чем меньше борда тем меньше анонимность. Поэтому анонимусы не должны бугуртеть от притока народа на борду, а совсем даже наоборот.
Вот задача как раз в том, чтобы этот пример выдумать.
Во первых, это что-то, что рядовому анонимусу будет полезно. Иначе он пользоватся этим не будет.
Можно и с другого конца зайти, проанализировать структуру борды, что в ней можно изменить?
Тут затрагывается ещё одна проблема.
Граница.
В топологии, объект который не имеет точного определения, называется объект заданный окрестностью или открытый объектоткрытая система
Зданию соответствуют его свойства.
Но здание представляет и квартиры, которые находятся в нем.
В здании необязательно должны быть квартиры, но, если они есть, они считаются частью "здания".
Значит зданий, домов, камней, деревьев не существует. Так как эти объекты предполагают то, что не входит в их определения.
Точнее, понятие "здание" не предполагает помещения с телевизорами.
Но мы то знаем, что телевизоры внутри, и они являются частью здания.
Следовательно зданий не существует.
Перед тем, как задавать свои вопросы, я посмотрел на даты твоих постов, и у меня такое чувство, что работаешь ты круглосуточно, и никаких интересных дел дома у тебя нет.
И ты не ответил на остальные вопросы, а они были очень важны. Такое чувство, что ты выбрал ответить на вопрос о распорядке дня только потому, что он выглядел как наезд и тебе хотелось немедленно пооправдываться (через 15 минут. видимо, этот треду тебя в закладках, приятно, что кто-то нас так сильно любит).
То есть, с тобой уже даже практически невозможна нормальная человеческая коммуникация. Чтобы что-то у тебя спросить, приходится использовать манипулятивные техники, вынуждать тебя оправдываться. Не представляю, каково твоей девушке. Двач, конечно, весёлое место, но некоторым он вреден. Тебя, например, он разрушает. Через какое-то время ты вовсе утратишь способность быть нормальным человеком, будешь как те полубезумные старики, что строчат чудовищные коменты на ютубе про политику и разврат современной молодёжи и вызывают у остальных мороз по коже. Ты уже почти там.
Спасибо за пояснение. Мне, правда, пока ещё не верится, что все инт/кон такие. Потому что я пока ещё воспринимаю это как течение мысли, а не как какой-то паттерн назревающих психических проблем.
>Интуиционисты которых я знаю на бордах и ИРЛ, просто придумали себе философскую надстройку над математическими теоремами и гасаждают её другим.
Отсюда рождается вопрос, как блюсти внутреннюю интеллектуальную чистоту? Что нужно делать, чтобы быть уверенным, что не построил подобные настройки? Различных течений мысли много, их активно описывают в разных книжках, но нигде не пишут про гигиену головы. Как не стать припижженным математиком?
Ты зря стараешься анон, он шизик.
> И ты не ответил на остальные вопросы, а они были очень важны.
Там все равно не было ничего по теме треда. Ты сам свои посты читаешь? Это же смешно. Теперь ты ещё пытаешься уговорить кого-то кроме себя что интуиционизм это заболевание. Все что угодно, только бы не признавать свою неправоту. У меня вообще серьёзные подозрения, что ты селедка. Причём, психолух какой-нибудь. Бывали у меня такие знакомые, твои посты прямо дежавю.
> Отсюда рождается вопрос, как блюсти внутреннюю интеллектуальную чистоту? Что нужно делать, чтобы быть уверенным, что не построил подобные настройки? Различных течений мысли много, их активно описывают в разных книжках, но нигде не пишут про гигиену головы. Как не стать припижженным математиком?
Если у тебя подобные вопросы вообще возникают, с тобой уже что-то не так.
Размышлять самому.
Если ты занимаешься математикой, то априорно ты не владеешь искажёнными надстройками.
Конструктивист тоже сам размышляет и занимается математикой(вычислениями).
Из чего ты взял, что Вербицкир тут сидит?
Читал, что если будет иное значние Pi, то будут другие законы геометрии.
Например, окружность будет квадратом.
И в том мире, не будет существовать "поворота".
Читал, что число Пи это пятый постулат евклида.
>Вообще у V постулата имеется огромное количество эквивалентных формулировок, многие из которых сами по себе кажутся довольно очевидными.
>Существует окружность (хотя бы одна), у которой отношение длины окружности к её диаметру равно числу Пи .
>Там все равно не было ничего по теме треда.
Не надо бояться и прикрываться такими формальными поводами как "это не по теме треда". Обзывать собеседников тоже не по теме треда, но тебя это не смущало ранее.
Но если ты просто не хочешь отвечать, я пойму, тебе не обязательно оправдываться.
>Ты сам свои посты читаешь? Это же смешно.
Рад, если смог повеселить.
>Теперь ты ещё пытаешься уговорить кого-то кроме себя что интуиционизм это заболевание.
Нет, я этого не делал и никогда даже так не думал. В тред пишу чтобы разобраться. У тебя холостое срабатывание оборонной позиции.
> Все что угодно, только бы не признавать свою неправоту.
Какую неправоту? Какой тезис я выдвигал? Можешь процитировать? Неправоту в чём? Я бы хотел, чтобы ты не игнорировал хотя бы этот вопрос, если снова будешь отвечать избирательно на мой пост, как тебе свойственно.
> У меня вообще серьёзные подозрения, что ты селедка.
Твоё дело. Ты ведь сможешь это пережить, надеюсь?
>Причём, психолух какой-нибудь.
Это ещё почему, потому что я задаю личные вопросы? Ты никогда ни с кем не общался на подобные темы и считаешь, что этим занимаются психологи, и что это что-то такое, от чего нужно защищаться? Слушай, когда я спрашивал, почему ты не с близкими, ты не хотел отвечать потому, что никаких близких у тебя и нет?
>Слушай, когда я спрашивал, почему ты не с близкими, ты не хотел отвечать потому, что никаких близких у тебя и нет?
Протестую. На дваче обвинять в хикканстве табу.
Как я уже успел убедиться, математика - колоссальная по своему объему наука и от обилия её разделов просто глаза разбегаются. Наиболее интересные для меня - дифференциальные уравнения и связанные/необходимые для них темы.
Хотелось бы дальнейшую свою судьбу связать с математикой, но вот как это сделать - не знаю. Поэтому не могли бы вы, анончики, ответить на следующие вопросы:
1. Что должен знать и уметь математик (в ключе интересующих меня тем)?
Если вам не трудно, приведите (или дополните мой) список разделов, которые с вашей точки зрения, нужно изучить. (Буду очень благодарен, если к каждому разделу вы приведете список учебников/задачников, которые стоит прочитать).
Теория множеств
Матанализ
Функан
Топология
Алгебра (линейная)
Алгебра (абстрактная)
Численные методы
ДУ
С каждым из этих разделов я знаком в той или иной мере. (Иногда мне кажется, что в никакой мере. Особенно, после некоторых тем в общем разделе форума математика) На какие разделы/подразделы стоит обратить дополнительное внимание, то есть, без них - никак. Какие ещё базовые разделы необходимо изучить (например, теория чисел - её нам не преподавали вообще, а я заметил, что всплывает она в самых разных местах). Какие более продвинутые разделы стоит изучить, чтобы стать математиком (например, теория хаоса, бифуркаций т. д.). Как проконтролировать достаточность своих знаний (например, математический тривиум Арнольда...)?
Если в остальных разделах список неплохой литературы я более-менее представляю, то в этих - не совсем/его расширение лишним не будет.
Я привел не весь список разделов математики, которые я изучал, только те, которые показались важными.
2. Как стать математиком?
Допустим, я таки изучил необходимый минимум. Как начать работать (начинающим) математиком? Куда нужно обращаться? И вообще, что из себя представляет работа математика? Ведь вряд ли это решение задач из задачника :) (Нет, я приблизительно представляю, как это, но хотелось бы узнать подробнее).
3. Могу ли я им стать?
Я сейчас не на первом курсе - на пятом. По уже изученным дисциплинам не считаю свои знания идеальными и дополнительных знаний, выходящих за рамки институтского курса, не имею (если и имею, то очень мало). Я неплохо программирую, поэтому вполне могу развиваться дальше как программист, но хотел бы стать всё же математиком. Но при этом как-то не хочется быть, что называется "ни рыба, ни мясо" - не программист и не математик. Стоит ли пытаться стать в моем случае математиком? Или я уже бесконечно отстал от выставляемых профессиональным математикам требованиям?
Приношу свои извинения, если мои вопросы звучат наивно или нагло. Сильно не бейте :cry:
Спасибо!
Как я уже успел убедиться, математика - колоссальная по своему объему наука и от обилия её разделов просто глаза разбегаются. Наиболее интересные для меня - дифференциальные уравнения и связанные/необходимые для них темы.
Хотелось бы дальнейшую свою судьбу связать с математикой, но вот как это сделать - не знаю. Поэтому не могли бы вы, анончики, ответить на следующие вопросы:
1. Что должен знать и уметь математик (в ключе интересующих меня тем)?
Если вам не трудно, приведите (или дополните мой) список разделов, которые с вашей точки зрения, нужно изучить. (Буду очень благодарен, если к каждому разделу вы приведете список учебников/задачников, которые стоит прочитать).
Теория множеств
Матанализ
Функан
Топология
Алгебра (линейная)
Алгебра (абстрактная)
Численные методы
ДУ
С каждым из этих разделов я знаком в той или иной мере. (Иногда мне кажется, что в никакой мере. Особенно, после некоторых тем в общем разделе форума математика) На какие разделы/подразделы стоит обратить дополнительное внимание, то есть, без них - никак. Какие ещё базовые разделы необходимо изучить (например, теория чисел - её нам не преподавали вообще, а я заметил, что всплывает она в самых разных местах). Какие более продвинутые разделы стоит изучить, чтобы стать математиком (например, теория хаоса, бифуркаций т. д.). Как проконтролировать достаточность своих знаний (например, математический тривиум Арнольда...)?
Если в остальных разделах список неплохой литературы я более-менее представляю, то в этих - не совсем/его расширение лишним не будет.
Я привел не весь список разделов математики, которые я изучал, только те, которые показались важными.
2. Как стать математиком?
Допустим, я таки изучил необходимый минимум. Как начать работать (начинающим) математиком? Куда нужно обращаться? И вообще, что из себя представляет работа математика? Ведь вряд ли это решение задач из задачника :) (Нет, я приблизительно представляю, как это, но хотелось бы узнать подробнее).
3. Могу ли я им стать?
Я сейчас не на первом курсе - на пятом. По уже изученным дисциплинам не считаю свои знания идеальными и дополнительных знаний, выходящих за рамки институтского курса, не имею (если и имею, то очень мало). Я неплохо программирую, поэтому вполне могу развиваться дальше как программист, но хотел бы стать всё же математиком. Но при этом как-то не хочется быть, что называется "ни рыба, ни мясо" - не программист и не математик. Стоит ли пытаться стать в моем случае математиком? Или я уже бесконечно отстал от выставляемых профессиональным математикам требованиям?
Приношу свои извинения, если мои вопросы звучат наивно или нагло. Сильно не бейте :cry:
Спасибо!
Да поздно спохватился, нужно было ответами оттуда отвечать.
http://hk.mathphy.googlepages.com/puremath.htm
Здесь огромный список, разбитый по разделам и уровням. Правда, все на английском.
>дифференциальные уравнения
Векторные поля на многообразии.
>приведите (или дополните мой) список разделов, которые с вашей точки зрения, нужно изучить
Алгебраическая к-теория, алгебраическая геометрия, топологическая к-теория.
>Теория множеств, Численные методы
В математике не используется.
>Функан, Алгебра (линейная)
Это одно и то же.
>Матанализ
Лоскутная область типа "дискретной математики", состоящая из криво пришитых друг к другу кусков алгебры, общей топологии и теории меры.
>ДУ
Раздел алгебры.
>Алгебра (абстрактная)
Что это? Впервые слышу.
>теория чисел - её нам не преподавали вообще
Под теорией чисел понимают обычно две вещи. "Аналитическая теория чисел" – это просто функциональный анализ. "Алгебраическая теория чисел" – теория полей классов, локальная и глобальная. Иногда так же под теорией чисел понимают арифметическую алгебраическую геометрию. Зависит от контекста. Все эти темы разбираются в обзоре Манина-Панчишкина.
В советских книгах типа Михеловича под теорией чисел понимали просто школьную алгебру, то есть делимость НОК и НОД, сравнения mod n в кольце вычетов, и т.д.
>Ведь вряд ли это решение задач из задачника
Как раз тут ты угадал. Надо решать задачи, и много. Стоит заметить впрочем, что задачи в математике могут быть только на доказательство утверждений, уж никак не на вычисление чего-либо.
>Я сейчас не на первом курсе - на пятом
В математике возраст не имеет значения, если тебе меньше 75-ти, конечно.
Там, кстати, один из ответ ведёт к Вербиту, и вот что он пишет.
Здравствуйте, мои дорогие маленькие друзья!
>1) Какие еще разделы математики тебе кажутся
> перспективными кроме алгебраической и дифференциальной
> геометрии и топологии?
Сейчас меня особенно прикалывает от теории
CAT-пространств, симплектической геометрии,
геометрического анализа и геометрической теории групп.
Но вообще - если где-то упоминают Громова или Перельмана,
это оно. Мне так кажется.
>2) Ты собираешься в дальнейшем обновлять свою программу?
Я надеюсь, о да. Надеюсь.
>3) Ты больше ценишь в девках - ум или сиськи?
Ум и сиськи. Ум и сиськи. Ум и сиськи. Ум и сиськи.
Сиськи и ум.
>4) Ты не собираешься больше писать что-нибудь такое же
> объемное про антикопирайт и трэш-культуру?
Надо бы, да.
>5) Миша, какие ты видишь перспективы в
>применении компьютеров в математике?
Думаю, что arxiv.org сам по себе уже колоссально
расширил область применения математики и компьютеров
в математике. В дальнейшем предвижу появление киборгов.
Сам бы не отказался иметь круглосуточный доступ к
Интернету непосредственно через череп.
>6) Правда, что теория множеств, математическая логика,
> теоретико-множественная топология, функциональный
> анализ, абстрактная алгебра (ну то есть то, что
> развивалось в первой половине 20го века) уже давно не
> актуальны?
Увы. Хотя я люблю эти науки. Но население их не ценит.
Подвергался критике за весьма скромные объемы этого
самого, когда учил первокурсников.
Впрочем, логика существует как отдельная от математики
наука, и в этом качестве весьма бурно развивается.
Но от математики (в традиционном смысле слова - алгебры,
геометрии и теории чисел) эти исследования довольно далеки.
>7) Нестандартный анализ - чепуха?
Нестандартный анализ это дикий прикол.
Население этого тоже не понимает, увы.
>8) Синергетики - совсем долбоебы, а синергетика - просто модное слово?
Угу.
>9) Нужно ли математику знание современной теорфизики?
Необходимо. Хотя я сам в этом плане урод и ничего не знаю.
>10) Миша, есть ли по твоему мнению сейчас что-то толковое
> в прикладной математике/сomputer science?
По-моему, дофига. P = NP например. Или учение о квантовом
компьютере.
О сем есть книжка Китаев-Вялый-Шень, чрезвычайно увлекательная.
>11) Как ты относишься к таким несостоявшимся
>наукам, как теория систем и кибернетика?
Жулье, по-моему. Унылое жулье.
>12) Как ты относишься к Бурбакам?
Бурбаки доставляют. Аутсайдеры (евреи и
протестанты) из ебеней и без должностей и регалий
основали пара-масонское общество и за 20 лет поставили
французскую математику на уши.
Книжки Бурбаков, за редкими исключениями,
отстой, но исторически немаловажные. Сами же
Бурбаки (к примеру: Картан, Серр, Эйленберг)
натурально гениальные чуваки.
>13) Правда, что для занятий математикой нужны охуенные
> способности и вообще все это невероятно сложно?
Не нужно особенных способностей, по-моему.
Нужно баранье упорство и отмороженность.
И толика вкуса, я думаю, иначе упорство и
отмороженность приведут к изучению конечных
групп порядка p^5, тканей в R^2 или какой-то
подобной ахинеи.
>14) Стоит ли, для того чтобы стать математиком, поступать
> на математическую специальность? Ведь в вузах по три
> года долбят матан, а общая топология - это для них
> потолок, в то время как в инете есть куча полезных
> книжек, есть колхоз, есть лекции нму, есть твоя
> программа, и т. п.
Опыт показывает, что в изоляции научиться
наукам невозможно. Исключения редки, а люди,
которые думали, что у них получится, заканчивали
в канаве. Фигурально выражаясь.
То есть нужно иметь группу, человек в 15 хотя бы,
с которыми постоянно общаться о науке. Я думаю.
Для этого недостаточно поступить на математическую
специальность, но это может помочь.
Последний абзац меня убил. Уже который раз слышу такое мнение. Неужели это правда.
Там, кстати, один из ответ ведёт к Вербиту, и вот что он пишет.
Здравствуйте, мои дорогие маленькие друзья!
>1) Какие еще разделы математики тебе кажутся
> перспективными кроме алгебраической и дифференциальной
> геометрии и топологии?
Сейчас меня особенно прикалывает от теории
CAT-пространств, симплектической геометрии,
геометрического анализа и геометрической теории групп.
Но вообще - если где-то упоминают Громова или Перельмана,
это оно. Мне так кажется.
>2) Ты собираешься в дальнейшем обновлять свою программу?
Я надеюсь, о да. Надеюсь.
>3) Ты больше ценишь в девках - ум или сиськи?
Ум и сиськи. Ум и сиськи. Ум и сиськи. Ум и сиськи.
Сиськи и ум.
>4) Ты не собираешься больше писать что-нибудь такое же
> объемное про антикопирайт и трэш-культуру?
Надо бы, да.
>5) Миша, какие ты видишь перспективы в
>применении компьютеров в математике?
Думаю, что arxiv.org сам по себе уже колоссально
расширил область применения математики и компьютеров
в математике. В дальнейшем предвижу появление киборгов.
Сам бы не отказался иметь круглосуточный доступ к
Интернету непосредственно через череп.
>6) Правда, что теория множеств, математическая логика,
> теоретико-множественная топология, функциональный
> анализ, абстрактная алгебра (ну то есть то, что
> развивалось в первой половине 20го века) уже давно не
> актуальны?
Увы. Хотя я люблю эти науки. Но население их не ценит.
Подвергался критике за весьма скромные объемы этого
самого, когда учил первокурсников.
Впрочем, логика существует как отдельная от математики
наука, и в этом качестве весьма бурно развивается.
Но от математики (в традиционном смысле слова - алгебры,
геометрии и теории чисел) эти исследования довольно далеки.
>7) Нестандартный анализ - чепуха?
Нестандартный анализ это дикий прикол.
Население этого тоже не понимает, увы.
>8) Синергетики - совсем долбоебы, а синергетика - просто модное слово?
Угу.
>9) Нужно ли математику знание современной теорфизики?
Необходимо. Хотя я сам в этом плане урод и ничего не знаю.
>10) Миша, есть ли по твоему мнению сейчас что-то толковое
> в прикладной математике/сomputer science?
По-моему, дофига. P = NP например. Или учение о квантовом
компьютере.
О сем есть книжка Китаев-Вялый-Шень, чрезвычайно увлекательная.
>11) Как ты относишься к таким несостоявшимся
>наукам, как теория систем и кибернетика?
Жулье, по-моему. Унылое жулье.
>12) Как ты относишься к Бурбакам?
Бурбаки доставляют. Аутсайдеры (евреи и
протестанты) из ебеней и без должностей и регалий
основали пара-масонское общество и за 20 лет поставили
французскую математику на уши.
Книжки Бурбаков, за редкими исключениями,
отстой, но исторически немаловажные. Сами же
Бурбаки (к примеру: Картан, Серр, Эйленберг)
натурально гениальные чуваки.
>13) Правда, что для занятий математикой нужны охуенные
> способности и вообще все это невероятно сложно?
Не нужно особенных способностей, по-моему.
Нужно баранье упорство и отмороженность.
И толика вкуса, я думаю, иначе упорство и
отмороженность приведут к изучению конечных
групп порядка p^5, тканей в R^2 или какой-то
подобной ахинеи.
>14) Стоит ли, для того чтобы стать математиком, поступать
> на математическую специальность? Ведь в вузах по три
> года долбят матан, а общая топология - это для них
> потолок, в то время как в инете есть куча полезных
> книжек, есть колхоз, есть лекции нму, есть твоя
> программа, и т. п.
Опыт показывает, что в изоляции научиться
наукам невозможно. Исключения редки, а люди,
которые думали, что у них получится, заканчивали
в канаве. Фигурально выражаясь.
То есть нужно иметь группу, человек в 15 хотя бы,
с которыми постоянно общаться о науке. Я думаю.
Для этого недостаточно поступить на математическую
специальность, но это может помочь.
Последний абзац меня убил. Уже который раз слышу такое мнение. Неужели это правда.
https://www.youtube.com/watch?v=zNXVDNAs1oY
>Сейчас меня особенно прикалывает от теории
Под "сейчас" следует читать "начиная с конца 90-х".
>абстрактная алгебра (ну то есть то, что развивалось в первой половине 20го века) уже давно не актуальны?
А что развивали до 1940-х? Модули над кольцами, ассиоциативные алгебры. Это настолько не актуально, что входит в обязательные курсы в любом приличном месте. Колоссальный бред, по-моему.
>Необходимо
угу, часто заканчивается фейлом
если студент в детстве читал ну типа Перельмана занимательную физику,
то не заканчивается, то есть ничего другого наверное и не надо
( Ответить) ( Уровень выше ) (Ветвь дискуссии)
kaledin
Я бы сказал, что даже и вредно. Т.е. картину в голове иметь полезно, но прочитать про нее хотя бы один учебник физики с формулами.... нафиг, нафиг
>О сем есть книжка Китаев-Вялый-Шень
Книг есть много и более вменяемых, например Garey&Johnson, но это теория алгоритмов, а не математика.
>>1231
2ch.hk/mu/
Есть люди, которые социоблядствуют, но глубоко одиноки. Слово "хикки" мало что значит.
Зачем скатывать тред в одно обсуждение конструктивизма? От него уже тошнит. Других тем нет?
Математика и есть конструктивизм, эти понятия неотделимы.
Чет в шепот с вас. Копротивляться непонятно зачем против интуиционизма, чтобы выяснить, что кроме него вам и поговорить не о чем. Какие же вы ущербы, прости господи. Я из всего вашего копротивления так и не понял, зачем в математике непостроимые, невычислимые верования.
 23 Кб, 720x1280
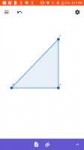
23 Кб, 720x1280>Существуют ли в математике примеры нарушения правила исключения третьего?
Существует. Например, это определение производной.
Производная, определяется, как сторону CA поделить на BA.[пикча]
Где BC — любой рисунок, любая картина, хоть нарисованные члены.
Фишка в том, что BC бесконечно старается стать отрезком, а не рисунком, а мы считаем, что эта бесконечность достигается.бесконечность недостижима по определению
Поэтому, говорим, что отношение[деление] двух сторон равняется тангенсу и производной.
Так как тангенс определяется точно также, т.е эта сторона поделить на эту, но только, если учесть что CB — просто отрезок. А для производной, CB — все что угодно.
Другими словами, противоречия просто нкжно допускать, чтобы раскрыть новые границы.
Истинность двух противоречивых высказаваний — инструмент.
Чем тебе не нравится матанализ? Здесь обсуждаются и более лёгкие вопросы, но ты их не осуждаешь.
Причём тут моё отношение к нему? "мат"анализ не является математикой, следовательно я не обязан знать его "определения". И не советую тут обсуждать хуйню не по теме. Для этого есть специальные доски.
Математика — это то, что не даёт спокойно спать конструктивистам.
Математика изучает саму себя.иначе математика изучает не-математические структуры
Значит, и придумала термин "модуль над кольцом". Но придумать этот термин невозможносто в рамках действий только модулей над кольцами.
ТВОЕ ОПРЕДЕЛЕНИЕ, ПРОТИВОРЕЧИВО
>структуры
Как там в сороковых?
>Но придумать этот термин невозможносто в рамках действий только модулей над кольцами
То есть по-твоему Дедекинд знал что есть не абелевы категории?
>Существуют ли в математике примеры нарушения правила исключения третьего?
Их очень много. Противоречие — инструмент математики.
Например, понятие площади.
Площадь — это то, сколько может вместиться квадратов в фигуру.
Сколько может вместиться в прямоугольный треугольник?
Площадь прямоугольного треугольника равна половине произведение катетов.
Пифагорова тройка (3, 4, 5) даёт площадь, как целое число.
Но фактически, мы никогда не сможем вставить в этот треугольник шесть квадратов. Другими словами, это фикция, которая противоречит нашему определению, зато применяется на практике.
Вообще, допускается это противоречие, чтобы изобрести меру плоской фигуры.
Т.е вначале важно, что площадь — количество квадратов в фигуре. А затем неважно.
Забыл, уточнить.
Единственное применение площади — это интеграл, так как тот позволяет оценить рисунок, относительно каждой точки, т.е интеграл — нечто(числа с буковками) являющая результатом всех точек рисунка. А то число с буковками, требует сумму площадей бесконечно-маленьких фигур.
В других случаях, лучше применить периметр. Он всегда целый и его легче считать, плюс он также характеризует площадь.
 25 Кб, 720x1280
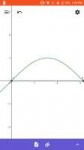
25 Кб, 720x1280Направильно сказал, слишком обобщил.
Интеграл, характерезует такую фигуру, где
Одна сторона — прямой отрезок, а вторая — произвольная кривая, где две точки не могут находиться на одной вертикали.
 27 Кб, 720x1280
27 Кб, 720x1280Первую фигуру, которая слева, невозможно описать, как интеграл, так как две точки лежат на одной абсциссеодинаково далеки от конца B или A, относительно F и E отрезка A и B
На втором рисунке, можно. Ведь нету на тоски абциссы двух координат.
Нет, я бы даже не сказал, что почти.
Ведь в фигуре, которая представлена интегралом, одна сторона должен быть прямой. А еще, кривая должна быть по определенному правилу.
Не понимаю. Как ты пришел к выводу, что треугольники — это синусы. Можешь объяснить?
Я лично пока не приходил, но вот человек в прикрепленном треде пришел, из твоих пространных объяснений. По-моему, лучше уж говорить что интеграл это гомоморфизм; чем что "интеграл это фигура", меньше заблуждений потом.
 158 Кб, 1280x1024
158 Кб, 1280x1024Если взять топологическую структуру, получается, чтобы описать рисунок, нужно бесконечное количество интегралов.
Под "рисунком" я имею ввиду, зависимость вещей от друг-друга. Количество того, сколько вещей зависят друг-от-друга, называются измерениями.
На тех рисунках, я рисовал двухмерное измерение, описывал зависимость двух величин.
Кстати, нужно уточнить, это работает, только, если топологическое пространство бесконечно-сложное.
Т.е нету какой-то элемента, атома, который будет бесконечно однообразен. В таком случае, можно использовать один интеграл, обобщающий эту бесконечность
>>1368
Кстати, в анализе, функция "интеграла", как раз и задана на топологическом пространстве.
То, есть, первое утверждение — тавтология. Зачем я это сказал?
Хотя, если говорить о бесконечно-сложных системах, тогда, действительно, для описания рисунка нужно бесконечное количество интегралов!
Как не очевидно!
Ну, натуральные числа.
Между единицей и нулем, нету бесконечного числа чисел, как в топологическом пространстве.
Я знаю бесконечно-много нетопологических пространств.
Нуль неоднозначно принадлежит натуральным числам, лучше выбрать что-то другое.
В натуральных числах, между 5 и 6 нету бесконечного количества других числел.
>Нуль неоднозначно принадлежит натуральным числам
Однозначно. Без нуля натуральные числа не образуют моноид, значит их нельзя пополнить до целых.
>нету бесконечного числа чисел, как в топологическом пространстве
https://en.wikipedia.org/wiki/Discrete_space
Блин, я забыл добавить.
Там стоит такое же ограничения, как и на интегралы. Т.е нельзя ставить точку на одной оси абцисс.
Чего читать? Интеграл это фигура, производная это гипотенуза деленная на катет, топологическое пространство бывает только гомеоморфрное R^n.
Иди нахуй. Выучи математику, потом пиши.
Ты делаешь неправильные выводы.
Интеграл описывает фигуру, где один отрезок — прямая, при этом, она должна идти всегда вперёд по горизонтали, не возвращаясь назад.
Производная описывает фигуру, где два отрезка — прямые, где третий, также идти всегда по горизонтали.
Производная, в отличии от интеграла, является самим углом фигуры, она её и описывает.
Нет, я потом, излишне обобщил про производную.
Там кроме двух прямых отрезок, там требуется прямой угол.
Всё верно сказал.
>анонимность на борде весьма условное понятие, чем больше постов оставляешь тем меньше твоя анонимность, чем меньше борда тем меньше анонимность
Понял вчера, что не только на борде. Скажем, можно же на фейсбуке создать страницу под своим реальным именем и фамилией. Формально вроде сдеанонился, но если больше никакой инфы не оставил, то там страниц с такими же иминем и фамилией - тысячи.
То есть, анонимность - это некое свойство сети (графа), и оно динамично. Можно сформулировать как игру двух агентов, Анона и дЕанона. Первый старется "слиться с сетью", стать неотличимым, второй - собирает отличия, фильтрует сеть.
Ватная алгебра.
Если под Демидовичем вы имеете в виду Хартсхорна, то все.
>Существуют ли в математике примеры нарушения правила исключения третьего?
Существуют.
Например единица соответствует определению простого числаделится на себя и единицу, но не относится к простым. Это, чисто из прагматической точки зрения.
Действительно. А ещё это является нарушением modus ponens.
https://en.wikipedia.org/wiki/Prime_number
> A prime number (or a prime) is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Ну да, если ты недоучка, то у тебя вся математика состоит из противоречий.
>>1476
Я выступал против прагматики.
Отказались от единицы, так как та необычным образом составляла составные числа.
Для меня, такой подход — неуместен, ведь имеет предвзятость, заинтересованность.
Математические понятия — это божественные структуры, делать в них исключения для удобства — плохой тон.
Ещё, большинство говорит, что числа имеют конечное количество делителей, так как "делителями могут быть лишь числа; тождества представляющие одно число — одно и тоже".
Ещё большинство говорят, что, если уравнение с нулевым дискриминантом имеют одно решение. Но я то знаю, что их неопределённое количество.
Так как тождества не равны между собой:
2+3≠3+2, даже, если оба равны "5", и у нас определённа коммутативность.
Истинную коммутативность нельзя выразить a+b=b+a, ведь тут понятие символа, которое не может быть определённо.
5≠2+3, так как написав "5" вместо "2+3", мы теряем информацию того, что в данном случае "2+3".
А выражения являются одинаковыми, если они одинаково содержательные, несут один смысл.
Какой я аутичен.
Я отвечу, что "2+3" содержит повышенного внимание "2+3", тогда в "5", " 2+3" и "1+4" равноценны.
Ты реально заебал со своим бессвязным бредом. Грамматические ошибки уровня пятого класса еще можно терпеть, но математического содержания у твоих высеров ноль, не осилил определения даже.
Значит, ты вводишь в математику понятие ценности?
Тип, всякий рассматриваемый объект имеет достаточную ценность, если рассматривается в данном выражении.
Если он не рассматривается, то он менее ценен.
Тогда "2+3" и "3+2" определить, как различные объекты.
В случае, отсутствия в выражении объекта, он становится менее ценен, а если его невозможно вывести, тогда он теряет свою ценность.
>нету связи с религией
Платонизм — религиозное учение Платона и его последователей, утверждающее, что универсальные понятия существуют независимо от их конкретных воплощений.
А если будет иначе, ведь будет противоречие.
>универсальные понятия существуют независимо от их конкретных воплощений.
1.Универсальные понятия существуют зависимо от конкретных воплощений.
2.Общие понятия существуют зависимо от частных воплощений
3.Общие понятия зависимые от частных воплощений
4.Общее зависит от частного.
зачкм столько флуда?
Общее — это что-то значимое(игнорируем все остальное)множество, класс, совокупность
Частное — это элемент общего, который, является общим. Значимый элемент значимого.элемент множества, объект категории
ТЫ УТВЕРЖДАЕШЬ, ЧТО СИСТЕМА ЗАВИСИТ ОТ ЕЕЭЛЕМЕНТОВ.
Но ты забываешь об возможной эмерджентности
Множества не являются элементами других множеств и объектами различных категорий? Понял.
Ты не к тому сопоставил скобки.
Частное — это элемент/элементы множества
Общее — само множество.
>Не математика. С этим в /b/.
Вербицкий в своей книге об этом пишет,
Даже пустоту вводит в определении множества подмножеств.
Тип, совокупность всех подсистем этой системы, равняется степени двойки, только тогда, когда пустота всегда считается элементом системы.
>Если он завтра напишет, что "взятие интегралов" является математикой, то ничего не поменяется.
Он рекомендует их решать для школьников.
Значит, это математика.
Привёл выше.
Могу более очевидные, тип, операции с пустотой и другими элементами.
Например, у пересечения системы и пустототы, нету общих элементов, или их пересечение — пустота.
Где про школьников
Математика. Официальные международные классификационные системы определяют, "теорию множеств", как часть математики.
.
>Дифференцирование, интегрирование, формула Ньютона-Лейбница. Дельта-эпсилон формализм, лемма о милиционере.
Отказались не от единицы, а от unit'ов.
В кольце главных идеалов, каким является, в частности, кольцо целых чисел, разложение на множители единственно с точностью до домножения на unit'ы. Продолжая пример, в целых числах любое число однозначно раскладывается на сомножители с точностью до домножения на плюс-минус единицу. В других кольцах unit'ы устроены куда как более сложно.
>формула Ньютона-Лейбница
Есть в программе любой общеобразовательной школы. В школах берут интегралы? Нет.
Статистику тоже некоторые объединяют с математикой. Международные системы классификации, и организации, которые их разрабатывают это обыкновенно толпа неграмотных бюрократов. Факультеты статистики, физики или еще какой-то хуйни с факультетами математики объединяют по соображениям финансирования, и только.
Если так рассуждать, то можно прийти, что объект A не равен A. Ведь, можно допустить, что всякий объект имеет различную ценностьили иначе, " различную рассматреваемость".
Любые символьные высказывания, в этом смысле — ложь. При этом, тут нету противоречий.
Для того, чтобы исполнялась коммутативность, т.е , a+b=b+a...
Ценность или "выделяемость"высказывния — характеристика уникальности, информативности.
Вводим новое требование к надэквивалентности — равноценность.
Вещи равноценны, если их рассмотрение по отдельности, даёт абсолютно одинаковую информативность.
a+b=b+a
Понятное дело, что при коммунативности a+b не даёт, такую же информацию, как b+a, так как не сохраняется порядок. А нам важны все черты.
При "сложении", каждый объект пространства ценностей, имеет порядковый номер, или ординал, который четко соответствует позиции.При этом, в ценностном пространстве никогда неопределены операции, а символ "+" ничем не отличается от "2" .
a[1] +[2] b[3]≠b+a
H никогда не равно H в ценностном пространстве, так как H[1] =[2] H[3], у них разные ординалы.
Кстати, тогда встаёт несколько проблем.
Какой одномерный рисуноккомбинация букв в строчку станет первым? На основе чего будет определяться порядок, тем более, если их бесконечно много? Если каждое тождество должно иметь новые/новые цифорки.
Что мы возьмём за "1"?
Значит ли это, что эта концепция доступна лишь в замкнутой системе?
Предположим, ценностное пространство задано в открытой системе.
Относительно замкнутой системы, мы вводим ограниченное кол-во символов, которые, будем считать, являющимся отличными и уникальными от всех остальных, в других тождествах.
И задаем относительно этих символов — порядок.
2[£] +[°] 3[×] = 5[π]
И вообще, такое замутить можно и из начала, проблемы нету.
Интегрирование обозначает алгебраическую операцию.
Учился у Крулля зато, а не у Маннури какого-то там.
> можно разделить математику на 2 части: логику и компьтерную.
Что одно и то же исходя из изоморфизма Карри Говарда. Но тут в такое не могут даже на уровне визуального сравнения соответствующих кубов Барендрегта.
Согласен, этот изамарфизм легко доказывается. Как и Аксиома Чёрча.
>специальная унитарная группа это то же самое, что серная кислота, согласно изоморфизму Пристли-Кавендиша. Но тут в это не могут даже на уровне электролиза
>танковая дивизия это то же самое, что тензорное произведение алгебр, согласно изоморфизму Триандафиллова-Тухачевского. Но тут в это не могут даже на уровне прикрытия фланга
Что, прасти?
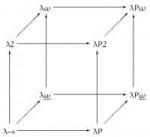 6 Кб, 321x294
6 Кб, 321x294И аксиоматическая теория международного права Ганса Кельзена тоже следует, если приглядеться. И принципы нравственности и основы законодательства Бентама. И манифест коммунистической партии Перу.
Начнём с того, что это не коммутативная диаграмма, так как не является даже просто диаграммой. Ибо не функтор.
Это бифунктор Гудериана из моноидальной категории Int в категорию PzDiv танковых дивизий.
Ты даже этого кубика не понимаешь, гейний гамалогий. Кубики это слишком сложно для мейлру.
>Ты даже электрохимической поляризации не понимаешь, гейний гамалогий
Прасти за вапрос, но ты точно не ошибся разделом?
Понимаю, это функтор из топаза Браузера-Гротендика в свободное копополнение категории функторов из Int в категорию Chrch (категорию церквей).
>>Ты даже электрохимической поляризации не понимаешь, гейний гамалогий
> Прасти за вапрос, но ты точно не ошибся разделом?
Причём тут поляризация, мань? В математику ты не можешь, это уже выяснили.
*Церкви
Ещё бы, даже Carry Coward'а не понимают.
 54 Кб, 807x646
54 Кб, 807x6461. Гамалогии не математика, а в лучшем случае частный третье культурный раздел, т.к основные понятия гамалогий невыводимы из самих гамалогий, а являются внешними по отношению к ним.
2. Изоморфизм Карри Говарда тут на мейлру непонятен никому кроме меня.
3. То же самое с конструктивизмом и вычислимостью. Машина Тьюринга так же никому тут непонятна.
4. Про более сложные вещи и говорить нечего, т.к MLTT упирается в вычислимость и вышеупомянутый изоморфизм. Тут просто некому понять как и почему automath де Брауна равнообьемен исчислению предикатов минус невычислимые верования, и каким образом данное лямбда исчисление позволяет проверять доказательства теорем, представимых в логике первого порядка.
Итого, мейлру, дегенераты, Нигерия в снегах. Ничего нового.
Сагласен, тут такие сложные темы никому не панятны к сожалению, тут тупицы сидят. Это же мейлру.
>automath де Брауна равнообьемен исчислению предикатов минус невычислимые верования
Почему ты ожидаешь знания цитологии и клеточной биологии от посетителей математической доски? Не все же смотрят аниме и саморазвиваются, чтобы быть разносторонними личностями, как ты.
Это доказательство изоморфизма между двумя рецептами великого повара Coward'a.
>Изоморфизм Паркинсона-Альцгеймера тут на мейлру непонятен никому кроме меня
Никто и не спорит.
> Ты же неграмотный просто
Вы тут в мейлру грамотные, ага. Кукарекать, петросянить и нести хуйню. У Барендрегта термин изоморфизм используется, встречается ещё correspondence, но вы ж тут грамотнее Барендрегта.
Грамотнее никому неизвестного голландского хипстера, в математике ничего не сделавшего? Да уж пожалуй.
На каппа-библиотеку Жемайтиса сослаться не забудь, аниме.
> никому неизвестного
Ты себя за всех считаешь, отсюда и твоё кукареканье. По существу тебе все равно сказать нечего, т.к в математике ты не понимаешь ровно нихуя.
Такой-то БАРЕНДРЕГТ.
Обосрался.
Определение гомологий выучи сначала, чмо анимешное, потом оценивай кто сколько понимает в математике.
> У Барендрегта термин изоморфизм используется
Используется у него, а чувства меры нет у тебя. Чисто идеологически я на твоей стороне, например. Но я всё же за конструктивный диалог. Ну если тебе с самого первого треда намекают, потом уже напрямую говорят, что "изоморфизм" - это в некоторых областях вполне конкректный термин, и просто чтобы не разжигать, не стоит его ставить где попало. В случае же тезиса Карри
и Ховарда - хоть изоморфизмом это явление назови, хоть соотношением, хоть void поставь - суть то не поменяется, суть там совсем в другом. Но ты продолжаешь упорно проявлять свою личностную твердолобость, а дискредитируешь целую область.
>"изоморфизм" - это в некоторых областях вполне конкректный термин
Он во всех областях математики конкретный.
>оппучканных категорных пынь
Это те, кто правильно использует математическую терминологию? То есть математики?
Пыня, ты совсем не палишься. Иди стрелки рисуй.
----> Hom(A;B) Ext(A;B)! ------> <----
^ ^
| |
| |
| |
> Определение гомологий
Не математика.
>>1635
> Но я всё же за конструктивный диалог
Называть меня "чмо анимешное" это конструктивный диалог?
> "изоморфизм" - это в некоторых областях вполне конкректный термин,
Это во всех областях конкретный термин. То, что на мейлру никто не понимает, в чем суть конкретно этого изоморфизма не делает этот термин неправильным.
Математика это мастурбация на японские мультики, you see.
По изоморфизму Микки Мауса – Дональда Дака это одно и то же.
>Итого, мейлру, дегенераты, Нигерия в снегах. Ничего нового.
Наконец-то! Ты абсолютно прав. Теперь, внимание, вопрос.
Почему ты до сих пор тут и как скоро ты наконец съебёшь в места более интеллектуальные?
>конструктивный диалог
Ты, верно, шутишь. Это же ебучий даун, какой с ним диалог.
В первом треде я ему еще пытался объяснить, где он неправильно понял философию Канта и т.д., но это бесполезно, так как ему похуй на самом деле. Он всё это время жонглировал заученными фразами и цитатами Мартинов-Лёфов, that is, пока не перешел на "тупое мейл ру".
Понятно что он никакой не конструктивист по убеждениям, а просто умственно неполноценный шизик. Конструктивисту была бы интересна такая тема как конструктивная гомологическая алгебра, perturbation lemma и т.д., как это реализуется и какие там трудности. У него же "гомологии не математика", как и всё остальное, что он не осилил, то есть 100% вузовской математики.
Я тут приводил на архиваче один из первых тредов про конструктивизм, так выяснилось что позиция этого дауна является просто менее содержательной вульгаризацией того, что мы могли видеть раньше. В 2013-м были дискуссии, сейчас одно кукареканье про неких авторитетов, которые кроме него никто не понял.
При чем важность этих работ просто постулируется.
Когда же речь заходит про философские следствия позиции Брауэра, например, наш товарищ не стесняется называть философов "никому неизвестными хипстерами", а если так сказать про его кумиров, которые вообще-то не философы и не математики, то сильно обижается. Адекватный человек был бы последователен здесь, но это не человек, а клоун.
>>1668
Так он в прошлом треде ещё сказал, что сюда потроллить заходит и "если у тупого мейл ру горит", то "он все правильно делает".
То есть как можно что-то говорить про любителей алгебры, если прямо здесь охуевшее говно сидит и "вся ваша математика не математика, математика это только вычислимость и что я ещё скажу, математики это те, кого я сейчас перечислю" без каких-либо намеков на аргументацию. В лучшее время мог ссылку на статью дать, которую сам не читал, сейчас просто оскорбления и всё.
Гражданин начинает разговаривать о философии, которую плохо понимает (отчасти потому, что не считает нужным читать что-то, кроме мнения создателя MLTT по этой теме). Ок, ему объясняют. Далее следует
– ОК, это все здорово, но какие применения у феноменологии в математике
На что, собственно, можно, оправившись от удивления, можно заметить:
– А какие применения у конструктивизма в математике, простите?
Здесь уже понятно, что будет дальше. "Математика это только конструктивизм". Я уже приводил ссылки, при обсуждениях в /sci еще, сторонники интуиционизма никогда не заявляли, что вся математика это вычислимость.
Это не одно и то же с позицией вся математика это алгебра. Во-первых, некоторые математики и правда так думают. Во-вторых, алгебра инклюзивна, и может включить в себя любую область, будь то логика, классический анализ или что ещё.
Конструктивизс не может, на аргумент "гомологическая алгебра в ряде случаев не является вычислимой" получаем "гамалогии это не математика". Можно перечислять длинный список результатов, полученных с использованием гомологической алгебры, но это бесполезно, потому что все эти результаты, вроде теоремы Ферма или еще чего, тут же объявят нематематикой.
Так было с топосами, гражданин их упоминал, пока ему не указали на опрелеление, потом заткнулся.
Математика это только вычислимость. Но почему?
Эндоморфизм Карри-Говарда в категории Int. Тезис Чёрча. Машина Тьюринга. Нумерация Гёделя. Диссертация Брауэра.
Пять уровней языка Маннури. Модель Миколова. Куб Барендрегта.
Если кто-то оспаривает значение этих идей и построений в самой математике, сразу объявляется, что сомневающийся ничего не понял, "тупое мейл ру, в математике не разбираешься нихуя".
Это жалкая пародия аргументации.
Говоря, что математика это только алгебра, можно хотя бы показать, почему это так.
Говоря, что математика это конструктивизм, можно только подменить понятие математики чем-то другим, типа химии, гистологии, вычислимости.
Разница понятна, надеюсь.
Гражданин просто рофлит, при чем, если шутить с ним за компанию, то обижается на "петросянство".
Гражданин начинает разговаривать о философии, которую плохо понимает (отчасти потому, что не считает нужным читать что-то, кроме мнения создателя MLTT по этой теме). Ок, ему объясняют. Далее следует
– ОК, это все здорово, но какие применения у феноменологии в математике
На что, собственно, можно, оправившись от удивления, можно заметить:
– А какие применения у конструктивизма в математике, простите?
Здесь уже понятно, что будет дальше. "Математика это только конструктивизм". Я уже приводил ссылки, при обсуждениях в /sci еще, сторонники интуиционизма никогда не заявляли, что вся математика это вычислимость.
Это не одно и то же с позицией вся математика это алгебра. Во-первых, некоторые математики и правда так думают. Во-вторых, алгебра инклюзивна, и может включить в себя любую область, будь то логика, классический анализ или что ещё.
Конструктивизс не может, на аргумент "гомологическая алгебра в ряде случаев не является вычислимой" получаем "гамалогии это не математика". Можно перечислять длинный список результатов, полученных с использованием гомологической алгебры, но это бесполезно, потому что все эти результаты, вроде теоремы Ферма или еще чего, тут же объявят нематематикой.
Так было с топосами, гражданин их упоминал, пока ему не указали на опрелеление, потом заткнулся.
Математика это только вычислимость. Но почему?
Эндоморфизм Карри-Говарда в категории Int. Тезис Чёрча. Машина Тьюринга. Нумерация Гёделя. Диссертация Брауэра.
Пять уровней языка Маннури. Модель Миколова. Куб Барендрегта.
Если кто-то оспаривает значение этих идей и построений в самой математике, сразу объявляется, что сомневающийся ничего не понял, "тупое мейл ру, в математике не разбираешься нихуя".
Это жалкая пародия аргументации.
Говоря, что математика это только алгебра, можно хотя бы показать, почему это так.
Говоря, что математика это конструктивизм, можно только подменить понятие математики чем-то другим, типа химии, гистологии, вычислимости.
Разница понятна, надеюсь.
Гражданин просто рофлит, при чем, если шутить с ним за компанию, то обижается на "петросянство".
> позиция этого дауна является просто менее содержательной вульгаризацией того, что мы могли видеть раньше
Постмодернизм такой постмодернизм.
"Математика может быть правильно понята только в терминах конструктивизма". Это позиция анона из 2013-го, тред с обсуждением я приводил.
"Основные положения гомологической алгебры невыводимы из неё, а являются внешними по отношению к ней. Но в математике не может быть зависимости от внешних теорий, следовательно гамалогии в лучшем случае применение математики, не первая культура даже."
Это профанация данной позиции, имеющая с ней мало общего.
При чем тут постмодернизм я не понял, тут любят употреблять это слово для описания разных явлений, ну и ладно.
Считаю это резким снижением содержания, ну и вульгаризацией, да.
Главное - математическое образование должно научить решать задачи, а не втиснуть в студента какой-то объём знаний. Как раз знания - дело наживное, тем более что математика более модульна, чем можно было бы представить.
> Это не одно и то же с позицией вся математика это алгебра. Во-первых, некоторые математики и правда так думают. Во-вторых, алгебра инклюзивна, и может включить в себя любую область, будь то логика, классический анализ или что ещё.
Тебе уже привели пример почему ты верунок в гамалогии и не более того. Алгебра не может быть всей математикой т.к основана на не алгебраических соображениях. Но ты слишком тупой чтобы понять даже этот аргумент.
> Конструктивизс не может
Может, и я сто раз приводил примеры. Даже чуть выше, automath де Брауна может все, что может логика первого порядка. Исчисление индуктивных построений может ещё больше. Но ты не понимаешь этих примеров, тебе горит и ты начинаешь кукарекать. И после этого обижаешься что тебя называют дегенератом.
>дифурщики могут жить без когомологий
Да и без групп Ли тогда могут. Да и без самих дифференциальных уравнений. Это какой-то театр абсурда уже получается.
> Вместо может быть понята в терминах вычислимости у нас теперь математика = вычислимость и маняотрицания любых возражений.
Возражений до сих пор не поступало. Кукареканья и петросянство это не возражения. Хотя бы тому факту, что любая формальная теория может рассматриваться как конструктивный объект в терминах алфавитов, термов и правил манипуляций с ними, что уже напрямую вычислимость на машине Тьюринга. Проблема будет только в значках не считающихся ни во что. Но с такими значками ничего не может поделать и человек, кроме как рисовать их и выводы из них. Вот на все это возражений я пока не видел. И не увижу, по очевидной причине.
Возражений на бессвязный бред, афазию и логорею?
>любая формальная теория может рассматриваться как конструктивный объект в терминах алфавитов, термов и правил манипуляций с ними, что уже напрямую вычислимость на машине Тьюринга
Не имеет никакого отношения к математике.
Давай лучше посчитаем, сколько премий Филдса и Абеля было присуждено за вычисления на машинах Тьюринга (и эквивалентные им операции). Теорема о модулярности и результат Перельмана не конструктивны, уже выяснили.
Пока ты наконец не признаешь маргинальность своей позиции, а именно, предположения "все что не вычислимо, не математика, а гомологии это третья культура".
>Давай лучше посчитаем, сколько премий Филдса и Абеля было присуждено за вычисления на машинах Тьюринга (и эквивалентные им операции).
Если ставить вопрос так - то вообще все.
>Теорема о модулярности и результат Перельмана не конструктивны, уже выяснили.
Невычислимые значки тоже можно гонять на машине Тьюринга, ровно с тем же результатом, как если бы это делал человек, т.к. человек принципиально неспособен сделать что-то чего не может машина Тьюринга, ты даже этого понять не в состоянии, хотя примеров полно у самого Тьюринга. И вот такие чучелоиды будут мне что-то пытаться доказать, лол. Еще и в спортлото на меня пишут >>1685>>1692 Дегенераты и есть.
>Если ставить вопрос так - то вообще все.
1954, Serre; Achieved major results on the homotopy groups of spheres, especially in his use of the method of spectral sequences
Спектральные последовательности не конструктивны, сам сказал
1966, Grothendieck; introduced the idea of K-theory (the Grothendieck groups and rings). Revolutionized homological algebra in his celebrated "Tohoku paper"
Гомологическая алгебра и К-теория не конструктивны, сам сказал.
1978, Deligne; Gave solution of the three Weil conjectures concerning generalizations of the Riemann hypothesis to finite fields.
Использовал топологию Гротендика и этальный топос, не конструктивно.
Плюс Милнор, Атья, Хиронака, Новиков, Квиллен, Воеводский и так далее.
Вопрос дня: почему на странице https://en.wikipedia.org/wiki/Fields_Medal
гамалогии и их производные упоминаются более 15 раз
А вычисления на машине Тьюринга ни одного?
>человек принципиально неспособен сделать что-то противоречащее воле Аллаха
Это понятно, математика тут при чем? Любой поступок можно представить как вычисления на машине последовательные, а любое высказывание как последовательность знаков.
Результаты где?
Где результаты применения конструктивизма в математике?
Почему за них не присуждают премии, не проводят конференции, не публикуют в журналах, преподаватели не сообщают о них студентам?
То есть конструктивных результатов не существует в природе? Единственный результат конструктивизма на данный момент, это то, что я дебил, а аниме это круто. Верно?
Если нет, я все еще жду список достижений конструктивизма.
То, что ты дебил, а аниме это круто - результат не конструктивизма, а совсем других вещей. На остальное отвечал уже, причем чуть выше, sapienti sat. По поводу конкретно аниме - я ни разу не видел анимехейтера, который не был бы дегенератом.
Я жду результатов конструктивизма.
In the meantime:
cohomology site:arxiv.org — About 89600 results
homology site:arxiv.org — About 75400 results
curry-howard site:arxiv.org — About 816 results
church thesis site:arxiv.org — About 17400 results, первая же ссылка "The rise and fall of the Church-Turing thesis"
godel numbering site:arxiv.org — About 15600 results
turing machine site:arxiv.org — About 13900 results
mannoury significa site:arxiv.org — 1 result, откуда узнаем, что твой "сингификационизм" это просто нидерландское слово, обозначающее семиотику, как я и предпологал
barendregt cube site:arxiv.org — About 56 results
>твой "сингификационизм" это просто нидерландское слово, обозначающее семиотику, как я и предпологал
Что ты там предполагал, ты даже правильного написания термина этого не осилил. Я даже не буду спрашивать, как из результатьв выдачи следует что сигнифика это семиотика, очевидно бесполезное занятие, учитывая уровень общения на мейлру.
>ты даже правильного написания термина этого не осилил
Я по своей наивности предполагал сначала, что твои слова это не пустой пиздеж; и подумал, точнее поверил наслово, что такая дисциплина действительно существует. Ну мало ли какие направления есть и т.д.
>как из результатьв выдачи следует что сигнифика это семиотика
did much research in semiotics (or in Dutch: significa). Mannoury explained already quite early what Ludwig Wittgenstein rediscovered and rephrased more succinctly: the meaning of a word is its usage (i.e. the notion of language games).
То есть это просто пересказ работ Витгенштейна, что я и понял, сразу после твоего указания, что это на самом деле significs, а не significationism. Было бы странно использовать название другой дисциплины.
Да будет тебе известно, тупой мрази, что сигнифика везде, начиная с dic.academic.ru и википедии, кончая всеми статьями и учебниками, обозначает семиотику.
Впрочем, я не сомневаюсь, что ни ты, ни твой Мартин Лёф не знаете, что такое семиотика, как уже было с эпистемологией, потому что являетесь образованцами и тупым быдлом.
В принципе, вся суть: пиздеть про Канта не читая Канта, пиздеть про Витгенштейна, не читая Витгенштейна.
Уровень мейл ру у него. До мейл ру тебе еще расти и расти.
Ты же не читаешь, хуесос ты ебаный. Я тебе приводил цитату из Философских исследований Витгенштейна, просто скопировал два абзаца. Ты это назвал, цитирую "хуйня на ровном месте без задач". А теперь выясняется, что расхваливаемый тобой Маннури это просто пересказ данной работы.
Реально, иди смотреть аниме лучше, борды это пока не твой уровень.
Гори дальше, чучело. Ты ж элементарных вещей понять не в состоянии, будто я сто раз не писал, как точка зрения Витгенштейна на язык связана с таковой Маннури, и в чем Маннури пошел гораздо дальше, в т.ч. в области оснований математики. Ты же не способен к пониманию, осмыслению чего-то, только цитатками трясти можешь, смысла которых все равно не понимаешь. Дегенерат эталонный.
Ты до сих пор даже не осознал, что словосочетание
>точка зрения Витгенштейна на язык
ничего конкретного не означает, потому что Витгенштейн "Логико-философского трактата" и Витгшенштейн "Философских исследований" это два разных философа, ничего общего.
>связана с таковой Маннури
Никак не связана. Связана с Э. Я. Брауэром, семинары которого Витгенштейн посещал, в результате чего и имеем "Философские исследования". Маннури не привёл его к этим идеям, он их лишь пересказал, при чём похоже очень криво.
>только цитатками трясти можешь
Лол блядь. Посчитай сколько раз ты тут приводил цитаты из Лёфа и т.д. Смысл был просто в выяснении того, что ты пиздел про Витгенштейна и не способен был узнать его же текст. То есть ты книг просто не читаешь, а учишься по аниме, что и было понятно ранее, но теперь просто очевидно.
Ай-да хуесос. Дегенераты у него вокруг, ну да.
>читать не в состоянии
А ты что-то в своей жизни прочитал, кроме субтитров к аниме и собственных постов? Должностную инструкцию охранника хоть освоил, которая у тебя в будке висит?
Какой же ты дебил, пиздец просто. Впрочем, у вас вся страна такая, живете хуже нигерии, при том что нейти больше чем у саудов.
Я жду ответа от "конструктивиста".
Я понимаю, что этот вопрос вызывает у тебя такую резкую анальную боль, что ты падаешь на пол и не можешь дотянуться до клавиатуры, но ты всё же постарайся.
>Я жду ответа от "конструктивиста".
Не стоит. Ты ничего не панимаешь и он уже на всё сто раз отвечал.
Пффф, если люди могут изучать те же динсистемы в R^2 и там до сих пор много нерешённых сложных проблем, то как зачем им сейчас рассматривать твои группы Лиувилля-Серпинского. Всё-таки обобщатели наивно думают что обобщение это вещь в себе почему-то, и что обобщать нужно всегда и везде даже если тогда нельзя сказать вообще ничего интересного. Да даже в самих гамологиях и тапалогиях обобщением просто ради обобщения никто не занимался (до нкатпетухов), даже Великий.
Частное важнее, содержательнее, интереснее общего. Но прежде, чем изучать частное нужно изучить общее. Анализ я буду изучать только после 3-4 лет изучения алгебры.
мимокрокодил
Вещи "на украине" или "в украине" меня тоже не интересуют.
>Великий
Это Гротендик? Так он широко известен тем, что был последним человеком, придумавшим схемы. Типа замена кольца многочленов с комплексными коэффициентами на произвольное коммутативное с 1, добавление нильпотентов и т.д. было в неявном виде у Эмми Нётер и в явном у Крулля, а потом у Андре Вейля и Картье, но не взлетело. Есть мнение, что использование теории категорий сделало успех неизбежным.
Гротендик вообще ничего не обобщал, таким образом, скорее наоборот.
Это типа Дария I кажется спросили:
– Why do you even want to conquer Greece?
– Cause it's there.
В математике оно не работает, как хорошо известно. У Крулля мотивация именно такая была.
Гротендик же скорее видел как можно применить методы одной теории к задачам другой, мало с ней связанной; ну либо на крайний случай придумать эти методы самому, и если же получается так, что методы столь мощные, что задачи под них ещё не появились (he already knew, that same idea would work for the cases yet unimaginable), так это и неплохо.
Что до нлаба, ну это аудитория такая, инфинити-топосами более всего интересуются те, кто не знает что такое многообразие. Stacks project более каноничный.
Мотивы, стэки и дериваторы это просто еще один концептуальный уровень после интегралов и когомологий; думаю мало кто спорит с тем, что этот путь развития правильный.
Например, производные функторы значительно проще спектральных последовательностей (как показано в residues and duality), позволяют записать в одну строчку многоэтажную спектралку так, что её потом можно по этой одной строчке восстановить – и при этом позволяют формулировать куда более сложные вещи, за счет упрощения языка; от спектралок же никто отказываться не призывает.
У сторонников Лури это и главный аргумент, типа "без нашего X нельзя изучать Y", на что им отвечают "а зачем изучать Y".
Вопрос здесь, конечно, к здравому смыслу, то есть теория должна удовлетворять ряду хороших требований, ну чтоб были результаты, которые можно сформулировать не пользуясь терминами этой теории и т.д.
Конструктивизм этим требованиям не удовлетворяет, кстати, легко видеть, и оказывается у параши вместе с теорией множеств, универсальной алгеброй и комбинаторикой.
>Великий
Это Гротендик? Так он широко известен тем, что был последним человеком, придумавшим схемы. Типа замена кольца многочленов с комплексными коэффициентами на произвольное коммутативное с 1, добавление нильпотентов и т.д. было в неявном виде у Эмми Нётер и в явном у Крулля, а потом у Андре Вейля и Картье, но не взлетело. Есть мнение, что использование теории категорий сделало успех неизбежным.
Гротендик вообще ничего не обобщал, таким образом, скорее наоборот.
Это типа Дария I кажется спросили:
– Why do you even want to conquer Greece?
– Cause it's there.
В математике оно не работает, как хорошо известно. У Крулля мотивация именно такая была.
Гротендик же скорее видел как можно применить методы одной теории к задачам другой, мало с ней связанной; ну либо на крайний случай придумать эти методы самому, и если же получается так, что методы столь мощные, что задачи под них ещё не появились (he already knew, that same idea would work for the cases yet unimaginable), так это и неплохо.
Что до нлаба, ну это аудитория такая, инфинити-топосами более всего интересуются те, кто не знает что такое многообразие. Stacks project более каноничный.
Мотивы, стэки и дериваторы это просто еще один концептуальный уровень после интегралов и когомологий; думаю мало кто спорит с тем, что этот путь развития правильный.
Например, производные функторы значительно проще спектральных последовательностей (как показано в residues and duality), позволяют записать в одну строчку многоэтажную спектралку так, что её потом можно по этой одной строчке восстановить – и при этом позволяют формулировать куда более сложные вещи, за счет упрощения языка; от спектралок же никто отказываться не призывает.
У сторонников Лури это и главный аргумент, типа "без нашего X нельзя изучать Y", на что им отвечают "а зачем изучать Y".
Вопрос здесь, конечно, к здравому смыслу, то есть теория должна удовлетворять ряду хороших требований, ну чтоб были результаты, которые можно сформулировать не пользуясь терминами этой теории и т.д.
Конструктивизм этим требованиям не удовлетворяет, кстати, легко видеть, и оказывается у параши вместе с теорией множеств, универсальной алгеброй и комбинаторикой.
>Частное важнее, содержательнее, интереснее общего
Ну иногда. Есть даже науки, построенные вокруг исключительных частных случаях, выбивающихся из общего, но это маргинальщина обычно (в хорошем смысле, то есть то, что помещают на полях страницы как сноску).
>>1726
Что характерно, продолжаешь демонстрировать своё незнание. Начать с того, что гомологиями, как ты выражаешься, то есть гомологической техникой, владеют все математики начиная с 1940-х, и советские/российские в том числе. Ты их устанешь перечислять, начиная с твоего же Колмогорова, Фаддеева, и т.д.
Теперь к твоим примерам.
Фоменко – третьеразрядный математик, долгое утверждавший что он решил задачу Плато, хотя он этого не делал. В смысле, по сравнению с Фоменко, ты и Мартин Лёф это ничто, пыль, пустое место; но Фоменко это мягко говоря не лицо российской математики, скорее в десятом ряду. Он конечно математику хорошо знает, но этого мало, phd только в сша десятки тысяч например, а математиков серьёзных на два порядка меньше. Хороший критерий: если человек в течение десяти лет после защиты ничего серьёзного не сделал, то и не сделает; Фоменко как раз не сделал.
А про историю, ну он это взял у своего учителя, Постникова; понятно что к математике это отношения не имеет никакого, я уже говорил, что среди математиков люди попадаются разные, и часто невежественные в других областях, хотя иногда нет. Гельфанд и Манин много занимались другими науками, Громов туда же.
Что до Ромы, то тут надо понимать, что он заранее выбрал такую область (гомотопические группы сфер) в которой в содержательном случае всё уже решено Серром (за что тому и дали Филдса), а остались очень сложные задачи уровня проблемы Гольдбаха, гипотезы Якобиана.
Ну он явно говорит своё мнение в первой лекции, типа так и так, в 50-х (десятилетие расцвета топологии) люди создавали миры, а сейчас вот они играют с конструкторами. И что это плохо, и лучше уж выбрать сложную задачу и решать её всю жизнь и не решить, но наткнуться на какую-то теорию в процессе, которая будет важнее самой задачи.
Это полная маргинальщина, но это сознательный выбор, человеку хочется быть маргиналом во всём. В математике это означает пытаться решать задачи тысячелетия комбинаторными методами.
То, что ты привёл, это полная хуйня. Ты не знаешь ни одного советского математика мирового уровня? Так это твои проблемы, имён вроде Новикова, Кириллова, Шафаревича, Манина, Бейлинсона, Дринфельда и т.д. у нас на десяток Швеций, это тебе не Маннури и Барендрегты.
То что ты путаешь применения когомологической техники, которые есть в любой науке, с такой специфической областью как алгебраическая топология (теория гомотопий, иначе), это может и простительно придурку. Первая началась в 40-х и закончится не скоро, если вообще; вторая началась давно, до конца 1930-х считалась маргинальной областью, в 50-е пережила расцвет и с 70-х стагнирует.
Напомню тебе, как гордому нигерийцу, что Воеводский, на которого ты надрачивал, карьеру сделал именно в области гамалогий.
https://en.wikipedia.org/wiki/Motivic_cohomology
На, жри, не подавись там.
Что касается разговоров про русскую культуру и т.д., то тут аргументов значительно больше, но это не по теме доски. По сути, ты просто показываешь в этом случае своё невежество и быдлянскую сущность охранника на полставки, впрочем, как и везде.
>Частное важнее, содержательнее, интереснее общего
Ну иногда. Есть даже науки, построенные вокруг исключительных частных случаях, выбивающихся из общего, но это маргинальщина обычно (в хорошем смысле, то есть то, что помещают на полях страницы как сноску).
>>1726
Что характерно, продолжаешь демонстрировать своё незнание. Начать с того, что гомологиями, как ты выражаешься, то есть гомологической техникой, владеют все математики начиная с 1940-х, и советские/российские в том числе. Ты их устанешь перечислять, начиная с твоего же Колмогорова, Фаддеева, и т.д.
Теперь к твоим примерам.
Фоменко – третьеразрядный математик, долгое утверждавший что он решил задачу Плато, хотя он этого не делал. В смысле, по сравнению с Фоменко, ты и Мартин Лёф это ничто, пыль, пустое место; но Фоменко это мягко говоря не лицо российской математики, скорее в десятом ряду. Он конечно математику хорошо знает, но этого мало, phd только в сша десятки тысяч например, а математиков серьёзных на два порядка меньше. Хороший критерий: если человек в течение десяти лет после защиты ничего серьёзного не сделал, то и не сделает; Фоменко как раз не сделал.
А про историю, ну он это взял у своего учителя, Постникова; понятно что к математике это отношения не имеет никакого, я уже говорил, что среди математиков люди попадаются разные, и часто невежественные в других областях, хотя иногда нет. Гельфанд и Манин много занимались другими науками, Громов туда же.
Что до Ромы, то тут надо понимать, что он заранее выбрал такую область (гомотопические группы сфер) в которой в содержательном случае всё уже решено Серром (за что тому и дали Филдса), а остались очень сложные задачи уровня проблемы Гольдбаха, гипотезы Якобиана.
Ну он явно говорит своё мнение в первой лекции, типа так и так, в 50-х (десятилетие расцвета топологии) люди создавали миры, а сейчас вот они играют с конструкторами. И что это плохо, и лучше уж выбрать сложную задачу и решать её всю жизнь и не решить, но наткнуться на какую-то теорию в процессе, которая будет важнее самой задачи.
Это полная маргинальщина, но это сознательный выбор, человеку хочется быть маргиналом во всём. В математике это означает пытаться решать задачи тысячелетия комбинаторными методами.
То, что ты привёл, это полная хуйня. Ты не знаешь ни одного советского математика мирового уровня? Так это твои проблемы, имён вроде Новикова, Кириллова, Шафаревича, Манина, Бейлинсона, Дринфельда и т.д. у нас на десяток Швеций, это тебе не Маннури и Барендрегты.
То что ты путаешь применения когомологической техники, которые есть в любой науке, с такой специфической областью как алгебраическая топология (теория гомотопий, иначе), это может и простительно придурку. Первая началась в 40-х и закончится не скоро, если вообще; вторая началась давно, до конца 1930-х считалась маргинальной областью, в 50-е пережила расцвет и с 70-х стагнирует.
Напомню тебе, как гордому нигерийцу, что Воеводский, на которого ты надрачивал, карьеру сделал именно в области гамалогий.
https://en.wikipedia.org/wiki/Motivic_cohomology
На, жри, не подавись там.
Что касается разговоров про русскую культуру и т.д., то тут аргументов значительно больше, но это не по теме доски. По сути, ты просто показываешь в этом случае своё невежество и быдлянскую сущность охранника на полставки, впрочем, как и везде.
>Ну и миша до кучи, чей вклад в математику
Начинается с защищенного в Гарварде тезиса, продолжается сотней статей в архиве и десятком прочитанных курсов в престижных вузах разных стран, от Бельгии до Бразилии. Понятно, что у тебя пригорело от его наездов на конструктивизм, но отрицать что он математик просто смешно, особенно если отрицающий – малолетний дебил с мейл ру, не имеющий диплома и работающий охранником 2 через 2.
Здесь практически бесконечный перечень прочитанных докладов, все лекционные курсы со слайдами, и т.д.
Хочешь показать что ты крутой – не надо петросянить про политику, просто открой рандомный курс, который он прочитал, и найди какую-нибудь ошибку/опечатку/оговорку/неточность в слайдах. Благо их дохуя.
Но ты этого не можешь, потому что ты говно. Докажи обратное.
Как ему дали диплом в аспирантуре Гарварда, если он не может в математику вообще? Как допустили до работы в Бельгии?
Alexander Grothendieck
Дурачок, ответь на вопрос, почему ты тусуешься среди людей, которых ненавидишь? Не подтверждай мои "фантазии", просто ответь на вопрос.
Почему ты здесь, мазохист ебаный? Я не против, это забавно, но почему ТЫ здесь?
1. Абасцать тупых эмпиристов в виде браузера и сочувствующих ему уёбков не-математиков.
2. Абасцать тупых грязноштанных любителей диамата под картофан в виде конструктивистов.
3. Закончить программу БОЖЕСТВЕННОГО Фреге в рамках неологицизма.
4. ???
5. PROFIT
>почему ТЫ здесь?
Если у мишы и остального мейлру так горит, а горение видно по вашим оскорблениям, то я всё правильно делаю.
Так ты будешь отвечать на вопрос-то? Если Миша не математик, почему у него диплом Гарварда, а у тебя никакого диплома нет?
Неужели нечего ответить?
Гамалогии элементарно понимаются с позиции вычислимости и я объяснял как но дегенераты с мейлру не поняли. Если имеем принципиальный отказ от вычислимости, то значит речь и не о математике, и т.о Гротендик рисователь гамалогий, не знаю, пусть будет гамалограф.
> и я объяснял как но дегенераты с мейлру не поняли
Значит хуёво объяснял/сам не понимаешь до конца.
> Дурачок, ответь на вопрос, почему ты тусуешься среди людей, которых ненавидишь?
А я разве говорил, что ненавижу? Нет, мейлру и дегенераты в естественной среде обитания не вызывают у меня таких эмоций. Зачем? Я давно на подтираче, ещё до мейлру. С2011 года. Так что привычка наверное.
> Значит хуёво объяснял/сам не понимаешь до конца.
Отнюдь. Нормально объяснил, даже со ссылками на Тьюринга, Мартин ЛЕФа, даже про арифметизацию теорий рассказал, про геделевскую нумерацию тут точно не слышали. А толку? В итоге одни кукареканья и врети.
>Если учёный не может объяснить уборщице, которая убирается у него в лаборатории, смысл своей работы, то он сам не понимает, что он делает.
Сейчас закидают говном, но практика показывает, что это действительно так. Если тебя не поняли, то это не проблема окружающих, это твоя проблема.
>элементарно понимаются с позиции вычислимости
Всё элементарно понимается с позиции религии. Просто берёшь любое явление X и утверждаешь "X есть, поскольку такова воля Аллаха". Объяснения твои ничего не показывают.
>Гротендик рисователь гамалогий, не знаю, пусть будет гамалограф
Согласно твоему определению Гротендик гамалограф, а Мартин Лёф – математик. Как так вышло, что у самого Гротендика, двух его коллег и трёх учеников есть премия Филдса, а у Лёфа нет (и комитет не знает, кто он такой)? Ты в состоянии ответить на простой вопрос, или сглотнешь и заткнешься, как обычно, анимепетух?
> Объяснения твои ничего не показывают.
Дебилу без мозгов вроде тебя.
> Ты в состоянии ответить на простой вопрос, или сглотнешь и заткнешься, как обычно, анимепетух?
Родители твои анимепетухи.
>>1761
> Если тебя не поняли, то это не проблема окружающих, это твоя проблема.
Ты забыл такой фактор как желание слушать и понимать. У сектантами веровающего в гамалогии его нет. Это вообще характерно для верунцов.
Ты не ответил на вопрос, говно.
Как так вышло, что у самого Гротендика, двух его коллег и трёх учеников есть премия Филдса, а у Лёфа нет (и комитет не знает, кто он такой)?
Нечего сказать?
По делу есть что сказать, говно?
Никак нет. Филдса дают только до сорока лет, а Лёф родился в 42-м. Может получить коммутативную премию, Нобелевскую или премию Притцкера (это если сконструирует что-то кроме безграмотного пиздежа, типа стадиона там, аэропорта, музея).
Его Пыня Пучкист получит. Кстати, следующий тред будет оппучканный. Философия математики ПУЧКИЗМ ЕДИШОН!
Ну хорошо, перефразирую. Зачем ты пишешь одно и то же людям, которые тебя не слушают а иногда и вовсе относятся к тебе как к мусору?
> Ну хорошо, перефразирую. Зачем ты пишешь одно и то же людям, которые тебя не слушают а иногда и вовсе относятся к тебе как к мусору?
Потому что могу. И что ты сделаешь? Так и будешь гореть и кукарекать. С чего ты взял что мне не похуй на чьето ко мне отношение?
Флуд и спам это опучкивание пыньки - это ни математика на любое упоминания анализа. Вот такая катигорная пыня. Hom(A;B)
Везде все враги.
Ну в формальной философии можно так отнестись. Это странное чувство, когда сам являешься частью уравнения.
НИ МАТЕМАТИКА ПУЧК ПУЧК!
Катеогрная пынька, иди монады в хачкеле считай. Горе-пограммист, а не математик.
>на математической доске
Хорошо, что ты это понимаешь. Уноси свои "UML" и "хачкеле" на другую доску, прагрпамист.
>категорный прогер
Что это такое? Это на русском?
>А тут математикой занимаются.
Любой раздел математики использует гомологическую алгебру, а следовательно и теорию категорий.
"What remains: the archiclassic structures (I don’t speak of sets, of course), linear and multilinear algebra, a little general topology (the least possible), a little topological vector spaces (as little as possible), homological algebra, commutative algebra, non-commutative algebra, Lie groups, integration, differentiable manifolds, Riemannian geometry, differential topology, harmonic analysis and its prolongations, ordinary and partial differential equations, group representations in general, and in its widest sense, analytic geometry. (Here of course I mean in the sense of Serre, the only tolerable sense. It is absolutely intolerable to use analytic geometry for linear algebra with coordinates, still called analytical geometry in the elementary books. Analytical geometry in this sense has never existed. There are only people who do linear algebra badly, by taking coordinates and this they call analytical geometry. Out with them! Everyone knows that analytical geometry is the theory of analytical spaces, one of the deepest and most dif cult theories of all mathematics.) Algebraic geometry, its twin sister, is also included, and nally the theory of algebraic numbers."
Jean Dieudonné
>гомологическая алгебра
>/pr/
Точно ебанулся. Пытаешься завербовать в свою прагармистскую секту?
Почему людям, использовавшим гомоалгебру дали более десяти медалей Филдса, а за классический анализ ни одной?
Куда?
Пиздато. И как успехи?
Помню что-то читал у Криспина Райта, вообще интересно, но под конец сложилось впечатления, что вместо реконструкции программы Фреге они занимаются какой-то хуйнёй, типа заиливания своей особой математики.
Я ничего не буду делать. Вот видишь, даже по твоей манере построения предложений ты как будто ожидаешь, что тебя начнут унижать, гнать прочь и всё такое. Я не буду этого делать, это борда, она мне не принадлежит. Если бы ты был у меня дома и так себя вёл, кончено я бы дал тебе позорного подсрачника и выставил бы.
И мы с тобой оба понимает, что ответ "потому что могу" на отъебись. Любой нормальный человек, глядя на твою ситуацию, скажет, что это очень странно. Тебя не слушают, тебя игнорируют, порой открыто презирают. Но ты остаёшься здесь. Словно у тебя нет людей ближе.
Ты понимаешь, скажи мне, ты понимаешь, что в данном случае ответ "мне всё равно, что обо мне думают", не работает? Потому что люди, которым всё равно, что о них думают, не тратят ни джоуля своей энергии на подобный онанизм.Ты понимаешь это? Или, хотя бы, понимаешь, что это понимают окружающие? И ты не можешь этого изменить, проговаривая свои аффирмации о том как тебе похуй на наше мнение? Тебе именно что болезненно не всё равно.
Я думаю ты очень нездоров, очень глубоко нездоров. И сам это знаешь. Любой твой ответ полон как минимум пассивной агрессии. Каждый тот ответ в защитной позиции. От тебя просто воняет гнилью. Я боюсь представить, в какой семье ты рос и как относишься к своим близким. И нет, я не призываю тебя убираться с борды и всё такое. Я не страдаю твоими комплексами и в твои игры тоже играть не стану, как не стал бы любой здоровый человек.
Я просто хочу выразить свою благодарность, что своим отвратительнейшим примером ты сразу даёшь возможным заинтересованным лицам понять, как следует относиться к таким увлечениям и образу мысли как у тебя. Это ценнее любых слов. Я не представляю, что кто-то посмотрит на твоё ядовитое горькое несчастное существование и подумает "Охуеть, хочу быть как крутой пацан! Даёшь конструктивизм, аниме и копрофилию!" Ты делаешь работу, которую не сделал бы десяток талантливых апологетов.
Спасибо тебе. Оставайся, конечно)
Ты лучше расскажи, как так получается, что в алгебре ничего нет кроме вычислений, а мне тут мозги ебут тп психолох и свидетель гамалогий (если это не один и тот же аутист).
Ты лучше расскажи, как ты недавно поливал Бурбаки дерьмом, а теперь вдруг хватаешься за его цитату обеими руками.
 177 Кб, 3450x2550
177 Кб, 3450x2550>Ты лучше расскажи, как ты недавно поливал Бурбаки дерьмом,
Бурбаков я дерьмом не поливал, они сами оподливились пикрелейтед в плане своего понимания интуиционизма Брауэра. Ну реально же хуйня написана, хотя там ссылочка на очень хорошую работу Брауэра, "интуиционизм и формализм".
> Наш разум по идее не бинарен,
А что, машина Тьюринга бинарна?
> квантовое сознание,
Не доказано же.
> Выходит создание ИИ алгоритмически неразрешимая задача?
В настоящее время не известно ничего в интеллекте человека, что не сводилось бы к алгоритму.
> Прямо как изамарфизм Карри.
Попробуй разобраться что это. Я не верю, что такие безмозглые существуют, даже на мейлру.
>бинарна
Вроде бы. Я не знаю.
>не доказано
>не известно
Ну хуй знает, короче, если такой пример найти, пример функции, которая на машине Тьюринга не вычисляется, то это будет означать невозможность создания ИИ?
 20 Кб, 604x340
20 Кб, 604x340Впрочем, если ты правда пизда психолох, это все объясняет. Сельдь - имитация человека.
>пример
Пример мышления что ли. Даже не знаю как сказать. Просто например человек способен парадоксально мыслить. Можно ли это эмулировать на машине Тьюринга?
О чём ты? На картинке коммутативный куб Барынрехта?
соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу одного множества ставится в соответствие некоторый элемент из другого множества.
> Вроде бы. Я не знаю.
Нет. Не бинарна.
> если такой пример найти, пример функции, которая на машине Тьюринга не вычисляется, то это будет означать невозможность создания ИИ?
Раз речь конкретно про ИИ, то логично искать нечто такое, что может интеллект человека, но не может машина Тьюринга либо любое равнообьемное ей уточнение понятия алгоритма.
>логично искать нечто такое, что может интеллект человека, но не может машина Тьюринга
Вот парадоксальное мышление. Можно его алгоритмически как-то это самое? Того?
> Пример мышления что ли. Даже не знаю как сказать. Просто например человек способен парадоксально мыслить. Можно ли это эмулировать на машине Тьюринга?
Парадоксально мыслить можно по типу чистого рандома, это машина Тьюринга может. Можно мыслить парадоксально исходя из каких-то правил. Это тоже может. Далее, парадоксальность может исходить из каких-то заданных констант, аксиом. Это тоже может. Затем, все выше перечисленное в любом сочетании, опять же не проблема.
То есть одновременно истинные противоположные вещи не проблема для неё? Машина Тьюринга не связана никак законами логики?
Хорошо, а проблема останова? Человек легко понимает, когда зацикливание, что программа никогда не завершит работу и стопает её. Алгоритмически неразрешимую проблему решает по сути.
Без понятия, лол. Но понимает же! Сотни программистов каждый день наёбываются в условии цикла или инкремент забывают, спустя какое-то время до них доходит, что они хуйню сделали.
Хотя если подумать, то со стороны работает то всё корректно, программа работает, всё ок. Вот как человек понимает, что произошло зацикливание?
Ты намекаешь на то, что человек не понимает на самом деле? Но как же тогда всё работает, как же тогда ошибки в коде исправляются?
Хорошо, а если бы я тебе предоставил доказательство оттуда следовало бы, что создание ИИ, равного человеку, алгоритмически неразрешимая задача?
Следовало бы, если принимать аксиому Чёрча. Тебе нужно предъявить доказательство, что он это может сделать во всех случаях. В частных случаях это и машина Тюринга может.
Понятно, спасибо.
>То есть одновременно истинные противоположные вещи не проблема для неё? Машина Тьюринга не связана никак законами логики?
Вообще не проблема. Машина Тьюринга связана только заданными алфавитами и правилами действия с элементами алфавитов и их сочетаниями. Другой вопрос, зачем нужны правила с истинностью противоположных суждений и к чему они приведут кроме возможности доказать вообще все, что угодно?
>в книге Манина "вычислимое и невычислимое"
Ты книгу-то читала? Там чуть не с самого начала про тезис Черча, и например, в 2.7, стр 23 перечислены аргументы в пользу этого тезиса. А где там аргументы против?
 344 Кб, 587x377
344 Кб, 587x377Между тем в математике широко используются функции, заданные неэффективными определениями. Столь же часты доказательства разрешимости задач, например оптимизации, не сопровождаемые алгоритмами их решения. В действительности класс задач, доступных классическим средствам, в некотором трудно уточняемом смысле строго шире класса задач, решаемых алгоритмически.
>читала
В отличие от тебя.
+ пикрил
Сводить математику к вычислимости будет только полный шизик.
 48 Кб, 472x450
48 Кб, 472x450Тезис Чёрча утверждает что вся математика сводится к вычислимости? Что, простите?
Будет тебе известно, что тезис Чёрча относится только к вычислимым функциям, дебил ты ебучий. На скриншоте, который ты не смог прочесть, указаны конкретные примеры невычислимых и полувычислимых функций.
Получай струю мочи, ты не конструктивист, просто манька безграмотная. Пародия, псевдоинтеллектуал.
>На скриншоте, который ты не смог прочесть, указаны конкретные примеры невычислимых и полувычислимых функций.
Мань, невычислимые функции не опровергают тезис Черча.
Тезис Черча не имеет никакого отношения к невычислимым функциям, он вообще не об этом. Естественно они его не "опровергают".
Осталось выяснить, в результате какого расстройства мышления ты считаешь, что из тезиса Черча следуют незамысловатые утверждения вроде "математика это вычислимость".
>Осталось выяснить, в результате какого расстройства мышления ты считаешь, что из тезиса Черча следуют незамысловатые утверждения вроде "математика это вычислимость".
Если функция невычислима, то с ней ничего нельзя сделать. Т.е. неразрешимые алгоритмически проблемы неразрешимы вообще никак. И я это писал много раз, вот только до местных дегенератов типа тебя это так и не дошло.
>Если функция невычислима, то с ней ничего нельзя сделать
Праграмисту может и нельзя, а математику можно. Читай книгу, там про это написано.
>И я это писал много раз, вот только до местных дегенератов типа тебя
От того, что ты напишешь ложное утверждение очень много раз, истинным оно не станет. Не знаю даже, откуда такие идеи могут возникнуть.
>Праграмисту может и нельзя, а математику можно.
Значки рисовать? Это и программисту можно ровно с тем же успехом, и любому умеющему рисовать.
Гамалогии, даже сколь угодно невычислимые - это точно такие же манипуляции над конечным алфавитом по определенным правилам, в какие может машина Тьюринга.
Для человека, который не знаком с кхмерским языком, процесс написания слов на этом языке выглядит как рисование значков. Для праграммиста, не знакомого с математикой, выписывание спектральной последовательности выглядит точно так же.
Argument from ignorance (дакажи что не Аллах и т.д.), это вообще не лучший довод, и в спорах о данной области с представителями этой области, то есть со специалистами, такого рода "аргументация" вообще не работает.
>над конечным алфавитом по определенным правилам, в какие может машина Тьюринга
Ну да, конечно. Интересно, почему математикой до сих пор занимаются люди, а не машины Тьюринга? Может потому, что люди существуют в реальной жизни, а машины Тьюринга – только в чьих-то фантазиях, прастите, лагических пастраениях.
Какой смысл упоминать здесь машину Тьюринга если это идея, не имеющая ни одного воплощения в реальной жизни?
>Интересно, почему математикой до сих пор занимаются люди, а не машины Тьюринга?
Пруверы в зачаточном состоянии потому что.
Все, чего ты не понимаешь, это рисование значков. Аргумент от собственной тупости это вообще твой конёк.
>Все, чего ты не понимаешь, это рисование значков.
И все, что понимаю - тоже. Потому что это факт. А понимание значков = их использование.
Они всегда будут в зачаточном состоянии, потому что физические ограничения. Это в твоих фантазиях машины Тьюринга и Поста, а ирл обоссаный комплюктер даже в операции с R^1 не может, обсирается сразу.
>Они всегда будут в зачаточном состоянии, потому что физические ограничения.
Какие ограничения?
>обоссаный комплюктер даже в операции с R^1 не может, обсирается сразу.
Ты будто можешь. Ну, значки нарисовать разве что, так и компьютер это может. И твое понимание значков ничем не отличается от знания как их использовать, что полностью совпадает с правилами манимуляций над значками машины Тьюригна.
 2,5 Мб, 2448x3264
2,5 Мб, 2448x3264> Я как раз могу. В отличие от floating point говна, мне известно сколько будет 2^54 + 2^54; тупому комплюктеру нет.
Пиздишь ты, это даже моему копеешному куркулятору известно.
> Машина Тьюринга имеет бесконечную ленту (и бесконечное время).
Это абстракция потенциальной осуществимости.
>>2398
> Не факт.
Ой ли? Как ты решишь задачу, для которой у тебя нет метода решения? Дзен мастер дохуя?
>Дзен-мастер дохуя?
Как вариант. Но я хотел сказать, что не доказано, что неразрешимые алгоритмически проблемы неразрешимы вообще никак. Может быть, а может и нет.
>я хотел сказать, что не доказано, что неразрешимые алгоритмически проблемы неразрешимы вообще никак. Может быть, а может и нет.
Ну смотри. Если есть решение, значит есть и путь к этому решению, как-то же оно было сделано и как-то же может быть повторено кем-либо еще. В англ. и не только языке слово "building" имеет двойственное значение - процесс построения и так же его итог - готовое построение. Потому что без процесса не будет и его результата.
А если решение внезапно пришло в голову как Рамануджану какому-нибудь? Богиня нашептала.
>Если есть решение, значит есть и путь к этому решению, как-то же оно было сделано и как-то же может быть повторено кем-либо еще
Вот, кстати, да, с Рамануджаном охуенный контрпример. Именно так в Англии и думали, но оказалось, что есть только ответ, а решения нет. Лол.
Я про тебя, своё петушиное мнение про этаниматиматику при себе держи, нахуй ты в чужой разговор встреваешь?
Ну вот некоторые его формулы доказаны, но многие так и остаются тупо ответом без решения, так что хз, хз. В любом случае он их не выводил никак, просто снились и всё. Так что не всякое решение(ответ) может быть получено в результате процесса. Иногда и такое бывает. Конечно, можно назвать вот эту вот работу подсознания, интуицию процессом, но как это формализовать? Алсо мне вот интересно, ты с одной стороны интуиционист, с другой же пишешь что всё суть есть значки и операции с ними, то есть формалист получается. Но интуиционизм же наоборот говорит, что никакая формальная система не годится полностью для интуиционизма, мол всегда будет место для интерпретации, двусмысленность, потому используется "интуитивное понятие". Да и ты помню писал что-то подобное насчёт Гёделя там. Как у тебя это в голове уживается без противоречий?
>ты с одной стороны интуиционист, с другой же пишешь что всё суть есть значки и операции с ними, то есть формалист получается. Но интуиционизм же наоборот говорит, что никакая формальная система не годится полностью для интуиционизма, мол всегда будет место для интерпретации, двусмысленность, потому используется "интуитивное понятие". Да и ты помню писал что-то подобное насчёт Гёделя там. Как у тебя это в голове уживается без противоречий?
И интуиционизм и формализм это операции со значками, но, интуиционизм предполагает построимость результатов этих операций, тогда как формализм таких требований не предъявляет. На примере того же исключенного третьего или дизъюнкции - классически дизъюнкция просто задана как общее правило, заповедь, верная всегда и везде, конструктивно же дизъюнкция принимается только при наличии доказательства (построения) одного из дизъюнктов. Наличие алгоритмически неразрешимых задач - это факт, как и проблема останова в случае машины Тьюринга, поэтому система, формализующая интуиционизм невозможна принципиально, т.к. такая система вместе с формализацией интуиционизма должна решать и проблему останова, и решать алгоритмически неразрешимые задачи.
Ну да. Я понял тебя теперь.
>поэтому система, формализующая интуиционизм невозможна принципиально
Как это следует из существования неразрешимых задач?
>Как это следует из существования неразрешимых задач?
Прямо и следует. Конструктивный объект - это построение, решение задачи конструктивно - это построение решения. Факт же в том, что существуют задачи, решения которых непостроимы. Поэтому формализация интуиционизма невозможна, т.е. не существует правил, которые в любом случае приводили бы к решению задачи (построению такого решения). Поэтому существование формальной системы, формализующей интуиционизм ровно то же самое, что существование формальной системы, решающей проблему останова машины Тьюринга.
Задумался над этим
У вас есть набор бильярдных шаров цвета красного, зеленого, синего, желтого, черного, белого, синего, фиолетового, голубого, сиреневого, азурного, перламутрового, лимонного, оранжевого, хаки, розового, детской неожиданности, серого, грязно-серого, ультрафиолетового, фосфор-зеленого, ярко-коричневого и бледно-коричневого. Эти шары разложили в 8 000 000 коробочек так, что в любой коробочке нет шаров одинакого цвета. Наблюдение показало: для любых двух взятых наугад коробочек имеется а возможно, и является одной из двух такая, что цветовой спектр ее шаров покрывает суммарный цветовой спектр взятых наугад коробочек (т.е. если в первой коробочке есть только один шарик, причем синего цвета, а во второй есть синий, да еще ультрафиолетовый и лимонный, то искомой спектропокрывающей коробочкой будет вторая; если же в первой коробочке кроме синего был еще и розовый шарик, то среди коробочек непременно есть содержащая синий, розовый, ультрафиолетовый и лимонный шарики. Вопрос: беретесь ли вы утверждать, что высыпав шарики в кучу и пересчитав их, мы найдем хотя бы 4 000 000 шариков одного цвета?
Интересно, можно ли построить алгоритм, который решал бы комбинаторные задачи. Определял вид задачи, важность порядка, составлял производящие функции и тд. Почему-то кажется, что алгоритм такой построить нельзя.
> Можно ли алгоритмически решить комбинаторную задачу ?
Можно. Задачу 4 красок так и решили.
>>2503
> Интересно, можно ли построить алгоритм, который решал бы комбинаторные задачи. Определял вид задачи, важность порядка, составлял производящие функции и тд. Почему-то кажется, что алгоритм такой построить нельзя.
У тебя пример задачи на идентификацию системы, алгоритмов, восстанавливающих такие функции многие тысячи.
 349 Кб, 200x131
349 Кб, 200x131> Прикольная херня.
Это не зерня, а алгоритмический подход к таким задачам, которые как тебе кажется, алгоритмически не решаются. Если кажется - креститься надо
Херня в хорошем смысле.







