344 Кб, 1680x1050
344 Кб, 1680x1050Мемы в сторону, я знаю, что на борде действует одиозный конструктивист и всё такое. Но давайте пока обойдёмся без инсайдовых шуток, потому что я и так ничего не понимаю.
Мне кажется, философия математики очень интересная тема. Думаю, она может приковать взгляды очень многих новичков, ведь речь идёт о совсем каких-то запредельных вещах, нетипичных для повседневной рутины.
Беглого взгляда на статью в википедии https://en.wikipedia.org/wiki/Philosophy_of_mathematics
достаточно, чтобы глаза разбежались. Сколько всяких течений! Как всё это заманчиво! Но вкурить это сходу очень тяжело. Даже просто вкуривать математику нубу непросто, что говорить про всякую мету?
Короче, здесь я предлагаю в ламповой атмосфере побеседовать о мете и лоре с учётом полного нубья (вроде меня), гуманитариев, сочувствующих и т.д.
Вот первый вопрос. Правильно ли я понял, что интуитивисты выступают против использования в математике объектов, которые человек не может интуитивно охватить? И одним из таких объектов является бесконечность.
Что с того, что её нельзя "охватить"? Мы знаем, что чисел бесконечно много. А значит, похер, можно ли её интуитивно понять, она как бы есть сама по себе.
Да и вообще, тот факт, что человек имеет некую идею об объекте, не достаточен ли, чтобы хотя бы попытаться им оперировать? Тем более математики ведь не делают с этой бесконечностью ничего такого ужасного.
Интуиция тут не при чем, там важна принципиальная построимость объекта, а не то что он конкретно построен или там интуитивно понятен. Но наш лучший друг брауэроеб думаю напишет более корректно, так что не буду пытаться.
Погугли про отличие актуальной бесконечности от потенциальной, финитизм Гильберта. Есть ещё ультрафинитизм, люди отрицающие очень большие числа (например я говорю что число не существует, если оно столь велико, что его невозможно записать используя любую нотацию), люди отрицающие континуум вообще и R в частности, и тд.
 109 Кб, 650x433
109 Кб, 650x433Философия математики и метаматематика - разные вещи. И философия математики таки существует, только там все заметно сложнее чем в самой математике, и смысла обсуждать ее на мейлру нет вообще никакого. Даже не очень сложный пример - диссертация Брауэра 1907 года требует гораздо большего бэкграунда (и не только в математике), чем его же интуиционизм. Если же брать что-то современное типа Мартин-Лёфа, там все еще печальнее для мейлру. Даже использование вполне конкретных философских идей в конкретной прикладной математике довольно сложно для понимания, у того же Вапника есть примеры использования в теории статистического обучения таких вещей как (не)фальсифицируемость Поппера, принципов Гегеля а куда без Гегеля человеку с советским образованием, которому в совковом вузике все мозги проканифолили политэкономией и т.д. Я тута пробовал пояснять разницу между конструктивным и неко нструктивным исходя из кантовских понятий аналитического и синтетического суждений (на примере мартинлефовской лекции) - стойкое ощущение, что кроме меня самого никто не понял вообще о чем речь. Короче, говоря проще - в философию математики без бэкграунда в самой математике смысла лезть нет.
Прилагаю скрин из книги Atten "Essays on Gödel", вообще в этой серии издано немало годноты, но если лень там копаться рекомендую статьи про Маха и Гуссерля на plato.stanford.edu
В философию нет смысла лезть без бэкграунда в философии, математика тут не при чем (интересно что ты под этим понимаешь, учитывая что основные достижения Брауэра на этом поприще это определение симплициального комплекса и несколько утверждений вроде теорем о неподвижной точке). А исследования какого-нибудь Витгенштейна по "основаниям математики" уж точно математических знаний не требуют, профессор сам её не знал, как бы.
Я неоднократно здесь указывал на увлечение таких людей как Гёдель или Герман Вейль феноменологией (при чем у последнего философия сыграла роль в исследованиях и привела к созданию калибровочной теории), и гегельянство Лойера. Так аргументы в духе "ну а Лайнус Роллинг рекомендовал витаминки", типа ни о чем не говорит.
Кстати мне ещё нормально зашла книжка Ralf Krömer Tool and object. Я сначала подумал что фуфло, исходя из названия, но потом увидел что он вполне вменяемо поясняет за прагматизм Пирса с философской стороны и про последовательность Майера-Виеториса и формулу Кюннета с математической. Ещё там есть много про Лере, Серра и Гротендика, но до этого я пока не дочитал, только бегло просматривал.
В этой же серии выходила похожая книга про теорию множеств, но там я за контент не ручаюсь, да и вообще от теоретиков множественных историй становится дурно, в случае с категориями хоть математика интересная.
Это я к разговору о "требуется знание математики", литералли чуть ли её единственная книга пока на эту тему, где мне потребовалось.
Особенно если учесть, что ты сам не понимаешь идей Канта и пытался разобраться в них с помощью экспертов с Доброчана.
 80 Кб, 566x403
80 Кб, 566x403>В философию нет смысла лезть без бэкграунда в философии, математика тут не при чем
Тут все "при чем". Чем больше всякого бэкграунда, тем больше дает философия. Как пример, если ты не в курсе последних достижений natural language processing, то тебе фраза Витгенштейна, касающаяся определения понятия смысла - "dont ask for meaning, ask for use" даст меньше, чем человеку, знакомому с моделью skipgram Миколова, которая по-сути, является реальным воплощением упомянутой цитаты Витгенштейна (вычисляет значение слова опираясь на его использование в контексте других слов в данном корпусе текстов). И наоборот, эта цитата позволяет лучше понять суть пикрелейтед.
>>6735
Я не столько не понимаю самих его идей, сколько мне интересно, из чего подобные идеи можно вывести и при этом не обосраться с их ценностью для науки, философии и т.д. На что нужно опираться, чтобы гарантированно выводить только правильные идеи, скажем так.
Понятно, но по-моему ты слишком осторожничаешь, тебе вроде интересны правильные вещи, но и оставлять привычные концепции вроде картезианского субъекта или например попперовского понятия научности тоже не хочется. Обидно тратить усилия, если с такими ограничениями далеко не продвинешься.
Витгенштейн о воплощении своих идей никак не знал, и пришёл к ним совсем из других соображений, при чем я так понял тебе не очень-то и интересно каких.
>Витгенштейн о воплощении своих идей никак не знал, и пришёл к ним совсем из других соображений, при чем я так понял тебе не очень-то и интересно каких.
Я примерно могу предположить, из каких соображений он пришел к вышеупомянутой цитате, хотя и не знаком с его работами. Зато я знаком с идеями сигнифики, а в педивикии Витгенштейн упоминается в одной статье с венским кружком, из чего я могу заключить, что идеи сигнифики были ему не чужды. Просто идеи сигнифицистов в то время были нереализуемы из-за состояния науки и техники, а вот сейчас некоторые из них переоткрываются или даже реализуются. Кант в этом смысле для меня менее понятен.
>оставлять привычные концепции вроде картезианского субъекта или например попперовского понятия научности тоже не хочется.
Мне как раз и интересны соображения, лежащие в основе чего-то, на что можно твердо опираться вне научного метода. Они есть, но их как-то нужно отделять от рандомной шизотерики. Т.е. нужны какие-то основания философии что ли.
>а в педивикии Витгенштейн упоминается в одной статье с венским кружком
Проиграл. Kind Sir,
Would you be willing to consider
At the very least,
Trouble thyself through reading an historical account
And learn about wise men's intentions
And affiliations.
приписывать Витгенштейна к сигнификационистам это вообще уже пушка, риальне, скачай что-то по истории философии, либо плато.стенфорд.эду
Ну вообще если не развешивать ярлычки, а смотреть на суть, то и упомянутая цитата Витгенштейна, и его же слова о том, что границы мира для человека определяются границами его языка, это вполне сигнифицистские воззрения.
Я не про ярлыки, а про то что Витгенштейн отказался от своих воззрений, выраженных в ЛФТ и этой фразе, это исторический факт. Витгенштейн раннего периода, по моему, вообще никакого интереса не представляет, нам важен Витгенштейн поздний и сам факт такого поворота совершенный, возможно, под влиянием Брауэра.
Впрочем, тот же Рамсей отказался от ультраплатонизма, но всего лишь за год до смерти.
Прочитал за эту вашу интенциональность, чем это отличается от ориентировочной рефлекса Павлова или простого внимания? Заслуга Брауэра прежде всего в том, что он показал, как на основе простого восприятия течения времени построить непротиворечивые основания математики, т.е. как использовать такое восприятие как основу для ментальных построений.
Философия математики не философия и не математика.
Ты не понимаешь сути философов. Лови алгоритм.
1. Вычитать в википедии редкий-редкий нескучный термин
2. Вычитать в википедии, кто его придумал
3. Щеголять этим термином, как будто это общеизвестная вещь.
Так философы и создают себе имидж. Пример - Лакан, любивший написать какую-нибудь чушь о топологических пространствах.
Я уже сбился со счета, сколько раз я пояснял за интенциональность (не только в этом разделе, впрочем). Если тебе лень читать что-то самостоятельно, довольствуйся хэндвэйвингом для умственно отсталых.
В философии Канта нельзя сказать ничего содержательного про какой-то предмет, а можно только про его атрибуты (объем, форма, цвет, проч), очевидно, не являющиеся частью самого объекта (ну например цвет это просто длина волны, и тд). Задавая вопрос "что такое X?" ты сталкиваешься с принципиально непознаваемым, трансцендентным.
Идея феноменологии в том, что ситуация выше это полная хуйня, и эту проблему как-то надо решить. Решается она применением новейших (для 1890-х годов) достижений психологии. Предмет X и восприятие этого предмета просто отождествляются, это называется феноменологическая редукция. Почему так можно, где обоснование? Обоснованием служит принцип интенциональности, то есть направленности мышления.
Это не вся правда, и даже не половина, но говноеду, не осилившему даже пары статей с сайта стэнфорда, больше и не надо.
Лакан это вообще не философия, а психоанализ и топологию он "применял" именно там.
>Я тута пробовал пояснять разницу между конструктивным и неко нструктивным исходя из кантовских понятий аналитического и синтетического суждений
Можешь ссылочку кинуть?
>в точности соответствуют основанию феноменологии – принципу интенциональности.
Кстати, у меня вопрос, который касается уже чисто философии. По Гуссерлю, сознание обладает свойством интенциональности, то есть, направленности на объект (причём, по его же словам, только сознание таким свойством и обладает, больше ничего в мире, но это мелочи).
Откуда такое утверждение? Как феноменологи это вывели? Интроспекцией собственного сознания? Какими-то наблюдениями? Можно сказать, что что-то в познавательной деятельности направлено на объект, но почему именно это считается сознанием? Мамардашвили потратил всю жизнь, чтобы очистить понятие "сознания" от примесей, и всё равно не закончил. А они так лихо делают такие утверждения?
И вообще, как можно утверждать что "что-то" присуще "чему-то" в таком случае? Может, это просто языковая иллюзия. Типа, мы так говорим о своей деятельности, что может сложиться впечатление, что сознание интенционально.
>(при чем у последнего философия сыграла роль в исследованиях и привела к созданию калибровочной теории)
Анон, ты бы не мог образно объяснить, как это вышло? Какова стратегия размышлений в феноменологии и как она в итоге выливается в калибровочную теорию в физике? Может я смогу понять эту феноменологию с помощью ассоциативных цепочек.
>Витгенштейн о воплощении своих идей никак не знал, и пришёл к ним совсем из других соображений, при чем я так понял тебе не очень-то и интересно каких.
Мне интересно, расскажи, плез.
Видят ли математики во сне бесконечных овец?
>Какова мотивация такого отрицания?
https://www.youtube.com/watch?v=WabHm1QWVCA
>>6885
Мое мнение, что предшественник Гуссерля это Мах, и его Анализ ощущений это почти феноменология.
Скопирую свой же пост:
Мах изучал физиологию органов чувств и пришел к выводу, что идея различения субъекта и объекта не является как необходимой, так и адекватной. Ощущения состоят из компонентов, объективная часть которых заключается в процессах, принадлежащих субъекту; граница между субъектом и объектом изменчива (для зрячего она идет по кончикам пальцев, для слепого по концу палки).
Мах заключает, что мир состоит из элементов и их отношений, элементы называются ощущениями. Граница между субъектом и объектом, феноменами и субстанцией, стирается.
Следующий шаг делает Гуссерль, опираясь на учение Маха и понятие интенциональности, введенное Брентано.
Замечу, что ничего общего с солипсизмом здесь нет. Солипсизм это производная той же догмы Декарта о дуализме (и порожденной ей mind-body problem). Нет субъекта, нет солипсизма.
>>6886
В основном осознанием того, что научная теория не обязана опираться на материальные субстанции. Gauge principle состоит в симметрии, то есть ты можешь все бозоны например заменить на фермионы, и стабильность мира сохранится.
В физике после Вейля, типа квантовой теории поля, например, понятие материи вообще не используется. Элементарные частицы это просто модель, описывающая возмущения квантового поля.
>>6890
Витгенштейн-1 мало интересен, можешь почитать про критику Рамсеем Principia Mathematica Рассела-Уайтхеда и переписку Рамсея и Витгенштейна.
Витгенштейн-2 это уже после Брауэра.
В который раз убедился, что любители поговорить про "теорему Гёделя" не вполне здоровы психически.
В ZFC есть аксиома бесконечности. Можешь отождествить латинский алфавит с натуральным числом 26.
Синтаксическое соглашение.
Gödel's ontological proof is a formal argument by the mathematician Kurt Gödel (1906–1978) for God's existence. More precisely, it presupposes the notion of positive and negative properties, and proves the necessary existence of an object which each positive property, but no negative property, applies to.
 69 Кб, 650x433
69 Кб, 650x433>Мах изучал физиологию органов чувств и пришел к выводу, что идея различения субъекта и объекта не является как необходимой, так и адекватной. Ощущения состоят из компонентов, объективная часть которых заключается в процессах, принадлежащих субъекту; граница между субъектом и объектом изменчива (для зрячего она идет по кончикам пальцев, для слепого по концу палки).
>Мах заключает, что мир состоит из элементов и их отношений, элементы называются ощущениями. Граница между субъектом и объектом, феноменами и субстанцией, стирается. Следующий шаг делает Гуссерль, опираясь на учение Маха и понятие интенциональности, введенное Брентано.
Ок, сделаем следующий шаг и спросим: 1) нахуя нам все это, если можно работать напрямую с нейрофизиологией? Ну раз все равно, все что мы вообще можем знать о мире - это только наши восприятия этого мира (к слову, ровно то же самое писал Брауэр и аргументировал примерно так же). Зачем философия, когда есть скажем fMRI высокого разрешения и методы работы со всем этим, не требующие каких-либо теорий для объяснения, кроме прямой интерпретации зависимости выходов от входов (идентификация систем). Но уже на этом этапе мы обнаружим, что и такой подход можно дальше свести к чему-то еще. А тот, следующий, еще и еще. В итоге мы рано или поздно опять придем к выводам Маха, потом Гуссерля и дальше по кругу. Т.е. какой-то абсолютной точки отсчета у нас нет, мы можем начать абсолютно откуда угодно и до куда угодно дойти. Но, может получиться и иначе - 2) мы включаем манямир и на этом возможности вышеописанных шагов заканчиваются, т.к. мы стоим на своих аргументах уровня "яскозал", а пытающихся их оспорить называем еврофашистами (как пример, маняматематик Рыбников, "опровергающий" Ньютона тем, тчо не понимает формулу тяготения, доступную 10-летнему школьнику, вместо чего несет какую-то дичь про мацу и жидов). Возникает естественный вопрос - в чем разница между 1 и 2 вариантами, и что нужно учитывать, чтобы не деградировать в своих рассуждениях до варианта 2?
 69 Кб, 650x433
69 Кб, 650x433>Мах изучал физиологию органов чувств и пришел к выводу, что идея различения субъекта и объекта не является как необходимой, так и адекватной. Ощущения состоят из компонентов, объективная часть которых заключается в процессах, принадлежащих субъекту; граница между субъектом и объектом изменчива (для зрячего она идет по кончикам пальцев, для слепого по концу палки).
>Мах заключает, что мир состоит из элементов и их отношений, элементы называются ощущениями. Граница между субъектом и объектом, феноменами и субстанцией, стирается. Следующий шаг делает Гуссерль, опираясь на учение Маха и понятие интенциональности, введенное Брентано.
Ок, сделаем следующий шаг и спросим: 1) нахуя нам все это, если можно работать напрямую с нейрофизиологией? Ну раз все равно, все что мы вообще можем знать о мире - это только наши восприятия этого мира (к слову, ровно то же самое писал Брауэр и аргументировал примерно так же). Зачем философия, когда есть скажем fMRI высокого разрешения и методы работы со всем этим, не требующие каких-либо теорий для объяснения, кроме прямой интерпретации зависимости выходов от входов (идентификация систем). Но уже на этом этапе мы обнаружим, что и такой подход можно дальше свести к чему-то еще. А тот, следующий, еще и еще. В итоге мы рано или поздно опять придем к выводам Маха, потом Гуссерля и дальше по кругу. Т.е. какой-то абсолютной точки отсчета у нас нет, мы можем начать абсолютно откуда угодно и до куда угодно дойти. Но, может получиться и иначе - 2) мы включаем манямир и на этом возможности вышеописанных шагов заканчиваются, т.к. мы стоим на своих аргументах уровня "яскозал", а пытающихся их оспорить называем еврофашистами (как пример, маняматематик Рыбников, "опровергающий" Ньютона тем, тчо не понимает формулу тяготения, доступную 10-летнему школьнику, вместо чего несет какую-то дичь про мацу и жидов). Возникает естественный вопрос - в чем разница между 1 и 2 вариантами, и что нужно учитывать, чтобы не деградировать в своих рассуждениях до варианта 2?
Надо осознать, что 1 и 2 в равной мере legitimate methods.
>не требующие каких-либо теорий для объяснения
>кроме прямой интерпретации
И перестать веровать в "объективные" и не зависящие от интерпретирующей теории данные. Это манямирок и есть как раз.
>т.к. мы стоим на своих аргументах уровня "яскозал"
В философии (не шизофрении типа психоанализа) такого как раз и нет, даже наоборот: там разбираются те понятия, которые у остальных людей считаются очевидными и например настолько глубоко внедрены в язык и мышление что их не так просто обнаружить; философия это в принципе деятельность математике обратная (лучше сказать: двойственная). Если в математике занимаются в основном прояснением семантики, то есть смыслового содержания понятий (определение Манина); то философы это содержание редицируют, выясняя, является ли оно необходимым или это просто очередная условность. Другого способа узнать, что фундаментально и есть на самом деле, по-видимому и нет.
То есть это не альтернатива, ты просто стоишь на позициях наивной веры в рационализм (объективность данных и возможность познания рациональным методом) это такое же "я сказал", просто не хочешь признавать это.
 40 Кб, 640x426
40 Кб, 640x426Ну а что тогда фундаментально и есть на самом деле, а что шизофрения и вера ни во что? Вернемся к Канту. Он в предисловии ("критика чистого разума") пишет, что его задача - установить все, что вообще можно твердо установить о разуме средствами самого разума. Для чего предлагается использовать как фундамент вещи неоспоримые и очевидные с любой точки зрения. Ок, ладно. Но дальше он выдает за таковые вещи, которые н-р мне не кажутся самоочевидными. Ладно, я понимаю, что я далеко не Кант и все такое, но вопроса о некоей точке опоры в своих выводах это не снимает.
>ты просто стоишь на позициях наивной веры в рационализм (объективность данных и возможность познания рациональным методом) это такое же "я сказал", просто не хочешь признавать это.
А что кроме рационализма можно использовать как основу для всех возможных выводов и суждений? Кант тот же разве не рационалист с этой точки зрения? Он, опять же, приводит пример аристотелевой логики, как нечто замечательного и незыблемого, на что можно опираться в своих суждениях. Аристотель не рационалист?
![quote-one-cannot-inquire-into-the-foundations-and-nature-of[...].jpg](/math/big/thumb/26720/15098031116020s.jpg) 71 Кб, 850x400
71 Кб, 850x400Аристотель точно не рационалист, поскольку рационализм вырос из переиначивания Декартом вопросов, которые впервые поставили схоласты из религиозных соображений.
Кант – да, но на Канте история не закончилась, и более того, для понимания феноменологии он тебе абсолютно не нужен, это просто чтобы знать с чем боролись и что было до этого, вообще. Это все равно что сейчас анализ по Эйлеру учить.
>>6968
Суть интуиционизма и схожесть его с феноменологией в том, что онтологические вопросы типа "существует ли X?" просто выбрасываются в мусорный ящик, и онтология сводится вместо этого к вопросу "можно ли показать эффективное построение X". Если можно, тогда и существует, при чем только тогда.
 74 Кб, 487x682
74 Кб, 487x682>Суть интуиционизма и схожесть его с феноменологией в том, что онтологические вопросы типа "существует ли X?" просто выбрасываются в мусорный ящик, и онтология сводится вместо этого к вопросу "можно ли показать эффективное построение X". Если можно, тогда и существует, при чем только тогда.
А вот Мартин-Лёф пишет, что онтологический по древним грекам, эпистемологический по Канту и Декарту и семантический в современной математике метод постановки вопроса - одно и то же (на примере первого суждения из MLTT - "A is a set"). Получается, что все это рационализм. А феноменология - разве не рационализм?
Мартин-Лёф это, кажется, известный специалист по греческой философии классического периода? По Канту вроде бы еще можно у Колмогорова почитать, а по Гуссерлю — Маркова.
>What is it that we must know in order to have the right to judge whether or not some X should be called a "set"?
Это не эпистемология, а история происхождения определений. В математике этот вопрос решается из чисто практических соображений.
Эпистемология происходит из дихотомии двух типов знания по Платону: божественного, истинного и определенного (episteme) и практического (doxa — common belief or opinon); при чём божественное знание, по Платону, получить невозможно.
Состояние науки к моменту жизни Канта (Ньютон, Лаплас и т.д.) позволяло ему отнести научное знание к первому типу, из чего собственно возникает вопрос "How can we have access to such knowledge?", ответ на который и является основной темой книги "Критика чистого разума". In short, по Канту, данные восприятия подлежат переработке разумом, что выражается формулой "мы налагаем законы на природу". Это, в свою очередь, ответ континентальному рационализму и одновременно британским эмпирикам в форме "you guys both right, but only partially".
По сравнению с эмпириками, Кант постулирует, что существуют концептуальные основания, от опыта независимые; поэтому познание (episteme) таки возможно. По сравнению с рационалистами, впрочем, знание у него все же ограничивается областью возможного опыта, и разум не имеет никакого доступа к трансцендентному.
Эта проблема разрешается уже в феноменологии.
>А феноменология - разве не рационализм?
Сколько можно рофлить.
Вместо адекватной литературы, коей невообразимо много, ты предпочитаешь читать бога и гения Лёфа, который оказывается не только has made virtually no contributions to the field of mathematics (в отличие от Брауэра и Колмогорова, у которых эти contributions хоть и minuscule, но есть) так ещё и не осилил элементарные понятия философии, на уровне что такое онтология, а что эпистемология. Типа я не совсем понял канеш чо там, но пожалуй напишу какую-то свою фразу, и ещё что-то про греков заверну, все равно мои читатели дебилы. Ну угадал, хули сказать, прокатило.
In a strict empiricist vein, what appears before the mind are sensory data or qualia: either patterns of one’s own sensations (seeing red here now, feeling this ticklish feeling, hearing that resonant bass tone) or sensible patterns of worldly things, say, the looks and smells of flowers (what John Locke called secondary qualities of things). In a strict rationalist vein, by contrast, what appears before the mind are ideas, rationally formed “clear and distinct ideas” (in René Descartes’ ideal). In Immanuel Kant’s theory of knowledge, fusing rationalist and empiricist aims, what appears to the mind are phenomena defined as things-as-they-appear or things-as-they-are-represented (in a synthesis of sensory and conceptual forms of objects-as-known).
…
Logic studies objective ideas, including propositions, which in turn make up objective theories as in the sciences. Psychology would, by contrast, study subjective ideas, the concrete contents (occurrences) of mental activities in particular minds at a given time. Husserl was after both, within a single discipline. So phenomena must be reconceived as objective intentional contents (sometimes called intentional objects) of subjective acts of consciousness. Phenomenology would then study this complex of consciousness and correlated phenomena. In Ideas I (Book One, 1913) Husserl introduced two Greek words to capture his version of the Bolzanoan distinction: noesis and noema, from the Greek verb noéō (νοέω), meaning to perceive, think, intend, whence the noun nous or mind. The intentional process of consciousness is called noesis, while its ideal content is called noema. The noema of an act of consciousness Husserl characterized both as an ideal meaning and as “the object as intended”. Thus the phenomenon, or object-as-it-appears, becomes the noema, or object-as-it-is-intended.
Добавлю к этому, что рационализм ПРОСТО ПО ОПРЕДЕЛЕНИЮ изначально, включает в себя идею объективности, из которой, к слову сказать, вытекает различие на субъект и объект. Которого ни у Маха, ни у Брауэра, ни у Гуссерля, вообще-то нет.
“Since, in philosophical literature, referemce is sometimes made to different levels of objectivity or subjectivity or even of reality, it may be stressed that the notion of an ultimate subject as well as conceptions like realism and idealism find no place in objective description as we have defined it” — Нильс Бор.
Мартин-Лёф это, кажется, известный специалист по греческой философии классического периода? По Канту вроде бы еще можно у Колмогорова почитать, а по Гуссерлю — Маркова.
>What is it that we must know in order to have the right to judge whether or not some X should be called a "set"?
Это не эпистемология, а история происхождения определений. В математике этот вопрос решается из чисто практических соображений.
Эпистемология происходит из дихотомии двух типов знания по Платону: божественного, истинного и определенного (episteme) и практического (doxa — common belief or opinon); при чём божественное знание, по Платону, получить невозможно.
Состояние науки к моменту жизни Канта (Ньютон, Лаплас и т.д.) позволяло ему отнести научное знание к первому типу, из чего собственно возникает вопрос "How can we have access to such knowledge?", ответ на который и является основной темой книги "Критика чистого разума". In short, по Канту, данные восприятия подлежат переработке разумом, что выражается формулой "мы налагаем законы на природу". Это, в свою очередь, ответ континентальному рационализму и одновременно британским эмпирикам в форме "you guys both right, but only partially".
По сравнению с эмпириками, Кант постулирует, что существуют концептуальные основания, от опыта независимые; поэтому познание (episteme) таки возможно. По сравнению с рационалистами, впрочем, знание у него все же ограничивается областью возможного опыта, и разум не имеет никакого доступа к трансцендентному.
Эта проблема разрешается уже в феноменологии.
>А феноменология - разве не рационализм?
Сколько можно рофлить.
Вместо адекватной литературы, коей невообразимо много, ты предпочитаешь читать бога и гения Лёфа, который оказывается не только has made virtually no contributions to the field of mathematics (в отличие от Брауэра и Колмогорова, у которых эти contributions хоть и minuscule, но есть) так ещё и не осилил элементарные понятия философии, на уровне что такое онтология, а что эпистемология. Типа я не совсем понял канеш чо там, но пожалуй напишу какую-то свою фразу, и ещё что-то про греков заверну, все равно мои читатели дебилы. Ну угадал, хули сказать, прокатило.
In a strict empiricist vein, what appears before the mind are sensory data or qualia: either patterns of one’s own sensations (seeing red here now, feeling this ticklish feeling, hearing that resonant bass tone) or sensible patterns of worldly things, say, the looks and smells of flowers (what John Locke called secondary qualities of things). In a strict rationalist vein, by contrast, what appears before the mind are ideas, rationally formed “clear and distinct ideas” (in René Descartes’ ideal). In Immanuel Kant’s theory of knowledge, fusing rationalist and empiricist aims, what appears to the mind are phenomena defined as things-as-they-appear or things-as-they-are-represented (in a synthesis of sensory and conceptual forms of objects-as-known).
…
Logic studies objective ideas, including propositions, which in turn make up objective theories as in the sciences. Psychology would, by contrast, study subjective ideas, the concrete contents (occurrences) of mental activities in particular minds at a given time. Husserl was after both, within a single discipline. So phenomena must be reconceived as objective intentional contents (sometimes called intentional objects) of subjective acts of consciousness. Phenomenology would then study this complex of consciousness and correlated phenomena. In Ideas I (Book One, 1913) Husserl introduced two Greek words to capture his version of the Bolzanoan distinction: noesis and noema, from the Greek verb noéō (νοέω), meaning to perceive, think, intend, whence the noun nous or mind. The intentional process of consciousness is called noesis, while its ideal content is called noema. The noema of an act of consciousness Husserl characterized both as an ideal meaning and as “the object as intended”. Thus the phenomenon, or object-as-it-appears, becomes the noema, or object-as-it-is-intended.
Добавлю к этому, что рационализм ПРОСТО ПО ОПРЕДЕЛЕНИЮ изначально, включает в себя идею объективности, из которой, к слову сказать, вытекает различие на субъект и объект. Которого ни у Маха, ни у Брауэра, ни у Гуссерля, вообще-то нет.
“Since, in philosophical literature, referemce is sometimes made to different levels of objectivity or subjectivity or even of reality, it may be stressed that the notion of an ultimate subject as well as conceptions like realism and idealism find no place in objective description as we have defined it” — Нильс Бор.
 70 Кб, 640x959
70 Кб, 640x959>Добавлю к этому, что рационализм ПРОСТО ПО ОПРЕДЕЛЕНИЮ изначально, включает в себя идею объективности, из которой, к слову сказать, вытекает различие на субъект и объект. Которого ни у Маха, ни у Брауэра, ни у Гуссерля, вообще-то нет.
У Брауэра "Creating Subject" - одно из основных понятий в его философии.
>>6975
>бога и гения Лёфа, который оказывается не только has made virtually no contributions to the field of mathematics
MLTT это далеко не "virtually no contributions to the field of mathematics". Тот, у кого ты взял эту цитату, похоже не понимает значения для математики вычислимых оснований.
>Вместо адекватной литературы, коей невообразимо много,
Например?
>У Брауэра "Creating Subject"
А у Гуссерля есть "радикальный субъективизм". Что с того? Слова "субъект" и "объект" введены схоластами, которые пытались описать сказки из священного писания в терминах категорий Аристотеля. Следуя твоему способу думать, Аристотель изобрел теорию категорий, кстати, а никак не Маклейн и Эйленберг. У него же есть книга с таким названием, "Категории".
Речь идёт о конкретном смысле, который вложил в эти термины Декарт, введя понятие дуализма. Это основа идеи объективности и, by extension, рационализма.
В Индии скажем века девятого нашей эры эти идеи опровергли, в Европе на девять с половиной столетий позже сделали то же самое, сначала в термодинамике (теория теплоты Маха), а потом, уже окончательно, в квантовой механике (копенгагенская интерпретация). Некоторым особо тупым европейцам это не мешает, и они продолжают верить, что взять с убогих.
Больцано, кстати, видел в одном месте Декарта и рационализм, и поэтому продолжал использовать термины "субъект" и "объект" в их изначальном значении.
>Тот, у кого ты взял эту цитату
Я её взял у себя. Теория типов это не математика, поекрати смеяться. Если людям вроде Воеводского, которые уже получили медаль Филдса за настоящую математику, вполне позволительно заниматься хоть теорией типов, хоть популяционной генетикой; то товарищам типа Лёфа, которые в принципе не способны понять даже формулировку теоремы об изоморфизме норменного вычета, let alone доказательство Воеводского, называться математиками можно только в альтернативной реальности, а не в этой.
Специалисту по алгебраической геометрии или к-теории от теории типов вообще ни холодно, ни жарко, значит это не математика.
Компьютер сайенс. То что 2.5 математика ей занимались не дает права специалистам только по теории типов примазываться к математике. Ну вот Гейзенберг был платонист, еще Дайсон и Пенроуз. Отсюда следует что все платонисты – физики? Лол что?
То, чем занимался Гротендик и/или Милнор – математика. Это определение смешное, но даже оно правдивее.
 75 Кб, 640x959
75 Кб, 640x959>Компьютер сайенс.
А через изоморфизм Карри-Говарда и математика. Что показал еще де Браун в 60-х. Однако, этого факта тут оценить не могут. В основе MLTT так же лежит этот изоморфизм, что и делает ее основаниями математики.
Сам по себе этот изоморфизм (так же как и версия этой эквивалетности в унивалетных основаниях) имеет в самой математике несоизмеримо меньшее значение, чем, скажем Rosetta Stone Андре Вейля и современные его версии типа геометрической програмы Ленглендса. Не надо забывать, что решение каких-то проблем это только одна сторона дела, деятельность математиков так же должна порождать новые интересные проблемы и области исследования, иначе наука загнется в принципе.
Поэтому когда людям типа Коэна, которые всю жизнь занимались специальными вопросами теории множеств, например, тоже дают Филдса, это вызывает колоссальное недоумение в сообществе.
Боюсь тут за википедию и обоссать могут, эти достопочтимые господа скорее всего читали оригинальные труды тех ребят, о которых говорят.
 88 Кб, 640x959
88 Кб, 640x959>Сам по себе этот изоморфизм (так же как и версия этой эквивалетности в унивалетных основаниях) имеет в самой математике несоизмеримо меньшее значение, чем, скажем
А таблица умножения в математике имеет значение больше или меньше чем численные методы интегрирования? Ты же сам понимаешь, что делаешь абсолютно беспредметные заявления уровня рекламы тонального крема, который улучшает цвет лица на 69%. Значение изоморфизма Карри-Говарда хотя его лучше бы называть изоморфизмом Карри - де Брауна в том, что он показывает соответствие 1 к 1му между математикой в ее обычном понимании и комплюктер саенс. Это значение на самом деле огромно, просто оценить его мало кто может, ибо как правильно заметил Максимка, ебанаты евривере. Именно этот изоморфизм позволяет показать, что логика первого порядка, которая используется как основания математики, это строго то же самое, что лямбда-П, специально для наркоманов, можно даже исключенное третье добавить (AUTOMATH де Брауна или соответствующее подмножество исчисления индуктивных построений в Coq'е). Единственный недостаток в том, что на нынешнем этапе развития пруверов выходит, что поменяли шило на мыло, т.к. возможность выразить всю математику в Коке выглядит пустым пердолингом на ровном месте, т.н. тактики немного улучшают ситуацию, но не сильно, как и прожекты типа deepmath. Если процесс автоматизировать полностью, это приведет к качественному скачку в развитии математики. Людишки математику уже не вывозят, дальше будет только хуже. Даже отдельные гении-аутисты типа Мочидзуки ситуацию не спасут, поскольку осилить подобную математику могут единицы из всего человечества. Это полный пиздец на самом деле. Единственный выход - использовать автоматизированные решения, которых пока нет. К счастью, теории типов не единственный вариант автоматизировать математику, есть равнообъемные формализмы, которые к тому же допускают полную автоматизацию процесса без костылей для Кока типа deepmath. В частности, я как раз пытаюсь запилить такой прувер.
 88 Кб, 640x959
88 Кб, 640x959>Сам по себе этот изоморфизм (так же как и версия этой эквивалетности в унивалетных основаниях) имеет в самой математике несоизмеримо меньшее значение, чем, скажем
А таблица умножения в математике имеет значение больше или меньше чем численные методы интегрирования? Ты же сам понимаешь, что делаешь абсолютно беспредметные заявления уровня рекламы тонального крема, который улучшает цвет лица на 69%. Значение изоморфизма Карри-Говарда хотя его лучше бы называть изоморфизмом Карри - де Брауна в том, что он показывает соответствие 1 к 1му между математикой в ее обычном понимании и комплюктер саенс. Это значение на самом деле огромно, просто оценить его мало кто может, ибо как правильно заметил Максимка, ебанаты евривере. Именно этот изоморфизм позволяет показать, что логика первого порядка, которая используется как основания математики, это строго то же самое, что лямбда-П, специально для наркоманов, можно даже исключенное третье добавить (AUTOMATH де Брауна или соответствующее подмножество исчисления индуктивных построений в Coq'е). Единственный недостаток в том, что на нынешнем этапе развития пруверов выходит, что поменяли шило на мыло, т.к. возможность выразить всю математику в Коке выглядит пустым пердолингом на ровном месте, т.н. тактики немного улучшают ситуацию, но не сильно, как и прожекты типа deepmath. Если процесс автоматизировать полностью, это приведет к качественному скачку в развитии математики. Людишки математику уже не вывозят, дальше будет только хуже. Даже отдельные гении-аутисты типа Мочидзуки ситуацию не спасут, поскольку осилить подобную математику могут единицы из всего человечества. Это полный пиздец на самом деле. Единственный выход - использовать автоматизированные решения, которых пока нет. К счастью, теории типов не единственный вариант автоматизировать математику, есть равнообъемные формализмы, которые к тому же допускают полную автоматизацию процесса без костылей для Кока типа deepmath. В частности, я как раз пытаюсь запилить такой прувер.
>Ну а что тогда фундаментально и есть на самом деле, а что шизофрения и вера ни во что?
Хороший вопрос.
> нахуя нам все это, если можно работать напрямую с нейрофизиологией?
Потому что тогда тебе надо как-то решать Трудную проблему сознания (уже 20 лет решаем)
>Потому что тогда тебе надо как-то решать Трудную проблему сознания
Зачем? Какая мне разница, почему "существует" "квалиа" и т.п., если речь о чисто практической работе с чисто практическими вещами? Дворнику нет надобности знать, почему идет снег, если его задача просто расчистить дорожки.
>Зачем? Какая мне разница, почему "существует" "квалиа" и т.п., если речь о чисто практической работе с чисто практическими вещами?
Может тебе тогда в тред прикладной математики пойти?
Математика вся прикладная, т.к. во всех случаях является результатом человеческой деятельности. Непонимание этого простого факта и ведет к постановке вопросов, не имеющих ответов с одновременным непониманием, что подобные вопросы, не имея ответов, не имеют и задач.
>Рома Михайлов со своим Равинагаром тут уместен.
>"Равинагар - состояние отождествления пространства, психики и грамматики"
Во, это уже на что-то интересное похоже. Удивительно, но факт, даже на мейлру иногда можно узнать что-то полезное.
Тебя даже вчерашний шторм не разбудил.
Нет, сейчас он находится в галлюцинации и в течении месяца выпустит про это текст.
А где он пишет текст-галлюцинацию? В Солнечном городе.
Солнечный город с хинди равинагар.
Да взял убил всю красоту доёбом до буквальности. Зачем, ради чего, и так вот во всём все. Бюрократы.
Слово не воробей же. Пусть останется напоминанием.
 202 Кб, 636x640
202 Кб, 636x640>А у Гуссерля есть "радикальный субъективизм". Что с того? Слова "субъект" и "объект" введены схоластами, которые пытались описать сказки из священного писания в терминах категорий Аристотеля.
Брауэр имеет в виду под "Субъектом" индивидуальность, эго. Скажем, очевидную очевидность собственного существования. Без отсылок к какому-то конкретному определению, а просто как нечто данное. Я это и есть я, безотносительно твоей игры в слова, что вот схоласты имели в виду одно, Гуссерль другое, Декарт пятое, Витгенштейн десятое. Так же вот сейчас пытаются вытуживать термины, не обозначающие ничего, типа "квалиа". Ну придумали, а что это дало для понимания того, что есть "я"? Ничего.
define понимание
Внеязыковая действительность существует и не может быть погружена в языковую целиком.
> Внеязыковая действительность существует и не может быть погружена в языковую целиком.
Дефайн "существует" тогда уж. Опять вера какая-то.
 271 Кб, 437x575
271 Кб, 437x575В философии математики плохое. В самой математике и вовсе пиздец. Поэтому, например Брауэр отказался от кантовских вещей самих по себе, т.к в математике они бесполезны. Предыдущий оратор правильно цитировал Маха и т.д про то, что кроме ощущений у человека о внешнем мире знаний никаких, то же писал и Брауэр о науке в целом. Понятие конструктивного объекта уже разбирали, это и есть дефайн, дефайн дефайн и т.д.
И может быть погружена в языковую действительность целиком, пользуясь словами предыдущего оратора.
Отнюдь. Это утверждение о существовании, оно не является объектом. Только объекты можно погружать.
Но не объект. Это строчка текста, у которой даже материальный носитель сложно найти - то ли пиксели на экране монитора, то ли набор байтиков на жестком диске, то ли ещё что-то.
Аргументировать в споре со структуралистами это примерно как на форуме flat earth society, удовольствие сомнительное.
Здоров ли ты?
> Но не объект. Это строчка текста, у которой даже материальный носитель сложно найти - то ли пиксели на экране монитора, то ли набор байтиков на жестком диске, то ли ещё что-то.
Текст это объект как раз. И дажеиконструктивный, например, тип List.
 59 Кб, 500x313
59 Кб, 500x313Текст не является объектом. Уже хотя бы потому, что один и тот же текст может находиться во множестве разных мест. С объектами так не бывает, объект не может находиться в двух местах одновременно.
Не, не интересный, уже скатили.
>С объектами так не бывает, объект не может находиться в двух местах одновременно.
Аргументировать не учили?
Что значит “не может находиться в двух местах одновременно”? Допустим, что ты имел в виду что-то вроде “две частицы не могут занимать одно и то же квантовое состояние”.
Утверждение, обратное этому, кстати, очевидным образом ложно.
Само же утверждение, как минимум, бессодержательно, потому что если не учитывать квантовое состояние, электроны абсолютно ничем друг от друга не отличаются. То есть имеет смысл говорить обо всех электронах как об одном объекте.
https://en.wikipedia.org/wiki/Identical_particles
https://en.wikipedia.org/wiki/One-electron_universe
Ты о чем вообще? При чем тут квантовое состояние?
Закон исключённого третьего - это "дёшево, быстро, качественно; выберите любые два слова из трёх".
Начни любой курс по мат. логике в интернетах, через пару лекций найдешь ответы на свои вопросы. Пиздос. У меня во дворе за такие вопросы убивают нахер.
Да разобрался уже.
Объясните полному нубу что такое феномен в феноменологии. Зачем нужно было вводить это понятие?
Понятие феномена вообще гораздо старше. Но в феноменологическом смысле явления первыми стал рассматривать Мах, у него они называются ощущениями.
В соответствующей книге (Анализ ощущений) это учение растолковано как раз исходя из физиологической мотивации.
Это не феноменология в строгом смысле (нет интенциональности), но гораздо понятнее.
Придумать можно какую угодно шизофрению, что уже показал Кантор своей теорией классификации недостижимых кардиналов, и потом сказать, что математика не сводится ни к чему. Это не аргумент.
 320 Кб, 719x403
320 Кб, 719x403> Есть невычислимые функции, неразрешимые множества
Где они есть? И в каком смысле, если даже правил вычисления у них нет? Реально заебало одно и то же сто раз по кругу обсуждать. Вы тута либо реально ебанаты, как максимка говорит, либо одно из двух. Ну нельзя же такими довнами быть.
Не всё. Гомологическая алгебра, вообще говоря, не конструктивна (если не затрагивать pertrubation theory).
>>7349
Нашел кого слушать. У него кстати, самое интересное, это разговоры про шуньяваду (мадхъямаку). "Математика это прикладная теория типов" вот это всё детсад просто. Типа, выучил бы для начала хоть что-то из математики, а потом уже говорил.
 298 Кб, 683x1024
298 Кб, 683x1024> "Математика это прикладная теория типов" вот это всё детсад просто.
Почему это детсад, а Бурбаки с их "математика это прикладная теория множеств" не детсад? Чем заповеди святого Гильберта лучше правил вычисления?
>Где они есть?
Существуют ли неразрешимые множества? Существуют — просто потому, что алгоритмов (и поэтому разрешимых подмножеств
натурального ряда) счётное число, а всех подмножеств натурального
ряда несчётное число.
Всё так, только над склонностью Бурбаки к теоретико-множественными конструкциям Гротендик посмеялся еще в 1957-м, когда придумал топосы. Современная алгебра к структурам не сводится
>в теории категорий изучается скорее "тип", можно взять циклическую группу как категорию с одним объектом, у которого все морфизмы это изоморфизмы и тогда все аксиомы группы вытекают из определения категории.
>вопрос "изоморфны ли две структуры?" имеет с категорной точки зрения столько же смысла, как вопрос "равны ли два числа?".
см. книгу Tool and Object.
Святого Гильберта уж точно не лучше, хотя вклад его в математику, конечно, неоспорим. В отличие от Кантора, чьи открытия относятся к истории психиатрии, а не математики.
Если уже есть слово "ощущение", зачем этот Мах выдумал ещё и феномен?
(я понимаю, что слово существовало и раньше, речь о контексте феноменологии, ну ты понел)
 91 Кб, 900x900
91 Кб, 900x900> Существуют ли неразрешимые множества? Существуют
Где и как они существуют, если даже правил построения нет? Даже максимкина дхармадхата и то ближе к математике чем весь этот ваш маняплатонизм.
> Если уже есть слово "ощущение", зачем этот Мах выдумал ещё и феномен?
А чтобы все охуели, как он может. И чтобы когда возникнет вопрос "нахуя это надо, когда есть нейрофизиология" обвинить оппонента в том, что он не шарит и научный метод и рационализм уже не в моде.
Читать научись. Мах не придумывал "феномены", "феномены" были еще у британских эмпириков. То, что я тебе указал, это конкретный источник появления феноменоменологии (их было несколько), а не она сама.
>>7373
Такого вопроса не возникает.
Как показали Кун и Лакатос, научная теория в принципе не может вступить в противоречие с фактами наблюдения, возможен только конфликт данной теории с другой, интерпретирующей факты наблюдения. Фейерабенд еще показал, что само существование фактов зависит от теории, то есть "естественного языка" для интерпретации не существует.
>научный метод и рационализм
А заодно Иисус Христос, апостол Павел и небесное царствие; все это является исключительно предметом слепой веры.
Научный метод полностью бессодержателен как набор рекомендаций, либо нарушается во всех важных случаях.
> Научный метод полностью бессодержателен как набор рекомендаций, либо нарушается во всех важных случаях.
Примеры можно, когда научный метод не работает? И я уже спрашивал, что вместо него есть ценного?
Может начнешь читать самостоятельно? В литературе этих трех авторов примеров достаточно, от исследовательской практики Галилея до принципа дополнительности у Бора. Не вижу смысла пересказывать аргументацию, да и стиль сохранить не получится.
На русском, например, есть тут:
http://www.psylib.ukrweb.net/books/kunts01/txt06.htm
http://www.gumer.info/bibliotek_Buks/Science/Lakatos/04.php
http://khazarzar.skeptik.net/books/feyerab/metod/10.html
>что вместо него есть ценного
Принцип пролиферации теорий и правило "anything goes", например, значительно лучше.
> Принцип пролиферации теорий и правило "anything goes", например, значительно лучше.
Ты первую часть вопроса проигнорировал, где же примеры не работоспособности научного метода? Ну и заодно, давай примеры использования того, что ты предложил.
А ты проигнорировал ответ.
Предполагается, что мне надо копипастить фрагменты параграфами, чтобы было понятно о чем идёт речь?
Или пересказать 1-2 отдельных примера? Допустим я могу это сделать, но где гарантия что ты будешь читать? То что по ссылкам ты не читаешь, уже выяснили, то есть мне искать их не стоило (я плохо ориентируюсь в русском переводе, к тому же; но на английском сходу найти смог только Фейерабенда).
То что ты не знаком с этими работами, это в принципе твоя личная проблема, учитывая что они до последнено времени (не знаю как сейчас) входили в кандилатский минимум, не говоря уже об остальном.
То есть с моей стороны не аргументация какая-то, не знаю как ты себе это представляешь, а ликбез для недоучки. Понятно что сие хорошо согласуется с идеей треда, но это него его тематика заведомо.
> Предполагается, что мне надо копипастить фрагменты параграфами, чтобы было понятно о чем идёт речь?
> Или пересказать 1-2 отдельных примера? Допустим я могу это сделать, но где гарантия что ты будешь читать?
Копипастить не надо, вопрос был показать пример где научный метод не работает. Все очень просто жи. Мне правда интересен пример ситуации, когда научный метод бесполезен, так что с удовольствием ознакомлюсь.
>Коперник
>Галилей
>Пристли и Лавуазье
>Проут
>Максвелл
>Мах и Эйнштейн
>Бор
>мне правда интересно
>игнорирует имена авторов и названия книг
>игнорирует ссылки на конкретные главы
>уже заявил о намерении проигнорировать копипасту
Понятно.
конкретных сюжетов из истории науки.
То есть искать там примеры не так уж и сложно, благо вся книга из них и состоит.
>Читать научись. Мах не придумывал "феномены", "феномены" были еще у британских эмпириков.
Читать научись.
>я понимаю, что слово существовало и раньше, речь о контексте феноменологии
>Научный метод полностью бессодержателен как набор рекомендаций, либо нарушается во всех важных случаях.
Ого, у нас тут постмодернистский критик науки.
Скажи честно, ты бы на каком самолёте предпочёл лететь? Который собрали учёные, или который собрали последователи секты аум синрикё? Я ожидаю конкретного ответа.
> Кто такой, чем знаменит?
Максим Сохацкий жи, видный специалист по лямбдам и прочей MLTT. Алсо немало шарит в буддизме. Знаменит тем, что называет всех ебанатами и разосрался со всеми соратниками пишет свой прувер на основе гомотопической теории типов.
Сохранить рационализм стремился только Лакатос, но у него он принимает столь утонченную форму, что от метода там остается мало. Фейерабенд отверг всякие попытки создания метода, и назвал себя "эпистемологическим анархистом" (анархизм обычный, как он шутя замечает, менее последователен, поскольку науку например Кропоткин не отвергал).
Кун предложил чисто социологическое объяснение науки как сообщества ученых.
>>7387
>Если уже есть слово "ощущение", зачем этот Мах выдумал ещё и феномен
Понятия не имею что ты несешь, я нигде не говорил что Мах выдумал это понятие или что вообще пользовался им.
>>7388
Постмодернизм – это состояние мышление манек вроде тебя, у которых в голове всё перемешалось и они не отличают а) инженерное дело от науки, б) реальную научную практику от рационалистического бреда, которому она никогда не соответствала. Сектант as is.
Фейерабенд, конечно, более радикален, и он открыто отвергает науку (не в принципе как способ познания, но как общественный институт с элементами тоталитаризма). Он заявляет в книге science in a free society, что "результаты науки не говорят в пользу её превосходства", причины на это две: 1) не показано, что достижения науки были получены исходя из "научного метода", без влияний из вне, 2) не было честного сравнения науки и альтернативных методов познания (в основном потому, что официальная наука не воспринимает всерьез ничего, кроме себя).
В книге against the method он рассматривает историю спора Галилея и католической церкви, показывая что многие аргументы со стороны церкви неотличимы от позиций современного рационалиста и "стороника науки".
Ну то есть я правильно понимаю, что практических результатов у всего этого хипстерства нет, а научный метод и рационализм они "критикуют" просто потому что так модно? Даже если рассматривать науку как тусовочку учёных, это же не отменяет научный метод. Короче, я примерно понял о чем ты, рандомное словоблудие без задач.
И вообще, всё больше замечаю такой пиздеж от людей, не имеющих отношение к инженерному делу в принципе. Точно так же как самые ярые "сциентисты" ни физики, ни химии не знают обычно совсем.
Видимо такое знание существенно препятствует образованию ложных связей.
>>7390
Он тут на правильном пути, у буддизма (мадхъямики по крайней мере, и похожей на неё адвайты-веданты, у Шанкары например) есть некоторые связи с феноменологией. Не в плане взаимодействия конечно, но соответствия идей. Например есть сборник переводов "Хайдеггер и восточная философия", при чем там статьи самих индийцев.
У восточных учений много общего с западной философией, ну не Канта, конечно, (и не Шопенгауэра).
Например open individualism в который верил Эрвин Шрёдингер, содержательно, это буддизм йогачары.
Такие дела.
Чет я не очень понял какие задачи тебе нужны от критиков. Типа, сам Фейерабенд лично какой самолет построил, что сам руками сделал? Ну он воевал на восточном фронте, и в результате стал инвалидом, например.
Вообще, инженерным делом и практическим вкладом много Витгенштейн увлекался, от работы учителем начальных классов в альпийской деревне до волонтерской работы в госпитале во вторую мировую. Еще хотел в ссср поехать чтобы устроиться работать на завод, но его не пустили.
>хипстерства
>модно
У тебя в голове какое-то говно, вдимо потому, что ты еблан.
Задача их была – показать что рационалистический бред не относится к реальной практике исследователя. Что они и сделали, обратившись к истории и рассмотрев действия ученых (принимая во внимание так же высказывания ученых по поводу этих действий) показали, как последовательно нарушаются рациональные стандарты во всех важных случаях. Например, указание Лакатоса на иррационализм Бора и стремление построить квантовую механику на противоречивых основаниях (что ему удалось, кстати).
Важно, однако, не нынешнее состояние этой науки, а именно действия конкретного исследователя в конкретной исторической ситуации.
> Чет я не очень понял какие задачи тебе нужны от критиков. Типа, сам Фейерабенд лично какой самолет построил, что сам руками сделал? Ну он воевал на восточном фронте, и в результате стал инвалидом, например.
Ну критика должна иметь какую- то цель, не? Я могу что то критиковать, потому что скажем, есть вариант получше, который при его применении даёт лучший результат, чем то, что я критикую. Это критика здорового человека. А то что описываешь ты это критика курильщика, сам же говоришь, что все,чего этот критик добился практически это инвалидность на восточном фронте. Так себе достижение, согласись. Но ок, может быть последователи этоикак то применяли? Или из последователей только ты и все практическое применение это назвать кого то ебланом на мейлру? Тоже иак себе достижениеипо сравнению с наукой.
 43 Кб, 291x256
43 Кб, 291x256> Задача их была – показать что рационалистический бред не относится к реальной практике исследователя. Что они и сделали, обратившись к истории и рассмотрев действия ученых (принимая во внимание так же высказывания ученых по поводу этих действий)
Вообще пушка. Ясно, что с таким подходом смешно ждать практических результатов. Короче, я тебя услышал, как альтернативу научному методу и рационализму ты предлагаешь псевдоумную критику этих явлений, которая сама по себе никаких практических применений не имеет кроме разве что впечатлить винишку ТП.
>>7401
>есть вариант получше, который при его применении даёт лучший результат, чем то, что я критикую
Он есть, и звучит так:
Anything goes.
Ну и что это такое, тезисно. Хотя, подозреваю, лучше спросить что такое по твоему научный метод и рационализм. По твоим постам чувствуется, начитался ты хуйни дальше некуда. Не то чтобы я против, просто чувствуется в тебе какой то манямир.
Принимаемые аксиматически нормы на основе которых, выводят исходящие формулы.
Можно ли назвать эти нормы научным методом? Нет, ведь, гипотетически, мы могли принять иные ввривнты
Вот это кукареканье тоже весьма замечательное
>медицина
>наука
Тут как с инженерным делом, только еще хуже. У медиков вершина науки это "биохимия", об обычной химии, и уж тем более, о физике с математикой, у них представления уровня 7-го класса обычно.
При чем можно подумать, что исследователей готовят лучше, и биофак вообще престижнее меда, но в реальности всё в точности наоборот.
Я даже не буду затрагивать такую тему, что можно пользоваться и знахарями и официальной медициной (например чтобы узнать что эффективнее в конкретной ситуации), и что обычный человек уж точно не связан "интеллектуальной честностью" обязывающей его встать на одну и только одну сторону, если даж ученый не всегда связан.
Ситуация нелепая совершенно:
Фанатики рационализма убеждают, что их учение верно, по той причине, что якобы используется наукой; при этом во всех случаях приводят как доводы примеры не из науки (биомедицина, авиация, и тд).
Но это не отвергает прикладной вклад научных познаний.
>позитивисты
Ты из 1840-х пишешь? Закопай это говно обратно.
Или имеется в виду "неопозитивизм" венского кружка?
Так тоже, в общем-то.
Вообще, на википедии даже Мах записан в позитивисты, что не может быть дальше от истины в принципе, он в своих работах позитивизм разобрал и отверг. В своё время их мало кто понял (одна книга Ленина чего стоит), а после как-то и перестали нужным читать.
>>7416
Тезисно: все годится, отсутствие предписаний лучше любых предписаний. Принцип пролиферации: чем больше у научной теории альтернатив, тем лучше.
Фейерабенд был релятивистом и считал, что вменяемого способа судить о том, какая альтернатива лучше все равно нет, и было бы из чего выбирать, а там уже практика покажет как оно получилось.
>что такое по твоему научный метод и рационализм
Первое – бессмысленный набор критериев (например критерий фальсифицируемости Поппера) которым, на поверку, не удовлетворяет ни одна научная теория.
Второе – более сложная идея, восходящая к Рене Декарту, основывается она на нескольких тезисах: идее объективности (которая вытекает из картезианской догмы о дуализме субъекта и объекта) и идее о руководящей роли разума в познании.
Как это было изначально, это вообще пиздос, Кант попытался хоть как-то совместить рационализм с реальной жизнью (я об этом писал в начале треда), после него были позитивисты, потом "аналитическая философия", критический рационализм Поппера, еще более утонченная версия от Лакатоса, и собственно всё.
> Тезисно: все годится, отсутствие предписаний лучше любых предписаний. Принцип пролиферации: чем больше у научной теории альтернатив, тем лучше.
> Фейерабенд был релятивистом и считал, что вменяемого способа судить о том, какая альтернатива лучше все равно нет, и было бы из чего выбирать, а там уже практика покажет как оно получилось.
Вот, практика. Т.е от практики все равно никуда. Потому что это единственный критерий ценности любой теории. Что вполне рационально и научно, как это ни назови. А то, что ты триггеришься от терминов этоиуже вторично. И сколько ни критикуй позитивистов или сигнифицистов, суть там в том же. Этот подход, опора на практические результаты, рационален и очевиден как правильный, т.к. есть внешний по отношению к теории критерий, практика. А речь изначально была не об этом, а о подходе Канта. Который не мог опираться на практику, т.к. в то время не было нейрофизиологии. Ему нечем было установить объективную правильность или неправильность своих выводов. Как и Брауэру. И тем не менее, они оказались правы. Вот из каких соображений исходил Кант кроме уверенности в своей правоте, мне это интересно.
Давай закончим заниматься подменой понятий.
Практика у Фейерабенда имеет ключевое значение, а именно, он призывает к взаимодействию разума и практики, в котором эти две вещи непрерывно связаны и ни одно не занимает руководящую роль. В рационализме, который он отвергает, разум всегда важнее и он руководит практикой, при чем практика не способна как-то повлиять или изменить его.
Собственно, именно в этом и было ключевое различие episteme и doxa у Платона, именно в этом отличие разума от изменчивого и приспособленного к ситуации здравого смысла (английский термин common sense куда лучше это подчеркивает).
Собственно, чем занимается любое приличное научное сообщество, это развитием собственного здравого смысла на техническом уровне.
Разум тут вообще не при чем. Если тебе не хочется признавать этих различий, а хочется смешать все в кучу и стоять на позициях "я за всё хорошее и против всего плохого", то вообще не понятно, к чему обсуждение.
>т.к. есть внешний по отношению к теории критерий, практика
И это тоже неверно. Рационализм представляет собой, жёсткий или нет, набор критериев, которые от практики никак не зависят. Говоря же о "подтверждениях" ты вообще скатываешься в джастификационизм.
Грубо говоря, фальсификационист утверждает, что хоть и подтверждающий пример для теории ни о чем не говорит (очевидно любому, знакомому с логикой), но опровержение имеет решающее значение, поскольку оно позволяет её отбросить и признать неверной. Значит, где можно потенциально много найти опровержений, но они не находятся до поры, там и наука.
Это наивный рационализм Поппера.
Перечисленные мной книги более чем на половину состоят из контрпримеров к этой позиции. Грубо говоря, требование это слишком жесткое, да и вообще фальсифицировать теорию напрямую фактами наблюдения невозможно (об этом я уже писал выше).
>ему нечем было установить объективную правильность или неправильность своих выводов
А про это я уже устал писать. То есть, ты собрался подтверждать правильность рационалистических взглядов, ссылаясь на "объективную правильность", которая основана на все том же рационализме (и имеет смысл только там). Brilliant.
Правилен ли рационализм с рациональной точки зрения? Ну даже не знаю, дай подумать.
Кант этим конечно не занимался, не потому что мрт еще не изобрели, а потому что клиническим идиотом он не был.
>Ситуация нелепая совершенно
Разумеется, куда нелепее.
Петухи-критики смеются над тупыми учёными в говне мочёными, не понимая что живы они до сих пор только по их милости.
Продолжай мастурбировать на ученых, я не запрещаю, но рационализм тут не при чём. Или все-таки рационализм тебя больше привлекает?
Сварщик из жэка это наука? Ну как, даже обычная электродная сварка это межатомное соединение, атомы открыл Резерфорд, значит наука.
Не смотря на то, что сварщик не знает что такое сила тока, качество его шва определенно говорит в пользу науки.
Медицина тоже наука, уже выяснили. Не сдох еще от инфекции? Значит жив по милости невидимой руки науки. Летал на самолете? Ну самолеты для боинга и аирбаса собирают исключительно физики-теоретики, это наука.
>кто из них
Так ты учёных имел в ввиду? Все вышеперечисленные, в тот или иной момент. За пруфами смотри литературу, ссылки были выше.
> А про это я уже устал писать. То есть, ты собрался подтверждать правильность рационалистических взглядов, ссылаясь на "объективную правильность", которая основана на все том же рационализме (и имеет смысл только там). Brilliant.
Ты лучше напиши, какая ещё есть правильность кроме объективной. Кант оказался прав именно объективно. Ты пишешь пустые слова, которые и тебе ни о чем не говорят, хотя ты уверен в обратном.
>какая ещё правильность кроме объективной
Ты про релятивизм что-то слышал?
https://ru.wikipedia.org/wiki/Релятивизм
Попробуй почитать, но я не уверен что поможет, случай в принципе клинический.
>Ты пишешь пустые слова
Я пытаюсь объяснить довольно простые вещи, которые до тебя не доходят из-за упертости твоей позиции.
Я знаю что такое релятивизм, более того, знаком с релятивизмом в математике, согласно идеям Маннури. Ты сам выше писал, что Кант рационалист, больше того, он и сам пишет о том, что у человека нет методов изучения своего разума кроме средств этого же разума. Отвлекаясь от ярлычков именно это я и называю рационализмом, не знаю, что под этим имеют в виду цитированные тобойихипстеры. Более того, правота Канта так же имелась в виду объективная, опять же это слово я использую в общепринятом значении, безотносительно того, что под ним подразумевают твои критики, не создавшие ничего.
>Отвлекаясь от ярлычков именно это я и называю рационализмом
Ну герой войны, которого ты называешь хипстером, имел в виду примерно то же самое, да.
>в общепринятом значении
Понятие объективности в рационализме предполагает что есть корректные способы установления истин, от практики (то есть чьих-то мнений, идей, ожиданий) не зависящие; и что существует некий универсальный стандарт оценки того, с каким утверждением можно согласиться, а с каким нет.
Релятивист не принимает этих предположений, и для него "X был прав объективно" смысла не имеет.
>твои критики, не создавшие ничего.
Это просто смешно.
Фейерабенд написал 5-6 иниересных книг, например одна его интерпретация космологии архаической Греции стоит больше, чем все рассуждения недоучки Лёфа про Канта, которого он никогда не читал.
>релятивизмом в математике, согласно идеям Маннури
Идеи Маннури, Мартина-Лёфа и прочих к математике имеют примерно такое же отношение, как новая хронология Постникова-Фоменко. Даже меньшее, поскольку она была создана математиком всё-таки, а не голландскими/шведскими хипстерами, которые в принципе не имели отношения к этой области.
Заметно, однако, что ты предпочитешь одних ничего не создавших болтунов другим.
This.
Не философия, и не математика. Область, состоящая из недоучек, которые не понимают ни того, ни другого, и производят по этой причине низкокачественную и в основном бессмысленную писанину прикрываясь терминами "математика", "логика", "теория типов".
Хуже астрологов в разы, те хотя бы никого не дискредитируют своей деятельностью.
 4 Кб, 211x220
4 Кб, 211x220> Идеи Маннури, Мартина-Лёфа и прочих к математике имеют примерно такое же отношение, как новая хронология Постникова-Фоменко. Даже меньшее, поскольку она была создана математиком всё-таки, а не голландскими/шведскими хипстерами, которые в принципе не имели отношения к этой области.
Ну я уж понял примерно уровень твоих познаний в математике. О чем тут говорить, если ты элементарщины типа изоморфизма Карри Говарда не понимаешь. Про релятивизм в математике и говорить нечего. Ты мыслишь ярлычками, предметной области не понимаешь вообще итд. Если по твоему это философия математики, то у меня для тебя плохие новости.
В ход снова пошли боевые картинки.
>если ты элементарщины типа изоморфизма Карри Говарда не понимаешь
Ты сделал вывод о том что я не понимаю из того факта, что я отказываюсь признавать значение этого результата для математики непосредственно? Так это совершенно очевидно, таких изоморфизмов можно придумать десятки. Максим твой уже писал что MLTT примерно соответствует мадхъямаке, а я например могу открыть Торчинова и прочитать там что мадхъямака соответствует феноменологии, продолжать надо?
При чем смешное, что ты и сам не видишь, что математические понятия есть только в изоморфизме Воеводского, а HoTT к MLTT отношения имеет чуть менее, чем никакого, то есть твое кукареканье wasn't valid in the first place.
>Про релятивизм в математике и говорить нечего
Естественно нечего, это высер очередного петуха из околоинтуиционистской тусовки, такой же как и "сигнификационизм". Внешние ссылки на оба эти термина просто отсутствуют.
При чем эти самые интуиционисты обычно не понимают смысла своего же учения. Взять того же Клини, который рассуждает в чисто реалистических терминах, Брауэр охуел бы, если бы дожил.
Замечу еще только, что переход Воеводского из математики в теорию типов хронологически совпадает с его высказываниями о том, что "математику необходимо уничтожить". Корреляция или каузальная связь, решай сам.
>Ты сделал вывод о том что я не понимаю из того факта, что я отказываюсь признавать значение этого результата для математики непосредственно?
Ты не можешь признавать или не признавать того, чего не понимаешь. Последнее же совершенно очевидно.
>таких изоморфизмов можно придумать десятки.
Хоть один придумай.
>При чем эти самые интуиционисты обычно не понимают смысла своего же учения. Взять того же Клини, который рассуждает в чисто реалистических терминах,
А в каких надо-то, если интуиционизм - это изначально построимые ментальные конструкции? То, что ты не понимаешь этого, как не понимаешь и того, что читаешь, тех авторов, которых ты цитируешь >>7476
>Отвлекаясь от ярлычков именно это я и называю рационализмом
>Ну герой войны, которого ты называешь хипстером, имел в виду примерно то же самое, да.
это абсолютно очевидно. Не понимаешь ты и элементарщины вроде отношения теории типов к математике, и опять же по то же самой причине - нулевые познания в предметной области, ты и отношения теории множеств к матлогике не понимаешь. Но, при этом ты высокопарно вещаешь аки глас самой истины в последней инстанции. Мартин-Лёф - недоучка, Маннури - петух. Как он может быть петухом, если он не русский? Ты даже этого понять не в силах, какая тебе философия.
>Внешние ссылки на оба эти термина просто отсутствуют.
Ты даже в гугл не можешь, давай уж назовем вещи своими именами.
>хоть один придумай
Уже придумал и привел выше. Еще парочка более полезных взаимно-однозначных соответствий уже из математики: André Weil's Rosetta Stone (с него началась этальная геометрия), geometric Langlands correspondence (более спорно, эта наука еще развивается).
Теперь сравни со своим Карри-Говардом, у которого применений в математике ровным счетом 0.
>А в каких надо-то, если интуиционизм - это изначально построимые ментальные конструкции
Из всех своих кумиров Брауэра ты, по видимому, понимаешь хуже всего. Пик релейтед.
>нулевые познания в предметной области
Тебе и твоим кумирам никто не давал права переопределять содержание математики таким образом, чтобы включить туда свою шизофрению. То же самое, что и с канторовской теорией множеств.
>ты и отношения теории множеств к матлогике не понимаешь
>теория множеств
>матлогика
Это не математика.
>Мартин-Лёф - недоучка
Если человек не смог узнать, что такое эпистемология и чем она занимается, то ему не стоило писать про это.
>Ты даже в гугл не можешь,
Ну учитывая что ты за несколько лет голословного пиздежа не предоставил ни одной внешней ссылки (а просто цитировал Лёфа и прочих напрямую), то куда уж мне-то?
Однако, тебе я предлагаю зайти в google books, набрать там "significationism" и посмотреть на выдачу. Со своей стороны я скажу, что специально просмотрел восемь книг издательства шпрингер на эти темы, и ни в одной из них сигнификационизм не упоминается. И вообще, из того, что я читал, упоминается это только у Гейтинга, если не путаю.
То есть ситуация какая, человек не осилил ни математики, ни философии, зато неплохо заучил пару книг типа очерков Лёфа и рофлит уже четвертый год.
При чем я не говорю что это плохо, только указываю на непоследовательность: от аналогичных по содержанию трудов о научном методе ты плюешься как от бесполезных.
>тебе я предлагаю зайти в google books, набрать там "significationism" и посмотреть на выдачу.
>"significationism"
Лол кек чебурек. Это слово пишеццо "significs", ты даже в термины не можешь. http://gen.lib.rus.ec/book/index.php?md5=80AF551F44776ADAE1F48D7DB259C5C0 вот книжка, конкретно по релятивизму Маннури и его вкладу в математику вообще -17. Relativism and Significs: Gerrit Mannoury on the Foundations of Mathematics (by Heijerman, Erik) статья крайне годная, обзор обеих работ Маннури по сигнифицистским основаниям математики.
>Это не математика.
Ты так сказал?
>не предоставил ни одной внешней ссылки
Я уже даже не помню, сколько их представлял. Только все и всегда развивалось по одному сценарию:
ПРИНЕС ТОЧНУЮ ЦИТАТУ
@
АРРЯЯАА НАХУЯ МНЕ СКРИНШОТЫ, ДАВАЙ ССЫЛКУ
ДАЛ ССЫЛКУ НА СТАТЬЮ / КНИГУ
@
АРРРЯЯАА ХУЛЕ ТЫ СВОИМИ ЕВРЕЯМИ ПУГАЕШЬ, ДАВАЙ ЦИТАТЫ / ТЕЗИСЫ СВОИМИ СЛОВАМИ
>Это слово пишеццо "significs"
Я думал этот термин обозначает теорию знака, например у Пирса, или Гуссерля или у Деррида, но окей. Признаю, по нидердландским хипстерам я не специалист.
>обзор обеих работ Маннури
>внешняя ссылка
Понятно. А так чтобы без самих петухов и их последователей, кто-то еще эти термины признает? Просто допустим сколько материала можно найти по феноменологии на plato.stanford.edu, а по твоей "сигнифике" ничего.
>Я уже даже не помню, сколько их представлял
Зато я помню, ни разу.
>АРРЯЯАА НАХУЯ МНЕ СКРИНШОТЫ, ДАВАЙ ССЫЛКУ
Ну вот я тебе только что дал скриншот с указанием на критику науки Брауэром и его явную антиреалистическую позицию. Маневрирование уже началось?
>АРРРЯЯАА
>АРРЯЯАА
Тебе больно, что ли?
>Из всех своих кумиров Брауэра ты, по видимому, понимаешь хуже всего. Пик релейтед.
>Ну вот я тебе только что дал скриншот с указанием на критику науки Брауэром и его явную антиреалистическую позицию. Маневрирование уже началось?
Я читал Брауэра, то, что на твоих скринах, он подробно разбирает в своем диссере 1907 года (2ая часть), который я тоже читал (в переводе Гейтинга на англ. ес-но, голландского я не знаю). И я в курсе его отношения к науке. Но вот эта его точка зрения, с какой стати считается, что она как-то противоречит реализму? Это наоборот же самый что ни на есть реализм, самая реалистическая позиция из всех возможных, т.к. она наиболее точно отражает существующую реальность. Брауэр признает, что внешний мир доступен человеку только через его восприятие. Это медицинский факт, где тут что-то против реализма или объективных фактов?
>>7497
>Я думал этот термин обозначает теорию знака,
В этом и проблема. Ты много чего думаешь, а на самом деле все иначе.
>А так чтобы без самих петухов и их последователей, кто-то еще эти термины признает?
Я же говорю, ты слишком зациклен на терминах, вместо того, чтобы разобраться к чему этот термин вообще применяет тот кто его использует.
>Просто допустим сколько материала можно найти по феноменологии на plato.stanford.edu, а по твоей "сигнифике" ничего.
> кто-то еще эти термины признает?
Тут видишь какое дело. Речь о вычислимых вещах, которые можно просто вычислить. Признание или непризнание не решает ничего. Для тебя большое значение имеют "авторитеты", в математике авторитет это ничто, зато доказательство - все. Ты даже этого не понимаешь. Твой аргумент о том, что на какой-то педивиккии за сигнифику ничего нет = хуйня, это вообще смешно.
>с какой стати считается, что она как-то противоречит реализму
Ты понимаешь что такое реализм? Скажи честно, что нет.
https://en.wikipedia.org/wiki/Philosophical_realism
Начать можешь со средневекового спора об универсалиях, который заключался в вопросе об онтологическом статусе — существуют ли универсалии, или же они являются всего лишь абстракциями, человеческими обобщениями вещей. Номинализм отрицает универсалии, признавая их только в качестве части языка. Реализм отрицает отдельные вещи, отводя им только акцидентные свойства.
Примеры реалистов в физике — Гейзенберг, Дайсон, Пенроуз. Не видишь разницы между позицией Гейзенберга и Брауэра? Ну можешь открыть например "Emperor's new mind" и посмотреть какими словами хуесосит Брауэра Пенроуз.
Но тебе это что божья роса, понятно.
>Ты много чего думаешь, а на самом деле все иначе.
Тебе не стыдно? Сколько раз ты уже обосрался со своим восприятием Брауэра, феноменологией, эпистемологией, Кантом, рационализмом, реализмом, хотя бы в этом треде? Значение ни одного из этих слов тебе не было известно.
>к чему этот термин вообще применяет тот кто его использует.
Кто-то его применяет и использует? Об этом и вопрос.
>Я же говорю, ты слишком зациклен на терминах
Скорее на их содержании. Ты же судишь об этом исключительно из названия термина, как происходит с "объективность", "реализм", "рационализм". У всех этих терминов существуют вполне определенные значения, и прописаны они практически везде, от википедии до популярной литературы. Ты их игнорируешь и задаешь вопросы в духе
"А феноменология это не рационализм?"
>>6974
До невежества такого уровня мне в любом случае еще очень далеко.
>Для тебя большое значение имеют "авторитеты",
Сказал человек, несколько лет подряд ссылающийся на Мартина-Лёфа.
>в математике авторитет это ничто, зато доказательство - все
Ну да, то есть не бывает ситуации в математике, чтобы опубликовали статью уважаемого человека, заведомо содержащую ошибку, только из уважения к этому человеку? Ты это хочешь сказать? Тогда ты обоссан, это случается регулярно. Например недавняя статья Атьи про 6-dimensional sphere packing.
>на какой-то педивиккии за сигнифику ничего нет
Как и нигде нет. А про алгебраическую геометрию есть везде. Чувствуешь разницу?
>с какой стати считается, что она как-то противоречит реализму
Ты понимаешь что такое реализм? Скажи честно, что нет.
https://en.wikipedia.org/wiki/Philosophical_realism
Начать можешь со средневекового спора об универсалиях, который заключался в вопросе об онтологическом статусе — существуют ли универсалии, или же они являются всего лишь абстракциями, человеческими обобщениями вещей. Номинализм отрицает универсалии, признавая их только в качестве части языка. Реализм отрицает отдельные вещи, отводя им только акцидентные свойства.
Примеры реалистов в физике — Гейзенберг, Дайсон, Пенроуз. Не видишь разницы между позицией Гейзенберга и Брауэра? Ну можешь открыть например "Emperor's new mind" и посмотреть какими словами хуесосит Брауэра Пенроуз.
Но тебе это что божья роса, понятно.
>Ты много чего думаешь, а на самом деле все иначе.
Тебе не стыдно? Сколько раз ты уже обосрался со своим восприятием Брауэра, феноменологией, эпистемологией, Кантом, рационализмом, реализмом, хотя бы в этом треде? Значение ни одного из этих слов тебе не было известно.
>к чему этот термин вообще применяет тот кто его использует.
Кто-то его применяет и использует? Об этом и вопрос.
>Я же говорю, ты слишком зациклен на терминах
Скорее на их содержании. Ты же судишь об этом исключительно из названия термина, как происходит с "объективность", "реализм", "рационализм". У всех этих терминов существуют вполне определенные значения, и прописаны они практически везде, от википедии до популярной литературы. Ты их игнорируешь и задаешь вопросы в духе
"А феноменология это не рационализм?"
>>6974
До невежества такого уровня мне в любом случае еще очень далеко.
>Для тебя большое значение имеют "авторитеты",
Сказал человек, несколько лет подряд ссылающийся на Мартина-Лёфа.
>в математике авторитет это ничто, зато доказательство - все
Ну да, то есть не бывает ситуации в математике, чтобы опубликовали статью уважаемого человека, заведомо содержащую ошибку, только из уважения к этому человеку? Ты это хочешь сказать? Тогда ты обоссан, это случается регулярно. Например недавняя статья Атьи про 6-dimensional sphere packing.
>на какой-то педивиккии за сигнифику ничего нет
Как и нигде нет. А про алгебраическую геометрию есть везде. Чувствуешь разницу?
Вот это я хуйню написал, переклинило. Там не упаковки шаров, а про отсутствие комплексной структуры S^6. Ну да ладно. В любом случае, сейчас есть целые области в комплексной геометрии, где с доказательствами ситуация не лучше. А до появления категорных методов в начале сороковых так было и с топологией; и с "классической" алгебраической геометрией до инфинитезимальных методов. Что приводит нас к мысли, высказанной явно Маниным, что определения все же важнее теорем, а теоремы доказательств. Но об этом уже слишком много написано, да и не к месту здесь.
Скажу только, что без этого понимания, нельзя отличить решение задачи ad hoc методами от применения к ней теории, построенной вообще говоря не для этой задачи и не зависящей от нее; соответственно нельзя уже отличить теорию множеств и универсальную алгебру от математики.
И вот теперь, спустя четыре года, мы здесь, громче всех орущий про конструктивищм человек назвал Брауэра платонистом.
На этом я думаю можно завершить.
> громче всех орущий про конструктивищм человек назвал Брауэра платонистом.
Да все с тобой понятно, даже смысла нет спрашивать, где я назвал Брауэра платонистом, все равно что-нибудь придумаешь, например, связав реализм (в определении какого-нибудь хипстера) с платонизмом. В общем, смысла обсуждать что-то дальше не вижу, мне видится полезнее потратить время на допиливание прувера, чем писать одно и то же на мейлру.
Платонизм и реализм это одно и то же.
>РЕАЛИЗМ
(от позднелат. realis — вещественный, действительный) — филос. направление, признающее находящуюся вне сознания реальность, которая истолковывается либо как бытие идеальных объектов (Платон, средневековая схоластика), либо как объект познания, независимый от субъекта, познавательного процесса и опыта (филос. Р. 20 в.).
>мне видится полезнее потратить время на допиливание прувера,
Ну я так и понял.
Насосался? Приходи как еще захочешь.
Максим?
>(от позднелат. realis — вещественный, действительный) — филос. направление, признающее находящуюся вне сознания реальность, которая истолковывается либо как бытие идеальных объектов (Платон, средневековая схоластика), либо как объект познания, независимый от субъекта, познавательного процесса и опыта (филос. Р. 20 в.).
Реальная вещь соответствует кантовской "вещи самой по себе"? С такой точки зрения ментальные конструкции Брауэра, конечно, нельзя назвать "реальными", как и ощущения, через который человек может получать информацию из окружающего мира. Однако, это не отменяет ни окружающего мира, ни нейрофизиологии. А значит, вопрос насчет Канта, поставленный в начале треда остается в силе. И вся та хуйня, что ты нес, на него не отвечает.
С чего ты взял, что "сознание" как место ментальных конструкций и "окружающий мир" это две разные вещи, а не части одного и того, например общего пространства ощущений (или феноменов)?
>кантовской "вещи самой по себе"
Это вообще костыль, использованный Кантом для частичного восстановления картезтансконо рационализма, от которого камня на камне не оставил Юм. С изобретением феноменологии, все эти "трансцендентное", "трансцендентальное", "априори", "апостериори", "вещи в себе", "антиномии" и прочее были упразднены, всё, это история.
Я про "сознание" вообще ничего не говорил. Чем плохо разделение действительности на внешние и внутренние относительно нервной системы явления? Причем, внутренние можно рассматривать как функции от внешних, так что разделение не абсолютно, а условно, для удобства.
>костыль, использованный Кантом для частичного восстановления картезтансконо рационализма, от которого камня на камне не оставил Юм.
Рассуждения о том, что "кто-то уничтожил Навального как политика Канта как философа" это вообще смех на палке. Мне известны примеры использования идей Канта в математике, в отличие от некоего Юма, думаю и ты таких примеров не приведешь.
То что кто-то приписал эти идеи Канту ни о чем по существу не говорит.
Кант был неглупым человеком и вовремя понял, что надо делать чтобы стать известным и популярным – писать объемные книги, в которых с педантичностью капитана очевидность разжевывать любую мысль до тривиальности.
На Юма я обращаю внимание, как на основную мотивацию, исходную точку для Канта.
Были конечно и неокантианцы, например Герман Коген, но это по сути извращенный позитивизм. От Канта там опять же, уже нет трансцентного, а от позитивизма не осталось фактов наблюдения, то есть теоретические принципы, извлекаемые из разума, первичны по отношению к любому опыту. Довольно чудовищное учение, что-то на уровне Фейербаха.
>Чем плохо разделение действительности
Ну кроме того, что мы становимся рационалистами; от введения разделения субъекта и объекта, материи и мышления и тд у нас сразу появляется куча неразрешимых вопросов: проблема тела и сознания (mind-body problem), проблема реальности внешнего мира, проблема измерений в квантовой механике и тд.
Еще это противоречит здравому смыслу, плохо согласуется с современной физикой (ктп и её альтернативами), ну и в целом некрасиво.
Разделение это не естественно, в античной европе и в средневековой азии его не было в принципе, и ничего, жили как-то. На самом деле, настоящие тёмные века в европе это как раз "эпоха просвещения", то есть условно от Гоббса и Декарта до Маха и Гуссерля.
Никакое христианство и тд не принесло столько вреда в интеллектуальном плане, сколько Декарт. Еще и проективную геометрию Дезарга и Паскаля похоронил своими координатами. А про работы по оптике и физиологии тот же Арнольд сказал исчерпывающе.
Реально, ни знаю ни одного положительного вклада за этим человеком, он даже в тридцатилетке воевал на стороне католиков.
Заслуга Маха основная в том, что он забил последний гвоздь в крышку гроба и закопал к хуям это учение.
>от введения разделения субъекта и объекта, материи и мышления и тд у нас сразу появляется куча неразрешимых вопросов:
Материю и мышление разделять не нужно, есть ионный ток в ЦНС, который одновременно и то и другое. А субъект и объект и так разные вещи.
>>7553
MLTT - это работающий пример того, что Лейбниц хотел запилить под названием characteristica universalis и calculus ratiocinator. В то время, естественно, это было невозможно. Но сами эти идеи сильно опередили свое время.
>субъект и объект и так разные вещи
Только у сектантов, sorry.
>characteristica universalis
Ой, ну это бесконечная тема, что в неявном виде было у Лейбница, от топологии (analysis situs его термин) и комбинаторики, до некоего прообраза теории категорий. Он еще и юристом был, вроде, неплохим.
Но нам интересно, конечно не это. Примерно в 1959 Курт Гёдель осознал, что если взять монадологию Лейбница и про возможные миры сказать, что они не создаются необходимым субъектом (боженькой), а конституируются непосредственно в сознании, то получится плюс минус феноменология Гуссерля, изучением которой Гёдель и занялся.
А так вообще Лейбниц не только в бога верил, но и, простите, в закон исключенного третьего. Ну время было такое.
>Понятия не имею что ты несешь, я нигде не говорил что Мах выдумал это понятие или что вообще пользовался им.
Блять ты мудазвон, своё же сообщение перечитай сука.
>Постмодернизм – это состояние мышление манек вроде тебя, у которых в голове всё перемешалось и они не отличают а) инженерное дело от науки, б) реальную научную практику от рационалистического бреда, которому она никогда не соответствала. Сектант as is.
Ты болеешь, тебе нужна помощь.
>рационалистический бред
>не относится к реальной практике исследователя
>рационалистический бред
>рационалистический
>бред
О как. А чё относится? Ты исследователь, поди? Можешь рассказать?
Или ты к науке имеешь такое же отношение, как, например, Ася Казанцева — то есть никакого?
>Фанатики рационализма убеждают, что их учение верно, по той причине...
Ты ошибся, манька нахуйная.
Сторонники (а не фанатики, фанатик тут только ты, судя по выбору слов) рационализма уверены в своём "учении", потому что маньки вроде тебя и петушков-критиков, на которых ты дрочишь, не предоставили НИКАКИХ веских оснований засомневаться в рационализме и рассмотреть другие варианты.
НИ
КА
КИХ.
И ты это сам прекрасно знаешь, потому в ответ на мой пост ты начнёшь писать про то что я еблан и сука, и что у меня говно в голове, вместо того, чтобы предоставить список хороших аргументов против рационализма. Ты будешь изо всех сил оскорблять меня, научный метод, ненаучный метод, учёных, мочёных, всё живое, всё неживое, языковые концепции и абстракции, будешь вести себя отвратительно, лишь бы никто не заметил, что тебе нечего сказать по делу. Лишь бы никто не заметил, что ты охуенно глубинно не прав и источаешь только пердёж в лужу всю свою сознательную жизнь.
Как ты его!
> Сторонники (а не фанатики, фанатик тут только ты, судя по выбору слов) рационализма уверены в своём "учении", потому что маньки вроде тебя и петушков-критиков, на которых ты дрочишь, не предоставили НИКАКИХ веских оснований засомневаться в рационализме и рассмотреть другие варианты.
Выяснили уже. Предыдущий оратор под рационализмом имеет в виду какую-то мутную философию 16 века, а не то, что этим словом называют обычно. То же самое с научным методом, он считает, что это нечто связанное чуть ли не со средневековой схоластикой. Реализм у него это платонизм. И так далее. Ну в стэнфордской педивикии так пишут.
> Только у сектантов, sorry.
Это опять же спор о терминах. Я уже сто раз приводил пример использования слова "Subject", "I", " Self" Брауэром. Ты же закатываешь глаза и начинаешь писать что субъект это какая-то хуйня, придуманная Декартом а на самом деле блабла... Я под разницей субъекта и объекта понимаю то, что даже ты не будешь отождествлять себя и свои тапки, разница очевидна, хотя с позиции твоих критиков, наверное и этоине так. Скажем, у человека есть области ЦНС ответственные за то, что считать собой и своим телом. У Рамачандрана про это подробно написано, повреждения их приводит к тому, что человек перестаёт например воспринимать свою руку своей и требует её ампутировать, раньше считалось, что это психическое заболевание, а оказалось что простая неврология.
Ты не читаешь половины того, что я тебе привожу.
>>7490
>his doctrine of the exterior world of the subject is a radical departure from the realist tradition
>>6733
>there is no subject-object distinction here
Для чего ты привязался к этому слову?
Я уже говорил, что субъект в контексте чего-то отдельного от объекта был только у Декарта и рационалистов; у схоластов, Брентано, Гуссерля и Брауэра под субъектом понимается совершенно другое понятие. Ну да, слово похожее. А у Аристотеля есть категории, значит Аристотель ввел понятие сопряженного функтора.
>отождествлять себя и свои тапки
Человек и его тапки являются частью общего мира ощущений, как и все существующее.
>>7571
>Реализм у него это платонизм
А у кого это не так? То что ты придурок и не учился в вузе, где философия обязательна, это твои проблемы. В любом учебнике, словаре, энциклопедии, дано именно такое определение.
>То же самое с научным методом, он считает, что это нечто связанное чуть ли не со средневековой схоластикой
Про то что "philosophy as a series of footnotes to Plato" слышал?
>а не то, что этим словом называют обычно
При этом здесь >>7476 мы выяснили что эти значения совпадают. То что мутная философия, ну она мутная и есть изначально, деятельность например Канта и других в принципе вся была направлена на то, чтобы эту муть убрать, успех как видно не был полным.
>ответственные за то, что считать собой и своим телом
Мах с этого и начал, что граница между собой и внешним миром у всех разная, у слепого одна, у зрячего другая, еще и может меняться.
> Мах с этого и начал, что граница между собой и внешним миром у всех разная, у слепого одна, у зрячего другая, еще и может меняться.
Однако граница эта есть. Это факт, даже если тебе печет от таких терминов как объективный. Как ты это ни назови, а разницу между субъектом и объектом опровергнуть невозможно.
> Человек и его тапки являются частью общего мира ощущений, как и все существующее.
Но ощущать может человек. Тапки ощущать не могут. Вот тебе и разница между субъектом и объектом. Так что и мир о котором ты говоришь субъективен. Однако, возвращаясь к математике, ни один из твоих хипстеров никакого вклада туда не сделал. Выше я показал, как работающая модель Миколова воплощает идеи сигнифики, то, о чем писал Маннури. Конструктивные основания МартинЛефа так же есть воплощение идей Брауэра. Как и последние есть развитие некоторых идей Канта. А то оичем пишешь ты, как это можно использовать в математике?
>ощущать может человек
Как он может ощущать, если человека невозможно выделить как отдельную часть из внешнего мира. Любой реальный объект в этом мире это комплекс ощущений, и человек тоже. С чего ты взял что ощущения ему принадлежат, что они вызваны его разумом, а не внешним миром?
>о котором ты говоришь субъективен
В смысле Декарта что-то может быть субъективно или объективно. Я этот смысл отвергаю.
>возвращаясь к математике
>ни один из твоих хипстеров никакого вклада туда не сделал
>модель Миколова
>писал Маннури
>основания МартинЛефа
Как ты верно заметил, ни один из этих хипстеров вклада в математику не сделал. Брауэр сделал, и его достижения можно перечислить:
С Брауэра начинается теория гомотопий: он занимался проблемой инвариантности размерности и для этих целей ввел гомотопическую классификацию непрерывных отображений S^2 —> S^2 и определил степень отображения; позже Хопф обобщил эту работу на политопы произвольной размерности, в значительной степени пользуясь наработками Брауэра. Брауэр так же доказал обобщение теоремы Жордана; теорему о неподвижной точке; теорему о симплициальной аппроксимации, и дал определение симлициального комплекса. Результаты эти не выглядят сейчас значительными, если не знать, в какое время они сделаны. До Брауэра топология (Жордан, Пуанкаре) была по существу бездоказательным мракобесием. Брауэр так же ввел понятие размерности до Лебега.
После этих достижений в области математики, Брауэр решил перейти в философию, где основал интуиционизм, отрицающий не конструктивные доказательства, основанные на принципе исключенного третьего. Funnily enough, основное достижение Брауэра — fixed point theorem как раз и являлась не конструктивным доказательством (в отличие от аналогичной теоремы Банаха, доказанной на 12 лет позже).
Что еще раз подчеркивает принципиальное различие в его деятельности как математика и как философа. Same goes for Voevodsky.
Отличие Лёфа-хуёфа, Манури-хуюри и прочих мужеложцев от Брауэра и Воеводского в том, что они сразу начали заниматься фуфлософией и периода занятий математикой, предшествующего этому, у них не было вовсе.
>ощущать может человек
Как он может ощущать, если человека невозможно выделить как отдельную часть из внешнего мира. Любой реальный объект в этом мире это комплекс ощущений, и человек тоже. С чего ты взял что ощущения ему принадлежат, что они вызваны его разумом, а не внешним миром?
>о котором ты говоришь субъективен
В смысле Декарта что-то может быть субъективно или объективно. Я этот смысл отвергаю.
>возвращаясь к математике
>ни один из твоих хипстеров никакого вклада туда не сделал
>модель Миколова
>писал Маннури
>основания МартинЛефа
Как ты верно заметил, ни один из этих хипстеров вклада в математику не сделал. Брауэр сделал, и его достижения можно перечислить:
С Брауэра начинается теория гомотопий: он занимался проблемой инвариантности размерности и для этих целей ввел гомотопическую классификацию непрерывных отображений S^2 —> S^2 и определил степень отображения; позже Хопф обобщил эту работу на политопы произвольной размерности, в значительной степени пользуясь наработками Брауэра. Брауэр так же доказал обобщение теоремы Жордана; теорему о неподвижной точке; теорему о симплициальной аппроксимации, и дал определение симлициального комплекса. Результаты эти не выглядят сейчас значительными, если не знать, в какое время они сделаны. До Брауэра топология (Жордан, Пуанкаре) была по существу бездоказательным мракобесием. Брауэр так же ввел понятие размерности до Лебега.
После этих достижений в области математики, Брауэр решил перейти в философию, где основал интуиционизм, отрицающий не конструктивные доказательства, основанные на принципе исключенного третьего. Funnily enough, основное достижение Брауэра — fixed point theorem как раз и являлась не конструктивным доказательством (в отличие от аналогичной теоремы Банаха, доказанной на 12 лет позже).
Что еще раз подчеркивает принципиальное различие в его деятельности как математика и как философа. Same goes for Voevodsky.
Отличие Лёфа-хуёфа, Манури-хуюри и прочих мужеложцев от Брауэра и Воеводского в том, что они сразу начали заниматься фуфлософией и периода занятий математикой, предшествующего этому, у них не было вовсе.
>В смысле Декарта что-то может быть субъективно или объективно. Я этот смысл отвергаю.
Ок, пусть будет не субъективно, а пынблективно. Факт есть, и от него никуда не денешься. Как это ни назови. ВЗять мой пример, алгоритм работает. Ты это не можешь отвергать, т.к. это уже чистый манямир. Пример проще - группы крови. Ты их можешь отвергать сколько угодно, но если ты себе по вене ебнешь гемокон несовместимой крови - почки у тебя отвалятся и ты уедешь ногами вперед. Безотносительно твоего и твоих хипстеров мнения о работах Ландштейнера, безотносительно ощущений, мира идей, феноменов, Декарта и всего остального.
>Любой реальный объект
>реальный
Атятяй, как же реальный-то? Это же от декартовского "res", я это отвергаю.
> в этом мире это комплекс ощущений, и человек тоже.
А человек это комплекс ощущений кого? Аллаха? Ощущения могут существовать отдельно от человека?
>С чего ты взял что ощущения ему принадлежат, что они вызваны его разумом, а не внешним миром?
А с чего это ты выделяешь внешний мир? Внешний относительно кого/чего?
>Отличие Лёфа-хуёфа, Манури-хуюри и прочих мужеложцев
Это ты так думаешь. Маннури (один из учителей Брауэра, к слову), математикой занимался, в т.ч. преподавал. Есть даже мнение, что это он подкинул Брауэру идею по поводу исключенного третьего.
Нельзя впрочем сказать, что Фейерабенд был недоучкой. Философии он научился у Витгенштейна (на семинарах Крафта), физике от Эренхафта, математике его обучил Ван-дер-Варден (взамен Фейерабенд объяснил ему философию Аристотеля).
>>7585
Вот это уже реально детский сад начался. Ты понимаешь, что любое наблюдаемое явление, например падение тел на землю, само по себе не относится никуда. Ты можешь его описать научно, с помощью гравитации, и тогда оно будет относиться к науке. А можешь сказать "тела падают, такова божья воля" и тогда это уже относится к религии. Не думал что придётся объяснять такие тривиальности.
По остальному, я уже говорил что термины для меня не имеют никакого значения, с картезианством я не согласен с точностью до семантики, если ты назовешь это "феноменологией", я с такой феноменологией не согласен. Впрочем, ты это давно уже делаешь, говоря о конструктивизме и при этом являясь чистым платонистом по убеждениям.
>Ощущения могут существовать отдельно от человека?
Только что дошло? Поздравляю. Они существуют сами по себе, при чем существуют только они. Я это пытался тебе объяснить 2.5 треда, наконец получилось.
>Они существуют сами по себе, при чем существуют только они.
Вот и дошли до религии. Что значит "существуют" по-твоему? Где они "существуют"? Ты еще меня в платонизме обвинять будешь, с такой-то швятою верою в "мир феноменов"?
Не видишь разницы? Платонизм утверждает что мир идей существует независимо от мира, в котором ты живёшь, именно отсюда идея объективности, которой ты так любишь пользоваться. Христианство и ислам в значительной мере на платонизма основаны (в первом случае так получилось, а во втором – выбрали создатель, так что чья бы корова мычала.
Современная физика утверждает, что ничего материального не существует, например элементарные частицы это просто модель, описывающая возмущения квантового поля.
В М-теории говорят о бранах (по сути поверхность, представляющая собой путь движения струны), с математической точки зрения это просто автоморфный пучок.
Если Мах знал алгебраическую геометрию, он бы говорил о морфизмах расслоений, а не об ощущениях. Но это, как ты выражаешься, спор о терминах. Не надо путать это с платонизмом Тегмарка. У них все математические идеи существуют реально, как идеи у Платона, но независимо от остального мира, что и делает их "объективными".
Любая научная идея всегда основана на философии, говорится об этом явно, или нет. То что ты привык мыслить опираясь на реалистические догмы говорит не в их пользу, а только о твоей религиозности.
 15 Кб, 267x310
15 Кб, 267x310Прежде чем говорить о моей религиозности, давай поговорим об ощущениях. Ты говоришь, >>7592 что они существуют, причем независимо от человека. Т.е. уже этим ты выделяешь субъекта, т.к. вот человек, а вот ощущения, которыми и сам человек является, но при этом которые в т.ч. независимы от него. Ты сам не видишь, что это все тот же субъективизм/объективизм только другими словами? Ты даже не можешь сформулировать, что есть "существование", а знаешь, почему? Потому что при этом неизбежно скатишься к столь нелюбимому тобой пикрелейтед господину.
Рационализм (картезианство это рационализм version point-o) это подмножество реализма (общепринято, в первую очередь среди сторонников, применять термин "платонизм" и к реализму 20-го века).
Каждый рационалист это платонист, обратное не верно хотя бы по историческим причинам, об этом ниже.
Даю иллюстрацию:
Платонизм это "в церковь не хожу, но пост соблюдаю и крестик ношу";
Рационализм это головой в пол и "верую во единого бога-отца, вседержителя-творца", ой, простите, "cogito ergo sum… cogito ergo sum", до полного исступления.
Примерно так.
>>7598
Если бы ты не был хроническим невеждой, уже бы понял что люди жили и до мистера Give-her-the-D, а те, кто жил после, могли о его бреднях просто не знать.
https://en.wikipedia.org/wiki/Monism
На, ознакомься.
>уже этим ты выделяешь субъекта, т.к. вот человек
Комплекс ощущений, а не субъект.
>Ты даже не можешь сформулировать, что есть "существование",
Да, ну конечно, онтологии до Рената Картезия не было. Что несет, блядь.
>Комплекс ощущений, а не субъект.
Тапки - тоже комплекс ощущений. Однако, себя ты от тапок отличаешь. Так?
>онтологии
Это общее название подхода к вопросу существования. А не ответ на него. От ответа же ты упорно уходишь, попутно пытаясь обмазать калом Картезия.
Все твои суждения оказываются чепухой, если принять тот факт, что любая религия - это просто платонизм для народа.
>Так?
И на этот вопрос нам ответит барабанная дробь.
В своих работах «О методе теоретической физики», «Физика и реальность» и «Основы теоретической физики» (перепечатано в сборнике «Идеи и мнения»; все ссылки даны по этой книге) Эйнштейн разъясняет, почему научные теории и понятия являются «фикциями» или «свободными созданиями человеческого мышления» и почему «только интуиция, опирающаяся на внимательное отношение к опыту, способна привести к ним». Согласно Эйнштейну, первым шагом в познании «реального внешнего мира» является формирование понятия телесных объектов, причем телесных объектов разного рода. Из всего многообразия наших чувственных восприятий мы мысленно выделяем и произвольно берем определенные комплексы ощущений, которые часто повторяются… и сопоставляем им некоторое определенное понятие – понятие телесных объектов. С логической точки зрения это понятие не тождественно совокупности ощущений, к которому оно относится; это – свободное творчество человеческого (или животного) разума. С другой стороны, смысл понятия и его оправданность определяются совокупностью ощущений, которые мы ассоциируем с ним. Второй шаг состоит в том, что в нашем мышлении (которое определяет наше ожидание) мы приписываем понятию телесного объекта смысл, который еще в большей мере независим от чувственного ощущения, первоначально его породившего. Именно это мы хотим выразить, когда приписываем телесному объекту «реальное существование». Оправдание такого утверждения основано исключительно на том факте, что с помощью таких понятий и установленных между ними мысленных отношений мы способны ориентироваться в лабиринте ощущений.
>Это общее название подхода к вопросу существования
Ну и?
>А не ответ на него
Ответ на чего? Что такое существование?
Так это экзистенцал просто, "presence", что понимается под Dasein у Хайдеггера или под Атманом в Упанишадах.
Пиздец уже, вот пёрлы пошли, без Декарта нельзя сказать, что существует, а что нет.
А я с этим спорю? Вообще, большинство народа под религией понимает именно "аврамическая религия" с персонифицированным богом и прочим. Называть разновидности буддизма или течения в рамках индуизма религией уже как-то некорректно.
Поэтому, например, по статистике самая атеистическая страна это Япония, хотя там 87% заявляют о своей причастности к синтоизму. А с конфуцианством как быть? Религия? Это правовая система, блядь, вообще-то.
Сказать же, что аврамическая хуита типа иудаизма/хрюстианства/излама это платонизм для народа, начит сказать тавтологию. Что мне в данном треде приходится делать все чаще.
Детектор почини, Вхорен, я из ридонли вылез.
>Так это экзистенцал просто, "presence", что понимается под Dasein у Хайдеггера или под Атманом в Упанишадах.
Ага, "веревка есть вервие простое". Дазайн, блядь, хайдеггер. Дупина еще принеси. Я же серьезно спрашиваю, а ты пытаешься с вопроса съехать таким толстым методом, как самореференция, "существование это существование".
То, что ты про Эйнштейна скопипастил, это называется "идентификация систем", то что таким методом можно открывать физические законы с помощью алгоритмов машинного обучения, было показано еще в совке академиком Ивахненко. Т.е. ты не ответил на собственно вопрос - чем комплекс ощущений "тапки" отличается от комплекса ощущений "Я".
>веревка есть вервие простое
А математика есть наука о модулях над кольцами. Контекстуальные определения самые содержательные.
>Я же серьезно спрашиваю, а ты пытаешься с вопроса съехать
Нет, ты хочешь чтобы я определил существование в твоих манякартезианских терминах. Это сделать конечно можно, но вовсе не обязательно. Существование – обозначение наличного бытия.
Что тут не ясно, я не понимаю.
>это называется "идентификация систем"
Да хоть как это называется, по сути это парафраз Маха, под влиянием которого Эйнштейн находился (хоть и не признавал этого).
Конкретно, он там описывает, почему тапки называются тапками, или что ты там спрашивал, в этой строчке:
>с помощью таких понятий и установленных между ними мысленных отношений мы способны ориентироваться в лабиринте ощущений
То есть у тебя ситуация уникальная, ты это видно читал и раньше, как и диссертацию Брауэра, но рационалистические убеждения заставили тебя всю содержательную часть проигнорировать. Что религия с людьми делает.
>Нет, ты хочешь чтобы я определил существование в твоих манякартезианских терминах.
Отнюдь. Я хочу увидеть альтернативу. А ее нет, один дазайн и прочие самореференции.
>Конкретно, он там описывает, почему тапки называются тапками, или что ты там спрашивал, в этой строчке:
Я не спрашивал, почему тапки называются тапками. Я спрашивал, как так получается, что себя ты от тапок отделяешь. Или себя от другого человека. И чем твои самореференции уровня "существую следовательно существую" лучше "cogito ergo sum".
>То есть у тебя ситуация уникальная, ты это видно читал и раньше, как и диссертацию Брауэра, но рационалистические убеждения заставили тебя всю содержательную часть проигнорировать.
"Рационалистические убеждения" можно заменить на "практическую применимость". У Брауэра и Канта я это вижу, (интуиционизм вообще начинается с определения существования математического объекта как построимой на основе интуиции движения времени ментальной конструкции, сложно придумать что-то более ясно понятное и практически применимое) у Эйнштейна из твоей цитаты это так же очевидно, "понятия и установление между ними мысленного отношения" это пости точное определение функциональной зависимости y = f(x) между входами и выходами в идентификации систем. А весь этот манядазайн и прочие самореференции и упанишады хуй знает как применять хоть для чего-то, не говоря о математике и науке.
>чем твои самореференции лучше "cogito ergo sum"
Тем, что если начать использовать слово "следовательно" для связки двух случайных слов, то это ровным счетом ничего не показывает. Откуда Декарту ясно, что мышление присуще именно ему, а не является чередой переживаний, вызванных внешним миром? Ниоткуда, он это просто постулирует. Значение этой максимы именно в этих неявных предположениях, которые делают высказывание "cogito ergo sum" осмысленным. То есть функция этой фразы это "смотри какие у меня догмы", а то что там не к месту вставлено "ergo", ну это джентельмен любил так выражаться.
Лошадь, следовательно, шпага.
>Я хочу увидеть альтернативу
Какая может быть альтернатива у догматов объективности и руководящей роли разума? Отсутствие этих догматов. Смысл феноменологии ровно в этом.
Шотландский экономист обложил хуями картезианство, Кант защитил рационализм от критики, но вылезло трансцендентное. Гуссерль взял шпагу и вырезал сие непотребство, называется феноменологическая редукция. Вся история.
Дазайн появляется если применить феноменологию к онтологическим вопросам, этим занялся уже Хайдеггер. Я не считаю, что ему следовало в это лезть, Упанишады с задачей объяснения бытия уже справились, а на то, что развел Хайдеггер быстро слетелись мухи в виде Мерло-Понти и Сартра. По деятельности этих мух, рядовой обыватель о философии и судит сейчас. Ну и еще по Лаканам всяким.
>хуй знает как применять
А математику как применять? Или оставить от нее только статистику, уравнения в частных производных и дискретное преобразование Фурье. Так и с этой точки зрения твои пруверы нахуй не усрались.
Охота знать кому нужна феноменология?
https://en.wikipedia.org/wiki/Phenomenology_(particle_physics)
Начиная с 60-х, это важная часть оснований физики (вспомнить историю с Г. Вейлем). Той части, которая про high energy и particles (есть еще condensed matter, astrophysics и прочее, где это не нужно, впрочем математика там не нужна тоже).
Да я понимаю, что с философией это связано лишь косвенно, но нет, это не просто совпадение названий, как например с феноменологической теорией теплоты (там это слово тупо значило что явления теория описывает, но не объясняет).
В общем я рад конечно, что тебе удалось себя убедить в том, что интуиционизм реально имеет массу практических приложений и даже найти 1-2 исследования по нейробиологии, но думаю, даже тебе понятно что в общей массе это, мягко говоря, не очень популярно.
>чем твои самореференции лучше "cogito ergo sum"
Тем, что если начать использовать слово "следовательно" для связки двух случайных слов, то это ровным счетом ничего не показывает. Откуда Декарту ясно, что мышление присуще именно ему, а не является чередой переживаний, вызванных внешним миром? Ниоткуда, он это просто постулирует. Значение этой максимы именно в этих неявных предположениях, которые делают высказывание "cogito ergo sum" осмысленным. То есть функция этой фразы это "смотри какие у меня догмы", а то что там не к месту вставлено "ergo", ну это джентельмен любил так выражаться.
Лошадь, следовательно, шпага.
>Я хочу увидеть альтернативу
Какая может быть альтернатива у догматов объективности и руководящей роли разума? Отсутствие этих догматов. Смысл феноменологии ровно в этом.
Шотландский экономист обложил хуями картезианство, Кант защитил рационализм от критики, но вылезло трансцендентное. Гуссерль взял шпагу и вырезал сие непотребство, называется феноменологическая редукция. Вся история.
Дазайн появляется если применить феноменологию к онтологическим вопросам, этим занялся уже Хайдеггер. Я не считаю, что ему следовало в это лезть, Упанишады с задачей объяснения бытия уже справились, а на то, что развел Хайдеггер быстро слетелись мухи в виде Мерло-Понти и Сартра. По деятельности этих мух, рядовой обыватель о философии и судит сейчас. Ну и еще по Лаканам всяким.
>хуй знает как применять
А математику как применять? Или оставить от нее только статистику, уравнения в частных производных и дискретное преобразование Фурье. Так и с этой точки зрения твои пруверы нахуй не усрались.
Охота знать кому нужна феноменология?
https://en.wikipedia.org/wiki/Phenomenology_(particle_physics)
Начиная с 60-х, это важная часть оснований физики (вспомнить историю с Г. Вейлем). Той части, которая про high energy и particles (есть еще condensed matter, astrophysics и прочее, где это не нужно, впрочем математика там не нужна тоже).
Да я понимаю, что с философией это связано лишь косвенно, но нет, это не просто совпадение названий, как например с феноменологической теорией теплоты (там это слово тупо значило что явления теория описывает, но не объясняет).
В общем я рад конечно, что тебе удалось себя убедить в том, что интуиционизм реально имеет массу практических приложений и даже найти 1-2 исследования по нейробиологии, но думаю, даже тебе понятно что в общей массе это, мягко говоря, не очень популярно.
>если начать использовать слово "следовательно" для связки двух случайных слов, то это ровным счетом ничего не показывает.
Ты, похоже, вообще не понимаешь смысла того, что пытаешься критиковать. Ergo в этой фразе из очевиднейших для любого школьника соображений - отождествление существования человека как человека с его мыслительной активностью. Скажем, с работоспособностью ЦНС. Человек с нефункционирующей ЦНС - это уже не человек, не личность, не субъект, а суповой набор секционный материал. Ты это пытаешься оспорить?
>А математику как применять?
Математика как раз для любой задачи применима. Идентификация систем, машинное обучение.
>Или оставить от нее только статистику, уравнения в частных производных и дискретное преобразование Фурье. Так и с этой точки зрения твои пруверы нахуй не усрались.
А ты на мои пруверы не гони, я как раз пытаюсь вымутить нечто, аналогов не имеющее, как раз на основе некоторых идей Маннури.
>high energy и particles (есть еще condensed matter, astrophysics и прочее, где это не нужно, впрочем математика там не нужна тоже).
Математика нужна везде. В любой науке ровно столько науки, сколько там математики. Остальное это не наука. Очевидно, что математику феноменологией не заменить, а в качестве ответа на все вопросы предлагать дазайн, это все равно, что говорить "бох так сотворил", разницы никакой, такая же религия.
>В общем я рад конечно, что тебе удалось себя убедить в том, что интуиционизм реально имеет массу практических приложений и даже найти 1-2 исследования по нейробиологии, но думаю, даже тебе понятно что в общей массе это, мягко говоря, не очень популярно.
Ты не понимаешь. Потому что не видишь дальше своих хипстеров. Жизнь - это не только дазайн. Прогресс идет, сложность наук и т.о. сопутствующих математических моделей растет, а человек уже не вытягивает математику, (открытые по несколько веков проблемы, IUTeich Мочидзуки, которую кроме него никто толком осилить не может и т.п. - это полный пиздец) нужна автоматизация. А автоматизация предполагает полную вычислимость, если позатыкать все дыры невычислимыми актуальными бесконечностями и исключенными третьими, в итоге любое сколько-либо сложное доказательство к этим дырам и сведется. Все больше областей, где требуются абсолютно корректно работающие программы, кроме языков с зависимыми типами так же нет методов писать такое ПО в большом объеме. И т.д.
>если начать использовать слово "следовательно" для связки двух случайных слов, то это ровным счетом ничего не показывает.
Ты, похоже, вообще не понимаешь смысла того, что пытаешься критиковать. Ergo в этой фразе из очевиднейших для любого школьника соображений - отождествление существования человека как человека с его мыслительной активностью. Скажем, с работоспособностью ЦНС. Человек с нефункционирующей ЦНС - это уже не человек, не личность, не субъект, а суповой набор секционный материал. Ты это пытаешься оспорить?
>А математику как применять?
Математика как раз для любой задачи применима. Идентификация систем, машинное обучение.
>Или оставить от нее только статистику, уравнения в частных производных и дискретное преобразование Фурье. Так и с этой точки зрения твои пруверы нахуй не усрались.
А ты на мои пруверы не гони, я как раз пытаюсь вымутить нечто, аналогов не имеющее, как раз на основе некоторых идей Маннури.
>high energy и particles (есть еще condensed matter, astrophysics и прочее, где это не нужно, впрочем математика там не нужна тоже).
Математика нужна везде. В любой науке ровно столько науки, сколько там математики. Остальное это не наука. Очевидно, что математику феноменологией не заменить, а в качестве ответа на все вопросы предлагать дазайн, это все равно, что говорить "бох так сотворил", разницы никакой, такая же религия.
>В общем я рад конечно, что тебе удалось себя убедить в том, что интуиционизм реально имеет массу практических приложений и даже найти 1-2 исследования по нейробиологии, но думаю, даже тебе понятно что в общей массе это, мягко говоря, не очень популярно.
Ты не понимаешь. Потому что не видишь дальше своих хипстеров. Жизнь - это не только дазайн. Прогресс идет, сложность наук и т.о. сопутствующих математических моделей растет, а человек уже не вытягивает математику, (открытые по несколько веков проблемы, IUTeich Мочидзуки, которую кроме него никто толком осилить не может и т.п. - это полный пиздец) нужна автоматизация. А автоматизация предполагает полную вычислимость, если позатыкать все дыры невычислимыми актуальными бесконечностями и исключенными третьими, в итоге любое сколько-либо сложное доказательство к этим дырам и сведется. Все больше областей, где требуются абсолютно корректно работающие программы, кроме языков с зависимыми типами так же нет методов писать такое ПО в большом объеме. И т.д.
>отождествление существования человека как человека с его мыслительной активностью
Отождествление лошади со шпагой, я и сказал.
>машинное обучение.
Ох, бой, хиа ве гоу агеин. Сколько в ML математики, ты в курсе? Половина андеград курса калькулюса.
Впрочем, примерно столько ты и знаешь.
> В любой науке ровно столько науки, сколько там математики
Сколько математики в condensed matter? Сколько её в химии? В биологии сколько? Впрочем, о чем спрашивать брейнлета, у которого ML, оказывается, использует математику.
>Математика нужна везде
И где нужна программа минимальных моделей? Гипотеза Морделла, проблема Бернсайда много где нужны, за пределами математики? Кристаллические когомологии уже применяются?
Ты хотя бы в курсе, сколько математики нужно для криптографии? Я тебе скажу, на всякий случай: ровно один факт, что перемножить два больших числа экспоненциально легче, чем разложить большое число на простые сомножители. И так в большинстве приложений. Математики уровня пятого класса там достаточно (в машинном обучении хватит и третьего).
> а в качестве ответа на все вопросы
Математика и не интересуются такими вопросами. На вопрос "что существует" отвечает философия.
>IUTeich Мочидзуки, которую кроме него никто толком осилить не может
Это простое применение к теории чисе геометрии Аракелова, которая сама по себе просто 11-я область из оставленных Гротендиком для математики 12-ти.
Учи математику лучше, не занимайся хуйней.
Или сразу так и заявляй: "Я – специалист по прикладной шизофрении (это интуиционистская теория типов, кто не понял)". Честнее и люди не будут путаться, сразу поймут с кем имеют дело. Собственно это ко всем умственно неполноценным относится, у кого "математика это раздел теории типов", не только к тебе.
Самому не смешно такое нести после признания, что кроме дазайна тебе на любой вопрос ответить нечего?
Разберись с тем, что такое дазайн, если хочется. Рекомендую "Основные понятия метафизики" Хайдеггера, книга куда более интересная и менее техничная чем Sein und Zeit (поэтому и переведена не так криво).
>>7631
Функциональный анализ тут это как США, на обоих сторонах карты? На самом деле это просто раздел К-теории C*-алгебр, после Гельфанда и Наймарка, по крайней мере.
 132 Кб, 640x959
132 Кб, 640x959>Математика и не интересуются такими вопросами. На вопрос "что существует" отвечает философия.
Математика начинается с вопроса "что значит существование математического объекта". Брауэр это понимал, в отличие от тебя.
>Ох, бой, хиа ве гоу агеин. Сколько в ML математики, ты в курсе? Половина андеград курса калькулюса.
>Математики уровня пятого класса там достаточно (в машинном обучении хватит и третьего).
Я ж говорю, ты дальше дазайна ничего не видишь. А я даже пример приводил, как типизированную лямбду можно использовать в теории статистического обучения Вапника для полностью автоматизированного, без участия человека, создания новых алгоритмов машоба. Тебе как и твоим хипстерам, такого и в голову бы не пришло.
>Математика начинается с вопроса "что значит существование математического объекта".
Метаматематика – не математика.
>типизированную лямбду можно использовать в теории статистического обучения Вапника
Для инженеров есть собственный раздел:
2ch.hk/pr
>Метаматематика – не математика.
Ты даже что такое метаматематика не знаешь. Это к тому, что ранее уже выяснили тоже самое про изоморфизм Карри-Говарда.
>Ты даже что такое метаматематика не знаешь
Мне интересна математика, а не религиоведение.
>Брауэр это понимал, в отличие от тебя
Брауэр, в отличие от тебя, не имел каши в голове и чётко разграничивал математику от её оснований. Именно поэтому основной результат Брауэра – теорема о неподвижной точке – противоречит его же принципам, то есть не является конструктивным (it doesn't describe how to find the fixed point).
Отличие же людей, по чьим книгам ты выучился в том, что никакой математики они в жизни не видели, и принимают разговоры о том, что в математической практике допустимо и обоснованно, а что нет, за саму практику.
Ни один работающий математик не задается такимм вопросами как "что такое математический объект". Есть два примера людей, которые после завершения математики перешли в область прикладной шизофрении (это если тебе не нравится термин "метаматематика") где подобные вопросы ставятся. Это Брауэр и Воеводский.
Остальные люди, которых ты называешь, математиками никогда не были, это медицинский факт.
>Мне интересна математика, а не религиоведение.
Феноменология и прочий дазайн с упанишадами - это как раз религиоведение, а не математика.
>основной результат Брауэра
Основной результат брауэра - непротиворечивые основания, что по тезису Черча то же самое, что основания вычислимые.
>Отличие же людей, по чьим книгам ты выучился в том, что никакой математики они в жизни не видели, и принимают разговоры о том, что в математической практике допустимо и обоснованно, а что нет, за саму практику.
Безапелляционность твоих заявлений и никакое их отношение к практике как бы намекает нам, что перед нами ебанат. Применение пруверов для самой что ни на есть математики начинается с самого де Брауна и его проекта AUTOMATH, конкретно - полная проверка книги Grundlagen Ландау. Собственно, пруверы как явление просто не существовали бы, если бы их нельзя было применять в математике.
>если тебе не нравится термин "метаматематика")
Мне не термин этот не нравится, мне не нравится, что ты его употребляешь абсолютно не к месту. Погугли хоть что это такое вообще. Ты и Брауэра не читал, иначе бы знал, что он вообще называет математикой и уж точно не нес бы хуйни про "прикладную шизофрению". Ты читал своих хипстеров, которые как и ты на пустом месте решили, что могут вместо Брауэра давать определения, что он считал субъектом и т.д.
Я где-то говорил что феноменология это математика? По-моему, как раз наоборот, i prefer to maintain distinction.
>Основной результат брауэра - непротиворечивые основания
Я имел в виду основной результат в математике.
Топология – это математика. Тезис Чёрча – нет.
>Grundlagen Ландау
Опять рофлишь, да? В предисловии к этой книге, которое ты видимо пропустил, ясно объясняется, что её цель – логически обосновать анализ, и что никакого анализа там нет. Впрочем это следует даже из названия.
Следуя твоей twisted logic, основное занятие математика это определять N, а не заниматься математикой. Однако в действительности, люди, которые определяют N, называются определяторами N. Чем собственно и занялся Ландау в этой книге (только не N, а R).
Но он был математиком, а ты и твои петухи – нет.
>Безапелляционность твоих заявлений
Уже предлагал тебе перечислить контрибьюции, например, Лёфа в такие области как топология, алгебраическая геометрия, к-теория, и т.д. Ты этого делать не стал. Поскольку лучшего специалиста по научной жизни Лёфа мы здесь вряд ли найем, предлагаю считать что этих контрибьюций не было.
 1,5 Мб, webm,
1,5 Мб, webm,480x360, 0:17
>Я где-то говорил что феноменология это математика?
Ты название треда видел вообще?
>Топология – это математика. Тезис Чёрча – нет.
То, что ты считаешь математикой только 1,5 раздела оттуда, не значит что так и есть на самом деле. И уж точно не значит, что даже эти 1,5 раздела не являются чем-то выразимым в основаниях. Основания для того и существуют, что это нечто, из чего можно вывести всю вообще математику. Этот вопрос, как и кризис оснований, тебе вообще не знаком, ты слышал только про те свои 1,5 раздела, которые и упоминаешь постоянно.
>Следуя твоей twisted logic, основное занятие математика это определять N, а не заниматься математикой.
Не наша, а ваша. N тут определяет N-петух, к нему я отношения не имею. Если бы ты понимал, что такое изоморфизм Карри-Говарда, ты бы понял и мою логику, которая не имеет ничего общего с тем, что ты мне пытаешься приписать.
>которые как и ты на пустом месте решили, что могут вместо Брауэра давать определения, что он считал субъектом
Моё отношение к Брауэру довольно простое, как и к Воеводскому.
Это люди, которые какой-то период своей жизни посвятили математике, и достигли там немалого. После чего перешли в другую область, которая к математике уже никак не относится.
Различие этих двух случаев вот в чём: если основные результаты Воеводского (символ норменного вычета и тд) в математике до сих пор актуальны и подлежат изучению, то есть являются частью стандартного курикуллума; то про результаты Брауэра (перечислены мною выше) так уже не скажешь: в течение двадцати лет после их получения они устарели безнадежно, сейчас же, спустя сто лет, читать работы Брауэра по математике будет интересно разве что историкам очень узкой специальности.
То есть, интересны сейчас только работы Брауэра по интиуиционизму, при всём уважении.
По моему же мнению, и эти работы интересны лишь постольку, поскольку их можно интерпретировать в терминах феноменологии. С работами "последователей" Брауэра типа Гейтинга, Клини, такого уже сделать нельзя (в отличие от Брауэра они реалисты-платоники) поэтому место им в мусорном ведре.
Феноменология это не математика, ни в каком месте.
Но, феноменология может представлять некий интерес, и выше я объяснил почему и для кого. В терминах феноменологии можно так же описать работы Лейбница, Маха, ряда других философов и ученых; а еще такие вещи как Упанишады, тексты Шанкары, Нагарджуны, Чандракирти.
При чем, как и в случае с интуиционизмом, необходимо тщательно выяснить где и в каких местах там феноменология, то есть содержательная часть, а где бред сумасшедшего, типа рассуждений о боге у Лейбница.
>Моё отношение к Брауэру довольно простое
Столь же простое, как и неправильное. Свой диссер по поводу интуиционизма он начал писать в возрасте около 24 лет. Сам как думаешь, многого он к такому возрасту достиг в том, что ты называешь математикой? Сборник его трудов под редакцией Гейтинга как раз и состоит из 2х томов, т.к. Гейтинг счел нужным разделить всю деятельность Брауэра на две "почти не пересекающиеся части". А разгадка проста - Брауэр занимался всем этим параллельно. Более того, тема его диссера как бы намекает нам, что из своей деятельности в математике он считал важнее.
>название треда видел вообще
После фразы "не философия и не математика" тред можно было закрыть. Не желая обсуждать бессмысленную хуйню, я счел уместным обсуждать здесь философию и математику по отдельности.
>ты считаешь математикой только 1,5 раздела оттуда
Я считаю математикой core mathematics. Это во-первых, не полтора раздела (лень все перечислять), во-вторых, в отличие от хуйни про вычислимость, которая скажем топологию никак не использует, там ничего за полсеместра не выучишь, и нужно знать все области сразу. Собственно поэтому их глупо перечислять, там масса пересеченй и взаимосвязей, любые границы будут произвольными. Науки, в которых это не верно (комбинаторика, динамические системы, твоя теория типов) то есть замкнутые в себе вещи, которым core mathematics не нужна и которые ничего ей не поставляют, выполняют в организме математики функцию ленточных червей и глистов.
>свои 1,5 раздела, которые и упоминаешь постоянно
Проекции, у тебя разделов не намного больше, чем 1,5, и все в лучшем случае инженерная хуйня.
>Брауэр занимался всем этим параллельно
Ну тогда ты его выставляешь в худшем виде, как бесчестного и безответственного кретина, говорящего про конструктивизм и доказывающего теоремы не конструктивно. Твоё мнение, я так не считаю.
>Гейтинга, Клини, такого уже сделать нельзя (в отличие от Брауэра они реалисты-платоники) поэтому место им в мусорном ведре
Ты и Гейтинга не читал, раз называешь его платонистом, коим он не был. Он же прямо пишет, почему предложенная им конструктивная логика не формализует интуиционизма и почему такой формализации в принципе быть не может. Дело как раз в отрицании платонизма. Но Гейтинг все равно платонист, раз так на мейлру пишут. Ясно, понятно.
>>7664
>Ну тогда ты его выставляешь в худшем виде, как бесчестного и безответственного кретина, говорящего про конструктивизм и доказывающего теоремы не конструктивно.
Прикинь, он именно это и делал. Доказывал теоремы неконструктивно и даже с исключенным третьим. Это называется "не мы такие, жизнь такая". Он так же писал, что чистая математика - это ментальные построения на основе интуиции движения времени, а любое практическое применение математики - это зло с точки зрения его принципов и взглядов на жизнь. Что не мешало ему неблохо зарабатывать на должности профессора кафедры математики и физики. Т.е. он, занимаясь математикой, ясно понимал, какой должна быть математика на самом деле, именно это привело его к идее реконструкции математики на основе идей интуиционизма, и он немало сделал для этого. Естественно, на самом деле такая работа, реконструкция всей математике, не по силам не то что одному, а сотне таких как он. Именно эта работа продолжается и сейчас в виде конструктивных оснований - MLTT.
>Проекции, у тебя разделов не намного больше, чем 1,5, и все в лучшем случае инженерная хуйня.
Еще раз замечу, что дело в твоем непонимании что такое изоморфизм Карри-Говарда. "У меня" разделов - вся математика ,т.к. я говорю об основаниях.
> в отличие от хуйни про вычислимость,
Математика - это и есть вычислимость. Вне вычислимости никакой математики быть не может, невычислимое в математике - это всякая вера в актуальные бесконечности, алефы-беты и прочий еврейский алфавит и исключенное третье.
>раз называешь его платонистом
Считаю использование реалистических терминов для выражения своих идей достаточным основанием для того, чтобы отличать Брауэра от его "последователей".
>Это называется "не мы такие, жизнь такая"
Ага, если бы только забыть факт, что в журнал Mathematische Annalen, который Брауэр считал своей собственностью, работы, использующие такие доказательства, не принимались.
https://en.wikipedia.org/wiki/Brouwer–Hilbert_controversy
http://www.cs.cornell.edu/courses/cs6110/2015sp/docs/brouwer.pdf
>а любое практическое применение математики - это зло
По сути так и есть, то есть не понятно для чего все кривляния с машинным обучением и прочей прикладной астрологией.
>"У меня" разделов - вся математика ,т.к. я говорю об основаниях
На примере Декарта уже было видно, что "следовательно" не является магическим словом. Я говорю об основаниях, следовательно,
Ой, нет, не следовательно.
Основания это деятельность бесполезная. Можно принимать ZF, ZFC, NBG, ETCS, или что угодно; начиная с 1920-х это абсолютно не важно.
Науки, в которых есть содержательные и полезные утверждения, останутся такими при использовании любых аксиом.
>Математика - это и есть вычислимость
Только у сектантов. Не помню, чтобы у Гротендика было что-то про вычислимость.
Придумать можно какую угодно хуйню, например, универсальную алгебру, и потом заявлять: "математика изучает структуры". На практике ничего содержательного из этих универсальных конструкций не вышло. Если математики не пользуются продуктами деятельности некой секты шизофреников, значит эти продукты к математике не относятся, хоть как это обосновывай.
>Вне вычислимости никакой математики быть не может
Если бы твои познания не ограничивались
>алефы-беты и прочий еврейский алфавит и исключенное третье
то ты бы знал что куча наук не являются конструктивными, например, гомологическая алгебра. У нас во дворе не все люди, заявляющие что гомологическая алгебра это не математика, живут долгой жизнью, если понимаешь о чем я.
>не понятно для чего все кривляния с машинным обучением
Конечно, тебе не понятно. Ты ж не признаешь значения таких вещей как практическое применение и практические результаты, это все придумал Картезий в 19-ом году. Тебе хватает дазайна. А математикой ты считаешь тапалогии с гамалогиями. Прикинь, необходимость машинного обучения для дальнейшего развития науки и техники стала очевидна еще в 60-х годах прошлого века, даже в совке этим занимались, не говоря о цивилизованном мире.
>На практике ничего содержательного из этих универсальных конструкций не вышло.
Вышло, MLTT хотя бы, только ты этого содержания оценить не можешь по той простой причине, что не знаком с простейшими вещами. Я даже не буду упоминать вышесторазупомянутый изоморфизм, ты поди не в курсе, что машина Тьюринга - это попытка автоматизировать процесс вычисления человеком натурального числа. И как только любой человек пытается что-либо вычислить, все что он делает, все, что способен сделать или хотя бы представить, равнообъемно машине Тьюринга. Поэтому в математике человек не способен перепрыгнуть возможности этой машины. Естественно, всегда можно начать рисовать невычислимую хуйню типа алефов, веровать в мировую душу и т.д. только это уже не математика.
>практическое применение и практические результаты
Люди, которым это интересно, обычно учатся на инженеров или медиков. В математику идти за этим странно.
>стала очевидна еще в 60-х годах прошлого века
Этим пытались заниматься на lisp вроде бы, но тогда не было а) такого количества данных б) такого количества вычислительных мощностей. Как только они появились, старая наёбка для быдла, закономерно выстрелила как коммерческий проект.
>пытается что-либо вычислить
В математике можно вычислить (compute) когомологии двойного комплекса с помощью спектральной последовательности, при этом не конструктивно.
Вычислить, и не конструктивно. В интуиционистской версии ислама это строго харам, я так понял, а в математике можно.
>Вычислить, и не конструктивно. В интуиционистской версии ислама это строго харам, я так понял, а в математике можно.
Почему же, 1 Аллах + 1 Аллах будет 2 Аллаха. Вот тебе и суть "неконструктивных вычислений". Можно алефы складывать, потенциальными бесконечностями обмазываться. Только это тапалогии с гамалогиями, а не математика. Вычислимость всегда кончтруктивна.
>Этим пытались заниматься на lisp вроде бы, но тогда не было а) такого количества данных б) такого количества вычислительных мощностей.
И данных было полно, и вычислительных мощностей хватало. Потому что тогда этим занимались академики, а не бородатые индусы-хипстеры на коворкингах как сейчас. Ивахненко я уже упоминал, его метод учета групповых аргументов позволял вычислять полиномиальную функцию от тысячи переменных на какой-нибудь допотопной ЭВМ Минск-6. Такой полином Вольтерры-Колмогорова-Габора и современное железо раком поставит. А при правильном подходе это можно вычислить на допотопном совковом хламе, который слабее, чем современный контроллер в микроволновке.
>старая наёбка для быдла,
Я уж понял, что для тебя все, что ты непонимаешь - наебка для быдла. Считай, все кроме дазайна и гамалогий.
>Вычислимость всегда кончтруктивна
В манямирке. В математике еще бывают такие вещи как extension problem, higher differentials, и проч.
Недавно ты заявлял, что под математикой понимаешь всю математику; теперь выяснилось что не всю, а только ту, которая удовлетворяет сектантским стандартам, на которые сам их создатель плевать хотел (в отношении практики доказательства теорем, а не философского пустословия).
Судя по твоим примерам вообще можно сделать вывод, что "математика" это у тебя что-то до третьего класса, пока умножают в столбик натуральные числа на машинах поста.
Ясное дело, что для столь любимых тобой приложений этого хватит с головой.
>для столь любимых тобой приложений
Вся математика - это деятельность человека, кроме приложений там нет и не может быть ничего.
Гамалогии не математика?
 3 Мб, 2560x1600
3 Мб, 2560x1600> Алсо всё это математика, просто разрыв на первую и вторую культуру оказался слишком глубоким.
Первая и остальные культуры это разве про данный случай?
> Похоже скоро придётся признать сущестование двух полноправных математик.
Математика это наиболее точное знание. О какой точности можно говорить в случае когда исключенное третье на актуальной бесконечности едет, алефами прогоняет и в платоновский мир идей верует, мне вообще непонятно.
Очень интересно узнать, что думают о технике спектральных последовательностей и какое определение математике дают прикладники с автотракторного факультета. Продолжай держать в курсе.
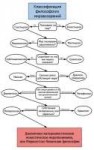 50 Кб, 383x604
50 Кб, 383x604Брауэр прикладником с тракторного университета не был, моё мнение о том, что есть математика полностью совпадает с точкой зрения Брауэра. Алсо, занимательная фуфлософия - найди себя на пике.
>>7707
Ну я и говорю. Математика, которой занимался Брауэр это 1910/20-е. Сегодня такая "математика" осталась только на картофельных плантациях, да в тракторных институтах.
> Ну я и говорю. Математика, которой занимался Брауэр это 1910/20-е. Сегодня такая "математика" осталась только на картофельных плантациях, да в тракторных институтах.
Я интуиционизм имею в виду. Именно этот подход Брауэр называл математикой. Но ты его не читал, поэтому откуда тебе знать. Зачем нужны основания тебе так же неясно, математика в твоём понимании это гамалогии.
То что твоя картинка абсолютно безграмотна, думаю, поснять не надо. Рационализма это по определению дуализм, картинка же предполагает, что может быть монистический рационализм.
От членинцев другого ждать не приходится. Все их учение это изврашенное "гегельянство наоборот", примерно как кантианский позитивизм Когена.
Философия делится на феноменологию и всё остальное.
 256 Кб, 1280x960
256 Кб, 1280x960> Философия делится на феноменологию и всё остальное.
Вот это точно слова сектанта. В философии полно всего, это просто с точки зрения феноменологии есть феноменология и остальная ебань.
Брауэр как тополог это математик. Как интуиционист – нет.
Нэш например был математиком и шизофреником. Но ни у кого нет трудности различать эти два аспекта.
Моё уважение к Брауэру исходит из первого, твоё видимо из второго. Ну кто виноват что фуфлософия тебе интереснее топологии.
> Брауэр как тополог это математик. Как интуиционист – нет.
При том, что сам он только интуиционизм и считал настоящей математикой. О чем и писал чуть менее чем на каждом шагу начиная с 1907 года. Но тебе виднее чем ему, я так и понял.
Аргумент 10/10. Ньютон уделял наибольшее количество своего времени алхимической лаборатории, а не физике. Кеплер считал самым важным фактом астрономии то, что орбиты пяти (известных тогда) планет соответствуют пяти платоновым телам.
Если вычесть из Нэша математика, останется рядовой пациент псих больницы. Логика думаю ясна.
> Ну религий тоже много, а атеизм один. So?
Демагогия. Атеизм это отрицание бога, т.е. очевидная противоположность любой религии, а феноменология просто одна из философских доктрин.
Нет, это твоя историческая безграмотность. Называл, и считал, учи историю. Более того: химии в нынешнем смысле науки о взаимодействиях электронов тогда ещё не было, а вот алхимия была. Лавуазье (создатель химии) родился через 16 лет после смерти Ньютона. И физики во времена Ньютона не было тоже, была philosophia naturalis, так что он философ, а не физик.
О занятиях Ньютона можно почитать у Куна, но поскольку ты не осилишь, рекомендую начать с Арнольда "Гюйгенс и Барроу". Там конечно рофлов много, но в целом по существу.
>>7720
Обе эти вещи схожи в том, что получаются отбрасыванием маня-догм. Буквально, выбрось из философии любую необоснованную эуйню, останется феноменология.
>Возможно придётся ввести понятие третьей культуры третьего пути .
Вообще Вавилов в одной из своих лекции говорил что-то о том что правильнее скорее рассматривать деление на четыре октанта как в political spectrum по осям
абстрактный/конкретный и общий/частный. Тогда конструктивистов куда-то в конкретный-общий, к пиночету надо засунуть.
>алсо
>любой религии
Зависит от того, что ты назовешь религией. Религия не требует утверждений о существовании бога, если что, и вообще такого понятия. 99% религий (по классификации, а не количеству последователей) таковы. Расширяй кругозор, что ли.
> Обе эти вещи схожи в том, что получаются отбрасыванием маня-догм. Буквально, выбрось из философии любую необоснованную эуйню, останется феноменология.
Нет конечно. То же самое тебе сказал бы членинец гегельянец, назвав манядогмами кантианство.
> Расширяй кругозор, что ли.
Как уже было сказано выше, все дело в том, что ты не читал Брауэра. Поэтому приплетаешь то, что тебе кажется аналогиями, типа с Ньютоном, однако на самом деле твояипозиция это демагогия.
То, за что оценивают исследователя другие люди и то, что сам исследователь считал в своих работах наиболее важным, почти никогда не пересекаются.
У тебя считается неоспоримым, что Брауэр – бох, а Лёф – пророк. Соответственно искать этому подтверждение или опровержение ты предлагаешь в работах самого Брауэра, что просто смешно.
Ну так кантианство и есть манядогмы, уже говорил почему. И материализм тоже, это тот же идеализм, только в профиль.
В феноменологии никаких догм нет, кто так думает, просто не разобрался. Кстати у Гегеля есть книга "феноменология духа" которая никакого отношенияч к предмету не имеет и написана задолго до Гуссерля, который этот термин ввел.
>еление на четыре октанта как в political spectrum по осям
>абстрактный/конкретный и общий/частный.
https://youtu.be/NgNRRI9s7uk?t=285
С 4:44 хорошо сказано про это.
на 7:44 деление математики на 4 части
> У тебя считается неоспоримым, что Брауэр – бох, а Лёф – пророк. Соответственно искать этому подтверждение или опровержение ты предлагаешь в работах самого Брауэра, что просто смешно.
> У тебя считается неоспоримым, что Брауэр – бох, а Лёф – пророк. Соответственно искать этому подтверждение или опровержение ты предлагаешь в работах самого Брауэра, что просто смешно.
У меня это считается вычислимым. Оспорить можно мнение, но не вычисление. И да, подтверждение этому сами работы авторов, а не рандомных хипстеров, которые лучше Брауэра знают чем и для чего он занимался.
> В феноменологии никаких догм нет, кто так думает, просто не разобрался.
Не уверовал в дазайн, ты хочешь сказать. Выше мы уже разобрались в ваших манядогмах.
Почему существуют закон противоречия?
Из чего он следует? Мог ли он несуществовать? Можно ли представить противоречивые структуры?
Противоречие всегда можно свести к форме "0=1" как показал Гейтинг. Суть в том, что в процессе доказательства выходит что А равно не А. Задача логических аксиом в том, чтобы такого не получалось при любом правильном их употреблении. Конструктивно все проще, т.к. там невозможно построить такую структуру.
Это не закон. Просто из такогй посылки можно доказать все что угодно. Ценность противоречивой теории т.о. нулевая. Для математики, в политике наоборот годнота, всегда можно доказать, что война это мир, свобода это рабство, чёрное это белое, деньги спиздили не чиновники а рептилоиды, воду в кране выпили жиды а в падике нассал Обама.
Это, я так понимаю, титан мысли из /ph приехал?
Что же такое вещь, титан мысли? И почему это должно волновать математику?
>Оспорить можно мнение, но не вычисление
Об играх, как о вычислениях/доказательствах ты конечно же не слышал.
кий оригинал говорит о Mengenlehre, а вовсе не Mengentheorie! Иными словами, о теоретико-множественной доктрине или учении, но не о теории!!! Основы этого учения были заложены в XIX веке Бернардом Больцано, Георгом, Кантором и Рихардом Дедекиндом. Как всякое учение, учение о множествах имеет фактические, теоретические, доктринальные и ритуальные аспекты. Основой этого учения, его символом веры является почти неограниченное принятие актуальной бесконечности. Нет сомнения, что это кредо в
значительной степени определило математику XX века и ответственно за все достижения.[жирным/курсивом выделил автор]
Кажется я нашёл учебник, по которому наш конструктивист учился.
Лол, там ещё сноска
>Доктрина — учение, вероучение, система философских, религиозных, идеологических или
теоретических взглядов.
Конечно, как мы теперь знаем, непротиворечивость систем Z, ZF и ZFC не может быть
установлена финитными средствами и, таким образом, в известном смысле, представляет
собой вопрос веры.Некоторые авторы шли настолько далеко, что даже определяли матема-
тика как того, кто верит в непротиворечивость системы ZF. Следует однако заметить, что
как чисто формальных, так и эпистемологических оснований для такой веры значительно
больше, чем оснований для веры в существование внешнего мира.
Лучше с Маха, "Анализ ощущений". Феноменология у Гуссерля появилась из двух источников: 1) понятия интенциальности в работе Брентано ("Психология с эмпирической точки зрения") 2) критика (на самом деле больше уточнения) Гуссерлем позиции Маха, Гуссерль называет её "феноменализмом". Этой критике в основном посвящен первый том "логических исследований" Гуссерля. Я следую Курту Гёделю, который был большим спецом по феноменологии и сказал что лучше всего у Гуссерля читать только "Идеи" и "Картезианские медитации", именно в таком порядке.
>>7738
Какая разница чем он занимался? Это вообще никого не волнует, кроме фанбоев Брауэра. Если бы не его деятельность в качестве тополога, никакого уважения к нему бы не было. Если бы не схожесть интуиционизма с феноменологией (разобранная в книге Essays on Gödel's reseption of Leibniz, Husserl and Brouwer) меня бы например и некоторых других людей, интуиционизм не интересовал бы в принципе. Это содержательная часть, остальное мусор. Лейбниц вот верил в бога. И что? Ничего, мне все равно.
>>7739
Разобрались? Штаны постирай.
Дазайн это не феноменология, а экзистенциализм, то есть деятельность Хайдеггера по приложению идей феноменологии к онтологическии вопросам. Которую потом спиздили французские петухи вместе с названием.
Из сборника переводов под ред. Торчинова и Корнеева ясно., что деятельность Хайдеггера была бесполезной, тк в Индии эти дазайны знали очень давно, со времен создания вед, просто называли иначе.
>>7745
/ph это раздел дебилов, в котором философию (феноменологию) никто не осилил, и принято обсуждать хуйню, в основном как раз с рационалистических позиций.
>>7747
В математике нет, конечно. Есть первая культура (Грассман, Дедекинд, Э. Нётер, Э. Картан, Э.Я. Брауэр как тополог, Лефшец, Дж.Г. Уайтхед, А. Вейль и Бурбаки, Гротендик и ученики, Милнор, Квиллен, и тд), остальное не математика.
>>7753
Только не надо Дедекинда сюда приписывать. Он создал наивную теорию множеств, дальше Кантор её увел, и на основе своей прогрессирующей болезни придумал классификацию букв еврейского алфавита.
Канторовская теория была окончательно упразднена Гротендиком в 1957-м.
Лучше с Маха, "Анализ ощущений". Феноменология у Гуссерля появилась из двух источников: 1) понятия интенциальности в работе Брентано ("Психология с эмпирической точки зрения") 2) критика (на самом деле больше уточнения) Гуссерлем позиции Маха, Гуссерль называет её "феноменализмом". Этой критике в основном посвящен первый том "логических исследований" Гуссерля. Я следую Курту Гёделю, который был большим спецом по феноменологии и сказал что лучше всего у Гуссерля читать только "Идеи" и "Картезианские медитации", именно в таком порядке.
>>7738
Какая разница чем он занимался? Это вообще никого не волнует, кроме фанбоев Брауэра. Если бы не его деятельность в качестве тополога, никакого уважения к нему бы не было. Если бы не схожесть интуиционизма с феноменологией (разобранная в книге Essays on Gödel's reseption of Leibniz, Husserl and Brouwer) меня бы например и некоторых других людей, интуиционизм не интересовал бы в принципе. Это содержательная часть, остальное мусор. Лейбниц вот верил в бога. И что? Ничего, мне все равно.
>>7739
Разобрались? Штаны постирай.
Дазайн это не феноменология, а экзистенциализм, то есть деятельность Хайдеггера по приложению идей феноменологии к онтологическии вопросам. Которую потом спиздили французские петухи вместе с названием.
Из сборника переводов под ред. Торчинова и Корнеева ясно., что деятельность Хайдеггера была бесполезной, тк в Индии эти дазайны знали очень давно, со времен создания вед, просто называли иначе.
>>7745
/ph это раздел дебилов, в котором философию (феноменологию) никто не осилил, и принято обсуждать хуйню, в основном как раз с рационалистических позиций.
>>7747
В математике нет, конечно. Есть первая культура (Грассман, Дедекинд, Э. Нётер, Э. Картан, Э.Я. Брауэр как тополог, Лефшец, Дж.Г. Уайтхед, А. Вейль и Бурбаки, Гротендик и ученики, Милнор, Квиллен, и тд), остальное не математика.
>>7753
Только не надо Дедекинда сюда приписывать. Он создал наивную теорию множеств, дальше Кантор её увел, и на основе своей прогрессирующей болезни придумал классификацию букв еврейского алфавита.
Канторовская теория была окончательно упразднена Гротендиком в 1957-м.
А определение множества? Просто кольца до него тоже рассматривали, например Гаусс, но опрелеление он же дал.
Теория множеств делится на наивную, канторовскодедекиндскую и аксиоматическую. Не понял тебя. Ну да. Дедекинд дал определение множеству.
Наивную теорию множеств. История наивной теории множеств насчи-
тывает по крайней мере 3–4 тысячи лет. Например, традиционный порядок
гексаграмм И-Цзин, приписываемый Фу-Си, содержит таблицы Кэли для буле-
вых операций на конечных множествах7
. Уже в совершенно современном виде
вся наивная теория множеств (принадлежность, включение, свойства булевых
операций, декартово произведение, конечная комбинаторика и т.д.) была раз-
вита в XVII – XVIII веках Пьером де Ферма, Рене Декартом, Готтфридом фон
Лейбницем, Якобом и Иоганном Бернулли и Леонардом Эйлером.
К этим идеям независимо и из разных соображений приходили такие люди как Г. Вейль, К. Гёдель, Брауэр, Брентано, Мах, Лейбниц и т.д.
Более того, Фейерабенд в своей интерпретации космологии Греции архаического периода показал, что основные идеи там тоже соответствуют феноменологии, а до него это сделал Эванс-Притчард с другими народами северо-восточной Африки, к примеру.
Сейчас ни для кого не секрет, что в Индии девятого века это прекрасно знали (Адвайта-Веданта Шанкары, буддизм мадхъямаки/шуньявады).
Феноменология это естественное состояние мышления у нормальных людей в других частях планеты, у европейского же биомусора мышление сильно засорено разными положениями веры в силу сложных исторических причин.
>>7766
Это из Вавилова? Он еще утверждал что линейная алгебра была в Китае в пятом столетии до нашей эры. Но если глубже копнуть, то там развитие идей Цзю чжан суаньшу, а не сам трактат (хотя и он был завершен в тртьем веке до н.э., а не в пятом), выполненное японским математиком в Seki Takakazu в 1690-х только (н.э.).
То есть это просто в духе Арнольда, типа "Лейбниц придумал гомологическую алгебру" а "Декарт изучал идеалы колец".
Смешно конечно, но буквально принимать не стоит.
У вавилова еще "теория групп" существуеь столько, сколько человечество, то есть Силов и Ли видимо не норвежцами были, а вавилонянами.
 373 Кб, 703x665
373 Кб, 703x665>Он еще утверждал что линейная алгебра была в Китае в пятом столетии до нашей эры
Ну тащемта я перешёл по ссылке, которую он указал, там тупо двоичная система счисления. Алсо Лейбниц двоичную систему тоже после фапа на И Цзин придумал.
Японец придумал определители (одновременно с Лейбницем) исходя из китайского трактата "девять книг по математике", я думаю заблуждение отсюда.
Посмотри на картинку, это двоичный код же, вверху 000000, внизу 111111, я про это. Картинке явно не 40 лет.
>Например, традиционный порядок
гексаграмм И-Цзин, приписываемый Фу-Си, содержит таблицы Кэли для булевых операций на конечных множествах7
>7Ю.К.Щуцкий, Классическая китайская ‘Книга перемен’. – Изд-во ‘Восточная Литерату-
ра’ РАН, М., 1997, с.1–605; см. форзац, схемы 8 и 10.
Это как раз схема 8.
 379 Кб, 750x983
379 Кб, 750x983>непротиворечивость систем Z, ZF и ZFC не может быть установлена финитными средствами и, таким образом, в известном смысле, представляет собой вопрос веры.Некоторые авторы шли настолько далеко, что даже определяли математика как того, кто верит в непротиворечивость системы ZF
К "математикам", верующим в математику за пределами вычислимости это определение относится на все 146%. Я с этой книжкой не знаком, но признаю, что в данном случае я бы не определил верунцов от математики лучше чем там, лол.
>>7761
>Какая разница чем он занимался? Это вообще никого не волнует, кроме фанбоев Брауэра.
Приехал ты, братец, совсем додвачевался.
ОБСУЖДЕНИЕ БРАУЭРА
@
АРРЯЯАА КОГО ВООБЩЕ ЕБЕТ ЧЕМ ОН ТАМ ЗАНИМАЛСЯ, ХИПСТЕРАМ ФЕНОМЕНОЛОХАМ ВИДНЕЕ
>Если бы не схожесть интуиционизма с феноменологией (разобранная в книге Essays on Gödel's reseption of Leibniz, Husserl and Brouwer) меня бы например и некоторых других людей, интуиционизм не интересовал бы в принципе.
Я об этом и говорю. Ты с первоисточниками не то что не знаком, ты считаешь это принципиально ненужным, вместо чего веруешь своим хипстерам. Сектантство как оно есть.
>Лейбниц вот верил в бога. И что? Ничего
Брауэр тоже верил, более того, давал определение, что для него есть бох. Дело в том, что в математику он эту веру не тащил.
>Дазайн это не феноменология, а экзистенциализм, то есть деятельность Хайдеггера по приложению идей феноменологии к онтологическии вопросам.
Я ж говорю, это просто очередная философская доктрина, не лучше любой другой. А ты мне тут проповедуешь что-то уровня "Ислам - истинная религия, а все остальные - фуфло, т.к. там в Аллаха не веруют".
>Штаны постирай.
Ты даже в смысл мемасов не можешь, какая тебе философия вообще?
>ОБСУЖДЕНИЕ БРАУЭРА
В /fag пожалуйста, окей?
Обсуждение достижений Брауэра.
>ХИПСТЕРАМ ФЕНОМЕНОЛОХАМ ВИДНЕЕ
Если бы не это, твой Брауэр вообще бы нахуй не усрался (мне по крайней мере), так понятно?
>ты считаешь это принципиально ненужным
В данном случае – да. Ты тоже не знаком, или нидерландский за ночь выучил? Ну вот и не пизди про пересказы Гейтинга.
>это просто очередная философская доктрина
Что именно?
>Если бы не это, твой Брауэр вообще бы нахуй не усрался (мне по крайней мере), так понятно?
Предельно понятно. Ты просто еще один верунок в очередную абсолютно верную религию (феноменология). Смысл интуиционизма Брауэра тебе понятен ровно никак, поскольку он точно так же понятен твоим хипстерам, на манямнения которых ты молишься.
>Что именно?
Феноменология. В которую ты швято уверовал как в единственную истину в последней инстанции.
>мой пересказ лучше твоего! То что ты читал писали неграмотные хипстеры, а у меня грамотные!
Ясно.
У тебя на все один ответ:
>АРРЯЯАА ХИПСТЕРАМ ВИДНЕЕ
Чем твои хипстеры лучше моих? То что Лёф неграмотен в философии, например, это видно на лицо.
>За все время обсуждения при чем не было ни одной конкретной претензии по этой интерпретации.
Ты даже не понимаешь, что тебе пишут. Больше того, и не способен понять. Даже если я напишу тебе еще миллион раз одно и то же - ты просто не поймешь сути претензии. Как и все остальные клованы на мейлру. Вот смотри: претензия в том, что ни твои хипстеры, ни тем более ты, не понимаете, почему интуиционизм - это математика. Понял? Нет, не понял. По той же самой причине ты никогда не поймешь, почему MLTT это математика. Это просто выше твоих способностей. А из того факта, что тут и способностей достаточно чуть выше плинтуса, я могу заключить, что перед нами очередной титан мысли, великий философ, который даже смысла мемаса про нестиранные штаны понять не в состоянии, не говоря о таких вещах как изоморфизм Карри-Говарда и уж тем более причин, побудивших Брауэра вобще поставить вопрос о реформе математики в сторону большей вычислимости. И такой вот мыслитель будет давать свои оценки Мартин-Лёфу, ой пиздец.
>Это просто выше твоих способностей
Если бы ты знал настоящую математику хотя бы в небольшом объеме, не называл бы теорию типов математикой. Человеку, который знаком только с first year calculus, понятно, сравнить не с чем.
>давать свои оценки Мартин-Лёфу
Ну по крайней мере мне прекрасно видно где он неправ, а тебе нет, потому что ты не знаешь философии (как и он).
А про интуиционизм в целом, ну твой сознательный выбор игнорировать какие у него есть философские следствия, мне же только это и интересно (как и в любой области, не являющейся математикой).
>Ну по крайней мере мне прекрасно видно где он неправ, а тебе нет, потому что ты не знаешь философии (как и он).
Что тебе видно-то? Несоответствие твоей вере? Так всем на нее похуй, особенно если есть вычислимый результат, а MLTT вычислимо непротиворечивые основания математики, т.е. то, в чем можно выразить любую математику, в том числе и гамалогии твои с тапалогиями.
>А про интуиционизм в целом
Ты вообще нихуя не понял и не поймешь никогда.
>нихуя не понял и не поймешь никогда
Что это особая форма третьекультурной математики? Вроде понял уже.
>Несоответствие твоей вере?
Подмена понятий и переопределение устоявшихся терминов под свои маня-представления, идущие в разрез с любым материалом по философии будь то монография, университетская методичка для сдачи сессии, учебник или интернет-энциклопедия.
>есть вычислимый результат
>Оспорить можно мнение, но не вычисление
>Вычислимость всегда кончтруктивна
Аллаху Акбар!
Надеемся, что в дальнейшем еще какой-нибудь приличный математик зашкварится об эту секту. Пока только Воеводский и сам Брауэр, что конечно маловато для поддержания репутации.
>в том числе и гамалогии твои с тапалогиями.
Предлагаю заняться конструктивизацией гомологической алгебры. Кто-то вроде это уже делает.
Как научишься считать Ext'ы на машине Поста, сообщи.
С введением единственно правильного конструктивного положняка вся содержательные и сложные проблемы для которых нужны гомологии просто отпадут. Не благодарите.
Какамалогии не нушны (ия ни знаю чоита)! все что не cuck-структивно нинажна! так скозел Брубер!
>единственно правильного конструктивного положняка Деуз вулт! изнгать еритиков!
>Как научишься считать Ext'ы на машине Поста, сообщи.
Я могу их и в голове посчитать. Применяем так называемый "тезис Чёрча" и видим, что он неконструктивен.
Как стать конструктивистом? Часто ли нужно посещать мессы? Как найти братьев-конструктивистов в своем городе? Что нужно еще говорить в рамках обряда отрицания содержательной математики, помимо "Это не конструктивно"? Сколько раз в день молиться Брауэру, а сколько Лёфу, можно ли делать это одновременно?
Не для себя интересуюсь.
Вот это поворот. Всю битву был за тебя, а теперь вижу, что ты обычный фашист
 1 Мб, 500x312
1 Мб, 500x312> Я могу их и в голове посчитать. Применяем так называемый "тезис Чёрча" и видим, что он неконструктивен.
Дурик, все что ты можешь посчитать в голове либо может посчитать машина Тьюринга либо твой счёт уровня "одна актуальная бесконечность плюс вторая будет две". Но на мейлру одни дегенераты и не понимают очевиднейших вещей. Каким надо быть аутистом, чтобы вербовать что понимаешь математику лучше Чёрча, Мартин ЛЕФа или Брауэра, вам самим с себя не смешно, фейлософы?
Не вижу в чём сложность. Лаплас например понимал математику лучше Наполеона. И это не удивительно, ведь Наполеон математиком не был. Как и все люди, которых ты перечислил.
Ты даже не понимаешь,что такое вычислимость и изоморфизм Карри Говарда, с чего ты решил чтотпонимаешь что такое математика? Думаешь, попетросянил как чуть выше в треде и сразу интуиционизм и конструктивный подход опроверг? Это аутизм настоящий. Как и веровать, что если назвал кого-то не математиком, этот кто-то сразу математиком быть перестал. Магическое мышление, сектантство, школьничество. К этому сводятся все твои аргументы. Для тебя Брауэр не математик потому что так хипстеры пишут и потому что он гамалогиями не занимался.
Алсо, тапалогиями Брауэр занимался, а значит он математик даже с точки зрения твоих хипстеров.
Кто из учеников и бывших коллег Гротендика был в курсе о существовании тезиса Чёрча или изоморфизма Карри-Говарда? Я думаю никто.
Карри это вообще кто такой? Специалист по fuzzy logic, в честь которого назвали язык программирования.
Математика это всё, что нужно знать, чтобы понимать теорему Атьи-Зингера, формулировку и доказательство. Или доказательство Делинем гипотез Вейля. Или теорему Воеводского об изоморфизме норменного вычета. Или любой другой аналогичный по ценности результат.
У твоего конструктивного пердежа ценности даже не ноль, она отрицательная, т.к. запрещает гомологическую алгебру, спектральные последовательности и прочие общеизвестные методы которыми пользуются математики.
> Математика это всё, что нужно знать, чтобы понимать теорему Атьи-Зингера, формулировку и доказательство. Или доказательство Делинем гипотез Вейля. Или теорему Воеводского об изоморфизме норменного вычета. Или любой другой аналогичный по ценности результат.
Ценность, разумеется, определяют твои хипстеры от феноменологии? А нечеткую логику ты к чему приплел вообще? Я так понимаю, с твоей точки зрения это тоже не математика? А не ты ли не так давно кукарекал, что результат в математике не нужон? И называл петухом Маннури, суть идей которого в том, что математика это деятельность человека, направленная на определённый результат, как и любая другая деятельность человека? Ты бы с собой разобрался для начала, потом лез бы кого-то поучать.
Математик развивает свою науку на фундаменте теорий, разработанных его предшественниками. Некоторые из этих теорий развились до такой степени, что для осмысленной работы с ними требуется несколько лет изучения.
Интересно, что если отбросить верхний этаж, то есть науки, которые требует год-другой нормальной работы, чтобы их освоить, останутся курсы, которые теснейшим образом переплетены друг с другом.
Алгебраическую топологию невозможно освоить без теории категорий и гомологической алгебры, они же играют ключевую роль в алгебраической геометрии, которая основана на коммутативной алгебре, теории чисел, дифференциальной геометрии и комплексном анализе, которые базируются на топологии и УрЧП. Именно это и называется core mathematics – совокупность тесно связанных предметов, лежащих в фундаменте большинства заметных достижений математики после начала 1960-х.
Прекрасной иллюстрацией к понятию core mathematics является теорема об индексе Атьи-Зингера; для ее понимания нужны фундаментальные знания в функциональном анализе, топологии, теории групп Ли, спинорной геометрии, К-теории и УрЧП, а ее основная область применения – алгебраическая геометрия, дифференциальная геометрия и топология. Для практических целей, можно определить core mathematics как "предметы, которые используются в доказательстве теоремы Атьи-Зингера". Это определение неточное, но настолько близкое к точному, что разница делается незначительна. Вместо Атьи-Зингера можно взять любое другое великое достижение математики: работы Делиня по гипотезам Вейля (и их развитие в книге Бейлинсона-Бернштейна-Делиня), доказательство Уайлсом теоремы Ферма, доказательство Гротендика
формулы Гротендика-Римана-Роха, доказательство Гивенталем зеркальной симметрии, или работы Дональдсона, Уленбек и Таубса по 4-мерной топологии. Для каждого из этих предметов, сущность "core mathematics" будет немного другой, но разница в десяток процентов непринципиальна, и никак не влияет на предмет обучения студентов первого и второго года.
Математик развивает свою науку на фундаменте теорий, разработанных его предшественниками. Некоторые из этих теорий развились до такой степени, что для осмысленной работы с ними требуется несколько лет изучения.
Интересно, что если отбросить верхний этаж, то есть науки, которые требует год-другой нормальной работы, чтобы их освоить, останутся курсы, которые теснейшим образом переплетены друг с другом.
Алгебраическую топологию невозможно освоить без теории категорий и гомологической алгебры, они же играют ключевую роль в алгебраической геометрии, которая основана на коммутативной алгебре, теории чисел, дифференциальной геометрии и комплексном анализе, которые базируются на топологии и УрЧП. Именно это и называется core mathematics – совокупность тесно связанных предметов, лежащих в фундаменте большинства заметных достижений математики после начала 1960-х.
Прекрасной иллюстрацией к понятию core mathematics является теорема об индексе Атьи-Зингера; для ее понимания нужны фундаментальные знания в функциональном анализе, топологии, теории групп Ли, спинорной геометрии, К-теории и УрЧП, а ее основная область применения – алгебраическая геометрия, дифференциальная геометрия и топология. Для практических целей, можно определить core mathematics как "предметы, которые используются в доказательстве теоремы Атьи-Зингера". Это определение неточное, но настолько близкое к точному, что разница делается незначительна. Вместо Атьи-Зингера можно взять любое другое великое достижение математики: работы Делиня по гипотезам Вейля (и их развитие в книге Бейлинсона-Бернштейна-Делиня), доказательство Уайлсом теоремы Ферма, доказательство Гротендика
формулы Гротендика-Римана-Роха, доказательство Гивенталем зеркальной симметрии, или работы Дональдсона, Уленбек и Таубса по 4-мерной топологии. Для каждого из этих предметов, сущность "core mathematics" будет немного другой, но разница в десяток процентов непринципиальна, и никак не влияет на предмет обучения студентов первого и второго года.
>Я так понимаю, с твоей точки зрения это тоже не математика
Не вижу смысла называть математикой все подряд. В алгебраической геометрии нечёткая логика не используется.
>результат в математике не нужон? И называл петухом Маннури
В математике нужен, имеются даже некоторые критерии.
Только вот приложимость результа, о которой ты говорил, к другим областям за пределами математики, в них явно не входит.
> Не вижу смысла называть математикой все подряд. В алгебраической геометрии нечёткая логика не используется.
Ты протестуешь против конструктивного подхода, отрицающего принадлежность к математике исключённого третьего и актуальной бесконечности, сам при этом выкидываешь из математики вообще все кроме гамалогий. При этом свою веру в гамалогии ты не считаешь ограничивающей математику.
> В математике нужен, имеются даже некоторые критерии.
Принадлежность к гамалогиям и чтобы Гротендик о них знал, я тебя понял.
> Только вот приложимость результа, о которой ты говорил, к другим областям за пределами математики, в них явно не входит.
А чем приложимость только к гамалогиям лучше приложимости к чему-то вне гамалогий? Математика такая же деятельность человека как и не математика, по Маннури математика это язык 5го уровня, выразимый во всех нижележащих. Которые тоже являются деятельностью человека и всегда направлены на какой-то результат. Даже гамалогии твои.
Хуя вы тут развели, тред анализа с прошлого года до бамп-лимита не дойдёт, а тут за две недели справились, да еще перекатов мильен будет ставьте ЛОПИТАЛЬ, если поняли, о чем я
Не нужно заниматься философией математики, нужно:
1) Просто решать новые содержательные задачи, любые, какие хочется.
2) Не зацикливаться на слишком однообразных.
3) Не врать самому себе, что ты что-то понимаешь, когда это не так.
4) Периодически повторять пройденнные темы: каждый раз открывается много нового.
Любая другая позиция - чушь, и я любому возражающему утырку поясню почему он не прав.
>Не нужно заниматься философией математики,
Еще один гигант мысли с мейлру. А ты чьих будешь, пророк али аниме? Заниматься можно чем угодно, если без фанатизма и не терять связь с ориентированностью на результат в пользу манямиров, чтобы в итоге не деградировать до швятой веры, что нечеткая логика это не математика, математика только гамалогии с тапалогиями.
>чтобы в итоге не деградировать до швятой веры, что нечеткая логика это не математика, математика только гамалогии с тапалогиями.
А можно деградировать до Брауредрочества? Типа что не Брауер то не математика. Тезис члена. Изаморфезм Харди-Литлвуда. Мортин-Лев. И прочее.
Ты даже возразить не смог, промямлил, растёкся мыслями, ушёл в частные случаи, и невнятно написал о том, о чём немножко слышал.
И что ты сделаешь? Будешь и дальше швято веровать, что опроверг MLTT и вообще конструктивный подход? Так я не против. Сейчас бы чьи-то манямиры опровергать.
Твоя проблема в том, что я с тобой НЕ ГОВОРИЛ ПРО КОНСТРУКТИВИЗМ И MLTT.
Это показывает, что ты либо просто дурачок, либо дурачок, ошибочно полагающий, что умеет троллить. Плохо быть тобой.
>"одна актуальная бесконечность плюс вторая будет две"
Что в этом неконструктивного? "актуальная бесконечность" является значком, значит её можно задать как индуктивный тип. Только в случае с подсчётом Ext'ов там посложнее будет.
Плутонисты.
> Что в этом неконструктивного? "актуальная бесконечность" является значком, значит её можно задать как индуктивный тип
Я так и понял, что ты понятия не имеешь, что такое вообще конструктивный объект. Разберись сначала, потом критикой, ок?
> консутикурвный объект
> Видимо что-то из философии, меня она не особо интересует.
Нет, из математики.
Представьте себе пространство всех языков программирования — понятно дело все знают про лямбда исчисление. Но не многие же рубисты или ПХП программисты задумываются, что они пишут на языке пространства — которое с точностью до битов моделируется теорией типов Мартина Лефа (надо только вселенные правильно отконфигурировать, это научились делать в 2001 году, когда Coq все дружно писали). Конечно я сам в это по началу не верил, и думал что есть все-таки ограничения и что Данила Мастер, который вручную все сам делает вместо того чтобы экстрактить это из Инфинити Топоса делает ненапрасный труд. Мне пришлось написать прувер чтобы понять — таки да, каждый Данила Мастер, который считает себя инженером — производит временный и бесполезный труд, давая ярлыки феноменам не видя их сути.
Пространство типов безгранично и все типы одновременно живут в этом бесконечномерном пространстве — где каждое его измерение наслаивается друг на друга, а сами типы образуют паттерны, похожие на гомотопические группы. Так как изоморфных типов в пространстве бесконечного топоса хватает, то в MLTT тоже есть что-то похожее на матрицу гомотопических групп. Они имеют разные имена и могут в принципе не проходить чеканье на равенство и т.д., но при компиляции в нетимизированную лямбду изоморфные типы будут генерировать совместимый код.
У всех типов есть четкая логика заселения пространства бесконечного топоса, подобно тому как жители самсары заселяют шесть лок. Начинается все с нижнего дна ада — Bottom типа. И потом по кирпичику начиная с Unit (), потом A -> A, потом Nat, потом Stream, потом List, потом ... и так далее вплоть до инфинити-групоида, потом все начинает повторятся и узор начинает меняться. Где у этого узора дырки я пока не вижу, и какая у него структура, но как бы чувствую немного дыхание этой мандалы. Эта мандала доступна впринципе всем программистам, которые могут писать циклы, складывать числа, больше уровня не нужно. Всю эту математику можно переформулировать так, чтобы MLTT преподавать 11 летним детям — считайте, что эксперимент начат.
Представьте себе пространство всех языков программирования — понятно дело все знают про лямбда исчисление. Но не многие же рубисты или ПХП программисты задумываются, что они пишут на языке пространства — которое с точностью до битов моделируется теорией типов Мартина Лефа (надо только вселенные правильно отконфигурировать, это научились делать в 2001 году, когда Coq все дружно писали). Конечно я сам в это по началу не верил, и думал что есть все-таки ограничения и что Данила Мастер, который вручную все сам делает вместо того чтобы экстрактить это из Инфинити Топоса делает ненапрасный труд. Мне пришлось написать прувер чтобы понять — таки да, каждый Данила Мастер, который считает себя инженером — производит временный и бесполезный труд, давая ярлыки феноменам не видя их сути.
Пространство типов безгранично и все типы одновременно живут в этом бесконечномерном пространстве — где каждое его измерение наслаивается друг на друга, а сами типы образуют паттерны, похожие на гомотопические группы. Так как изоморфных типов в пространстве бесконечного топоса хватает, то в MLTT тоже есть что-то похожее на матрицу гомотопических групп. Они имеют разные имена и могут в принципе не проходить чеканье на равенство и т.д., но при компиляции в нетимизированную лямбду изоморфные типы будут генерировать совместимый код.
У всех типов есть четкая логика заселения пространства бесконечного топоса, подобно тому как жители самсары заселяют шесть лок. Начинается все с нижнего дна ада — Bottom типа. И потом по кирпичику начиная с Unit (), потом A -> A, потом Nat, потом Stream, потом List, потом ... и так далее вплоть до инфинити-групоида, потом все начинает повторятся и узор начинает меняться. Где у этого узора дырки я пока не вижу, и какая у него структура, но как бы чувствую немного дыхание этой мандалы. Эта мандала доступна впринципе всем программистам, которые могут писать циклы, складывать числа, больше уровня не нужно. Всю эту математику можно переформулировать так, чтобы MLTT преподавать 11 летним детям — считайте, что эксперимент начат.
> Объяснишь тогда, что это такое? Можешь в терминах теории типов.
Я уже не помню сколько раз объяснял. Причём это ребёнку в детском саду можно объяснить с помощью счетных палочек. Но не фейлософам на мейлру. Тут сразу начинаются закатывания глаз и кукарекания. Даже у максимки был пример как перенумеровать типы их байткодом, т.е. ребёнку можно объяснить даже что такое MLTT. Мейлру хуже детсада, официально. Это лайк, господа. И репост.
>Я уже не помню сколько раз объяснял.
Мне ты ничего не объяснял. И видимо не можешь.
>максимки
Праграмист какой-то? Причём тут не-математики?
 17 Кб, 469x480
17 Кб, 469x480>математика
Определение будет? У тебя оно какое-то нестандартное, раз гомологическая алгебра ей не является.
Каким образом это лучше делать? Желательно более менее скрытно.
> Определение будет? У тебя оно какое-то нестандартное, раз гомологическая алгебра ей не является.
Я уж понял, что стандартное определение - математика это гамалогии. Определение Брауэра я давал, и что такое математика и что можно считать математическим объектом и почему, но ты его не понял.
>математика это гамалогии
Гамалогии (согласно стандартному определению) являются её частью.
>Определение Брауэра
Я знаю только английский и русский.
>но ты его не понял.
Действительно. Сложно понять то, чего ты не читал.
>Феноменология не способна объяснить
>из каких соображений исходил Кант
Это и без феноменологии всем понятно. Кант исходил из а) рационализма Декарта и Гоббса б) критики этого рационализма британскими эмпириками, в частности Юмом. Это в начальной школе объясняют.
>Брауэр
Относительно чего? Deepest home in our consciousness (фраза самого Брауэра)? Так способна. И это не математика.
>>7882
>Максим
Собираешься комментировать его рассуждения про топосы дхарм, или проигнорируешь, как с примордиальной интуицией Брауэра?
>Deepest home in our consciousness (фраза самого Брауэра)
Да, это фраза Брауэра. Вот только тебе твои хипстеры не объяснили, к чему она вообще у Брауэра и причем тут математика. И ты сам без хипстеров никогда не угадаешь, хотя я сто раз об этом говорил.
>>7895
Охуеть, ты похоже, начинаешь понимать суть релятивизма Маннури. О котором я уже полгода здесь талдычу. Следующим шагом скажи, что это не гамалогии и к математике не относится.
>по Маннури математика это язык 5го уровня, выразимый во всех нижележащих
Примерно совпадает с идеями Пенроуза в "новом разуме императора":
Таким образом, абстрактное мышление превращается в нечто вроде эксперимента в физической лаборатории, имя которой -- мозг -- а результатом эксперимента оказывается научная истина.
Конечно, эта натур-философская модель может оказаться совершенно неверна. Тем не менее, разделение мышления на четыре уровня (симулятивный, дедуктивный, визионерский и мистический) есть нечто несомненное и данное нам в ощущении.
Интересно, что язык оперирует только с низшими уровнями мышления -- никакой возможности передать мистический и визионерский опыт словами нет (кроме разве что в стихах). Для коммуникации же необходимо жесткое владение языком, т.е. дедукцией и риторикой -- двумя самыми примитивными уровнями. Языком математики являются логические построения (а языком других точных наук -- логические и формальные языковые конструкции, взятые из математики).
>Охуеть, ты похоже, начинаешь понимать
Что ты платонист, у которого mathematics is the language of the universe? Давно понял.
>Да, это фраза Брауэра. Вот только кококо хипстеры, кудах-тах-тах хипстеры, кукареку хипстеры!
Это считается возражениями по существу уже, или ещё нет?
Чтобы разобрать писанину Брауэра и не стать хипстером, необходимо сначала получить у тебя лицензию, авторизацию, разрешение, верно?
>Что ты платонист, у которого mathematics is the language of the universe? Давно понял.
Нихуя ты не понял. Нести вот такую хуйню про платонизм после того, как я сто раз написал, что математика это деятельность человека и даже более конкретно, с точки зрения Маннури (язык 5 уровня в его теории уровней языка) и с точки зрения Брауэра (ментальные построения на основе интуиции движения времени и манипуляции над ними) это показатель только того, что ты не понимаешь даже что такое платонизм.
>Чтобы разобрать писанину Брауэра и не стать хипстером, необходимо сначала получить у тебя лицензию, авторизацию, разрешение, верно?
Мозги нужно получить сначала.
Маннури и Брауэр это два разных человека?
По-моему да. Тогда давай разбирать эту хуйню по-порядку.
>Брауэр
Я уже привёл страницы из двух разных книг. Конструктивной критики не было, обвинения сводятся к "писали не те люди, которые мне нравятся".
>Маннури
Поясняй чем это отличается от Пенроуза, раз такой знаток. Я разницы не увидел.
>Маннури и Брауэр это два разных человека?
Да, ты прикинь. Карл Маркс и Фридрих Энгельс - это 2, а не 4 человека, а Слава КПСС - это вообще не человек! Думаю, на фотачках видно, что это разные люди, более того, Маннури был одним из учителей Брауэра. Маннури, к слову, интуиционистом не был и не поддерживал основные идеи Брауэра.
>Поясняй чем это отличается от Пенроуза, раз такой знаток. Я разницы не увидел.
То, что подобные идеи были не просто высказаны в научпопе, но и было подробно с примерами расписано, как это можно использовать в математике для получения результатов более чем за полвека до Пенроуза, считается за отличие?
>Я уже привёл страницы из двух разных книг. Конструктивной критики не было, обвинения сводятся к "писали не те люди, которые мне нравятся".
Была, только ты ее не увидел.
>была
Первую треть треда мы разбирались с тем, что такое рационализм, почему приведённая на скриншотах интерпретация не является рационалистической. То есть тут аргументов быть не могло, потому что ты тупо не понял чем это отличается от твоей позиции. Потом выясняли что такое математика, теперь просто перешли к "тот хипстер, это петух, купи мозги, если ума хватит".
>Маннури, к слову, интуиционистом не был
Это ясно, как ни странно. Не ясно зачем ты его откопал
>подобные идеи были не просто высказаны в научпопе
Научпоп is beside the point. Пенроуз это 100% платонист, дальше некуда, я к этому.
>Не ясно зачем ты его откопал
Откопал я его затем, что некоторые его идеи доказывают (или показывают, как доказать в полностью вычислимом и т.о. реализуемом в виде программного обеспечения) некоторые мои соображения по поводу прувера. То, что ты в его релятивизме увидел платонизм - это вообще пушка, учитывая, что основной его тезис в том, что язык - это деятельность человека и значение слова - это всегда его использование. Подобную цитату Витгенштейна я приводил, как и показывал конкретную реализацию этой идеи - модель word2vec Миколова. Ни о каком платонизме и прочей вере тут изначально не может идти речи, все напрямую вычислимо (а подобная задача ставилась еще в манифесте венского кружка). А вот насчет твоих гамалогий, тут предъявы за патонизм вполне уместны, т.к. ты утверждаешь, что что-то там невычислимо/неконструктивно, то возникает резонный вопрос, а в каком смысле, отличном от платонизма, может существовать непостроимый математический объект, в т.ч. решение?
Да, на слово "реализуемо" можешь не триггериться и не вспоминать Декарта, "реализация" использовано в значении "implementation".
(∞,B)-топос
>подобную цитату Витгенштейна
Very flawed logic.
Когда речь идёт о Брауэре, для тебя большой аргумент, какой из двух противоречащих друг другу видов деятельности он считал более важным.
А с Витгенштейном так же можно рассуждать? Повзрослевший и поумневший Витгенштейн периода "Философских исследований", например, утверждает что слова это всего лишь ярлыки:
11. Представь себе инструменты, лежащие в специальном ящике. Здесь есть молоток, клещи, пила, отвертка, масштабная линейка, банка с клеем, гвозди и винты. Насколько различны функции этих предметов, настолько различны и функции слов. (Но и там и здесь имеются также сходства.)
Конечно, нас вводит в заблуждение внешнее подобие слов, когда мы сталкиваемся с ними в произнесенном, письменном или печатном виде. Ибо их применение не явлено нам столь ясно. В особенности когда мы философствуем!
12. Это похоже на то, как, заглянув в кабину локомотива, мы бы увидели там рукоятки, более или менее схожие по виду. (Что вполне понятно, ибо все они предназначены для того, чтобы браться за них рукой.) Но одна из них пусковая ручка, которую можно поворачивать плавно (она регулирует степень открытия клапана); другая рукоятка переключателя, имеющая только две рабочие позиции, он либо включен, либо выключен; третья рукоятка тормозного рычага, чем сильнее ее тянуть, тем резче торможение; четвертая рукоятка насоса, она действует только тогда, когда ее двигают туда"сюда.
13. Когда мы говорим: "Каждое слово в языке что-то означает", то этим еще совсем ничего не сказано; до тех пор пока мы точно не разъясним, какое различие при этом хотим установить. (Ведь возможно, что мы хотим отличить слова языка (8) от слов, "лишенных значения", вроде тех, какие встречаются в стихотворениях Льюиса Кэррола, или слов, подобных "ювиваллера" в песне.
14. Представь себе, что кто-то говорит: "Все инструменты служат преобразованию чего-то. Так, молоток меняет положение гвоздя, пила форму доски и т.д.". А что видоизменяют линейка, банка с клеем, гвозди? "Нашу осведомленность о длине вещи, температуре клея, прочности ящика". Разве подобным истолкованием выражения достигался бы какой-то эффект?
15. Слово "обозначать" употребляется наиболее прямым образом, по-видимому, тогда, когда на обозначаемом предмете проставляется знак. Представь себе, что на инструментах, применяемых А в строительстве, проставлены определенные знаки. Когда А показывает помощнику один из таких знаков, тот приносит ему инструмент, помеченный этим знаком.
Так или примерно так имя обозначает некоторую вещь, имя дается вещи. Занимаясь философией, часто бывает полезно напоминать себе: наименование чего-то подобно прикреплению ярлыка к вещи.
>подобную цитату Витгенштейна
Very flawed logic.
Когда речь идёт о Брауэре, для тебя большой аргумент, какой из двух противоречащих друг другу видов деятельности он считал более важным.
А с Витгенштейном так же можно рассуждать? Повзрослевший и поумневший Витгенштейн периода "Философских исследований", например, утверждает что слова это всего лишь ярлыки:
11. Представь себе инструменты, лежащие в специальном ящике. Здесь есть молоток, клещи, пила, отвертка, масштабная линейка, банка с клеем, гвозди и винты. Насколько различны функции этих предметов, настолько различны и функции слов. (Но и там и здесь имеются также сходства.)
Конечно, нас вводит в заблуждение внешнее подобие слов, когда мы сталкиваемся с ними в произнесенном, письменном или печатном виде. Ибо их применение не явлено нам столь ясно. В особенности когда мы философствуем!
12. Это похоже на то, как, заглянув в кабину локомотива, мы бы увидели там рукоятки, более или менее схожие по виду. (Что вполне понятно, ибо все они предназначены для того, чтобы браться за них рукой.) Но одна из них пусковая ручка, которую можно поворачивать плавно (она регулирует степень открытия клапана); другая рукоятка переключателя, имеющая только две рабочие позиции, он либо включен, либо выключен; третья рукоятка тормозного рычага, чем сильнее ее тянуть, тем резче торможение; четвертая рукоятка насоса, она действует только тогда, когда ее двигают туда"сюда.
13. Когда мы говорим: "Каждое слово в языке что-то означает", то этим еще совсем ничего не сказано; до тех пор пока мы точно не разъясним, какое различие при этом хотим установить. (Ведь возможно, что мы хотим отличить слова языка (8) от слов, "лишенных значения", вроде тех, какие встречаются в стихотворениях Льюиса Кэррола, или слов, подобных "ювиваллера" в песне.
14. Представь себе, что кто-то говорит: "Все инструменты служат преобразованию чего-то. Так, молоток меняет положение гвоздя, пила форму доски и т.д.". А что видоизменяют линейка, банка с клеем, гвозди? "Нашу осведомленность о длине вещи, температуре клея, прочности ящика". Разве подобным истолкованием выражения достигался бы какой-то эффект?
15. Слово "обозначать" употребляется наиболее прямым образом, по-видимому, тогда, когда на обозначаемом предмете проставляется знак. Представь себе, что на инструментах, применяемых А в строительстве, проставлены определенные знаки. Когда А показывает помощнику один из таких знаков, тот приносит ему инструмент, помеченный этим знаком.
Так или примерно так имя обозначает некоторую вещь, имя дается вещи. Занимаясь философией, часто бывает полезно напоминать себе: наименование чего-то подобно прикреплению ярлыка к вещи.
>...многобукв... Занимаясь философией, часто бывает полезно напоминать себе: наименование чего-то подобно прикреплению ярлыка к вещи.
>имя обозначает некоторую вещь, имя дается вещи.
То, что ты там столь многословно описал, укладывается в понятие номинальной дефиниции, вычислимому отношению. Т.к. имя дается вещи не боженькой, а связью этой вещи с ее использованием. Я тебе уже раза два привел в пример модель, которая вычисляет смысл слова только на основе его использования, причем, различает даже использование одного и того же слова в разных контекстах, как и нахоид связь между разными словами, использующимися в похожем значении. Можно закатывать глаза и отказываться от фактов, алгоритм есть и он работает, против этого никакая философия ничего поделать не сможет.
>насчёт гамалогий
Ну например это
https://math.stackexchange.com/questions/805180/extension-problem-of-a-spectral-sequence
Ты просто исходишь из принципов, типа указано явно построение/не указано, и т.д., а надо исходить из практики.
>where you don't even know X
И это один конкретный случай, есть ещё.
Если принципы не работают на практике, значит принципы говно, не наоборот.
Знал что не осилишь, поэтому процитирую только нужный фрагмент
>Представь себе, что кто-то говорит: "Все инструменты служат преобразованию чего-то. Так, молоток меняет положение гвоздя, пила форму доски и т.д.". А что видоизменяют линейка, банка с клеем, гвозди? "Нашу осведомленность о длине вещи, температуре клея, прочности ящика". Разве подобным истолкованием выражения достигался бы какой-то эффект?
>нужный фрагмент
Это нечто из серии "сам шучу - сам смеюсь". Сам придумал пример - сам опроверг, заебись. Значение слова есть его использование, вот и все. Больше того, это вычислимое определение. То, что ты пишешь - хуйня на ровном месте без задач.
>>7919
>Ты просто исходишь из принципов, типа указано явно построение/не указано, и т.д., а надо исходить из практики.
Вот именно. А какая математическая практика может быть с непостроимыми объектами? Как ты с ними будешь практиковаться, если они не вычислимы? Что они в таком случае вообще такое, если не элементы платоновского мира идей / любой другой хуйни из этой же оперы?
Сразу видно веруна в Аллаха и ZFC. А мог бы Браузера читать, а не алефы рисовать. Плутонисты соснули в очередной раз. Типа Браузер чето доказал с движением времени интуиции платоновских тел, которые существуют ментально, аксиоматически.
|
||
|||
||||
|||||
||||||
Вот такие палочки, не то что ваши хомологии.
Ещё по изамарфизму Кронекера-Хопфа можем рисавать стрелочки
->
-> ->
-> -> ->
-> -> ->
-> -> -> ->
Можем рисовать даже такое:
0 -> -> -> 0
^ ^ ^ ^
0 -> -> -> 0
причём бесконечно в обе стороны!
Это из последней книги Витгенштейна, если чо.
>А какая математическая практика может быть с непостроимыми объектами?
Если я могу практиковаться с чем-то, например с функторами Tor, то являются ли они "вычислимими"? Или про это запрещено думать даже согласно известному изамарфизму? В какой категории кстати этот изамарфизм?
 55 Кб, 707x919
55 Кб, 707x919Понятие вычислимости определял сто раз, как и отличия канонического от неканонического элемента вычисления. В том или ином виде все это с подробными примерами и пояснениями было еще у Тьюринга в "on computable numbers" в 1937 году.
В какой категории имеет место быть тот самый изамарфизм?
Потому что без неё не получится доказывать изамарфизмы в несуществующих категориях.
>полями
Какими именно? Канструктивно по изоморфизму Квиллена-Улама в неопределённой категории есть несколько неэквивалентных определений.
>Тьюринга
> пеиуха спросить забыли
> У каких еще биологов были интересные статьи по математике?
Правильный у тебя метод вести дискуссию, нечего возразить - включай Евгения вагиныча. Только все это не отменяет простого факта, в обсуждаемую тему ты не можешь. И все твои невычислимые гамалогии это платонизм простой. Поскольку, если математический объект не существует в смысле построимости, значит существует в каком-то религиозном смысле.
> Понял, ℤ это плутонический/религиозный объект.
То, что ты нарисовал, это просто буква. В само такое множество ты можешь только веровать. У тебя его нет. У Аллаха есть, но это не математика.
Я вообще не верую в множества, в данном случае я верую в начальный объект категории алгебр для эндофунктора X ↦ X + 1 + X на любом подходящем топосе, ну или по-деревенски в "объект целых чисел", а то есть в частности и "тип целых чисел".
Все равно как ты это назовешь. Либо есть построимый объект, либо вера во всякий платонизм. Для твоей как и для любой другой задачи нужны отдельные элементы такого множества, вот только с ними ты и можешь что-то сделать практически. И все, что ты можешь с ними сделать это вычисления, алгоритмические преобразования. Либо не сводимые к таковым верования. Все очень просто и машину Тьюринга в любой математике никак не обойти. Ты либо делаешь что-то равнообьемное соотв. МТ либо веруешь.
>множества
Причём тут множества? Я в них не верю.
>элементы
Я не верую в элементы, я верую только в стрелки из терминального объекта.
Во что бы ты там ни веровал, это либо построимо, либо и правда швитая вера, либо пока неизвестно, куда отнести, например, построения ннет, но и достаточных оснований считать это принципиально непостроимым тоже нет. Как-то так. А веровать можешь во что угодно, свободу вероисповедания не отменяли.
>это либо построимо, либо и правда швитая вера
Ну получается, что либо построимо, либо непостроимо?
Есть ли доказательство этого? Или на веру нужно принимать?
> Ну получается, что либо построимо, либо непостроимо?
Читай все, а не из контекста вырывай. Там ещё третий вариант, его нельзя простоивзять и априори отбросить. Конкретные примеры такого приводил и Брауэр и Гейтинг и много кто.
> Есть ли доказательство этого? Или на веру нужно принимать?
Вот бы сейчас по сотому разу объяснять чем конструктивное отрицание отличается от неко нструктивного. Маннури вообще 4 вида отрицания показывал, я и их приводил с пояснениями. Толку-то, это мейлру.
> Что нельзя вычислить на компуктере то не ко-ко-консруктивная мотиматика.
Ты ж совсем деревянный. То, что нельзя вычислить на машине Тьюринга, нельзя вычислить вообще никак. Гонять значки можно и на МТ. По той простой причине, что МТ есть автоматизация вычислений чего-то человеком. Отсюда и тезис Чёрча, который пока что ни одному верунцу опровергнуть не удалось. Это факты, мань. Математика равнообьемна с вычислимостью.
>То, что нельзя вычислить на машине Тьюринга, нельзя вычислить вообще никак.
Хуя ты верун плутократонист.
>Ты ж совсем деревянный.
Ты просто тупой, я уже сто раз говорил про Браузера, а ты понять не можешь. Мейлуру вообще математикой заниматься не могу. Я вот сайтик на php сделал, теперь мне дадут phd по математике?
>Отсюда и тезис Чёрча, который пока что ни одному верунцу опровергнуть не удалось.
Существования бога тоже не одному аметисту опровергнуть не удалось. Это факты, мань. Математика равноьёмна с вичеславостью.
>опровергнуть не удалось
То есть ты веришь, что если его двойное отрицание верно, то и сам тезис верен?
Это в церкви нужно делать, а не в математике.
>Я вот сайтик на php сделал, теперь мне дадут phd по математике?
Нет, нужно написать Браузер на php. После этого уже должны дать.
Вот же не лёгкая задача. Современная математика с Браузерами такая сложная, не то что хомологии. Браузер не каждый и написать может.
> То есть ты веришь, что если его двойное отрицание верно, то и сам тезис верен?
Я ж говорю, у тебя аргументы уровня "сам шучу - сам смеюсь". Ни про веру в этот тезис, ни про двойное отрицание его я ни слова не говорил. Этот тезис просто констатация факта. Веришь ты в него или нет, несущественно. Ты можешь не верить в группы крови, это никак не повлияет на тот простой факт, что если ты себе перельешь несовместимую - почки отвалятся. Можно называть это как угодно, сам факт никуда не денется. Так и тут, веруй, не веруй, разницы 0.
То что никто пока не доказал, что бага не существует это тоже
>констатация факта
Выходит, ты не верешь в бога?
Точнее, веришь в его отсутствие.
Ты хоть и обмазываешься своими хипстерами, по факту никуда не ушёл от того же платонизма и веры в исключенные третье. Кроме веры и неверия есть ещё как минимум вариант "похуй", который в частности соответствует моему представлению о бытии бога. Вот реально, мне строго до бороды.
>Кроме веры и неверия есть ещё как минимум вариант
Противоречивость конструктивизма уже давно понятна.
>Этот тезис просто констатация факта.
То есть он является теоремой? Где можно прочитать доказательство?
>Отсюда и тезис Чёрча, который пока что ни одному верунцу опровергнуть не удалось
Гипотезу Римана никто пока не опроверг. Она верна, получается?
>Если докажешь, что верна, будет верна.
Вот и тезис свой доказывай, пока не докажешь, он беспруфная хуйня, на которую нельзя опираться.
>Кому? Кловну с мейлру?
Так этих клованов! Падали на мейлру развилось! Браузера ни четали! Мортина Льва не знают. Программировать не умеют! Говно какое-то, а не прогеры.
> Вот и тезис свой доказывай, пока не докажешь, он беспруфная хуйня, на которую нельзя опираться
Ты и правда тупой. В настоящее время все известные факты о вычислимости подтверждают тезис Чёрча. И я их приводил неоднократно. Даже чуть выше, когда говорил о соображениях Тьюринга, из которых он исходил, предлагая эту модель. Любое существующее уточнение понятия алгоритма равнообьемно МТ, это так же вычислимый факт. Не известен ни один факт, опровергающих тезис Чёрча. Более того, не известен ни один подход, который мог бы его опровергнуть хотя бы теоретически.
>Ты и правда тупой.
А ты любишь переходить на личности, когда прилюдно обсираешься на весь тред.
>В настоящее время все известные факты о вычислимости подтверждают тезис Чёрча.
Подтверждение не равно доказательства. Гипотезу Римана тоже многое подтверждает. И что, она верная?
>Не известен ни один факт, опровергающих тезис Чёрча.
То же и с гипотезой Римана.
> А ты любишь переходить на личности, когда прилюдно обсираешься на весь тред
Где?
> Подтверждение не равно доказательства. Гипотезу Римана тоже многое подтверждает.
Перечитай ещё раз то, что я написал, и подумай. Какая связь с гипотезой Римана вообще?
>Перечитай ещё раз то, что я написал, и подумай. Какая связь с гипотезой Римана вообще?
Такая, что у твоего тезиса нет доказательства, как и у неё.
>нет доказательства
Зато этот тезис вычислим и является каноническим элементом типа натуральных чисел, а значит по изоморфизму Уайтхеда-Постникова можем посчитать палочки и легко получить, что он доказан.
> Такая, что у твоего тезиса нет доказательства, как и у неё.
А ты говоришь, я на личности перехожу. Не льсти себе, я просто факт констатирую. Ты даже то что сам пишешь не читаешь, не говоря о том на что отвечаешь. Хотя, кому я пытаюсь что-то объяснить.
В катигории всех палочек которые можно посчитать в столбик.
Загляни в свои пифагоровы штоны, платонист несчастный.
Да ладно, знание Мартина Льва и Манори еще не делает из человека дегенерата. Про тебя Витгенштейн давно сказал, что "трудно взбираться на гору математики с рюкзаком, набитым философией". Черча читает, Карри читает, Тьюринга, Рассела-Уайтхеда еще надо и Гильберта-Кон Фоссена. А мог бы математикой заниматься.
Я бы сказал, с чёрным мешком для мусора скорее.
Мейлу же. Даже тезис Чёрта не понимают.
>А мог бы математикой заниматься.
Так философия вычислима же, значит по изамарфизму Евклида-Гаусса она является математикой.
>вычислима
Не математика.
По изоморфизму Гёделя-Лейбница все вычисления сводятся к вычислениям на машине Раймунда Луллия, а это, простите за выражение, cultura secundaria.
ОПИСАНИЕ ДЕЯТЕЛЬНОСТИ
Калькулятор – это технический работник предприятий общественного питания. Он знает все технологии приготовления блюд. В начале каждой своей смены он составляет план-меню. В нем калькулятор указывает название блюда, его номер в сборнике рецептур и количество намеченных к приготовлению блюд. Пока повара чистят овощи, разделывают мясо, рыбу, замешивают тесто, калькулятор вычисляет потери массы готовых изделий при механической и тепловой обработке продуктов. Затем калькулятор составляет калькуляцию (определяет цену) блюд, кулинарных и кондитерских изделий с учетом их особенностей. Если в заведении есть бар, то винную и барную карты также составляет калькулятор. Обычно для наиболее точного определения цены ее составляют из расчета стоимости сырья на сто блюд. А для торжественных вечеров, банкетов и т.п. стоимость блюд определяется в зависимости от количества гостей.
Технолог-калькулятор составляет для каждого вида изделия калькуляционную карточку, где указывает используемое сырье, цену на них, изменения в ценах или наборе продуктов.
Хотя этот специалист напрямую не участвует в приготовлении блюд, но знает все рецептуры и технологии. Он может сделать блюдо высококалорийным или диетическим, улучшить его вкусовые качества, помочь в разработке новых изделий.
Калькулятор должен уметь пользоваться сборниками рецептов, знать нормы раскладки готовой продукции, правила образования наценок. Ему не обойтись в своей работе без применения специальных компьютерных программ, например, Store-House и 1C-Общепит.
Не знаю такого. Есть изоморфизм Квиллена-Вальдхаузена, там про то что математика и алгебраическая к-теория это одно и то же.
Ну это Гёдель доказал ёще в 20-х, разбирают даже в школе. Я про более сложные вещи сейчас говорю, про вычислимасть.
Вычислимость это в "1С: предприятие", ей в оснлвном бухгалтеры интересуются, а не математики. Я про вычислимость помню читал как-то специально, у нас в вузе довольно приятные женщины работают в бухгалтерии, хотел понравиться им. Оказалось читать Чёрча и Тьюринга было не обязательно, красивого лица достаточно.
>Оказалось читать Чёрча и Тьюринга было не обязательно
Надо было читать Браузера. Я слышал, что он им нравится намного больше.
>ей в оснлвном бухгалтеры интересуются, а не математики
как?? Тезис же доказывает вычислимасть/канструктивность математики? разве нет?!
К Браузеру восторженные молодые мужчины более склонны, часто программисты. Женщин среднего возраста он отнюдь не трогает, по-моему.
Нашел тут кстати книгу по конструктивизму, где в полный рост используется теория категорий. Это вообще законно?
Как умма к такому относится?
>Это вообще законно?
Так большая часть теории категорий конструктивна, только канструктивистам-вычислителям этого видимо не понять.
Но ведь катагории это то же рисование алефов и бетов. Например у них даже есть непостижимый кардинал, как в теории множеств, катагористы говорят что это топос Кратондика. Не канструктивно! Только тезис Церкви (church) канструктивен и все, что из него вытекает. А у Кратондика аксиома универсума. Сектант сразу видно.
Топасы Кратындика это вообще "объект" (не канструктивный) поклонения секты Кратындика. Тезис опровергает их существование, но сектанты все равно веруют.
Только Church святая, соборная и апостольская конструктивна!
Что придумали, безбожники! Топазы Картотеки у них, актуальные бесконечности, гамма-логии, ироды, платонисты!
Аксиому Церкви не принимают! Исключают третье, понимаешь.
Во имя отца, сына и святого духа, да не будет исключено ни одно из трёх!
 10 Кб, 360x225
10 Кб, 360x225Захотелось вебмку сделать с нарезками ответов конструктивиста. Только я безрукий.
>Возможно ли это сделать без PhD по программированию?
Возможно, но тогда потребуется PhP по программированию.
В такой тезис я ещё могу уверовать.
>>8093
Программирование это наука о модулях над кольцами.
https://en.wikipedia.org/wiki/ML_(programming_language)
>Modules are ML's system for structuring large projects and libraries. A module consists of a signature file and one or more structure files.
>Module systems are central to the construction of large-scale programs, and there is a rich and highly-developed theory devoted to the study of type systems for modules
http://people.mpi-sws.org/~skilpat/modsem/
http://mlton.org/PolymorphicEquality
Ну и книга Роберта Харпера:
https://www.cs.cmu.edu/~rwh/introsml/
 12 Кб, 480x360
12 Кб, 480x360>>7881
>мандала
>сансара
>тибетские тексты
>дхарма
> Эта мандала доступна впринципе всем программистам, которые могут писать циклы, складывать числа, больше уровня не нужно. Всю эту математику
>всю эту математику
>критикует веру в актуальную бесконечность
>мандала и сансара это математика, ZFC не математика
Не надо дискредитировать движение.
На шуньяваду наезжать будет только тупой, это предельно логичное учение.
Насчет zfc и актуальной бесконечности конструктивист тоже прав, думаю. Просто он не догнал еще, что начиная с 1957-го эти темы относятся к истории древнего мира, Гротендик их упразднил.
И тупо продолжает свою критику на приличную математику типа гомологической алгебры, не понимая, что это не теория множеств и старые аргументы больше не канают.
Никто и не говорит что математика. Прост если человеку смешно от слова "буддизм", то это немного странно. Если разбираться, там довольно интересно.
Смешно не от слова буддизм, а от критика веры в актуальную бесконечность верящего в мандалы и прочую сансару. Двойные стандарты as is.
>веры в актуальную бесконечность
Но канторовская теория множеств это дрисня изначально, сейчас при чем еще и окаменевшая. Так что если конструктивист начинает пинать этот копролит для самоутверждения, то, кроме того, что это занятие не слишком достойное уважающего себя человека, других возражений нет.
>>8105
> верящего в мандалы и прочую сансару
Западные люди в этом отношении потрясающе невежественны. Их представления о религии основаны на восприятии аврамических религий, то есть иудаизма, ислама и христианства. Соответственно они смотрят на этот кал, и дальше думают что все религии такие.
Я собственно даже не могу назвать разновидности индуизма религией, тк это вызовет некорректные ассоциации.
В этих учениях верить ни во что не нужно, вообще. Не больше чем в философии. Шуньявада и адвайта-веданта (не путать с адвайтой) по сути атеистические учения.
А йогачар-буддизм (второй популярный вариант махаяны, наряду с мадхъямакой-шуньявадой) это дословно "открытый индивидуализм" Шрёдингера, тупо все основные положения совпадают.
Собственно конструктивист этого как раз и не понимает, его позиция в разы более догматична, чем то, что описано у Максима. Но я это уже расписал выше.
>рря вы все тупые вируны в аллаха
>харе кришна харе рама шри шри чёрчтьюринг
Вас понял. Всё это не более, чем вопрос веры. Что и требовалось доказать, тащемта.
Кого вас? Я ни про Чёрта, ни про Тьюнинга ничего тут не говорил.
>кришна
Ну оно и ясно. Будет тебе известно, что гаудия-вайшнавизм (так это на самом деле называется) это самый настоящий рак и говно, грамотными людьми обоссаное уже пятнцать тысяч раз, и с самого начала существует только как наёбка для белых туристов-неофитов (типа Ромы Михайлова) как какое-нибудь Ошо.
Это примерно как о философии судить по Лакану, который философом не является и никогда не был.
>>8109
Теория множеств Кантора это вторая культура.
Схемы, топосы и этальные когомологии – core mathematics. В отличие от "тезис Церкви" и "изоморфизм Абеля-Руффини" это аргумент, с которым спорить трудно.
>Кого вас?
Это устойчивое выражение, тебя, мой милый друг, тебя, конструктивиста, гомологического анона, того, кто спорит
тезисом Церкви, всех вас, короче. Основания, деление на первую, вторую, двадцать третью культуры, на математику и не математику и так далее. Всё это не более, чем вопрос веры. Есть философия, есть математика, а есть философия математики ака религия.
>философия математики ака религия
Я с этим вообще не спорил никогда:
>Собственно, чем занимается любое приличное научное сообщество, это развитием собственного здравого смысла (common sense) на техническом уровне.
>>7425
А то что "вторая культура" – это просто ярлык, надо же бесполезное говно как-то называть.
Махаяна в Индии (да и буддизм вообще, за пределами Шри Ланки) сейчас практически не представлена, см. картинки.
Что до индусов, то есть разные. Отличить просто:
>Начиная с десятого века н.э. и раньше, ситуация такая: север и индо-арийские регионы – отсталая пердь, юг – цивилизация и культура. С распространением ислама различие ещё более усилилось.
>То есть designated shitting streets и прочее, это индоевропейцы как раз местные. С грамотностью 50%. А в двух-трех штатах вся промышленность, грамотность 95%.
В этом отношении показательны такие ебанаты как Вербицкий, который съездил в Мадрас и по своей невнимательности принял чёрных господ-тамилов за под-людей, хотя всем давно ясно, что под-людьми могут быть только индоевропейцы.
Ну и Михайлов, который из всей Индии (страна размера трёх западных европ по населению, да и по площади тоже) выбрал такую shithole, как Колькатта. Еще и пропагандирует это дело.
Мрази в общем, ненавижу за это.
>"вторая культура" – это просто ярлык
Что именно к ней относится? Я примерно представляю, но не знаю полного списка.
Да кому нужно составлять такие списки. Все что за пределами "ядра", то и относится.
Не, Индию я уважаю, братишка, и религию их не меньше, мантры меня прут, например.
https://www.youtube.com/watch?v=_3EoRFDzDoU
https://www.youtube.com/watch?v=-i4S2wT_vqc
> Михайлов выбрал shithole
Ну так братишка, ему ж другие не особо интересны, человек такой, всякую гадость любит разглядывать, думает, что во всякой гадости истина прячется, тоже свой путь, своя религия-философия.
>их
Ну это примерно как объединить в одну группу жителей Андалусии и Норвегии. Даже хуже: и те и другие индо-европейцы, дальние потомки германских племён.
А в Индии живут представители разных не только языков, но этносов, рас можно сказать.
Как и везде, там есть охуенная и интересная часть (юг) и есть сраное говно и пидорасы (все остальное).
Так мог бы не уезжать из своей прибалтики или че там у него. Не сильно и отличается.
Ну вот меня танцевать прёт под кишори цуче эйзаа интеджам хоо джаеее, значит заебись, а они индусы же, причём это мантра какая-то, не Кришне, Радхе, но прёт же. Уважаю. Понимаю.
Видать там уже все места противные исходил, притоны цыганские да подвалы героиновые.
>нахуя нам все это, если можно работать напрямую с нейрофизиологией
>Зачем философия, когда есть скажем fMRI высокого разрешения
Верун-плутонист никак не смог понять, что нейрофизологию можно интерпретировать не только реалистически, но и феноменологически, и вообще как угодно.
Группы крови у него как факт существуют, алгоритмы работают, охуеть вообще.
Что должны были показать эти картинки?
>Интуиционисты и конструктивисты предлагают заменить выражение ‘множество X конечно’ на ‘множество X не может не быть конечным’. Я не вижу в этом ничего, кроме ман[ь]еризма. Человек может следить либо за тем, что он говорит, либо за тем, как он это
говорит, но не за тем и другим сразу.
ханики. Уже одна только роль теории множеств в истории нашей науки обязывает каждого серьезного студента – и, тем более, преподавателя – математики попытаться постичь дух и пафос этой теории, а не просто научиться использовать пару теоретико-множественных значков. Кроме того, не видно никаких симптомов того, что роль понятия актуальной бесконечности в качестве основы и сущности математического мышления может подвергнуться
ревизии в ближайшие столетия.
 38 Кб, 807x581
38 Кб, 807x581Ситуацию, которая возникла затем, социологи описали бы в терминах
культурной отсталости(mental retardation). Несмотря на наличие непротиворечивой теории множеств, математики продолжали беспокоиться о непротиворечивости. Некоторые сомневались даже в непротиворечивости самой арифметики! Ситуацию еще более ухудшали гротескные попытки Л.Э.Я.Брауэра превратить математику в религию.
К.Сморинский
do rightaway, the finite may take a little bit longer’.
Вот теперь точно /thread.
>Феерическая расстановка точек
Ты даже не понял о чём этот тред был.
>Канторовская теория множеств – независимо от того, как к ней относиться – представляет собой самое важное из всего, что до сих пор произошло в математике.
For one, теория множеств Кантора не имеет никакого отношения к математике.
>одно из трех самых важных событий произошедших в истории человечества за последние 6000 лет
В /re/ –––>
"Nobody will ever drive us out of Cantor's paradise" – David Hilbert.
"For if one person can see it as a paradise, why should not another see it as a joke?" – Ludwig Wittgenstein.
>открытием квантовой механики
Линейной алгебры тогда уж (частью которой является КМ) в работах Лейбница, Грассмана и Дедекинда.
дед.
>о чём этот тред был
О том, что конструктивизм/интуиционизм не нужен.
Совершенно особое место во всей околоматематической литературе, по существу промежуточное между религией, идеологией, логикой и философией, занимают труды по логицизму, интуиционизму, конструктивизму и другим сектантским направлениям в области ‘оснований математики’, которые поддерживались их представителями с фанатизмом и религиозным рвением (‘война мышей и лягушек’), со всеми атрибутами идеологической борь-
бы, типа ссылок на марксизм и пр. В мировоззренческом плане дискуссии об основаниях
не оказали никакого влияния на позицию подавляющего большинства математиков, но на определенном этапе своего развития конкретные исследования в области интуиционистской и конструктивной математики были инкорпорированы в классическую математику и в настоящее время являются вполне респектабельными, хотя и весьма эзотерическими разделами теории алгоритмов, теории булевых алгебр и топосов
помощью туманного.
Когда конструктивист говорит, что натуральное число выражается в алфавите, состоящем из одного символа |, ||, |||, и заявляет, что этот процесс можно неограниченно продолжать, мне кажется, он не учитывает чего-то весьма существенного. А именно, того, что в процессе написания таким образом уже крошечных чисел, ну хотя бы 101010 мы собъемся со счета, кончатся чернила,
кончится бумага, кончится время, но главное все-таки, состоит в том, что если мы будем писать все дальше и дальше, то под действием гравитации чернила и бумага превратятся в чер[ниль]ную дыру. Словом, требуемого количества черточек ему написать не удастся.
Конструктивная математика опирается на тысячи неявных предположений, подразумеваемых, но не сформулированных аксиом. Кто может гарантировать, что за ночь в тексте не появляются новые символы и не исчезают старые, что мы в состоянии отличить один символ от другого
>>8176
Да, охуенно он расписывает.
Охуенно он расписывает в книге "не совсем наивная линейная алгебра", а здесь жидко обсирается.
Вавилов сам назвал причину своего баттхерта: это решение слить специальность математическая логика со специальностью алгебра. В итоге ему пришлось досдавать. Но этих вещей он как не знал никогда, так и не выучил (а я и не говорю что надо было).
А по-моему он не обсирается, а совсем наоборот.
Например в этих местах
>понятия элемента, множества, функции, бесконечности, числа требуют дальнейшего анализа и обоснования, в то время как понятия символа, текста, конструктивного объекта,правильно составленной формулы, формального языка, выводимости, доказуемости, истинности ясны сами по себе
> по существу промежуточное между религией, идеологией, логикой и философией, занимают труды по логицизму, интуиционизму, конструктивизму и другим сектантским направлениям в области ‘оснований математики’
>Наша интуиция больших конечных объектов вторична по отношению к интуиции бесконечности. В большинстве осмысленных и правильно поставленных вопросов трактовка бесконечного проще или много проще, чем трактовка конечного: ‘the infinite we’ll
do rightaway, the finite may take a little bit longer’.
>Все попытки логиков и философов осесть между двумя этими стульями со своей ‘абстракцией потенциальной бесконечности’ бесславно провалились, и я верю, что так будет и впредь. Я склонен соглашаться с Кантором, что никакая математически последовательная трактовка понятия бесконечности, отрицающая актуальную бесконечность, невозможна.
И особенно здесь
>Интуиционисты и конструктивисты предлагают заменить выражение ‘множество X конечно’ на ‘множество X не может не быть конечным’. Я не вижу в этом ничего, кроме ман[ь]еризма.
Очень чётко и по делу сказано как по мне. С чего бы символ, текст, формула, алгоритм и тд вдруг ясны сами по себе? Конструктивисты действительно сектантов напоминают(яркий пример ИТТ). С большим конечным действительно сложнее работать, чем с бесконечным, в этом, похоже, и есть главный обсёр в количестве и качестве результатов в конструктивизме, все попытки сесть между двух стульев действительно провалились, ну и последнее. Где же он обосрался? По мне так всё чётко и по делу.
То что он расписывает и критикует с конструктивизмом имеет лишь небольшое сходство, но это пусть браузерофаг обосновывает, мне лень за ним повторять.
От себя только скажу, что конструктивизм имеет к математике примерно такое же отношение как медицина (ну например математики тоже люди и иногда болеют, ясно что им это важно в какой-то степени) и не более, и смысла Вавилову рассуждать про вещи которые он не понимает нет никакого, еще бы про геологию начал писать.
>То что он расписывает и критикует с конструктивизмом имеет лишь небольшое сходство
Спорно.
>но это пусть браузерофаг обосновывает, мне лень за ним повторять.
Да мне самому лень спорить, тихо вбросил и ушёл, потом посмотрю на аргументы, которые приведёт браузерофаг, интересно посмотреть на его спор с Вавиловым.
А математика — экспериментальная наука.
Ведь выводы, ты берёшь на основе опыта, из окружающей среды.
Ты можешь формализировать хоть каждый шаг, но вне опыта познаний нет.
Почему есть более классные и более плохие математики? Это зависит от кол-ва литературы и задач.
действительна...
я каждый раз когда даказываю теоремы просто делаю экспермиент и говорю, что всё доказано.
Ты доказывая, делая эксперимент, вспоминая аналогичные ситуации, пытаешься подобрать нужный вариант на основе опыта.
7+8
1.7+(8-5)= 10
2.10 + (8-3) = 15
Либо, ты знаешь, данное значение, как факт, либо разбираешь его до того момента, на основе заполненного правила, пока тебе то станет известным, как факт.
Это частный случай.
Главное, что ты либо запоминаешь, либо выводишь из того, что было запомнено, по запомненному правилу.
На самом деле, это тезис Арнольда.
Можно на любой формализм сказать, что нельзя быть уверенным, что этот тезис верен, ибо из чего я взял, что, если я считаю это утверждение истинным, а формализм достаточным? Возможно, что я допускаю ошибку?
Это круто. Я на одной конференции недавно сказал, что вся математика конструктивна, это тоже мой Тезис.
Если формализм порождает субъект, и субъект может порождать суждения лишь из своего опыта. Можно ли назвать математику экспрементальной?
Давай поделим математику на два вида.
1.Божественная математика
2.Математика, которой касается субъекта.
Всякий тезис субьект может утверждать лишь то, что в рамках его опыта.
Но также можно поделить и физику.
Одна, божественная.
До второй коснулся субъект.
Но ведь всю физику называют экспериментальной, так как её коснулся субъект.
>Главное, что ты либо запоминаешь, либо выводишь из того, что было запомнено, по запомненному правилу.
А как же интуиция?
Бурбаки не пользовался такими "определениями".