Это копия, сохраненная 18 января 2017 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.


Если вы хотите задать вопрос типа "как мне взять этот интеграл", это не сюда. Вам нужен тред "для начинающих", он плавает неподалёку.
Предыдущий: >>381147 (OP)
1. https://arhivach.org/thread/18638/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
46. https://arhivach.org/thread/156244/
47. https://arhivach.org/thread/159628/
48. https://arhivach.org/thread/165872/
49. https://arhivach.org/thread/183576/
50. https://arhivach.org/thread/187447/
51. https://arhivach.org/thread/188358/
52. https://arhivach.org/thread/197703/
1. https://arhivach.org/thread/18638/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13v1. https://arhivach.org/thread/76561/
13v2. https://arhivach.org/thread/92428/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. https://arhivach.org/thread/109198/
30. https://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
33v1. https://arhivach.org/thread/122613/
33v2. https://arhivach.org/thread/122615/
34. https://arhivach.org/thread/123717/
35. https://arhivach.org/thread/128822/
36. https://arhivach.org/thread/129039/
37. https://arhivach.org/thread/131462/
38. https://arhivach.org/thread/138362/
39. https://arhivach.org/thread/138429
40. http://arhivach.org/thread/140404/
41. https://arhivach.org/thread/142386/
42. https://arhivach.org/thread/145879/
43. https://arhivach.org/thread/146833/
44. https://arhivach.org/thread/152600/
45. https://arhivach.org/thread/153157/
46. https://arhivach.org/thread/156244/
47. https://arhivach.org/thread/159628/
48. https://arhivach.org/thread/165872/
49. https://arhivach.org/thread/183576/
50. https://arhivach.org/thread/187447/
51. https://arhivach.org/thread/188358/
52. https://arhivach.org/thread/197703/
>Известно, что адепты абстрактной алгебры могут доказать, что 2+2=1 (в кольце вычетов по модулю 3).
Объясните, пожалуйста.
4 дает остаток 1 при делении на 3
Аноны, а поясните в чем цимес истории с ℕ-петухом?

Тредик-то его читни. Суть в том, что он затралил парашу, а это и несложно, т.к. неконструктивная математика на самом деле не может определить N. Т.н. аксиомы Пеано исходят из того, что нам уже дано натуральное число, а оно нам нихуя не дано, т.к. не имеет формального определения. В математике здорового человека N определяется элементарно, по Маркову - натуральное число это слово в алфавите |. В математике же курильщика есть н-р бурбаковское "определение" из астрономического числа символов, разумеется, абсолютно бесполезное.
>н-р бурбаковское "определение" из астрономического числа символов, разумеется, абсолютно бесполезное.
Но ведь оно не определено через ℕ?
Да. Но практической пользы от такого "определения" нет. Его вообще, походу, только сами бурбаки и понимали. Тогда как по факту понятие натурального числа абсолютно ясно даже ребенку. Более того, есть нейрофизиологические доказательства, что натуральные числа и операции над ними - естественная возможность мозга, точнее правой нижней париетальной коры (rIPC) и конкретного типа нейронов - т.н. "нумероны". Причем, речь не только о мозге человека, обезьяны и даже крысы могут в N без всяких бурбаков и верований в актуальную бесконечность и т.п. фофудью. Причем, восприятие числа основано на восприятии времени, что доказано Уолшем в его модели ATOM (A Theory Of Magnitude) на основе данных нейровизуализации и наблюдению больных с повреждением в этой области мозга. Что прямо доказывает правильность подхода пикрелейтед (1 акт интуиционизма).
Почему тогда в некоторых культурах нет понятия числа? Что-то мнеттвои рассуждения кажцтся сомнительными.
>в некоторых культурах нет понятия числа
У мартышек тоже нет понятия числа, однако они могут в N, арифметику и т.д (на что есть нейрофизиологические пруфы). Подозреваю, те культуры, о которых ты говоришь, весьма недалеко ушли от бабуинов. Тут суть как раз в том, что число - изначальное, долингвистическое, доязыковое понятие. Для операций с числами не нужен язык (опять же, все по Брвуэру, 1 акт интуиционизма). Поэтому в числа могут и новорожденные дети и даже зверушки, не могущие в язык.


Я не понимаю. Объясни. Вот проводили много экспериментов с какими-то там индейцами. Показывали им предметы и просили объяснить, как на их языке это количество предметов называется. Получилось, что у них есть несколько категорий (ну, что-то вроде "ноль, один, много", совсем как у программистиков, хи), и что одно и тожеколичество они относят к разным категориям в зависимости от того, добавили предмет к группе или убрали. То есть мы видим три банана, а они видят много бананов. Или немного бананов, если их только что было четыре.
То есть считать они не умеют, вообще. Людей тоже считать не могут. Я уже не помню деталей, давно читал, но было что-то про то, что вот ушли несколько человек из племени рыбу ловить - и оставшиеся не понимали, что ушли, например, Джон, Пит и Мэри, а могли только размышлять в стиле "Джон здесь? Нет, Джона здесь нет". Короче, у них вообще понятия множества, объединения, коллекции как будто нет.
Вот были эксперименты, которые показали, что муравьи могут в арифметику, да? Хотя это та еще антропоморфизация, на самом деле это показывает, как мне кажется, не то, что они могут в арифметику, а то, что они могут сжимать информацию, если оптимальное поведение этого требует. То есть некорректно говорить, что они могут в эн и арифметику, потому что для эн нужны числа, это именно понятийная концепция. А они просто могут в определенные паттерны поведения, которые мы можем объяснить с помощью концепции числа. Но это не говорит о том, что они могут в эту же концепцию. Если о чем это и могло бы говорить, то о некой материальности (и неизбежности, ечли хочешь) понятия числа. Но и это утверждение мне видится недостаточно обоснованным. Все-таки нельзя отождествлять некое свойство материальной системы с концепцией, помогающей нам это свойство абстрагировать.
Вот. Поведение муравьев требует сжатия информации, которое мы можем объяснить с помощью нашей концепции числа. А поведение индейцев этого не требует, например. Поэтому я не понимаю, в чем тут фундаментальность.
Алсо, говорить о том, что некоторые другие, отличные от нашей, культуры недалеко ушли от бабуинов - это тот еще шовинизм, как мне кажется. Если ты придерживаешься мнения о том, что (европейский) человек - венец творения, эволюционный прогресс движется поступательно и т.п. - то мы вряд ли найдем общий язык, как мне кажется. Извини, если что, я не осуждаю, просто выражаю опасения.
Я не понимаю. Объясни. Вот проводили много экспериментов с какими-то там индейцами. Показывали им предметы и просили объяснить, как на их языке это количество предметов называется. Получилось, что у них есть несколько категорий (ну, что-то вроде "ноль, один, много", совсем как у программистиков, хи), и что одно и тожеколичество они относят к разным категориям в зависимости от того, добавили предмет к группе или убрали. То есть мы видим три банана, а они видят много бананов. Или немного бананов, если их только что было четыре.
То есть считать они не умеют, вообще. Людей тоже считать не могут. Я уже не помню деталей, давно читал, но было что-то про то, что вот ушли несколько человек из племени рыбу ловить - и оставшиеся не понимали, что ушли, например, Джон, Пит и Мэри, а могли только размышлять в стиле "Джон здесь? Нет, Джона здесь нет". Короче, у них вообще понятия множества, объединения, коллекции как будто нет.
Вот были эксперименты, которые показали, что муравьи могут в арифметику, да? Хотя это та еще антропоморфизация, на самом деле это показывает, как мне кажется, не то, что они могут в арифметику, а то, что они могут сжимать информацию, если оптимальное поведение этого требует. То есть некорректно говорить, что они могут в эн и арифметику, потому что для эн нужны числа, это именно понятийная концепция. А они просто могут в определенные паттерны поведения, которые мы можем объяснить с помощью концепции числа. Но это не говорит о том, что они могут в эту же концепцию. Если о чем это и могло бы говорить, то о некой материальности (и неизбежности, ечли хочешь) понятия числа. Но и это утверждение мне видится недостаточно обоснованным. Все-таки нельзя отождествлять некое свойство материальной системы с концепцией, помогающей нам это свойство абстрагировать.
Вот. Поведение муравьев требует сжатия информации, которое мы можем объяснить с помощью нашей концепции числа. А поведение индейцев этого не требует, например. Поэтому я не понимаю, в чем тут фундаментальность.
Алсо, говорить о том, что некоторые другие, отличные от нашей, культуры недалеко ушли от бабуинов - это тот еще шовинизм, как мне кажется. Если ты придерживаешься мнения о том, что (европейский) человек - венец творения, эволюционный прогресс движется поступательно и т.п. - то мы вряд ли найдем общий язык, как мне кажется. Извини, если что, я не осуждаю, просто выражаю опасения.
ты аргументируешь практическую пользу устройством мозга? Это же даже звучит глупо. В математике полно неинтуитивных и тяжелых для восприятия структур, которые на поверку оказываются удобными для работы с объектами. Да та же позиционная система исчисления, те же алгебраические структуры, те же категории. Так почему же мы должны отталкиваться не от них, а от нашего восприятия?
Если почитать ту терминологию, которую использовал Кант, то он скорее угадал.
>Показывали им предметы и просили объяснить, как на их языке это количество предметов называется. Получилось, что у них есть несколько категорий (ну, что-то вроде "ноль, один, много",
Вопрос - неправильно построенный ответ. Вот ты сам себе и ответил - дело в языке. Человек может в натуральные числа и арифметику с рождения, это медицинский, прямо скажем, факт. Но вот человек растет, обучается языку. Хорошо, если язык развитый. А не такой, что вся математика на этом языке уровня "один, два, много".
> А они просто могут в определенные паттерны поведения, которые мы можем объяснить с помощью концепции числа. Но это не говорит о том, что они могут в эту же концепцию.
Нет, там речь именно о восприятии натурального числа в конструктивном смысле - как слова в алфавите | или т.п., а так же восприятия операций с числами. Концепция числа в интуиционизме и конструктивизме ничем не отличается от самого числа, существует только тот математический объект, который может быть построен. В противном случае "существование" чего-то есть мистика и т.п.
>>389586
>В математике полно неинтуитивных и тяжелых для восприятия структур, которые на поверку оказываются удобными для работы с объектами. Да та же позиционная система исчисления, те же алгебраические структуры, те же категории. Так почему же мы должны отталкиваться не от них, а от нашего восприятия?
Восприятие числа - фундамент всех остальных построений, которые сами по себе могут быть сколь угодно тяжелыми для восприятия. Зависимые типы и правила вывода в MLTT сложно назвать интуитивно простыми, однако они конструктивны, т.е. построимы и выводимы из базовой интуиции. Основывая математику на теории множеств и логике, невозможно обойтись без парадоксов, которые из этих построений вытекают. Можно выдумывать сколько угодно костылей, в конечном счете формально-аксиоматический подход просто сталкивается с теоремой Геделя о неполноте - либо придуманные костыли неполны, либо противоречивы. В обоих случаях это бесполезные костыли.
>Восприятие числа - фундамент всех остальных построений, которые сами по себе могут быть сколь угодно тяжелыми для восприятия.
Собственно, вопрос был о том, почему, а ты просто повторил эту мантру. Почему не восприятие паттерна, более фундаментальное?
>Более того, есть нейрофизиологические доказательства, что натуральные числа и операции над ними - естественная возможность мозга, точнее правой нижней париетальной коры (rIPC) и конкретного типа нейронов - т.н. "нумероны". Причем, речь не только о мозге человека, обезьяны и даже крысы могут в N без всяких бурбаков и верований в актуальную бесконечность
А с каких пор убогие костыли эволюции как оптимизационного процесса с достаточно хуёвой эвристикой стали оправданием хуёвых определений чего-либо в математике?
>Почему не восприятие паттерна, более фундаментальное?
Ну ок, дай определение восприятию паттерна. И покажи его нейрофизиологические основы, позволяющие говорить о наличии такого восприятия независимо от возраста особи и даже от ее вида. для начала хотя бы определение паттерна Со своей стороны я пруфы назвал - модель ATOM Уолша, если Брауэр и Кант не канают.
>>389592
>А с каких пор убогие костыли эволюции как оптимизационного процесса с достаточно хуёвой эвристикой стали оправданием хуёвых определений чего-либо в математике?
Сами эти костыли для интуиционизма несущественны. Я о них говорю потому что они есть и вполне материальны, интуиционизм без них обходится более века. И я сомневаюсь, что у тебя есть возражения по существу к MLTT например. Да даже какие-нибудь нормальные алгорифмы Маркова ты вряд ли сможешь покритиковать. О чем тогда вообще разговор.
>Я о них говорю потому что они есть и вполне материальны, интуиционизм без них обходится более века.
Неконструктивная математика обходится без этой хуйни уже больше двух тысячелетий. И что?
>И что?
И даже N определить не может. Даже непротиворечивость арифметики до сих пор не доказана.
>И даже N определить не может.
Ну бурбаки определили.
>Даже непротиворечивость арифметики до сих пор не доказана.
P ≠ NP уже доказал, доказатель мамкин?
>О чем тогда вообще разговор.
О том, что это абсолютно неприменимо в современной математике, когда не формализованы даже положения математики двухвековой давности? И определения диктуются именно реалиями актуальной практики.
>Ну ок, дай определение восприятию паттерна. И покажи его нейрофизиологические основы, позволяющие говорить о наличии такого восприятия независимо от возраста особи и даже от ее вида.
Ты так залихвацки предполагаешь решенной трудную проблему сознания, отождествляя число в формальной теории и нечто связанное с числами в теории нейрофизиологической.
А ответы на твои вопросы есть в гугле по запросу pattern recognition physiology.

>бурбаки определили.
Заебись определили))) Давай поговорим об этом "определении". Что же такое единица согласно бурбакам? И вот это вот определение из квинтиллионов знаков или сколько там, его в аксиомы Пеано подставлять или что?
>>389597
>Ты так залихвацки предполагаешь решенной трудную проблему сознания, отождествляя число в формальной теории и нечто связанное с числами в теории нейрофизиологической.
А в чем проблема? Число - изначальная интуиция времени. Об этом говорил Брауэр, это подтверждают современные исследования. На основе идей Брауэра созданы даже конструктивные основания (HoTT). А "паттерн" это нечто из области гуманитарной психологии, смешно и думать что у этих горе-психолохов будут хоть какие-то определения, не сводящиеся к мутной фуфлософии ниочем.
>А в чем проблема
В том, что вещь не определяется ее описанием.
https://en.wikipedia.org/wiki/Hard_problem_of_consciousness
На основе "доказанной" гипотезы Римана тоже много что создано.
>нечто из области гуманитарной психологии
термин из машинного обучения так-то.
>И вот это вот определение из квинтиллионов знаков или сколько там, его в аксиомы Пеано подставлять или что?
Да, а в чем проблема? Всяко лучше чем РАСПЕЧАТКУ ДОКАЗАТЕЛЬСТВА хроматического числа планарного в квинтиллион шагов вручную проверять.
>И вот это вот определение из квинтиллионов знаков или сколько там, его в аксиомы Пеано подставлять или что?
Ну если ты хочешь пользоваться минимумом символов (зачем?) и чисто формальной записью без использования естественного языка (какой нет ни в одной работе бурбакистов), то дерзай.

>вещь не определяется ее описанием.
Так именно с этих слов начинается 1 акт интуиционизма Брауэра. Математический объект определяется возможностью его построения. В противном случае это просто аутизм или вера во что-то.
>термин из машинного обучения так-то.
В машинном обучении нет слова "психология". И "паттерны" там - вещественнозначные векторы, матрицы или тензоры. Т.е. конструктивные объекты, как ни крути.
>>389601
>Да, а в чем проблема?
Проблема в том, что это определение не дает возможности построить на нем арифметику и доказать или опровергнуть ее непротиворечивость.
Ви таки будете смеяться, но эта задача решена методами конструктивной математики. https://ru.wikipedia.org/wiki/Проблема_четырёх_красок
Я имею ввиду словами, по старинке, без ЭВМ. Кто-нибудь до сих пор пытается её так решить, или нет?
>Так именно с этих слов
Именно с этих слов начинается шестая книга глава евангелия... Походит на религиозный догматизм, не считаешь ли?
>И "паттерны" там - вещественнозначные векторы, матрицы или тензоры. Т.е. конструктивные объекты, как ни крути.
А персептрон об этом в курсе? Ему то все равно, может ли быть сведено что-то к математическому объекту. Ну или, если ты так уверен, то расскажи что представляет собой там тональность сообщения или картинки для google deep dream. Ну, а то, что он получает информацию в виде компьютерных данных, это не тайна мадридского двора.
Существует большой класс задач, решаемых только перебором, особенно в комбинаторике. Люди не решают их, потому что делать простую проверку для сотни тысяч вариантов это проблематично. Саму задачу о красках просто свели к доступному перебору.
Отлично. А кто-нибудь рецензировал код переборщика вместе с кодом компилятора которым софтинка была скомпеляна? Ну мало ли, сейчас время такое, сложные программы - баги живут в конпеляторах годами если не десятилетиями....
>Именно с этих слов начинается шестая книга глава евангелия... Походит на религиозный догматизм, не считаешь ли?
Религиозный догматизм - это актуальная бесконечность, например. В интуиционизме существование чего-то означает возможность это что-то построить. Никакого догматизма абсолютно.
>догматизм это когда много богов, как в индуизме. у нас же есть только троица: отец, сын и святой дух, что означает возможность воскресения христова. Никакого догматизма абсолютно.
Блажен, кто верует.
Ладно, ты меня не услышал и просто еще раз повторил свои изначальные установки. Ладно.
Эта строка из википедии выглядит как-то совсем неправдоподобно. Вроде там намного меньшее число.

Есть соотношение: s/d = 0.7, d - известно.
Чему будет равно s?
А теперь докажи правомерность перехода от вещественного чисда к рациональному.
Что за хуйню ты несёшь, наркоман?
Мне надо выразить S из приведённой формулы. Отношение S к D должно быть 0.7 (в идеале). D известно, надо найти S.
Нахуй иди. Умник нашёлся тут, блядь.
Мамку свою вырази. Анон всё верно сказал.
Скоро, очень скоро.

На самом деле они определяли число 1 вот так. Пикрелейтед - скрин из книги.
Так никто не может понять, что дает этот факт? Никто же не строит "конструктивные основания" на основе их формализма, он скорее нужен для интуитивного восприятия.
Кому "нам"? Ты тред читал перед тем, как спрашивать? Речь о том и шла, что она не нужна.
Кстати, раз двощ теперь филиал мейлсру - куда перекатываться? На доброчане вроде аж несколько годных маттредов.
Анон, интересует ситуация в топологии. Мне тут сказали, что общая топология умирает и нет смысла ей заниматься или даже углублённо изучать. Что думаете?
Взяли хорошее, годное определение Бурбаков, зачем-то развернули его до самого низа, а потом кудахтают, что то, что получилось, нинужно. Странные люди.
Чета мне здесь услышалось созвучное, словам о физике, сказанное в начале 20 века.

>>389854
>Где ты конструктивистов увидел?
Бесноватого так корежит, что конструктивистов видит даже у себя под кроватью.
У бурбаков в предисловии к первой книге написано, что сокращенные записи и вольности речи только для удобства читателя, по факту "говорим ленин - подразумеваем партия", у них там претензия именно на полную формализацию.
Встанут на колени перед барским домом и стоят подлецы!
И ведь знают, что бунтуют и всё равно стоят!"
Так зачем надо раскладывать все до минимальных термов, объясни? Бурбаки все нормально делают, а не переопределяют все в каждом определении, у них нет страха введения новых символов.
Опять верующий пришел со своей проповедью, "опровержением всех ересей"? Но, если мы спросим тебя, почему это все присутствует в материальном мире, ты можешь сказать только "потому что верую". При этом как типичный религиозный догматик тебе кажется абсурдным (абсолютно такая же) вера других, как христианам казалась абсурдна вера язычников.
>а как иначе трактовать его исходную часть - чистую интуицию времени, не основанную на языке, опыте и прочих внешних явлениях
А почему, собственно, солипсизм, а не другой вид субъективного идеализма, например, кантовский? Почему не объективный идеализм, где чистая идейная интуиция и определяет бытие? Почему не диалектический материализм, где это отражение материи в сознании? Если ты знаком только с одной недалекой философской концепцией, это не повод приписывать ее куда не следует.

>зачем надо раскладывать все до минимальных термов, объясни?
Потому что как-то манипулировать можно только с изначальными термами. Т.е. с каноническими элементами. Их можно заменить более высокоуровневыми абстракциями, неканоническими элементами, номинальными определениями и т.п. для удобства, но вычисляются все равно канонические элементы. Вот и подумай, как это должно выглядеть, если таковые состоят из каких-то там квинтиллионов знаков. Хотя, о чем это я, бурбакизм не предполагает возможности построить описанное. Но тогда встает вопрос, какая от него практическая польза.
>>389882
>Но, если мы спросим тебя, почему это все присутствует в материальном мире, ты можешь сказать только "потому что верую".
Что именно присутствует? Ты о чем?
>А почему, собственно, солипсизм, а не другой вид субъективного идеализма, например, кантовский? Почему не объективный идеализм, где чистая идейная интуиция и определяет бытие?
Тут не суть на самом деле, просто у Брауэра ближе к солипсизму, это даже не особо моя мысль, хотя я и согласен с этим утверждением. Дело-то не в этом, а в том, почему такой аутизм гораздо лучше подходит для оснований математики, чем собственно математика?
>Потому что как-то манипулировать можно только с изначальными термами.
Манипулировать кому и зачем? Человеку определенно неудобно, большинство математиков даже не в курсе, как канонично формализуются те абстракции, которые они используют.
>Что именно присутствует? Ты о чем?
Ну ты же задаешься вопросом: "почему дело так, а не иначе". При этом, как мне кажется, подразумеваешь, что математика должна быть построена на каких-то законах материального мира или от них отталкиваться, или я плохо понимаю? Собственно, от ответа на этот вопрос принципиально зависит и позиция. Если математика совершенно оторвана от бытия, то зачем ее какой-то земной критерий, вместо интуитивного?
>Манипулировать кому и зачем? Человеку определенно неудобно, большинство математиков даже не в курсе, как канонично формализуются те абстракции, которые они используют.
А ты не видишь, что именно в этом вся проблема? В частности с тем, что неконструктивная математика до сих пор не может доказать непротиворечивости арифметики.
>Если математика совершенно оторвана от бытия, то зачем ее какой-то земной критерий, вместо интуитивного?
Конструктивный объект всегда может быть построен, в этом смысле интуиционизм гораздо больше привязан к бытию, чем какая-нибудь бурбакистика. Прикол в том, что интуиционизм основывается на солипсизме, что с точки зрения неконструктивной математики шизофрения какая-то. И тем не менее, по факту выходит, что это более годные основания, чем логицизм и формализм.
>А ты не видишь, что именно в этом вся проблема? В частности с тем, что неконструктивная математика до сих пор не может доказать непротиворечивости арифметики.
Я не вижу в этот проблемы. Невозможность что-то доказать это же уже результат. Может ли конструктивная математики помочь, например, десятой проблеме Гильберта?
Да и про непротиворечивость ты лукавишь, не объясняя почему мы должны пользоваться средствами теории, а не метатеории.
>Конструктивный объект всегда может быть построен, в этом смысле интуиционизм гораздо больше привязан к бытию, чем какая-нибудь бурбакистика
Построение же чисто умозрительное, какая-то связь с реальность даже не предусмотрена постановкой вопроса. При этом, насколько я знаю, критерии конструктивности совершенно неопределенны (вера в тезис черча, например). И именно от того, как мы поставим обоснуем этот критерий, и зависит само наше построение. Возникает вопрос, а почему такая система претендует на формализацию всей математики? Доступно ли ей это?
Ты бы почитал их хоть для начала, ох.
>>389869
Доброчан же. Все будет хорошо. Сделай первый шаг.
Энивей, никакая более лучшая формализация математики невозможна. У Бурбаки минимально достаточный набор знаков.
> никакая более лучшая формализация математики невозможна.
Формализация математики - тупиковый путь, что доказывается теоремой Геделя о неполноте. Уже после этого формализм можно списывать на свалку истории. Однако, несвежий труп поебывают до сих пор. Закопали бы уже обратно.
>>389893
>Построение же чисто умозрительное, какая-то связь с реальность даже не предусмотрена постановкой вопроса.
Предусмотрена, возможность построения объекта - это как раз постановка вопроса.
>Возникает вопрос, а почему такая система претендует на формализацию всей математики? Доступно ли ей это?
Доступно. HoTT как раз из этой области. Проблема только в том, что там еще полно работы, по-сути, конструктивными основаниями никто и не пытался заниматься до относительно недавнего времени, все веровали в формализм, да и сейчас большинство веруют.
Пожалуйста, сформулируй теорему Гёделя о неполноте и объясни, о каком тупике ты говоришь.

Все элементарно настолько, что есть даже в предисловии к первой книге бурбаков. Любая формальная система либо неполна, либо противоречива. Сами бурбаки отнеслись к этому вопросу в стиле пикрелейтед. Прежде всего, надо думать, по той причине, что никогда и не надеялись что вся математика будет когда-то формализована, н-р на основе той же теории множеств.
>Любая формальная система либо неполна, либо противоречива
Это неверно: существует обширный класс полных непротиворечивых формальных систем. Ты выставил себя идиотом, дальнейший разговор с тобой лишён смысла.
>существует обширный класс полных непротиворечивых формальных систем.
Вся математика к ним не относится.

А, я думал. что это овервьюшка всей математической философии, типа шапировского The Oxford Handbook of Philosophy of Mathematics and Logic. Тогда читать не буду.
>Предусмотрена, возможность построения объекта - это как раз постановка вопроса.
С чего вдруг возможность построения определяет реальный объект? Это наоборот максимальный отрыв от реальности, ведь вместо связи с ней берется совершенно оторванный от реальности критерий возможности построения. Но это я повторяюсь.
>Доступно
Да неужели, а что делать с результатами в классическом анализе, это у конструктивистов объявляется неверным? Я уж не знаю сколько нужно "работы", чтобы с такими убогими вещественными числами идти дальше.
>>390009
И в скольких из них можно определить арифметику?
>С чего вдруг возможность построения определяет реальный объект?
А что по-твоему, определяет существующий объект в математике?
>Это наоборот максимальный отрыв от реальности, ведь вместо связи с ней берется совершенно оторванный от реальности критерий возможности построения.
Ты читаешь что пишешь-то? Что может быть реальнее фактически построенного объекта? Расскажи.
>а что делать с результатами в классическом анализе, это у конструктивистов объявляется неверным?
С какими результатами, например?
>существующий объект в математике
Если мы говорим в математике, то я бы с большим интересом поискал "несуществующий" объект, прежде чем делать дистинкции.
>Ты читаешь что пишешь-то? Что может быть реальнее фактически построенного объекта? Расскажи.
Ну не верю я в тезис Черча, представь себе. Следовательно, конструктивная математика работает по какому-то невменяемому критерию, непонятно почему именно такому.
>С какими результатами, например?
Лемма о конечном покрытии, например, да и вообще все теоремы касательно сходимости и непрерывности. Весь анализ можно в помойку выкинуть.
>Если мы говорим в математике, то я бы с большим интересом поискал "несуществующий" объект,
И тут мы опять приходим к изначальному вопросу - что есть существование в математике?
>Лемма о конечном покрытии, например, да и вообще все теоремы касательно сходимости и непрерывности. Весь анализ можно в помойку выкинуть.
Конструктивный анализ никто не отменял, например.
>Конструктивный анализ
Что-то среднее между "вегетарианская котлета" и "православный коммунист".
С чего ты взял существование в реальном мире имеет какое-то отношение к существованию в математике?
Например, бесконечность в математике существует. В реальности ещё не факт, что она есть. Или аксиома выбора, чем она так непонравилась ко-ко-конструктивистам?
Так и скажи, что не знаком с темой. Это будет хотя бы честно. Есть там и лемма о покрытиях, и интегральчики и все остальное при месте.
>>390056
>Например, бесконечность в математике существует.
Существует в каком смысле? Я в это уверовать должен? Или что?
То есть вот у бурбаков написано "существует бесконечное множество", а вот в коране написано, что существует Аллах. В чем разница между этими определениями существования?
А почему я должен уверовать в то, что её нет? Взять хотя бы мощьность действительных или натуральных чисел.
>>390059
>То есть вот у бурбаков написано "существует бесконечное множество", а вот в коране написано, что существует Аллах. В чем разница между этими определениями существования?
>У констррутивистов написанно "не существует бесконечного множество", а вот в коране написано, что не существует бога кроме Аллаха. В чем разница между этими определениями не существования?
>И тут мы опять приходим к изначальному вопросу - что есть существование в математике?
Тогда ответный вопрос: ты считаешь возможно построить заведомо нереальный объект?
>Конструктивный анализ никто не отменял, например.
Так толку от него, если современные ученые, ушедшие далеко далеко вперед, отталкиваются от понятий классического анализа, до которых конструктивный еще даже не добрался (а некоторые опроверг или переделал, что подразумевает огромный массив "плохо доказнного").
>У констррутивистов написанно "не существует бесконечного множество",
Нигде такого не написано, господин соврамши. Даже принцип исключенного третьего не отвергается в тех случаях, когда он может быть непосредственно доказан на конструктивном объекте.
>А почему я должен уверовать в то, что её нет? Взять хотя бы мощьность действительных или натуральных чисел.
Это случай абстракции потенциальной бесконечности. Если есть правила конструирования бесконечного объекта, никто не отрицает его бесонечность (N или н-р шкала множеств у бурбаков). Ты же веруешь в актуальную бесконечность, т.е. бесконечность саму по себе, в отрыве от конкретного объекта, который можно построить. И такая вера то же самое что вера в домовых.
Ты свел все к своей вере в частично рекурсивную функцию и обвиняешь кого-то в ереси.
>ты считаешь возможно построить заведомо нереальный объект?
Реален тот объект, который можно построить. В отрыве от построимого объекта, что есть реальность?
>конкретного объекта, который можно построит
Хорошо, как построить точку? По определению:
Точка есть то, что не имеет частей.
Формулу Эйлера можно построить? Насколько объекты в ней реальны?
Неа, не фига. Это биекция между координатами и самой точкой, что нарисованна на плоскости.
>>390064
В реальности ты не построишь не одной точки. Хоть одну нарисуй, построй.
> Это биекция между координатами и самой точкой, что нарисованна на плоскости.
А кто сказал, что надо рисовать? Координаты задают объект - точку. Задают однозначно. Т.е. имеем конструктивный объект.
>В реальности ты не построишь не одной точки. Хоть одну нарисуй, построй.
Еще раз, что по-твоему есть реальность в математике?
Ты не можешь даже точки посторить, получаеться, что геометрия не ко-ко-консруктивная?
Какой мне смысл писать десятый раз одно и то же. Не понимаешь - попробуй религию. Конструктивные определения евклидова пространства, как и его подмножеств, мало отличаются от неконструктивных. Возможность построить объект не равна возможности нарисовать его.
>парадоксы похлеще удвоение шара.
Но это не парадокс, это лишь "удивительный факт".
>тоже считали непротиворечивой
А она противоречива? Можно пруф?
>Но это не парадокс, это лишь "удивительный факт".
Я знаю.
>Можно пруф?
Парадокс Рассела. Раньше считали, что есть множество всех множеств.
>когда теория множесТв набирала обороты то её хвалили, типа там рай для математиков и т.д.
Кто хвалил-то? Тот самый Гильберт, который обокакавшись со своей программой, быстренько переобулся в конструктивизм?
>Но потом бац и парадоксы!
Какой нежданчик, а?
>Я на 100% уверен, что в этой молодой теории будут свои парадоксы
Этой молодой теории больше сотни лет. Напомню, что диссертация Брауэра была написана в 1907 году. Пока ни одного парадокса.
Теперь уже и не будет, расслабься. Раньше надо было. С появлением же MLTT все вычисляется на камплюктерах.
Я говорил про ранюю теорию множеств.
>В ZF нет никаких множеств всех множеств.
Игнорировать источник парадоксов тоже выход, да. Если проблему не замечать - само как-нибудь рассосется.

Задать правила его построения. Например, на основе алфавитов (знаков и переменных) и производящих схем (примеры - каноническая система Поста, алгорифмы Маркова). Это классика, это знать надо.
В чем игнорирование? Это я бы сказал конструктивное изменение, воспрещающее строить множества из еще непостроенных элементов.
>Это я бы сказал конструктивное изменение, воспрещающее строить множества из еще непостроенных элементов.
Если множества считаются заведомо существующими математическими объектами (ведь требование их построимости не фигурирует в ZF), почему не может существовать множество их подмножеств?
Ох лол, а ведь несколько сотен лет до появление конструктивизма думали, что в действительных числа нет ничего противоречивого!
В теории NBG (конечно аксиоматизируемой) есть класс всех множеств.
Не вижу проблемы. Как известно, непротиворечивость ZFC эквивалентна утверждению о существовании одного большого кардинала. То есть, по сути, непротиворечивость ZFC эквивалентна утверждению "ZFC непротиворечива". Если вы можете сделать это утверждение по каким-либо, каким угодно, причинам, то вы спокойно можете заниматься математикой.
>В теории NBG (конечно аксиоматизируемой) есть класс всех множеств.
А в коране есть Аллах. Класс всех множеств может быть построен? Или в каком смысле он "есть"?
Да. Я же выше назвал примеры - алгорифмы Маркова, системы Поста. Они сами по себе конструктивные объекты.
>А в коране есть Аллах
А коструктивно математике есть построение.
Чем построение не являеться Аллахом?
Мы можем взять и построить Аллаха по своему желанию.
>ведь требование их построимости не фигурирует в ZF
Чет не очень понимаю, а само ZF это что? Давай так множество это объекты построимые в ZF, зачем путаться с каким-то интуитивным определением начала века?
Но ведь есть контруктивные объекты, построение которых неконструктивно!!!
Как ты построишь число 1?
А можно построить тот факт, что алгоритмические вычислимые объекты исчерпываются этими системами? А, я же забыл, веру нельзя построить конструктивно, ее можно строить только в своем сердце.

>А коструктивно математике есть построение.
Есть. И оно само по себе построимо. Третий раз скажу про алгорифм Маркова.
>Чем построение не являеться Аллахом?
Тем, что оно конструктивный объект и построимо, а Аллах - нет.
>Мы можем взять и построить Аллаха по своему желанию.
Не можем, нет правил построения.
>>390100
>Но ведь есть контруктивные объекты, построение которых неконструктивно!!!
Нету таких.
>Как ты построишь число 1?
Натуральные числа по Маркову - это слова в алфавите |. Т.е. | - это 1, ||| это 3. Если совсем просто - счетные палочки.
>А можно построить тот факт, что алгоритмические вычислимые объекты исчерпываются этими системами?
Возможно построить то, что построимо. Все очеь просто, не нужно ни во что веровать и делать глобальных априорных утверждений.
СТОП! Ты берёшь и считаешь, что существую какие-то абастрактые счётные палочки и слова в алфавите маркова, так? Разве это не верунство? С чего ты взял, что они существуют вообще? И как ты мне построишь число 1 и главное из чего?! Если вся конструктивная математика строиться на натуральных числах, тогда из чего строятся они?! А? Для построения еденицы нужно больше, чем нарисовать палку.
>С чего ты взял, что они существуют вообще?
С того, что их можно построить.
>И как ты мне построишь число 1 и главное из чего?! Если вся конструктивная математика строиться на натуральных числах, тогда из чего строятся они?! А?
Из счетных палочек. Понятие натурального числа базовое, понятное любому человеку и не зависит от языка. Нейрофизиологическая основа - модель ATOM, некоторые нейроны в rIPC, т.н. нумероны. Ну или базовая интуиция времени по Брауэру.
>Для построения еденицы нужно больше, чем нарисовать палку.
Не нужно. Палка - конструктивный объект.
>С того, что их можно построить.
Построй мне число 1, а не эту ёбанную палку!
>Из счетных палочек. Понятие натурального числа базовое, понятное любому человеку и не зависит от языка. Нейрофизиологическая основа - модель ATOM, некоторые нейроны в rIPC, т.н. нумероны. Ну или базовая интуиция времени по Брауэру.
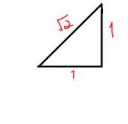
Ага, а я возьму и строию sqrt(2), как гипотенузу треугольника, ПОСТРОЕННОГО из трёх ПАЛОК двух длины 1 и одной длины sqrt(2). Найс. Я только что построил корень из двух и он коструктивный объект! Палки-то использованны. Может для построенния этого числа нужно что-то ещё?
>Не нужно. Палка - конструктивный объект.
Действительно.
Ах да, я всё ещё жду построения числа 1.
>Построй мне число 1, а не эту ёбанную палку!
Это одно и то же.
>Ага, а я возьму и строию sqrt(2), как гипотенузу треугольника, ПОСТРОЕННОГО из трёх ПАЛОК двух длины 1 и одной длины sqrt(2).
>Ах да, я всё ещё жду построения числа 1.
Я говорю о равенстве палки и слова в алфавите |. Это и есть конструктивное построение. Из палок числа строятся дробями (2 палки делим на 3) и т.д.
>Перед его описанием стоит квантор существования.
Ну точно, как в коране. Нарисуй квантор существования перед словом "Аллах" и будет то же самое. Или ты из вкантора существования можешь получить правила построения того, что этот квантор объявляет существующим?
Почему ты считаешь правилами построения только то, что назвал правилами построения священный Марков? Я вот считаю универсум фон Неймана построимым.
>Почему ты считаешь правилами построения только то, что назвал правилами построения священный Марков?
Почему "только"? Это просто один из примеров.
>Я вот считаю универсум фон Неймана построимым.
Если у тебя есть правила его построения, то он и построим. В противном случае встает вопрос, почему ты так считаешь.
Продолжая продолжать.
В начале конструктивный бог сотворил понятие натурального числа.
Земля же была безвидна и пуста, и тьма над бездною, и Дух Брауэра носился над текстом.
И сказал конструктивный бог да будет нормальный алгоритм Маркова, и был нормальный алгоритм Маркова.
И увидел конструктивный бог, что он хорош, и отделил им построимые объекты от непостроимых.
И назвал конструктивный бог построимые объекты интуитивными, а непостроимые тьмой.
И сказал конструктивный бог, да будет частично рекурсивная функция посреди текста, и да отделяет она текст от текста.
И создал конструктивный бог твердь, и отделил текст который под твердью, от текста, который над твердью. И стало так.
И назвал конструктивный бог твердь машиной Тьюринга.
...
И создал конструктивный Господь Бог человека из праха земного, и вдунул в лице его дыхание интуиции времени, и стал человек душею конструктивною.

Так почему же слово| в алфавите "|" не определяет натуральное число 1? Поясни. Я же пояснил, почему таки определяет.
Я нашел нашего конструктивиста на dxdy! Деанон по маске Гая Фокса! И высказывания такие же.
Потому что понятие натурального числа дал человеку конструктивный господь в виде интуиции времени (в трактовке преподобного Брауэра)? Или тебе нужны какие-нибудь нейроны актуальной бесконечности?

Какой годный ответ. Всё это время мы занимались философией, а не математикой.

>Какой годный ответ.
И правда годный. Назвать все неудобные вопросы философией, и вроде как нет проблемы.
Если бы все было так просто. Но нет. MLTT, конструктивные основания (HoTT) это не философия. Брауэра можно попытаться объявить философией, но не конкретные языки программирования с зависимыми типами, например.
Но все равно все сводится к построимости. У Брауэра это свободно становящиеся последовательности, у дальнейших конструктивистов тезис Черча-Тьюринга, а без решение этого сугубо философского вопроса, такая теория просто не претендует на формализацию математики, а просто развивает какую-то область.
>Если у тебя есть правила его построения
У меня есть правила его построения. Смотри, берём пустое множество. Оно будет верум-нуль. Далее берём его булеан - это будет верум-1. Потом булеан булеана - это верум-2. И так далее. На каждом шаге n получаем верум номер n. Если шаг n предельный, то за верум-n считаем объединение всех ранее построенных верумов. За ультимате-верум принимаем объединение всех верумов.
>Как же я проиграваю над этим дрочем на Брауэра,
А что с ним не так? Единственный кто понял как и на чем нужно основывать математику, показал несостоятельность программы Гильберта задолго до Геделя.
>А что с ним не так
>прямо пророк-господь-бог
Слишком много его упоминаний сектантами в своей речи.
Бесконечность "сама по себе", в отрыве от конкретного бесконечного объекта. В классической математике веруют в ее существование, даже если называют вопрос существования философией.
Что значит бесконечность сама по себе и как она выглядит в классеческой математике?

Так ты посмотри, >>390127 какой няшный :3 Такой-то истинный ариец, сычует на дачке, ссыт за шиворот всяким гильбертам, ну как его не упоминать.
>>390131
>К какому объекту привязан алфавит конструктивной математики?
К конструктивным элементам алфавита.
>>390132
Никак не выглядит, в нее веровать надо. Абстракция актуальной бесконечности - одна из базовых абстракций классической математики. Вопрос ее построимости принципиально не ставится, типа это философия. Поэтому остается веровать.
>>390133
С точки зрения MLTT математика это и есть программирование.
Ага, там ключевая фраза, что "я не знаю за конструктивный анализ, но считаю, что ты вот фанатик". Очень умный аргумент.
>какой няшный
Я не тня чтобы внешность мужиков оценивать и не гей.
>сыт за шиворот всяким гильбертам
А я сейчас возьму и нассу за шиворот Брауэру. Гилберт пизже и сделал для математики гораздо больше.
>я не знаю за конструктивный анализ
Он такого не говорил.
>но считаю, что ты вот фанатик
По твоему то же упонимание пророка пять раз за сообщение не сектанство?
>К конструктивным элементам алфавита.
А длина строки конечна или бесконечна? А вариантов символов в ней конечное число или бесконечное? А как это доказать?
Двачую!
Ну берем 0, определяем функцию следования succ. Дальше все это объединяем. Если получилось что-то отличное от пустого типа, то объект построен.
>>390139
>Гилберт пизже и сделал для математики гораздо больше.
Метаматематику, придуманную Брауэром? Или свою программу, несостоятельность которой показал сначала Брауэр, а потом Гедель?
>>390142
>А как это доказать?
Построить. Иначе никак.
Почитать про то что и где сделал Гильберт, можно хотя бы в той же википедии. По значимости это перекрывает всех нынешних погроммистопетушков.
>Я дал описание, как построить верум. Верум построен?
Если в результате применения этих правил он построится - то да.

Как бы не восхвалял своего пророка, по сравнениюю с Гилбертом он так-себе учённый.
Я сомневаюсь, что булеан нуля это вообще конструктивный объект, так скажем. Нуль он в африке нуль, какие у него могут быть множества подмножеств, отличные от него самого, т.е. того же нуля?

Как же тошнит от этих ванаби-интеллигентных петухов. Вы через Вы и Вы погоняет.
МНЕ КАЖЕТСЯ ВЫ НЕНАМЕРЕННО ДОПУСТИЛИ ОШИБКУ; БОЮСЬ, ЧТО ВАМ ПОМЕРЕЩИЛСЯ ЛИШНИЙ НУЛЬ В ЧИСЛЕ.
Готов поспорить процентаж девственников там выше, чем у нас раз в 10.
А меня так конструктивисты бесят!
Готов поспорить процентаж девственников там выше, чем у нас раз в 10.
В булеане нуля содержится ровно один элемент: нуль.
Да. Брауэр так скозал!
Нет, бесконечное. Доказательство Евклида конструктивное, представь себе. Как уже сказано выше, никто не отрицает потенциально бесконечные объекты, если даны правила их построения.
А количество способов ебли твоей мамаши - то конструктивный объект.
Тебе дали правила построения верума. Ты их принимаешь? Если да, то вопрос закрыт.
>Булеан - это множество всех подмножеств.
Ну. А какие подмножества у нуля? Булеан нуля есть 0. И любое их объединение и пересечение тоже 0. Чтобы получилось N, надо брать функцию следования от нуля, s(0) = 1, s(s(0)) = 2 и т.д. Вот это будет конструктивно. А нули гонять смысла нет.
>Булеан нуля есть 0.
Это неверно. У нуля есть подмножество: пустое. Булеан нуля - одноэлементное множество.
Одноэлементное множество, содержащее нульэлементное множество. В качестве нуля можно использовать любой праэлемент.
А не проще взять алфавит | и строить натуральные числа как слова в этом алфавите? А то уже праэлементы какие-то.
Праэлемент - термин, которым можно назвать в том числе твою палочку. Совершенно неважно, каким символом обозначается нуль. Важно, что символ для множества без элементов у нас имеется.
Более минималистичная нотация. Итак, ты принимаешь верум?
Но в том доказательстве не конструируется еще одно простое число, а просто показывается, что должно быть еще одно. Правила, по которому его найти можно, там нет.

Пикрелейтид. Братья, я всё правильно расписал (голубым выделено)? Нужно было тип формально доказать то, что голубым не выделено, но автор учебника уёбок какой-то и примеров даже не дал, не знаю, правильно ли я всё это делаю.
Помогите!
>>390230
Действительно ли, если перемножить все простые числа, следующие по порядку, и прибавить к ним единицу - в результате получится простое число.
Интересно, есть ли какой-либо закон, позволяющий гарантированно на выходе получить простое число, не обязательно всю последовательность. Слышал их много, но интересует такой, самый результативный, чтоб мало пропусков было...
Вот значит, нарыл квадратичный трёхчлен Эйлера:
x² + x + 41, где x - от 1 до 2398
41^2 + 41 + 41 = 1763 = 41·43 (составное)
Ну да. Без актуальной бесконечности какой-то отсос выходит, ведь мы не можем конструктивно построить ВСЕ простые числа.
Ну, вообще-то...
43 не следует за 7, а 7 не следует за 3 в списке простых чисел.
И...
1·2·3·5 + 1 = 31 - простое,
1·2·3·5·7 + 1 = 211 - простое,
Однако,
1·2·3·5·7·11·13·17·19·23·29·31·37·41·43·47·53·59·61·67·71 + 1 = 557940830126698960967415391
= 1063·303049·598841·2892214489673 (составное)
Причем тут актуальная бесконечность? Потенциальная (построимая) бесконечность - совсем другое дело, сто раз уже было сказано. Разница в том, что в нее веровать не нужно, т.к. есть правила ее получения для потенциально бесконечного объекта. А актуальная бесконечность - это догмат веры о существовании бесконечности самой по себе.
Походу, эту вашу теорию множеств и правда можно построить в прувере. https://coq.inria.fr/V8.2pl1/contribs/ZFC.html https://www.ps.uni-saarland.de/Publications/documents/Kaiser_2012_Formal.pdf Т.е. она выводима в зависимых типах, в MLTT. Тогда встает вопрос, зачем она нужна в неконструктивном варианте, если все возможные следствия из нее можно получить на камплюхтере?
Ни одной. Бурбаки писались не для того чтобы их читали а чтобы показать как охуенно они могут.
А разве это не правда с любыми ОСНОВАНИЯМИ МАТЕМАТИКИ?
Всмысле кто вообще за всю историю прочел например Расселовский высер?
>А разве это не правда с любыми ОСНОВАНИЯМИ МАТЕМАТИКИ?
С любыми -нет, не правда. Правда только с сортами добреца типа бурбаков с расселом.
У Бурбаки же больше, чем одна книга. https://en.wikipedia.org/wiki/Nicolas_Bourbaki#Books_by_Bourbaki
Наркоман ты штоле? У бурбаков про основания только первая книга. Остальное уже на основе теории множеств. Н-р, алгебра. Там внезапно про алгебру, а не про основания.
Всё в математике - про основания.
Читай Колмогорова 6-8 класс. Там на основе теории множеств и преобразований про это говорят.

В основном идеи рождаются на конференциях, в неформальных беседах. В наши дни - просто в скайпике говорят и по ходу что-то изобретают.
>Откуда они берут темы для статей?
Даёт научный руководитель.
>У них возникают собственные идеи, и они самостоятельно выводят и доказывают теоремы?
Да.
мимо-со-статьей
Поэтому Вербицкий говорит, что одному математикой невозможно заниматься?
Конечно, одному можно заниматься только аутизмом.
Да хуйня всё это. Если хочешь, чтобы спиздили твои идеи или просто потратить время на бухло и блядей - работай в коллективе. Если хочешь результатов - работай один.
https://terrytao.wordpress.com/career-advice/attend-talks-and-conferences-even-those-not-directly-related-to-your-work/
Если бы он мог, он бы их всех нахуй послал.
>В.В. В деловом отношении Америка меня сразу поразила. В первый же день, когда я приехал в Гарвард, мне вручили ключи от квартиры, от офиса и чек на тысячу долларов. А я был обычным, никому неизвестным аспирантом. Уже тогда на факультете было много математиков из России. Деканом был Дмитрий Каждан. С ним я тоже должен разделить свою премию. Он и его коллеги поддерживали меня в тот период, когда в России я жить уже не мог, а в Америке еще не мог. Помню, как во время своего первого Рождества в Бостоне я в сильном подпитии попал в какой-то негритянский квартал. Там меня обобрали, избили и выбросили на снег. Это, конечно, добавило неприятных ощущений, но и вообще я тогда с жуткой тоской почувствовал, как мне не хватает московских дворов, как мне противно «их» Рождество. Хотелось, чтобы был мой Новый год – елка, мама, подарки.
Однажды пидораха - навсегда пидораха. Ностальгия симптом аутизма. Блядь, убил бы за ключи от квартиры и чек.
А вы говорите жизнь... Не жизнь, а сплошная метафизика!
Конечно. Что есть эта тяга к крайне специфичной зоне комфорта? Оно и есть. Обратный трейт - тяга к новизне (один из биг файва), обусловленный скукой по отношению к прошлому. Но если ты тревожная омежка-аутист, то ты слишком боишься нового и как результат стремишься зарыться в старом. Это форма эскапизма.
Приятно иногда вспомнить прошлое а Володю ещё и негры отпиздили, такой-то стресс; но всё время пребывать в ностальгии, да, аутизм.
Это кусок интервью Воеводского, вот полностью:
http://www.polit.ru/article/2006/08/22/voevod/
> Тем более, что я действительно не специалист
Охуенно.
Я, кстати, ничего не понимаю в этой вашей математике, ребята, но по-моему вы все тут фанатики, и вас всех надо забанить - от греха подальше.
Еще один охуенный аргумент. "А вот пацаны, которых считают крутыми, сказали, что он самый крутой, поэтому результат его работы правильный, а результат работы другого, на букву бэ, - неправильный, и все, кто не считают его плохим и неправильным, - фанатики."
Заебись, чо.
Да это хороший аргумент. Или по-твоему тот же Рыбников, которого пацаны считают полным фриком может быть прав?
Кстати, этот ваш Мотидзука, с ним учОные разобрались? Поняли о чем он писал и что это дает? Или все еще в процессе?
Рыбников просто великовозрастный еблан. В свои-то годы не осилить формулу тяготения Ньютона, которую 10-летняя школота понимает, это просто верх альтернативной одаренности. Покажи хоть один результат работ Рыбникова кроме 1,5 смишных плаката про "русское объемное мышление".
Брауэр просто великовозрастный еблан. В свои-то годы не осилить формулу записи действительныъ чисел, которую 10-классники понимают, это просто верх альтернативной одаренности. Покажи хоть один результат работ Брауэра кроме 1,5 смишных результата про "M встречаеться в записи числа пи".
С каждым уравнением можно связать геометрический образ, например x²=0 — парабола. Это называется алгебраическая геометрия. Некоммутативная геометрия пытается её расширить на случай xy≠yx.
Так и запишем: математику руссов не знает.

В первую очередь у меня горит жопа с верунов, которые считают, что есть понятия истинности и ложности вне человека. В этом плане они ничем не отличаются от каких-нибудь христиан, которые считают, что бог есть вне их воображения.
ай, молодца! даже такому как я понятно
Раз нет формулы, для скатерти Улама, тогда вот...
1.4 млрд. простых чисел:
magnet:?xt=urn:btih:C73C4E9F00AD46369A5893B615AF2790ECD2F8A7&dn=hostingaccounts_bigprimes.net_1400000000-primes.7z
На самом деле, там 1302397653 простых чисел, последнее из которых 30057700549
Это один текстовый файл, размером овер 14 ГБ.
Не каждым блокнотом открывается.
Разделитель - байт 0A. Символ сброса строки.
Резалку построчную на питоне - нашел здесь. https://gist.github.com/anonymous/3d73ab56f61ac9efa85f7898cb6881ff
С её помощью разрезал файл на 13024 txt-шника по 100000 строк в каждом.
Каждая строка - простое число.
.join(chunk)[:-1] вместо .join(chunk) - удаляет сброс строки в конце каждого файла при разрезании.
Кто будет резать всё это - %03d.txt следует заменить на %05d.txt чтобы имена файлов были по порядку и имели одну длину (00000.txt - 13024.txt)
Иначе, при запаковывании в архив, файлы не будут читаться по порядку, а будут паковаться так:
[001, 010-019, 100-199, 1000-1999, ..., 002, 020-029, 200-299,...] а надо по порядку.
Ну да ладно...
Дело вот ещё в чем, анон...
Большинство длинных простых чисел - отличаются незначительно, и их можно было бы упаковать с меньшим объемом,
например, выразив их как последовательность интервалов между простыми числами.
Вот она, эта последовательность: A001223 в OEIS. https://ru.wikipedia.org/wiki/Интервалы_между_простыми_числами
Большинство интервалов (если не все) - являются четными числами, поэтому если разделить эти интервалы на 2, можно было бы ещё более сжать эту последовательность.
Короче, как бы так красиво забить в минимальный объем максимально возможное количество простых чисел последовательно,
ну чтобы развернуть скатерть Улама в 11-ти измерениях из M-теории, в многомерном массиве, например?..Может что-то и получится, лол
Я тебе больше скажу, он ещё и на русском есть.
Где тред нат-петуха?
Что за хуйня? Почему нельзя, как обычно, взять пустое множество и натравить на него аксиомы Пеано?
Поцыки, по чём учить гомоалгебру?
>натуральное число это слово в алфавите |
Здесь порочный круг. Чтобы определить слово, тебе уже нужно понятие числа.
Чтобы что угодно сделать, тебе нужен пространственно-временной континиум, а доказать его ты не можешь, потому что сам им являешься.
Не знаю, чем вам не нравятся аксиомы и определения - мы просто допускаем, воображаем, принимаем на веру. Ты же принял на веру то, что ты разумен и твои выводы могут иметь смысл?
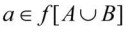
Что обычно в математической литературе подразумевают под записью на пикрелейтед?
Имеют в виду, что элемент a принадлежит функции f вообще - то есть, может лежать как в области заданий X, так в области значений Y? Либо имеют в виду, что a - это именно "выходное значение", то есть, элемент только Y?
Пусть f - функция A->Y, X - подмножество A.
Под символом f(X) понимается множество всех таких y из Y, что существует x из X такой, что f(x)=y.
бамп вопросу, ну



Буду игнорировать этого фанатика и запощу вот такую конструктивную книжку.
http://iphras.ru/uplfile/logic/log17/Li_17_Nepeivoda.pdf
Поехавшие считают нормальную математику грязной и упоминают Брауэра по 7-8 раз на странице. Пиздец. Как же им мозги промывают. Секта ей-богу.
ty.
А когда говорят, что элемент принадлежит функции вообще, без image или pre-image, просто функция от х, это что значит?
Не знаю, нестандартная терминология. Вообще, функция иногда рассматривается как множество пар. Когда говорят, что x - элемент функции f, могут понимать под этим, что x - упорядоченная пара, являющаяся элементом f как множества.
Пусть А -какое-нибудь множество, тогда f(A) - множество, значениями которого являются f(x), где x - элемент из А. В твоём примере. a - элемент множества f(A ОБЪЕДИНЕНИЕ B), тогда существует элемент s принадлежащий A ОБЪЕДИНЕНИЕ B, такой, что f(s)=a. Ясно?
Ты на каком уровне? Если классика: Weibel, но это хардкорчик. Как вариант, можно начать, например, с главы в Лэнге.
это же непейвода, он ваще не математик, а CS-специалист. Этим ребятам надо было преподать чуть-чуть гомологической алгебры, чтоб они похоронили свои конструктивистские бредни.
Ну так, с категориями знаком, с группами тоже вроде бы. А какие пререквизиты к этому Weibel'ю,
А как же N-объект в категории?
Другими словами, начальный объект категории диаграм вида 1->X->X.
Ты так говоришь, как будто сиэс - не математика.
Ты так говоришь, как будто в России Удмуртии есть сиэс.
>будто сиэс - не математика.
Вроде как и математика, но от неё петушиным зашкваром конструктивизма веет.
Конкретно Непейводе это бы не помогло. Он ебнутый, Николай Непейвода.
p.s. вспомнил, что это вроде начальный объект в категории N-алгебр


>Здесь порочный круг. Чтобы определить слово, тебе уже нужно понятие числа.
Понятие числа - интуиция времени, пикрелейтед 1. Никакого порочного круга нет, N-пивень.
>>390765
>Поехавшие считают нормальную математику грязной
Немного неверное определение. Более точное - пикрелейтед2. Дело не в грязи, а в порядке. Математика 1 порядка - чистые ментальные конструкции, созданные методом 2го акта интуиционизма на основе первичной интуиции времени со свойствами из 1 акта интуиционизма. Соотв-но математика 2 порядка - это лингвичтическое описание конструкций 1го порядка. Математика 3го порядка - метаматематика. И т.д.
От того, что ты на ровном месте придумал "порочный круг", он не появляется. Есть алфавит |. Есть производящие схемы построения слов из него. Все ясно определено, просто и понятно.
Есть функция следования, succ. Как пример, наверни нумералы Черча. Попытка свести математику к каким-то аксиомам, оторванным от конкретного конструктивного, построимого, объекта - это изначальный фейл и путь в никуда.
Причем здесь Гаусс? Я тебе говорю: неконструктивные аксиомы обрекают математику.
Строим зависимый тип по этому правилу. Если он не нулевой, имеем готовое доказательство.

Мат индукция - это весьма сомнительная хуйня. Вот смотри: у меня нет ферари. Я спрашиваю своего друга - у него тоже нет ферари, Мой друг спрашивает своего друга - у его друга тоже нет ферари. Таким образом, выстраивая цепочку друзей, я делаю вывод, что ферари не может быть ни у кого.
Мат индукция неявно подразумевает некую предсказуемость математических сущностей, которая, однако, не была доказана.
>>390806
Человек есть мера всех вещей: существующих - в том, что они существуют, и несуществующих - в том, что они не существуют (Протагор)
Понятие чисел интуитивно и просто воспринимается человеком как данность, вроде "два - это когда корова и еще корова".
А все кобылы чёрные, да, знаем. Проследуй под шконку.
Забудь про индукцию. У тебя из-за нее все проблемы. Тебе же сказали, есть заданный алфавит, есть заданные производящие схемы. Хоть формула Гаусса, хоть что.
>Понятие чисел интуитивно и просто воспринимается человеком как данность, вроде "два - это когда корова и еще корова".
Вообще, не только человеком. Я уже упоминал нейрофизиологическую модель ATOM, подобное понятие числа есть и у животных.
>>390817
Я тебе уже подсказал, как это сделать на любом языке с зависимыми типами.
А не надо подсказывать, ты тут не пророк. Просто покажи готовое доказательство. 100% в нём будет метаиндукция.
В нормальной математике формулу Гаусса можно доказать парой строчек, а в вашей секте как с этим дела обстоят?
>100% в нём будет метаиндукция.
Будет зависимый тип, конструктивный объект. Третий раз тебе говорю - все эти твои псевдоумные слова, не привязанные к конструктивному объекту - ментальный онанизм.
Доказательство без возможности построить объект - это манядоказательство. Тебе сто раз сказано, что единственный способ доказать - это построить. Покажи, как построить твою формулу Гаусса и сам увидишь ответ.
Это я от тебя доказательство прошу, алё. В вашей "математике" формула Гаусса вообще есть?
Я тебе больше скажу, конструктивис и есть N-петух.
За шиворот слили, да.
>>390826
Давно дал и неоднократно. Кукарекать что ваши пруфы не пруфы можно сколько угодно.

Пикрелейтед твой N, пивень. Алфавит | и слова из него и есть натуральные числа по Маркову. Кукарекай сколько угодно, факт есть факт.
Понимаешь, конструктивисты - ебанутые. У них вообще остутствует доказательства в их исходном смысле.
Второй пик обазац снизу.
>>390765
По позиции, блядь.
>У них вообще остутствует доказательства в их исходном смысле.
Что есть "доказательство в исходном смысле"? Доказать что-то можно только построением этого чего-то. Иначе что ты доказываешь? Пустоту? Аллаха?
>>390832
А зачем отличать? Одна палка - это число 1. Две - число 2 и т.д. 1 ничем не отличается от 1.
Чувак, вот смотри. Формула для суммы первых n натуральных чисел. Классическая формула, её все знают. Любой первокурсник доказывает её на первом курсе. Гаусс её в школе доказал. В этом треде почти любой анон без труда сможет написать доказательство этой формулы, которое любой нормальный математик без возражений примет.
В чём для тебя проблема просто ВЗЯТЬ И ДОКАЗАТЬ эту несчастную формулу? Если в твоей "конструктивной математике" эта формула вообще имеет место, конечно. Просто, блядь, покажи, как вы эту формулу доказываете. Если вообще доказываете, сектанты ебаные.
Тебе же говорят - формула в данном случае производящая схема. Ее элементы - слова алфавита. Строим зависимый тип из заданного алфавита по заданной производящей схеме в любом языке с зависимыми типами. Получаем тип. Если он не пустой - формула доказана, если пустой - она ложна. Что именно из этого тебе непонятно?
>Что есть "доказательство в исходном смысле"? Доказать что-то можно только построением этого чего-то. Иначе что ты доказываешь? Пустоту? Аллаха?
Вот про это я и говорю, поехавшие. Просто отбитые люди. Доказать в исходном смысле - вывести из аксиом тоерему. Ещё и ссылаеться постоянно на пустоту, Аллаха и веру. Как же беднягам мозги промыли.
>>390835
Что значит зачем? Ты не хочешь отвечать на этот вопрос, потому что, в нём используются натуральные числа для упорядочевания множества палок. И для нумерации палок нужны числа, иначе ты не отличишь одну палку от другой.
Ты сам ее написал. Формула - это и есть доказательство. Вопрос только в том, что из нее построится. Если непустой тип - то она верна.
>>390839
>Доказать в исходном смысле - вывести из аксиом тоерему.
Аксиомы откуда возьмешь?
>>390840
Мне специально ради тебя программирование осваивать? Согласись, крайне шаткий аргумент ты притащил. Тебе ж говорят, в любом случае что-то построится, даже если пустой тип.
>Ты не хочешь отвечать на этот вопрос, потому что, в нём используются натуральные числа для упорядочевания множества палок. И для нумерации палок нужны числа, иначе ты не отличишь одну палку от другой.
Тебе уже сказали про нумералы Черча. Не нужны никакие мистические понятия, оторванные от конкретного построения.
>Ты сам ее написал.
Нет, я не писал никакого конструктивного доказательства. Я призываю тебя взять и написать конструктивистское доказательство того, что у вас понимается под формулой Гаусса.
>Мне специально ради тебя программирование осваивать? Согласись, крайне шаткий аргумент ты притащил. Тебе ж говорят, в любом случае что-то построится, даже если пустой тип.
Просто охуеть. Что-бы доказать такую простую формулу нужно столько ебатни. Нахуй тогда ваше говно вообще нужно? Оно того не стоит.
Исследования продолжаются.
Заскринил твой пост. Буду использовать его для унижения конструктивистов.
Не в защиту петуха будет сказано, но это аргумент уровня /b/. Всё-таки чтобы abc-гипотезой обмазаться придётся поебаться с IUT и никто не даже не вопрошает нахуя это говно нужно.
Ну так формула Гаусса - это не abc-гипотеза как бе, её доказательство все знают.
Формула верна для n=1, очевидно. Если формула верна для k, то она верна и для k+1, так как 1+2+...+k+k+1 = k(k+1)/2 + (k+1) = (k(k+1) + 2(k+1))/2 = (k+2)(k+1)/2. Следовательно, формула верна для любого натурального числа n.
Теперь ты докажи на свой манер.
Сам спросил - сам принес пик с ответом. Не может быть никаких аксиом вне реализующих эти аксиомы объекта. Поэтому следующий раз не неси хуйни, что я какие-то там аксиомы принес, окда?
>>390856
Ну вот видишь, ты же сам и написал производящие схемы для построения этой формулы. Очевидно, что для любого k получается результат отличный от нуля. Это и есть построение, т.е. конструктивное доказательство.
Функцией следования, например, схемами построения нумералов Черча.
>>390860
Я же попросил, не неси хуйни.
Ну и как ты из этой Succ выводишь, что формула верна для каждого натурального числа?
>Третий раз прошу - хватит нести хуйню. Читай, что тебе пишут.
Ебанько, тебе тоже самое посоветовать. Получаеться, в конструктивной математике есть аксиомы. И она ничем не лучше формализма.
От тебя просят предъявить конструкцию, которая из множества гипотез {P(1), P(k)→P(k+1)} позволяет вывести формулу ∀nP(n).
>Если она верна для k, то она верна и для следующего за k.
И что с того? Как ты получаешь, что она верна для всех натуральных чисел?
Допустим, заменил. Получилось множество гипотез {P(1), P(k)→P(Succ(k))}
Дальше что? Квантор всеобщности как возникает?
>Ну если так яскозал даун с мейлру, то значит точно есть.
Ага, ЕСЛИ ТАК ЯСКАЗАЛ БРАУЭЕР, ЗНАЧИТ ТАК ОН ЕСТЬ!
ЕСЛИ ТАК ЯСКАЗАЛ КО-КО-КОНСТУРКТИВИСТ С ДВАЧЕ, ЗНАЧИТ ТАК ОН ЕСТЬ
ВЕРУНЫ ВСЮДУ ВЕРНУ, АКСИОМ НЕТУ, АКСИОМЫ ЭТО АЛЛАХ, ВЕРУНЫ, ДОКАЗАТЬ ЧТО-ТО ЭТО ЕГО ПОСТРОЕНИЕ
СЧИТАЕМ НА ПАЛОЧКАХ
БРАУЭР
Построением соответствующего ей объекта. Т.е. применением ее подряд ко всем натуральным числам. Т.к. реально на это не хватит никаких ресурсов, результат вычисляется только для заданных чисел (lazy evaluation).
>>390875
>Квантор всеобщности как возникает?
Только непосредственным построением. Иначе никак, остается только веровать.
>Только непосредственным построением.
То есть чтобы утверждать, что формула Гаусса верна для n=100500, тебе нужно построить 100500 формул? Ты серьёзно?
Да, я абсолютно серьезно. А ты серьезно считаешь, что вот написал квантор всеобщности, и что-то доказал? А я вот возьму коран и нарисую там квантор существования возле слова "Аллах", и чем такое "доказательство" будет хуже твоего?
Понимаешь, тут полтреда спора с этим ебланом. Ты хочешь, чтобы мат-тред так выглядил? Даже мемасы лучше этого.
Поддерживаю этого оратора. Пожаловался что конструктивистопетух всех заебал.
Нет, это репрессии и подлость.

У тебя на пике констуктивист спит, которому снится о том, что Гилберт не прав?

Ясно, я понял. На пике конструктивист, который думает о том, как бы ему в мат-тред обоссать Гилберта.
А чего ты ждал от фанатика конструктивизма?
>Что-бы доказать такую простую формулу нужно столько ебатни. Нахуй тогда ваше говно вообще нужно? Оно того не стоит.
Стоит. Вся математика - про ебатню. Поскольку всю простую ебатню уже исследовали вдоль и поперек, мы вступаем в новую эпоху математики - мы будем писать книгу с доказательством теоремы "1+1 = 2". Главное, что математикам есть чем заняться, и они могут поныть о том, что им не дают финансирования/мест.
>мы будем писать книгу с доказательством теоремы "1+1 = 2". Главное, что математикам есть чем заняться, и они могут поныть о том, что им не дают финансирования/мест.
А что, уже есть неконструктивные доказательства, что 1+1=2, т.е. непротиворечивости арифметики?

Так и представляю Вейля в роли N-петуха!
Не угадал оба раза.
У них, кстати, проблемы с Арнольдом были, как тут пишут.
http://mathoverflow.net/questions/153604/the-arnold-serre-debate
Нет, он - ℕ-петух
Только в английской литературе.
А он здесь причём?
Только в математике людей. У животных своя расчеты.
Неконструктивные, маня. Метаматематику Брауэр придумал, >>390889 еще до того, как Гильберт в нее переобулся, не зашквар ли вам такими методами пользоваться?
Врядли Вейль был таким веруном, и помимо этого если бы среди Бурбаков был N-петух они бы нихуя не написали бы, только срались о мета-индукции на каждом собрании.
>8-9 октября(суббота-воскресенье) будет открыт набор в модераторы. Не пропустите возможность попасть в молодой, стремительно развивающийся коллектив! Об открытии набора будет сообщено дополнительно.
Аноны, которые хуесосят модера, а чего бы вам самим не подать заявку? Будите конструктивиста терепть.
Мне нельзя, я - вахтёр.
Не стоило петю петей называть, он может ещё больше обидеться и пощёчину дать. дело Курина
А если без ерунды - пусть будет, меня, например, очень веселит этот тред.
Да.
>до того
>переобулся
А чем он раньше занимался? Смешно говорить, что один из основателей метаматематики в нее переобулся.
А красные палочки - мусорские?
Ты хотел сказать дауна? Или это тред математики 1930 года, где все в ахуе сидят еще?

Ну ща я на смотрящего подамся, и мы с пацанами будем решать нарушаешь ты что-то или нет.
мимо-вахтёр
Пацаны решат.

>Программа Гильберта, слышал? Опять же, Брауэр доказал ее неработоспособность еще до Геделя.
Доказал? Тащи сюда пруф, навроде теорем Геделя. Или просто петушился, что "не выйдет"? Так таких скептиков было дохуя, тот же Пуанкаре.
>Хуйней, если одним словом. Программа Гильберта, слышал?
По этой программе работали Цермело, Фон Нейман, Гедель, Борель, Аккерман, генцен... Хуйня в общем, раз вася так сказал.
Однако остаётся еще один вопрос: какие конструктивные доказательства вообще бывают, ибо конструктушок не привёл ни одного.
Например, с помощью трансфинитной индукции Генценом.
Двачую, ко-ко-консрутивист только свои клювом чесать может.

Ты просто читать не умеешь, какая тебе математика. Я же неоднократно упоминал Маркова. Алфавит | и производящие арифметические схемы, вот и все что нужно для построения.
>>390967
Я тебе принес ссылку на эту его работу, статья 1928А. Сама статья есть в сборнике его работ под редакцией Гейтинга, но на немецком.
Ты мне скажи, там есть доказательство или там просто кукареку? Я же уже сказал, что среди кукареку Брауэр далеко не первый.
Если же там есть доказательство, то получается Гедель незаслуженно украл славу у Брауэра, что вряд ли.
Только кукареку. В конструктивной математике вообще нет такого понятия, как доказательство. Ко-ко-косруктивист считает, что если что-то можно построить, то он что-то доказал. Еблан он, короче.
>Ты мне скажи, там есть доказательство или там просто кукареку?
Ты не понял. Там объяснение, почему такой подход в принципе неработоспособен с точки зрения интуиционизма. Как позже выяснилось, Брауэр был прав.
>>390974
>В конструктивной математике вообще нет такого понятия, как доказательство.
Куда ты лезешь, клован? Выше ты кукарекал про какие-то аксиомы, в которые я верую, так и не привел пример. Теперь очередные кукарекания школотрона? Я уже сто раз объяснял, что есть доказательство. Если оно не подразумевает возможности построить то, что оно доказывает, то что оно вообще доказывает?

>Ты не понял. Там объяснение, почему такой подход в принципе неработоспособен с точки зрения интуиционизма. Как позже выяснилось, Брауэр был прав.
Ну повторил за умными дядями, молодец. Правда интуиционизм тут не причем, Гёдель ведь был формалистом.
И да, вот тебе в догонку - с чего ты взял, что твоё доказательство вообще правильно? Чем доказательство от противного неправильное? Или те же аксиомы? Твоя конструктивная математика основывается на аксиоме, что объект можно построить, то он доказан. Просто ты не называешь её аксиомой. Даун.
>Там объяснение, почему такой подход в принципе неработоспособен с точки зрения интуиционизма.
>Там объяснение, почему такой подход в принципе неработоспособен с точки зрения христианства.
Ясно.
Вот этого двачну!

А теперь смотри внимательно на пикрил, шваль, голубое - это то, что нужно было формально доказать.
Ниже три строки под голубым - моё доказательство.
У меня всё получилось правильно, обезьяны? Ясно, что мысль правильна и доказывать надо именно так, я говорю именно о записи - правильно ли я всё формально записал и оформил? Можно так записывать? С местного уёбка брал пример, если что.
Сосите.
Зарепортил.
>так и не привел пример
Что все частичные алгоритмические функции частично рекурсивны. Можно назвать это главной догмой современных интуиционистов. Ну, а там делить уже на веру в физическую машину или веру в какой-нибудь автомат.
>У меня всё получилось правильно, обезьяны?
Нет.
>правильно ли я всё формально записал и оформил?
Нет.
>Можно так записывать?
Нет.
Возможность построить объект этот объект и доказывает. Т.е. доказывает возможность его существования.
>>390979
>с чего ты взял, что твоё доказательство вообще правильно?
С того, что есть фактически построенный объект, соответствующий доказательству.
>Чем доказательство от противного неправильное?
Тем, что не дает возможность построить объект. Если такой возможности нет, чем ты докажешь правильность твоего доказательства?
>>390986
Это не догма. Знаешь почему? В нее веровать не нужно. То, что какое-то правило работает в каждом отдельном случае, никак не означает, что его необходимо обобщать на все случаи и потом уже исходить из обобщения, а не из конкретного случая. То же самое можно сказать про "аксиому" выше. Это не аксиома.
Ты думаешь мой пост ему сильно помог?
А как его можно переформулировать, тварь? Элемент из A не принадлежит объединению А и другого множества B. Ебанат тупой, как это записать формально?
>Возможность построить объект этот объект и доказывает. Т.е. доказывает возможность его существования.
Наличие первородного греха показывает что Иисус не зря умер за наши грехи
Не кудахтай тут, ублюдок. Напиши мне решение лучше.
> Или те же аксиомы? Твоя конструктивная математика основывается на аксиоме, что объект можно построить, то он доказан. Просто ты не называешь её аксиомой. Даун.
А чего ты на это ничего не написал? Ах, да ведь в ко-ко-консруктивной математике нет аксиом. А вот хуй, есть.
Ты и правда дебил, если не видишь разницы между этими утверждениями.
>То, что какое-то правило работает в каждом отдельном случае, никак не означает, что его необходимо обобщать на все случаи и потом уже исходить из обобщения, а не из конкретного случая
Получается нельзя вывести никакого физического закона? Интересная вера, ядреная.
>>390997
Разница действительно есть. Утверждение про иисуса это теорема, а у тебя аксиома, определяющая существование.
>Мы с матерью как-то изобрели для него насмешливое прозвище, и с тех пор, в разговорах между собой, никогда не называли его по имени. Это прозвище глубоко врезалось в мою память; еще долгое время после смерти матери я так и называл его (разумеется, про себя). Сейчас мне кажется, что мое пренебрежительное отношение к нему сформировалось определенно не без участия моей матери. Она всю жизнь отличалась сильным характером, и даже после ее смерти я еще лет двадцать, быть может, по-прежнему находился под ее влиянием. Я безоговорочно перенял ее систему ценностей, во многом определившую ее образ жизни. Мягкий, приветливый, нисколько не воинственный характер моего друга без лишних слов был сочтен «ничтожным» - и немедленно стал объектом насмешки.
Шурик та альфачем у нас был, обоссал бы всех ИТТ

МНЕ НУЖЕН ОДИН ЕБУЧИЙ ПРИМЕР НАХУЙ! СОСАТЬ МОЙ ХУЙ, БЛЯДЬ!
>С чего ты взял, что это аксиома?
А из чего она следует? Если принимаеться безаговорочно, и не подлежит критике, значит аксиома.
>>391004
Cuck, please.
>>391001
Разделяй язык высказываний и множеств. Есть высказывание P, исходное утверждение. Есть знаки этого языка. Во второй строчке у тебя икс принадлежит высказыванию, но это не имеет никакого смысла в рамках языка множеств.
Ты говоришь чего-то про непротиворечивость арифметики, но тем не менее подразумеваешь, что (возможно) существует класс задач, недоступный конструктивной математике вообще. Как с таким противоречием можно жить?
>А из чего она следует?
Ты скажи, из чего она следует. Ты же и придумал, что это аксиома. Т.е. перевернул все с ног на голову. Хотя изначально это вопрос существования в математике. Объект существует, если может быть построен. В противном случае, о существовании можно говорить только в каком-то мистическом смысле, оторванном от конкретного существующего объекта.
Ты просто не называешь это аксиомой, но эта аксиома. Назовём её аксиомой существования.
Когда я тебе в прошлый раз подробно расписовал, ты даже мне спасибо не сказал. Неужели ты думал, что я тебе буду помагать после такого?
Блядь, друг, прости. Учусь самостоятельно теории множеств третий день, но в учебниках для начинающих cuck'и даже примеров не дают. Ни одного просто нахуй примера за всю тему. Вот и выходит у меня такая хуйня в упражнениях.
Как это нужно написать, скажи, пожалуйста.
>тем не менее подразумеваешь, что (возможно) существует класс задач, недоступный конструктивной математике вообще.
Ты можешь прямо назвать этот класс задач?
>>391012
>Ты просто не называешь это аксиомой, но эта аксиома. Назовём её аксиомой существования.
И что это за аксиома, если от нее можно просто отказаться? Существование построенного объекта есть его существование. Зачем мне какая-то аксиома для этого?
Зачем тебе это надо? Забей на эти задачи.
Вообще: х в А и не(х в А и х в В) = х в А и (х не в А или х не в В) = (х в А и х не в А) или (х в А и х не в В) = х в А или х не в В.
Не выёбывайся знанием английского и иди читать Пратусевича. Как прочтёшь первую главу пересаживайся на свои английские учебники.
>Ты можешь прямо назвать этот класс задач?
Конечно, не частично-рекурсивные алгоритмически вычислимые функции.
>Зачем мне какая-то аксиома для этого?
Ну тогда пусть построение объекта не есть его существование. Dixi.
Начинается блядь. Ну зачем ты проецируешь своё незнание английского на меня? Мне вообще похуй, от зубов отлетает. Я русский знаю хуже. Чего ты начал? Хуй соси.
Или листочки решать для матшкольников 57 школы.
>И что это за аксиома, если от нее можно просто отказаться
Попробуй.
>Существование построенного объекта есть его существование
То есть непостроенный объект, который можно построить, не существует? Ух ты. Например, нельзя построить число Грэма в степени числа Грэма. У тебя не хватит бумаги, как минимум. Здорово, не все натуральные числа существуют и могут быть конструктивными объектами.
С какой стати алгоритмически вычислимая функция не конструктивна? Если есть алгоритм для ее построения?
>Ну тогда пусть построение объекта не есть его существование.
Еще одна аксиома?
Еблан, там просто понят написанно. С основ логики до примеров с доказательствами. Подробно. Лучше для таких cuck'ов, как ты, просто нет варианта.
>>391023
А что ты запостил?
Помню. Мне плохо видно было, я тебе ещё говорил про ручку. Сложно читать из-за освещения и карандаша. Так бы проверил.
ИТТ одни тянки. Мы не обращаем внимания на тихих хикк, нам нужны буйные альфачи!
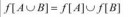
Спасибо! Забыл про эту хуйню с отрицанием всего выражения. Глупо.
>Зачем тебе это надо?
По сути мне это не надо, но это же просто оргазмъ, когда докапываешься до правильного решения.
Я вот сам правильно доказал пикрелейтид. Пол дня оргазмъа!
Да и, блядь, как я понимаю, в высшей математике начального уровня множества везде, почему бы не уметь очень хорошо с ними работать, знать основные свойства? Да и я так скилл доказательства развиваю.
>>391017
Нахуй с ним иди, друг. Алсо, это >>391020 тоже мой друг. Который тоже идёт нахуй.
>С какой стати алгоритмически вычислимая функция не конструктивна? Если есть алгоритм для ее построения?
Есть, но его нельзя записать в терминах частично рекурсивной функции или машины Тьюринга.
>Еще одна аксиома?
Отрицание твоей. Считаешь, ответ не нужен? Но тогда чем конструктивная математика отличается от библии, там же тоже можно верить и не верить?
Оргазмы надо получать ебя баб, cuck, а не решая математические задачи.
Во всех учебниках начального уровня необходимая ТМ даётся во введении(множества, операции над ними[пересечение, объединение, разность, симметрическая разность], отображения, классы эквивалентности, законы Де-Моргана).
Чтобы поддерживать баланс. Если прибывать в состоянии омеги 24/7, то и до куколда недалеко.
Получается, альфачи в интернете омегами притворяются? Создают еот треды, поёбывая тянок в пердачелло?
А я думал, что кукодлами становятся алфачи, чтобы поддерживать баланс и не стать омегами.
93.7% альфачей какнуты религией и всякой социальной поеботней вроде педоистерии. Еще больше омег правда.

>>391041
Им не нужно поддерживать баланс. Они будут скатываться в сторону альфачества, это не зашкварно, в отличии от скатывания в омеганство.
Понимаешь, когда альфачество переполняеться, то оно меняет свой знак и становится омеганством. И для разрядки аьфач становится куколдом.
Какой ужос! И что теперь делать?
Зачем ты отвечаешь говорящей собаке?
Спасибо.
Аноны, не вычисляете интегралы всю жизнь - не стать вам великими математиками! Топосы, схемы какие-то неправославные! Фу! От лукавого!
ПОНТРЯГИН НАША ГОРДОСТЬ! ПРАВОСЛАВИЕ!
Зарепортил уёбка
Это копия, сохраненная 18 января 2017 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.