Это копия, сохраненная 22 ноября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.




Общие курсы
М. И. Сканави: "Элементарная математика".
Алгебра
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
С. Б. Гашков: “Современная элементарная алгебра”.
Геометрия
А. Д. Александров, А. Л. Вернер, В. И. Рыжик: “Геометрия”. Учебник для 10-11 классов. Базовый и углубленный уровни.
Я. П. Понарин: “Элементарная геометрия” в двух томах. Первый том - это планиметрия, а второй том - это стереометрия.
А. Ю. Калинин, Д. А. Терешин: “Геометрия”, 10-11 классы. Годный учебник.
Тригонометрия
И. М. Гельфанд, С.М. Львовский, А. Л. Тоом: “Тригонометрия”. Название говорит само за себя. Много геометрических и физических интерпретаций + комплексные числа, как бонус.
Начала анализа
Б. М. Давидович: “Математический анализ в 57 школе“.
БАЗОВЫЕ КУРСЫ ДЛЯ СТУДЕНТОВ:
Общая алгебра
Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
М. Атья, И. Макдональд : "Введение в коммутативную алгебру".
А. Л. Городенцев: "Алгебра. Учебник для студентов-математиков". Вырос из лекций НМУ. Читать параллельно с Винбергом (Винберга читать в первую очередь).
И.Р. Шафаревич: “Основные понятия алгебры“. Замечательный обзор вообще того, что такое алгебра, как она выглядит и какое место она занимает в математике. Примеры, приложения и прочая конкретика.
E. Connell: Elements of Abstract and Linear Algebra". Хорошая первая книга по алгебре, да и математике вообще.
P. Grillet: "Abstract algebra". Очень лаконичный и понятный учебник. Надо знать элементарную теорию чисел, про индукцию, про множества и функции. Линейной алгебры нету.
J. Rotman: "Advanced modern algebra". Ротман сильно разжевывает. Задачи слишком простые для уровня учебника. Линейная алгебра есть.
M. Artin: "Algebra". Американский Винберг. Группы Ли, упор на геометрию. Задачи неудачные.
I. Herstein: “Topics in Algebra“. Прекрасные задачи, отбор материала очень устарел, почти что Ван дер Варден.
P. Aluffi: "Algebra, Chapter 0". Если ты в состоянии ее осилить, бери и забывай про остальные книжки из списка. Линейная алгебра есть.
Линейная алгебра
В. А. Ильин, Э. Г. Позняк: “Линейная алгебра“. Один из классических и самых популярных курсов линейной алгебры.
Д. В. Беклемишев: “Курс аналитической геометрии и линейной алгебры“.
И. М. Гельфанд: "Лекции по линейной алгебре". Не даётся определение определителя.
А. И. Кострикин, Ю. И. Манин: "Линейная алгебра и геометрия". Затрагивается темы геометрий и связей с квантовой механикой. Не даётся определение определителя.
S. Axler: "Linear algebra done right". Подход без определителей (почти). Одна из самых популярных книг за рубежом.
S. Treil: "Linear algebra done wrong". Не такая популярная, как Axler, но тоже хвалят, да. Определители есть.
G. Shilov: "Linear Algebra". Определитель появляется на первой странице.
K. Hoffman, R. Kunze: "Linear Algebra". Классика за рубежом.
P. Halmos: "Finite-Dimensional Vector Spaces". Тоже классика.
P. Peterson: "Linear Algebra". Не особо знаком, но выглядит аккуратно. Что-то вроде Акслера.
S. Roman: "Advanced Linear Algebra". Хороший учебник по линалу. Но нужно знать элементарные свойства матриц и определителей.
Математический анализ
T. Tao: “Real analysis“. Один из самых популярных курсов математического анализа на английском языке.
C. Pugh: "Real Mathematical analysis". Более простая версия Рудина с картинками. Норм книга, но не самая лёгкая.
У. Рудин: "Основы математического анализа".
В. А. Зорич: "Математический анализ". Первый том посвящен классическому анализу. Много примеров, много материала, в том числе даются в начале основы матлогики и теории множеств, а также функций между ними.
Р. Курант: "Курс дифференциального и интегрального исчисления". Идеален с точки зрения первого знакомства с теорией, но имеет достаточно сложные упражнения.
Г. М. Фихтенгольц: "Курс дифференциального и интегрального исчисления". Хорош как повторительный курс.
С. М. Львовский: "Лекции по математическому анализу". Записки лекций из НМУ. Нужно знать основы калькулюса.
Г. Г. Харди, Д. Е. Литтлвуд, Г. Пойа: "Неравенства".
Н. Н. Лебедев: "Специальные функции и их приложения".
Г. П. Толстов: “Ряды Фурье“.
Дифференциальные уравнения
С. Фарлоу: “Уравнения с частными производными для научных работников и инженеров“.
Вариационное исчисление
И. М. Гельфанд, С. В. Фомин: " Вариационное исчисление".
Топология
V. Runde: "A taste of topology". Неплохая книга по метрическим пространствам и общей топологии, затрагивает фундаментальную группу.
J. Strom: "Modern classical homotopy theory".
T. Dieck: "Algebraic topology".
M. Crossley: "Essential Topology". Пререквизит для изучения алгебраической топологии. Не затрагивает тему метрических пространств.
КУРСЫ ДЛЯ ПРОДВИНУТЫХ МАТЕМАТИКОВ
Математический анализ
А. И. Маркушевич: "Теория аналитических функций".
S. Ramanan: "Global calculus".
H. Amann, J. Echer: "Analysis".
W. Fidcher, I. Lieb: "A Course in Complex Analysis: From Basic Results to Advanced Topics".
Дифференциальные уравнения
В. И. Арнольд: “Обыкновенные дифференциальные уравнения”. Книга для уверенных в себе математиков. Диффеоморфизмы, фазовые потоки, гладкие многообразия. Слава Гермесу Трисмегисту!
Теория категорий
С. Маклейн: "Категории для работающего математика".
Р. Голдблатт: "Топосы. Категорный анализ логики".
Дифференциальная Геометрия
К. Номидзу: "Основы дифференциальной геометрии".
J. Lee: "Manifolds and DIfferential Geometry".
L. Nicolaescu: "Lectures on the Geometry".
P. Michor "Topics in Differential Geometry".
Алгебраическая геометрия
Д. Мамфорд: "Красная книга о многообразиях и схемах".
В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”.
В. И. Арнольд: “Вещественная алгебраическая геометрия”.
Ю. И. Манин: Введение в теорию схем и квантовые группы“.
R. Vakil: "Foundations of algebraic geometry".
S. Bosch: "Algebraic Geometry and Commutative Algebra".
U. Gotz, T. "Wedhorn: Algebraic Geometry".
E. Harris: "The Geometry of Schemes".
Топология
А. Хэтчер: "Алгебраическая топология".
J. Munkres: "Topology". Книга - жесткий учебник по теоретико-множественной топологии. Много ненужного для других областей математики.
ИНТЕРЕСНОЕ:
Цикл “Manga guide to...“. Популярное изложение различных областей математики (и не только), оформленное в виде манги. Увы, без фансервиса.
Н. А. Вавилов: “Конкретная теория групп I: основные понятия“. И вообще все остальные книги (и лекции!) Вавилова.
П. С. Александров: “Введение в теорию групп“. Просто о сложном. Несколько вольный язык изложения, местами затрудняющий восприятие.
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”.
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
Н. Я. Виленкин: "Рассказы о множествах". Теория множеств для широкого круга читателей.
М. М. Постников: “Теорема Ферма. Введение в теорию алгебраических чисел”.
Н. Стинрод: “Первые понятия топологии“.
А. Я. Хинчин: “Три жемчужины теории чисел“.
О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов: “Элементарная топология”.
Я. П. Понарин: “Алгебра комплексных чисел в геометрических задачах”.
А. А. Заславский: “Геометрические преобразования”.
В. Акопян, А. А. Заславский: “Геометрические свойства кривых второго порядка”.
В. И. Арнольд: “Геометрия комплексных чисел, кватернионов и спинов”.
В. В. Прасолов: “Геометрия Лобачевского”.
Д. В. Аносов: “Дифференциальные уравнения: то решаем, то рисуем”.
В. В. Прасолов: “Наглядная топология”.
Д. В. Аносов: “От Ньютона к Кеплеру”.
М. Клайн: “Математика. Поиск истины“.
Д. Пойа: “Математическое открытие“.
Л. Кэрролл: “Логическая игра“.
Д. Пойа: “Как решать задачу“.
О. Я. Виро, Д. Б. Фукс: "Введение в теорию гомотопий. Гомологии и когомологии".
A. Ostermann, G. Wanner: "Geometry by its history".
T. Sundstrom: "Mathematical reasoning writing and proof". В книге объясняется что такое математическое доказательство, математический факт и каким образом их можно придумывать. Начала теории множеств.
D. Dummit R. Foote: “Abstract Algebra“. Много примеров, задач, но страшно скучный учебник, его нужно держать как справочник.
ПОЛЕЗНЫЕ РЕСУРСЫ:
Библиотка "Квант": math.ru/lib/ser/bmkvant
Высшая математика просто и доступно, по 2 курс включительно: mathprofi.net
Необъятная онлайн библиотека: gen.lib.rus.ec
Обсуждаем и дополняем!
Интересно, почему Ибн Ал-Хайсам не отображается?
А можно поподробнее, я думаю, для многих было бы интересно.
2. https://arhivach.org/thread/157894/
3. https://arhivach.org/thread/165665/
4. https://arhivach.org/thread/175432/
5. https://arhivach.org/thread/175434/
6. https://arhivach.org/thread/174050/
7. https://arhivach.org/thread/181477/
8. https://arhivach.org/thread/177783/
9. https://arhivach.org/thread/180129/
10. https://arhivach.org/thread/185246/
11. https://arhivach.org/thread/188615/
12. https://arhivach.org/thread/190551/
Хуй пизда апокалипсис, не правда ли?
Мы уже тринадцать битых тредов поливаем говном манясписок манялитературы из оппоста, а тут прибегает еще один даун и говорит "надо бы еще говна в список запихнуть"
Раз уж в ОП-пик Александров, то почему из списка была удалена его книга "Введение в теорию множеств и общую топологию"?
Есть два стула. На одному гомологии точены, на другом гмологии дрочены.
На какой стул сам сядешь, на какой алексндрова посадишь?

Ну построй так чтобы была биекция из компакта, разобрались же вроде в прошлом треде.
Ниче не разобрались, никто не смог даже приблизиться к решению.
Заливали уже, и не раз. Перекотчик ложил на списки хуй и копировал прошлые.
А ти сам и перекоти
Чому параша? Довольно годно и интересно поясняет, в форчановской /sci/ вики ее тоже советуют.
>Заливали уже, и не раз
Лол, это те самые знаменитые списки, где полторы книги + ссылки на программу Вербицкого и 4chan? Потому, Я СКОЗАЛ ЧТО АСТАЛЬНОЕ НИНУЖНО РЯЯЯ!!!!
Ну повесьте кто-нибудь кнопку vote или че-нить такое. Пусть народ волю изъявит по каждой книжке. Говно или охуенно.
Так в этом и была задумка изначально, представь себе. Этот список - компиляция рекомендаций 5 (по крайней мере я столько насчитал) анонов + еще двух математиков из реальной жизни, которую из треда в тред предлагалось обсуждать и дополнять. Увы, главный аргумент против той или иной книги, до сих пор, был "говно". Даже умственно неполноценному очевидно, что "говно" не является конструктивной аргументацией. Причем одни говорят говно про одни книги, другие - про другие. Всех сделать довольными не получится никогда.
>еще двух математиков из реальной жизни
Этот факт добавить в шапку и посылать даунвотеров на хуй.
Биопроблемник осознал что матаном друзей не найдешь, найс, теперь самое время создавать треды уровня "мне адиноко, хачу тяночку" в /b/ и /rf/
Только вот сразу всплывет батина фраза "твои друзья в интернете в трудную минуту не помогут", тут только реальные.
Почему не помогут, мне в /b на телефон бросили чуть чуть рублей когда я проебал вписку и уснул на лавочке в хуй знает каком раёне без денег и телефон кончался. Скажешь это мелочь, но в ирл когда у тебя серьезные проблемы не факт что какие-то друзья будут за тебя вписываться...
Ну ведь батя то жизнь повидал, он то точно прав.
В и Арнольд
Однако, здравствуйте
Забавно, но я привел цитату арнольда, который цитировал Петровский, как собсно и указано в цитате, приведенной мною. Ты просто триггеред
То есть Арнольд считает, что математики должны быть одинокими титанами.
Есть задача: есть 10 критериев с определенными значениями. Значения могут быть разными, но есть ограничения, что первый критерий не может иметь значение больше 100 и меньше 14, у следующего критерия другие ограничения на значение, у следующего новые и т.д.
Для каждого критерия нужно подобрать коэффициент от 1 до 10, который умножается на значение критерия. После критерии как аргументы принимаются в функцию и функция выдает число в процентах от 0 до 100.
Необходимо найти такие коэффициенты, при которых достигается экстремум функции. При попытки сделать это дело банальным перебором всех значений столкнулся с проблемой, что количетсво возможных комбинаций при таком подходе будет 10^10 = 10000000000. Приближенный подсчет показал, что мне придется ждать несколько лет.
Нет ли более простого способа найти экстремум функции кроме метода перебора? Читал на вики про то метод множителей Лангранжа, но не смог разобраться как ту теорию привести к моему случаю. Буду рад вашей помощи.
>Этот список - компиляция рекомендаций 5 (по крайней мере я столько насчитал) анонов + еще двух математиков из реальной жизни
А еще толще можешь?
Скажи что аксиомы пеано не определяют натуральные числа.
Или вот, скажи что математика нинужна, ведь есть комлюктеры.
Можеть так натолстить*

Малаца. Ткнул местным маняматикам на ихнюю парашу у теории струн.
>Они могут объединяться по разным принципам (будь то сверхабстрактность, антисемитизм или "прикладная и индустриальная" проблематика)
Ммммм.... запахло ГАМАТОПЕЯМИ и историями ромы михайлова про его друга математика, упореблявшего всякие препараты и разговаривающего со средами...

Вот у меня есть задачки на эту тему.
Я правильно понял что их решать нужно с конца, тобишь с элемента около которого икс?
первый ответ : корень(4х-8/4)
второй : корень(4х-8)/4
третий : корень(х-8)
четвертый : 4корня(х/4)-8
пятый : корень(х)-8
шестой : 4корня(х/4)-8
Это что. Меня давеча четверг нахуй послал.
>Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
>А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
Кукушка хвалит петуха, за то что хвалит тот кукушку.
Виттен в треде, все в 12-мерное пространство.
А каковы твои? Вот как только ты ответишь на этот вопрос я тебе сразу скажу почему эта теория говно ебаное.

Вот тебе несколько примеров:
f(x) = x x
f(5) = 5 5 = 25
f(-4) = (-4) (-4) = 16
g(x) = x + 1
g(3) = 3 + 1
g(-6) = (-6) + 1 = -5
g(f(5)) = g(5 5) = g(25) = 25 + 1 = 26
f(g(-1)) = f((-1) + 1) = f(0) = 0 0 = 0
g(f(x)) = g(x x) = x x + 1
f(g(x)) = f(x + 1) = (x + 1) (x + 1)
Я значит что то не понимаю. У меня все равно получается на второй пример ответ корень(4х-8)/4.
У параболы есть 1 увеличивающийся отрезок и 1 уменьшающийся. Окружность в 1 мерном сечении относительно луча является двумя точкаки. С какой бы стороны не взглянешь. 2 умножить на 2 равно 4. Но это при условии что окружность правильная.
Алгебраически. Рассмотрим систему
{
y = ax^2 + bx + c
(x - x_0)^2 + (y - y_0)^2 = R^2
}
Подставляя правую часть (1) вместо y в (2), получаем уравнение вида p(x) = 0, где p(x) - многочлен не выше 4й степени, поэтому у него не более 4х корней. Каждый x однозначно определяет y через уравнение (1), поэтому у нас не более четырех пар точек.
Необычный у тебя вопрос, слишком практический, об этом здесь не говорят. Здесь ведь сидят в основном N-векторнопространственные гамологоебы, которые и лампочку небось ввернуть не могут.
Учусь программить уже второй год. Охуенно вставляет - прикладная математика рулез. Вещи щупаются нараз. Цифровые методы например. Программить можно все, от интегральчиков до чудных аттракторов. Потом визуализация всяких еба функций, но это чисто для лулзов. Пытался запилить ellipse fit но получилось криво, и в матлабе это все есть. Кстати популярна реализация нашего соотечествинника yuri . Он наверное на дваче не сидит, эн не оперделяет, делом занимается. А я разбираюсь с калманофильтрами сейчас: есть два датчика... а может даже 3. Ну ты понил. Если из raw data при помощи ёба-фьюжн получить самому euler angles - это же так вставляет охуенно, лучше забористой травы. Тут тебе и цифровые методы, и фильтры, и векторные дела, и кватерниончики ваши любимые. Без пруфоебства, только практические результаты - это мегаохуенно. Вот это и есть математика а не
Вот это разрыв технобыдла. Технобыдло очень гордится тем, что может вбить в комп формулу, которую умные люди придумали сотни лет назад. К пониманию математики 20 века технобыдло даже не приближается (если это не какие-нибудь CS-разделы типа теории графов). Технобыдло на полном серьезе думает, что чистые математики не умеют кодить, в то время как в 2016 кодить может любой дебил, никакой специальной подготовки для этого не надо.
>Здесь ведь сидят в основном N-векторнопространственные гамологоебы, которые и лампочку небось ввернуть не могут.
Вот щас обидно было.
Тянучка уже давно мозг ест на тему того чтобы я СВАЕЙ МАТИМАТИКАЙ начал деньги делал, а религия ничего кроме лекций ромы михайлова смотреть не позволяет.
>кодить может любой дебил, никакой специальной подготовки для этого не надо.
Сделай мне игру, суть токова. Есть картофан бегающая по гаматапическим плоскостям. Можно дифференцировать функции, домики леревянные набегают
Так же как и я, наверное.
Помылся, побрился, постригся и пошел в центр на какой то праздник.
>говорит про разрыв
>у самого пердак лопнул конкретно
:))) Конечно, есть только два стула - чистые математики и остальное "технобыдло".
А я кстати про деньги ничего не говорил. Все что я описал - это тоже некое длясебяёбство, только в другом ключе. Можно пощупать результаты.
Вот только я нихуя не делаю и сижу втыкаю в рому. Пробовал на бирже играть, но понял что мои познания теор. математики в этом деле не выдерживают проверки действительностью.
>Тянучка уже давно мозг ест на тему того чтобы я СВАЕЙ МАТИМАТИКАЙ начал деньги делал
Сочувствую и ей и тебе. Ей, потому что вместо практичного Ашота с рынка она себе нашла мойтиматика абсолютно ненужного недоразвитой стране, у которой нет излишков, чтобы их давать мойтиматикам. А тебе известно почему. Тянучка Ромы Михайлова ездила вместе с ним в секты. Тебе такое видимо не грозит.
>>Кукушка хвалит петуха, за то что хвалит тот кукушку.
>Профессиональное сообщество математиков не имеет единого критерия, а если бы и имело его, это было бы только хуже, наверное, потому что он был бы основан на невнятных властных играх по принципу ты почеши мне, а я почешу тебе, а ля академия наук.
Про биржу я сразу ньютона вспоминаю, как он проиграл существенную часть своего состояния и наконец понял, что на бирже нет никакой математики, а есть только greed и fear.
Ну тащем-то я тоже теоретической хуйней маюсь, просто кроме этого еще в прикладушки играю. Такие периоды бывают у меня, как месячные примерно.
Анон, напиши мне на фейко-мыло свои контакты:
zavimufu,7axiANUSlackmA3dailPUNCTUMgceru
Сам занимаюсь похожими вещами.
>Что за секты?
Да всякие ебанутые секты из 90-х. Вот эти вроде:
https://ru.wikipedia.org/wiki/Звенящие_кедры_России_(движение)
Технобыдло - это не род деятельности, это определенный майндсет, набор взглядов на жизнь вообще. Это утилитаристский взгляд на жизнь, дроч на "практические результаты". Чтобы не быть технобыдлом, совсем не обязательно быть математиком.
Ну и что ты тут загринтекстил?
Ты понимаешь что есть литература написанная учителями от бога, а есть литература написанная вербитками и картофанами?
Что сказать то хотел?
>Пробовал на бирже играть, но понял что мои познания теор. математики в этом деле не выдерживают проверки действительностью.
А мог бы запрограммировать генетический алгоритм, как бывшие выпускники 239 школы гугли Григория Фишмана и уже стать миллиардером.
>Живу в говне, но зато духовность гамалогею знаю
Знаешь кого ты мне напоминаешь с такими взглядами?
Я смотрю ты силен в терминологии. А как называется дроч на стремление всех разложить по полочкам, категоризировать согласно своих личных проекций? "Дроч на результаты" кек.
Технобыдло — это единственные полезные люди на планете. Чтобы стать технобыдлом обязательно нельзя становиться мойтиматиком.
поправил тебя
как считаете норм книжка?
В секте, вроде, он рассказывал в своём посте про сектанских личностей.
Да у меня и фейкомыла нет. Сегодня где-то создал, но ближе к ночи забыл еба, где создал то его я, ну его нах. Кстати можно же тред отдельный прямо тут в саентаче запилить. Или давай здесь если не совсем оффтоп, смотря о чем. В радиаче например васяны такого не обсуждают. Еще есть 1.5 человека где-то в хобби что ли, коптеростроители которые. В /b теперь петушня борится с тематикой. Как начнешь номерные треды - сразу выпилят. Там только диванон шкур номерной разрешается. Вообще все говно так то, но выбора нет - меня с обычных форумов давно пидорнули, так как я люблю пошутить, а они там шуток не понимают.

А че такого. Мат треды же бывают иногда в "ночном" (хз по какому времени, видимо ДС). И всякие быстро вопросы, пока в тематике пусто.
Сейчас я буду доказывать все теоремы.
Ну как бы /b/ самый зашкварный раздел двача, там обычно полный пиздец и летние каникулы.
Удваиваю реквест этого анона. Как задачник к Зоричу хорошо пойдёт или нет? Просто в Демидовиче одни производные и интегралы.
Конечно же лямбда исчислением
По индии они шароебились очень много. Почитай его "книгу" чуток, проникнись этим пиздецом. Я вот вчера открыл, так пробеать, очнулся блять заполночь, с мыслью что же я нахуй читаю?
Вовсе не гоню, это восхищение напополам с ужасом.
Которую? У него их уже несколько. Наверное ты про "Улицу Космонавтов".
Есть ролеплейная игра, в игре есть недосимуляция атмосферы - идеальный газ и все дела, можно использовать эту симуляцию, чтобы соединит баллон горючего газа и кислорода с очевидными последствиями. Пытаюсь решить систему уравнений, чтобы найти параметры наимощнейшей возможной бомбы, вот система:
E1 = 101.3251070 == Nhp8.314Th
E2 = 101.3253070 == (Ncp + Nco)8.314Tc
E3 = 373.15(200(Nhp + Ncp) + 20Nco) ==
200(ThNhp + TcNcp) + 20TcNco
E4 = Ncp + Nhp == 2 Nco
E5 = Pcp70 == Ncp8.314Tcp
E6 = Pco70 == Nco8.314Tco
E7 = Tc(200 Ncp + 20 Nco) == TcpNcp + 20 TcoNco
E8 = Pcp + Pco == 101.32510
E9 = Pres270 == Nco8.314Tres
E10 = Tres30Nco == Th200Nhp+Tc(20Nco + 200Ncp) + 550000Nco/2
В первом уравнении записываю уравнение Клапейрона-Менделеева для нагретого баллона, 101.32510 - давление, до которого можно накачать горячий баллон в кПа - 10 атмосфер, Nhp - молей горючего газа, "Плазмы", в горячем баллоне, Th - температура горячего баллона.
Во втором уравнении то же для охлаждённого баллона, Ncp - молей горючего газа в холодном баллоне, Nco - молей кислорода, Tc - температура холодного баллона. Давление в холодном баллоне - 30 атмосфер, потому что, путём хитростей и обмана, в баллонах, в которых смешаны газы с разными теплоёмкостями можно получить давление выше наибольшего накачиевомого насосом, но не больше 30 атмосфер: давление выше разорвёт баллон.
В третьем уравнении задаю условие прохождение реакции - температура после смешивания газов из двух баллонов более 100°C через уравнение сохранения тепловой энергии. Теплоёмкость газов принимается за константу: 200 для горючего газа, 20 для кислорода.
В четвёртом уравнении устанавливаю соотношение молей горючего газа и кислорода в реакции горения: на два моля кислорода один моль горючего газа.
В пятом, шестом, седьмом и восьмом уравнениях описываю процесс получения давления в 30 атмосфер в холодном баллоне: смешивание горючего газа и кислорода при разных температурах.
В девятом уравнении описываю Клапейроном-Менделеевым образовавшийся сразу после сгорания, за момент перед взрывом, углекислый газ, в него обратились весь горючий газ и кислород, по два моля кислорода и одному молю горючего газа на два моля углекислого газа. Pres - результирующее давление, а Tres - результирующая температура.
В последнем уравнении записано уравнение сохранения тепловой энергии для смешанного газа двух баллонов, теплоёмкость углекислого газа - 30, каждые два моля сгоревшего кислорода выделили 550000 единиц тепловой энергии.
Таким образом у меня есть десять уравнений и одиннадцать переменных, что должно давать возможность составить функцию Pres от, допустим, Th, вычислить её максимум и подставить его значение в систему уравнений, тем самым сделав её решаемой. Проблема вся в том, что я не знаю как добиться желанного результата. Я пытался орудовать Вольмрамом: Альфа напрочь отказывается от таких длинных запросов, а с математикой выходит непонятная белиберда. Стоит ли попробовать какую-нибудь МатЛаб или нечто пострашнее? Как сделать так, чтобы компьютер сказал мне те цифры, которые я хочу от него услышать?
Есть ролеплейная игра, в игре есть недосимуляция атмосферы - идеальный газ и все дела, можно использовать эту симуляцию, чтобы соединит баллон горючего газа и кислорода с очевидными последствиями. Пытаюсь решить систему уравнений, чтобы найти параметры наимощнейшей возможной бомбы, вот система:
E1 = 101.3251070 == Nhp8.314Th
E2 = 101.3253070 == (Ncp + Nco)8.314Tc
E3 = 373.15(200(Nhp + Ncp) + 20Nco) ==
200(ThNhp + TcNcp) + 20TcNco
E4 = Ncp + Nhp == 2 Nco
E5 = Pcp70 == Ncp8.314Tcp
E6 = Pco70 == Nco8.314Tco
E7 = Tc(200 Ncp + 20 Nco) == TcpNcp + 20 TcoNco
E8 = Pcp + Pco == 101.32510
E9 = Pres270 == Nco8.314Tres
E10 = Tres30Nco == Th200Nhp+Tc(20Nco + 200Ncp) + 550000Nco/2
В первом уравнении записываю уравнение Клапейрона-Менделеева для нагретого баллона, 101.32510 - давление, до которого можно накачать горячий баллон в кПа - 10 атмосфер, Nhp - молей горючего газа, "Плазмы", в горячем баллоне, Th - температура горячего баллона.
Во втором уравнении то же для охлаждённого баллона, Ncp - молей горючего газа в холодном баллоне, Nco - молей кислорода, Tc - температура холодного баллона. Давление в холодном баллоне - 30 атмосфер, потому что, путём хитростей и обмана, в баллонах, в которых смешаны газы с разными теплоёмкостями можно получить давление выше наибольшего накачиевомого насосом, но не больше 30 атмосфер: давление выше разорвёт баллон.
В третьем уравнении задаю условие прохождение реакции - температура после смешивания газов из двух баллонов более 100°C через уравнение сохранения тепловой энергии. Теплоёмкость газов принимается за константу: 200 для горючего газа, 20 для кислорода.
В четвёртом уравнении устанавливаю соотношение молей горючего газа и кислорода в реакции горения: на два моля кислорода один моль горючего газа.
В пятом, шестом, седьмом и восьмом уравнениях описываю процесс получения давления в 30 атмосфер в холодном баллоне: смешивание горючего газа и кислорода при разных температурах.
В девятом уравнении описываю Клапейроном-Менделеевым образовавшийся сразу после сгорания, за момент перед взрывом, углекислый газ, в него обратились весь горючий газ и кислород, по два моля кислорода и одному молю горючего газа на два моля углекислого газа. Pres - результирующее давление, а Tres - результирующая температура.
В последнем уравнении записано уравнение сохранения тепловой энергии для смешанного газа двух баллонов, теплоёмкость углекислого газа - 30, каждые два моля сгоревшего кислорода выделили 550000 единиц тепловой энергии.
Таким образом у меня есть десять уравнений и одиннадцать переменных, что должно давать возможность составить функцию Pres от, допустим, Th, вычислить её максимум и подставить его значение в систему уравнений, тем самым сделав её решаемой. Проблема вся в том, что я не знаю как добиться желанного результата. Я пытался орудовать Вольмрамом: Альфа напрочь отказывается от таких длинных запросов, а с математикой выходит непонятная белиберда. Стоит ли попробовать какую-нибудь МатЛаб или нечто пострашнее? Как сделать так, чтобы компьютер сказал мне те цифры, которые я хочу от него услышать?

Уравнения из, как их записал я, получились нечитаемыми, надеюсь, на этот раз всё иначе:
E1 = 101.325×10×70 == Nhp×8.314×Th
E2 = 101.325×30×70 == (Ncp + Nco)×8.314×Tc
E3 = 373.15×(200×(Nhp + Ncp) + 20×Nco) ==
200×(Th×Nhp + Tc×Ncp) + 20×Tc×Nco
E4 = Ncp + Nhp == 2 Nco
E5 = Pcp×70 == Ncp×8.314×Tcp
E6 = Pco×70 == Nco×8.314×Tco
E7 = Tc×(200 Ncp + 20 Nco) == Tcp×Ncp + 20 Tco×Nco
E8 = Pcp + Pco == 1013
E9 = Pres×2×70 == Nco×8.314×Tres
E10 = Tres×30×Nco == Th×200×Nhp×+Tc×(20×Nco + 200×Ncp) + 550000×Nco/2
Короч, смотри. Если будешь решать через fsolve, то у тебя может быть бесконечное множество решений в зависимости от начальных посылок. Тебе надо параметризовать одну из переменных иначе ты ничего не решишь. Выбери переменную от которой избавляемся и я тебе решу сейчас.
Я выбрал за тебя Tco = 0.5.
Не ведаю хорошо это или плохо. Получился такой результат:
http://pastebin.com/f1uLTkgW
Мне важно только чтобы Pres был максимален, а Pcp, Pco, Tcp, Tco и Th известны. Можно параметризировать Ncp или Nhp? Или мешает то, что они линейно зависимы от нужных?
Tco - это температура для смешивания, её я хотел узнать, и по результатам получается, что конечное давление 18 кПа, что низко. А никак не поможет, если я введу массу неравенств, чтобы ограничить количество решений? Например, все переменные - температура, давление или количество вещества, значит положительные, Th>Tc, Tc<373, Tcp<Tco. Я пытался так же убрать одну переменную в вольфраме, но он напрочь отказывается её признавать, выдаёт пустые строки в ответе
Можно ничего не параметризовывать и оставить 11 неизвестных на 10 уравнений. Но тогда скажи приблизительные желаемые значения каких-то переменных. Тогда оно будет итерационно решать оптимизационную задачу, пока не превысит лимит на итерации. Или можно заранее от какой-то переменной избавиться и тогда будет тупое решение в лоб (единственное).
> Можно параметризировать Ncp или Nhp?
Любую переменную.
>введу массу неравенств, чтобы ограничить количество решений
Хз. Надо читать документацию. Наверное, можно сделать.
Я отрыл свои кривые экселевские заметки, в них наилучший результат был с Ncp+Nhp около 17, значит для лучших результатов Ncp+Nhp должно оказаться выше 17, значит Nco больше 34. Можешь попробовать на это или, если так можно, на большее решить?
>Nco больше 34
Поставил 37.7. Получился такой результат (алсо некоторые переменные изменились в сравнениии с прошлым разом 11 <--> 6):
http://pastebin.com/62eQXUKY
Вроде судя по цифрам большое давление и температура теперь.
Давление на выходе отличное, но появились отрицательные значения, то есть нет способа получить такую смесь реально. Может быть я напортачил с уравнениями? Я пытался создать таблицу в экселе, там тоже постоянно минусы вылезали, такие значения я вручную исключал.
В вольфраме есть тип документа Testing Notebook, в нём такое можно провернуть? Были попытки брутфорсом провести мириаду экспериментов каким-нибудь C# или Pearl, вроде как не безуспешно.
>но появились отрицательные значения
Сделал несколько тестов с разными значениями Nco (25.7...75.7). В каждом есть отрицательные значения, но у разных переменных. Посмотри, может что-то сгодится:
http://pastebin.com/9Rwgf8gt
Я сегодня попробую соорудить что-нибудь на основе этого, спасибо! Если не выйдет сразу, попробую подставить в экселевскую таблицу и поправить, чтобы чуть чуть в положительные значения выходило, спасибо большое!
Хочу поставить себе на дверь китайские замки, это которые прокручиваются в обе стороны. Тобишь есть четыре положения у них, из которых только одно открыто.
Суть в том чтобы поставить кучку замков и все закрыть на разную "закрытость" или вообще не закрывать.
Сколько надо поставить замков чтобы их нельзя было перебрать за адекватное время. За одну секунду может крутится только один замок.
Как они связанны?
Это не маняматический ответ.
А счего ты взял, что шифроманные то? обычные циферки же. Не догоняю, чего ты хочешь
Дай ссылку на замки, которые ты собрался ставить. Но заранее можно уже сказать, что если тебе захотят дверь вскрыть, то сделают это за 10 минут независимо от типа замков.

https://en.wikipedia.org/wiki/Transportation_theory_(mathematics)
Что-то я проиграл с различия статей.
Рашка реально сильно отстала от развития математики?
Или, слава Арнольду, всё норм, и это тупые пиндосы не туда идут с их нинужной формализацией?
Кто ж знает, как оно в юудующем обернется.
Это новая реальность, открытая эзотериком из 11 треда. Не будешь читать Воеводского - велком ту практические результаты, гнида!
>слава арнольду
Конечно, а еще удивляются, почему наши соотечественники на всех вокруг смотрят как на говно, а уж тем более в области НАУКИ, это же наше, а не косоглазых пидоров. А чего удивляться, если даже Арнольды говорили то же самое - на каком-то видео он объясняет, что тупые пиндосы специально не учат своих пиндосов, потому что обществу потребителей нужны тупые пиндосы, и тп. Примерно такие же мерзости читал в какой-то книжечке с мемуарами про МГУ. Все там известные личности, авторы учебников, а говорят такие же вещи, как в политаче.
1-ый же пост истории тредов на архиваче. 11 тред, ключевые слова - воеводский, пучки, к-теория.
Видимо, необязательно быть хорошим человеком, чтобы быть хорошим математиком.
Бинго. Более того, ты физически не можешь быть хорошим человеком, 24/7.
Он же в край ебанутый.
http://ezotera.ariom.ru/2014/04/14/voevodskij.html
>К психиатрам я с этим не обращался. Как-то с самого начала было ясно, что это никакая не шизофрения.
>не обращался
А надо бы.
>навык вот этой вот мелкой алгебры
Но это же в 6-м классе приобретается. Или никогда. А если приобретается, то не теряется. Ты же ручкой писать не разучишься по клавишам пиздяча. Так то ты же не умножаешь в уме двузначные числа, а пользуешься калькулятором. Так что норм.
>математического обучения
Какого обучения. Как с дробями обращаться что ли и тп.
>>379477
>ебанутый
А разве это не помогает в абстрактных науках? Нет нужды отвлекаться на бытовуху.
>Примерно такие же мерзости читал в какой-то книжечке с мемуарами про МГУ. Все там известные личности, авторы учебников, а говорят такие же вещи, как в политаче.
Академик Н. Н. Моисеев писал о Рудольфе Калмане: «Мне он показался человеком не очень образованным, во всяком случае, по московским математическим меркам, надутым и с огромным самомнением — свойством, весьма обычным для американцев»
Чёт по-моему ты неправ насчёт навыков. Имхо, теряются со временем, если не использовать. Таких мелких навыков вообще дохерища, помимо таблицы умножения.
Я имею в виду, если человек верит в попобаву, но при этом не просто считает, что он есть и что он что-то о нём знает, а думает, что стоит его зафиксировать и проанализировать с помощью научного метода, то ебанутость этого человека не является индикатором его умственной несостоятельности. Ну и вообще, на фоне Ромки он весьма адекватно выглядит, хотя Ромка же норм.
>Общая топология, или теоретико-множественная топология — раздел топологии, в котором изучаются понятия «непрерывности» и «предела» в наиболее общем смысле.
Это из за этой хуйни
>«непрерывности»
>«предела»
местные юродивые натолкали в шапку говна несусветного и требуют, и не просто требуют, а агрессивно кидаются, чтобы все учили гомотопию с начальных классов по вырвиглазным учебникам!?
Поясню суть.
Когда топологию сделали оказалось что она поглощает чуть ли не всю математику. Из за этого выкинули к хуям всю предыдущую математику. При этом забыв что без предыдущей математики, даже с сраной теорией множеств, топологию никто нихуя не понимает.
Они же говорят вам не нужна предыдущая математика. Только уясните что дифференциал - это линейный оператор. И забудьте уже про определение предела через епслион дельта или шары. Это слишком сложно и неинтуитивно. Вот вам простое интуитивное определение (и далее какой-то пиздос).
А какое там у них определение предела?
То что в метрических пространствах куда лучше понимается чем то что в анализе.
Я ньюфаг, но я пролистывал учебник по матану до последних глав и там есть КОГОМОЛОГИИ, что-то там клеят, какие-то торы и всякая такая хуйня. Т. е. топология нужна для анализа на многообразиях. А еще если ты полистаешь книгу Арнольда по дифурам, то увидишь, что там много упражнений в духе "приклеим ручки к сфере", а что может быть связано с реальностью больше чем дифуры?
Нужен гаусс современности который СМОЖЕТ пояснить топологию по хардкору как для даунов. И то не факт что она нужна будет где то кроме как в глубинах ума поехавших математиков.
>То что в метрических пространствах куда лучше понимается чем то что в анализе.
Неистово двачую, на метрических пространствах всё гораздо понятнее, потому что выделяются только ключевые моменты. Хотя они у меня были как раз на анализе.
Так теоретико-множественная топология это и так самый простой раздел математики. Там иногда встречаются сложные вещи, но если сравнить с матаном, то топология - это легкая прогулка, а матан - это бесконечные боль и страдания.
>Какого обучения. Как с дробями обращаться что ли и тп.
Ну у меня речь идёт о калькулюсе, от которого неимоверно бомбит.
>>379498
А как вообще можно изучать R^n без метрических пространств? Типа через евклидову норму и эпсилоны с дельтами?
Пояснил, проверяй.
>>379502
Да блядь, там просто определения и теоремы, следующие прямо из определений, без всяких трюков. Да, определений много, но доказательства простые и красивые, как привыкнешь к терминологии, всё кристально ясно. По крайней мере в point-set topology
Ну да, как-то так. Сначала на R, потом обобщать на многомерный случай. Ничто не мешает проделать всё это в обход метрических пространств, но конечно лучше с ними.
>Да блядь, там просто снял трусы и всунул, следующие движения тазом, без всяких трюков. Да, движений много, но результаты простые и красивые, как привыкнешь к движениям, всё кристально ясно. По крайней мере в обычной ебле.
Так я просто думаю может не решать все то, что я могу решить с помощью матпакета?
Ты мне все еще не пояснил за топологию.
Из самого слова я могу сказать только то что это некая плоскость по типу местности.
Колотушкин. Это же калкулус. Плаг энд чаг.
>>379514
Хуем тыкать КУДА не уточняете вы.
Я пока тыкал только в руку. Со временем думаю попробовать что-то еще. Можете провести параллель с математическими дисциплинами?
Я тебе пояснил уже. Бери учебник или какие-нибудь конспекты лекций по топологии. После моего пояснения все должно быть понятно.
За щеку что ли? Так я не понял.
Либо диктуй названия учебников по топологии либо проследуй к И петуху искать ошибку в определениях пеано.
А ну так тебе еще рано топологию тогда. Сначала листву сбрось, без этого в топологии никак.
Ты не можешь даже нагуглить какие есть учебники?
Munkres: Topology
Листки Вербита
Лекции НМУ (в группе в вк есть видеозаписи лекций, на сайте нму есть конспекты лекций и листки с задачами).
Пусть X и Y - топологические пространства, f - функция из X в Y, x - точка X.
Пределом f в точке x называется такая точка y из Y, что частью любой окрестности этой точки y является f-образ некоторой проколотой окрестности точки x.
Ну не знаю насчет НМУ, но я лично ебался 1 раз в жизни и только через пару месяцев после этого скачал учебник по топологии и начал читать.
>Вербита
АААААААААААААААААААА, СУКААААААААААААААААААААААААААААААААААА, АААААААААААААААААААААААААААААААААААААААААААААААААААААААААА
На лекториуме курс есть. А вообще, ты поехавший что ли? За целую теорию ему на дваче поясните.
Чё ты начинаешь, нормально же общались.
Хм. Задумался. У меня есть мысль попробовать наоборот - скачать учебник, и может получится попробовать поебаться. Если эти два события коррелируют, то порядок не важен м.б. Нужно поспрашивать анонов и построить chi square fit.
Поскольку их написал Лузин, они должны быть очень старыми. Дай ссылку, скажу подробнее.
Снаружи или изнутри?
И листом медиуса между ног протягивают потом, до разрыва ленты.
Топологией можно пикапить гиковых школьниц. Только их найти трудно. за базар отвечаю, у самого такая есть
Так то я сам жиробас но мне нравятся тонкие тянучки. 50кг макс. Но это в теории я так расчитал.
> У меня есть мысль попробовать наоборот - скачать учебник, и может получится попробовать поебаться.
Ни в коем случае, если будешь действовать в таком порядке, ты безнадежен. Тянки чувствуют, когда кто-то изучает топологию. Ко мне они сами подкатывают, потому что я красивый, но потом быстро понимают кто я есть и как бы все, ноу вэй.

По-твоему то что в статье на вики был использован подход через топологию не означает что это общепринятый в этой стране подход к этой задаче?
Довольно приличные книги. Читай, если тебя не пугает устаревший язык олдскульного автора.
Представил, что в треде только я и Хеллер и он со мной обсуждает еблю и топологию как бы от разных лиц.
Задумался, что бы выбрал анон, черенок в жопу или понять и принять это: >>379521
хотя как я понимаю у самых успешных получается и то и то
Как можно смотреть на тёлок меньше сотки кг массой? Не понимаю.
С пределом-то что не так? Вполне естественное обобщение.
М-м. Трудно сказать. Короче, в наши дни таким языком не говорят и не думают. Не яти.
Да, это не модно.
В вузах на анализе преподают это, насколько мне известно.

> Пусть X и Y - топологические пространства
Ясно, мог не продолжать.
Раз 20 уже читал на википедии определение топологического пространства, но так и не понял его. Хотя метрические/нормированные/гильбертовы - вроде норм осознал.

Берёшь и понимаешь короч. Интуитивно.
Мотивировка этого дерьма, все дела.
В принципе понимание всегда хорошо проверяется предлагаемыми задачами.
Без понимания ты видишь просто символы, максимум - манипуляции символами.
Ну блин примеры посмотри. Достаточно рассмотреть несколько метрических пространств, которые тривиальным образом соответствуют топологическим (все открытые множества включены в топологию, остальные не включены) + несколько вырожденных случаев просто так. А приведённое определение можно всё равно понять, если знаешь, что такое окрестность.
>>379557
Как же вы заколебали с этим вопросом. Или это всё один и тот же человек спрашивает?
> Объединение произвольного семейства множеств
> Пересечение конечного семейства множеств
так? Мне кажется что конструктивно разницы вообще нет ведь как известно бесконечных множеств не существует.
мимопробегал
Представь себе бесконечное множество вложенных интервалов на R, таких, что первый - это (-a,a), а каждый последующих строго вкладывается в предыдущий. В пересечении будет точка 0.
Может ты сначала доказательство сам разберёшь там где тебе это встретилось?
А, или это из определение топологии?
Ну короч в топологии я не могу, но в метрических пространствах доказывается что объединения открытых множеств - всегда открыто, но пересечение - только конечного кол-ва гарантированно открыто.



>>379569>>379571
Тебе копипастить определение из википедии? А потом ещё и разжёвывать его, ведь сам ты ничего не поймёшь?
А может просто нахуй иди, а?
Тупой здесь ты. Я тебе только что объяснил, что пересечение бесконечного числа открытых множеств может быть не открыто. А ты, уёбок, даже определение посмотреть не можешь.
Нахуя ты притащил это говно?
>>379574>>379575
Во-первых - давайте определение по которому точка не может быть открытым множеством
Хинт: его нет и не может быть
Хинт2 для самых тупеньких:дискретная топология
Я же предлагаю поварьировать определения и понять почему они именно такие а не какие другие. На с такими тупорылым контингентом это занятие заведомо провальное.
Блять, ну ты совсем упоротый. Я тебе уже задал конкретную топологию, которая не является дискретной, что ты мне блять втираешь?
В R со стандартной метрикой (которая, естественно, подразумевалась) синглтон НЕ ЯВЛЯЕТСЯ открытым множеством. По определению открытых множеств в метрических пространствах.
Ну вот, с этой точки зрения понимание - это такой непрерывный процесс и нет деления между пониманием и непониманием. Это некий метауровень. А если имеется в виду понимание определения на уровне формальной системы, то для него достаточно знать значение (пит буль) символов этой системы, которые используются в определении. Если понимания на метауровне нет, не стоит думать, что оно появится, если ныть на дваче. Стоит на первое время ограничиться пониманием на уровне формальной системы, поработать с объектом, и тогда, может быть, появится какая-то интуиция.
Алсо, интуиция необязательно должна быть геометрической или иметь какую-то другую естественную природу. Интуиция вполне может вырабатываться от манипуляции с символами, если манипулировать с умом.

Можете не благодарить. Я обратно на небеса.
Я тебя умоляю, анон, добавь в свой лексикон словосочетания "интуитивная ясность" и "дискурсивная ясность", как же так жить-то можно
Подробнее об этом вы можете прочитать вот здесь:
http://link.springer.com/article/10.1007/s00407-014-0144-6
http://homepages.math.uic.edu/~hurder/math445/handouts/Moore_Historia2008.pdf
И тут:
http://www.mathnet.ru/rus/sm5526
Рома Михайлов объяснил уже.
Не троль, тут серьезные вещи обсуждают на приличном уровне.
> Я же предлагаю поварьировать определения и понять почему они именно такие а не какие другие.
Рассмотрим евклидово пространство R^n и топологию на нем, которая индуцирована обычной евклидовой метрикой. Это пространство полностью соответствует нашей геометрической интуиции. В нем объединение произвольного числа открытых множеств открыто (это доказывается в матане). Пересечение произвольного числа открытых множеств открытым быть не обязано. Если мы возьмем последовательность открытых шаров радиуса 1/n с центром в начале координат, они стягиваются в точку, то есть их пересечение по n от 1 до бесконечности замкнуто.
Почему одноточечное множество должно быть замкнутым? (в общем случае это не так, но в большинстве топологических пространств это так) Потому что оно содержит свою единственную граничную точку, совпадает со своим замыканием, дополнение к нему открыто - выбери причину, которая тебя больше привлекает интуитивно.
Вообще, в любом хаусдорфовом пространстве одноточечное множество замкнуто, а какой-нибудь первокурсник, который только начал изучать топологию, вообще не сможет привести пример нехаусдорфового пространства из реальной жизни, так что интуитивно это должно устраивать.
Так метаиндукцией же петли рвутся.
А ещё можно попробовать поискать открытый шар с центром в точке одноточечного множества, который бы содержался в этом множестве, чтобы увидеть, что такого шара нет.
Фу, мы тут обсуждаем искусство математики, а не грязную животную еблю.
поправил своё пенсне, и затянул потуже модный шарфик
Что это блядь. Какое еще external use, в глаза ебаться что ли? А если adventurous, то что можно придумать?
Еще вот что. Пусть X - хаусдорфово пространство и пусть для этого пространства верно, что произвольное пересечение открытых множеств открыто. Тогда по законам де Моргана произвольное объединение замкнутых множеств замкнуто. Так как любое множество можно представить как объединение одноточечных множеств, любое множество замкнуто, а значит, любое множество открыто. Поэтому если бы мы так определили топологическое пространство, для большинства пространств мы бы не получили никакой новой структуры, а получили бы просто множество всех подмножеств X.
Не предназначено для сования внутрь, но если ищешь приключений, то можно.
Пусть B - семейство подмножеств X. B называется базой, если
1) B покрывает X;
2) если B_1, B_2 ∈ B, то для любой x ∈ B_1 ∩ B_2 найдется B_3 ∈ B такой, что x ∈ B_3 ⊂ B_1 ∩ B_2.
Можно думать про X как про евклидово пространство, а про B как про открытые шары, но этот случай ничуть не проще общего.
Элемент базы, содержащий p, будем называть окрестностью точки p.
Назовем точку множества E внутренней, если она содержится в E вместе с некоторой окрестностью. Назовем p предельной точкой E, если любая окрестность p содержит точки E. Назовем множество открытым, если все его точки внутренние. Назовем множество замкнутым, если оно содержит все свои предельные точки.
Полученное семейство открытых подмножеств X называется топологией, порожденной базой B.
Пример: стандартная топология на R^n порождается открытыми шарами.
Теперь докажем, что выполняются свойства из определения топологического просранства.
(i) Пусть { E_α } - семейство открытых множеств.
Пусть x ∈ ∪ E_α. Тогда x принадлежит какому-то E_α, а значит, входит в объединение вместе с какой-то окрестностью. Таким образом, все точки ∪ E_α внутренние и ∪ E_α открыто.
(ii) Достаточно доказать интересующее нас утверждение для двух открытых множеств E, F.
Пусть x ∈ E ∩ F. Тогда x ∈ B_1 ⊂ E и x ∈ B_2 ⊂ F для каких-то элементов базы B_1 и B_2. По определению базы найдется B_3 ∈ B такой, что x ∈ B_3 ⊂ B_1 ∩ B_2 ⊂ E ∩ F. Это показывает, что любая точка E ∩ F внутренняя.
Заметим, что стандартная топология на R^n порождается не только открытыми шарами, но и открытыми квадратами, ромбами и другими семействами подмножеств X. Несложно проверить, что подмножество R^n открыто тогда и только тогда, когда любая точка содержится в нем вместе с открытым квадратом. Получается, что у нас одна топология порождается разными базами, но при этом у нас есть "привелегированная" база, через которую мы определяем открытые множества. Это некруто, хочется говорить об открытых множествах, не выделяя какой-то конкретной базы. Люди экспериментировали и выяснили, что удобно принять свойства (i), (ii) за определение.
В итоге окрестностью p называют любое открытое множество, содержащее p.
Пусть B - семейство подмножеств X. B называется базой, если
1) B покрывает X;
2) если B_1, B_2 ∈ B, то для любой x ∈ B_1 ∩ B_2 найдется B_3 ∈ B такой, что x ∈ B_3 ⊂ B_1 ∩ B_2.
Можно думать про X как про евклидово пространство, а про B как про открытые шары, но этот случай ничуть не проще общего.
Элемент базы, содержащий p, будем называть окрестностью точки p.
Назовем точку множества E внутренней, если она содержится в E вместе с некоторой окрестностью. Назовем p предельной точкой E, если любая окрестность p содержит точки E. Назовем множество открытым, если все его точки внутренние. Назовем множество замкнутым, если оно содержит все свои предельные точки.
Полученное семейство открытых подмножеств X называется топологией, порожденной базой B.
Пример: стандартная топология на R^n порождается открытыми шарами.
Теперь докажем, что выполняются свойства из определения топологического просранства.
(i) Пусть { E_α } - семейство открытых множеств.
Пусть x ∈ ∪ E_α. Тогда x принадлежит какому-то E_α, а значит, входит в объединение вместе с какой-то окрестностью. Таким образом, все точки ∪ E_α внутренние и ∪ E_α открыто.
(ii) Достаточно доказать интересующее нас утверждение для двух открытых множеств E, F.
Пусть x ∈ E ∩ F. Тогда x ∈ B_1 ⊂ E и x ∈ B_2 ⊂ F для каких-то элементов базы B_1 и B_2. По определению базы найдется B_3 ∈ B такой, что x ∈ B_3 ⊂ B_1 ∩ B_2 ⊂ E ∩ F. Это показывает, что любая точка E ∩ F внутренняя.
Заметим, что стандартная топология на R^n порождается не только открытыми шарами, но и открытыми квадратами, ромбами и другими семействами подмножеств X. Несложно проверить, что подмножество R^n открыто тогда и только тогда, когда любая точка содержится в нем вместе с открытым квадратом. Получается, что у нас одна топология порождается разными базами, но при этом у нас есть "привелегированная" база, через которую мы определяем открытые множества. Это некруто, хочется говорить об открытых множествах, не выделяя какой-то конкретной базы. Люди экспериментировали и выяснили, что удобно принять свойства (i), (ii) за определение.
В итоге окрестностью p называют любое открытое множество, содержащее p.
Тем же, чем круг от окружности.
ЧЁ блять за слова непонятные, умный такой штоле? Специально так говорит, шоб умным показаться, свои маттермины бля, а на самом деле он пидор, ууухх сука
Эх, тебе бы книжки писать.
Нихуя тащемта не получишь, если не начнёт люто доставлять.
Никогда не понимал такой утилитаризм ко всем знаниям человечества. Познание - это самая высшая деятельность человека. Если твоя жизнь не будет связана с математикой, то никак, но разве понимание одной из самых фундаментальных наук человечества не великолепно само по себе? Я вот ещё историю изучаю, что даст мне знание первых тринадцати императоров Рима? Ничего. Само знание великолепно, но самая великолепная вещь - это колонизация тех областей понимания нашего мира, которые нами ещё не познаны. Такое чувство, что словно эпохи "Возрождения" и не было, где человеческий разум был самой совершенной вещью, словно и не было такого "Фаустовского" человека, который стремится познать всё сущее и сделать мир вокруг себя лучше своей безграничной инициативностью.
По-моему очевидно, что статью писали программисты, а не математики, и для программистов на практике эта задача решается исключительно макспотоком, вне зависимости от страны. Охуеваю, каким нужно быть тупым, чтобы этого не знать.
> Мне говорят старших иногда нужно слушать - занимайся чем то толковым, перестань тратить время на кинцо и худ.литературу. Так что я получу с точки зрения прагматики от изучения математики?
С точки зрения прагматики ничего, но если хочешь получать удовольствие и чтоб от тебя отъебались, то норм. По моим наблюдениям к математикам отношение такое: аутист, но вроде не совсем дегенерат, так что не надо его трогать. Алсо, имей в виду, что есть прикладная и чистая математика. Прикладная математика - нуднейшее говно, но можно с помощью нее работу найти, а чистая математика интересная, но с ней можно только хуй сосать (профессиональным математиком ты не станешь в 26 лет).
И блядь никакой связи с топологией макспоток не имеет.
Не понимаю, как кинцо и худлит мешают заниматься той же математикой. Что за долбоёбы у тебя в советчиках?
Насоветуйте записей видео, на которых решают всякие примеры и задачи из школьного курса математики, желательно с объяснениями. Можно и лекций по биологии, физике и химии, с разбором и решением задач. Что-то вроде видеоучебников. А если будут ещё и приведённые в шапке материалы для новичков в таком формате - вообще будет очень хорошо. Спасибо, милые мои математики.
> гайд по топологии для даунов.
> 1) B покрывает X;
Хм, ни разу, по крайней мере в совковых учебниках не встречал термина "покрывает".
Отсюда следует что они для не даунов, т.е. даунам этот термин должен быть известен.
Бинго, в этом и проблема. Русские термины очень сложно понимать. Что такое покрывать? Cover? Или свиней покрывать? (бастиан швайнштайгер says hi). И тоже самое с нотацией. Это как акцент в языке. Чем абстрактнее математика, тем больше разных акцентов. Ну, про Зорича мы уже тут обсуждали. Это охуенный deterrent.
Успенский так считает.
http://trv-science.ru/2014/01/28/v-a-uspenskijj-matematika-ehto-gumanitarnaya-nauka/
я уже загуглил этот профиль и даже прочёл полтора его интервью (на половине второго подумал "нахуя я этого хуесоса читаю, ведь ни на грам полезной информации, одна белиберда и самолюбование", из всех математиков всего два человека так считает - это из того интервью, да пошёл он нахуй блядь, все эти на -ский должны заткнуться нахуй, например, окей)

Что-то в этом есть. Математика, которую мы изучаем это математика людей, а не математика per se. Мы пытаемся понять бесконечного Б-га ограниченным умом и наталкиваемся на парадоксы и противоречия
Вот Каждан говорит примерно о том же
https://www.youtube.com/watch?v=ETlTsK1Qeh4
Лол, минут 5 решал задачу про Швейцарцев.
Это не наука, а инструмент, вобще-то.
возможно виной поиску утилитариности - некая фрустрация у меня. Довольно часто говорили "что читаешь своего палтона и витгиштена, шел бы на улицу пробзделся да работу нашел".
>>379632
хм, хороший ответ. Пожалуй так и сделаю. Действительно, к технарям получше отношение чем к гуманитариям.
>>379637
наверно не мешает, но совмещать это все плюс работу в 24 часах уже как то не очень. Итак не высыпаюсь и чувствую себя как гуано.
В чем проблема читать худлит максимум два часа, а лучше час? Никакой проблемы тут нет
А сколько у тебя есть? Или ты как нюфаги из пр, "буду задротить по 8 часов в день"? Есть 4 часа-уделяй их.
А я уже полтора года задрочу по 8 часов в день. Иногда больше, иногда меньше, пока не надоест. Из математики мне надоедает только ебучий картофанный матан, его через силу заставляю себя читать, а красивые разделы никогда не надоедают.
Знаний 0.
Начал проходить курсы в Khan academy. Все легко, доступно и без доказательств. Нормально или лучше по книге?

>Все легко, доступно и без доказательств.
Пиздец! В нумерологии 13 - это не ужасное число, а очень хорошее и поэтому я не понимаю, от куда вся нечисть с уравнениями, криптографией и data scienceом повылазила. Аве вербит!
нахуя мне доказательства, если я не чистый математик? или я чего то не понимаю?
> Хочу стать спортсменом. Начал смотреть гайды на ютубе. Все легко, доступно и без тренировок. Нормально или лучше тренироваться?
для того, чтобы число было в степени, делайте [ sup] [/sup] или [/sub ]
А то достали со своими 2^2 22 , епта.
>Насоветуйте записей видео, на которых решают всякие примеры и задачи из школьного курса математики
https://www.youtube.com/user/MADreval/playlists?shelf_id=0&view=1&sort=dd
Когда ты читаешь книгу – ты должен забыть о себе, погрузиться в книгу. Или же ты должен постоянно сохранять бдительность, и постоянно держать руку на пульсе – какими методами пользуется автор? Цельность достигается двойным чтением – изнутри и снаружи.
Забывая о себе и целиком погружаясь в книгу – можно лучше ее почувствовать, проникнуть в ее дух и смысл. Но иногда расстояние между тобой и книгой велико, и ты не обращаешь внимания, что ты переживаешь происходящее с собственной точки зрения, не обращая внимания на то, что то, что написано в книге – написано с другим духом, из другого мира, совершенно отличного от твоего собственного.
Можно утверждать, что любое духовное творение состоит из самоидентификации с одной из сторон. Алтер Ребе объясняет, как творится открытие. Есть методическая работа. Человек трудится систематически, и достигает изначально поставленных целей. Как компьютер, который не создает ничего принципиально нового, но работает по заложенной в него программе. Творение чего-то, что не существовало ранее, это творение «из ничто» происходящее из сущности. Ты находишься внутри, и даешь вещам течь самим собой, и можно углубиться в это. Творение требует вовлеченности. Но если ты только стоишь снаружи и наблюдаешь – ты никогда не станешь творцом. Ибо наблюдатель – это называется вещественный взгляд, и само собой, то, что есть – есть в нем, но ничего нового не выйдет из него. Поэтому творение и открытие нового требуют самоидентификации и вовлеченности. С другой стороны, возможно, ты сделал великое открытие, но если ты не способен привести его в порядок, аргументировать его, перед другим человеком, который не пережил это, это, очевидно, большой недостаток, и не только в отношении того вопроса, который ты пытаешься объяснить, но в самом тебе. У тебя нет сосудов, чтобы вместить собственное открытие. Поэтому с этой точки зрения человек должен приучить себя смотреть на вещи с двух точек зрения – изнутри и снаружи.
Есть более лучший способ читать книги по математике. Сразу начинать решать задачки, не читая предварительно параграфов.
Водовку из картофана делают только в МФИ
Да, так же как пидорство...как его там, рейпер что ли, или вейпер, или шейкер...
ШК ШК
ГОМОлогия, даже само название зашкварное, ПИДОРОизучение, в залупу всяким пидорам залезать.
Теорема Сосницкого # 2: Твоя ЕОТ – шлюха.
Доказательство:
Пусть ЕОТ, ШЛЮХИ, НЕ ШЛЮХИ - множества
(ЕОТ С ШЛЮХИ) = (ЕОТ) + (ШЛЮХИ) – (НЕ ШЛЮХИ)
Left side: (ЕОТ С ШЛЮХИ) = (ЕОТ) U (ШЛЮХИ) + (ЕОТ) ∩ (ШЛЮХИ)
Right side: (ЕОТ) + (ШЛЮХИ) – (НЕ ШЛЮХИ) = (ЕОТ) U (ШЛЮХИ) + (ЕОТ) ∩ (ШЛЮХИ) – (НЕ ШЛЮХИ)
Таким образом:
(ЕОТ) U (ШЛЮХИ) + (ЕОТ) ∩ (ШЛЮХИ) = (ЕОТ) U (ШЛЮХИ) + (ЕОТ) ∩ (ШЛЮХИ) – (НЕ ШЛЮХИ)
НЕ ШЛЮХ не существует ИРЛ
Тогда:
(ЕОТ) U (ШЛЮХИ) + (ЕОТ) ∩ (ШЛЮХИ) = (ЕОТ) U (ШЛЮХИ) + (ЕОТ) ∩ (ШЛЮХИ)
Теорема доказана.
лол, пару дней назад ленга читал и орнул с этого. там еще сноска охуенная
Хоспади, двач кладись информации.То, что нужно, сяп анончики:3. Забил хуй на математику с 6 класса, сейчас буду исправляться, благо время есть, 18 лвл.
Учи сразу гомологии, теорию категорий и абстракную алгербру. Чтобы потом не переучиваться.
Но если "НЕ ШЛЮХ" не существует, то теорема не может существовать, потому что не хватает этих самых "НЕ ШЛЮХ", потому что их просто нет. Не бывает. то есть твоя теорема неприменима к жизни, на практике.
Шах и мат, ТННисты!
Опять Шифт не сработал, извиняюсь.
интуитивист в треде. факт существования шлюх не может быть доказан опираясь на несуществование не шлюх. вы инвокаете law of excluded middle а за это бьют канделябром
пару часов вечером, начну понемногу со школьных учебников, ибо есть дома
Я понял, точнее ты просто не сказал ничего не того же. А вот кстати интересно, как математический язык согласуется с естественным разных в языках, ведь не везде возможно двое отрицание. Как говаривал Жванецкий, давно там был, эээ, то есть хотел сказать давно там не был, а впрочем это то же самое.
Смотри, параграф - это несколько предложений. Полстранички. Они не нумеруются. Между параграфами есть отступы из одной пустой строки. Вот это был параграф.
А вот сейчас я начал второй параграф.
А главы состоят из параграфов и они нумеруются. После глав идут упражнения.
>параграф - это несколько предложений. Полстранички. Они не нумеруются.
Лишь бы что-нибудь спиздануть.
>>379785
Алсо, я задачки пропустил и перешл дальше читать и я встал на том как они там предел вводят.
А как они там предел вводят, медленно и осторожно через arbitrary and sufficiently close, или сразу втыкают со всей дури через дельта эпсилон?
Я понял в чем дело. Пишут:
Параграф и абзац
Абзац - не то же самое, что параграф
Хватит называть абзацы «параграфами». Слово paragraph в большинстве случаев переводится на русский язык: «абзац». А слово «параграф» означает другое и в большинстве случаев переводится на английский язык: section
У меня батарея в планшете села и он пока заряжается.

Судя по тому что я читаю по первому способу.
Где найти моар такого чтива?
>Ведь смысл НМУ — плодить самовлюбленных сектантов, которые потом будут срать на сосаче.
С чего ты так решил? Ты с самим Львовским на эту тему общался?
Можешь не пародировать мой стиль, у тебя ничего не получится.

Ааа, еба, ЕфремОвич! Понял свою ошиьку.
Коммутативность и ассоциативность. Деление a на b - это умножение a на b^(-1);
ac : b = ac * b^(-1) = ab^(-1)c = (ab^(-1))c
Твой пример можно по другому решить, если сомневаешься.
5=5x | - 5
5-5 = 5x - 5 | дистрибутивность
0 = 5(x-1) => x-1 = 0
x-1 = 0 | +1
x - 1 + 1 = 1
x = 1
Получилось, надо же!
https://crazymath.gitbooks.io/mathemix/content/index.html
проект незаконченный, если что
По-моему здорово.
Денех ему чтоли закинуть? А если мало закину, так он обидится, скажет ты бля лучше себе оставь это бля, лучше не тревожь меня.
Какой-то несвязный набор фактов, не ориентированный на читателя какого-то одного уровня. Википедия уже есть, зачем нужна еще одна?
Сука лол.
1. Общая логика. Форма мышления. Знак и семиотика. Понятие - денотат, концепт. Суждение. Умозаключение. Истинность. Корректность. Синтаксис и семантика. Правила вывода. Силлогизм. Modus ponens. Modus tollens. Именная функция. Пропозициональная функция. Содержание понятия. Объём понятия. Абстрактные и конкретные понятия. Термины. Определения, реальные и номинальные. Остенсивные определения. Родовые и видовые понятия. Деление понятий. Классы. Операции с классами. Дедуктивные умозаключения. Необходимость и достаточность. Аналогии. Гипотезы. Теории. Верифицируемость, фальсифицируемость. Научный метод. Операционализм. Позитивизм.
2. Математическая логика. Формальные системы. Формальные языки. Формальные логики. Буквы, слова, термы, атомы, формулы. Суждения. Вывод. Аксиоматические системы. Языки первого порядка. Переменные. Функции и предикаты. Кванторы. Логические аксиомы. Теории с равенством и без равенства. Тавтология, теоремы о ней. Дедукция. Структура. Модель. Теорема компактности. Изоморфизм и гомоморфизм моделей. Подструктуры. Мощность моделей. Непротиворечивость, выполнимость. Категоричность. Арифметика Пеано. Математическая индукция. Генетическое, рекурсивное определение. Аксиоматическое определение.
3. Теория множеств. Наивная теория множеств. Множества, элементы, подмножества, семейства. Дополнение, объединение, пересечение, степень, законы де Моргана и др. Пара. Произведение. Отношение. Функция, операция. Структуры. Равномощность. Мощность. Теоремы о мощностях. Счётные, несчётные множества. Объёмное определение кардинала. Арифметика кардиналов. Упорядоченные множества. Подобие порядков и порядковый тип. Вполне упорядоченные множества. Ординалы, конечные и бесконечные. Натуральные числа. Кардиналы как ординалы. Алефы. Теорема Цермело. Мощность как алеф. Парадоксы. Аксиоматическая теория множеств. ZFC. Интерпретация всего вышесказанного в ZFC. Схема замены и её следствия. Аксиома выбора и её следствия, лемма Цорна. Интуитивный смысл классов, предикат как класс. NBG. Универсумы, аксиома Гротендика.
4. Общая алгебра. Алгебраические структуры. Моноид, группа, кольцо, тело, поле. Подструктуры. Модуль над кольцом, векторное пространство, базис Гамеля. Действие группы. Морфизмы групп, морфизмы модулей. Нормальные подгруппы, факторгруппы, теоремы о группах (гомоморфизм, Лагранж, Кэли и т.д.). Идеалы, двусторонние идеалы, факторкольца, вычеты. Кольцо частных. Целые числа, рациональные числа. Нормальные и композиционные ряды. Алгебры. Свободные группы, свободные модули, свободные алгебры. Многочлены, целые рациональные функции. Алгоритм Евклида. Алгебраические расширения, сепарабельные расширения. Трансцендентные расширения, базис трансцендентности. Пополнения и нормирования.
5. Линейная алгебра. Векторные пространства, линейные многообразия. Матрицы. Линейные операторы. Опеределители. Двойственность. Формы, билинейные и полуторалинейные формы. Жорданова форма. Квадратичные формы, симметрические формы, скалярное произведение, ортогональные базисы. Алгебры Клиффорда. Знакопеременные формы. Эрмитовы формы. Спектральные теоремы. Геометрия пространств со скалярным произведением. Алгоритм ортогонализации. Евклидовы и унитарные пространства. Ортогональные, унитарные, самосопряженные операторы. Геометрия квадратичных форм. Пространство Минковского. Аффинные пространства. Проективные пространства. Кэлерова метрика. Алгебраические многообразия.
6. Полилинейная алгебра. Тензорное произведение модулей. Тензорное произведение алгебр. Тензорная алгебра модуля. Симметрическая алгебра. Алгебра Грассмана. Теоремы о внешнем произведении. Определители. Двойственность. Историческое определение тензора, связь с формами. Тензорные поля.
7. "Аналитическая" геометрия. Прямоугольные и косоугольные координаты, полярные, сферические и цилиндрические координаты. Уравнения прямой. Расположение прямых. Конические сечения. Кривые второго порядка. Плоскость. Расположение плоскости и прямых. Поверхности второго порядка. Касательная плоскость. Ортогональные, аффинные, проективные преобразования. Однородные координаты. Тангенциальные координаты.
1. Общая логика. Форма мышления. Знак и семиотика. Понятие - денотат, концепт. Суждение. Умозаключение. Истинность. Корректность. Синтаксис и семантика. Правила вывода. Силлогизм. Modus ponens. Modus tollens. Именная функция. Пропозициональная функция. Содержание понятия. Объём понятия. Абстрактные и конкретные понятия. Термины. Определения, реальные и номинальные. Остенсивные определения. Родовые и видовые понятия. Деление понятий. Классы. Операции с классами. Дедуктивные умозаключения. Необходимость и достаточность. Аналогии. Гипотезы. Теории. Верифицируемость, фальсифицируемость. Научный метод. Операционализм. Позитивизм.
2. Математическая логика. Формальные системы. Формальные языки. Формальные логики. Буквы, слова, термы, атомы, формулы. Суждения. Вывод. Аксиоматические системы. Языки первого порядка. Переменные. Функции и предикаты. Кванторы. Логические аксиомы. Теории с равенством и без равенства. Тавтология, теоремы о ней. Дедукция. Структура. Модель. Теорема компактности. Изоморфизм и гомоморфизм моделей. Подструктуры. Мощность моделей. Непротиворечивость, выполнимость. Категоричность. Арифметика Пеано. Математическая индукция. Генетическое, рекурсивное определение. Аксиоматическое определение.
3. Теория множеств. Наивная теория множеств. Множества, элементы, подмножества, семейства. Дополнение, объединение, пересечение, степень, законы де Моргана и др. Пара. Произведение. Отношение. Функция, операция. Структуры. Равномощность. Мощность. Теоремы о мощностях. Счётные, несчётные множества. Объёмное определение кардинала. Арифметика кардиналов. Упорядоченные множества. Подобие порядков и порядковый тип. Вполне упорядоченные множества. Ординалы, конечные и бесконечные. Натуральные числа. Кардиналы как ординалы. Алефы. Теорема Цермело. Мощность как алеф. Парадоксы. Аксиоматическая теория множеств. ZFC. Интерпретация всего вышесказанного в ZFC. Схема замены и её следствия. Аксиома выбора и её следствия, лемма Цорна. Интуитивный смысл классов, предикат как класс. NBG. Универсумы, аксиома Гротендика.
4. Общая алгебра. Алгебраические структуры. Моноид, группа, кольцо, тело, поле. Подструктуры. Модуль над кольцом, векторное пространство, базис Гамеля. Действие группы. Морфизмы групп, морфизмы модулей. Нормальные подгруппы, факторгруппы, теоремы о группах (гомоморфизм, Лагранж, Кэли и т.д.). Идеалы, двусторонние идеалы, факторкольца, вычеты. Кольцо частных. Целые числа, рациональные числа. Нормальные и композиционные ряды. Алгебры. Свободные группы, свободные модули, свободные алгебры. Многочлены, целые рациональные функции. Алгоритм Евклида. Алгебраические расширения, сепарабельные расширения. Трансцендентные расширения, базис трансцендентности. Пополнения и нормирования.
5. Линейная алгебра. Векторные пространства, линейные многообразия. Матрицы. Линейные операторы. Опеределители. Двойственность. Формы, билинейные и полуторалинейные формы. Жорданова форма. Квадратичные формы, симметрические формы, скалярное произведение, ортогональные базисы. Алгебры Клиффорда. Знакопеременные формы. Эрмитовы формы. Спектральные теоремы. Геометрия пространств со скалярным произведением. Алгоритм ортогонализации. Евклидовы и унитарные пространства. Ортогональные, унитарные, самосопряженные операторы. Геометрия квадратичных форм. Пространство Минковского. Аффинные пространства. Проективные пространства. Кэлерова метрика. Алгебраические многообразия.
6. Полилинейная алгебра. Тензорное произведение модулей. Тензорное произведение алгебр. Тензорная алгебра модуля. Симметрическая алгебра. Алгебра Грассмана. Теоремы о внешнем произведении. Определители. Двойственность. Историческое определение тензора, связь с формами. Тензорные поля.
7. "Аналитическая" геометрия. Прямоугольные и косоугольные координаты, полярные, сферические и цилиндрические координаты. Уравнения прямой. Расположение прямых. Конические сечения. Кривые второго порядка. Плоскость. Расположение плоскости и прямых. Поверхности второго порядка. Касательная плоскость. Ортогональные, аффинные, проективные преобразования. Однородные координаты. Тангенциальные координаты.
9. Математический анализ. Дифференциальная форма. Координаты формы. Внешний дифференциал формы. Интеграл формы. Форма объёма. Формулы Грина, Остроградского-Гаусса, Стокса. Скалярные и векторные поля на R^3. Градиент, ротор, дивергенция в дифференциальных и интегральных формах, набла. Криволинейные координаты. Потенциальные поля, векторный потенциал, точные и замкнутые формы. Примеры уравнений - теплопроводность, неразрывность, динамики сплошной среды, волновое. Абстрактные многообразия, грассманиан, локальные кольца, лемма Адамара. Компактные многообразия. Интегрирования плотностей. Дифференциальная форма в аффинном пространстве. Дифференциальная форма на многообразии. Интегрирование форм по цепям. Интеграл от формы по многообразию. Формула Стокса. Теорема Пуанкаре, гомологии и когомологии. Когомологии де Рама. Теорема де Рама. Интеграл от коцикла по циклу. Гомологические циклы. Гомотопия. Топологическая степень. Теорема Фробениуса. Свойства преобразований. Распределения. Обобщенные функции. Пространства Соболева. Эллиптические операторы. Оператор Коши-Римана. Теорема регулярности.
10. Комплексный анализ. Голоморфные функции. Формулы Коши. Ряд Тейлора. Ряды Хартогса и Лорана. Теорема Лиувилля. Мероморфные функции. Псевдовыпуклость. Оболочки голоморфности. Проблемы Кузена. Группы гомологий, точные последовательности пучков. Вычеты. Поверхности Римана. Свертки. Теоремы Бэра и Банаха-Штейнгауза. Свойства Монтеля. Теорема Миттаг-Лефлера. Теорема Вейерштрасса. Задача Дирихле. Теоремы Коши-Пуанкаре, Мартинелли-Бохнера, Лере, Севери, Вейла.
11. Обыкновенные дифференциальные уравнения. Задача Коши. Теоремы существования и единственности. Априорная оценка. Непрерывность решения. Фазовые пространства, фазовые потоки. Действие диффеоморфизмов. Теоремы о выпрямлении. Классические дифференциальные уравнения - разделяющиеся, однородные, линейные, Бернулли, Якоби, Риккати, Лагранжа, Клеро. Устойчивость по Ляпунову. Фазовый поток, заданный векторным полем. Дифференциальное уравнение, определенное векторным полем. Дифференциальное уравнение на многообразии. Особые точки, индексы особых точек.
12. Уравнения с частными производными. Линейное однородное урчп с производными первого порядка. Системы уравнений. Уравнение Пфаффа. Уравнение теплопроводности, уравнение струны. Задача Штурма-Лиувилля, задача Коши. Характеристика. Полный, общий и особый интегралы, интеграл Пуассона. Методы Лагранжа и Коши. Преобразование Лежандра. Теорема Коши-Ковалевской. Уравнение Монжа. Уравнение Эйлера. Эйконал. Поле экстремалей. Уравнние Гамильтона-Якоби. Конструкция Гюйгенса. Интеграл Гильберта. Теория возмущений. Уравнения высших порядков. Гиперболичность. Уравнения Дарбу, Максвелла и Дирака. Фундаментальные решения. Плоские, бегущие, цилиндрические и сферические волны. Принцип Дюамеля. Запаздывающие потенциалы. Приведенное волновое уравнение, условие Зоммерфельда. Теорема Реллиха. Оценки Шаудера. Уравнение Бельтрами. Характеристическая нормальная форма для гиперболических систем первого порядка. Динамика сжимаемой жидкости. Представление решений в форме Римана. Исчисление Хевисайда, метод Хевисайда. Дифференциальные уравнения гидродинамики, кристаллодинамики, магнитной гидродинамики. Асимптотические разложения решений. Уравнения физики, примеры и контрпримеры, пример Адамара.
9. Математический анализ. Дифференциальная форма. Координаты формы. Внешний дифференциал формы. Интеграл формы. Форма объёма. Формулы Грина, Остроградского-Гаусса, Стокса. Скалярные и векторные поля на R^3. Градиент, ротор, дивергенция в дифференциальных и интегральных формах, набла. Криволинейные координаты. Потенциальные поля, векторный потенциал, точные и замкнутые формы. Примеры уравнений - теплопроводность, неразрывность, динамики сплошной среды, волновое. Абстрактные многообразия, грассманиан, локальные кольца, лемма Адамара. Компактные многообразия. Интегрирования плотностей. Дифференциальная форма в аффинном пространстве. Дифференциальная форма на многообразии. Интегрирование форм по цепям. Интеграл от формы по многообразию. Формула Стокса. Теорема Пуанкаре, гомологии и когомологии. Когомологии де Рама. Теорема де Рама. Интеграл от коцикла по циклу. Гомологические циклы. Гомотопия. Топологическая степень. Теорема Фробениуса. Свойства преобразований. Распределения. Обобщенные функции. Пространства Соболева. Эллиптические операторы. Оператор Коши-Римана. Теорема регулярности.
10. Комплексный анализ. Голоморфные функции. Формулы Коши. Ряд Тейлора. Ряды Хартогса и Лорана. Теорема Лиувилля. Мероморфные функции. Псевдовыпуклость. Оболочки голоморфности. Проблемы Кузена. Группы гомологий, точные последовательности пучков. Вычеты. Поверхности Римана. Свертки. Теоремы Бэра и Банаха-Штейнгауза. Свойства Монтеля. Теорема Миттаг-Лефлера. Теорема Вейерштрасса. Задача Дирихле. Теоремы Коши-Пуанкаре, Мартинелли-Бохнера, Лере, Севери, Вейла.
11. Обыкновенные дифференциальные уравнения. Задача Коши. Теоремы существования и единственности. Априорная оценка. Непрерывность решения. Фазовые пространства, фазовые потоки. Действие диффеоморфизмов. Теоремы о выпрямлении. Классические дифференциальные уравнения - разделяющиеся, однородные, линейные, Бернулли, Якоби, Риккати, Лагранжа, Клеро. Устойчивость по Ляпунову. Фазовый поток, заданный векторным полем. Дифференциальное уравнение, определенное векторным полем. Дифференциальное уравнение на многообразии. Особые точки, индексы особых точек.
12. Уравнения с частными производными. Линейное однородное урчп с производными первого порядка. Системы уравнений. Уравнение Пфаффа. Уравнение теплопроводности, уравнение струны. Задача Штурма-Лиувилля, задача Коши. Характеристика. Полный, общий и особый интегралы, интеграл Пуассона. Методы Лагранжа и Коши. Преобразование Лежандра. Теорема Коши-Ковалевской. Уравнение Монжа. Уравнение Эйлера. Эйконал. Поле экстремалей. Уравнние Гамильтона-Якоби. Конструкция Гюйгенса. Интеграл Гильберта. Теория возмущений. Уравнения высших порядков. Гиперболичность. Уравнения Дарбу, Максвелла и Дирака. Фундаментальные решения. Плоские, бегущие, цилиндрические и сферические волны. Принцип Дюамеля. Запаздывающие потенциалы. Приведенное волновое уравнение, условие Зоммерфельда. Теорема Реллиха. Оценки Шаудера. Уравнение Бельтрами. Характеристическая нормальная форма для гиперболических систем первого порядка. Динамика сжимаемой жидкости. Представление решений в форме Римана. Исчисление Хевисайда, метод Хевисайда. Дифференциальные уравнения гидродинамики, кристаллодинамики, магнитной гидродинамики. Асимптотические разложения решений. Уравнения физики, примеры и контрпримеры, пример Адамара.
14. Статистика. Классическая статистика. Исчерпывающие статистики. Доверительные границы и доверительные вероятности. Гипотезы. Вероятности и частоты. Биномиальное распределение. Бета- и гамма-функции. Кривая Кетле. Оценки функций распределения. Характеристические функции, хи-квадрат, предельные теоремы, прямоугольное распределение. Гауссова теория ошибок, s-квадрат, критерий Стьюдента. Метод наименьших квадратов. Средние значения и дисперсии. Оценка дисперсии. Линии регрессии. Метод наибольшего правдоподобия Фишера. Неравенство Фреше. Свойства нормального распределения. Асимптотические свойства. Оценка параметров по наблюденным частотам. Проверка гипотез с помощью статистических критериев. Гипотезы однородности, независимости, случайности. Параметрические гипотезы, простые и сложные. Дисперсионный анализ. Порядковые критерии. Корреляция, ковариация. Коэффициенты корреляции.
15. Классическая неквантовая механика. Законы Ньютона. Терминология. Энергия, связи, обобщенные координаты, конфигурационное пространство, принцип возможных перемещений, принцип Даламбера. Теорема Нётер. Уравнения Лагранжа. Консервативные и неконсервативные системы. Функция Рэлея. Сила Кориолиса, центробежная сила, задача двух тел, теорема Лармора, симметричный волчок, главные колебания. Обобщенные импульсы, циклические координаты, фазовое пространство, функция Гамильтона. Интегралы движения. Диссипативные системы. Принцип Гамильтона. Уравнения Гамильтона, метод Гамильтона-Якоби. Движение частиц, столкновение частиц, рассеяние частиц. Формула Резерфорда. Малые колебания. Колебания систем со многими степенями свободы. Параметрический резонанс. Ангармонические колебания. Движение твердого тела. Тензор инерции. Волновое уравнение, принцип Ферма. Функция Рауса, скобки Пуассона, тождество Якоби. Принцип Мопертюи. Теорема Лиувилля. Непрерывные среды. Переменные поля, уравнения Гамильтона для поля. Законы сохранения плотности. Симплектические многообразия, классическая механика как структура на симплектическом многообразии.
16. Классическая термодинамика. Термодинамические системы. Идеальные газы. Первый закон. Адиабатические процессы в газах. Второй закон. Цикл Карно. Абсолютная температура. Тепловые машины. Энтропия. Уравнение Клапейрона. Уравнение Ван-дер-Ваальса. Термодинамические потенциалы. Свободная энергия. Правило фаз. Химическое равновесие в газах. Принцип ле Шателье. Термодинамика разбавленных растворов. Осмотическое давление. Химическое равновесие в растворах. Связь энтропии и температуры. Теорема Нернста. Энтропийная константа. Третий закон термодинамики. Фактор Больцмана. Распределение Максвелла по скоростям. Экспериментальные подтверждения.
17. Классическая гидродинамика. Модель Эйлера. Уравнение состояния. Граничные условия. Уравнение энергии. Перенос количества движения. Уравнение неразрывности. Безвихревое движение, поток, циркуляция. Несжимаемая жидкость. Трубка тока. Источники и стоки. Функция тока Лагранжа. Теория Максвелла о полюсах. Зональные функции, гипергеометрические ряды, тессеральные и секторальные функции. Уравнение Лапласа. Линии тока на эллипсоиде, диполь. Движение твердых тел в жидкости. Гидрокинетическая симметрия. Вихревое движение. Постоянство вихрей. Изолированный вихрь. Потенциал, создаваемый вихрем. Импульс вихря. Прямолинейные вихри. Вихревая дорожка. Теоремы Кирхгофа. Вихревые кольца, их устойчивость. Приливные волны. Поверхностные волны. Стоячие волны в ограниченной массе воды. Капиллярные волны. Плоские волны. Звуковые волны. Вязкость. Диффузия вихря.
18. Классическая электродинамика. Электрические явления и приборы. Заряд. Закон Кулона. Электростатическое поле. Проводники. Уравнение Лапласа. Уравнение Лежандра. Полиномы Лежандра. Граничные задачи. Функции Бесселя. Разложение по мультиполям. Изотропные диэлектрики. Поляризуемость молекул и диэлектрическая восприимчивость. Магитостатика. Закон Био-Савара. Закон Ампера. Векторный потенциал. Магнитная индукция, магнитное поле, магнитный момент. Внешнее магнитное поле. Макроскопические уравнения. Электромагнитное поле. Закон Фарадея. Энергия магнитного поля. Максвелловский ток. Уравнения Максвелла. Векторный и скалярный потенциалы. Калибровочные преобразования. Лоренцовская, кулоновская калибровка. Функция Грина для волнового уравнения. Интегральное представление Кирхгофа. Теорема Пойтинга. Плоские электромагнитные волны. Волны в непроводящей среде. Линейная, круговая поляризации. Суперпозиция волн. Групповая скорость. Распространение импульсов в диспергирующей среде. Отражение и преломление электромагнитных волн. Поляризация. Волны в проводящей среде. Простая модель проводимости. Волноводы. Поля на поверхности и внутри проводника. Цилиндрические резонаторы. Диэлектрические волноводы. Поле ограниченного колеблющегося источника. Электрическое дипольное поле. Излучение. Магнитные дипольное и квадрупольные поля. Линейная антенна. Интеграл Кирхгофа. Дифракция на круглом отверстии. Дифракция на малых отверстиях. Рассеяние коротких волн проводящей сферой.
19. Классическая геометродинамика. Специальная теория относительности. Группа Лоренца. Сокращение Фицджеральда. Замедление времени. Опыт Физо. Допплеровское смещение. Прецессия Томаса. Собственное время и световой конус. Ковариантность уравнений электродинамики. Преобразование электромагнитного поля. Импульс и энергия релятивистской частицы, её лагранжиан и гамильтониан. Кинематика осколков. Движение в однородном статическом поле. Дрейф частиц. Излучение движущихся частиц. Общая теория относительности. Уравнение Эйнштейна. Решение Шварцшильда. Тензор энергии-импульса. Действие для электромагнитного поля. Гравитационные волны. Поток и плотность энергии. Особенности уравнений Эйнштейна.
20. Классическая квантовая механика. Поляризация фотонов. Интерференция фотонов. Принцип суперпозиции. Динамические переменные и наблюдаемые. Правила квантования Бора-Зоммерфельда. Соотношения сопряженности. Шредингеровское представление. Импульсное представление. Принцип Гейзенберга. Операторы сдвига. Уравнения движения в формулировках Шредингера, Гейзенберга. Стационарные состояния. Свободная частица. Движение волнового пакета. Ансамбль Гиббса. Гармонический осциллятор. Момент количества движения. Спин. Движение в центральном силовом поле. Уровни энергии атома водорода, классические серии. Эффект Зеемана. Изменение уровней энергии возмущением. Переходы. Излучение. Аномальный эффект Зеемана. Системы нескольких частиц. Перестановки как динамические переменные, как интегралы движения. Электроны. Статистические ансамбли. Ансамбль бозонов, ансамбль фермионов. Испускание и поглощение бозонов. Фотоны. Энергия взаимодействия между фотоном и атомом. Волновое уравнение, волновое уравнение электрона. Движение электрона. Релятивистская форма квантовых условий. Шредингеровские переменные. Электроны и позитроны в присутствии поля.
14. Статистика. Классическая статистика. Исчерпывающие статистики. Доверительные границы и доверительные вероятности. Гипотезы. Вероятности и частоты. Биномиальное распределение. Бета- и гамма-функции. Кривая Кетле. Оценки функций распределения. Характеристические функции, хи-квадрат, предельные теоремы, прямоугольное распределение. Гауссова теория ошибок, s-квадрат, критерий Стьюдента. Метод наименьших квадратов. Средние значения и дисперсии. Оценка дисперсии. Линии регрессии. Метод наибольшего правдоподобия Фишера. Неравенство Фреше. Свойства нормального распределения. Асимптотические свойства. Оценка параметров по наблюденным частотам. Проверка гипотез с помощью статистических критериев. Гипотезы однородности, независимости, случайности. Параметрические гипотезы, простые и сложные. Дисперсионный анализ. Порядковые критерии. Корреляция, ковариация. Коэффициенты корреляции.
15. Классическая неквантовая механика. Законы Ньютона. Терминология. Энергия, связи, обобщенные координаты, конфигурационное пространство, принцип возможных перемещений, принцип Даламбера. Теорема Нётер. Уравнения Лагранжа. Консервативные и неконсервативные системы. Функция Рэлея. Сила Кориолиса, центробежная сила, задача двух тел, теорема Лармора, симметричный волчок, главные колебания. Обобщенные импульсы, циклические координаты, фазовое пространство, функция Гамильтона. Интегралы движения. Диссипативные системы. Принцип Гамильтона. Уравнения Гамильтона, метод Гамильтона-Якоби. Движение частиц, столкновение частиц, рассеяние частиц. Формула Резерфорда. Малые колебания. Колебания систем со многими степенями свободы. Параметрический резонанс. Ангармонические колебания. Движение твердого тела. Тензор инерции. Волновое уравнение, принцип Ферма. Функция Рауса, скобки Пуассона, тождество Якоби. Принцип Мопертюи. Теорема Лиувилля. Непрерывные среды. Переменные поля, уравнения Гамильтона для поля. Законы сохранения плотности. Симплектические многообразия, классическая механика как структура на симплектическом многообразии.
16. Классическая термодинамика. Термодинамические системы. Идеальные газы. Первый закон. Адиабатические процессы в газах. Второй закон. Цикл Карно. Абсолютная температура. Тепловые машины. Энтропия. Уравнение Клапейрона. Уравнение Ван-дер-Ваальса. Термодинамические потенциалы. Свободная энергия. Правило фаз. Химическое равновесие в газах. Принцип ле Шателье. Термодинамика разбавленных растворов. Осмотическое давление. Химическое равновесие в растворах. Связь энтропии и температуры. Теорема Нернста. Энтропийная константа. Третий закон термодинамики. Фактор Больцмана. Распределение Максвелла по скоростям. Экспериментальные подтверждения.
17. Классическая гидродинамика. Модель Эйлера. Уравнение состояния. Граничные условия. Уравнение энергии. Перенос количества движения. Уравнение неразрывности. Безвихревое движение, поток, циркуляция. Несжимаемая жидкость. Трубка тока. Источники и стоки. Функция тока Лагранжа. Теория Максвелла о полюсах. Зональные функции, гипергеометрические ряды, тессеральные и секторальные функции. Уравнение Лапласа. Линии тока на эллипсоиде, диполь. Движение твердых тел в жидкости. Гидрокинетическая симметрия. Вихревое движение. Постоянство вихрей. Изолированный вихрь. Потенциал, создаваемый вихрем. Импульс вихря. Прямолинейные вихри. Вихревая дорожка. Теоремы Кирхгофа. Вихревые кольца, их устойчивость. Приливные волны. Поверхностные волны. Стоячие волны в ограниченной массе воды. Капиллярные волны. Плоские волны. Звуковые волны. Вязкость. Диффузия вихря.
18. Классическая электродинамика. Электрические явления и приборы. Заряд. Закон Кулона. Электростатическое поле. Проводники. Уравнение Лапласа. Уравнение Лежандра. Полиномы Лежандра. Граничные задачи. Функции Бесселя. Разложение по мультиполям. Изотропные диэлектрики. Поляризуемость молекул и диэлектрическая восприимчивость. Магитостатика. Закон Био-Савара. Закон Ампера. Векторный потенциал. Магнитная индукция, магнитное поле, магнитный момент. Внешнее магнитное поле. Макроскопические уравнения. Электромагнитное поле. Закон Фарадея. Энергия магнитного поля. Максвелловский ток. Уравнения Максвелла. Векторный и скалярный потенциалы. Калибровочные преобразования. Лоренцовская, кулоновская калибровка. Функция Грина для волнового уравнения. Интегральное представление Кирхгофа. Теорема Пойтинга. Плоские электромагнитные волны. Волны в непроводящей среде. Линейная, круговая поляризации. Суперпозиция волн. Групповая скорость. Распространение импульсов в диспергирующей среде. Отражение и преломление электромагнитных волн. Поляризация. Волны в проводящей среде. Простая модель проводимости. Волноводы. Поля на поверхности и внутри проводника. Цилиндрические резонаторы. Диэлектрические волноводы. Поле ограниченного колеблющегося источника. Электрическое дипольное поле. Излучение. Магнитные дипольное и квадрупольные поля. Линейная антенна. Интеграл Кирхгофа. Дифракция на круглом отверстии. Дифракция на малых отверстиях. Рассеяние коротких волн проводящей сферой.
19. Классическая геометродинамика. Специальная теория относительности. Группа Лоренца. Сокращение Фицджеральда. Замедление времени. Опыт Физо. Допплеровское смещение. Прецессия Томаса. Собственное время и световой конус. Ковариантность уравнений электродинамики. Преобразование электромагнитного поля. Импульс и энергия релятивистской частицы, её лагранжиан и гамильтониан. Кинематика осколков. Движение в однородном статическом поле. Дрейф частиц. Излучение движущихся частиц. Общая теория относительности. Уравнение Эйнштейна. Решение Шварцшильда. Тензор энергии-импульса. Действие для электромагнитного поля. Гравитационные волны. Поток и плотность энергии. Особенности уравнений Эйнштейна.
20. Классическая квантовая механика. Поляризация фотонов. Интерференция фотонов. Принцип суперпозиции. Динамические переменные и наблюдаемые. Правила квантования Бора-Зоммерфельда. Соотношения сопряженности. Шредингеровское представление. Импульсное представление. Принцип Гейзенберга. Операторы сдвига. Уравнения движения в формулировках Шредингера, Гейзенберга. Стационарные состояния. Свободная частица. Движение волнового пакета. Ансамбль Гиббса. Гармонический осциллятор. Момент количества движения. Спин. Движение в центральном силовом поле. Уровни энергии атома водорода, классические серии. Эффект Зеемана. Изменение уровней энергии возмущением. Переходы. Излучение. Аномальный эффект Зеемана. Системы нескольких частиц. Перестановки как динамические переменные, как интегралы движения. Электроны. Статистические ансамбли. Ансамбль бозонов, ансамбль фермионов. Испускание и поглощение бозонов. Фотоны. Энергия взаимодействия между фотоном и атомом. Волновое уравнение, волновое уравнение электрона. Движение электрона. Релятивистская форма квантовых условий. Шредингеровские переменные. Электроны и позитроны в присутствии поля.
Это не Вербит, а какой-то хуй из /b. Хочет учиться по этом списку.
https://2ch.hk/b/res/133365332.html (
Нахуя так расписывать на столетия вперед, никогда не понимал
Гомологии есть? 10/10 курс, станешь сверхчеловеком.
Что из оп-списка определённо годнота и нужно читать?
А то я начитался тут критики в его адрес.
Годнота все по отдельности, но все вместе-ужас
Я конечно понимаю, что Вербит ебанутый, но будет ли он на двочах притворяться ньюфагом и кидать список, изучения математики?
От профессора математики чего угодно можно ждать. Они ебнутые все.
Они скоро сотрут либген, а бекап никто из вас не сделал. Тоже будешь за книги платить.
Вот я вынес из списка для начала
1) Э. Б. Винберг: “Курс алгебры”
2/3) В. А. Ильин, Э. Г. Позняк: “Линейная алгебра“
В. А. Зорич: "Математический анализ"
4) И. М. Гельфанд, С. В. Фомин: " Вариационное исчисление"
Норм? Или я идиот? как ангельский нормально выучу, перейду на ваших заморских
норм
Я пендосский плохо знаю(((( Как, кстати, маттермины учить? Сразу или по ходу?
Посмотри видосы на кханакадеми с субтитрами с самого начала ( с арифметики), он там поясняет за термины, так их сразу на пиндоском поймешь, в будущем это тебе охуенную пользу сыграет
>>379894
Не тупые, а просто белые люди у которых адекватная зарплата, и которым не жалко денег за книги
Нашел кого слушать, они тут такое говно иногда едят что ты даже не представляешь, тысячи довольных анонов с других борд советуют кханакадеми и нормас.
инб4 фраза про тысячу мух
Нашёл кого слушать, они ничего не понимают.
> для серьезных книжек по программировани/элекроники, матан пригодиться
> пригодиться
Во-первых, русский язык тебе пригодится, если ты не заводишь трактор в ближайшее время. Советую подучить. Во-вторых, гугли MIT: Mathematics for Computer Science.
да говорю же, мне не только для погроммирования, для той же схемотехники и другой годноты, но за линк спасибо, ато я только про конкретную математику кнута знал.
Вики до энциклопедии не дотягивает ну совсем никак, увы. Местами больше похоже на сборник фанфиков.
Им жалко денег на книги. Книги очень дорогие и они разборчивы при их выборе из-за этого.
Ну это хорошая привычка не понакупать всякого говна сразу, а потом в нем копаться, а лучше сделать небольшой research и покупать сразу годноту
Пушо потребляди, ни то что мы, русские, которым похуй на формат, лишь бы информацию передать.
на самом деле потому что это удобно, ну вот сидишь ты в очереди, делать нехуй, а так можно книгу достать и на полях задачи решать, а с электронной версией тебе надо и планшет доставать и блокнот, и не повыебываешься перед людьми что они тут без дела сидят, а ты такой как илита сидишь и матан решаешь, не легетимно в общем
Мне почему-то кажется, что из калькулюса среднему инженеру или программисту не нужно вообще ничего. Можно на пальцах объяснить, что да зачем, игнорируя все формальные построения, и послать сразу в матлаб.
Дык говорю же, открыл the art of electronics (на фочан-вики поговаривают лютая годнота, а там lim, интегралы вот это все, потом открыл какой-то неплохой гайд по написанию электронной музыки, а тут снова lim, синусоиды и прочая годнота
Маттермины не надо учить, просто берешь и читаешь смысл. Ты же легко запомнил иностранный термин дилдак, например. Никто же его не нызывал для тебя резиновым хуем. Просто увидел его и запомнил как есть - это дилдо. Кстати на русском мат терминология адский пиздец. Вон почитай бурбаков выше. "Покрывает". "Порождает". И проч . Что такое порождает кстати, span? Spanning set? Или give birth?
Как по мне, так это cast, типо cast spells/fireballs
Ну дык открой википедию, почитай. Я не вижу смысла пару недель идти к понятию предела, а потом еще пару месяцев к понятию какого-нибудь интеграла, чтобы понять саму сущность понятий для конкретной книжки.
Ну неплохой такой материал для школьника, очень плохо изложенный и вообще литературно бездарный, будто реферат.
Есть лекции Awodey'а (и книга у него тоже есть), есть TheCatsters на ютубе. Awodey начинает сначала, но я не уверен, что его курс претендует на хоть какую-то полноту, возможно просто введение. TheCatsters тоже не похож на полный курс, скорее на сборку важных тем, когда уже знаешь базу https://byorgey.wordpress.com/catsters-guide-2/
Понять что и как в электронике, научиться паять электронику самому, и тому подобное.
Хоровиц хорош, но он же заточен под курс EE, там много всяких gory details которые тебе вряд ли понадобятся. Анон выше прав - просто гугли по мере необходимости или пропускай непонятные места. Не понимаю от чего такой дроч именно на эту книжку. Есть много похожих, с разным уровнем деталей и сложности. Просто она наиболее полная и "котируется" в определенных кругах (как гамологии здесь). Алтернативы попроще:
Boylestad & Nashelsky 7th.pdf
Floyd 9th. Floyd.pdf
Malvino Bates 7th.pdf
Robbins Miller 2012.pdf
Все есть на либгене.
Спасибо, обязательно просмотрю твой список
Не вижу книг по доказательствам, мат. логике и теории множеств. Или ты не совсем нуб?
>Не вижу книг по доказательствам, мат. логике и теории множеств.
Отдельные книжки, ты не шутишь? Может тогда с учебника метаматематике и металогике начать?
Не обязательно отдельные, если там эти темы есть, то ок. По мат. логике есть полукнижки How to Prove it Веллемана и Introduction to Mathematical Thinking by Keith Devlin. Не бесполезно будет полистать, особенно если никто не рассказывал про математические доказательства в школе/универе.
Ну в зориче есть нормальное введение. А в плане доказательств есть норм книжки Пойа, даже на русик переведенные.
А я наоборот как-то стесняюсь матан и прочий энтрилевел решать в очередях. Стесняюсь, потому что в моем возрасте уже давно пора гомологии считать, а я с такой детской хуйней.
Абсолютное большинство совсем не видят разницы между интегралами с первых курсов и твоими гомологиями. Да и стыдно быть взрослым и переживать что о тебе думают, тем более незнакомые люди.
>В юностьи у меня был дин знакомый математик. Он неправильно жил, решал интегралы первого курса в очередях... И вот один раз, в какой то очереди, он увидел пред собой рому михайлова, который сказал ЗАДАВАЙ МНЕ ЛЮБЫЕ ВОПРОСЫ
Потом Рома Михайлов сказал ему, что зря потратил время на гомологии и они в очереде вместе решали интегралы.
>Многие, впрочем, знают меня под другими именами (кои я предпочёл бы умолчать здесь).
Хеллер, ты? Или это другой поехавший?
Лол, не дописав один учебник взялся бы он за другой? Впрочем, кто знает чего ждать от шлюхоеба
Спасибо!
А какие тебе нужны темы в категориях? Все категорные темы - в алгеме и гамалогиях. Изучаешь котегории, функторы, аджойнты, базовые конструкции, инъективные-проективные объекты и начинаешь хуярить гамалогии. Всё.
Аводи попытался исправить то, что запорол его учитель. Тот самый Маклейн, более упоротого изложения предмета которого трудно найти. Получилось ли это у него? Да хуй знает, честно говоря. Что-то - да, а что-то не менее упорото. Есть охуенные abstract and concrete categories, с кучей букав без особой лирики, примеров и ебанутых задач. но там немного устаревшая терминология как минимум в одном моменте квазикатегории, которые не считаются квазикатегориями сейчас вроде бы. Основы есть в достаточно неплохом "Basic category theory" Leinster'а.

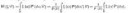
ты сначала скидывай, а потом спрашивай
Вот двачую, разведут хайпу, а потом бросают не доделав. Чмы бесхарактерные
Докажи сперва что доказал, а то я вот тебе не верю

> Тупо подставлять полчаса, пока не совпадет?
Даже если ты найдешь какие то x,y,z которые удовлетворяют этому уравнению, тебе надо будет показать что других решений нет.
Теорию меры очевидно же, посмотри в Колмогорове Фомине соответствующие параграфы.
Пусть они сначала дадут определение натуральных чисел, тогда решу
Я бы сначала действительно поподставлял числа, ведь факториал очень быстро растёт.


Ну вот скриншот подобных упражнений в конце урока. Решил я их, а как сверить ответы?
ох блядь, вот оно как.
Просто я точно все не смогу загуглить.
Репетитора конечно я себе найду, но до этого еще как минимум месяц.
Exercise 1.13 asks us to prove that Fib(n) is the closest integer to φn/√5, where
φ = (1 + √5)/2.
The exercise also gives us the following hint:
Let ψ = (1 - √5)/2. Use induction and the definition of Fibonacci numbers to prove that
Fib(n) = (φn - ψn) / √5
Школьную программу
Метод математической индукции
Определение чисел фибоначчи
Определение золотого сечения
Все правильно сказал.
Можно через линейную алгебру доказать. Типа вектор [φ_n φ_{n-1}] - это линейное преобразование вектора [φ_{n-1}, φ_{n-2}]. Матрица этого преобразования диагонализуема, за счет чего можно получить явную формулу для n-й степени матрицы.
проиграл с пояснения про восклицательный знак. советская школа преподавания как она есть? то есть стюдент может не знать про ! но задачку ему все равно задать надо.
Я доказал что в /b все пидоры. Не могут решить задачу для китайского 6-го класса.
это чтобы не дискриминировать на олимпиадах ребят из обычных школ
А что, для решения задачи требуются еще какие-то знания про факториал кроме его определения?
Это другой вопрос, требуется или нет. Просто это странный подход - вводить определение чего-то в задачке про это самое.
Дети в обычных школах не учат факториалы. Задачка школьная-то школьная.
Че странного? А если порядок предложений изменить и написать сначала определение факториала, а потом условие задачи, что-то изменится?
При чем тут порядок предложений. Это вообще про порядок процесса. ordnung muss sein. Изучаешь тему, читаешь определения, абзацами, или параграфами. Потом решаешь задачи. А ты утверждашь что наоборот это норм? Аноны о чем угодно готовы спорить.
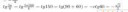
Там нужно было в конце в условии задачи дописать в скобках, что такое тангенс и схемку нарисовать малюсенькую. От этого бы ничего не изменилось. Конечно он меняет знак. atan2 для этого есть. Квадранты учитывает.

Ну она у меня нарисована. tg 150, вторая четверть. -sgrt3/2 поделить на 1/2, получается -sgrt3 же. С катангенсом все наоборот и получается как раз правильный ответ.
Попробуем доказать, что решений конечное количество (потому что обычно в таких задачах решений конечное количество). Можно попробовать посмотреть на делимость: для достаточно больших z, z! делится на любое n, а вот 3^x + 5^y - 14 может не делиться.
Если левая и правая части уравнения равны, они должны быть сравнимы по модулю n (давать одинаковый остаток при делении на n) для любого n >= 2. Начинаем перебирать и видим, что при z >= 4 правая часть делится на 4, а левая нет: 3^x (mod 4) = 3 или 1, 5^y (mod 4) = 1 и 14 (mod 4) = 2.
3 + 1 + 2 != 0
1 + 1 + 2 != 0
Остается только перебрать варианты с z <= 3.
То есть задача типовая для олимпиад: факториал здесь хуйнули, чтобы это делилось на все числа, а слева что-то хуйнули, чтоб оно делилось не на все числа. Вообще, советую не тратить время на олимпиады, а читать вузовские учебники, изучать что-то вперед программы, потому что для математики навык решения олимпиадок абсолютно бесполезнен.
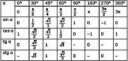
Пиздос у тебя рисунок, это ж мозги раком станут. Смотри на простенький пикрил и на свою сумму и все поймаешь. Минус тебе дает tg(90)
>Попробуем доказать, что решений конечное количество (потому что обычно в таких задачах решений конечное количество)
Лольнул почему-то.
> 1 + 1 + 2 != 0
Ой, чет я не выспался седня, лол. Но я уверен, что решение должно быть в таком духе.
>Пиздос у тебя рисунок, это ж мозги раком станут.
в тетрадке другой совсем.
>Минус тебе дает tg(90)
Какого хуя он мне что то дает? Минус это который от -sgrt3/2? ну и нахуй он мне нужен? он же только знак ответа менять.
>Смотри на простенький пикрил и на свою сумму и все поймаешь
Ну у меня тангенс 150, 90 грят что это 2 четверть, 60 - крайнее положение на таблице, если делить синус на косинус получается -sgrt3, прямо как в таблице tg60-sgrt3, только знак другой из за четверти.
Но откуда берется катангенс?
>>380166
Исправил. Из сравнения по модулю 3 видно, что y четное. Из сравнения по модулю 4 видно, что x четное. Посмотрим на сравнение по модулю 7: 3^x дает остатки [3, 2, 6, 4, 5, 1], 5^y дает [5, 4, 6, 2, 3, 1]. С учетом того, что x и y четные, это [2, 4, 1] и [4, 2, 1]. Отсюда видно, что при z >= 7 решений нет.
Остается перебрать варианты для z < 7. Чтобы сократить перебор, надо использовать сравнения.
Ну это же просто тождество такое tan (90° + Э) = - cot Э. Во втором квадранте (90< Э < 180) тан отрицателен. А tan(90) не определен - деление на нуль. Просто глядя на сумму (90+60) ты видишь какой квадрант и какой будет знак.
То есть если косинус отрицательный, то тангенс меняется на котангенс?
Ну я вроде бы понял, спасибо.
Это же не учебник, а какая-нибудь олимпиадка.
Там три решения всего вроде.
Какие параграфы ты собираешься про факториал читать? Ты че аутист? К какой теме по-твоему относится определение факториала?
>К какой теме по-твоему относится определение факториала?
К интегральному исчислению. Гамма-функция, сэр.
Вне зависимости от истинности твоего высказывания, для определения факториала всё ещё не нужна гамма-функция.
> А ты утверждашь что наоборот это норм?
Не наоборот, а одновременно. Да, я считаю что норм. Но лучше, конечно, давать доказать какое-то утверждение, а не задавать вопрос, потому что если человек не понял определение, это утверждение может его как-то скорректировать. Пример: дается определение хаусдорфова пространства и предлагается доказать, что любое метрическое пространство хаусдорфово. Очень простая задача, которая помогает понять определение (хотя че в нем можно не понять?).
Затем, чтобы не ебаться с матаном, наверное? Человек учится от частного к общему, а не наоборот, к сожалению.
Ну хорошо не параграф, но хотя бы абзац.
Что за вопросы ты задаешь, ты что аутист? Факториалы изучаются напримере в discrete math, в статистике, биномиалз, counting, wot это все. У них до ебени страсти всяких свойств, тождеств, в тч с тригонометрическими функциями, всякие косекансы (не помню конкретно, что-то про переходы от факториалов к биномиалам), recurrence indenities хуева туча. Еще запишем сюда разные функциональные уравнения, логарифмические выпуклости/впуклости. Целый том можно написать про факториалы, только дискретные при том, не касаясь гамма функций. Да, еще в дискретном калькулюсе ебошат производные с факториалами, напичканные всякими синусами в перемешку с логарифмами.
> И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
Вкатываюсь с нуля, начну с этого пожалуй, посоветуйте еще чего-нить схожего, а то по школьным учебникам как-то не охота работать.
>В. Б. Алексеев: “Теорема Абеля в задачах и решениях”
Дальше уже берешь университетские учебники.
Так это не школьный учебник вроде.
ханакадеми, там даже задачки есть.
Читай учебники Колмогорова 80-х годов.

Посоветуйте лучшие учебники для новичков по комбинаторики и по теории вероятностей (интересные, понятные, с задачами+решениями)
Киселев А П
А еще - дискретная математика - каков уровень вхождения в нее? Есть ли области применения?
Вообще, при занятиях математикой стоит отключить поиски связи с внешнем миром и отдаться математике как своему, ни на что не похожему мирку?
тут за все кроме гамологий убивают нахер.
Обьяснитесь, или дуэль
Да. Невеликий. Есть.тут нужно поступать сообразно своим ощущениям
рекомендую umbral calculus. это не мединицский термин как может интуитивно померещиться. совершенно неутилитарно, так что бурбакисты камень не бросят. umbral proofs вставляют. охуеешь от всяких совпадений. с другой стороны не так абстрактно, как гомологии. все таки многочлены бернули и тп можно пощупать и мысленно окинуть. хотя там есть и много возможностей чуток обмазаться алгеброй с векторными пространствами, функционалами, короч всех как у наших гамологоведов.
Твоя мамка
Двухточечное метрическое пространство, отображенное в одну из точек.
Пиздец ты даун. Мы обсуждали задачу для 5 класса, а ты начал нести какую-то хуйню не имеющую отношения к делу, чтобы выебнуться своими знаниями уровня слабенького пту. Это просто смешно - совершенно не улавливать нить дискуссии и не понимать что к чему относится, но при этом пиздеть на традиции преподавания и говорить, что учебники у нас пишутся неправильно, а вот на швитом западе все заебись.
Послать во все губернии по нескольку человек из школ математических, чтобы учить дворянских детей, кроме однодворцов, приказного чина цифири и геометрии, и положить штраф такой, что невольно будет жениться, пока сего выучится. И для того о том к архиереям о сем, дабы памятей венчальных не давали без соизволения тех, которым школы приказаны
Полное собрание законов Российской империи с 1649 года, СПб., 1830. - Т. V. -№ 2762. - С. 78
"Пошел нахуй". Завершающий залп в 500+ м посте, гранд финале треда. И долгие раскаты. А потом - тишина. Тред завершен. Это сигнал к перекату.
Есть книга на 300 страниц без воды где математика и физика в объёме всей школы и немного за первый курс. Аленицын, Бутиков, Кондратьев.
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
Книжка хуйня, если что.
гугли учебники С.М.Никольского
можешь объяснить почему? У него там только философия?

Дляя чего она тебе нужна? Чтобы лекции ромы михайлова понимать только бурбаков читать
Там минус в правой части, конечно же.
Ой, там не от 0, а от 1. А то ведь не сойдется.
https://ru.wikipedia.org/wiki/Интегральная_показательная_функция
У вас интегральная экспонента, сэр.
>Следует заметить, что вычисление подобных интегралов (в особенности при комплексных значениях параметров) опасно доверять коммерческим системам компьютерной алгебры. Из-за неразберихи с обозначенияминельзя полностью доверять также и справочникам.
>Следует заметить, что вычисление подобных интегралов (в особенности при комплексных значениях параметров) опасно доверять коммерческим системам компьютерной алгебры
Петухи, кричащие, что 1001 способов брать интегралы не нужны соснули.
Я правильно понял, что легче аппроксимировать разложением (e^x)/x в ряд?
1. Берешь какой-то список попонтовее. Не дай бог прочитать книгу, которой там нет, рисково это, можно зашквариться.
2. Заучиваешь наизусть определения. Не пытайся обдумывать прочитанное, это занимает слишком много времени, а тебе нужно успеть дойти до настоящей современной математики.
3. Раз в неделю заходи на архив, выбирай рандомную статью и несколько секунд читай несколько первых строк. Особый шик — запомнить название. Так ты приобщаешься к современным исследованиям. На забудь скачать статьи Мочидзуки.
4. Ежедневно посещай блог вербита и математические треды. Глубокие обсуждения математических проблем в среде настоящих специалистов помогут повысить уровень математической культуры для недосягаемых академическому быдлу высот.
5. Настоящая математика только на английском. Постепенно прекращай читать книги, написанные по-русски, да и вобще любые, зато показывай всем, как ты знаешь английский, а не то примут за картофана.
6. Интегралы, которые тебе задают на первом курсе, решать не обязательно, это называется вторая культура.
7. Ну и что, что тебя выперли из вузика? Это и вузом то назвать было нельзя, так, картофельная плантация, работники которой реконструируют математику допотопных времен. Вон, вербита тоже выперли. Настоящее образование только за границей. Злая судьба забросила тебя в водочный ад, но рано или поздно, благодаря своему упорному труду ты выберешься в Гарвард, где будешь раз в неделю ходить на семинары по теарам Ходжа по выбору.
8. К этому моменту можно самому составлять списки, давать советы, отвечать на вопросы. Списки составляются очень легко: берешь готовый от вербита и меняшь местами названия. Можно взять парочку и перемешать.
9. Отвечать на вопросы тоже очень просто: если увидел знакомые слова — перепечатывай соответствующие определения из книги. Если незнакомые — это картофан, гони его ссаными тряпками.
В точности следуя этим советам ты станешь Настоящим Первокультурым Математиком и сможешь посвящать свободное от жалоб мамки время на улучшение научной атмосферы в парашке путем остроумных дискуссий в сети.
1. Берешь какой-то список попонтовее. Не дай бог прочитать книгу, которой там нет, рисково это, можно зашквариться.
2. Заучиваешь наизусть определения. Не пытайся обдумывать прочитанное, это занимает слишком много времени, а тебе нужно успеть дойти до настоящей современной математики.
3. Раз в неделю заходи на архив, выбирай рандомную статью и несколько секунд читай несколько первых строк. Особый шик — запомнить название. Так ты приобщаешься к современным исследованиям. На забудь скачать статьи Мочидзуки.
4. Ежедневно посещай блог вербита и математические треды. Глубокие обсуждения математических проблем в среде настоящих специалистов помогут повысить уровень математической культуры для недосягаемых академическому быдлу высот.
5. Настоящая математика только на английском. Постепенно прекращай читать книги, написанные по-русски, да и вобще любые, зато показывай всем, как ты знаешь английский, а не то примут за картофана.
6. Интегралы, которые тебе задают на первом курсе, решать не обязательно, это называется вторая культура.
7. Ну и что, что тебя выперли из вузика? Это и вузом то назвать было нельзя, так, картофельная плантация, работники которой реконструируют математику допотопных времен. Вон, вербита тоже выперли. Настоящее образование только за границей. Злая судьба забросила тебя в водочный ад, но рано или поздно, благодаря своему упорному труду ты выберешься в Гарвард, где будешь раз в неделю ходить на семинары по теарам Ходжа по выбору.
8. К этому моменту можно самому составлять списки, давать советы, отвечать на вопросы. Списки составляются очень легко: берешь готовый от вербита и меняшь местами названия. Можно взять парочку и перемешать.
9. Отвечать на вопросы тоже очень просто: если увидел знакомые слова — перепечатывай соответствующие определения из книги. Если незнакомые — это картофан, гони его ссаными тряпками.
В точности следуя этим советам ты станешь Настоящим Первокультурым Математиком и сможешь посвящать свободное от жалоб мамки время на улучшение научной атмосферы в парашке путем остроумных дискуссий в сети.
А я уж было подумал, что что-то не так делаю.
Когда встретитесь с Демидовичем, у вас может не найтись общих тем для беседы
А если я ему про топологии расскажу?
В голос.
Что означает форма записи
> I(x, y)dx + J(x, y)dy = 0
? Что за dx? Что за dy?
Все, я походу понял. Мы записали производную как dy/dx и переписали уравнение так, как будто dy/dx - это просто дробь.

http://www.ozon.ru/context/detail/id/31431876/
Спасибо, гляну
Продолжаю чтение.
Так запретили мат треды перекатывать, будут удаляться. Сперва первый, а теперь вот и этот. Создавайте лучше в ночном.
Тогда давайте определим!
ХЗ, думаю в следствие низкого уровня контента, шитпостинга, повышения градуса утилитарности, засилие гомологий и тп
А пруф можно?
Это копия, сохраненная 22 ноября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.