Это копия, сохраненная 16 ноября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.




Общие курсы
М. И. Сканави: "Элементарная математика".
Алгебра
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
С. Б. Гашков: “Современная элементарная алгебра”.
Геометрия
А. Д. Александров, А. Л. Вернер, В. И. Рыжик: “Геометрия”. Учебник для 10-11 классов. Базовый и углубленный уровни.
Я. П. Понарин: “Элементарная геометрия” в двух томах. Первый том - это планиметрия, а второй том - это стереометрия.
А. Ю. Калинин, Д. А. Терешин: “Геометрия”, 10-11 классы. Годный учебник.
Тригонометрия
И. М. Гельфанд, С.М. Львовский, А. Л. Тоом: “Тригонометрия”. Название говорит само за себя. Много геометрических и физических интерпретаций + комплексные числа, как бонус.
Начала анализа
Б. М. Давидович: “Математический анализ в 57 школе“.
БАЗОВЫЕ КУРСЫ ДЛЯ СТУДЕНТОВ:
Общая алгебра
Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
М. Атья, И. Макдональд : "Введение в коммутативную алгебру".
А. Л. Городенцев: "Алгебра. Учебник для студентов-математиков". Вырос из лекций НМУ. Читать параллельно с Винбергом (Винберга читать в первую очередь).
И.Р. Шафаревич: “Основные понятия алгебры“. Замечательный обзор вообще того, что такое алгебра, как она выглядит и какое место она занимает в математике. Примеры, приложения и прочая конкретика.
E. Connell: Elements of Abstract and Linear Algebra". Хорошая первая книга по алгебре, да и математике вообще.
P. Grillet: "Abstract algebra". Очень лаконичный и понятный учебник. Надо знать элементарную теорию чисел, про индукцию, про множества и функции. Линейной алгебры нету.
J. Rotman: "Advanced modern algebra". Ротман сильно разжевывает. Задачи слишком простые для уровня учебника. Линейная алгебра есть.
M. Artin: "Algebra". Американский Винберг. Группы Ли, упор на геометрию. Задачи неудачные.
I. Herstein: “Topics in Algebra“. Прекрасные задачи, отбор материала очень устарел, почти что Ван дер Варден.
P. Aluffi: "Algebra, Chapter 0". Если ты в состоянии ее осилить, бери и забывай про остальные книжки из списка. Линейная алгебра есть.
Линейная алгебра
В. А. Ильин, Э. Г. Позняк: “Линейная алгебра“. Один из классических и самых популярных курсов линейной алгебры.
Д. В. Беклемишев: “Курс аналитической геометрии и линейной алгебры“.
И. М. Гельфанд: "Лекции по линейной алгебре". Не даётся определение определителя.
А. И. Кострикин, Ю. И. Манин: "Линейная алгебра и геометрия". Затрагивается темы геометрий и связей с квантовой механикой. Не даётся определение определителя.
S. Axler: "Linear algebra done right". Подход без определителей (почти). Одна из самых популярных книг за рубежом.
S. Treil: "Linear algebra done wrong". Не такая популярная, как Axler, но тоже хвалят, да. Определители есть.
G. Shilov: "Linear Algebra". Определитель появляется на первой странице.
K. Hoffman, R. Kunze: "Linear Algebra". Классика за рубежом.
P. Halmos: "Finite-Dimensional Vector Spaces". Тоже классика.
P. Peterson: "Linear Algebra". Не особо знаком, но выглядит аккуратно. Что-то вроде Акслера.
S. Roman: "Advanced Linear Algebra". Хороший учебник по линалу. Но нужно знать элементарные свойства матриц и определителей.
Математический анализ
T. Tao: “Real analysis“. Один из самых популярных курсов математического анализа на английском языке.
C. Pugh: "Real Mathematical analysis". Более простая версия Рудина с картинками. Норм книга, но не самая лёгкая.
У. Рудин: "Основы математического анализа".
В. А. Зорич: "Математический анализ". Первый том посвящен классическому анализу. Много примеров, много материала, в том числе даются в начале основы матлогики и теории множеств, а также функций между ними.
Р. Курант: "Курс дифференциального и интегрального исчисления". Идеален с точки зрения первого знакомства с теорией, но имеет достаточно сложные упражнения.
Г. М. Фихтенгольц: "Курс дифференциального и интегрального исчисления". Хорош как повторительный курс.
С. М. Львовский: "Лекции по математическому анализу". Записки лекций из НМУ. Нужно знать основы калькулюса.
Г. Г. Харди, Д. Е. Литтлвуд, Г. Пойа: "Неравенства".
Н. Н. Лебедев: "Специальные функции и их приложения".
Г. П. Толстов: “Ряды Фурье“.
Дифференциальные уравнения
С. Фарлоу: “Уравнения с частными производными для научных работников и инженеров“.
Вариационное исчисление
И. М. Гельфанд, С. В. Фомин: " Вариационное исчисление".
Топология
V. Runde: "A taste of topology". Неплохая книга по метрическим пространствам и общей топологии, затрагивает фундаментальную группу.
J. Strom: "Modern classical homotopy theory".
T. Dieck: "Algebraic topology".
M. Crossley: "Essential Topology". Пререквизит для изучения алгебраической топологии. Не затрагивает тему метрических пространств.
КУРСЫ ДЛЯ ПРОДВИНУТЫХ МАТЕМАТИКОВ
Математический анализ
А. И. Маркушевич: "Теория аналитических функций".
S. Ramanan: "Global calculus".
H. Amann, J. Echer: "Analysis".
W. Fidcher, I. Lieb: "A Course in Complex Analysis: From Basic Results to Advanced Topics".
Дифференциальные уравнения
В. И. Арнольд: “Обыкновенные дифференциальные уравнения”. Книга для уверенных в себе математиков. Диффеоморфизмы, фазовые потоки, гладкие многообразия. Слава Гермесу Трисмегисту!
Теория категорий
С. Маклейн: "Категории для работающего математика".
Р. Голдблатт: "Топосы. Категорный анализ логики".
Дифференциальная Геометрия
К. Номидзу: "Основы дифференциальной геометрии".
J. Lee: "Manifolds and DIfferential Geometry".
L. Nicolaescu: "Lectures on the Geometry".
P. Michor "Topics in Differential Geometry".
Алгебраическая геометрия
Д. Мамфорд: "Красная книга о многообразиях и схемах".
В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”.
В. И. Арнольд: “Вещественная алгебраическая геометрия”.
Ю. И. Манин: Введение в теорию схем и квантовые группы“.
R. Vakil: "Foundations of algebraic geometry".
S. Bosch: "Algebraic Geometry and Commutative Algebra".
U. Gotz, T. "Wedhorn: Algebraic Geometry".
E. Harris: "The Geometry of Schemes".
Топология
А. Хэтчер: "Алгебраическая топология".
J. Munkres: "Topology". Книга - жесткий учебник по теоретико-множественной топологии. Много ненужного для других областей математики.
ИНТЕРЕСНОЕ:
Цикл “Manga guide to...“. Популярное изложение различных областей математики (и не только), оформленное в виде манги. Увы, без фансервиса.
Н. А. Вавилов: “Конкретная теория групп I: основные понятия“. И вообще все остальные книги (и лекции!) Вавилова.
П. С. Александров: “Введение в теорию групп“. Просто о сложном. Несколько вольный язык изложения, местами затрудняющий восприятие.
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”.
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
Н. Я. Виленкин: "Рассказы о множествах". Теория множеств для широкого круга читателей.
М. М. Постников: “Теорема Ферма. Введение в теорию алгебраических чисел”.
Н. Стинрод: “Первые понятия топологии“.
А. Я. Хинчин: “Три жемчужины теории чисел“.
О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов: “Элементарная топология”.
Я. П. Понарин: “Алгебра комплексных чисел в геометрических задачах”.
А. А. Заславский: “Геометрические преобразования”.
В. Акопян, А. А. Заславский: “Геометрические свойства кривых второго порядка”.
В. И. Арнольд: “Геометрия комплексных чисел, кватернионов и спинов”.
В. В. Прасолов: “Геометрия Лобачевского”.
Д. В. Аносов: “Дифференциальные уравнения: то решаем, то рисуем”.
В. В. Прасолов: “Наглядная топология”.
Д. В. Аносов: “От Ньютона к Кеплеру”.
М. Клайн: “Математика. Поиск истины“.
Д. Пойа: “Математическое открытие“.
Л. Кэрролл: “Логическая игра“.
Д. Пойа: “Как решать задачу“.
О. Я. Виро, Д. Б. Фукс: "Введение в теорию гомотопий. Гомологии и когомологии".
A. Ostermann, G. Wanner: "Geometry by its history".
T. Sundstrom: "Mathematical reasoning writing and proof". В книге объясняется что такое математическое доказательство, математический факт и каким образом их можно придумывать. Начала теории множеств.
D. Dummit R. Foote: “Abstract Algebra“. Много примеров, задач, но страшно скучный учебник, его нужно держать как справочник.
ПОЛЕЗНЫЕ РЕСУРСЫ:
Библиотка "Квант": math.ru/lib/ser/bmkvant
Высшая математика просто и доступно, по 2 курс включительно: mathprofi.net
Необъятная онлайн библиотека: gen.lib.rus.ec


мне теперь везде эти петухи мерещатся. вот еще из коллекции. это кафе аист напротив саранского политеха мы там с пацанами N определние обсуждали. заскучал, смотрю на стену - а там гениталии петуха. в смысле сверху гребень а снизу яйца и уретра. может спьяни померещилось. а вы аноны что на этой картине видите?
Сук, ну ты уже задал психологическую установку. Теперь всем, кто ее прочтет придется усилие делать, чтобы то же самое не увидеть.
Ну да, ну а помнишь всякие картинки на обман зрения - типа кого видишь, молодуху или старуху. Сперва увидишь одну, а потом другую, и можешь переключаться. А здесь кроме гениталий петуха я ничего не вижу, как ни старался!
Если бы я был психоаналитиком, то, скорее всего, сказал бы, что тебе стоит поменьше с сидеть на дваче.
Когда то мне перестанет быть лень и я создам тред математики для не математиков.
Это символ Франции, le coq.
А ты?
N-петух, почему не отвечаешь на вопрос? Тебя приз ждет на пике, если правильно ответишь. У тебя же хирш и публикации!
некоторые вообще танчики клеят и чуствуют себя прекрасно. но у них же все свободное пространтсво говном забито. а тут блокнот и карандаш, и лаптоп. и весь lebensraum.
Да. Чет мегагодная книжка.
Как нет проку, можно тянкам в уши заливать, они текут, когда парень умнее их, еще можно аутировать в голове безо всякого интернета, сплошные плюсы.
> можно тянкам в уши заливать, они текут, когда парень умнее их
И что именно ты тянкам рассказываешь? Типа как в видосах numberphile? Мне бы западло было такую хуйню рассказывать.
Чтобы "парень умнее их" достаточно посмотреть с десяток фильмов и почитать с десяток книг, плюс анализ всего этого. Математическими концепциями, даже "интересными" можно доказать, что ты скучный мудак.
> Математическими концепциями, даже "интересными" можно доказать, что ты скучный мудак.
А если тянку научить правильному счету (ноль, целковый, полушка, четвертушка, осьмушка, пудовичек, медячек, серебрячек, золотнячек), она потечет?
Напомнили - меня как-то недавно затащили на концерт на открытом воздухе, на лужаечке епта. Я чуть не охуел - столько народу давно не видел вместе! И громко, что пиздец. И приперлись как-то сильно заранее, хотя я заметил, что необязательно прямо лезь к сцене. Можно неподалеку лежать на травке, не так громко и все равно все видно хотя хули там смотреть. Я тем временем вытащил блокнотик и стал прикидывать за сколько до начала лучше всего приходить, чтобы от скуки не охуеть и видно было нормально. Я пытался объяснить, что по идее sweet spot должен быть на пересечении двух графиков - функции заполняемости (размер толпы от времени) и ф-ции "кайфа" в завимости от удаленности от сцены. Функция заполняемости мне кажется какой-то long tailed sigmoid (только не гуглите в images умоляю, страшные картинки выползают), вернее не Long tailed но с перекосом не знаю как назвать, основная масса народа приходит "внезапно" и сравнительно незадолго до начала, а потом асимптотически приближается к full house. А функция кайфа еще интереснее - оказывается практически похую где находиться, кроме самых задворков, где нихуя не видно. Так что пересечение приходится на примерно 30 мин до начала. А пускать начинают часа за 3, это охуеть, и есть ебланы которые к открытию приходят.
Короче я попытался это все рассказывать, но меня никто не слушал и смотрели как на мудака. Хм, а мне кажется это интересно.
Когда меня люди спрашивают, чем занимаешься, я обычно отвечаю "ничем", потому что если ответить "математика", то есть небольшой риск, что спросят чем конкретно, и тут придётся придумывать неимоверно скучную научно-популярную историю, чтобы как-то оправдаться, типа "представь себе бублик, есть значит такие пространства..."
лол, жызненно
Нет, потечет Юрий Степанович.
Верно, потому что ты занимаешься ненужным дерьмом. Так что ответ "ничем" даже более точен.
в чем критерий "нужности"? вот нужник действительно нужен. остальное спорно.
Перельман пять лет отработал в США на маленьких должностях. Заработал столько денег, что до сих пор ими свою семью кормит.
Говорить о нужности чего-либо бессмысленно, так как нужность обуславливается субъективным отношением человека к объекту дискуссии.
Ясно епта?!
Глупости. Сейчас во всех областях человеческих знаний очень высокая степень специализации. Часто даже компетентному человеку нужно прослушать целый доклад, чтоб хотя бы в общих чертах понять, чем другой занимается.

Пикрелейтед. Но читать его следует строго на английском, в русском переводе есть убийственно безобразные опечатки.
1. Сложение беззнаковых чисел в программировании. Z/2^2Z, Z/2^8Z, Z/2^16Z, Z/2^32Z.
2. Целые числа. Z
> Сложение беззнаковых чисел в программировании. Z/2^2Z, Z/2^8Z, Z/2^16Z, Z/2^32Z.
Слишком простые группы. У них даже подгрупп нет кроме тривиальной.
> 2. Целые числа. Z
Это не из жизни.
>Слишком простые группы.
Все циклические группы слишком простые
>У них даже подгрупп нет кроме тривиальной.
Есть. Уже у Z/2^8Z 7 нетривиальных подгрупп.
Минуты Z/60Z, часы Z/24Z.
Давай сравним нужность тупой пизды с айфончиком и бабы нюры из деревни.
>О, вася привет, чем занимаешься?
>Да вот гамалогии с гаматопияями считаю.
>ЩИТО?
>Ну короче считаю просто.
>А что такое гамалогии с гаматопиями?
>... Ой бля иди нахуй
>О вася привет, что делаешь?
>на скорителе работаю
>ЩИТО?
>Ну атомы по кругу гоняю под сабатон
>ясн)
Ты понимаешь что это просто гнилые отмазки!?
Тот же уровень ответа на вопрос "зачем ты качаешься?" будет "вон ероха выиграл на мистере олимпия и уже десять лет кормит семью"
>О, вася привет, чем занимаешься?
>Да вот гамалогии с гаматопияями считаю.
>ЩИТО?
>Ну короче считаю просто.
>А что такое гамалогии с гаматопиями?
>... Ой бля иди нахуй
Какая-то нереальная ситуация. Обычный человек больше всего на свете боится че-то новое узнать, он просто ненавидит знания. Когда он чего-то не понимает, он просто ждет пока тема разговора сменится или сам пытается перевести разговор в другое русло. Сильно сомневаюсь, что он будет спрашивать, что такое гомологии. Тянка может спросить для поддержания разговора, но ей будет абсолютно похуй на твой ответ, потому что вы с ней не общаетесь, а просто выполняете ритуал.
>Обычный человек больше всего на свете боится че-то новое узнать
Как там диван? Не сильно жмет?
Ну хз, может это специфика Мухосранска, в котором я живу, но все мои знакомые обсуждают вещи типа как они на велике покатались, новый расфорсенный пиндосский фильм про супергероев (suicide squad или как его), футбол и прочую даунскую хуйню. Я как-то на вписке объяснил, почему Q счетно, а R несчетно. Люди послушали, поняли (это любой школьник поймет, если на пальцах рассказывать), а потом мне саркастически так говорят: "Охуенно. Вот я приду на собес, у меня спросят, что я умею, а я скажу, что могу доказать, что вещественных чисел больше чем натуральных". То есть, у 99% людей отношение к интеллектуальной деятельности чисто утилитарное: если что-то требует умственных затрат, но не приносит денег - этим занимаются только долбоебы и аутисты.
>Пришло в голову рассказывать диагональный аргумент на вписке
Тебе когда-нибудь говорили, что ты долбоёб?
Обычно просто нажираемся, происходит какой-то трэшак, а на следующий день смешно. Но меня заебало каждый раз одно и то же делать, решил разнообразие внести.
> Тебе когда-нибудь говорили, что ты долбоёб?
Only too often.
Я не он, но отвечу.
Он имеет в виду, что большинство людей поглощены собой и им похуй на тебя и твои интересы. 1 из 10 задаст тебе пару осмысленных вопросов и выслушает ответы. 1 из 1000 пойдёт потом и почитает что-то там сам по этой теме будь то математика или разведение скота. Где-то 3 из 10 просто сядут тебе на уши и будут нон-стоп рассказывать как у них дела и про свою работу. А с остальными можно говорить только об общих для всех людей интересах: бабло, еда, отношения etc.
Я могу ебать детей 10 лет и мои друзья не узнают, потому что они никогда не спрашивают чем я вообще занимаюсь и как у меня дела.
Естественно, это мой личнный опыт. Может мне не везёт просто.
> Я могу ебать детей 10 лет и мои друзья не узнают, потому что они никогда не спрашивают чем я вообще занимаюсь и как у меня дела.
К тебе уже выехали.
> А с остальными можно говорить только об общих для всех людей интересах: бабло, еда, отношения etc.
Да, именно это я и хотел сказать.
>мои друзья никогда не спрашивают чем я вообще занимаюсь и как у меня дела.
Заебись у тебя друзья)
Похоже мы тут открыли филиал бэ, но да и похуй
> мы тут открыли филиал бэ
Ну так тут все такие аутисты-маргиналы из Мухосрансков, которые не могут общаться в нормальном математическом коммьюнити. Без обид анон, но если бы мне было с кем в жизни обсуждать математику, я бы тут не сидел.
Я бы сидел. Нужно 2-3 норм персонажа, чтобы создать коммунити. Ну и сама идея -- сосака оплот современной математики -- почему-то забавляет.
Да и чисто идеалистически: на каком-нибудь форуме с аватарками начинается ЧСВшное брожение, а тут ононимные посты -- главное идеи, а не люди.
>почему Q счетно, а R несчетно
Вангую аргументацию в духе
"Ну кароч вот числа адин джва три есть, да, а есть дроби 0.999999999999......9 нутыпонял. Так вот, таки чисел дохуя, а все остальные посчитать можно"
Сосака - оплот эзотерико-мистической математики.
> Да и чисто идеалистически: на каком-нибудь форуме с аватарками начинается ЧСВшное брожение
На форуме да. А если в жизни общаться, то все збс будет, наверное. Если кто-то будет вести себя как Мунин на dxdy, я ему просто пизды дам.
Спасибо тебе, анон
>не могут общаться в нормальном математическом коммьюнити
Говно без задач. Если не в курсе, советую посмотреть какой-нибудь "буквальная геометрия" (есть на рутрекре), вполне отражает суть.
Это ты долбоёб, а не они, реплику-то их ты так и не понял. Естественно, их твоя школьная хуйня не впечатлила (вангую, они в любом быдлонаучпопном видосике уже это всё слышали). Они очевидно ждали чего-то более крышесносящего, типа вопросов об основаниях математики и обосновании ряда натуральных.
> типа вопросов об основаниях математики и обосновании ряда натуральных
Почему ты думаешь, что он выступал перед N-петухами?
Так это наполовину их, бездуховное скучное комньюнити.
Не то что наше, с каледиными; геями, наркоманами, художниками, активистами лгтб c матфака и преподами-педофилами из 57.
Интересные личности это здорово конечно, вот только общение с ними ровно такое же будет, как в этих коммьюнити. Причем кем бы ты ни был, хоть их родственником.
Типичная ошибка сознания, тащем-то. В смысле думать, что с людьми вроде Вербицких или Михайловых в реале приятно общаться.
Все люди рождаются N-петухами.
С Вербицким приятно, кстати. Очень вежливый и умный собеседник с хорошим голосом. Я так не умею.
>вот только общение с ними ровно такое же будет, как в этих коммьюнити
Что-то я не увидел, а в чём говённость того комьюнити?
Все что ни делается в этой жизни, делается для себя, маня. Вот ты, сразу видно, мышлением обделен, математикой не занимался
Молодец.
>>377451
> советую посмотреть какой-нибудь "буквальная геометрия" (есть на рутрекре), вполне отражает суть
Пиздец у них там нудная картофанская область. Никогда не понимал, что за аутисты таким занимаются.
Благодарю покорно
Пока еще нет, но думаю что в течение полугода начну понимать. Я сейчас почти изучил пререквизиты к алгебраической топологии.
Что именно? Каким путём идёшь к успеху? Давай, делись опытом. Я тоже хочу понимать лекции Ромы Михайлова. Кстати, а нахуя тебе лекции Ромы Михайлова?
> Кстати, а нахуя тебе лекции Ромы Михайлова?
Ну я посмотрел видосы с ним, подумал: "вот это чувака штырит, хочу, чтоб меня так же штырило" и скачал учебник по топологии, начал изучать всякую элементарщину, которую по-хорошему надо было в школе пройти: непрерывность, компактность, связность. Почитал че такое quotient topology, понял как "склеивать" всякие хуевины друг с другом, но пока этим почти не занимался. Ну меня вштырило в принципе.
Какие-то элементарнейшие факты про группы, кольца и поля я знаю, поэтому, если собраться с силами и ебаться с книгой Хэтчера каждый день, попутно восполняя пробелы из других областей, можно уже сейчас ее осилить. Но я думаю, что нет смысла дрочить на абстрактную хуйню, не понимая общего контекста. Сейчас прочитаю простенький учебник по анализу на многообразиях, в котором в конце есть когомологии. Как раз узнаю что это и зачем они нужны.
Исправляют ошибки, добавляют упражнения, добавляют материал (могут целые главы добавить).
>>377514
Алсо, ты что, ебанутый? Не проще скачать и посмотреть в чем разница чем на дваче спрашивать?
>>377514
Я верю двачу больше чем себе.
Плюс 13 издание я в сети не нашел, а 12 валяется на первой странице гугла.
ЧТо то там нету того что надо.
Да хуйня это, отговорки. Единственная цель этих переизданий - бабла срубить авторам. Борьба с торрентами, только и всего. Но борьбу то все равно проигрывают поэтому уже давно прибегают к другой тактике - дофига книжек продаются с пасскодом для "домашки онлайн" или еще какой-нибудь такой хуйни. Получается похуй если ты купил б/у учебник задешево или скачал его, будь добор купить пасскод.
У меня так было с занятиями йогой. Начал было но застеснялся и забросил. Коврик себе купил, все дела.
Читал Маклейна, каротьш. Там такой пиздец лютый, ну я чет воспламенился и дропнул. Было досадно Потом опять, кстати, начал, но снова онхолднул, правда без дропа - прост нашёл чуть-чуть более удобоваримые книжки для начала, а потом может и адвансед стафф из Маклейна лучше пойдёт Ещё Зорича читал и даже не дропнул, а просто в какой-то момент забил, поняв, что гамалогии - сила, картофан - магила.
Ну чево ты начинаешь, нормально же общались)
Потом может вернешься. А так ТЧ ИМХо скучнейшая область математики.
И тут возник спор вероятность попадания в одну из точек. Чем он равен? Мне утверждают, что ноль, потому что площадь точки равна нулю. Но разве это верно?
Да, объясню суть вопроса ещё немного.
То есть, для примера - попадание в половину отрезка равно 1/2, потому что отношение той площади отрезка, куда нам надо попасть и всех возможных вариантов. А вот что если надо попасть в точку. В одну точку из бесконечного числа точек некоторой ограниченной области. Площадь одной точки, как мне утверждают - ноль, потому и вероятность ноль. Но по логике теории вероятности - это недостоверное событие.
Ты путаешь необходимость с достаточностью. Вероятность невозможного события равна нулю. Но из того, что вероятность события равна нулю, вовсе не вытекает, что оно невозможное. Идея, что событие нулевой вероятности - невозможное, ошибочна. В эксперименте могут произойти события, вероятность которых нулевая.

Да, вероятность попадания в данную конкретную точку равна нулю. Пикрелейтед (с.в. - случайная величина, д. - дискретная, н. - непрерывная).
То, что надо было. Спасибо тебе.
Письменный, конспект лекций по теории вероятностей, статистике и случайным процессам.
Огромное спасибо.
http://new.math.msu.su/content_root/programs/kaf/matstat.htm
Программы мехмата. По ссылкам - документы со списком учебников в конце.
Благодарю.
Каротыш. Коротышка тип.
Вот меня удивляет, что можно какой-то кусок математики систематизировать так, что довольно нетривиальные результаты можно получить на 2х страницах и это будет выглядеть очень естественно и легко. Причем я не просто поверил каким-то умным людям, а посмотрел, и мне все видно. Магия какая-то. Жаль, что в матане такого не бывает.
Читал вот учебничек по линалу, а там задание "покажите, что матрица В является обратной для А". Понятное дело, надо искать произведение BxA=E. Вот я его нашел. Могло ли в теории получиться, что AxB≠Е?
Просто не хочется лишний раз надрывать жопу и считать второе произведение.
Толсто в смысле про матан, или ты не веришь, что кто-то таким простым вещам может радоваться?
Ну-ка, если все так просто сделай видос и покажи мне что ты там доказываешь. Читать Винберга мне западло. А ты уже все понял. Можешь и ирл рассказать, готов приехать послушать если ты из дс/околодс.
> Читать Винберга мне западло
С таким подходом мне что-то не хочется тебе ничего рассказывать.
>мне что-то не хочется тебе ничего рассказывать
Такова суть любого матано-петуха. Что и требовалось доказать.
В том то и суть, что ты нихуя сказать не можешь по существу. Тебя попросили сказать чтоты узнал, а ты в духе "ДА Я ТЕБЯ СВОИМ КАРОННЫМ ПАХАРОННЫМ, ПРОСТА СВЯЗЕВАТСЯ НИАХОТА" слился.
Так а зачем мне что-то кому-то доказывать на анонимном форуме? Все что хотел, я уже сказал.
Уже второй трейдж я вас посещаю, и всенепременно вижу эту шапку. Меж тем эта шапка рикому в треде не нравится, о чем всегда мимокрокодил не приминет сказать. Либо вы тут балбесы, либо болтуны
Конкретная математика кнута мб
>шапка не нравится
Почему тебе не нравится шапа?
>Либо вы тут балбесы, либо болтуны
И то, и другое.
Вон в википедии написанно что комплексные числа это числа решения уравнений, график которых не пересекает ось иксов. Как это понимать? Что почитать чтобы понять?
>комплексные
На курсере есть ща оч хороший курс по кмоплексному анализу. Тебе хватит лекций первой недели, чтобы ответить на все свои вопросы. Но надо будет въябывать.
Физик-кун? Расскажи, где они там в физике, так чтобы прямо не обойтись. Интересно чисто, слыхал что такое есть.
Ладно, буду курить.
>>377652
Ну, я из википедии все взял.
Я так понял, поле это все числа которые можно "взять в руку" и которые можно собрать в кучу введя пару простых правил.
Ну и поясни мне тогда что там такое с ними особенного, раз там все так просто.
>>377655
Проще всего думать про них как про вектор. Просто вектор, в прямоугольных или полярных координатах. По одной оси Re по другой Im. Такая модель используется например в электричестве (переменный ток, импеданс вот этот все). В синусах косинусах считать неудобно, поэтому используются комплексные числа. В полярной форме их легче умножать, в прямоугольной - складывать. Потом переходишь обратно к синусам и получаешь результат. Вот и все.
Ну, физика. Квантувую механику кури тогда. Там не обойтись, мало не покажется. Я думал вопрос был просто "что с ними делать" на простом примере типа импеданса и фазоров.
Кстати не обойтись в КМ без комплексных чисел вовсе не потому, что это какая-то физическая сучность. Просто Шредингер так придумал. Он долго хуй к носу подгонял и колебался. В итоге пришел к уравению первого порядка по времени. И пошло и поехало, так что конечно уже не обойтись. Но приглядись - если из гамильтониана убрать V (потенциал не зависит от времени), то оно сведется к двум уравнениям - от координаты и от времени, причем последнее будет иметь вид dФ/dt = aФ. Понятно что тогда для осциллирующего решения а должно быть комплексным числом. Для сравнения, в классической физике уравнение колебаний струны - второго порядка (как по времени так и по координате) и его решением является действительная функция. Короче говоря, точно так же как и в электричестве, переход к комплексным числам в КВ - это трюк для удобства вычислений. Сам Шредингер признал, что если бы комплексные числа были необходимы В ПРИНЦИПЕ, это означало бы что состояние системы описывается какими-то двумя волновыми функциями (действительной и мнимой) которые нужно принципиально рассматривать вместе, что есть полная тащемта хуйня.
>В итоге пришел к уравению первого порядка по времени.
Искалось, с самого начала уравнение первого порядка по оператору дифференцирования по времени( просто из-за принципа суперпозиций)
>Сам Шредингер признал
Ссылку
>что состояние системы описывается какими-то двумя волновыми функциями (действительной и мнимой)
Какой-то бред городишь, сама волновая функция физического смысла не имеет, вот квадрат ее модуля, это да.

Прибавь к третьей строке вторую, умноженную на -1.
Прибавь к четвертой строке вторую, умноженную на -2.
Элементарно, в 4.4 2 строчка такая же как и 3 и 4, таким образом из 4 вычитают 3, а потом из 3 вычитают 2.
На последнем шаге из 4 строчки вычли 3 умноженную на два И из 3 строчки вычли 2
...
Может есть где то физики тред?
Нашел хорошую книгу косаткиной Физика для старшеклассников и абитуриентов: интенсивный курс подготовки к ЕГЭ, с темами объяснения законов на понятном языке и все нужные формулы
После каждой темы идут задачи по этой теме со сложностью A, B и C.
Но эта книга 2012 года и егэ там все 2012 и раньше. Не старо ли? Не проебусь ли я?




Да не в этом дело, задания то остались.
>>377683
Смотрел задачники, они даже не по темам, тупо кимы, а мне бы хотелось поступательно все решать, а не сначала всю теорию, а потом только решать, я так многое забуду да и скучно будет.
>>377684
Вот, это КИНЕМАТИКА, дальше динамика и статика и такая же проверочная работа.
И так ~700 страниц все темы. Более свежих аналогов даже других авторов не нашел..
>>377685
Часть из этих могут попасться в первых заданиях, но ощущение, что много левой хуйни.
Бля и что делать? Ахуеть конечно, я думал это вброс, хотя бы примерные варианты выложили.
И что теперь, только B и С будет? Тоесть только средней и высокой сложности? Только их решать? Даже на решуегэ изменений нет.
>>377691
> могут попасться в первых заданиях
Да так как это первые темы.
>что много левой хуйни.
видимо так и есть(
Что не так?
В твоем задачнике конкретно один вариант сколько заданий содержит? В реальном ЕГЭ 32 задания.
Да нет там вариантов. Там берется из сборников задач только определенные задания после пройденной темы.
Да уже все равно, вон какой пиздец через год на физике будет, буду решать тогда только B и С задания. А что еще делать? Вот именно что хуй знает.

Ты доебываешься до формулировок, я же не доклад пишу. Если хочешь from the horse's mouth, это есть в книжке, перевод шредингера с немецкого, называется Collected Papers on Wave Mechanics: Third Edition By Erwin Schrödinger стр 123. Поразительно, он говорит слово в слово тоже самое что и я, так что доебывайся до него.
Окей ссылочку посмотрю, благодарю
>Да нет там вариантов
Хуйня какая-то. Бери нормальные варианты и смотри, а то на ЕГЭ шары вылупишь.
Ты не понял не меня, не задачника. задания из ВАРИНАТОВ, только все в порядке по темам, а не в разброс как в обычных в вариантах. Кароче забей.
>Бери нормальные варианты и смотри
Даже книжки 2017 года для подготовки по физике говно, в них везде тестовая часть. А как блять ебанный егэ по физике будет выглядеть без тестовой части? вот хуй знает как именно.
А сейчас рассматривают маняфункции, которые имеют смысол только при возведении в квадрат.
Десять гауссов из десяти на кончиках декартов.
Потому что СКОЗАЛ
Он по-моему сбалансирован. Покрывает много материала из современной ТМ, написан по делу, без лукавых мудрствований, некоторые доказательства оттуда более лаконичны и прозрачны, чем в более старых работах. ХЗ.
Так это даже не программа, так, свалка книг.
Программа мехмата.
666 из хуев не так зловеще
Проще всего представить комплексные числа как поле линейных многочленов по модулю x^2+1.
>Полярные координаты объясняют. И формула эйлера. Из полярных координат легко переходить к декартовым и наоборот. Куда еще проще.
Ничуть не проще. Так же. Алгебраический подход очень удобен тем, кто ок с алгеброй.
Это что, мне надо зарисовать весь кружок в радиусе 3 от центра координат!?
Да
Задание узнать расстояние между двумя точками по теореме пифагора про штаны.
Нормально.
Если всё так просто то найди при помощи векторов или полярных координат произведение двух комплексных чисел (a, b) и (c, d).
При помощи многочленов всё получается просто:
(a + bx)(c + dx) mod (x^2+1) = bdx^2 + (ad +bc)x + ac mod (x^2+1) = (ad + bc)x + ac - bd
Это может понять любой семиклассник
>Из чего следует твоя формула?
Смотри в любом учебнике по комплексному анализу(даже по математическому, в тех курсах, где комплексные числа затрагиваются)
>Где вывод, как в >>377920?
Я бы написал, но мне пиздец как лень рисовать очевидные вещи, оставляю тебе в качестве упражнения.
Я хз что тот анон имел в виду под полярными координатами, в моем понимании это то, что я написал.
Проблема в том, что ты пытаешься вывести своё умножение из умножения экспонент с комплексным показателем, то есть объяснить непонятное неизвестным.
Бро с R[X]/(X^2+1) двощую и одобряю.
Я мог бы с тем же успехом нарисовать косинус и синус вместо экспоненты. Как известно под этой записью имеется вполне очевидная геометрическая подоплека.
Уножить на 4. И вычесть.
Дошел до 50 страницы. Полет отличный. Проблем только в терминах, уровня точка начала координат у пиндосов называется оригинс и подобные.
вкинь ссылку на книгу ради лулза
ну когда в учебнике поясняют что такое знак суммы сигма, это такое. Интеграл Римана тоже неправильно введен судя по всему.
страница 263 из которой следует что интеграл римана вводится как предел римановских сумм при n->\inf но всем известно что ТАКЖЕ шаг разбиения должен при этом идти в нуль, у томаса я этого не вижу.
Что значит хз. rcosЭ + isinЭ.
>>377930
Да, через косинус синусы/ триг identities вывод кучерявее получается, и что. Зачем подменять понятия. Степень сложности выводимости не имеет никакого отношения к простоте восприятия. Вопрос же был в том, как проще ПРЕДСТАВЛЯТЬ а не выводить правила действий над ними.
>Что значит хз
Это называется тригометрическая форма.
>как проще ПРЕДСТАВЛЯТЬ
Тут я на стороне формалистов, в мире много вещей которые не имею "представления" в житейском смысле этого слова.
Просто непривычно видеть, чтобы в учебнике пояснялся значок суммы или что то подобное, это довольно странно для меня.
Ну ты алёша.
Попадись он мне на первом курсе, матан прошел бы легче наверное, хотя в конце концов и фихтенгольца хватило заглаза
Но сам же апологет алгебраического подхода сформулировал свою мысль так:
>Проще всего представить комплексные числа как поле линейных многочленов по модулю x^2+1.
То есть мы о представлении говорим или о чем?
>>377948
ну если ты в математику можешь и в логику наверное, зачем обобщаешь как баба срака
>ну если ты в математику можешь и в логику наверное, зачем обобщаешь как баба срака
Изначально был негативно настроен.
>То есть мы о представлении говорим или о чем?
В общем, кому-то проще осознавать через линейные многочлены по модулю, кому-то через показательную форму, вопрос вкуса.
У него просто все поясняют подробно. Учебник написан так сказать с позиции дауна который хочет понимать лекции ромы михайлова и выебываться этим на сосачах.
Просто меня слегка припекает, что многие почему-то не понимают, или не хотят понять, что калькулюс - это учебник для инженеров. Это не матан. Строгостей там не надо искать. Матану там учат по другим учебникам. См. шапку Ж)
А ведь у них еще вроде есть и прекалькулюс. Да, все время почему-то идет отождествеление калькуюса с матаном у нас.
Прекалькулус - это high school обычно, ну или рефрешер для ебланов в community college кто SAT неасилил чтобы им можно было calculus брать.
Им только за щеку брать можно.
Помню, Рома в видосе рассказывал как у него в детстве не было интернета и он трехтомник Фихтенгольца выменял у друга.
> Полет отличный.
Еще бы. Этот учебник даже для школы слабоват. Такое классе в 6-7 еще норм читать, но где-то 8 классе уже пора завязывать с математикой без доказательств.
Не мешай третьекуру выёбываться перед второкурами))
Ненавижу лютой ненавистью таких, как ты. И не читаю русских учебников и русских статей по той же причине. Русские должны сдохнуть.
Какой ты умный
При этом ты пишешь на русском, любопытный диссонанс, вас шизофрения случаем не мучает?
Щас нам этот анон пояснит зе лекции ромы михайлова.
Что начинается? Западные общеобразовательные программы объективно слабее российских, патриотизм здесь не при чём.
Почему объективно? И какие ещё "западные общеобразовательные программы", ведь на западе такого явления вообще нет?

Это (а также книги Клини) - must read по дефолту.
Давай, обосновывай свои слова или тостейший лев когда либо заходивший на сци

И это доказательство!?
И этот пацак потом что то кукарекает про херовые доказательства в нижке!?
Доказательство уровня маттреда
Вонючий школотун, как же хочется выпнуть тебя из треда пинком под зад.
Это был не я. А в чем проблема, собственно? Я определяю косинус через ряд, если че.
Алсо, по первой же ссылке в гугле нашел
https://proofwiki.org/wiki/Cosine_Function_is_Even
Первое доказательство именно такое же как мое. В чем проблема-то?
Я вполне серьёзно.
Нигде кроме маняматики не применяется.
Как ты себе вообще представляешь её применение? Группа электронов? Группа тел с массой эмжэквадрат?
Какой здоровый калькулюс
Применяется в современной физике.

И вопрос:
При построении x^2(2x^2 + 1) степени складываются, а при возведении многочлена в степень - перемежаются, так?
У тебя во втором не так, в скобках там основание должно быть не 1, а 4. А в первом что непонятно? (x^2 - 1) можно ещё разложить на (x + 1)(x - 1)
погуглил group theory biology|chemistry|physics
не знаю если тебе это нужно
Review and application of group theory to
molecular systems biology
http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3149578/pdf/1742-4682-8-21.pdf
MOLECULAR SYMMETRY, GROUP THEORY, & APPLICATIONS
http://vallance.chem.ox.ac.uk/pdfs/SymmetryLectureNotes2009.pdf
в самом верху есть список книг.
Спасибо
> S. Axler: "Linear algebra done right".
Книга очень простая (первые несколько глав), но не для дебилов.
Надо, конечно, добавить, что книга немного упоротая:
1) Обозначения немного нестандартные: null space вместо kernel, list вместо n-tuple и другие.
2) В некоторых ситуациях, когда можно рассматривать произвольное поле нулевой характеристики или вообще произвольное поле, там используется R или C.
3) Из-за того, что определители выпихнуты в последнюю главу, характеристический многочлен определяется через треугольную форму матрицы отдельно для матриц над C и отдельно для матриц над R.
Но в целом годнота, рекомендую.
Ты 15 рублевый что ли? "Западные программы". "Эти земляне такие тупые".
Базовые школьные по математике - да, слабее, но заинтересованный американский школьник с легкостью идёт на дополнительные занятия, превосходя ту школьную программу, что навязывается в российских мат. классах.
А вот высшего математического образования в России нет: оно застряло на уровне 1920-х (брать интегралы из Демидовича), а США имеет сотни ведущих математических высших учреждений, лучших в мире, где обучают современной математике.
666 на капче.
Заинтересованный российский студент с легкостью идет на спецкурсы, превосходя ту университетскую программу, которая навязывается в американских бакалавриатах.
Элементарщина с конечными группами в простых алгоритмах на теорию чисел (тип обратное по модулю) + в группах галуа (например док-во неразрешимости уравнения в радикалах).
Они же уже существенно используются в комбинаторных играх (кубик рубика и почти любые другие), шифрах, задачах.
В физике по теореме нётер каждый закон сохранения = симметрия => группа симметрий. Группы симметрий это совсем другие группы, они большие и непрерывные, как группа лоренца или пуанкаре, теория совсем другая.
В алгебраической топологии основные инварианты -- абелевы группы. Гомотопические, гомологии, иногда когомологии.
Пидора ответ.
Двачую. В отличие от традиций совка, там никто ничего не навязывает. Можешь просидеть high school c 9 по 12 класс и заниматься всякой хуйней, лепить дилдаки на уроках лепки из глины. Это и есть core aka "базовая хуйня если тебе все пох лишь бы выпустится и пойти на ферму работать". А можешь брать AP классы по математике, в тч за колледжные кредиты. То же самое дальше в колледжах, выбора еще больше, от матана для сварщиков до межпланетных мочедзук. Поэтому ссу на бинарных ебланов обобщающих про "западное образование". Тупые обмудки еще имеют наглость сидеть в маттреде, хотя даже в элементарную логику не умеют со своими однобитными мозжечками.
Теперь вот имею наглость попросить вашего совета.
По алгебре - Винберг или Кострикин. Или вообще что-то другое?
По геометрии думаю брать
Калинина.
Что по линалу что посоветуете?
Заранее спасибо.
В геометрии изучаются свойства фигур относительно той или иной группы преобразований пространства.

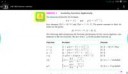

Почему две картинки суммы функций не совпадают? Или это просто пример как функции плюсуются?
Почему они должны совпадать? Две разные картинки, разные функции, на первой +, на второй + . для двух других фций.
Ну хорошо. А первая пикча тогда почему с ошибками? Или это ошибки для точности?
https://ru.wikipedia.org/wiki/Вложенные_радикалы
Наверное там ключевое слово reasonably support the proportionality assumption. И дальше от тебя требуется estimate. То есть примерно 6. Не знаю, у тебя же учебник, может там речь идет об экспериментальных результатах и нужна примерная оценка? Это же для инженеров :)

Приноси эти спецкурсы. Ведь должны же они существовать в природе, раз ты такое утверждаешь.
странно, ты 1988 инстинктивно не дополняешь до 2000? ты сразу не видишь 12 которые складываешь с 16?
Да, про это я и говорю. Всегда в математике были проблемы со счетом в уме. В принципе не особо мешает, даже в универе, но напрягает меня самого, лично.
Такая же хуйня. В шкалке всегда считал на черновике. Даже двухзначные числа складывал. Боялся проебаться где-нибудь.
>В геометрии изучаются свойства фигур относительно той или иной группы преобразований пространства.
Пиздеж теоретико-групповиков. Ни разу не видел, чтобы геометрию изучали с помощью групп.
А вот теорию групп с помощью геометрии хорошо так изучают.
Пиз-дёж. Открой любой учебник по геометрии. Где там U(1)? Где там SO(2)? Старый добрый Евклид со своими аксиомами.
*можно
Бумажные можно перед сном читать, а за комплюктером сидеть надо. С другой стороны, можно планшет какой-нибудь купить или читалку, но мне как-то удобней лежа в кровати читать бумажную книгу.
Ты аутист?
>Открой любой
Лелон-Ферран Основания геометрии, Берже Геометрии. Куда же пропал старый добрый Евклид?


это Г.М. Фихтенгольц "Курс дифференциального и интегрального исчисления". мне непонятно, почему из-за возможности увеличить а, а', b, b' пропадает знак равенства
Это как спросить, почему параллельные прямые не пересекаются. Мы ВЫБИРАЕМ числа a, a', b, b' так, чтобы выполнялось неравенство 1. Числа, не удовлетворяющие неравенству, не рассматриваем.

Открыл. А где тут, собственно, геометрия? Я хочу задачи из ЕГЭ решать, зачем вы мне лемму Цорна принесли?
Издательства тобой недовольны. Жди счет за нарушение копирайта.
Так вся суть чтения учебника - это быстрый поиск нужных мест. Это же не детективчик.
>Я хочу задачи из ЕГЭ решать
Любую задачи из школьного курса можно решить методами линейной алгебры.
Меня дедушка научил на 11 умножать двузначные числа - раздвигаааешь и вставляешь между ними их сумму. Например 23x11 = 253. Думал тянок этим фактом поражать, но им как-то пох.
>на 11 умножать двузначные числа - раздвигаааешь и вставляешь между ними их сумму
Задачка для треда. В скольких процентах случаев методика деда дает верный результат?
Чо-то около сорокета в процентах.

>Думал тянок этим фактом поражать, но им как-то пох.
Тянки текут от топологических векторных пространств, инфа 100%
Это в военное время. А для small angles в смысле небольших значений методика деда отлично работает!
>>378269
Ну это слишком абстрактно. А тут умножаешь и получаешь, например, длину чего-нибудь важного. Например у тебя 11 инчей а ты хочешь перевести свой размер в сантиметры. Умножай смело на 25 и откидывай последнюю цифру. Огого!

Вопрос в чем, О(1) и о(1) - это сколько секунд?
> О(1)
Константа, независимо от размера входных данных. Если алгоритм программа обрабатывает вход за O(1), то она за одно и то же время обработает и килобайт, и петабайт.
>о(1)
Нуль или неразличимо малая величина.
Спасибо за ответ.
Иной раз нужн вбивать конкретную фразу, причем в гугл даже а не в учебник, и многократно ее менять чтобы выскочило конкретно то что ищешь, например в google books. Это метода 2016. Мой дед так не умеет например. У него только бумажный фихт 1966 года издания.
Срыв покровов: иногда нужно быстро нагуглить что-то по фразе, а иногда люди читают книги подряд.
Посоны, помогите решить эту задачку алгебраическими методами. Вроде все просто, но чет не получается пока.
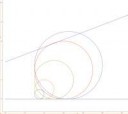
Пока не знаю как выразить координаты точки касания с наклонной линией. Радиус должен быть чуть меньше 3. А значит там в ответе будут или радикалы или арксинусы.
Но это тупо, читать учебник от корки до корки как худ лит. Да даже если читаешь, все равно нужно бывает быстро откинуться назад и найти ключевые места.
> Но это тупо, читать учебник от корки до корки как худ лит.
Во-первых, читать подряд не означает читать от корки до корки. Можно пропускать параграфы или даже целые главы, если они кажутся неинтересными.
Во-вторых, не нравится читать подряд - не читай. Че доебался-то?

>почему бы так и не записать, что остаток одинаковый?
Потому что это понятие нужно отдельно вводить. Проще и логичнее сказать, что a и b принадлежат к одному классу mod n если их разность кратна n.
> Почему даётся не эквивалентность двух чисел a и b, а эквивалентность a и остатка от деления?
Даётся именно эквивалентность двух чисел a и b. Просто запись такая. "а равно b по модулю n".
>>378335
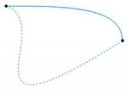
Кривая в пространстве X = непрерывное отображение [0,1]->X.
Если одну кривую в другую можно "плавно" (=непрерывно по всем параметрам) перевести, то они гомотопичны.
Гомотопичность относительно концов кривых -- это когда все рассматриваемые кривые должны иметь фиксированные концы (пикрелейтед гомотопия с фикс концами).
Какую книгу читаешь?
Появилась новая идея как решить эту задачку. Все точки начала окружности походу лежат на одной прямой. А вектор от точки касания до точки начала окружности ортогонален линии касания.
По сути у нас будут два вектора:
(0,0);(x_точка касания, y_точка_касания)
(x_начало_окружности,y_начало_окружности);(x_точка касания, y_точка_касания)
Берем скалярное произведение и оно равно нулю.
Как это выразить формульно пока не знаю.
Посоны, помогите.
Да не доебался, нормально общаемся же. Тред надо поднимать, он на второй строчке болтается второй день. А должен быть в тройке всегда.
Мне удобно. Две вкладки одинаковые открываю, одну для собственно чтения и одну для референсов

Радиус внутри (2.95...3). Точное значение пока не могу найти. Помогите составить уравнение скалярного произведения.
>Кривая в пространстве X = непрерывное отображение [0,1]->X.
>Если одну кривую в другую можно "плавно" (=непрерывно по всем параметрам) перевести, то они гомотопичны.
>Гомотопичность относительно концов кривых -- это когда все рассматриваемые кривые должны иметь фиксированные концы (пикрелейтед гомотопия с фикс концами).
>Какую книгу читаешь?
То есть это как бы двумерное отображение? Где-то видел, что гомотопию деформацией называют. Только зачем для этого вводится прямоугольник, одна из сторон которого отображается в одну кривую, противоположная - в другую?
Читаю, в основном, интернет. Наслышан, что книга Рунде неплохая, но взяться за чтение математики на бусурманском языке пока немного очкую.

>Только зачем для этого вводится прямоугольник, одна из сторон которого отображается в одну кривую, противоположная - в другую?
Это просто способ рисовать, как устроено отображение гомотопии.
Ведь как ты эту деформацию задашь? Деформация будет функцией от времени от t = 0 до 1, на каждом значении t задающая свою кривую [0,1]->X. То есть некая g(t, x) : [0,1]x[0,1]->X, которая на t=0 одна кривая, на t=1 другая. Это и обозначают рисуя прямоугольник. Хуй знает, мне кажется и так понятно, что такое гомотопия, без дурацких прямоугольников. В английской википедии например нормальное описание, без всяких прямоугольников долбоебических)
В книге какого-то препода из НМУ подобная штука называлась слоем, но тут переводчик про какие-то волокна говорит.
Двачую, так же делаю. У меня еще 2 моника, один 27 дюймов, другой 20.
>>378479
> fiber of f over q
Прообраз q при отображении f.
Fiber - это просто fancy word. Обычно говорят inverse image of {q} under f, а по-русски: прообраз {q} при отображении f.
> fiber over q is a singleton
Прообраз q состоит из 1 элемента.
Вообще, забей на переводы. Русские термины очень быстро выяснятся по ходу дела, когда ты начинаешь читать что-то на русском. Никаких проблем от незнания русских терминов у тебя не будет.
Спасибо.

Никакого второго ответа я там не вижу. Вариант с окружностью внутри треугольника условием задачи не предусмотрен.
>матеша.
где ты такое слово выцепил дебильное пиздец. иди лучше днюху справляй с пацанами. правильно понял - лучше идти на хуй.
> Так вот, топология интересна или мне идти на хуй?
на, изучай. Потом решишь - интересно, или нахуйвпизду.
http://gen.lib.rus.ec/book/index.php?md5=5CD3A3DB7FC638EAC684359D7551A036

>Чего вообще в матеше такого пиздец интересного, что люди занимаются ею всю жизнь?
Теория чисел. Самый годный раздел математики
>Khetcher_Algebraicheskaya_Topologia_2011
Проиграл. Эта книга для graduate students. Ты там даже 2 страниц не осилишь.
То, что ты дал - энтри левел? Тогда норм.
>Че пижже будет, твоя ссылка или эта книженция?
моя научно-популярная для даунов. Это чисто почитать для общего развития, не учебнтк.

Это автор про додекаэдр чтолей?
Хуль там такого интересного? Вики ничего такого охуенного не рассказывает, так что давай ты.
Я сам пока в неё вкатоваюсь, читаю Прахар Распределение простых чисел.
Просто меня удивляет, сколько всего скрывается за такими простыми вещами, как натуральные числа.
Например, почему одни числа содержат в разложение на простые множители только два множителя, а другие три. Почему блядь?! Как так происходит? И почему именно эти числа?
v(n) - количество простых множителей.
v(4)=v(6)=v(10)=v(15)=2, почему именно эти числа? Есть ли какай-нибудь общая формула для таких чисел? И сколько их на отрезке [1;n]?
Тоже и для чисел a, таких, что v(а)=m. Тебе не кажеться это интересным?
Хуя тебя понесло. Меня такая хуита интересует в физике, в связи времени и пространства. Только там нет пруфов и одфа философия.
И да, и нет. Меня оно интересует как альтернативные основания математики тащемта
Ты же сам спросил - идти на хуй или нет. И не говори матеша. Просто не говори так. Ты же в мат треде, а не в б. Здесь многие с публикациями.
>Здесь многие с публикациями.
УУУУ, прямо в ежегодных сборникх статей Усть-Пиздюйского училища математики? Ого прямо.
А ты думаешь даже в вестнике усть пиздюйского политеха кого угодно публикуют что ли. А вообще ты не допонял, никакой агрессии, тут все твои друзья.
>А ты думаешь даже в вестнике усть пиздюйского политеха кого угодно публикуют что ли
Кончено. Знаком с такой хуйней в универе. На конференции ходят со всякой хуитой (не все офк) ради бесплатной публикации для магистратуры, например.
>никакой агрессии, тут все твои друзья
Я знаю.

Отображение π:E→B проецирует все точки щетины на расчёске в их корень.
Прообраз точки на цилиндре будет одной щетинкой, волокном. У нас это называют слоем.
Ага, хуевый перевод. Для Hopf fibration выбрать перевод как расслоение Хопфа - пиздец. Нормальные люди перевели бы как фибрация Хопфа, но нет.
Иди нахуй, школьник. Вот по такому школьному пафосу можно гарантированно детектировать школьников либо особо туповатых первокурсников.
А с чего ты взял, что это вообще перевод, и тем более что это перевод с английского, а не французского?
Хатчер норм. Но зависит от того, что ты знаешь вообще в математике. А что ты знаешь, кстати?
>топология интересна или мне идти на хуй?
Хуй ответишь на этот вопрос. Кто-то скажет, что на двачах неинтересно сидеть. Кто-то скажет, что это единственное, что интересно в жизни. И как теперь отвечать на
>каково сидеть на двачах, интересно или мне идти на хуй?
Открыл-то Хопф. Вообще похуй, какой язык в оригинале. Тут же проблема как с переводом термина quantum entanglement в квантовой механике - переводят его как квантовая запутанность, хотя лучше передает смысл перевод как квантовая сцепленность.
>А что ты знаешь, кстати?
А нихуя. Школьный курс + пара семестров высшей математики уровня забытых интегралов и ангема. Заценю ту книженцию, что челик выше кинул, сам себе отвечу.
>каково сидеть на двачах, интересно или мне идти на хуй?
Интересно, дохуя разных людей, хорошо что есть тематика.
Подождите минуточку, я же только что на хуй кого-то послал, и тут же меня послали, даже не выдержав паузу? Это подрывает авторитет обсуждений.
Кстати а че вы так к школьникам отрицательно относитесь. Веди сами же практически школьники. Хули тебе три-джва года универа ума прибавит что ли. Все равно мамке трусы стирает и картофан жарит. Весь б забит магами которые ноют что им только вчера было 18. Возраст это полная хуета. Я сформировался лет в 12. И дальше мне похуй, автопилот
у фрейда немецкий, как и русский, с падежами ебаными. а в английском таких оговорок невозможно.
Да нормально мы к школьникам относимся)
Блин, так теперь же всё понятно. А я-то голову ломал, почему так называется.
Сначала подумал, что это пост шизика или перевод промптом, а потом понял глубинный смысл.

долбоебы fiber это клетчатка. у меня дедушка пикрил употребляет, чтобы газы не мучали.
http://libgen.io/book/index.php?md5=3FB5F62D057564BC97AB9254F5DA6465
>Language:German
>German
>GERMAN
>GERMAN
Алсо, классная шапка, выглядит внушительно
>О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов: “Элементарная топология”.
Совсем не идет.
Брат по несчастью. Тоже с этого начал (после Куранта загорелся) и был дико удивлён такой скучной аксиоматикой и разжёвыванием.
Прасолов с его наглядной топологией нормас. Первые задачи интересно в уме решать, прокачиваешь пространственное мышление. Пятая глава о топологии в курантовской "Что такое математика?" - то, с чего я начал и тебе рекомендую. И наглядная топология от Болтянского хорошо заходит, особенно мне, ибо про графы я и так знаю и главы про них пролистал. Если хочешь прям с аксиом - на лекториуме есть курс лекций.
Нет. Русского материала хватит только чтобы докачаться до уровня семидесятых. Дальше придётся читать научные статьи, а они на английском.
Докажи.
>Я не говорю глупости.
>Русского материала хватит только чтобы докачаться до уровня семидесятых
>семидесятых
Угу.
Разве всё не так? Именно до семидесятых, потому что дальше идут статьи. А статьи на ангельском.
> он у мамы и антифа
> и математишн
> и учебник свой пишет,
> но в основном про проституток
Не вижу ничего безумного в вышеперечисленном.
Вообще, мне кажется, математикой занимаются люди, которых мало заботит мнение общества о них, потому что это не самая престижная профессия при капитализме. Если человек независим от мнения общества и у него творческий склад ума, то, скорее всего, у него будут какие-то необычные интересы и необычное поведение, вот и все. Но безумие тут ни при чем.
ну ты сравнил жопу с пальцем. вербицкий это голова и ваще. не то что этот вниманиеблядь дрищ.
Ты ахуел? Математика - отдельная хуйня, она, как мне кажется, от физики сильно отличается. Без математики не было бы физики, без физики - математика возможна.
Алсо, математика очень странная штука, ну, в совокупности с физикой - то есть всякие уравнения и равенства. Она описывает падающее яблоко, но ведь природа не решает никаких уравнений, яблоко просто падает.
Все так.
Как я и говорил, обычным людям доказательства на примерах и образах, для математиков доказательства с полным отрывом от реальности и удвоения объема шара разрезанием.
Как я и говорил, математика везде одна, только технарям и школьникам дают урезанную версию, первым для вычислений, а вторым просто так. И не надо думать, что студентом-математикам не дают хороших примеров и не объясняют "на пальцах".
Алсо, если бы была цель технарям или школоте объяснить все те же доказательства, что и студентам-математикам, изложение тоже было бы запутанное, от этого никуда не денешься. А удвоение шара разрезанием внезапно считается контринтуитивным среди математиков, они же не шизофреники поголовно, блять. Некоторые из них даже стараются не пользоваться аксиомой выбора, чтобы не было таких парадоксов.
покормил
Живые существа миллиарды лет эволюционировали, чтобы развивать фантазию - способность моделировать окружающий мир. Кто хорошо моделировал - много жрал. Кто плохо моделировал - того сжирали.
По-видимому, человек - одно из умнейших существ, созданных эволюцией. Человеческая способность моделировать мир в своем воображении очень высока. Люди -- хорошие фантазёры. В человеческом воображении есть очень много фантастических образов - звезда, человек, яблоко, человек Петя Иванов, непосредственно наблюдаемое мною прямо сейчас яблоко, etc. Важно понимать, что никто никогда не видел звезду; звезда - это фантастическая конструкция.
Математика - это деятельность человека по оттачиванию способности моделировать. Математики профессионально работают с фантастическими объектами, созданными человеческой фантазией. Они подвергают эти объекты многократному разложению и синтезу, смешивая их в причудливых сочетаниях. Математики - это профессиональные фантазёры.
Поэтому неудивительно, что математика иногда пригодна для описания реальности. Всё дело в миллиардах лет планетарной эволюции и капельке рефлексии.
>звезда - это фантастическая конструкция
Че ты говоришь такое, на улице давно был? В окно посмотри, там солнце на небе. Солнце - это звезда.
>Математики - это профессиональные фантазёры.
Да ну, это слишком расплывчато сказано.
Я бы сказал, что математика - инструмент для предсказаний (моделирования, как ты сказал), но есть одна хуйня - схуя ли математика вообще работает, и хуйня еще удивительнее - схуя ли с её помощью можно предсказывать-моделировать? То есть, грубо говоря, почему сначала математик пишет систему уравнений, а потом физик находит в природе явление/объект, который и был предсказан той системой. Это же пиздец, природа не решает уравнений, ты только вдумайся в курсив, и в то, что схуя ли математика работает, она ж никому ничего не должна.
>>378644
Ага, как же. Тот же парадокс про шар появился из за того что теория множеств напрочь оторванна от реальности.
И математиков так же учат, в полном отрыве от реальности, чтобы они тоже оторвались от реальности и начали на многообразия дрочить и обмазываться гомотопическим хаосом.
Потомк что матемтика это образ физики, которая в свою очередь образ наблюдаемой вселенной.
Что такое образ? Типа бледная копия? Даже если так, из того, что ты написал, не следует, что математика со своими уравнениями должна работать во вселенной.
Возьми книжку по математике для математиков и для технарей и сравни их.
Если бы у одних была урезанная версия а у вторых полная, в первой книжке было бы написанно больше текста со следствиями и причинами.
Но на деле получается что в книжкх для математиков все написанно мутно и непонятно.
Во-первых, кому непонятно-то? Мне понятно. А во-вторых, книжка по математике "для технарей" -
это сборник руководств по решению задач тащемта. Откуда эти руководства берутся, по-твоему? Из какой-то другой математики или из воздуха?
Зайдем с другой стороны.
Дай определение дифференциала с точки зрения математики для математиков.
https://www.youtube.com/watch?v=w-I6XTVZXww
То, что это makes no fucking sense следовательно матиматика это хуита.
4 МИЛЛИОНА просмотров блять.
Есть объективная реальность, существующая независимо от твоего мышления, а есть образы, существующие в твоей голове. Когда на твои органы чувств действует некоторое ощущение, в твоей голове возникает восприятие. Когда ты фантазируешь, в твоей голове возникает представление (термины позаимствованы из учебника логики Гетмановой).
Восприятие - сложная вещь. Если на один и тот же луг выйдут генерал, крестьянин, художник и травник, то они воспримут его по-разному. Генерал прикинет, сколько можно нарыть окопов. Крестьянин оценит, сколько можно посадить картошки. Художник восхитится красотой. Травник присмотрится к траве, которая растёт на этом лугу. Одни и те же ощущения вызовут у этих людей разные восприятия.
Восприятие индивидуально, в нем участвует не только то, что непосредственно действует на органы чувств, но вообще весь опыт человека. У разных людей опыты разные, поэтому восприятия у них тоже разные. Фантазия о звезде, которая есть у меня, сильно отличается от фантазий о звездах, которые были у моих предков тысячи лет назад. Я воспринимаю звезду как шарообразный сгусток плазмы. Мои предки воспринимали звезду как дырку в твердом куполе. Мои потомки, возможно, будут воспринимать звезду как решение некоторого уравнения.
Конечно, ввиду большого генетического сходства, люди воспринимают мир в основном одинаково. Мозг всех людей способен работать со временем и выделять в пространстве разнообразные геометрические формы. У всех людей есть представление о стабильном объекте (оно, кстати, не врожденное, а формируется на первом году жизни). Почти у всех людей есть отделы мозга, отвечающие за речь и арифметику. Все люди оборудованы памятью и некоторой фантазией. Кроме того, все люди, живущие в достаточно цивилизованном государстве, имеют один и тот же набор книг, смотрят один и тот же телевизор, упарываются одной и той же фантастикой. Поэтому у всех людей, проживающих в одно и то же время на одной и той же территории, фундаментальные фантазии, типа как о звезде, похожи. Но фантазия о звезде - это всё-таки фантазия.
Когда я смотрю на Солнце, я ощущаю ощущения, а не звезду. Звезда возникает в моей фантазии на основе всего моего жизненного опыта и некоторых аппаратных особенностей моего мозга.
Есть объективная реальность, существующая независимо от твоего мышления, а есть образы, существующие в твоей голове. Когда на твои органы чувств действует некоторое ощущение, в твоей голове возникает восприятие. Когда ты фантазируешь, в твоей голове возникает представление (термины позаимствованы из учебника логики Гетмановой).
Восприятие - сложная вещь. Если на один и тот же луг выйдут генерал, крестьянин, художник и травник, то они воспримут его по-разному. Генерал прикинет, сколько можно нарыть окопов. Крестьянин оценит, сколько можно посадить картошки. Художник восхитится красотой. Травник присмотрится к траве, которая растёт на этом лугу. Одни и те же ощущения вызовут у этих людей разные восприятия.
Восприятие индивидуально, в нем участвует не только то, что непосредственно действует на органы чувств, но вообще весь опыт человека. У разных людей опыты разные, поэтому восприятия у них тоже разные. Фантазия о звезде, которая есть у меня, сильно отличается от фантазий о звездах, которые были у моих предков тысячи лет назад. Я воспринимаю звезду как шарообразный сгусток плазмы. Мои предки воспринимали звезду как дырку в твердом куполе. Мои потомки, возможно, будут воспринимать звезду как решение некоторого уравнения.
Конечно, ввиду большого генетического сходства, люди воспринимают мир в основном одинаково. Мозг всех людей способен работать со временем и выделять в пространстве разнообразные геометрические формы. У всех людей есть представление о стабильном объекте (оно, кстати, не врожденное, а формируется на первом году жизни). Почти у всех людей есть отделы мозга, отвечающие за речь и арифметику. Все люди оборудованы памятью и некоторой фантазией. Кроме того, все люди, живущие в достаточно цивилизованном государстве, имеют один и тот же набор книг, смотрят один и тот же телевизор, упарываются одной и той же фантастикой. Поэтому у всех людей, проживающих в одно и то же время на одной и той же территории, фундаментальные фантазии, типа как о звезде, похожи. Но фантазия о звезде - это всё-таки фантазия.
Когда я смотрю на Солнце, я ощущаю ощущения, а не звезду. Звезда возникает в моей фантазии на основе всего моего жизненного опыта и некоторых аппаратных особенностей моего мозга.
Но дело не только в научнпопе, а в том что они через научпоп каналы сеят мракобесие - "присваивание" результата расходящимся рядам это только в дурке можно додуматься делать. Всякие гранди-хуянди чезаро-хуяро это полная абстракная чушь, сектарианство, не имеющее ничего общего с объективной реальностью.
А интересно, это в универе проходят? Мне бы сука СТЫДНО было бы преподу такую хуету сдавать, и гнать не краснея что сумма 1-1+1-1... равна 1/2 потому что ебучий чезаро так решил. Это же унижение, как в джинсиках с подворотом ходить и с косичкой.
Это не мракобесие, это легально. Но в этом-то и проблема, что несведущий человек толком и не поймёт, почему это так и как это вообще нужно понимать, и сделает пародоксальный вывод о том, что это не он не понял, а ему хуйни наплели.
Define понимание. Можно "понять" - просто выучить ПРАВИЛА и применять их. И что такое "легально"? Просто кто-то придумал некие правила суммирования. Можно ведь придумать как разделить на ноль и назвать эту теорию своим именем. Вот это утверждение как согласуется с фокусами с рядами? >>378649
Ну вот бывает так, что ты чего-то не понимаешь и думаешь что это хуета. И считает наверное это потому что ты не обладаешь ЗНАНИЯМИ. Тогда ты изучаешь вопрос, веришь выкладкам и у тебя наступает ОЗАРЕНИЕ. Наконец то я понял! Но через некоторое время когда все отложится, ВНЕЗАПНО осознаешь, что нет, все таки хуета это. Зато теперь ты знаешь почему это хуета. Потому что ты понял ход мысли автора, но не купился. Как то так.
>>378682
Почему тралю, меня реально раздражают несходящиеся ряды и вольное обращение с ними.
Какой раздражительный. Это вольное обращение придумали люди поумнее тебя.
Что ещё за "вольное обращение"? Просто ввели обозначение такое, не хуже других
>манга гайд ту...
>без фансервиса
Безполезно.

Годная книжка? Стоит ли тратить на неё время?
Ну вдруг я не понял чаго.
Пусть V и W - нормированные векторные пространства, полные по метрике, порождённой нормой. Нормы обозначим как nV и nW.
Пусть U - открытое подмножество V. Пусть f - функция из U в W. Пусть x - точка U.
Ограниченная линейная функция L из V в W называется дифференциалом Фреше функции f в точке x, если предел отношения nW(f(x+h) - f(h) - L(h)) / nV(h) равен нулю при h стремящемся к нулю по множеству x+h ∈ U.
Упрощая, дифференциал - это линейный оператор, приближающий функцию с малой погрешностью.
Если пространства V и W конечномерны и в них выбраны базисы, то всякое линейное отображение из V в W биективно соответствует некоторой матрице. Матрица дифференциала Фреше называется производной Фреше. В случае когда V=W=R эта матрица отождествляется с числом, которое и оказывается, очевидно, обычной производной функции в точке.
Реквестирую книгу по теории колец главных идеалов

Как считают подобное?

Бля, перепутал пикчи
Всего 10 столбцов, каждый из 10 строк. Первая строчка выбирается из первого столбца, т. е. есть 10 различных первых строчек. Для каждой первой строчки можно выбрать одну из возможных вторых строчек, их тоже десять. Стало быть, комбинаций первых и вторых строк всего 10*10. Таким образом, получается, что вариантов стиха из 10 строк будет 10^10.
А можно таким макаром себе речь на выступление сделать?
Больше, чем люди написали за всю свою историю. В одной какой-то дурацкой картинке 300х400. На Дваче.
>Я идиот, потому что прогуливал школу
>рисовать множество Мандельброта
В школе его не проходят.
И в пту тоже. Даже в университе наврядли, только если в спец-курсе каком-нибудь.
Естественно я прочитал это. Но я настолько туп, что не понял даже вот этот мануал.
http://www.wikihow.com/Plot-the-Mandelbrot-Set-By-Hand
Бамп
А теперь скажи чем это определение отличается от того которое изобрел ньютон с лейбницем.
Ньютон с Лейбницем не знали о множествах, метрических пространствах и нормах. У них он для R, а в определении обобщении на большее количество пространств.
>А теперь скажи чем это определение отличается от того которое изобрел ньютон с лейбницем.
>Ты не к словам придирайся, а к сути.
>Ты тролируешь двач так?
>Суть дифференциала поменялась или нет?
Ты сначала с вопросом определись.
Тебе ещё блять растолковать надо, существуют полные метрические пространства помимо R? Или что общие определения и теоремы лучше частных, потому что они могут быть более широко применимы?
Ну давай, примени мне производную на какой то, любой, случай.
Начнём с главного. Ни Ньютон, ни Лейбниц не использовали дифференциал в смысле "линейное отображение". Такой смысл начал вкладывать в этот термин лишь Коши.
Так, давай с самого начала появления фиддеренциала
>Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке)
Вот теперь из этой точки показывай дорожку к нормированным векторным пространствам.
>>378785
Уточню, я не прошу чтобы ты мне сказал "вот пал палыч палкин сказал это", а показал где, в каком месте пал палычу палкину пришлось столкнуться с тем чтобы прийти к векторным пространствам.
Уже просто R - векторное пространство.
1. Изучал функции Rm->Rn
2. Перешёл к функциям Cm->Cn
3. Решил не ограничиваться конечномерным случаем
1. Линейные функции из вещественных чисел в вещественные числа - это всегда умножение на какое-то число. Обратно, о каждом числе можно думать как о линейной функции. Более того, линейная функция из R^m в R^n биективно соответствует матрице размера m на n.
2. Функции из R в R мы будем называть числовыми функциями одного аргумента. Функции из R^m в R мы будем называть числовыми функциями нескольких аргументов. Функции из R^m в R^n мы будем называть векторными функциями нескольких аргументов.
3. Известно, как определить производную числовой функции одного аргумента. Производная таких функций - это число. Умножение на это число - по пункту 1 линейная функция. Она называется дифференциал в точке. У дифференциала есть главное свойство: дифференциал приближает функцию с малой погрешностью. Это свойство следует из определения производной.
4. Для векторных функций нескольких аргументов тоже бы хотелось иметь дифференциал. Для этого нужно
а) указать линейную функцию
б) уточнить понятие "приближать с малой погрешностью"
5. Рассмотрим сначала числовые функции нескольких аргументов. Известно, что для таких функций введено понятие "частной производной" в точке.
6. Заметим, что векторную функцию нескольких аргументов можно рассмотреть как несколько скалярных функций (от тех же самых аргументов). То есть перейти к координатам. Например, функцию в пространство можно рассмотреть как три числовые функции - координаты по осям OX, OY, OZ. Функцию из R^m в R^n можно рассмотреть как n функций из R^m в R.
7. Возьмём векторную функцию нескольких аргументов. Рассмотрим её как несколько скалярных функций. У каждой из скалярных функций возьмём все частные производные. Составим из них матрицу. Так как всякая матрица однозначно соответствует линейному оператору, тем самым получим линейный оператор. Он называется якобиан.
8. Зафиксируем некую точку, назовём её a. Пусть у нас есть какая-то функция. В точке a у неё одно значение. Если мы немного сдвинемся от точки a, у функции станет другое значение.
9. Пусть у нас есть две функции, f и L. Скажем: функция L приближает функцию f в точке a, если для любого маленького сдвига от точки a расстояние между изменившимися значениями f и L мало по сравнению со сдвигом. Что значит мало? Сдвиг - это вектор. Расстояние между двумя точками - тоже вектор. Под малостью мы будем понимать малость длин этих векторов, или малость норм. Т.е. просто малость чисел.
10. Малость чисел мы будем понимать в нотации o малое. Смысл предыдущих пунктов, стало быть, таков. Функция L приближает функцию f в точке a, если существует такая числовая функция r, что
а) r бесконечно-малая
б) |f(a+x)-f(a) - L(a+x)-L(a)| = |x|r(x).
Под x понимается сдвиг от точки a.
f(a+x)-f(a) - это приращение функции f при сдвиге x от точки a.
L(x+a)-L(a) - это приращение функции L при сдвиге x от точки a.
Если функция L линейна, то L(x+a)-L(a) = L(x).
В дальнейшем будем предполагать, что L линейна.
11.Разделив обе части на |x| и перейдя к пределу x->0, получим выражение, которое очень напоминает аналогичное выражение для производной числовых функций.
lim |f(a+x)-f(a) - L(x)|/|x| = 0.
12. В п. 7 мы получили линейный оператор, якобиан. Если он приближает функцию в смысле п. 11, то якобиан называется дифференциал.
1. Линейные функции из вещественных чисел в вещественные числа - это всегда умножение на какое-то число. Обратно, о каждом числе можно думать как о линейной функции. Более того, линейная функция из R^m в R^n биективно соответствует матрице размера m на n.
2. Функции из R в R мы будем называть числовыми функциями одного аргумента. Функции из R^m в R мы будем называть числовыми функциями нескольких аргументов. Функции из R^m в R^n мы будем называть векторными функциями нескольких аргументов.
3. Известно, как определить производную числовой функции одного аргумента. Производная таких функций - это число. Умножение на это число - по пункту 1 линейная функция. Она называется дифференциал в точке. У дифференциала есть главное свойство: дифференциал приближает функцию с малой погрешностью. Это свойство следует из определения производной.
4. Для векторных функций нескольких аргументов тоже бы хотелось иметь дифференциал. Для этого нужно
а) указать линейную функцию
б) уточнить понятие "приближать с малой погрешностью"
5. Рассмотрим сначала числовые функции нескольких аргументов. Известно, что для таких функций введено понятие "частной производной" в точке.
6. Заметим, что векторную функцию нескольких аргументов можно рассмотреть как несколько скалярных функций (от тех же самых аргументов). То есть перейти к координатам. Например, функцию в пространство можно рассмотреть как три числовые функции - координаты по осям OX, OY, OZ. Функцию из R^m в R^n можно рассмотреть как n функций из R^m в R.
7. Возьмём векторную функцию нескольких аргументов. Рассмотрим её как несколько скалярных функций. У каждой из скалярных функций возьмём все частные производные. Составим из них матрицу. Так как всякая матрица однозначно соответствует линейному оператору, тем самым получим линейный оператор. Он называется якобиан.
8. Зафиксируем некую точку, назовём её a. Пусть у нас есть какая-то функция. В точке a у неё одно значение. Если мы немного сдвинемся от точки a, у функции станет другое значение.
9. Пусть у нас есть две функции, f и L. Скажем: функция L приближает функцию f в точке a, если для любого маленького сдвига от точки a расстояние между изменившимися значениями f и L мало по сравнению со сдвигом. Что значит мало? Сдвиг - это вектор. Расстояние между двумя точками - тоже вектор. Под малостью мы будем понимать малость длин этих векторов, или малость норм. Т.е. просто малость чисел.
10. Малость чисел мы будем понимать в нотации o малое. Смысл предыдущих пунктов, стало быть, таков. Функция L приближает функцию f в точке a, если существует такая числовая функция r, что
а) r бесконечно-малая
б) |f(a+x)-f(a) - L(a+x)-L(a)| = |x|r(x).
Под x понимается сдвиг от точки a.
f(a+x)-f(a) - это приращение функции f при сдвиге x от точки a.
L(x+a)-L(a) - это приращение функции L при сдвиге x от точки a.
Если функция L линейна, то L(x+a)-L(a) = L(x).
В дальнейшем будем предполагать, что L линейна.
11.Разделив обе части на |x| и перейдя к пределу x->0, получим выражение, которое очень напоминает аналогичное выражение для производной числовых функций.
lim |f(a+x)-f(a) - L(x)|/|x| = 0.
12. В п. 7 мы получили линейный оператор, якобиан. Если он приближает функцию в смысле п. 11, то якобиан называется дифференциал.
не ругайтесь, я мимошкольник
Для 1-9 непосредственной проверкой. Многозначное число представлять как сумму числа, оканчивающегося на 0, и однозначного числа.
phi(10)=4, поэтому по теореме Эйлера в Z/10Z a^5=a. ЧТД.
>Пусть у нас есть две функции, f и L. Скажем: функция L приближает функцию f в точке a, если для любого маленького сдвига от точки a расстояние между изменившимися значениями f и L мало по сравнению со сдвигом. Что значит мало? Сдвиг - это вектор. Расстояние между двумя точками - тоже вектор. Под малостью мы будем понимать малость длин этих векторов, или малость норм. Т.е. просто малость чисел.
Ты только доказываешь
>У дифференциала есть главное свойство: дифференциал приближает функцию с малой погрешностью
как на него не смотри.
Это копия, сохраненная 16 ноября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.