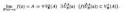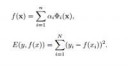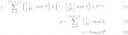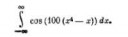Математика, тред 51 - Наука

Двач.hk не отвечает.
Вы видите копию треда, сохраненную 16 ноября 2016 года.

Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее

Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

Математика, тред 51 17 Июл, 04:17 #376017 В конец треда | Веб

Этот тред посвящён pure mathematics. Здесь из нескольких разных доказательств выбирают самое концептуально правильное, доказывают задачи из листочков для первого курса НМУ, а также читают научные статьи (пытаются).

Если вы хотите задать вопрос типа "как мне взять этот интеграл", это не сюда. Вам нужен тред "для начинающих", он плавает неподалёку.

Предыдущий: >>372131 (OP)

Ответы>>376196 >>377801 >>378728 >>379662

Архивы 17 Июл, 04:19 #2 #376022

Архивы 17 Июл, 04:19 #2 #376022

Показать весь текст

17 Июл, 09:52 #3 #376183

Сидим тута? Математика хуёва грамматика.

17 Июл, 10:23 #4 #376196

>>376017 (OP)
Что на пикрелейтед (я не про анимэ)?

Ответы>>376205 >>376208

17 Июл, 10:46 #5 #376205

>>376196
Программа Вербицкого, третий курс, одна из книжек, пара страниц из неё.

Ответы>>376208

17 Июл, 10:56 #6 #376208

>>376205
>>376196
Артур Бессе это. В программе вербицкого второй курс, а не третий.

Ответы>>376209

17 Июл, 10:58 #7 #376209

>>376208
В самом деле.

17 Июл, 12:52 #8 #376242

Только non вербитосрач.

17 Июл, 14:32 #9 #376258

Маняматики, какой по вашему способ наиболее лучшего изучения маняматики?
Я вот читаю что есть два способа, первый с времен лейбница, когда студиозу все рассасывают и пережевывают по десчять раз, чтобы даже сосачер из буэ все понял.
Второй, как бы нынешний молодежный, популярный, и т.д., бросить каникуляру основные определения чтобы он дальше сам выводил из них следствия и теоремы.

Ответы>>376263 >>376264 >>376269

17 Июл, 14:53 #10 #376263

>>376258
Для получения людей, который гарантированно знают хоть что-то, нужен первый.
Второй сильно поможет усердным и способным(но из них важнее первое, ибо способный лентяй может забить), но утопит остальных. Если это сочетается с жёстким экзаменационным контролем, то получаем толпы неосиляторов. Если же нет, то просто толпу с корочками со знаниями математики в лучшем случае чуть больше нормальных физиков.

Ответы>>376413 >>376460

17 Июл, 14:55 #11 #376264

>>376258
Нужно представить, будто окунаешься в океан говна с открытым ртом - и математика идёт как по маслу.

Ответы>>376404

17 Июл, 15:28 #12 #376269

>>376258

> Маняматики, какой по вашему способ наиболее лучшего изучения маняматики?

Если бы я знал, давно бы уже ее изучил.

17 Июл, 17:47 #13 #376339

Как вы относитесь к собственному удивлению? Вот есть какое-то утверждение, доказательство которого вы знаете; знаете, что утверждение верное, но оно вас удивляет даже спустя какое-то время. Первое, что в голову пришло: лемма о лебеговом числе. Я когда прочитал ее формулировку, я удивился. Потом порисовал шары и думаю: "ага, ясно". Сам без учебника придумал доказательство. Но вот геометрически она мне кажется какой-то неочевидной. То есть я сам придумал доказательство, оно совпало с тем, что в учебнике, но мое естество почему-то не хочет ее принимать.

Я всегда думал, что если сам придумал доказательство, то ты реально понимаешь материал. Но сейчас я думаю, что, быть может, я придумываю доказательства не потому, что все прочувствовал, а потому что авторы учебников разбивают все на короткие леммы и как бы за руку подводят тебя к нужным вещам. Как вы заставляете свой мозг что-то принять?

Ответы>>376405

57 Кб, 1920x1080

17 Июл, 20:29 #14 #376404

>>376264
Двачую! Я так и изучаю математику, полёт нормальный!

17 Июл, 20:33 #15 #376405

>>376339
Потому что большая часть человеческих доказательств -- это не более чем убедительные рассуждения. Реально же это может быть не более чем математической демагогией.

Короче, пока ты не написал док-во, принимаемое пруф ассистентом, знай, это нихуя не док-во.

Ответы>>376418 >>376437

17 Июл, 21:43 #16 #376413

>>376263
Почему тогда форсится сейчас второй способ?

Ответы>>376416

17 Июл, 21:50 #17 #376416

>>376413
Потому что дешевле и проще нихуя не делать, чем уделять время на реальное общение с учениками.

17 Июл, 23:07 #18 #376418

>>376405
Но есть риск дохуя всего написать и все равно ничего не понять. Особенно если ассистент хорошо ассистирует и сам половину фактов за тебя подбирает.

Ответы>>376437

18 Июл, 07:01 #19 #376437

>>376405
>>376418

Съеби в тред для новичков, пожалуйста, не шкварьте этот тред.

Ответы>>376485

18 Июл, 12:15 #20 #376460

>>376263
Твой пост огорчает физиков.
Они что, не знают ничего по твоему?

Ответы>>376468

18 Июл, 13:45 #21 #376468

>>376460
А что именно знают физики? По темам.

Ответы>>376473

18 Июл, 14:32 #22 #376473

>>376468
Если брать вообще всю физику то интригалы, тапалогии, векторы, матрицы, эвклидовые и неэвклидовые геёметрии, многомерные пространства, например.

Ответы>>376477 >>376480

18 Июл, 15:01 #23 #376477

>>376473
То есть то, что математики, по-хорошему, должны знать на первом семестре первого курса.

Ответы>>376479

18 Июл, 15:38 #24 #376479

>>376477
а также: комплексный анализ, теория групп, уравнения математической физики, основы теории интегральных уравнений и.т.д

Ответы>>376480

18 Июл, 15:52 #25 #376480

>>376473

>тапалогии

Point-set topology определяется в курсе анализа задолго до интеграла.

>матрицы

Линейная алгебра.

>эвклидовые и неэвклидовые геёметрии

Нет такого в 21-м веке. Евклидова геометрия называется аффинной, чтобы знал. Её обобщение - проективная геометрия. Математики изучают метрическую геометрию (и топологию).

>многомерные пространства,

Лол. То есть ты предполагал что исключительно для одномерного пространства вся математика строится?
>>376479

>комплексный анализ, теория групп

Опять же первый семестр. На старших курсах изучают теорию колец, в том числе некоммутативную. А действительный анализ вообще нахер не всрался никому.

>уравнения математической физики

Этим термином называют уравнения в частных производных, то есть опять же, ты предполагаешь что сначала нужно изучать функции одной переменной.

Ответы>>376481 >>376482 >>376497

18 Июл, 15:59 #26 #376481

>>376480

>ФСЕНИТАК

Давай тогда пиши что они знают по твоему.

18 Июл, 16:00 #27 #376482

>>376480
Опускаю вербитодетей в прямом эфире.

> Евклидова геометрия называется аффинной, чтобы знал.

Аффинная геометрия не то же самое, что евклидова, чтобы знал, не обсирайся на уровне терминологии хотя бы.

>Математики изучают метрическую геометрию

Метрическая геометрия - мем, зафорсенный Вербицким, никто её не изучает. Было пару экспериментальных спецкурсов от Иванова и тусовки и одна книжечка от них же и форс Вербицкого этой темы, на том всё и закончилось.

>На старших курсах изучают теорию колец, в том числе некоммутативную.

Ой не могу блять. Теорию колец на старших курсах. Дай угадаю, а на ещё более старших - теорию алгебр?

>А действительный анализ вообще нахер не всрался никому.

Ой ли? А почему в qual exams Гарварда на graduate наряду с тапалогиями и гамалогиями требуется знать вещественный анализ и теорию вероятностей?

Ответы>>376486

18 Июл, 16:06 #28 #376485

>>376437
дибилка блядь это вопрос фундаментальнейшей важности

18 Июл, 16:09 #29 #376486

>>376482

>не то же самое,

Строго говоря нет. На уровне "аффинная геометрия - геометрия линейки и циркуля, проективная - только линейки".

>Метрическая геометрия - мем

Вот тут я тебя обосрал.

>никто её не изучает

Можешь открыть например трехтомник по анализу Herbert Amann, внезапно начинается с метрической геометрии. Можешь хоть Шварца посмотреть, я не знаю что ты вообще читал, чтобы придти к такому выводу. Ничего, скорее всего.

>экспериментальных спецкурсов от Иванова

Спбгу

>форс Вербицкого этой темы

Вышка/нму
То есть то, что это изучается по меньшей мере в двух разных городах и школах в принципе, тебя не смущает

>и одна книжечка от них же

Это Бураги-то?

>Теорию колец на старших курсах

Ну это просто говорит о том, как мало ты знаешь о кольцах, если думаешь что там нечего изучать

>qual exams Гарварда на graduate

По АГ вопросы в духе "What is a scheme", "State Riemann-Roch". Могу представить какой там детский сад по твоей любимой комбинаторике. Могу еще и посмотреть, но лень.
http://math.harvard.edu/graduate/quals/topics/

Ответы>>376506 >>376675

18 Июл, 16:22 #30 #376488

>Можешь открыть например трехтомник по анализу Herbert Amann, внезапно начинается с метрической геометрии. Можешь хоть Шварца посмотреть, я не знаю что ты вообще читал, чтобы придти к такому выводу. Ничего, скорее всего.

Это не то, что называется метрической геометрией, это просто общая теория метрических пространств, это естественно учат даже в провинциальных ВУЗах на инженерных специальностях, илитка ты наша.
Ну и соответственно:

>Спбгу

>Вышка/нму

ни там, ни там метрическая геометрия не входит в обязательные курсы (в НМУ вообще нету обязательных курсов, конечно, я про стандартные курсы геометрия/алгебра/топология/анализ).

>Ну это просто говорит о том, как мало ты знаешь о кольцах, если думаешь что там нечего изучать

Знаю достаточно, чтобы утверждать, что никому не придёт в голову выделить время на "старших курсах" для теории колец под обязательные курсы, потому что тот кусок структурной теории, который нужен всем математикам рассказывают на первом курсе, а алгебраических тем, которые нужно рассказать на старших курсов итак очень много, и теория колец в них не войдёт.

>По АГ вопросы в духе "What is a scheme", "State Riemann-Roch". Могу представить какой там детский сад по твоей любимой комбинаторике. Могу еще и посмотреть, но лень.

Лол, нашёл самые простые (= которые можно нагуглить) вопросы из списка и скинул. А ну ответить на "What is the connection between H1 and line bundles?", алгебраический геометр мамкин.

Ответы>>376489 >>376675

18 Июл, 16:44 #31 #376489

>>376488

>это естественно учат даже в провинциальных ВУЗах

Нет, не учат. Я не знаю, правда, что в твоем понимании провинциальный вуз, ратгерс и глазго или саратовский государственный университет.

>не входит в обязательные курсы

В спбгу в обязательные курсы с недавнего времени даже категории входят. При чем не в элементарном виде как часть введения в АГ и не на третьем курсе, как это было в вышке например.

>в НМУ вообще нету обязательных курсов

Ну вообще-то есть, но ладно.

>которые можно нагуглить

Нагуглить можно что угодно. Или ты думаешь, что я не смогу нагуглить про первые гамалогии линейного расслоения? Определение схемы через пучки или формулировку римана-роха для кривых можно знать by heart не будучи серьезным математиком при этом. На самом деле, изучение алгебраической геометрии с этого и начинается. Сначала ты интуитивно понимаешь, что важно, а уже потом изучаешь это.

Ответы>>376493

18 Июл, 16:57 #32 #376493

>>376489

>Нет, не учат. Я не знаю, правда, что в твоем понимании провинциальный вуз, ратгерс и глазго или саратовский государственный университет.

В Донецком НУ на специальности "прикладная математика" определения метрических пространств дают и основные свойства учат. (Есть знакомые)

>В спбгу в обязательные курсы с недавнего времени даже категории входят.

Конкретно метрической геометрии в понимании Вербицкого:

Геодезические. *Теорема Хопфа-Ринова (локальная
компактность в полном метрическом пространстве равносильна
существованию геодезических). Внутренние метрики.

нету и там.

>Определение схемы через пучки или формулировку римана-роха для кривых можно знать by heart не будучи серьезным математиком при этом.

Уход от ответа уровня /б/. Ты бы ещё про "напоминание в платоновском смысле" вспомнил; факт в том, что связь первых гомологий пространства с линейными расслоениями над ними - это азы топологической К-теории, и то, что ты этого не знаешь как бы характеризует твою осведомлённость в АГ в целом. Зато выёбываться мастер.

Ответы>>376495 >>376496

18 Июл, 17:07 #33 #376495

>>376493

>Конкретно метрической геометрии в понимании Вербицкого

Я мало вижу различия между "общей теорией метрических пространств" и "метрической геометрией" в реальном курсе. Риманова геометрия тоже форс вербицкого?

>напоминание в платоновском смысле

Речь вообще не об этом. У нормального человека обучение математике происходит примерно так: "Мне попалась книга Фоменко-Фукса по гомотопической топологии, завершающаяся кратким эскизом про теорему Атиа-Зингера. Видимо ещё из каких-то книг я понял, что эту теорему хорошо бы понять."
То есть пока ты сам не поймешь интуитивно, что классы черна или когомологии пучков это важно, тебя в этом никто не сможет убедить в принципе.

>азы топологической К-теории

Топологическая к-теория занимается классификацией векторных расслоений, и это не совсем алгебраическая геометрия. Это что-то больше из книг адамса скорее. Гамалогии и спектралки - АТ, другие же области математики больше интересуются гамалогиями с приставкой ко. Есть еще алгебраическая к-теория, занимающаяся проективными модулями над кольцами, и это тоже не совсем алгебраическая геометрия.

Ответы>>376621

18 Июл, 17:16 #34 #376496

>>376493

>В Донецком НУ на специальности "прикладная математика"

Кстати, а какого образца у них там дипломы сейчас? Украинского? Российского? ДНРовского?

Ответы>>376503

18 Июл, 17:26 #35 #376497

>>376480

>изучают метрическую геометрию

Вай-вай, без метрики уже никуда?

18 Июл, 18:08 #36 #376503

>>376496
Обещают сделать российского, но пока ДНРовского, как я понял.

Ответы>>376509

51 Кб, 1280x720

18 Июл, 18:50 #37 #376506

>>376486

>На уровне "аффинная геометрия - геометрия линейки и циркуля, проективная - только линейки".

18 Июл, 19:05 #38 #376509

>>376503
Кто им это даст сделать, лол?

21 Кб, 1004x107

18 Июл, 22:58 #39 #376522

Ответы>>376524 >>376538 >>376553

18 Июл, 23:10 #40 #376524

>>376522
Я помню это упражнение. Его решение сравнительно замороченное, нужно хорошо разбираться в ординалах и индикаторных функциях.

Пусть у нас есть равенство, в которое входят множества x₁, x₂, ... , x_n. Объединение этих множеств обозначим как X, его мощность как ℵ. Зафиксируем биекцию φ: ℵ → X. Таким образом, все элементы множеств, участвующих в формуле, каноничным образом расположены в виде трансфинитной строки Φ длины ℵ. В этой строке на месте i, где i - ординал, стоит элемент φ(i).

Рассмотрим множество всех функций из ℵ в ℤ₂ - поле вычетов по модулю 2, состоящее из элементов 0 и 1. Как известно, такие функции называются характеристическими, или индикаторными. С помощью нашей зафиксированной функции φ множество индикаторных функций биективно соответствует множеству всех подмножеств X. В самом деле, если χ - характеристическая функция, то сопоставим ей множество {φ(x) | x∈ℵ и χ(x) = 1}. Если же M - подмножество X, то сопоставим ему функцию χ такую, что χ(x) = 1, если φ(x)∈M, и χ(x) = 0, если φ(x)∉M. Таким образом, о строке Φ можно думать как о трансфинитной строке длины ℵ из сплошных единиц, а всякому множеству x_i соответствует трансфинитная строка длины ℵ, в которой на части позиций стоят нули. То есть чтобы получить из множества X множество x_i, нужно часть позиций затереть нулями.

Два множества равны тогда и только тогда, когда их характеристические функции совпадают во всех точках. Если множество ординалов, в которых характеристические функции не равны, не пусто, то оно (как и вообще всякое непустое множество ординалов) имеет наименьший элемент, скажем, n.

Операциям ∪, ⋂ и \ над двумя множествами соответствуют известные поточечные операции над характеристическими функциями в поле ℤ₂. То есть если χ₁ и χ₂ - две характеристические функции, то объединению соответствует функция χ, во всех точках задаваемая как χ(x) = max(χ₁(x), χ₂(x)), пересечению соответствует функция χ(x) = min(χ₁(x), χ₂(x)), разности соответствует функция "χ(x) = 1, если χ₁(x) = 1 и χ₂(x) = 0, и χ(x) = 0 в противном случае".

Поскольку эти операции поточечные, на результат их применения к позиции номер i в строке Φ не влияет результат их применения ко всем остальным позициям.

Докажем теорему индукцией по количеству операций в формуле. Пусть в формуле имеется только одна операция. По условию теоремы, найдется контрпример к формуле. Это значит, что характеристические функции левой и правой части поточечно не совпадают. Пусть i - первый ординал, в котором они различаются. Рассмотрим трансфинитные битовые строки, соответствующие множествам нашего контрпримера. В них все позиции, кроме i-й, затрём нулями, а i-ый элемент не тронем. Тогда если в строке, соответствующей данному множеству из контрпримера, на i-м месте стоял нуль, то оно станет пустым множеством, иначе - одноэлементным множеством. Поскольку рассматриваемые операции - поточечные и применяются не более чем к паре множеств, контрпример не перестанет быть контрпримером. Таким образом, база индукции доказана. Совершенно аналогично доказывается шаг индукции. Поэтому теорема верна для формулы, содержащей любое конечное количество операций ∪, ⋂ и \.

18 Июл, 23:10 #40 #376524

Показать весь текст

Ответы>>376538

19 Июл, 01:03 #41 #376538

>>376522
>>376524
Пиздец ты ебан.
Достаточно найти всего лишь один набор множеств, где равенство обломалось, посмотреть, в каком элементе части различаются, и пересечь множества с этим элементом. Рез-т будет требуемым.

Пиздец сколько понаписал.

Ответы>>376540

19 Июл, 01:25 #42 #376540

>>376538
Во-первых, мне не очевидно.
Во-вторых, разбирать частные случаи, когда есть общее решение, - это так уродливо.

Ответы>>376543

19 Июл, 01:43 #43 #376543

>>376540
Не понял, в каком месте ты разбираешь сколько-нибудь более общую задачу?

Ответы>>376545

19 Июл, 01:55 #44 #376545

>>376543
Кроме ∪, ⋂ и \, есть и другие поточечные операции. Моё доказательство без изменений проходит для любой булевой функции от двух переменных. А тебе придётся долго ебаться с раскрытием скобок.

Ответы>>376550

19 Июл, 02:21 #45 #376550

>>376545
Лолчто
Моё док-во требует только знания факта, что пересечение с множеством можно выносить за скобки (дистрибутивность). Для всех операций, для которых это верно, это банальнейший факт.

19 Июл, 02:43 #46 #376553

>>376522
возьмем контрпример вида
F(A, B, C, ...) /= G(A, B, C, ...)
имеется некий элемент а, который содержится в левом множестве и не содержится в правом (или наоборот)
введем операцию Т - которая выбрасывает из множества все элементы кроме а
операции ∪, ⋂ и \ коммутируют с T
теперь мы применяем эту операцию к неравенству и вносим ее внутрь
F(T(A), T(B), T(C), ...) /= G(T(A), T(B), T(C), ...)
получаем контрпример с требуемыми свойствами

Ответы>>376680

19 Июл, 12:21 #47 #376580

Пусть T: V -> W - линейное отображение нормированных векторных пространств . Я доказал, что следующие утверждения экивалентны:
1) |T| < Inf
2) T равномерно непрерывно
3) T непрерывно
4) T непрерывно в 0.

Помогите доказать, что если V и W конечномерные, то T непрерывно, используя только этот факт. В учебниках какая-то смекалочка вместо нормального доказательства.

Ответы>>376581 >>376584

19 Июл, 12:22 #48 #376581

>>376580
Норма здесь |T| = sup{|Tv|/|v|, v != 0}, если че.

19 Июл, 13:40 #49 #376584

>>376580
Там нужно использовать факт компактности единичной сферы.

Ответы>>376585

19 Июл, 13:45 #50 #376585

>>376584
Я это и имел в виду под смекалочкой. По моим ощущениям, связь между компактностью единичной сферы и непрерывностью T очень косвенная.

19 Июл, 16:55 #51 #376608

Зачем нужно разбирать доказательства при чтении книг? Вот я вижу 2 причины:
1) В доказательстве может быть какой-то концептуальный пример применения штук, которые мы изучаем.
2) Часто доказательство запомнить проще чем утверждение. Иногда оно очевидное и даже запоминать ниче не надо (как большинство доказательств в point set topology, например).
Может быть на некрасивые доказательства забивать полностью, а для запоминания утверждений решать задачи? Так-то я задачи не люблю и почти никогда их не решаю, но, может быть, решать задачи эффективнее, чем пытаться прочувствовать хуевое доказательство, которое непонятно вообще как можно было придумать?

Ответы>>376669 >>376690

19 Июл, 18:55 #52 #376621

>>376495
Я вообще мимо проходил и в целом поддерживаю твою позицию, что физики математики не знаю, а гарвадские exams хуйня.
Но, блджадь, запомните уже, алгемщики херовы, что линейные расслоения это H^1 от пучка обратимых функций. А то без этого никуда. Сам же говоришь про классы Черна, которые, например, тот Вербяшка любит определять, используя этот факт.
А еще про теорию колец какую-то хуйню спизданул. Не видел такого курса никогда. Но, может, это моя неграмотность.

19 Июл, 21:38 #53 #376657

Почему русскосоветские учебники по мтану такое говно ебаное?
Открываю русский учебник, читаю про экспоненту
"Ну вишь, братишка, экспонента короче, ну функция предела бесконечного. Вот хочешь, я для тебя предел задам а ты её посчитаешь, хочешь, братишка?"
Открываю английский учебник
"Вот есть сто клеток у тебя. Каждую секунду они производят одну такую же клетку. За сто секунд количество клеток удвоится. Но это если не считать вклад в работу тех клеток которые уже появились на свет. Вот если считать этот вклад то и получается экспонента. Рассчитывается она по формуле бинома, из которой же следует её самоподобие при дифференцировании и обоснование для натурального логарифма"

Почему такой разрыв между учебьниками? В одном тянут тему на пять страниц и нихуя толком не объясняют а в другом за эти же пять страниц все разжжуют и в рот положат.

Ответы>>376658 >>376666 >>376682 >>376704 >>376723 >>376756 >>376766

19 Июл, 21:47 #54 #376658

>>376657
Есть разные определения и разные подходы, ищешь что тебе нравится, изучаешь. Английский матан - калькулус, он рассчитан именно на то, чтобы обучить народ брать производные, интегралы и прочую муть, наш калькулус, это как правило тяжеловесная фигота с кучей теорем и доказательств(через эпсилон формализм), традиция, хули.

Ответы>>376659 >>376766

19 Июл, 21:50 #55 #376659

>>376658
Тато, чому я постсовок...
Нахуй так жить тогда? Почему никто не напишет книжко чтко, годно, чтобы батя малаца сказал и руку пожал, быдло забоялось, тянучки потекли? Почему надо городить хуиту какую то настолько непонятную, что та же хуита на другом языке более понятна?

Ответы>>376661 >>376664 >>376766

19 Июл, 21:58 #56 #376661

>>376659

>Почему надо городить хуиту какую то настолько непонятную, что та же хуита на другом языке более понятна?

Ну, ты же понимаешь, что это тебе СЛОЖНА понять что такое экспонента через предел, другой народ справляется и ничего.

>Почему никто не напишет книжко чтко

четко в подъезде у пацанов, тут ты либо находишь нужную тебе литературу либо идешь нахуй, ты удовлетворил свою надобность в англоязычном сегменте, молодец.

Ответы>>376662

19 Июл, 22:00 #57 #376662

>>376661
Но ведь в нашей литературе не говорится почему экспонента самая быстрорастущая функция. Говорят это только как факт. Хотя это еще доказать и показать надо.

Ответы>>376663

19 Июл, 22:16 #58 #376663

>>376662

>Хотя это еще доказать и показать надо.

Упражнение.

Ответы>>376714

19 Июл, 22:19 #59 #376664

>>376659

>Почему никто не напишет книжко чтко

Для этого нужны три вещи.
1. Деньги.
2. Квалификация.
3. Спрос.

Деньги может выдать либо рыночек, либо государство. Но рынка математической литературы в России нет, даже Фихтенгольца уже не купить. А государство выдаёт деньги только в виде грантов, а грантов ограниченное количество и все они быстро расхватываются на более приоритетные вещи.

Квалифицированных математиков, способных потратить несколько лет своей жизни на учебник матана, тоже нет. Они либо занимаются более интересными вещами, либо уехали из России в более цивилизованные места.

Наконец, кто будет читать такой учебник? Вообще-то в России есть жесткие стандарты высшего образования, и любой вуз, кроме НИ, должен следовать этим стандартам, иначе он не получит лицензию на образовательную деятельность. А по законам России образовательная деятельность без лицензии - преступление. Поэтому вузы учат только по тем книгам, которые соответствуют стандарту на математика. А этот стандарт писал говноед Лупанов с мехмата. Таким образом, вузам не нужны учебники, которые не релевантны говноедству. Студентам же нужны только те учебники, которые будут полезны для учебы в вузе. Хорошие учебники нужны только тем студентам, которые учатся не ради диплома, а ради знаний. То есть спрос на хороший учебник матана исчерпывается буквально несколькими десятками людей на всю страну. Причем в местах скопления математиков, например на матфаке, такой учебник даже не нужен, обитающие там люди уже знают все нужное из каких-то своих собственных источников. Спрос на такой учебник может быть только в далеких от математики местах.

Ответы>>376668 >>376714

19 Июл, 23:17 #60 #376666

>>376657

>учебники по мтану такое говно ебаное

>читаю про экспоненту

Ты ошибся тредом.

Ответы>>376714

19 Июл, 23:32 #61 #376668

>>376664
Ну не может же все быть так плохо. Меня от твоего поста такая беспросвтеная тоска обуяла, что хоть в гроб не ложись. Ну мы ведь тоже хорошие люди, почему никому ничего не нужно-то нахуй?

Ответы>>376670

19 Июл, 23:56 #62 #376669

>>376608
Так доказательства, а точнее говоря идеи доказательств - это самая суть. Когда ты действительно разобрался в доказательстве, прочувствовал его, то можешь прилагать идеи заложенные в нем в других местах, а это именно то, что нужно для исследовательской деятельности.
Впрочем, если, например, понятно, что кусок какого-то доказательства - это безыдейный счет, то пропустить его весьма разумно.

20 Июл, 00:08 #63 #376670

>>376668
Я не знаю.

20 Июл, 01:03 #64 #376675

>>376488
>>376486
лол что такое теория колец? теория колец in коммутативная алгебра = аффинный алгем

Ответы>>376683

sage 20 Июл, 01:54 #65 #376680

>>376553
Естественно ни спасибо ни блядь пожалуйста. Чтоб я еще ебаным первокурсникам помогал домашку делать. Нахуй.

Ответы>>376737 >>376738

20 Июл, 02:05 #66 #376682

>>376657
Потому что в России принято людей мучить и учить соответствующе. Т.е. пиздить как можно сильнее, чтобы выжили сильнейшие (а слабые и середнячки при этом просто подохли). То же самое и в других областях же. Например, спорте или балете.
А разница между обучением физиков в СССР и США уже стала определенного рода мемом в этом плане.
В математике это приводит к тому, что отдельные гении есть (и те по большей части моментально съебывают), а науки нет.

Ответы>>376705 >>376766

25 Кб, 300x456

11 Кб, 200x284

20 Кб, 200x295

20 Июл, 02:09 #67 #376683

>>376675

Ответы>>376685

20 Июл, 02:20 #68 #376685

>>376683
Это называется функциональный анализ в первых двух случаях. А в третьем случае это называется результаты алгебраиста Туганбаева.

sage 20 Июл, 03:03 #69 #376690

>>376608

>Так-то я задачи не люблю и почти никогда их не решаю

Удваиваю. В частности потому что с вероятностью 100% авторы ввернут несколько задач которые невозможно решить в принципе на основе пройденного материала. Нужна смекалочка - как кажется авторам - на самом же деле огромное количество дополнительного материала, до которого читатель еще не дошел и никогда не дойдет если будет попадаться на каждую такую бомбу.

Ответы>>376707 >>376733

20 Июл, 07:23 #70 #376704

>>376657

>Почему русскосоветские учебники по мтану такое говно ебаное?

Чем тебя зорич не устроил?

Ответы>>376708 >>376714

20 Июл, 07:32 #71 #376705

>>376682
Хуйня беспруфная

20 Июл, 07:41 #72 #376707

>>376690
Например, особенно радует такими вещами Львовский, непринужденно вворачивая в задачи формулы Рамануджана.

7 Кб, 811x87

20 Июл, 07:42 #73 #376708

>>376704
Ты его читал? Он предел определяет пикрелейтед.

Ответы>>376711 >>376732

20 Июл, 08:11 #74 #376711

>>376708
Вполне валидное определение.

Ответы>>376712

20 Июл, 08:19 #75 #376712

>>376711
во-первых нет, потому что без дополнительных оговорок окрестность, которая стоит после квантора существования, не обязана быть той же самой окрестностью, которая стоит слева от значка подмножества.

Во-вторых, это не определение, а долбоебизм, мечта безумной стенографистки. Это даже не формальная конструкция (формативной последовательности не предъявлено), это именно что тупая, бессмысленная и беспощадная стенография.

Ответы>>376716

20 Июл, 08:25 #76 #376713

https://www.youtube.com/watch?v=r0pzGzoo8kY
Давно не было такого.

20 Июл, 08:49 #77 #376714

>>376663
Давай, придумай мне упражнение кот орое это показывает. Покажи что ты круче вербицкого.

>>376664
Тогда почему бы группе анонимусав не написать такой учебник? И назваться как бурбакисты какими то гайофоксистами.

>>376666
Я привел банальнейший пример. Или мне надо было в залупу гомологий лезть?

>>376704

>Пусть дано множество M и отношение порядка < на нём

Определи мне теперь это множество.

Ответы>>376717

20 Июл, 09:00 #78 #376716

>>376712

>окрестность, которая стоит после квантора существования, не обязана быть той же самой окрестностью, которая стоит слева от значка подмножества.

Понятно, с формальной записью через кванторы поциент не знаком.

>это не определение, а долбоебизм, мечта безумной стенографистки

...

>формативной последовательности

Что такое формативная последовательность?!

А главное покажи мне правильное на твой взгляд определение, и мы с радостью обсудим, как оно отсасывает у этого.

Ответы>>376718

20 Июл, 09:01 #79 #376717

>>376714

>Я привел банальнейший пример. Или мне надо было в залупу гомологий лезть?

Шапку треда почитай.

Ответы>>376724

20 Июл, 09:02 #80 #376718

>>376716

>Что такое формативная последовательность?!

И етот человек называет других поциентами.

Ответы>>376719

20 Июл, 09:11 #81 #376719

>>376718
Хотя бы поэтому ты и есть поциент, если ты не понял.

Ответы>>376720

20 Июл, 09:22 #82 #376720

>>376719
Символ U у Зорича обозначает какую-то функцию, U(x), где x - вектор параметров. Если Зорич для вектора параметров t может получить символ ∃U(t), то логика, которой он пользуется, сильно отличается от общечеловеческой. Ну или он вообще не пользуется логикой, а его "формализм" - всего лишь стенография.

Ответы>>376722 >>376723 >>376751

20 Июл, 09:25 #83 #376722

>>376720

>Символ U у Зорича обозначает какую-то функцию, U(x), где x - вектор параметров

Ты болен. Лечись!

Ответы>>376727

20 Июл, 09:32 #84 #376723

>>376720
>>376657
Вам сюда >>374531 (OP)
Не срите здесь, блджадт.

Ответы>>376724 >>376727

20 Июл, 09:35 #85 #376724

>>376723
>>376717
Поясняй давай почему нам туда а не сюда.

20 Июл, 09:46 #86 #376727

>>376723
Обсуждение Зорича вполне соответствует теме этого треда. В треде для начинающих логику не знают. Впрочем, конкретно с этим >>376722 я разговаривать больше не буду.

Ответы>>376736

20 Июл, 09:51 #87 #376728

Вы все больны. Лечитесь!

20 Июл, 10:14 #88 #376732

>>376708
Как же ты заебал.

Ответы>>376735

20 Июл, 10:16 #89 #376733

>>376690
И ты тоже заебал. Одни и те же темы гоняете по пол-года. Долбоёбы бля.

20 Июл, 10:30 #90 #376735

>>376732
Просто не люблю, когда стенографию выдают за формализм. Это убивает саму идею формального метода.

Ответы>>376745

20 Июл, 10:41 #91 #376736

>>376727
Поясняй давай почему не прав.

20 Июл, 10:42 #92 #376737

>>376680
До тебя уже два доказательства привели - то, которое ты написал, и более общее ТРАНСФИНИТНОЕ, в глаза-то не ебись.

20 Июл, 10:42 #93 #376738

>>376680
Спасибо. Пожалуйста.

20 Июл, 11:18 #94 #376745

>>376735
Мы уже поняли в предыдущих 10 тредах твоё важное мнение (которое, к тому же, ты прекращаешь отстаивать как только тебя тыкают лицом в тот факт, что это определение - не определение, а определение у Зорича другое). Можешь теперь нахуй пойти?

Ответы>>376746

20 Июл, 11:25 #95 #376746

>>376745
Это определение. Символ := означает определение.

Ответы>>376747

20 Июл, 11:27 #96 #376747

>>376746
Пошёл нахуй.

Ответы>>376748

58 Кб, 1432x191

94 Кб, 1422x393

20 Июл, 11:33 #97 #376748

>>376747
Послушай, добрый человек, ведь сам Зорич пишет, что это определение. Он даже специально подписал: "Определение".

Ответы>>376749

20 Июл, 11:37 #98 #376749

>>376748
Пошёл нахуй.

Ответы>>376750

20 Июл, 11:49 #99 #376750

>>376749
Аргументируй как-то. Я вот хоть картинки вырезаю.

20 Июл, 12:12 #100 #376751

>>376720
По-моему Ю от икс - это не функция, это просто такая (аргюабли не слишком удачная) запись, нет?

Ответы>>376753

20 Июл, 12:32 #101 #376753

>>376751
Нет, U - это функция от трёх аргументов. Пусть M - метрическое пространство, T - множество открытых в нём подмножеств, тогда U - это функция из 2^M×M×ℝ₀→T. Каждой тройке из подмножества пространства, точки пространства и положительного вещественного числа эта функция сопоставляет одно конкретное открытое множество.

Ответы>>376754

20 Июл, 12:40 #102 #376754

>>376753
Хотя нет, что я говорю. U - это функция всё-таки в 2^M. Функция сопоставляет тройке <E, x, d> не открытое множество, а пересечение открытого множества с E.

В любом случае ставить квантор существования перед символом U очень странно.

103 Кб, 746x919

77 Кб, 746x633

20 Июл, 12:47 #103 #376756

>>376657

> Почему русскосоветские учебники по мтану такое говно ебаное?

Англоязычные тоже. Просто матан говно.

> "Ну вишь, братишка, экспонента короче, ну функция предела бесконечного

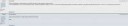
Неудачное определение. Пикрелейтед (Львовский) - самое хорошее.

Ответы>>376757 >>376767

20 Июл, 12:57 #104 #376757

>>376756
Двачую, братишечка. Под каждым словом подписался.

24 Кб, 1847x397

12 Кб, 707x179

20 Июл, 13:09 #105 #376758

К обсуждению выше.

20 Июл, 13:59 #106 #376766

>>376657
Calculus - это курс для даунов, он абсолютно бесполезен. Зачем инженеру уметь считать интегралы? Незачем. Ему надо уметь пользоваться соответствующим ПО. Зачем математику считать интегралы? Тоже незачем (кроме маленького процента людей, занимающихся довольно специфическими областями).

>>376658

> наш калькулус, это как правило тяжеловесная фигота с кучей теорем и доказательств

Это называется аксиоматический метод. Он используется во всех областях математики.

>>376659

> Почему надо городить хуиту какую то настолько непонятную, что та же хуита на другом языке более понятна?

Во-первых, я не вижу как язык может влиять на сложность восприятия математической литературы. Сложность заключается в том, что надо воспринять какие-то новые для себя концепции, а это никак не зависит от языка.
Во-вторых, это тебе непонятно, а кому-то норм. В пиндостане просто слишком много денег, людям можно вообще не работать, поэтому пиндостанские вузы могут себе позволить тратить время на студентов, которые заведомо непригодны к интеллектуальной деятельности, вот они и придумывают всякие калькулюсы.

>>376682

> Потому что в России принято людей мучить и учить соответствующе. Т.е. пиздить как можно сильнее, чтобы выжили сильнейшие (а слабые и середнячки при этом просто подохли).

Все правильно, так и надо. Слабым студентам от этого будет только лучше: они поймут, что надо сменить род деятельности, пойдут писать сайты на пхп и жизнь у них наладится. А представь, что такого слабого студента недостаточно пиздили и он выжил. Вот он закончил вуз - и че? К творчеству-то он неспособен, он умеет только конспектировать лекции, делать домашки и сосать хуй преподам. В итоге он в лучшем случае все равно пойдет писать сайты (при этом он какое-то время будет довольно несчастен от осознания проебанного времени), а в худшем станет преподавателем и пронесет свой даунизм в следующее поколение, будет создавать такую систему, в которой поощряются не хорошие студенты, а терпилы как он.

Ответы>>376768 >>376772

20 Июл, 14:12 #107 #376767

>>376756

>Англоязычные тоже. Просто матан говно.

>Пикрелейтед (Львовский)

Парашей повеяло

Ответы>>376773

20 Июл, 14:13 #108 #376768

>>376766
Да да, мы все прекрасно поняли что математика не нужна.

Ответы>>376773

20 Июл, 14:45 #109 #376772

>>376766
Калькулюс - это не про "считать интегралы", это про понимать, как оно все работает и почему.

Ответы>>376773

20 Июл, 15:04 #110 #376773

>>376768

> Да да, мы все прекрасно поняли что математика не нужна.

Как ты из моего поста пришел к такому выводу? Я не понимаю.

>>376772

> Калькулюс - это не про "считать интегралы", это про понимать, как оно все работает и почему.

Calculus - это такой курс без доказательств (у пиндосов самый популярный учебник - Stewart, Calculus: Early Transcendentals). Есть еще real analysis. Там не считают интегралы, там, например, дают определение интеграла, доказывают, что интегрируемые функции образуют векторное пространство над R, а интеграл - линейный функционал на нем, и много еще всяких хороших штук делают.

>>376767

> > Пикрелейтед (Львовский)

> Парашей повеяло

Ты Львовского не осилил что ли? Или в чем проблема?

Ответы>>376774 >>376789

20 Июл, 15:08 #111 #376774

>>376773
Докажи мне теперь число два, доказатель.

Ответы>>376775 >>376780

20 Июл, 15:09 #112 #376775

>>376774
У тебя каша в голове.

Ответы>>376777

20 Июл, 15:23 #113 #376777

>>376775
Гречневая или овсяная?

Ответы>>376779 >>376790

20 Июл, 15:26 #114 #376779

>>376777
Пшённая.

Ответы>>376790

20 Июл, 15:27 #115 #376780

>>376774
1+1=2

20 Июл, 16:47 #116 #376786

А как доказать, что K[X] - кольцо? Как, например, доказать, что умножение многочленов ассоциативно?

Ответы>>376787

20 Июл, 16:48 #117 #376787

>>376786
Открытая проблема.
Есть же тред для начинашек, ну

Ответы>>376788

20 Июл, 17:01 #118 #376788

>>376787
Ну я имел в виду как красиво и концептуально доказать

20 Июл, 17:05 #119 #376789

>>376773
Ну вот на курсее есть курс калькулюса от пенна. Глянь его, пожалуйста, выскажи свое мнение.

Ответы>>376792 >>376797

20 Июл, 17:05 #120 #376790

>>376779
>>376777
Горшочек не вари

Ответы>>376812

20 Июл, 17:08 #121 #376792

>>376789

>думать что кто то напишет свою личную математику, без разрывов второго рода и преобразований

Советую навернуть рыбникова.

Ответы>>376794

20 Июл, 17:09 #122 #376794

>>376792
Чего блядь?

Ответы>>376795

20 Июл, 17:10 #123 #376795

>>376794
Зачем тебе мнение того анона о какой то книжке по матану?

20 Июл, 17:23 #124 #376797

>>376789
Там регаться надо. Мне лень. Кроме того, я не обладаю нужной компетенцией, чтобы сравнивать какие-то курсы. Я просто говорил о том, что калькулюсом называется что-то типа нашего матана, но без доказательств, и что математика без доказательств никому не нужна (кроме студентов, которые хотят сдать задачи и чтоб от них отъебались).

Ответы>>376813 >>376821

20 Июл, 18:18 #125 #376812

>>376790
Ладно, варить не буду. Лушче картошки пожарю, тебе водовфки налить?

20 Июл, 18:18 #126 #376813

>>376797

>математика без доказательств никому не нужна

Еще раз, докажи мне число два.
Число один бурбаки уже доказали.

20 Июл, 18:55 #127 #376821

>>376797
Математика "без доказательств" нужна инженерам и физикам - для которых, собственно, калькулюс и предназначен.

Ответы>>376822

20 Июл, 18:58 #128 #376822

>>376821
И сейчас ты мне такой говоришь, в каком году последний раз инженер сидел и вручную считал интеграл. Только не говори, что для того, чтобы понять интеграл, нужно его много раз вычислить по формуле Ньютона-Лейбница.

Ответы>>376823

20 Июл, 19:06 #129 #376823

>>376822
Слушай, ты настойчиво не хочешь читать то, что тебе пишут. Мне уже неинтересно, это просто глупо. Хлчешь спорить с голосами в голове - спорь сам. И почитай что-нибудь популярное про теорию обучения - ну, с нейропсихостороны.

Ответы>>376825 >>376827

20 Июл, 19:15 #130 #376825

>>376823
Ты утверждаешь, что в курсе калькулюса что-то объясняют? Я даже не представляю, что там без доказательств можно объяснять. Что интеграл - это площадь под графиком? Так это даже пятикласснику можно объяснить. Кратные интегралы можно за 5 минут объяснить любому школьнику, который по физике прошел плотность, массу и объем. Если, конечно, не заставлять их считать эти интегралы, со всякими заменами переменных, интегрированием по частям и прочей ебалой. Но блять, что в калькулусе можно 3 семестра рассказывать 18летним лбам, если там даже доказательств нет? Вангую, что в курсе калькулуса занимаются пикрелейтедом

Ответы>>376829

20 Июл, 19:26 #131 #376827

>>376823

> теорию обучения

> с нейропсихостороны.

Ты вообще ебан что ли? Ты бы мне еще посоветовал педагогический вуз закончить.

20 Июл, 19:28 #132 #376828

Ясно.

20 Июл, 19:39 #133 #376829

>>376825

>РЯЯЯЯ, ВСЬО ИЗААБРИЛИ МАТИМАТИКИ, ФИЗЕКИ НИНУЖНЫ

20 Июл, 19:49 #134 #376830

Поцыки, а объясните-ка популярно за ети ваши гамалогии/когомологии. Что это такое, как их щитать и зачем оне нужны.

Ответы>>376831 >>376835 >>376842

20 Июл, 19:51 #135 #376831

>>376830
Чтобы выёбывать перед второкультурщиками.

Ответы>>376832 >>376833

20 Июл, 19:54 #136 #376832

>>376831
выёбыватьСЯ
Блядь, на клаве кнопки плохо работают.

20 Июл, 19:56 #137 #376833

>>376831
Это типа как хуесосить тиаретика-множественных дидов категориями и топосами?

Ответы>>376834

20 Июл, 19:58 #138 #376834

>>376833
Да. И ещё выёбываться на дваче, без этого никуда.

20 Июл, 20:03 #139 #376835

>>376830
Почти все математические объекты - гамалогии. Кроме некоторых исключительных случаев, которые - когамалогии и (совсем редко) тапалогии, они тоже очень важны.

Ответы>>376836

20 Июл, 20:05 #140 #376836

>>376835
Гамалогии приминяются в теории чисел?

Ответы>>376839

20 Июл, 20:34 #141 #376839

>>376836
Да, разнообразные теории чисел - это отдельные гамалогии.

20 Июл, 20:51 #142 #376842

>>376830
Прочитай в статьи на вики же, там написано очень хорошо. Кратко - это алгебраические инварианты топологических объектов с которыми, в большинстве случаев, гораздо легче работать, чем с изначальными топ. объектами.

Ответы>>376848

20 Июл, 21:24 #143 #376848

>>376842
Я почитал в общих чертах. Ну я так понимаю, там каротьш топ.пространству сопоставляется группа. Причем одному объекту сопоставляется аж пачка групп - гамалогии разных размерностей. Говорят наивное толкование гамалогий - это число дырок n-й размерности. Правда я не ебу, как формализм цепей и границ совмещается с дырками, стягиваемостью циклов и всей этой поебенью. В общем, на самом деле ничего толком непонятно, как в частности щитать эти гамалогии. А примеры использования - ну хоть один? Котегории связывают собственно топ.прост-ва с группами, H_n - группа гамалогий n-й размерности - это попутно ещё и функтор из Top в Ab, так? А что с неабелевыми группами? Ещё котегории связывают гамалогии и когамалогии, так?

Ответы>>376854 >>376865 >>377113 >>377116

20 Июл, 21:31 #144 #376854

>>376848

>В общем, на самом деле ничего толком непонятно, как в частности щитать эти гамалогии.

Это ведь уже технический уровень, а не мистический, для этого нужно последовательно структурную теорию учить, а не руками размахивать.

>А примеры использования - ну хоть один?

Доказать, что R^n и R^m гомеоморфны титтк n=m.

>Котегории связывают собственно топ.прост-ва с группами, Hn - группа гамалогий n-й размерности - это попутно ещё и функтор из Top в Ab, так? А что с неабелевыми группами?

По сути да.

Ответы>>376860

20 Июл, 21:36 #145 #376860

>>376854

> Доказать, что R^n и R^m гомеоморфны титтк n=m.

Точно? По-моему тут тапалогии вообще вроде не нужны, достаточно доказать изоморфизм пространств и на всё про всё хватит линейкиезо всяких тапалогий.

А как эту теорию учить вообще? По каким соусам там и все дела?

59 Кб, 807x515

20 Июл, 21:45 #146 #376865

>>376848

>каротьш

Ответы>>376872

20 Июл, 21:47 #147 #376867

>Точно? По-моему тут тапалогии вообще вроде не нужны, достаточно доказать изоморфизм пространств и на всё про всё хватит линейкиезо всяких тапалогий.

Да. Попробуй, не получится.

>А как эту теорию учить вообще? По каким соусам там и все дела?

Любой курс по АТ.

Ответы>>376872

20 Июл, 21:58 #148 #376872

>>376865
Ну чиво ты, нормально же общялись, ну))

>>376867
Курс курсу рознь. Вон выше да и вообще часто и много где спорят о Зорич вс Stewart's calculus, Ромич предостерегал от Хэтчера и ычё такое.

Ответы>>376877

20 Июл, 22:00 #149 #376875

> и всё такое

Чет кнопки путаются в потьмах.

20 Июл, 22:02 #150 #376877

>>376872
Курс Вилдберга на ютубе + Хэтчера.

Ответы>>376880 >>376883

20 Июл, 22:12 #151 #376880

>>376877
Последовательно или параллельно? Какие пререквизиты нужны из СТ?

Ответы>>376881

20 Июл, 22:13 #152 #376881

>>376880
Никаких, грамотность первого курса.

Ответы>>376882

20 Июл, 22:18 #153 #376882

>>376881
Cпасибо. Посмотрим, что из этого получится.

20 Июл, 22:19 #154 #376883

>>376877

> Курс Вилдберга на ютубе

Это который в вещественные числа не верит?

Ответы>>376884 >>376885 >>376889

20 Июл, 22:20 #155 #376884

>>376883
Да.

20 Июл, 22:20 #156 #376885

>>376883
лолшто?

Ответы>>376889

20 Июл, 23:12 #157 #376889

>>376883
Это который Вайлдбергер?
>>376885
Рациональная тригонометрия

Ответы>>376894

20 Июл, 23:18 #158 #376892

поясните, пожалуйста, ньюфагу: есть какое-нибудь общее название для отображений X^n -> X где n - любая декартова степень?

кажется, где-то видел такое, но не могу вспомнить - в русской и английской википедии сходу не нашёл

Ответы>>376893

20 Июл, 23:20 #159 #376893

>>376892
n-арная алгебраическая операция на X.

Ответы>>376897

20 Июл, 23:22 #160 #376894

>>376889
Чему равна длина гипотенузы треугольника с катетами длины 1?

Ответы>>376899 >>376900

20 Июл, 23:22 #161 #376897

>>376893
хуясе, оперативненько
а я копался в разделах про функции

спасибо

Ответы>>376898

20 Июл, 23:24 #162 #376898

>>376897
Да я просто хикка без друзей, который самореализовывается за счёт ответов на вопросы по энтрилевельной математике. :3

Ответы>>376988

20 Июл, 23:24 #163 #376899

>>376894
Современная наука не в состоянии ответить на этот вопрос

20 Июл, 23:30 #164 #376900

>>376894
британские учёные целый видос специально для тебя запилили https://youtu.be/5sKah3pJnHI

Ответы>>376901 >>376931

20 Июл, 23:41 #165 #376901

>>376900
Прикольно, я не знал про бумагу.

20 Июл, 23:57 #166 #376902

А я тем временем напоминаю, что вещественные числа не нужны ни одной прикладной дисциплине.

Ответы>>376903 >>376904

20 Июл, 23:59 #167 #376903

>>376902
Нужны во всех прикладных дисциплинах.

Ответы>>376905

21 Июл, 00:04 #168 #376904

>>376902
Как меня учил один анон здесь, прежде чем ответить на вопрос о нужности/важности, нужно зафиксировать языковую игру.

Ответы>>376905 >>376934

21 Июл, 00:07 #169 #376905

>>376903
Это ложь.

>>376904
Давай.

Ответы>>376907

21 Июл, 00:14 #170 #376907

>>376905
Ну ты и фиксируй. Ты же утверждаешь, что не нужны. Я вот ничего не могу утверждать про прикладные дисциплины, я ими не занимаюсь.

Ответы>>376908

21 Июл, 00:17 #171 #376908

>>376907
Хорошо.

А я тем временем напоминаю, что представление о бесконечном количестве натуральных чисел противоречиво.

Ответы>>376910

21 Июл, 00:22 #172 #376909

Хочу сформулировать непрерывность числовой прямой как факт того, что каждая ее точка лежит в достаточно малой окрестности хотя бы одной другой ее точки. Какие подводные камни?

Ответы>>376913

21 Июл, 00:23 #173 #376910

>>376908
Подробней?

Ответы>>376916

21 Июл, 00:28 #174 #376913

>>376909
На нормальном языке это называется "отсутствие изолированных точек", а не "непрерывность".

Ответы>>376914

21 Июл, 00:30 #175 #376914

>>376913
В чем разница этих понятий?

Ответы>>376915

21 Июл, 00:32 #176 #376915

>>376914
Непрерывными могут быть отображения, а то свойство пространств, которое ты хочешь сформулировать, называется полнотой, интуитивно - это "отсутсвие дырок". Разница в том, что рацилнальные числа не содержат изолированных точек, но "дырки" в них присутствуют, поэтому это не полное пространство.

Ответы>>376917

21 Июл, 00:35 #177 #376916

>>376910
Множества натуральных чисел не существует.

Ответы>>376930

21 Июл, 00:39 #178 #376917

>>376915
Так почему Дедекинд так странно формулирует полноту вещественных чисел? Чем мое определение хуже?

Ответы>>376919

21 Июл, 00:44 #179 #376919

>>376917
Тем, что по твоему определению рациональные числа тоже "полные", а они не.

Ответы>>376920

21 Июл, 00:50 #180 #376920

>>376919
Тогда почему у Дедекинда все ок? Чем его определение через минимальный и максимальный элементы классов лучше?

Ответы>>376921

21 Июл, 00:55 #181 #376921

>>376920
Оно эквивалентно теореме о промежуточном значении, а это ровно то, как мы "чувствуем" вещественные числа - как нечто такое, что мы можем нарисовать не отрывая руки.

Ответы>>376922

21 Июл, 00:58 #182 #376922

>>376921
Чет нихрена не понятно, если честно.

Ответы>>376923

21 Июл, 01:01 #183 #376923

>>376922
Тогда пока забей на этот вопрос и просто считай, что оно лучше, потому что некоторые умные люди решили, руководствуясь своей интуицией, что оно лучше. Когда начнешь чуть глубже понимать анализ, то появится понимание того, откуда у этой интуиции растут ноги.

Ответы>>376924

21 Июл, 01:04 #184 #376924

>>376923
Так подожди. Разве строгого доказательства этого не существует? Не хочу полагаться на интуицию. Я у мамки бурбакист.

Ответы>>376925 >>376970

21 Июл, 01:06 #185 #376925

>>376924
Строгое доказательство бывает у строгих утверждений. А вопрос "почему определение Х лучше определения У" нестрогий и неутверждение.

Ответы>>376926

21 Июл, 01:16 #186 #376926

>>376925
Но "я так сказал" - тоже не ответ.

Ответы>>376927

21 Июл, 01:19 #187 #376927

>>376926
Проблема в том, что ты думаешь, что понять почему то или иное определение можно прочитав пост на дваче длиною в пару абзацев. Ан нет, это можно понять, повъёбывав пару месяцев те разделы математики, где это определение "работает" и увидев тем самым, какие задачи с его помощью можно формулировать и решать и какой язык с его помощью можно строить.

Ответы>>376929

21 Июл, 01:20 #188 #376928

>что понять почему то или иное определение

что понять, почему то или иное определение именно такое, какое есть

21 Июл, 01:29 #189 #376929

>>376927
Но раньше посты на дваче мне помогали.

21 Июл, 01:29 #190 #376930

>>376916
Что значит "не существует"? Чему противоречит его существование?

21 Июл, 01:38 #191 #376931

>>376900
Бесит это чмо. Хочется ему в еблет прописать все время.

Ответы>>376933

21 Июл, 01:40 #192 #376933

>>376931
сука блядь он бы еще в сортире снимал и говном по полу рисовал

21 Июл, 01:53 #193 #376934

>>376904

>языковую игру

Специально освежил в памяти статью:

>Пародист Евгений Венский, пародируя Андрея Белого, использует фонетические средства — повторение одного звука:

>Тоща, как мощи ты. Тоща, кащей те во щи! Как теща, тощи мощи. Ты тщетность красоты.

>Комическое впечатление производит шутливо-надрывное обращение А. Чехова в письме к брату Александру: «Братт!» Любопытны также шутливые подписи, например подпись одного из Полторацких, совмещающая буквы и цифры: 1,5цкий, или подпись переводчика Федора Федоровича Фидлера — Ф. Ф. Ф. либо: Ф3 (эф в кубе).

Умоляю объясните по-человеческий что это за хуйня такая и нахуя она может пригодиться математику?

Ответы>>376943

21 Июл, 04:10 #194 #376943

>>376934
https://ru.wikipedia.org/wiki/Философские_исследования

>Основное понятие «Философских исследований» — языковая игра: язык представляется совокупностью языковых игр. Ключевые тезисы: значение слова есть его употребление в рамках языковой игры, а правила такой игры есть практика. Главный вывод: философские проблемы — следствие неправильного словоупотребления.

21 Июл, 13:07 #195 #376970

>>376924

> Разве строгого доказательства этого не существует? Не хочу полагаться на интуицию. Я у мамки бурбакист.

Ты сейчас говоришь про работу в формальной системе. В формальной системе ты можешь только выполнять манипуляции со строками по определенным правилам. Вопрос "какое определение лучше" не вписывается в формальную систему, это уже некий метауровень, на котором математики используют интуицию и здравый смысл. На этом уровне обсуждения такие же как и в повседневной жизни, никаких доказательств там быть не может, по крайней мере, в том смысле, который мы вкладываем в формальные доказательства.

Ответы>>376972

21 Июл, 13:20 #196 #376972

>>376970
Ну так вот, выбор определения обусловлен субъективными соображениями удобства. Как уже писал анон выше, не поработав с определением какое-то время, ты не можешь понять, насколько оно удобно. Подход должен быть такой: опытные люди много всего пробовали и со временем выявили самое удобное определение.

102 Кб, 604x453

21 Июл, 14:32 #197 #376988

>>376898
А бывают хикки с друзьями? inb4: Здесь все мои друзья.
Учитывая специфику треда, жду ответ в виде математического доказательства. :3

Ответы>>376990

21 Июл, 14:45 #198 #376990

>>376988
Определим хикку h как измеримое подмножество некоторого пространства M такое, что оно инвариантно относительно действующей на пространстве группы трансляций (хикка домосед). Потребуем, чтобы пространство было топологическим, и будем говорить, что если в некоторой окрестности множества h содержится измеримое множество t, отделимое от h, то t является другом h относительно этой окрестности. Очевидно, что существуют примеры хикк, у которых есть друзья относительно всего пространства.

Ответы>>376992

21 Июл, 15:15 #199 #376992

>>376990

>оно инвариантно относительно действующей на пространстве группы трансляций

Что-то слишком суровое условие.

Ответы>>376994

21 Июл, 15:18 #200 #376994

>>376992
А ты думал, хиккой быть легко?

Ответы>>376996

21 Июл, 15:20 #201 #376996

>>376994
В смысле, что для группы R^n ты получаешь все пространство на орбите. То есть, все друзья хикки тривиальны.

Ответы>>377002 >>377099

21 Июл, 15:28 #202 #377002

>>376996
Щито поделать.

21 Июл, 20:11 #203 #377068

Почему в физике не используется теория множеств?

Ответы>>377069 >>377082

21 Июл, 20:14 #204 #377069

>>377068
А зачем она там?

Ответы>>377075

21 Июл, 20:41 #205 #377075

>>377069
Знал бы не стал страшивать, почему не используется.

21 Июл, 21:36 #206 #377082

>>377068
В сявязи с её поразительной неэффективностью

21 Июл, 22:27 #207 #377099

>>376996

>все друзья хикки тривиальны.

Это же и есть истина, объясняющая столь многое о хикках.

21 Июл, 23:03 #208 #377113

>>376848

>Правда я не ебу, как формализм цепей и границ совмещается с дырками, стягиваемостью циклов и всей этой поебенью.

Это очень понятно как раз.
n-тая гомология = векторное пространство на n-мерных дырках. n-мерные дырки -- это n-мерные симплексы (=шарики) на пространстве с точностью до гомотопии.

почему бля это верно? вообще шарики-дырки это ровно то пространство, что уходит в 0 граничным оператором, так он специально сделан. дальше понятно что прибавление образа граничного оператора переводит вектора в гомологичные, это потому что он сдвигает n-мерные объекты вдоль n+1-мерных. и наоборот. если два хуйни на пространстве гомотопичны, их можно соединить образами сфер размерности повыше. так что всё чики-пуки, h(this)=ker(this b)/im(+1 b) это ровно векторное пространство шариков-дырок этой размерности, с точностью до гомотопии.

21 Июл, 23:08 #209 #377116

>>376848

>Правда я не ебу, как формализм цепей и границ совмещается с дырками, стягиваемостью циклов и всей этой поебенью.

Короче я чё-та много накатал.

Просто гомотопичные n-мерные объекты в X <=> объекты которые можно соединить n+1-мерным объектом в X <=> объекты которые переводятся друг в друг прибавлением граничного оператора из размерности +1.

дырки <=> то, что уходит в 0 граничным оператором.

Вот всё что я там писал так долго.

Поэтому гамалогии это векторное пространство дырок с точностью до гомотопии. охуенно жи.

Ответы>>377121

22 Июл, 00:37 #210 #377121

>>377116
бля я проебался с векторным пространством. ну то есть векторные тоже можно, но осмысленнее просто абелевы свободные группы.

22 Июл, 10:02 #211 #377159

Я вот не понимаю, почему везде говорят о теориях гомологий и когомологий как о различных теориях? Разве цепной комплекс не отличается от коцепного просто перенумерованием и пусканием стрелок в другую сторону?

Ответы>>377162

22 Июл, 10:38 #212 #377162

>>377159
Ну, строго говоря цепной комплекс и граничные операторы там не те же, а дуальные.
Cn = Hom(Cn, Z)
dn_-1 = Hom(Cn_-1, Z) --d*--> Hom(Cn, Z)

Про остальное пусть ПЕРВОКУЛЬТУРЩИК-петух расскажет.

22 Июл, 10:50 #213 #377165

А кто-то едет в Ярославль?

Ответы>>377170 >>377178

22 Июл, 11:18 #214 #377170

>>377165
Я в прошлом году был. жди что никто НИХУЯ не будет понимать.

Ответы>>377173

22 Июл, 11:20 #215 #377173

>>377170
Я нихуя не буду понимать в первую очередь. 3:

43 Кб, 366x493

22 Июл, 11:41 #216 #377178

>>377165

> тчк не взяли

22 Июл, 17:14 #217 #377268

Поясните, зачем в Винберге такая длинная глава про многочлены? Я думал многочлены изучают в контексте алгебраической геометрии (я до нее еще не дошел) или чего-то такого.

Ответы>>377282 >>377283

22 Июл, 17:27 #218 #377282

>>377268
Действительно, нахуй полиномиальные представления функций.

22 Июл, 17:32 #219 #377283

>>377268
Алгебраическую геометрию, в идеале, нужно изучать имея крепкое знание коммутативной алгебры. Азы коммутативной алгебры - это "коммутативная алгебра над полями" или "теория Галуа", у которой основные объекты изучения - это фактор кольца многочлена по чему-нибудь. Чтобы уметь работать с такими объектами, желательно пройти курс общей алгебры и хорошо понимать, что кольцо многочленов над полем евклидово и КГИ и всё такое.

Ответы>>377311

22 Июл, 19:37 #220 #377311

>>377283
Ясно, спасибо.

> кольцо многочленов над полем евклидово и КГИ и всё такое.

Это я знаю.

Ответы>>377317

22 Июл, 19:43 #221 #377317

>>377311

>Это я знаю.

Тогда не читай Винберга, а читай книжки посерьзнее. Винберг для начинашек же.

Ответы>>377331

22 Июл, 20:56 #222 #377331

>>377317
Ну хз, я много нового из него узнаю, хоть он и вялотекущий какой-то для меня. Просто стараюсь по диагонали читать, потому что там как бы вширь а не вглубь.

23 Июл, 23:18 #223 #377530

Поцыки, смотрите какая беда. Вот нулевые и вторые гамалогии S² H_{0, 2}(S²) = ℤ. 2-сфера - это комплекс, склеенный из 2 клеток - одной точки и прилепленной к ней 2-мерной мембраны, неформально говоря. Так? А что значит равенство ℤ? Почему, скажем, не (ℚ, +) или (ℝ, +), а вот именно ℤ?

Ответы>>377604

24 Июл, 13:35 #224 #377604

>>377530
Циклическая группа с одной образующей.
k-мерные гомологии = k-мерные дырки (не стягиваемые k-мерные сферы) с точностью до гомотопии.

В случае 2-сферы это просто "обмотки" её обычной сферой. Не бывает нецелых обмоток.

Ответы>>377627

24 Июл, 15:56 #225 #377627

>>377604

>не стягиваемые k-мерные сферы

Только на самом деле нет. k-мерные дырки это не сферы.

Ответы>>377629

24 Июл, 16:09 #226 #377629

>>377627
Сферы, которые не ограничивают шара.

Ответы>>377631 >>377635

24 Июл, 16:21 #227 #377631

>>377629
Не, скорее k-мерные замкнутые многообразия, которые при этом не границы k+1-мерного многоорбазия.

Например, у тора вторые гомологии Z, но вторая гомотопическая группа тривиальна.

24 Июл, 16:45 #228 #377635

>>377629
А 0-вые гомологии это компоненты линейной связности, как раз потому что 0-мерные многоообразия = точки, а любые две точки, соединённые отрезком (1-мерным многообразием), можно перевести в одну точку, т.к. граница отрезка = разность точек на концах.

16 Кб, 761x82

24 Июл, 16:52 #229 #377638

Как следует понимать, что отношение не транзитивно? Как "транзитивность необязательно выполняется" или "транзитивность никогда не выполняется"?

Ответы>>377642 >>377697 >>377743

24 Июл, 16:59 #230 #377642

>>377638
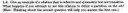
Существуют такие a,b,c, что пары (a,b) и (b,c) находятся в отношении, но пара (a,c) - нет.

24 Июл, 18:08 #231 #377663

Есть тут те, кто реально учится/учился в НМУ? Расскажите, в каком вузе учитесь, с какого курса начали, сложно ли совмещать, помогает ли как то при изучении официальной универской(не нмушной) программы?

24 Июл, 19:37 #232 #377690

Как у математиков с индексом Хирша? Дрочат на него? Какой среди математиков считается нормальным в 30, 40, 50, 60, 70 лет? Или всем плевать?

Ответы>>377694

24 Июл, 19:41 #233 #377694

>>377690
На хирши дрочат все.

Ответы>>377696

24 Июл, 19:50 #234 #377696

>>377694
А что насчёт конкретных цифр? В 50 иметь индекс равный 20 нормально или так себе? Или, к примеру, в 35 — равный 10? Можно ли по этим цифрам с некоторой погрешностью отличить труматематика от не тру?

Ответы>>377852

24 Июл, 19:53 #235 #377697

>>377638
Алуффи что ли?

Ответы>>377733

24 Июл, 20:39 #236 #377716

Анон, какой вообще активной деятельностью ты занимаешься в математике? Вот я раньше задачи решал, но потом осознал, что это хуйня. Потом доказывал теоремы сам, не смотря в учебник. Сейчас понял, что и это хуйня и тоже особо ниче не дает. Сейчас просто читаю и вникаю, но просто читать - такое себе удовольствие.

Ответы>>377724 >>377742 >>377775 >>378077

24 Июл, 21:44 #237 #377724

>>377716
Пытаюсь придумать формализм для одной оккультной системы и доказать две теоремы о ней.

Ответы>>377726

24 Июл, 21:52 #238 #377726

>>377724
Проиграл. Трави прохладную.

24 Июл, 22:28 #239 #377733

>>377697
Да. Что можешь сказать о книге? Мне нравится, задач хоть и немного, но для их решения надо понимание всего параграфа.

Ответы>>377744

24 Июл, 23:17 #240 #377742

>>377716
Веду разработки в академии, руковожу, сам разрабатываю целую новоую область.

Ответы>>377752

24 Июл, 23:17 #241 #377743

>>377638
необязательно

никогда бы называлось антитранзитивностью

24 Июл, 23:18 #242 #377744

>>377733
Хз, я пока только 1 главу про категории прочитал. Если хочешь, можем вместе разбираться.

25 Июл, 00:30 #243 #377752

>>377742
Мамка не ругает?

Ответы>>377784

25 Июл, 04:47 #244 #377775

>>377716
Есть мнение что чтение книг тоже лютая хуита. Наебка какая-то. И когда кто-то дает тебе охуительный список - скорее всего сам он прочитал из этого списка ну максимум по главе из половины книг, не более.

Ответы>>377788

25 Июл, 08:55 #245 #377784

Бабах >>377752

25 Июл, 09:49 #246 #377788

>>377775
А что тогда не хуета, как математику то саму изучать, если даже книги хуита?

Ответы>>377800 >>377863

25 Июл, 11:40 #247 #377800

>>377788
По-хорошему, надо получить базу, т. е. образование, чтоб иметь представление. А потом изучать нацеленно. Нк и задача нужна - для чего ты это делаешь. иначе трата времени. Всё забывается со временем. Это игривое зучивание красивых терминов, вроде гомологий и алг. многообразий - лишь выпендрёж. А задача такая: либо ты этим себе заработаешь денег (например, экзотический фрилансом), либо статус - а это публикации. Не зарабатываешь, не публикуешься -- стало быть, позёр с поверхностными знаниями.

Ответы>>377811 >>377907

25 Июл, 11:48 #248 #377801

>>376017 (OP)
Аноны, поясните по легкому за интерполяцию кубическим сплайном, пожалуйста, как оно происходит?

Ответы>>377802 >>377803 >>377845

6 Кб, 292x154

25 Июл, 11:50 #249 #377802

>>377801
На основе вот этих вот двух формул.

Ответы>>377803 >>377845

25 Июл, 12:29 #250 #377803

>>377802
>>377801
Шок, двачи не могут в это, блядь.

Ответы>>377845

25 Июл, 13:00 #251 #377811

>>377800

> Нк и задача нужна - для чего ты это делаешь. иначе трата времени.

Интересно потому что. Че тебе еще надо?

25 Июл, 14:59 #252 #377845

>>377801
>>377802
>>377803
Это не математика.

Ответы>>377850

25 Июл, 15:06 #253 #377850

>>377845
С каких это пор интерполяция перестала быть математикой? Или сплайны?

Ответы>>377855

25 Июл, 15:08 #254 #377852

>>377696
Бамп. Что насчёт Хирша?

25 Июл, 15:11 #255 #377855

>>377850
С тех пор, как они стали жалким приложением математики. Т.е. всегда.

Ответы>>377857

25 Июл, 15:14 #256 #377857

>>377855
И математики не умеют мат.стат?

25 Июл, 15:37 #257 #377863

>>377788
Ну есть такое подозрение, что сам ты нихуя не наизучаешь. Математика передается от учителя ученику при прямом общении. А так твой максимум будет - уровня дяди Вани, который в пятьдесят решает школьные задачки из Кванта. Если тебя это устраивает, то ОК.

Ответы>>377886 >>377888 >>377905

25 Июл, 17:17 #258 #377886

>>377863

>в пятьдесят решает школьные задачки из Кванта

как что-то плохое

25 Июл, 17:20 #259 #377888

>>377863
Если бы не устраивало я бы пошёл на математический факультет учиться в свои 30

25 Июл, 19:13 #260 #377905

>>377863

>Математика передается от учителя ученику при прямом общении.

Подожди. Ведь через учебник тоже идёт общение. Хороший учебник, как мне кажется, может заменить живого учителя. Многое гораздо легче понять самому: достаточно просто вдумчиво прочитать и пофантазировать. С другой стороны, когда ты выйдешь на какой-то уровень тебе придётся общаться с коллегами, чтобы понять, в какую сторону вообще двигаться, какие задачи актуальны. В общем, я хочу сказать, что роль преподавателя именно в том, чтобы направлять, а получать новые знания и осознавать их ты должен сам. Во всяком случае, я лично заметил, что мне гораздо проще что-то учить самому, а уже потом с преподавателем это можно обсудить, рассмотреть интересные задачи, более детально проникнуться. Хотя, конечно, могу предположить, что не всем может хватить усидчивости/настойчивости. Или это всё мои маняфантазии?

Ответы>>377916

25 Июл, 19:29 #261 #377907

>>377800
А вот я, кстати, не понимаю вообще таких вопросов в этом итт треде. Даже когда я был на первом курсе, у меня уже была вполне конкретная задача, которая была мне интересна, и по которой можно было бы писать (никому не нужные) пейперы. Собственно, поэтому я на этот первый курс и пошел. Не очень представляю, как вообще может быть по-другому и в чем тогда смысл. С другой стороны, я в итоге полностью забросил и универ, и то свое увлечение, так что может быть итт анон все правильно как раз таки делает, хех.

25 Июл, 20:44 #262 #377916

>>377905
Раньше я думал - нахуя нужны лекции, когда все можно спокойно в книжке прочитать? И кажется до меня дошло, что главный профит лекций - в их ограниченности по времени. Есть N занятий по M минут, и какие бы охуительные истории не хотелось рассказать лектору, ему приходится себя ограничивать и выбирать самое важное. С книгой же таких ограничений нет и некоторые вообще уходят в разнос. Некоторые книги это просто шедевры графомании. Книга на треть может состоять из "метадискурса" - всякие вводные, выводные, вода, отсылки назад, отсылки вперед, абсолютно бесполезные комментарии, типа что по данному вопросу спизданул Платон, подведения итогов и прочее. И на половину из того что в общем-то не является прямым предметом, а только косвенно с ним связано e.g. какая-нибудь глава по комбинаторике в учебнике по анализу, теория вероятностей в учебнике по алгоритмам и т.п.
Главная проблема для меня - что я ебаный аутист и не могу просто взять и прочитать то что нужно. Я читаю вообще все от введения на обложке, благодарности, краткие содержания, потом охуительные вещи типа определения пересечения множеств. И когда дело доходит то того что действительно нужно, я уже так заебался, что перестаю понимать вообще что-либо.

Ответы>>377917 >>377958

8 Кб, 645x773

25 Июл, 20:46 #263 #377917

>>377916

> Главная проблема для меня - что я ебаный аутист и не могу просто взять и прочитать то что нужно. Я читаю вообще все от введения на обложке, благодарности, краткие содержания, потом охуительные вещи типа определения пересечения множеств. И когда дело доходит то того что действительно нужно, я уже так заебался, что перестаю понимать вообще что-либо.

Очень жизненно. Ты, это я, бро.

Ответы>>377918 >>377958

25 Июл, 20:53 #264 #377918

>>377917
Утраиваю. Из-за этого не могу дочитать ни одну книжку, потому что если начал не с начала - некошерно, и в итоге приходится перечитывать то, что уже и так знаю, из-за чего теряется интерес; если сделал перерыв на несколько дней - некошерно и надо начинать сначала. Если не осилил какое-нибувдь упражнение в первой главе - некошерно, читать дальше нет смысла, переключаюсь на другое. </биопроблемы>

Ответы>>377958

25 Июл, 22:22 #265 #377958

>>377918
>>377917
>>377916
Лоллировал с вас. Как успехи, матан за 1 курс прошли?

Ответы>>377962

25 Июл, 22:31 #266 #377962

>>377958
Нет.

Ответы>>377967

25 Июл, 22:50 #267 #377967

>>377962
Тогда советую перестать так делать. Я когда перестал так делать, за 2 недели стал узнавать столько же математики, сколько раньше узнавал за полгода.

Ответы>>377968

25 Июл, 22:52 #268 #377968

>>377967
Я не могу, это часть характера. Не так-то просто отказываться от своей идентичности. Сразу в голову лезут мысли про всякие лодочки.

Ответы>>377971 >>377975 >>377977

25 Июл, 22:59 #269 #377971

>>377968
Обычно людям экзамены в универе помогают с перфекционизмом бороться.

Ответы>>377974 >>377998

25 Июл, 23:04 #270 #377974

>>377971
Но не всегда.

25 Июл, 23:32 #271 #377975

>>377968
Ты о парадоксе Тесея? Пфф. На одном уровне детализации ты из вчерашнего дня - это не ты из сегодняшнего дня. На другом уровне детализации ты и Юлий Цезарь - одно. А избранного уровня детализации нет. Я вот воспринимаю себя как один частный случай Общего Себя, а некоторых других людей - как другие частные случаи. Просто стараюсь об этом не распространяться, а то некоторые собеседники могут не оценить глубину этих философских построений и сдать меня бездушным докторам.

Ответы>>377976 >>377978

25 Июл, 23:34 #272 #377976

>>377975
лол

25 Июл, 23:34 #273 #377977

>>377968
Ну ты и ебан. Прикрываешь "своими особенностями" банальную омежью сущность, которая не даёт тебе делать то, что ты сам хочешь, а не что Ерох Ерохыч сказал.

Ответы>>377978 >>377980

25 Июл, 23:38 #274 #377978

>>377975
Это все хорошо и очевидно, но ты говоришь про искусственные, мысленные построения, а я - про обыденные, чувственные ощущения. Я за ними могу наблюдать и я их могу описывать, но влиять на них я не в силах. Часто ли ты задумывался о том, что, быть может, следует перестать ощущать зеденый цвет зеленым, и начать видеть его, например, синим?

>>377977
Ты ошибся временем и местом.

Ответы>>377979 >>377984

25 Июл, 23:41 #275 #377979

>>377978
Не ошибся я ни разу, а описал твою т.н. склонность к обсессивно-компульсивному чтению книг от корки до корки.

Ответы>>377982

25 Июл, 23:42 #276 #377980

>>377977
Я не он, но поясню. Дело не в этом. Дело в желании сделать что-то добросовестно, полностью. Типа есть вера, что если ты сам решил все задачи, у тебя абсолютное понимание этой темы и эти знания с тобой на всю жизнь. Есть только один способ победить этот глупый предрассудок: прорешать на 100% несколько глав из какого-нибудь учебника и где-то через полгода понять, что нахуй не нужно было ебаться с этими задачами со звездочками.

Ответы>>377981

25 Июл, 23:44 #277 #377981

>>377980
Ну в общем допускаю, что это по молодости, да.

25 Июл, 23:46 #278 #377982

>>377979
Пожалуйста, не употребляй термины, значения которых не понимаешь до конца - хотя бы в этом треде. Спасибо.

Ответы>>377983

25 Июл, 23:50 #279 #377983

>>377982
Угораю с того, как ты безуспешно пытаешься прикрыть свой баребух)))) при помощи псевдо-интеллектуальности)).

Ответы>>377986

25 Июл, 23:50 #280 #377984

>>377978
Да, часто. Даже периодически пробую. Пока не получается, впрочем.

25 Июл, 23:52 #281 #377986

>>377983
Угорают в /б. Если вам хочется угорать - проследуйте, пожалуйста, в /б, и там угорайте, а здесь тред про математику и философию, спасибо.

Ответы>>377987 >>377995

43 Кб, 604x288

29 Кб, 604x321

25 Июл, 23:55 #282 #377987

>>377986
Глупости какие.

26 Июл, 00:37 #283 #377995

>>377986
Можете возвращаться на dxdy, спасибо. )))

26 Июл, 01:10 #284 #377998

>>377971
Так и получается что нужна крепкая рука. Чтобы умный дядя за тебя составил программу и оставил то что нужно. Правда возникает маленькая проблемка если ты с этим дядей в чем-то несогласен.
Или если у экзаменующего дяди другой набор жизненных установок. Правда, это уже совсем другая история.

Ответы>>378002

512 Кб, 872x720

26 Июл, 01:47 #285 #378002

>>377998
Сам ж пошёл в это рабство. Выкручивайся теперь как хочешь.

Либо меняй вуз на тот, где люди адекватны.

Ответы>>378008

26 Июл, 02:30 #286 #378008

>>378002
Не бывает такого. Особенно в рашке.
К тому же я уже отучился.

Ответы>>378018

26 Июл, 03:56 #287 #378018

>>378008
Бывает такое. Особенно вне рашки.

> я уже отучился.

Прихуел. Сочувствую, если это правда, и у тебя такие мысли не на первом курсе.

Ответы>>378020

26 Июл, 04:15 #288 #378020

>>378018
Да угадаю - ты на первом курсе и твои мысли

> нахуя нужны лекции, когда все можно спокойно в книжке прочитать?

26 Июл, 11:04 #289 #378038

Ребятки, поясните пожалуйста, почему дифференциальные формы нужны были математике именно такими, какие они есть?

Ответы>>378044 >>378089

26 Июл, 12:04 #290 #378044

>>378038
Пример приведи

Ответы>>378050

26 Июл, 12:23 #291 #378050

>>378044
Пример чего? Меня интересует только объект полностью.

Ответы>>378065

26 Июл, 14:22 #292 #378065

>>378050
Ты невнятно сформулировал вопрос. Не понятно чего ты хочешь.
Твой вопрос на одному уровне с вопросом "почему слово квадрат не квадратное"

Ответы>>378073

26 Июл, 14:41 #293 #378073

>>378065
Тебя это ебёт что ли?
Человек, задавший вопрос - последователь Бурбаки: для него общие понятия премного важнее частных. Вот и всё. Чего тут не ясного? Зачем примеры?
Пиздос!

26 Июл, 14:58 #294 #378077

>>377716
специально взял неоплачиваемый отпуск от погромирования, чтобы запилить свою логику с блэкджеком и шлюхами, расширяющую область значений характеристических функций множеств

после пары месяцев луркания осознал, что я хуй простой в математике - в нашей шаражке хоть и был хардкорный матан, но топологию и категории нам почему-то не преподали, а осилить их самостоятельно уже не могу - мозг заплыл жиром за долгие годы говнокодинга

в общем, свожу всё, что смог получить хуита хуит, тащемта, в несколько статей и буду напрашиваться на работу в институты своего мухосранска - с целью подкачать свои скиллы по матану на практике статьи постараюсь преподнести не как достижения, а как пример того, как я могу оформлять свои мысли

Ответы>>378078

26 Июл, 15:15 #295 #378078

>>378077
Зачем?

Ответы>>378085

26 Июл, 15:54 #296 #378085

>>378078
если зачем относится к логике, то изначально цель была разработать консистентную логическую систему, в рамках которой можно было бы работать с предикатами, описывающими дуалистические феномены якобы взаимоисключающие

цель оказалась для меня недостижимой, поэтому я ограничился расширениями булевой алгебры - многомерными, но со специальным правилом конъюнкции, похожим на правило умножения мнимых единиц в гиперкомплексных алгебрах

как применить полученные алгебры хоть в какой-то практической задаче - ума не приложу

26 Июл, 16:09 #297 #378089

>>378038
Чтобы ухватить геометрию инфинитсемального объёма. Фактически ты применяешь определитель к касательным векторам.

19 Кб, 180x330

26 Июл, 20:00 #298 #378115

Как проверить, является ли алгебра групповой алгебры некоторой группы?

Ответы>>378156

27 Июл, 02:06 #299 #378156

>>378115
ноу вей

27 Июл, 12:14 #300 #378198

Анон, если я буду называть матрицу линейным отображением, а линейное отображение (конечномерных пространств) матрицей - это норм или так не принято делать?

Ответы>>378228

103 Кб, 662x904

27 Июл, 14:02 #301 #378210

Поясните за доказательство утверждения 3.78, чому оно такое наркоманское? Я его понял, но почему нельзя просто взять базисы для каждого U_k, хуйнуть их вместе и сказать, что если U_1 + ... + U_m - не прямая сумма, то найдется нетривиальная линейная комбинация, которая равна 0, а значит, мы можем из базиса выкинуть какой-нибудь вектор, что противоречит предположению о сумме размерностей?

Или у этого отображения Г есть какой-то важный смысл, который я не знаю?

Ответы>>378230

27 Июл, 15:11 #302 #378228

>>378198
ненорм, даже канонического соответствия нет, только после выбора базиса.

Ответы>>378244

27 Июл, 15:17 #303 #378230

>>378210
равенство конечных размерностей = изоморфизм лин. пр-в, т.е. существование биективного лин. отображения, т.е. сюръективного и инъективного. Это и доказывается.

101 Кб, 531x769

43 Кб, 555x340

27 Июл, 15:18 #304 #378232

я думаю здесь много компетентных людей, которые могли бы мне помочь. я не до конца понимаю обоснование строгости неравенства (1).

Ответы>>378241 >>378243

27 Июл, 16:00 #305 #378241

>>378232
Это Фихтенгольц. Ждать от него большой строгости — нет смысла. Тебя смущает, что не обосновано существование чисел больше или меньше какого-то наперёд заданного? Читал давно, поэтому могу ошибаться, но ранее должна была быть аксиома Архимеда. Думаю, именно из неё это вытекает напрямую.

Ответы>>378247

27 Июл, 16:11 #306 #378243

>>378232
Не читал Фихтенгольца, но слышал, что там вещественные числа определяются через бесконечные десятичные дроби. Это долбоебизм, советую пропустить вообще все обоснования действий с вещественными числами либо прочитать их в другом учебнике, а потом вернуться к Фихтенгольцу (не знаю, нужно ли вообще к нему возвращаться).

Ответы>>378248

27 Июл, 16:12 #307 #378244

>>378228
Ну базис же понятен из контекста.

27 Июл, 16:18 #308 #378247

>>378241
я не точно выразился. меня смущает, каким образом он исключил случай равенства сумм с гаммой. я понимаю, что из условия точной границы гамма может быть равна какому-то элементу ограниченного сверху множества сумм рац. чисел а,b, что в самом начале под (2), когда ввелось определение суммы вещ. числа там записано строгое неравенство. но почему из того, что любые удовлетворяющие условиям (1) а, a', b, b' можно увеличить, следует, что равенства быть не может ни справа, ни слева ?

Ответы>>378258

27 Июл, 16:19 #309 #378248

>>378243
что не так с фихтенгольцом ?

Ответы>>378258

27 Июл, 16:51 #310 #378258

>>378247
С трудом тебя понимаю, если честно. Если ты о том, почему из a < α < a' ; b < β < b' ; α + β = γ следует, что a + b < γ (именно меньше, но не равно), то могу предположить, что это выводится примерно так:
(1) a < α ⇒ a + β < α + β = γ ⇒ a + β < γ;
(2) b < β ⇒ a + b < a + β (из 1) < γ ⇒ a + b < γ;

>>378248
Немного устаревший подход к матану. Мне кажется, лучше сначала прочитать что-нибудь более современное, а уже потом для дополнительного понимания в построении анализа читнуть и сего автора. Строгости вряд ли стоит от него ждать.

Ответы>>378261 >>378295

28 Кб, 471x189

27 Июл, 17:12 #311 #378261

>>378258
вот предложение, и мне совершенно непонятно почему "равенства быть не может с одной и с другой стороны".

Ответы>>378275 >>378283

27 Июл, 17:49 #312 #378275

>>378261
Пусть A и B - вещественные числа, a и b - рациональные. Пусть a < A и b<B. Пусть S - супремум с твоей пикчи.

1. Существуют рациональные числа p и q такие, что a<p<A и b<q<B.

2. Предположим, что a+b = S. Тогда по аксиомам рациональных чисел a+b < p+b и p+b < p+q, т.е. a+b<p+q.

3. Так как a+b=S, это означает, что S < p+q. Но по условию S - супремум таких сумм. Значит, предположение (2) было ошибочным.

Ответы>>378281

27 Июл, 18:10 #313 #378281

>>378275
спасибо что ты есть, анон

27 Июл, 18:19 #314 #378283

>>378261
Ладно, попробую ещё пованговать. Значит, попробуем так.
Что делаем сначала? Задаём γ = sup {a + b}. Теперь мы пытаемся доказать, что это именно то γ, которое нам нужно для условия (1). Дальше. Почему можно увеличить (уменьшить) числа с сохранением условия (1)? Примерно так (напомню, что γ мы уже сделали вполне конкретным числом и суммировать рациональные числа вроде как умеем, по мнению Фихтенгольца):
a + b = c < γ ⇒ ∃d ∈ ℚ, c < d < γ ⇒ a + (b + e) = d < γ.
Здесь я воспользовался какой-то лемой выше из этого Фихтенгольца, гласящей, что между двумя вещественными числами существует рациональное. То же самое делается с a и со вторым случаем. Значит, конспектируем:
(∀a, b ∈ ℚ, a + b < γ) ∧ (∀a', b' ∈ ℚ, γ < a' + b'). [1]
Что у нас уже известно? А вот что:
(a + b ≤ γ) ∧ (γ ≤ a' + b'). [2]
Как это понимать? Вот так:
(a + b < γ ∨ a + b = γ) ∧ (γ < a' + b' ∨ γ = a' + b'). [3]
Дальше. Из [1] следует, что ситуация равенства невозможна, поэтому из [3] и получается то, что нужно.

Ответы>>378284 >>378288

27 Июл, 18:21 #315 #378284

>>378283

>∈ ℚ

Вот с этим я правда обосрался, но, думаю, ты понял.

27 Июл, 18:36 #316 #378288

>>378283
добра тебе

27 Июл, 20:56 #317 #378295

>>378258

>Мне кажется, лучше сначала прочитать что-нибудь более современное

Что, например?

Ответы>>378305

27 Июл, 21:06 #318 #378296

Допустим, хэш-функция выдает только 64-битные хеши, а нам нужно, скажем, 100 байт.
hash(A) = 64-битное число
Если мы вызывем ее несколько раз:
hash(A+1) = ...
hash(A+2) = ...
hash(A+3) = ...
и конкатенируем выходы, ухудшится ли качество?

27 Июл, 22:07 #319 #378305

>>378295
Да вариантов много. Я не знаю, зачем тебе анализ нужен. Можно буками на английском закидываться, но в этом я, честно говоря, толком не понимаю, но помню Тао. Из русскоязычных учебников, подходящих новичкам, можно посмотреть на того же Зорича (хотя у него бывает много лирики, да и обозначения многим не нравятся). Рудин опять-таки. Ну и там дальше уже всякие Шварцы, Камынины, Смирновы. Ну и всякие лекции для «двинутых».

Ответы>>378308 >>378321

27 Июл, 22:29 #320 #378308

>>378305
Спасибо. Начну с Рудина

Walter Rudin principles of mathematical analysis
(эта же книга имелась ввиду)

Ответы>>378314

27 Июл, 23:07 #321 #378314

>>378308
Не советую. Он немного всратый и неоправданно хардкорный. Это такой показательный пример учебника, цель которого в первую очередь разорвать тебе жопу и только потом уже обучить разделу математики.

Вот годнота

> C. Pugh: "Real Mathematical analysis".

> С. М. Львовский: "Лекции по математическому анализу".

Львовский хардкорней, но там тем меньше, оставлены наиболее важные.

Ответы>>378316

27 Июл, 23:17 #322 #378316

>>378314
Добра тебе.

Жаль у Львовского ответов к задачам нет. Но если что тут спрошу

Ответы>>378317

27 Июл, 23:23 #323 #378317

>>378316
А ты их еще решать пытаешься? Я даже не пытаюсь.

Ответы>>378318 >>378561

27 Июл, 23:33 #324 #378318

>>378317
Я только начал читать. Посмотрим насколько меня хватит.

27 Июл, 23:56 #325 #378321

>>378305
А вот поясни, почему советуют один учебник на первое чтение, а другой на второе? Не будет ли неинтересно читать Шварца, когда все известно?

Ответы>>378325

28 Июл, 00:34 #326 #378325

>>378321
Шварц очень абстрактен и не утруждает себя ни комментированием теорем, ни тем более мотивировками. Если у тебя не будет глубокого опыта изучения матана, то учебник Шварца покажется тебе белибердой.

28 Июл, 04:50 #327 #378354

Посоветуйте книг по компьютерной алгебре
Пока наткнулся на
Кузнецов М.И. и др. Компьютерная алгебра.
Лукач Ю.С. Основы компьютерной алгебры.

Ответы>>378501 >>378780

28 Июл, 12:51 #328 #378396

"Научное сообщество населяют орлы, стервятники, шакалы как из мультика про Маугли «а мы пойдем на север», пантеры, питоны. У меня есть друзья — волки. Сам я ближе к постапокалиптическим кротам. Кротам не интересно участвовать в обсуждении обустройства науки, очень не люблю научпоп, например, и то, что связано с каким-то околонаучными официозными тусовками, ну и тяжело воспринимаю всяких научных функционеров-прилипал, которые сами нихуя не сделали, но везде видны, мы пойдем на север, короче."

Планирую в середине сентября написать туда статью о людях-насекомых, которые двигаются под шорохи и шипения. Так называемый insect-dub-punk. Субкультура муравьев итд.

Короче, я знал человека-кота, человека-собаку и человека-робота. Жаль, не получится с ними интервьюшки сделать.

Отвечаю на вопрос об имиджбордах. Ок, посмотрел внимательно двач, 4chan итд. Если бы там японские слова заменить хинди. Няша - прия или пьяра. И еще там нет содержательного квеста, в который мог бы броситься анонимный интеллект. Разоблачать девушек, снимавшихся в порно - это не очень как-то. Создать новый язык, например! Который не возьмут электронные переводчики. Создать грамматику, (плавающий, меняющийся) словарь, писать на нем что-угодно. Сделать город, населенный носителями этого языка. Тогда да.

Вот, про встречу с человеком без зубов.

"Ну давай, ну давай, научи меня индийскому. Он сел напротив и начал ерзать, вглядываясь мне в лицо.

-- Гханта - колокол, звон, звонок, а сленговое значение - пустота, ничто. Чамча - ложка, а сленгово - жополиз. Фудду - вагина, идиот. А всякие ругательства типа fuck - это обычно чутия, чутан, чод. Если в резкой форме звучит чут.. или чод - явно что-то не то. Хотя чутна - это отслаивать или отрезать. Классную девушку могут назвать маал, тхарки, а могут и саман, что не очень.

-- Типа если скажу, слышь маал, ты норм. То да?

-- Типа да.

-- А че ты там в Индии делал вообще? Трава там, да? А как спросить, слышь, подкинь мелочи.

-- Тхора кхарча пани милега. Это более мумбаиское.

У него нет зубов спереди, но он все равно улыбается из себя всему миру. Он как израненная собачка, шавка со слюной, по рынкам-базарам, может кого куснуть и отбежать с лаем и хохотом. Ну что, делайте теперь уколы от бешенства."

28 Июл, 12:51 #328 #378396

Показать весь текст

Ответы>>378397 >>378399 >>379616

28 Июл, 13:03 #329 #378397

>>378396
Урааа, Рома ЖЖ восстановил. Теперь заживем.

28 Июл, 13:09 #330 #378399

>>378396
Да он же про /фл! И битардск! Это все было, что он описывал! Эх, не сумел найти жемчужин в трясине бэ-говна!

Ответы>>378401

28 Июл, 13:32 #331 #378401

>>378399
/fl ? А что там?

Ответы>>378409

28 Июл, 13:56 #332 #378407

Правильное ли это доказательство того, что любое открытое подмножество R представляется в виде счетного объединения открытых интервалов?

Шары с рациональными центрами и радиусами - база для стандартной топологии R. Теперь представим открытое U как объединение всех B_x, где B_x - элемент базы, содержащий x и содержащийся в U. Так как база счетное, количество различных B_x счетно.

Ответы>>378408

28 Июл, 14:06 #333 #378408

>>378407
Правильное, но сказано несколько лишних слов.
Во-первых, множество шаров с рациональными центрами и радиусами счётно, то есть база счётная.

Во-вторых, любое открытое множество представляется как объединение подмножества базы, по определению базы.

Из этого следует, что любое открытое множество представляется в виде не более чем счётного объединения рациональных интервалов.

28 Июл, 14:09 #334 #378409

>>378401
Там создавали как раз новый язык имаджборд, например. Да и в целом атмосфера, кстати, гораздо выше уровнем, чем здесь (в сци, не в треде), но это уже другой вопрос.

Ответы>>378560

28 Июл, 20:47 #335 #378501

>>378354
Бамп

29 Июл, 01:19 #336 #378560

>>378409
На всём Дваче нет такой атмосферы, как в мат. тредах.

29 Июл, 01:19 #337 #378561

>>378317
Почему не пытаешься?

Ответы>>378601

55 Кб, 695x818

65 Кб, 646x684

29 Июл, 11:55 #338 #378601

>>378561
Потому что они там приведены не для того, чтобы читатель мог закрепить пройденный материал, а чтоб читатель жопу себе разорвал. Я знаю, что есть люди, которые любят, когда им анус рвут, но я не из таких.

Ответы>>378602

29 Июл, 12:01 #339 #378602

>>378601
Ну а что, задача 1.105, например, именно на пройденный материал. Она элементарна, если подумать.

Ответы>>378604 >>378628

29 Июл, 12:25 #340 #378604

>>378602
Ну да. Типа предположим, что такое отображение f существует. Так как R \ {0} несвязно, f(R \ {0}) тоже должно быть несвязно, но f(R \ {0}) - это R^2 \ { f(a) }, а оно связно.

Но, во-первых, то, что одно упражнение из листка легкое, еще не означает, что в целом листок нормальный. Во-вторых, не такое оно и легкое, это просто баян, мы с тобой его заранее знали.

Ответы>>378605 >>378606

29 Июл, 12:26 #341 #378605

>>378604

> R^2 \ { f(a) }

фикс: R^2 \ { f(0) }

29 Июл, 12:39 #342 #378606

>>378604

>тоже должно быть несвязно

Почему? Это же не гомеоморфизм.

Ответы>>378607 >>378613

29 Июл, 12:43 #343 #378607

>>378606
Непрерывное отображение отображает связные множества в связные.

Ответы>>378608

29 Июл, 12:47 #344 #378608

>>378607
Но не несвязные в несвязные.

Ответы>>378609

29 Июл, 12:48 #345 #378609

>>378608
Согласен, я неправильно решил.

Ответы>>378610

29 Июл, 12:50 #346 #378610

>>378609
Просто не в ту сторону. Таким рассуждением можно доказать отсутствие непрерывной биекции из плоскости в прямую.

29 Июл, 14:02 #347 #378613

>>378606
Непрерывная биекция в компакт является гомеоморфизмом. Мемс в том, что нужно просто рассуждать не для всех R и R^2, а выбрать компакт в R^2 и его прообраз.

Ответы>>378620

29 Июл, 15:19 #348 #378620

>>378613
Это неверно. Самый простой пример f: [0, 1) → S¹, f(t) = (cos t, sin t.

Непрерывная биекция f из компактного пространства X в хаусдорфово пространство Y является гомеоморфизмом.
Доказательство. Покажем, что f переводит замкнутые подмножества в замкнутые. Пусть K ⊂ X замкнуто. Тогда оно компактно. Так как f непрерывна, f(K) компактно. f(K) замкнуто, потому что Y хаусдорфово.

Ответы>>378639

29 Июл, 15:50 #349 #378628

>>378602
Я уже 3.5 часа решаю эту задачу. Спрашивается, нахуя мне знать, существует ли непрерывная биекция из R в R^2? А вот у Львовского все задачи такие. Поэтому я их не решаю в принципе.

Ответы>>378635

29 Июл, 15:57 #350 #378635

>>378628

>нахуя мне знать, существует ли непрерывная биекция из R в R^2?

Ну а нахуя тебе матан учить тогда? Ты же специально приобретаешь способность быстро отвечать на вопросы, из чего в куда какое отображение есть.

Ответы>>378640

29 Июл, 16:04 #351 #378639

>>378620
Да, я перепутал.

29 Июл, 16:05 #352 #378640

>>378635
Во-первых, это вообще даунский аргумент. Это как человеку, который не хочешь решать школьные олимпиады, говорить: "Нахуя тебе математику учить тогда? Ты же специально приобретаешь способность быстро решать задачи". Во-вторых, если такой умный, реши мне эту задачу.

Ответы>>378641

29 Июл, 16:07 #353 #378641

>>378640
Ну а зачем ты учишь матан? Что конкретно ты хочешь узнать? Какие знания обрести?

Ответы>>378664

29 Июл, 16:56 #354 #378664

>>378641
Какие-то нормальные темы, очевидно, которые используются в других разделах математики. Покажи мне хоть один результат, который использует эту ебанутую задачу.

По поводу задачи: я понял, что если такая f существует, то прообраз любого открытого шара неограничен. Потому что иначе мы можем взять отрезок [a, b] такой, что
f([a, b]) содержит этот шар. Так как [a, b] компактен, он гомеоморфен f([a, b]). Выберем из открытого шара такую точку, прообраз которой не равен a или b (это можно сделать, потому что у нас всего 2 точки a, b и несчетное количество точек внутри шара). Если эту точку выколоть, f([a, b]) останется связным, а [a, b] нет.

> прообраз любого открытого шара неограничен

Казалось бы, бред полный, но я не могу доказать что это невозможно.

Ответы>>378677 >>379371

29 Июл, 17:41 #355 #378677

>>378664

>Покажи мне хоть один результат, который использует эту ебанутую задачу.

Тот факт, что R нельзя непрерывной биекцией, а следовательно и гомоморфизмом отобразить на R^2 это частный случай "инвариантности размерности": того что R^n не гомеоморфно R^k.

Ответы>>378680

29 Июл, 17:45 #356 #378680

>>378677
Какой частный случай? Утверждение R^2 негомеоморфно R более слабое чем утверждение этой задачи.

Ответы>>378683

29 Июл, 17:50 #357 #378683

>>378680
Ну да, более слабое, ну и что?

Ответы>>378686

29 Июл, 18:02 #358 #378686

>>378683
Ну то что ты не ответил на вопрос, нахуя эта задача нужна.

Ответы>>378689 >>378690

29 Июл, 18:16 #359 #378689

>>378686
Чуть более сильная версия используемого утверждения.

29 Июл, 18:23 #360 #378690

>>378686
Один факт из серии.
— существует биекция между отрезком и квадратом
— существует непрерывная сюръекция отрезка на квадрат
— не существует непрерывной биекции отрезка на квадрат
...

30 Июл, 09:05 #361 #378728

>>376017 (OP)
Реквестирую книгу по теории колец главных идеалов

Ответы>>378803 >>378822 >>378841

30 Июл, 22:45 #362 #378780

>>378354
>>378354
Бамп

31 Июл, 03:06 #363 #378803

>>378728
нет такой теории

Ответы>>378813

31 Июл, 08:29 #364 #378813

>>378803
Кольца главных идеалов существуют? %существуют% Значит и теория по ним тоже существует.

Ответы>>378814 >>378836

31 Июл, 08:30 #365 #378814

>>378813
Проебался с разметкой :(

31 Июл, 10:06 #366 #378818

Хуле у тапалогии такая всратая аксиоматика, нельзя попроще сделать? Не из теории множеств её вывести, а из категорий, например.
А, ещё хотелось бы задать вопрос. Здесь наверняка есть люди, которые защитили кандидатскую. По каким темам по чаще всего пишут? И по каким писали вы, просто интересно.

Ответы>>378838 >>378841

31 Июл, 10:29 #367 #378822

>>378728
http://gen.lib.rus.ec/book/index.php?md5=33BACCBFD8D054FEEE5532A66F077D3A

31 Июл, 13:27 #368 #378836

>>378813
Пусть дано множество линейно связных замкнутых множеств в R^n, которые мы называем хуями. Анусом твоей мамаши сегодня вечером для данного набора хуёв мы называем класс окрестностей в R^n, допускающих неплотную упаковку хуями; т.е. окрестностей, которым принадлежит объединение множеств, попарно пересекающихся не более чем по кускам границ (такая упаковка называется пидорской), каждое множество взято из орбиты какого-то хуя из набора ( все хуи взяты и взяты по одному разу ) под действием группы аффинных преобразований. Сами окрестности называются состояниями ануса твоей мамаши сегодня вечером. Анусом твоей мамаши данной размерности n называется объединение классов анусов твоей мамаши сегодня вечером для всех конечных наборов хуёв в R^n. Очевидно, для любого конечно набора хуёв анус твоей мамаши сегодня вечером существует => значит должна быть содержательная теория! Предлагаю всем итт заняться её разработкой, я вот уже немного вглубь продвинулся.

Ответы>>378837 >>378858

31 Июл, 13:29 #369 #378837

>>378836
*конечное множество линейно связных замкнутых подмножеств

31 Июл, 13:38 #370 #378838

>>378818

>Хуле у тапалогии такая всратая аксиоматика, нельзя попроще сделать? Не из теории множеств её вывести, а из категорий, например.

Выведи кольца/группы/алгебры/векторные пр-ва/... "из категорий", долбоёб.

Ответы>>378854

31 Июл, 13:58 #371 #378841

>>378728
Считается, что там нечего изучать.
>>378818

>Хуле у тапалогии такая всратая аксиоматика, нельзя попроще сделать?

Содержит всё и ничего, конечные пересечения и любые объединения. Что сложного? Скорее слишком просто.

>Не из теории множеств её вывести, а из категорий, например.

Не вывести, а выразить на языке. Можно, например: ncatlab.org/nlab/show/locale. Фундаментальные понятия все более-менее эквивалентны.

Ответы>>378849 >>378854

31 Июл, 15:45 #372 #378849

>>378841

>Содержит всё и ничего

Избыточное требование. Смотри.

>любые объединения

Объединение пустого семейства открытых множеств даст открытость пустого множества.

>конечные пересечения

Пересечение пустого семейства подмножеств M даст M, т.е. всё пространство открыто.
мимошёл

Ответы>>378870

31 Июл, 15:51 #373 #378851

Объясните почему действие Эйнштейна-гильберта именно такое, какое оно есть, какого хуя там скаляр Риччи? Кто не сможет объяснить, тот пидар зашкваренный.

31 Июл, 15:57 #374 #378854

>>378838
Вывел эти понятия из широкого очка твоей мвмки, проверяй.
>>378841
Аксиомы простые, имелось ввиду, что они слишком, на первый взгляд оторваны от того, что принято считать топологией в глазах любителя (как у Прасолова в наглядной топологии). От них нужно долго шагать до чего-то действительно интересного. Неужто нельзя никак сократить данный путь? Тут просто был анон, который пытался читать элементарную топологию, и ему не впёрло именно по этой причине - вместо обещанной красоты нагромождение определений и скучных заданий.

Ответы>>378857 >>378870

31 Июл, 16:17 #375 #378857

>>378854
Блядь какой там длинный путь-то?
Ты вообще Хатчера-то открывал?

Ответы>>378859

31 Июл, 16:19 #376 #378858

>>378836
Ну вот зачем так обидно-то? Я тебя обижал?

Ответы>>378876

31 Июл, 16:46 #377 #378859

>>378857
Толсто. Предлагаешь детям начать своё обучение с Хатчера? Ты его сам открывал?

Ответы>>378860

31 Июл, 16:47 #378 #378860

>>378859
Не вижу ни единой проблемы с ним. А вот с другими авторами - да.

31 Июл, 17:16 #379 #378870

>>378849
Ок. На самом деле это просто наличие нейтральных элементов относительно этих операций. 1 и 0, α и ω.
>>378854
Все претензии к понятию непрерывной функции, оно тут главное, а «топология» нужна только чтобы придать ему смысл.

22 Кб, 361x358

31 Июл, 17:23 #380 #378876

>>378858

Ответы>>378880

31 Июл, 17:27 #381 #378880

>>378876
Вот и именно, бля. Стыдно должно быть!

31 Июл, 19:20 #382 #378899

Манон, что можно почитать по эпистемологии/гносеологии? И в целом насчёт разных подходов к математике (логицизм, интуиционизм, конструктивизм, формализм, etc.)?

Ответы>>378902 >>378910 >>378945 >>379332

29 Кб, 1174x265

75 Кб, 890x1013

31 Июл, 19:26 #383 #378901

Посаны, можно как-то покороче доказать пикрелейтед 1 чем на пикрелейтед 2? Че-то слишком длинно и как-то смекалисто что ли для таких простых утверждений.

Ответы>>378903 >>378906

31 Июл, 19:28 #384 #378902

>>378899

>логицизм, интуиционизм, конструктивизм, формализм

Это мемы философов. Только философы с ними носятся сейчас. К математике вся эта дребедень имеет даже меньше отношения, чем философский "наблюдатель" к физике.

Ответы>>378907

31 Июл, 19:29 #385 #378903

>>378901
Куда ещё короче-то? Это буквально чуть ли не по определению вещественных чисел доказательство.

Ответы>>378905

31 Июл, 19:33 #386 #378905

>>378903
Ну видимо я тупой. Я его где-то час придумывал.

31 Июл, 19:33 #387 #378906

>>378901
По-моему утверждение очевидно, тут доказывать нечего. Этот размер отображения это константа Липшица чтоли?

31 Июл, 19:34 #388 #378907

>>378902
Так мне для общего развития. Хочу копнуть чуть глубже.

31 Июл, 19:37 #389 #378910

>>378899
Манин
Мунин
Манон

Ответы>>378916

31 Июл, 20:16 #390 #378916

>>378910
Менона забыл

Ответы>>378948

31 Июл, 22:29 #391 #378945

>>378899
Вилдербергер.

31 Июл, 22:36 #392 #378948

>>378916
И мунина

Ответы>>378958

31 Июл, 23:17 #393 #378958

>>378948
И Манина.

135 Кб, 1058x933

65 Кб, 1080x576

01 Авг, 10:57 #394 #379041

Поясните за строчку

> By the one-dimensional chain rule and mean value theorem applied to the differentiable real-valued function g(t) = f_i σ_j(t)

Тут же ошибка, да? Типа σ_j - это функция из [0, 1] в R^n, а f_j - функция из R^n в R, поэтому надо применять многомерный chain rule, который в этом месте книги еще не доказан.

Ответы>>379319

01 Авг, 11:17 #395 #379042

Блин, что вербит так носится с кооперативами своими и прочими выкидышами "сибирского панка". Говно же ебаное.

Ответы>>379088

01 Авг, 13:30 #396 #379058

Матаны, поясните мне за картафан. Вот вербитомразь постоянно топит за уродливость интеграла Римана и калькулюса в целом. А что используют благородные доны на замену? Вон вся ссаная физика (ну кроме мож ОТО где жид-эйнштей впервые прогрессивную математику заюзал) на калькулюсе с закорючками основана, что делать братьям нашим меньшим?

Ответы>>379060 >>379061 >>379062 >>379277

01 Авг, 13:33 #397 #379060

>>379058

>А что используют благородные доны на замену?

Калькулятор.

Ответы>>379067

01 Авг, 13:38 #398 #379061

>>379058
Рациональный анализ.

102 Кб, 644x894

61 Кб, 544x901

104 Кб, 581x906

01 Авг, 13:47 #399 #379062

>>379058

> Вот вербитомразь постоянно топит за уродливость интеграла Римана и калькулюса в целом.

Неправда. Никакой уродливости нет, просто интеграл Римана и всякие критерии интегрируемости по Риману занимают 20-30 страниц учебника, а потом все равно люди изучают интеграл Лебега и благополучно интеграл Римана забывают. По крайней мере, это верно для тех, кто читает доказательства в учебниках. Для остальных людей интеграл Римана - это оверкилл, им достаточно понимания интеграла на уровне 17 века, типа разбили на бесконечно малые кусочки и хуйнули сумму.

Калькулусом называется вычислительная часть, типа задач из Демидовича. Такое все нормальные люди ненавидят. Я не физик, но я думаю, что физики тоже не тупые и могут освоить техники, используемые в матане, не решая сотни вычислительных примеров на каждую тему.

Ответы>>379063 >>379167

01 Авг, 14:12 #400 #379063

>>379062

>Калькулусом называется вычислительная часть, типа задач из Демидовича. Такое все нормальные люди ненавидят. Я не физик, но я думаю, что физики тоже не тупые и могут освоить техники, используемые в матане, не решая сотни вычислительных примеров на каждую тему.

Ну я называл калькулюсом интегрально-дифференциальное исчисление, не только задрачивание примерчиков. Про задрачивание примерчиков даже физику понятно что всё можно в какую-нибудь максиму или вольфрам сунуть или на худой конец запрогать алгоритм Риша на фортране (физики ведь ничего другого не знают?). А вот вопрос нужно ли интегрально-дифференциальное исчисление и если нет то что сунуть на его замену - остаётся открытым.

Ответы>>379098

01 Авг, 14:22 #401 #379067

>>379060

>Калькулятор.

Т.е. интегральчики всё-таки нужны, но только в вольфраме?
Ибо я слышал мнение что всю эту интегрально-дифференциальную хуйню в том виде в котором её высрал Ньютон и подхватил Риман можно закопать.

01 Авг, 15:30 #402 #379088

>>379042
Просто ты не понимаешь. С возрастом хочется перенестись мечтами в свою юность, которая у Вербицкого ассоциируется с Летовым, у Медведева с Дип Перплом, а у Путина с группой Любе. Абсолютно каждый из них говноед, но хуй ты это сможешь доказать. Ты тоже через 20 лет будешь переноситься мечтами в какое-то говно. Что ты сейчас слушаешь?

Ответы>>379092 >>379097 >>379099

01 Авг, 15:37 #403 #379092

>>379088
Шнитке и Сорабджи в основном, а что?

01 Авг, 16:05 #404 #379097

>>379088
Вэйпор, советскую эстраду и российский поп 90х.

01 Авг, 16:10 #405 #379098

>>379063
Какие темы по-твоему входят в дифференциально-интегральное исчисление и какие из них Вербит предлагает выпилить?

Ответы>>379101

01 Авг, 16:11 #406 #379099

>>379088
патимэйкер
энджойкин
Это самое любимое, а так еще много чего

Ответы>>379278

01 Авг, 16:16 #407 #379101

>>379098

>Какие темы по-твоему входят в дифференциально-интегральное исчисление и какие из них Вербит предлагает выпилить?

Ну к примеру дифуры. Мне за них больше всего интересно, как же бедные физики без них обойдутся...

Ответы>>379104 >>379105

01 Авг, 16:25 #408 #379104

>>379101
выпилить в смысле, выделить в отдельный курс.

Ответы>>379131

01 Авг, 16:28 #409 #379105

>>379101
Ну, во-первых, я не слышал, чтоб он предлагал выпилить дифуры из программы. Во-вторых, я не представляю в каком контексте он мог обсуждать программу по математике для физиков, мне казалось, его интересует только программа для математиков. Если оттуда выпилить дифуры, это будет норм, потому что дифуры нужны далеко не всем. Те, кому они нужны, смогут довольно быстро вкатиться при наличии хорошей базы (анализ на многообразиях, группы Ли и всякое такое).

Ответы>>379131

01 Авг, 17:23 #410 #379131

>>379104

>выпилить в смысле, выделить в отдельный курс.

Выпилить от слова "нахуй"

>>379105

>Ну, во-первых, я не слышал, чтоб он предлагал выпилить дифуры из программы.

Ну я со слов анонов утверждаю. Я не трал.

>Во-вторых, я не представляю в каком контексте он мог обсуждать программу по математике для физиков, мне казалось, его интересует только программа для математиков. Если оттуда выпилить дифуры, это будет норм, потому что дифуры нужны далеко не всем.

Это не он обсуждал, это я обсуждаю сейчас. Если выпилить дифуры из математиков то что сунуть на их место?

>Те, кому они нужны, смогут довольно быстро вкатиться при наличии хорошей базы (анализ на многообразиях, группы Ли и всякое такое).

Отсюда поподробнее можно?

Ответы>>379134

01 Авг, 17:25 #411 #379134

>>379131
http://imperium.lenin.ru/~verbit/MATH/programma.html

Ответы>>379145 >>379151 >>379927

01 Авг, 17:37 #412 #379145

>>379134
А Вербит сам-то это всё осилил?

Ответы>>379150 >>379155

01 Авг, 17:46 #413 #379150

>>379145
Судя по наличию у него PhD Гарварда, в бытность студентом он осилил гораздо больше.

01 Авг, 17:46 #414 #379151

>>379134

>http://imperium.lenin.ru/~verbit/MATH/programma.html

А можно подчеркнуть то что на замену картофана идёт?

Ответы>>379152

01 Авг, 17:50 #415 #379152

>>379151
Всё.

01 Авг, 17:53 #416 #379153

Вопрос к тем кто изучал теорию меры. В каких местах у вас там вводились весовые функции? Зачем они у вас были нужны?

01 Авг, 17:54 #417 #379155

>>379145
Вербит учась в школе уже публиковался по теме функционального анализа. Логично, что он это все осилил к 25 годам.

Ответы>>379328

01 Авг, 17:56 #418 #379156

Кто-нибудь тут программирует? Часто матаном пользуетесь? Какими областями?

Ответы>>379157 >>379159

01 Авг, 17:56 #419 #379157

>>379156
Я программирую.
Не просто нечасто - никогда.

Ответы>>379161

01 Авг, 17:58 #420 #379159

>>379156

>Часто матаном пользуетесь? Какими областями?

Пользуюсь преобразованиями Фурье каждый божий день. Остальной матан НЕ НУЖЕН.

Ответы>>379161

01 Авг, 18:13 #421 #379161

>>379157
>>379159
А матан чего тогда изучаете? Просто нравится?

Ответы>>379163

01 Авг, 18:16 #422 #379163

>>379161
Чтобы не быть безмозглым быдлом вроде тебя

Ответы>>379170

01 Авг, 18:33 #423 #379167

>>379062
Что за добрая книжка? Прям какой-то антипод Демидовича.

Ответы>>379215

01 Авг, 18:41 #424 #379170

>>379163

> имлаинг что решение абстрактных задачек сделает тебя умнее

Ответы>>379173

01 Авг, 18:47 #425 #379173

>>379170

>сделает тебя умнее

Не обязательно, но скатывание в говно вроде тебя сильно замедляет.

Ответы>>379176

01 Авг, 18:50 #426 #379175

В каком году рефьюджис завезли в Европу десятичные числа? Как до этого священники считали церковный налог? Римскими числами? В каких числах считали налоги монголы с русских рабов?

01 Авг, 18:52 #427 #379176

>>379173
Бля, как решение задачек поможет тебе не скатиться в говно? В житейских проблемах она не поможет, на кой хуй она нужна?

Ответы>>379177 >>379180

01 Авг, 18:56 #428 #379177

>>379176

>этот охуевающий от собственно тупости быдларий

Благодарю за иллюстрацию и мотивацию.

Ответы>>379191

01 Авг, 18:56 #429 #379178

матаны, вопрос по терминологии:

как можно назвать или может уже есть готовое название формулу для получения всех элементов множества из подмножества натуральных чисел в любой декартовой степени?

если выражаться программерским языком - то, что может быть сосчитано с помощью одного или более вложенных циклов

хочется назвать это индуктивной или конструктивной формулой, но судя по всему эти термины не очень подходят

также интересует: есть ли какое-то название для множеств, элементы которого не могут быть так выражены inb4: счётные и несчётные множества - речь идёт не о сопоставлении элементов, а о выразимости их в виде формулы

Ответы>>379189

01 Авг, 18:58 #430 #379180

>>379176
Тупому быдлу НЕПРИЯТНО, запасаемся попкорном.

Ответы>>379191

01 Авг, 19:03 #431 #379189

>>379178

>как можно назвать или может уже есть готовое название формулу для получения всех элементов множества из подмножества натуральных чисел в любой декартовой степени?

https://en.wikipedia.org/wiki/Cardinal_number

01 Авг, 19:05 #432 #379191

>>379177
>>379180
Ну что же вы, господа илитарии, ну занимаетесь вы безполезной хуйней, ну не стоит так реагировать, я понимаю это чувство когда вас опрокидывают в реальность, ну ничего, привыкните что ваш матан уже никому не нужен.

Ответы>>379204

179 Кб, 500x211

01 Авг, 19:21 #433 #379204

>>379191

>ваш матан уже никому не нужен

01 Авг, 20:12 #434 #379215

>>379167
Spivak: Calculus

02 Авг, 07:52 #435 #379277

>>379058
Интеграл Лебега есть как бе. Очевидно, что Римана сосёт, это даже не обсуждается.

02 Авг, 07:56 #436 #379278

>>379099
Ну вот и будешь такой подходить через 30 лет к детям и такой "патимейкер! шейкер-шейкер! иххихихихих ну вы поняли да?", а детки такие смотрят на тебя как на еблана и у виска крутят.

13 Кб, 378x361

02 Авг, 12:10 #437 #379294

есть один псевдокод пикрелейтед, который выкусывает из i биты, которые включены в b

можно ли превратить его в адекватную математическую формулу?

или это тот самый случай, когда псевдокод лаконичнее и понятнее математического эквивалента? как тут например https://en.wikipedia.org/wiki/Bitwise_operation#Mathematical_equivalents

Ответы>>379334 >>379362

02 Авг, 13:45 #438 #379310

В последнее время целыми днями читаю математическую литературу и у меня началась какая-то хуйня с головой: я могу начать че-то делать и через 2 минуты забыть, что я делаю. Эта проблема по жизни а не в математике, в математике все норм. У вас такого не было?

Алсо, я весь день ботаю, а когда заебывает, смотрю мемы. Так у меня почти каждый день проходит. Может быть такое, что у меня мозг охуел от количества информации? Меня чет эта хуйня пугает.

Ответы>>379316 >>379322

02 Авг, 14:08 #439 #379316

>>379310
Иди на велике покатайся, поплавай, отдохни от умственного труда. Мемасики и кинцо только хуже сделают. А что конкретно изучаешь/читаешь?

Ответы>>379319

02 Авг, 14:21 #440 #379319

>>379316
Ну я ньюфаг, Винберга читаю где-то на середине. Еще изучаю матан, вот, например, я вопрос задал >>379041

Причем я задачи почти не решаю по минимуму, стараюсь как можно быстрее получить представление и дойти до анализа на многообразиях, потому что там, вроде как, используется алгебра и топология, а это то, что мне больше всего нравится в математике. Пока что из всей математики мне больше всего понравились point-set topology (всякую алгебраическую топологию еще не изучал) и алгебра (алгебра мне пока вся нравится). В итоге последние несколько недель получается так, что я целыми днями читаю и поглощаю информацию. Моя активность заключается в том, что я пытаюсь сам доказать теоремы из учебника, не читая доказательство. Как только я начинаю более-менее комфортно себя чувствовать с какой-то темой, я сразу же перехожу к следующей, в итоге мозг постоянно охуевает.

>>379316

> Иди на велике покатайся, поплавай, отдохни от умственного труда.

Я это все не люблю. Я бегаю, чтоб жирным не быть, но это занимает всего 1 час в день.

Ответы>>379321

02 Авг, 14:22 #441 #379321

>>379319

> задачи почти не решаю по минимуму

фикс: задачи решаю по минимуму

02 Авг, 14:23 #442 #379322

>>379310
Какой смысл все это делать. Ты что собираешься матан в ВУЗе преподавать? Если ты не будешь все это использовать, то со временем забудешь большую часть.
Попробуй лучше теоремы самостоятельно доказывать.

Ответы>>379323

02 Авг, 14:27 #443 #379323

>>379322
Я и так дохуя пропускаю. Если что-то мне не нужно для дальнейшего понимания, я это читаю по диагонали или вообще пропускаю. У меня есть конкретная цель - получение пререквизитов для анализа на многообразиях.

02 Авг, 15:23 #444 #379328

>>379155

>Вербит учась в школе уже публиковался по теме функционального анализа. Логично, что он это все осилил к 25 годам.

Но ведь функан это тоже картафан? Или в школе он еще не прозрел?

02 Авг, 15:34 #445 #379332

>>378899
Бамп, манон.

10 Кб, 732x203

02 Авг, 15:50 #446 #379334

>>379294
сам напейсал

выглядит пугающе, но кусок псевдокода посреди кучи формул - ещё хуже

02 Авг, 22:51 #447 #379362

>>379294

>https://en.wikipedia.org/wiki/Bitwise_operation#Mathematical_equivalents

Что за ёбанный пиздец? Какого хуя они решили что битовая последовательность обязательно является целым положительным числом в двоичной системе? Почему блядь не рассматривать её как вектор или многочлен над GF(2). Вообще непонятен предмет этой статьи.
Твой алгоритм надо выразить в виде обработки битовой последовательности, тогда он примет более удобочитаемый вид

03 Авг, 00:58 #448 #379371

>>378664
Если прообразы всех шаров неограничены, то образ любого отрезка - нигде не плотное множество. Тогда R^2 можно представить в виде счетного объединения нигде не плотных множеств (образов [-n, n]), но это не так по теореме Бэра (в учебнике Львовского это теорема 1.47 из 5-го листка)

Ответы>>379442

45 Кб, 1118x360

03 Авг, 13:46 #449 #379418

Что вообще означает последнее предложение на пикрелейтед? Я вообще ни разу ничего подобного не встречал. У меня догадка такая: рассмотрим изоморфизм: T(e_k) = s_k, где s_1, ..., s_m -стандартный базис R^m. Тогда должно выполняться следующее:
1) U открыто в V <=> T(U) открыто в R^m;
2) U открыто в R^m <=> T^{-1}(U) открыто в V;
3) T - гомеоморфизм.

Ответы>>379441

82 Кб, 641x874

03 Авг, 14:45 #450 #379441

>>379418
Короче, помогите понять доказательство. Что вообще за хуйня тут написана?

Ответы>>379444 >>379470

03 Авг, 14:53 #451 #379442

>>379371

> Если прообразы всех шаров неограничены, то образ любого отрезка - нигде не плотное множество.

Почему? Возьмем какой-нибудь шар. Почему не может быть, например, так, что прообразы рациональных точек шара лежат в отрезке, а прообразы иррациональных точек разбросаны по R каким-то непонятным образом?

Ответы>>379453 >>379592

03 Авг, 15:06 #452 #379444

>>379441

>Короче, помогите понять доказательство. Что вообще за хуйня тут написана?

Так а что собственно непонятно?

Ответы>>379445

03 Авг, 15:12 #453 #379445

>>379444
Ну, допустим, я понял как отождествить V с R^m. Введем такую топологию, что изоморфизм V на R^m - гомеоморфизм. А почему норма непрерывна в этой топологии?

Ответы>>379454 >>379456

03 Авг, 16:13 #454 #379453

>>379442
Непрерывности не будет?

03 Авг, 16:20 #455 #379454

>>379445

>Ну, допустим, я понял как отождествить V с R^m

Что значит допустимс? Это одно из основных утверждений линейной алгебры курс за первый.

Ответы>>379461

03 Авг, 16:35 #456 #379456

>>379445

>А почему норма непрерывна в этой топологии?

Почему норма непрерывна в стандартной топологии R^{k}? На этот вопрос дает ответ первая выкладка в твоем пике.

Ответы>>379461

03 Авг, 17:02 #457 #379461

>>379454
Ну я не тупой, я про топологию спрашиваю, а не про изоморфизм векторных пространств.

>>379456
Ну вопрос в том и заключается: почему эта выкладка показывает, что норма непрерывна?

03 Авг, 17:42 #458 #379470

>>379441
Короче, местные эзотерики только кукарекать умеют и не могут даже понять доказательство из учебника для 1 курса. Что у Львовского написано я так и не понял, но немного модифицировал.

Рассмотрим изоморфизм T: R^n -> V.
1) Покажем, что T непрерывно в 0.
2) Для любого линейного отображения непрерывность в 0 эквивалентна непрерывности. Это доказывается через неравенство ||x| - |y|| <= |x - y|.
3) Так как T непрерывно, оно отображает компактное подмножество R^n { x_1 e_1 + ... + x_n e_n : max|x_i| = 1 } в компактное подмножество V { x_1 v_1 + ... + x_n v_n : max|x_i| = 1 }, где v_1, ..., v_n - базис V.
4) Дальше доказательство такое же как в книге.

Ответы>>379471 >>379472

03 Авг, 17:47 #459 #379471

>>379470
Забыл написать доказательство пункта 1:
|Tx| = |T(sum x_k e_k)| = |sum x_k T(e_k)| = |sum x_k v_k| <= sum |x_k| |v_k| <= (max |x_k|) (sum |v_k|).
Пусть sum |v_k| = M. Тогда для любого eps > 0 если max |x_k| < eps/M, |Tx| < eps.

03 Авг, 17:54 #460 #379472

>>379470

>Что у Львовского написано я так и не понял, но немного модифицировал.

>не понял, но модифицировал

Ответы>>379476

03 Авг, 18:05 #461 #379476

>>379472
Проблемы?

Ответы>>379480

03 Авг, 18:11 #462 #379480

>>379476
Забавляют подобные обороты речи.

03 Авг, 21:09 #463 #379592

>>379442

> Почему не может быть, например, так, что прообразы рациональных точек шара лежат в отрезке, а прообразы иррациональных точек разбросаны по R каким-то непонятным образом?

Потому что образ отрезка замкнут

22 Кб, 512x384

03 Авг, 22:20 #464 #379616

>>378396

>Так называемый insect-dub-punk

Кем называемый? Даже гугл про такое не слышал.

04 Авг, 02:53 #465 #379662

>>376017 (OP)
Насоветуйте записей видео, на которых решают всякие примеры и задачи из школьного курса математики, желательно с объяснениями. Можно и лекций по биологии, физике и химии, с разбором и решением задач. Что-то вроде видеоучебников.

Ответы>>379682

04 Авг, 05:25 #466 #379672

Как статьи пишутся, гомологи мамины?

Ответы>>379675

04 Авг, 07:30 #467 #379675

>>379672
Вчера статью написал о маскимальном расширении ануса твоей мамаши

04 Авг, 09:06 #468 #379682

>>379662
В /u посоветуют, у нас студенты не могут интегралы брать и поэтому пытаюсь оправдать свою безграмотность знанием топологии и гомологии.

Ответы>>379683 >>379686 >>379702 >>379738

04 Авг, 09:09 #469 #379683

>>379682
Набрался этих интегралов в универе, а тут извольте что-нибудь новенькое

04 Авг, 09:54 #470 #379686

>>379682
Вот ты серьезно думаешь, что кто-то итт не может взять интеграл? Или ты думаешь, что нужно уметь решать интегралы из тривиума Арнольда?

04 Авг, 12:03 #471 #379696

Пусть T: V -> W - линейное отображение. Что такое интеграл от T по V? Нагуглить не получается.

10 Кб, 368x168

3 Кб, 207x61

04 Авг, 13:27 #472 #379702

>>379682
Ну бери, раз такой умный.

Ответы>>379706

04 Авг, 13:58 #473 #379706

>>379702
Забористого картофана, ты Петрович принес, чует моя водофная глотка, что 50 и 51 это упражнения на вычеты, а во твой второй пик вообще обобщенная функция какая-нибудь.

Ответы>>379710

04 Авг, 14:19 #474 #379710

>>379706
Водовка с картофана.

Ответы>>379721

04 Авг, 15:11 #475 #379721

>>379710
На картофанных очистках.

323 Кб, 1280x1024

04 Авг, 16:56 #476 #379738

>>379682
/u&
Ничего не перепутал?

Ответы>>379742

04 Авг, 17:42 #477 #379742

>>379738
/un
У меня клава хуёвая, кнопки залипают.

Ответы>>379770

6 Кб, 144x155

04 Авг, 19:21 #478 #379760

Связаны ли как-нибудь теории гомологий координатного кольца многообразия и теории гомологий самого многообразия?

04 Авг, 20:09 #479 #379770

>>379742
Ого! Что-то я и забыл про такой раздел. Спасибо.

Ответы>>379819

05 Авг, 00:19 #480 #379819

>>379770
Тоже самое Воеводский сказал про калькулюс.

Ответы>>379821 >>379863

53 Кб, 892x508

05 Авг, 00:36 #481 #379821

>>379819

05 Авг, 12:57 #482 #379863

>>379819
Тоже самое Арнольд сказал про про вычисление интегралов на компьютере.

05 Авг, 16:53 #483 #379927

>>379134
http://verbit.ru/Job/HSE/Curriculum/all.txt
ТЫ СТАЛ МЕДЛЕННЕЕ

Ответы>>379947

05 Авг, 18:33 #484 #379947

>>379927

> В. Пополнение. P-адические числа. *Теорема Островского.

Дак кто-нибудь в итоге может объяснить, кому кроме теоретико-числовых петухов нужны p-адические числа? Почему Вербит так на них дрочит?

Ответы>>379954 >>379963 >>379983 >>380001

05 Авг, 19:31 #485 #379954

>>379947
Это элементарная грамотность, p-адические сюжеты встречаются всюду - от математической физики до алгебраической геометрии и теории представлений.

Ответы>>379961

05 Авг, 20:13 #486 #379961

>>379954
А нахуя их изучать за несколько лет до того, как они понадобятся? Вербит же их предлагает изучать одновременно с вещественными.

05 Авг, 20:20 #487 #379963

>>379947
Удваиваю вопрос, хотя не в курсе интимной жизни Вербита, кроме эпизода с дилдаком, и не знаю, на что он там дрочит и дрочит ли конкретно на падики.

05 Авг, 21:30 #488 #379983

>>379947
ПСИХОЛОГАМ!

Ответы>>379987

05 Авг, 21:49 #489 #379987

>>379983
Но зачем?

Ответы>>380193

17 Кб, 1068x129

41 Кб, 1107x588

05 Авг, 21:51 #490 #379988

Давайте еще задачу из Львовского решим. Ответ я уже знаю: (D Inv)_X(∆) = -X^-1∆X^-1. Я погулил inverse of matrix sum и на MSE дают ссылку на статью с формулой для (A + B)^-1. (A + B) невырождена для невырожденной A и достаточно малых B, так как GL_n(R) открыто. В итоге я получил решение на пикрелейтед 2.

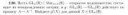
Но скачать статью нельзя, поэтому я не знаю доказательство этой формулы. Наверное, Львовский че-то другое имел в виду? Как без этой формулы решить?

Ответы>>379991 >>380014

05 Авг, 22:11 #491 #379991

>>379988
Бля, я объебался, нет такой формулы для trace. Но ничего страшного: все элементы ∆ стремятся к 0, поэтому trace ∆X^-1 -> 0.

05 Авг, 23:38 #492 #380001

>>379947
Это просто единственный результат, который могут предложить "первокококультурщики" в качестве примера своей собственно кококультуры новичкам так, чтоб у них глаза из орбит не вылезли и они не забросили всю математику вообще нахер. И то так себе примерчик, на олимпиадчину похоже.

06 Авг, 00:46 #493 #380014

>>379988
Проще вывести, дифференцируя X*X^-1 = Id

Ответы>>380659

22 Кб, 800x600

06 Авг, 16:02 #494 #380123

Есть формула для Липшицевойо функции из, скажем, R² в R², проведённой через заданные точки? Что-то ничего в голову не приходит.

Надо как на рисунке

Ответы>>380128 >>380129 >>380190

06 Авг, 16:07 #495 #380128

>>380123
Если что, слева регулярная сетка. Справа произвольный набор точек (удов. липшицеву словию, конечно)

06 Авг, 16:08 #496 #380129

>>380123
А, придумал, кажись. Буду отображать треугольники в треугольники при помощи барицентрических координат. Должно србаотать?

1179 Кб, Webm

06 Авг, 20:48 #497 #380177

06 Авг, 21:18 #498 #380190

>>380123
y=Σ(yk•П(|x-xm|/|xk-xm|, m≠k)), подойдёт? Тут yk, x, xk обозначает весь набор координат, суммирование по k, умножение по m.

Ответы>>380213

06 Авг, 21:32 #499 #380192

Концепцию бесконечности поясните мне.

06 Авг, 21:35 #500 #380193

>>379987
Психоанализ формализовывать.

338 Кб, 1280x1024

06 Авг, 22:35 #501 #380205

Помогите найти текст.
Несколько недель назад начал читать довольно интересно и просто написанную ПДФ-ку (кажется), озаглавленную примерно как "Современный анализ", или может "введение в анализ" или что-то в этом роде.
На русском.

Начиналась с краткого изложения топологии, понятий непрерывных функций, пределов и прочего, как в это треде любят.

Но я её потерял, блжад! Ни в истории браузера, ни в документах не найти. Может, у кого есть в закладках похожее?

Ответы>>380209 >>380212

06 Авг, 22:48 #502 #380209

>>380205
Единственное что приходит на ум это Дьедонне "Основы современного анализа"

Ответы>>380211 >>380214

06 Авг, 22:55 #503 #380211

>>380209
Не, там что-то недавно написанное было и довольно маленькое. По объёму скорее большая методичка чем полноценный учебник.

168 Кб, 631x1080

06 Авг, 22:56 #504 #380212

>>380205
Объём какой?
Пригодно для чтения без знания обычного изложения анализа? Или изложения уровня введения гамма-функции не зная обычный факториал?

Ответы>>380214 >>380215

06 Авг, 22:57 #505 #380213

>>380190
Что-то я не думаю, что оно будет не "растягивать"

06 Авг, 22:59 #506 #380214

>>380209
<- >>380212

06 Авг, 23:07 #507 #380215

>>380212
Чем тебе гамма-функция не угодила?!

48 Кб, 634x765

09 Авг, 12:52 #508 #380568

Нигилизм и низовой юмор неразделимы, но последняя волна т.н. edgy (острый, неудобный) content (сетевой креативчик) это уже совсем экстрим. речь даже не о баттл-предъявах за мамку, нет, каждый третий мем намекает на суицид — эти шутки как игры с бритвой, действительно, острее не придумаешь. Смерть выступает в сверхкоротких анекдотах единственно существующей реальностью, к которой палитра перснажей — всех полов и возрастов — стремится изо всех сил.

По семантике мемов не так много исследований и очень редко они бывают своевременными — академическое запаздывание в два-три года обесценивает усилия в случае со сверхмобильной и еженедельно мутирующей средой. В потоке ярких картинок можно вычленять ключевые образы для поколения го: лягушки на велосипедах и без, покемон цирроз, абстрактный асбест, ликующий Дональд Трамп и стрелки из школы в Колумбине. Мемы это намного больше чем просто фольклор, это среда коммуникаций для миллионов по всему свету — хуматон общается мемами, нанизывая их друг на друга, их анализ — это не интерпретация отражений мыслевспышек из внутреннего мира, а непосредственный доступ к сознанию. На эту тему высказывался Пепперштейн, подражая Проппу пытался выявить морфологию мема музыкальный критик Горбачев, но что может сделать один человек с фрактальным пространством, извивающимся в непрерывной рекомбинации панчлайнов? Осенью закончу большую работу о пространстве мемов, сделанную в соавторстве в московскими коллегами — похоже, что нам удалось подобрать точную топологическую модель. Но сейчас хочется бросить взгляд по ту сторону означаемого — вот, познакомьтесь, Грэм, гуманоид, который переживет любую автокатастрофу; даже самую яростное соитие машин не сможет переломить его отсутствующую шею.

За несколько недель Грэм стал новым символом интернет-сообщества, его последовательно — так во Франции носили победителя турнира на руках — встраивают во все существующие мем-контексты, его любят и ненавидят, в нем видят свое будущее и пытаются от него отшутиться. Соль шутки в том, что Грэм — это уже настоящее.

Недавно я был в гостях у такого Грэма — мы встретились на улице: здоровяк, настоящая мясная машина, с широким подбородком и размашистыми плечами. В его фигуре было что-то нескладное, что я понял, только когда мы вошли к нему — он упал на диван как трансформер, приняв истинное обличье. Его живот оказался удобной подставкой для ноутбука, подбородок ушел в грудь, полностью скрыв шею, а спина согнулась дугой — одной рукой он стучал по клавиатуре, отвечая на сообщения в неисчислимых чатах, а другой скручивал косяк. Он спросил меня, не знаю ли я где нанять людей, которые бы собрали его вещи для переезда — я покачал головой. Он плаксиво заметил, что не хочет тратить время на такую ерунду, ведь у него есть много более интересных занятий — и затянулся так, что обжег пальцы. В процессе разговора, который — если время ото времени его не выравнивать — спиралью уходил к воспроизведению мемов, кубов и вайнов, он обмолвился о своем слабом темпераменте, мол, у него не получается останавливаться: и впрямь, большего кайфожора мне сложно представить — за полтора часа он успел приделать пару литриконов пива, полграмма химического гашиша и несколько дорожек какого-то порошка. Наркотики, впрочем, он предпочитает исключительно те, что не имеют психоделического эффекта — больше всего он дорожит своим видением мира, ведь ему и так стоило стольких часов бизнес-тренингов и чтения мотивационной литературы, чтобы выстроить систему координат. Он не считает денег, но вместе с тем неразборчив в еде и в развлечениях, предпочитая всем видам искусства лихие атракционы, которые давно оккупировали кинотеатры и постепенно захватывают театральную сцену. Свой профессиональный род занятий он характеризирует не иначе как "полезного паразита", перекачивая потоки рекламы, давно уже ставшей самостоятельным ресурсом, из одних мест в другие — "все просто, ты идешь в контору, даже если не справляешься за три месяца, тебя берут в следующую на должность повыше и с лаве пожирнее, там еще три месяца и через год у тебя может быть поллмиллиона в месяц при том, что никто не будет понимать за что", — посмеиваясь, обронил мой собеседник.

Таких и впрямь любит современный мир, они идеальные реципиенты будущего, его баловники и пророки. Хуматоны, вечно сидящие в смартфонах, передвигающиеся только на такси, заказывающие еду на дом — они интериоризировали все функции кроме зарабатывания денег, которую тоже следует рассматривать как переработку сырья — колоссальной индустрии производства нужны свои ударники потребления, спасающие переполненные склады и магазины. Тем страннее читать, что кто-то считает их проводниками революции — Пол Мейсон пишет о том, что глобальное переустройства придет не слева и не справа, оно выпрыгнет из нашего кармана, где свил гнездо мегамощный смартфон; что интернет похоронит капитализм; что Грэм — это гражданин дивного нового мира, где не будет денег и насилия. К своей идее техноутопии Мейсон приплетает Маркса, ссылаясь на его малоизвестную работу «Отрывку о машинах», написанной в 1858 году. Автор «Капитала» описывает экономику, основанную на «автоматической системе машин», которая целиком бы обеспечивала производительность, людям бы оставалось лишь «наблюдать и предохранять от помех». Главная производительная сила в такой экономике — это «всеобщее общественное знание» или «всеобщий интеллект», то есть достижения науки и прогресса, обеспечивающие производительную мощь машин. Понятно, к чему клонит Мейсон, но он хитрый адвокат новой технокаббалы, призванный польстить Грэмам из золотого миллиарда тем, что заказывая пиццу по телефону, которую повезет сквозь толчею в метро узбек в униформе, они приближают конец капитализма. Маркс писал совсем о другом, он писал об освободительной классовой борьбе, без которой не может произойти изменение общества — и мы уже начинаем понимать, кто на кого пойдет с булыжником и вирусным контентом — чтобы перепрошить его в нужную сторону и нужно понять, как работает пространство мемов. Да, Грэмы не погибают в автокатастрофах, они вообще кого угодно переживут, они могут мучаться фантомными болями в шее и утренними отходняками хоть до ста лет, напихав в себя консервантов и антибиотиков до полной муммификации — но настанет день, и мы им поможем. Пусть терапия мемами о смерти подготовит их к этому дню.

48 Кб, 634x765

09 Авг, 12:52 #508 #380568

Показать весь текст

Ответы>>380606

09 Авг, 14:29 #509 #380606

>>380568
Но мумификация пишется без удвоенной "м".

55 Кб, 822x592

09 Авг, 14:37 #510 #380612

посоны, как относитесь к такому http://www.chronos.msu.ru/old/RREPORTS/kaminskiy_incompleteness_book.pdf ?

сначала, подумал, что он наркоман, а с другой стороны наркоманы ведь тоже люди

Ответы>>381080 >>381084

09 Авг, 16:40 #511 #380659

>>380014
Спасибо, получилось.

11 Авг, 18:56 #512 #381080

>>380612
это не science, это философия, возможно, псевдо-.

Ответы>>381084

11 Авг, 19:53 #513 #381084

>>380612
Это было один-в-один у одного чувака из американского университета, имя забыл. Что-то там по тегам quantum physics consciouusness conscious agents

>>381080
Не.

Ответы>>381105

11 Авг, 22:54 #514 #381105

>>381084

>Это было один-в-один у одного чувака из американского университета, имя забыл. Что-то там по тегам quantum physics consciouusness conscious agents

напоминает название обосанной со всех сторон теории пенроуза и хамероффа

Ответы>>381139

12 Авг, 09:15 #515 #381139

>>381105
Да оно вообще много чего напоминает, дело же в формализации.

А оп что, сдох, кстати?

Ответы>>381143 >>381145

# OP 12 Авг, 11:19 #516 #381143

>>381139
См. удалённую дискуссию в конце треда.
https://arhivach.org/thread/188358/

Ответы>>381155

12 Авг, 11:38 #517 #381145

>>381139
Анимеха-оп обиделась что запретили срать нерелейтедом и хлопнула дверью но по прежнему сидит итт

Ответы>>381155

12 Авг, 11:40 #518 #381148

https://2ch.hk/sci/res/381147.html (

М)
https://2ch.hk/sci/res/381147.html (

М)
Перекатил.

Ответы>>381155

12 Авг, 12:19 #519 #381155

Хм. Ну я тогда тоже сваливаю с этой параши. Маттред был почти единственным островком интересных вещей в этом море школобалаболов, и маттред у меня четко ассоциируется с его опом. Он молодец хоть мы с ним и срались часто, а на аниме-картинки мне как-то похер. Я их так и не заметил, кстати, даже в архиваче.

>>381143
Оставь здесь ссылку, если перекатишься на другой ресурс.

>>381145
Ну и правильно сделал.

>>381148
НЕЛИГИТИМНАА!!11

Ответы>>381156 >>381172 >>381176

12 Авг, 12:24 #520 #381156

>>381155

>НЕЛИГИТИМНАА!!11

Ты предлагаешь ждать, когда ОП-анимеха одумается и начнёт создать треды?

Ответы>>381157

12 Авг, 12:26 #521 #381157

>>381156
Нет, я ничего не предлагаю. Я же написал все выше, посмотри. Ну или лучше не смотри, а забей.

# OP 12 Авг, 13:50 #522 #381172

>>381155
Перееду в /u/ Доброчана.

Ответы>>381176 >>381220

12 Авг, 14:31 #523 #381176

>>381155
>>381172
Да скатертью по жопе уже, задолбали. Такие люди всегда прощаются десять тредов и не уходят.

12 Авг, 17:59 #524 #381220

>>381172
Окай.

Обновить тред