Это копия, сохраненная 5 января 2017 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.

Смотри, хуйня какая.
Есть у нас, скажем, точка А (x1, y1). Кроме того у нас есть еще и точка B (x2, y2). Есть еще и угол alf.
Надобно нам найти точку C (ейные координаты x3, y3), причем такую точку, чтобы угол CAB = alp, а угол ACB = 90°.
Путем нехитрых умозаключений получаем вот такую формулу:
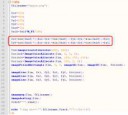
x3=cos(alf)((x2-x1)cos(alf)-(y2-y1)sin(alf))+x1;
y3=cos(alf)((x2-x1)sin(alf)+(y2-y1)cos(alf))+y1;
если разметка похерится - вторая пикча (на символ $ внимание не обращай - специфика PHP). Вполне себе получается найти такую точку - первая пикча.
Это все круто, хорошо и отличненько. А как мне туда еще координату Z добавить? Ну, понятно, что теперь кроме угла alp (который в плоскости поворачивает вектор) добавить еще угол bet (который саму плоскость вращает). Только я че-т туплю немношк, как его туда добавить)))



Ну вот и как ты догадался-то?
Короче, вот эту херню
http://xcontcom.livejournal.com/6010.html
хочу сделать для 3-х измерений, ну и чтобы его прям в браузере можно было вращать, как вот здесь:
http://xcont.com/3d.php
Жалко, что только 3Д в перспективе, нет конопочки "изометрического 3Д", это было бы в 100 раз информативней

Вокруг линии должна красная сфера получиться: http://xcont.com/sphere.html причем так, чтобы линия через центр сферы проходила.
Не получается. Че-т вообще какой-то бред выходит.
О, так ты прям он, видел твой пост на хабре, вдохновил тогда :3 У меня есть такое впечатление, что у твоей штуки есть практическое применение, именно потому что она простая, но о фракталах. В последнее десятилетие появились работы в медицине, о диагностике раковых опухолей по их фрактальной размерности. Анализ картин от сканирующего микроскопа показывает четкое отличие опухолей от здоровой ткани по этому параметру.
Ну, и если абстрагироваться, как мы там получаем эти картины (тут массовые технологии ещё не доползли), то их анализ можно проводить сетью, наученной строить фракталы твоим алгоритмом и сличать с заданной картинкой. Как только сети кажется, что она нашла фрактал размерностью "похожей" на то что на картинке - выдается результат. Тут в чем удобство, элемент построения твоим способом - это же просто бинарная матрица 2х2. А значит рассчеты можно проводить очень быстро и анализировать огромные массивы.
Если б ещё была хорошая технология получения данных, что-то типа УЗИ, но с разрешением на порядки выше, чем сейчас.
Ну это всё просто мысли вслух.
Лол, отрыл бумажные очки, порадовался 3Д

>>355241
Таки получилось.
Зеленая линия проходит через центр сферы. Синие линии сходятся в центр оси вращения.
Каких-то несчастных 1296 точек, а ресурсы отжирает ппц. Походу WebGL надо курить.
Не специально, не специально, без злого умысла. Впрочем читать не очень хочется, но код чего-то подобного в триде посмотреть очень хочется.
Ну про фракталы-то про свои что-то знаешь. Ну я вот 2д повозюкал мышкой. Получатся, генерируется какая-то группа фракталов, но она конечная? Ну, если бы у меня был бесконечный монитор и я все вел и вел мышку, куда-то в сторону, я бы увидел что фракталы повтояются, просто более детальные?
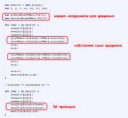
>Не понимаю как вообще подключать канвас в похпе, через что подключается
В похапе канваса нет. В похапе можно чего-то посчитать, в цикле через echo сформировать массив (не html-код, а JS) и в браузере, через JS с ним уже работать. Ну или если Ajax используешь - упаковал массив на сервере с помощью json_encode и дальше его используешь в JS как обычный массив.
>как строить тридерисунок.
На примере вот этой сферы: http://xcont.com/sphere.html
Есть у нас массив точек с разными координатами (x, y, z), которые нам надо за-3d-шить. Просто так нам их 3d-шить скучно - мы их хотим мышкой вращать. Поэтому подключаем addEventListener('mousemove', function), в котором считаем координаты мауса (стандартный код, я его вообще из википедии где-то дернул). Функция возвращает X и Y координаты мышки. Координату X будем использовать для вращения по одной оси (угол альфа), координату Y - для вращения по другой оси (бетта). Берем эти координаты и тупо умножаем на какой-то коэффициент (скорость вращения, грубо говоря). Получаем соответствующие углы. Далее, путем нехитрой тригонометрии, для каждой из точек (x, y, z) применяем формулы вращения из википедии:
yy=y∙cos(alfa)-z∙sin(alfa);
zz=z∙cos(alfa)+y∙sin(alfa);
z=zz;
xx=x∙cos(betta)+z∙sin(betta);
zz=z∙cos(betta)-x∙sin(betta);
y=yy;
x=xx;
z=zz;
Получаем новые координаты для каждой точки. Теперь надо нарисовать 3d-проекцию каждой точки. Как проекция работает? Все, что дальше - меньше, все что ближе - больше. Соответственно, координаты дальних объектов находятся ближе к центру (к оси, через которую якобы твой глаз проходит). Как сделать такое колдунство в канвасе? делим координату x на z и делим координату y на z. Получается, чем больше z (чем дальше от нас точка находится) - тем меньше координаты x и y, относительно центра координат. Ну а поскольку все эти вычисления мы производили относительно центра координатных осей, остается нам к каждой x добавить canvas.width/2 и к каждой y добавить canvas.height/2. После чего используем функции JS (moveTo, lineTo - если точки линиями надо соединять или fillRect - если рисовать одни точки) для рисования внутри канваса.
>Что прочитать для этого нужно?
Википедию

>Не понимаю как вообще подключать канвас в похпе, через что подключается
В похапе канваса нет. В похапе можно чего-то посчитать, в цикле через echo сформировать массив (не html-код, а JS) и в браузере, через JS с ним уже работать. Ну или если Ajax используешь - упаковал массив на сервере с помощью json_encode и дальше его используешь в JS как обычный массив.
>как строить тридерисунок.
На примере вот этой сферы: http://xcont.com/sphere.html
Есть у нас массив точек с разными координатами (x, y, z), которые нам надо за-3d-шить. Просто так нам их 3d-шить скучно - мы их хотим мышкой вращать. Поэтому подключаем addEventListener('mousemove', function), в котором считаем координаты мауса (стандартный код, я его вообще из википедии где-то дернул). Функция возвращает X и Y координаты мышки. Координату X будем использовать для вращения по одной оси (угол альфа), координату Y - для вращения по другой оси (бетта). Берем эти координаты и тупо умножаем на какой-то коэффициент (скорость вращения, грубо говоря). Получаем соответствующие углы. Далее, путем нехитрой тригонометрии, для каждой из точек (x, y, z) применяем формулы вращения из википедии:
yy=y∙cos(alfa)-z∙sin(alfa);
zz=z∙cos(alfa)+y∙sin(alfa);
z=zz;
xx=x∙cos(betta)+z∙sin(betta);
zz=z∙cos(betta)-x∙sin(betta);
y=yy;
x=xx;
z=zz;
Получаем новые координаты для каждой точки. Теперь надо нарисовать 3d-проекцию каждой точки. Как проекция работает? Все, что дальше - меньше, все что ближе - больше. Соответственно, координаты дальних объектов находятся ближе к центру (к оси, через которую якобы твой глаз проходит). Как сделать такое колдунство в канвасе? делим координату x на z и делим координату y на z. Получается, чем больше z (чем дальше от нас точка находится) - тем меньше координаты x и y, относительно центра координат. Ну а поскольку все эти вычисления мы производили относительно центра координатных осей, остается нам к каждой x добавить canvas.width/2 и к каждой y добавить canvas.height/2. После чего используем функции JS (moveTo, lineTo - если точки линиями надо соединять или fillRect - если рисовать одни точки) для рисования внутри канваса.
>Что прочитать для этого нужно?
Википедию
Не при чем вообще. Я его использую, если что-то по быстрому нарисовать надо - он удобнее, чем JS.
Сейчас понял, что смущает. У тебя в 3д алгоритм отражает луч от стенок двух плоскостей, а стенки третьего измерения не замечает.
Ну тогда хз, значит какое-то свойство. Если смотреть без перспективы и перпендикулярно (т.е. всего 6 таких точек обзора), то периоды и линии, понятное дело, сливаются в решетку. Но на одной из осей эта решетка всегда намного реже, "выглядит проще", чем на остальных осях, вне зависимости от чисел

>>355456
Вот об этом я говорю. Вся сложность фрактала как бы остается в двумерной плоскости, а сама эта плоскость приломляется в 3д. А мне казалось, что должны то получаться кубические структуры
У вас синусы-косинусы зря столько раз рассчитываются. Их можно посчитать один раз на поворот.
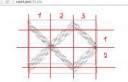
На пикче две стороны имеют общий делитель (7х3 и 7х2)

Как? Тригонометрию в школе прогулял. В /pr/ пишут, что я шизик.
>Скажи, насколько ясно ты понимаешь, что ты шизик?
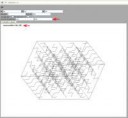
Как-то так. Можно указать параметры камеры по умолчанию
Ну это, ты вообще с синусами-косинусами делаешь, потому что планируешь в расширениях модели менять угол отражения? Потому что, если всегда будет 90 градусов, ты мог просто сделать трехмерный бинарный массив [x,y,z], задать бинарную матрицу, которая диагонально ставит true в точках этого массива, задать правила перемещения этой структуры - которые есть просто диагональное смещение по массиву и задать правило поворота , если матрица достигла границы массива, там просто симметричный поворот "красящих элементов матрицы" (всего два варианта - диагоналей то в матрице две) + изменения правила перемещения матрицы (всего 6 вариантов, для каждой границы). Ну и всё, как алгоритм завершился, рендеришь массив - каждая точка это пиксель. Будет намного быстрее всё.
Собственно говоря, если накодишь структуру матрицы довольно абстрактно и потом ещё подумаешь немного, то ты можешь матрицу делать не квадратную, это и будет изменением угла падения, если оно тебе понадобиться.
А, Серега, ты, ну привет.
Похер на тригонометрию. Ты тупо считаешь 100500 раз то что можно посчитать один раз. Например генеришь сферу каждый такт. Нахуя? Сгенерь ее один раз в массив точек и потом вращай ее готовую как хочешь. Потом ты считаешь поворот для каждой точки, когда можно посчитать один раз поворот сразу для всех точек. Еще можно упростить отрисовку точки не прямоугольником, а сразу пикселем.
Ну ладно тебе, перфекционист. Это все детали, важные только для прикладного применения. Не думаю, что у кого-то калькулятор настолько, что тормозит (хотя сфера торомозит заметно, лол). Человек показал красивую структуру. Я второй день любуюсь, уже столько всяких применений придумал, и распознавание образов, и конструирование микро-фильтров, клапанов, логических наноэлементов, работающих на статическом электричестве. Я тебе говорю, эта штука ляжет в основу многих вещей, но технологии ещё не дошли. Можешь скринить.
Ок. Сферу отдельно можно посчитать, упаковать в массив и уже туда в функцию передать, где ее вращать мышкой.
>Потом ты считаешь поворот для каждой точки, когда можно посчитать один раз поворот сразу для всех точек.
kak?
>сразу пикселем.
Канвас не может же в пиксели.
А вот если тот паттерн на стеклышко маленькими штришками нанести, аки решетка дифракционная и лазером туда потом светонуть?
>Сферу отдельно можно посчитать, упаковать в массив и уже туда в функцию передать, где ее вращать мышкой.
http://xcont.com/sphere_test.html
Не заметил разницы.
Лол, ну нет. А за наводку спасибо, отряд космодесанта уже вылетел покарать еретика.
/me троллил этого мудака ещё до того, как это стало мейнстримом.
>kak?
Просто считай все косинусы-синусы отдельно от цикла перебора точек. Они долгие эти синусы их частый расчет нужно избегать.
>Канвас не может же в пиксели.
Да, но можно применить хитрый костыль.
Вот небольшой пример как можно быстро вращать 100500 точек на холсте.
https://jsfiddle.net/zxv7gL8b/
Если быстроты все же не хватает то нужно юзать WebGl.
Наверное вывод точки в виде прямоугольника значительно более тормозной чем расчет синуса.
Таки прямоугольники больше всего ресурсов отъедают.


Кубик с таким паттерном можно гораздо проще сделать.
Заполняем пространство точками с одинаковыми интервалами между ними (по всем трем осям). Применяем преобразования 3D-перспективы:
xx = x ∙ focus/z
yy = y ∙ focus/z
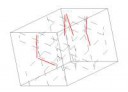
http://xcont.com/cube.html


3 dimensions
Все 6 -один и тот де " квадрат". уже не помню, что-то воде 81 82 83. А дальше - крутишь и ищешь
Круто
>>356077
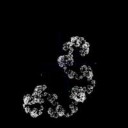
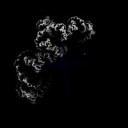
Cмотри, как интересно получается. Очевидная одинаковость этих двух структур происходит из одного правила, правила построения перспективы. А вот эти фракталы >>356026 произошли от того правила, которым браузер рендерит наложившиеся друг на друга точки структуры. Вот эти http://xcont.com/ фракталы получается простым правилом задания границы. Не может ли быть так, что в общем случае, задание любого правила - это и есть задать фрактал?
Множества - это фракталы, потому что правило построения теории множеств - это задание его элементов, а элемент любого множества - это элемент множества, лол, самоподобие же.
>>356151
Вы с ног на голову-то не ставьте. Фрактал - это частный случай множества с заданной на нем структурой, но не наоборот.
Ну ладно тебе, ну на секундочку поставили, все ж мы люди. Просто, ну если ставится, то это не проблема никакая, а просто провод задуматься. А структуры можно задавать, вообще не вдаваясь в теорию множеств, с этим хоть спорить не будешь?


>Возьмем, для примера, самую простую систему счисления - двоичную. Запишем цифры от 0 до 255 в столбик и раскрасим 1 черным цветом, а 0 - белым. Получим вот такой вот паттерн, который вполне обладает свойствами самоподобия
Да, ты крут, давно хотелось увидеть в повороте

Забавно. Углы чередуются на по порядку (45, -45, 45, -45), а как в последовательности Морса-Туэ (45, -45, -45, 45, -45, 45, 45, -45)

Похуй, так и оставлю. Всё выравнивается, если вместо двух углов указать 4 (45, -45, -45, 45)
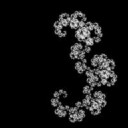
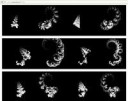
Ого! Объясни, что хоть происходит. Ну, там треугольник - это начало посторения, ну и дракон. А в кадрах между ними вообще происходит ?
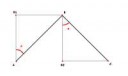
Ну смотри, как дракон Хартера-Хейтуэя строится.
Есть две точки A и C. Третья точка B - это пряма AC повернутая на угол 45° (альфа) и умноженная на косинус этого угла.
Получаем новые точки AB и BC. Для них проделываем ту же операцию (но чередуем углы 45° и -45°). (первая пикча).
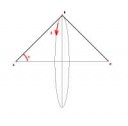
Для новых точек проделываем ту же операцию, в цикле, пока не надоест.
Это всё на плоскости. Как сюда третье измерение добавить? После поворота прямой AC на угол (альфа) получаем новую точку B и далее ее (точку B) еще раз поворачиваем на угол (бетта), но уже вокруг самой прямой AC (вторая пикча)
На гифке выше >>357128 угол альфа = 45° (и -45°). Угол бетта меняется от 180° до -180° с шагом 10°
Только я че-т не пойму, откуда там треугольник берется. Где-то направление вращения вокруг АС (по часовой/против) неправильно считается.




>неправильно считается
Признаться честно, лень искать. Назовем это не багом, а фичей)))
В том виде, как сейчас - больше вариантов фракталов получается.

>Они техмерные?
Те, что выше - двухмерные.
>Их можно повертеть онлайн на твоем сайте?
Вот сюда закинул:
http://xcont.com/geom3d/
Углы тупо через слеш (альфа/бета/альфа/бета/...):
http://xcont.com/geom3d/45/90/45/90/45/90/45/-90/ (пикча)
Дракон Хартера-Хейтуея, например:
http://xcont.com/geom3d/45/180/-45/180/-45/180/45/180/
Или вот этот >>356412 с первой гифки:
http://xcont.com/geom3d/45/90/
Если дохуя тормозит, вот тут:
http://xcont.com/geom3d_low/
"лайт"-версия. Можно на ней углы подбирать.
Угол альфа в пределах (-90°, 90°). Угол бета - от 0 до 360 (ну или от -180 до 180)
Еще пример: http://xcont.com/geom3d/45/210/
Количество углов можно любое вбивать:
http://xcont.com/geom3d/30/90/-60/90/-30/90/60/90/-30/90/60/90/30/90/-60/90/45/180/45/180/
Самые "ровные" фракталы получаются с углами:
30°, 45°, 60°, -30°, -45°, -60° (альфа)
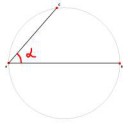
Наглядно. С любым углом альфа, точка C лежит на окружности (диаметр которой - AB).
Если угол альфа = 90° - точка C совпадает с точкой A
Если угол альфа = 0° - точка C совпадает с точкой B
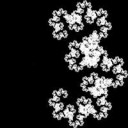
45,180
45,180
45,0
http://xcont.com/geom3d/45/180/45/180/45/0/
Последняя очень красивая.
>дохуя тормозит
Да, чуть тормозит.
Если тормоза критичны, то вместо вывода линиями воспользуйся вот такой оптимизацией:
https://jsfiddle.net/jkage0db/embedded/result/


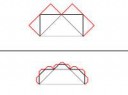
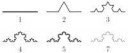
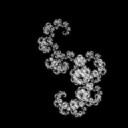
Не, смотри прикол. Тут, на каждой итерации, к каждым двум точкам только одна добавляется (верхняя часть пикчи - одна точка, нижняя - две).
В той же "Снежинке Коха" (вторая пикча) таких точек три.

[45, 0], [45, 0], [45, 0], [45, 0], [45, 0], [45, 0]
[45, 0], [45, 0], [45, 0], [45, 0], [45, 0], [45, 180]
[45, 0], [45, 0], [45, 0], [45, 0], [45, 180], [45, 0]
...
[45, 180], [45, 180], [45, 180], [45, 180], [45, 180], [45, 180]
Или ОП открыл общий способ строить любые фракталы? Или это просто так проявляется самоподобие, то общее, что есть у любого фрактала, вне зависимости от способа построения?

30, 30, 30, 60, 60, 60
Тормозит сам вывод context.putImageData(canvasData, 0, 0);
Короче при больших размерах холста эта гореоптимизация не поможет.
Если нужны просто четкие пиксели, то рисуй однопиксельные прямоугольники четко на пикселе.

Та не, норм оптимизация. Удобно цвета можно указывать.
Ты JS хорошо шаришь? Не могу сообразить, как мне канвас с аяксом подружить. При нажатии на кнопочку сервак должен отдавать новую порцию углов, которые надо передать туда в канвас. На пикче исходник (или вот тут http://pastebin.com/GJnc49np )
На ум приходит только сделать скрытое текстовое поле - туда ответ аякса записывать и каждый раз в канвасе оттуда углы дергать.
>Ты JS хорошо шаришь?
Я его практически не знаю. Так только немного базовый уровень. Спроси лучше в программаче или вебаче.
Все. Разобрался.
Там надо было var angls вынести перед window.onload=function() и в Ajax-ответе убрать var перед angls
Трудно сразу на двух языках программировать. В PHP глобальные переменные работают иначе.
>Трудно сразу на двух языках программировать
Ох...
Не позорься, прочитай хоть какую-нибудь книжку про программирование, пожалуйста.
ага
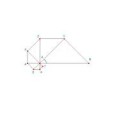

Мне кажется, все не так просто.
Кстати, смотри прикол. Точка 1 - это поворот точки B вокруг точки A на угол альфа. Следующая точка 2 - поворот точки 1 на этот же угол (!!!). Точка 3, 4 и т.д. - тот же угол.
Если, после каждого поворота, увеличивать (уменьшать) этот угол на определенное число?
На гифке уменьшаю этот угол на 0.0001° (!) в диапазоне от 0° до 0.009°
Да хоть через imagecreatetruecolor - какая хер разница? Проекция каждой точки высчитывается по формулам.
Но рисую я через JS canvas - там мышку можно приделать, в отличии от php
Мужииик, если тебе не трудно, а ты можешь вращение повесить на клавиши WSAD, а на мышку - изменение углов? Вот это будет вообще полное погружение.

>Какие именно изменять?
Ну да, задачка не простая, прямо скажем, дизайнерская. Пример интерфейса на пикрелейтед
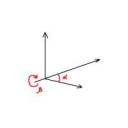

Углы парами идут. Таки лучше делать, чтобы один из углов менялся кнопками A, D, а второй - W, S. Но над этим завтра буду соображать.
>>361539
>анаглиф
Цвета не могу корректно подобрать для черного фона: http://xcont.com/geom3d_anagl/60/255/70/15/35/105/75/195/
>>361610
>Добавь автоматическую перерисовку
Done
>Цвета не могу корректно подобрать для черного фона
Есть немного, но в целом, быстро перестаешь шум замечать. Все равно фигура сразу внимание поглощает. Очень красиво, прям ух.
Если кому сильно мешает, вот можно контрастность монитора убавить - помогает; с цветностью поиграться ещё можно
Фон заменил на белый
Углов слишком дофига и все разные. Отсюда больше хаоса.
И таки да, если увеличить количество точек подобие будет легче заметить.
Вот тут:
http://xcont.com/geom3d_21/60/270/45/105/30/315/10/180/25/120/20/255/20/165/20/135
вместо 32770 точек, 2097154. Браузер может зависнуть.
По ссылке - не сильно тормозит, а вот уже на следующих фракталах - тормозит нереально, даже если довольно простые попадаются. Где-то что-то не оптимизировано
Походу, после отправки запроса на сервер, старый массив не успевает выгрузится из памяти до того, как сформируется новый. Засоряется кеш. Браузеры не предназначены для подобных вычислений.
Ну так, на вскидку, массив на 2^21 точек - 2097154 точек. Каждая точка записана 3-мя координатами - 6291456 значений. Каждое значение весит в JS 8 байт - 50.331648 мегабайт. Плюс еще 33.554432 мегабайт после рендеринга. 83.886080 мегабайта. Канвас тоже массивом отрисовывается (canvasData.data) - еще 67 метров... А вообще, у меня Firefox 500 мегабайт куда-то сливает. Скриптовые языки программирования - это черный ящик. Одному бозе известно, как реализованы доступ в память и сборка мусора в том или ином браузере.
Фракталы, фракталы повсюду
Да не то слово. Ты строил как в ролике, но убирал отрезки через один? А фрактал получается тот же. Отрежь от фрактала половину - получится тот же фрактал.
Даже не так. Как-то сложно эту мысль софрмулировать. Ну в общем это наблюдение. Как мы получаем фракталы? мы берем какой-то объект и задаем на нем какое-то правило построения, получаем другой объект - фрактал. Два разных правила - два разных фрактала. Но если мы задаем композицию двух таких правил, то получаемый третий фрактал, который содержит оба предыдущих фрактала в целости. И хоть миллион их скомбинируй, они друг друга "не испортят", всегда можно распознать любой отдельный фрактал, учавствовавший в построении исходного. Так мне кажется.
Или, блджад, не берем мы никакой объект изначально, а только правило построения примненное на себя - дает фрактал. Сука, с ним очень сложно, но фрактал - он о чем-то таком глубоком, об источнике, основаниях всего.
Почему но? Делал как в ролике. Разделил круг на n точек (количество - xMouse). Каждую точку соединил с точкой*k (k - yMouse/10). А где там фрактал?
У меня на этот счет немношк другое наблюдение)
Раз в месяц, чтобы не утонуло.
Самое время бампнуть!
Это копия, сохраненная 5 января 2017 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.