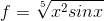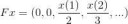Это копия, сохраненная 28 июля 2022 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
Программа Вебрита.
http://verbit.ru/Job/HSE/Curriculum/all.txt
http://imperium.lenin.ru/~verbit/MATH/programma.html
В этом треде мы изучаем математику, ну или начинаем это делать. Если ты школьник или студент, и тебя есть задача, то в здесь тебе помогут её решить или хотя бы скажут, в каком направлении двигаться для её решения.
Также приветствуется обсуждения самого процесса изучения и учебников/задачников
Архивы тредов
http://pastebin.com/kiRZGVHW
ВНИМАНИЕ! ВНИМАНИЕ!! ВНИМАНИЕ!!!
On-line LaTex. Формулы пишем в нём, а после прикрепляем картинками к посту
http://www.codecogs.com/latex/eqneditor.php
Львовский Набор и вёрстка в системе latex
http://www.mccme.ru/free-books/llang/newllang.pdf
Если ты только зашел в тред и хочешь спросить, какую книжку прочитать, то ответ, скорее всего, будет в этих списках, анон.
Список от ОП-а, бывшего тут до меня. Был составлен на протяжении 13 тредов, к ознакомлению обязателен.
http://pastebin.com/4iMjfWAf
Список от анона с dxdy. Довольно внушителен, тоже рекомендуется к прочтению. Является дополнением к списку старго ОП-а.
http://pastebin.com/YP1uaUyd
Goodbook.txt список книг с dxdy, рекомендованный тамошними обитателями.
http://pastebin.com/4FngRj6n
Литература - НМУ
https://docs.google.com/spreadsheets/d/1UWwIIAFwSwOQLK3m--LOaMOvHUivFDEz-JAnLa87i7Q/edit#gid=0
ОП-список 2. Составляйте список в реальном времени! Предлагайте в тред книги, критикуйте уже имеющиеся!
http://pastebin.com/szzZfkCM
Форчановский список, книги на английском.
http://4chan-science.wikia.com/wiki/Mathematics
Список с видеолекциями(в разработке):
http://pastebin.com/S3d7Jj6J
Качать книги тут:
http://libgen.io
А статьи тут(в разработке):
http://pastebin.com/3BfHPskz
Мемасы(в разработке):
http://pastebin.com/e38Yuj5V
СПИСКИ В РАЗРАБОТКЕ, НУЖНА ПОМОЩЬ АНОНА, ПОЖЕЛАНИЯ ОСТАВЛЯЕМ В ТРЭДЕ.
Книги из списков.
 267 Кб, 1280x956
267 Кб, 1280x956Правило Лопиталя, продифференцируй числитель и знаменатель.
Я вам математической этики принёс:
http://iphras.ru/uplfile/ethics/seminar/Lobovikov_15_12_2010.html
http://philosophy.nsc.ru/site/journals/55/В.О. Лобовиков.pdf
вот есть симплектическое многообразие (M, \omega)
как найти связность на TM без кручения, чтобы \omega была параллельной для связности, индуцированной на \Lambda^2 M?
долго смотрел на доказательство существования Леви-Чивита
не помогло
 79 Кб, 600x450
79 Кб, 600x450Хочу начать брать места на олимпиадах и вообще стать не обычным дношным отличником, который математики на самом деле не знает, а монстром. Хотя бы классе в 11 съедить на зэ всеросса, уже к 10 классу выступить на олимпиадах первого уровня за 11 класс или хотя бы половину из этого.
Те же просьбы и стремления у меня и в физике, я понимаю конечно, что тут доска для математиков, но даже Вербицкий писал, что математика нужна только как приложение к физике.
Поправка на то, что я живу в очень дальних ебенях и возможности ездить в летние школы и тем более ходить на олимпиадные кружки у меня нет.
Ну тогда сиди дома и выучивайся.
Пратусевичь Алгебра и анализ - очень много различных тем, которые могут тебе попастя на олимпиаде. Далее тебе нужно выучить олимпиадную алегбру и теорию чисел и комбинаторику, ну может ещё и олимпиадную геометрию. Книжку можешь сам погуглить книжки по тегам, но конкретно, я сказать не могу.
Что касается абитуриентских олимпиад -- это как ЕГЭ, только сложнее. Так что задрачивай уравнения с параметрами и прочую залупу, ну и просто задания прошлых лет посмотри.
Бля, тупой двач случайно отправил сообщение.
Так вот. Если будешь шарить в математике, то и с этой мерзостью скорее всего справишься.
Что касается всероса и нормальных олипиад (типа Турнира Городов), то там нужно знать комбинаторику, теорию чисел, графы. Ну и самое главное, нужно уметь быстро придумать хитровыебанное решение, потому что там шаблонных решений нет. Вообще, даже касаемо их, можно нихуя не знать математики кроме вышеперечисленной и всё тащить, главное сообразительность.
Насчёт физики -- я канешн забил на неё в своё время, но там вроде достаточно математический анализ знать и интегральчики брать. Ну и физику тоже знать. Учебник Ландсберга немного для даунов и слишком большой, но хороший и там есть всё необходимое.
А ещё если можешь деньги с обедов сэкономить, посмотри курсы на Фоксфорде, там мб есть что-то подходящее. Даже всякие поцанчики из илитных московских школ пользуются, так что это годнота должно быть.
>5503
Перебором x, очевидно же.
При x = 100,
твоё a уже будет иметь значение большее,
чем число Шеннона.
>А ещё если можешь деньги с обедов сэкономить, посмотри курсы на Фоксфорде, там мб есть что-то подходящее. Даже всякие поцанчики из илитных московских школ пользуются, так что это годнота должно быть.
Видимо потому что там преподователи -- авторы олимпиад. Хитрый план: делаю задачи для раскрученной индустрии @ продаю свои услуги по обучению решать эти задачи.
Аналитическая геометрия - линейная алгебра размерности меньше или равной три. По сути, частный случай.
Тот же вопрос к программе Миши Вербицкого:
Где брать литературу и годные лекции для изучения оного? Mathus не шибко катит, там самом разбираться и много времени терять.
На аналитической геометрии изучают аналитические многообразия, а нна линейной - линейные.
Собсна, сама задача: является ли множество поворотов правильного равностороннего треугольника подгруппой группы самосовмещений того же треугольника? Если да, то найти левые и правые классы эквивалентности, правостороннее и левостороннее разложение группы по подгруппе и выяснить, является ли группа нормальным делителем?
Является, ибо поворот - это самосовмещение, делаешь два различных поворота - снова получаешь поворот, обратный повороту - другой поворот.
В группе у тебя только 6 элементов, а подгруппа поворотов состоит из 3 элементов. Следовательно, могут быть только два класса - сами повороты и 3 отражения. Других быть попросту не может, ибо классы не пересекаются, а одним из классов точно является подгруппа поворотов.
Из этого следует нормальность.
Все самосовмещения треугольника - это группа S3, а повороты - это циклическая подгруппа в нём.
>>5561
Ты же знаешь, что такие классы не пересекаются, равны по количеству элементов (количеству элементов в той подгруппе, по которой ты разлагаешь) и охватывают всю группу? Группа порядка 6, подгруппа порядка 3. Разбиение на классы тут может быть только одно, неважно, лево или право - это сама подгруппа и три оставшихся элемента.
>Все самосовмещения треугольника - это группа S3, а повороты - это циклическая подгруппа в нём.
Ты путаешь понятия поворота и самосовмещения. Поворот в плоскости может быть на угол и не кратный 120 градусам, в то время как группа самосовмещений, являясь циклической, как раз-таки предполагает повороты исключительно на 120 градусов. Множество самосовмещений - подмножество множества поворотов.
Нет, он задавал вопрос по теории групп, я так понимаю? В геометрии повороты могут быть и не на 120, но в теории групп имеются ввиду те повороты, которые являются самосовмещениями. Все же самосовмещения включают в себя ещё и зеркальные отражения относительно 3 осей. Погугли группу Диэдра.
Это геометрическое представление теории групп, а не сама теория групп. Сложившейся терминологии не существует, каждый автор пользуется своими объяснениями. Поэтому естественно, в целях унификации, пользоваться геометрическими понятиями.
>Все же самосовмещения включают в себя ещё и зеркальные отражения относительно 3 осей
Ты изоморфные преобразования между собой различаешь? Зачем?
Нет, не различаю. Анон спросил про группу D3~S3, про неё и отвечаю.
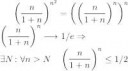 2 Кб, 254x142
2 Кб, 254x142Если нужно именно сравнивать, то можно с геометрическим рядом
root test, очевидно. увидь, что \sqrt{n}{a_n} это "второй замечательный предел", и стремится к 1/e < 1, так что всё сходится.
Про математику можно.
 229 Кб, 720x1280
229 Кб, 720x1280Подставь вместо AOC AOB.
Как его брать, и что если число a не целое?
 483 Кб, 850x1192
483 Кб, 850x1192Какие ваши советы мне будут? Конкретно интересует учебный материал.
Сейчас вот листаю Гашкова из оп поста.
Помогу, только расскажи немного как выбрался в зарубежный вуз?
Завтра 100% отвечать по частным производным функции. Матпрофи пролистал полностью. Понятного мало.
Где еще для дебилов на пальцах раскладывают?
 98 Кб, 937x244
98 Кб, 937x244лемма:
если p^2=2q^2, то p число четное. Предположим обратное, тогда p представимо в виде 2n+1, (2n+1)^2=2q^2
4n^2+4n+1 = 2q^2
2(2n^2+2n)+1=2q^2 - противоречие
 62 Кб, 627x436
62 Кб, 627x436И в последних двух не выходит найти несмещенную оценку: параметр не вынести. Как привести к виду b*A выражение вида http://www.wolframalpha.com/input/?i=((1-n)b+b^(1/2))/n ? Или что с ним вообще сделать
 19 Кб, 913x128
19 Кб, 913x128Упорядоченная пара - это (как ни странно) пара элементов, одна из которых из первого множества, а вторая - из второго.
Неупорядоченная пара - это когда {x,y} и {y,x} не различаются.
Если что-то найдешь дай знать.
Сперва это меня не слишком волновало, потому что это касалось вещей, которые я и так знаю, типа функции Эйлера etc, но в последнее время вдруг оказалось, что теорему о гомоморфизме например тоже доказывали в листочках, и я сильно опасаюсь, что скоро это выйдет за пределы моего знания.
Что это за листочки такие блядские?
в России это распространённый метод преподавания, когда часть материала выносится в списки задач (листочки), которые все обязаны прорешивать и сдавать.
придумал это Н. Константинов
http://polit.ru/article/2010/09/29/matheducation/
Один вопрос про базис пересечения подпространств, может помочь кто нибудь?
да
решений у этих задач нет, потому что это обесценило бы саму цель этих задач: они НЕ на изобретение изъёбистых трюков, а на применение только что введённых понятий.
Не буду. Мне надо к дифф. уравнениям в частных производных подобраться, в частности к Уравнениям мат. физики Самарского- Тихонова, зачем мне Вербит?
Упорядоченная пара - это социальный конструкт, никаких пар не существует, есть только морфизмы и объекты.
Есть какая-то возможность посмотреть на них, ну или хотя бы увидеть список теории, которую туда вынесли?
не знаю, кто такие самарский и тихонов, но решать PDE без знания линейной алгебры и какой-нибудь теоремы арцела-асколи точно невозможно
у вербита кстати есть курс по эллиптическим операторам в листковом формате, оч. хороший. назывется "теория ходжа" что ли.
а, вот
http://imperium.lenin.ru/~verbit/MATH/LISTKI/HODGE/
и более лайтовая версия того же
http://ium.mccme.ru/s10/funcan.html
Возьмем два элемента x и у. Построим, используя одну из аксиом zfc, такое множетво {{x},{x,y}}. Будем обозначать его так (x,y) и называть упорядоченной парой. Все.
Тебе нужно твои пространства в неявном виде переписать, так, чтобы получились две системы уравнений, и решить их объединенную.
Если ты прекратишь хипешить и подождешь еще полчасика, то я даже соображу как, для этого мне придется вспомнить линейную алгебру, поскольку я ее уже сто лет в глаза не видел. Может, за это время сам поймешь.
Да в том то и делоо, что я не могу понять. Хотя эта задача далеко не самая сложная, другие с матрицами легко решаю, а эту уже неделю не могу дорешать
>подождешь еще полчасика, то я даже соображу как, для этого мне придется вспомнить линейную алгебру
Жду
Ну ландсберг довольно годно объясняет всю школьную физику, хотелось бы найти такой же учебник по математике
А чем обычные школьные учебники не подходят? В голову только шень приходит и прасолов, охватывающие алгебру и геометрию.
>Элементы математики в задачах
>Математический анализ в 57-й школе
Тут http://www.mccme.ru/free-books/
Нигде нет. Только в печатном виде.
Есть в одном pdf файле?
Нахуя Бурбаки, когда есть ncatlab?
Смотри, немного через жопу, потому что я теории нихуя не помню, но как бы делал я.
Например, если тебе нужно найти плоскость, проходящую через две точки и начало координат в трехмерном пространстве, то ты просто берешь ax+by+cz=0, подставляешь туда две точки вместо (x,y,z), и находишь уравнение.
Тут так же само, только в первом случае одно уравнение с 4 неизвестными, в него нужно подставить три точки. Подойдут тупо значения базиса этого пространства.
Во втором случае размерность пространство не 3, а 2, значит уже нужно 2 уравнения.
Находишь коэффициенты в каждом случае, получаешь свои пространства в неявном виде, в первом случае одно уравнение, во втором - система из двух. Решаешь их совместно, и получаешь свое пересечение.
100 процентов можно как-то легче, через ядро отображения, я думаю, но это мне нужно вспомнить полностью теорию, а я ебал. Ну может еще подумаю, но попытайся пока что так.
через тор пробуй
Определить число троек слов (a,b,c) длины 12 в латинском алфавите, таких что:
a. два слова имеют 4 общих буквы и 2 слова имеют 3 позиции, символы в которых совпадают;
Как решать такое дерьмо?
Суть решения такова. Надо построить "дерево" возможных вариантов, и одну из ветвей надо довести до конца.
 38 Кб, 843x539
38 Кб, 843x539Все, вспомнил.
Каждую из матриц с базисными векторами просто реши как систему, я их красным обвел. Потом напиши общее решение через базисные вектора пространства решений. В первом случае это один вектор, во втором случае - два.
В принципе, по построению, эти вектора суть коэффициенты тех уравнений, про которые я говорил. Просто составь из всех троих матрицу и реши ее.
Как ты это будешь объяснять это формально, это уже другой вопрос.
Вы великолепны, спасибо, то что надо
Ну и ебанутое задание, не завидую. Проиграл с оговорки f = 0 когда решений нет.
Алимов 7-11 класс.
Справа минус синус пи на восемь.
Слева разность косинусов. Если его преобразовать в произведение синусов, то одно из слагаемых как раз и будет синус пи на восемь.
А вообще говоря, ты биомусор, ты понимаешь это?
Ах, да суммарная длина 52.
Пздц, ботаю математику С НУЛЯ, даже 0.01 Гротендика в день не набирается. Что же делать?
ты определись бля как можно определить множество упорядоченных пар, не используя слово "множество" вообще. хочу то, не знаю чего
Ну так котягориями низзя? Знач картоха.
 74 Кб, 650x800
74 Кб, 650x800О себе: 23 лвл дебил-вкатывальщик.
В школе был круглым дебилом и ничего не учил, собсна за недельку освоил программу 7 классов, научился решать уравнения, дроби, многочлены, графики, вот это все, но есть проблемка! Никак не могу решать задачки и составлять уравнения следуя условию, это фиксится вообще? Как лечить недуг?
>7 классов
Примерно такие задачи?
Расстояние между городами А и В равно 120 км. Город С находится между городами А и В. Из города А в город В выехал автомобиль, а через 36 минут следом за ним со скоростью 75 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из C в А, автомобиль прибыл в В. Найдите расстояние от А до С.
Охуенная тёлка, кстати.
На самом деле, меня самого от них воротит, ещё со школы. Топологию ботаю, а эти задачки раза с третьего решить получается.
Нам с восьмого класса примерно такие часто давали. Я долго разобраться с ними не мог.
Мне помог сайт этот:
https://math-oge.sdamgia.ru/test?theme=76
Там можно потренироваться варианты порешать по предметам и есть ГИА по математике, там как раз задачи такого плана есть.
С2, можно сразу в кучу выбрать их и решать, сразу же решение и ответ есть. Линк я дал на задачи на движения, есть ещё на работу например.
 195 Кб, 1500x1045
195 Кб, 1500x1045C.И.Туманов - Элементарная алгебра - 1970
Хуярю следуя этому учебнику + школьные учебники по алгебре Мордковича.
https://www.youtube.com/channel/UCOSK7BOX_onFvQiyj6Z_WrQ годнота, чек плейлисты, найдешь школьную алгебру и проч для нубасов.
https://www.youtube.com/channel/UCU5UBxAOqcXtviP3EsJrQ7A у этого чела есть каналы 7-11 класс, нормец поясняет.
 55 Кб, 751x210
55 Кб, 751x210Забыл пикчу
>ТОЛСТО.
Ну удачи йопта с соткой однотипных упражнений на каждую тему. При решение возникает чувство что из тебя делают калькулятор.
P=0=Q
Вполне неплохой учебник для лоу левела, не выебистый: Киселёв А.П. – Элементарная алгебра – 1906.
>Подлинной гуманизацией было бы именно возвращение к Киселеву. Он сделал бы математику вновь понятной детям и любимой. И этому есть прецедент в нашей истории: в начале 30-х годов прошлого века "устаревший" "дореволюционный" Киселев, возвращенный "социалистическим" детям, мгновенно поднял качество знаний и оздоровил их психику. И, может быть, помог одержать победу в Великой войне.
Что за шизофазию с сейчас прочел, ебаный насос!
>Зуланке, Городенцев, Кострикин, Ленг, Вандер Варден.
Я имел в виду лоу-лвл алгебру, которая описана в том же туманове
 18 Кб, 678x369
18 Кб, 678x369помогите пожалуйста, я не понимаю, почему wolframalpha мне строит график так странно, есть функция , и мне не понятно, почему она не определена на (3.14;6.28)? ведь там корень пятой степени, то есть нечётной, и следовательно,корень из отрицательного числа должен извлекаться. Так почему так странно строится график?
да, синус отрицателен, но корень у меня НЕЧЁТНОЙ степени, а корень нечётной степени должен извлекаться из отрицательного числа.
Конечно, дауны говорящие, КО-КО-КО КАЛЬКУЛЯТОР ВСЕГДА ИНТЕГРАЛЫ ПОСЧИТАЕТ КУДАХ, как всегда обосрались.
Скорее наоборот, вольфрам то считает всё как надо, просто кто-то вольфрамом пользоваться не умеет.
Корень - многозначная функция, ты должен указать вольфраму какое значение корня ты берешь.
напиши пожалуйста подробней, как мне задать функцию, чтобы она вывела правильный график.
https://www.wolframalpha.com/input/?i=surd(x^2*sin(x),5)
Функция surd принимает два аргумента, первый это функция, второй это тот корень который извлекаешь.
>Это выглядит убого
Твои эстетические переживания - последнее что меня волнует, пиздуй на нахуй, щегол ебанный.
 22 Кб, 952x385
22 Кб, 952x385теория меры
>это означает, что ты даун.
Логические суждения имбецилов меня мало волнуют, извольте пиздовать нахуй.
Ты хоть понимаешь насколько жалко видеть оскорбления в интеренете от человека, сагающего в тематики, при этом называющего кого-то имбецилом?
Загугли уже учебник по теории меры и просвещайся.
Это по определению. Можешь считать по-другому:
https://en.wikipedia.org/wiki/Whitehead's_point-free_geometry
 466 Кб, 1366x768
466 Кб, 1366x768Я нашел через медиану точку В(10,5)
И уравнение стороны АВ: 6x-7y-25=0
ЧТо делать с этой бисектрисой ебучей? Как через неё найти С или ВС
В кпи такому не учат штоле?
При нажатии на номер появляется решение, ну ты и сам это знаешь. Так зачем ты сюда пришел? Могу переслать решение с того сайта
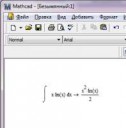
Маткад не может взять простой интеграл. Это баг такой или я уже ебанулся?
Нормальные люди не используют маткад, а делают либо сами (как и необходимо), либо через Математику (Максима, AXIOM).
>а делают либо сами (как и необходимо)
так и делаю. Просто есть привычка проверять себя в задачах на вычисление. И здесь всплыло вот это.
В данной ссылочке
http://www.antirelativity.dp.ua/pseudo_mathematic_01.htm
Парень утверждает, цитата
>Очевидно, что умножение является ускоренным сложением. При умножении двух отрицательных чисел мы получаем положительное число, т.е. здесь логика ускоренного умножения чё блядь? Он сам же и забыл о чём пишет, там должно было быть сложение, вероятно у парнихи каша в голове, но так у него указано не работает.
Короче он вроде логично всё объясняет, несмотря на косяки, на самом же деле выходит так что нельзя взять и перемножить что-то отрицательное с положительным, выходит тут у нас косяк и это действие, по идее, не имеет ничего общего с "стандартным умножением"? да и не похож, он, вроде, на шизика, или поехавшего какого
![1442869238050042032[1].jpg](/math/big/thumb/5474/14822437467700s.jpg) 162 Кб, 800x450
162 Кб, 800x450>Черт, я вижу математику лишь как символы, над которыми наперсточники работают. Я не вижу математику, как красоту и количественное описание мира и работу с количественными отношениями. Помогите мне.
 137 Кб, 629x778
137 Кб, 629x778Нет, я предложил тебе в систем шок поиграть хуй знает чё он хочет сказать на самом деле, без знакомства с этой хуйнёй ничо и не понять.
Ты зачем насрал? Ну-ка быстро блядь под струю, мойся, мойся, сука блядь.
>да и не похож, он, вроде, на шизика, или поехавшего какого
Вот и толстота подъехала.
У тебя есть вещественная прямая. Сложение/вычитание это сдвиг прямой вправо/влево, умножение это растяжение в n раз.
Епта, все эти операции низкий уровень где ускорение равно обрабтнопропорциональному кодированию
Да, годно объяснил, спасибо, а почему тогда возможно возведение в отрицательную степень? почему мне сообщили про вещественные прямые в начальных классах? Всё бы стало намного понятнее.
>>5855
>все эти операции низкий уровень где ускорение равно обрабтнопропорциональному кодированию
А вот это вообще не понял.
>>5854
Я не тот анон, ему вообще похуй поймёшь ты его или нет
>>5851
Там скрытый текст для кого? Можешь ознакомиться с ним ещё раз.
>Мимо-нематематик из философача на связи
Можешь рассматривать это как "даун гумманитарий", но никаких толковых аргументов в том что ты на кого-то нассал кроме своего манямирка я не увидел. А значит ты обоссал только себя. Обоссать можно только того кто неформально с этим согласится, или будет вынужден это сделать. Вот оно истинное унижение, а не школьные обзывалки.
>Мимо-нематематик из философача на связи
Окей поясняю для особо-любознательных. Ты набрел на сайт обыкновенного фрика помешанного на теории относительности, его опусы, при детальном рассмотрении не выдерживают никакой критики. Более того, я полистал его сайтик и наткнулся на следующую строку "философские вопросы естествознания", опять же поясняю, что это за тип людей: как правило, это окончившие философский( и то не всегда), которые возомнили себе, что они в чем то разбираются, т.е дилетанты и шарлатаны, впредь будь аккуратней.
Более того он просто еще чсвшник еще то, постоянные в честь себя называет, самоцитирует себя дохуя, в общем обыкновенный сумасшедший.
>впредь будь аккуратней
Сорре, я не суперспец, чтобы брать и делать такие выводы как может сделать спец, именно поэтому я спросил относительно сущности задачи в своём первом посте, а не спросил стоит ли мне верить этому сайту. Также в том посте я заметил
>Он сам же и забыл о чём пишет, там должно было быть сложение, вероятно у парнихи каша в голове, но так у него указано
Возможно ещё тогда следовало забить на тот его текст, но всё таки, данные лучше сначала проверять, и именно этого я сделать не смог, поэтому и спросил то что спросил, заодно и понял что же такое умножение, лично мне никогда этого нормально не объясняли. На уровне чисто - умножай сука, сказано умножать - умножай. Неча вопросы задавать, ты чё, самый умный?
В философии нет вычислимости, это меня всегда бесило. Как корректно проверять данные, которые кто-то высрал, как найти все ошибки, все те места где кто-то кого-то наебал, себя, других, а все согласились?
Плагин такой на фаер, меняет цвета у всего подряд, но и у мелких изображений, которые становится такими как на том скрине возможно стоит черкануть автору чтоб добавил кнопку, убирающую эту "фичу"
При беглом взгляде, в своих "статьях" он показывает не только незнание и непонимание теории относительности, но даже электродинамики. Что до опусов по математике, то я вообще промолчу.
>заодно и понял что же такое умножение
в школе вроде, раньше поясняли за связь между сложением и умножением.
>забить на тот его текст
мой совет забит на него совсем и внести термин пострелятивизм в списке фричества.
Как вообще решаются задачи по геометрии? Хотя бы скажите, по какому алгоритму их решать?
Спасибо, конечно, но этот метод мне точно не поможет.
Если бы доп.лит-ру посоветовал какую-нибудь
>и внести термин пострелятивизм в списке фричества.
Так сайт о антирелятивизме, вот в чём дело. Сам пострелятивизм так и не могу нагуглить в нормальной форме с шлюхами, блекджеком и вычислимостью.
таких говноедов же надо ставить на место, иначе они превратятся вот в это - https://www.youtube.com/watch?v=18cRnqS9rxo
Вот как, как можно этого пидора поставить на место в случае чего? Это же пиздец, ещё и буйный, книги публикует, по ящику выступает. Чтоб оно заткнулось ему же как-то доходчиво надо пояснить что он несёт хуйню
>>5867
В школе не учат искать решения, в школе учат их клонировать. Думать тебя врядли тут и тут в разделе научат.
>Так сайт о антирелятивизме
Так это вроде как фричество чистой воды.
>таких говноедов же надо ставить на место
не разводить хайпа вокруг них, сами подохнут.
>ему же как-то доходчиво надо пояснить что он несёт хуйню
от этого хуйню он не перестанет нести, они же, в большинстве своём, психически больные люди.
>Спасибо, конечно, но этот метод мне точно не поможет.
доп литература не поможет, берешь атанасяна вдумчиво читаешь, доходишь до упражений( они так по нарастающей сложности), пытаешься доказывать утверждения, имея теоремы доказанные в учебнике ранее.
Я их [решения] не клонировал, думал и в итоге получал тройки по матем., так как училке уже девятый десяток пошел (она типа учит решать только по тому, как она показывает. Любые отступления от ее правил караются двойкой или тройкой в дневник + звонок родителям или какая-нибудь кляуза классному руководителю)
>больные люди
...Которые уверены в том что они великие и правые, а все остальные - дартаньяны.
Очень просто такое говорить, но я считаю что больных не существует, есть лишь те кто выполняет по каким-то причинам ошибочную программу, и особенно страшно что они считают что эта программа верная, а особенно грустно если они превращаются в особо буйных как феминаци, к примеру. Ктож лечить-то их будет?
>>5870
Тут много вариантов, можешь строчить правдоподобные доносы директору, если пошлёт - в более высшие инстанции, типа РОНО, но лучше забить хуй, предлагать правдоподобные решения, а самому отдельно как-то "постигать истину".
Учёба в Роиссе это наука об имитации правдоподобной деятельности. Имитации корректного поведения, имитация написания дипломов, имитация знаний, имитация учительствования. Ничего кроме имитации. Умеешь имитировать - молодец, не умеешь - идёшь нахуй. а истина как всегда идёт в пизду
Посчитают неправдоподобным твоё поведение, не соответствует "слепку верного поведения"/"корректного решения" - садись два/уволен.
>так как училке уже девятый десяток пошел
Она уже непригодна. Сама наверное матешу ели осиливает.
Зависит-то зависит, но статистике пофиг на погрешности. То что лежит в пределах погрешности - имеет ли какое-то значение для обычного рандомного человека или для исследователя?
 136 Кб, 763x566
136 Кб, 763x566Только не перетрудись. За один день не въедешь. За месяц. За два. Рассчитывай на пиздец долгие сроки.
В целом ты говоришь правду, если ты тот философ-кун, но давай завязывай с тезисами про "Учёбу в России", так как такое кол-во фриков, в число коих ты записал и феминаци, огромно как раз там, также и человеческие ресурсы для фундаментальных наук портятся во многих областях еще сильнее чем здесь (про уровень студентов и их способности ума), а уровень интеллектуального, системного воспитания психически здорового человека в этих ваших Скандинавиях и North America-x вообще способен превратить человека в, пользуясь твоей терминологией, имитацию с бесконечным уровнем вложенности значимости имитируемого и с бессмысленной дегенерирующей эмпатией. Этот тоже прав >>>5877
Бамп вопросу.
Сразу подумал, что Эйнштейн не мог такой хуйни сказать, нагуглил - и действительно http://quoteinvestigator.com/2013/04/06/fish-climb/
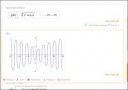
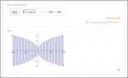
помогите пожалуйста разобраться с равномерной непрерывностью функции. Вот есть функция. Объясните пожалуйста, является она равномерно-непрерывной или нет, и как это доказать. Судя по графику, а точнее по тому, как медленно растут значения функции, эта функция является равномерно-непрерывной. Моё предположение верно? Как его доказать, подскажите пожалуйста.
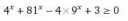 1 Кб, 174x29
1 Кб, 174x29МАТЕМАТИКА ДЛЯ НАЧИНАЮЩИХ?
Отлично, предлагаю создать ещё один тред:
МАТЕМАТИКА ДЛЯ УЖЕ КОНЧЕННЫХ.
 13 Кб, 1110x828
13 Кб, 1110x828Добрый Вечер. Принес вам задачку на поиск координат точки прямоугольного треугольника. Итак
ДАНО :
Ax = 574
Ay = 79
Cx = 595.30914588
Cy = 92.60862514
Угол С - прямой
AB = 72
BC = 67.4145802
AC = 25.28387582
Найти :
Bx =
By =
Очень нужно, застопорился немного.
тем что для любого эпсилон больше нуля найдется дельта, зависящая от эпсилон, и только от эпсилон, то есть от х не зависящая, такая что из
|x1-x2|<дельта следует что |f(x1)-f(x2)|< эпсилон
а в случае непрерывности, дельта зависит и от x и от дельта.
Предположи что равномерно непрерывная, выбери дельту, а потом покажи, что есть точка икс такая что разность значений функций больше эпсилон.
то есть функция всё-таки не является равномерно-непрерывной? я не знаю, как это показать, объясни подробнее пожалуйста.
>всё-таки не является равномерно-непрерывной
Зависит от того, где она задана, на всей ли вещественной оси, или на каком то отрезке.
Не является равномернонепрерывной - это видно по графику если мы возьмём очень маленький интервал и будем смещать его вправо - то разброс на этом интервале будет бесконечно расти. А это и значит неравномерную непрерывность. (Равномерная непрерывность, соотв. наоборот - если мы взяли маленький интервал, то разброс на нём можно ограничить некоторым числом.
рассмотреть предел некого приращения
хули расписывать? Боревич, Шафаревич Теория чисел
Ну по графику видно, что в окрестности нулей этой функции самый пиздец происходит. Докажи, что для любого eps. f(x_n + eps) стремится к бесконечности, где x_n - ноль этой функции. Это и докажет, что равномерной непрерывности быть не может.
Какие практические применения у частичных сумм ортогонального ряда? Зачем кому-то может понадобиться их считать? Прошу без шуток про студентов и прочего.
Охуенные курсачи. Напиши, что для термодинаамики, электрофизики, биомеханики, биопсихологики, сажания картошки, жарки картошки, math is very sexual, математика очень нужна в народном хозяйстве, мотивные когомологии для борьбы с раком, сосания хуёв и Арнольд математика это часть физики.
Не прокатит, нужны конкретные примеры.
Сам проигрываю, ибо специальность-то не инженерная. Но сдавать надо завтра сегодня утром, блядь.
Программа школьной математики, в большинстве своём, не на то заточена. В предыдущем треде аноны уже поясняли по этому вопросу.
На калькуляторы.
 213 Кб, 731x417
213 Кб, 731x417Я примерно правильно понимаю? Меня не наебывают? Определение кардинальных чисел такое и есть?
zfc
В NBG - да. В ZFC там кое-каким хитровыебанным способом выбирают из каждого класса по представителю не называя его словом "класс".
Что значит "познать математику"? Конкретные цели назови.
Можно конечно, но очень долго. Хотя ты ещё успеваешь занятся комбинаторикой.
объясни пожалуйста, почему после модуля разности значений функции x'' и x'(3 снизу строка) идёт вынесенный за модуль (2npi)^2/5 (на 2-ой строке снизу)? Как он получился?мне не понятно, откуда это следует. И откуда следует, что модуль разности sin^2/5(2npi) и sin^2/5(2npi-1/2npi) равен sin^2/5(2n*pi) в самой нижней строке? По какой формуле это посчитано?
объясните пожалуйста, что значит линейное отображение из одного метрического пространства в другое. Вот есть отображение F:l_2 -> l_1. Это отображение является линейным? Почему? И скажите пожалуйста, что можно сказать о непрерывности, равномерной непрерывности и условии Липшица для этого отображения?
 205 Кб, 720x1280
205 Кб, 720x1280Вместо r подставили 4.
45/360 = 1/8 (сорок пять градусов - одна восьмая часть полного оборота).
Что непонятно?
Смотри, у нас есть проективные модуми и когомологии де рама. Мы берём транзитивные интегралы Галуа и тензорно умножае пучок на кватернион, после чего получаем линейное представление функтора свободной категорий вращений квадрата в сопряженом пространстве гомотопической размерности 6. Далее вполне очевидно, нужно провести преобразование фурье над кольцом эндоморфизмов группы гоморфизмов, получается интеграл, который считается на колькуляторе, ответ число пи. Собственно твоя формула частный случай леммы Вебрита-Картофена о кручении кольца интегралов симпликсов.
>>5992
Аналогично, только производи преобразование лапласса над категория локалей.
ну помогите же, почему модуль разности значений функции x'' и x'(3 снизу строка) равен (2npi)^2/5 (на 2-ой строке снизу)? Разве так можно делать?
вытащил за скобки, то что осталось в скобках разложил в ряд тейлора, оставил только первый член( единицу)
мне не понятно, как можно вытащить за скобки (2npi)^2/5 и (2npi+1/(2npi))^2/5, потому что после них стоят разные выражения, то есть (2npi+1/(2npi))^2/5 умножен на sin^2/5(2npi+1/(2npi)), а (2npi)^2/5 умножен на sin^2/5(2npi). То есть, разве можно так выносить за скобки множители? Ты разложил в ряд Тейлора разность синусов? Можно более подробно это объяснить? И где тут единица? И у тебя неправильно записана функция, синус в этой функции должен быть в степени (1/5), а у тебя синус в степени (2/5). Напиши пожалуйста доказательство для правильно записанной функции, только более подробно.
 197 Кб, 1632x1224
197 Кб, 1632x1224>И у тебя неправильно записана функция, синус в этой функции должен быть в степени (1/5)
Проглядел бывает.
После по модулю больше 1/2 для любых натуральных n, но на самом деле нужна более аккуратная оценка.
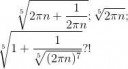 1 Кб, 188x102
1 Кб, 188x102ну я не понимаю, как ты вынес из корня пятой степени квадрата из (2pin+1/2pin) корень пятой степени из квадрата (2pin), объясни пожалуйста подробнее этот момент. Sin(2pin+1/2pin)=sin(1/2pin) так как синус это периодическая функция, так? Откуда следует, что разность sin^1/5(1/2pin) и sin^1/5(2pin) равна sin^1/5(1/2pin)? И можно поподробнее, куда делать (2pin)^(-7/5)? Почему это О большое?
>После по модулю больше 1/2 для любых натуральных n, но на самом деле нужна более аккуратная оценка.
распиши этот момент подробнее, пожалуйста.
>Sin(2pin+1/2pin)=sin(1/2pin) так как синус это периодическая функция, так?
Так.
>разность sin^1/5(1/2pin) и sin^1/5(2pin) равна sin^1/5(1/2pin)?
Так как sin(2pi n) = 0 для любого натурального n.
>И можно поподробнее, куда делать (2pin)^(-7/5)?
ну я функцию (1+x)^{a} раскладываю при малых x.
Туманов.
 44 Кб, 604x453
44 Кб, 604x453Без всех этих ебучих теорем и формул, а человеческим языком.
 78 Кб, 480x640
78 Кб, 480x640Оливер решил угостить всех коллег шоколадом. Он взял список сотрудников и решил, что человеку под номером n достанется T(n) долек, где T(n) возвращает остаток от деления 2^(2016 + n) на 11. Сколько всего долек достанется Виталику и Вере, если их номера 3 и 5 соответственно?
 38 Кб, 510x408
38 Кб, 510x4082(mod11)=2
2^2(mod11)=4
2^3(mod11)=8
2^4(mod11)=16-11=5
2^5(mod11)=2(16)=25=10
2^6(mod11)=2(32)=210=9
2^7(mod11)=29=7
2^8(mod11)=27=3
2^9(mod11)=23=6
2^10(mod11)=26=1
2^11(mod11)=2
2^(11t+k)=2^k(mod11)
T(n)=2^(2016+n) (mod11)=2^(3+n) (mod11)
T(3)=2^6=9 (mod11)
T(5)=2^8=3(mod11)
Блядь. Макаба звёздачки съела. Там умножение кароче.
Спасибо, очень ценный совет. Пригодиться мне в учебе.
Вот поэтому у вас и нет финансирования, серьезных покровителей и живёте как бомжи в россии
>>6016
Изучи ка вот это.
http://www-math.mit.edu/~djk/calculus_beginners/
>Вот [...]
Не злись на него. Он либо шутканул, либо просто не хотел тебе отвечать, но надо было соблюсти, так сказать, "этикет раздела /math/".
то есть эта функция ТОЧНО не является равномерно-непрерывной? потому что если посмотреть на её график, то видно, что скорость роста функции очень медленная относительно изменения аргумента функции, например, на промежутке от (-100;100) функция меняет своё значение всего лишь в пределах от -6 до 6. Может она всё-таки равномерно-непрерывная?
Пиздец вы поехавшие. Домножение на ограниченную непрерывную не меняет факта равномерной непрерывности, а неравноменрная непрерывность x^p (для p != 0, 1) очевидна.
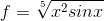 2 Кб, 104x21
2 Кб, 104x21и что это означает? эта функция является равномерно-непрерывной или нет?
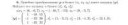 25 Кб, 729x149
25 Кб, 729x149Сап, помогите решить. Знаю как сделать, но не могу привести к единичной матрице этими ебаными элементарными преобразованиями, как их нахуй можно видеть, где делить, где отнимать?
Ну как я понял, мы найдем матрицу перехода, затем полученную матрицу умножим на это линейно преобразование ф и умножим на обратную матрицу и получим матрицу в новом базисе.
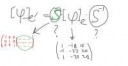 52 Кб, 1140x593
52 Кб, 1140x593Я вот блять и не могу её найти, это надо быть ёбаным экстрасенсом и знать заранее куда прибавить куда отбавить, чтобы ее привести к нужному виду, как я блять не пытался, получается хуйня. И вот еще пикча сама отвалилась. Вот мне и нужна помощь, чтобы помогли найти матрицу перехода.
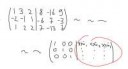 47 Кб, 1086x597
47 Кб, 1086x597Ну по примеру вот так получается, и путём ЭЛЕМЕНТАРНЫХ преобразований получаем матрицу перехода Красным
>если посмотреть на график
Это не является доказательством. Либо ебать определение, либо утверждения типа >>6024
>>6036
Хуйня какая-то нарисована. По определению новый базис выражается через старый E'=AE, где E' матрица состоящая из векторов нового базиса, E - матрица состоящая из векторов старого базиса. Отсюда несложно найти, что A - матрица перехода есть A=E' E^{-1}, таким образом надо найти обратную матрицу состоящую из старых векторов и потом умножить две матрицы.
 70 Кб, 960x719
70 Кб, 960x719>омножение на ограниченную непрерывную не меняет факта равномерной непрерывности
На самом деле меняет, я ошибся (сорян-борян).
я как то с недоверием посмотрел на это, но проверять не стал, вообще лично я мало знаю утверждения позволяющих говорить о неравномерности непрерывности.
тогда доказывай. Бери дельту, допустим, в 2pi (больше 6) и устремляй предел к бесконечности.
я что то вообще неправильно воспринял пост, тут надо подумать более тщательно.
Ну если функция отделена от нуля и от бесконечности (т.е. c<|f(x)| < C 0<c<C) то домножение на неё уж точно ничего не меняет (потому что тоже самое, что домножение на константу).
Но так-то рукомахательством доказать тоже как-нибудь можно. Но мне лень думать.
Бамп вопросу
Анон, ты тут?
 13 Кб, 657x53
13 Кб, 657x53 78 Кб, 482x202
78 Кб, 482x202А нахуй оно нужно? ТФ интересна в той мере, в какой она связана с гипотезами Ленглендса, простое доказательство (даже если оно существует) - никому не нужная ебола.
https://www.youtube.com/watch?v=yqyzD4bfw7k
https://www.youtube.com/watch?v=WfibjWbInC4
https://www.youtube.com/watch?v=WfibjWbInC4
https://www.youtube.com/watch?v=hmHz0Hrw4JA
я ныне совершенно случайно наткнулся. Вроде нормально показал мужик
 298 Кб, 1098x379
298 Кб, 1098x379Как вывести уравнение кривой перемещения? Мои вычисления не совпадают с тем, что я вижу на пикриле.
Есть уравнение скорости v = Δs\Δt (1)
Есть уравнение ускорения a = Δv\Δt (2)
Уравнение 2 мы можем выразить, как v = v0 + aΔt (3)
Уравнение 1 можно выразить, как s = s0 + vΔt (4)
Подставив скорость (уравнение 3), можно получить такое уравнение s = s0 + (v0 + aΔt) Δt
Раскрыв все это получим s = s0 + v0Δt + a(Δt^2)
А теперь смотрим на картинку и там формула показана как s = s0 + v0Δt + 1/2 a*(Δt^2)
Как такое может быть? Что я делаю не так?
no is u meme
Строго можно записать так:
s = s0 + vt + o(t^2)
v = v0 + at + o(t^2)
откуда следует только
s = s0 + v0 t + o(t^2)
если не выёбываться и говорить нормально, то
>Есть уравнение скорости v = Δs\Δt (1)
неверно.
 50 Кб, 405x720
50 Кб, 405x720двачик,помоги 5 6 и 7 строку привести к нулевому виду
От минуса обязательно избавляться нужно или и так пойдет? Чет совсем не понимаю нихуя, в учебнике ничего сказано.
Теоремой Пифагора возьми
Я и не в вольфарме смотрел. Сначала попробуй привести к квадрату разности, прибавив и убавив y^2. Дальше разложить, как разность квадратов.
x^2-2xy-4xy+8y=0
Решается обычной квадратной формулой, а ты похоже туповат.
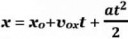 1 Кб, 227x70
1 Кб, 227x70>s = s0 + vt + o(t^2)
Не понимаю, что за "о".
>s = s0 + v0 t + o(t^2)
А куда было потеряно at?
>уравнение скорости неверно
Расстоянние, деленное на время - м\с. Само собой речь идет о равномерном движении или средней скорости.
Этот 1 час видео > 6 лет жизни, потраченных в школе на "уроках" "математики".
Ёбаная пидарашка с ёбаной системой "образования"
Нужна небольшая помощь с матанализом ,первый курс
Пропустил много пар по формуле Тейлора и разложению, с ними нужна помощь, остальное норм
Через 20 мин, если может кто помочь - отпишитесь, не бесплатно офк
https://ru.wikipedia.org/wiki/Логарифмическая_производная
Используй этот приём для вычисления производной.
 1,8 Мб, 3264x2448
1,8 Мб, 3264x2448Бл, уже нашел производные (вроде не обосрался)
А что делать дальше? Не понимаю
Сорян за почерк, тороплюсь
http://www.webmath.ru/poleznoe/formules_8_19.php
По определению делай - коэффициент, производная в точке.
Подставить туда ноль.
 84 Кб, 1328x819
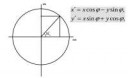
84 Кб, 1328x819Если с полярными координатами и окружностью фиксированного радиуса все понятно, то никак не могу сообразить как формируются вторые слагаемые в пикрелейтед?
ДЦПшник
>Кто такой мунин
Самый дерзкий дед на dxdy, за то что он там вытворяет других банят а ему лишь пальчиком грозят.
>И что вообще за разборки с dxdy
На dxdy жОсткая модерация. Можешь зайти и почитать их правило. А пичот от того, что местные, дорвавшиеся до власти, типа Мунина могут вытворять беспредел, который неположено делать.
>А пичот от того, что местные, дорвавшиеся до власти, типа Мунина могут вытворять беспредел, который неположено делать.
Странная причина. Собачечки говорят гав-гав, кошечки мяу-мяу, а моча на мочерируемых форумчиках, в зависимости от своих заморочек, творит мочебеспредел. Всегда так было. Даже на сосаче, где вроде как должно быть наоборот.
С каких это пор ананасы вдруг стали борцами за справедливость?
ладно, вобщем ситуацию я понял
Поворот линейный оператор. А значит нам достаточно понять, куда перейдут базисные вектора при повороте, т.е. куда перейдёт (1,0) и (0,1).
(1,0) перейдёт в (сos a, sin a), (0,1) перейдёт в (сos pi/2 + a, sin pi/2 + a).
Думаю, отчасти это желание поглимутся над дидами, отчасти форс местного дегенерата Хорена. Да и народ тут либеральные левачки, а на dxdy строят комунизм, вот местным и подгорает, кричат о злых совках гулаге и швабоде.
Формулы - это картоха. Математика о словах, а не о формулах.
пикрил - выведено для постоянного ускорения. Постоянное ускорение эквивалентно уравнению x''=const, его решение тривиальная задача, приводящая к пику, при надлежащих граничных условиях.
 382 Кб, 2710x618
382 Кб, 2710x618Почему так?
Почему в ебучих школьных учебниках пишут какую-то хуйню и не поясняют почему именно так они это делают?
Он домножил уравнение на -1? Да так.
ДОГАДАЙТЕСЬ САМИ МОЛОДОЙ ЧЕЛОВЕК!!!!!!!!!
А вдруг мне это не очевидно что тогда? Ебись конем и фрустрируй.
Ну, тут это умножение как бы напрашивается. Но да, согласен, бывает, напишут что-то, выведенное из чего-то, и оно совсем не само собой разумеющееся.
>Он домножил уравнение на -1? Да так.
ДОГАДАЙТЕСЬ САМИ МОЛОДОЙ ЧЕЛОВЕК!!!!!!!!!
Это же очевидно.
>А вдруг мне это не очевидно что тогда?
Тогда тебе неочевидно и ты ебешься показывая что это так.
 95 Кб, 640x818
95 Кб, 640x818Более того дебилизм - относителен, а так терпение и труд как известно всё перетрут.
Воистину так, профессор.
Если кто захочет помочь - тому даже готов бабла отвалить или пикселей из контры.
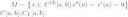 1 Кб, 330x46
1 Кб, 330x46помогите пожалуйста разобраться, как делать задание по функциональному анализу, по теме топология метрических пространств. Вот есть два пространства С[a,b](пространство непрерывным на отрезке [a,b] функций) и C_L[a,b](пространство интегрируемых на [а,b] функций) и есть множество M. Нужно ответить на вопросы, является ли это множество M открытым, замкнутым, ограниченным в пространствах С[a,b] и С_L[a,b]. А также найти его замыкание, внутренние и граничные точки в каждом указанном пространстве. Подскажи пожалуйста, как сделать это задание, хотя бы с чего начать.
всякую непрерывную функцию можно приблизить многочленами, так что M открыто в C[a,b]
вернее говоря, оно точно не замкнуто, но раз стоит вопрос "или", то наверно открыто :D
а можно это как-нибудь по другому доказать, то есть без многочленов? Используя термины вроде открытого шара или чего-то подобного.
ну с помощью |x|, который приближается x^2, должно быть можно доказать, что оно таки открытое
А давай так. Возьмём C[a,b]=C[0,1]. Пусть f - функция из M. Тогда функция f + 1/n Sqrt[x] не имеет производной в нуле, однако она приближает f. Получается, любой шар в C[0,1] вокруг f содержит функции, которых нету в M. Значит, М не открыто. Правильно вроде? Не такая простая оказалась у тебя задачка
Далее, полагаю, рядом с любой функцией, которая не лежит в М, можно обнаружить функцию, которая лежит в M. Для этого надо произвольную функцию суметь приблизить функцией, которая в окрестности 0 постоянна. Убеждён, что можно. Так что M таки не замкнуто. Далее надо, наверно, доказать, что M всюду плотное, это даст его граничные точки. А множество внутренних точек у него пустое, т.к. нету точек, которые в него входят со своей окрестностью
Ты прав, ZF и ZFC тоже ненужная ебола, а АБЦ-теории несуществует, есть АБЦ-гипотеза (которая может, максимум что, стать АБЦ-теоремой).
Очевидно что функция неравномерно непрерывная, чтд
Ну попутал чутка, с кем не бывает.
Из за этого я углубился в маняматику чуть поглубже и нашел лузина. Ваще чотко расписано все про интригалы. Однако у лузина та же база только с полным погружением.
Мне же сейчас требуется книжка которая по сложности тем стоит между калькулусом и началом теории множеств, чтобы объяснялись всякие тензоры, частные производные энной степени терминами обычное, не множественной, математики.
Смотри в топология треде.
Ускорение это по определению a=d^{2}x/dt^{2}. Так как ускорение постоянно, то это определение превращается в простой диффур. d^{2}x/dt{2}=a. Решая его получаем твой пик.
что-нибудь по real analysis, например, рудина.
Вторая теорема Гёделя о неполноте, фактически, говорит, что для того, чтобы обосновать некоторые методы математических рассуждений нужно использовать более мощные средства. Но к математической практике для арифметики, да и конечных объектов вообще, это имеет мало отношения, т.к. за пределами специально сконструированных логиками примеров, не было случаев, чтобы выяснилось, что придуманное математиками доказательство утверждения про натуральные числа нельзя было бы переделать в доказательство, использующее лишь средства обычной первопорядковой арифметики Пеано.
>>6253
Формальные доказательства - это вполне адекватная модель обычных доказательств. Теоремы Гёделя говорят о математике (и, кстати, это вполне проявилось, но не в теории чисел, а в теории множеств).
А что я должен аргументировать? Что ТМ не нужна? Пожалуйста: сколько филдсовских лауреатов получили филдсовку за работы в ТМ и в каких годах? Сколько абелевских? (Вопросы риторические, поэтому это аргумент [ты туповат просто, мог и не понять])
И там и тут ты хочешь сообщить, что теория множеств - это немодно (в последнем сообщение, по крайней мере, более конкретно, отсылаясь ко вкусам филдсовского комитета). Отлично, ты обрисовал группу людей (себя и филдсовский комитет), которые не очень интересуются теорией множеств. Но каким путем ты хочешь от сюда сделать далеко идущие выводы о ненужности теории множеств для меня загадка - если посмотреть на комьюнити людей занимающихся теорией множеств, то представления о ценности будут совсем другие.
А что ты понимаешь под нужностью? Я понимаю нужность для математики -> нужность для математиков -что частично отражается в-> решения филдсовского/абелевского комитета.
> если посмотреть на комьюнити людей занимающихся теорией множеств, то представления о ценности будут совсем другие.
Посмотрел - 0.5 толковых человека и какие-то философы. Полный зашквар короч. Что дальше делать?
>Я понимаю нужность для математики -> нужность для математиков
Будучи аккуратным, я бы скорее говорил о ценности. Применяя твой подход, мы подменяем содержательный вопрос о том, чем является некоторая область на чисто социологический о том, насколько область популярна среди математиков. Кстати, вполне вероятно окажется, что наиболее популярны окажутся вовсе не те области, которые ты любишь и ценишь, например прикладников, занимающихся какими-нибудь численными методами очень даже много.
>Посмотрел - 0.5 толковых человека и какие-то философы.
Не думаю, что ты сколь-нибудь подробно вникал. Но отмечу, что в современной теории множеств имеется развитая система понятий и довольно много технически сложных результатов.
 21 Кб, 643x490
21 Кб, 643x4901. как использовать ММП конкретно для данной задачи (№1)? Я не понимат абстрактную хуиту из учебников/интернетов.
2. допустим, формулы оценок найдены. Если оценки точечные, то это значит, что они имеют какое-то одно числовое значение, правильно? Ну и откуда у чисел дисперсия и прочее из № 3? Я нихуя не понял.
3. зачем в условии дан закон распределения погрешности? Где его нужно использовать?
Да, я пиздец тупой. Анончики, я в отчаянии, помогите
> Применяя твой подход, мы подменяем содержательный вопрос о том, чем является некоторая область на чисто социологический о том, насколько область популярна среди математиков.
Содержание из пальца высосано. Математика - чисто социологическое понятие, поэтому и ценность математики может быть только чисто социологическая.
>Кстати, вполне вероятно окажется, что наиболее популярны окажутся вовсе не те области, которые ты любишь и ценишь, например прикладников, занимающихся какими-нибудь численными методами очень даже много.
Прикладникам не дают Филдса.
>Не думаю, что ты сколь-нибудь подробно вникал. Но отмечу, что в современной теории множеств имеется развитая система понятий и довольно много технически сложных результатов.
Нахуй не нужные остальному мат. сообществу.
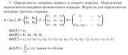 174 Кб, 2064x898
174 Кб, 2064x898Подействовал на единичный куб оператором и посмотрел на его ориентированный гиперобъём, что непонятно-то, бля.
Никто не знает про хроматическое число графа или просто лень отвечать?
А также приведение матрицы к треугольной и куча других методов.
>Математика - чисто социологическое понятие, поэтому и ценность математики может быть только чисто социологическая.
Демагогия уровня /b
>Содержание из пальца высосано. Математика - чисто социологическое понятие, поэтому и ценность математики может быть только чисто социологическая.
Математика, конечно, завязана на людей и оценивается людьми. Но сейчас ты фактически заявляешь, что вместо того, чтобы в качестве отдельного математика оценивать область в том числе исходя из внутренних критериев (красота математических конструкций, важность мотивации за постановкой задач и т.п.) ты исключительно смотришь на то, что думает "математическое сообщество". В рамках такой позиции мне честно-говоря не ясно, почему тебя вообще волнует, скажем медаль Филдса - можно же просто смотреть на индекс цитирования, являющийся отражением нужности статьи математическому сообществу, а не лишь нескольким конкретным математикам из комитета.
>Прикладникам не дают Филдса.
И что? У тебя определение математики это что-то в духе "математика - это те разделы науки за достижения в которых можно получить медаль Филдса"?
>(красота математических конструкций, важность мотивации за постановкой задач и т.п.)
Это тоже социальные конструкты, что красиво и что важно решает математическое сообщество.
>почему тебя вообще волнует, скажем медаль Филдса - можно же просто смотреть на индекс цитирования, являющийся отражением нужности статьи математическому сообществу, а не лишь нескольким конкретным математикам из комитета.
Можно и так - теория множеств что так что так соснёт.
>И что? У тебя определение математики это что-то в духе "математика - это те разделы науки за достижения в которых можно получить медаль Филдса"?
Да.
Бамп. Ну что же вы, аноны, тут есть шарящие 100 проц.
Может ли быть параллельный перенос по одной координате и может ли C распологаться на координате Y у фокусов?
>решает математическое сообщество
>>"математика - это те разделы науки за достижения в которых можно получить медаль Филдса"?
>Да.
Математическое сообщество не субъект и ничего не решает. Что-то оценивать могут конкретные математики, ну или формально принимающие решения группы, в частности тот же филдсовкий комитет. Ну а тебе, как видно ничего не остается, кроме как отождествить решения математического сообщества с решениями последнего. Ну и тем самым ответ на вопрос что такое математика начинает существенно зависеть от чисто процессуального вопроса о составе филдсовского комитета... Если серьезно, то я полагаю, что математика состоит из тех областей в которых применяется математический метод исследований.
Измерение ценности математических работ по индексу цитирования я привел чисто для указания на то, что твоя позиция приводит к совершенно абсурдным выводам.
Да, вполне.
>>6315
Советую попробовать связку http://www.springer.com/us/book/9783540225256 + http://www.springer.com/us/book/9783540642435 - Я серьёзно. Это будет лучшим выбором; книга по алгебре писалась лучшими алгебраистами прошлого века, нет по упражнениям, набору материала и доказательствам книги по начальной алгебре лучше, чем Algèbre I.
Theory of Sets необходима (ведь ты ноль, как Я вижу), но её можно получитать: просматривать, выделяя только основные синтаксические моменты (но будет нужно видеть важное: иначе затем не поймёшь, что к чему, к примеру, почему Бурбаки не используют нотацию Гильберта для эпсилон-оператора и в подобном паттерне); со второй книгой ты будешь обязан вырывать гнилые сосуды, с потом и кровью продираясь, — Horen.
Как скачивать со Springer, надеюсь, знаешь.
Horen.
Я хотел узнать, что такое логарифм, производная и интеграл, а ты мне дал говно
Ало ,роботы.Подсобите
>Что-то оценивать могут конкретные математики, ну или формально принимающие решения группы, в частности тот же филдсовкий комитет. Ну а тебе, как видно ничего не остается, кроме как отождествить решения математического сообщества с решениями последнего.
Это более-менее одно и то же.
>Ну и тем самым ответ на вопрос что такое математика начинает существенно зависеть от чисто процессуального вопроса о составе филдсовского комитета...
Да, ответ на вопрос, что такое математика зависит от людей, которые образуют сообщество, называющее себя "математиками". Не вижу ничего удивительного.
>Если серьезно, то я полагаю, что математика состоит из тех областей в которых применяется математический метод исследований.
Это рекурсивное определение. Объясни тогда, что такое "математический метод исследований".
>Измерение ценности математических работ по индексу цитирования я привел чисто для указания на то, что твоя позиция приводит к совершенно абсурдным выводам.
Не вижу ничего абсурдного в индексе Хирша. Есть, конечно, коррупционные схемы его накрутки, но так-то вполне адекватный измеритель.
 174 Кб, 1280x960
174 Кб, 1280x960определенной интеграл определен на замкнутом отрезке.
Натуральные числа - более-менее понятно
Дроби - тоже можно представлять в виде пирогов и тд
Целые числа - ну, деньги бывают с минусом и тд
Функция - зависимость одной переменной от другой, все ясно
На каком уровне уже нельзя представлять себе что-то бытовое?
Можешь привести пример? А я вообще слушал недавно лекцию такого физика Фейнмана о связи математики и физике. И он говорил, что нет бытового пояснения закона гравитации Ньютона, есть только формула. Может сказал какой-то бред, не знаю
> И он говорил, что нет бытового пояснения закона гравитации Ньютона, есть только формула
Да он просто не шарил нихуя. Все знают, что R-действия высшего slice топоса над moduli стэком круговых главных связностей окружности эквивалентен топосу законов движения. Подробнее тут https://ncatlab.org/nlab/show/Higher+toposes+of+laws+of+motion
Ну бля, берешь ты гладкий cohensive (infty,1)-топос, значит, а его internal notion of cohomology уже кодирует всю кинематику. Естественно - пиздец, естественнее определения натуральных чисел, BTW.
https://yandex.ru/referats/?t=mathematics
для меня то, что ты сказал аналогично тому, что выдал яндекс реферат
Да там картохи какой-то нагенерило. Интегралы, арифметическая прогрессия, пределы, чего блять... Это генерирует реферат по математике или по картофелеводству? Вот в чём главный вопрос...
https://yandex.ru/referats/?t=mathematics+physics
стоить чуть добавить физики... и выйдет типичный ландавшиц
Давай так. Я помню арифметику вроде и чуть школьной алгебры. Как мне ступить на путь истинный?
Много заниматься. Желательно на хорошем факультете (Матфак ВШЭ), но если факультет не очень хороший, то заниматься нужно ещё больше, чем много. Во-о-от.
Дано: длина вектора а = длина вектора б = 1. Длина вектора c = 2.
вектор а перпендикулярен вектору с. Угол между векторами а и б равен 60. Угол между векторами б и с тоже равен 60.
Узнать: Перпендикулярны ли вектора а-2б и а-с
Нарисуй (прости боже, но да, ты лучше нарисуй) всё станет видно. Просто уметь графически складывать вектора, легче и быть не может.
перпендикулярность это по определению означает, что скалярное произведение равно нулю
можешь отложить их от одной точки и ввести координаты, можешь посчитать по теореме косинусов. и помни, что а-б=а+(-б).
спасибо огромное
 399 Кб, 2688x1520
399 Кб, 2688x1520 124 Кб, 1521x689
124 Кб, 1521x689после стрелки какая-то муть. Дробь на простейшие разложи
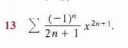 8 Кб, 271x104
8 Кб, 271x104Бурбаки, "Теория множеств" – если ты начинающий и логика тебе для математики чистой, логика там в достаточном свете.
Если ты всё же грязный: нет никакой "дискры", как отдельной области; это миф, придуманный педагогами. Если тебе для CS, советую сначала "Concrete Matematics" Кнута ("Конкретная математика") – теория графов, автоматов, алгоритмы и всё минимально нужное. Затем бери для теории конечных групп любой простой классический учебник по общей алгебре.
Нужна для CS, но в силу особенностей изучения на факультете, лучшее ее учить как чистую. Нужна теория множеств, логика 1 порядка, интуиционистская логика и тд. в принципе, программа соответствует Верещагину-Шеню, но там иногда довольно сжато все описано.
>>6514
Спасибо, попробую.
Может есть какие то англоязычные учебники, в них обычно все очень хорошо разжевано?
Прочитай в словаре, что такое абстракция.
Ответ: вся математика является абстракцией по своей сути, начиная с самых простых вещей, которые ты привел в своих прмерах.
Математика отрывается от бытового довольно быстро. Например в алгебре при переходе от группы перестановки множества к абстрактной группе. Комплексные числа тоже тяжеловато уже объяснить. "a + ib яблок, это как?", ну можно 2D плоскость показать, можно убедить, что есть такое число корень из -1, но это уже минимально оторвано от бытовухи.
В анализе вроде можно как-то на бытовом уровне рассказать про базовые определения, но довольно не строго и бытовые аналогии слишком тяжело использовать при решении задач (например, дифференциальных уравнений).
В геометрии всё что про 4-х (и выше) мерные пространства уже тяжело, некоторые вещи про неевклидову геометрию можно рассказать.
Ну и плюс к этому: когда речь про бесконечности, бытовуха даёт отказ довольно быстро.
Т.е. уже в средних классах школы приходится отказываться от мышления в терминах яблок и пирогов. Хороший школьник начинает манипулировать уравнениями, не думая про яблоки.
>Хороший школьник начинает манипулировать уравнениями, не думая про яблоки.
И потом хуев нахватывается в алгебре и анализе, потому что умножает яблоки на пироги и пироги на яблоке. Почему у вас деление на ноль? Почему вы так умножаете в некоммутативной группе? Почему у вас объем как площадь поверхности?
ТМ Бурбаки надо читать с минимальными preliminaries, хотя бы в виде матлогики Клини.
Только если человек не хочет уж слишком сильно медленно читать ТМ от Бурбаки, то можно, но не необходимо ввиду самодостаточности трактата. Сами Бурбаки говорят, что начинать читать можно "на втором университетском курсе вашей системы образования".
На самом деле при чтении этого французского творения нужно просто войти в абстрактный транс: свести уже полученные математические знания к минимуму, а полученные математические умения к максимуму.
выписать перемножение матриц. Например, чтобы получить первый элемент K при умножении A на X, надо посчитать произведение первой строчки матрицы А на вектор X.
А есть универсальный способ, чтобы Х найти через эти 2 матрицы, вроде бы можно как-то получить уравнение X=A^-1*K Это я так, к примеру?
Точки единичной окружности на комплексной плоскости, являющиеся вершинами правильного n-угольника, где n количество корней, а одна точка принадлежит вещественной прямой.
при условии, что A обратима, можно домножить на обратную слева и получить такое выражение.
>>6771
деды изначально их придумали, чтобы строить равносторонние многоугольники.
http://kvant.mccme.ru/pdf/1998/01/kv0198senderov.pdf
Не деды только а Gauß вроде
Вот за пдф спасибо огромное. А то в лекциях примеров нет, при этом препод требует понимание™
Наоброт молодец, школьников егэ учит решать. На Доктора Кто похож и пилит всякие популярные ролики.
ЕГЭ нинужно, популярные ролики плохого качества (а ещё иногда сам он говорит какую-то хуйню). Если хочется посмотреть хорошие популярные ролики, то лучше какого-нибудь 3blue1brown глянуть, там хоть видно, что люди заморачиваются - продумывают что и как говорить, делают анимацию и т.д.
Есть дохуя всего, просто ты калоед
Тот же Шестопалов в 700 раз лучше
Не говоря уже о Harpreet Bedi например
>Harpreet Bedi
>Шестопалов
Это же курсы лекций, а не популистика. При том оба не то, чтобы сверхвысокого качества. Если Bedi хотя бы работающий математик, то Шестопалов просто студиозис который закончил какой-нибудь мехмат. Лучше уже на лекториуме и канале ВШЭ что-то смотреть.
ps Я не тот анон, который форсит того хуесоса.
Ну это понятно, у них ЦА разные, Шестопалова я привел как стримера. А на лекториуме ехал Вавилов через Вавилова, тошнит уже. При чем даже самые интересные курсы по чисто питерским форсам типа мотивов Панина или метрической геометрии Иванова. Но хоть качество хорошее.
самое охуенное, когда этот вавилов идет по кафедре и пиздит с кем-то, у него голос еще узнаваемый такой
Пусть
x_i ~ binom(n_i, q_i)
q_i ~ beta(a, b)
По X нужно найти a, b
Если решать максимальным правдоподобием то после интегрирования по Q получается произведение кучи Beta-функций по которым хуй что прооптимизируешь
если использовать x_i/n_i в для нахождения моментов то матожидание может и норм а дисперсия явно завышена
Как это таки можно сделать?
Здесь такое не знают, лучше в мат-треде /sci спроси.
> А на лекториуме ехал Вавилов через Вавилова
Потому что он умеет читать лекции, в отличие от 95% препода матмеха. Особенно спецкурсы у него отлично получаются.
Еще про Вавилова добавлю. Пытайтесь подсосаться к нему с первого курса, ходите на все его спецкурсы, даже если тема вам не слишком интересна и вы нихуя не понимаете на моем четвертом курсе на вавиловскую теорию категорий ходило куча перваков, часть из них даже поняла, что теория категорий это стрелочки и буковки, берите курсачи. Во-первых, серьезно прокачаете алгебру. Во-вторых, Вавилов любит таких студентов, возит в Гермашку и помогает попасть в гейропейские аспирантуры.
Знаю минимум одного человека, который благодаря Вавилову от червя-пидора из зажопинской средней школы докачался до аспиранта европейского неплохого вузика. Лол, я же из всероса-дипломника превратился в долбоеба, с 3 курса вечно находящегося на грани вылета.
Метачитать, как в букаче. Допустим в книге 300 страниц, значит 300 раз отжимаешься от пола. Это значит метапрочитал выбранную книгу. Или 300 фрикций в рот и попу, что больше нравится.
Советую начать с метачтения трактата бурбаки.
с 3 курса еще можно вылететь, но вот с 4ого уже анрил, не знаю как ты проебываешься.
Tak ona ne tochna.
1. google "how to read math books"
2. прочитать Velleman "How to prove it"
3. во всех книгах делать упражнения, доказывать теоремы из текста самостоятельно, медитировать над определениями и доказательствами до просветления
Линпространство - множество стрелочек из нуля, подпространство - плоскости/прямые - проходящие через ноль. Линейный оператор - растяжения и вращения. Чё там связывать-то.
Закончил 3.5 года назад.
На 3-4 курсах была матфа, которую все боялись. Урчп, урчп в обобщенных функциях, Назаров со значком "каждой тваре по паре".
 836 Кб, 2448x3264
836 Кб, 2448x3264книги арнольда по оду в помощь
Порекомендуйте задачник к курсу Ландау-Лифшица. Желательно с ответами.
Коткин-Сербо
Кароль, наверн. Осмоловский вообще хуже всех, заставлял формулировки билетов наизусть учить.
Это копия, сохраненная 28 июля 2022 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.











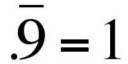

![images[1]](/math/big/thumb/5474/14822440045870s.jpg)