В этом треде мы объясняем любителям Демидовича что такое дифференциал и операция дифференцирования, как определить модуль не обращаясь к понятию группы, определяем когомологии и Ext на языке точных последовательностей. Прошу воздержаться от диаграммного поиска и метания стрелок, для этого есть отдельный тред >>2473 (OP).
Классической гомологической алгебры нить стартует тут.
Известный московский бурбакист В.И. Арнольд в своей книге "Что такое математика" на 17-й странице определяет нормальную подгруппу через точную последовательность расширений.
Арнольду, как и нам, совершенно очевидно, что гомологическая алгебра в её классической форме как нельзя лучше подходит для педагогических целей, например для объяснения формулировки теоремы Абеля в начальной школе.
>что такое дифференциал и операция дифференцирования
Рассказывай. Хороший тред. Надеюсь не пропадет.
Инварианты т.е., а не коинварианты.
Let's go.
Начнем мы, пожалуй, с базовой терминологии.
Отображение двух модулей h: A —> A1 называется гомоморфизмом, если
h (x1 + x2) = hx1 + hx2,
h (ax) = ahx.
Множество элементов модуля, удовлетворяющих условию hx = 0 называется ядром гомоморфизма Ker h, мн-во элементов вида y = hx называется образом Im h.
По-человечески. Ядро — все элементы, переходящие в нейтральный (ноль). Образ — все элементы, в которые что-то переходит. Отображение с нулевым ядром называется мономорфизмом (иначе: вложение), отображение на весь модуль — эпиморфизмом (стягивание). В случае если выполняются оба условия, это изоморфизм.
Теперь рассмотрим пару гомоморфизмов h1, h2, при чём Im h1 = Ker h2. Такая пара называется точной. Последовательность, в которой каждая соседняя пара точна, называется точной последовательностью.
Ослабим это условие: пусть Im h1 — подмножество Ker h2. Отсюда следует, что h1 h2 = 0 (это еще называют ортогональностью). Такую последовательность назовем комплексом.
Рассмотрим цепной комплекс:
... —> C(3) —> C(2) —> C(1) —> C(0) —> 0,
группы C(n) назовем n-мерными цепями, а гомоморфизмы (стрелки) назовем граничными операторами ..., d(3), d(2), d(1), d(0).
Комплекс этот неточен, и нам хотелось бы знать насколько именно.
Для измерения этой неточности определим гомологии.
Hn (C) это фактор-группа Ker dn по Im dn+1. Легко видеть, что условие точности эквивалентно всюду нулевым гомологиям. Аналогично определяются когомологии, положив вместо этого фактор Ker dn / Im dn-1. По сути мы просто избегаем отрицательных коэффицентов и подписываем их сверху, а не снизу, комплекс же разворачивается в противоположную сторону и идёт от нуля, а не к нулю.
Топологический смысл гомологий в том, что берется фактор группы циклов по группе границ, что позволяет нам находить дырки на различных симплициальных объектах. C(0) это нуль-мерные точки, C(1) линии, далее двумерные клетки, и т.д.
Но это же алгебраическая топология, а вы пришли сюда за анализом. Behold.
Рассмотрим для разнообразия такой комплекс:
... —> C(n−1) —> C(n) —> C(n+1) —> ...
где C это дифференциальные формы — то есть элементы алгебры, порожденной символами dx(1), ... dx(n) с соотношениями
(dx)^2 = 0,
dx1 dx2 = - dx1 dx2.
Называется он комплексом де Рама.
Отображение d(n) называется дифференциалом. Сие означает, что дифференцирование это гомоморфизм модуля. Условие же d(n-1) d(n) = 0, означает что дифференциал это нильпотент по умножению со степенью два.
Многие авторы учебных пособий так и определяют комплекс, мол последовательность гомоморфизмов абелевых групп, такая что композиция двух соседних нулевая. На самом деле это можно доказать через равенство смешанных производных, в частности окажется что d является антидифференцированием.
Перейдем к более интересным вещам.
Как и в топологическом случае выше, у нас есть последовательность модулей и гомоморфизмов. Только теперь модули это не n-мерные симплициальные цепи, а n-формы; d — не граничный оператор, а "внешнее дифференцирование".
Для C(0) — 0-форм — d это градиент, для C(1) — ротор, для C(2) — дивергенция. Использование внешнего дифференцирования, помимо прочего, позволяет заниматься физикой без координат и покомпонентного разложения тензора, что, например, позволяет узнать что такое электромагнитное поле как объект, а не набор различных параметров. Физики с их "тензорным анализом" этой роскоши, конечно, лишены.
А теперь обещанное определение дифференцирования.
Положим R — кольцо, A — R-модуль. Отображение d: R —> A называется дифференцированием, если оно удовлетворяет правилу Лейбница:
d(fg) = fdg + gdf,
для f, g из R.
На этом пока всё.
А про когомологии-то и не написал.
Итак, когомологии определялись выше фактором Ker d(n) / Im d(n–1); группа циклов по группе границ.
В теории де Рама когомологии это фактор замкнутых форм по точным формам. Комплекс можно представить как систему дифференциальных уравнений, решением которых будут замкнутые формы. Если комплекс точен, все когомологии нулевые и формы априори замкнуты, это не интересно. Когомологии показывают, насколько много интересных решений.
Раз уж есть категории без гомологий, пусть будут гомологии без категорий. Стоит признать, что исторически именно категории сделали топологию приличной и уважаемой наукой, и тридцатые для гомологической алгебры были не самым лучшем временем.
Тем не менее, сейчас, прекрасно понимая эффективность и даже утилитарность метода спектральных последовательностей, давно оставившего концептуальный фронт производным категориям, мы можем обратиться к пропедевтике и педагогике. Сейчас не тридцатые и теперь ясно, что это не general nonsense, а объединяющий алгебру, анализ и топологию аппарат, без которого невозможно понимание и даже формулировка ключевых понятий этих дисциплин.
Не элемент, n-тая гомология это и есть H(n). H(n) это фактор группы циклов по группе границ, обе эти группы лежат в C(n). То есть каждой из групп C(n) соответствует своя группа гомологий H(n).
Когомологии это еще и кольцо, при чем операции там бывают интересные и не обязательно сводятся к умножению.
Есть двойственность Пуанкаре, по которой H^k (k-тые когомологии) изоморфно (n-k)-тым гомологиям.
У гомологий стрелки в сторону нуля, у когомологий в противоположную, по сути когомологии это гомологии с отрицательными индексами.
Кроме того, гомологии это функтор.
А еще гомологии можно определить через Tor (функтор кручений), а когомологии через Ext (функтор расширений). Необходимо будет рассмотреть точные справа и слева функторы и продолжить их в соответственно левую или правую сторону производными функторами.
В этом разделе очень часто делают нелепые ремарки о том, что модуль это группа с дополнительными аксиомами, следовательно группы фундаментальны в алгебре.
Некоторые из этих ремарок делал я. Но, как скажешь, я не буду спорить с тобой, что фундаментальней. Абелевы группы - отдельная наука о модулях? Ок.
Но в чем профит модулей без групп? В том, что для изучения модулей не обязательно знать теорию групп? И всё?
В чем профит групп без моноидов? Модуль это базовый объект в таких областях как линейная алгебра, гомологическая алгебра, теория представлений, к-теория, функциональный анализ (банаховы алгебры) и вообще любая наука про абелевы категории (то есть такая, где есть точные последовательности).
Изложение такой дисциплины как линейная алгебра в группах или кольцах не нуждается, правильно сразу определять модули и гомоморфизмы, прямую сумму и произведение, и дальше переходить к формулировке теоремы о жордановой форме на этом языке.
Те же фактор-пространства удобно определять через коядра и кообразы.
Выглядит ахуенно, но много чего непонятно. Буду дальше учить.
Меня вопрос терзает, может знаешь ответ, как Галуа вводил разрешимые группы? Почему они определяются так, как придти к такому определению? Как не гуглил, везде только определениянашел только что коммутанты и прочее ввел вообще не Галуа, а после него
Имеем кубическое уравнение общего вида, пусть x, y, z – его корни, a – кубический корень из -1.
Обозначим t = x + a y + a^2 z.
t принимает шесть значений, каждое из которых является решением уравнения шестой степени f(X) = (X – t1) (X – t2) … (X – t6) = 0. Это резольвента Вандермонда (не в смысле треда, просто слово похожее).
Лагранж заметил что произведение любых двух t, например (x + a y + a^2 z) (x + a^2 y + 2 z) симметрично относительно перестановок x, y, z. Это знание позволяет свести резольвенту как многочлен шестой степени к квадратному.
В случае n = 4, 5, резольвенты получаются многочленами соответственно 24-й и 120-й степеней, но используя симметрию сводятся к 6-й и 24-й.
Теперь рассмотрим резольвенты Галуа.
Пусть K множество, например рациональных чисел. Обозначим K (x, y, z, …) множество, содержащее K и корни x, y, z, … уравнения f(a) = 0 с коэффициентами в K. K(t) это множество всех (x, y, z, …), которые можно рационально выразить через t.
То есть:
K(t) содержит K;
K(t) содержит t, такое что G(t) = 0;
Каждый элемент из K(t) можно записать как многочлен от t с коэффициентами в K.
Это расширение поля, но Галуа о том что такое поле, конечно, не знал.
Основная идея теории Галуа в соответствии между расширениями полей и подгруппами групп их автоморфизмов.
A, A1, A2 – модули над R. Пусть h1 принадлежит Hom (A, A1), h2 – Hom (A1, A2).
Примем для x из A:
hx = h2 (h1 x)
Произведение h2 и h1 это гомоморфизм
h: A –> A2. Определив единичный элемент, умножение на скаляры и внешнюю и внутреннюю дистрибутивность, можно говорить об алгебре эндоморфизмов.
Теперь M – подмодуль A, h принадлежит Hom (M, A1). Для x из M
g из Hom (A, A1) это продолжение h, если gx = hx.
Математика это наука о модулях над кольцами; это базовое предположение, которое я не хочу сейчас обсуждать.
Ничего не понял.
Если M это A (из моего поста), A1 = B, A это первые коцепи комплекса для A, а A2 это первые (гипотетического) комплекса для A1, то откуда взять отображение из A в A1, как построить A2 и как задаётся морфизм из A1 в A2.
>это базовое предположение
ну оно неверное просто по той причине, что математика наукой не является.
Про Лагранжа я знаю.
>ур. разрешимо в радикалах, если группа перестановок его корней разрешима.
Что направило Галуа на то чтобы разбирать группу на коммутанты?Коммутанты Жордан вроде ввёл, но суть та же
Что такое k-теория?
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe
Топологическая к-теория это функтор из компактных хаусдорфовых пространств в коммутативные кольца, переводящий операции прямой суммы и тензорного произведения векторных расслоений в сложение и умножение в кольце. Самая естественная теория когомологий.
Но я говорил об алгебраической. Общего у них мало, а именно, только K(0).
Рассмотрим коммутативный моноид Pr(R) конечно-порожденных проективных модулей над кольцом (R), с операцией прямой суммы. Мы хотим сделать из него абелеву группу, добавив обратимость элементов.
K(0) это пополнение Pr(R), а именно, фактор свободной абелевой группы F порождаемой элементами Pr(R), по соотношениям [m] + [n] ~ [m + n]; для m, n из R.
Если R – локальное кольцо, кольцо главных идеалов или поле, то K(0) изоморфно целым числам. А если дедекиндово – то прямая сумма Z с группой классов идеалов R.
Вообще, это изучают еще в начальных классах. Идея – обобщить пополнение моноида до группы, частный пример это пополнение натуральных чисел до целых. Это описано в брошюре Кириллова "Что такое число".
Опять же, функтор из колец в абелевы группы. Высшая К-теория в принципе такая же, но бьет в категорию с более богатой структурой.
K(0) ввел Гротендик; K(1), K(2) и высшие – Милнор, после него все K определил Квиллен. Но об этом хорошо написал Миша Вербицкий, сейчас я найду цитату.
К-теория (топологическая) для пространства это группа, порожденная расслоениями, с операцией прямой суммы. Эквивалентным нулю объявляется тривиальное расслоение. Этот функтор когомологический, то есть является нулевым членом обобщенной теории когомологий (обобщенная теория когомологий – функтор из топологических пространств в группы, для которого имеют место точные последовательности вырезания и Майера-Виеториса).
Оказывается, что эта теория когомологий – периодическая (K^n=K^{n+k}, k=2 или 8). Это видно оттого, что соответствующее классифицирующее пространство (BGL(∞), где GL(∞) понимается как H-топологическая группа, а BGL ее распетливание) обладает свойством периодичности: оно эквивалентно своему n-кратному пространству петель (n=2 для комплексных расслоений, 8 для вещественных). Это называется периодичность Ботта. Очень удобно в алгебраической геометрии и анализе и является ключом к пониманию формулы индекса и Римана-Роха-Хирцебруха-Гротендика, за которые разные люди получили несколько филдсовских медалей.
Алгебраическая К-теория гораздо труднее. Имеется "плюс-конструкция Квиллена". Это функтор в гомотопической категории, который делает из CW-комплекса CW-комплекс с теми же когомологиями, но с абелевой фундаментальной группой. Это универсальный функтор при отображениях в пространства с абелевой фундаментальной группой. Строится явно путем доклеивания клеток.
Пусть дано кольцо R, рассмотрим группу GL(R, ∞) как дискретную группу, и пусть BGL(R) это соответствующее K(\p, 1). Гомотопические группы BGL(R)^+ – это
алгебраическая К-теория для R.
>>26334
Попрошу не засорять тред, под наукой конкретно в том посте я подразумевал любую человеческую деятельность, за которую дают гранты. На мой взгляд это довольно удобное определение, но спорить об этом я не хочу, интересующимся же этим вопросом могу посоветовать почитать Маха, Джулиан Барбур и Фейерабенда с Лакатосом.
модульный дед
Есть четыре определения векторного расслоения, все довольно полезные. Большинство наших студентов знают, что векторное расслоение есть расслоенное пространство со слоем $\R^n$; если добавить к этому "и групповой структурой, гладко зависящей от базы", получается правильное определение, но довольно неудобное, потому что "гладкую зависимость от базы" прописать весьма трудно. Другой минус этого определения (пожалуй, решающий) – если мы думаем про расслоение как про расслоенное пространство, совершенно непонятно, что есть дифференциальный оператор на расслоении: это оператор на сечениях, который на тотальном пространстве расслоения вообще не определен. Топологическая интуиция, которая формируется из определения расслоений через расслоенные пространства, затрудняет понимание связности как дифференциального оператора на сечениях (и дифференциала де Рама, естественно). Поэтому этим определением ограничиваться невозможно. Коль скоро мы уже начали рассказывать студентам про пучки, глупо останавливаться на полдороге. На языке пучков, векторное расслоение есть локально свободный пучок модулей над кольцом гладких функций. Также можно определить расслоение на языке коциклов и функций переклейки. Это очень удобно для локальных аргументов, примерно как определение в терминах карт, атласов и функций перехода удобно для работы с многообразиями. Эквивалентностью чеховских коциклов, как и эквивалентностью атласов, очень трудно пользоваться, но если перевести ее на язык пучков, оно становится понятнее. Четвертое определение (особенно удобное для К-теории): расслоение есть проективный модуль над кольцом гладких функций на многообразии. Эквивалентность этого определения и всех остальных называется "теорема Серра-Суонна". Ее доказательство вытекает из версии теоремы Уитни для векторных расслоений, которая сама по себе полезна для закрепления разбиения единицы и основных операций с расслоениями.
Открытые проблемы есть. Эрмитова K-теория и гипотезы Новикова, многомерная теория узлов и L-теория, ну про связи с мотивами и прочим я умолчу
>высшие гомотопические пацаны
Кто это
Сизигиях же!
В чем отличие пучка от модуля?
a sheaf has also topological meaning, while module is but pure algebraic notion
Математика это наука о резольвентах модулей и производных категориях когерентных пучков, что хорошая замена понятию пространства вообще (это замечательно описано в книге гомологическая алгебра Гельфанда и Манина, во второй части).
И что лучше всего выбрать по гомологической алгебре: "Introduction to homological algebra" Weibel'а или "Методы гомологической алгебры"/"Гомологическая алгебра" Гельфанда-Манина (или что-нибудь другое вообще)?
>какие
Любой хороший textbook по топологии (Прасолов, Мэй, Дик, Фукс-Фоменко, Кирк-Дэвис) либо книга о векторных расслоениях (Хьюзмюллер, Мищенко, Болтянский-Дынкин-Постников). Еще не помешает хорошо знать внешнюю алгебру, но это не обязательно.
>лучше всего выбрать
Вайбель более простой и с мемчиками, ГМ это standard reference. Только именно "Методы", обзор в ВИНИТИ значительно беднее на содержание.
Но это только если ты уверенно чувствуешь себя рядом с гладкими многообразиями.
вообще там была старая техника Лагранжа, когда из исходного уравнения строились уравнения для произведения корней более низкого порядка. например, для квадратног уравнения переходят к линейному уравнению первого порядка.
от произведения корней Галуа перешел к коммутаторам. и тогда схема решения уравнения превратилась в построение коммутаторов крней все большего порядка, а степень уравнения для коммутаторов должна падать до первой - если уравнение разрешимо в радикалах.
вообще Галуа творил не на пустом месте, как принято считать.
Da. Я сначала накорябол свой ответ, но тебе не понравилось и пришлось скопировать пост другого анона из прошлого треда для начинаек.
Overrated, lacks rigor yet annoying
Сука, я уже на стену от него лезу; встретил бы ирл - ёбыч бы сломал нахуй. То у него CW-пары обладают НЕР, а то он уже рассматривает ретракции цилиндров на консервные банки. Что за нахуй? Граница диска - это подкомплекс разве? Какая вообще ретракция Dn×I на Dn×0 ∪ ∂Dn×I. Пусть n=2, тогда Dn×I это ж цилиндр и он гомеоморфен шару, какая нахуй ретракция? Брауэр завещал, что не существует ретракции шара на его границу. А этот пидор нихуя толком не обесняет, только знай себе переписывает одно и то же по пять раз. Сука, ненавижу.
>В чем профит групп без моноидов?
Тогда в чем профит в анализе колец? Не надо говорить, что анализ это C*-алгебры.
Так я и написал, что моноиды не нужны, вообще-то. C*-алгебры, как и алгебры фон Неймана, это частный пример. Основной объект анализа это нормированные кольца, они же линейные метрические кольца, они же Банаховы алгебры. Гельфанд стал их изучать и применил теорию представлений как более мощный метод для получения простых доказательств в области, ранее называвшейся Фурье-анализом.
https://en.wikipedia.org/wiki/Gelfand_representation
Как уже было замечено, Банаховы пространства это плохой объект изучения, из-за обилия патологических примеров, большую часть которых предоставили некто Bernard Maurey и более известный здесь Timothy Gowers.
Вообще, говорят еще Колмогоров имел мысль, что объект, в котором задана алгебраическая и аналитическая структура при чем последняя непрерывна, должен быть очень конкретным.
Так более того, было доказано что при некоторых условиях типа полупростоты (с нулевым радикалом Джекбсона) аналитическая структура уникальна, то есть
для банаховой алгебры норму можно задать единственным способом.
>>26565
Преследование стеков это 1983 год, а не просто "реалии после 19 века", при чем неизвестно когда эта работа будет завершена.
Ну вот облиле вы сову говном, а она не взлетит теперь никогда!
>что такое дифференциал и операция дифференцирования, как определить модуль не обращаясь к понятию группы
Сверстай все нормально в TeX'е и выложи pdf.
Так и знал что этим ответишь. Во-первых, есть большая разница между "создать тред и неторопливо отвечать в него пару месяцев" и единовременной еботней на пару дней в LyX. Во-вторых, кто это оценит? Долбоебы вроде тебя, называющие раковым все подряд? Ты другие треды видел? Протри глаза и посмотри. Я бы ещё понял такие предъявы в другом месте на форуме для обсуждения сериалов и гороскопов типа dxdy, но не тут.
Кроме того, я поиском проверил, про те же комплексы де рама ни в /sci, ни тут никто не пояснял, а вопросы при этом были (буквально в нескольких тредах до этого, например "производная дифференциал и интеграл"-тред). Давали пару раз определение когомологий, но и то без упоминания точной последовательности.
Если кто-то хочет написать лучше, пусть напишет, но начать с чего-то надо было.
Вообще, я был бы более заинтересован в написании мифологии типа арнольдовских рассказов про Тота-ГерместаТрисмегиста, только про соответствующих деятелей алгебры. Единственная проблема с нарративом Арнольда, это то что прочитав у него одну книгу, ты прочитал тем самым все, тупо повторяются одни и те же телеги.
Я видел достаточно много материалов по Дедекинду, как монографий так и коротких статей, но это все разные источники, а хотелось бы в одном месте.
В частности глава 2 (кажется) "Что такое математика", Абель и Пуанкаре, где он рассказывает идею "группа Галуа = фундаментальная группа римановой поверхности", и под это дело начинает с расширений групп (см второй пост в этом треде).
То есть выбрать конкретный сюжет и под это дело изложить необходимое, 5-6 страниц макс, с хорошей порцией анахронизмов и видимо абсурдных заявлений, на самом деле открывающих суть.
С темой я пока не определился.
Математика, на самом деле, всегда была наукой о модулях, тут я ничего нового не придумал. Кем был Декарт? Философом. Ферма? Юристом. Дезарг? Архитектором. Гаусс?
Когда жили эти люди математика еще не была профессией. Не было тех, кто занимался всю жизнь только математикой и ничем другим, то есть математиков в современном смысле. А теперь возьми Дедекинда. Разве он занимался чем-то кроме математики? Нет, никогда. Столетием раньше подобных Дедекинду просто не было и не могло быть. Оно и понятно, поскольку даже к 1850-м население земли не превышало миллиарда. Общество было недостаточно развитым. С другой стороны, все центральные понятия современной математики появляются одновременно с первыми профессиональными математиками: матрицы и кватернионы в 1840-х; гомотопия голоморфных функций, фундаментальное множество и понятие абстрактной группы в 1850-х; кольца, поля, идеалы и модули в 1870-х; тогда же -- групповые алгебры и ассоциативные алгебры; аксиоматика натуральных чисел, теория множеств, и т.д. История математики до 19-го века это история чего? Решения квадратных уравнений? Было ровно одно исключение в лице того же Дезарга, то, что он открыл, относилось к области чистой математики, которой тогда еще просто не существовало.
Чего? Точная последовательность это последовательность гомоморфизмов, таких что для двух соседних гомоморфизмов h1 и h2, образ h1 равен ядру h2.
Потому что часто возникает ситуация, когда im h1 лежит в ker h2, то есть композиция h1 h2 = 0. Буквально, все утверждения гомологической алгебры выводятся отсюда.
Это комплекс, он не точен, и степень его отклонения от точности это, например, количество нетривиальных решений системы дифференциальных уравнений или например количество дырок (читай: циклов без границы) в разных объектах. Ну это полезная информация в некоторых случаях.
Ты что, вообще тред не читал что ли?! Это все расписано выше было.
дед
Что, все два года сознательной жизни и только математикой? А как же революционные кружки, дуэли? Дедекинд хоть до седин дожил.
>>26740
Еще вспомни смысл понятий ядра и образа
>Ядро — все элементы, переходящие в нейтральный (ноль). Образ — все элементы, в которые что-то переходит.
>Отображение с нулевым ядром называется мономорфизмом (иначе: вложение), отображение на весь модуль — эпиморфизмом (стягивание)
То есть ядро показывает насколько гомоморфизм не инъективен, а образ – насколько он не сюръективен.
А бывают такие примеры что есть три комплекса и есть длинная точная последовательность в их гомологиях, но короткой точной последовательности комплексов нету?
В каком смысле?
Я имею ввиду у нас нет 0 -> A. -> B. -> C. -> 0
Но есть
... -> H_{i}(C) -> H_{i}(A) -> H_{i}(B) -> H_{i}(C) -> H_{i-1}(A) -> ...
не приходящая оттуда.
Спасибо. Теперь ясно.
Написал херню.
Ядро гомоморфизма A–>B это множество элементов A, которые гомоморфизм переводит в нейтральный. Коядро – всё остальное (то есть фактор B по его образу). Тогда ядро измеряет не инъективность (если Ker = 0, это мономорфизм), а не сюръективность измеряет коядро (если Coker = 0, это эпиморфизм).
Так! Нашел ответ в книжке Harold Edwards Galois theory, может кого тоже волнует, могут прочитать. Простите за спам не по теме треда.
Странно, я вроде эту книгу тоже смотрел, но того что тебе надо найти не смог.
У Эдвардса есть еще про последнюю теорему Ферма книга, следуя идеям Куммера. Еще в таком историческом жанре писал Stillwell, про другие области.
Там есть. В общем группа Галуа уменьшается при расширениях поля, и в последнем расширении, когда в поле добавили все корни, она ровна {e}. Я ещё не всё прочитал.
Об эргодической теории ничего не известно, но есть эргодическая теорема. Правда она не для модулей, а для нормированных алгебр.
Пусть U – изометрия на такой алгебре, A – подалгебра решений уравнения Ux = x, тогда последовательность эндоморфизмов V(n) = 1/n (1 + U + … + U^n–1) сходится при n –> ∞ к перпендикулярному проектору E = P(A).
Доказательство есть в книге Халмоша.
Итнегральный пучок в гомологическом спектре кольца свободных результантов. Открытый симплекс высшей когомологии пространства петель ростков полей. Расслоение тривиально, проверяется через замкнутое сепарабельной расширение малых категорий.
Огонь! А теорему Пуанкаре о возвращении в таком же духе можна?
Это понятно, а что имеют ввиду люди из деревни когда говорят про "дифференцирование"? Хочется понимать их язык, на всякий случай.
Интер-универсальную? Так там как раз всё логично и ясно.
>>28165
Тогда заменяй "модуль над кольцом" на "векторное пространство над вещественными числами".
Например не все деревенские знают что производной как линейному оператору соответствует матрица, аналогичное же утверждение на моем языке абсолютно тривиально.
>"векторное пространство над вещественными числами"
Этим серьёзно кто-то пользуется?
>производной
Есть нормальное определение? Я слышал про деревенское, но не знаю его.
>кто-то пользуется
Боющиеся сизигий люди, в основном, предпочитающие не выходить за пределы полей.
>Я слышал про деревенское, но не знаю его
Ну там два, визуальное и геометрическое. Визуальное я уже называл в начале треда, а геометрическое это производная как наилучшая (отличающаяся на o-small) линейная аппроксимация функции вблизи точки.
>Интер-универсальную? Так там как раз всё логично и ясно.
Сепарабельные топосы универсальных расширений комутанта этальной подгруппы. Расширение локального кольца гомологий полилинейного интграла Фробениуса. Ординалы достигаются при наименьшей инволюции дифференциального оператора компакта.
Там топологические пространства инвариативны относительно свободного функтора сужения когомологий.
Решение диффуров в элементарных функциях? Особо нет.
Вообще калькулюсу на многообразиях примерно соответствует коммутативная алгебра.
Есть еще такой новомодный термин как differential algebraic topology, это типа характеристические классы и прочие "гладкие многообразия в теории гомотопий"; такое конечно много используется и везде, что в той к-теории, что в этой.
>>28201
Ну плиз, хватит.
>Ну плиз, хватит.
Прекращаю только потому что ты сказал плиз.
Кстати, что скажешь о комутативной алгебре Зарисского?
Не прекращай плиз.
 53 Кб, 514x698
53 Кб, 514x698https://math.stackexchange.com/questions/1784262/how-is-the-derivative-truly-literally-the-best-linear-approximation-near-a-po
+ пикрил
>>28206
Учиться по ней довольно трудно, терминология устарела. Я вообще даже не думаю, что есть нужда в книгах только по коммутативной алгебре, это уже какая-то "теория чисел" получается.
Ну это как у Атьи-Макдональда, где значительная часть задач посвящена категорному языку вообще и гомологической алгебре (хотя ничо из этого там толком не объясняется, вроде).
>это типа характеристические классы и прочие "гладкие многообразия в теории гомотопий"
Ну ладно, а как вообще k-theory к теории высшихвысших гомотопий и прочей ncatlab-stuff? Есть пересечения? Сори за ЛАМЕРский вопрос, просто я вообще как-то запутался.
>Я вообще даже не думаю, что есть нужда в книгах только по коммутативной алгебре
Что посоветуешь тогда?
Решил изучать Алг. топ. , с какого учебника начать?
Спеньер не плох?
И G-модули.
Мы хотим классифицировать билиненые отображения вида U × V –> W, где U, V, W – модули над K. Пусть U, V свободны, выберем в них базисы соответственно {u(1), …, u(n)} и {v(1), …, v(m)}. Тогда F: U × V –> W однозначно определяется значениями F(u(i), v(j)) = w(ij).
W и есть тензорное произведение U на V, если оно удовлетворяет аксиомам, которые я выпишу ниже.
Пусть у нас теперь A – алгебра над полем K.
Представлением A называется гомоморфизм T: A –> E(M), где E(M) алгебра эндоморфизмов модуля M, удовлетворяющее аксиомам (для a, b из A, λ из K):
T(a+b) = T(a)+T(b);
T(λa) = λT(a)
T(ab) = T(a)T(b).
Образ T, то есть совокупность T(a), образует подалгебру в E(M). Если T – мономорфизм, то эта подалгебра изоморфна A.
Так вот тензорное произведение это, по существу, аналогичная представлению конструкция, только для бимодулей.
Что ты несешь, больной? Все знают, что тензоры - это таблица с числами. Придумал их великий Эйнштейн!
Ну если говорить честно, то чтобы нормально математически определить те тензоры которые нужны физикам, т.е. набор чисел, изменяющийся определённым образом при гладкой замене координат, недостаточно просто понятия тензорного произведения пространств. Как минимум нужно определять гладкое многообразие и тензорное поле на нём как сечение соответствующего расслоения. Неочевидно зачем той куче нематематических физиков, пользующихся тензорами как действительно просто массивами с числами, которые можно сворачивать по индексам, вообще это всё сдалось.
Конечно. Не очевидно, зачем физику знать, что такое электромагнитное поле (связность в главном расслоении)?
Зачем людям вообще знать, чем они занимаются, в чем состоит объект изучения, и т.д. Нет, людям-то, конечно, это знать всегда надо. Но вот физикам не обязательно.
Физики очень агрессивно реагируют на любые попытки их просвещать. В лучшем случае просто ругаются на "бесполезную абстрактность", в худшем - могут и уебать.
Электромагнитное поле это электромагнитное поле, физический концепт к которому маняматику подкрутили уже после.
>физический концепт
… который нельзя выразить иначе, как на языке математики. Можно, конечно, сказать про шесть окошек со стрелочками, которые что-то там регистрируют, это в жизни так выглядит. Как один объект – нет, надо использовать дифф. формы.
В принципе, физик-теоретик переводится примерно как "пиздабол-собеседник", а физика это такая математика без доказательств (и внятных определений), так что у них может и можно говорить что-то содержательное о том, чего не знаешь, somehow.
Я разобрался. Перед этим открывал много книг. Самое лучшее, это >>27477 Stillwell Galois theory for beginers, 4 странички. Но там много упущено, и нормальность подгрупп и абелевость факторов предполагается известным, как и гомоморфизмы/ядра, но доказательство коммутативности фактора хорошее. Пробелы пришлось заполнять самостоятельно.
> Хорошо известно, что математика это раздел алгебраической к-теории.
Дегенератами с мейлру. Основные положения этой теории невыводимы из неё, а являются внешними по отношению к ней. Но в математике не может быть зависимости от внешних теорий, следовательно гамалогии в лучшем случае применение математики, не первая культура даже.
Зарепортил.
Но вот тапалогии - это не гамалогии.
Тип, непрерывному[где несуществует самого маленького, можно бесконечно уменьшать предмет] пространству ставится какая-та структура на алгебре. Типа, вещественных чисел, где считается, что между двойкой и тройкой бесконечное-много значений.
Ну возьми неопределённый функторинтеграл, узнаешь.
Они не производные, а копроизводные. А именно копроизводные вложения Йонеды.
Хома в категорию предпучков. Тензорного умножения на R, если рассматриваем R-модули.
праигрунькал тож! xD
Составил бы список, чё как куда двигаться.
Пока что решаю Глазмана-Любича параллельно с учебником Вербитского, по твоей наводке.
новобранец в армии пынь
Math curriculum очень неплох в качестве такого списка, написать что-то лучше будет очень сложно.
В /pr/, кстати, делали аналогичную копипасту (программисткая программа должна быть устроена…) перегруженную теоретической compoter science и инженерными дисциплинами, но там, как мне кажется, не смогли понять сути.
Смысл текста программы в минималистичности, а не в разнообразии. Вопрос не в том, что можно было бы выучить, а в том, что нужно.
>>33282
Ну Гротендик и оставил свои 12 подвигов, из которых не менее половины еще далеки от реализации.
Упоминаются Кострикин-Манин и Кириллов-Гвишиани же, а это примерно одно и то же. Допускаю, что он про эту книгу просто забыл (вообще на тифаретнике её упоминали пару раз всего).
Sowa, вроде бы, писал что "на линейную алгебру можно смотреть исключительно как на раздел функционального анализа".
Что-то глубокое тут есть, но к этому нужно добавить, что функциональный анализ это раздел к-теории операторных алгебр. Типа как в введении у Wegge-Olsen'а, где он как пример указывает на теорию Фредгольма.
В этом же ключе, теорию представлений в смысле Брауэра думаю стоит рассматривать как раздел алгебраической к-теории. В принципе термин representation theory означает объединение непересекающихся множеств, ну примерно как "теория чисел".
Гармонический анализ это вроде 100% RT, но включают этот материал только в курсы анализа. С другой стороны, для модулей над алгебрами ли теорема Машке не выполняется (она только для представлений конечных групп, по-моему), а это влечет много гомологической алгебры, операции Стинрода и т.д.
Высказывание Гельфанда "i used to say: everything is representation theory" представляется чем-то вроде фразы Гаусса про "теорию чисел – царицу математики", с существенной разницей, что Гаусс наук про пространства Харди (аналитическая теория чисел это чистый анализ по сути) не знал. А вот Гельфанд аналитическую теорию представлений изобрёл. Отсюда и продолжение фразы "…now i say nothing is representation theory". Потому что этот термин ничего конкретного не значит сам по себе уже, "аналитическая т.пр." и "полупростая т.пр." две разные области, ничего общего.
:3
Модуля над кольцом ответ.
В чём цимес?
 121 Кб, 847x275
121 Кб, 847x275Спасибо, интересная штука.
Как сгенерировать полугруппу группы точек эллиптической кривой в конечном поле?
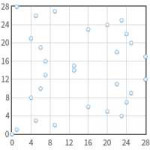 9 Кб, 300x300
9 Кб, 300x300На пикрелейтед - вся группа. Видно, что точки обеих полугрупп - симметричны. А надо сгенерировать одну полугруппу и проверить принадлежность точки ей.
Анон, какие в 2к19-м существуют алгоритмы, эффективнее этого:
https://ru.wikipedia.org/wiki/Алгоритм_Гельфонда_—_Шенкса
и применяемые для решения этой же задачи:
>в теории групп детерминированный алгоритм дискретного логарифмирования в мульпликативной группе кольца вычетов по модулю простого числа.
Есть вот кольцо по модулю простого числа.
Характеристика его - простое число.
Это абелева группа, и поле Галуа.
В этом поле/кольце - определены операции сложения, умножения, деления, вычитания.
Задача: по элементу - найти индекс элемента в кольце, кратчайшим путём.
Слышал есть pollard rho с поиском циклов методом Флойда, методом Брента, и методом kangaroo,
но чё-то не раздуплю суть того, как оно всё там работает.
мехмат прогнали к чубарикову х)
>На официальном сайте механико-математического факультета МГУ по состоянию на 2013 год утверждается, что В. Н. Чубариков дал полное решение проблемы Варинга—Гольдбаха в 2009 году[7]. Однако в единственной статье 2009 года, посвящённой этой теме[8], дается решение задачи, лишь в некотором смысле сходной с проблемой Варинга — Гольдбаха
Господи, когда это говно уже закроют. То у них Фоменко решил задачу Плато, то Садовничий еще до Атьи с Зингером теорему об индексе доказал. Что, без приписывания сотрудникам несуществующих результатов вообще работать не получается? Клоуны.
Ну тогда россиянское государство денег плотить не будет, очевидно же.
впервые слышу про влкад садовничего в теорему об индексе
про фоменко - да, известная история. а вот это таки новость
>про фоменко - да, известная история
Кто-нибудь может затравить эту кулстори? Викимусорка до сих пор утверждает, что Фоменко решил задачу Плато.
кулстори заключается в том, что фоменко издал на ангельском книжку, у которой на обложке было написано, что автором решена проблема Плато, а внутри оказывалось, что разобран только частный случай. рецензент с недоумением на это указал, на что фоменко ответил, мол, на обложке может быть что угодно и служит лишь для рекламы, а внутри книжки типа всё правильно.
история поимела известность в ходе публичных препирательств Новикова и Фоменко, когда они производили довольно своеобразные тексты с наездами друг на друга (а в случае Новикова -- до кучи и на многих других); в одном из таких наездов Новиков про указанную рецензию рассказал (и фоменко отвечал не на рецензию, а именно ему)
Всё это лежит в сети повсюду, можно легко найти и устроить себе увлекательное досуговое чтение
речь, правда, не совсем про теорему об индексе, но смотрится заявление всё равно неплохо
садовничий, а воняет как физтех
О том, что что "математика это раздел алгебраической к-теории"?
Вон в треде МАТЕМАТИКА ДЛЯ НАЧИНАЮЩИХ N+1 Арнольд-петух образовался, он объяснит. Думаю, что наверно больше нигде
полно же источников
Из доступных -- Rotman,
Из известных -- Weil
Из канонических -- Гротендик (а также Бурбаки, а также Маклейн)
Из хороших -- Гельфанд-Манин (но их немного неуютно читать из-за большого количества опечаток)
Выбор на любой вкус
Про Вейля что конкретно имеется в виду? Может ты хотел сказать Вейбель?
>Гротендик (а также Бурбаки, а также Маклейн)
Полная каша из говна 67-го года издания с неиспользуемыми уже нигде терминологией и обозначениями. Странно что Картана-Эйленберга забыл.
В книге Бурбаки Алгебра X по собственно гомологической алгебре очень мало.
ГМ нормальный учебник, лучше пока не написали.
>>61252
Мне понравилась Heart of Cohomology by Kato.
Есть еще лекции:
https://youtube.com/playlist?list=PLul8LCT3AJqS_-MNTC7jPhQP0QAj_w6yd
Ну да, вейбель. Сорри
 37 Кб, 782x390
37 Кб, 782x390> Heart of Cohomology by Kato.
Посмотрел по диагонали, выглядит интересно, думаю подробнее ознакомиться, кажется я начинаю догадываться, почему у местного пучкиста такой барендрегт от конструктивизма, лол. Там походу все эти гамалогии тапалогии можно просто на HoTT переписать и в пруверах тилибонить почти без участия лысых обезьян. Гомологическую алгебру ещё до Воеводского пытались в коке вымутить, но CoIC для этого не оче, а вот HoTT - то, что доктор прописал.
По этому вопросу мнение двачера, который даже введение в алгтоп не осилил, никого не интересует.
Что пучкист шизик, что ты. Иди уже в свой /pr/.
>мнение двачера,
Манюнь, это ты автора этого https://tel.archives-ouvertes.fr/tel-01486550/document двачером называешь? Вообще, если опучкаться в MLTT / CoIC напрямую не получится, нужно много хуйни дописывать, то в HoTT с гамалогиями проблема только в том, что этим занимается 1,5 человека.
>Что пучкист шизик, что ты.
Один ты весь в белом? Сам-то чьих будешь?
>то в HoTT с гамалогиями проблема только в том, что этим занимается 1,5 человека.
вот математики тупыыыые, только 3,5 фрика знают, что на самом деле нужно
ну чего ты доебался
в мёртвом старом треде анон написал "мне понравилось вот это", ну понравилось ему, ну и что? он же не попытался насрать везде, где мог, а вот ты на пустом месте срач разводишь
У меня есть к тебе вопрос. Считаешь ли ты CoIC конструктивно-приемлемой системой? И если да, то как ты обосновываешь полиморфные типы?
Это полностью непредикативная штука. Мы хотим иметь типы функций, которые имеют аргумент-тип и должны корректно работать (всегда завершать свою работу) при подстановке произвольного типа (включая тип этой функции и более сложные типы). Мне совершенно непонятно как такое можно обосновать с чисто конструктивистских позиций.
На самом деле это больше для удобства программирования, чтобы не перечислять явно все допустимые в данном случае типы. И произвольность там кажущаяся. "Произвольный" тип это в любом случае тип, правильнотипизированный в имеющемся контексте, иначе он, как и любая функция с его участием, просто чекаться не будет. Как и гипотетическое суждение x:A в MLTT, где х - произвольный и не обязательно существующий объект, в процессе применения правила с таковым суждением отменяется конкретным термом a:A, где a это уже не переменная, а конкретный элемент конкретного типа, правильнотипизированного в имеющемся контексте.
Ну так я же говорю о полиморфных типах в CoIC, а не о гораздо менее выразительных полиморфных типах хаскелла (без расширений), которые и в самом деле суть свободные переменные по типам (и вывода типов в CoIC в отличие от хаскелла все-равно нет). И меня интересовала не утилитарная сторона дела - понятно, что более выразительная система типов удобнее. А обоснование CoIC как конструктивно приемлемой системы - как минимум, почему, например, с помощью полиморфных типов мы же докажем, что 0=1.
Обсуждать HoTT - себя не уважать, это очередная "я настоящий математик!"-игрушка для горе-программистов.
> как минимум, почему, например, с помощью полиморфных типов мы же докажем, что 0=1.
Потому что тип Eq(0,1) пуст. И никакие сколь угодно полиморфные типы, допустимые в CoIC этого не изменят, если сознательно и явно не прописать что-то такое в виде аксиомы, не выводимой из чего-то ранее построенного. Ну так-то там и десять заповедей можно прописать. Да, типы в CoIC в общем случае невыводимы. Поэтому эта система неразрешима чисто на одних тактиках.
 43 Кб, 453x604
43 Кб, 453x604> Обсуждать HoTT - себя не уважать, это очередная "я настоящий математик!"-игрушка для горе-программистов.
А в исходной теории типов Мартин-Лёфа был непуст. И это произошло по-существу именно из-за очень сильной формы полиморфизма. Если бы ты не знал об этом изяне исходной теории Мартин-Лёфа, то с успехом бы произносил эти мантры и по её поводу.
> А в исходной теории типов Мартин-Лёфа был непуст.
С чего бы? В какой это версии MLTT 0 = 1? Надеюсь, ты хоть не парадокс Жирара имеешь в виду?
Martin-Löf 1971 и да, конечно, парадокс Жирара. Так у тебя есть объяснение почему полиморфизм в U с конструктивной точки зрения плохой, а в CoIC хороший?
Самая смехота в том, что для чекающейся типизации гамалогий в HoTT пришлось таки искусственно ввести заповедь, вызывающую парадокс Жирара (Type i : Type i), что прямо доказывает неизбежную противоречивость этих ваших гамалогий, на данный момент времени других решений нет. Вот и прикинь, чего стоят ваши гамалогии, если могут существовать только в изначально и гарантированно противоречивой системе. Кантор в свое время даже заболел от переживаний после того, как Бурали-Форти показал противоречивость его теории множеств. А нынешним свидетелям гамалогий все похую, достаточно сказать что "математика подвешена в воздухе" и неебет. Ваши пруфы не пруфы и не математика, азаза)))
>Я ничего не могу сказать по существу
Ну ладно, все с тобой понятно. Кстати, вообще непонятно для кого должно было бы оказаться неприятно твое последнее замечание. Видимо это должен был бы быть кто-то кто одновременно угорает по алгебраической топологии и теории типов. Но что-то я таких здесь не припомню.
Я угораю по алтопу, но мне абсолютно похуй.
и чо? аксиома унивалентности тоже долго отношения к вычислимости не имела, и всем заебок было
я это к чему говорю, придумают чонить, а наш товарищ уже гогочет
Так я по существу. Ты ж серьезно спрашиваешь, чем конструктивно плоха MLTT с парадоксом Жирара. При этом понимая, что всем плоха. Зато гамалогии в такой можно типизировать.
Меня интересовало есть ли у тебя внятное конструктивное обоснование полиморфных типов из CoIC. А MLTT71 возникла в контексте твоего "аргумента" из >>61817, который никоим образом не адресовал особенности системы типов CoIC и (если бы ты не знал о парадоксе Жирара), то с тем же успехом мог бы в нем заменить CoIC на MLTT71 и прийти к ошибочному результату.
>Кантор в свое время даже заболел от переживаний после того, как Бурали-Форти показал противоречивость его теории множеств.
У Кантора не было никаких противоречий, у него понятие множества было сильно урезано, противоречия появились уже после Фреге.
> У Кантора не было никаких противоречий,
Пиздец. Ты б хоть педивикию читнул. Парадокс Бурали-Форти касается именно теории множеств Кантора и показывает именно ее противоречивость.
>>61859
> Меня интересовало есть ли у тебя внятное конструктивное обоснование полиморфных типов из CoIC
Ну так есть же.
> аксиома унивалентности тоже долго отношения к вычислимости не имела,
Всегда имела. Ещё в HoTT book в 13 году писали, что конструктивность аксиомы унивалентности это просто открытая на тот момент проблема, вряд ли кто-то сомневался в возможности ее конструктивного доказательства, иначе HoTT вообще не имела бы смысла как конструктивные основания.
Открыл, посмотрел
>Несуществование множества всех порядковых чисел противоречит концепции наивной теории множеств, разрешающей построение множеств с произвольным свойством элементов, то есть термов вида «множество всех x таких, что P» ({x|P}).
Вот эту хуйню с произвольным свойство Фреге и добавил, тем самым расширив изначальное понятие "множество" у Кантора до противоречивого. Сам Кантор считал множеством такую совокупность, что для каждой вещи в мире известно принадлежит она ей или нет, там никаких противоречий не было, но понятие было очень узким, математику на нём построить нельзя было.
>По этому поводу стоит заметить, что сам Кантор не только никогда не пользовался предположениями, подобным аксиоме Фреге, но уже лет за 20 до парадокса Рассела тщательнейшим образом различал множества (Mengen) и совокупности81 (Gesamtheiten, Vielheiten, Totalit¨aten, Unmengen), которые слишком велики для того, чтобы быть множествами и чтобы к ним можно было применять стандартные процедуры образования новых множеств. Совокупности, к которым неприменима его теория трансфинитных множеств, Кантор называл абсолютно бесконечными. Иными словами, уже в 1880-х годах Кантору были известны не только сами парадоксы, но и способ их преодоления, по существу эквивалентный предложенной Дж.фон Нейманом теории классов.
Короче не надо гнать на Кантора.
тащемта, ну вот впилили в CCHM (вроде как) Glue types, тупо ради kan composition и док-ва унивалентности, а что в них, собственно, конструктивного? то что оно редуцируется это хорошо, конечно, но я мог бы и ввести в теорию beta редукцию (типа ua (idEquiv) A A == refl A), от этого же унивалентность конструктивной не стала, так?
> то есть термов вида «множество всех x таких, что P» ({x|P}).
> Сам Кантор считал множеством такую совокупность, что для каждой вещи в мире известно принадлежит она ей или нет,
А ты сам не видишь, что оба определения выше - это одно и то же? Речь в обоих случаях о функции принадлежности. Алсо, вроде Кантор определял множество не так. Энивей, его теория множеств для математики не подходит.
>что оба определения выше - это одно и то же?
Не, там говорится, что для любого свойства P существует множество всех х таких, что P, ну и понятно, что это неправда, можно много свойств напридумывать, когда получается противоречие типа Бурали-Форти, парадокса Рассела, вот, а Кантор не считал, что для любого свойства, вот взять то же множество всех множеств, мы не можем сказать принадлежит ли оно самому себе или нет, поэтому оно не является множеством. С другой стороны множество нечётных совершенных чисел тоже не будет являться множеством с такой точки зрения, ну ты понел, слишком узко получается, поэтому Фреге объявил, что для любого свойства П блаблабла, но так получилось противоречиво, поэтому пришли к ZFC.
Вавилов утверждает, со ссылкой на канторовские статьи на немецком, что Кантор разделял множества и "поистине бесконечные совокупности". Так что оригинальная канторовская теория скорее напоминает NBG.
>>61883
>>61887
Как то я спросил кококонструктивиста какой вычислительный смысл у равенства ( refl : 1 = 1 ) или индуктивных конструкторов ( O : Nat ), на что получил ответ
>он тривиальный, кукареку
Собственно что мешает про ту же аксиому унивалентности так сказать, да хоть про любую другую хуйню?
Ситуация мне кажется сходной с тем как доказывали пятый постулат Евклида. Казалось бы - вы че ебанутые, как вы его докажете - это ж постулат. А потом вон оно как вышло интересно.
 313 Кб, 418x502
313 Кб, 418x502С точки зрения конструктивного понимания кванторов аксиома выбора верна. В самом деле, с точки зрения конструктивной утверждение вида "для любого x из A существует y из x" означает, что есть метод построения y-ков по x-ам, а этот метод построения и есть искомая функция выбора для A.
>"для любого x из A существует y из x" означает, что есть метод построения y-ков по x-ам, а этот метод построения и есть искомая функция выбора для A.
это какая-то хуйня из под коня, а не AC, ознакомься
https://ncatlab.org/nlab/show/axiom+of+choice
Я имел ввиду эту форму ∀A(∀ x ∈ A∃ y(y∈ x)→ ∃ f(dom(f)=A ∧ ∀ x∈ A(f(x)∈ x))). Понятно, что встречаются незначительные вариации. Если ты считаешь, что с этим вариантом что-то фундаментально не так, то можно предметнее.
>>61978
As discussed above, in ZFC, the axiom of choice is able to provide "nonconstructive proofs" in which the existence of an object is proved although no explicit example is constructed. ZFC, however, is still formalized in classical logic. The axiom of choice has also been thoroughly studied in the context of constructive mathematics, where non-classical logic is employed. The status of the axiom of choice varies between different varieties of constructive mathematics.
In Martin-Löf type theory and higher-order Heyting arithmetic, the appropriate statement of the axiom of choice is (depending on approach) included as an axiom or provable as a theorem.[10] Errett Bishop argued that the axiom of choice was constructively acceptable, saying
A choice function exists in constructive mathematics, because a choice is implied by the very meaning of existence.[11]
In constructive set theory, however, Diaconescu's theorem shows that the axiom of choice implies the law of excluded middle (unlike in Martin-Löf type theory, where it does not). Thus the axiom of choice is not generally available in constructive set theory. A cause for this difference is that the axiom of choice in type theory does not have the extensionality properties that the axiom of choice in constructive set theory does.[12]
Чего скажите про аксиому детерминированности? Когда и вообще вытеснит ли она аксиому выбора?
Никогда. Аксиомы класса definable determinacy совместимы с ZF+AC, а вся AD целиком не нужна.
>вполне упорядочить аксиома детерминированности разрешает не любые, а лишь только конечные и счётные множества, лишается основания нестандартный анализ
никогда.
Нестандартный анализ сейчас все-равно не слишком популярен. И кроме того, с AD несовместен только подход на основе ультрафильтров, а с аксиоматическим подходом к нестандартному анализу все в порядке и без аксиомы выбора. С AD другие проблемы - она релевантна только в областях с большой теоретико-множественной составляющей, а там у людей уже выработалась интуиция существенно опирающаяся на AC. Например, любители детерминированности в качестве приложения иногда продают результат о том, что L_1 - это двойственное пространство для L_\infty. Но с точки зрения собственно людей занимающихся функциональным анализом, это довольно абсурдная вещь.
бля, вот у нас короче есть пространство, шестимерное, шесть классов когомологий на нем.
допустим это пространство минковского где одна компонента это ЧЕТЫРЕСФЕРА, а вторая МЕРА ортоцентра триангуляции гранатомета, а третья это интеграл.
Для объяснения расслоения не нужны ни алгебра, ни топология. Ближайший и простейший изоморфизм расслоения, который сам по себе может является логикой -- это зависимый Пи-тип, квантор всеобщности. Расслоение --- это основание современной математики, покуда математики используют кванторы и выражение "для всех х ..."
Definition (Section). A section of morphism f:A→B in some category is the morphism g:B→A such that f∘g:B→gA→fB equals the identity morphism on B.
Definition (Fiber). The fiber of the map p:E→B in a point y:B is all points x:E such that p(x)=y.
Definition (Fiber Bundle). The fiber bundle F→E→pB on a total space E with fiber layer F and base B is a structure (F,E,p,B) where p:E→B is a surjective map with following property: for any point y:B exists a neighborhood Ub for which a homeomorphism f:p^{−1}(U_b)→U_b×F and p:U_b×F→U_b and pr_1:U_b×F→U_b.
Definition (Trivial Fiber Bundle). When total space E is cartesian product Σ(B,F) and p=pr1 then such bundle is called trivial (F,Σ(B,F),pr1,B).
Theorem (Fiber in a trivial total space is a family over base). Inverse image (fiber) of fiber bundle (F,B∗F,pr1,B) in point y:B equals F(y).
На практике математики пользуются четырьмя видами расслоений (два с зависимым кодоменом и два без):
-- Definition (1) Dependent
isFBundle1 (B: U) (p: B -> U) (F: U): U
= (_: (b: B) -> isContr (Path U (p b) F))
((x: Sigma B p) -> B)
-- Definition (2) Dependent
isFBundle2 (B: U) (p: B -> U) (F: U): U
= (V: U)
(v: surjective V B)
((x: V) -> Path U (p (v.1 x)) F)
-- Definition (3) Non-Dependent
im1 (A B: U) (f: A -> B): U = (b: B) propTrunc ((a:A) Path B (f a) b)
BAut (F: U): U = im1 unit U (\(x: unit) -> F)
unitIm1 (A B: U) (f: A -> B): im1 A B f -> B = \(x: im1 A B f) -> x.1
unitBAut (F: U): BAut F -> U = unitIm1 unit U (\(x: unit) -> F)
isFBundle3 (E B: U) (p: E -> B) (F: U): U
= (X: B -> BAut F)
(classify B (BAut F) (\(b: B) -> fiber E B p b) (unitBAut F) X) where
classify (A' A: U) (E': A' -> U) (E: A -> U) (f: A' -> A): U
= (x: A') -> Path U (E'(x)) (E(f(x)))
-- Definition (4) Non-Dependent
isFBundle4 (E B: U) (p: E -> B) (F: U): U
= (V: U)
(v: surjective V B)
(v': prod V F -> E)
* pullbackSq (prod V F) E V B p v.1 v' (\(x: prod V F) -> x.1)
На практике математики пользуются четырьмя видами расслоений (два с зависимым кодоменом и два без):
-- Definition (1) Dependent
isFBundle1 (B: U) (p: B -> U) (F: U): U
= (_: (b: B) -> isContr (Path U (p b) F))
((x: Sigma B p) -> B)
-- Definition (2) Dependent
isFBundle2 (B: U) (p: B -> U) (F: U): U
= (V: U)
(v: surjective V B)
((x: V) -> Path U (p (v.1 x)) F)
-- Definition (3) Non-Dependent
im1 (A B: U) (f: A -> B): U = (b: B) propTrunc ((a:A) Path B (f a) b)
BAut (F: U): U = im1 unit U (\(x: unit) -> F)
unitIm1 (A B: U) (f: A -> B): im1 A B f -> B = \(x: im1 A B f) -> x.1
unitBAut (F: U): BAut F -> U = unitIm1 unit U (\(x: unit) -> F)
isFBundle3 (E B: U) (p: E -> B) (F: U): U
= (X: B -> BAut F)
(classify B (BAut F) (\(b: B) -> fiber E B p b) (unitBAut F) X) where
classify (A' A: U) (E': A' -> U) (E: A -> U) (f: A' -> A): U
= (x: A') -> Path U (E'(x)) (E(f(x)))
-- Definition (4) Non-Dependent
isFBundle4 (E B: U) (p: E -> B) (F: U): U
= (V: U)
(v: surjective V B)
(v': prod V F -> E)
* pullbackSq (prod V F) E V B p v.1 v' (\(x: prod V F) -> x.1)
На Агде доказан изоморфизм всех четырех структур, дозательство равности раслоения и квантора есть на всех HoTT пруверах.
- гамалогии в общем неконструктивном случае сами по себе противоречивы, т.к чекаются только при искусственном добавлении в прувер парадокса Жирара. А раз так, то их нельзя использовать в математике вообще.
- в объеме, не требующем специального введения парадоксов, гамалогии конструктивны.
- других результатов пока не поступало.
Из чего можно сделать выводы:
- HoTT пока единственный инструмент для работы с гамалогиями, использование которого не ведёт к противоречиям.
- модульный дед таки поел говна на обед.
Я ничего не упустил?
Я б не сказал, шо модульный дед поел говна, я сюда захожу только его читать. С Гомологиями проблем нет особо, проблемы разве что с когомологиями, ну и просто чё-то никто не хочет Алгебру переписывать, так как есть уже KENZO, GAP/HAP. Ну и производные категории с инвертированными квази-эквивалентностями громоздкие. Удобного MLTT фреймворка для работы с Tor Ext пока нет.
> никто не хочет Алгебру переписывать, так как есть уже KENZO
А это вообще что за народное творчество? Какой-то кринж-прувер на Лиспе или что-то в этом роде? https://www-fourier.ujf-grenoble.fr/~sergerar/Kenzo/
Это не прувер, но оно может работать с прувером ACL2, так как написано тоже на Common Lisp. KENZO --- это CAS система для (ко)-гомологической алгебры.
Вот в GAP можно такое писать:
gap> F:=FreeGroup(4);;w:=F.1;;x:=F.2;;y:=F.3;;z:=F.4;;
gap> rels:=[w^8, wxw(xwx)^-1, y^2, zx(xz)^-1,z^-1yzy, (xy*x)^2];;
gap> G:=F/rels;
<fp group on the generators [ f1, f2, f3, f4 ]>
gap> N2:=[]; N3:=[];
[ ]
[ ]
gap> for u in GeneratorsOfGroup(G) do
> Add(N2,u^2);
> Add(N3,u^3);
> for v in GeneratorsOfGroup(G) do
> Add(N2,Comm(u,v));
> Add(N3,Comm(u,v));
> od;;
> od;;
gap> N2:=NormalClosure(G,Group(N2));
Group(<fp, no generators known>)
gap> N3:=NormalClosure(G,Group(N3));
Group(<fp, no generators known>)
gap> AbelianInvariants(N2);
[ 0, 0, 3, 3, 3, 3, 4 ]
gap> AbelianInvariants(N3);
[ 0, 2, 4 ]
Дед старый, может не осилить. Там же свои модули нужно писать, а так он дернет пару фукнций и скажет "не математика".
И да и нет, ты же не понимаешь чем CAS система от прувера отличается, что ты вообще тут делаешь. Так то конечно на любом языке можно построить модел чекер любого языка.
А если хотя бы теоремы дифференциальной геометрию не можешь записать в прувере то о какой Мочидзуке мы тут говорим.
> на Бейсике можно Мочидзуку написать, если знаешь что писать.
Опять же, хотелось бы узнать позицию модульного деда по этому вопросу.
def localization (α : Type u) [comm_ring α] (S : set α) [is_submonoid S] := quotient $ localization.setoid α S
class is_noetherian (R M) [ring R] [add_comm_group M] [module R M] : Prop := (noetherian : ∀ (s : submodule R M), s.fg)
@[class] def is_noetherian_ring (R) [ring R] : Prop := is_noetherian R R
@[class] def is_maximal (I : ideal α) : Prop :=
I ≠ ⊤ ∧ ∀ J, I < J → J = ⊤
собери определение регулярного локального кольца своими руками
10 LOCALIZATION COMMRING A, SET S, QUOT= A S
20 NOETHERIAN RING R MODULE M, SUBMODULE S, S.F.G
30 IS_MAXIMAL IDEAL I ≠ ⊤ ∧ ∀ J, I < J → J = ⊤
пофиксал кольца на Бейсике
> если на человеческом можно, то и на Бейсике тоже, не?
Ну в соседнем треде модульный дед говорит, что с гамалогиями так нельзя, бохнакажет. Вот мне и интересно.
он просто режектить будет все, что не понимает или не хочет понимать, даже если вы ему нарисуете конструктивный топос Зарисского и афинную теорию гомотопий имени Воеводского, все равно диалога не получится.
 915 Кб, 1208x1840
915 Кб, 1208x1840Кстати, чё Эмми Нетер нет на фотка, кольцейобы?!
Обпучкался чёт.
Модульный дед, ты по делу ответь - почему бейсик или пистон для гамалогий это ДРУГОЕ.
 60 Кб, 1000x1507
60 Кб, 1000x1507God Tier
Да.
че почитать по гомологическое алгебре, но чтобы не только гомологическая алгебра, а еще что-то дальнейшее, интересное было.
Если вообще ничего не знаешь, то просто почитай алгтоп.
А так мне понравилась книжка Ротмана.
Не представляю, что ты имеешь ввиду. Почти наверняка нет.
Можно, наверное, сказать, что кольцо это аналог целых чисел, в том смысле, что с целыми числами можно делать всё то же, что и с элементами кольца(складывать, умножать, вычитать, но не делить!, дистрибутивность сложения относительно умножения и тд)
>Нормированные кольца тоже арифметика?
Это как спрашивать про евклидово пространство - а это арифметика? Ну там структур дохуя же напичкано, от кольца/поля до формы объёма и римановой метрики. Складывать и умножать нам же никто от этого не запрещает, лол.
Нормированное кольцо это векторное пространство прежде всего. Но таки да, это тоже арифметика, естественно, хотя бессмысленно её сравнивать с другими кольцами из-за дополнительной структуры (в контексте вопроса анона выше).
в английском переводе стоит автором гутенмахер и значит это перевод другой книги, первой, оригинальной, самиздатовской. В издании без гутенмахера картинок нет.
>про евклидово пространство - а это арифметика?
У тебя тогда и вещественные числа - арифметика.
>>69690
http://libgen.is/book/index.php?md5=48258D3C46D719970D2372946811DA66
Есть там всё. В английском издании даже пояснения для этих картинок имеются.
Сейчас проверил, в советском издании 89-го года без Гутенмахера тоже есть картинки, на 497-й странице.
http://libgen.is/book/index.php?md5=99D116BF0B592C91771774B96933A4FF
очень легко:
1) доказываем, что в кольце многочленов одной переменной имеется операция дифференцирования d: R[x] -> R[x], заданная известной школьной формулой (элементарная проверка)
2) применяем формулу
забавно приставать с такими тупыми вопросами к ответу 2,5-годичной давности
До неё нетрудно догадаться, если размышлять как деды "допустим точка движется по графику, её скорость...", или "проведя касательную прямую к графику мы сможем вычислить приближенное значение в окрестности...". Если размышлять как бурбакисты, то до неё никогда не догадаешься.
я проверил, чтобы получить школьную формулу, достаточно записать d(x^1) = 1
при этом дифференцирование на кольце многочленов не единственное: для d(x^1) можно назначать разные значения (например, положить d(x^1) = x^2), будут получаться разные дифференцирования
чтобы догадаться, что d(x) =1, действительно можно рассуждать как деды, но рассуждение получится такое: "если точка движется с постоянной скоростью, то её скорость постоянна". нетрудно же?
или получить её из основного определения производной: d(f)(a) = f(a) + f'(a) x + o(|x-a|)
>достаточно записать d(x^1) = 1
А как поступить с тригонометрическими функциями?
в Львовский "тригонометрия" производная косинуса выводится без рядов
>или получить её из основного определения производной: d(f)(a) = f(a) + f'(a) x + o(|x-a|)
Это определение легко переварить зная производную как предел. Для тех кто его не знает это определение абсолютно не перевариемое.
>А как поступить с тригонометрическими функциями? в Львовский "тригонометрия" производная косинуса выводится без рядов
для сначала надо как-то ввести эти функции
я не читал эту указанную книжку Львовского, но в бурбаках эти функции определяются через ряды
>Это определение легко переварить зная производную как предел
извини, но без этого определения или чего-нибудь подобного тебе вообще будет трудно понять, что такое "гладкая функция", так что полностью обойтись не получится
в то же время мне лично это определение кажется более наглядным, чем то, которое через предел, поскольку оно ясно выражает главное: производная -- это линейное приближение функции в данной точке (понятие "скорость" у физиков означает то же самое)
кроме того, оно годится для отображений между банаховыми пространствами; осознать, что семейство операторов может быть гладким и его можно дифференцировать, - это классно. но это уже оффтопик
Так это и есть определение через предел, в словосочетании "о-малое" содержится предел. Другое дело что такая запись гораздо понятнее традиционной.
Про все возможные определения производной можно посмотреть короткую статью "On proof and progress in mathematics" Тёрстона.
>Про все возможные определения производной можно посмотреть короткую статью "On proof and progress in mathematics" Тёрстона.
Хуита, конечно - во-первых, в статье нет "всех вохможных определений", во-вторых, те, которые есть, даны там хуй черех плечо без какой-либо точности совершенно.
Статья отличная, конечно, но по другим причинам.
Она понятней только если ты знаешь традиционную. Лучше всего использовать сначала "производная в точке это угловой коэффициент касательной". Чтобы его высчитать, можно использовать "треугольник приращения с катетами dy и dx". Тогда чисто школьно-геометрически можно вывести правила взятия производной суммы и произведения.
Катет dy для суммы f+g будет равен df+dg, тогда dy/dx=df/dx+dg/dx=f'+g'
Катет dy для произведения равен эти вычисления наглядны, если нарисовать прямоугольник (fx+df)(gx+dg)-fxgx=f(x)dg+g(x)df+dfdg, так как dfdg ничтожно мало, то им можно пренебречь, получаем dy=fdg+gdf, и производная dy/dx=fdg/dx+gdf/dx=fg'+gf'
Уже после этого можно легко вывести, что приращение функции можно посчитать по этой самой касательной: dy=y'dx+o(dx)
>Хуита, конечно - во-первых, в статье нет "всех вохможных определений", во-вторых, те, которые есть, даны там хуй черех плечо без какой-либо точности совершенно.
Они и не даны как логические определения, они даны как разные интуитивные понятия для разных применений, и которые обобщаются в разных направлениях.
В школе нет даже элементарных понятий из современной алгебры. Что тебе можно сказать о современной алгебре, если ты не знвешь что такое кольца/модули/группы/поля/категории и никогда не видел примеров в геометрии, физике, топологии, etc, где современная алгебра оставила глубокий отпечаток и является базовой составляющей.
в школе рассказывают векторы, ничего не говоря об линейную алгебру.
в школе учат делать перенос при сложении в столбик, ничего не поясняя за расширение модулей.
в школе какой-то позор.
первый класс нужно начинать с определения цепного комлекса, а дальше уже как получится.
и даже какой-то вербицкий в это верит.
Не нужно делать образование стандартным для всех и одинаковым во всех школах. Пусть разных людей учат по-разному - так, как им лучше.
Если не занимать мемные позиции вроде шуток вот этого анона >>80035, то Арнольд именно за это и топил, а эта дсока топит против Арнольда, так что обсуждение здесь бессмысленно. Всем же известен его курс про теорему Абеля для школьников, или книжка про группы из кванта (александрова?). Вполне можно было бы порассказывать про симметрии, ввести определние группы, порешать простейшние задачки, и помахать ркуами насчёт кристаллов и теоремы Нётр, и всё это в 9-10 классах (на факультативе, ессно).
В наглядной топологии уйма интересных вещей, которые можно просто послушать в старших классах.
Ну и obligatory основная функция школы - обучение обучению, на сосбственно контент похуй.
>а эта дсока топит против Арнольда
ну что ты, это только любители-фундаменталисты определять определитель
а вообще его фото на самом верху висит, и мы все ему радуемся
его физическая форма пускай волнует его жену, его тренера, его врача.
для матемача интересна только его математическая работа. ну и лулзы, само собой.
да ничего не серьезно, он за годы реального обучения уже понял, что зря абстрагировал свою уникально элитную маттусовку на всех. Его программа подходит, чтобы выращивать жидоспартанцев в элитном потоке элитной матшколы, а учителями должны быть не иначе как Гельфанд, Арнольд и Гинзбург, иначе может и не получиться.
>Его программа подходит, чтобы выращивать жидоспартанцев в элитном потоке элитной матшколы
так правильно, именно для это тифарет-программа и нужна: для людей, которые будут работать в математике.
остальным математика совсем побоку, за них калькулятор считает и телевизор обосновывает.
>для людей, которые будут работать в математике.
ну если ты считаешь, что этому достойны только несколько человек в год со всей России, то безусловно. Я же считаю, что количество математиков не менее важно, чем качество, даже если они не решат фундаментальных проблем за свою жизнь.
>Я же считаю, что количество математиков не менее важно, чем качество
Для начала, кого считать математиком?
Проблема в том (и об этом говорили люди гораздо умней меня или Миши), что наука становится всё более специализированной. Тут уже говорили, в 2021м году нельзя быть чистым математиком и не знать теоремы об индексе, например. С другой стороны, эта теорема не цель, так что тратить 6 лет обучения + постдок на то, чтобы её понять - это просто хуёвое образование и трата времени, потому что ну охуеть, теперь ты на уровне 50тилетней давности вот в этой конкретной теме. С похожим сталкиваются теорфизики, потому что нужно знать очень много всего для топологических и алгебраических методов КТП.
Единственное решение - кидать студентов в котёл как можно раньше, ну курса с 3его хотя бы, ценой других фундаментальных вещей сразу их специализировать, давать ликбез галопом по европам "аналитическая ТЧ за две недели", гнать на семинары. Но всё равно это приводит к китайской комнате, манипулировать объектами могут, но связей между областями не понимают.
Реальность такая - шансов понять актуальную статью с архива у выпускников вузов рфии практически нет.
Вообще, странно, что об этом так мало говорят: текущая система образования (не только здесь) одна для всех специальностей. Глупо полагать, что время, требуемое для каждой специальности, одинаковое. Чтобы писать статьи в социологии и экономике этого хватит (основы экономики, статистика, эконометрика, да куда быстрей можно справиться). Для математики этого тупо не хватает, для таких областей как чистая математика и теорфизика нужно делать обучение 8 или 10 лет. Но это деньги, идеи просвещения и поска научного грааля уже давно никого не волнуют. Гранты идут, клпипастные статьи про сферическую задачу матфизики в вакууме пишутся, малафья льётся.
Бакалавриат + магистратура + аспирантура - ровно 10 лет. Только вот чтобы защититься в аспе, надо иметь какое-то количество статей УЖЕ, то есть подразумевается, что на начало аспирантуры ты достаточно образован, чтобы их писать.
>Бакалавриат + магистратура + аспирантура - ровно 10 лет.
Ну так и в других областях (той же экономике) также! Смысл-то в том, что какого хуя вообще должен быть паритет? В реальности его нет, а рамки одни для всех. Когда ты поступаешь на аспирантуру, то ты в ЛУЧШЕМ случае прочитал какого-нибудь хартсхорна или фукса-фоменко. Это в лучшем. Даже если и так, ты всё равно нихуя не готов к собственно реальной актуальной математике.
Проблема в том, что количество переходит в отсутствие качества.
Что реально и возможно в идеальной воображаемой России? Два конкурирующих факультета, суммарно набирающих 100-150 студентов в год. Из них 30 доживет до аспирантуры. Из них несколько станет полноценными математиками, а остальные, в идеальном мире, пойдут зачищать другие университеты от ретардов.
В реальной России, еще совсем недавно, я учился на мехмате среди толпы в 300 рыл, две трети из которых в принципе не было дано - нейронов не доложили, а еще у 50 просто был другой путь, и серьезная математика им изначально была не нужна.
Да я согласен. Про то и пишу - ожидается, что к аспе ты уже способен вести исследовательскую деятельность, что далеко не всегда так.
Отличная идея, разом вынесет 90% желающих в математику, но не хотящих перебираться в такую пердь.
>что наука становится всё более специализированной
>Единственное решение - кидать студентов в котёл как можно раньше
>Реальность такая - шансов понять актуальную статью с архива у выпускников вузов рфии практически нет.
Тут как мне кажется еще перестать верить в существование общей математики, которую "нельзя не знать"
именно этим и руководствовались создатели уебищной программы мехматов, которые заставляют математиков проходить набор аналитических дисциплин 19 века, а еще заодно и физику с механикой, чтобы не скучали. Может лет 100 назад это еще и было обьятно студентам, сейчас же очевидно, что нет, да и это устарело. Миша зачем-то предложил новый курикуллум, не менее объемный. В этом я никогда не видел ни малейшего смысла, в рамках моей специальности я бы пытался избежать и той программы, и другой, какие вещи мне действительно нужны я понял только к магистратуре. Очевидно, что нужна большая академическая свобода, с возможностью перекатиться в смежную дисциплину на любом этапе. Обязательным может быть что-то уж совсем базовое типа линейной алгебры и анализа для пту.
А читать статьи в архиве, сомнительное удовольствие. "Чистый математик", но это вообще хрен пойми кто, если ты аналитик, то ты не понимаешь алгебру на архиве, если алгебраист, то не понимаешь анализ, в таком контексте математиком может быть кто-то с уникальной специализацией, которая вбирает себя дофига смежных дисциплин, типа как раз современной матфизики.
В чем проблема описания "гладкой зависимости от базы " ? Обязательно нужно куда-то присобачить свои модули и категории, я правильно понимаю?
>нужно куда-то присобачить свои модули
без модулей никак, полюбому:
"Я без милого гулять не выхожу, Во прекрасный сад в окошко не гляжу. Мне не милы в саду розовы цветы, Не веселят меня мелки пташки на кустах. Только весел в саду зелёненький лужок, На лужку гуляет миленький дружок. Как ты знатен, как преславен, молодец!"
В координатах потому-что, неудобно, там дальше написано про это
А в Новосибирске есть результаты?
А то говорят, что после того, как крупные величины там поумирали или разъехались, то дела там так себе.
>>80503
>в таком контексте математиком может быть кто-то с уникальной специализацией, которая вбирает себя дофига смежных дисциплин, типа как раз современной матфизики
Ну так Вербицкий и Ко. и ориентируются на матфизику в основном. Это секрет Полишинеля.
Где раздобыть эту школьную программу по мотивам Бурбаков?
С какой книги нАчять?
Так деление в столбик это численный метод и при том не самый эффективный.
 514 Кб, 580x689
514 Кб, 580x689>Где раздобыть эту школьную программу по мотивам Бурбаков?
Литературы на эту тему - тьма
Называется new math
Во Франции самая жесть была, в Америке поменьше, ещё Колмогорова не забудем, программу которого пришлось потом отменить и вернуть, как было
Собственно, все анти-Бурбакистские комментарии Арнольда именно против new math и против реформы его научрука, а не против гамалогий и пучков, как тут некоторые считают, потому что Арнольд это всё в 1970ые застал вживую
Вот эта серия книг была во Франции https://www.amazon.co.uk/Aleph0-Géométrie-plan-affine-vectoriel/dp/B003X7AM82 - шесть томов (геометрия х2, алгебра х2, анализ х2)
Отрывки из школьного (!) общего (!!) учебника - на пике (переведены на англ)
 65 Кб, 1414x1902
65 Кб, 1414x1902Для сравнения, вот современный русскоязычный учебник (Мордкович).
"Заглатывающая ловушка", однако.
Та хуёвый текст ужасно, первое же определение хуёвое "подмножество $I$ называется интервалом если оно удовлетворяет формуле $\phi$", во-первых не подмножество а его элементы, во-вторых там x, y и z входят свободно из-за чего может сложиться впечатление что определение зависит от выбора x,y и z, в-третьих там какого-то хуя проверка типа стоит "$x \in I \text{ and } y \in I$ ..." хотя если мы уже сказали "если его элементы удовлетворяют формуле" то она не нужна.
Ты какой-то неграмотный. Всё там правильно. Формула - на букву I, а не на x или y. Ср. с "множество M называется открытым, если любая точка m \in M входит в M вместе с некоторой окрестностью".
>простой
Я, когда отвечал, такого ответа ожидал на 99%.
Ну ясен хуй для меня это просто, я профессионально математикой занимаюсь годами. Очевидно, что посыл другой. У тебя какой опыт преподавания непрофильной математики школьникам (желательно не ЕГЭ)?
 102 Кб, 1280x720
102 Кб, 1280x720А зачем учить всех одному и тому же по одним и тем же книгам? Такие тексты должны быть учебниками для избранных.
Простите великодушно, что вклиниваюсь, а нахера это обсуждать? Вот вы сударь, который профессионально математикой занимается годами, подвезли бы какую-нибудь проблему нам, что вас волнует, а то все эти школьники да егэ опостылели уже до чертиков, честно говоря, и без того вся доска ими полна.
>опыт преподавания непрофильной математики школьникам (желательно не ЕГЭ)
Вёл курсы по подготовки к EGA для молодых пучкистов.
ну типа модуль это группа по сложению
да и кольцо (которое действует на модуле) тоже есть группа по сложению
но вопрос идиотский, нужные аксиомы можно перечислить и не произнося слова "группа"
>>83159
>как определить модуль не обращаясь к понятию группы
думал есть идеи по интереснее чем просто слово убрать
нет ничего интересного в том, чтобы бездумно переопределять элементарные базовые понятия. если так неймётся, займись лучше определением числа N тебя обоссут ещё раз
 4,1 Мб, 3264x2448
4,1 Мб, 3264x2448Пролистал. Действительно выглядит неплохо - например, подчёркивается, что группы важны из-за действий, или что модуль это абелева группа с действием кольца.
До идеального всё равно не дотягивает - такие же проблемы, как и в Chapter 0. Если это совсем с нуля, то нужно больше интересных примеров и больше интуиции. Например, уравнение классов сопряжённости и лемму Бёрнсайда можно проиллюстрировать, рассмотрев автоморфизмы куба. Для многих понятий нет интуиции (та же сопряжённость, по аналогии с линалом, это просто вгляд на группу со стороны какого-то элемента). Многих важных и интересных базовых тем/утверждений нет (например, теоремы о нулях).
Учебник хороший, один из лучших даже. Но всё равно, если кто-то захочет с нуля читать алгебру, ему нужно будет читать и другие книжки тоже.
Более того, в учебнике есть много задач и решения к большинству из них, можно быстро валидировать знания самостоятельно.
Для совсем нулей есть еще записки лекций от Aluffi: Introduction to Advanced Mathematics, как упрощенная альтернатива матшкольной литературе.
>Aluffi: Introduction to Advanced Mathematics
Посмотрел, похоже на сильно расширенную версию appendix A в этом учебнике >>99708 возможно, на основе и писалось.
>>99720
>Для многих понятий нет интуиции (та же сопряжённость, по аналогии с линалом, это просто вгляд на группу со стороны какого-то элемента). Многих важных и интересных базовых тем/утверждений нет (например, теоремы о нулях).
Насколько это вообще необходимо для учебника undergraduate уровня? Как я понял, там только самое общее введение в предмет.
>Насколько это вообще необходимо для учебника undergraduate уровня?
Я бы поспорил, что для начинающих лучше дать меньше понятий, но с интуицией, чем больше, но сухо.
Теорема о нулях проста и фундаментальна. Хорошо иллюстрирует, как можно через идеалы выйти на что-то геометрическое.
А что тебе даст эта интуиция? Ну будешь ты знать, как можно проиллюстрировать уравнения классов сопряжённости и лимму какого-то там хуя. И что?
Для меня всё это звучит как диалектика в духе гегеля или феноменология гуссерля.
Зачем вам это надо? Лучше идите на завод, дома стройте, отопление проводите, а не хуйнёй занимайтесь, ей богу.
мимо программист
Ну правда, расскажи, зачем вам это нужно? Ну вот я могу решать бизнесовые задачки, а ещё более туповатые чем я дядечки мне готовы платить за это неплохие деньги.
В свободное время я могу изучать гамалогии и натягивать сову на глобус, только зачем. Вы всё равно не построите топологические пространства инвариантные пространству, в котором мы с вами обитаем, дорогие эскаписты.
Пока считаю, что математики - это просто философы бездельники с математической оптикой.
 29 Кб, 795x307
29 Кб, 795x307>Почему они определяются так, как придти к такому определению?
Древний вопрос, но раз уж никто не ответил и ответ не гуглится, то возьмусь.
"Наивную" теорию Галуа можно вывести из формул Кардано. Далее речь лишь об буквенных, общих уравнениях.
Чтобы решить общее куб. уравнение нужно сначала решить квадратное, а затем простое кубическое(вида x^3=a). То есть вычислить сначала квадратный корень, а затем кубический.
Лагранж заметил, что решение и квадратного и кубического уравнения выражаются через корни исходного уравнения. Причём каждое выражение получается из другого простой перестановкой корней. Сами коэффициенты уравнения так же являются функциями от корней.
Зная об этом, не нужно быть гением, чтобы догадаться, что функции от корней(и как они меняются при перестановках) имеют связь с разрешимостью в радикалах.
Далее каждой функции от корней сопоставляется группа тех перестановок корней, что не меняют её. Например дискриминанту(решению кв. уравнения)
(x1-x2)(x2-x3)(x1-x3) соответствует знакопеременная группа, а резольвенте(решению куб. ур)
x1+wx2+w^2x3 соответствует единичная.
Тем самым схема решения кубического уравнения такая: из 1-значных(симметричных) функций строим 2-значную(дискриминант), из 2-значных и 1-значных строим 6-значную.
Как из 1-значных построить 2-значную?
Пусть f двузначна: f1 и f2. Рассмотрим уравнение (x-f1)(x-f2). Мы можем выразить f1 и f2 через коэффициенты этого уравнения. Сами коэффициенты равны
f1+f2 и f1f2. Тем самым коэффициенты являются симметрическими функциями от корней исходного уравнения, а, значит, выражаются через однозначные функции.
Как построить 6-значную? Решать уравнение с 6 корнями мы не умеем. Но можно рассмотреть лишь те её значения, что получаются при перестановках знакопеременной группы. В случае куб. уравнения 6-значная функция принимает
f1, f2, f3 значения. Вроде опять тупик, куб. уравнения мы решать не можем. Но в случае резольвенты
x1+wx2+w^2x3 её 3 значения под "действием" знакопеременной группы равны тому, если просто домножать на w.
Тогда имеем три значения: f1, wf1, w^2f3. Уравнение (x-f1)(x-wf1)(x-w^2f1) мы решать умеем, так как оно равно (x^3-f1^3)
f1^3 2-значна. Лагранж доказал, что если ф и ф' имеют одну и ту же группу, то они выражаются рационально одна через другую. Значит зная 2-значную функцию, например дискриминант, мы можем выразить f1^3 через неё и ивзлекая куб получаем 6-значную. Вдобавок, зная 6!-значную мы можем рационально выразить корни уравнения.
Начиная с 1-значных функций мы построили более "могущественные" 6-значные в 2 шага. Параллельно с этим группы самих функций, наоборот, уменьшались. Сначала имели S, затем A, а затем 1.
Потому Галуа заострил внимание ни на функциях, а на их группах.
Пусть ф имеют группу H, H подгруппа G и под действием G ф принимает 3 значения: ф1, ф2, ф3.
Пусть t отображает ф1 в ф2: t(ф1) = ф2. Что если t применить уже к ф2? Оставит ли t ф2 на месте или куда-то переведет?
Для ответа на этот вопрос нужно вычислить группу ф2, зная группу ф1(H). Легко вычислить, что каждая перестановка G, оставляющая ф2 на месте имеет вид: tHt^-1. Если группы ф1, ф2 и ф3 все совпадают, то перестановку t, а точнее класс tG, можно рассматривать уже никак перестановку аргументов функции, а перестановку самих функций. Чтобы группы ф1 и ф2 и ф3 совпадали необходимо, чтобы gHg^-1 = H, то есть чтобы H была нормальной подгруппой группы G. В этом случае у нас существует фактор-группа G/H, которая переставляет сами функции между собой.
Рассмотрим дискриминант куб. уравнения (x1-x2)(x2-x3)(x1-x3). Он принимает 2 значения: d и -d. Их группы совпадают, значит A_3 нормальна в S_3. Мы можем перевести d в -d двумя способами: переставив буквы или домножив на -1. Фактор-группа состоит из класса транспозиций.
Теперь x1+wx2+w^2x3. Под действие A эта функция принимает 3 значения: z1, z2, z3. Группа {e} очевидно нормальна в A. Значит существует фактор-группа, как-то переставляющая буквы z1, z2, z3.
Мы знаем, что z2=wz1, z3=w^2z1. Тогда у нас есть два способа переставить буквы: действуя перестановками из A, или домножением всех букв на w или на w^2.
Тем самым мы каждой перестановке можем сопоставить соответствующее домножение на w или w^2. Так как домножение на w циклично, то и фактор-группа циклична. Тогда переходя от n-значной функции к m-значной n < m с помощью радикала, мы понижаем группу и мы можем переставлять значения m-значной функции с помощью домножения на корни из единицы. Такое домножение действует циклично, а значит фактор-группа циклична.
Поэтому можно выдвинуть гипотезу(и определить разрешимые группы): уравнение разрешимо в радикалах, если существует цепочка групп S - G - H - ...- 1 такая, что каждая след. группа является норм. подгруппой предыдущей и фактор-группа циклична. К этому нужно добавить, чтобы порядок фактор-группы был простой, т.к. проще рассматривать корень не (mn) степени, а сначала вычислить корень степени m, а затем n.
Если рассматривать конкретные численные уравнения, а не буквенные, то мы можем вычислять каждую функцию, а не рассматривать их как буквенное выражение. Здесь появляется большая преграда. Может оказаться так, что какое-то число можно выразить, например, и симметричной и какой-нибудь k-значной функцией. Поэтому мы не можем с самого начала рассматривать группу S, нужно выбрать группу, соответствующую k-значной функции. Каждому конкретному уравнению можно сопоставить такую группу. Эта группа и называется группой Галуа уравнения.
Работы Галуа забраковали именно поэтому. Для решения уравнения его методом требовалось уже заранее знать корни, так как нужно рассматривать функции от корней и вычислять их симметрии. Так же вычисление группы уравнения это задача, не имеющая общее решение, для каждого уравнения эти вычисления индивидуальны и почти всегда невозможны.
>Почему они определяются так, как придти к такому определению?
Древний вопрос, но раз уж никто не ответил и ответ не гуглится, то возьмусь.
"Наивную" теорию Галуа можно вывести из формул Кардано. Далее речь лишь об буквенных, общих уравнениях.
Чтобы решить общее куб. уравнение нужно сначала решить квадратное, а затем простое кубическое(вида x^3=a). То есть вычислить сначала квадратный корень, а затем кубический.
Лагранж заметил, что решение и квадратного и кубического уравнения выражаются через корни исходного уравнения. Причём каждое выражение получается из другого простой перестановкой корней. Сами коэффициенты уравнения так же являются функциями от корней.
Зная об этом, не нужно быть гением, чтобы догадаться, что функции от корней(и как они меняются при перестановках) имеют связь с разрешимостью в радикалах.
Далее каждой функции от корней сопоставляется группа тех перестановок корней, что не меняют её. Например дискриминанту(решению кв. уравнения)
(x1-x2)(x2-x3)(x1-x3) соответствует знакопеременная группа, а резольвенте(решению куб. ур)
x1+wx2+w^2x3 соответствует единичная.
Тем самым схема решения кубического уравнения такая: из 1-значных(симметричных) функций строим 2-значную(дискриминант), из 2-значных и 1-значных строим 6-значную.
Как из 1-значных построить 2-значную?
Пусть f двузначна: f1 и f2. Рассмотрим уравнение (x-f1)(x-f2). Мы можем выразить f1 и f2 через коэффициенты этого уравнения. Сами коэффициенты равны
f1+f2 и f1f2. Тем самым коэффициенты являются симметрическими функциями от корней исходного уравнения, а, значит, выражаются через однозначные функции.
Как построить 6-значную? Решать уравнение с 6 корнями мы не умеем. Но можно рассмотреть лишь те её значения, что получаются при перестановках знакопеременной группы. В случае куб. уравнения 6-значная функция принимает
f1, f2, f3 значения. Вроде опять тупик, куб. уравнения мы решать не можем. Но в случае резольвенты
x1+wx2+w^2x3 её 3 значения под "действием" знакопеременной группы равны тому, если просто домножать на w.
Тогда имеем три значения: f1, wf1, w^2f3. Уравнение (x-f1)(x-wf1)(x-w^2f1) мы решать умеем, так как оно равно (x^3-f1^3)
f1^3 2-значна. Лагранж доказал, что если ф и ф' имеют одну и ту же группу, то они выражаются рационально одна через другую. Значит зная 2-значную функцию, например дискриминант, мы можем выразить f1^3 через неё и ивзлекая куб получаем 6-значную. Вдобавок, зная 6!-значную мы можем рационально выразить корни уравнения.
Начиная с 1-значных функций мы построили более "могущественные" 6-значные в 2 шага. Параллельно с этим группы самих функций, наоборот, уменьшались. Сначала имели S, затем A, а затем 1.
Потому Галуа заострил внимание ни на функциях, а на их группах.
Пусть ф имеют группу H, H подгруппа G и под действием G ф принимает 3 значения: ф1, ф2, ф3.
Пусть t отображает ф1 в ф2: t(ф1) = ф2. Что если t применить уже к ф2? Оставит ли t ф2 на месте или куда-то переведет?
Для ответа на этот вопрос нужно вычислить группу ф2, зная группу ф1(H). Легко вычислить, что каждая перестановка G, оставляющая ф2 на месте имеет вид: tHt^-1. Если группы ф1, ф2 и ф3 все совпадают, то перестановку t, а точнее класс tG, можно рассматривать уже никак перестановку аргументов функции, а перестановку самих функций. Чтобы группы ф1 и ф2 и ф3 совпадали необходимо, чтобы gHg^-1 = H, то есть чтобы H была нормальной подгруппой группы G. В этом случае у нас существует фактор-группа G/H, которая переставляет сами функции между собой.
Рассмотрим дискриминант куб. уравнения (x1-x2)(x2-x3)(x1-x3). Он принимает 2 значения: d и -d. Их группы совпадают, значит A_3 нормальна в S_3. Мы можем перевести d в -d двумя способами: переставив буквы или домножив на -1. Фактор-группа состоит из класса транспозиций.
Теперь x1+wx2+w^2x3. Под действие A эта функция принимает 3 значения: z1, z2, z3. Группа {e} очевидно нормальна в A. Значит существует фактор-группа, как-то переставляющая буквы z1, z2, z3.
Мы знаем, что z2=wz1, z3=w^2z1. Тогда у нас есть два способа переставить буквы: действуя перестановками из A, или домножением всех букв на w или на w^2.
Тем самым мы каждой перестановке можем сопоставить соответствующее домножение на w или w^2. Так как домножение на w циклично, то и фактор-группа циклична. Тогда переходя от n-значной функции к m-значной n < m с помощью радикала, мы понижаем группу и мы можем переставлять значения m-значной функции с помощью домножения на корни из единицы. Такое домножение действует циклично, а значит фактор-группа циклична.
Поэтому можно выдвинуть гипотезу(и определить разрешимые группы): уравнение разрешимо в радикалах, если существует цепочка групп S - G - H - ...- 1 такая, что каждая след. группа является норм. подгруппой предыдущей и фактор-группа циклична. К этому нужно добавить, чтобы порядок фактор-группы был простой, т.к. проще рассматривать корень не (mn) степени, а сначала вычислить корень степени m, а затем n.
Если рассматривать конкретные численные уравнения, а не буквенные, то мы можем вычислять каждую функцию, а не рассматривать их как буквенное выражение. Здесь появляется большая преграда. Может оказаться так, что какое-то число можно выразить, например, и симметричной и какой-нибудь k-значной функцией. Поэтому мы не можем с самого начала рассматривать группу S, нужно выбрать группу, соответствующую k-значной функции. Каждому конкретному уравнению можно сопоставить такую группу. Эта группа и называется группой Галуа уравнения.
Работы Галуа забраковали именно поэтому. Для решения уравнения его методом требовалось уже заранее знать корни, так как нужно рассматривать функции от корней и вычислять их симметрии. Так же вычисление группы уравнения это задача, не имеющая общее решение, для каждого уравнения эти вычисления индивидуальны и почти всегда невозможны.
 48 Кб, 802x195
48 Кб, 802x195Будто бесконечные это что-то кроме нарисованной нотации, или для них аксиоматика другая. Или как Савватеев будешь лечить, что актуальнобесконечные объекты у боженьки где-то в кладовке валяются?
Ты ж сам признаешь различие между тем, что ты называешь "численными" и "буквенными" уравнениями
>>99830
>Если рассматривать конкретные численные уравнения, а не буквенные, то мы можем вычислять каждую функцию, а не рассматривать их как буквенное выражение
И понимаешь, что не всегда можно просто перейти от буквенного к численному. Проще всего сказать, что буквенные уравнения это первая культура, а численные - картофан и вообще не математика. Но проблем это не снимает. Гамалогии в буквенном виде прекрасно работают, а попытки перейти к численному виду приводят к тому, что начинают вылезать всякие проблемы Уайтхеда. Причина этого давно известна, и подробно рассмотрена ещё Брауэром например в кембриджских лекциях.
алсо
>Из-за этого многие математики «олимпиадного типа», которые считают, что цель математики — решение задач, по возможности с минимумом введения новых понятий, его (классического «создателя теорий») недолюбливают.
>математики «олимпиадного типа»
угарнул немножко
>охват тем - от теории множеств и категорий
Никто, кто этих тем не знает, из этих заметок их и не поймёт. А те, кто знают, в подобном не нуждаются.
Вообще у всех таких проектов (был по синтетической геометрии, по теоркату, по алгебре, ну можно нкатлаб сюда же пихнуть) одна и та же проблема. Они никакую интуитицию не предоставляют, нет обсуждения, нет "ковыряния". Определение теорема лемма. А нахуя? Ну просто symbol pushing а-ля теоркатщики из CS. Создаётся некая песочница, и в ней строятся замки. Всё анально изолировано от других областей чистой математики, да и собственно от интересных интерпретаций внутри алгема тоже.
Вкатывальщику в алгем я посоветую почитать хотя бы обзор истории итальянской школы и классических проблем, потом какую-нибудь хорошую вводную книжку без схем, потом Vakil (+Хартсхорн), в потом можно и неиронично вдумчиво полистать EGA. После уже можно пытаться в специализированные подтемы.
Сколько я повидал постдоков, которые годами изучают всё в схемах и ебошат когомологии квазикогерентных пучков, но не могут решить даже простейших задач про алгебраические кривые.
>inb4 "кривые это вторая культура"
Ну вот серры и гротендики могли это всё решить. Может, надо задуматься о структуре современного математического образования вообще.
Открыл что то там почитать уже не помню что и дристанул с того что детали они предлагают посмотреть в другой книге. Хотя казалось бы 7500 страниц - можно было бы написать вообще про все на свете.
>Они никакую интуитицию не предоставляют, нет обсуждения, нет "ковыряния"
А надо? Вся алгебра как явление, была выведена из множества Z. Любая аксиоматика чего угодно, любые леммы, теоремы итд. Просто кто-то понимает логику того, как от Z можно дойти до модулей над кольцами, а кто-то нет. И вот тот, кто понимает, вполне может увидеть то, чего до него не увидели. Собственно, именно этим какой-нибудь условный Гротендик и отличается от пупкина-залупкина, который на лекциях в тиктаке сидел и в носу ковырялся.
>>102990
>вдумчиво полистать EGA
Парле ву франсе? Или есть в переводе?
> какой-нибудь условный Гротендик
У какого-нибудь условного Гротендика хорошая база, ему такая "книга" была бы не нужна, потому что ему про Z и модули уже рассказали в хороших книжках и на хороших лекциях/семинарах.
Идея математика-самоучки, который читает 8,000 страниц и становится королём алгема, это романтизация двачеров.
Всё, на что самоучка способен, это что-то на уровне Рамануджана ковыряться в картофане.
Мне очень помогает при изучении.
>Парле ву франсе? Или есть в переводе?
Принято читать по-французски, не зная французского.
Но теперь, кажется, делается перевод.
https://github.com/ryankeleti/ega
>Сколько я повидал постдоков, которые годами изучают всё в схемах и ебошат когомологии квазикогерентных пучков, но не могут решить даже простейших задач про алгебраические кривые.
Что в этом плохого, если конкретный математик не занимается кривыми? Мне конкретно геометрическая интуиция нужна, знаю лично известного геометра, которому это помогает писать абстрактные статьи по триангулированным категориям, но знаю и тех, кто занимается "symbol pushing-ом", им хватает языковой интуиции, полученной из формализма, при этом их деятельность вполне осмысленна, а результатами пользуются другие математики.
>Что в этом плохого
Всё зависит от критерия "плохости". Если, как ты говоришь, критерий -
>результатами пользуются другие математики.
то, конечно, ничего плохого. Даже китайская комната полезна, никто же не спорит.
Но если критерий - понимание, то тот, кто знает абстрактный формализм + геометрическую интуитицию всегда будет понимать лучше, чем тот, кто знает только абстрактный формализм. Есть какая-то ирония в том, что именно это и позволило бурбакам так сильно развить математику - у условного Картана или Шевалле естественный интуитивный fallback - это геометрическая интуитиция.
Опять же, это 1:1 китайская комната, вопрос только в критерии - полезность или "настоящее понимание" (чтобы это ни значило).
Хотя не понимаю, как можно утверждать, что непонимание фундаментальных фактов - это нормально, если
>если конкретный математик не занимается кривыми?
Это как говорить "что плохого в том, чтобы не знать гомологии сферы, если конкретный математик не занимается сферами?". Если у тебя такой большой разрыв между symbol pushing и интуицией, то результаты обречены быть чисто техническими (хоть и полезхными).
Сравнение с китайской комнатой весьма странное. Я говорил скорее о том, что интуицию и понимание можно развить внутри конкретной области (гомологическая алгебра давно является самостоятельной дисциплиной со своими глубокими вопросами и методами, а не просто инструментарием), эти вещи не обязательно должны быть внешними по отношению к ней, хотя другой угол обзора и может помочь.
Если развиваешь интуицию\понимание изнутри, то ты себя заведомо ограничиваешь, и никогда не сможешь обрести понимание, возможное при изучении области изнутри И снаружи. Ну понятно, что время ограничено и всё такое, поэтому лучше уж так, чем никак.
Гомологическая алгебра это просто замечательный пример, потому что вот буквально недавно тут в каком-то треде обсуждали самые базовые вещи и их интуитивное понимание, напр. то, что точные последовательности естественным образом появлялись уже у Гильберта в 1890м в изучении сизигий, а об этом практически ни слова ни в одном учебнике.
Нам всем известен пример задачки из Ланга на доказательство всех утверждений из произвольной книги по гомологической алгебре, это же неспроста уже тогда было понятно, что symbol pushing может быть очень эффективным.
Если выбирать между условными формами математики того же Арнольда с изящным перемежанием геометрии и абстракных идей, и ncatlab со смысловым наполнением статей уровня чатжпт, то ящитаю, что первое по духу ближе к математике - и нет, это не завуалированный дискурс о первых культурах.
ты же осознаёшь, наверно, что Арнольд очень специфичный автор и его "изящности" далеко не всем заходят
>точные последовательности естественным образом появлялись уже у Гильберта в 1890м в изучении сизигий
мало ли что было у Гильберта в 1890
об этом наверно и не задумывался никто, потому в учебниках нет
>ты же осознаёшь, наверно, что Арнольд очень специфичный автор и его "изящности" далеко не всем заходят
Это так, но даже те, кому не заходит, думаю могут оценить, как он использует геометрическую интуицию для другого взгляда на вещи. Я просто хотел подчеркнуть, что если сидеть исключительно в абстракции, то у тебя этот взгляд по определению более ограниченный. Ну хорошо, не нравится китайская комната, пусть будет платоновская пещера и тени (хотя первокультурщик может сказать, что тень это как раз таки геометрическая интуиция..)
>об этом наверно и не задумывался никто, потому в учебниках нет
Так об этом и речь - с каждым новым поколением математиков и учебников, потихоньку теряются интересные связи. Это становится кристально ясным, если читать оригинальные статьи 19го\начала 20го веков.
Ну конечно же тут нет одного правильного ответа, я твои аргументы тоже понимаю.
>напр. то, что точные последовательности естественным образом появлялись уже у Гильберта в 1890м в изучении сизигий, а об этом практически ни слова ни в одном учебнике
>>114027
>об этом наверно и не задумывался никто, потому в учебниках нет
Не понимаю, о чём вы, об этом буквально в каждом учебнике написано ведь, просто обычно ближе уже к производным категориям.
Мне тоже больше нравятся такие танцы от "наглядной" геометрии и топологии к какой-нибудь теории гомотопий или кобордизмам и обратно. Тем не менее периодически я встречал очень красивые и изящные вещи, полностью лежащие внутри казалось бы комплекса "лингвистических" экзерсисов.
ты всё с гельфандом-маниным своим носишься, в котором два предложения мимоходом что-то сказано
 98 Кб, 634x537
98 Кб, 634x537>напр. то, что точные последовательности естественным образом появлялись уже у Гильберта в 1890м в изучении сизигий, а об этом практически ни слова ни в одном учебнике
Буквально это и сказано, что в ГМ, что в Вейбеле, Ротмане, Эйзенбаде (это не гомалгебра, но всё равно туда при изучении алгема заглядывать приходится), везде доказывается теорема Гильберта о сизигиях, в последних двух подробнее, но и в первых двух достаточно, чтобы общую идею уловить и решить что-то на тему почитать, если заинтересовался. Вот только а есть ли там что-то сильно глубже?
Наверное он имел в виду, что, скажем, \Z/100 можно воспринимать как расширение \Z/10 с помощью \Z/10, и, таким образом, складывая числа в столбик в десятичной системе счисления, мы как-бы взаимодействуем с нетривиальными расширениями модулей и гомологиями. Но это больше прикол такой.