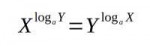78 Кб, 505x599
78 Кб, 505x599Ну и пусть вообще будет математики тред, не лишний же, правильно? Может, кто-нибудь еще заинтересуется этой темой, а тут будет уже тред. Если же и не нужен, сам его и затоплю. Будь что будет.
На картинке:
1) Тарн Адамс, доктор философии по математике, создатель Dwarf Fortress, и просто очень хороший человек, хоть и жаба.
Спасибо, кстати
В старых книгах всё более доходчиво разъяснено, в целом выше уровень, плюс много плюшек для мотивации: научат извлекать квадратный корень в столбик, например.
Фишка ещё именно в методологии. Важно читать теорему, закрывать книгу и пытаться самостоятельно её доказывать. После того, как ты её докажешь или просто сдашься (в чём, в принципе, нет ничего постыдного), открываешь учебник и читаешь доказательство там, анализируешь и делаешь выводы. Решать задачи так же нужно, но не как это принято в школе: вот вам 9000 однотипных заданий, а чтоб все немного разные и желательно на смекалку. Дополнительно к задачнику находишь книги из серии "пособие по математике для поступающих в вузы", так же 70х годов, когда ещё никакого ЕГЭ и в помине не было, он сплошь состоит из таких полуолимпиадных задач с решениями.
Спасибо огромное за рекомендации. Буду обязательно пытаться и пробовать.
Вот, раздачу нашел: http://rutracker.org/forum/viewtopic.php?t=4505920
Что-то подходящее? А то книжек таких физически у меня пока нету, да долго придется искать.
Пойдёт, ага. Сейчас на твоём уровне можно брать абсолютно любую книгу, не заморачиваясь элитными подборочками. Открываешь и если слишком сложно/просто/уныло, дропаешь и берёшь другую.
Знаешь, мне кажется, что в любом случае сначала будет сложно и уныло. Это же не просто развлечение, как компьютерные поигрушки, допустим. Если бы я мог просто взять и изменить свое отношение к этому, было бы намного проще. Но так не бывает, увы. Или бывает?
А что касается мотивации, то тут хуй знает. У каждого она своя. Кого-то прёт, что он может синус любого числа без калькулятора на листочке посчитать. Кого-то манит красота изоморфизмов и обобщение теорий. Как правило, это всё появляется при наличии уже каких-то знаний, совсем новичка хрен знает чем можно заинтересовать.
Ну можно тешить своё ЧСВ, когда самостоятельно получается доказать что-то. Или решить что-то хитрожопое. Меня всегда дико пёрло с этого, например. Если ты не 6-классник, а просто проспал все уроки в школе и у тебя уже была тригонометрия, я могу тебя мотивировать, например, тем, что она абсолютно вся может быть выведена и понята из одной единственной формулы. Практически то же с оговорками касается и школьной геометрии.
Ну как. Не проспал. Классическая история - один или два раза пропустил (классе в 7, там как раз геометрия и прочее) или что-то не понял, пытался понять, но не получилось, забил, появилось злость на предмет - и покатилось. Это по геометрии. Потом тоже самое произошло и с алгеброй. За одиннадцатый класс мне можно было двойку ставить, но как-то вывернулся. Жаль, что так случилось, конечно. А тригонометрию - вообще не знаю. Совсем.
Ну я к тому, что ты хоть приблизительно знаешь, что значат эти слова и сколько школота тратит на их изучение времени. А твоя история совершенно типична, к сожалению.
Ну да. Эхх, дурак, не надо было тупить тогда. Как жаль, что все свои ошибки и глупости мы осознаем гораздо позже.
Сканави задачник ищи. Для поступающих во ВТУЗы. Вот это хорошая вещь для новичка. Там много тем. И задачи по нарастающей.
>Кого-то прёт, что он может синус любого числа без калькулятора на листочке посчитать
Лол, а я ведь как-то почти осилил метод. Зная углы специальных треугольников а также золотое сечение это и вправду возможно, вплоть до всех 90 градусов с шагом в градус. 30, 90, 45, 36, и комбинируя их всех в бесконечных формулах приведения и тригонометрических правилах оно так и выходит.
Удачи тебе, анон.
x-x^3/6+x^5/120 уже 3-4 знака даёт.
>знатоки математики
Я во весь во внимании.
>Никакие графики, косинусы-синусы, квадратные там уравнения - этого я ничего не знаю
Пиздос
>Кто-нибудь может мне порекомендовать хорошую литературу там, дать советов, наставлений, и прочего? Мотивировать (не люблю это слово, ну да ладно) как-нибудь может. Все это я хочу для себя. Ведь можно же это сделать?
Ты должен сам всего достичь
>Ну и пусть вообще будет математики тред, не лишний же, правильно?
Это наука для быдла ограничивающаяя воображение, уноси это говно.
>На картинке:
Какой-то питурд, нахуй
(Автор этого поста был забанен. Помянем.)
Маня, ты опоздала.
http://interneturok.ru/ru/school/algebra/7-klass
http://interneturok.ru/ru/school/geometry/7-klass
https://ru.khanacademy.org/ лучше конечно на английском
Есть значит люди, и их средний уровень интеллекта мы проецируя свой личный опыт примерно можем прикинуть,можно обозначить эту величину какой-то буквой.
Есть раса А и она имеет 2/3 интеллекта от уровня людей.
Есть раса Б и она в 3 раза превосходит уровень рас А.
Вопрос: На сколько раса Б умней расы людей?
ебучий автор этого сам не написал, видимо оставил читателям на вычисление
UPD
Решение [СПОЙЛЕР]
пиздец, я пока этот текст писал и увидел инфу наглядно мне сразу очевидным стало умножение расы А на число 3 и получаем ответ:
В 2 раза.А пока сидел и читал и пытался прикинуть в уме чуть стул не пржег
Анончик, мне кажется, что не совсем так.
Допустим, интеллект людей - x. Тогда интеллект расы А равен 2x/3. Интеллект расы Б в 3 раза превосходит интеллект расы А. Значит интеллект расы Б равен 3*2x/3, то есть 2x. Нам нужно узнать насколько раса Б умнее расы А. То есть из интеллекта расы Б отнимаем интеллект расы А, то есть 2-2/3, поэтому ответ 4/3.
Но про то, насколько Б > люди не сказано, известно только, что А в три раза меньше, то есть из трех вычетам два получается правильный ответ - 1.
>Вопрос: На сколько раса Б умней расы людей?
Ой, а я пишу "нужно узнать насколько раса Б умнее расы А. "
Тогда в 2 раза, всё верно. Но вопрос " На сколько раса Б умней расы людей?" по-прежнему смущает.
"Что такое математика" Куранта и Роббинса
"Что такое математика" Аргольда
Это для общего понимания.
"Математика не для отличников" скачиваешь на рутрекере. Мультимедийный курс для учащихся средней школы 6-11 классов разработан на базе программы средней школы в НИИ экономики авиационной промышленности. Реально для дебилов. Решай по часу в день.
Что не понятно, смотри тему на Interneturok - тут выше была ссылка.
"Элементарная алгебра. Пособие для самообразования" С.И. Туманова. Покупаешь в букинисте (что лучше) или скачиваешь на крайний случай из сети.
Сканави задачник тут посоветовали уже, но еще лучше найди (опять же, лучше на бумаге):
Сканави М.И. Элементарная математика. Подготовительный курс, где-то 1965-67 год
Поставь последние две книги в туалет и читай каждый раз, когда сядешь срать по 4-5 страниц. Я серьезно.
Вот, собственно, все.
>На практике существует такая вещь, как способности к математике?
Я думаю, что есть, но эти способности, зачастую, были развиты, а не предоставлены свыше. Как говорится, успех — это капля таланта и море труда. У нас в группе есть две девчонки, которые прекрасно разбираются в высшей математике, схватывают новый материал очень быстро, подготовиться к экзамену на отлично для них не составляет большого труда. Примечательно, что обе они с детства обучались в физико-математических гимназиях. Но программирование даётся им тяжело, начинали они в начале курса с нуля и без должного энтузиазма. В итоге программирование объяснял им я — человек, со скрипом пролезший в институт, поскольку готовился несерьёзно к поступлению. А кодингом увлекаюсь уже не один год.
Резюмирую: если долго в чём-то разбираться/упражняться, то в любом слючае когда-нибудь да поймёшь/сможешь это сделать. Ведь всё сложное — совокупность простого, разделяешь на маленькие кусочки и изучаешь.
>А вот мне говорят, что я долбоеб и не имею способностей к точным наукам, но все равно лезу в математику. Я правда долбоеб?
Нет. Мне говорили тоже самое на протяжении 5 лет в школе.
Но после того, как начал готовиться к быдло Егэ, когда адекватный преподаватель начал все грамотно объяснять и у меня хоть что-то начало получаться, мне это все понравилось. Т.е., как сказал анон выше, если упражняться, то все получится, да еще и интересно станет.
Поступил, кстати, на математика, 3 года назад. Первые 2 курса охуевал просто, но затем быдло матаны сошли на нет. А я стал ближе к специальности. В итоге сейчас у меня все довольно не плохо, учитывая, что в организациях моей кадрами моей специальности очень даже интересуются.
Задавай свои ответы, если интересно.
> вот вам 9000 однотипных заданий
Тащемта, ровно так же готовились к поступлениям и так же - к олимпиадкам. Сам доходил до всероса в 2008, тот же дроч, разве что стандартных алгоритмов решения сильно больше и иногда нужно применить сразу несколько из них.
Пожалуй, во всех этих олимпиадках были полезными лишь летние мат.школы. А самым вредным - до невероятных размеров распухшее самомнение.
ОПчик, если твоя цель изучения математики не сводится к поступлению, забивай хуец на все это школьное дерьмо. Лучше посмотри пару видео по топологии (там, где будут интересные картиночки со склеивающимся листиком) и почитай книжки серии "библиотека мат.кружка" и "Популярные лекции по математике".
Могу посоветовать почитать да посмотреть всякий красивый научпоп по математике. Типа "математических этюдов", они красивые и понятные.
Если будет переть — приступай к каким-нибудь простеньким курсам. По матану могу тебе Зельдовича и Ялома (вышмат для начинающих физиков и математиков), там более-менее понятно. Хотя уверен, что есть получше пособия.
По этой теме Пойа хорош, у него книги именно по эвристикам, рассказывает и показывает, как эффективно думать (в решении математических задач, а не вообще).
> Ф И Х Т Е Н Г О Л Ь Ц
Только если ты инженер.
В Фихтенгольце отсутствует куча важных тем. Те же теория меры, дифференциальные формы, гладкие многообразия.
Стартуй с Мякишева, Буховцева, а потом садись на что-нибудь тяжелее, вроде Козела + сборники, архивы олипмпиад.
Двачую.
Второй вопрос, связанный с первым. Назовите набор мастхейв пособий по алгебре (назначение указано выше) или онлайн, видеокурсов грамотных. Задачник Сканави уже есть.
Нужно подтянуть себя (просто стало интересно) и помочь старшекласснику ПОНИМАТЬ предмет (это не профиль, ЕГЭ не так важно, важно именно понимать).
>задач Сканави
Годный сборник задач?
Алсу, если всё так плохо как у меня - то можешь начать как и я с самых азов - кхан академия или курсы. В данный момент я прохожу вот этот курс https://www.udacity.com/course/visualizing-algebra--ma006
который рассчитан на самые азы и идет аж 4 месяца (но ничего не мешает закончить быстрее). Мне нравится как объясняют, лучше чем в школе, а так же много заданий, приходится посидеть с тетрадкой и ручкой, а так же и таблицу умножения поучить, чтобы быстрее решать. В общем, рекомендую.
Я не знаю, но в школе его вроде используют и таже здесь в треде советовали.
Тут у меня геоблок, похоже, будем что-то думать. Алсо, мне понравился http://betterexplained.com/
Так и не посоветовали нихуя.
Вот тут говорят, что математика - это не синусы, косинусы и страшные формулы.
https://www.youtube.com/watch?v=rQJMT9nbFhk
> "Элементарная алгебра. Пособие для самообразования" С.И. Туманова. Покупаешь в букинисте (что лучше)
Да ты охуел, она несколько тысяч рублей стоит :3 Однако есть отличный скан. Лучше эта книга или сканави элементарная математика?
Туманов - это 900 стр. по всей школьной программе. Слышал много хвалебных отзывов о нем, главное, чтобы издание было 1970 года.
Алсо, сам по нему начал заниматься недавно.
 77 Кб, 700x714
77 Кб, 700x71401.03.01 - Математика
02.03.01 - Математика и компьютерные науки
На какой сам сядешь, на какой мать посадишь? Хочу на вторую ололо погромист, но у просто математики весьма значительно меньше проходной бал и я думаю она могла бы быть альтернативой. Или учат там одной и той же хуйне и разница в несколько предметов? Может на 3-4 курсе будет возможность выбрать/заменить несколько курсов и получить то же самое?
На финишной прямой. Осталось сдать тест за последнюю треть. Мог бы быстрее намного, но слишком много прокастинирую. Мне понравилась интерактивность и краткость объяснений. За учебником или сборником задач я бы уснул ещё на 2-й странице. А тут за пару минут буквально объясняют концепцию и тут же дают пример для опробования.
Что и где учить дальше пока не знаю. Найти бы подобные курсы по плани-, стерео- и тригонометрии. А там уже и за пределы школьного курса двигаться можно.
Поздравляю, далеко дошел!
Эх, а я не могу одну задачку понять и забросил, начал другое проходить, и прокрастинация, само собой, но иногда и банально времени не хватает (вместе с силами).
Я вообще-то хотел с тобой списаться (например, через почту), может быть ты бы смог мне с задачкой помочь, а я тебе тоже как-нибудь. Как тебе идея?
Написал.
А руками я отучился писать, только печатаю.
LaTeX немного знаю, но вот ставить какие-то дополнительные кривые утилиты нет ни воли, ни желания.
Потому решаю задачи на знания.ком. Но там всё школьное, почти всегда на вычисление.
Собственно, сабж:
Сфера технического и естественно-научного должна обществом восприниматься как первичная по отношению к сфере гуманитарного. То есть, технократия - это норма. Но, крайне важная деталь: сфера технического и естественно-научного должна обязательно содержать в себе концепты и нарративы, лежащие на стыке технических/естественных и гуманитарных, а также социальных наук.
Дам несколько пояснений.
К примеру, на сознание Эйнштейна очень сильно повлияла вторая волна позитивизма, а конкретно философия Э.Маха. Принцип относительности, лежащий в основании научного наследия Эйнштейна, изначально был им почерпнут именно из махизма. То есть, в основе крупнейшей естественно-научной теории, имеющейся у человечества, лежит конкретная философская концепция. Советский биолог, философ, методолог науки А.А. Любищев написал целую монографию, в которой показал, что всё многовековое развитие науки, к примеру, математики, может быть интерпретировано через влияние на данное развитие двух философских систем - Платона и Демокрита. А на формирование физики Ньютона решающее воздействие оказали социокультурные положения Модерна, в которых одной из главных установок являлась десакрализация и деманифестационализация взглядов на мироздание. Отсюда и теологический унитаризм Ньютона, отсюда и его физика в русле концепции механической вселенной. То есть, наивно-поверхностно сциентистские и архаично-позитивисткие взгляды, что существует объективный мир объективного технического знания, свободный от гуманитарщины - они очень милы и романтичны, но, увы, неверны. В реальности же сфера технического зачастую определяется некоторыми вещами гуманитарного толка. Это важно.
В СССР господствовал марксизм, которому совковая научная "элита" не давала обновляться. То есть, марксизм был догматизирован, причём не в какой-то аутентичной форме, а в форме его ленинской интерпретации, притом, что эта интерпретация тоже несколько зауживалась. Это всё было нелепо ещё и потому, что некоторые взгляды Маркса менялись по ходу его жизни, но в совке к Марксу относились как к некому пророку, получившему объективное знание от какого-то коммунистического Бога. То есть, в совке считалось, что марксизм - это предел философии, науки и прочего, весь марксизм - он окончательно истинный, потому он не может развиваться, меняться и т.д. Соответственно, взгляд на сферу научного постулировался именно наивно-позитивисткий и вульгарно-сциентистский, мол существует объективный мир объективного технического и естественно-научного знания, и он не определяется какими-либо гуманитарными положениями.
Пока в мире Запада развивались сферы технического/естественно-научного, а также гуманитарного/социального, причём они переплетались между собой, то есть, некоторые номинально технические штуки применялись в сфере гуманитарного, и наоборот, то в совке взаимодействие этих сфер между собой ограничивалось марксисткой и, соответственно, позитивистски-сциентистской догматикой, в итоге это привело к развалу СССР. На Западе вовсю развивалась социальная инженерия, в состав которой входило, к примеру, наследие легендарного химика И. Пригожина, то есть все эти его труды по термодинамике неравновесных структур, нелинейности, диссипативным структурам, точкам бифуркации и т.д., они вовсю осмысливались в контексте социальных процессов. А в совке - нихуя, так как Маркс про это не писал, значит это всё - ложное говно. В свою очередь физика в западном обществе стала уходить от наивного сциентистского редукционизма и материализма, в итоге некоторые направления и концепты "западной" физики в совке интерпретировали как буржуазную диверсию через внедрение в физику идеализма. В итоге, в позднем совке мы начали отставать от Запада даже и в некоторых сферах технических и естественных наук, а про гуманитарные я и вовсе молчу. В итоге мы получили то, что получили.
Таким образом, наивный позитивизм, вульгарный сциентизм и т.д. - они приводят к не самым лучшим результатам. Посему, хоть сфера технического и естественно-научного и должна быть первичной, но она обязательно должна включать в себя гносеологию, методологию науки, когнитивистику и т.д.
Собственно, сабж:
Сфера технического и естественно-научного должна обществом восприниматься как первичная по отношению к сфере гуманитарного. То есть, технократия - это норма. Но, крайне важная деталь: сфера технического и естественно-научного должна обязательно содержать в себе концепты и нарративы, лежащие на стыке технических/естественных и гуманитарных, а также социальных наук.
Дам несколько пояснений.
К примеру, на сознание Эйнштейна очень сильно повлияла вторая волна позитивизма, а конкретно философия Э.Маха. Принцип относительности, лежащий в основании научного наследия Эйнштейна, изначально был им почерпнут именно из махизма. То есть, в основе крупнейшей естественно-научной теории, имеющейся у человечества, лежит конкретная философская концепция. Советский биолог, философ, методолог науки А.А. Любищев написал целую монографию, в которой показал, что всё многовековое развитие науки, к примеру, математики, может быть интерпретировано через влияние на данное развитие двух философских систем - Платона и Демокрита. А на формирование физики Ньютона решающее воздействие оказали социокультурные положения Модерна, в которых одной из главных установок являлась десакрализация и деманифестационализация взглядов на мироздание. Отсюда и теологический унитаризм Ньютона, отсюда и его физика в русле концепции механической вселенной. То есть, наивно-поверхностно сциентистские и архаично-позитивисткие взгляды, что существует объективный мир объективного технического знания, свободный от гуманитарщины - они очень милы и романтичны, но, увы, неверны. В реальности же сфера технического зачастую определяется некоторыми вещами гуманитарного толка. Это важно.
В СССР господствовал марксизм, которому совковая научная "элита" не давала обновляться. То есть, марксизм был догматизирован, причём не в какой-то аутентичной форме, а в форме его ленинской интерпретации, притом, что эта интерпретация тоже несколько зауживалась. Это всё было нелепо ещё и потому, что некоторые взгляды Маркса менялись по ходу его жизни, но в совке к Марксу относились как к некому пророку, получившему объективное знание от какого-то коммунистического Бога. То есть, в совке считалось, что марксизм - это предел философии, науки и прочего, весь марксизм - он окончательно истинный, потому он не может развиваться, меняться и т.д. Соответственно, взгляд на сферу научного постулировался именно наивно-позитивисткий и вульгарно-сциентистский, мол существует объективный мир объективного технического и естественно-научного знания, и он не определяется какими-либо гуманитарными положениями.
Пока в мире Запада развивались сферы технического/естественно-научного, а также гуманитарного/социального, причём они переплетались между собой, то есть, некоторые номинально технические штуки применялись в сфере гуманитарного, и наоборот, то в совке взаимодействие этих сфер между собой ограничивалось марксисткой и, соответственно, позитивистски-сциентистской догматикой, в итоге это привело к развалу СССР. На Западе вовсю развивалась социальная инженерия, в состав которой входило, к примеру, наследие легендарного химика И. Пригожина, то есть все эти его труды по термодинамике неравновесных структур, нелинейности, диссипативным структурам, точкам бифуркации и т.д., они вовсю осмысливались в контексте социальных процессов. А в совке - нихуя, так как Маркс про это не писал, значит это всё - ложное говно. В свою очередь физика в западном обществе стала уходить от наивного сциентистского редукционизма и материализма, в итоге некоторые направления и концепты "западной" физики в совке интерпретировали как буржуазную диверсию через внедрение в физику идеализма. В итоге, в позднем совке мы начали отставать от Запада даже и в некоторых сферах технических и естественных наук, а про гуманитарные я и вовсе молчу. В итоге мы получили то, что получили.
Таким образом, наивный позитивизм, вульгарный сциентизм и т.д. - они приводят к не самым лучшим результатам. Посему, хоть сфера технического и естественно-научного и должна быть первичной, но она обязательно должна включать в себя гносеологию, методологию науки, когнитивистику и т.д.
На каком языке правильно описывать периодичность арифметических остатков?
Т.е. у меня есть число 7, если его возводить в степень, то оно будет давать разные остатки при делении на десять (будет оканчиваться на разное число).
7^1 - 7 = 10A
7^2 - 9 = 10B
7^3 - 3 = 10C
7^4 - 1 = 10D
A, B, C, D - натуральные.
Я понимаю, что четвёртая строка особенная, но не знаю, как об этом сказать.
Теперь ясно, что степени семёрки разбиваются на несколько групп, в зависимости от остатка, который показатель степени даёт при делении на четыре.
Так, степени с показателем 1, 5, 9, ..., 4m + 1 оканчиваются на 7. С показателем 4m+2 оканчиваются на 9. Показатели степени 4m+3 оканчиваются на 3, а 4m на единицу.
Так вот, мы получили какое-то разбиение. Как такие называются? В чём особенность 4 в данном случае?
Моя догадка: 4 равно функции Эйлера для 10.
Т.е. если у нас есть число А взаимнопростое с 10, то в силу теоремы Эйлера для этого числа у нас всегда получается разбиение его степеней на четыре класса? (Для 11 это точно не так. Там один класс, т.к. остаток при делении на 10 всегда равен 1).
@
Демидович
ДА В ШКАЛКЕ И ПОЛОВИНЫ ТОГО НЕ ПРОХОДЯТ, ВЫ СОВСЕМ ОХУЕЛИ ЧТОЛИ ? КИДАЙТЕ МНЕ СЮДА УЧЕБНИКИ ПО ВСЕМУ ЭТОМУ ВОТ В СТУДИЮ, БЫСТРОБЛЕЯТЬ
Ищи самостоятельно. Никто тебе тут ничего на блюдечке подавать не станет.
https://youtu.be/Nb2tIzK5SdM
Все возможно!
Зарепортил за ложную тревогу
Ага, например, -3
Последовательно.
Анон, если ты хочешь получать ответы на свои вопросы, вопросы всё-таки надо задавать.
А то хочется ответить "разобраться с жордановой нормальной формой можно открыв любимый учебник по линалу и найдя там раздел про эту тему"
Палю годноту: "повторяем и систематизируем школьный курс алгебры/геометрии" Крамор В.С
потому что доступно описано для тех кто нихуя не сечёт
В каком вузе?
Переведено далеко не все, лучше англ
научная библиотека находится по адресу gen.lib.rus.ec
Но не в этом дело. Суть в том, что для меня математика это сука испытание от которого я легко увернулся, но мне почему-то хочется к нему вернуться. Хочется вернуться к уровню 10 класса. Ебнуть его. Потом ебнуть подготовку к егэ и после - вузовский курс. Как? Ну теперь у меня есть смартдраги, те что работают. То есть у меня не будет проблем с пониманием и запоминанием. Остается только вопрос: нахуя. Я ощущаю себя очень очень странно, ощущаю отстающим от своих сверстников лет на 5, т.к. они то это говно осилили в свое время. Пиздец какой-то ребятки. Я какой-то мазахист. Надо как-то выбить это говно из головы и забыть, но не получается. Думаю об этом уже полгода наверное. Представляю как могу в своей голове думать о всяких гомологиях и прочем. Но я собрал вокруг себя совершенно других людей. Успешные карьеристы, бизнесмены, которые уже на последнем курсе очень и очень неплохо устроены. Они не поймут если я отобьюсь от них и уйду в это. Странно это все. Ну да ладно. Может чуть по позже, я смогу это замутить под предлогом "шоп мозг не костенел".
Беклемишев
ОП, сразу скажу что тред не читал, но сам в одно время заинтересовался математикой, и по отзывам наткнулся на старинные, но доходчивые учебники под авторством Фихтенгольца Г.М. http://rutracker.org/forum/viewtopic.php?t=667021
попробуй, может зайдут.
Можно, конечно, перепроверять, но не каждый же раз? Да и даже если перепроверить, хоть пальцем тыкни -- могу ошибку не видеть... Как пофиксить такую рассеянность? Из-за этого на всяких самостоятельных/контрольных были тройки-четвёрки, хотя теорию знаю.
давай себе отдохнуть, делай перерыв после решения и проверяй только когда отвлечешься, можешь попробовать помедетировать
>вундеркинд
>Вся школьная математика и физика учатся
Дальше этого места не читал твой пост, Мистер Косноязычность 2016.
Go back to /b, быдлан.
>70х годов
Эпоха Колмогорова? Вообще, всякие старперы с ЖЖ дико срутся с учебников Колмогорова и яростно надраивают Андрею Киселеву. Кто что думает по этому поводу? На дворе 2016-ый, неужели за то время нельзя было сделать 12 совершенных школьных книг (математика 5-6, алгебра 7-11, геометрия 7-11)?
Нельзя. Для начала: кому это надо?
За плечами пара курсов вузовской математики (тервер, дискретка, дифуры, аналитическая геометрия) онли.
 130 Кб, 720x960
130 Кб, 720x960 130 Кб, 720x960
130 Кб, 720x960какое же ты тупое уёбище
закончил школу 6 лет назад и до сих пор всё это помню... как любой нормальный человек
Сейчас на курсере годный курс идет, правда ты не успел к началу. Он вообще простой, но интересный, на русском. Называется "Математика для всех", поможет научиться получать удовольствие от математики
https://www.coursera.org/learn/matematika-dlya-vseh/
> 02.03.01 - Математика и компьютерные науки
Учусь тут, фундаментальная годнота как по программам, так и по математике. Как минимум с++ в качестве первого языка мне внушил
Киселев кстати норм, есть переизданные физматлитом в современном, так сказать, виде учебники элементарных алгебры и геометрии. Жалею, что ничего подобного не было в поле зрения, когда учился в 7-9 классах, точнее, мучался.
Вообще обычная школа больше отбивает желание заниматься математикой, чем учит. Апофеоз сего есть ЕГЭ с его абсолютно унылыми и не подчиненными никакой систематичности вычислительными задачами, внущающими отвращение и стремление как можно скорее забыть эту горе-науку.
>>53374
Кто их любит, лол.
DEUS VULT
сука, анон, вот тоже самое
Учился на математика 4 года, понял только азы вышмата на первых двух курсах еле-еле. Чувствую себя дауном и хочу добить математику после учёбы.
Только в геоме Киселёву добавили задачи совсем не к месту, если не ошибаюсь.
 96 Кб, 998x409
96 Кб, 998x409Помогите мне, учебник "Высшая математика для инженеров" я читал, не помогло. Биореактор?
Разбиением на прямоугольники. Численное интегрирование.
Какие американские школьные учебники по математике являются самыми лучшими сегодня?
вольфрам альфович твой верный друг
schoolyourself.org как базовое введение по математике. Использует небольшую дозу программируемого обучения.
Почти как ОП. Закончил пять лет назад универ по тех.специальности, синий диплом. Но знания о высшей математике испарились сразу после сдачи лабораторных (потому что задрачивал в основном программерскую часть, лишь бы формула работала).
Теперь вот хочу подтянуть знания по ВышМату, МатАналу, и т.д..
Знающие аноны, поясните за intuit.ru - годный веб-универ? Стоит ли обучаться по их лекциям?
И да - спасибо всем, кто накидал ссылок/авторов годных учебников!
Решение твоей проблемы: 2ch.hk/math/
>>54496
Удваиваю вас господа, только я еще и пытаюсь в кодинг вкатиться, а это вообще охуеть сложно оказалось. К лету мать работать погонит, а я не хочу снова идти в общепит или в продажи. Пытаюсь хотя бы в начального уровня веб-макакинг ворваться, но все равно трудности испытываю и чувствую себя тупым. И тоже как и вы в школе страдал от математики, у нас даже всякие спортивные ерохи и быдланы, и те могли в математику, а я уже пустым взглядом смотрел в листок с контрольной и ежедневно приносил домой двойки, которые вместе с истеричной жирной учительницей математики/алгебры еще больше отбивали желание постигать математику. А еще я всегда весьма хуево играл в игры где требуется реакция/координация. От этого еще больше начинаю думать что я тупой и не приспособлен к высокоинтеллектуальному труду.
Которые не нужны для человека, который занимается самообразованием.
спасибо тебе, добра тебе, надеюсь ты жив и хоть что то тут ещё напишешь)
>"Математика не для отличников" скачиваешь на рутрекере
всем привет. Может быть есть у кого-нибудь ссылка? Вчера вечером все торренты обыскал
Нахуй тебе математика? Почему быдло видит в ней что-то сакральное. Изучай что-нибудь полезное для жизни и работы
мимо-закончил-мехмат
Нуу как тебе сказать, есть люди которые после работы пьют пиво, есть которые лепят из пластилина. Я после работы решаю задачи из учебника 8 класса (инженер энергетик 26 лет.)
Так это же круто, многие так делают на самом деле
Сап математики.
Посоветуйте годных интересных учебников по линалуможно и ангему.
Слава богу скоро кончится сессия и будет время почитать на досуге.
мимо-2-курс
/math/
Гельфанд же
Оп, как твои успехи... Столько лет прошло
Охренеть, мой тред еще живой! Несмотря на то, что он в тематике, я думал, что его смыло уже давным давно. Вау.
Как успехи... Да хрен его знает даже, оцениваю, что не очень. Сейчас учусь на 3-м курсе, на (очень) естественной специальности, в которой из математики только матстатистика (в научной работе, типо всякие выборки, сравнения, коэффициент Стьюдента и прочее. в котором особо нихуя не понимаю). Больше знаний в химии, геологии и картографии появились.
В январе устроился на работу, на полставки, в госучреждение, времени мало стало совсем + я еще нихуя не организован. Математикой особо не занимаюсь, как ты понял, наверно, сейчас уже другие вещи заботят. Вот, курсовую на этой неделе (завтра-послезавтра тезисы надо сдать), можно сказать, сдавать, а у меня нихуя не сделано, буду всю ночь корпеть над отчетами.
А лет действительно уже столько прошло.. Особенно, если учесть, что тред создал я еще в 11 классе, когда я эгэ сдавал. Сейчас это егэ такой мелочью кажется, хотя нихуя не так, наверно. Грустно на самом деле, взрослым как-то тяжко становиться, особенно-то с моим инфантилизмом. Надо как-то себя преобразовывать, научиться планировать и через нехочу делать дела. Но до сих пор себя школьником чувствую, хотя недалеко и ушел-то, лол. Вот как-то так, собственно, и дела, себя душой так себе ощущаю.
Интересно, получится ли ОП-марку прилепить, хотя вряд ли, уже столько провайдеров переменял.
В целом готовлюсь к ЕГЭ, хочется научиться 14,16, но без базы и смысла нет пытаться решать. Помогите, с чего начать. До егэ месяц =3
Есть какая-нибудь статья вроде "Изучение математики позволяет решать кучу проблем"?
Бамп вопросу
Ну математика в целом развивает логику и аналитический ум, это та причина по которой математику стоит изучать нематематикам. Но не могу сказать уверенно насколько тут необходима математика дальше школьной программы.
Я хочу стать дата сайенсом. А вообще, мне просто интересно. Кто-то играет игры, кто-то переодевается в девочку, а я доказываю теоремы.
Анон, но зачем нужны эти теоремы? Для чего они пригодятся в жизни? Я ни в коем случае не говорю, что это плохо. Просто хочу тебя понять.
Спасибо что ответил, анон
А хуле должны пригодиться? Мне нравится их доказывать, мышление развивает, Альцгеймер не так быстро настигнет. Прост делаю, и так все умрем.
Для чего в жизни пригодятся компьютерные игры? Для чего в жизни пригодятся аниме, сериалы, художественные книжки?
Для нормального социального взаимодействия.
Но я рассказываю истории с двачей, немного изменяя их и этого мне хватает. Дома формулы хуярю.
Чтобы ловить ништяики с людей, ну. Попиздел с одногруппниками -> свой человек -> получаешь албы нахаляву.
>для чего в жизни необходимо искусство?
Для получения удовлетворения как минимум, не говоря уже о том что это один из работающих способов познания и перевоспитания. Далеко как не все в этой жизни измеряется только одной шкалой "пригодится ли в будущем".
мимо инженер, в принципе тоже много не знаю, но умею пользоввться нужными формулами и таблицами, кайфа от подсчетов вручную не испытываю категорически
А мне оно нахуя? Последнее, что я проектировал это подъемный кран, и все, что требовалось это расчёты в онлайн-калькуляторах и данные из справочников
Ну как знаешь. Просто вдруг спросят тебя, почему 0.(9) = 1, а ты не сможешь объяснить.
Нет, строго равно. 0.(9) и 1 - это одно и то же число, без шуток. Никаких приближений или округлений тут нет. Просто бывает так, что две разные строки цифр изображают одно и то же число.
Говоря более наукообразным языком, представление вещественных чисел в виде строк десятичных цифр не является однозначным - у многих чисел бывают два разных представления. Например, 0.(9) = 1, 7.3(9) = 7.4 и т.п.
Есть даже наглядный аргумент.
1/9 = 0.(1)
2/9 = 0.(2)
3/9 = 0.(3)
...
8/9 = 0.(8)
9/9 = 0.(9)
Я не объяснял, я иллюстрировал. У тебя тоже не объяснение, поскольку ты пользуешься бесконечными суммами. Но понятие бесконечной суммы чисел нельзя использовать, пока не сконструировано понятие одного числа. Очевидно же.
>почему так.
А чтобы объяснить, почему так, нужно на самом деле очень неслабо углубиться в математику. Ввести множества и действия над ними, постулировать существование какой-нибудь вселенной множеств, потом в этой вселенной соорудить непрерывно упорядоченное поле (в обычных вселенных множеств такое поле только одно), это поле и будет R. И только после всего этого можно пытаться объяснять, какова же всё-таки взаимосвязь строк цифр и вещественных чисел.
Обычно пытаются объяснить равенство 0.(9) и 1 с помощью какого-нибудь предельного перехода (вот как у тебя, например, через ряд). Но предельный переход во множестве существенно опирается на топологическую структуру этого множества. А пока R у нас не построено, никакой топологией на R, понятное дело, мы пользоваться не имеем права. Нельзя пользоваться тем, чего пока ещё нет. Причины равенства 0.(9) и 1 лежат глубже, чем предельные переходы.
Ещё один вопрос из той же серии.
Понятно, как возводить положительное число в рациональную степень. Например, x^3 = xxx. x^5 - это x, умноженное на себя пять раз. x^(-3) = 1/x^3. x^(1/2) = квадратный корень из x, x^(7/3) = кубический корень из x в седьмой. А вот что такое x в степени пи? Число пи ведь нельзя выразить в виде обыкновенной дроби p/q, пи иррационально.
Таки нет. Ты путаешь объяснение и доказательство (причём в самом строгом смысле доказательство).
Объяснение может быть интуитивным. Например, я могу объяснить равенство (a+b)^2 = a^2 + b^2 + 2ab, нарисовав квадрат и поделив на части. Но чтобы доказать, мне придется доказать, что такой квадрат есть, что я могу его делить на части и т.д.
Я утрирую, но тем не менее.
Можно объяснить, почему lim 1/x = 0 при x->inf (объяснить=сделать очевидным), пользуясь при этом интуитивным пониманием предела, но вот доказательство требует определения и много букв.
Ты отчасти прав: вовсе не очевидно, что суммируется оно именно так. Но с дойти до топологии, имхо, ты загнул).
Ненатуральную степень наверное проще считать искуственным обобщением натуральной (исходя из a^b * a^c = a^(b + c)), которое упрощает многие вещи. Ну как и отрицательные числа или комплексные (которые по сути на самом деле вектора на плоскости и удобный способ работать с ними).
Иными словами, ты иллюстрировал, что оно работает, а я иллюстрировал, почему оно работает.
ок
Отличная книга "Мир математики. Трудности доказательств", советую ознакомиться. Поможет глубже понять (как неожиданно) тонкости доказательств, что является неотъемлемой частью всех разделов математики
Пиздец, не получилось нормально показать
Арнольд, "Задачи для детей от 5 до 15 лет" к ознакомлению рекомендую.
Упорство и целеустремлённость делают чудеса. Тебе нужно не ныть на анонимных форумах про аниме, а ботать.
Khan academy, потом MIT OCW.
Для МГУ лучше всего задрочить учебники Мякишева (определения в ДВИ по физике берутся из них)и сборник задач Сканави для поступающих в ВУЗы (это уже математика). Для ЕГЭ по обоим предметам советую сайт mathus.ru.
По определению, натуральными числами называется класс конечных ординалов.
0 - пустое множество, 1 - множество, единственным элементом которого является пустое, 2 = {0,1}, 3={0,1,2} и т.п. Каждое очередное число n имеет в качестве своих элементов все числа от 0 до n-1.
Это не может являться строгим определением так как использвует аналогичные понятия вроде конечных ординалов, или конструкции "и т.д.".
Определение было в первой строке, в последующих строках было пояснение. В принципе, могу определить вообще с нуля.
Определение 0. Класс называется множеством, если он является элементом какого-нибудь класса. Класс называется собственным, если он не является множеством.
Определение 1. Отношением на множестве M называется подмножество декартова произведения MxM. Если ф - отношение на M, то вместо (x,y)∈ф пишут xфy.
Определение 2. Отношение ф множестве M называется порядком, если для любых элементов x, y, z из множества M выполнено:
a) xфx (рефлексивность)
б) xфy И yфx → x=y (антисимметричность)
в) xфy И yфz → xфz (транзитивность)
Порядок называется линейным, если вдобавок для любых x,y из M выполнено
г) xфy ИЛИ yфx (линейность)
Множество, на котором задан порядок, называется упорядоченным.
Множество, на котором задан линейный порядок, называется линейно упорядоченным.
Определение 3. Пусть N - непустое подмножество M.
x∈N называется наименьшим элементом в N, если для любого y∈N верно xфy.
Определение 4. Линейно упорядоченное множество называется вполне упорядоченным, если в любом подмножестве есть наименьший элемент. В этом случае порядок называется полным порядком.
Определение 5. Эпсилон-порядок на множестве M - это такой порядок ф на нём, что xфy ⇔ x∈y.
Соглашение 1. Определения с 1 по 5 сформулированы для множеств. Чтобы получить аналогичные определения для собственных классов, следует вместо "множество" написать "собственный класс". Читатель пусть проделает это самостоятельно, я не буду разъяснять, что такое "вполне упорядоченный класс". Определения ниже уже не допускают переформулировки для классов.
Определение 6. Множество M называется ординалом, если эпсилон-порядок на нём является полным порядком.
Теорема 1. Каждый элемент ординала - ординал.
Теорема 2. Класс всех ординалов вполне упорядочен эпсилон-порядком.
Определение 7. Последователем x' множества x называется множество x∪{x}.
Теорема 3. Последователь ординала - ординал.
Теорема 4. Класс всех ординалов не является множеством.
Определение 8. Ординал M называется индуктивным, если:
a) ∅∈M
b) x∈M → x'∈M
Аксиома 1. Существует хотя бы один индуктивный ординал.
Определение 9. Наименьший элемент класса всех индуктивных ординалов называется ω.
Определение 10. Элементы ω называются конечными ординалами.
Определение 11. Натуральными числами называются конечные ординалы.
Определение 12.
0 = ∅
1 = 0' = {∅}
2 = 1'= {0,1}
3 = 2' = {0,1,2}
4 = 3' ={0,1,2,3}
5 = 4' = {0,1,2,3,4}
6 = 5' = {0,1,2,3,4,5}
7 = 6' = {0,1,2,3,4,5,6}
8 = 7' = {0,1,2,3,4,5,6,7}
9 = 8' = {0,1,2,3,4,5,6,7,8}
На классе ординалов определены сложение и умножение с обычными свойствами.
Это позволяет любой строке десятичных цифр сопоставить вполне определенное натуральное число.
Исчерпывающе?
Определение было в первой строке, в последующих строках было пояснение. В принципе, могу определить вообще с нуля.
Определение 0. Класс называется множеством, если он является элементом какого-нибудь класса. Класс называется собственным, если он не является множеством.
Определение 1. Отношением на множестве M называется подмножество декартова произведения MxM. Если ф - отношение на M, то вместо (x,y)∈ф пишут xфy.
Определение 2. Отношение ф множестве M называется порядком, если для любых элементов x, y, z из множества M выполнено:
a) xфx (рефлексивность)
б) xфy И yфx → x=y (антисимметричность)
в) xфy И yфz → xфz (транзитивность)
Порядок называется линейным, если вдобавок для любых x,y из M выполнено
г) xфy ИЛИ yфx (линейность)
Множество, на котором задан порядок, называется упорядоченным.
Множество, на котором задан линейный порядок, называется линейно упорядоченным.
Определение 3. Пусть N - непустое подмножество M.
x∈N называется наименьшим элементом в N, если для любого y∈N верно xфy.
Определение 4. Линейно упорядоченное множество называется вполне упорядоченным, если в любом подмножестве есть наименьший элемент. В этом случае порядок называется полным порядком.
Определение 5. Эпсилон-порядок на множестве M - это такой порядок ф на нём, что xфy ⇔ x∈y.
Соглашение 1. Определения с 1 по 5 сформулированы для множеств. Чтобы получить аналогичные определения для собственных классов, следует вместо "множество" написать "собственный класс". Читатель пусть проделает это самостоятельно, я не буду разъяснять, что такое "вполне упорядоченный класс". Определения ниже уже не допускают переформулировки для классов.
Определение 6. Множество M называется ординалом, если эпсилон-порядок на нём является полным порядком.
Теорема 1. Каждый элемент ординала - ординал.
Теорема 2. Класс всех ординалов вполне упорядочен эпсилон-порядком.
Определение 7. Последователем x' множества x называется множество x∪{x}.
Теорема 3. Последователь ординала - ординал.
Теорема 4. Класс всех ординалов не является множеством.
Определение 8. Ординал M называется индуктивным, если:
a) ∅∈M
b) x∈M → x'∈M
Аксиома 1. Существует хотя бы один индуктивный ординал.
Определение 9. Наименьший элемент класса всех индуктивных ординалов называется ω.
Определение 10. Элементы ω называются конечными ординалами.
Определение 11. Натуральными числами называются конечные ординалы.
Определение 12.
0 = ∅
1 = 0' = {∅}
2 = 1'= {0,1}
3 = 2' = {0,1,2}
4 = 3' ={0,1,2,3}
5 = 4' = {0,1,2,3,4}
6 = 5' = {0,1,2,3,4,5}
7 = 6' = {0,1,2,3,4,5,6}
8 = 7' = {0,1,2,3,4,5,6,7}
9 = 8' = {0,1,2,3,4,5,6,7,8}
На классе ординалов определены сложение и умножение с обычными свойствами.
Это позволяет любой строке десятичных цифр сопоставить вполне определенное натуральное число.
Исчерпывающе?
Чёрт, меня подглючило. В определении 2 я дал определение нестрогого порядка, а там должно было быть определение строгого.
Определение 2': Отношение ф множестве M называется строгим порядком, если для любых элементов x, y, z из множества M выполнено:
а) xфy → НЕ yфx (асимметричность)
б) xфy И yфz → xфz (транзитивность)
Ниже имеются в виду именно строгие порядки.
В определении 3 y не равен x.
Не лезь, оно тебя сожрет. Там вон какой тред оснований математики в math, а ты хочешь это прямо здесь определить...
Нет, не исчерпывающе.
1. Нет определения класса.
2. Нет определения декартова произведения.
3. Нет определения знаков принадлежности и объединения.
Это для начала.
Я-то знаю, лол. Просто я думал ты хочешь from the ground up из базовой аксиоматики построить. Но у тебя не хватило усердия. Впрочем, забей.
Для полного счастья осталось только перечислить аксиомы NBG и дать определение формальной теории.
> Определение было в первой строке, в последующих строках было пояснение.
Это не определение, ты заюзал более мощное неопределяемое интуитивное понятие множества (оно, кстати, в таком виде противоречиво) и взял из него интуитивное понимание натурального числа как частный случай. Надеюсь не надо пояснять что это не строгое определение а чит?
> В принципе, могу определить вообще с нуля.
Валяй. Пока я в этом треде его не увидел.
> Это позволяет любой строке десятичных цифр сопоставить вполне определенное натуральное число.
Что такое строка десятичный цифр в общем случае? Ты опять рекурсивно аппелируешь к интуитивному понятию натурального числа которое хочешь определить. Т.е. ты занимаешься иллюстрацией, как и было выше, а не даешь строго определение.
> Исчерпывающе?
К сожаленю не только не исчерпывающе, а просто не верно.
>неопределяемое интуитивное понятие множества
Сфигали интуитивное? Про аксиоматические теории множеств не слышал?
Киселев писал, так, чтобы научить, Колмогоров писал потому что Партия приказала написать.
Ты использовал эти учебники, можешь сделать некий отзыв?
К слову мне в math дали эту ссылку: http://vk.com/wall-94378522?owners_only=1&q=киселев Раньше ведь писал кто-то, что нужны были отдельные задачники к пособиям, а не всё в кучу. Впечатляет, что есть довольно неплохо проработанный задачник даже по арифметике. Книги есть на libgen.io вроде.
Интересно побольше отзывов и рекомендаций, что ли.
Просветов Г.И. Учимся считать быстро: задачи и решения
— Вроде неплохо написано, но пока не нашел полной книги в интернете, возможно стоит лучше поискать. Хотя в целом интересно что можно почитать о быстром счете.
Выгодский М.Я. Геометрия для самообразования
— Книга 1950 года. В книге написано, что она написана просто.
 33 Кб, 600x654
33 Кб, 600x654как научиться использовать многомерные интегралы в повседневной жизни?
как влезть в топологию?
каждый раз как серьёзно берусь за эти темы не могу зайти дальше маняпримерчиков на листочке. как это всё осиливают настоящие учёные, строчащие вайтпейперы?
У тебя губа не дура, лол. Тут натуральные числа не могут определить, а ты в топологию собрался.
с любого учебника по математике с 5 по 11 класс. Если понимаешь, что слишком сложно - понижаешь уровень. Слишком легко - повышаешь.
Или же смотришь варианты, пытаешься решать. Если что-то непонятно, смотришь в интернете, как это решается. Сейчас полно видео разборов.
Возьми один вариант и попробуй решить - велика вероятность, что ты и так его напишешь на 3-4, потому как он очень простой. Если нет - гуглишь видеоразборы заданий и запоминаешь.
Когда на бумаге считаю, все ок. Как только надо у доски что-то решить или в уме посчитать, сразу жопа.
Не тупой, но, по всей видимости, числа в башке перемешиваются, как только прерывается зрительный контакт с промежуточными выкладками.
Вообще говоря счет не относится к математике, математики обычно обижаются когда от них требуют быстрый счет.
Но все же.
>>66678
Это где же вы учитесь? Получается, что с такими знаниями поступили как-то. Короче, есть два пути, долгий и чуть короче.
1) Я могу тебе посоветовать книги и/или сайты, где можно бесплатно и без смс пройти путь от неуча, до человека понимающего эльфийский в рамках школьной программы оф корс. Но тут нужно будет много читать и много решать РУЧКАМИ, а не тесты клацать. И еще, нельзя будет пропускать темы в духе "а, я понял, дальше пошел". Как минимум, самые интересные и сложные задачи и примеры по теме нужно будет решать.
2) Путь попроще. Берем твои насущные проблемы и смотрим, что и почему у тебя не получается, закрывая конкретно эти пробелы. Но тут без первого пути будет сложно, так как без посторонней подсказки или бэкграунда ты можешь ошибаться.
Сейчас думал тут список навалять, но передумал. Тем более, что оказывается в треде уже упоминали многое. Короче, то, что тебе поможет в ближайшее время:
Интернетурок. Сейчас там почти все видео лекции платные, но стоит подписка на месяц ~100р., я точно не помню. Вся школьная программа в конспектах, очень доходчивые объяснения. В конце урока есть домашние задания + задания в учебниках. Последние легко загуглить, как и ГДЗ к ним. В подписке есть вариант с тестиками, но задания там слабее.
Туманов "Элементарная математика" - опять же, все, что тебе нужно. Но в отличии от вышеупомянутого сайта язык там более сложный, читай для расширенного понимания тем. Но это не обязательно.
Этого тебе хватит. Далее можешь зайти в этот тред и почитать, что тут советовали выше. Когда именно? Когда будешь на этапе класса 8-9. Например, тот же Курант сегодня, скорее всего, тебе покажется мутью, хотя когда ты освоишься им даже будешь зачитываться. Поэтому в качестве полезного развлечения лучше бери того же Перельмана.
Ок. Спасибо тебе.
А второе ты как видишь? Репетитора нанимать какого-то? Это уже не совсем будет образования. Или так подскажет кто?
Если есть время и возможность следуй первому совету. Если нет, то даже будучи потерянным в математике ты должен хотя бы примерно представлять какой фундамент нужен для решения той или иной задачи или понимания того или иного предмета. Но даже если ты хз, гугли примеры, которые ты на учебе разбирал последними, смотри в каких книгах они встречаются и что в этих книгах по содержанию предшествует твоей задаче. Если ВСЕ непонятно, то читай предисловие в той же книге, там могут писать, что "бла-бла-бла для старшеклассников" или "бла-бла-бла для младших курсов физмата" и т.д. Вот это то, к чему ты должен стремиться, чтобы обрести понимание. И решай письменно. Никогда не выебывайся тем, что ты прочитал и все понял. Всегда хоть чуть чуть, но закрепляй решением примеров и повторяй периодически. Регулярно занимайся и будет тебе профит. И еще, если вдруг возникнут проблемы с эго, мол ты тут детские задачки пачками решаешь, будучи лбом здоровым, то такая позиция тебя не приведет туда куда ты хочешь. Это я на всякий случай сказал.
Ну где я задачи возьму чтобы от простого к сложному? Небось для арифметики надо тыщу порешать...
>>66711
>>66712
Слышал выражение о том, что в математике нет царского пути? Не обязательно решать тысячу примеров арифметики. Скорее всего, ты справишься быстрее. Отторжение у тебя может быть вызвано скорее всего тем, что математика у тебя ассоциируется с угнетением, болью, комплексом неполноценности из-за ее незнания и парашных оценок. Но всю это можно победить, если прикладывать усилия и работать над собой. Это как заниматься спортом. Может конкретно ты олимпийским чемпионом, охуенным бодибилдером или МС не станешь, но не быть дрыщом и иметь нормальные силовые под силу каждому у кого нет противопоказаний по здоровью. Можешь для энтузиазма почитать наупоп какой-нибудь по математике, говорят, некоторых вдохновляет.
Ну вроде все правильно, даже сказать нечего на твои посты... Но опиши подробнее путь два. Как понять свои слабые стороны... Что-то и правда при всей этой математике такое состояние, что мысли путаются. Чувствую себя тупее всего двоща. В школе посещал уроки иногда и даже что-то получал, но не могу сказать, что что-то основательно знаю. Экзаменов не сдавал.
Науч-поп не помогает совсем, даже хуже чувствую себя от этих всех логических загадок.
Сканави вот пробовал решать... Как не стыдно, как-то за один месяц порешал арифметические задачи с дробями и всем этим (не знаю сколько там дней это заняло, можно будет посмотреть). Потом перешёл на алгебраические преобразования и сразу выпал, не знал как подступиться даже... Как-то так и забросил до сегодняшнего момента... Прошло уже много времени...
Вот такой крик души...
 20 Кб, 299x215
20 Кб, 299x215>Как понять свои слабые стороны... Что-то и правда при всей этой математике такое состояние, что мысли путаются. Чувствую себя тупее всего двоща. В школе посещал уроки иногда и даже что-то получал, но не могу сказать, что что-то основательно знаю. Экзаменов не сдавал.
Расскажи о своих отношениях с математикой по жизни, а так же с учителями. Я насколько понимаю, все было плохо и ты числился в довенах? Опиши так же состояние на текущий момент, в частности конкретно, зачем тебе знание математики?
>Науч-поп не помогает совсем, даже хуже чувствую себя от этих всех логических загадок.
Я не про загадки, а про что-то вроде "Удовольствие от Х".
>Как не стыдно, как-то за один месяц порешал арифметические задачи с дробями и всем этим
Вот сразу то, о чем я говорил выше:
вдруг возникнут проблемы с эго, мол ты тут детские задачки пачками решаешь, будучи лбом здоровым, то такая позиция тебя не приведет туда куда ты хочешь
Приведу пример с той же качалкой. Ты приходишь туда чмошным дрыщем, который всю жизнь не подымал ничего тяжелее бутылки пива, и естественно, начинать ты будешь с маленьких весов, постепенно подбираясь к чему-то посерьезнее. Но это не значит, что тебя должно угнетать такое положение вещей, так как ты уже как минимум поднял жопу, чтобы это исправить и это делает тебя не таким говном, как раньше.
>Потом перешёл на алгебраические преобразования и сразу выпал, не знал как подступиться даже
Ты смотришь на свою задачу в масштабе, а надо дробить по частям. Не ставь себе цель - ВЫУЧИТЬ ВСЕ. Хотя, конечно, такое можно иметь в качестве мотивации, но цель должна быть проще. Например, начинаю я сегодня с такого: научиться решать рациональные уравнения. Научился, прорешал n-количество, ставишь следующую цель. Это такой механизм психики, когда ты смотришь на глобальную цель, то руки сразу опускаются, так как ты начинаешь думать о том, как решить ее РАЗОМ, а тут ебать сил нужно, ой бляяяя. Тем более, если ты в этой сфере был лузером.
1) теории групп
2) теории меры и интегралам Лебега
3) тензорному анализу
4) топологии
5) дифференциальной геометрии
закончил первый курс, как-то касались первых четырех пунктов. сдал, проблем не было, но глубокого понимания не получил. пятый пункт хотелось бы почитать перед/в ходе изучения в институте
Этот тред появился раньше раздела /math/. Да и тут делается акцент на самообразование, наверное.
 176 Кб, 312x312
176 Кб, 312x312скопипастил себе из саентача пару лет назад список основного материала
До большей части из этого так и не добрался, но может тут кому-то полезно будет:
ДЛЯ САМЫХ МАЛЕНЬКИХ:
Общие курсы
М. И. Сканави: "Элементарная математика".
Алгебра
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
С. Б. Гашков: “Современная элементарная алгебра”.
Геометрия
А. Д. Александров, А. Л. Вернер, В. И. Рыжик: “Геометрия”. Учебник для 10-11 классов. Базовый и углубленный уровни.
Я. П. Понарин: “Элементарная геометрия” в двух томах. Первый том - это планиметрия, а второй том - это стереометрия.
А. Ю. Калинин, Д. А. Терешин: “Геометрия”, 10-11 классы. Годный учебник.
Тригонометрия
И. М. Гельфанд, С.М. Львовский, А. Л. Тоом: “Тригонометрия”. Название говорит само за себя. Много геометрических и физических интерпретаций + комплексные числа, как бонус.
Начала анализа
Б. М. Давидович: “Математический анализ в 57 школе“.
БАЗОВЫЕ КУРСЫ ДЛЯ СТУДЕНТОВ:
Общая алгебра
Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
М. Атья, И. Макдональд : "Введение в коммутативную алгебру".
А. Л. Городенцев: "Алгебра. Учебник для студентов-математиков". Вырос из лекций НМУ. Читать параллельно с Винбергом (Винберга читать в первую очередь).
И.Р. Шафаревич: “Основные понятия алгебры“. Замечательный обзор вообще того, что такое алгебра, как она выглядит и какое место она занимает в математике. Примеры, приложения и прочая конкретика.
E. Connell: Elements of Abstract and Linear Algebra". Хорошая первая книга по алгебре, да и математике вообще.
P. Grillet: "Abstract algebra". Очень лаконичный и понятный учебник. Надо знать элементарную теорию чисел, про индукцию, про множества и функции. Линейной алгебры нету.
J. Rotman: "Advanced modern algebra". Ротман сильно разжевывает. Задачи слишком простые для уровня учебника. Линейная алгебра есть.
M. Artin: "Algebra". Американский Винберг. Группы Ли, упор на геометрию. Задачи неудачные.
I. Herstein: “Topics in Algebra“. Прекрасные задачи, отбор материала очень устарел, почти что Ван дер Варден.
P. Aluffi: "Algebra, Chapter 0". Если ты в состоянии ее осилить, бери и забывай про остальные книжки из списка. Линейная алгебра есть.
Линейная алгебра
В. А. Ильин, Э. Г. Позняк: “Линейная алгебра“. Один из классических и самых популярных курсов линейной алгебры.
Д. В. Беклемишев: “Курс аналитической геометрии и линейной алгебры“.
И. М. Гельфанд: "Лекции по линейной алгебре". Не даётся определение определителя.
А. И. Кострикин, Ю. И. Манин: "Линейная алгебра и геометрия". Затрагивается темы геометрий и связей с квантовой механикой. Не даётся определение определителя.
S. Axler: "Linear algebra done right". Подход без определителей (почти). Одна из самых популярных книг за рубежом.
S. Treil: "Linear algebra done wrong". Не такая популярная, как Axler, но тоже хвалят, да. Определители есть.
G. Shilov: "Linear Algebra". Определитель появляется на первой странице.
K. Hoffman, R. Kunze: "Linear Algebra". Классика за рубежом.
P. Halmos: "Finite-Dimensional Vector Spaces". Тоже классика.
P. Peterson: "Linear Algebra". Не особо знаком, но выглядит аккуратно. Что-то вроде Акслера.
S. Roman: "Advanced Linear Algebra". Хороший учебник по линалу. Но нужно знать элементарные свойства матриц и определителей.
Математический анализ
T. Tao: “Real analysis“. Один из самых популярных курсов математического анализа на английском языке.
C. Pugh: "Real Mathematical analysis". Более простая версия Рудина с картинками. Норм книга, но не самая лёгкая.
У. Рудин: "Основы математического анализа".
В. А. Зорич: "Математический анализ". Первый том посвящен классическому анализу. Много примеров, много материала, в том числе даются в начале основы матлогики и теории множеств, а также функций между ними.
Р. Курант: "Курс дифференциального и интегрального исчисления". Идеален с точки зрения
первого знакомства с теорией, но имеет достаточно сложные упражнения.
Г. М. Фихтенгольц: "Курс дифференциального и интегрального исчисления". Хорош как повторительный курс.
С. М. Львовский: "Лекции по математическому анализу". Записки лекций из НМУ. Нужно знать основы калькулюса.
Г. Г. Харди, Д. Е. Литтлвуд, Г. Пойа: "Неравенства".
Н. Н. Лебедев: "Специальные функции и их приложения".
Г. П. Толстов: “Ряды Фурье“.
Дифференциальные уравнения
С. Фарлоу: “Уравнения с частными производными для научных работников и инженеров“.
Вариационное исчисление
И. М. Гельфанд, С. В. Фомин: " Вариационное исчисление".
Топология
V. Runde: "A taste of topology". Неплохая книга по метрическим пространствам и общей топологии, затрагивает фундаментальную группу.
J. Strom: "Modern classical homotopy theory".
T. Dieck: "Algebraic topology".
M. Crossley: "Essential Topology". Пререквизит для изучения алгебраической топологии. Не затрагивает тему метрических пространств.
КУРСЫ ДЛЯ ПРОДВИНУТЫХ МАТЕМАТИКОВ
Математический анализ
А. И. Маркушевич: "Теория аналитических функций".
S. Ramanan: "Global calculus".
H. Amann, J. Echer: "Analysis".
W. Fidcher, I. Lieb: "A Course in Complex Analysis: From Basic Results to Advanced Topics".
Дифференциальные уравнения
В. И. Арнольд: “Обыкновенные дифференциальные уравнения”. Книга для уверенных в себе математиков. Диффеоморфизмы, фазовые потоки, гладкие многообразия. Слава Гермесу Трисмегисту!
Теория категорий
С. Маклейн: "Категории для работающего математика".
Р. Голдблатт: "Топосы. Категорный анализ логики".
Дифференциальная Геометрия
К. Номидзу: "Основы дифференциальной геометрии".
J. Lee: "Manifolds and DIfferential Geometry".
L. Nicolaescu: "Lectures on the Geometry".
P. Michor "Topics in Differential Geometry".
Алгебраическая геометрия
Д. Мамфорд: "Красная книга о многообразиях и схемах".
В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”.
В. И. Арнольд: “Вещественная алгебраическая геометрия”.
Ю. И. Манин: Введение в теорию схем и квантовые группы“.
R. Vakil: "Foundations of algebraic geometry".
S. Bosch: "Algebraic Geometry and Commutative Algebra".
U. Gotz, T. "Wedhorn: Algebraic Geometry".
E. Harris: "The Geometry of Schemes".
Топология
А. Хэтчер: "Алгебраическая топология".
J. Munkres: "Topology". Книга - жесткий учебник по теоретико-множественной топологии. Много ненужного для других областей математики.
ИНТЕРЕСНОЕ:
Цикл “Manga guide to...“. Популярное изложение различных областей математики (и не только), оформленное в виде манги. Увы, без фансервиса.
Н. А. Вавилов: “Конкретная теория групп I: основные понятия“. И вообще все остальные книги (и лекции!) Вавилова.
П. С. Александров: “Введение в теорию групп“. Просто о сложном. Несколько вольный язык изложения, местами затрудняющий восприятие.
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”.
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
Н. Я. Виленкин: "Рассказы о множествах". Теория множеств для широкого круга читателей.
М. М. Постников: “Теорема Ферма. Введение в теорию алгебраических чисел”.
Н. Стинрод: “Первые понятия топологии“.
А. Я. Хинчин: “Три жемчужины теории чисел“.
О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов: “Элементарная топология”.
Я. П. Понарин: “Алгебра комплексных чисел в геометрических задачах”.
А. А. Заславский: “Геометрические преобразования”.
В. Акопян, А. А. Заславский: “Геометрические свойства кривых второго порядка”.
В. И. Арнольд: “Геометрия комплексных чисел, кватернионов и спинов”.
В. В. Прасолов: “Геометрия Лобачевского”.
Д. В. Аносов: “Дифференциальные уравнения: то решаем, то рисуем”.
В. В. Прасолов: “Наглядная топология”.
Д. В. Аносов: “От Ньютона к Кеплеру”.
М. Клайн: “Математика. Поиск истины“.
Д. Пойа: “Математическое открытие“.
Л. Кэрролл: “Логическая игра“.
Д. Пойа: “Как решать задачу“.
О. Я. Виро, Д. Б. Фукс: "Введение в теорию гомотопий. Гомологии и когомологии".
A. Ostermann, G. Wanner: "Geometry by its history".
T. Sundstrom: "Mathematical reasoning writing and proof". В книге объясняется что такое математическое доказательство, математический факт и каким образом их можно придумывать. Начала теории множеств.
D. Dummit R. Foote: “Abstract Algebra“. Много примеров, задач, но страшно скучный учебник, его нужно держать как справочник.
ПОЛЕЗНЫЕ РЕСУРСЫ:
Библиотка "Квант": math.ru/lib/ser/bmkvant
Высшая математика просто и доступно, по 2 курс включительно: mathprofi.net
Необъятная онлайн библиотека: gen.lib.rus.ec
 176 Кб, 312x312
176 Кб, 312x312скопипастил себе из саентача пару лет назад список основного материала
До большей части из этого так и не добрался, но может тут кому-то полезно будет:
ДЛЯ САМЫХ МАЛЕНЬКИХ:
Общие курсы
М. И. Сканави: "Элементарная математика".
Алгебра
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
С. Б. Гашков: “Современная элементарная алгебра”.
Геометрия
А. Д. Александров, А. Л. Вернер, В. И. Рыжик: “Геометрия”. Учебник для 10-11 классов. Базовый и углубленный уровни.
Я. П. Понарин: “Элементарная геометрия” в двух томах. Первый том - это планиметрия, а второй том - это стереометрия.
А. Ю. Калинин, Д. А. Терешин: “Геометрия”, 10-11 классы. Годный учебник.
Тригонометрия
И. М. Гельфанд, С.М. Львовский, А. Л. Тоом: “Тригонометрия”. Название говорит само за себя. Много геометрических и физических интерпретаций + комплексные числа, как бонус.
Начала анализа
Б. М. Давидович: “Математический анализ в 57 школе“.
БАЗОВЫЕ КУРСЫ ДЛЯ СТУДЕНТОВ:
Общая алгебра
Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
М. Атья, И. Макдональд : "Введение в коммутативную алгебру".
А. Л. Городенцев: "Алгебра. Учебник для студентов-математиков". Вырос из лекций НМУ. Читать параллельно с Винбергом (Винберга читать в первую очередь).
И.Р. Шафаревич: “Основные понятия алгебры“. Замечательный обзор вообще того, что такое алгебра, как она выглядит и какое место она занимает в математике. Примеры, приложения и прочая конкретика.
E. Connell: Elements of Abstract and Linear Algebra". Хорошая первая книга по алгебре, да и математике вообще.
P. Grillet: "Abstract algebra". Очень лаконичный и понятный учебник. Надо знать элементарную теорию чисел, про индукцию, про множества и функции. Линейной алгебры нету.
J. Rotman: "Advanced modern algebra". Ротман сильно разжевывает. Задачи слишком простые для уровня учебника. Линейная алгебра есть.
M. Artin: "Algebra". Американский Винберг. Группы Ли, упор на геометрию. Задачи неудачные.
I. Herstein: “Topics in Algebra“. Прекрасные задачи, отбор материала очень устарел, почти что Ван дер Варден.
P. Aluffi: "Algebra, Chapter 0". Если ты в состоянии ее осилить, бери и забывай про остальные книжки из списка. Линейная алгебра есть.
Линейная алгебра
В. А. Ильин, Э. Г. Позняк: “Линейная алгебра“. Один из классических и самых популярных курсов линейной алгебры.
Д. В. Беклемишев: “Курс аналитической геометрии и линейной алгебры“.
И. М. Гельфанд: "Лекции по линейной алгебре". Не даётся определение определителя.
А. И. Кострикин, Ю. И. Манин: "Линейная алгебра и геометрия". Затрагивается темы геометрий и связей с квантовой механикой. Не даётся определение определителя.
S. Axler: "Linear algebra done right". Подход без определителей (почти). Одна из самых популярных книг за рубежом.
S. Treil: "Linear algebra done wrong". Не такая популярная, как Axler, но тоже хвалят, да. Определители есть.
G. Shilov: "Linear Algebra". Определитель появляется на первой странице.
K. Hoffman, R. Kunze: "Linear Algebra". Классика за рубежом.
P. Halmos: "Finite-Dimensional Vector Spaces". Тоже классика.
P. Peterson: "Linear Algebra". Не особо знаком, но выглядит аккуратно. Что-то вроде Акслера.
S. Roman: "Advanced Linear Algebra". Хороший учебник по линалу. Но нужно знать элементарные свойства матриц и определителей.
Математический анализ
T. Tao: “Real analysis“. Один из самых популярных курсов математического анализа на английском языке.
C. Pugh: "Real Mathematical analysis". Более простая версия Рудина с картинками. Норм книга, но не самая лёгкая.
У. Рудин: "Основы математического анализа".
В. А. Зорич: "Математический анализ". Первый том посвящен классическому анализу. Много примеров, много материала, в том числе даются в начале основы матлогики и теории множеств, а также функций между ними.
Р. Курант: "Курс дифференциального и интегрального исчисления". Идеален с точки зрения
первого знакомства с теорией, но имеет достаточно сложные упражнения.
Г. М. Фихтенгольц: "Курс дифференциального и интегрального исчисления". Хорош как повторительный курс.
С. М. Львовский: "Лекции по математическому анализу". Записки лекций из НМУ. Нужно знать основы калькулюса.
Г. Г. Харди, Д. Е. Литтлвуд, Г. Пойа: "Неравенства".
Н. Н. Лебедев: "Специальные функции и их приложения".
Г. П. Толстов: “Ряды Фурье“.
Дифференциальные уравнения
С. Фарлоу: “Уравнения с частными производными для научных работников и инженеров“.
Вариационное исчисление
И. М. Гельфанд, С. В. Фомин: " Вариационное исчисление".
Топология
V. Runde: "A taste of topology". Неплохая книга по метрическим пространствам и общей топологии, затрагивает фундаментальную группу.
J. Strom: "Modern classical homotopy theory".
T. Dieck: "Algebraic topology".
M. Crossley: "Essential Topology". Пререквизит для изучения алгебраической топологии. Не затрагивает тему метрических пространств.
КУРСЫ ДЛЯ ПРОДВИНУТЫХ МАТЕМАТИКОВ
Математический анализ
А. И. Маркушевич: "Теория аналитических функций".
S. Ramanan: "Global calculus".
H. Amann, J. Echer: "Analysis".
W. Fidcher, I. Lieb: "A Course in Complex Analysis: From Basic Results to Advanced Topics".
Дифференциальные уравнения
В. И. Арнольд: “Обыкновенные дифференциальные уравнения”. Книга для уверенных в себе математиков. Диффеоморфизмы, фазовые потоки, гладкие многообразия. Слава Гермесу Трисмегисту!
Теория категорий
С. Маклейн: "Категории для работающего математика".
Р. Голдблатт: "Топосы. Категорный анализ логики".
Дифференциальная Геометрия
К. Номидзу: "Основы дифференциальной геометрии".
J. Lee: "Manifolds and DIfferential Geometry".
L. Nicolaescu: "Lectures on the Geometry".
P. Michor "Topics in Differential Geometry".
Алгебраическая геометрия
Д. Мамфорд: "Красная книга о многообразиях и схемах".
В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”.
В. И. Арнольд: “Вещественная алгебраическая геометрия”.
Ю. И. Манин: Введение в теорию схем и квантовые группы“.
R. Vakil: "Foundations of algebraic geometry".
S. Bosch: "Algebraic Geometry and Commutative Algebra".
U. Gotz, T. "Wedhorn: Algebraic Geometry".
E. Harris: "The Geometry of Schemes".
Топология
А. Хэтчер: "Алгебраическая топология".
J. Munkres: "Topology". Книга - жесткий учебник по теоретико-множественной топологии. Много ненужного для других областей математики.
ИНТЕРЕСНОЕ:
Цикл “Manga guide to...“. Популярное изложение различных областей математики (и не только), оформленное в виде манги. Увы, без фансервиса.
Н. А. Вавилов: “Конкретная теория групп I: основные понятия“. И вообще все остальные книги (и лекции!) Вавилова.
П. С. Александров: “Введение в теорию групп“. Просто о сложном. Несколько вольный язык изложения, местами затрудняющий восприятие.
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”.
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
Н. Я. Виленкин: "Рассказы о множествах". Теория множеств для широкого круга читателей.
М. М. Постников: “Теорема Ферма. Введение в теорию алгебраических чисел”.
Н. Стинрод: “Первые понятия топологии“.
А. Я. Хинчин: “Три жемчужины теории чисел“.
О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов: “Элементарная топология”.
Я. П. Понарин: “Алгебра комплексных чисел в геометрических задачах”.
А. А. Заславский: “Геометрические преобразования”.
В. Акопян, А. А. Заславский: “Геометрические свойства кривых второго порядка”.
В. И. Арнольд: “Геометрия комплексных чисел, кватернионов и спинов”.
В. В. Прасолов: “Геометрия Лобачевского”.
Д. В. Аносов: “Дифференциальные уравнения: то решаем, то рисуем”.
В. В. Прасолов: “Наглядная топология”.
Д. В. Аносов: “От Ньютона к Кеплеру”.
М. Клайн: “Математика. Поиск истины“.
Д. Пойа: “Математическое открытие“.
Л. Кэрролл: “Логическая игра“.
Д. Пойа: “Как решать задачу“.
О. Я. Виро, Д. Б. Фукс: "Введение в теорию гомотопий. Гомологии и когомологии".
A. Ostermann, G. Wanner: "Geometry by its history".
T. Sundstrom: "Mathematical reasoning writing and proof". В книге объясняется что такое математическое доказательство, математический факт и каким образом их можно придумывать. Начала теории множеств.
D. Dummit R. Foote: “Abstract Algebra“. Много примеров, задач, но страшно скучный учебник, его нужно держать как справочник.
ПОЛЕЗНЫЕ РЕСУРСЫ:
Библиотка "Квант": math.ru/lib/ser/bmkvant
Высшая математика просто и доступно, по 2 курс включительно: mathprofi.net
Необъятная онлайн библиотека: gen.lib.rus.ec
Такой же список и в math есть. Но что список, если нужна система...
>теории групп
Надо бы добавить до кучи книжку Dummit, Foote, "Abstract algebra" и брошюрку П. Александрова "Введение в теорию групп" (для самых маленьких).
Упс, какие-то нигде не дифференцируемые господа запихнули указанное не в раздел алгебры, а в раздел "Интересное". Вообще, коль скоро речь зашла о самообразовании, то нужно что-то вроде кооперативного треда, где анон мог бы отчитываться по тому, какую книжку/статью читает, какую задачу разбирает и задавать вопросы (вроде поблизости проплывал общий мотивационный тред такого толка, но забивать его математикой было бы, наверное, слишком). Самое досадное - это затыки в непонятных местах, а когда спросить не у кого, мотивация падает мгновенно.
P.S. был в /math, чет там совсем негусто.
По-хорошему, нужно как раз задавать больше вопросов. А то видели мы таких студентов, улыбаются, кивают, "халасо, халасо, все понятно, нет вопросов", а потом скобки раскрыть по-человечески не могут.
Типа не умеешь раскрывать скобки и надо больше вопросов почему задача не получается
С какого уровня? Хотя бы 7 класс есть? (т.е. нет проблем с арифметикой и решением простейших уравнений).
Простейшие уравнения это 2x=2?
В /math были недавно аналогичные дискуссии. Попробуй для начала Киселева "Элементы алгебры и анализа", (где-то вконтактике валяется издание 20-х годов в двух томах, там начало с переместительных, сочетательных и других законов арифметики, т.е. примерно с 5-6 класса). К этому учебнику там есть еще задачник. Если не пойдет, попробуй сменить учебник, но мне пока Киселев кажется самым подробным.
Не хочу
Спасибо!
К киселевским Элементам алгебры есть сборник задач и упражнений. Это получается материал за 6-10 класс. Терминология там, я смотрю, немного устарела (относительные числа мы сейчас называем просто целыми числами), но сами задачки любопытные. Есть типовые, есть не очень.
Ох, ебать. Ну ты хоть срок реальнее моего выставил, лол. Я за год хотел подготовиться в MIT, лол. Там всего-то нужно сдать TOEFL и SAT по математике и физике. Ебашил каждый день с сентября по апрель, потом заебался и бросил. Такие дела.
Удачи, блядь, не будь таким хуйлом как я.
>Я за год хотел подготовиться в MIT, лол.
Так это же ведь более чем реально, при условии если у тебя присутствуют весьма ёбкие цели которые понравятся приемной комиссии и хоть какие то да сподвижки в этом направлении уже сейчас. А если не будет этого, хоть Intel ISEF выиграй - не возьмут.
другой анон
Какие учебники читать если необходимо научиться формальной логике? Интересует как теоретическая часть так и задачники для практики. Может быть кто нибудь в курсе и подскажет мне.
>Так это же ведь более чем реально,
какое там количество денег на счету надо подтвердить для годовой визы? тысяч 20? +билеты еще тысячу.
Анончики, хочу нормально изучить всю школьную геометрию. Буду себе пилить колоду для анки. Как вам идея?
Разбирать теоремы и использовать карточники для более эффективного запоминания доказательства. Ну и точные формулировки определений.
Недавно начал пробовать методикой из первых постов, где надо самому доказывать или хотя бы пробовать, и столкнулся с тем, насколько важны мелочи в формулировках и доказательствах.
Или я что-то не так делаю?
Есть такая книжка: Всё что надо знать Матшкольнику Гордин.
Не имея никакого опыта в школьной геометрии тупо начал её конспектировать попунктно, разбирая то, что не понимаю.
За два месяца конспектирования, помимо массы удовольствия, смог подготовиться к Экзамену.
Всем советую, ощущения интересные да и, по сути, там вся школьная геометрия с углублёнными случаями.
Так я в анки и делаю. Пока для теста одну главу учебника забил, как закончу поделюсь впечатлениями.
https://www.mccme.ru/free-books/shen/shen-logic-part1-2.pdf
https://www.mccme.ru/free-books/shen/shen-logic-part2-2.pdf
https://www.mccme.ru/free-books/shen/shen-logic-part3-2.pdf
Вкуришь логику настолько, насколько это возможно для не-математика.
Был же вот только в октябре или летом, вроде бы. Не могу найти, но вот ещё пара кандидатов, можно даже не создавать.
https://2ch.hk/se/res/62763.html (
https://2ch.hk/se/res/672.html (
Лучше уметь выводить самому или хотя бы развивать пространственное мышление и понимать что откуда берется.
Ну и рисовать в тетрадке не помешает.
Я сам освоил только школьную и соснул в тригонометрии правда, надеюсь восполнять.
mathematician's delight
Так книжка называется. Основная проблема нежелания в математику - неспособность препода тебя заинтересовать. Отчасти потому что преподу это нахуй тоже не упало и он сам не понимает чему тебя учит и нахуй оно надо.
После прочтения книжки загорается искра заниматься матешей потому что это естественная наука, позволяющая не складывать ебучие цифирки, а менять окружающий мир и себя.
И нету никакого "технического" или "гуманитарного" склада мышления. Технари сами очень легко ведутся на подобные суеверия, против которых выступают.
> машинное обучение
Нужна математика
> дата саенс
Нужна математика
> системное программирование
Нужна математика
> создание всякой технической поебени
Нужна математика
> финансовый аудит
Нужна математика
> в жизни не пригодится
Конечно, если ты собираешься быть столяром, дворником, уборщиком, официантом, физруком, спортсменом, маркетологом, философом, теоретиком кино, актером, режиссером, оператором, писателем, певцом, музыкантом, медиком, дизайнером, веб-макакой, журналистом и т.д и т.п, - то, конечно же, математика и та же физика тебе нахуй не всрались.
 75 Кб, 600x220
75 Кб, 600x220Моё мнение - ерунда это всё. Математика проста сама по себе.
Я до 10-го класса нихрена не вёз математику. Потом надоело - взял книгу Цыпкин, Пинский - Справочник по математике для средней школы. Там всё прекрасно и коротко было обьяснено. От алгебры до логики. После прочтения книги я стал решать задачи и ставить их сам. После этого я был лучшим в школке по математике и прочему. Учился на математика-программиста.
Сейчас могу посоветовать:
1. Учи логику. То, что в школе учат доказывать, без логики - бред. Именно логика скажет почему надо доказывать так, а не иначе. В математику без логики желательно не лезть.
2. Книги о мышлении математика:
Вейль - Математическое мышление,
Пуанкаре - О науке,
Пойя - Математика и правдоподобные суждения,
Лакатос - Доказательства и опровержения,
Гротендик - Урожаи и посевы.
Арнольда и Куранта уже посаны советовали. Кстати, у Арнольда есть лекция - её гуглим по запросу "Алексеев - Теорема Абеля в задачах" и читаем.
Прекрасно понимаю, что тому, кому отвечаю - это больше не актуально. Но этот ответ адресую больше анонам, которым говорят так же.
Пример вам, ананы - гуглите чувака-математика по фамилии Лузин. Про него строчка из вики
Поначалу обнаружил полную неспособность к математике в той форме, в которой она преподавалась (заучивание правил и действия по шаблонам). Положение спас репетитор, студент Томского политехнического института, который обнаружил и развил у Н. Н. Лузина способность к самостоятельному решению сложных задач и страсть к этому занятию.
То, что парят вам в школке - не обязательно математика. Это достижения математики. Но умение мыслить вам могут и не привить, т.к. многие учителя математики сами не могут в математику больше программы. Читайте математиков и учитесь у них. Авторы книг, которые я упомянул - гении математики. Особенно Пуанкаре и Гротендик.
У меня был кореш - математик от природы, но не волок в программировании. Я его пытался учить, но он выучил и стал в этом рубить только тогда, когда сам захотел этого.
Так же смотрите фильмы:
Агора(о Гипатии),
Выстоять и сделать(о том, как учили математике быдло),
и проч.
 75 Кб, 600x220
75 Кб, 600x220Моё мнение - ерунда это всё. Математика проста сама по себе.
Я до 10-го класса нихрена не вёз математику. Потом надоело - взял книгу Цыпкин, Пинский - Справочник по математике для средней школы. Там всё прекрасно и коротко было обьяснено. От алгебры до логики. После прочтения книги я стал решать задачи и ставить их сам. После этого я был лучшим в школке по математике и прочему. Учился на математика-программиста.
Сейчас могу посоветовать:
1. Учи логику. То, что в школе учат доказывать, без логики - бред. Именно логика скажет почему надо доказывать так, а не иначе. В математику без логики желательно не лезть.
2. Книги о мышлении математика:
Вейль - Математическое мышление,
Пуанкаре - О науке,
Пойя - Математика и правдоподобные суждения,
Лакатос - Доказательства и опровержения,
Гротендик - Урожаи и посевы.
Арнольда и Куранта уже посаны советовали. Кстати, у Арнольда есть лекция - её гуглим по запросу "Алексеев - Теорема Абеля в задачах" и читаем.
Прекрасно понимаю, что тому, кому отвечаю - это больше не актуально. Но этот ответ адресую больше анонам, которым говорят так же.
Пример вам, ананы - гуглите чувака-математика по фамилии Лузин. Про него строчка из вики
Поначалу обнаружил полную неспособность к математике в той форме, в которой она преподавалась (заучивание правил и действия по шаблонам). Положение спас репетитор, студент Томского политехнического института, который обнаружил и развил у Н. Н. Лузина способность к самостоятельному решению сложных задач и страсть к этому занятию.
То, что парят вам в школке - не обязательно математика. Это достижения математики. Но умение мыслить вам могут и не привить, т.к. многие учителя математики сами не могут в математику больше программы. Читайте математиков и учитесь у них. Авторы книг, которые я упомянул - гении математики. Особенно Пуанкаре и Гротендик.
У меня был кореш - математик от природы, но не волок в программировании. Я его пытался учить, но он выучил и стал в этом рубить только тогда, когда сам захотел этого.
Так же смотрите фильмы:
Агора(о Гипатии),
Выстоять и сделать(о том, как учили математике быдло),
и проч.
Философ должен знать логику. Как и математик. Иначе этот философ будет пиздоболом уровня Фихте, а не гением типо Канта.
Кстати, добавляю в список "Кант - Критика чистого разума". Тоже годная весчь, хоть и не математика. Но это близко.
Обращайся, если что.
ну привет Анон. На связи все тот же инженер энергетик, только уже 27 лвл. В Январе того года я решал задачки 8 класса. Сейчас я уже в универе не торопясь ковыряюсь в дифурах и рядах, первую сессию закрыл с 5 по матану. Но замечаю, что с физикой болото. Динамика сложно дается. Где? Куда? Какая сила? не очень понятно. ( может подскажете годный ресурс?) Ну думаю после динамики молекулярка, которая, вроде-как не очень сложная. А потом электричесто в котором, в силу совей работы, я разбираюсь.
 20 Кб, 441x440
20 Кб, 441x440>Теория хаоса гласит, что сложные системы чрезвычайно зависимы от первоначальных условий, и небольшие изменения в окружающей среде могут привести к непредсказуемым последствиям.
>Математические системы с хаотическим поведением являются детерминированными, то есть подчиняются некоторому строгому закону, и, в некотором смысле, являются упорядоченными.
Как хаос может вести к строгой причинно-следственной упорядоченности, если это противоречит энтропия системы
Поясни матанончик за энтропию и в чем её различие в разных дисциплинах(да, вики себе сама противоречит, а если открыть обсуждение мозг просто улетит от срача)
- Энтропия динамических систем всегда Обязательно растет лишь в математике? А ирл можно примеры равновесия энтропии или её уменьшения?
- Должен ли происходить прирост энергии используемой для уменьшения энтропии системы или энергии всегда уходит равное количество?
- Всегда ли энтропия динамической системы ведет к её деформации и уничтожению(относительно её первоначального состояния)?
- Применима ли понятие энтропии к виртуальной сфере, т.е к динамической замкнутой системе как Операционная система или Глобальная Сеть? И если ДА то какой там эквивалент энергии поддерживающей систему
Это в Ткачуке есть.
Решать интересно, но я не нашёл волшебного способа, который быстро поднимет хотя бы довузовского уровня, учитывая что ещё и физику нужно дрочить. Так что увы.
Все дело в методологии.
Можно весело в свободное время решать задачки в течении пары месяцов и задрочить все что тебе нужно, а можно неделю рвать волосы на жопе по 4 часа к ряду каждый день, ахуеть и подумать,мол НУ НЕ МОЁ,ХУЛЕ
Кто-нибудь будет вместе со мной учить алгебру по Городенцеву?
Этот учебник кажется мне лучшим из того, что есть сейчас на русском языке. Интересные упражнения.
Где? Ну, лучше бы, конечно, здесь. Читат @ обсуждат. Можно в отдельный тред укатиться.
Сейчас я разбираю параграф про нётеровость колец. Если кто-то хочет присоединиться, самое время.
Ну и ладно.
>"Математика не для отличников"
Этого будет достаточно, если мне нужно изучить математику не углубляясь? И достаточно ли этого будет для дальнейшего перехода на высшую математику?
Надеюсь ответят, очень хочется знать..
Я прав?
Для особо въедливых сейчас уже говорят уменьшился/увеличился "на x процентных пунктов" вместо "на x%". Т.е. играло 100 человек, через год - 110, еще через год - 115.
Долго мучился с установкой и запуском этого курса, для 1998 года выглядит неплохо
Можно ещё это вспомнить: https://www.youtube.com/watch?v=eURtTV_qKw8
 41 Кб, 1329x661
41 Кб, 1329x661Когда ты скачиваешь это, то у тебя загружаются файлы mdf и mds. Это всё надо добавить в Daemon Tools (его сложновато установить, но всё же), он сам распознает, склеит эти файлы в такие ALGEBRA и так далее. В самой программе надо выбрать "Монтировать" и оно создаст новый диск на компьютере.
На этом диске будет такой файл INSTALL.EXE Windows 10 не поддерживает 16 бит программы (поддерживает 32 бит и 64 бит), компонент по этому поводу уже нельзя установить. По этому надо скачивать чужую программу. https://github.com/otya128/winevdm/releases тут скачиваешь zip-архив в Assets, распаковываешь где-то. Жмакаешь install.reg (хотя может не нужно, там есть ещё настройки, я не разбирался), далее можешь нажать otvdmw.exe и тебе откроется окно с выбором файла. Там переходишь в диск к этому INSTALL.EXE и тебе должно открыться что-то такое как на картинке. Далее уже надо ярлык запустить с помощью этой программы или может даже прописать в самом ярлыке и запустится то, что на скриншотах выше.
Возможно, что гораздо проще было бы запустить на какой-то виртуальной машине. Да и в целом вряд ли целесообразно это всё... Возможно стоит поискать иные средства.
Да, вообще не идет. В школе сидел и нихуя не понимал, видео на ютубе нихуя не объясняют, текстовых курсов нихуя нет.
Установил? А как думаешь, в чем могут быть трудности? В том, что не видно картинки за всем этим? Как у тебя с арифметикой?
>Этого будет достаточно, если мне нужно изучить математику не углубляясь?
Углубляясь куда? В школьную математику?
>И достаточно ли этого будет для дальнейшего перехода на высшую математику?
Из школьной математики нужна только тригонометрия и навык обращения с алгебраическими выражениями. Всё. Математика никак в общем то не коррелирует со школьной математикой от слова совсем.
И последний вопрос, нахуя тебе вообще всё это сдалось.
Начальное запаривание мозгов. Ученики постигнут, что математика — это не то, что ты делаешь, а то, что делают за тебя. Внимание уделяется дисциплине на занятиях, аккуратному заполнению прописей и тщательному исполнению инструкций. Дети изучат сложную систему алгоритмов для манипуляции символами непонятного алфавита, не имеющую отношения к тому, что им интересно и любопытно, несколько столетий назад считавшуюся слишком сложной для среднего взрослого. Особые усилия прикладываются к заучиванию таблицы умножения, а также к родителям, учителям и самим ученикам.
Средняя школа
Ученики обучатся взгляду на математику как совокупность шаманских ритуалов, вечных и неизменных. Ученикам будут выданы Священные Таблички учебников, и они обучаются говорить о старейших шаманах в третьем лице (например, «чего от меня хотят? они хотят, чтобы я что поделил?»). Искусственные, вымученные «текстовые задачи» будут введены, чтобы, по сравнению с ними, безумная зубрежка арифметики показалась приятной и интеллектуальной. Ученики сдают экзамены на знание бессмысленных технических терминов, таких, как «целое число», «правильная дробь», вводимых без малейших на то причин. Данный курс полностью подготовит ученика к курсу алгебры-1.
Алгебра-1
Чтобы избежать потерь времени на размышления над числами и закономерностями, курс построен вокруг символов и правил манипуляции ими. Плавное и постепенное введение в предмет, начиная с задач месопотамских табличек и заканчивая высоким искусством алгебры эпохи Возрождения, заменяется фрагментарным постмодернистским пересказом без действующих лиц, сюжета и линии повествования. Требование записывать все числа и выражения в стандартной форме создаст дополнительные трудности в понимании смысла тождества и равенства. Ученики по непонятной причине также заучат наизусть формулу для решений квадратного уравнения.
Геометрия
Не связанный с остальной программой, этот курс даст ученикам надежду на осмысленные математические действия, а затем не оправдает эту надежду. В курсе дается неуклюжая и непонятная система записи. Ученики будут напряженно работать над запутыванием простого до сложного. Целью курса является изведение остатков естественного математического любопытства для подготовки к курсу алгебры-2.
Алгебра-2
Предметом курса является немотивированное и неуместное применение аналитической геометрии. Конические сечения вводятся в системе координат, надежно скрывающей их простоту и эстетику. Учащиеся обучатся переписывать квадратичные формы в различные стандартные форматы без какой-либо цели. В курсе также вводятся экспоненциальные и логарифмические функции, несмотря на то, что они не являются алгебраическими объектами, просто потому, что больше их воткнуть было некуда. Название курса выбрано с целью закрепить мифологию о лестнице. Почему между алгеброй-1 и алгеброй-2 включается геометрия, в курсе не рассматривается.
Тригонометрия
Две недели содержания курса растянуты на полугодие самоценной игрой в определения. Интересные и красивые явления, например, как стороны треугольника зависят от его углов, будут даны с упором на бесполезные сокращения и устаревшие обозначения, чтобы не допустить возникновения у учащихся ясной идеи о предмете. Учащиеся изучат также бесполезные мнемоники, заменяющие естественные и интуитивные понятия о симметрии. Измерение треугольников объясняется без упоминания трансцендентности тригонометрических функций, а также лингвистических и философских проблем, возникающих при подобных измерениях. Калькуляторы обязательны, чтобы запутать эту тему еще больше.
Начала анализа
Курс представляет собой винегрет из несвязанных между собою тем. Производится безуспешная попытка дать ученикам понятия о методах мат. анализа второй половины XIX в. на совершенно неподходящих примерах. Вводятся технические определения предела и непрерывности, заменяющие собою интуитивно ясное понятие плавного изменения. Как показывает название курса, он предназначен для подготовки учащихся к полному курсу мат. анализа, в котором будет завершено систематическое затуманивание идей формы и движения.
Мат. анализ
Курс предназначен для изучения математики движения и лучшего способа похоронить ее под горой формализма. Несмотря на то, что курс является введением в дифференциальное и интегральное исчисление, простые и глубокие идеи Лейбница и Ньютона будут заменены более сложным функциональным подходом, разработанным в ответ на некоторые аналитические кризисы, которые не относятся к данному уровню изложения и, разумеется, не будут упомянуты. Этот курс будет также слово в слово повторен в колледже.
*
Итак, перед вами рецепт для неизлечимого поражения юных умов, надежное излечение от любознательности. Что же они сделали с математикой!
В математике, древней форме искусства, есть и захватывающая дух глубина, и щемящая сердце красота — а вышло так, что люди противопоставляют математику творчеству. Они проходят мимо формы искусства, что древнее книги, глубже поэмы и абстрактнее любой абстракции. И ведет их именно школа! О скорбный замкнутый круг невинных учителей, несущих беду невинным ученикам! А ведь нам могло бы быть весело и интересно.
Начальное запаривание мозгов. Ученики постигнут, что математика — это не то, что ты делаешь, а то, что делают за тебя. Внимание уделяется дисциплине на занятиях, аккуратному заполнению прописей и тщательному исполнению инструкций. Дети изучат сложную систему алгоритмов для манипуляции символами непонятного алфавита, не имеющую отношения к тому, что им интересно и любопытно, несколько столетий назад считавшуюся слишком сложной для среднего взрослого. Особые усилия прикладываются к заучиванию таблицы умножения, а также к родителям, учителям и самим ученикам.
Средняя школа
Ученики обучатся взгляду на математику как совокупность шаманских ритуалов, вечных и неизменных. Ученикам будут выданы Священные Таблички учебников, и они обучаются говорить о старейших шаманах в третьем лице (например, «чего от меня хотят? они хотят, чтобы я что поделил?»). Искусственные, вымученные «текстовые задачи» будут введены, чтобы, по сравнению с ними, безумная зубрежка арифметики показалась приятной и интеллектуальной. Ученики сдают экзамены на знание бессмысленных технических терминов, таких, как «целое число», «правильная дробь», вводимых без малейших на то причин. Данный курс полностью подготовит ученика к курсу алгебры-1.
Алгебра-1
Чтобы избежать потерь времени на размышления над числами и закономерностями, курс построен вокруг символов и правил манипуляции ими. Плавное и постепенное введение в предмет, начиная с задач месопотамских табличек и заканчивая высоким искусством алгебры эпохи Возрождения, заменяется фрагментарным постмодернистским пересказом без действующих лиц, сюжета и линии повествования. Требование записывать все числа и выражения в стандартной форме создаст дополнительные трудности в понимании смысла тождества и равенства. Ученики по непонятной причине также заучат наизусть формулу для решений квадратного уравнения.
Геометрия
Не связанный с остальной программой, этот курс даст ученикам надежду на осмысленные математические действия, а затем не оправдает эту надежду. В курсе дается неуклюжая и непонятная система записи. Ученики будут напряженно работать над запутыванием простого до сложного. Целью курса является изведение остатков естественного математического любопытства для подготовки к курсу алгебры-2.
Алгебра-2
Предметом курса является немотивированное и неуместное применение аналитической геометрии. Конические сечения вводятся в системе координат, надежно скрывающей их простоту и эстетику. Учащиеся обучатся переписывать квадратичные формы в различные стандартные форматы без какой-либо цели. В курсе также вводятся экспоненциальные и логарифмические функции, несмотря на то, что они не являются алгебраическими объектами, просто потому, что больше их воткнуть было некуда. Название курса выбрано с целью закрепить мифологию о лестнице. Почему между алгеброй-1 и алгеброй-2 включается геометрия, в курсе не рассматривается.
Тригонометрия
Две недели содержания курса растянуты на полугодие самоценной игрой в определения. Интересные и красивые явления, например, как стороны треугольника зависят от его углов, будут даны с упором на бесполезные сокращения и устаревшие обозначения, чтобы не допустить возникновения у учащихся ясной идеи о предмете. Учащиеся изучат также бесполезные мнемоники, заменяющие естественные и интуитивные понятия о симметрии. Измерение треугольников объясняется без упоминания трансцендентности тригонометрических функций, а также лингвистических и философских проблем, возникающих при подобных измерениях. Калькуляторы обязательны, чтобы запутать эту тему еще больше.
Начала анализа
Курс представляет собой винегрет из несвязанных между собою тем. Производится безуспешная попытка дать ученикам понятия о методах мат. анализа второй половины XIX в. на совершенно неподходящих примерах. Вводятся технические определения предела и непрерывности, заменяющие собою интуитивно ясное понятие плавного изменения. Как показывает название курса, он предназначен для подготовки учащихся к полному курсу мат. анализа, в котором будет завершено систематическое затуманивание идей формы и движения.
Мат. анализ
Курс предназначен для изучения математики движения и лучшего способа похоронить ее под горой формализма. Несмотря на то, что курс является введением в дифференциальное и интегральное исчисление, простые и глубокие идеи Лейбница и Ньютона будут заменены более сложным функциональным подходом, разработанным в ответ на некоторые аналитические кризисы, которые не относятся к данному уровню изложения и, разумеется, не будут упомянуты. Этот курс будет также слово в слово повторен в колледже.
*
Итак, перед вами рецепт для неизлечимого поражения юных умов, надежное излечение от любознательности. Что же они сделали с математикой!
В математике, древней форме искусства, есть и захватывающая дух глубина, и щемящая сердце красота — а вышло так, что люди противопоставляют математику творчеству. Они проходят мимо формы искусства, что древнее книги, глубже поэмы и абстрактнее любой абстракции. И ведет их именно школа! О скорбный замкнутый круг невинных учителей, несущих беду невинным ученикам! А ведь нам могло бы быть весело и интересно.
>теоремы
Ах да, школьная геометрия, пожалуй, единственное, что есть полезного в школьной программе.
>И как ты предлагаешь даже это усвоить?
Главный вопрос для чего тебе это нужно. Если для себя, то это бесполезно. Если для всяких егэ и прочего, брать задачник сканави и дрочить его.
> брать задачник сканави и дрочить его
Лежит на полочке, слишком сложно для меня, каждый пример на страницу и думать весь день. Даже дроби эти. Но я правда без учебника пытался это и давно ещё. Опять обратиться к этому что ли? Но не одним задачником же обойтись, что ещё взять-то?
А сам ты как достиг успеха в этом? Или же просто хорошо учился, постоянно ходил и всё шло своим чередом?
>каждый пример на страницу и думать весь день.
Ну сканави полностью прорешивать дело гиблое. Но по 10-20 примеров из каждой секции вполне реально.
>Даже дроби эти.
Дроби надо понимать. Без этого никуда.
>Но я правда без учебника пытался это и давно ещё. Опять обратиться к этому что ли?
Это должно приносить хоть какое-то удовольствие. Иначе быть не может.
>что ещё взять-то?
Школьные учебники по алгебре-геометрии. Причем необязательно продрачивать учебник математики за 5 класс, нужно обращаться к нему, если чувствуешь, что где-то дыры в твоих знаниях. Так что оптимал взять учебники по алгебре за 9, 10-11 класс, учебник по геометрии за 7-9(Атанасян очень неплох), 10-11(Погорелов но это на любителя) и работать, каждый день. Тут как с языком.
>А сам ты как достиг успеха в этом?
Успех понятие относительное. До 10 класса, мне на всё было похуя,я умело заучивал рецепты не вдаваясь в подробности. Летом после 9 класса случился этакий катарсис. После которого всё и завертелось. Оглядываясь назад, а минуло уже почти 10 лет, сложно поверить в реальность произошедшего со мной.
Это сложно выразить в словах. Только прочувствова это на собственном опыте понимаешь, что это такое.
Стереотип. На уровне руководства образованиям в то время озаботились крайне низким уровнем образовательной литературы того времени. И это известный факт. Чего Колмогоров один стоил. Он учил одарённых, брал высокую планку. В итоге никто нихера не понимал и всё скатилось к ебеням. Вот, https://www.google.com/sorry/index?continue=https://webcache.googleusercontent.com/search?q=cache:FdbGihOE20YJ:https://mat.univie.ac.at/~neretin/misc/reform/reforma1965.html+&cd=1&hl=ru&ct=clnk&gl=ru&client=firefox-b-d&hl=ru&q=EgRfHiOOGLvC7uwFIhkA8aeDS4pwF-Y2POTTFx1WWV0f8fuBYw0LMgFy, читай, пока из кэша не пропало. И убеждайся сам. Хороший.
Есть монография "Проблема качества математического образования в свете исторической ретроспективы"
Спасибо за рекомендацию, мне она интересна.
Читай школьные учебники.
Я 30лвл закончил когда то физмат, примрено лет 10 назад, но нихуя не помню, так как работал программистом веб-макакой.
Решил взять себя в руки и составил себе расписание когда я буду заниматься и вступил в курсы по ввеедение в матан на степике.
Всё что забыл ещё со школы внимательно гуглю, догоняю, в остальном даже если совсем нихуя не понимаешь, нужна только дисциплина.
Лично я учусь на факультете математики. И я не считаю, что учебник, в котором категория определяется на странице 19, а функтор - на странице 484, может рассматриваться иначе как анекдот.
Тем более в этом треде.
Для n=1 верно: 2 - (1+2)/2 = 2 - 3/2 = 1/2
Пусть верно для n=k. Рассмотрим для n=k+1:
1/2 + ... + k/2^k + (k+1)/2^(k+1) =
= 2 - (k+2)/2^k + (k+1)/2^(k+1) =
= 2 - 2(k+2)/2^(k+1) + (k+1)/2^(k+1) =
= 2 - (2k+4 - k-1)/2^(k+1) =
= 2 - (k+3)/2^(k+1) =
= 2 - ((k+1)+2)/2^(k+1)
Получили, что верно и для n=k+1.
По принципу индукции верно для всех натуральных n.
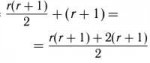 13 Кб, 388x164
13 Кб, 388x164И еще. Есть ли какие-то математические чаты в телеге, где ньюфагу помогут и не обложат хуями?
Всё, я понял. Тут (r+1) представлена как (2(r+1))/2, а по правилам сложения дробей, со знаменателем не делается ни чего, а числитель складывается.
Просто привели к общему знаменателю и сложили числители
---------------------------------------------------------------------------
Аналитик в компании за день написал некоторое количество
SQL-запросов. Все запросы можно охарактеризовать количественной
характеристикой сложности выполнения - условная “память”.
Три “тяжелейших” (7/20 общей затраченной памяти) запроса превысили
максимальное время выполнения и были отключены системой.
Три “легчайших” (5/13 затраченной памяти всех оставшихся запросов)
выполнялись менее 10 минут каждый. Остальные запросы выполнялись
менее получаса каждый.
1)Найдите общее количество запросов, которое написал аналитик
2) Дайте оценку на среднее время успешно выполненного запроса
----------------------------------------------------------------------------------
С какой стороны подойти? Заранее спасибо
1) Время легчайших = (1-7/20)5/13 = 1/4
Время средних = (1-7/20)(1-5/13) = 2/5
Минимальное время тяжелого 7/20 / 3 = 7/60
Максимальное время легкого 1/4 / 3 = 5/60
Тогда время среднего запроса в пределах 5/60 < t < 7/60.
Сколько таких можно уложить в 2/5?
(2/5 / 7/60) < N < (2/5 / 5/60)
24/7 < N < 24/5
3.4 < N < 4.8
Ответ: N = 4
2) M=(4Tmid + 3Tlight)/7 = (430+310)/7~ 21 мин, это верхняя оценка.
 322 Кб, 480x298
322 Кб, 480x298> "Что такое математика" Куранта и Роббинса "Что такое математика" Аргольда
Хуйня для тех, кто шарит на нормальном уровне в элементарной математике и в курсе о некоторых разделах университетской математики.
> "Элементарная алгебра. Пособие для самообразования" С.И. Туманова
Пойдет для поверхностного ознакомления.
> Сканави М.И. Элементарная математика. Подготовительный курс, где-то 1965-67 год
Не подойдет для тех, кто полный 0 в математике. Язык и подача материала сложна для восприятия и не совсем для новичков.
> Сканави для поступающих во ВТУЗы
На самом деле мастхэв(особенно для пидорашкинских вузов), но уже немного морально устарел, если вы собираетесь поступать в топовые тех. вузы зарубежом, так как придется учить еще и некоторые разделы университетской математики(вроде аналитической геометрии, комбинаторики и теорвер).
Я учился по Мордковичу(курс 7-11 класс), там очень хорошая подача материала и все разжевывается. По тригонометрии читать "Тригонометрия" Гельфанд. По геометрии трехтомник Понарина "Планиметрия", "Стереометрия", "Треугольники и тетраэдры".
По нициативе /math поднят дискорд для желающих совместно учить какую-нибудь математику.
>/math/res/63525.html
Там есть свежая и непротухающая discird,gg/ZPEmccT
Тут скорее не врождённые способности, а что-то близкое к этому, некоторые крепко усвоенные понятия. Вряд ли человек достигнет успеха, если он крепко не знает базовых понятий типа произведение, слагаемое, пропорция, бис сектриса (рассекающая надвое). Не понял одно слово и дальше уже всё пропустил, будешь в хвосте тянуться.
https://www.youtube.com/watch?v=n9nfTxp_APM
Попробуй что-нибудь практичное, наглядное. Когда совмещаешь математику с программированием, можешь визуализировать результат, проверить, как все в действительности работает. Получается такая экспериментальная математика.
https://www.udemy.com/course/fundamentals-of-math/
Я делаю у нее курс по статистике и он весьма разжеванный. Так что думаю курс по основам математики тоже будет подробным и понятным. Может быть где-то есть на него сабы или переводы курса на торрентах есть.
 125 Кб, 513x789
125 Кб, 513x789Если вообще нихуя не знаешь, то читай школьный учебник. А потом читай какой нибудь вузовский учебник для 1-2 курса. Это такой базовый курс для начинающих. Если вообще лень и нужно что то прививающее интерес, то могу посоветовать книги Гельфанда и Шеня, отличные книги по простейшей математике и алгебре, тоже в своё время узнал о них с двачей. Так же "Энциклопедия Юного математика" хороший научпоп про всякие термины, да и просто интересно, ну и Савватвеева книги часто хвалят, но я не читал. Сам не шибко математик, но просто знаю что наука охуеть какая большая, и тут нужно изначально знать зачем тебе. Если ты пидорас которому нравиться сидеть и пиздеть про гомологические пространства и супер-элитные мемы для нетаких как все элитнийших математиков, то тебе в /ga/, надеюсь ты найдёшь себе актива. Если ты информатикой занимаешься, то тебе нужно конкретно заняться всем что связано с числами, теорией вероятности, булевой логикой и вот это всё. Если ты радиотехник какой нибудь, то тебе нужно дифференциальное исчисление более углублённо изучить, теория функции комплексной переменной, операционное исчисление итд и тп. Если ты экономист то это дискретная математика. А в быту больше чем базовых знаний не пригождается
Дак это ты самое начало включил. Конечно тут будут основы.
Первая глава вообще для совсем незнаек.
Это и есть большая проблема. Когда нет плана занятий и не знаешь какие статьи НУЖНЫЕ. А в курсах человек собрал инфу и разжевал и привел примеры.
Вот такой вопрос. 30 лет, ума нет, поступил в вуз на бюджет, после десяти лет в макдаке, лол. Недоволен тем, что сдав ЕГЭ, кекаю на уроках "вышмата" и теорвера: никакого напряжения ума, задрочил формулы и вперед: никаких доказательств, никакого блядь вдохновения.
Математика по специальности нужна пипец как, а вот с какой стороны зайти, не знаю.
Хочу с самого начала поставить все на строгую основу, чтобы для любой херни, которую использую, мог написать внятное математическое доказательство.
План на два года такой:
1. Мат. логика
2. Теория множеств
3. Теория отображений
4. Абстрактная алгебра
5. Линейная алгебра
6. Анализ
7. Теория вероятностей и статистика.
8. Ряды Фурье.
9. Комплексный анализ.
10. Вариационное исчисление.
Посоветуйте книжек мудрых, на русском или английском, желательно с ответами.
 61 Кб, 494x365
61 Кб, 494x365>никакого напряжения ума, задрочил формулы и вперед: никаких доказательств, никакого блядь вдохновения
Что за вуз такой? У нас математика была далеко не основным предметом, но при этом мы разбирали все доказательства и, соответственно, нужно было всё выводить и доказывать на экзаменах, если хотелось оценку выше, чем "3".
По вопросу тебе не подскажу, так как сам не математик разве что любитель. Но если живёшь в ДС, рассмотри поступление в НМУ.
Вуз хороший, с кафедрой социологии повезло. Но у кафедры фатальный недостаток - готовят молодое мясо для маркетинговых и статистических контор. Готовят заебись, только распиздяи не устраиваются еще на старших курсов.
Вопрос только в том, что готовят жестких прикладников и математика подается не как наука а как набор инструментов. Типа "такую-то формулу на такой-то набор данных подходящий по признакам а), б), в), г)". Доказательство теоремы почитайте для общего развития, вам важно уметь ее применять, а не выводить.
Математика - наука о математических структурах.
Алгебра - наука о модулях над кольцами.
Арифметика - наука о соответствиях Ленглендса.
Про величины (количества) короче
Алгебра и арифметика - разделы математики.
Это как
>Объясните отличия птиц, голубей и снегирей
Дружище, никак не могу въехать во второй случай. На 7 мы делим так как в совокупности 3+4 = 7 запросов. А откуда мы получаем 430 и 310? Подскажи, добрый человек.
Это 430 (в условии менее 30) и 310 (менее 10 в усл) / 7 = 150 / 7 = 21,4. очевидно, что там сторого меньше, поэтому немножечко секунд отбираем с запросов и по сути, просто округляем в меньшую сторону.
Не знаю математику класса с 5-го. То есть совсем. Даже уравнения и дроби. Что можете посоветовать?
Не сказал бы, что не люблю математику - если я понимаю, то мне очень интересно. Но я не понимаю нихуя, в чем и суть проблемы.
Берешь учебник 5-го класса и читаешь/решаешь задачи оттуда. Неужели это так трудно?
Вместо того чтобы такие вопросы задавать, лучше бы тред с начала почитал.
И ещё раз.
Более конкретно по изучению математики. Все книги выглядят как сборник капитанских советов, но ничего лучше для старшеклассников и студентов пока не нашел. (Хотя их восприятие как "очевидных" тоже является когнитивным искажением. Не так уж они очевидны, на самом деле.)
Kevin Houston, "How to think like a mathematician".
Lara Alcock, "How to Study as a Mathematics Major".
J. Mason, L. Burton, K. Stacey, "Thinking Mathematically".
Кринжовая методичка чисто по техническим инструментам.
Bindner D., Erickson M., "A student's guide to the study, practice, and tools of modern mathematics".
Можешь еще посмотреть серию книг от Steven G. Krantz по изучению математики, ее преподаванию и проч. Он много чего понаписал, некоторым нравится.
Довольно известные в узких кругах книги, ориентированные на методологию.
Акцент на примерах и их самостоятельной генерации.
Anne Watson, John Mason, "Mathematics As A Constructive Activity: Learners Generating Examples".
Акцент на самостоятельной генерации проблем.
Stephen I. Brown, Marion I. Walter, "The art of problem posing".
 18 Кб, 370x500
18 Кб, 370x500И ещё.
Разве не будет достаточно просто принципов?
Есть, просто дело не из простых.
Хорошо, что напомнили, тред хотел сохранить, а то вдруг утонет.
http://arhivach.net/thread/100689/
Нормально будет всё это прочитать что бы вкатиться в математику в старших классах школы? Я в ней полный ноль.
Вроде темы простые. Теорема Виета доказывается остальное не смотрел, поэтому должно быть не совсем говном. Думаю, что знания получишь. А так возьми учебник Колмогорова по алгебре.
Предлагаю кому-нибудь начать. Прям с определения "числа". И там же упражнения сделать. Страниц под десяточку тысяч выйдет, я думаю, пилить будем несколько лет.
Но зато хоть оживим тему! И важную тему, безграмотность 21 века - это математическая безграмотность.
И тред предлагаю перекатить в более широкую так сказать тему, "самообразование". Тут и математика, и кодинг, и физика с теорфизикой, и ремесленничество какое. Дело ж!
https://drive.google.com/drive/folders/1IYWYAZ2AGP1rNmpkalck38uhi0I-0Qom?usp=sharing
В латехе что-то напечатать вроде бы несложно, только вот что, чтобы не получился очередной учебник, может быть с вкраплениями ехидных колобков (думаю и йобы бы наскучили, если бы вместо яблок на них объяснили десятилетиями)? Что, к примеру, пихать в первую главу, если так назвать? Аксиомы рациональных чисел? Таблицу истинности для всех 16 булевых операций двух переменных вместо классических и, или, не? Числовую прямую и циферблат? Код на питоне? Матрицы как таблички с числами? Задания на преобразования физических формул? Переводы в иные системы счисления? Непонятно что именно туда написать. Обычно этот вопрос решается тем, что напишем то, что давали на экзаменах.
Никола Бурбаки. Начало.
Тогда можно с принципов математического доказательства, логики, множеств, функций, матиндукции, инвариантов. Меты, короче.
Так даже лучше, я думаю, ибо сразу же даёт весь инструментарий, которым анон в математических рассуждениях должен пользоваться. Но не слишком ли это сложно для анона, который математику на уровне детского садика только помнит?
Мне такое не нравится(
Прикольная и красивая штука, которой можно учить детишек в детском саду -- комбинаторная теория групп. Там никакая логика не нужна. Просто есть фигурки, и они красиво вращаются.
а зачем? в саморазвитии, первый шаг - английский, как международный язык, и только потом все остальное
оставаясь в границах русского, тебе достанутся толкьо крошки знаний
К каким опечаткам?
>оставаясь в границах русского, тебе достанутся
>оставаясь
>достанутся
Т.е. крошки знаний будут оставаться в границах русского и достанутся тебе, именно так ты и написал. Это не опечатка. То, что мелкобуква и опечатки это похуй
 2,1 Мб, 1332x850
2,1 Мб, 1332x850Начал с самых азов, скачал алгебру 7 класса Макарычева, ну хоть углублённый уровень, думаю, что это лучше. Интуитивно понятные упражнения пропускаю, на задачках со звёздочкой и некоторых непонятных моментах типа телескопического суммирования останавливаюсь и прорешиваю.
Всем добра.
Старый же учебник.
https://drive.google.com/folderview?id=1Pn_BqsqmxC_Zvoo9OoR0GvfLtnFhxnQY
Вот тебе новые (2020) и супернаглядные.
Всё красиво и понятно.
Ну как "понятно" - если совсем математикой не занимался, то сначала будет непонятно, но это у всех так, посиди с полгодика, поварись в математической теме, и всё будет довольно очевидно.
Тебе ведь никуда торопиться не надо, как я понял, поэтому в размеренном темпе, без фанатизма, сиди, изучай, решай. Решать тут ключевое, иначе никак нельзя.
Спасибо за совет, тут хотя бы линейка до 11-го сразу. Ну как не занимался, в школьной и вузовской программе всё это хорошо решал, но как то не вникал особо. А сейчас хочется чисто мозги размять. Спасибо ещё раз!
А математику и решение задачек нельзя рассматривать как хобби?
А зачем ты учился читать?
Математика на школьном углублённом уровне - это моральная обязанность, минимум уважающего себя человека это если ты безнадёжный гуманитарий в 21 веке.
В освоении этого нет совершенно ничего сложного, так как в 90% случаев не предполагает математической интуиции, креативности или чего-то, что эвристикой называют, а предполагает тупое "прочитал - обдумал - понял - применил. Что интересно, эта "математическая интуиция" и "креативность" начинает понемногу просыпаться в человеке, чем больше он занимается даже "тупой" математикой (школьной).
Отвечая конкретно на твой вопрос. Незнание школьной математики автоматически ставит крест на твоих попытках вкатиться во многие хобби. Наоборот, чем больше ты понимаешь математику, тем больше дверей в самые разные интересные хобби для тебя открыты.
>Математика на школьном углублённом уровне - это моральная обязанность, минимум уважающего себя человека
Почему?
>Незнание школьной математики автоматически ставит крест на твоих попытках вкатиться во многие хобби.
Почему?
 36 Кб, 564x696
36 Кб, 564x696Хотя и в школе математика с трудом давалась (виню в этом лично Петерсон, которая привила лютую НЕНАВИСТЬ!11 к предмету, хотя до этого учился по позднесоветским учебникам и все норм было)
Школьный курс помню где-то на уровне восьмого класса и то отрывками, хотя иногда простейшая арифметика в тупик ставит
Задача - прокачаться до такого уровня, чтобы решать Демидовича и Колмогорова
Времени - да хоть всю жизнь, потому что зато скучно не будет
Пока что планирую повторить школьный курс и потом буду реквестировать литературу
Советы?
Никогда не понимал людей, у которых математика проблемы вызывает. Особенно школьный курс и первые пару курсов - там все по "алгоритмам" делается.
Бери примеры и решай их. Не знаешь как решить? Смотри как решаются подобные. Так в итоге от частных случаев можно и к общему придти, если теория совсем не дается.
Очень интересно, спасибо!
Да любая. Или для например анализа и тригонометрии разный подход?
Тут вот в чём вопрос. Вот есть допустим формулы сокращенного умножения или бином Ньютона. Мне их просто выучить и использовать? Мне некомфортно от такого. Есть чувство, что я что-то упустил. Мне хочется понять, почему они работают так, а не иначе. И в целом такая хуйня, что если я не понимаю чего-то (например алгебру) на 146%, то мне кажется, что я ничего не знаю и руки опускаются
>Мне их просто выучить и использовать?
Смысла в этом не много. Понимать какое-то утверждение = знать, понимать и уметь воспроизвести доказательство. Если ты чего-то не знаешь, значит ты не понимаешь откуда это берётся, значит ты не знаешь/понимаешь доказательство.
>Никогда не понимал людей, у которых математика проблемы вызывает. Особенно школьный курс и первые пару курсов - там все по "алгоритмам" делается.
А как прокачаться по олимпиадным задачам? Они все сука как будто к общему курсу никакого отношения не имеют. Есть какие либо учебники которые сортируют задачи от простой к сложной и обьясняют подходы?
В каком направлении ботать по олимпиадам.
https://vk.com/postypashki
Классическая кружковая литература. Олимпиадный фольклор, баяны, штучки, дрючки, фокусы и покусы без которых никуда.
Серия "Школьные математические кружки".
Генкин С.А., Итенберг И.В., Фомин Д.В., "Ленинградские математические кружки. Пособие для внеклассной работы".
Фридман, Турецкий, "Как научиться решать задачи".
Сборники листочков прежних лет, в которых покрывается школьная программа, кружково-олимпиадные темы, материал первого курса университета.
Давидович Б.М., Пушкарь П.Е., Чеканов Ю.В, "Математический анализ в 57-й школе. 4-годичный курс".
Голенищева-Кутузова Т.И., и др., "Элементы математики в задачах", Ч.1, 2.
Доценко В. (ред.), "Задачи по математике, предлагавшиеся ученикам 57-й школы".
Алгебра и анализ для матшкольников. Каждый сборник (кроме Алексеева) содержит порядка 1000 задач. Чтобы стать перельманом на минималках, достаточно решить хотя бы 70-80% из них.
Алексеев В.Б., "Теорема Абеля в задачах и решениях".
А.А. Заславский, А.Б. Скопенков, М.Б. Скопенков, "Элементы математики в задачах: через олимпиады и кружки - к профессии" (на либгене висит черновая версия от 2017.04.15).
Алфутова Н.Б., Устинов А.В., "Алгебра и теория чисел для математических школ".
Гашков С.Б., "Современная элементарная алгебра в задачах и упражнениях".
Прасолов В.В., "Задачи по алгебре, арифметике и анализу".
Плюс нужно знать азы теории множеств - ибо это язык, на котором будет идти изложение предмета на начальных курсах.
Виленкин (совсем для детишек).
Шень, "Начала теории множеств".
Вавилов, "Не совсем наивная теория множеств".
>графики, косинусы-синусы, квадратные там уравнения
Вся эта хуйня забывается на раз-два, если ты постоянно ее не дрочишь.
Да я бы не сказал. Синус - отношение противолежащего катета к гипотенузе в прямоугольном треугольнике?
Ну и всякие син2 + кос2 = 1
Вроде помню. Да и выведу сам, если что забыл.
15 лет назад школу закончил.
Ну тут надо чтобы это интересно было, офк.
 88 Кб, 360x480
88 Кб, 360x480Я тупой долбаеб,который в школе не учил ровным счетом ничего.Серьезно,откинув сейчас все,я даже не умею в дроби.То есть,уровень математики у меня на уровне чуть ниже 5 класса.Не особо хочу углубляться в причины,просто меня тогда пиздили и я совершенно ничего не хотел,кроме как поскорее уйти домой.Но понимание того,что математика нужна пришла мне только сейчас.И у меня появился закономерный вопрос:какой учебник 5 класса мне выбрать?По которому учился я?Или какой...Посоветуйте что ли
Или лучше вообще пойти к репетитору,объяснить ему все и пусть он к моему корыту цепляет колеса,и оттолкнет.А разгонюсь я уже сам.Что думаете?
Ч правда в отчаянии
Картинка для привлечения внимания
Берешь советские учебники и задачники по математике за нужные тебе классы и без задней мысли учишься. Если ты безволен и ленив, то можешь в качестве внешней палки нанять репетитора. Но его задача будет не учить тебя, а пиздить. Учиться ты будешь (или не будешь) сам.
Бери книги Киселева. Арифметика, алгебра обе части, геометрия. Занимательную математику от Перельмана ещё возьми, чтобы скучно не было. Это те самые советские учебники, на которые дрочат анонсы в треде. Они были написаны так, чтобы даже Ванька-колхозник кое-как понял материал.
Книги Колмогорова не бери, именно из-за него пошла мода писать хуевые учебники по математике с усложненным изложением, чтобы потешить ЧСВ авторов.
Короче, речь шла про среднеквадратическое значение и среднеквадратическое отклонение. Формула одна, просто в одном случае в переменную ноль подставляется.
Есть тут господа, умеющие считать на соробане? Подскажите годный гайд, а то я уже многие посмотрел и каждый лепит отсебятину (например, сколько отступать рядов в том или ином случае, многие даже не поясняют свои действия), должна же быть какая-то система.
Пока взял себе дешевый китайский пластик на 13 столбиков. Если что это для общего развития мне необходимо и прокачки оперативки и концентрации. Сейчас делаю обычное умножение двузначных на двузначные громоздким способом, а чтобы дополнительно грузануть оперативку, представляю цифры на внутреннем экране (что для меня адски трудно, потому что ментальный экран мутный и плохо контролируемый, цифры прямо разлетаются, как буйные птицы и норовят занять место друг друга, их приходится удерживать, и это требует напряжения).https://abakus-center.ru/img/blog/soroban-2.jpg
 1 Мб, 1156x755
1 Мб, 1156x755Чёт ссылку случайно вставил вместо картинки.
Если хочешь повысить читаемость своих комментариев со стороны других людей - перестань закрывать всё в спойлер. Рили, уже тупо лень мышкой все открывать и я скипаю.
Это дружеский совет, я не наезжаю
Спасибо за совет, мне бы туториал по соробакусу, но не по комментариям под спойлером. Там под спойлером второстепенное же, главное на виду.
НМТ на носу
И что мне даст математика - абстрактное мышление? Понимание сего мира? Его установ? 3д мышление?
Какие книги читать, что смотреть, чтобы это решить/ать?
Представляю что блять на конкурсах по матике в рашке.
[1] Решение квадратного уравнения (просто не паришься по поводу знака неравенства и решаешь как обычное уравнение, не забывая, что можно переносить левую часть в правую и наоборот). Переносишь правую часть налево с обратным знаком, выносишь за скобку х и решаешь. получается два корня: X>= 0 & X<=2 т.е. [0,2]
[2] сложение логарифмов с разными основаниями
log2(1/8) = в какую степень нужно возвести 2, чтобы получилось 1/8? Очевидно, что в отрицательную, т.к. значение дробное получается. В знаменателе 8 это 2^3. Значит 2 в степени -3 будет равно 1/8. (Если степень отрицательная, то значит x^(-a) = 1/x^a - простое правило) Значит = -3
log5(25) = в какую степень нужно возвести 5, чтобы получилось 25? Во 2ю. Значит = 2
-3 + 2 = -1
[3] Лень читать на иностранном
[4] Брутфорсом берешь ответы (точки) и чекаешь на графике где они находятся. Если лежит на графике, вот тебе и ответ. Если я правильно понял задачу. (-3, 1)
Все очень просто. Что тебе тут непонятно вообще могло быть? Вопрос не риторический.
Имхо, скорее всего ты до этого многое забивал на математике, а потом одумался в последующих классах, что ничего не понимаешь. А уже и не будет непонятно, потому что математика по ступенькам изучается, где каждая следующая ступенька состоит из всех предыдущих и добавляет новое. И вот ты успешно пропустил мимо ушей все предыдущие ступеньки, что текущие, более высокие, тебе непонятны.
Это как читать войну и мир, не зная алфавит. А ведь тебя учили алфавиту, но ты забивал на него.
Какие книги?
Учебники по математике за предыдущие классы. По порядку. И задачники. Изучай "алфавит" с самого начала, чтобы понять каких "букв" ты не знаешь.
>Имхо, скорее всего ты до этого многое забивал на математике, а потом одумался в последующих классах, что ничего не понимаешь. А уже и не будет непонятно, потому что математика по ступенькам изучается, где каждая следующая ступенька состоит из всех предыдущих и добавляет новое. И вот ты успешно пропустил мимо ушей все предыдущие ступеньки, что текущие, более высокие, тебе непонятны.
Так и есть, а теперь аналог ЕГЭ на носу.
Пиздец вы умные, но где эти знания использовать, кроме самой математики?
В технических науках такие фундаментальные знания используются везде. Да и в целом чем шире твой багаж знаний, тем проще тебе будет вкатываться во что-то новое.
Вот щас ты математику будешь скипать, а через 20 лет у тебя мозги будут скрипеть от того, что тебе девочка в банке объясняет про ипотеку и кредит или когда начнешь считать свой домашний бюджет и смотреть где ты тратишь много. Или когда тебе предстоит плитку класть в ванной и понять, сколько тебе брать штук, чтобы не переплатить.
Это много где стрельнет в итоге, и тут не важна конкретика, мол "где я буду этот лагарифм использовать?", тут важен сам принцип мышления, который тебе математика дает. Да, ты не будешь логарифмы нигде считать, но принцип мышления подсчета логарифмов будет такой же, как в некоторых бытовых задачах, с которыми тебе предстоит в жизни столкнуться.
 134 Кб, 420x280
134 Кб, 420x280Спасибо, что поясняешь такому неучу ничтожному как я.
Я сквозь своё нытьё, нашёл что искал. - https://drive.google.com/file/d/1BxMknigFz9L0Ai73zVMx-UpGUBhmrXya/view
Всё таки PDF версия этого учебника - есть.
То о чём ты говорил.
И автор нужный, который вебинары ведёт на ILearn (главный вроде бы по матеше в укр.)
И с 5 по 11 класс.
И это задачник одновременно, или это просто задачник 5-11?
Остальные учебники обязательно наверну, но с какого класса начинать? И начинать ли этот учебник-задачник первым?
А это плейлист с ответами, к этому учебнику - на русском, 2014 года плейлист... Ух.
https://www.youtube.com/playlist?list=PLk91qesJngSK8tu025oH-3OMaRBXwOmes
Его я просмотрю как пройду учебник (тесты).
Осталось всё это скачать... (ибо я параноик)
Уже у меня так и канал с музыкой, которую я слушал - удалился и пропал навсегда, не зря всё оттуда скачал, и тут скачаю и поделюсь со всеми жаждущими.
Слишком сука ценная информация.
Невероятно благодарю Вас (Тебя)
Ваше умственное развитие, многократное превышает наше (либо я имею слизком узкий круг людей, сужу по школе)
Пока думаю купить эту (щас доучиваю Историю Украины, и то с 20 по 32 темы только нужно , вот так)
https://rozetka.com.ua/259539816/p259539816/?gclid=Cj0KCQjw-daUBhCIARIsALbkjSZk8gwcEnCr1rDkAoEGpXS4sxJhWPN9eJNIJgSxbuvW4WngM9Y-oDwaAlRAEALw_wcB
Там 5-11 класс задачник
И эти каналы
https://www.youtube.com/watch?v=qyQHRjW5YZc&list=PLk91qesJngSK8tu025oH-3OMaRBXwOmes&index=1
https://www.youtube.com/channel/UCwIC75LZ578z6T9w33SS5Tg/playlists
Хватит этого?
Кто же тебе ответит, что тебе хватит, а что нет? Тем более ты спрашиваешь какую-то конкретику, не думаю что люди, давно закончившие школу, могут тебе ответить каких авторов покупать.
Я бы учебники изучал, а только потом задачи из задачников решал. Те самые учебники, которые у тебя были, т.к. там все разжевывается, дается теория и идет по-порядку. Но если ты думаешь, что тебе задачника хватит - ок, пробуй. Возможно так.
>Я бы учебники изучал
Тоже так думаю.
Как учебник, училка эта сойдёт? https://www.youtube.com/channel/UCwIC75LZ578z6T9w33SS5Tg/playlists
С 5 по 11 класс
Учебник это бумажная шершавая субстанция вперемешку с чернилами.
Как можно записать математические символы, мешанные символы и тд, на пк?
Я использую TeXstudio. На техстудио.орг скачиваешь инсталлятор. В ютубе гайды есть.
Чтобы писать документ с матемематическими формулами - да. Можно ТеХовский файл преобразовать в пдф, так ты сможешь его на любом устройстве открыть.
По поводу приложения не знаю, но полагаю, что нет.
Вот бы бесплатный и с шагами...
MathType. Классическая прога, встраивается в word. Постепенно запоминаешь основные горячие клавиши и достаточно быстро набираешь формулы + есть автонумерация формул и ссылок на формулы. Удобно.
А ТеХи всякие слишком для задротов, ну или тех, кому надо статьи верстать в научные журналы.
 6 Кб, 534x55
6 Кб, 534x55https://1progs.ru/mathtype-portable-russkaya-versiya-s-klyuchom/
Скачаю отсюда
Вроде бы топ
Блять а почему тех для задротов, навучные статьи и тд? Нихера не шарю.
> Блять а почему тех для задротов, навучные статьи и тд? Нихера не шарю.
Потому что чтобы начать пользоваться ТеХом тебе надо потратить время на обучение этому прекрасному инструменту. И если тебе просто формулы набирать надо, то это как из пушки по воробьям стрелять имхо, ведь там еще куча всяких штук есть по оформлению документов.
А на рутрекере с вирусами, я блядь 0 и не знаю что сука ставить.
Есть же ещё Matlab и OpenCV
Какую версию лучше MathType поставить? Может кто-то дать проверенную?)
>Не принципиально. Та которая поставится - ту и ставь. Я на 6й работал.
Сам скачал Math Type 6.9 и 7+, с только что упавшего рутрекера.
На 7+ жаловались, что постоянно падала активация, куча входящих/исходящих подключений нужно блокировать и тд. И что все равно слетает активация через месяц. Поставил 6.9
Есть гайд как работать в нём? В Math Type
Понял только как пробел поставить, зажав Ctrl
А как абзац и тд...
Маттайп работает в связке с Word. В ворде появится вкладка с маттайпой, откуда можно будет его запускать и набирать формулы сразу в документ.
Горячие клавиши указываются при наведении курсора на соотвествующую кнопку.
Основные запомни. Например дробь, верхний индекс, нижний индекс, интеграл, дифференциал, знак производной, производная по времени (точка), знак вектора, греческие буквы (они там изи вводятся, вроде надо нажать ctrl+G, а потом латинскую букву, напримр "a" и напечатается альфа. ctrl+G и после "b" - бетта. Удобно.
Просто наводи мышкой и снизу вроде будут горячие клавиши указываться. Если горячая клавиша через запятую идет, что вроде Ctrl+K, L — это значит нажимает сначала Ctrl+K, потом отпускаешь их и жмешь L.
Тебе вообще что набирать то надо? Физика, математика? С лекции, курсовая, диплом?
 512 Кб, 1093x854
512 Кб, 1093x854Такая вкладка
>математика
Да. Бля жестко. А зачем Word?... Когда просто Маттайп...
Если бы он был на мобиле и синхронизация то да..
>Набрал ты формулу, дальше что? Зачем? Странный ты.
Для запоминания...
Кстати как убрать запоминания пробела?
И эту чёрточку
Которая постоянно мигает
Можешь тут еще поиграться (smath - есть на телефоне и пк + облачная версия. Это бесплатный аналог Mathcad), раз тебе просто для запоминания и печатания ради печатания.
https://ru.smath.com/cloud/sheet/B4FWNuGrz7
Desktop обычный. Это же не сложно, что же ты такой нерешительный?
Есть еще облачная версия
https://ru.smath.com/cloud/sheet/
 76 Кб, 725x869
76 Кб, 725x869Вот пример с квадратным уравнением, чтобы тебе было проще разобраться
https://ru.smath.com/cloud/worksheet/S4vrPp22
 47 Кб, 687x464
47 Кб, 687x464>что же ты такой нерешительный?
Тоже самое мне учительница говорит.... На дополнительных...
Почему я такой деградант блять... Квадратные уравнения решить не могу даже...
Не забудь перекат сделать. ДА ты!
Назови Математики Тред #2, шапку напиши и картиночку подбери хорошую.
Этот тред заархивируй https://arhivach.ng/add/ и ссылку вставь в новый тред в шапку.
Да прибудет с тобой сила, анон.
Вот такой вот график в 6.9 (наверное и в следующих) - делается по индусошвайновски.
Представляю если щас буду делать координатную прямую... Муахахха...
>>105962
А зачем? Если он прикреплён к тематике.
Чтобы анон рандом зашёл, и по 300 раз в будущем искал перекат?
Ни один тред не видел здесь, чтобы перекрепляли заново.
Все равно сюда почти никто не пишет, и уж точно по "Бампам" в тематике - не заглядывает. А лишь тем кому нужно.
Может и в Smath перейду, но параноя насчёт облачности - браузерной, без сохранения данных на устройстве + лагает. Но там аж такие графики можно делать. Коими я сейчас уже и занимаюсь.Парабола точнее.
Как же мне воплотить 4 пик в MathType... Не говоря о просто координатной площине. За каракули сори, работаю над этим.
> се равно сюда почти никто не пишет, и уж точно по "Бампам" в тематике - не заглядывает. А лишь тем кому нужно
Тред утонет, будешь один сюда писать. Я захожу с главной.
В маттайпе нельзя строить графики - это не программа для вычислений, а текстовый редактор.
Smath можно и без облака юзать, тем более там есть возможность скачать то, что ты написал и открыть через десктоп версию. Да и вроде на андроиде тоже можно установить и эти файлы открывать. А если хочешь синхронизацию между десктопом и телефоном, то можешь использовать какой-нибудь дропбокс.
Зачем перекат? Для математики есть отдельная доска. Что в этом треде такого, чего нет в /math?
>Что в этом треде такого, чего нет
Не тот вопрос. Надо так: "чего в math такого, чего нет в этом треде". И ответ напрашивается сразу же - жутчайшего чсв обитателей. Math это про писькомерство, этот тред - про обучение.
То есть просто перекат с ссылкой книг сделать? Если да, то после сессии через 21 день сделаю.
Хотя нет, раньше смогу. Но не позднее, чем написал выше.
>Тред утонет, будешь один сюда писать. Я захожу с главной.
А в чем проблема сделать закладку этого треда и не ипать мозги? Плюс плашка с этим тредом выше, чем спускаться вниз...
>В маттайпе нельзя строить графики - это не программа для вычислений, а текстовый редактор.
Уже понял, мог бы быть очень классный софт, все равно спасибо за этот опыт. Лишь бы Ctrl C; Ctrl V перенеслось в Smath.
>Smath можно и без облака юзать, тем более там есть возможность скачать
Скачать или установить как приложение с помощью Edge?
>Да и вроде на андроиде тоже можно установить и эти файлы открывать.
?
>А если хочешь синхронизацию между десктопом и телефоном, то можешь использовать какой-нибудь дропбокс.
Ух, синхронизация своими руками.. Хорошо, спасибо, не вижу пока никаких альтернатив твоего предложения.
А это вроде бы просто решалка, фотаешь уравнение ну и ты понял.
Записывать туда и через историю смотреть, было бы совсем по индусошвайнвоски.
Зашёл кстати в /math и приахуел, от одних только названий и описаний тредов, куча информации кидается на новычка, любой, не понятно зачем, чтобы сразу напугать, и все очень всрато и неудобно оформлено через тот же пастбин.
Копроготово https://2ch.hk/se/res/106044.html (
>>106040
Хелп ми плиз
Сегодня к училке по матеши наверное не пойду, Др все таки... ПЛюс хуево.. Я уже стар..
Перекат
https://2ch.hk/se/res/106044.html (
https://2ch.hk/se/res/106044.html (
https://2ch.hk/se/res/106044.html (
https://2ch.hk/se/res/106044.html (
https://2ch.hk/se/res/106044.html (
А то единичную ссылку могут провтыкать
>Важно читать теорему, закрывать книгу и пытаться самостоятельно её доказывать. После того, как ты её докажешь или просто сдашься (в чём, в принципе, нет ничего постыдного), открываешь учебник и читаешь доказательство там, анализируешь и делаешь выводы
++++
Всё верно говорит. Это основной источник прокача.
Насчет английского. Посоветуй годных англоязычных учебников аналогов наших 8-11 классов. Где-то может дальше программа идет как в германии 12, тоже интересно. Мало ли где светоч педагогики выстрелил, тут же не только америка и англия.
Объясни как ты так подставил x в 2/3. Это контринтуитивно для меня. Понятно, что это свойство перестановки и так работает, но две третьих ведь изначально это (x/3)*2? Ты просто помнишь это свойство?
2/3 x = 2/3 x/1 = (2x)/(31) = 2x/3
Он решил не пояснять...