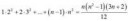Это копия, сохраненная 15 февраля 2017 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.
О чём пикча с говном на лопате? Пахом принёс покушать олимпиадникам?
Нет, дед с dxdy просеевает числа через решето эратосфена.


Сумма всех натуральных чисел равна -1/12, а число всех натуральных чисел равно -1/2. Последний факт совсем легко понять: "ясно", что число всех целых чисел -- ноль; соответственно, среди них -1/2 отрицательных, один ноль, и -1/2 положительных.
Число всех натуральных чисел -- это сумма 1+1+1+..., где единицы занумерованы натуральными числами. То есть индекс суммирования варьируется от единицы до бесконечности. Эту сумму следует отличать от суммы 1+1+1+..., где единицы занумерованы неотрицательными целыми числами (индекс суммирования варьируется от нуля до бесконечности). Вторая сумма, естественно, на единицу больше первой. Первая равна -1/2, а вторая 1/2.
Число натуральных чисел равно числу четных натуральных чисел, т.к. между ними есть естественное соответствие n <-> 2n. Следовательно, число нечетных натуральных чисел равно 0. С другой стороны, число четных натуральных чисел минус число нечетных натуральных чисел -- это просто сумма -1 + 1 - 1 + 1 - ...; она равна -1/2. Значит, четных натуральных чисел -1/2, соответственно и всех натуральных чисел -1/2.
Кстати, таким же образом можно установить, что сумма 1 + 4 + 9 + 16 + ... равна нулю. "Ясно", что сумма n^2 по всем целым n равна нулю, а сумма n^2 по всем натуральным n есть половина суммы n^2 по всем целым n.
А на этого еблана, у меня скорее ляжет.
Не число, а сумма. Потому что для каждого числа a есть число -a, в сумме они дают ноль.
Кстати а есть какая-нибудь интуитивная не путать с интуиционистской интерпретация всех этих петушений с суммами расходящихся рядов?
В голову лезут только мысли про векторные расслоения, вроде теоремы Серра-Суона и идей в духе "функтор из векторных пространств в векторные расслоения представим, делаем эквивалентность категорий, смотрим на точные последовательности", но реализовать это не получается.
А зачем ты это изучаешь? Домашка от препода в институте или есть какая-то более интересная мотивация? Ты не стесняйся, выкладывай всю подноготную, мы люди тут толерантные, плюрализм допускаем.
Да у вас, батенька, параноидный психоз.
В чём может быть мотивация узнавания причин фактов? Год назад научился считать функтор Tor, полгода назад узнал за классифицирующие пространства, а сегодня прочитал статью group cohomology на Википедии, где было указано, что определения гомологий групп эквивалентны.
Стало интересно, что же от меня жидорептилоиды скрывали-то, мешая развитию руSSкой математики!
Как вычитать бинарные числа суммированием?
Вот, есть формула: X - Y = X_2 + ¬Y_2 + 1, однако:
(10100 - 100)_10 =
(10011101110100 + 1100100)_2 =
(10011101110100 + ¬1100100 + 1)_2 =
(10011101110100 + 11011 + 1)_2 =
10011110010000 = 10128_10 ≠ 10000_10
>Как вычитать бинарные числа суммированием?
Перевести в десятичные, вычесть, снова перевести в двоичные.
Да ну тебя. Вот сам так и считай.
Помогла
$hex = unpack('H٭',$bytestring);
$big = new BigInteger('$hex', 16);
$sub = $big->subtract('$value');
$result = pack('H٭', $sub->ToHex())
Это - по числам.
А теперь вопрос: как отнять две точки на эллиптической кривой с помощью удвоений и суммирований с использованием аддитивных и мультипликативных инверсий?
Хочу уметь криптить точками и декриптить байтами на элиптик курве, да.
Много интересного хомякам говна в своем бложике. В основном о том как ебал себя в пердическое пространство объектами третьего уровня гомологичности.
Понимаешь, что он действительно полезного написал утопает в той куче графоманского дерьма, что из себя представляют его бложики.
Может здесь кто знает, как выразить число через сумму удвоенных единиц в различных степенях?
Не, уже разобрался.
1. 123456 dec
2. в bin 11110001001000000,
3. Читать с конца
5. Если 1, то +2^N, где N - номер разряда минус 1
(1 разряд - нулевой)
6. Если ноль, то 0^N, или просто 0, или пропустить.
123456 = 2^10+0^9+0^8+2^7+0^6+0^5+0^4+2^3+2^2+2^1 = 2^10+2^7+2^3+2^2+2^1, вот.
>123456 = 2^10+0^9+0^8+2^7+0^6+0^5+0^4+2^3+2^2+2^1 = 2^10+2^7+2^3+2^2+2^1, вот.
Не, и тут накосячил.
123456 (10) = 11110001001000000 (2) =
2^16+2^15+2^14+2^13+0^12+0^11+0^10+2^9+0^8+0^7+2^6+0^5+0^4+0^3+0^2+0^1+0^0 =
2^16+2^15+2^14+2^13+2^9+2^6
= 65536 + 32768 + 16384 + 8192 + 512 + 64 = 123456.
Вот так будет.

Вот и всё. Никакие интегралы не нужны.
> Один анон говорил мне что интегралы нужны, например, для вычисления числа пи. Но зачем если можно просто воспользоваться пикрилейтедом? Просто задать комптьютеру каждый добавлять/минусовать/умножать следующее число и дальше будет просто вопрос времени и памяти компьютера.
> Вот и всё. Никакие интегралы не нужны.
Ты ведь понимаешь, что пользуясь этими формулами ты пользуешься интегралами?
Просто потому, что в их знаменатели входят простые числа.
А ты разводишь демогогию, лол. >>392451
Ты не говорил о какой именно писанине идёт речь. Но из всей писанине статьи в архиве малая часть всего, что он написал. А написал, он чертовски много говна. Просто представь сколько времени на математику Вебритом было проёбано, когда он писал свою графоманию.
Утверждение б): две прямые параллельны.
Вопрос: какое из данных двух утверждений считается общим, а какое – частным?
Ну, это следствия всяких аналитических продолжений гипергеометрии, зета и тд и некоммутативности пределов. То есть, в зависимости от способа суммирования ответы могут быть разными, и интуиция не оче.
>ты разводишь демогогию
Нет, демагогию разводишь ты. Речь о том, что
>он написал очень много интересного
>Нет, демагогию разводишь ты. Речь о том, что
> он написал очень много интересного
А я говорю, что процент интересного от обшего процента его графомании стремится к нулю. Он так мал, что мы можем им пренебречь и считать, что Вербит не написал ничего интересного.
Речь не об этом. Не о проценте годноты среди всех написанных им текстов. Речь о том, что он написал гораздо больше годноты, чем Зорич.
Понимаешь, дерьма он написал больше. Один "Гитлер-Гитлер-Гитлер" или "Сдохнуть" чего стоит.
>Не о проценте годноты среди всех написанных им текстов
>Речь о том, что он написал гораздо больше годноты, чем Зорич
Понимаешь, в процентном соотношении именно Зорич написал больше годноты.
Я предлагаю засунуть тебе свои процены в анус своей мамаши, юный демагог. Потому что речь о том, что
>он написал гораздо больше годноты, чем Зорич
>Секреты Математики:
>Правило 4-х знаков
Поясните.
Очевидно же, что 2 - частный случай первого, ибо прямые параллельны, если они пересекаются в бесконечно удалённой точке.
Программа Посметьего его не найдёт. Она может найти корень в промежутке от -1000 до 1000.
Тогда, предлагаю, забить в массив все корни от -1000 до 1000 и выискивать с помощью random. Лол.
У него какая-то обида детская на математику. Будто препод по матанализу его в очко драл на сессии. Успешным он точно не выглядит.
Просто он в душе ультрафинитист, пускай и слов таких не знает. Причём, радикальный! Для него существуют только натуральные числа + некоторые рациональные, которые меньше четырёх знаков после запятой.
Хотя, стоп. Не все натуральные числа для него существуют. А только те, которые можно посчитать на компе.
Неа, он в таких границах только квадратные корни считает.
Целые у него в диапозоне -2147483648 +2147483647.
Не, думаю, что ему нужны большие числа в работе. Числа, абсолютные величины которых больше 2147483647, для него это что-то мистическое.
Двачую. Читаю тифарета только из-за подобных выражений "Так ненавижу, что кушать не могу".
Не подскажете ли, чему равно множество N?
Точнее множеству, состоящему из числа его одноэлементных подмножеств. Лол.
axiom of specification + axiom of pairing + axiom of power set + axiom of extensionality
Он главное в Определения N тред перекатился, а от сюда ушел. Боится уже заглядывать сюда. Хуями же накормят.
Посметьев < Ультрафинитисты < Конструктивисты < Интуиционисты < Математики < Фанаты больших кардиналов
Конструктивисты < Посметьев < Ультрафинитисты < Интуиционисты < Математики < Фанаты больших кардиналов
Пофиксил.
Нет, почему. Это шкала допустимых сущностей же. Ультрафинитисты радикальнее конструктивистов. Посметьев гораздо ебанутее конструктивистов.
>Посметьев гораздо ебанутее конструктивистов.
Ну не знаю. Пока конструктивисты срутся на двочах со своими противниками, Посметьев гребёт бабло лопапатами, ненапрягаясь, решая всё методом перебора.
>Посметьев гребёт бабло лопапатами
Поправка: он пишет во вконтакте, что гребёт бабло лопапатами.
Ну и у конструктивистов есть какая-никакая наука, а Посметьев просто ебонашка.

>манятред на мейлру скатывается в обсуждение конструктивизма даже без моего участия
Лол, до сих пор печет? Ну ок, тогда еще тезисы.
1) Любая практическая математика конструктивна. Для практических целей абстракция актуальной бесконечности в принципе не нужна, т.к. все практические вычисления конечны и производятся над конечными объектами, существующими именно в конструктивном смысле. Даже если какой-то математический объект считается бесконечным, конкретные рассчеты в практическом отношении идут только с определенным количеством знаков после запятой, например.
2) Любые формулы и доказательства в формальной системе так же являются конструктивными объектами, если записываются конечным числом знаков.
3) Таким образом, настоящая неконструктивнаяч математика, с маняверой в актуальную бесконечность - это только основания, ZFC там и т.п. Но в предыдущем треде много кукарекалось, что основания это вообще не математика.
Ну и?
Ну наконец-то! Я тебя заждался уже, присаживайся, родной!
Так... На чем же остановились?
А... Ак... Акси... Аксиоматика конструктивной математики! Ты говоришь, что в конструтивной математики не аксиом, но очень многое ты принимаешь на веру. Даже не на веру, а на интуицую. Зачем ты так делаешь?
Слушай, а как связаны алгоритмы Маркова и арифметика? Здесь что-то мелькало такое в одном из прошлых тредов.
Я тебе RAGE поставил.
Тогда дай ссылку на пост или ответь ещё раз. Правила знаешь.
Я бы хотел поговорить об основаниях конструктивной математики.
>Напрямую, арифметика выразима через алгорифмы Маркова.
Не, это понятно, но какая связь то? То есть вот есть арифметика, есть ном, через которые она выражается, и что? Мб у тебя какие-нить статьи есть, книги на эту тему? Я просто даже не знаю, как вопрос то сформулировать нормально.
>но какая связь то?
Ну, скажем, арифметические правила - частный случай алгорифмов Маркова и любых идентичных с ними подходов (машина Тьюринга, система Поста, лямбда-исчисление Черча).
>какие-нить статьи есть, книги на эту тему?
Почти все что угодно на тему алгорифмов Маркова и всего вышеупомянутого. Как вариант http://neerc.ifmo.ru/wiki/index.php?title=Лямбда-исчисление нумералы Черча.
Объясни, почему мы должны строить всю математику на алгоритмах и машине Тьюринга?
Не обязательно. Только в конечном итоге все равно получится нечто вроде частного случая этого. Ну или актуальная бесконечность и во что вы там еще из неконструктивных оснований веруете. Любые конечные формулы и доказательства в любой формальной системе - кончтруктивные объекты, я жи даже цитату Лёфа принес >>392676
>Ну или актуальная бесконечность и во что вы там еще из неконструктивных оснований веруете
Смотри, твоя конструктивная математика основана на аксиомах, так что обхывания нас верунами некоретно. Ты можешь доказать, что в твоей математики нет аксиом?
То есть подожди. Если задачу рассматривать как цепочку шагов A => B => C => ... =>Z, то только последний шаг должен быть конструктивным, так? Дозволено ли использовать неконструктивные доказательства на предшествующих шагах? Например, при доказательстве, что тот или иной алгоритм завершается. То есть разрешено ли конструктивисту использовать неконструктивные рассуждения, если они в итоге приводят к конструктивным доказательствам?
Один, похоже, начал понимать, лол. У Лёфа в цитате выше ничего не сказано про обязательную конструктивность рандомной формулы. Речь только о том, что она должна быть объектом из конечного числа знаков. Тогда она будет конструктивным объектом. Конечно же, записанная в виде зависимого типа и т.п. такая формула может выдавать и жопу _|_ в качестве результата работы.
>разрешено ли конструктивисту использовать неконструктивные рассуждения, если они в итоге приводят к конструктивным доказательствам?
А будут ли такие рассуждения именно неконструктивными, а? Если итог - конструктивный объект, то очевидно, что в рассуждениях нет ничего нарушающего вычислимость.
Да, допустим они будут принципиально неконструктивными. Например, в промежуточных шагах от алгоритма к алгоритму я использую ультрафильтры и аксиому выбора.
Он использовал математику только для формализации своей теории и специально совершал ошибки, показывая свою "отдаленность" от дискурса математики.
мимо проходил
>маняверой
>>392677
>на веру
>Даже не на веру, а на интуицую.
>>392687
>кроме веры
Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык.
Как можно вообще изучать эти воображаемые, идеальные объекты, если не принимать на веру их существование и аксиомы, позволяющие конструировать их конструктивно?
Как вообще можно изучать соотношения между ними и их системы, не принимая на веру существование критериев, на которых конструктивно основаны эти соотношения?
Анон, ты не врубился в наш спор. Понструктивист пытается доказать, что его математика единственная правилная и что сам критерий существования нашего мира построен на ней.
И показать, что мы тупые веруны.
Я же указываю ему достойное его место - у параши. И что он тоже верит, чего он никак не хочет признавать.
Тогда скорее всего вычислимость пойдет по пизде и в качестве итога работы получим жопу.
Алгоритм-то получим, по условию рассматриваемой гипотетической ситуации. Неконструктивное доказательство доказывает, что алгоритм считает ровно то, что нам нужно.
Тогда возникает вопрос, настолько ли это доказательство неконструктивное, как принято считать.
Ну если что-то представимо в виде алгоритма, зависимого типа и не нарушает вычислимости, выдавая при проверке этого типа конструктивный объект, то почему это что-то нельзя считать конструктивным объектом?
Он даже пояснял в одном из случаев, что так высказывания не записываются в математике, но ему на это похуй. Ну и да, дискурсы то разные - учитывай.
Ей богу, кому его "обсирать" - его теорию уже критиковали другие люди (которые читали его полностью), а уж на какие-то там претензии со стороны науки он клал.
Не злись, пуся.
И проблему останова, невзначай.
Пиздец, в гугле ничего не могу найти, что за бред
Да, наслышан.
Пусть f : X -> k регулярное отображение и мы знаем, что
1) для любого x \in k x != 0 верно, что f^-1(x) неприводимо
2) Х неприводимо
хначит ли это, что слой f^-1(0) неприводим?
у кого есть идеи, как раскрутить?
полилинейная и кососиметричная штуковина, т-щ начальник!
>по двум строкам
Не понял, у тебя только две строки есть и ты по ним узнаёшь определитель или как?
Заменой sqrt(x)=t >=0. Как обычное квадратное.
sqrt(x) = x^(1/2) = y;
x = y^2 = x^(2/2) = x^1;
-3y^2 -12y = 11, значит
3y^2 + 12y + 11 = 0 - квадратное уравнение.
Ты путаешь алгебраический и арифметический корень. Алгебраический корень - +. Арифметический только +. Чтобы легче считать было и убрать необдозначность корня.
https://ru.wikipedia.org/wiki/Корень_(математика)
Потому что корня четной степени (sqrt это square root, т.е. корень второй степени, он же квадратный корень) из отрицательного числа в области ℝ не существует, так как при возведении в четную степень не может получиться отрицательное число (опять же, в области ℝ).
Но ведь не говориться что x - это отрицательное число, а говорится только что корень из x отрицательный
>>393104
Понял, спасибо, значит просто чтобы было удобно и определенно.
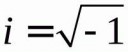
>почему при sqrt(x)=-1 не существует ответа
Ищи его в комплексной плоскости.
>ведь и 1 и -1 в квадрате могут быть однеркой
Однёрка - не минус однёрка.
>У корня n-ной степени есть n возможных решений.
Ну, пускай n будет 4.
3^4 = 81;
4√81 = {3, -3, где остальные 2?}
3^4 = 81;
(-3)^4 = 81;
Где остальные 2?
Хочешь сказать, что на самом деле корни имеют вид: 4√81 = {3+0i; -3+0i, 0+3i, 0-3i} ?
Т. е. это как-бы отражённый,
относительно оси Im,
пятиугольник, для 5-й степени, где одна из вершин - минус 1?
Для чётной степени он совпадает.
Да, и вот ещё...
{3+0i; -3+0i, 0+3i, 0-3i} - неправильно.
Радиус круга равен 3, значит {3+3×0i; -3+3×0i, 0+3×i, 0-3×i}
Так, что-ли?..
Ну вот, например, 4-я степень...
Корень четвертой степени - это квадрат с вершинами (Re, Im):
(+1, 0), (0, +1), (-1, 0), (0, -1) - координаты их.
И одна из его вершин, третья - совпадает со значением алгебраического корня -1.
Отражая его получится тот же квадрат.
А вот пятиугольник 5-й степени не пересекает -1, если не отразить его
относительно вертикальной оси, получив 10 вершин, верно?

a-корень четвёртой степени из b.
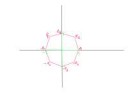
Тогда (ae_i)^4=(-ae_i)^4=b*1. Ясно? Все корни четвёртой степени из единицы на пикче.
А последнего ответа нет, потому что ни косинус, ни синус не могут дать отрицательное. =)
У тебя там, знак умножения между i и синусом стоит?
Я не стараюсь их визуализировать, но скорее получаются два четырёхугольника, а не восьмиугольник.
ИМХО, они совпадают.
А если нет, то может в одном из слагаемых числитель со знаменателем надо менять?
Хотя, нет! Он должен выть вогнут во внутрь. Я сонный, и рисовав его посчитал, что sqrt(2)/2>1. Сейчас перерисую.
>- косинус
-синус, хотел сказать
>может
> числитель со знаменателем надо менять
Чтоб было вот так:
e1 = cos((пи×0)/4) + i×sin((пи×0)/4);
e1 = -cos((пи×0)/4) + i×sin((пи×0)/4);
e1 = cos((пи×0)/4) - i×sin(4/(пи×4));
e1 = -cos((пи×0)/4) - i×sin(4/(пи×4)); -кажется тут вариантов уже 16
e1 = -cos((пи×0)/4) + i×sin(4/(пи×4)); -а тут 32



Пошел нахуй отсюда, мы тут комплексные числа обсуждаем.
Добро пожаловать на комплексную плоскость.
Анон, у тебя проблеммы с тригонометрией. Поскольку в твоих формулах
e1 = cos((пи×0)/4) + i×sin((пи×0)/4);
e1 = -cos((пи×0)/4) + i×sin((пи×0)/4);
e1 = cos((пи×0)/4) - i×sin(4/(пи×4));
e1 = -cos((пи×0)/4) - i×sin(4/(пи×4)); -кажется тут вариантов уже 16
e1 = -cos((пи×0)/4) + i×sin(4/(пи×4)); -а тут 32
Только два числа +1 -1.
Это получается из cos((пи×0)/4)=1 sin((пи×0)/4)=0.
Серьёзно, ты поебень написал. Да и если cos((пи×k)/n) + i×sin((пи×k)/n) - корень, не факт что все остальные тоже.
Если n-четное, то 2n. Т.к. (-1)^n=(1)^n=1
>корень, не факт что все остальные тоже
В смысле, те которые ты написал:
e1 = cos((пи×0)/4) + i×sin((пи×0)/4);
e1 = -cos((пи×0)/4) + i×sin((пи×0)/4);
e1 = cos((пи×0)/4) - i×sin(4/(пи×4));
e1 = -cos((пи×0)/4) - i×sin(4/(пи×4)); -кажется тут вариантов уже 16
e1 = -cos((пи×0)/4) + i×sin(4/(пи×4)); -а тут 32
>Откуда берутся правила построение? И откуда берутся формулы?
Из постановки задачи, которую требуется решить.
Ну, это я от балды.
Ты же прогишь там - так и проверь заодно...
А ещё, вот, угол ты какой берёшь?
Пи. Относительно каких на окружности?
Могут ли углы, входящие в слагаемые косинусы и синусы изменяться при расчёте корня?
Если да, то симметричны ли эти углы?
Если симметричны, то относительно каких осей?
Может ли, например,
cos(пи×1/4) + i×sin(пи×3/4) давать корень 4-й степени в комплексной плоскости?
а -cos(пи×4/4) + i×sin(пи×1/4)?
В общем, ещё и углы можно пошатать, вдруг там комплексные корни найдутся?
Матрично-алгоритмическим.
>А ещё, вот, угол ты какой берёшь?
Из формулы муавра.
https://ru.wikipedia.org/wiki/Корни_из_единицы
>Относительно каких на окружности?
Окружность с центром в начале координат.
>Могут ли углы, входящие в слагаемые косинусы и синусы изменяться при расчёте корня?
Формула Муавра. Там всё написанно.
>Если да, то симметричны ли эти углы?
Относительно комплексного сопряженного.
>Относительно каких на окружности, имелось в виду.
точек, имелось в виду.
>Окружность с центром в начале координат.
И радиусом, равным длине от начала координат до значения подкоренного выражения.
Это понятно.
>Относительно комплексного сопряженного.
z = a + bi; z = a - bi - комплексно-сопряженное, по определению.
Т. е. ты отражаешь вторую точку на окружности относительно горизонтальной оси координат?
А почему бы её не отразить относительно вертикальной?
z = a + bi; z = -a + bi
Или ваще, так: z = a + bi; z = -a - bi? Лол.
Если тебе нужно поделить 2 компл. числа: (a+bi)/(c+di), то непонятно, как это делать.
Если числ. и знаменатель домножить на одно и то же число, то значение дроби не изменится. Если домножить на сопряженное к (c+di), то в знаменателе появится действительное число[(c+di)(c-di) = (c^2+d^2)], а поделить комплексное на действительное уже можно.
Поэтому вот так вот сопряжение определяется.
Твоя мамаша.
>Какие подводные?
Это сложный вопрос, но подводные...
___КАМНИ___
___А________
___М________
___Н________
___И________
"Правда, такая ерунда получается".
В классической математике это тоже всего лишь формула.
>>393117
>>393118
>>393120
>>393121
>С чего это 8?
>>393122 >>393165
Из этих формул вытекает, что корней из единицы всегда ровно n, и все они различны.
>>393122 >>393125
-1^5 не даст 1, поэтому отражать не нужно. Это же корни из 1, а не из (-1).
Степень - нечётная.
>>393123
Да.
>>393131
4√1 = {1, -1, i, -i};
1^4 = 1;
(-1)^4 = (-1)×(-1)×(-1)×(-1) = 1×1 = 1;
i^4 = i×i×i×i = i^2 × i^2 = (-1)×(-1) = 1;
(-i)^4 = (-i)×(-i)×(-i)×(-i) = i^2 × i^2 = (-1)×(-1) = 1;
Вот это - проверить можно.
А остальное, >>393126>>393127>>393128>>393148>>393150>>393161
как проверить?
>>393138>>393142
Все точки лежат на окружности, радиусом 1, для корня n-й степени из 1.
>>393173
А зачем делить?
>>393117
>>393118
>>393120
>>393121
>С чего это 8?
>>393122 >>393165
Из этих формул вытекает, что корней из единицы всегда ровно n, и все они различны.
>>393122 >>393125
-1^5 не даст 1, поэтому отражать не нужно. Это же корни из 1, а не из (-1).
Степень - нечётная.
>>393123
Да.
>>393131
4√1 = {1, -1, i, -i};
1^4 = 1;
(-1)^4 = (-1)×(-1)×(-1)×(-1) = 1×1 = 1;
i^4 = i×i×i×i = i^2 × i^2 = (-1)×(-1) = 1;
(-i)^4 = (-i)×(-i)×(-i)×(-i) = i^2 × i^2 = (-1)×(-1) = 1;
Вот это - проверить можно.
А остальное, >>393126>>393127>>393128>>393148>>393150>>393161
как проверить?
>>393138>>393142
Все точки лежат на окружности, радиусом 1, для корня n-й степени из 1.
>>393173
А зачем делить?
Слова "две прямые параллельны" значат "две прямые не пересекаются". Прямые, которые не пересекаются, - не пересекаются.
В не Евклидовой геометрии, возможно, да - в зависимости от кривизны пространства.
>ОП, где шапка?
Постоянной шапки для этого треда никогда и не было. Надо бы сделать.
>Почему с вопросом о корнях приходят сюда, а не в тред для начинающих?
Аноны с самого начала путают треды. Как с этим бороться не знаю. Да и нужно ли? Может две ветви снова в одну объединить?
А, я здесь с тредов, когда в шапке было типа - обсуждение листков НМУ; новички идите в тред для начинающих.
Вообще да, мне кажется хорошо бы объединить. В шапку накидать списки, рекомендации, архив мемасов и сказку какую-нибудь.
>А, я здесь с тредов, когда в шапке было типа - обсуждение листков НМУ; новички идите в тред для начинающих.
Так и было. Работало не сильно, как помню.
Два треда протекали в друг-друга(да и сейчас так делают), а потом и вовсе аноны перебрались в тред для начинающих. Обычный мат-тред почти умер. Возможно, сейчас он жив только потому что я не стал писать это предупреждение.
Тогда вопрос как именно? Можно продолжить одну из ветвей и закрыть другую. А можно закрыть обе и начать новую ветвь "Объединенный мат-тред".
Пусть G - группа.
Требуется доказать, что произведение g1 g2 ... gn не зависит от расстановки скобок.
Док-во:
по индукции. база n=3 - верно (аксиома)
предположим, что верно для n = k,
докажем, что верно для n = k+1
(g1 g2 ... gk)gk+1 = ((g1 g2...gm)(gm+1...gk))g_k+1
Пусть g1 g2...gm = a
gm+1...gk = b
Тогда (ab)g k+1 = a(b*g) в силу аксиомы
Верно?
Это ещё почему?
Они базируются на уже готовых числах N и сами натуральные числа не определяют.
>>393340
>ты не можешь юзать индукцию до её определения.
Я ее построить могу. Это и есть определение. Определение индукции, оторванное от самой индукции - это мистика.
А я в них не верю, я их применяю. Верой было бы нечто оторванное от самих правил построения.
>Неконструктивная шляпа.
А я могу сказать, что конструктивизм - дерьмо. Ты по существу что-то сказать можешь?
>Их применение дает в итоге конструктивный объект - N.
Я задал вопрос не про N, а в общих чертах. Как ты докажешь, что правила построения и есть определение?
>Ты по существу что-то сказать можешь?
Могу. Логика - часть математики. Она может применяться как часть математики, но не может служить обоснованием математики.
>Я задал вопрос не про N, а в общих чертах. Как ты докажешь, что правила построения и есть определение?
Разницы нет, в общих или не в общих. Правила построения определяют объект непосредственно его построением, в результате которого и получаем построенный объект, который т.о. исчерпывающе определяется правилами своего построения.
>Могу. Логика - часть математики. Она может применяться как часть математики, но не может служить обоснованием математики.
Почему? А грамматика слово "грамматика" описывать может?
>А грамматика слово "грамматика" описывать может?
Может. Но в отрыве от грамматических правил это просто слово.
>>393355
Ой, не надо по новой. Каждый тред одно и то же. Будто я не писал что такое конструктивный объект, не писал про системы Поста, алгорифмы Маркова, лямбда-исчисление Черча и протчая и протчая. Мне в каждом треде с этого начинать?
>Логика - часть математики.
Смелое заявление. На чём оно основывается?
>Она может применяться как часть математики, но не может служить обоснованием математики.
Почему нет? Разве ты в своей конструктивной параше разве не исользуешь логику для описания правил построения?
>Разницы нет, в общих или не в общих.
Есть.
>Правила построения определяют объект непосредственно его построением, в результате которого и получаем построенный объект, который т.о. исчерпывающе определяется правилами своего построения.
Ты доказал, только что из правил построение можно что-то построить. Всё. Это не определение. Например, строитель может построить дом, у него есть правила построения(четрём там все дела). Но он может ничего не знать о молекулах, атомах, кварков и т.д, тех материалов, которые использует при строительстве. Ему не нужно определения того, с чем он работает. Так же и ты.
Не знаю. Я здесь не один. Спроси у ОПа треда для начинающих; спроси у анончиков обоих тредов; проведите голосование. Может они и объединяться не захотят.
Да на все это сто раз отвечено, трюле. Я даже в этом треде >>393144 уже пояснял. Принес вот нумералы Черча, а все опять скатывается к бесконечному повторению азов.
Не знаю в общем, решай сам, ТЫЖЕОП.
Я просто не понимаю что значит "дать основания", по мне так к этому многие люди приплетают какую-то ненужную метафизику. По мне так "дать основания" значит свести математику к каким-то более простым и более понятным любому человеку концепциям. Классическая математика (формализм типа Гильберта) сводит к "теории первого порядка" и в ней уже "правилам вывода" одних строк из других; конструктивизм типа Маркова сводит к алгоритмам - неважно в какой формализации - через нумералы Чёрча или через программы на pure C. В упор не вижу по каким причинам один подход это "основания" а другой "не основания.
> Разве ты в своей конструктивной параше разве не исользуешь логику для описания правил построения?
Есть логика и логика. Я же специально >>393144 пояснил в чем разница, третий пик. Неконструктивная логика либо неполна, либо противоречива по Геделю, там написано почему так.
>Ты доказал, только что из правил построение можно что-то построить. Всё. Это не определение. Например, строитель может построить дом, у него есть правила построения(четрём там все дела). Но он может ничего не знать о молекулах, атомах, кварков и т.д, тех материалов, которые использует при строительстве. Ему не нужно определения того, с чем он работает. Так же и ты.
Будто для того чтобы построить дом, нужно знать за каждый кварк в стройматериалах. Дом будет построен и без этого. А кварками ядерная физика занимается, а не строители домов. Какая задача, такое и решение.

>Неконструктивная логика либо неполна, либо противоречива по Геделю, там написано почему так.
Пик.
>Будто для того чтобы построить дом, нужно знать за каждый кварк в стройматериалах. Дом будет построен и без этого. А кварками ядерная физика занимается, а не строители домов. Какая задача, такое и решение.
Я рад, что ты понимаешь, что правило построение - не определения объекта. Мы пришли к согласию?
Генцена тоже разбирали уже, у него там конструктивизм на конструктивизме едет и конструктивизмом погоняет, потому у него и получилось доказать непротиворечивость арифметики. На одном формализме до сих пор бы не доказали что 1+1=2. Построение - это определение объекта, я уже сто раз объяснял почему.
>Построение - это определение объекта, я уже сто раз объяснял почему
Ты пытался объснить, а не доказать. Я хочу доказательство этого. Пример с домом опроверг твоё доказательство здесь >>393353
>Генцена тоже разбирали уже, у него там конструктивизм на конструктивизме едет и конструктивизмом погоняет
Он ученик Гилберта, а не Брауэра. Зачем ученику Гилберта заниматься констркутивной математикой?
>Зачем ученику Гилберта заниматься констркутивной математикой?
А Гильберту зачем? Метаматематика -конструктивный подход. Как и почти вся остальная математика, опять же я объяснял почему и даже Мартин-Лёфа цитировал. Говорю же, обсуждалось все это.
>Пример с домом опроверг твоё доказательство
Ну раз ты так сказал, то ладно. Даже лень объяснять, почему дом это не аналогия с конструктивными математическими объектами, настолько все очевидно и однозначно.
Ты говоришь, что определение объекта - правила его построения.
Тогда какие правила построения у фотона, например? Как ты будешь строить фотон? Или какие правила построения у бозона Хигса? Если их нет, то эти элементарные частицы неопределены и значит физика сплошное вернуство?

Ты не очень умный, да? Мы про математику и про математические объекты, а не про кобзон Хиггса.
>настолько все очевидно и однозначно
>очевидно
Обычно, когда пишут очевидно в мматематике, то всё не так уж и очевидно. Ты не ленился писать "Брауэр" несколько сотен раз, а написать доказательство лень.
> лень объяснять
Мне нужно ДОКАЗАТЕЛЬСТВО, а не ОБЪЯСНЕНИЯ! Ты видишь между этими понятиями разницу?!
Если математические объекты не имеют ничего общего с реальностью, то почему бесконечность не может существовать в математике? Ведь приминение твоих констурктивных приёмчиков к реальности полностью их дискредитирует.
>Мне нужно ДОКАЗАТЕЛЬСТВО, а не ОБЪЯСНЕНИЯ! Ты видишь между этими понятиями разницу?!
А ты видишь разницу между математическим объектом и фотонами и бозонами? Какие могут быть математические правила построения у элементарных частиц, совсем уже школота тутошняя поехала.
>>393380
И на это отвечал. Существование в математике = построение. Существование в математике чего-то, не сводящееся к построению этого чего-то = мистика. Что значит "существует бесконечность", объясни? И чем такое "существование" отличается от существования Аллаха?
>Что значит "существует бесконечность", объясни?
Значит, что соответствующая формула выводится из аксиом ZFC.

>Значит, что соответствующая формула выводится из аксиом ZFC.
А из корана выводится существование Аллаха. Чем твоя вера в KFC ZFC лучше? В обоих случаях какие-то там аксиомы, не дающие возможности построить объект, "определяемый" ими. Впрочем, это тоже уже обсуждалось.
>А ты видишь разницу между математическим объектом и фотонами и бозонами? К
Стоп.
>Существование в математике = построение.
Ну если так сказал анон с мейл.ру, то да.
http://ponjatija.ru/node/800 Тут другие определения существования.
>А ты видишь разницу между математическим объектом и фотонами и бозонами? Какие могут быть математические правила построения у элементарных частиц, совсем уже школота тутошняя поехала.
То есть мы обсуждаем не реальный мир а абстрации? Что-то вроде платоновского мира, так. Где объекты существуют сами по себе, оторванные от реальности.
>Существование в математике чего-то, не сводящееся к построению этого чего-то = мистика.
Раз уж мы оторвались от реального физического мира, то какое это имеет значение? И как же непротиворечимость теории? Мы всеравно говорим об астрациях, причём твои правила к примению в физическом мире приводят к породоксам похлеще удвоения шара.
Все это тоже было уже. Правда, мне лень по десять раз писать одно и то же. На сей раз я пришел с конкретной темой - определение N через нумералы Черча.
Физика не может быть ложной, значи ложна конструктивная математика, а значит и логика, значит, только, что выведенное ложно. Если оно ложно, то констуквтиная математика истинна, если она истинна, то высказывание ложно. Парадокс. Значит, логика - не часть математики.
>>393387
Не ври. Про физику я только сейчас сказал. Это новая тема.
— Потому.
— Ты ебанутый?
— На это неоднократно давался ответ.
— Ты можешь доказать формулу Гаусса?
— Твоя вера не нужна.
— Пошёл нахуй, ебанашка.
— Ты не воспринимаешь объективные аргументы.
— Какие?
— Хватит спрашивать одно и то же.
— Ты издеваешься. Ты не можешь писать это всерьёз.
— Я не виноват, что ты такой тупой.

>Значит либо физика ложна, либо констктивнмая математика.
Честно скажу, на этот бред кроме пикрелейтед даже не знаю что ответить. Вся суть школьной манялогики.
>ты сказал, что логика не использутся для констктивной математики, но констуктивная математика используеться для логики
Твои цытатки?
>Могу. Логика - часть математики. Она может применяться как часть математики, но не может служить обоснованием математики.
>констуктивная математика - основания математики
Просто признайся, что ты обосрался.
Верно ли следующее доказательство обобщённого закона ассоциативности?
Пусть G - группа.
Требуется доказать, что произведение g1 g2 ... gn не зависит от расстановки скобок.
Док-во:
по индукции. база n=3 - верно (аксиома)
предположим, что верно для n = k,
докажем, что верно для n = k+1
(g1 g2 ... gk)gk+1 = ((g1 g2...gm)(gm+1...gk))g_k+1
Пусть g1 g2...gm = a
gm+1...gk = b
Тогда (ab)g k+1 = a(b*g) в силу аксиомы
Верно?
Я бы проверил, но до сих пор не врубаюсь в доказательство этой теоремы. И я просто забил на неё вообще. Можешь сверить своё доказательство с доказательством и з Теорим Абеля в Задачах.
Можешь посмотреть у Кострикина доказательство.
>(g1 g2 ... gk)gk+1 = ((g1 g2...gm)(gm+1...gk))g_k+1
С этим соглашусь.
>Тогда (ab)g k+1 = a(b*g) в силу аксиомы
С этим тоже.
Каким образом из этого следует, что в изначальном произведении можно выбирать любую расстановку скобок?
>>392366 (OP)
Ну, вот, взять например,
5√1;
Пускай это будет cos(2П4/5)+i×sin(4П/5).
Как правильно возвести это всё в 5-ю степень, может кто-нибудь расписать?
> На одном формализме до сих пор бы не доказали что 1+1=2. Построение - это определение объекта, я уже сто раз объяснял почему.
Ты ебанашка необучаемая, иди читай учебники блядь! Формализм это желание максимально подробно описать математику формальным языком. Самые ярые формалисты: Бурбаки и создатели HoTT. Противники формализма: Брауэр, который поэтому даже не формализовал интуиционистскую логику, пришлось другим за него это делать. Что ты несешь то блядь?
Далее, Гентцен использовал трансфинитную индукцию. Какой конструктивизм блядь? Что ты несешь? Можно ли представить что-то более невероятное из области бесконечного, чем трансфинитную индукцию?
>определение N через нумералы Черча.
Где-то есть тред Computer Science, тут же занимаются математикой, а не компьютерной поеботой.
>Самые ярые формалисты: Бурбаки
На самом деле нет, они не формалисты. Для них эстетика всегда важнее формальности.
Ты так говоришь, как будто современная математика - это не компьютерная поебота.
В принципе да. Компьютерные формалисты зашли куда дальше.

>А ты видишь разницу между математическим объектом и фотонами и бозонами? Какие могут быть математические правила построения у элементарных частиц, совсем уже школота тутошняя поехала.
Математика - часть физики.
-В.А. Арнольд
А ты вредный.
всё произведение вырождается в три сомножителя, среди которых мы можем ставить скобки как угодно, не?
Вообще скучное доказательство и сама теорема, но хочется разобраться, Винберг потому что сказал "легко видеть"
Доказательство подробное и лёгкое, поймёт любой, знакомый с комплексным анализом.
1. Идёшь на bitcoin brain wallet generator.
2. walletgenerator.net
3. Генеришь биткоин адрес. (Туда же можешь запросить и эти свои лиммионы)
4. Сохраняешь приватный (СЕКРЕТНЫЙ) ключ у себя.
5. Вбиваешь биткоин адрес в http://wallet-2sx53n.sakurity.com/#sign
6. Вместо message - своё доказательство.
7. Нажав кнопку sign message подписываешь сообщение приватным ключем.
8. Проверить цифровую подпись можно здесь: http://wallet-2sx53n.sakurity.com/#verify - в результате, будет адрес.
9. Т. к. никто, кроме тебя не знает приватный ключ - никто не сможет сгенерировать новое сообщение, подписанное твоим адресом.
Ведь сообщение подписывается приватным ключом.
Подписанное сообщение выглядит примерно так:
-----BEGIN BITCOIN SIGNED MESSAGE-----
This is an example of a signed message.
-----BEGIN SIGNATURE-----
1HZwkjkeaoZfTSaJxDw6aKkxp45agDiEzN
G464uQHxQKFoM5REYcTJN6JOd4Ezzg2bDY7E7VIa0ICwRf/CS9hs9f/F3i/SF7b5of6le6+BWVaUnqE3wyAjvL0=
-----END BITCOIN SIGNED MESSAGE-----
Можешь также, юзать трипкоды.
https://2ch.hk/dr/res/97.html (
10. Постишь подписанное сообщение здесь.
11. И можешь ссылаться на него, даже когда тред уйдёт в бамплимит.
12. Твоё доказательство с цифровой подписью наверняка будет на архиваче.
(http://arhivach.org/)
Там же, сможешь найти и этот тред по ссылке, и свой пост.
13. Не забудь вставить дату в подписанное сообщение. Она как-бы докажет, что ты опубликовал это раньше.
14. ?????
15. PROFIT!
>>393488
Алсо, brainwallet генератор можешь слить в zip-архиве, в виде JS и HTML-кода и открыть его у себя в браузере с диска. Он работает локально, и не требует сетевого подключения, по сути.
https://github.com/MichaelMure/WalletGenerator.net/archive/master.zip
Вот он, на github'e.
А вот тебе bitcoin signature tool, на JS, которая тоже работает локально.
https://github.com/ReinProject/bitcoin-signature-tool/archive/master.zip
>чтобы получить свой
Вообще-то обещают выплату Математический институт Клэя, значит - тебе туда.
Но доказательство - лучше всё-равно подпиши. И даже время с микросекундами вставь. =)
Ещё раз:
1. Допустим, walletgenerator.net, при генерации, выдал:
5JdYN7qdXEFnC6hrbPCQV9UdE4jX6Zvj2YWfAx9Lo4dzGrso71c - приватный ключ. Знаешь только ты.
1CcdZSAVDvHBaZdmZygWEKcKd6zZyY3eSt - биткоин адрес.
2. Вбиваешь всё это http://wallet-2sx53n.sakurity.com/#sign или же в bitcoin signature tool:
Private key: 5KYZdUEo39z3FPrtuX2QbbwGnNP5zTd7yyr2SC1j299sBCnWjss
address - получается из приватного ключа, но не наоборот.
message
"Доказательство Васи Пупкина.
Дата: Wednesday, October 19, 2016
Время: 13:41:37
Курлык-курлык-курлык."
Нажимаешь "sign message" -> получаешь подписанное сообщение:
"-----BEGIN BITCOIN SIGNED MESSAGE-----
Доказательство Васи Пупкина.
Дата: Wednesday, October 19, 2016
Время: 13:41:37
Курлык-курлык-курлык.
-----BEGIN SIGNATURE-----
1HZwkjkeaoZfTSaJxDw6aKkxp45agDiEzN
GyJbLY3gaq8sRsVKI1AguEoptP8qY6vVuRL9FndVLbWuYUGVrY/AhSf8s3NjFPOS1Dhqlg0pBBLI4OFxHp8CeJw=
-----END BITCOIN SIGNED MESSAGE-----"
Вот его и постишь везде и всюду, и во все поля,
пока институт Клея - сам к тебе не прийдёт.
Можешь запостить и здесь своё доказательство [spoielr]и никто его не спиздит, потому что подписанное[/spoiler], а мы замутим "одобрение" - нас легион.
Ещё раз:
1. Допустим, walletgenerator.net, при генерации, выдал:
5JdYN7qdXEFnC6hrbPCQV9UdE4jX6Zvj2YWfAx9Lo4dzGrso71c - приватный ключ. Знаешь только ты.
1CcdZSAVDvHBaZdmZygWEKcKd6zZyY3eSt - биткоин адрес.
2. Вбиваешь всё это http://wallet-2sx53n.sakurity.com/#sign или же в bitcoin signature tool:
Private key: 5KYZdUEo39z3FPrtuX2QbbwGnNP5zTd7yyr2SC1j299sBCnWjss
address - получается из приватного ключа, но не наоборот.
message
"Доказательство Васи Пупкина.
Дата: Wednesday, October 19, 2016
Время: 13:41:37
Курлык-курлык-курлык."
Нажимаешь "sign message" -> получаешь подписанное сообщение:
"-----BEGIN BITCOIN SIGNED MESSAGE-----
Доказательство Васи Пупкина.
Дата: Wednesday, October 19, 2016
Время: 13:41:37
Курлык-курлык-курлык.
-----BEGIN SIGNATURE-----
1HZwkjkeaoZfTSaJxDw6aKkxp45agDiEzN
GyJbLY3gaq8sRsVKI1AguEoptP8qY6vVuRL9FndVLbWuYUGVrY/AhSf8s3NjFPOS1Dhqlg0pBBLI4OFxHp8CeJw=
-----END BITCOIN SIGNED MESSAGE-----"
Вот его и постишь везде и всюду, и во все поля,
пока институт Клея - сам к тебе не прийдёт.
Можешь запостить и здесь своё доказательство [spoielr]и никто его не спиздит, потому что подписанное[/spoiler], а мы замутим "одобрение" - нас легион.
Спасибо, конечно, за такой надёжный способ подтверждения авторства, но если я опубликую док-во сюда, то как Математический Институт Клэя сможет о нём узнать?
Здесь вообще есть хоть пара ананонов, кто знает на среднем уровне комплексный анализ? Или только множество N обсуждать горазды?
У них в правилах написано, что перед вручением премии научное сообщество моё док-во должно проверить и признать. Для этого нужна публикация в журнале, а не на окраине интернета. Наверное.
Вот Перельман свои потоки Риччи на arxiv.org опубликовал, у меня даже на архиве нет разрешения на публикацию.
Миша Вербицкий может посмотреть, если аноны одобрят, кто-нибудь скинет ссылку на тифаретчик.
>научное сообщество моё док-во должно проверить и признать
Ну так, чтобы это было, надо ж распиарить это дело значит - в среде научного сообщества, разумеется.
Чё ты сидишь-то, а?
Подпиши и вайпай треды, лол.
Можешь подписанное сообщение почтой на бумажке в институт Клея отправить.
Вот ихний адрес: Clay Mathematics Institute
70 Main St
Suite 300
Peterborough, NH 03458
USA
CMI President’s Office
Andrew Wiles Building
Radcliffe Observatory Quarter
Woodstock Road
Oxford OX2 6GG, UK
Можешь его на билборды прицепить, на форумы всякие запостить, чаты заспамить и т. д.
На википедию прицепить, в конце-концов...

Решал за бабосы контрольную, препод поставил за задание минус. кто из нас в глаза ебётся? не вижу ошибки в упор
У них что, Интернета нет?
Сослаться на пост можешь с помощью
символа #
https://2ch.hk/sci/res/392366.html#393498 (
393498 - номер поста.
Или, например, вот так: http://arhivach.org/thread/206244/#393264
на архиваче, когда тред уйдёт в бамплимит или его выпилят.
>>393488
>>393491
>>393493
>>393497
>>393498
Да, и вот ещё... Подпись нужна для проверки того, что сообщение отправлено именно от адресата, а не от какого-то рандом анона.
Адрес - открытая информация (хеш публичного ключа), приватный ключ - закрытая инфа.
Текст - открытая инфа.
Т. к. рандом анон может извлечь инфо и подписать её другим ключём, с другим адресом в результате проверки подписи, позже причём,
значит адрес надо опубликовать прежде чем будет опубликовано сообщение содержащее цифровую подпись.
Такие дела.
>Ты с тифаретника что ли?
>Ты нахуй на моём тифаретнике
Хрень какая-то без https и SSL. Двощи рулят.
>Пепка прыгни
Аж туда прокинул этим?
Вербит говорил о какой-то альтернативе архиву для ноунейм бомжей. Правда я не помню, как называется
Верно ли следующее доказательство обобщённого закона ассоциативности?
Пусть G - группа.
Требуется доказать, что произведение g1 g2 ... gn не зависит от расстановки скобок.
Док-во:
по индукции. база n=3 - верно (аксиома)
предположим, что верно для всех n меньших k,
докажем, что верно для n = k
(g1 g2 ... g_k-1)gk = ((g1 g2...gm)(gm+1...g_k-1))g_k
Пусть g1 g2...gm = a
gm+1...g_k-1 = b
Тогда (ab)g_k = a(b*g_k) в силу аксиомы
т.е. наше произведение из n cомножителей выродилось в произведение трёх сомножителей, среди которых мы можем ставить скобки как угодно. Т.е. мы доказали, что результат не зависит от расстановки скобок, а значит обобщённый закон ассоциативности доказан.
бля я понимаю, что это пиздецки скучная теорема и доказательство чисто техническое и без идеи, но мне надо его усвоить, чтобы двигаться дальше.
алсо вторую задачу из учебника винберга (доказать что любая подгруппа Z имеет вид nZ ) я спокойно решил
Забей на это гавно, блядь.
И ты доказал, что g1g2g3...gn+1 = (((g1g2g3...gm)(gm+1gm+2...)g_k)
А нужно для любой расстановки скобок.
К примеру для (g1g2g3...)(gk1gk2gk3...*gk) ты нихуя не доказал. Хотя, возможно, я тупой дебил несу хуйню
vixra.org
я такой аутист, что пока с этим говном не разберусь дальше не смогу нормально книгу читать.
и я доказал, что g1...gk = ((g1...g_m)(g_m+1...g_k-1))g_k = (g1...g_m)((g_m+1...g_k-1)g_k)
бля. теперь я понял где соснул.
какого хуя винберг говорит тогда "нетрудно вывести". ну да, для него нетрудно наверное. петухан бля
>я такой аутист, что пока с этим говном не разберусь дальше не смогу нормально книгу читать.
Избавься от этой привычки, она очень сильно тормозит и не факт, что ты решишь задачу.
>На dxdy вас бы всех обоссали и перебанили, особенно "доказавшего" Римана - его бы ещё и выебли.
Дед, плис, обоссали бы может да, у половины дедов там энурез, а вот что выебали не факт, чирикалка в таком приклоном возрасте просто не работает.
>Соси хуй.
Твоя мать-шлюха будет его сосать.
>То есть, ты защищаешь "доказавшего" Римана? правильно понял, петушок?
Дед, в твоём возрасте делать логичные выводы сложно и я действительно сочувствую тебе. Но я имел в виду, что таких поехавших, как решишвий задчу, на dxdy полно, один Мунин чего стоит с его тензорами, которые придумал Эйнштейн. И никто его не обоссывает и не ебёт, говорю же у дедов чирикалка давно не работает.
Я на это и намекал здесь (>>393396). Тебе нужно доказать, что (g_1 × g_2 × … × g_m) × (g_{m+1} × … × g_n) = (g_1 × g_2 × … × g_l) × (g_{l+1} × … × g_n). Вот тогда ты докажешь, что скобки можно расставлять как угодно. Чтобы это доказать, удобно воспользоваться левонормированной формой произведения. Короче, ничего сложного у Кострикина нет, но пишет он запутанно.
Дед, ты обосрался иди смени памперс, просто представь сколько правил dxdy ты нарушил этими постами:
>>393548
>>393555
>>393559
Так, что обоссали бы именно тебя там а не решателя гипотезы римана.
Нет, в учебники хуёво написали.
Конечно, можешь учить всё сразу.
Теория категорий абстрактна, но перед ней лучше изучить мотивировку этих всех обозначений, т.е. алгебру.
Топология, теория узлов как ее часть, теория графов, они вообще довольно независимы, применяются в других местах, но сами посторонних знаний не требуют.
Есть Aluffi, Algebra Chapter 0. Там алгебра (которая пригодится по-любому) вводится на языке категорий, отличная вещь. Пререквизитов никаких не надо. Имхо, чтобы учить теорию категорий с ходу нужно быть невообразимым аутистом - слишком абстрактно - мотивации и применения будут непоняты как мне кажется.
>вас спросили не о теории категорий
>Можно ли скипнуть этот ваш анализ и сразу перейти к годноте вроде теории категорий ...
Я ответил на эту часть - что да, можно, но через алгебру.
А предыдущий анон вообще один в один на поставленный вопрос ответил полностью.
А вдруг он её решил?
*того
Теоретико-категорное обобщение понятия функции это пучок. Функции работают с числами, пучки с векторными пространствами. Анализ нужно учить на языке пучков. Начни с понятия векторного расслоения.
Основное понятие в алгебре это модуль. Модули бывают над кольцом, так что начни с изучения колец. Группы (не абелевы) не нужны, это отдельная область. Кольцо это абелева группа по сложению + ассоциативное умножение + дистрибутивность. Модуль это обобщение понятий абелевой группы и векторного пространства. Скаляры в векторном пространстве образуют поле, для модуля достаточно кольца. Модуль над кольцом, который сам является кольцом, называется алгеброй.
Векторное расслоение это обобщение понятия векторного пространства. Если слои в векторном расслоении являются алгебрами, то оно называется когеретным пучком, но это в алгебраической геометрии.
Пучок бывает над топологическим пространством. Группа сечений пучка определена для каждого открытого подмножества пространства, плюс отображение ограничения для каждого включения. Локально тривиальное векторное расслоение (fibre bundle) локально гомеоморфно декартову произведению, пучок же локально гомеоморфен самому пространству. Пучок колец это способ сопоставить гомоморфизмы колец включениям открытых множеств. Конверсия глобальных данных в локальные.
Теория категорий и ее мотивация лежат в гомологической алгебре. И гомологическая алгебра, и теория представлений, и алгебраическая к-теория изучают модули. В последней области модули нужны проективные, поскольку hom functor is exact они дают локально свободный пучок.
Про анализ пусть расскажет кто-то другой, мне он нахуй не нужен лично. Или читай Касивара, Шапира.
Матаны, нужен учебник/пособие по механике сплошных сред, жидкость. И задачник к нему. На дхду ничего не нашел, выручайте.
По количеству интересного хардкора - программа Вербицкого, с большим запасом. По количеству фолловеров - Бурбаки.
Верно, это я.
>>393695
Обосрался, по следующей причине: один человек заверил меня, что полнота по дедекинду и архимедовость это эквивалетные требования. А про теорему Островского я просто забыл. Что касается R, то оно и правда не нужно, мне по крайней мере.
>>393685
Программа Вербицкого достаточно хороша для самостоятельного изучения, по причине разообразия тем. Схематически её можно представить так:
2 курс: спектралки, хар классы, коммутативная алгебра.
3-й: топологическая к-теория, гомотопическая алгебра, алгебраическая геометрия
4-й: алгебраическая к-теория, этальные когомологии
5-й: программа мори, гипотезы вейля.
Плюс процентов 30 того, что интересно Михаилу Сергеевичу.
Когомологии Галуа уже можно заменить мотивными когомологиями им. Воеводского. Каледин мог бы в этом манифесте написать про циклические гомологии, поскольку у него нет такой боли, как у тифарета (утверждающего что когомологии де рама проще сингулярных и вообще топологическая мотивация не нужна).
Этальные когомологии на четвертом курсе нужны для последующего изучения работы Делиня. По мнению Вербицкого геометрический ленглендс это и есть современная математика.
Эллиптические когомологии, топологические модулярные формы и вообще производную математику оба дружно отрицают, тут лучше слушать более адекватных людей.
Что интересно в имеющемся списке -- последовательное изучение сначала топологической к-теории, потом алгебраической к-теории. Общего у них только К0. Топологическая это про операторные С* алгебры, алгебраическая же раздел линейной алгебры. Это экстремизм, это хорошо и правильно. В этом смысле его же программа для ВШЭ уныла и не интересна, поскольку экстремизма уже нет, а вкусовщина и неосиляторство остались.
Ты всё ещё считаешь, что математик должен быть мистиком и эзотериком?
Ко-ко-консурктивист нас тут верунами и мистиками обзывает, как ты к этому относишься?
>11!
>!
>11!=39916800
Полегче со знаками восклицания, мужик. Навряд ли столько мат-тредов вообще будет.
Алгебраическая крайне сложна и интересна -- BGL(R)+ Квиллена, категория Вальдхаузена, те же мотивы появляются отсюда.
А вот теория представлений в контексте геометрического Ленглендса это ультрамейнстрим, каждый желающий попасть в Гарвард обязан этим заниматься, перефразируя Арнольда можно говорить о гельфандской мафии в московской школе, находясь вне которой можно быть только очередным маргиналом с нлаба.
Я понял, что ты хотел сказать.
Конструктивисту кстати можно было бы форсить Вайлдбергера, отрицающего слишком большие числа и не употребляющего R вообще. Серьезно, у него есть только rational, decimal и complex. Это охуенно, по моему. Общая топология и то, что считается основами анализа, достаточно легко вытекают из теории множеств Кантора и достаточно нахуй никому не нужные за её пределами.
Отношусь так: Кантор спиздил все у более гениального Дедекинда (который еще и первым ввел определение N понятие мат. индукции, дал определение поля, кольца и идеала, алгебраически построил римановы поверхности и тд). А Брауэр, например, за один семинар сформировал Витгенштейна-2 как философа. После написания трактата тот разочаровался в позитивизме и считал философию бесполезным занятием.
Ну наш конструктивист отрицает матиндукцию и аксиому выбора в принципе, заодно с исключенным третьим, так что и топология у него pointless, и анализ конструктивный, что маргинальщина невероятная.
В смысле про Витгенштейна? Расскажи про него. Он применял математическую нить в своей философии языка?
Конечно же нет, математика у него на таком же иллюстративном уровне, как и у Канта. А философские исследования он написал через 20 лет после злополучной лекции.
Что двачеры будут обсуждать в математическом треде под номером 39916800? Конструктивиста?
А во время войны он в дневнике писал, что типа потерял математическую нить своего философского рассуждения. Врал, собака?
Отрицание аксиомы выбора не такая уж и редкость, почитай блог Павлова, например. Да и сам Вербит говорит, что многие важные результаты можно получить и без нее, см его лекцию про Банаха-Тарского.
>>393719
После лекции он написал синюю и коричневую книги, из которых выросли философские исследование, при жизни так и не опубликованные. А математика его была на уровне Фреге и Рассела-Уайтхеда, потому что с ними он общался.
Эй, я вилдербергера форсю, а конструктивист - петух и ненастоящий конструктивист. Но вы все еще хуже, фанатики ебаные.
Домашку с интегралами и производной.
Будут плеваться от того, что мы называли современной математикой и первой культурой. А нас будут называть дедами.
А после всей этой программы от Вербицкого можно начать понимать современные работы в алгебраической геометрии и теории чисел (те, что на arxiv.org) и работать с ними? А после книг Бурбаки, для сравнения?
Сам я по глупости инженегор четвёртого курса. Хотя всегда хотел стать математиком (первокультурным, а не интеграло-обезьяной, как сейчас).
Да, и гораздо раньше. По Бурбаки нельзя, там алгебраической геометрии нет. Зато второй том по группам Ли хороший.
Так, а евклидова геометрия нужна? У него в программе есть. Вообще, весь этот первый его блок "Матшкольник (школьная программа)" мне, нешкольнику, нужен? Не говорю, что знаю хотя бы половину тем в нём, просто он оторван от программы и эти вещи далее, вполне вероятно, прояснятся в предложенных им же учебниках не на школьном, а уже нормальном уровне.
Вот программа сама, если что: http://imperium.lenin.ru/~verbit/MATH/programma.html
Евклидовой, аффинной и проективной геометрий достаточно в объеме книги Прасолова и Тихомирова. Про ортогональную и симлектическую можно читать у Артина (геометрическая алгебра) или Коксетера (введение в геометрию).
>>393746
В 2004 в НМУ Миша с Димой вели спецпоток, где учили тому, что нужно было выучить в школе. Большинство тем из программы соответствуют тому, что дано в листочках(нет анализа, логики и ТМ).
http://ium.mccme.ru/f04/experimental.html
Здесь можешь pdf-ки скачать, но не все в pdf
http://imperium.lenin.ru/~verbit/MATH/LISTKI/TRIVIUM/
Конвертер из ps в pdf
https://online2pdf.com/convert-ps-to-pdf
Есть опечатки в некоторых местах, но ты их заметишь, скорее всего.
имхо это все бесполезно. Когда это объясняет лектор, потом приходишь обсуждать задачки с другими ребятами, решения проверяют, то это годнота, а в отрыве от людей нет.
Dead s dxdy, pliz
Скажем, закончил человек магистратуру, идёт в аспирантуру, учится там три года. Что дальше?
И как эти степени транслируются в американские стандарты? В phd что переводится?
>закончил человек магистратуру, идёт в аспирантуру, учится там три года.
И master degree и phd получают в graduate school. Магистр для индустрии, phd для академии. Поступают туда бакалавры. На phd учатся пять лет, в первые два из которых ты проходишь обязательные курсы, а далее работаешь над тезисом.
В рф магистр обязателен, сделано это чтобы не убить специалитет в местах типа мехмата мгу. И магистры и специалисты могут поступить в аспирантуру и получить там phd -- кандидата наук. Дальше можно через какое-то время защитить докторскую. У нас это называется доктор наук, в Германии -- габилитация.
>Дальше можно через какое-то время защитить докторскую.
То-есть, там нихуя не надо делать, кроме диссертации?
Основные научные результаты докторской диссертации должны быть опубликованы в ведущих рецензируемых научных журналах и изданиях, перечень которых определяет ВАК.
Спасибо, что помогаешь моей мама с математикой.
Кстати, пока вы с ней занимались математикой, мы с твоей мамкой занимались сексом. Я ебал её во все щели, засовывал ей свой хуец в очко, а потом она слизывали с его говно. Ещё она облизала мне анус. Твоя мам развратная женщина, я такого, что она вытроряет даже в порно не видел.

Мне не с кем и я не понимаю зачем их обсуждать? Если твоё решение тебя удовлетворяет, то мне кажется этого достаточно.
Обвинение в мистицизме было довольно привычным делом для канторовской теории, которая в итоге рухнула под грузом парадоксов. Воскресить ее не удалось и более поздние математики решили притвориться, что так и надо.
Источник таких обвинений -- вы берете логику, справедливую в отношении финитных объектов, и необоснованно начинаете применять ее к инфинитным.
Под эзотерикой и мистикой я понимал не это, а отход от рационализма прежде всего.
Ясно.
Ну лично я так много неверных и неточных доказательств сочинил, шаги какие-то пропустил, важные проверки. А еще товарищ может придумать более изящное доказательство и за какую-то очень сложную теорему можно взяться вдовем.
>берете логику, справедливую в отношении финитных объектов, и необоснованно начинаете применять ее к инфинитным
Покажи несколько примеров такого.
Существование недостижимого кардинала. Первая проблема Гильберта. Вообще любое бесконечное множество.
Classical logic was abstracted from the mathematics of finite sets and their subsets …. Forgetful of this limited origin, one afterwards mistook that logic for something above and prior to all mathematics, and finally applied it, without justification, to the mathematics of infinite sets. This is the Fall and original sin of [Cantor's] set theory.
Это список buzzword'ов. А ты покажи, пожалуйста, именно то, как математики "берут логику, справедливую в отношении финитных объектов, и начинают применять её к инфинитным". На конкретных примерах. Желательно без больших кардиналов, так как для их содержательного изучения необходимы аксиомы, отличающиеся от канона ZFC, и я уверен, что с этими аксиомами в этом треде никто не работает.
поункукаре-кун
Я специально купил пасскод и отправил заявку на /math, но ответа нет. С Абу свяжитесь, если хотите, попросите обезьяну мою заявку одобрить.
непроеби, Саш
Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.
Через две точки можно провести одну и только одну прямую.
Это, кажется, аксиома принадлежности, из Начал Евклида.
>>393835
Если прямая лежит на плоскости, значит она пересекается с ней в точках этого конкретного отрезка, не?
Существуют точки прямой, не лежащие в этом отрезке, но принадлежащие пересечению.
Ну, пускай у тебя будет неевклидова геометрия
и кривое пространство с неким коэффициентом кривизны.
И пускай в этом пространстве будет плоскость.
Ты сможешь нарисовать прямую, удовлетворяющую твоим условиям?
Или даже не прямую, а кривую, потому что пространство кривое же.
В этих лекциях было: http://ium.mccme.ru/f15/algebra-3.html
Задачи там же и, например, в Атье-Макдональде, с. 47.
Ещё в книжке Прасолова есть про Tor_1 (там он назван просто функтором Tor).
Ещё - английская Википедия и какие-то книги и записки лекций, найденные по запросу "tor/ext functor" и "group cohomology".
Внятного последовательного изложения в книгах, увы, не знаю.
А ответ на свой вопрос нашёл здесь, 10 страница: http://www.mi.ras.ru/~kazarian/papers/chcl06.pdf

Ах ты лживый хуесос, статья у него по функану. А сам-то даже в интегралах не может разобраться, вот же питух. И хуй дед твой сосёт.

Ты у ко-ко-консруктививиста местного спрости, когда он штанишки постирает, то сюда придёт.
Это пример функции. А не пример определения функции как объекта/явления вообще.
Для разнообразия аксиома подстановки. Какой наркоман её придумал? Типа, если есть множество M и есть функциональное высказывание f, в которое можно подставлять множества, - то f-образ M снова множество, как?! Что за бред, объясняйтесь веруны. С фига ли у вас можно преобразовать одно множество в другое, просто указав правило преобразования элементов?
Желательно на английском. Их много, не знаю, что выбрать.
Спасибо.
Да, это сарказм. Второй том зорича на голову полезнее первого. Как минимум интереснее.
Спасибо. Пойду читать.
Только в случае неконструктивных множеств. Я же сто раз давал ссылку на реализацию ZFC через зависимые типы. Все там конструктивно, если не основано на вере в бесконечность саму по себе, вне хотя бы и потенциально построимого объекта.
Algebra chapter 0 буквально пару постов назад советовали на аналогичный вопрос.
Хочешь сказать, что
(cos(2П4/5) + i×sin(8П/5))5 =
15×(cos(5×2П4/5) + i×sin(5×8П/5)) =
15×(cos(8П) + i×sin(8П))?
А дальше что?
Пиздец, с кем я на борде сижу. Просто посмотри определение интеграла простой функции, тогда, если не последний даун, поймешь, как это доказывается. Там и доказывать то нечего.
Нет. Я тополог, а та картофан!
Да. Поэтому и прошу помощи.
как закатиться в алгебру "для себя"с возможными профитами? Знание нулевоену складывать вычитать да делить могу, но допустим таблицу умножения так себе знаю. Откуда начать? Даст ли школьная программа что-то полезное? Пните в нужном направлении, как освою прибегу дальше спрашивать.
Алгебра Гельфанд Шень, Гашков Элементарная алгебра, Алексеев теорема Абеля в задачах и решениях, рандомный учебник по алгебре.
Понял, чтопроебался. Зачем несколько тредов для математики?
Спасибо!
Так как я я не распознал, буквально каким формализмом ты пользуешься в >>393937, я не берусь судить, что ты понимаешь под "реализацией", где именно ты её проводишь и нет ли у тебя ошибок. Но хочу обратить внимание на то, чем это быть не может. Как несложно показать, ZFC доказывает непротиворечивость базовой теории типов Мартин-Лёфа, как впрочем и ряда её вариаций с аксиома вселенных (кстати, относительно недавно было доказано, что это имеет место даже если добавить аксиому унивалентности). Но если бы твоя "реализация" сводила бы вопрос о непротиворечивости ZFC к непротиворечивости одной из перечисленных выше теорий, то ZFC доказывала бы свою непротиворечивость и была бы противоречива в силу второй теоремы Гёделя о неполноте. Вообще говоря, нет никаких причин полагать, что какие-либо разумные с концептуальной точки зрения теории зависимых типов окажутся сильнее ZFC или хотя бы, что они будут непротиворечивы, но это нельзя будет установить в ZFC (см. https://www1.maths.leeds.ac.uk/~rathjen/typeOHIO.pdf ). Тем самым здесь не может выходить сведение непротиворечивости, а тем самым довольно странно называть это реализацией.
Извиняюсь, не та статья - должна быть эта http://www1.maths.leeds.ac.uk/~rathjen/EHPanthology.pdf
Смотря для каких прикладных задач, для некоторых придёться самому подбирать разделы.
Опять же для вычислений чего? Гугли численные методы, для разных задач они разные.
Не нужно.
>нет никаких причин полагать, что какие-либо разумные с концептуальной точки зрения теории зависимых типов окажутся сильнее ZFC или хотя бы, что они будут непротиворечивы
Я же тут >>393144 3ий пик, привел тезис Мартин-Лёфа насчет того, почему конструктивная форма суждений полна в отличие от неконструктивной. За твою "концептуальную точку зрения" ничего не могу сказать, что ты там взял и откуда. С парадоксами и противоречиями в конструктивной математике все просто - посылки, ведущие к противоречиям просто выбрасываются как бесполезные, нарушающие вычислимость и все. Так было с парадоксом Жирара в MLTT.
>довольно странно называть это реализацией.
А что это https://coq.inria.fr/V8.2pl1/contribs/ZFC.html если не реализация? Этот Акцель, насколько мне известно, вообще предлагал конструктивный вариант ZFC использовать вместо MLTT, там целая книжка есть, я не читал правда.
Там капча сломана, треды не создаются.
>>довольно странно называть это реализацией.
>А что это https://coq.inria.fr/V8.2pl1/contribs/ZFC.html если не реализация?
Честно говоря, здесь еще надо разбираться, что именно там реализовано - настоящая ZFC над классической логикой или тот или иной ограниченный вариант (скажем CZF в самом деле погружается в теорию типов). Кстати прямо в абстракте там указывается, что нужны неконструктивные аксиомы
> A non-computational type-theoretical axiom of choice is necessary to
prove the replacement schemata and the set-theoretical AC.
Так что может и правда здесь самая обычная ZFC, но не в базовом Calculus of Inductive Constructions, а в его расширение неконструктивными аксиомами. Но если это так, то конечно занятно взглянуть, чем именно является теоретико-типовая аксиома выбора и почему она столь сильно усиливает теорию, но заявлять, что ZFC конструктивно реализована полностью некорректно.
>За твою "концептуальную точку зрения" ничего не могу сказать, что ты там взял и откуда.
Еще раз, я привел вовсе не случайную ссылку (http://www1.maths.leeds.ac.uk/~rathjen/EHPanthology.pdf). Автор (кстати, крупный специалист по интуиционистским теориям множеств) довольно подробно анализирует возможные расширения MLTT, которые лежат в рамках изначального подхода. Он формулирует некоторую систему T и неформально аргументирует, что в неё погружаются всевозможные концептуально правильные потенциальные расширения MLTT (она сама уже лежит за рамками этого подхода), а далее оказывается, что по силе T находится на уровне некоторого фрагмента арифметики второго порядка (теорема 6.3), т.е. гораздо ниже ZFC.
>настоящая ZFC над классической логикой или тот или иной ограниченный вариант (скажем CZF
А чем "настоящая" лучше? И вообще, не та ли настоящая, которую можно построить, а не веровать в нее?
>И вообще, не та ли настоящая, которую можно построить, а не веровать в нее?
Пользуйся теми теориями которые тебе нравятся, никто ведь не мешает, но аббревиатура ZFC имеет общепринятое понимание и не нужно пытаться его подменить.
>А чем "настоящая" лучше?
Скажем, CZF и ZFC - это разные системы, решающие разные задачи. ZFC - это формализация неформальной канторовской теории множеств. Поэтому она прекрасно подходит (хотя зачастую и крайне избыточна) для формализации областей математики построенных в теоретико-множественном духе (т.е. большей части математики) и также для собственно изучения теории множеств. CZF - это попытка сохранить фрагмент теории множеств, оставаясь в рамках интуиционистской парадигмы.
В /d/ зайди. Да, ты знаешь куда.
>CZF и ZFC - это разные системы, решающие разные задачи.
Ой, всё. А не разные подходы к одному и тому же, не?
К основаниям.
>А не разные подходы к одному и тому же, не?
Одна теория полноценная формализация канторовской теории множеств, другая нет (что там насчет диагонального метода в CZF? ах да, ведь в CZF даже нет нормальной аксиомы степени).
У меня время до утра, чтобы понять. Хуево напишу завтра - хуево пройдёт все полугодие.

Блять как же проигроваю с коментов этого опущенного репера.
Школьник, угомонись.
Да.
Когда вы съебете наконец то можно будет создать нормальный тренд математики для нематематиков.
Тред для новичков перекатывается в /math.
Обычный мат-тред, остаётся в /sci и превращается в тред математики для не математиков, ну или филиал /math в /sci.
Перекатываемся =======> https://2ch.hk/math/res/200.html (
Посмотрел эту новую доску, мда-мда, оп чсвшное мудило и пошел нахуй со своей доской в пизду.
Дурачок? Где там ЧСВ?
>оп чсвшное мудило и пошел нахуй со своей доской в пизду.
Это ты про меня или про создателя доски?
Я так и не пойму зачем ставиться коэффициент 1, когда нету числа рядом с буквою?
Тся.
потому что цифры это многочлен, а буквы прост для удобства
С 30й минуты, поясните поцаны, я понимаю что он доказывает на пальцах, но почему он использует в доказательстве windinw numbers? Разве не достаточно что у него между малым кругом вокруг проекции нуля и большим-большим кругом - непрерывная функция и она покроет собой область нуля? Причем здесь winding numbers?
Осторожно, в видео - сектанство.
Добавь к скорости отрицательное ускорение.
Поясните за процесс синтеза молекул нуклеиновых кислот, гомологичных вирусному геному с точки зрения гомологий и когомологий.
Гомологии — одно из основных понятий алгебраической топологии.
Так что без топологий тоже не обойтись.
А чтоб вкатиться в когомологии, надо походу котопологии.
Полностью с тобой согласен.
С мейлру все адекваты кроме меня давно съебали. Нет ничего интересного в общении со школуйней, чей предел - аргументация уровня "азаза мамку твою ебал, поссал на опущенца)))".
Потому что все по делу. У тебя получается написать больше пяти постов о математике в неделю?
С чего это друг? Или ты представляешь беседу в мат-треде в виде онли решения задачи школьникам?
Нет, просто смехуечки неотъемлимая часть мат-треда. А сейчас ты просто пытаешься оправдать мёртвость доброчана тем, что там якобы говорят только по делу. Если бы там было больше анонов, то и смехуечки были бы.
Гротендик нассал на тебя только что.
Не ври. На всём /math поста четыре с домашней из трёхсот. Модератор /math может удалять и такие редкие просьбы о школьной домашней, но вряд ли это нужно, если ты не ебанутый.
/math сейчас - просто отображённый в доску мат. тред.
>На всём /math поста четыре с домашней из трёхсот.
Да, остальные посты - в треде рыбникова или ℕ-петуха.
Там только 34 поста. Причём, это нафлудили два анона(один из которых я). И да Рыбников-тред как раз и создан ради того, чтобы там можно было бы оттянутся и мальца пошитпостить.
Я не вру. А ты не оправдывайся. Гоните нахуй школьников оттуда (хотя это все равно не поможет).
Второй вариант.
Вопрос по теории вероятностей, и комбинаторике.
Пусть есть число 42.
Задача - найти количество способов его разложения на различные множители.

помогите сделать задание по функциональному анализу. Есть пространство l∞, и есть условие:
∀k∈N существует предел числовой последовательности x_n(k).
Необходимо ответить на вопросы, является ли заданное условие
a) необходимым;
б) достаточным;
в)необходимым и достаточным
для сходимости последовательности x_n в метрическом пространстве X?
Объясните пожалуйста, как сделать это задание?

Анон, я сегодня охуел, когда на паре посчитали функцию Римана для минус единицы и получили ответ - 1/12, меня просто как молнией ударило. Одно дело, когда ты читаешь это как какой-то рандомный факт, а другое дело - когда логически выводишь и понимаешь, от чего у Чебышёва взрывался мозг, и испытываешь похожие ощущения. Математика - ты замечательная.

Вроде на стаке поясняли, но линалом. А тут без линала должна решаться задача, так что нахуй то говнорешение.
Альзо как доказать биноманальную формулу ньютана индукцией без всякой комбинаторики?
Хуй соси, говно. Если не можешь буквально доматан решить, тебе здесь нехуй делать. По-крайней мере, назад в ро съеби, говнарь.
Хуеплёт, тебе уже три раза всё сказали, а ты продолжаешь выёбываться.
>Если не можешь буквально доматан решить, тебе здесь нехуй делать.
Когда решишь, тогда и приходи. А пока ты хуя собачьего не стоишь.

Так и не выложил, хотя я его просил. Может кто-то восполнить этот пробел?
Потому что ему похуй на это.
В /math
И что?
Это копия, сохраненная 15 февраля 2017 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.