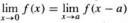Это копия, сохраненная 23 ноября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.




Общие курсы
М. И. Сканави: "Элементарная математика".
Алгебра
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
С. Б. Гашков: “Современная элементарная алгебра”.
Геометрия
А. Д. Александров, А. Л. Вернер, В. И. Рыжик: “Геометрия”. Учебник для 10-11 классов. Базовый и углубленный уровни.
Я. П. Понарин: “Элементарная геометрия” в двух томах. Первый том - это планиметрия, а второй том - это стереометрия.
А. Ю. Калинин, Д. А. Терешин: “Геометрия”, 10-11 классы. Годный учебник.
Тригонометрия
И. М. Гельфанд, С.М. Львовский, А. Л. Тоом: “Тригонометрия”. Название говорит само за себя. Много геометрических и физических интерпретаций + комплексные числа, как бонус.
Начала анализа
Б. М. Давидович: “Математический анализ в 57 школе“.
БАЗОВЫЕ КУРСЫ ДЛЯ СТУДЕНТОВ:
Общая алгебра
Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
М. Атья, И. Макдональд : "Введение в коммутативную алгебру".
А. Л. Городенцев: "Алгебра. Учебник для студентов-математиков". Вырос из лекций НМУ. Читать параллельно с Винбергом (Винберга читать в первую очередь).
И.Р. Шафаревич: “Основные понятия алгебры“. Замечательный обзор вообще того, что такое алгебра, как она выглядит и какое место она занимает в математике. Примеры, приложения и прочая конкретика.
E. Connell: Elements of Abstract and Linear Algebra". Хорошая первая книга по алгебре, да и математике вообще.
P. Grillet: "Abstract algebra". Очень лаконичный и понятный учебник. Надо знать элементарную теорию чисел, про индукцию, про множества и функции. Линейной алгебры нету.
J. Rotman: "Advanced modern algebra". Ротман сильно разжевывает. Задачи слишком простые для уровня учебника. Линейная алгебра есть.
M. Artin: "Algebra". Американский Винберг. Группы Ли, упор на геометрию. Задачи неудачные.
I. Herstein: “Topics in Algebra“. Прекрасные задачи, отбор материала очень устарел, почти что Ван дер Варден.
P. Aluffi: "Algebra, Chapter 0". Если ты в состоянии ее осилить, бери и забывай про остальные книжки из списка. Линейная алгебра есть.
Линейная алгебра
В. А. Ильин, Э. Г. Позняк: “Линейная алгебра“. Один из классических и самых популярных курсов линейной алгебры.
Д. В. Беклемишев: “Курс аналитической геометрии и линейной алгебры“.
И. М. Гельфанд: "Лекции по линейной алгебре". Не даётся определение определителя.
А. И. Кострикин, Ю. И. Манин: "Линейная алгебра и геометрия". Затрагивается темы геометрий и связей с квантовой механикой. Не даётся определение определителя.
S. Axler: "Linear algebra done right". Подход без определителей (почти). Одна из самых популярных книг за рубежом.
S. Treil: "Linear algebra done wrong". Не такая популярная, как Axler, но тоже хвалят, да. Определители есть.
G. Shilov: "Linear Algebra". Определитель появляется на первой странице.
K. Hoffman, R. Kunze: "Linear Algebra". Классика за рубежом.
P. Halmos: "Finite-Dimensional Vector Spaces". Тоже классика.
P. Peterson: "Linear Algebra". Не особо знаком, но выглядит аккуратно. Что-то вроде Акслера.
S. Roman: "Advanced Linear Algebra". Хороший учебник по линалу. Но нужно знать элементарные свойства матриц и определителей.
Математический анализ
T. Tao: “Real analysis“. Один из самых популярных курсов математического анализа на английском языке.
C. Pugh: "Real Mathematical analysis". Более простая версия Рудина с картинками. Норм книга, но не самая лёгкая.
У. Рудин: "Основы математического анализа".
В. А. Зорич: "Математический анализ". Первый том посвящен классическому анализу. Много примеров, много материала, в том числе даются в начале основы матлогики и теории множеств, а также функций между ними.
Р. Курант: "Курс дифференциального и интегрального исчисления". Идеален с точки зрения первого знакомства с теорией, но имеет достаточно сложные упражнения.
Г. М. Фихтенгольц: "Курс дифференциального и интегрального исчисления". Хорош как повторительный курс.
С. М. Львовский: "Лекции по математическому анализу". Записки лекций из НМУ. Нужно знать основы калькулюса.
Г. Г. Харди, Д. Е. Литтлвуд, Г. Пойа: "Неравенства".
Н. Н. Лебедев: "Специальные функции и их приложения".
Г. П. Толстов: “Ряды Фурье“.
Дифференциальные уравнения
С. Фарлоу: “Уравнения с частными производными для научных работников и инженеров“.
Вариационное исчисление
И. М. Гельфанд, С. В. Фомин: " Вариационное исчисление".
Топология
V. Runde: "A taste of topology". Неплохая книга по метрическим пространствам и общей топологии, затрагивает фундаментальную группу.
J. Strom: "Modern classical homotopy theory".
T. Dieck: "Algebraic topology".
M. Crossley: "Essential Topology". Пререквизит для изучения алгебраической топологии. Не затрагивает тему метрических пространств.
КУРСЫ ДЛЯ ПРОДВИНУТЫХ МАТЕМАТИКОВ
Математический анализ
А. И. Маркушевич: "Теория аналитических функций".
S. Ramanan: "Global calculus".
H. Amann, J. Echer: "Analysis".
W. Fidcher, I. Lieb: "A Course in Complex Analysis: From Basic Results to Advanced Topics".
Дифференциальные уравнения
В. И. Арнольд: “Обыкновенные дифференциальные уравнения”. Книга для уверенных в себе математиков. Диффеоморфизмы, фазовые потоки, гладкие многообразия. Слава Гермесу Трисмегисту!
Теория категорий
С. Маклейн: "Категории для работающего математика".
Р. Голдблатт: "Топосы. Категорный анализ логики".
Дифференциальная Геометрия
К. Номидзу: "Основы дифференциальной геометрии".
J. Lee: "Manifolds and DIfferential Geometry".
L. Nicolaescu: "Lectures on the Geometry".
P. Michor "Topics in Differential Geometry".
Алгебраическая геометрия
Д. Мамфорд: "Красная книга о многообразиях и схемах".
В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”.
В. И. Арнольд: “Вещественная алгебраическая геометрия”.
Ю. И. Манин: Введение в теорию схем и квантовые группы“.
R. Vakil: "Foundations of algebraic geometry".
S. Bosch: "Algebraic Geometry and Commutative Algebra".
U. Gotz, T. "Wedhorn: Algebraic Geometry".
E. Harris: "The Geometry of Schemes".
Топология
А. Хэтчер: "Алгебраическая топология".
J. Munkres: "Topology". Книга - жесткий учебник по теоретико-множественной топологии. Много ненужного для других областей математики.
ИНТЕРЕСНОЕ:
Цикл “Manga guide to...“. Популярное изложение различных областей математики (и не только), оформленное в виде манги. Увы, без фансервиса.
Н. А. Вавилов: “Конкретная теория групп I: основные понятия“. И вообще все остальные книги (и лекции!) Вавилова.
П. С. Александров: “Введение в теорию групп“. Просто о сложном. Несколько вольный язык изложения, местами затрудняющий восприятие.
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”.
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
Н. Я. Виленкин: "Рассказы о множествах". Теория множеств для широкого круга читателей.
М. М. Постников: “Теорема Ферма. Введение в теорию алгебраических чисел”.
Н. Стинрод: “Первые понятия топологии“.
А. Я. Хинчин: “Три жемчужины теории чисел“.
О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов: “Элементарная топология”.
Я. П. Понарин: “Алгебра комплексных чисел в геометрических задачах”.
А. А. Заславский: “Геометрические преобразования”.
В. Акопян, А. А. Заславский: “Геометрические свойства кривых второго порядка”.
В. И. Арнольд: “Геометрия комплексных чисел, кватернионов и спинов”.
В. В. Прасолов: “Геометрия Лобачевского”.
Д. В. Аносов: “Дифференциальные уравнения: то решаем, то рисуем”.
В. В. Прасолов: “Наглядная топология”.
Д. В. Аносов: “От Ньютона к Кеплеру”.
М. Клайн: “Математика. Поиск истины“.
Д. Пойа: “Математическое открытие“.
Л. Кэрролл: “Логическая игра“.
Д. Пойа: “Как решать задачу“.
О. Я. Виро, Д. Б. Фукс: "Введение в теорию гомотопий. Гомологии и когомологии".
A. Ostermann, G. Wanner: "Geometry by its history".
T. Sundstrom: "Mathematical reasoning writing and proof". В книге объясняется что такое математическое доказательство, математический факт и каким образом их можно придумывать. Начала теории множеств.
D. Dummit R. Foote: “Abstract Algebra“. Много примеров, задач, но страшно скучный учебник, его нужно держать как справочник.
ПОЛЕЗНЫЕ РЕСУРСЫ:
Библиотка "Квант": math.ru/lib/ser/bmkvant
Высшая математика просто и доступно, по 2 курс включительно: mathprofi.net
Необъятная онлайн библиотека: gen.lib.rus.ec
Обсуждаем и дополняем!
ОП, все верно, только фоточку прикладника и гомологического петуха надо поменять местами. Обычно первый ест устрицы, а другой живет на мамину пенсию.
Во! Даже еще лучше. Запрещенных барабанщиков математегов кружок. Кто знает почему ^ не работает как страйк? Или это вакабазим? В мат форуме это конечно хорошо. А то бы и степень не могли рисовать, не только умножение. Впрочем степени кажется уже не очень популярны в 2016.
Прекрасная подборка литературы, все кристально ясно и никаких вопросов. У всех бы так.
Двачую. 14 тред - самый лучший. 1
И подписи нужно изменить. Слева что-нибудь про сектарианство и манямирок и презрение к утилитаризму, а справа - про двигатель прогресса
Чем дерево отличается от берёзы? Множество всех подмножеств является сигма-алгеброй, но, вообще говоря, есть дофига других сигма-алгебр.
Кусок говна, а не подборка литературы.
Это ты из-за этого их винишь? За то что они, как и положено умняшкам, видели всю неотвратимость краха наперёд?
http://lib.ru/POLITOLOG/lubimow.txt
Там не с 85 года.
>Итоги науки и техники. Алгебра. Алгебра. Топология. Геометрия т.14
Вот это 76-ой вообще.
>Там не с 85 года.
Вся серия целиком издавалась незначительными частями с 1962 года, однако в 1985 году произошло массовое увеличение числа издаваемых сборников. По математике, например, была создана серия "Современные проблемы математики. Фундаментальные направления". Издавалась с 1985 по 1993 год. Всего издано 67 томов.
http://www.mathnet.ru/php/archive.phtml?jrnid=intf&wshow=contents
У вас заговор головного мозга.
1. У меня в кармане штанов лежит пятирублевая монета.
2. У меня в кармане штанов НЕ лежит пятирублевая монета.
Закон исключенного третьего говорит, что одно из этих двух утверждений является ложью, а второе истиной. Исключен вариант, что сразу два утверждения ложны. Тут все понятно.
Но интуиционистская логика отказывается от этого закона и допускает варианты, при которых два этих утверждения являются ложь. И вот тут мои мозги начинают заворачиваться в трубочку, а жопа раскаляется, потому что я не могу себе вообразить таких вариантов! Как? Кааак Гильберт меня подери, возможно, что пятирублевая монета одновременно и лежит и не лежит у меня в кармане штанов?!
Помогите, объясните.
Правильно ли я понимаю, что если T1 = {∅ ,{1},{0,1}}
А T2 = {∅ ,{1},{0},{0,1}}, то T1 ⊂ T2, а множеств на которых они заданы можно придумать бесконечно много?
>В интуиционистской математике суждение считается истинным, только если его можно доказать. То есть истинность утверждения «Существует объект x, для которого верно суждение A(x)» доказывается построением такого объекта, а истинность утверждения «A или B» доказывается либо доказательством истинности утверждения A, либо доказательством истинности утверждения B. Отсюда, в частности, следует, что утверждение «A или не A» может быть не истинным, а закон исключённого третьего неприемлем.
Педивикию я и сам прочитал, только понятнее не стало. Вот в классической логике если я доказал ложность первого утверждения (то что у меня в кармане штанов лежит пятирублевая монета), то считается доказанной истинность второго. В интуиционистской хуй! Если я доказал ложность первого (вывернул карманы и нихуя не нашел), то истинность второго не считается доказанной!
Еще раз спрашиваю, приведите мне варианты, при которых одновременно 2 утверждения являются ложью.
В интуиционизме истинным считается доказанное. Ну пускай ты не доказал, что у тебя в кармане монетка. Пускай ты не доказал даже и того, что у тебя в кармане её нет. Тогда ни то, ни другое утверждение мы не считаем истинными.
Короче всё дело в том, что считать истиной, конкретное построение или (также) противоречивость его отрицания. Пятый постулат Евклида тоже когда-то казался неебаца очевидным, однако ж и без него можно жить, так же, как без закона исключённого третьего (на самом деле нет).
Все иди нахуй, ты еще тупее, чем я. Ты опять пересказываешь педивикию с умным видом. только понимания в тебе еще меньше чем во мне!
Ты смешал в кучу принцип двузначности и закон исключения третьего. А это разные вещи. Ключевым элементом в законе исключения третьего является отрицание ¬p. С ним отдельно безотносительно закона исключения третьего тоже не все в порядке. Подробнее в книжке Карри.
Классическая логика предполагает, что утверждение:
У меня в кармане или лежит, или НЕ лежит монета - всегда истинно.
Интуиционистская логика допускает варианты, когда это утверждение является ложью. Я прошу описать мне такие варианты!
Твой карман порванный, и потому монета частично в подкладке, а частично в кармане.
>Интуиционистская логика допускает варианты, когда это утверждение является ложью.
Ничего подобного интуиционистская логика не утверждает. Ты это сам придумал. Не хочешь читать Карри -- иди читай Колмогорова:
http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=sm&paperid=7425
Ещё в прошлом треде надо было сказать: раз тут все такие тупые, по твоему убеждению, почему ты постишь свои сраные вопросы сюда, а не в другое место?
В надежде, что хотя бы один умный человек сюда заглянет. Но похоже эти надежды напрасны, в период летних каникул ИТТ одни школьники, способные только на копипаст педивикии, и отсылке к книгам (я слишком умен, и занят чтобы тебе ответить, вот тебе книга ищи сам в ней ответ). На самом деле никаких ответов не знают, а книги нагуглили первые попавшиеся.
Какой же ты баран всё-таки. Никто тебе здесь не будет разжёвывать то, что гуглится за три секунды, потому что бессмысленно объяснять тому, кто не намерен сам что-либо делать. Мимопробегал - беги дальше.
Вообще-то Колмогоров доказал даже более сильный результат. Он доказал, что в интуиционистской логике отрицание истинного утверждения попросту бессмысленно. То есть если доказано, что в штанах есть монета, то предложение "в штанах нет монеты" нельзя даже сформулировать.
http://arxiv.org/abs/1511.01113
>Вообще-то Колмогоров доказал даже более сильный результат. Он доказал, что в интуиционистской логике отрицание истинного утверждения попросту бессмысленно. То есть если доказано, что в штанах есть монета, то предложение "в штанах нет монеты" нельзя даже сформулировать.
А чё так? А зачем?
Брауэр выступает против лингвистического аксиоматизма в духе Бурбаки. А также против того, что с помощью специально подобранных аксиом и логических правил вывода можно построить общематематически корректные утверждения. По его мнению подобные лингвистические здания не имеют никакого отношения к интуитивным математическим истинам в арифметике или геометрии.
Относительно закона исключения третьего Брауэр высказывает следующее: в системах, где речь идет о бесконечности ЗИТ пока еще ненадежен.
В качестве мотивации почему он так считает он строит так называемые слабые контрпримеры Брауэра. А именно: любым слабым контрпримером Брауэра является любая открытая математическая проблема на данный момент. Например: https://en.wikipedia.org/wiki/List_of_unsolved_problems_in_mathematics
Для того, чтобы не рассматривать конкретную открытую проблему, которая может быть решена с минуты на минуту Брауэр придумал методику построения слабых контрпримеров. Она зависит только от того, что открытые проблемы все еще существуют, а от точного содержания самих этих проблем.
Слабые контрпримеры Брауэра -- это такие утверждения, где мы можем утверждать только слабое отрицание некого высказывания, но не истину или сильное отрицание.
Пример: семейство, состоящее из пустого множества и всего R, является сигма-алгеброй на R.
> То что у нее есть конструктивная схема построения?
Это че вообще значит?
> что означает запись T1 ⊂ T2
⊂ почти в любом контексте означает одно и то же.
> Правильно ли я понимаю, что если T1 = {∅ ,{1},{0,1}}
> А T2 = {∅ ,{1},{0},{0,1}}, то T1 ⊂ T2
да
> а множеств на которых они заданы можно придумать бесконечно много?
Нет. Топология содержит все пространство X, поэтому в качестве X здесь подойдет только {0, 1}.
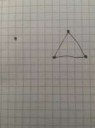
> Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу. (ср. Гамильтонов путь)
> Эйлеров цикл — эйлеров путь, являющийся циклом. То есть замкнутый путь, проходящий через каждое ребро графа ровно по одному разу.
> Эйлеров граф — граф, содержащий эйлеров цикл.
> эйлеров цикл существует тогда и только тогда, когда граф связный и в нём отсутствуют вершины нечётной степени.
По этой теореме получается, что граф пикрелейтед не является эйлеровым, так как он несвязный. Почему так? Разве треугольник не образует эйлеров цикл?
Прорешай задачки, чтобы откладывалась. Прочитал, через пару дней прорешал задачки - закрепил.
А еще какое то неудовлетворение что ли. Типо я вот вожусь со школьной программой а хочу прыгнуть выше.
Тогда попробуй почиать раздел, для которого не нужны элементарные знания.
Можешь ещё порешать олимпиадные задачки, прокачаешь смекалочку.
А на какой ты теме, кстати?
Я на все подряд разбрасываюсь.
> А еще какое то неудовлетворение что ли
Это естественное состояние не только для математика, но и вообще для любого человека, который занимается интеллектуальной деятельностью. Ты постоянно батхертишь от своей тупости и это заставляет тебя больше работать.
А что делать, если это заставляет тебя не ещё больше работать, а заминать фрустрацию всякой хуитой, пока не пройдёт?
2. Математическая логика. Формальные системы. Формальные языки. Формальные логики. Буквы, слова, термы, атомы, формулы. Суждения. Вывод. Аксиоматические системы. Языки первого порядка. Переменные. Функции и предикаты. Кванторы. Логические аксиомы. Теории с равенством и без равенства. Тавтология, теоремы о ней. Дедукция. Структура. Модель. Теорема компактности. Изоморфизм и гомоморфизм моделей. Подструктуры. Мощность моделей. Непротиворечивость, выполнимость. Категоричность. Арифметика Пеано. Математическая индукция. Генетическое, рекурсивное определение. Аксиоматическое определение.
3. Теория множеств. Наивная теория множеств. Множества, элементы, подмножества, семейства. Дополнение, объединение, пересечение, степень, законы де Моргана и др. Пара. Произведение. Отношение. Функция, операция. Структуры. Равномощность. Мощность. Теоремы о мощностях. Счётные, несчётные множества. Объёмное определение кардинала. Арифметика кардиналов. Упорядоченные множества. Подобие порядков и порядковый тип. Вполне упорядоченные множества. Ординалы, конечные и бесконечные. Натуральные числа. Кардиналы как ординалы. Алефы. Теорема Цермело. Мощность как алеф. Парадоксы. Аксиоматическая теория множеств. ZFC. Интерпретация всего вышесказанного в ZFC. Схема замены и её следствия. Аксиома выбора и её следствия, лемма Цорна. Интуитивный смысл классов, предикат как класс. NBG. Универсумы, аксиома Гротендика.
4. Общая алгебра. Алгебраические структуры. Моноид, группа, кольцо, тело, поле. Подструктуры. Модуль над кольцом, векторное пространство, базис Гамеля. Действие группы. Морфизмы групп, морфизмы модулей. Нормальные подгруппы, факторгруппы, теоремы о группах (гомоморфизм, Лагранж, Кэли и т.д.). Идеалы, двусторонние идеалы, факторкольца, вычеты. Кольцо частных. Целые числа, рациональные числа. Нормальные и композиционные ряды. Алгебры. Свободные группы, свободные модули, свободные алгебры. Многочлены, целые рациональные функции. Алгоритм Евклида. Алгебраические расширения, сепарабельные расширения. Трансцендентные расширения, базис трансцендентности. Пополнения и нормирования.
5. Линейная алгебра. Векторные пространства, линейные многообразия. Матрицы. Линейные операторы. Опеределители. Двойственность. Формы, билинейные и полуторалинейные формы. Жорданова форма. Квадратичные формы, симметрические формы, скалярное произведение, ортогональные базисы. Алгебры Клиффорда. Знакопеременные формы. Эрмитовы формы. Спектральные теоремы. Геометрия пространств со скалярным произведением. Алгоритм ортогонализации. Евклидовы и унитарные пространства. Ортогональные, унитарные, самосопряженные операторы. Геометрия квадратичных форм. Пространство Минковского. Аффинные пространства. Проективные пространства. Кэлерова метрика. Алгебраические многообразия.
6. Полилинейная алгебра. Тензорное произведение модулей. Тензорное произведение алгебр. Тензорная алгебра модуля. Симметрическая алгебра. Алгебра Грассмана. Теоремы о внешнем произведении. Определители. Двойственность. Историческое определение тензора, связь с формами. Тензорные поля.
7. "Аналитическая" геометрия. Прямоугольные и косоугольные координаты, полярные, сферические и цилиндрические координаты. Уравнения прямой. Расположение прямых. Конические сечения. Кривые второго порядка. Плоскость. Расположение плоскости и прямых. Поверхности второго порядка. Касательная плоскость. Ортогональные, аффинные, проективные преобразования. Однородные координаты. Тангенциальные координаты.
8. Элементарный анализ. Аксиоматика вещественных чисел. Аксиома полноты, принцип Архимеда. Конструкция R по Симону Стевину, по Рихарду Дедекинду. Комплексные числа. Топологические пространства, метрические пространства. Открытые множества и базы топологии. Замкнутые множества, замыкание. Непрерывность, гомеоморфизмы, теоремы о непрерывности. Пределы. Хаусдорфовы пространства. Топология Александрова на натуральных числах, последовательности. Замыкание в метрическом пространстве. Последовательности Коши, критерий Коши. Определение R по Коши-Кантору. Пополнение. Компакты. Леммы Гейне-Бореля-Лебега, Больцано-Вейерштрасса, Коши-Кантора, Вейерштрасса о функции на компакте, Больцано-Коши, Вейерштрасса о монотонности. Связность, линейная связность. Секвенциальная компактность, лемма о лебеговом числе. Топология произведения. Характеристические функции, максимальный идеал, лемма Александера о предбазе. Теорема Тихонова о компактности. Нормы на векторных пространствах, стандартная норма на R^n. Фильтры, базы фильтров, предел вдоль фильтра (ака по базе множеств). Локальные и глобальные свойства непрерывных функций, разрывы. Бесконечно-малые и бесконечно-большие функции, асимптотическое поведение функций, O-большое и o-малое. Производная функций R->R, дифференциал, классы гладкости. Теоремы Ферма, Ролля, Коши, Лагранжа, Тейлора. Формула конечных приращений, формула Тейлора. Топологическое векторное пространство, базис Шаудера. Элементарная теория банаховых пространств. Линейные непрерывные отображения, их ядро и образ. Произведения нормированных пространств, непрерывные билинейные и мультилинейные отображения произведения пространств в нормированное пространство. Равномерная сходимость, равномерная непрерывность, теорема Кантора. Функциональные ряды, ряд Тейлора как обобщение производной. Абсолютная сходимость и теорема о перестановке, условная и безусловная сходимость и теорема Римана, числовые ряды, знакопеременные ряды, признаки сходимости. Действие линейного непрерывного отображения на ряд. Произведение двух рядов, применение билинейного непрерывного отображения к двум рядам. Примеры функциональных пространств. Локально равномерный предел последовательности непрерывных функций. Контрпримеры. Бесконечные произведения, логарифмические ряды. Определения элементарных функций, формула Эйлера, таблица производных. Аналитические функции, их свойства. Круг сходимости. Аналитическое продолжение. Голоморфные функции. Интеграл Коши (от кусочно-непрерывных функций), его линейность, аддитивность и монотонность. Формула Ньютона-Лейбница, таблица первообразных, техника интегрирования. Несобственный интеграл. Выпуклые и вогнутые функции. Исследование функций. Аффинные пространства. Аффинные многообразия. Аффинные отображения. Норма и выпуклость. Евклидовы и эрмитовы аффинные пространства. Двойственное пространство, ортонормированные базисы. Производная аффинного отображения. Производная вдоль вектора. Частная производная. Матрица Якоби. Якобиан. Производная Гато. Производная Фреше. Дифференцируемое многообразие. Линейное касательное многообразие. Градиент вещественной функции в евклидовом пространстве. Векторное поле. Произведения аффинных пространств. Производная билинейного непрерывного отображения. Теорема о сложной функции. Производные высших порядков. Обобщенная формула Тейлора. Экстремумы. Теорема о неявной функции. Лемма Морса. Разложение диффеоморфизма в композицию простейших. Поверхности в R^n. Кратный и повторный интегралы Коши, криволинейный и поверхностный интегралы. Параметрическое представление дифференцируемого многообразия. Неявные уравнения многообразия. Вещественные, комплексные, абстрактные многообразия. Теория условных экстремумов, неравенства Гёльдера и Минковского. Вариационное исчисление. Лемма Хаара. Геодезические. Канонические уравнения Гамильтона. Мера, пространства с мерой, измеримые отображения. Мера Жордана. Суммы и интегралы Дарбу. Интеграл Римана. Мера Радона. Векторные меры.
2. Математическая логика. Формальные системы. Формальные языки. Формальные логики. Буквы, слова, термы, атомы, формулы. Суждения. Вывод. Аксиоматические системы. Языки первого порядка. Переменные. Функции и предикаты. Кванторы. Логические аксиомы. Теории с равенством и без равенства. Тавтология, теоремы о ней. Дедукция. Структура. Модель. Теорема компактности. Изоморфизм и гомоморфизм моделей. Подструктуры. Мощность моделей. Непротиворечивость, выполнимость. Категоричность. Арифметика Пеано. Математическая индукция. Генетическое, рекурсивное определение. Аксиоматическое определение.
3. Теория множеств. Наивная теория множеств. Множества, элементы, подмножества, семейства. Дополнение, объединение, пересечение, степень, законы де Моргана и др. Пара. Произведение. Отношение. Функция, операция. Структуры. Равномощность. Мощность. Теоремы о мощностях. Счётные, несчётные множества. Объёмное определение кардинала. Арифметика кардиналов. Упорядоченные множества. Подобие порядков и порядковый тип. Вполне упорядоченные множества. Ординалы, конечные и бесконечные. Натуральные числа. Кардиналы как ординалы. Алефы. Теорема Цермело. Мощность как алеф. Парадоксы. Аксиоматическая теория множеств. ZFC. Интерпретация всего вышесказанного в ZFC. Схема замены и её следствия. Аксиома выбора и её следствия, лемма Цорна. Интуитивный смысл классов, предикат как класс. NBG. Универсумы, аксиома Гротендика.
4. Общая алгебра. Алгебраические структуры. Моноид, группа, кольцо, тело, поле. Подструктуры. Модуль над кольцом, векторное пространство, базис Гамеля. Действие группы. Морфизмы групп, морфизмы модулей. Нормальные подгруппы, факторгруппы, теоремы о группах (гомоморфизм, Лагранж, Кэли и т.д.). Идеалы, двусторонние идеалы, факторкольца, вычеты. Кольцо частных. Целые числа, рациональные числа. Нормальные и композиционные ряды. Алгебры. Свободные группы, свободные модули, свободные алгебры. Многочлены, целые рациональные функции. Алгоритм Евклида. Алгебраические расширения, сепарабельные расширения. Трансцендентные расширения, базис трансцендентности. Пополнения и нормирования.
5. Линейная алгебра. Векторные пространства, линейные многообразия. Матрицы. Линейные операторы. Опеределители. Двойственность. Формы, билинейные и полуторалинейные формы. Жорданова форма. Квадратичные формы, симметрические формы, скалярное произведение, ортогональные базисы. Алгебры Клиффорда. Знакопеременные формы. Эрмитовы формы. Спектральные теоремы. Геометрия пространств со скалярным произведением. Алгоритм ортогонализации. Евклидовы и унитарные пространства. Ортогональные, унитарные, самосопряженные операторы. Геометрия квадратичных форм. Пространство Минковского. Аффинные пространства. Проективные пространства. Кэлерова метрика. Алгебраические многообразия.
6. Полилинейная алгебра. Тензорное произведение модулей. Тензорное произведение алгебр. Тензорная алгебра модуля. Симметрическая алгебра. Алгебра Грассмана. Теоремы о внешнем произведении. Определители. Двойственность. Историческое определение тензора, связь с формами. Тензорные поля.
7. "Аналитическая" геометрия. Прямоугольные и косоугольные координаты, полярные, сферические и цилиндрические координаты. Уравнения прямой. Расположение прямых. Конические сечения. Кривые второго порядка. Плоскость. Расположение плоскости и прямых. Поверхности второго порядка. Касательная плоскость. Ортогональные, аффинные, проективные преобразования. Однородные координаты. Тангенциальные координаты.
8. Элементарный анализ. Аксиоматика вещественных чисел. Аксиома полноты, принцип Архимеда. Конструкция R по Симону Стевину, по Рихарду Дедекинду. Комплексные числа. Топологические пространства, метрические пространства. Открытые множества и базы топологии. Замкнутые множества, замыкание. Непрерывность, гомеоморфизмы, теоремы о непрерывности. Пределы. Хаусдорфовы пространства. Топология Александрова на натуральных числах, последовательности. Замыкание в метрическом пространстве. Последовательности Коши, критерий Коши. Определение R по Коши-Кантору. Пополнение. Компакты. Леммы Гейне-Бореля-Лебега, Больцано-Вейерштрасса, Коши-Кантора, Вейерштрасса о функции на компакте, Больцано-Коши, Вейерштрасса о монотонности. Связность, линейная связность. Секвенциальная компактность, лемма о лебеговом числе. Топология произведения. Характеристические функции, максимальный идеал, лемма Александера о предбазе. Теорема Тихонова о компактности. Нормы на векторных пространствах, стандартная норма на R^n. Фильтры, базы фильтров, предел вдоль фильтра (ака по базе множеств). Локальные и глобальные свойства непрерывных функций, разрывы. Бесконечно-малые и бесконечно-большие функции, асимптотическое поведение функций, O-большое и o-малое. Производная функций R->R, дифференциал, классы гладкости. Теоремы Ферма, Ролля, Коши, Лагранжа, Тейлора. Формула конечных приращений, формула Тейлора. Топологическое векторное пространство, базис Шаудера. Элементарная теория банаховых пространств. Линейные непрерывные отображения, их ядро и образ. Произведения нормированных пространств, непрерывные билинейные и мультилинейные отображения произведения пространств в нормированное пространство. Равномерная сходимость, равномерная непрерывность, теорема Кантора. Функциональные ряды, ряд Тейлора как обобщение производной. Абсолютная сходимость и теорема о перестановке, условная и безусловная сходимость и теорема Римана, числовые ряды, знакопеременные ряды, признаки сходимости. Действие линейного непрерывного отображения на ряд. Произведение двух рядов, применение билинейного непрерывного отображения к двум рядам. Примеры функциональных пространств. Локально равномерный предел последовательности непрерывных функций. Контрпримеры. Бесконечные произведения, логарифмические ряды. Определения элементарных функций, формула Эйлера, таблица производных. Аналитические функции, их свойства. Круг сходимости. Аналитическое продолжение. Голоморфные функции. Интеграл Коши (от кусочно-непрерывных функций), его линейность, аддитивность и монотонность. Формула Ньютона-Лейбница, таблица первообразных, техника интегрирования. Несобственный интеграл. Выпуклые и вогнутые функции. Исследование функций. Аффинные пространства. Аффинные многообразия. Аффинные отображения. Норма и выпуклость. Евклидовы и эрмитовы аффинные пространства. Двойственное пространство, ортонормированные базисы. Производная аффинного отображения. Производная вдоль вектора. Частная производная. Матрица Якоби. Якобиан. Производная Гато. Производная Фреше. Дифференцируемое многообразие. Линейное касательное многообразие. Градиент вещественной функции в евклидовом пространстве. Векторное поле. Произведения аффинных пространств. Производная билинейного непрерывного отображения. Теорема о сложной функции. Производные высших порядков. Обобщенная формула Тейлора. Экстремумы. Теорема о неявной функции. Лемма Морса. Разложение диффеоморфизма в композицию простейших. Поверхности в R^n. Кратный и повторный интегралы Коши, криволинейный и поверхностный интегралы. Параметрическое представление дифференцируемого многообразия. Неявные уравнения многообразия. Вещественные, комплексные, абстрактные многообразия. Теория условных экстремумов, неравенства Гёльдера и Минковского. Вариационное исчисление. Лемма Хаара. Геодезические. Канонические уравнения Гамильтона. Мера, пространства с мерой, измеримые отображения. Мера Жордана. Суммы и интегралы Дарбу. Интеграл Римана. Мера Радона. Векторные меры.
Значит не судьба. Чтобы заниматься математикой, нужно быть упрямым как баран. Сложности должны у тебя вызывать спортивную злость. Омегам в математике не место, короч.
У меня вызывают, но я на все подряд внимание распределяю. Можешь примерный план написать для новичка. Ничего не пойму что за чем учить.
Не я её писал. Я просто спинул сюда.
вот я школу бросил в 7 классе. ну и до седьмого не особо учился. хочу почитать "Рассказы о множествах". я там че-та пойму?
Теория множеств - это самодостаточный раздел, тебе для его понятия не нужны другие.
Почитай, если не поймёшь, спрашивай.
А что вообще читать, чтобы овладеть всеми доказательствами по индукции, от обратного и т.д.
Может с мат логики начать?
Точно не с матлогики. Лучше какую книжку для новичков типа "How to prove it".
ты няшка. обязательно спрошу.
Ну совсем новичку-дурачку стоит начать с теории множеств, например, первые главы Зорича. Можно прочитать "Дискретная математика для программистов" Рода Хаггарти, выборочно. Основы логики там в тех же разделах.
читаю. пишут "множество точек на окружности бесконечно". это как так? чому так?
Спасибо.
Странный вопрос какой-то. Ну, если их не бесконечное число, то значит конечное. А сколько именно? Почему больше быть не может, если между любыми двумя точками можно запихнуть третью?
Можешь прочитать маленькую книжку (63 стр) Кутасов Элементы математической логики 9-11 классы. Задачи там довольно сложные правда.
>>380871
Окружность можно биективно отобразить в отрезок [0;2pi), в котором бесконечно точек.
> если между любыми двумя точками можно запихнуть третью
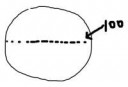
а так разве можно? почему? но если взять сто точек пикрелейтед и запихнуть между каждой парой по еще одной точке, то разве это не потребует, ну увеличения размера окружности?
>>380875
>Окружность можно биективно отобразить в отрезок [0;2pi), в котором бесконечно точек.
нихуя не понял
>>380876
почему не понятно? точка же конечной величины? имеет она какой-то размер?
Ничего странного нет. Это настоящее математическое доказательство — доказательство „по-индукции”.
>нихуя не понял
Мы разрываем окружность в одной точке, получаеться отрезок. В отрезке бесконечное количество точек.
>точка же конечной величины? имеет она какой-то размер?
Если размер есть, то какой он? Непонятно. А раз так, то его нет.
вот у нас конкретная окружность из 1000 пикселей, точка в ней размером 1 пиксель. хуле непонятного-то? непонятно.
Смотря какой отрезок.
>а так разве можно?
Ну почти. Под "запихнуть" я имел в виду не прямо взять и запихнуть, а то, что между любыми двумя точками найдётся обязательно какая-нибудь третья, ведь в противном случае там была бы пустота (на окружности же нет пустоты).
>Окружность можно биективно отобразить в отрезок [0;2pi)
Тут имелось в виду, что для каждого числа из интервала [0;2pi) можно выбрать соответствующую точку на окружности и наоборот, для каждой точки на окружности можно выбрать точку из интервала. Раз так, то в интервале и на окружности количество точек одинаковое, а в интервале их бесконечно много, что очевидно.
>точка же конечной величины?
Точка не имеет радиуса, объёма и всяких таких вещей. Она как бы бесконечно маленькая, если приближать.
>почему в отрезке бесконечное кол-во точек? отрезок конечен же?
Вот про то что он бесконечен как раз и говориться в теории множеств.
Но смотри, между двумя любыми точками a,b мы можем найти точку s=(b-a)/2. Потом, между точками a,b находим точку t=(b-a)/2 и т.д. этот процесс можно поторять до бесконечности.
Приблизим эту окружность немножко, тогда пикселей станет больше. Хотя это та же самая окружность.
Вся путаница оттого, что под словом "точка" понимается число, в данном случае.
2. элементарная алгебра
3. элементарная геометрия: планиметрия и стереометрия
4. теория элементарных функций и элементы анализа
и высшую математику, изучаемую в ВУЗе. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности. Программа обучения по специальности математика образована следующими учебными дисциплинами:
5. Математический анализ
6. Алгебра
7. Аналитическая геометрия
8. Линейная алгебра и геометрия
9. Дискретная математика
10. Математическая логика
11. Дифференциальные уравнения
12. Дифференциальная геометрия
13. Топология
14. Функциональный анализ и интегральные уравнения
15. Теория функций комплексного переменного
16. Уравнения с частными производными (вместо этого курса физикам читаются Методы математической физики)
17. Теория вероятностей
18. Математическая статистика
19. Теория случайных процессов
20. Вариационное исчисление и методы оптимизации
21. Методы вычислений, т.е. численные методы
22. Теория чисел
Как такой план?С вики утащил.
Нашёл уже.
Некоторые разделы из списка следует изучать параллельно, например алгебру, аналитическую геометрию и матан.
Никогда не задавался этим вопросом и уделял сколько мог. Теперь интересно стало.
Бля не замерял даже. Думаю, не больше часа в день (считая вообще все дни, даже те, когда вообще ничего не делал)
Я не он, но может ты мне подскажешь? Мне интересна теория типов, языки программирования, автоматическое доказательство теорем, вот это всё. Как бы мне вообще к успеху-то прийти?
Логику, английский учу.А вообще мне все науки интересны и я постоянно от одной к другой бегаю.
Я не знаю какие разделы нравятся. Хочу абстрактное мышление улучшить и научится понимать красоту математики.
> Хочу абстрактное мышление улучшить
Тогда тебе нужны области типа алгебры, топологии, теории категорий. Но вообще, не занимайся хуйней, в современном обществе математика нужна где-то 1 проценту людей, если ты не собираешься ее использовать, она тебе будет мешать жить.
Уйдёшь в мистику и будешь говорить с разными сущнастями ну или выебешь себя в зда резиныновым членом.
в университет
А еще чем то фракталы привлекают.
Формирует определенный склад мышления. После красивых абстрактрных концепций тебе будет неприятно работать с уебищными концепциями из реальной жизни, тебе все будет казаться скучным и некрасивым. Во-вторых, тебе будет хотеться пообщаться, обсудить математику с кем-то, но будет не с кем и ты будешь чувствовать себя одиноким.
Мне даже не с кем прочитанную книгу обсудить.
А уж красивые абстрактные концепции хотел бы понимать.
ЛОЛ. Я тоже недавно читал эту книгу, картинки там охуенные.
Я сам в неё вкатываюсь, и как я понял нужно - алгебра от самых низов до алгебраической геометрии (Теорема Ферма с её помошью доказна), анализ и ТФКП.
Янке Специальные функции.
Ты это я. Я после 8 го ушел у бати в магазине работать. Так и работаю по 15 часов практически без выходных. По ночам читаю математику. Зато мопед себе купил, чего у многих тут нет.
Предел - не понимают что такое математика. Думают если бы не ебланили, а выучили интегральчики на четверочку, то знали бы математику.
Имелось в виду, чего можно в лучшем случае достичь, если ты тупой, но старательный.
Сука лол. Вопрос ниже пояса.
Я же и говорю - максимум можешь научиться в интегральчики. Многие будут думать, что ты знаешь математику. Хотя это еще не математика. Но выше не сможешь.
А как узнать что тупой и выше интегралов не поднимешься?Какие ограничения?
Открой любой учебник выше из шапки и попробуй почитать. Абстрактные вещи тяжело даются. Старанием можно запомнить формулы и надрочиться их применять в решении однотипных задач. Но это тупик.
>>380942
См. шапку:
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
>в двух словах не описать
>Открой любой учебник выше из шапки и попробуй почитать. Абстрактные вещи тяжело даются. Старанием можно запомнить формулы и надрочиться их применять в решении однотипных задач. Но это тупик.
Вот теперь по настоящему будет страшно изучать математику, боюсь в один прекрасный день понять что я дурак.

Tauglich!
мопедобляди соснули у велобогов
Хуй знает. Читаю HoTT и Алуффи, полёт нормальный, в вузике за анализ секу на отличненько. А вот интегралы с горем пополам даются. Не вписываюсь в систему.
А у меня по математике и физике в школе двойки были и внимание плохо держал когда учитель рассказывал.
подскажите за оценку эффективности (в контексте - были такие-то показатели, а стали - такие то. типа вычислить прогресс )
в какую сторону смотреть?
В школе по математике стабильный тройбан был, ни хвоста собачьего не понимал. А щас теоремы доказываю в институте, в основном на отл. Я тупой или нет?
Я еще и к доске боялся выходить и постоянно пугали математикой в младших классах Вот и результат.Суки.
вычесть второй результат из первого. если положительное число получится - значит прогресс.
то есть наоборот лол 2-1
Тредом не ошибся? Тут для начинающих.
> Старанием можно запомнить формулы и надрочиться их применять в решении однотипных задач.
Я стараюсь ничего не запоминать вообще. Когда порешаю пару задачек, всё само запоминаеться. А что не запоминаеться, то сам стараюсь выводить.
Самый простой пример, вместо задчивания сранных формул по тригонометрии нужно запомнить лишь три синус(косинус) суммы и основное тринометрическое тождество а дальше из них всё выводить.
Или же формула корней квадратного уравнения, не мог её запомнить и поэтому выводил через дополнение до квадрата суммы.
Как считать геодезическую кривизну, которая в гаусс-бонне? Как нормально её определять? В википедии бред какой-то про ковариантные производные.
Немного об авторе: Эдуард Френкель — американский математик, занимающийся теорией представлений, алгебраической геометрией и математической физикой. В настоящее время он работает профессором математики в Калифорнийском университете в Беркли.
Эдуард Френкель родился в Коломне, в семье инженера. После того как его не приняли на мехмат МГУ из-за его еврейского происхождения, Френкель по-ступил в университет нефти и газа. Во время учебы он посещал семинар Израиля Гельфанда, работал с Борисом Фейгиным и Дмитрием Фуксом. По окончании университета, Эдуарда пригласили преподавать в Гарвард.
1. Логика
А. Д. Гетманова. Логика.
К. К. Жоль. Логика.
А. И. Липкин. Философия науки.
2. Математическая логика
Н. Н. Непейвода. Прикладная логика.
С. К. Клини. Введение в метаматематику.
А.Н. Колмогоров, А.Г. Драгалин. Математическая логика.
Д. Шенфилд. Математическая логика.
3. Теория множеств
А. В. Архангельский. Канторовская теория множеств.
П. С. Александров. Введение в теорию множеств.
Ф. Хаусдорф. Теория множеств.
К. Куратовский, А. Мостовский. Теория множеств.
Thomas Jech. Set Theory. The Third Millennium Edition.
Н. А. Вавилов. Теория множеств.
4. Общая алгебра
А. И. Кострикин. Введение в алгебру.
Э. Б. Винберг. Алгебра.
Б. Л. ван дер Варден. Алгебра.
С. Ленг. Алгебра.
С. Маклейн. Категории для работающего математика.
Paolo Aluffi. Algebra: Chapter 0.
5. Линейная алгебра
А. И. Кострикин, Ю.И.Манин. Линейная алгебра и геометрия.
В.А. Ильин, Э.Г. Позняк. Линейная алгебра.
И. Р. Шафаревич, А. О. Ремизов. Линейная алгебра и геометрия.
И. М. Гельфанд. Линейная алгебра.
6. Полилинейная алгебра
К. Фейс. Алгебра: кольца, модули и категории
М. Атья, И. Макдональд. Введение в коммутативную алгебру.
М. А. Акивис, В. В. Гольдберг. Тензорное исчисление.
П. А. Широков. Тензорное исчисление. Часть 1.
Д. С. Широков. Алгебры Клиффорда и спиноры.
7. Аналитическая геометрия.
И. И. Привалов. Аналитическая геометрия.
П. С. Александров. Лекции по аналитической геометрии.
П. С. Александров. Курс аналитической геометрии и линейной алгебры.
А. В. Погорелов. Аналитическая геометрия.
А. Ю. Оболенский, И. А. Оболенский. Лекции по аналитической геометрии.
Н. В. Ефимов, Э. Р. Розендорн. Линейная алгебра и многомерная геометрия.
8. Элементарный анализ.
У. Рудин. Основы анализа.
В. А. Зорич. Математический анализ.
Г. Е. Шилов. Математический анализ.
Ж. Дьедонне. Основы современного анализа.
П. Халмош. Теория меры.
С. М. Львовский. Лекции по математическому анализу.
И. П. Натансон. Теория функций вещественной переменной.
Л. Шварц. Анализ.
А. Н. Колмогоров, С. В. Фомин. Элементы теории функций и функционального анализа.
У. Рудин. Функциональный анализ.
И. М. Гельфанд, С. В. Фомин. Вариационное исчисление.
9. Математический анализ
М. Спивак. Математический анализ на многообразиях.
А. Картан. Дифференцальное исчисление, Дифференцальные формы.
С. М. Львовский. Введение в когомологии пучков.
С. М. Натанзон. Пучки и гомологическая алгебра.
Д. Хьюзмоллер. Расслоенные пространства.
10. Комплексный анализ.
Б. В. Шабат. Введение в комплексный анализ.
С. М. Львовский. Лекции по комплексному анализу.
W. Rudin. Real and complex analysis.
11. Обыкновенные ДУ.
В. И. Арнольд. Обыкновенные дифференциальные уравнения.
В. В. Степанов. Курс дифференциальных уравнений.
М. В. Федорюк. Обыкновенные дифференциальные уравнения.
12. Уравнения с частными производными.
М. В. Федорюк. Дифференциальные уравнения с частными производными.
Р. Курант. Уравнения с частными производными.
В. И. Арнольд. Лекции об уравнениях с частными производными.
А. Зоммерфельд. Дифференциальные уравнения в частных производных физики.
13. Теория вероятностей.
Дж. Андерсон. Дискретная математика и комбинаторика
Б. В. Гнеденко, А. Я. Хинчин. Элементарное введение в теорию вероятностей.
Б. В. Гнеденко. Курс теории вероятностей.
А. Н. Ширяев. Вероятность.
14. Статистика.
Б. Л. ван дер Варден. Математическая статистика.
Э. Леман. Проверка статистических гипотез.
1. Логика
А. Д. Гетманова. Логика.
К. К. Жоль. Логика.
А. И. Липкин. Философия науки.
2. Математическая логика
Н. Н. Непейвода. Прикладная логика.
С. К. Клини. Введение в метаматематику.
А.Н. Колмогоров, А.Г. Драгалин. Математическая логика.
Д. Шенфилд. Математическая логика.
3. Теория множеств
А. В. Архангельский. Канторовская теория множеств.
П. С. Александров. Введение в теорию множеств.
Ф. Хаусдорф. Теория множеств.
К. Куратовский, А. Мостовский. Теория множеств.
Thomas Jech. Set Theory. The Third Millennium Edition.
Н. А. Вавилов. Теория множеств.
4. Общая алгебра
А. И. Кострикин. Введение в алгебру.
Э. Б. Винберг. Алгебра.
Б. Л. ван дер Варден. Алгебра.
С. Ленг. Алгебра.
С. Маклейн. Категории для работающего математика.
Paolo Aluffi. Algebra: Chapter 0.
5. Линейная алгебра
А. И. Кострикин, Ю.И.Манин. Линейная алгебра и геометрия.
В.А. Ильин, Э.Г. Позняк. Линейная алгебра.
И. Р. Шафаревич, А. О. Ремизов. Линейная алгебра и геометрия.
И. М. Гельфанд. Линейная алгебра.
6. Полилинейная алгебра
К. Фейс. Алгебра: кольца, модули и категории
М. Атья, И. Макдональд. Введение в коммутативную алгебру.
М. А. Акивис, В. В. Гольдберг. Тензорное исчисление.
П. А. Широков. Тензорное исчисление. Часть 1.
Д. С. Широков. Алгебры Клиффорда и спиноры.
7. Аналитическая геометрия.
И. И. Привалов. Аналитическая геометрия.
П. С. Александров. Лекции по аналитической геометрии.
П. С. Александров. Курс аналитической геометрии и линейной алгебры.
А. В. Погорелов. Аналитическая геометрия.
А. Ю. Оболенский, И. А. Оболенский. Лекции по аналитической геометрии.
Н. В. Ефимов, Э. Р. Розендорн. Линейная алгебра и многомерная геометрия.
8. Элементарный анализ.
У. Рудин. Основы анализа.
В. А. Зорич. Математический анализ.
Г. Е. Шилов. Математический анализ.
Ж. Дьедонне. Основы современного анализа.
П. Халмош. Теория меры.
С. М. Львовский. Лекции по математическому анализу.
И. П. Натансон. Теория функций вещественной переменной.
Л. Шварц. Анализ.
А. Н. Колмогоров, С. В. Фомин. Элементы теории функций и функционального анализа.
У. Рудин. Функциональный анализ.
И. М. Гельфанд, С. В. Фомин. Вариационное исчисление.
9. Математический анализ
М. Спивак. Математический анализ на многообразиях.
А. Картан. Дифференцальное исчисление, Дифференцальные формы.
С. М. Львовский. Введение в когомологии пучков.
С. М. Натанзон. Пучки и гомологическая алгебра.
Д. Хьюзмоллер. Расслоенные пространства.
10. Комплексный анализ.
Б. В. Шабат. Введение в комплексный анализ.
С. М. Львовский. Лекции по комплексному анализу.
W. Rudin. Real and complex analysis.
11. Обыкновенные ДУ.
В. И. Арнольд. Обыкновенные дифференциальные уравнения.
В. В. Степанов. Курс дифференциальных уравнений.
М. В. Федорюк. Обыкновенные дифференциальные уравнения.
12. Уравнения с частными производными.
М. В. Федорюк. Дифференциальные уравнения с частными производными.
Р. Курант. Уравнения с частными производными.
В. И. Арнольд. Лекции об уравнениях с частными производными.
А. Зоммерфельд. Дифференциальные уравнения в частных производных физики.
13. Теория вероятностей.
Дж. Андерсон. Дискретная математика и комбинаторика
Б. В. Гнеденко, А. Я. Хинчин. Элементарное введение в теорию вероятностей.
Б. В. Гнеденко. Курс теории вероятностей.
А. Н. Ширяев. Вероятность.
14. Статистика.
Б. Л. ван дер Варден. Математическая статистика.
Э. Леман. Проверка статистических гипотез.
Ты путаешь прикладников со стартаперами и успешными манагерами вроде Цукерберга и Стива Джобса. Прикладные математики именно что бомжи с бутылкой водки, которые поясняют за то, как они охуенно интегральчики берут. Математики же изредка добиваются успеха.
Смотрите, что нашел. Проект заброшен?
Анализ изи, а вот калькулус напрягает.
Пусть существуют два бесконечных множества A и B с общей единицей дискретности (например, состоящие из целых чисел). На обоих множествах изначально определена функция следования, которая является базовой функцией. Пусть существует отображение A в B по произвольному, но неизменному на всем множестве, правилу. Отображение не меняет порядок следования. Такие множества назовем параллельными.
Пусть на множестве A можно установить определенное элементарное правило 1, которое устанавливает связь между некоторыми элементами множества A, и существует бесконечное количество примеров применения этого правила. Правило неизменно на всем множестве А и обусловлено закономерностями и свойствами множества, то есть примеры не являются случайными.
Отображения элементов А, связанных правилом 1, на B будут являться элементами множества B и будут связаны между собой, элементарным правилом 2, которое может отличаться от правила 1. Правило 2 будет самодостаточным для множества B. То есть сформулировано через ранее определенные на множестве B функции и правила. И один из примеров правила 2 будет состоять из следующих друг за другом членов множества.
Доказательство
Если B - отображение A, то A - отображение B тоже. Примеры правила 1 на множестве A не случайны. Следовательно, они не могут быть отображениями случайных примеров 2 на множестве B. Следовательно, примеры 2 не случайны и связаны определенным правилом 2.
Если A является отражением B, то правило 2 не должно обосновываться правилами и функциями множества A. Следовательно, правило 2 будет самодостаточным для множества B, то есть его можно сформулировать только через функции и правила множества B.
На множестве B изначально определена базовая функция следования. Следовательно, правило 2 должно быть сформулировано через функцию следования, то есть на примере последовательных членов множества.
Следствие 1 (теорема о неполноте Гёнделя)
На множестве В определены некоторые функции и правила изначально. Однако через них могут быть сформулированы любые правила, которые зависят от множества А и функции отображения A на B. Но каждое такое правило должно быть самодостаточным для множества В. Таким образом, на множестве В одни и те же правила и аксиомы, могут порождать любые правила. Следовательно, эти новые правила не основываются только на существующих аксиомах. И одновременно, исходя из этих аксиом, нельзя доказать, что новые правила основаны не только на них, потому что это нарушало бы условие самодостаточности новых правил на множестве В.
Следствие 2 (Великая теорема Ферма)
B - бесконечное множество целых чисел x. A - бесконечное множество, каждый элемент которого равен xn . A и B - параллельные множества На множестве A действует элементарное правило 1 : $a^n+b^n=c^n$ . Если существует один пример для этого правила, то существует и бесконечное количество примеров. Следовательно существует бесконечное количество отображений на множество B. Например, при n=2 на множестве A: $ 9+16=25$, а на множестве B: $3+4=5$ По теореме параллельных множеств существует правило 2, которое связывает все отображения на множестве B, то есть связывает все корни уравнения $a^n+b^n=c^n$ в целых ненулевых числах. И один из примеров должен состоять из последовательных элементов.
И, следовательно, наоборот, если нет решения в последовательных элементах, то нет и любого решения. Для $n>2$ легко показать, что не существуют корней уравнения в целых последовательных числах. Следовательно, нет решений в целых ненулевых числах вообще.
Следствие 3 (физика)
Пусть миры всех наблюдателей – параллельные множества, которые взаимно отображаются. Каждый мир – самодостаточен.
Отображения могут быть разными и порождать разные правила. Так одно и то же явление для одного наблюдателя может быть проявлением электростатической силы, а для другого – магнитной.
Но базовой функцией параллельных миров является функция следования, и никакое отображение не меняет порядок следования. Поэтому при отображении может меняться абсолютно все (пространство, время и т.д.), но всегда и для всех наблюдателей останется неизменным порядок событий (теория относительности). И любой закон, может быть проиллюстрирован на примере последовательных событий, между которыми нет других событий (квантовая механика).
Следствие 4 (философия)
Параллельные множества могут объединяться в подмножества. Наш мир является одним из таких подмножеств. Он является отражением других множеств и миров, но в тоже время является самодостаточным. Это приводит к противоречивому Следствию 1.
Философы давно обнаружили это противоречивую суть всех элементарных суждений нашего мира:
«Выскажем же это утверждение, а также и то, что существует ли единое или не существует, и оно и иное, как оказывается, по отношению к самим себе и друг к другу безусловно суть и не суть, кажутся и не кажутся.» (Платон, «Парменид»)
Пусть существуют два бесконечных множества A и B с общей единицей дискретности (например, состоящие из целых чисел). На обоих множествах изначально определена функция следования, которая является базовой функцией. Пусть существует отображение A в B по произвольному, но неизменному на всем множестве, правилу. Отображение не меняет порядок следования. Такие множества назовем параллельными.
Пусть на множестве A можно установить определенное элементарное правило 1, которое устанавливает связь между некоторыми элементами множества A, и существует бесконечное количество примеров применения этого правила. Правило неизменно на всем множестве А и обусловлено закономерностями и свойствами множества, то есть примеры не являются случайными.
Отображения элементов А, связанных правилом 1, на B будут являться элементами множества B и будут связаны между собой, элементарным правилом 2, которое может отличаться от правила 1. Правило 2 будет самодостаточным для множества B. То есть сформулировано через ранее определенные на множестве B функции и правила. И один из примеров правила 2 будет состоять из следующих друг за другом членов множества.
Доказательство
Если B - отображение A, то A - отображение B тоже. Примеры правила 1 на множестве A не случайны. Следовательно, они не могут быть отображениями случайных примеров 2 на множестве B. Следовательно, примеры 2 не случайны и связаны определенным правилом 2.
Если A является отражением B, то правило 2 не должно обосновываться правилами и функциями множества A. Следовательно, правило 2 будет самодостаточным для множества B, то есть его можно сформулировать только через функции и правила множества B.
На множестве B изначально определена базовая функция следования. Следовательно, правило 2 должно быть сформулировано через функцию следования, то есть на примере последовательных членов множества.
Следствие 1 (теорема о неполноте Гёнделя)
На множестве В определены некоторые функции и правила изначально. Однако через них могут быть сформулированы любые правила, которые зависят от множества А и функции отображения A на B. Но каждое такое правило должно быть самодостаточным для множества В. Таким образом, на множестве В одни и те же правила и аксиомы, могут порождать любые правила. Следовательно, эти новые правила не основываются только на существующих аксиомах. И одновременно, исходя из этих аксиом, нельзя доказать, что новые правила основаны не только на них, потому что это нарушало бы условие самодостаточности новых правил на множестве В.
Следствие 2 (Великая теорема Ферма)
B - бесконечное множество целых чисел x. A - бесконечное множество, каждый элемент которого равен xn . A и B - параллельные множества На множестве A действует элементарное правило 1 : $a^n+b^n=c^n$ . Если существует один пример для этого правила, то существует и бесконечное количество примеров. Следовательно существует бесконечное количество отображений на множество B. Например, при n=2 на множестве A: $ 9+16=25$, а на множестве B: $3+4=5$ По теореме параллельных множеств существует правило 2, которое связывает все отображения на множестве B, то есть связывает все корни уравнения $a^n+b^n=c^n$ в целых ненулевых числах. И один из примеров должен состоять из последовательных элементов.
И, следовательно, наоборот, если нет решения в последовательных элементах, то нет и любого решения. Для $n>2$ легко показать, что не существуют корней уравнения в целых последовательных числах. Следовательно, нет решений в целых ненулевых числах вообще.
Следствие 3 (физика)
Пусть миры всех наблюдателей – параллельные множества, которые взаимно отображаются. Каждый мир – самодостаточен.
Отображения могут быть разными и порождать разные правила. Так одно и то же явление для одного наблюдателя может быть проявлением электростатической силы, а для другого – магнитной.
Но базовой функцией параллельных миров является функция следования, и никакое отображение не меняет порядок следования. Поэтому при отображении может меняться абсолютно все (пространство, время и т.д.), но всегда и для всех наблюдателей останется неизменным порядок событий (теория относительности). И любой закон, может быть проиллюстрирован на примере последовательных событий, между которыми нет других событий (квантовая механика).
Следствие 4 (философия)
Параллельные множества могут объединяться в подмножества. Наш мир является одним из таких подмножеств. Он является отражением других множеств и миров, но в тоже время является самодостаточным. Это приводит к противоречивому Следствию 1.
Философы давно обнаружили это противоречивую суть всех элементарных суждений нашего мира:
«Выскажем же это утверждение, а также и то, что существует ли единое или не существует, и оно и иное, как оказывается, по отношению к самим себе и друг к другу безусловно суть и не суть, кажутся и не кажутся.» (Платон, «Парменид»)
Вот это спасибо тебе.
Хуйня какая-то хуйнющая. Кто-то тебе это сказал чтобы выебнуться, наверное.
Дифференциал, как линейный оператор на дифф. формах, в квадрате 0. Вот и всё.
>Очень гордится тем что может считать интегралы
Эй, мани, посчитайте мне интригал (e^x)/x
Хочу ресурс какой-нибудь исчерпывающий, желательно с алгеброй, топологией, теорией игор и матстатом. Чтобы онлайн можно было скроллить. Ну или годный курс на крайняк
Помню был один сайт, году в 2006 или даже 7-м на нем сидел
Ну и что там получается? Интеграл равен ингералу + константа? Какая хуета, браток. Ничего не посчитано!
зачем тебе топология? теория игори и матстат как-то более в тему к дисперсиям.
Не совсем дебил может, просто симплициальный чуток
(В случае многообразия с краем)
Я не читал, но хочу вас обскакать. Сейчас пытался запомнить этот рисунок и воспроизвести его по памяти. Хуй там. Все-таки тяжелая наука.
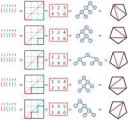
Клини в 2016 году НЕ НУЖЕН. Можно сразу учить гомотопическую теорию типов и coq. Зачем каждый раз по-новой изучать свойства изоморфных структур типа пикрилейтед, если это можно сделать один раз?
не знаю, я люблю до самых низов докопаться. и до сих пор НЕДОВОЛЕН, что не нашёл любимый учебник/сайт/методичку
слушай, а что посоветуешь по другим разделам математики актуального? как ищешь?
Может кому нужно, то вот сделал pdf одним файлом все страницы.
http://rgho.st/private/8vdyZCtLB/d4dee6751fb0f31815de4279b2fa6035
Хорошая малварь. Зиродей.
Спасибо, анон.
Не ну чо серьёзно никто не понимает гаусса бонне?( Это ж такое, что обязан знать и "первокультурщик", и картофан, и перельман?
Доложите мне всё, что вы про него знаете в случае многообразия с краем.
Хотя стой. Это для N -> N
А надо в {1;2;...;n} -> {1;2;...;n}, так? g - такая биекция.
Если n=2m g(k)=f(k), 1 <= k <= n
f - из предведущего поста.
Если n=2m+1
g(k)=f(k), 1<= k <= 2m=n-1
g(n)=g(2m+1)=2m+1
Не понял вопроса, если это множество, то биекций можно придумать дохуя (n!) другой вопрос, если ты задал на множестве операцию. Например, f(n) = 1, f(n-k+1) = k для всех k<n+1

Допустим я придумал такую биекцию:
1↦16
2↦17
3↦18
4↦19
5↦20
6↦1
7↦2
8↦3
9↦4
10↦5
11↦11
12↦12
13↦13
14↦14
15↦15
16↦6
17↦7
18↦8
19↦9
20↦10
...
И теперь проверяю произведние для \nu = 1...7. Нихуя же не выходит. Что он имеет тут в виду?
Он тут имет виду что ты пидор
Так как phi биективно, то элементы n и phi(n) просто меняются местами в произведении, но произвдение остаёться тем же.
Для коммутативного моноида - очевидно. Ты поменял местами множители, поменяется произведение?
Если произведение бесконечное, то я согласен. А если оно конечное, то я нихуя не согласен.
У человека уже на этом мусоре серьёзное непонимание.
Посмотри внимательное, что у тебя в произведении. Ты меняешь n членов друг с другом и их же перемножаешь. Не часть от n, не больше чем n, а ровно n.
А я наоборот, чем больше читаю тем больше понимаю что тут сидят поехавшие гомотопы которые хуй от векторного пространства не отличат.

http://puu.sh/qzc8a/b65a08172c.png
То есть указанного тебе мало? Вся элементарная математика есть в этих книгах.
Материал в нём хороший, но некоторые параграфы - атас.
Они гомотопии от гомологий не отличат, хуле. Тут же шкальники выпендривающиеся. Словечки новые выучиInxSAOxsYzw
https://www.google.ru/url?sa=t&source=web&rct=j&url=http://www.mccme.ru/free-books/mmmf-lectures/book.10.pdf&ved=0ahUKEwje8vX78b3OAhWHjSwKHejCBJsQFggjMAI&usg=AFQjCNFZF5hgkA_7_E3FN9lriVKZl8ITtg&sig2=A-RK6OaP0a_InxSAOxsYzw
По этой ссылке - брошюра с теорией кос и узлов. Ещё в школе читал, дико понравилось, а сейчас ещё больше. Хоть и поверхностно, уровня наглядной топологии Прасолова, даже ещё более научно-популярно, но многим здесь это будет полезнее попытки разобраться сразу с hott и учёбы тапалогии по ангельским учебникам.
Бамп вопросу
Читай дальше. Решай проблемсы

Я думал, что интегралы это что-то невъёбно сложное, что даже Вербит брать не умеет, но на самом деле довольно просто.
Я прочел "Алгебру" Гельфанда и Шень, потом начал Гашкова, но там достаточно много новых понятий, которых у Шень не было, но с которыми я при этом уже должен быть знаком. А все книги из раздела геометрия вообще для тех, кто с базовыми понятиями геометрии уже знаком.
Ух, 63 интеграла за день, ну я и молодец.

Неопределённые же неинтересно. Лучше считай площади фигур под графиками.
Что же ты наделал? Теперь если встретишь Демидовича, то у вас не будет общих тем для беседы.
>>381289
Я же только начал. Всего из ~4000 задач прорешал 500, скоро до площади дойду.
>>381290
Не выражаеться в элементарных функциях.

Ой, точно. Спасибо. Перед скобкой же минус.
А еще есть гомотетия ебта. А ее тут ни разу не упоминали со времен образования саентача. Ну и homopolar мотор еще. На русский гомо стыдливо перевели как уни.
>гомотетия
Всю эту гомосятину завез в Россию из Европы Александров. А потом с помощью своего гей-лобби внедрил повсеместно.
Дерни себе анус, «пёс».
Имея ph.d по математике ты можешь стать CTO вконтакте и получить несколько миллионов долларов.
Имея диплом матмеха ты можешь устроиться на работу в JetBrains и купить себе квартиру по-быстрому.
Имея диплом НМУ ты можешь начать долбиться в туза и писать на сосаче.
Имея диплом Заборостроительного ты можешь начать пить горькую и писать сайты на пхп.
Вылетев со второго курса Заборостроительного ты можешь пойти работать грузчиком и мечтать по вечерам, как ты пишешь сайты на пхп.
сурово говоришь. Так получается , рассказы про саморазвиванцев верны лишь только к самым упорным , задротящим предмет и матан 24/7 ?
Получить нужную для работы подготовку не выходя из дому крайне трудно, тут нужна не только воля и некоторая врождённая способность, но ещё и удача. Впрочем, про пхп он загнул, пхп можно выучить ещё в школе вместе с жаваскриптом и пойти писать сайты мимо шараги, вообще как нехуй.
Вообще, в научной стреде я вижу принято тонко шутить, причем с давних пор
math.MG - Metric Geometry (new, recent, current month)
Euclidean, hyperbolic, discrete, convex, coarse geometry, comparisons in Riemannian geometry, symmetric spaces
Шок архивом Корнельского униве рситета управляют вербитомрази! Сенсация!
А смысл старый журнал брать? Бери актуальное. Я сам тут третий тред, вроде это не особо нормально тут
>Аноны, можно взять какой-нибудь старый математический журнал и, начиная с первого номера, изучать математику по нему? С какого-нибудь 1900-ого года.
Аноны, можно взять каких-нибудь старых русских летописей и, начиная с первой, изучать русский язык по ним? С какого-нибудь 900-ого года.
1. пройти этот курс https://www.khanacademy.org/math/algebra-home
2 прочитать и сделать все упражнения Stewart : Precalculus
3 Прочитать Algebra: Chapter 0
рейт
> нужна ли погромисты математика ?
Не только не нужна, но даже вредна. Увлечение математикой приведет тебя к тому, что вместо того, чтобы делать че-то реальное, ты будешь по вечерам писать на хаскеле, доказывать теоремы с помощью пруф асистантов, решать задачи с codeforces, в то время как Ерохин будет писать сайты на пыхе и будет абсолютно счастлив в отличие от тебя.
Только свой анус для силиконовых фаллосов.
Если конкретно что мне надо, вот я читал про интригалы а мне пишут "как можно увидеть по формуле о суммировании бесконечного числа членов прогрессии мы получим хуй+пизда_умножить_дельта+сковорода_умножать_дельтаквадрат площадь площади формулы джигурда" и вот там не понятно как они эту формулу получили, не поясняется нихуя. И там еще много такого КАК МОЖНО УВИДЕТЬ, ОЧЕВИДНО, ЧТО И ТРЕБОВАЛОСЬ ДОКАЗАТЬ
Сканави.
И лекции это конечно хорошо, но лектор говорит слишком долго а я читаю со скоростью 400 знаков в минуту.
Значит, у тебя не откладывается в голове материал. Чтобы понимать все эти очевидности, нужно постоянно держать в голове абсолютно всё, что было уже пройдено. Если ты этого не можешь, значит, либо у тебя проблемы с памятью, либо — с пониманием материала, а то и вовсе оба пункта сразу. Снижай скорость чтения или выбери книгу легче. Если у тебя нет понимания только при использовании результатов из школьного курса математики (тригонометрия, прогрессии, биномы), то можешь просто в каждом отдельном случае гуглить эти темы и немного повторять. Если у тебя возникают проблемы при оперировании теоремами из других разделов математики (к примеру, в учебнике анализа используется какая-нибудь теорема о матрицах), то начни читать книги по этому разделу, чтобы идти примерно вровень. Что рекомендовать конкретно в твоём случае, я сказать не могу. Скорее всего, тебе просто не хватает математической культуры.
>Скажите название учебников по алгебре и геометрии
Дьёдонне Ж. Линейная алгебра и элементарная геометрия.
По крайней мере до теории групп включительно сможет. Я проверял.
Повторяю: школьные учебники.

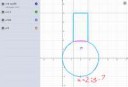
Найти по отдельности у круга и прямоугольника, а потом у получившихся двух точек (с соответствующими массами)? То есть делать нечего.
>потом у получившихся двух точек (с соответствующими массами)?
Не понял смысла предложения, поясни плиз
>Найти по отдельности у круга и прямоугольника
что мне это даст? Здесь же не должно канать среднее арифметическое.
Ну это само собой через двойные решается, а что мне делать с пределами интегрирования? У круга область определения видно из рисунка. В какую сторону копать эту сраную фигуру?
Круг заменить точкой в его центре такой же массы как и круг.
То же самое с прямоугольником.
Потом легко найти итоговый центр по правилу рычага.
Самый простой способ — повернуть твою фигуру. Она как раз симметричная — будет удобно. Иначе придётся разбивать интеграл и ебаться с пределами интегрирования.
счастлив не будет никто. ни математик ни погромист. оба придут ныть на дваче и хуесосить себе подобных
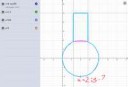
Хорошо. С иксом все ясно, даже не будем о нем говорить. Что делатьс игреком? При вычислении площадей получается нюанс: заштрихованная область является общей для обеих фигур. Что с этим делать?
Я знаю, что хуево повернул без полярных координат, суть не в этом, а в координате по игреку.
Из первых мыслей: опустить заштрихованную площадь до 0 по игреку, проинтегралить ее, а потом отрезать от какой-либо фигуры и далее посчитать. Так пойдет?
Я думал, ты повернёшь её наоборот (набок): там было бы только два интеграла. Если ты повернул её таким образом, то интеграла будет четыре, но два из них равны, третий — площадь полукруга, а четвёртый — площадь прямоугольника. Считаешь интеграл от 0 до 1,2, считаешь интеграл от 1,2 до 2,8 (площадь прямоугольника), считаешь площадь оставшейся части круга (она уже посчитана, поэтому первый интеграл можешь просто на два умножить). Короче, положи набок свою фигуру.
Может, на случайной дуэли закололи, как перепела
>читает бурбаков со скоростью 400 знаков в минуту
Вот это охуенная постановка вопроса. Я здесь на двачах много всякой хуйни прочитал, но про скоростное чтение математики вижу впервые. Так прочитай полный курс из списка вербита, у тебя не больше пары дней должно занять. Можно конкурсы устраивать, кто быстрее прочитает фсю матешу.
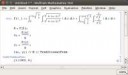
Вот центр для твоего первого примера. Я положил фигуру на бок и просчитал точки пересечения. Надеюсь, нигде не ошибся. Знатно поел картошечки.
Только координаты я получил для лежащей фигуры, но не составит труда перевести.
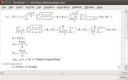
Вот как считается центр, если фигуру не вращать. Здесь координаты переводить не нужно. Можно убедиться, что оба решения эквивалентны, поэтому либо оба верны, либо оба неверны.

У тебя есть функция sin(x). Пределы этой функции во сех точках равны значениям этой функции. Теперь у тебя есть функция sin(x)/x. В точке 0 у нее нет значения (т.к. деление на 0), но есть предел, который равен 1.
Тебе рассказывают формальное определение того, что же собственно есть предел функции в точке x.
Для общего развития почитай эту страницу:
https://ru.wikipedia.org/wiki/Предел_вдоль_фильтра
Определение предела функции.
>>381528
Не знаю английского, но, видимо, просят найти δ. Например, в первом случае δ = 0,01.


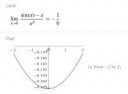
Вот смотри. Есть две функции. Во всех "обычных" точках предел равен значения этой функции. В необычных точках (в данном случае у геперболы таких точек 3: +inf, -inf, 0; а у синусной функции одна такая точка: 0) функция может иметь предел, а может и не иметь.
Для синусной функции предел есть, т.к. функция с двух сторон подбирается к одной и той же точке.
Для гиперболы в +inf и -inf пределы есть, а для 0 нет. Т.к в нуле функция с двух сторон подбирается совершенно к разным точкам. Говорят, что у нее есть предел слева и справа. А просто предела в точке 0 нет.
И все?
Это я и так понял

Сегодня ночью мне было видение.
Ко мне спроецировался Вербит и сказал что я готов.
Так вот, я пришел спросить - какой там топовый учебник по топологии на русском?
Только не листки Вербита. Вербит сказал что листки - это не учебник и вообще говно.
А, точно, это же сборник листков. Тогда хз, лекции на лекториуме и можно анализ Барри Саймона глянуть, хотя это не совсем то.
Спасибо!
а не, это у меня просвечивается на картинке

Ну нормально в общем, мой ответ разница на 0.1 примерно, думаю, проканает. А то я с двойными интегралами день знаком, считал другие фигуры, а тут мне приспичило такую посчитать.
Попробуй со школьных учебников пятого класса.
Скинь оставшиеся плис, и оставшиеся советы по книгам! (ты написал, мол, 19 было)
Тащемта, например, это и так очевидно что синус бесконечно млого деленный на бесконечно малое будет адын из самого свойства синуса, который при малом икс дает примерно такой же икс.
Нахуя это доказывать надо?
8. Элементарный анализ. Аксиоматика вещественных чисел. Аксиома полноты, принцип Архимеда. Конструкция R по Симону Стевину, по Рихарду Дедекинду. Комплексные числа. Топологические пространства, метрические пространства. Открытые множества и базы топологии. Замкнутые множества, замыкание. Непрерывность, гомеоморфизмы, теоремы о непрерывности. Пределы. Хаусдорфовы пространства. Топология Александрова на натуральных числах, последовательности. Замыкание в метрическом пространстве. Последовательности Коши, критерий Коши. Определение R по Коши-Кантору. Пополнение. Компакты. Леммы Гейне-Бореля-Лебега, Больцано-Вейерштрасса, Коши-Кантора, Вейерштрасса о функции на компакте, Больцано-Коши, Вейерштрасса о монотонности. Связность, линейная связность. Секвенциальная компактность, лемма о лебеговом числе. Топология произведения. Характеристические функции, максимальный идеал, лемма Александера о предбазе. Теорема Тихонова о компактности. Нормы на векторных пространствах, стандартная норма на R^n. Фильтры, базы фильтров, предел вдоль фильтра (ака по базе множеств). Локальные и глобальные свойства непрерывных функций, разрывы. Бесконечно-малые и бесконечно-большие функции, асимптотическое поведение функций, O-большое и o-малое. Производная функций R->R, дифференциал, классы гладкости. Теоремы Ферма, Ролля, Коши, Лагранжа, Тейлора. Формула конечных приращений, формула Тейлора. Топологическое векторное пространство, базис Шаудера. Элементарная теория банаховых пространств. Линейные непрерывные отображения, их ядро и образ. Произведения нормированных пространств, непрерывные билинейные и мультилинейные отображения произведения пространств в нормированное пространство. Равномерная сходимость, равномерная непрерывность, теорема Кантора. Функциональные ряды, ряд Тейлора как обобщение производной. Абсолютная сходимость и теорема о перестановке, условная и безусловная сходимость и теорема Римана, числовые ряды, знакопеременные ряды, признаки сходимости. Действие линейного непрерывного отображения на ряд. Произведение двух рядов, применение билинейного непрерывного отображения к двум рядам. Примеры функциональных пространств. Локально равномерный предел последовательности непрерывных функций. Контрпримеры. Бесконечные произведения, логарифмические ряды. Определения элементарных функций, формула Эйлера, таблица производных. Аналитические функции, их свойства. Круг сходимости. Аналитическое продолжение. Голоморфные функции. Интеграл Коши (от кусочно-непрерывных функций), его линейность, аддитивность и монотонность. Формула Ньютона-Лейбница, таблица первообразных, техника интегрирования. Несобственный интеграл. Выпуклые и вогнутые функции. Исследование функций. Аффинные пространства. Аффинные многообразия. Аффинные отображения. Норма и выпуклость. Евклидовы и эрмитовы аффинные пространства. Двойственное пространство, ортонормированные базисы. Производная аффинного отображения. Производная вдоль вектора. Частная производная. Матрица Якоби. Якобиан. Производная Гато. Производная Фреше. Дифференцируемое многообразие. Линейное касательное многообразие. Градиент вещественной функции в евклидовом пространстве. Векторное поле. Произведения аффинных пространств. Производная билинейного непрерывного отображения. Теорема о сложной функции. Производные высших порядков. Обобщенная формула Тейлора. Экстремумы. Теорема о неявной функции. Лемма Морса. Разложение диффеоморфизма в композицию простейших. Поверхности в R^n. Кратный и повторный интегралы Коши, криволинейный и поверхностный интегралы. Параметрическое представление дифференцируемого многообразия. Неявные уравнения многообразия. Вещественные, комплексные, абстрактные многообразия. Теория условных экстремумов, неравенства Гёльдера и Минковского. Вариационное исчисление. Лемма Хаара. Геодезические. Канонические уравнения Гамильтона. Мера, пространства с мерой, измеримые отображения. Мера Жордана. Суммы и интегралы Дарбу. Интеграл Римана. Мера Радона. Векторные меры. Разложение единицы. Склейка мер. Продолжение меры. Внешняя мера. Внутренняя мера компакта. Мера Лебега. Произведение мер. Борелевские множества. Интеграл Лебега. Теорема Беппо Леви, лемма Фату, теорема Фубини. Теория Лебега. Теорема Фишера-Рисса. Умножение меры на функцию. Широкая сходимость. Тензорное произведение мер. Кратный интеграл Лебега. Повторный интеграл Лебега. Теорема Арцела-Асколи, интегрирование рядов. Теорема Сарда. Тригонометрический ряд Фурье, преобразование Фурье, преобразование Лапласа.
9. Математический анализ. Дифференциальная форма. Координаты формы. Внешний дифференциал формы. Интеграл формы. Форма объёма. Формулы Грина, Остроградского-Гаусса, Стокса. Скалярные и векторные поля на R^3. Градиент, ротор, дивергенция в дифференциальных и интегральных формах, набла. Криволинейные координаты. Потенциальные поля, векторный потенциал, точные и замкнутые формы. Примеры уравнений - теплопроводность, неразрывность, динамики сплошной среды, волновое. Абстрактные многообразия, грассманиан, локальные кольца, лемма Адамара. Компактные многообразия. Интегрирования плотностей. Дифференциальная форма в аффинном пространстве. Дифференциальная форма на многообразии. Интегрирование форм по цепям. Интеграл от формы по многообразию. Формула Стокса. Теорема Пуанкаре, гомологии и когомологии. Когомологии де Рама. Теорема де Рама. Интеграл от коцикла по циклу. Гомологические циклы. Гомотопия. Топологическая степень. Теорема Фробениуса. Свойства преобразований. Распределения. Обобщенные функции. Пространства Соболева. Эллиптические операторы. Оператор Коши-Римана. Теорема регулярности.
10. Комплексный анализ. Голоморфные функции. Формулы Коши. Ряд Тейлора. Ряды Хартогса и Лорана. Теорема Лиувилля. Мероморфные функции. Псевдовыпуклость. Оболочки голоморфности. Проблемы Кузена. Группы гомологий, точные последовательности пучков. Вычеты. Поверхности Римана. Свертки. Теоремы Бэра и Банаха-Штейнгауза. Свойства Монтеля. Теорема Миттаг-Лефлера. Теорема Вейерштрасса. Задача Дирихле. Теоремы Коши-Пуанкаре, Мартинелли-Бохнера, Лере, Севери, Вейла.
11. Обыкновенные дифференциальные уравнения. Задача Коши. Теоремы существования и единственности. Априорная оценка. Непрерывность решения. Фазовые пространства, фазовые потоки. Действие диффеоморфизмов. Теоремы о выпрямлении. Классические дифференциальные уравнения - разделяющиеся, однородные, линейные, Бернулли, Якоби, Риккати, Лагранжа, Клеро. Устойчивость по Ляпунову. Фазовый поток, заданный векторным полем. Дифференциальное уравнение, определенное векторным полем. Дифференциальное уравнение на многообразии. Особые точки, индексы особых точек.
12. Уравнения с частными производными. Линейное однородное урчп с производными первого порядка. Системы уравнений. Уравнение Пфаффа. Уравнение теплопроводности, уравнение струны. Задача Штурма-Лиувилля, задача Коши. Характеристика. Полный, общий и особый интегралы, интеграл Пуассона. Методы Лагранжа и Коши. Преобразование Лежандра. Теорема Коши-Ковалевской. Уравнение Монжа. Уравнение Эйлера. Эйконал. Поле экстремалей. Уравнние Гамильтона-Якоби. Конструкция Гюйгенса. Интеграл Гильберта. Теория возмущений. Уравнения высших порядков. Гиперболичность. Уравнения Дарбу, Максвелла и Дирака. Фундаментальные решения. Плоские, бегущие, цилиндрические и сферические волны. Принцип Дюамеля. Запаздывающие потенциалы. Приведенное волновое уравнение, условие Зоммерфельда. Теорема Реллиха. Оценки Шаудера. Уравнение Бельтрами. Характеристическая нормальная форма для гиперболических систем первого порядка. Динамика сжимаемой жидкости. Представление решений в форме Римана. Исчисление Хевисайда, метод Хевисайда. Дифференциальные уравнения гидродинамики, кристаллодинамики, магнитной гидродинамики. Асимптотические разложения решений. Уравнения физики, примеры и контрпримеры, пример Адамара.
8. Элементарный анализ. Аксиоматика вещественных чисел. Аксиома полноты, принцип Архимеда. Конструкция R по Симону Стевину, по Рихарду Дедекинду. Комплексные числа. Топологические пространства, метрические пространства. Открытые множества и базы топологии. Замкнутые множества, замыкание. Непрерывность, гомеоморфизмы, теоремы о непрерывности. Пределы. Хаусдорфовы пространства. Топология Александрова на натуральных числах, последовательности. Замыкание в метрическом пространстве. Последовательности Коши, критерий Коши. Определение R по Коши-Кантору. Пополнение. Компакты. Леммы Гейне-Бореля-Лебега, Больцано-Вейерштрасса, Коши-Кантора, Вейерштрасса о функции на компакте, Больцано-Коши, Вейерштрасса о монотонности. Связность, линейная связность. Секвенциальная компактность, лемма о лебеговом числе. Топология произведения. Характеристические функции, максимальный идеал, лемма Александера о предбазе. Теорема Тихонова о компактности. Нормы на векторных пространствах, стандартная норма на R^n. Фильтры, базы фильтров, предел вдоль фильтра (ака по базе множеств). Локальные и глобальные свойства непрерывных функций, разрывы. Бесконечно-малые и бесконечно-большие функции, асимптотическое поведение функций, O-большое и o-малое. Производная функций R->R, дифференциал, классы гладкости. Теоремы Ферма, Ролля, Коши, Лагранжа, Тейлора. Формула конечных приращений, формула Тейлора. Топологическое векторное пространство, базис Шаудера. Элементарная теория банаховых пространств. Линейные непрерывные отображения, их ядро и образ. Произведения нормированных пространств, непрерывные билинейные и мультилинейные отображения произведения пространств в нормированное пространство. Равномерная сходимость, равномерная непрерывность, теорема Кантора. Функциональные ряды, ряд Тейлора как обобщение производной. Абсолютная сходимость и теорема о перестановке, условная и безусловная сходимость и теорема Римана, числовые ряды, знакопеременные ряды, признаки сходимости. Действие линейного непрерывного отображения на ряд. Произведение двух рядов, применение билинейного непрерывного отображения к двум рядам. Примеры функциональных пространств. Локально равномерный предел последовательности непрерывных функций. Контрпримеры. Бесконечные произведения, логарифмические ряды. Определения элементарных функций, формула Эйлера, таблица производных. Аналитические функции, их свойства. Круг сходимости. Аналитическое продолжение. Голоморфные функции. Интеграл Коши (от кусочно-непрерывных функций), его линейность, аддитивность и монотонность. Формула Ньютона-Лейбница, таблица первообразных, техника интегрирования. Несобственный интеграл. Выпуклые и вогнутые функции. Исследование функций. Аффинные пространства. Аффинные многообразия. Аффинные отображения. Норма и выпуклость. Евклидовы и эрмитовы аффинные пространства. Двойственное пространство, ортонормированные базисы. Производная аффинного отображения. Производная вдоль вектора. Частная производная. Матрица Якоби. Якобиан. Производная Гато. Производная Фреше. Дифференцируемое многообразие. Линейное касательное многообразие. Градиент вещественной функции в евклидовом пространстве. Векторное поле. Произведения аффинных пространств. Производная билинейного непрерывного отображения. Теорема о сложной функции. Производные высших порядков. Обобщенная формула Тейлора. Экстремумы. Теорема о неявной функции. Лемма Морса. Разложение диффеоморфизма в композицию простейших. Поверхности в R^n. Кратный и повторный интегралы Коши, криволинейный и поверхностный интегралы. Параметрическое представление дифференцируемого многообразия. Неявные уравнения многообразия. Вещественные, комплексные, абстрактные многообразия. Теория условных экстремумов, неравенства Гёльдера и Минковского. Вариационное исчисление. Лемма Хаара. Геодезические. Канонические уравнения Гамильтона. Мера, пространства с мерой, измеримые отображения. Мера Жордана. Суммы и интегралы Дарбу. Интеграл Римана. Мера Радона. Векторные меры. Разложение единицы. Склейка мер. Продолжение меры. Внешняя мера. Внутренняя мера компакта. Мера Лебега. Произведение мер. Борелевские множества. Интеграл Лебега. Теорема Беппо Леви, лемма Фату, теорема Фубини. Теория Лебега. Теорема Фишера-Рисса. Умножение меры на функцию. Широкая сходимость. Тензорное произведение мер. Кратный интеграл Лебега. Повторный интеграл Лебега. Теорема Арцела-Асколи, интегрирование рядов. Теорема Сарда. Тригонометрический ряд Фурье, преобразование Фурье, преобразование Лапласа.
9. Математический анализ. Дифференциальная форма. Координаты формы. Внешний дифференциал формы. Интеграл формы. Форма объёма. Формулы Грина, Остроградского-Гаусса, Стокса. Скалярные и векторные поля на R^3. Градиент, ротор, дивергенция в дифференциальных и интегральных формах, набла. Криволинейные координаты. Потенциальные поля, векторный потенциал, точные и замкнутые формы. Примеры уравнений - теплопроводность, неразрывность, динамики сплошной среды, волновое. Абстрактные многообразия, грассманиан, локальные кольца, лемма Адамара. Компактные многообразия. Интегрирования плотностей. Дифференциальная форма в аффинном пространстве. Дифференциальная форма на многообразии. Интегрирование форм по цепям. Интеграл от формы по многообразию. Формула Стокса. Теорема Пуанкаре, гомологии и когомологии. Когомологии де Рама. Теорема де Рама. Интеграл от коцикла по циклу. Гомологические циклы. Гомотопия. Топологическая степень. Теорема Фробениуса. Свойства преобразований. Распределения. Обобщенные функции. Пространства Соболева. Эллиптические операторы. Оператор Коши-Римана. Теорема регулярности.
10. Комплексный анализ. Голоморфные функции. Формулы Коши. Ряд Тейлора. Ряды Хартогса и Лорана. Теорема Лиувилля. Мероморфные функции. Псевдовыпуклость. Оболочки голоморфности. Проблемы Кузена. Группы гомологий, точные последовательности пучков. Вычеты. Поверхности Римана. Свертки. Теоремы Бэра и Банаха-Штейнгауза. Свойства Монтеля. Теорема Миттаг-Лефлера. Теорема Вейерштрасса. Задача Дирихле. Теоремы Коши-Пуанкаре, Мартинелли-Бохнера, Лере, Севери, Вейла.
11. Обыкновенные дифференциальные уравнения. Задача Коши. Теоремы существования и единственности. Априорная оценка. Непрерывность решения. Фазовые пространства, фазовые потоки. Действие диффеоморфизмов. Теоремы о выпрямлении. Классические дифференциальные уравнения - разделяющиеся, однородные, линейные, Бернулли, Якоби, Риккати, Лагранжа, Клеро. Устойчивость по Ляпунову. Фазовый поток, заданный векторным полем. Дифференциальное уравнение, определенное векторным полем. Дифференциальное уравнение на многообразии. Особые точки, индексы особых точек.
12. Уравнения с частными производными. Линейное однородное урчп с производными первого порядка. Системы уравнений. Уравнение Пфаффа. Уравнение теплопроводности, уравнение струны. Задача Штурма-Лиувилля, задача Коши. Характеристика. Полный, общий и особый интегралы, интеграл Пуассона. Методы Лагранжа и Коши. Преобразование Лежандра. Теорема Коши-Ковалевской. Уравнение Монжа. Уравнение Эйлера. Эйконал. Поле экстремалей. Уравнние Гамильтона-Якоби. Конструкция Гюйгенса. Интеграл Гильберта. Теория возмущений. Уравнения высших порядков. Гиперболичность. Уравнения Дарбу, Максвелла и Дирака. Фундаментальные решения. Плоские, бегущие, цилиндрические и сферические волны. Принцип Дюамеля. Запаздывающие потенциалы. Приведенное волновое уравнение, условие Зоммерфельда. Теорема Реллиха. Оценки Шаудера. Уравнение Бельтрами. Характеристическая нормальная форма для гиперболических систем первого порядка. Динамика сжимаемой жидкости. Представление решений в форме Римана. Исчисление Хевисайда, метод Хевисайда. Дифференциальные уравнения гидродинамики, кристаллодинамики, магнитной гидродинамики. Асимптотические разложения решений. Уравнения физики, примеры и контрпримеры, пример Адамара.
13. Теория вероятностей. Комбинации. Сочетания, размещения, перестановки. Наивное понятие вероятности. Правило сложения вероятностей, полная система. Условная вероятность, правило умножения вероятностей, независимые события. Формула полной вероятности. Формула Байеса. Схема Бернулли. Теорема Бернулли. Случайная величина, закон распределения, средние значения. Рассеяние, среднее квадратичное уклонение. Закон больших чисел. Нормальные законы. Случайные процессы. Свойства специальных функций теории вероятностей. Аксиоматика Колмогорова. Вероятностное пространство. Локальные предельные теоремы. Интегральные предельные теоремы. Теорема Пуассона. Цепи Маркова. Непрерывные и дискретные распределения, многомерные. Функции от случайных величин. Интеграл Стилтьеса. Матожидание, дисперсия, моменты. Закон больших чисел в форме Чебышева. Характеристические функции. Теорема Хелли. Преобразование Лапласа-Стилтьеса. Теорема Линдеберга. Безгранично делимые законы. Стохастические процессы. Процесс Пуассона. Уравнения Колмогорова. Стационарный случайный процесс. Теорема Хинчина. Эргодическая теорема Биркгофа-Хинчина.
14. Статистика. Классическая статистика. Исчерпывающие статистики. Доверительные границы и доверительные вероятности. Гипотезы. Вероятности и частоты. Биномиальное распределение. Бета- и гамма-функции. Кривая Кетле. Оценки функций распределения. Характеристические функции, хи-квадрат, предельные теоремы, прямоугольное распределение. Гауссова теория ошибок, s-квадрат, критерий Стьюдента. Метод наименьших квадратов. Средние значения и дисперсии. Оценка дисперсии. Линии регрессии. Метод наибольшего правдоподобия Фишера. Неравенство Фреше. Свойства нормального распределения. Асимптотические свойства. Оценка параметров по наблюденным частотам. Проверка гипотез с помощью статистических критериев. Гипотезы однородности, независимости, случайности. Параметрические гипотезы, простые и сложные. Дисперсионный анализ. Порядковые критерии. Корреляция, ковариация. Коэффициенты корреляции.
15. Классическая неквантовая механика. Законы Ньютона. Терминология. Энергия, связи, обобщенные координаты, конфигурационное пространство, принцип возможных перемещений, принцип Даламбера. Теорема Нётер. Уравнения Лагранжа. Консервативные и неконсервативные системы. Функция Рэлея. Сила Кориолиса, центробежная сила, задача двух тел, теорема Лармора, симметричный волчок, главные колебания. Обобщенные импульсы, циклические координаты, фазовое пространство, функция Гамильтона. Интегралы движения. Диссипативные системы. Принцип Гамильтона. Уравнения Гамильтона, метод Гамильтона-Якоби. Движение частиц, столкновение частиц, рассеяние частиц. Формула Резерфорда. Малые колебания. Колебания систем со многими степенями свободы. Параметрический резонанс. Ангармонические колебания. Движение твердого тела. Тензор инерции. Волновое уравнение, принцип Ферма. Функция Рауса, скобки Пуассона, тождество Якоби. Принцип Мопертюи. Теорема Лиувилля. Непрерывные среды. Переменные поля, уравнения Гамильтона для поля. Законы сохранения плотности. Симплектические многообразия, классическая механика как структура на симплектическом многообразии.
16. Классическая термодинамика. Термодинамические системы. Идеальные газы. Первый закон. Адиабатические процессы в газах. Второй закон. Цикл Карно. Абсолютная температура. Тепловые машины. Энтропия. Уравнение Клапейрона. Уравнение Ван-дер-Ваальса. Термодинамические потенциалы. Свободная энергия. Правило фаз. Химическое равновесие в газах. Принцип ле Шателье. Термодинамика разбавленных растворов. Осмотическое давление. Химическое равновесие в растворах. Связь энтропии и температуры. Теорема Нернста. Энтропийная константа. Третий закон термодинамики. Фактор Больцмана. Распределение Максвелла по скоростям. Экспериментальные подтверждения.
17. Классическая гидродинамика. Модель Эйлера. Уравнение состояния. Граничные условия. Уравнение энергии. Перенос количества движения. Уравнение неразрывности. Безвихревое движение, поток, циркуляция. Несжимаемая жидкость. Трубка тока. Источники и стоки. Функция тока Лагранжа. Теория Максвелла о полюсах. Зональные функции, гипергеометрические ряды, тессеральные и секторальные функции. Уравнение Лапласа. Линии тока на эллипсоиде, диполь. Движение твердых тел в жидкости. Гидрокинетическая симметрия. Вихревое движение. Постоянство вихрей. Изолированный вихрь. Потенциал, создаваемый вихрем. Импульс вихря. Прямолинейные вихри. Вихревая дорожка. Теоремы Кирхгофа. Вихревые кольца, их устойчивость. Приливные волны. Поверхностные волны. Стоячие волны в ограниченной массе воды. Капиллярные волны. Плоские волны. Звуковые волны. Вязкость. Диффузия вихря.
18. Классическая электродинамика. Электрические явления и приборы. Заряд. Закон Кулона. Электростатическое поле. Проводники. Уравнение Лапласа. Уравнение Лежандра. Полиномы Лежандра. Граничные задачи. Функции Бесселя. Разложение по мультиполям. Изотропные диэлектрики. Поляризуемость молекул и диэлектрическая восприимчивость. Магитостатика. Закон Био-Савара. Закон Ампера. Векторный потенциал. Магнитная индукция, магнитное поле, магнитный момент. Внешнее магнитное поле. Макроскопические уравнения. Электромагнитное поле. Закон Фарадея. Энергия магнитного поля. Максвелловский ток. Уравнения Максвелла. Векторный и скалярный потенциалы. Калибровочные преобразования. Лоренцовская, кулоновская калибровка. Функция Грина для волнового уравнения. Интегральное представление Кирхгофа. Теорема Пойтинга. Плоские электромагнитные волны. Волны в непроводящей среде. Линейная, круговая поляризации. Суперпозиция волн. Групповая скорость. Распространение импульсов в диспергирующей среде. Отражение и преломление электромагнитных волн. Поляризация. Волны в проводящей среде. Простая модель проводимости. Волноводы. Поля на поверхности и внутри проводника. Цилиндрические резонаторы. Диэлектрические волноводы. Поле ограниченного колеблющегося источника. Электрическое дипольное поле. Излучение. Магнитные дипольное и квадрупольные поля. Линейная антенна. Интеграл Кирхгофа. Дифракция на круглом отверстии. Дифракция на малых отверстиях. Рассеяние коротких волн проводящей сферой.
19. Классическая геометродинамика. Специальная теория относительности. Группа Лоренца. Сокращение Фицджеральда. Замедление времени. Опыт Физо. Допплеровское смещение. Прецессия Томаса. Собственное время и световой конус. Ковариантность уравнений электродинамики. Преобразование электромагнитного поля. Импульс и энергия релятивистской частицы, её лагранжиан и гамильтониан. Кинематика осколков. Движение в однородном статическом поле. Дрейф частиц. Излучение движущихся частиц. Общая теория относительности. Уравнение Эйнштейна. Решение Шварцшильда. Тензор энергии-импульса. Действие для электромагнитного поля. Гравитационные волны. Поток и плотность энергии. Особенности уравнений Эйнштейна.
20. Классическая квантовая механика. Поляризация фотонов. Интерференция фотонов. Принцип суперпозиции. Динамические переменные и наблюдаемые. Правила квантования Бора-Зоммерфельда. Соотношения сопряженности. Шредингеровское представление. Импульсное представление. Принцип Гейзенберга. Операторы сдвига. Уравнения движения в формулировках Шредингера, Гейзенберга. Стационарные состояния. Свободная частица. Движение волнового пакета. Ансамбль Гиббса. Гармонический осциллятор. Момент количества движения. Спин. Движение в центральном силовом поле. Уровни энергии атома водорода, классические серии. Эффект Зеемана. Изменение уровней энергии возмущением. Переходы. Излучение. Аномальный эффект Зеемана. Системы нескольких частиц. Перестановки как динамические переменные, как интегралы движения. Электроны. Статистические ансамбли. Ансамбль бозонов, ансамбль фермионов. Испускание и поглощение бозонов. Фотоны. Энергия взаимодействия между фотоном и атомом. Волновое уравнение, волновое уравнение электрона. Движение электрона. Релятивистская форма квантовых условий. Шредингеровские переменные. Электроны и позитроны в присутствии поля.
21. Сосать толстые писосы.
13. Теория вероятностей. Комбинации. Сочетания, размещения, перестановки. Наивное понятие вероятности. Правило сложения вероятностей, полная система. Условная вероятность, правило умножения вероятностей, независимые события. Формула полной вероятности. Формула Байеса. Схема Бернулли. Теорема Бернулли. Случайная величина, закон распределения, средние значения. Рассеяние, среднее квадратичное уклонение. Закон больших чисел. Нормальные законы. Случайные процессы. Свойства специальных функций теории вероятностей. Аксиоматика Колмогорова. Вероятностное пространство. Локальные предельные теоремы. Интегральные предельные теоремы. Теорема Пуассона. Цепи Маркова. Непрерывные и дискретные распределения, многомерные. Функции от случайных величин. Интеграл Стилтьеса. Матожидание, дисперсия, моменты. Закон больших чисел в форме Чебышева. Характеристические функции. Теорема Хелли. Преобразование Лапласа-Стилтьеса. Теорема Линдеберга. Безгранично делимые законы. Стохастические процессы. Процесс Пуассона. Уравнения Колмогорова. Стационарный случайный процесс. Теорема Хинчина. Эргодическая теорема Биркгофа-Хинчина.
14. Статистика. Классическая статистика. Исчерпывающие статистики. Доверительные границы и доверительные вероятности. Гипотезы. Вероятности и частоты. Биномиальное распределение. Бета- и гамма-функции. Кривая Кетле. Оценки функций распределения. Характеристические функции, хи-квадрат, предельные теоремы, прямоугольное распределение. Гауссова теория ошибок, s-квадрат, критерий Стьюдента. Метод наименьших квадратов. Средние значения и дисперсии. Оценка дисперсии. Линии регрессии. Метод наибольшего правдоподобия Фишера. Неравенство Фреше. Свойства нормального распределения. Асимптотические свойства. Оценка параметров по наблюденным частотам. Проверка гипотез с помощью статистических критериев. Гипотезы однородности, независимости, случайности. Параметрические гипотезы, простые и сложные. Дисперсионный анализ. Порядковые критерии. Корреляция, ковариация. Коэффициенты корреляции.
15. Классическая неквантовая механика. Законы Ньютона. Терминология. Энергия, связи, обобщенные координаты, конфигурационное пространство, принцип возможных перемещений, принцип Даламбера. Теорема Нётер. Уравнения Лагранжа. Консервативные и неконсервативные системы. Функция Рэлея. Сила Кориолиса, центробежная сила, задача двух тел, теорема Лармора, симметричный волчок, главные колебания. Обобщенные импульсы, циклические координаты, фазовое пространство, функция Гамильтона. Интегралы движения. Диссипативные системы. Принцип Гамильтона. Уравнения Гамильтона, метод Гамильтона-Якоби. Движение частиц, столкновение частиц, рассеяние частиц. Формула Резерфорда. Малые колебания. Колебания систем со многими степенями свободы. Параметрический резонанс. Ангармонические колебания. Движение твердого тела. Тензор инерции. Волновое уравнение, принцип Ферма. Функция Рауса, скобки Пуассона, тождество Якоби. Принцип Мопертюи. Теорема Лиувилля. Непрерывные среды. Переменные поля, уравнения Гамильтона для поля. Законы сохранения плотности. Симплектические многообразия, классическая механика как структура на симплектическом многообразии.
16. Классическая термодинамика. Термодинамические системы. Идеальные газы. Первый закон. Адиабатические процессы в газах. Второй закон. Цикл Карно. Абсолютная температура. Тепловые машины. Энтропия. Уравнение Клапейрона. Уравнение Ван-дер-Ваальса. Термодинамические потенциалы. Свободная энергия. Правило фаз. Химическое равновесие в газах. Принцип ле Шателье. Термодинамика разбавленных растворов. Осмотическое давление. Химическое равновесие в растворах. Связь энтропии и температуры. Теорема Нернста. Энтропийная константа. Третий закон термодинамики. Фактор Больцмана. Распределение Максвелла по скоростям. Экспериментальные подтверждения.
17. Классическая гидродинамика. Модель Эйлера. Уравнение состояния. Граничные условия. Уравнение энергии. Перенос количества движения. Уравнение неразрывности. Безвихревое движение, поток, циркуляция. Несжимаемая жидкость. Трубка тока. Источники и стоки. Функция тока Лагранжа. Теория Максвелла о полюсах. Зональные функции, гипергеометрические ряды, тессеральные и секторальные функции. Уравнение Лапласа. Линии тока на эллипсоиде, диполь. Движение твердых тел в жидкости. Гидрокинетическая симметрия. Вихревое движение. Постоянство вихрей. Изолированный вихрь. Потенциал, создаваемый вихрем. Импульс вихря. Прямолинейные вихри. Вихревая дорожка. Теоремы Кирхгофа. Вихревые кольца, их устойчивость. Приливные волны. Поверхностные волны. Стоячие волны в ограниченной массе воды. Капиллярные волны. Плоские волны. Звуковые волны. Вязкость. Диффузия вихря.
18. Классическая электродинамика. Электрические явления и приборы. Заряд. Закон Кулона. Электростатическое поле. Проводники. Уравнение Лапласа. Уравнение Лежандра. Полиномы Лежандра. Граничные задачи. Функции Бесселя. Разложение по мультиполям. Изотропные диэлектрики. Поляризуемость молекул и диэлектрическая восприимчивость. Магитостатика. Закон Био-Савара. Закон Ампера. Векторный потенциал. Магнитная индукция, магнитное поле, магнитный момент. Внешнее магнитное поле. Макроскопические уравнения. Электромагнитное поле. Закон Фарадея. Энергия магнитного поля. Максвелловский ток. Уравнения Максвелла. Векторный и скалярный потенциалы. Калибровочные преобразования. Лоренцовская, кулоновская калибровка. Функция Грина для волнового уравнения. Интегральное представление Кирхгофа. Теорема Пойтинга. Плоские электромагнитные волны. Волны в непроводящей среде. Линейная, круговая поляризации. Суперпозиция волн. Групповая скорость. Распространение импульсов в диспергирующей среде. Отражение и преломление электромагнитных волн. Поляризация. Волны в проводящей среде. Простая модель проводимости. Волноводы. Поля на поверхности и внутри проводника. Цилиндрические резонаторы. Диэлектрические волноводы. Поле ограниченного колеблющегося источника. Электрическое дипольное поле. Излучение. Магнитные дипольное и квадрупольные поля. Линейная антенна. Интеграл Кирхгофа. Дифракция на круглом отверстии. Дифракция на малых отверстиях. Рассеяние коротких волн проводящей сферой.
19. Классическая геометродинамика. Специальная теория относительности. Группа Лоренца. Сокращение Фицджеральда. Замедление времени. Опыт Физо. Допплеровское смещение. Прецессия Томаса. Собственное время и световой конус. Ковариантность уравнений электродинамики. Преобразование электромагнитного поля. Импульс и энергия релятивистской частицы, её лагранжиан и гамильтониан. Кинематика осколков. Движение в однородном статическом поле. Дрейф частиц. Излучение движущихся частиц. Общая теория относительности. Уравнение Эйнштейна. Решение Шварцшильда. Тензор энергии-импульса. Действие для электромагнитного поля. Гравитационные волны. Поток и плотность энергии. Особенности уравнений Эйнштейна.
20. Классическая квантовая механика. Поляризация фотонов. Интерференция фотонов. Принцип суперпозиции. Динамические переменные и наблюдаемые. Правила квантования Бора-Зоммерфельда. Соотношения сопряженности. Шредингеровское представление. Импульсное представление. Принцип Гейзенберга. Операторы сдвига. Уравнения движения в формулировках Шредингера, Гейзенберга. Стационарные состояния. Свободная частица. Движение волнового пакета. Ансамбль Гиббса. Гармонический осциллятор. Момент количества движения. Спин. Движение в центральном силовом поле. Уровни энергии атома водорода, классические серии. Эффект Зеемана. Изменение уровней энергии возмущением. Переходы. Излучение. Аномальный эффект Зеемана. Системы нескольких частиц. Перестановки как динамические переменные, как интегралы движения. Электроны. Статистические ансамбли. Ансамбль бозонов, ансамбль фермионов. Испускание и поглощение бозонов. Фотоны. Энергия взаимодействия между фотоном и атомом. Волновое уравнение, волновое уравнение электрона. Движение электрона. Релятивистская форма квантовых условий. Шредингеровские переменные. Электроны и позитроны в присутствии поля.
21. Сосать толстые писосы.
21. - конечная остановка.
ебать, что это за текстик такой в вольном стиле? как будто бложик, но формат с закосом под книгу.
Раскладываем синус бесконечно малого в ряд, видим что он равен бесконечно малому ЧТД

Например берем a, b,
a<b, значит а СТРОГО меньше b. Например если a=3, b=4.
Берем a<=b. а=3 и b=4 прокататит. Но при этом a=b тоже прокатит. Короче гугли, ебал элементарные вещи разжевывать.
>почему эти учебники такое говно и не дают конкретных примеров наглядно демострирующих целесообразность этих ебучих понятий?
вся математика такая, как только чуток абстракциями обмажешься. раз пошла за гаражи, не ори и не визжи.
это тред для начинающих. Я думаю, что большинство местных гамологов не сможет решить такое уравнение.
Это формализация концепции, которой ты и так постоянно пользуешься, но не замечаешь. Пример: комплексные числа определяются как пары вещественных чисел с соответствующими операциями сложения и умножения. Хочется, чтобы вещественные числа были в том числе комплексными, то есть чтобы R было подполем С. Но x и пара (x, 0) это не одно и то же. Однако, множество { (x, 0) } образует в C подполе изоморфное R, поэтому мы можем отождествить его с R и говорить, что R - подполе C (это abuse of notation, но так все делают).
Такое происходит всюду. Скажем, вещественные числа - это классы эквивалентности фундаментальных последовательностей, поэтому, строго говоря, рациональные числа не являются вещественными, но опять же, R содержит подполе изоморфное Q.
Так-то есть дохуя более содержательных примеров, но пока что ты их не сможешь воспринять.
Двачую, зато гамолог скажет что это и не надо решать, если калькулятор есть.
>это abuse of notation
Ни разу. Изоморфные объекты в вышележащих теориях являются тождественными, это аксиома.
>какой отождествляющий смысл этого понятия? изоморфные структуры типо эквивалентны и находя какой-то элемент в одной структуре мы находим эквивалентный первому элемент в другой? почему эти учебники такое говно и не дают конкретных примеров наглядно демострирующих целесообразность этих ебучих понятий?
Расскажу то, что узнал вчера. В школе рассказывают, что углы измеряются в градусах или радианах. Радианы -- это вещественные числа из R которые образуют класс эквивалентности относительно прибавления констант типа 2×pi×k. Вся вещественная прямая образует аддитивную группу (это к радианам отношения не особо имеет; просто само по себе). Т.е. сумма любых двух числе из R снова принадлежит множеству R.
Также можно рассмотреть множество комплексных чисел, по модулю равных 1. Грубо говоря окружность с радиусом 1 в комплексной плоскости. Это множество образует мультипликативную группу. Т.е. произведение любых двух чисел из такого множества снова оказывается в этом множестве.
Теперь можно построить гомоморфизм из аддитивной группы R в мультипликативную группу комплексных чисел, по модулю равных 1 (эта группа в разных книжках называется или группой T или группой U(1)). Т.е. для того, чтобы сложить два угла представленных в радианах достаточно в случае комплексных чисел по модулю равных 1 перемножить два таких числа. Причем умножение коммутативное. Т.е. без разницы в какой последовательности умножать, слева направо или справа налево: xy=yx.
По-моему охуительная конструкция.
мимокрокодил с группой T
>>381734
Бля я вчера уставший был и тупо не смотрел что вы мне написали. Теперь я просто проорал с того что вы мне написали, блять это понятно что больше, меньше, меньше либо равно и т.д.
Я имел ввиду откуда они задаются? Ну блять трудно объяснить. Вот "При x "знак" 4/7" А откуда они взяли что x меньше этого числа, ведь x это у нас неизвестная. Есть например другое уравнение там вместо = между уравнениями стоит больше либо равно, хотя само полностью аналогичное, только цифры другие, так там уже совсем другие то есть например "При x "<" 4/7
Надеюсь вы поймете что я написал.
>>381801
Нахуй иди долбаеб.

Если тебе интересно, откуда именно мы взяли, что одно число больше другого, то гугли отношения порядка. У Зорича про написано это в главе про действительные числа. Там ещё из этих аксиом дальнейшие следствия выводиться.
Если считать, что g(x) = f(x-a), то символы на той картинке означают, что предел функции f в точке 0 равен пределу функции g в точке a. Чтобы это доказать, мне достаточно предположить, что lim g(x) = m при x -> a для некоторого m, а потом показать, что lim f(x) = m при x -> 0?
Я просто припоминаю что эти знаки При x<4/7 берутся сразу из уравнения, т.е. никак аксиом не было. Ну вот уравнение и там сразу можно сказать что x больше 1 или сразу промежуток записать ввиде 4/7<=x<3/5, то есть уже сразу известно знак строгий или нет.
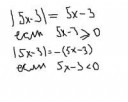
там же используется тупо определение модуля. Какие там отношения порядка?
А ты хочешь знать, почему именно такие числа в неравестве?
В уравнени с модулями, мы разбиваем R на промежутки, в которых модули превращаються в линейную функцию.
При x<4/7 |7x-4|= 4-7x, а при x>= 4/7 |7x-4|=7x-4. Так же и со вторым модулем.
У тебя даже есть рисунок прямой, на которой показан знак первого и второго модуля.
Просто он зачеркнул самое важное. Я подумал, что он про сами знаки неравенств спрашивает.
>>381891
Все теперь понял, этот знак зависит от раскрытия модуля и от полученных + и - на прямой.
>>381894
Ну да, что то я с краской переборщил
Теперь я могу прорешать все сам, это круто.
Еще мне интересно какого хуя в учебнике Золоторева сначала в главе 1.3 дают параметры, которые понятное дело я не знаю еще, а следующей темой объясняют что такое дискриминант. Чет пиздец какой то.
То есть там даже их не объясняют тупо запихнули в задание после пройденной темы

Хотя смотри, ты раскрываешь модуль если 5x-3 больше либо равно нулю, а здесь расскрыли строго больше, почему? Там тоже модуль не меняет знак
Просто от этого зависит ответ, какая будет скобочка. Не правильно написал - ошибка
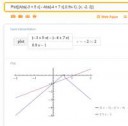
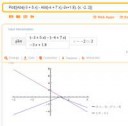
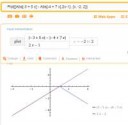
>>381729
В твой поток мыслей и поток мыслей тех кто отписывался я не вдавался. Отпишу, как эту задачу можно решать геометрическими методами.
У тебя есть уравнение с 3-мя функциями:
Abs[-3 + 5 x]
-Abs[-4 + 7 x]
2x-1
Для каждой из этих функций можно построить ее график. Затем первые две функции можно сложить поточечно. Получится новая функция. Решить исходной уравнение -- значит найти точки пересечения двух функций. Таких пересечений как может не быть вовсе, так и быть конечное число, так и бесконечное число. В твоем случае составители задачи выбрали бесконечное число пересечений (прямая линия 2x-1 совпадает с частью точек функции суммы первых двух).
На картинках твой вариант последний. И две альтернативы.
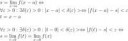
Вот на картинке всё написанно. Сначала раскрываем предел по определению. Потом делаем замену переменной. После видим, что после замены это предел при t->0.
Самое важно, что переменные x в первом и втором пределе по сути разные. В первом пределе x~0, а во втором x~a.
Это довольно формальное доказатество.
Ясно.
Пусть, в уравнении с модулями ты разбиваешь R на три интервала и две точки: (-inf;a) U (a;b) U (b;+int) U {a;b}.
В каждой точке модуль обращаеться в 0, а у другого определён знак. Вся соль в том, что можно продставить эти точки по отдельности и посмотреть будут ли они решениями или можно объеденит их с интервалами, например, (-inf;a) U [a;b] U (b;+int), это не важно на самом деле.


Ну почему же троллинг. Берешь и от руки чертишь какой-нибудь график. Вот я тебе нарисовал график функции с разрывами. Теперь рисуй график производной и график интеграла.

пиздец какая поебень, это и есть "тривиум"? картофан какой-то ебучий. и не зашкварно это прорешивать? это ж только на заебаться тест. типа развяжи сто узлов.
Там типо задачи на смекалочку. Влоб будешь долго ебаться с картофаном, применишь смекалочку всё пойдёт как по маслу.
Так, примерно график производной я могу построить. Я думал, что надо нарисовать с охуенной точностью этот график. Хотя похуй, в условиях задач не сказанно с какой точностью, спасибо.
То есть сто раз не нужно производную брать, на ста страницах? Фух. ну пошутил пошуил Но все равно, наверное нужно дробь разложить, чтобы в числитиле не осталось х или че-нить в этом духе, чтобы свести к какой-нибудь простой поебени типа 100! Но это же пиздец как лень делать. Лучше что-нибудь из гамологий доказать попробовать.
Начал как три дня изучать эту вашу хуйню. Наткнулся на Декартово произведение. Понимаю, что это произведение состоит из всевозможных упорядоченных пар вида (a, b), помню, что A×B ≠ B×A.
Но не понимаю, почему эта упорядоченная пара, когда автор её расписывает на языке теории множеств - (a, b) = {{a}, {a, b}) - вторым элементом имеет {a, b}, а не просто {b}! Ну, почему, ебать? Почему у первого элемента есть своё собственное множество, а второму элементу приходится делить его со всё тем же первым элементом? Как так получается? Почему (a, b) не равно {{a}, {b}}?
>Но это же пиздец как лень делать
Лол. Сейчас решил задачу за минуты три. Долго ебаться будешь, если смекалочки нет.
Антонии, жду от вас ответа, а сейчас мне пора на завод. Ночью вернусь к вам.
Подожди, а какая там нахуй смекалочка в 4-й задачке, там же нужно видимо тупо применить формулу разложения дроби на 1/.... + 1/..... Это же дроч а не смекалочка. Или это по-другому делается?
>за сколько лет можно осилить весь курс матиши с нуля ?
Лет за 200 умаю можно управиться до состояния 2016 года.
>Почему (a, b) не равно {{a}, {b}}?
Потому что тогда ты не сможешь отличать (a,b) от (b,a). А при предложенном способе задания ты легко построить биекцию:
(a,b) ↦ {{a}, {a, b})
(b,a) ↦ {{b}, {a, b})
> Почему у первого элемента есть своё собственное множество, а второму элементу приходится делить его со всё тем же первым элементом
Чтобы выделить какой элемент первый а какой второй. Убедись, что (a, b) = (c, d) тогда и только тогда, когда a = c и b = d.
Вооо))) Нормас) Мне всего лишь 577 год пошёл.
Арнольд прав. Есть две большие разницы — владеть математикой и быть математиком. Это как водитель и механик, как переводчик и лингвист. Один использует — второй разбирается. Тут каждому своё: кому-то достаточно всю жизнь перебирать движки, ни разу не сев за руль, а кому-то нужно быстро ездить, не думая о том, почему двигатель стучит.
>Чем отличается элементарная алгебра от алгебры?
Элементарная алгебра -- это то чему женщин учат в педвузах, чтобы они потом становились школьными учителями. Алгебра -- это то чему мужчин учат на мехмате, чтобы они потом становились высокомерными петухами.
>переводчик и лингвист
Не понял, кто по твоему круче в этой аналогии.
Лингвисты же не говорят на языках. Они знают ПРО языки. Про много языков. Но двух слов на них не свяжут без гугла.
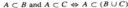

Почему базы индукции не требуется?
Т.е. почему верно P1 для которого множество "предыдущих утверждений" пусто?
Если прочтешь весь, не будет общих тем для разговора с Борисовичем.
Думаю будет тяжеловато его читать, если нюфак. Но можешь попробовать почитать вместе с видосами отсюда:
https://www.lektorium.tv/course/27206

Сначала написал длинное формальное доказательство, но оно всё равно сводилось к этому.
Никто. У каждого свой путь, своё предназначение. Переводчик языки использует — лингвист языки изучает.
Сперва only-if часть докажи, а потом if. Или наоборот.

>>381973
>Думаю будет тяжеловато его читать, если нюфак.
В том смысле того что нужен определённый уровень мат.культуры или там без пояснений используются факты из других разделов математики?
>Но можешь попробовать почитать вместе с видосами отсюда:
Я очень плохо отношусь к лекциям, и мои чувства по-моему весьма обоснованы.
Для реального изучения предмета лекции всегда и всем хуже учебника.
Лекции подходят либо для того чтобы окинуть беглым взглядом предмет который ты ещё не учил (при этом у тебя останется много сущностных пробелов), либо чтобы вспомнить уже изученный материал и может быть получить немного другой взгляд на него.
Я их представил. Получается что одна точка является решением, другая нет. Но что это мне дает? Все равно от этого < > не зависит никак, я пробовал в другом уравнении, не сходится. То есть вся моя проблема в том, что я не могу определить что мне ставить > или <, >= или <= в записи "При x "больше или меньше" ТОЧКИ из уравнения". А от этого зависит ответ. Кароче какой то пиздец. И ведь я помню что как то легко это делается.
Лично я всегда разбиваю так : (-inf;a) U (a;b) U (b;+int) U {a;b}. Ты сказал, что одна точка - рещение другая нет.
Пусть (-inf;a) U (b;inf) U {a} - решение, тогда можно записать так : (-inf;a] U (b;inf), понял?
Вообще (-inf;a) U (a;b) U (b;+int) это понятно
но
>{a;b}
это нет.
>решение
Но решение я знаю как записывать и разбираюсь в скобках, мне важен сам знак "При x "< или >" число"
Точка сама по себе. То есть не надо ставить знаки для неё, она самодостаточна.



Бляяяяяяяяяяяяяяяяяяяяяяяяяяяяяядд.
Ну БЛЯДЬ в этих ебанных примерах их же берут не с потолка же блядь?
ХОТЯ Ладно, я сдаюсь, ты меня победил, пойду в другое место спрашивать нахуй
Проиграл с бугурта. Давай я тебе уравнение подробно решу? А не так как на пикчах.
Да решать не надо мне, у меня ответы такие же получаются, а от знаков < > будет скобка круглая квадратня овальная блядь
Мне важно откуда они берут Меньше или Больше когда пишу "при ыпВТЖЛ)УФЦОЛУДРЫПВМЗОрУЩОЫГЖРидоуеаф
ябялдь заебался уже писать одно и тоже, мне уже плохо блядь я не знаю это такое недопонимание или очень тонкий троллинг?
лол. попабуль
Все равно мимо на втором пике в 3) решении >, хотя по определению должен быть > либо равно.
Да даже если бы модуль получался с отрицательным знаком было бы тогда <, а тут вообще строго >. И так во всех примерах чистая путаница
Пересекаються решения неравенства с областью, откуда мы выбирали знак модуля.
Ну, а на первом пике в 3) не пересекаются и поэтому знак не строгий? Но там же одинаковые + и - уравнений. Они вообще аналогичные.
>>381992
>может тебе более поянтную книгу почитать?
Нахуй мне читать кингу если я помню что в школе мы такое решали за минуту, я просто не помню способ который подсказывал какой знак ставить. А тетрадки проебал походу, хотя пойду еще полистаю, от вас все равно ничего не добьешься
только блядь время потерял и нервы
>от вас все равно ничего не добьешься
Не надо бомбить, просто я не совсем понимаю, что ты вообще хочешь сказать, потому что выражаешся неясно.
да у него просто нервный припадок, боюсь как вы вены себе не порезал. нужно водички попить и успокоиться лол
> нужно водички попить и успокоиться лол
Ага прямо сразу помогло, я уже второй день сижу над этим дерьмом, дальше темы не могу идти изучать ибо ебанные задачи там тоже идут с модулями, только еще к тому же усложненные
да норм, у меня тоже так было когда мочезуку пробовал читать. прочитал один абзац и меня скрутило пиздец.
у меня сроки и строгий план, я не ожидал что наткнусь на такой сильный барьер, был бы учитель под рукой..
Так спрашивай здесь, модули то говно вопрос, с этим не должно быть затыка! Давай мы тебе протолкнем если не заходит, поясним.
>Скажи, что за книга.
Базовый курс с решениями и указаниями Золотарева
>>382006
Попробуй еще тоньше плиз.
Анон, так чо те непонятно? Давай сначала. Просто сформулируй свой вопрос информативнее, ибо, когда пытаешься сформулировать какой-то вопрос, внезапно может прийти решение. Собственно, половина решения задачи — это правильно поставленный вопрос.
Анон, посмотрел я твою книжку...
Это какая-то йоба. Даже не учебник, а пособие. Которое подрузумивает, что ты уже знаком НА ДОСТАТОЧНОМ УРОВНЕ с элементарной математикой! И оно нацелено на подготовку к ЕГЭ! УХ, БЛЯДЬ! Скачай УЧЕБНИК, а не пособие. Могу скинуть пару годных учебников, где всё понятно. Сам поним учил элементарную.

Я НЕ толщу. Ты не видел как тут толстят видимо. На невинный вопрос что такое производная базового определения тебе естественно не дадут и на пальцах не пояснят, а так ненавязчиво приведут одно из обобщений (а их дохуя), например наплетут про линейное отображение на кольце удовлетворяющее правилу произведения лол. Вот за это мошенничество нужно пиздить конечно при встрече. Но тебе то помочь пытаются.
Ты тролишь так? Тебя не удивляет строкой ниже откуда берется 1+cos2t (inb4 это тождество), го удивляет что 2x2 =4 ?
Ну да я на целен на подготовку к ЕГЭ, у меня есть полноценные знания за 10 класс, я просто все вспоминаю, а то за лето забыл уже. Мне элементарнее не надо, там и так блядь объясняют как считать дискриминант, куда еще легче то. И я за это время просто забыл как там в 1 ход определять какой знак ставить, я собственно там спокойно решаю все, ответы сходятся, только скобки другие из-за знаков больше меньше, ибо мне кажется они их вообще с потолка берут, а под определение модуля вообще не подходит это все.
Алсо мне уже советовали учебник "ткачука", так там вообще даже ответов(!) нету.
>>382012
Не знаю, я как то уже устал все по сто раз рассписывать, вверху все написанно. В любом случае завтра с новыми силами попробую вкатиться за советами в какой нибудь образовательный ресурс где подскажут что да как.
>>382017
>Я НЕ толщу
Ну я уже вроде как смог так рассписал все свехру.
> что такое производная
Так есть же годный сайт http://mathprofi.ru/
там за вышмат на пальцах поясняют
Ой что-то еще и ошибок наклепал не посмотрев
>линейное отображение на кольце удовлетворяющее правилу произведения лол
Сам виноват. Ты спрашивал про само понятие производной. Надо было сузить вопрос до производной на R и евклидовой метрике.
Ты можешь совершенно рандомно выбирать больше или равно или строго больше в рассматриваемых случаях.
НО тебе нужно убедиться, что если ты до этого выбрал строго меньше, то дальше будешь использовать больше или равно.
И наоборот, если использовал меньше или равно, то в следующем неравенстве у тебя будет строго больше.
Суть процедуры решения твоих уравнений с модулями состоит в том, что ты разбиваешь вещественную прямую на куски. И рассмотреть тебе надо абсолютно все точки этой прямой. Т.е. ты не можешь оба раза взять строго меньше точки N, а затем строго больше точки N -- иначе у тебя эта точка проебется. А последовательность не важна.
У тебя умножение 2 cos(t) на 2 cos(t). Два умножается на два равно 4. А сосинус на косинус равен косинус в квадрате.
Насколько я понял, суть в том, что импликация эквивалента P1. Сейчас я нафантазирую, а ты разбирайся. Короче, при n=1 у нас будет пустое множество. Следовательно, посылка ложная, а значит, следует верность всей импликации. Мне кажется, истина где-то рядом.
Опять маняврирования.
Производная — фундаментальное
математическое понятие, используемое в различных вариациях (обобщениях)
Общее между различными вариациями и обобщениями заключается в том, что производная отображения характеризует степень изменения образа отображения при (бесконечно) малом изменении аргумента.
Понял бля? Все что нужно сказать нубу - это последнее предложение или даже его интерпретация своими словами
>>382026
Я тоже сперва подумал про дважды два, но унего вроде другой вопрос - как из 2сost выше ("выясним во что превратится) два таких (там нет пояснения про смену пределов интегрирования)
А дальше
В зависимости от рассматриваемых математических структур конкретизируется содержание данного понятия.
это уже отдельный вопрос. А пидорки начинают с заднего прохода сперва.
Сначала читаешь книгу Кантора. Это прямо обязательно. Затем Куратовский Мостовский или какую-нибудь современную на английском. Например, Jech, T. Set Theory. Затем читаешь драфт лекций Вавилова посмеяться.
>ибо мне кажется они их вообще с потолка берут
>>382025
>Ты можешь совершенно рандомно выбирать
Лол, я был очень близко
>иначе у тебя эта точка проебется
Но взять нестрого больше я могу, после того как я взял строго меньше?
А и поясни как поступать с промежутком а-ля a/b<x<=y/z, он еще обычно посередине стоит обычных.
замена переменных x->t (и пределов соответственно)
Но ведь то определение, которое дается в школе и на 1 курсе реально плохое. Почему нельзя дать нормальное определение производной, а потом сказать, что любое линейное отображение из R в R - это умножение на вещественное число, поэтому можно отождествить производную с этим числом?
Поясните еблану за дифференциал в таком случае. Мне всегда казалось, что это означает пердолинг по Х в случае dx. А в итоге это какое-то число или выражение? Какого тогда хуя в интеграле суммы все выражения не берут в скобки, чтобы не оказалось, что только одно домножено на dx
Kaplansky
У тебя замена переменной в интеграле. Но ты должен заменить не только выражение, но ещё и дифференциал.
x=2sin(t)
dx/dt=x'(t) - определение производной. Отсюда dx=dtx'(t)=
dt2cos(t). Вот и твой косинус.
Это приращение, не парься, ответ на твой вопрос - у тебя же там замена переменных выше, переход от х к t.
>Поясните еблану за дифференциал
Дифференциал -- это нильпотентный элемент на коммутативном кольце.
Докажи сука!
Или дилдаком выебать его в анальное кольцо. Будет потом говорить, что ощущения странные.

>Свойство импликации. a->b <=> не a или b. Дальше сам разбирай.
Сукаблять, что в качестве 'a' будет в случае P1?
Там же просто не будет утверждений, вообще. Ни верных, ни ложных, никаких.

А схуяли пустое множество утверждений - ложное утверждение?
Смотри, f - какая-та поебень, её истинность неизвестна, тогда f->1, что равносильно неf или 1= 1, так?
Дополняю список разделов математики (возможно какие-то повторяются)
1. Автоматов теория – раздел теории управляющих систем, изучающий математические модели преобразователей дискретной информации, называемой автоматами. Возникла в середине 20 века.
2. Аксиоматическая теория множеств – раздел математической логики, изучающий множеств теорию как аксиоматическую теорию. Впервые аксиоматическая теория множеств была построена Э. Цермело (1908). К. Гёдель, П. Коэн.
3. Алгебра – часть математики, принадлежащая наряду с арифметикой и геометрией к числу старейших ветвей этой науки.
4. Алгебра логики – раздел математической логики, изучающий логические операции над высказываниями. Основоположником является Дж. Буль.
5. Алгебраическая геометрия – раздел математики, изучающий геометрические объекты, связанные с алгебраическими уравнениями: алгебраические многообразия (алгебраические кривые, алгебраические кривые, алгебраические поверхности, абелевы многообразия), и их различные обобщения (схемы, алгебраические пространства). Возникла в 17 веке. Р. Декарт, И. Ньютон.
6. Алгебраическая теория чисел – раздел теории чисел, основной задачей которого является изучение свойств целых чисел полей алгебраических чисел. Э. Куммер, Э Галуа.
7. Алгебраическая топология – область математики, возникшая для изучения таких свойств геометрических фигур и их отображений друг в друга, которые не меняются при непрерывных деформациях (гомотопиях).
8. Алгоритмов анализ – раздел математической теории программирования, изучающий характеристики исполнения алгоритмов. (1987)
9. Аналитическая геометрия – раздел геометрии, в котором простейшие геометрические образы (прямые, плоскости, линии и поверхности второго порядка) исследуется средствами алгебры на основе метода координат. 17век Р. Декарт, П. Ферма, Г. Лейбниц, И. Ньютон, Л. Эйлер, И. Бернулли, Ф. Виет.
10. Аналитическая теория чисел – раздел теории чисел. Включает в себя вопросы распределения простых чисел, аддитивные проблемы, теорию алгебраических чисел и трансцендентных чисел.
11. Арифметика – часть математики, наука о числах, в первую очередь о неотрицательных рациональных числах (целых и дробных), и действия над ними. Возникла за 2-3 тысячи лет до нашей эры.
12. Аффинная геометрия – раздел геометрии, в котором изучаются свойства фигур на плоскости (или в пространстве), сохраняющиеся при любых аффинных преобразованиях плоскости (или пространства), т.е. инвариантные относительно таких преобразований. Впервые изучалась в первой половине 19 века А. Мёбиусом. Само понятие возникло в 1872 году.
13. Булева алгебра – это частично упорядоченное множество специального вида. Дж. Буль 1847-54 года.
14. Вариационное исчисление – раздел математики, посвящённый исследованию методов отыскания экстремумов функционалов, зависящих от выбора одной или нескольких функций при разного рода ограничениях (фазовых, дифференциальных, интегральных, и т.п.), накладываемых на эти функции. 18 век Л. Эйлер, Ж. Логранж, Г. Лейбниц, Я. и И. Бернулли.
15. Векторная алгебра – раздел векторного исчисления, в котором изучается простейшие операции над (свободными) векторами.
16. Векторное исчисление – раздел математики, в котором изучаются свойства операций над векторами. Середина 19 века У. Гамильтон, Г. Грассман, Дж. Гиббс.
17. Векторный анализ - раздел векторного исчисления, в котором изучаются средствами математического анализа векторные и скалярные функции одного или нескольких аргументов (векторные поля и скалярные поля). 1981 Дж. Гиббс, О. Хевисайд.
18. Вероятностей теория – математическая наука, позволяющая по поверхностям одних случайных событий находить вероятности других случайных событий, связанных каким – либо образом с первыми.
19. Винтовое исчисление - раздел векторного исчисления, в котором изучаются операции над винтами.
20. Внутренняя геометрия – раздел геометрии, изучающий только те свойства поверхности и фигур на ней, которые могут быть получены лишь при помощи изменений на самой поверхности без обращения к объемлющему пространству. Основы созданы К. Гауссом в 1827 году. Б. Риман.
21. Выпуклое программирование – раздел математического программирования, в котором используется задача максимизации вогнутой целевой функции f(x) векторного аргумента x=(x1,…,xn), удовлетворяющего ограничениям gi(x)?0, i=1,2,…,n; x?X, где gi – вогнутые функции, X – выпуклое множество.
22. Вычислительная математика – раздел математики, включающий круг вопросов, связанных с использованием ЭВМ. Появилась и развилась с развитием ЭВМ.
23. Галуа теория – созданная Э. Галуа теория алгебраических уравнений высших степеней с одним неизвестным, устанавливает возможность (или невозможность) сведения решения таких уравнений к решению цепи других алгебраических уравнений (обычно более низких степеней). 19 век Э. Галуа, Э. Безу, Ж. Лагранж, Н. Абель.
24. Гармонический анализ – раздел математики, объединяющий методы теории Фурье рядов и Фурье интегралов. Развивался в 18-19 веках, сформировался в дисциплину в конце 19 – первой половине 20 веков.
25. Геометрия – часть математики, изучающая пространственные отношения и формы, а так же другие отношения и формы, сходные с пространственными по своей структуре. Зарождение в Древнем Египте, Вавилоне, Греции примерно до 5 века до нашей эры.
26. Геометрия чисел – раздел теории чисел, изучающий теоретико-числовые проблемы с применением геометрических методов. 1896 год Г. Минковский.
27. Гомологическая алгебра – раздел алгебры, основным объектом изучения которого являются производные функторы на различных категориях алгебраических объектов. Середина 40-х годов 20 века.
28. Дескриптивная теория множеств – раздел теории множеств, изучающий внутренние строение множеств в зависимости от тех операций, при помощи которых эти множества могут быть построены и множеств сравнительно простой природы. 20 век Э Борель, Р. Бэр, А. Лебег. П. С. Александров, Ф. Хаусдорфом, М. Я. Суслин.
29. Динамическая логика – раздел теоретического программирования, в рамках которого исследуются аксиоматические системы, представляющие средства для задания семантики программирования языков, а также для программ синтеза и программ верификации.
30. Динамическое программирование – раздел математического программирования, посвящённый исследованию многошаговых задач принятия оптимальных решений. Р. Беллман 50-е годы 20 века.
31. Диофантова геометрия – раздел математики, изучающий целочисленные и рациональные решения алгебраических уравнений методами алгебраической геометрии. Г. Фалтингс начало 20 века.
32. Диофантовы приближения – раздел теории чисел. Изучающий приближения действительных чисел рациональными числами или, при более широком понимании предмета. Вопросы, связанные с решениями в целых числах линейных и нелинейных неравенств или систем неравенств с действительными коэффициентами. Г. Минковский, И. М. Виноградов, А. Туэ, К. Зигель 19 век.
33. Дискретная математика – область математики, занимающаяся изучением свойств дискретных структур, которые возникают как внутри математики, так и в её приложениях.
34. Дискретное программирование – раздел математического программирования, посвящённый нахождению экстремумов функций, заданных на конечных множествах.
35. Дискриминантный анализ – раздел многомерного статистического анализа, изучающий методы классификации объектов, представленных многомерными наблюдениями. Р. Шифер (1936).
36. Дифференциальная геометрия – раздел геометрии, в котором геометрические образы изучаются методами математического анализа, в первую очередь – дифференциального исчисления. 2-я половина 17 века И. Ньютон, Г. Лейбниц, Х. Гюйгенс, Я. и И. Бернули, Э, Ейлер, Г. Монж, К. Гаусс, Н. И. Лобачевский, Б. Римман, Г. Ламе, Э. Бельтрам, Э Кристоффель, Г. Риччи–Курбастро, Я. Схоутен, Г. Вейль, Л. А. Люстерник, Л. Г. Шнирельман, А. Д. Александров, А. В. Погорелов, Н. В. Ефимов.
37. Дифференциальная топология – раздел топологии, изучающий топологические проблемы теории дифференцируемых многообразий и дифференцируемых отображений. 30-е годы 20 века А. Пуанкаре.
Дополняю список разделов математики (возможно какие-то повторяются)
1. Автоматов теория – раздел теории управляющих систем, изучающий математические модели преобразователей дискретной информации, называемой автоматами. Возникла в середине 20 века.
2. Аксиоматическая теория множеств – раздел математической логики, изучающий множеств теорию как аксиоматическую теорию. Впервые аксиоматическая теория множеств была построена Э. Цермело (1908). К. Гёдель, П. Коэн.
3. Алгебра – часть математики, принадлежащая наряду с арифметикой и геометрией к числу старейших ветвей этой науки.
4. Алгебра логики – раздел математической логики, изучающий логические операции над высказываниями. Основоположником является Дж. Буль.
5. Алгебраическая геометрия – раздел математики, изучающий геометрические объекты, связанные с алгебраическими уравнениями: алгебраические многообразия (алгебраические кривые, алгебраические кривые, алгебраические поверхности, абелевы многообразия), и их различные обобщения (схемы, алгебраические пространства). Возникла в 17 веке. Р. Декарт, И. Ньютон.
6. Алгебраическая теория чисел – раздел теории чисел, основной задачей которого является изучение свойств целых чисел полей алгебраических чисел. Э. Куммер, Э Галуа.
7. Алгебраическая топология – область математики, возникшая для изучения таких свойств геометрических фигур и их отображений друг в друга, которые не меняются при непрерывных деформациях (гомотопиях).
8. Алгоритмов анализ – раздел математической теории программирования, изучающий характеристики исполнения алгоритмов. (1987)
9. Аналитическая геометрия – раздел геометрии, в котором простейшие геометрические образы (прямые, плоскости, линии и поверхности второго порядка) исследуется средствами алгебры на основе метода координат. 17век Р. Декарт, П. Ферма, Г. Лейбниц, И. Ньютон, Л. Эйлер, И. Бернулли, Ф. Виет.
10. Аналитическая теория чисел – раздел теории чисел. Включает в себя вопросы распределения простых чисел, аддитивные проблемы, теорию алгебраических чисел и трансцендентных чисел.
11. Арифметика – часть математики, наука о числах, в первую очередь о неотрицательных рациональных числах (целых и дробных), и действия над ними. Возникла за 2-3 тысячи лет до нашей эры.
12. Аффинная геометрия – раздел геометрии, в котором изучаются свойства фигур на плоскости (или в пространстве), сохраняющиеся при любых аффинных преобразованиях плоскости (или пространства), т.е. инвариантные относительно таких преобразований. Впервые изучалась в первой половине 19 века А. Мёбиусом. Само понятие возникло в 1872 году.
13. Булева алгебра – это частично упорядоченное множество специального вида. Дж. Буль 1847-54 года.
14. Вариационное исчисление – раздел математики, посвящённый исследованию методов отыскания экстремумов функционалов, зависящих от выбора одной или нескольких функций при разного рода ограничениях (фазовых, дифференциальных, интегральных, и т.п.), накладываемых на эти функции. 18 век Л. Эйлер, Ж. Логранж, Г. Лейбниц, Я. и И. Бернулли.
15. Векторная алгебра – раздел векторного исчисления, в котором изучается простейшие операции над (свободными) векторами.
16. Векторное исчисление – раздел математики, в котором изучаются свойства операций над векторами. Середина 19 века У. Гамильтон, Г. Грассман, Дж. Гиббс.
17. Векторный анализ - раздел векторного исчисления, в котором изучаются средствами математического анализа векторные и скалярные функции одного или нескольких аргументов (векторные поля и скалярные поля). 1981 Дж. Гиббс, О. Хевисайд.
18. Вероятностей теория – математическая наука, позволяющая по поверхностям одних случайных событий находить вероятности других случайных событий, связанных каким – либо образом с первыми.
19. Винтовое исчисление - раздел векторного исчисления, в котором изучаются операции над винтами.
20. Внутренняя геометрия – раздел геометрии, изучающий только те свойства поверхности и фигур на ней, которые могут быть получены лишь при помощи изменений на самой поверхности без обращения к объемлющему пространству. Основы созданы К. Гауссом в 1827 году. Б. Риман.
21. Выпуклое программирование – раздел математического программирования, в котором используется задача максимизации вогнутой целевой функции f(x) векторного аргумента x=(x1,…,xn), удовлетворяющего ограничениям gi(x)?0, i=1,2,…,n; x?X, где gi – вогнутые функции, X – выпуклое множество.
22. Вычислительная математика – раздел математики, включающий круг вопросов, связанных с использованием ЭВМ. Появилась и развилась с развитием ЭВМ.
23. Галуа теория – созданная Э. Галуа теория алгебраических уравнений высших степеней с одним неизвестным, устанавливает возможность (или невозможность) сведения решения таких уравнений к решению цепи других алгебраических уравнений (обычно более низких степеней). 19 век Э. Галуа, Э. Безу, Ж. Лагранж, Н. Абель.
24. Гармонический анализ – раздел математики, объединяющий методы теории Фурье рядов и Фурье интегралов. Развивался в 18-19 веках, сформировался в дисциплину в конце 19 – первой половине 20 веков.
25. Геометрия – часть математики, изучающая пространственные отношения и формы, а так же другие отношения и формы, сходные с пространственными по своей структуре. Зарождение в Древнем Египте, Вавилоне, Греции примерно до 5 века до нашей эры.
26. Геометрия чисел – раздел теории чисел, изучающий теоретико-числовые проблемы с применением геометрических методов. 1896 год Г. Минковский.
27. Гомологическая алгебра – раздел алгебры, основным объектом изучения которого являются производные функторы на различных категориях алгебраических объектов. Середина 40-х годов 20 века.
28. Дескриптивная теория множеств – раздел теории множеств, изучающий внутренние строение множеств в зависимости от тех операций, при помощи которых эти множества могут быть построены и множеств сравнительно простой природы. 20 век Э Борель, Р. Бэр, А. Лебег. П. С. Александров, Ф. Хаусдорфом, М. Я. Суслин.
29. Динамическая логика – раздел теоретического программирования, в рамках которого исследуются аксиоматические системы, представляющие средства для задания семантики программирования языков, а также для программ синтеза и программ верификации.
30. Динамическое программирование – раздел математического программирования, посвящённый исследованию многошаговых задач принятия оптимальных решений. Р. Беллман 50-е годы 20 века.
31. Диофантова геометрия – раздел математики, изучающий целочисленные и рациональные решения алгебраических уравнений методами алгебраической геометрии. Г. Фалтингс начало 20 века.
32. Диофантовы приближения – раздел теории чисел. Изучающий приближения действительных чисел рациональными числами или, при более широком понимании предмета. Вопросы, связанные с решениями в целых числах линейных и нелинейных неравенств или систем неравенств с действительными коэффициентами. Г. Минковский, И. М. Виноградов, А. Туэ, К. Зигель 19 век.
33. Дискретная математика – область математики, занимающаяся изучением свойств дискретных структур, которые возникают как внутри математики, так и в её приложениях.
34. Дискретное программирование – раздел математического программирования, посвящённый нахождению экстремумов функций, заданных на конечных множествах.
35. Дискриминантный анализ – раздел многомерного статистического анализа, изучающий методы классификации объектов, представленных многомерными наблюдениями. Р. Шифер (1936).
36. Дифференциальная геометрия – раздел геометрии, в котором геометрические образы изучаются методами математического анализа, в первую очередь – дифференциального исчисления. 2-я половина 17 века И. Ньютон, Г. Лейбниц, Х. Гюйгенс, Я. и И. Бернули, Э, Ейлер, Г. Монж, К. Гаусс, Н. И. Лобачевский, Б. Римман, Г. Ламе, Э. Бельтрам, Э Кристоффель, Г. Риччи–Курбастро, Я. Схоутен, Г. Вейль, Л. А. Люстерник, Л. Г. Шнирельман, А. Д. Александров, А. В. Погорелов, Н. В. Ефимов.
37. Дифференциальная топология – раздел топологии, изучающий топологические проблемы теории дифференцируемых многообразий и дифференцируемых отображений. 30-е годы 20 века А. Пуанкаре.
38. Дифференциальное исчисление – раздел математики, в котором изучаются производные и дифференциалы функций и их применение к исследованию функций. И. Ньютон, Г. Лейбниц 17 век.
39. Дифференциальные игры – раздел математической теории управления, в котором изучается управление в конфликтных ситуациях и управление с гарантированным результатом в условиях неопределённости. 50-е года 20 века Н. Н. Красовский.
40. Евклидова геометрия – геометрическая теория, основанная на системе аксиом, впервые изложенной в “Началах” Евклида (3 в. до н. э.). Д. Гильберт (1899).
41. Игр теория – раздел математики, предметом которого является изучение математических моделей принятия оптимальных решений в условиях конфликта. Теория игр была разработана Дж. Нейманом и О. Моргенштерном (1944).
42. Интегральное исчисление – раздел математики, в котором изучаются свойства интегралов и связанных с ними процессов интегрирования. 5 век до н. э.
43. Интервальный анализ – раздел вычислительной математики, посвящённый учёту ошибок округления при проведении расчётов на цифровых ЭВМ.
44. Информации теория – раздел математики, исследующий процессы хранения, преобразования и передачи информации. Основы были заложены в 1948-49 К. Шенноном. А. Н. Колмогоров, А. Я. Хинчин, В. А Котельников.
45. Исследование операций – научный метод выработки количественно обоснованных рекомендаций по принятию решений. Конец 30-х годов 20 века.
46. Комбинаторная логика – раздел логики, посвящённый изучению и анализу таких понятий и методов, как переменная, функция, операция подстановки, классификация предметов по типам или категориям и др.
47. Комбинаторный анализ – раздел математики, посвящённый решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами. Б. Паскаль, П Ферма, Г Лейбниц, Я. Бернулли, Л. Эйлер.
48. Коммутативная алгебра – раздел алгебры, изучающий свойства полей, коммутативных колец, и связанных с ними объектов (идеалов, модулей, нормирований и т. д.). В первой половине 19 века К. Гаусс, Э. Куммер, Р. Дедекинд, Л. Кронекер, Д. Гильберт.
49. Конечных разностей исчисление – раздел математики, в котором изучаются функции при дискретном изменении аргумента, в отличии от интегрального и дифференциального исчислений, где аргумент изменяется непрерывно. 18 век Б. Тейлор.
50. Конструктивная математика – абстрактная наука о конструктивных процессах, человеческой способности осуществлять их и об их результатах – конструктивных объектах.
51. Конструктивный анализ – название, объединяющее различные течения в основаниях математики и математическом анализе.
52. Конформная геометрия – раздел геометрии, в котором изучаются свойства фигур, инвариантные относительно конформных преобразований.
53. Линейная алгебра – часть алгебры, изучающая векторные (линейные) пространства и их подпространства, линейные отображения (операторы), линейные, билинейные и квадратичные функции (функционалы или формы) на векторных пространствах. 18 век Г. Фробениус, Крамер, Гаусс.
54. Линейное программирование – раздел математического программирования, посвящённый теории и методам решения задач об экстремумах линейных функций на множествах, задаваемых системами линейных неравенств и равенств.
55. Линейчатая геометрия – раздел геометрии, в котором рассматриваются в качестве элементов пространства прямые линии.
56. Лобачевского геометрия – одна из неевклидовых геометрий; основана на тех же основных посылках, что и обычная – евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на противоположную. 1826 год.
57. Логика высказываний – раздел математической логики, изучающий логические законы, в которых учитывается лишь логическая структура высказываний, а именно, как одни высказывания получены из других с помощью таких логических операций, как конъюнкция ,дизъюнкция, импликация, эквивалентность, отрицание.
58. Логика предикатов - раздел математической логики, изучающий логические законы, общее для любой области объектов исследования (содержащей хоть один объект) с заданными на этих объектах предикатами (т. е. свойствами и отношениями).
59. Массового обслуживания теория – раздел теории вероятностей, изучающий потоки требований на обслуживание, поступающие в системы обслуживания и выходящие из них, длительности ожидания и длины очередей и т. п. и их зависимость от правил (дисциплины) обслуживания. 20-е годы 20 века.
60. Математическая лингвистика – математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков. Возникла в 50-х годах 20 века.
61. Математическая логика – раздел математики, посвящённый изучению математических доказательств и вопросов оснований математики.
62. Математическая статистика – раздел математики, посвящённый математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. 18-19 века Р. Фишер, Э. Пирсон, Е. Нейман, А. Вальд и др.
63. Математическая экономика – раздел математики, объединяющий задачи, которые возникают при исследовании математических моделей производства, распределения, обмена и других протекающих в экономике процессов.
64. Математический анализ – часть математики, в которой функции и их обобщения изучаются методом пределов. 17 век.
65. Математическое программирование – математическая дисциплина, посвящённая теории и методам нахождения экстремумов (максимумов или минимумов) функций многих переменных при наличии дополнительных ограничений на эти переменные, имеющих форму равенств или неравенств. Сформировалось в 50-х годах 20 века.
66. Метаматематика – раздел математической логики, изучающий формализованные математические теории. 19-20 века Д. Гильберт, Г. Кантор, Л. Брауэр и др.
67. Метрическая теория функций – раздел теории функций действительного переменного, в котором изучаются свойства функций на основе понятия меры множества. Начало 20 века Э. Борель, Р. Бер, А. Лебег.
38. Дифференциальное исчисление – раздел математики, в котором изучаются производные и дифференциалы функций и их применение к исследованию функций. И. Ньютон, Г. Лейбниц 17 век.
39. Дифференциальные игры – раздел математической теории управления, в котором изучается управление в конфликтных ситуациях и управление с гарантированным результатом в условиях неопределённости. 50-е года 20 века Н. Н. Красовский.
40. Евклидова геометрия – геометрическая теория, основанная на системе аксиом, впервые изложенной в “Началах” Евклида (3 в. до н. э.). Д. Гильберт (1899).
41. Игр теория – раздел математики, предметом которого является изучение математических моделей принятия оптимальных решений в условиях конфликта. Теория игр была разработана Дж. Нейманом и О. Моргенштерном (1944).
42. Интегральное исчисление – раздел математики, в котором изучаются свойства интегралов и связанных с ними процессов интегрирования. 5 век до н. э.
43. Интервальный анализ – раздел вычислительной математики, посвящённый учёту ошибок округления при проведении расчётов на цифровых ЭВМ.
44. Информации теория – раздел математики, исследующий процессы хранения, преобразования и передачи информации. Основы были заложены в 1948-49 К. Шенноном. А. Н. Колмогоров, А. Я. Хинчин, В. А Котельников.
45. Исследование операций – научный метод выработки количественно обоснованных рекомендаций по принятию решений. Конец 30-х годов 20 века.
46. Комбинаторная логика – раздел логики, посвящённый изучению и анализу таких понятий и методов, как переменная, функция, операция подстановки, классификация предметов по типам или категориям и др.
47. Комбинаторный анализ – раздел математики, посвящённый решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами. Б. Паскаль, П Ферма, Г Лейбниц, Я. Бернулли, Л. Эйлер.
48. Коммутативная алгебра – раздел алгебры, изучающий свойства полей, коммутативных колец, и связанных с ними объектов (идеалов, модулей, нормирований и т. д.). В первой половине 19 века К. Гаусс, Э. Куммер, Р. Дедекинд, Л. Кронекер, Д. Гильберт.
49. Конечных разностей исчисление – раздел математики, в котором изучаются функции при дискретном изменении аргумента, в отличии от интегрального и дифференциального исчислений, где аргумент изменяется непрерывно. 18 век Б. Тейлор.
50. Конструктивная математика – абстрактная наука о конструктивных процессах, человеческой способности осуществлять их и об их результатах – конструктивных объектах.
51. Конструктивный анализ – название, объединяющее различные течения в основаниях математики и математическом анализе.
52. Конформная геометрия – раздел геометрии, в котором изучаются свойства фигур, инвариантные относительно конформных преобразований.
53. Линейная алгебра – часть алгебры, изучающая векторные (линейные) пространства и их подпространства, линейные отображения (операторы), линейные, билинейные и квадратичные функции (функционалы или формы) на векторных пространствах. 18 век Г. Фробениус, Крамер, Гаусс.
54. Линейное программирование – раздел математического программирования, посвящённый теории и методам решения задач об экстремумах линейных функций на множествах, задаваемых системами линейных неравенств и равенств.
55. Линейчатая геометрия – раздел геометрии, в котором рассматриваются в качестве элементов пространства прямые линии.
56. Лобачевского геометрия – одна из неевклидовых геометрий; основана на тех же основных посылках, что и обычная – евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на противоположную. 1826 год.
57. Логика высказываний – раздел математической логики, изучающий логические законы, в которых учитывается лишь логическая структура высказываний, а именно, как одни высказывания получены из других с помощью таких логических операций, как конъюнкция ,дизъюнкция, импликация, эквивалентность, отрицание.
58. Логика предикатов - раздел математической логики, изучающий логические законы, общее для любой области объектов исследования (содержащей хоть один объект) с заданными на этих объектах предикатами (т. е. свойствами и отношениями).
59. Массового обслуживания теория – раздел теории вероятностей, изучающий потоки требований на обслуживание, поступающие в системы обслуживания и выходящие из них, длительности ожидания и длины очередей и т. п. и их зависимость от правил (дисциплины) обслуживания. 20-е годы 20 века.
60. Математическая лингвистика – математическая дисциплина, предметом которой является разработка формального аппарата для описания строения естественных и некоторых искусственных языков. Возникла в 50-х годах 20 века.
61. Математическая логика – раздел математики, посвящённый изучению математических доказательств и вопросов оснований математики.
62. Математическая статистика – раздел математики, посвящённый математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. 18-19 века Р. Фишер, Э. Пирсон, Е. Нейман, А. Вальд и др.
63. Математическая экономика – раздел математики, объединяющий задачи, которые возникают при исследовании математических моделей производства, распределения, обмена и других протекающих в экономике процессов.
64. Математический анализ – часть математики, в которой функции и их обобщения изучаются методом пределов. 17 век.
65. Математическое программирование – математическая дисциплина, посвящённая теории и методам нахождения экстремумов (максимумов или минимумов) функций многих переменных при наличии дополнительных ограничений на эти переменные, имеющих форму равенств или неравенств. Сформировалось в 50-х годах 20 века.
66. Метаматематика – раздел математической логики, изучающий формализованные математические теории. 19-20 века Д. Гильберт, Г. Кантор, Л. Брауэр и др.
67. Метрическая теория функций – раздел теории функций действительного переменного, в котором изучаются свойства функций на основе понятия меры множества. Начало 20 века Э. Борель, Р. Бер, А. Лебег.

>Смотри, f - какая-та поебень, её истинность неизвестна, тогда f->1
>1
Под 1 ты подразумеваешь True?
>СХУЯЛИ ОНО ИСТИННО-ТО СУКАБЛЯТЬ?
68. Метрическая теория чисел – раздел теории чисел, в котором изучаются и метрически (т. е. на основе теории меры) характеризуются множества чисел, обладающих определёнными арифметическими свойствами.
69. Минимизация вычислительной работы – раздел вычислительной математики, посвящённый конструированию и исследованию методов, позволяющих находить приближённое с заранее указываемой точностью ?>0 решение поставленной задачи P из класса {P} при наименьших затратах вычислительной работы.
70. Многозначная логика – обобщение классической логики, при котором наряду с обычными истинностными значениями “истина” и “ложь” рассматриваются и другие (“промежуточные”) значения. 1920-21 года Я. Лукасевич, Э. Пост.
71. Многокритериальная оптимизация – раздел математического программирования, посвящённый проблемам выбора принципов оптимальности и методов нахождения их реализаций в экстремальных задачах с несколькими критериями.
72. Многомерная геометрия – геометрия пространств размерности, большей трёх. 18-19 века И Кант, Ж. Д’Аламбер, А. Кели, Г. Гриссман, Л. Шлефли.
73. Многомерный статистический анализ – раздел математической статистики, объединяющий методы изучения статистических данных, которые являются значениями многомерных качественных или количественных признаков.
74. Множеств теория – учение об общих свойствах множеств, преимущественно бесконечных. 19 век Г. Кантор.
75. Модальная логика – область логики, в которой наряду с обычными высказываниями рассматриваются модальные высказывания, то есть высказывания типа «необходимо, что …», «возможно, что …» и т. п.
76. Моделей теория – раздел математической логики, изучающий взаимосвязи между формализованными логико-математическими языками и математическими структурами, описываемыми с помощью этих языков. Э. Бельтрами, Ф. Клейн, Д. Гильберт.
77. Надёжности теория – направление прикладной математики, в которой разрабатываются методы обеспечения эффективной работы изделий (систем).
78. Начертательная геометрия – раздел геометрии, в котором пространственные фигуры, а также методы решения и исследования пространственных задач изучаются при помощи построения их изображений на плоскости. Ж. Дезарг, Г. Монже.
79. Неевклидовы геометрии – в буквальном понимании - все геометрические системы, отличные от геометрии Евклида.
80. Нелинейное программирование – раздел математического программирования, посвящённый теории и методам нахождения экстремумов нелинейных функций многих переменных при наличии дополнительных ограничений на эти переменные, имеющих форму равенств и неравенств.
81. Общая алгебра – часть алгебры, занимающаяся изучением тех или иных алгебраических систем, включающая в себя теории групп, колец, модулей, полугрупп, решёток и т. п. 19 век О. Ю. Шмидт, Б. Л. Ван.
82. Оптимальное управление – раздел математики, изучающий неклассические вариационные задачи. 20 век Л. С. Понтрягин, Р. Беллман.
83. Основания геометрии – раздел геометрии, в котором исследуются основные понятия геометрии, соотношения между ними и связанные с ними вопросы.
84. Очередей теория – раздел теории массового обслуживания. Изучает системы обслуживания, в которых требования, застающие систему занятой, не теряются, а ожидают его освобождения и затем обслуживаются в том или ином порядке.
85. Ошибок теория – раздел математической статистики, посвящённый построению выводов о численных значениях приближённо измеренных величин и об ошибках (погрешностях) измерений.
86. Параметрическое программирование – раздел математического программирования, посвящённый исследованию задач оптимизации, в которых условия допустимости и целевая функция зависят от некоторых детерминированных параметров.
87. Планиметрия – часть элементарной геометрии, в которой изучаются свойства фигур, лежащих в плоскости.
88. Планирование эксперимента – раздел математической статистики, изучающий рациональную организацию измерений, подверженных случайным ошибкам.
89. Поверхностей теория – раздел дифференциальной геометрии, в котором изучаются свойства поверхностей. 19 век Л. Г Шнирельман, Л. А Люстерник, А. Д. Александров, А. В Погорелов.
90. Приближение функции – раздел комплексного анализа, изучающий вопросы приближённого представления (аппроксимации) функций комплексного переменного посредством аналитических функций специальных классов.
91. Программирование теоретическое – математическая дисциплина, изучающая математические абстракции программ, трактуемых как объекты, выраженные на формальном языке, обладающие определённой информационной и логической структурой и подлежащие исполнению на автоматических устройствах.
92. Проективная геометрия – раздел геометрии, изучающий проективные свойства фигур, те есть те свойства, которые не меняются при проективных преобразованиях, например при центральном проектировании. Основы были заложены в 17 веке Ж. Дезаргом и Б. Паскалем. Г. Монжа, Ж. Понселе (в 19 веке изложил как самостоятельную дисциплину).
93. Размерности теория – часть топологии, в которой для каждого компакта, в последствии и для более общих классов топологических пространств тем или иным естественным образом определяется числовой топологический инвариант – размерность, совпадающий, если Х есть полиэдр, с его числом измерений в смысле элементарной и дифференциальной геометрии. Л. Брауэр (1913).
94. Разностных схем теория – раздел вычислительной математики, изучающий методы приближённого решения дифференциальных уравнений путём их замены конечно – разностными уравнениями (разностными схемами).
95. Расписаний теория – раздел исследования операций, в котором строятся и анализируются математические модели календарного планирования (т.е. упорядочения во времени) различных видов целенаправленных действий. Появилась в 50-х годах 20 века.
68. Метрическая теория чисел – раздел теории чисел, в котором изучаются и метрически (т. е. на основе теории меры) характеризуются множества чисел, обладающих определёнными арифметическими свойствами.
69. Минимизация вычислительной работы – раздел вычислительной математики, посвящённый конструированию и исследованию методов, позволяющих находить приближённое с заранее указываемой точностью ?>0 решение поставленной задачи P из класса {P} при наименьших затратах вычислительной работы.
70. Многозначная логика – обобщение классической логики, при котором наряду с обычными истинностными значениями “истина” и “ложь” рассматриваются и другие (“промежуточные”) значения. 1920-21 года Я. Лукасевич, Э. Пост.
71. Многокритериальная оптимизация – раздел математического программирования, посвящённый проблемам выбора принципов оптимальности и методов нахождения их реализаций в экстремальных задачах с несколькими критериями.
72. Многомерная геометрия – геометрия пространств размерности, большей трёх. 18-19 века И Кант, Ж. Д’Аламбер, А. Кели, Г. Гриссман, Л. Шлефли.
73. Многомерный статистический анализ – раздел математической статистики, объединяющий методы изучения статистических данных, которые являются значениями многомерных качественных или количественных признаков.
74. Множеств теория – учение об общих свойствах множеств, преимущественно бесконечных. 19 век Г. Кантор.
75. Модальная логика – область логики, в которой наряду с обычными высказываниями рассматриваются модальные высказывания, то есть высказывания типа «необходимо, что …», «возможно, что …» и т. п.
76. Моделей теория – раздел математической логики, изучающий взаимосвязи между формализованными логико-математическими языками и математическими структурами, описываемыми с помощью этих языков. Э. Бельтрами, Ф. Клейн, Д. Гильберт.
77. Надёжности теория – направление прикладной математики, в которой разрабатываются методы обеспечения эффективной работы изделий (систем).
78. Начертательная геометрия – раздел геометрии, в котором пространственные фигуры, а также методы решения и исследования пространственных задач изучаются при помощи построения их изображений на плоскости. Ж. Дезарг, Г. Монже.
79. Неевклидовы геометрии – в буквальном понимании - все геометрические системы, отличные от геометрии Евклида.
80. Нелинейное программирование – раздел математического программирования, посвящённый теории и методам нахождения экстремумов нелинейных функций многих переменных при наличии дополнительных ограничений на эти переменные, имеющих форму равенств и неравенств.
81. Общая алгебра – часть алгебры, занимающаяся изучением тех или иных алгебраических систем, включающая в себя теории групп, колец, модулей, полугрупп, решёток и т. п. 19 век О. Ю. Шмидт, Б. Л. Ван.
82. Оптимальное управление – раздел математики, изучающий неклассические вариационные задачи. 20 век Л. С. Понтрягин, Р. Беллман.
83. Основания геометрии – раздел геометрии, в котором исследуются основные понятия геометрии, соотношения между ними и связанные с ними вопросы.
84. Очередей теория – раздел теории массового обслуживания. Изучает системы обслуживания, в которых требования, застающие систему занятой, не теряются, а ожидают его освобождения и затем обслуживаются в том или ином порядке.
85. Ошибок теория – раздел математической статистики, посвящённый построению выводов о численных значениях приближённо измеренных величин и об ошибках (погрешностях) измерений.
86. Параметрическое программирование – раздел математического программирования, посвящённый исследованию задач оптимизации, в которых условия допустимости и целевая функция зависят от некоторых детерминированных параметров.
87. Планиметрия – часть элементарной геометрии, в которой изучаются свойства фигур, лежащих в плоскости.
88. Планирование эксперимента – раздел математической статистики, изучающий рациональную организацию измерений, подверженных случайным ошибкам.
89. Поверхностей теория – раздел дифференциальной геометрии, в котором изучаются свойства поверхностей. 19 век Л. Г Шнирельман, Л. А Люстерник, А. Д. Александров, А. В Погорелов.
90. Приближение функции – раздел комплексного анализа, изучающий вопросы приближённого представления (аппроксимации) функций комплексного переменного посредством аналитических функций специальных классов.
91. Программирование теоретическое – математическая дисциплина, изучающая математические абстракции программ, трактуемых как объекты, выраженные на формальном языке, обладающие определённой информационной и логической структурой и подлежащие исполнению на автоматических устройствах.
92. Проективная геометрия – раздел геометрии, изучающий проективные свойства фигур, те есть те свойства, которые не меняются при проективных преобразованиях, например при центральном проектировании. Основы были заложены в 17 веке Ж. Дезаргом и Б. Паскалем. Г. Монжа, Ж. Понселе (в 19 веке изложил как самостоятельную дисциплину).
93. Размерности теория – часть топологии, в которой для каждого компакта, в последствии и для более общих классов топологических пространств тем или иным естественным образом определяется числовой топологический инвариант – размерность, совпадающий, если Х есть полиэдр, с его числом измерений в смысле элементарной и дифференциальной геометрии. Л. Брауэр (1913).
94. Разностных схем теория – раздел вычислительной математики, изучающий методы приближённого решения дифференциальных уравнений путём их замены конечно – разностными уравнениями (разностными схемами).
95. Расписаний теория – раздел исследования операций, в котором строятся и анализируются математические модели календарного планирования (т.е. упорядочения во времени) различных видов целенаправленных действий. Появилась в 50-х годах 20 века.
96. Регрессионный анализ – раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.
97. Римана геометрия – одна из неевклидовых геометрий, т. е. геометрическая теория, основанная на аксиомах, требования которых отличны от требований аксиом евклидовой геометрий. Б. Римман 1854.
98. Статистический анализ – раздел математической статистики, посвящённый методам обработки и использования статистических данных, относящихся к случайным процессам.
99. Стереометрия – часть элементарной геометрии, в которой изучаются пространственные фигуры, в отличии от планиметрии, где рассматриваются фигуры лежащие в плоскости.
100. Стохастическое программирование – раздел математического программирования, посвящённый исследованию стохастических экстремальных задач, т. е. задач, в которых условия допустимости и целевая функция зависят от случайных параметров.
101. Сферическая геометрия – математическая дисциплина, изучающая геометрические образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрические образы, находящиеся на плоскости.
102. Сферическая тригонометрия – математическая дисциплина, изучающая зависимости между углами и сторонами сферических треугольников. 1-2 века Менелай, Птоломей, Насирэддин, Тусси, Абу-ль-Вефа, Л. Эйлер.
103. Тензорное исчисление – математическая теория, изучающая величины особого рода – тензоры, их свойства и правила действий над ними. Г. Риччи – Курбастро 19 век.
104. Топологическая алгебра – раздел алгебры, который занимается изучением различных топологических алгебраических систем, наделённых топологиями, в которых алгебраические операции этих систем непрерывны. 20-е годы 20 века.
105. Топология – раздел математики, имеющий своим назначением выяснение и исследование в рамках математики идеи непрерывности.
106. Тригонометрия – раздел геометрии, в котором метрические соотношения между элементами треугольника описываются через тригонометрические функции, а также устанавливаются соотношения между тригонометрическими функциями.
107. Факторный анализ – раздел многомерного статистического анализа, объединяющий методы оценки размерности множества наблюдаемых переменных посредством исследования структуры ковариационных или корреляционных матриц.
108. Функций теория – раздел математики, в котором изучаются общие свойства функций.
109. Функциональный анализ – раздел математики, главной задачей которого является изучение бесконечно-мерных пространств и их отображений. 20-30 годы 20 века.
110. Чисел теория – наука о целых числах.
111. Элементарная геометрия – часть геометрии, входящая в элементарную математику. 3 век до нашей эры.
112. Элементарная теория чисел – раздел чисел теории, изучающий свойства чисел элементарными методами.
96. Регрессионный анализ – раздел математической статистики, объединяющий практические методы исследования регрессионной зависимости между величинами по статистическим данным.
97. Римана геометрия – одна из неевклидовых геометрий, т. е. геометрическая теория, основанная на аксиомах, требования которых отличны от требований аксиом евклидовой геометрий. Б. Римман 1854.
98. Статистический анализ – раздел математической статистики, посвящённый методам обработки и использования статистических данных, относящихся к случайным процессам.
99. Стереометрия – часть элементарной геометрии, в которой изучаются пространственные фигуры, в отличии от планиметрии, где рассматриваются фигуры лежащие в плоскости.
100. Стохастическое программирование – раздел математического программирования, посвящённый исследованию стохастических экстремальных задач, т. е. задач, в которых условия допустимости и целевая функция зависят от случайных параметров.
101. Сферическая геометрия – математическая дисциплина, изучающая геометрические образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрические образы, находящиеся на плоскости.
102. Сферическая тригонометрия – математическая дисциплина, изучающая зависимости между углами и сторонами сферических треугольников. 1-2 века Менелай, Птоломей, Насирэддин, Тусси, Абу-ль-Вефа, Л. Эйлер.
103. Тензорное исчисление – математическая теория, изучающая величины особого рода – тензоры, их свойства и правила действий над ними. Г. Риччи – Курбастро 19 век.
104. Топологическая алгебра – раздел алгебры, который занимается изучением различных топологических алгебраических систем, наделённых топологиями, в которых алгебраические операции этих систем непрерывны. 20-е годы 20 века.
105. Топология – раздел математики, имеющий своим назначением выяснение и исследование в рамках математики идеи непрерывности.
106. Тригонометрия – раздел геометрии, в котором метрические соотношения между элементами треугольника описываются через тригонометрические функции, а также устанавливаются соотношения между тригонометрическими функциями.
107. Факторный анализ – раздел многомерного статистического анализа, объединяющий методы оценки размерности множества наблюдаемых переменных посредством исследования структуры ковариационных или корреляционных матриц.
108. Функций теория – раздел математики, в котором изучаются общие свойства функций.
109. Функциональный анализ – раздел математики, главной задачей которого является изучение бесконечно-мерных пространств и их отображений. 20-30 годы 20 века.
110. Чисел теория – наука о целых числах.
111. Элементарная геометрия – часть геометрии, входящая в элементарную математику. 3 век до нашей эры.
112. Элементарная теория чисел – раздел чисел теории, изучающий свойства чисел элементарными методами.

А почему да?
Ладно, бесполезный разговор. Может быть ты ебанулся, может быть я, в любом случае моего понимания мы не добьёмся.
Окей. Сколько примерно недель/месяцев уйдёт на изучение в объёме этих нескольких книг?
>— Слушай, а… сколько сейчас времени, ты не знаешь? Так, примерно, можешь почувствовать?
Часть ключевых статей Кантора можно прочитать за пару дней. Куратовского-Мостовского вряд ли можно осилить целиком за полгода. Вавилова можно прочитать за пару вечеров.

>ообще ничего по теории множеств не могу найти под его авторством. Ни на русском, ни на английском.
Название знаешь?
Испытал биекцию.
Мимо Кантор
Бляд, так это же именно его труды, не учебник. Я больше половины написанного не пойму, я же обычный undergraduate-левел, ниже среднего.
Зачем он вообще нужен?
Читай, там все понятно. Базарю.

Замаскированный Вербит.
https://en.wikipedia.org/wiki/Cantor's_diagonal_argument
Или в книжке Клини по логике. Там где-то в середине все это разжевывается.
Или смотришь этот видос:
https://www.youtube.com/watch?v=elvOZm0d4H0
Если ничего не получается, то берешь книжку Шеня:
http://www.mccme.ru/free-books/shen/shen-logic-part1-2.pdf
Попробую. Видео, кстати, давно смотрел когда-то.
Кстати, на другом сайте мне порекомендовали это: http://golibgen.io/view.php?id=4480. Мол, читать нужно только в современном изложении. Undergraduate ниже среднего осилит эту книгу?

А вот почему бы ему не взять книжку Шеня сразу?
gap> G:=Integers mod 4;
(Integers mod 4)
gap> M:=MultiplicationTable(G);
[ [ 1, 1, 1, 1 ], [ 1, 2, 3, 4 ], [ 1, 3, 1, 3 ], [ 1, 4, 3, 2 ] ]
gap> Display(M);
[ [ 1, 1, 1, 1 ],
[ 1, 2, 3, 4 ],
[ 1, 3, 1, 3 ],
[ 1, 4, 3, 2 ] ]
То в таблице ко всем числам прибавлена единица? Не понимат.
-------------------ZmodnZObj(0,4) ZmodnZObj(1,4) ZmodnZObj(2,4) ZmodnZObj(3,4)
-------------------------------------------------------------------------------------------------
ZmodnZObj(0,4)|ZmodnZObj(0,4) ZmodnZObj(0,4) ZmodnZObj(0,4) ZmodnZObj(0,4)
ZmodnZObj(1,4)|ZmodnZObj(0,4) ZmodnZObj(1,4) ZmodnZObj(2,4) ZmodnZObj(3,4)
ZmodnZObj(2,4)|ZmodnZObj(0,4) ZmodnZObj(2,4) ZmodnZObj(0,4) ZmodnZObj(2,4)
ZmodnZObj(3,4)|ZmodnZObj(0,4) ZmodnZObj(3,4) ZmodnZObj(2,4) ZmodnZObj(1,4)
Если A = {1}, B = {1,2} (2 на случай, если A - proper subset) и C = {}, то утверждение ложно.
Я читаю halmos naive set theory. Очень хорошая книга.
Смотри, если ты возьмёшь в этой строчке логической n=1, у тебя в первой скобке будет всегда истинна предпосылка (а с хуя ли он ложна, если в ней ничего не проверяется), а из 1 у тебя выходит 1, следовательно, p1 тоже должна быть 1. Надеюсь, понятно объяснил.
Наверное, Арнульд имел тут в виду разложение синуса в ряд Тейлора.
Среднее = сумма / количество слагаемых = интеграл / область интегрирования.
Вот этот прав. В какой системе можно подобную хуйню опровергать? В coq? Покажите. В вольфраме нельзя нихуя, у него сабсетов нет.

Арнольд имел в виду, что любой кто не способен за пять минут выписать ответ к математике не имеет способностей.
Расскажите про альтернативную арийскую математику, где нет понятия бесконечности. Что почитать по теме?
Это копия, сохраненная 23 ноября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.