Это копия, сохраненная 5 октября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.




Общие курсы
М. И. Сканави: "Элементарная математика".
Алгебра
И. М. Гельфанд, А. Шень: “Алгебра”. Весь курс школьной алгебры по 9 класс.
С. Б. Гашков: “Современная элементарная алгебра”.
Ю. М. Алимов, М. В. Колягин: "Алгебра и начала анализа".
Геометрия
Г. Коксетер: “Введение в геометрию“. Годная книга для уровня "продвинутый школьник".
А. Д. Александров, А. Л. Вернер, В. И. Рыжик: “Геометрия”. Учебник для 10-11 классов. Базовый и углубленный уровни.
Я. П. Понарин: “Элементарная геометрия” в двух томах. Собственно, первый том - это планиметрия, а второй том - это стереометрия.
А. Ю. Калинин, Д. А. Терешин: “Геометрия”, 10-11 классы. Годный учебник.
Тригонометрия
И. М. Гельфанд, С.М. Львовский, А. Л. Тоом: “Тригонометрия”. Название говорит само за себя. Много геометрических и физических интерпретаций + комплексные числа, как бонус.
БАЗОВЫЕ КУРСЫ ДЛЯ СТУДЕНТОВ:
Общая алгебра
Э. Б. Винберг: “Курс алгебры”. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Введение в алгебру" Кострикина.
А. И. Кострикин: “Введение в алгебру“. Пожалуй, лучший из известных учебников, соперничать с которым может разве что "Курс алгебры" Винберга.
М. Атья, И. Макдональд : "Введение в коммутативную алгебру".
А. Л. Городенцев: "Алгебра. Учебник для студентов-математиков". Вырос из лекций НМУ. Читать параллельно с Винбергом (Винберга читать в первую очередь).
И.Р. Шафаревич: “Основные понятия алгебры“. Замечательный обзор вообще того, что такое алгебра, как она выглядит и какое место она занимает в математике. Примеры, приложения и прочая конкретика.
E. Connell: Elements of Abstract and Linear Algebra". Хорошая первая книга по алгебре, да и математике вообще.
P. Grillet: "Abstract algebra". Очень лаконичный и понятный учебник. Надо знать элементарную теорию чисел, про индукцию, про множества и функции. Линейной алгебры нету.
J. Rotman: "Advanced modern algebra". Ротман сильно разжевывает. Задачи слишком простые для уровня учебника. Линейная алгебра есть.
M. Artin: "Algebra". Американский Винберг. Группы Ли, упор на геометрию. Задачи неудачные.
I. Herstein: “Topics in Algebra“. Прекрасные задачи, отбор материала очень устарел, почти что Ван дер Варден.
P. Aluffi: "Algebra, Chapter 0". Если ты в состоянии ее осилить, бери и забывай про остальные книжки из списка. Линейная алгебра есть.
Линейная алгебра
В. А. Ильин, Э. Г. Позняк: “Линейная алгебра“. Один из классических и самых популярных курсов линейной алгебры.
Д. В. Беклемишев: “Курс аналитической геометрии и линейной алгебры“.
И. М. Гельфанд: "Лекции по линейной алгебре". Не даётся определение определителя.
А. И. Кострикин, Ю. И. Манин: "Линейная алгебра и геометрия". Затрагивается темы геометрий и связей с квантовой механикой. Не даётся определение определителя.
S. Axler: "Linear algebra done right". Подход без определителей (почти). Одна из самых популярных книг за рубежом.
S. Treil: "Linear algebra done wrong". Не такая популярная, как Axler, но тоже хвалят, да. Определители есть.
G. Shilov: "Linear Algebra". Определитель появляется на первой странице.
K. Hoffman, R. Kunze: "Linear Algebra". Классика за рубежом.
P. Halmos: "Finite-Dimensional Vector Spaces". Тоже классика.
P. Peterson: "Linear Algebra". Не особо знаком, но выглядит аккуратно. Что-то вроде Акслера.
S. Roman: "Advanced Linear Algebra". Хороший учебник по линалу. Но нужно знать элементарные свойства матриц и определителей.
Математический анализ
T. Tao: “Real analysis“. Один из самых популярных курсов математического анализа на английском языке.
C. Pugh: "Real Mathematical analysis". Более простая версия Рудина с картинками. Норм книга, но не самая лёгкая.
У. Рудин: "Основы математического анализа".
В. А. Зорич: "Математический анализ". Первый том посвящен классическому анализу. Много примеров, много материала, в том числе даются в начале основы матлогики и теории множеств, а также функций между ними.
Р. Курант: "Курс дифференциального и интегрального исчисления". Идеален с точки зрения первого знакомства с теорией, но имеет достаточно сложные упражнения.
Г. М. Фихтенгольц: "Курс дифференциального и интегрального исчисления". Хорош как повторительный курс.
С. М. Львовский: "Лекции по математическому анализу". Записки лекций из НМУ. Нужно знать основы калькулюса.
Г. Г. Харди, Д. Е. Литтлвуд, Г. Пойа: "Неравенства".
Н. Н. Лебедев: "Специальные функции и их приложения".
Г. П. Толстов: “Ряды Фурье“.
Дифференциальные уравнения
С. Фарлоу: “Уравнения с частными производными для научных работников и инженеров“.
Вариационное исчисление
И. М. Гельфанд, С. В. Фомин: " Вариационное исчисление".
Топология
V. Runde: "A taste of topology". Неплохая книга по метрическим пространствам и общей топологии, затрагивает фундаментальную группу.
J. Strom: "Modern classical homotopy theory".
T. Dieck: "Algebraic topology".
M. Crossley: "Essential Topology". Пререквизит для изучения алгебраической топологии. Не затрагивает тему метрических пространств.
КУРСЫ ДЛЯ ПРОДВИНУТЫХ МАТЕМАТИКОВ
Математический анализ
А. И. Маркушевич: "Теория аналитических функций".
S. Ramanan: "Global calculus".
H. Amann, J. Echer: "Analysis".
W. Fidcher, I. Lieb: "A Course in Complex Analysis: From Basic Results to Advanced Topics".
Дифференциальные уравнения
В. И. Арнольд: “Обыкновенные дифференциальные уравнения”. Книга для уверенных в себе математиков. Диффеоморфизмы, фазовые потоки, гладкие многообразия. Слава Гермесу Трисмегисту!
Теория категорий
С. Маклейн: "Категории для работающего математика".
Р. Голдблатт: "Топосы. Категорный анализ логики".
Дифференциальная Геометрия
К. Номидзу: "Основы дифференциальной геометрии".
J. Lee: "Manifolds and DIfferential Geometry".
L. Nicolaescu: "Lectures on the Geometry".
P. Michor "Topics in Differential Geometry".
Алгебраическая геометрия
Д. Мамфорд: "Красная книга о многообразиях и схемах".
В. В. Острик, М. А. Цфасман: “Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые”.
В. И. Арнольд: “Вещественная алгебраическая геометрия”.
Ю. И. Манин: Введение в теорию схем и квантовые группы“.
R. Vakil: "Foundations of algebraic geometry".
S. Bosch: "Algebraic Geometry and Commutative Algebra".
U. Gotz, T. "Wedhorn: Algebraic Geometry".
E. Harris: "The Geometry of Schemes".
Топология
А. Хэтчер: "Алгебраическая топология".
J. Munkres: "Topology". Книга - жесткий учебник по теоретико-множественной топологии. Много ненужного для других областей математики.
ИНТЕРЕСНОЕ:
Цикл “Manga guide to...“. Популярное изложение различных областей математики (и не только), оформленное в виде манги. Увы, без фансервиса.
Н. А. Вавилов: “Конкретная теория групп I: основные понятия“. И вообще все остальные книги (и лекции!) Вавилова.
П. С. Александров: “Введение в теорию групп“. Просто о сложном. Несколько вольный язык изложения, местами затрудняющий восприятие.
В. Б. Алексеев: “Теорема Абеля в задачах и решениях”.
Р. Курант, Г. Роббинс: “Что такое математика?”. Очень интересная книга, в двух словах не описать. Но вас захватит, надолго.
Н. Я. Виленкин: "Рассказы о множествах". Теория множеств для широкого круга читателей.
М. М. Постников: “Теорема Ферма. Введение в теорию алгебраических чисел”.
Н. Стинрод: “Первые понятия топологии“.
А. Я. Хинчин: “Три жемчужины теории чисел“.
О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов: “Элементарная топология”.
Я. П. Понарин: “Алгебра комплексных чисел в геометрических задачах”.
А. А. Заславский: “Геометрические преобразования”.
В. Акопян, А. А. Заславский: “Геометрические свойства кривых второго порядка”.
В. И. Арнольд: “Геометрия комплексных чисел, кватернионов и спинов”.
В. В. Прасолов: “Геометрия Лобачевского”.
Д. В. Аносов: “Дифференциальные уравнения: то решаем, то рисуем”.
В. В. Прасолов: “Наглядная топология”.
Д. В. Аносов: “От Ньютона к Кеплеру”.
М. Клайн: “Математика. Поиск истины“.
Д. Пойа: “Математическое открытие“.
Л. Кэрролл: “Логическая игра“.
Д. Пойа: “Как решать задачу“.
О. Я. Виро, Д. Б. Фукс: "Введение в теорию гомотопий. Гомологии и когомологии".
A. Ostermann, G. Wanner: "Geometry by its history".
T. Sundstrom: "Mathematical reasoning writing and proof". В книге объясняется что такое математическое доказательство, математический факт и каким образом их можно придумывать. Начала теории множеств.
D. Dummit R. Foote: “Abstract Algebra“. Много примеров, задач, но страшно скучный учебник, его нужно держать как справочник.
ПОЛЕЗНЫЕ РЕСУРСЫ:
Библиотечка "Квант": math.ru/lib/ser/bmkvant
Высшая математика просто и доступно, по 2 курс включительно: mathprofi.net
Необъятная онлайн библиотека: gen.lib.rus.ec
Пойду составлю списочек пока. Для этого придется читать и читать, но думаю к десятому треду создам отдельный, с НОРМАЛЬНЫМ спискомлитературы, а не говном, которое мало кто кроме писателя и редактора читал.
Ох, лол, шел бы ты отсюда с таким мировоззрением, петушок. Это тред для ПАСАВЕТУЙТЕ КНИЖКУ как раз и создан.
Ну и похуй. Зато будет нормальная активность, без этого всего типа ЗА ЧИСТОТУ МАТЕМАТИКИ ЗИГ ХАЙЛЬ ZFC или ВСЕХ ФИЗИКОВ НАДО УНИЧТОЖИТЬ!! ОНИ РАК УБИВАЮЩИЙ МАТЕМАТИКУ
Я же не подразумевал своей фразой буквализм "в списке все школьное говно", у меня типичная гипербола, означающая, что слишком много материала для школьника (т.е. ограниченного в области школы, не имеющего дальнейшего развития; или составляющего долгое топтание на месте), хотя это /sci, а не /un.
Так тут начинающие. По-твоему, они сразу должны пространствами тейхмюллера оперировать? У всех начальный уровень разный. Считать умеют - уже хорошо.
>слишком много материала для школьника
Например? Для школьников 9 книг. Все остальное выходит за рамки необходимого не интересующимся математикой.
Ну е-мое. Почему в этом треде всегда проблемы с осознанием факта, что разные люди воспринимают информацию по-разному? То, что тебе кажется говном кому-то может быть самым понятным изложением.
Ты ебанулся? Хотя чего я спрашиваю это у математика...
То что они написанны разными людьми не значит что они отличаются друг от дружки. Там все описывается одинаково. Если тебе не понятно что то то надо перечитать еще раз. Или спросить в этом треде, в котором тебя по привычке смешают с говном и начнут задвигать за чистоту арийской рассы математики
Я правду говорю. Я тут когда спрашивал про книги меня говном закидали, а потом оправдались "да у меня прост в жизни проблемы) че ты репортишь то?"
Ну мне тут много раз поясняли. Правда специфическим языком, но с символьной разметкой и, вроде бы, от души.
По мне, начинающие никогда не дойдут до алгеома, если будут действовать по списку, а именно ебашить школьную геометрию (имхо вообще бесполезную, которую можно вычеркнуть, потеряв при этом нихуя), школьную алгебру (разве что для развития навыка записи в тетрадочке, но не на таком же блевотно-однотипном материале, гельфанд шень это выше крыши); при этом не получат никакой общематематической культуры и самого важного навыка: доказательства.
После этого начинать Винберга, Рудина, Кострикина-Манина, это будет как удар лбом об стену. Потому что надо доказывать, надо теоретизировать, а родных циферок и выводов из евклида нету.
Нужен 2ch.hk/math.
Подобно тому, как /ftb вырос в отдельный раздел из /sp, математика уже не вмещается в /sci. Половина мат. тредов - срачи между истинными хозяевами треда - математиками - и грязными физиками, сующими свой грязный нос-обрубок туда, куда не следует.
Ноудискасс.
Кому-то и школьный курс освоить по каким-либо соображениям надо. Да и не подразумевает список, что по нему от начала до конца доходить надо. Разумеется, какую-нибудь теорию гомотопий освоить самостоятельно крайне тяжело. Но это не проблема списка, а проблема сложности и контринтуитивности некоторых разделов математики. Помочь тут может разве что наставник, разбирающийся в теме, который и подскажет и исправит и задач задаст порешать. А в остальном по этому списку вполне реально учиться математике. Я смог в Винберга с Тао вкатиться с, можно сказать, школьными знаниями (учился в языковой школе, поэтому с математикой было плохо). Не такое уж достижение, но уже что-то. Единственное что, я бы листки какого-нибудь сунца в школьный список добавил. Но они же вроде без названий.
>>367099
Обсуждать. Вежливо, тактично, аргументированно. Без "выкинуть все нахуй, и оставить только вот эти три книги". Без срача "Вербицкий против всех" или "Дифференциальная геометрия не нужна".
Мразь молчала два месяца назад. Попробуйте сейчас кто-нибудь.
>они же вроде без названий
Да ну?
http://www.mccme.ru/free-books/
Тем не менее большинству полезно освежить школьные знания, дополнить их продвинутым уровнем. А школьный учебник на 80% состоит из воды и жевания. А самое главное, не учит конструктивности, там все построено на обучению каким-то конкретным методам.
Соглашусь. Тут вон даже обычный тред математики неактивным стал. На целую доску не потянет.
>>367108
>Да ну?
Ну ок, че. Мне их всегда просто отдельными листками кидали.
>Тем не менее большинству полезно освежить школьные знания, дополнить их продвинутым уровнем. А школьный учебник на 80% состоит из воды и жевания. А самое главное, не учит конструктивности, там все построено на обучению каким-то конкретным методам.
Ни одного плохого школьного учебника в списке нет. Да, подход изложения не везде с заделом на профессиональную карьеру математика. Но и не всем это нужно.
Даже хороший школьный учебник обязан:
1) быть распределенным на определенное количество часов
2) охватывать все темы для егэ
Так что в итоге оказывается растянутым, с большим количеством лишней инфы.
У него было несколько коллег и учеников, которых он постоянно оскорблял во время их докладов. Они были милейшие люди и это терпели. Причем оскорбления были явными, а не только «это – глупость» или «ты делаешь не то, что нужно». Мне запомнился такой яркий эпизод, на котором я присутствовал, и уверен, что он был не единственным в этом роде.
На семинаре Гельфанда делал доклад известный математик средних лет по своей тематике. Давайте назовем его профессором Ивановым. Иванов начал выступать, пару раз его перебивал Гельфанд, а где-то минут через 15 Гельфанд остановил речь Иванова и заявил, что тот подход, который предлагает профессор Иванов, совершенно никуда не годится, что это глупость, что здесь нужно делать не так, а нужно делать совершенно по-другому. Дальше Израиль Моисеевич обратился к одному из школьников и сказал. Назовем школьника Мишей. «Миша, Вам понятно то, что я сейчас объяснил?» Мише это было понятно, тогда И.М. стал объяснять дальше, как это нужно делать и сказал следующее. «Продолжать слушать этот доклад мы не будем, это совершенно бессмысленно, перейдем к следующему докладу. А на следующем заседании семинара Миша расскажет, как нужно на самом деле расправляться с этой тематикой».
И действительно, на следующем заседании Миша, который впоследствии стал очень известным математиком, рассказал, как это нужно делать. Я уверен, хотя не был этому свидетелем, что школьник Миша приезжал к Гельфанду домой, они там вместе поработали и разобрались в проблеме. Однако внешне это выглядело таким образом, что бедному Иванову была публично нанесена пощечина, объяснено, что он ничего не понимает в своей собственной области, что он не знал, как делать правильно, а вот школьник Миша может это сделать, как следует.
У него было несколько коллег и учеников, которых он постоянно оскорблял во время их докладов. Они были милейшие люди и это терпели. Причем оскорбления были явными, а не только «это – глупость» или «ты делаешь не то, что нужно». Мне запомнился такой яркий эпизод, на котором я присутствовал, и уверен, что он был не единственным в этом роде.
На семинаре Гельфанда делал доклад известный математик средних лет по своей тематике. Давайте назовем его профессором Ивановым. Иванов начал выступать, пару раз его перебивал Гельфанд, а где-то минут через 15 Гельфанд остановил речь Иванова и заявил, что тот подход, который предлагает профессор Иванов, совершенно никуда не годится, что это глупость, что здесь нужно делать не так, а нужно делать совершенно по-другому. Дальше Израиль Моисеевич обратился к одному из школьников и сказал. Назовем школьника Мишей. «Миша, Вам понятно то, что я сейчас объяснил?» Мише это было понятно, тогда И.М. стал объяснять дальше, как это нужно делать и сказал следующее. «Продолжать слушать этот доклад мы не будем, это совершенно бессмысленно, перейдем к следующему докладу. А на следующем заседании семинара Миша расскажет, как нужно на самом деле расправляться с этой тематикой».
И действительно, на следующем заседании Миша, который впоследствии стал очень известным математиком, рассказал, как это нужно делать. Я уверен, хотя не был этому свидетелем, что школьник Миша приезжал к Гельфанду домой, они там вместе поработали и разобрались в проблеме. Однако внешне это выглядело таким образом, что бедному Иванову была публично нанесена пощечина, объяснено, что он ничего не понимает в своей собственной области, что он не знал, как делать правильно, а вот школьник Миша может это сделать, как следует.
Не вижу ничего плохого в том, чтобы научиться решать уравнения с параметрами и упрощать выражения. Или что там еще сейчас в ЕГЭ. В крайнем случае можно что-нибудь пропустить. В реал анилизисе Тао тоже много воды, однако это не минус, а плюс. Так иногда понятнее.
>>367112
Это откуда?
Еще и забывает кто маняматику двигает а кто дрочит ZFC теории.
Давай более наглядно, в Алимове из оп-списка 114 страниц посвящено тригонометрии, в них содержатся 375 упражнений.
Охватываемые темы: определения основных функций, их свойства, основные тождества и разнообразные выводы из них.
Охуенно, да? Это, конечно, не учебник геометрии, где на протяжении 1000 упражнений неуверенно разрабатывается аксиоматика Евклида, но тоже достойно.
• логикофанатики
• физикомафиозы
• платонобоги
То есть тебе не нравится, что много упражнений и мало тем? По мне так лучше уж это, чем наоборот.
что я сделал. я нашел в computer algebra обратную матрицу простой матрицы 2на2. потом построил, как я понял, из объяснения ниже, столбец матрицы Х. решил ее в computer algebra и сравнил с столбцом обратной матрицы.
но это фигня какая-то, учитывая что из доказательсва я должен понять как находить обратные матрицы.
мне бы хотелось книгу где понятнее.
это из Винберг - курс алгебры.
Теорема 7. Квадратная матрица обратима тогда и только тогда, когда она невырожденна.
Доказательство.
...
Обратно, пусть матрица А невырожденна. Будем искать
обратную матрицу как решение матричного уравнения АХ = Е. Для
элементов k-ro столбца матрицы X это дает систему линейных
уравнений с матрицей коэффициентов А и столбцом свободных членов,
равным k-му столбцу матрицы Е.
Можно только say, что ты extremely bad умеешь обращаться с computer algebra, потому что, если бы ты всё делал correctly, то получил бы right answer.
Когда ты строишь обратную матрицу, то делишь каждый элемент транспонированной матрицы алгебраических дополнений на определитель исходной матрицы. У вырожденной матрицы определитель равен нулю, поэтому нельзя построить ее обратную. Или ты не про это?
Упражнений просто ПИЗДЕЦ много, на такую малополезную и необъемную тему. А уж содержание этих упражнений... Почти все посвящены подставлению тождеств и прочим комбинаторным говном.
Не нужно, кстати, недооценивать простые упражнения на использование формул. Для меня, в свое время, тождественные преобразования были понс асинорум для понимания алгебры вообще.

На кой это надо вообще? Система компьютерной алгебры все равно знает больше трюков (чем пикрелейтед) и не совершает ошибок.
Шпора по тригонометрии.
Понятно.
che
Я think, что у вас butthurt, советую do a barell roll, и suck a dick. Я вообще мамкин русофоб, нахуй иди.
А что тут может быть непонятно? Есть вектор-столбец переменных из X, при умножении строк-коэффициентов из A на него получается система уравнений. Уравнений столько, сколько строк. Переменных в каждом уравнении столько, сколько элементов в столбце из X.
Недавно возникло ощущение, что я просёк "фишку" математики. Хотя никаких глубоких знаний у меня нет - обычный университетский курс матан+линал+диффуры(включая урматы)+теорвер+стохи+вычислялка+тфкп. Сдавал все на 3-4, теоремы сам не доказывал, но таки интересовался и пытался все связать воедино.
Стоит ли далее углубляться в математику, если сфера моих интересов - межмолекулярные взаимодействия, нелинейные эффекты на таких масштабах (0.1-100нм), моделирование систем типа белок-белок-раствор?
Какие могут еще ждать за поворотом откровения? Типа дуализма элементов множеств и операторов, типа базиса, типа линейных пространств, типа колец и алгебр и типа фурье и типа банаховых пространств и групп ли? Какие еще есть ништяковые идеи в математике, которые пригодятся прикладнику? Спасибо.
> прошел кучу университетских курсов
> базисы, линейные пространства, кольца, алгебры называет откровениями
Вся суть университетского образования.
Скорее всего нет. Можно прогуляться по топологии, но основную часть недостающей математики лучше уже черпать из тематических курсов и книг. Никаких откровений ты больше не прочтешь, а что-то недостающее наверстаешь когда понадобится.
Группы с функаном можно, конечно, поковырять для интересу и сомообразования, но лучше лезть в численные и приближенные методы и дрочить кодинг.
И да, я не математик, математики не умеют различать полезные абстракции от бесполезного воспаления фантазий.
Да и нет тут работающих математиков. Только воннаби, домоседы сраные, мнящие себя икспертами.
Быстра блять, какой раздел математики изучает нашу реальность напрямую? Топология?
Не во всех учебниках по физике есть вводный курс в математику. Открываешь черные дыры и прочий майндфак-уже идут какие-то ебанутые формулы. системы и хуяк хуяк.
Очевидно, метаматематика.
Физика - это раздел математики. Предполагается, что ты достаточно компетентен, чтобы самостоятельно доказать всё, что тебе нужно.
Арнольд, вы умерли. Отстаньте.
Это ерунда.
> икосаэдр не гладкий
Гладкость - это структура, которую мы задаём, а не что-то данное свыше. Мы можем её просто перенести со сферы через гомеоморфизм, тогда всё будет диффеоморфно.
Как же с помощью анализа получаются правильные результаты? Беркли пришёл к мысли, что это объясняется наличием в аналитических выводах взаимокомпенсации нескольких ошибок, и проиллюстрировал это на примере параболы. Как ни странно, некоторые крупные математики (например, Лагранж) согласились с ним.
Сложилась парадоксальная ситуация, когда строгость и плодотворность в математике мешали одна другой. Несмотря на использование незаконных действий с плохо определёнными понятиями, число прямых ошибок было на удивление малым — выручала интуиция. И всё же весь XVIII век математический анализ бурно развивался, не имея по существу никакого обоснования. Эффективность его была поразительна и говорила сама за себя, но смысл дифференциала по-прежнему был неясен. Особенно часто путали бесконечно малое приращение функции и его линейную часть.
В течение всего XVIII века предпринимались грандиозные усилия для исправления положения, причём в них участвовали лучшие математики столетия, однако убедительно построить фундамент анализа удалось только Коши в начале XIX века. Он строго определил базовые понятия — предел, сходимость, непрерывность, дифференциал и др., после чего актуальные бесконечно малые исчезли из науки. Некоторые оставшиеся тонкости разъяснил позднее Вейерштрасс. В настоящее время термин «бесконечно малая» математики в подавляющем большинстве случаев относят не к числам, а к функциям или последовательностям.
Как иронию судьбы можно рассматривать появление в середине XX века нестандартного анализа, который доказал, что первоначальная точка зрения — актуальные бесконечно малые — также непротиворечива и могла бы быть положена в основу анализа. С появлением нестандартного анализа стало ясно, почему математики XVIII века, выполняя незаконные с точки зрения классической теории действия, тем не менее получали верные результаты.
Как же с помощью анализа получаются правильные результаты? Беркли пришёл к мысли, что это объясняется наличием в аналитических выводах взаимокомпенсации нескольких ошибок, и проиллюстрировал это на примере параболы. Как ни странно, некоторые крупные математики (например, Лагранж) согласились с ним.
Сложилась парадоксальная ситуация, когда строгость и плодотворность в математике мешали одна другой. Несмотря на использование незаконных действий с плохо определёнными понятиями, число прямых ошибок было на удивление малым — выручала интуиция. И всё же весь XVIII век математический анализ бурно развивался, не имея по существу никакого обоснования. Эффективность его была поразительна и говорила сама за себя, но смысл дифференциала по-прежнему был неясен. Особенно часто путали бесконечно малое приращение функции и его линейную часть.
В течение всего XVIII века предпринимались грандиозные усилия для исправления положения, причём в них участвовали лучшие математики столетия, однако убедительно построить фундамент анализа удалось только Коши в начале XIX века. Он строго определил базовые понятия — предел, сходимость, непрерывность, дифференциал и др., после чего актуальные бесконечно малые исчезли из науки. Некоторые оставшиеся тонкости разъяснил позднее Вейерштрасс. В настоящее время термин «бесконечно малая» математики в подавляющем большинстве случаев относят не к числам, а к функциям или последовательностям.
Как иронию судьбы можно рассматривать появление в середине XX века нестандартного анализа, который доказал, что первоначальная точка зрения — актуальные бесконечно малые — также непротиворечива и могла бы быть положена в основу анализа. С появлением нестандартного анализа стало ясно, почему математики XVIII века, выполняя незаконные с точки зрения классической теории действия, тем не менее получали верные результаты.
>Как иронию судьбы можно рассматривать появление в середине XX века нестандартного анализа, который доказал, что первоначальная точка зрения — актуальные бесконечно малые — также непротиворечива и могла бы быть положена в основу анализа. С появлением нестандартного анализа стало ясно, почему математики XVIII века, выполняя незаконные с точки зрения классической теории действия, тем не менее получали верные результаты.
Хуйня жи. Нестандартный анализ очень слабо связан с Лейбницевым "dx".
Так а в чём пафос быть физиком? Они-то просто подгоняют модели под результаты экспериментов и ставят новые эксперименты. Никакой глубины в этом нету.
как выводится время разряда конденсатора через сопротивление?
Зельдович - высшая математика для начинающих.
Укажи этот диффеоморфизм.
Опять начинаешь, ебучий шакал.
>У математики в принципе нету связи с реальностью
Такое дегенеративное утверждение мог произнести только физический пропагандон.
>да и понятия реально-нереально в математике нету как такового
Ещё одна часть мифа-псевдоопределения «математики», спорить с подобными описаниями-определениями — дело сомнительное, но, тем не менее.
Есть, ещё как. Парадокс Банаха-Тарского почему называется «парадоксом»?
Математики не изучают произвольные структуры (как должны были бы делать, если бы игнорировали так называемую «реальность»), математические образы чрезвычайно наглядны и суггестивны. Все они исходят из единого источника с физикой, только точнее и яснее. Что поделать, если вкус у математиков тоньше, а воображение — богаче, разве это недостаток?
>используя математику как один из инструментов.
Как единственный нетривиальный „инструмент“. Физика — это такой монстр франкенштейна, сшитый из краденых обрывков настоящей фундаментальной науки — математики, опьянённый лоботомит, гарцующий между двумя противоположными стульями, то подставляя очко публике для сбора средств, то эксплуатируя единственный источник доброго, чистого, светлого.
>подставляя очко публике для сбора средств
Как и математика-кукаретика, как и вообще все науки сейчас. Аутисты могут говорить о том что НАУКА НУЖНА САМА ДЛЯ СИБЯ!! сколько угодно, но они будут сидеть без денег если не объяснят серьёзным дядям зачем это всё нужно.
мимоаутист
Ебанутся, кем надо быть чтобы такую хуйню городить? Вас там на мехмате промывают что ли?
> если использовать радикалы - решения уравнений x n =a, то можно явно получить решения произвольных уравнений 2-й, 3-й и 4-й степеней. Уже уравнения 5-й степени неразрешимы в радикалах.
О чём он?
О теореме Абеля о неразрешимости в радикалах уравнений выше четвёртой степени, видимо.
Не понял доказательство с википедии. Поясни для человека прошедшего только школьную программу. Он говорит что решение у уравнений ax^5+bx^4+cx^3+dx^2+ex+f=0 не может быть иррациональным. Но ведь если x=0, то решение есть при f=0. А ноль это радикал если верить определению из википедии.
Теорема утверждает, что для уравнения ax^5+bx^4+cx^3+dx^2+ex+f=0 нельзя написать общую формулу, зависящую только от a,b,c,d,e,f и содержащую только операции +-*/ и корни любой степени. В то время как для ax^2+bx+c = 0 такую формулу написать можно: x= (-b +- sqrt(b^2-4ac)) / 2a.
Элемент без переменной тоже должен быть нулем.
Тобишь, решение есть, но только если и переменная равна нулю и константа без переменной равна нулю. А это не распространяется на ВСЕ уравнения пятой степени.
Если так судить, то вообще все уравнения разрешимы, если их элементы равны нулю.
Но какова мощность у такого множества уравнений, по сравнению с остальными...
>Правда? А как тогда их решают?
Численно, когда нужно проводить какие-то рассуждения просто говорят "пусть x0 - какой-то из корней такого уравнения" и проводят рассуждения с ним (так делают и для квадратных уравнений, btw). На самом деле "в реальном мире" очень редко когда что либо можно аналитически решить, поэтому это не очень удивительно.
>И почему именно начиная с 5ой степени?
Фундаментальная причина этого: это то, что S_4 (группа перестановок из 4х элементов) ещё содержит нетривиальные нормальные подгруппы, а S_5 уже нет (под тривиальными я понимаю и знакопостоянную A_n которая есть у любой S_n).
Теорема не утверждает, что любое уравнение выше пятой степени неразрешимо в радикалах, она утверждает, что нельзя выписать одну общую формулу для всех уравнений.
Понял это. Он тут >>367267 сказал, что это не считается т.к. частный случай.
Хотя ещё 1 вопрос. Это говорит теорема Абеля или то предложение которое я запостил? Просто в том предложении не говорится про отсутствие формулы, а говорится именно то, что уравнение выше пятой степени неразрешимо в радикалах. Это ошибка?
>>367270
Ничего не понял, но всё равно спасибо.
Нету ОБЩЕГо решения.
Для тупых, с каждым уравнением пятой степени надо ебаться в сракотан, каждый раз, с каждым уравнением, по разному, чтобы найти решение.
Для всех уравнений степенью ниже есть формулы в которые просто надо поставить цифры и посчитать столбиком.
Под неразрешимостью в радикалах и понимают отсутствие формулы. Правда нужно было добавить "уравнение выше четёртой степени в общем виде не разрешимо в радикалах", чтобы уже совсем придирок не было.
>Ничего не понял, но всё равно спасибо.
Есть хорошая книга Алексеева "Теорема Абеля в задачах и решениях", как раз для уровня "постшкольника". Если тебя это правда заинетересовало - можешь почитать её (там не только теорема Абеля, но и много хорошей и глубокой математики вокруг неё).
Понял. Спасибо.
Разумеется мы можем сделать многозначную функцию "F(a,b,c,d,e,f)=все решения уравнения ax^5+bx^4+cx^3+dx^2+ex+f=0" и исследовать её. И получать о ней даже какие-то содержательные аналитические утверждения: приближения, разложения в ряды, неравенства, быстрые алгоритмы, вычисляющее её, и так далее. Так и делают, собственно.
А, я чуть по-другому твой вопрос воспринял. Интуиция нам подсказывает, что если формулы в радикалах не существует, то и формулы, использующей всякие экспоненты, логарифмы, синусы/косинусы и прочие стандартные школьные функции тем более не существует, но строгих теорем на этот счёт нету.
На дхду съеби. Там ты будешь чувствовать себя в своей стихии, как говно в унитазе.
Это другой.
Тут вся проблема в том, что считать под "явно заданы". Вот (арифметический) квадратный корень (вещественного) неотрицательного числа определяется как положительное решение уравнения x^2 = a. Насколько это можно считать "явным заданием"?
>Насколько я нагуглил, для гипергеометрических и тета функций потенциально такие формулы существуют.
Не знаю ничего об этом, вполне возможно.
А вот и оскорбления пошли, ещё dxdy приплёл. Там что, кто-то озвучивал схожие взгляды?
>математические образы чрезвычайно наглядны и суггестивны
Сколько можно уже это обоссывать? Математика зиждется на теории множеств и дальнейшей метаматематике, которая представляет собой скопление совершенно ненаглядных и трудных для восприятия образов. Притом к реальности и интуитивности эти области совершенно не тяготеют, им негде черпать эту реальность.
dxdy говно, там пидоры. дискас.
Неформально - функции, которые приходят из других теорий, в контексте которых есть рецепты их вычисления.
Если так хочется формально - в разложении в ряд явно заданы коэффициенты.
>Математика зиждется на теории множеств
Абсолютно неправда, теория множеств нужна только как общий язык для обоснования основ математики, и без неё прекрасно обходились вплоть до конца ХХ века. Если завтра логики выяснят, что теория множеств иррелевантна по каким-то их логическим причинам (например, окажется противоречивой), то 99.99% математических результатов всё равно сохранятся и им будет абсолютно похуй. Знаю мощного аналитика, который не знает, что такое кардинал и кроме алеф-нуль и континуума мощностей не знает. И жив как-то.
Ну так для функции "F : R^5 -> R^5" которая равна всем корням уравнения общего уравнения пятой степени тоже можно вычислить коэффициенты разложения в ряд тейлора по теореме о неявной функции. По крайней мере в тех точках, где все корни различны.
>Абсолютно неправда, теория множеств нужна только как общий язык для обоснования основ математики, и без неё прекрасно обходились вплоть до конца ХХ века.
Расскажи мне поподробнее как без нее обходились и кто все-таки припилил к математику эту нелепую канторову выдумку?
>Если завтра логики выяснят, что теория множеств иррелевантна по каким-то их логическим причинам (например, окажется противоречивой), то 99.99% математических результатов всё равно сохранятся и им будет абсолютно похуй. Знаю мощного аналитика, который не знает, что такое кардинал и кроме алеф-нуль и континуума мощностей не знает. И жив как-то.
Ну какой-нибудь отшельник тоже может революции не заметил, но это же ничего не говорит о революции.
>Расскажи мне поподробнее как без нее обходились
А что нужно от теории множеств рядовому математику? Конструкция функции, отношения эквивалентности и фактора по нему, декартового произедения множеств и всё. Всё это можно объяснить нетупому школьнику 7-8 класса абсолютно не вдаваясь ни в какие аксиоматические детали.
>Ну какой-нибудь отшельник тоже может революции не заметил, но это же ничего не говорит о революции.
Это не единичный случай, а типичный; может этот слегка гипертрофирован тем, что хорошие математики всё же знает поглубже теоретико-множественный фреймворк, но абсолютно адекватен тому факту, что математику можно его не знать. Факт в том, что в теории множеств, как и в понятии о множестве нету ничего фундаментального. Вместо теории множеств могли быть типы и конструкторы типов (что сейчас продвигается некоторыми чуваками), могли быть точки и стрелки (что сейчас продвигаетсся категорщиками), могли быть фундированные деревья, могло быть что угодно - математику можно строить на любом достаточно гибком лингвистическом фреймворке, результаты о том, что существует ровно пять платоновых тел и ровно 17 wallpaper groups (из которых и состоит математика) не потеряют ни капли своей значимости, глубины и даже "природности" от этого.
опять же, ты твоя аргументация вообще ничего не проясняет. Ну и что, что она не нужна какому-то определенному математику? Она это этого перестала быть частью математики, перестала "отражать реальность и черпать из нее"?
Есть, например [a,c) и (c,b], где a<c<b. Окрестности всегда есть, всё пространство — окрестность каждой своей точки.
Вот это поворот. А я почему-то думал, что окрестности должны быть симметричны во всех направлениях и представлять на плоскости внутренность окружности, а на прямой - равные интервалы в обе стороны от точки.
Покажу только для случая n=2
Рассмотрим функцию f:R^2->R^2 которая отображает (b,c) -> (x1,x2) коэффициенты уравнения x^2+bx+c в его корни.
У нас есть система уравнений вида
F = 0
F(b,c,x1,x2): R^4 -> R^2
F1(b,c,x1,x2) = c - x1x2
F2(b,c,x1,x2) = b + x1 + x2
теорема о неявной функции утверждает что в окрестности хороших точках существуют единственные гладкие функции x1(b,c) x2(b,c) которые решают это уравнение F(b,c,x1(b,c),x2(b,c))=0
при этом дифференциал функции f' = - F'_ab / |F'_x1x2|, иначе говоря, в координатах это будет выглядеть так:
(dx1/da, dx1/db)
(dx2/da, dx2/db) =
-
(dF1/dx1 dF1/dx2)^-1
(dF2/dx1 dF2/dx2)
x
(dF1/da dF1/db)
(dF2/da dF2/db)
вот и первый член ряда тейлора.
>>367312
Тогда я не очень понял твоей мысли; я думал твой тезис примерно следующий: "математика часть теории множеств, теория множеств абстрактна и мало связей имеет с реальным миром, следовательно, математика абстрактна и не имеет связи с реальным миром". Так вот, у теории множеств и математики (а именно: геометрии, алгебры и анализа) связей примерно столько же, сколько у лингвистики и литературы. Если завтра лингвисты введут новую систему падежов, то на произведениях Кафки это никак не отразится.
На отрезке [a,b] шар радиуса r, меньшего b-a, с центром в точке a выглядит так: [a,a+r). Шар, определённый с помощью расстояния — это множество точек, расстояние которых до его центра меньше радиуса. Окрестность точки должна содержать шар с центром в этой точке, если топология определена расстоянием, конечно.
ты все время пытаешься у меня найти аргумент, что теория множеств определяет или даже является (что вообще абсурд) основой математической науки. Я же утверждаю, что она является частью этой науки, причем немаловажной, но тем не менее не черпает свои знания из реальности. Мы же не можем выкинуть просто так теорию множеств, или найти ей реальную замену. Значит и математика не может быть наукой о реальности, раз содержит такую часть.
Но это же половина шара. А как же точки с координатой c<a<b? Они должны же лежать в шаре, чтобы он получился шаром. Как же я туп(
> Значит и математика не может быть наукой о реальности, раз содержит такую часть.
Очень странное суждение, как по мне. В фундаментальной физике есть toy models с n пространственными и m временными измерениями, которые тоже к реальности отношения не имеют, разве из этого следует, что физика не может быть наукой о реальности, если содержит такую часть?
>не черпает свои знания из реальности
О какой реальности идёт речь? Понятия теории множеств вполне наглядны — конечное множество букв алфавита, счётное множество связано с образом натурального ряда, континуум — вещественная линия, дальше идёт пространство, точками которого являются функции на прямой. Декартово произведение, множество подмножеств — всё это понятия, которые можно легко иллюстрировать.
Я же не зря отметил неотьемлемость ТМ, что потеряет физика без этих моделей? Математике же все равно нужен метааппарат (хоть какой-то), иначе непонятно насколько ее суждения будут истинны и проверяемы.
>>367344
В чем состоит отличие множеств:
{{},{},{}} {{{}},{},{}} {{{},{}},{}} {}
и как это отражается в реальности?
А как иллюстрировать понятие мощность бесконечного множества какой-либо реальной аналогией?
Ну и про наглядность Банаха-Тарского тоже очень интересно. Все-таки это не парадокс, а верное суждение.
>Математике же все равно нужен метааппарат (хоть какой-то), иначе непонятно насколько ее суждения будут истинны и проверяемы.
Ты опять же воспринимаешь теорию множеств как "аппарат для математики", мне кажется это несколько некорректно. Мне кажется до того, как Бурбаки расфорсили ТМ, тоже все прекрасно без неё обходились.
>В чем состоит отличие множеств:
>{{},{},{}} {{{}},{},{}} {{{},{}},{}} {}
>и как это отражается в реальности?
Это странный вопрос, отражается тем, что коробка, в которой есть пустая коробка это не то же самое, что коробка, в которой коробка, в которой пустая коробка.
>А как иллюстрировать понятие мощность бесконечного множества какой-либо реальной аналогией?
Отрезок и натуральный ряд, вполне реальные аналогии, как по мне.
>Ну и про наглядность Банаха-Тарского тоже очень интересно. Все-таки это не парадокс, а верное суждение.
Мне кажется, что парадокс Банаха-Тарского просто иллюстрирует, что при интерпретации мат. моделей (и, соответственно, мат. теорем) на реальность нужно быть аккуратнее. Это и так было понятно: например уравнения "показывают" что игла может стоять вертикально на столе, тогда нужно учитывать ещё и такое свойство как "устойчивость", но и не все устойчивые решения могут иметь физический смысл, тогда нужно учитывать что-то ещё, и так далее.
>Кудах-бабах!!
Банах-Тарский как пример связи с реальностью, лол. Уж лучше бы молчал.
>>367255
Математики-кукаретики так не делают. Я уже показывал в каком-то старом треде на конкретных примерах (ERC) как математикам-кукаретикам приходится подставлять очко физикам, химикам и биологам, а те уже работают с публикой. Чистого математика публика даже ебать не станет, а другие науки делают это исключительно из жалости.
>>367258
Это не специально, это побочка от перегруженности мозга математикой.
>>367342
toy models это немножко не то что ты думаешь. Это продукт ленивости физиков и от строгой математики он сидит еще дальше чем простые модели.
>>367347
> коробка, коробка
Только вот коробок в тех примерах нету. Это тебе как математику наличие коробки эквивалетно отсутствию, ты просто не можешь различить эти два случая. Для тебя "коробка" - абстрактная хуета, которую можно добвить или убрать в зависимости от того какой способ удобней для понимания конструкции.
>Только вот коробок в тех примерах нету. Это тебе как математику наличие коробки эквивалетно отсутствию, ты просто не можешь различить эти два случая. Для тебя "коробка" - абстрактная хуета, которую можно добвить или убрать в зависимости от того какой способ удобней для понимания конструкции.
Не понял. Вложенные относятся к абстракции конечного множества так же, как и линия нарисованная карандошом к абстракции прямой в геометрии - то есть это просто очень хорошая аналогия неоторого математического конструкта.
Вложенные коробки*
В видео типичный физик.
Их используют. Просто никто уже давно не занимается решением уравнений степени n над полем вещественных чисел - давно всё решили.
>но тем не менее не черпает свои знания из реальности
Канон теории множеств прямо зависит от реальности. Потенциальных аксиом теории множеств так много, что они даже не образуют множество; но избраны из них только девять. Как раз из-за реальности.
Что ты ординалами нумеровать собрался? Подмножества множества всех строк над алфовитом логики первого порядка?
Даже ZFC не является чистой теорией первого порядка, в ней есть схемы аксиом. Почему бы не рассмотреть схемы схем, схемы схем схем и так далее? Технически это означает построение w-логики для каждого ординала w.
Я может что-то не понимаю, но всегда думал, что схема аксиом - это просто вычислимое подмножество аксиом, нет?
Схема аксиом языка X - это метаматематический текст, который считается достаточно понятным, чтобы породить бесконечное множество формул языка X (которые называются соответствующими схеме). Эти формулы затем объявляются аксиомами.
Всё-таки если определять чуть более строго, то это множество формул порождаемое некоторым алгоритмом, то есть - вычислимое. В любом случае, что в твоём варианте, что в моём, это никак нельзя назвать чем-то, что принадлежит логике второго порядка.
Определить "алгоритм" очень сложно, и при попытках определить его всё равно всплывут слова "понятный метаматематический текст". Ну и зачем тогда использовать понятие алгоритма для определения схемы аксиом?
>>367316
Просто тред математики отобразился сам в себя через функцию треда математики для начинающих
Единственное что лезет в голову морфизм hom(a,b)= b если |a|<|b|
>Банах-Тарский как пример связи с реальностью, лол.
Употребление слова „парадокс“ в названии математической теоремы как пример связи с реальностью мышления математиков.
Подготовьте пики.
Зеркальное приписывание своих промахов другим — не самая лучшая стратегия.
Топология, нужно построить атлас на грассманиане (2, 5)
Прочитал про построение карт вот тут
http://people.math.umass.edu/~tevelev/5-20.pdf
раскурил, обьяснил их преподу по этому образцу, все норм.
Теперь нужно написать функции склейки между картами, и тут я как-то плохо понимаю, что делать. Я же, вообще говоря, не знаю вроде бы как у меня выглядят матрицы A_{ij}, чтобы просто написать что-то вроде A_{i'j'}^{-1} A_{ij} A
Что такое ненулевая/нулевая окрестность? Ответ зависит от твоего определения окрестности.
Самое хорошее определение: окрестностью точки называется любое открытое множество, содержащее точку. Любая точка имеет хотя бы одну окрестность - все пространство (см. определение топологического пространства).
Если не изучал топологические пространства, то в метрическом пространстве окрестность точки x - это открытый шар с центром в точке x.
Если не изучал метрические пространства, то eps-окрестностью точки x из R называется множество
{ y из R | |x - y| < eps }.
>>367438
То есть, в смысле определения 1 любая точка имеет окрестность.
В смысле определения 3 твой вопрос некорректен. Потому что в этом смысле не бывает окрестностей в чем-то, все окрестности только в R.
В определении 2 легко запутаться, если ты не понимаешь, что такое шар в метрическом пространстве, но на самом деле все легко.
Короче, если путаешься, разбирайся с определением 1, оно самое хорошее и общее.
Смотря какая топология. Если метрическая, то эти точки не имеют окрестности, кроме тривиальных.
>>367440
>>367446
Ну вот есть тот же отрезок [a, b] прямой действительных чисел. Он замкнут в R. У него есть минимальное значение a, и максимальное - b. Есть ли у точек a и b ненулевая окрестность, содержащаяся в [a, b]? Собственно это вся задача, через которую я пытаюсь прийти к осознанию понятия локальной компактности и локальной связности. Это какая топология?
>Ещё раз повторяю что школьная программа о трёх мерном мире не верна, мир многомерный! Трёх мерное пространство есть в трёх мерном мире. В нашем мире минимум 5 измерительных качеств пространства. Зрение-Слух-Вкус-Осязание- Обаняние и ими мы соизмеряем всю жизнь. А вам втюривают что наш мир это только длинна ширина и высота.
Ты заебал уже со своим птушным определением. Что такое ненулевая окрестность? Это во-первых. Во-вторых, ты сам должен знать какая топология, раз спрашиваешь. Если не знаешь, то вопросы об открытости/замкнутости не имеют смысла.
>Бурбаки расфорсили ТМ
Когда ТМ форсилась в математике Бурбаки еще не родились, а точкой начала ее власти можно считать первый математический конгресс. Да и это очевидно, если почитать математические труды, например, по анализу, середины 19 века и начала 20ого.
>Это странный вопрос, отражается тем, что коробка, в которой есть пустая коробка это не то же самое, что коробка, в которой коробка, в которой пустая коробка.
ну а теперь вопрос, содержится ли пустая коробка в которой пустая коробка в множестве присутствующих в этом треде? А если предположить, что это коробка, где содержится Гитлер, она получается тоже среди нас (ведь коробка пуста)?
>Отрезок и натуральный ряд, вполне реальные аналогии, как по мне.
И так, у нас есть натуральный ряд, натуральный ряд откуда мы выкинули несколько чисел, и множество всех подмножеств натурального ряда, как же нам интуитивно их расставить?
>Мне кажется, что парадокс Банаха-Тарского просто иллюстрирует, что при интерпретации мат. моделей (и, соответственно, мат. теорем) на реальность нужно быть аккуратнее.
Вполне. Однако, он затрагивает собой неизмеримые множества, аксиому выбора, свойства натурального ряда... Что и приводит к странному результату. Но где же в этом всем реальность? Откуда же она берется во всех этих преобразованиях?
Чтобы ввести ZFC, нужно располагать понятием схемы аксиом. Поэтому определение схемы аксиом не должно зависеть от понятия алгоритма.
Конечно.
>>367458
В смысле обещанный? Я тебе ничего не обещал явно построить. А ты явно гомеоморфизм построить сможешь тогда, раз утверждаешь что они гомеоморфны? Давай гомеоморфизм - получишь диффеоморфизм.
Лол, а к определению обычной аксиомы, строки, символа, правила вывода, терма, wwf почему подобный критицизм не относится? Когда мы строим логику, мы предполагаем, что работаем в достаточно мощной метатеории. В частности, достаточно мощной для того, чтобы ввести понятие алгоритма.
Нет, не предполагаем. В метаязыке, с помощью которого ZFC вводится впервые, есть только понятия "символ", "строка", "текст" (конечная последовательность строк), и с ними можно делать стандартные операции - проверять наличие данного символа в данной строке, сравнивать две данные строки, проверять наличие данной строки в данном тексте, заменять в данном тексте один символ на другой символ, совершать конкатенацию и т.п. Модели ZFC в самой ZFC - отдельный разговор.
Это какой-то сверхнаивный взгляд. Даже чтобы определить, что такое wwf в логике первого порядка нужно уже построить кое-какой парсер, тобишь иметь по силе нечто эквивалентное алгоритму.
Почитай на досуге http://math.stackexchange.com/questions/201703/an-apparently-vicious-circle-in-logic
Тем не менее, именно такой подход успешно реализован в книге Бурбаки. Понятие "символ" они, кстати, определять отказались, так как предполагали-де, что их книгу не будут читать марсиане.
Это уже какая-то апилляция к авторитетам.
Скажу только, что книжка Бурбаки является безусловным авторитетом в вопросах того, сколько отображений существует из пустого множества в пустое. Но это не книжка по мат. логике.
апелляция*
Поначитаются Вавилова, понимаешь.
Да, это не книжка по матлогике. Это книжка по математике, причём хорошая книжка. Я, кстати, склонен считать, что логика и математика - это вообще две разные науки, которые не имеют абсолютно ничего общего. И то, что ты не обнаружил в книге Бурбаки матлогики, служит аргументом в пользу моего мнения.
Вавилов няша :3
Твоё мнение расходится с мнением научного сообщества. Мне вполне очевидно, что математическая логика в отрыве от математики никому не интересна (что очевидно из названия).
Да мне всё равно, в принципе, понял ты или нет, в любом учебнике по логике (Cori Lascar; Манин; Мендельсон) написано ровно то же, что сказал я, и что написано на stackexchange. Если хочешь продолжать учить логику по Бурбаки и путать схемы аксиом и аксиомы в языке второго порядка - то пожалуйста.
Есть довольно много логиков (например, Непейвода), которые занимаются логикой, открывают всякие там логические теоремы, делают учёные и хитрые вещи, но ничего не понимают в математике. Есть, аналогично, довольно много математиков, которые знать не знают, чем модальная логика отличается от темпоральной. Этого бы не было, если бы две науки, - математика и логика, - являлись одной и той же наукой.
Логика в математике не используется никак. На первый взгляд это заявление кажется неверным, да. Но как только ты окинешь взглядом всё то, что логики создали за последние сто лет, ты с ним согласишься, я думаю.
>Есть довольно много логиков (например, Непейвода), которые занимаются логикой, открывают всякие там логические теоремы, делают учёные и хитрые вещи, но ничего не понимают в математике. Есть, аналогично, довольно много математиков, которые знать не знают, чем модальная логика отличается от темпоральной. Этого бы не было, если бы две науки, - математика и логика, - являлись одной и той же наукой
Это вполне нормально, что специалисты в одной области не знают некоторых специальных вещей из другой области. Не вижу, где утверждение сломается если заменить логиков на КК-теоретиков, а модальную логику на функтор Каспарова.
>Логика в математике не используется никак. На первый взгляд это заявление кажется неверным, да. Но как только ты окинешь взглядом всё то, что логики создали за последние сто лет, ты с ним согласишься, я думаю.
Я не очень понимаю, что ты понимаешь под "математикой". В любом случае, помимо логики есть достаточно мощные попарно не использующие друг друга разделы. Btw, вот такой вот пост нагуглил http://mathoverflow.net/questions/7018/model-theoretic-applications-to-algebra-and-number-theoryiwasawa-theory
В таком случае вообще всю науку логиков придётся записать в "некоторые специальные вещи", потому что она вся является неведомой для математиков.
Ссылку открывал, не?
Диффеоморфизм - это гомеоморфизм, который переводит гладкие функции в гладкие. Задаём гладкую структуру (т.е. атлас) на икосаэдре так, что гладкие функции на нём - это гладкие функции на сфере как на гомеоморфном образе. Тогда этот гомеоморфизм - диффеоморфизм по построению.
Математическая логика - часть математики в силу того, что с методологической точки зрения она совершенно неотделима от других разделов чистой математики и имеет более-менее общее с ними происхождение. Сразу отмечу, что теоретическая информатика тоже часть математики.
Да, безусловно, она несколько изолирована от остальных частей математики. Тем не менее, перечислю некоторые связи. Есть наука про теории типов, их категорные и топологические семантики. Есть множественные связи с теоретической информатикой и теорией множеств (но для людей не считающих логику это видимо неинтересно, т.к. эти разделы математикой скорее всего они также не считают). Есть ряд связей между комбинаторикой (а может и это не математика?) и логикой - это в основном либо обобщения в логических терминах комбинаторных задач, либо логический анализ аксиом нужных для доказательства комбинаторных теорем. Есть упомянутые выше приложения теории моделей, правда, с логической точки зрения, они, как правило, весьма элементарны и находятся где-то на уровне применения теоремы о компактности. Есть ряд пересечений с универсальной алгеброй (либо со стороны теории моделей, либо со стороны неклассических логик).
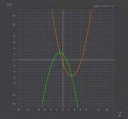
Ну, всмысле выше. Бля, я хз, как тебе объяснить. Я просто решаю чертов интеграл, и мне нужно вычесть большую функцию из меньшей.
Я не тот анон, но ты реально даун, у тебя с элементарным мышлением проблемы.
Хоть ты и даун полнейший, я попробую предположить, что ты хочешь сделать, и помочь. Мне кажется, ты хочешь посчитать площадь фигуры ограниченной зеленой и оранжевой кривыми. Для этого тебе надо найти левую точку пересечения (a) и правую (b); ответом будет интеграл от зеленой на [a, b] минус интеграл от оранжевой на [a, b].
Спасибо, антош, я просто выразился хуево. От души спасибо.
Как себе представить четвертое измерение? Три измерения это когда три палки перпендикулярны друг другу. А как сюда приткнуть еще одну палку, чтобы она была перпендикулярна трем остальным?
Представь себе трехмерный объект, изменяющийся во времени. Так вот если взять какой-то отрезок времени, то это четырехмерный объект.
>>367506
Ну т.е. как я и сказал >>367204 нет никакой "гладкости" которая идёт с топологическим многообразием "вообще", что типа сфера и какой-то элипсоид "гладкий", а куб, икосаэдр, тетраэдр или что там ещё "не гладкие". Когда мы говорим, что дано гладкое многообразие мы имеем ввиду что берётся топологическое многообразие и говорится что значит что функция "гладкая" на нём. Это делается через задание гомеоморфизма окрестности каждой точки некоторой окрестности R^n особым образом, и гладкой функцией считается функция, которая получается гладкой "в координатах" - т.е. то что композиция с заданным гомеоморфизмом гладкая в смысле обычного анализа как функция из R^n в R^k. Поэтому говорить диффеоморфен или нет куб икосаэдру, а икосаэдр сфере бессмысленно без фиксирования этой структуры, эти многообразия топологически неотличимы - поэтому естественно требуемые гомеоморфизмы в R^n можно задать просто перенеся их со сферы после того как зафиксируем какой-то гомеоморфизм икосаэдра со сферой, и он будет диффеоморфизмом по построению тогда.
Если качественные - это не про качество записи посмотри лекции Смирнова в НМУ 2015 года.
Ключевое слово "подмногообразие".
https://ru.wikipedia.org/wiki/Гладкое_многообразие#.D0.9F.D0.BE.D0.B4.D0.BC.D0.BD.D0.BE.D0.B6.D0.B5.D1.81.D1.82.D0.B2.D0.B0_.D0.B8_.D0.B2.D0.BB.D0.BE.D0.B6.D0.B5.D0.BD.D0.B8.D1.8F
А откуда дровишки?
Цветом можно. От красного до синего.
Сука, стиль как у Рыбникова.
Это философский пердёж, а не математика. К тому же подмена понятий, мол, я такой альтернативно умный, буду все понятия переопределять как мне хочется.
Но профессор действительно дебил. Все знают, что подмножества R^n имеют (или не имеют) канонические гладкие структуры, а то, что на подмножестве R^n можно ввести структуру не индуцированную из R^n - никого не ебёт.
> Это философский пердёж, а не математика.
Именно что математика, покажи мне где вообще кто-то строит гомеоморфизмы между сферой и икосаэдром явно в математике.
> понятия переопределять
https://ru.wikipedia.org/wiki/Гладкое_многообразие
Топологическое многообразие X, наделенное C^k -структурой, называется C^k -гладким многообразием.
дебил уровня двача, где каждый кого угодно может назвать дебилом. как "крупный математик" - по оценке самого обвиняющего - может быть одновременно дебилом?

Какие подводные?
Для большинства людей прочтение даже одной книги по математике является подвигом. Тебе придётся прочитать сотни книг и статей.
Подводные камни в том, что это не программа, а список тем. Они не упорядочены, а просто скинуты в одну корзину.
Я изредка посматриваю и наблюдаю как количество непонятных слов падает.
Они упорядочены.
Двачую адеквата
В чём сложность?
а вот про этот курс что скажете? стоит по нему заниматься например параллельно с Давидовичем? (Давидовича я в любом случае не брошу, он охуенный)
Ну и хуле в мат-треде делаешь? Иди в свой загон! Тут физика лишь часть математики.
Все, уже не надо. <= верно, если X first-countable.
Просто ты не знаешь определение N. Поэтому, ты не можешь нормально считать. Определи N, после ещё раз посмотри.
P.S.
Определение N тоже у тебя за щекой.
Мы нуждаемся в новой науке - замене математики. Математика умерла. Она мертва. Давайте создавать новое знание.
Да. Ты читаешь мои мысли. Сделаем новую математику на основе программы Вербицкого! А Вербицкого сделаем пророком и будем внимать каждому его слову!
Согласен с Вами, друг.
Потому что дебил я? Или вербит дебил? Давайте конкретно говорить, отталкиваясь от дебилов.
Оба хороши.
Откуда математики так подкованы в тюремном жаргоне? Прямо сыпят им в каждом сообщении. Петухи маня два стула. Это только для российской интеллигенции свойственно или это мировая тенденция?
Может, потому что одному сложной математикой сложно заниматься.
Это двач. Тут каждый второй так говорит.
Программа абсолютно анреал для студентов. И, на самом деле, слишком специальная, всем математикам нужно знать только первые два курса и некоторые темы из третьего, дальше, специализация именно в вербитоговне.
То есть дебил все таки ОН. А не Я. Для кого тогда этот список, тралит он так?
Очевидно для тех, кто хочет заниматься теми же областями, что и Вербит.
> Математика лишь постольку интересна, поскольку она связана со струнной теорией; это базовое предположение, которое я не хочу сейчас обсуждать. Релевантность для физики это единственный критерий, который у нас остался; а почти вся математика, относящаяся к физике, относится к струнной геометрии. Этот тезис хорошо подтверждается наблюдением, приведенным выше: (почти) все интересные идеи последних 20 лет связаны с физикой струн.

1) принцип Дирихле
2) обобщенный принцип Дирихле
3) нелинейное уравнение Пуассона
4) минимальная поверхность
Вербит ни разу не авторитет, что все так на него равняются. Есть и были гораздо более сильные и глубокие математики, просто они не постят в жж.
этиХ, а не эти. дебил.
Ряд подынтегральной функции в данном примере? То есть мне не нужно подбирать еще одну функцию и искать предел их отношений?
Буду очень благодарен если напишешь пошаговое пояснение на этом примере. Я чрезвычайно туплю и уже запутался.
Двач нынче обмельчал. Очевидно, что твоя подинтегральная функция на бесконечности ~ x^(λ - 2).
Очевидно, что твоя функция должна убывать быстрее чем 1/n, чтобы интеграл сходился. Вспоминаем, что ряд Дирихле Σ 1/n^a сходится при a > 1. Т.е для нашего случая 2 - λ > 1 => λ < 1.
В этом и проблема. Через свой журнальчик и дешевый эпатаж посредством страпона навязывает свои понятия о том, "что такое математика и как ее изучать". Очередной нуб, перечитав вербита, решит что гамалогии и тп и есть "правильная современная математика". А на самом деле это какой-то узкий набор тем из миллиона различных направлений.
Это фамилия.
нет, сорян, я только знаю есть кажется земля франка и мизеса. вроде там дубак и льды.
Ну ты дальше прочитай. Какие должны быть отображения. Ты же спорол хуйню, мол у тебя карты состоят из композиций гомео на сферу, а потом там диффео.
>Вербит ни разу не авторитет
Всего-то был одним из четырёх делегатов от России на недавнем международном математическом конгрессе. Подумаешь. У меня эти делегаты каждую ночь под окнами бегают.
>>367666
Лучше онтологически разделять определение интеграла и методы его вычислений. Для некоторых хороших классов функций удаётся подогнать годные методы вычисления, для некоторых - нет, соу ват?
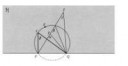
Элементарная геометрия. Как доказать, что угол y меньше угла b?
конгресс по гамологиям был поди. тем более там небось тоже разборчивые - обычных математиков переели уже, привези-ка им этакова некаквсе, с журнальчиком и страпончиком.
Это я к тому, что нужно ли мне изучать интеграл Римана? Вот я читал Рудина, дошел до интегралов, а там даже не интеграл Римана, а интеграл Римана-Стильтеса, то есть вообще какой-то упоротый. Я решил изучить нормальный интеграл Лебега, а потом дальше читать Рудина, но доказывать все теоремы оттуда с помощью интеграла Лебега. Это норм подход?
Блядская иисусня, я наконец-то понял! Угол "b" больше угла "y" вследствие свойства, что внешний угол треугольника всегда больше любого из противоположных ему углов в этом треугольнике.
Норм подход, так и делай. Могу посоветовать ещё Львовский "Лекции по математическому анализу", там вводится так называемый "Интеграл Коши", который потом всё равно заменяется интегралом Лебега.
Норм. Только вот с "доказывать все теоремы оттуда с помощью интеграла Лебега" у тебя будут проблемы. У Рудина Риман-Стилтьес не зря.
Львовского тоже читаю, но там многие вещи пропускаются как сами собой разумеющиеся и как-то бегло все. Скачал еще пару книг, которые советовали на MSE и выбрал Folland: Real analysis modern techniques, там вроде довольно подробно все расписывается. На Львовского посматриваю в качестве ориентира.
Почему вместо того чтобы сказать что ряд сходится если общий член ряда приближается к нулю мне начинают задвигать про сходимость по коши для сердца и души, по даламберу, по ньютону, по эйнштейну, по минковскому, по гауссу, по небу и по аллаху? Зачем все это? Кому нужна эта жопоебля?
При чём тут это? Если тебе интересен некоторый кусок математического знания, то можешь изучать его, если неинтересен - то и ненужно. Теория расходящихся рядов весьма специфическое знание, и вполне можно быть хорошим математиком и ничего об этом не знать. Или ты про что?
Я про то, почему меня сразу грузить надо кошелками с дамблдорами? Почему просто не сказать что ряд сходится если он стремится к нулю, прицепить к этому притчу про производные и натуральный ряд, через который проходит сам ряд, и только потом начать уточнять что мол "ряд может и не сходится, даже если он в передел равен нулю, что доказал нянькин-бабский в соавторстве с ногой-макарониной в своей теории кранца начиханца в супрематическом году от дня рождения тети сраки" и потом уже начинать грузить коши и даламбером.
То же самое и с интегралом. Сперва можно было обосновать его как подсчет квадратиков на листочке в клеточку, потом сказать что квадратики считать тяжело и на производные съехать, а потом съехать уже на интегралы.
ПроЭкцией переносится на плоскость, небо, аллаха, проекцией на пятое измерение, которое проекцией на четвертое, проекцией на третье, проекцие на второе измерение экрана монитора комьпютера.
Собрать бесконечное количество мушкетеров, чтобы они каждый кардинал лично пересчитали и сказали какой больше, нарисовав на кардинальной плоскости, в масштабе, какой размер у какого кардинала.
Ну смотри, если у нас вселенная бесконечная, то множество мыслящих существ, получившихся в результате эволюции, будет бесконечно.
Так же само будет бесконечно множество мыслящих существ получившихся в результате больцмановского мозга, тобишь из говна и палок напрямую.
И то и то бесконечно, но вероятность, а следовательно и кардинал, того что на какой то занюханной планете появятся лысые макаки сильно больше вероятности того что где то в далекой галактике кучка газа соберется в мыслящий самоосознающий конструктив.
Бесконечности разных размерностей, во.
И если представить себе что у нас есть кардинальное пространство, содержащееся на балансе его королевского величества, то на ней можно обозначить что множество А меньше множества Бэ в корень из двух раз.
Если ты самоосознающий и мыслящий конструктив из кучки газа, то мой совет - пиздуй с саентачей, тут всё, что не понимают хуесосят и называют вербитоговном.
Тобишь, и то и то бесконечность, но вот эта бесконечность больше.
https://en.wikipedia.org/wiki/Boltzmann_brain
>A Boltzmann brain is a hypothesized self aware entity which arises due to random fluctuations out of a state of chaos.
Это вам не бурбакистов читать, да.
Ну ты смотри, моё дело предупредить.
> Почему вместо того чтобы сказать что ряд сходится если общий член ряда приближается к нулю
Потому что это неверно. Самый простой пример: гармонический ряд.
Научись отличать необходимое условие от достаточного условия. Сходимость общего члена ряда к нулю - необходимое условие сходимости ряда. Но отнюдь не достаточное.
>>367704
Гармоничный ряд это не вообще все ряды.
Тут как в ебле все, сперва бухой в говно пытаешься ебюаться, потом без алкоголя, потом не крокодилов, а потом и топ моделей.
А мне тут предлагают, девственнику неопытному, сразу начать ебать джесику альбу, или кто там щас популярен, и удивляются почему у меня полшестого.
Так-то джессика альба норм, я не знаю почему у тебя полшестого.
мимо ебался один раз в жизни по пьяне
Ты походу совсем тупой, с элементарным мышлением проблемы, математика тут ни при чем.
Еще раз, для контуженных жизнью даунов.
Да, сходимость к нулю ряда джостаточное, но не обязательное условие сходимости, гармонические ряды это опровергают.
НО, гармонические ряды это специфические ряды. Для какого то ряда икс куб или два икс делить на три икс увидеть сходимость, есть она или нет, можно только по этому правилу. И вот уже с этого правила извлекать исключения и уточнения.
> И вот уже с этого правила извлекать исключения и уточнения.
Ну так и делают. Когда видят ряд, сначала проверяют, стремится ли общий член к 0. Если не стремится, ряд расходится. Если стремится, то нужно использовать другие инструменты, чтобы выяснить, сходится ли он. В чем проблема?
>сходимость к нулю ряда джостаточное, но не обязательное условие сходимости
Ты в состоянии прочитать пост, на который отвечаешь? Сходимость общего члена ряда к нулю - необходимое условие сходимости ряда. Но отнюдь не достаточное.
> Ну ты дальше прочитай. Какие должны быть отображения
Какие? Если ты про то, что там про непрерывные функции ничего не сказано, а только ебля с атласами - ну так это же русская википедия. Ты прав в том что есть куда более человеческое определение гладкого многообразия через пучки, эквивалентное данному. Можно посмотреть например в английской википедии https://en.wikipedia.org/wiki/Differentiable_manifold#Structure_sheaf
Когда я тут объяснял интуицию всего этого дела, я конечно использовал то что о гладком многообразии разумно думать таким образом, а не через какую-то муть с картами и атласами. Гладкость отображения в первом смысле эквивалетна тому что гладкие функции переводятся в гладкие - достаточно очевидно после первой минуты размышлений.
Но, даже если ты против, это всё вообще можно считать лирическим отступлением. То что при переносе структуры с помощью гомеоморфизма со сферой этот гомеоморфизм оказывается гладким и биективным - это в общем-то тавтология, хоть в первом определении, хоть во втором. Это то же самое когда ты говоришь что, взяв в качестве топологии X прообразы открытых множеств из Y при отображении f из X в Y, это отображение f у тебя получается непрерывным по построению.
Можешь Тао навернуть, он лучше переваривается.
Твоей мамки
Кек.
Мне не понравилась идея называть гладкими картами композиции из гомео на сферу и диффео на сфере. Проблема в том, что всё равно придётся отображать сами точки икосаэдра, включая "углы". Либо тогда надо слишком много всего "переопределять"
Но ведь можно тупо прямые по всем целым числам и сказать что это график такой функции.
Опять перепутал. По всем рациональным имел ввиду. Получится настолько густая частота линий, что нам она будет казаться плоскостью декартовой.
Или если мы на числовой прямой обозначаем то той же прямой.
Ну тогда как пример - какая-нибудь фрактальная линия. Мы сможем увидеть её график только приближенно, и чем больше будем приближать тем сложнее будет становится участок приближения.
Че так? Фрактал он и в африке фрактал. Как ты его ни приближай он все равно будет однообразной загогулиной, бесконечной загогуленности но конечной длинны.
> И я имел ввиду чтобы сперва пояснить что такое за хуйня этот ряд
Ты реально олигофрен. Покажи мне учебник, в котором не дается определение ряда, но даются признаки сходимости.
Все математические объекты можно отобразить. Если математический объект нельзя отобразить, значит о нем нельзя сказать, и значит такой объект существует только в манямирке ощущающего его математика, а остальные о нем никогда не узнают.
Детский же вопрос о том, все ли можно нарисовать - да, все, если не учитывать силы, которые потратишь на придумывание способа отображения и доказывание остальным, что этот способ - верный.

https://en.wikipedia.org/wiki/Order_topology
Пикрелейтед правильное определение.
Разница будет, например, если вводить order topology на extended real numbers (что я пытался сделать и долго тупил).
А ничего, что по твоему определению порядковая топология на вещественных - это дискретная топология (для всякого a, пересечение (a-1,a] и [a,a+1) - это сама точка a)?
Да, в самом деле, - не прав. У тебя X - это множество на котором задан порядок.
Но думаю, что лучше определять, как топологию с предбазой из всех открытых лучей.
Всё нормально по его определению, полинтервалы разрешается брать когда конец полуинтервала - наименьший или наибольший соответственно.
Так нет топологически никаких углов. А координаты, которые должны быть гладкими, ты задаёшь именно топологически через гомеоморфизм с R^n. И если ты это делаешь через сферу, все отображения переклейки у тебя получается в точности такими как на сфере, т.е. гладкие.
это не ты доказывал что trollface pi = 4? где-то этот пидор тут сидит. опять по целам числам прямые строятся.
Я.
Умри.
_Кек_
да, все лица двачерские. их травили в шкалке похоже. и вот они отомстили. здесь бы они наверняка друг друга бы хуесосили и N определяли.
Хуй соси.
Что-то я тебя плохо понимаю, слишком размыто. Дай-ка лучше ссылку на что-нибудь похожее на то, что ты имеешь ввиду.
Есть интеграл Римана, который позже не заменяется на интеграл Лебега, бывают размытые задания. Во втором томе есть дебильные главы, вроде равномерной сходимости. Так-то учебник годнота лютейшая.
мимо зоричеёб
> дебильные главы, вроде равномерной сходимости
Поясни за это. Как без нее обосновать почленное интегрирование ряда?
Monotone/bounded convergence theorem для общих пространств с мерой.
Не знаю, не было никогда желания читать на ангельском то, что в оригинале на русише. Это же аллогично.
Разве? Ведь все современные мат. работы на ангельском, а держать в уме два пакета терминов - русские определения из литературы и аналогичные им английские для понимания современных статей, как раз-таки аллогично. Лучше всё сразу на английском учить.
Кстати, а в чем на том пике ошибка? То, что к негладкой функции предельный переход применяют?
Мимо-нематематик
Там строится последовательность линий, потом на этих линиях каким-то таинственным образом совершается магический переход, и далее объявляется, что пределом является окружность. Хотя на самом деле, так как топология на множестве линий не указана, операция предельного перехода не определена.
А каким образом указывается топология? Как должна выглядеть та картинка, чтобы быть правильной?
Очевидно, что там топология индуцированная метрикой Хаусдорфа.
>>367864
Если очень просто на пальцах. То чтобы говорить, что одна кривая сходится к другой, мы должны выбрать модель сходимости. В одной модели сходимости (которая называется "метрикой Хаусдорфа", например) последовательность ступенчатых функций будет стремится к окружности. Но это не означает, что последовательность длин будет стремится к длине предельной кривой.
В других модельях (например в C^(1)) последовательность тех ступенчатых штук вообще не будет сходится.
И да, если тебе будут затирать что-то про "бесконечно малые" ступеньки - бей в ебало. Классическая математика построена на теоретико-множественном формализме, что означает ровно то, что кривую мы задать можем только тогда, когда сможем ответить на вопрос - какие точки принадлежат ей, а какие нет (по модулю некоторых логических тонкостей), естественно, координаты ни одной нетривиальной точки у этой "кривой с бесконечно малыми ступеньками" никто не назовёт.
Спасибо за пояснение. А если мы определили такую кривую со ступеньками, например, по Хаусдорфу, то как определить к чему сходится сумма их "длин"? Это вообще реальная задача?
Их, то есть ступенек.
Ну вот у тебя (или это не твой пост?) написано:
>В одной модели сходимости (которая называется "метрикой Хаусдорфа", например) последовательность ступенчатых функций будет стремится к окружности. Но это не означает, что последовательность длин будет стремится к длине предельной кривой.
Вот в этой модели, если последовательность длин (я так понимаю это длины ступенек?) не обязательно стремится к длине предельной кривой (это, я так понял, окружность?), то как понять когда она будет стремиться (если это вообще возможно), а когда нет? И к чему в общем случае стремится такая последовательность длин?
>я так понимаю это длины ступенек?
Да.
>о, я так понял, окружность?
Да.
>то как понять когда она будет стремиться (если это вообще возможно), а когда нет?
Для дифференцируемых кривых достаточное условие - сходимость в C^(1) смысле. То есть сходится должны не только кривые, но и их производные.
> И к чему в общем случае стремится такая последовательность длин?
Может ни к чему не стремится, а может стремится к какому-то числу которое смысла особо не имеет. Например в случае ступенчатых функций она стремится к 4 (потому как каждый элемент последовательности равен 4).
А где можно про это почитать? Лучше назови конкретную главу книжки, если можно.
Спасибо. То есть с длиной окружности такая последовательность никак не связана?
Окей, спасибо, а сборники задач не посоветуешь, пожалуйста?
В общем случае нет (кроме того, что длина предельной <= lim inf длин допредельных), откуда можно получить, что pi < 4. Но опять же, при некоторых хороших условиях она может непосредственно стремится к длине предельной кривой.
>>367886
Это очень специфический вопрос. Во-первых всё-таки классически рассматривают не кривые, а функции с которыми связаны их графики - функциональные кривые.
Про модели сходимости функций можно почитать в блоге Тао https://terrytao.wordpress.com/2010/10/02/245a-notes-4-modes-of-convergence/ (или в его книжке "an introduction to measure theory" или как-то так)
Про то, почему функционал длины полунепрерывен снизу на непрерывно дифференцируемых функциях с нормой ||f||=max{||f||,||f'||}:
http://math.stackexchange.com/questions/70509/can-anyone-tell-me-why-the-arclength-integral-is-a-lower-semicontinuous-function
>Edit, 12/10/15: An earlier version of this answer claimed that no such map can be smooth. In fact this is false; a counterexample can be constructed by slowing down as you hit each corner using a bump function
Вот это уже ближе к делу. Но опять же не достаточно для ответа (как он именно применяет сглаживание). Хотя Киачу и заслуживает доверия.
Еще вопрос кароч. Рассмотрим топологию порядка на расширенной вещественной прямой. Рассмотрим, например, функцию f(x) = 1/x^2. Доопределим ее: пусть f(0) = ∞. Тогда получается, что f непрерывна, если ее область значений имеет описанную выше топологию. Теперь расширим область определения f и положим f(-∞) = f(∞) = 0. Тогда f все еще непрерывна. Я правильно понимаю?
Да.
еб вашу мать, мне про это кто-нибудь блять ответит гавно ебаное сука нахуй !?
Курс очень милый. Стоит.
Не плоскость а прямая. Расширенная вещественная прямая R' - это R и еще +- ∞. Операции определены по очевидным правилам (∞ - ∞ не определено; есть неочевидное правило: 0∞ = 0). Обычно так не делают, потому что R' теряет алгебраические свойства R. Это не поле и есть пары элементов, для которых даже сложение не определено. Но пацаны пишут, что в теории меры так делать удобно. В качестве топологии я беру топологию порядка.
Это я писал. Так делать удобно только на полупрямой [0..inf], а не на прямой [-inf..inf].
1/x^2 не непрерывно на [-inf..inf] потому что непонятно, куда отправлять 0 (в inf или -inf?)
Очевидно же, что да, стоит. Каледин вообще редко пишет хуйню.
Страницу где он определяет 0 inf = 0.
Прообраз (открытого) полуинтервала (1 +inf] будет [0..1) - не открытое множество.
Да, ты прав. Тогда будет.
Замечание только, что это не совсем тот вопрос. Это не про диффеоморфность окружности и квадратика вообще, а как подмногообразий в R^2.
Топология дает возможность ВСЕМ пройти к успеху.
Тополооооогия дает возможность всем пройти к успеху, реально.
Топология - это тема. Топология -
это
наша
тема.
Еще интересная тема про эту топологию (почему она плохая). Если f, g: X -> R' непрерывны, их произведение fg не обязано быть непрерывным:
Пусть, например f(x) = 1/x^2 при x != 0 и inf при x = 0, g(x) = x^2. Тогда обе эти функции непрерывны в описанной выше топологии, но fg = 1 при x != 0 и 0 при x = 0. Короче, юзлесс топология, не буду ее использовать.
Так что я про эту топологию забуду и не буду вспоминать никогда. Жалко, что вообще думал про нее несколько часов.
Тпология это йоба, а YOBA ETO TI




R с чертой означает R и +- inf. BX означает борелевскую сигма-алгебру на X. Измеримость на подмножестве определяется на пикрелейтед 3. Борелевская сигма-алгебра на R с чертой определяется на пикрелейтед 4.
У меня 2 вопроса: есть ли более простое решение и какого хуя такое, казалось бы, простое утверждение так сложно доказывается? До этого я еще полдня пытался ввести топологию на R с чертой так, чтобы она порождала сигма-алгебру на пикрелейтед 4 и доказать это утверждение для R с чертой точно так же как его доказывают для R, обрадовался, когда ввел, а потом оказалось, что в этой топологии умножение не является непрерывной операцией.

А теперь посмотри на себя. Замечаешь сходство? То-то и оно.
На вскидку можете сказать, по скольким точкам минимум нужно считать (порядок), чтобы получилось близко к 1/sqrt(2), хотя бы до 3-го знака 0.707?
Написал прогу, которая считает всего по 10 точкам. Получил на удивление точный результат:
1: deg 0.0, rad 0.0
2: deg 36.0, rad 0.6283185307179586
3: deg 72.0, rad 1.2566370614359172
4: deg 108.0, rad 1.8849555921538759
5: deg 144.0, rad 2.5132741228718345
6: deg 180.0, rad 3.141592653589793
7: deg 216.0, rad 3.7699111843077517
8: deg 252.0, rad 4.39822971502571
9: deg 288.0, rad 5.026548245743669
10: deg 324.0, rad 5.654866776461628
nsteps: 10, rms: 0.7071067811865476
Но как видите не хватает последней точки 2PI, то есть интервал получился от 0 до 18pi/10. Если ее добавить, получим в ней нуль, но кол-во шагов будет 11, и если разделим на 11 то получим 0.67, что даже неблизко. ОДНАКО! Если увеличивать кол-во точек, то 0.67 начнет приближаться к 0.707 где-то после 10000 шагов. Что в принципе имеет смысл - чем больше итераций, тем точнее. Но почему я же тогда в 1-м случае я получил такой точный результат за 10 шагов, на интервале от 0 до 18pi/10? Это читинг?
На изучение одной теоремы придётся тратить два-три дня.
Причем без учета упражнений.
Да ладно, это слишком медленно. Я вот первый том Зорича на english сейчас читаю. Примерно пять минут-семь на страницу. Разве дальше должно стать настолько
>час на 1 страницу
хуже?
Анон, чему равна мера Жордана множества N?
Что-то я запутался. С одной стороны, нижняя мера равна 0, верхняя inf, а потому множество неизмеримо, с другой же — граница N состоит только из одной точки, потому мера границы равна нулю и множество измеримо. Где ошибка, помоги плз.
> Граница N есть N
Хм, почему? Это следует из того, что окрестность точки n не проколотая, потому пересечение с N содержит точку n?
Внутренность множества M - множество таких точек x∈M, что существует открытое множество U такое, что x∈U и U⊂M. Внутренность M обозначается как IntM.
Граница множества M - множество M\IntM. То есть граница M - множество таких точек x∈M, что x∉IntM. Граница M обозначается BnM.
В стандартной топологии вещественной прямой не существует такого непустого открытого множества U, что U⊂ℕ. Поэтому Intℕ = ∅. Поэтому Bnℕ = ℕ\∅ = ℕ.
>граница M - множество таких точек x∈M
Не обязательно. Границей открытого интервала (a;b) есть множество {a;b}, хотя ни а, ни b интервалу не принадлежат.
Я отталкивался от определения, данного в википедии, где граничной точкой множества А называется точка, окрестность которой имеет непустое пересечение как с самим множеством А, так и с его дополнением. То есть для x найдется окрестность U (не проколотая) такая что
U ∩ A ≠ ∅ и U ∩ A^c ≠ ∅, при чем сама точка х не обязана принадлежать множеству А.
В таком случае я согласен, что граница N есть N, так как окрестность U содержит точку х и некоторые точки, не являющиеся элементами N, потому любое натуральное число есть граничная точка N.
Но все же, что это говорит об измеримости N? Оно не измеримо?
Ну если эти концепции тебе более-менее знакомы, то понятно, что быстро читаешь. Я могу вообще за 20-30 секунд страницу просмотреть, если там для меня ничего нового. А если что-то новое, то и больше часа можно думать. Не потому что какую-то строчку не понял, а просто надо самому себе задавать вопросы и ставить задачи во время чтения.
Кроме того, f(x) = g(x) для всех x. Равны ли эти функции? По идее функции - это подмножества декартовых произведений. Могут ли подмножества X x Y и X x Z быть равны, если Y != Z?
Если f(x) = g(x) для всех x, то Im(f)=Im(g), области значений функций равны как множества. Вообще говоря, Im(f)≠ Y, Im(g)≠ Z, они лишь подмножества этих множеств (которые могут и совпадать с ними, но необязательно). То есть главное, чтобы области значений совпадали и условие "f(x) = g(x) для всех x" выполнялось. Обычно равенство функций так и задается имхо
Верно ли тогда, что любое счетное множество или имеет меру нуль, или неизмеримо?
Для любого элемента x∈X существует единственный такой элемент y∈Y, что пара (x,y) ∈ f. Обозначается y = f(x).
Для любого элемента x∈X существует единственный такой элемент z∈Z, что пара (x,z) ∈ g. Обозначается z = g(x).
Предположим, что f != g. Тогда существует такая пара (x',p), которая является элементом одной из этих функций, но не является элементом другой. Но это невозможно, так как из условия следует, что f(x') = g(x').
Но как же классический пример множества рациональных чисел из отрезка [0;1], которое неизмеримо по Жордану?
Все счётные множества измеримы по Лебегу. Мера Жордана равна мере Лебега, если она есть.
>Ограниченное множество измеримо по Жордану тогда и только тогда, когда его граница имеет меру Жордана нуль (или, что равносильно, когда его граница имеет меру Лебега нуль).
Граница множества рациональных чисел из отрезка [0;1] очевидно, это множество как ограничено, так и счетно равна 1, из чего следует, что это множество неизмеримо по Жордану. Также это следует из того, что верхняя мера этого множества равна 1, а нижняя 0, потому оно неизмеримо. Если ты говоришь, что любое счетное множество измеримо, то вот тебе пример неизмеримого счетного множества.
или мы говорим о разном, лол?
>Граница множества рациональных чисел из отрезка [0;1] очевидно, это множество как ограничено, так и счетно равна 1
Мера границы.
фикс
Если множество измеримо по Жордану, то оно измеримо по Лебегу, и меры равны.
Любое счётное множество измеримо по Лебегу.
Мера Лебега счётного множества равна нулю.
Поэтому если счётное множество измеримо по Жордану, то оно имеет меру нуль.
>если счётное множество измеримо по Жордану
Согласен, но из этого не следует, что любое счетное множество измеримо по Жордану. Те, что измеримы, имеют меру нуль, это я уже понял, спасибо.
Я сам нуб и многое забыл, но вспомнить хотя бы ряд Тейлора / Лорана -- разложили функцию в ряд и нашли приближенное значение в окрестности точки.
Потому что точка 2пи сумму не меняет, зато числитель уменьшается в силу увеличения знаменателя, ты сам об этом сказал.
В чем вообще основная задумка-то? Сумма в числителе сходится, или что?
Просто не понимаю почему без включения 2пи то есть типа на [0, 2pi[ сходится к 1/sqrt(2) мгновенно при достаточно грубой дискретизации - это подозрительно. Если же делать "честно" [0, 2pi] то требуется несколько тысяч итераций. Думаю может ошибка в программе? Думал может какой теоретический инсайт мне дадите, уровня duh.
public class Rms2
{
public static void main (String[] args)
{
double step = 36.;
double sum = 0.;
int nsteps = 0;
for (double i = 0; i < 360; i += step)
{
double r = i Math.PI / 180.;
System.out.println ((nsteps+1) + ": deg " + i + ", rad " + r);
sum += Math.sin(r)Math.sin(r);
++nsteps;
}
double rms = Math.sqrt(sum/nsteps);
System.out.println ("\nnsteps: " + nsteps + ", rms: " + rms);
}
}
> Если же делать "честно" [0, 2pi] то требуется несколько тысяч итераций
Ну вот у тебя 11 член суммы это квадрат синуса 2пи, насколько я понял? Из какого интервала остальные тысячи? Возможно, ты каждый раз захватываешь точку 2kpi, каждая из которых ухудшает результат. Исключи из повторений значения 2kpi и посмотри, что получится.
Два варианта
1) На интервале [0, 2pi[ делим интервал на 10 частей и это достаточно для получения супер точного результата
2) На интервале [0, 2pi] для получений похожей точности внезапно требуется дельту уменьшить в 1000 раз.
Если сделать i=< 360, то есть включаем 2pi, получаем 11 шагов и результат 0.6??.
public class Rms2
{
public static void main (String[] args)
{
double step = 36.;
double sum = 0.;
int nsteps = 0;
for (double i = 0; i < 360; i += step)
{
double r = i Math.PI / 180.;
System.out.println ((nsteps+1) + ": deg " + i + ", rad " + r);
sum += Math.sin(r)Math.sin(r);
++nsteps;
}
double rms = Math.sqrt(sum/nsteps);
System.out.println ("\nnsteps: " + nsteps + ", rms: " + rms);
}
}
Исключи точки, в которых синус равен нулю 2kpi, они только ухудшают результат. В первом случае попробуй исключить еще и ноль.
Да, я наверную могу подfudgить чуток, но мне просто интересно - теоретически RMS синуса равно 1/sqrt(2) на интервале [0, 2pi], так?
То есть мы не должныев принципе ничего выкидывать а честно подставлять 0<=360 в градусах. И ведь в конечном итоге получается правильный результат - только требуется существенно увеличивать частоту дискретизации. Что в принципе имеет смысл.
Так что я склоняюсь что мой результат с выколотой 2pi это какой lucky coincidence который наверное можно объяснить, но я не знаю как.
>RMS синуса равно 1/sqrt(2) на интервале [0, 2pi]
Хуй знает, пруф есть? Просто не совсем представляю предельный переход в данном случае.
Если ты про среднее квадратическое, то его значение в твоем случае зависит не только от итераций, но и от разбиения.
Такая же. Вытекает из необходимости высчитывать эквивалент потребляемой мощность для DC на интервале t. P(t) = I(t)^2 x R.
И если вместо I подставить интеграл, или сумму, то как раз получится RMS. Прикол в том, что многие долбоебы объясняют необходимость использовать RMS "потому что синус меняет знак" - то есть якобы это блять такой математический трюк. Это у статистов трюки и форексов. А тут матушка природа.

Хм, пруф не задумывался, но вот интеграл посчитал вроде все сходится. sin^2 преобразовал через power reduction и под интегралом остается 1-cos , после интегрирования 1-sin и подстановки пределов sin=0, короче получается 1/2. wicked.
В математике нет направлений.
Анализ 1го курса, пиздец пакет терминов, ya ebal.
>После этого начинать Винберга, Рудина, Кострикина-Манина, это будет как удар лбом об стену
Нет. После миллионов вычислительных задач, отличающихся только кол-вом чисел и правилами, как их между собой скрещивать; Винберг, Рудин и Костркин-Манин будут манной небесной.
Хорошо разбираюсь в теории множеств.

Как выучить семестровый курс за 1.5 дня? Экзамен в субботу.
da
Ну там теорию прям перед преподом садишься писать, даже не знаю...
>>368318
Пинал как раз.
>>368320
Не знаю, даун видимо. Поначалу прям учусь целую неделю, а потом как-то хуй забиваю и всё тут.
Вообще в первом семестре тоже нихуя не делал и прокатило, но вроде и материал был полегче...
Буду Аллаху, молиться, мда уж.
Если там ещё доказательства надо писать, то надорвётся.
Я два семестра не верил, что между двумя отрезками разной длины может быть биекция, и срался с преподом из-за этого.
Да. Школьная математика нахуй не нужна, разве только при сдаче егэ. Физматовцы только в начале тащат, потом курсу к 2 у всех примерно один и тот же уровень.
Утешил.
Я вообще на механику идти собираюсь, но первые два курса у них программа идентичная с математиками.
Смерти тебе.
У меня был такой себе. Ничего кроме школьной не знал, гомологии как Вербила в 9ом классе не считал. Ещё рано говорить, выжил или нет, но статейки какие-то есть, правда в ожидании рецензии, но такое.
1/3=0,(3)
1/7=0,(142857)
1/11=0,(09)
1/13=0,(076923)
Дроби 1/2, 1/5 не образуют периодов наверняка как-то связано с тем, что 2 и 5 есть делители 10 И так далее.
При умножении получившихся дробей на другие натуральные числа получаются дроби с другими периодами. Но, при умножении дроби 1/7 на n она не меняет период, а лишь терпит некоторые перестановки. Например: 2/7=0,(285714)
3/7=0,(428571)
То есть, можно сказать, что в некотором смысле период этой дроби образует группу относительно операции перестановок. Может ли кто-то объяснить, почему деление на 7 так примечательно? Или это вообще школьная истина, а я долблюсь в глаза?
Что не так?
чому кек, как правильно
Короче хз как. Но любая дробь это бесконечная дробь, то есть 1 = 1.(0). Докажи, что произведение периодических дробей есть периодическая дробь. Потом если дробь непериодическая, то дробь нерациональная. Может я неправ, но это сходу.
> Докажи, что произведение периодических дробей есть периодическая дробь
Это уже доказано, если вводить вещественные числа как бесконечные дроби.
>Потом если дробь непериодическая, то дробь нерациональная.
В любом случае они периодические, тк числа вида n/p рациональны. Но для других р период зависит от числителя n. Вопрос в том, почему при делении на 7 период не меняется, а при делении на другие простые числа — меняется.
Ап вопроса.
Нашел вот такое
https://books.google.ru/books?id=KxBCpzyNi_IC&lpg=PA22&ots=_-TKcyPF6b&dq=grassmannian transition charts&pg=PA22#v=onepage&q&f=false
Но тут чот без поллитры не разберешься.
Никто не встречал обьяснения попроще, для конкретной размерности?
Может там что-то написано будет https://en.wikipedia.org/wiki/Repeating_decimal#Fractions_with_prime_denominators
yasobe.ru/na/flores
Ебанарот, это не для самых маленьких.
То есть, у меня есть конечное множество {x(n)} и множество {f(x(n))}.
Спасибо.
Нука накидали что про вариационное исчисление
Почему математика так важна?
АААА, понял какой я еблан, просто ж нужно как обычный интеграл кодить например через mid point считать, а я тупо суммирую f(x) не умножая на ∆x!!!!
Меня смутило что, когда про площадь я думаю, то очевидно что кодить надо ∑ f(x)∆x.
А вот про среднее у меня брейнфарт приключился, ведь в дискретном виде сумма ∑ai, то есть просто суммируем значения. Вот я и просуммировал сука. А для непрерывной функции среднее эта та же площадь, деленная на интервал. Нужно было в программерском форуме спрашивать, здесь похуй на прикладные дела, здесь же N определяют.
В общем на 3 сдал, нормас. 3 вопроса сам написал, а 2 кое-как скатал. Вооот.
просто поделилися
Молодец.
удваиваю. хуйня какая-то
*просрались
Это копия, сохраненная 5 октября 2016 года.
Скачать тред: только с превью, с превью и прикрепленными файлами.
Второй вариант может долго скачиваться. Файлы будут только в живых или недавно утонувших тредах. Подробнее
Если вам полезен архив М.Двача, пожертвуйте на оплату сервера.





