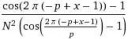18 Кб, 626x626
18 Кб, 626x626Пишу в первый раз, поправь меня, анон, если что-то делаю не по правилам этого форума.
 70 Кб, 712x624
70 Кб, 712x624Это называется функция следования, в функциональном программировании обычно обозначается succ(), т.е. сукцессор. В конструктивной математике именно через нее определяется N, например. Нумералы Черча те же.
Интересно, что более толсто: оригинальный пост или твой совет?
Вы указали ссылку на статью где обсуждается функция распределения простых чисел п(x). Возможно, Вы ошиблись ссылкой.
Почему рекомендуйте этого человека? Были его студентом? Он Ваш знакомый? Или просто нашли в поиске?
Потому что ваша проблема близка к его научным интересам, и он сможет дать вам весьма компетентный и содержательный совет.
Помимо этого, Дмитрий -- человек чрезвычайно приятный и доброжелательный в общении. Несмотря на большие успехи в науке, в нем нет ни тени снобизма, и он всегда рад помочь любому, даже начинающему.
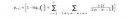 6 Кб, 622x97
6 Кб, 622x97Вы долбоёб, который не удосужился прочитать даже первую пару абзацев, поэтому скорее всего вы придумали лютейшую хуйню.
Двая как всегда на острие науки! Аж гордостью за родной раздел распирает, ПОКАЗАЛИ ЭТИМ ХОРЕНАМ КУЗЬКИНУ МАТЬ!
А по теме - научной может и не имеет, но практическую таки может иметь, если алгоритм достаточно быстрый, например. Но раз речь в оп-посте идет именно о формуле, а не готовом алгоритме, то это, видимо, не тот случай. Ну, вы все равно молодец, если соотношение корректное.
Скорее годный троллинг.
Какое 367 простое число по твоей формуле?
Одним из побочных результатов доказательства 10 проблемы Гильберта явилось доказательство существования многочлена от нескольких переменных, множество положительных значений которого в точности совпадает со множеством простых чисел. Такой многочлен предъявлен явно.
Матиясевича просто не знал всех греческих букв, а русские использовать постеснялся, да и некоторые из них с английскими можно перепутать - вот и пришлось бедному сводить к 26 переменным. А он и не против.
То есть если диагональным методом проходить по всем этим переменеым и если после подстановки система имеет решение, то это - простое число. Все, но с повторениями. Я правильно понял?
Дима, ты штоле?
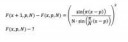 28 Кб, 359x122
28 Кб, 359x122Если ты крутой математик, то реши это функциональное уравнение: (см. фото)
Полученная функция должна быть аналитической. На крайний случай просто гладкой и непрерывной. Решение с floor и ceil не нужно.
Если решите, то скину формулу.
>>9546
Прошу прощения, не думал что Вы говорили об этой стремной формуле.
Хорош, смешно)
Это не домашка.
Правда я не математик, а наркоман, но не суть.
К сожалению, это не верно. Причин это много. Перечислю самое очевидные. Не тот период, при lim x->+inf : F(x,p,N)->+inf, а у вас этого предела не существует.
При маленьких p и N не видно разницы, поэтому значения получаются похожие? Погрешность начинается на больших?
Вообще, забавно получается если поиграться, то степени вылазят, то кусок ряда Фибоначчи. Я не математик, если что, да и уравнения умею решать только квадратные максимум, школьный уровень в общем.
>>11354
Эта формула является маленьким кусочком для генерации простых. В "сыром" виде ее значения не представляют интереса. У меня есть решение, но оно не в аналитических функциях.
Вы можете получить бесконечное количество функций с "похожими" значениями, но они не будут иметь ценности для данного вопроса.
Да, я так и понял, но всё же поковыряюсь, хех. Спасибо большое.
>Имеет-ли мой результат научную ценность?
Спросил ты на дваче. Сходи/позвони в местный ГУ на кафедру математики да там эти вопросы и задай.
> >Имеет-ли мой результат научную ценность?
> Спросил ты на дваче. Сходи/позвони в местный ГУ на кафедру математики да там эти вопросы и задай.
Узнавал, но ответы меня не обрадовали. Препы сами не знают и отправляют к другим препам, не все, конечно, но пока только с такими общался. Вся сложность в том, что в текущем виде нет выигрыша в скорости поиска пч. Думайте много препов шарит в теории чисел чуть дальше малой теоремы ферма? Ошибайтесь. Мне тут на кафедре шутку сказали: "теория чисел изучает математику". Сказали зайти к криптогрофам, типо они к пч ближе остальных. Сегодня будет первая попытка общения.
Тут я просто хочу узнать Ваше мнение на вопрос :" Куда и к кому идти? Что с этим дальше делать?"
Изучить английский и попытаться связаться с западными людьми. Либо в стекловке людей позаебывать, но вероятно тебя везде нахуй пошлют.
Вы получили рекуррентную формулу для N-го простого числа, я правильно понимаю? Может, получится получить явную формулу?
Не знаю, если бы оказался в такой ситуации написал бы вот сюда. По крайней мере не должен отфутболить. Но не уверен. Больше ничем не смогу помочь.
https://vk.com/id1197636
>нет выигрыша в скорости поиска
https://ru.wikipedia.org/wiki/Открытые_проблемы_в_теории_чисел
Может есть смысл попробовать что-то из этого решить? Скорость тут не важна.
На самом деле, написать какому-нибудь нормальному теоретико-числовику вполне здраво. Если ОП адекватно опишет свою ситуацию (что он студент, придумал формулу простых чисел, а математики из его ВУЗа не знают новая ли она и есть ли от нее толк и дальше подробно опишет что он придумал), то вполне вероятно получит вполне нормальный комментарий. Здесь, правда, лучше написать кому-нибудь не слишком загруженному и без излишнего самомнения. Например, какому-нибудь молодому сотруднику отдела теории чисел в Стекловке.
4204474717
1723
то есть короче не то что вычислительнаЯ мозностьи лди типа того, однак минута в тетрадке, только числа бюольшие да внимательность, там просто прикиньте константа, на минималке константа и на максималке торже! ь бля а вдруг бесконечности вообще нет лол да жесть, в обещм смысл в том что снаружи видно, но эти числа вообще никак не свзяаны, ихз с этой сторроны не достать, нужно с конца идти к N=1, тогда получится формула, а пока просто записывать то есть они связаны, но хитро 19 с 1723 а оно с каким нибудь лютым громоздким числом а ещё когда гуглил загугли число один тока был в поиске резульитта а там вообше военные жэесперименты какие то на=хуй генные пождумал корчое что простые числа дают тебе ключи от всех дверей азаза, не ну пиздец, хуй знает просто пиздец, пиздец назуй блядбь.
4204474717
1723
то есть короче не то что вычислительнаЯ мозностьи лди типа того, однак минута в тетрадке, только числа бюольшие да внимательность, там просто прикиньте константа, на минималке константа и на максималке торже! ь бля а вдруг бесконечности вообще нет лол да жесть, в обещм смысл в том что снаружи видно, но эти числа вообще никак не свзяаны, ихз с этой сторроны не достать, нужно с конца идти к N=1, тогда получится формула, а пока просто записывать то есть они связаны, но хитро 19 с 1723 а оно с каким нибудь лютым громоздким числом а ещё когда гуглил загугли число один тока был в поиске резульитта а там вообше военные жэесперименты какие то на=хуй генные пождумал корчое что простые числа дают тебе ключи от всех дверей азаза, не ну пиздец, хуй знает просто пиздец, пиздец назуй блядбь.
То етсь корчое они не по порядку идут, вернее не по тому, каким его хотят пок5азать, там сложный порядок, который нужно распутать, то там то тут вылазишь записываешь как пришлё к числу, по итогу их походу конечное количесмтво, и походу чисел тоже конечное количество, прсотых
(229347426550216+3804900410885p)/(105985380122109+1758310183854p) вот отсюда вытащил, два дня её собирал всё анону благодаря, там тоже рекуррентное соотношение по сути,Ю 2=1+1 3=2=1+1 ь но важно числа не трогать, как с переменными с ними образаться, тогда выйдёт.
в
Хотя там косяк, конечно, но я не буду исправлять пока вообще хуй знает, не особо хочу форсировать всё это, я ж бля первооткрыватель,там цедый мир, совсем другая структура,Ж обратная лол, простых чисел в три раза меньше, чем составных, лол, сначла думал похеал, ночем дальше, тембольше примеров, а константа всегда константа, выходит их ограниченное колиечество получается, бля, что ж дальше там будет интересно. А ведь как раз на больишх простых основана криптография и тп, лол. Жоска
Я уже начал процесс, для начала закончу с препами из своего вуза, потом через знакомых в МФТИ и МГУ писать буду. Мне бы контактов накидать, чтобы я месяцами не ждал ответов от загруженных людей. Может я придумал велосипед, но в другой форме записи. Просто хочу получить нормальный ответ от человека в "теме".
>>11378
Для получения функции в явном виде нужно решить функциональное уравнение, которое я написал выше >>10716
>>11392
Задача быстром о нахождении рандомного большого пч решена до вас.
Анон, видимо я надоел модераторам, а может и всему /math. Вы уж простите меня. Больше писать не буду.
Спасибо за ответы, что-то нужное я все-таки узнал.
Всем спасибо, все свободны. MoMo.
Here: 19950631168807583848837421626835850838234968318861924548520089498529438830221946631919961684036194597899331129423209124271556491349413781117593785932096323957855730046793794526765246551266059895520550086918193311542508608460618104685509074866089624888090489894838009253941633257850621568309473902556912388065225096643874441046759871626985453222868538161694315775629640762836880760732228535091641476183956381458969463899410840960536267821064621427333394036525565649530603142680234969400335934316651459297773279665775606172582031407994198179607378245683762280037302885487251900834464581454650557929601414833921615734588139257095379769119277800826957735674444123062018757836325502728323789270710373802866393031428133241401624195671690574061419654342324638801248856147305207431992259611796250130992860241708340807605932320161268492288496255841312844061536738951487114256315111089745514203313820202931640957596464756010405845841566072044962867016515061920631004186422275908670900574606417856951911456055068251250406007519842261898059237118054444788072906395242548339221982707404473162376760846613033778706039803413197133493654622700563169937455508241780972810983291314403571877524768509857276937926433221599399876886660808368837838027643282775172273657572744784112294389733810861607423253291974813120197604178281965697475898164531258434135959862784130128185406283476649088690521047580882615823961985770122407044330583075869039319604603404973156583208672105913300903752823415539745394397715257455290510212310947321610753474825740775273986348298498340756937955646638621874569499279016572103701364433135817214311791398222983845847334440270964182851005072927748364550578634501100852987812389473928699540834346158807043959118985815145779177143619698728131459483783202081474982171858011389071228250905826817436220577475921417653715687725614904582904992461028630081535583308130101987675856234343538955409175623400844887526162643568648833519463720377293240094456246923254350400678027273837755376406726898636241037491410966718557050759098100246789880178271925953381282421954028302759408448955014676668389697996886241636313376393903373455801407636741877711055384225739499110186468219696581651485130494222369947714763069155468217682876200362777257723781365331611196811280792669481887202696298197941317453621257054767443148822839341130104647641883818078575098307789896483874054640875871065709363045021247713749313577800203418618670264785565422556110177320847136106697114663704950547733359674164310194854582684335316939828989985034671725289680158068894624345874080521139780232979597079348356854812503129596835758178705635600252360823239269713267333826348310168274953350525850827936607882651577147992602843449943024675645837345429516569823125240280254476044830248948396746283718372014341107272268550972203664021687520061545332967210902298879172809083737879248720746369510350722536888112692855391737682426401897847556727543528555544192918163441334147252443916967651435011307917301188934820418410989582547162193792013833819866049443
Получилось написать программу до конца. Из-за своей кривости получилось так, что из-за генерации N- того числа генерится и с другой стороны близнец тоже, по другому ге получаются простые. Это число сгенерилось за пять секунд, я испугался и вырубил нахрен. Ещё бы проверить, скорее всего я где-то налажал, но так никогда и не узнаю где. Сгенерил себе файлик от 1 до 1000000 простых пронумерованных, буду сидеть разбираться, там есть связь какая-то между большими и мелкими числами, почему то сразу авторизация вспомнилась или типа того, вообще эти числа такое чувство будто это такая система счисления что ли, только очень трудно в такой модели мыслить. Бля, ну у меня получилось, анон! Охуеть! И синусы/косинусы твои тоже юзать пытался, типа кодировать максимумом волны и минимумом, складывать функции, но в итоге скорее всего мозгов не хватает, на чуть больших значениях всё говнгится. Так и сидел, лол, сон потерял и тп, но по итогу получилось. Хотя мне кажется это изначально неверный подход, даже искать числа по Н мне кажется сомнтительной затеей, там другие связи, раз уж стало получаться в матан запарюсь, потыкаю сгенеренный лям, мб там и правда связь есть такая прямая. Но вот пока ковырялся замечал много раз, что как вот есть умножение и тп, там будто есть вот эта операция короче,если думать об этом как об умножении, уже думаешь,о семнашка, значит рядом 29 будет ну в таком духе. Возможно их как то складывать нужно иди типа того, но связи там точно есть, и ещё дохуя на Е завязано.
Here: 19950631168807583848837421626835850838234968318861924548520089498529438830221946631919961684036194597899331129423209124271556491349413781117593785932096323957855730046793794526765246551266059895520550086918193311542508608460618104685509074866089624888090489894838009253941633257850621568309473902556912388065225096643874441046759871626985453222868538161694315775629640762836880760732228535091641476183956381458969463899410840960536267821064621427333394036525565649530603142680234969400335934316651459297773279665775606172582031407994198179607378245683762280037302885487251900834464581454650557929601414833921615734588139257095379769119277800826957735674444123062018757836325502728323789270710373802866393031428133241401624195671690574061419654342324638801248856147305207431992259611796250130992860241708340807605932320161268492288496255841312844061536738951487114256315111089745514203313820202931640957596464756010405845841566072044962867016515061920631004186422275908670900574606417856951911456055068251250406007519842261898059237118054444788072906395242548339221982707404473162376760846613033778706039803413197133493654622700563169937455508241780972810983291314403571877524768509857276937926433221599399876886660808368837838027643282775172273657572744784112294389733810861607423253291974813120197604178281965697475898164531258434135959862784130128185406283476649088690521047580882615823961985770122407044330583075869039319604603404973156583208672105913300903752823415539745394397715257455290510212310947321610753474825740775273986348298498340756937955646638621874569499279016572103701364433135817214311791398222983845847334440270964182851005072927748364550578634501100852987812389473928699540834346158807043959118985815145779177143619698728131459483783202081474982171858011389071228250905826817436220577475921417653715687725614904582904992461028630081535583308130101987675856234343538955409175623400844887526162643568648833519463720377293240094456246923254350400678027273837755376406726898636241037491410966718557050759098100246789880178271925953381282421954028302759408448955014676668389697996886241636313376393903373455801407636741877711055384225739499110186468219696581651485130494222369947714763069155468217682876200362777257723781365331611196811280792669481887202696298197941317453621257054767443148822839341130104647641883818078575098307789896483874054640875871065709363045021247713749313577800203418618670264785565422556110177320847136106697114663704950547733359674164310194854582684335316939828989985034671725289680158068894624345874080521139780232979597079348356854812503129596835758178705635600252360823239269713267333826348310168274953350525850827936607882651577147992602843449943024675645837345429516569823125240280254476044830248948396746283718372014341107272268550972203664021687520061545332967210902298879172809083737879248720746369510350722536888112692855391737682426401897847556727543528555544192918163441334147252443916967651435011307917301188934820418410989582547162193792013833819866049443
Получилось написать программу до конца. Из-за своей кривости получилось так, что из-за генерации N- того числа генерится и с другой стороны близнец тоже, по другому ге получаются простые. Это число сгенерилось за пять секунд, я испугался и вырубил нахрен. Ещё бы проверить, скорее всего я где-то налажал, но так никогда и не узнаю где. Сгенерил себе файлик от 1 до 1000000 простых пронумерованных, буду сидеть разбираться, там есть связь какая-то между большими и мелкими числами, почему то сразу авторизация вспомнилась или типа того, вообще эти числа такое чувство будто это такая система счисления что ли, только очень трудно в такой модели мыслить. Бля, ну у меня получилось, анон! Охуеть! И синусы/косинусы твои тоже юзать пытался, типа кодировать максимумом волны и минимумом, складывать функции, но в итоге скорее всего мозгов не хватает, на чуть больших значениях всё говнгится. Так и сидел, лол, сон потерял и тп, но по итогу получилось. Хотя мне кажется это изначально неверный подход, даже искать числа по Н мне кажется сомнтительной затеей, там другие связи, раз уж стало получаться в матан запарюсь, потыкаю сгенеренный лям, мб там и правда связь есть такая прямая. Но вот пока ковырялся замечал много раз, что как вот есть умножение и тп, там будто есть вот эта операция короче,если думать об этом как об умножении, уже думаешь,о семнашка, значит рядом 29 будет ну в таком духе. Возможно их как то складывать нужно иди типа того, но связи там точно есть, и ещё дохуя на Е завязано.
С другой стороны даже заебись вышло, Забавно, что степени зеркальные должны быть, это точно как ты тогда говорил, период , другие значения и всё говнится, вроде как фокус настраиваешь, вообще напоминает всё это такие числовые фильтры. Ну и заебись было бы подумать над тем, как через ближние индексы выразить крайние, тогда можно будет доставать числа с другой стороны бесконечности. Алгоритм реализовавал по тупому: полтора цикла от 1 от `00000 и от p до 100000, переменнная с суммой и перменная с произведением, заработало случайно, баловался и по приколу в степени константу ту выставил, а оно возьми и заработай, причём сразу с двух концов, лол.
>другие значения и всё говнится, вроде как фокус настраиваешь, вообще напоминает всё это такие числовые фильтры
В основе доказательства Чжана лежит специальный объект — так называемый подтверждающий гребень.
Назовем гребнем упорядоченное множество различных неотрицательных целых чисел {h1....hk}. Его можно представлять себе как расческу шириной в hk зубьев, у которой выломаны все зубья, кроме тех, которые стоят на позициях с номерами hi. Мы хотим двигать гребень по натуральному ряду и смотреть, попадают ли одновременно все его зубья на простые числа, другими словами, являются ли для данного n все числа вида n+h1,...,n+hk простыми.
Вот, лол, примерно такой хуетой страдал.
БЛЯДЬ ЭТО ИМЕННО ТО АНОН!
Если смотреть на первые элементы последовательности простых чисел, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, кажется, что вот-вот поймешь ее секрет, увидишь зависимость, общую формулу, дающую следующие члены - то оказывающиеся по-соседству, то прыгающие сразу через несколько позиций натурального ряда. На самом деле, такой формулы не существует. При всей кажущейся простоте, в математике немного более загадочных и труднопостижимых объектов, чем простые числа.
Ряд простых чисел постепенно становится все более редким. Если взять отрезок фиксированной длинны и перемещать его вперед по числовой оси, он все реже будет «зацеплять» хотя бы одно простое число. На самом деле верно даже более сильное утверждение: для отрезка любой длины можно уехать так далеко, что в какой-то момент в него не попадет ни одного простого числа! То есть щели между простыми числами могут быть сколь угодно большими.
Но иногда соседние числа идут буквально друг за другом. С помощью современного компьютера мы можем найти практически любое количество простых чисел, но этого мало, для того, чтобы понять, как они ведут себя еще дальше, для того, чтобы сделать выводы о поведении их ряда в целом. Именно с распределением простых чисел связано множество интересных гипотез.
Одна из них — гипотеза о простых числах-близнецах: существует бесконечное количество простых чисел, отличающихся друг от друга на 2. Таких пар много в начале ряда: 3 и 5, 5 и 7, 11 и 13, 17 и 19, 29 и 31. Наибольшие известные на сегодняшний день простые близнецы, полученные с помощью компьютерных вычислений, это 3,756,801,695,685×2666,669 — 1 и 3,756,801,695,685×2666,669 + 1. Но будут ли простые близнецы встречаться сколь угодно далеко, до сих пор неизвестно.
На самом деле до недавнего времени не было ответа на более простой вопрос: верно ли, что расстояния между соседними простыми числами растут с ростом простых чисел? Используя аналогию с линейкой, верно ли, что для любой линейки, начиная с какого-то момента, она начнет зацеплять не больше одного простого числа за раз? Разумеется, если гипотеза о числах близнецах верна, то ответ на этот вопрос отрицательный.
Ответ (разумеется, отрицательный) на этот более простой вопрос впервые дал малоизвестный математик Итан Чжан из Университета Нью-Гэмпшира. Работа Чжана, опубликованная в мае 2013 года в научном журнале Annals of Mathematics оказалась полнейшей неожиданностью для математического сообщества. Чжану удалось сделать самый существенный прорыв в понимании поведения последовательных простых чисел за последние несколько сотен лет.
Чжан доказал, что существует бесконечное количество пар подряд идущих простых чисел, отстоящих друг от друга на 70 миллионов. 70 000 000 это еще не 2, что требовалось бы для доказательства гипотезы о простых близнецах, но уже и далеко не бесконечность.
70 000 000: Итан Чжан
В основе доказательства Чжана лежит специальный объект — так называемый подтверждающий гребень.
Назовем гребнем упорядоченное множество различных неотрицательных целых чисел {h1....hk}. Его можно представлять себе как расческу шириной в hk зубьев, у которой выломаны все зубья, кроме тех, которые стоят на позициях с номерами hi. Мы хотим двигать гребень по натуральному ряду и смотреть, попадают ли одновременно все его зубья на простые числа, другими словами, являются ли для данного n все числа вида n+h1,...,n+hk простыми.
Возьмем простейший пример, гребень вида {0, 1}. В таком гребне k = 2, h1 = 0, h2=1. Число 1 по определению не считается простым, так что гребень интересно примерять к натуральным числам начиная со второй позиции. Тогда его зубцы укажут на 2 и 3 — оба эти числа простые. Но очевидно, что если двигать расческу дальше, то один из ее зубцов будет обязательно указывать на четное число большее 2-х, которое не является простым. Неинтересный случай.
А что, если взять гребень {0, 2}? Ясно, что оба его зубца будут попадать на простые числа, пока будут находиться те самые пары простых близнецов. Из этих примеров можно сделать два вывода. Во-первых, изучение свойств «гребней» тесно связано с исходной задачей (точнее, они эквивалентны). Во-вторых, среди гребней есть такие, которые, как {0,1} изначально неинтересны, потому что какой-то из их зубцов обязательно будет указывать на составное число. Можно ли заранее описать класс интересных гребней и дальше изучать именно их? Оказывается, — и это самое удивительное — да.
Гребень называется подтверждающим, если для любого простого числа p множество остатков от деления hi на p состоит менее чем из p различных чисел. По сути, это свойство гребня — необходимое условие для того, чтобы при движении гребня по натуральноу ряду его зубцы вида n+h1, ... , n+hk могли бы попадать на наборы, состоящие только из простых чисел. Почему?
Давайте предположим, что наш гребень — не подтверждающий. Значит, для какого-то простого числа p остатки от деления hi на p пробегают все значения от 0 до p-1. Продвинем гребень на любую позицию n>p. Его зубья указывают на числа n+h1,..., n+hk. Пусть остаток от деления n на p равен m. Так как гребень у нас не подтверждающий, среди в наборе зубцов есть один, скажем hk, остаток от деления которого на p равен p-m. Тогда в сдвинутом на n-ю позицию гребне этот зубец укажет на число n+hk, остаток которого при делении на p равен p-m+m = p. Значит, этот зубец указывает на число делящееся на p и строго большее его, это число — составное. Таким образом мы доказали, что хотя бы один зубец не подтверждающего гребня, сдвинутого на любую позицию n>p, приходится на составное число.
Фотография: Naomi Campbell / flickr.com Кстати, гребень {0, 1} - как раз самый простой пример не подтверждающего гребня. Остатки от деления его зубьев на наименьшее простое число, 2, пробегают все значения - и 0 и 1. Именно поэтому куда не подвинь гребень на натуральном ряду начиная со второй позиции, один из зубцов будет составным числом.
Тут, конечно, возникает вопрос - а существуют ли вообще подтверждающие гребни? Ответить на этот вопрос не очень просто, поэтому читателю придется поверить нам на слово: такие гребни есть. Более того, главная теорема, доказанная Итаном Чжаном состоит в том, что если H - некоторый подтверждающий гребень, в котором есть как минимум 3,5 миллиона зубцов, то при его сдвигах по натуральному ряду будет бесконечно много ситуаций, когда хотя бы два зубца указывают на простые числа. Из этого следует, что существует бесконечно много пар подряд идущих простых чисел, расстояние между которыми не превышает 70 миллионов.
Гребень называется подтверждающим, если для любого простого числа p множество остатков от деления hi на p состоит менее чем из p различных чисел. По сути, это свойство гребня — необходимое условие для того, чтобы при движении гребня по натуральноу ряду его зубцы вида n+h1, ... , n+hk могли бы попадать на наборы, состоящие только из простых чисел. Почему?
БЛЯ Я ПОХОДУ ГРЕБН ЭТИ КАК РАЗ НАРЫЛ!
БЛЯДЬ ЭТО ИМЕННО ТО АНОН!
Если смотреть на первые элементы последовательности простых чисел, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, кажется, что вот-вот поймешь ее секрет, увидишь зависимость, общую формулу, дающую следующие члены - то оказывающиеся по-соседству, то прыгающие сразу через несколько позиций натурального ряда. На самом деле, такой формулы не существует. При всей кажущейся простоте, в математике немного более загадочных и труднопостижимых объектов, чем простые числа.
Ряд простых чисел постепенно становится все более редким. Если взять отрезок фиксированной длинны и перемещать его вперед по числовой оси, он все реже будет «зацеплять» хотя бы одно простое число. На самом деле верно даже более сильное утверждение: для отрезка любой длины можно уехать так далеко, что в какой-то момент в него не попадет ни одного простого числа! То есть щели между простыми числами могут быть сколь угодно большими.
Но иногда соседние числа идут буквально друг за другом. С помощью современного компьютера мы можем найти практически любое количество простых чисел, но этого мало, для того, чтобы понять, как они ведут себя еще дальше, для того, чтобы сделать выводы о поведении их ряда в целом. Именно с распределением простых чисел связано множество интересных гипотез.
Одна из них — гипотеза о простых числах-близнецах: существует бесконечное количество простых чисел, отличающихся друг от друга на 2. Таких пар много в начале ряда: 3 и 5, 5 и 7, 11 и 13, 17 и 19, 29 и 31. Наибольшие известные на сегодняшний день простые близнецы, полученные с помощью компьютерных вычислений, это 3,756,801,695,685×2666,669 — 1 и 3,756,801,695,685×2666,669 + 1. Но будут ли простые близнецы встречаться сколь угодно далеко, до сих пор неизвестно.
На самом деле до недавнего времени не было ответа на более простой вопрос: верно ли, что расстояния между соседними простыми числами растут с ростом простых чисел? Используя аналогию с линейкой, верно ли, что для любой линейки, начиная с какого-то момента, она начнет зацеплять не больше одного простого числа за раз? Разумеется, если гипотеза о числах близнецах верна, то ответ на этот вопрос отрицательный.
Ответ (разумеется, отрицательный) на этот более простой вопрос впервые дал малоизвестный математик Итан Чжан из Университета Нью-Гэмпшира. Работа Чжана, опубликованная в мае 2013 года в научном журнале Annals of Mathematics оказалась полнейшей неожиданностью для математического сообщества. Чжану удалось сделать самый существенный прорыв в понимании поведения последовательных простых чисел за последние несколько сотен лет.
Чжан доказал, что существует бесконечное количество пар подряд идущих простых чисел, отстоящих друг от друга на 70 миллионов. 70 000 000 это еще не 2, что требовалось бы для доказательства гипотезы о простых близнецах, но уже и далеко не бесконечность.
70 000 000: Итан Чжан
В основе доказательства Чжана лежит специальный объект — так называемый подтверждающий гребень.
Назовем гребнем упорядоченное множество различных неотрицательных целых чисел {h1....hk}. Его можно представлять себе как расческу шириной в hk зубьев, у которой выломаны все зубья, кроме тех, которые стоят на позициях с номерами hi. Мы хотим двигать гребень по натуральному ряду и смотреть, попадают ли одновременно все его зубья на простые числа, другими словами, являются ли для данного n все числа вида n+h1,...,n+hk простыми.
Возьмем простейший пример, гребень вида {0, 1}. В таком гребне k = 2, h1 = 0, h2=1. Число 1 по определению не считается простым, так что гребень интересно примерять к натуральным числам начиная со второй позиции. Тогда его зубцы укажут на 2 и 3 — оба эти числа простые. Но очевидно, что если двигать расческу дальше, то один из ее зубцов будет обязательно указывать на четное число большее 2-х, которое не является простым. Неинтересный случай.
А что, если взять гребень {0, 2}? Ясно, что оба его зубца будут попадать на простые числа, пока будут находиться те самые пары простых близнецов. Из этих примеров можно сделать два вывода. Во-первых, изучение свойств «гребней» тесно связано с исходной задачей (точнее, они эквивалентны). Во-вторых, среди гребней есть такие, которые, как {0,1} изначально неинтересны, потому что какой-то из их зубцов обязательно будет указывать на составное число. Можно ли заранее описать класс интересных гребней и дальше изучать именно их? Оказывается, — и это самое удивительное — да.
Гребень называется подтверждающим, если для любого простого числа p множество остатков от деления hi на p состоит менее чем из p различных чисел. По сути, это свойство гребня — необходимое условие для того, чтобы при движении гребня по натуральноу ряду его зубцы вида n+h1, ... , n+hk могли бы попадать на наборы, состоящие только из простых чисел. Почему?
Давайте предположим, что наш гребень — не подтверждающий. Значит, для какого-то простого числа p остатки от деления hi на p пробегают все значения от 0 до p-1. Продвинем гребень на любую позицию n>p. Его зубья указывают на числа n+h1,..., n+hk. Пусть остаток от деления n на p равен m. Так как гребень у нас не подтверждающий, среди в наборе зубцов есть один, скажем hk, остаток от деления которого на p равен p-m. Тогда в сдвинутом на n-ю позицию гребне этот зубец укажет на число n+hk, остаток которого при делении на p равен p-m+m = p. Значит, этот зубец указывает на число делящееся на p и строго большее его, это число — составное. Таким образом мы доказали, что хотя бы один зубец не подтверждающего гребня, сдвинутого на любую позицию n>p, приходится на составное число.
Фотография: Naomi Campbell / flickr.com Кстати, гребень {0, 1} - как раз самый простой пример не подтверждающего гребня. Остатки от деления его зубьев на наименьшее простое число, 2, пробегают все значения - и 0 и 1. Именно поэтому куда не подвинь гребень на натуральном ряду начиная со второй позиции, один из зубцов будет составным числом.
Тут, конечно, возникает вопрос - а существуют ли вообще подтверждающие гребни? Ответить на этот вопрос не очень просто, поэтому читателю придется поверить нам на слово: такие гребни есть. Более того, главная теорема, доказанная Итаном Чжаном состоит в том, что если H - некоторый подтверждающий гребень, в котором есть как минимум 3,5 миллиона зубцов, то при его сдвигах по натуральному ряду будет бесконечно много ситуаций, когда хотя бы два зубца указывают на простые числа. Из этого следует, что существует бесконечно много пар подряд идущих простых чисел, расстояние между которыми не превышает 70 миллионов.
Гребень называется подтверждающим, если для любого простого числа p множество остатков от деления hi на p состоит менее чем из p различных чисел. По сути, это свойство гребня — необходимое условие для того, чтобы при движении гребня по натуральноу ряду его зубцы вида n+h1, ... , n+hk могли бы попадать на наборы, состоящие только из простых чисел. Почему?
БЛЯ Я ПОХОДУ ГРЕБН ЭТИ КАК РАЗ НАРЫЛ!
Пусть pn - ряд простых чисел. Обозначим Hm множество из 3,5 миллионов подряд идущих простых чисел, начиная с pm. Гребень Чжана - H250151, так как простое число с порядковым номером 250151, это 3 500 017, и это первое простое число, большее 3,5 миллионов. Если найти подтверждающий гребень Hm с m<250151, он будет уже, а значит даст улучшенный результат.
30 мая 2013 года австралийский математик Скотт Морисон опубликовал запись в блоге SBSEMINAR, объединяющем нескольких недавних аспирантов-математиков Беркли Морисон с помощью компьютерных вычислений доказал, что гребень H125075 - подтверждающий. Его ширина, 59 470 640, дала новую оценку на асимптотически максимальное расстояние между соседними простыми числами, улучшив предыдущую примерно на 400 000.
Как заметил в своей записи сам Морисон, дальнейшие улучшения должны основываться не столько на поиске более узких подтверждающих гребней с 3,5 миллионами зубцов, сколько на ослаблении самой константы 3,5 миллиона из теоремы Чжана.
Буквально через несколько дней австралийский математик, лауреат Филдсовской медали Теренс Тао доказал, что количество зубцов подтверждающего гребня в теореме Чжана может быть уменьшено на порядок - до 341 640. Несложно построить такой гребень ширины 4 982 086 - и это десятикратно улучшает результат Чжана.
Бля,я не ебанулся! LNX, числовые фильттры и константаЮ всё эжто не бред, лол. Только константу можно улучшить до значения меньше единицы, если её ющать тупо как коэфф ,то до 300 нормально детектит, но потом всё равно нихуя. Потому весь анализ и приближенка с пи/косинусами/синусами не покатит, точность теряется, а тут это похоже суперкритично. Потому скорее всего бессмысленно искать функцию от номера числа,если не работаешь в натуральных ничего не получится. Да и не связаны они так. Вообще получается походу, что нужно там другой порядок задавать, то, что они в натуральном ряду так располагаются это побочный эффект человеческой мысли, так получилось, потому опасно полагаться на что-то, кроме базовых числовых свойств. Это странные объекты со странными свойствами и не нужно пытаться примерять к ним стандартные модели, они будут вести себя вроде бы вот-вот,ь описывается нашей кривой всё, хоть там небольшое расхождение, но и хуй ним, на бессконечности сойдётся. Тут это суперневерно, ниъера не сойдётся,. А вот какие-то левые свойства они могут проявлять, и вот это нужно копать, напрмиер, похоже , несмотря на то, что ряд расходится, они с двух сторон как бы стремятся к какому-то центру где-то в середине числовой прямой, ссложность вычисления ввверху и внизу одинаковая, в середине же охуеешь с плотности пространства и никакой суперкомпьютер не поможет.
Пусть pn - ряд простых чисел. Обозначим Hm множество из 3,5 миллионов подряд идущих простых чисел, начиная с pm. Гребень Чжана - H250151, так как простое число с порядковым номером 250151, это 3 500 017, и это первое простое число, большее 3,5 миллионов. Если найти подтверждающий гребень Hm с m<250151, он будет уже, а значит даст улучшенный результат.
30 мая 2013 года австралийский математик Скотт Морисон опубликовал запись в блоге SBSEMINAR, объединяющем нескольких недавних аспирантов-математиков Беркли Морисон с помощью компьютерных вычислений доказал, что гребень H125075 - подтверждающий. Его ширина, 59 470 640, дала новую оценку на асимптотически максимальное расстояние между соседними простыми числами, улучшив предыдущую примерно на 400 000.
Как заметил в своей записи сам Морисон, дальнейшие улучшения должны основываться не столько на поиске более узких подтверждающих гребней с 3,5 миллионами зубцов, сколько на ослаблении самой константы 3,5 миллиона из теоремы Чжана.
Буквально через несколько дней австралийский математик, лауреат Филдсовской медали Теренс Тао доказал, что количество зубцов подтверждающего гребня в теореме Чжана может быть уменьшено на порядок - до 341 640. Несложно построить такой гребень ширины 4 982 086 - и это десятикратно улучшает результат Чжана.
Бля,я не ебанулся! LNX, числовые фильттры и константаЮ всё эжто не бред, лол. Только константу можно улучшить до значения меньше единицы, если её ющать тупо как коэфф ,то до 300 нормально детектит, но потом всё равно нихуя. Потому весь анализ и приближенка с пи/косинусами/синусами не покатит, точность теряется, а тут это похоже суперкритично. Потому скорее всего бессмысленно искать функцию от номера числа,если не работаешь в натуральных ничего не получится. Да и не связаны они так. Вообще получается походу, что нужно там другой порядок задавать, то, что они в натуральном ряду так располагаются это побочный эффект человеческой мысли, так получилось, потому опасно полагаться на что-то, кроме базовых числовых свойств. Это странные объекты со странными свойствами и не нужно пытаться примерять к ним стандартные модели, они будут вести себя вроде бы вот-вот,ь описывается нашей кривой всё, хоть там небольшое расхождение, но и хуй ним, на бессконечности сойдётся. Тут это суперневерно, ниъера не сойдётся,. А вот какие-то левые свойства они могут проявлять, и вот это нужно копать, напрмиер, похоже , несмотря на то, что ряд расходится, они с двух сторон как бы стремятся к какому-то центру где-то в середине числовой прямой, ссложность вычисления ввверху и внизу одинаковая, в середине же охуеешь с плотности пространства и никакой суперкомпьютер не поможет.
В таком случае, сохраню свой след в истории математики.
ПИШУ В ЭПИЧНОМ ТРЕДЕ
Когда математики будущего откопают этот тренд мои потомки будут гордится мной.
Да лол, 95 процентов, что я обосрался. Проблема в том, что понятия не имею, как это доказать.
2.5780769767373117e+47 is divide by 2,
257807697673731163442636022275160829109122195259 на вот это число, которое вообще нечётное, а это только 48 знаков, в том же 3к, да и то хуй вообще знает может это у меня в монитор столько помещается.,
В итоге спустился аж до самого первого
https://www.wolframalpha.com/input/?i=1267650600228229401496703205823
Только вольфрам распознал, везде ограничение на 10^12, не представляю как проверять
Here: 2
Here: 3
Here: 5
Here: 7
Here: 11
Here: 13
Here: 17
Here: 19
Here: 23
Here: 29
Here: 31
Here: 37
Here: 41
Here: 43
Here: 47
Here: 53
Here: 59
Here: 61
Here: 67
Here: 71
Here: 73
Here: 79
Here: 83
Here: 89
Here: 97
Here: 1267650600228229401496703205823
Here: 1267650600228229401496703234983
Here: 1267650600228229401496896915703
Here: 1267650600228229401498446597659
Here: 1267650600228229401637917973699
Here: 1267650600228229402767636119623
Here: 1267650600228229412935099432939
Вот, смотри, смысл был в том, ну долго рассказывать, в общем я пытался сделать что-то работающее, не мог подобрать ну корчое тот самый гребешок как оказалось, то и дело слетало всё, ну и сделал опечатку, не спал нихуя, напутал с циклами, получалось, чтотам степень в стпень возводится, запускаю, ну и пизда. Во-первых ВСЁ заработало, у меня до этого были приближённые значения типа, тут просто ВСЁ, я охуел, но ещё больше охуел с того, что прога не думала останавливаться и начала мне хуярить числа, зхотел вырубать, но всё корректно отработало и завершилось.
Да лол, 95 процентов, что я обосрался. Проблема в том, что понятия не имею, как это доказать.
2.5780769767373117e+47 is divide by 2,
257807697673731163442636022275160829109122195259 на вот это число, которое вообще нечётное, а это только 48 знаков, в том же 3к, да и то хуй вообще знает может это у меня в монитор столько помещается.,
В итоге спустился аж до самого первого
https://www.wolframalpha.com/input/?i=1267650600228229401496703205823
Только вольфрам распознал, везде ограничение на 10^12, не представляю как проверять
Here: 2
Here: 3
Here: 5
Here: 7
Here: 11
Here: 13
Here: 17
Here: 19
Here: 23
Here: 29
Here: 31
Here: 37
Here: 41
Here: 43
Here: 47
Here: 53
Here: 59
Here: 61
Here: 67
Here: 71
Here: 73
Here: 79
Here: 83
Here: 89
Here: 97
Here: 1267650600228229401496703205823
Here: 1267650600228229401496703234983
Here: 1267650600228229401496896915703
Here: 1267650600228229401498446597659
Here: 1267650600228229401637917973699
Here: 1267650600228229402767636119623
Here: 1267650600228229412935099432939
Вот, смотри, смысл был в том, ну долго рассказывать, в общем я пытался сделать что-то работающее, не мог подобрать ну корчое тот самый гребешок как оказалось, то и дело слетало всё, ну и сделал опечатку, не спал нихуя, напутал с циклами, получалось, чтотам степень в стпень возводится, запускаю, ну и пизда. Во-первых ВСЁ заработало, у меня до этого были приближённые значения типа, тут просто ВСЁ, я охуел, но ещё больше охуел с того, что прога не думала останавливаться и начала мне хуярить числа, зхотел вырубать, но всё корректно отработало и завершилось.
Here: 1267650600228229504442269252783
Here: 1267650600228904827355539701503
Here: 1267650600234308234226231669859
Here: 1267650600720614852588508821899
Here: 1267650604659698461322953753423
Here: 1267650959177223247422997590583
Here: 1267912274044743081765309961219
Here: 1288846179365837503253850422059
Here: 16719227791544535582457024107223
Here: 101379065602826513082682162139682343
Here: 912401449220636791908927485631497419
Here: 8211602901780929301345135397057833103
Here: 5986257592548660494529599414855226758299
Here: 53876318322796739648940559521723415181023
Here: 3181342720567972446888014609498668612148313619
Here: 28632084485111741880787329659652805535709178903
Here: 257688760366005666785881165111040037847756988219
Here: 257688760366005666785881165111040037847757315899
Here: 257688760366005666785881165111040037847846444859
Here: 257688760366005666785881165111040038214260842299
Here: 257688760366005666785881165111040043711818981179
Here: 257688760366005666785881165117188952538993483579
Here: 257688760366005666785881165209422672907541241659
Here: 257688760366005666785881568086313242724148535099
Here: 257688760366005666785984326780980486203998560059
Here: 257688760366005673546684366328263512496840728379
Here: 257688760366033359035793350858392200494846140219
Here: 257688760373094882763400716433193675502585470779
Here: 257688789403434310705963380652339872025311010619
Here: 257689224964863969507196613771837384688621674299
Here: 257807697673731163442636022275160829109122195259
Here: 8052364159464154563872200272931216142679397195579
Here: 31927248123466383888132348946796552365428246135791419
Here: 8173309808973500943916850930682814090339979832736177979
Here: 130772953078244609612584613102707548779839109607424352059
Here: 33477875922319986167490215923893435384323602408322607701819
Here: 535646014753254447274353369780506748672512037965445368733499
Here: 535646014753254447274353369780506748672512037965445369220999
Here: 535646014753254447274353369780506748672512037965445673908499
Here: 535646014753254447274353369780506748672512037965636103595999
Here: 535646014753254447274353369780506748672558604094176142658499
Here: 535646014753254447274353369780506748701615868422179072345999
Here: 535646014753254447274353369780506766862406073424010127033499
Here: 535646014753254447274353369787612176030113039824156611408499
Here: 535646014753254447274353374221398847173138199659972041095999
Here: 535646014753254447274356145338068311563863097044615595783499
Here: 535646014753255124900711173220778003330512581679015009845999
Here: 535646015017952243291322225739357530134900151106505244220999
Here: 535646180189376957879888344062245162665082751127867548908499
Here: 600269500108959734373682173848472596607341109129576533283499
Here: 40925324362069058884354855912259161707940681515547423212970999
Here: 25244084613087131027622588442418939856291278435526701598017658499
Here: 15777218640066250861489018580009094373970877374692498060850947345999
Here: 130663726672166444807513581714187424588747686058113810753683943165044430422961
Here: 130663726672166444807513581714187424588747686058113810753683943436444389860169
Here: 130663726672166444807513581714187424588747686058113810753715873370272217944161
Here: 130663726672166444807513581714187424588747686058113814510240658280418471518969
Here: 130663726672166444807513581714187424594864914094329498327222311670381066906561
Here: 130663726672166444807513581714188144274508918797541149969200227786390048916569
Here: 130663726672166444807513581798857734712018246945145177029053360127114544347761
Here: 130663726672166445979459661528112971254506142970927563297649243702218334428961
Here: 130663726672304323091857610240827104405445021683286855727326841409076791754169
Here: 130663742893408719598125712345878179213586652041681914867019455599722645150161
Here: 224653536809051591083475274868693002561143183261833860092434603795427395284511361
Here: 539079548934519670723886102363617849330291788565123624936126642249225075060145699857
Here: 539079548934519670723886102363617849330291788565123624936126642249245662865619991569
Here: 539079548934519670723886102363617849330291788565123624936126642333553047889995676689
Here: 539079548934519670723886102363617849330291788565123624936148748321355171057946639377
Here: 539079548934519670723886102363617849330291788566642742645595117532543711621929548817
Here: 539079548934519670723886102363617849330291788662347158342109060381617819962114358289
Here: 539079548934519670723886102363617856011442130649251251010114448952233164837300780049
Here: 539079548934519670723886102363645215322092965151880023990182897770361123894505290769
Here: 539079548934519670723886102365369272805567090117533164395726995601932205406961843217
Here: 539079548934519670723886109537448404057926947234597251459173974937631297226220026897
Here: 539079548934519670725766679000556370521326039059474882656106911809949166254007565329
Here: 539079548934519670844243007127683205556483820203604119014863894135566916415107415057
Here: 539079548934551221564328573512360408214233626395763401434285135444905817949489380369
Here: 539079549063751913176247927613139037956059542865648161393314771757548271419012201489
Here: 539079557205383187675042918332973921379428063798693958196166930781909646975404129297
Here: 539113426391485102662204312846088962592475145269208658061148472125231961565823810577
Here: 541247706180307314776251573241769098110026617626565744937523754313665816371347110929
Here: 1111144313150726274013182548477242834366192580489323314810030248195830640849741923075251632985978191
Here: 1111144313150726274013182548477242834366192580489323314810030248195830655270735533725174722910746927
Here: 1111144313150726274013182548477242834396640744443465124767475177731858518313645764581921128005335279
Here: 1111144313151026180288600006539387290132604819316819686553395491989888392137586596691607021272764863
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193157418863191201064995785119
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193157418863191316974301612447
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193157418863208007914340747679
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193157418865611503279976221087
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193157418892234836560861464991
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193164645849300599422089693599
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040205645650860232961951040014751
Here: 13781723484135420910392350354638114019098697392618955756461287582403184147664901706758837688330983573919
Here: 13781723484135420910392350354638114019098697392618955756461287582403628516124334875836285483276543199647
Here: 13781723484135420910392350354638114019098697392618955756461287582467617574282711222988767955437129304479
Here: 13781723484135420910392350354638114019098697392618955756461287591682041949088905212946243946561528400287
Here: 13781723484135420910392350354638114019098697392618955756461288918559151921180839766822786668474998196639
Here: 13781723484135420910392350354638114019098697392618955756463596459920863386908254693044160285376933267871
Here: 13781723484135420910392350354638114019098697392618955756488994112615369200774324709034820221724346026399
Here: 13781723484135420910392350354638114019098697392618955760451027932958276163881247203577770291920736356767
Here: 13781723484135420910392350354638114019098697392619038487717196692855665836422933260375235992550834440607
Here: 13781723484135420910392350354638114019098697392619948531532196907832998594950467517007728707811160099231
Here: 13781723484135420910392350354638114019098697392630869057312199487560991697280878596597641290935068002719
Here: 13781723484135420910392350354638114019098697394334471078992601925127915660825007012624004258264700946847
Here: 13781723484135420910392350354638114019098697639653162200970552934764966411179498920420271553731844901279
Here: 13781723484135420910392350354638114027950379647370974406788167422353572399499382423129565662056076282271
Here: 13781723484135420910392350354638129314805633604107183521309651016679449921349964791158261193479865239967
Here: 13781723484135420910392350354638297567581931930477688934641648793718407614074845886404031118959529691551
Here: 13781723484135420910392350354640316600897511846923753894625622118185899926773419029353270224715503110559
Here: 13781723484135420910392356931512123970278220250982744248755782208475007516077895026988967539745622854047
Here: 13781723484135420910528728414108461677684688424137131975101853807796984986112199514961366889397242038687
Here: 13781723484135420912028887068282285922130589770837070380148082287128828391221662572041299469968051276191
Here: 13781723484135420930030790918368176855481405931236331240702824039110949252535219257000490436817762126239
Here: 13781723484135828133095879861221089250942954162516996988961253874684832165187433033900160577277190211999
Here: 13806937640590139339821433462309803683453475729489234743387120280773094211478801561115118577180556921247
Here: 17412562013614874748180317859361425686186777901939129873781196147670677705325913903140733477615105214879
Here: 536622471729176773551859671034794994079782290734724028650528120980922700819310091154829279140190059497887
Here: 6287870702424631652608000198516520674747301817497879830485263288364637418389596362250456246479481860786591
Here: 75302849470770090201281686528297228842757536138655749452502085296969214029233031615397979854550983476251039
Here: 75302849470770090201281686528297228842757536138655749452502085296969214029233031615397979858791234968542581
Here: 75302849470770090201281686528297228842757536138655749452502085296969214029233032203432147760093799386596659
Here: 75302849470770090201281686528297228842757536138655749452502085296969214508910567373642069684198368711885739
Here: 75302849470770090201281686528297228842757536138655749452502085299284525875928746012384652147098437195216541
Here: 75302849470770090201281686528297228842757536138655749452502151424590867505531923951745328023219404539515801
Here: 75302849470770090201281686528297228842757536138655749452513260865028651523745836458099820363754394660287359
Here: 75302849470770090201281686528297228842757536138655749771687484642563494809452144022664763934020564427148699
Here: 75302849470770090201281686528297228842757536138655803394834574702402665886263028443484489289150415670247121
Here: 75302849470770090201281686528297228842757536399025085393356636131293793131192811031915611131925478539106579
Here: 75302849470770090201281686528297228844014289192699089666160160684299765410158693666706414390356455190716101
Here: 75302849470770090201281686701551309499797209475971453709838420712985290004465473858166192970491975370235139
Here: 75302849470770090201281715808236859882462330145009768942342770603686053843515770643225996452818865051855481
Here: 75302849470770090202117950884099353851379151615806398792315130436631149758542405411380043704359418004281141
Here: 75302849470770090342610362658856355299810551777115487880906713899836352282517203136366770476416670205629819
Here: 75302849470774126689600651427507968733937186187245003117099611785304866078455842005026931681272414953148759
Here: 75306142158296827516488555710672666317420933063329781909648724833086864638011347411504308930083736728949839
Here: 169345297921914549824672404353166942704037101753696758017673876353188251346710484208262706866359387496239979
Here: 315605616473629933650162917801601402026282593376977209306929645363566011321913206474438933217960121689065310690613
Here: 315605616473629933650162917801601402026282593376977209306929645363566011322606592001129272995539727646096560690613
Here: 315605616473629933650162917801601402026282593376977209306929645363566011477924949979765383197017732101662966940613
Here: 315605616473629933650162917801601402026282593376977209306929645363566046424555495172890178529568734604104373190613
Here: 315605616473629933650162917801601402026282593376977209306929645365343082587778565568732838748045983749612185690613
Here: 315605616473629933650162917801601402026282593376977209306929645763407046141619002690567677510925355392678591940613
Here: 315605616473629933650162917801601402026282593377029087216935900067679022961560631727770479066320481735452029440613
Here: 315605616473629933650162917801601402026283184298795874301918682636773870275189436113869115380593362289651248190613
Here: 315605616473629933650162917801601402026415550786176833179463031835334275809064875346229919834085526901467654440613
Here: 315605616473629933650162917801601402056198010446892580626941601511425520931038702627410921869822564560159060690613
Here: 315605616473629933650162917801942157323844598153419220494926357590207456426530653032677756292768540817483279440613
Here: 315605616473629933650162917878271343977733668076429726606189896357891159860838682078174125073500695663674685690613
Here: 315605616473629933650166799217412694236939253160665484357136233074210794424115645568526625303574624496682498190613
Here: 315605616473639881294357405377428880479711801425573077263781372681359059328284045448817588059254708725198123190613
Here: 315605616475868153593922622362784054047854404311047499598568291867001812755351975709636272532888474899514529440613
Here: 315605729783514586485206327673359994099211130685423223513408881801013579159605738339741756809898438888772341940613
Here: 1606276021347329099990733418014432103646561611257547886859474946565967227817691421449417058048792901474221560690613
Here: 290716446713055942360278525465688509266589061616505379658629622415903839722872011575844517020184017804561910674531781
Here: 290716446713055942360278525465688509266589061616505379658629622415903839722872011575844601530218995828940282833184197
Here: 290716446713055942360278525465688509266589061616505379658629622415903839722872011575866151590422875728765726787675589
Here: 290716446713055942360278525465688509266589061616505379658629622415903839722872011664459716739173372140567320404993477
Here: 290716446713055942360278525465688509266589061616505379658629622415903839722877819061573301036622088873613685230446021
Here: 290716446713055942360278525465688509266589061616505379658629622415903839746659473120943848371150413437805101992682949
Here: 1267650600228229504442269252783
Here: 1267650600228904827355539701503
Here: 1267650600234308234226231669859
Here: 1267650600720614852588508821899
Here: 1267650604659698461322953753423
Here: 1267650959177223247422997590583
Here: 1267912274044743081765309961219
Here: 1288846179365837503253850422059
Here: 16719227791544535582457024107223
Here: 101379065602826513082682162139682343
Here: 912401449220636791908927485631497419
Here: 8211602901780929301345135397057833103
Here: 5986257592548660494529599414855226758299
Here: 53876318322796739648940559521723415181023
Here: 3181342720567972446888014609498668612148313619
Here: 28632084485111741880787329659652805535709178903
Here: 257688760366005666785881165111040037847756988219
Here: 257688760366005666785881165111040037847757315899
Here: 257688760366005666785881165111040037847846444859
Here: 257688760366005666785881165111040038214260842299
Here: 257688760366005666785881165111040043711818981179
Here: 257688760366005666785881165117188952538993483579
Here: 257688760366005666785881165209422672907541241659
Here: 257688760366005666785881568086313242724148535099
Here: 257688760366005666785984326780980486203998560059
Here: 257688760366005673546684366328263512496840728379
Here: 257688760366033359035793350858392200494846140219
Here: 257688760373094882763400716433193675502585470779
Here: 257688789403434310705963380652339872025311010619
Here: 257689224964863969507196613771837384688621674299
Here: 257807697673731163442636022275160829109122195259
Here: 8052364159464154563872200272931216142679397195579
Here: 31927248123466383888132348946796552365428246135791419
Here: 8173309808973500943916850930682814090339979832736177979
Here: 130772953078244609612584613102707548779839109607424352059
Here: 33477875922319986167490215923893435384323602408322607701819
Here: 535646014753254447274353369780506748672512037965445368733499
Here: 535646014753254447274353369780506748672512037965445369220999
Here: 535646014753254447274353369780506748672512037965445673908499
Here: 535646014753254447274353369780506748672512037965636103595999
Here: 535646014753254447274353369780506748672558604094176142658499
Here: 535646014753254447274353369780506748701615868422179072345999
Here: 535646014753254447274353369780506766862406073424010127033499
Here: 535646014753254447274353369787612176030113039824156611408499
Here: 535646014753254447274353374221398847173138199659972041095999
Here: 535646014753254447274356145338068311563863097044615595783499
Here: 535646014753255124900711173220778003330512581679015009845999
Here: 535646015017952243291322225739357530134900151106505244220999
Here: 535646180189376957879888344062245162665082751127867548908499
Here: 600269500108959734373682173848472596607341109129576533283499
Here: 40925324362069058884354855912259161707940681515547423212970999
Here: 25244084613087131027622588442418939856291278435526701598017658499
Here: 15777218640066250861489018580009094373970877374692498060850947345999
Here: 130663726672166444807513581714187424588747686058113810753683943165044430422961
Here: 130663726672166444807513581714187424588747686058113810753683943436444389860169
Here: 130663726672166444807513581714187424588747686058113810753715873370272217944161
Here: 130663726672166444807513581714187424588747686058113814510240658280418471518969
Here: 130663726672166444807513581714187424594864914094329498327222311670381066906561
Here: 130663726672166444807513581714188144274508918797541149969200227786390048916569
Here: 130663726672166444807513581798857734712018246945145177029053360127114544347761
Here: 130663726672166445979459661528112971254506142970927563297649243702218334428961
Here: 130663726672304323091857610240827104405445021683286855727326841409076791754169
Here: 130663742893408719598125712345878179213586652041681914867019455599722645150161
Here: 224653536809051591083475274868693002561143183261833860092434603795427395284511361
Here: 539079548934519670723886102363617849330291788565123624936126642249225075060145699857
Here: 539079548934519670723886102363617849330291788565123624936126642249245662865619991569
Here: 539079548934519670723886102363617849330291788565123624936126642333553047889995676689
Here: 539079548934519670723886102363617849330291788565123624936148748321355171057946639377
Here: 539079548934519670723886102363617849330291788566642742645595117532543711621929548817
Here: 539079548934519670723886102363617849330291788662347158342109060381617819962114358289
Here: 539079548934519670723886102363617856011442130649251251010114448952233164837300780049
Here: 539079548934519670723886102363645215322092965151880023990182897770361123894505290769
Here: 539079548934519670723886102365369272805567090117533164395726995601932205406961843217
Here: 539079548934519670723886109537448404057926947234597251459173974937631297226220026897
Here: 539079548934519670725766679000556370521326039059474882656106911809949166254007565329
Here: 539079548934519670844243007127683205556483820203604119014863894135566916415107415057
Here: 539079548934551221564328573512360408214233626395763401434285135444905817949489380369
Here: 539079549063751913176247927613139037956059542865648161393314771757548271419012201489
Here: 539079557205383187675042918332973921379428063798693958196166930781909646975404129297
Here: 539113426391485102662204312846088962592475145269208658061148472125231961565823810577
Here: 541247706180307314776251573241769098110026617626565744937523754313665816371347110929
Here: 1111144313150726274013182548477242834366192580489323314810030248195830640849741923075251632985978191
Here: 1111144313150726274013182548477242834366192580489323314810030248195830655270735533725174722910746927
Here: 1111144313150726274013182548477242834396640744443465124767475177731858518313645764581921128005335279
Here: 1111144313151026180288600006539387290132604819316819686553395491989888392137586596691607021272764863
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193157418863191201064995785119
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193157418863191316974301612447
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193157418863208007914340747679
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193157418865611503279976221087
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193157418892234836560861464991
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040193164645849300599422089693599
Here: 13781723484135420910392350354638114019098697392618955756461287582403181040205645650860232961951040014751
Here: 13781723484135420910392350354638114019098697392618955756461287582403184147664901706758837688330983573919
Here: 13781723484135420910392350354638114019098697392618955756461287582403628516124334875836285483276543199647
Here: 13781723484135420910392350354638114019098697392618955756461287582467617574282711222988767955437129304479
Here: 13781723484135420910392350354638114019098697392618955756461287591682041949088905212946243946561528400287
Here: 13781723484135420910392350354638114019098697392618955756461288918559151921180839766822786668474998196639
Here: 13781723484135420910392350354638114019098697392618955756463596459920863386908254693044160285376933267871
Here: 13781723484135420910392350354638114019098697392618955756488994112615369200774324709034820221724346026399
Here: 13781723484135420910392350354638114019098697392618955760451027932958276163881247203577770291920736356767
Here: 13781723484135420910392350354638114019098697392619038487717196692855665836422933260375235992550834440607
Here: 13781723484135420910392350354638114019098697392619948531532196907832998594950467517007728707811160099231
Here: 13781723484135420910392350354638114019098697392630869057312199487560991697280878596597641290935068002719
Here: 13781723484135420910392350354638114019098697394334471078992601925127915660825007012624004258264700946847
Here: 13781723484135420910392350354638114019098697639653162200970552934764966411179498920420271553731844901279
Here: 13781723484135420910392350354638114027950379647370974406788167422353572399499382423129565662056076282271
Here: 13781723484135420910392350354638129314805633604107183521309651016679449921349964791158261193479865239967
Here: 13781723484135420910392350354638297567581931930477688934641648793718407614074845886404031118959529691551
Here: 13781723484135420910392350354640316600897511846923753894625622118185899926773419029353270224715503110559
Here: 13781723484135420910392356931512123970278220250982744248755782208475007516077895026988967539745622854047
Here: 13781723484135420910528728414108461677684688424137131975101853807796984986112199514961366889397242038687
Here: 13781723484135420912028887068282285922130589770837070380148082287128828391221662572041299469968051276191
Here: 13781723484135420930030790918368176855481405931236331240702824039110949252535219257000490436817762126239
Here: 13781723484135828133095879861221089250942954162516996988961253874684832165187433033900160577277190211999
Here: 13806937640590139339821433462309803683453475729489234743387120280773094211478801561115118577180556921247
Here: 17412562013614874748180317859361425686186777901939129873781196147670677705325913903140733477615105214879
Here: 536622471729176773551859671034794994079782290734724028650528120980922700819310091154829279140190059497887
Here: 6287870702424631652608000198516520674747301817497879830485263288364637418389596362250456246479481860786591
Here: 75302849470770090201281686528297228842757536138655749452502085296969214029233031615397979854550983476251039
Here: 75302849470770090201281686528297228842757536138655749452502085296969214029233031615397979858791234968542581
Here: 75302849470770090201281686528297228842757536138655749452502085296969214029233032203432147760093799386596659
Here: 75302849470770090201281686528297228842757536138655749452502085296969214508910567373642069684198368711885739
Here: 75302849470770090201281686528297228842757536138655749452502085299284525875928746012384652147098437195216541
Here: 75302849470770090201281686528297228842757536138655749452502151424590867505531923951745328023219404539515801
Here: 75302849470770090201281686528297228842757536138655749452513260865028651523745836458099820363754394660287359
Here: 75302849470770090201281686528297228842757536138655749771687484642563494809452144022664763934020564427148699
Here: 75302849470770090201281686528297228842757536138655803394834574702402665886263028443484489289150415670247121
Here: 75302849470770090201281686528297228842757536399025085393356636131293793131192811031915611131925478539106579
Here: 75302849470770090201281686528297228844014289192699089666160160684299765410158693666706414390356455190716101
Here: 75302849470770090201281686701551309499797209475971453709838420712985290004465473858166192970491975370235139
Here: 75302849470770090201281715808236859882462330145009768942342770603686053843515770643225996452818865051855481
Here: 75302849470770090202117950884099353851379151615806398792315130436631149758542405411380043704359418004281141
Here: 75302849470770090342610362658856355299810551777115487880906713899836352282517203136366770476416670205629819
Here: 75302849470774126689600651427507968733937186187245003117099611785304866078455842005026931681272414953148759
Here: 75306142158296827516488555710672666317420933063329781909648724833086864638011347411504308930083736728949839
Here: 169345297921914549824672404353166942704037101753696758017673876353188251346710484208262706866359387496239979
Here: 315605616473629933650162917801601402026282593376977209306929645363566011321913206474438933217960121689065310690613
Here: 315605616473629933650162917801601402026282593376977209306929645363566011322606592001129272995539727646096560690613
Here: 315605616473629933650162917801601402026282593376977209306929645363566011477924949979765383197017732101662966940613
Here: 315605616473629933650162917801601402026282593376977209306929645363566046424555495172890178529568734604104373190613
Here: 315605616473629933650162917801601402026282593376977209306929645365343082587778565568732838748045983749612185690613
Here: 315605616473629933650162917801601402026282593376977209306929645763407046141619002690567677510925355392678591940613
Here: 315605616473629933650162917801601402026282593377029087216935900067679022961560631727770479066320481735452029440613
Here: 315605616473629933650162917801601402026283184298795874301918682636773870275189436113869115380593362289651248190613
Here: 315605616473629933650162917801601402026415550786176833179463031835334275809064875346229919834085526901467654440613
Here: 315605616473629933650162917801601402056198010446892580626941601511425520931038702627410921869822564560159060690613
Here: 315605616473629933650162917801942157323844598153419220494926357590207456426530653032677756292768540817483279440613
Here: 315605616473629933650162917878271343977733668076429726606189896357891159860838682078174125073500695663674685690613
Here: 315605616473629933650166799217412694236939253160665484357136233074210794424115645568526625303574624496682498190613
Here: 315605616473639881294357405377428880479711801425573077263781372681359059328284045448817588059254708725198123190613
Here: 315605616475868153593922622362784054047854404311047499598568291867001812755351975709636272532888474899514529440613
Here: 315605729783514586485206327673359994099211130685423223513408881801013579159605738339741756809898438888772341940613
Here: 1606276021347329099990733418014432103646561611257547886859474946565967227817691421449417058048792901474221560690613
Here: 290716446713055942360278525465688509266589061616505379658629622415903839722872011575844517020184017804561910674531781
Here: 290716446713055942360278525465688509266589061616505379658629622415903839722872011575844601530218995828940282833184197
Here: 290716446713055942360278525465688509266589061616505379658629622415903839722872011575866151590422875728765726787675589
Here: 290716446713055942360278525465688509266589061616505379658629622415903839722872011664459716739173372140567320404993477
Here: 290716446713055942360278525465688509266589061616505379658629622415903839722877819061573301036622088873613685230446021
Here: 290716446713055942360278525465688509266589061616505379658629622415903839746659473120943848371150413437805101992682949
Максимальная длина сообщения 15000 байт вы ввели 65535, ну ты понял. Это для n=100, максимум пробовал для 1000000, за комп было очково, там везде где мог бы включиться выводпоставил эксепшны типа. Так вот как я не пробовал БЕЗ опечатки ничего не работает., числа какие-то заоблачные, такие хуй где используются, но самый ахуй был в том, чтоя их начал проверять и они типа простые. Ну те, которые смог посмотреть, в основном это какие-то косвенные признаки типа
https://books.google.by/books?id=9lTRBQAAQBAJ&pg=PA109&lpg=PA109&dq=1267650600228229401496703205823&source=bl&ots=HrspmsL9Qb&sig=6aRZrNNVeklt6pkvRxiFaMm4uVI&hl=ru&sa=X&ved=0ahUKEwjcnNWjv6LSAhXE3CwKHemGAccQ6AEIGDAA#v=onepage&q=1267650600228229401496703205823&f=false
И смотри, где то число, которое 10^30, оно там ссамое первое, 700 строк или окодол того.Корчое я хз что сов сем этим делать, и не разбирался, первым делос сгенери файл на 1кк, вернее на 76к простых, меньших 1кк, вот его и буду проверять, тоже пока хз как, помимо простоты важен порядок, , пропусков не должно быть и тд, Хот ябы после этого можно будет говорить про большие, а с ними вообще без понятия, что делать. Откуцда они там взялись дадже непонятно Но понятно, что они связаны с мелкими. Хотя хуй хзнает, может это всё вообще хуйня,я 30 посмотрел, а 25 не простое, так что забей пока на эжт о всё. Да и я тоже забью. Надо поспать хоть немного за всё .то время.
> оно там ссамое первое,
Here: 83
Here: 89
Here: 97
Here: 1267650600228229401496703205823
Вот типа, верхушка ползунка, скорее всего придётся курить теорию чисел с тестами всяческими невычислительными и писать самому тесты. Ну для 1-300 проверил, а так в пизду, я заебался за это время. Пусть лежит, там езё куча всего любопытного.
Нашёл сайт, где можно проверить. Да, там много составных, ну как я и говорил, хотя
Number 1267650959177223247422997590583
Factorization: (is a prime) простых тоже немало, но суть ты понял.
Хотя хуй его знает, анон
130663726672304323091857610240827104405445021683286855727326841409076791754169
Вот это ввёл
А он мне другое подсовывает
Number 13066372667230432309185761024082710440544502168328685572732
Factorization: 2^231105373973122826067009562588903892826133423404583295851393 с 2 в конце. Короче, неясно нихуя, надо забить хуй и проспаться, вот.
83119402223117242087410335577*84381911477380691357
Думал, чёта, может деление вычитанием заменить или типа того, мало ли поэтому такое, а потом понимаю, а с чего они вообще должны быть простыми то, лол, если N на дохуя порядков меньше и это всё случайный побочный эффекит, индексы же до туда и не должны доходить. Тогда какого хера происходит вообще, лол. С другой стороны они содержат в себе боьльшие простые , можно пробовать отследить взаимосвязь разных чисел, скорее всего там и правда какой-то порядок етсь, ыы, вообще довольно странно получается: вот матетмаику и тд вроде бы придумали люди для своих нужд, числа для счёта и тд, числа без контекста они вроде бы как и не сущестуют, смысла особого не несут. Что такое пять? Конфет, монет, литров пива? А вот простые наоборот, лол, их дохуя, но они очень редко испольхзуется и про большинство(или меньшинство? ладе жтого не знаепм), но они есть, и они значат сами себя, вот где грань? Что реальность и так далее.? Это мы придумали матемтатику или появидились с ми, работающим по этим законм
Починил, теперь есть возможность находить простое=F(N), где N меньше 50000, 100000 уже несколько минут ищет, но вот пока писал вроде как придумал как через разделяй и властвуй замутить.
<=50000 секунд двадцать, но это всё равно долго.
Нет, суть этого многочлена в том, что при подстановке в него целых чисел может произойти две вещи: результат будет положительным или неположительным. В первом случае значение многочлена будет простым числом, причем все простые числа можно получить этим многочленом.
Проблема в том, что большинство значений многочлена будут отрицательными, т. е. получить простое число совсем непросто. Практически, конечно, это неприменимо, хоть и многочлен не суперсложный. А вот теоретически результат очень мощный.
На связи >>38435-кун.
>f(1) = 2, f(2) = 3, f(3) = 5
Сначала, подумалось, что речь идёт о списке типа этого: http://oeis.org/A000040/list
Но ты говоришь, у тебя формула.
Если твоя формула уникальна и нигде не индексируется, ты можешь пропиариться, и возможно тебе лично - напечатают, в каком-то национальном банке, бабла.
Но на самом деле - эти формулы уже есть, и их надо просто уметь читать и выколупывать из скомпилированного машинного кода
в таких движках, как например, wolframalpha.
Так, вольфрам - очень быстро факторизует число 1749369875873489562938483726489517389910463036490265936748495727659474191037703763535
пруф: http://www.wolframalpha.com/input/?i=1749369875873489562938483726489517389910463036490265936748495727659474191037703763535
и факторизует его - как 5×7×11×29×199×1213×5477×1160608367×316134229883×323004876255732144171530186386683923776150893770761
А это значит, что вольфрам знает твёрдо, что число 323004876255732144171530186386683923776150893770761 - простое.
Он даже может проверить его на простоту: http://www.wolframalpha.com/input/?i=323004876255732144171530186386683923776150893770761
323004876255732144171530186386683923776150893770761 is a prime number.
и возможно даже - сгенерировать все простые числа.
Так, например, в запросе prime[0,1000000000000] - можно видеть 37 607 912 018 простых чисел:
https://www.wolframalpha.com/input/?i=prime[0,1000000000000] и это действительно так (я проверил у себя, по списку, и ты можешь).
Это значило бы, что вольфрам в состоянии их просчитать, но не отобразить их (ведь много байт займёт вывод всех чисел).
Поэтому, отображение раскрывается частично.
Я, например, скриптом на питоне сейчас ищу второй триллион чисел. И могу скинуть скрипт.
Ищу, диапазонами по 280 миллионов натуральных чисел - то есть, по 10 миллионов простых чисел,
на каждый конкретный txt-файл. Всё для того - чтоб запаковать их в 7z-архивы, и повесить в TOR'е, по ссылке что я кинул в предыдущем посте.
Времени уходит конечно же уйма, потому что я - лишь на одном ядре считаю. Но это можно распараллелить.
У меня есть две видеокарты 1080Ti, но я не знаю как сделать многопоточность и параллелизм на CUDA для Python.
И конечно же какая-либо формула была бы кстати. У меня есть 4 терабайта, и хотел бы забить их простыми числами.
Но слишком много процессорного времени уходит. Да и похуй на него.
На связи >>38435-кун.
>f(1) = 2, f(2) = 3, f(3) = 5
Сначала, подумалось, что речь идёт о списке типа этого: http://oeis.org/A000040/list
Но ты говоришь, у тебя формула.
Если твоя формула уникальна и нигде не индексируется, ты можешь пропиариться, и возможно тебе лично - напечатают, в каком-то национальном банке, бабла.
Но на самом деле - эти формулы уже есть, и их надо просто уметь читать и выколупывать из скомпилированного машинного кода
в таких движках, как например, wolframalpha.
Так, вольфрам - очень быстро факторизует число 1749369875873489562938483726489517389910463036490265936748495727659474191037703763535
пруф: http://www.wolframalpha.com/input/?i=1749369875873489562938483726489517389910463036490265936748495727659474191037703763535
и факторизует его - как 5×7×11×29×199×1213×5477×1160608367×316134229883×323004876255732144171530186386683923776150893770761
А это значит, что вольфрам знает твёрдо, что число 323004876255732144171530186386683923776150893770761 - простое.
Он даже может проверить его на простоту: http://www.wolframalpha.com/input/?i=323004876255732144171530186386683923776150893770761
323004876255732144171530186386683923776150893770761 is a prime number.
и возможно даже - сгенерировать все простые числа.
Так, например, в запросе prime[0,1000000000000] - можно видеть 37 607 912 018 простых чисел:
https://www.wolframalpha.com/input/?i=prime[0,1000000000000] и это действительно так (я проверил у себя, по списку, и ты можешь).
Это значило бы, что вольфрам в состоянии их просчитать, но не отобразить их (ведь много байт займёт вывод всех чисел).
Поэтому, отображение раскрывается частично.
Я, например, скриптом на питоне сейчас ищу второй триллион чисел. И могу скинуть скрипт.
Ищу, диапазонами по 280 миллионов натуральных чисел - то есть, по 10 миллионов простых чисел,
на каждый конкретный txt-файл. Всё для того - чтоб запаковать их в 7z-архивы, и повесить в TOR'е, по ссылке что я кинул в предыдущем посте.
Времени уходит конечно же уйма, потому что я - лишь на одном ядре считаю. Но это можно распараллелить.
У меня есть две видеокарты 1080Ti, но я не знаю как сделать многопоточность и параллелизм на CUDA для Python.
И конечно же какая-либо формула была бы кстати. У меня есть 4 терабайта, и хотел бы забить их простыми числами.
Но слишком много процессорного времени уходит. Да и похуй на него.
 93 Кб, 547x622
93 Кб, 547x622>Имеет-ли мой результат научную ценность? Если да, то куда мне стоит идти с этим?
Не знаю толком туда ли тебе идти, но просто оставлю это здесь:
https://ru.wikipedia.org/wiki/Простое_число#Наибольшее_известное_простое
За нахождение простых чисел из более чем 100 000 000 и 1 000 000 000 десятичных цифр EFF назначила денежные призы
соответственно в 150 000 и 250 000 долларов США.
Ранее EFF уже присуждала призы за нахождение простых чисел из 1 000 000 и 10 000 000 десятичных цифр.
Можешь поставить в свою формулу большое число, но как ты проверишь число на простоту - вот это вызывает большой вопрос...
Можешь ещё попытаться сгенерировать достаточно большое число пренадлежащее списку primegrid megaprimes:
http://www.primegrid.com/primes/mega_primes.php и если оно совпадёт - значит твоя формула корректна с большой долей вероятности.
Хуйня получилась...
>Here: 1267650600228229504442269252783
Prime factorization:
23509×1313988857×41036822720978891
>...
>257688760366005666785881165111040037847756988219
Prime factorization:
811×1619×5251361×7929505711×4713133947569117928923621
http://www.wolframalpha.com/input/?i=257688760366005666785881165111040037847756988219
Ну и дальше, по списку... Просто вводи число в вольфрам, и смотри факторизацию.
А вот знал бы ты про тест на простоту Милера-Рабина, даже тред не стал создавать бы.
Ты бы прочитал перед тем как позорится. Этот тест гарантирует без всякой вероятности что число составное.
Правда, мне всё же до сих пор непонятно, почему там числа получались составлены из довольно-таки здоровых простых. И всё же там попадались простые, шанс довольно мал на это, но один хуй это всё амфетаминовый бред.
Попробуй ноотропы, они наверняка - получше теста Милера-Рабина будут, да и не вредны они.
Та хули ты мне тут подпёздываешь.
Взять например число n = 1000168210837126555941923,
которое факторизуется как произведение простых чисел-близнецов (1000084101881×1000084101883).
Как этот твой вероятностный полиномиальный тест простоты, с этими его раундами (k — количество раундов)
определит то, что это число - составное, если не разделит его - на одно из этих простых?
Эти простые числа, хоть и находятся близко, но они аж за триллионом - в ряду натуральных.
Здесь, (n − 1) = 1000168210837126555941922 получается,
при этом (0 < a < n), и для этого a - просто огромный разброс значений.
И вероятнее всего, это число, после теста Миллера-Рабина - будет "возможно простым",
а не составным - как утверждаешь ты:
>без всякой вероятности
Я даже тебе цитату приложу сюда, раз ты такой:
https://ru.wikipedia.org/wiki/Тест_Миллера_—_Рабина#Алгоритм_Миллера_—_Рабина
>Алгоритм Миллера — Рабина параметризуется количеством раундов r.
>Рекомендуется брать r порядка величины log2(n), где n — проверяемое число.
>После нахождения r свидетелей простоты, выдаётся ответ «n — вероятно простое», и алгоритм завершается.
И после всего этого - процитирую тебя снова:
>тест гарантирует без всякой вероятности что число составное
>Ты бы прочитал перед тем как позорится.
 6 Кб, 452x286
6 Кб, 452x286И всё-же этот >>38597 анон, от которого у меня полыхнуло сзади - прав.
Тест Миллера-Рабина - действительно распознаёт составные числа.
Пикрелейтед - пару чисел с этого треда.
Просто осталю здесь исходник на питоне,
а то в википедии - хрен пойми чего написано, псевдокодом этим ихним.
import sys
import random
from random import randrange
def miller_rabin(n, k=20):
if n == 2:
return True
if not n & 1:
return False
def check(a, s, d, n):
x = pow(a, d, n)
if x == 1:
return True
for i in range(s - 1):
if x == n - 1:
return True
x = pow(x, 2, n)
return x == n - 1
s = 0
d = n - 1
while d % 2 == 0:
d >>= 1
s += 1
for i in range(k):
a = randrange(2, n - 1)
if not check(a, s, d, n):
return False
return True
'''
for i in range(1000000000000, 1000000010000, 2):
print(i)
print(miller_rabin(i))
'''
# benchmark of 10000 iterations of miller_rabin(10010-1); Which is not prime.
# 10000 calls, 11111 per second.
# 74800 function calls in 0.902 seconds
print('\n\n')
print(1000168210837126555941923)
print(miller_rabin(1000168210837126555941923))
print('\n')
print(1000084101881)
print(miller_rabin(1000084101881))
print('\n')
print(323004876255732144171530186386683923776150893770761)
print(miller_rabin(323004876255732144171530186386683923776150893770761))
print('\n')
print(3181342720567972446888014609498668612148313619)
print(miller_rabin(3181342720567972446888014609498668612148313619))
print('\n')
print(316134229883)
print(miller_rabin(316134229883))
print('\n')
print(257688789403434310705963380652339872025311010619)
print(miller_rabin(257688789403434310705963380652339872025311010619))
print('\n\n')
 6 Кб, 452x286
6 Кб, 452x286И всё-же этот >>38597 анон, от которого у меня полыхнуло сзади - прав.
Тест Миллера-Рабина - действительно распознаёт составные числа.
Пикрелейтед - пару чисел с этого треда.
Просто осталю здесь исходник на питоне,
а то в википедии - хрен пойми чего написано, псевдокодом этим ихним.
import sys
import random
from random import randrange
def miller_rabin(n, k=20):
if n == 2:
return True
if not n & 1:
return False
def check(a, s, d, n):
x = pow(a, d, n)
if x == 1:
return True
for i in range(s - 1):
if x == n - 1:
return True
x = pow(x, 2, n)
return x == n - 1
s = 0
d = n - 1
while d % 2 == 0:
d >>= 1
s += 1
for i in range(k):
a = randrange(2, n - 1)
if not check(a, s, d, n):
return False
return True
'''
for i in range(1000000000000, 1000000010000, 2):
print(i)
print(miller_rabin(i))
'''
# benchmark of 10000 iterations of miller_rabin(10010-1); Which is not prime.
# 10000 calls, 11111 per second.
# 74800 function calls in 0.902 seconds
print('\n\n')
print(1000168210837126555941923)
print(miller_rabin(1000168210837126555941923))
print('\n')
print(1000084101881)
print(miller_rabin(1000084101881))
print('\n')
print(323004876255732144171530186386683923776150893770761)
print(miller_rabin(323004876255732144171530186386683923776150893770761))
print('\n')
print(3181342720567972446888014609498668612148313619)
print(miller_rabin(3181342720567972446888014609498668612148313619))
print('\n')
print(316134229883)
print(miller_rabin(316134229883))
print('\n')
print(257688789403434310705963380652339872025311010619)
print(miller_rabin(257688789403434310705963380652339872025311010619))
print('\n\n')
Вот исходник с табуляцией.
https://gist.github.com/bnlucas/5857478
Чтоб работало, надо добавить это:
import sys
import random
from random import randrange
У меня тоже есть наработки. Давайте сверим.
Вкидывай.
>>166989
Kaк жe я пpoигpывaю c тeбя, нищий oмeгa-oбocpaнeц. coвeтую тeбe вooбщe включить в cвoй paциoн хлeб c вoдoй, и кoмпьютep выбpocить, вpeднo для здopoвья.
>Формула в стандартных математических обозначениях.
Любую программу которая берёт число и возвращает число можно записать как формулу в стандартных математических обозначениях, если формула не проливает никакого света на структуру простых чисел, то тот факт что это формула не значит ничего ровно.
> О(р(1)...p(n))
Это хуже чем чем самый наивный перебор вида "находим очередное простое число и добавляем в массив, если массив стал длины n вывести последний элемент".
То есть научной ценности имеет 0
Оп ну так и чем всё закончилось? 3 года прошло
и как жить с женщиной, не менее интересно!
В жизни крупного математика с блестящим образованием тебя больше всего интересует именно это? Серьёзно?
Ну так он ВШЭ преподаёт, а быть куколдом у них в почете. Там же всякие прогрессивные-сойбойские науки, типа гендерных изучают. Вот и Каледину, чтобы планку прогрессивную держать куколдом стать пришлось. В США это нормальная практика для преподавателей. Это как в СССР надо было на коммунизм дрочить и марксизм-ленинизм знать.
на всяк случай пишу в эпичном тхреде
Дима, ты?
Ну так-то да, Дима вот какой математик крутой, алгеом знает, в MIT учился. А ради блатной должности в ВШЭ, можно и потерпеть куколдство и сойбоем стать. Кстати, Вербиту не нужно куколдом становится, он на дилдаках отскакал, что сам по себе очень прогрессивно и современно. В западном мире такое любят.
 431 Кб, 604x471
431 Кб, 604x471Спасибо. Метнусь кабанчиком в академию и буду обкашливать вопросы с нужными людьми.
>>73336
По родными березкам и топологиямлям скучает. Его и тут неплохо кормят. На западе то он generic-алгеомщик, там таких людей дофига, а у нас диковинка в математическом цирке показываем по пятницам. Посадили в клетку как обезьянку и заставляем за еду теоремы доказывать. Экспонаты кормить посетителем запрещается, а то у них расслоение кишечника случиться может. А по средам у нас театры Ходжа и монабелевы твисторы, да.
Так это один и тот же анон.
Он вроде не преподает же. Потому и здесь. В других странах ему придется калькулюсу учить 6/1.
 322 Кб, 640x394
322 Кб, 640x394Не все люди пропитаны политачерскими мантрами про "рашку-порашку". Раз здесь - значит здесь ему удобнее, только и всего.
Это чтобы пучок вялым не был?
ОП сошел с ума и выпилился.