Так же планируем набег на dxdy.
Второй вопрос: как задеть лично Мунина?
А если просто хуёв ему в ЛС покидать? Там же хотя бы личную почту вахтёры не читают, лол?
Он в интернете дольше чем ты и на гомонигр насмотрелся поболее твоего, поверь. Ещё и подрочит.
Были уже набеги двача на dxdy (мунину чего только не слали). Ничего интересного из этого не вышло.
Тред для разработки операции более выского толка, чем простое кидание хуями в личку.
Думаю, мы одинаково году в 2004 в сеть вышли.
И не забывай, что это, наверное, дед. Нужно что-нибудь, что доведёт его до инсульта.
Да отъебитесь вы от него.
Удовольствие от обучения = отказ от собственного развития
Сколько он статей написал?
Надо их почитать.
И покритиковать сами работы.
Он же математик! А статьи где?
Наверное надо разузнать кто чем занимается, какие статьи пишет.
Деанон офк.
Как на это развести?
@
ЗАКИДЫВАЕМ В ЛИЧКУ ГОМОНИГР
@
ОБЗЫВАЕМ ЕГО, СОЗДАЕМ ПРОВОКАЦИОННЫЕ ТРЕДЫ
@
СДЕАНОНИЛИ, МУНИН - ПЕРЕЛЬМАН
@
"ИЗВИНИТЕ РАМЗАН ГРИГОРИЙ"
ЛОЛ! Кто-то успел сохранить мою пикчу до того, как ее потерла моча :3
один антон давал ссылку на маттрэд и на списки, бруквалюб (препод МГУ) не был в восторге :), а потом одного пидора забанили на месяц за то, что начал поливать говно тролля с 2ча, вот вам кст пример, как их можно обосрать
и это было уже почти 7 лет назад...
 31 Кб, 256x366
31 Кб, 256x366Ред Херринг, залогинтесь, на dxdy его нахваливать будете.
Генуэзской. Юрий Манин, персонаж рассказа братьев пиздим-все-у-акутагавы Стругатских.
Рассказ об обеспеченной семье, которая осталась без всего и лишилась сына. Он должен был сделать всё возможное, чтобы семья осталась семьёй. Сначала может показаться, что Юрий Манин только один в семье, у которого всё нормально с головой. Ему приходиться проживать в Оранж-Каунти и быть управленцем семейного дела. Отца его упрятали за решётку, ведь тот не выплачивал налоги. Юрий Манин собирается упорядочить семейный бизнес, а чтобы тот был рациональным, Юрий Манин собирается урезать расходы своей семьи. Надо жить как нужно. Ко всему прочему у Юрий Манин растёт 14-тилетний сын Джордж-Юрий Манин. Сын его работает продавцом замороженных бананов. Каждая серия богата множеством весёлых моментов, а поэтому сериал не будет скучен.
Другой, там по сюжету до конца света остается миллиард лет, а первокультурные математики решают что с этим делать.
http://dxdy.ru/topic77263.html
Труднее запоминать, что с дырой название одно, а без неё другое. Для других многообразий такого нет: просто говорят "с дырой" и всё.
— С дырой… Кто тебя научил так говорить «с дырой»? А? Здесь, ёпта! Ты на кафедре работаешь, блядь, надо говорить правильно, ты же тополог, блядь! Не позорь, блядь, диплом, нахуй, не позорь, блядь! Чё ты нагомеоморфировал-то, блядь? С меня содрали, блядь, ему написали, нахуй. Охуенно, блядь. Охуенно. Дай сюда, блядь… Ещё пизды получишь, блядь…
— Ну чего ручку-то бросил, это потом…
— Блядь, всё, тебе, блядь… тебя защита ждёт, блядь, а он ручки приделывает.
— Они ругаться потом будут на меня.
— Кандидат, блядь. Пидорас ты, а не кандидат, блядь.
— Ну чё ты… оторвал ручку-то?
— Ручку. Какую ручку, бля? Гомеоморфное отображение шара в M^n, нахуй. Пара, блядь, образа и отображения.
— Ты же хороший математик…
— Я хороший математик, и ты, бля, охуенный парень просто, бля…
—…весёлый такой.
— Ой, бля, а ты какой весёлый, я просто, блядь, тащусь. Просто веселюсь, блядь, весь день, блядь, Задорнов, нахуй, здесь сижу и смеюсь, блядь, как на концерте, блядь.
А затем и до Мунина не далеко!
Кстати, за коверканье ника Red_Herring меня бы уже забанили на дхлду.
Пока нет, но у него же там дохуища сообщений, где-нибудь точно спалился по совокупности.
Просто нужно с поиском поработать.
Как травить-то будем? Если использовать Tor, можно создавать множество аккаунтов без опасности бана по IP от совковой мочи дхлду.
Удачи, школьники :3
(Автор этого поста был предупрежден.)
Чуханчик - эталонная крыса. Гротедик ссыт тебе в ротешник. Свободный человек так бы не поступил.
СВОБОДА, ЧАСТНАЯ СОБСТВЕННОСТЬ, РАВЕНСТВО, ПРАВА ВСЁ ЭТО ДЛЯ НЕГО НИЧЕГО НЕ ЗНАЧИТ, ПОСКОЛЬКУ ОН ЛОЖИТСЯ ПОД КРОВАВЫЙ СОВКОВЫЙ РЕЖИМ И СТУЧИТ ИМ О НАШЕМ ТРЕДЕ. ПОДЛОЕ ГАДКОЕ СУЩЕСТВО, КОТОРОЕ НЕ ДОСТОЙНО НАХОДТСЯ В НАШЕЙ УЮТНОЙ ДОСКЕ. ЛИЦЕМЕРНАЯ МРАЗЬ, ГОТОВАЯ ЛЕЧЬ ПОД ДЕДОВ.
Привет.
>этот внезапный удар в псину
Ох лол, пиздец.
Уж на что мунин старый дурак без чувства юмора - а и то угорает с вас, долбоебов.
Во первых, анон сделав топик на dxdy кинул его сюда. Этого не надо было делать, поскольку они поняли откуда автор. Во вторых только два сообщения и те о дваче. Максимальное палево.
Смешно, учитывая, насколько математики замкнуты.
Это не только филиал /po, но и /rf.
В то время как деды с дхдилды наверняка социо~.
>грустно
Да ты угораешь. Хеллер это же эталон позера. Слушаю Шопена в коралловой рубашечке. В другом посте пишет, что начал изучать Erlang. Вся жизнь – сплошной выебон, и в НМУ ходил за этим же.
Вот, про его товарища по несчастью:
>Капинус относится к длинному списку героев, активно увлекавшихся математикой, доросших по уровню примерно до начала второго курса НМУ, >а затем по тем или иным причинам махнувших рукой.
>Death lies before us as we sail through the Ocean of Youth.
Разница в том, что Хеллер в принципе никуда не дорос.
Еще посмотри его посты из 2009: "В НМУ умнейшие люди из тех что я видел, место прекрасное и удивительно замечательное", читать проотивно.
Да, есть такое - сам по себе чувствую, как только баксы начал зарабатывать - сразу интерес к математике и математической тусовке начал стремитьельно тускнеть. Последний раз я учил шо-то такое математическое пару месяцев назад. Это давно.
Да не, не пизди, Рома норм чувак. Может он и выебывается чем-то, но тщеславие всем присуще.
И то правда, согласен.
У Манина Ю.И. есть кстати сын, Д.Ю., кандидат наук по computer science, строчил статьи в бюллетень комиссии по борьбе с лженаукой. Редкостный уебок. Со своим батей борится, кстати, тот же угорал по компаративистике и ностратическим гипотезам.
Напомню, что на форуме действует иммунитет к толстоте, так что нужно очень осторожно и неявно действовать
Аки >>1007
Дважды добившийся бана одного деда. хоят судя по постам сделал это ненамеренно
Есть идеи? Может создать какую-нибудь говнофилософскую тему и брызать в ней дерьмом? На dxdy философия (свободный полет) - одно из главных мест, откуда люди отправляются в баню.
 89 Кб, 555x933
89 Кб, 555x933>>410151
>ну а это уже жир
Пикрелейтед, раздел для дискуссий о математике. Темы не меняются с лета. Это же какой-то бред, а не математика. В обсуждениях бабок у подъезда ценности больше, чем в этих дискуссиях.
>50/50, тобишь кто как
— Миша Вербицкий высказался, что из программ по анализу надо изгонять эпсилон-дельта язык и всё надо переводить на язык топологии. Как думаете, насколько в этом есть смысл? По мне так ерунда всё это.
— я уже приводил примеры, Миша иногда довольно грубые ошибки и несуразицы лепит и именно в анализе. Интересно, как он полноту собирается определять в чисто топологических терминах :mrgreen:
— Миша Вербицкий писал, что Цитата:
Хуже Куроша просто нет, это финиш, припадочный бред, а не учебник
— Попугайничать за всяким там вербицкими, тупо переписывая сказанные ими в припадке безумия гадости, каждый может.
— Психи преследуют Александра Геннадиевича и после смерти.
— споткнувшись о лежавшую на его пути книгу Куроша, Вербицкий упал, нелепо взмахнув руками, после чего грязно выругался
— Предупреждение за использование неубедительного и неаргументированного тезиса для голословного обвинения в адрес проф. Куроша А.Г. и его известного учебного пособия.
— Профессор Снэйп в сообщении #316720 писал(а): Мне почему-то Вербицкий подозрителен.
— Если эта программа -- и впрямь тов. Вербицкого (кстати, не в курсе, кто он такой), то он -- нисколько не подозрителен. Он -- просто идиот, не имеющий ни малейшего представления насчёт того, за что взялся.
— Да программа - чушь. Однобокая сильно.
— Еще раз. Программа Вербицкого в любом (даже гения педагогики Макаренко) изложении не работает. Теперь понятно?
— TL;DR: Если классическую программу Вербицкого можно рассматривать как троллинг, то эта программа вполне себе ок.
— Михаил Вербицкий, которого Вы процитировали, - известный экстремист. Не удивлюсь, если завтра он предложит выкинуть из программы 1-го класса "совсем уж бессмысленную и никому совсем не нужную тупую фигню, типа" таблицы умножения.
— Как понять что такое предел?
— У Вербицкого очень наглядное объяснение
— про Вербицкого, если это Миша Вербицкий, слышал в основном negative
— Похоже, что Миша Вербицкий не знает, что такое пространство Фреше: http://ium.mccme.ru/postscript/s08/top10.ps.gz И, вообще, судя по другим лекциям, весьма смутное представление имеет о роли сходящихся последовательностей в общих ЛТП
— Вербицкий дает определение пространств Фреше. По сравнению со стандартным определением, Вербицкий пропускает условие метризуемости пространства. В результате этого, например, теорема об открытости отображения делается, вообще говоря, неверной для тех пространств, которые Вербицкий называет пространствами Фреше.
—программа Миши Вербицкого по математике
— Он хотя бы ее сам знает? :D Попробуйте почитать Фихтенгольца, там очень хорошо написано
— Чтобы стать математиком, по мнению Вербицкого, требуется НЕ решать задачи из Демидовича, Филиппова и прочих, не читать Фихтенгольца, ибо это вредно.
— А мне, немного математику, уверенно видится, что при планировании программы по изучению математики не стоит руководствоваться этими "записками сумасшедшего", который за свою жизнь никого ничему не выучил
— Вспомнился старый пост М. Вербицкого о том же: Взял интеграл? Положи его на место!
— Не так это просто, как утверждает Вербицкий. Именно поэтому он не прав. Имхо наоборот - в учебных программах должно быть как можно больше задач на получение первообразной с физическим, геометрическим и любым другим смыслом, какой только можно придумать в связи с этим. Именно для развития у обучающегося нативной осознанности аналитического труда и искоренения операторнутой однобокости.
— Мне почему-то Вербицкий подозрителен. Слищком много времени уделяет "политической жизни" для того, чтобы быть серьёзным математиком. Хотя профессионально судить его не возьмусь. Всё-таки в очень разных областях с ним работаем. А программа его --- полная чушь. Как план Путина :-)
— Тут мне импонирует мнение Вербицкого о core mathematics(Вербицкий не всегда адекватен, но мнение совершенно серьёзное и, как минимум, имеющее право на жизнь).
— Это он пытается разумным способом объяснить те многочисленные человеконенавистнические, обильно пересыпанные ненормативной лексикой пассажи в блоге Вербицкого, за которые Роскомнадзор заблокировал его блог, признав тот экстремистским.
— Миша Вербицкий - математик, и с его колокольни ему это позволено. В физику со своими критериями он не лезет, и хорошо. Если бы (гипотетически!) какой-то математик с такими критериями в физику полез, ему бы быстро по рукам надавали.
— Статья by Миша Вербицкий? Это круто, на "крутом" сайте. Я когда-то вроде читал, по-моему ахинея с большими понтами и гипертрофированной категоричностью. ОТ товарища имеющего только Ph.D. рассуждения о том, что в России нет математиков, способных заниматься научной работой, звучит убого. Молодость.
— Возможно, зря топикстартер на входе помянул Вербицкого. Ибо Вербицкий, очевидно, также отчасти понтуется. Правда Вербицкий понтуется а-ля Ландау.
— Взгляды Вербицкого на этот вопрос ортогональны мнению большинства преподавателей математики и, если я не ошибаюсь, мнению большинства работающих математиков. То, что Вербицкий громче всех кричит и матерится, не значит, что он прав (впрочем, и того, что он не прав - тоже). И уж во всяком случае на этом форуме взгляды Вербицкого разделяют очень немногие, так что Вы выбрали не ту площадку, чтобы искать "правильную" по его критериям математическую программу. Это лучше в тифаретник, там будет у кого спросить. Но если с изучением этой программы что-то пойдет не так - не говорите, что Вас не предупреждали.
 89 Кб, 555x933
89 Кб, 555x933>>410151
>ну а это уже жир
Пикрелейтед, раздел для дискуссий о математике. Темы не меняются с лета. Это же какой-то бред, а не математика. В обсуждениях бабок у подъезда ценности больше, чем в этих дискуссиях.
>50/50, тобишь кто как
— Миша Вербицкий высказался, что из программ по анализу надо изгонять эпсилон-дельта язык и всё надо переводить на язык топологии. Как думаете, насколько в этом есть смысл? По мне так ерунда всё это.
— я уже приводил примеры, Миша иногда довольно грубые ошибки и несуразицы лепит и именно в анализе. Интересно, как он полноту собирается определять в чисто топологических терминах :mrgreen:
— Миша Вербицкий писал, что Цитата:
Хуже Куроша просто нет, это финиш, припадочный бред, а не учебник
— Попугайничать за всяким там вербицкими, тупо переписывая сказанные ими в припадке безумия гадости, каждый может.
— Психи преследуют Александра Геннадиевича и после смерти.
— споткнувшись о лежавшую на его пути книгу Куроша, Вербицкий упал, нелепо взмахнув руками, после чего грязно выругался
— Предупреждение за использование неубедительного и неаргументированного тезиса для голословного обвинения в адрес проф. Куроша А.Г. и его известного учебного пособия.
— Профессор Снэйп в сообщении #316720 писал(а): Мне почему-то Вербицкий подозрителен.
— Если эта программа -- и впрямь тов. Вербицкого (кстати, не в курсе, кто он такой), то он -- нисколько не подозрителен. Он -- просто идиот, не имеющий ни малейшего представления насчёт того, за что взялся.
— Да программа - чушь. Однобокая сильно.
— Еще раз. Программа Вербицкого в любом (даже гения педагогики Макаренко) изложении не работает. Теперь понятно?
— TL;DR: Если классическую программу Вербицкого можно рассматривать как троллинг, то эта программа вполне себе ок.
— Михаил Вербицкий, которого Вы процитировали, - известный экстремист. Не удивлюсь, если завтра он предложит выкинуть из программы 1-го класса "совсем уж бессмысленную и никому совсем не нужную тупую фигню, типа" таблицы умножения.
— Как понять что такое предел?
— У Вербицкого очень наглядное объяснение
— про Вербицкого, если это Миша Вербицкий, слышал в основном negative
— Похоже, что Миша Вербицкий не знает, что такое пространство Фреше: http://ium.mccme.ru/postscript/s08/top10.ps.gz И, вообще, судя по другим лекциям, весьма смутное представление имеет о роли сходящихся последовательностей в общих ЛТП
— Вербицкий дает определение пространств Фреше. По сравнению со стандартным определением, Вербицкий пропускает условие метризуемости пространства. В результате этого, например, теорема об открытости отображения делается, вообще говоря, неверной для тех пространств, которые Вербицкий называет пространствами Фреше.
—программа Миши Вербицкого по математике
— Он хотя бы ее сам знает? :D Попробуйте почитать Фихтенгольца, там очень хорошо написано
— Чтобы стать математиком, по мнению Вербицкого, требуется НЕ решать задачи из Демидовича, Филиппова и прочих, не читать Фихтенгольца, ибо это вредно.
— А мне, немного математику, уверенно видится, что при планировании программы по изучению математики не стоит руководствоваться этими "записками сумасшедшего", который за свою жизнь никого ничему не выучил
— Вспомнился старый пост М. Вербицкого о том же: Взял интеграл? Положи его на место!
— Не так это просто, как утверждает Вербицкий. Именно поэтому он не прав. Имхо наоборот - в учебных программах должно быть как можно больше задач на получение первообразной с физическим, геометрическим и любым другим смыслом, какой только можно придумать в связи с этим. Именно для развития у обучающегося нативной осознанности аналитического труда и искоренения операторнутой однобокости.
— Мне почему-то Вербицкий подозрителен. Слищком много времени уделяет "политической жизни" для того, чтобы быть серьёзным математиком. Хотя профессионально судить его не возьмусь. Всё-таки в очень разных областях с ним работаем. А программа его --- полная чушь. Как план Путина :-)
— Тут мне импонирует мнение Вербицкого о core mathematics(Вербицкий не всегда адекватен, но мнение совершенно серьёзное и, как минимум, имеющее право на жизнь).
— Это он пытается разумным способом объяснить те многочисленные человеконенавистнические, обильно пересыпанные ненормативной лексикой пассажи в блоге Вербицкого, за которые Роскомнадзор заблокировал его блог, признав тот экстремистским.
— Миша Вербицкий - математик, и с его колокольни ему это позволено. В физику со своими критериями он не лезет, и хорошо. Если бы (гипотетически!) какой-то математик с такими критериями в физику полез, ему бы быстро по рукам надавали.
— Статья by Миша Вербицкий? Это круто, на "крутом" сайте. Я когда-то вроде читал, по-моему ахинея с большими понтами и гипертрофированной категоричностью. ОТ товарища имеющего только Ph.D. рассуждения о том, что в России нет математиков, способных заниматься научной работой, звучит убого. Молодость.
— Возможно, зря топикстартер на входе помянул Вербицкого. Ибо Вербицкий, очевидно, также отчасти понтуется. Правда Вербицкий понтуется а-ля Ландау.
— Взгляды Вербицкого на этот вопрос ортогональны мнению большинства преподавателей математики и, если я не ошибаюсь, мнению большинства работающих математиков. То, что Вербицкий громче всех кричит и матерится, не значит, что он прав (впрочем, и того, что он не прав - тоже). И уж во всяком случае на этом форуме взгляды Вербицкого разделяют очень немногие, так что Вы выбрали не ту площадку, чтобы искать "правильную" по его критериям математическую программу. Это лучше в тифаретник, там будет у кого спросить. Но если с изучением этой программы что-то пойдет не так - не говорите, что Вас не предупреждали.
Я думал Вербитка шутит и преувеличивает любовь определённых кругов к матанализу, но судя по первому пику они там совсем ебнутые. Как они сами для себя обосновывают анальную фиксацию на матанализе? Это ж какая-то секта.
Вы просто не понимаете этой манящей сладости засовывания себе в задницу интеграла и последующей слепой, башибузуковой беготни с растопыренными руками по всем лестницам здания МГУ. Вверх-вниз, вверх-вниз.
Свисающий дифференциал стучит по яичкам.
Дык таблицу умножения нужно выкинуть нахуй. Помню как нас по одному вызывали к доске и спрашивали её наизусть.
>— Вспомнился старый пост М. Вербицкого о том же: Взял интеграл? Положи его на место!
— Не так это просто, как утверждает Вербицкий. Именно поэтому он не прав. Имхо наоборот - в учебных программах должно быть как можно больше задач на получение первообразной с физическим, геометрическим и любым другим смыслом, какой только можно придумать в связи с этим. Именно для развития у обучающегося нативной осознанности аналитического труда и искоренения операторнутой однобокости.
С этого ахуел. Пиздец.
И что плохого в том, что ее наизусть спрашивали? Или ты хочешь сказать, что у тебя от этих вызовов к доске травма на всю жизнь осталась, и теперь ты ненавидишь интегралы? Или что?
А в официальной конфе телеграмма для первокурсников НМУ этого года была ссылка на 2ch.hk. Мне после чтения обсуждений конфы как-то неприятно стало ходить туда. Впечатления как у Хеллера "умнейшие люди посещают", только наоборот.
Одна из цитат: "Шабат вообще отжатый в край".
Tl;dr местные студенты это сраное быдло из подворотен.
>делать выводы по первокурсникам
хуево луркёбил, сначала быдла много, очень много, но уже ко второму курсу большинство из них уходит, к 3 остается 0
Нахуй это надо, если на обратной стороне многих тетрадей есть эта таблица? Ещё существуют калькуляторы, специально для этого придуманные. Лучше бы его схему разбирали, чем тысячи примеров на умножение решали.
Однажды ехал в электричке, рядом сидели девица и парень. Говорили о всеросе, вожатстве в летней школе для аутистов, репетиторстве. Проиграл, когда тня с ненавистью рассказывала, как какие-то трюкачи отказали ей репетиторствовать их сыночка, потому что "хотели бы видеть мужчину".
Но это неважно. Важно, что в какой-то момент девушка произнесла примерно следующее: "Там хорошо, такая ламповая атмосфера". Парень тут же спросил: "А что такое "ламповая"?".
Сразу так приятно стало. Существуют еще молодые люди, плюющие на модные мемчики, луркояз, сосачи, раковые конфочки, популярные бордопаблики, смищные видосики и картиночки.
Ну... Следуя твоей логике, получается, что детям не нужно учиться считать до десяти, например. В тетради же есть таблица. Лучше бы правильное определение N искали, чем тыщу раз считать до десяти.
Под аутистами ты подразумевал математиков или настоящих аутистов, то есть детей с этой болезнью?
Хороший рассказ, кстати; мне отчего-то тоже стало приятно и тепло после его прочтения
До десяти и не нужно, достаточно до 2-ух. Потом про системы счисления рассказать и всё хорошо.
Раз тут у нас /math, а не /mehmath, то объясни, что такого зазорного в 2016 году не уметь считать? Где вообще в математике нужно считать? Возможно, это необходимый навык для специалистов в области составления олимпиад или подражатель Рамануджана, но для остального есть "численные методы".
Летние матшколы я имел ввиду, конечно.
Да математика тут вообще не при чем. Считать (не только до десяти) нужно любому обычному человеку. И таблицу умножения зашить в мозг тоже нужно. Идиотский пример про "деньги в магазине посчитать" тут как раз вполне уместен. Читать, писать, считать, алфавит, таблица умножения. Анон выше ведь от этого предлагал отказаться, а ты про олимпиады говоришь.
>подражатель Рамануджана,
Как что-то плохое. Между прочем, он нашел много пиздатых формул только из-за своего пиздатого умения считать. Просто если умеешь считать, перед тобой открываются больше возможностей.
>И таблицу умножения зашить в мозг тоже нужно.
Потом будет "И таблицу производных зашить в мозг тоже нужно" и т.д.
>Идиотский пример про "деньги в магазине посчитать" тут как раз вполне уместен.
У каждого сейчас есть телефон, где как раз можно и подсчитать. Да и умножение редко требуется, там, в основном, сложение.
Я тебе сказал, достаточно до двух считать, а потом рассказать про системы счисления. Таблица умножения для двоичной системы запоминать не нужно.
Ты меня совершенно не слышишь. Проехали.
Смотрите, мунен наезжает на Бурбаки и получает закономерный вопрос, который в итоге пытается игнорировать - а сам то он читал их книги.
Но тут честь хозяина приходит защитить красная сельдь!
Ну так-то манин прав вроде.
"Назжает"? Он справедливо со своим подсосом замечает, что Бурбаки не учебная литература, а справочник и упражнение в объединении разных областей математики в единую систему.
http://dxdy.ru/topic113539.html
очередной микрохоливар вокруг двощей
алсо, кидаем жалобы на art9
Блять, не понимаю как на той параше можно вообще общаться? За одну безобидную картинку - ворнинг и выпиливание поста (картинки). А вы блядь смеете еще на местную мочерастию жаловаться.
картинка - оффтопик, вот почему
к тому же там ведь КАНФИРЕНЦИЙА™ УВАЖИТИЛЬНА АТНАСИТИСЬ К УЧАСНИКАМ ФОРУМА™, поэтому мат запрещен
в принципе твои придирки необоснованны ну разве что с позиции двача, нужно отдавать отчет, что сюда люди приходят в первую очередь поугарать, во вторую - за какими-то сведениями и помощью, на дхдв порядок обратный
Я уверен, что там модерация косячит, но это не тот случай. Чуваки потёрли обсуждение хуйни про культуру и оставили всё по теме топика, даже линк на двощ оставили.
Пожалуйста, продолжай.
вот это чсв
Тот самый.
Нас тут несколько, но имелся в виду шизоидный дед, расписавший апгрейд вербитопроги
https://2ch.hk/math/res/3784.html (
кулстори, плиз
А вот в /матх ты можешь даже сказать, что Кадыров - пидор, и ничего тебе за это не будет.
(Автор этого поста был забанен. Помянем.)
Точно, а если факты принести - получишь бан за клевету и подделку фкатической информации. Значем-знаем.
Ну ведь всегда есть отмазка "факты подделаны"!
А они тут причём?
 62 Кб, 1850x536
62 Кб, 1850x536>>4976
>И Холокост.
Либираха перепутала страны, лол.
Да - он точно стукнутый, но это ещё ничего. Я тут а dxdy столкнулся с интересным методом безграмотных ублюдков. Когда они не смогли ни чего мне возразить, а возразить там было невозможно, так как я в математике обсуждал совершенно общепризнанную теорию. Эти дураки по своей безграмотности (команда с названием Мунин) пытались меня уверить, что они смогут измерить плоскость Лобачевского рулеткой, что им не удалось. Тогда они голосованием местных тупиц лишили меня доступа к теме (банить было невозможно, так как не за что) с последующим её удалением. А вы говорите, что на астрофоруме дураки. Настоящие дураки и подонки на dxdy.
Эти идиоты на dxdy решили, как французы, создавшие сообщество математиков с фамилией Бурбаки, создать сообщество идиотов-полуматематиков у себя на форуме с фамилией Мунин.
Не спорю, что на dxdy просто секта МУНИНА. И доказывать им бесполезно, только встретят серьёзный аргумент, тут же накладывают БАН.
Не стал бы эту тему открывать, но ради справедливости надо упомянуть.
Открыли тему на dxdy http://dxdy.ru/topic88641.html
Обсуждать там бесполезно. Набегут всякие Шведки с Маниными и давай как психбольные орать.
Значит, что имеем - сей гражданин используя примитивные арифметические действия получает некоторые кратные решения уравнений.
Я ему пытался несколько раз объяснить, что это уровень 8 класса.
Задача обычно сводится к линейному уравнению - то есть он степенное заменяет линейным - которое и решает.
Понятно, что вопрос сводится к выяснению есть ли другие решения?
Или же только такой подход даёт решения?
Наша же банда математиков заявляет, что это не решения!
Странно!
Они считать разучились? Или же в облом признать, что некоторые кратные решения можно легко получать?
Я заметил фальсификацией эта банда занимается широко - вот это типичный случай.
Хотя лженаучности можно больше найти в тех работах которая эта банда напечатала.
Но с этой толпой тяжело бороться!
Значит они заявили, что это не решения! То есть формула которая приведена не даёт решений.
Это наглая ложь! Требую чтоб они сделали официальное опровержение!
individ! Если вам кажется что ото всех попахивает гавницом принюхайтесь к себе, не обосрались ли вы?
Tozhe tak kazhetsa.
с самого создания здесь не было такого застоя и говна
Хорен, ты ебанулся? С самого начала тут было просто дохуя говна.
 56 Кб, 1162x925
56 Кб, 1162x925Чтобы выучить алгеом, нужно решить ~250 упражнений из Хартсхорна: всю вторую главу (про схемы) и всю третью (про когомологии пучков). Больше ничего не нужно, в принципе.
>проективные коники
Как там в Италии 19-го века, нормально? Доказывать утверждения уже научились?
Утверждения - да. Категорные переливания из пустого в порожнее - ну уж извините, до такого аутизма пока не скатились.
http://dxdy.ru/topic117119-180.html
>Интересным вопросом был бы другой: перечислить науки, для занятия которыми можно вообще не знать теории категорий.
Я хочу попробовать! Итак, начнем. Пойдем прямо по кафедрам.
1. Кафедра ТФФА. ТФДП-ники, школа которых берет начало от Лузина, Колмогорова, Меньшова, Бари если и используют категории, то только в смысле Бэра. :D ТФКП-шники одной переменной тоже их не используют. В большинстве разумных разделов ТФКП многих переменных, типа пространств функций в шаре, граничных свойств, геометрии областей и т.п категории не используются. В функане, теории операторов категории, если и используются, то сбоку-припеку, как новомодная дань, но новых результатов они не приносят.
2. Теория вероятностей и мат.статистика. Вот уж где нет категорий, так там.
3. ОДУ и УРЧП, Динамические системы. Категории не используются.
4. Общие проблемы управления. Категории не используются.
5. Дискретная математика и МАТИС. Категории не используются.
6. ОТГ, ВГТ, ДГи приложения - если категории и используют, то мал-мало, совсем не видно, нужно долго искать.
7. Матлогика и теория алгоритмов. Где же там категории??? Ау?
8. Кафедра теоретической информатики. Вот где категории живут? Или нет? :D
9. Теория чисел. Эти дня не проживут, чтобы категориями не воспользоваться! :D
10. Кафедра вычмата. Вот здесь без категорий точно все рухнет! :D
Фу, устал.
Жду новых вопросов от читателей, возмущенных низким уровнем профессорско-преподавательского состава мехмата в стиле:
"Я смотрел в эти лица и не мог им простить
Того, что у них нет тебя знания категорий и они могут жить!"
ну это же бруквалюб :)
Иногда читаешь его, кажется, что троллинг,
а потом вспоминаешь, что это типичный дiд
мало того, что второкультурщик, так еще и оголтелый ватник
в общем, классический для препода этой параши набор
Он не второкультурщик. Насколько я понимаю, он математикой профессионально уже давно не занимается.
Зато последняя статья в ВЕСТНИКЕ МАСЬКОВСКАГО УНИВЕРСИТЕТА в 2016. Топовый рисерчер.
Она называется "К восьмидесятилетию Валериана Ивановича Гаврилова", это не считается.
Ты ничего не понимаешь в ИССЛЕДОВАНИЯХ МИХМАТА МГУ
Школота ебаная.
Смысл аргументов категородаунов, что в современноё матёшке без категорий нечего делать. Изи.
>в современноё матёшке
Просто в математике, не только современной. Современная - это последние лет десять, а категориям уже сто лет.
2017-1940 = 77.
Но категории были до маклейна. Просто они не назывались категории.
https://en.wikipedia.org/wiki/Timeline_of_category_theory_and_related_mathematics
Да ну, глупости это всё. Этак можно договориться до того, что уже у Платона были категории.
В "современной математике" (в одно слово) а не в современной математике. Так-то в современной нам математике и комбинаторика и вещественный анализ есть и много чего ещё, для чего категории нужны.
Какой, в жопу, Манин? Мунин.
Вот чувак ввел Ext functor в 1934 году. До Маклейна.
Двачер Вербицкий зафорсил на тифаретнике
Охуенная дискуссия
http://dxdy.ru/post1210173.html
нигерийские математики профессора мехмата рассуждают
о пагубности теории категорий, мотивируя это тем, что
в Нигерии на мехмате МГУ теории категорий
совершенно никому не нужны. В качестве козырного
аргумента приводится список кафедр мехмата с
комментариями в духе
Общие проблемы управления. Категории не используются.
Дискретная математика и МАТИС. Категории не используются.
Кафедра вычмата. Вот здесь без категорий точно все рухнет! :D
В Нигерии, кстати, действительно очень продвинутая математика,
там где-то 10,000 профессиональных математиков и 7 математических
журналов
Возмутил не сам срач, а коммент какела в самом низу
>русскоязычного материала
<sarcasm>Щас бы в 2к17 вкатываться в науку на языке отсталых диких пидорашек</sarcasm>
Сам поди годноту на человеческом языке читает, а русскому народу блины с лопаты... Русофобы. Русофобы эвривэа.
и там ВНЕЗАПНО вылезает коммент Мунина
вот его ЖЖ-ак
http://firtree.livejournal.com/
он оказывается с совой и старожилами ЖЖ много общался, и кстати судя по возрасту его друзей он никакой не дед, там 40-50 лет (а когда ЖЖ вел совсем молодой был)
ща увлеченно просматриваю посты с надеждой на какую-то зацепку, предлагаю присоединиться и общими усилиями его сдеанонить
сразу говорю, что некто Павел Иванович Мунин - не Munin
судя по друзьям он мб из МИЭТа (но это совсем не точно)
разве что вот этот его древний паблик
http://mmt-lecturehall.livejournal.com/2004/
и 2 его друга
http://santiaga.livejournal.com/profile?socconns=mutual_friends
http://wad-white.livejournal.com/profile
они больше всех срали у него в ЖЖшке
Через них, однако, найти ничего удалось
можете, кстати, написать в ВК второму и спросить про мунина
алсо, он дикий толкиенодрочер очень много спамил тут https://tolkien.su/forum/
2 мунина, которых обычно выдают:
(уже упомянутый) Павел Иванович Мунин и Мунин Анатолий Григорьевич - не он.
Но судя по тому, что его ни разу (из тех постов, что я чекал, а проверил лишь малую часть) не называли по имени, но часто обращались "Мунин" - это может все-таки его реальная фамилия (но вряд ли, иначе бы загуглив "Мунин" и название вуза можно было бы найти, а нихуя не вышло)
Короче, сплошные догадки и вопросы, ни одного ключа по сути.
Если возьметесь за это дело, то почаще юзайте веб архив, а также пробивайте сохраненные копии сайта в яндексе и гугле.
А я спать
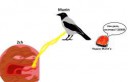
Мунин - это один из воронов Одина. Другого звать Хугин. Если б он себя "Торин" обозвал, ты бы тоже думал, что это фамилия?
Я, блядь, знаю.
Просто действительно есть фамилия у людей Мунин. Логично предположить, что это могла быть его фамилия. Я ничего конкретного не утверждал, только рассматривал варианты
Хули ты всё ещё онлайн? пиздуй спать
Мунин - это Манин, давно уже задианонили.
Дед-доцент Brukvalub с МГУ объявил себя "Патриотом России" и начал постить ватную пропаганду. Молодой адепт категорий с Киева послал его нахуй; адепта тотчас забанили пожизненно.
Репрессии поразили даже приученных к бутылке форумчан. Вспыхнул и продолжает полыхать срач, в результате которого бан словили ещё несколько любителей категорий.
Доцент ехидно хихикает и продолжает патриотизм.
начало: http://dxdy.ru/topic123625.html
полыхание 1: http://dxdy.ru/topic123631.html
полыхание 2: http://dxdy.ru/topic123694.html
дед: http://dxdy.ru/topic123632.html
> Для начала: У нас нет ни демократии, ни конституционного суда на форуме. Все решения субъективны и понятие прецедента не имеет такой же силы, как в суде США.
А вообще, Брюкволюб всё правильно сделал. Давно этого категорного пониёба забавнить следовало.
- Мимо Патриот России, поддерживаю Брюкволюба
А ведь война "Категории Vs диды" реально идёт.
Понятие преценда вообще есть только в англо-саксонской правовой системе, непонятно к чему он это спизданул.
*прецедента
Гомоморфизм изобрели?
Что еще за эпи, моно? Мы в России или в Греции?! Стягивание и вложение это называется, соответственно.
Это конкретный сорт эпиморфизмов, а не вообще любой эпиморфизм.
На стриме Светова с Пожарским говорил.
Так я не понял кто там тролль Brukvalub или топикстартер?
Я порылся в www.topuniversities.com и ни Шанинки, ни ЕУСПб там в лидерах нет, у них там вообще нет рейтингов.
Про ЕУСПб я сам слышал полярные мнения.
 5 Кб, 356x142
5 Кб, 356x142Подожди-ка, то есть и вся эта афа хуета, вегетерианство и йога тоже позерство?
Хотя я это почти начал подозревать
ну да. но он писал, что после того, как его бложик стал немного известен, ему стали писать множество тянок и все умоляли их выебать; чем он с радостью занимался
так что он поймал удачу да и вообще, сейчас переехал в западную страну, окончив там университет. наверно, для многих его бложик служит источником мотивации и вдохновения.
для меня скорее -- больше источником боли, потому что он как личность мне очень неприятен, а я сам, между тем, лох и неудачник. завидую, наверно
А вот что такие, как он, находят в творчестве некого Бродского и обязательно о нём упоминают? Это мода среди некой "интеллигенции"?
Неправильно, на столе должна быть "Путинка" и картофан.
Тебе же сказали, Хеллер — эталон позера, ничего он там не находит.
> Когда я там бывал, Мунин тоже был только заслуженный участник. Админом или хотя бы модератором на этом форуме он вряд ли мог бы быть. Он мне однажды сознался, что не имеет по физике не только университетского, но и вузовского образования. Он физику осваивал самостоятельно по учебникам, составленным по программе Ландау-Лифшица. Отсюда его дурные манеры: он никогда не выступал на семинарах, никогда не сдавал экзамены по физике, т.е. не приучен искать научные аргументы в споре. Выбор учебников для самообучения привёл к провалам в его знаниях. В частности, он совершенно не знал теорию моего излюбленного уравнения Дирака, поэтому поначалу, пока мы с ним на форуме Естественных Наук, где он действительно был админом, пытались спорить, он против моих доводов выдвигал единственный:"Ложь!", поэтому быстро оказался в игноре.
> не имеет по физике не только университетского, но и вузовского образования
>В 1953 году окончил среднюю школу с золотой медалью и поступил на механико-математический факультет МГУ.
Прочитал самое начало, а уже прололировал.
http://www.newtheory.ru/mathematics/novaya-zakonomernost-v-teorii-chisel-t4279.html
Неизвестная математика.
Какие секреты прячет всем известный ряд чисел — 123456789 ?
1 + 2 + 3 = 6
4 + 5 + 6 = 15 = 1 + 5 = 6
7 + 8 + 9 = 24 = 2 + 4 = 6
Все числа связаны безконечными взаимосвязями, впрочем как и весь Мир.
По самому маленькому признаку можно восстановить абсолютно все.
Так же как поступки того или иного человека могут многое рассказать о нем, о его родителях, о более дальних предках и даже о положении всей его рассы и человечестве в целом, так и числа открывают свои тайны в самом удивительном и на первый взгляд незаметном месте !!!
Стоит только чуть чуть присмотреться и задуматься над увиденным.
На мехмате физику не изучают.
>Лучше бы правильное определение N искали, чем тыщу раз считать до десяти.
Мне кажется, что следует определять N, после определения Z,
так как множество Z - является группой, да ещё и абелевой,
а вот множество N даже группой не является.
У любого числа из N нет обратного элемента, дающего ноль - а это одно из основных свойств группы.
Зато коммутативным моноидом является, если считать ноль натуральным числом. К-теория описывает пополнение коммутативного моноида до кольца, то есть переход от N к Z.
Ты не забывай, о том, что этот коммутативный моноид является ещё и аддитивным.
Более того, всё множество натуральных чисел с операцией сложения образуют
аддитивную полугруппу натуральных чисел.
А вот множество Z - полноценная абелева группа.
Если вывести определение Z, тогда определение N,
как полугруппы и аддитивного коммутативного моноида -
оно просто вытечет из этого определения Z.
А вот без нуля, множество натуральных чисел не то что моноидом,
(коммутативным и/или аддитивным), а даже группой не является.
Поэтому при определении N надо обязательно включить туда ноль, как натуральное число,
хотя натуральным оно и не является (всё-же является, относительно -1, но уже - во множестве Z).
>У любого числа из N нет обратного элемента, в сумме - дающего ноль. А это одно из основных свойств группы.
А у Z - есть. -5 + 5 = 0;
С натуральными числами такое не прокатит, даже если это множество N - включает в себя ноль.
>>55893
Цитата отсюда: https://ru.wikipedia.org/wiki/Моноид#Свойства
>Не каждый моноид можно вложить в группу.
>Например, вполне возможно что в моноиде существуют элементы a и b,
>такие что a×b = a и при этом b не является нейтральным элементом.
Для натуральных чисел, возьмём b = 1, и a = любое число из N, допустим - это 5.
Тогда: a×b = a; (5×1 = 5); при этом (b == 1) и (b !== 0);
Продолжаю цитату:
>Если бы этот моноид являлся подмножеством некоторой группы,
>мы могли бы домножить обе части равенства на a−1 слева
>и получили бы противоречие.
Предположим, что N является подгруппой группы целых чисел Z.
Для N, мы взяли ранее: a = 5; считаем: a-1 = 5^-1 = 1/5.
Это число уже и ни в N и ни в Z - оно во множестве R,
то есть - за пределами и полугруппы N и всей группы Z.
Дальше, продолжение цитаты
>Говорят, что моноид M обладает свойством сокращения, если, для любых его элементов,
>ab = ac => b=c
>и
>ba = ca => b=c.
Для множества натуральных чисел, при a = 1, и различных b и c (b = 2, c = 5),
оба равенства - не выполняются, а следствия вытекающие из них - не соответствуют действительности,
потому что a = 1 - не является нейтральным элементом:
>ab = ac => b=c; 1 2 = 1 5 => 2 != 5, то есть (b != c)
>ba = ca => b=c; 2 1 = 5 1 => 2 != 5; опять же (b != c)
Если для N с нулём - взять a = 0 - нейтральный элемент, и различные b и c,
то равенства тоже не выполняются, а следствия из них - опять же не соответствуют действительности:
>ab = ac => b=c; 0 2 = 0 5 => 2 != 5, то есть (b != c)
>ba = ca => b=c; 2 0 = 5 0 => 2 != 5; опять же (b != c)
Всё это, как мне кажется, означает то, что N, как коммутативный моноид - не обладает свойством сокращения.
Дальше, продолжаю цитату:
>Коммутативный моноид со свойством сокращения можно вложить в группу,
>используя конструкцию группы Гротендика.
Очевидна необходимость для этого - наличия у моноида вышеописанного свойства.
>Это обобщает способ, по которому аддитивную группу целых чисел
>можно восстановить по аддитивной группе натуральных чисел.
Тут я уже не пойму о какой аддитивной группе может идти речь,
в случае с аддитивным коммутативным моноидом - множеством N, ведь это не группа,
а полугруппа абелевой группы, а именно - множества Z.
И хотя любая группа является моноидом, это вовсе не значит, что любой моноид - является полноценной группой.
>У любого числа из N нет обратного элемента, в сумме - дающего ноль. А это одно из основных свойств группы.
А у Z - есть. -5 + 5 = 0;
С натуральными числами такое не прокатит, даже если это множество N - включает в себя ноль.
>>55893
Цитата отсюда: https://ru.wikipedia.org/wiki/Моноид#Свойства
>Не каждый моноид можно вложить в группу.
>Например, вполне возможно что в моноиде существуют элементы a и b,
>такие что a×b = a и при этом b не является нейтральным элементом.
Для натуральных чисел, возьмём b = 1, и a = любое число из N, допустим - это 5.
Тогда: a×b = a; (5×1 = 5); при этом (b == 1) и (b !== 0);
Продолжаю цитату:
>Если бы этот моноид являлся подмножеством некоторой группы,
>мы могли бы домножить обе части равенства на a−1 слева
>и получили бы противоречие.
Предположим, что N является подгруппой группы целых чисел Z.
Для N, мы взяли ранее: a = 5; считаем: a-1 = 5^-1 = 1/5.
Это число уже и ни в N и ни в Z - оно во множестве R,
то есть - за пределами и полугруппы N и всей группы Z.
Дальше, продолжение цитаты
>Говорят, что моноид M обладает свойством сокращения, если, для любых его элементов,
>ab = ac => b=c
>и
>ba = ca => b=c.
Для множества натуральных чисел, при a = 1, и различных b и c (b = 2, c = 5),
оба равенства - не выполняются, а следствия вытекающие из них - не соответствуют действительности,
потому что a = 1 - не является нейтральным элементом:
>ab = ac => b=c; 1 2 = 1 5 => 2 != 5, то есть (b != c)
>ba = ca => b=c; 2 1 = 5 1 => 2 != 5; опять же (b != c)
Если для N с нулём - взять a = 0 - нейтральный элемент, и различные b и c,
то равенства тоже не выполняются, а следствия из них - опять же не соответствуют действительности:
>ab = ac => b=c; 0 2 = 0 5 => 2 != 5, то есть (b != c)
>ba = ca => b=c; 2 0 = 5 0 => 2 != 5; опять же (b != c)
Всё это, как мне кажется, означает то, что N, как коммутативный моноид - не обладает свойством сокращения.
Дальше, продолжаю цитату:
>Коммутативный моноид со свойством сокращения можно вложить в группу,
>используя конструкцию группы Гротендика.
Очевидна необходимость для этого - наличия у моноида вышеописанного свойства.
>Это обобщает способ, по которому аддитивную группу целых чисел
>можно восстановить по аддитивной группе натуральных чисел.
Тут я уже не пойму о какой аддитивной группе может идти речь,
в случае с аддитивным коммутативным моноидом - множеством N, ведь это не группа,
а полугруппа абелевой группы, а именно - множества Z.
И хотя любая группа является моноидом, это вовсе не значит, что любой моноид - является полноценной группой.
 26 Кб, 225x300
26 Кб, 225x300Ящитаю, вы все неправы. Сначала нужно определять R - как непрерывно упорядоченное поле. Существует только одно такое поле. Потом нужно определять индуктивные подмножества в R - такие подмножества, что вместе с каждым x содержат x+1. Множество N - пересечение всех индуктивных подмножеств, содержащих 0.
>Сначала нужно определять R - как непрерывно упорядоченное поле.
Мало того, что множества бесконечны, так ты ещё и непрерывность решил пришпандорить.
Если бесконечность можно ужать на моделях, до какого-нибудь, условного Алеф Нуль,
то вот с непрерывным упорядоченным полем - может возникнуть проблема...
Поясню... Определение этого множества, как поля, и определение аксиоматики в этом поле -
нужно будет не просто формализовать, но ещё и проверить соответствие этого определения -
при помощи формальной верификации.
Однако, здесь, мы имеем дело с непрерывностью,
поэтому оставлю вот это: https://ru.wikipedia.org/wiki/Тезис_Чёрча_—_Тьюринга
>сильный тезис Чёрча — Тьюринга (тезис Чёрча — Тьюринга — Дойча):
>любой конечный физический процесс, не использующий аппарат,
>связанный с непрерывностью и бесконечностью,
>может быть вычислен физическим устройством.
Но постой... А что, если взять определение множества Q?
Тогда, упорядоченное поле тогда - что, будет прерывным?
Ведь если взять бесконечность за условное число א0,
то число 1/∞ = 1/א0 - оно будет ненулевым рациональным числом,
а всё поле - прерывным и дискретным.
Таким образом, определение множества Q, а также свойств его (как группы, или поля, или что там ещё за свойства),
выводимых из аксиоматики - логическим выводом,
это определение должно бы пройти валидацию - в результате той же формальной верификации. Не?
Если так, то всё это, ещё и возможно будет проверить - при помощи вычислительной техники,
обладающей полнотой по Тьюрингу.
>Сначала нужно определять R - как непрерывно упорядоченное поле.
Мало того, что множества бесконечны, так ты ещё и непрерывность решил пришпандорить.
Если бесконечность можно ужать на моделях, до какого-нибудь, условного Алеф Нуль,
то вот с непрерывным упорядоченным полем - может возникнуть проблема...
Поясню... Определение этого множества, как поля, и определение аксиоматики в этом поле -
нужно будет не просто формализовать, но ещё и проверить соответствие этого определения -
при помощи формальной верификации.
Однако, здесь, мы имеем дело с непрерывностью,
поэтому оставлю вот это: https://ru.wikipedia.org/wiki/Тезис_Чёрча_—_Тьюринга
>сильный тезис Чёрча — Тьюринга (тезис Чёрча — Тьюринга — Дойча):
>любой конечный физический процесс, не использующий аппарат,
>связанный с непрерывностью и бесконечностью,
>может быть вычислен физическим устройством.
Но постой... А что, если взять определение множества Q?
Тогда, упорядоченное поле тогда - что, будет прерывным?
Ведь если взять бесконечность за условное число א0,
то число 1/∞ = 1/א0 - оно будет ненулевым рациональным числом,
а всё поле - прерывным и дискретным.
Таким образом, определение множества Q, а также свойств его (как группы, или поля, или что там ещё за свойства),
выводимых из аксиоматики - логическим выводом,
это определение должно бы пройти валидацию - в результате той же формальной верификации. Не?
Если так, то всё это, ещё и возможно будет проверить - при помощи вычислительной техники,
обладающей полнотой по Тьюрингу.
У любой теории, описывающей R, есть счётная модель. Даже несмотря на то, что R несчетно.
Q действительно упорядочено разрывно, любое иррациональное число - разрыв в Q.
Ну так вот вопрос, достаточно ли определить множество Q, чтобы уже из него - вывести определение множества N?
Если множество N (с нулём),
являясь аддитивным коммутативным моноидом,
не может быть вложено в абелеву группу R,
по причине отсутствия свойства сокращения,
и если этот моноид является подмножеством какой-либо группы (не только R),
и если это требует домножения обоих частей равенства
>a×b = a
из поста >>55896
на a-1, где a - произвольный ненулевой элемент,
то очевидно, что a-1 = 1/a ∈ Q.
Значит ли это, что множество N вложено не столько в группу R,
сколько по сути своей - в группу Q?
Ну и соответственно, основной вопрос: Достаточно ли определения множества Q, как группы? Или всё-же - как прерывного поля?
Или нужно выйти ещё дальше, вплоть до определения всего множества Z, именно как непрерывного поля, а не группы?
>Сначала нужно определять R - как непрерывно упорядоченное поле.
Что значит <<непрерывно>> в этом контексте, и почему под это определение не подходит поле $p$-адических чисел.
Да известно уже, кто он.
Кстати, Мунина в прошлом году банили на несколько месяцев. Может кто знает по какой причине?
Да. А почему нет-то? Тебе вот неинтересно?
Конечно. Звучит будто у дедов на форуме локальный конфликт из-за власти произошел. Лидеры интегральных и диффурных группировок борются за власть обладанием форума МГУ.
Интеграл не поделили.
Дался вам этот Munin. Чувак полезным делом занят: ссаными тряпками гоняет дураков, которые возомнили себя галилеями, по территории рунета. Оставьте его в покое.
 100 Кб, 640x640
100 Кб, 640x640Ну, это уже довольно давний и один из немногих случаев. Хотя к слову о говнах, этот бруквалуб мразотнее Манина и стоит дюжины местных обитателей.
>один из немногих случаев.
Так там же чуть ли не каждый третий активный участник забанен пожизненно.
Так то так, но он сам иногда нихуя не знает. Несколько лет назад толтко начал читать алгтоп и уже лезет с ошибками учить других, как считать гомологии. Это из того, что помню я. Может, физик из него и неплохой. Не к лицу быть высокомерным, когда у тебя самого пробелы.
>Несколько лет назад толтко начал читать алгтоп и уже лезет с ошибками учить других, как считать гомологии.
Можешь пример скинуть? Просто это так угарно звучит что захотелось самому взглянуть
 89 Кб, 1080x285
89 Кб, 1080x285Другой анон, но вот например (пик)
У него ещё были посты, где он какую-то андерград чушь говорит в оффтопике
Ну физикам не надо деталей знать, нет проблем, но он же каждой бочке затычка
Как-то походил в это ваше нму, охуел от задачек на алгебре и бросил после третьего занятия.
Быдло
поч
записываться туда не надо, посещение свободное
По поводу сдачи курса, наверно, нужно договариваться индивидуально с преподом
Ну в течение семестра отправляют ведь задачи, на сами экзамены я могу приехать, я живу в 6 часах езды на поезде от Москвы, только что он меня видеть не будет до этого, в обычном вузе на посещения смотрят.
Мне до сих пор стыдно. Писал хуйню в решениях листочков и стеснялся потом сдавать. Как-то брякнул хуйню на семинаре. Хорошо, что прошли года, и про меня забыли.
думаю, на посещения всем наплевать, и если придёшь на экзамен, к тебе номрально отнесутся и позволят сдавать
>>64234
Сейм шит, бро
А ещё тоже на одном курсе под конец набрался смелости и стал что-то брякать. Один раз даже заржали всей группой надо мной. Ладно бы, забыли, так ведь запись в интернете осталась
>А ещё тоже на одном курсе под конец набрался смелости и стал что-то брякать. Один раз даже заржали всей группой надо мной. Ладно бы, забыли, так ведь запись в интернете осталась
Ебать они токсичные, я бы никогда над тобой не посмеялся, /b/ро.
Скримеры посылай.
они вроде были хорошие
мне кажется, они подумали, что я шучу так
отчего мне ещё хуже, по правде
Frequently, in fact, it is conversely true that all herrings are red herrings. This often leads to mathematicians speaking of “non-red herrings,” and sometimes even to a redefinition of “herring” to include both the red and non-red versions.
https://ncatlab.org/nlab/show/red+herring+principle
>Хорошо, что прошли года, и про меня забыли.
Пиздец ты омега. Один раз оступился и с тех пор больше ничего в жизни не пробовал делать. Ору с /math
Полностью поддерживаю.
По мне так это конкретно Бруквалюб туповат. Ред_херринг, не смотря на приличный возраст, иногда вполне внятные вещи говорит, хотя и специалист по матфизике. Многие остальные вообще ок.
Так он же ватник из мгу. Херринг же вроде вообще в Канаде преподаёт, причем насколько я понимаю он выходец из питерской школы матфизиков.
Смысл пиздеть о математике, если можно вкатываться в неё? Я тут года пол посидел, попиздел, а теперь только вопросы иногда задаю, когда не могу нагуглить ничего.
>Смысл пиздеть о математике, если можно вкатываться в неё?
Смысл сидеть на борде, если не пиздеть? Естественно у всех нас есть хобби и это не обязывает сидеть на тематических бордах, но раз ты тут, то хули тут делать-то ещё блядь? Если нужна информация, то есть куда более полезные площадки, чем эта дыра.
Лол, конечно. К тому же, ты подразумеваешь, что пиздеть на двоще автоматически исключает вкатывание. Представь себе, многие двачуют в каком-нибудь транспорте на работу, охуеть же, да - там не то, что карандаш с бумагой, телефон-то еле держишь в набитом троллейбусе. Ну и в 7 утра мозгу не до спектралок.
>Смысл пиздеть о математике, если можно вкатываться в неё?
одно другому не мешает жи
тут некоторын треды годами висят
запостил что-то, что тебе кажется интересным - хоть через год можешь вернуться
как будто обсуждать что-то реально интересное - это многчасовой ежедневный труд
зашел на доску раз в неделю, за одну минуту полистал неприкрепленные треды, еще пара минут на ответы, если захочется - вот и все
но нет, это мешает "вкатываться", что за охуительные истории
>К тому же, ты подразумеваешь, что пиздеть на двоще автоматически исключает вкатывание.
Не подразумеваю, просто если у тебя есть время на двачевание, то почему бы его не потратить на что-то более полезное.
На что, например? Какие нахуй задачи? Типа тысяча и один интеграл? Для решения нормальных задач обычно не требуется сидеть в напряжении за столом и морщить лоб. Часто хорошие идеи приходят во время отвлеченной деятельности: спорта, чтения вской левой хуйни, просмотра кино, прогулок.
>Какие нахуй задачи?
Докажите то, докажите сё. Докажите, что групп порядка 6 только 2. Сидишь, пердишь. Думаешь.
И такое тоже не будешь обсуждать тут, иначе подсказку получишь случайно и удовольствие испортишь. А в спорах уровня конструктивисты против классиков участвовать не хочется. Я просто думал, что и другие аноны точно так же, поэтому и не пишет никто ничего.
Делится на два и на три. Если только одна подгруппа порядка 2, то такая подгруппа нормальна. Если нет, то таких подгрупп 3.
>И такое тоже не будешь обсуждать тут, иначе подсказку получишь случайно и удовольствие испортишь.
Нахуя?
Я сам может и не пиздец сделал, но многие мои знакомые действующие математики высказывали аналогичное мнение. Я не про то что нужно нихуя не делать и ждать озарения, а про то что нужно сначала напряженно читать, а потом ходить думать о прочитанном. Прогресс во второй фазе происходит. У тебя как-то иначе работает?
>>69728
>И такое тоже не будешь обсуждать тут, иначе подсказку получишь случайно и удовольствие испортишь. А в спорах уровня конструктивисты против классиков участвовать не хочется. Я просто думал, что и другие аноны точно так же, поэтому и не пишет никто ничего.
Лично я неоднократно задавал вопросы, которые лично мне казались интересными и нетривиальными, и которые не были ни задачей типа "1001 интеграл", ни доказательством теоремы, ни околофилософскими беседами. Ответа я, кстати, не получил ни на один свой вопрос.
Пример из недавнего - вопрос про косы, искать уже не буду.
Наверное слишком специальный вопрос, не думаю, что тут много кто косами занимался.
Там достаточное количество пучкистов-модулистов, которые просто не пишут десять тысяч сообщений и в дурацкие споры не ввязываются.
Это что пучкисты ведут подрывную деятельность на dxdy тайно, руша dxdy изнутри. Ну прямо как америкосы совок развалили.
Мунин начал изучать модули в конце прошлого года. Пожелаем ему удачи.
ну тогда не надо с него строго спрашивать, я думаю
вкатыш до ленга докатился, правда, только на одну страницу хватило, но хотя бы фамилию выучил
Не просто дед, а ЗАСЛУЖЕННЫЙ УЧАСТНИК dxdy. Собственно, может чуть ли не хуями крыть других участников форума, и ему за это ничего не будет. А если нахамить ему в ответ, то забанят.
Ну и название треда - НАБЕГ НА dxdy Травля и дианон мунина №1
Так что до конца не ясно кто он такой. Не сдеанонили пока.
ну если бы действующий математик такое написал, как там, это был бы кошмар и позор, а если вкатывальщик -- ради бога
>На прикреплённой в конце настоящего сообщения фотографии математическая программа для итогового становления профессиональным математиком.
>Сначала (I этап) все книги Бурбаки, затем Elements of Algebraic Geometry - трактат Гротендика (II этап), затем профессиональные статьи с семинаров Бурбаки с 50х годов до 2000х (III этап, всего там ~1300 статей).
>Что думаете насчёт неё? После изучения этих книг и семинаров можно начать современные математические исследования и проблемы? На какую область математики сделан упор в программе? У меня получится её осилить?
Собственно программа:
Диды не дают проходу первокультурному математику, желающему освоить EGA. ВТОРОКУЛЬТУРЩИКИ ПРОТИВ ГРАТЕНДИКА И БУРБУЛЯТОРОВ ПОШЛИ ДИЛДЫ!!! НЕ ДАЮТ АЛГЕОМ ИЗУЧАТЬ МАТЕМАТИКАМ!!!
>нет, как и вы
Лол
У Мунина классическая спесь головного мозга, что с его-то бэкграундом просто смехотворно
Селёдка хоть математику где-то в штатах преподаёт, а Мунин вообще хуй с горы
проиграл с первокультурщика
шо dxdy хуйня, шо math.
в фундаментальной группе поищи препятствия
В смысле вряд ли? Большой тред был про это на дхду в разделе для ЗУ. Что-то, по-моему, утекло в общедоступные треды.
Жаль ЗУ нету на двощах, хотелось бы слив почитать.
Занятно, благодарю
https://dxdy.ru/topic93474.html
Здесь Мунин спалил свой акк на physics.stackexchange
https://physics.stackexchange.com/users/24124/firtree
В анкете нихуя не написано. Ни длины члена, ни сексуальных предпочтений, ни диаметра очка. Никакой свежей информации(
Написано, что он состоит в комьюнити по японскому языку и аниме с мангой. Мунин анимешник, лол.
>Базоны Ферма - это те кирпичики, из которых строятся степени натуральных чисел. Они наполняют степени "математической массой", определяют их структуру.
>Таким образом, квантовые числа или степени натурального числа представляют собой сумму базонов Ферма для этой степени.
>Для анализа думаю достаточно. Мы видим, что базоны Ферма для чётных и не чётных степеней отличаются, и это является первым намёком на то, что в квантовых числах имеет место нарушение симметрии по чётности т.е. квантовая структура у степеней с чётными и не чётными показателями разная, в то время, как классическая линейная структура симметрична относительно четности показателя степени. Посмотрим - подтвердится ли это в дальнейшем.
Проиграл.
Норм аккаунт кстати, респект мунину.
Чел заслужил.
Пиздец. Там же совок нахуй. Не так ляпнул всё пиздец растрел. Как же хуево быть совком
Знай своё место, быдло. Порядок может быть только при диктатуре. Даже просто законы это диктат. Свободы нет нигде. Веди себя корректно.
То есть ты хочешь делать что угодно, но чтобы за это не били?
Свободы нет нигде, школотрон. Если есть законы, это уже несвобода. Живи по правилам, одинокий социально неадаптированный ссыкун.
эх, сдох блог, только на веб-архиве теперь можно старые посты с ностальгией перечитывать. бля, было время...
да ну и нахуй этого мудака
от его рассказов о том, как он людям сзади головы разбивал с целью грабежа, а теперь весь из себя такой правильный и клёвый, меня жёстко корёжило
Плюсую, жуткий долбоёб.
 103 Кб, 1117x869
103 Кб, 1117x869https://dxdy.ru/topic146572.html
https://dxdy.ru/topic146697.html
Скорее всего просто не до конца понял. Бесконечный список из строк бесконечной длинны - это не совсем интуитивно понятная конструкция. И его нельзя рассматривать как квадрат или как квадратную матрицу. Так что слово диагональ там скорее как метафора. Раньше в принципе в культуре доминировало представление, что актуальная бесконечность - это, блядь, хуита какая-то, так что тут ничего удивительного нет.
 15 Кб, 268x289
15 Кб, 268x289Тут надо человеку что-то про пределы объяснить, но я лично не берусь это сделать.
> В этом доказательстве, по-моему, вообще непонятно, что используется, потому что используются какие-то мистические представления о бесконечности -- я имею в виду представление о матрице, которая при любом конечном $n$ не квадратная, да еще и с ростом $n$ все больше вытягивается по вертикали, а при бесконечном $n$ (еще один мистический момент -- $n=\infty$) вдруг становится квадратной.
Вот непонятно. Может, всё-таки зелёный.
Ну вот ему тоже непонятно, что за зверь такой - актуальная бесконечность. Ты лучше почтай Кравецкого https://22century.ru/popular-science-publications/infinity
Зелёный знает о том, что он зелёный, если ему что-то непонятно, он вежливо просит ему разъяснить. А когда он с остервенением бросается опровергать всем известные и общепринятые основы столетней давности, это он не зелёный, он долбоеб
Кравецкий скучный. Какие-то жалкие попытки переизобрести теорию рекурсии и ультрафинитизм.
 9 Кб, 118x216
9 Кб, 118x216>Зелёный знает о том, что он зелёный, если ему что-то непонятно, он вежливо просит ему разъяснить.
привет из будущего
зеленый значило тролль, а не неискушенный
Жаль, что это шизик на двачах неизвестен. Персонаж-то поехавший похлеще Мицгола. Лет 10-15 назад любил почитывать его ЖЖ.