465 Кб, 1864x2780
465 Кб, 1864x2780Теория множеств ничего не привнесла, просто пересказ того как думали древние греки заумными словами очкариков из престижных университетов. Просто пересказ обычных интуитивных вещей, запихнутых в кванторы с логикой, опять же обычной, просто с апгрейдом в виде обозначений.
Теория множеств ничего не доказывает. Как была основа математики всей интуитивной, она такой и осталась. Просто вместо равно сделали красивое слово «эквивалентно» и вместо чертежей пишут буковки в фигурных скобках. Только пошли дальше и начали сравнивать бесконечности, а родоначальник этой идеи был душевнобольным, о чем это говорит?
>частичный порядок
>там наглядно показывается это на отрезках, как равенство и неравенство соответственно
Частичный порядок бывает не только линейный как на отрезке. Не думаю, что греки думали об этом.
>Теория множеств ничего не доказывает.
Она выступает удобным языком для математических понятий как и теория категорий. Без существования подобного языка было бы трудно формализовать многие теоремы.
>вместо чертежей пишут буковки в фигурных скобках
А как ты собрался рисовать чертежи пространств размерности больше 3?
Спасибо, что разъясняешь мне. Но только учитывай, что я закончил матмех и теоремы сдавал на экзаменах. А нет этих пространств размерности больше трех, они не существуют, поэтому их и не нарисовать. Это даже не пространство это просто пара: Множество+множество его подмножеств - удовлетворяющие трем условиям - опять простой пересказ интуитивных вещей.
Про удобный язык я уже расписал, что это тоже классическая логика , написанная значками (кванторы, импликации и т.д). Вся математическая логика тоже пересказ древнегреческой логики.
Про удобство языка я и не говорил, они как раз полезны. Я говорю про весь этой бред с ординалами, кардинальными числами, континум и прочий бред.
> весь этой бред
Так грекоинтуитивные вещи взяты за аксиомы, а весь этот бред просто следствие грекоинтуитивных аксиом. Ты предлагаешь отказаться выводить следствия, мол, вот до сюда мы идём, а дальше не идём или что? Да и равенство не то же самое, что эквивалентность, более общее понятие, математика вообще со времён греков по пути обобщения понятий и идёт, довольно естественное стремление по моему, хуй знает, короче, не понял твоего посыла.
Если эквивалентность не то же, что и равенство, то что оно тогда? Что тебе напоминают эти три условия того, что можно назвать эквивалентностью:
1) рефлексивность
2) симметричность
3) транзитивность
Это равенства отрезков в книге «Начала».
Теорию множеств преподносят, как формализация математики, где нет места интуиции. Но все определения, идеи, они взяты с интуиции, у них нет доказательств и не будет.
А мой посыл вот какой: теория множеств наебалово. Утверждается, что всё из математики строится только из аксиом теории множеств, но определения внутри этой теории содержит все аксиомы, которые так и не доказаны внутри неё. Никакой формализации математики в 20 веке так и не произошло, как с гордостью заявляют те балбесы, вроде Гильберта со своей программой (заметь что у Гильберта сын родился психически нездоровым, высокая вероятность что и сам Гильберт был нездоров, но скрывал это, а он был предводителем этой армии формализаторов). Они так и не доказали начала арифметики, более того внутри своей же тупой теории они и доказали это сами. Гёдель это сделал, тоже душевнобольной.
>то что оно тогда?
Оно, внезапно, эквивалентность, т.е. что какие-то вещи относятся к одному какому-то виду вещей(классу эквивалентности), равенство это две вещи совпадают. Не одно и то же.
Ну да не одно и то же. А как фактор множества разбивают на классы? Именно так и понимают, что в множествах лежат одни и те же объекты, в смысле равенства.
>родоначальник этой идеи был душевнобольным, о чем это говорит?
Не на момент создания теории. Дедекинд к ней тоже руку приложил, не один Кантор всё делал. Дедекинд здоровым был.
>Гильберта сын родился психически нездоровым
Гильберт основаниями занялся уже под конец жизни, лет в 70. Он работал в теориии инвариантов изначально, после 35 перешел в теорию чисел, в 47 начал заниматься функциональным анализом в 47, а в 50 физикой.
>Гёдель это сделал, тоже душевнобольной
Еще и еврей помойму! Как и Кантор с Гильбертом.
>Но все определения, идеи, они взяты с интуиции
Да.
>них нет доказательств и не будет
А у чего есть "доказательства" в твоем понимании данного слова? У бессмысленных тавтологий, а дальше это:
https://en.wikipedia.org/wiki/Infinite_regress
> в множествах лежат одни и те же объекты, в смысле равенства.
Мне такой взгляд на эквивалентность чужд, похожие объекты, да, но не равные.
>лемму Цорна
>трансфинитную индукцию
Тащемта довольно интуитивные понятия, доказать не смогли бы, конечно, но оспаривать бы тоже не стали.
>классификацию бесконечных мощностей
Ну тут да.
У меня стандартное понимание доказательств. Я поддерживаю аксиомы Пеано. Но то что теория множеств претендует какую-то роль на обоснование начал математики, абсурд. Там создается видимость, что нет порочного круга, а он в каждом определении (типа, если прямыми словами, не сказано, то так не считается). В конечном итоге я все равно должен принять определения на веру, что они имеют смысл.
Дедекинд как раз был полностью адекватным, он и действительные числа отождествлял чисто с прямой. Свое определения бесконечных множеств полностью преподносил, как абстрактные. А Кантор всерьез охуевал, когда находил биекцию двух множеств и думал, что он считает дальше бесконечности. Он здорово бесил Кронекера этими высерами, который более адекватно смотрит на арифметику целых чисел.
Вот моя тема и об этом. Трансфинитная индукция, ординалы, аксиомы выбора - всё это говно.
>>535
Потому что Дедекинд построил наивную теорию множеств, а ординальную арифметику уже развил Кантор. Кронекер вообще многими считается первым конструктивистом.
>конечном итоге я все равно должен принять определения на веру, что они имеют смысл
Так это с любыми определениями так. Сначала область интенсивно развивается, потом подводятся аксиомы под уже сложившуюся ситуацию. С гомологической алгеброй так же. Таким образом аксиомы в известной степени обосновываются своими результатами в той же мере, в какой практика на акстомы ссылается. Порочный круг или нет решай сам.
>Но то что теория множеств претендует какую-то роль на обоснование начал математики, абсурд
А так никто и не считает. Математике основания не нужны, читай Манина.
В самой же теории множеств Кантора результатов, применимых в остальной математике крайне мало и ни для какого математика изучение её не является необходимым, кроме 2-3 людей, работающих в этой области. Но такое про многие разделы математики можно сказать.
>Тащемта довольно интуитивные понятия, доказать не смогли бы, конечно, но оспаривать бы тоже не стали.
Они интитивные в рамках современных представлений. Греки существовали в другом понятийном контексте и ничего подобного не рассматривали.
>Вот моя тема и об этом. Трансфинитная индукция, ординалы, аксиомы выбора - всё это говно.
Пока ты работаешь с математическими объектами не сложнее индивидуальных непрерывных функций, то можно все это игнорировать. Если же перейти, скажем, к функциональному анализу, это все становится весьма важным.
Что важным, что ординалы берутся в качестве индексов? Это говно посмотрел и забыл.
Помощь анализу идет из топологии.
Именно что равные в точности смысле этого слова. Но как будто бы смотришь на это по-другому. Подчеркиваю как будто бы. Отношения эквивалентности типа гомеоморфизма и прочая поеботина бесполезная хуйня.
>Что важным, что ординалы берутся в качестве индексов?
Если ты про греков, то они не знали про ординалы и вообще не работали с бесконечными объектами. Ну а так если дойти до такой абстракции то дальше все, конечно, полностью интуитивно.
>Помощь анализу идет из топологии
В которой, наверное, не используется такая экзотическая вещь как аксиома выбора.
>Отношения эквивалентности типа гомеоморфизма и прочая поеботина бесполезная хуйня.
Гомоморфизм тоже хуйня?
Вообще-то она используется. Стоят пометки в теоремах AC, когда её юзают. И она же приводит к строго доказанной теореме что из одной сферы можно получить две, причем вторая будет с идентичной метрикой (одного размера короче говоря, что в реальности не бывает).
А что такое ординалы? Это типа даже бесконечности считаешь, но точно также: к следующему числу прибавляешь единицу. Бредятина, чтобы восполнить то что действительные числа нельзя индексировать натуральными. Но само существование ординалов доказывает, что действительные числа можно вполне упорядочить, то есть каждое подмножество будет иметь минимальный элемент, что бред.
Еще какая хуйня. Она была создана чтобы можно было считать что дроби со знаменателем представляют целые и натуральные. Я напишу 5/1 и не буду задумываться, что это был образ из Z который передал свою структуру.
Изоморфизм тем более хуйня, получается, мало того, что гомоморфизм, так ещё и отношение эквивалентности?
Я про изоморфизм и сказал. Он да - дикая хуйня. Имеет прямое отношение к кардинальным числам, как нижним сегментам ординалов.
>Вообще-то она используется.
Кажется, мой сарказм оказался непонят, ну да ладно.
>И она же приводит к строго доказанной теореме что из одной сферы можно получить две, причем вторая будет с идентичной метрикой (одного размера короче говоря, что в реальности не бывает).
Еще без неё нельзя доказать теорему Тихонова, построить компактефикацию Стоуна-Чеха и т.д.
>А что такое ординалы?...
Трансфинитная индукция и ординалы за пределами логики действительно используются довольно редко. Но вполне бывает, например для построения алгебраического замыкания поля произвольной мощности или для доказательства свойств борелевской сигма-алгебры трансфинитной индукцией до omega_1.
ммм картофанчег
> действительные числа можно вполне упорядочить
Любое множество можно вполне упорядочить по АС, ну я хз, отказывайся от АС, тогда даже то, что любые два множества по мощности сравнимы, доказать не получится по идее.
А впрочем может ZFC на самом деле противоречива, тогда всё на места становится.
Просто вот как от неё отказаться, ну ок, теорема Цермело действительно нифига не интуитивна, но есть другие эквивалентные АС утверждения, которые очень уж интуитивны, например что прямое произведение непустых множеств непусто или что для любого бесконечного множества существует биекция между ним и его декартовым квадратом. От этого ведь тоже придётся отказаться.
Не все множествы построены на отношениях.
И какие не построены?
 1 Мб, 1468x1129
1 Мб, 1468x1129> Математике основания не нужны, читай Манина.
Это Панину твоему основания не нужны, а не математике. Потому что он занимается очень малой частью прикладной околоматематики. То же самое, Греф вскукарекнул, что ему не нужны программисты. Из чего никак не следует, что программисты не нужны банковской сфере. Они не нужны только грефовскому наебанку. Чувствуешь разницу?
 452 Кб, 1920x1148
452 Кб, 1920x1148>Потому что он занимается очень малой частью прикладной околоматематики
https://arxiv.org/search/?searchtype=author&query=Manin,+Y+I
https://genealogy.math.ndsu.nodak.edu/id.php?id=44207
https://www.mpim-bonn.mpg.de/node/99
Очень малой частью прикладной шизофрении занимались твои кумиры Брауэр и Лёф. Последний вообще не математик.
Манин же занимался в разное время практически всем, вычислимостью тоже. Не выставляй себя и свой воинственный идиотизм на посмешище, уйди отсюда лучше.
 96 Кб, 900x800
96 Кб, 900x800Ого, да это же сам множества-господин нас навестил. Давно не виделись ;)
> Очень малой частью прикладной шизофрении занимались твои кумиры Брауэр и Лёф. Последний вообще не математик.
Что же тогда на твоей картинке HoTT делает прямо рядом с гамалогиями? Это ты слепой пиздабол или авторы твоей картинки?
Это ты слепой. Гомологическая алгебра там ровно в центре. Потому что она применяется везде: в теории представлений, алгебраической геометрии, дифференциальной геометрии, алгебраической топологии, функциональном анализе.
Конструктивизм и вычислимость ни в одной из этих областей не применяются, о чем тебе уже говорили на конкретных примерах.
Так что твоя параша есть в лучшем случае периферия, смирись или продолжай отрицать.
Доказательства бывают разные, не только явное построение и перебор, это самые примитивные примеры. Прочитай на википедии что такое доказательство. Пример из школьной программы:
У тебя есть конструктивное определение функции, например как закона соответствия. Пространство таких функций не полно. Пространство интегрируемых по Лебегу функций, к примеру, полно. То есть там есть все функции, а не только конструктивно определяемые явной формулой или еще как. Поэтому у меня сразу все строго и я могу брать интегралы, а тебе еще надо доказать их существование.
В математике строгость ортогональна конструктивности или вычислимости. В твоём манямирке это не так, и 95% того что на картинке выкидывается на помойку, а математика в твоем понимании это бесполезная гуманитарная хуйня типа формальной логики у которой ноль внешних приложений. Так что иди палочки перекладывать в песочнице с другими "математиками" из ясельной группы.
В твоей вычислимой математике нельзя даже числа сравнивать, нахуй она нужна вообще? Допустим, есть алгоритм, который сравнивает вычислимое число x с каким-то числом, например 5, допустим он вычисляет x всё более точно, получается что-то типа 5.0000000...(n нулей), и наконец решает, что они равны и выдаёт ДА.
Нет никакой гарантии, что через n+1 шагов алгоритм, вычисляющий x не выдаст 5.0000000000...000000000001.
Я ничего не приписывал, просто говорю, что в вычислимой математике нельзя даже числа сравнивать, настолько это хуйня без задач.
В том смысле, в каком ты написал, числа нельзя сравнить ни в какой вообще математике. А в том смысле, в котором числа можно сравнить в неконструктивной математике, ровно это же возможно и в конструктивной.
>числа нельзя сравнить ни в какой вообще математике
Если не опираться на понятие алгоритма, то можно, а в конструктивной числам соответствуют алгоритмы, их вычисляющие, поэтому нельзя узнать равны ли два числа, ещё нет алгоритма, который выдаёт да, если x < a и нет, если x >= a, только если заведомо известно, что числа неравны, можно сказать какое больше, а какое нет. Короче, конструктивная математика это каличная матеша))
> в конструктивной числам соответствуют алгоритмы, их вычисляющие, поэтому нельзя узнать равны ли два числа,
Хуйню не неси. Числа это числа, алгоритмы это алгоритмы. 1:N или 1.0:Double это не алгоритмы.
> Короче, конструктивная математика это каличная матеша))
Свою каличность на конструктивизм не перекладывай.
>В том смысле, в каком ты написал
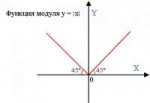
Ну вот функция модуля,
f(x) = x, если x >= 0, -x, если x < 0
в обычной математике мы можем с ней работать, в конструктивной она будет невычислима, лол. Каличная матеша.
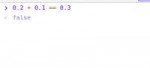
Натуральные числа это конструктивный объект? Рациональные числа это конструктивный объект? Целые числа это конструктивный объект? Для каждого конструктивного объекта должен существовать алгоритм, их строящий. Короче, можно как в компах, ограничиться точностью какой-то и не париться, но тогда точно так же как в компах 0.2 + 0.1 == 0.3 будет false. Такую математику оставь себе.
А для вещественных чисел смотри wiki: computable number.
> точно так же как в компах 0.2 + 0.1 == 0.3 будет false.
Это ты пистон как прувер используешь? Гениально, апплодирую стоя.
Я ж написал, если по честному, то вычислимая функция, сравнивающая вычислимое число с каким-то заданным числом, не будет всюду определена, можно вычислять с какой-то точностью, но тогда будут вот такие приколы, там плюсы, жс и питон на скринах, ну и такая математика это говно.
А ты из тех, для кого и аксиомы поля аксиомы?
Да что вы за козлы такие. Мальчика сломали и теперь он решает тавтологические задачи.
Равенство - это самое дробное отношение эквивалентности. Просто для равенства классы эквивалентности тождественны самим элементам. Это, блядь, знать надо, неучи.
>Просто для равенства классы эквивалентности тождественны самим элементам
>равенство это две вещи совпадают
Ну а я что сказал? Равенство это отношение эквивалентности, но не каждое отношение эквивалентности это равенство, не одно и то же.
Да и вообще, разговор как раз и был о том, что эквивалентность обобщение понятия равенства, понятие равенства появилось до понятия эквивалентности, уже потом его обобщили до эквивалентности, ну и это не то же самое, что и равенство.
 17 Кб, 1689x43
17 Кб, 1689x43>эквивалентность и есть равенства.
Нет. Взять хотя бы эквивалентность множества людей по полу. Почему людей 7 млдр, а классов эквивалентностей все два - мужской и женский?
Или же социальные классы. Пролетариаты, буржуазии там всякие.
>вы тупые.
Нет, ты.
>1/2 = 2/4 вот как пишут, а не так 1/2 ~ 2/4.
Под дробью понимают класс эквивалентностей. 1/2 и 2/4 лежат в одном классе. Сравниваются сами классы.
Открываем википедию
https://ru.wikipedia.org/wiki/Кольцо_частных
Вообщем, узнай для начала построение рациональных числе из целых.
А этот класс эквивалентности и есть равенство!
>Вообщем, узнай для начала построение рациональных числе из целых.
я еще их в первом классе построил, а 0 у меня был двусторонний идеал!
>А этот класс эквивалентности и есть равенство!
Нет. Пары эквиваленты, но не равны. Состоят из разных элементов.
(1,2)~(2,4) но (1,2) не равно (2,4).
Или пример с людьми. Два мужчины имеют однинаковый пол, но это не означает, что они идентичны. Один из них может быть рыжый, а другой блондин. Или два представителя буржуазии могут иметь разные фабрики одна по производству хлопьев, другая бензина.
И таких примеров можно привести множество, сорри за каламбур.
Если примеры со "скобками" тебе не ясны, рассмотри другие. Они легче для понимания, и показывают различие между равенством и эквивалентностью наглядней.
Я понимаю, что ты отослал к "почти всем элементам бесконечного множества", но ведь множество математиков не бесконечное.
9 из 999 это тоже все, за исключением конечного числа
Если не коммунист, то идиот. Математика не нужна рыночку. Потому платить яйцеголовым при свободном рынке никто не будет. Разве что какой-нибудь меценат выделит немного денег раз в десятилетие для 5-6 человек, кек.
С этой стороны пучкист прав, что первый математик это Дедекинд и его современники. В прошлом все математики занимались чем-то дополнительно.
>Если не коммунист, то идиот
Но ведь есть математики-пифагорейцы, которые считают, что надо в пещеры уйти и аутировать над сакральным знанием там в эзотерических культах.
Так да. Более того, мне кажется это зависит от общего количества человеческой популяции например. Выше население, выше специализация. Если население не превосходит миллиарда, как это было до 1800-х, математика просто никому не будет нужна как самостоятельная область. Сейчас в мире например защищается примерно 4000 кандидатских диссертаций по математике ежегодно, это при населении 7.5 млрд. В далеком будущем с конвертированием всех планет солнечной системы в материал для постройки цилиндров О'Нилла и прочих rotating habitats и постепенным заполнением улея Дайсона на орбите вокруг Солнца, возможно будет общее население в 200-300 трлн человек, согласно оценкам футуристов. Тогда под любую самую незначительную проблему в математике найдется миллион желающих заниматься ей, и соответствующее финансирование тоже найдется.
А в обществе конца XVI - начала XVII века с населением Земли в районе 500 миллионов было бы странно ожидать что кто-то будет заниматься эксклюзивно математикой. Дезарг архитектор, Паскаль и Декарт философы, Лейбниц и Ферма юристы, Бернулли физик. Дедекинд уже в 1860-х был одним из первых профессиональных математиков.
Есть кстати такая книга, The First Professional Scientist: Robert Hooke.
>Если не коммунист, то идиот
А я не хочу коммунизм, там заставят пользу приносить, интегралы считать под картофан и водофку за еду, ракеты строить, а откажешься сошлют в Сибирь. При капитализме, конечно, тоже за еду, но хоть занимаешься тем, что нравится.
В смысле шизаны? Конкретизировать свои претензии можешь?
Во первых, в ссср не было коммунизма. Во вторых, в 60-х в том же МГУ занимались чем хотели. В третьих, во время войны и на западе считали интегралы первокультурщики.
Университеты получают деньги от государства. При свободном рыночке ты будешь получать деньги как раз ради разработки всякого говна, чтобы айфон быстрее работал.
Ломают себе мозг кривыми прямыми, нетрадиционной геометрией и прочим. Это нельзя осмыслить, это можно только зазубрить уходя от здравого смысла.
Только перед этим они вдоль и поперёк изучат реальный мир.
Меня больше бесят авторы учебников. Эти петухандрэ оставляют в качестве упражнения задачи, над которыми трахались 2000 лет.
>петухандрэ
Так в этом фишка, тебе предоставляют концептуальный котекст в рамках которого серьезные достижения за которые бились предшествующие поколения математиков оказываются просто упражнениями.
Ты что думаешь, они из благих побуждений оставляют упражнения? У упражнений в книге две функции - просто сказать, что доказательства не будет в книге, дабы её не сделать слишком толстой, ибо никто её не купит, во вторых чтобы усыпить бдительность читателя, мол не моя книг хуйня, это ты дурак.
Маклейн, которого ты упомянул, во время войны занимался прикладными вещами для военных, если что.
И зачем ты Лерэ упомянул? Был бы он в штатах, то сидел бы рядом с Маклейном и интегрировал, скорее всего.
Так раньше не было многих инструментов. Сейчас есть, и с помощью них легко доказывать то, над чем бились раньше кучу лет.
Например пифагоровы тройки. Сейчас ты без труда сможешь выписать их всех, используя комплексные числа или аг.
Что тебе дает знание, что есть инструменты, если автор в книге не покажет их?
Будешь пробовать доказывать даже простейшую теорему, не будешь знать, что ты не рассмотрел все случаи (например).
Книги нужны, чтобы дали мощную теорию и познакомили с доказательствами всех важных вещей. Ладно, можно пропустить некоторые доказательства, но как минимум теоремы сформулировать правильно и все другие док-ва какие есть доказывать строго, а даже этого в большинстве книг нет. Возьми учебник по матану Кудрявцева - это пиздец чё он творит.
И вообще в наше время когда есть программирование и интернет будет полезнее выпустить книги с решениями упражнений, чем создавать книгу с упражнениями. Почему никто так не делает? Потому что суки все.
Лере тоже занимался прикладными вещами для военных, но в плену перестал, видимо не хотел помочь противнику.
То есть публикации первой статьи по теории категорий никакая работа не предшествовала, статья сама написалась?
Были наработки до войны. Думал о ней на толчке и перед сном во время войны.
Ты будешь что ли отвергать, что Маклейн занимался прикладными задачами во время войны?
Зависит от книги. Если в упражнение вынесено что-то до чего подавляющее большинство потенциальных читателей книги не догадаются, то это действительно не очень. Но если в упражнение, выносятся нецентральные с точки зрения учебника, но интересный результат, идея доказательства которого легко восстанавливается, то это очень хорошо и правильно.
Что я терпеть не могу, это когда долго расписывает нудные детали за которыми теряются содержательные идеи.
А как же учебники состоящие только из упражнений? Тот же Глазман-Любич?
Хуя блатной учебник, схоронил.
Ну а Ньютон имел собственную алхимическую лабораторию, толковал священное писание и вообще казначеем был. Кого волнует эта побочная активность? Лабрюйер в "Характерах" где-то писал, что мы часто подражаем великим людям в их недостатках. Ну типа дед с dxdy подобен Маклейну в этом смысле, оба брали интегралы.
Как вот можно считать дальше натуральных чисел? Это изначально ясно, что бред. Если нужно показаться умным, то можно хоть анализом заняться, но это говнище мало того, что легкое, так оно и не нужно никому. Почему в нормальный универ не брали? Потому что аутировал над этой херней - ни сложности, ни мысли в ней нет.
не брали в универ Кантора*
Пятитомный высер, который еще и зрение посадит? Ты чё охуел?