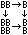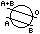https://pastebin.com/96XPBCEs
Если найдёте ошибки или
возникнут вопросы --- пишите.
Определения:
$a^b = b^{-1}ab$
$[a,b] = a^{-1}b^{-1}ab$
Мы используем "правонормированные" коммутаторы.
В тождествах с "левонормированными" коммутаторами
надо использовать сопряжение слева, а не справа
(что трудно записать в компьютерном тексте),
а так же группировать кратные коммутаторы влево:
$[[ , ], ]$, а не вправо: $[ ,[ , ]]$.
Эквивалентная характеризация:
$ab = ba^b$
$a[a,b] = a^b$
$ba[a,b]=ab$
$abc = (bc)a^{bc}$
$abc = ba^bc = bc(a^b)^c$
=> $a^{bc} = (a^b)^c$
$abc = c(ab)^c$
$abc = acb^c = ca^cb^c$
=> $(ab)^c = a^cb^c$
$[a,b]^{-1} = [b,a]$ (кососимметричность)
$[a,b]^g = [a^g,b^g]$ (функториальность)
$a[a,bc] = a^{bc} = (a^b)^c = (a[a,b])^c
= a^c [a,b]^c = a[a,c][a,b]^c$
=> $[a,bc] = [a,c][a,b]^c$ (дистрибутивность)
Обращением получаем: $[bc,a] = [b,a]^c [c,a]$.
Подставив в первое $b=c^{-1}$, получаем:
$[c,a] = [a,c^{-1}]^c$.
Лёгкое тождество Якоби:
$a(bc)[bc,a] = (bc)a$
(циклическая перестановка $(a,b,c)$).
Поэтому: $abc[bc,a][ca,b][ab,c]=abc$
=> $[bc,a][ca,b][ab,c]=1$.
Тяжёлые тождества Якоби (тождества Холла и Холла-Витта):
$a^b[a^b,[b,c]] = (a^b)^{[b,c]} = a^{b[b,c]} = a^{b^c}$
$[ ] := [a^b,[b,c]] = [a^b,[c,b^{-1}]^b] = [a,[c,b^{-1}]]^b$
$bca^b[ ] = bca^{b^c} = cb^ca^{b^c} = cab^c$
(циклическая подстановка $(a,b,c)$)
Поэтому:
$[a^b,[b,c]] [b^c,[c,a]] [c^a,[a,b]] = 1$
(тождество Холла)
$[a,[c,b^{-1}]]^b [b,[a,c^{-1}]]^c [c,[b,a^{-1}]]^a = 1$
(тождество Холла-Витта).
Определения:
$a^b = b^{-1}ab$
$[a,b] = a^{-1}b^{-1}ab$
Мы используем "правонормированные" коммутаторы.
В тождествах с "левонормированными" коммутаторами
надо использовать сопряжение слева, а не справа
(что трудно записать в компьютерном тексте),
а так же группировать кратные коммутаторы влево:
$[[ , ], ]$, а не вправо: $[ ,[ , ]]$.
Эквивалентная характеризация:
$ab = ba^b$
$a[a,b] = a^b$
$ba[a,b]=ab$
$abc = (bc)a^{bc}$
$abc = ba^bc = bc(a^b)^c$
=> $a^{bc} = (a^b)^c$
$abc = c(ab)^c$
$abc = acb^c = ca^cb^c$
=> $(ab)^c = a^cb^c$
$[a,b]^{-1} = [b,a]$ (кососимметричность)
$[a,b]^g = [a^g,b^g]$ (функториальность)
$a[a,bc] = a^{bc} = (a^b)^c = (a[a,b])^c
= a^c [a,b]^c = a[a,c][a,b]^c$
=> $[a,bc] = [a,c][a,b]^c$ (дистрибутивность)
Обращением получаем: $[bc,a] = [b,a]^c [c,a]$.
Подставив в первое $b=c^{-1}$, получаем:
$[c,a] = [a,c^{-1}]^c$.
Лёгкое тождество Якоби:
$a(bc)[bc,a] = (bc)a$
(циклическая перестановка $(a,b,c)$).
Поэтому: $abc[bc,a][ca,b][ab,c]=abc$
=> $[bc,a][ca,b][ab,c]=1$.
Тяжёлые тождества Якоби (тождества Холла и Холла-Витта):
$a^b[a^b,[b,c]] = (a^b)^{[b,c]} = a^{b[b,c]} = a^{b^c}$
$[ ] := [a^b,[b,c]] = [a^b,[c,b^{-1}]^b] = [a,[c,b^{-1}]]^b$
$bca^b[ ] = bca^{b^c} = cb^ca^{b^c} = cab^c$
(циклическая подстановка $(a,b,c)$)
Поэтому:
$[a^b,[b,c]] [b^c,[c,a]] [c^a,[a,b]] = 1$
(тождество Холла)
$[a,[c,b^{-1}]]^b [b,[a,c^{-1}]]^c [c,[b,a^{-1}]]^a = 1$
(тождество Холла-Витта).
>ЛЕММА УРЫСОНА
В указанной формулировке неверна
>Вложим белое множество в чёрное, затем чёрное в белое и так до бесконечности (рис. 1), после чего применим отображение к чёрным слоям, а остальное оставим на месте.
Пиздец
Как памятка мб и норм, я сразу понял, о чём речь.
Матрицу, определитель которой должен оказаться нулём, можно интерпретировать
как матрицу, элементами которой являются коммутирующие эндоморфизмы. Если
умножить её на строку, элементами которой являются базисные векторы, то
получится нулевая строка. Домножив это равенство справа на присоединённую
матрицу, получим, что определитель (который является эндоморфизмом) зануляет
базисные векторы.
Не обязательно было использовать базис, матрицу преобразования можно записать
в любых образующих и умножить на строку из этих образующих.
У меня тоже такое есть, но я никому не покажу!
 51 Кб, 790x624
51 Кб, 790x624Добавил теорему Пуанкаре-Биркгофа-Витта.
Доказательство из книги Серра об алгебрах Ли, только там он, вроде бы, неясно проговаривает предположение индукции.
Отправил 50 рублей.
 970 Кб, 2048x1147
970 Кб, 2048x1147Кстати, вспомнил, где я видел эту теорему Архимеда.
Пикрелейтед, "мера Сато-Тейта", --- это ведь это и есть?
Добавил теорему Джекобсона о плотности.
Всё в LaTeX.tex. Картинки записаны текстом в METAPOST.
Компилирую это всё онлайн на https://www.overleaf.com
Или ты имеешь в виду старые пиксельные? Это GIMP, но наверное что угодно подойдёт.
METAPOST похоже то что мне нужно, спасибо. Про твой вопрос о векторных полях: я его не совсем понял если честно, экспонента берётся у тебя не от векторного поля. а от "преобразования" (оператора) ровно как у тебя и написано. Как ты правильно заметил, так можно определить взятие целой функции от любого элемента в любой банаховой алгебре (= C-алгебре с нормой, полной по норме). Это по-учёному называется holomorphic functional calculus.
>Про твой вопрос о векторных полях: я его не совсем понял если честно
Не важно, не актуально уже.
>Натуральные числа, представимые в виде суммы двух квадратов
Напомнило мне, смотрел одно видео о жизни и творчестве Эйлера, довольно интересное, там была ссылка на архив его работ, которых не счесть.
http://eulerarchive.maa.org/
Наугад ткнул в одну и увидел там такую красотулю.
Добавил сумму геометрической прогрессии и конструкцию Лиувилля трансцендентных чисел.
Хуита.
Подправил за бесплатно. А самое хуевое то что 99% литературы сейчас пишутся ровно по такому принципу - как хуевенько сбитая выжимка разных охуительных историй до которых горюшко-автор сумел дотянуться. И вот ты читаешь-читаешь и вообще нихуя не понятно. Как результат был достигнут, как вообще ко всему этому пришли и для чего это надо, овердохуя деталей до которых тебе предлагают додуматься самому. Ты открываешь другую книгу, вторую, третью - но там все то же самое, абсолютно то же самое.
>овердохуя деталей до которых тебе предлагают додуматься самому.
А тебе всё разжуй и в рот положи. И упражнения ещё с ответами и решениями чтобы, да? От такого обучения толку почти 0.
![Screenshot2019-05-09 Lorentz-invariant phase space for 2- 2[...].png](/math/big/thumb/52498/15573996821880s.jpg) 2 Кб, 537x38
2 Кб, 537x38>Это не учебник, а памятка.
Хуя се а я и не заметил
>>53209
>Лекции смотреть не пробовал, умник?
Не по всем интересующим меня вещам есть. К тому же гораздо быстрее и удобнее было бы прочитать то что оформлено в текстовом виде. Но вот ведь какая хохма - когда автор берется переложить свои мысли в письменный вид на него будто нападает какое то психическое расстройство - половина выкладок идет нахуй, важные заметки сказанные по ходу лекции идут нахуй, но бля... чет текста маловато получается - надобно его разбавить водой и добавить еще дополнительных глав. Такая то пушка.
>>53211
>А тебе всё разжуй и в рот положи. И упражнения ещё с ответами и решениями чтобы, да? От такого обучения толку почти 0.
Говно в голове, мышление искалеченного учебной дедовщиной.
На пикриле терминальная стадия например. Ох и припекло у меня. Чувак, тебе задают вопрос -
>ну не знаю... как бы я не объяснил через чур понятно, какбы чего не вышло.
может дойти до
>Я придумал тут одну теорию - но рассказывать ее никому не буду, ведь все и так ясно, а вам пидорасам подумать не помешает.
inb4 ты не понимаешь по англицки он совсем не то написал ко-ко-ко-ко-ко-кукареку
>>53212
>Даже не пытаюсь написать учебник
Это правильно
>Тем более не может быть претензий.
Просто наболело, это не к тебе лично претензия, попробуй прочитать внимательнее. По поводу же твоей памятки я выразил свое мнение первым словом. Тебе уже писали оценки в треде, ну и я решил добавить свое мнение для статистики.
>Хочешь лучше --- напиши сам.
Утютютю.
>И вот ты читаешь-читаешь и вообще нихуя не понятно.
У тебя просто хуёвый мозг, бывает. Заметки эти, очевидно, не для таких как ты.
Ну все, перданул - полегче стало?
Если тебе все понятно что ты читаешь то значит ты сидишь на уровне кашки для даунов типа заметочек в итт треде и не пытаешься даже с него рыпаться.
>Если тебе все понятно что ты читаешь то значит ты сидишь на уровне кашки для даунов типа заметочек в итт треде и не пытаешься даже с него рыпаться.
>>53197
>А самое хуевое то что 99% литературы сейчас пишутся ровно по такому принципу - как хуевенько сбитая выжимка разных охуительных историй до которых горюшко-автор сумел дотянуться. И вот ты читаешь-читаешь и вообще нихуя не понятно.
Так ты определись --- понятно или непонятно.
>>53219
>Просто наболело
Сри в другой тред.
Такие заметки, очевидно, полезны только одному человеку – тому кто их составил.
>очевидно
Для меня это было неочевидно. Что, совсем ничего не понятно? Или имеется в виду что-то другое?
>Так ты определись --- понятно или непонятно.
Определился уже
>Сри в другой тред.
Лучше буду срать тебе в ротешник.
>>53303
В заметках очень сжатое изложение. Ты подчеркиваешь те моменты, которые лично тебе были непонятны и пропускаешь другие до которых, по твоему мнению, легко догадаться. То есть в случае другого человека может оказаться иначе, начальные знания ведь могут быть другие. Я даже уверен, что более половины отписавшихся не понимают львиную долю того что ты написал, но хвалят за effort. Я с ними соглашусь тоже.
Сделал (в разделе "Элементарная геометрия и топология").
Сравните, где понятнее, --- у меня, или у Бугаенко:
https://mccme.ru/free-books/dubna/bugaenko.pdf ?
Это какая-то хуйня комбинаторноолимпиадная. Лучше б этого другого хуя на В про строение полупростых алгебр нормально изложил.
>Это какая-то хуйня комбинаторноолимпиадная.
Ну, есть много теорем такого типа: "Теоремы типа Рамсея":
https://www.ihes.fr/~gromov/wp-content/uploads/2018/08/problems-sept2014-copy.pdf
>Лучше б этого другого хуя на В про строение полупростых алгебр нормально изложил.
Доказательство в книге Шафаревича "Основные понятия алгебры" мне нравится.
Стараюсь не использовать ничего, кроме базовых тавтологий, то есть вещей, которые надо не доказывать, а осознавать.
>>53304
>Я даже уверен, что более половины отписавшихся не понимают львиную долю того что ты написал, но хвалят за effort.
Серьёзно? Хотелось бы знать, что конкретно непонятно.
К тому же можно задавать вопросы ITT, постараюсь ответить.
1) воздержаться от оценочных суждений вроде "не трудно доказать что...", "легко видеть что..."
2) в качестве познавательного упражнения все высказывания вида "очевидно что Х" заменить по формуле "Х непосредственно следует из У поскольку З"
3) больше определений богу определений - каждый термин должен быть определен
extra - выложить это где-нибудь, хуй знает где но только не на меге, уж больно мозгоебно
Доказательство. Убедитесь в этом сами.
пушка
>опечатка в 9.8.1 должна быть лямбда в кубе вместо единицы
Спасибо.
>Доказательство. Убедитесь в этом сами.
>пушка
Написал кое-что. Смысл этой заметки состоит в том, чтобы не использовать нумерацию множества переменных и показать, что количество переменных нас вообще не волнует. А то даже когда определяют алгебру симметрических функций обычно нумеруют переменные, да и само существование этой алгебры преподносят как какой-то сюрприз.
>>53370
>хуй знает где
В том-то и дело.
Уравнение маятника это прежде всего:
x''=-\omega^{2}Sin(x)
То что написано там, это уравнение малых колебаний.
Хуишко у тебя малый. Думай еще.
Почему? Неплохо выходит же! Что значит перерыв? Я думал ты умненький второкур вышечки, или ты про перерыв в написании твоих заметок, а не в математике?
>>53417
>Я думал ты умненький второкур вышечки
Давным-давно отчислили со второго курса физфака.
>или ты про перерыв в написании твоих заметок, а не в математике?
Да.
Например, доказательство теоремы Джекобсона о плотности я взял отсюда:
https://youtube.com/watch?v=bR4zxIXNBcI
но только не понял, зачем нужны все эти аннигиляторы, да и явное выписывание матрицы.
Может быть, я действительно чего-то не понимаю, и они действительно нужны?
>Если его ядро равно нулю, то обратный гомоморфизм даст со-отношение xn=\sum_1^{n-1} x_id_i, где d_i \in D - противоречие. Поэтому ядро равно M.
Так A(x1,...,xn) не простой.
Элементы ядра этого отображения имеют вид (0,0,...,0,x), то есть ядро содержится в последнем слагаемом произведения, которое изоморфно M, а M --- простой.
>Вообще, хочу сделать перерыв на несколько лет.
Опа опапа, я то думал что эти говно-заметочки ваяются в перерывах между почесыванием яиц и скролированием двачей, а оказывается вон оно как - перерыв нужен, да еще на несколько лет, ну нихуя себе.
>Опа опапа, я то думал что эти говно-заметочки ваяются в перерывах между почесыванием яиц и скролированием двачей
Да, это так.
Утихни гребешок
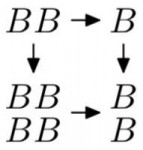
Назовём симплексами множества, а подсимплексами --- подмножества. Определим ориентацию симплекса и оператор границы одновременно, используя индукцию по размерности симплекса (количеству точек). Ориентированный симплекс --- это симплекс, снабжённый оператором границы $\partial$ в абелеву группу своих ориентированных подсимплексов, т. ч. $\partial^2=0$. Ориентации фиксированного симплекса очевидным образом образуют абелеву группу. Абелева группа ориентированных симплексов определяется образующими --- ориентированными симплексами --- и соотношениями --- сумма ориентаций на фиксированном симплексе даёт уже известную нам ориентацию того же симплекса. Оператор границы продолжается на неё по аддитивности.
Граница нульмерного симплекса (точки) --- это ориентированный "пустой симплекс", то есть просто элемент абелевой группы коэффициентов.
 56 Кб, 1000x2300
56 Кб, 1000x2300>используя индукцию по размерности симплекса
Попытался написать формальное определение (пикрелейтед).
Кажется, лучше продолжить комплекс вправо нулями и определить supp для всех элементов C_0 как пустое множество.
 58 Кб, 1100x2170
58 Кб, 1100x2170Вот более правильное определение.
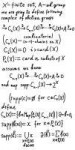 62 Кб, 1100x2170
62 Кб, 1100x2170Кто-то понял это определение? Оно стандартное?
 48 Кб, 416x647
48 Кб, 416x647Кайфую.
Добавил в папку новую PDF-ку для всякого мусора и записал это туда.
В основной текст добавил теорему о существовании и единственности поля разложения.
В данном конкретном случае я хочу определить цепной комплекс для абстрактного симплициального комплекса, не используя нумерации вершин симплексов. В частности для A=Z/3Z это даёт понятие ориентированного симплекса и его границы, не использующее нумерации вершин.
Чисто мой загон, можно не обращать внимания.
Есть какие-то применения этой штуки?
 17 Кб, 194x203
17 Кб, 194x203Какие?
Пикрелейтед диаграмма для биалгебр очень похожа на диаграмму тут: https:/youtube.com/watch?v=gI2csQaKJDk (10:40).
Может быть, это всё обобщается на биалгебры и что-то значит для них. Они естественно в связи с действиями возникают, а там тоже $G$-множества.
 203 Кб, 301x725
203 Кб, 301x725>хочу сделать перерыв на несколько лет.
ПЕРЕНИМАЮ ЭСТАФЕТУ
https://filecloud.me/3k3440wws6rs.html
ПУЧК
Гениально!
Обпучкался в голосину чёт.
Как раз добавил свой концептуальный взгляд на пучки и ростки в черновик. Не знаю, насколько он правилен или стандартен.
>Добавил в папку новую PDF-ку для всякого мусора и записал это туда.
Переписал. Теперь действительно норм.
Во избежание возможных недоразумений поясню, что я и есть оп.
Парциальные отображения $M \leftrightarrow M \times \{x} \subset M \times M \to \mathbb{R}$ должны быть непрерывны, поэтому открытые шары открыты (как прообразы отрезков $(0,r)$). Этого и достаточно.
Тут нет ошибки?
Просто это определение мне кажется менее ad hoc, чем просто декларация открытых шаров открытыми.
Алсо, ещё один педагогический принцип: сразу же после определений топологии и непрерывности должны даваться два примера: метрическая топология и топология Зарисского. Иначе вообще не понятно, в чём смысл рассатривать многие понятия из общей топологии. А так сразу понятно.
>Кажется, нашёл интересное определение топологии метрического пространства <..>
Ну очень интересное определение, попробуй теперь с помощью него что-нибудь доказать
>Это такое не абсолютно тривиальное упражнение.
Тривиальное же: утверждение очевидно следует из того факта, что система открытых интервалов на R образует базу стандартной топологии на R. Обратно: тот факт, что топология открытых шаров удовлетворяет твоему универсальному свойству, влечёт этот факт про R
>>55153
>Иначе вообще не понятно, в чём смысл рассатривать многие понятия из общей топологии
Какие, например?
>педагогический принцип
Круто звучит, внушительно
>Какие, например?
Порядок специализации: $x$, лежащий в замыкании $y$ называется специализацией $y$.
Вообще --- зачем рассматривать нехаусдорфовы пространства.
>Ну очень интересное определение, попробуй теперь с помощью него что-нибудь доказать.
Оно естественное, а это главное.
Топология произведения определяется условием непрерывности проекций. Затем даётся явное описание.
Топология фактор-пространства определяется условием непрерывности факторизации. Затем даётся явное описание.
Топология подпространства определяется условием непрерывности вложения. Затем даётся явное описание.
Топология метрического пространства определяется условием непрерывности метрики. Затем даётся явное описание.
>Тривиальное же
Это верно, что для любой функции на $X \times X$ есть универсальная топология $X$, относительно которой она непрерывна?
>Это верно
верно, что топология открытых шаров удовлетворяет твоему определению. если ты не то имел в виду, выражаться надо яснее, я же по конктесту
>Порядок специализации: $x$, лежащий в замыкании $y$ называется специализацией $y$.
В первый раз о таком понятии слышу. Если не браться за топологию Зарисского, какой смысл его рассматривать?
>Вообще --- зачем рассматривать нехаусдорфовы пространства.
Ну ясно, что в общем положении незачем. У кого они появились, тот пусть и изучает. При первом знакомстве совершенно не нужно их рассматривать, только ради пары наглядных примеров, как бывает
>верно, что топология открытых шаров удовлетворяет твоему определению
Чего верно-то? Почему она самая слабая?
ты же хотел пример нехаусдорфовой, нет?
примеры неметризуемых топологий есть более простые, чем зарисского, хотя это уже субъективно
в общем, я ничего против зарисского не имею, но там всё надо доказывать, начиная уже просто с того, что это топология. я бы не стал в первом (или втором) примере такого делать
>>55178
она самая слабая потому что определена через базу топологии (базу открытых шаров)
>Круто звучит, внушительно
На самом деле есть ещё кое-что. Замкнутые подмножества метрических пространств --- это нули непрерывных функций (например, функции рассояния до данного замкнутого подмножества). Поэтому логично рассмотреть нули алгебраических функций, а это примерно и есть топология Зарисского.
если у тебя не курс алгебраической геометрии, то выбор для этого именно именно алгебраических функций не совсем ясен да и зачем сразу нули функций вообще, это довольно техническое рассуждение
всё же примеры можно изготовить и попроще
но я не настаиваю, вообще извините, что ввязался
Кстати, кто-нибудь знает, как определить образ квадратичной формы (при сюръективном отображении, скажем)? Просто для положительной формы $Q$ мы можем взять функцию $e^{-Q}$, у которой определён образ (интегрированием по слоям), который тоже является экспонентой формы. Но это только для знакоопределённых форм. А есть абстрактное определение?
Кажется, для любой формы можно определить образ, если у нас есть фоновая евклидова форма: мы берём ортогональное дополнение ядра отображения и ограничиваем на него. Но для образа знакоопределённой формы с помощью этого интегрирования экспоненты нам нужно меньше структуры --- нужна только евклидова форма на ядре отображения. Странно. Ладно, плевать.
1. Зачем он тут ссылается на теорему Вейля о полной приводимости представлений? Разве не естественнее сразу начать классификацию простых представлений? Пусть прдставление $V$ простое. Пусть $V_\lambda = \{v \in V \mid hv = \lambda v\}$. Мы берем сумму $V_\lambda$. Она не равна нулю, т.~к. над полем характеристики $0$ у каждого оператора есть собственный вектор. Она инвариантна относительно действия алгебры Ли, т.~к. $x V_\lambda \subset V_{\lambda+2}$, $y V_\lambda \subset V_{\lambda-2}$. Поэтому она совпадает с $V$. Сумма прямая, так как собственные векторы с разными собственным значениями линейно независимы.
2. Фраза <<факт из линейной алгебры>> абсолютно идиотская. Это общий алгебраический факт: если $y^n=0$, $xy=yx$, то $(xy)^n = x^n y^n = 0$.
>Добавил в "черновик" интересную связь между нормальным распределением и стандартным примером не аналитической гладкой функции.
От чего так получилось, совпадение? не думаю
Понятия не имею.
>Зачем он тут ссылается на теорему Вейля о полной приводимости представлений? Разве не естественнее сразу начать классификацию простых представлений?
Так всё равно придётся, он-то начинает с произвольного L модуля. Кроме того он рассматривает строение над любым алгебраически замкнутым полем, а теорема Вейля только над char 0 работает.
>Так всё равно придётся, он-то начинает с произвольного L модуля.
Выясняем строение неприводимых, затем говорим: по теореме Вейля любой разлагается на неприводимые.
>Кроме того он рассматривает строение над любым алгебраически замкнутым полем, а теорема Вейля только над char 0 работает.
Не понял. Это всё по-любому в характеристике $0$.
>Фраза <<факт из линейной алгебры>> абсолютно идиотская.
Это факт из линейной алгебры, доказываемый элементарно. Если просто сказать, что из y^n = 0 в любом коммутативном кольце следует (xy)^n = 0, то приложение к эндоморфизмам не приходит на ум автоматически - с тем же успехом можно подумать о любом другом приложении.
>Не понял. Это всё по-любому в характеристике $0$.
То что h действует полупросто и поэтому любое представление расскладывается в прямую сумму h-пространств верно и в положительной.
Следует? Это одномерный случай просто, доказательству плевать на размерность.
[Не уверен, что в доказательстве Артина-Веддербарна использовал именно артиновость (господи, как же ненавижу условия конечности). Для конечномерных всё ок.]
Похоже, что и для артиновых ок. Попробовал прояснить.
Это верно, что объединение цепочки подмодулей $M_1 < M_1 \oplus M_2 < M_1 \oplus M_2 \oplus M_3 < \ldots$ равно бесконечной прямой сумме $\bigoplus_{i=1}^\infty M_i$?
P.S. Разлагается в прямую сумму или разлагается на прямую сумму?
На прямую сумму и липовый мёд.
Нет, вот теперь нормально.
Нет. Похоже на длинный учебник, а у меня короткие фрагментарные доказательства отдельных фактов.
Я, кстати, до сих пор пишу эти заметочки.
Теперь оформляю короткими кусками, а не в одну псевдокнигу.
Ссылка тут:
>>52591
всё ещё рабочая.
[Сказал и пошёл отсюда, чтобы не видеть этого позора.]
Выглядит как интересный набор фактов и сюжетов. Интересно, есть ли у этого метаматематическая ценность или в большинстве своём эти факты только в своей области нужны?
Надо будет почитать.
Нифига не понятно из Ваших щаписок.
 72 Кб, 670x310
72 Кб, 670x310ОП, объясни интерпретацию. Каким образом элементы матрицы это эндоморфизмы и эндоморфизмы чего это?
 417 Кб, 1366x905
417 Кб, 1366x9051. Читать старые заметки в тех случаях, когда на эту тему есть более свежие — не очень разумно, в частности, как раз по причине подобного рода расплывчатых текстовых описаний. Скриншот более свежей версии данного доказательства приложен. Может быть, так будет понятнее.
2. Не очень понимаю, с какого места объяснять. Вот, скажем, четыре факта:
а) Пусть V — абелева группа, R — ассоциативное унитальное кольцо. Продолжить структуру абелевой группы на V до структуры R-модуля на V — это то же самое, что задать кольцевой гомоморфизм R \to \End(V), где \End(V) — это кольцо эндоморфизмов V как абелевой группы.
б) Пусть V — модуль над ассоциативным унитальным кольцом R. Задать эндоморфизм \varphi : V \to V R-модуля V — это то же самое, что задать отображение множеств {X} \to \End(V), где {X} — это множество с единственным элементом X, а \End(V) — это кольцо эндоморфизмов V как абелевой группы, такое что образ {X} в \End(V) поэлементно коммутирует с образом R. Образ X и соответствует \varphi.
с) Пусть R — ассоциативное унитальное кольцо, V — абелева группа. Задать отображение {X} \to \End(V) и гомоморфизм R \to \End(V), образы которых поэлементно коммутируют, — это то же самое, что задать гомоморфизм R[X] \to \End(V), где R[X] — это кольцо многочленов от переменной X с коэффициентами в кольце R. Это так по универсальному свойству многочленов.
Замечание. Если X переходит в \varphi, то образ R[X] в кольце \End(V) иногда обозначают R[\varphi]. Это про смысл обозначения на картинке.
д) Пусть V — модуль над ассоциативным унитальным кольцом R. Тогда на абелевой группе V^{\oplus I}, где I — конечное множество, индуцируется структура модуля над кольцом (I на I)-матриц с коэффициентами в R.
Скажем, среди этих четырёх фактов что-то конкретно непонятно?
Но вообще, это очень утомительно, такие длинные пояснительные тексты писать.
Это не учебник.
P. S. Отмечу, кстати, что по теореме Гамильтона-Кэли у меня нет ощущения какого-то глубокого понимания. Но это к теме имеет мало отношения.
 417 Кб, 1366x905
417 Кб, 1366x9051. Читать старые заметки в тех случаях, когда на эту тему есть более свежие — не очень разумно, в частности, как раз по причине подобного рода расплывчатых текстовых описаний. Скриншот более свежей версии данного доказательства приложен. Может быть, так будет понятнее.
2. Не очень понимаю, с какого места объяснять. Вот, скажем, четыре факта:
а) Пусть V — абелева группа, R — ассоциативное унитальное кольцо. Продолжить структуру абелевой группы на V до структуры R-модуля на V — это то же самое, что задать кольцевой гомоморфизм R \to \End(V), где \End(V) — это кольцо эндоморфизмов V как абелевой группы.
б) Пусть V — модуль над ассоциативным унитальным кольцом R. Задать эндоморфизм \varphi : V \to V R-модуля V — это то же самое, что задать отображение множеств {X} \to \End(V), где {X} — это множество с единственным элементом X, а \End(V) — это кольцо эндоморфизмов V как абелевой группы, такое что образ {X} в \End(V) поэлементно коммутирует с образом R. Образ X и соответствует \varphi.
с) Пусть R — ассоциативное унитальное кольцо, V — абелева группа. Задать отображение {X} \to \End(V) и гомоморфизм R \to \End(V), образы которых поэлементно коммутируют, — это то же самое, что задать гомоморфизм R[X] \to \End(V), где R[X] — это кольцо многочленов от переменной X с коэффициентами в кольце R. Это так по универсальному свойству многочленов.
Замечание. Если X переходит в \varphi, то образ R[X] в кольце \End(V) иногда обозначают R[\varphi]. Это про смысл обозначения на картинке.
д) Пусть V — модуль над ассоциативным унитальным кольцом R. Тогда на абелевой группе V^{\oplus I}, где I — конечное множество, индуцируется структура модуля над кольцом (I на I)-матриц с коэффициентами в R.
Скажем, среди этих четырёх фактов что-то конкретно непонятно?
Но вообще, это очень утомительно, такие длинные пояснительные тексты писать.
Это не учебник.
P. S. Отмечу, кстати, что по теореме Гамильтона-Кэли у меня нет ощущения какого-то глубокого понимания. Но это к теме имеет мало отношения.
Каждый из перечисленных фактор мне понятен, кажется, но откуда они взялись и почему это естественный взгляд — абсолютно точно нет.
Ок.
Насчёт пункта а) ещё небольшое пояснение.
Пусть R — ассоциативное унитальное кольцо.
Обычно структура R-модуля на абелевой группе V определяется с помощью отображения множеств
R \times V \to V,
удовлетворяющего каким-то аксиомам.
Но отображения
R \times V \to V
естественно биективны отображениям
R \to \Map(V,V),
где \Map(V,V) — это множество отображений из V в V.
Функция от двух аргументов — это то же самое, что функция от одного аргумента в функции от другого аргумента.
Это соответствует биекции между множествами X^{Y \times Z} и (X^Y)^Z, где X, Y и Z — множества, из теории множеств.
Важнейший факт, различные проявления которого встречаются в математике постоянно, буквально везде, и без которого нельзя понять ничего.
Так вот, описание модуля как гомоморфизма в эндоморфизмы отсюда и берется. Это один взгляд.
Точно так же действие группы G на множестве X можно задавать с помощью отображения G \times X \to X, удовлетворяющего неким аксиомам, а можно задавать с помощью гомоморфизма группы G в группу перестановок множества X — это одно и то же.