1) Сриниваса Рамануджан показал, что традиционные методы доказательств не являются объективными и неоспоримыми. Будучи самоучкой, он имел собственный стиль математического мышления и получил уникальные результаты в теории чисел. Самый глубокий - сумма натурального ряда равна -1/12, что с точки зрения традиционной математики звучит абсурдно, следовательно, доказывает, что математика есть лишь выдуманная ОДНИМ человеком абстракция, которая ДРУГИМ человеком может быть воспринята иначе, и в той же степени может претендовать на истинность. Общепринятая математика, таким образом, неполная.
2) А Курт Гёдель показал, что полной математики в принципе не может существовать. Вернее, что "в любой формальной системе существует утверждение, которое нельзя ни доказать, ни опровергнуть". Отсюда фразы о том, что математика - язык бога, что через неё можно познать мир - неверны. Гёдель фактически доказал, что мир не познаваем в полной мере с помощью формальных систем с конечным набором аксиом.
Прошу прощения за некоторое дилетантство, я не профессионал, математического образования не имею и занимаюсь математикой как хобби. Хотел бы услышать мысли грамотных людей по этому поводу.
Я, к несчастью, тоже любитель, но рискну прокомментировать прочитанное. Самым величайшим математиком в истории был Архимед, потому что именно его профиль изображён на одной из сторон филдсовской медали.
>что с точки зрения традиционной математики звучит абсурдно
Аналитическое продолжение дзета-функции не звучит абсурдно.
Рамануджан мыслил как современник Эйлера, а жил в 20 веке.
>доказал, что мир не познаваем в полной мере с помощью формальных систем с конечным набором аксиом
Не имеет отношения к содержательной части математики: основной прогресс пришелся на промежуток между концом 1950-х началом 1970-х, дискуссии же по основаниям заглохли к середине 1930-х.
Впечатление, что твои знания ограничиваются прочтением книги "Дядя Петрос и проблема Гольдбаха".
Платина
Что значит значительнее? Абель уже жил во времена Гаусса, Коши. А Архимеду в его времена равных, судя по всему, не было.
Чего не Пифагор сразу. Полумифические люди, про научную деятельность которых достоверно ничего не известно.
Работы Абеля, с другой стороны, еще при жизни получили высокую оценку от того же Гаусса.
Я бы сказал Лагранж, но если подумать, то все хороши.
Хорош! Жду продолжение, особенно выступления "Сознание и квантовая суперпозиция", "Эфир и теория относительности: столетний еврейский заговор", и "Тайны чисел, до сих пор не раскрытые математиками: 0.(9)".
Эйлер был самым продуктивным.
Эрдеш вроде был продуктивнее.
>>50475
Ну потому что Пифагору могли присвоить результаты его учеников, а "полумифический" Архимед реально довёл до пределов стиля древнегреческую математику, шутка ли в одиночку изобрести аналог дифференциального и интегрального счисления в эпоху геометрических построений. В этом плане сильно выделяется также Диофант, но Архимед разностороннее.
Гротендик и Дедекинд конечно!
члены?
И по этим тоже. ;)
Очевидный Галуа очевиден. Live fast, die young. Герой поколения.
>You shouldn’t have mentioned the stuff about Benzedrine. It’s not that you got it wrong. It’s just that I don’t want kids who are thinking about going into mathematics to think that they have to take drugs to succeed.
Такое милое лицемерие. Я вот сам на спидах сижу, но лучше об этом никому не рассказывайте - а то кабы чего не вышло.
К слову о том, как написать 1525 статей за жизнь.
На отходняках сильно способности падают? Без них на сколько оценишь результативность (приблизительно)?
 271 Кб, 500x485
271 Кб, 500x485Если не переставать марафонить, то и отходняков не будет.
"Отсюда фразы о том, что математика - язык бога, что через неё можно познать мир - неверны"
Из теоремы Гёделя (в более общей современной формулировке) вытекает лишь то, что не существует тьюринговый алгоритм, который выдаёт все истинные и только истинные высказывания. Но кто доказал, что в нашем мире невозможны сверхтьюринговые вычисления?
Спиды высвобождают запасённую энергию из клеток. Если ничего не запасенно то и высвобождать нечего. Т.е. я так понимаю залог успеха в математике это занятия спортом что бы повысить скорость метаболизма, затем много есть, заниматься спортом(чтобы поддерживать характеристики метаболизма) и употреблять спиды.
Такая то пушка что кто то подумал что это я употреблял, хотя это была очевидная отсылка к цитате. Сам то я никакого допинга серьезнее чем шоколадка на олимпиаде даже из далека не видел никогда.
Кто же тебя знает, родной? Сегодня ты пишешь с юмором, а завтра раздосадованно набираешь строки. Текст эмоций не передаёт.
>Если не переставать марафонить, то и отходняков не будет.
Не. Интеллектуальный ресурс ограничен. Легко можно стать слабоумным при чрезмерной нагрузке.
Типичная промытая зожка, на Эрдеша ровняться не стоит,
>Мазги разные у всех.
поэтому нужно всем дружно молиться, поститься, и слушать радио Радонеж.
Ты ёбнутый какой-то, что ли? Или Эрдешем себя возомнил? Ещё и зож приплесть успел, шизофреник.
Ну и в чем же я конкретно не прав, ничего кроме ко-ко-кукарек-кукареку не высрал а уже в мамкины психотерапевты заделался.
>ничего кроме ко-ко-кукарек-кукареку не высрал
Напомнило тебя, только ещё плюсом
>ряяя промытка
Побольше вкачивай в себя всяких НаРкоТиКоВ))), обязательно станешь великим математиком Романом. Прыгающим, правда, а не Михайловым. Хотя, ты и так уже хорош.
>Типичная промытая зожка, на Эрдеша ровняться не стоит,
О, вот же типичный анимешник. Ты небось ещё и в силу усердия веришь? Так продемонстрируй ссылку на свои научные статьи.
Но спортсмены выходят из строя. В случае математики самый пик карьеры с допингами припал бы на вычисления интегралов.
Фу пидор куда подъехать?
>>50981
Ну это просто утверждение ни на чем не основанное. Точнее основанное на ЗОЖной пропаганде. Я вот возьму и скажу что - любой Васян из падика под марочкой будет ебошить теоремы лучше этих ваших Перельманов. И если бы мы жили в дивном новом мире то такая же промытка уже бы утверждала что - да, мол, только так и может быть, а как же еще?
Чёт не думаю, что они именно из-за допинга выходят из строя.
>>50984
Да, медицинских исследований у меня нет. Но их и у тебя нет, так что мы оба тут бросаемся догадочками и машем руками.
Про любого васяна vs Перельмана ты утверждать не можешь, потому что не любой васян успешно это делает. Про среднего васяна под марочками vs среднего васяна без марочек - пожалуй можешь, это будет такой же уровень обоснования, как и у меня.
>А может лучше ты соснешь моего хуйца?
Нет. Так где статьи твои, быдло? Ты топишь за наркотики, но не имеешь результатов на их основе. Может ты первокурсник?
Это малолетний ебанат, у которого в голове мейнстримная повестка, что наркотики помогают в творчестве.
 46 Кб, 544x600
46 Кб, 544x600Позволь объяснить почему ты хуй, а Рамануджан и Гёдель не самые великие математики. Обоснованные претензии к формализму как основаниям математики были задолго до работ Гёделя. Брауэр тот же. Рамануджан хоть и понимал математику не так как это делают другие, не сделал из своего подхода внятной программы / направления. Т.е ценность для математики с него сомнительна.
>Гёдель не самые великие математики
У меня нет желания начинать холивар на тему какие разделы математики важны/неважны. Но вклад Гёделя в основания математики (как область собственно математических исследований) и математическую логику очень велик и фундаментален. И с моей точки зрения явно более существенен чем у какого-либо другого математика работавшего в этой области. Это вовсе не ограничивается теоремами о неполноте. Практически все его работы либо являлись концептуальным прорывом в существующем подразделе, либо создали новый.
>Но вклад Гёделя в основания математики и математическую логику очень велик и фундаментален
Я согласен с этим утверждением. Вот ещё утверждения, с которыми я согласен:
Вклад Дейкстры в компьютер саенс велик и фундаментален.
Вклад Гуссерля в философию велик и фундаментален (Гёдель его тоже ценил).
Вклад Дирака в физику велик и фундаментален.
Речь, однако, шла о математике.
Почему ты считаешь, что основания не математика? Там есть теоремы и тд, очень похоже на математику.
 447 Кб, 640x640
447 Кб, 640x640> Почему ты считаешь, что основания не математика?
Потому что основания это не гамалогии и не тапалогии, очевидно же. Фейерабенд завещал, что наука это то, что считают наукой те, кто считает что занимается наукой. Вербицкий основаниями не занимается, при этом считает себя математиком. Значит, основания не математика. Как-то так.
Потому что в основаниях не используется математика, и основания не используются в математике.
Математика определяется как всё, что необходимо для формулировки и доказательства теоремы Атьи-Зингера, великой теоремы Ферма, гипотез Вейля, теоремы об изоморфизме норменного вычета (гипотеза Милнора) и т.д. Математика это то, чем занимались Маклейн, Серр, Гротендик, Кан, Милнор, Квиллен, и др. То, чем сейчас занимаются Хитчин, Концевич, Шольце, Бхатт; любой математик знает, что такое математика.
>Там есть теоремы и тд,
Теоремы даже у Спинозы в "Этике" есть.
>51346
>наука это то, что считают наукой те, кто считает что занимается наукой
Это ещё у Куна было, но в остальном согласен. Что признается самим научным сообществом как наука, то и есть наука.
Из последних примеров можно вспомнить разве что Коэна, которому дали премию полей за доказательство независимости гипотезы континуума (существование промежуточного кардинала между алеф нуль и алеф один) от zfc. Этим вопросом, если не путаю, Гёдель тоже интересовался. Но дело в том, что данная гипотеза оказалась по не совсем понятным причинам включена в список проблем Гильберта, да ещё и первым номером. Другой аспект, что доказательство было произведено применением новой техники форсинга, которая вроде как не вполне бесполезна и даже применяется где-то в теории топосов. Если бы не эти два аспекта (включение в престижный список проблем и использование нового метода) вполне возможно что премию бы не дали.
> Гёдель тоже себя математиком считал.
И что? Тебе вон выше клован с мейлру сказал, что Гёдель не математик и математикой не занимался. Ты что, не веришь клованам с мейлру?
 93 Кб, 512x512
93 Кб, 512x512Т.е:
- математик это тот, кто занимается математикой.
- математика это то, чем занимается математик.
Ничего не упустил? Такой матерой хуйни даже у Рыбникова нет и у авторов "православной арифметики".
> проверка теорем компом
Этим вообще кто-то пользуется не из специалистов по основаниям? Или это очередная вещь в себе?
А куда деваться? Руками проверять теоремы по 3к страниц по теме, где 3.5 специалиста существуют, у которых своих дел полно? Без движения в этом направлении математика вообще заглохнуть может, вон работы Мочидзуки уже сколько проверяют? Другое дело, что охуеешь формализовывать, но Воеводский мутил что-то по этому поводу, ХоТТ, если доведут до конца будет збс.
> Или это очередная вещь в себе?
Вообще такие вот нападки очень напоминают дидов с их "нахуй вашу алгебру, котягории, а вот пользу они принести могут, м?". Стареете, матаны?
>>51360
> проверка теорем компом,
Просто проверка это 60е годы и automath де Брауна. Пруверы это гораздо более мощная вещь. И гамалогии с тапалогиями туда ещё Воеводский завез. А сейчас есть уже cubicaltt, где аксиома унивалентности это уже не аксиома а доказуемая теорема. Другой вопрос, что во все это могут полтора человека помимо Мортберга, ещё и Воеводский помер.
Конструктивист до сих пор не выяснил, что такое "контекстуальное определение". Я не только написал очевидную вещь, но еще и привел примеры. Маклейн про это говорил сто раз, что серьезную математику можно выучить только на конкретных примерах. Браузера ты уже прочитал, теперь пора взяться за Маклейна. Начни с form and function.
>>51360
Да вроде нет. Ну какие-то единичные примеры есть, например Хана-Банаха проверили на прувере mizar system, или там кукарекун сверху может тебе рассказать про "Основы Анализа" Ландау, проверенные автоматом Дебрауна.
В основном это, очевидно, бессмысленная деятельность, проверка той или иной теоремы на очередном говнопрувере нужна в основном для рекламы этого прувера. Математикам от этого пользы никакой.
О, я угадал про Дебрауна, даже пост не успел дописать. Что насчет ХОТТ, никаких гамалогий нет, не было, не может быть и не будет. Разве что на уровне названий, примерно как эндофункторы в Хаскеле у сойбоев-программистов.
>работы Мочидзуки уже сколько проверяют? Другое дело, что охуеешь формализовывать
1) работы Мотидзуки уже проверил Шульце
2) перевести введенный в IIUT формализм на язык унивалетных гомотопических сойбоев займет где-то 10^500 лет, по консервативным оценкам, т.е. совершенно not feasible.
Конструктивистам доступны только объедки вроде очень ограниченного числа теорем, доказанных математиками ещё до 1920-го года.
>уже проверил
>В августе 2012 года опубликовал на своем сайте четыре статьи, которые развивают арифметическую теорию Тейхмюллера (арифметическую теорию деформации)
Не прошло и 7 лет.
>Другой вопрос, что во все это могут полтора человека помимо Мортберга, ещё и Воеводский помер.
>>51370
> т.е. совершенно not feasible.
Ну так это печально, если проверка каждой теоремы с переднего края математики будет занимать 7 лет( а ведь Уайлз 10 лет потратил на док-во теоремы Ферма), то математика превратится в свалку никем не проверенных результатов, большинство из которых тупо затеряется во времени. Так что основания/ математическая логика играют важнейшую роль для нормальной жизнедеятельности всей математики в целом, нужно больше специалистов в этих областях.
>а ведь Уайлз 10 лет потратил на док-во теоремы Ферма
К тому, что проверка теоремы заняла почти столько же времени, сколько доказательство теоремы Ферма.
 246 Кб, 400x402
246 Кб, 400x402> 1) работы Мотидзуки уже проверил Шульце
Фесенко тоже. И не только. И что? Они свою проверку у нотариуса заверят пикрелейтед? Какая польза науке от того, что один аутист разобрал писания другого аутиста?
> 2) перевести введенный в IIUT формализм на язык унивалетных гомотопических сойбоев займет где-то 10^500 лет, по консервативным оценкам, т.е. совершенно not feasible.
Ты ебнутый, понимаешь это? Мочидзукины писания это уже готовые формализмы, их никуда переводить не надо.
>Пруверы это гораздо более мощная вещь
И все еще никому не нужная. Вещь ради вещи. Никто в здравом уме не будет равнять свою деятельность на это.
>>51366
Если кому то интересно заниматься пруверами и прочим. Окей никаких проблем. Но если же куча этих сойбойчиских животных хочет навязать своё говно остальному миру, то тут так сказать пора заряжать наган. Любое дерьмо прекрасно пока не начинается навязывание.
>Руками проверять теоремы по 3к страниц по теме
Почему бы и нет. Если тебя интересует объект то можно и 10к страниц осилить. Вопрос мотивации.
>Вопрос мотивации.
Да ладно, у тебя одна жизнь и ты, вместо пиздиловки с открытой проблемой потратишь её на проверку чужого решения? Ладно, если бы это работа для бесталанного аспиранта была, так нужен именно светила, лютый спец в своей области. Да кто на такое пойдёт в здравом уме?
Хотя может он вечерами по выходным час уделял, тогда да, может потому и вышло 7 лет, так или иначе это совсем не круто тратить такие человеческие ресурсы на то, с чем машина справится.
А кто навязывает? По моему как раз вы навязываете, основания не математика, не нужно, вещь в себе, какой-нибудь анализ тоже вещь в себе, так что же, не математика?
>их никуда переводить не надо.
Ну-ка давай хотя бы первую строчку какой-нибудь статьи на Coq или Agda, раз не надо.
Алсо теория множеств или категорий сами по себе являются предметами оснований, но без них выстроить формальные взаимосвязи между различными разделами математики не представляется возможным.
Я в курсе, но дидам похуй, они как хуесосили котягории так и хуесосят, пушо и нахуй она не нужна нам, алгебра ваша, первым делом матанализ, ну а алгебра потом. Вот вы тут тоже уподобляетесь дидам, вещь в себе, ничего себе предъява.
Если что-то оскорбляет твои религиозные чуйства, это не доказательство ненужности этого чего-то. Как бы тебя ни корежило, математика автоматизируема. С Брауэра ты зря горишь, к слову. Он как раз считал человека неотъемлемой частью математики и логику Гейтинга, на которой основаны пруверы, не одобрял ("интересный, но бесплодный пример").
>>51347
Все бы хорошо, но с чего вы называете очерчиваемый вами предмет математикой. Довольно очевидно, что в течение 20 века математика, бывшая относительно единым предметом существенно разрослась и сейчас состоит из довольно большого конгломерата областей многие из которых довольно слабо связанны между собой. И видимо кроме теоретической информатики, в остальных разделах этого разросшегося здания люди, как правило, считают себя математиками. И у всех них есть для этого полные основания так как все эти области восходят к тому что считалось математикой ранее.
>у тебя одна жизнь и ты, вместо пиздиловки с открытой проблемой потратишь её на проверку чужого решения?
Жизнь жестока и если кто-то решил открытую проблему первым, то тебе некуда так сказать деваться. Потому что даже если представить, что будет создан какой-то оракул-прувер который магическим образом скажет тебе верно чужое решение или нет, поверишь ли ты ему? Если да, то это тоже самое, что с самого начала принять это решение за верное. Если нет, то тебе придется разбираться, что под капотом у этого оракул-прувера, а на этой уйдет времени как на 100к страниц, а то и больше. Пойдешь ли ты на это? А если окажется, что в прувере багулинка, которая стоила тебе кучи времени? Сможешь ли ты пережить свой разрыв очка, от осознания, что всё это время ты потратил впустую?
>>51392
>А кто навязывает?
Шизоиды. Так то сообщество как правило, каждый в своем угле и занимается своими задачами. Хорошо, если возникают так сказать пересечения между областями, из этого, как правило рождается, что-то фундаментально новое.
>основания не математика, не нужно, вещь в себе
Опять же, если кто-то хочет заниматься основаниями, пруверами, копанием дилдой у себя в жопе, то хорошо, в этом нет ничего плохого. Дихотомия вида математика, не-математика, это локальный рофел пары шизоидов.
>>51405
>это не доказательство ненужности этого чего-то.
Ну я в том посте допустил неточность. Под ненужностью я имел в виду, ненужность за пределами работ по основаниям и построениям пруверов.
>Как бы тебя ни корежило, математика автоматизируема.
Абсолютно безосновательное утверждение. Впрочем вера в святой компьютер это самый настоящий бич нашего времени, поэтому я не осуждаю тебя.
> С Брауэра ты зря горишь, к слову.
Ты явно перепутал меня с кем-то другим. На заре раздела, помнится тут было много кидания говна по коконструктивизму и прочему. Я тогда дипломатично сидел в ридонли, потому что уже тогда понимал, что это не обсуждение, а самый, что ни на есть, шитпостинг.
>в течение 20 века математика, бывшая относительно единым предметом существенно разрослась и сейчас состоит из довольно большого конгломерата областей многие из которых довольно слабо связанны между собой
Да. Поэтому мы выделяем ту часть, которая связана довольно тесно, и говорим, что это core mathematics. То есть вышеописанное.
Конструктивизм дал нам компьютеры, компьютеры привели к развитию разнообразной комбинаторики, большая часть которой не интересна никому в принципе, но есть исключения в виде например тропической геометрии. Не то что бы дискретными штуками не интересовались раньше, просто раньше вычислительных мощностей не было. Примерно как с машинным обучением, которое придумали в начале 1960-х, а взлетело только сейчас. Аналогично комбинаторикой ещё Гаусс интересовался, просто руками там много не посчитаешь.
>в остальных разделах этого разросшегося здания люди, как правило, считают себя математиками. И у всех них есть для этого полные основания
Это понятно. Просто согласись с тем, что если два представителя одной области ничего не понимают в работах друг друга, то это не совсем область? Ну вот Поппер сказал, что каждый человек философ. Ну мы здесь решили что каждый человек математик. Дело-то не в этом. Имеется некоторое количество людей, знающих некоторый условно стандартный материал, не обязательно использующих его в своей работе, но тем не менее, они прекрасно поймут друг друга. Это всё уже было описано 17 лет назад тут:
http://imperium.lenin.ru/~verbit/MATH/programma.html
Помимо создания нового знания, есть еще такая вещь как систематизация. Концептуальная математика об этом. Если не заниматься систематизацией, и не развивать язык, то доступ к знаниям затруднится и знания будут утеряны.
Поэтому нахуй это надо. С административной точки зрения: имеется очень расширенное определение математики, как ты предлагаешь. Хорошо. В одном департаменте сидят комбинаторщики, чистые математики, физики, компьютер саентисты. Никто из них не понимает друг друга, но все конкурируют за одни ресурсы. Что дальше? Полное вырождение. Если невозможно вести беседу, нет общих точек соприкосновения, предметом дискурса станет наличие академических регалий, цитируемость, и т.д. а от этой ситуации выигрывают только жулики и профанаторы. Имеем науку как в Мавритании.
>в течение 20 века математика, бывшая относительно единым предметом существенно разрослась и сейчас состоит из довольно большого конгломерата областей многие из которых довольно слабо связанны между собой
Да. Поэтому мы выделяем ту часть, которая связана довольно тесно, и говорим, что это core mathematics. То есть вышеописанное.
Конструктивизм дал нам компьютеры, компьютеры привели к развитию разнообразной комбинаторики, большая часть которой не интересна никому в принципе, но есть исключения в виде например тропической геометрии. Не то что бы дискретными штуками не интересовались раньше, просто раньше вычислительных мощностей не было. Примерно как с машинным обучением, которое придумали в начале 1960-х, а взлетело только сейчас. Аналогично комбинаторикой ещё Гаусс интересовался, просто руками там много не посчитаешь.
>в остальных разделах этого разросшегося здания люди, как правило, считают себя математиками. И у всех них есть для этого полные основания
Это понятно. Просто согласись с тем, что если два представителя одной области ничего не понимают в работах друг друга, то это не совсем область? Ну вот Поппер сказал, что каждый человек философ. Ну мы здесь решили что каждый человек математик. Дело-то не в этом. Имеется некоторое количество людей, знающих некоторый условно стандартный материал, не обязательно использующих его в своей работе, но тем не менее, они прекрасно поймут друг друга. Это всё уже было описано 17 лет назад тут:
http://imperium.lenin.ru/~verbit/MATH/programma.html
Помимо создания нового знания, есть еще такая вещь как систематизация. Концептуальная математика об этом. Если не заниматься систематизацией, и не развивать язык, то доступ к знаниям затруднится и знания будут утеряны.
Поэтому нахуй это надо. С административной точки зрения: имеется очень расширенное определение математики, как ты предлагаешь. Хорошо. В одном департаменте сидят комбинаторщики, чистые математики, физики, компьютер саентисты. Никто из них не понимает друг друга, но все конкурируют за одни ресурсы. Что дальше? Полное вырождение. Если невозможно вести беседу, нет общих точек соприкосновения, предметом дискурса станет наличие академических регалий, цитируемость, и т.д. а от этой ситуации выигрывают только жулики и профанаторы. Имеем науку как в Мавритании.
> Имеется некоторое количество людей, знающих некоторый условно стандартный материал, не обязательно использующих его в своей работе, но тем не менее, они прекрасно поймут друг друга.
И разумеется, стандартность материала определяет некий сойбой, на которого у тебя ссылка. Ну вот онскозал, внемлите.
> Это понятно. Просто согласись с тем, что если два представителя одной области ничего не понимают в работах друг друга, то это не совсем область?
Если игнорировать факт существования оснований, к которым все в области сводится. Только такой игнор это следствие непрофессионализма. Конечно, некоему сойбою проще сказать "то что я знаю это кор математикс, а чего я не знаю это хуйня бородня", но это опять же школьничество и непрофессионализм.
>под капотом у этого оракул-прувера
Так смысл пруверов в том, что они основаны на простых правилах, в которых очень тяжело ошибиться при его написании.
> Мне не кажется, что все области математики одинаково ценные; я уверен, что самоценности математика сама по себе не имеет.
Классика, "тут играем, тут не играем".
https://www.youtube.com/watch?v=ZlCed-6GkAM
>стандартность материала определяет некий сойбой, на которого у тебя ссылка
С этим описанием согласится любой математик. Выше я уже упоминал Маклейна, могу еще посоветовать почитать Дьедонне. Да хоть Вавилова. Везде то же самое.
>Если игнорировать факт существования оснований, к которым все в области сводится
У математики вообще нет оснований. По словам Манина, математика "висит в воздухе". Более того, нахождение связей, наведение мостов между этими парящими островами знания, это то что определяет деятельность математика.
>но это опять же школьничество и непрофессионализм
Школьничество это подкреплять свои высеры несуществующими цитатами Браузера, потом упрекать оппонента ссылками на авторитеты, а на встречные аргументы отвечать бредом в духе "слова Брауэра вычисляются, а Манина или Гротендика нет, потому что они сойбои-хипстеры".
>чего я не знаю это хуйня бородня
Я уверен что ты даже линейную алгебру не в состоянии выучить, дело не в этом, тебя просто интересует игра в названия. Типа, Максимка сказал слово "топос", в Хачкеле есть термин "монада", а в унивалентном сойбойстве "гомотопия".
Этого достаточно для обоснования важности твоей хуйни.
"Математика это вычислимость". Как насчет невычислимых функций? Или неконструктивных вычислений? Ррряя, не математика, яскозал, я привел цитаты и сослался на авторитеты, а тебе нельзя, мои авторитеты вычислимы в автоматах Дебраузера/теории обучения Ватника/представимы в модели Миколова, и всё, дальше элементарное следствие изоморфизма Карри-Говарда в категории Int интуиционистских типов.
Содержательная математика тебе в принципе не интересна, тебе интересны её несуществующие "основания". При чём, тебя тут много раз называли праграммистом, но это большой комплимент, потому что область, интересная тебе, т.е. пруверы, это даже не программирование, это тестирование программ.
>>51416
Я еще понимаю дiдов с диэксдиуай, которые не зная контекста данного произведения вытаскивают отдельные фразы и утверждения и начинают гоготать над ними. Но я же выше объяснил, что там имелось в виду, и к чему это написано.
Математика изолируется до некоторого сообщества понимающих друг друга людей. А то что общее у этих людей это язык пучков, производных категорий, спектральных последовательностей, характеристических классов и т.д., ну извините как бы, так получилось.
Можно, конечно, определить иначе, исходя из оснований, но тогда размер математического сообщества сузится с нескольких десятков тысяч профессионалов до трех анальных клоунов, два из которых уже умерли.
Что признает сам унивалентный сой-тестировщик тут:
>>51367
>Другой вопрос, что во все это могут полтора человека помимо Мортберга
Такие дела.
>стандартность материала определяет некий сойбой, на которого у тебя ссылка
С этим описанием согласится любой математик. Выше я уже упоминал Маклейна, могу еще посоветовать почитать Дьедонне. Да хоть Вавилова. Везде то же самое.
>Если игнорировать факт существования оснований, к которым все в области сводится
У математики вообще нет оснований. По словам Манина, математика "висит в воздухе". Более того, нахождение связей, наведение мостов между этими парящими островами знания, это то что определяет деятельность математика.
>но это опять же школьничество и непрофессионализм
Школьничество это подкреплять свои высеры несуществующими цитатами Браузера, потом упрекать оппонента ссылками на авторитеты, а на встречные аргументы отвечать бредом в духе "слова Брауэра вычисляются, а Манина или Гротендика нет, потому что они сойбои-хипстеры".
>чего я не знаю это хуйня бородня
Я уверен что ты даже линейную алгебру не в состоянии выучить, дело не в этом, тебя просто интересует игра в названия. Типа, Максимка сказал слово "топос", в Хачкеле есть термин "монада", а в унивалентном сойбойстве "гомотопия".
Этого достаточно для обоснования важности твоей хуйни.
"Математика это вычислимость". Как насчет невычислимых функций? Или неконструктивных вычислений? Ррряя, не математика, яскозал, я привел цитаты и сослался на авторитеты, а тебе нельзя, мои авторитеты вычислимы в автоматах Дебраузера/теории обучения Ватника/представимы в модели Миколова, и всё, дальше элементарное следствие изоморфизма Карри-Говарда в категории Int интуиционистских типов.
Содержательная математика тебе в принципе не интересна, тебе интересны её несуществующие "основания". При чём, тебя тут много раз называли праграммистом, но это большой комплимент, потому что область, интересная тебе, т.е. пруверы, это даже не программирование, это тестирование программ.
>>51416
Я еще понимаю дiдов с диэксдиуай, которые не зная контекста данного произведения вытаскивают отдельные фразы и утверждения и начинают гоготать над ними. Но я же выше объяснил, что там имелось в виду, и к чему это написано.
Математика изолируется до некоторого сообщества понимающих друг друга людей. А то что общее у этих людей это язык пучков, производных категорий, спектральных последовательностей, характеристических классов и т.д., ну извините как бы, так получилось.
Можно, конечно, определить иначе, исходя из оснований, но тогда размер математического сообщества сузится с нескольких десятков тысяч профессионалов до трех анальных клоунов, два из которых уже умерли.
Что признает сам унивалентный сой-тестировщик тут:
>>51367
>Другой вопрос, что во все это могут полтора человека помимо Мортберга
Такие дела.
>тебя просто интересует игра в названия. Типа, Максимка сказал слово "топос", в Хачкеле есть термин "монада", а в унивалентном сойбойстве "гомотопия".
we have a winner
самоутверждайтесь в Computer Science, не трогайте мои пучки
Тестирование сой-программ это не совсем компьютер саенс, но в целом да. А математика и пучки это более-менее синонимы.
 52 Кб, 960x720
52 Кб, 960x720> С этим описанием согласится любой математик.
Ага, а кто не согласится, тот не настоящий. Есть такой прикол - "ненастоящий шотландец". Вот такие приколы, самореференции, постсойбойство от Фейерабенда, ссылка на " авторитетов" маргиналов и т.п трешак уровня рыбникова типа отрицания оснований - твой уровень понимания математики. Ну и швитая вера в абсолютную правоту, кудаж школоте без этого
> У математики вообще нет оснований. По словам Манина, математика "висит в воздухе".
> Более того, нахождение связей, наведение мостов между этими парящими островами знания, это то что определяет деятельность математика.
Это и называется "основания". То, из чего можно вывести все разделы математики или к чему можно свести любой раздел. Ты понимаешь, что противоречишь сам себе? Манин блядь какой-то, математика у него в воздухе висит. Че несешь-то?
>приколы, самореференции, постсойбойство
Чем твоё определение отличается от моего? Тем что я могу сослаться на десяток учёных, которые дофига чего сделали, что признано людьми, а не только на Брауэра и Лёфа (при чём второй к науке ну совсем никаким боком)?
Какой вес имеет твой пиздёж здесь? Математики ты не знаешь совсем никакой, это выяснили ещё семь тредов назад. Про вычислимость священного интуиционистского писания и сведение гомологической алгебры к нумерации Гёделя мы уже слышали, реальные аргументы можно? Или вся возможная аргументация сводится к усмотрению в моих или чьих-то ещё словах риторических приёмов, которыми ты сам регулярно пользуешься? Вера в вычислимость вычислима, а вера в что-то другое это платонизм, Аллах и т.д.
>а кто не согласится, тот не настоящий
Кто не знает пучков, тот не математик. Ты не знаешь ничего кроме Quality Assurance, поэтому не математик. В свете этого особенно смешны твои нападки на Вербицкого или ещё кого-то, как будто он не знает что такое интуиционизм или ты понимаешь хотя бы два слова в любой из его работ.
Ты тупой, это не называется "основания". Основания это попытка подвести фундамент, то есть вопросы типа какая аксиома важнее, аксиома выбора или аксиома детерминированности, или ZF без C но с аксиомой недостижимого кардинала, или ещё хуй знает что. Содержательной математики это не касается. Основания это изамарфизм Карри-Говарда грубо говоря, то есть абсолютно бессмысленный результат.
Наведение мостов это например "Rosetta Stone" Вейля, словарь "Fonctions – faisceaux" Гротендика, и т.д.
Я могу приводить десяток примеров, ни один из которых ты не поймёшь, потому что у тебя отсутствует целиком и полностью математическая культура, и знаний в математике у тебя никаких нет.
>Манин блядь какой-то
>Манин
>какой-то
Можно было бы сказать, что ты не умеешь пользоваться Гуглом, но это тебе не поможет, по выше названным причинам даже простое перечисление результатов какого-то конкретного ученого это пустой звук для тебя, ты их значения никогда не поймешь.
Анон, какой у тебя уровень понимания математики? Ты вообще изучал когомологии и пучки, или просто научпопом обмазался?
> Кто не знает пучков, тот не математик.
Тыскозал? Сойбой какой-то? Покажи хоть святое писание, где эта хуерга озвучена. Или реально сам придумал?
>Довольно очевидно, что в течение 20 века математика, бывшая относительно единым предметом существенно разрослась и сейчас состоит из довольно большого конгломерата областей многие из которых довольно слабо связанны между собой.
Я тебя огорчу, но всё как раз наоборот. Математика стало единой как никогда в 20 веке.
Этот деятель либо просто дрочит на давно всеми забытого вербицкого, либо сам Вербицкий и есть. Все его маняидеи по поводу математики дословно как раз из жжшечки вышеупомянутого сойбоя.
От нее оч сильно оторван CS, до такой степени, что в CS переоткрываются забытые области математики и именуются навроде "вычислимая дискретная теория хуйни". Люди которые в этой теме находятся они вообще начисто оторвано от какой-либо математической реальности, для них вся математика это наличие соответствующего алгоритма.
У нас на кафедре (прикладная математика) недавно читали семинар по какой-то новой статье о симметричных линейных программах, так там оратор 40 минут доказвал хитровыебанными CS методами один из базовых результатов теории групп для Sn. CS-наркоманы варятся в своём чане прямо как в известном скриншоте статьи из то ли медицины то ли биологии про инновационный метод расчёта площади под графиком. Куда уж там понять абстракции вроде пучков.
А что за результат?
Смысл?
>кококо cs наука
- переоткрываем решетку конечных множеств
- переоткрываем функцию над конечным телом
- переоткрываем конечную меру
- переоткрываем симплициальные комплексы ("теория графов")
- открываем новые результаты в комбинаторике методом тупого перебора
ну и всякие там теории алгоритмов, теории кодирования, которые сугубо прикладные инженерные дисциплины, такая же наука как сопромат.
Т.е претензии только к названиям? Гамалогии бездуховно называют, потеря потерь, что же делать.
В этом и состоит трагедия нашего времени, когда из программирования ушли все люди с истинно математическим образованием, в эту пустоту влились тысячи кс-мартыханов.
>в школе подать соответствие Карри-Говарда?
С тем же успехом можно давать в школу аксиому выбора.
да и в университете это оч забавно давать, не зная что полезнее, аксиома выбора или вторая теорема об изоморфизме, обе пригодились мне ниразу
Говночист жалуется, что науки ему не пригодились.
И хочет чтобы образовательную программу подстроили под говночистов.
 662 Кб, 650x532
662 Кб, 650x532Для кого же это трагедия?
Откуда ты знаешь, что есть в пучках, если ты не в состоянии понять определение пучка?
>In the nontrivial cases, it is often a deep geometric idea that is caught up in the knowledge of a differential. In most cases, it is in fact a matter of computability: the higher differentials of the spectral sequence are mathematically defined, but their definition is not constructive.
>mathematically defined, but not constructive
Что не удивительно, поскольку конструктивность не имеет никакого отношения к математике.
С точки зрения конструктивизма не верна даже фундаментальная теорема арифметики. Данная теорема утверждает, что для любого целого числа, большего 1 и не простого, существует единственное разложение на простые множители. Возьмём сравнительно небольшое число 10^(10^10^10^10^10^10^10^10^10^10)+23. Какое у него разложение? Никакое, поскольку тепловая смерть вселенной наступит раньше, чем мы сможем его вычислить, учитывая принцип Ландауэра.
Для конструктивиста нет никакой разницы между достаточно большими числами (даже теми, для записи которых не требуются стрелки Кнута или стрелки Конвея) и недостижимым кардиналом.
Между вычислением спектралок и верой в Аллаха. Между топосами Гротендика и ловлей покемонов.
> С точки зрения конструктивизма не верна даже фундаментальная теорема арифметики. Данная теорема утверждает, что для любого целого числа, большего 1 и не простого, существует единственное разложение на простые множители. Возьмём сравнительно небольшое число 10^(10^10^10^10^10^10^10^10^10^10)+23. Какое у него разложение? Никакое, поскольку тепловая смерть вселенной наступит раньше, чем мы сможем его вычислить, учитывая принцип Ландауэра.
Ну если так, на каком основании ты заявляешь, что вышеупомянутая теорема верна? Сам же привёл случай, для которого она недоказуема на практике. Значит, ты веруешь в то, что она верна? Поди и умным себя считаешь, новости смотришь?
Я просто продемонстрировал два случая, один посложнее другой попроще, в которых математики считают некоторые утверждения математически корректным и верными, а шизики-конструктивисты те же самые утверждения отрицают и орут "ррря врёти, нет такого". Ты же верун и есть, верун в вычислимость. Есть невычислимые функции? Нет такого, не верю. Понятно. Запишись на конференцию сторонников теории плоской земли, найдешь там единомышленников.
Дык я про это как бы и говорил. Товарищ на протяжении девяти тредов утверждает, что математика это есть вычислимость. Других аргументов, кроме того что данное утверждение вычислимо, пока не было.
> Я просто продемонстрировал два случая, один посложнее другой попроще, в которых математики считают некоторые утверждения математически корректным и верными,
А на каком основании ты считаешь корректным то, что невозможно доказать? Вероваешь? А математика к твоей вере какое отношение имеет?
>>51520
> Математикам вообще на вычислимость глубоко наплевать,
Раз пукнутый такскозал, ок
Какое отношение к математике имеет твоя вера в вычислимость? Если ты даже фундаментальную теорему арифметики отрицаешь, какой из тебя математик?
Мой прикол оказался слишком сложным для тебя. Доказать-то возможно, но только это не конструктивное доказательство. Почему? Потому что явное построение отсутствует, это критерий конструктивности. Таким образом показано, что конструктивность не имеет отношения к математике.
>Значит, само число делится на 3
Речь шла про выписывание факторизации, но ладно, не важно.
Ну тебе выше показали, что можно доказать невычислимое утверждение. Какой из тебя математик, если ты не понимаешь, что является доказательством, а что нет?
В чем проблема? Можно просто запретить очень большие числа. Они в общем-то и не нужны. И даже не особо-то числа.
А зачем их запрещать? У математиков нет проблемы с этими числами. Как и с высшими дифференциалами в спектральных последовательностях. Как и с топосом Гротендика, в аксиомы которого входит утверждение эквивалентное существованию недостижимого кардинала. Как и с невычислимыми функциями.
У конструктивиста есть проблемы со всем этим. Поэтому ему надо запретить. С таким мышлением лучше депутатом в гос думе работать, никак не математиком.
Если рассуждать как конструктивист, то практически все содержательное из математики упраздняется, остаётся разве что перекладывание палочек в машине Поста. В принципе понятно, у человека есть желание называть и считать себя математиком, а не QA-тестером или охранником на соевом складе; при этом желания или возможности выучить хоть что-то из математики нету, надо же ведь и аниме смотреть и вообще жизнь тяжелая. Вот и приходится запретить всю математику, кроме палочек.
>И даже не особо-то числа
А, ну да, элемент \mathfrak$Z$ кольца целых чисел это не особо-то и число. Вас понял.
>ак и с топосом Гротендика, в аксиомы которого входит утверждение эквивалентное существованию недостижимого кардинала
Какое? Знаю только, что юниверсумы Гротендика влекут существование недостижимого кардинала.
>юниверсумы Гротендика влекут существование недостижимого кардинала
Угу, я про это
https://en.wikipedia.org/wiki/Grothendieck_universe#Grothendieck_universes_and_inaccessible_cardinals
Непосредственно же в аксиомы топоса входит понятие малой категории, которое опирается на упомянутые выше основания
https://ncatlab.org/nlab/show/small+category
https://ncatlab.org/nlab/show/locally+small+category
htps://ncatlab.org/nlab/show/size+issues
>Непосредственно же в аксиомы топоса входит понятие малой категории, которое опирается на упомянутые выше основания
Понял, спасибо.
> Ну тебе выше показали, что можно доказать невычислимое утверждение. Какой из тебя математик, если ты не понимаешь, что является доказательством, а что нет?
Ты про потенциальную бесконечность что-нибудь слышал? Ах да, ты ж в неё не можешь.
>>51538
Недостижимые кардиналы и прочее такое это просто буковки. Их можно и на машине Тьюринга переставлять. Элементы алфавита теории соевых гамалогий, типы, для которых определены конструкторы итд. Никакого другого содержания за ними не стоит. Но вы веруете, что у таких обьектов есть какое-то ещё значение, смысл кроме конструктивного (элементы алфавита и сочетания элементов). Вы сколько ни выебуйтесь, а выше машины Тьюринга не прыгнете, это ещё в 30х годах прошлого века доказано. Все ваши гамалогии это просто программы для универсальной машины Тьюринга.
Я-то слышал. Последовательный и честный конструктивист её тоже отрицает, непоследовательный и нечестный начинает что-то говорить про машину Тьюринга в этом месте. Как же получается, что разложение на простые гуглп лекса или числа Грэма существует, если его нельзя явно построить?
> оследовательный и честный конструктивист её тоже отрицает
Хуйни не неси, её даже Брауэр не отрицал. Как вариант, ты как обычно не знаешь того, о чем пытаешься спорить и путаешь конструктивизм с финитизмом.
>Никакого другого содержания за ними не стоит
Вообще-то стоит, просто ты не в состоянии его понять.
>выше машины Тьюринга не прыгнете, это ещё в 30х годах прошлого века доказано
Кем доказано? Тезисом Чёрча? Ты понимаешь, что такое доказательство? При чём никто в здравом уме этого не утверждал, сам тезис сводит только лямбда-калькулюс к вычислениям машине Тьюринга, чтобы утверждать что математика эквивалентна лямда-калькулюсу, надо очень серьёзно упороться.
>Все ваши гамалогии это просто программы для универсальной машины Тьюринга
Угу, все ваши гамалогии это символы, нарисованные мелом на доске, значит математика это раздел каллиграфии. Понятно. Главное что тебе учить ничего не надо. Палочки выучил складывать, всё, математик.
http://www.math.harvard.edu/quals/index.html
Можешь объяснить почему сюда входят гамалогии, но не входят лямбда-функции? И почему там вообще есть что-то кроме перекладывания палочек?
>её даже Брауэр не отрицал
"Даже". Браузер, тот который сначала защитил диссертацию про интуиционизм, а потом доказал свои основные математические результаты, типа теорем о неподвижной точке, неконструктивно? Этот? Ну как бы он своими работами показал, чего стоит конструктивизм (ничего) и насколько он применим в математике (ни насколько).
> Вообще-то стоит, просто ты не в состоянии его понять.
Да-да, новое платье короля не видят только ебланы. Давай, поясни за это невидимое содержание. Во что я там не вероваю, в каких пучковых покемонав.
> Можешь объяснить почему сюда входят гамалогии, но не входят лямбда-функции?
Потому что это не курс по основаниям? А только по частному случаю оснований?
> И почему там вообще есть что-то кроме перекладывания палочек?
А есть ли?
> "Даже". Браузер, тот который сначала защитил диссертацию про интуиционизм, а потом доказал свои основные математические результаты, типа теорем о неподвижной точке, неконструктивно?
Потому что конструктивно на тот момент мало что доказать можно было? Это сложно вообще-то. И одному человеку полную реформу математики не потянуть.
>его нельзя явно построить
Нет, ну алгоритм-то есть, берёшь все простые, не превосходящие N(тоже алгоритм существует), потом делишь на максимальное, пока остаток 0, увеличиваешь степень на 1, потом берёшь следующее и так, пока не дойдёшь до последнего. То, что это работать будет вечность не значит, что нельзя явно построить. Явно построить значит предоставить алгоритм, отрабатывающий за конечное время.
По ироническому утверждению В. И. Арнольда, разница между чистой и прикладной математикой не научная, а социальная и залючается в том, что чистому математику платят за открытие математических фактов, в то время как прикладному математику платят за решение практических задач. Арнольд также замечает, что в России почти каждый математик сочетал «чистую» и «прикладную» математику.[2]
Прикладной математики вообще не существует, потому что вся математика прикладная. Если математическая теория не помогает доказать утверждения, для формулировки которой не требуются понятия этой теории, то это говно, а не теория.
То есть с одной стороны оказывается весь core mathematics вокруг теоремы Атьи-Зингера; с другой не имеющая никаких внешних применений параша, вроде классического анализа с оценками, "очень общей алгебры" в духе теории квазигрупп, комбинаторики, изучения специальных эллиптических функций и тэта-функций, мат. логики вроде теории моделей, n-категорий и прочих попыток построить "гомотопическую алгебру", и т.п., можно долго ещё перечислять.
В данном треде наблюдаем очередной пример, т.е. конструктивизм:
>>51367
Здесь мы выяснили, что заниматься конструктивными основаниями могут из ныне живущих где-то 1.5 человека,
>>51548
А здесь, что конструктивные принципы очень сложны в реализации, и поэтому не применимы на практике в данный момент.
Осталось понять, зачем ими вообще заниматься. Чтобы коммунизм наступил? В математике и так все работает.
> Бертран Рассел о чистой математике: «Чистая математика — это такой предмет, где мы не знаем, о чём мы говорим, и не знаем, истинно ли то, о чём мы говорим».
Ну я и говорю. Без конструктивного подхода математика это раздел богословия.
>>51555
> А здесь, что конструктивные принципы очень сложны в реализации,
> и поэтому не применимы на практике в данный момент.
На данный момент как раз применимы, сейчас не 1907 год.
Лучше уж раздел богословия, чем сойбойства.
https://otr-online.ru/programmy/gamburgskii-schet/mihail-tsfasman-fenomen-20790.html
>Что делает теология? Она рассуждает о столь же общих проблемах, связанных с Богом, со Священным Писанием, с церковным преданием. И почему первое должно считаться наукой, а второе – нет, я не понимаю.
>Я участвовал пару раз в таких семинарах, посиделках с богословами. И оказывается, что, по крайней мере в этих конкретных сообществах, мы с ними думаем одинаково. Я имею в виду сейчас не предмет рассмотрения, а именно стиль мышления, вплоть до отношения ко всяким общественно острым фактам.
Можешь начинать рваться.
>На данный момент как раз применимы
В манямирке? Теорему Коши о среднем доказали конструктивно уже? Вообще хоть какую-нибудь теорему, полученную после 1920-го?
Вся актуальная математика доказана конструктивно. Разумеется, кроме невнятного бреда про большие кардиналы и прочих подобных вещей.
"Актуальная математика" в твоём смысле это ~0.000001% от всей математики.
>Без конструктивного подхода математика это раздел богословия.
Да с ним, тоже раздел богословия.
> Да с ним, тоже раздел богословия.
Отнюдь. Брауэр показал что такое математика на самом деле. А всякие веруны до сих пор хуйней страдают.
>Бертран Рассел
Охеренный чел!
>Годфри Харди
Красава бля!
>В. И. Арнольда
Мой личный математический кумир, ёпта.
Я и говорю, доказал что интуиционистский пиздеж ничего не стоит тем, что сам не пользовался им на практике. И Воеводский тоже не пользовался в доказательстве теоремы об изоморфизме норменного вычета. За перекладывание палочек премию Филдса не дадут, это только в коррекционной школе, куда ты ходил, такие упражнения.
О, а вот и пророк Брауэр появился. Это у вас новое ветвь родилась я смотрю? Брауэризм.
ыы основания ыхыхы
Комбинаторика, теория графов, теория чисел
Автор ты сука?
первая волна илитблядства: хаскiль, дрочка на мощные системы типов и кокотегориальность, утверждение о прикладной пользе всего этого в повседневном программировании
вторая волна илитблядства: дрочка на завтипы, пруверы, начало интуиционистского маразма
третья волна илиблядства, предтерминальная: отход в кококонструкивистский манямир с кукарекам про полную автоматизацию математики, постоянная фокусировка на основаниях
по всей видимости, четвёртая финальная стадия: полная деградация до ультрафинитизма и понимания математики на уровне древних греков
тут можно провести аналогию с фемками
первая волна - задачи чисто прикладные, движение по законодательно-правовому направлению
вторая волна - направление тоже вроде прикладное, хотя задачи весьма расплывчатые, уже появляются какие-то обощения и теор. обоснования, вроде теории пересечений
третья волна - полнейший пиздец с gender science и privilege theory, и прочими фундаментальными открытиями, которые должны изменить мир
в обоих случаях имеем типичный криптомарксизм: всё плохо, потому что всё с самого основания ниправильна, нужно всё изменить, мы знаем как это сделать, ко-ко-ко ривалюция нужно привозмогать и высрать нового человека, и новое общество, без классов, полового диморфизма и модус понес, аминь
ну и конечно же бесконечный самоподдув, заключающийся в ощущении себя неибаца прогрессивным
Спизданул как господь, сохранил.
>полная деградация до ультрафинитизма и понимания математики на уровне древних греков
Разве древние греки были ультрафинитистами?
На уровне пещерных людей, скорее.
Да и то, какой там уровень был у пещерных людей --- мы не знаем.
Может они и представляли актуальную бесконечность (во снах).
Архимед однажды написал книгу "Псаммит", в которой проиллюстрировал, что самого большого натурального числа нет. Был срач, с Архимедом много спорили.
Не только ультрафинитистами, еще не верили в отрицательные числа, ноль и вообще числом считали только то, что выражает какое-то геометрическое отношение. Унаследовали науки от вавилонян и египтян и проебали всё из-за дремучего догматизма.
У них были отдельно числа - это 1, 2, 3, 4, ... , и отдельно были отношения - это положительные рациональные числа. Отношения не воспринимались как числа, это были совсем отдельные сущности.
Бб двумя блоками ниже.
В быдломатематике перекладывают палочки и проверяют на прувере полученные 60 лет назад и используемые с тех пор ежедневно результаты;
В илитоматематике доказывают теоремы.
Кстати, прямо сейчас тебе могу доказать, что конструктивная математика это не математика. Назовем функцию f(x) конструктивной, если её можно задать некоторой формулой или правилом, описываемым текстом конечной длины; это соответствует вычислимой на машине Тьюринга функции.
Легко видеть, что множество таких функций не более чем счётно (проверка предоставляется читателю); в то время как множество функций непрерывных на отрезке [0; 1] уже имеет мощность континуум, а множество всех функций не меньше гиперконтинуума; (даже функций, возвращающих лишь два значения, уже гиперконтинуум, потому что можно построить биекцию в 2^{R}).
Таким образом, весь функциональный анализ попадает под запрет бешеной религиозной секты конструктивизма, ведь функциональное пространство по определению полно, и включает в себя все функции, а не только одобренные лично Чёрчем. Гомологическую алгебру запретили несколько тредов назад из-за того что в спектральных последовательностях высшие дифференциалы вычисляются неконструктивно; теорию топосов упразднили из-за понятия малой категории, и т.д.
В общем все содержательное, что позволяет доказывать теоремы и получать результаты, под запретом, остается подбирать давно используемые в математиками теоремы и передоказывать их на компьютере раз в 50 лет.
То есть ты приходишь в уже устоявшуюся традицию, и говоришь что это не так, то нельзя, и вообще всё надо ограничить; вот есть мои принципы, в которые я верю, в данном случае вычислимость, всё остальное под запрет.
Религиозный фундаментализм как он есть, ваххабизм из таких же посылок исходит и так же действует.
Вот, у нас истинное понимание ислама математики, оно было со временем утеряно из-за всяких кафиров Канторов и Пеано, но ничего, мы пришли чтобы запретить всё плохое и заодно перечеркнуть последние 400 лет прогресса вашей науки. Круто.
Вопрос не в тему, но стоит читать "Логику" Чёрча? Актуально? Полно?
Доказательства несоизмеримости некоторых величин привели к расширению понятия числа; доказательство неразрешимости в радикалах уравнения общего вида со степенью ≥5 привели к теории Галуа, аналогично кстати к ней привели доказательства невозможности построения циркулем и линейкой правильных n-угольников для некоторых n (оставляя в стороне искусственные ограничения, поставленные в этих задачах, кому вообще может быть принципиально в радикалах решено уравнение или нет, в тэта-функциях уравнение любой степени кстати можно решить); конструктивизм в принципе не приведет ни к какому расширению, потому что он уже содержится в математике.
В математике дофига построимого и вычислимого. Просто если ей заниматься не только на школьном уровне, а хотя бы векторное пространство пополнить по норме, то всё, пиздец, там будут функции которые никак нельзя описать конечным правилом, при чем несчётное количество таких функций.
У тебя неправильная аналогия, конструктивизм это наоборот, как если бы мы запретили иррациональные числа и скатились на уровень древних греков. Вайлдбергер собственно уже запретил.
Чего не охватывают такие подходы, они не пытаются охватить что-то содержательное и сохранить это, им в принципе плевать на содержание, святые принципы важнее. Хотя там есть способы. Например ну ты не любишь иррациональные числа, но pi или e тебе все равно нужны. https://en.wikipedia.org/wiki/Ring_of_periods
>осталось ровно тем же, чем и было: пропорцией
Пропорцией чего является элемент произвольной ассоциативной алгебры? Потому что это и есть то, к чему привело обобщение понятия числа.
>взятие корня - это операция, обратная возведению в степень
Чего? Взятие корня это и есть возведение в степень, буквально, просто степень с дробным показателем. Обратное к операции возведения в степень это логарифмирование.
>Казалось бы, зачем вводить лишние сущности
Зачем вводить какие-то произвольные ограничения на методы, доступные для решения нужной тебе задачи? Ну если из догматических соображений, что тебе лично не нравятся какие-то методы, например доказательства от противного или чисто экзистенциальные доказательства, и ты поэтому не хочешь ими пользоваться и предлагаешь другим отказаться тоже, то понятно, но это сектантская позиция, изначально.
>Речь о том, что некоторые задачи неразрешимы в той конкретной форме, в которой они сформулированы
Не, ну это ясно. Гипотеза континуума например невыводима из ZFC. Впрочем есть мнение что где-то 100% содержательных математических результатов, выводимы и верны в любой возможной аксиоматике, данное убеждение подтверждается на практике тем что проблемы оснований ни одного серьезного математика не интересовали уже лет 80 как.
>представления об отрицательных числах, нуле и уж тем более комплексных числах возникли позже
Комплексные числа ~1545, отрицательные числа ну смотря где, примерно IX век в Индии или III в Китае, в Европе же не раньше Фибоначчи, а скорее всего, того же Кардано. Но математика в средневековой Европе до Кардано это довольно чудовищное явление в принципе, легче сказать что её просто не было.
>Вопрос в том, как такие абсурдные задачи можно было бы распознавать заблаговременно
Да оно кажется проще, не иметь научруком какого-нибудь Лузина, который выдает тебе задачи вроде той же гипотезы континуума. А вообще, здравый смысл исследователя и всё такое. У Маклейна есть про это.
>Гипотеза континуума например невыводима из ZFC.
Это доказано, по существу, с применением теоретико-топосовых методов. Непротиворечивость которых под сомнением.
>ни одного серьезного математика
И тут такой ХОБАНА, ХОБАНА! Воеводский.
Это доказано методом форсинга. Позже оказалось, что форсинг имеет применение в теории топосов. Сама теория топосов не относится к core mathematics, при чём, даже; топосы изначально придумал Гротендик как основания для этальных когомологий, а сами этальные когомологии придумал чтобы доказать гипотезы Вейля. Аналогично, как выяснилось что этальные когомологии можно применить за пределами алгебраической геометрии (см. Сулливан Геометрическая топология), так же оказалось что можно ввести понятие элементарного топоса (топос пучков на пространстве с одной точкой эквивалентен категории множеств), которое не нуждается в топологии Гротендика, хотя современные деятели в этой области вроде как раз предлагают вернуться так сказать к истокам:
https://www.oliviacaramello.com/Unification/HDROliviaCaramello.pdf
>Воеводский
Воеводский доказал теорему об изоморфизме норменного вычета, за что получил премию Филдса. После этого результата математикой он больше не занимался. Сначала он избрал себе популяционную генетику, но не преуспел в ней, затем переключился на основания и придумал там ХоТТ. В последние годы он вообще говорил что математика больше не нужна и ей осталось лет 50 максимум.
Можно привести много примеров, Перельман после гипотезы геометризации тоже больше ничего не сделал кроме общения с журналистами, Николай Дуров после своей диссертации про геометрию Аракелова написал одну соцсеть и мессенджер. Не вижу какую мысль нужно извлечь из этих примеров.
>Это доказано методом форсинга.
Который не "имеет применение в теории топосов", а по существу теоретико-топосовый. Это как если бы ты увидел аналитическое доказательство того, что C алгебраически замкнуто, и сказал бы, что "основная теорема алгебры применима в матанализе". См. Peter T. Johnstone, Topos Theory и Sketches of an Elephant.
>топос пучков на пространстве с одной точкой
На антидискретном пространстве, мы же не маленькие и про локали в курсе.
Общеизвестно что "основная теорема алгебры" не имеет никакого отношения к алгебре
>ты увидел аналитическое доказательство того, что C алгебраически замкнуто
а что, есть хоть одно не аналитическое? Если это аналитический факт, в принципе, какое там еще может быть доказательство.
>Topos Theory и Sketches of an Elephant
Ок, не спорю, like I've said, it's not part of core mathematics. Насчёт непротиворечивости предложенной Гротендиком изначально конструкции, впрочем, никаких сомнений нет.
Нет. Hask не является категорией. Поскольку в хаскеле нельзя определять новые категории, в хаскеле нет категорий.
>Не вижу какую мысль нужно извлечь из этих примеров.
Матан отжирает кучу сил и становится не интересным.
>Курт Гёдель показал, что полной математики в принципе не может существовать.
>Вернее, что "в любой формальной системе существует утверждение, которое нельзя ни доказать, ни опровергнуть".
>Отсюда фразы о том, что математика - язык бога, что через неё можно познать мир - неверны.
>Гёдель фактически доказал, что мир не познаваем в полной мере с помощью формальных систем с конечным набором аксиом.
Не совсем так.
Во-первых, есть https://ru.wikipedia.org/wiki/Теорема_Гёделя_о_неполноте
Их там две, ты написал о первой. Но они обе - про формальные арифметики, а не про формальные системы вцелом.
Во-вторых, есть https://ru.wikipedia.org/wiki/Теорема_Гёделя_о_полноте
Там как-раз про истинность и доказуемость прочитай.
И сразу - пара вопросов:
Разве логика предикатов первого порядка не является формальной системой?
Разве логика предикатов первого порядка не имеет конечный набор аксиом?
В-третьих, ты пишешь о том, что
>в любой формальной системе существует утверждение, которое нельзя ни доказать, ни опровергнуть
Что же из этого следует? Или должно бы следовать? Что вся формальная система некорректна что-ли?
Смотри. Есть геометрия Евклида, например. В ней есть аксиома. Это пятый постулат.
Цитата, отсюда: https://ru.wikipedia.org/wiki/Евклидова_геометрия
>Если прямая, пересекающая две прямые,
>образует внутренние односторонние углы,
>меньшие двух прямых углов,
>то, продолженные неограниченно,
>эти две прямые встретятся с той стороны,
>где углы меньше двух прямых углов.
И есть, допустим, утверждение:
>C какой-либо конкретной стороны
>встретятся прямые,
>для которых внутренние углы пересекающей их прямой - ПРЯМЫЕ. Это параллельные прямые.
Да, это утверждение нельзя ни доказать ни опровергнуть.
Но это вовсе не значит, что вся геометрия перестаёт, внезапно, работать,
и уж тем более, что она поэтому - перестаёт существовать.
>>50673
>Из теоремы Гёделя (в более общей современной формулировке) вытекает лишь то,
>что не существует тьюринговый алгоритм, который выдаёт все истинные и только истинные высказывания.
>Но кто доказал, что в нашем мире невозможны сверхтьюринговые вычисления?
Сверхтьюринговые вычисления - связаны с "проблемой останова".
Тот же парадокс лжеца на одном лишь отрицании.
Лжец говорит, что он лжет.
Вопрос: Лжёт ли он?
TRUE: Если он лжец, то лжёт;
FALSE: Если он лжёт, что он лжёт, то он говорит правду.
TRUE: Правда про то, что он лжёт - значит ложь...
FALSE: Если он лжёт, что он лжёт, то он говорит правду.
TRUE: Правда про то, что он лжёт - значит ложь...
FALSE: Если он лжёт, что он лжёт, то он говорит правду.
...
И так - до бесконечности.
Эту шнягу, не то что тьюринговыми, но ИМХО, даже сверхтьюринговыми вычислениями не вычислить,
если ими не будет доказано, что последовательные вычисления - ВНЕЗАПНО, закольцовываются, или не застопорится.
Также, как и с попыткой проверить - где пересекутся ПАРАЛЛЕЛЬНЫЕ прямые.
Вдруг они пересекутся где-то в миллиардах гигапарсек, из-за какой-нибудь кривизны пространства.
>Курт Гёдель показал, что полной математики в принципе не может существовать.
>Вернее, что "в любой формальной системе существует утверждение, которое нельзя ни доказать, ни опровергнуть".
>Отсюда фразы о том, что математика - язык бога, что через неё можно познать мир - неверны.
>Гёдель фактически доказал, что мир не познаваем в полной мере с помощью формальных систем с конечным набором аксиом.
Не совсем так.
Во-первых, есть https://ru.wikipedia.org/wiki/Теорема_Гёделя_о_неполноте
Их там две, ты написал о первой. Но они обе - про формальные арифметики, а не про формальные системы вцелом.
Во-вторых, есть https://ru.wikipedia.org/wiki/Теорема_Гёделя_о_полноте
Там как-раз про истинность и доказуемость прочитай.
И сразу - пара вопросов:
Разве логика предикатов первого порядка не является формальной системой?
Разве логика предикатов первого порядка не имеет конечный набор аксиом?
В-третьих, ты пишешь о том, что
>в любой формальной системе существует утверждение, которое нельзя ни доказать, ни опровергнуть
Что же из этого следует? Или должно бы следовать? Что вся формальная система некорректна что-ли?
Смотри. Есть геометрия Евклида, например. В ней есть аксиома. Это пятый постулат.
Цитата, отсюда: https://ru.wikipedia.org/wiki/Евклидова_геометрия
>Если прямая, пересекающая две прямые,
>образует внутренние односторонние углы,
>меньшие двух прямых углов,
>то, продолженные неограниченно,
>эти две прямые встретятся с той стороны,
>где углы меньше двух прямых углов.
И есть, допустим, утверждение:
>C какой-либо конкретной стороны
>встретятся прямые,
>для которых внутренние углы пересекающей их прямой - ПРЯМЫЕ. Это параллельные прямые.
Да, это утверждение нельзя ни доказать ни опровергнуть.
Но это вовсе не значит, что вся геометрия перестаёт, внезапно, работать,
и уж тем более, что она поэтому - перестаёт существовать.
>>50673
>Из теоремы Гёделя (в более общей современной формулировке) вытекает лишь то,
>что не существует тьюринговый алгоритм, который выдаёт все истинные и только истинные высказывания.
>Но кто доказал, что в нашем мире невозможны сверхтьюринговые вычисления?
Сверхтьюринговые вычисления - связаны с "проблемой останова".
Тот же парадокс лжеца на одном лишь отрицании.
Лжец говорит, что он лжет.
Вопрос: Лжёт ли он?
TRUE: Если он лжец, то лжёт;
FALSE: Если он лжёт, что он лжёт, то он говорит правду.
TRUE: Правда про то, что он лжёт - значит ложь...
FALSE: Если он лжёт, что он лжёт, то он говорит правду.
TRUE: Правда про то, что он лжёт - значит ложь...
FALSE: Если он лжёт, что он лжёт, то он говорит правду.
...
И так - до бесконечности.
Эту шнягу, не то что тьюринговыми, но ИМХО, даже сверхтьюринговыми вычислениями не вычислить,
если ими не будет доказано, что последовательные вычисления - ВНЕЗАПНО, закольцовываются, или не застопорится.
Также, как и с попыткой проверить - где пересекутся ПАРАЛЛЕЛЬНЫЕ прямые.
Вдруг они пересекутся где-то в миллиардах гигапарсек, из-за какой-нибудь кривизны пространства.
 44 Кб, 740x721
44 Кб, 740x721> Но кто доказал, что в нашем мире невозможны сверхтьюринговые вычисления?
А кто сказал, что возможны? Ты что ли?
Подводный камень в том, что хотелок тут мало.
В каких интересных одеждах раньше учёные ходили..
> Эту шнягу, не то что тьюринговыми, но ИМХО, даже сверхтьюринговыми вычислениями не вычислить,
Этот парадокс касается только двузначной логики, т.е исключённого третьего в конечном счёте. В той же нечёткой логике парадокса лжеца нет, там просто получается по 50% правды и пиздежа. Исключенное третье это вообще не математический принцип, от его использования в математике одна хуйня и парадоксы на ровном месте.
Нечеткая логика в физике применяется (в Копенгагенской интерпретации, в many worlds коллапса волновой функции не происходит и соответственно вероятность не имеет смысла вообще); но в математике у неё применений нет.
>в many worlds коллапса волновой функции не происходит и соответственно вероятность не имеет смысла вообще
Ну да, ну да. Правило Борна-то всё равно нужно костылить, никуда от него не деться независимо от интерпретации.
> в математике у неё применений нет.
В гамалогиях что ли? Я уверен, что её можно применить в основаниях вместо каличной бинарной логики. Этого точно никто не пробовал. Наверное даже лучше сразу брать конструктивную нечеткую логику Атанасова вместо оригинальной Заде.
Основания математики относятся к математике так же, как метафизика к физике. Или философия науки к науке. Никак то есть.
>Этого точно никто не пробовал
Не сомневаюсь, в области оснований за всё время её существования трудились от силы 3 человека.
Очевидные определения по рекурсии. Трансфинитная рекурсия и, вообще говоря, нётерова рекурсия. Обобщений нётеровой рекурсии ещё не придумано.
Потенциальная бесконечность
> Основания математики относятся к математике так же, как метафизика к физике.
Ну раз Панин или Манин, кто бы они ни были, так сказал, наверное так и есть.
Вот да, трансфинитная рекурсия, но мне что-то казалось, что это не то немного, думал есть её алгоритмический аналог какой-то, ну а хотя да, он и не нужен, наверное. Спасибо
Существуют разные обобщения понятия вычислимости на бесконечные множества. Среди относительно популярных: альфа-рекурсия, E-рекурсия и машины Тьюринга с трансфинитным временем.
Идея альфа рекурсии примерно такая. Вычислимые функции из N в N это в точности те функции график которых определяется Σ₁ формулой. И если вместо N рассматривать другие структуры, в определенном смысле похожие на N, то Σ₁-определимые функции там должны быть обобщениями вычислимости. Как правило в качестве таких структур используют уровни конструктивной иерархии L_α для допустимых ординалов α.
E-рекурсия говорит о вычислительных процессах манипулирующих с произвольными множествами. Название машин Тьюринга с бесконечным временем объясняет само себя.
Спасибо.
> Основания математики относятся к математике так же, как метафизика к физике
Не пизди. Основания это фреймворк, потреблядское отношение только у прикладников.
 86 Кб, 604x584
86 Кб, 604x584О, N-петуха из дурки выписали. Неожиданно. Года 2 лечился, все забыл? На выбор: нумералы Чёрча, ординалы фон Неймана, ординалы Брауэра.
Ты я смотрю так и не нашел определение за 3 года? Ни что из перечисленной тобой хуйни не является определением. Усёк?
Фреймворк это гомологическая алгебра, пучки, теория категорий. Если у тебя ZFC это фреймворк, то ты не математик, а петух. Иди гипотезу континуума докажи или чем вы там, долбоебы, занимаетесь.
> Фреймворк это гомологическая алгебра, пучки, теория категорий
С точки зрения малолетнего долбоёба - безусловно.
> Ни что из перечисленной тобой хуйни не является определением
Если бы ты не был ебланом, ты бы догадался упомянуть ABC-гипотезу и сказал бы, что ни одно из существующих определений N не позволяет вывести свойства умножения из свойств сложения даже в простейшем случае, и чтобы это сделать, нужно рассматривать сложение и умножение в разных театрах Ходжа, а их свойства связывать через всякую эталь тета хуергу. Вот это действительно хуй знает почему так.
Ты выообще не в теме, ничего из того что ты перечислил не имеет ни малейшего отношения к определению натурального числа (подозреваю ты тупое школоло нахватавшееся модных терминов а сам понятия не имеешь о чём они).
На самом деле определние N дать невозможно так как не умея оперировать счетными множествами на метаязыке ты не сможешь корректно определить N в объектном языке.
Ты ж сказочный долбаеб. Никакого "определения" N вне его построения быть не может, во всех этих метаязыках ты просто запутаешься, потому что определения на метаязыке сами требуют определения и так до бесконечности.
Школотрон ебучий, подумай почему в нормальной (конструктивной) математике не используется никаких определений, внешних по отношению к самой теории (лямбда исчисления, например), никаких метаязыков и прочей бесполезной хуерги. Только то, что выразимо на языке самой теории.
>никаких метаязыков и прочей бесполезной хуерги.
никаких машин тьюринга там или поста все реальное)))
> Ну так хули ты тогда пиздел про ABC, пеано и прочую хрень якобы они являются определениями? Ась???
Ты ещё раз перечитай, что там написано. Хотя, думаю смысла нет, мозги у тебя все равно не отрастут.
> Используется, например марков на первой странице учит рисовать палочки на бумаге.
Опять же, ты даже не понимаешь о чем речь, не понял приведенного примера. Думаешь, если начитался какой-то хуйни, умным стал?
> Ты ещё раз перечитай, что там написано. Хотя, думаю смысла нет, мозги у тебя все равно не отрастут.
Ты пытался подменить дискурс первичного определения N какой-то экзотикой, ну и кто из нас мудак?
> Опять же, ты даже не понимаешь о чем речь, не понял приведенного примера.
Тогда пусть подробнее расписывает что имел ввиду или примера там никакого нет. Ткни в любую конструктивисткую книжку с последовательным изложением материала, получишь вначале метаязыковое описание конструктивисткого языка.
> Ты пытался подменить дискурс первичного определения N какой-то экзотикой, ну и кто из нас мудак?
Мань, я тебе привёл пример в какую сторону доказывать, что все определения N это не определения. Ты даже этого не понял.
> Ткни в любую конструктивисткую книжку с последовательным изложением материала, получишь вначале метаязыковое описание конструктивисткого языка.
Для общего неформального описания происходящего. Которое нужно только для введения в предмет и общих пояснений, а в самих теориях (собственно, построениях и вычислениях) не используется. Барендрегт тот же, lambda calculus with types. Там есть примеры того, как метаязыковые определения операции отбрасываются использованием нотации самой теории.
>ни одно из существующих определений N
>не позволяет вывести свойства умножения
>из свойств сложения даже в простейшем случае
Если умножение - это многократное сложение,
то почему нельзя вывести свойства умножения
из свойств операции сложения, и свойств операции повтора этого сложения?
Ведь чтобы умножить a на b - нужно просто повторять сложение a к результату - b раз?
Мне кажется можно как-то ещё быстрее и проще реализовать умножение,
например, умножение Карацубы, или вот это:
https://studfiles.net/preview/4258611/page:10/
По сути, здесь просто повтор фиксированных правил,
но через них уже реализовано умножение в унарной системе счисления.
Так вот, разве ИЗ СВОЙСТВ этих правил нельзя вывести свойства умножения.
А ещё вот эту статью разберите: https://habr.com/ru/post/451860/
Там какое-то алго для умножения придумали, невъебенное. Я не могу вникнуть туда, но pdf-ку скачал.
Гляньте на этот алго через призму этих ваших теорем.
 1,7 Мб, 2715x2748
1,7 Мб, 2715x2748> Если умножение - это многократное сложение,
> то почему нельзя вывести свойства умножения
> из свойств операции сложения, и свойств операции повтора этого сложения?
> Ведь чтобы умножить a на b - нужно просто повторять сложение a к результату - b раз?
Казалось бы, все так, т.е просто как 3 копейки. А на деле есть ABC-conjecture, неразрешимая вот таким образом. Повторяется ситуация с теоремой Ферма, которую местами доказали относительно недавно. Более 300 лет изьебств впустую. Очень похоже, что её так же доказать в полной мере можно только в IUTeich, в разных театрах Ходжа.
Колупни суть того быстрого алго для умножения, и главное - как к нему пришли.
Может быть через какие-то магические квадраты, сможете чё-нибудь формализовать и таки доказать.
Подозреваю, что умножение намного проще и короче можно выразить как-то, пытаясь его определить,
и не важно, что эта операция будет не очень быстрой с точки зрения эффективности,
но сама структура её, и конструкция - может открыть много чего интересного.
Главное понять КАК к этому приходили математики, и там вокруг ещё глянуть что оно всё это значит,
можно ли это оптимизировать, и главное будет ли это всё - конвертируемо в логику предикатов первого порядка,
и верифицируемо ли всё это - посредством формальной верификации.
Это все численные методы же. Это в матанализе просто значок интеграла нарисовал и доволен. А по факту вычисление нужно, и методов есть немало, что как бы намекает нам, что идеального нет. Тут похожая ситуация. Формализация численных методов в общем привела бы к увеличению скорости умножения больших чисел. Но результат-то будет тот же. 100500100500100500 в итоге даст одно значение, как его ни считай.
А мне кажется, что при определении операции умножения, через другие операции,
и выводе самих свойств этой операции умножения из свойств всех этих операций,
основной вопрос, на который нужно ответить - это КАК ИМЕННО её проводить,
то есть КАК ПРАВИЛЬНЕЕ эту операцию проводить, чтобы её полностью ОПРЕДЕЛИТЬ её,
не задействуя сложные механизмы, и теории.
То есть найти - такое фундаментальное и основополагающее определение,
которого было бы достаточно для умножения - на том же множестве N,
а не всякие неведомые производные от этого определения,
к которым оно же-таки, по мере расширения функциональности множества - изоморфно сводится.
В таком случае, было бы целесообразно рассмотреть свойства тех же групп чисел,
по которым производится разбиение в алгоритме Карацубы,
и не прост рассмотреть, а рассчитать их гомологии.
Типа на некоторых компах умножение получается быстрее сложения, лол, и в перспективе сложение будет через умножение вычисляться.
Долблюсь в шары, лол.
Это кодировки, а не определения. Что бы их сформулировать метаязык уже должен уметь оперировать счётными наборами объектов, а если ты умеешь это делать можно сразу "определить" N через конструкции с "и т.д." и даже множества тебе не понадобятся.
>>54707
> Мань, я тебе привёл пример в какую сторону доказывать, что все определения N это не определения. Ты даже этого не понял.
Вообще-то операции определяются после операндов, если мы операнды не определили, как ты можешь вообще рассуждать про проблематику определения операции, лол? Сам-то понял что сказал?
> Для общего неформального описания происходящего.
Ты походу о чём-то своём кукарекаешь. Вообще-то метаязык в конечном счёте это всегда неформальное математическое арго как любит говорит Манин.
А, так ты и есть тот же дебилок, который на гамалогии, сойбоя Вербицкого, Панина или манина дрочит. Оснований нет, математика подвешена в воздухе и прочая такая щиза. Ну это многое объясняет, два таких клоуна - пучкнутый и N петух это многовато.
>Вообще-то операции определяются после операндов, если мы операнды не определили,
>как ты можешь вообще рассуждать про проблематику определения операции, лол?
>Сам-то понял что сказал?
Ещё скажи что все SHA512-хэши и ключи RSA-8192
рассчитываются прежде
чем варганятся сами алго для их рассчёта.
Вот тут: https://ru.wikipedia.org/wiki/Натуральное_число#Аксиомы_Пеано_для_натуральных_чисел
Вторая аксиома, как-бы намекает на предварительное - определение операции следования.
И если многократно лишь её повторять - то получишь N вплоть до алеф-нуль.
 959 Кб, 1688x1688
959 Кб, 1688x1688Охлол, таки угадал. Ебать ты жалкий клован. Вот смотри, ты тут
>>54765
> метаязык в конечном счёте это всегда неформальное математическое арго как любит говорит Манин.
Ты соглашаешься, что метаязык в математике в целом дело не первой важности. Чуть выше >>54707 я привёл пример теорий, в которых метаязык не используется, но в которых возможно определить N (нумералы Чёрча). Т.е определения отличные от построения, например на метаязыке, если и есть, то в самой теории ненужны. И к чему тогда вся твоя многолетняя клоунада про определение N? Ты ж шизик, лол.
Какое же ты шизло, твой пример говно и вообще не в тему. Ни одна теория не существует без метатеории, иначе ты тупо не можешь обговорить о правилах и средствах вывода в этой теории.
> Ни одна теория не существует без метатеории,
Мань, в таком случае теорий как таковых вообще существовать не может, т.к для любой метатеории нужна метаметатеория итд до бесконечности. И определения нет вообще ни у чего. Ты ж дебил, лол.
И тут из сумрака вышли Бурбаки со своим тау-символом.
> Неопределяемые понятия? Не, не слышали.
Ты не понял. С таким подходом определяемых понятий вообще существовать не может. Потому что у определения должно быть определение. И так до бесконечности.
Это ты не понял. Когда говорят о неопределяемых понятиях как раз имеют ввиду, что нужно выделить набор неопределяемых понятий и явно объявить их таковыми а не мухлевать с переформулировками того же самого на метаязыке.
> Когда говорят о неопределяемых понятиях как раз имеют ввиду, что нужно выделить набор неопределяемых понятий и явно объявить их таковыми
PN, "primitive notion" в automath'е де Брауна так помечаются строки, где просто вводится некий объект без его определения выше. Естественно, смысл этого только в упрощении доказательства, то что можно объявить примитивным объектом в одной теореме, может быть доказательством в другой. Ты же походу уверовал в какие-то абсолютно неопределяемые сущности в виде гномика. Какой смысл в такой религии, непонятно.
> не мухлевать с переформулировками того же самого на метаязыке.
Ну и ты видишь метаязык там, где его нет, либо где он есть для пояснений и общего развития, но самой системой не используется. Например, нумералы Чёрча. Это прямое построение, хотя, разумеется, выразимое на метаязыке. Который однако же не используется в собственно вычислениях. Т.е у тебя ещё и проблемы с пониманием, где язык, а где метаязык.
Но ламбада-калкулус определяется с использованием бесконечного множества переменных (x, x', x'', ...) - суть те же натуральные числа. Вот если бы взять SKI комбинаторы за основу. Но может и там есть свои подводные, хз.
Боюсь, про эту хуйню они спорят уже тыщи три лет.
Моя версия - рассматривать умножение и деление чисел, как единую сущность, множество (одно число, разбитое на процессы).
То есть 2+3 5 это 2+ множество 3 5, нельзя отодрать 3 от множества и сложить ее с немножеством "2", а потом умножить на 5. При операциях вычитания и сложения мы можем представить течение времени - последовательно, друг за другом выполняем операции с ОДИНАКОВЫМИ сущностями. При операциях деления и умножения мы имеем, по сути, одну сущность, которую, чтобы сложить или вычесть, сначала нужно привести к ОДИНАКОВОСТИ одного числа. Как то так.
Просвещайте.
>>55841
>Вариант-так договорились - не канает
На этом "просвещение" можно заканчивать.
Ты можешь определять всё как тебе захочется коль скоро твоя система непротиворечива и даёт какие-то новые интересные результаты.
 54 Кб, 702x298
54 Кб, 702x298Извинись!
> Ты сначала натуральное число определи, а потом уже с операциями разбирайся.
N-петух, тебе ж пояснили, что с твоим маняподходом получается, что понятие определения принципиально невозможно, так как в любом случае требует бесконечное количество метаязыков.
> эта мысль не нова
Не нова, конечно. Странно считать, что N-петух может сказать что-то новое в математике. Просто наступил на очередные грабли, на что я и указал.
Лол, операционный петух закукарекал. А ничего, что это я утверждал насчёт невозможности определения N? Маняподход у вас, так как он отличается от строгого и общепринятого определения математических понятий, это вы должны пояснять про свои мнимые определения N.
Ты пойми уже, что никакие определения не нужны. Нужно построение. Правила этого построения работают без метаязыков и сами являются определением. Вот и все. А весь аутизм с "определениями" в бесконечных метаязыках никакого отношения к объекту определения не имеет и для работы с ним не нужен. Поэтому, ординалы Брауэра, фон Неймана, нумералы Черча итд это непосредственное определение N. Работающее без метаопределений.
Назови хоть одну книгу, где вместо математических определений идут математические построения
Любая вообще. Объяснения на метаязыках нужны чисто для удобства пользователя и не являются неотъемлемой частью самой математической нотации. У тех же бурбаков об этом на каждом шагу говорится прямым текстом.
Этот пидор еще и теорему скоммуниздил про ежа.
Манямир двачного дурика, лол. Брауэр прямым текстом писал почему формализм не подходит для оснований, когда Геделю 1 год был, про неразрешимость того, что Гильберт назвал Entscheidungsproblem за 20 лет до того как Гильберт сформулировал эту проблему и за 30 лет до того, как Тьюринг доказал ее неразрешимость. То, что до кого-то это дошло на 30 лет позже, чем до Брауэра, это уж точно не проблема Брауэра. Мозги дело такое, если уж нет, то не купишь.
> Так почему он не доходит до оснований?
Почему формализм не подходит? Потому что любая сколько-нибудь подходящая для оснований аксиоматика либо неполна либо противоречива. На этом и Гильберт обосрался, и чуть позже - бурбаки. А системы, соответствующие теореме Гёделя о полноте, для оснований недостаточны.
>Брауэр прямым текстом писал почему формализм не подходит для оснований, когда Геделю 1 год был, про неразрешимость того, что Гильберт назвал Entscheidungsproblem за 20 лет до того как Гильберт сформулировал эту проблему и за 30 лет до того, как Тьюринг доказал ее неразрешимость
Но никто не заметил петуха, увы, не того масштаба личность, как Гильберт или Гедель.
Бравера твоего, пиздившего теоремы. Он хоть что-то в жизни своей доказала, у него есть оригинальные математические результаты?
Ты ебнутый. Неси оригинальные результаты или будешь нахуй послан со своим феласафом.
> или будешь нахуй послан со своим феласафом.
Мнение зумер-кринж дегенерата очень важно для меня.
Нашёл пока только такое, хоть и не понимаю:
Первым серьёзным критиком Аристотелевской логики был Пьер Рамэ, погибший во время Варфоломеевой ночи. Во второй части его «Диалектики» говорится о силлогизме; учение его о силлогизме, однако, существенных отступлений от Аристотеля не представляет. Начиная с Бэкона и Декарта философия идёт по новым путям и отстаивает методы исследования: непригодность силлогистического метода в смысле метода получения нового знания становится всё более и более очевидной.
Тем не менее, решение силлогизмов составляет важнейшую часть любого учебника по традиционной логике.[2] Несмотря на то, что использование силлогизмов само по себе не даёт новое знание, использование правил построения силлогизмов позволяет избежать логических ошибок, софизмов, в рамках имеющегося знания (см. Демагогия).
Силлогизм преобладал в логике до XIX века и имел ограниченное приложение в частности из-за привязки к категорическому силлогизму. Заменой силлогизму служит более простая и мощная логика первого порядка, а также теория кванторов.
>зачем сейчас преподают аристотелевскую логику
Этим занимаются люди с факультетов философии, а они в целом любят преподавать всякую давно устаревшую муть. Ладно уж аристотелевскую логику, они ведь и о философии Гегеле любят поговорить.
>и как от неё перешли к математической
Просвещайся:
https://plato.stanford.edu/entries/logic-firstorder-emergence/
>а также почему существует так много логик с разными основаниями, а не выводятся они вроде из одного.
В современной логике люди формулируют разные логические системы исходя из разных мотиваций. Мотивации могут быть сильно разные: в одних случаях система отражает более правильный, в глазах своего создателя, метод рассуждений, в других случаях речь может идти об изоляции алгоритмически разрешимых, но в тоже время достаточно выразительных, фрагментов существующей системы, который сами по себе неразрешимы.
>Этим занимаются люди с факультетов философии, а они в целом любят преподавать всякую давно устаревшую муть. Ладно уж аристотелевскую логику, они ведь и о философии Гегеле любят поговорить.
Ну, если бы это честно подавалось как история философии, то ничего особенно страшного, на мой взгляд, нет. Другое дело, что часто (особенно в Раиссе) преподают совершенную кашу и студенты не понимают, например, актуальны ли сейчас идеи Гегеля.
Аристотеля ставить в один ряд с Гегелем я бы не стал, потому что считаю, что чтение классических греков (именно чтение, а не идиотская зубрёжка и экзамены) были бы полезны в подростковом возрасте. Гегель же никакой ценности, кроме исторической, не представляет.
А чем они собственно полезны? Я читал множество всего в подростковом возрасте, в том числе и греков. Пользу не ощущаю
> Объясните, пожалуйста, зачем сейчас преподают аристотелевскую логику и как от неё перешли к математической
Никто не преподаёт (разьве что у гумусов облегчённый курс какой нибудь, так как матлог они не осилят). Аристотелевская логика это древнее гамно, к современному матлогу относится примерно как планиметрия древних греков к современным же разделам геометрии.
>Аристотеля ставить в один ряд с Гегелем я бы не стал, потому что считаю, что чтение классических греков (именно чтение, а не идиотская зубрёжка и экзамены) были бы полезны в подростковом возрасте. Гегель же никакой ценности, кроме исторической, не представляет.
Ну так я и оценил Аристотеля позитивнее Гегеля. Аристотель на мой взгляд все-таки был важным с исторической точки зрения мыслителем, который, конечно, продвинул человеческую мысль в свое время. Гегель же, на мой взгляд, просто нес муть с самого начала.
Прогать.
> "в любой формальной системе существует утверждение, которое нельзя ни доказать, ни опровергнуть"
В логике высказываний/предикатов таких утверждений нет, прикинь?
У него Гёдель головного мозга, забудь.
Ты конченый дебил. Ты серьёзно решил, что истинность суждений зависит от субъекта?
Рамуджан лишь в очередной раз показал, что интуиция и здравый смысл -- хуйня ебаная, и что понятие бесконечности вообще штука тяжёлая. Если бы то, что ты сказал, было правдой, это значило бы противоречивость математики, а значит, её бессмысленность. Об этом, кстати, формальные системы. И ты понятие полноты вообще не понимаешь. И суёшь не туда. Пиздец, да ты дебил.
Гёдель говорил лишь про конкретные формальные системы, а не про все. Кроме того, формальные системы -- лишь способ представления математики, а не математика, и всё, что он доказал -- что этот способ хуёвый. Кроме того, его теорема не работает для формальных систем с хотя бы счётным количеством аксиом.
>дилетанство
>хобби
Чел, прочитать википедию про математиков, или посмотреть фильм на дискавери, это не хобби, и ты далеко даже не дилетант. Ты очередной клоун, решивший, что математика -- это просто.
>считаю
Всем поебать на твоё мнение и оно неверное.
Гаусс общепринято лучший математик истории. Кроме того, результаты Гёделя узкие, хоть и значительные, и его творчество в силу его сумасшествия оборвалось, он не слишком много сделал. Тот же Тарский заслуживает больше. Гротендик.
>Эйлер
Всегда интересовало - он когда по-русски разговаривал, то представлялся как Ойлэ или сам коверкал до Эйлера?
Лукойлэ
Или не нужно? Но как я смогу тогда доказывать теоремы и знать, что им можно верить?
Опыт, большое количество примеров. Хочешь научиться плавать, плавай. Хочешь научиться доказывать, ну здесь аналогично. Не получается доказать самому, разбирай чужие доказательства. Пробуй рассказывать аргументы кому-то. Пытайся записать их. Честное рассуждение отличить от не совсем честного в принципе можно.
Можешь что угодно писать и говорить, но лучше не на этой доске.
> Есть ли какая-то пропедевтика по отношению к математике, философское введение или какое-то другое
Основания.
Кооооококо ниматиматика, матиматика только пучки, гамалогии и тапалогии, так сойбой вербитский скозал!!11
Кооооококо матиматика, матиматика не только пучки, гамалогии и тапалогии, так сойбой мартин лёф скозал!!11
А для оснований не нужно ли изучать историю вопроса, какие проблемы были, как всё это развивалось, историю математики вообще? Что нужно знать, чтобы начать изучать основания? Разве с них можно начать изучение математики на текущем этапе всей этой темы?
Слышал правда, что какой-то гений-математик всё изучил по какой-то книге с истории математики и энтому Principia Mathematica, но подозреваю себя слегка туповатым для такого пути.
Странно вроде в высшей математике изучают множества и алгоритмы...
> Слышал правда, что какой-то гений-математик всё изучил по какой-то книге с истории математики и энтому Principia Mathematica, но подозреваю себя слегка туповатым для такого пути.
Ну это и есть путь просветлённого, лол. Если никак, остаётся путь слесаря - задрачивай конкретные области, как тут советуют >>57100 здесь главное не лезть за пределы задроченного и не пытаться понять, как все работает, ато вон выше цитировали какого-то сказочного свидетеля гамалогий, который заявлял, что математика висит в воздухе и никаких оснований не имеет.
Principia mathematica провалилась же, кроме исторического никакого интереса не представляет, не стоит тратить на неё время
> Principia mathematica провалилась же, кроме исторического никакого интереса не представляет
Так и весь формализм как подход тоже провалился, после попыток Гильберта и теоремы о неполноте Гёделя для математики он не представляет интереса кроме исторического. По-сути кроме конструктивизма вообще все остальные подходы к основаниям либо провалились, либо просто не изучались достаточно для того, чтобы сказать, провалились они или нет.
> Основание - перекладывать палочки.
Что значит перекладывать палочки? Сколлько палочек у меня есть? Это всё эквивалентные понятий поэтому основанием не является.
Палочки это физическая реализация концепции потенциальной бесконечности, которая трансцендентальна и следовательно дана нам a priori в отличие от скажем трансцендентной актупальной бесконечности, которая просто вернуство. Читай Мартин-Лёфа, Критику интуиционистского разума.
Т.е. ты обычный верун, который уверовал в потенциальную бесконечность, с какого-то перепоя отверг актуальную и кукарекаешь тут про обоснование? Ну так нихуя ты не дал обоснование, ты всего лишь уверовал в N как исходное неопределяемое понятие
Все положения конструктивизма, включая потенциальную бесконечность истинны, потому что вычислимы. Актуальная бесконечность, гамалогии и тапалогии это просто бессмысленные значки, то есть они тоже тривиально вычислимы как простейшие манипуляции символами в рамках логики предикатов, равно как и Аллах и вообще что угодно, то есть это не математика даже. Интуиционистская теория типов, с другой стороны, реализована и проверена в Автомате Де Брауна, в этом вся разница.
>Да.
Тогда почему сойбои не возятся с тапалогиями и не начинают переделывать математику на конструктивных основаниях?
>истинны, потому что вычислимы.
Истинно верую, говорю вам братцы!
>>57292
вот тут, например.
https://ncatlab.org/nlab/show/HomePage
Т.е. что бы "обосновать" потенциальную бесконечность вы уверовали в ещё более неведомую хуету под названием вычислимость?
Сейчас поле исследования теории вычислимости расширилось — появляются новые определения понятия вычислимости и идёт слияние с математической логикой, где вместо вычислимости и невычислимости идёт речь о доказуемости и недоказуемости (выводимости и невыводимости) утверждений в рамках каких-либо теорий.
> Т.е. что бы "обосновать" потенциальную бесконечность
Не устаю поражаться твоему дебилизму, серьезно.
А мы твоему, "палочник". Принимаешь на веру тезис черча и не можешь доказать тривиальные математические факты, при этом считаешь это будущим математики.
Тебе от математики вообще что нужно с таким уровнем понимания вопроса? Что ты несёшь вообще, ты сам свои посты читаешь хоть? Какая "вера в тезис Черча", ты хоть почитай что такое этот тезис. А потом попытайся подумать, причем тут вера вообще.
Тезис Церкви - вычислимые функции суть машины Тьюринга. Этому тезису можно противопоставить другой: вычислимые функции суть индуктивные машины Тьюринга.
Френкель, Бар-Хиллел. Основания теории множеств.
Бурбаки. Очерки по истории математики.
Прасолов. История математики.
> Френкель, Бар-Хиллел. Основания теории множеств.
Вот это удвою. Написано очень профессионально, Френкель тот самый, который один из авторов аксиоматики Цермело-Френкеля. Алсо, в переводном варианте этой книжки единственное внятное на русском языке изложение интуиционизма без хуеты и пиздежа. Автор не придерживается этого подхода, но точно понимает что это и о чем, в отличие всяких чумаходов-псевдоматематиков типа, ну не будем пальцем показывать.
> Этот вопрос является частью тысячелетней дискуссии "платоновский реализм vs коснтруктивистский номинализм", лучше не трогать данную тему.
Поподробнее?
>Поподробнее?
Перечитай последние шесть тредов на ОСНОВАНИЯМ МАТЕМАТИКИ
https://2ch.hk/math/res/40955.html (
Подробнее некуда. Кратко - >>57693
 946 Кб, 2500x2500
946 Кб, 2500x2500>Вся вообще возможная математика выразима в унивалентных основаниях
Те есть швитые гамалогии не математика. Интересно в какой раздел тогда таполагов гнать. В /sci? В /ph? А может быть в /re?
Так а что почитать нормальному человеку для вката в конструктивизм интуиционизм?
Так этих сойбоев проклятых с окрестностями проткнутыми, веруны хуевые.
> Так а что почитать нормальному человеку для вката в конструктивизм интуиционизм?
HoTT book и читай. Что непонятно - читай по ссылкам в конце глав. Можно для наглядности параллельно вот с этим https://www.cs.bham.ac.uk/~mhe/HoTT-UF-in-Agda-Lecture-Notes/index.html и в агде все разбирать.
>>58275
Вообще мимо.
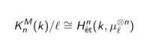 12 Кб, 415x135
12 Кб, 415x135пойду поем
 169 Кб, 1041x700
169 Кб, 1041x700Единственное в чем Брауэр был прав, это в том что он насрал на собственную философию тем что приводил неконструктивные доказательства теорем.
Он не срал на собственную философию, дело в том, что при его жизни она была недостаточно развита, чтобы в ней можно было доказать все. Для одного человека, даже Брауэра, это неподьемная задача.
https://www.frontiersin.org/articles/10.3389/fncom.2017.00048/full
>Гамалогии и тапалогии, их представление в мозгу:
Так а ты не зумер что ли? Совершенно примитивная с точки зрения математики статья, они просто считают числа Бетти и всё. Куда более продвинутые методы описаны даже в уже устаревшей книжке "Computational Homology", не говоря уже о каком-нибудь cohomological feature extraction, который используется в свежих статьях по нейрофизиологии.
Вот, например, свежее ревью, зотя многого тут нет
https://www.mitpressjournals.org/doi/pdf/10.1162/netn_e_00096
Вобщем, пока что ты похож на того самого "флексящего зумера".
Т.е. ты даже не понимаешь разницы между структурами в ЦНС, ответственными за кодирование математики как явления и применением методов гамалогий к описанию структур в ЦНС?
Иди сам что-нибудь поучи, зумер. Каждый школотрон что-то из себя корчит и обязательно считает, что может указывать другим, что им делать.
нет ты :)
В том-то и дело, что я вполне вправе указывать петухам, которые пытаются указывать мне как правильно думать, при этом не зная элементарщины.
Ну если под умным ты имеешь ввиду просто не пиздеть лишнего если в чём-то не разбираешься, как делают невежественные петухи вроде тебя, то да.
Судя по наблюдениям ни в чём о чём пиздишь. Ни математику нормально выучить не пожелал, ни даже гамалогии освоить, ни усвоить самую базовую информацию которая выпадает в первой ссылке когда гуглишь "what is machine learning".
По каким наблюдениям? Твои кукареканья это не наблюдения и не мнение, это просто кукареканья обиженного.
Не с презрением, просто не нужно делать вид, что это хоть как-то имеет отношение к настоящей математике.
Потому что логика это не математика, математик постоянно пользуется логикой, да, а ещё он должен уметь писать и читать, но никто не говорит, что умение писать и читать это математика.
>в чём принципиальная разница между авиалайнером и яблоком
Я не знаю как на такие вопросы отвечать.
Сейчас бы слушать шизика. Логика это и есть математика, т.к вся математика сводится к основаниям, а основания это логика. Но полтора сектанта веровают, что оснований нет, а математика это только гамалогии.
Приведи пример теоремы из оснований, которая имеет приложение в математике. Обратных примеров выше крыши.
основания не сводятся к логике. гугли обсёр рассела и фреге и их программы логицизма
Ну так и приведи пример раз не спишь, нет такого, чтобы теорема из логики применялась где-то в математике.
Любые возможные объекты и действия над ними в гамалогиях являются таковыми исходя из определенной аксиоматики или набора правил вывода, ты ведь не будешь с этим спорить. Если ты за гамалогиями не видишь логики, значит ты ее просто принимаешь по умолчанию.
Любые возможные объекты и действия над ними являются значками на доске исходя из правил чистописания, ты ведь не будешь с этим спорить. Следовательно, математика это часть каллиграфии.
Один и тот же "аргумент" повторяешь, за семь лет мог бы что поумнее придумать.
Сейчас напишет: я в разделе со вчерашнего дня
> Следовательно, математика это часть каллиграфии.
Математика это язык. Со своими правилами. Поэтому сигнифика - допустимый вариант оснований, что показал ещё Маннури. Что сказать-то хотел? Каллиграфия причем? Погугли хоть что это. Факт в том, что в любой математике все допустимые действия исходят из соответствующей аксиоматики либо набора правил вывода. Без этого никакая математика в принципе не возможна.
Конструктивист должен знать:
- изоморфизм Карри-Говарда и тезис Чёрча;
- содержание диссертации Брауэра в переводе Гейтинга;
- пять уровней языка и четыре способа отрицания по Маннури;
- интерпретацию логических констант по Брауэру-Гейтингу-Колмогорову;
- теорию статистического обучения Вапника и модель spikgram Миколова;
- отличия машины Тьюринга от машины Поста.
Конструктивист обязан:
- отрицать закон исключённого третьего;
- отрицать любую математику, не выразимую через типизированную лямбду в MLTT или нормальные алгорифмы Маркова;
- переписать на прувере AUTOMATH де Брауна книгу "Основы математического анализа" Ландау;
- представить все формальные теории в терминах алфавитов, термов и манипуляций с ними;
- свести гомологическую алгебру к исчислению предикатов, используя нумерацию Гёделя.
> Математику можно представить в терминах логики = математика это часть логики.
Не "можно представить", а "исходит исключительно из". Ты даже этого не понимаешь.
>Математика это язык. Со своими правилами
Нет, не язык. Гомологическая алгебра это язык. Со своими правилами, которые являются теоремами, кстати.
>Поэтому сигнифика - допустимый вариант оснований, что показал ещё Маннури
Не показывал. Ссылку, где он показал? Ты же сам его работы не читал.
>Факт в том, что в любой математике все допустимые действия исходят из соответствующей аксиоматики либо набора правил вывода
Только "соответствующая аксиоматика" (= соответствующие теоремы) бывает разная, поэтому это пустые слова.
Математику невозможно записать не пользуясь значками, значит часть каллиграфии.
> Пример утверждений, которые "исходят чисто из" логики
Само понятие "утверждения" или "высказывания" это элемент логики
>>58489
> Гомологическая алгебра это язык.
Боженька на Синае его выдал? В воздухе висит язык, да?
> Только "соответствующая аксиоматика" (= соответствующие теоремы) бывает разная,
Аксиомы и теоремы это разные вещи. Ты даже не знаешь, чем аксиома от теоремы отличается.
>Само понятие "утверждения" или "высказывания" это элемент логики
То есть до логики утверждений не высказывали? Математика пользуется словами, значит это раздел лингвистики. У Баруха Спинозы в "Этике" есть теоремы и схолии, этика значит тоже часть логики?
>Боженька на Синае его выдал
Гильберт и Нётер в Гёттингене.
>Ты даже не знаешь, чем аксиома от теоремы отличается.
Это ты не знаешь. Любая аксиома является теоремой. Пример: d^2 = 0. Аксиома и теорема. Приведи пример аксиом из математики, не являющихся теоремами.
> То есть до логики утверждений не высказывали?
Ты и разницу между дедуктивным и индуктивным выводом не знаешь?
> Гильберт и Нётер в Гёттингене.
Гильберт обосрался с формализмом в качестве оснований.
> Это ты не знаешь. Любая аксиома является теоремой.
Хоспаде как у тебя в голове насрано. Аксиому можно рассматривать как теорему без посылок, т.е что-то взятое с потолка, а не вытекающее из чего-то другого. Теорему можно доказать, аксиому нет, ее можно только использовать в дальнейших построениях.
Гильберт помимо "оснований" занимался ещё физикой, функциональным анализом, алгебраической геометрией и гомологический алгеброй. Как и Брауэр, кстати, основной его вклад в математику отнюдь не в шизофренических высерах (вне зависимости от того, что он сам думал или говорил по этому поводу; Ньютон так же алхимиком был, Кеплер астрологом, ну а Брауэр вот интуиционистом).
>Ты и разницу между дедуктивным и индуктивным выводом не знаешь?
В теологии и юриспруденции выводы тоже дедуктивны. Это разделы логики?
>Аксиому можно рассматривать как теорему без посылок, т.е что-то взятое с потолка
То, что в одной области аксиома, в другой это теорема. В математике так по крайней мере. Основное положение гомологической алгебры не только можно доказать, в любом нормальном курсе его доказывают. Несколькими способами. То, что гомологическая алгебра является языком математики, не значит что основные её принципы нельзя проверить средствами других разделов. Более того, это справедливо по отношению к любой области. Только в "основаниях" берется бред с потолка. В математике любая аксиома имеет длинную историю в качестве теоремы.
> Только в "основаниях" берется бред с потолка.
Например?
> В математике любая аксиома имеет длинную историю в качестве теоремы.
Я ж говорю, ты даже разницы между аксиомой и теоремой не понимаешь. Аксиома недоказуема, если ее можно доказать, это теорема. Например, аксиома унивалентности Воеводского это аксиома в HoTT, но доказуемая теорема в cubicaltt.
>Аксиома недоказуема, если ее можно доказать, это теорема
Получается, что вычислимость - это аксиома? Ну то есть, мы можем рисовать палочки какое-то конечное число раз, но бесконечное не можем, и для бесконечного случая алгоритмы не являются доказательством... Тогда вычислимость - аксиома.
 99 Кб, 511x407
99 Кб, 511x407> Получается, что вычислимость - это аксиома?
Вычислимость это не аксиома, а процесс, я же приводил определение.
> для бесконечного случая алгоритмы не являются доказательством...
Так ты и не осилил понять в чем разница между актуальной и потенциальной бесконечностью. Вот ты не понимаешь вещи, которые можно объяснить 10 летнему ребенку, при этом хочешь показать, что понимаешь в гамалогиях.
Просто потому что для матлогики на уровне того чтобы кукарекать про то что никто ничего не понимает и копаться в строгом доказательстве каких-то элементарных утверждений не нужно ни какой-то особой подготовки, ни особого ума. Тупеньким прогерам как раз подходит для того чтобы тешить комплекс "я тоже умный!!".
> копаться в строгом доказательстве каких-то элементарных утверждений не нужно ни какой-то особой подготовки, ни особого ума.
Ага, то ли дело просто веровать без доказательств, тут дохуя ума надо.
 102 Кб, 1000x700
102 Кб, 1000x700> кукарекать про то что никто ничего не понимает и копаться в строгом доказательстве каких-то элементарных утверждений
Картинка отвалилась.
>процесс
Который ты можешь проводить только для конечного числа шагов. Ты же аксиомой постулируешь, что вычислять можно бесконечное число раз, когда на деле существует константа, которая ограниченная сверху числом атомов во вселенной, что дальше неё вычислять уже не получится. Нельзя бесконечно рисовать палочки рано или поздно мел кончится. И да, это аксиома, ты не приводишь доказательства, что можно рисовать палочки бесконечно много раз.
> Ты же аксиомой постулируешь, что вычислять можно бесконечное число раз,
Что ты несёшь... Какие аксиомы, кто что постулирует? Есть правило, число шагов которого не задано. Вот и все. Зачем додумывать хуйню на ровном месте и выдумывать то, чего в понятии потенциальной бесконечности нет и никогда не было?
> существует константа, которая ограниченная сверху числом атомов во вселенной
И причем тут вычислимость? Смешно читать эти аппеляции к физическому смыслу математических понятий от веровающего в актуальные бесконечности. Ещё расскажи, что вещественные числа ограничены постоянной Планка и для величин меньше нее физического смысла не имеют.
 45 Кб, 1200x642
45 Кб, 1200x642>Какие аксиомы
Аксиома того, что вычисление можно провести.
>кто что постулирует?
Ты.
>Есть правило, число шагов которого не задано.
Разве оно по умолчанию не меньше той константы о которой я упомянул? Назовём её константой Браузера. И обозначим алефом.
>И причем тут вычислимость?
Вычислимость подразумивает вычисление на чём-либо, те же самые палочки рисовать. Уж тут ты вилять жопой не будешь.
>потенциальной бесконечности
А вот и аксиома существования потенциальной бесконечности подъехала. Доказательство её существования ты привести не сможешь.Тут сплошная вера. Вера в том, что вычисление можно провести в потенциальной бесконечности, постулат-аксиома Браузера.
И что, результатов-то это никаких не даёт, я ж не отрицаю, что как способом описания этим пользуются, но точно так же и русским языком пользуются и умением писать и читать, без этого математик не может, но это не значит, что всё это можно назвать математикой, так как всё это никак не помогает находить новые факты.
>как способом описания этим пользуются, но точно так же и русским языком пользуются и умением писать и читать, без этого математик не может,
Ты не видишь разницу между правилами русского языка и правилами математики как языка.
>>58509
>Разве оно по умолчанию не меньше той константы о которой я упомянул?
Отсутствие числа шагов в правиле это отсутствие, никаких "констант" и ничего другого оно под собой не подразумевает. Сама постановка вопроса про число шагов там, где никакого числа нет, не имеет смысла, ты сам этого не видишь? >>58509
>А вот и аксиома существования потенциальной бесконечности подъехала. Доказательство её существования ты привести не сможешь.
Еще раз. Это не аксиома. Аксиома - это правило без посылок. Вычислимость - процесс. Если рассматривать это как правило, то посылки в нем есть, а это уже выводит вычислимость из определения "аксиома".
>>58509
>Вера в том, что вычисление можно провести в потенциальной бесконечности,
Если бы было можно, в названии не было бы слова "потенциальная". Ты не носитель русского языка или что?
 28 Кб, 844x97
28 Кб, 844x97>Ты не видишь разницу между правилами русского языка и правилами математики как языка.
Во, я понял какую аналогию привести, логика/основания это типа орфографии, конечно писать грамотно это ок, но писателем тебя это не сделает, фантазии не прибавит, мозгов не даст, в то же время очень многие писатели, тот же Г.Х.Андерсен, с ошибками писали и это никак не мешало им и не помогало. Логика примерно из той же области, да и вообще ей интересны совсем другие вещи, как разрешимость, противоречивость и тд, можно конечно найти применение логики к математике, типа из модельной полноты алгебраически замкнутых полей характеристики 0 можно получить теорему Гильберта о нулях, ну так её можно и без этого получить и все примеры хоть какого-то применения логики из той же оперы, даже если и применяется, то давным-давно есть аналог доказательства без использования оснований.
> Это не аксиома.
Нет. Как раз аксиома.
>процесс
Который ты можешь проводить только для конечного числа шагов. Иначе у нас используется аксиома существовании потенциальной бесконечности. Чистая вера. Ты ведь так и не предоставил её доказательства существования. Значит аксиома, ты сам говорил -
>Аксиома недоказуема, если ее можно доказать, это теорема.
>Если бы было можно, в названии не было бы слова "потенциальная".
Значит, ты признаёшь я прав и алгоритмы можно проводить только для конечного числа шагов? Так называемая алеф-константа Браузера. Для каждого алгоритма она своя.
Замечу, что вычислить константу Браузера для конкретного алгоритма может быть невозможно. Т.е. проблема алгометрически неразрешима, невычислима. Поскольку вычисление константы Браузера может затребовать количество шагов больших чем атомов во вселенной.
 1 Мб, 1280x720
1 Мб, 1280x720В голосину просто.
> марио
Вот это реально твой уровень. Математика не твое.
>>58514
> Который ты можешь проводить только для конечного числа шагов. Иначе у нас используется аксиома
Как понятие аксиомы вообще связано с конечностью? Чёт ты совсем запизделся.
Ещё раз, не можешь понять, что такое "потенциально" и чем отличается от "фактически", ну я даже не знаю, училку по русскому спроси.
Хватит вилять жопой!
Бери и доказывай, что существование потенциальной бесконечности не аксиома. Но ты не сможешь, а знаешь почему? Потому что ты в неё веришь и всё. Потенциально можно и до больших кардиналов перебором добраться. К чему ты вообще о потенциальности говоришь? Потенциально можно решать математические задачи без вычислимости вообще. Но ты сам говоришь, что это просто значки. Чем твои значки лучше? Ты говоришь именно об актуальной бесконености. Алгоритм нельзя рассматривать для произвольного числа шагов. Только для конкретного для данного алгоритма числа Браузера, которое строго меньше числа атомов во вселенной. Иначе идёт потенциальная бесконечность о которой ты и толкуешь. Можно написать алгоритм, но это просто значки.
Кстати, если Числа Браузера больше числа атомов во вселенной, то алгоритм невычислим. Сорри. Но твои значки с вычислимостью тут бессильны. То есть, это что получается, не все алгоритмы вычислимы!!!
>Который ты можешь проводить только для конечного числа шагов
Конечным должен быть набор инструкций, алгоритм может просто никогда не останавливаться на данном входе и это не запрещено.
Вот конечный набор инструкций - выичслить 9^903, т.е. 903 разf умножить 9на себя. Однако результа не будет никогда. Это пример невычислимого алгоритма для данных чисел. Как думаешь, какое у него числа Браузера? Думаю, для всех невычислимых алгоритмов можно считать число Браузера равным бесконечности.
>алгоритм может просто никогда не останавливаться
Кстати, нет. Ещё одна аксиома. Не факт, что во вселенной бесконечное время. И сейчас ты делаешь на этом допущение. Сплошная вера.
Нет, во-первых что значит невычислимый алгоритм, такого понятия нет, есть понятие вычислимая функция, это такая функция, для которой существует алгоритм, такой что если f(x) определено, то алгоритм останавливается на входе x и печатает f(x), если не определено, то он никогда не останавливается на входе x. Например такой алгоритм
если x >= 0 то печатай корень из x
иначе бесконечный цикл(while(1))
будет вычислить функцию sqrt(x). Набор инструкций конечен, но если передать отрицательное число он никогда не остановится.
>>58523
Ну понятно, что когда-то компьютер сломается или ещё чего, но мы же всё это проделываем на гипотетической автономной вечной машине, так что.
 594 Кб, 1200x900
594 Кб, 1200x900> во-первых что значит невычислимый алгоритм
Алгоритм с бесконечным числом Браузера. Который нельзя вычислить, пример я приводил. Вычислить 9^903 нельзя.
>Набор инструкций конечен, но если передать отрицательное число он никогда не остановится.
Анон, это просто значки. Вот смотри, значок Аллах.jpg
>такого понятия нет
Теперь есть. Надо будет статью в archiv.org загрузить.
>он никогда не остановится
Вот она аксиома - существования бесконечного времени. Нельзя такое вычислить. По сути, алгоритм остановится рано или поздно. Всюду скрытые постулаты.
>гипотетической автономной вечной машине
Что это такое? Вера в гипотетическую вечную машину. Быть такого не может. Это что ещё одна аксиома!!! Так дело не пойдёт. Алгоритмы у них бесконечные. Напрогаются, а потом мерещится им вычислимость там, где её и не пахнет. Не все алгоритмы вычислимые, кстати.
Или другой пример, теорема Левенгейма-Сколема, типа вот есть алгебраически замкнутое поле С, "алгебраически замкнутое поле" можно записать счётным числом аксиом по теореме ЛС если конечная интерпретация имеет бесконечную модель, то она имеет элементарную подмодель. Значит существует алгебраически замкнутое подполе поля С, но опять же, это и так всем понятно(корни многочленов с целыми коэффициентами). Типа даже то, что из логики можно получить в математике это всегда можно получить другим путём, более простым, и давно уже получено, ничего нового она не даёт, полезности кроме проверки на компе доказательств нет, да и то там тоже скорее гипотетической проверки. Хуита без задач короче.
>>58525
Ты типа рофлишь, я понял, ну так я не конструктивист же, просто нет такого вычислимый/невычислимый алгоритм, а так мне пох, не хочу отвечать на рофлы.
> Бери и доказывай, что существование потенциальной бесконечности не аксиома
Ты дебил, реально. Потенциальная бесконечность это правило с посылками, аксиома это правило без посылок. Сколько мне раз это написать, чтоб ты понял? Потенциально не равно фактически, никто не утверждает, что возможно построить то, что задано правилом без ограничения числа шагов. Поэтому можно говорить об абстракции потенциальной бесконечности, а не о построении, ей соответствующей. Опять же, сколько раз ещё надо это написать, чтобы ты понял?
> Алгоритм нельзя рассматривать для произвольного числа шагов
Можно, именно такому по оритму соответствует правило без указания точного числа шагов. И таких правил дохуя и больше.
> Можно написать алгоритм, но это просто значки.
Гамалогии это так же значки, все правильно.
>>58520
> Кстати, если Числа Браузера больше числа атомов во вселенной, то алгоритм невычислим.
Надо же, неужели начал понимать, что далеко не все вычислимо фактически? Я больше скажу, не всегда можно сказать, завершится ли алгоритм. Проблема останова, слышал, не?
> Машина не может, человек может.
Хуйню не неси, пжлст. Есть полторы эвристики для 1,5 случаев, когда человек может. В некоторых случаях это может и прувер. Но в общем случае - нет. Ничего в тебе нет волшебного, зумерок. И значки переставлять ты можешь не лучше машины Тьюринга.
Не знаю, человек же может понять, когда прога зациклилась. Ну хотя ок, это простые случаи, в общем случае непонятно может или не может.
> в общем случае непонятно может или не может.
Давно понятно, что не может. Тьюринг ещё в 30х годах доказал. Даже если к машине Тьюринга приколхозить боженьку, решающего алгоритмически неразрешимые задачи, это не снимает проблемы останова.
Turing Oracle machine гугли. Точное название работы не помню, это была его пхд диссертация, 1939 год.
Ок, мерси.
>A machine with an oracle for the halting problem can determine whether particular Turing machines will halt on particular inputs, but they cannot determine, in general, if machines equivalent to themselves will halt.
Это?
Тем, что ты зумер без мозгов? Любой мошонлернинх это просто разновидности EM алгоритма, но тебе не хватит мозгов понять, почему. Так что ебал я твой зумерский рот, маня.
Кстати, ты не феминист случайно? А то есть один клоун... Или на мейлру для каждого раздела отдельных шизиков нанимают постинг поднимать?
 88 Кб, 660x300
88 Кб, 660x300ИЗОМОРФИЗМ КАРРИ-ГОВАРДА ПРИСУТСТВУЕТ
О узнаю конструктивного петушка с первой ноты. Ну как дела, все резвишься?
С формализацией алгоритма разобрался или все еще живешь в маня-мирке из духа Брауэра?
>>58552
> феминисты клоуны зумиры ааааа сасать лизать твари уууу
Пиздец, покажи где зумеры тебя трогали?
> Любой мошонлернинх это просто разновидности EM алгоритма
Да-да, а математика это разновидность каллиграфии.
Мы уже поняли что основной твой мотив это редукционизм первоклашки, потому что позволяет заглушить комплекс неполноценности от того что ты ничего на самом деле не знаешь.
knn кстати это k nearest neighbors, можешь рассказать чем он от kmeans отличается?
 126 Кб, 439x510
126 Кб, 439x510> комплекс неполноценности от того что ты ничего на самом деле не знаешь.
Да-да, полный бред и хуйню несёшь ты, а ничего не знаю я. Я тебя услышал, поди подмойса, маня.
Конец второкультурной параши.
Какойто кнн невнятный, ничего не получитца
 76 Кб, 680x510
76 Кб, 680x510https://techcrunch.com/2019/08/01/dasha-ai-is-calling-so-you-dont-have-to/
https://dasha.ai/
Если коротко: бот симулирующий человеческую речь.
Послушал примеры, по моему там что-то вроде технопранка, т.е. мужик заранее наговаривает фразы, а не симуляция речи.
>у вас указано
>восточная
>кухня
>верно
>японская кухня
>есть?
До теста Тьюринга им срать и срать, лол.
В том смысле, что там каждое слово отрывками идёт, будто записали заранее и вырезали, и потом после каждого пункта есть есть есть есть, понятно, что это робот.
залетный
Официально да, по факту ближе к программированию, чем к математике, и я не пыня гротендиковская какая-нибудь, мне самому основания нравятся, вот сейчас эту книжку прорешиваю
https://www.mccme.ru/free-books/shen/shen-logic-part3-2.pdf
, но отрицать очевидное смысла нет.
>по факту ближе к программированию, чем к математике
В каком плане? Что апологеты оснований не доказывают теоремы на бумажке, а ебутся с пруверами? Вопрос без провокации, просто интересно.
тот же самый залетный петух
Олсо, для меня "программирование" это асм и императивщина вроде Си какого-нибудь, максимум ООП а ля сисярп, все, что творится в хацкеле и подобных языках, для меня уже выглядит, как математика, т.е. как непонятная загадочная хуйня. Поэтому и переспрашиваю, для меня разница не очевидна.
Трудно объяснить, применяются те же интуиции, что и в программировании или что-то в таком духе. А математика это другое, ты это прямо сразу чувствуешь. Ну и сложность, основания/программирование/логика они все как бы количественные, там сложность в объёме, типа как вот выкопать одну картошку просто, а вскапывать целое поле заебёшься, вот там такая примерно сложность, плоская что-ли, сложность вширь. А в математике сложность вглубь как бы, качественная, и усилия совсем другого рода применяются, не усилие воли, а усилие осознания что ли.
>, а усилие осознания что ли.
https://www.youtube.com/watch?v=NIOyMHO0DHY
Вот как тут, перед тобой каша, ты смотришь на неё со всех сторон и с определённого угла перед тобой возникает картина, задача найти этот угол зрения и готовых рецептов нет в отличие от алгоритмов вскапывания картошки. Ну по крайней мере я именно так разницу воспринимаю, может кто дополнит.
Я понял, к чему ты ведешь, просто на мой взгляд, даже в том же программировании можно встретить задачу, которую вообще хуй знает как решать, подступиться неоткуда (т.е. это именно поиск нужного угла зрения). Наверняка такие задачи есть и в основах. Получается, что граница все равно очень размытая.
Кстати, чем вы, математики, занимаетесь в основном? Читаете учебники/научные статьи и потом доказываете теоремы (как уже доказанные, чисто чтобы потренироваться, так и придумываете новые)?
Из-за этого представления о глубоком внутреннем мире нужном для понимания математики многие математику и отказываются понимать.
Нужно описывать математическое поведение.
>можно встретить задачу, которую вообще хуй знает как решать
Да понятно, а в математике есть чисто технические задачи, это просто моё ощущение, не более. Я не математик, просто дома сижу задачки решаю.
>>59356
> о глубоком внутреннем мире нужном
Не, я вообще не о том. Просто это разное, не то, что одно лучше, другое хуже, а просто разное. Математика это шизофрения, а программирование/логика/основания это аутизм, как-то так.
>Ну и сложность, основания/программирование/логика они все как бы количественные, там сложность в объёме, типа как вот выкопать одну картошку просто, а вскапывать целое поле заебёшься
Это довольно странный взгляд на логику/основания (наверное происходящий из-за существенной переоценки веса людей, занимающимися формализацией математики в пруверах). Основной прогресс там, как и во многих других частях математики, происходит от обнаружения оригинальных идей и инкрементарного увеличение понимания, а вовсе не в таком ключе, что заранее все в целом ясно и остается только произвести большой объем работы.
>Кстати, чем вы, математики, занимаетесь в основном? Читаете учебники/научные статьи и потом доказываете теоремы (как уже доказанные, чисто чтобы потренироваться, так и придумываете новые)?
В целом да. Хотя если описывать, как я занимаюсь математикой, то скорее я в основном пытаюсь разобраться в каких-нибудь интересных мне вещах. Передоказывание известных теорем и придумывание новых при этом составляют естественную часть такой деятельности. При этом, статьи я сколь-нибудь детально обычно не читаю, а фокусируюсь на том, чтобы выловить из статьи новые для меня идеи для чего обычно нужно понять, где в статье происходит что-то удивительное, а дальше понять, как именно оно происходит.
>что заранее все в целом ясно и остается только произвести большой объем работы.
Я имел ввиду, что сложные задачи в "computer science", буду там всё
это называть, это увеличенные копии простых задач что ли, грубо говоря ты описал так, будто я имею ввиду, что сложность с увеличением объёмом растёт линейно, но она растёт по экспоненте и вот тут уже применяются оригинальные идеи и тд. Но отличаются эти задачи от своих простых собратьев только увеличенным "объёмом" в формулировке. Все умеют копать картошку, но попробуй вскопай всё поле, все умеют собирать кубик рубика 2 на 2, но попробуй собери 6 на 6, вот такого плана что-то, это не значит, что 6на6 ровно в три раза проще собрать, нельзя просто взять и применять те же интуиции, что и в 2 на 2, но общие принципы всё равно сохраняются, хотя сложность возрастает.
Пункт 2ой курт гёдель пересечение с физикой и логикой
Любая мыслящая система структурно отличная от среды носителя ее сознания, должна и будет иметь постулатные утверждения формальной системы понятий в ее науке
Так как у любой системы форм из квантового вакуума должна быть ограниченность по векторам пространства времени и познаваемой сложности.Вследствие бесконечности Большой Вселенной.
Для прикола рекомендую просмотреть книгу авадхута гита где Бог несмог познать себя до конца.Можно воспринимать это как филосовское и логическое прозрение древних философов индии.
Есть два стула. Программа магистратуры в европке по логике/основаниям математики (могу закончить за год вроде) и пытаться в науку или забить хуй и быть погромистом 300кк/сек
Расскажите че как, кто в тусовке. Есть ли реальная возможность тусить с отцами Лефами или буду сидеть в Канаде как лох по итогу? Математику знаю оч.хуево. Ну до схем, примерно.
К математике за 3-4 месяца можно более менее привыкнуть. Чтобы читать как обычный текст, как первоклассник. Но ты пиздун, и ни в какую Канаду не едешь, ясное дело.
Как научиться? Я открываю любой текст и впадаю в ступор где-то на сопряженных функторах. Может я просто тупой, хз
А Канада, это шуточка. У них там какой-то дрочь на хотт, но абсолютно бессодержательный (ну опять, это мнение со стороны от человека, который нихуя не знает толком).
я предлагаю не читать на русском. У всех математических терминов в переводе на русском нелогичный бред: на нашем языке таких слов нет, а если и есть, то аналогию провести нельзя.
Я не думаю, что проблема в языке. Да и читаю я обычно на английском. Читал. Для магистратуры нужно денег накопить, работаю сейчас просто.
тогда не знаю, что ты это слово "функторы" сказал. Я вот не знаю, как на русском из мат.анализа что называется, а я только его и знаю, но знаточества хорошо, благодаря тому что не читал никогда русских книг.
Начну с очевидного - при равных усилиях быть программистом это гораздо более денежная деятельность.
>Есть ли реальная возможность тусить с отцами Лефами
Конкретно Мартин-Лёф сейчас уже весьма пожилой и на пенсии. Хотя в принципе он пока ездит на конференции и участвует в семинарах у себя в Стокгольме. В принципе, попасть на PhD в каком-нибудь центральном месте в Европе, например в Вене или Амстердаме (если ты не хочешь учить сколь-нибудь нетривиальной математики, но хочешь как-бы заниматься логикой, Амстердам как раз подходит) довольно просто. Но как и везде в науке, чем ты старше, тем сложнее с позициями. Еще, видимо, если притвориться, что ты занимаешься Theoretical Computer Science, это улучшает карьерные перспективы.
Хм, а почему Амстердам? Что-то не припомню там никого стоящего. Ну а формально я и так буду theoretical CS (вот только мне непонятно, почему с таким дипломом легче найти позицию, ведь это ж проще математики).
И да. Что значит "чем старше"? Именно, количество лет, или уровень позиции? Я слышал, что " отсчет годов " идёт с момента PhD.
>Хм, а почему Амстердам?
Я сам не особый фанат амстердамской логики (что можно было заметить из моего комментария), но тамошний ILLC по численности людей занимающихся логикой вполне может быть самым крупным местом в Европе, хотя я это не проверял.
>вот только мне непонятно, почему с таким дипломом легче найти позицию, ведь это ж проще математики
Я имел ввиду, что проще получить позицию в TCS (так как их банально больше).
>Я слышал, что " отсчет годов " идёт с момента PhD.
В формальных критериях в основном именно с момента защиты. Хотя, иногда есть и явно возрастные ограничения.
> Что значит "чем старше"? Именно, количество лет, или уровень позиции?
Не берусь судить, насколько обращают внимание собственно на возраст (хотя, конечно, могут и обращать). И да, чем выше уровень позиции, тем сложнее её получить.
> Все, дискутировать больше не о чем, вся математика конструктивна
Не понимаю, почему? Типа ты берёшь их формализм, добавляешь некую аксиому требуюмую для "обычной математики" (ну например аксиому выборки) и дальше все выводится то же самое ? Но где гарантия, что эта доп.аксиома и аксиом униваленостни не противоречивы?
>>60400
А что они там вообще делают, впринципе? Идейно может написать?
В остальном понял, спасибо, анон.
>А что они там вообще делают, впринципе? Идейно может написать?
По большей части модальную логику. Но, в принципе, там есть люди занятые и другими вещами.
Из большой российской энциклопедии уже убрали эту часть, но разве математика не действительный мир изучает?
В математике изучают много такого, чего не может быть в действительном мире, думаю нет.
Конечно нет. Она изучает отношения между идеальными объектами с помощью формальной логики. Действительный мир тут ни при чем.
То, что математику применяют естественные науки в своих моделях, не означает, что математика изучает мир. Математика для них - это инструмент.
>Конечно нет.
>Она изучает отношения между идеальными объектами с помощью формальной логики.
Кек. Математика - раздел физики же. Ладно, как минимум обусловлена физической реальностью. "Идеальные объекты", ну возьмем тогда числа, они существуют только потому что ты можешь в физической реальности взять N каких то объектов - вроде N стульев или перекладывать N палочек. А что бы было если реальность состояла из аморфных блобов переливающихся друг в друга? Или абсолютно уникальных сущностей без возможности обобщения? Никаких бы чисел тогда не было.
То же и с логикой. Логика это всего лишь ментальное построение некоторого механизма который перекладывал бы логические выражения и совершал прочие логические действия. При этом "предполагается" что этот механизм действует по Ньютоновским законам. Этот пример особенно занятен потому что как известно в микромире действуют квантовые законы, и если бы люди обитали в микромире до рассуждали бы по непоколебимым законам квантовой логики.
Ты неправ на 100%. Можно например взять аксиоматику евклида, а можно взять аксиоматику лобачевского. Они взаимоисключющие, а значит как минимум одна точно не про этот мир. Да и все твои доводи инвалидны - то, что для представления прямой или точки или числа можно использовать аналогию реального мира не влечет за собой то, что математика мир описывает. А про физику мне вдвойне смешно слышать, как физик говорю.
Нет просто я мыслю на более высоком уровне и вижу как даже самые абстрактные теории обусловлены физической реальностью в которой они разрабатываются. Еще и евклидову геометрию притащил - это ничего что она вся состоит из черчения линий по линейке на бумаге. Вот если бы там какие размышления об ангелах были еще было о чем поговорить.
>Они взаимоисключющие, а значит как минимум одна точно не про этот мир.
А что на счет ОТО и КМ. Они тоже "не про этот мир" совсем тогда?
>А про физику мне вдвойне смешно слышать, как физик говорю.
Нет причин для смеха. Я тоже физик. Поебемся теперь?
 272 Кб, 480x320
272 Кб, 480x320>Поебемся теперь?
Давай.
На книжной полке рядом стоят две задницы:
первая и вторая. Булки каждой заднцы имеют вместе толщину 2 см, а обложка –– каждая –– 2 мм. Червь прошел(перпендикулярно булкам) от первой заднцы до последней. Какой путь он прошел?
>>58525
> Вычислить 9^903 нельзя.
Почему?
Ну хорошо. Но мы же в состоянии вычислить 10903×10903 без малейших усилий с точностью до последнего знака? Почему же число атомов может принципиально помешать вычислить 9903?
> Но мы же в состоянии вычислить 10903×10903 без малейших усилий с точностью до последнего знака?
Нет. Число атомов примерно 10^80. И наши вычислительные мощности ограничены им.
Ты, верно, тралишь. Как число атомов воспрепятствует тебе выписать число с 903 + 903 нулями после единицы?
А куда это число выписывать собрался? Если что, то речь идёт про десятичную запись. У тебя атомов для записи не хватит просто.
И что, что десятичную? Легко можно выписать хоть 903, хоть 1806 ноликов убористым почерком на одной странице твоей школьной тетради, хотя можно и не выписывать, конечно. При чём тут атомы какие-то вообще? Охуеть.
Речь идёт про 9^903 ноликов. Это число превышает 10^80. Выписать его десятичную запись в нашей вселенной нельзя, атомов для записи ноликов не хватит.
Он вооще невменяем. Целую книжку написал где пафосно всем доказывал будто наивная теория множест Кантора не противоречива, просто все дурачки неправильно перевели с немецкого термины множест и супермножеств-классов.
>Нет просто я мыслю на более высоком уровне и вижу как даже самые абстрактные теории обусловлены физической реальностью в которой они разрабатываются.
У вас физикализм головного мозга
https://ru.wikipedia.org/wiki/Физикализм
Схуяли это правда? По сути он "разрешает" противоречие простой наивной формулировкой но с запретом на построение "множеств всех множеств". Это хуйня полнейшая а не определение, страусиная позиция.












![15651539737980[1].jpg](/math/big/thumb/50442/15656126489100s.jpg)







