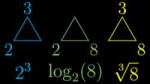 6 Кб, 300x168
6 Кб, 300x168https://www.youtube.com/watch?v=sULa9Lc4pck
Если вкратце, в нем аффтар обкладывает хуями современную систему обозначения в математике по поводу того что она....как бы это сказать....не связана с математикой.
Конкретно в этом видео речь идет о том что факт 2х2х2 = 8 можно записать как 2^3=8 как log2(8)=3 как root3(8)=2 и эти записи символьно никак не связаны. И это не смотря на то что по сути мы имеем дело с одним и тем же математическим фактом, но под разными углами.
Имеется ввиду что личинке математика-учащемуся, да и иногда всяким уважаемым математикам типа гауссов с бурбаками, это один и тот же факт из математики но под разными соусами нифига не очевиден.
По этому поводу там давалась ссылка на сайт на котором, по мнению автора видео, предлагается простой способ решения этой проблемы для степеней и логарифмов, вот она
https://www.science4all.org/article/the-triangle-of-power/
Суть ясна по картинке.
Союственно судь треда в чем, не кажется ли вам что все эти log с корнями нужно менять на другие символы, которые больше связаны с математическим смыслом действия которые они описывают? Самой математике конечно похеру как мы будем символ корня рисовать, да.
Или может кто то знает похожие обозначения, связаные с математическим смыслом действия которое они представляют? Помню тут где то давали ссылку на книжку по геометрии для дошкольнят в котором теоремы выделялись цветом, который соответствовал цвету линии в треугольнике/на картинке который отражался в написанной теореме. Это тоже давайте сюда если знаете похожее. Будем собирать памфлет на нынешнюю систему обозначений.
>>861 (OP)
> Помню тут где то давали ссылку на книжку по геометрии для дошкольнят в котором теоремы выделялись цветом, который соответствовал цвету линии в треугольнике/на картинке который отражался в написанной теореме.
Евклид?
Это типографически намного более сложный способ записи, подходит он только для того, чтобы наглядно показать тот факт, что логарифм является обратной функцией для показательной.
Чтобы понять, что происходит при 2^3 всё-равно придется разбираться со степенями, как бы ты не записал это(ну кроме 222)
А если ты разберешься - то тебе уже похуй, как обозначается это, ты это запомнишь наизуть через пару дней-недель
Опять блять приехали, школьники начали изучать алгебру восьмого класса и решили что их идеи ниибацо крутые
Вдогонку: какое-то абсолютно ублюдское обозначение через треугольник, я не понимаю какому дауну так будет проще
Что ты запишешь треугольник 2-3-8, который будет занимать дохуя места, что ты запишешь 2^3=8, разницы никакой
Изобретаем квадратный велосипед короче опять
>не кажется ли вам что все эти log с корнями нужно менять на другие символы, которые больше связаны с математическим смыслом действия которые они описывают?
Нет.
>Самой математике конечно похеру как мы будем символ корня рисовать, да.
Да.
Бля, ну и шизофрения.
До Декарта вроде так и было.
Ну и хуита. Угарнул с «о-плюса», «который часто встречается в физике». Такие вещи максимум подходят для визуализации, для мнемоники, но не для математики. Я, когда пишу a / b = c или a / c = b или bc = a, представляю себе a в вершине треугольника, поэтому никогда не напишу a в знаменателе, но я же не предлагаю дроби через треугольники записывать.
>Союственно судь треда в чем, не кажется ли вам что все эти log с корнями нужно менять на другие символы, которые больше связаны с математическим смыслом действия которые они описывают?
Я, может, тупой, но всё равно не понимаю, как треугольник «больше связан с математическим смыслом»? Как замена одних символов другими может помочь? Что с log, sqrt запоминать какие-то свойства, что с треугольниками. Понимания эти треугольники не прибавят, а если есть понимание, то тебе вообще без разницы, как это всё обозначается.
>Или может кто то знает похожие обозначения, связаные с математическим смыслом действия которое они представляют?
Как может обозначение быть связанным с математическим смыслом? Как иероглифы китайские?
>Будем собирать памфлет на нынешнюю систему обозначений.
https://en.wikipedia.org/wiki/Abuse_of_notation
Лично мне не нравятся в сегодняшних обозначениях (помимо ссылки выше):
Замена ∈, например:
1) f : X → Y (логичнее f ∈ X → Y или даже f ∈ YX).
2) f(x) = o(x) (логичнее f(x) ∈ o(x)).
3) ∫f(x)dx = g(x) + c (логичнее g(x) ∈ ∫f(x)dx).
Использование → во всех мыслимых и немыслимых смыслах. (Хотя этот знак неединственный в этом смысле.)
Неоднозначность записи fn(x). Это f(f(...f(x))) или (f(x))n. Логичнее fn(x) = f(f(...f(x))), а f(x)n = (f(x))n.
Ну и ещё, наверно, что-нибудь по мелочи, чего не вспомнил.
 39 Кб, 511x509
39 Кб, 511x509>Вот всегда раздражают такие тошнотные индивиды, как автор видео. "Вот я сижу и мне не нравится что-то, давайте всё дедушкино говно выкинем нахуй, я сейчас всё новое поставлю как мне удобно будет, и похуй мне на тридцатилетнюю историю, я сейчас мой план вам опишу, будем ими пользоваться".
Улавливаешь?
>Угарнул с «о-плюса», «который часто встречается в физике».
Единственная полезная часть ролика.
loga(bc)=loga(b)+loga(c)
loga(b)logb(c)=loga(c)
в частности loga(b)=logb(a)-1
благодаря чему первое тождество превращается в
logbc(a)-1=logb(a)-1logc(a)-1
Делай свои видео с мемасами, авось откроешь людям истину. А то так о твоих теория знают полтора гомопучкиста и натурала.
>1) (логичнее f ∈ X → Y)
нет, это плохо, потому что через X → Y обозначается морфизм, а не всё множество морфизмов сразу. обозначения морфизмов через стрелочки хорошее, т.к. категории визуализируются через графы
>2) (логичнее f(x) ∈ o(x)).
это неудобно, когда работаешь с прямыми вычислениями (а только для них, по существу, этот символ и нужен), например
(1+x+o(x^2))^2=1+2x + o(x^2)
если тебя напрягает запись f(x) = o(x), считай, что ты работаешь в фактор-пространстве и через o(x) там обозначается нулевой элемент, тогда всё в порядке (всё логично)
>3) ∫f(x)dx = g(x) + c (логичнее g(x) ∈ ∫f(x)dx).
то же самое, что и в случае 2): ∫f(x)dx = g(x) + c есть представитель функции g(x) в фактор-пространстве