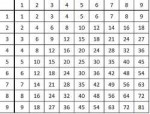
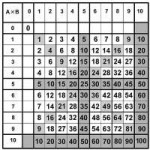
Зачем зубрить таблицу умножения и как правильно считать? Как сформировать и развить "математическое чутьё"? Сколько и каких задач надо решать для понимания? Что значит понимать математику? Нужны ли сложные задачи и науч-поп по математике или это развлекательный контент? Как сформировать мотивацию к математике или вообще отбить всякий интерес ("Плач математика")? Почему уровень математических познаний падает? Нужно ли возвращаться с старым учебникам? Как вообще можно обучать математике, какая тут связь с условными рефлексами и основаниями математики? Как написать экзамен по математике, если ничего не понимаешь? Как производственными масштабами выпускать математиков если "Нет царских путей к геометрии"? Можно ли используя измененные состояния сознания (речь не идёт о лихорадке) и современные представления стать как Сриниваса Рамануджан Айенгор?
✵ Эти и подобные вопросы можно будет обсудить в данном треде. ✵
В тред приглашаются учителя/преподаватели математики, со своими прохладными историями.
по аналогии с /fl/
>Зачем зубрить таблицу умножения и как правильно считать?
Чтобы довести банальные действия до автоматизма и не тратить на них лишние ресурсы мозга. Банальная аналогия: все мы задрочили набор текста на клавиатуре и теперь не тратим время на поиск нужной клавиши, а просто набираем текст. В математике тоже самое.
>Как сформировать и развить "математическое чутьё"?
Одна часть — зубрёжка, вторая — глубокое многостороннее изучение. Без первой части вторая часть бесполезна и быстро забывается.
>Сколько и каких задач надо решать для понимания?
Это уже во многом индивидуально. Понимание — это осознание некоторых общих схем, алгоритмов, методов; это поднятие на новой общностный уровень. Иногда бывает достаточно одной трудной задачи, чтобы выйти на него. Решение листков — типичный
>Что значит понимать математику?
Ничего.
>Нужны ли сложные задачи и науч-поп по математике или это развлекательный контент?
Сложные задачи нужны. Чем концептуальнее сложная задача, тем лучше. Науч-поп не нужен: нужны хорошие учебники для школьников.
>>45033 (OP)
>Как сформировать мотивацию к математике или вообще отбить всякий интерес ("Плач математика")?
>Зачем зубрить таблицу умножения и как правильно считать?
Чтобы довести банальные действия до автоматизма и не тратить на них лишние ресурсы мозга. Банальная аналогия: все мы задрочили набор текста на клавиатуре и теперь не тратим время на поиск нужной клавиши, а просто набираем текст. В математике тоже самое.
>Как сформировать и развить "математическое чутьё"?
Одна часть — зубрёжка, вторая — глубокое многостороннее изучение. Без первой части вторая часть бесполезна и быстро забывается.
>Сколько и каких задач надо решать для понимания?
Это уже во многом индивидуально. Понимание — это осознание некоторых общих схем, алгоритмов, методов; это поднятие на новый общностный уровень. Иногда бывает достаточно одной трудной задачи, чтобы выйти на него. Решение листков — неплохой пример.
>Что значит понимать математику?
Ничего.
>Нужны ли сложные задачи и науч-поп по математике или это развлекательный контент?
Сложные задачи нужны. Чем концептуальнее сложная задача, тем лучше. Науч-поп не нужен: нужны хорошие учебники для школьников, которые будут служить мостом от школы к университету.
>Как сформировать мотивацию к математике или вообще отбить всякий интерес ("Плач математика")?
Чтобы сформировать, можно показывать всякие интересные и неожиданные результаты. Например, меня в своё время очень сильно удивило, как можно вычислить сумму квадратов корней уравнения (квадратного) без вычисления самих корней. Такого много в математике. Чтобы отбить, особо стараться не надо.
>Как вообще можно обучать математике, какая тут связь с условными рефлексами и основаниями математики?
Можно быть лишь проводником в мир математики. Если кто-то не захочет идти, ты его не заставишь.
>Как написать экзамен по математике, если ничего не понимаешь?
Лучше не писать.
>Как производственными масштабами выпускать математиков если "Нет царских путей к геометрии"?
В этом нет нужды.
>Можно ли используя измененные состояния сознания (речь не идёт о лихорадке) и современные представления стать как Сриниваса Рамануджан Айенгор?
Без каких-то начальных данных, располагающих к этому, вещества тебе не помогут (слишком грубо действуют), но какая-нибудь медитация, развитие геометрической или скорее даже визуальной (это когда ты, к примеру, можешь представить визуально устройство факторгруппы) интуиции очень может помочь, а уже потом…
>Зачем зубрить таблицу умножения и как правильно считать?
Чтобы довести банальные действия до автоматизма и не тратить на них лишние ресурсы мозга. Банальная аналогия: все мы задрочили набор текста на клавиатуре и теперь не тратим время на поиск нужной клавиши, а просто набираем текст. В математике тоже самое.
>Как сформировать и развить "математическое чутьё"?
Одна часть — зубрёжка, вторая — глубокое многостороннее изучение. Без первой части вторая часть бесполезна и быстро забывается.
>Сколько и каких задач надо решать для понимания?
Это уже во многом индивидуально. Понимание — это осознание некоторых общих схем, алгоритмов, методов; это поднятие на новый общностный уровень. Иногда бывает достаточно одной трудной задачи, чтобы выйти на него. Решение листков — неплохой пример.
>Что значит понимать математику?
Ничего.
>Нужны ли сложные задачи и науч-поп по математике или это развлекательный контент?
Сложные задачи нужны. Чем концептуальнее сложная задача, тем лучше. Науч-поп не нужен: нужны хорошие учебники для школьников, которые будут служить мостом от школы к университету.
>Как сформировать мотивацию к математике или вообще отбить всякий интерес ("Плач математика")?
Чтобы сформировать, можно показывать всякие интересные и неожиданные результаты. Например, меня в своё время очень сильно удивило, как можно вычислить сумму квадратов корней уравнения (квадратного) без вычисления самих корней. Такого много в математике. Чтобы отбить, особо стараться не надо.
>Как вообще можно обучать математике, какая тут связь с условными рефлексами и основаниями математики?
Можно быть лишь проводником в мир математики. Если кто-то не захочет идти, ты его не заставишь.
>Как написать экзамен по математике, если ничего не понимаешь?
Лучше не писать.
>Как производственными масштабами выпускать математиков если "Нет царских путей к геометрии"?
В этом нет нужды.
>Можно ли используя измененные состояния сознания (речь не идёт о лихорадке) и современные представления стать как Сриниваса Рамануджан Айенгор?
Без каких-то начальных данных, располагающих к этому, вещества тебе не помогут (слишком грубо действуют), но какая-нибудь медитация, развитие геометрической или скорее даже визуальной (это когда ты, к примеру, можешь представить визуально устройство факторгруппы) интуиции очень может помочь, а уже потом…
Извиняюсь за сумбурность.
Но ведь устный счёт это не мышечная память как с слепой печатью. У обычной аудиомоторной технологии устного счёта есть весьма много недостатков и от нее со всякими ухищрениями (метод Трахтенберга), говорят, необходимо переходить к визуальной технологии устного счёта. Это уже ближе к некому чувству числа и должно помочь. Вообще о визуальной технологии счёта нашел следующее:
> Владимир Борисович ТВОРОГОВ (род. в 1951 г.)
> Окончил с отличием механико-математический факультет Московского государственного университета им.М.В.Ломоносова. Кандидат физико-математических наук.
> Однажды, занимаясь с сыном повторением таблицы умножения, случайно заметил закономерность поворота цифр на телефонной матрице. Глубокое математическое исследование удивительного факта заняло немало времени. Результатом явились многочисленные статьи и патенты, посвященные классу цифровых вертушек, а также настоящая книга о наглядной арифметике и быстром счете.
Вот подобный и человек и пишет себе тихонько книги пока в интернете процветают различные франшизы типа зубрежки абакуса: https://www.youtube.com/watch?v=cYw3ppgibxQ
А ведь эти книги весьма интересны, там и теоремы различные и проблем с будущей математикой (в отличии от зубрежки абакусов) не создаст, а даже должно наоборот помочь. Вот еще почти что фокусы (в книгах упоминается о феноменальных счетчиках): https://www.youtube.com/watch?v=y7fcb-WFuUA Правда Шелушков, говорят, сошел с ума, но это потому что он чересчур увлекся невзирая на советы, а так методы ментальной гигиены были предложены еще в 30-х годах немецкой психиатрией. А потом получил распространение "метод Трахтенберга". И так о всех подобных сверхспособностях снимают кино типа "Человек дождя", а тайну даже не пытаются раскрыть. В общем я ссылок и отсылок накидал.
А о зубрежке таблицы умножения это тоже интересный вопрос. Как правило зубрят обычно примеры "2x2=4 7x8=56" даже не пытаясь найти определенные закономерности. Подробнее тут: https://kukina-kat.livejournal.com/354584.html
И если уже на таком уровне всё происходит, то что дальше? Сколько было убито математиков?
Извиняюсь за сумбурность.
Но ведь устный счёт это не мышечная память как с слепой печатью. У обычной аудиомоторной технологии устного счёта есть весьма много недостатков и от нее со всякими ухищрениями (метод Трахтенберга), говорят, необходимо переходить к визуальной технологии устного счёта. Это уже ближе к некому чувству числа и должно помочь. Вообще о визуальной технологии счёта нашел следующее:
> Владимир Борисович ТВОРОГОВ (род. в 1951 г.)
> Окончил с отличием механико-математический факультет Московского государственного университета им.М.В.Ломоносова. Кандидат физико-математических наук.
> Однажды, занимаясь с сыном повторением таблицы умножения, случайно заметил закономерность поворота цифр на телефонной матрице. Глубокое математическое исследование удивительного факта заняло немало времени. Результатом явились многочисленные статьи и патенты, посвященные классу цифровых вертушек, а также настоящая книга о наглядной арифметике и быстром счете.
Вот подобный и человек и пишет себе тихонько книги пока в интернете процветают различные франшизы типа зубрежки абакуса: https://www.youtube.com/watch?v=cYw3ppgibxQ
А ведь эти книги весьма интересны, там и теоремы различные и проблем с будущей математикой (в отличии от зубрежки абакусов) не создаст, а даже должно наоборот помочь. Вот еще почти что фокусы (в книгах упоминается о феноменальных счетчиках): https://www.youtube.com/watch?v=y7fcb-WFuUA Правда Шелушков, говорят, сошел с ума, но это потому что он чересчур увлекся невзирая на советы, а так методы ментальной гигиены были предложены еще в 30-х годах немецкой психиатрией. А потом получил распространение "метод Трахтенберга". И так о всех подобных сверхспособностях снимают кино типа "Человек дождя", а тайну даже не пытаются раскрыть. В общем я ссылок и отсылок накидал.
А о зубрежке таблицы умножения это тоже интересный вопрос. Как правило зубрят обычно примеры "2x2=4 7x8=56" даже не пытаясь найти определенные закономерности. Подробнее тут: https://kukina-kat.livejournal.com/354584.html
И если уже на таком уровне всё происходит, то что дальше? Сколько было убито математиков?
>Одна часть — зубрёжка, вторая — глубокое многостороннее изучение. Без первой части вторая часть бесполезна и быстро забывается.
Что именно желательно зазубрить?
> Это уже во многом индивидуально. Понимание — это осознание некоторых общих схем, алгоритмов, методов; это поднятие на новый общностный уровень. Иногда бывает достаточно одной трудной задачи, чтобы выйти на него. Решение листков — неплохой пример.
Как иначе сказать что такое понимание? Это какие-то возникающие образы и представления? Хоть круги Эйлера, хоть "геометрическая интуиция"? Если человек решил тысячу задач и прекрасно решает некие уравнения, то будет ли тут понимание? Переходить к доказательствам уже?
Чем существенно отличается "решение листков"?
> Можно быть лишь проводником в мир математики. Если кто-то не захочет идти, ты его не заставишь.
Это вопрос мотивации и учебы из под палки или более общий вопрос вообще? Можно ли выдрессировать человека на математику? Для успешной работы с математикой человек должен умело работать с фантазией осознанно?
> В этом нет нужды.
Но ведь математики могут закончиться. Разве не так?
> Без каких-то начальных данных, располагающих к этому, вещества тебе не помогут (слишком грубо действуют), но какая-нибудь медитация, развитие геометрической или скорее даже визуальной (это когда ты, к примеру, можешь представить визуально устройство факторгруппы) интуиции очень может помочь, а уже потом…
Вот об этом во многом и идет речь.
>Что именно желательно зазубрить?
Я не он, мимохуй, но считаю, что зубрить плохо, гораздо лучше попытаться понять, почувствовать то, что ты хочешь изучить. Из аналогий в голове только видеорелейтед.
https://www.youtube.com/watch?v=W5wVyUWy7qA
Обрати внимание, как он втирает говно себе в лицо в попытке понять его секрет, вот это отличная метафора к тому, о чём я пытаюсь тебе сказать. Обмазывающий стиль, понимаешь? А, без толку.
>Как иначе сказать что такое понимание?
Проведя много времени с чем-то ты начинаешь понимать как оно может себя вести, как не может, мягкое оно, вонючее или твёрдое и сладкое, понимаешь? Свойства, ощущения, они остаются в памяти сами.
Тупо покрутить с разных сторон, убирать-добавлять свойства?
Как предлагалось "наглядный пример—контрпример—нужда в формализме"?
Скорее набрать 50-100 задачек по теме разной сложности и доказывать, доказывать, каждое доказательство будет проливать больше света на то, с чем ты работаешь, в итоге появится интуиция.
Ну в смысле пока будешь пытаться что-то доказать так или иначе по много раз перекрутишь так и сяк во все стороны.
>Как производственными масштабами выпускать математиков если "Нет царских путей к геометрии"?
Интересно, а сколько математиков выпускают в год российские вузы. Предположу, ответ где-то в промежутке 1-3.
> Что значит понимать математику?
Понимать значит "уметь использовать". Хоть математику, хоть что угодно другое. Заметим, это определение не подразумевает наличие человека. В этом смысле пруверы тоже в какой-то мере математику понимают
>развитие геометрической или скорее даже визуальной (это когда ты, к примеру, можешь представить визуально устройство факторгруппы
Что тут представлять? Разве можно знать что такое фактор-группа или идеал на уровне определения, но не иметь в голове визуального образа, картинки? Как? Ещё раз убеждаюсь что словосочетание "геометрическая интуиция" обозначает обычное понимание того, о чем говоришь. В других учебных дисциплинах почему-то такие фразы не придумывают.
Это очень легко выяснить: посмотри сколько мест в аспирантуру института Стеклова РАН. Как раз, по моему, три и будет. Многие, впрочем, уезжают.
Геометрия это не то, тут скорее визуальная, а не геометрическая. И да, можно на уровне определения, чисто как лингвистический артефакт, кто-то так и воспринимает, как язык.
Интересная тема со всеми этими ментальными арифметиками, но и здесь не обойтись без зубрёжки. Всё равно нужно в той или иной мере зубрить эти методы, алгоритмы, образы, но другой вопрос, что такая зубрёжка гораздо эффективнее и полезнее, чем зубрёжка таблицы умножения.
>Подробнее тут:
С одной стороны, хочется согласиться, что правильную таблицу умножения интереснее исследовать, чем столбцы 2х2=4. С другой стороны, таблица умножения отдаляет концептуальный уровень достаточно далеко. По сути это и есть обобщение в результате понимания, поэтому, чтобы выучить таблицу умножения, сперва нужно понять, почему она именно такая. Поэтому нужно начинать не с зубрёжки таблицы умножения в той или иной форме, а с собственного составления этой самой таблицы. Сперва ребёнку нужно дать задание составить таблицу умножения с помощью обычных палочек, а уже потом её учить. Также с помощью палочек можно легко заметить коммутативность умножения. Пусть имеется 5 кучек по 3 палочки (5x3). Возьмём две кучки (6 палочек) и добавим по две палочки в оставшиеся три кучки. Получится 3 кучки по 5 палочек (3x5). Вот это гораздо интереснее, чем какая-то сухая безжизненная таблица.
>Что именно желательно зазубрить?
Тут надо сделать оговорку по поводу слова «зубрить». Для меня «зубрить» — это какое-то количество раз вспомнить, повторить, применить. Например, прочитал анон какую-то теорему с доказательством. Он её несколько раз вспомнил, несколько раз повторил ход доказательства и несколько раз где-нибудь применил. Поэтому желательно зубрить всё, что так или иначе может быть полезным. В любом случае чем больше математическая эрудиция, тем лучше и проще.
>Как иначе сказать что такое понимание?
Тут нужно сделать оговорку. Понимание — это лестница, каждая ступенька которой — новый уровень абстрактности, общности, однако расстояние между ступеньками нефиксированное, поэтому иногда бывает трудно сделать шаг выше. Нельзя понять «до конца», но можно подниматься по этой лестнице всё выше и выше.
>Это какие-то возникающие образы и представления?
В том числе.
>Если человек решил тысячу задач и прекрасно решает некие уравнения, то будет ли тут понимание? Переходить к доказательствам уже?
Без сомнения тут есть понимание и без сомнения нужно переходить на новый уровень понимания, но, как я и сказал выше, это может быть трудной задачей из-за полного или частичного отсутствия нужного слоя абстракции или отсутствия самого аппарата абстрагирования, как такового. Первое — решаемо при наличии «проводника», но, как правило, не очень быстро. Второе тоже решаемо, но это уже индивидуальный, личный и в некоторой степени даже интимный процесс, окончание которого даёт человеку возможность идти дальше без «проводника».
>Чем существенно отличается "решение листков"?
Хорошо составленные листки снабжают множеством примеров на «повторение/использование», но в то же время наводят на некоторые общие идеи, рассуждения, как бы слегка подталкивают человека вверх — на новую ступень, но не делают это грубо.
>Это вопрос мотивации и учебы из под палки или более общий вопрос вообще?
Более общий. Человек вполне может иметь выбор между несколькими путями (например: математика, биология, физика), а выберет в конечном итоге что-то одно (и не факт, что это будет математика).
>Можно ли выдрессировать человека на математику?
Думаю, что можно. Во всяком случае школа и университет именно этим и занимаются. Другой вопрос — насколько это правильно и нужно.
>Для успешной работы с математикой человек должен умело работать с фантазией осознанно?
Это сложный вопрос. Что значит работать с фантазией осознанно? Можно ли работать с ней неосознанно?
>Но ведь математики могут закончиться. Разве не так?
Я считаю, что это может произойти только в результате очень сильного культурного сдвига, а в этом случае вряд ли что-то поможет.
>Что именно желательно зазубрить?
Тут надо сделать оговорку по поводу слова «зубрить». Для меня «зубрить» — это какое-то количество раз вспомнить, повторить, применить. Например, прочитал анон какую-то теорему с доказательством. Он её несколько раз вспомнил, несколько раз повторил ход доказательства и несколько раз где-нибудь применил. Поэтому желательно зубрить всё, что так или иначе может быть полезным. В любом случае чем больше математическая эрудиция, тем лучше и проще.
>Как иначе сказать что такое понимание?
Тут нужно сделать оговорку. Понимание — это лестница, каждая ступенька которой — новый уровень абстрактности, общности, однако расстояние между ступеньками нефиксированное, поэтому иногда бывает трудно сделать шаг выше. Нельзя понять «до конца», но можно подниматься по этой лестнице всё выше и выше.
>Это какие-то возникающие образы и представления?
В том числе.
>Если человек решил тысячу задач и прекрасно решает некие уравнения, то будет ли тут понимание? Переходить к доказательствам уже?
Без сомнения тут есть понимание и без сомнения нужно переходить на новый уровень понимания, но, как я и сказал выше, это может быть трудной задачей из-за полного или частичного отсутствия нужного слоя абстракции или отсутствия самого аппарата абстрагирования, как такового. Первое — решаемо при наличии «проводника», но, как правило, не очень быстро. Второе тоже решаемо, но это уже индивидуальный, личный и в некоторой степени даже интимный процесс, окончание которого даёт человеку возможность идти дальше без «проводника».
>Чем существенно отличается "решение листков"?
Хорошо составленные листки снабжают множеством примеров на «повторение/использование», но в то же время наводят на некоторые общие идеи, рассуждения, как бы слегка подталкивают человека вверх — на новую ступень, но не делают это грубо.
>Это вопрос мотивации и учебы из под палки или более общий вопрос вообще?
Более общий. Человек вполне может иметь выбор между несколькими путями (например: математика, биология, физика), а выберет в конечном итоге что-то одно (и не факт, что это будет математика).
>Можно ли выдрессировать человека на математику?
Думаю, что можно. Во всяком случае школа и университет именно этим и занимаются. Другой вопрос — насколько это правильно и нужно.
>Для успешной работы с математикой человек должен умело работать с фантазией осознанно?
Это сложный вопрос. Что значит работать с фантазией осознанно? Можно ли работать с ней неосознанно?
>Но ведь математики могут закончиться. Разве не так?
Я считаю, что это может произойти только в результате очень сильного культурного сдвига, а в этом случае вряд ли что-то поможет.
>Я не он, мимохуй, но считаю, что зубрить плохо, гораздо лучше попытаться понять, почувствовать то, что ты хочешь изучить. Из аналогий в голове только видеорелейтед.
Понять/почувствовать — это как раз таки многосторонне изучить, а уже после этого можно «зубрить», то есть повторять/использовать.
>>45057
>>45058
Это пример зубрёжки совмещённой с многосторонним изучением.
>>45069
>Что тут представлять? Разве можно знать что такое фактор-группа или идеал на уровне определения, но не иметь в голове визуального образа, картинки? Как?
Можно. Я лично видел таких людей (когда человек знает определение на аудиомоторном уровне, но не имеет визуальной опоры). Даже ты наверняка таблицу умножения знаешь именно на аудиомоторном уровне. Вряд ли, умножая числа, ты себе в голове кучки представляешь или прямоугольники.
>такая зубрёжка гораздо эффективнее и полезнее, чем зубрёжка таблицы умножения.
>полезнее
Можно клоуном в цирке выступать?
Можно. Так-то в жизни возникают иногда ситуации умножения трёхзначных чисел, когда гораздо быстрее было бы посчитать произведение в уме, чем доставать компуктер и вбивать в него числа.
Не настолько оно субъективное, чтобы тратить время на объективно глупые занятия по типу ментальной арифметики.
Но ты и вправду неправ, понимать и использовать - вообще говоря это разные вещи. На низких уровнях это практически одно и то же, но чем дальше в лес...
Ну если подразумевать под зубрёжкой тупое механическое повторение, то это не зубрёжка, конечно. Но для меня зубрёжка — это в принципе какое-то повторение, использование несколько раз. Просто зубрёжка может быть более концептуальной (задачи на доказательство) или менее (примерчики).
>это в принципе какое-то повторение, использование несколько раз
В таком случае вообще всё зубрёжка, ты постоянно повторяешь использование слов, определений и тд. Не, по мне так зубрёжка именно тупое выучивание наизусть.
При поиске информации о быстром счёте находится метод Трахтенберга (чтобы умножить на 11...) и ментальная арифметика™ (почти что товарный знак). Второе представляет из себя франшизу (бизнес под ключ, развивающие центры) с коммерческой тайной и как оказывается страшной зубрежкой, которая даже может помешать математике в дальнейшем. Ведь дети долгое время передвигают эти косточки на абакусе пока оно не засядет в голове. И вообще всё весьма сомнительно, забава для небожителей больше.
Напротив после копаний я обнаружил работы некого кандидата физико-математических наук. Статья об этом была удалена из Википедии из-за непопулярности. Называется "Наглядная арифметика", выше обложки книг. Вот скан первой книги: http://libgen.io/book/index.php?md5=244EFDCDAAA810412A5D64C490D0025A
То есть сидит себе кандидат физико-математических наук и спокойно себе изучает быстрый счёт со всеми теоремами пока остальные люди успешно зарабатывают на каких-то обрубках. Думаю ситуация вполне обыденная. В связи с этим призываю сообщество /math/ изучить эту тему.
>>45080
Не понимаю где я написал, что одна зубрежка лучше другой. Просто может я написал странно.
А польза самая разная, об этом говорил ещё Лев Толстой. Можно, конечно, и в цирке выступать, только это ближе к фокусникам, чем к клоунам.
>>45081
Да, Лев Толстой говорил, что это довольно хорошо даже просто уйти в себя и поразмыслить. Так, наверное, и делал Рамануджан, хотя и этот вопрос надо изучить подробнее. И я сомневаюсь, что он зубрил таблицу умножения.
>>45082
О, ошибки тут уменьшаются в разы. Помимо самой сути навыка в виде того, что при тренировке даже большие числа будут чувствоваться примерно также как считаешь пару сапог (не надо же задумываться, что сапог двое) приходит и более осознанная работа с числами. Не просто 20x10=200 и знание правила умножения на 10, но и более глубокие принципы. Стать Рамануджаном можно, конечно же, инфа 100%!!1
А о скорости и говорить нечего. Визуальный канал восприятия самый-самый и именно он лежит в основе мышления во многом.
>>45098
Ментальная арифметика это во-многом бренд, я упоминал её в качестве некой порочности.
При поиске информации о быстром счёте находится метод Трахтенберга (чтобы умножить на 11...) и ментальная арифметика™ (почти что товарный знак). Второе представляет из себя франшизу (бизнес под ключ, развивающие центры) с коммерческой тайной и как оказывается страшной зубрежкой, которая даже может помешать математике в дальнейшем. Ведь дети долгое время передвигают эти косточки на абакусе пока оно не засядет в голове. И вообще всё весьма сомнительно, забава для небожителей больше.
Напротив после копаний я обнаружил работы некого кандидата физико-математических наук. Статья об этом была удалена из Википедии из-за непопулярности. Называется "Наглядная арифметика", выше обложки книг. Вот скан первой книги: http://libgen.io/book/index.php?md5=244EFDCDAAA810412A5D64C490D0025A
То есть сидит себе кандидат физико-математических наук и спокойно себе изучает быстрый счёт со всеми теоремами пока остальные люди успешно зарабатывают на каких-то обрубках. Думаю ситуация вполне обыденная. В связи с этим призываю сообщество /math/ изучить эту тему.
>>45080
Не понимаю где я написал, что одна зубрежка лучше другой. Просто может я написал странно.
А польза самая разная, об этом говорил ещё Лев Толстой. Можно, конечно, и в цирке выступать, только это ближе к фокусникам, чем к клоунам.
>>45081
Да, Лев Толстой говорил, что это довольно хорошо даже просто уйти в себя и поразмыслить. Так, наверное, и делал Рамануджан, хотя и этот вопрос надо изучить подробнее. И я сомневаюсь, что он зубрил таблицу умножения.
>>45082
О, ошибки тут уменьшаются в разы. Помимо самой сути навыка в виде того, что при тренировке даже большие числа будут чувствоваться примерно также как считаешь пару сапог (не надо же задумываться, что сапог двое) приходит и более осознанная работа с числами. Не просто 20x10=200 и знание правила умножения на 10, но и более глубокие принципы. Стать Рамануджаном можно, конечно же, инфа 100%!!1
А о скорости и говорить нечего. Визуальный канал восприятия самый-самый и именно он лежит в основе мышления во многом.
>>45098
Ментальная арифметика это во-многом бренд, я упоминал её в качестве некой порочности.
Если человек сдал государственный экзамен на высокий балл, то он понимает математику? Это безусловно можно проверить некоторыми объективными тестами? Человека надо учить каким-то навыкам определенным? В это хорошо вписывается наука о поведении (бихевиоризм), прикладной анализ поведения, с высокой эффективностью можно применять "Программированное обучение"?
На фото:
Умный Ганс (нем. Kluger Hans) — лошадь породы орловский рысак, жившая в Германии в начале XX века и получившая известность из-за того, что якобы обладала высочайшим интеллектом и могла производить в уме арифметические операции и решать другие математические (и не только) задачи, давая верные ответы на задаваемые ей людьми вопросы[1]. Представления с её участием проводились при широкой публике.
>>45069
>>45073
Вообще образы это весьма важная часть. Их используют даже для тренировки спортсменов, смотрите идеомоторная тренировка.
[...]
«Оказалось, что и Адамар мыслит подобным образом. Едва он приступает к решению задачи, все слова вылетают у него из головы и возвращаются лишь после того, как задача решена. Думает он пятнами неопределенной формы. В их причудливых сочетаниях отражается процесс комбинирования идей. Чтобы доказать, например, что существует простое число больше 11, он должен рассмотреть все простые числа от 2 до 11. В это время перед его взором находится неопределенная масса. Потом числа надо перемножить друг на друга.
Так как их произведение большое число, Адамар представляет себе точку, удаленную от этой массы. Он прибавляет к произведению единицу и видит поблизости еще одну точку. Наконец перед его глазами возникает некое место, расположенное между массой и первой точкой. Это делитель – признак числа, полученного после сложения. Некое место – чем это хуже дырки в море энергий! Не велика заслуга – представить себе атом или электрон, представьте-ка место, где был электрон! Какова изощренность воображения! И если бы прилагались хоть какие-нибудь усилия, а то ведь эти «места» появляются сами собой, в процессе мышления. Рассматривая сумму бесконечного числа слагаемых, Адамар видит не формулу, а «место, которое она занимала, если бы ее написали». Как же все-таки выглядит это «место»? Как лента, "более широкая или более темная в тех местах, где должны быть самые важные члены формулы..."»
Ж. Адамар в своей книге «Исследования психологии изобретения в области математики» [9] много раз повторяет свои и чужие слова, что он не мыслит словами над проблемами и даже математические знаки ему тяжелы.
[...]
>>45100
По нарастающей? Значит необходим определенный уровень умения (навыки + знания) для перехода на следующий уровень?
>>45078
> Это сложный вопрос. Что значит работать с фантазией осознанно? Можно ли работать с ней неосознанно?
Сам Рамануджан говорил, что формулы ему во сне и в молитве (в индуизме: в мантра-йоге, медитации)[1] внушает богиня Намагири Тхайяр (англ.) (Махалакшми) (хинди नामगिरी), почитаемая в Намаккале (там. நாமக்கல்).[2][3]
Есть различные техники.
>>45079
>Понять/почувствовать — это как раз таки многосторонне изучить, а уже после этого можно «зубрить», то есть повторять/использовать.
Разве не с зубрежки начинается? А то после запоминания это уже будет повторение. Тут уже о искусстве запоминания (мнемотехнике) речь.
Вообще странно, что педагогическая мнемотехника это "Каждый охотник желает знать где сидит фазан", хотя возможности мнемотехники намного шире, а цвета радуги надо запоминать именно зубрежкой. Будто специально вводят в заблуждение, хотя это по и незнанию, инерции.
> Можно. Я лично видел таких людей (когда человек знает определение на аудиомоторном уровне, но не имеет визуальной опоры). Даже ты наверняка таблицу умножения знаешь именно на аудиомоторном уровне. Вряд ли, умножая числа, ты себе в голове кучки представляешь или прямоугольники.
Это и есть та самая несчастная зубрежка с заметными последствиями. Даже стихи лучше учить с...
>>45105
>доказательство
Кто-то хочет аккуратно потрогать основания?
Если человек сдал государственный экзамен на высокий балл, то он понимает математику? Это безусловно можно проверить некоторыми объективными тестами? Человека надо учить каким-то навыкам определенным? В это хорошо вписывается наука о поведении (бихевиоризм), прикладной анализ поведения, с высокой эффективностью можно применять "Программированное обучение"?
На фото:
Умный Ганс (нем. Kluger Hans) — лошадь породы орловский рысак, жившая в Германии в начале XX века и получившая известность из-за того, что якобы обладала высочайшим интеллектом и могла производить в уме арифметические операции и решать другие математические (и не только) задачи, давая верные ответы на задаваемые ей людьми вопросы[1]. Представления с её участием проводились при широкой публике.
>>45069
>>45073
Вообще образы это весьма важная часть. Их используют даже для тренировки спортсменов, смотрите идеомоторная тренировка.
[...]
«Оказалось, что и Адамар мыслит подобным образом. Едва он приступает к решению задачи, все слова вылетают у него из головы и возвращаются лишь после того, как задача решена. Думает он пятнами неопределенной формы. В их причудливых сочетаниях отражается процесс комбинирования идей. Чтобы доказать, например, что существует простое число больше 11, он должен рассмотреть все простые числа от 2 до 11. В это время перед его взором находится неопределенная масса. Потом числа надо перемножить друг на друга.
Так как их произведение большое число, Адамар представляет себе точку, удаленную от этой массы. Он прибавляет к произведению единицу и видит поблизости еще одну точку. Наконец перед его глазами возникает некое место, расположенное между массой и первой точкой. Это делитель – признак числа, полученного после сложения. Некое место – чем это хуже дырки в море энергий! Не велика заслуга – представить себе атом или электрон, представьте-ка место, где был электрон! Какова изощренность воображения! И если бы прилагались хоть какие-нибудь усилия, а то ведь эти «места» появляются сами собой, в процессе мышления. Рассматривая сумму бесконечного числа слагаемых, Адамар видит не формулу, а «место, которое она занимала, если бы ее написали». Как же все-таки выглядит это «место»? Как лента, "более широкая или более темная в тех местах, где должны быть самые важные члены формулы..."»
Ж. Адамар в своей книге «Исследования психологии изобретения в области математики» [9] много раз повторяет свои и чужие слова, что он не мыслит словами над проблемами и даже математические знаки ему тяжелы.
[...]
>>45100
По нарастающей? Значит необходим определенный уровень умения (навыки + знания) для перехода на следующий уровень?
>>45078
> Это сложный вопрос. Что значит работать с фантазией осознанно? Можно ли работать с ней неосознанно?
Сам Рамануджан говорил, что формулы ему во сне и в молитве (в индуизме: в мантра-йоге, медитации)[1] внушает богиня Намагири Тхайяр (англ.) (Махалакшми) (хинди नामगिरी), почитаемая в Намаккале (там. நாமக்கல்).[2][3]
Есть различные техники.
>>45079
>Понять/почувствовать — это как раз таки многосторонне изучить, а уже после этого можно «зубрить», то есть повторять/использовать.
Разве не с зубрежки начинается? А то после запоминания это уже будет повторение. Тут уже о искусстве запоминания (мнемотехнике) речь.
Вообще странно, что педагогическая мнемотехника это "Каждый охотник желает знать где сидит фазан", хотя возможности мнемотехники намного шире, а цвета радуги надо запоминать именно зубрежкой. Будто специально вводят в заблуждение, хотя это по и незнанию, инерции.
> Можно. Я лично видел таких людей (когда человек знает определение на аудиомоторном уровне, но не имеет визуальной опоры). Даже ты наверняка таблицу умножения знаешь именно на аудиомоторном уровне. Вряд ли, умножая числа, ты себе в голове кучки представляешь или прямоугольники.
Это и есть та самая несчастная зубрежка с заметными последствиями. Даже стихи лучше учить с...
>>45105
>доказательство
Кто-то хочет аккуратно потрогать основания?
 110 Кб, 1349x625
110 Кб, 1349x625> Ж. Адамар в своей книге «Исследования психологии изобретения в области математики» [9] много раз повторяет свои и чужие слова, что он не мыслит словами над проблемами и даже математические знаки ему тяжелы.
Забавная книженция даже, кстати.
Тпшка использует ипхоне, тырнет, фотик, но едва ли понимает, как что-либо из этого работает.
> Рассматривая сумму бесконечного числа слагаемых, Адамар видит не формулу, а «место, которое она занимала, если бы ее написали». Как же все-таки выглядит это «место»? Как лента, "более широкая или более темная в тех местах, где должны быть самые важные члены формулы..."»
Ой, клёво, а то я думал я один такой поехавший мудак.
>О, ошибки тут уменьшаются в разы.
По сравнению с калькулятором?
>Помимо самой сути навыка в виде того, что при тренировке даже большие числа будут чувствоваться примерно также как считаешь пару сапог
Не будут из-за объёма внимания или чего-то в этом духе.
> Тпшка использует ипхоне, тырнет, фотик, но едва ли понимает, как что-либо из этого работает.
А для того, чтобы это использовать для нужд ТП и не нужно знания того, как оно работает. Ты даже не понял, что я вообще написал, судя по твоей левой аналогии. Точно так же и повару не нужно знать уравнение Шрёдингера чтобы погасить соду уксусом. Все эти примеры никак не опровергают того, что значение чего-то это использование этого чего-то.
Чтобы использовать не нужно, чтобы понимать нужно. Чтобы найти результат 1023х63, не нужно уметь считать, достаточно уметь нажимать на кнопки со значками, так что, по твоему такой человек будет понимать счёт? Всё это мне напоминает мысленный эксперимент с китайской комнатой.
> Чтобы использовать не нужно, чтобы понимать нужно. Чтобы найти результат 1023х63, не нужно уметь считать, достаточно уметь нажимать на кнопки со значками, так что, по твоему такой человек будет понимать счёт?
Ты опять приводить левые примеры. Почитай мой предыдущий пост и подумай. Если человек умеет пользоваться калькулятором - это значит что он умеет пользоваться калькулятором. Само по себе умение пользоваться калькулятором не предполагает умения понимать счёт в уме. Это разные вещи, зачем их валить в одну кучу?
> Всё это мне напоминает мысленный эксперимент с китайской комнатой.
Основанного на вере, что существует какое-то понимание, отличающееся от использования.
>Если человек умеет пользоваться калькулятором - это значит что он умеет пользоваться калькулятором.
Это бессмысленное утверждение.
>Само по себе умение пользоваться калькулятором не предполагает умения понимать счёт в уме
Есть объект, есть понимание этого объекта(на каких принципах он работает, как он устроен и тд), а есть использование этого объекта, использовать значит выполнить какие-то действия с объектом по алгоритму и получить нужный результат, совершенно необязательно понимать, чем на самом деле объект является, эти вещи вообще никак не связаны, микроскоп можно использовать для рассмотрения бактерий, для забивки гвоздей или для анальных утех. Ну и вообще, смысла спорить нет, так как у тебя по определению понимание это использование.
>Основанного на вере, что существует какое-то понимание,
Да в смысле, хочешь сказать, что составляя иероглифы как тебе скажут ты китайский выучишь? По такой схеме и цирковые лошади понимают человеческий язык и счёт.
> Да в смысле, хочешь сказать, что составляя иероглифы как тебе скажут ты китайский выучишь?
Ну ты ж русский выучил, составляя слова и фразы как тебе сказали сначала родители, а потом общество, литература там. Просто использовал так как это принято и все. Знаешь ли ты русский язык с точки зрения твоего предыдущего поста? Т.е можешь ли составить алгоритм построения общения из слов и предложений, применимый к любой возможной ситуации?
>Ну ты ж русский выучил, составляя слова и фразы как тебе сказали сначала родители, а потом общество, литература там
Они мне говорили слово, а потом показывали на предмет, который это слово означает. Без показывания я бы хуй пососал.
То есть лошадь понимает, что если взять вот эту буковку, то она получит сладкое, она понимает как использовать буковки, но не понимает сам язык. Понимать как использовать что-то и понимать, что ты используешь это разное понимание, первое почти не проливает свет на второе, а вот поняв что-то, конечно, ты поймёшь как это можно использовать.
> Они мне говорили слово, а потом показывали на предмет, который это слово означает. Без показывания я бы хуй пососал.
>>45273
> Вот кстати момент построения ассоциации и есть момент понимания.
Фейсбуковский StarSpace ровно так и работает - строит ассоциации, в т.ч между словами и фичами картинок. Так что из этого китайская комната - ты или софт для NLP?
>>45275
> То есть лошадь понимает, что если взять вот эту буковку, то она получит сладкое, она понимает как использовать буковки, но не понимает сам язык.
Лошадь понимает язык ровно на том уровне, что ты описал. Ты - на более сложном (если возьмешь такието буковы, слова и фразы, то получишь работу после собеседования итд). Тут чисто количественная разница, не качественная.
> Понимать как использовать что-то и понимать, что ты используешь это разное понимание,
Буквы и в Африке буквы, как и слова и фразы и связи между ними и чем-то ещё. Что ты там такого мистического за буковы понимаешь, чего не может понять алгоритм или лошадь?
> ты или софт для NLP
Софт, конечно. Программы не могут строить ассоциации, там просто обсчитывается то, что в них заложил человек и интерпретировать тоже человек будет.
>на более сложном
>количественная
Качественная, если лошади добавить в мозг нейронов она умнее не станет, сотня лошадей вместе тоже не даст прироста интеллекта.
>понять алгоритм или лошадь
Лошадь не может в сложные ассоциации, это уже к биологам, наверное, пример был приведён для того, чтобы проиллюстрировать, что научить использовать что-то можно даже лошадь научить, в то время как понимаем там дело и не пахнет, а значит, это всё же разные вещи. Хотя, повторюсь, если у тебя по опредлению понимание=использование, то с этим спорить невозможно, просто из этого всякие странные следствия получаются, ну так что с того. про алгоритм вообще не понял, ты считаешь, что алгоритмы обладают волей, они разумны?
>не может в сложные ассоциации
Хотя обезьяна может, наверное. Фиг знает ещё, что такое эти ассоциации, как они строятся. Так-то обучение математике по сути это тоже усвоение некоторого набора ассоциаций, любое понимание к этому сводится, просто понять как использовать что-то легче, чем понять чем является та или иная вещь. Пониманием как использовать занимаются в приложениях математики, в отличие от чистой, где рассматриваются вещи сами по себе, безотносительно их возможных приложений.
https://www.youtube.com/watch?v=CCUXwT4vdW8
Блядь, какой-то пидарас свой пиздёж вставил как всегда.
https://www.youtube.com/watch?v=spMkaJp975s
> ровно так и работает - строит ассоциации, в т.ч между словами и фичами картинок.
Ну и в китайской комнате картинок не было, только наборы иероглифов, картинки уже какую-то инфу дают(человеку, который понимает, что на них изображено). А просто наблюдая за перемешиванием иероглифов ничего ты не узнаешь о том, что они значат, даже, мне кажется, ты можешь грамматику выучить, найти закономерности в том, как они располагаются относительно друг друга, но семантика будет недоступна. Вот это прикол, как говорится, лет за 10 такого эксперимента получится человек, отлично знающий язык, но не понимающий ровно нихуя. Напоминает как нас в унике учить таблицы интегралов заставляли, кого ни спроси никто не ебёт в душе, что такое интеграл или производная, максимум хуево заученное определение из вики, да и то с неточностями, тебе выдадут, но зато все знают правила работы с ними, примеры решают. Молодцы.
С другой стороны зачем это знать, когда они геологи, умеют применять и ладно. Интеграл это такая буква с змейкой, его можно по формулам преобразовывать в другие формулы. В логике такого много, формально-логический подход, но там это обоснованно, смысл как раз в том, чтобы абстрагироваться от док-ва, сделать из док-ва математический объект и с ним работать, использовать его, логика это как раз понимание как использовать, но потом-то нужно от полученного спуститься обратно, к пониманию что. Ладно, нахуй двачи.
Заводы стоят, примеры надо решать уже сейчас. А смысл производной можно и в науч-попе пояснить.
 38 Кб, 495x576
38 Кб, 495x576> Софт, конечно. Программы не могут строить ассоциации, там просто обсчитывается то, что в них заложил человек и интерпретировать тоже человек будет.
Ясно. Сразу видно, что ты в глаза не видел ничего типа fasttext, word2vec итд и тем более не представляешь принципов работы подобного, но школомнение, разумеется, имеешь. А мне лениво объяснять суть какого-нибудь skipgram итп. Сам же понимаешь, что с моей стороны это типа как спорить о творчестве Достоевского с тем, кто ни о Достоевском, ни о русском языке не слышал.
> про алгоритм вообще не понял, ты считаешь, что алгоритмы обладают волей, они разумны?
Я ровно наоборот считаю. Всякие термины ни о чем, не имеющие и принципиально не могущие иметь предметного обоснования, типа "душа, квалиа, разум" итд абсолютно лишние и бесполезные сущности. Я скорее с буддистами соглашусь, что нихуя нет и природа разума это пустота, чем со всякой мутной гуманитарщиной, не объясняющей ничего.
Учить таблицу умножения надо только потому, что умножая любые числа достаточно уметь умножать числа от 1 до 9 (включая первое и последнее). Так как операция умножения делается по частям: сначала умножаются единицы, потом десятки, потом сотни и т.д. И НИКОГДА эти разрядные единицы не будет нужно умножать больше чем на 9. Например, чтобы умножить 5090 нужно узнать только сколько будет 59 и результат умножить на 100 - это только приписать два нуля. Это основной пример на котором строится всё умножение.
(a∙10n)∙(b∙10k) = (a∙b)∙10n+k
a,b,n,k ∈ N0
fasttext это нейросеть, то есть поиск максимума функции многих аргументов, вот это и обсчитывается, что я не так сказал? Причём тут ассоциации, скорее уж для тебя самого это какая-то магия, понимающие компьютеры и тд.
Ой, какой же ты неприятный человек.
Ну как бы, нельзя утверждать, что ассоциации - это не "поиск максимума функции многих аргументов" на биологическом уровне.
Можно.
 75 Кб, 579x347
75 Кб, 579x347И вообще, это редукционизм, а его давным-давно обоссали уже. Глупо сводить какую-нибудь сложную хуйню к простой и верить, что ничего при таком лютом упрощении не потеряется. Раньше организм сводили к механизмам, теперь к компьютерам, нейросетям, потом ещё к чему-то будут, суть та же.
Учение о рефлексах самое лучше среди этого всего. Но рефлексы это именно кирпичики.
Бихевиоризм тоже несостоятелен. Всё это прошлый век, в общем. Нужно учиться рассматривать системы целиком, наблюдать за взаимодействием всех их частей, а не выцеплять одну какую-то и провозглашать её причиной всех вещей. И не нужно проводить вообще никак не обоснованные аналогии между фактами из одной области знания и совершенно другой, ну хотя если долго занимаешься чем-то, то один хер невольно начинаешь смотреть на вещи через призму того, чем занимаешься, занимаешься механикой организм превращается в механизм, программированием мозг в компьютер, у любителей машоба нейроны начинают экстремумы функций искать, а у любителей теории хаоса сознание это аттрактор ну и всё в таком духе.
> не нужно
А почему не нужно? Ну потому что такие теории очень отвлекают человечество, дают ложный след, они моментально захватывают умы, люди бросаются их развивать, находят кучу подтверждений, игнорируя мелкие несоответствия действительности, фурор, бум, хайп, ну а потом постепенно несоответствия копятся, развитие теории тормозится, пока совсем не остановится и не станет понятно, что это тупик, многие ещё по инерции пытаются что-то сделать, веря, что это временные трудности, но в конечном счёте всё равно усилия ничего не дают. Так было с бихевиоризмом в психологии, сейчас вот нейросети(ИИ же, ну почти, ну надо только больше мощности, ну чуть-чуть ещё и ИИ) и тд. В итоге максимум этого "ИИ" лица знаменитостей к порноактрисам пририсовывать, да и то коряво, ну и всякие мелкие функции выполнять, где частые ошибки не критичны.
>>45415
В чем несостоятельность и прошлый век бихевиоризма? Только он и работает. Всё остальное это фантазии о том, что мозг это компьютер или квантовый телевизор, замена "удовольствие" на "дофамин" в науч-попе, поиск извращений у человека, фантазии философов сознания о суперсуперсуперспартанцах и прочие странные вещи.
Есть мнение, что достаточно продвинутый демагог может все что угодно обозвать редукционизмом.
>В чем несостоятельность и прошлый век бихевиоризма?
Гугли cognitive revolution, правда тут говно победило мочу, по сути одна форма редукционизма сменилась другой, раньше сводили к рефлексам, теперь к информации и вычислениям, ну то, что выше писал. Это та же хуйня, только вид сбоку.
>>45424
Ну, достаточно продвинутый демагог может что угодно обозвать чем угодно и никто не заметит подвоха, что с того?
Ну, решай задачи.
>Нужно учиться рассматривать системы целиком, наблюдать за взаимодействием всех их частей, а не выцеплять одну какую-то и провозглашать её причиной всех вещей.
Двачую. Именно это я называю пониманием, о котором спришваетсяв ОП-посте. Т. е. понимание это когда человеку ЛЕГКО найти ответ на любой о вопрос о моделе/системе/задаче, и он может рассказать этот ответ с разным степенем абстракции. Например: дана матрица преобразования плоскости, человек ЛЕГКО ответит на вопросы типа: а какое ей соответсвует комплексное число? А кватернион если плоскость в пространстве? А нарисовать? А во что это преобразование переводит данную функцию? А на сфере Римана что будет ? и т. д. чем больше механических, статистических интерпртаций данной матрицы человек знает и чем больше ответов верно даёт тем выше его понимание, это такой блиц-опрос, но не обязательно в уме и не на время. Про степень абстракции: мне интуитивно ясно, что преобразование 1/z переводит в прямую в непрерывную функцию,ну кроме точки 0, но почему это так я не знаю, принимаю это как данность, могу по уравнению прямой найти в какую прямую или окружность она перейдёт, но это не совсем ответ на вопроспочему функция останется непрерывной. Чем меньше в ответах человека таких интуитвных моментов и больше раскладывания до самых простых аксиом(если была дана установка максимально подробно рассказывать) тем выше его понимание. Нужно "свободно ходить" по структуре.
Блять, для сколь угодно простой структуры найдется вопрос, на который не то что конкретный математик не сможет ЛЕГКО дать ответ, а вообще ни один математик не сможет дать ответ вообще никак, как и тысячи уже пытавшихся.
Определенно в этом есть смысл, грамотно написал. Только как это внедрить в учёбе помимо очевидного "добавим/изменим/удалим аксиому и бежим доказывать пятый постулат Эвклида"?
Сдаётся мне, что никак. Ну кроме индивидуального подхода к каждому ученику, то есть выбирается одарённый ученик и лет десять-пятнадцать обучается у учителя, перенимает интуицию. Как у ситхов, короче. А на поток поставить никак.
Не тупо же зубрить всю математику до конца. Определенно должен быть путь.
Я когда писал 2 момента имел ввиду: чтобы обязательено была интерпретация из практической области(механика,статистика, визаулизация и т. п.); чтобы человек не символами мыслил а семантикой.
1. В начальной школе все учатся норм(кроме тех кому совсем пофиг) Почему так ? Потому что легко просто ? Нет. Потому что сначала на яблоках а уже потом на числах. Даже задачи в началке типа "было то-то отняли стало столько", а чем дальше тем больше просто "решите уравнение". Многие люди рили не понимают что решение по действиям как в началке и решение линейного уравнения это одно и тоже. Отсюда простейший вариант изменений в учёбе это сначала ставить задачу реального мира, а потом показывать как её можно формализовать в символах(числах). Греки строят сарай, нужна его площадь - квадратые уравнения; Физикам нужно силу обозначить - вектор; площадь параллелограмма-матрица, ну для матриц нужно подумать с чего начать лучше. А как сейчас учат ? Сначала зазубривают форму на математике, потом показывают приложение в физике и ты либо опять зубришь эти соответствия либо натягивашь физику на математику по крупицам решая задачи с частными случаями. Зубрёшка подводит ко второй проблеме.
2. Мышление символами или по прецеденту. Это когда чедовек зазубрил что так можно а вот так нельзя, а объяснить почему не может. Как в анекдоте: под пределом выражение с цифрой 8 равен он инфинити, блондинке дали такой же где вместо 8 цифра 5, она написала равно цифре 5 повёрнутой набок. Если человек поймёт что символы запоминать на самом деле сложнее чем семантику(потому что их тупо больше и запоминаются они зубрёшкой, а не озарением, без эмоций) он уже впредь сам будет нормально себя контролировать. Если у детей триггернулось "зачем так усложнять простые вещи", думаю, спасёт просто пример расчёта в учебнике - без новой абстракции на 1 лист, и с ней на треть листа(писать меньше, никто не любит писать). Можно ещё реформировать нотацию. Тут где-то тред на доске, где степень и логарифм треугольником обозначают, ИМХО, очень хорошая затея.
>>46352
Подумаю над этим постом ещё.
Я когда писал 2 момента имел ввиду: чтобы обязательено была интерпретация из практической области(механика,статистика, визаулизация и т. п.); чтобы человек не символами мыслил а семантикой.
1. В начальной школе все учатся норм(кроме тех кому совсем пофиг) Почему так ? Потому что легко просто ? Нет. Потому что сначала на яблоках а уже потом на числах. Даже задачи в началке типа "было то-то отняли стало столько", а чем дальше тем больше просто "решите уравнение". Многие люди рили не понимают что решение по действиям как в началке и решение линейного уравнения это одно и тоже. Отсюда простейший вариант изменений в учёбе это сначала ставить задачу реального мира, а потом показывать как её можно формализовать в символах(числах). Греки строят сарай, нужна его площадь - квадратые уравнения; Физикам нужно силу обозначить - вектор; площадь параллелограмма-матрица, ну для матриц нужно подумать с чего начать лучше. А как сейчас учат ? Сначала зазубривают форму на математике, потом показывают приложение в физике и ты либо опять зубришь эти соответствия либо натягивашь физику на математику по крупицам решая задачи с частными случаями. Зубрёшка подводит ко второй проблеме.
2. Мышление символами или по прецеденту. Это когда чедовек зазубрил что так можно а вот так нельзя, а объяснить почему не может. Как в анекдоте: под пределом выражение с цифрой 8 равен он инфинити, блондинке дали такой же где вместо 8 цифра 5, она написала равно цифре 5 повёрнутой набок. Если человек поймёт что символы запоминать на самом деле сложнее чем семантику(потому что их тупо больше и запоминаются они зубрёшкой, а не озарением, без эмоций) он уже впредь сам будет нормально себя контролировать. Если у детей триггернулось "зачем так усложнять простые вещи", думаю, спасёт просто пример расчёта в учебнике - без новой абстракции на 1 лист, и с ней на треть листа(писать меньше, никто не любит писать). Можно ещё реформировать нотацию. Тут где-то тред на доске, где степень и логарифм треугольником обозначают, ИМХО, очень хорошая затея.
>>46352
Подумаю над этим постом ещё.
Че? Я вот не знаю чего так.
Это хорошо для детей, но черевато для математиков. Сперва человек начнёт задавать вопросы из разряда "а как представить четырёхмерное пространство", потом будет пытаться нарисовать множество Витали, и в итоге ёбнется наглухо при подготовке к экзамену по топологии. Иногда придётся выключать воображалку и переставлять буковки по правилам, как бы это ни было неприятно.
> а как представить четырёхмерное пространство
Представляем n-мерное пространство и задаем n=4
А что надо?
Да, но при этом некоторые люди всё равно получают прозрение когда узнают, что можно не переносить (по аналогии с весами), а добавлять/отнимать с двух сторон как в Америке записывают.
>А что надо?
Смотря кому и по какому предмету. В школе - яблоки и немножко буковки. В вузе в первую очередь буковки, а если есть приложения или можно нарисовать - то рисовать и показывать приложения. Но обязательно сопровождать это буковками.
Есть ещё такой вопрос: что сперва излагать - мотивировку или формальное определение. Но это уже очень зависит от студентов и того, через какую призму им удобнее мыслить. Либо это "а как бы мне строго смоделировать такое-то явление", либо "а на что похож этот набор буковок".
Чтобы ими потом пользоваться, зная, что они верные. А чем одно на другое похоже, по-твоему?
Не согласен с тем, что это самое важное (в контексте вопроса).
>>46772
Несколько причин. Предположу, что ты в математике не силён, поэтому для тебя самая релевантная - научиться обращаться с объектом, привыкнуть к нему и к тому, что с ним можно делать; увидеть, как используются предыдущие теоремы.
Полезно подходить к теоремама следующим образом. Сначала предположить, почему утверждение вообще должно быть верно - на пальцах/интуитивном уровне (не всегда работает по началу). Потом подумать, а как вообще можно доказать. Потом пробежать доказательство и составить его план, опуская технические детали - спустить его до интуитивного уровня. Потом подумать, почему твоё доказательство не сработало бы. Ну и проделать все шаги самому.
Это одна из причин, но я её выделил исходя из собственного опыта обучения и преподавания.
>в контексте вопроса
Мда. Я почему-то сразу подумал, что это философский наброс в духе "мотемотика не ноука, кому нужны ваши пустопорожние перелевания из одних терминов в другие". Каюсь, твой вариант разумнее.
>Полезно подходить к теоремама следующим образом. Сначала предположить, почему утверждение вообще должно быть верно - на пальцах/интуитивном уровне (не всегда работает по началу). Потом подумать, а как вообще можно доказать. Потом пробежать доказательство и составить его план, опуская технические детали - спустить его до интуитивного уровня. Потом подумать, почему твоё доказательство не сработало бы. Ну и проделать все шаги самому
Ой как двачую.
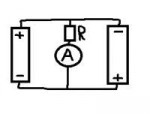 3 Кб, 312x238
3 Кб, 312x238Человек на видео скорее балуется, чем "меняет точку зрения", но в конце он высказывает очень хорошую мысль про эмаптию. В конце поста вернусь к этому.
Я сам далёк от математики моё понимание слова "понимание" калибровалось на предмете схемотехники и разделах школной физики связанной с электричеством, хотя с ними я тоже не связан. Взгляните на пикрил. Вам только что впервые объяснили как течёт ток и показали схему с 1 батарейкой и ампером, теперь вам показывают что будет с током если подключить вторую батарейку как на пикрил - он уменьшится. Вопрос а что с электронами ? Они бегут по двум циклам, т. е. через амперметр идёт два потока электронов в разные стороны или 1 замедленный ? У человека ищущего понимания ДОЛЖЕН возникнуть этот вопрос на автомате. А дальше два варианта один интуитивно не задумываясь найдёт ответ - таких я зовуталантами, остальные должны будут пройти калибровку понмания, котораятребует времени. Это значит что онилибо должны решить задачу на проверку обоих гипотез, не важно в числах или практическую задачу построения схемы для измерения. Отсюда я сделал вывод такой: понимание не передаётся от человека к человеку, оно либо создаётся сразу, либо калибруется(долго, мучительно). Задачи - инструмент калибровки. Они отсекают возможные гипотезы по одной за раз(это важно), но тут есть и опасность в виде мышления по прецеденту - ошибка второго рода в понимании. Два потока электроном или один медленный - изначально не однозначно, требует проверки. Когда таких неоднозначностей не останется - возникло понимание. Выходит нужен полный перебор неоднозначностей и решение по одной задаче убирающей на каждую из них по одной. Но это не так, иногда задача всё же может однозначно разрешить сразу несколько неоднозначностей. Здесь задачи в смысле пример, не важно будет учащийся сам решать или ему дадут как готовое. И теперь о мысли из видео про эмпатию. Человек точно обладает пониманием когда способен сходу придумать для объясения некоторой темы минимальную серию задач(примеров) однозначно разрешающую все ноднозначности в теме, т. е. калибрующую понимание у тех кто изучает в первые эту тему, т. е. создать эмпатию, о которой говорится в видосе.
Почему я топлю за схемотехнику: с одной стороны схемы состоят из отдельно описанных функциональных элементов(транзистор, диод, каскад усилка), с другой - изменение параметров схемы в одном месте(сопротивления, напряжения, ёмкости) приводит к изменению параметров во всех частях схемы(если не были предприняты меры защиты от этого). Это ведёт к тому, что когда вы изучили ряд элементов(они все хорошо описаны графиками и формулами и словесно как они внутри устроены физически/химически) и вам показали схему приборчика из них у вас ДОЛЖНЫ возникать вопросы типа: а точно ли i-ый функциональнй элемент поведёт во всех кейсах работы приборчика поведёт себя так как предполагается ? Ответ на этот вопрос приведёт вас к том, то я писал тут: >>46089
>Чем меньше в ответах человека таких интуитвных моментов и больше раскладывания до самых простых аксиом(если была дана установка максимально подробно рассказывать) тем выше его понимание. Нужно "свободно ходить" по структуре.
Свободно ходить значит заглядывать на уровень абстракции работы каждого функционального элемента в схеме и наглядно словесно описывать что всё будет нормально работать как задумано.
Мне пока сложно придумать примеры из математики, но я ещё подумаю.
 3 Кб, 312x238
3 Кб, 312x238Человек на видео скорее балуется, чем "меняет точку зрения", но в конце он высказывает очень хорошую мысль про эмаптию. В конце поста вернусь к этому.
Я сам далёк от математики моё понимание слова "понимание" калибровалось на предмете схемотехники и разделах школной физики связанной с электричеством, хотя с ними я тоже не связан. Взгляните на пикрил. Вам только что впервые объяснили как течёт ток и показали схему с 1 батарейкой и ампером, теперь вам показывают что будет с током если подключить вторую батарейку как на пикрил - он уменьшится. Вопрос а что с электронами ? Они бегут по двум циклам, т. е. через амперметр идёт два потока электронов в разные стороны или 1 замедленный ? У человека ищущего понимания ДОЛЖЕН возникнуть этот вопрос на автомате. А дальше два варианта один интуитивно не задумываясь найдёт ответ - таких я зовуталантами, остальные должны будут пройти калибровку понмания, котораятребует времени. Это значит что онилибо должны решить задачу на проверку обоих гипотез, не важно в числах или практическую задачу построения схемы для измерения. Отсюда я сделал вывод такой: понимание не передаётся от человека к человеку, оно либо создаётся сразу, либо калибруется(долго, мучительно). Задачи - инструмент калибровки. Они отсекают возможные гипотезы по одной за раз(это важно), но тут есть и опасность в виде мышления по прецеденту - ошибка второго рода в понимании. Два потока электроном или один медленный - изначально не однозначно, требует проверки. Когда таких неоднозначностей не останется - возникло понимание. Выходит нужен полный перебор неоднозначностей и решение по одной задаче убирающей на каждую из них по одной. Но это не так, иногда задача всё же может однозначно разрешить сразу несколько неоднозначностей. Здесь задачи в смысле пример, не важно будет учащийся сам решать или ему дадут как готовое. И теперь о мысли из видео про эмпатию. Человек точно обладает пониманием когда способен сходу придумать для объясения некоторой темы минимальную серию задач(примеров) однозначно разрешающую все ноднозначности в теме, т. е. калибрующую понимание у тех кто изучает в первые эту тему, т. е. создать эмпатию, о которой говорится в видосе.
Почему я топлю за схемотехнику: с одной стороны схемы состоят из отдельно описанных функциональных элементов(транзистор, диод, каскад усилка), с другой - изменение параметров схемы в одном месте(сопротивления, напряжения, ёмкости) приводит к изменению параметров во всех частях схемы(если не были предприняты меры защиты от этого). Это ведёт к тому, что когда вы изучили ряд элементов(они все хорошо описаны графиками и формулами и словесно как они внутри устроены физически/химически) и вам показали схему приборчика из них у вас ДОЛЖНЫ возникать вопросы типа: а точно ли i-ый функциональнй элемент поведёт во всех кейсах работы приборчика поведёт себя так как предполагается ? Ответ на этот вопрос приведёт вас к том, то я писал тут: >>46089
>Чем меньше в ответах человека таких интуитвных моментов и больше раскладывания до самых простых аксиом(если была дана установка максимально подробно рассказывать) тем выше его понимание. Нужно "свободно ходить" по структуре.
Свободно ходить значит заглядывать на уровень абстракции работы каждого функционального элемента в схеме и наглядно словесно описывать что всё будет нормально работать как задумано.
Мне пока сложно придумать примеры из математики, но я ещё подумаю.
https://youtu.be/uiSIqSuDms8?t=1301
https://youtu.be/uiSIqSuDms8?t=1140
Дискасс.
Что-то я не особо понял эти видео. Как-то печально этот доктор психологических наук говорит.
С другой стороны выше в треде было упоминание о книге с наблюдениями математиков о своем мышлении >>45135 >>45136
Ж. Адамар «Исследования психологии изобретения в области математики». Да и другое.
Что, собственно, обсуждать?
Красавчик.
Ээее, зашквар же.
Какие типы математического мышления существуют?
Математика — царица наук, пожалуй, самая точная и въедливая наука из всех, которые есть в распоряжении у человечества. Но и здесь не всё так просто, как кажется, ученые-психологи пришли к интересному выводу. В общей структуре мышления, по предложению И. Я. Каплуновича, можно выделить пять пересекающихся подструктур — типов математического мышления. Доминирующий тип и определяет мыслительную деятельность человека в разных практических случаях.
Топологическое мышление. Этот тип появляется у человека в самую первую очередь, примерно в 2−3 года. Он отвечает за целостность и связанность логических операций. Они склонны проделывать постоянные преобразования с объектом. В подходе к делу доминируют такие принципы: непрерывно или разорвано, внутри или снаружи, целое или части. Люди-топологи не любят действовать наобум и с бухты-барахты. Им необходимо всегда начать действие с начала, ухватить нить следствия, не пропуская ни одной детали, скрупулезно, не торопясь, довести до конечного результата. В жизни топологи очень аккуратны, живут размеренно, по определенному циклу. Нередко они очень консервативны, плохо привыкают к новшествам. Их основной недостаток: редкая дотошность и медлительность.
Порядковое мышление. Формируется в мозгу почти сразу же после топологического и отвечает за точное следование логических операций. «Порядковцам», в отличие от топологов, не важно объединение операций в одно целое; они любят строгий линейный порядок, от начального к конечному. В деятельности им важна форма и размер объектов (больше или меньше), их соотношение (правее, левее, выше, ниже), направление движения (по или против, вверх или вниз). Люди с таким типом мышления стремятся чётко следовать порядку, в любых действиях стараются выработать алгоритм, который зависит от какого-то одного объективного принципа. В повседневной жизни абсолютные порядковцы педантичны, редко отступают от общепринятых правил и всегда чётко следуют инструкциям.
Метрическое мышление. Эта структура руководствует в человеке количественными запросами. Метристы в деле считают самым главным точное математическое значение — цифры, цифры и ещё раз цифры. Всегда и во всем они пытаются сводить к конкретным величинам и постоянно оперируют такими параметрами как ширина, высота, дальность, цена, количество, время и т. д. Метристы не любят образность и общность — им сложно представить какую-то абстрактную величину, не выраженную определённостью; они всегда ясно представляют себе, что выйдет в результате работы, сколько придётся затратить, и сколько от этого получишь. Такие люди осторожны и предусмотрительны, неизвестность пугает их — пока человек не выяснит досконально все подробности и нюансы — действовать не начнёт.
Алгебраическое мышление. Люди с доминирующим мышлением этого типа — прирождённые комбинаторы и конструкторы. Они постоянно стремятся к представлению объекта через структурное восприятие. То есть, постоянно разбирают и собирают предмет, пытаются выстроить из частей разные комбинации. К решению каких-либо задач подходят с хаотическим настроем — начинают с того места, которое им нравится, потом перескакивают куда-то в середину, минуя промежуточные этапы, и заново возвращаются в начало, предварительно исследовав часть, которая должна завершать процесс. Таких людей сложно заставить делать что-то по правилам и в рамках. В жизни они чаще всего рассеянны, часто опаздывают, склонны упрощать ситуацию. Они видят предмет одновременно и целиком и каждую его часть, что позволяет им быстро находить единственно нужное в данной ситуации.
Проективное мышление. Самое сложное из всех пяти. Тот, у кого преобладает структура данного типа, склонен рассматривать предмет с разных точек зрения, под разными углами. Его интересуют все варианты применения предмета в теории и на практике. Такой человек мыслит нестандартно, удивляет окружающих многовариантностью решений, казалось бы, банальной проблемы. «Проективист» стремиться найти оптимальное применение любого явления, его волнует не характеристики, а степень применяемости и полезности. В жизни эти люди обладают неординарным интеллектом, любят везде и во всем искать выгоду, это отличные идейные лидеры, которые могут мгновенно оценивать ситуацию и поворачивать её в нужное русло. Самый большой недостаток проективистов в том, что, рассматривая предмет как не статичную структуру, они забывают об абсолютных характеристиках и значительных подробностях.
Разумеется, в каждом человеке присутствуют в разных количествах все эти типы мышления. Кстати, у большинства людей порядковое мышление является главным, доминантным — всё это объясняется тем, что обучение в школе все 10 лет проходит по этой системе. Доминант определяет многие аспекты мыслительной и, соответственно, практической деятельности. Причём не только на поприще математики. Даже по тому, как человек пропалывает грядки, расставляет предметы в комнате, одевается, можно вычленить информацию о преобладающей структуре, хотя существует множество простых тестов, которые позволяют это определить. Например, достаточно попросить человека описать свою комнату. Метрист начнёт перечислять количество стульев, габариты комнаты; топограф будет перечислять по группам, сначала про стулья, кресла, диваны, и уже потом про магнитофон, компьютер, телефон; алгебраист просто выльет на бумагу все свои мысли, в любом порядке, перескакивая с места на место; порядковец особое внимание уделит расположению предметов относительно друг друга, их формам и размерам; а у проективиста получится самая большая по объёму работа — он постарается расписать применение наиболее важных вещей его квартиры.
Учёные выяснили, что люди с одинаковыми типами мышления сами тянутся друг к другу, так как им бывает сложно понять «математически других» людей. Следите за собой и развивайте в себе все виды мышления! Всего хорошего!
Какие типы математического мышления существуют?
Математика — царица наук, пожалуй, самая точная и въедливая наука из всех, которые есть в распоряжении у человечества. Но и здесь не всё так просто, как кажется, ученые-психологи пришли к интересному выводу. В общей структуре мышления, по предложению И. Я. Каплуновича, можно выделить пять пересекающихся подструктур — типов математического мышления. Доминирующий тип и определяет мыслительную деятельность человека в разных практических случаях.
Топологическое мышление. Этот тип появляется у человека в самую первую очередь, примерно в 2−3 года. Он отвечает за целостность и связанность логических операций. Они склонны проделывать постоянные преобразования с объектом. В подходе к делу доминируют такие принципы: непрерывно или разорвано, внутри или снаружи, целое или части. Люди-топологи не любят действовать наобум и с бухты-барахты. Им необходимо всегда начать действие с начала, ухватить нить следствия, не пропуская ни одной детали, скрупулезно, не торопясь, довести до конечного результата. В жизни топологи очень аккуратны, живут размеренно, по определенному циклу. Нередко они очень консервативны, плохо привыкают к новшествам. Их основной недостаток: редкая дотошность и медлительность.
Порядковое мышление. Формируется в мозгу почти сразу же после топологического и отвечает за точное следование логических операций. «Порядковцам», в отличие от топологов, не важно объединение операций в одно целое; они любят строгий линейный порядок, от начального к конечному. В деятельности им важна форма и размер объектов (больше или меньше), их соотношение (правее, левее, выше, ниже), направление движения (по или против, вверх или вниз). Люди с таким типом мышления стремятся чётко следовать порядку, в любых действиях стараются выработать алгоритм, который зависит от какого-то одного объективного принципа. В повседневной жизни абсолютные порядковцы педантичны, редко отступают от общепринятых правил и всегда чётко следуют инструкциям.
Метрическое мышление. Эта структура руководствует в человеке количественными запросами. Метристы в деле считают самым главным точное математическое значение — цифры, цифры и ещё раз цифры. Всегда и во всем они пытаются сводить к конкретным величинам и постоянно оперируют такими параметрами как ширина, высота, дальность, цена, количество, время и т. д. Метристы не любят образность и общность — им сложно представить какую-то абстрактную величину, не выраженную определённостью; они всегда ясно представляют себе, что выйдет в результате работы, сколько придётся затратить, и сколько от этого получишь. Такие люди осторожны и предусмотрительны, неизвестность пугает их — пока человек не выяснит досконально все подробности и нюансы — действовать не начнёт.
Алгебраическое мышление. Люди с доминирующим мышлением этого типа — прирождённые комбинаторы и конструкторы. Они постоянно стремятся к представлению объекта через структурное восприятие. То есть, постоянно разбирают и собирают предмет, пытаются выстроить из частей разные комбинации. К решению каких-либо задач подходят с хаотическим настроем — начинают с того места, которое им нравится, потом перескакивают куда-то в середину, минуя промежуточные этапы, и заново возвращаются в начало, предварительно исследовав часть, которая должна завершать процесс. Таких людей сложно заставить делать что-то по правилам и в рамках. В жизни они чаще всего рассеянны, часто опаздывают, склонны упрощать ситуацию. Они видят предмет одновременно и целиком и каждую его часть, что позволяет им быстро находить единственно нужное в данной ситуации.
Проективное мышление. Самое сложное из всех пяти. Тот, у кого преобладает структура данного типа, склонен рассматривать предмет с разных точек зрения, под разными углами. Его интересуют все варианты применения предмета в теории и на практике. Такой человек мыслит нестандартно, удивляет окружающих многовариантностью решений, казалось бы, банальной проблемы. «Проективист» стремиться найти оптимальное применение любого явления, его волнует не характеристики, а степень применяемости и полезности. В жизни эти люди обладают неординарным интеллектом, любят везде и во всем искать выгоду, это отличные идейные лидеры, которые могут мгновенно оценивать ситуацию и поворачивать её в нужное русло. Самый большой недостаток проективистов в том, что, рассматривая предмет как не статичную структуру, они забывают об абсолютных характеристиках и значительных подробностях.
Разумеется, в каждом человеке присутствуют в разных количествах все эти типы мышления. Кстати, у большинства людей порядковое мышление является главным, доминантным — всё это объясняется тем, что обучение в школе все 10 лет проходит по этой системе. Доминант определяет многие аспекты мыслительной и, соответственно, практической деятельности. Причём не только на поприще математики. Даже по тому, как человек пропалывает грядки, расставляет предметы в комнате, одевается, можно вычленить информацию о преобладающей структуре, хотя существует множество простых тестов, которые позволяют это определить. Например, достаточно попросить человека описать свою комнату. Метрист начнёт перечислять количество стульев, габариты комнаты; топограф будет перечислять по группам, сначала про стулья, кресла, диваны, и уже потом про магнитофон, компьютер, телефон; алгебраист просто выльет на бумагу все свои мысли, в любом порядке, перескакивая с места на место; порядковец особое внимание уделит расположению предметов относительно друг друга, их формам и размерам; а у проективиста получится самая большая по объёму работа — он постарается расписать применение наиболее важных вещей его квартиры.
Учёные выяснили, что люди с одинаковыми типами мышления сами тянутся друг к другу, так как им бывает сложно понять «математически других» людей. Следите за собой и развивайте в себе все виды мышления! Всего хорошего!
[...]
Еще один интересный пример профанации педагогики специалистами-математиками. Пример, неожиданно приоткрывший одну поистине "тайну" Киселевских книг. Лет десять назад присутствовал я на лекции крупного нашего математика. Лекция посвящалась школьной математике. В конце задал лектору вопрос, — как он относится к учебникам Киселева? Ответ: "Учебники хорошие, но они устарели". Ответ банален, но интересно было продолжение, — в качестве примера лектор нарисовал Киселевский чертеж к признаку параллельности двух плоскостей. На этом чертеже плоскости резко изгибались для того, чтобы пересечься. И я подумал: "Действительно, какой нелепый чертеж! Нарисовано то, чего быть не может!" И вдруг отчетливо вспомнил подлинный чертеж и даже его положение на странице (внизу-слева) в учебнике, по которому учился почти сорок лет назад. И почувствовал связанное с чертежем ощущение мускульного напряжения, — будто пытаюсь насильственно соединить две непересекающиеся плоскости. Сама-собой возникла из памяти четкая формулировка: "Если две пересекающиеся прямые "одной плоскости параллельны -..", а вслед за ней и все короткое доказательство "от противного".
Я был потрясен. Оказывается, Киселев запечатлел в моем сознании этот осмысленный математический факт навечно (!).
[...]
Собственно как удалось запомнить именно таким образом, что оно впечаталось в память? В чем особенность такого запоминания или даже понимания, которое
[...]
Замечательный Воронежский математик Ю. В. Покорный, "болеющий школой", установил, что методическая архитектура учебников Киселева наиболее согласована с психолого-генетическими законами и формами развития юного интеллекта (Пиаже-Выготский), восходящими к Аристотелевой "лестнице форм души". "Там (в учебнике геометрии Киселева — И.К.), если кто помнит, изначально изложение нацелено на сенсо-моторное мышление (наложим, т.к. отрезки или углы равны, другой конец или другая сторона совпадают и т.д.).
Затем отработанные схемы действий, обеспечивающие начальную (по Выготскому и Пиаже) геометрическую интуицию, комбинациями приводят к возможности догадок (инсайту, ага-переживанию). При этом наращивается аргументация в форме силлогизмов. Аксиомы появляются лишь в конце планиметрии, после чего возможны более строгие дедуктивные рассуждения. Не зря в когдатошние времена именно геометрия по Киселеву прививала школьникам навыки формально-логических рассуждений. И делала это достаточно успешно" .
Вот где еще одна тайна чудесной педагогический силы Киселева! Он не только психологически правильно подает каждую тему, но строит свои учебники (от младших классов к старшим) и выбирает методы соответственно возрастным формам мышления и возможностям понимания детей, неторопливо и основательно развивая их. Высший уровень педагогического мышления, недоступный современным дипломированным методистам и преуспевающим авторам учебников.
[...]
?
[...]
Еще один интересный пример профанации педагогики специалистами-математиками. Пример, неожиданно приоткрывший одну поистине "тайну" Киселевских книг. Лет десять назад присутствовал я на лекции крупного нашего математика. Лекция посвящалась школьной математике. В конце задал лектору вопрос, — как он относится к учебникам Киселева? Ответ: "Учебники хорошие, но они устарели". Ответ банален, но интересно было продолжение, — в качестве примера лектор нарисовал Киселевский чертеж к признаку параллельности двух плоскостей. На этом чертеже плоскости резко изгибались для того, чтобы пересечься. И я подумал: "Действительно, какой нелепый чертеж! Нарисовано то, чего быть не может!" И вдруг отчетливо вспомнил подлинный чертеж и даже его положение на странице (внизу-слева) в учебнике, по которому учился почти сорок лет назад. И почувствовал связанное с чертежем ощущение мускульного напряжения, — будто пытаюсь насильственно соединить две непересекающиеся плоскости. Сама-собой возникла из памяти четкая формулировка: "Если две пересекающиеся прямые "одной плоскости параллельны -..", а вслед за ней и все короткое доказательство "от противного".
Я был потрясен. Оказывается, Киселев запечатлел в моем сознании этот осмысленный математический факт навечно (!).
[...]
Собственно как удалось запомнить именно таким образом, что оно впечаталось в память? В чем особенность такого запоминания или даже понимания, которое
[...]
Замечательный Воронежский математик Ю. В. Покорный, "болеющий школой", установил, что методическая архитектура учебников Киселева наиболее согласована с психолого-генетическими законами и формами развития юного интеллекта (Пиаже-Выготский), восходящими к Аристотелевой "лестнице форм души". "Там (в учебнике геометрии Киселева — И.К.), если кто помнит, изначально изложение нацелено на сенсо-моторное мышление (наложим, т.к. отрезки или углы равны, другой конец или другая сторона совпадают и т.д.).
Затем отработанные схемы действий, обеспечивающие начальную (по Выготскому и Пиаже) геометрическую интуицию, комбинациями приводят к возможности догадок (инсайту, ага-переживанию). При этом наращивается аргументация в форме силлогизмов. Аксиомы появляются лишь в конце планиметрии, после чего возможны более строгие дедуктивные рассуждения. Не зря в когдатошние времена именно геометрия по Киселеву прививала школьникам навыки формально-логических рассуждений. И делала это достаточно успешно" .
Вот где еще одна тайна чудесной педагогический силы Киселева! Он не только психологически правильно подает каждую тему, но строит свои учебники (от младших классов к старшим) и выбирает методы соответственно возрастным формам мышления и возможностям понимания детей, неторопливо и основательно развивая их. Высший уровень педагогического мышления, недоступный современным дипломированным методистам и преуспевающим авторам учебников.
[...]
?
>>47602
Как по мне всякие такие статейки про околоматематическое мышление и всё в таком духе ебучий графоманский кал, а обсуждение этого ещё больший кал. Задачи надо решать, теоремы доказывать, а не хуйнёй заниматься, хуй дрочить на то как бы найти эффективную методику обучения или там проходить ололотесты "какой ты маняматик?" или что там, классифицировать себя по шкале какого-то психолуха, для которого топология, алгебра и тд просто умные слова. Говно, крайне недоволен, раньше лучше было, такой хуйни не было на доске.
>Это определение напечатано жирным шрифтом, значит, для обязательного заучивания
>психолого-генетическими законами и формами развития юного интеллекта (Пиаже-Выготский), восходящими к Аристотелевой "лестнице форм души".
>Киселев, возвращенный "социалистическим" детям, мгновенно поднял качество знаний и оздоровил их психику. И, может быть, помог одержать победу в Великой войне.
Будешь за две копейки вычислять интегралы в своём НИИ пока прогресивные люди становятся новыми Рамануджанами и изобретают ИИ размышляя об основаниях математики.
>вычислять интегралы в своём НИИ
Чини детектор.
>Рамануджан
>ИИ
Ясно, понятно, очередной научпопный хайпожор. Особенно смешон Рамануджан мистер "яскозал", за которого другие люди всё доказывали в одном предложении с основаниями.
>люди становятся новыми Рамануджанами
Стать новой реинкарнацией Эйлера чтобы переизобрести аналитическое продолжение, но не суметь сформулировать в виде содержательной теории, только баловаться различными нелепыми преобразованиями чтобы все математики считали тебя шизиком? Охуенно.
Ну раз математики считают...
>как бы найти эффективную методику обучения
Это стоит того, зря ты так.
>проходить ололотесты "какой ты маняматик?" или что там, классифицировать себя по шкале какого-то психолуха
Это параша, солидарен полностью.
>Это стоит того, зря ты так.
Но не вместо собственно обучения. Хотя имхо никакой общей методики нет и не может быть, а индивидуальную ты сам для себя выработаешь так или иначе.
Собственное обучение и разработка методик (сиречь педагогика, обучение других) - это задачи из разных плоскостей.
Что ты хочешь обсудить?
Какую только гуманитарную чушь не принесут, иногда кажется, что гуманитарии ничего ясно не видят, в всё в полутьме ощупывают, обнюхивают, да в анал засовывают.
Мимо алгебраист, метящий в проективисты
Я не могу просто прочитать определение, прочитать свойства, прочитать формулы, и врубиться. Как только до задачи доходит, все эти знания существуют словно в разных манямирках, формулы и определения в своём, а задача - в своём, и эти два манямирка не пересекаются. Зато если я сам "изобрету", то мне сразу всё понятно что к чему.
А какое же истинное?
Ни в каком, нужно владеть теорией, тогда задачи будут решаться считай автоматически в твоей голове. Для этого теорию и учат, так-то с нуля можно весь матан заново придумать, но зачем, если умные люди за тебя это уже сделали? Твоя задача - правильно всосать эту теорию так, чтобы она могла приносить тебе профит, например, в решении задач.
Задача зачастую сама в себе маленькая теория. Ты должен соединить теорию задачи, с теорией, которую изучил. Так ты придёшь к решению.
>Ни в каком, нужно владеть теорией, тогда задачи будут решаться считай автоматически в твоей голове.
Интересная теория. Немного отходит от тупого дроча на задачки до упаду превалирующего в текущем образовательным дискурсе. Меня как человека которого этот задачкодроч просто доебал это не может не радовать.
>например, в решении задач
Надеюсь тут ты имеешь в виду реальные задачи возникающие в жизни (ну конечно у каждого это может быть своя очень необычная "жизнь"), а не решение говен из учебников как самоцель.
мимопроходил
>до упаду превалирующего в текущем образовательным дискурсе
Школьники считаются слишком тупыми для теории, да и не заинтересованы в ней. У технарей слишком мало часов математики и опять же нет интереса, а им нужно в короткие сроки научиться решать некоторое количество типовых задач. Отсюда и дроч.
>реальные задачи возникающие в жизни
Реальные задачи, возникающие у тебя в голове.
Потому что для решений задач "из жизни" нужно в основном не умение решать математические задачи, а умение их ставить в соответствии с задачами "жизненными", то есть строить математические модели. Да и даже это редко, как правило нужно просто двигать тазом и рычать-урчать.
>Уделив 20% времени теории можно решать 80% задач?
Это бессмысленный вопрос. 20% и 80% от чего? Если ты в сумме занимался один час, то ты не прорешаешь 80% Демидовича, сколько бы процентов ни уделял теории.
Если у тебя круг задач довольно узкий, то напирать на теорию в принципе неэффективно, так как это очень трудоёмкое дело. Теория пригодится либо если ты мастер на все руки и должен уметь решать любую задачу, либо если ты сам составляешь техзадания, переводя с языка заказчика на человеческий и определяя, что возможно сделать, что невозможно и что было бы лучше сделать.
Тогда к чему ты это написал? В чём тогда проявляется теория и практика? А может никакой теории не существует?
Не получается решать их хоть убей. На что в первую очередь нужно обращать внимание?
На сколько я понял, в дифференциальных все время выполняется замена - в этом у меня сильный пробел, так как я просто навсего не понимаю что заменять. Единственное, что извлек из этой темы, так это замена y' = dy/dx, дальше иксы в одну, игорей в другую и у нас получаются два красивых интеграла. Но как только я пытаюсь применять эту процедуру на практике, у меня получается не замена, а хуйня какая-то. Понимаю, что это применяется только в однородных уравнениях, вроде как. В остальных - не ясно.
Смотрю решения задач - голова взрывается: почему заменили это, почему другое не заменяли...
В общем, реквестирую годную методику решения несложных диффуров. По типу:
(x^2 - 1)y' + 2xy^2 = 0.
y' = y/cos^2 5x.
y'' = 1/(sin^2)5x + 6.
Короче, можете кидаться в меня говном, я попробую поймать.
Если эти примеры не можешь решить, значит, неопределенные интегралы брать не умеешь. С них и надо начинать. Там видно будет, что в этой жизни, а что в следующей.
 828 Кб, 700x543
828 Кб, 700x543Традиционная история курса светского обучения в средние века. Уже в эпоху поздней античности они объединялись в группу. Они отделялись, с одной стороны, от философии — «матери» всех их, а с другой — от технических (или механических) искусств, таких, как архитектура и земледелие, которые были сферой деятельности ремесленника или работника физического труда.
Свободные искусства делились на две группы:
trivium (лат. — тривий) — учебный цикл из трех словесных наук (грамматика, логика (или диалектика) и риторика) и quadrivium (лат. — квадривий) — учебный цикл из четырех математических наук (геометрия, арифметика, астрономия и музыка).
Риторику обычно символизирует Цицерон;
Логику — Аристотель (который может держать экземпляр своей «Этики», как это изображено на фреске Рафаэля «Афинская школа»;
Грамматику — либо Присциан, грамматик императорского двора в Константинополе (нач. VI в.), либо Донат (IV в.), чей трактат «Ars Grammatica» (лат. — «Искусство грамматики» стал основой средневековой грамматики;
Геометрию — Евклид, держащий циркуль;
Арифметику — Пифагор, который может также служить олицетворением Музыки, как указание на ее математические основы (Музыка иногда представлена Тувалкаином, потомком Каина, которого средневековая традиция считала изобретателем музыки и который держит музыкальный инструмент);
Астрономию — александрийский астроном Птолемей (которого нередко путают с представителями египетских царских династий, носивших то же имя, и который по этой причине может изображаться с короной на голове).
https://alindomik.livejournal.com/5475715.html
Реквестирую таблицу по распорядку решения Демидовича.
Под "грамматикой" в средние века понималось изучение классической латыни. Её можно заменить или дополнить изучением санскрита.
Логику по Аристотелю учить не стоит, он придавал слишком большое значение силлогизмам, не смотря на то что в математике, например, силлогизмы практически не используются. Аристотель впрочем не весь плох, "Метафизика" к примеру достаточно интересная, особенно четвертая книга:
http://classics.mit.edu/Aristotle/metaphysics.html
Геометрию лучше начать изучать с Introduction to smooth manifolds Джона Ли.
Двачую, меня в дурке так и обучали.
>Геометрию лучше начать изучать с Introduction to smooth manifolds Джона Ли.
до сих пор не верю, что без классического дифгема (например в листочках у скопенкова) возможно в это вкатиться. Как никак, геометрическая интуиция должна быть.
Как тебе классический дифгеом поможет предоставить что такое, скажем, перенос Ли? Нужно просто попыхтеть над определениями, поделать упражнения. Может, почитать ещё книжек, например геометрические методы Шутца, или того же Ли, но первую книжку про топологические многообразия, или твои "листочки" - это, считай, Fecko (не помню названия).
> не смотря на то что в математике, например, силлогизмы практически не используются
А как же Эвклид? Да и разве не выросло всё из силлогистики?
>скопенков
Это который Аркадий Борисович? До сих пор из-за него уже 18 лет спустя после выпуска из сунца случаются вьетнамские флешбеки в холодном поту по ночам.
ну я только в нму его слушал и не сдавал ничего, а книжки вроде норм пишет
Ебали жестко.
Больные фантазии уровня РЕН ТВ или реально существующий метод?
https://maxpark.com/community/603/content/2499632
первое
 5 Кб, 225x224
5 Кб, 225x224ТРЕД НЕ ЧИТАЙ - СРАЗУ ОТВЕЧАЙ
Где-то на пятом посте началась какая-то шиза. Вы из гуманитарки вылезли, чтобы демагогию разводить или че.
ПЕРВАЯ ПРОБЛЕМА
Барьер между естественным языком и математикой.
Объяснения в терминах недостаточно, если человек с ними незнаком, а зачастую авторы книг по вышмату любят писать книги, содержащие только формулы без какого-либо объяснения или численного примера, что не позволяет читателю провести аналогию между искусственным языком и реальными концептами.
Это подводит нас ко
ВТОРОЙ ПРОБЛЕМЕ
Язык математики содержится сам в себе и интерпретируется человеком. Это явление опять же затрудняет познание в силу невозможности найти возможную ошибку в тексте, если читатель уже не обладает соответствующими знаниями, сама мысль такого парадоксальна.
ТРЕТЬЯ ПРОБЛЕМА
Искусственный язык математики не поддается проверкам с помощью интерактивных систем( исключение пруверы ) и соответственно нельзя методом проб и ошибок придти к пониманию предмета, ведь любая проверка проводится читателем и соответственно не несет большой пользы.
КАК ЭТО РЕШИТЬ
Включить программирование в список требуемых знаний для математика, в конце концов, ЭВМ построена на принципах математики. Чего стоит математик, который не может объяснить шайтан-машине как вычислить предел?
Оптимизировать процесс получения знаний. Не у всех есть роскошь учится в престижных вузах. В отличии от научпокства это означает не только поверхностное объяснение на пальцах, но и дальнейшее введение в изучаемый материал.
Создание атмосферы заинтересованности в получении знаний, будь то создание форумов, рассылочных листов или любого другого централизованного способа распространения информации.
>Барьер между естественным языком и математикой.
Шиз, иди нахуй. Ты сначала учебник математики осиль, прежде чем пиздеть о том, что язык тебе говна в жопу залил и мешает тебе изучать математику.
Ты сам открывал чето сложнее таблицы умножения?
Если да, возьми хоть определение предела. Этот набор дурацких букв ниче не дает. Чтоб понять что это, нужно разобрать кучу примеров
точка A называется пределом последовательности x_n, если в каждой открытой окрестности точки A содержатся все члены последовательности x_n с номерами, начиная с некоторого. что непонятно? ни одной буквы нет, кроме тех, что входят в определение
 3 Кб, 311x111
3 Кб, 311x111Вот стандартное определение предела без окрестности. Чтобы в него въехать надо потратить как минимум больше времени чем на твое определение словами
это не стандартное определение, а говно, которое тупо кодирует настоящее определение, которое я выписал (к тому же лишь частный его случай, когда вместо произвольного топологического пространства рассматривается убогое R)
Не стоит настаивать на своём невежестве, производя из него какие-то теории. Пучок на воротничок получается
Ты видимо совсем тупой, раз не понимаешь, что в этом треде обсуждают методики изучения математики, а не выбирают лучшее определение предела.
То, что я скинул - есть стандартное определение, которое изучают во всех вузах
В нормальных вузах, дают два определения, топологическое и это. И доказывают(а что оставляют как тривиальное утверждение) их эквивалентность.
Из-за таких дебилов все и в жопе, когда профессор пишет определения в чистых терминах, которые сам уже воспринимает как данное, а потом удивляется почему студентики, кроме как отзеркалить учебник нихуя не могут.
Сейчас задавать вопрос ответу 2-х летней давности.
> пару минут
> 20 единиц символьной информации, каждый из которых имеет под собой пласт теории, взаимоотношения между которыми не определены
> нет контекста
Простоблядок, пошёл нахуй. Из-за таких как ты ракеты падают.
От темы уходишь, петушок.
я точно не знаю, но подозреваю, что большинство современных людей по факту глупее шумеров
По-моему, верить в то, что древние люди (представители древних цивилизаций) априори были тупее современных, — это само по себе тупость. Как минимум, они были такими же
Удвою этого, древние РУССЫ так вообще были на порядок умнее современных, считали правильно, сложение и умножение не путали.
>Методик изучения математики тред
> Зачем зубрить
Чтобы "не нмытём так катаньем" запомнить то, что само не всосалось, но при этом имеет значимость даже без понимания. Понимание может прийти в процессе зубрёжки или позже, когда в мозгу уложатся все необходимые для сбора паззла кусочки и пройдёт соответствующая работа по их объединению. А чтобы собрать пазл необходим чтобы соответствующие кусочки были в наличии и доступны все, а иногда одновременно. Если память их не держит то либо процесс освоения и анализа будет проходить последовательно и несистематично, опираясь на внешнее запоминающее устройсто либо о возможности понимания вообще речь не идёт. Как нельзя понять смысл предложения, забывая слова сразу после прочтения/услышания
> таблицу умножения
Именно таблицу умножения стоит вызубрить лишь для того, чтобы не запинаться на таких мелочах при решении более сложных, продвинутых и интересных задач, чем само по себе умножение двух однозначных чисел. Чтобы сэкономить самый ценный ресурс - время, целенаправленно уделив его заранее и сконцентрировавшись на этой задаче. Иначе в дальнейшем будет потрачено намного больше усилий, внимания и времени на возвращение к этому вопросу и изобретение велосипеда каждый раз заново. В любом случае отдельные фрагменты в памяти осядут, но привычка "не помнить и перевычислять заново" во-первых, по сути та же зубрёжка, только менее осмысленная, во-вторых, частое переключение контекста и отвлечение от основной задачи негативно сказывается на общем ходе решения и возможности концептуализации.
Вообще, зубрёжка это механическое повторение, протаптывание нейронных путей "грубой силой", как делает та же ебучая реклама. К ней прибегают от нетренированности ума, недостатка концентрации. Когда мышление сдаётся или даже не пытается в силу привычки. тогда действует лишь дрессировка.
> и как правильно считать?
Тут нет царских путей в смысле методики. Есть разные способы и методики, их все придумали люди, потому что они так видели, им было так удобно и понятно, это их ход и форма рассуждения. Всё это в той или иной мере костыли для тех, кто не может просто получить результат непосредственно. Так же как мнемоники дая памяти или слова для мыслей. Если имеется в виду корректность вычислений, то проверять себя. Для этого можно делать одно и то же действие разными способами, либо использовать специальный способ проверки вроде контрольной суммы, который достаточно прост и прозрачен, чтобы быть уверенным в корректности результата.
> Как сформировать и развить "математическое чутьё"?
Чутьё, интуиция - это опыт помноженный на эвристику, работающую без непосредственного сознательного контроля самого процесса.
Опыт набирается примерами (не только в смысле примеры задач для решения, а знакомство с экземплярами объектов различных классов и их отношениями). Эвристика включает все доступные человеку инструменты мышления и навык их комбинации для решения конкретных задач. Это и концепции и алгоритмы. В общем, это собственно всё и есть. Так же как для самосознания необходима нейронная сеть достаточного объёма и сложности для образования соответствующей структуры, так и для чутья.
В этом и состоит суть изучения не только математики - узнавать новые пути понимания и ходить по этим путям, чтобы это понимание закрепилось на уровне смысловых ощущений.
> Сколько и каких задач надо решать для понимания?
Столько сколько денег нужно на покупку еды.
> Что значит понимать математику?
Вопрос неоднозначно определён. Если как действие - то понимать=познавать. Если "математика" в том же смысле что "логика" в словосочетании "логика вещей", то есть математика чего-то, некого объекта, то "понимать математику" чего-то - значит знать (или познавать - см. пред. предл.), понимать концепцию устройства и действия этого объекта в рамках заданного уровня абстракции.
> Нужны ли сложные задачи
да
> и науч-поп
да
> по математике
да
> или это развлекательный контент?
Или! Таки снова да!
Задачи нужны всякие, всевозможных степеней сложности. Простые - для наглядности и мотивации к обучению, отдыха от сложных. Сложные нужны чтобы прощупать границы и расширять их, чтобы дать мозгу причину к размышлению. То что не сложно совсем становится неинтересно и автоматично.
> Как сформировать мотивацию к математике?
Дать возможность получать от неё удовольствие.
> Почему уровень математических познаний падает?
В среднем? Потому что незачем, да и не только математических. Есть же сами знаете кто, у которого все всё в интернете спрашивают. Получается как в вказке "а вы что, и есть за меня будете? ага". Но не у всех же.
> Нужно ли возвращаться с старым учебникам?
Сама по себе старость ничего не говорит. Изучать их нужно, но не ученикам, а учителям, как культурное наследие, и использовать по своему усмотрению. Необходимо иметь разные типы учебной литературы. Каждый думает по-своему. Кто-то с удовольствием читает справочник в алфавитном порядке или сухое изложение теории и всё у него укладывается, сами рисуются примеры и выстраиваются связи, а другому нужно пошагово, от практики к концептуализации, по мере применимости новой порции материала, а третьему сразу нужно показать общую структуру, схему, а затем разбирать вглубь, спускаясь всё глубже, пока не выберешься из кроличьей норы абстракций в мир привычных конкретных вещей.
> Как вообще можно обучать математике,
С удовольствием можно, с любовью.
> какая тут связь с условными рефлексами
Прямая и обратная.
> и основаниями математики?
Основания реагируют с кислотами.
> Как написать экзамен по математике, если ничего не понимаешь?
Но зачем, есть ли в этом смысл?
Если кажется, что ничего не понимаешь сейчас в математике и есть желание научиться понимать то учиться, всего-навсего, честно и добросовестно.
Если действительно ничего не понимаешь вообще, то это вопрос медицинский. Тут, как гриться, "не до жиру, быть бы живу".
> Как производственными масштабами выпускать математиков
И кто ентих производственников буить в их масштабах кормить, а, масляков?
Если математиков не в смысле профессии, а в смысле оснащать всех и каждого радостью мышления и навыкам применения математического аппарата, то это вопрос реформации общественного сознания. Человечество (можно и в узком смысле, локальное такое человечество, народ, страна, город хотя бы или поселение, короче самовоспроизводящаяся единица обладающая достаточными ресурсами и автономией для целенаправленного назначения и реализации курса общественного развития) должно прийти к соответствующему миропониманию в массе своей.
> Можно ли используя измененные состояния сознания (речь не идёт о лихорадке) и современные представления стать как Сриниваса Рамануджан Айенгор?
Сознание постоянно меняет своё состояние, но некоторые более-менее устойчивы и нам знакомы.
Если речь о веществах, то нет, нельзя. Насыпав металлические опилки в системный блок и встряхивая его можно добиться разных интересных эффектов, но надеяться проапгрейдить таким образом комп глупо.
Подытожу:
Чтобы пройти путь, надо по нему идти, шаг за шагом. Кто делает тот и научается, кто ест, тот и насыщается. (Да-да,услышат имеющие уши, обрящут ищущие, отворят стучащим, без труда из пруда...)
Сухая теория как чай без воды.
Теория и практика, запоминание и осмысление - это как инь и янь, не существующие друг без друга. Как две ноги, которыми далеко не уйдёшь -оодиночке. В зависимости от развитости ног (мышления), привычки, местности (изучаемого материала) или случайных обстоятельств можно идти прямо, криво, боком, с прискоком. Но если одна нога останется на месте, то далеко не уйдёшь, в лучшем случае будешь топтаться по кругу на месте. Также и ноги крепнут в процессе. Дорогу осилит идущий.
Чутьё это неосознанное понимание, которое формируется и развивается как напрямую через непосредственный опыт, так и через осознание.
Как речь не является мышлением, так язык математики не является математикой. При этом, языковые средства выражения мыслей и смыслов выполняют роль не только коммуникации между людьми, но и с самим собой, как вспомогательное средство мышления и организации памяти как внутренней так и внешней.
>Методик изучения математики тред
> Зачем зубрить
Чтобы "не нмытём так катаньем" запомнить то, что само не всосалось, но при этом имеет значимость даже без понимания. Понимание может прийти в процессе зубрёжки или позже, когда в мозгу уложатся все необходимые для сбора паззла кусочки и пройдёт соответствующая работа по их объединению. А чтобы собрать пазл необходим чтобы соответствующие кусочки были в наличии и доступны все, а иногда одновременно. Если память их не держит то либо процесс освоения и анализа будет проходить последовательно и несистематично, опираясь на внешнее запоминающее устройсто либо о возможности понимания вообще речь не идёт. Как нельзя понять смысл предложения, забывая слова сразу после прочтения/услышания
> таблицу умножения
Именно таблицу умножения стоит вызубрить лишь для того, чтобы не запинаться на таких мелочах при решении более сложных, продвинутых и интересных задач, чем само по себе умножение двух однозначных чисел. Чтобы сэкономить самый ценный ресурс - время, целенаправленно уделив его заранее и сконцентрировавшись на этой задаче. Иначе в дальнейшем будет потрачено намного больше усилий, внимания и времени на возвращение к этому вопросу и изобретение велосипеда каждый раз заново. В любом случае отдельные фрагменты в памяти осядут, но привычка "не помнить и перевычислять заново" во-первых, по сути та же зубрёжка, только менее осмысленная, во-вторых, частое переключение контекста и отвлечение от основной задачи негативно сказывается на общем ходе решения и возможности концептуализации.
Вообще, зубрёжка это механическое повторение, протаптывание нейронных путей "грубой силой", как делает та же ебучая реклама. К ней прибегают от нетренированности ума, недостатка концентрации. Когда мышление сдаётся или даже не пытается в силу привычки. тогда действует лишь дрессировка.
> и как правильно считать?
Тут нет царских путей в смысле методики. Есть разные способы и методики, их все придумали люди, потому что они так видели, им было так удобно и понятно, это их ход и форма рассуждения. Всё это в той или иной мере костыли для тех, кто не может просто получить результат непосредственно. Так же как мнемоники дая памяти или слова для мыслей. Если имеется в виду корректность вычислений, то проверять себя. Для этого можно делать одно и то же действие разными способами, либо использовать специальный способ проверки вроде контрольной суммы, который достаточно прост и прозрачен, чтобы быть уверенным в корректности результата.
> Как сформировать и развить "математическое чутьё"?
Чутьё, интуиция - это опыт помноженный на эвристику, работающую без непосредственного сознательного контроля самого процесса.
Опыт набирается примерами (не только в смысле примеры задач для решения, а знакомство с экземплярами объектов различных классов и их отношениями). Эвристика включает все доступные человеку инструменты мышления и навык их комбинации для решения конкретных задач. Это и концепции и алгоритмы. В общем, это собственно всё и есть. Так же как для самосознания необходима нейронная сеть достаточного объёма и сложности для образования соответствующей структуры, так и для чутья.
В этом и состоит суть изучения не только математики - узнавать новые пути понимания и ходить по этим путям, чтобы это понимание закрепилось на уровне смысловых ощущений.
> Сколько и каких задач надо решать для понимания?
Столько сколько денег нужно на покупку еды.
> Что значит понимать математику?
Вопрос неоднозначно определён. Если как действие - то понимать=познавать. Если "математика" в том же смысле что "логика" в словосочетании "логика вещей", то есть математика чего-то, некого объекта, то "понимать математику" чего-то - значит знать (или познавать - см. пред. предл.), понимать концепцию устройства и действия этого объекта в рамках заданного уровня абстракции.
> Нужны ли сложные задачи
да
> и науч-поп
да
> по математике
да
> или это развлекательный контент?
Или! Таки снова да!
Задачи нужны всякие, всевозможных степеней сложности. Простые - для наглядности и мотивации к обучению, отдыха от сложных. Сложные нужны чтобы прощупать границы и расширять их, чтобы дать мозгу причину к размышлению. То что не сложно совсем становится неинтересно и автоматично.
> Как сформировать мотивацию к математике?
Дать возможность получать от неё удовольствие.
> Почему уровень математических познаний падает?
В среднем? Потому что незачем, да и не только математических. Есть же сами знаете кто, у которого все всё в интернете спрашивают. Получается как в вказке "а вы что, и есть за меня будете? ага". Но не у всех же.
> Нужно ли возвращаться с старым учебникам?
Сама по себе старость ничего не говорит. Изучать их нужно, но не ученикам, а учителям, как культурное наследие, и использовать по своему усмотрению. Необходимо иметь разные типы учебной литературы. Каждый думает по-своему. Кто-то с удовольствием читает справочник в алфавитном порядке или сухое изложение теории и всё у него укладывается, сами рисуются примеры и выстраиваются связи, а другому нужно пошагово, от практики к концептуализации, по мере применимости новой порции материала, а третьему сразу нужно показать общую структуру, схему, а затем разбирать вглубь, спускаясь всё глубже, пока не выберешься из кроличьей норы абстракций в мир привычных конкретных вещей.
> Как вообще можно обучать математике,
С удовольствием можно, с любовью.
> какая тут связь с условными рефлексами
Прямая и обратная.
> и основаниями математики?
Основания реагируют с кислотами.
> Как написать экзамен по математике, если ничего не понимаешь?
Но зачем, есть ли в этом смысл?
Если кажется, что ничего не понимаешь сейчас в математике и есть желание научиться понимать то учиться, всего-навсего, честно и добросовестно.
Если действительно ничего не понимаешь вообще, то это вопрос медицинский. Тут, как гриться, "не до жиру, быть бы живу".
> Как производственными масштабами выпускать математиков
И кто ентих производственников буить в их масштабах кормить, а, масляков?
Если математиков не в смысле профессии, а в смысле оснащать всех и каждого радостью мышления и навыкам применения математического аппарата, то это вопрос реформации общественного сознания. Человечество (можно и в узком смысле, локальное такое человечество, народ, страна, город хотя бы или поселение, короче самовоспроизводящаяся единица обладающая достаточными ресурсами и автономией для целенаправленного назначения и реализации курса общественного развития) должно прийти к соответствующему миропониманию в массе своей.
> Можно ли используя измененные состояния сознания (речь не идёт о лихорадке) и современные представления стать как Сриниваса Рамануджан Айенгор?
Сознание постоянно меняет своё состояние, но некоторые более-менее устойчивы и нам знакомы.
Если речь о веществах, то нет, нельзя. Насыпав металлические опилки в системный блок и встряхивая его можно добиться разных интересных эффектов, но надеяться проапгрейдить таким образом комп глупо.
Подытожу:
Чтобы пройти путь, надо по нему идти, шаг за шагом. Кто делает тот и научается, кто ест, тот и насыщается. (Да-да,услышат имеющие уши, обрящут ищущие, отворят стучащим, без труда из пруда...)
Сухая теория как чай без воды.
Теория и практика, запоминание и осмысление - это как инь и янь, не существующие друг без друга. Как две ноги, которыми далеко не уйдёшь -оодиночке. В зависимости от развитости ног (мышления), привычки, местности (изучаемого материала) или случайных обстоятельств можно идти прямо, криво, боком, с прискоком. Но если одна нога останется на месте, то далеко не уйдёшь, в лучшем случае будешь топтаться по кругу на месте. Также и ноги крепнут в процессе. Дорогу осилит идущий.
Чутьё это неосознанное понимание, которое формируется и развивается как напрямую через непосредственный опыт, так и через осознание.
Как речь не является мышлением, так язык математики не является математикой. При этом, языковые средства выражения мыслей и смыслов выполняют роль не только коммуникации между людьми, но и с самим собой, как вспомогательное средство мышления и организации памяти как внутренней так и внешней.
Либо в MIT. У них листки получше, и все курсы выложены на сайте (видео, конспект, разборы, библио)
В НМУ больше курсов на сложные темы. В НМУ все на русском (для некоторых это большой плюс). НМУ даёт тебе ту среду, которой нет у самоучки с книгами/конспектами/видеозаписями лекций. Поэтому тут НМУ однозначно лучше. Кстати, насколько я помню, у МИТ не все курсы снабжены задачами, например, курс по геометрии многообразий.
>прорешать
Дежурно напоминаю что когда ты решаешь задачу ты по определению не узнаешь ничего нового. Задачи - пустая трата времени для дауничей.
>ты по определению не узнаешь ничего нового
Твоё определение не учитывает, что механизмы анализа речи и синтеза речи в человеческом мозге разделены (см. центр Вернике и центр Брока). Если читать математические тексты, но не будешь решать задачи, - создавать что-то новое не научишься. Симметрично: обучаясь только по листкам, можно остаться без навыка чтения.
Задачи прокачивают навык синтеза, задачи нужны.
Мелкобуквенная прошмандовка опять вылезла кукарекать. Ты почему экзамены не пошел сдавать, бляденыш? Это же как раз решение твоих любимых задачек. Рассказывать лохам как ты дрочишь на дристочки и задачки это самое лучше что есть в мире. А на экзамены не пойти... как я ОРУ
>>110060
>механизмы анализа речи и синтеза речи в человеческом мозге разделены (см. центр Вернике и центр Брока)
Обоссано-переобоссаная псевдо-теория, потребляй научпокеров посвежее.
https://en.wikipedia.org/wiki/Wernicke%27s_area
https://en.wikipedia.org/wiki/Broca%27s_area
>псевдо
Только по мнению опровергаторов натуральных чисел.
Читать свое говно не пробовал? Например
>Neuroimaging suggests the functions earlier attributed to Wernicke's area occur more broadly in the temporal lobe and indeed happen also in Broca's area.
В любом случае твои охуительные "измышления" на уровне "дофаминового детокса" и прочей паранаучной поебистики.
>>110074
Ты же та ебанашка не осилившая НМУ? Теперь на детях отыгрываешь свою неполноценность, все с тобой понятно. А детей жаль.
>Читать
Процитированное тобой не является даже возражением на обсуждаемый тезис, не то что опровержением. Ну да, в деталях мозг работает не совсем так, как думали пятьдесят лет назад. Но принципы работы уловили правильно.
Ты не сможешь выучиться кон фу без практики, всего лишь прочитав книжку.
>не является даже возражением
Ну если ты дебил без мозгов то не является.
Но для любителей охуительных теорий у меня есть одна своя весьма охуительная. Она состоит в том что задачеблядство это всего на всего такая форма наркомании. Ведь никто не будет спорить с тем что когда ты долго бился над задачей и наконец ее решил бывает испытываешь неземной приход. Вот только что если объективно оценить потраченное время. Наркоман в принципе не способен признаться даже самому себе что тупо бесполезно проебывает время. Он будет всем упорно доказывать что по другому никак нельзя и предлагать дозу самым маленьким.
 15 Кб, 380x450
15 Кб, 380x450MY BRAIN IS OPEN
Наркомрази печет, иди срочно бахни говнозадачку, может попустит.
Потому что ты прав, и они существуют в разных мирках. Между формулами и конкретными задачами существует определённый логический "пробел", который пидорасы-преподаватели, пидорасы-писатели учебников, пидорасы-объяснятели хуйни в интернете НИКОГДА не заполняют. Так что анон, твои мозги работают как надо, и ты ни в чём не ошибся. Действительно, знание теории не означает умения эту теорию грамотно применить.
Думай как матсматмк? Шта?
 773 Кб, 750x563
773 Кб, 750x563вроде Эндрю Уайлс (по крайней мере в известной книге о теореме Ферма это цитируют, и он вроде не оспаривал)
вау, почти 5 лет тебе понадобилось, чтобы его утешить