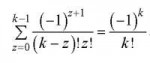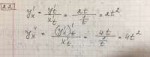226 Кб, 500x619
226 Кб, 500x619Алсо, анализ не нужен.
Пропущу себя через поток Риччи. Мать выкину.
Натуральные числа определив, взялися определять анализ?
Это математики сами оставили этот гниющий /sci с его модератором. Это математики пидорнули из себя /sci, а не наоборот.
Не осилил?
 12 Кб, 575x54
12 Кб, 575x54Вроде на стаке поясняли, но линалом. А тут без линала должна решаться задача, так что нахуй то говнорешение.
Альзо как доказать биноманальную формулу ньютана индукцией без всякой комбинаторики?
Братишка, там вообще не нужна индукция. Можно и так, но, при переходе от бинома к мультиному, ты жидко обосрешься.
Там проще рассуждение. (a+ b)^ n = (a+b)(a+b)...(a+b). Что будет, если попытаться раскрыть все скобки сразу? Сумма мономов вида a^ib^(n-i), осталось найти коэффициент. А сколько будет таких мономов с фикс. степенью? Число сочетаний из n по i, ну ты понел.
Vot Mariya Vyazovskaya nedavno poluchila resultat pro 8 i 24 spheri:
https://www.researchgate.net/profile/Maryna_Viazovska/publication/298738892_The_sphere_packing_problem_in_dimension_8/links/56eaa98008ae95fa33c8340a.pdf
vot eto kak bi analiz. A cohomologii puchkov na diff mnogoobraziyah schitat', eto konechno toje veselo (Eshe veselee daje!), no ne analiz.
 114 Кб, 977x818
114 Кб, 977x818Kaledin, eto ti, suka?
слушь, мудак
x->x+a
y->y+b
x->(x+a)cost+(y+b)sint
y->-(x+a)sint+(y+b)cost
x->k((x+a)cost+(y+b)sint)
y->k(-(x+a)sint+(y+b)cost)
неподвижная точка
x=k((x+a)cost+(y+b)sint)
y=k(-(x+a)sint+(y+b)cost)
x(1-kcost)-yksint=k(acost+bsint)
xksint+y(1-kcost)=k(-sint+bcost)
чтобы решение существовало, детерминант должен быть отличен от нуля
det=(1-kcost)^2+(ksint)^2=1+k^2-2kcost!=0
очевидно что если k>0, найдется t, что det=0
сл., при k<0 всегда есть неподвижная точка
обрати внимание на казенку
У меня так с алгебраической геометрией было. Открыл, а там какие-то цепные комплексы, расслоения, ну и санина же. Закрыл сразу.
Это не так скучно. Любой от бесконечных мантр аля "Найдется такой э > 0, что начиная с некоторого N a_n - a_m < э для любых n, m > N" сойдет нахуй с ума.
Ну это только для извращенцев. Я предпочитаю более традиционную математику, с интегралами и производными. Алгебраическая геометрия - зашквар.
Я надеюсь, что ты не заражен алгебраическим спидом.
1) Почему в учебниках по анализу вводятся аксиомы ТМ, потом аксиомы N, а потом (sic!) аксиомы R, не связывая их между собой, когда по сути после аксиом ТМ остальное теоремы?
2) Почему предполагается, что тупые читатели анализа не знаю азов алгебры, и им надо как дебилам жевать R это линейно упорядоченное нетривиальное архимедово поле, вместо одной этой фразы? Мало того, что R1 это сам по себе просто интересный частный случай, так он еще и расписывается через такой же интересный частный случай алгебры.
3) Зачем давать три разных определения вещественных чисел (опять же, не связывая это с натуральными), доказывать их эквивалентность, а потом рассказывать, что вещественные числа это пополнение рациональных? Разве это все не должно быть в книжке по истории анализа, а не по самому анализу?
4) Зачем давать три разных определения непрерывности вещественных чисел, затем выводить их через друг-друга ("полезное упражнение"), хотя этим свойством уже обладают рациональные числа?
5) На кой нужны именные теоремы, если можно просто писать Коши-Вейерштрасс-Дедекинд-Кантор-Гильберт-Гейне-Больцано-Борель к каждой?
>потом (sic!) аксиомы R,
Что тут не так?
>Почему предполагается, что тупые читатели анализа не знаю азов алгебры, и им надо как дебилам жевать R это линейно упорядоченное нетривиальное архимедово поле, вместо одной этой фразы?
Чтобы читетаель мог в катится в анализ не зная алгебры, идиот. Ещё скажи, что первое что должен учить математи - алгебра.
>Зачем давать три разных определения вещественных чисел (опять же, не связывая это с натуральными), доказывать их эквивалентность, а потом рассказывать, что вещественные числа это пополнение рациональных?
Чтобы у человека сложилось более общее представление о предмете.
>Разве это все не должно быть в книжке по истории анализа, а не по самому анализу?
Нет.
>Зачем давать три разных определения непрерывности вещественных чисел, затем выводить их через друг-друга ("полезное упражнение"), хотя этим свойством уже обладают рациональные числа?
А что ты предлагаешь дать одно для рационального? А потом для действительного?
> На кой нужны именные теоремы, если можно просто писать Коши-Вейерштрасс-Дедекинд-Кантор-Гильберт-Гейне-Больцано-Борель к каждой?
Хуёвая идея. Очень хуёвая.
>Что тут не так?
Пропущены рациональные числа. Даются ничем не обоснованные аксиомы с пометкой: поверь в них.
>Чтобы читетаель мог в катится в анализ не зная алгебры, идиот. Ещё скажи, что первое что должен учить математи - алгебра.
Далеко он без алгебры не уйдет.
>Чтобы у человека сложилось более общее представление о предмете.
Это не ответ. Человеку прежде всего надо знать как работать с действительными числами, а не изучать как их строили динозавры.
>А что ты предлагаешь дать одно для рационального? А потом для действительного?
Доказательство аксиомы? Верность для R при верности для Q это прямое следствие.
>Очень хуевая
Да я зуб даю никто нихуя не помнит, о чем там Кантора-Гейне, Гейне-Бореля, Больцано-Коши и прочие бессмысленные сочетания фамилий, доказывавших какую-то тривиальщину.
>Пропущены рациональные числа. Даются ничем не обоснованные аксиомы с пометкой: поверь в них.
>Доказательство аксиомы? Верность для R при верности для Q это прямое следствие.
Ты обосрался.
https://ru.wikipedia.org/wiki/Непрерывность_множества_действительных_чисел
войство системы действительных чисел R , которым не обладает множество рациональных чисел Q .
Там ниже специально для таких как ты показано, что не хватает рациональным числам для этого. Зато аксиома архимеда ака архимедовость поля определена и там, и там.
Что думаешь по поводу этой - http://bookfi.net/md5/129555D966FD704B63E578B05218BCDE - книжонки?
А там именно Advached Calculus или Real Analysis? Не пойму.
Ещё не пойму, зачем он добавил дифференциальные уравнения. Какой смысл?
Тогда всё ясно.
дифференциальной геометрией и матфизикой.
Иди нахуй, мудак.
это тред о функциональном анализе или о математическом?
 145 Кб, 794x619
145 Кб, 794x619Ну вот есть множество непрерывных функций на [0..1], C([0..1]->R). Это, конечно, кольцо и даже R-алгебра, но это и нечто чуть чуть больше. Ведь если у нас есть функция f \in C([0..1] -> R) мы можем её ограничить и получить функцию f|_(1/3..2/3) \in C( (1/3..2/3) -> R). С другой же стороны, если у нас есть две функции g \in C([0..2/3) -> R) и h \in C((1/3..1] -> R) такие, что они равны на 1/3..2/3 то мы можем их "склеить" и получить функцию f \in C([0..1] -> R).
Вот эти две дополнительные структуры (ограничение у функции области определения и склейка по нескольким функциям одной) и определяют некоторую дополнительную структуру - структуру пучка.
> Почему в учебниках по анализу вводятся аксиомы ТМ, потом аксиомы N, а потом (sic!) аксиомы R, не связывая их между собой, когда по сути после аксиом ТМ остальное теоремы?
Проиграл с алгебраиста. А аксиомы группы у тебя, случайно, не теоремы?
Какой ещё объект? Вот у тебя в учебнике написано, группой называется пара (G,*) с аксиомами такими-то такими-то. Это аксиомы или теоремы?
 6 Кб, 585x323
6 Кб, 585x323Ясно, спасибо. Я так понял пучки позволяют, например, как-то проще говорить о топологии пространств, в частности о непрерывности, переходя от непрерывности на открытых подмножествах к непрерывности на всём пространстве и наоборот? Ну и вообще переносить локальные свойства на всё пространство и глобальные свойства на куски пространства.
Алсо, глупый вопрос: почему использовали слово "пучки"? Потому что если нарисовать, что они делают по сути получится пикрелейтед?
Вообще трудный вопрос. Для теории групп, наверное, аксиомы, а в более сильной теории теоремы.
Да, вроде того.
>Алсо, глупый вопрос: почему использовали слово "пучки"? Потому что если нарисовать, что они делают по сути получится пикрелейтед?
Ну Гротендик вообще любил аграрную терминологию. Если грубо, то значение функции f : R^2 -> R в точке можно представить как росток торчащий из этой точки, а совокупность таких вот ростков связанных как-то между собой - это пучок.
Я высказал своё мнение. Чтобы говорить "разберись с этим трудным вопросом", надо прежде всего пояснить, почему мнение неверно.
Ты пока ничего не высказал. Если это теоремы в более сильной теории, то предъяви эту более сильную теорию и предъяви вывод из аксиом этой теории этих теорем.
Пусть это будет ZFC. Тогда, я полагаю, утверждение о том, что множество является группой не является аксиомой, следовательно является теоремой. Мое сомнение заключается лишь в том, что я не знаю как строго доказать, что утверждения теории групп не эквивалентны аксиомам.
Утверждение о том, что множество с бинарной операцией является моделью для аксиом теории групп является теоремой. Но аксиомы теории групп, всё-таки, остаются аксиомами теории групп.
>Утверждение о том, что множество с бинарной операцией является моделью для аксиом теории групп является теоремой.
Ну вернее даже не теоремой, а одноместным предикатом, так что ты что так что так не прав.
Ну не прав я в этом конкретном факте. При этом общее утверждение, что имхо при преподавании анализа рациональней сначала выводить некую модель чисел, потом доказывать, что она является алгебраической структурой, а затем расширять ее для дальнейший нужд, чем сразу давать в лоб какое-то непонятное поле.
А смысл? Это есть очевидно, что существует одно и лишь одно непрерывно упорядоченное поле. Какая же тут общая ситуация?
>Это есть очевидно, что существует одно и лишь одно непрерывно упорядоченное поле
Очевидно для тебя, но не для читателя учебника, в котором этого факта нет.
Ситуация проста, мы пытаемся строго для читателя уложить понятие числа. После некоторой возни с определением N, мы обнаруживаем полугруппу. Но полугруппы недостаточно для комфортной работы. Тогда мы несложным жестом замыкаем N, чтобы получить кольцо. Но мы не можем делить. Тогда дополняем нашу структуру до поля. И вроде бы все хорошо, но ведь есть вещи вроде корня из двух. Мы исследуем их, приходим к сечениям и непрерывности. И получившаяся структура тоже поле, и теперь у нас есть фундамент для дальнейшей работы. И главное, все наши построения единственны с точности до изоморфизма, и именно это составляем понятие числа, а не какие-то конкретные примеры.
Или же мы доказываем, что R это поле, совершенно непонятными рассуждениями про сложение нулей и прочей казуистикой. Зачем это вообще делать? Какая глубина в таком результате?
А с хуя ли эти рассуждения непонятные? Вот вы дали аксиоматику какого-то объекта(так называемых вещественных чисел), а потом проверяете, существует ли вообще модель, удовлетворяющая вашей аксиоматике. Мы же не философы, чтобы о глубине кукарекать
>эти рассуждения непонятные
Потому что у человека (который хочет узнать про действительные числа) нет алгебраического мышления. Человек на этом этапе знает теорию множеств, получил какие-то топологические термины, а теперь ему дают привычные числа и дают проверять непонятные факты: следствия из аксиом. Как ему понять, что он работает с какой-то там моделью? Он узнает об этом намного позже, когда откроет хороший учебник.
Этот аргумент можно обратить: необходимость дополнения натуральных до целых, перехода к кольцу частных и исследования сечений абсолютно не мотивирована. Зачем нам это делать? У нас и другие дела могут быть. Какова конечная цель?
Тоже этого не особо понимал, вынужден признать.
Выходит, проблема здесь в том, что эти числа для него "привычные". Не думаю, что было бы столько возмущений, если бы пришлось проверять аксиомы не для "привычных нам с детского сада" действительных чисел, а для какой-то более абстрактной(хотя, по-моему, действительные числа-это уже довольно абстрактное понятие) неведомой хуеты, которую ты второй раз за всю жизнь видишь
Почитай этот тред http://mathoverflow.net/questions/14877/how-much-of-differential-geometry-can-be-developed-entirely-without-atlases если коротко, то совсем инвариантного бескоординатного языка для анализа ещё не построили; так что особой разницы нет, что рассматривать локальный пучок, изоморфный пучку гладких функций на R^n, что рассматривать соответствующую карту в атласно-картовом языке. Дмитрий Павлов в комментариях намекнул, что для того, чтобы разница появилась, нужно переосмыслять пониятие многообразия.
Поэтому пока, я бы советовал, учить дифгеом в терминах атласов и карт.
В таком случае придётся понимать функцию f как частично определенную функцию R->R. Законно ли в этом случае делать предельный переход?
Собственно, в этом и был вопрос. Спасибо.
 46 Кб, 500x449
46 Кб, 500x449Видел где-то охуенные гифки с интегралами. Хочу моар таких. Где искать?
Там были поля, в них S потом было наглядно показано в какой плоскости смотреть и как. В общем наглядного матана дайте, пожалуйста.
Функция, непрерывная в любой точке Q.
Это значит, что для любого рационального числа q подмножеством любой окрестности точки f(q) является f-образ некоторого рационального шара с центром в q.
В этом конкретном случае язык последовательностей удобнее (мне кажется). Возьмём x0, возьмём последовательность рациональных q_n, сходящуюся к x0. Теперь нужно показать сходимость f(q_n). То есть что непрерывное отображение переводит фундаментальные последовательности в фундаментальные. Но это же очевидно, isn't it?
И в самом деле. Хотя у нас функция непрерывна во всех рациональных числах, то есть это не какая-нибудь непрерывная вообще, а вот именно конкретная. Вдруг она переводит.
А, ну да, это просто неверно, потому что функция 1/(x-sqrt(2)) непрерывна на Q но не продолжается на R; извини, что запутал.
Вообще, это должно быть так. Это из листочков для НМУ по матану, и я уже нагуглил, что это должно быть частным случаем теоремы Титце-Урысона. Ведь должно же? R - нормальное пространство, правильное?
*правильно?
R - нормальное пространство; к теореме Титце-Урысона это не имеет никакого отношения; автор листочка из НМУ по матану ошибся, так бывает.
Спасибо.
Обращайся еще.
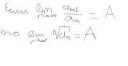 24 Кб, 698x365
24 Кб, 698x365И вот ещё доказать пикрелейтед.
Пожалуйста.
> топ специальность
> программная инженерия
Вуз-то тоже такой же "топовый"? Переводись на мехмат или физфак, чего ты. Гораздо проще и эффективнее учить математику в вузе, а девелопмент самостоятельно, чем наоборот.
чччерт, я опечатался, хотел спросить про непрерывность равностепенную и сходимость равномерную, но я спрашивал зачем они вобще нужны для рассмотрения, а не что проще доказывать
низачем, в природе бывают такие функции, а бывают такие.
полиномы uniformly continuous, а экспонента уже нет, просто непрерывна в каждой точке
а, ну вот например где возникает
uniformly continuous это условие типа "нет такого, что дико быстро растёт в одом месте, а в другом нет", что в каких-то случаях можно понимать как условие чуть послабее интегрируемости (в смысле сходимости несобственных интегралов)
если у тебя функция L_1, то её преобразование Фурье uniformly continuous, хотя может быть и не интегрируемым
терминологию "пучки" придумал не Гротен, а Лерэ (по легенде, когда в концлагере сидел)
Гротен знаменит тем, что придумал их применить к алггему, и родил теорию схем взамен промудохуеблядского формализма Вейля с "универсальной областью".
я плоха владей рускай терминология, сори
это equicontinuous sequence?
тогда полезность более осязаема: это необходимое условие существования предела в sup-норме
Математическая грамотность:
https://www.amazon.com/Mathematical-Proofs-Transition-Advanced-Mathematics/dp/0321797094/
https://www.amazon.com/Naive-Set-Theory-Paul-Halmos/dp/1781394660/
Velleman "How to prove it"
Сам калькулюс:
Зельдович Я.Б., Яглом И.М. "Высшая математика для начинающих физиков и техников"
Зорич "Математический анализ"
https://www.coursera.org/learn/single-variable-calculus
И делай упражнения в книгах. Это очень важно.
не оч же
Пацаны, посоветуйте простого в понимании для Преобразований Лапласа, способы нахождения оригиналов и изображений.
Препод говорит, что курсач должен быть понятен даже школьнику.
Спасибо, я уже всё.
Какой-то там поиск решения уравнений в виде ряда каких-то определённых функций с параметрами какими-то.
Нужно бросить институт. Анализ прочти по Рудину, но не всё. Дальше изучай анализ на многообразиях.
 517 Кб, 2592x1552
517 Кб, 2592x1552как говаривал наш семинарист по математическому анализу: дифференцировать можно научить даже обезьяну.
Открою тебе секрет, любой математик это скорее гуманитарий, чем технарь.
Его интересует семантика понятий, придуманных человеком:
>Humanities are academic disciplines that study aspects of human culture
Заебали со своим "я гуманитарий", а мы тут все кто, тогда?
Гуманитарии изучают человеческую культуру. Математики изучают математику. То есть петь ртом, рисовать, писать стихи- гуманитарищина. Математика же не волнует, как математика относится к человеческой культуре, ему интересна математика само по себе.
А художника волнует, как живопись относится к человеческой культуре?
>Математика же не волнует, как математика относится к человеческой культуре
Особенно это не волновало Арнольда, к примеру
1)производная это предел отношения приращения функции к приращению аргумента.
lim x0->0 (f(x+x0)-f(x))/x0
подставляешь функцию сюда, упрощаешь выражение
2) считаешь производную по формулам. не забывай, про производную композиции:
(f(g(x)))'=f'(g(x))g'(x)
т.е. например (sin(x^2))'=sin(x^2)'(x^2)'=cos(x^2)2x
неочевидны разве что примеры 5 и 6. в 5 надо не забыть, что дифференцируешь по x, в 6 представить выражения как x^(1/x).
3) считаешь производную, а потом снова считаешь производную. неочевидно, что имел в виду препод в третьем примере, учитывая текст задании
Спасибо
Но более всего меня удивил их страх перед "построением фазовых портретов"! Вроде бы, курс динамических систем там должен был организовать Ю.С. Ильяшенко. Я сам когда-то учил УРЧП на семинарах у Ильяшенко, он хорошо знает и объясняет материал, четко проговаривает все скользкие моменты, так неужели, как пишут студенты, есть такие трудности в построении фазовых портретов, что и сами преподы на вопросы только разводят руками? :shock: Мне всегда казалось. что построение фазовых портретов - давно полностью алгоритмизированный раздел качественной теории ОДУ, во всяком случае, ни от кого из студентов мехмата я ни разу не слышал о немыслимой сложности этой задачи, более того, ввиду ее рутинности кафедра дифуров обычно не включает подобную задачу в задачи письменного экзамена в 4-м семестре...
-Brukvalub
Интересно, почему же, скажем, курс анализа Уиттекера и Ватсона считается основополагающим, ведь он тоже состоит, в основном, из вычислительных рецептов и упражнений?
Да и математика - это, прежде всего, наука о вычислениях, приносящих пользу людям. В дифференциальной геометрии, теории чисел, урчп, методах оптимизации, тфкп, вычмате все основано на преобразованиях и вычислениях...
А уж "умников-первокуров", готовых учить профессуру, как и чему тем нужно учить студентов, я такую кучу перевидал... До сих пор вспоминаю, как мне досталась группа, почти целиком сформированная из "второшкольников", ух, и натерпелся же я в боях с теми умниками и умницами! :cry:
Великолепные учебники Куроша, Колмогорова и Фомина, кирпич Александрова, Петровского, Маркушевича, Привалова, Зорича, Шабата, Винберга, Хелемского, Шубина, Филиппова, Алексеева, Тихомирова и Галеева, Ульянова и Дьяченко, Богачева и Смолянова, Ильина, Садовничего и Сендова, Архипова, Садовничего и Чубарикова, Нестеренко, Архангельского, и еще многая и многая возникли именно как результат чтения обязательных курсов на мехмате МГУ.
Более того, именно обязательные семинарские занятия на мехмате породили всемирно известные задачники, такие как:
задачник Демидовича по матану, задачник Филиппова по ОДУ, задачник Проскурякова по линалу, задачник под ред. Кострикина по высшей алгебре, задачник Моденова и Пархоменко по ангему, задачник кафедры ВГТ по ангему и линалу, задачник Тихомирова и Галеева по ОПУ, задачник кафедры ТФФА по действительному анализу, только что в МЦНМО издан задачник коллектива авторов кафедры ТФФА по функану, в 2016-2017 г. в МЦНМО переиздается переработанный энциклопедический трехтомный задачник по мат.анализу Виноградовой, Олехника и Садовничего и еще много чего.
Каким еще математическим факультетом во всяких там Оксвордах-Гарвардах написано такое большое количество великолепных задачников, по которым учатся студенты всего мира?
Так что умерьте свой пыл в охаивании мехмата, и без вас критиков хватает, но караван-то все идет и идет!
Анон, объясни пожалуйста, почему из дифференцируемости функции следует непрерывность функции. Только, молю, не как в википедии, а нормально. Без упрощений вроде "приращение аргумента" и "приращение функции".
С меня что-нибудь.
Если функция дифференцируема, значит в ней в каждой точке существуют пределы справа и слева, и эти пределы имеют одинаковое значение. То есть, все значения функции справа и слева (на малом расстоянии) ничтоже сумлящеся отличаются от значения функции в самой точке.
>значит в ней в каждой точке существуют пределы справа и слева
Почему?
>ничтоже сумлящеся отличаются
Из существования пределов слева и справа и их равенства следует только существование предела. Непрерывность отсюда не следует же.
>Непрерывность отсюда не следует же.
Определение непрерывности знаешь?
>Почему?
прямо следует из определения производной.
Функция непрерывна в точке, если её значение в точке равно её пределу в этой точке. Предел может быть не равен значению.
>прямо следует из определения производной.
Но как? Производная f в точке a - это предел функции f(a+x)/x в нуле. Как отсюда можно вывести непрерывность f в a?
>Предел может быть не равен значению.
В каком случае? Почему такая функция дифференцируема в этой точке?
>Производная f в точке a - это предел функции f(a+x)/x в нуле
чему равна производная x^3 в точках 0, 1, 2, 3 по данной формуле?
>В каком случае?
В принципе. Бывают такие функции.
>чему равна производная
*предел (f(a+x) - f(a))/x в нуле.
((a+x)^3 - a^3)/x = 3a^2 + 3ax + x^2.
Равна соответственно 0, 3, 12, 27.
>*предел (f(a+x) - f(a))/x в нуле.
что эквивалентно f'(x) + o(x)x = (f(a+x) - f(a))/x, где о - б.м.
можно ли из этого вывести условие непрерывности?
>В принципе
Раз уж мы нашли производную, скажи, дифференцируема ли функция, если она имеет производную в данной точке?
Подожди, почему эквивалентно?
o(f) - это такая функция g, что найдется бесконечно малая функция h, что g=hf. Разве нет?
Функция называется дифференцируемой в точке, если у нее есть производная в точке.
>Функция называется дифференцируемой в точке, если у нее есть производная в точке.
Это не правда. Не так дифференцируемость в точке определяется.
>почему эквивалентно
чтобы доказать эквивалентность понятий 1 и 2, надо доказать, что 1 => 2 и 2 => 1. Нетрудно, например, доказать, в случае с пределом, что 2 => 1, просто взяв предел от двух частей. Почему 1 => 2, подумай сам.
>>10414
Функция дифференцируема если имеет производную (производная это отдельное понятие) в точке и наоборот, эти понятия эквивалентны. Производную ты уже определил.
А вот дифференцируемость функции в точке означает, наивно, что ее можно приблизить линейной функции. Т.е. взяв какую-то окрестность, ты можешь заменить функцию на ломаные линии, которые будут точно определять точки функции в такой окрестности.
Более точно, функцию в точке x0 можно представить в виде:
f(x0)+A(dx)+o(dx), где A - некая константа
 42 Кб, 598x700
42 Кб, 598x700Нет. Только двухтомники.
Есть. Называется John Lee.
 188 Кб, 1032x134
188 Кб, 1032x134Ну так разложение показывай.
Второе определение - частный случай первого.
Доказательство - вырвиглазное.
Непонятно что ты там доказываешь. Тебе стоит писать предложения с подлежащими, сказуемыми и дополнениями. Просто формулы - не читаются. Да и сам ты потом ничего не поймёшь.
И да, ты кванторы нормально пиши. Не сокращай так голимо.
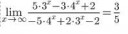 3 Кб, 198x53
3 Кб, 198x53Я понимаю что там у 4^x -3 в числителе и -5 в знаменателе, но такое правило же вроде должно быть если x^4 а не 4^x? там через логарифмы че-то?
помогите плз срочно
Выносишь 4^{x} сверху и снизу и медитируешь до просветления.
lim x->∞ 4^x бесконечно больше lim x->∞ 3^x, хули тут непонятного то?
Приблизительно понимаю это, как С*-алгебру с какой-то доп.структурой - особое произведение, норма, и т.д.
Не знаю ничего про квантовые деформации, но должен заметить, что норма не является доп. структурой на C^*-алгебре
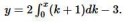 2 Кб, 191x36
2 Кб, 191x36> Найдите медиану упорядоченной выборки первых девяти целых чисел из области значений функции
Что это значит?
Как понимать предел "limΔx→0Δy"? О каких окрестностях, в каких пространствах, с какими элементами тут идёт речь?
Посмотрел у Рудина, похожей символики не увидел. Или я в глаза ебусь?
Помогите разобраться, пожалуйста.
Какие функции? Δx и Δy - разности:
Δx=x-x0
Δy=y(x)-y(x0).
Они стремятся к нулю при увеличении количества вот этих точек, узлов. Мы имеем право писать Δx→0. Мат. анализ - это классическая дисциплина и в ней уже давно всё истоптано вдоль и поперек, не понимаю откуда тебе привиделись функции и почему тебя это смущает.
По определению, число A называется пределом функции f в точке a, если для любой открытой окрестности U точки A найдется такая открытая проколотая окрестность V точки a, что f(V) - подмножество U.
А что значит Δx→0?
По определению, число A называется пределом функции f(x) в точке a, если для любого ε>0 существует такое δ=δ(ε) > 0, что для всех x, для которых |x-a|<δ выполняется неравенство |f(x)-f(a)|< ε
Нет, неправильно, у тебя ошибка. Окрестность точки a должна быть выколотой, т.е. сама точка a не должна в неё входить. А у тебя - входит.
Чтобы не было таких косяков, лучше определять предел с помощью топологических пространств, а не с помощью эпсилон и дельта.
Вот сейчас обидно было. Сам ты поехавший, а у меня нормальный вопрос. Δx и Δy не вписываются в определение предела.
>Я могу дописать, что x неравно a
Зачем? Это определение уже включает в себя возможное отсутствие f(a) (δ>0 а не ≥0)
>Это определение уже включает
блядь я облажался, ничего оно не включает
там |x-a|<δ а должно быть 0<|x-a|<δ
похоже тополог прав
Энивей это не имеет к изначальному вопросу никакого отношения.
ты дэбил? не можешь расписать delta(x)=x-x0 и потом подставить в предел? Слабоумный? Или что с тобой не так?
(Автор этого поста был предупрежден.)
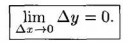 2 Кб, 319x109
2 Кб, 319x109Да. Я знаю, что такое предел. Мне непонятно, что означает символ пикрелейтед. Символ lim определен так, что под ним внизу можно писать только аргумент функции, стоящей справа от lim.
Дельта y - это и есть функция от дельта x:
Δy = f(x0 + Δx) - f(x0), где x0 - это конкретное число. Если ты все еще чувствуешь туман в голове, когда размышляешь об этом, скорее всего ты прорешал недостаточно задач на пределы. Антидемидович в помощь
Дальше будет хуже, чел. Понимаю, что хочется поскорее перейти к чему-то серьезному, но если ты тратишь больше времени на чтение учебника, чем на решение задач на понимае, сосать подано.
Просто помоги понять, что за хрень там написана, пожалуйста. Не надо нести какую-то дичь про антидемидовича.
Δx - не переменная. Под lim можно писать только переменную. Как понимать символ limx-x0 → 0Δy?
Антидемидович -- это сборник задач. Если он тебе не нравится, можешь выбрать, например Виноградову или что-нибудь на английском. Ты же решаешь задачи для закрепления, верно? Мы тебе всем двачем все пояснили так, что уже не представляем, как ты можешь не понять. Мб нормальный препод в вузе умеет справляться с таким непониманием, но мы нет. Поэтому я могу только посоветовать вернутся и начать решать задачи, которые ты пропускал.
Извини, но объяснений не было. С твоей стороны были только советы решать антидемидовича.
>>21863
С чего вдруг? Пусть f - отображение P→Q, где P и Q - топологические пространства. Символ limx→af=A означает "для любой открытой окрестности U точки A найдется такая открытая проколотая окрестность V точки a, что f(V) - подмножество U". Его можно переписать как limBf=A, где B - база проколотых окрестностей точки a. В этом определении x - немая переменная, её можно заменить любой другой буквой.
А как определяется символ limx-x0→0f=A? Как его расписать словами? Как понимать x-x0→0? Это какая-то база, которую Зорич забыл упомянуть?
Ну рассмотрим изначальную Δx->0, для любого эпсиллона больше нуля, существует такая дельта больше нуля, что для любого x такого что 0<|Δx|<дельта следует что |Δy|<эпсиллон. Подставим Δx = x-x0, значит условие 0<|Δx|<дельта перепишется как 0<|x-x0|<дельта, а это и есть тоже самое что предел при x->x0
Это неформальные рассуждения, к ним вопросов нет. Вопрос в том, как записать всё это, пользуясь формальным определением предела. Символ "x→x0" - это просто обозначение базы проколотых окрестностей точки x0, он не несет никакого самостоятельного смысла и может быть заменен любым другим символом, например буквой B. А обозначением какой базы множеств является символ "x-x0→0"? И как строго доказать, что предел по базе B влияет на неё, на эту загадочную базу?
>формальным определением предела
Формальное определение предела как раз и дается через эпсиллон-дельту. Своё базо-дрочерство и прочее оставь при себе или неси к тапалагам.
Ну вот когда ты говоришь "перепишем" и "подставим", где у тебя гарантия, что ничего не изменится? Когда ты переписываешь, ты, по сути, берешь композицию функций и пользуешься тем, что предельный переход перестановочен с непрерывной функцией.
0 = limh→0f(x0+h)-f(x0) = limx-x0→0f(x0+x-x0)-f(x0) = f(limx-x0→0(x0+x-x0))-f(x0) = f(x)-f(x0) - твоё рассуждение.
Ну а с фига ли f непрерывна, если мы как раз пытаемся доказать, что f непрерывна?
>пытаемся доказать
На тех пиках речь идет о определении. Что ты там доказываешь, одному тебе известно.
И да, мочератор - петух.
(Автор этого поста был забанен. Помянем.)
Ты бы хоть прочитал, прежде чем отвечать. На тех пиках даётся два определения и утверждается, что эти определения эквивалентны.
Блин, интересная задача. Скинь контекст что ли, тему.
x,y принадлежащего R*
Хуя ты. Олимпиады по матану?
Это вторая задача с недавно прошедшей межнар олимпиады в Рио. где,
кстати, парашка заняла позорное 11-ое место, при этом 42 балла (max) не набрал никто, какие-то задроты из вьетнама еле-еле наскребли 35. Возможно, это была самая сложная IMO за всю её историю.
Самая сложная была 3-я
обсуждения всех задач есть на artofproblemsolving в специальном топике про IMO
Хотя, погоди. Линейная функция не может удовлетворять решению, у меня есть контрпример. Ты видишь, что я не так делаю?
ты вышел на мета-уровень
а платить не по карману
>невозможность самостоятельного доказательства
Это норма.
Вот если ты еще и считать не умеешь по теории, то это пизда.
Со счетом норм. Все со временем должно прийти?
y''+ (a^2)y = tg(x)
При каких а существует единственное непродолжаемое решение с областью определения (-1;3/2).
Я так понимаю, что раз все функции на этом промежутке непрерывны => мы можем поставить сколько угодно задач Коши и каждая будет решаться. И ответ ни при каких. Мне кажется слишком простое решение, чтобы быть правдой. Да и предыдущая задача решалась точно так же, что меня собственно и настораживает. Все выделенное жирным шрифтом - точное задание, возможно я как-то неправильно понимаю область определения?
А тут могут подсказать по однопараметрической оптимизации?
Не помогайте ему, этот даун отдельный тред для своего листика запилил.
Q замкнуто относительно сложения и умножения(сумма любых рациональных чисел рациональна; произведение любых рациональных чисел рационально)
a+2b=(a+b)+b=r, пусть r - рациональное число, тогда b=r-(a+b) тоже рационально число, что противоречит условию
a-b=(a+b)-2b=r, пусть r - рациональное число, тогда b=((a+b)-r)/2 рационально число, что противоречит условию.
Не могу понять, как это может быть возможно, что для каждого E выполняется |Xn-Xm|<E ? Допустим, E = 6, и есть последовательность, в которой Xn = 40, Xm = 50. |40-50|=10 10>E. И такой эпсилон, меньший, чем разность членов последовательности, я могу подобрать к любой последовательности. Следовательно, ни одна последовательность не является фундаментальной. Вот, в общем-то мои рассуждения, которые, очевидно, не верны. Но я не понимаю, в чем ошибка. Не закидывайте какахами
Фундаментальная последовательность - такая, что для любого r>0 почти все её члены содержатся в каком-нибудь интервале длины r.
Пример фундаментальной последовательности - это 0.1, 0.01, 0.001, ... В ней xn = 10^(-n).
Во-первых, n и m переменные. Ты не можешь написать xn = 40, xm = 50, потому что n и m - это любые натуральные числа, которые больше No. А не какие-то конкретные числа. Впрочем, твою идею можно исправить и сказать, что последовательность 40, 50, 40, 50, 40, 50, ... действительно не будет фундаментальной.
Во-вторых, из того, что некоторые последовательности не являются фундаментальными, не следует, что фундаментальных не бывает вообще. Пример фундаментальной тебе уже привели в посте выше.
 5 Кб, 257x196
5 Кб, 257x196Дело в том, что как мне кажется, матанализ В ПРИНЦИПЕ - это набор каких-то отдельных тем, причем зачастую разрозненных но каким-то хуем переплетающимися в некоторых местах. Мне совершенно непонятно, например, нахуя пихать в один курс диференциальное и интегральное исчисление.
Но ладно, две стороны медали, пусть будет.
Но НАХУЯ ТУДА ПИХАТЬ РЯДЫ?
Это вообще блять какой-то школьный уровень математики.
А теория поля? Каким хуем она делает в матане, если это вообще блять тема алгебры.
Поясните по хардкору почему я неправ и как все-таки организовать этот биомусор, который дают в вузах
>Но НАХУЯ ТУДА ПИХАТЬ РЯДЫ?
Ряды - это те же самые последовательности, вид сбоку. Всякий ряд - некоторая последовательность, и всякая последовательность может быть преобразована в ряд. Нельзя изучать последовательности без рядов. А последовательности - основной инструмент классического анализа, все объекты анализа изучаются через последовательности. Поэтому последовательности нужно изучать.
Чтобы можно было определить, какой элемент в паре первый, а какой второй. Т.к. множество {a,b} = {b, a}, то без хитростей подобных {a,{a,b}}, ты этого не сделаешь.
> это вообще блять тема алгебры
Ну тут есть простое объяснение. Матан - это по большей части алгебра + предельный переход. Вот потому темы и пересекаются. Берешь алгебру, веришь, что если подойти близко-близко, но не до конца, то окажешься прямо там, где надо и получаешь матан.
Почему его изучают до алгебры и до мат. логики или это у меня такой ебанутый вуз попался?
Велкам ту рашка. Везде так.
lim (sin(11x)/sqrt(1-cos(x)), x - 0)
Я понимаю что sin (11x) ~ 11 x , но что делать дальше?
Как мне преобразовать sqrt(1-cos(x))?
Спасибо
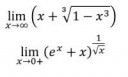 8 Кб, 456x277
8 Кб, 456x2771 / бесконечность = 0
Ага, осталось это грамотно записать.
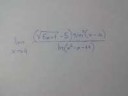 1,7 Мб, 2592x1944
1,7 Мб, 2592x1944Через эквивалентные.
Да что же это за издевательство над людьми такое...
>Хоть кто-нибудь мне скажет где столько матана применяется?
Твой утилитаристский вскукарек тут не нужен.
>что же это за издевательство
Кто виноват, что ты даун, который не может сесть и разобраться в том, что ему непонятно. Ты понимаешь насколько ты дегенеративен? Ты не можещь сесть и разобраться в разделе математики, который оформился к концу 19 века, тебе должно быть стыдно, великовозрастному дылде, который имея при себе весь необъятный интернет, не научился находить информацию, окромя порнухи.
сделай замену x\to x+4 и не еби себя большим дилдаком и по лицу и везде сперма
Пиздец какой онанизм. Почему нельзя просто сказать, что это упорядоченное множество?
В таком случае, нужно будет вводить понятие "натурального множества" и "соответствия"
{a; b, …}
{a} ~ 1
{b} ~ 2
{…} ~ n+1
В общем, семпаи, помогите первокуру-физтеху-будущему-физику(?!) выбрать книгу по матану. Гугл, как и личные опросы, дал чересчур полярные ответы.
Зорич + какой нибудь старый учебник( Фихтенгольц).
Что за ВУЗ? Лучшее, что есть для самосостоятельного чтения - Зорич + Лоран-Шварц.
Мимо: аспирант ПОМИ после питерского говновуза
Если пойдешь в теорию, то после говноучебника (Фихтенгольц, например) придется переучиваться. А это очень больно и долго. Делай так: бери список вопросов на семестр у лектора (по матанализу и потом, по матфизике) и разбирай их самостоятельно по книге. Будет уходить 10-12 часов в неделю, зато потом у тебя не будет проблем с аспирантурой. Терфизику слушай в том объеме, в котором дают - обычно, ее читают те, кто ей непосредственно занимаются, а не эти ушлемпки с кафедр математики во всяких СПбГУ.
*по нормальной книге. Матфизику можно разбирать по Морсу-Фешбаху. +Обязательно к прочтению после первого курса книжка НЯ Виленкина - Теория представлений и Спец. функции (погугли, вроде так). После Морса-Фешбаха нужно будет срочно искать лектора по ОТО, ибо книжек по ОТО нормальных и понятных нет (есть или понятные или нормальные). Возьмешь книжку Вайнберга (ОТО) и, если понравится ее читать - то добро пожаловать в мир теоретической физики (то, что за бугром называется ТФ, не у нас - по сути, та самая Теория струн и вот этот весь наш онанизм). Если не понравилось, то можно идти во всякие Квантовые Оптики и Твердые Тела (что такое твердое тело хорошо поясняет нечитаемая книжка трех японцев - Термополевая Динамика, но ее нужно читать только после курса КТП - 5-6 курсы). На худой конец, если вообще ничто не вкатило, можно за год-полтора переучится на Software Design или Machine Learning и ебашить прогером.
Тебе же еще линейная алгебра нужна. Есть книжка И Гельфанда и курс лекций Постникова.
Любой государственный ВУЗ с бюджетной зачной формой, и учиться самостоятельно. В магистратуру поступить проще все равно, это же не математика.
А в ведущих базовых институтах практику тоже в любом ВУЗе можно проходить? Или тоже по учебникам это изучать, лол?
>практику проходить
Ну это в пед, либо в мед. Не вижу при чем тут физика, тем более теоретическая.
*заочной
Если пройдешь - СПбАУ. Но туда хрен пробьешься. Есть еще НМУ, но это особое заведение, а также, как ни странно, магистратура в Сколково. На худой конец физфак МГУ есть - там не так плохо, как в МФТИ.
А в чем отличие? Препод может двадцати группам по двадцать человек читать свой предмет. Об индивидуальном подходе, указании на ошибки и их исправление речи нет.
Понятность материала зависит от человека, а не от формы подачи. Лучше хорошая книга, чем плохой лектор. А еще бывают случаи когда один и тот же человек пишет интересно, но объяснять в формате лекций совершенно не умеет.
Лектор - в первую очередь человек, которого можно спросить - другие просто быдло и идут в сторону. Лектор, читающий дисциплину, которую он никогда не затрагивал в своих исследованиях идет туда же.
Мне вот интересно, люди которые подобное утверждают, сами были в университетах хоть раз? Ну на дне открытых дверей хотя бы. Я не говорю про твоих одногруппников, которые косо смотрят на любого задающего вопросы.
Большинство преподов, читающих лекции по учебнику, сами это не приветствуют. При чем если ты шибко умный, могут начать открыто гнобить. Даже если сами плохо знают предмет и обсираются – преподу ты априори ничего не докажешь, хоть в книгу тычь, хоть куда.
>Лектор, читающий дисциплину, которую он никогда не затрагивал в своих исследованиях
То есть 99% лекторов.
Ну если ты думаешь что это не про мгу сказано, то спешу огорчить.
"Шарага" кстати это КБ изначально подпольные в ссср. Так что ты еще комплимент сделал.
>знакомцев с физфака и они такой дичи не рассказывали
Я на физфаке не был. Но думаю что они, скорее всего, сами недалекие и соответственно им нормально.
Алсо, сам пример выглядит так z = u^2 - v^2u, где u = xsiny, v = ycosx
 47 Кб, 782x72
47 Кб, 782x7225+15=40
40-12=28
30-28=2 - ответ.
А как будут выглядеть эти диаграммы? Решил по памяти.
 23 Кб, 583x275
23 Кб, 583x275Анон, спасибо. Если оформлять по канонам (с окружностями), то получается будет выглядеть вот так?
 119 Кб, 960x720
119 Кб, 960x720Спасибо, анон.
Есть еще вопрос. Никак не могу найти в интернете вот этот знак (на втором пике детально выделил). В гугле криво выделяется. Может кто-нибудь сюда скинуть?
Лол, вообще все лекции проебал? Это девочки так (некорректно) записывают строчную ёбсилен, греческий аналог буквы Е.
Анон, ты не понял. Мне именно в таком варианте и нужно. Чтобы прописными были. В интернете есть варианты, но почему-то не распознаются.
А так, да, все лекции проебал.
Спасибо, анон.
Не зря в МФТИ сильный уклон в сторону изучения английского, горжусь. Если серьёзно, то на русском выбор литературы гораздо меньше, особенно это касается книг изданных после 1980-х.
На русском лучшая книга по анализу это Глазман-Любич.
Хмм, я открыл все-таки "действительный и комплексный анализ", как оказалось, его-то я и читал... это что значит, я могу к функциональному анализу переходить?..
>>29261
На первом курсе откровенно ноль прогресса, даже близко не интенсив во вшэ.
Что я нашёл от Глазмана-Любича -- в предисловии сказано, что это взгляд на линейную алгебру с точки зрения функана -- где ж здесь анализ? Хотя метод изложения меня впечатлил.
Алсо, что читать по линалу, если эту область охота вдоль и поперёк изучить? Прочитал Беклемишева, думаю о допглавах.
>где ж здесь анализ
А чего именн не хватает? Топология есть, нормированные пространства есть, дифференциальное исчисление для операторов есть, спектральная теория есть. Вряд ли в средней книге по анализу особо больше.
Теории меры нет, но она к анализу вообще никаким боком (анализ строится на банаховых и гильбертовых пространствах, они по определению бесконечномерные).
>взгляд на линейную алгебру с точки зрения функана
Взгляд на X с точки зрения X. Линал от функана отличается тем, что алгебры конечномерные. Всё.
>что читать по линалу
Глазман-Любич.
Ну, в таком случае, вопрос меняется на "какой смысл мне это читать после Рудина и Беклемишева?". Я не спорю, что там есть существенная часть, которой я не знаю, но вместо этого я мог бы прочитать что-то более важное на моём этапе образования.
По поводу линала -- лол, ну это уж перебор. Бо'льшая часть того материала есть в Беклемишеве, однако там нет линейного программирования, например.
>>29425
У Рудина вообще есть три книги. Одна undergraduate, "основы математического анализа", там в целом Фихтенгольц, только короче.
Другая "real and complex analysis". Она по-моему не переведена.
И ещё "функциональный анализ", перевод есть. Первые 2 книги брейнлеты с другой стороны океана именуют как baby rudin и papa rudin соответственно.
Функциональный анализ не требует знания "математического анализа"; "математический анализ" это бессмысленная дисциплина, что-то вроде дискретной математики.
Он состоит из дифференциального и интегрального исчисления. Дифференциальное исчисление это, по существу, часть алгебры (дифференцирование – гомоморфизм модуля, дифференциал – оператор в комплексе де Рама), Картан ещё в 1910-м показал, что дифференциальные формы это элементы алгебры Грассмана, у которых есть геометрический смысл (сечение кокасательного расслоения).
Любой (абсолютно любой) неопределенный интеграл это интеграл от дифференциальной формы. Определяется он чисто алгебраически, как отображение, сопоставляющее внешнему произведению цепи на коцепь – скаляр, то есть элемент \mathbb {R}.
Собственно, это получается из двойственности Пуанкаре. Работает она только для гладких ориентируемых многообразий, соответственно весь "calculus" и происходит там обычно; это раздел дифференциальной геометрии – науки про векторные поля, расслоения и связности.
Определённый интеграл (в многомерном случае, по крайней мере) это совсем другое, там не про решения дифференциальных уравнений, а про меру. Это не анализ, уже говорил выше, скорее раздел общей топологии.
Есть ещё интегралы от функционалов в бесконечномерных пространствах, например Фейнмана Березина, но это уже "суперанализ".
>линейного программирования
Не математика.
>Бо'льшая часть того материала есть в Беклемишеве
Курс аналитической геометрии? Смотрел как-то, по-моему там нихуя нет, но ладно, поверю.
Почти все вменяемые учебники по алгебре на английском, например двухтомник Rowen. Из переведенного ещё хорошее Бурбаки, три тома про алгебру и "топологические векторные пространства".
Примеров много, те же кватернионы это банахова алгебра. Ещё, в отличие от банаховых пространств, алгебры можно строить не только над R или C, но и над Q(p); то есть неархимедов анализ тоже имеется.
Гельфанд применил к нормированным кольцам методы теории представлений, и получил обобщение Фурье-анализа:
https://en.wikipedia.org/wiki/Gelfand_representation
Из литературы очевидные Гельфанд и Наймарк, на русском ещё неплохая книга Пирс "Ассоциативные алгебры".
>Любой (абсолютно любой) неопределенный интеграл это интеграл от дифференциальной формы.
Это частный случай интеграла по мере.
Неопределенный частный случай определенного?
У Рудина гораздо больше чем три книги. Например, он написал "Fourier Analysis on Groups".
Да; еще у него есть "Function Theory in the Unit Ball", например. Я это знаю, но имел в виду стандартный материал.
Ну охуеть теперь. И что это мне дало? Может, тогда скажешь, что вся математика -- разделы теории множеств и стоит изучать только её? Я же должен следовать какой-то программе. Нашёл программу Вербицкого и оценил книжку Шварца. Занимательно, даже готов потратить время на то, чтобы прочитать то, что уже по большей части знаю, однако столкнулся с проблемой -- где упражнения? Брать из Зорича? В списке упоминаются и Зорич, и Шварц, это значит, что они взаимозаменяемы, или что дополняют друг друга? Без упражнений не катит, через месяц забуду, как было с алгоритмами перед всероссом по информатике.
Теория множеств это вообще не математика.
У Зорича во втором томе написано ровно то, что я тебе сказал, но не так хорошо, как в других книнах; менее внятно и с уродскими выкладками.
Гораздо лучше Ботт, Ту Дифференциальные формы в топологии, первая глава. Еще хорошая книга: Федерер Геометрическая теория меры.
>Нашёл программу Вербицкого
Программа отличная, но список книг говно. Сам Вербицкий говорил, что "хороший студент выучится по самой хуевой книге; а плохой не выучится вообще". Он этот материал давно знает и 99% учебников новых или нет, ни разу не открывал, а советует в основном то, по чему выучился сам. Это не обязательно лучшее, чаще всего наоборот.
>книжку Шварца
Уебищное говно.
>где упражнения?
Самый тупой вопрос на доске про математику. Единственные упражнения, которые нужны, это упражнения на доказательство утверждений. Соответственно любая книга, где есть хоть какие-то теоремы это задачник: просто бери и доказывай всё сам.
>через месяц забуду
Хуй знает как ты читаешь тогда, видимо не понимаешь вообще ничего. Собственно, упражнения нужны только для того, чтобы "объективно" проверить, усвоил ты тему или нет.
>перед всероссом
Ну я бы не стал сравнивать тупой проблем-солвинг на скорость с математикой. Это скорее что-то вроде судоку, или шахмат, говно в общем.
Кстати чуть не забыл, есть вполне вменяемая книга другого Шварца и Данфорда "Линейные операторы" в трех томах. Там как раз весь анализ есть, первый том элементарная теория как в Глазмане-Любиче, а вот второй уже с банаховых алгебр начинается.
Про теорию множеств вообще странная ремарка, будто методами теории можно что-то содержательное сказать про анализ (а вот методами алгебры и топологии про него можно сказать практически всё).
Почему Шварц говно? Ботта и Федерера смогу читать, если по топологии в жизни книжки не открывал, а только то, что в Шварце было во второй главе?
Во-первых, мне надо сдавать экзамены, включая письменные (хотя для этого хватит и вузовского списка, уже решённого), во-вторых, сам я заниматься математикой не хочу (я подразумеваю профессиональную деятельность) и математическое образование получаю для "гимнастики ума", сам я в консалтинг и data science.
Большинство теорем из учебников либо тривиальны, либо слишком сложны, задач, подходящих для набивания руки, там мало, да и вообще, их просто мало. Я ставлю перед собой цель научиться хорошо и _быстро_ оперировать матаппаратом, чтобы мне не приходилось сидеть и что-то вспоминать, будь то при решении задачи (любого характера -- от взятия интеграла до доказательства сформулированных самостоятельно теорем в кандидатской/дипломной работах) или сдаче экзамена.
Причем здесь понимание? Ты не сможешь через месяц так же эффективно пользоваться аппаратом, как через день, это объективно, в этом вообще весь прикол обучения -- образованные связи надо отрабатывать. Естественно, я смогу рассказать определения/теоремы/доказательства и через месяц, и через два, но на это потребуется больше сил и времени.
Проблем-солвинг на время -- это то, что меня интересует как в математике, так и от неё.
Чтобы была понятнее моя позиция: допустим, мне дали задачу по физике -- мало того, чтобы я ее быстро решил, мне надо, чтобы я мог так же быстро доказать верность применённых теорем и методов решения, чтобы в голове выстраивалось дерево решения до аксиом ТМ (я утрирую, естественно).
>Почему Шварц говно?
Дохуя страниц про всякие интегралы Римана, меры Радона, вариационное исчисление для кратных интегралов; дифф. формы же определяются на 300-й странице второго тома. Еще у него какие-то бурбакистские взгляды на то, как называть подмножества, но это мелочи.
>по топологии в жизни книжки не открывал
Весь необходимый в математике материал по общей топологии занимает примерно пять страниц.
>Большинство теорем из учебников либо тривиальны, либо слишком сложны
Да. Бывает непонятно что и доказывать, настолько всё очевидно; а иногда даже не ясно в чем состоит смысл утверждения.
Что поделать.
>Проблем-солвинг на время -- это то, что меня интересует как в математике
В математике этим не занимаются. Вообще. Умение понимать нужно при чтении чужих работ и конечно, при написании своих. Хорошо усвоенный материал предмета предоставляет некоторую интуицию, полезную, в том числе, и для взятия интегралов. Само же взятие интегралов ничего не дает.
Нет, это развлечение для слабоумных кретинов, вроде игры в кости. Про шахматы всё сказал ещё Эдгар По:
Между тем рассчитывать, вычислять - само по себе еще не значит анализировать. Шахматист, например, рассчитывает, но отнюдь не анализирует. А отсюда следует, что представление о шахматах как об игре, исключительно полезной для ума, основано на чистейшем недоразумении. И так как перед вами, читатель, не трактат, а лишь несколько случайных соображений, которые должны послужить предисловием к моему не совсем обычному рассказу, то я пользуюсь случаем заявить, что непритязательная игра в шашки требует куда более высокого умения размышлять и задает уму больше полезных задач, чем мнимая изощренность шахмат. В шахматах, где фигуры неравноценны и где им присвоены самые разнообразные и причудливые ходы, сложность (как это нередко бывает) ошибочно принимается за глубину. Между тем здесь решает внимание. Стоит ему ослабеть, и вы совершаете оплошность, которая приводит к просчету или поражению. А поскольку шахматные ходы не только многообразны, но и многозначны, то шансы на оплошность соответственно растут, и в девяти случаях из десяти выигрывает не более способный, а более сосредоточенный игрок. Другое дело шатки, где допускается один только ход с незначительными вариантами; здесь шансов на недосмотр куда меньше, внимание не играет особой роли и успех зависит главным образом от сметливости. Представим себе для ясности партию в шашки, где остались только четыре дамки и, значит, ни о каком недосмотре не может быть и речи. Очевидно, здесь (при равных силах) победа зависит от удачного хода, от неожиданного и остроумного решения. За отсутствием других возможностей, аналитик старается проникнуть в мысли противника, ставит себя на его место и нередко с одного взгляда замечает ту единственную (и порой до очевидности простую) комбинацию, которая может вовлечь его в просчет или сбить с толку.
По первым двум пунктам понятно. Интеграл Римана и прочая хуйня меня интересует, ибо мне ещё экзамены сдавать.
Я понимаю, к чему ты клонишь, но что такое "доказать" я понимаю. Я про то, что в большинстве теорем либо одна и та же идея, либо идея встречается единожды и пиздец непростая -- пока не прочитаешь, не догадаешься. А среднее положение имеет количество утверждений ещё меньшее, чем количество сложных, при том, что всего теорем и лемм в учебнике не так много, как должно быть, на мой взгляд, задач.
Хорошая усвоение материала слабо помогает скорости -- скорее, решишь более сложную задачу, но время решения средних изменится не сильно. Повторюсь, передо мной задача дроча до рефлексов.
В общем, я все понял, спасибо. Задачи в "линейных операторах" есть, хех.
Теперь меня интересует ещё учебник по диффурам и вариационному исчислению.
 64 Кб, 330x410
64 Кб, 330x410>вариационному исчислению
У математиков это называется "теорией Морса".
https://en.wikipedia.org/wiki/Morse_theory
В зачаточном виде эти идеи были еще у Максвелла, см. статью.
Ключевой факт там – клеточное разбиение в терминах геодезических. Из литературы очевидный Милнор (на английском есть ещё Matsumoto и Nicolaescu).
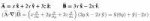 17 Кб, 652x93
17 Кб, 652x93>какие-то бурбакистские взгляды на то, как называть подмножества
Он иногда позволяет себе называть их "части". Очень удобное слово, как по мне. Отвергаю ваши претензии.
мимошёл
Какие конкретно книги?
В Algebra: Groups, Rings, and Fields by Louis Rowen и в Basic Linear Algebra Blyth, T.S., Robertson, E.F. ни слова про дифференцирование и интегрирование.
>Rowen
Graduate algebra же, второй том 19 глава и добавление к 6 главе первого тома.
>Blyth
Module theory, это пререквизиты (Rowen на линейной алгебре подробно не останавливается, а без нее в анализе делать нечего).
Спасибо, глянул.
> это пререквизиты
К чему? В этих двух книгах тоже нет ничего непосредственно аналитического, ведь так? Должна же быть книга с названием вроде Algebraic Approach to Real and Complex Analysis?
Единственное, что нагуглилось пока это Dieudonné "Foundations of modern analysis".
>Real Analysis
Differential geometry
>Compex Analysis
Algebraic geometry
Книга Дьедонне тоже плохая, во всяком случае не лучше Шварца.
"Мат анализ" это лоскутная дисциплина, состоящая из криво пришитых друг к другу кусков дифференциальной геометрии, функционального анализа, теории меры; химера типа "дискретной математики".
Дифференциальное исчисление и неопределенный интеграл (читай: интеграл от дифференциальных форм на многообразиях) это часть дифференциальной геометрии. Фундаментом здесь опять служит полилинейная алгебра (дифф форма это элемент внешней алгебры, по определению).
Про это можно читать у John Lee introduction to smooth manifolds, либо у Ботта и Ту дифф формы в топологии (1 глава). Чисто алгебраическая экспозиция этого же самого дана в 16 главе commutative algebra Eisenbud'а.
Функциональный анализ это другая тема; но основанная так же на линейной алгебре. Линал это наука об операторах в конечномерных линейных пространствах, функан отличается тем, что пространства там бесконечномерные и нормированные. Впрочем, удобнее смотреть на эти пространства как на ассоциативные алгебры. Соответственно основные темы: спектральная теория операторов, банаховы алгебры, ядерные пространства, обобщённые функции, теория Фурье-анализа Гельфанда.
Читать про это можно у Пирковского (но там довольно кратко); Шварца-Данфорда, еще есть современные книги, например Kaniuth Eberhard.
С более общей точки зрения весь функциональный анализ является разделом К-теории С*-алгебр. Даже такая простая вещь, как теоремы Фредгольма, на самом деле опирается на К-теорию операторной алгебры.
Мне кажется, что выделение анализа как отдельной области это историческое недоразумение, все равно что выделять теорию множеств или универсальных алгебр, исследование асимптотик бесселевых функций никакой "теорией" не является.
>интеграл от дифференциальных форм на многообразиях
А криволинейный интеграл типа B тогда как понимать?
Открыть к примеру Зорича, увидеть что там криволинейный интеграл типа В определяется как интеграл от дифференциальной формы, некоторое время думать, осознать что отличия его от знакопеременного случая чисто косметические.
Не получилось? Ну пробуй еще, может выйдет со временем.
 75 Кб, 352x333
75 Кб, 352x333подскажите по каким правилам произошло это преобразование(если можно распишите)
Разложение дроби на простейшие
 15 Кб, 565x114
15 Кб, 565x114Ну ёбона, бином Ньютона же. Распиши (1-1)^k и все увидишь.
Хотя, раз первая найдена, можно просто продифференцировать.
Благодарю по-братски, ежже. Всех благ.
It is not easy to give a comprehensive definition of this subject, and the name 'geometric analysis' has only been in common currency for the last 25 years or so. Loosely speaking, this field involves the many interlocking relationships between geometry and partial differential equations. These interconnections go both ways. For example, a 'purely geometric' problem, such as finding the optimal shape of a manifold, can be translated into an equivalent problem which involves solving a PDE. If a solution of that equation can be found, this can then be translated back into a solution of the original geometric problem. A classic instance is the uniformization theorem, where one seeks optimal (constant curvature) metrics on surfaces. There are several different analytic approaches, the earliest involving complex analysis and later ones involving semilinear elliptic PDE's. In the other direction, new perspectives in the field of PDE and many new techniques to solve various classes of equations have been inspired by the geometry underlying these equations. Among the many examples here, deep advances in fully nonlinear elliptic equations originated in the fundamental breakthroughs by Yau and others on Monge-Ampere equations arising in geometry. In a different direction, the entire modern theory of linear partial differential using microlocal analysis, pioneered by Hörmander, Kohn, Nirenberg and others, relies on a new way of viewing linear PDE through a geometric lens and exploiting the deep connections with symplectic geometry.
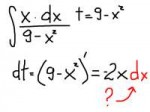 44 Кб, 800x600
44 Кб, 800x600Неправильна формула второй производной в [2.1] y''xx в числителе должно быть Fxx(Fy)^2-2FxyFxFy+Fyy(Fx)^2.
В задании [2.1] в формуле y''x Fyy неправильно подсчитана, вторая производна от tg''(y) = 2sin(y)/cos^3(y) по y. [2.2] вроде правильно
Щас бы прислушиваться к высерам поехавшего, который даже в орангутанах разобраться не в состоянии.
Я посмотрел, там аксиоматическое введение действительных чисел, а я бы хотел что то более высокого уровня (если есть такое)
ей чё за хуйня неруский
Ну посмотри в другой книжке конкретно этот вопрос. Особой разницы нет.
Алсо аксиомтически подход это и есть "более высокий уровень", т.к. абстрагируется от деталей конструирования объекта.
А в какой книжке можно этот вопрос увидеть подробно?
А что насчёт Винберга?
Я пытался найти, куда мне вбить мой пример с помощью Гоогле Транслите, но так ничего и не вышла. Видимо, это злой рок. Судьба. Апокалипсис.
В главное поле ввода:
integrate ((x^2-2x)/(x^3-блабла))dx from 0 to 1
Если брать предел, то limit (f(x)) at x=+inf (+ бесконечность, к примеру)
Ряд Тейлора:
taylor e^x at x=0
Если какой-нибудь пример решить или уравнение, то просто его ввести и всё.
Жизнеутверждающе благодарю тебя. Думаю, разберусь.
хз на самом деле. в задании так указано. Скорее всего подразумевается С2[0;1], т.к. нужно найти резольвенту второй производной
Оператор $d/dx - \lambda \colon C^2[0,1] \rightarrow C^1[0,1]$ не является ограниченным, соответственно, его резольвента есть пустое множество
Что?
Сорян, некоторому. Грубо говоря, нужно построить такую биекцию, но как ее строить и в какое конкретно множество непонятно
Возьми каждый второй элемент
Каждому элементу x сопоставим элемент x', где x' - элемент, следующий за x. У Зорича x' определяется как x∪{x}, емнип. Легко видеть, что это биекция на собственное подмножество.
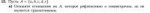 11 Кб, 532x50
11 Кб, 532x50ТРАНЗИТИВНОСТЬ := (x, y) ∈ R ⋀ (y, z) ∈ R → (x, z) ∈ R
Пусть A = { a, b, c } и есть такое отношение на А:
R = { (a, a), (b, b), (c, c), (a, b), (b, a) }
Нигде в определении транзитивности не сказано, что x ≠ z. Тогда отношение R рефлексивно, симметрично И в любом случае транзитивно. Т.е. в случае, если отношение рефлексивно и симметрично, то оно не может быть НЕ транзитивным. Чому тогда пикрелейтед?
R = { (a, a), (b, b), (c, c), (d, d), (e, e), (a, b), (b, a), (a, c), (c, a) }
(a,b) ∈ R ⋀ (a,c) ∈ R, но (b,c) ∉ R
но нигде и не сказано, что x=z
Твой контраргумент не соответствует определению транзитивности. Впрочем, мне уже провели хуем по губам объяснили всё в прикреплённом треде, а пост я удалить не могу, поэтому неважно.
Я тебя неправильно понял. Ты спрашивал только про множество A={ a, b, c }, да?
Чекнул прикреплённый, и, кажись, это ты нормально выразиться не можешь.
Мой контраргумент как раз задаёт НЕ транзитивное отношение, всё по определению.
>(a,b) ∈ R ⋀ (a,c) ∈ R, но (b,c) ∉ R
Есть (a, b) и (a, c). Второй элемент первой упорядоченной пары не равен первому элементу второй упорядоченной пары, поэтому отсутствие (b, c) в отношении не связано в этом контексе с его транзитивностью никак. Если бы были пары (b, a) и (a, c), то тогда да, это выражение бы указывало на нетранзитивность R. Это просто опечатка, скорее всего. Ну там реально вопрос решённый, но всё равно спасибо за интерес.
Бля, проебался, да.
просто распиши все определения и станет очевидно
Замыкание содержит все предельные точки.
Насколько знаю в R у каждой сходящейся последовательности есть только одна предельная точка.
Но зависит ли это от топологии X?
не у всех последовательностей есть предел
в нехаусдорфовом пространстве у последовательности может быть больше одного предела
думаю ещё, можно придумать множество, у которого есть предельные точки, не являющиеся пределами никаких последовательностей в этом множестве. но это что-то хитрое
Нельзя. Беру окрестности 1/n, в каждой выбираю по точке и последовательность готова.
шабат
Ну это в метрическом пространстве радиусы окрестностей, а в общем случае просто семейство вложенных окрестностей.
>а в общем случае просто семейство вложенных окрестностей.
Ты уверен, что в общем случае такое семейство можно найти?
Думаю, что в Хаусдорфовом пространстве это всегда так. В другом случае нужно придумать пример.
Не понял утверждения. Чтобы вычислить интеграл по поверхности, нужно иметь диф. форму на ней. Каким образом диф. формы на разных поверхностях связаны?
Видимо, неправильно сформулировал. Тогда сначала частный случай.
Есть вектор S=∫dS, равный векторному интегралу от dS по поверхности, натянутой на замкнутый контур, где dS - вектор элементарной площадки поверхности (dS=dS*n, где n - нормаль элементарной площадки).
Удтверждается, что этот интеграл не зависит от выбора натянутой на этот контур поверхности, а только от самого контура
неновижу все эти обозначения. Разве интеграл по dS от поверхности это не тупо её площадь? Это не наводящий вопрос, если что, я сам не знаю.
Можно, но нам нужно не абы какое семейство, а счётное. Без первой аксиомы счётности не факт, что оно обязательно существует, но я тупой и пример выдумать не могу.
Смотря что ты интегрируешь по поверхности. Если dω какую-то, то не зависит по Стоксу (интеграл dω по S = интеграл от ω по ∂S). Если произвольную, то вообще говоря должен зависеть.
Там не интеграл не по скаляру, а по вектору dS
Я написал полное условие, больше ничего не дано.
Собственно я сейчас электромагнетизм учу и там часто на какой-то контур натягивают какую-то поверхность и говорят, что поверхность может быть произвольной.
Мне ещё одно непонятно. Почему телесный угол, под которым видна поверхность, натянутая на контур, тоже не зависит от выбора этой поверхности, а только от контура? Разве нельзя так "выпучить" нятянутую поверхность, что она выйдёт за пределы телесного угла, из-под которого виден сам контур?
Можно чуть подробнее про Стокса? Можно такой же вывод сделать не из общей формулы, а из той, которая с ротором?
>Почему телесный угол, под которым видна поверхность, натянутая на контур, тоже не зависит от выбора этой поверхности, а только от контура?
Не ебу, что там в электромагнетизме, но может быть дело в том, что там, где поверхность "выпячевает", наш взгляд проходит через неё дважды?
Вообще, физики любят подразумевать и недоговаривать. Если они подразумевают, что ты интегрируешь какое-то dω, а в определении телесного угла имеют в виду правило "два раза - не пидорас", то всё сводится к Стоксу. Если нет, то хуйню несут, контрпримеры можно составить.
>там, где поверхность "выпячевает", наш взгляд проходит через неё дважды
Блин, точно.
>Если они подразумевают, что ты интегрируешь какое-то dω
Может ли dS=n*dS (n - нормаль к элементарной площадки поверхности, dS - её площадь) являться дифференциалом какой-то формы ω?
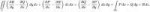 13 Кб, 764x63
13 Кб, 764x63>Может ли dS=n*dS (n - нормаль к элементарной площадки поверхности, dS - её площадь) являться дифференциалом какой-то формы ω?
Нет, это вообще не дифференциальная форма в R^3. Это описание самой поверхности, по которой ты интегрируешь. "Элементарная площадка" у физиков идёт вместо карты поверхности, а нормаль - вместо ориентации.
Тебе же важно понимать, что именно ты по этой поверхности интегрируешь, например какой-то оператор от какого-то поля. Вот он должен быть дифференциалом какой-то формы, чтобы Стокс работал.
То есть смотри, у тебя в учебнике по электродинамике утверждение: "Интеграл от хуйнянейм_1 по поверхности S, натянутой на контур T, не зависит от выбора такой поверхности." Не зависит почему? Скорее всего, потому что этот интеграл равен интегралу от хуйнянейм_2 по контуру Т, а контур T не меняется. Первый интеграл равен второму почему? Потому что хуйнянейм_1 - это дифференциал от хуйнянейм_2, T - край S, а тут и Стокс подъехал.
Пикрил пример из википедии. хуйнянейм_1 - это первое подинтегральное выражение (вместе со всеми dxdy), хуйнянейм_2 - второе выражение. И действительно, первое - это дифференциал второго, что можно легко доказать чистописанием, пользуясь правилами дифференцирования функции нескольких переменных и учитывая, что dxdx=dydy=dzdz=0.
Сигма и дэ сигма здесь - это как раз поверхность и её граница.
>Тебе же важно понимать, что именно ты по этой поверхности интегрируешь
Ну, в том-то и прикол, что интегрирую я единицу, умноженную на dS и больше ничего.
Есть векторный интеграл, который целиком выглядит вот так и берётся по поверхности, натянутой на какой-то фиксированный контур: S=∫dS. Удтверждается, что S зависит только от контура.
Это полное условие удтверждения.
Возможно, конечно, что я чего-то в упор не понимаю.
*S и dS - вектора, если не видно.
Можно на этот интеграл от вектора dS посмотреть покомпонентно. То есть, S_x = ∫e_x dS, где e_x - единичный вектор по оси x. Теперь нужно показать, что e_x - ротор какого-то векторного поля. Можно взять в качестве такого поля, например, a=y e_z. Стокс теперь говорит, что ∫e_x dS = ∫y dz, где интегрирование идет вдоль контура. То же самое для компонент у и z работает. Независимость интеграла от выбора поля, ротором которого является e_x, будет обеспечиваться тем же Стоксом.
Спасибо за разъяснение
дифференциальное уравнение -- это задача об описании ядра некоторого (дифференциального) оператора, действующего в определённых (функциональных) пространствах, которые, по-честному, должны быть заданы в условии задачи
что именно ты понимаешь под "нормальной формой", не очень понятно
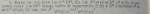 671 Кб, 4146x404
671 Кб, 4146x404Это теорема Соболева о вложении по сути, ты можешь передоказать её небольшой кусочек самостоятельно, там несложно.
Тривиальная часть 0: Если бы f была многочленом - задача решалась бы тривиально.
Нетривиальная часть 1: покажи, что любую l-гладкую во внутренности шара и непрерывную на его границе можно приблизить многочленами по норме W_inf^l (за определениями в википедию, но для того чтобы это доказать, ничего кроме определений знать не нужно).
Тривиальная часть 2: покажи, что предел многочленов по такой норме будет l-дифференцируемой функцией.
Тривиальная часть 3: используя часть 1 приблизь функцию f многочленами, после чего заметь, что многочлены у тебя продолжаются тривиально (часть 0), предел продолжений приближающих многочленов по части 2 и будет исккомым продолжением.
Спасибо. Я немного знаю соболевские пространства, но не может быть, чтобц Зорич подразумевал такое решение. Это же всего лишь учебная задачка по матану, да и в Зориче нет соболевских пространств.
А их тут тоже по сути нет нет, нужно всего лишь показать что гладкая функция равномерно приближаема многочленом, вместе со своими первыми l производными, используя теорему об аппроксимации Вейерштрасса (которая у зорича, думаю, есть)
Даже если я найду такую аппрксимацию на компакте, где функция задана, то с чего бы на каком-то большем компакте эта последовательность должна быть фундаменьальной?
И я про такую аппроксимацию (в C^l, а не в C) первый раз слышу, ты уверен, что они существуют?
ты прав, сорян бротан, не онолитик по жизни, я ещё подумаю
Такое есть? Там есть тонкости или как обычный интеграл брать? Где почитать про это? Вариационное исчисление через полгода только начнётся в универе.
> Там есть тонкости
Ну да, по сути, ничего кроме функционального гауссова интеграла точно взять нельзя.
>— Нас, — говорил он, — всегда интересует именно отношение конечных приращений, а производные математиков — это просто приближённые математические формулы для вычисления отношений этих конечных приращений.
почему нет? критическая точка -- это явление локальное, так что, если взять критическую точку, что там функция, кроме неё имеет ещё, уже неважно
возьми постоянную функцию, в окрестностях трёх изолированных точках продеформируй её, как тебе надо, будет пример.
можно взять три функции, каждая с нужной тебе точкой, умножить их всех на срезающие функции с носителями в окрестностях этих точек, получившиеся новые три функции сложить
В данной задаче особые точки +-2i лежат на контуре, теорема о вычетах вроде как неприменима.
Но я, конечно же, обосрался, не лежат они.
Спасибо.
Это называется теорема Бореля.
Borel theorem. Encyclopedia of Mathematics. URL: http://www.encyclopediaofmath.org/index.php?title=Borel_theorem&oldid=30977
Σakxk/k!
так на весь раздел 1,5 шизоида и те сидят в треде про основания переливая одно и тоже говно. Нахуя делали доску, непонятно.
 124 Кб, 1511x274
124 Кб, 1511x274Где про это почитать?
>ух сука ненавижу подобное
люто поддерживаю
А имеется в виду разложение Гельмгольца (его и гугли)
что авторам мешало написать напрямую название теоремы вместо того самого подобного, не ведаю. видимо, то же, что и всегда в подобных случаях
Спасибо.
>что авторам мешало написать
Нет, что ты, куда лучше вместо двух слов написать две строчки про то, насколько это очевидно))0)
 180 Кб, 1020x894
180 Кб, 1020x894Утверждение: разность двух телесных углов одинакова, если:
1) Сместить на какой-то вектор вершину угла
2) Сместить на этот же вектор сам контур (в этом случае разница будет равна телесному углу, под которым видна цилиндрическая поверхность, описанная точками контура при смещении).
Это идейно очевидно в каком-то смысле, но ни геометрически, ни математически не очевидно лично для меня.
Может кто что подсказать на эту тему?
пикрил
Дичь страшная, сомневаюсь, что кто-то даже попытается это прочитать, сорри. Если герой найдётся, не скупись на благодарности
А чё не очевидно-то?
1. Одинакова, поскольку вершина относительно контура расположена так же.
2. Телесный угол - это площадь высекаемого конусом участка на единичной сфере. Нарисуем хрень, которая добавилась/убавилась - это будет как раз телесный угол, под которым видна цилиндрическая поверхность. С учетом ориентации, если надо.
>Одинакова, поскольку вершина относительно контура расположена так же.
Так было бы при смещении на противоположный вектор, а не на тот же самый.
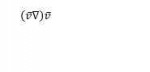 2 Кб, 185x90
2 Кб, 185x90возможно, имеется в виду, что оператор, умноженный на функцию, тоже есть оператор (точнее: композиция двух операторов -- данного оператора и оператора умножения функцию)
Пример: оператор x d/dx (дифференцирует и умножает результат на х)
Из-за каких трюков получаются оценки со множественными логами логов логов логов?
Спасибо, анон
Правильно ли я понимаю, что дивергенция суть разность между скалярами векторов, входящих в некую бесконечно малую точку?
А ротор - геометрическая разность между векторами.
Антон, ты? https://www.youtube.com/watch?v=PboWBq-MsRI
Или сам лидер атаки? https://www.youtube.com/watch?v=_DN2mrHnJxo
Что это за опущ и при чем здесь ротор и дивергенция?
Наверное, в каждой области свои приемы.
Возможно, но всё равно интересно, что имел ввиду.
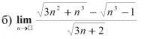 22 Кб, 724x191
22 Кб, 724x191Как решать подобные пределы? Точно так же как и другие неопределенности типа бесконечность деленная на бесконечность -- разделив числитель и знаменатель на старшую степень n или же как-то иначе?
(N стремится к бесконечности, символ бесконечности почему-то не отображается на картинке)
Конкретно в твоем примере надо домножить числитель и знаменатель на сумму корней из числителя. А дальше уже выносить старшую степень.
 6,5 Мб, 2885x2885
6,5 Мб, 2885x2885Вначале проверяем на полноту, а потом на открытые множества.
Возьмём метрику на R: r=|f(x)-f(y|, f - инъективны.
Обязательно ли оно должно быть полным. Берём arctg(x) и получаем что необязательно.
Правда ли, что в каждом открытом шаре есть точка из множества. Взял открытый шар с f(x_1) и f(x_2). |f(x_1)-f(x_2)|<r, но в этом шаре x_1 и x_2 и есть точки этого множества. Что не так?
Как сказал этот джентльмен: >>59336 , подобные примеры решаются удалением кхуям корней из числителя.
Делается это путём умножения на т.н. "сопряжённое выражение". По сути - нам нужно получить в числителе разность квадратов:
(a-b) x (a+b) = a2-b2
Тогда в числителе кубы уходят сами
А знаменатель всё также положительный - то есть никакой неопределённости. И вот теперь можно выносить старшие степени.
Сейчас я учусь и прямо реально кайфую от охуенности выводов и построений. Само понятие предела это же надо было додуматься! Это же настолько элегантно точный метод приближений... а студенты, школота вчерашняя, этого не понимают, им бы побыстрей с пар съебать. Им под нос суют настоящее сокровище, достояние величайших умов человечества, а они...
 110 Кб, 1373x922
110 Кб, 1373x922Пытаюсь понять, как выводится формула распределения Максвелла. За основу взял вот это пособие: https://portal.tpu.ru/departments/kafedra/tief/method_work/method_work2/lab1/LabsMechMolecFiles/ModT-04.pdf
И не могу понять начало страницы 5 (оно же и на пике).
По сути в этой системе есть два понятия: вектор и норма. И берутся частные производные по одной из переменных (допустим, x).
Для того, чтобы потом прийти к равенству, нужно, чтобы дифференциалы у обоих уравнений были одинаковые. Как я понимаю, это дифференциал нормы/дифференциал х.
Почему такой дифференциал существует во втором уравнении - это понятно. Но как нужно продифференцировать первое уравнение, чтобы получить его там? И существует ли он вообще?
Заранее огромная благодарность.
Ты берешь 1000$ с собой к букмекеру, ставишь 1$ выигрываешь - ставишь ещё, проигрываешь - удваиваешь, до тех пор, пока не выиграешь
Какова вероятность того что я стану миллионером и того что проебу всю 1k$?
Блять. А хули у меня формула всратая?
А если так:
[mаth]/forall x/in dom f /forall n , m /in /mathbb{Z} : f(x+n+m /sqrt{2}=f(x)[/mаth]
$H(p1, p2, ...) = -\sum_{n=1}^{\infty}p_n log(p_n)$
Вопрос, могу ли я ее оптимизировать с помощью уравнения Лагранжа-Эйлера? Если да, то почему? Меня конкретно смущает то, что у нее счетное количество аргументов, и то, что про Лагранжа-Эйлера для интегралов везде написано. Препод говорит, что надо решать задачу через множители Лагранжа, но для бесконечномерных функций обычный метод не применим, а других вариантов решения подобной задачи я не нашел и не знаю.













![depositphotos37046619-stock-photo-two-manual-workers-shakin[...].jpg](/math/big/thumb/4/15116360452790s.jpg)