 14 Кб, 480x360
14 Кб, 480x360Итак, пачаны, я прошел один математический тест для дошкольнят.
Предлагаю местным мат-и-мат-икам тоже попробовать решить его.
Проходил я его ирл и правильные ответы знаю, так что буду постить вопросы по мере продвижения по ним.
Зачем? Чтобы посмотреть как двачные математики будут справляться с ящичным для песка демоном, с применением топологии над модулями колец в бесконечномерных пространствах.
Предлагаю местным мат-и-мат-икам тоже попробовать решить его.
Проходил я его ирл и правильные ответы знаю, так что буду постить вопросы по мере продвижения по ним.
Зачем? Чтобы посмотреть как двачные математики будут справляться с ящичным для песка демоном, с применением топологии над модулями колец в бесконечномерных пространствах.
Вопрос первый.
Группа школьников купила в буфете несколько пирожков, каждый стоимостью 30 рублей, а пять штук булочек, каждая стоимостью Х рублей.
Какое из следующих чисел может выражать общуую сумму покупки
А 91
Б 92
В 93
Г 94
Д 95
Группа школьников купила в буфете несколько пирожков, каждый стоимостью 30 рублей, а пять штук булочек, каждая стоимостью Х рублей.
Какое из следующих чисел может выражать общуую сумму покупки
А 91
Б 92
В 93
Г 94
Д 95
Вопрос второй
Чему равно 1 - sin(a)ctg(a)cos(a)
А cos(2a)
Б 1-sin(2a)
В 0
Г cos^2(a)
Д sin^2(a)
>>39657
Конечно же разное. Пирожок это изделие из теста с начинкой внутри, а булочка это просто изделие из теста.
Чему равно 1 - sin(a)ctg(a)cos(a)
А cos(2a)
Б 1-sin(2a)
В 0
Г cos^2(a)
Д sin^2(a)
>>39657
Конечно же разное. Пирожок это изделие из теста с начинкой внутри, а булочка это просто изделие из теста.
>>39656
Пусть куплено a пирожков и x - целое.
Тогда сумма покупки s = 30a + 5x = 5(6a +x).
Поскольку Z факториально, s должно делиться на 5
Ответ д.
Пусть куплено a пирожков и x - целое.
Тогда сумма покупки s = 30a + 5x = 5(6a +x).
Поскольку Z факториально, s должно делиться на 5
Ответ д.
 22 Кб, 467x409
22 Кб, 467x409>>39675
>>39674
>>39670
Пока все правильно решаете. Но это так, ерунда.
Третий вопрос.
Тут понадобится мое безумное умения рисования в пейнте.
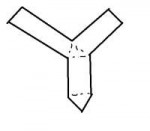
Есть развертка правильной треугольной призмы по типу рисунка. Представьте что она нарисована правильно и со всеми пропорциями, пунктиры это линии изгиба
Нужно определить площадь боковой поверхности призмы, когда известно что периметр этой развертки составляет 52 сантиметра, а периметр основания призмы 12 сантиметров.
>>39674
>>39670
Пока все правильно решаете. Но это так, ерунда.
Третий вопрос.
Тут понадобится мое безумное умения рисования в пейнте.
Есть развертка правильной треугольной призмы по типу рисунка. Представьте что она нарисована правильно и со всеми пропорциями, пунктиры это линии изгиба
Нужно определить площадь боковой поверхности призмы, когда известно что периметр этой развертки составляет 52 сантиметра, а периметр основания призмы 12 сантиметров.
>>39693
Чаво блядь такое площадь боковой поверхности? Площадь всей хуйни? Нет верного ответа.
Площадь только 1 боковой боковой стенки 72см^2, а всех 3 в 3 раза больше.
Чаво блядь такое площадь боковой поверхности? Площадь всей хуйни? Нет верного ответа.
Площадь только 1 боковой боковой стенки 72см^2, а всех 3 в 3 раза больше.
 20 Кб, 467x409
20 Кб, 467x409>>39696
Небось мем с ящиком так же появился. Но правильно.
>>39733
Правильно.
Дальше, четвертый вопрос.
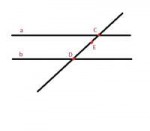
Есть две паралельные прямые а и б.
Есть секущая, проходящая через них. На секущей есть точка Е. Расстояние от точки E до точки D равно 5 сантиметров, а от точки E до точки C два сантиметра.
Требуется найти расстояние между параллельными прямыми, если расстояние от точки Е до прямой а равно 1 сантиметр.
Варианты ответов
А 2.5 см
Б 3 см
В 3.5 см
Г 4 см
Д 4.5 см
Небось мем с ящиком так же появился. Но правильно.
>>39733
Правильно.
Дальше, четвертый вопрос.
Есть две паралельные прямые а и б.
Есть секущая, проходящая через них. На секущей есть точка Е. Расстояние от точки E до точки D равно 5 сантиметров, а от точки E до точки C два сантиметра.
Требуется найти расстояние между параллельными прямыми, если расстояние от точки Е до прямой а равно 1 сантиметр.
Варианты ответов
А 2.5 см
Б 3 см
В 3.5 см
Г 4 см
Д 4.5 см
>>39741
Опустим перпендикуляр из D. Назовём его основание точкой W. Опустим перпендикуляр из E, основание назовём точкой V. Из подобия понятно каких треугольников вытекает, что EC:DC = EV:DW, откуда DW = EV DC/EC = 1x7/2 = 3.5
В
Опустим перпендикуляр из D. Назовём его основание точкой W. Опустим перпендикуляр из E, основание назовём точкой V. Из подобия понятно каких треугольников вытекает, что EC:DC = EV:DW, откуда DW = EV DC/EC = 1x7/2 = 3.5
В
>>39745
Примем a за действ ось с центром в C, тогда секущая задаётся функцией y=kx. Обозначим за l длину CE.
Чтобы обосновать, нужно доказать, что l пропорциональна y. То что a пропорционально b будем обозначать a~b. Это отношение эквивалентности.
l2=x2+y2; y можно выразить через x, получается : l2=2k2x2, потому l=sqrt(2)kx. Потому l~x. y=kx, потому x~y. Т.к. ~ отношение эквивалентности, то оно транзитивно, потому l~y.
Примем a за действ ось с центром в C, тогда секущая задаётся функцией y=kx. Обозначим за l длину CE.
Чтобы обосновать, нужно доказать, что l пропорциональна y. То что a пропорционально b будем обозначать a~b. Это отношение эквивалентности.
l2=x2+y2; y можно выразить через x, получается : l2=2k2x2, потому l=sqrt(2)kx. Потому l~x. y=kx, потому x~y. Т.к. ~ отношение эквивалентности, то оно транзитивно, потому l~y.
Докажите, что каждое чётное число больше 2 может быть представлено в виде суммы двух простых. Например, 4 = 2+2, 6 = 3+3, 8 = 5+3 и т.д.
Можно по индукции.
Можно по индукции.
>>39763
Это тривиально следует того факта, что точная категории фильтрованных модулей над этальной фундаментальной группой регулярного локального кольца с циклотомическими присоединенными факторами является ретрактом точной категории фильтрованных этальных пучков на спектре этого кольца с присоединенными факторами, получающимися подкруткой пучков, поднятых с сайта Зарисского, на циклотомические этальные пучки. Этот ретракт надо построить (простое упражнение), а дальше разберёшься сам.
Это тривиально следует того факта, что точная категории фильтрованных модулей над этальной фундаментальной группой регулярного локального кольца с циклотомическими присоединенными факторами является ретрактом точной категории фильтрованных этальных пучков на спектре этого кольца с присоединенными факторами, получающимися подкруткой пучков, поднятых с сайта Зарисского, на циклотомические этальные пучки. Этот ретракт надо построить (простое упражнение), а дальше разберёшься сам.
>>39764
Уважаемый Корчеватель, уходи.
Уважаемый Корчеватель, уходи.
>>39763
Открытая проблема.
Открытая проблема.
>>39763
УХАДИ ПРАТИВНЫЙ))))))
>>39744
>>39745
Правильно.
Теперь уже вопросы посложнее пошли.
Пятый вопрос.
В прямоугольном треугольнике АВС (С = 90 градусов) расстояние от середины медианы ВМ к катетам АС и ВС равно 15 и 10 сантиметров соответственно.
Найдите длинны этих катетов и радиус описанного вокруг треугольника круга.
Тут как бы нужно упомянуть что пользоваться интернетами и вольфрамами нельзя. Просто чтобы посмотреть сколько гомологических алгебраистов тоже сольются на этом вроде бы простом вопросе.
УХАДИ ПРАТИВНЫЙ))))))
>>39744
>>39745
Правильно.
Теперь уже вопросы посложнее пошли.
Пятый вопрос.
В прямоугольном треугольнике АВС (С = 90 градусов) расстояние от середины медианы ВМ к катетам АС и ВС равно 15 и 10 сантиметров соответственно.
Найдите длинны этих катетов и радиус описанного вокруг треугольника круга.
Тут как бы нужно упомянуть что пользоваться интернетами и вольфрамами нельзя. Просто чтобы посмотреть сколько гомологических алгебраистов тоже сольются на этом вроде бы простом вопросе.
>>39832
катет BC равен 20 см, а дальше мне лень считать
катет BC равен 20 см, а дальше мне лень считать
>>39832
И что это докажет? Что специалист в своей области не разбирается в другой области? Ты бы ещё задачи по биологии принёс и потешался над математиками, которые не могут в биологию.А школьная математика так же далека от как и биология.
>колько гомологических алгебраистов тоже сольются на этом вроде бы простом вопросе
И что это докажет? Что специалист в своей области не разбирается в другой области? Ты бы ещё задачи по биологии принёс и потешался над математиками, которые не могут в биологию.А школьная математика так же далека от как и биология.
>>39832
Так же, как и в прошлой задаче. На медиане возьмем точку E, и будем двигать её от B до M.
Тогда если E на центре и d(E,BC)=10, то d(M,BC)=20, т.к. M середина AC, то AC=40
Точно так же, если на центре d(E, AC)=15, то d(B,AC)=30, потому BC=30.
Теперь докажем, что гипотенуза = диаметр описанной окружности.
Тогда центр окружности лежит на середине гипотенузы. Обозначим его O. OA=OB, т.к. O середина. Пусть O' середина BC, то O и O' лежат на одной прямой l, перпендикулярной BC, доказательство точно такое же, как выше: будем двигать точку от B до A...
Потому треугольник OCB равнобедренный: O'OB=O'OC по двум сторонам и углу между ними.
Потому OC=OB=OA
По теореме Пифагора вычисляем гипотенузу = 50, тогда радиус = 25
Ответ: 25, 30, 40
Так же, как и в прошлой задаче. На медиане возьмем точку E, и будем двигать её от B до M.
Тогда если E на центре и d(E,BC)=10, то d(M,BC)=20, т.к. M середина AC, то AC=40
Точно так же, если на центре d(E, AC)=15, то d(B,AC)=30, потому BC=30.
Теперь докажем, что гипотенуза = диаметр описанной окружности.
Тогда центр окружности лежит на середине гипотенузы. Обозначим его O. OA=OB, т.к. O середина. Пусть O' середина BC, то O и O' лежат на одной прямой l, перпендикулярной BC, доказательство точно такое же, как выше: будем двигать точку от B до A...
Потому треугольник OCB равнобедренный: O'OB=O'OC по двум сторонам и углу между ними.
Потому OC=OB=OA
По теореме Пифагора вычисляем гипотенузу = 50, тогда радиус = 25
Ответ: 25, 30, 40
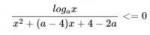 21 Кб, 316x75
21 Кб, 316x75>>39881
У меня куда то проебался листок с решениями. Будем считать что правильно.
Хотя я так пытался примерно так же, тупо брут форсом подобрать и тоже набросал от руки график примерный, но мои ответы неправильными оказались.
Шестой вопрос.
Решить неравенство на картинке относительно параметра а.
У меня куда то проебался листок с решениями. Будем считать что правильно.
Хотя я так пытался примерно так же, тупо брут форсом подобрать и тоже набросал от руки график примерный, но мои ответы неправильными оказались.
Шестой вопрос.
Решить неравенство на картинке относительно параметра а.
>>39914
Много писать, потому решать не буду.
Я честно не знаю, как решить её дедовским методом, да и зачем. Могу только обратно дедовским взять. Возьмём треугольник с AC=4 и BC=3. Проведём медиану BM. В треугольнике BMC стороны MC=2 и BC=3, длина BM=sqrt(13). Из центра BM опустим перпендикуляры OB' и OA'. 1)треугольники BMC и OB'B подобны, тогда 2/OB'=sqrt(13)/0.5sqrt(13)
sqrt(13)=OB'sqrt(13)=>OB'=1
2) Треугольники BMC и OA'M подобны. Потому 3/OA'=sqrt(13)/0.5sqrt(13)
OA'sqrt(13)=1.5sqrt(13)
OA'=1.5
Много писать, потому решать не буду.
>Будем считать что правильно
Я честно не знаю, как решить её дедовским методом, да и зачем. Могу только обратно дедовским взять. Возьмём треугольник с AC=4 и BC=3. Проведём медиану BM. В треугольнике BMC стороны MC=2 и BC=3, длина BM=sqrt(13). Из центра BM опустим перпендикуляры OB' и OA'. 1)треугольники BMC и OB'B подобны, тогда 2/OB'=sqrt(13)/0.5sqrt(13)
sqrt(13)=OB'sqrt(13)=>OB'=1
2) Треугольники BMC и OA'M подобны. Потому 3/OA'=sqrt(13)/0.5sqrt(13)
OA'sqrt(13)=1.5sqrt(13)
OA'=1.5
 5 Кб, 614x15
5 Кб, 614x15>>39914
Лень самому решать.
Лень самому решать.
 1,7 Мб, 2048x1536
1,7 Мб, 2048x1536>>39914
Лениво накатал графическое решение в заметках.
Лениво накатал графическое решение в заметках.
Блеать, это 9 класс? Что вы тут решаете? К ЕГЭ готовитесь?