78 Кб, 752x501
78 Кб, 752x501Но "ничто" - это не число.
Т.е. ряд натуральных чисел начинается с "1", а не с "0" и не с "ничего".
Но возникает множество проблем.
И поэтому, вероятно, и применяетcя ошибочная модель, где "ничто" превратилось в число "0", с которого начинаетcя числовой ряд натуральных чисел.
Говоря "ничего", мы обозначаем что-то.
В аксиомах пеано, 0 — это первичный объект.
А потом S0 — один.
Дальше SS0 — два.
SSS0 — три.
Для нуля, в отличии от " ничего", установлены операции
5+0=5
6×0=0
Свойства "ничего" установлены двумя аксиомами пеано. Другими словами, те дополняются дополнительно. Ведь само понятие пустоты не требует этого.
Х
 22 Кб, 623x677
22 Кб, 623x677/тред
Да хацкель же!
Видите в реале один камень? Я да, а два? И это я вижу и все это видят. А что такое "0 камней"? И чем "0 камней" от "0 палок" отличается?
0 камней нельзя потрогань, нельзя посчитать, мы это не видим и не слышим. А вы уверены в том, что это именно 0 камней у вас на столе, а не 0 палок? Вы даже доказать это не сможете. У вас это ноль всего и сразу, ноль бесконечности, прикиньте?
Вот и не хер нести бредятину. В натуральных числах вместо нуля должно быть "ничего", а "ничего" посчитать нельзя и перед 1 его можно поставить личшь чисто условно, теоретически. Но вряд ли мы имеем право притащить "ничего" в ряд натуральных чисел. Он совсем не похож на них. Он из области "бесконечность", только наоборот и всё ещё хуже.
"Ничего" - не число.
 69 Кб, 960x878
69 Кб, 960x878> Видите в реале один камень? Я да, а два? И это я вижу и все это видят. А что такое "0 камней"? И чем "0 камней" от "0 палок" отличается?
Я тебе выше даже код написал. Не надо разводить аутизм на ровном месте, 0 - такой же конструктор типа, ну или элемент в ординалах фон Неймана. Для которого определены свойства. Никакая пустота или бесконечность там рядом не валялась. Если ты даже такого примитивна понять не в состоянии, нахуя тебе вообще математика? С тем же успехом можно сказать, что одну палку или одно яблоко видят все, а что такое косинус или тангенс от одной палки?
Вы даже с множествами не знакомы, но лезете что-то такое
обсуждать.
> И чем "0 камней" от "0 палок" отличается?
>
Но ведь отличаются же.
0 палок - у нас нет палок
0 камней - у нас нет камней
покормил
>0 камней
Это когда не вижу ни одного камня.
>чем "0 камней" от "0 палок" отличается
Не стоит вскрывать эту тему.
хуево объясняешь
С кардинальной.
Анон, он же очередной залетный дебил, математика ему и не нужна.
Алсо, если уж на то пошло, то нулевой конструктор должен быть полиморфным. То есть Z :: forall a. Num a => a; так что в каком-то смысле идею про камни и палки интерпретировать можно.
Одна палка, две палки, куда уж проще?
А теперь покажите мне число в реале "ноль палок".
"Ноль палок" - это конкретно "ничего". Это отсутствие палок.
2 камня и ноль палок - это 2 камня и "ничего" палок, а ещё это 2 камня, ничего палок, ничего овец, ничего...
И выходит, что 0 - это полное отсутствие чего-либо, а не количество палок. Нельзя подсчитать количество палок, если палок нет, т.е. число ответом быть не может. А 0 - это число.
Так что нет никакого нуля в натуральных числах, так как мы не можем видеть его в реальности и мы не можем доказать его существование. Мы видим только "ничего".
>0 - это полное отсутствие чего-либо
Это полное отсутствие всего.
А в той точке пространства, где находится камень, отсутствует всё остальное в мире натуральных чисел.
Как доказать, что в первой коробке у нас палки и их количество ноль? В ряду только палки? А ты уверен, что эта коробка вписывается в ряд палок? Докажи. И ты не доказал.
Все мы прекрасно видим, что палок в первой коробке нет, нет там и всего остального (упрощённая модель).
Там нет не только палок, там ничего нет или нет всего. Пустота пустот или ничего ничего (отсутствие всего).
И эта "пустота" в данном случае - это штука универсальная для всего и для палок и для камней и для всего остального.
Это одна штука, которая подходит для чего угодно в этом мире. А числа "1 камень", "2 камня" подходят только для камней, аналогично с остальными - "1 палок" - только для палок.
А то, что в пустой коробке, подходит для всего сразу.
Но "любое_число камней" подходит только, чтобы подсчитать камни и 0 - число, короче, не 0 у нас в первой коробке а некий универсальный показатель полного отсутствия чего-либо, которые называется "ничего".
Я доказываю, а вы тупо утверждаете.
А вы докажите свои слова. Докажите, что это перед нами на столе "лежит" именно ноль палок, а не "ничего".
Два объекта существуют в двух разных точках пространства итд.
В пустом пространстве нет объектов.
Пустота - это "ничего", а не "ноль конкретно палок".
Если принять, что "ноль" - это "полное отсутствие", то можно сказать, что пустота - это "ноль всего", ноль бесконечности видов объектов, полное отсутствие любого вида объектов.
В первой коробке полное отсутствие любого вида объектов, а не отсутствие только палок.
Разумеется, второе множество входит в первое бесконечное множество.
А первое множество называется "ничего".
Но второе множество существует только в теории, в реальности нет "нуля палок" или "нуля камней", в реале есть только "ничего", пустое пространство.
А когда в точке пространства есть камень, тогда в этой точке "полное отсутствие всего, исключая камень". Т.е. полное отсутствие любого вида объектов, за исключением камней. Двух камней или двух объектов разных видов в одной точке пространства быть уже не может. Один объект - одна точка.
Это шизофазия, а не математика. Объект, точка итд, все это требует определений, более того, с натуральными числами не связанных. Тебе твоя бредятина кажется чем-то содержательным, но это не так. И уж конечно, все что ты несешь, к математике вообще не относится.
Гротендика тоже когда-то не признавали
> И чем "0 камней" от "0 палок" отличается?
Допустим, ничем, то есть 0 камней и 0 палок одно и то же. Тогда у нас, например, есть коробка с камнями. Там 0 палок, но не 0 камней. Противоречие.
Тоже взлольнул с этого формалиста, который подменяет свои желания требованиями точки
точки в пространстве, ебань
Да вся математика сплошная шизофрения.
В пустой коробке 0 чего угодно и 0 всего сразу, ноль бесконечно возможных видов реальный вещей (теоретически). Там ничего.
В коробке с камнями 0 чего угодно, исключая камни.
И чо?
Не существует в реале и 2D объектов и 1D, а 0D и тем более не существут (точек).
Не существует точек и в 2D и в 1D мире.
И сфер в реале нет по той же причине.
И это ещё даже без рассмотрения 4D пространства-времени.
Кроме того, в реале невозможно создать идеальные объекты, идеальный круг итд. Найдите два одинаковых атома во всей Вселенной, сомневаюсь, что они существуют.
А если верна теория о минимальной длине (длина Планка), тогда при мельчайшем приближении любой идеальный круг превратится в правильный многоугольник и максимальный реально возможный пи будет отличаться от теоретического.
Причём
Причём точно его будет уже не найти.
https://ru.wikipedia.org/wiki/Число#Иерархия_чисел
Тонко у него получилось.
Твоя ошибка в том, что ты рассматриваешь какие-то "0 палок". В математике нет никаких палок. Она не рассматривает "эн чего-то", она рассматривает просто "эн", в отрыве от любого "чего-то". Иными словами, тебе нужно немножко абстракции.
Не может, потому что без identity элемента ты даже группы не построишь. То есть арифметика у тебя кривая получится, если ты ее всю начнешь вот так строить.
А если ты таким заниматься не собираешься - конечно может. Некоторые авторы определяют натуральные числа с единицы, если в контексте их работы это удобно. No big deal, исключительно вопрос удобства.
Ну тут конечно совсем шизоглупость пошла, даже не знаю, как прокомментировать. Но анон, я так понимаю, что ты школьник, так что ты молодец, что пытаешься думать и искать какие-то противоречия. Если ты в 6-7 классе, то я бы тебе рекомендовал заниматься и решать побольше задачек, плюс почитать что-нибудь по формальной логике. Можешь даже попросить родителей поискать вот прям хорошего препода, если ты в обычной СОШ, походить и позаниматься. Это того стоит и в будущем окупится. Удачи.
Эх, а в реале то у нас обязательно "эн чего-то" должно быть, а не твои абстракции. А натуральные числа хоть немного да должны реальностью отдавать.
Но как я уже не раз говорил, натуральных чисел не существует в реальности и всё это чистейшие теоретические модели. Натуральные числа условны и относительны.
ещё один даун.
 653 Кб, 1709x744
653 Кб, 1709x744/тред
Ты бы и мужчиной отдался
Кантор не считал, что множество всех множеств - обычное, регулярное множество. Он изобрёл классы - такие же, как у фон Неймана, Гёделя и Бернайса. Поэтому парадокс Бурали-Форти улетает в молоко. Более того: Кантор, по-видимому, додумался даже до универсумов Гротендика.
Подробности и цитаты у Вавилова.
Внимательно рассмотри человека на прилагающейся фотографии. Можешь ли ты представить себе, как этот мужчина плачет и набирает дрожащими пальцами доказательство Аллаха, чтобы рассказать о своих чувствах по его поводу? Можешь представить, что он пропускает в очереди жирного эмпириста с томиком Арнольда в руках? А то, что он работает пол-года, прорешивая Демидовича, чтобы сдать зачет по анализу? Ты видишь в нем человека, который стесняется сказать родителям, что на свой двадцать четвертый день рождения он хочет обсудить реализацию HoTT в coq с друзьями?
Теперь посмотри на него еще раз. Видишь ли ты на нем стильные брендовые (или вообще хоть какие-нибудь) вещи? Может он покрыт огромной лысиной и очками а-ля "советский инженер"? Он обладает внешностью ботаника или еврея-задрота?
Позади него стоит доска с объявлением о каком-то ненужном семинаре?
Посмотри снова на этого мужчину и спроси самого себя, что с ним не так?
Почему в его взгляде железо, в его осанке сталь, а вместо кожи свинец?
мудак, скрыл
 1,2 Мб, webm,
1,2 Мб, webm,360x480, 0:14
>Кантор не считал, что множество всех множеств - обычное, регулярное множество.
Он вообще по этому поводу до Бурали-Форти ничего не считал.
>Он изобрёл классы - такие же, как у фон Неймана, Гёделя и Бернайса.
Охуительные истории. Одна охуительнее другой. Кантор - основоположник NBG, универсумов Гротендика, Аллаха... Впрочем,
>у Вавилова.
Ясно, понятно.
>>8273
>ещё один даун нарисовался
Мань, у тебя вебкамера включилась пшел нахуй, школьник ебучий.
Просто идите дружно на хуй, если вы не верите ОПу, и в жопу засуньте себе все эти абстракционные модели о числах.
Так ты хуйню несешь уровня православной арифметики или Рыбникова.
Результат любой математического достижения, является результатом игры символов.
Охуеть теперь. Добавь к этому требование непротиворечивости результатов символьных комбинаций, и считай ты в 21 веке до формализма додумался. Мейлру просветляет.
 148 Кб, 973x1074
148 Кб, 973x1074Что это за такое волшебное пустое число "0"? Как его создать? Волшебство да и только!
0 - это "ничего".
3 + "ничего" [и мы пишем] = 3.
На деле же у нас в правой части осталось 3 + "ничего".
Просто мы этого не замечаем.
ПОТОМУ ЧТО мы не можем сложить число и нечисло.
А [3 - 0] - это [3 - "ничего"].
Мы пишем:
3 - 0 = 3, на деле же: 3 - "ничего" = 3 - "ничего".
А ничего мы не замечаем, ведь оно ничего и не меняет.
И вот именно поэтому нельзя делить на "0" и именно поэтому и возникает множество попросов связанных с этим.
Когда мы делим на "0", мы на самом деле делим на "ничего".
А "ничего" - не число и поделить на него нельзя.
Поэтому "на ноль делить нельзя".
И не важно, натуральные числа у нас или нет.
0 - это везде "ничего" и везде нечисло.
3/0 = 3/0
Теперь рассмотрим умножение на 0.
3 x 0 = Как вы думаете, что должно быть здесь?
Да то же, что и слева!!!
3 x 0 = 3 x 0
О, но как же так, ведь все математики говорят, что на ноль можно умножать и получим ноль.
Да они в жизнь этого не докажут!
Мы не можем умножить 3 на 0, вот правильный ответ.
Аналогично и с 3^0.
Итого, мы не можем складывать, вычить, умножать, делить, возводить в степень число и/на/в "0".
Ох, как же так, ты сломал мои волшебные детские миры, как ты мог!?
Вот так-то, сучки, знайте своё место!
 148 Кб, 973x1074
148 Кб, 973x1074Что это за такое волшебное пустое число "0"? Как его создать? Волшебство да и только!
0 - это "ничего".
3 + "ничего" [и мы пишем] = 3.
На деле же у нас в правой части осталось 3 + "ничего".
Просто мы этого не замечаем.
ПОТОМУ ЧТО мы не можем сложить число и нечисло.
А [3 - 0] - это [3 - "ничего"].
Мы пишем:
3 - 0 = 3, на деле же: 3 - "ничего" = 3 - "ничего".
А ничего мы не замечаем, ведь оно ничего и не меняет.
И вот именно поэтому нельзя делить на "0" и именно поэтому и возникает множество попросов связанных с этим.
Когда мы делим на "0", мы на самом деле делим на "ничего".
А "ничего" - не число и поделить на него нельзя.
Поэтому "на ноль делить нельзя".
И не важно, натуральные числа у нас или нет.
0 - это везде "ничего" и везде нечисло.
3/0 = 3/0
Теперь рассмотрим умножение на 0.
3 x 0 = Как вы думаете, что должно быть здесь?
Да то же, что и слева!!!
3 x 0 = 3 x 0
О, но как же так, ведь все математики говорят, что на ноль можно умножать и получим ноль.
Да они в жизнь этого не докажут!
Мы не можем умножить 3 на 0, вот правильный ответ.
Аналогично и с 3^0.
Итого, мы не можем складывать, вычить, умножать, делить, возводить в степень число и/на/в "0".
Ох, как же так, ты сломал мои волшебные детские миры, как ты мог!?
Вот так-то, сучки, знайте своё место!
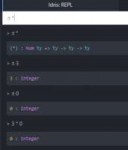 8 Кб, 290x338
8 Кб, 290x338>3 x 0 = Как вы думаете, что должно быть здесь? Да то же, что и слева!!!
>но как же так, ведь все математики говорят, что на ноль можно умножать и получим ноль.
>Да они в жизнь этого не докажут!
Пикрелейтед доказательство. А теперь ты докажи, что оно неправильное.
По определению.
A + 0 = A. Это АКСИОМА
Деление на нуль, это исключение из правил.
Оно порождает парадокс.
И чтобы решить его, вводят аксиому,
A×0=0
Есть другой парадокс[который решается договором], например умножение отрицательных чисел.
-5 × -4.
По определению, нужно взять -4 раза -5 и добавить. НО КАК МОЖНО ДОБАВИТЬ ОТРИЦАТЕЛЬНОЕ КОЛ-ВО РАЗ?
И сайты объясняют, ЭТО СДЕЛАНО ДЛЯ УДОБСТВА. ЕБ ТВОЮ МАТЬ. ВВЕЛИ НЕВОЗМОЖНОЕ, ДЛЯ УДОБСТВА, БЛЯДИ. РАДИ ЗАКОНА ДИСТРУБУТИВНОСТИ
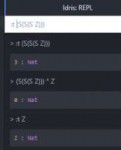 6 Кб, 218x269
6 Кб, 218x269Точнее, так, чтобы с натуральными числами.
Таблетки выпей. Твоя манятеория ломается уже на -3 палках, поэтому дальше можешь не продолжать. Кроме того, выше уже сказано, что твое маняопределение натуральных чисел противоречиво. Т.о. вся твоя шиза не нужна.
А теперь покажу вам математический фокус и математическую шизофрению.
Как из ничего получить чего? Самое натуральное волшебство!
Лицезрейте и боготворите!
0^0 = 1
Апофеоз дегенерации и Анталогия шизофрении.
>0^0 = 1
Нихуя ты дебил братишка, царствие те небесное. Не 0^0 а (0, {0}} тогда уж, если ты об ординалах фон Неймана. Ну или (S Z) в теориях типов. Короче, из всего, что ты высрал, можно сделать только один вывод - ты вообще нихуя не понимаешь в том, о чем пытаешься рассуждать, поэтому рассуждения твои на уровне детского сада максимум.
Мань, но там не было ничего. Суть ординалов фон Неймана в том, что пустое множество - это 0, но т.к. оно одно, то {0} - это множество, один единственный элемент которого - пустое множество. Т.е. пустое множество пусто, но оно одно, поэтому {0} - одноэлементное множество, содержащее пустое множество, т.е. 1. Далее, добавим в это одноэлементное множество еще одно пустое {0, {0}}, тут уже множество, содержащее два элемента (пустых множества). И так далее. Я просто непонимаю, каким нужно быть чучелом, чтобы не понять суть ординалов фон Неймана, это же просто как 3 копейки.
Бесплатная энергия, нароооод!
Этот прав, Кантор считал множеством только такие совокупности, что для любой вещи в мире можно сказать принадлежит ли она, а впрочем похуй, всё это тысячу раз обсуждалось.
1 - 1 = "ничего"
Какой вариант более правильный?
3^2 : 3^2 = 1
3^2 : 3^2 = 3^(2-2) = 3^0
3^0 = 1
Какое классное доказательство.
Следовательно, 0 не "ничего". (это мы и так знаем)
А когда мы получаем "ничего"?
3 - 3 = 0 на бумаге (где 0 число).
3 - 3 = "ничего" в реале (где "ничего" не число, вообще не посчитать полное утсутствие чего-либо).
Выходит, что всё что мы знали о математике из школы, институтов и интернета, всё полная ложь!
Может, уже кто-то раскрыл её.
0^-1 x 0^1 = 0(-1+1) = 0^0
0^-1 x 0^1 = 1/0 x 0 = 0/0
не факт, что можно делить
Я нет.
Ноль раз чего-то это "ничего".
x^0 = "ничего"
в данном случае не могут.
ноль раз чего-то это "x умножить на 0", сути не меняет.
x^3 = xxx (умножение) - три раза перемножаем х
x^2 = xx - два раза перемножаем x
x^1 = x - один раз "перемножаем" x
x^-1 = 1/x
x^-2 = 1/(xx)
А x^0 это с каких-то хренов 1.
x^0 - ноль раз "перемножаем" x, кто сказал, что это 1?
Откуда взялся этот 1? Почему мы должны не просто умножать x количество раз, которое соответствует степени, но и умножать всё каждый раз на 1?
Смотри.
a^x. Объект x показывает, сколько нужно записать a.
Например:
a^3 =aaa
2^3 = 2×2×2
Пусть a` будет противоположность a.
Тогда a×a`=1, подобно как (+a) + (-a) = 0.
Запись a^(-x). Тогда объект (-x) показывает, сколько нужно записать a`.
0 является, ни положительным, ни отрицательным. Сам себе противоположен.
Мы знаем, что x^1=x, но, что если мы запишем ноль раз, т.е x^0? Должно быть ноль? Но тогда, как записать x^0 x^2?
Если x^0 x^2 = 0 × x^2 = 0.
Получается, мы вначале записываем x 0 раз, а затем два, но получаем ноль!!!
>Кто верит, что ноль раз по x (x^0), это 1 в реальности?
>Я нет.
Мощность множества A - это то, сколько в нём элементов.
В множестве A n элементов, тогда это записывается |A|=n.
Множества называются равномощными, если в них одинаковое
количество элементов.
Функция f задана на множестве A со значениями в B, если каждому a из A поставлено
в соответствие b из B.
Если представить, что мы не умеем считать, но умеем рисовать стрелочки,
тогда |A|=|B|, если между ними существует взаимно-однозначное соответствие.
Вместо сложения чисел, можно объединять непересекающиеся множества и смотреть
их мощность.
Ну это так, отступление неважное.
Пусть |B|=b и |A|=a. Тогда ab это мощность множества функций из B в A.
Тогда для любого a) x0=1 и если x ненулевое, то b) 0x=0.
a) По определению, это множество отображений из пустого множества в какое-то
множество X. В пустом множестве нет ни одного элемента, которому функция не ставит
соответствие. Поэтому существует функция из пустого множества в любое другое.
Она единственна, потому что иначе f(x)!=f(x), но это не так.
b) Опять же по определению, это множество функций из X в пустое множество. Но функции
нечего сопоставить любому элементу х из Х. Поэтому множество функций пусто.
>Кто верит, что ноль раз по x (x^0), это 1 в реальности?
>Я нет.
Мощность множества A - это то, сколько в нём элементов.
В множестве A n элементов, тогда это записывается |A|=n.
Множества называются равномощными, если в них одинаковое
количество элементов.
Функция f задана на множестве A со значениями в B, если каждому a из A поставлено
в соответствие b из B.
Если представить, что мы не умеем считать, но умеем рисовать стрелочки,
тогда |A|=|B|, если между ними существует взаимно-однозначное соответствие.
Вместо сложения чисел, можно объединять непересекающиеся множества и смотреть
их мощность.
Ну это так, отступление неважное.
Пусть |B|=b и |A|=a. Тогда ab это мощность множества функций из B в A.
Тогда для любого a) x0=1 и если x ненулевое, то b) 0x=0.
a) По определению, это множество отображений из пустого множества в какое-то
множество X. В пустом множестве нет ни одного элемента, которому функция не ставит
соответствие. Поэтому существует функция из пустого множества в любое другое.
Она единственна, потому что иначе f(x)!=f(x), но это не так.
b) Опять же по определению, это множество функций из X в пустое множество. Но функции
нечего сопоставить любому элементу х из Х. Поэтому множество функций пусто.
ты чего сказать то хотел?
Ой дегрод... 0 это 0, {0} - это множество, содержащее один элемент - одно блядь пустое множество, единственный 0. Т.е там один элемент, пидор ты, ну что тут непонятно-то, маня?!
 18 Кб, 657x539
18 Кб, 657x539> пошёл нах уёбок, ноль есть ноль
Ноль может быть элементом множества, и тогда элементов будет уже не ноль а один. То, что ты этого не понимаешь, доказывает только то, что ты еблан. Это проблема твоей безмозглости, а не математики, что бы ты там о себе ни возомнил.
пиздец дегенерат один элемент, который равен нулю, у тебя становится равен 1, еблан.
мм, путать порядок со значением. Это тред дебилов?
 175 Кб, 1748x985
175 Кб, 1748x985> пиздец дегенерат один элемент, который равен нулю, у тебя становится равен 1, еблан.
Маня, ты сам почитай, что написал. Ключевое слово - один элемент. Один равен одному, проснись, хуйлопанушка. Ноль равен нулю, и я нигде не утверждал обратного. Понял, нет, чучело?
ИДИОТ, КАКАЯ РАЗНИЦА СКОЛЬКО ЭЛЕМЕНТОВ, ЕСЛИ ОНИ ВСЕ НОЛЬ И БУДЕТ НОЛЬ, ГЛАВНОЕ ЗНАЧЕНИЕ!!!
3^4 - возьмём 4 раза по 3 и перемножим их между собой.
0^0 - возьмём 0 раз по 0 и перемножи их между собой.
Как может получиться 1 ?
Легко обобщить эту формулу для любой степени.
Возьмем, например, y=0. Тогда отсюда (да и не только) для алгебраистов возникает желание определить 0^0=1.
Оп, читай до тех пор, пока не поймёшь http://lj.rossia.org/~dmitri_pavlov/11307.html
и не еби приличным людям мозги зачем вы его вообще кормите
> ИДИОТ, КАКАЯ РАЗНИЦА СКОЛЬКО ЭЛЕМЕНТОВ, ЕСЛИ ОНИ ВСЕ НОЛЬ И БУДЕТ НОЛЬ, ГЛАВНОЕ ЗНАЧЕНИЕ!!!
Ну ты и еблан... Само количество, если оно не нулевое, не может быть равно нулю, тупое ты хуйло. 10 не может быть равным нулю, тупень. Открой для себя понятие ординала, школьник тупой. И не пиши всякую хуйню, если вообще не в теме. Вместо того, чтобы кукарекать, лучше разберись в теме, говно.
> значит 0 - это когда нет количества?
Чего угодно, в том числе и количества. Если множество непусто и содержит элементы, этих элементов сколько-то, безотносительно их содержания. Ну и уже говорилось, что 0 это конструктор типа с определенными свойствами, а не какая-то пустота в буддистском или каком-то ещё смысле. Школуйня элементарных вещей не понимает, поэтому и шизеет на ровном месте.
>Математика не ограничивается конструктивной
Вместо типов тут уже сто раз упоминали ординалы фон Неймана.
x^0 = x
0^0 = 0
Отличие от ^1 заключается в том, что там мы возвели в степень, а при ^0 в степень не возводится и всё остаётся по прежнему.
Спорить нет смысла, обратное вы не докажете. А доказывать предстоит реальными примерами, а не теоретическими.
> Но {} это 1
Это пустое множество, ноль. И элементов там тоже 0. Один - это число элементов в одноэлементном множестве {0}.
> Пустое это пробел, а { } это 1.
Пиздец даун. Ты хоть учебник почитай, нотацию посмотри прежде чем лезть спорить, школотрон. Вся суть школуйни, нихуя не знают, но своё ценное манямнение имеют по всем темам.
 182 Кб, 640x480
182 Кб, 640x480Попался.
Как получить x?
(x^n)^1/n = x^(n/n) = x^1
Эта формула должна работать для любого числа.
А теперь подставляем ЧИСЛО "0":
x^0 = 1
x = 1^(1/0) - получаем деление на ноль, и это не неопределённость.
x = (x^0)^(1/0) = x^(0/0) - а вот тут уже неопределённость.
При этом они равны. И получается, что делить всё-таки нельзя. Но как так, если должна сработать наша формула для любого числа?
А вот так, "0" не число!
Число "x" в степень число "0" возвести можно, а обратно получить начальное число "x" нельзя, это просто смешно.
x/x = x^(1-1) = x^0 = 1
А теперь ничего поделим на нечиго и что же мы получим? Мы получили ничего, вместо 1, чистое волшебство ваша математика.
А пока всё указывает на то, что 0 - это всё же что-то, а не ничего.
И как вы заметили ничего легко делится на ничего в реальности. С нулём же мы получим неопределённость в лучшем случае (смотря какой пример), а в худшем мы не сможем поделить из-за деления на ноль.
А теперь возникает ещё один вопрос, можем ли мы в реальности поделить что-то само на себя и получить 1?
И речь тут идёт не о подсчёте вещей, а об операции деления. Как можно поделить один камень на один камень?
Он же не делится.
А раз он не делится, тогда и в степень "0" никакое число не возводится.
x/x = x^0
x/x - не делится.
x^0 - в степень ноль не возвести.
Заметьте, когда мы сравнили две кучи камней поделив их друг на друга (допустимые значения), в итоге мы получили не реальные камни, а абстракционное число.
Это, наверное, и есть корень проблемы.
Когда мы работаем с реальными объектами у нас одни правила, а когда мы переходим в мир абстракций, там уже можно практически что угодно. Единственное ограничение - ваше воображение.
И разумеется, ни одну реальную задачу нельзя решать абстракциями и реальное устройство мира нельзя будет описать ни одной абстракционной теорией.
только заменим "абстракционный" на "абстрактный".
Абстракции
Абстрактные числа
Абстрактные модели
Абстрактные теории.
>чтоб существовал элемент, у которого нет предшественника,
То есть нулем может быть что угодно? 1, например.
Докажи, агрессивная школота.
 31 Кб, 604x408
31 Кб, 604x408В реальности, когда мы делим камни на камни, мы получаем абстрактное число, а не камни.
Когда камни умножаем на камни, мы получаем абстрактные камни в квадрате (и в других степенях).
Камни в степени - умножение.
Когда мы умножаем камни на абстрактное число, мы почему-то получаем камни, хотя явно, что мы не имели права умножить камни на "вкусный", например.
Аналогично с делением и степенью, сложение, вычитание, да всё.
А вот сложить (следовательно и отнять) камни с камнями можно без проблем.
А как же абстрактные числа?
Абстрактные числа при умножении дадут степень:
2 x 3 = 6 абстрактных_чисел^2
итд
Камни делим на камни, получаем ач.
Следовательно, что? Знаменатель, т.е. камни, умножим на результат ач и получим, что это = камни? Херня какая-то.
Значит камни на камни не делятся!
Мы не можем умножать камни, только складывать.
6 камней разделить на три равные части.
Получится две группы камней по три в каждой.
6 камней разделить на три равные камня.
Как мы можем 6 камней превратить в 3 камня
Точнее, как получить камень-группу камней, а не число-групп камней.
 273 Кб, 700x400
273 Кб, 700x400Ты почти догадался.
Говоря о сложении камней вы так же складываете не камни, а их количество. Камень+камень вы не определили, вы определили только количество(камень)+количество(камень)=количество(камень, камень).
Поэтому все невероятные тождества, типа x0=1, нельзя распространить на камни.
Если представить, что камни — это векторы.
То, сложение камней образуют кольцо.
Но линейное пространство всегда стоит над полем скаляров.
Тогда, умножение/деление будет умножение и деление на скаляр.
Т.е вектор в данном контексте, — это "число" с единицей измерения. Например, количество камней.
А скаляр, это некие абстрактные "числа", которые можно использовать
Рекомендую назвать нулем элемент, у которого нет предшественника, а единицей - тот, который следует за нулем.
Это всё понятно, но делить камни на абстрактное число, это как камни поделить на яблоки.
А если можно подсчитать отношение камней к яблокам, тогда можно и умножать камни на яблоки, но как умножить камни на яблоки в реальности?
я об этом и говорю
Мы обязаны использовать тип объекта.
Но не нужно путать "античисла" с другой шизофренией вроде "противочисла", т.е. что-то диаметрально противоположное числам. Таких штук бесконечное количество видов даже.
А когда возводим, что-то реальное в степень "ничего" ("0"), при условии, что у нас уже что-то было, тогда мы и получаем это то, что у нас было (если было ничего, тогда остаётся ничего), т.к. возвести в эту степень нельзя.
Но есть и другой вариант, когда мы что-то (отличное от "ничего") собирались получить, но это было только в теории и мы эту теорию возвели в степень "ничего" (0), тогда у нас ничего и не появится. Т.е. когда решаем реальные задачи и примеры нужно ещё прослеживать, где у нас реальные, а где теоретические числа.
Возьми множество, удоволетворяющее моим условиям, и для каждого элемента кроме нуля заебашь еще один элемент, например соответствующий элемент для 1 назовешь -1, для 2 назовешь -2 и так далее.
Умножая камни на яблоки, получаем новую единицу измерения.
Деля перемещения на время, получаем скорость.
Определяем отрицательные, как противоположные положительным. На базе операции "сложение".
Умножая камни на яблоки, мы никакой размерности не получаем кроме "камни x яблоки", и само умножение не происходит, потому что в реале мы не можем получить такую штуку, как камень-яблоко, поэтому умножение и не идёт.
Где в реальности ты видел время?
>Т.е. ряд натуральных чисел начинается с "1", а не с "0" и не с "ничего".
Мань, у немцев ряд натуральных чисел и так с 1 начинается, это французики ебанутые туда ноль всрали.
Дай определение "натуральности", что ли.
Разделяя тесто на вишни, получаем количество пирожков с вишнями.
Я вот тут Бояршинова процитирую: вот пошли мы по грибы, взяли с собой три корзины, в лес зашли и испугались медведя, одну корзину даже потеряли. Сколько грибов мы собрали?
Вот это да!
А сколько у нас грибов в первой корзине? Тоже нисколько? А во второй? А сколько в первой и второй? Нисколько плюс нисколько получается тоже нисколько?
Мань, меня совершенно не ебут твои лингвистические выебоны, иди об этом с Витгенштейном спорь.
Ты сам выше назвал какое-то явление "нисколько", вот и используй его в математике.
Что такое "жётский анализ" и чем он отличается от "мягкого"?
>Сумма пустого множества чисел есть 0.
>Произведение пустого множества чисел есть 1.
Смелое заявление.
мимо-алгебраист
Чему там будет равно произведение пустого множества элементов кольца без единицы, ммм?
ну оно будет просто не определено в кольце
Зато они образуют semiring.
По факту так и есть в математике чаще всего применяются абстрактные модели и некоторые теоремы доказываются лишь через несколько веков после их открытия, да что там вспомните хотя бы Лобачевского, с его утверждением о том что 2 параллельные прямые могут пересекаться
Объясняешь прям как чиновники говорящие о повышении зарплаты
Ты идиот? Параллельные прямые не пересекаются по определению. Лобачевский в отличие от тебя идиотом не был. Он вывел теоремы геометрии исходя из отрицания пятого постулата, а не то, что ты написал.
А как можно всё это заменить чем-то универсальным?
Да. Использовать буквы вместо чисел.
Операции для нуля отдельно определены просто, долбан. Забыл учебник по которому к зимней сессии готовился, но там был вывод "определения" натуральных чисел через теорию множеств. Так там сначала рассматривались 1, 2 ... n, а потом 0 добавлялся.
мудак, ещё больше мудацких учебников уровня букварей почитай, опущ, будешь таким же защеканским хуесосом, как и 99% матемпидоров.
1) Есть двухмерное пространство и в нём у нас две параллельные прямые
2) Добавляем третье измерение, и в этом третьем измерении одну прямую или обе сразу поворачиваем так, чтобы они пересекались.
Короче говоря, прямые будут пересекаться, но сбоку будет казаться, что они параллельны, вот вам и вся геометрия Лобачевского с его пересекающимися прямыми.
И так понятно, что если начать городить, да ещё и пространства искревлять, блядь, чего только не произойдёт в таком пространстве. Но кого это ебёт, если к реальному миру это отношения не имеет?
кого ебёт реальный мир?
>Параллельные прямые у Лобаческого пересекаются
Ты опять выходишь на связь?
Ну не пересекаются прямые у Лобачевского, сука! Если 2 прямые параллельные, то они не пересекаются, это определение такое. Если прямые пересекаются, то они не параллельные.
У Лобача для каждой прямой и точки существует несколько прямых, проходящих через точку и параллельными данной прямой. У Евклида только одна прямая, у Лобача несколько прямых.
Зато, любые паралельные прямые пересекаются в проективной геометрии, на бесконеночности.
Нет, он даун не поэтому. Он даун, потому что попытался ответить тебе осмысленно, а тебя надо было просто сразу нахуй слать.
в проективной геометрии любые 2 прямые пересекаются
ОП, что про категории думаешь? А про пучки?
Я говорю с ОПом. Если ты оп, то подтверди это, если нет, то я не хочу с тобой говорить.
Запрашиваешь подтверждение, прям как коллектор.
Опровергать нечего, про них нет ни одного содержательного утверждения. Все эти «категории являются частным случаем пучков» и «этониматематика» местного пыни все это не более чем тугой шизофренический бред, миммикрирубщий под ворох аксиом и определений, из которого никаких ощутимых следствий нет
>про них нет ни одного содержательного утверждения
Действительно. Тоже считаю анализ и алгеом не содержательным.
Я бы послушал про то, как функтор является частным случаем вероятностного пространства.
Что за бред я только что прочитал? Это психобольные написали?
Что тебе непонятно?
Далеко не любой функтор является вероятностным пространством, т.е. объектом вероятностного топоса. Это понятно интуитивно, так как произвольный функтор не обязан сохранять локальную структуру твоего пространства.
А строго это следует из частного случая известного результата Гротендика, который говорит нам, что только функторы имеющие открытое покрытие многообразиями в гладкой топологии (т.е копроизведение всех гладких отображений покрытия будет локальным диффеоморфизмом) являются пучками на вероятностном сайте.
>>9819
ZFC в математике обычно не рассматривается, слишком слабая система даже для описания категории функторов из гладкого топоса алгебраических пространств в категорию категорий.
В каком плане?
ты прав, если автор сначала определил "морфизм между (малыми) категориями", а потом пишет
>Функтор — особый тип отображений между категориями.
то он хуесос, и ему надо ссать в лицо.
Если же он понятие "морфизм между категориями" не определил, хули он пытается что-то с его помощью объяснить? так делает только обоссанный хуесос
Мы доказали, что автор хуесос, ему надо нассать в лицо
Тебя интересуют конечно-мерные ассоциативные алгебры с делением. Их всего три, что лучше всего доказывается в топологии
это всё частные случаи пучковых фашистов, кроме планеметрических. последних правильно называть евклидовыми фашистами
ой, дурак
Книжка Милнор-Сташеф, характеристические классы. Ещё это доказывается с помощью К-теории, но ссылок не подскажу.