 324 Кб, 499x713
324 Кб, 499x713Вопросы вот какие - возможно ли это вообще? Что такое функтор между двумя играми? Если игры не укладываются в категории, возможно ли шагнуть ещё дальше в абстракцию?
Ты спросишь, анон, зачем я задаюсь такими глубокими вопросами на матаче? А у меня вот есть такая интуиция, что анонимная организация общения может дать свои плоды, которые академическому миру и не снились. Тут мы освобождены от гнета авторитета, вопрос поставлен, давайте посмотрим куда это нас приведет.
>вторая культура
Это довольно бессмысленное выражение, ведь она в математике только одна.
Просил же без теории игр. Она, внезапно, изучает стратегии в играх, а не сами игры.
Под теорией игр понимается изучение функторов между играми, а то есть изучение самих игр. Стратегии естественным образом дают теорию когомологий игр, что и изучается классически.
лол, это какой-нибудь генератор рандомных статей?
Вот основная проблема, мне кажется, именно в последнем, в концепции того, что игра задается стратегическим выбором, что это какая-то статичная структура. А давайте взглянем иначе. Пусть существования игрока достаточно, чтобы задать игру.
Конечно игра что в этом провокационного? Причем, игра в том числе и формализованная, так как это ещё и компьютерная программа. Ну и что теория игр нам может сказать о майнкрафте? А вот хочется иметь такую теорию, на языке которой можно говорить о майнкрафте, о патчах, о читерстве. Но при этом ещё и об игре актеров, о театре, о зрителе, о дваче и социальных сетях, в конце концов. То есть, хочется поймать эту абстракцию, которая объединяет всё вышеперечисленное.
Нет, подожди, ты не путай. Формализована не игра minecraft. Формализована программа "minecraft.jar". Сама по себе программа игрой не является, так как в такой "формализации" отсутствует субъект.
>хочется поймать эту абстракцию, которая объединяет всё
Ну... нутыпонел и так, наверное.
Игры в том понимании, о котором ты говоришь, изучает такая прикладная дисциплина, как геймдизайн. И там нет четкого консенсуса по поводу того, что считать играми. Тот же майнкрафт многие геймдизайнеры откажутся признать игрой, классифицировав его как песочницу. Обычно в "определение" не настоящее, а гуманитарное включают критерий наличия цели, а если цели нет, то это и не игра. Происходит это оттого, что если цель (и соревновательность, например) есть, то понятно, что нужно балансировать, можно записать циферки и получить некую понятную систему. Если же цели нет, то получается, что настоящей "целью" "игры" является тупо получение игроком удовольствие, а формализация этого понятия - дело нейронаук и всяких психологий.
Так что давай ты попробуешь мне объяснить, что ты вообще понимаешь под словом "игра".
Языковая игра.
Так я же уже дал определение, игра - это существование игрока.
Четкого консенсуса у геймдизайнеров и не будет, иначе их и не нужно столько будет )
Цель игры тоже помещается в понятие игрока, я пока не хочу забегать так далеко вперед. Мы же ищем категорную интерпретацию, а значит начинаем с самого абстрактного.
Если выразим игру через категории - это получится само собой.
Это не определение.
>Мы же ищем категорную интерпретацию, а значит начинаем с самого абстрактного.
Это бессмысленный набор слов.
Это же не Теория Всего, я просто предлагаю согласиться с очевидной вещью - без игроков игры немыслимы. Но вот действия игроков, и даже раньше - существование игроков - это можно в той или иной степени формализовать. Я понимаю, что всем привычней думать об играх как о структурах с заданной наперед целью. Но тогда целый пласт явлений, которые как мне кажется игровые по сути, остаются вне осмысления - когда цель формируется в процессе игры.
>игры без игроков немыслимы
Я тебя понимаю, но что есть игрок? Определи игрока как-нибудь, тогда можно через него игру определить. Алсо
>В любой игре всегда есть соперник и всегда есть жертва, вся хитрость — вовремя осознать, что ты стал вторым, и сделаться первым
>но что есть игрок?
Вот как мне видится, процесс формального ответа на этот вопрос - это и есть категоризация той или иной игры. То есть в каждом случае мы отвечаем на этот вопрос заново. В классических примерах теории игр, игрок - это набор стратегий. В примере с майнкрафтом - всё сразу НАМНОГО сложнее, но с ходу можно выделить первого игрока - это сам Нотч, созидающий игру игрок.
Интересно, то есть ответ на вопрос кто такой игрок и есть полное описание игры? Интересно.
Понял меня, няша :3 Вот, а язык категорий имеет понятие функтора - "стрелки" между категориями. То есть, можно будет раскрывать такие темы, как меняется игрок при переходе от одной игры к другой (в классической теории игр это не решается вообще)
Ответ на вопрос Кто Я? и есть полное описание мира. Ты меня загрузил.
Есть два игрока, задача каждого из них определить второго игрока и в то же время не дать определить себя. То есть как только враг тебя пытается описать ты должен измениться, иначе тебя полностью опишут и ты проиграешь. Что это будет за игра?
>Есть два игрока
Что такое "игрок"?
>определить
Что такое "определить"?
>Что это
Что такое "игра"?
А если тоже самое, но игрок один? Игрок выиграет, когда полностью себя опишет, игрок проиграет, когда полностью себя опишет. Описывая себя, узнавая своё новое свойство игрок одновременно изменяется и усложняется. Поэтому процесс будет продолжаться бесконечно.
>Что такое "игрок"?
Некая структура, динамический набор аксиом, два таких набора, описывающих два неких процесса, которые могут менять чужие аксиомы. Изначально есть два набора аксиом, описывающих работу с текстом, игроки могут работать с текстом, могут изменять аксиомы друг друга, изменять свойства. Цель игры сделать так, чтобы процесс прекратился, полное описание то есть.
Круто. Думаю да, ведь игрок не обязан являться игроком. Следовательно если попытаться определить, то игра сразу же закончиться. Это только если игроку интуитивно ясно, что он на самом деле является игроком.
В противном случае всё намного сложнее.
>Некая структура
Что это?
>набор аксиом
Такое в математике не изучается.
>неких процесса
>менять чужие аксиомы
>работать с текстом
>игры
Что это? В твоём тексте ни одного внятного определения.
Ты прям настойчиво хочешь чужих определений, ты правда не умеешь двигаться без них? Я так не думаю.
Структура, ну как кольцо, группа, поле. Структура. Нужно придумать такую структуру, которая могла бы изменять свойства объекта, переписывать его аксиомы. Например какой-нибудь забывающий функтор превращает одну структуру в другую посредством деформации набора аксиом.
Непонятно, какие именно свойства должна иметь категория игр. Если нет даже этого, то это уже что-то вне математики.
>>36959
>ну как кольцо, группа, поле
Они не являются структурами. Это лишь объекты некоторой категории, для которых существуют определённые морфизмы и имеет место коммутативность определённых диаграмм.
>Нужно придумать такую структуру, которая могла бы изменять свойства объекта, переписывать его аксиомы.
Функторы придуманы уже давно.
Алгебраические структуры, алгебраические системы. Почему не являются?
>какие именно свойства должна иметь категория игр
Возможность изменять свои свойства, добавлять и удалять новые свойства.
>я в этом не шарю, категории, функторы
Может тогда почитаешь начальные учебники по математике перед посещением доски по ней?
Этот набор слов не имеет смысла. Что такое "изменение" или "удаление" свойств категории? И как она может это делать "сама"?
Была одна категория, стала другая.
>сама
коммутативность, например, буквы сами могут переставляться.
Что может делать игрок это аксиомы, что может делать игрок и есть правила игры, и есть игра. Например можно переставлять буквы, можно раскрывать скобки, это будет одна игра. Ещё что-то другая игра. Нужно, чтобы эти объекты были одного рода. Два игрока. И чтобы они могли изменять друг друга. Как это сделать?
Можно так, например, два игрока, два набора аксиом, первый игрок доказывает какую-то штуку своим набором аксиом и эта штука автоматически становится истиной для второго игрока, второй игрок уже с этой штукой может доказать ещё что-то для первого игрока и так повторяется, пока у какого-то игрока не получится противоречие, тогда он проиграл.
>Была одна категория, стала другая.
Это не имеет математического смысла. Каким образом это является доказуемым "свойством" категории игр?
>коммутативность
Коммутативность (в кольце, например) это существование определённой коммутативной диаграммы, причём тут переставление букв?
>>36968
>>36969
Это что-то вне математики.
>Это что-то вне математики.
Вот и я думаю, что игры вне математики. Так же, как и логика вне математики. Теория категорий тоже вне математики, кстати. Но соприкосновения есть.
>Теория категорий тоже вне математики, кстати
Она используется примерно в 99% математики. Математика теперь вне математики?
Но категории - на 99% математика, как ты писал выше, так что категоризацию игр тут можно обсуждать.
>Но категории - на 99% математика
Я писал, что теория категорий используется примерно в 99% математики. Значит есть всего примерно 1% математики, где она не используется.
Не понимаю, как ты вывел из этого то, что у тебя выше. В любом случае, она является областью математики, так что на 100% состоит из неё.
Просто у тебя нет фантазии. Как можно быть математиком и не иметь фантазии? Не хотеть мечтать?
Давайте полный текст напишем и в архив
И что же он имел?
>залётные обыватели нахватались умных слов и теперь хочут казаться умными
Это. Хуже пидорасов.
Внезапно, тут есть о чем порассуждать. Вот ребята делают нескушный видос для своего канала. Как тему выбирают теорию игр, берут пару каноничных примеров. Но если спросить строго, как они решили эти игры? Они упоминали Нэша, но они не использовали его метод. Вместо этого они явно задали игроков, установили между ними отношения, и именно эти отношения решали игры, причем одни и те же игроки переходили к разным играм, эти переходы и приводили к решениям.
>под объектами нашей категории игр подразумевать игрока
Тут видно, что ты не понимаешь определения категории, а это примерно третий-четвёртый класс. Можешь сразу нахуй идти.
Она выражает собой идею естественных преобразований, а не "композиции".
Он вообще-то про тебя.
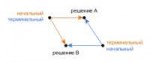 16 Кб, 345x147
16 Кб, 345x147Ну тут такое, на одну и ту же игру можно смотреть и как на игру одного игрока, а можно выделять в ней нескольких, если нужно - это позволяет двойственность категорий. Ну вот например способ решать игры без табличек.
Ну такое, мне это не видится центральным вопросом игр. Ну просто вибирай критерий, и если пришел к нему - значит выиграл. Меня заботит то, что всякая игра - это эпистемологический процесс для игрока.
Подумал тут, что математика это игра, в которой тебе даны некоторые правила (игры) и смысл игры в том, чтобы создавать из этих новые правила. И так делать до тех пор, пока изначальные правила себя не исчерпают. Тогда можно опять ввести новые фундаментальные правила и снова играть. Если так думать, то игра шире, чем математика даже.
Понятие игры в смысле.
Игра с образами с помощью языка. Структурированное воображение. Воображение по правилам.
Игра - это постоянное движение, значит и граф, описывающий игру, должен постоянно трансформироваться. К сожалению, картинки не умеют трансформироваться сами, но у нас есть воображение для этого.
У игрока по всем представлениям должна быть цель, обычно это цель выиграть. Но есть сотни игр-песочник, где выиграть или проиграть невозможно, ты просто открываешь мир, исследуешь игру, открыта новая локация=доказана новая теорема. А потом наступает момент, когда уже нечего исследовать.
Я бы клеточные автоматы тоже отнес к таким типам игр
Вы реально что-ли не понимаете что то что в естественном языке две разные вещи называются одним словом (это я еще не уверен в любом ли) то это еще совершенно не значит что где-то за этим есть математический смысл?
Вам в тред философии, в общем.
Все имеет математический смысл.
Математика — это наука, которую можно изучить не видев никакой мир вокруг.
А как же геометрия?
Как человек не познавши форму, может о ней размышлять?
Значит геометрия — раздел физики.
Человек должен удостовериться в возможности линий.
В существования графической науки не прийти.
Тогда остается только алгебра?
Все ли есть концепты для возможности ее понимания?
Если есть субъект, то есть и алгебра.
Алгебра выходит из субъекта.
Ведь, можно понять, что единственный, что может быть много меня. Что есть нечто, где меня нет. Что я могу иметь определенные отношение к другим я.
Хаха. Ошибаешься. Чтобы познать "много", нужно видеть то, что вещи могут быть не единственными.
Арифметика не математика.
Чтобы познать "отличное от меня", нужно иметь такой опыт, созерцать такое.
Алгебра — это изучение структур и их отношений.
Когда единственный субъект — ты.
Ты узнаешь ограниченное кол-во алгебр.
Чтобы узнать про эквивалетность, нужно получить опыт, когда вещи различаются
Чтобы узнать преобразование, нужен опыт.
Конечно, кроме того, что в результате бездействия ты становишь самим собой.
Биология ничем не отличается от математики, в этом плане.
Биологии не существует.
>Все имеет математический смысл.
>
>Математика — это наука, которую можно изучить не видев никакой мир вокруг.
Из второго утверждения (вне зависимости от его правдивости) не следует первое. Как видим, лично тебе бы не помешало видение мира, а то совсем никакой математики не знаешь. Или лучше философией тогда уж занимайся.
>Как человек не познавши форму, может о ней размышлять?
Поседи в полной темноте пару дней - начнешь такие формы видеть, что свое очко проиграешь. В том то и дело, что формы возникают из самого человека.
Я не смогу разделить с тобой твою радость, анон. Сейчас голова совсем занята другим, к сожалению.
Да вот, один из интересных вопросов об играх. Инициатива задана наперед, не меняется в ходе игры - что это дает?
Всегда выигрывают. Доказывается тривиально, так как белая пешка является симплициальным объектом в категории схем.
>There’s still an unfortunate stigma against addressing mental health in academia, and I’m going to try to do my part to break it here: I would unquestionably not have finished my Ph.D. without therapy for anxiety and depression. Thanks to Dr. W for her incredible skills.
>My mother has been the one constant in my life, and she has made her love known the whole way. Growing up, my “village” consisted of grandparents, aunts and uncles, teachers, and my mother’s romantic partners, all of whose love and guidance deserve my profound thanks. But my mother shaped who I am today more than anyone else; it’s hard to thank her without a touch of narcissism. Mom: thanks for showing me how to be fearless, opinionated, independent, creative, hard-working, vulnerable, selfless and
selfish (as the situation warrants).
>Finally, while it is clearly possible to be a successful academic without a partner who shoulders a large burden of domestic and emotional labor, it is abundantly clear to me that Rob’s efforts to be an equitable and generous partner to me while juggling his own teaching career have made a huge dif-
ference in my productivity, creativity, and happiness. And furthermore, I am
in the rare position to have a partner who understands and enjoys my thesis work, even to the point of putting up with my rambling about narrative structure after every television show, movie, and play we see together.
Что это за хуйню он написал? Там так принято, что ли, такое дерьмо в дисер вставлять? Мрак какой, совсем ебанулись
Игра есть добровольное действие или занятие, которое осуществляется в определенных временных и пространственных границах с свободно принятыми, но абсолютно обязательными правилами, имея ограниченную собственными рамками цель и сопровождаясь чувствами напряжения и радости, а также сознанием пребывания в «другом бытии», отличном от «повседневной жизни». По нашему мнению, определенное таким образом понятие игры способно охватить все, что мы у животных, детей и взрослых называем «игрой»: соревнования на силу и ловкость, игры на выдумку, на отгадывание, азартные игры, всевозможные показы и представления. Мы осмелились назвать игру одной из найфундаментальниших категорий жизни.
Я к тому, что никто не познал математику чисто по книгам. Всегда есть инициация, фигура учителя, который производит неформальное введение в очко математику. А после этого уже можешь кукарекать про формальные системы сколько хочешь.
Да я понял тебя, я не имел ввиду формальность в смысле формальных систем, я имел ввиду формальность как в миру говорят, формальное общение, неформальное общение, ты понял. Есть очко, есть дилдак, дилдак входит в очко, туда-сюда, ну и что, уравнение составлять? Как выиграть в эту игру, как проиграть? Что это такое с точки зрения математики? Какие-то ощущения, чувства, это всё вне математики, не сможешь ты это описать более-менее формально. Но это ведь игра, игра с очком. Вот я и говорю, что игры вне математики.
Ты нормальный?
Попа — ключ, условие по отношению к...
Партнер — объект.
Если для объекта А найдется такой объект B, для которого существует ключ C, то объект A доминирует над объектом B, а B подчиняется A.
Пусть, "∆" — символ страсти.
Тогда он станет аналогичной попой, требованием по отношению к возникновению подобных отношений.
Можно вводить понятия "продожительности акта", "удовольствия", "цели объектов", "любовные отношения", "сперма, член и прочая биология" Для хорошей формализации, следует писать целые трактаты. Связей ключей и следствий будет много. Но примеры этой формализации, можно увидеть во всех компьютерных играх, которые содержат эти понятия. Чем больше ввести понятий, тем более общей.
Чтобы составить уравнение, нужно немного разбираться в алгебраической геометрии.
Если примерно, то, это множество кадров сопоставления движения + геометрическая форма, в зависимости от степени обобщения, можно представить, как элипс и тор. Иначе, использовать продвинутые методы анализа, использовать всякие интегральные, дифференциальные уравнения.
Классно. Я тебя обожаю.
Ладно, ты меня убедил. Игры внутри математики, но тут для каждой игры нужно будет придумывать своё описание, а как описать саму игру? Что есть общего у всех игр?
Смотри, ты можешь действовать различным образом. Делать разное. Это тоже самое, что "иметь разные стратегии". " Пользоваться стратегиями".
У тебя, могут быть разные потребности, желания. Это тоже самое, что и "разные цели игры".
Теория игр, это раздел теории операций. Операция — это действие.
Теория операций изучает возможные осуществимые действия, т.е все твои возможности. Все, чем ты можешь заниматься.
Общего у всех игр?
Тут нужно уточнять, но обычно применяется полный резервуар математических средств
Но, вообще, кроме цели и возможных стратегий, существуют игроки.
Игрок — это условно недетерменированная машина.
Другими словами, игрок может применять различные стратегии, и какую он нам приймет, нам неизвестно.
Всегда существует самая эффективная стратегия для достижения цели. Если игрок ей не последует, то дурочка, либо не ценит цель, либо из-за факторов она недостижима.
Выбор определенной стратегии, предлагает всегда трату ресурсов. Другими словами, выбирая что-то[и только одно], ты отрицаешь все другие варианты.
Игроки, всегда могут иметь ограниченное кол-во стратегий одновременно.
В играх всегда, используются множества для любых сущностей. А также теория вероятностей для любого поведения.
Еще, в играх, всегда используются[непроизвольным образом], такие разделы, как топология, анализ, алгебра. Шучу, на самом деле, НЕСУЩЕСТВУЕТ РАЗДЕЛА МАТЕМАТИКИ, КОТОРЫЙ НЕ ЗАТРАГЫВАЕТ ВСЕ ИГРЫ . И я даже больше скажу, АБСОЛЮТНО ЛЮБОЕ МАТЕМАТИЧЕСКОЕ ПОНЯТИЕ, СОДЕРЖИТСЯ В АБСОЛЮТНО-ЛЮБОЙ ИГРЕ.
В этом свете интересно выделить такую стратегию, как "попробовать все стратегии".
Нетрудно написать, что что-то затрагивает все понемногу, когда стоит четкая задача формализовать это. 0 усилия.
>Что есть общего у всех игр?
Только то что на русском языке они обозначаются словом "игра". В английском, кстати, уже не все так однозначно, потому что есть "game" и "play".
Довольно много верных утверждений формулируется с таким "модификатором". Например, только полный имбецил либо философ может искать скрытый смысл в случайных совпадениях одного из естественных языков, сложившихся спонтанно.
>Например, только полный имбецил либо философ может искать скрытый смысл в случайных совпадениях одного из естественных языков, сложившихся спонтанно.
Когда рассуждаешь о том, в чем ни ухом ни рылом.
Цитируй уж тогда все свои посты.
>из одного состояния стремится прийти к другому, по вариативному пути.
Не математика. В КА, например, нет никаких путей, а есть тройки ф-ии переходов.
Создание всегда более сложного ритма на выходе чем на входе
Т.е. степень усложнения
Показательно тут то, что игры есть, а с точки зрения науки - это пустышка (ты же тут от лица науки?)
Ну не дает современная наука нам языка для рассуждений об играх - приходится самим искать, щито поделать
Классический путь - формализовать несколько конкретных игр, потом искать общее в формализмах.
Та ну они уже все и так формализованы матрицей монитора. Различие в режимах, т.е. как читать матрицу. Ну и тут опять возникет игра между понятиями текста, изображения и символа.
 74 Кб, 360x570
74 Кб, 360x570>Ну и тут опять возникет игра между понятиями текста, изображения и символа.
Если возникает, то это не математика. И значит нихуя еще неформализировано
Вот теорема какая-нибудь, выиграть=доказать теорему, есть аксиомы преобразования текста=правила игры.
Боюсь, что твоё.
И это он перефразировал Гротендика. Ну и хули? Ты решил, что Рома - ровный пацик и ему можно верить и если он хуй достанет и скажет "сосать - это соль математики, ёпта", начнёшь хуй сосать?
Если что и отличает математиков, так это умение думать, ёпта.
Алсо, тут хуесос с "пуком", тоже уёбок, но он меня ваще не трогает.
>так это умение думать,
) и снова гуманитарии со своими терминами без определений и оснований.
Содержимое в математике, вприниципе непознаваемое, является суть мистичностью.
Вот, когда мы говорим "прямая", это может быть и любая кривая[на самом деле, все, что угодно], но главное, чтобы исполнялись свойства планиметрии. А вот, познание прямой, которую мы рисуем, является невозможным, мистичным.
И священные тексты SGA
Ты про научпоп пизданул чё-то, потому и сказал. Так я с ним согласен, причём тут верить/думать, просто наши мнения совпадают. Есть аксиомы, есть вывод из аксиом, всё остальное хуйня уровня физической интуиции. Текст не описывает объект, текст и есть объект.
Почему странно? Просто он меня понял, а я его нет.
>>37775
>содержимое
>это что?
>оно впринципе непознаваемо
Если содержимое непознаваемо, то какой смысл о нём говорить? Если оно впринципе непознаваемо, то как ты узнал, чем оно является? Хуйня какая-то, шизотерика, это потому, что нет никакого содержимого. Нет ничего, кроме символьной игры.
>легче принебречь содержимым, чем ОСОЗНАТЬ
>Содержимое в математике, вприниципе непознаваемое
И опять же, как ты собрался осознавать непознаваемое?
Линейная логика прикольна тем, что там есть знак "Par", о котором сам создатель этой логики говорит, что не может подобрать словесной интерпретации. Но это и хорошо, мы можем интерпретировать его как "непознаваемое".
Непознаваемое нельзя познать, всё, что мы о нём не скажем не будет им являться, я про это. О нём вообще нет смысла говорить. О чём невозможно говорить, о том следует молчать.
И опять же, символ-то есть, объекта нет. Тут нужен пример, когда объект есть, а символа для него нет. Например "нечто, невыразимое символами". Только что мы выразили его символами, значит это не оно. А что оно? Непонятно. Но разве такие конструкции имеют отношение к математике?
Для согласованности, через комбинации с другими символами можно делать логический вывод.
И что же? Мне вот нет. Понятно это нечто, невыразимое никакими словами, кроме этих. То есть это просто неопределяемое понятие. Точка это точка. А вот без приписки кроме уже непонятно.
>>37788
Ну так клёво, это совсем осмысленная штука, далеко не непознаваемое. Так-то и плюс можно описать только относительно операции сложения, через комбинации с другими символами можно производить вычисления. А что такое плюс сам по себе? Крестик вертикальный, я хз.
Где ты видел в математике операцию без определения над чем эта операция? С кем я сижу...
>Где ты видел в математике операцию без определения над чем эта операция?
>Так-то и плюс можно описать только относительно операции
О том и говорю. Символ плюса сам по себе ничего не значит, точно так же, как символ par, поэтому неудивительно, что его не смог тот чел описать.
>там есть знак "Par", о котором сам создатель этой логики говорит, что не может подобрать словесной интерпретации.
Так и про + можно сказать, в этом нет ничего удивительного. Понимаешь? Но у par есть смысл, это
>⅋ is called "multiplicative disjunction
>Для согласованности, через комбинации с другими символами можно делать логический вывод.
Поэтому он никаким боком не относится к непознаваемому.
В математике у символов есть смысл, а символы сами по себе неинтересны - можно заменить их любыми другими, в отличии от смысла.
В математике правила работы с символами, с текстом и есть смысл, запиши их другими символами ничего не изменится. Нет никакого содержимого/непознаваемого за этими правилами. Математика это язык.
А у символов смысла никакого нет. Символы имеют смысл только в контексте их применения.
>Символы имеют смысл только в контексте их применения.
Символы имеют смысл только в контексте смысла
Доказательства, впринципе невозможны.
Аксиома: A=A
1.Как доказать, что A=A?
Ты мудак? Аксиома A=A, значит, A=A.
2.Докажи, что из аксиомы A=A, следует, что A=A.
3. Аксиома — это факт, утверждение об истине.
Говоря, что A=A аксиома, мы говорим, что она истинна. Значит и A=A истинна.
...
616.Докажи, что говоря, что A=A истинна, A=A истинна.
617.Не говоря, а превозглашая!
...
4001.Докажи, что, если A=A истинна, то A=A истинна.
4002. Это же очевидно, из A=A, следует A=A!
...
8616. Из A -> A. Утверждение следует из самого себя!!!!
8167. Ты не сможешь это доказать.
...
10000. Ничего нельзя доказать, если не признать магию, процесс того, как мы
становимся быть уверенными, что при принятии A, следует А.
Нет, тут ситуация сложнее, чем с плюсом. Par известно над чем определен, тем не менее никто не смог ещё подобрать адекватную семантику. Мультипликативная конъюнкция - "могу взять/мне дадут А и В сразу". Аддитивная конъюнкция - "Могу выбрать между А и Б". Аддитивная дизъюнкция - "Мне дадут А или Б". Мультипликативная дизъюнкция (par) - "Ну хуй знает. "А и Б "сообщающиеся сосуды" (с) Жирар""
Если бы ты изучал основания,
Ты бы понял, что смысла нету вне символов.
А аксиомы утверждают об свойствах символов.
Известно, как с ним работать, с этим пар, известны свойства. ИРЛ интерпретация нахуй не нужна. В математике. Бытовая интерпретация. Ну пиздец. А КОКОЙ ФЕЗИЧЕСКЕЙ СМЫСЛ МММ?? ММММММ????!!!
Приведи контрпример
Это так. Доказательства невозможны без постулирования. Но я не понимаю, к чему ты это. Да, мы задаём правила игр, задаём структуру текста, затем мы можем его изменять внутри этого пространства и получать другой текст, тот, который нам нужно было получить.
Не понял, что ты имеешь ввиду.
Ну тут такое дело, если воспринимать математику как игру, то ты только что выбрал сдаться, проиграть. Ты выбрал закрыть глаза на семантику, и заниматься только синтаксисом (тем, чем компьютеры занимаются заведомо лучше тебя).
Если из A-> A, из этого не следует, что из A->A.[иначе бы требовалась осуществимая бесконечная цепь]
Следовательно, любые математические утверждения полагаются на интуитивную очевидность, магию.
Пример кубик Рубика или доказать, что A
U B U C U D=A\B U B\C U C\D U D\A U AПBПCПD это для n=4, а надо для любого n, пользуясь только свойствами разности, пересечения и объедигнения
>>37809
Нет, почему? Семантика и свойства символов, аксиомы, это одно и то же. Ты не описываешь абелеву группу набором аксиом, ты её вводишь, она не существует где-то там, а в тексте её отражение, она прямо в тексте, вот она.
>она не существует где-то там, а в тексте её отражение, она прямо в тексте, вот она.
пошла феласофия
Они принимают на веру, что существует выводимость из аксиом.
А если принимают, как аксиому выводимость, то принимают вывод выводимости из аксиомы выводимости
>аниматься только синтаксисом (тем, чем компьютеры занимаются заведомо лучше тебя).
Компьютеры не могут доказывать теоремы, они могут их только проверять.ну ладно, четыре краски, перебором решили, но это такое
Видимо, да. Или нет. Вывод выводимости, зачем на выводить выводимость, если это аксиома?
Потому что никто не может признать, что задача ему не по силам. А умничать хочется.
Нужно бесконечное кол-во аксиом выводимости, чтобы вывод существовал.
А бесконечность не может достигнуться
Другими словами с такой точкой зрения я вообще ничего не теряю, весь смысл уже записан, это и есть абелева группа, в этом её смысл.
>>37819
Так я с самого начала треда пишу, что игры вне математики, потому что математика сама является игрой.Хотя мне ответили тут, что даже игру с очком можно математизировать. Возможно игры являются математикой. Тогда игра и математика это одно и то же.
Зачем выводить выводимость, если она постулируется?
> вообще ничего не теряю
Даже больше, я абстрагируюсь от субъективного "понимания", которое на самом деле является упрощением, аналогией или ещё чем-то таким, интуиция вообще перестаёт действовать во многих случаях, полагаться на неё бредово. Интуитивно даже 4-мерный вектор не представишь. Можно цветом, конечно, кодировать, но понятно, что это уловка.
>Интуитивно даже 4-мерный вектор не представишь.
Представляешь как объект, который ведет себя под операциями неким образом.
>объект , который ведёт себя неким образом
Так это тоже самое, что и аксиоматическое описание. Объекта нет, зато есть свойства. Свойства=объект.
Нечто, "не имеющее свойств", звется объектом с пустым множеством свойств. А пустое множество имеет свойства.
/0
>свойства=объект
Да я ж вроде не разделяю. Это же ты стал писать про непознаваемое содержимое, которое кроется за аксиомами. Я топлю за то, что нет никакого непознаваемого содержимого объекта, объективная реальность, в то время как мы все субъективно мыслим, потому объект не познаваем, есть познаваемые аксиомы, они записаны символами, они определяют правила преобразования символов, правила символьной игры, пространство игры, ну как шахматная доска с тем, как ходят фигуры, блядь.
Я говорю о дед морозе. Дед мороз мужчина, с белой бородкой. У него есть свойства. Он существует?
Получается так. Как образ, часть народного эпоса, вот это всё. Хотя, ты же опять языком воспользовался, аксиомы деда мороза задал.
Ну на самом деле аксиомы белобородых мужчин, но не суть.
По-моему, это было очень в тему треда
Да я говорил уже, математика подмножество игр, с другой стороны анон выше писал, что игры, даже игры с очком, подмножество математики. Может математика и игра одно и то же? Действительно, есть правилы игры-аксиомы, есть цель игры-теорема, задача вывести теорему из аксиом.
>Математик Владимир Воеводский о своем мистическом опыте и "игре, хозяйкой которой является страх"
>хозяйкой
>страх
>смерти нет если бы была смерть то меня бы не было под смертью мы понимаем страх смерти
>Cowards die many times before their deaths
Зачем разделять? Ну, как нечто временное я такое разделение могу понять (для целей оубчения, например), но по существу - это тупой подход
Не знаю, для меня разные вещи. В математике нет времени, страха, других ограничений.
В математике нет Я, в общем. Для меня реальность проекция математики на несовершенное человеческое сознание. Я не шизик, честно.
пульсирующий анус
Ну, это как проиграть листу бумаги. Если этот лист - повестка в армию, то конечно можно подумать, что ты проиграл. В общем, я к тому, что за компом всегда стоит другой человек, как и за Теоремой Ферма стоит сам человек Ферма, и конечно же, математика - это всегда игра между людьми (даже если оба - это две твои личности, например). И те, кто (по)думают, что искусственный интеллект может быть обособлен от естественно стоящих за ним людьми - это и есть заведомо проигравшие. Это те лохи, с которых будут стричь в ближайшие десятилетия.
Ну то ладно. У меня тут созрел термин, чего же мне так не хватает в классической теории игр - Тактический уровень. Теория игр сейчас только стратегическая, всё внимание приковано к цели - выигрышной стратегии. Но то, как она достигается - выставлено за рамки, словно бы игры герметичны. И нет, развернутая форма - это не то, она все равно статична. Если говорить о формальных вещах, то вот обогатить развернутую форму теорией трансформации графов - было бы круто. Но тогда понятие стратегии летит к чертям, или нет?
А насколько эффективно применять теорию игр к сток трейдингу?
>В общем, я к тому, что за компом всегда стоит другой человек
Ну это как думать, что за доказательством теоремы Ферма стоит Диофант у которого, согласно википедии, появились первые примеры эллиптических кривых
Пардон, только там не два игрока будет. Или можно рассматривать художника как первого игрока, а общество - как второго.
>>38333
>>38334
Кстати, еще пара мыслей. Определяем противника как победителя. Надеюсь, понятно. Чтобы противостоять такой стратегии с его стороны, заранее определяем его как того, кто определит нас как победителя, наше определение своевременнее, поэтому если он его применит, мы по идее выиграли, потому что раньше дали определение. Тут формализовать надо правила, какие утверждения вообще должны быть возможны. Вырисовывается и самый слабый ход - определить противника как проигравшего. В общем, может неплохая игра выйти, если хорошо обдумать ее, кмк.
Вот вам и категория, кстати. Ход обоих противников - стрелка, а когда они оба определяют как проигравшего - идентичность.
нихуя не понял
>того, кто определит нас как победителя
Хотя получается тут, что победитель этот тот, кто определяет нас как победителя, не?
Тут Нео определил Смита как победителя.
Позиция проигравшего позволяет учиться. В позиции победителя нет доступа к поиску новой выигрышной стратегии. Такая вот игра получается, ты ищешь победную стратегию, пока её не находишь, потом, если её применишь - сам станешь победителем. Но теперь тебя могут так же сместить.
То есть если ты победитель твой проигрыш лишь дело времени.
https://www.youtube.com/watch?v=PX2H6UtCpjY
Блядь, тоже не тот отрывок. Короче текстом
>В любой игре всегда есть соперник и всегда есть жертва, вся хитрость — вовремя осознать, что ты стал вторым, и сделаться первым
Почему? В тему же, по сути то же самое другими словами.
>Позиция проигравшего позволяет учиться. В позиции победителя нет доступа к поиску новой выигрышной стратегии
>вся хитрость — вовремя осознать, что ты стал вторым, и сделаться первым
двачую, из гугла сюда попал
когда пошел с корешем в макдак, вспоминали, как воеводский пытался теорвер категоризировать, и как лурье гармонический анализ категорил
я пошутил, что неплохо бы тигры в порядок привести
сейчас вспомнил и решил гуглануть - пусто
Просто для тебя это не актуально. Ты хочешь на все готовенькое прийти, а я же сразу сказал, что тут настоящая наука делается, а не её профанация. Я ждал обмена мнениями, но нашлось всего пара анонов, которым было что сказать.
Описать всевозможные ходы.
Вообще, написать майнкрафт на языке математики, это написать код игры, но очень понятно.
Ну а если игра такая, что действие не описать, пока оно не произойдет?
>Dank Learning: Generating Memes Using Deep Neural Networks pdf
Зачем нужны формализации, если все необходимое уже умеют делать нейроночки без всяких формализаций?




