54 Кб, 398x600Ребят подскажите как решать это, нихера не могу понять
С меня что нибудь, нужно хотя бы мат аппарат под это дело заточить, а я уже третий день голову ломаю и нихера сообразить не могу.
Нужно запрогать этот алгоритм на С++. Запрогаю сам, но алгоритм расчёта, до сих пор не нашёл. В интернетах нашёл вот что. Если кто то сможет помочь - не забуду\возмещу время в эквиваленте\добрым словом.
Собственно ресурсы где я что то похожее нашёл
1) http://www.cyberforum.ru/pascal/thread1591818.html
2) https://acmp.ru/index.asp?main=task&id_task=619
2.1) https://acmp.ru/asp/gb.asp?id=619 (комментарии)
3) http://opennotes.ru/knowledge/vba-knowledge/algoritm-poiska-vsex-kombinacij-chisel-dayushhix-zadannuyu-summu-na-vba/
4) похожие задачи в англ учебнике в "разделе 2"
http://www.madandmoonly.com/doctormatt/mathematics/dice1.pdf
5) похожее задание на "интуите" https://www.intuit.ru/studies/courses/648/504/lecture/17184?page=11&keyword_content=SMS
Кубик, грани которого помечены цифрами от 1 до 6, бросают N раз. Найти вероятность того, что сумма выпавших чисел будет равна Q.
Ограничения: 1 <= N <= 500, 1 <= Q <= 3000.
Входные данные
В первой строке находятся числа N и Q через пробел.
Выходные данные
Вероятность того, что сумма выпавших чисел будет равна Q.
Примеры
Входные данные
1 1
Выходные данные
1.66666666666667E-0001
Входные данные
2 2
Выходные данные
2.77777777777778E-0002
С меня что нибудь, нужно хотя бы мат аппарат под это дело заточить, а я уже третий день голову ломаю и нихера сообразить не могу.
Нужно запрогать этот алгоритм на С++. Запрогаю сам, но алгоритм расчёта, до сих пор не нашёл. В интернетах нашёл вот что. Если кто то сможет помочь - не забуду\возмещу время в эквиваленте\добрым словом.
Собственно ресурсы где я что то похожее нашёл
1) http://www.cyberforum.ru/pascal/thread1591818.html
2) https://acmp.ru/index.asp?main=task&id_task=619
2.1) https://acmp.ru/asp/gb.asp?id=619 (комментарии)
3) http://opennotes.ru/knowledge/vba-knowledge/algoritm-poiska-vsex-kombinacij-chisel-dayushhix-zadannuyu-summu-na-vba/
4) похожие задачи в англ учебнике в "разделе 2"
http://www.madandmoonly.com/doctormatt/mathematics/dice1.pdf
5) похожее задание на "интуите" https://www.intuit.ru/studies/courses/648/504/lecture/17184?page=11&keyword_content=SMS
Кубик, грани которого помечены цифрами от 1 до 6, бросают N раз. Найти вероятность того, что сумма выпавших чисел будет равна Q.
Ограничения: 1 <= N <= 500, 1 <= Q <= 3000.
Входные данные
В первой строке находятся числа N и Q через пробел.
Выходные данные
Вероятность того, что сумма выпавших чисел будет равна Q.
Примеры
Входные данные
1 1
Выходные данные
1.66666666666667E-0001
Входные данные
2 2
Выходные данные
2.77777777777778E-0002
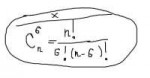22 Кб, 390x205в знаменателе я получаю количество всех комбинация при N бросках, а вместо X[/b] - Количество комбинаций дающих значение Q
>>825 (OP)
Кидаем шестигранный кубик какое-то кол-во раз.
Какая вероятность того, что сумма будет равна заданному числу?
Возможность выбора числа, 500.
Возможностей правильно отгадать из 3000
500/3000=5/30=1/6
Вероятность, что в 1/6 будет что-то из 500/3000 будет 1/6 1/6 = 1/36.
Вероятность, что результат броска будет положителен, и того, что выборка из множества будет нужным числом, равно произведению вероятностей этих событий.
2) Кинем два раза.
6+6=12 — максимальная сумма
1+1=2 — минимальная сумма
12-2+1=11 — число возможных вариантов.
1/11 — вероятность кубиков, теперь домножим на вероятность выборки.
1/111/6=1/66
Теперь, можно сформулировать принципы;
Даны N и Q
1. Умножаем N на шесть образовывая новое число
2.Плюсуем 6×N с самим собой, т.е удваиваем, т.е достаточно умножить на 12, получим 12×N. Это максимальная сумма.
3.Берём число N. Это минимальная сумма
4.12×N-N+1 — число возможных вариантов
5. (12×N-N+1)*(1/6) — конечный вариант.
Кидаем шестигранный кубик какое-то кол-во раз.
Какая вероятность того, что сумма будет равна заданному числу?
Возможность выбора числа, 500.
Возможностей правильно отгадать из 3000
500/3000=5/30=1/6
Вероятность, что в 1/6 будет что-то из 500/3000 будет 1/6 1/6 = 1/36.
Вероятность, что результат броска будет положителен, и того, что выборка из множества будет нужным числом, равно произведению вероятностей этих событий.
2) Кинем два раза.
6+6=12 — максимальная сумма
1+1=2 — минимальная сумма
12-2+1=11 — число возможных вариантов.
1/11 — вероятность кубиков, теперь домножим на вероятность выборки.
1/111/6=1/66
Теперь, можно сформулировать принципы;
Даны N и Q
1. Умножаем N на шесть образовывая новое число
2.Плюсуем 6×N с самим собой, т.е удваиваем, т.е достаточно умножить на 12, получим 12×N. Это максимальная сумма.
3.Берём число N. Это минимальная сумма
4.12×N-N+1 — число возможных вариантов
5. (12×N-N+1)*(1/6) — конечный вариант.
>>840
Случайно отправил
Случайно отправил
>>839
удалить
удалить
>>825 (OP)
Зачем ты пишешь про вещи вне математики на математической доске?
Ну так на /pr/ и спрашивай. Не нужно тут испражняться.
Зачем ты пишешь про вещи вне математики на математической доске?
>Нужно запрогать
Ну так на /pr/ и спрашивай. Не нужно тут испражняться.
>>854
Просто у нас тут так загажено воинствующим конструктивистом, что ОП подумал, что тут можно прям так, не снимая брюк.
Я сам очень люблю поработать в интуиционистких теориях множеств, но этот "охранник" позорит своим фанатизмом на самом деле крутую вещь.
Просто у нас тут так загажено воинствующим конструктивистом, что ОП подумал, что тут можно прям так, не снимая брюк.
Я сам очень люблю поработать в интуиционистких теориях множеств, но этот "охранник" позорит своим фанатизмом на самом деле крутую вещь.
>>839
а как решать то? Говорят что это элементарная задача комбинаторики..., Я не могу понять. ПОмогите анонимы, я заплачу за алгоритм. Прото печёт с этого. У меня комбинаторики в вузе не было.
а как решать то? Говорят что это элементарная задача комбинаторики..., Я не могу понять. ПОмогите анонимы, я заплачу за алгоритм. Прото печёт с этого. У меня комбинаторики в вузе не было.
>>876
Не думаю, что он вообще в состоянии что-либо кроме себя опозорить.
>но этот "охранник" позорит своим фанатизмом на самом деле крутую вещь
Не думаю, что он вообще в состоянии что-либо кроме себя опозорить.
>>854
Лол, алгоритмы такая же математика, как и теория чисел. Он же написал, что запрогать сам может, проблема в математической части задачи.
Лол, алгоритмы такая же математика, как и теория чисел. Он же написал, что запрогать сам может, проблема в математической части задачи.
>>880
Нет, "алгоритмы" это раздел CS. Обсуждай свою хуйню на своей доске.
То, что ты считаешь "теорией чисел" не является теорией чисел.
В его задаче нет никакой математической части.
>алгоритмы такая же математика
Нет, "алгоритмы" это раздел CS. Обсуждай свою хуйню на своей доске.
>как и теория чисел
То, что ты считаешь "теорией чисел" не является теорией чисел.
>проблема в математической части задачи
В его задаче нет никакой математической части.
>>825 (OP)
Обязательно было срать этим в каждый ебаный тред, дебил?
Обязательно было срать этим в каждый ебаный тред, дебил?
>>879
А как думаешь, почему он получает извращённое удовольствие от своего идиотизма?
Мне кажется, потому что он краем сознания понимает, что это всё хуйня, что он пишет, что ему надо учиться, решать задачи, самосовершенствоваться, но он отвергает эти мысли как невыносимые.
Может это в силу того, что он не научился получать от этой деятельности удовольствие, но при этом очень хочет уважения.
А как думаешь, почему он получает извращённое удовольствие от своего идиотизма?
Мне кажется, потому что он краем сознания понимает, что это всё хуйня, что он пишет, что ему надо учиться, решать задачи, самосовершенствоваться, но он отвергает эти мысли как невыносимые.
Может это в силу того, что он не научился получать от этой деятельности удовольствие, но при этом очень хочет уважения.
>>891
Динамическое программирование.
dp[j] - количество способов получить сумму j из i слагаемых, каждый из которых принадлежит множеству {1, 2, 3, 4, 5, 6}.
dp[j] = dp[i - 1][j - 1] + dp[i - 1][j - 2] + dp[i - 1][j - 3] + dp[i - 1][j - 4] + dp[i - 1][j - 5] + dp[i - 1][j - 6].
Изначально dp[1][1] = 1 ... dp[1][6] = 1, остальное равно нулю.
j можно считать до i умножить на 6.
Можно хранить только два слоя, т.е. завести массив dp[2][3001], и заполнять dp[i & 1][j] = dp[(i - 1) & 1][j - x].
Ответом будет 1/6 в степени dp[N & 1][Q].
На будущее, съеби нахуй с /math с подобными вопросами
Динамическое программирование.
dp[j] - количество способов получить сумму j из i слагаемых, каждый из которых принадлежит множеству {1, 2, 3, 4, 5, 6}.
dp[j] = dp[i - 1][j - 1] + dp[i - 1][j - 2] + dp[i - 1][j - 3] + dp[i - 1][j - 4] + dp[i - 1][j - 5] + dp[i - 1][j - 6].
Изначально dp[1][1] = 1 ... dp[1][6] = 1, остальное равно нулю.
j можно считать до i умножить на 6.
Можно хранить только два слоя, т.е. завести массив dp[2][3001], и заполнять dp[i & 1][j] = dp[(i - 1) & 1][j - x].
Ответом будет 1/6 в степени dp[N & 1][Q].
На будущее, съеби нахуй с /math с подобными вопросами
>>906
Твой ответ на его вопрос в этом особо не поможет. Скорее наоборот.
>На будущее, съеби нахуй с /math с подобными вопросами
Твой ответ на его вопрос в этом особо не поможет. Скорее наоборот.