>>2892 (OP)
Продолжайте.
Продолжайте.
63 Кб, 847x829>>4704
Нет.
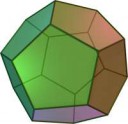
Лучше посмотри, какой охуенный я нашёл додэкаэдр.
Обожаю додэкаэдры, сука. Какие они правильные, с 12-ю гранями. Когда работал трудовиком - заставлял детей всех возрастов делать из всевозможных материалов додэкаэдры - чтобы у них мозги работали. Нужно БОЛЬШЕ додэкаэдров!
Нет.
Лучше посмотри, какой охуенный я нашёл додэкаэдр.
Обожаю додэкаэдры, сука. Какие они правильные, с 12-ю гранями. Когда работал трудовиком - заставлял детей всех возрастов делать из всевозможных материалов додэкаэдры - чтобы у них мозги работали. Нужно БОЛЬШЕ додэкаэдров!
>>4757
Почему не икосаэдр? Поясни-ка
Да и вообще, зачем ограничиваться правильными? В них всё уже изучено, ничего интересного не осталось
Почему не икосаэдр? Поясни-ка
Да и вообще, зачем ограничиваться правильными? В них всё уже изучено, ничего интересного не осталось
>>4757
Четырехмерный еще сделай, у которого шлефли {5,3,3}
Четырехмерный еще сделай, у которого шлефли {5,3,3}
Что там говорил Гротендик о теоретико-схемной точке зрения на правильные конфигурации в элементарной геометрии?
>>4702
Одна из моих любимых книг.
Одна из моих любимых книг.
>>4926
А что он говорил? Напомни.
А что он говорил? Напомни.
66 Кб, 687x502А есть кстати более концептуальное объяснение существование исключительных правильных многогранников в dim = 3,4 кроме "ну просто конечные подгруппы есть такие))))".
>>7058
Серьёзно? Спасибо.
Серьёзно? Спасибо.
>>7063
Да, есть теорема Шлефли, см., например, второй том Берже
Да, есть теорема Шлефли, см., например, второй том Берже
>>9494
Ебать ты даун. Если я получаю эмоции от склеивания - значит я УЖЕ не нолайфер, потому что жизнь - это положительные эмоции, ДАУН. И нет особой разницы, как их получать - на тусовке или за компьютером. Всё зависит от человека.
Ебать ты даун. Если я получаю эмоции от склеивания - значит я УЖЕ не нолайфер, потому что жизнь - это положительные эмоции, ДАУН. И нет особой разницы, как их получать - на тусовке или за компьютером. Всё зависит от человека.
![zadrot11288291orig[1].jpg](https://2ch.life//math/src/2892/14855296575420.jpg)
134 Кб, 603x444>>9503
>Ебать ты даун. Если я получаю эмоции от склеивания - значит я УЖЕ не нолайфер, потому что жизнь - это положительные эмоции, ДАУН.
А можно, с помощью высокой науки типа торических тапалогий явно выписывать целые точки внутри многогранников или хотя бы поставить им что-то в соответствие?
72 Кб, 640x432Нате вам древнего.
Мой любимый тред на всей доске, правда.
Что значит "не хочу додэкаэдр"? Не лги, додэкаэдрчиков все хотят. Не медли, заводи себе, часики-то тикают! Дал бох плоскость, даст бох и ребро.
>>6980
Моё почтение. Когда в школе трудовиком работал - тоже всех учеников запрягал клеить и выпиливать. Мозги детям неплохо развивает.
Моё почтение. Когда в школе трудовиком работал - тоже всех учеников запрягал клеить и выпиливать. Мозги детям неплохо развивает.
>>2892 (OP)
Я просто напишу здесь, что Сабитов Иджад Хакович плохой семинарист. Спасибо за внимание, у меня все.
Я просто напишу здесь, что Сабитов Иджад Хакович плохой семинарист. Спасибо за внимание, у меня все.
>>12119
На третьей кубы можно просмотреть! Удивительно
На третьей кубы можно просмотреть! Удивительно
>>19105
А! Завуалированный Экзибит. Понятно.
А! Завуалированный Экзибит. Понятно.
Бамп моему любимому треду.
Не понимаю ничего кроме куба. Чувствую себя быдлом. Как им перестать? Или, вы в большинстве просто созерцаете красоту без особого анализа?
>>21695
Да. Втыкай и обрящешь.
Да. Втыкай и обрящешь.
>>21695
Параллелограмм — это четереугольник у которого противоположные стороны попарно параллельны.
Призма — это фигура, где две грани — произвольные равные многоугольники, звутся основаниями, а все остальные — параллелограммы.
Параллепитед — это призма, основания которых — параллелограммы.
Куб — параллелитед, где параллелограммы являются правильными квадратами.
Правильная фигура — фигура, где все стороны равны.
Теперь ЧИТАЙ интересное:
Пять тел Платона.
Во всем мире, в трехмерном пространстве, существует лишь пять правильных форм, форм, где все стороны равные.
1.Тетрадэдр— многогранник, у которого четыре грани — треугольники.
2.Октаэдр — многранник имеющий восемь граней
3. Гексоэдр, или куб — многогранник, каждая грань которого — квадрат.
4. Икосаэдр — двадцатигранник, фигура имеющая двадцать граней.
5.Додекаэдр — фигура, составлена из двенадцати правильных пятиугольников.
ЭТО ЕДИНСТВЕННЫЕ ФИГУРЫ, ГДЕ ВСЕ СТОРОНЫ МОГУТ БЫТЬ РАВНЫ.
Параллелограмм — это четереугольник у которого противоположные стороны попарно параллельны.
Призма — это фигура, где две грани — произвольные равные многоугольники, звутся основаниями, а все остальные — параллелограммы.
Параллепитед — это призма, основания которых — параллелограммы.
Куб — параллелитед, где параллелограммы являются правильными квадратами.
Правильная фигура — фигура, где все стороны равны.
Теперь ЧИТАЙ интересное:
Пять тел Платона.
Во всем мире, в трехмерном пространстве, существует лишь пять правильных форм, форм, где все стороны равные.
1.Тетрадэдр— многогранник, у которого четыре грани — треугольники.
2.Октаэдр — многранник имеющий восемь граней
3. Гексоэдр, или куб — многогранник, каждая грань которого — квадрат.
4. Икосаэдр — двадцатигранник, фигура имеющая двадцать граней.
5.Додекаэдр — фигура, составлена из двенадцати правильных пятиугольников.
ЭТО ЕДИНСТВЕННЫЕ ФИГУРЫ, ГДЕ ВСЕ СТОРОНЫ МОГУТ БЫТЬ РАВНЫ.
>>35237
Вот, в двухмерном пространстве существует бесконечное кол-во фигур, которые являются правильными.
А тут только пять...
Вот, в двухмерном пространстве существует бесконечное кол-во фигур, которые являются правильными.
А тут только пять...
83 Кб, 226x240>>2892 (OP)
Ромбокубоктаэдр ван лав.
Ромбокубоктаэдр ван лав.
>>35237
Вот в этой серии видео тема правильных форм раскрыта чуть более, чем полностью:
https://www.youtube.com/watch?v=pWOMDm6ejlw
Алсо, обратите внимание на использованную музыку: http://www.florentghys.com/
Вот в этой серии видео тема правильных форм раскрыта чуть более, чем полностью:
https://www.youtube.com/watch?v=pWOMDm6ejlw
Алсо, обратите внимание на использованную музыку: http://www.florentghys.com/
>>35360
Платоновые тела:
если — то
1.Тетрадэдр— состоит из четырёх правильных треугольников
2.Октаэдр — состоит восьми правильных треугольников
3. Гексоэдр, или куб — состоит из шести квадратов
4. Икосаэдр — состоит из двадцати правильных треугольников
5.Додекаэдр — состоит из двенадцати правильных пятиугольников
Платоновые тела:
если — то
1.Тетрадэдр— состоит из четырёх правильных треугольников
2.Октаэдр — состоит восьми правильных треугольников
3. Гексоэдр, или куб — состоит из шести квадратов
4. Икосаэдр — состоит из двадцати правильных треугольников
5.Додекаэдр — состоит из двенадцати правильных пятиугольников
>>35237
Ты лох короче, уебок, шлюха и не прав
Ты лох короче, уебок, шлюха и не прав
>ЭТО ЕДИНСТВЕННЫЕ ФИГУРЫ, ГДЕ ВСЕ СТОРОНЫ МОГУТ БЫТЬ РАВНЫ.
>>35238
Забавное наблюдение в том что в размерности 4 тоже есть исключительные и всего многогранников получается шесть, а начиная с пяти и дальше их всегда только три: куб, октаэдр и тетраэдр.
Забавное наблюдение в том что в размерности 4 тоже есть исключительные и всего многогранников получается шесть, а начиная с пяти и дальше их всегда только три: куб, октаэдр и тетраэдр.