 15 Кб, 427x302
15 Кб, 427x302>Но в интернете об этом ни слова.
Ты шутишь?
>Но то есть там полно информации об этой теореме и как её доказывать
Этого не достаточно для тебея?
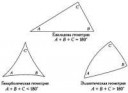
>Почему углы треугольника складываются в прямую линию.
Следствие теоремы.
>Помню задавал этот вопрос преподавателю еще в школе, она меня даже не поняла.
Либо ты плохо объяснил, либо твоя учительница плохо знает математику.
Учитель не может знать математику.
>Почему сумма углов треугольника равна прямой линии
представь треугольник, который складывается из 2 параллельных линий и пересекающего их перпендикуляра. третий угол - угол пересечения параллельных на бесконечнности, равен нулю. очевидно что сумма всех углов треугольника равна 180 градусов. поскольку каждый тругольник можно трансформировать в такой треугольник, и это преобразование сохраняет сумму углов, поэтому у каждого треугольника сумма углов - 180 градусов.
С такими вопросами гугли сакральную геометрию
Использовать для объяснения простого геометрического факта предельный переход? Некрасиво.
"простой геометрический факт" это постулат эквивалентный параллельности
Кстати, а если треугольник огромный, а мимо Юпитер там проплывёт или ещё какая хуйня. Тогда уже не 180 градусов будет, так как треугольник исказится? Ну вы поняли
Извините за глупый вопрос. Но это же двач, здесь все мои друзья, да ещё и такая доска ламповая теперь появилась
Поясни плез насчет трансформации, и где на эту тему прочитать на понятном языке.
Одно из допущений Евклида. Я являясь мимо-школьником доказать не могу, но точно знаю, что доказательство есть.
накрест-лежащие углы...
>Почему углы треугольника складываются в прямую линию. Что такое есть треугольник что у него такое интересное свойство? Почему геометрия нашего пространства так решила?
Ооооочень хороший вопрос. Уже вижу как у математиков затрещало.
Пиздец даунский вопрос. Математика не задается вопросом почему, она строится аксиоматически, и если так уже получилось, что из аксиом и теорем, на них доказанных, сумма углов в треугольнике равна 180, это принимается, как факт. В геометрии Лобаческого эта сумма может быть от нуля до 180, и ты же не спрашиваешь "а почему это так?", потому что так получилось из аксиом. Короче иди нахуй, осел, со своими тупыми вопросами, удали это.
Пожалуйста, либо вернись в тред для начинающих, либо распиши, из каких аксиом и как именно вытекает тот факт, о котором спрашивает оп.
>что из аксиом и теорем, на них доказанных, сумма углов в треугольнике равна 180
>теорем
Тебя в начальный класс вернуть?
Ты меня не понял. Ты пишешь: "потому что так получилось из аксиом". Сказал А - говори и Б: напиши, как именно это получилось. В противном случае твои слова не имеют никакой ценности. Мы все-таки в /матх, а не в /б.
Гугли "постулат Евклида о параллельной прямой". Оттуда шагай прямиком в раздел математики под названием "дифференциальная геометрия" и будет тебе счастье.
Какая геометрия, такие и треугольники.
Я не знаю, зачем тебе это надо, свчешный ебанат, но так уж и быть.
>Мы все-таки в /матх, а не в /б.
Пиздец честь, долбоеб.
Аксиома принадлежности. Через любые две точки на плоскости можно провести прямую и притом только одну.
Аксиома порядка. Среди любых трёх точек, лежащих на прямой, есть не более одной точки, лежащей между двух других.
Аксиома конгруэнтности (равенства) отрезков и углов. Если два отрезка (угла) конгруэнтны третьему, то они конгруэнтны между собой.
Аксиома параллельных прямых. Через любую точку, лежащую вне прямой, можно провести другую прямую, параллельную данной, и притом только одну.
Аксиома непрерывности (аксиома Архимеда). Для любых двух отрезков AB и CD существует конечный набор точек A1, A2, …, An, лежащих на прямой AB, таких, что отрезки AA1, A1A2, …, An-1An конгруэнтны отрезку
CD, a точка B лежит между A и An .
Теорема 3.1.
Если внутренние накрест лежащие углы равны, то прямые параллельны.
Доказательство:
Докажем теорему так называемым методом от противного: предположим, что условие теоремы выполнено, а именно: прямые AB и CD образуют с секущей AC равные внутренние накрест лежащие углы, но вопреки утверждению теоремы прямая AB не параллельна прямой CD и, следовательно, они пересекаются в точке O, которая лежит в одной из полуплоскостей от прямой AC.
Отложим от луча АC треугольник AO1C, равный COА, так, что вершина O1 лежит в другой, нежели точка O, полуплоскости. Из равенства этих треугольников следует, что ^OAC = O1CA, ^OCA = ^O1AC; по условию: ^OAC = ^ACD и тогда точки O, C, O1 лежат на одной прямой, и, аналогично, из равенства по условию углов OCA и смежного к BAC следует, что точки O1, A, O лежат также на одной прямой. Отсюда следует, что через две различные точки O и O1 плоскости проходят две различные прямые AB и CD. Это противоречит аксиоме параллельных прямых. Полученное противоречие доказывает теорему.
Теорема 3.2.
Две прямые, параллельные третьей, параллельны.
Это свойство называется транзитивностью параллельности прямых.
Доказательство:
Пусть прямые a и b одновременно параллельны прямой c. Допустим, что a не параллельна b, тогда прямая a пересекается с прямой b в некоторой точке A, не лежащей на прямой c по условию. Следовательно, мы имеем две прямые a и b, проходящие через точку A, не лежащую на данной прямой c, и одновременно параллельные ей. Это противоречит аксиоме аксиоме параллельных прямых. Теорема доказана.
Теорема 3.4.
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
Доказательство:
Пусть (AB) || (CD). Предположим, что ^ACD ≠ ^BAC. Через точку A проведем прямую AE так, что ^EAC = ^ACD. Но тогда по теореме 3.1 (AE) || (CD), а по условию – (AB) || (CD). В соответствии с теоремой 3.2 (AE) || (AB). Это противоречит аксиоме параллельных прямых, по которой через точку A, не лежащую на прямой CD, можно провести единственную прямую, параллельную ей. Теорема доказана.
Теорема о сумме углов треугольника — сумма углов треугольника на евклидовой плоскости равна 180°
Доказательство:
Пусть ABC' — произвольный треугольник. Проведём через вершину B прямую, параллельную прямой AC (такая прямая называется прямой Евклида). Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC.Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD.Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Что и требовалось доказать.
Я не знаю, зачем тебе это надо, свчешный ебанат, но так уж и быть.
>Мы все-таки в /матх, а не в /б.
Пиздец честь, долбоеб.
Аксиома принадлежности. Через любые две точки на плоскости можно провести прямую и притом только одну.
Аксиома порядка. Среди любых трёх точек, лежащих на прямой, есть не более одной точки, лежащей между двух других.
Аксиома конгруэнтности (равенства) отрезков и углов. Если два отрезка (угла) конгруэнтны третьему, то они конгруэнтны между собой.
Аксиома параллельных прямых. Через любую точку, лежащую вне прямой, можно провести другую прямую, параллельную данной, и притом только одну.
Аксиома непрерывности (аксиома Архимеда). Для любых двух отрезков AB и CD существует конечный набор точек A1, A2, …, An, лежащих на прямой AB, таких, что отрезки AA1, A1A2, …, An-1An конгруэнтны отрезку
CD, a точка B лежит между A и An .
Теорема 3.1.
Если внутренние накрест лежащие углы равны, то прямые параллельны.
Доказательство:
Докажем теорему так называемым методом от противного: предположим, что условие теоремы выполнено, а именно: прямые AB и CD образуют с секущей AC равные внутренние накрест лежащие углы, но вопреки утверждению теоремы прямая AB не параллельна прямой CD и, следовательно, они пересекаются в точке O, которая лежит в одной из полуплоскостей от прямой AC.
Отложим от луча АC треугольник AO1C, равный COА, так, что вершина O1 лежит в другой, нежели точка O, полуплоскости. Из равенства этих треугольников следует, что ^OAC = O1CA, ^OCA = ^O1AC; по условию: ^OAC = ^ACD и тогда точки O, C, O1 лежат на одной прямой, и, аналогично, из равенства по условию углов OCA и смежного к BAC следует, что точки O1, A, O лежат также на одной прямой. Отсюда следует, что через две различные точки O и O1 плоскости проходят две различные прямые AB и CD. Это противоречит аксиоме параллельных прямых. Полученное противоречие доказывает теорему.
Теорема 3.2.
Две прямые, параллельные третьей, параллельны.
Это свойство называется транзитивностью параллельности прямых.
Доказательство:
Пусть прямые a и b одновременно параллельны прямой c. Допустим, что a не параллельна b, тогда прямая a пересекается с прямой b в некоторой точке A, не лежащей на прямой c по условию. Следовательно, мы имеем две прямые a и b, проходящие через точку A, не лежащую на данной прямой c, и одновременно параллельные ей. Это противоречит аксиоме аксиоме параллельных прямых. Теорема доказана.
Теорема 3.4.
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
Доказательство:
Пусть (AB) || (CD). Предположим, что ^ACD ≠ ^BAC. Через точку A проведем прямую AE так, что ^EAC = ^ACD. Но тогда по теореме 3.1 (AE) || (CD), а по условию – (AB) || (CD). В соответствии с теоремой 3.2 (AE) || (AB). Это противоречит аксиоме параллельных прямых, по которой через точку A, не лежащую на прямой CD, можно провести единственную прямую, параллельную ей. Теорема доказана.
Теорема о сумме углов треугольника — сумма углов треугольника на евклидовой плоскости равна 180°
Доказательство:
Пусть ABC' — произвольный треугольник. Проведём через вершину B прямую, параллельную прямой AC (такая прямая называется прямой Евклида). Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC.Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD.Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Что и требовалось доказать.
>Почему геометрия нашего пространства так решила?
С точки зрения физики это не верно в общем случае из-за того, что энергия-импульс искривляет пространство.
Так что с точки зрения общей теории относительности ответ на этот вопрос: потому что человечество живёт в почти плоской геометрии (рядом с нами нет достаточно сильных концентрированных гравитационных полей).
Но тебя возможно это не удовлетворит. Потому что можно спросить: почему низкогравитационный предел это плоское пространство? Ответа на этот вопрос нет. Даже не ясно имеет ли смысл такой вопрос. Может нет, может пока нет.
Очевидно, что аксиома параллельности так же выводима из теоремы о сумме углов.
знаем мы ваши конструктивные дискуссии. Кончается все тем, кто кого как и что куда сделал.
> кто кого как и что куда сделал
Я, твою мамашу, решительно, свой хуй, за щеку. :3
Нет, ну правда. Вот не спровоцировал бы я того анона - в треде так бы и не было ничего, кроме ебания твоей и моей мамаши. А так - и в треде появился контент, и тот анон сделал полезное, хорошее дело. Видишь, я сею разумное, доброе, вечное - и вовсе никакой не жиробас!
потому что пи - это прямая линия, очевидно же
l=2pir, r=1, l=2pi, pi=l/2=3,14=180градусов, l=6.28=360градусов
тут всё понятно
pi=l/2=3,14=180градусов=сумма углов треугольника при r=1
А теперь нах всё, что мы писали, потому что мы вспомнили, что кто-то когда-то предложил поделить круг на 360 условных секторов - градусов.
на замену этому постулату существует около 20-ти альтернатив, эквивалентных по значению
в геометрии Лобачевского 5-ый постулат совершенно другой(не равный по значению). Но тем не менее, задачки решаются без конфликтности и в традиционной геометрии Евклида, и в Неевклидовой ЫЫЫЫЫЫЫЫЫЫЫАААААЫЫ
Потому что прямую можно рассматривать как частный случай треугольника. Если у нас есть 2 угла по 0 градусов, то третий будет равен 180, и никак иначе.
вот тебе ответ по хардкору
по теореме Гаусса-Боннэ, если у тебя есть компактная ориентированная
риманова поверхность M с кусочно глаким краем dM, со скалярной
кривизной K, и геодезической кривизной границы k, то
\int_M K + \int_dM k + \sum a_i = 2\pi \chi(M)
где a_i --- сумма внутренних углов между гладкими кусками и \chi(M)
--- эйлерова характеристика (альтернированная сумма чисел бетти).
треугольник плоский, с эйлеровой характеристикой 1 (1 - 0 + 0),
поэтому первые два члена в левой части зануляются, а справа 2\pi.
это кстати объясняет, почему в сферической и гиперболической
геометриях сумма углов треугольника может отличаться от 2\pi.
осталось поверить в формулу Гаусса-Боннэ!
и всё-таки налажал: a_i внешние углы, конечно же. поэтому \sum a_i =
2\pi влечёт \sum (\pi - b_i) = 3\pi - \sum b_i = 2\pi, где b_i
внутренние углы. и тогда норм, получается.
айм сорри.
> И сразу энова уан: "Почему верна теорема Гаусса-Боннэ?"
ну это шутка как бы
очевидно есть две части вопроса: как входят кривизны, и как входят
углы
вначале надо разобраться, что происходит около одного угла, а потом
склеить и получить глобальную формулу.
доказательство не поместится на этих узких полях, увы.
если всё время полагать кривизны нулевыми, то можно просто порезать
всё на стандартные симплексы.
тогда по ходу мы и сумму углов плоского треугольника посчитаем, но ещё
--- гораздо больше! свяжем подсчёты сумму углов с эйлеровой
характеристикой.
есть такое концептуальное доказательство
пусть X наша поверхность, рассмотрим сферизацию касательного
расслоения, STX, это S^1-расслоение, обозначим проекцию на X за p. На
STX есть форма a, которая на касательном векторе \ksi к точке x даёт
скалярное произведение \ksi и x (x понимается как единичный вектор в
TX, касательное пространство к STX идентифицируется с TX). Главное
наблюдение, и это некоторое чудо: da это пуллбэк вдоль p 2-формы K из
формулы Г-Б.
Пусть \Delta треугольная область на X. возьмём у неё внутри маленький
диск C_e. Рассмотрим незануляющееся векторное поле на \Delta_e, оно
задаёт сечение q: X \to STX проекции p, и напишем стокса для \Delta_e:
\Delta без C_e (надеюсь я не намудрил с ориентацией)
\int_\Delta_e K = \int_q(\Delta_e) p^ K = \int_q(\Delta_e) da =
= \int_\partial(q(C_e)) a - \int_\partial(q(\Delta)) a
где \partial обозначает границу. Если e устремить к нулю, левая часть
достремится до \int_\Delta K dV, одно из слагаемых в формуле
Гаусса-Боннэ.
интеграл в правой части, обрати внимание, идёт не по \partial\Delta, а
по его образу в STX, то есть весОм вклад не от векторного поля вдоль
треугольника, который граница \Delta, а от изменения* этого
векторного поля, как мы идём вдоль сторон.
теперь подберём векторное поле так, чтоб оно касалось и границы C_e и
границы \Delta, с одной ориентацией. тогда первый член будет
интегрироваться до 2\pi (длина окружности), а второй интеграл, по
\partial\Delta, будет вдоль сторон давать нули, и влад будет ровно
внешние углы при вершинах. вообще, это неаккуратно, потому что поле
должно быть гладким, ну значит возьмём гладкое поле и будем его
стремить к такой ситуации, одновременно стремя C_e к нулю.
с картинкой было бы понятней, рисовать лень. сори
есть такое концептуальное доказательство
пусть X наша поверхность, рассмотрим сферизацию касательного
расслоения, STX, это S^1-расслоение, обозначим проекцию на X за p. На
STX есть форма a, которая на касательном векторе \ksi к точке x даёт
скалярное произведение \ksi и x (x понимается как единичный вектор в
TX, касательное пространство к STX идентифицируется с TX). Главное
наблюдение, и это некоторое чудо: da это пуллбэк вдоль p 2-формы K из
формулы Г-Б.
Пусть \Delta треугольная область на X. возьмём у неё внутри маленький
диск C_e. Рассмотрим незануляющееся векторное поле на \Delta_e, оно
задаёт сечение q: X \to STX проекции p, и напишем стокса для \Delta_e:
\Delta без C_e (надеюсь я не намудрил с ориентацией)
\int_\Delta_e K = \int_q(\Delta_e) p^ K = \int_q(\Delta_e) da =
= \int_\partial(q(C_e)) a - \int_\partial(q(\Delta)) a
где \partial обозначает границу. Если e устремить к нулю, левая часть
достремится до \int_\Delta K dV, одно из слагаемых в формуле
Гаусса-Боннэ.
интеграл в правой части, обрати внимание, идёт не по \partial\Delta, а
по его образу в STX, то есть весОм вклад не от векторного поля вдоль
треугольника, который граница \Delta, а от изменения* этого
векторного поля, как мы идём вдоль сторон.
теперь подберём векторное поле так, чтоб оно касалось и границы C_e и
границы \Delta, с одной ориентацией. тогда первый член будет
интегрироваться до 2\pi (длина окружности), а второй интеграл, по
\partial\Delta, будет вдоль сторон давать нули, и влад будет ровно
внешние углы при вершинах. вообще, это неаккуратно, потому что поле
должно быть гладким, ну значит возьмём гладкое поле и будем его
стремить к такой ситуации, одновременно стремя C_e к нулю.
с картинкой было бы понятней, рисовать лень. сори
самофикс: формула покорёжилась, потому что звёздочка у пуллбэка вдоль p дала курсив
\int_\Delta_e K = \int_q(\Delta_e) p^* K = \int_q(\Delta_e) da =
= \int_\partial(q(C_e)) a - \int_\partial(q(\Delta)) a
Херню какую-то пишет, пц.
То, что сумма углов треугольника равна 180 градусов - простая случайность, с такой же вероятностью в другой вселенной, она может оказаться равна любому количеству любых мер.
не
в аргументе выше я налажал, конечно
может соберусь переписать
главное, анон, дырок там в треугольнике делать не надо, а векторное поле брать просто постоянное гор зонтальное. тогда всё получается
Два чая
Сумма углов треугольника равна длине окружности единичного радиуса в радианах (на плоскости), то есть числу Пи.
А на эллиптических, сферических поверхностях сумма углов будет равна отношению длинны описанной окружности к радиусу, в радианах?
Теорема о вписанном угле там будет или не будет выполняться?
Дело в том, что и отношение длинны окружности к радиусу там будет другое, должно ли оно соответствовать сумме улов?
ответ на етот вопрос будет зависеть от гауссовой кривизны твоей поверхности, анонче.
Какой расплывчатый ответ, анонче.
Нет чтобы просто написать: выполняется для такой-то кривизны поверхности и не выполняется для такой-то.
Ведь я это и спрашивал, потому что сам не проходил это, гуглил и не нашел.
Все, до чего я смог докопаться, это то, что тригонометрия не работает при ненулевой кривизне.
при круге всё отлично работает, не знаешь темы, возьми да освой, через пару недель может отркрытие сделаешь
Я тебя не понимаю, отношение длины описанной окружности к радиусу - это 2пи.
Или ты длину окружности к диаметру хочешь, что будет пи?
В радианах? Ну r берём равным одному, получаем, что 2пи = длине окружности и пи равен половине окружности.
Дальше, что конкретно ты хочешь узнать, есть рисунок?
Открытие... Я бы лучше в физике сделал открытие, чем в математике.
>>6606
Да, ты прав, я тут ошибся.
Вряд ли я смогу нарисовать, попробую так написать:
Длина окружности равна диаметру умножить на X
На эллиптической поверхности X < пи (при усилении кривизны поверхность как бы сжимается, при неизменном диаметре длина окружности уменьшается)
На гиперболической поверхности X > пи (при усилении кривизны поверхность как бы растягивается, при неизменном диаметре длина окружности увеличивается)
Ну это понятно.
Вот этот Х - будет 2X радиан аналогом 360 градусов на полном круге? Угол с X/2 радиан можно считать прямым углом на этой поверхности (для тригонометрии)?
Сумма углов треугольника, построенного на этой окружности будет ли равна X?
Вот это я хотел узнать.
P.S. Но вот что меня смущает:
На эллиптической поверхности в какой-то момент при увеличении диаметра длина окружности уменьшается. Сначала в ноль, а потом что, в минус?
Я уже запутался.
Если взять поверхность планеты и ее экватор, его длина равна двум диаметрам. (X=2)
Эти меридианы с 360 градусами долготы, это же совсем не те 360 градусов, что на плоскости. Прямой угол тут равен X/2 = 1 радиан? (И это угол у треугольника, одна из сторон которого - диаметр окружности. А если вторая сторона почти диаметр? Не диаметр, но близко к нему. То есть один из углов стремится к нулю, то сумма остальных к X, а они оба почти одинаковы, то есть каждый по X/2, по 1 радиан. Но если рассматривать маленький участок поверхности, где они рядом, там поверхность то почти плоская, и этот 1 радиан превращается в пи пополам. Всё, я уже чувствую себя поехавшим.)
Пытаюбсь осмыслить.
Осмыслил пока в пределах сферы.
Отношение радиуса окружности к радиусу сферической поверхности играет большую роль. При уменьшении отношения, Х, а так же сумма углов треугольника, приближается к пи, так как кривизна участка приближается к нулевой.
Это наводит на мысль, что маленький участок пространства, которое нам доступно в пределах в всей вселенной, кривизну которого мы считаем нулевой, не позволяет судить о кривизне пространства в масштабах всей вселенной.
блять, ну выше же по треду упоминается формула гаусса-бонне, она ровно про это.
если ненулевая гауссова кривизна, то к пи надо прибавить интеграл её по треугольнику (если треугольник предполагается геодезическим)
Скажу тебе по секрету, ни одна из ныне существующих геометрий вообще ничего общего с реальностью не имеет, включая геометрию Евклида.
Ты прямо сейчас можешь написать программу, которая тебе тысячу новых геометрий создаст с любыми законами, которые тебе только вздумаются.
А всего их - бесконечное количество.
Все эти геометрии - изобтретения людей и все они либо попытки создать модель похожую на реальный мир - модель-урезка реальности, либо вообще плод воображения автора ни капли не имеющий отношение к реальности.
Если хочешь изучать математику, тогда учи английский и иди на лучшие англоязычные математические форумы.
Установи и изучи математические пакеты, они на любой твой вопрос новичка ответят.
Если учишься, тогда подкати с вопросами к какому-нибудь одинокому старику-математику с мат. кафедры, старики рады поговорить о чём угодно и с кем угодно.
Или я тупой, но на пике же и есть ответ на твой вопрос лул.
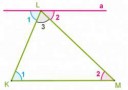
Гугли неевклидову геометрию. Там сумма углов треугольника может быть не равна 180 гр.
KM может быть и не параллельно а, но сумма углов все равно будет 180. Короче говоря, пик нихуя не объясняет.
Если по сабжу - потому что пи.
Параллельность КМ и a (в случае если углы 2 и 3 в сумме 90) и "сумма углов в треугольнике равна 180" эквивалентные постулаты. ОП каритнка скорее всего именно про это.
 78 Кб, 341x791
78 Кб, 341x791на 207 странице сразу припомнился этот тред
>Хорошо известно
Это точно учебник по математике? Хорошо известно у них, вообще охуеть. Что я читаю.
Ну как-бе есть формула для всех правильных многоугольников: (n-2)*180=сумма всех углов, где n=число сторон.
Вообще ничего интересного в этом нет.
А что если поставить вопрос иначе?
Например, почему в равностороннем треугольнике, где все углы равны, максимальное значение каждого угла 60 градусов?
Для квадрата - 90 градусов.
прав 5-ти угольник -108 градусов.
6 - 120
7 - 128 4/7
8 - 135
9 - 140
10 - 144
затем увеличение градусов на угол замедляется всё сильнее
360 - 179
После чего, т.е. в случае > 360 сторон и до бесконечности включительно (круг), количество градусов приближается к 180. На круге 180 градусов.
А вот и формулы:
180г(n-2)/n=180г-360г/n=180г(1-2/n)
Это количество градусов на угол в правильном n-угольнике.
Я делаю вывод, что мы должны копать в сторону площади.
при n<3
180г(n-2)
2 - 0
1 - -180
0 - -360
-1 - -540
-2 - -720
-3 - -900
-4 - -1080
180г-360г/n
2 - 0
1 - -180
0 - минус бесконечность
-1 - 540
-2 - 360
-3 - 300
-4 - 270
-360 - 181
А при минус бесконечность (отрицательный круг) - 180 градусов на угол.
Как видим, хуйня какая-то, и либо формула не универсальная, либо всё в числах правильно и это не хуйня.
И тогда в отрицательном треугольнике сумма всех углов = -900 градусов, но при этом в равностороннем каждый угол = 300 градусов.
И начинать стоит с создания адекватных универсальных формул. Причём сделать и варианты с площадями.
Пиздец даунский ответ. Сначала решается, зачем нужна та или иная модель, потом уже придумывают аксиомы, которые могут создать алгебраическую структуру, годящуюся для описания этой модель. Или, по-твоему, сначала задавалист аксиомы комплексного поля, а потом вдруг обнаружили, что i^2=-1?
Задаеться, хотя зависит от уровня "погружения" в неё
Ага, а ещё сначала появилась аксиоматика Пеано, а потом люди поняли, что натуральными числами можно СЧИТАТЬ.
>Ага, а ещё сначала появилась аксиоматика Пеано, а потом люди поняли, что натуральными числами можно СЧИТАТЬ.
кстати, по существу так и было. поскольку для того, чтобы научиться считать, надо научиться прибавлять 1. посмотри, как учат счёту детей
Ты же тролишь, да? Прибавление единицы - это естественное свойство счёта, историческое, так сказать. Потом эти естественные свойства уже загоняют в строгие рамки аксиом.
>Прибавление единицы - это естественное свойство счёта,
и оно же есть самая суть аксиом Пеано -- они просто формализуют понятие, ясное интуитивно. а откуда оно ясно интуитивно? выучено потому что. т.е. твой мозг о нём уже знал, когда тебе было 10, оно просто не было сформулировано в явном осознанном виде
>они просто формализуют понятие, ясное интуитивно. а откуда
Ну я про то и говорю, что аксиомы просто формализуют. Поэтому чаще всего сначала появляется (или становится необходимой) модель, обладающая какими-то свойствами, а потом математики её строго задают.
>Математика не задается вопросом почему, она строится аксиоматически
Так что это утверждения не верное же в общем случае. Все начинается с вопроса, потом строятся аксиомы, чтобы соответствовать цели. А вот что потом уже получается, это да, это уже вытекает просто.
>Ну я про то и говорю, что аксиомы просто формализуют.
Я мыслю, что аксиомы, формализующие простые, естественные понятия, они в мозге уже есть, но в сидят там не осознанном виде, не сформулированные словами, но всё равно они там уже существуют.
мыслю, что в мозгу человека, который может считать, уже содержатся аксиомы пеано может быть, кроме аксиомы индукции, которая обслуживает бесконечность, а человек, который знает отрицательные числа, он знает и группу Гротендика
мыслю, что "свойства" модели и соответствующие аксиомы в таких случаях это по сути одно и то же
Вавилов плиз
Представь себе что ты идешь по треугольнику и тебе нужно обойти его полностью. Ты будешь идти и по пути сделать 3 поворота, каждый на какой-то угол. В сумме эти повороты дадут 360 градусов, это очевидно, ведь ты закончишь в той же точке, в которой начал. Каждый из эти поворотов будет равен 180 - угол1, 180 - угол2, 180 - угол3 и в сумме они дают 360. Видно что сумма этих углов получается 180. Таким образом тот факт что сумма углов треугольника равна 180 градусам, есть ни что иное как прямейшее следствие из того что мы придумали считать углом в 180 градусов, никакой эзотерики, просто прямой вывод. Определение развернутого угла и сумма углов треугольника это суть одно и то же, лишь сказанное разными словами.
Вот за такие ответы я люблю math
>почему низкогравитационный предел это плоское пространство?
Полуторалетней давности пост на сосаче заставил меня задуматься над перпендикулярностью связанных пространственных размерностей как базовом принципе или это наше субъективное восприятие? xd мироздания, кайф
дополнение: Вот в "принятом" доказательстве например фигурирует такое понятие как "полуплоскость". Что это? И почему прямая разбивает плоскость на две этих самых полуплоскости. Очевидно? Я так не думаю.
Не понимаю как можно построить строгое формальное доказательство без строгого формализма.
А так конечно, приложим хуй к носу хуе-мое. Я и сам так доказываю всегда и доволен как слон.
Нет, знаю
> Аккуратненько переносим прямую и видим что перекрестные углы равны
вот и вся "аксиоматика". Можешь себе на хуй лазерным резаком расписать.
![Square20n20Comps,20Eye20in20Triangle,20JPEG20file[1].JPG](/math/big/thumb/2311/14823283042140s.jpg)
![images[1]](/math/big/thumb/2311/14823283042171s.jpg)
![4004-eae58c[1].jpg](/math/big/thumb/2311/14823283042172s.jpg)