41 Кб, 200x261
41 Кб, 200x261Сап, матач. Аноном на коленке абсолютно корректно, просто, точно и изящно решена "неразрешимая" задача на построение трисекции угла, а заодно не менее корректно и точно опровергнута теорема Гаусса-Ванцеля о построении многоугольников. Но анон не математик и не знает, куда с этим идти и можно ли вообще с этого поиметь хоть какой то профит. Подскажите уж.
>>21606
примерно такого ответа я и ожидал. но решение абсолютно точное и корректное, вот прям комар носа не подточит базарю. так что чисто гипотетически, если хотя бы просто представить, что анон это сделал, что ему с этим можно делать дальше?
примерно такого ответа я и ожидал. но решение абсолютно точное и корректное, вот прям комар носа не подточит базарю. так что чисто гипотетически, если хотя бы просто представить, что анон это сделал, что ему с этим можно делать дальше?
>>21605 (OP)
Ну, касательно теоремы, опровергнута часть, добавленная Ванцелем. Построения самого Гаусса то, как раз, верны и справедливы.
Ну, касательно теоремы, опровергнута часть, добавленная Ванцелем. Построения самого Гаусса то, как раз, верны и справедливы.
>>21605 (OP)
Пости здесь со сканом паспорта
Пости здесь со сканом паспорта
>>21605 (OP)
Ну тут несколько вариантов: нахуй, впизду, на бутылку, в жопу, в кащенко, выбирай с умом.
>анон не математик
>точно и изящно решена
>анон не математик
>не знает, куда с этим идти
Ну тут несколько вариантов: нахуй, впизду, на бутылку, в жопу, в кащенко, выбирай с умом.
>>21616
ну может тут кто нибудь заметит тогда. мало ли. ща выложу.
ну может тут кто нибудь заметит тогда. мало ли. ща выложу.
>>21619
cерьезно, набирай в LaTeX
cерьезно, набирай в LaTeX
Я тебе что, Конфуций - в вёрстке разбираться? Нахуярил в paint.net наспех, суть то ясна все равно будет.
>>21621
Тогда всё таки проследуйте нахуй.
>Нахуярил в paint.net наспех
>абсолютно корректно, просто, точно и изящно решена
Тогда всё таки проследуйте нахуй.
>>21622
бля, какая разница где чертить?
бля, какая разница где чертить?
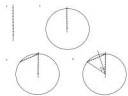
Кароче. Сначала Гаусс-Ванцель. Согласно теореме, правильный n-угольник возможно построить с помощью циркуля и линейки без делений тогда и ТОЛЬКО тогда, когда n=2k p 1p 2 *.....p i, где p i -различные числа Ферма. Что простейшим образом опровергается. Есть метод, который позволяет с помощью циркуля и линейки без делений строить правильные многоугольники с абсолютно ЛЮБЫМ числом сторон. Рассмотрим его на примере правильного девятиугольника.
1.Проводим прямую, и с помощью циркуля откладываем на ней девять равных отрезков.
2.Взяв сумму всех отрезков как радиус, строим окружность.
3.Проводим из точки пересечения хорду, равную радиусу, аналогично состоящую из девяти равных отрезков.
4.Через общую точку шестого и седьмого отрезка на хорде проводим из центра окружности прямую. Также достроим третью сторону равностороннего треугольника из двух радиусов и равной им хорды. Получится, что угол в 60 градусов при центре окружности разделяется прямой на углы в 20 и 40 градусов соответственно.
5.Понятно, что в сущности, задача по построению многоугольника сводится к построению соответствующего угла, который мы уже получили за счет хорды, разделенной на равное количеству сторон искомого многоугольника одинаковых отрезков. Далее, соединив точку пересечения последней проведенной прямой и окружности с дальней вершиной равностороннего треугольника, то есть построив новый треугольник с одним сорокоградусным углом, мы получим сторону искомого многоугольника, откладывая которую внутри окружности, построим этот самый многоугольник.
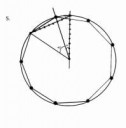
По этой схеме можно строить без ограничений любые правильные многоугольники, каждый раз проводя таким образом линию из центра через общую точку шестого и седьмого отрезков и аналогично строя хорды. Все дело — в количестве откладываемых мерок. Строятся абсолютно любые многоугольники. метод имеет чуть отличающийся алгоритм для построения правильного пятиугольника: в этом случае нужно получить угол в 72 градуса. Необходимо построить аналогичный радиус и хорду, разделенные на 5 равных отрезков. Это, согласно алгоритму, позволит нам получить пять углов по 12 градусов внутри угла в 60 градусов. Далее один из таких углов нужно добавить к углу в 60 градусов, чтобы получить искомый угол в 72 градуса. Пикча кривовата, но достаточно ясно всё отражает. Прошу критики, если есть признаки кащенизма) скан паспорта тоже тут.
1.Проводим прямую, и с помощью циркуля откладываем на ней девять равных отрезков.
2.Взяв сумму всех отрезков как радиус, строим окружность.
3.Проводим из точки пересечения хорду, равную радиусу, аналогично состоящую из девяти равных отрезков.
4.Через общую точку шестого и седьмого отрезка на хорде проводим из центра окружности прямую. Также достроим третью сторону равностороннего треугольника из двух радиусов и равной им хорды. Получится, что угол в 60 градусов при центре окружности разделяется прямой на углы в 20 и 40 градусов соответственно.
5.Понятно, что в сущности, задача по построению многоугольника сводится к построению соответствующего угла, который мы уже получили за счет хорды, разделенной на равное количеству сторон искомого многоугольника одинаковых отрезков. Далее, соединив точку пересечения последней проведенной прямой и окружности с дальней вершиной равностороннего треугольника, то есть построив новый треугольник с одним сорокоградусным углом, мы получим сторону искомого многоугольника, откладывая которую внутри окружности, построим этот самый многоугольник.
По этой схеме можно строить без ограничений любые правильные многоугольники, каждый раз проводя таким образом линию из центра через общую точку шестого и седьмого отрезков и аналогично строя хорды. Все дело — в количестве откладываемых мерок. Строятся абсолютно любые многоугольники. метод имеет чуть отличающийся алгоритм для построения правильного пятиугольника: в этом случае нужно получить угол в 72 градуса. Необходимо построить аналогичный радиус и хорду, разделенные на 5 равных отрезков. Это, согласно алгоритму, позволит нам получить пять углов по 12 градусов внутри угла в 60 градусов. Далее один из таких углов нужно добавить к углу в 60 градусов, чтобы получить искомый угол в 72 градуса. Пикча кривовата, но достаточно ясно всё отражает. Прошу критики, если есть признаки кащенизма) скан паспорта тоже тут.
Кароче. Сначала Гаусс-Ванцель. Согласно теореме, правильный n-угольник возможно построить с помощью циркуля и линейки без делений тогда и ТОЛЬКО тогда, когда n=2k p 1p 2 *.....p i, где p i -различные числа Ферма. Что простейшим образом опровергается. Есть метод, который позволяет с помощью циркуля и линейки без делений строить правильные многоугольники с абсолютно ЛЮБЫМ числом сторон. Рассмотрим его на примере правильного девятиугольника.
1.Проводим прямую, и с помощью циркуля откладываем на ней девять равных отрезков.
2.Взяв сумму всех отрезков как радиус, строим окружность.
3.Проводим из точки пересечения хорду, равную радиусу, аналогично состоящую из девяти равных отрезков.
4.Через общую точку шестого и седьмого отрезка на хорде проводим из центра окружности прямую. Также достроим третью сторону равностороннего треугольника из двух радиусов и равной им хорды. Получится, что угол в 60 градусов при центре окружности разделяется прямой на углы в 20 и 40 градусов соответственно.
5.Понятно, что в сущности, задача по построению многоугольника сводится к построению соответствующего угла, который мы уже получили за счет хорды, разделенной на равное количеству сторон искомого многоугольника одинаковых отрезков. Далее, соединив точку пересечения последней проведенной прямой и окружности с дальней вершиной равностороннего треугольника, то есть построив новый треугольник с одним сорокоградусным углом, мы получим сторону искомого многоугольника, откладывая которую внутри окружности, построим этот самый многоугольник.
По этой схеме можно строить без ограничений любые правильные многоугольники, каждый раз проводя таким образом линию из центра через общую точку шестого и седьмого отрезков и аналогично строя хорды. Все дело — в количестве откладываемых мерок. Строятся абсолютно любые многоугольники. метод имеет чуть отличающийся алгоритм для построения правильного пятиугольника: в этом случае нужно получить угол в 72 градуса. Необходимо построить аналогичный радиус и хорду, разделенные на 5 равных отрезков. Это, согласно алгоритму, позволит нам получить пять углов по 12 градусов внутри угла в 60 градусов. Далее один из таких углов нужно добавить к углу в 60 градусов, чтобы получить искомый угол в 72 градуса. Пикча кривовата, но достаточно ясно всё отражает. Прошу критики, если есть признаки кащенизма) скан паспорта тоже тут.
1.Проводим прямую, и с помощью циркуля откладываем на ней девять равных отрезков.
2.Взяв сумму всех отрезков как радиус, строим окружность.
3.Проводим из точки пересечения хорду, равную радиусу, аналогично состоящую из девяти равных отрезков.
4.Через общую точку шестого и седьмого отрезка на хорде проводим из центра окружности прямую. Также достроим третью сторону равностороннего треугольника из двух радиусов и равной им хорды. Получится, что угол в 60 градусов при центре окружности разделяется прямой на углы в 20 и 40 градусов соответственно.
5.Понятно, что в сущности, задача по построению многоугольника сводится к построению соответствующего угла, который мы уже получили за счет хорды, разделенной на равное количеству сторон искомого многоугольника одинаковых отрезков. Далее, соединив точку пересечения последней проведенной прямой и окружности с дальней вершиной равностороннего треугольника, то есть построив новый треугольник с одним сорокоградусным углом, мы получим сторону искомого многоугольника, откладывая которую внутри окружности, построим этот самый многоугольник.
По этой схеме можно строить без ограничений любые правильные многоугольники, каждый раз проводя таким образом линию из центра через общую точку шестого и седьмого отрезков и аналогично строя хорды. Все дело — в количестве откладываемых мерок. Строятся абсолютно любые многоугольники. метод имеет чуть отличающийся алгоритм для построения правильного пятиугольника: в этом случае нужно получить угол в 72 градуса. Необходимо построить аналогичный радиус и хорду, разделенные на 5 равных отрезков. Это, согласно алгоритму, позволит нам получить пять углов по 12 градусов внутри угла в 60 градусов. Далее один из таких углов нужно добавить к углу в 60 градусов, чтобы получить искомый угол в 72 градуса. Пикча кривовата, но достаточно ясно всё отражает. Прошу критики, если есть признаки кащенизма) скан паспорта тоже тут.
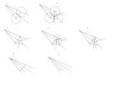
Трисекция. Задача проста - с помощью циркуля и линейки без делений разделить заданный угол на три равных.
1) С помощью циркуля отметить на лучах угла равные отрезки и соединить их концы. Построить перпендикуляр к получившемуся отрезку, опущенный из вершины угла, используя точки пересечений равных окружностей с центрами в его концах.
2)Отложить от концов отрезка и построить еще два отрезка, равных первоначально построенному так, чтобы одни их концы лежали на опущенном из вершины угла перпендикуляре, а другие - совпадали с концами первоначального. Затем провести в образованном равностороннем треугольнике высоты, используя точки пересечений равных окружностей с центрами в его вершинах.
3)Для удобства убрать вспомогательные окружности, использованные для построения перпендикуляров.
4)Построить еще один перпендикуляр к стороне треугольника.
5) Отложить на нем отрезок, равный меньшей части разделенной центром треугольника высоты. Таким образом, проведенная через его конец и центр треугольника прямая будет параллельна одной из его сторон и точкой пересечения разделит другую сторону в соотношении 1/3, так как в этом же общеизвестном соотношении центр равностороннего треугольника делит высоту.
6)Для удобства и наглядности убрать все лишние построения, оставив только первоначально построенный отрезок с точкой, делящей его 1 к 3. Отложив расстояние этой трети, получить вторую точку. Через полученные точки провести прямые из вершины угла.
7) Убрать все прочие построения, оставив только полученные трисектрисы.
8) В случае, если заданный угол не является острым, его следует произвольно поделить, получив острые углы, проделать с каждым описанную выше операцию и путем сложения долей разделенных на три части первоночально строимых отрезков, отмерить трети первоначально строимого отрезка всего заданного угла, затем аналогично проведя через них лучи из его вершины и разделив его таким образом на три равные части.
Тут вообще няшно всё.
1) С помощью циркуля отметить на лучах угла равные отрезки и соединить их концы. Построить перпендикуляр к получившемуся отрезку, опущенный из вершины угла, используя точки пересечений равных окружностей с центрами в его концах.
2)Отложить от концов отрезка и построить еще два отрезка, равных первоначально построенному так, чтобы одни их концы лежали на опущенном из вершины угла перпендикуляре, а другие - совпадали с концами первоначального. Затем провести в образованном равностороннем треугольнике высоты, используя точки пересечений равных окружностей с центрами в его вершинах.
3)Для удобства убрать вспомогательные окружности, использованные для построения перпендикуляров.
4)Построить еще один перпендикуляр к стороне треугольника.
5) Отложить на нем отрезок, равный меньшей части разделенной центром треугольника высоты. Таким образом, проведенная через его конец и центр треугольника прямая будет параллельна одной из его сторон и точкой пересечения разделит другую сторону в соотношении 1/3, так как в этом же общеизвестном соотношении центр равностороннего треугольника делит высоту.
6)Для удобства и наглядности убрать все лишние построения, оставив только первоначально построенный отрезок с точкой, делящей его 1 к 3. Отложив расстояние этой трети, получить вторую точку. Через полученные точки провести прямые из вершины угла.
7) Убрать все прочие построения, оставив только полученные трисектрисы.
8) В случае, если заданный угол не является острым, его следует произвольно поделить, получив острые углы, проделать с каждым описанную выше операцию и путем сложения долей разделенных на три части первоночально строимых отрезков, отмерить трети первоначально строимого отрезка всего заданного угла, затем аналогично проведя через них лучи из его вершины и разделив его таким образом на три равные части.
Тут вообще няшно всё.
>>21625
с помощью циркуля, лол.
с помощью циркуля, лол.
>>21629
циркуля нет под рукой. всё будет точно так же, как описано выше. если я не вижу какую то проблему - скажи, какую.
циркуля нет под рукой. всё будет точно так же, как описано выше. если я не вижу какую то проблему - скажи, какую.
>>21631
ты мне объясни что не так? если что то не так. Я точно так же отложу отрезки, построю равносторонний треугольник и прочее. в чем проблема то должна возникнуть по твоему?
ты мне объясни что не так? если что то не так. Я точно так же отложу отрезки, построю равносторонний треугольник и прочее. в чем проблема то должна возникнуть по твоему?
>>21633
почему не поделится? поэтапно. 1. отмерили равные отрезки на лучах, соединили концы. 2. Построили на этом основании равносторонний треугольник. 3. распилили основание на три равные части. 4. провели через точки "распила" лучи из заданного угла.
что именно должно не получиться?
почему не поделится? поэтапно. 1. отмерили равные отрезки на лучах, соединили концы. 2. Построили на этом основании равносторонний треугольник. 3. распилили основание на три равные части. 4. провели через точки "распила" лучи из заданного угла.
что именно должно не получиться?
>>21633
если еще и изначально, по условию, знать, что это угол в 60 градусов, то можно вообще обойтись без вспомогательного треугольника, кстати.
если еще и изначально, по условию, знать, что это угол в 60 градусов, то можно вообще обойтись без вспомогательного треугольника, кстати.
>>21636
ну где ж я тебе его в пол десятого возьму? давай сделаем так. ты возьмешь циркуль и все сделаешь сам, продемонстрировав, что именно не выходит. уж если ты не можешь словесно это выразить.
ну где ж я тебе его в пол десятого возьму? давай сделаем так. ты возьмешь циркуль и все сделаешь сам, продемонстрировав, что именно не выходит. уж если ты не можешь словесно это выразить.
>>21637
у меня линейка была последний раз, лет десять назад, тем более это нужно тебе, я то прекрасно осознаю, что трисекция произвольного угла линейкой и циркулем невозможна.
у меня линейка была последний раз, лет десять назад, тем более это нужно тебе, я то прекрасно осознаю, что трисекция произвольного угла линейкой и циркулем невозможна.
>>21638
если осознаешь и понимаешь - сформулируй почему не выйдет. потому что у меня складывается четкое впечатление, что ты просто априорно принимаешь, но ни в коем случае не осознаешь.
если осознаешь и понимаешь - сформулируй почему не выйдет. потому что у меня складывается четкое впечатление, что ты просто априорно принимаешь, но ни в коем случае не осознаешь.
>>21639
Если в кратце, то это следует из простого факта: Нет такой степени 2, которая бы делилась без остатка на 3. Можешь у Тао в его бложике по этому поводу почитать, вполне доступно объяснено.
Если в кратце, то это следует из простого факта: Нет такой степени 2, которая бы делилась без остатка на 3. Можешь у Тао в его бложике по этому поводу почитать, вполне доступно объяснено.
>>21640
Любопытно) Но я, как видишь, любых алгебраических выражений при решении избежал. Так что объясни мне на каком этапе моего решения и почему у меня не выйдет. Без привязки к числам и степеням. Любой угол. Любые условия. И мой метод. Он же прост, доступен даже школьнику. В нём обязана быть ошибка, не ускользающая от твоего зоркого глаза, если это действительно невозможно. Дай мне её.
Любопытно) Но я, как видишь, любых алгебраических выражений при решении избежал. Так что объясни мне на каком этапе моего решения и почему у меня не выйдет. Без привязки к числам и степеням. Любой угол. Любые условия. И мой метод. Он же прост, доступен даже школьнику. В нём обязана быть ошибка, не ускользающая от твоего зоркого глаза, если это действительно невозможно. Дай мне её.
>>21626
1 к двум, конечно же, не к трём. невнимательный я опять.
>разделит другую сторону в соотношении 1/3
>Для удобства и наглядности убрать все лишние построения, оставив только первоначально построенный отрезок с точкой, делящей его 1 к 3
1 к двум, конечно же, не к трём. невнимательный я опять.
>>21642
впрочем, на чертеже это видно. что именно 1 к 2. да и так понятно.
впрочем, на чертеже это видно. что именно 1 к 2. да и так понятно.
>>21615
Дебил сука, ты нахуя самый годный вариант, нахуй и впизду не написал?
Дебил сука, ты нахуя самый годный вариант, нахуй и впизду не написал?
>>21646
задача - построить три угла, а не делить какую то хуйню нацело. мы рассматриваем не Гауссовско-Ванцелевские методы построения, а конкретный, который я описал. ты мне, блять, объясни геометрически, в каком конкретно моменте построения и что не так? Что именно некорректно и почему?
задача - построить три угла, а не делить какую то хуйню нацело. мы рассматриваем не Гауссовско-Ванцелевские методы построения, а конкретный, который я описал. ты мне, блять, объясни геометрически, в каком конкретно моменте построения и что не так? Что именно некорректно и почему?
>>21648
деды меня тоже в кащениты запишут)
деды меня тоже в кащениты запишут)
>>21647
Потому что ты пидор, епта
Тебе же сказали, дебилу, берешь линейку с циркулемм и рисуешь как сказано а потом меряешь транспортиром какой там у тебя получился угол. А потом приходишь сюда чтобы насосаться трансцендентное число хуйцов.
Потому что ты пидор, епта
Тебе же сказали, дебилу, берешь линейку с циркулемм и рисуешь как сказано а потом меряешь транспортиром какой там у тебя получился угол. А потом приходишь сюда чтобы насосаться трансцендентное число хуйцов.
что ж, соснул хуйца, выполняя построение в автокадоподобной программе. не понимаю откуда там может быть погрешность, все же идеально в соотношениях, епта.
>>21624
Не получится. То что отрезок разделен на равные части, не значит, что углы тоже будут равные.
>4.Через общую точку шестого и седьмого отрезка на хорде проводим из центра окружности прямую. ... Получится, что угол в 60 градусов при центре окружности разделяется прямой на углы в 20 и 40 градусов соответственно.
Не получится. То что отрезок разделен на равные части, не значит, что углы тоже будут равные.
>>21655
Ну вот, учи алгебру, чтобы не быть баттхертом.
Ну вот, учи алгебру, чтобы не быть баттхертом.
>>21655
Эти программы пишутся "учеными", которые расчитывают например что трисекуия угла невозможно. отсюда и ошибки погрешности
Эти программы пишутся "учеными", которые расчитывают например что трисекуия угла невозможно. отсюда и ошибки погрешности
>>21605 (OP)
ОП, остановись. Потом не отмоешься от этого.
ОП, остановись. Потом не отмоешься от этого.
>>21698
сволочи
сволочи
>>21698
и инженегры с планеты нибуру проектируют линейки, траспортиры и циркули так, что трисекция угла становится невозможна.
и инженегры с планеты нибуру проектируют линейки, траспортиры и циркули так, что трисекция угла становится невозможна.
>>21605 (OP)
А ты хорошо подумал? А то я тут на спидах как-то формулу простых чисел нашёл и гипотезу Римана доказал. Хорошо ума хватило до утра подождать, пока отпустит.
А ты хорошо подумал? А то я тут на спидах как-то формулу простых чисел нашёл и гипотезу Римана доказал. Хорошо ума хватило до утра подождать, пока отпустит.
>>21634
И сколько у него углы будут тогда градусов? Ты только что поделил 60/3.
> построили равносторонний треугольник
И сколько у него углы будут тогда градусов? Ты только что поделил 60/3.
В голос с треда. И не лень же ему было все это писать и строить.
>>21753
братан, узнаю себя
братан, узнаю себя
>>21652
На самом деле пидар ты. Вопрос же простой: указать ошибку. Если ты её не можешь указать, значит, как минимум, ты его решения не понимаешь (скорее всего, не понимаешь также и почему задача нерешаема), а если не понимаешь, нефиг его оскорблять, изображая из себя умного
Элементарная этика же
На самом деле пидар ты. Вопрос же простой: указать ошибку. Если ты её не можешь указать, значит, как минимум, ты его решения не понимаешь (скорее всего, не понимаешь также и почему задача нерешаема), а если не понимаешь, нефиг его оскорблять, изображая из себя умного
Элементарная этика же
>>23192
Тебе уже выше точно сформулировали ошибку. Ты где-то поделил сторона напротив угла на равные части и решил, что прямые из вершины угла к этим частям тоже разделят угол поровну. Это неверно
Тебе уже выше точно сформулировали ошибку. Ты где-то поделил сторона напротив угла на равные части и решил, что прямые из вершины угла к этим частям тоже разделят угол поровну. Это неверно
>>23204
Истинно так, это неверно
Истинно так, это неверно
>>21624
Выкладывать на сосаче свой паспорт... Тебе стоило сделать это в /b
Выкладывать на сосаче свой паспорт... Тебе стоило сделать это в /b
>>23433
На тебе Римана, например https://riemannhypothesisproof.files.wordpress.com/2017/08/latexfra51.pdf
На тебе Римана, например https://riemannhypothesisproof.files.wordpress.com/2017/08/latexfra51.pdf
>>23493
С этого места поподробнее.
> считаем её, считаем количество простых чисел и сравниваем с количеством нулей
С этого места поподробнее.
>>23532
Братишка, так доказательство о количестве простых чисел, а не о поиске простых чисел.
Братишка, так доказательство о количестве простых чисел, а не о поиске простых чисел.
>>23611
Ну так распиши подробнее плс, какое количество, какие нули, ничего не понятно.
Ну так распиши подробнее плс, какое количество, какие нули, ничего не понятно.
 596 Кб, 1573x1568
596 Кб, 1573x1568 599 Кб, 1564x1568
599 Кб, 1564x1568>>25817
Пофиксил же, ну.
Пофиксил же, ну.
Проигранно.
https://arhivach.org/thread/307173/
>>21641
>>21647
Рыбников Юрий Степанович, залогиньтесь. И верните парню паспорт, не по-людски это.
https://arhivach.org/thread/307173/
>>21641
>>21647
Рыбников Юрий Степанович, залогиньтесь. И верните парню паспорт, не по-людски это.
Обновить тред