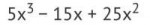Тред используется для любых вопросов, связанных с современной алгеброй и её ответвлениями (но не ограничивается оными).
Для начала предлагаю следующую задачу на пикрелейтид.
Это самоконтрольный тест. Не можешь её решить - не владеешь алгебраической геометрией.
Заниматься алгеброй — значит, по существу, вычислять, т. е. выполнять над элементами некоторого множества "алгебраические операции".
Несомненно, именно возможность этих последовательных операций, при которых форма вычислений оставалась одной и той же, но природа математических объектов, над которыми производились вычисления, существенно менялась, позволила постепенно выявить руководящий принцип современной математики: математические объекты сами по себе не столь существенны — важны их отношения.
Архивач
В теории квантового поля, в некоторых изложениях пол-курса затирают про эти группы Ли. Преобразования Лоренца/Пуанкаре образуют группу Ли, а их (унитарные) представления соответствуют частицам с разными спинами. (и это чертовски занятный факт имхо)
Вот тебе еще какая-то мутная теоремка из квантовой механики
https://en.wikipedia.org/wiki/Wigner–Eckart_theorem
Да, имеют. Вращения — это группа Ли. Сдвиги пространства — это группа Ли. Уже по этим примерам видно, насколько это (простое и) важное понятие. Классификация элементарных частиц использует группы Ли, например, кварки — это просто какое-то представление какой-то из SU (комплексный аналог вращений), а то, что всё состоит из кварков — это то, что все представления получаются из этого «простого» представления с помощью произведений (тензорных). Подробнее, например, в книге И.Р. Шафаревич «Основные понятия алгебры» (там есть пункт про это).
Представление — сопоставление элементам группы линейных преобразований, вроде представления перестановок трёх букв как симметрий равностороннего треугольника; тензорное произведение — полный аналог перехода от однородных многочленов степени 1, которые можно отождествить с векторами, к многочленам произвольной степени, только абстрактно аксиоматически описанный для абстрактно аксиоматически заданных линейных пространств. Это если кто-то не знает, вдруг.
Если под Zp имеется в виду Z/pZ, то количество базисов равно Π(p^n - p^i), i=0,...,n. Но это упорядоченных базисов.
ему базис L^tt, A ∈ Hom(L, L^tt ) — такое отображение, что A(e_i) = g_i. Зависит ли A от выбора базиса (e_i)?
Верно, что дважды двойственный базис L^tt это базис L? Значит, A от выбора базиса не зависит.
Забей на базисы.
Смотри. Есть линейное пространство L. Пространство функционалов f(v) на нём есть двойственное к нему L'.
Выберем какой-нибудь определенный v из L, и подставим его во все функционалы в L'. Не совсем строго можно теперь считать, что это не функционал ставит число вектору v, а вектор v ставит функционалам числа, тем самым такое отображение есть функционал. Тем самым вектора в L это функционалы для пространства L'.
Чтобы записать это строго нужно построить функцию, которая каждому вектору v ставит соответствующий ей функционал на L'. h: v = gv(f) где gv(f)=f(v). Так как все двойственные пространства имеют одинаковую размерность, то нужно всего лишь доказать, что h мономорфизм, оттого h изоморфизм.
>математические объекты сами по себе не столь существенны — важны их отношения.
Что это значит?
 134 Кб, 1113x771
134 Кб, 1113x771G={e,a,b,c} — абелева группа с таблицей умножения пикрил.
Не могу понять, почему перестановка элементов a, b, c является автоморфизмом G с указанной операцией (той, которая таблице задаётся, да?).
Почему в перестановке участвуют только a, b, c, что делать с e?
Как строить-то этот автоморфизм?
При автоморфизме e в любом случае переходит в e, так что ясно, что с ней делать.
Таблица умножения по сути говорит, что каждый элемент обратен сам себе и что произведение двух разных неединичных элементов равно третьему неединичному элементу, она симметрична относительно всех перестановок неединичных элементов. Поэтому эти перестановки и определяют автоморфизмы.
Автоморфизм строится аналогично тому, который встречается при доказательстве теоремы Кэли?
f(g_j): g_i → g_j⋅g_i, где f суть есть перестановка.
Автоморфизм, естественно, не f (перестановка, описанная выше), а другое отображение, к примеру, L: g_j → f(g_j).
Это всё ещё вопрос, а не удтверждение. Верно?
Любая подгруппа абелевой группы нормальна.
Движение -- это конгруэтность.
Две фигуры подвижны(одна переходит в другую), если равны параметры фигуры.
Очевидно, что движение без расстояния, значит форму без метрики.
Значит единичный куб представляет ту же фигуру, что и стократный куб.
Подводные в том, что в машинке это не применяется.
я купил биткойны в прошлом декабре
x = 2pi/5
Подсказка: cos(2x) = cos(3x), следовательно можно выразить cosx через формулы двойного и тройноог угла и получится уравнение.
Сделал несколько преобразований получил:
2q^3(1/x1^3+1/x2^3+1/x3^3)+6q^2-q^2(x1^2/x3^2+x1^2/x2^2+...)-2q^2(x1/x2+x1/x3+...)+2q(x1^3+x2^3+x3^3). Дальше увяз.
Правильно понимаю, что (x_1-x_2)^2(x_1-x_3)^2(x_2-x_3)^2 - дискриминант кубического уравнения?
Вопрос в том как грамотно от (x_1-x_2)^2(x_1-x_3)^2(x_2-x_3)^2 перейти к -27q^2-4p^3. Под спойлером у меня записано на чём я остановился.
Раз это и правда дискриминант, тогда ещё один вопрос. Почему именно это число связано с корнями многочлена? Положим, я не знаю, что (x_1-x_2)^2(x_1-x_3)^2(x_2-x_3)^2 - дискриминант кубического уравнения. Тогда как к нему прийти от редуцированного уравнения x^3+px+q?
Какие там есть интересные задачи?
Руками, по определению, непосредственно.
 56 Кб, 655x1024
56 Кб, 655x1024это было так тонко, что даже толсто. лол
Знает кто доказательство теоремы о определителе треугольной матрицы
>Определитель матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали.
Как доказать?
Берёшь и расписываешься по столбцу или строчке, замечая, что если дополнительный минор содержить нулевой столбец, то он равен 0.
свою безграмотность, очевидно же
https://en.wikipedia.org/wiki/Derivation_(differential_algebra)
ВО 1ых, найди в той статье слово "гомоморфизм", ты его не найдешь знаешь почему? Потому что дифференциал произведения не равен произведению дифференциалов.
Во-вторых, научи так же шутить "что я за хуйню прочитал?" - "свою безграмотность, очевидно же"! просто АХУЕТЬ! Как ты только блять додумался до такого, ебучий придурок сука!
все, обтекаю
спасибо
И поэтому это гомоморфизм кольца? Или к чему ты это пизданул?
Манин.
И как вывести общую формулу для тензора чётного ранга, инвариантного относительно вращений и симметричного относительно перестановки любой пары индексов? Там сумма произведений символов Кронекера должна быть.
Во втором полагаю, что надо произведенией n/2 символов кронекера симметрировать, где n - ранг тензора + ещё учесть числовой множитель как-то.
Какие ориентированные на упражнения книги можете посоветовать (желательно с решениями или ответами для самопроверки, можно на английском)?
да он сам не знает, потому и спрашивает у нас
только мы сами не физики и ответить не можем. странный он, какой ответ он ждал-то?
Я вообще мимо прохоил и решил пошутить.
Наверное топология просто вылезла в каком то неожиданном месте в металлофизике, раз её реквестируют.
В общем-то в condensed matter всё уже пропитывается всякими гомотопиями и категориями, см. например, https://arxiv.org/pdf/1810.12965.pdf
модуль это и есть представление.
пусть m и n имеют общий делитель a...
Конечно, это очень легко. Централизатор перестановки состоит из перестановок, которые переставляют&прокручивают её циклы.
Скиньте плез билеты по алгебре первый семестр для матфака, условной вышки или мгу. Если можно то все 3 семестра. Буду благодарен, если скинете также по дискретке/графам/алгоритмам и прочей информатике.
Ну если ты знаешь слово "группа", то конечно.
|2 0|
|0 2|
Существуют четыре прямые, вдоль которых она растягивает вектора, не меняя их направления: по горизонтали/вертикали с коэффициентом 2; по диагоналям с коэффициентом (8)^(1/2).
Почему же утверждают, что у неё может быть не больше 2 неколлинераных собственных вектора?
>Существуют четыре прямые, вдоль которых она растягивает вектора, не меняя их направления: по горизонтали/вертикали с коэффициентом 2; по диагоналям с коэффициентом (8)^(1/2).
Уверен, что только 4?
>Почему же утверждают, что у неё может быть не больше 2 неколлинераных собственных вектора?
Кто утверждает? Сам же опроверг это утверждение.
>Уверен, что только 4?
Вроде, да. Вектора, направленные вдоль других прямых, изменят угол наклона.
>Кто утверждает? Сам же опроверг это утверждение.
"Оператор A (матрица A) имеет не более n различных собственных значений (в n-мерном линейном пространстве)" - например, тут:
http://twt.mpei.ac.ru/math/LARB/Linoper/LA_04050000.html
Твой оператор тупо умножает вектор на два, поэтому для него ВСЕ ненулевые векторы собственные. Смысл в том, что нельзя взять больше двух векторов так, чтобы они были линейно независимы . Даже если взять только те, что ты перечислил, то для них это выполняется.
Когда ты ищещь собственные векторы, ты, вообще говоря, ищешь собственные подпространства, т.е. базисы подпространств, векторы которых растягиваются в число раз, соответсвующее числу соответствующего собственного значения.
У тебя любой базис двумерного простраснтва состоит из двух векторов. Так что очевидно, что совокупность базисных векторов собственных подпространств не может превзойти совокупность базисных векторов всего пространства.
>собственных значений
а не собственных векторов
>Вроде, да. Вектора, направленные вдоль других прямых, изменят угол наклона.
Никакие углы не меняются. Ты знаешь, как перемножаются матрицы?
Вряд ли, недаром же у нас теорема классификации есть только для конечно-порождённых
Зайди на сайт.
Спасибо, добрый анон.
А есть подобное от Чебышевки?
Не пиздите меня пожалуйста, я знаю, что я тупой, но я только начал изучать вышмат, параллельно готовясь к ЕГЭ это не так просто
Векторное пространство строится над полем (частным случаем кольца). Разъясни для себя хорошенько этот момент.
Какой есть учебник, написанный понятным языком? А то как не начну читать ваших Винбергов и прочих, так удушить себя хочется, какая же сложносформулированная залупа там
Хз, что может быть проще Винберга или Кострыкина (вводные курсы ведь), в любом случае надо учиться воспринимать такую подачу. Там вроде бы и примеры приводятся + гугол есть.
Нет. В линейном пространстве нет умножения элементов, вместо этого - умножение на элементы основного поля.
Алуффи
M. Artin
 4 Мб, webm,
4 Мб, webm,1280x720, 0:20
Ты можешь взять и придумать множество (например расширение Q каким-нибудь иррациональным числом; ещё можешь наложить дополнительные условия в виде тождеств которым должны удовлетворять любые два элемента твоего множества), и можешь придумать себе операцию, простой пример это "сложение с нулем", или например последовательную комбинацию сложения, умножения и возведения в степень, или ещё что-то.
И потом проверить, какие аксиомы выполняются, является ли то что ты придумал кольцом или группой. Здесь в принципе два варианта. Либо это уже известный пример и ты изобрел вещественные или комплексные числа; либо оно вообще никакой разумной структуры не образует и не является в алгебраическом смысле ничем.
Это в принципе мало интересное упражнение. Интереснее находить известные структуры там, где их, казалось бы, нет. Например то что кобордизмы можно умножать и складывать и выполняются все аксиомы кольца. Или там нетривиальные операции в когомологиях, квадрат Стинрода, произведение Масси. Внешнее произведение поливекторов, или дифф. форм, или скобка Пуассона. В принципе это фундаментальной важности было открытие, что как алгебраическая структура, алгебра дифференциальных форм изоморфна внешней алгебре. По сути ты показываешь, что что-то до сих пор плохо и недостаточно понятое оказывается можно описать в известных и привычных терминах. В целом, исторически, нахождение соответствующей структуры позволяло а) исправить ошибочные утверждения б) перейти к более общей ситуации (например понятие модуля сначала возникло в работах Дедекинда, и только потом выяснилось что если векторное пространство определить над кольцом, то получится идентичная конструкция), в) найти двойственные объекты и операции (ковариатные и контравариантные векторы, полупрямое произведение и т.д.)
Это очень условное деление. Например, топологическое пространство - это тоже множество с заданной некоторыми аксиомами структурой, но само по себе оно алгебраическим объектом не считается.
Если очень нужно простое и ёмкое определение, то можно, к примеру, с натяжкой определить алгебру как науку об ассоциативных бинарных операциях на множествах. Что-то мы при таком определении упустим, но на то это и условное деление.
>>52282
Я имел в виду не только числа, а вообще любые объекты в том числе и топологические. Значит я не правильно понял, что алгебра изучает структуры, которые существуют вообще в любой структурированной системе? Раз есть системы неалгебраические. А можно ли любую систему сделать алгебраической не включая в нее ограничения и операции, которых там не было?
>об ассоциативных
а что такое ассоциативных?
Ещё я хотел спросить. Саватеев на своей первой лекции сказал что в математике не бывает правильных и неправильных дробей. И что типа дробь 48/16 это типа нормальная крутая дробь. Но какого хуя то? Как можно думать таким понятием?
Операцию предельного перехода, понятие непрерывности и всё такое, невозможно описать алгеброй. Для этого придумали топологию. 99% математики это переплетение алгебры и топологии. Например, функциональный анализ. Берем алгебраический объект (векторное пространство), добавляем топологическую структуру (пополняем по норме).
Или гомологическая алгебра. И т.д.
>ассоциативных
Ну тех где выполняется аксиома ассоциативности, очевидно, a (b c) = (a b) c.
>правильных и неправильных дробей
Про рациональное число лучше всего думать как про класс эквивалентности, 5/15 и 1/3 это не разные числа, просто разный способ записи одного и того же числа. То же можно сказать про 0.99999… и 1.
а числа 0,(9) не существует. это дыра на числовой прямой. Это я ещё у одного блогера узнал
Тогда получается можно в любой системе с любыми объектами найти одинаковые принципы. А это либо топологические либо алгебраические принципы? То есть алгебра и топлогия занимается этими универсальными принципами?
>можно в любой системе с любыми объектами найти одинаковые принципы
А можно и не найти. Но найти это всегда хорошо.
>либо топологические либо алгебраические принципы
Теоретико-категорные.
Начинаю путаться. Короче, если я хочу универсальных принципов, то мне надо теорию категорий изучать. А алгебра и топлогия это частные случаи.
Ты хотел сказать "полно", а не "всюду плотно".
>>52296
Да, тебе надо изучать теорию категорий. Ещё можно математическую логику, это в принципе тоже об универсальных принципах, но с другого бока.
Алгебру и топологию придётся изучать в любом случае, без базовых знаний в этих областях ты не вдуплишь большую часть примеров, которые будут тебе нужны для тех же категорий.
Савватеев имеет ввиду, что в большинстве случаев к неправильным дробям в ответе доёбываются по беспределу. С корнями в знаменателе такая же история.
Я алгебру воспринимаю как прерывную математику, а топологию как непрерывную. Алгебра кубик Рубика, топология пластилин, чета такое.
А любое упоминание о группах Ли или топологических векторных пространствах причиняет тебе мучительную боль? Или, вероятнеё, ты с такими понятиями не сталкивался
Мне кажется это уже алгебраическая топология/геометрическая алгебра или что-то такое, комбомикс. Полностью разделить невозможно ведь.
Ну хорошо, а вот комбинаторика не связана с непрерывностью, она тоже к алгебре относится?
Но можно ли подобным образом определить, например, полугруппу или модуль? Полугруппа, возможно, вкладывавется в полугруппу всех отображений множества в себя, но я не видел доказательств этого факта. А с модулем вообще сложно. Например, любое ли кольцо вкладывается в кольцо эндоморфизмов абелевой группы?
Половина языкочесательных выступлений Арнольда - о преподавании. У тебя есть опыт преподавания? У многих тут есть, как ни странно, в том числе и у меня.
Если тебе нужно рассказывать про полугруппы или модули, то студенты, вероятно, уже обладают достаточной математической культурой для понимания таких понятий. Тем более, полугруппа - плохой пример, это просто множество с ассоциативной операцией, там не нужно (было бы) танцевать, объясняя это школьникам.
И да, Арнольд так определял группу в своих лекциях школьникам о теории Галуа, и оно действительно интуитивнее и полностью обосновано в этом случае.
Ещё меня веселит тот факт, что вербито-адепты ненавидят/презирают Арнольда за такие вот определения, хотя они по духу куда ближе к категорному языку, чем традиционные.
Любой критикующий арнольда это вербитоадепт?
>действительно интуитивнее и полностью обосновано в этом случае
Оно интуитивно, конечно, и не бесполезно как иллюстрация, особенно если речь о конкретных примерах, например группе симметрий тетраэдра и её подгруппах. См. "Что такое математика", он отсюда и приходит к понятию короткой точной последовательности. Более того, ещё было бы небесполезно сказать пару слов о подстановках, и показать что симметрии и подстановки это одно и то же (можно просто пронумеровать грани), чего Арнольд например не делает, но зато делают другие авторы, например Александров который П.С. в своей брошюре для старшеклассников. При чем у него там есть аксиоматическое определение группы. И теоремы Нётер об изоморфизме он доказывает.
>Арнольд так определял группу в своих лекциях школьникам о теории Галуа
Только дело в том, что это вообще не определение. И тот факт, что ты не понимаешь, что такое определение, полностью объясняет то, что ты не математик, а тупой пиздобол, который ищет вербитодетей на дваче, у себя под кроватью, и в прочих местах.
И критика в адрес Арнольда вообще не на этом основалась, а на ахинее, которую он не только изложил в многочисленных брошюрах, названных кем-то "сборником анекдотов", но еще и прочитывал неоднократно в школьником на летней школе в Дубне и в других местах, и если бы не было пиетета вокруг академической репутации Арнольда, его бы по-хорошему следовало послать нахуй с такими лекциями.
Полегче, я не залупаюсь на Арнольда, маленький ещё. Мне просто интересно, есть ли аналогичные теоремы для других классов алгебраических объектов.
>Любой критикующий арнольда это вербитоадепт?
ну ты-то совсем не палишься, у тебя посты как у димки с мишкой один в один
мимо-анон, арнольда не читал
Нет, да, ладно, плохое разделение.
>Только дело в том, что это вообще не определение.
хуле нет то? Группа это нечто + тройка морфизмов.
Сходи тифаретничка ещё наверни, шизик. Ему арнольд только что явно морфизмы не называет, а он продолжает яро защищать убогое дефолтное определение. Теоркат вообще читал дальше введения? Пиздуй в /sci/ нубов гонять, здесь ты никого своими знаниями википедии не поразишь.
>Пиздуй в свои родные разделы - ну там /b/, /pol/, жж, лурк.
>Пиздуй в /sci/ нубов гонять, здесь ты никого
>Сходи тифаретничка ещё наверни, шизик
Не то что? Порвешься совсем, свинья безмозглая?
>Теоркат вообще читал дальше введения
Ну ты категории по Арнольду учил, я уже понял. Какое у него определение категории, кстати?
>убогое дефолтное определение
Убогое в твоем арнольдистском манямирке разве что, у Маклейна такое же определение группы, как у меня.
забавно, что ты не понимаешь даже прямого текста, с которым к тебе обращаются, зато пихаешь пафосные выверты типа
>И тот факт, что ты не понимаешь, что такое определение, полностью объясняет то, что ты не математик, а тупой пиздобол
понаблюдал за тобой из соседнего треда
и чего тебя так разрывает любое упоминание арнольда? он до тебя домогался, когда тебе было 9 лет? так об этом надо на фейсбуке писать, вот это был бы наброс
Представляешь, здесь сидит более одного анона, которые считают, что ты глупенький. Ясное дело, что это вызывает у тебя когнитивный диссонанс и легче всё списать на семёнство, чем на собственное невежество.
Группа это нечто, да. А ещё группа это точка. А дифференциал это стрелочка.
Если ты хочешь чтобы твои
>глубокомысленные выверты
сравнивали с определениями, которые были у Нётер и Гильберта, потрудись, во всяком случае, выражаться внятно.
>>52371
>более одного анона, которые считают, что ты
Тащемта только ты и ещё один ворвавшийся в тред поборник категорий по Арнольду, который, видимо, скоро расскажет нам, что такое группоид.
Впрочем
>когнитивный диссонанс
>гонять нубов
>свои родные разделы, жж, лурк
Ты жертва Пикабу что ли? Так бы и сказал. В принципе это интересно, конечно, больше ебанатов с разных ресурсов, живее раздел, вот уже обсуждения какие-то. Правда довольно однообразные в твоём случае.
>скоро расскажет нам, что такое группоид
Под «нами» ты имеешь в виду «я и моя прелесть»? Ты же здесь один такой юродивый
подвести группоид под какие-нибудь преобразования едва ли должно быть хоть чуть-чуть трудно, если уж захочется; просто преобразования будут локального характера, и все
Про Арнольда ничего не знаю и в этом трэде отписывался давно по совершенно другой теме, но упомянутое выше определение группы действительно идейно близко к категорному мышлению. Это очевидно, думаю, всем, кто доказывал коммутативность более одной диаграммы в своей жизни. Со стороны именно ты выглядишь нелепо, честно говоря, игнорируя аргументы других и используя fallacies. Но мне так вы все тут долбоёбы.
>же здесь один такой юродивый
В том смысле, что опустился до разговора с тобой, что ли? И не с такими дебилами сталкивался.
>подвести группоид под какие-нибудь преобразования едва ли должно быть
Угу, можешь подавать заявку на грант уже, напишешь учебник по алгебре с позиций Арнольда, упразднив аксиомы группы и кольца окончательно. Безусловно, твой высер разделит судьбу двухтомника Ван дер Вардена и со временем я стану горд тем что имел честь общаться с тобой, тупым клоуном, на анонимной имиджборде. Ещё есть что сказать, или это всё?
Наверно ты не заметил (да и вряд ли заметишь, хотя я тебе сейчас прямо на это укажу) у тебя самого давно не находится ничего сказать, кроме разнообразных оскорблений собеседников. Тем самым у меня есть сказать как минимум не меньше, чем есть у тебя. Поскольку, очевидно, ты сам останавливаться не будешь, не откажу себе и далее вставлять какие-нибудь реплики, если захочется
>Я понимаю, что многие сейчас сначала узнают английские термины, типа "abelianization", а потом механически переносят их в русский язык. Давайте всё-таки безжалостно выкидывать таких монстров, как "абелианизация", и ставить нормальные давно существующие русские слова. В данном случае - абелизация.
Так я-то согласен. Ну абелианизация, ну и что. Я, по крайней мере, только такое произношение слышал вживую. Меня это меньше коробит, чем "специальная" теория относительности или "линейная оболочка, натянутая на вектора".
Цитата, если что, из обсуждения на педивикии.
У него видимо частная теория относительности, из серии "категории частных и теория гомотопий".
Прошу помощи с сингулярными значениями.
Каков смысл сингулярных значений? Собственные значения и вектора, например, определяют одномерные подпространства, инвариантные относительно оператора. То есть дают возможность разложить оператор. А сингулярные?
Как от SVD оператора переходим к SVD произвольного линейного отображения?
Я всегда понимал что линейное отображение = поворот масштабирование другой поворот. Сингулярные значения - то самое масштабирование.
В догонку вопрос алгебраистам - интерпретацию svd в geometric algebra кто-нибудь ковырял. Есть где почитать чего?
Двач, мне нужен сайтец или архивы кровавой гэбни со всякими там примерами, логарифмами, уравнениями за все классы и сё такое.
Не хочется искать в поисковиках прост.
Скачай учебники за все классы
Купи Киселёва арифметику и алгебру. В трёх небольших книгах есть все необходимое
Модульная арифметика, это такой пиздец, но я поясню вам:
Компьютеры не очень хорошо справляются с произвольно большими числами. Эту проблему можно решить, если выбрать максимальное значение и иметь дело только с числами, которые меньше максимума. Работает это как в часах с циферблатом и стрелками. Как перевести их, например, на 37 часов? Очевидно, разделить 37 на максимум — то есть 12 — и докрутить остаток. Так и здесь: любые вычисления, дающие результат больше максимума, мы «докручиваем» до числа в допустимом диапазоне.
а что он написал общую алгебру?
Ну не совсем с произвольными, а просто с рациональными. То есть любое деление они представляют в виде большой десятичной дроби. И поэтому сравнивают результаты деления взаимно простых чисел не с помощью знака равно а с помощью больше-меньше погрешности. Ты об этом?
Из за этого включается так называемая Floating-point arithmetics, которая даже не может правильно сравнить результат сложения двух десятичных дробей
0.1 + 0.2 == 0.3 // false
Приветствую, я паста. Вот мы и поговорили. https://xakep.ru/2019/08/27/elliptic-curve-cryptography/
>console.log(0.1 + 0.2 == 0.3); //false
Бле, внатуре. Чё за нах? Опять новый браузер ставить что-ли?
Аа я понял к чему ты клонишь. Могу сказать про это то что идея шифрования рса тоже имеет интересную историю, заключающуюся в том, что сначала был придуман принцип, по которому банк поставляет кейс, ключ от которого есть у банка, в который клиент кладёт свои данные и запирает, и много позже был придуман математический принцип с множителями, который смог воплотить его в жизнь.
Раз уж ты про RSA, держи это, моешь слить в zip: https://username1565.github.io/pgp/
После распаковки, работает локально, client-side на скриптах.
А вообще, эллиптическая криптография гораздо интереснее. Там ключи поменьше, а взломать так хуй.
Однако ECC ещё не завезли, потому что кодировать-декодировать сообщения в точки на эллиптической кривой - не понятно как.
Но у меня уже, по мере изучения, чё-то уже вырисовывается в мозгах, правда сформулировать толком не могу ещё.
Дело не в браузерах, просто конструктивная математика каличная.
>конструктивная математика каличная
В том смысле, что нет алгоритма, который бы мог два числа произвольных сравнить, поэтому если дробь не степень двойки, как 0.5, 0.25, 0.125 и тд, то там будет период, ну и на каком-то знаке после запятой округление(например 0.2 + 0.1 в двоичной это 0.0(0110) + 0.0(0011) и по идее должно получаться 0.0(1001) то есть 0.3, но где-то происходит округление и 0.2+0.1 = 0.30000000000000004 != 0.3 получается)
Произвольных вычислимых.
 136 Кб, 1059x125
136 Кб, 1059x125Понимаю, что a порождает базис в факторкольце многочленов над Fp, в принципе если постараюсь, докажу, что элементы из Fp порождаются (хотя хз), но как линейные комбинации получить -- не представляю.
Ну ты хоть номер-то назови, ёпта, прояви элементарное уважение к сосачерам.
Если №10, то очевидная индукция + разложение по одной строке.
>надо потом будет через многочлены ещё порешать
>можно равенство частей слева и справа проверить
Заебёшься. Типа ничего дельного из этого из этого не выйдет.
А если хочешь посмотрел доказательство, где в определителе используется то свойство, что он многочлен - смотри
https://ru.wikipedia.org/wiki/Определитель_Вандермонда
Хз. Это вообще решается??
> Сап,двач.Помогите с задачей,хуй знает что с ней вообще делать:найти число классов эквивалентности над С и над R квадратичных форм от n переменных.
Число классов эквивалентности - число видов нормированных диагональных матриц, соответствующих этим формам. Почему и сколько их сам догадаешься.
Конечно, некорректная, но остальные инварианты вряд ли доступны в курсе алгебре мухосранскгу.
А которая из теорем де Рама неизвестна нормальным аналитикам?
Теорема. Для любой таблицы (1) интерполяционный многочлен существует в единственном виде. На (1) таблица инт. многочлена в общем виде
Доказательство:
Действительно, легко видеть что мн-н заданный ф-лой
(Тут формула форма Лагранжа)
это инт. мн-н в форме Лагранжа.
... (дальше единственность доказываем)
Почему так нахуй? Я не понимаю вообще откуда эта форма взялась. Подозреваю что препод разрешит это ей не рассказывать, но мне просто интересно. Как эту формулу нашли?
Я не совсем понял вопрос и за историю этой формулы не шарю, но, может быть, ты что-то осознаешь, если подставишь в эту формулу какой-нибудь из узлов xi и поймёшь, почему этот многочлен является интерполяционным.
Все слагаемые формулы, кроме i-го, обнулятся, потому что в числителе окажется множитель xi-xi. А в i-м слагаемом этого множителя не будет, зато все xi-xj в числителях и знаменателях сократятся, и в итоге i-е слагаемое окажется просто равным f(xi).
Сборник задач по алгебре, Кострикин
Короче, в программе есть участок, где к разложенной по Холецкому матрице (LLT разложение) нужно прибавить другую, не разложенную матрицу R. Причем ответ тоже должен быть разложенный.
Есть вроде какое-то решение, и предполагает qr разложение R, но я не знаю нихуя, сложно пиздец. Спасибо.
Сверни разложенную матрицу, сложи и разложи результат снова.
Листки Независимого за любой год. Впечатление от Независимого как от места для матбогов неверное, не переживай. Проблема просто сдавать листки ПО ВСЕМ предметам, особенно если в своём вузе не проходишь эти предметы. Листки по алгебре адекватные.
Почему схему (понятие из алгебраической геометрии) можно назвать системой уравнений? Что такое схема?
А где-нибудь есть решения для этих листков?
>можно назвать системой уравнений?
Только локально, схема - локально окольцованное пространство, то есть, только ограничения пучка на открытые подмножества аффинны (те изоморфны спектру какого-то кольца).
>кодировать-декодировать сообщения в точки на эллиптической кривой - не понятно как
Сообщение разбивается на блоки и каждый блок преобразуется в длинное число с системе считсления с основанием 256
Запили сам.
Пишешь любому НМУшному семинаристу по алгебре в соцсеточках/на мыло и просишь попринимать листки. Кто-нибудь да откликнется, особенно сейчас, когда все дома хуи пинают.
Это то же самое, что декодировать сообщение в байты.
Каждый байт - это цифра в 256-ричной системе исчисления. А дальше-то что делать с байтами?
В общем, ты некропостер ещё тот... Лол. Хорошо что я заметил твой ответ.
Я уже реализовал некое подобие эллиптической криптографии - тут:
https://github.com/username1565/mini_ecdsa/blob/master/ECC.py
>А дальше-то что делать с байтами?
Ну вот у тебя есть массив zhopa = { 0x01, 0x02, 0xFF, 0xDD } это твое сообщение. А дальше кручу-верчу наебать хочу, перегоняешь все это в длинное число примерно так, в зависимости от порядка байт (endianess): 01h x 256 + 02h x 256^2 + FFh * 256^3 + DDh x 256^4 = 123456789101112 (мне лень считать). И уже этот результат передаешь на вход криптосистемы, например, в виде точки (123456789101112, 1). Я уже забыл лекции по криптографии
Поправка: отсчет начинается с нуля, поэтому вместо 01h * 256 будет 256 в степени 0, то есть 1, получаем просто 01h
>>67300
То есть, ты, предлагаешь просто засунуть инфу в виде длинного числа - в x-координату, а y-координату точки - вычислить?
Прикол в том, что как видно отсюда:
>>67297
>https://github.com/username1565/mini_ecdsa/blob/master/ECC.py
на маленькой эллиптической кривой (y^2) mod 211 = (x^3 + 7) mod 211
с генераторной точкой (150, 22)
лежит всего 199 точек (198 + O), при этом 198 / 2 = 99,
и 99 точек имеют x-координаты одинаковые, а y-координаты - разные.
При этом, значения x-координат лежат в диапазоне [0, 211),
То есть не все числа от [0,211) являются x-координатами точек на кривой в конечном поле,
а лишь 99 чисел из этого диапазона.
То же самое, и для больших кривых, и для очень больших.
вот так:
https://ru.wikipedia.org/wiki/Свободная_группа
Стоит заметить ещё, указанная операция есть функтор, сопряжённый забывающему Группы -> Множества (см. Алуффи)
На любом непустом множестве можно ввести структуру группы, да. Достаточно ввести её на кардиналах. На конечном n можно рассмотреть Z\nZ. На бесконечном k - прямую сумму k экземпляров Z\2Z. Это множество последовательностей длины k из нулей и единиц, в которых лишь конечное количество элементов отлично от 0, с покомпонентным сложением по правилам 0+1=1+0=1, 0+0=1+1=0.
>на любом непустом множестве
>Достаточно ввести её на кардиналах
А у нас уже кардиналы множество образовывать стали?
Ты берешь 1000$ с собой к букмекеру, ставишь 1$ выигрываешь - ставишь ещё, проигрываешь - удваиваешь, до тех пор, пока не выиграешь
Какова вероятность того что я стану миллионером и того что проебу всю 1k$?
1000 же, я забыл уточнить, вероятность 1\2
а ты про.. ну да
Чтобы ввести структуру на каждом из кардиналов, совсем не нужно объединять все кардиналы в какое-то единое множество.
В принципе, подобные большие образования не запрещены. Например, класс всех множеств V является моноидом (очень большим) относительно операции объединения. Просто в ZFC такое сложновыразимо.
 36 Кб, 795x135
36 Кб, 795x135помоги решить задачу по гладким многообразиям.
Я пока рассуждал так. Допустим, L!=[L,L]. Тогда существует базисный вектор e такой, что он не равен коммутатору. Тогда можно получить, что его дуальная форма w имеет нулевой дифференциал, т.е. dw = 0. Препод задал встречный вопрос, является ли форма точной, т.е. существует ли функция f: w = df
Разве это не следует тривиально из того, что скобка есть дифференцирование (которое можно отождествить с каким-то гладким векторным полем)?
Может и следует, но мне это не очевидно... (
Или ты имеешь ввиду, что коммутатор векторных полей снова векторное поле?
Коммутатор есть производная Ли, но есть ли в этом толк?
Из односвязности следует, что первые когомологии де Рама нулевые. То есть, любая замкнутая 1-форма точна. В твоём случае это как раз и означает, что для w, где dw=0, найдётся f такое, что w=df.
Корни 1/2 и -3.
Блин, точно, что-то я напутал с корнями, 1/2 и -3, правильно. Бтв почему дискриминант? Разве разность корней - это дискриминант?
ну, ещё умноженная на $a_n^{2n-2}$
(A\B)\C=(A\C)\(B\C)
нужно доказать тождество используя алгебру множеств
 78 Кб, 556x364
78 Кб, 556x364Там нужно учитывать, помимо прочего, что (a,b)=1, a>0, b>0.
тоже не догоняю, хуйня какая-то, факт из ТЕОРЕМЫ(пиздец) проще доказать либо через табличку m на n, а лучше - через изоморфизм из КТО(ну типа надо показать что образ группы обратимых по умножению в Z/mnZ - это в точности группа обратимых по умножению в Z/mZ x Z/nZ, а порядок последней легко посчитать)
А блядь понял короче там опечатка: "взаимно прост с b" конечно. Ну на картинке какое-то нагроможденное доказательство через табличку, но без таблички, найди норм в инете.
БЛЯТЬ, Анон, СПАСИБО огромное, как я сам не заметил опечатку.
Можно даже подобрать числа, удов. условиям, например a=12, b=5, r=2, q=2 - получается, что 0<=r<b, 0<=q<a, (a,b)=1, (b,r)=1, значит, по этому долбаебскому утверждению, на попытку доказать которое у меня вчера ушло больше 2х часов драгоценного времени, получается, что (12, 12)=1, пиздец. Но это
я только теперь заметил. Спасибо еще раз.
Доказательство с табличкой видел, но скипнул, т.к. времени нет разбираться с новым доказательством. В итоге потратил еще больше с этой опечаткой, МДА.
cпаcибо оп
Конечно имеют, они фундаментальны в современной теорфизике
В частности, представления группы Лоренца (и группы Пуанкаре) очень тесно связаны с понятием элементарной частицы
Генераторы групп Ли это важнейшие операторы/наблюдаемые в квантовой механике
Операторы Казимира играют важную роль
Теорема Нётер конечно же
Вобщем, если одним словом описать развитие теорфизики в ХХ веке, то это будет 'симметрии', и группы Ли описывают непрерывные симметрии
>Если математика - царица наук, то алгебра - венец самой математики. Этот тред посвящён ей! ссым в нём на тех, кто занимается анализом и не знает теорему де Рама
А обязательно ли ссать на тех, кто занимается анализом?
если они занимаются анализом, но не знают теорему де рама, то наверно не помешало бы
> Генераторы групп Ли это важнейшие операторы/наблюдаемые в квантовой механике
Расскажи пожалуста подробнее об этом
Серьёзно, неиронично
Про индексы нужно любому чистому математику знать, это фундаментальная вещь
И тогда мы упираемся в пререквизиты и хуевые университетские курсы
Поэтому мы приходим к тому, что есть и в других областях - каждый разбирается только в своей ультра-узкой области и отрабатывает гранты высирая никому не нужные статьи про (H¨⇐N)-exact natural transformations arising from fibrant arrows over the co-hypercover of reflective bi-categories
>Поэтому мы приходим к тому, что есть и в других областях - каждый разбирается только в своей ультра-узкой области и отрабатывает гранты высирая никому не нужные статьи про (H¨⇐N)-exact natural transformations arising from fibrant arrows over the co-hypercover of reflective bi-categories
Арнольд кстати говорил, что разговоры про то, что сегодня уже ни один мощный математик не способен хотя бы общим пониманием охватить всю математику - это херня.
Типа проблема просто в том, что высираются тонны статей типа "об одном частном решении одного дифференциального уравнения" (примерно такая цитата была), которые одно по одному обсасывают.
Миша примерно так же считает, вроде. По крайней мере, насчёт ненужных статей.
>"об одном частном решении одного дифференциального уравнения"
Или статей об
"об одном топологическом пространстве и его гомологиях"
Да.
>"об одном топологическом пространстве и его гомологиях"
"об одном старом топологическом пространстве и одной его гомологии, посчитанной еще одним новым способом" - вот так надо!
Можно здесь задавать вопросы по алгебре? по моему моя проблема алебраического характера, в плане там простой матанализ
Проблема такова:
Вот есть функция f(u,v) она пока что абстрактная
Самое важное требование к этой функции - ассоциативность, то есть
f( f(u,v), w ) = f( u, f(v, w) )
Есть также дополнительные требования к ней во первых монотонное возрастание по u и по v
или иными словами df/du > 0 и df/dv>0
во вторых оно должно быть continuous and twice differentiable, не совсем понятно второе выражение но я полагаю возможность дифференциировать по первой переменной а потом по второй
Понятное дело, что даже с такими ограничениями подходящих функций бесконечное множество. Сам автор перед началом долгого поиска общей функции заранее говорит что если у вас есть любая invertible и монотонная функция G(u) то общим решением является
f(u,v) = G^-1( G(u)G(y) )
Я хотел убедиться в этом и решил взять arctan(u) как G(u). Она invertible и монотонная.Теперь имеем функцию f(u,v) = tan(arctan(u)arctan(v)), она ассоциативна
просто из за ее общей формы G^-1( G(u)G(v) ). Проверяю теперь ее монтонное возрастание по двум переменным
f(u,v)/du = tan'(arctan(u)arctan(v)) = 1/cos^2(arctan(u)arctan(v) ) ( arctan'(u)arctan(v) )= 1/cos^2(arctan(u)arctan(v) ) constant(v)
1/1+u^2
вроде бы при любых u производная от u будет строго больше нуля
и тоже самое будет со вторым
Теперь вопрос: почему когда рисую график этой функции tan(arctan(u)*arctan(v)) получается лютый кошмар, он вовсе не монтонен он скачет верх и вниз как бешенная. Почему так? Где мой прокол?
Проблема такова:
Вот есть функция f(u,v) она пока что абстрактная
Самое важное требование к этой функции - ассоциативность, то есть
f( f(u,v), w ) = f( u, f(v, w) )
Есть также дополнительные требования к ней во первых монотонное возрастание по u и по v
или иными словами df/du > 0 и df/dv>0
во вторых оно должно быть continuous and twice differentiable, не совсем понятно второе выражение но я полагаю возможность дифференциировать по первой переменной а потом по второй
Понятное дело, что даже с такими ограничениями подходящих функций бесконечное множество. Сам автор перед началом долгого поиска общей функции заранее говорит что если у вас есть любая invertible и монотонная функция G(u) то общим решением является
f(u,v) = G^-1( G(u)G(y) )
Я хотел убедиться в этом и решил взять arctan(u) как G(u). Она invertible и монотонная.Теперь имеем функцию f(u,v) = tan(arctan(u)arctan(v)), она ассоциативна
просто из за ее общей формы G^-1( G(u)G(v) ). Проверяю теперь ее монтонное возрастание по двум переменным
f(u,v)/du = tan'(arctan(u)arctan(v)) = 1/cos^2(arctan(u)arctan(v) ) ( arctan'(u)arctan(v) )= 1/cos^2(arctan(u)arctan(v) ) constant(v)
1/1+u^2
вроде бы при любых u производная от u будет строго больше нуля
и тоже самое будет со вторым
Теперь вопрос: почему когда рисую график этой функции tan(arctan(u)*arctan(v)) получается лютый кошмар, он вовсе не монтонен он скачет верх и вниз как бешенная. Почему так? Где мой прокол?
>twice differentiable, не совсем понятно второе выражение но я полагаю возможность дифференциировать по первой переменной а потом по второй
Неправильно полагаешь. Имеется в виду, что данная функция из класса $C^{2}$ то есть имеет все частные производные до второго порядка включительно.
понял тебя кстати я там производные посчитал не правильно, у функции tan(arctan(u)*arctan(v)) производные от обоих переменных не строго больше нуля
Но еще есть такой вопрос, вообще есть ли функция f(u,v) которая обладает строго положительными производными и также обладает ассоциативностью f( f(u,v), w ) = f( u, f(v, w) )?
На уме только f(u,v) = u + v
Ахаахахаа
анон я туплю страшно
мне надо поделить arctan(u) на pi/2?
тогда будет функция tan((arctan(u))/(pi/2)*(arctan(v))/(pi/2))
как это сделает производные строго позитивными? я тупой
tan((pi/2)(arctan(u))/(pi/2)(arctan(v))/(pi/2))
там чуть сокращается, конечно
у тебя уже всё есть
производные будут какие надо при аргументе до pi/2
ты сам написал hint к решению, но не до конца понял.
его идея в том, что можно "деформировать" множество, на котором задана операция, при помощи любой обратимой функции (сохраняющей то, что нам надо сохранить по условию - порядок, непрерывность, гладкость)
но анон
смотри, производная функции tan((pi/2)(arctan(u))/(pi/2)(arctan(v))/(pi/2)) от u
f(u,v) = 1/cos^2( arctan(u) arctan (v)/(pi/2) ) arctan(v)/(pi/2) * 1/(1+u^2)
тут u не может сделать значение функции негативным, но все портит константа arctan(v)/(pi/2), если она негативна а она, негативна если v от минус бесконености до нуля, то производная вся тоже больше нуля
вопрос: причем тут нормализация?
меньше нуля
тут u не может сделать значение функции негативным, но все портит константа arctan(v)/(pi/2), если она негативна а она, негативна если v от минус бесконености до нуля, то производная вся тоже меньше нуля*
даже когда просто x*y то, внезапно, одна из производных тоже может быть меньше нуля, когда x<0 или y<0.
что там с условием задачи?
>Вектор - направленый отрезок с точностью до параллельного переноса
>с точностью до параллельного переноса
Пожалуйста объясните последнюю фразу.
это означает, что все направленые отрезки, которые можно получить друг из с друга с помощью до параллельного переноса, считаются одним и тем же объектом
т.е. операция параллельного переноса не изменяет твой объект
Два параллельных одинаково направленных отрезка одинаковой длины представляют один и тот же вектор
Понял.
Анон, а можно уточню про базис: правильно ли я понимаю, что любые 2 непропорциональные векторы будут базисом R2?
Работает ли такое же для любого пространства (то есть любые N непропорциональные векторы базис N-мерного пространств)?
>любые 2 непропорциональные векторы будут базисом R2?
правильно
>Работает ли такое же для любого пространства (то есть любые N непропорциональные векторы базис N-мерного пространств)?
представь себе R^3, горизонтальную плоскость и любые три вектора на ней. а теперь нарисуй вектор, торчащий из этой плоскости вертикально вверх, можно его через них выразить?
Благодарю.
угол между векторами - это дополнительная характеристика, которая определена только в пространствах со скалярным произведением. про базисы можно говорить, не упоминая углы вообще (работая в линейных пространствах, в которых скалярное произведение не определено)
 14 Кб, 650x156
14 Кб, 650x156ну как варианты рассуждений:
1. или общий множитель равен нулю, или на него можно поделить
2. просто перенести все налево и разложить на множители
P.S. не знаю, что вопрос про тригонометрические уравнения делает в треде алгебра, но это, вероятно, из-за того, что школьный предмет, который по сути на 90% начала анализа (непрерывные аналитические функции, действительные числа и операции с ними, ...) называют почему-то алгеброй
главное - тригонометрия должна быть исключена полностью
это какой-то дикий атавизм, неприемлемый вообще
Домножь на sin6x
(cos(6x)cos(2x))sin6x=cos6x
Если cos(6x)!=0, то на него можно поделить, и получим cos(2x)sin(6x)=1. Если cos(6x)=0, то равенство так же выполняется.
>>81805
Для решения школьных уравнений не нужно ничего из анализа. Это та же школьная алгебра, манипулирование значками, просто вместо qx пишут cos(qx), вместо формул сокращенного умножения формулы сумм углов и тд.
ну полностью тригонометрию исключать нельзя - оставить ее с большим уклоном в геометрию и физику
я бы
1. вернул бы комплексные числа, может быть как раз через них и рассказал тригонометрию в курсе алгебры (в геометрии пусть будет как есть)
2. добавил бы введение в группы - ну это просто, интересно и красиво
3. можно добавить немного про многочлены типа локализации корней, раз уж говорим про комплексные числа
4. можно попробовать рассказать про другие алгебраические структуры - жаль, до Галуа вряд ли получится дотянуть
5. анализ рассказал бы описательно - выкидываем нафиг всю главу про пределы, производную вводим как скорость - через махание руками, так же и про интегралы. вметсо этого хоть как-нибудь постараться впихнуть что-то про ряды - опять же для физики и без доказательств
ну п. 5, конечно, не в тему треда
Короче, после того как детей научили считать, я бы превратил курс математики в описательный типа природоведения, без строгих доказательств. Вроде того как в школе про теорию относительности и квантовую физику рассказывают - чисто красивые факты, чтобы интерес развивался.
Мне нравится, как чаще всего вводят разные тригонометрические формулы, типа вот смотрите косинус-синус и вот такие правила выполняются, без доказательства, без нихера. Потом заставляют их формально применять. Какой в этом смысл? Да абсолютно никакого, через год это абсолютно начисто забывается.
не знаю, зачем школьникам ряды и группы
а вот про комплексные числа рассказать дело хорошее
имхо
 72 Кб, 500x733
72 Кб, 500x733Какие-то люди, само собой, выберут никуда не ходить и ничему не учиться. Ну и пусть, это их дело. Такие люди и в общеобразовательной школе ничему не учатся. Они там и сами страдают, и остальным мешают, сковывают чужие таланты.
>Зачем учить этих людей одному и тому же одинаковыми способами?
$$$
нанимать вдвое или втрое больше преподавателей/администрации/уборщиков, арендовать или выкупать новые помещения для школ, составлять разные программы, и т.д., это всё деньги
если с одних налогов это финансировать, то non-sustainable очевидно, отсюда и частные школы
ты должен был это проходить классе в 9-ом на уроке условного обществознания
если постарше, то можешь почитать серьёзные экономические статьи (как, кстати, хороший пример применения базового матанализа, гладкости, выпуклости, и проч.), где налогообложение обсуждается с точки зрения deadweight loss и прочих externalities
если рассуждать идеалистически, то конечно материально-одарённые государства (например, полезными ископаемыми, ну понятно кто имеется ввиду) должны бы были все эти лишние деньги вкладывать в пенсионное обеспечение, здравоохранение, и образование, а не в ебаные тaнки и прочую хуйню (например то же ОАЭ расписало свой мега-план траты нефтебаксов на образование, науку, и проч вплоть до колонизации марса в 2100 году)
но что есть то есть
В школьной математике есть пропасть между античной математикой и математикой 18 века.
Лучше программу забить средневековой математикой. Она и нетривиальная, не слишком уж сложная, и полезная. Логарифмы, задачи на максимум и минимум и т.п. Короче всем что позже убил, основанный на этих вещах, матанализ.
Какая жуткая картина. Эмоции охуенно переданы. Дед будто с плаката слезет и орать начнёт. Есть ещё?
>один знакомый дед называет темными людей, которые не угадывают, из какого совкового фильма он в очередной раз произнес цитату.
это действительно так. Это называется культурный уровень. Нормальные математики такие как Вербицкий или Громов очень много знают помимо своей специальности. А узкие специалисты с кругозором зубочистки нужны лишь ушлым капиталистам, чтобы люди не бухтели и сидели в своей яме.
а что они должны уважать? тем более в данном случае зумер даже поленился погуглить, хотя происхождение восхитившей его картинки прямо на ней написано
>один знакомый дед называет темными людей, которые не угадывают, из какого совкового фильма он в очередной раз произнес цитату.
правильно делают, тащемта.
>>81854
+
Считать чем-то равноценным советскую культуру и нормальную всё-таки не следует. Есть мнение, что во многих случаях там та же ситуация, что с The Winner Takes It All и Позвони мне, позвони.
стоит
>во многих случаях там та же ситуация, что с The Winner Takes It All и Позвони мне, позвони.
культура это палимпсест (c)
Именно поэтому в российской науке (и в алгебре в частности, раз уж мы в алгебра-треде) так распространен переводной плагиат. Ачотакова.
>так распространен переводной плагиат. Ачотакова.
в первый раз слышу
но если даже и так, то вообще ничего, ящитаю
>золотой век культуры
Ты сказал?
Музыка того же Варга, периода когда он сидел в тюрьме и имел лишь синтезатор, намного качественней, чем вся та дрисня из 60х. Исключений единицы, типа малинового короля.
>Музыка того же Варга <..> намного качественней, чем вся та дрисня из 60х
нет
"музыка варга" вообще довольно примитивная, во все периоды
> Ну и для того, чтобы понимать, что говорят алгебраисты, когда они выёбываются.
Для того, чтобы это понять, одного учебника (и даже двух) недостаточно
>Посоветуйте
Для начинающих - Hungerford, например, или Винберг
>Очень желательно с применением полученных знаний на практике
Хорошо, а причём здесь алгебраисты? Алгебраистам, как и всем математикам, на приложения похую.
Попробуй Gallian, по-моему там было что-то прикладное.
Или ещё Abstract Algebra with Applications
>о бросил потому что не понял, нахуя вообще нужно.
Странно, учитывая что эти вещи как раз-таки прикладываются и используются на ура, в отличие от каких-нибудь резольвент модулей
Группы и теория представлений - это ключевые компоненты теорфизики уже лет 100 как
Группы ещё используются в химии и программировании, например
Группы дохуя где применяются, приложения в какой области тебе интересны?
Так или иначе, сначала разберись с теорией. Читай Кострикина или уже предложенного Винберга.
Для начинающих David Lay Linear Algebra with applications, там даже школьники вывезут
Сап двач, если я вообще не вывожу анализ но кайфую от алгебры, это нормально? Или чтобы замастерить второе нужно обяз ахуенно шарить в первом
Мне кажется, абсолютно нормально
Вот не знать топологию и кайфовать от алгебры — это, по-моему, какой-то аутизм, а анализ не знать норм
Пусть стоит задача отыскать образ и ядро такого гомоморфизма(очевидно) $f \colon (Z/pZ)^ \to (Z/pZ)^*$, $f(n)=n^{10}$.
Возникает эвристика: а давайте смотреть не на данный гомоморфизм, а на такой: $\tilde f \colon Z/(p-1)Z \to Z/(p-1)Z$, $\tilde f(n)=10n$.
Для последнего легко найти образ и ядро, ну значит такие же образ и ядро у исходного гомоморфизма. Но как это формально доказать, т.е. что $Im \tilde f \cong Imf$ и $Ker \tilde f \cong Kerf$?
Че-то туплю, мб диаграмму какую-то нарисовать?
Пусть стоит задача отыскать образ и ядро такого гомоморфизма(очевидно) $f \colon (Z/pZ)^ \to (Z/pZ)^$, $f(n)=n^{10}$.
Возникает эвристика: давайте смотреть не на данный гомоморфизм, а на такой: $\tilde f \colon Z/(p-1)Z \to Z/(p-1)Z$, $\tilde f(n)=10n$.
Для последнего легко найти образ и ядро, ну значит такие же образ и ядро у исходного гомоморфизма. Но как это формально доказать, т.е. что $Im \tilde f \cong Imf$ и $Ker \tilde f \cong Kerf$?
Имеется в виду математический анализ? Я хочу в алгебру вкатиться, но в калькулусе я полный ноль.
Можешь аргументировать? Планирую пройти начала множеств Шеня и штурмовать алгебру, а тут ты говоришь, что надо сначала матан заботать.
Так я хочу чисто алгеброй заниматься, а не матанализом.
Скажи еще что алгебра нужна чтобы генерализировать решение линейных уравнении для R^n
еще приведение квадратичных форм к каноническому виду, второе высшее достижение алгебры
>при этом математический смысл сего действа ты вряд ли расскажешь
Не он, но я даже пытаться не буду, потому что на 99% будет подъёб про какую-нибудь "жутко полезную и фундаметнальную" хуйню вроде следа в расширении поля, когомологий Понтрягина, или скобки Уайтхэда, в которых "на самом деле" проясняется смысл приведения формы к каноническому виду
Не удивлюсь, если на шиз-нкатлабе есть 10тистраничный опус о связи канонического вида с (∞,1)-категориями
удобно потенциальную энергию представлять, вторую вариацию, формы колебаний, для нас прикладников это ценно
Зачем Шень, если ты хочешь только алгебру изучать? Шень будет в тему перед анализом или топологией, но не обязателен.
Не на таком уровне, как у Шеня.
> Половину лекций проебал и вообще не понимаю что происходит.
> помогите
Каким образом можно вложить материала объемом в половину, хотя кого ты наебываешь малыш. Ты проебал вообще все лекции и не появлялся в вузике. До осени, до пересдачи, у тебя будет маса времени.
> Ты проебал вообще все лекции
Половину да, половину не понял наполовину
> не появлялся в вузике.
Меня бы и не пустили. Короновирус хуле
Я просил помочь, а не нахуй послать. Мне хотя бы темы по номерам узнать чтоб найти аналогичные примеры
> Мне хотя бы темы по номерам узнать
У тебя совсем какие-то проблемы? На твоих пиках, 1 номер билета, в нем название тем.
Ну ты спросил типа, как мне нихуя не делать, дрочить-бухать и все сразу уметь и знать? Ответ "пошел нахуй" вполне уместный, бро. Никак.
Если какая-то мотивация/интуиция у идеала, по которому мы берём фактор в определении алгебры? Вот например во внешней алгебре мы берём фактор по идеалу [math] x \otimes x [/math] и это легко мотивировать (если мы хотим построить что-то, что "измеряет" площади, то "коллинеарные" объекты будут схлопываться в нуль).
В определении алгебры Клиффорда (с билинейной формой B) можно рассмотреть два идеала (которые совпадают, конвенции знака бывают разные):
1) [math] x \otimes y + y \otimes x = 2B(x,y) [/math] - знаю, что похожая штука появилась у Дирака при попытке разложить оператор Клейна-Гордона. Но всё-таки алгебра Клиффорда видится более фундаментальной (да и появилась раньше), так что это так себе мотивация;
2) [math] x \otimes x = B(x, x) [/math] - уже получше и поестественней. Мы хотим, чтобы наше новое умножение схлопывалось в скалярное для y=x. Но.. почему?
Я уже почитал вперёд и увидел, что из одной только этой аксиомы (ну и ассоциативности/дистрибутивности) можно вывести всю алгебру, и как много чего (вроде C и H) красиво вкладывается. Я полезность под вопрос не ставлю. Из моего опыта, если мотивация "так будет удобно в дальнейшем", то я просто что-то не понимаю из других областей или не знаю исторического контекста.
У самого Клиффорда в статьях определяется по другому (через фактор определяли в 50х Бурбаки и Шевалле).
Так есть какая интуиция/интерпретация у идеала #2) вроде простой интерпретации идеала для внешней алгебры?
все определения хорошо задавать инвариантно, то есть через универсальные свойства и потом из этого выводить другие равносильные определения типа вот таких явных построений. Посмотри тут какое универсальное свойство алгебр клиффорда: https://en.wikipedia.org/wiki/Clifford_algebra#Universal_property_and_construction.
И в конце говорится вот это Namely, Cl can be considered as a functor from the category of vector spaces with quadratic forms (whose morphisms are linear maps preserving the quadratic form) to the category of associative algebras. The universal property guarantees that linear maps between vector spaces (preserving the quadratic form) extend uniquely to algebra homomorphisms between the associated Clifford algebras.
так что всё очень естественно
Это всё интересно (хоть и повторяет изложенное в моём теоркат-ориентированном учебнике), но не отвечает на мой, совершенно конкретный, вопрос совершенно. Впрочем, я уже нашёл ответ в другом учебнике для хлебушков.
матрица квадратичной формы диагонализуется (приводится к диагональному виду)
для этого ищешь собственные вектора матрицы для твоей формы, затемх их ортоганализуешь
диагонолизовать и найти собственные вектора вообще без проблем, а ортогонализовать как?
Cобственные векторы, соответствующие разным собственным значениям ортогональны друг другу.
а если они отвечают одинаковым с.з., то необязательно
а если собственное значение одно, у него 2 собственных вектора. Далее характеристический многочлен в ноль идет и у него базис ijk палучаеца. Допустим один вектор я беру из собственных, второй из ijk, а третий откуда брать, чтобы матрицу перехода получить?
я не очень понял, что ты хочешь сказать.
у диагонализуемой матрицы всегда столько линейно независимых собственных векторов, какова размерность пространства
на то она и диагонализуема
Клиффорд, который один из немногих догадался, как связать алгебру Грассманна и алгебру Гамильтона, не смог в сбалансированный распорядок дня и рано умер от туберкулёза, оставив нам полторы странички про свои идеи.
В итоге имеем монстра Гиббса-Хевисайда, которого до сих пор преподают аж в школе нахуй, вместе с неассоциативным выкидышем произведения Клиффорда/Грассманна.
Чем больше читаю про историю алгебры, тем больше понимаю, сколько я не понимаю.
 303 Кб, 480x333
303 Кб, 480x333Пару раз смотрел его ролики, не впечатлило, ну нормально так обьясняет, многовато болтовни. Но потом...как я понял его странности, а то есть его непринятие действительных чисел, мне стало крайне странно смотреть его математику.
1) Кроме его странностей, насколько полезны его видео?
2) Как вы относитесь к его идеям, имеено к его отношению к дейст числам. ?
>1) Кроме его странностей, насколько полезны его видео?
Если тематика не сильно связана с его шизой - то видео как видео. Например, по вводному алгтопу или проективной геометрии.
>2) Как вы относитесь к его идеям, имеено к его отношению к дейст числам. ?
Так же, как и 99.999% остальных математиков. Основная проблема даже не в его позиции, а в её популяризации - он-то базовую математику знает сносно, а вот типичные слушатели - нет. Он просто деньги же делает.
Вторая часть вроде издана в бумаге издательством ОЦЭиМ СПбГУ в 2006 году (232 страницы) и не существует в электронном виде, про остальные части вообще ничего не известно. Можешь попробовать написать самому Вавилову, других вариантов походу нет. А будь бы в России свой Спригер, то возможно такой хуйни с поиском книжки изданной хуй-знает-когда хуй-знает-кем не было.
А есть ссылка на финальную, ну или хотя бы самую последнуюю версию pdf'ки Вавилова "не совсем наивная теория множеств"? То, что с ходу гуглится, какое-то совсем сырое и не законченное.
Хз, попробуй самому Вавилову письмо написать.
Возник один вопрос, который связан с разделом алгебры, в который я почти не заглядывал (пусть это и основы).
Проблему свою оформлю в несколько постов.
Первый пик — это вопрос, который возник у меня.
Второй - это ответ, который мне дали.
Последний пик — это изначальное утверждение, которое я увидел.
1) $\mathbb{Q}(X)(x_0)$ - это поле частных (дробей, составленных из двух полиномов с рациональными коэффициентами, где переменная принимает значение в $X\sqcup \{x_0\}$. Трансцендентный базис $\mathbb{R}$ над $\mathbb{Q}$ по определению это такое множество $A=X\sqcup \{x_0\}$, что $\mathbb{R}$ алгебраично над $\mathbb{Q}(X)(x_0)$.
2) Потом, кажется, так как в любой точке из $X\sqcup \{x_0\}$ $\mathbb{Q}(X)(x_0)$ принимает значение в $\mathbb{R}$, то $\mathbb{Q}(X)(x_0)\subseteq \mathbb{R}$, поэтому на $\mathbb{Q}(X)(x_0)$ можно задать дифференцирование, которое потом можно продлить на всё $\mathbb{R}$ единственным способом.
3) Нетривиальное дифференцирование в области целостности можно расширить на поле частных, поэтому дифференцирование можно рассмотреть просто на кольце многочленов с рациональными коэффициентами, где переменная принимает значение в $X\sqcup \{x_0\}$.
Если всё вышеперечисленное мною понято правильно, то мне непонятно, почему коэффициента там из $\mathbb{Q}(X)$, а не из $\mathbb{Q}$.
Потому, что в лемме "here" предполагается, что L алгебраично над k (если применять её в нужном тебе направлении (1)=>(3)). По этой причине взять k=\mathbb{Q} и L=\mathbb{R} не получится.
Но ведь $\mathbb{Q}(X)(x_0)$ — это же дроби, где наверху и внизу многочлены с коэффициентами из $\mathbb{Q}$, а значениями переменной в $X\sqcup \{x_0\}$, если я правильно понимаю. Казалось бы, что многочлены на последнем шаге мы тоже должны рассматривать с коэффициентами из $\mathbb{Q}$.
Понял тебя, кажется. Ты хочешь думать о \mathbb{Q}(X)(x_0) как о поле частных кольца \mathbb{Q}[X\sqcup \{x_0\}], а не кольца \mathbb{Q}(X)[x_0]. Тогда при построении ненулевого дифференцирования D нужно будет описывать как оно действует на многочлены с коэффицентами из \mathbb{Q}, как ты хочешь, но с переменными из X\sqcup \{x_0\}, вместо многочленов с коэффициентами из \mathbb{Q}(X), но с одной переменной x_0, как тебе написали. Видимо, можно и так тоже. По линейности и по правилу Лейбница достаточно определить D на каждом элементе из X\sqcup \{x_0\}. Например, D(x_0)=1 и D(x) = 0 для всех x\in X.
Кстати, я ранее неверно написал, что тебе нужно (1)=>(3). Нужно (1)=>(2).
>а не кольца \mathbb{Q}(X)[x_0]
Хм, я просто думал, что по определению трансцендентного базиса $A$ расширения $L/K$ у нас $L$ должно быть алгебраично именно над $K(A)$. А в данном случае у нас ведь $A=X\sqcup\{x_0\}$. Или тут как-то можно совершить переход от частных кольца $\mathbb{Q}[X\sqcup \{x_0\}]$ к частным кольца $\mathbb{Q}(X)[x_0]$? Я просто в этой области только несколько определений знаю, не более.
Хотя они, наверное, изоморфны ведь, как, например, $\mathbb{Q}[x]$ изоморфно $\mathbb{Q}[a]$ для любого выбранного $a$, поэтому так сделать можно.
>Хотя они, наверное, изоморфны
Да. Оба поля изоморфны $\mathbb{Q}(X\sqcup \{x_0\})$. Можно, например, воспользоваться универсальным свойством поля частных. Более наивно, отношение $\frac{p}{q}$, где $p, q\in \mathbb{Q}[X\sqcup \{x_0\}]$ можно, "собрав коэффициенты" перед степенями $x_0$ представить себе как отношение элементов из $\mathbb{Q}(X)[x_0]$, и аналогично в обратную сторону.
>например, Q[x] изоморфно Q[a] для любого выбранного a
Только если $a$ трансцендентно над $\mathbb{Q}$. Иначе, $Q[a]\simeq Q[x]/(p(x))$, где $p(x)$ - минимальный многочлен для $a$.
Спасибо, анон. Это как раз то, что мне нужно.
Я, вообще, приятно удивлён, насколько алгебраическая теория чисел красивая, хоть и заглянул туда совсем чуть-чуть. Раньше-то я думал, что это что-то наподобие рамануджанщины.
 96 Кб, 963x417
96 Кб, 963x417Ну вот например пик(общий перпендикуляр к двум прямым), векторное произведение понятно - ищем перпендикуляр, почему в первой строке какая то хуйня? почему во второй строке направляющий вектор?
Есть чувство что эти формулы довольно просто выводить если понять как это делать, но этого я еще не понял. Что почитать чтобы понять как составлять такие системы для разных случаев, в зависимости от того что ищем?
>Есть чувство что эти формулы довольно просто выводить
все эти формулы выводятся по определению через разложения векторов по базису. что именно происходит в твоём случае, понять нельзя
общий перпендикуляр к двум прямым (если речь идёт о векторе) даётся векторным произведением направляющих векторов
выписываем эти вектора (их разложение по базису),
вычисляем векторное произведение (есть формула)
получаем ответ
на пике просто пример
мне интересно как в целом выводятся разные формулы в ангеме, что почитать чтобы понять как их правильно раскладывать, какие системки составлять?
ещё раз, эти формулы получаются напрямую из определений путём (несложных) вычислений; основной инструмент - представление участвующих в вычислении векторов через координаты; потом и результирующие формулы получаются в координатах
годно, грац
так это определитель матрицы, какая там формула быть должна?
всякие функторы внешней степени и прочая ерунда - это всё относится к линейным операторам, а не к матрицам.
>Чтоб с аджоинтами и модулями, но как для продвинутых первокуров.
Нахуя, если потом все группы порядка 4 не можешь найти?
>Нахуя, если потом все группы порядка 4 не можешь найти?
Так это отражение сегодняшних реалий мат образования вообще. Тут на доске приводили примеры, когда люди всякие схемы и квазикогерентные пучки знают, а на простейшие вопросы по классическому алгему, ну то есть про собственно кривые, ответить не могут. То же и с гомологической алгеброй vs интуитвное геометрическое представление на основе "дедовской" комбинаторной топологии.
Когда у тебя есть всего 6-7 лет, чтобы проехаться по верхам и основам устаревшей математики и выбрать тему для пхд (и начать понимать хотя бы абстракты актуальных статей в своей области), то сидеть и ковыряться в каждой теме и её истории просто невозможно. Алюффи позволяет перепрыгнуть через частное сразу к обобщениям и мастурбации в своей китайской комнате. Особая ирония в том, что именно на это и сетовал всеми тут ненавистный Арнольд.
> Тут на доске приводили примеры, когда люди всякие схемы и квазикогерентные пучки знают, а на простейшие вопросы по классическому алгему, ну то есть про собственно кривые, ответить не могут.
Так пучки это первокультурная математика, а алгем ваш - картофан.
> Алюффи позволяет перепрыгнуть через частное сразу к обобщениям и мастурбации в своей китайской комнате.
А почему собственно китайская комната? Есть аксиоматика, можно взять объект, который ей соответствует и доказать какие-то его свойства. По своей сути это очень условно отличается от частного примера, просто не все могут в абстрактное мышление.
>Тут на доске приводили примеры, когда люди всякие схемы и квазикогерентные пучки знают, а на простейшие вопросы по классическому алгему, ну то есть про собственно кривые, ответить не могут
Не напомнишь ссылку на такой пример?
А то выглядит как сказка из публицистики Арнольда
>Не напомнишь ссылку на такой пример?
Как минимум я приводил такие примеры в новичковом треде как из своей преподавательской практики так и из времён обсуждения с однокурсниками на семинарах. Если кинешь ссылку на его архив, я может и поковыряюсь на досуге.
>А то выглядит как сказка из публицистики Арнольда
Из этого можно сделать вывод, что у тебя собственного опыта преподавания или хотя бы обсуждения нет. Также я с этим сталкивался при чтении некоторых обсуждений вопросов на матх иксчендж и всяких ирс каналов (может, уже дохлых).
Хотя по твпему ответу уже сразу ясно, что даже если бы я тебе видео записал, ты бы ушёл в перманентный вывсёврёти.
>>95620
>просто не все могут в абстрактное мышление.
Это нелепая отговорка, а "абстрактное мышление" - придумка вроде "математического таланта". Либо ты можешь применить свои абстракции к базовым вещам, которые рассказывают школьникам на кружках, либо нет. Если нет, это значит, что у тебя неполное понимание темы. Ну и конечно же уже пошли оправдания, что у школьников просто нет гена абстрактного мышления, или что это вообще не нужно и картофан.
По поводу абстрактного мышления я хочу сказать, что есть правильная, арийская физика/математика, а есть подлая, еврейская физика/математика с геодезическими линиями и двадцатимерными пространствами.
Знаете ли Вы, что до поражения Германии во Второй Мировой, было два вида математики, - арийская и еврейская, - названные так по национальности своих сторонников?
Арийская Математика брала пример с естественных наук, склонялась к эмпирицизму, конечности и познаваемости мира, и работала исключительно c объектами, которые можно построить физически (например, в памяти ЭВМ или на бумаге).
Еврейская Математика же слоняется к религиозной абстракции и казуистике: всеохватывающей бесконечности, множествам, и порождаемым ими апориям. Так Еврейская Математика постулирует, что можно удвоить объект, путём перекладывания его частей, пространство делимо на "бесконечно малые", а для любого числа, Бог может создать большее число (аксиома о бесконечности).
Основатель Еврейской Математики, Гидеон Кантор, писал, что работает с "Абсолютом - непознаваемым человеком Актус Пьюриссимус, именуемым многими Богом". Примечательно, что Кантор окончил свою жизнь в психиатрической лечебнице, однако дело Кантора поддержали сионистские организации и католическая церковь, доведя до того, что сознательные германские студенты и профессора протестовали, требуя убрать еврейскую заразу из ВУЗов.
После войны, евреи сделали все возможное, чтобы уничтожить Арийскую Математику, удалив ее сторонников и подменив ее Теорией Множеств - центральной опорой Еврейской Математики. Так основатель интуиционизма, Лёйтзен Брауэр, подвергся изоляции, а результаты Русских и Английских финитистов умалчивались и не получили распространения. В русской истории от рук евреев пострадали математики Егоров (умер в гулаге), Лузин (подвергся травле и был отстранен), Флоренский (расстрелян), Есенин-Вольпин (репрессирован).
Добавлено через 9 минут
Сегодня математика стала еврейской даже по-цвету. Государства поддерживают так называемую "анти-расистскую математику", требующую например использовать еврейские имена в примерах и задачках, рассказывая при этом о великом "вкладе" еврейства в развитие математики.
Евреи, занимающиеся математикой, предпочитают всё специфическое-эльфийское. Причём презирают тех, кто занимается вещами, имеющими практическое применение. Поэтому в Советском Союзе вышел закон, по-которому в ВУЗах должно учиться евреев пропорционально их населению. Лишних отчисляли. Преподаватели евреи на мехмате в знак протеста ушли из университета и образовали НМУ (Независимый Московский Университет). Отсюда и название в мехматянском простонародье ``еврейская секта''.
Еврейские дети в СССР часто учились отдельное от детей гоев, в специальных элитных школах. Одной такой была Московская 57-й спецшкола, ученики которой не без оснований называют себя "пятидесятисемитами". Там часто преподавали выдающиеся преподаватели с мехмата.
В основании математики последнего столетия лежит знаменитая теория множеств Георга Кантора. Если вы откроете большую часть современных серьезных учебников математического и функционального анализа или топологии, или теории вероятности, то в начале почти наверняка увидите экскурс в теорию множеств. Почти вся современная математическая литература написана на теоретико-множественном языке. Камень теории множеств лежит в основании грандиозного здания современной науки.
Но в самом сердце этой самой фундаментальной вроде бы теории, лежащей в основе "царицы наук", почти сразу после ее создания были обнаружены очень серьезные парадоксы и проблемы, не преодоленные до сих пор. Уже сто лет с тех пор математика находится в состоянии перманентного кризиса, который остро воспринимается самыми выдающимися учеными. Великий немецкий математик Герман Вейль писал по этому поводу: "Мы менее чем когда-либо уверены в незыблемости наиболее глубоких оснований логики и математики. Как у всех и всего в мире, сегодня у нас есть свой кризис".
Математика говорит, что у шпекеровой последовательности есть предел? Говорит. Практика говорит, что его нет? Тоже говорит. Математика говорит, что апельсин можно удвоить путём перекладывания его частей? Говорит. Удалось кому-нибудь с новозаветных времён повторить эту процедуру? Наблюдения раз за разом показывают, что при такого рода операциях закон сохранения вещества неукоснительно соблюдается. Математика предсказывает наличие в бесконечномерном гильбертовом пространстве базиса Гамеля. Наблюдать оный пока вообще никому не удалось. Так что математика - именно лженаука, и никак иначе.
Именно уверенность в нематериальности математических объектов влечёт за собой веру в возможность "приближённых" вычислений (что чушь - вычисления бывают либо точные, либо неверные). Да, самолёты летают и при засилье Теории Множеств. Но если бы математика была конструктивной, они летали бы лучше, потому что конструкторы не забивали бы себе голову теоретико-множественным мусором, на практике бесполезным и дезориентирующим.
Аксиомы имеют смысл только тогда, когда они выражают свойства объективно существующих предметов. Так, если мы введём аксиому "на каждой руке человека содержится 3.1415… пальцев" и построим на базе этой аксиомы формальную теорию, то положения этой теории будут бессмысленны и даже вредны.
По поводу абстрактного мышления я хочу сказать, что есть правильная, арийская физика/математика, а есть подлая, еврейская физика/математика с геодезическими линиями и двадцатимерными пространствами.
Знаете ли Вы, что до поражения Германии во Второй Мировой, было два вида математики, - арийская и еврейская, - названные так по национальности своих сторонников?
Арийская Математика брала пример с естественных наук, склонялась к эмпирицизму, конечности и познаваемости мира, и работала исключительно c объектами, которые можно построить физически (например, в памяти ЭВМ или на бумаге).
Еврейская Математика же слоняется к религиозной абстракции и казуистике: всеохватывающей бесконечности, множествам, и порождаемым ими апориям. Так Еврейская Математика постулирует, что можно удвоить объект, путём перекладывания его частей, пространство делимо на "бесконечно малые", а для любого числа, Бог может создать большее число (аксиома о бесконечности).
Основатель Еврейской Математики, Гидеон Кантор, писал, что работает с "Абсолютом - непознаваемым человеком Актус Пьюриссимус, именуемым многими Богом". Примечательно, что Кантор окончил свою жизнь в психиатрической лечебнице, однако дело Кантора поддержали сионистские организации и католическая церковь, доведя до того, что сознательные германские студенты и профессора протестовали, требуя убрать еврейскую заразу из ВУЗов.
После войны, евреи сделали все возможное, чтобы уничтожить Арийскую Математику, удалив ее сторонников и подменив ее Теорией Множеств - центральной опорой Еврейской Математики. Так основатель интуиционизма, Лёйтзен Брауэр, подвергся изоляции, а результаты Русских и Английских финитистов умалчивались и не получили распространения. В русской истории от рук евреев пострадали математики Егоров (умер в гулаге), Лузин (подвергся травле и был отстранен), Флоренский (расстрелян), Есенин-Вольпин (репрессирован).
Добавлено через 9 минут
Сегодня математика стала еврейской даже по-цвету. Государства поддерживают так называемую "анти-расистскую математику", требующую например использовать еврейские имена в примерах и задачках, рассказывая при этом о великом "вкладе" еврейства в развитие математики.
Евреи, занимающиеся математикой, предпочитают всё специфическое-эльфийское. Причём презирают тех, кто занимается вещами, имеющими практическое применение. Поэтому в Советском Союзе вышел закон, по-которому в ВУЗах должно учиться евреев пропорционально их населению. Лишних отчисляли. Преподаватели евреи на мехмате в знак протеста ушли из университета и образовали НМУ (Независимый Московский Университет). Отсюда и название в мехматянском простонародье ``еврейская секта''.
Еврейские дети в СССР часто учились отдельное от детей гоев, в специальных элитных школах. Одной такой была Московская 57-й спецшкола, ученики которой не без оснований называют себя "пятидесятисемитами". Там часто преподавали выдающиеся преподаватели с мехмата.
В основании математики последнего столетия лежит знаменитая теория множеств Георга Кантора. Если вы откроете большую часть современных серьезных учебников математического и функционального анализа или топологии, или теории вероятности, то в начале почти наверняка увидите экскурс в теорию множеств. Почти вся современная математическая литература написана на теоретико-множественном языке. Камень теории множеств лежит в основании грандиозного здания современной науки.
Но в самом сердце этой самой фундаментальной вроде бы теории, лежащей в основе "царицы наук", почти сразу после ее создания были обнаружены очень серьезные парадоксы и проблемы, не преодоленные до сих пор. Уже сто лет с тех пор математика находится в состоянии перманентного кризиса, который остро воспринимается самыми выдающимися учеными. Великий немецкий математик Герман Вейль писал по этому поводу: "Мы менее чем когда-либо уверены в незыблемости наиболее глубоких оснований логики и математики. Как у всех и всего в мире, сегодня у нас есть свой кризис".
Математика говорит, что у шпекеровой последовательности есть предел? Говорит. Практика говорит, что его нет? Тоже говорит. Математика говорит, что апельсин можно удвоить путём перекладывания его частей? Говорит. Удалось кому-нибудь с новозаветных времён повторить эту процедуру? Наблюдения раз за разом показывают, что при такого рода операциях закон сохранения вещества неукоснительно соблюдается. Математика предсказывает наличие в бесконечномерном гильбертовом пространстве базиса Гамеля. Наблюдать оный пока вообще никому не удалось. Так что математика - именно лженаука, и никак иначе.
Именно уверенность в нематериальности математических объектов влечёт за собой веру в возможность "приближённых" вычислений (что чушь - вычисления бывают либо точные, либо неверные). Да, самолёты летают и при засилье Теории Множеств. Но если бы математика была конструктивной, они летали бы лучше, потому что конструкторы не забивали бы себе голову теоретико-множественным мусором, на практике бесполезным и дезориентирующим.
Аксиомы имеют смысл только тогда, когда они выражают свойства объективно существующих предметов. Так, если мы введём аксиому "на каждой руке человека содержится 3.1415… пальцев" и построим на базе этой аксиомы формальную теорию, то положения этой теории будут бессмысленны и даже вредны.
>как из своей преподавательской практики так и из времён обсуждения с однокурсниками на семинарах.
мало ли, что ты там вспоминаешь из своей практики
мы же не знаем, как было на самом деле, что ты имеешь в виду под "простейшими примерами", что ты считаешь "ответить не могут", да и было ли что-нибудь вообще. как бы твоё, анона, частное мнение относительно твоего личного (гипотетического) экспириенса это не очень убедительно, сорри. Я-то подумал, прямо тут в треде кто-то про пучки задвигал, а потом на простой ерунде посыпался, вот было бы интересно посмотреть
>Из этого можно сделать вывод, что у тебя собственного опыта преподавания или хотя бы обсуждения нет.
быстро ты выводы делаешь
>я с этим сталкивался при чтении некоторых обсуждений вопросов на матх иксчендж
тоже было бы интересно посмотреть
>Хотя по твпему ответу уже сразу ясно
я смотрю ты у нас прошаренный
свидетельству вербита я, конечно, доверяю полностью,
но думаю, что студент, осиливший схемы, таблицу умножения для такой группы нарисует (если его очень сильно заставят, правда, потому что это дико уныло)
 208 Кб, 799x694
208 Кб, 799x694>>95644
Вы просто недостаточно обпучкались, раз приводите такие аргументы. Абстрактная алгебра тем и хороша, что не опускается до численных примеров, а манипулирует только отношениями, и этого достаточно. Алюффи буквально это пишет на странице 52 в сноске 10 к своему примеру с группами перестановок.
 113 Кб, 1280x720
113 Кб, 1280x720Вопрос. Как теперь украинцу обозначать множество целых чисел???
Векторное пространство над полем $F$ - это фактически абелева группа $G$ плюс гомоморфизм $\phi$ (как колец) поля $F$ в $End(G)$, кольцо эндоморфизмов $G$.
Я не понимаю, как определить, какой именно эндоморфизм соответствует какому-то элементу $F$. В общем случае, как я понял, этот гомоморфизм не сюръективен, то есть будут какие-то эндоморфзимы, которым вообще никакой элемент поля не соответствует. Также в общем случае ядро может быть нетривиально, то есть каждому эндоморфизму будет соответствовать несколько элементов поля. Верно?
Но я всё равно не могу описать для себя эндоморфизмы, не привлекая умножение на скаляр. Я же определяю умножение на скаляр как применение какого-то элемента $End(G)$. Мне всё кажется, что я использую круговое рассуждение и в итоге ссылаюсь на знакомое мне умножение на скаляр.
Вот пусть например есть векторное пространство $\mathbb{R}^2$. Тогда для $\alpha \in \mathbb{R}$ и $v \in $\mathbb{R}^2$, $\alpha v$ это применение $\phi ( \alpha) \in End(G)$ к $v$. Я про это $\phi ( \alpha)$ фактически ничего не знаю же, ну просто какой-то эндоморфизм.
Я что-то не так понимаю? Или надо дальше изучать модули, чтобы познакомиться с интересными нетривиальными примерами?
Только что читал тред где чел рассуждал про талант и труд, а тут твой пост. Надо бы самому историю математики почитать, интересно стало. Пока по твоему посту сложилось ощущение, что математики такие же в бытовом плане люди. Часто раздолбаи, но только с большим интузиазмом и сообразительные
> Я не понимаю, как определить, какой именно эндоморфизм соответствует какому-то элементу $F$.
Очень просто. Берёшь элемент F, применяешь к нему гомоморфизм \phi и получаешь искому эндоморфизм.
*искомый
Так тебе прошаренный или эстетически приятный?
Хочешь почувствовать себя "умным", слушай какого-нибудь Шабата (он там без прелюдий начинает на категорном языке базарить, после чего 9/10 слушателей уёбывают в ахуе) или Городенцева (он тебе за полторы лекции весь первый семестр алгебры расскажет и ещё сверху насыпет, только ты нихуя не успеешь понять, разумеется).
А вообще выскажу возможно не очень популярное мнение, но базовые курсы в нму лучше не слушать. Они там очень... странные. Они обладают всеми теми же минусами, которыми обладают базовые курсы на математических факультетах, только в них ещё и подборка тем порой очень специфическая. Так что слушая базовые курсы только в нму ты очень сильно рискуешь не выучить вообще никакую базу. Всякую алгебру, геометрию и анализ лучше всё-таки ботать самому, параллельно слушая курс в своём вузе. Так шансы, что ты не проебёшь базу намного выше.
А в нму всё-таки лучше приходить за спец. курсами.
> Что почитать чтобы понять
Учебник по арифметике за 5 класс.
Хуею с местных математиков. Теперь понятно, почему вам тут всем мерещится, что программировании много математики. Для вас же два числа перемножить - уже проблема.
Блядь, тред перепутал. Прошу прощения. Троллинг отменяется.
>Шабата
>Дали концептуально правильный курс: категории, когомологии групп, точные последовательности и вообще, строжайшие определения (то есть там эпиморфизм не всегда сюрьективен, например). Умерли в итоге все, а задачи сдавали более-менее только те, кто знал алгебру уже до этого. Доходило до смешного: человек имел на матфаке автомат за алгебру, а в курсе НМУ с трудом сдавал хотя бы одну задачу из листка. Зато концептуально правильно!
А почему ты "умным" в кавычках написал? Это ты считаешь тоже плохим базовым курсом? Чего там не хватает?
> Это ты считаешь тоже плохим базовым курсом?
Я считаю плохой дидактической находкой накачивать непуганных перваков категорным языком с самого порога. Люди научатся умным словами вроде функтор, нормальное преобразование, копроизведение, пулбэк и т.д., но при этом абсолютно не будут понимать сути и зачем вообще всё это нужно.
Теория категорий хороша в тот момент, когда у студента уже накоплен хотя бы минимальный багаж конструкций из разных областей математики и он уже самостоятельно начинает подозревать, что конструкции эти не настолько разнородны, насколько казалось в самом начале. В идеале студент сам начинает говорить на языке диаграмм, когда ему ещё ничего не сказали про категории.
На матфаке в этом плане преподы ведут себя очень грамотно. Никакого насилования категориями не происходит, но при этом и на алгебре, и на геометрии, и уж тем более на топологии преподы мягко подводят студентов к формулировкам на категорном языке
Шабатовский же подход из разряда "группа - это однообъектный группоид, ебитесь с этим как хотите" немного неконструктивен, как по мне.
>Люди научатся умным словами вроде функтор, нормальное преобразование, копроизведение, пулбэк и т.д., но при этом абсолютно не будут понимать сути и зачем вообще всё это нужно.
Абсолютно с этим согласен. Дроч андерградов-математиков (а часто ещё и погромистов) на Алюффи всё это только усугубляет.
Всему своё время. Нет смысла в обобщениях, когда не знаешь примеров, которые собственно и обобщаются.
>при этом абсолютно не будут понимать сути и зачем вообще всё это нужно
Первые две лекции посвящены вводным сюжетам про системы полиномиальных уравнений. Предлагается поверить, что их исследование становится проще при использовании соответствующего языка.
>минимальный багаж конструкций из разных областей математики
По сути, для примеров хватает знаний конструкций из экзамена Матшкольник Вербита.
>насилования категориями
>группа - это однообъектный группоид, ебитесь с этим как хотите
Группы, кольца, модули определяются (и обсуждаются) сначала на теоретико-множественном, а потом и категорном языках.
>>97885
>Нет смысла в обобщениях, когда не знаешь примеров, которые собственно и обобщаются
Есть, дальнейшее изложение и доказательства станут проще.
Необходимые примеры в курсе есть. Не все хотят двигаться от частного к общему. Можно и нужно наоборот.
Уже неактуально, но может кому-то тоже интересно: ответ есть в книжке Cox Galois Theory в первых параграфах.
Правда подстановка Виета там берется из ниоткуда. До неё можно додуматься так:
Если есть общее уравнение 3 степени P(x) мы можем его попытаться упростить какой-то подстановкой x=y+k, где y новая неизвестная.
Подставив P(y+k) и разложив на множители при одинаковых степенях y увидим, что от y^2 можно избавиться, положив k=-b/3.
Получаем редуцированное уравнение y^3+py+q. Попытаемся повторить трюк, y=z+d;
:(z+d)^3=z^3+d^3+3d^2z+3z^2d=z^3+d^3+3dz(z+d)
сложив это с p(z+d) выносим (z+d)
z^3+d^3+(z+d)(3dz+p)+q
От сюда видно, что можно избавиться от (z+d) если (3dz+p)=0
Тогда d=-p/3z.
Получим z^3 - (p/3z)^3 + q
С уравнением 4 степени так уже, к сожалению, не выйдет. Обычной подстановкой можно избавиться только от кубического одночлена. Применяя подобный трюк повторно куб неизвестного будет возвращаться. Это видно, если (x+d) возвести в 4 степень, всегда будет одночлен 3 степени неизвестного.
Понял, спасибо.
>Что за "Modules with algebraic K-theory in mind,"
Думаю, Berrick - An Introduction to Rings and Modules: With K-Theory in View
> Модуль можно определять до кольца
Дальше даже не читал. Самое естественное понимание модуля - это действие, т.е. гомоморфизм кольца в кольцо эндоморфизмов абелевой группы.
>Модуль можно определять до кольца
Вообще говоря, это будет не модуль, а абелева группа с операторами. Модуль всегда является коммутативной группой с операторами. Не менее естественно чем то, о чём ты говоришь.
Очевидно в любой книжке о теории Галуа.
Вроде как кажется, что интуитивно это из-за антисимметричности. С одной стороны, a∧b=-b∧a, так как меняется ориентация (или что аналогично - площадь параллелограмма, натянутого на линейно зависимые вектора, есть нуль). С другой стороны, для элементов алгебры so(n) есть косая симметрия A'=-A (где A' - транспонирование), которая есть бесконечно малый аналог определения поворотов (R'R=1).
Но это очень нестрого, и антисимметричность в этих двух случаях совершенно другая, так что это просто махание руками.
Собственно сам изоморфизм обычно приводится такой:
(a∧b)(с) = (a,c)b-(b,c)a
И это тоже мне не очень помогает. То есть это очевидно на уровне матриц, но хочется понять интуитивно почему так получается.
да вроде это не совсем махание руками, внешний квадрат у тебя определяется как фактор тензорной алгебры по тому соотношению что ты написал, а so(n) это типа матрицы, удовлетворяющие твоему второму условию, ну и видно, что и там и там соотношения то одинаковые: выделенная инволюция(х)=-х. Но важно понимать, что в тензорном квадрате мы факторизуем по соотношениям, а в so(n) мы не факторизуем, а выбираем из более общего объекта элементы, удовлетворяющие соотношению и изоморфизм очевидным образом получается. Более простая ситуация когда появляется такой эффект - это изоморфизм между симметрической степенью и алгеброй разделенных степеней, но там уже например если мы работаем не над полем а над кольцом, то это не верно.
Ну и да я ниче не прояснил, просто накинул говна на вентилятор.
Схожу к вам на практику
Спасибо. Я гуглил uplift, raise и всякие другие вариации, а про самый простой вариант забыл
 218 Кб, 1555x452
218 Кб, 1555x452 251 Кб, 730x346
251 Кб, 730x346Че посоветуете? Какие-то статьи, учебники, разделы в учебниках, лекции ютубовские. Хз, хоть как-то меня направьте.
>(this) definition behaves poorly when one considers topological groups and continuous group actions, since in general it may not be possible to put a nice topology on \text{Aut}(Z) such that continuous actions are precisely continuous group homomorphisms G \to \text{Aut}(Z). The situation is even worse for, for example, algebraic groups and algebraic group actions.
Может кто прокомментировать?
Я могу объяснить на пальцах, через аналогию.
Есть в лингвистике такая штука, как теория семантических ролей. Рассмотрим в качестве примера какое-нибудь предложение с переходным глаголом, например "кузнец бьет молотом по наковальне". Его схема выглядит как "агент X действует способом Y на объект Z с помощью объекта Q". В нашем случае понятийная структура аналогична, "структура G действует на структуру Z с помощью своего элемента g способом, описанным аксиоматикой действия группы".
Действие - это обобщение понятия операции. Операция работает внутри структуры (аналогия с двумя химическими элементами, которые складываясь, превращаются в третий), а действие позволяет элементам из внешней структуры управлять поведением элементов в текущей. Способ этого внешнего воздействия описывается (или регулируется, что, в общем-то, одно и то же) некоторой аксиоматикой. Понятно, что управляющая и управляемая структуры могут быть весьма различны по уровню своей внутренней сложности - и аксиоматика, дающая некоторую "естественную" интерпретацию действия в одном случае, может не иметь ее в другом.
Группа, как абстрактный механизм, собранный из симметрий, может легко шаффлить обычное множество и вдобавок отображаться в его симметрическую группу - потому что множество, по сути, бесструктурно (если не считать "теневой структуры" попарного различия всех его элементов). Но когда ты закутываешь управляющие и управляемые структуры в некоторые дополнительные тряпки типа топологий, и при этом эти тряпки оче сильно отличаются, то начинаются всякие неожиданности. Например, далеко не факт, что две структуры, шаффлящие без разрывов третью структуру, гомеоморфны.
А примеры есть? И насколько часто всё идёт по пизде?
То есть допустим у нас есть действие группы G на топологическом пространстве X. Гомеоморфизмы X образуют группу Aut(X). Согласно определению выше, действием будет гомоморфизм групп G->Aut(X). Что именно здесь пойдёт не так, если на G нет топологической структуры?
В категории топологических пространств, насколько знаю, нет внутреннего Hom-а, то есть на множестве непрерывных отображений из произвольного топологического пространства X в произвольное топологическое пространство Y нельзя ввести структуру топологического пространства таким образом, чтобы получилась естественная биекция между Mor(X \times Y, Z) и Mor(X, Mor(Y, Z)) (Mor --- морфизмы --- это непрерывные отображения). А именно так и отождествляются два определения действия (через гомоморфизм в эндоморфизмы и через гомоморфизм из произведения). От этого «недостатка» можно избавится, ограничив класс рассматриваемых топологических пространств:
https://en.m.wikipedia.org/wiki/Compactly_generated_space
>топовые геометры
>This paper is the second in a series of five
>439 страниц
где-то я это уже видел только геометр был один
Лурье?
 1,1 Мб, mp4,
1,1 Мб, mp4,512x640, 0:12
Есть вариант поступить в магистратуру на кафедру алгебры и топологии, скорее всего не на бюджет (да и как-то похуй). В голове держим что меня не надо отговаривать. Разделы математики сдавал на средние баллы, но уже ничего не помню, т.е. разобраться если захочу - могу. Посоветуйте, на ваш взгляд, самые подходящие прелиминарии в виде книг, видео-лекций, которые подготовят меня на моем пути. Хочу туда поступить шутки ради, оказаться в абсолютно новом пространстве ахуевше непонятных вещей, среди людей стоящих за такими дверями знаний, ключ для которых есть странное любопытство с долей аутизма.
там экзамены вступительные нужны? их и готовь
ван дер варден
Какие разделы математики ты сдавал? Что планируешь изучать на кафедре?
это ты куда поступать собрался? никогда не слышал, чтобы где-то была кафедра "алгебры и топологии"
Алгебра и топология:
«Algebra» - Michael Artin
«Abstract Algebra» - David S. Dummit, Richard M. Foote
«Algebra» - Serge Lang
«Topology» - James R. Munkres
«General Topology» - Stephen Willard
«Topology» - Klaus Jänich
Курсы:
MIT OpenCourseWare
Coursera и edX
Признаться, не вижу смысла отдельно изучать общую топологию. Не лучше в процессе изучения многообразий её пройти? Или в процессе изучения функционального анализа.
Почему не лучше?
>«Algebra» - Michael Artin
Хорошая книга. Хочу купить ее себе. Доставка книг с амазона в Россию сейчас работает?
Выглядит как чатжпт высер на основе нкатлаба. Все плевались на бурбаков, и тем не менее статьи и книги условных дьедонне, серра, или гротендика читаются комфортно и по сей день, с интересными идеями и комментариями.
А эта статья - какой-то симулякр математики.
Я пробовал читать учебники для новичков от Дьедонне и мне не зашли. Книги по истории: функан и аг, хорошие.
мочечмо съебись
пососи
Давеча увлёкся изучением теории Галуа. И возник вопрос, который без помощи цепких лап не разрешить.
Одним из центральных понятий теории Галуа являются поля разложений одного полинома
Поля разложений строятся через построения Башни расширений:
Берём фактор по главному идеалу искомого полинома, пока молоко из жопы не польётся. Когда полилось, т.е. когда у полинома появилось степень его корней, процесс прекращается
И, вроде как конструкция выше алгоритмизуется.
Мол... У нас есть жадный перебор по неприводимым факторам полинома
И... Процесс в какой-то момент обрывается. И... Промежуточными результами являются какие-то конечномерные алгебры над основным полем, о которых можно думать, как о вполне вычислимом объекте, а именно как об квадратных матрицах коэффициентами в основном поле (ну, типа, умножение в конечномерных алгебрах --- билинейно)
Значит, что по идее должно быть алгоритмизируемо всё. Но... Простейший гугл не выдал мне алгоритма построения башни расширения стандартных полей (рациональных чисел т.е.). И, явно можно придумать трудно-алгоритмизируемую задачу, вроде факториального разложения многочлена в соответствующем ему фактор-кольце.
Короче... Алгоритм-то этот есть? Знает ли кто о нём? Если кто знает --- где можно было бы о нём прочитать?
Я не знаю, но вот что-то есть, вроде башни тоже вычисляются
https://dl.gi.de/server/api/core/bitstreams/1b9b74e9-c205-42fc-a757-7704b1367114/content
Я подозреваю, что поля разложений не особо полезны для вычислительных целей, а ценны чисто теоретически. В любом случае, если что-то такое про них и есть, то это должно быть в книжках по компьютерной алгебре и/или вычислительной алгебре, т.е. смотреть можно в сторону Cox'а (у него и книжка по теории Галуа есть), Sturmfels'а, Edwards'a (у этого тоже есть про Галуа).
>Cox
>Sturmfels
>Edwards
Я, немного, слаб в литературе. Анон, можешь ли ты указать конкретные книги, в которых стоит поискать?
Вроде самая сложная часть твоего алгоритма это факторизация полинома (или нахождение хотя бы одного неприводимого фактора).
Факторизация в Q[x] это +- то же самое, что факторизация в Z[x], но для того, чтобы сделать это за полиномиальное время потребовалось изобрести LLL алгоритм, то есть даже над Q задача нетривиальная.
По теме алгоритмов в алгебраической теории чисел есть очень хорошая книжка, автор достаточно известный специалист в области теории чисел
H.Cohen A Course in Computational Algebraic Number Theory
В ней написано про факторизацию над Z. Строго говоря, предъявленный там алгоритм экспоненциальный, но для практических целей пойдет, про факторизацию через LLL см. оригинальные статьи.
Более того в PARI/GP есть функция nfsplitting, которая принимает на вход многочлен P над Q и возвращает многочлен S, который задает поле разложения P, то есть такой, что Q[x]/(S(x)) есть поле разложения P. https://pari.math.u-bordeaux.fr/dochtml/html/General_number_fields.html#se:nfsplitting
лет в 8
Если тебе что-то нравится, то не размышляй поздно или не поздно, а занимайся этим. 17 лет это очень молодой возраст, так что далеко не поздно. Галуа вон в 16 лет начал вкатываться в математику а в 20 уже умер.
Вот у нас есть действие группы $G$ на множестве $X$. Скажем, пусть $G=D_8=\langle r,s | r^4=s^2=(sr)^2=1 \rangle $, и $X$ это квадрат. Чтобы указать действие группы $G$ на $X$, нам нужно установить соответствие между элементами $G$ и элементами $Aut(X)$.
Квадрат пусть будет с вершинами как на следующей диаграмме
BA
CD
Возьмём например элемент $r$, и сопоставим ему автоморфизм $\phi \in Aut(X)$ такой (поворот на $\pi/2$):
BA AD
CD -> BC
И вот тут у меня возникает вопрос. Как мы "внутренне" задаём этот автоморфизм? Мы же должны как-то пронумеровать (или обозначить буквами) вершины? То есть у нас есть какое-то индексное множество $I$ и "координатная" функция $\i: X \to I$?
То же самое если мы будем записывать автоморфизмы как вложенные в $S_4$, то есть в виде перестановки $(1,2,3,4)$. Тут вот эти $1$, $2$ - это же какое-то отображение $X \to [1,2,3,4]$ подразумевается?
Или мы просто думаем об элементе $\phi \in Aut(X)$ как о подмножестве декартова квадрата $X$?
Вопрос возникает вот почему: применим к исходному $X$ другой автоморфизм, например соответствующий $s \in D_8$ (отражение), то есть перестановка $(1,3)$. Квадрат будет выглядить как
DA
CB
Но поскольку это автоморфизм, то мы не можем отличить элементы $X$. То есть если мы не знаем, что мы до этого примениили $s$, то для применения автоморфизма $r$, то есть $\phi$, нужно на самом деле применить не $r$, а сопряжённый $srs^{-1}=r^3$:
DA CB
CB -> DA
То есть если мы хотим повернуть квадрат в направлении от А к В, то уже нужен поворот не на $\pi/2$, а на $-\pi/2$, потому что квадрат отражён.
Но с другой стороны, если задать автоморфизм $\phi$ как "поворот на $\pi/2$", то он становится как бы "инвариантным" к истории действий. Не знаю, как даже объяснить, в чём я запутался.
То есть что такое сопряжение я прекрасно понимаю. Мой вопрос не про то, что такое сопряжение, и какой у него смысл. А про то, что, чтобы сопряжение обрело свой смысл как аналога "замены координат", эти координаты (отображение $I \to X)$ должны же быть введены.
Для себя нашёл объяснение такое. Есть понятие эквивалентности G-множеств. И если мы применим какой-то элемент $g \in G$ на $X$, то пара $G, g(X)$ не будет эквивалентна $G, X$ как G-множества. Для эквивалентности на $G$ индуцируется сопряженный автоморфизм $\h \to ghg^{-1}$, и тогда уже новая пара будет эквивалентна.
Знаю, что сумбурно, но может кто-то поймёт, в чём у меня загвоздка.
Вообще на это всё меня вывел дифгем, потому что я вдруг узнал, что коммутатор - это фактически локальное "приближение" сопряжения в контексте групп Ли. И я стал копать в сопряжение, но сам себя запутал.
Вот у нас есть действие группы $G$ на множестве $X$. Скажем, пусть $G=D_8=\langle r,s | r^4=s^2=(sr)^2=1 \rangle $, и $X$ это квадрат. Чтобы указать действие группы $G$ на $X$, нам нужно установить соответствие между элементами $G$ и элементами $Aut(X)$.
Квадрат пусть будет с вершинами как на следующей диаграмме
BA
CD
Возьмём например элемент $r$, и сопоставим ему автоморфизм $\phi \in Aut(X)$ такой (поворот на $\pi/2$):
BA AD
CD -> BC
И вот тут у меня возникает вопрос. Как мы "внутренне" задаём этот автоморфизм? Мы же должны как-то пронумеровать (или обозначить буквами) вершины? То есть у нас есть какое-то индексное множество $I$ и "координатная" функция $\i: X \to I$?
То же самое если мы будем записывать автоморфизмы как вложенные в $S_4$, то есть в виде перестановки $(1,2,3,4)$. Тут вот эти $1$, $2$ - это же какое-то отображение $X \to [1,2,3,4]$ подразумевается?
Или мы просто думаем об элементе $\phi \in Aut(X)$ как о подмножестве декартова квадрата $X$?
Вопрос возникает вот почему: применим к исходному $X$ другой автоморфизм, например соответствующий $s \in D_8$ (отражение), то есть перестановка $(1,3)$. Квадрат будет выглядить как
DA
CB
Но поскольку это автоморфизм, то мы не можем отличить элементы $X$. То есть если мы не знаем, что мы до этого примениили $s$, то для применения автоморфизма $r$, то есть $\phi$, нужно на самом деле применить не $r$, а сопряжённый $srs^{-1}=r^3$:
DA CB
CB -> DA
То есть если мы хотим повернуть квадрат в направлении от А к В, то уже нужен поворот не на $\pi/2$, а на $-\pi/2$, потому что квадрат отражён.
Но с другой стороны, если задать автоморфизм $\phi$ как "поворот на $\pi/2$", то он становится как бы "инвариантным" к истории действий. Не знаю, как даже объяснить, в чём я запутался.
То есть что такое сопряжение я прекрасно понимаю. Мой вопрос не про то, что такое сопряжение, и какой у него смысл. А про то, что, чтобы сопряжение обрело свой смысл как аналога "замены координат", эти координаты (отображение $I \to X)$ должны же быть введены.
Для себя нашёл объяснение такое. Есть понятие эквивалентности G-множеств. И если мы применим какой-то элемент $g \in G$ на $X$, то пара $G, g(X)$ не будет эквивалентна $G, X$ как G-множества. Для эквивалентности на $G$ индуцируется сопряженный автоморфизм $\h \to ghg^{-1}$, и тогда уже новая пара будет эквивалентна.
Знаю, что сумбурно, но может кто-то поймёт, в чём у меня загвоздка.
Вообще на это всё меня вывел дифгем, потому что я вдруг узнал, что коммутатор - это фактически локальное "приближение" сопряжения в контексте групп Ли. И я стал копать в сопряжение, но сам себя запутал.
говно какое-то бесполезное, гомологии где?
Мне кажется, в таких случаях обычно смотрят сначала на фигуру, вложенную в плоскость, а потом устанавливают изоморфизм действий подгруппы поворотов плоскости и перестановок вершин или типа того.
>обычно смотрят сначала на фигуру, вложенную в плоскость
Ну то есть вводят координаты, я про это писал.
Это не сработает, если $X$ - множество со структурой, которая не вкладывается в многообразие, например, алгебраическая структура, или просто множество.
>а потом устанавливают изоморфизм действий подгруппы поворотов плоскости и перестановок вершин или типа того.
Такого изоморфизма не существует, если что. $D_{2n}$ не вкладывается в $SO(n)$.
И вообще, квадрат был просто примером же.
>Такого изоморфизма не существует, если что.
D_2n вкладывается в O(2) и следовательно в SO(3), что анон которому ты отвечаешь скорее всего и имел в виду.
мимо
Бтв, мой ответ на твой вопрос: аналогия между сопряжением и заменой координат это прежде всего просто аналогия, которая становится строгой только в конкретных ситуациях, где есть смысл говорить о координатах.
Так это понятно, что $O(n)$ вкладывается в $SO(n+1)$.
>что анон которому ты отвечаешь скорее всего и имел в виду
Ну сказано было
>устанавливают изоморфизм действий подгруппы поворотов плоскости и перестановок вершин
Я на что написано, на то и отвечаю.
Вопрос мой вообще был не об этом. Ладно короче, похуй.
> это прежде всего просто аналогия, которая становится строгой только в конкретных ситуациях, где есть смысл говорить о координатах.
Так в том то и дело, что нет, потому что мы фактически и выбираем "координаты", когда (неявно) думаем об автоморфизме как об элементе симметрической группы. Я же об этом и писал.
Так что это не "просто аналогия". Как только у нас есть какое-то отображение $X \to I$ для множества индексов $I$ (которое либо индуцируется вложением $Aut(X)$ в $Sym(X)$, либо выбирается изначально), то уже имеет смысл об этом говорить.
Такой взгляд часто вижу в книгах 1890-1930х годов (в соответствующих терминах, конечно). Другое дело, что удобней/принято так не делать
Ты ничего нового, прости, не сказал, потому что ты не понял вопроса (но это моя вина, потому что я сумбурно написал). Ты отвечаешь на вопрос "что такое автоморфизмы в этих случаях", я этого не спрашивал, и более того, из моего поста понятно, что всем понятно, что за автоморфизмы тут будут.
>В общем виде через категории понять можно
Теория категорий тут не причём. Группу как структуру множества "симметрий" определяли ещё более 100 лет назад.
>Ну а действие некой группы это как раз
Да я об этом уже писал же, это понятно.
Короче, вопрос снимается из-за моего косноязычия.
Дивизоры нужны, например, чтобы из информации, какие точки кривой являются нулями или полюсами желаемой функции, построить собственно эту желаемую функцию. Группа классов дивизоров это мера того, насколько возможно из произвольной формальной линейной комбинации точек кривой, кодирующей, какие точки должны быть нулями и какие полюсами желаемой функции, построить такую функцию. Если группа тривиальна, то это возможно для любой комбинации.
libertine
>>120610
>>120609
>>120663
>Раз уж про ударения заговорили
Вот кстати тоже недавно искал, почему комплЕкс, комплЕксные числа. Ну думал корни латинские, там комплЕксус, оттуда в европейские языки, ну и сильное французское влияние было на российскую науку в, скажем, 17-18 веке (ну это предполжение, если кто знает точно - пишите).
Не суть, вобщем дошёл до цепных комплЕксов, и тоже думал что их нахреначили ожидаемые личности типа серров и гротендиков. Ан нет, вроде как первым, кто использовал, был Майер, тот который из Майера-Вииториса. А Майер - австриец, писал на немецком. Но там тоже комплЕкс читается, так что разницы для заимствования (видимо) нет.
Кстати, интересный слабо связанный факт: Вииторис умер в 110 лет.
Ещё один интересный факт про названия, который я недавно узнал: Арнольд был за использования русскоязычных аналогов, например струя, а не джет. Он спорил с Виноградовым на эту тему (который потом организовал коллектив Джета Неструева).
Давно хотел запилить тред про математические названия и интересности в истории математики в принципе. Но всё что-то откладывал, день, месяц, джва года, а тут уже и раздел почти дохлый...
Из книжек Вавилова по этому поводу.
У него про это не так много, это просто заметки на полях скорее, по-моему скринами его высказывания по этой теме и исчерпываются.
Конкретная теория групп, Конкретная теория колец.
 434 Кб, 853x1280
434 Кб, 853x1280> Вавилов
Вместе с Успенским - биба и боба, вока и жока совковой псевдоматематики. У одного N неопределяемое понятие, у другого - алгебру можно понять только читая оригиналы 19 века на староколпакском. Самое смешное, что местные подбородочные гении на это ведутся. Вы же реально конченые
>У одного N неопределяемое понятие,
Любой, кто это эссе, предназначенное для широкой публики, действительно прочитал, должен хорошо понимать, в каком смысле N "неопределяемо". Математически ничего неправильного или вводящего в заблуждение Успенский не говорит, всё это покрывается в первом курсе матлогики.
>у другого - алгебру можно понять только читая оригиналы 19 века на староколпакском
Очевидный эпатаж, в стиле Арнольда того же, причем содержащийся исключительно в "книгах", которые он сам просил не распространять.
>псевдоматематики
Оба очень хорошие математики.
Серр-Свон?
>приходится всё самому придумывать.
Это да. Но зато когда придумаешь, обретаешь более глубокое понимание.
>Серр-Свон?
Не. Понятно, что морально модуль над кольцом нужно понимать как пространство сечений векторного расслоения над спектром кольца, и теорема Серра про то, в каких случаях это не аналогия, а строгое соответствие. Но это не особо объясняет геометрическую природу разложения к.п. модулей (=когерентных пучков) над кольцом г.и. (=аффинной схемой с размерностью $\leq 1$) в целом и конкретных примеров (кольцо K[T] для линейного оператора T) и как это связано с вещами вроде носителя пучка, линейными расслоениями, группой Пикара, геометрической интерпретацией примарного разложения, хотя связи эти есть. У меня получается понять отдельные детали (они все на поверхности на самом деле), но понятной общей картины не возникает и нормальной интуиции нет.
Брооооо