 71 Кб, 500x930
71 Кб, 500x930Ломаю голову над аксиомой выбора.
Мы не можем выбрать из любого множества по объекту, так как не для любого множества определена функция выбора. Вроде так.
Вопрос: почему нельзя просто выбрать любой попавшийся объект из множества, так сказать наугад, рандомно?
И поступив таким образом со всеми множествами. В итоге получим новое множество.
В чем ошибка?
Мы не можем выбрать из любого множества по объекту, так как не для любого множества определена функция выбора. Вроде так.
Вопрос: почему нельзя просто выбрать любой попавшийся объект из множества, так сказать наугад, рандомно?
И поступив таким образом со всеми множествами. В итоге получим новое множество.
В чем ошибка?
>>114 (OP)
Но разве суть не в том, что для составление иных подмножеств (даже если они singleton) нам нужен конкретный элемент, а не случайный?
Но разве суть не в том, что для составление иных подмножеств (даже если они singleton) нам нужен конкретный элемент, а не случайный?
>>123
конкретный - то есть, чтобы при взгляде на этот элемент, мы сразу поняли из какого множества мы его взяли?
конкретный - то есть, чтобы при взгляде на этот элемент, мы сразу поняли из какого множества мы его взяли?
Сложность я вижу в этом (поправьте, может быть я ошибаюсь):
У нас например есть множество из ста красных яблок.
Ок...мы берем "второе яблоко" и добавляем его в новое множество. То есть мы применили функцию типа как "из линии всех яблок выбрать второе по счету и изъять его"
Итак с первым множеством из семейства мы разобрались.
Беремся за второе: У нас есть множество всех действительных чисел.
Мы не можем вообще никакую функцию здесь придумать, потому что если мы воспользуемся функцию "выбрать десятое по счету действительне число", мы даже ведь не знаем от какого числа считать!
А если, мы из множества действительных чисел выбрали наугад любое, то:
Во-первых, не существует такой функции "выбрать любое"
Во-вторых, невозможно потом по этому числу, посмотрев на неего сказать" ааа, да это же десятое число из мноества натуральных".
Я уловил суть или хрень?
У нас например есть множество из ста красных яблок.
Ок...мы берем "второе яблоко" и добавляем его в новое множество. То есть мы применили функцию типа как "из линии всех яблок выбрать второе по счету и изъять его"
Итак с первым множеством из семейства мы разобрались.
Беремся за второе: У нас есть множество всех действительных чисел.
Мы не можем вообще никакую функцию здесь придумать, потому что если мы воспользуемся функцию "выбрать десятое по счету действительне число", мы даже ведь не знаем от какого числа считать!
А если, мы из множества действительных чисел выбрали наугад любое, то:
Во-первых, не существует такой функции "выбрать любое"
Во-вторых, невозможно потом по этому числу, посмотрев на неего сказать" ааа, да это же десятое число из мноества натуральных".
Я уловил суть или хрень?
 71 Кб, 500x930
71 Кб, 500x930В Википедии прочитал подпись еще раз к пике:
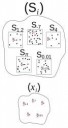
Где (Si) семейство непустых множеств, проиндексированных множеством действительных чисел R. То есть для каждого действительного числа i существует множество Si. На рисунке приведен пример выбора элементов множеств. Каждое такое множество Si непусто, а возможно и бесконечно. Аксиома выбора позволяет нам произвольно тыкать в один элемент из каждого множества, формируя соответствующее семейство элементов (xi), также проиндексированных множеством действительных чисел R, где xi выбраны из Si.
Произвольно тыкать!!!
Так что же нам мешает, например, в примере Бертрана Рассела с носками, тупо выбрать из каждой пары носков ЛЮБОЙ?
Где (Si) семейство непустых множеств, проиндексированных множеством действительных чисел R. То есть для каждого действительного числа i существует множество Si. На рисунке приведен пример выбора элементов множеств. Каждое такое множество Si непусто, а возможно и бесконечно. Аксиома выбора позволяет нам произвольно тыкать в один элемент из каждого множества, формируя соответствующее семейство элементов (xi), также проиндексированных множеством действительных чисел R, где xi выбраны из Si.
Произвольно тыкать!!!
Так что же нам мешает, например, в примере Бертрана Рассела с носками, тупо выбрать из каждой пары носков ЛЮБОЙ?
>>130
Так множества же считаются равными, если в них равное количество элементов.
Ткните носом плиз, где я туплю.
Так множества же считаются равными, если в них равное количество элементов.
Ткните носом плиз, где я туплю.
Нужно понимать, что все примеры семейств множеств для которых аксиома выбора по-существу нужна (т.е. таких, что нельзя доказать без использования аксиомы выбора существования функции выбора для этого семейства) довольно сложны, а для простых и естественных семейств, знакомых условному первокурснику матфака это не по-существу. В частности без использования аксиомы выбора можно установить, что
1. для всех семейств из конечного числа множеств существует функция выбора;
2. для всех семейств составленных из подмножеств некоторого одного данного счетного множества существует функция выбора;
3. для всех семейств составленных из открытых и замкнутых подмножеств R^n существует функция выбор.
Для того, чтобы увидеть примеры семейств для которых аксиома выбора по-существу нужна рекомендую посмотреть на доказательство леммы Цорна или теоремы Цермело (чтобы получить совсем конкретный пример семейства можно посмотреть на конструкцию из теоремы Цермело, применительно к вполне-упорядочиванию вещественной прямой).
Отвечая на изначальный вопрос, о том, почему нельзя "выбирать наугад". "Выбор наугад" - это метод интуиция к которому исходит от работы с конечными множествами. К сожалению, многие исходящие из такой интуиции "естественные" методы работы, применительно к абстрактным бесконечными множествами, либо приводят к противоречиям, либо, что мы видим в случае с аксиомой выбора, приводят к полностью контр-интуитивным последствиям (см. теорема Банаха-Тарского).
Здесь стоит отметить, что вообще теория множеств основана на исторически довольно долго устанавливавшейся интуиции, касательно устройства абстрактных бесконечных множеств, которая позволяет довольно удобно с ними работать, сохраняет довольно большую часть интуиции, касательно конечных множества и, насколько на текущий момент известно, не содержит противоречий.
1. для всех семейств из конечного числа множеств существует функция выбора;
2. для всех семейств составленных из подмножеств некоторого одного данного счетного множества существует функция выбора;
3. для всех семейств составленных из открытых и замкнутых подмножеств R^n существует функция выбор.
Для того, чтобы увидеть примеры семейств для которых аксиома выбора по-существу нужна рекомендую посмотреть на доказательство леммы Цорна или теоремы Цермело (чтобы получить совсем конкретный пример семейства можно посмотреть на конструкцию из теоремы Цермело, применительно к вполне-упорядочиванию вещественной прямой).
Отвечая на изначальный вопрос, о том, почему нельзя "выбирать наугад". "Выбор наугад" - это метод интуиция к которому исходит от работы с конечными множествами. К сожалению, многие исходящие из такой интуиции "естественные" методы работы, применительно к абстрактным бесконечными множествами, либо приводят к противоречиям, либо, что мы видим в случае с аксиомой выбора, приводят к полностью контр-интуитивным последствиям (см. теорема Банаха-Тарского).
Здесь стоит отметить, что вообще теория множеств основана на исторически довольно долго устанавливавшейся интуиции, касательно устройства абстрактных бесконечных множеств, которая позволяет довольно удобно с ними работать, сохраняет довольно большую часть интуиции, касательно конечных множества и, насколько на текущий момент известно, не содержит противоречий.
>>149
Всё так.
Всё так.
Попробую подытожить.
Есть такие множества, для которых легко или точнее возможно найти функцию выбора. Наша интуиция без труда позволит нам это сделать, используя конечные множества. Для реальной жизни этого хватит сполна.
Сложности начинаются при переходе к бесконечным множествам, например множествам пронумерованным вещественными числами и так далее.
При выборе нужна будет специальная ФУНКЦИЯ (функция выбора), если её не удается подобрать, то у нас возникает соблазн произвести интуитивный выбор (как мы успешно делали в случае конечных множеств), но произведя этот интуитивный выбор и, вроде как, справляясь с задачей (принимая аксиому выбора), мы получаем "странные" следствия, такие как парадокс Банаха-Тарского, в качестве побочных эффектов.
Вот, что я понял.
Есть такие множества, для которых легко или точнее возможно найти функцию выбора. Наша интуиция без труда позволит нам это сделать, используя конечные множества. Для реальной жизни этого хватит сполна.
Сложности начинаются при переходе к бесконечным множествам, например множествам пронумерованным вещественными числами и так далее.
При выборе нужна будет специальная ФУНКЦИЯ (функция выбора), если её не удается подобрать, то у нас возникает соблазн произвести интуитивный выбор (как мы успешно делали в случае конечных множеств), но произведя этот интуитивный выбор и, вроде как, справляясь с задачей (принимая аксиому выбора), мы получаем "странные" следствия, такие как парадокс Банаха-Тарского, в качестве побочных эффектов.
Вот, что я понял.
>>151
В упор не вижу, что в нём странного. Ведь объём приписывается не отдельным точкам, а множествам точек.
>парадокс Банаха-Тарского
В упор не вижу, что в нём странного. Ведь объём приписывается не отдельным точкам, а множествам точек.
>>148
элемент множества это такой x который принадлежит множеству
элемент множества это такой x который принадлежит множеству
>>155
Когда ты узнал, что бывают равномощные отрезки, имеющие разную длину, то ты должен был перестать считать подобные явления удивительными.
Когда ты узнал, что бывают равномощные отрезки, имеющие разную длину, то ты должен был перестать считать подобные явления удивительными.
>>156
давай на примерах, я только учусь)))
Возьмем два отрезка: 1см и 2см.
Отложим на каждом из отрезков столько точек, сколько всего натуральных чисел.
Получим в обоих вариантах одинаковые бесконечности. Отрезки будут равномощные, но при этом разной длины. Я верно понимаю?
давай на примерах, я только учусь)))
Возьмем два отрезка: 1см и 2см.
Отложим на каждом из отрезков столько точек, сколько всего натуральных чисел.
Получим в обоих вариантах одинаковые бесконечности. Отрезки будут равномощные, но при этом разной длины. Я верно понимаю?
>>158
понимаю, что без метрики хрень получится. Но всё же. Смысл, мне кажется, я уловил.
понимаю, что без метрики хрень получится. Но всё же. Смысл, мне кажется, я уловил.
>>114 (OP)
Ты поломай голову над аксиомой пустого множества, блин.
Ты поломай голову над аксиомой пустого множества, блин.
множеств
>>1800
А чего там ломать? Мне, как богослову с естественнонаучным образованием, она самоочевидна.
А чего там ломать? Мне, как богослову с естественнонаучным образованием, она самоочевидна.
>>1800
А чего там ломать? Мне, как богослову с естественнонаучным образованием, она самоочевидна.
А чего там ломать? Мне, как богослову с естественнонаучным образованием, она самоочевидна.
>>71733
Лучше поздно, чем никогда.
Лучше поздно, чем никогда.
>>71733
Профессор читает лекцию по математике. Выписывает на доске длиннющую, совершенно необозримую формулу и заявив: "Отсюда с очевидностью следует..." выписывает еще более громоздкую формулу. Вдруг, на минуту задумывается, потом, извинившись, выходит из аудитории. Примерно через полчаса возвращается и, небрежно бросив на кафедру кипу исписанной бумаги, заявляет: "Да, это действительно очевидно" и продолжает лекцию.
Профессор читает лекцию по математике. Выписывает на доске длиннющую, совершенно необозримую формулу и заявив: "Отсюда с очевидностью следует..." выписывает еще более громоздкую формулу. Вдруг, на минуту задумывается, потом, извинившись, выходит из аудитории. Примерно через полчаса возвращается и, небрежно бросив на кафедру кипу исписанной бумаги, заявляет: "Да, это действительно очевидно" и продолжает лекцию.
но ответил хорошо
Как выучить все эти заповеди Цемело-Френкеля